8.26--8.30
\title {Logic I \\ Fast Lecture 04}
\maketitle
\def \ititle {Logic I}
\def \isubtitle {Fast Lecture 04}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
\section{Get Some Quantifiers: Don't Economise}
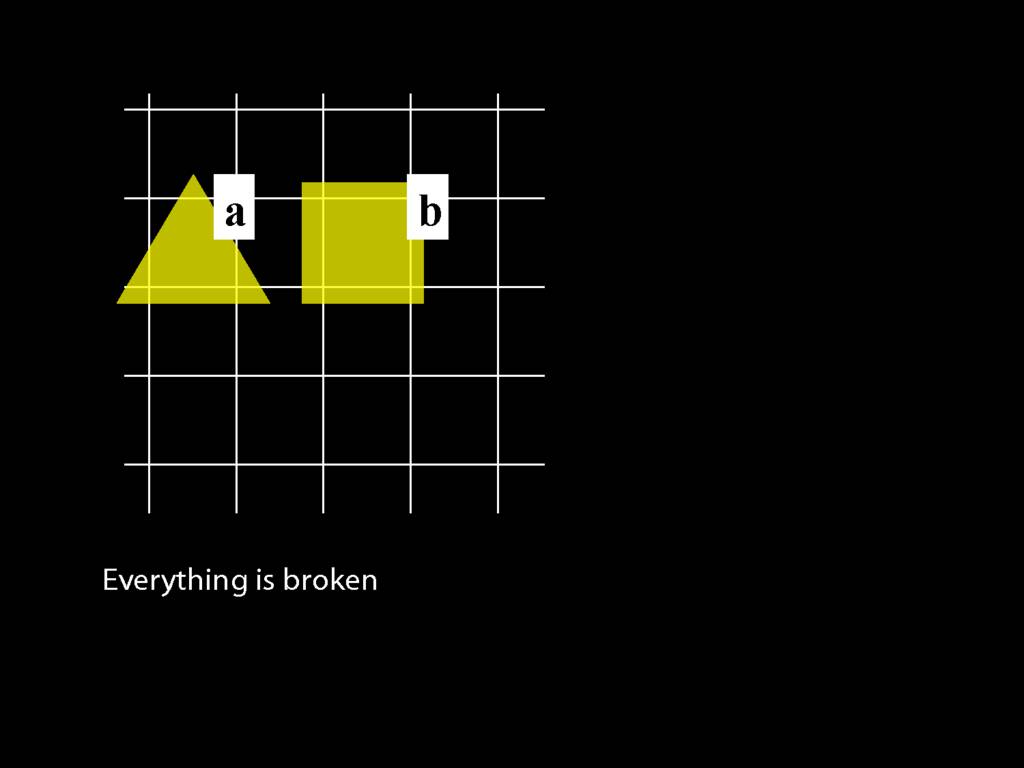
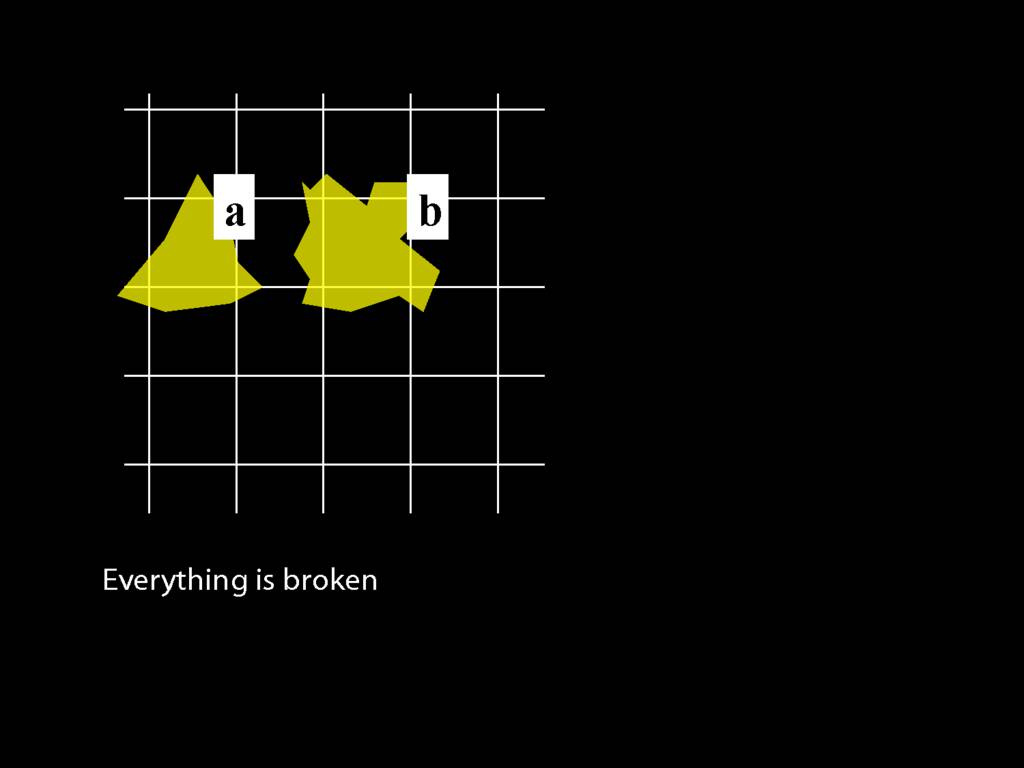
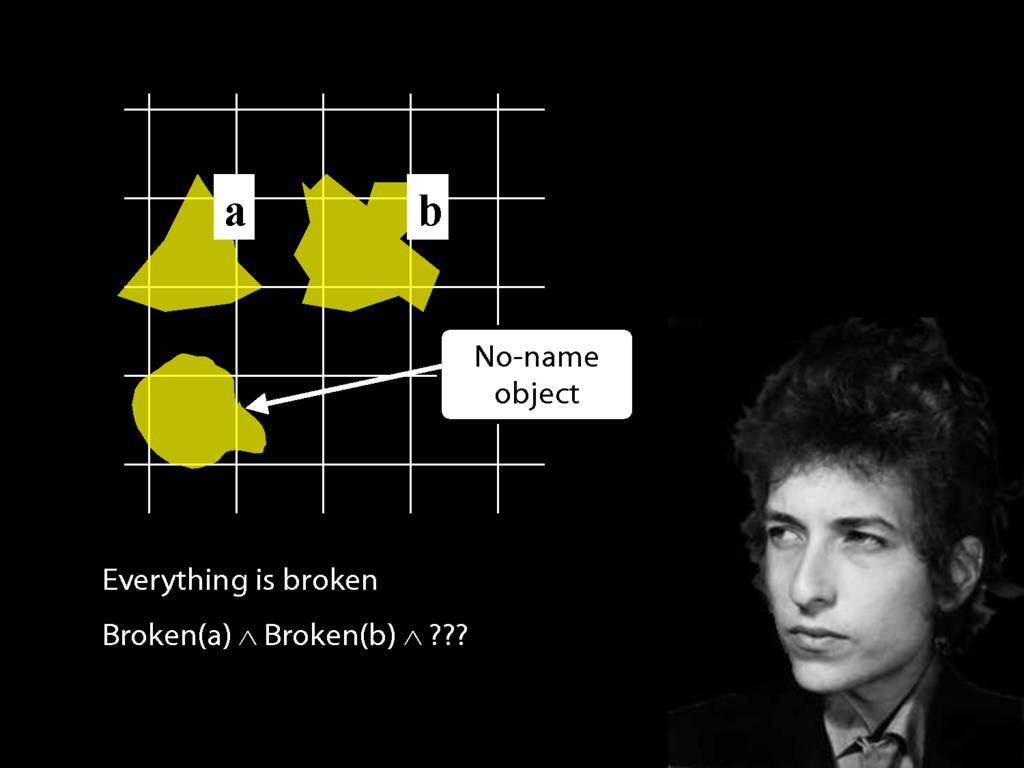
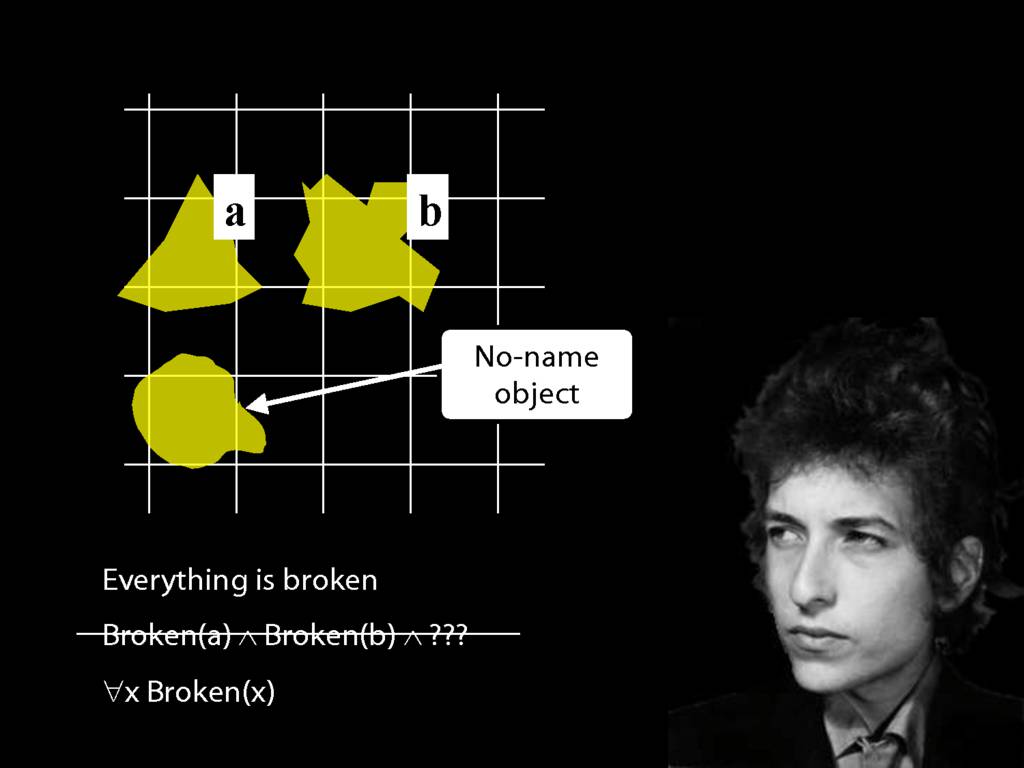
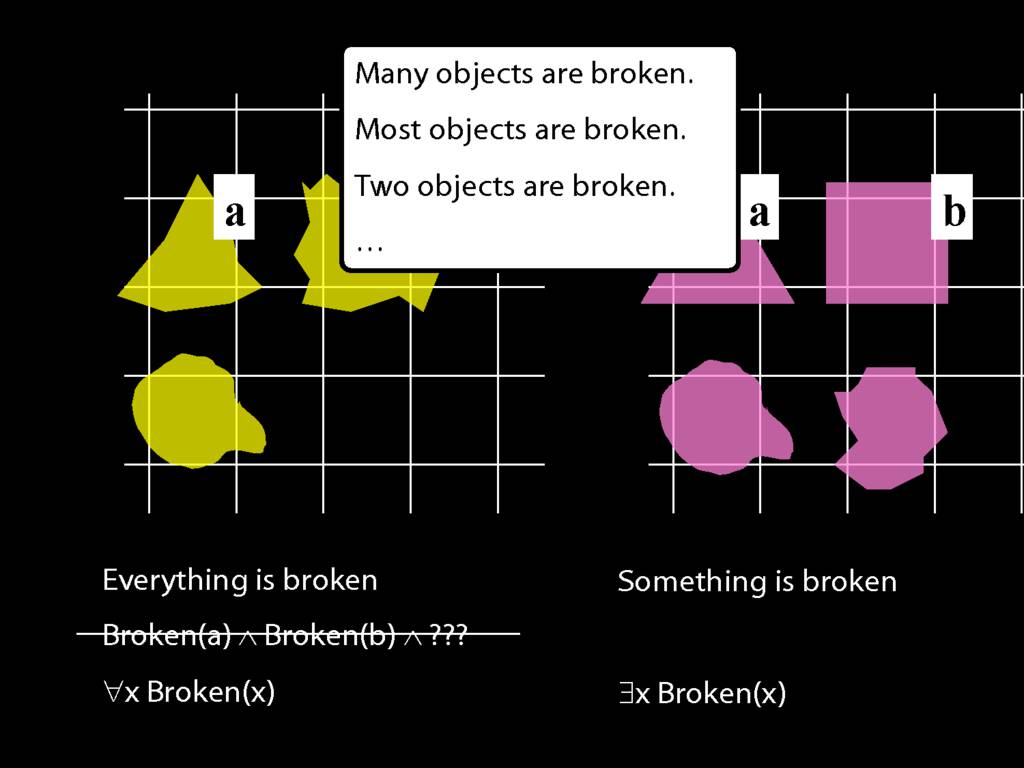
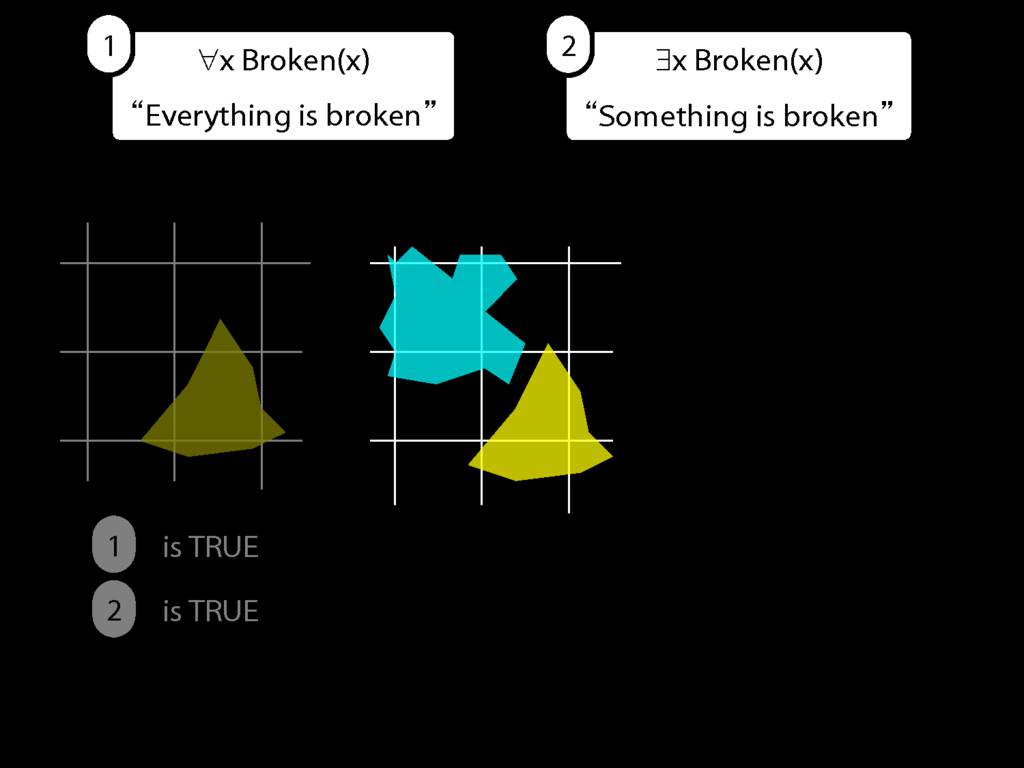
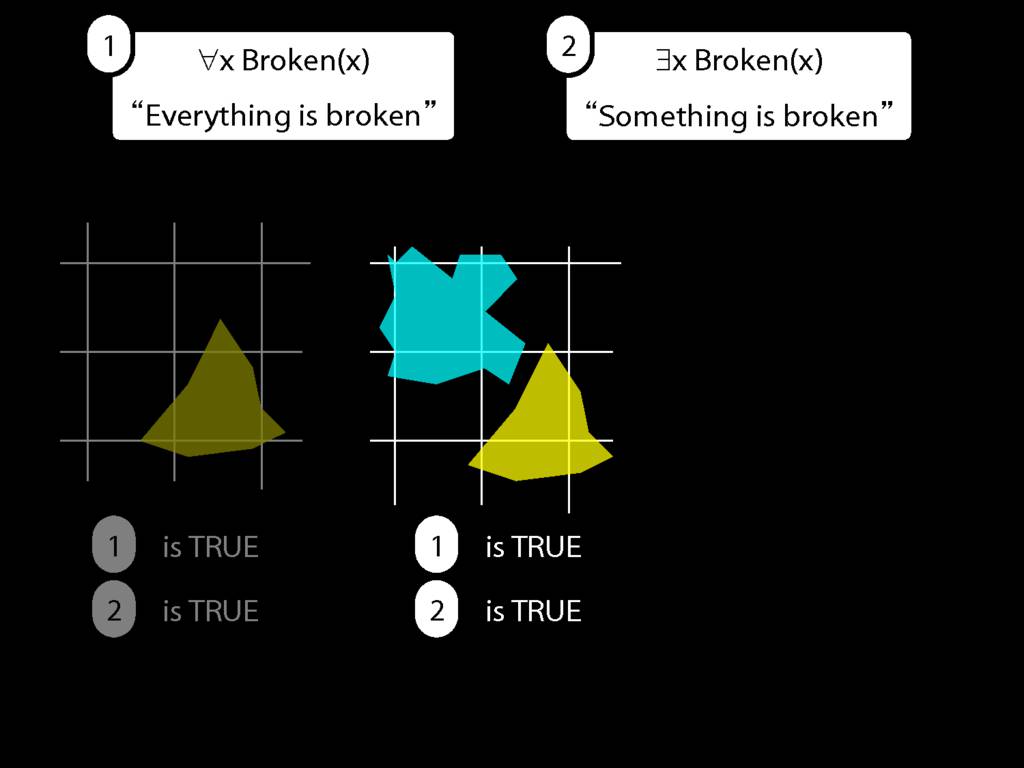
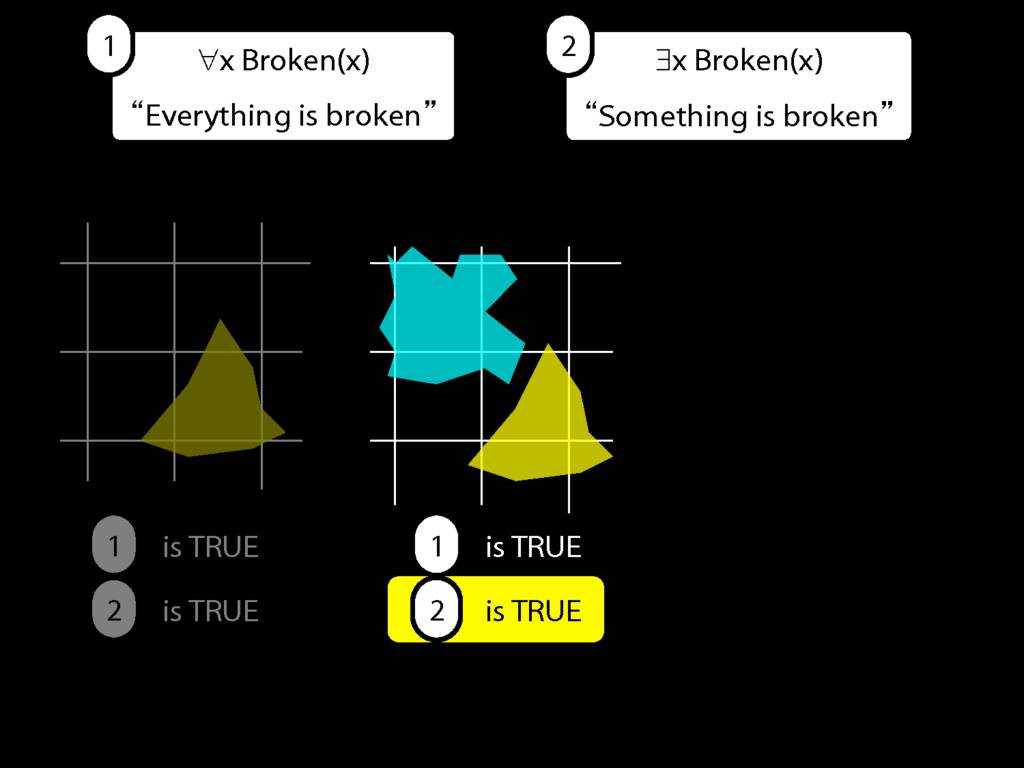
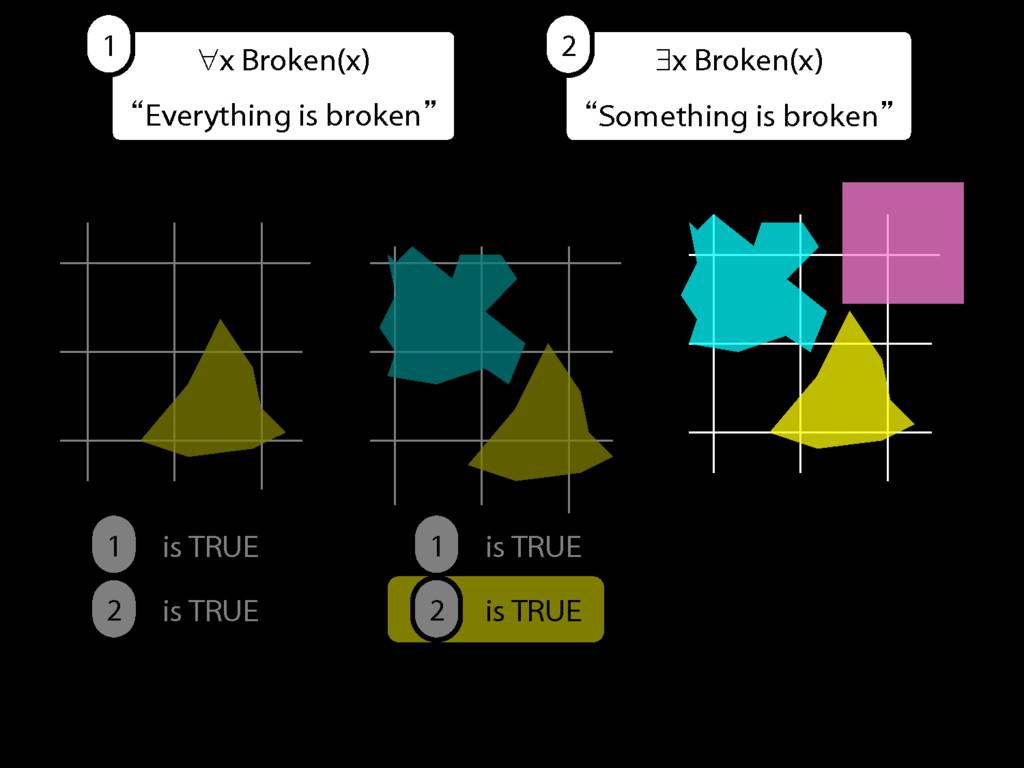
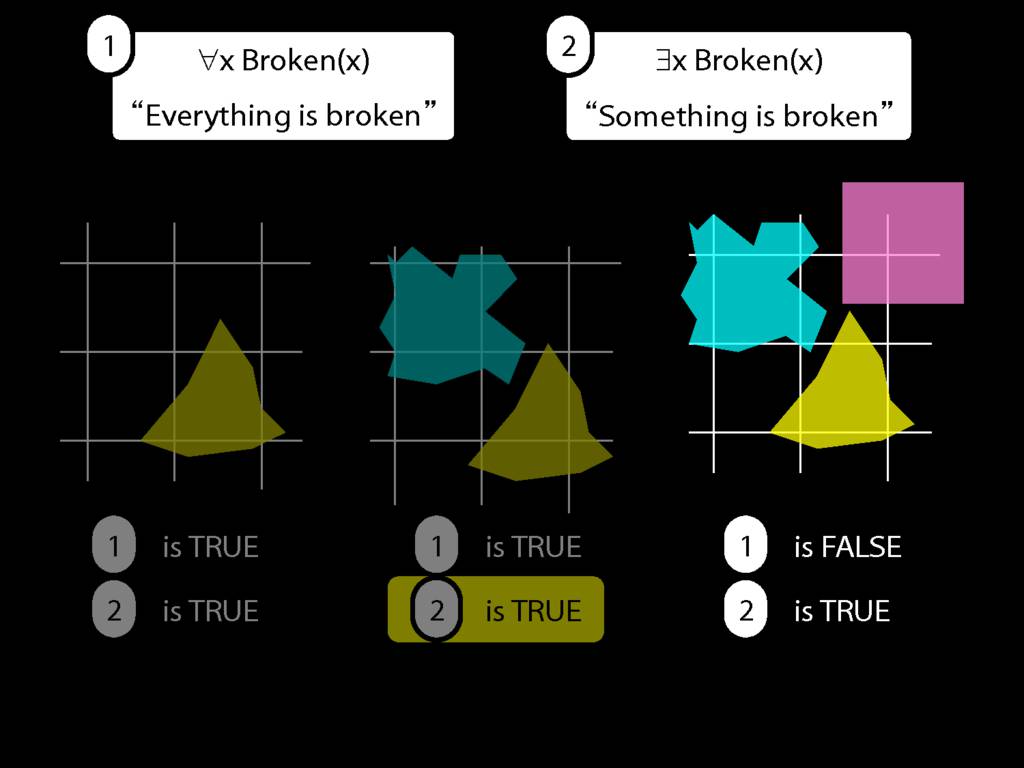
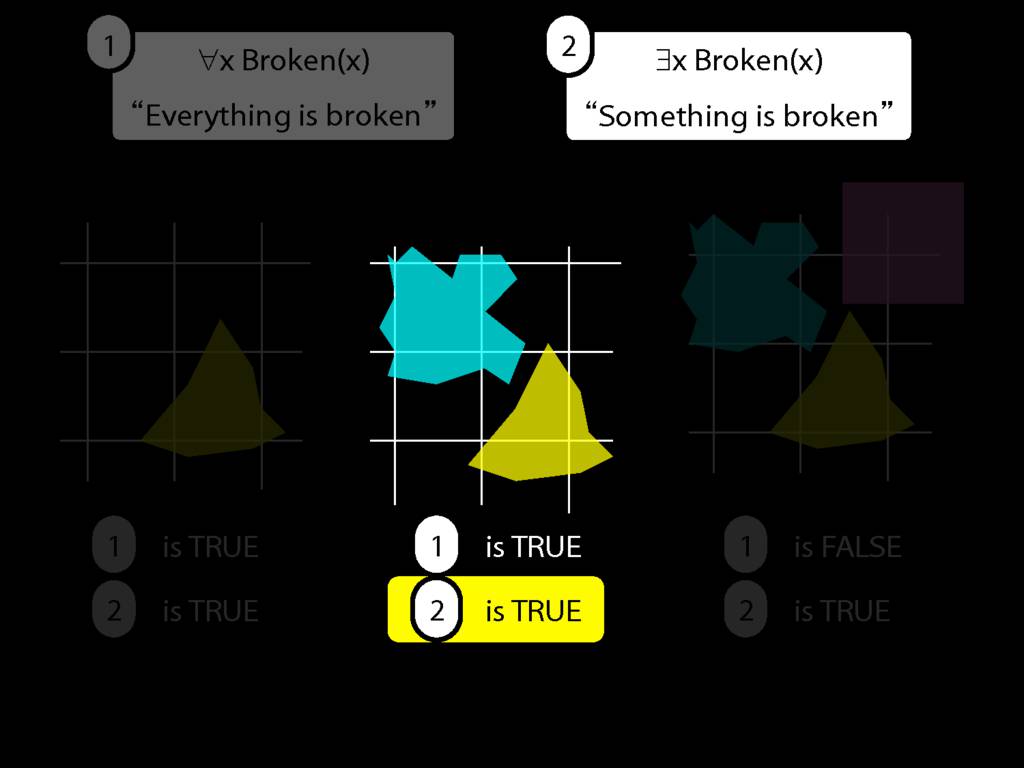
\section{Everything Is Broken}
\emph{Reading:} §9.1, §9.2
\section{Everything Is Broken}
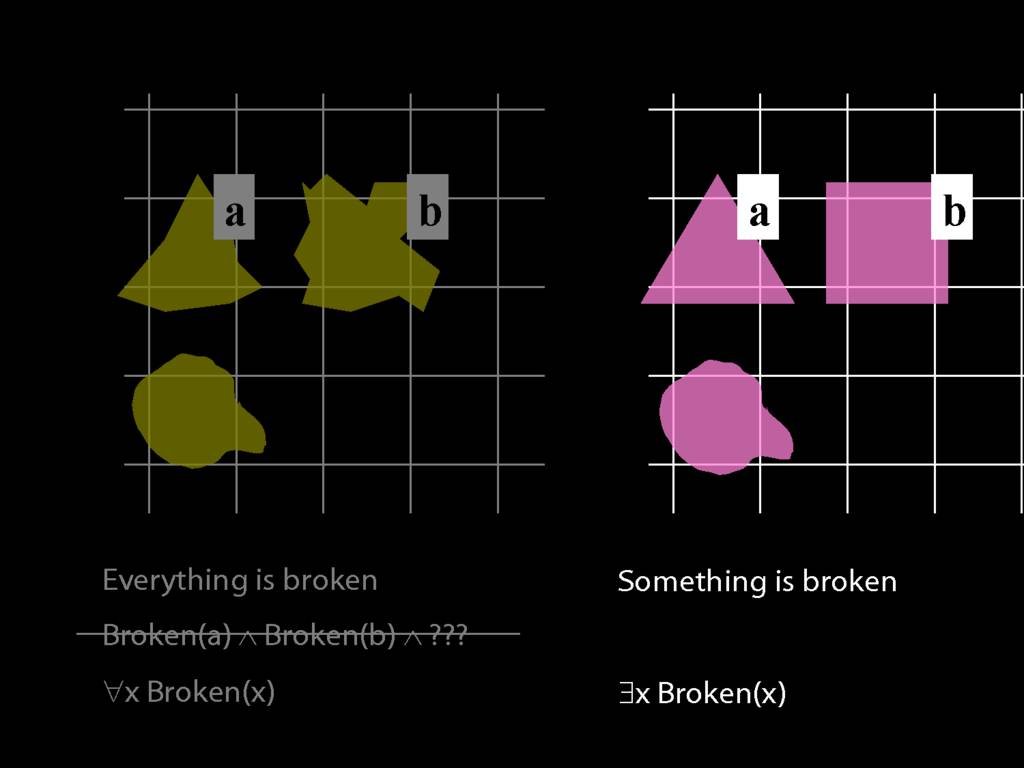
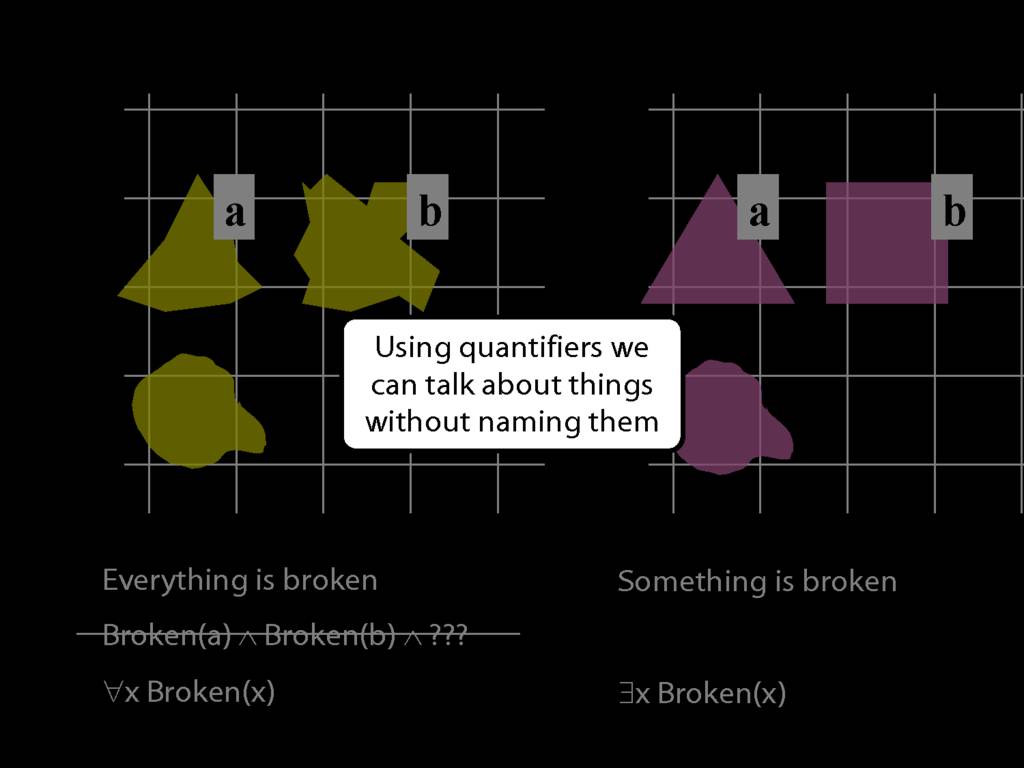
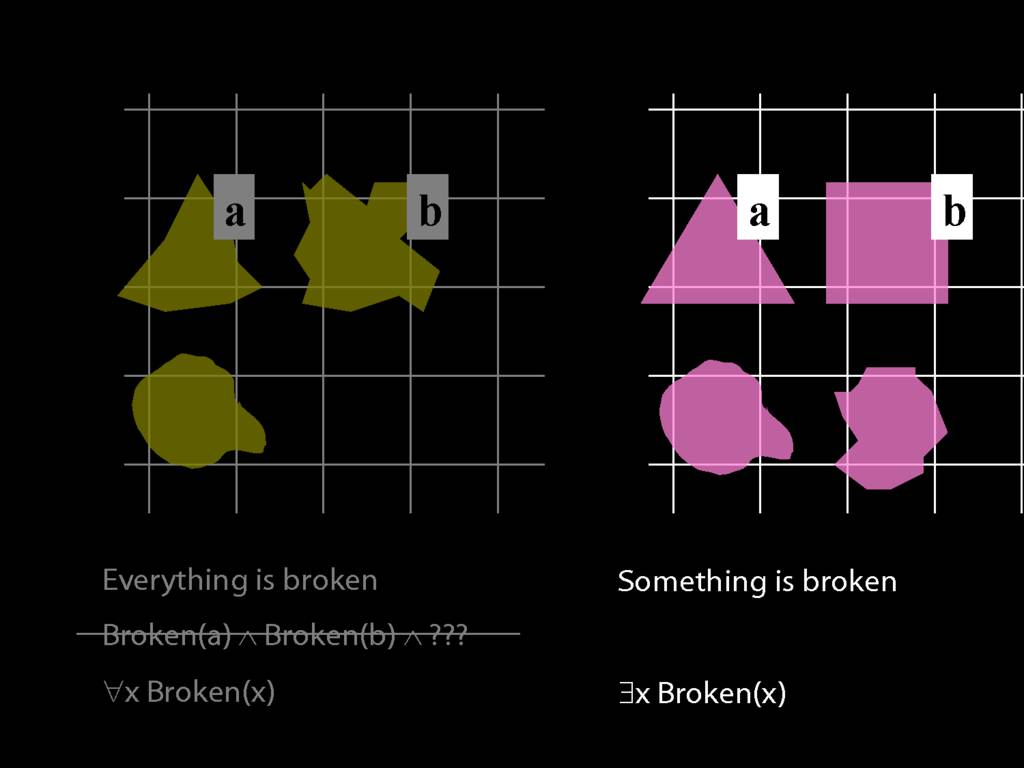
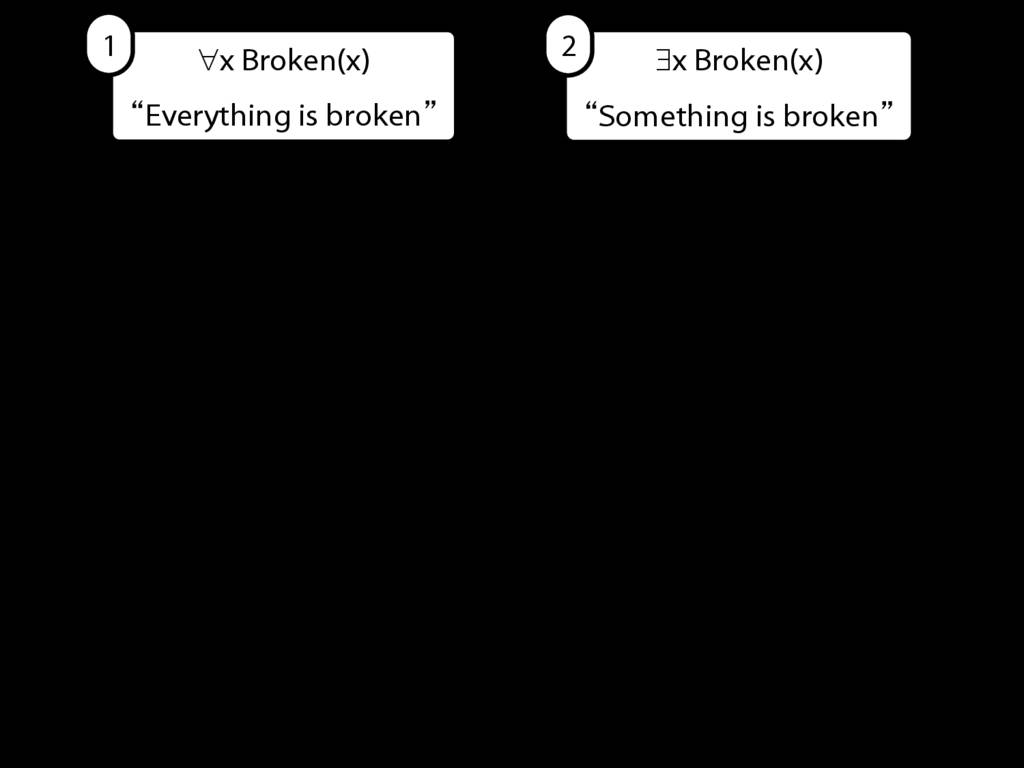
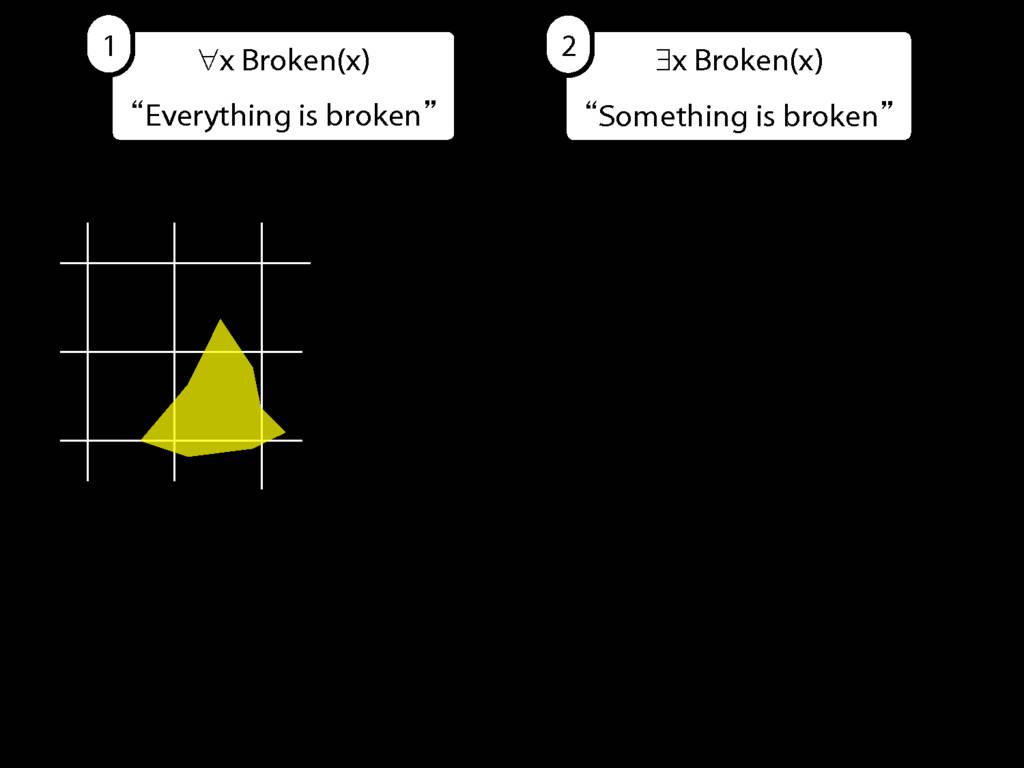
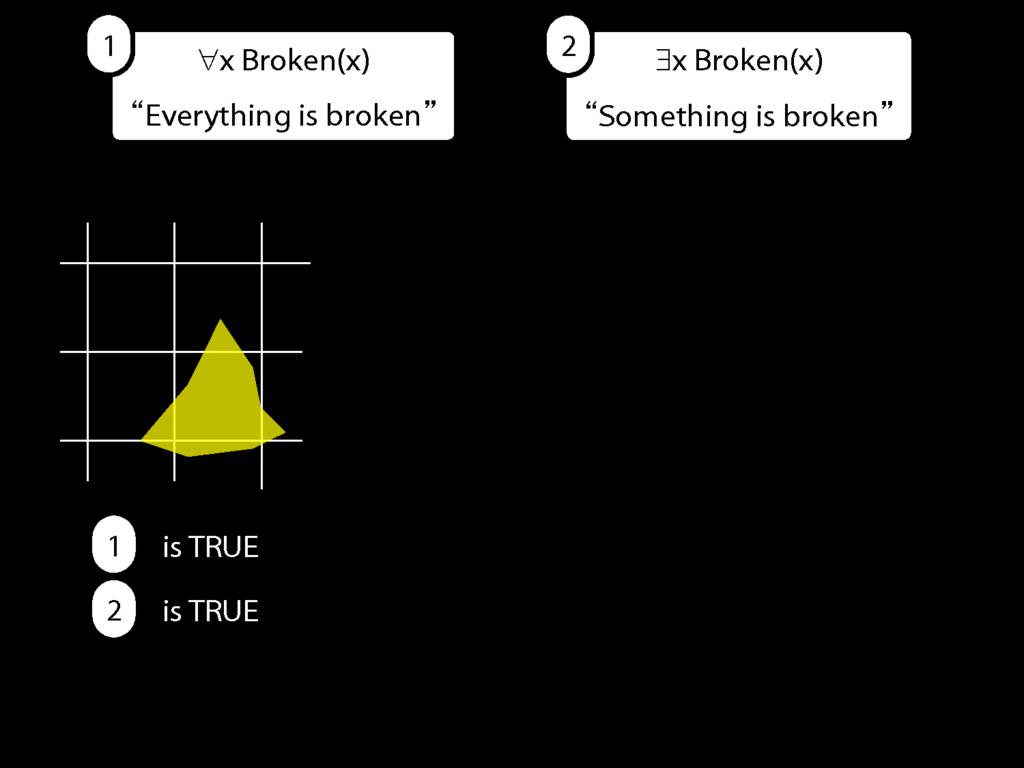
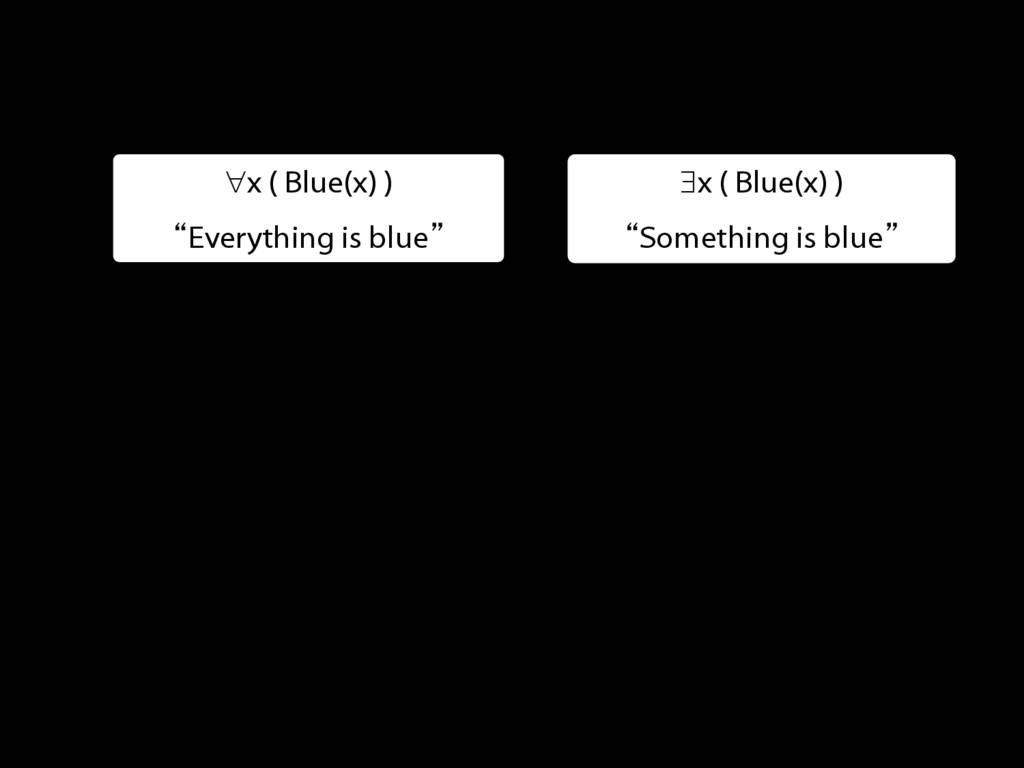
Everything is broken: ∀x Broken(x)
Something is broken: ∃x Broken(x)
9.1 odd numbers only
9.2 even numbers only
9.8–-9.10
∃Elim
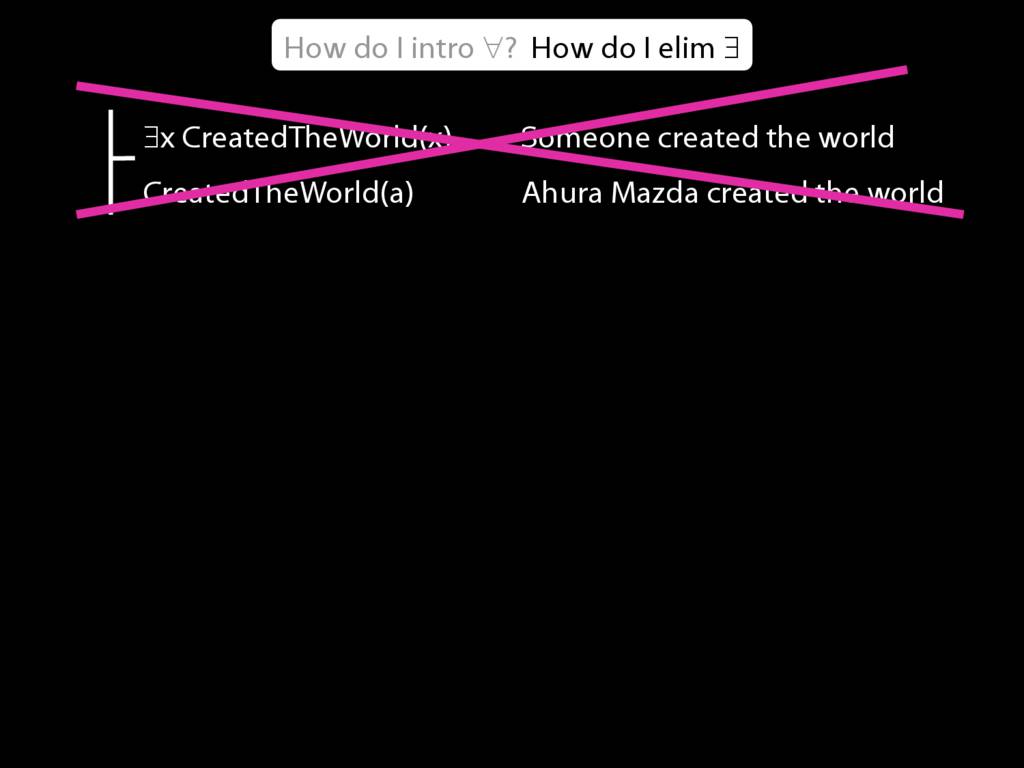
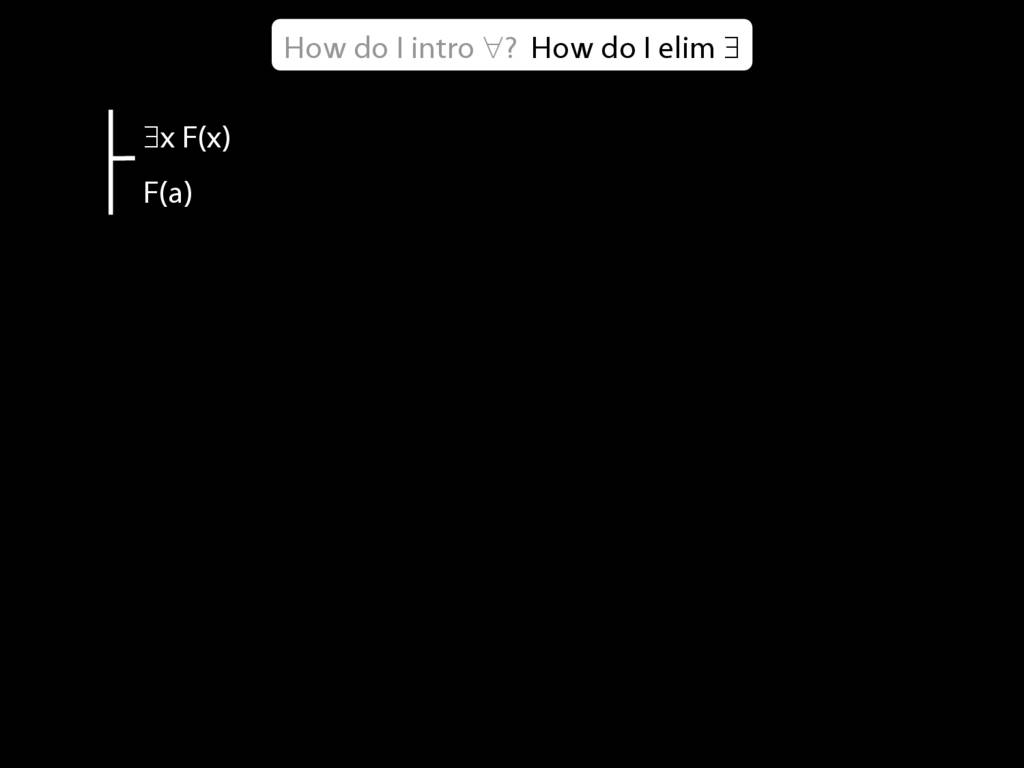
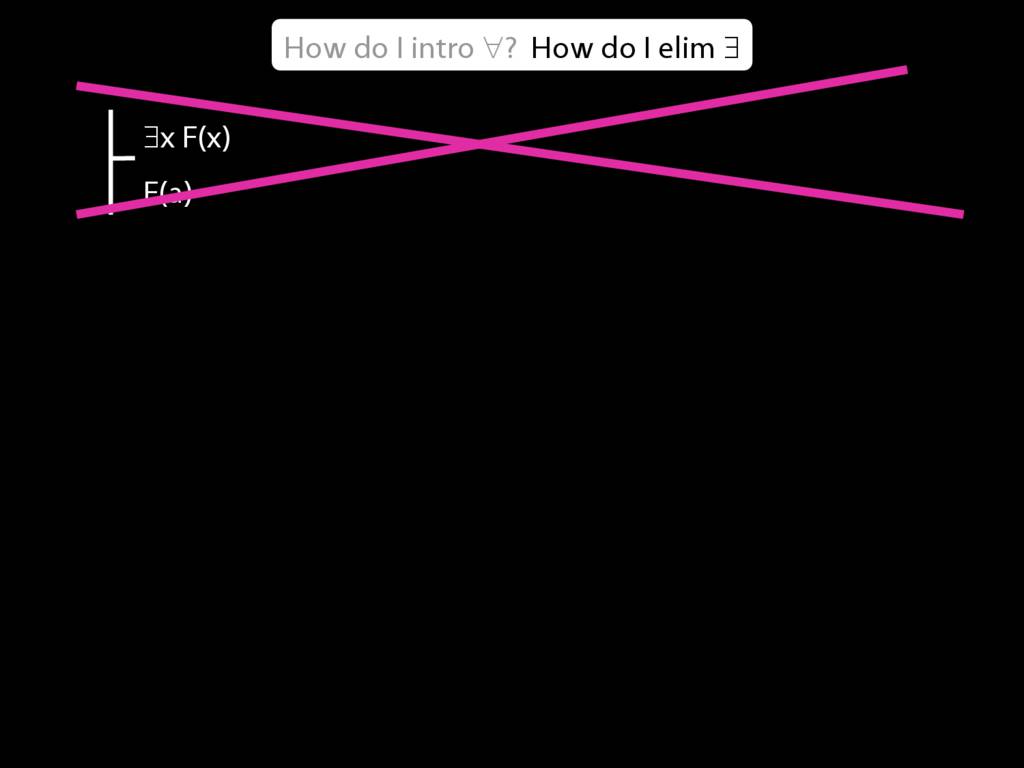
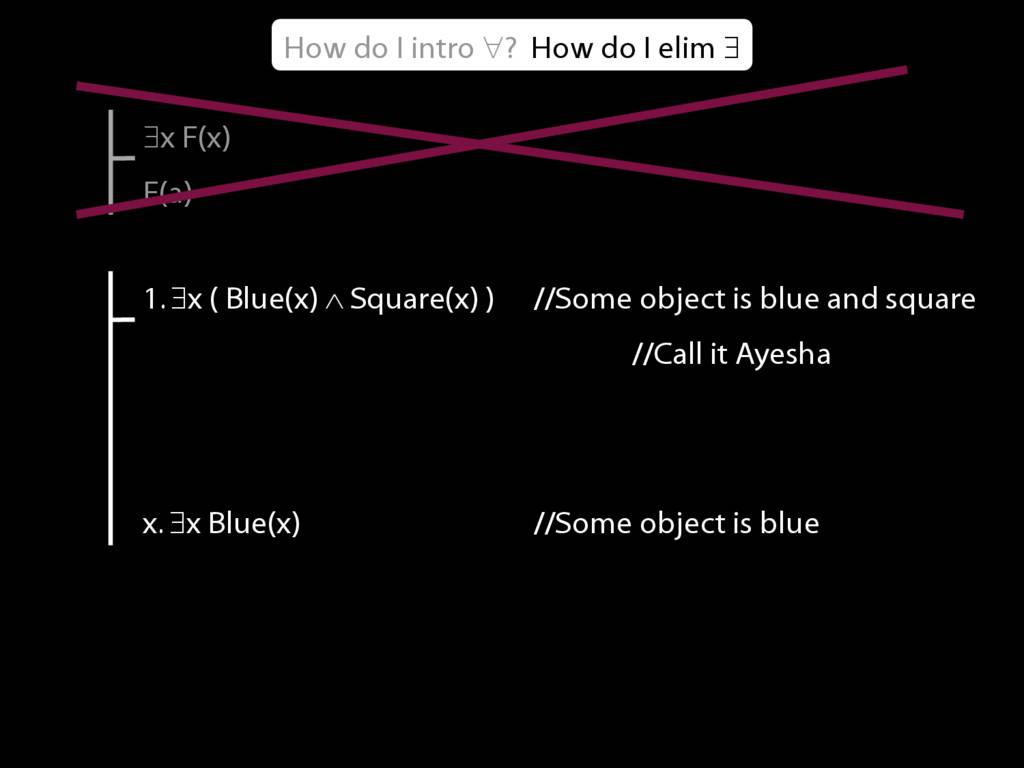
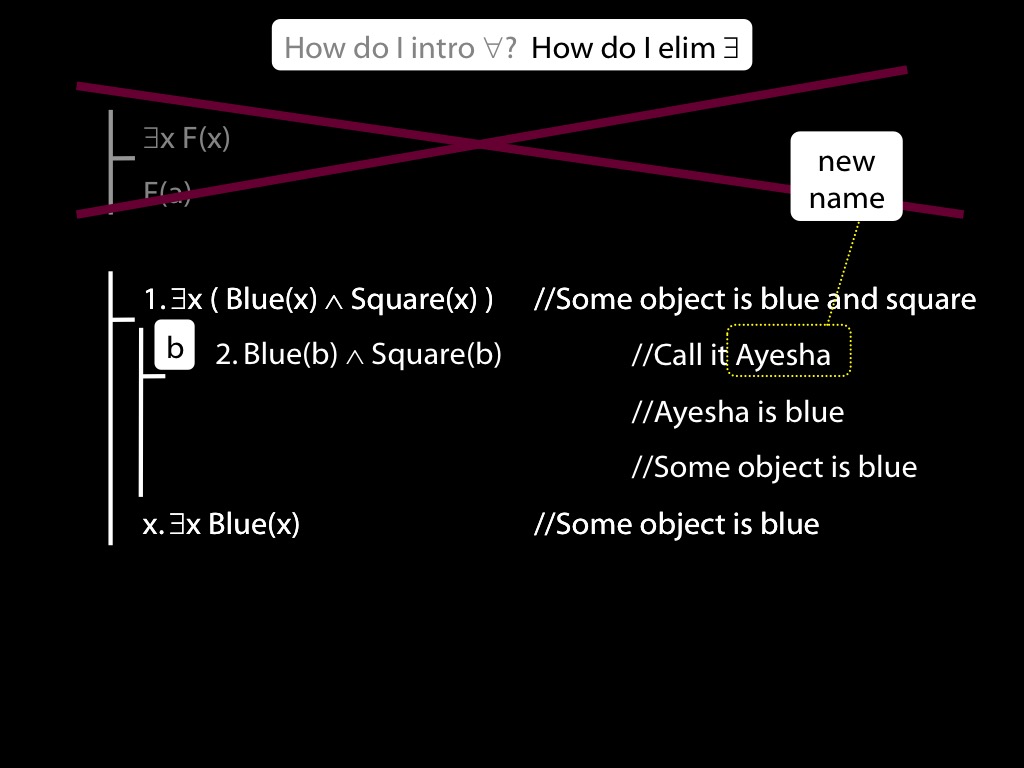
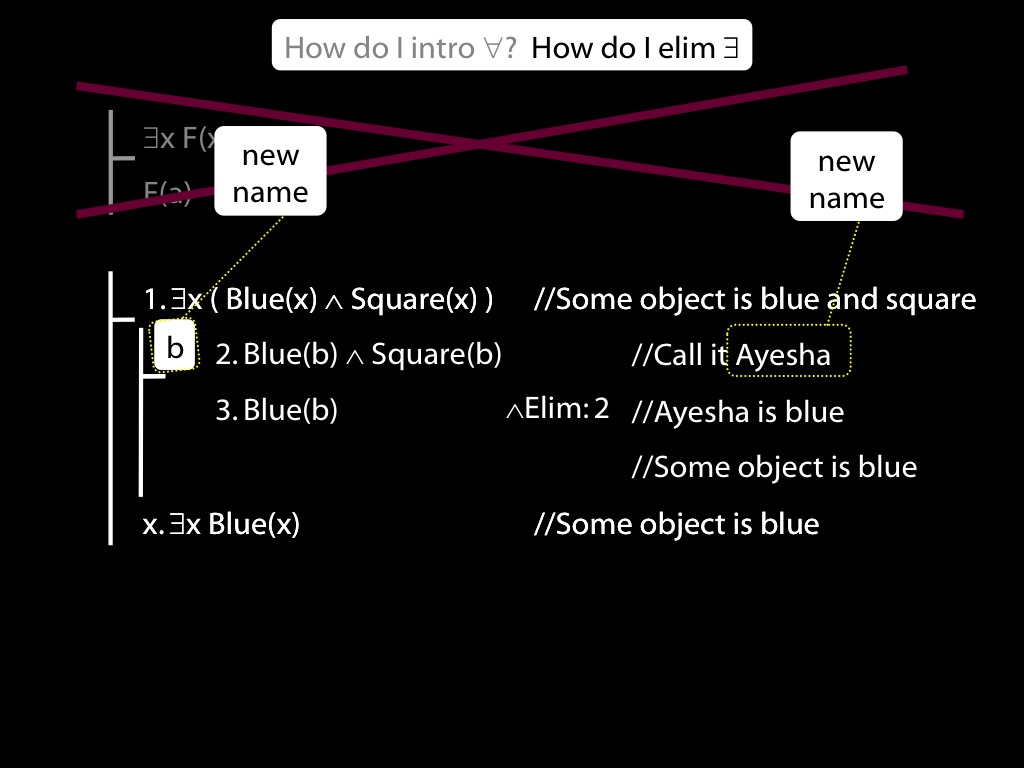
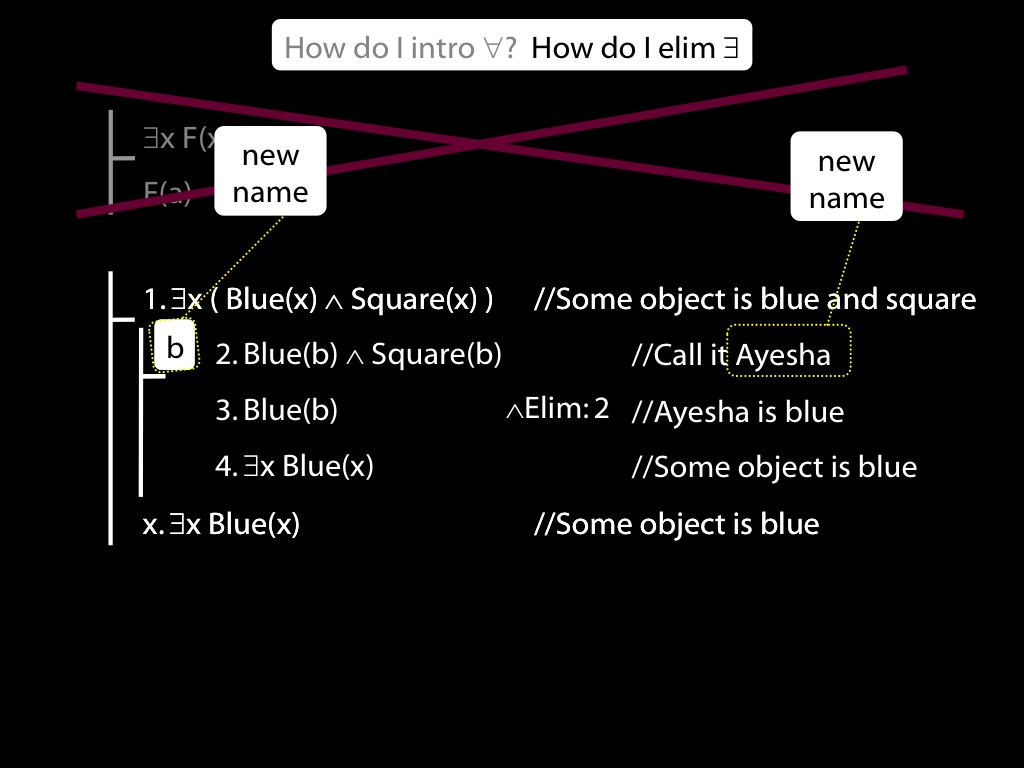
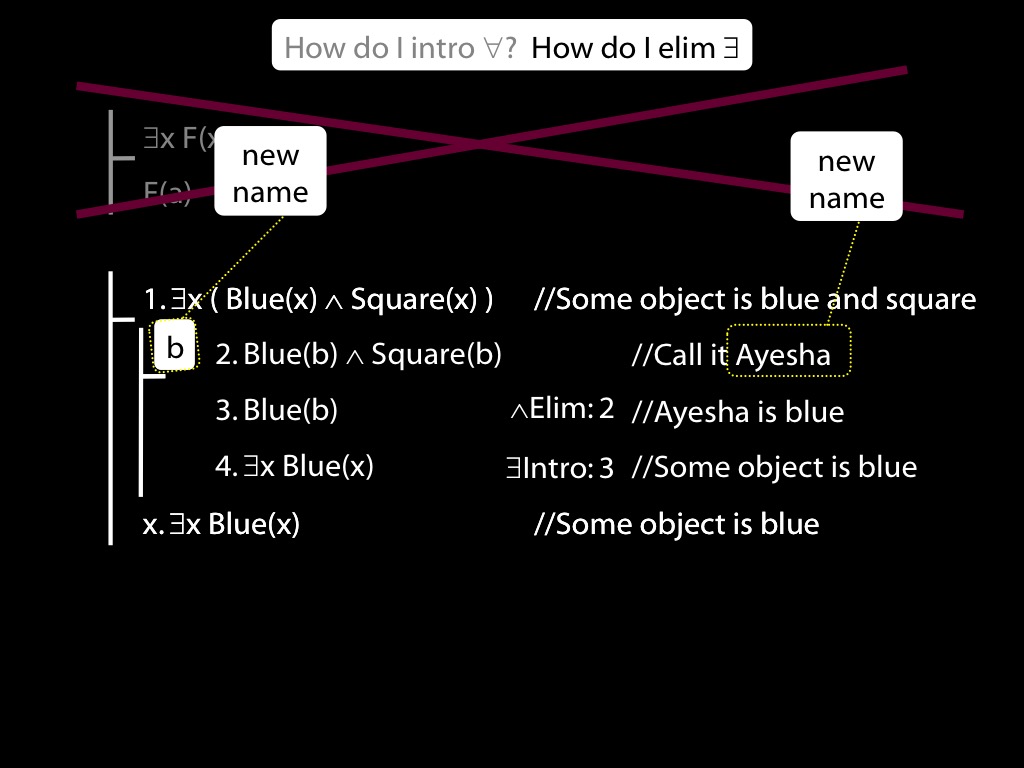
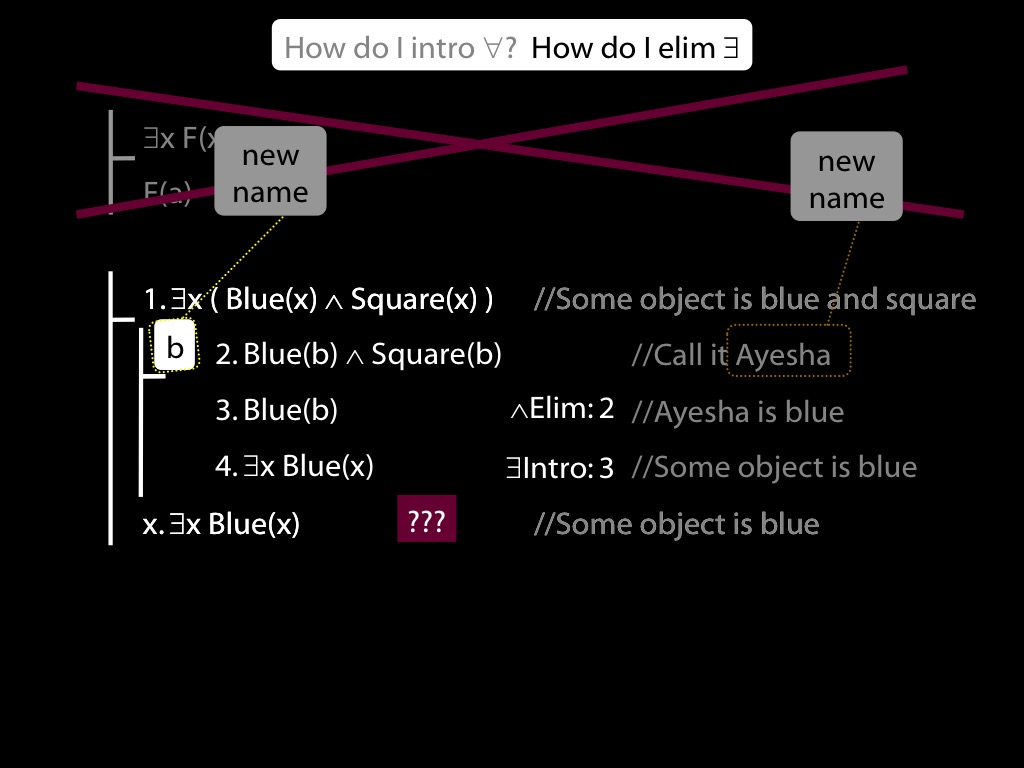
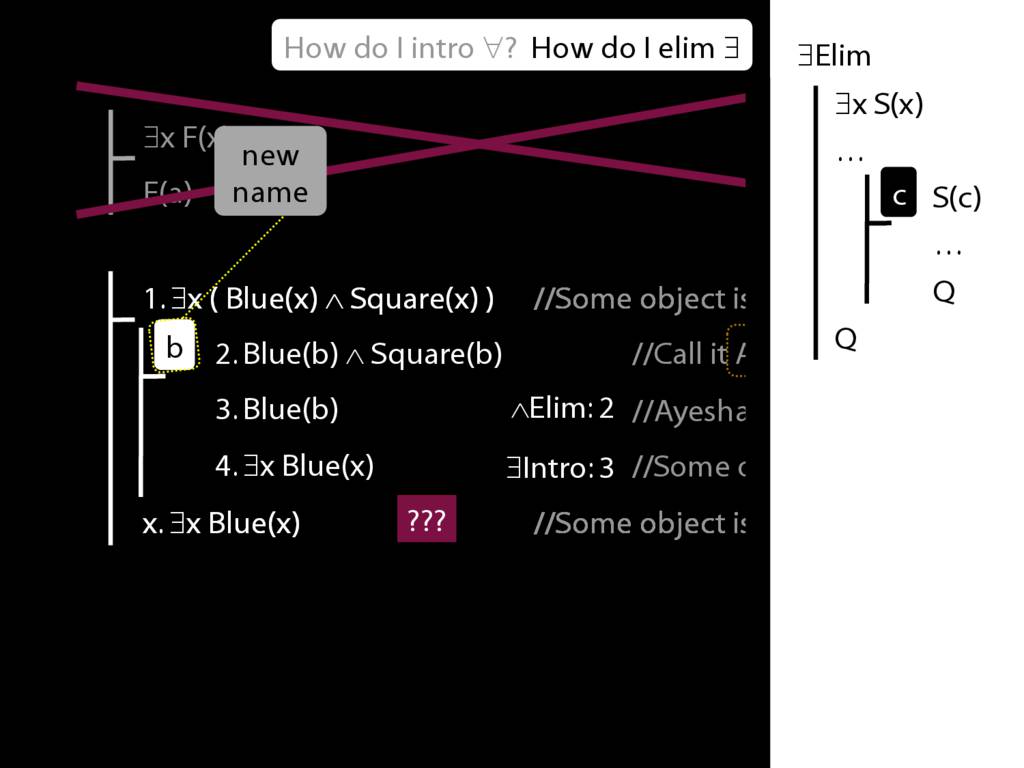
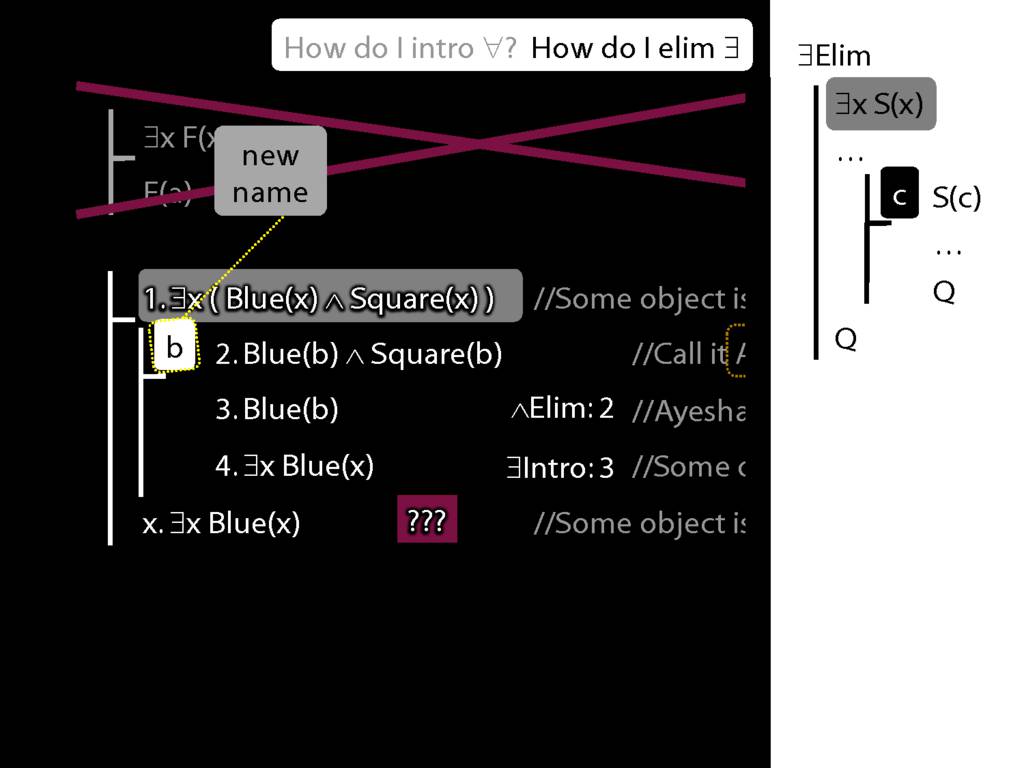
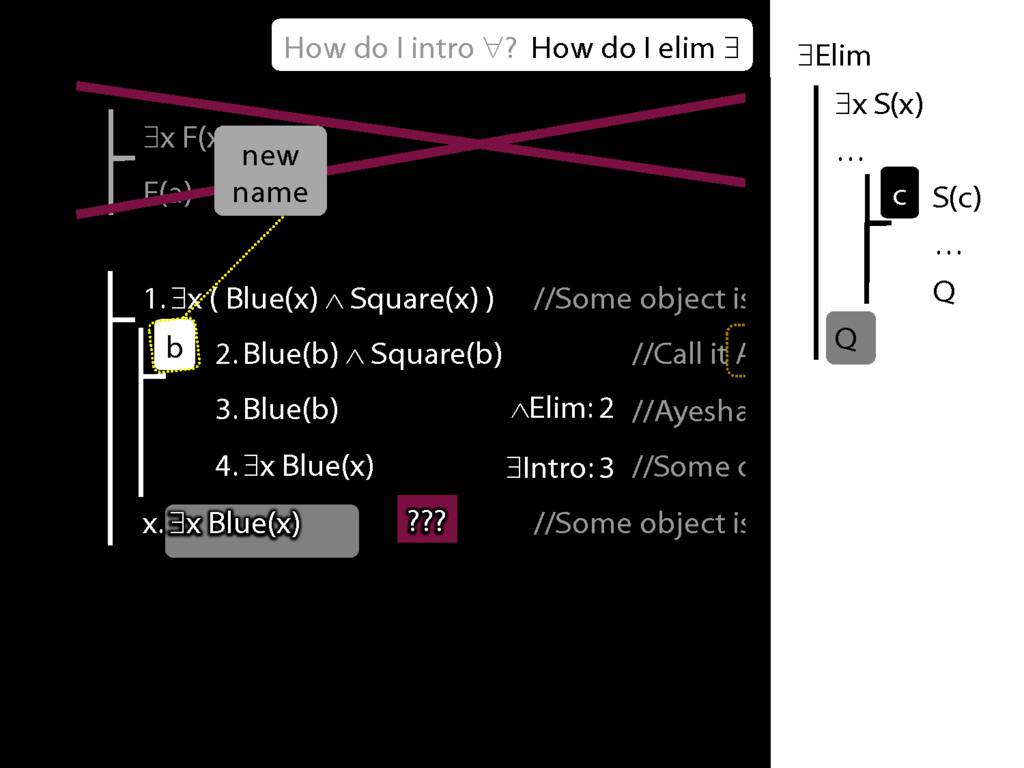
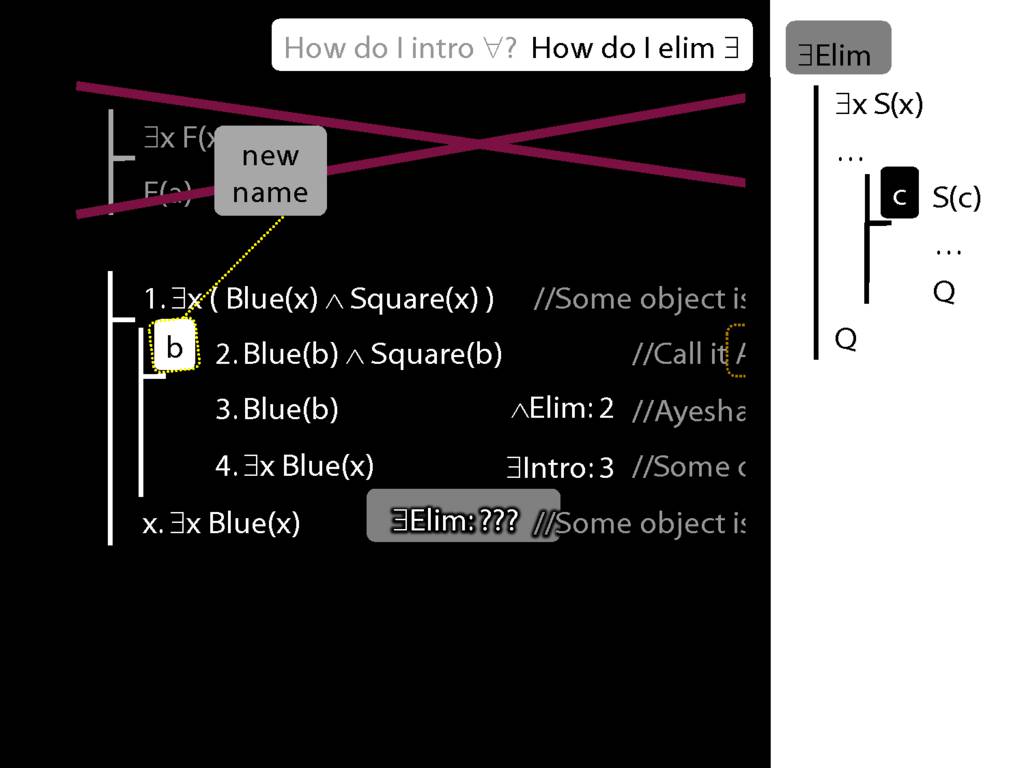
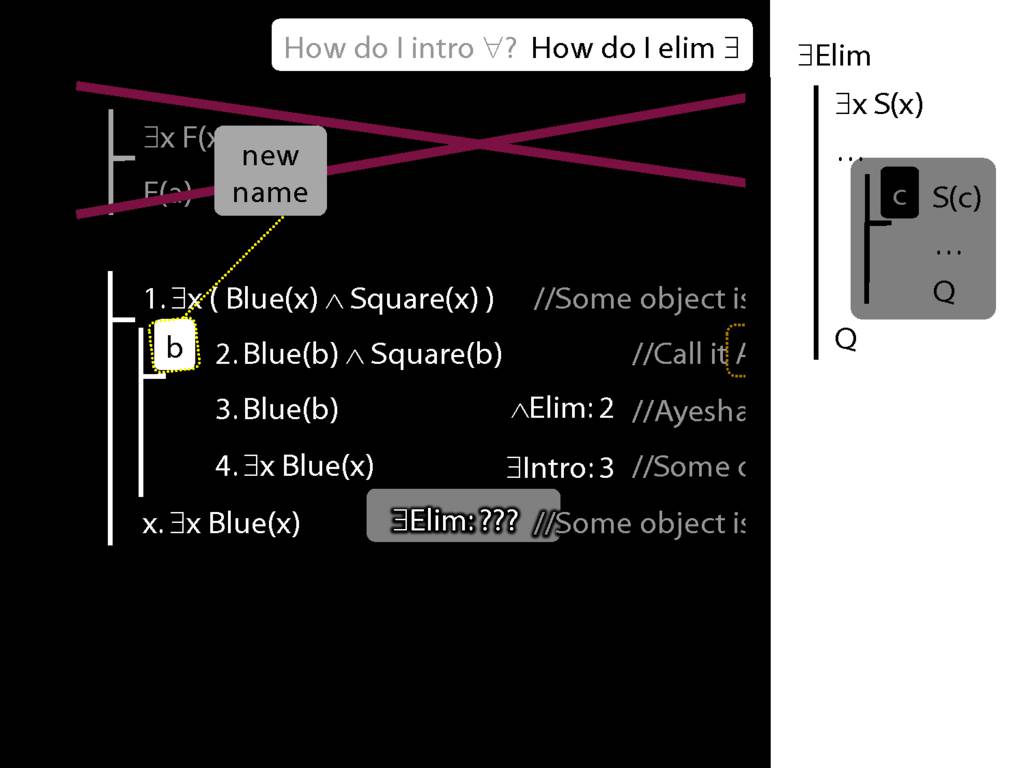
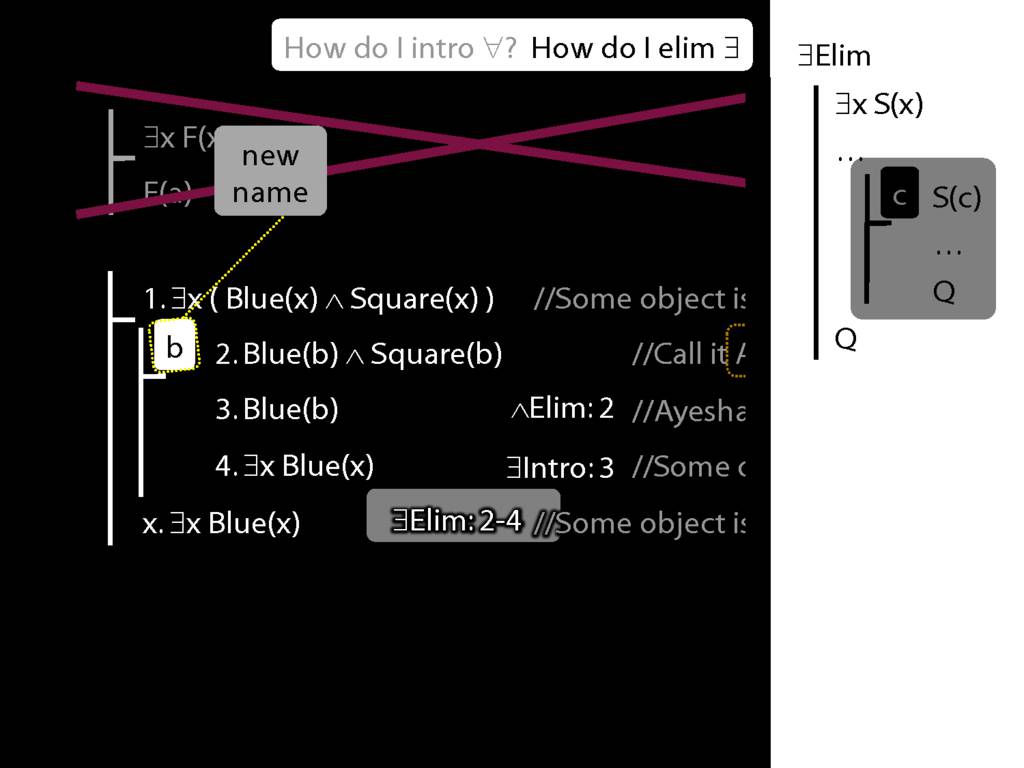
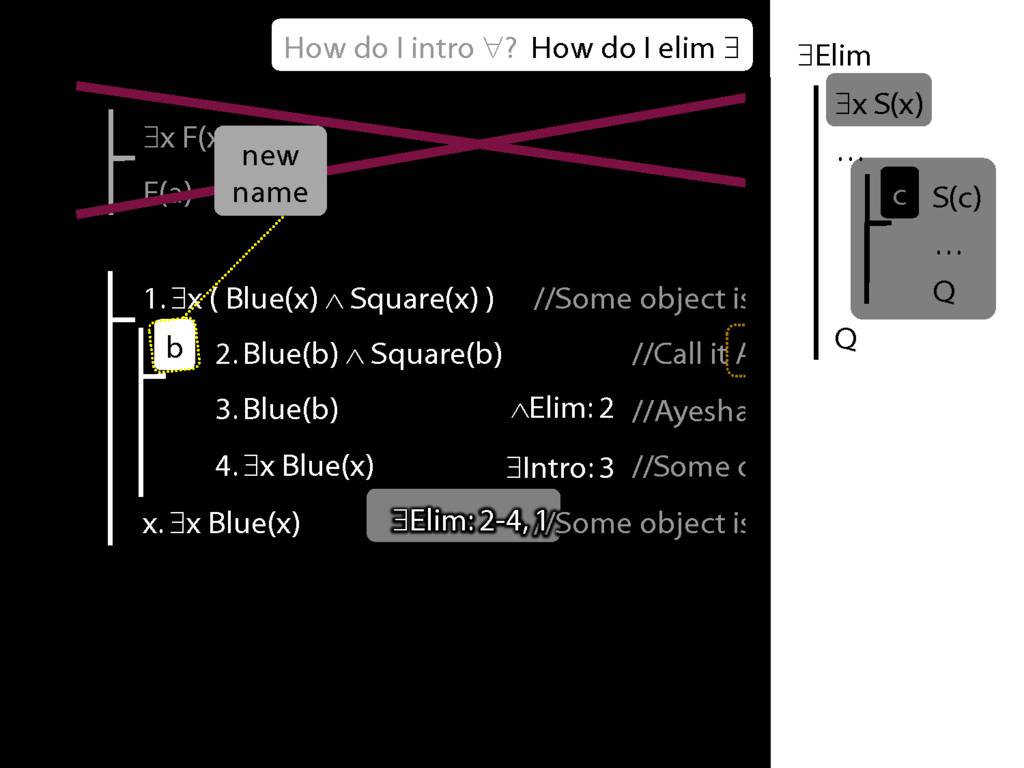
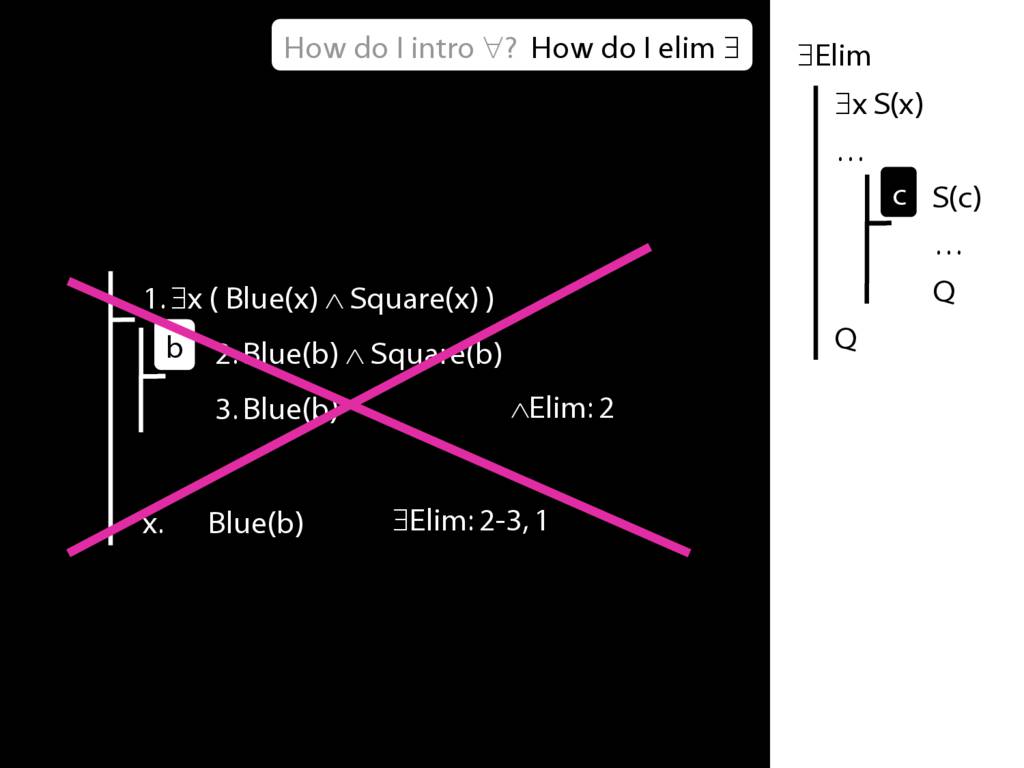
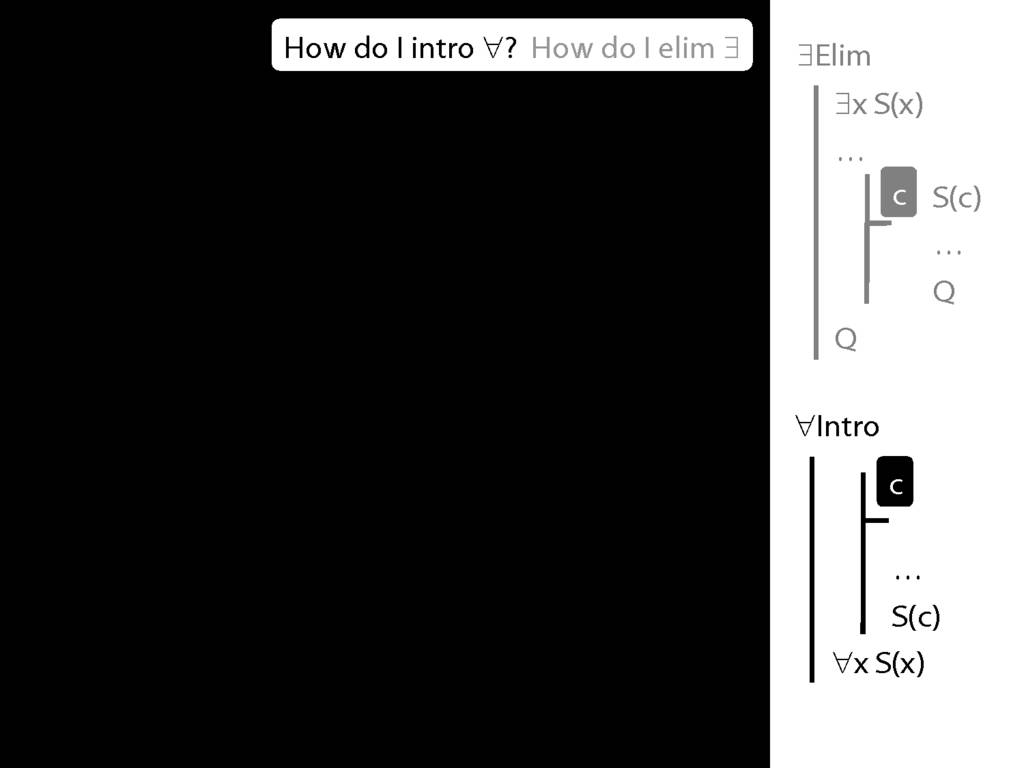
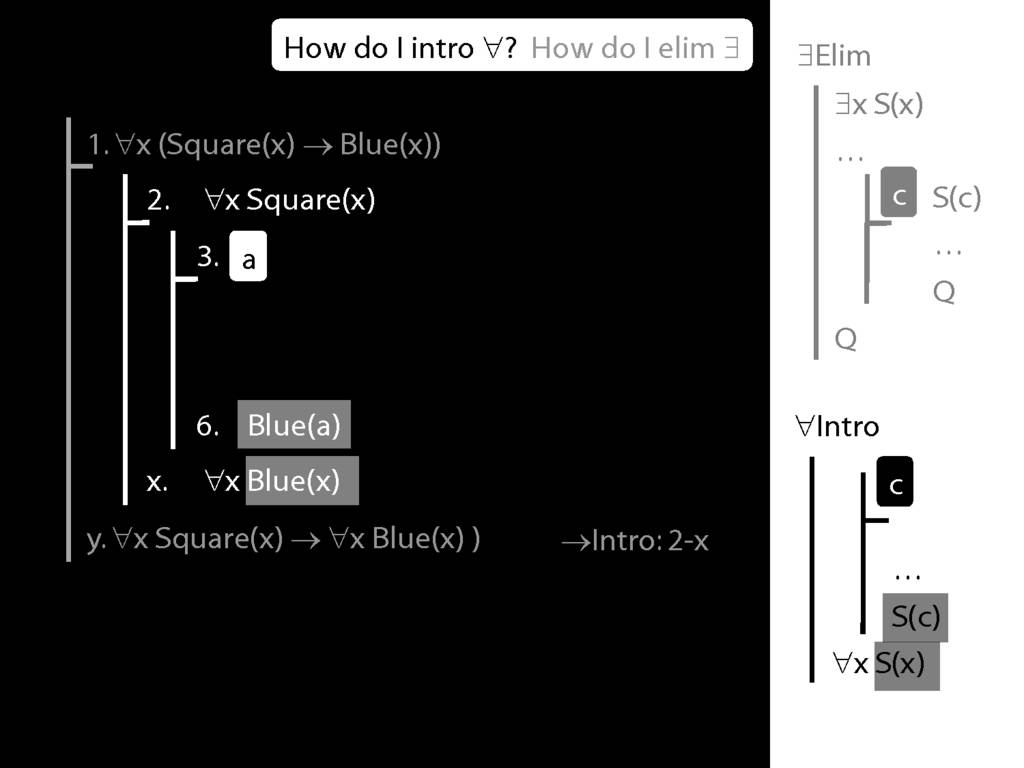
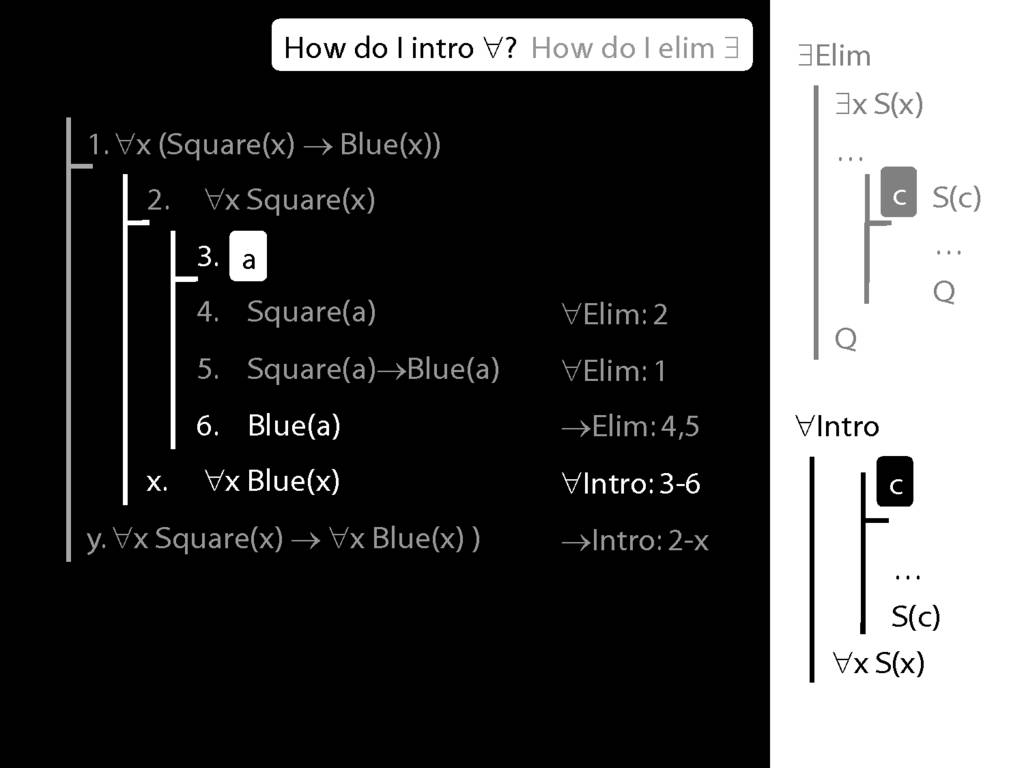
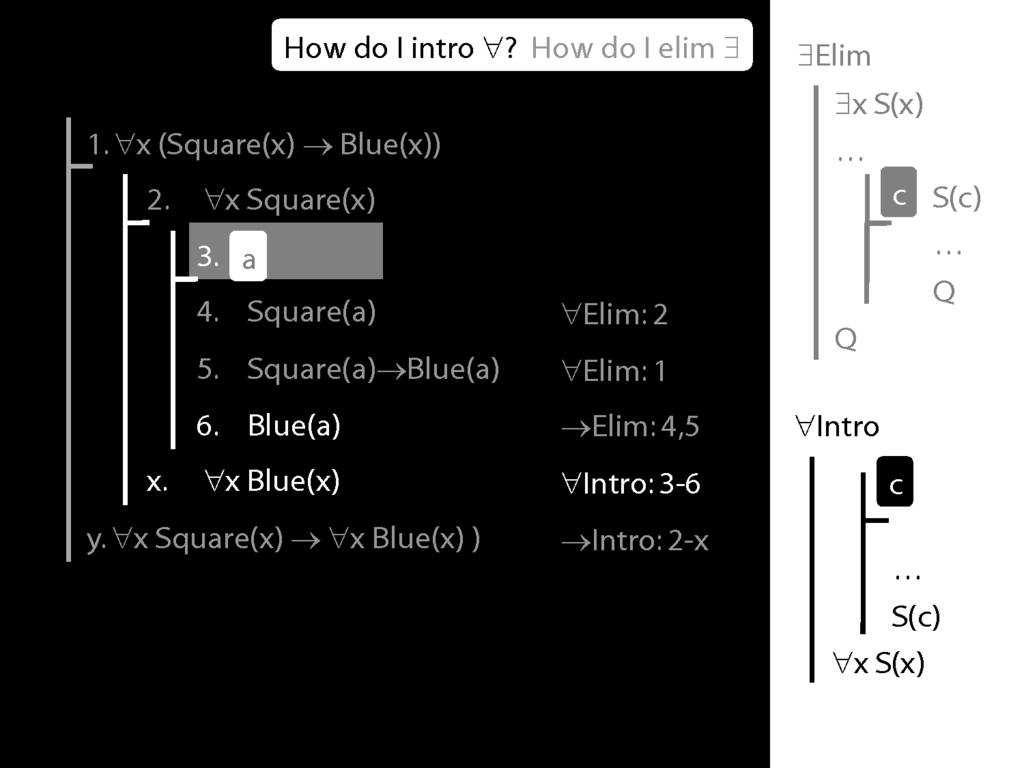
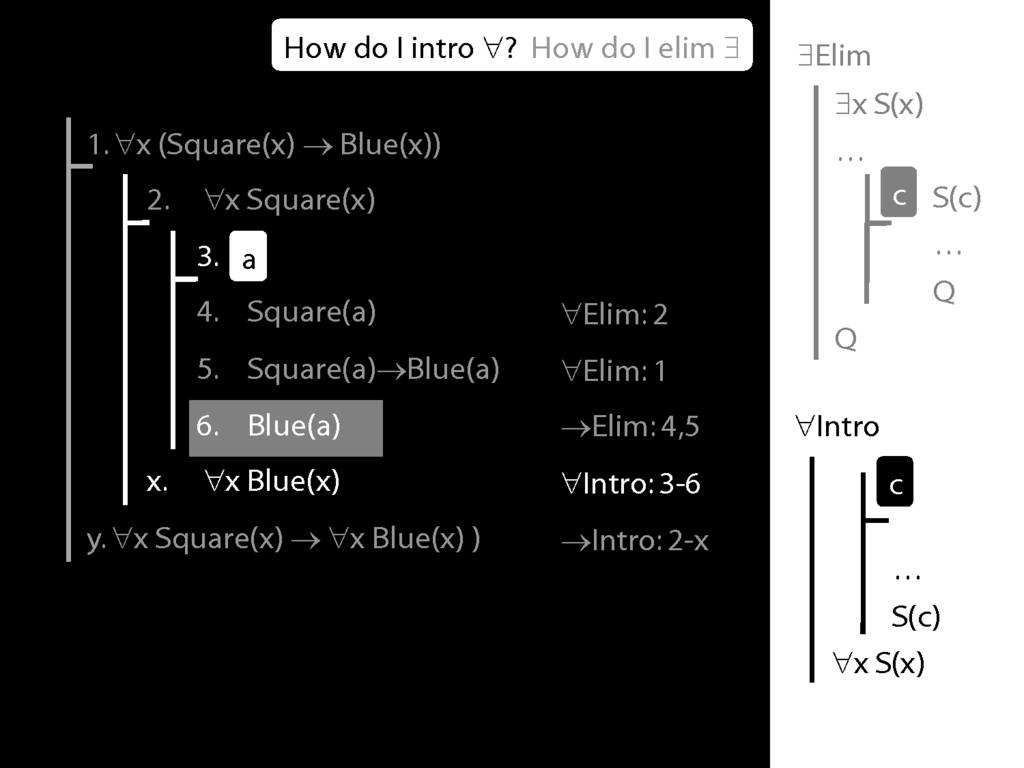
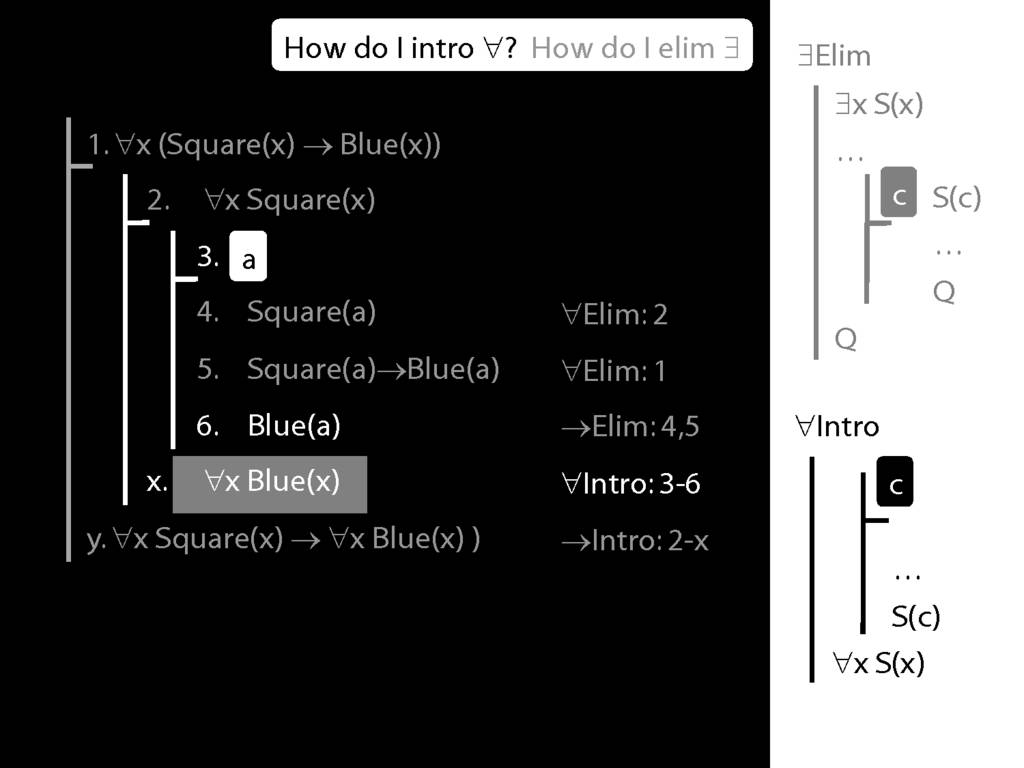
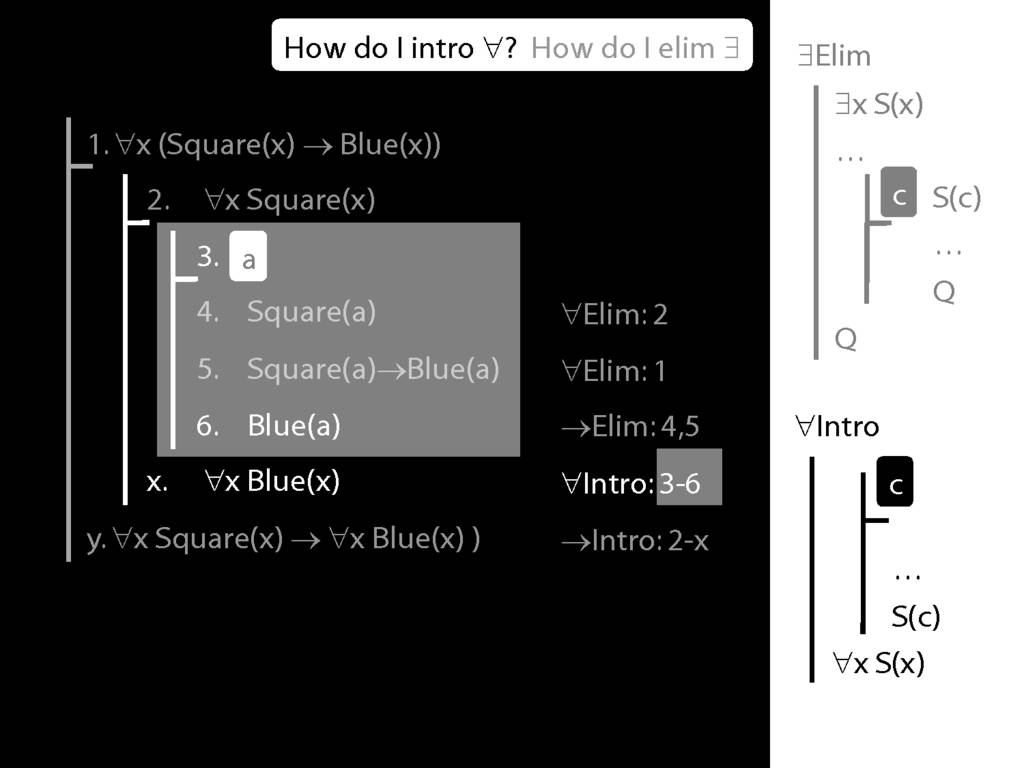
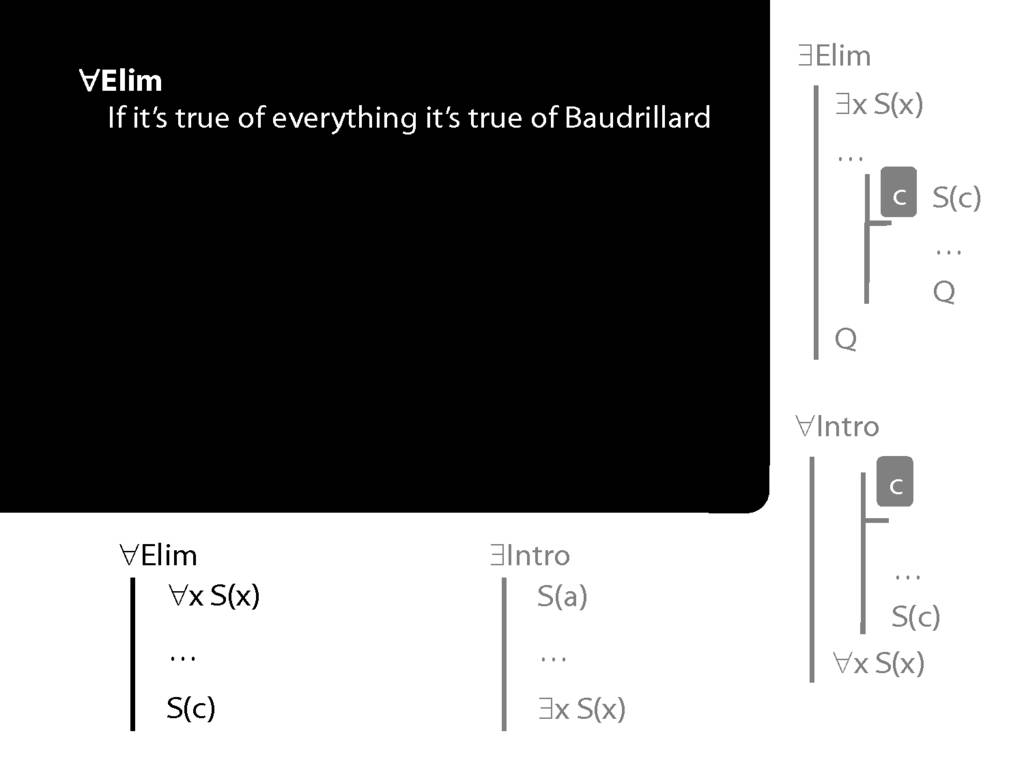
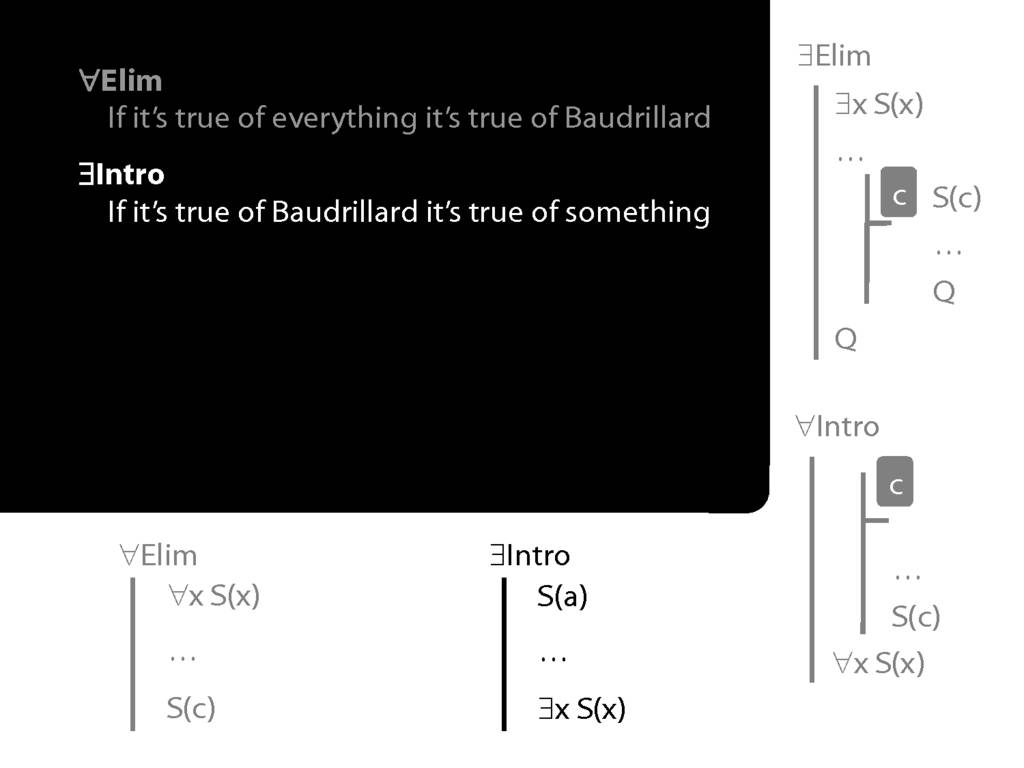
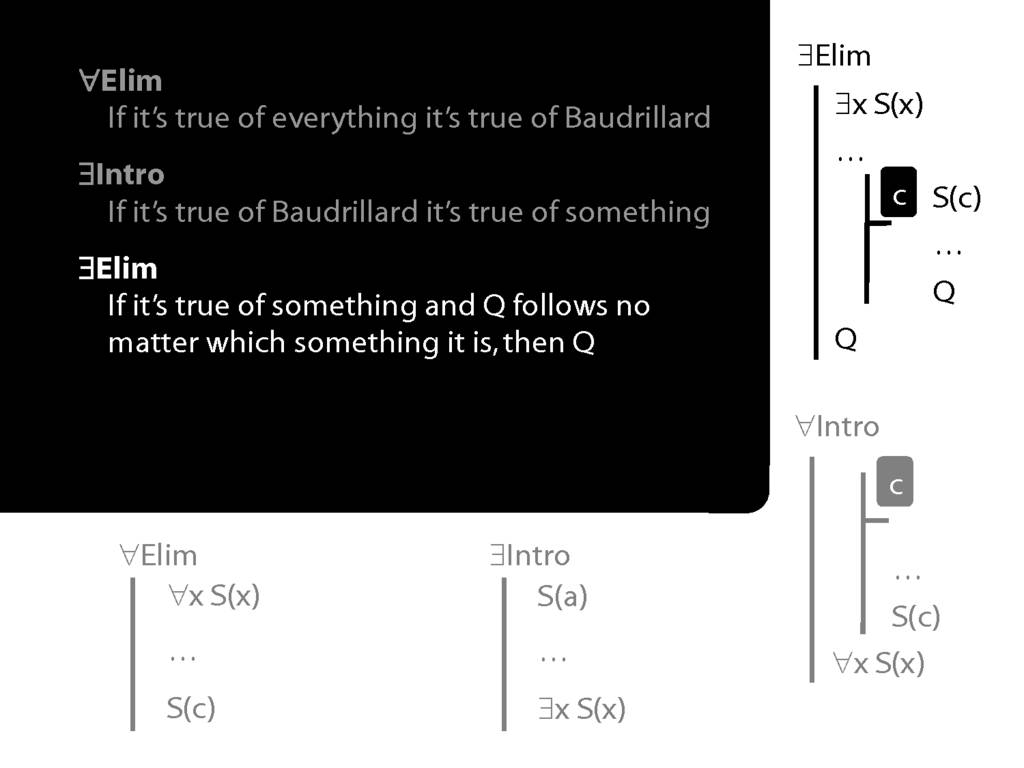
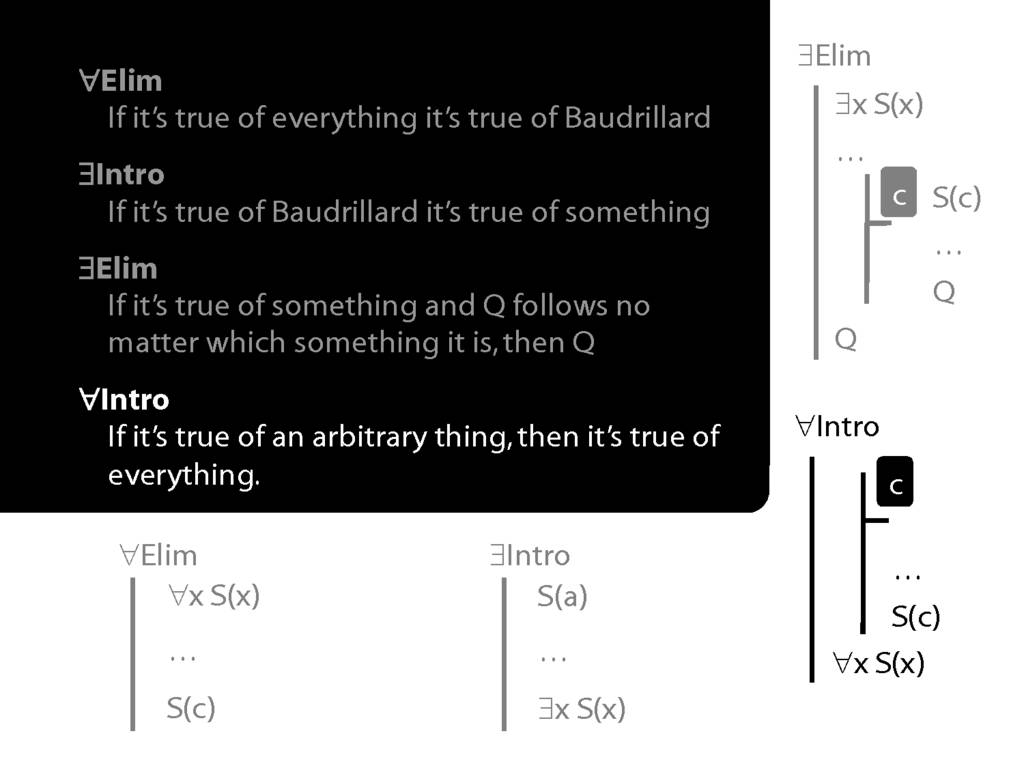
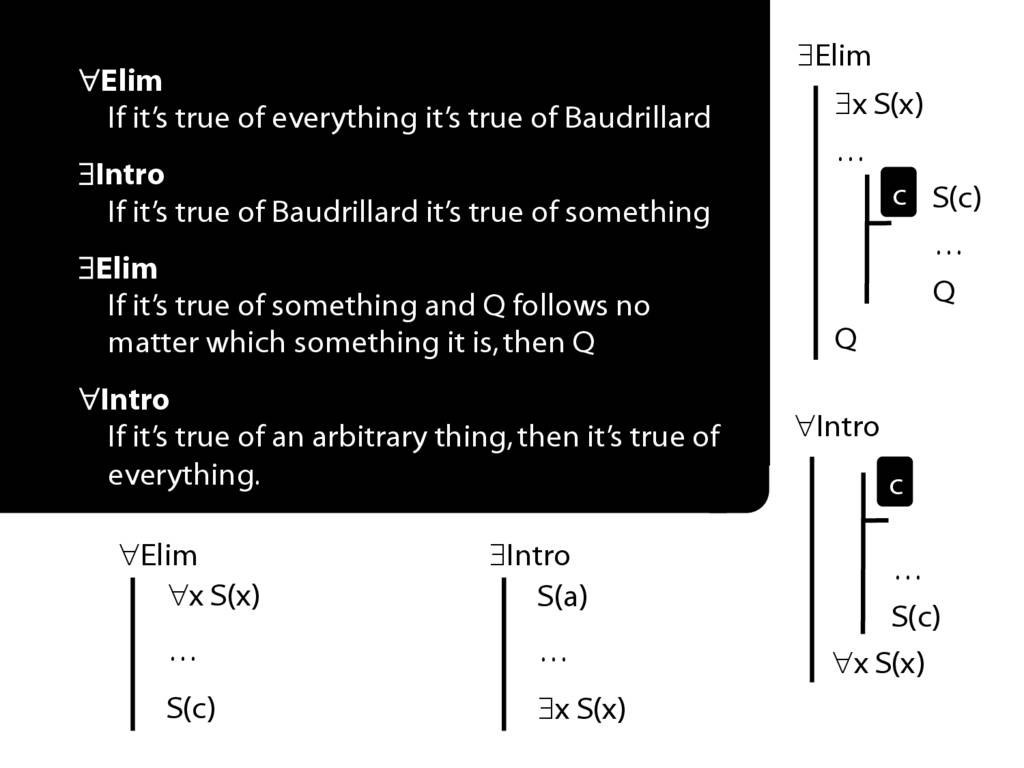
\section{∃Elim}
\emph{Reading:} §12.2, §13.2
\section{∃Elim}
\begin{minipage}{\columnwidth}
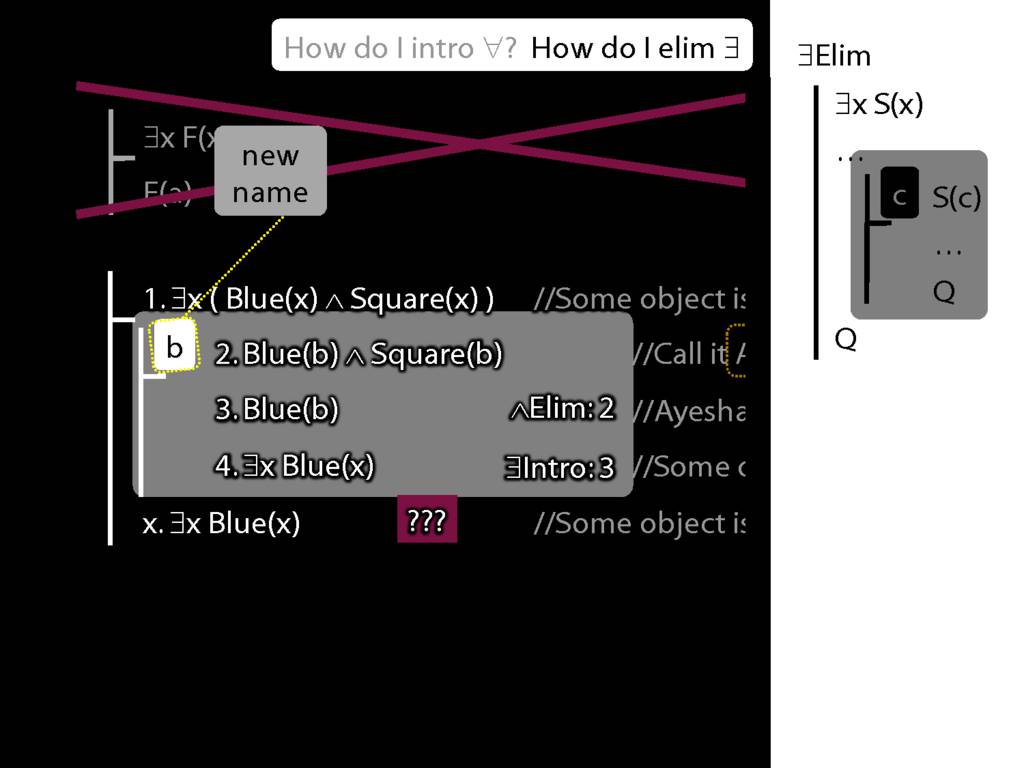
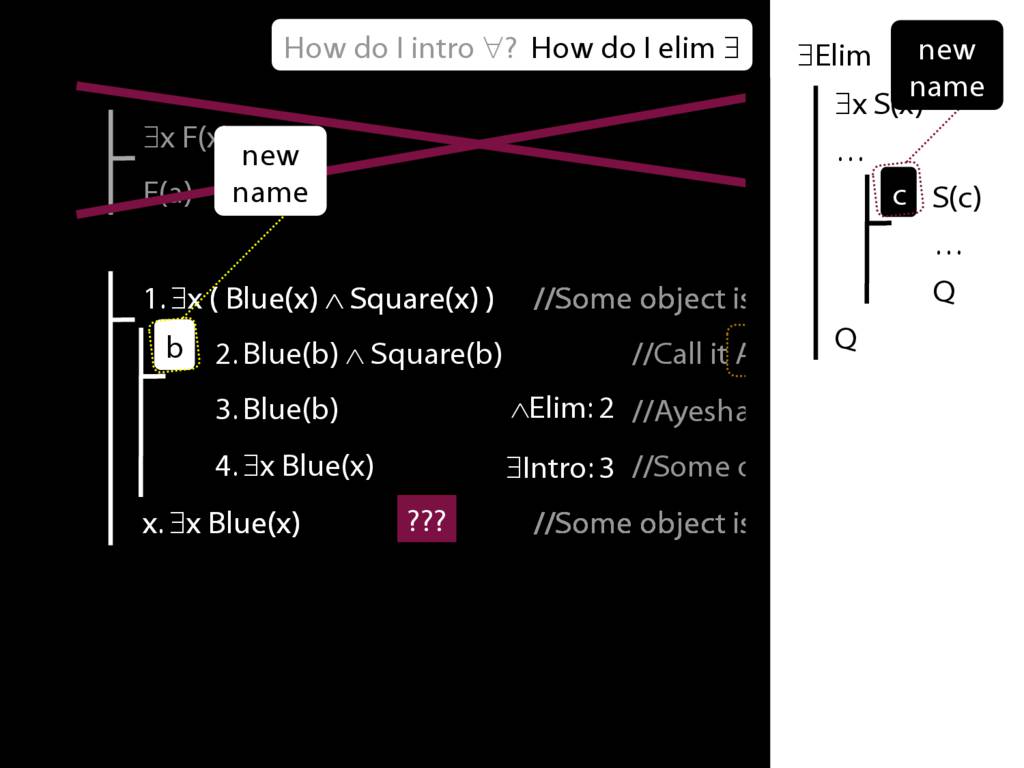
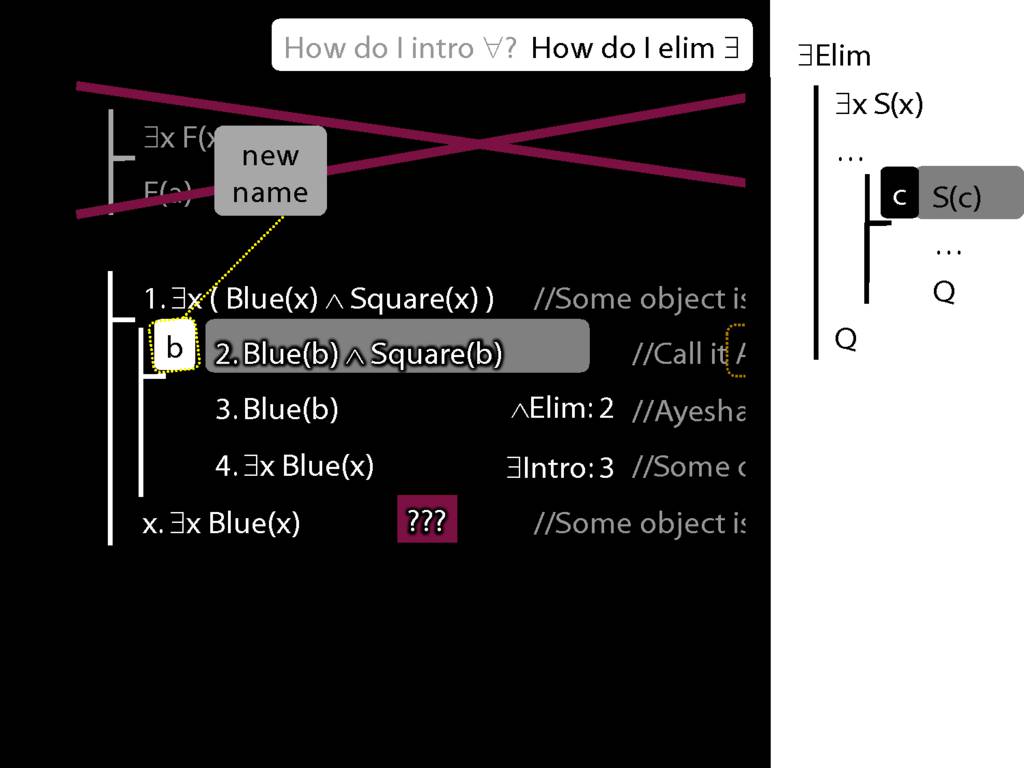
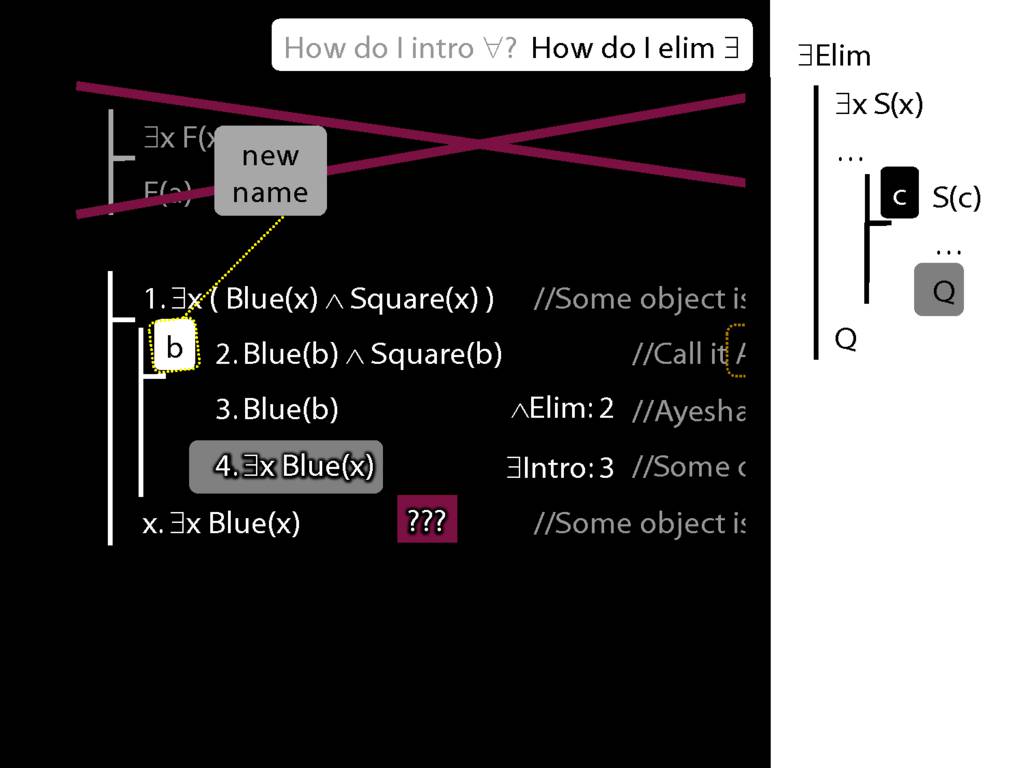
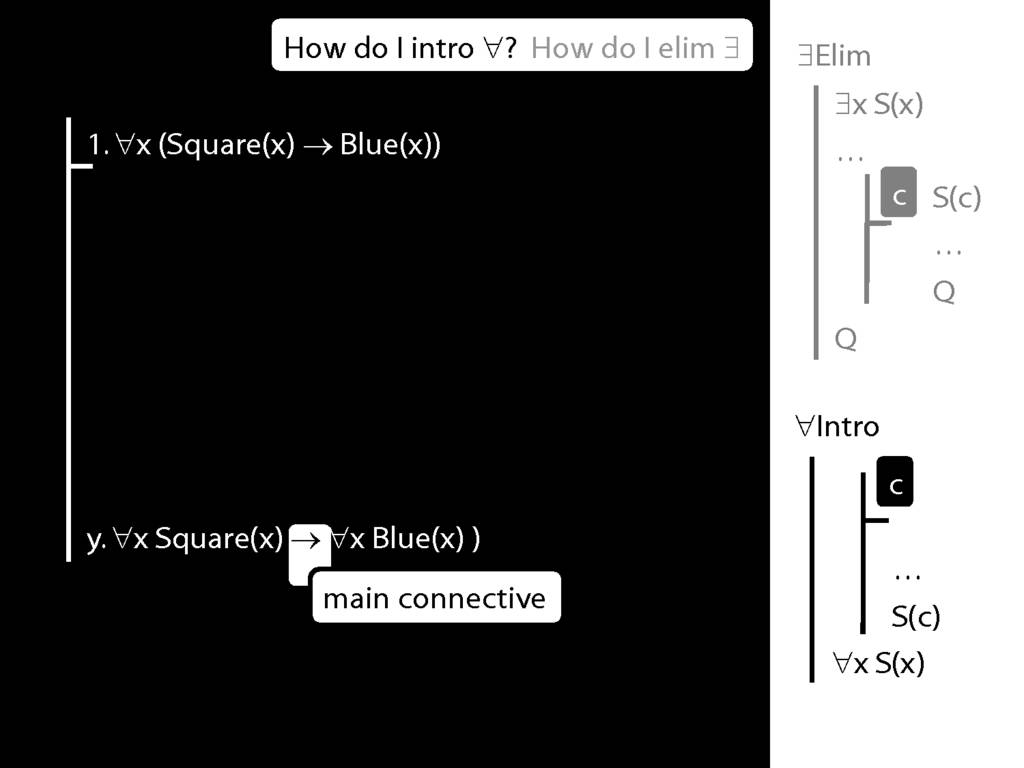
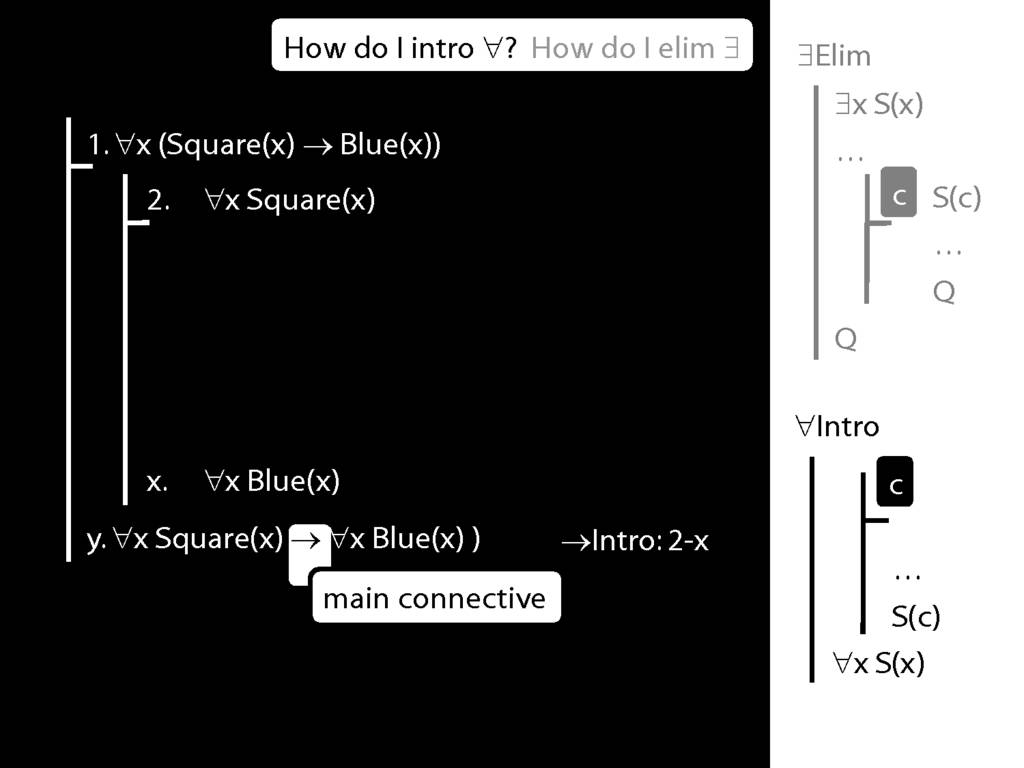
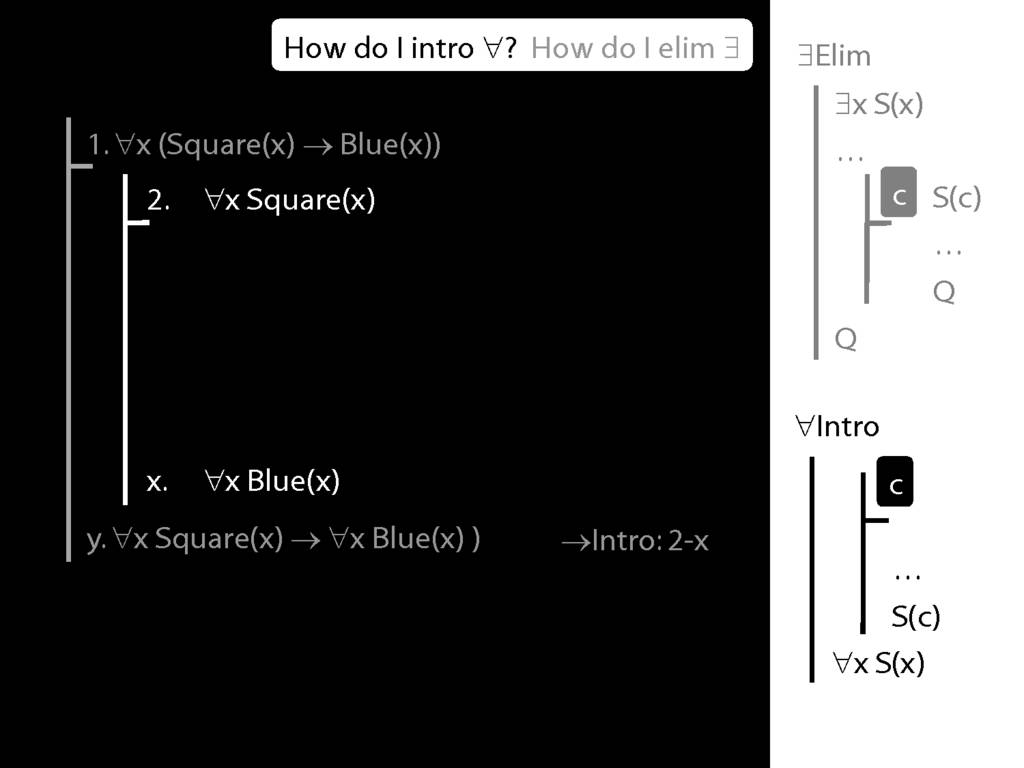
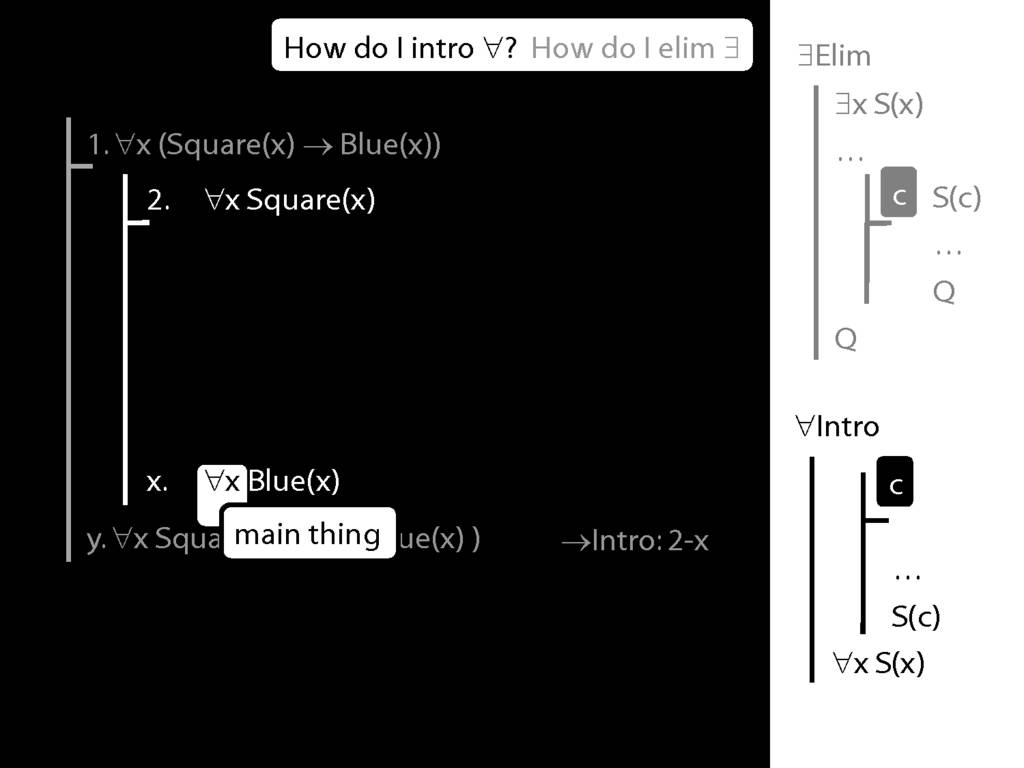
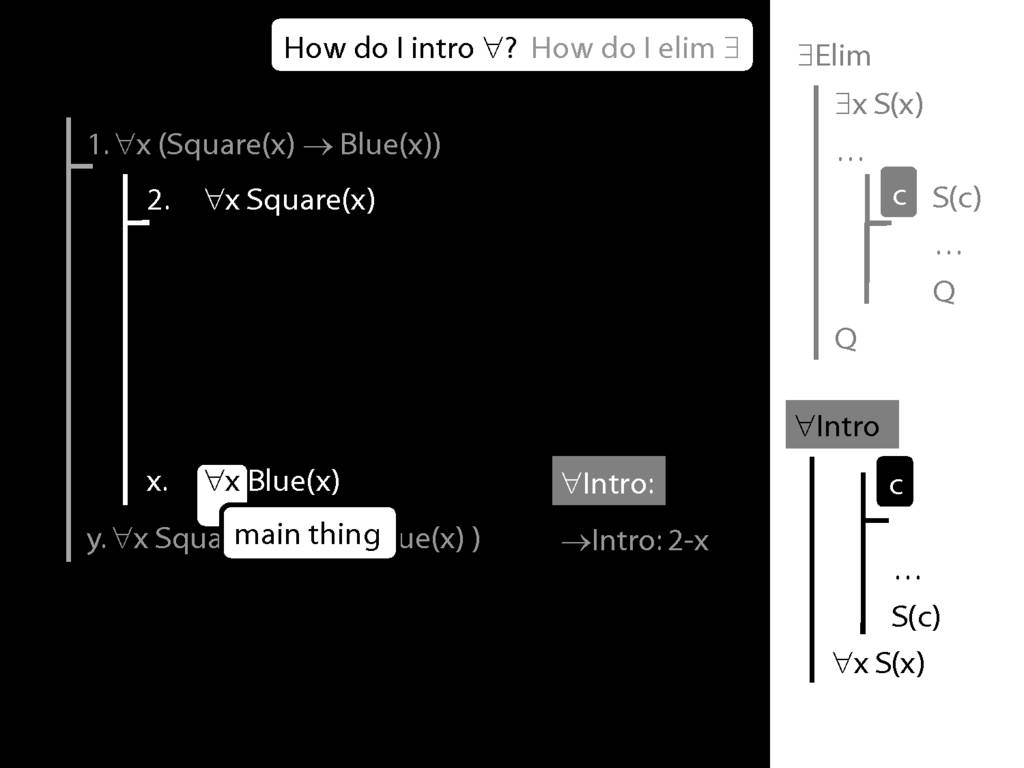
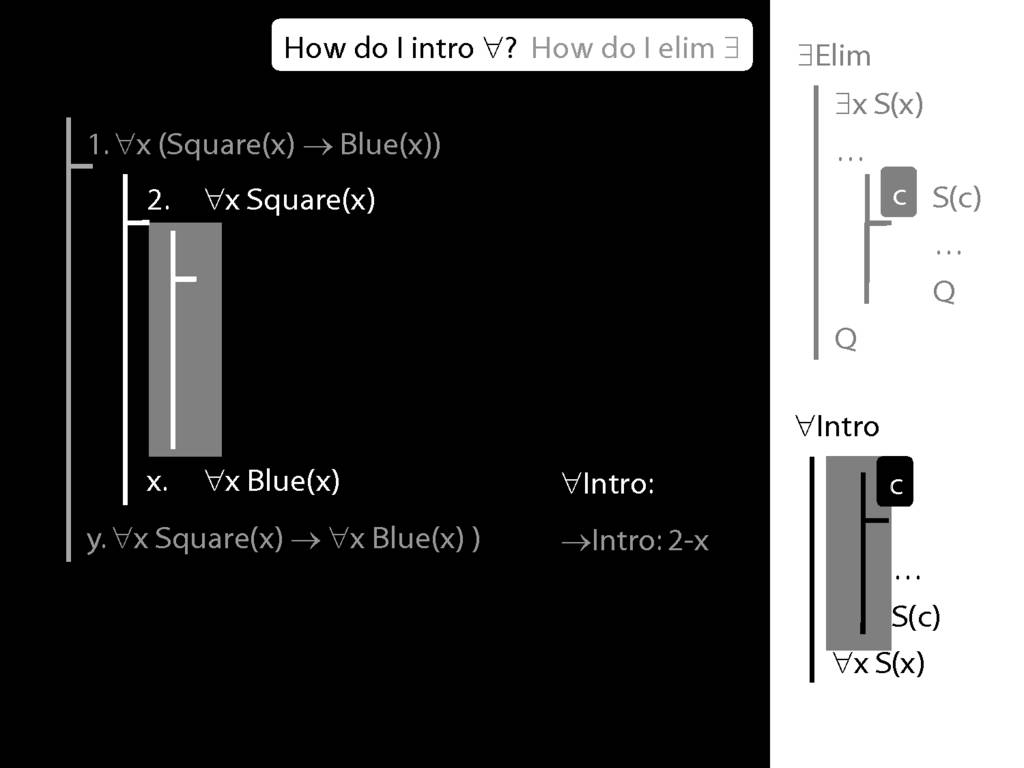
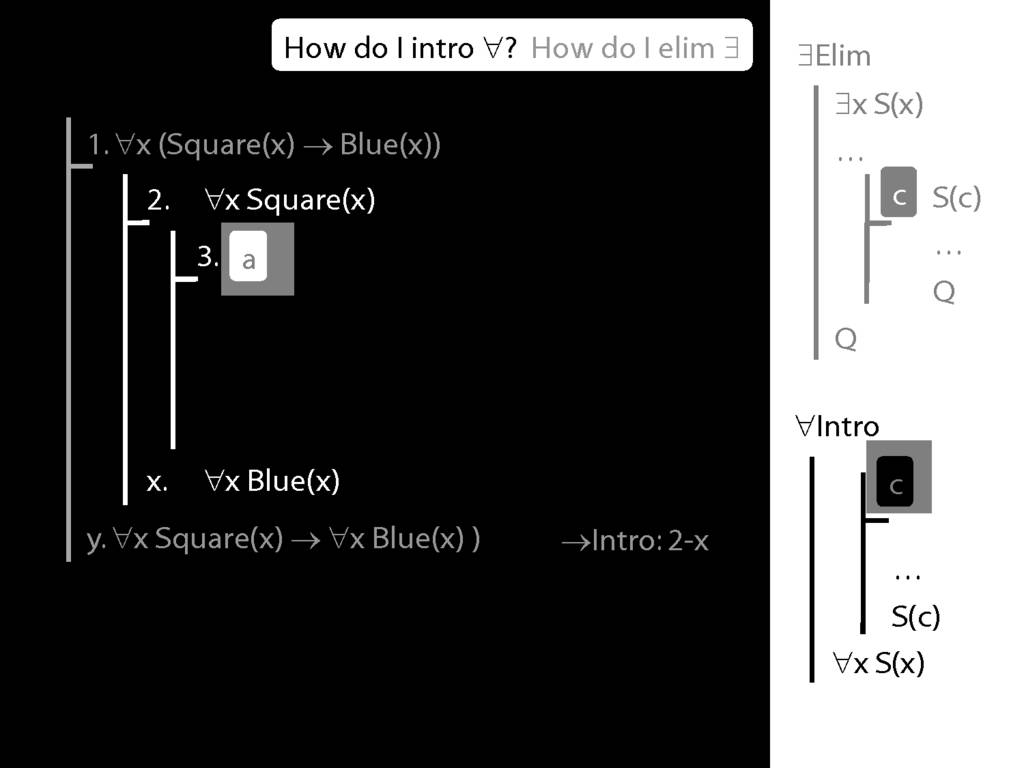
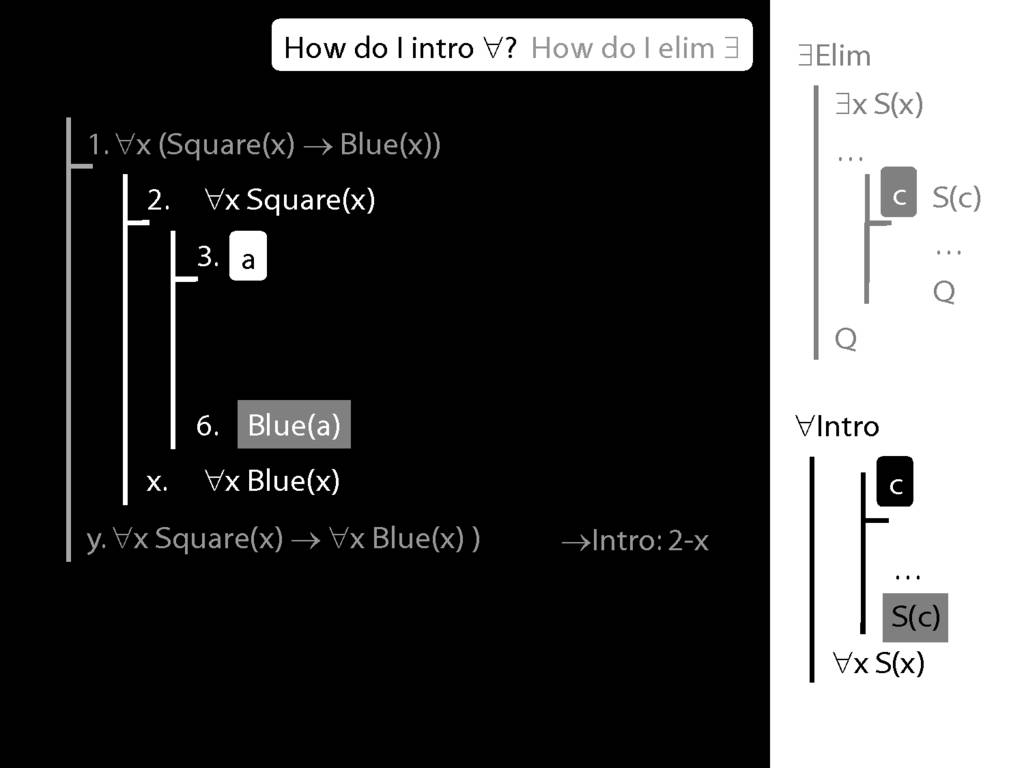
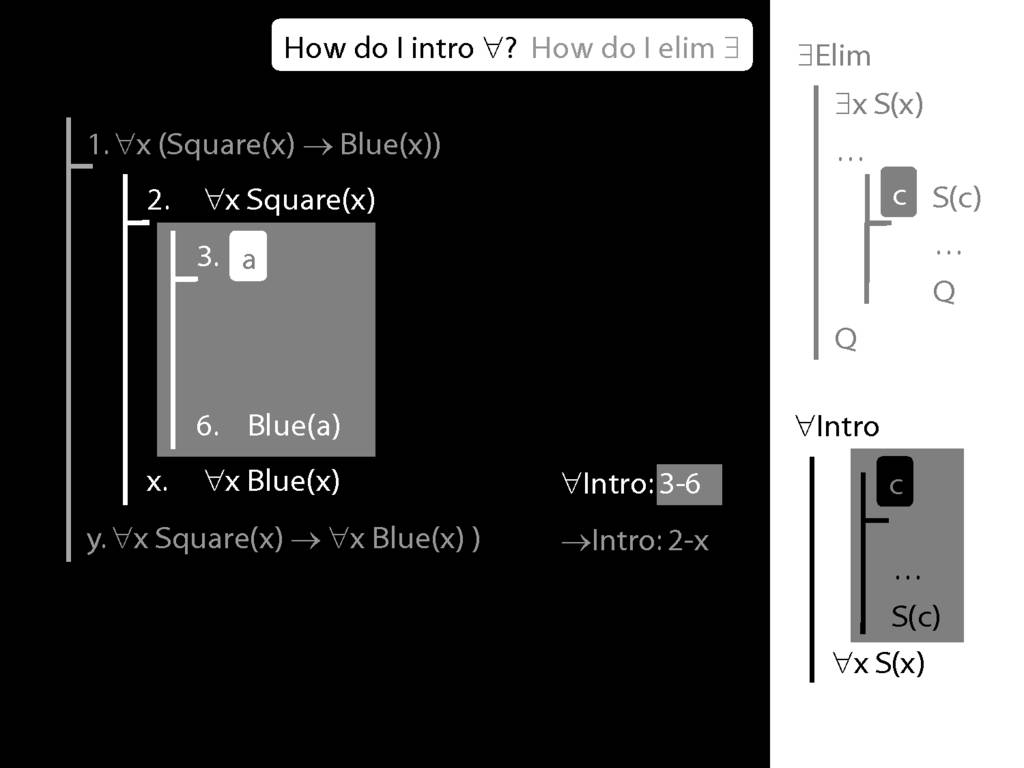
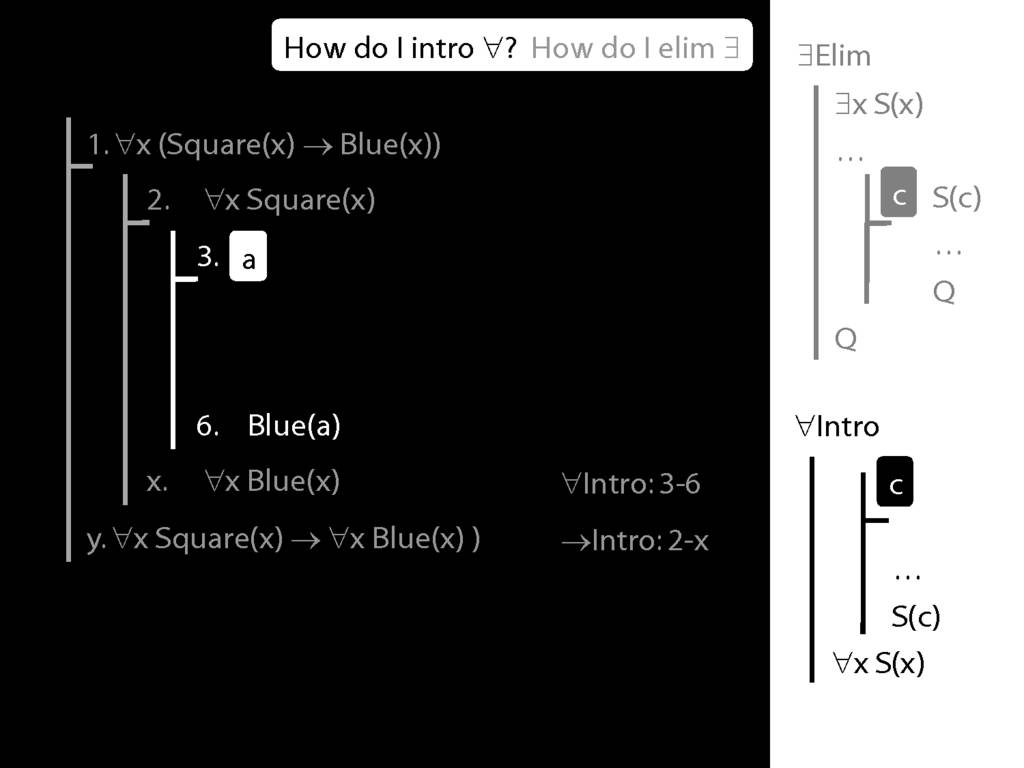
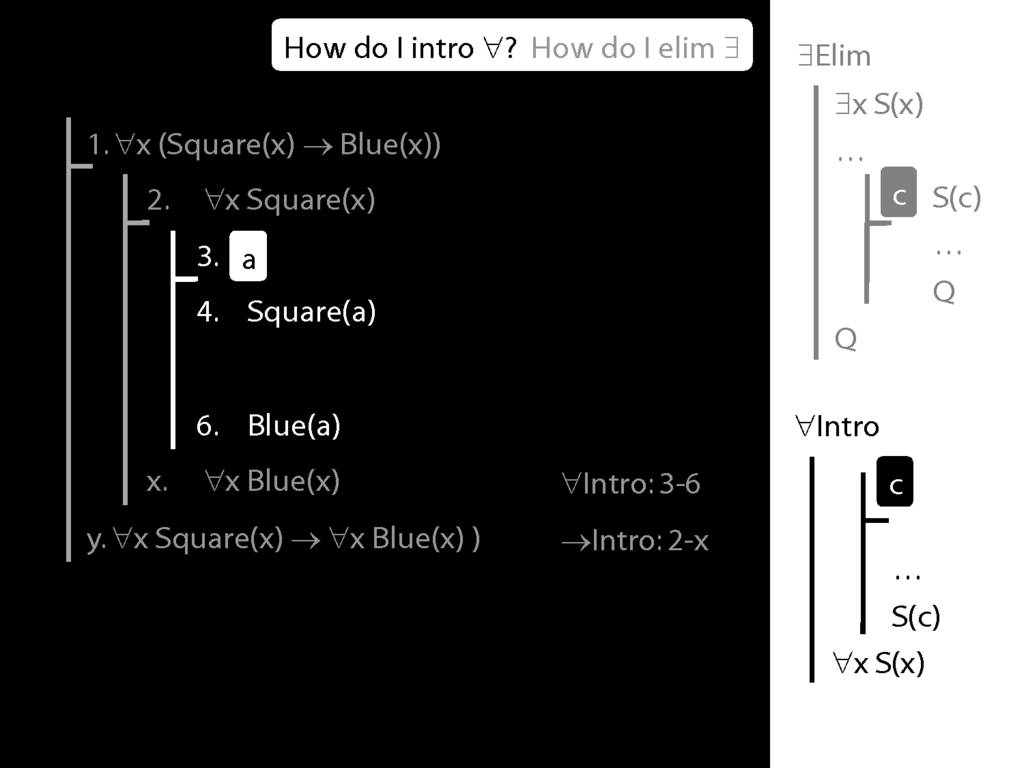
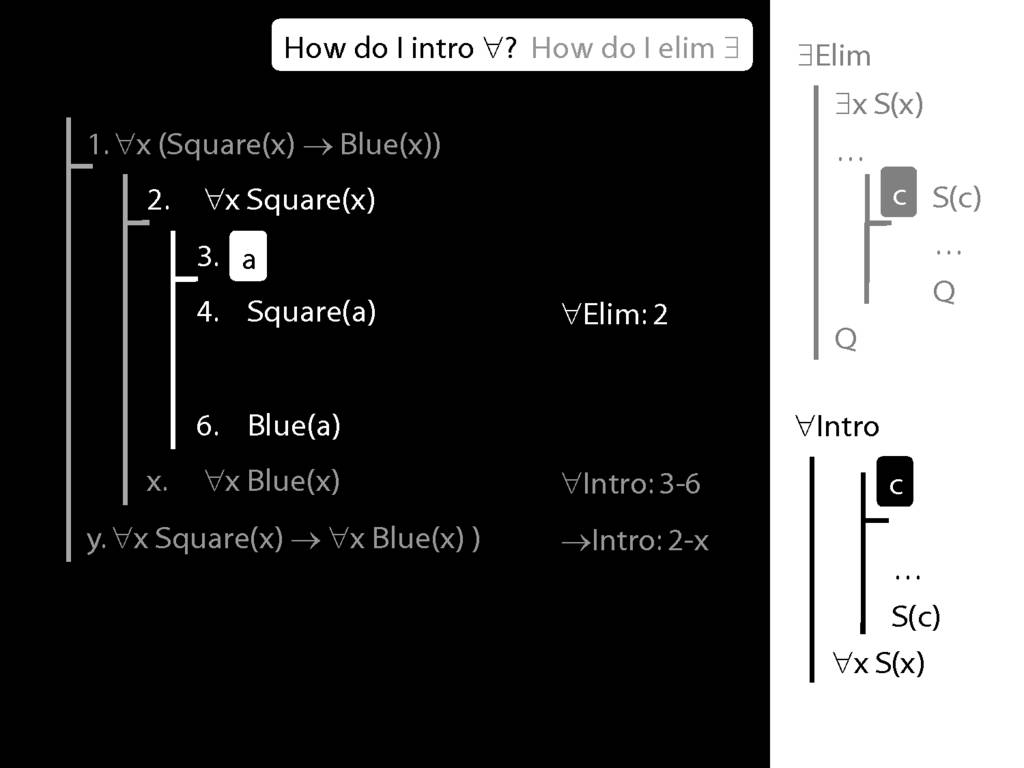
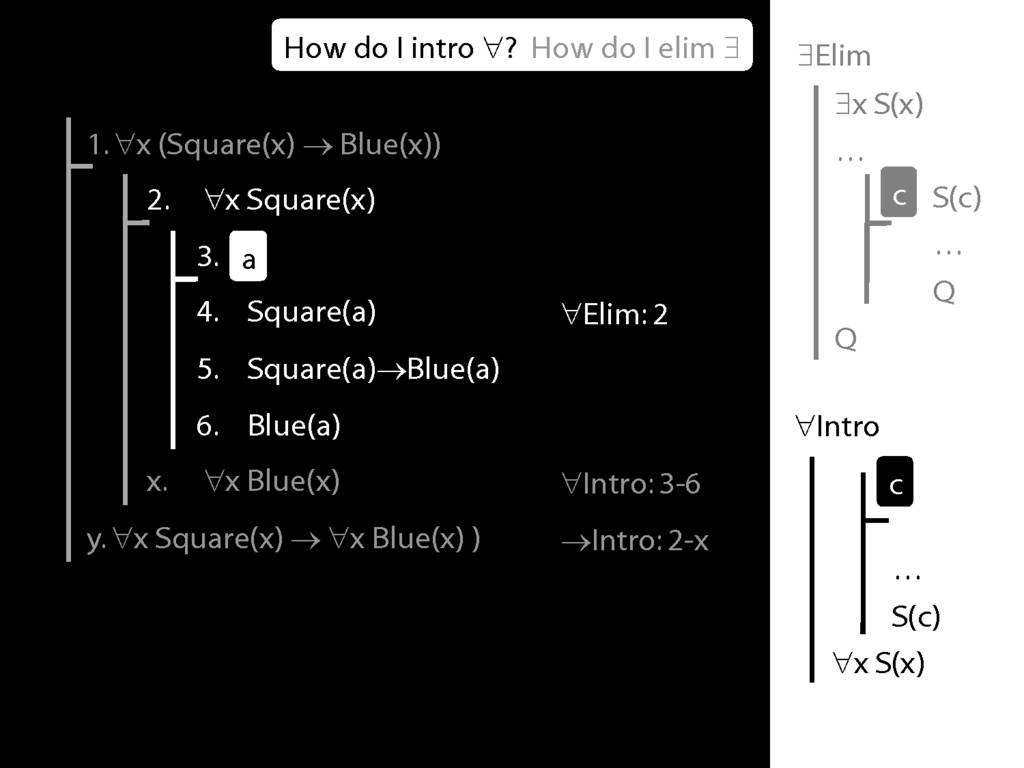
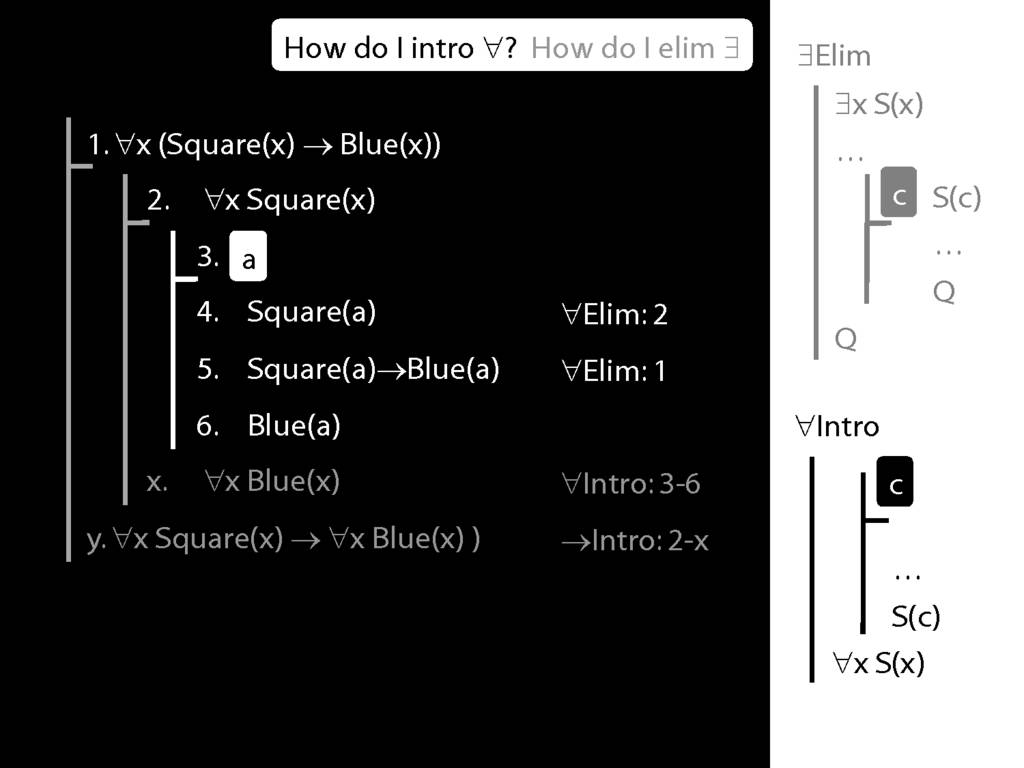
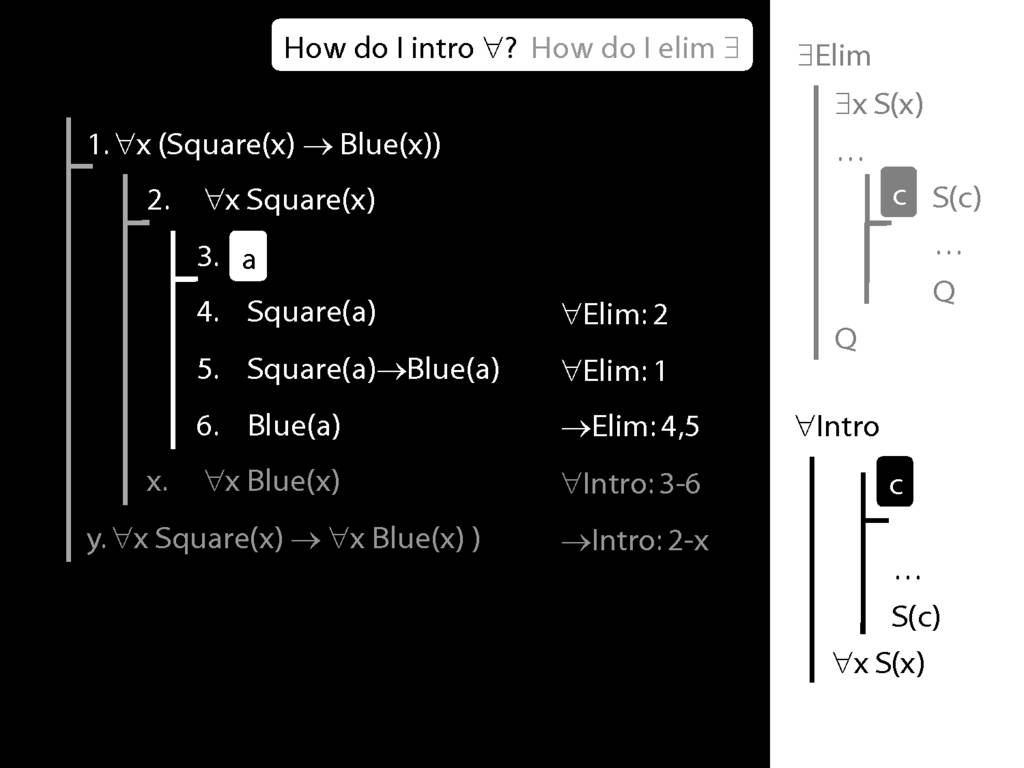
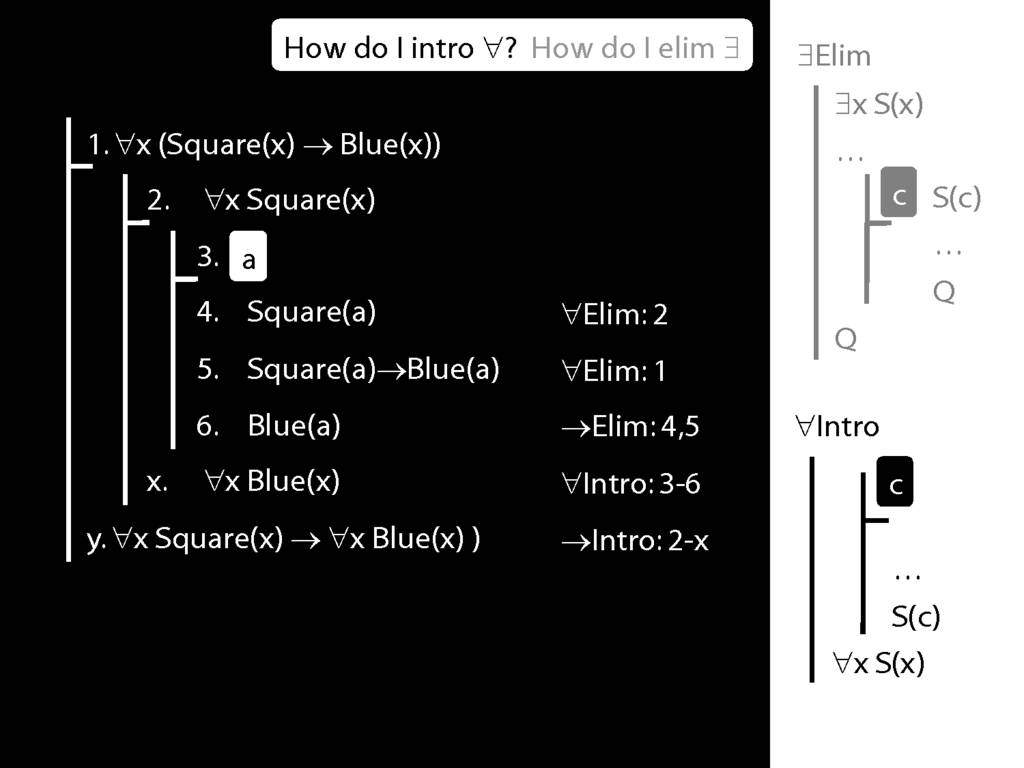
Note this restriction on the use of ∃Elim:
\end{minipage}
Quantifer Rules: ∃Elim with zoxiy
\section{Quantifer Rules: ∃Elim with zoxiy}
\section{Quantifer Rules: ∃Elim with zoxiy}
The rules of proof exists elim and universal intro each
require you to put a name in a box in the premise of a subproof.
How can you do this with zoxiy?
Where you see a name in a box, just enclose it in square brackets.
For example: [a]
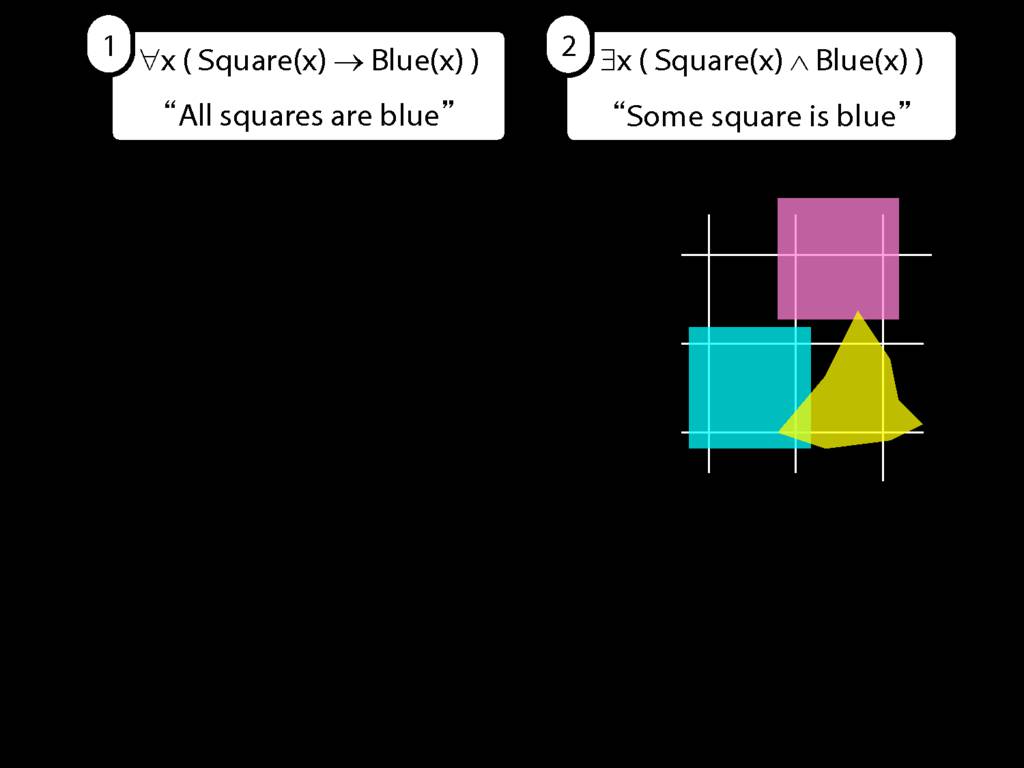
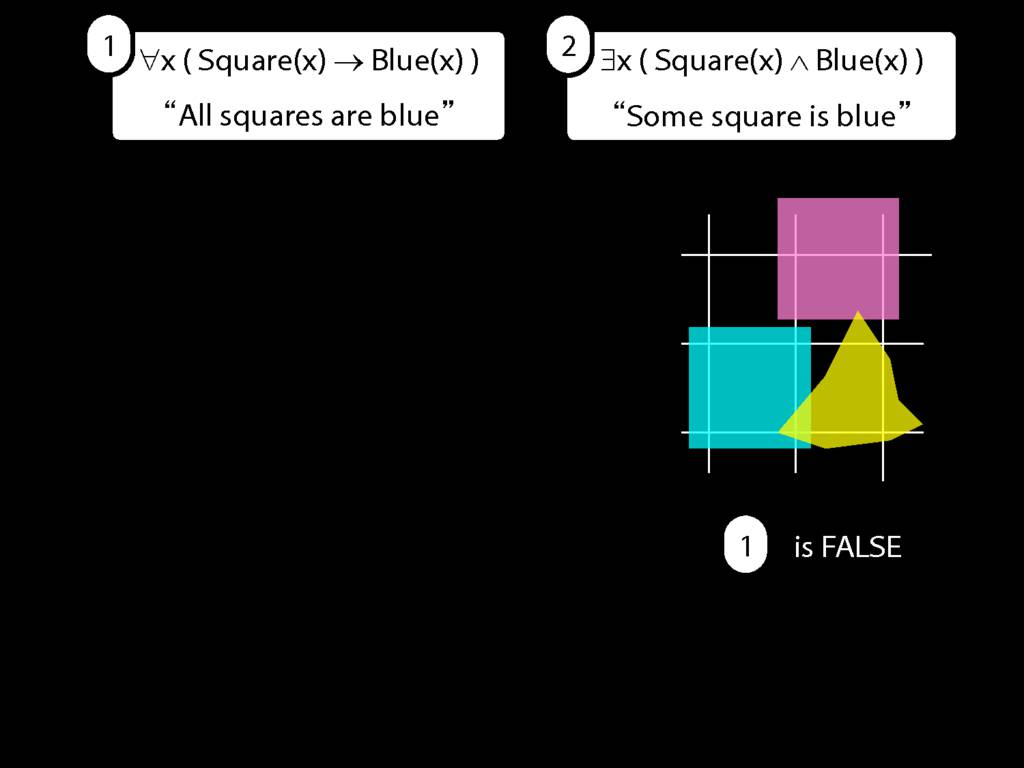
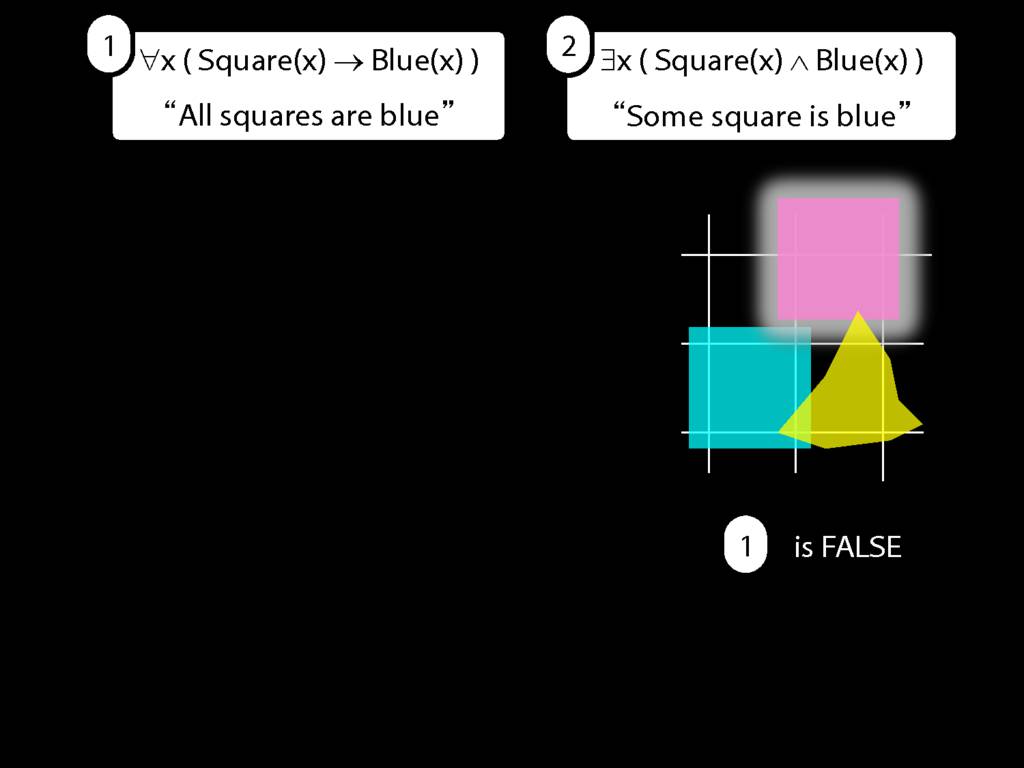
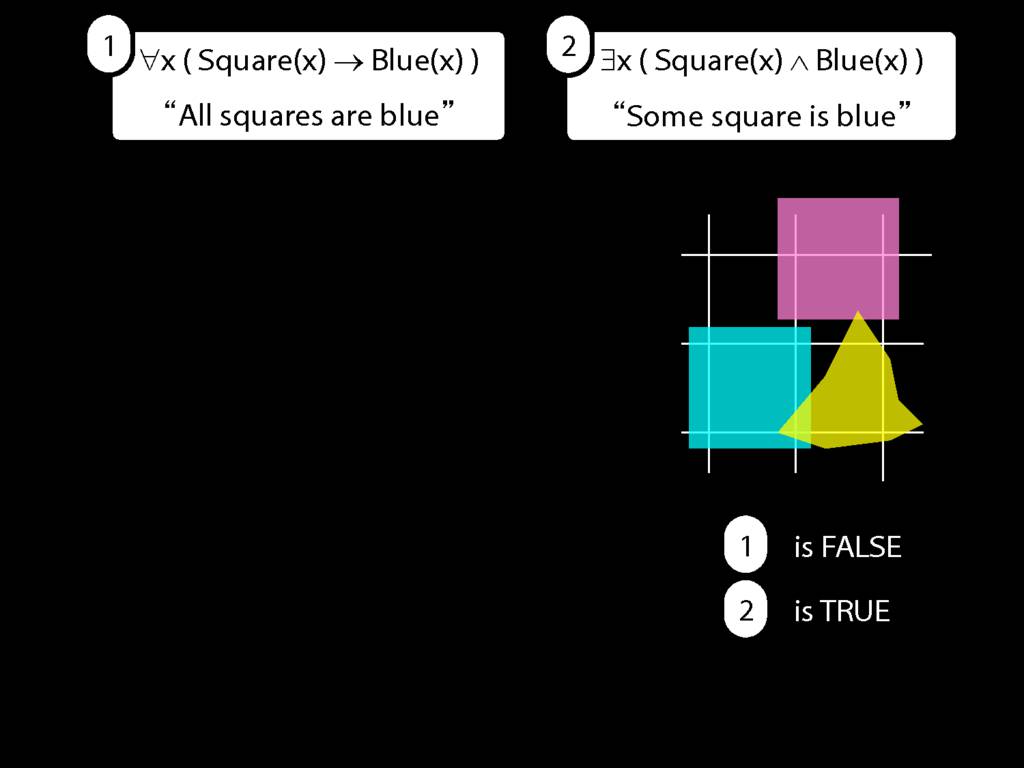
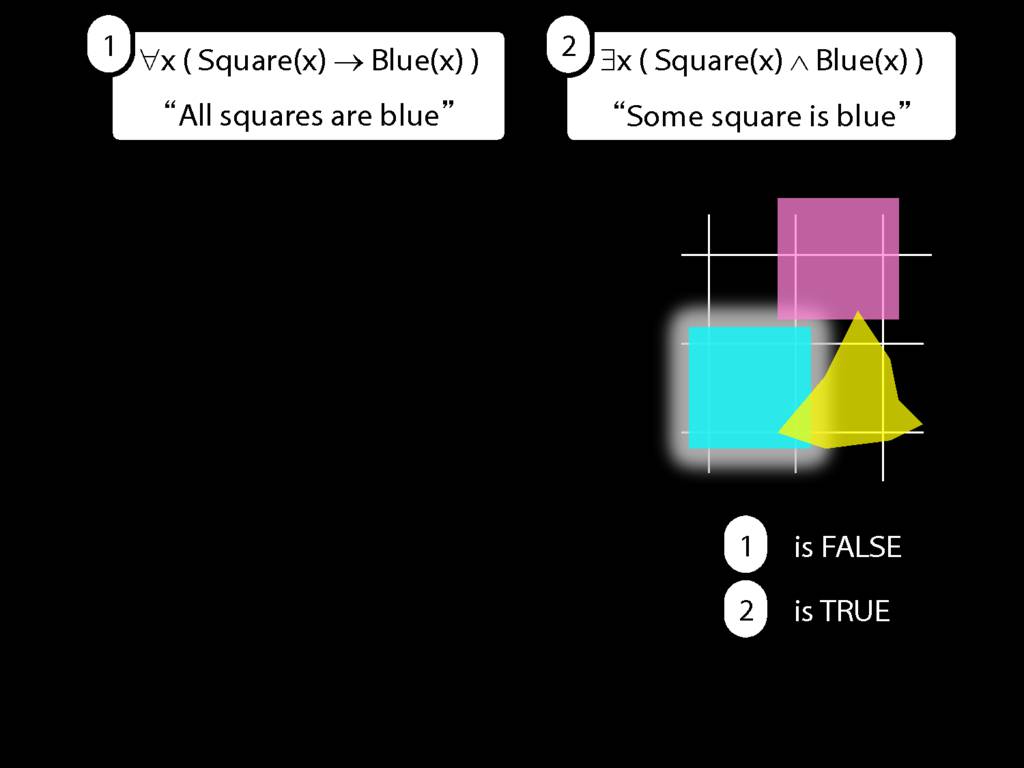
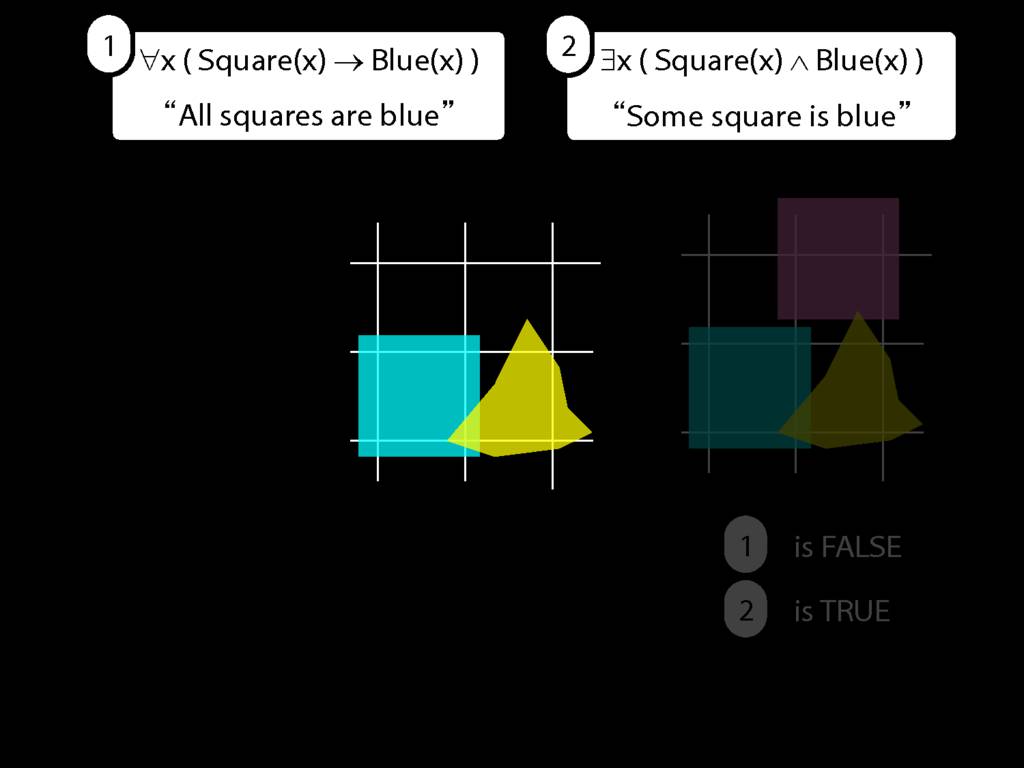
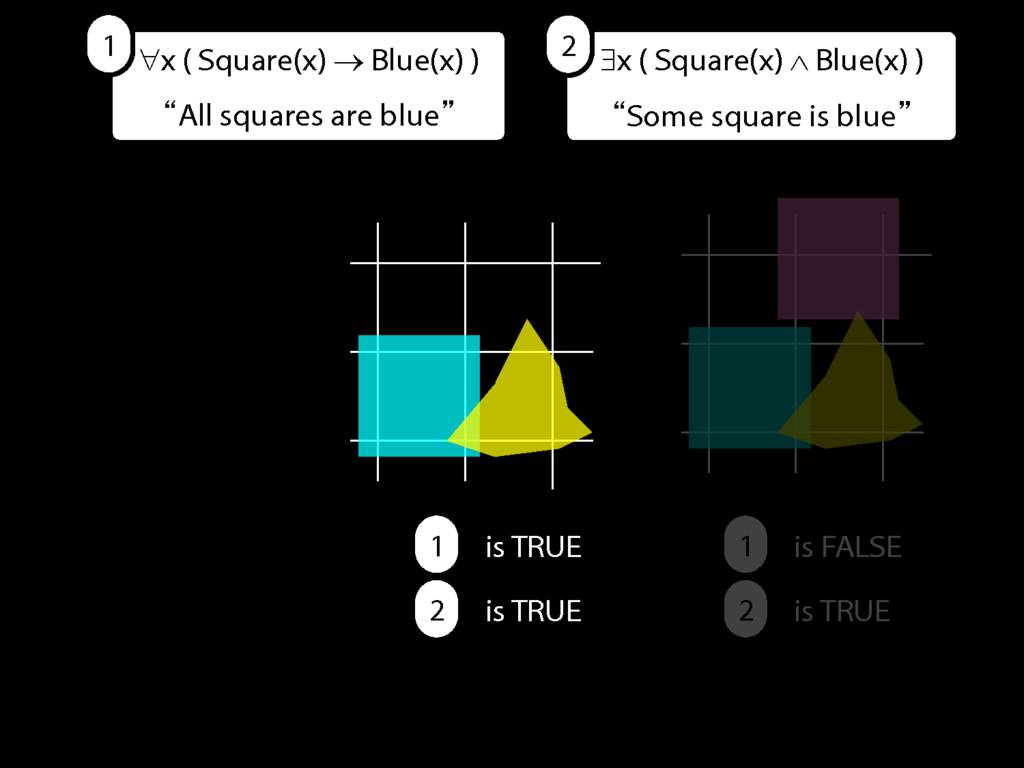
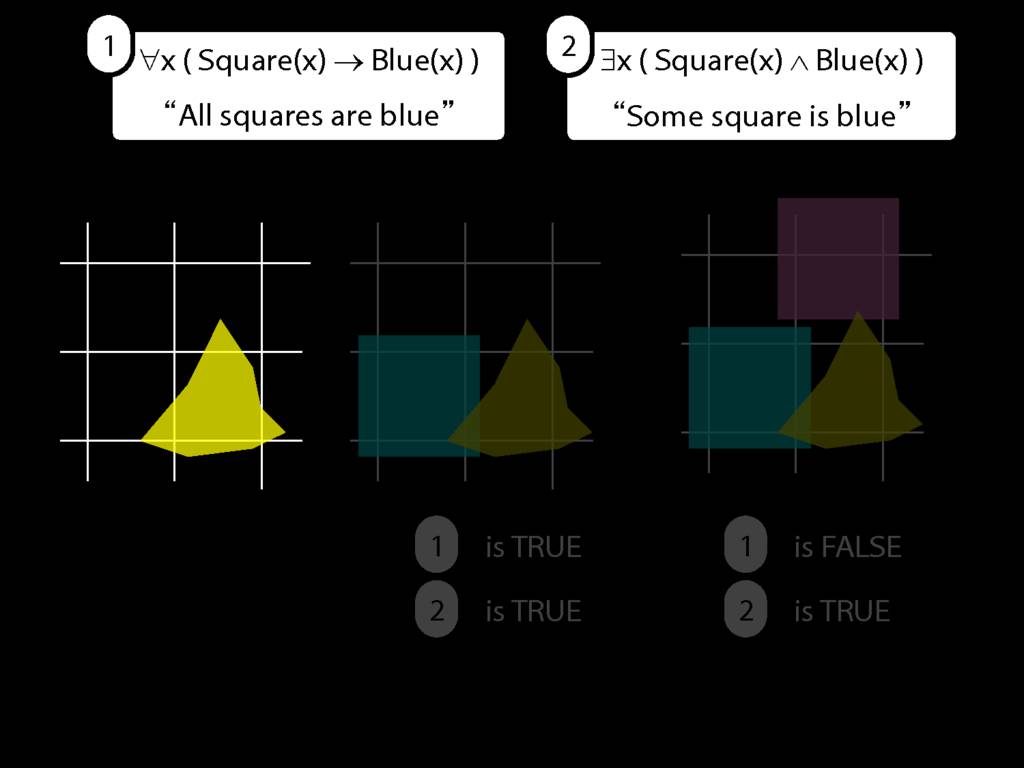
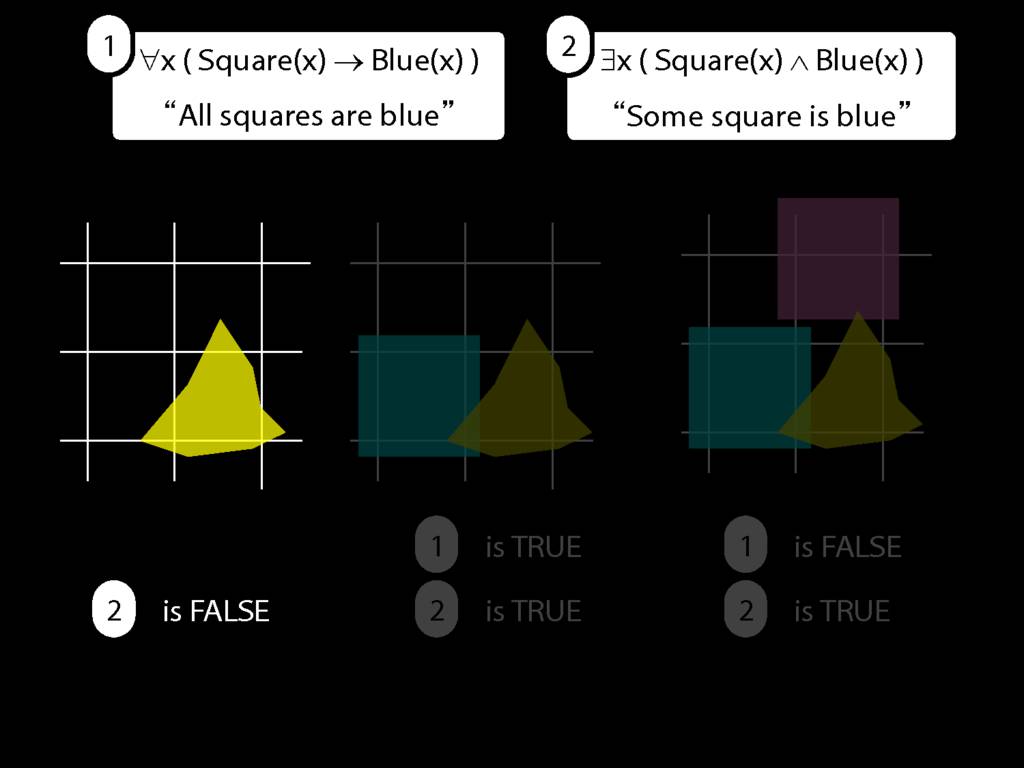
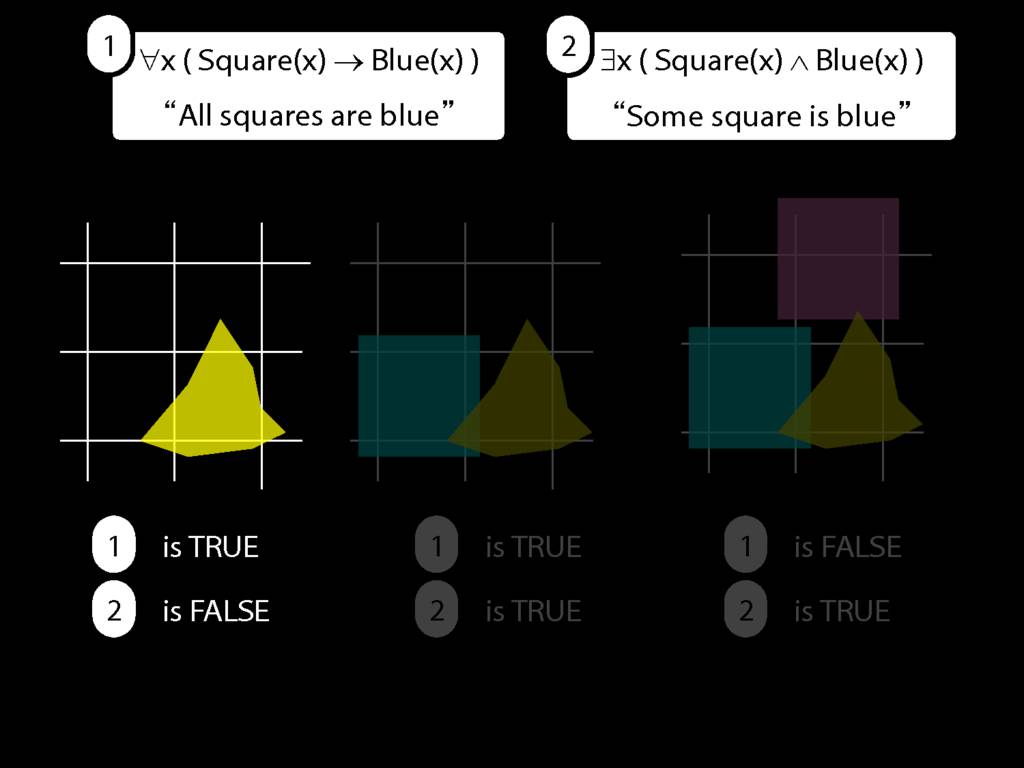
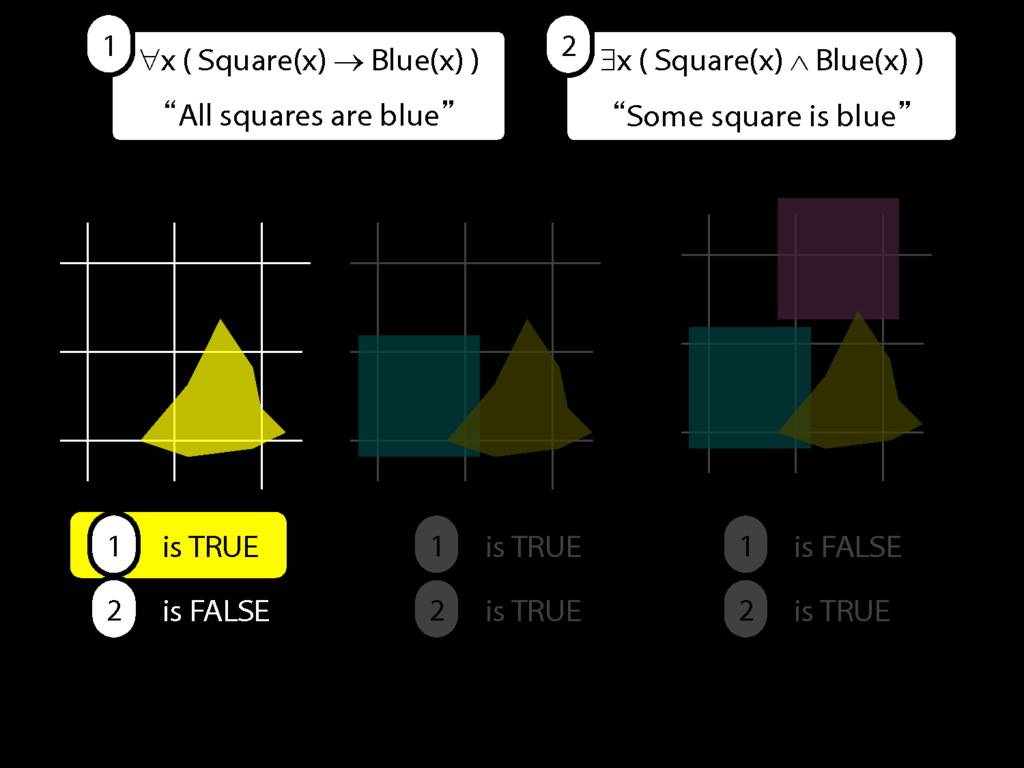
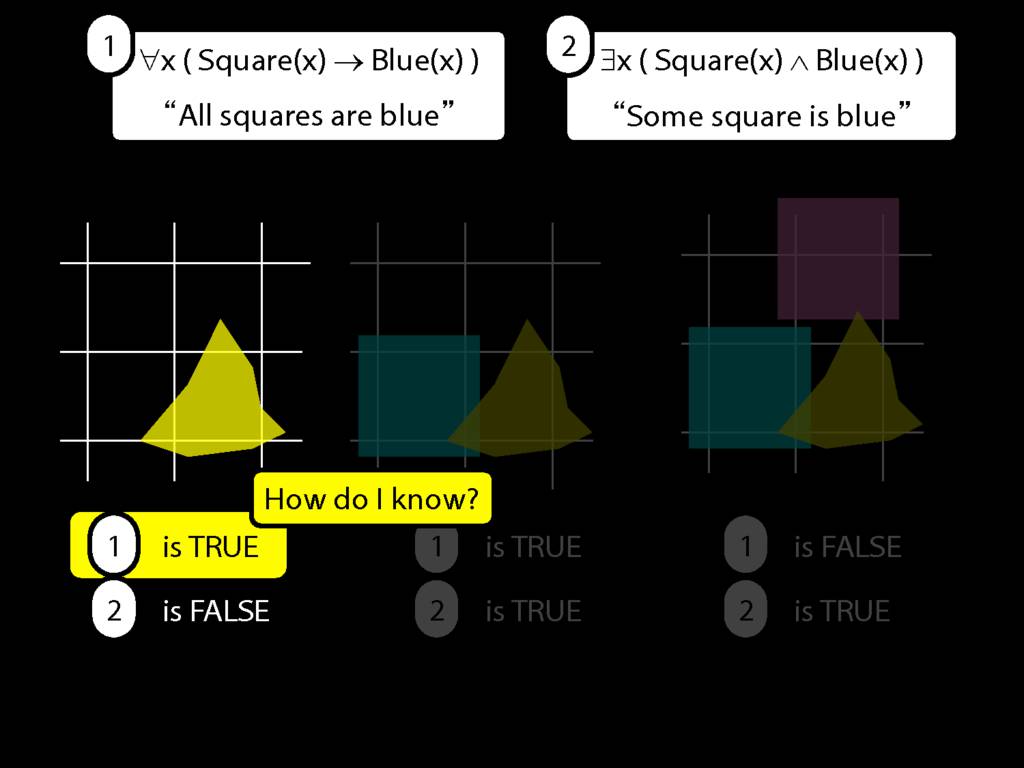
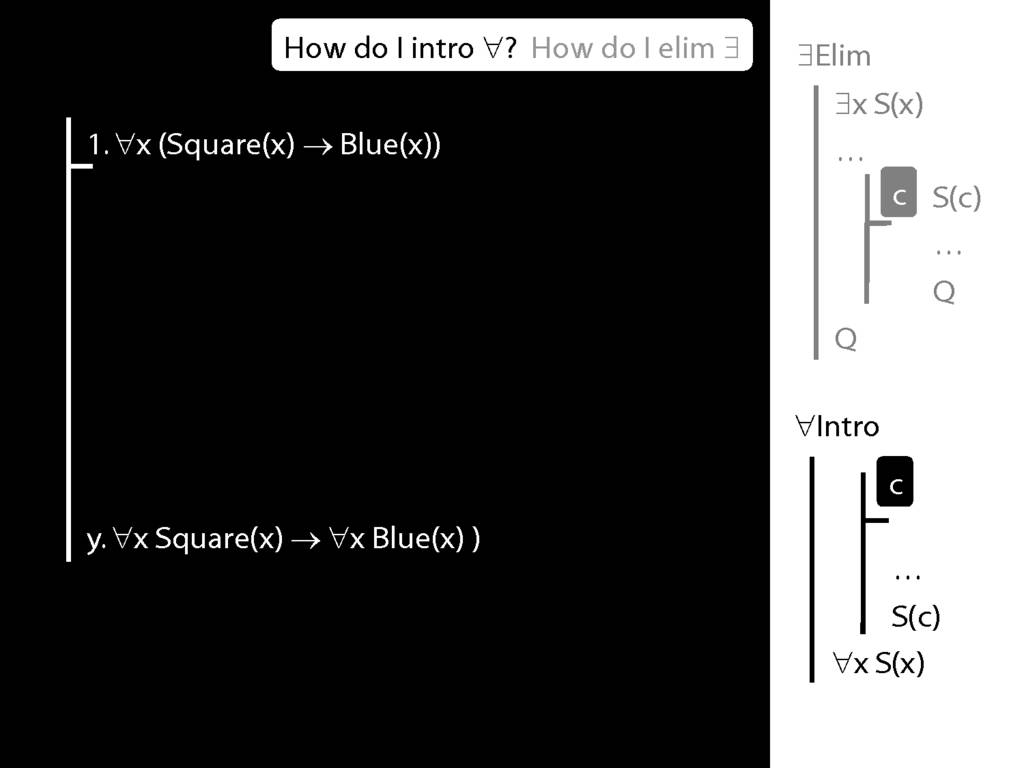
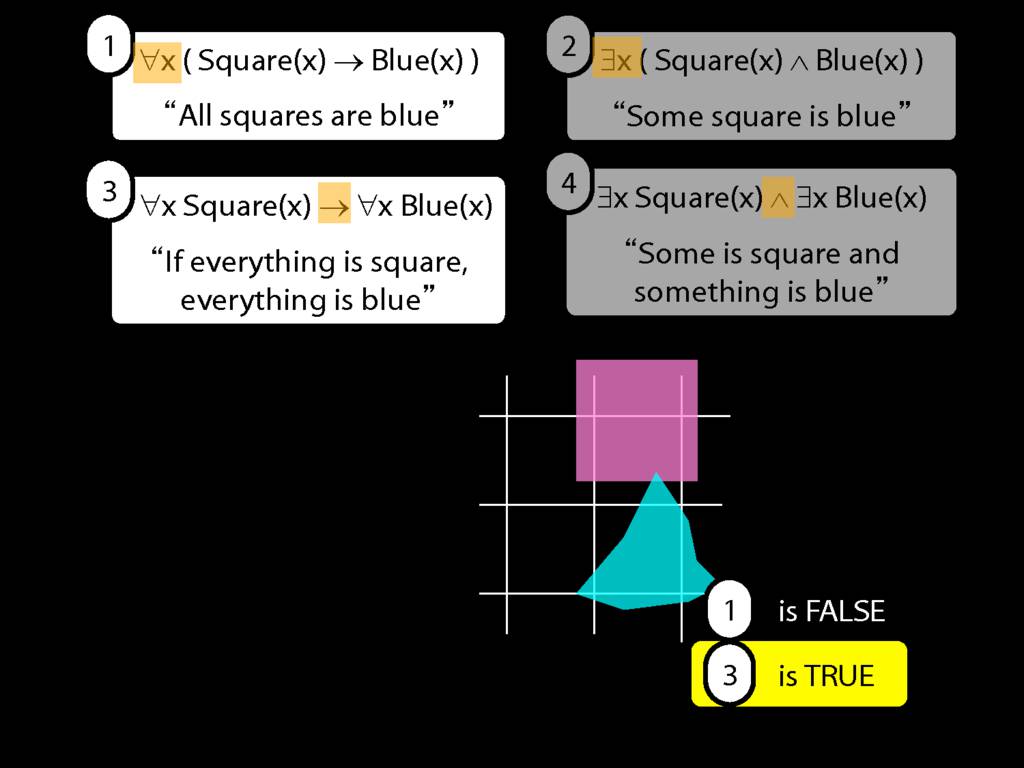
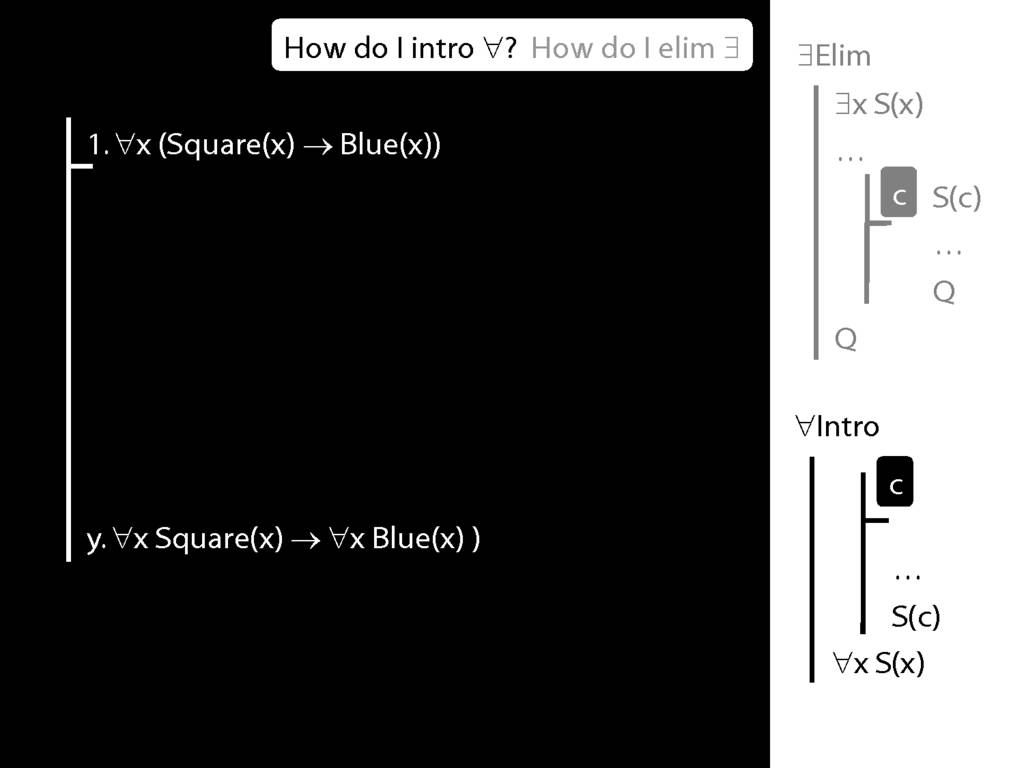
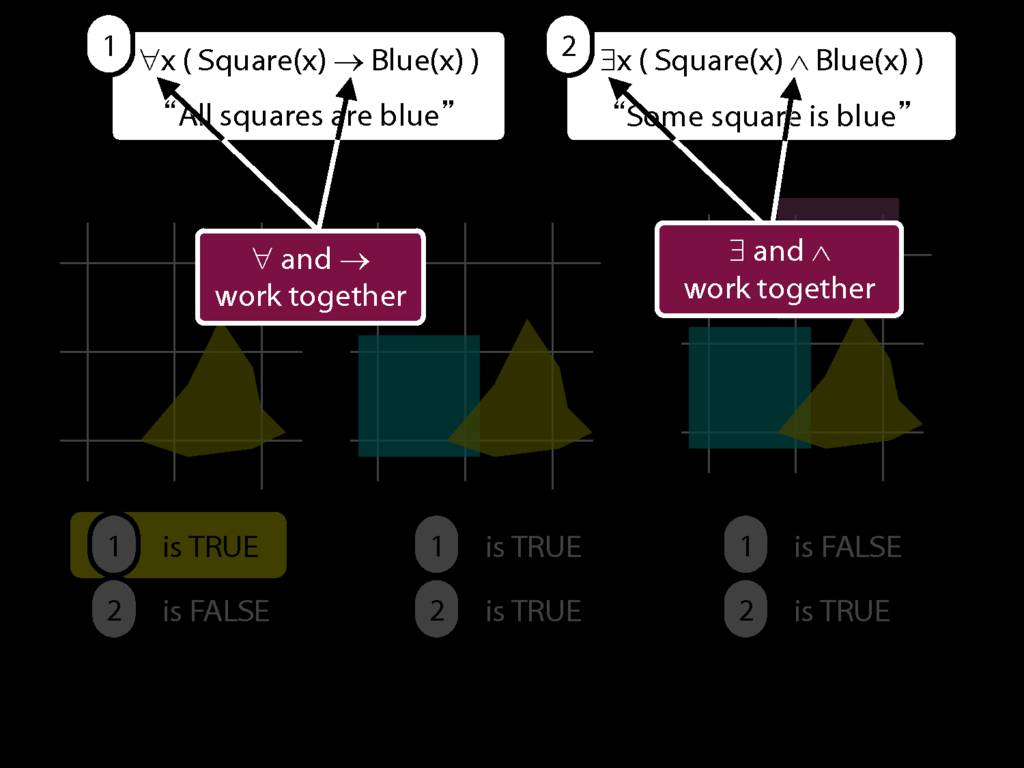
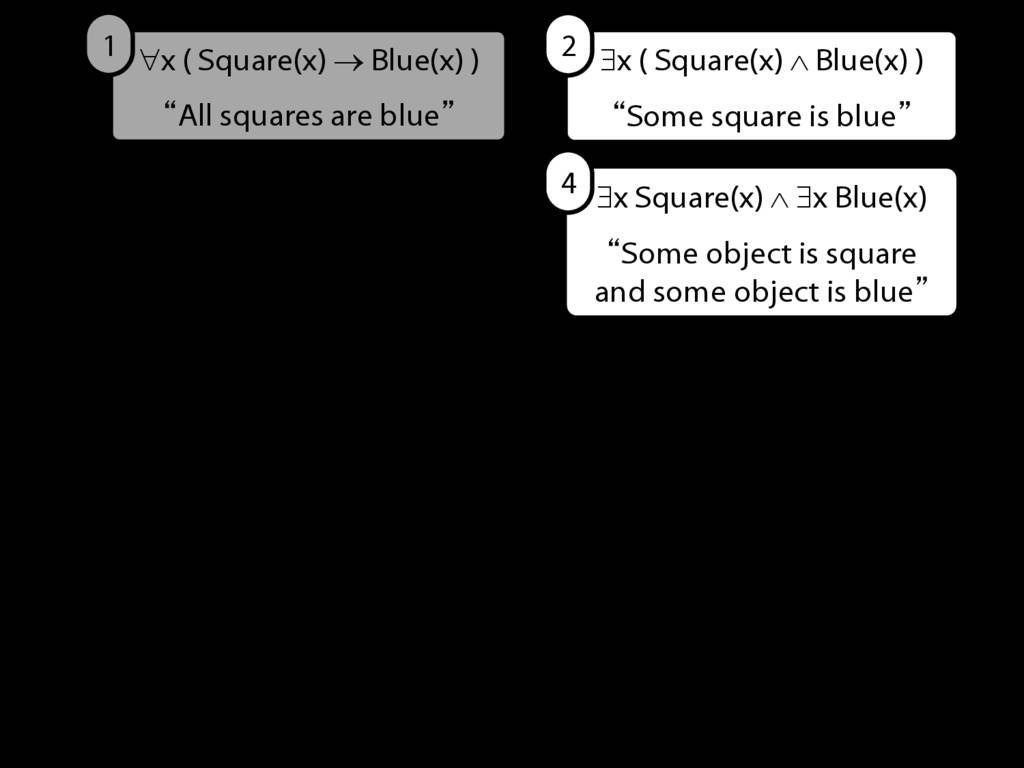
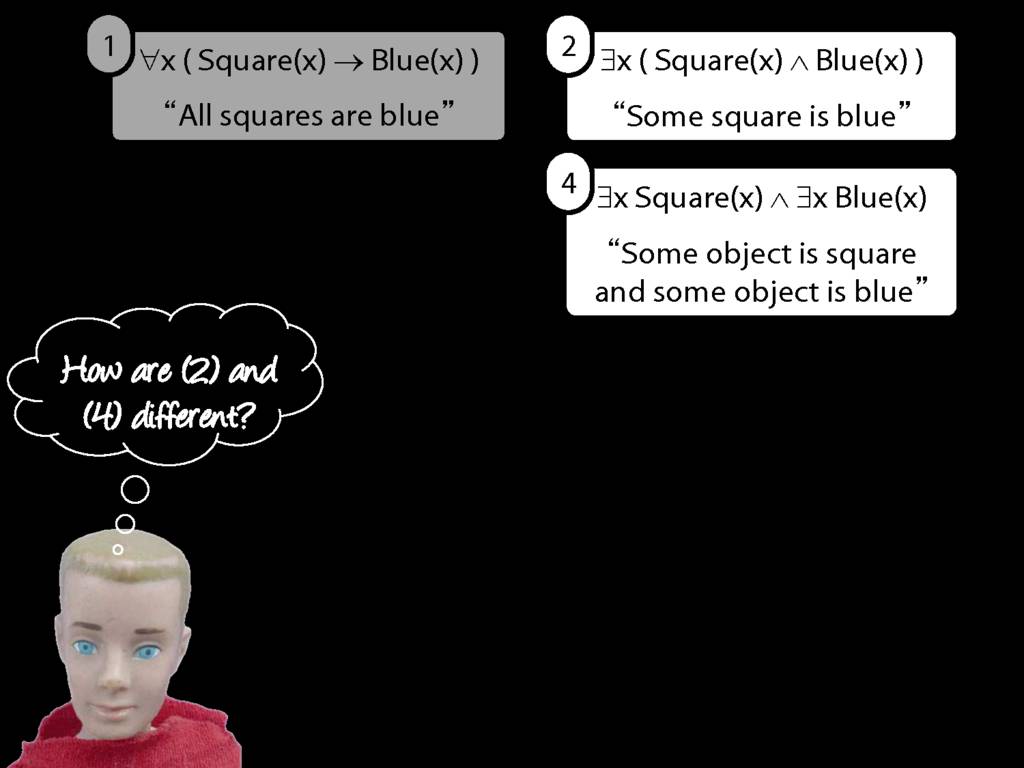
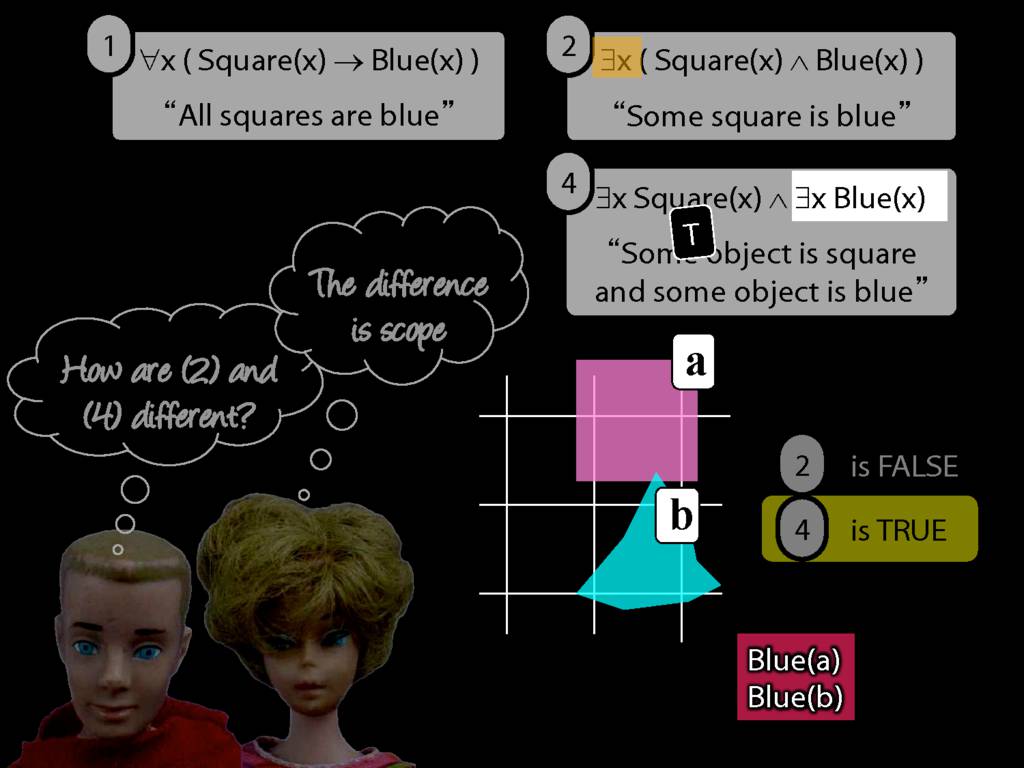
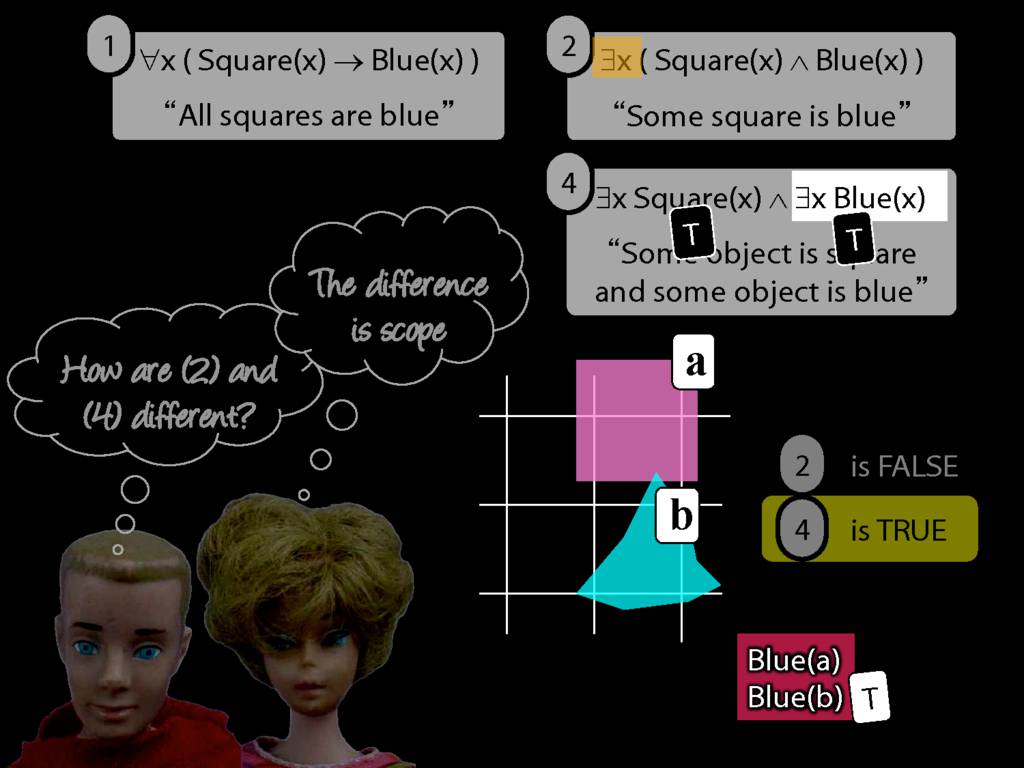
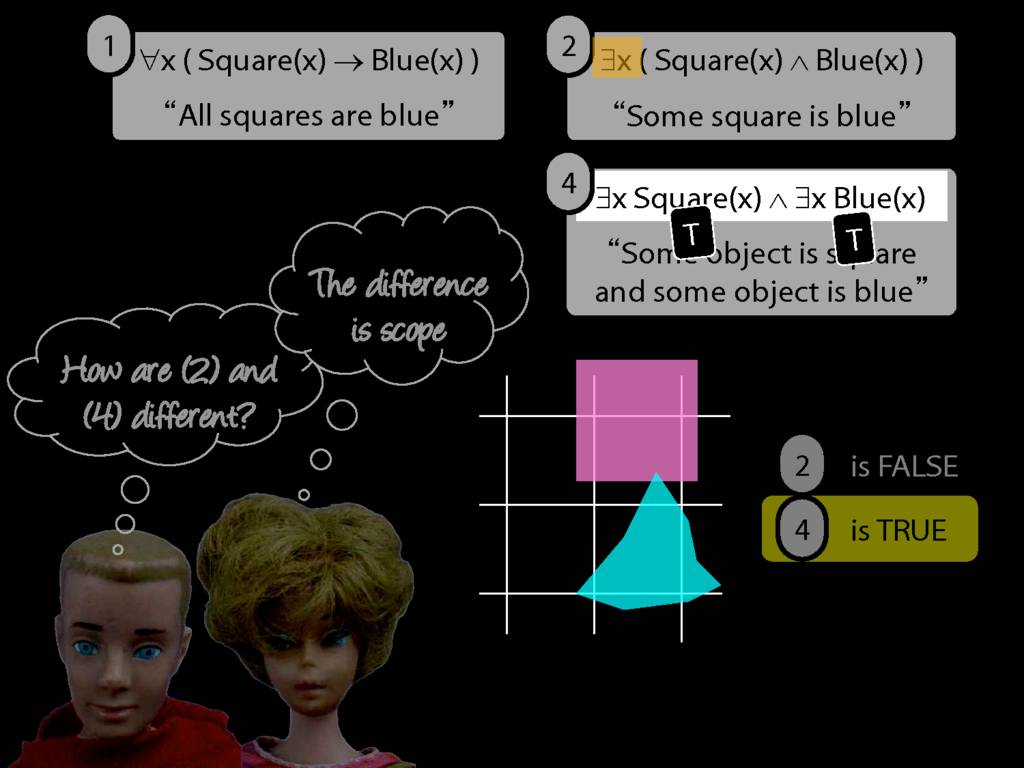
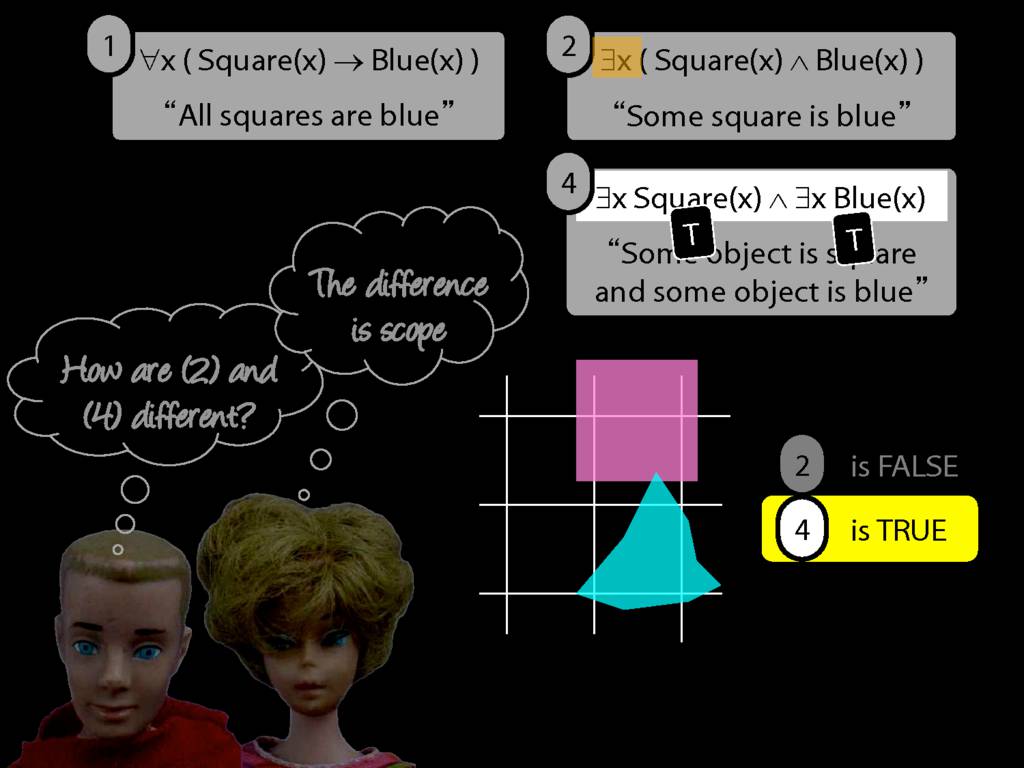
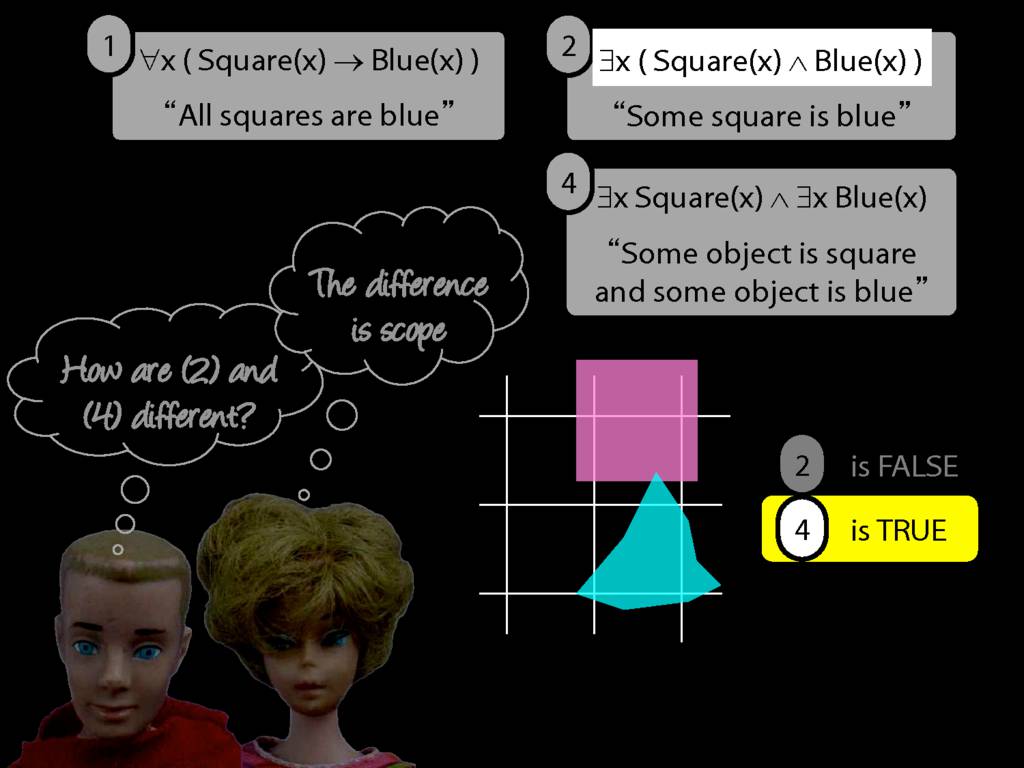
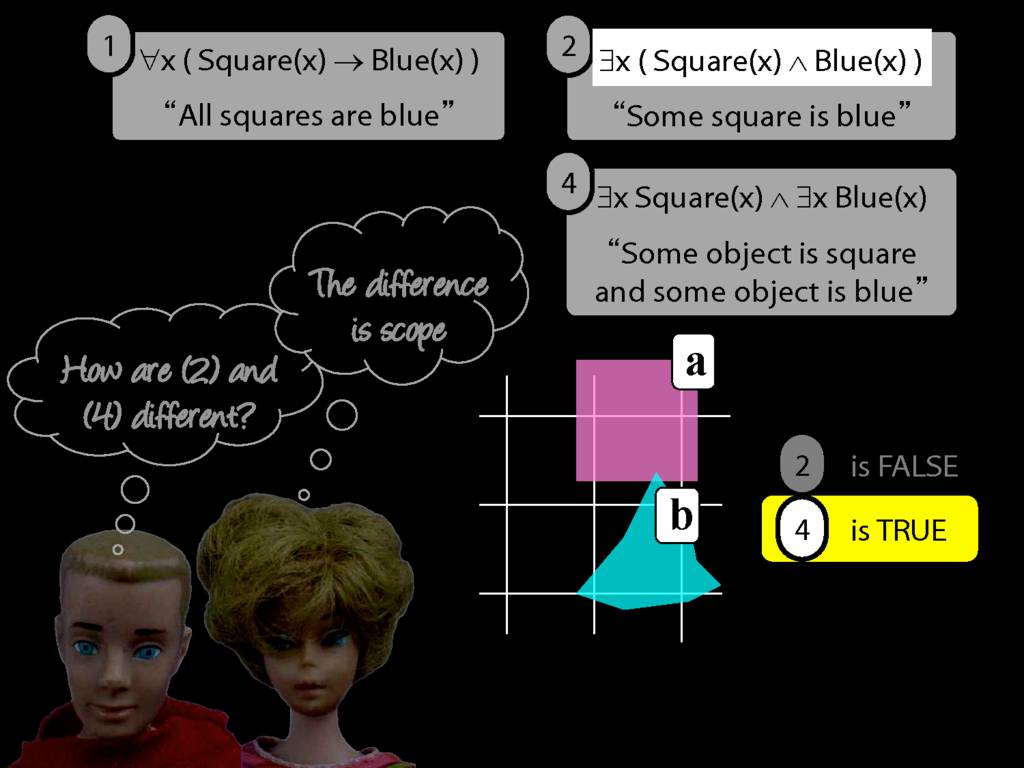
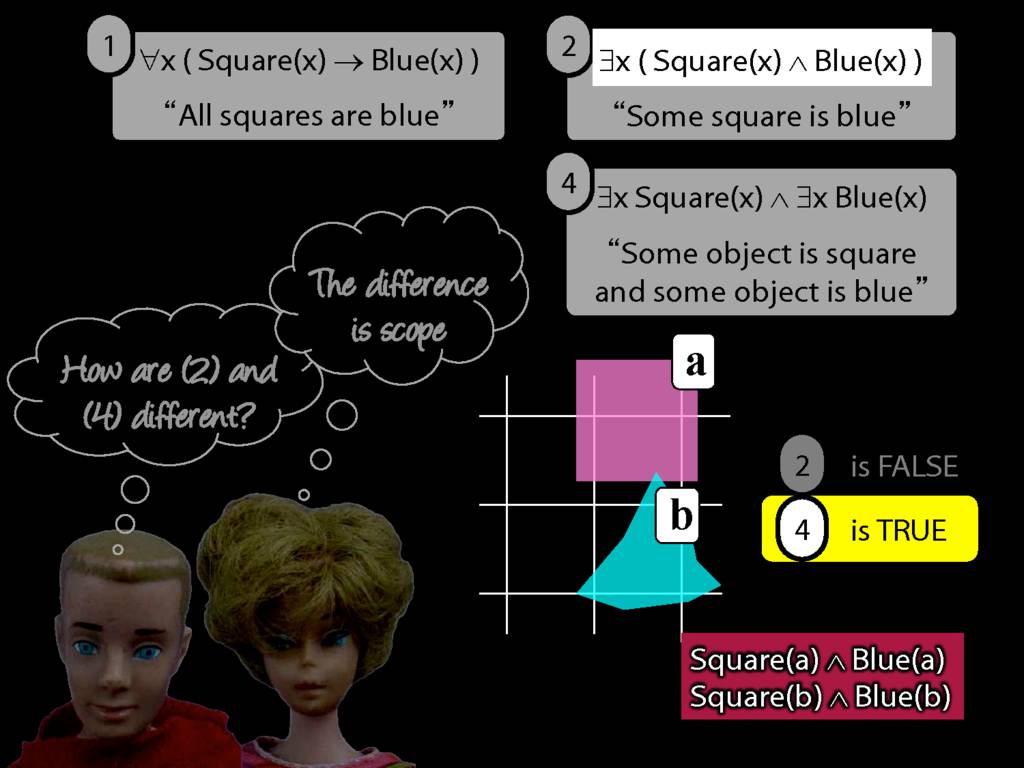
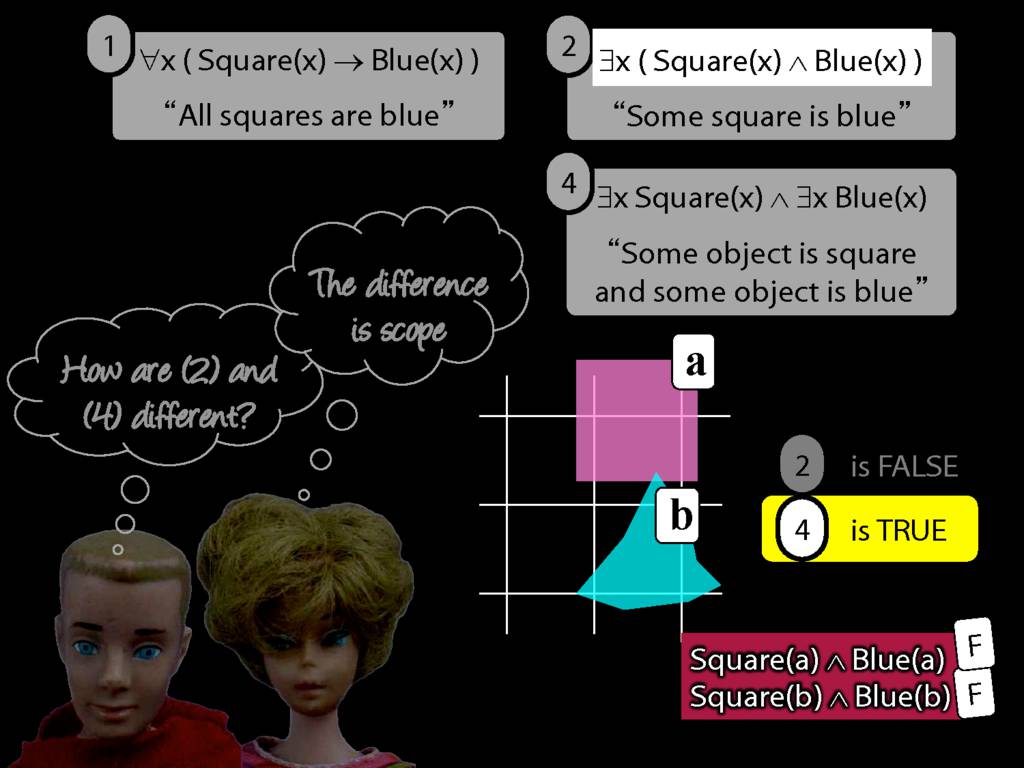
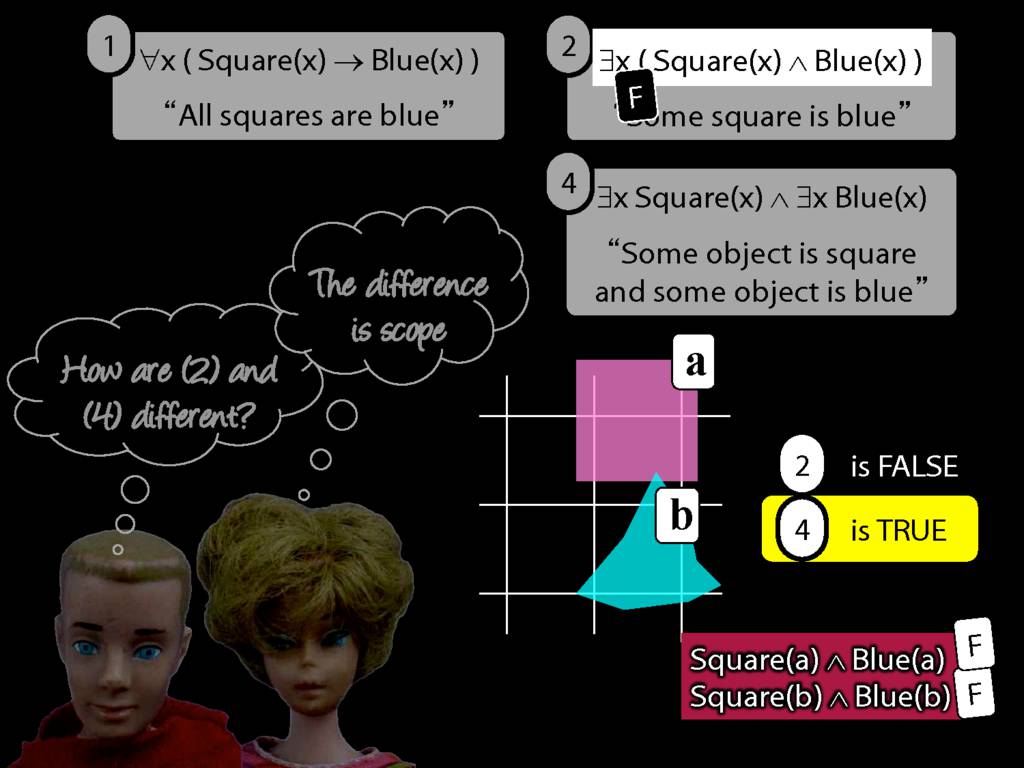
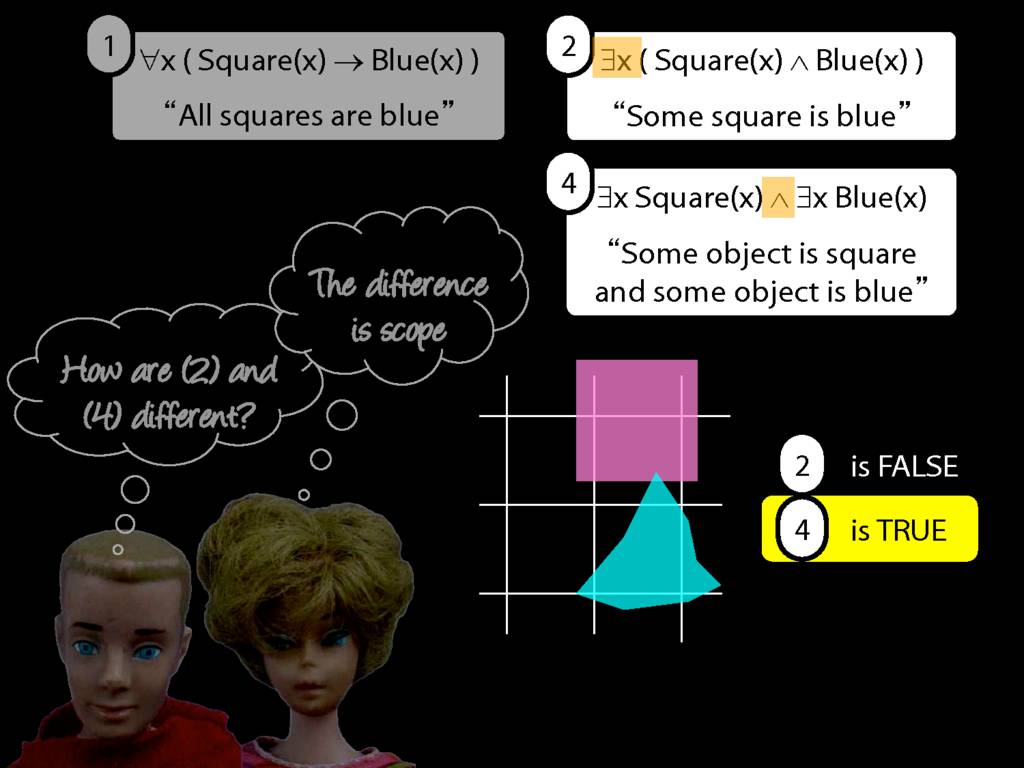
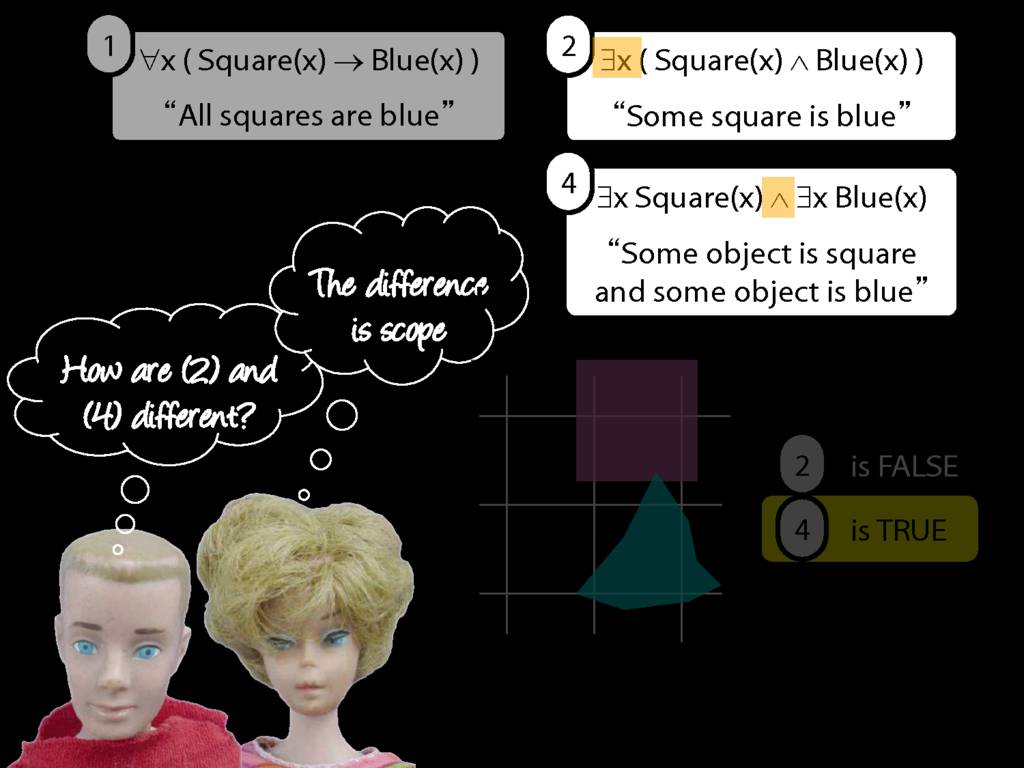
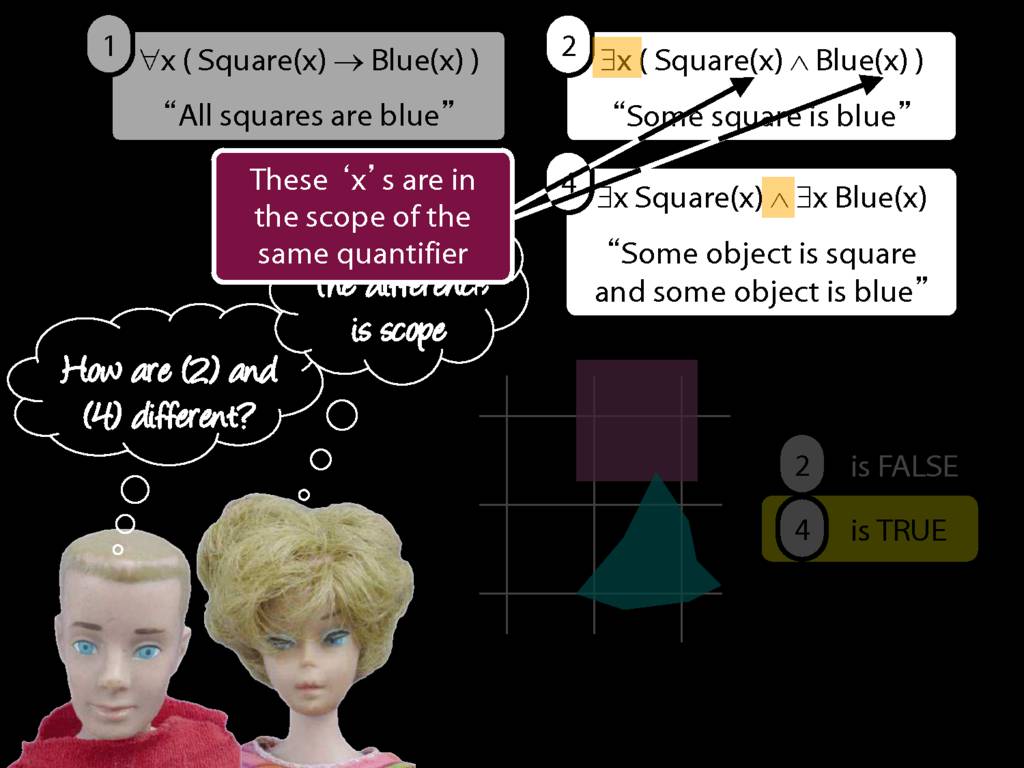
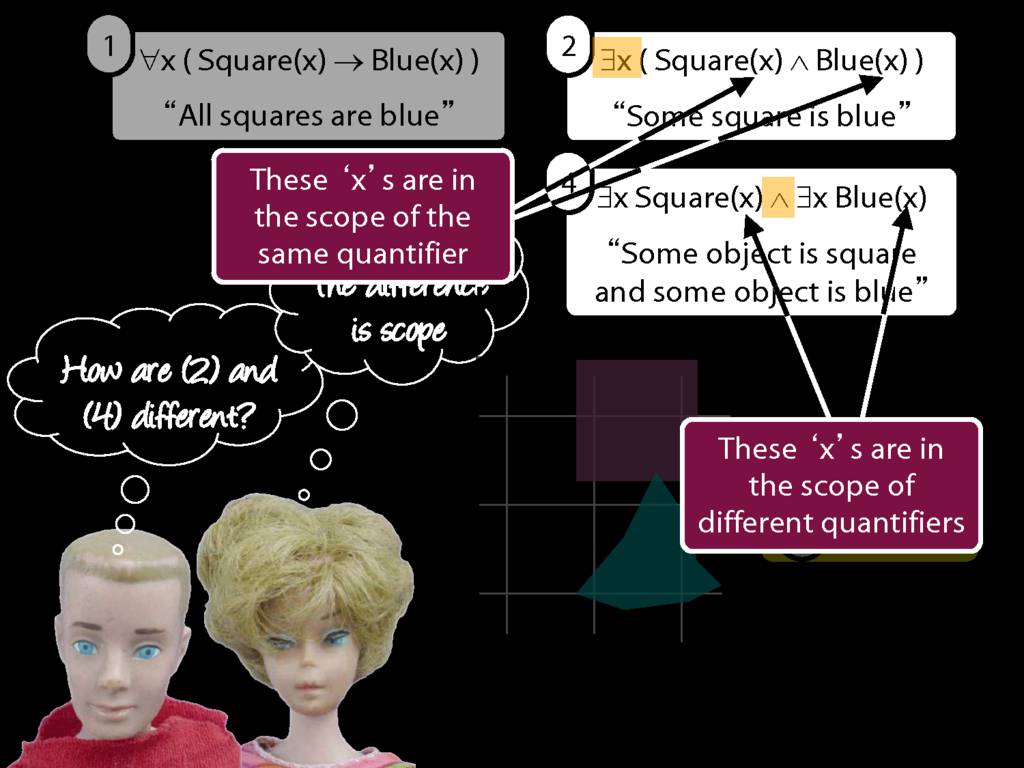
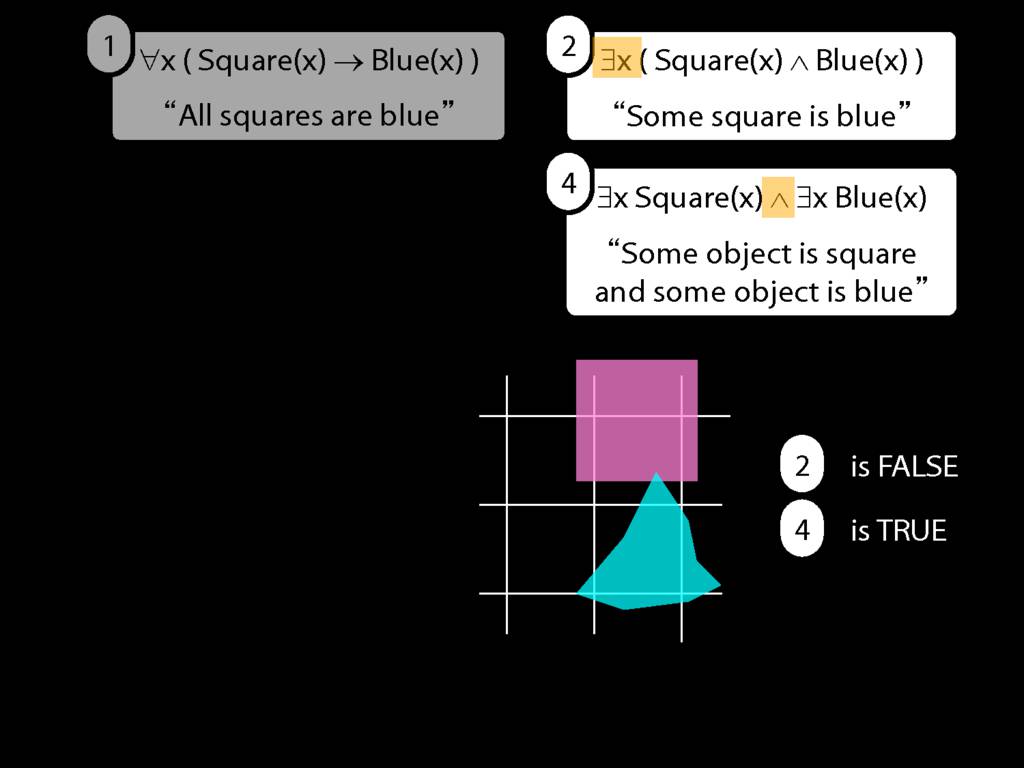
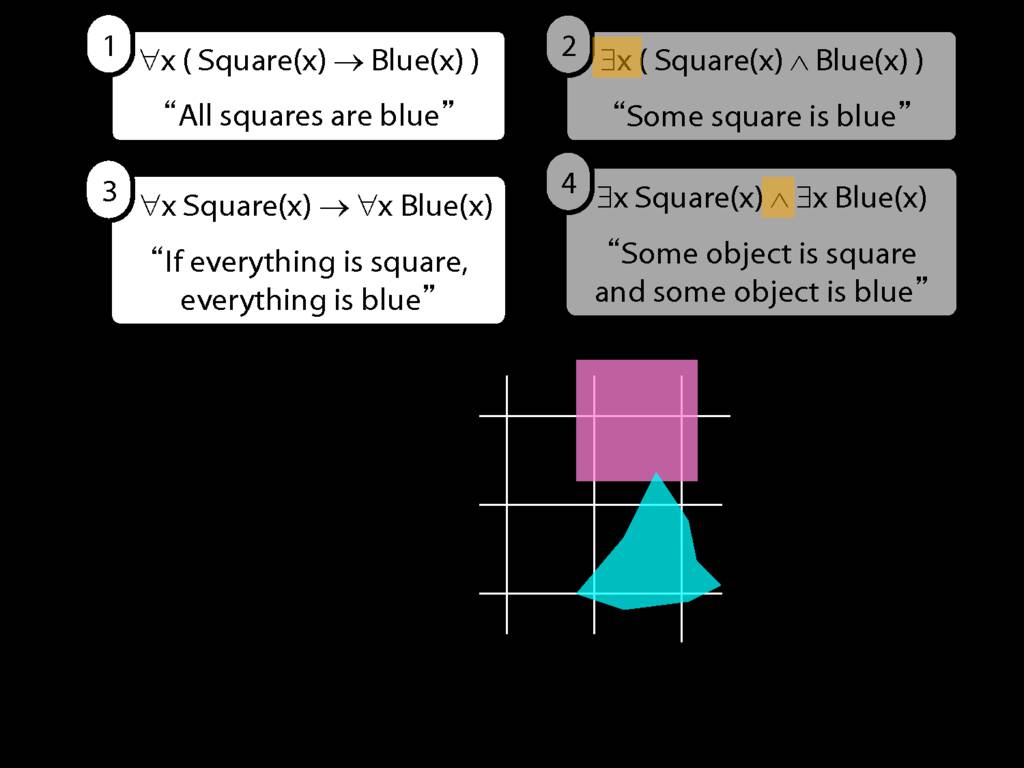
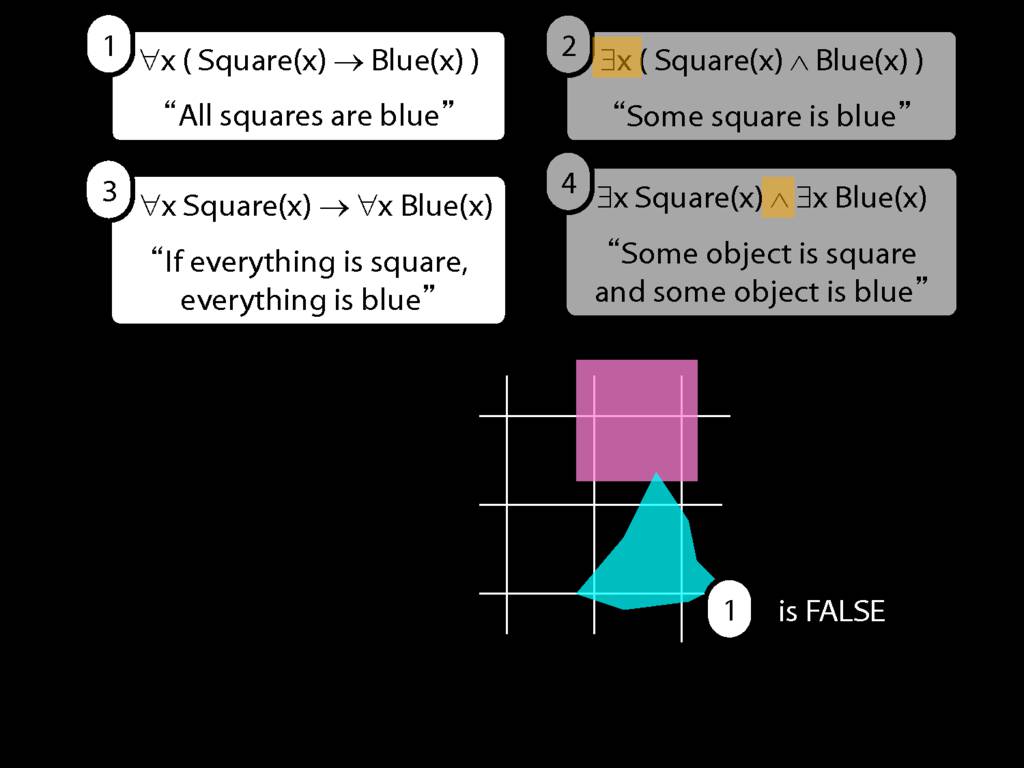
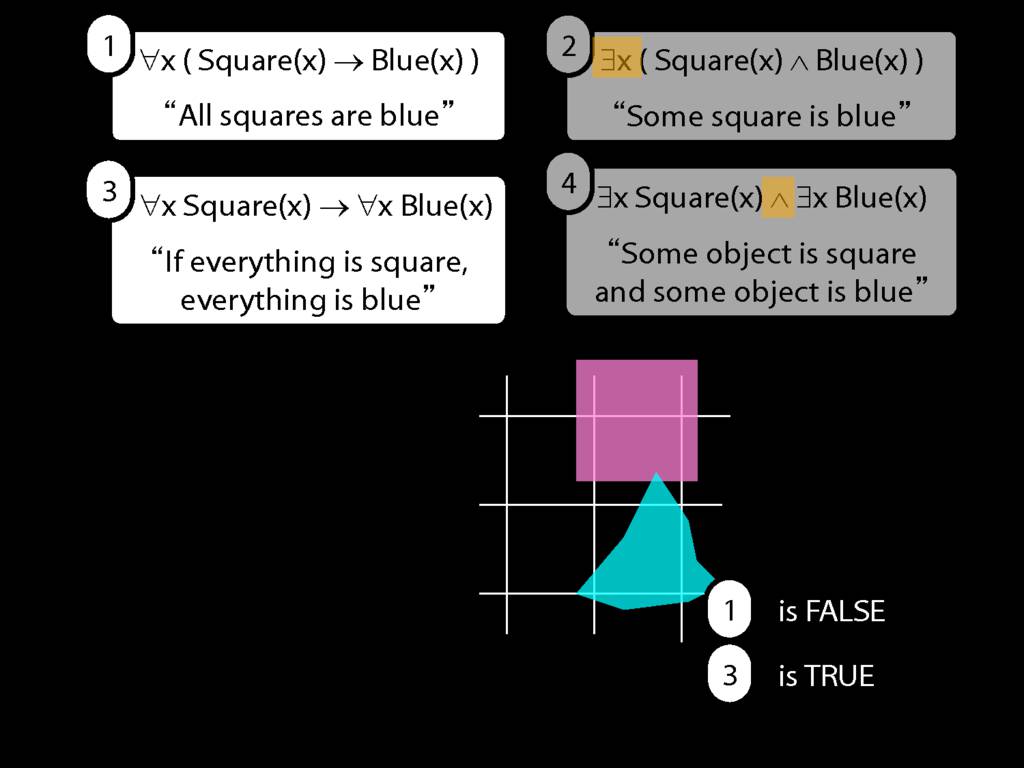
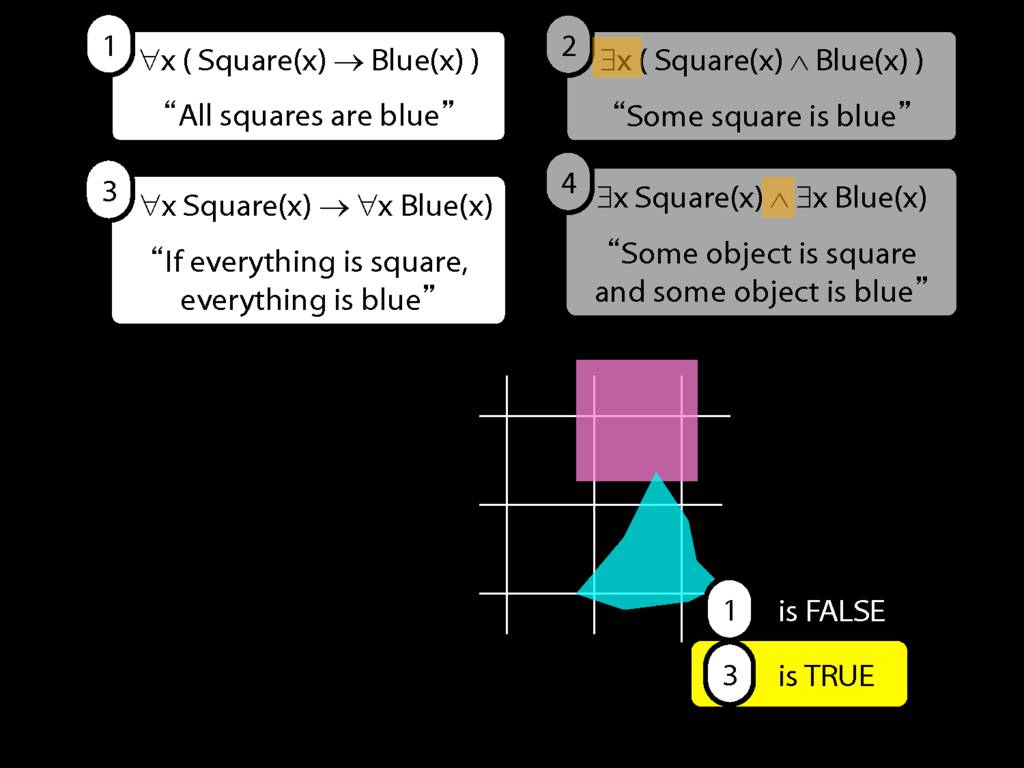
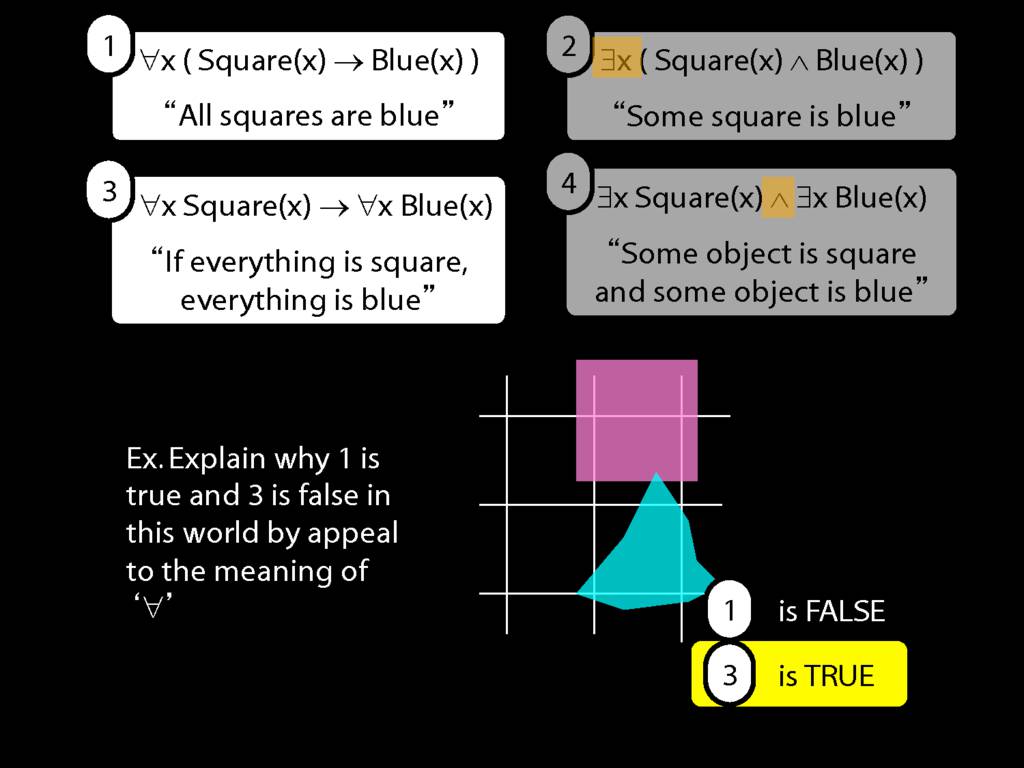
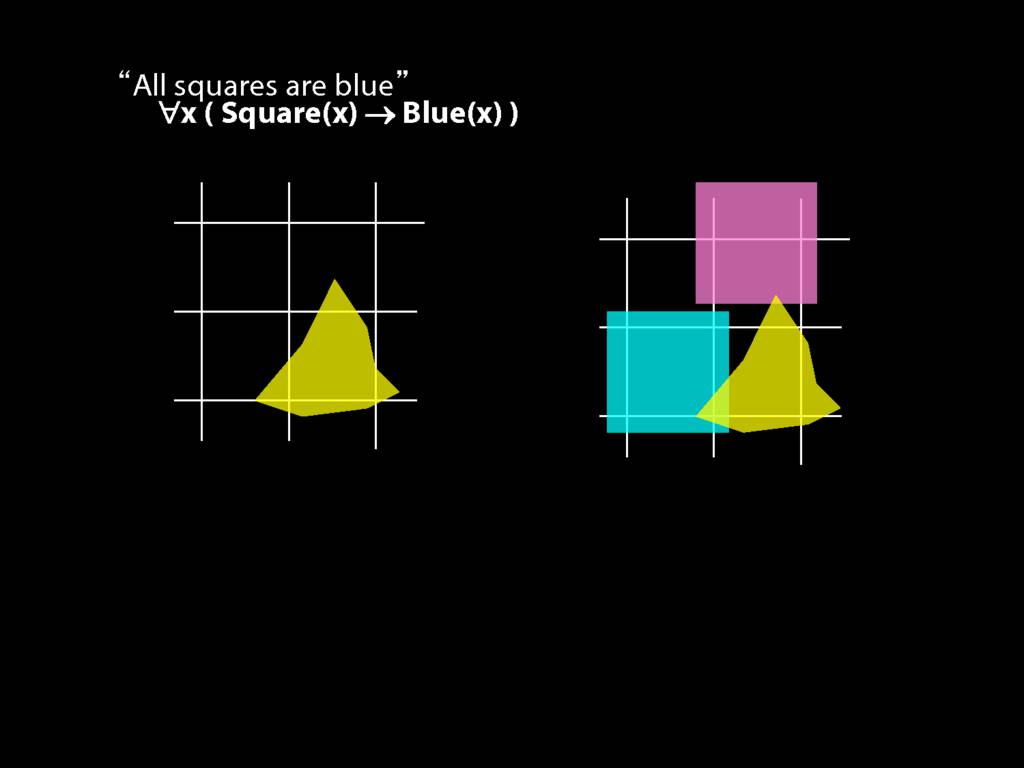
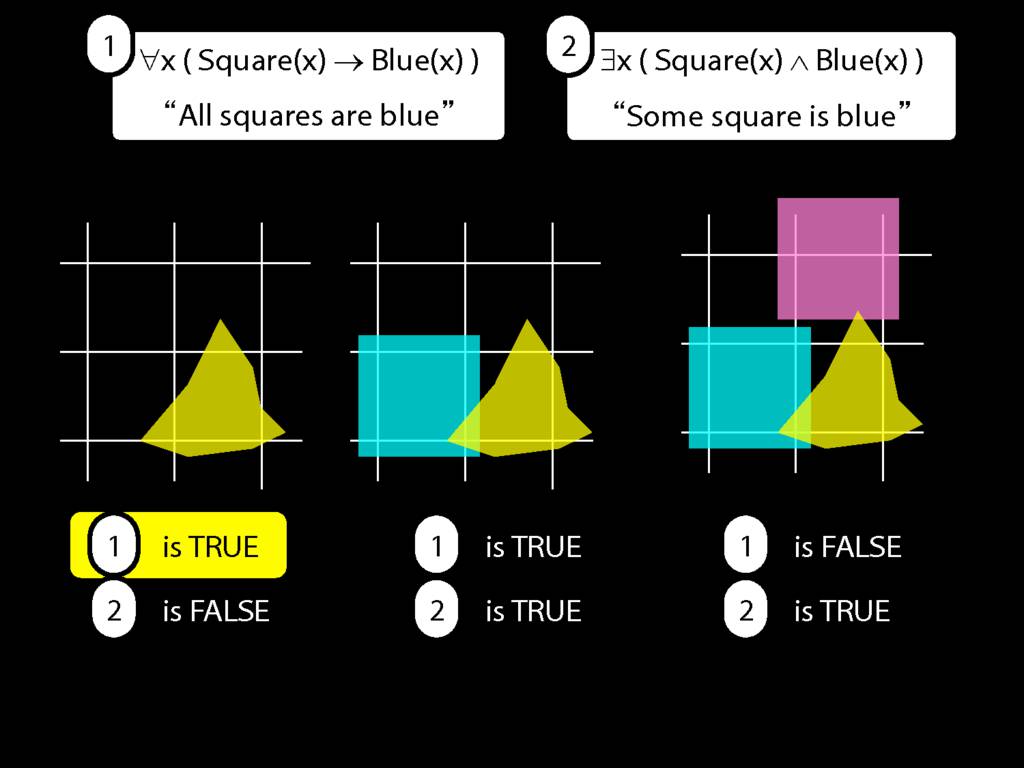
All Squares Are Blue (Fast Version)
\section{All Squares Are Blue (Fast Version)}
\emph{Reading:} §9.2, §9.3, §9.5
\section{All Squares Are Blue (Fast Version)}
\begin{minipage}{\columnwidth}
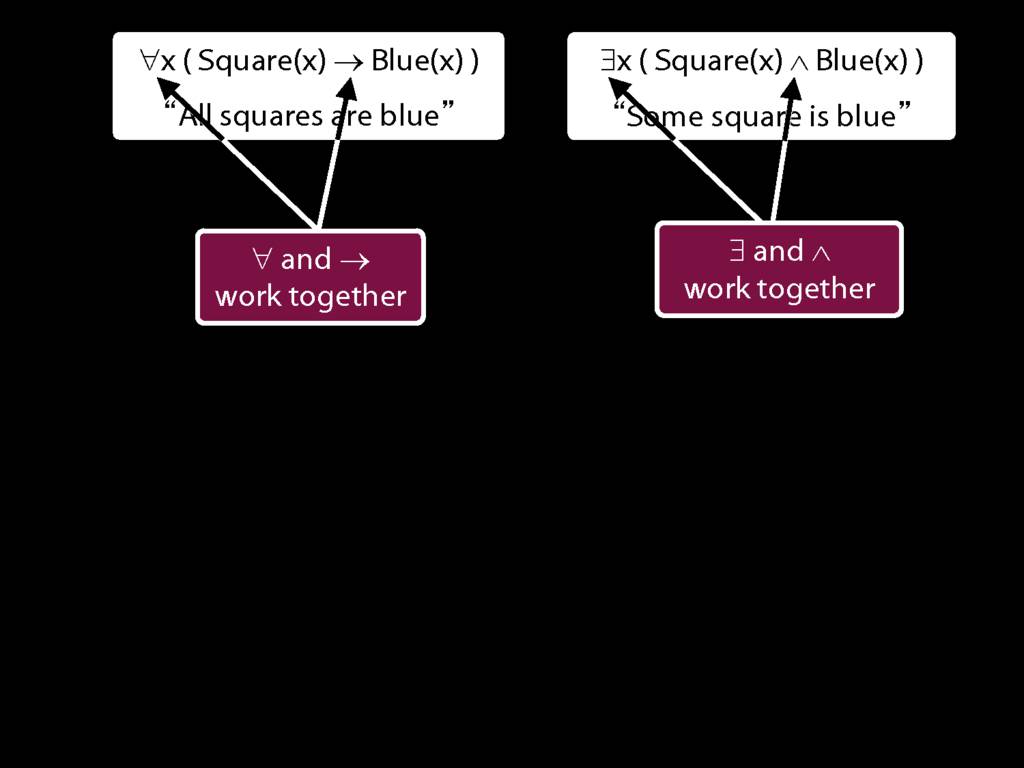
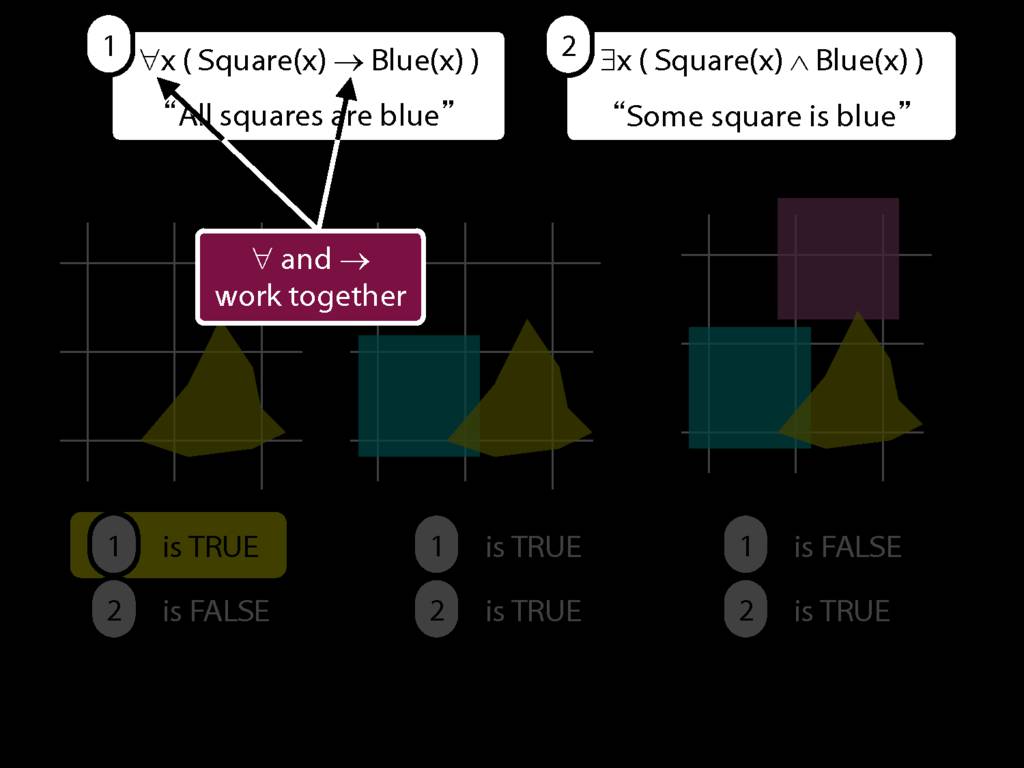
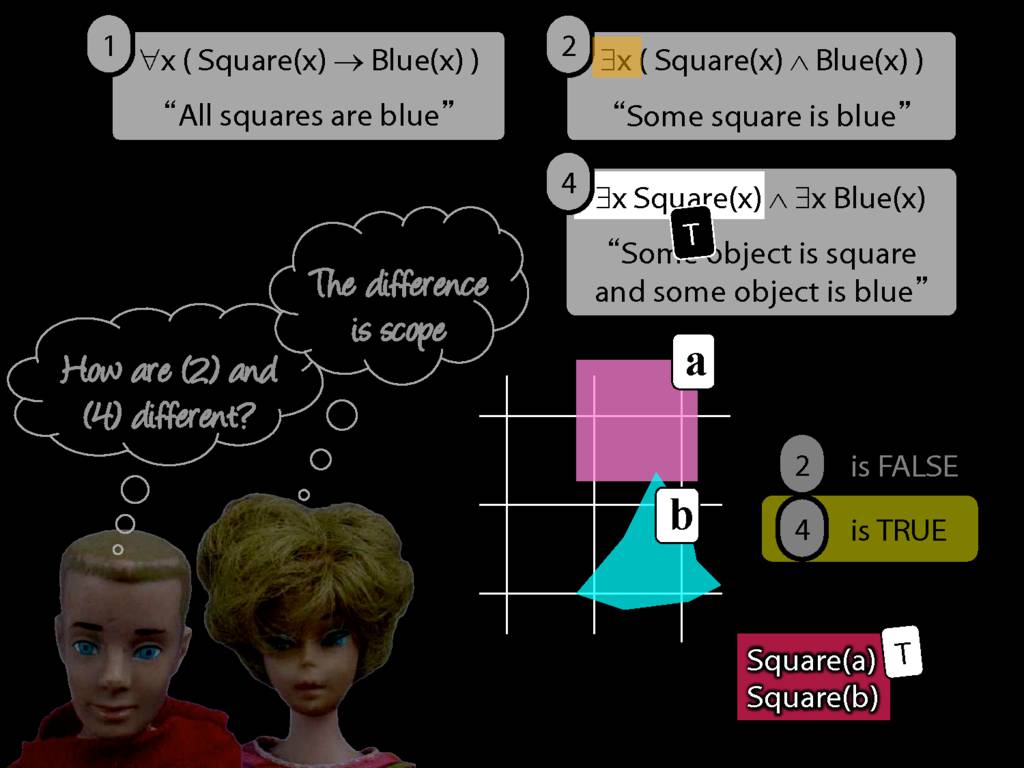
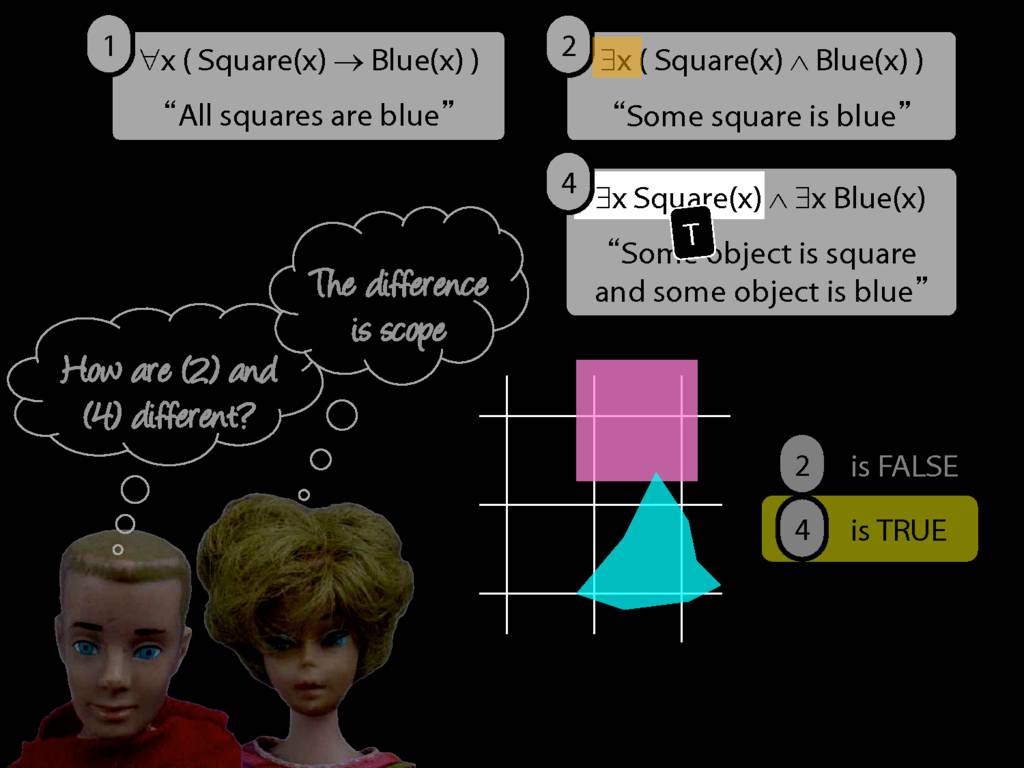
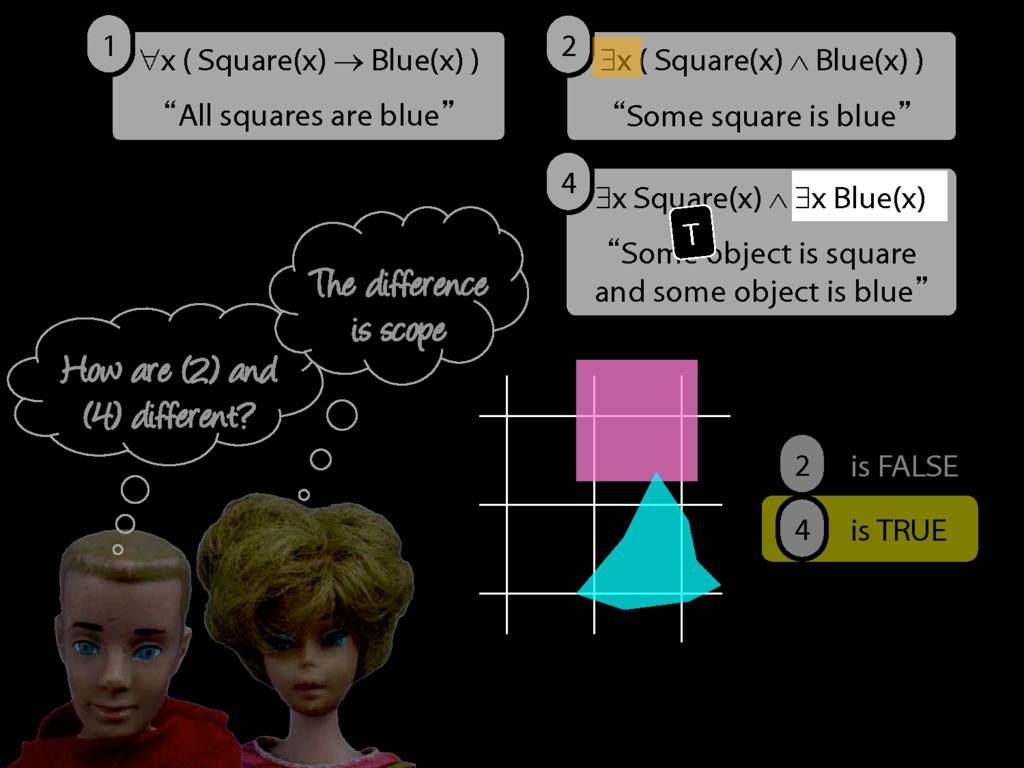
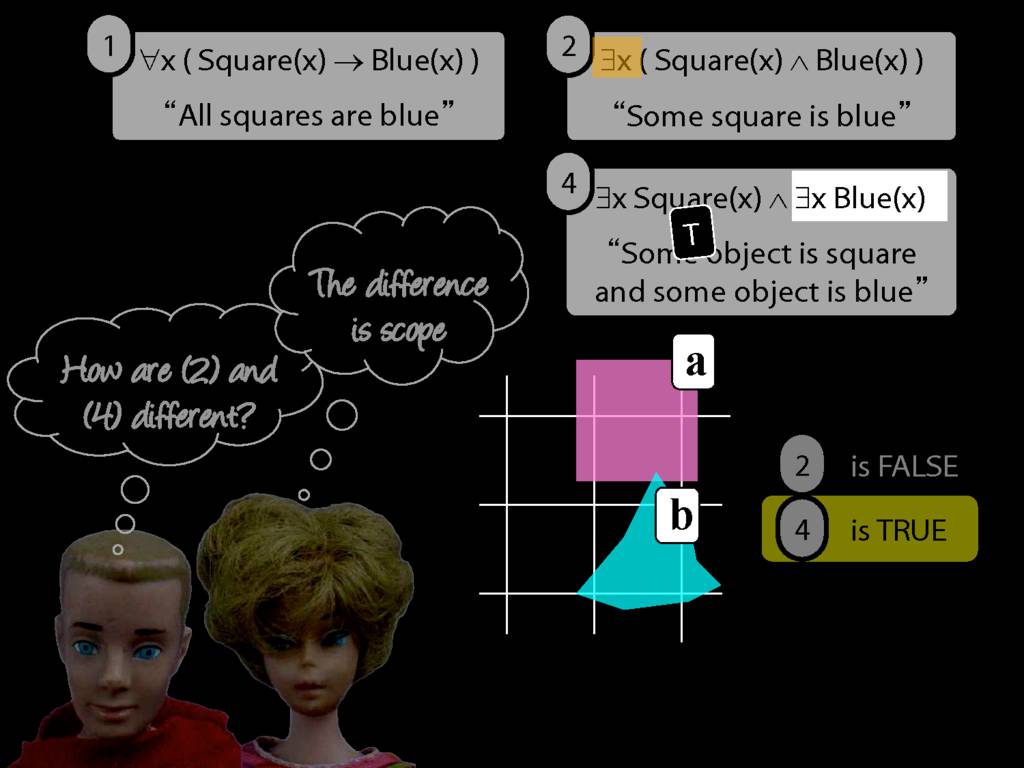
\emph{∃ and ∧ work together}
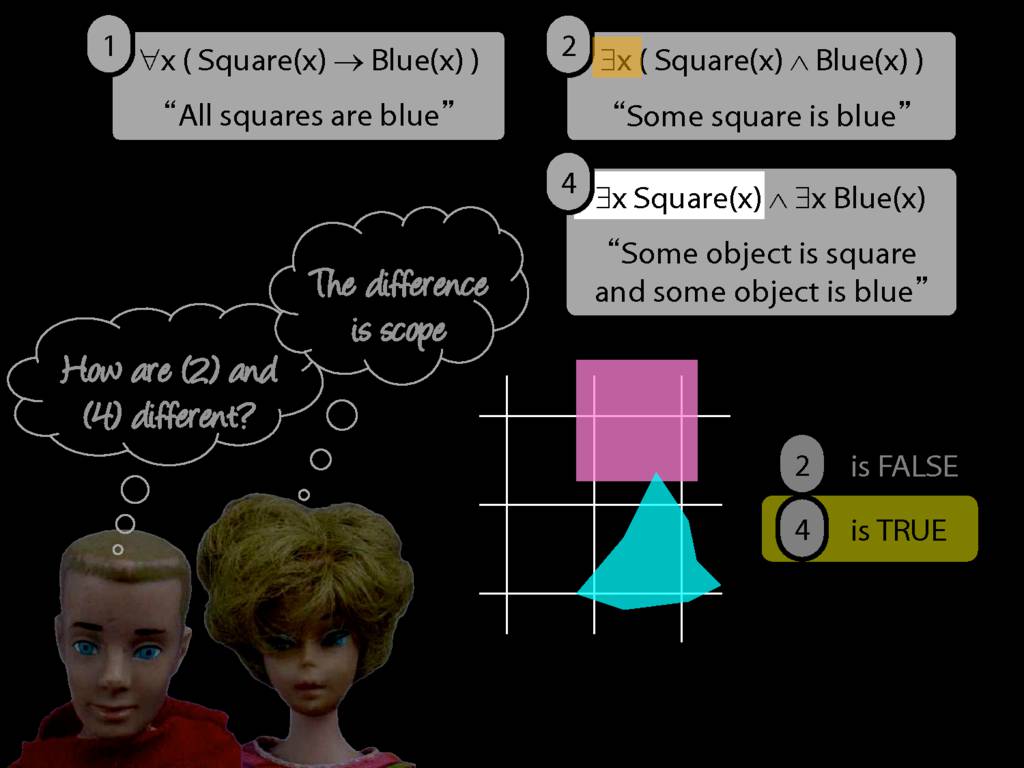
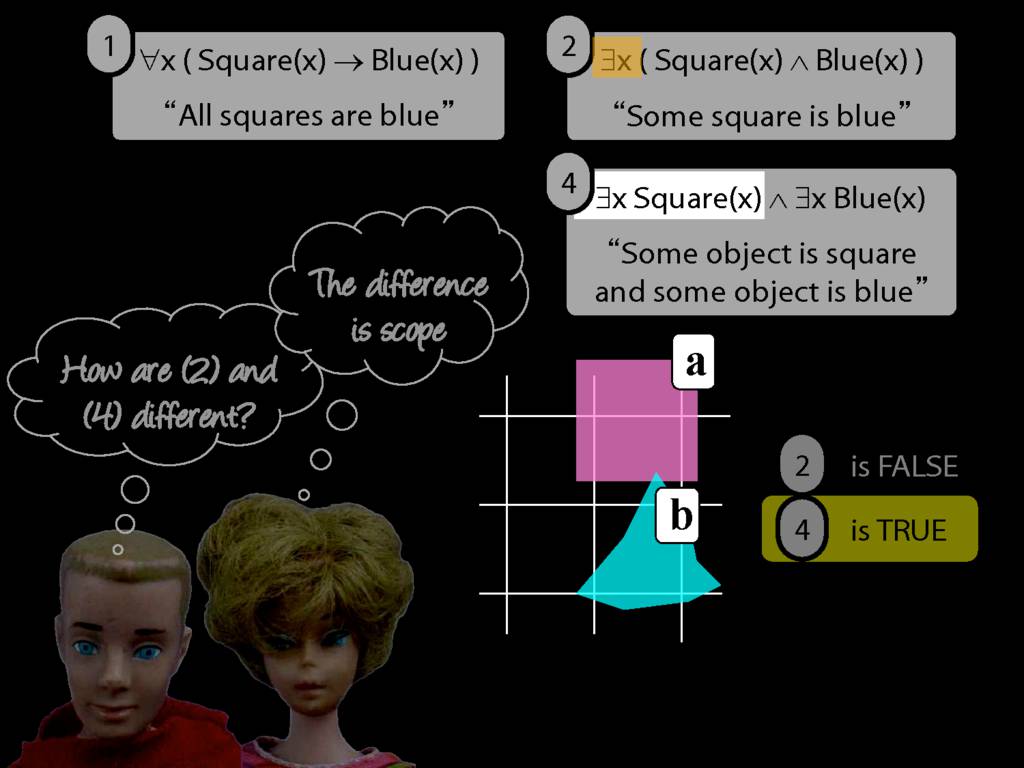
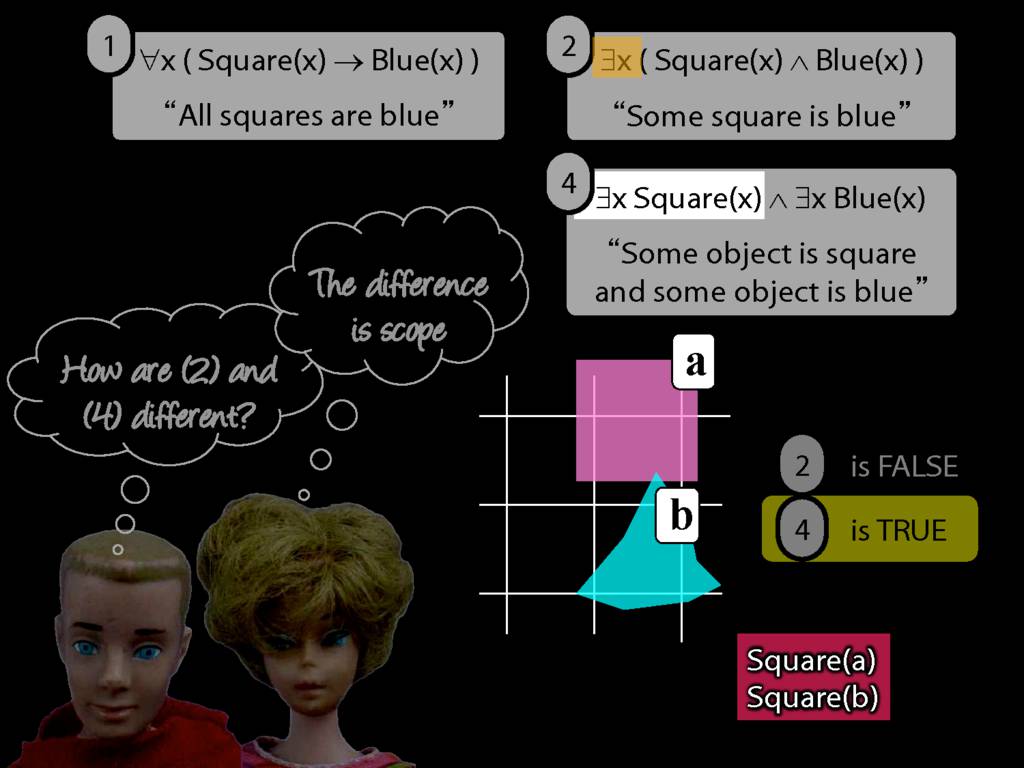
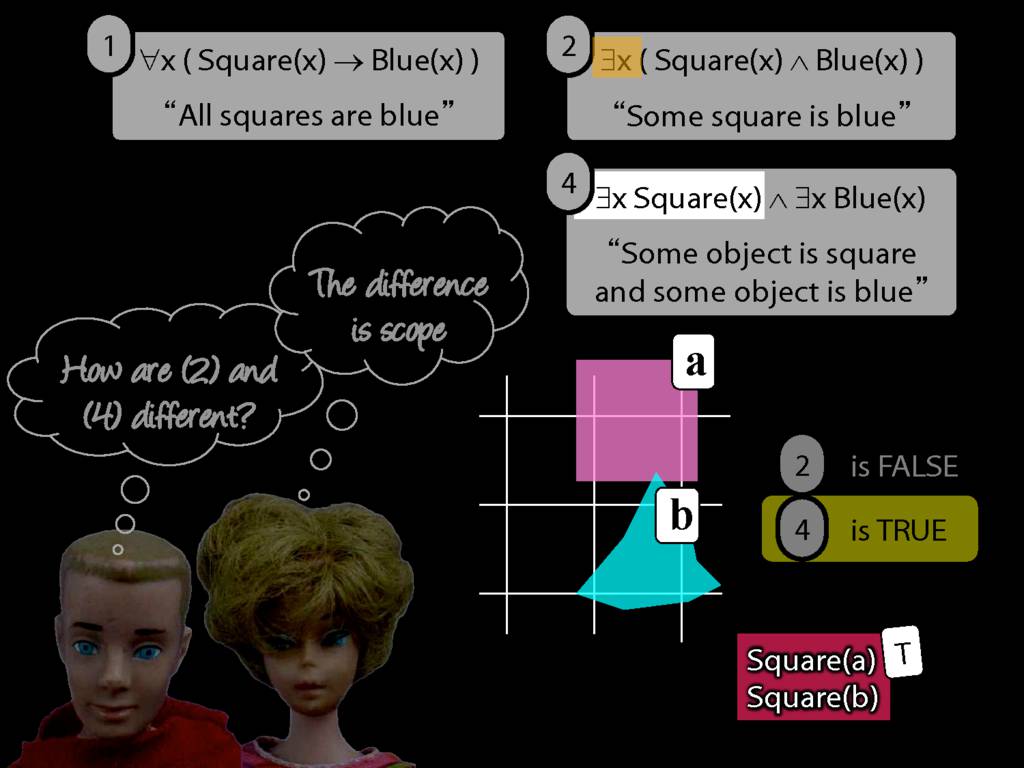
Some square is blue:
∃x ( Square(x) ∧ Blue(x) )
Some of my things are broken:
∃x ( Belongs(a,x) ∧ Broken(x) )
\end{minipage}
\begin{minipage}{\columnwidth}
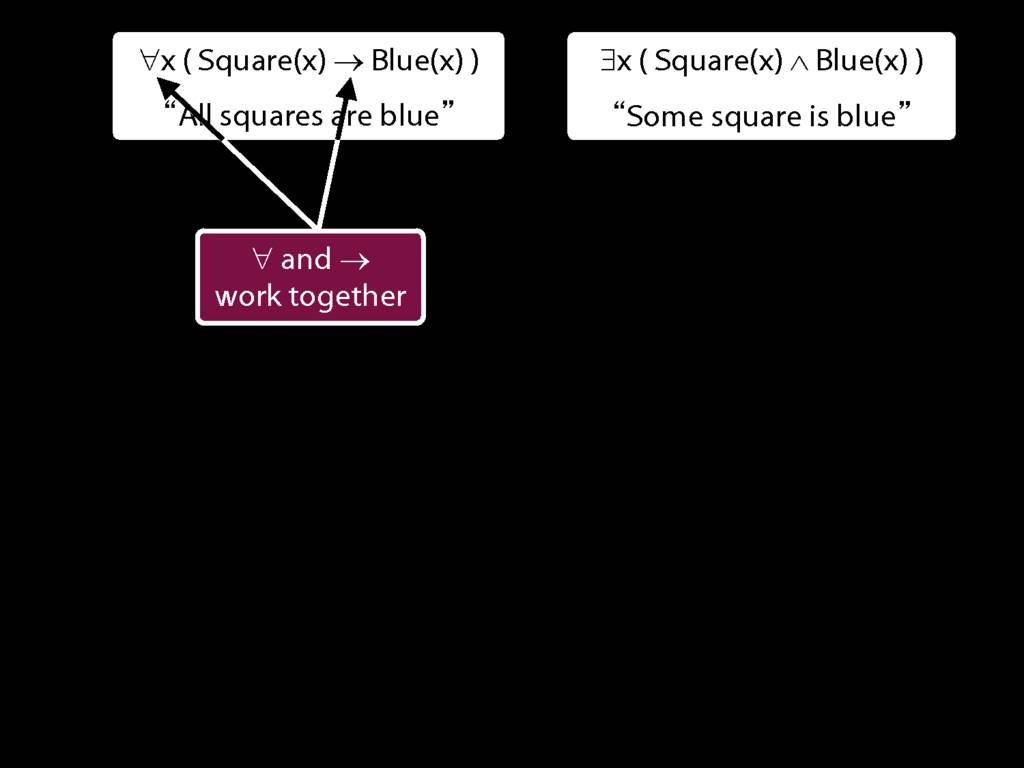
\emph{∀ and → work together}
All squares are blue:
∀x ( Square(x) → Blue(x) )
All my things are broken:
∀x ( Belongs(a,x) → Broken(x) )
\end{minipage}
9.16.10--9.16.15
9.17.7--9.17.15
What does ∀ mean?
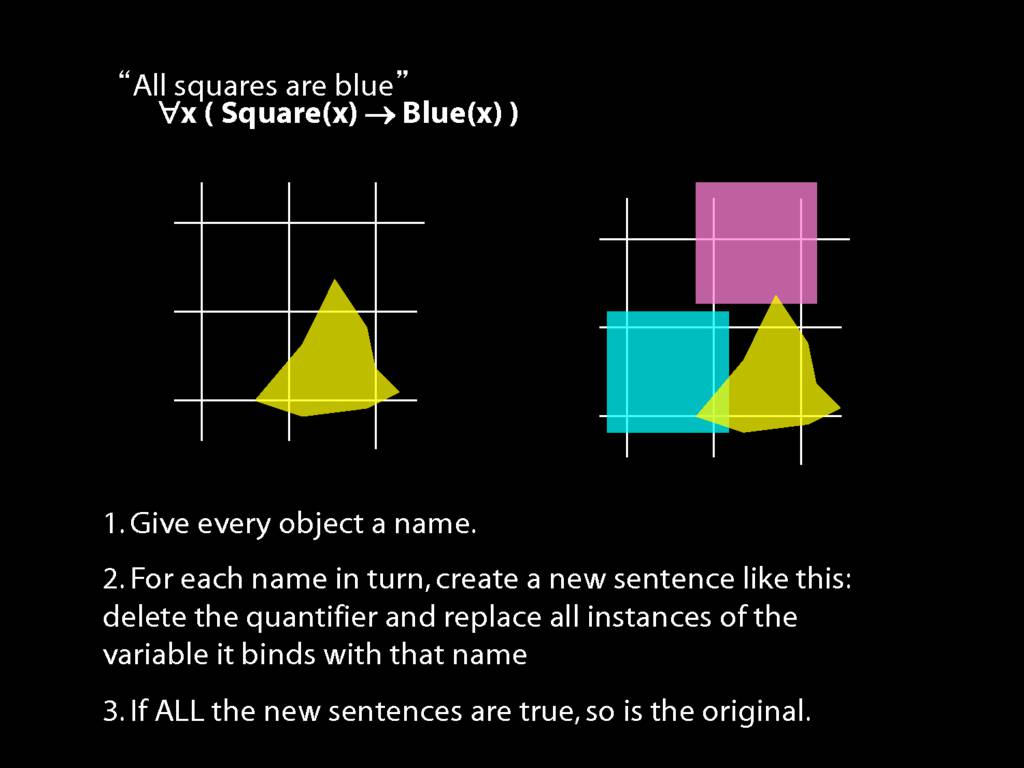
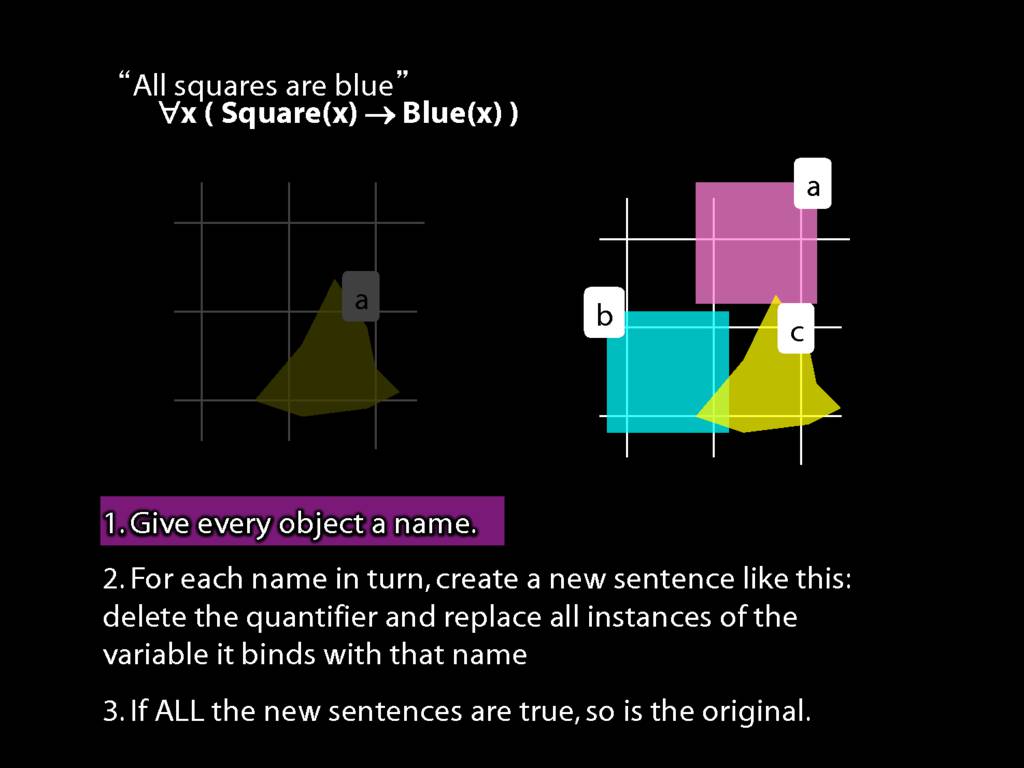
\section{What does ∀ mean?}
\emph{Reading:} §9.4
\section{What does ∀ mean?}
We give the meaning of ∀ by specifying what it takes for a sentence containing ∀ to be true:
\begin{enumerate}
\item Give every object a name.
\item For each name in turn, create a new sentence like this: delete the quantifier and replace all instances of the variable it binds with that name.
\item If ALL of the new sentences are true, so is the original sentence.
\end{enumerate}
∀Intro
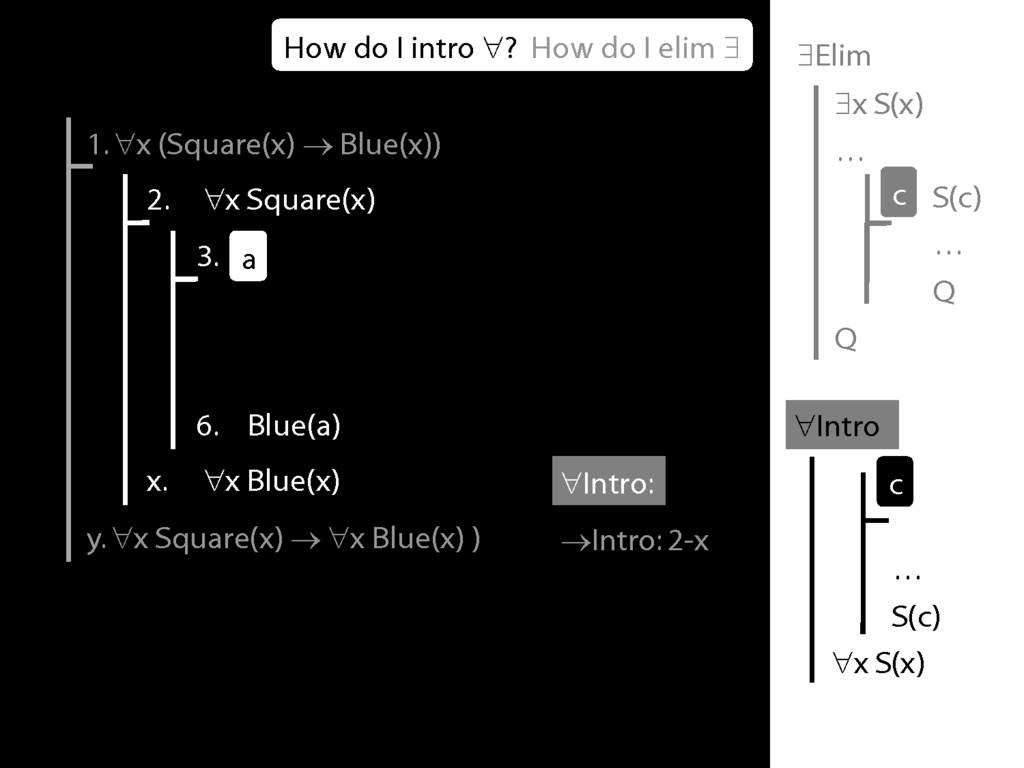
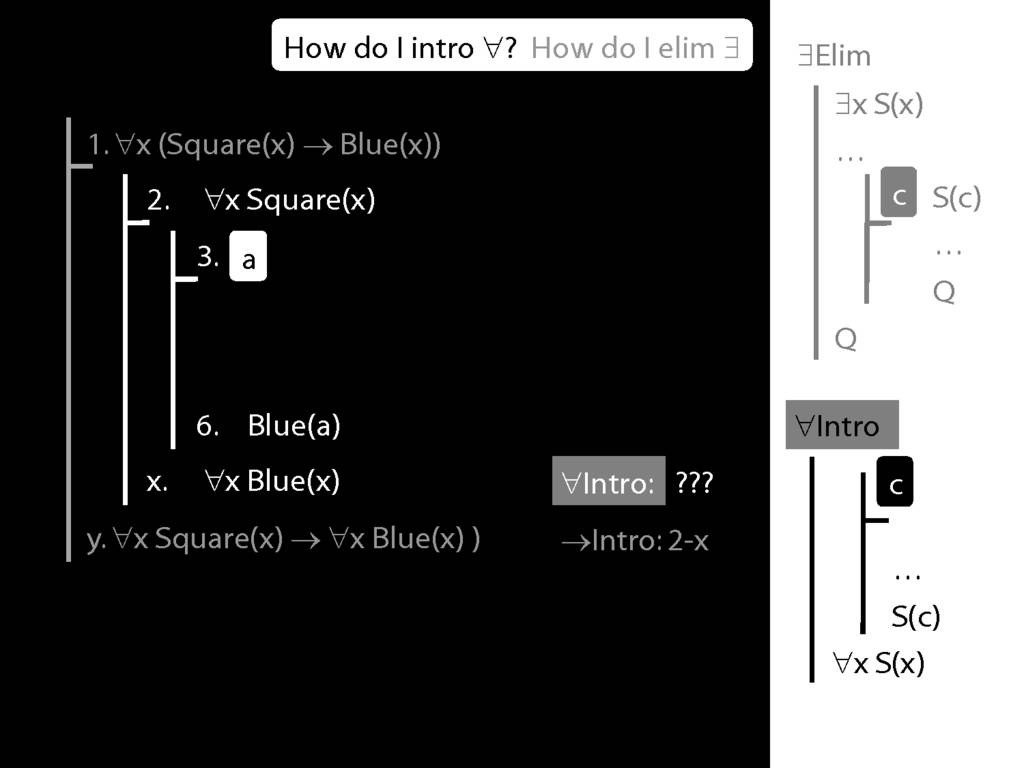
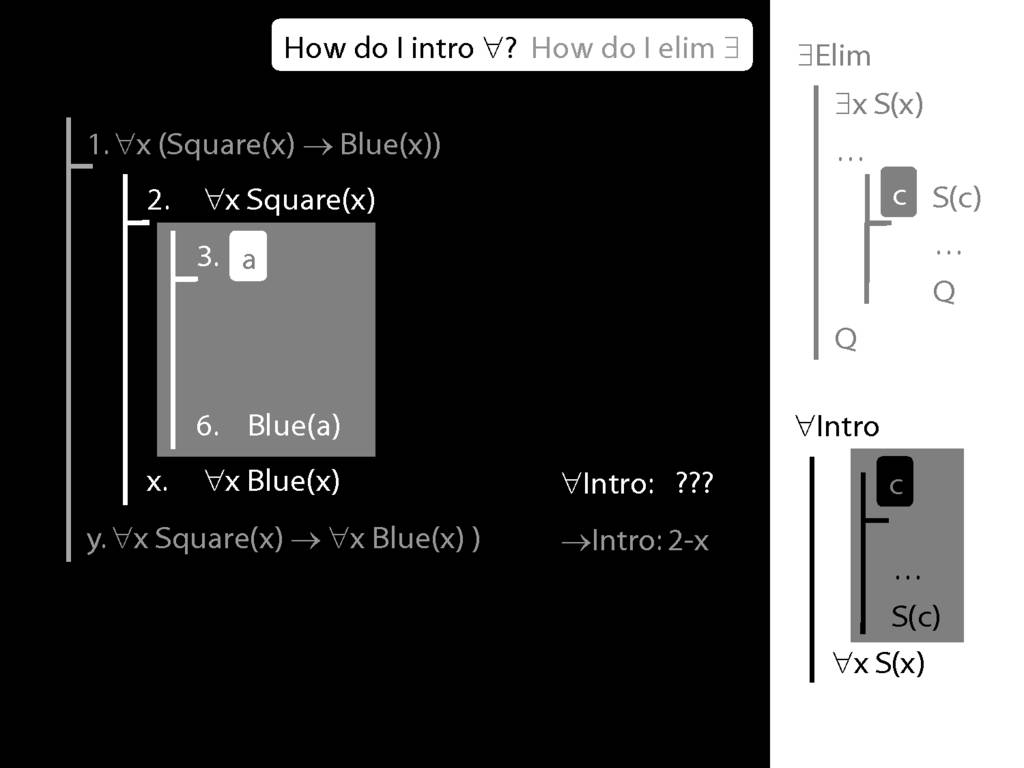
\section{∀Intro}
\emph{Reading:} §12.1, §12.3, §13.1
\section{∀Intro}
\begin{minipage}{\columnwidth}
Why is this proof incorrect?
\end{minipage}
12.4--12.5
*12.6--12.7
12.9--12.10
Summary of Quantifier Rules
\section{Summary of Quantifier Rules}
\emph{Reading:} §13.1, §13.2
\section{Summary of Quantifier Rules}
10.20
*10.24--10.7
10.28--10.29
13.2--13.3, 13.8--13.9
13.11, 13.13, 13.15
Translation with Quantifiers
\section{Translation with Quantifiers}
\emph{Reading:} §9.5, §9.6
\section{Translation with Quantifiers}
9.4–-9.5
9.8–-9.9
9.12-–9.13
What does ∃ mean?
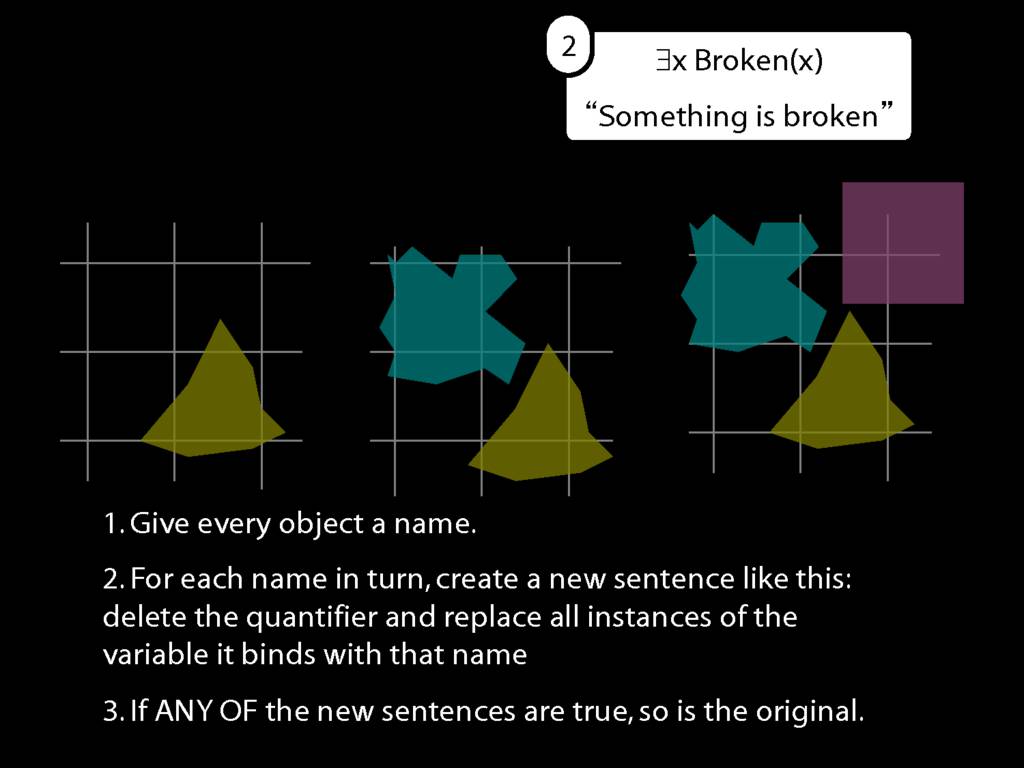
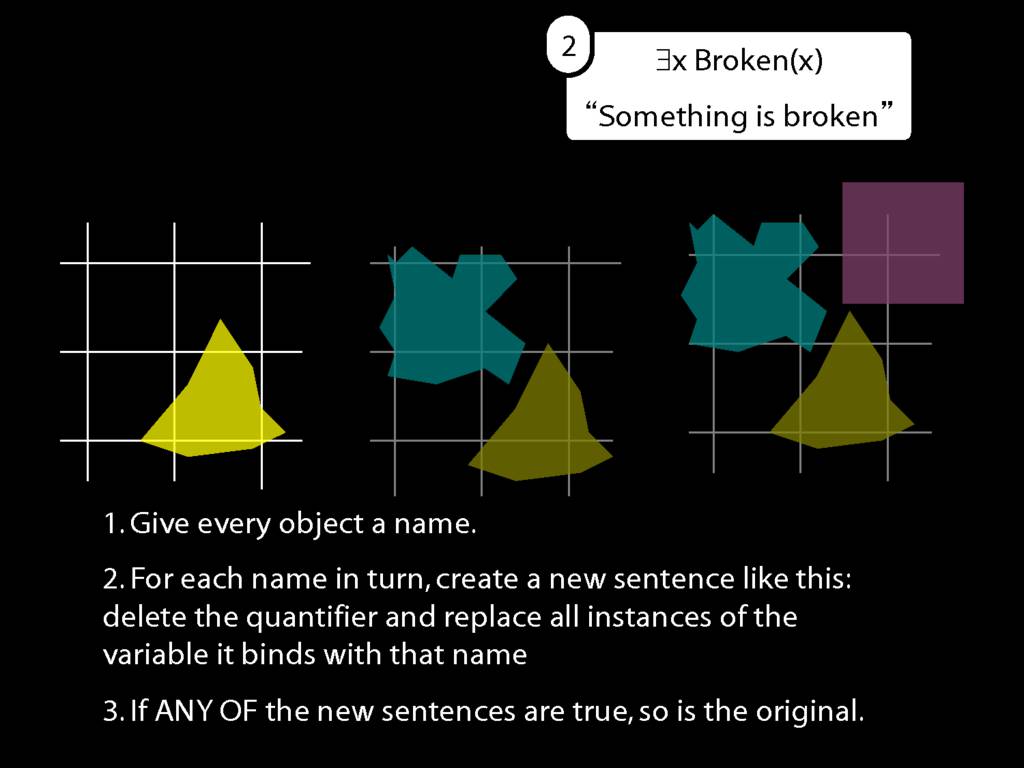
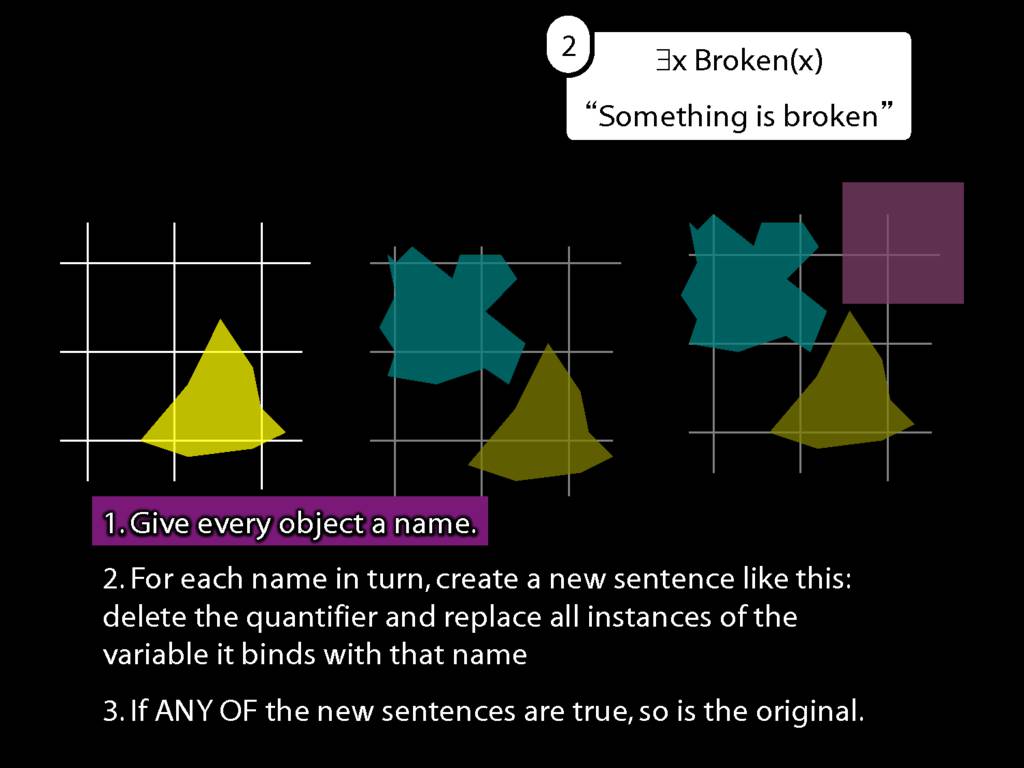
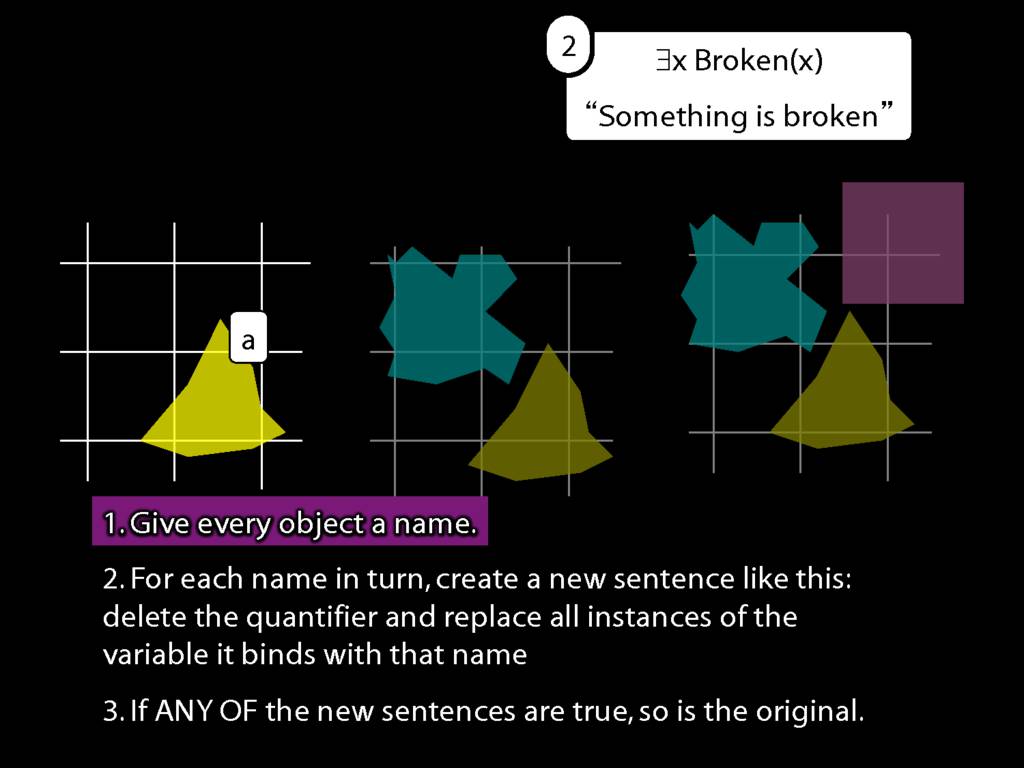
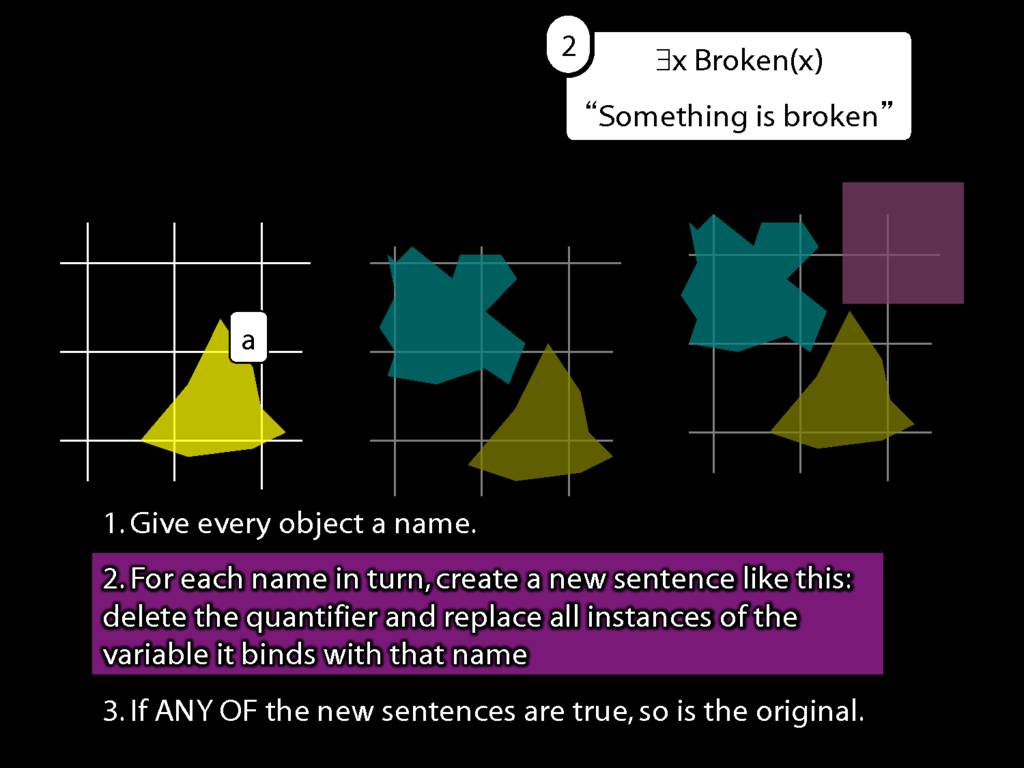
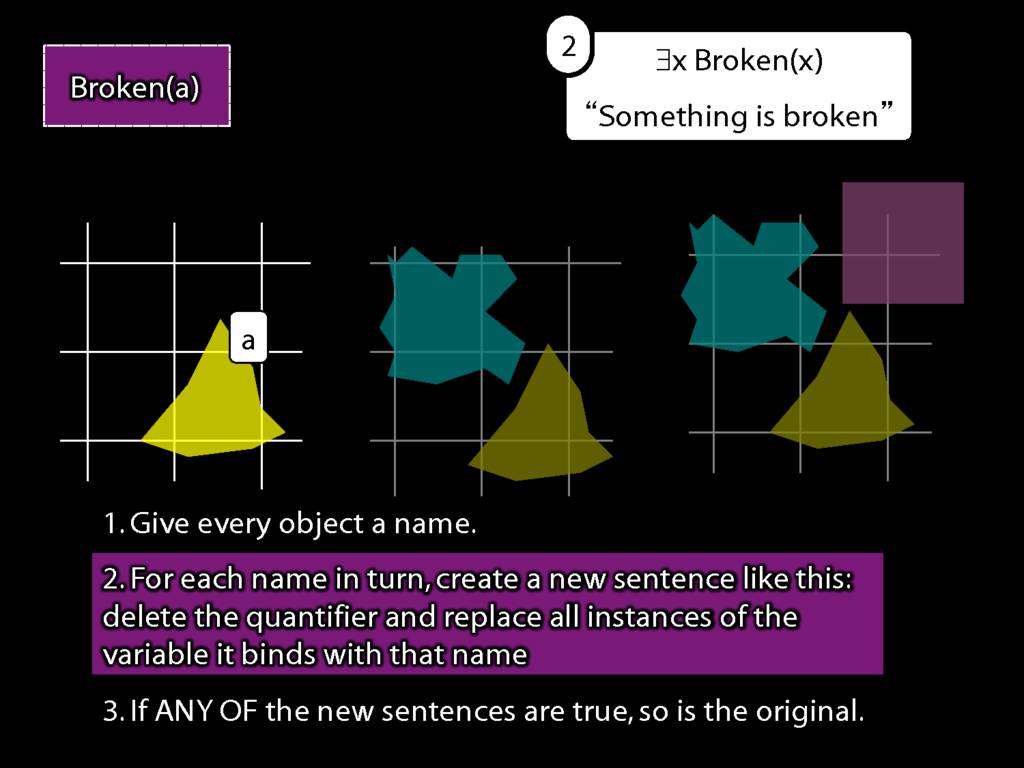
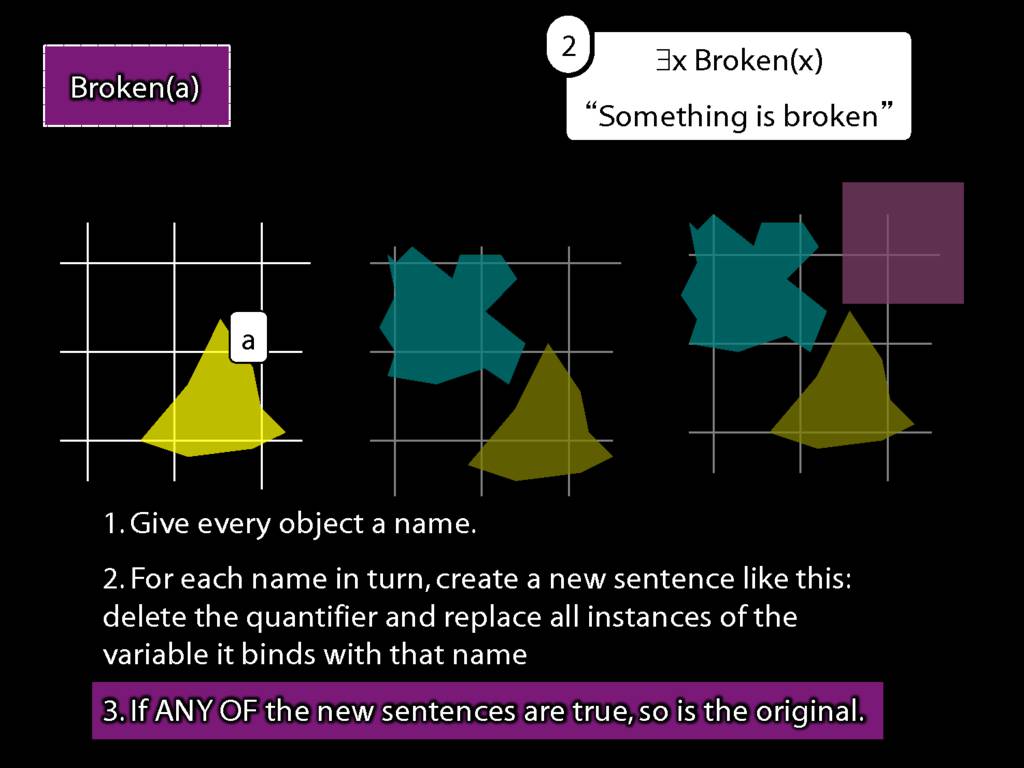
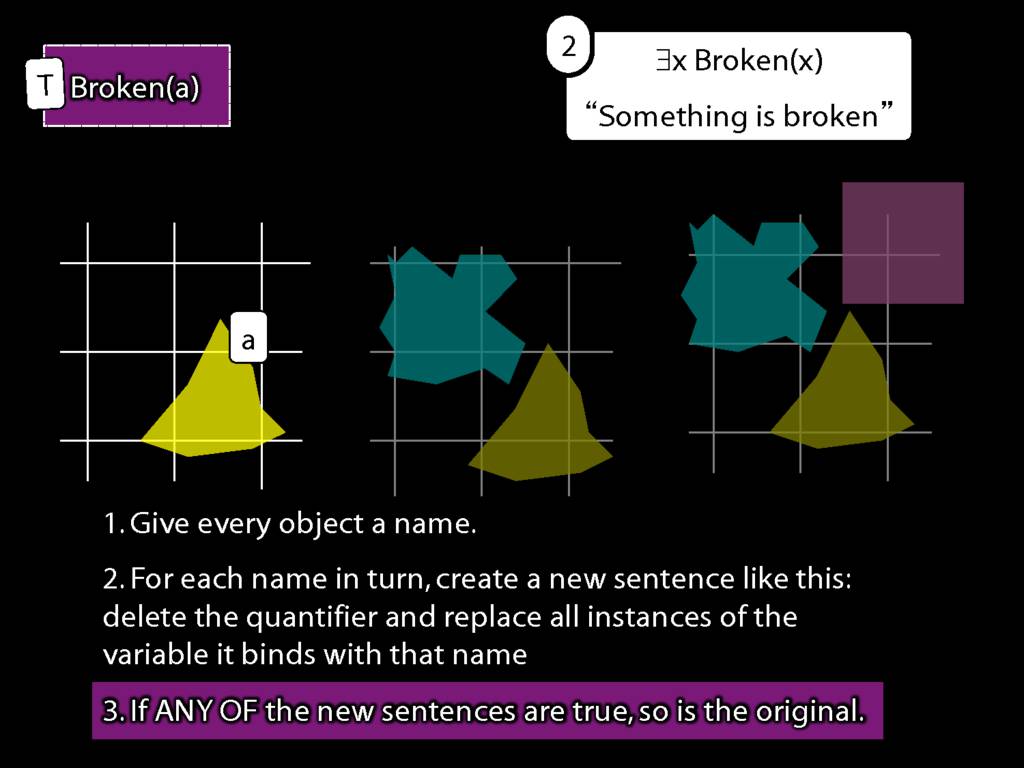
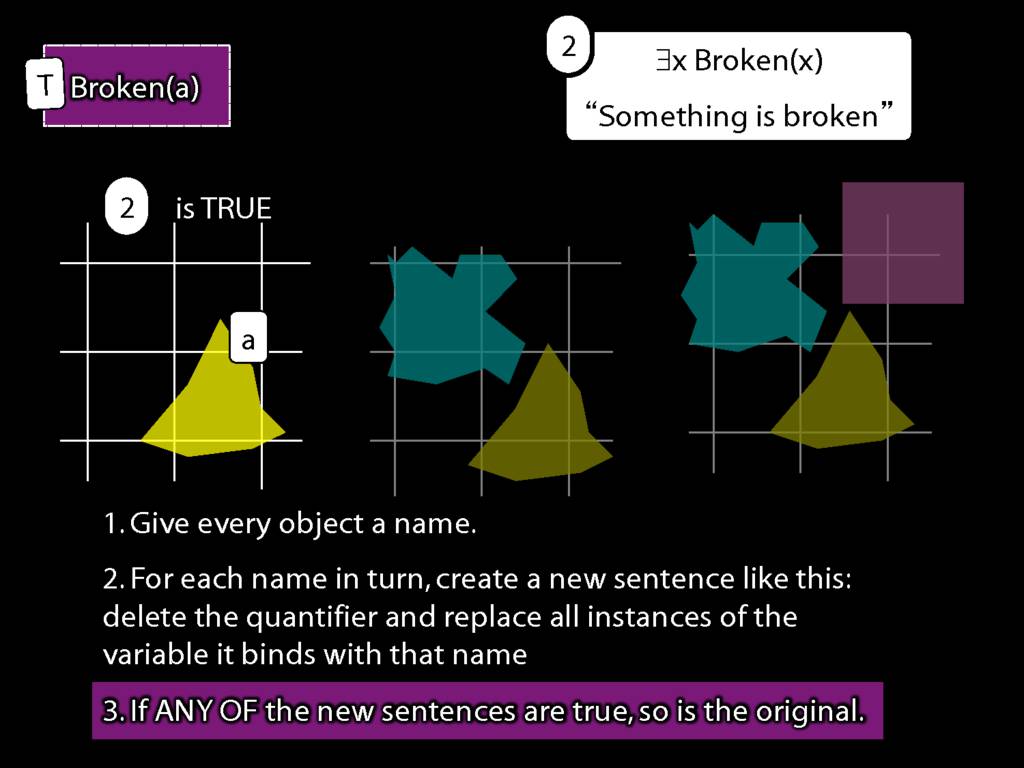
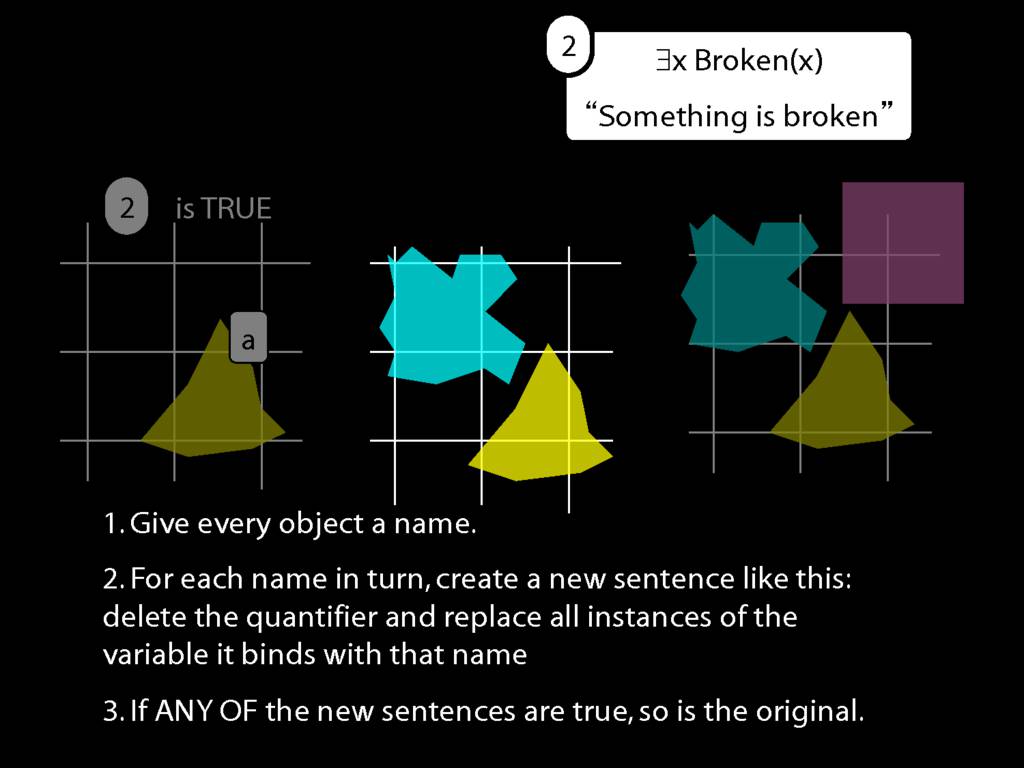
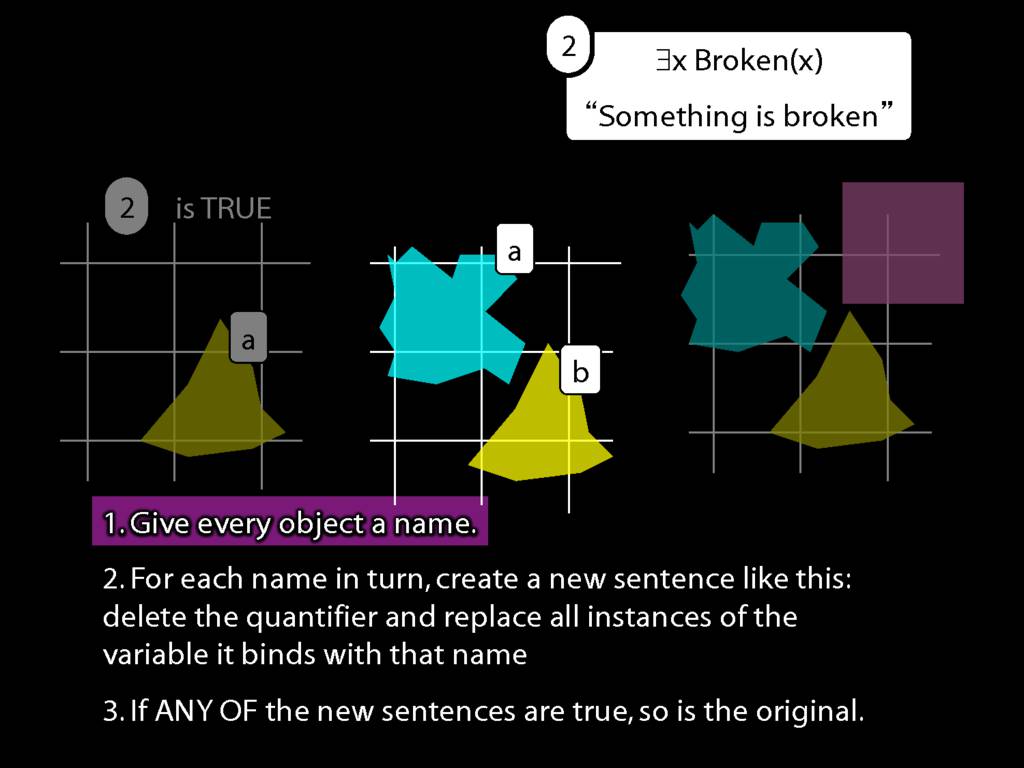
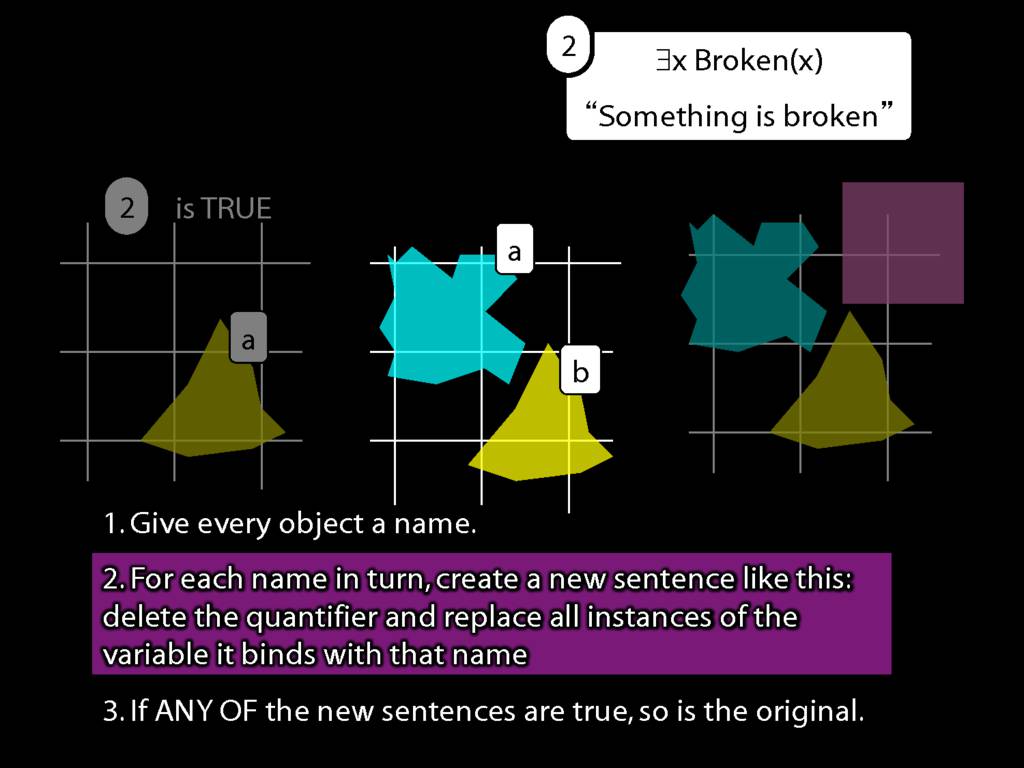
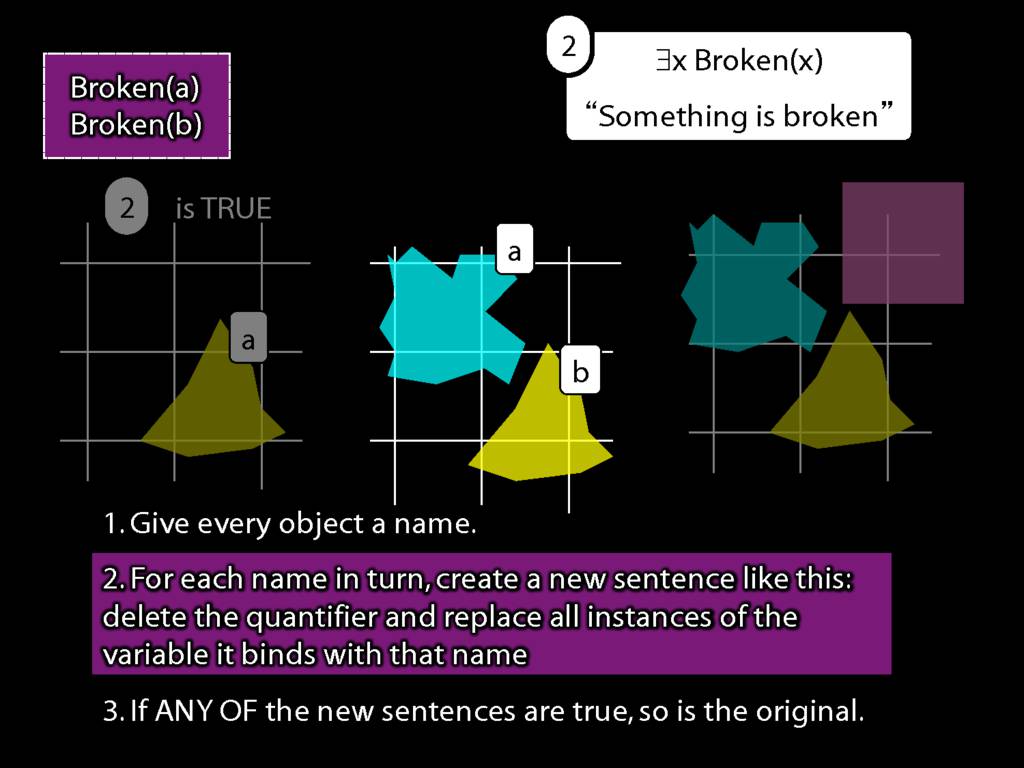
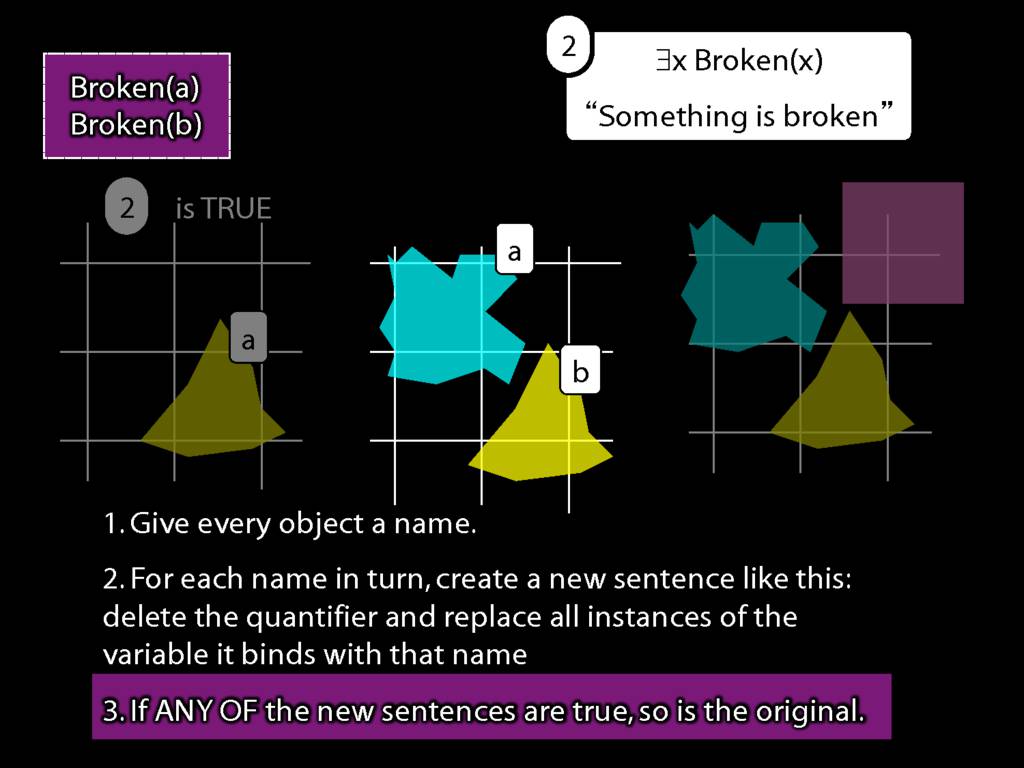
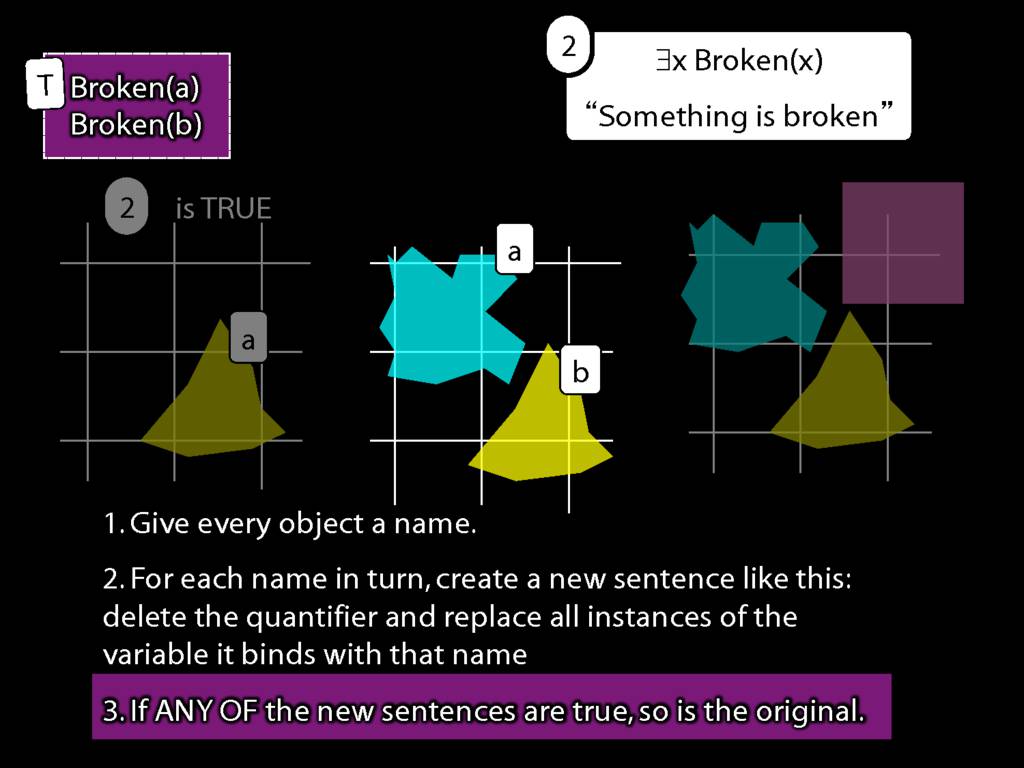
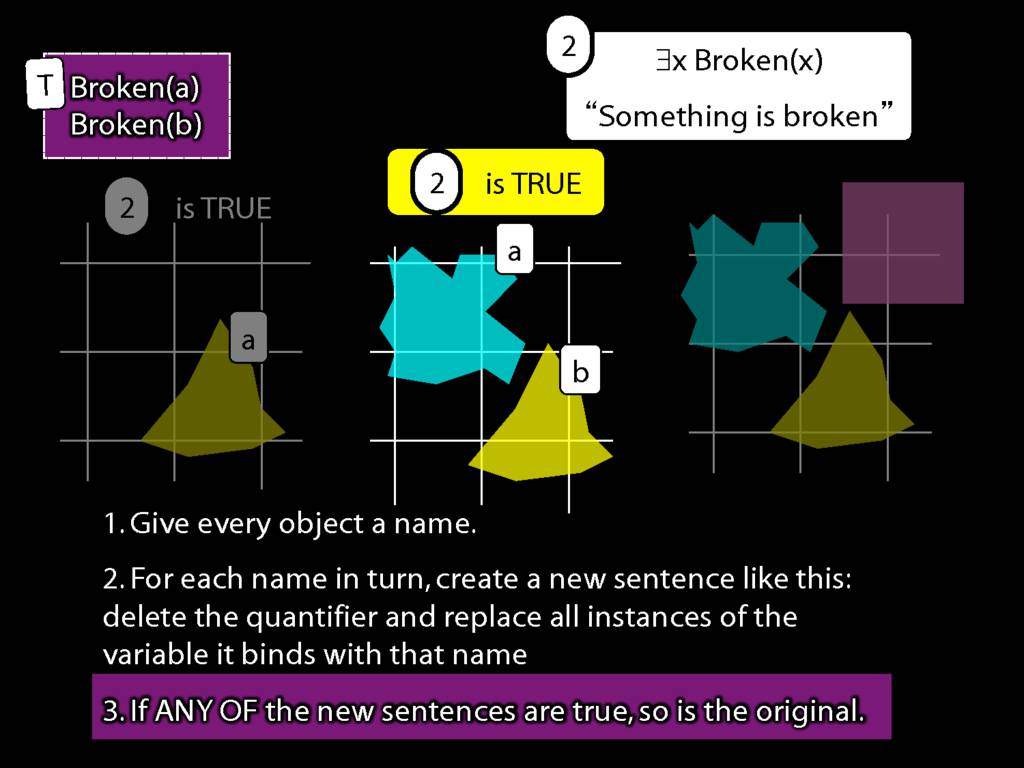
\section{What does ∃ mean?}
\emph{Reading:} §9.4
\section{What does ∃ mean?}
We give the meaning of ∃ by specifying what it takes for a sentence containing ∃ to be true:
\begin{enumerate}
\item Give every object a name.
\item For each name in turn, create a new sentence like this: delete the quantifier and replace all instances of the variable it binds with that name.
\item If ANY of the new sentences are true, so is the original sentence.
\end{enumerate}
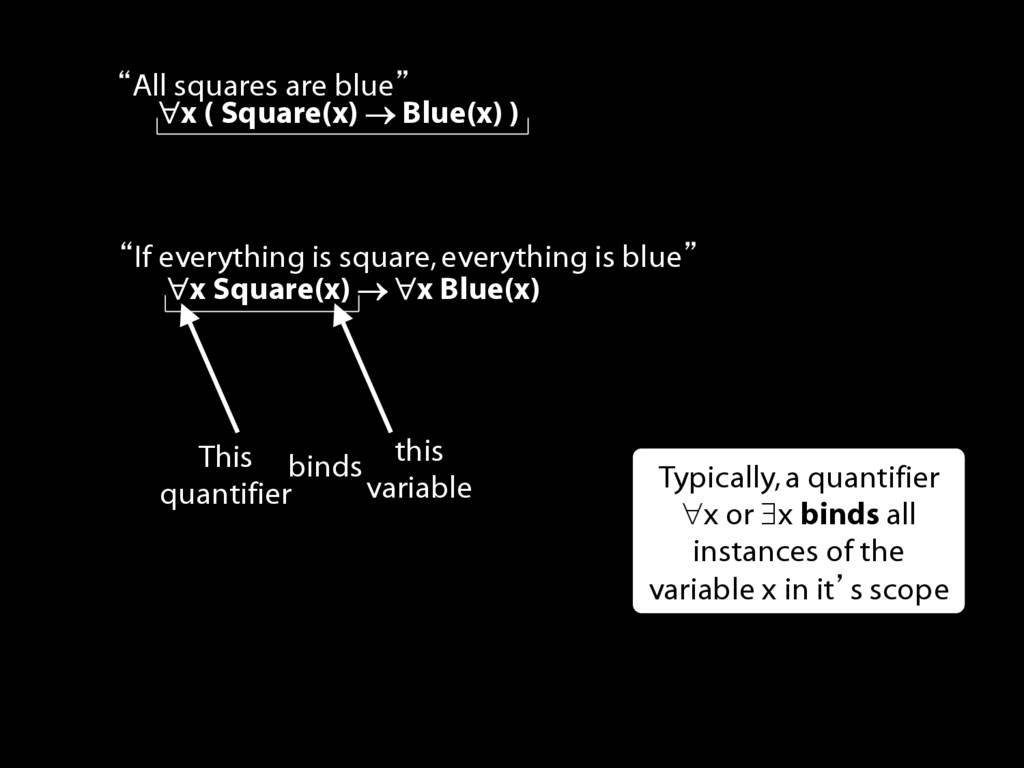
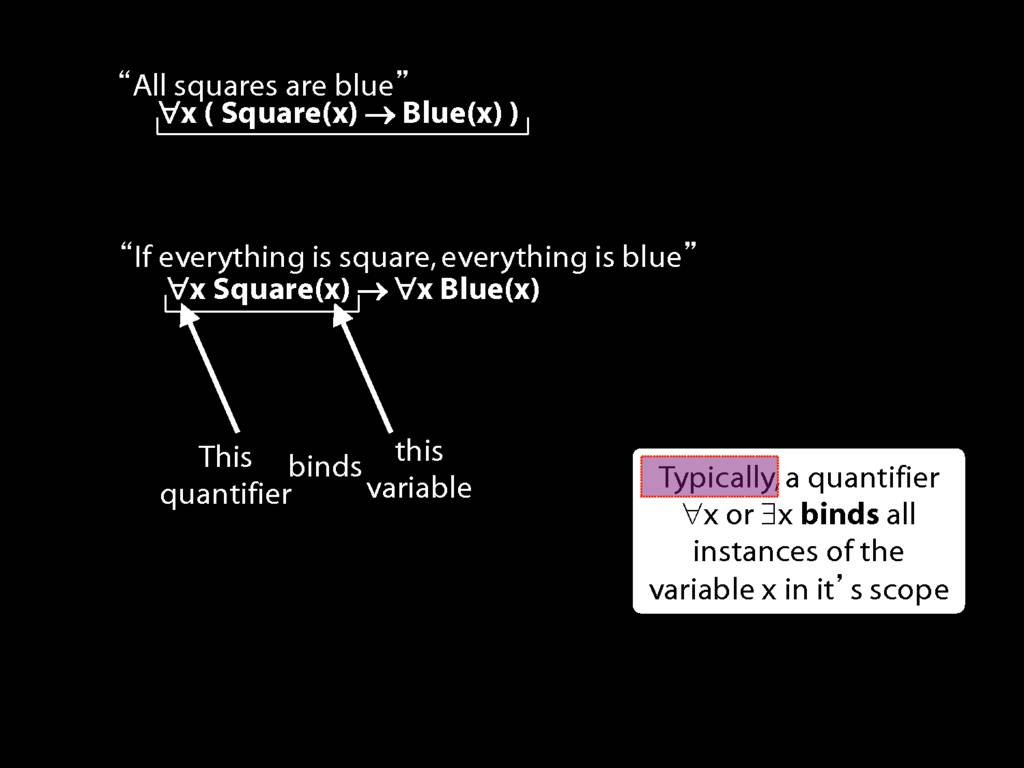
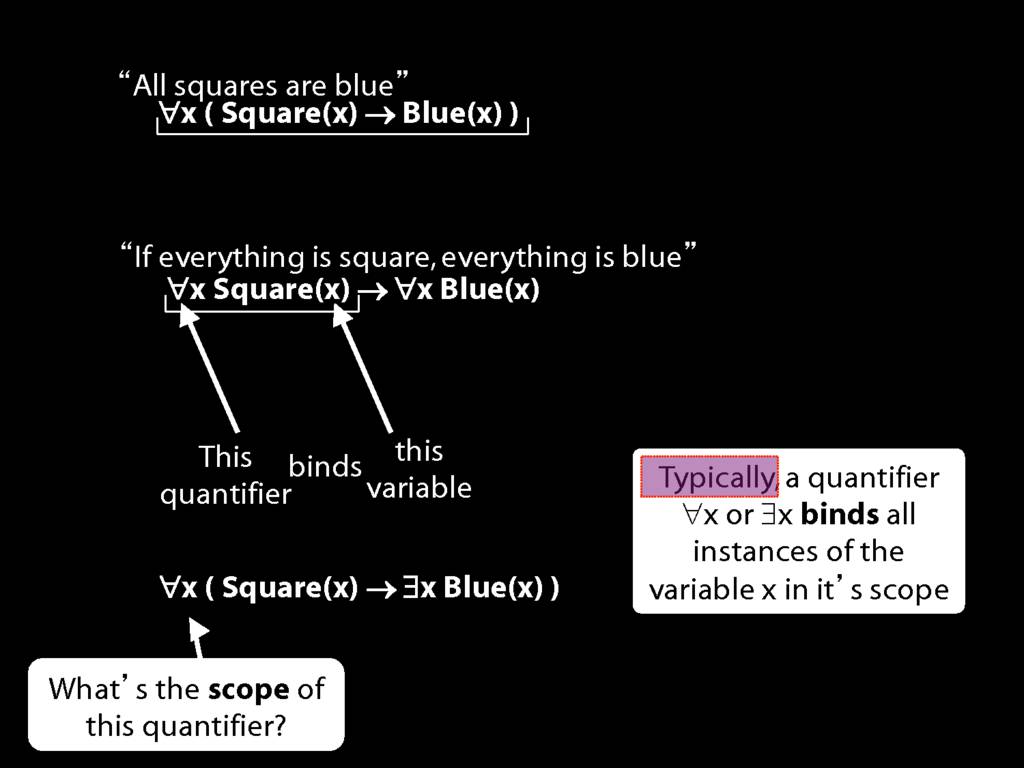
Quantifiers Bind Variables
\section{Quantifiers Bind Variables}
\emph{Reading:} §9.3
\section{Quantifiers Bind Variables}
Scope and Quantifiers
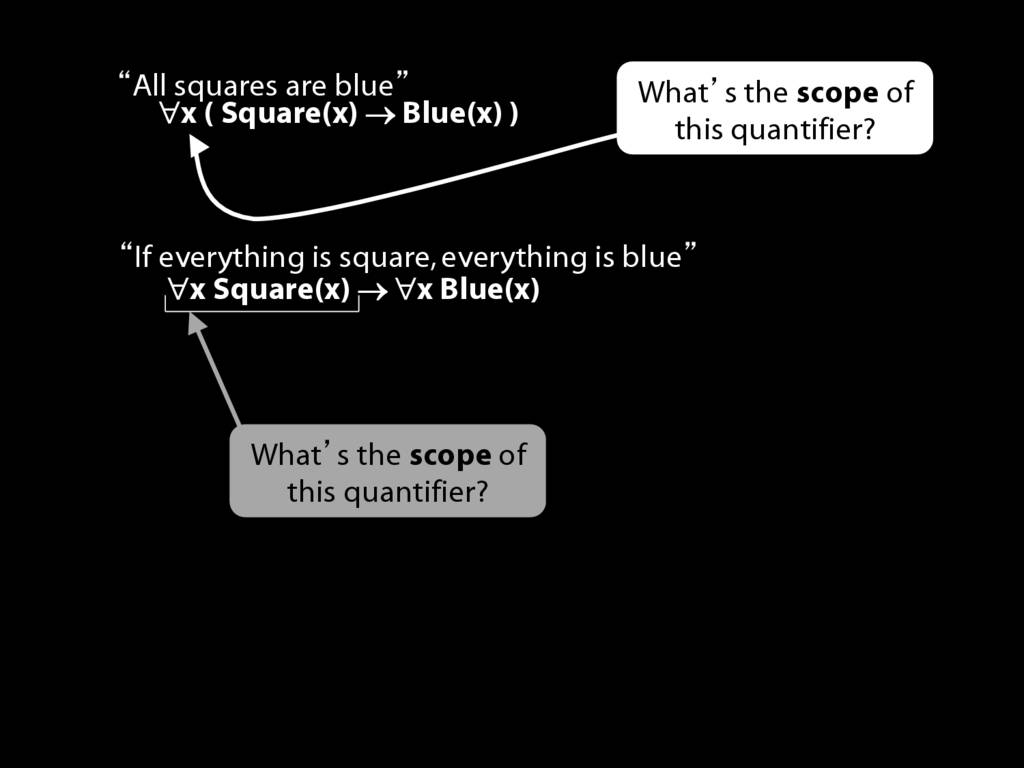
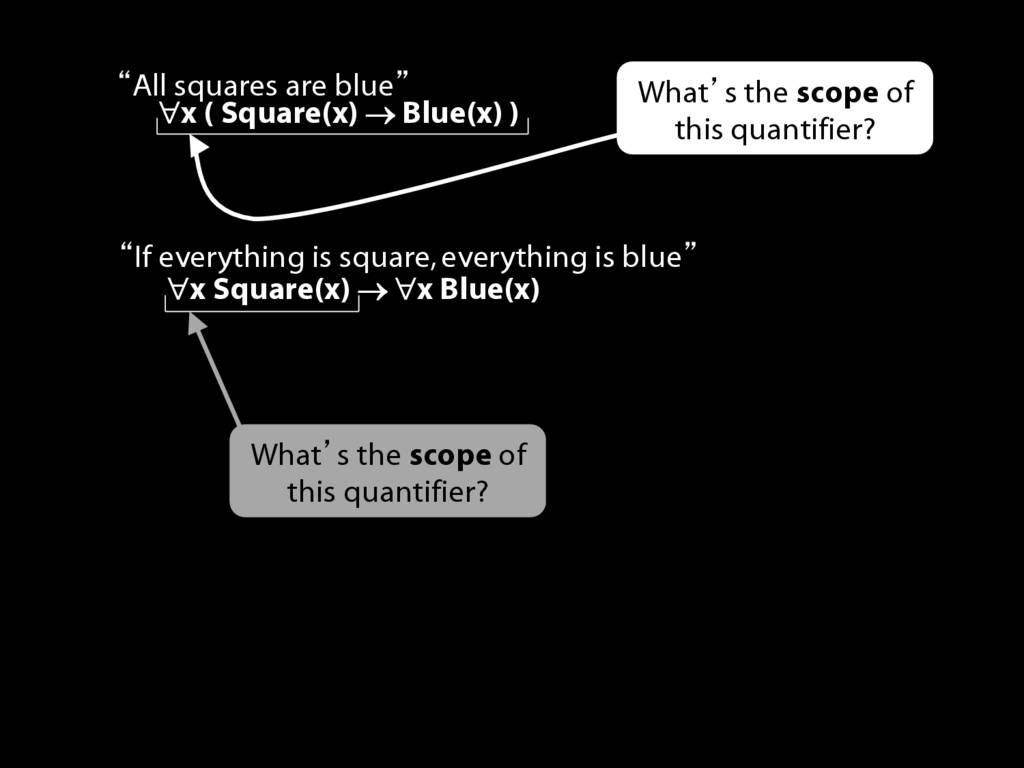
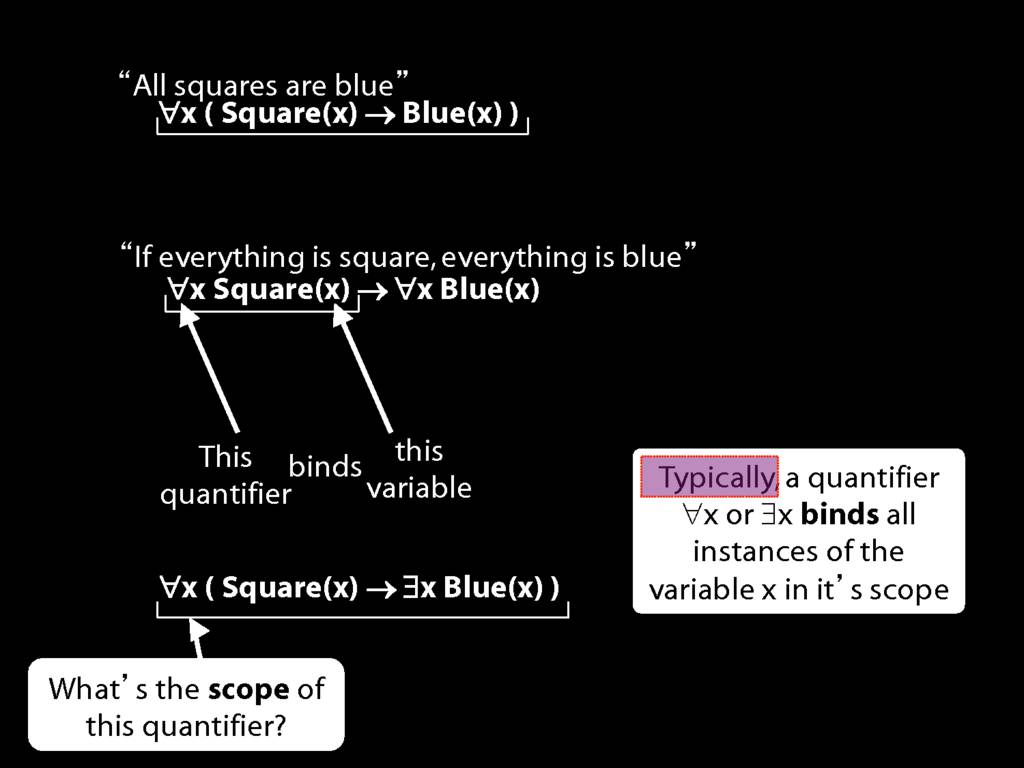
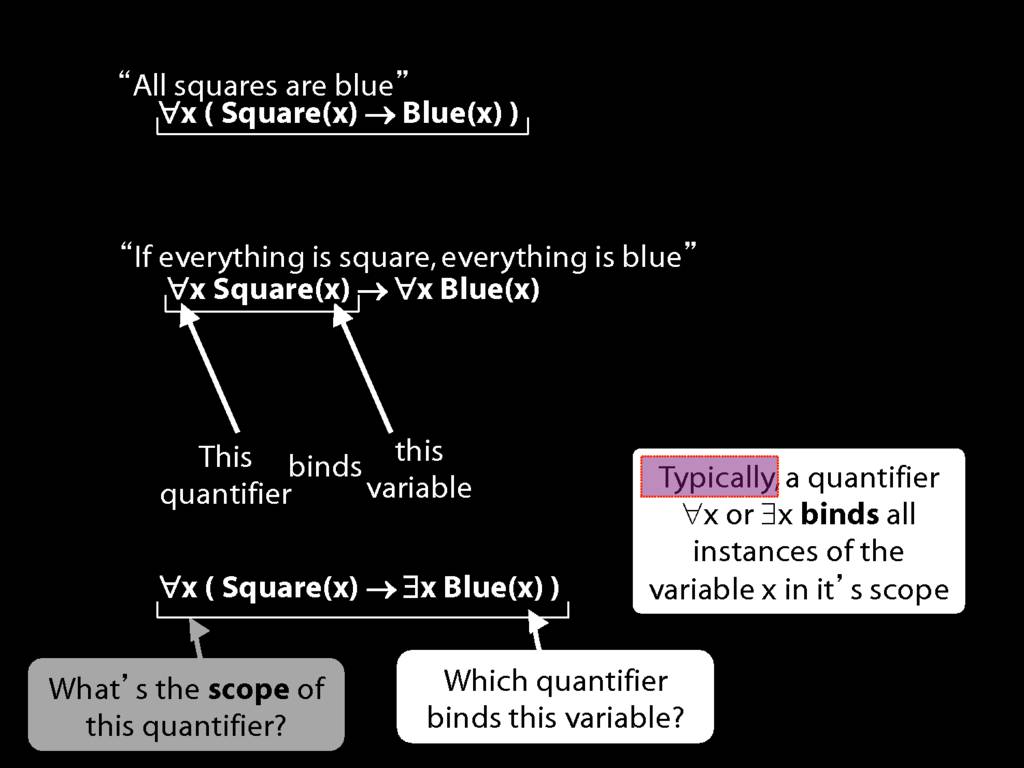
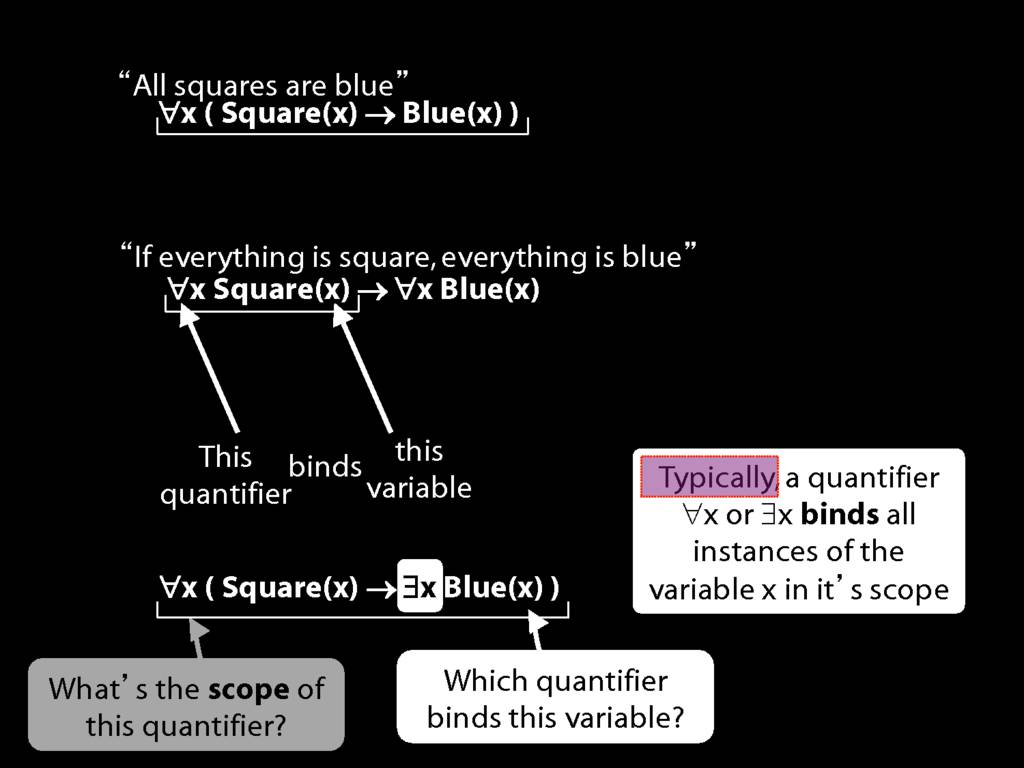
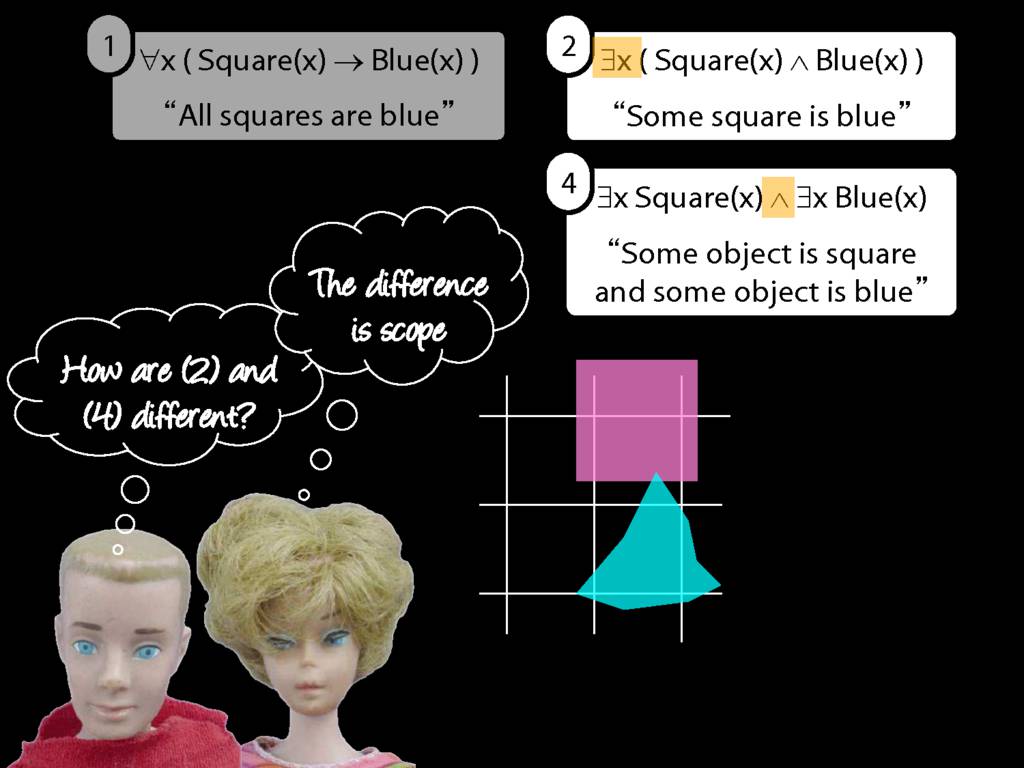
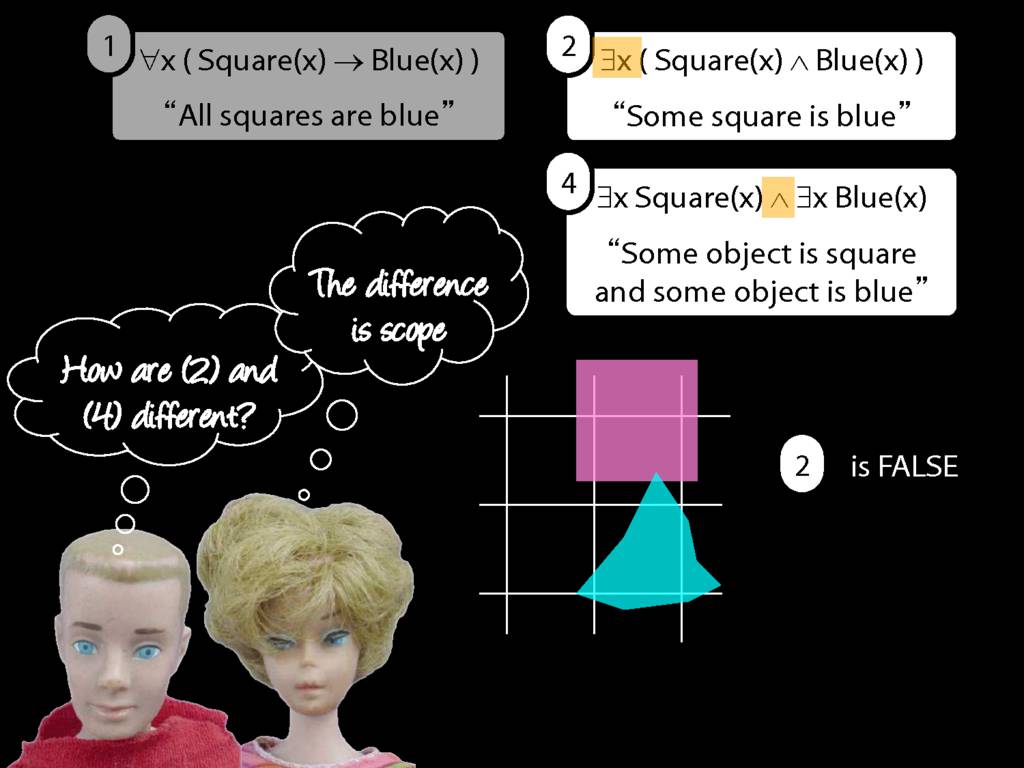
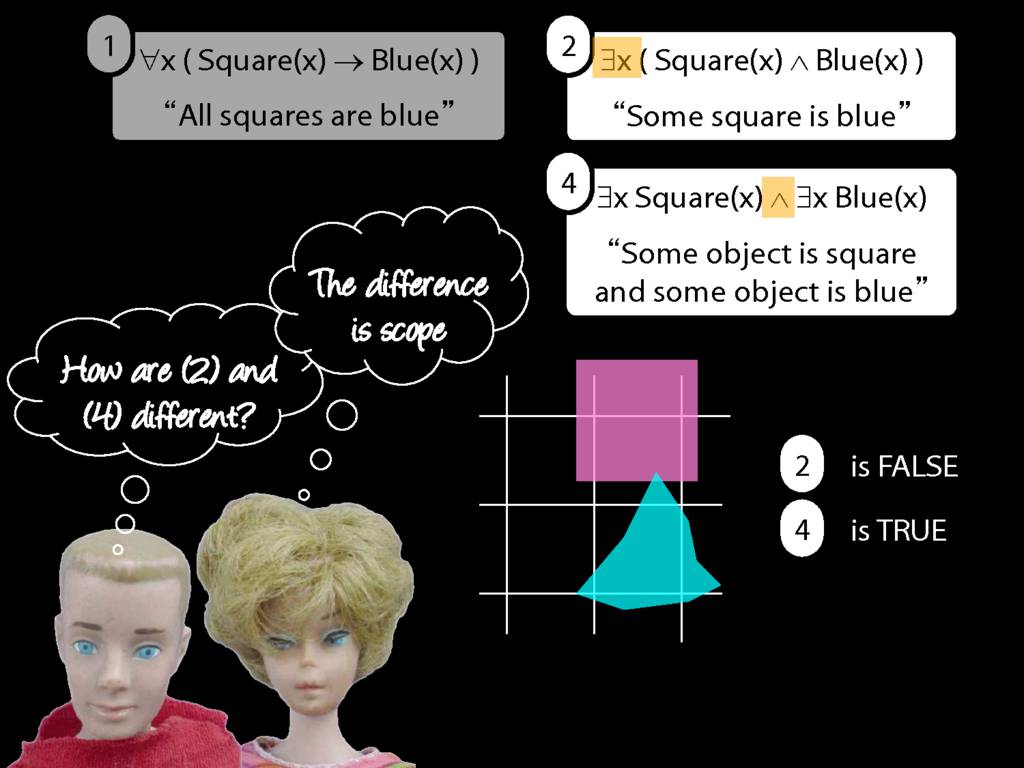
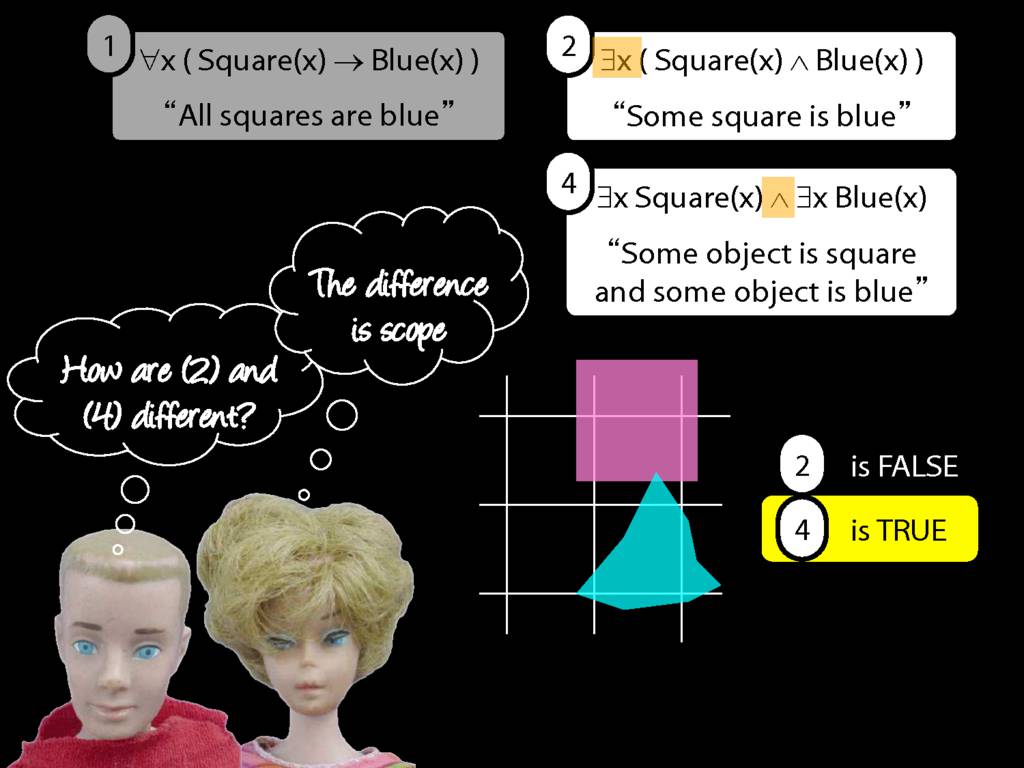
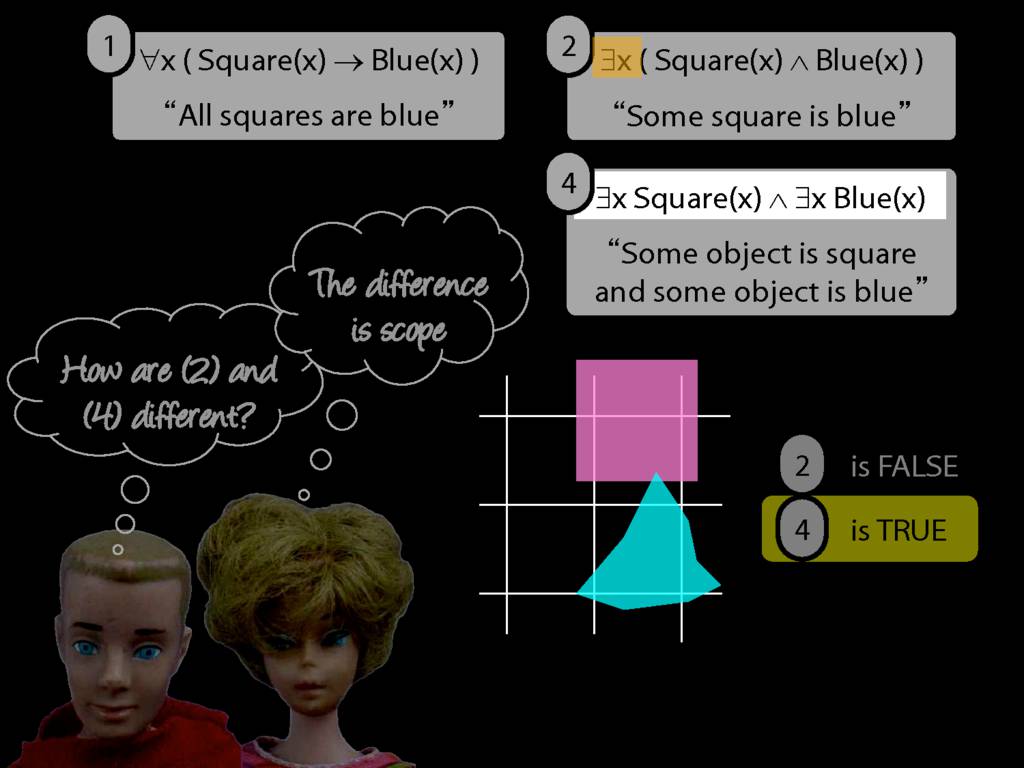
\section{Scope and Quantifiers}
\emph{Reading:} §9.5, §9.6
\section{Scope and Quantifiers}
\begin{minipage}{\columnwidth}
Underlining shows the scope of the quantifiers:
\end{minipage}
