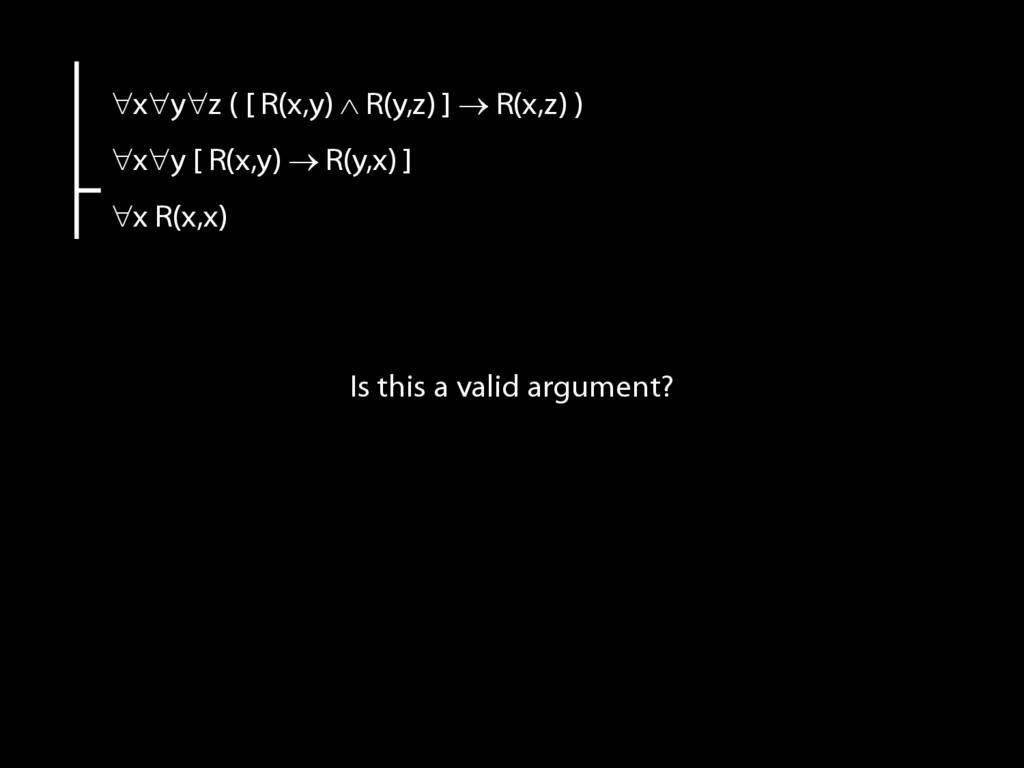Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides

\def \ititle {Logic I}
\def \isubtitle {Fast Lecture 05}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
13.28--13.31
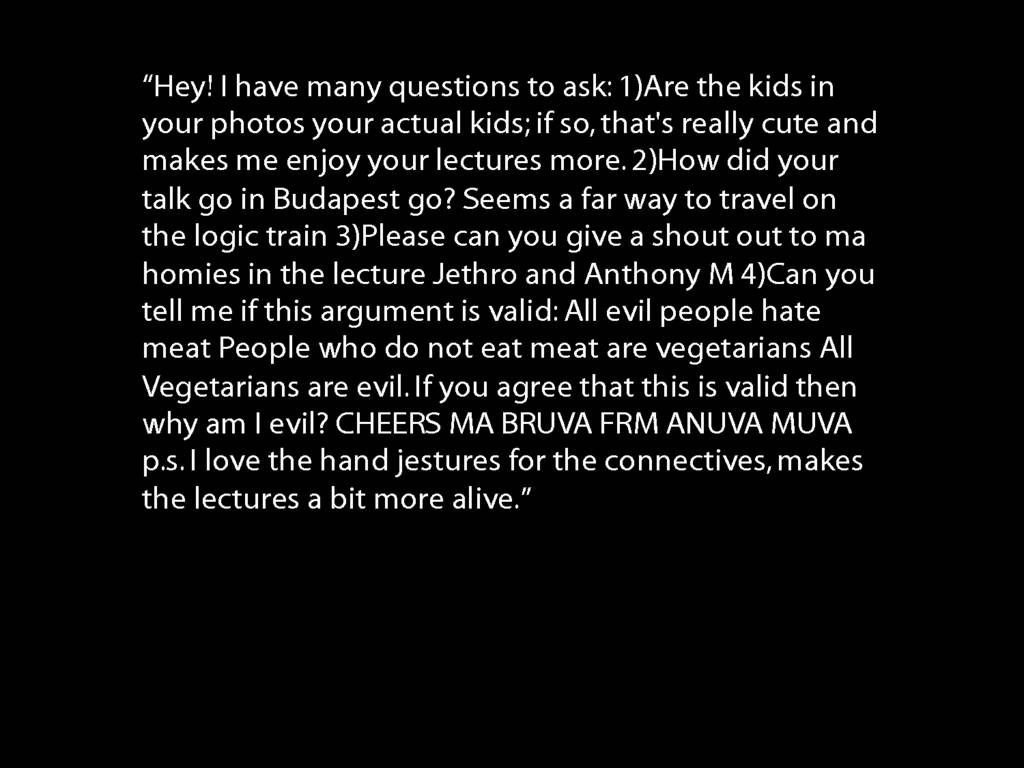
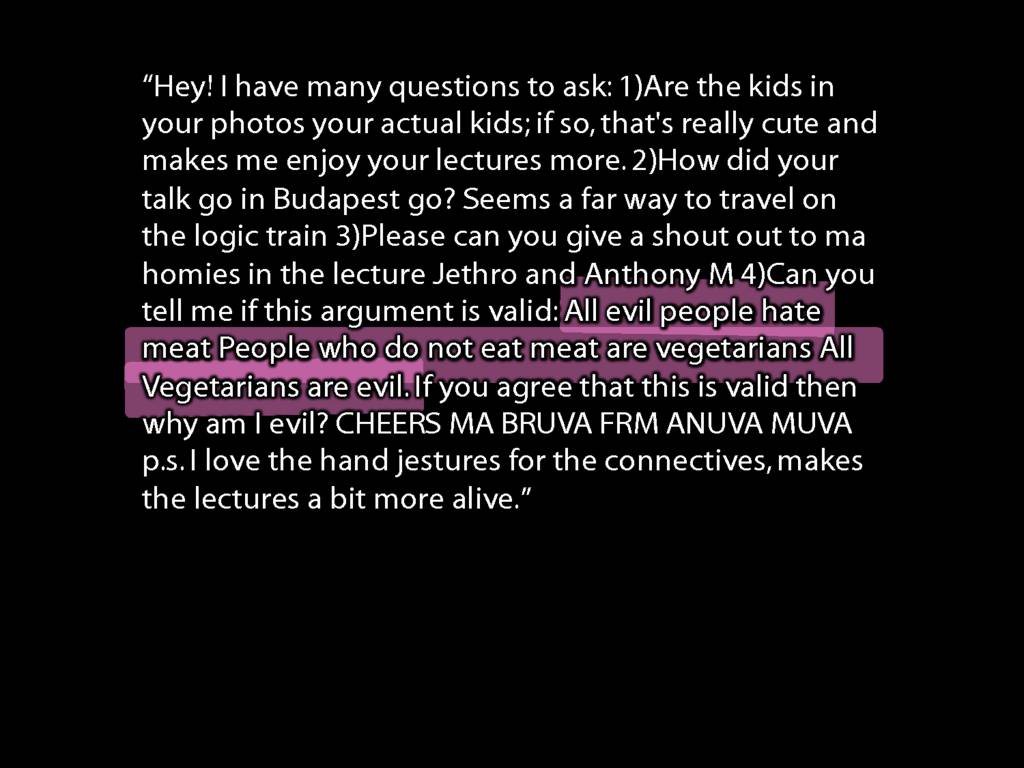
\section{Vegetarians Are Evil}
\emph{Reading:} §9.2, §9.3, §9.5

Counterexamples with Quantifiers
\section{Counterexamples with Quantifiers}

| | Evil(x) | HatesMeat(x) | Vegetarian(x) |
| Ayesha (a) | no | ?no | yes |
HatesMeat(a) → Vegetarian(a)
No lectures or seminars in reading week (Week 6).

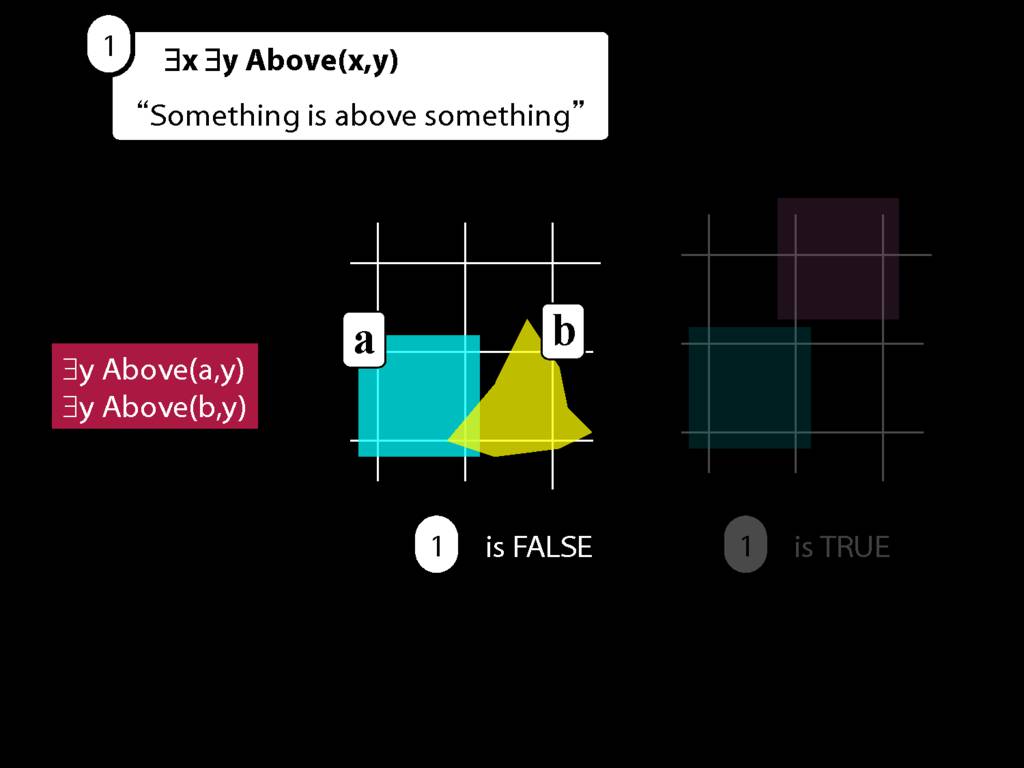
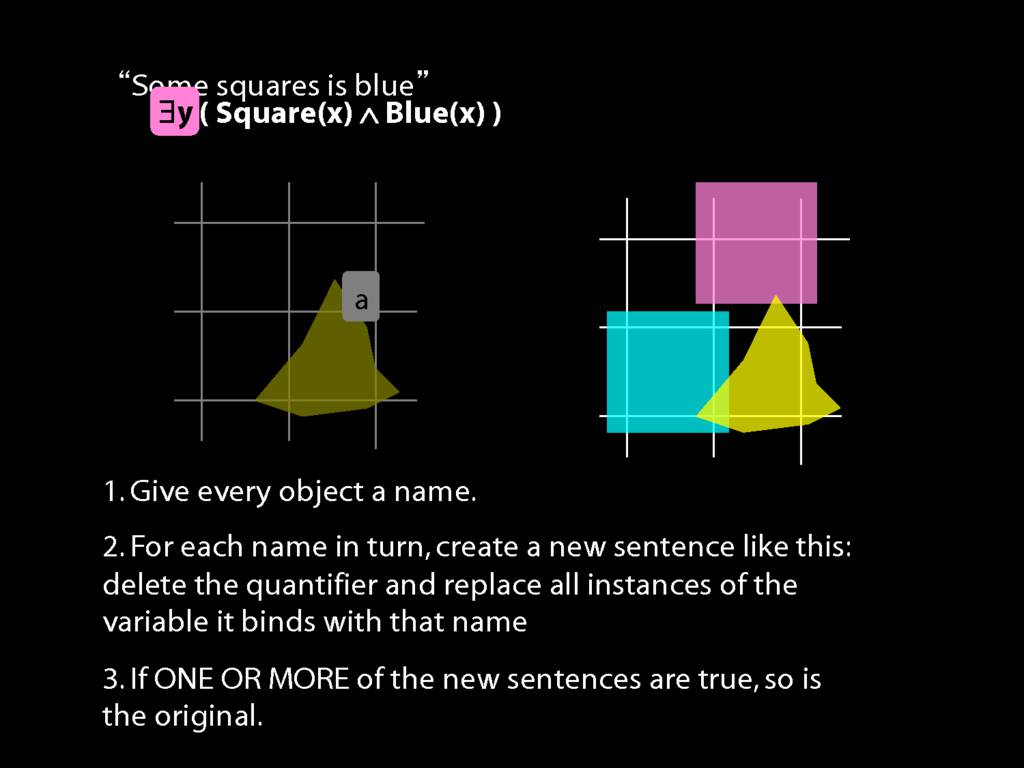
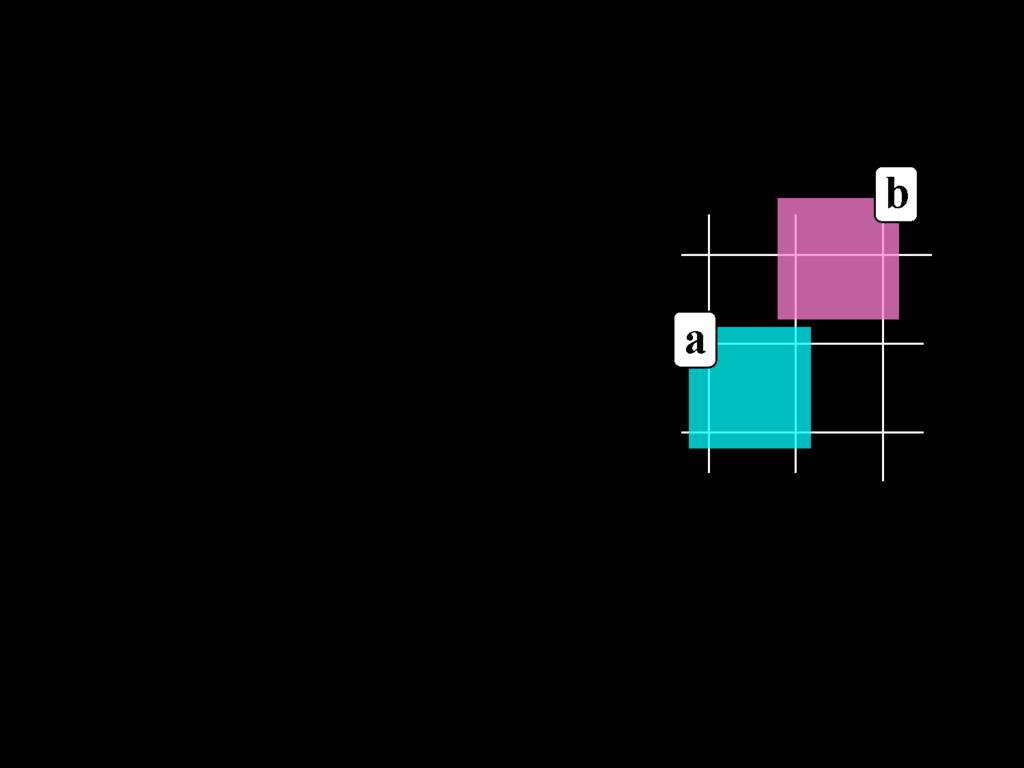
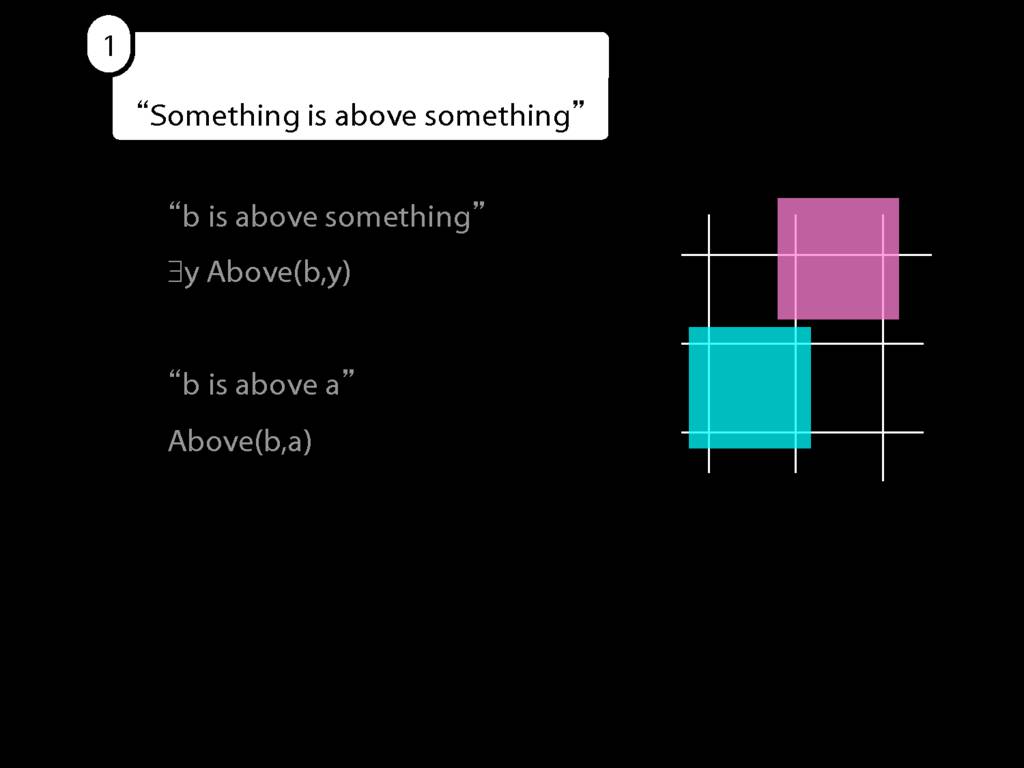
Something Is Above Something
So how can we start thinking about sentences with multiple quantifiers in our formal language, awFOL?
\begin{minipage}{\columnwidth}
Something is above something:
\hspace{3mm} ∃x ∃y Above(x,y)
\end{minipage}

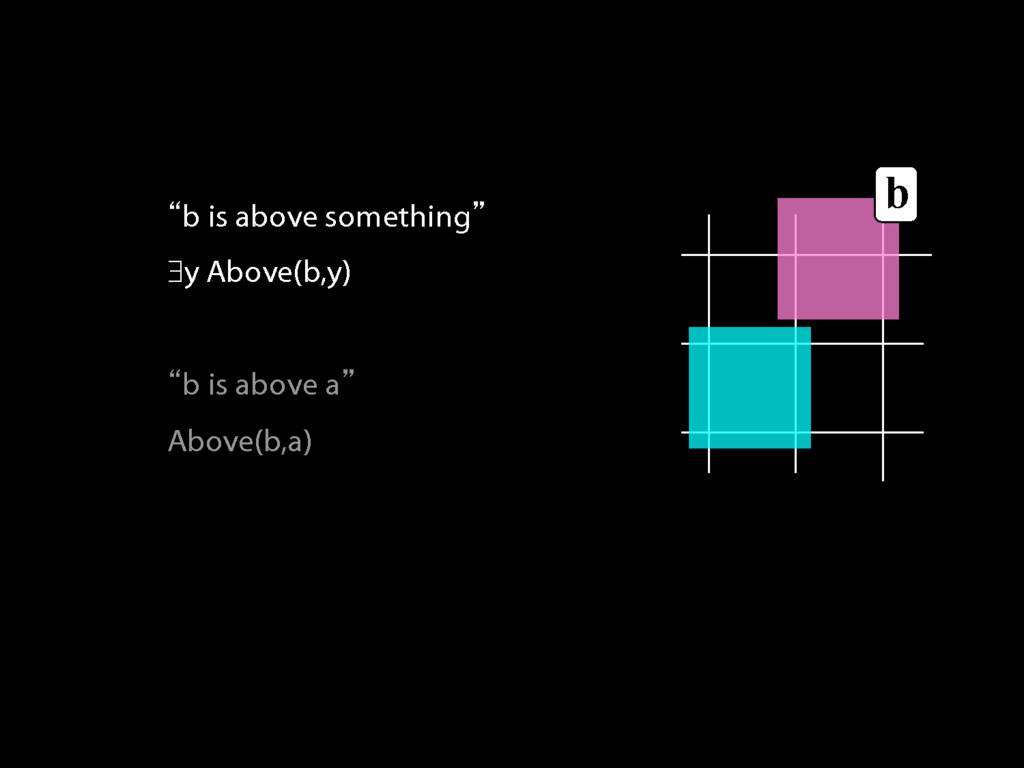
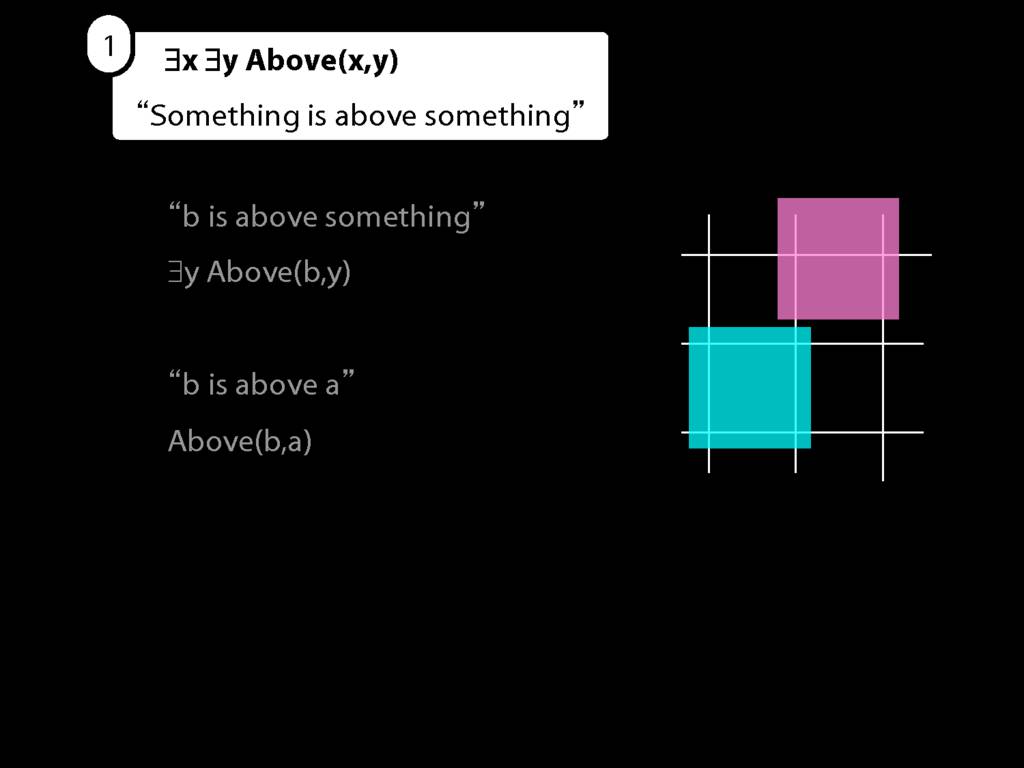
Here's a very simple possible situation in which b is above a.
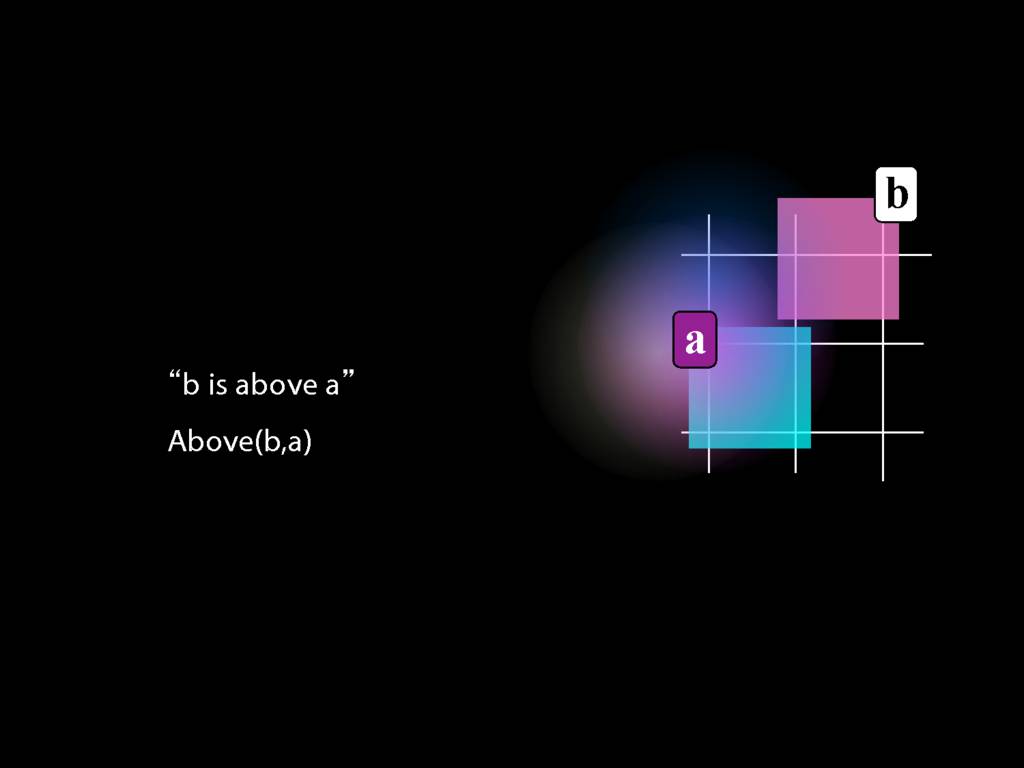
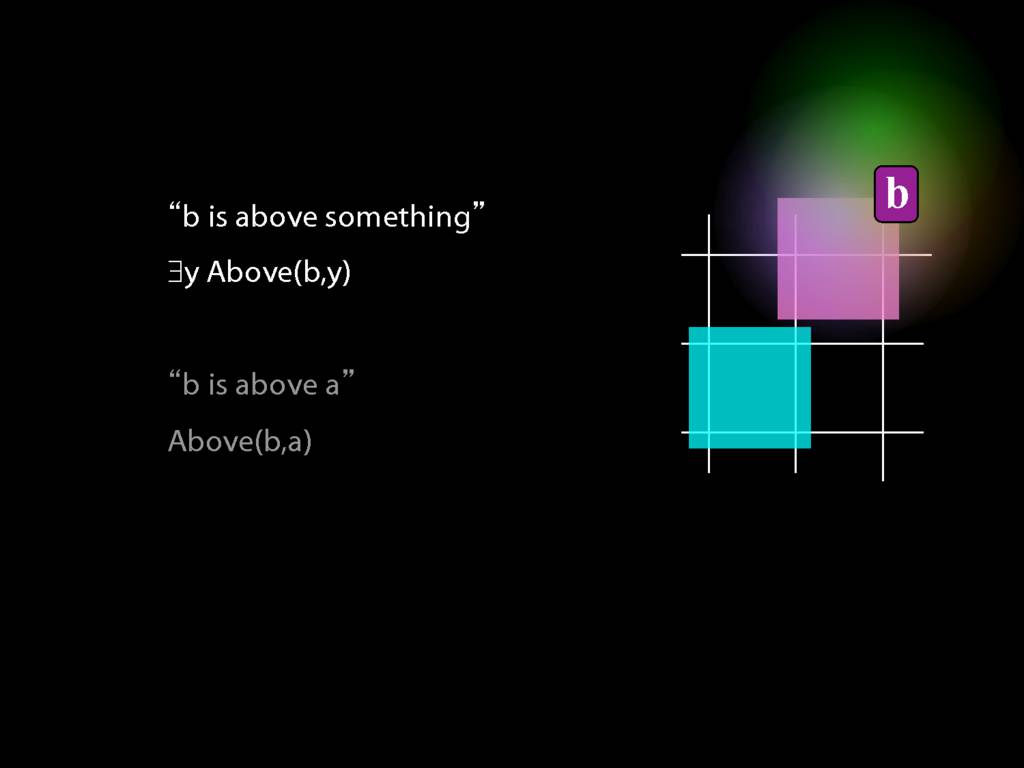
Now suppose that we lost the name a.

Actually, we didn't really lose it. There were some terrorists, the logical equivalent of Hezbollah,
(here they are pictured in Southern Lebanon looking all military and disciplined)
and they were taking a break from doing their good work for Bashar Assad in his war on Syria
and Bashar had given them some cool weapons
and they were like, let's destroy the name a.
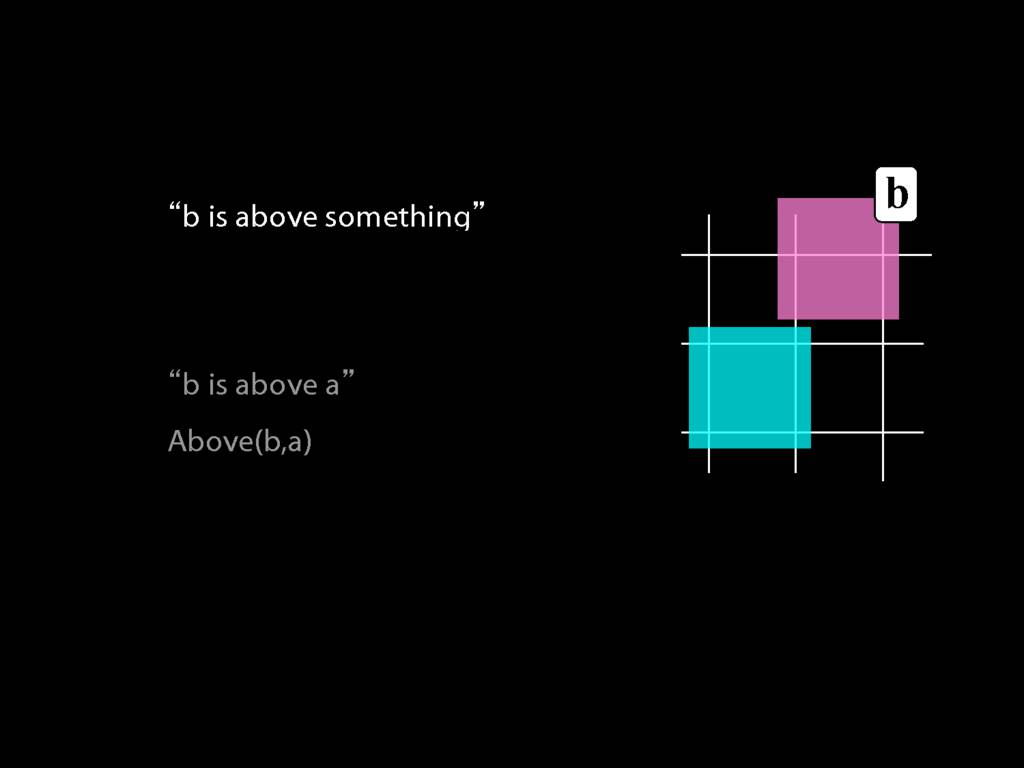
So we can't say b is above a anymore. We can only say that b is above something.
Luckily we know how to do this. We just drop the a, replace it with a variable (in this case, y), and add an existential quantifier.
Why existential? Because we're talking about something, not everything.
But look what happened next.

This time is wasn't Hezbollah.
It was my terrible twins, just back from training with the taliban.
(You may laugh but it's just very hard to get quality childcare without religion these days.)
Yes, and they destroyed the name b.
So now we can't name that object either, we can only say that something is above something.
But, look, we already know how to do this. We just remove the name b from the sentence we last had, replace it with a variable (in this case, x) and add an existential quantifer out the front.

Now we've got a sentence with multiple quanifiers without doing anything new, just replacing names with quantifiers.
Let's consider translation the other way, from awFOL back to English.
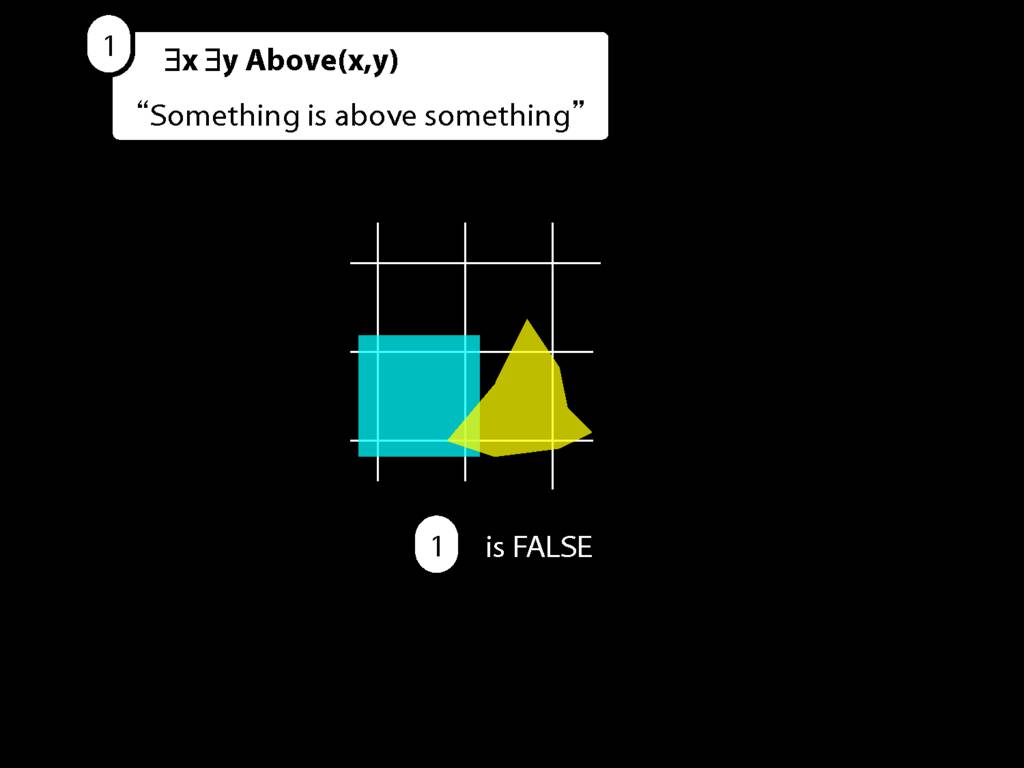
Do we understand this sentence of awFOL?
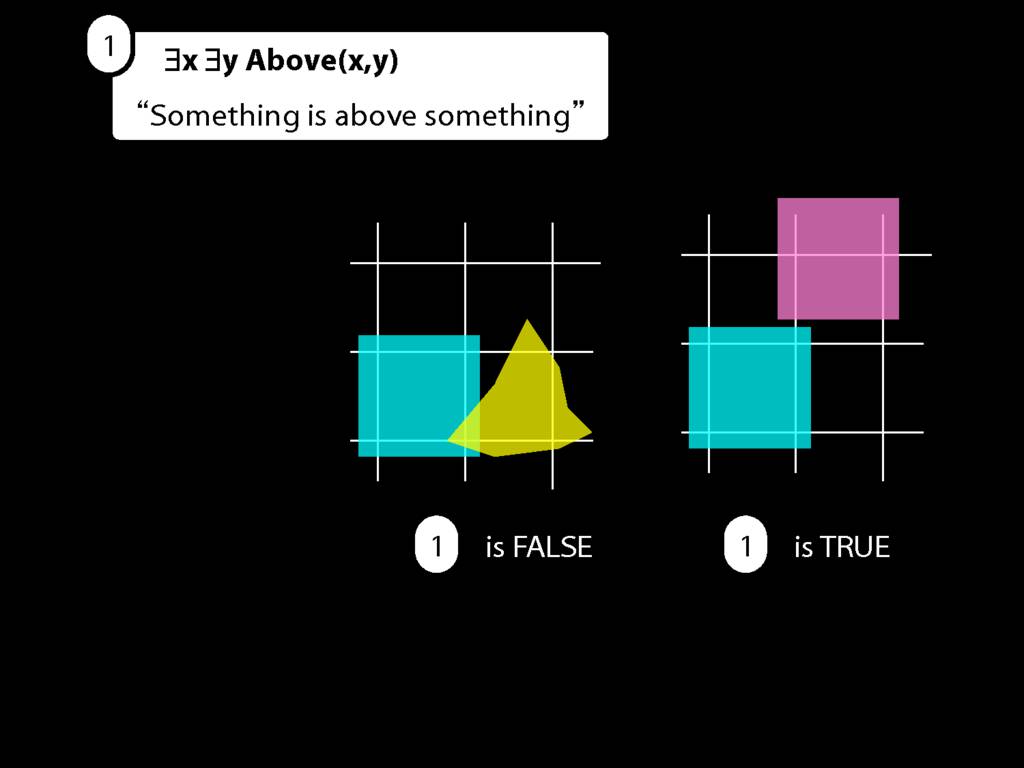
Well, is it true in this possible situation?
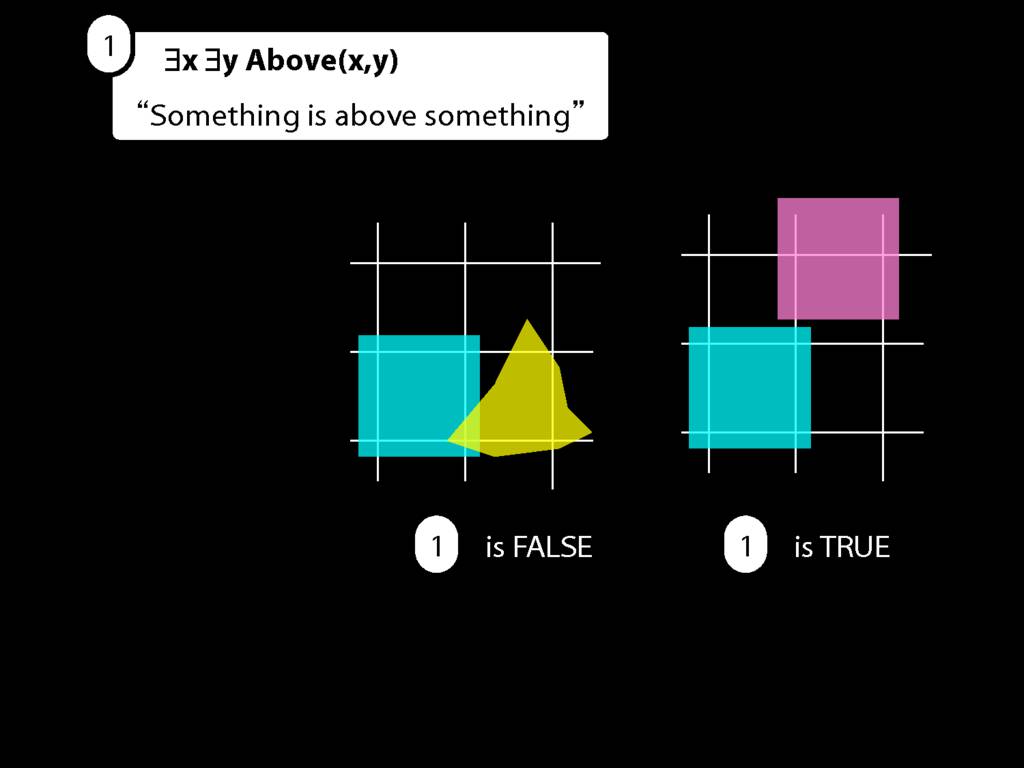
And is it true in this possible situation? How do we know?
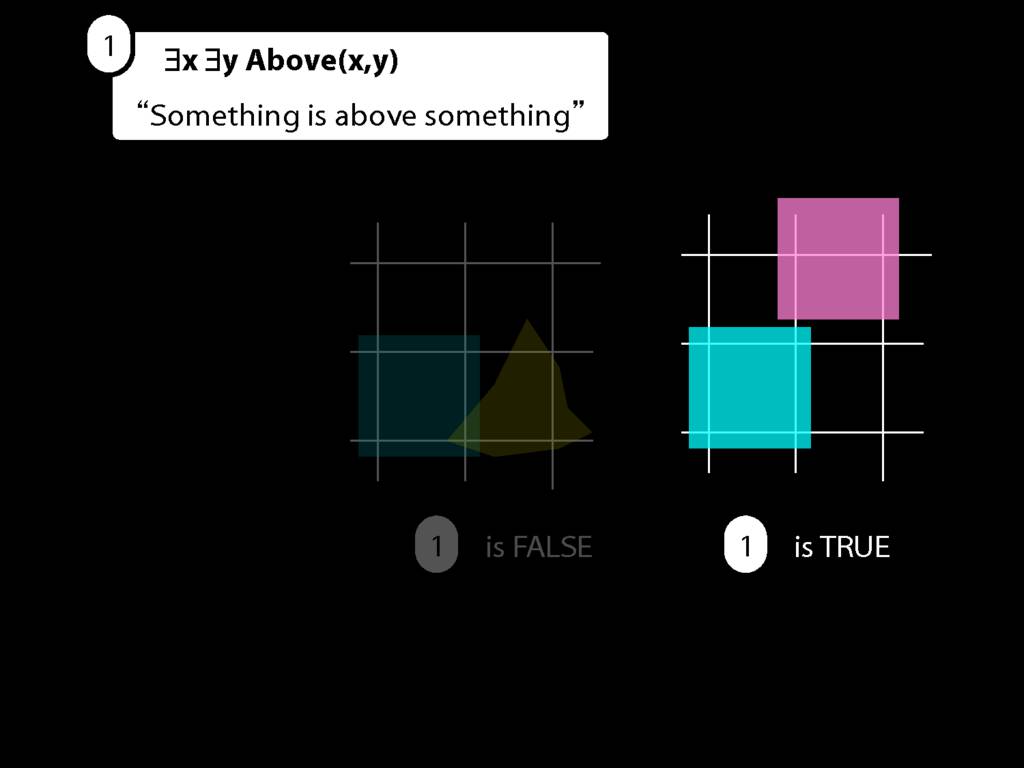
Take this possible situation first.
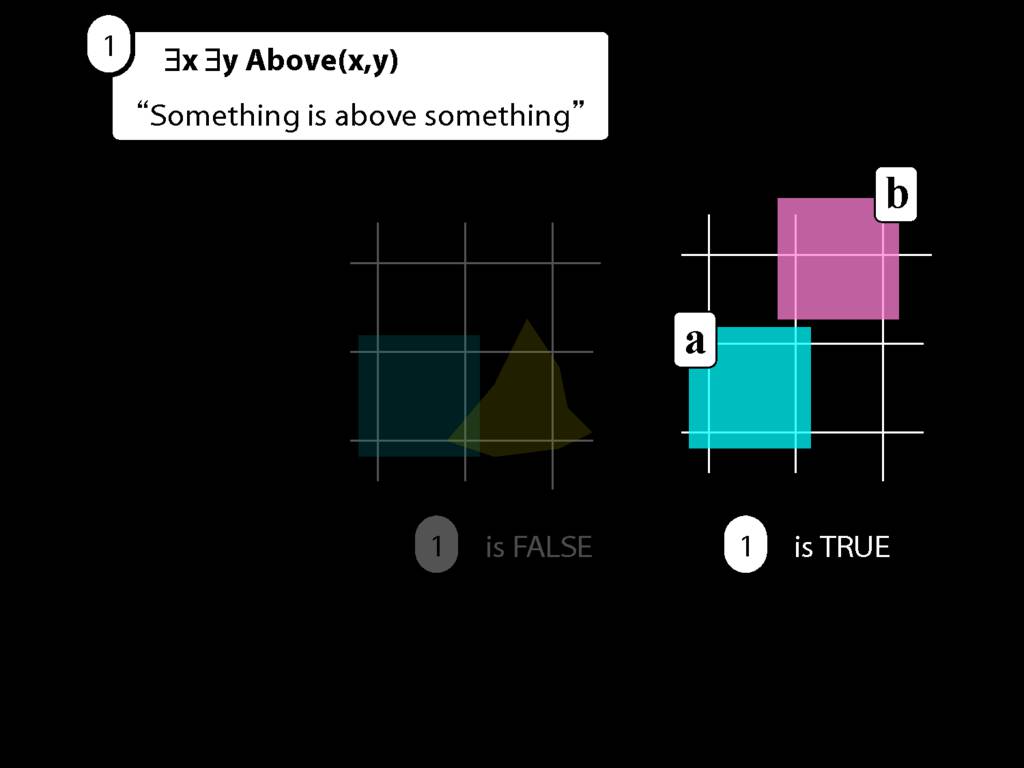
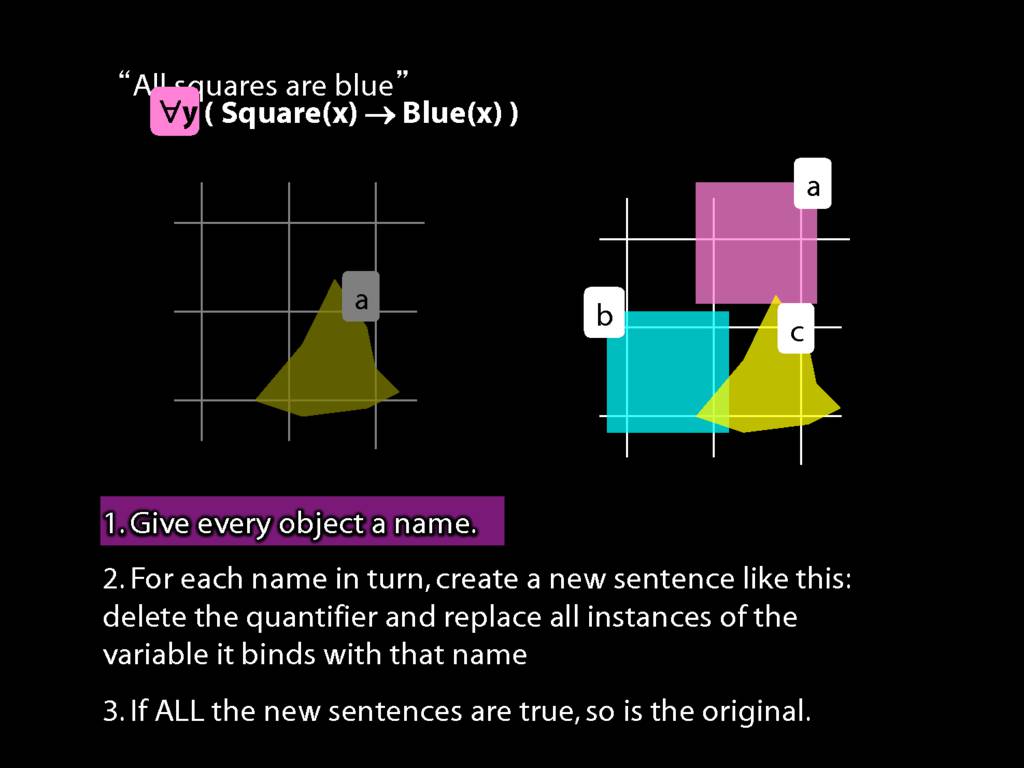
There is a procedure for determining the truth or falsity of an existentially quantified sentence.
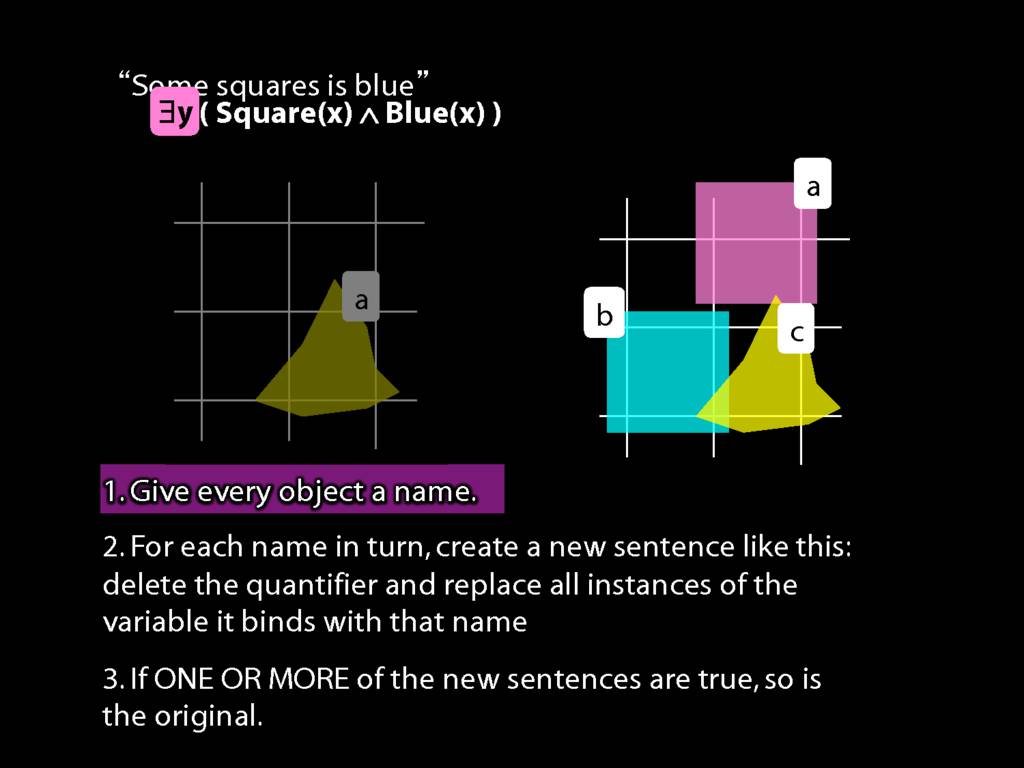
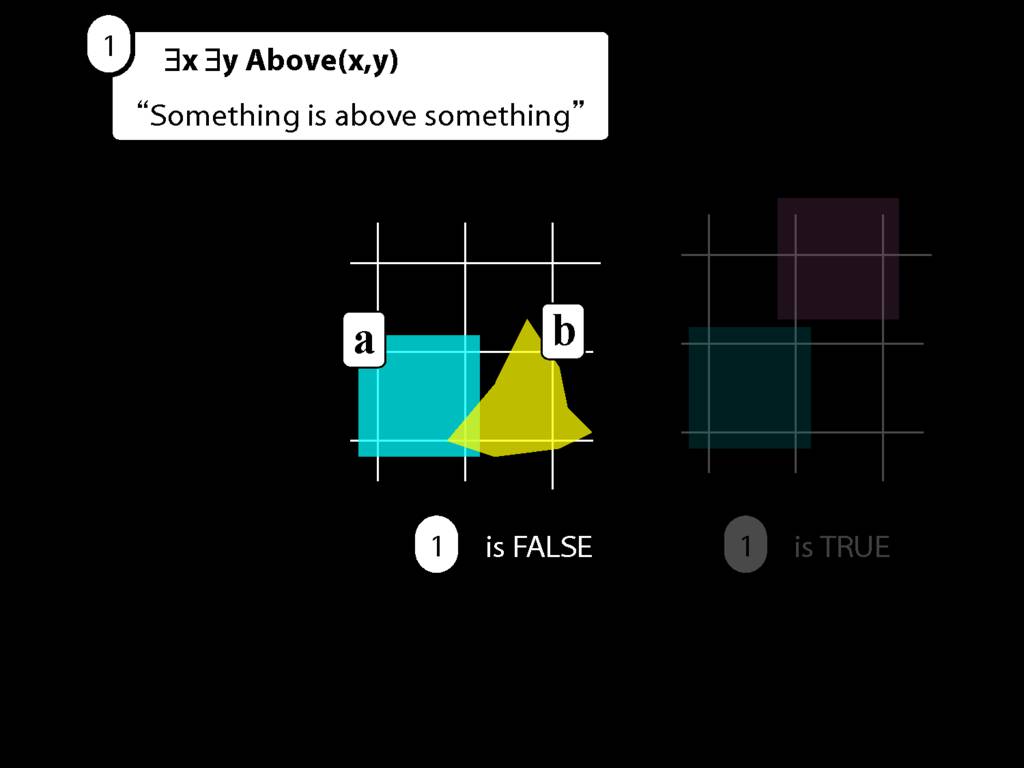
We first give every object a name.
In this possible situation there are two objects so there we assign two names.
(Look, here are a and b again. I guess they weren't destroyed forever. Maybe we had a little war on terror and got them back.)
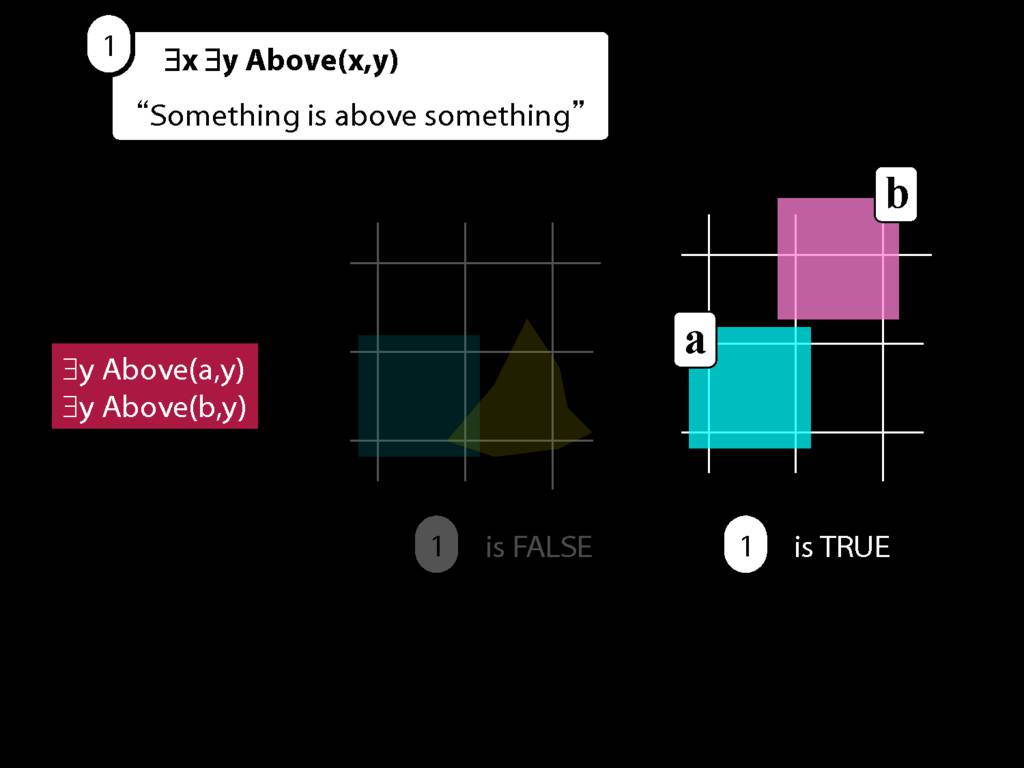
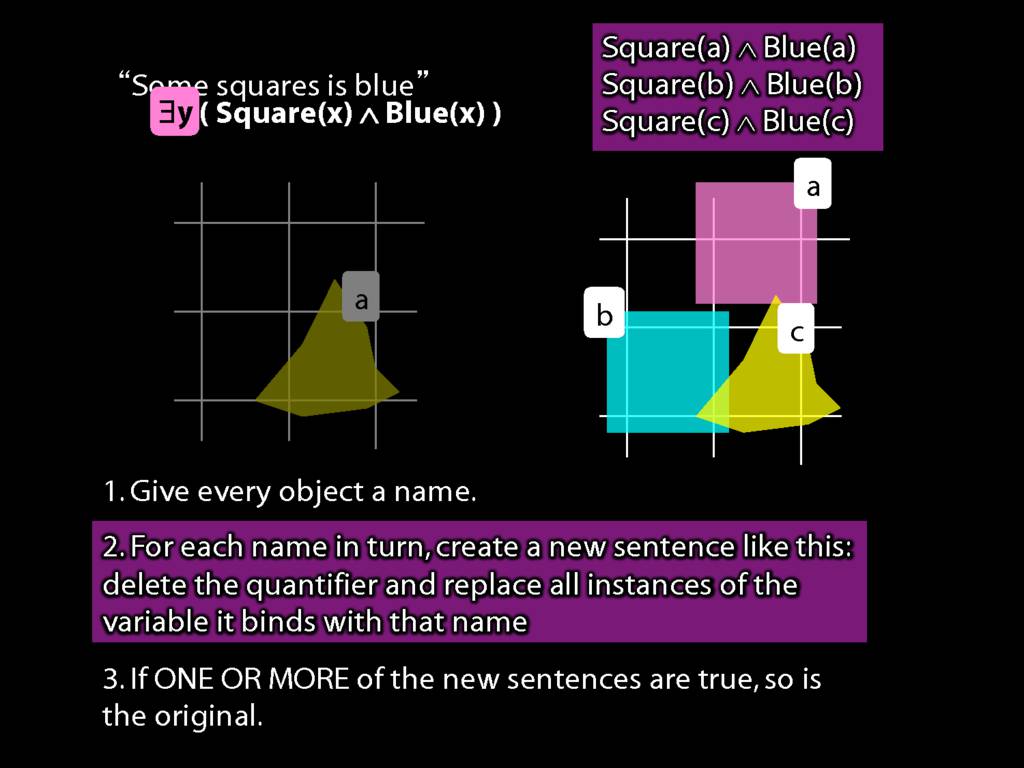
Then we make new sentences by removing an existential quantifier and replacing the variable with each name in turn.
Look here: two objects so two names so two sentences.
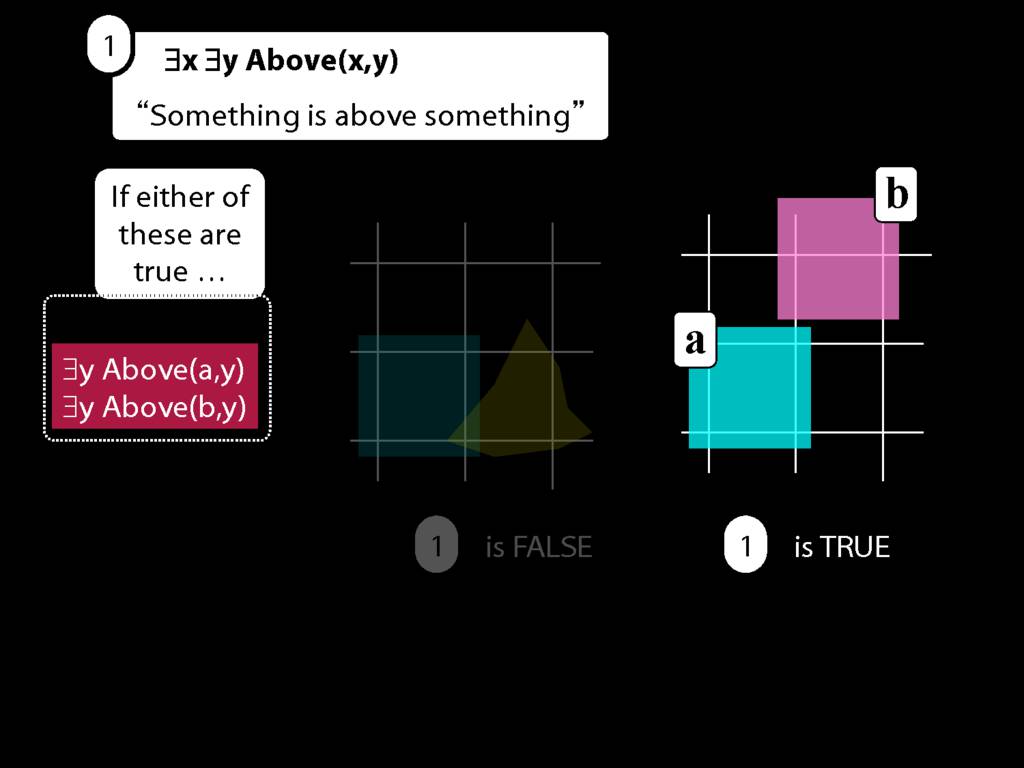
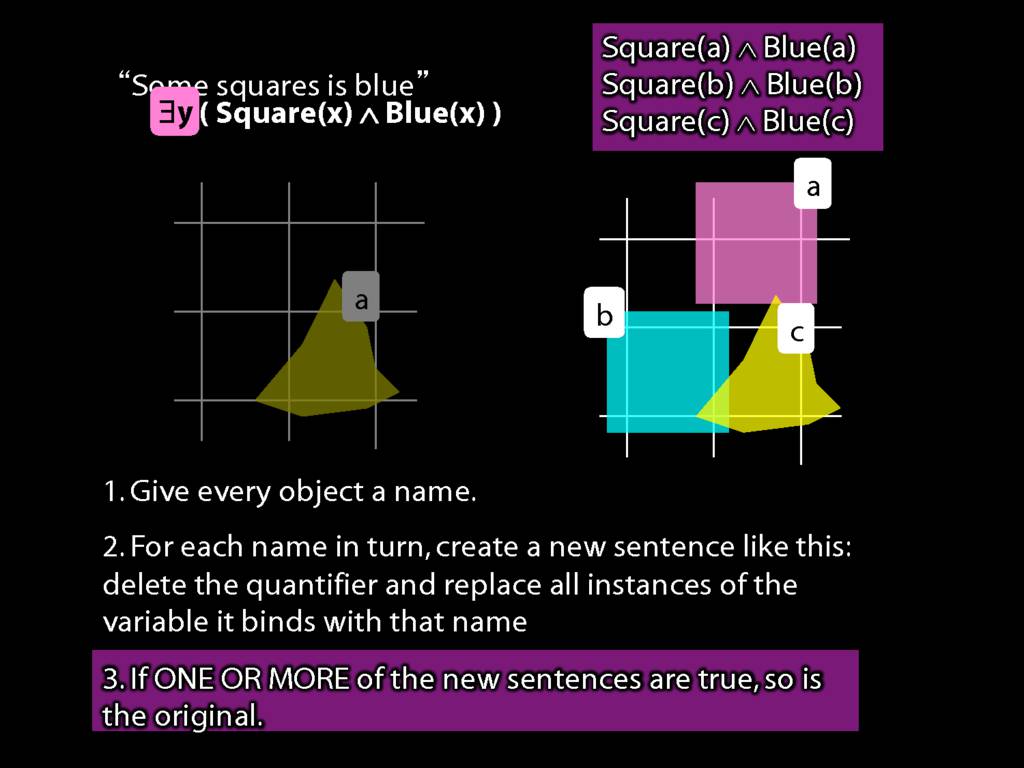
Now if either of these are true, ...
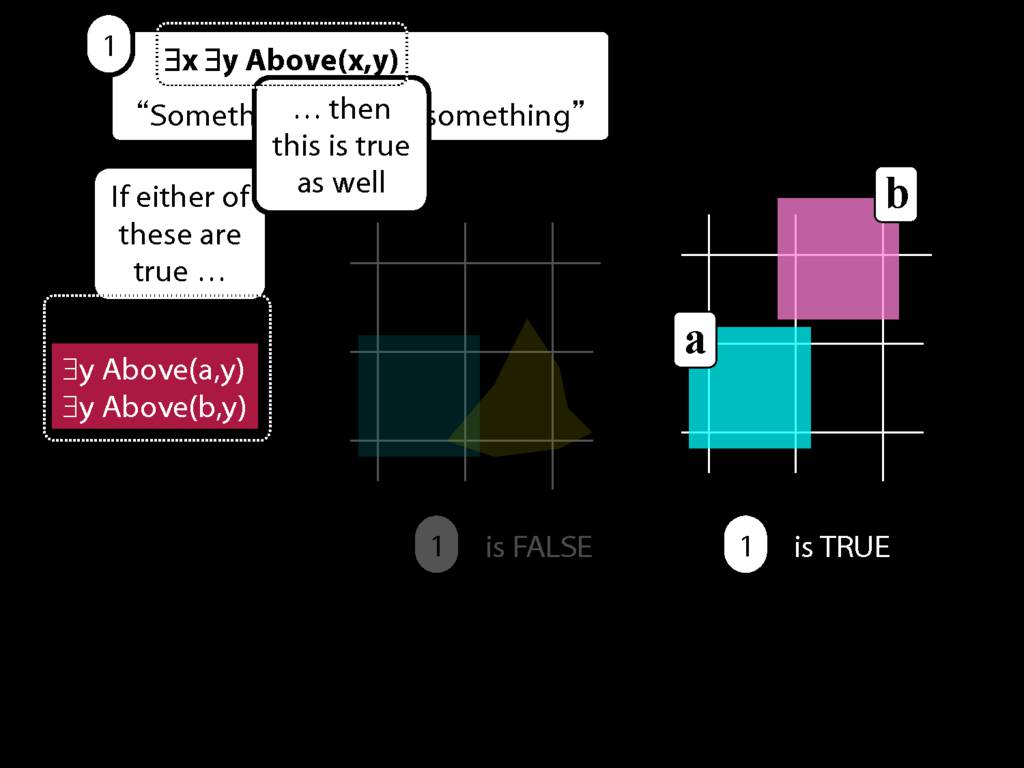
... then so is the sentence we started with, ∃x ∃y Above(x,y).
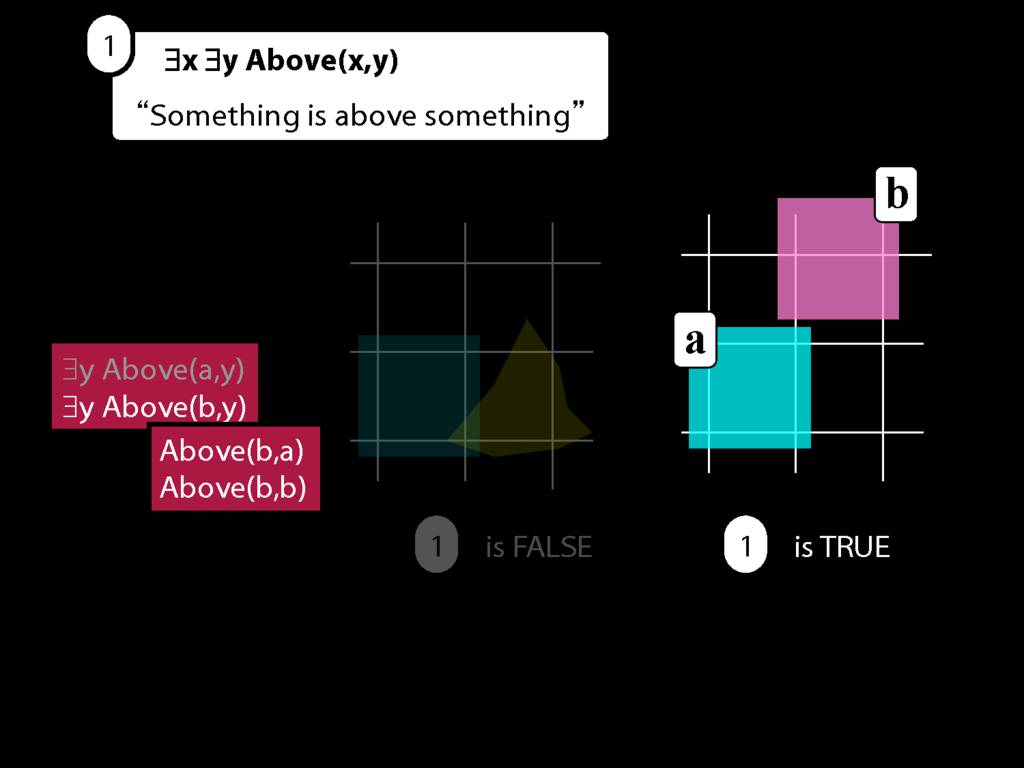
But what does it take for one of these to be true?
Consider the second.
To work out whether it's true we have to apply the same procedure again.
The first step is to give everything a name, but since everything already has a name there's nothing we need to do.
Then we make new sentences by removing an existential quantifier and replacing the variable with each name in turn.
This gives us these new sentences, Above(b,a) and Above(b,b)
Now if either of these are true, then so is the sentence we started with, ∃y Above(b,y).
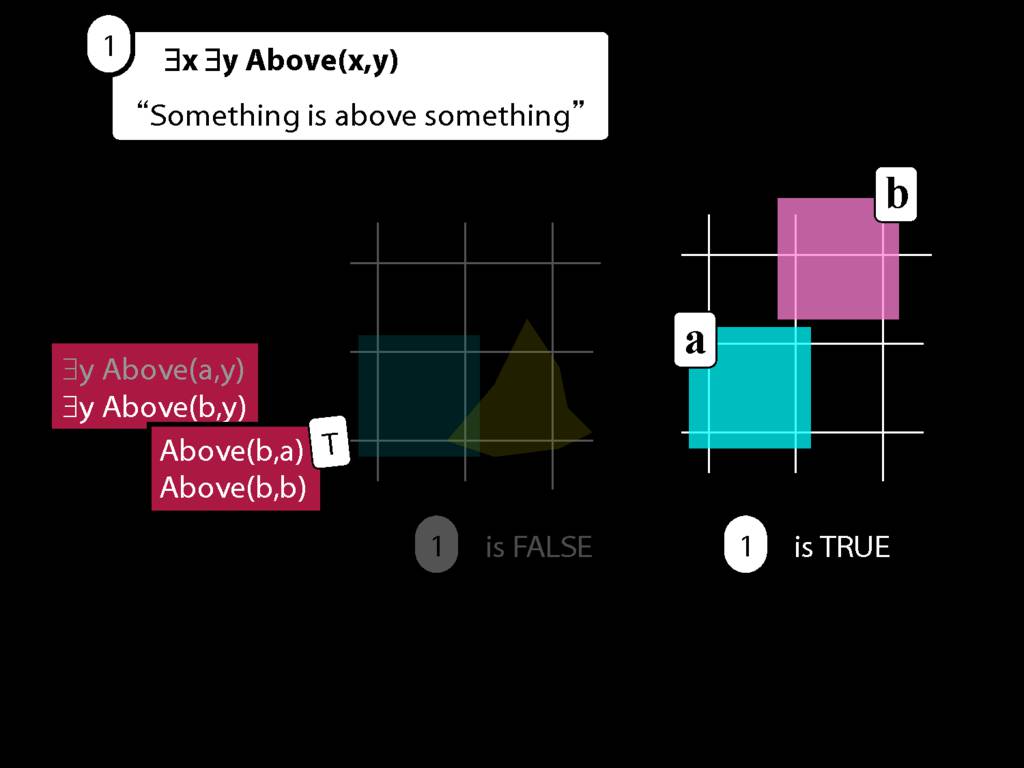
But the first of these is true!
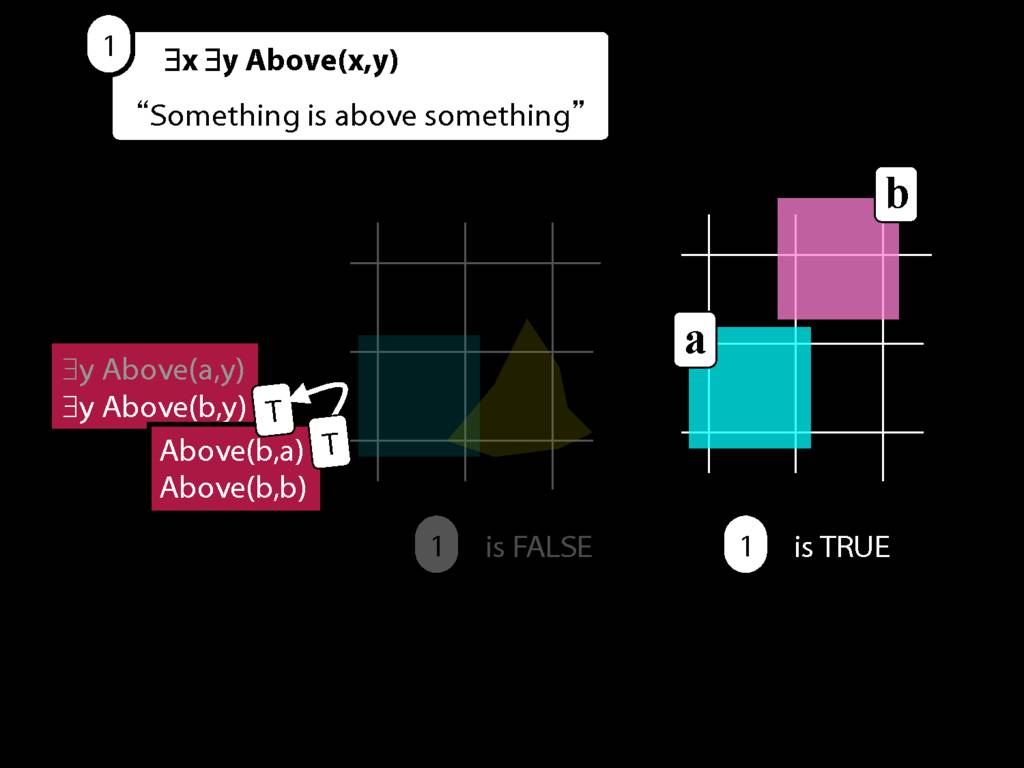
This tells us that ∃y Above(b,y) is true.
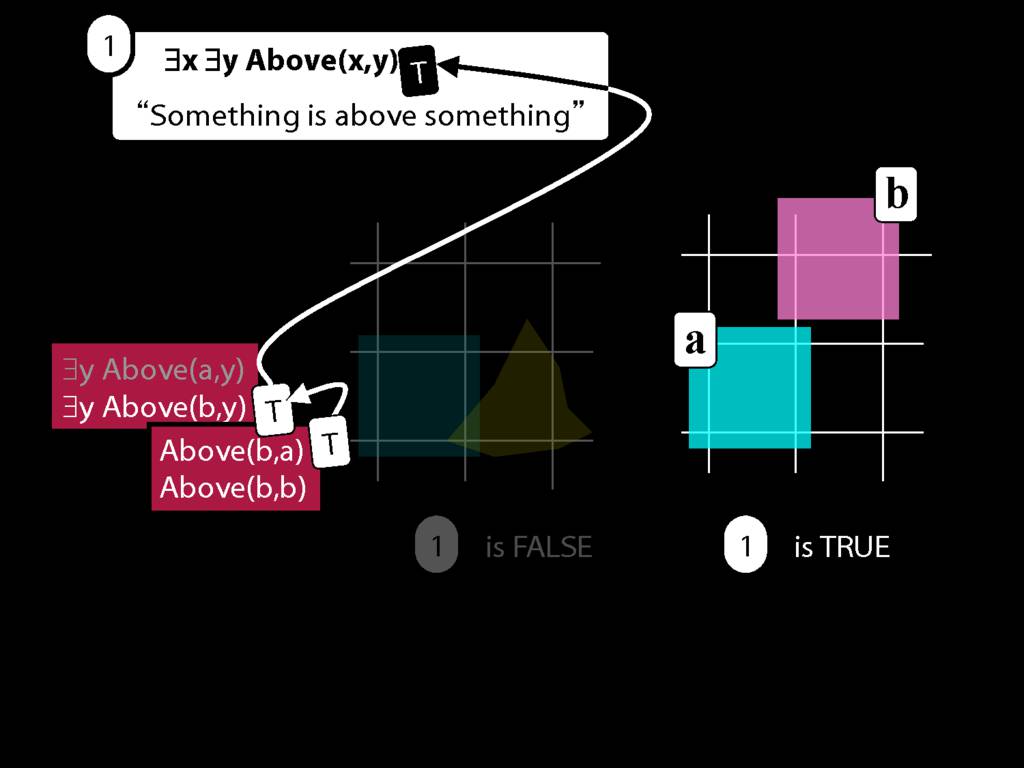
And that tells us that ∃x ∃y Above(x,y) is true as well.
This is how we can understand sentences of awFOL involving multiple quantifiers.
To work out whether they are true, we apply the procedure for determining the truth of an existentially quantified statement removing just one quantifer.
And we keep applying these procedures until not quantifiers are left.
This is much like doing complex truth-tables.
Magic, no?
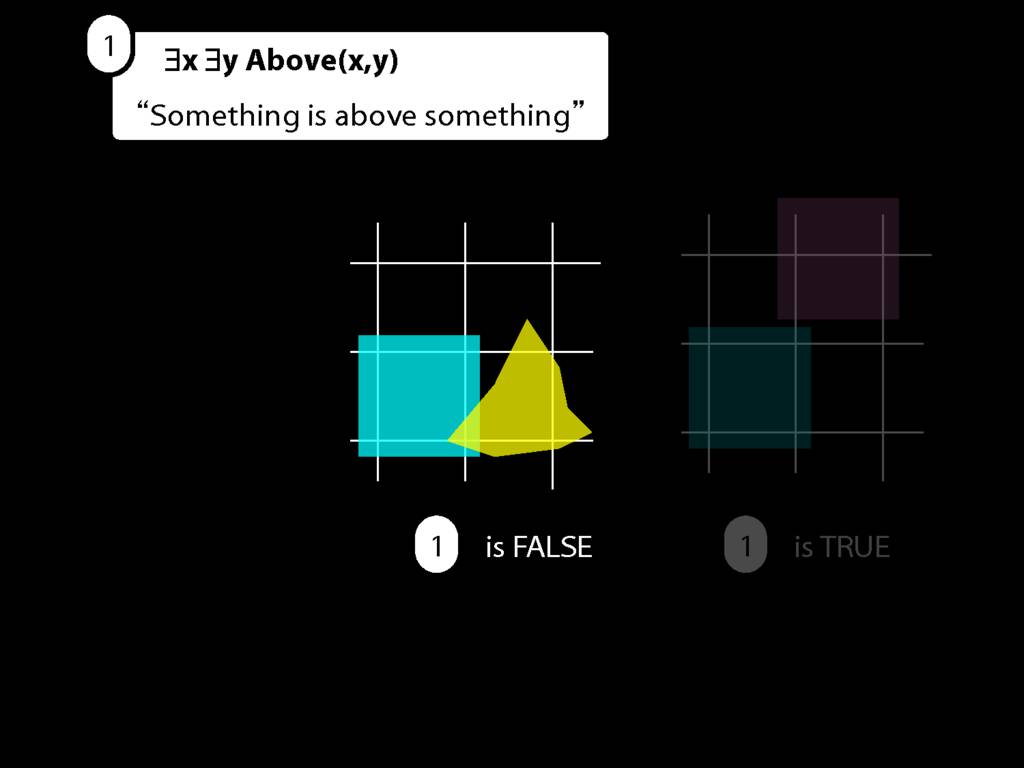
If you've been following along you should be able to do the same in any other possible situation like this one.
The procedure has three steps. First ... well, you know what the procedure is.
... and you can see whether the sentence is true or false.
11.2, 11.4

Multiple Quantifiers: Everyone Likes Puffins
\section{Multiple Quantifiers: Everyone Likes Puffins}
\emph{Reading:} §11.1
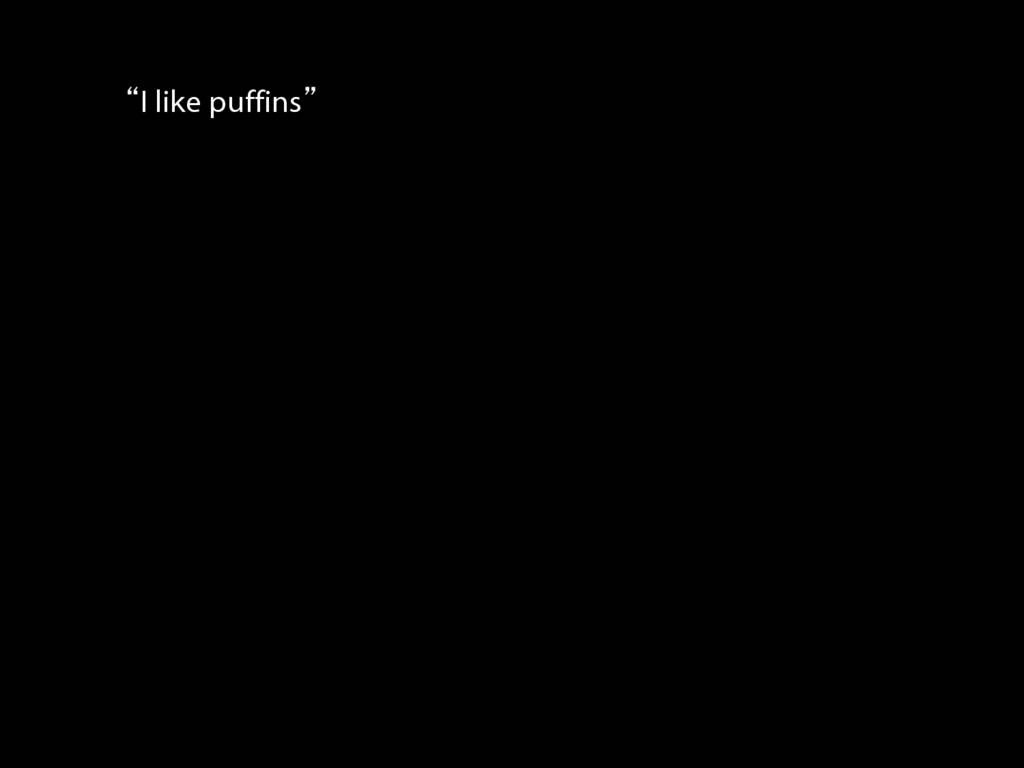
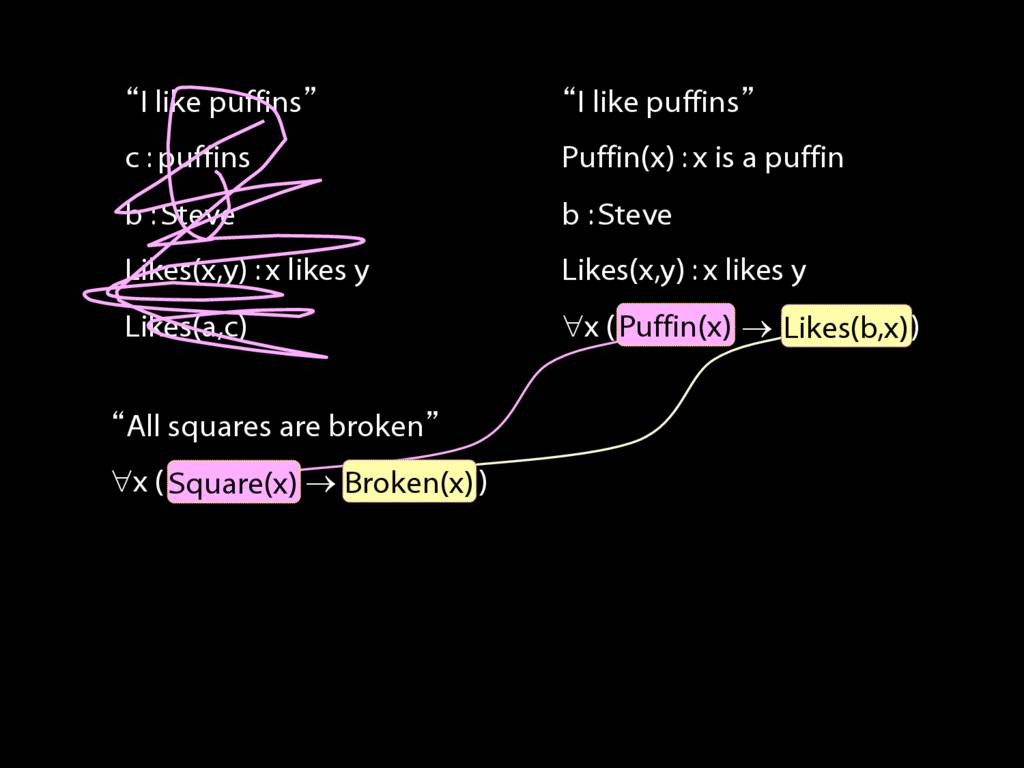
I like puffins:
\hspace{3mm} ∀x ( Puffin(x) → Likes(a,x) )
y likes puffins:
\hspace{3mm} ∀x ( Puffin(x) → Likes(y,x) )
Everyone likes puffins:
\hspace{3mm} ∀y ∀x ( Puffin(x) → Likes(y,x) )
11.2
\section{Relations: Transitivity}
\emph{Reading:} §15.1, §15.6

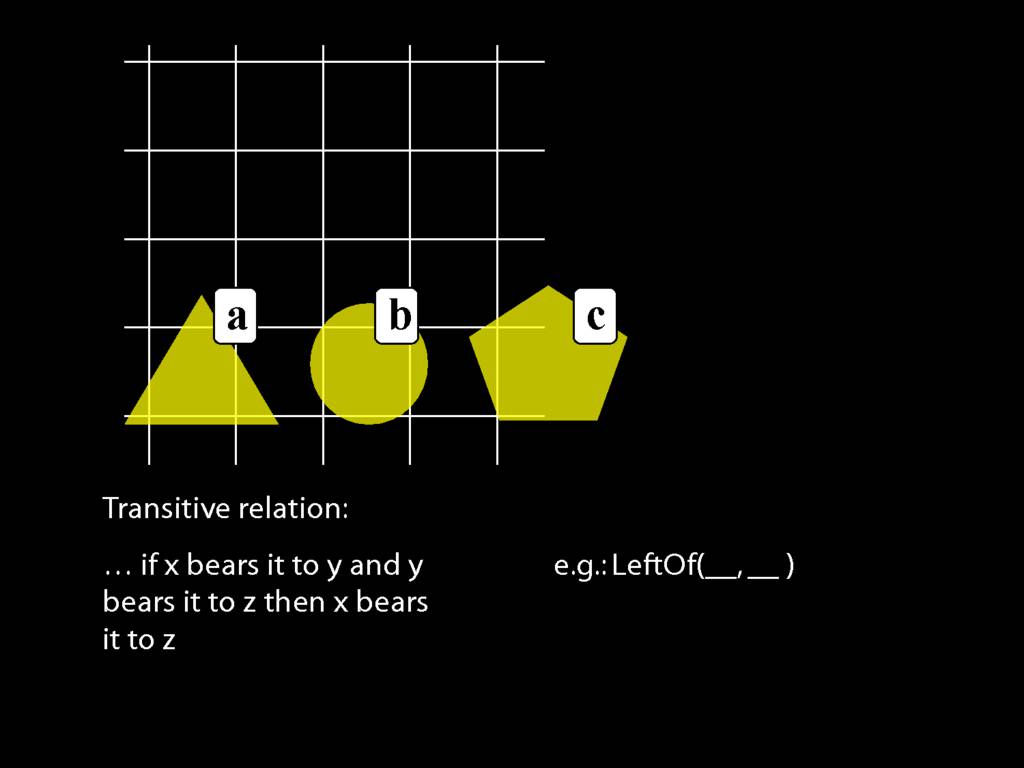
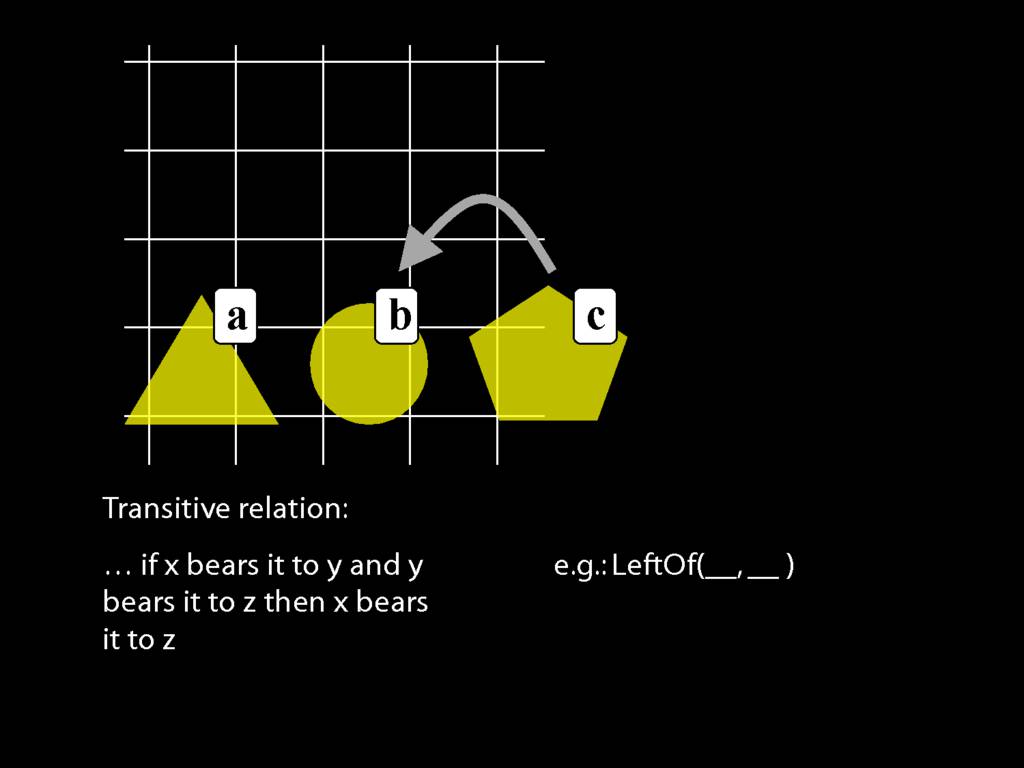
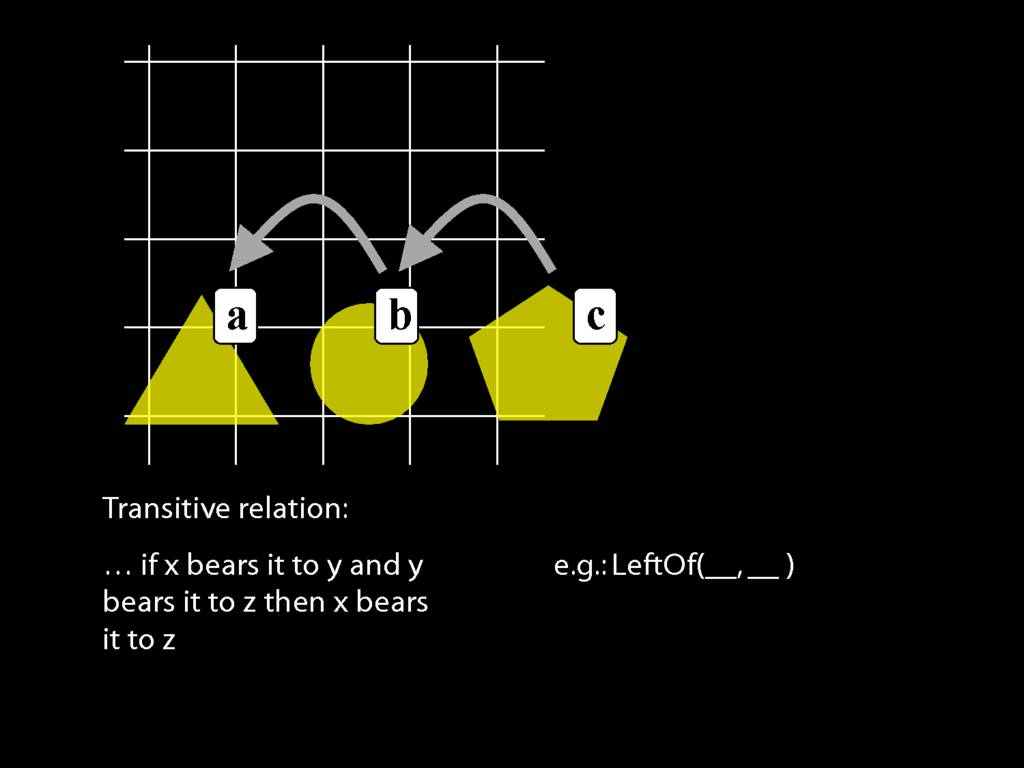
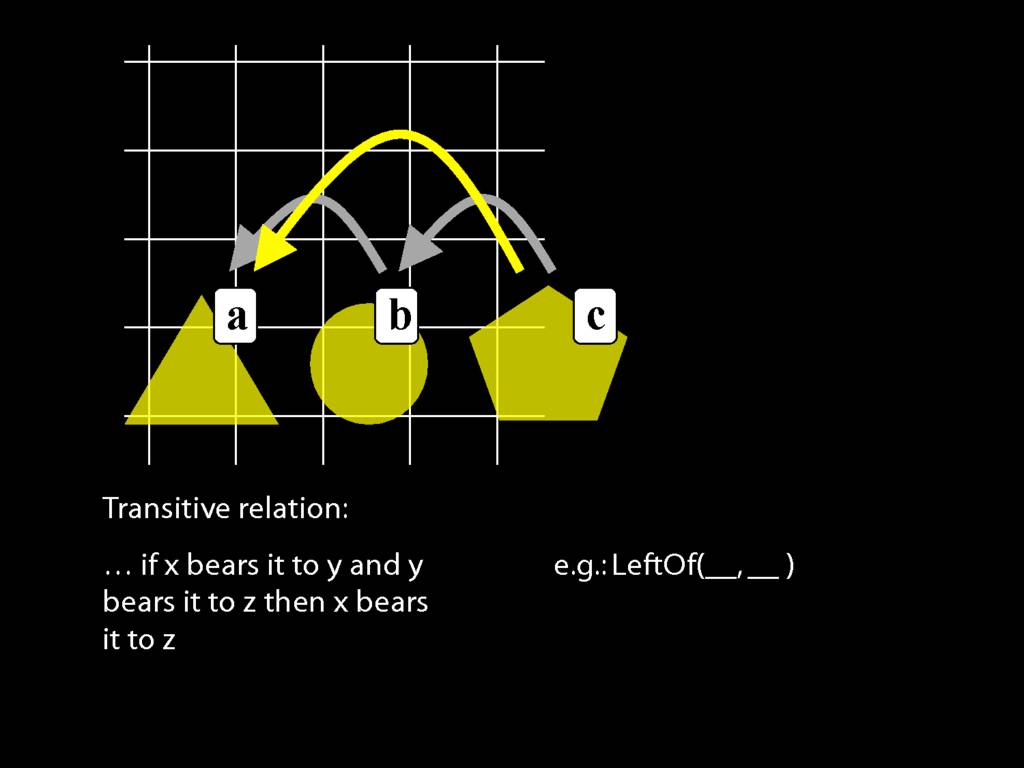
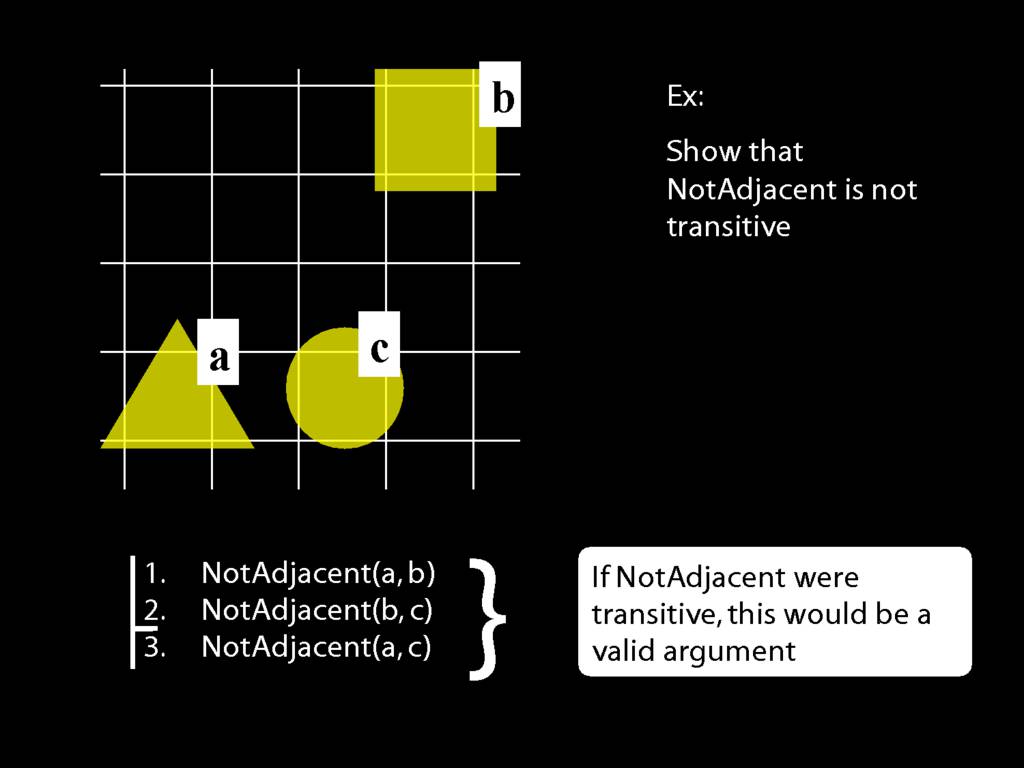
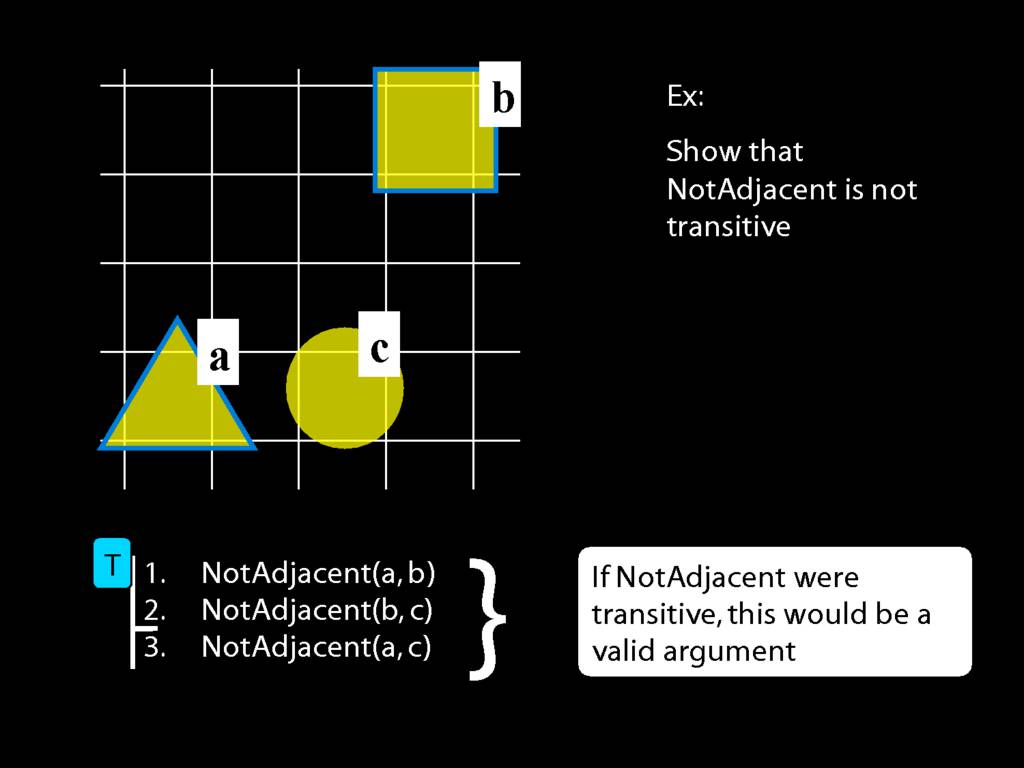
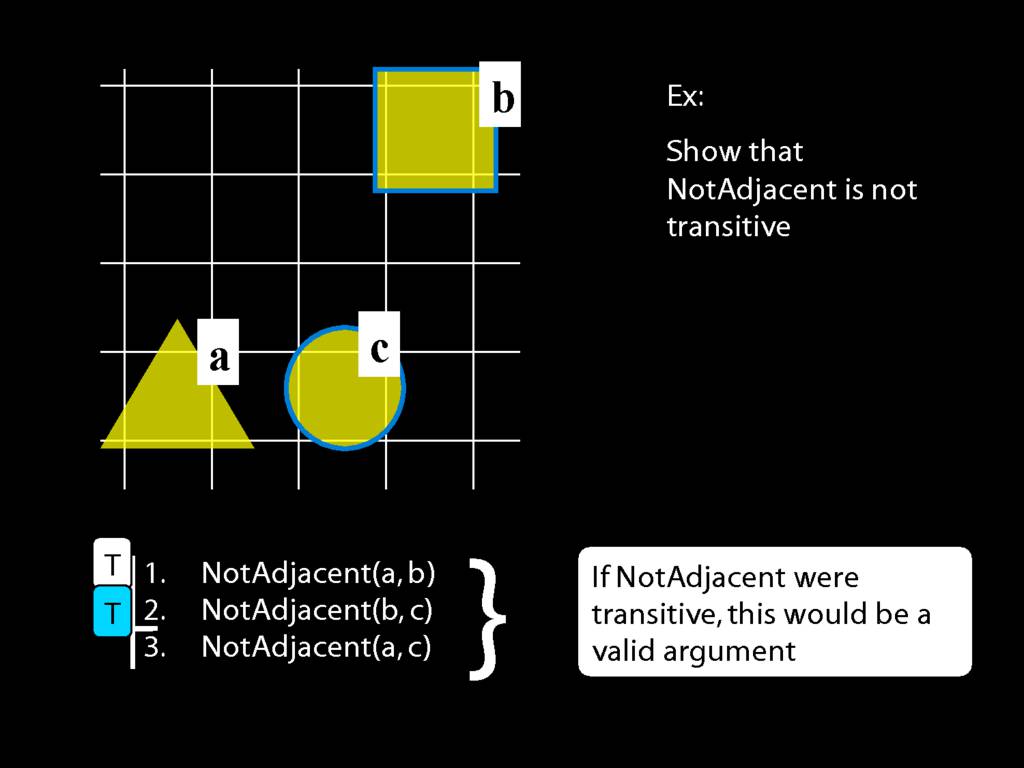
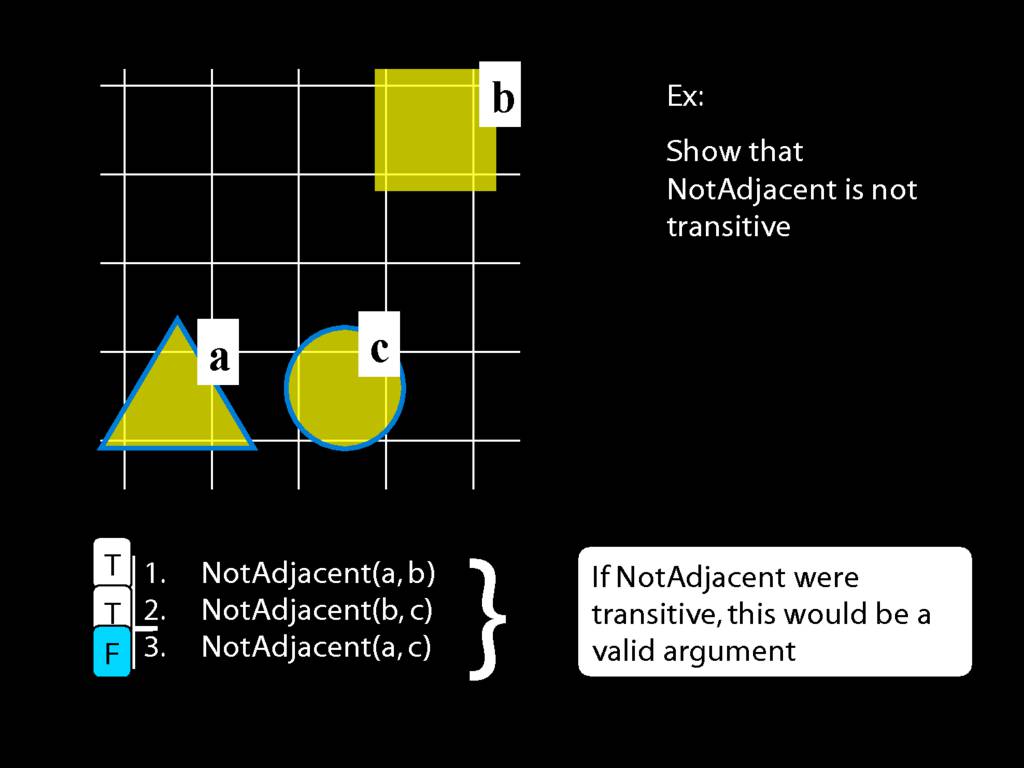
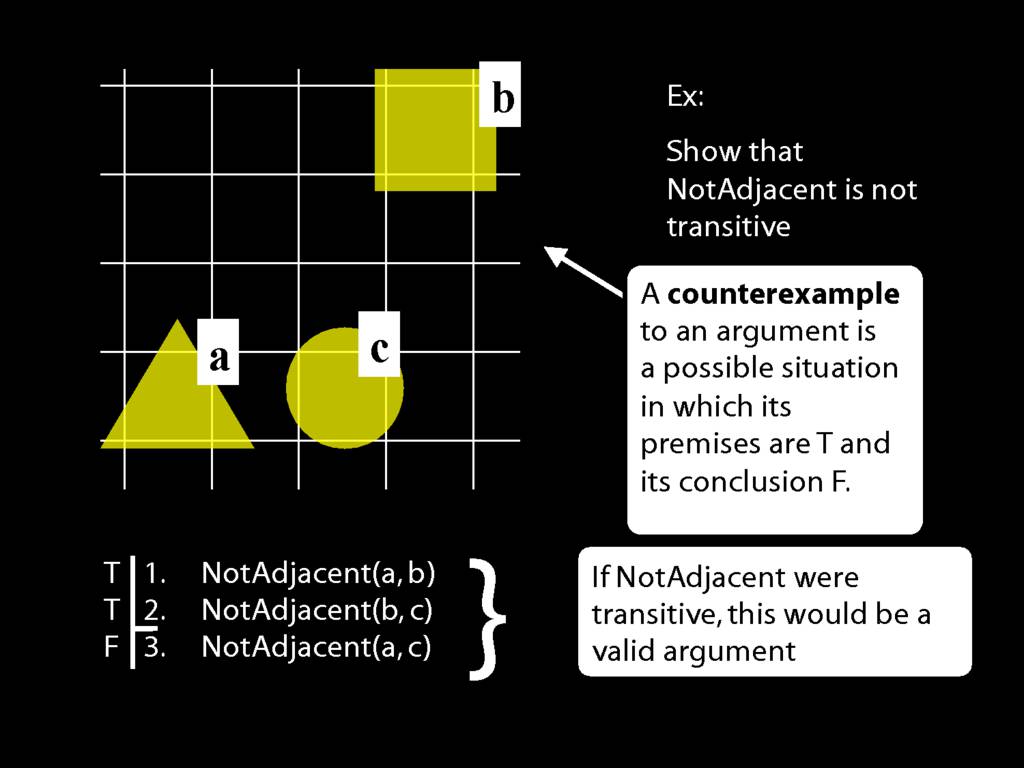
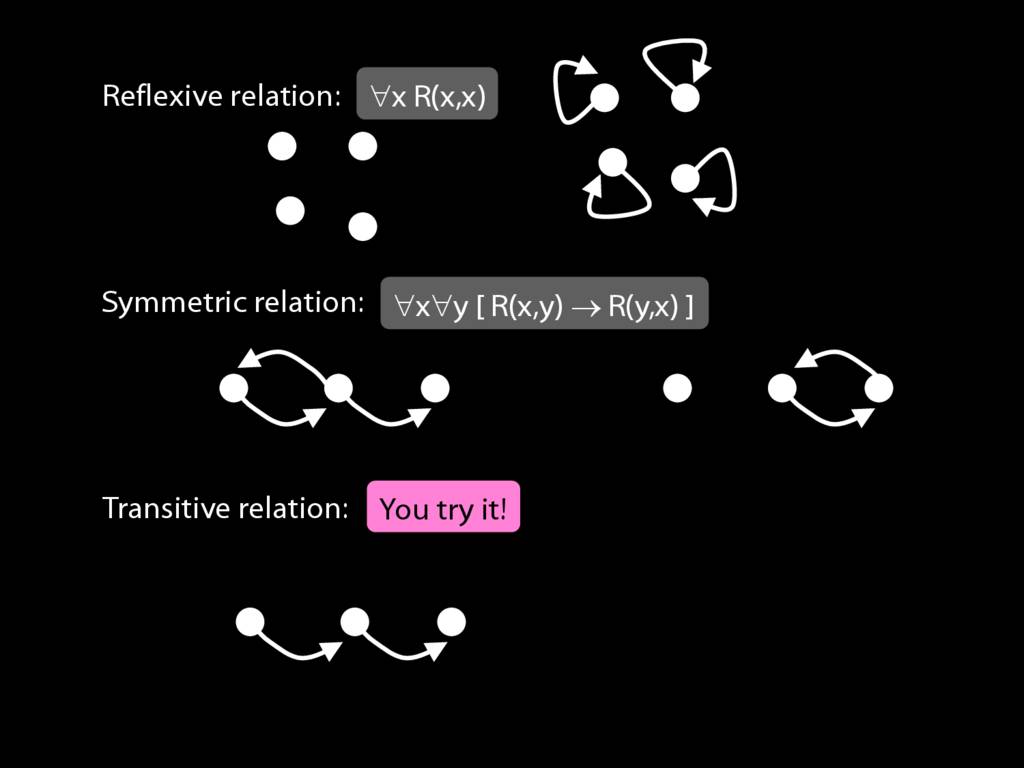
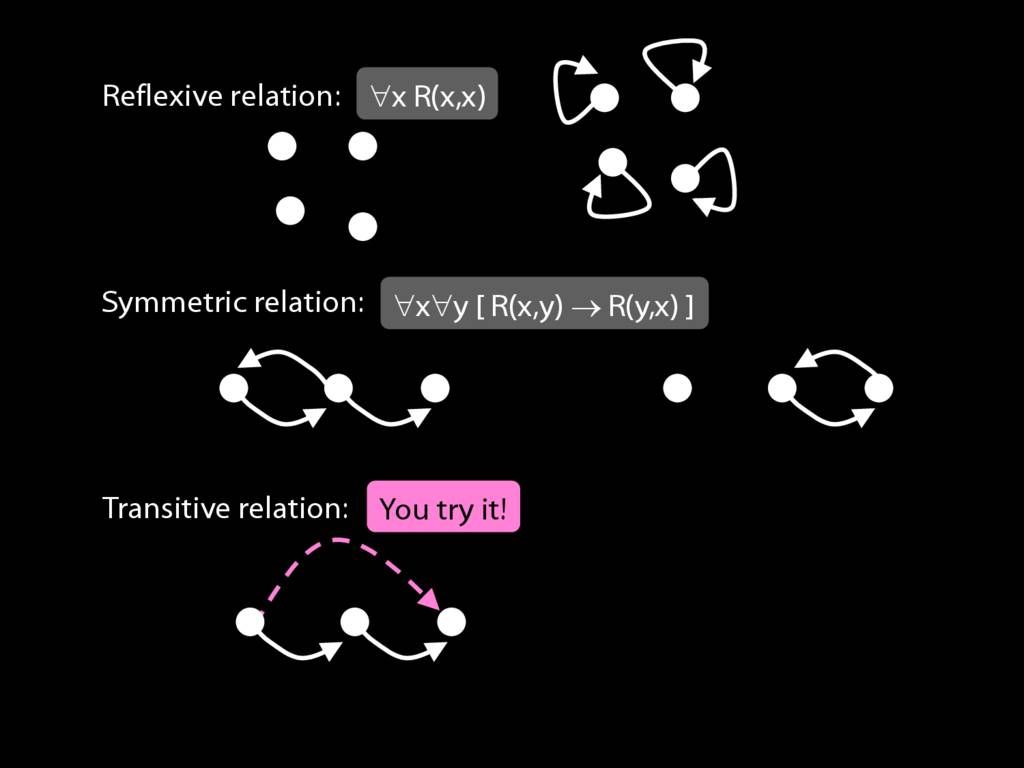
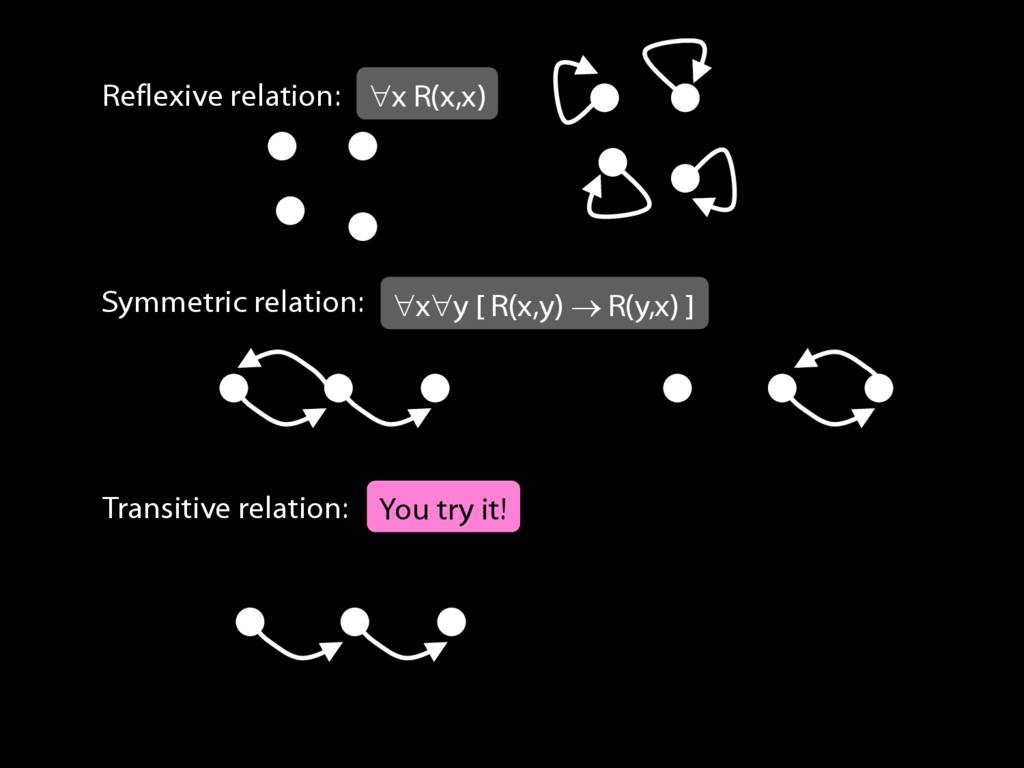
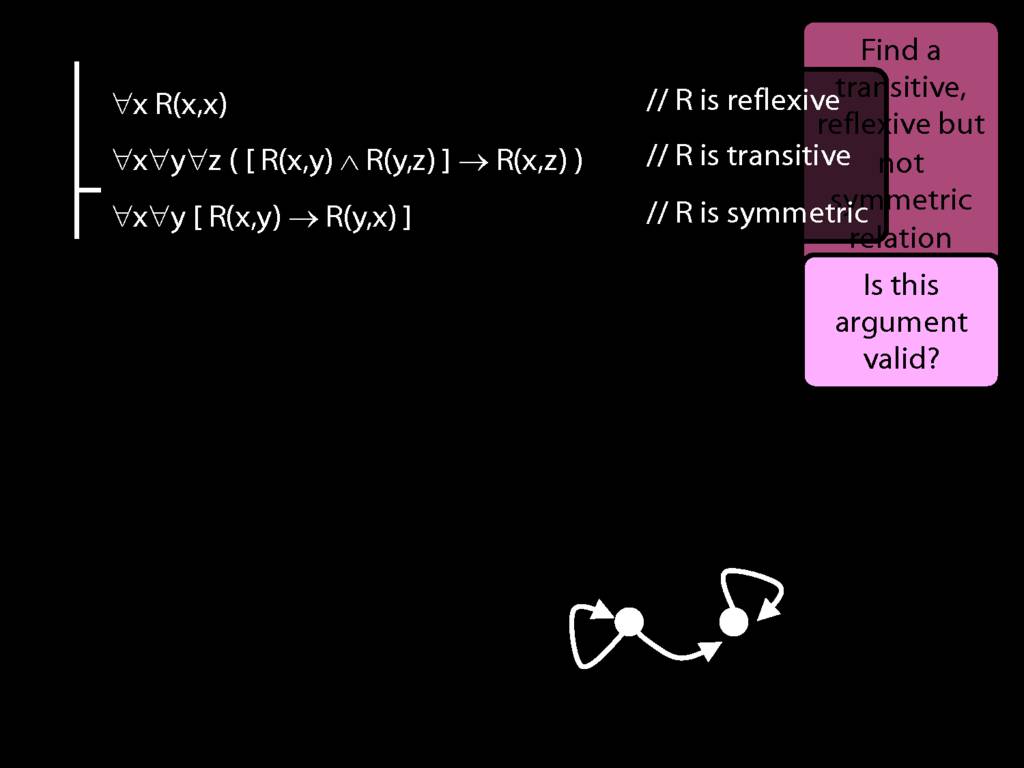
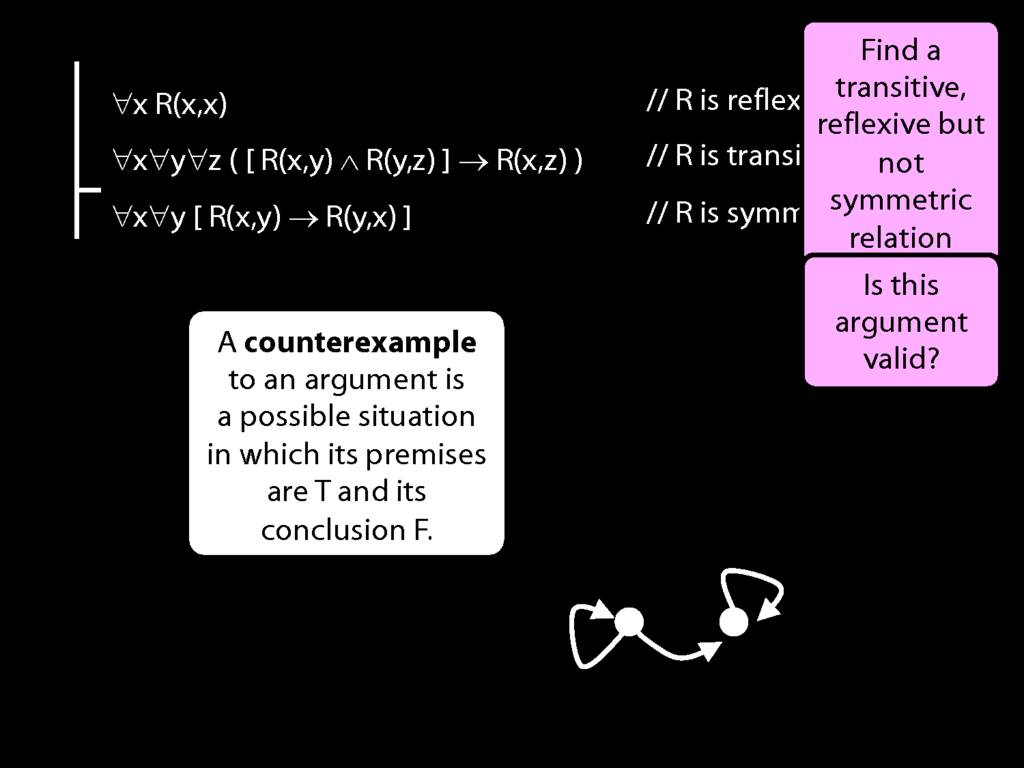
A \emph{transitive} relation is one such that if x bears it to y and y bears it to z then x bears it to z. (E.g. LeftOf is transitive; NotAdjacent is not transitive.)
\begin{minipage}{\columnwidth}
If NotAdjacent were transitive, the following argument would be logically valid:
\end{minipage}
\begin{minipage}{\columnwidth}
A counterexample to this argument:
\end{minipage}
express the counterexample formally
Domain
{0, 1, 2}
Names
a : 0
b : 1
c : 2
Predicates
NotAdjacent : {
<0,1>, <1,2>,
<1,0>, <2,1>
}
Domain
{0, 1, 2}
Names
a : 0
b : 1
c : 2
Predicates
NotAdjacent : {
<0,1>, <1,2>,
<1,0>, <2,1>
}
Domain
{0, 1, 2}
Names
a : 0
b : 1
c : 2
Predicates
NotAdjacent : {
<0,1>, <1,2>,
<1,0>, <2,1>
}

Expressing Relations with Quantifiers
\section{Expressing Relations with Quantifiers}
\emph{Reading:} §15.1, §15.6

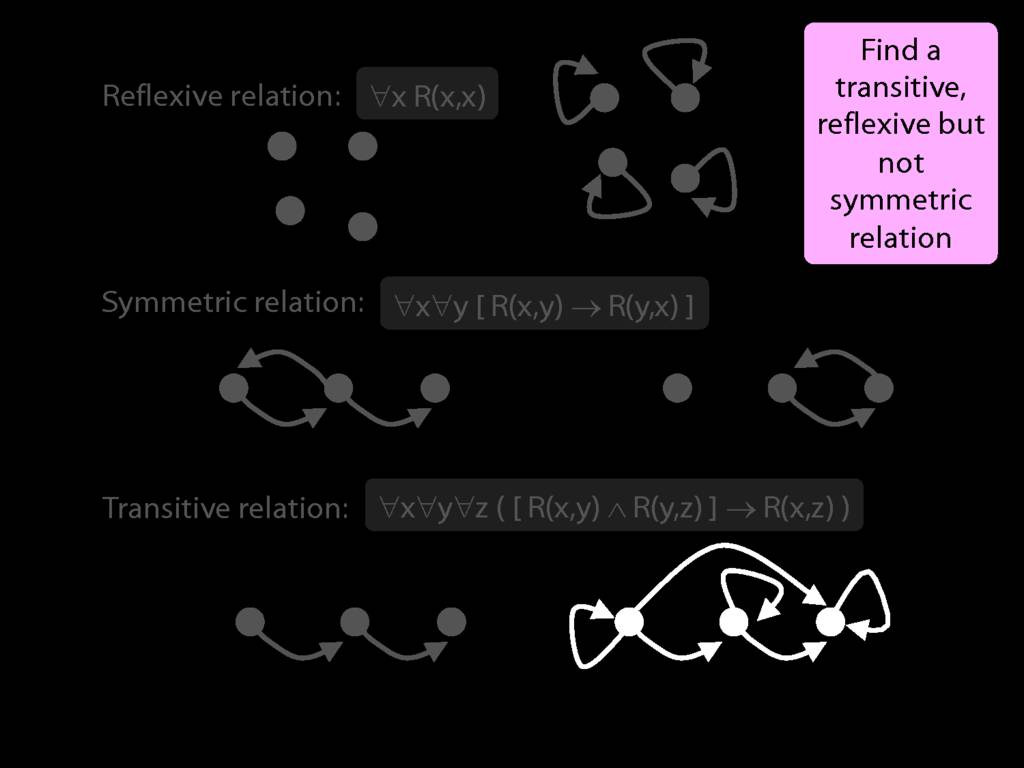
\begin{minipage}{\columnwidth}
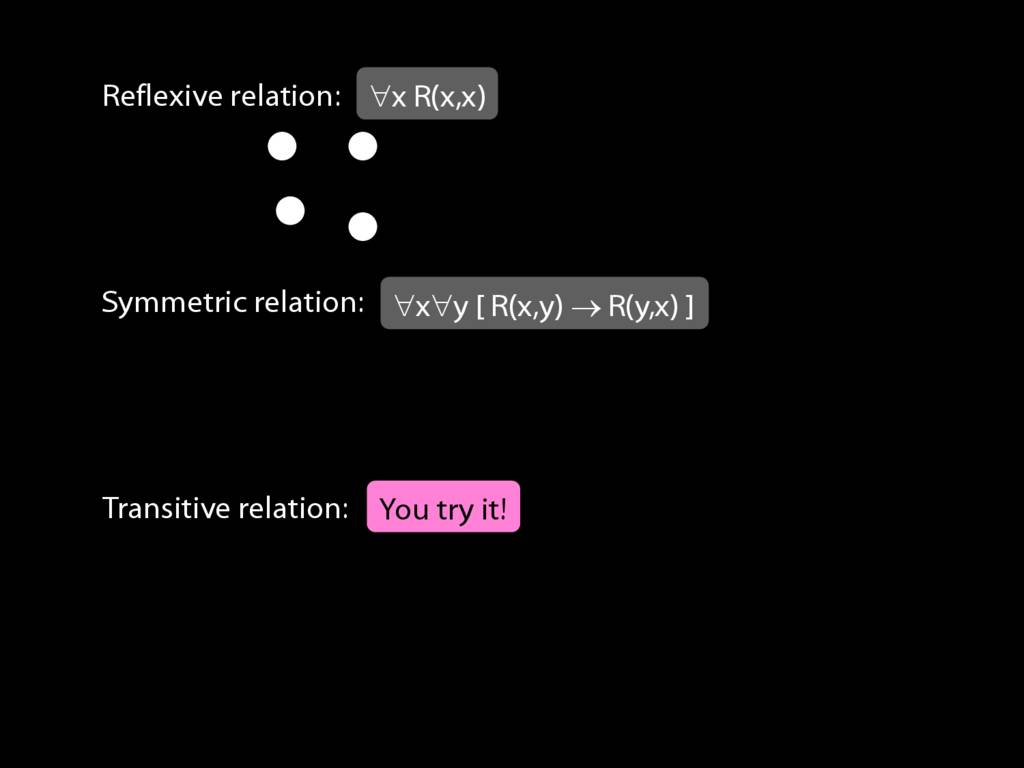
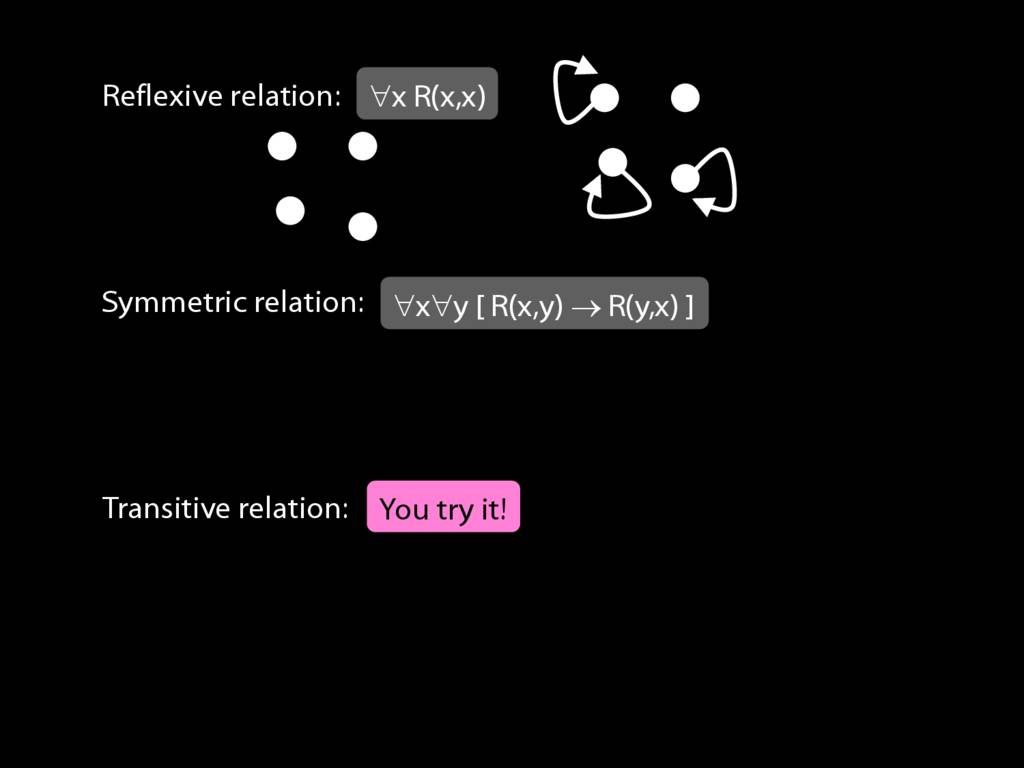
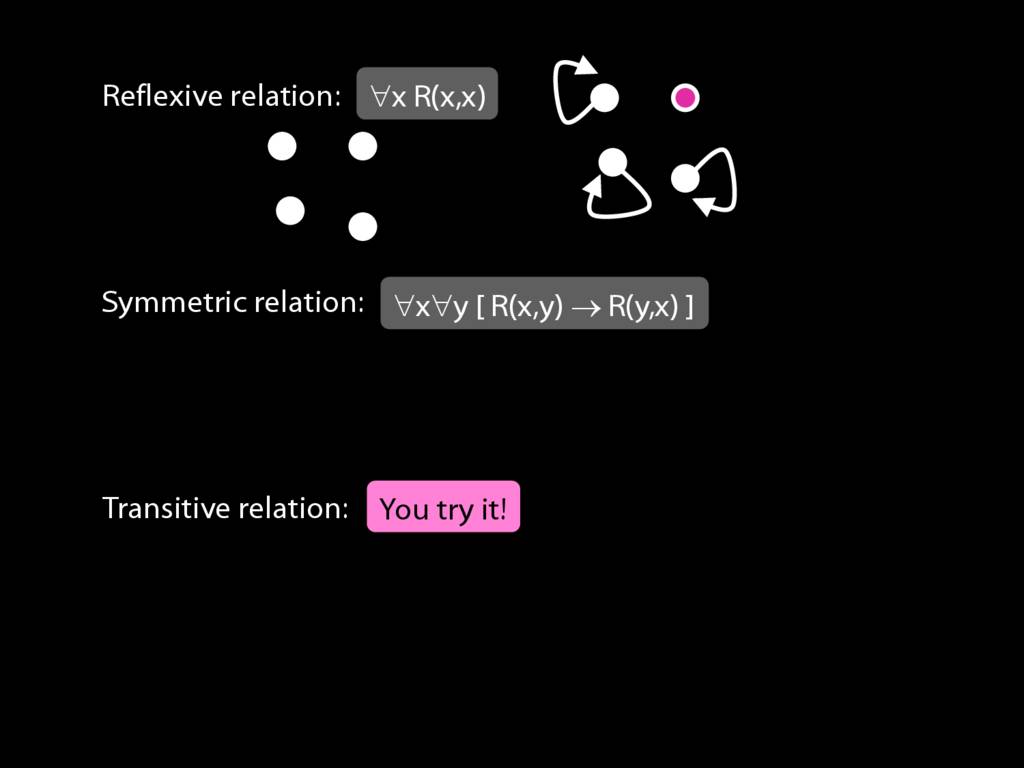
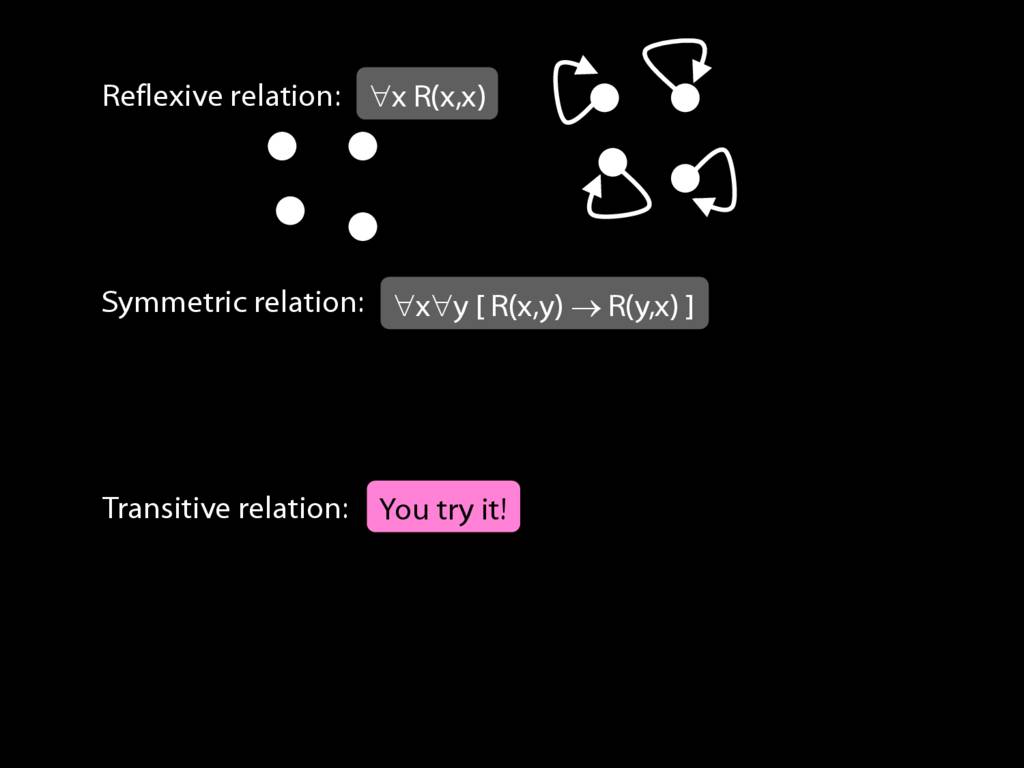
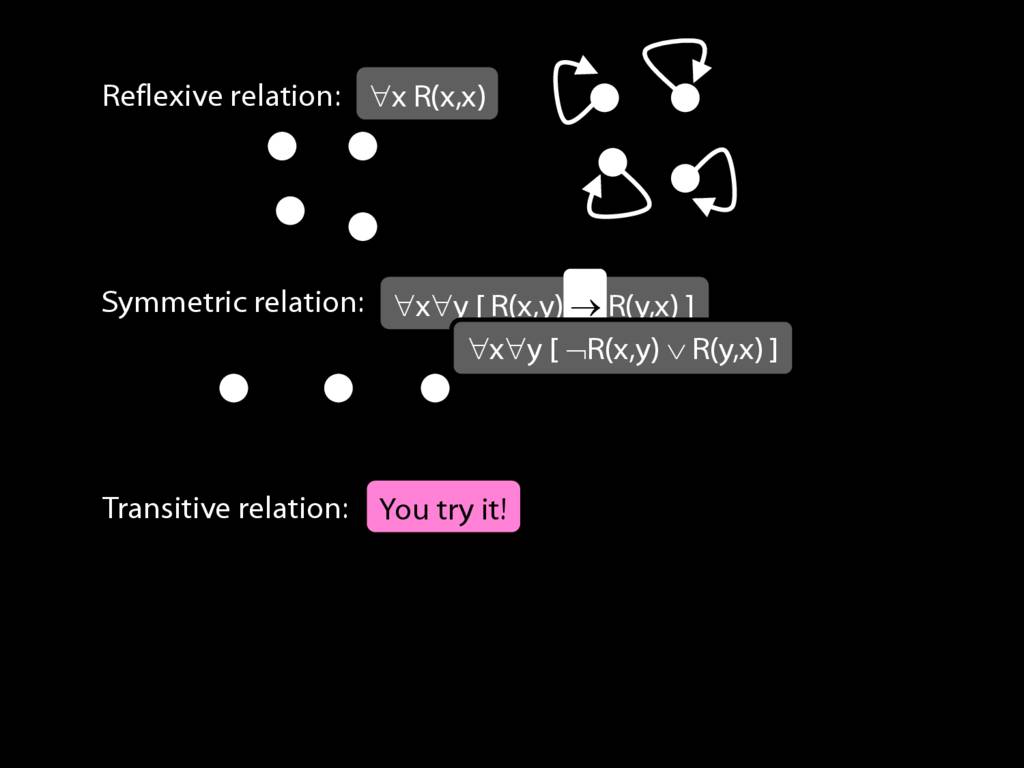
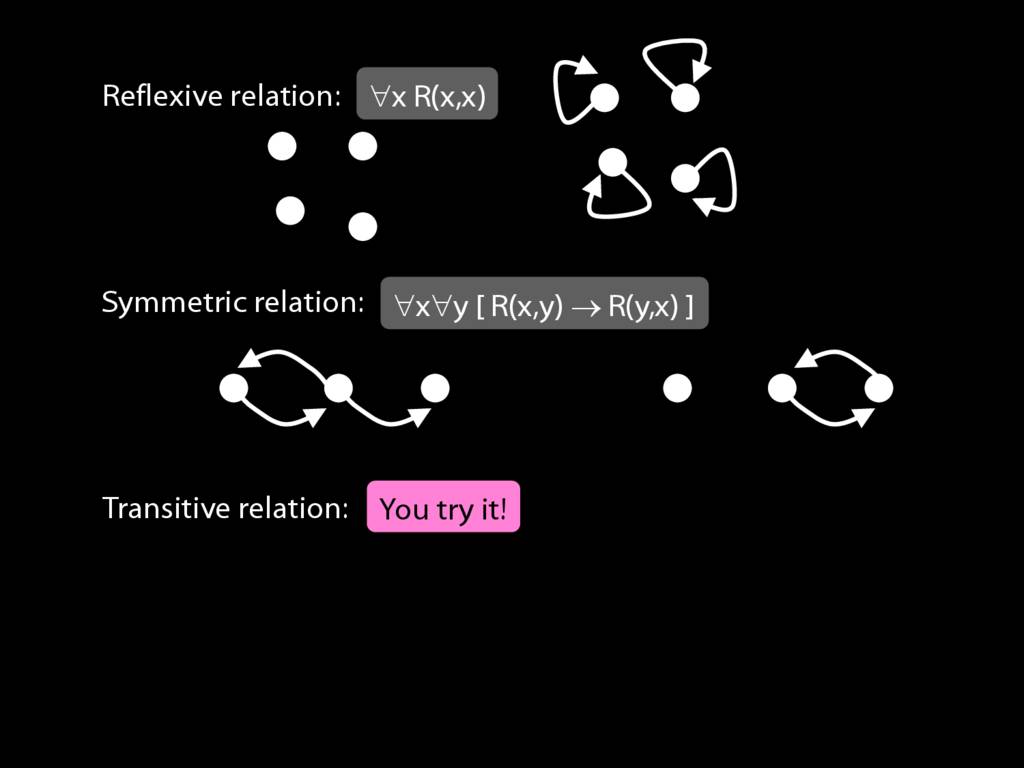
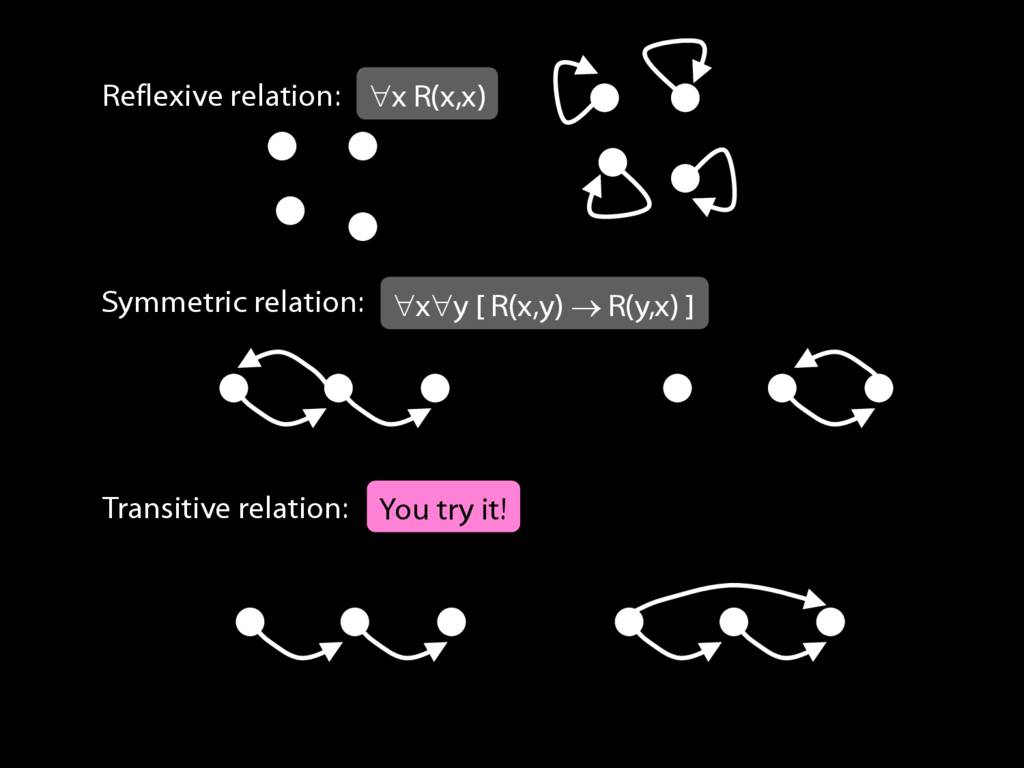
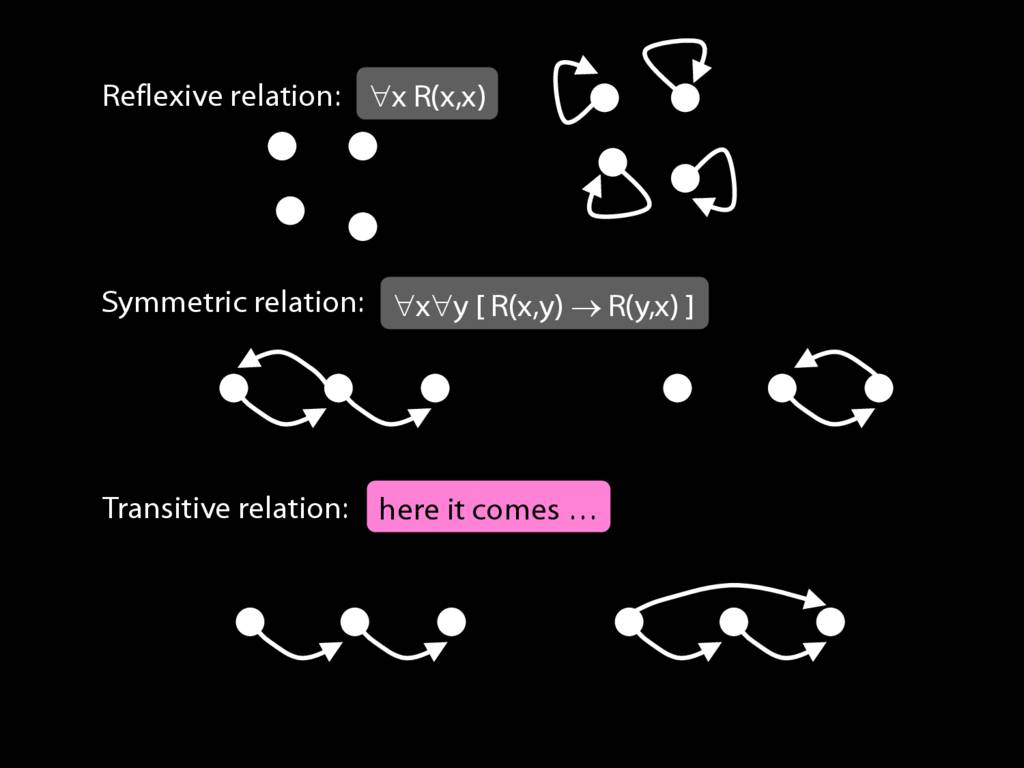
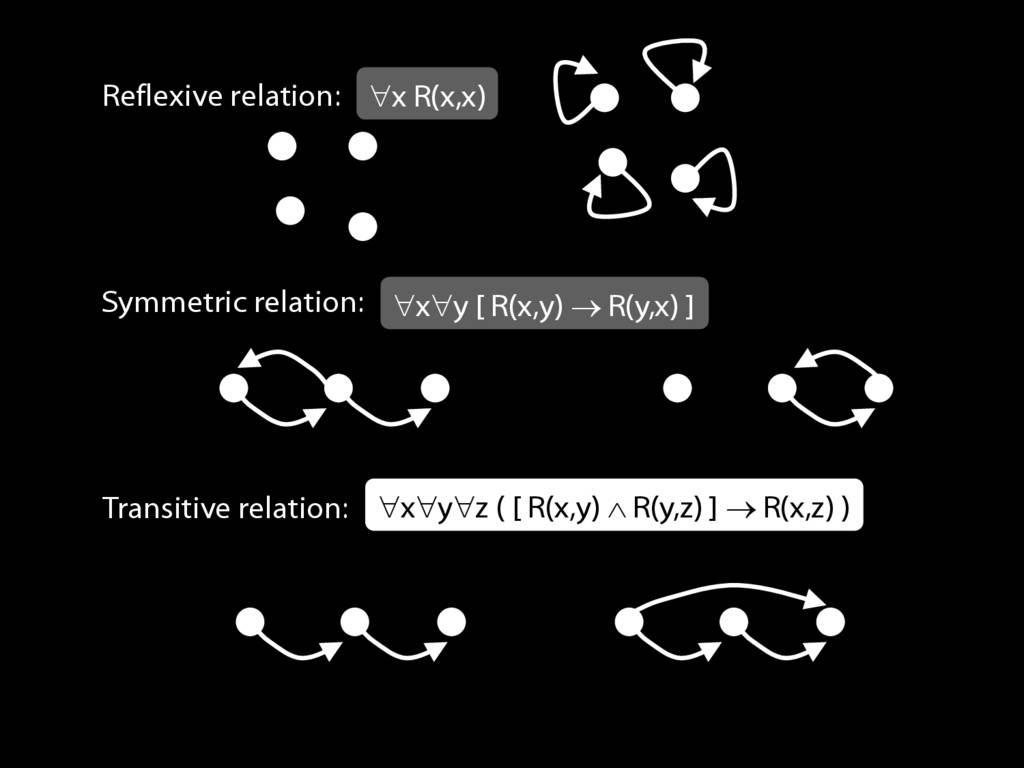
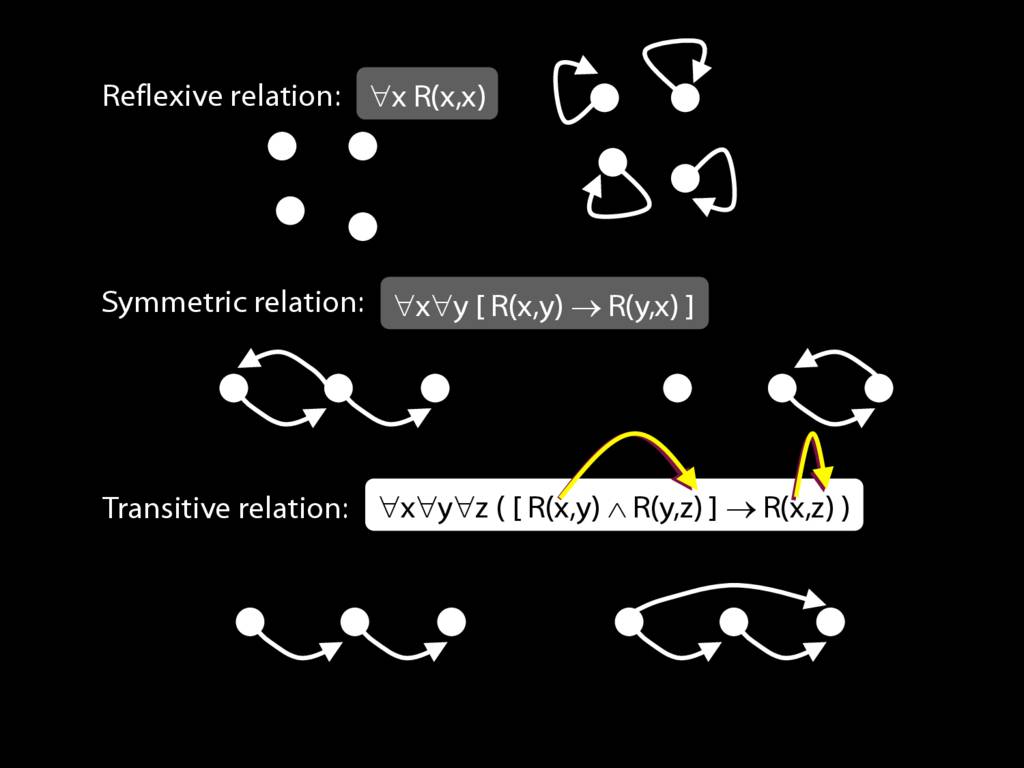
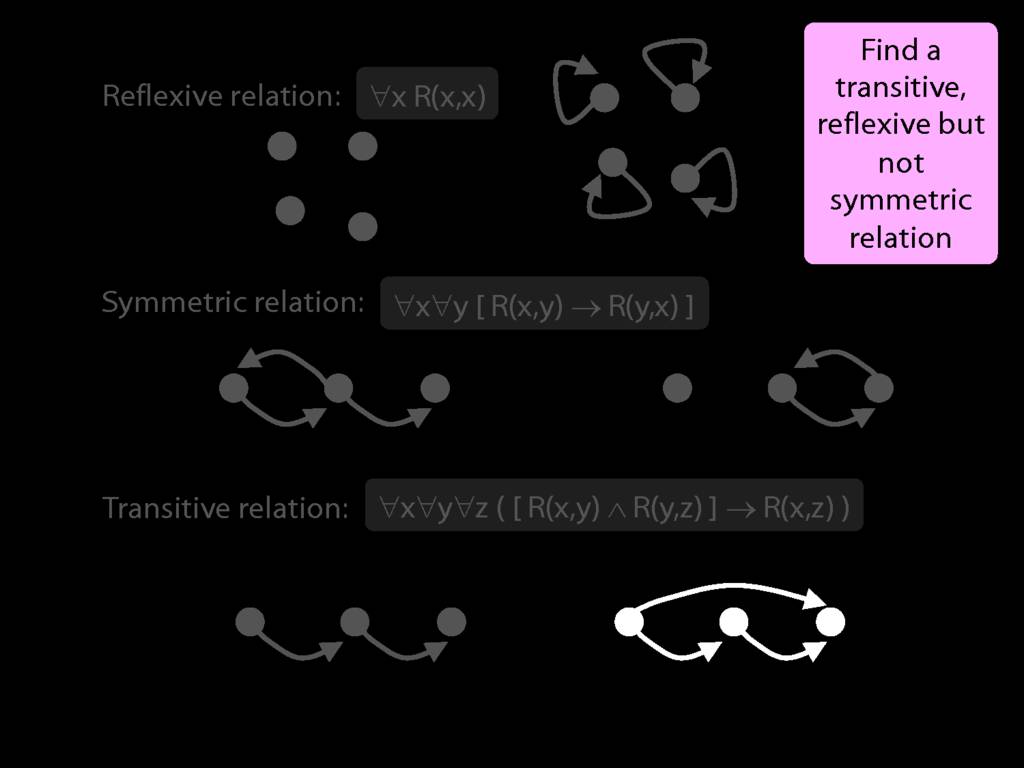
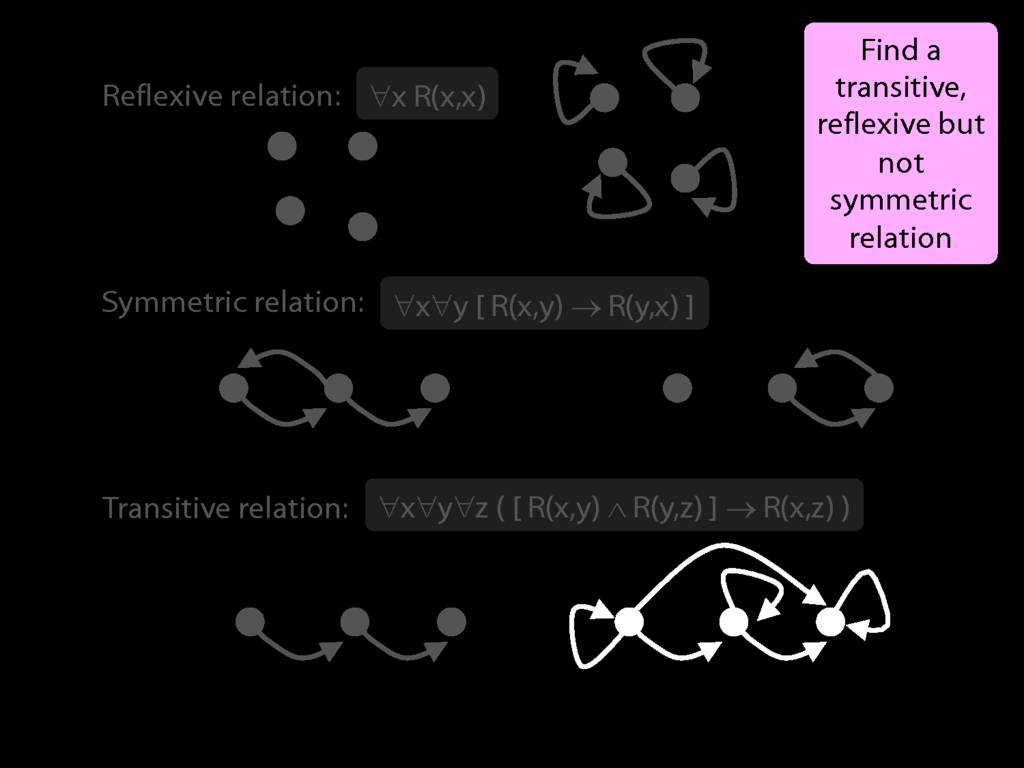
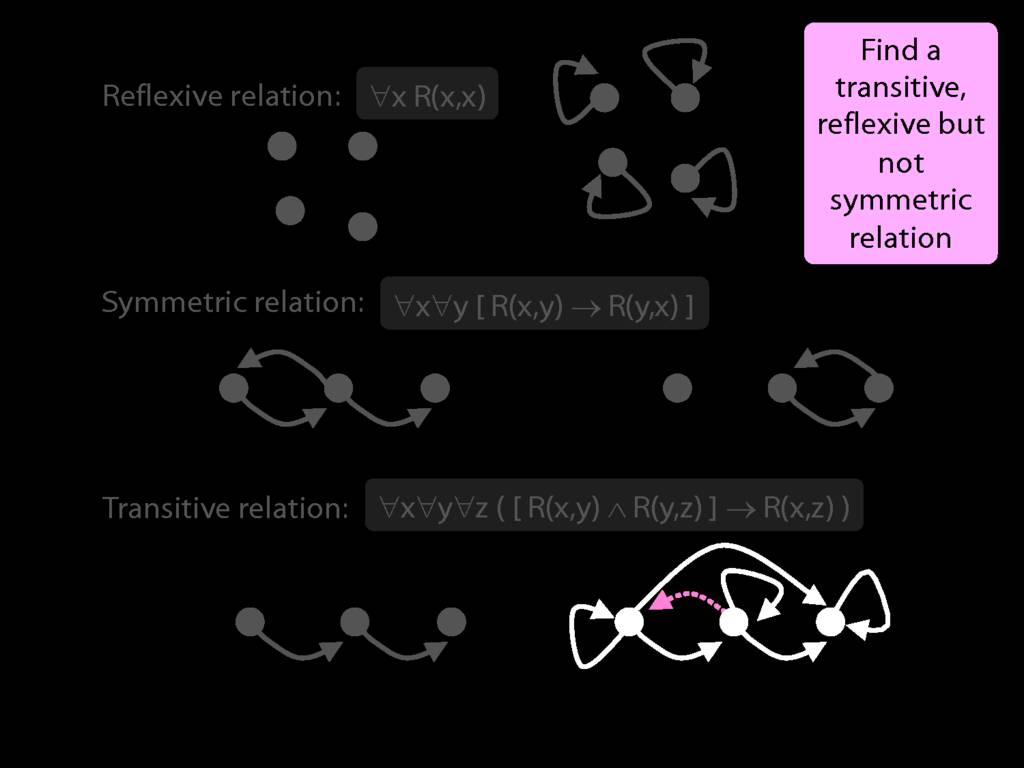
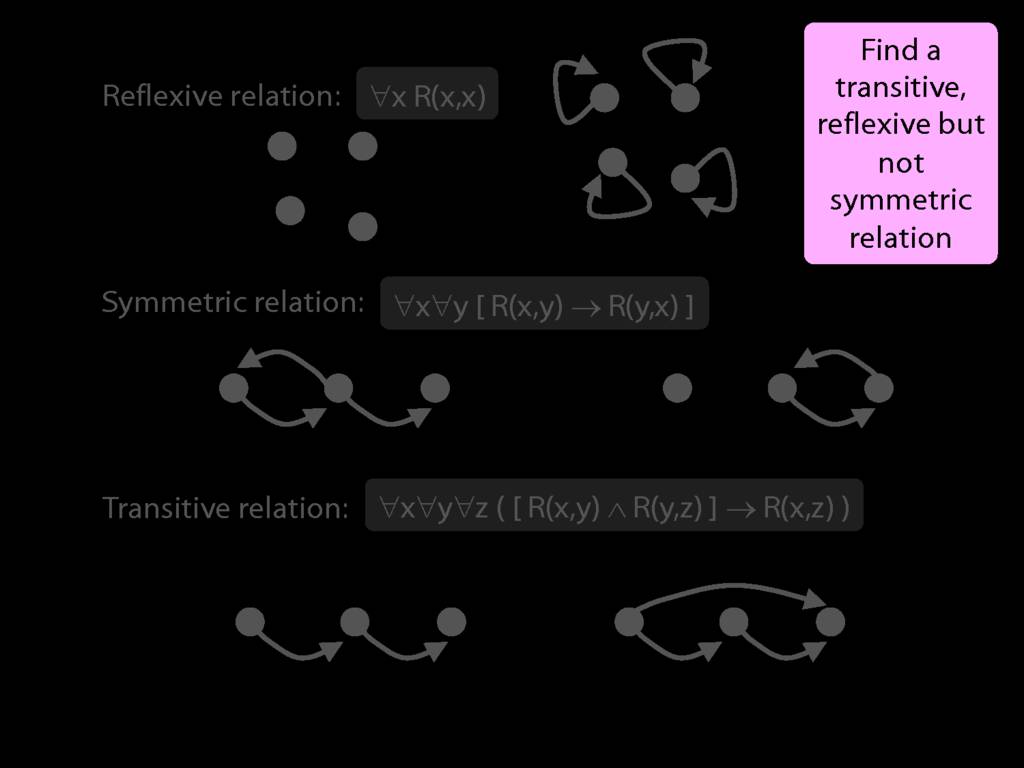
A \emph{reflexive} relation is one that everything bears to itself. (E.g. SameShape)
reflexive: ∀x R(x,x)
\end{minipage}
\begin{minipage}{\columnwidth}
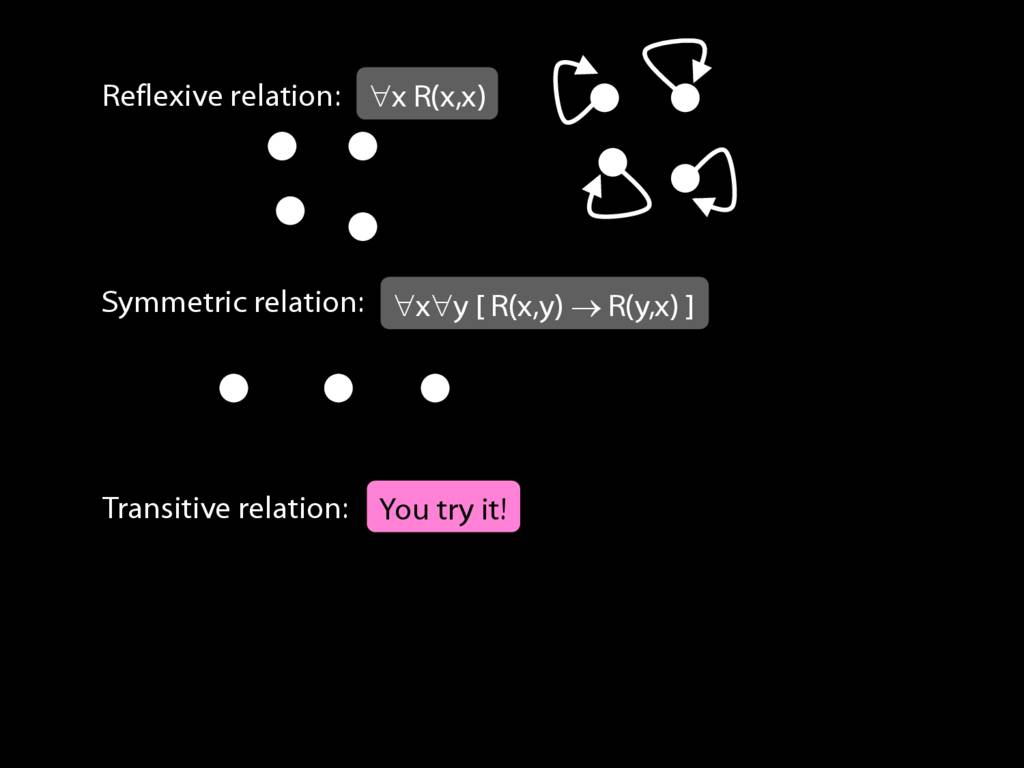
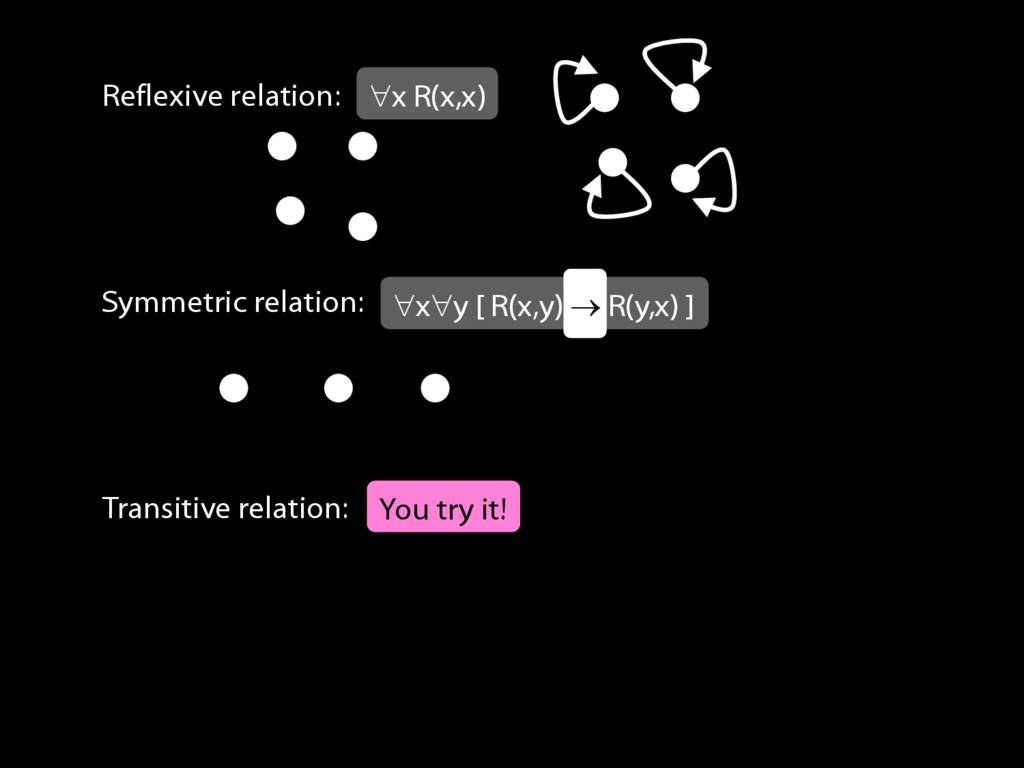
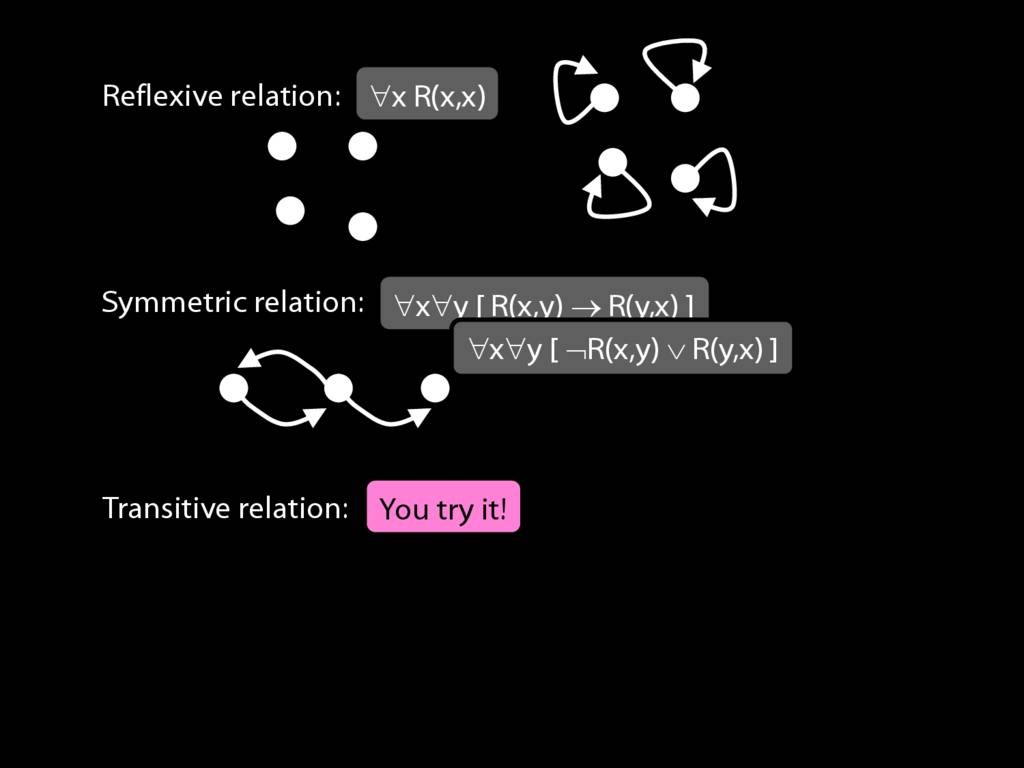
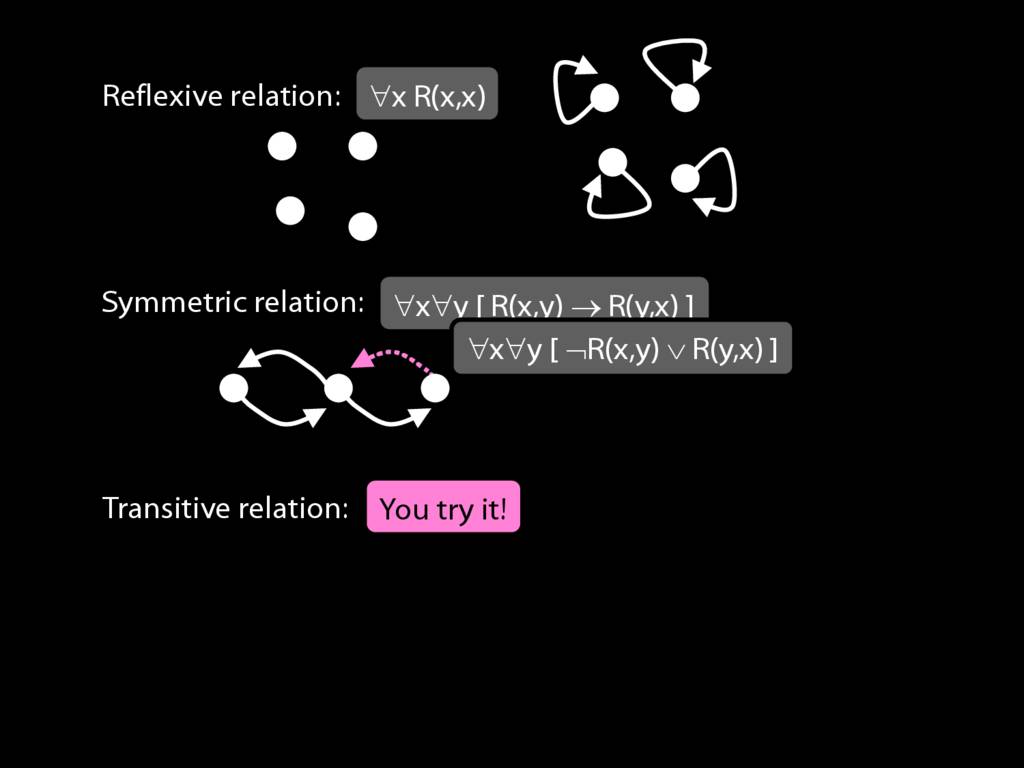
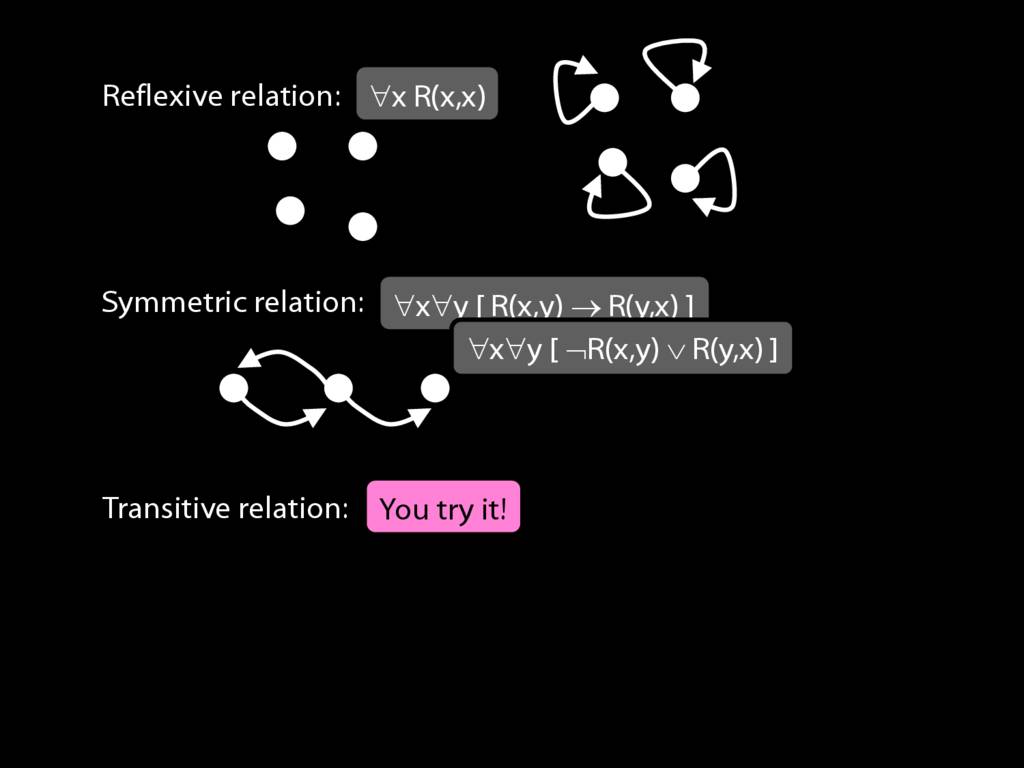
A \emph{symmetric} relation is one such that if x bears it to y, then y bears it to x. (E.g. Adjacent(x,y))
symmetric: ∀x∀y ( R(x,y) → R(y,x) )
\end{minipage}
\begin{minipage}{\columnwidth}
A \emph{transitive} relation is one such that if x bears it to y and y bears it to z then x bears it to z. (E.g. LeftOf is transitive; DifferentShape is not transitive)
transitive: ∀x∀y∀z ( ( R(x,y) ∧ R(y,z) ) → R(x,z) )
\end{minipage}
15.33--15.40 (second edition)
15.33, 15.37--15.39 (second edition)

Expressing Counterexamples Formally
\section{Expressing Counterexamples Formally}
\emph{Reading:} §15.1, §15.6
Give a counterexample to this argument:
Informally:
Formally:
\hspace{3mm} Domain: \{a, b\}
\hspace{3mm} R: \{<a,a>, <a,b>, <b,b>\}
Here’s a quick look at how to enter the counterexample in
zoxiy. If you want more detail, please see the user guide
(which is linked to on the home page of zoxiy).
No lectures or seminars in reading week (Week 6).
office hours
Tuesdays:
16-17 in S2.40 (Barney)
Wednesdays:
11-12 in S2.40 (Hemdat)
12-13 in S2.40 (Hemdat)
13-14 in S2.40 (Alfonso)
15-16 in S2.40 (Dino)
16-17 in H3.45 (Barney*)
Thursdays:
10-11 in S2.33 (Joe)
12-13 in S2.33 (Joe)
13-14 in S2.40 (Barney)
15-16 in S2.40 (Dino)

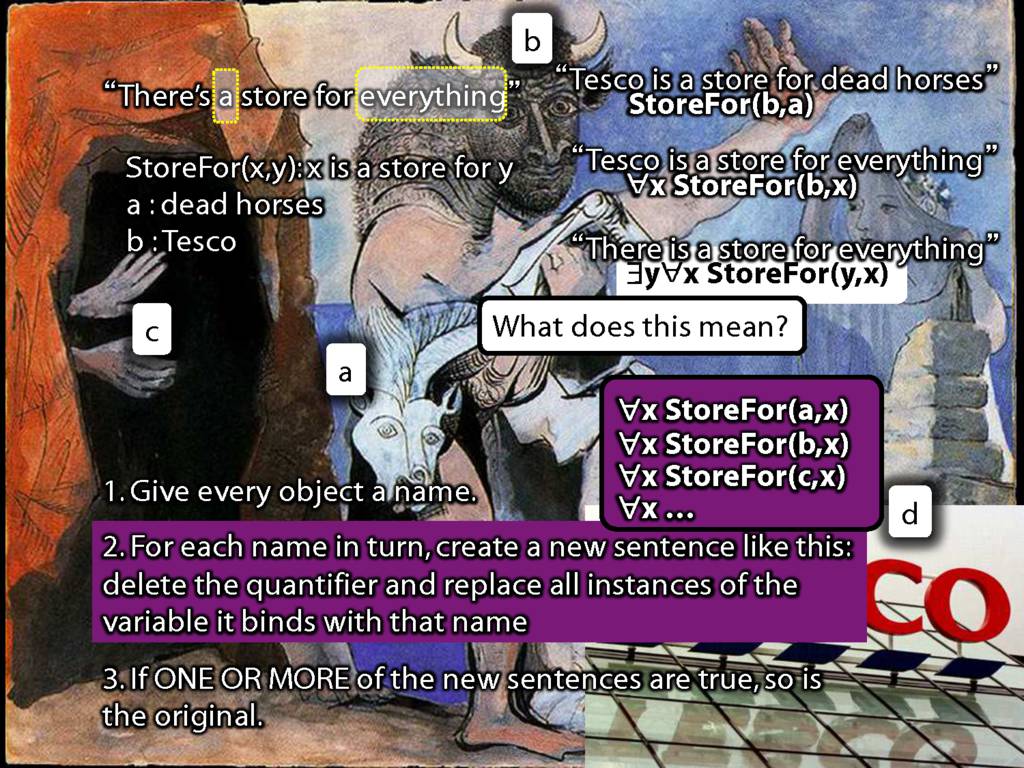
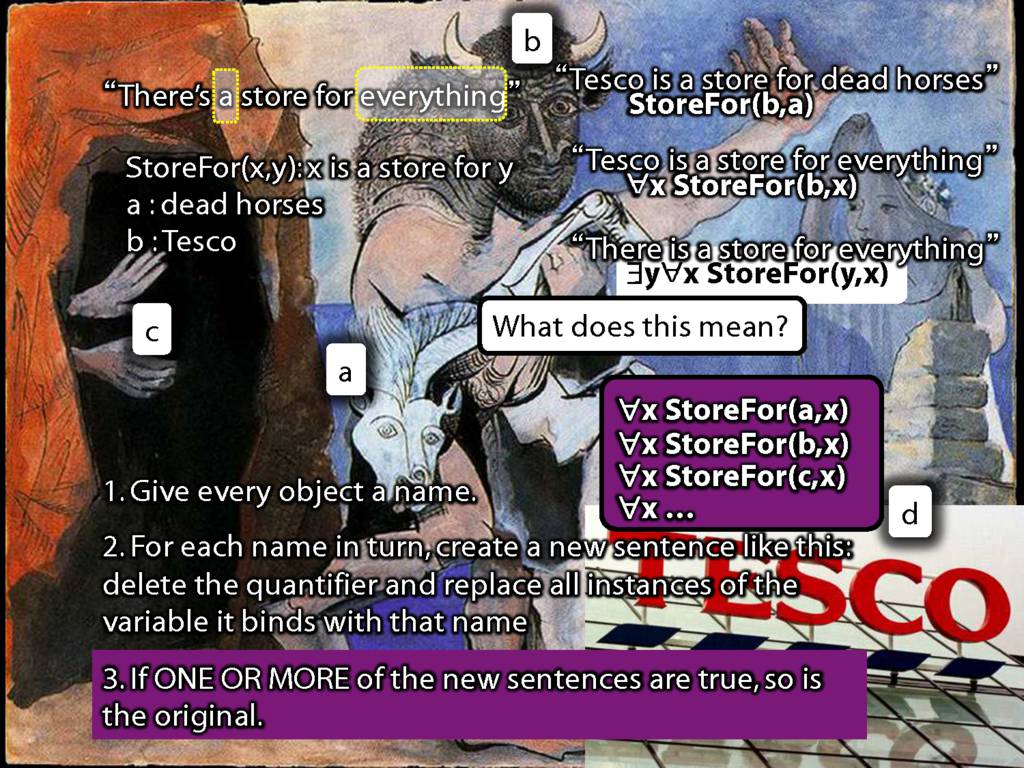
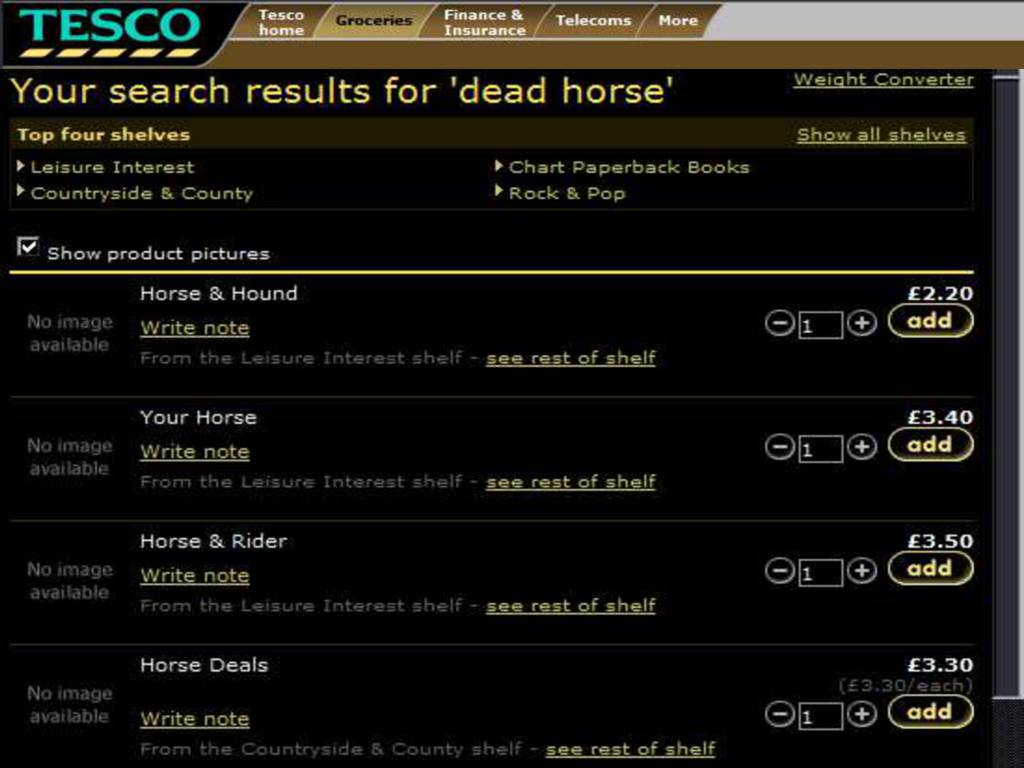
There Is a Store for Everything
\section{There Is a Store for Everything}
\emph{Reading:} §11.2, §11.3

There is a store for everything:
\hspace{3mm} ∃y∀x StoreFor(y,x)
\hspace{3mm} ∀y∃x StoreFor(x,y)
Other sentences to translate:
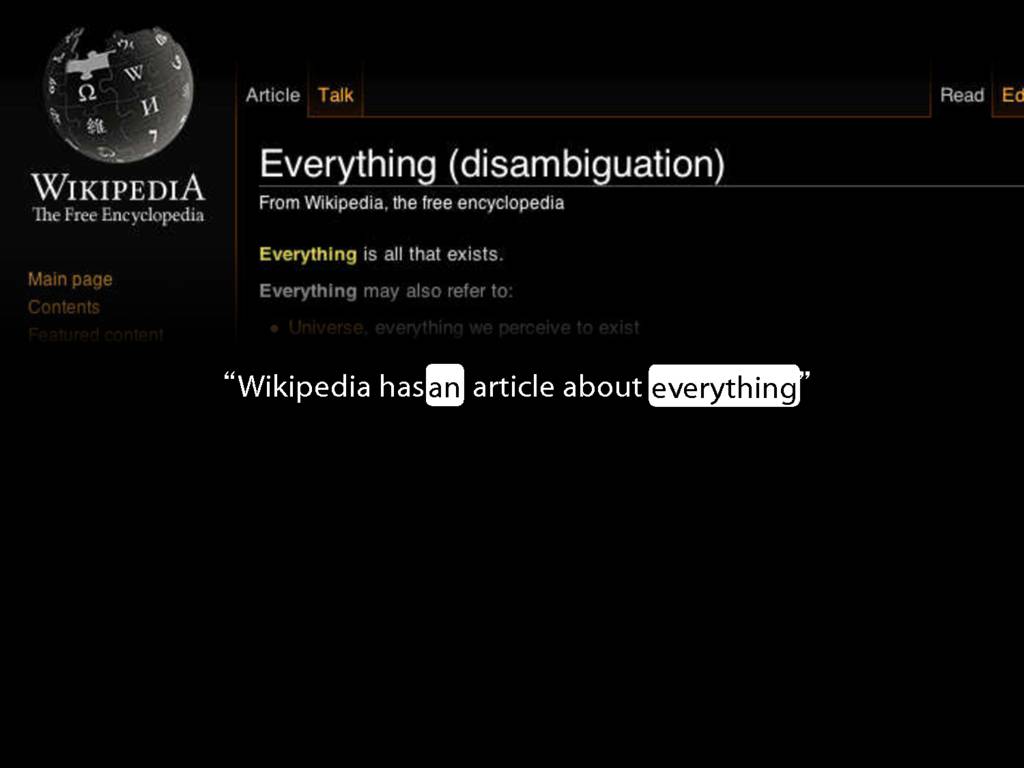
\hspace{3mm} Wikipedia has an article about everything
\hspace{3mm} Everyone hurts someone they love
\hspace{3mm} Someone hurts everyone she loves
11.3
11.4, 11.8, 11.9
11.11, 11.13, *11.10
11.8, 11.9, *11.11
No lectures or seminars in reading week (Week 6).
\section{There Does Not Exist}
Something is not dead:
\hspace{3mm} ∃x ¬Dead(x)
Nothing is dead:
\hspace{3mm} ¬∃x Dead(x)
Everything is not broken:
\hspace{3mm} ∀x ¬Broken(x)
Not everything is broken:
\hspace{3mm} ¬∀x Broken(x)


Something is dead.
∃x Dead(x)
Something is not dead.
∃x ¬Dead(x)
Nothing is dead.
¬∃x Dead(x)
| | 1. | | |
| | 2. | a=a | =Intro |
| | 3. | ∃x (x=x) | ∃Intro: 2 |
Everything is broken.
∀x Broken(x)
Everything is not broken.
∀x ¬Broken(x)
Not everything is broken.
¬∀x Broken(x)
| | 1. | ¬∃x Dead(x) | |
| | | | 2. | Dead(a) | | | | 3. | ∃x Dead(x) | ∃Intro: 2 | | | 4. | ⊥ | ⊥Intro: 1,3 |
|
| | 5. | ¬Dead(a) | ¬Intro: 2-4 |
| | 6. | ∃x ¬Dead(x) | ∃Intro: 5 |
| | 1. | ∃x ¬Dead(x) | |
| | 2. | ¬∃x Dead(x) | |
Counterexample:
Domain: {Ayesha, Beatrice}
Dead : { <Beatrice> }
a : Ayesha ; b : Beatrice
... Dead(b) is true; so the conclusion, ¬∃x Dead(x), is false
... and ¬Dead(a) is true; so the premise, ∃x ¬Dead(x), is true
9.12
9.18--9.19
No lectures or seminars in reading week (Week 6).