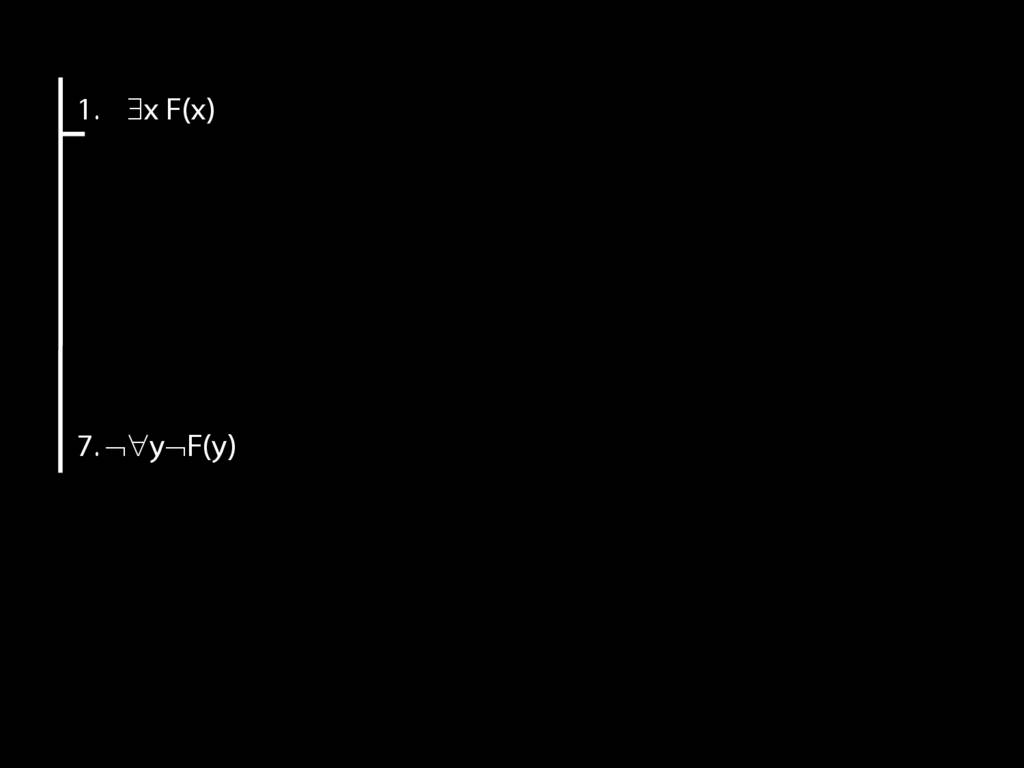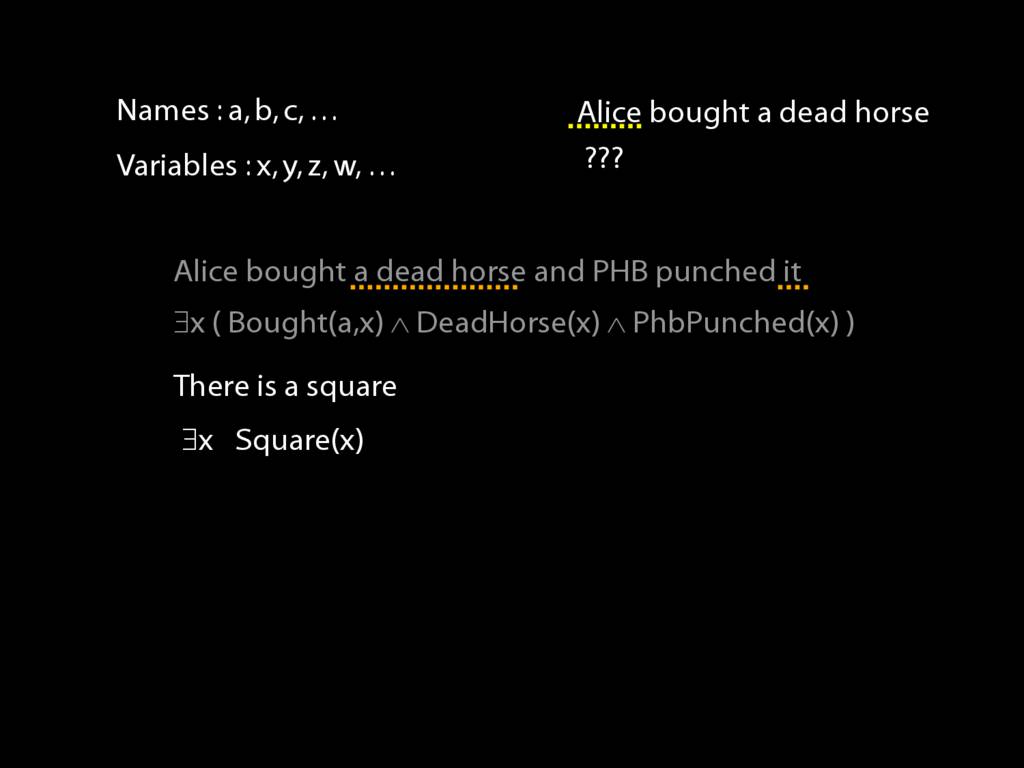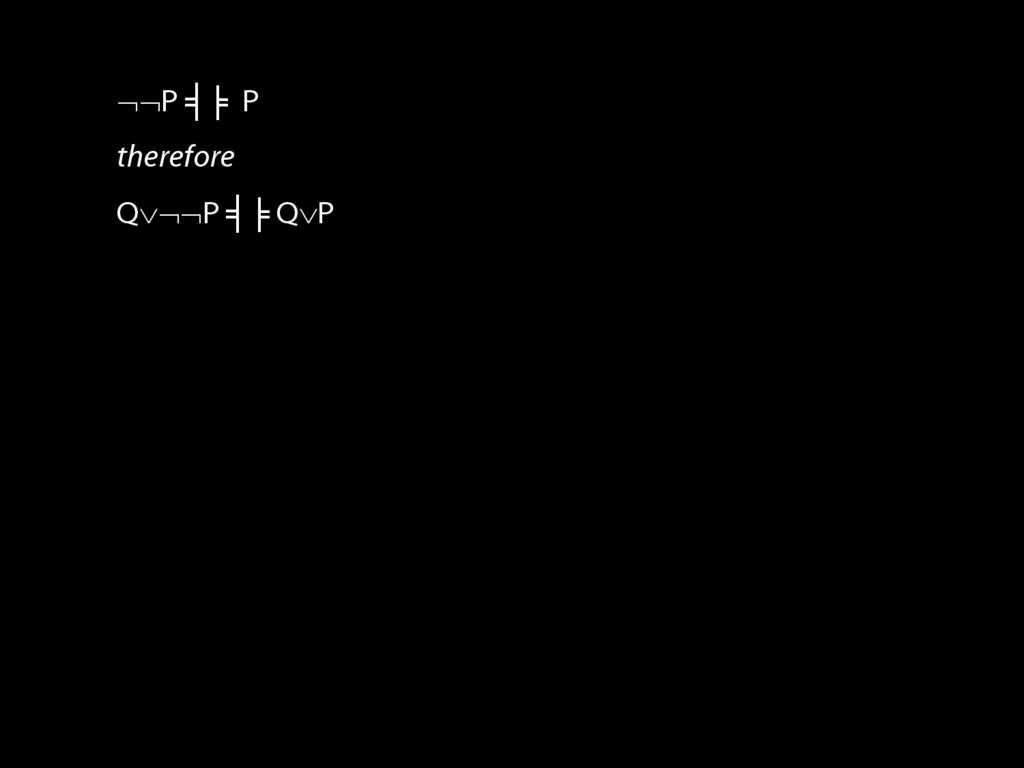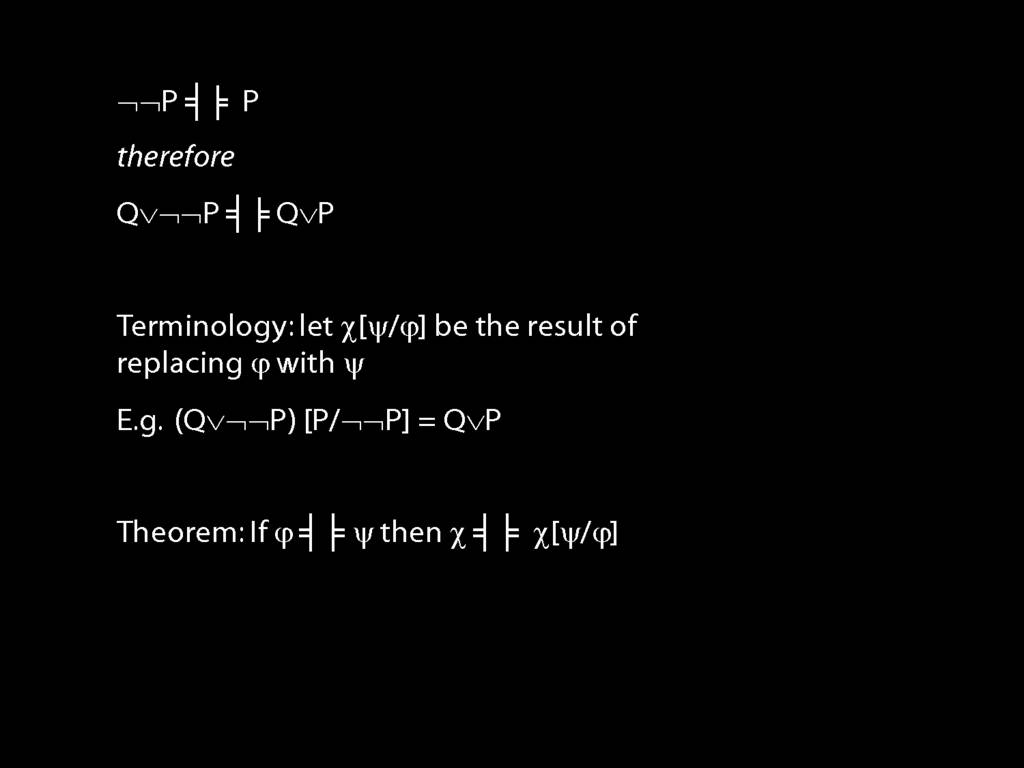Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

13.12, 13.14, 13.16
\title {Logic I \\ Fast Lecture 06}
 
\maketitle
 

Logic I

Fast Lecture 06

\def \ititle {Logic I}
\def \isubtitle {Fast Lecture 06}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
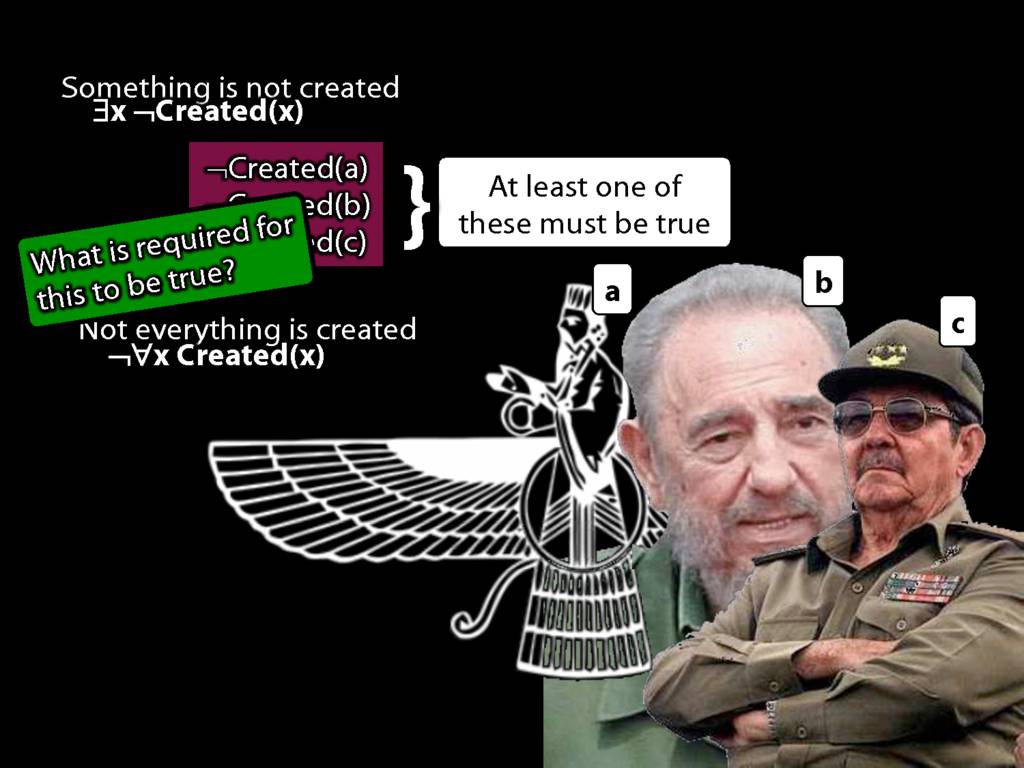
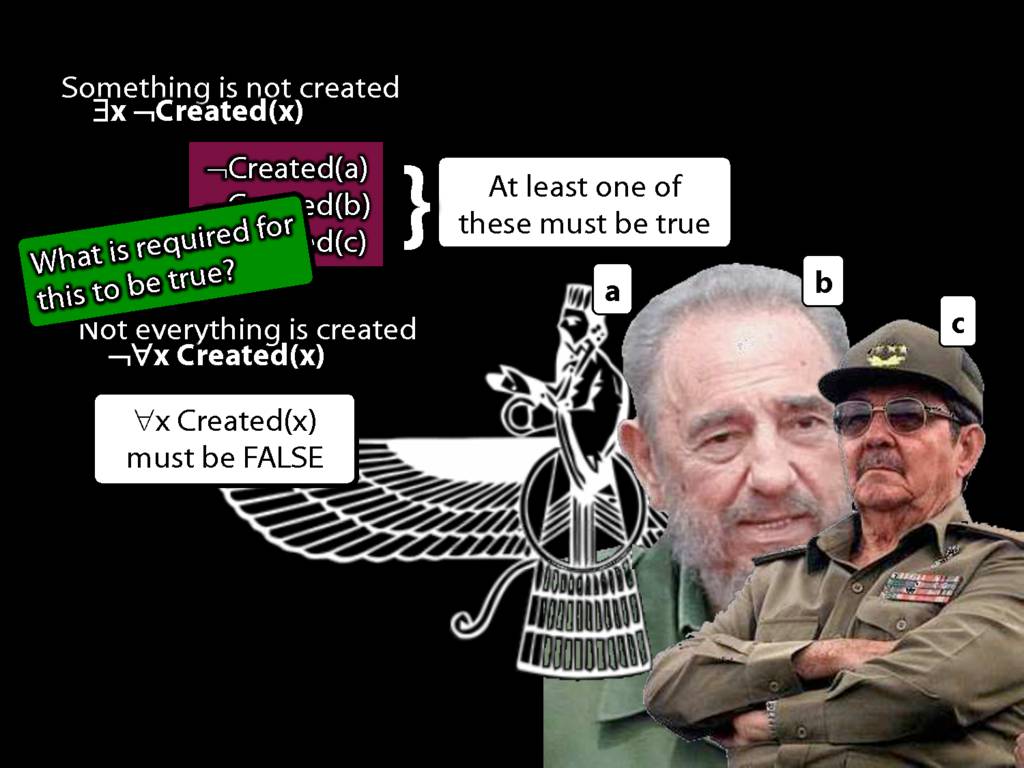
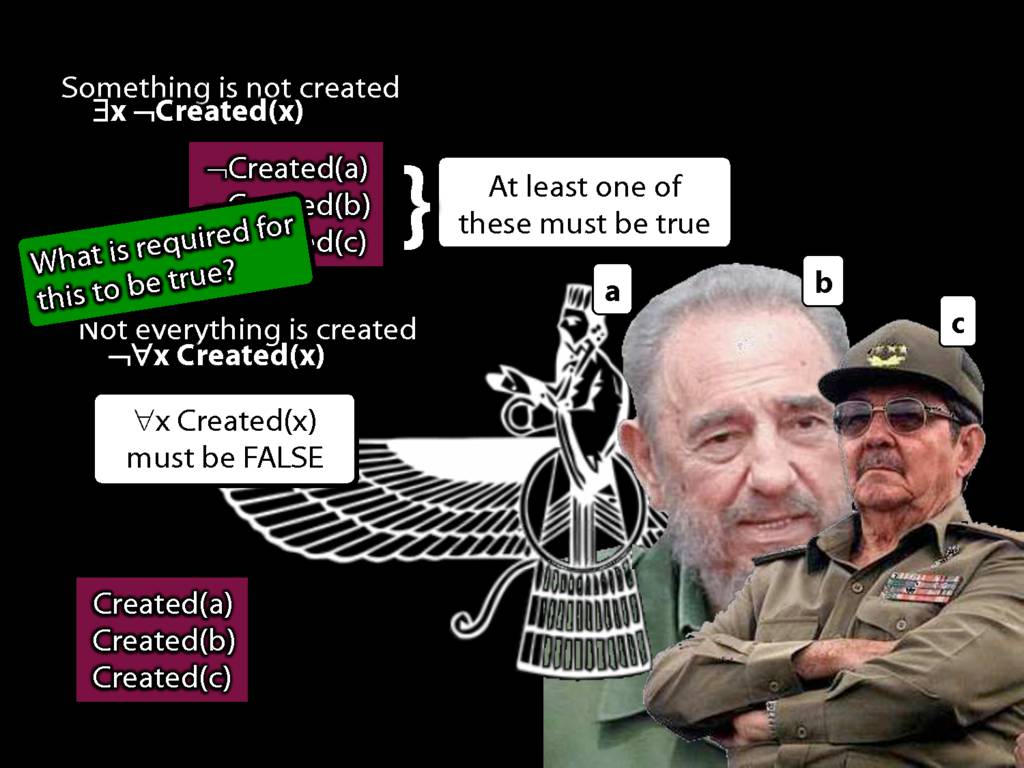
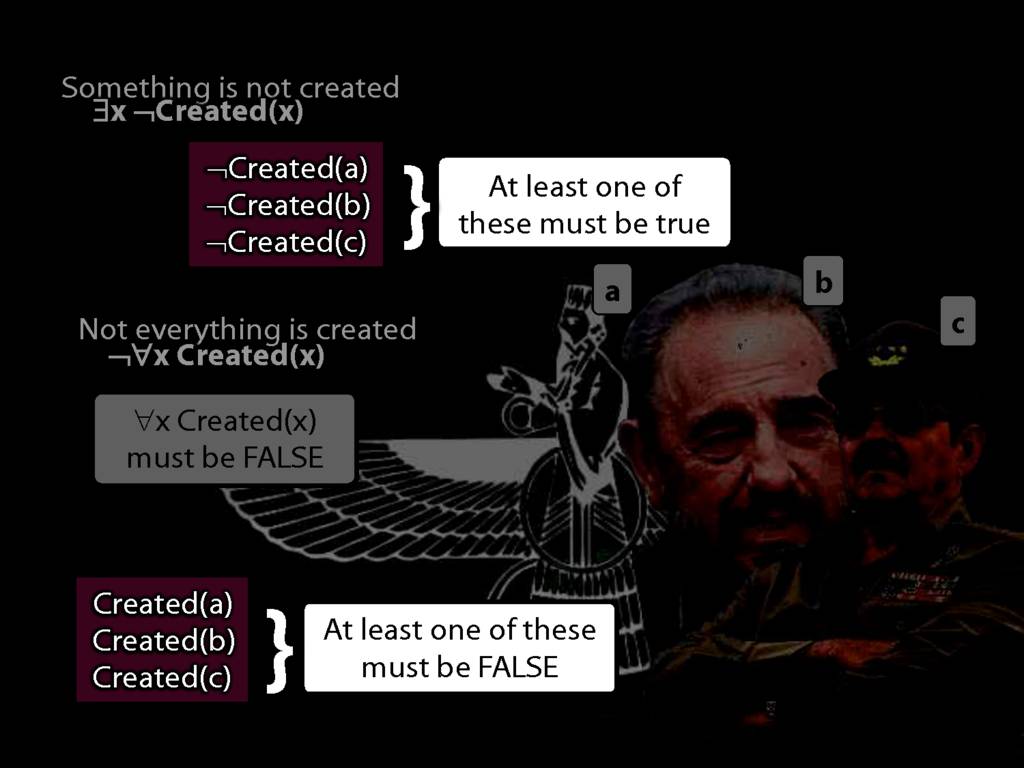
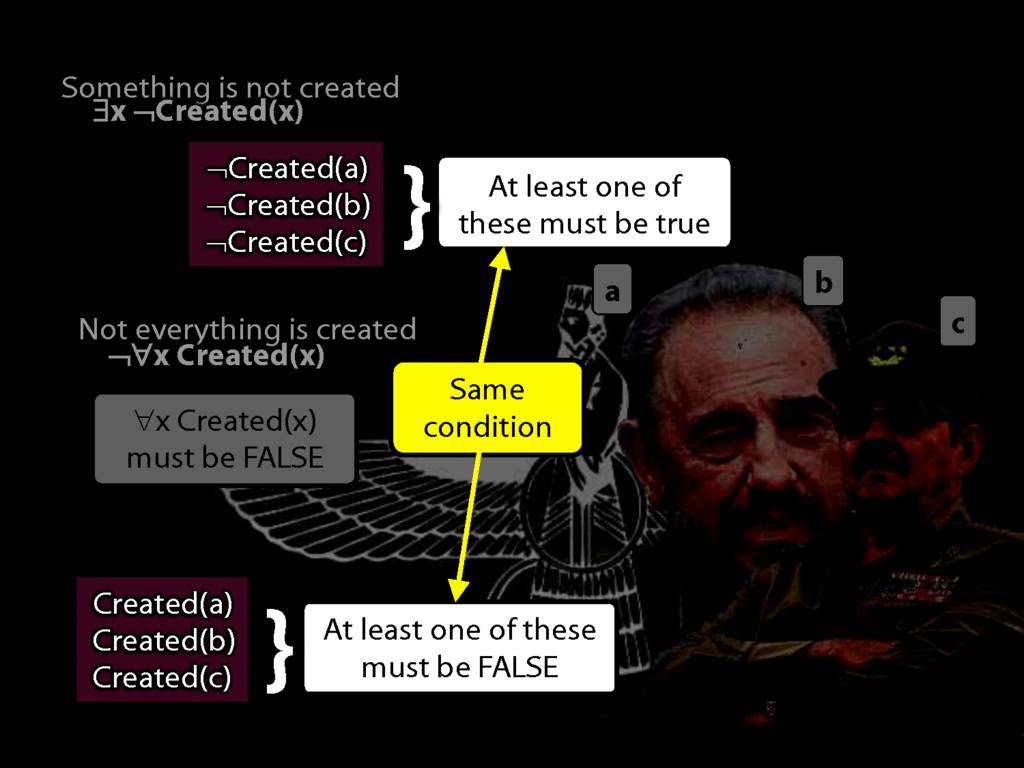
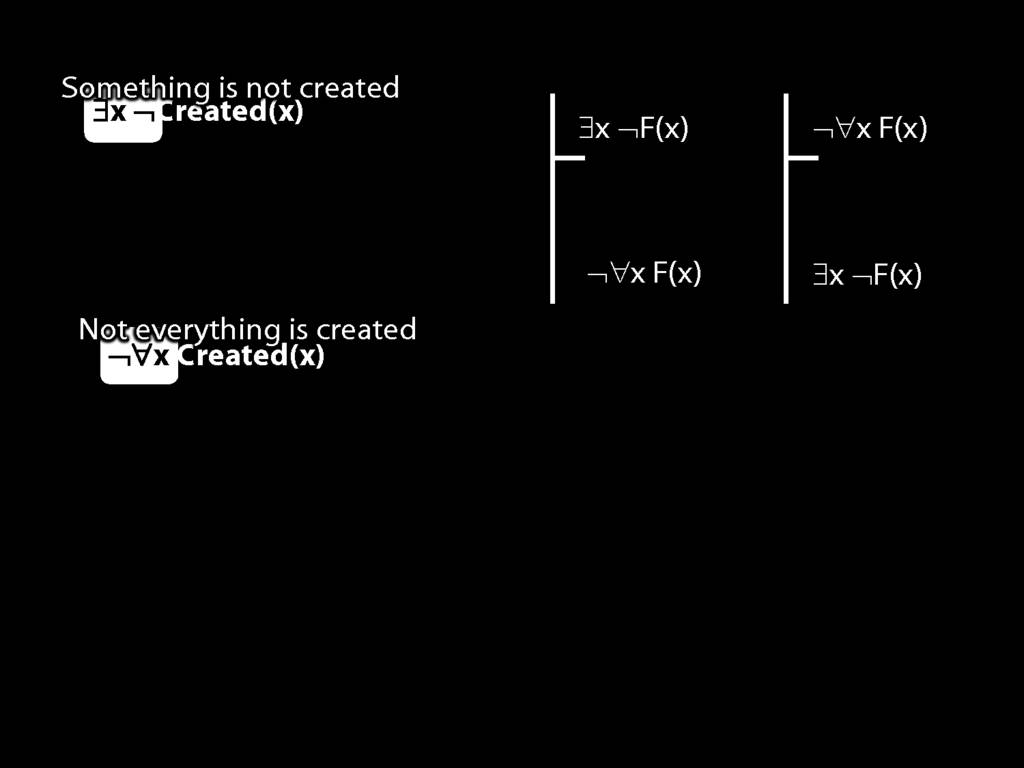
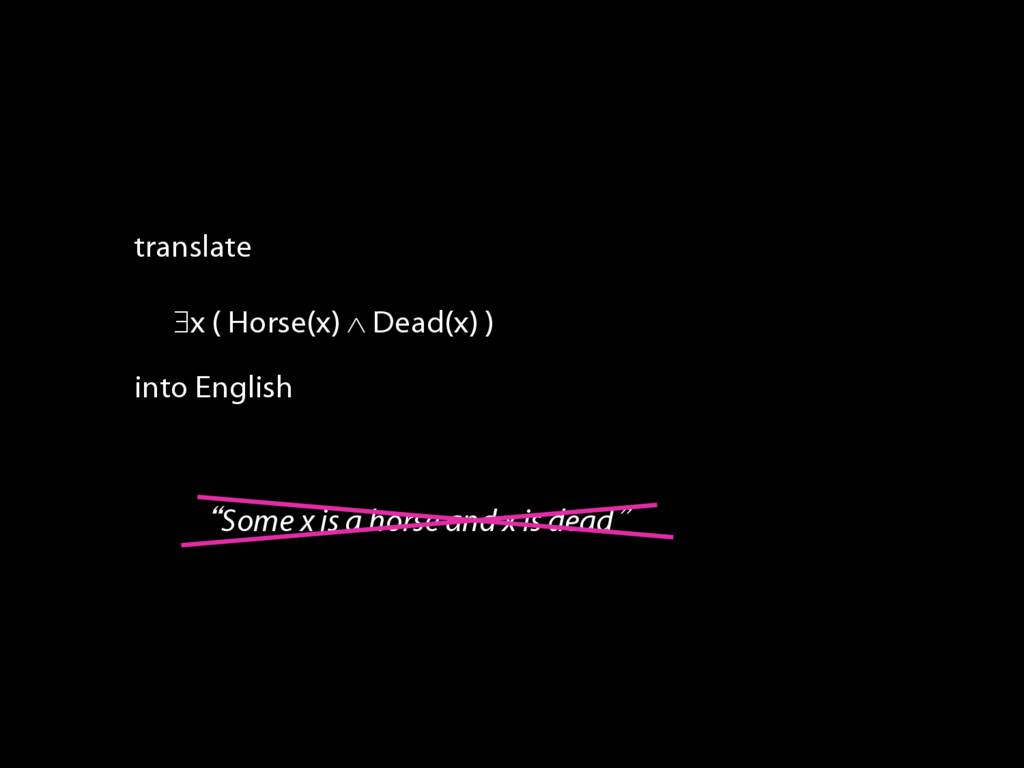
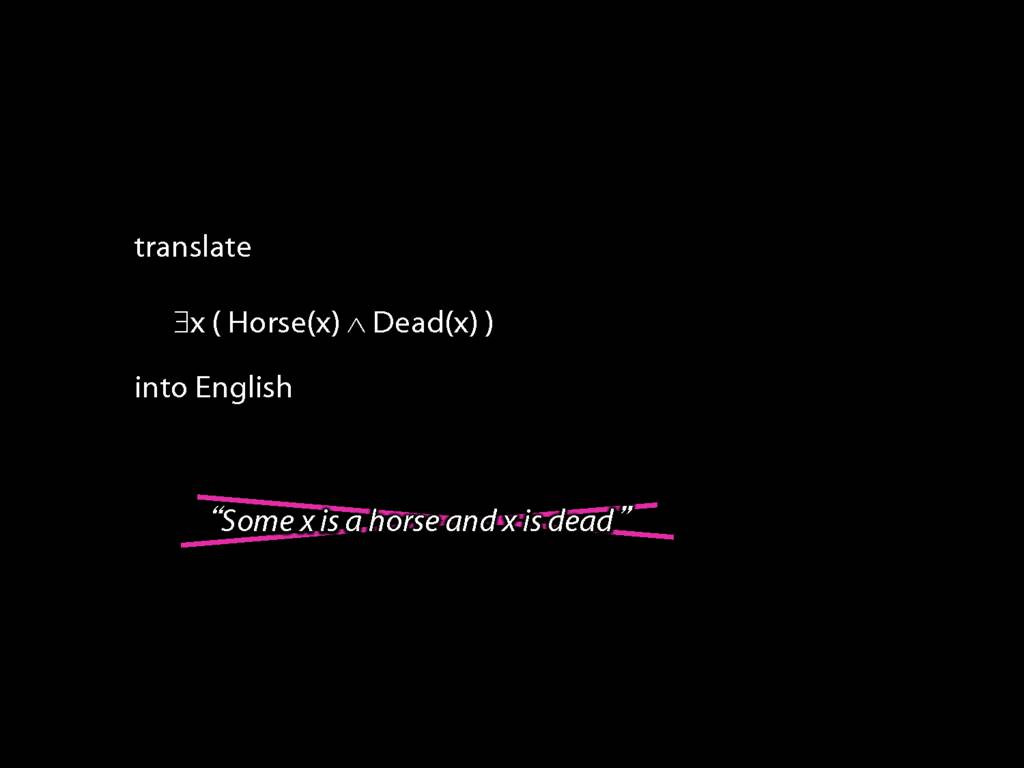
\section{Quantifier Equivalences: ¬∀x Created(x) ⫤⊨ ∃x ¬Created(x)}
\emph{Reading:} §10.1, §10.3, §10.4
 
\section{Quantifier Equivalences: ¬∀x Created(x) ⫤⊨ ∃x ¬Created(x)}
 

Proof Example: ∃x Dead(x) ⊢ ¬∀x¬ Dead(x).

 
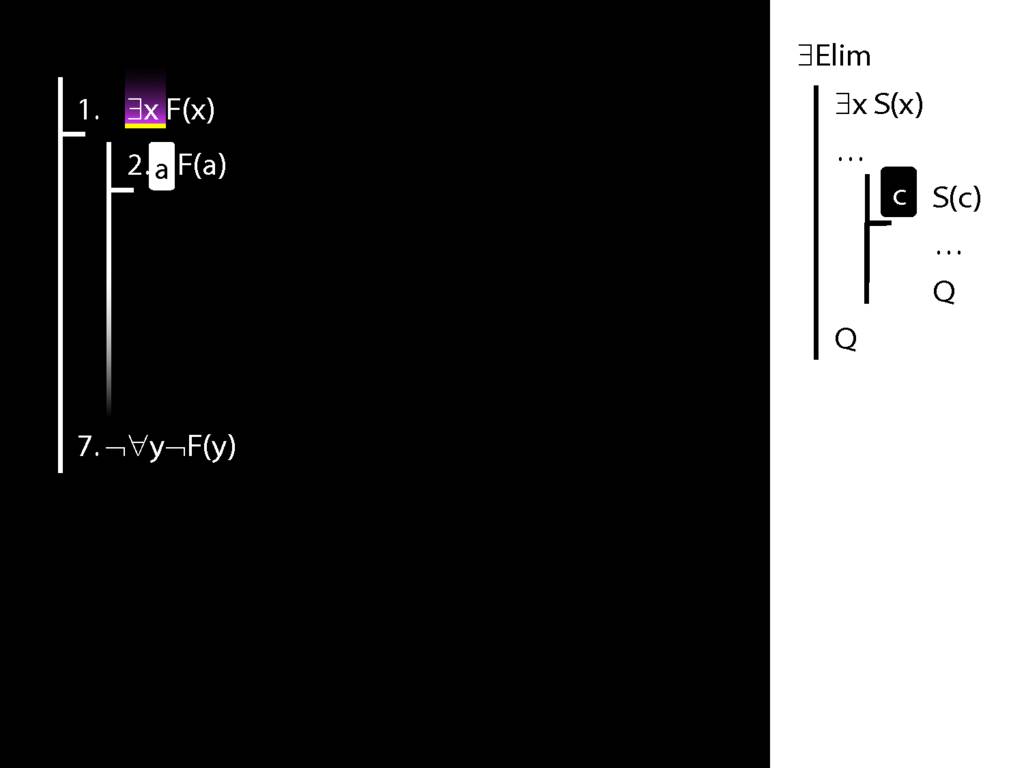
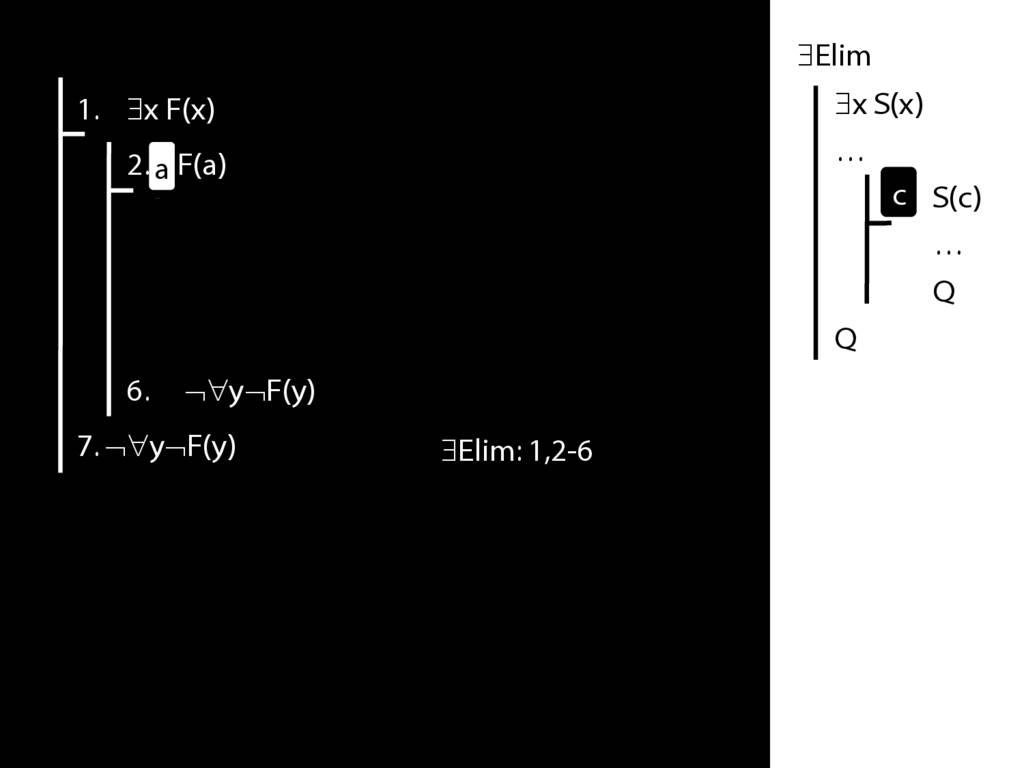
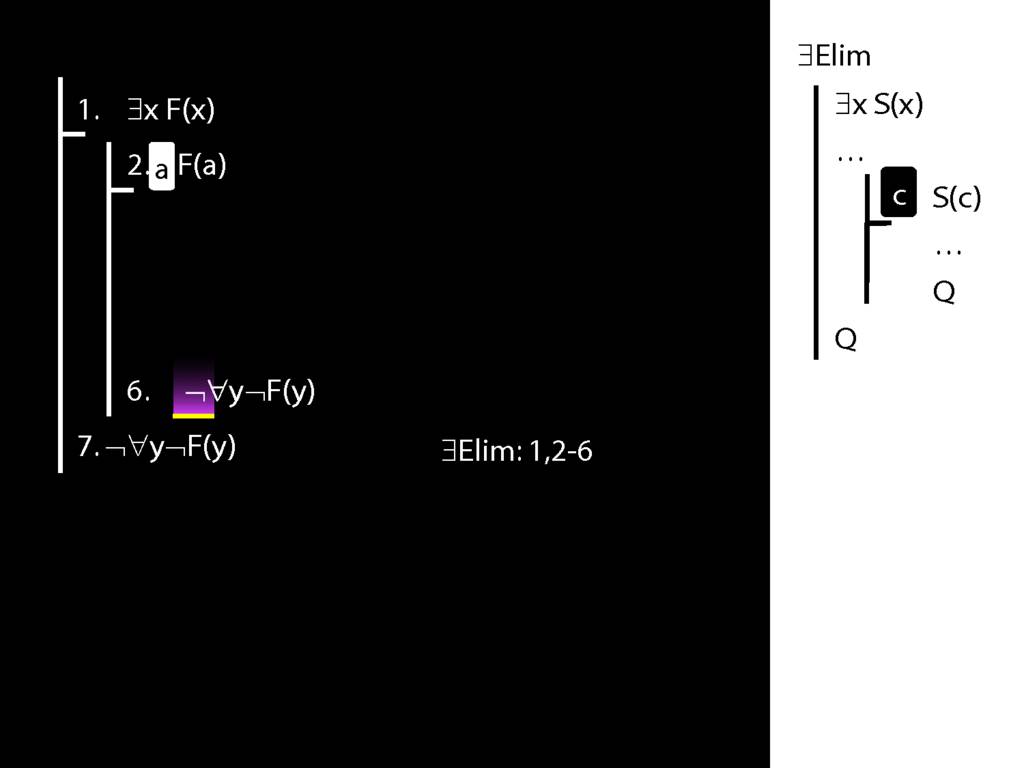
\section{Proof Example: ∃x Dead(x) ⊢ ¬∀x¬ Dead(x).}
 
\section{Proof Example: ∃x Dead(x) ⊢ ¬∀x¬ Dead(x).}
13.43--13.45
 

Proof Example: ¬∀x Dead(x) ⊢ ∃x¬ Dead(x).

 
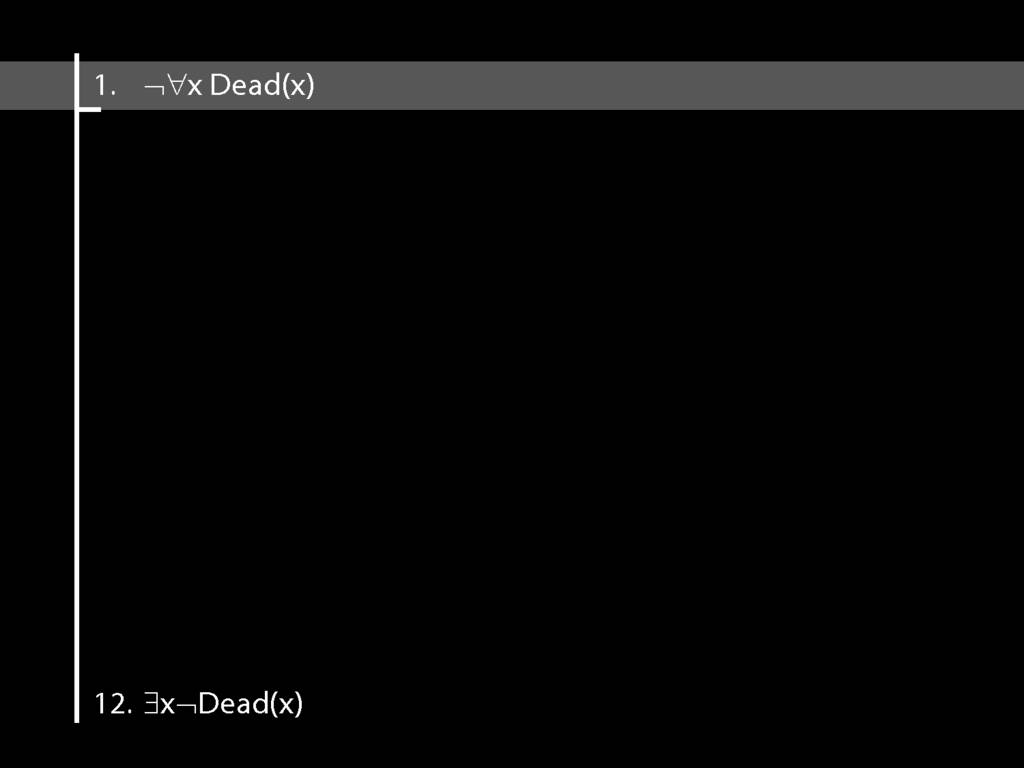
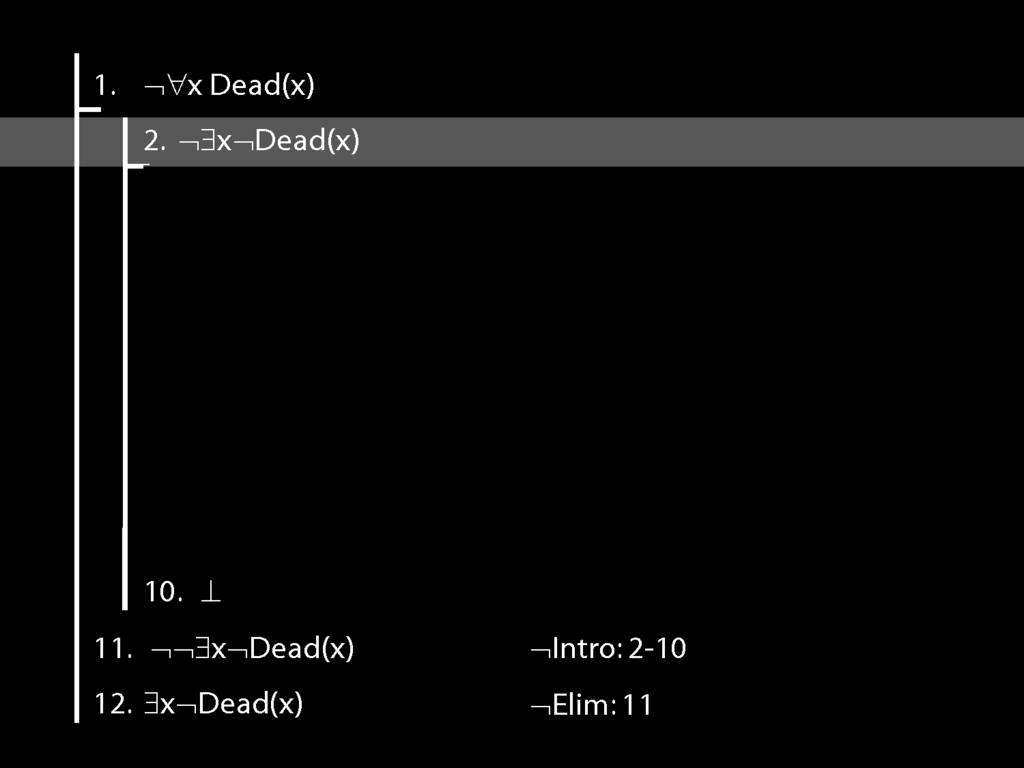
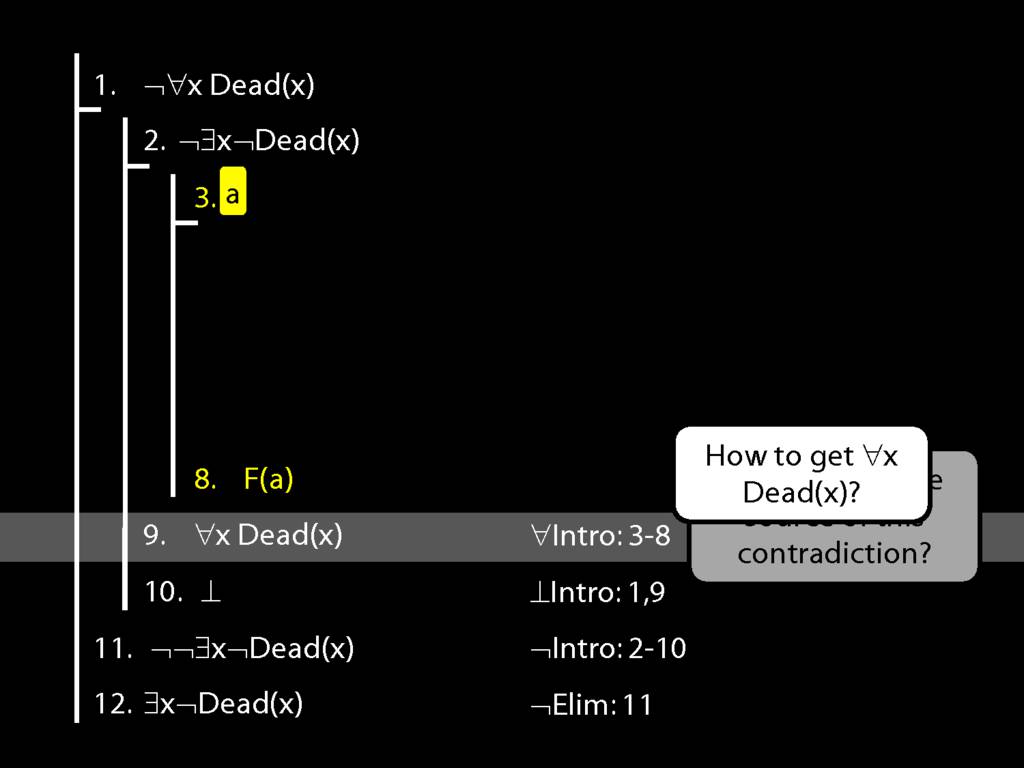
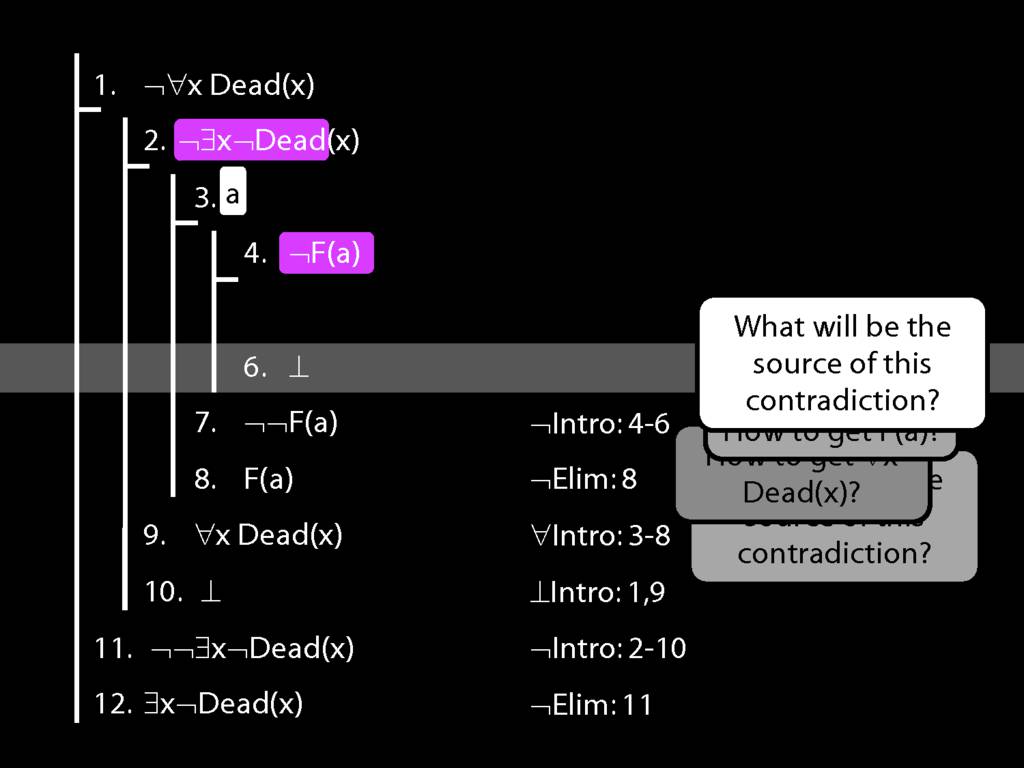
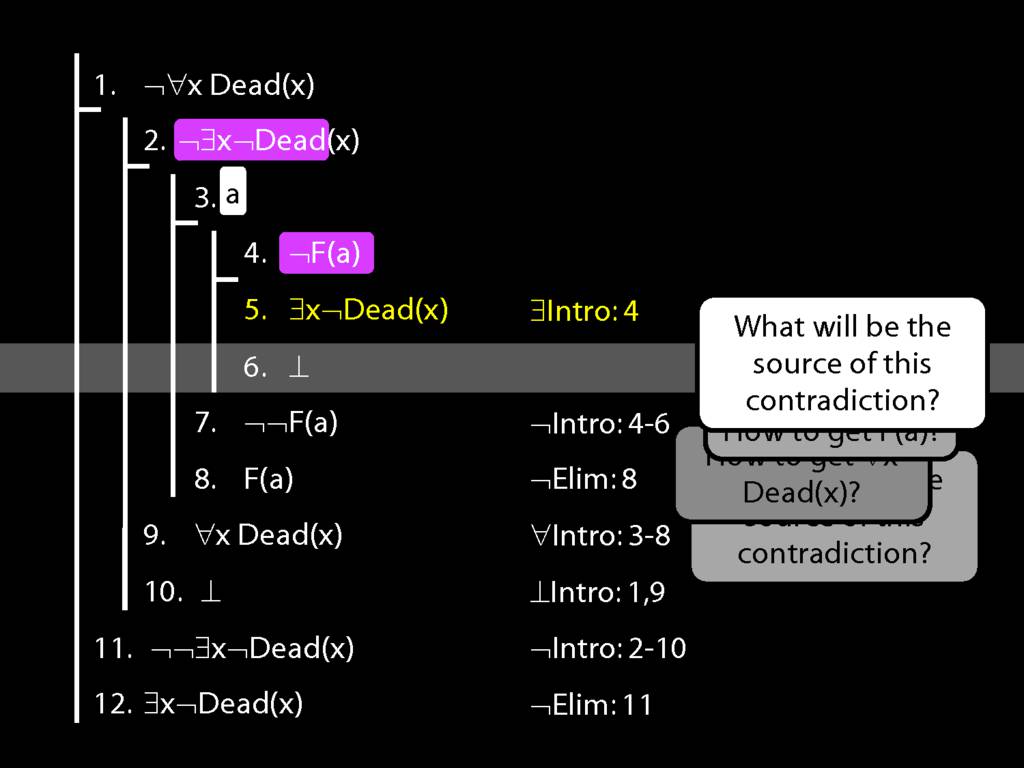
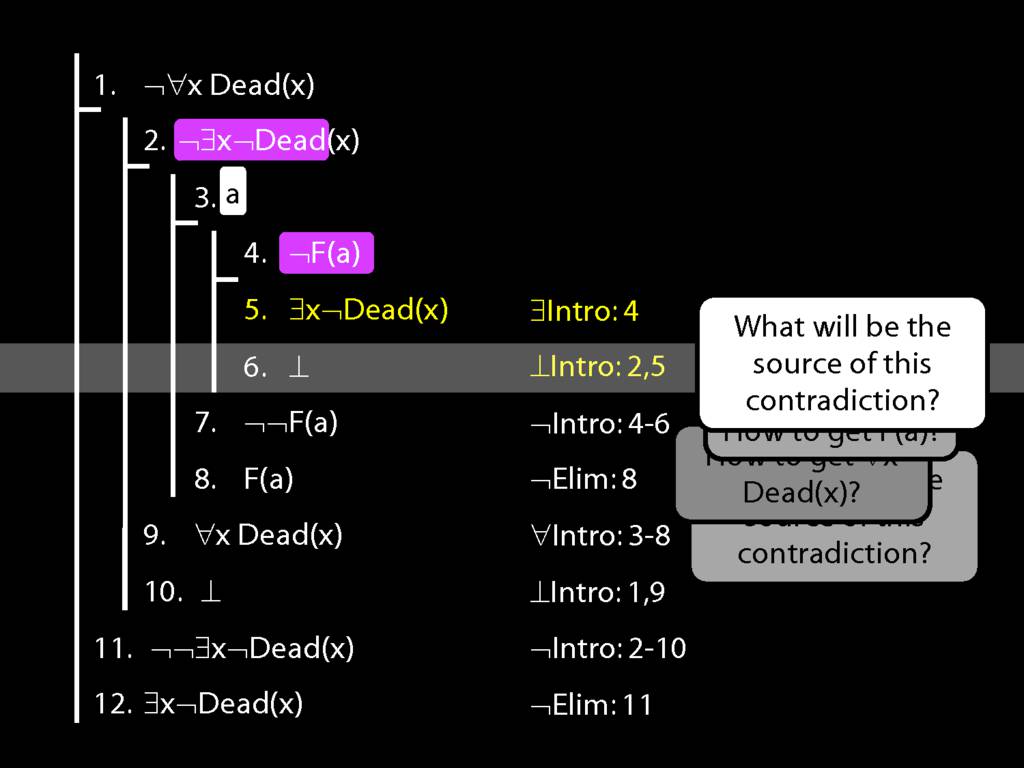
\section{Proof Example: ¬∀x Dead(x) ⊢ ∃x¬ Dead(x).}
 
\section{Proof Example: ¬∀x Dead(x) ⊢ ∃x¬ Dead(x).}
13.49--13.50
 

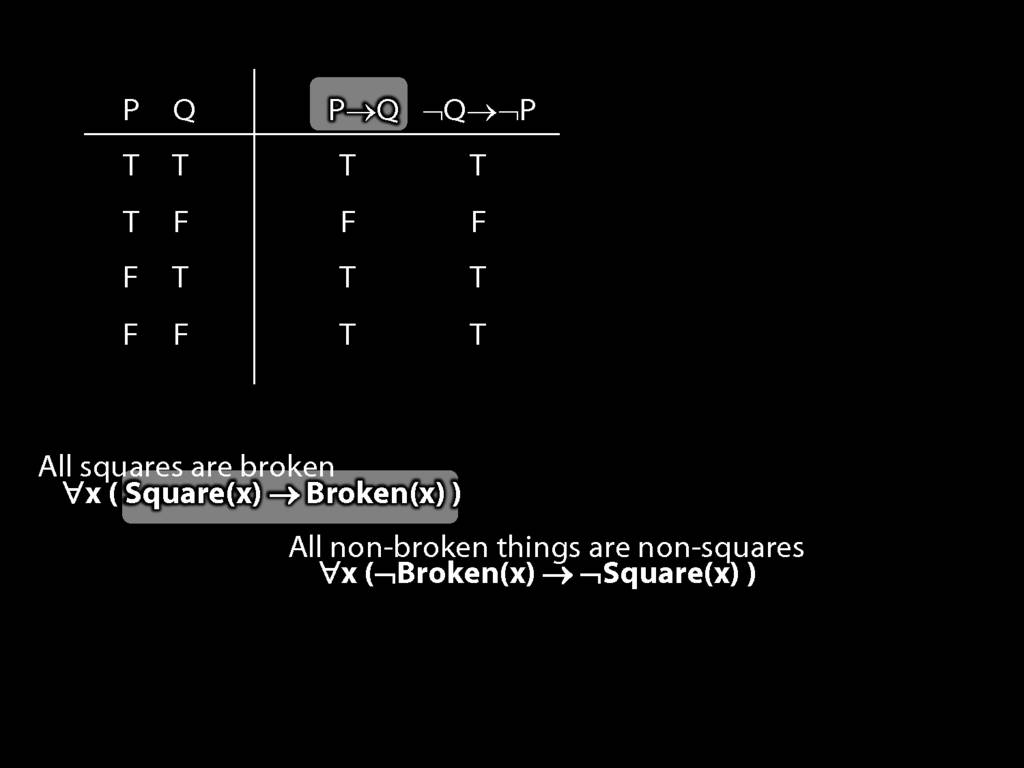
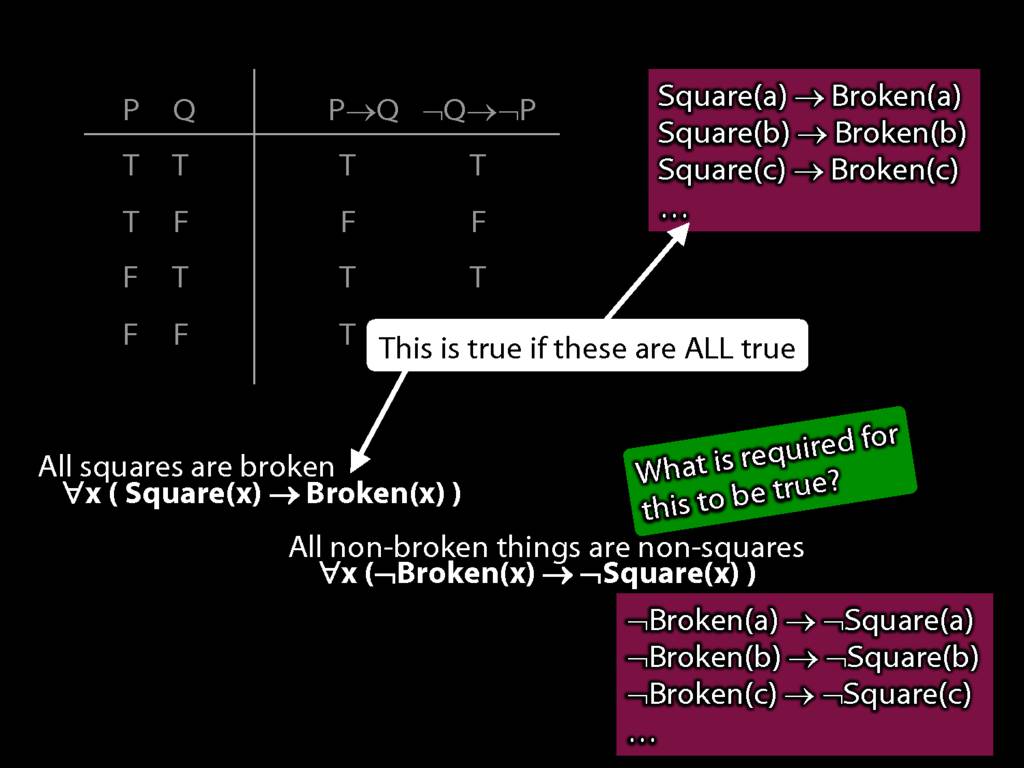
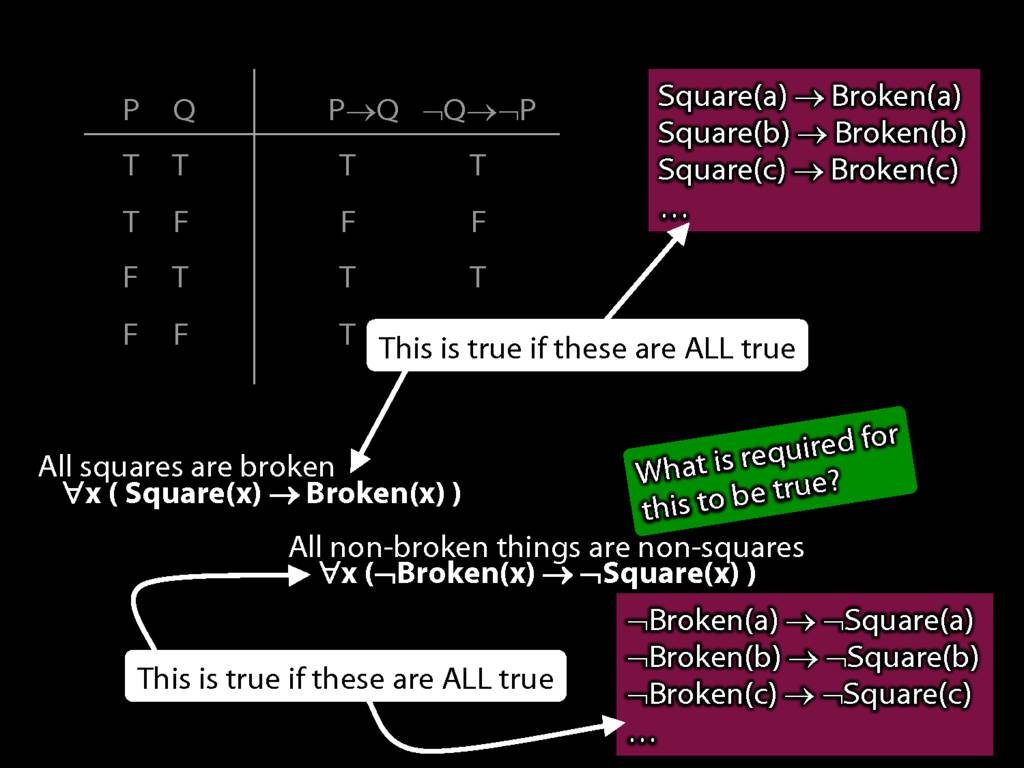
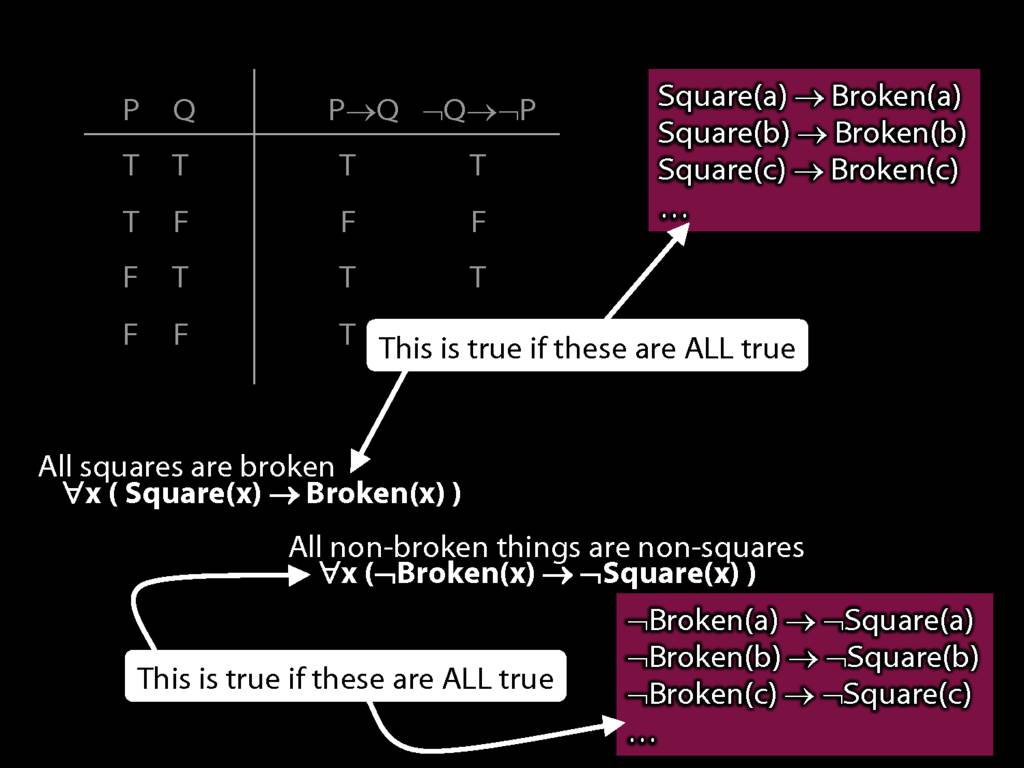
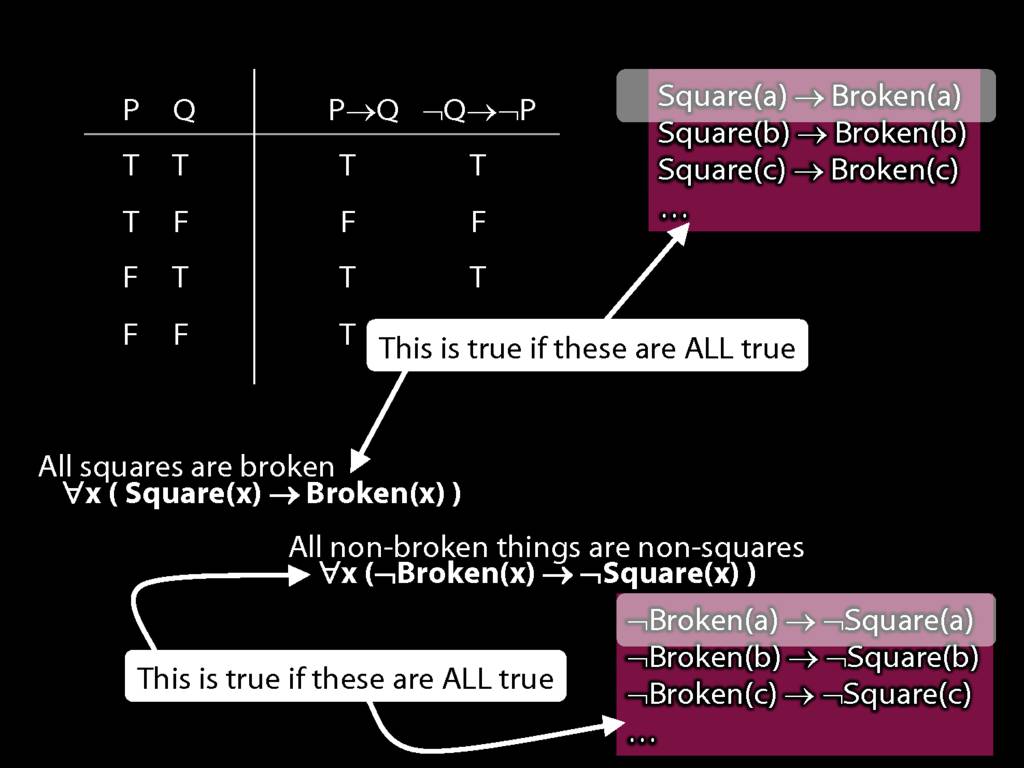
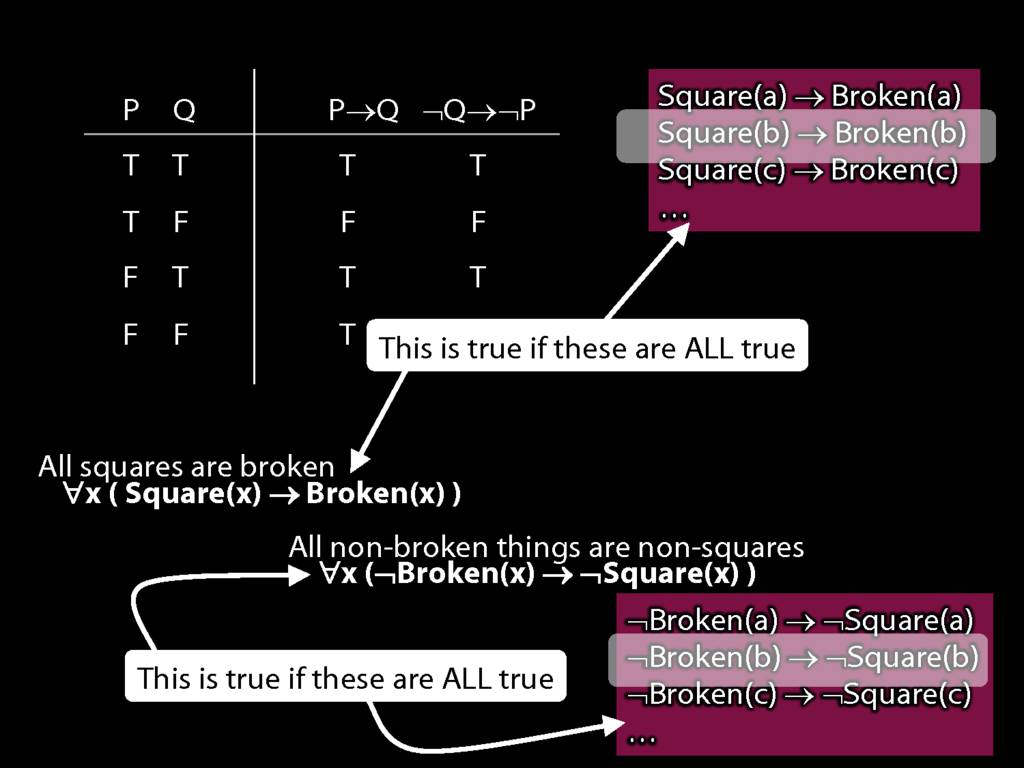
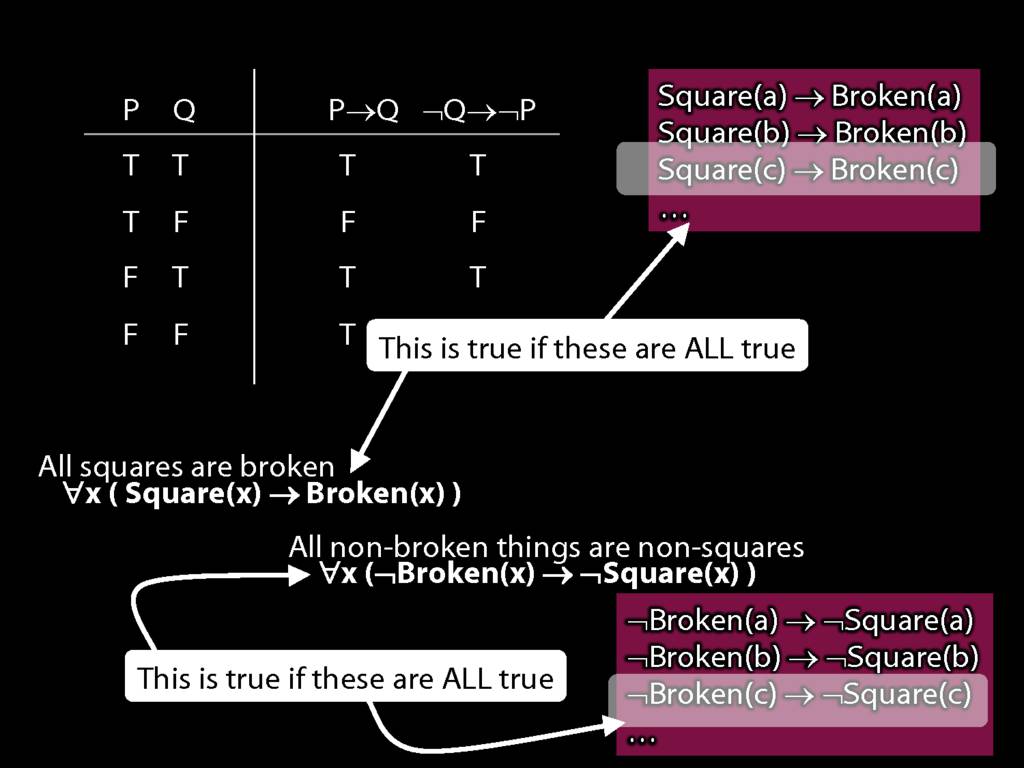
Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))

 
\section{Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))}
\emph{Reading:} §10.3
 
\section{Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))}
10.20, 10.22
 

Two Things Are Broken

 
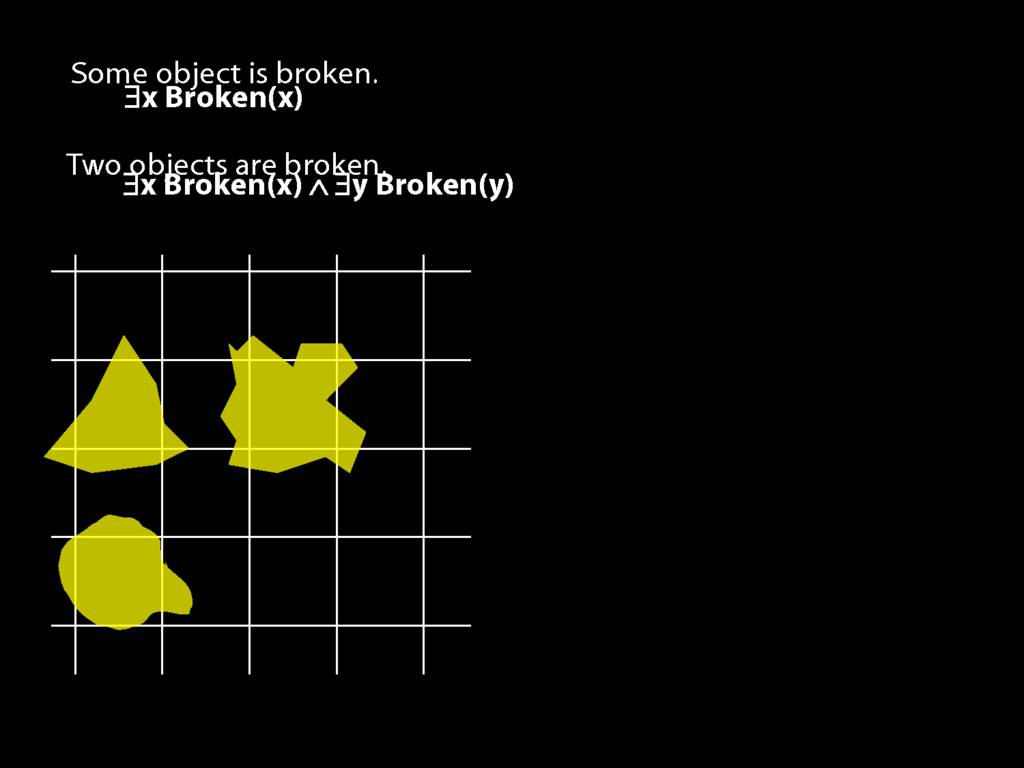
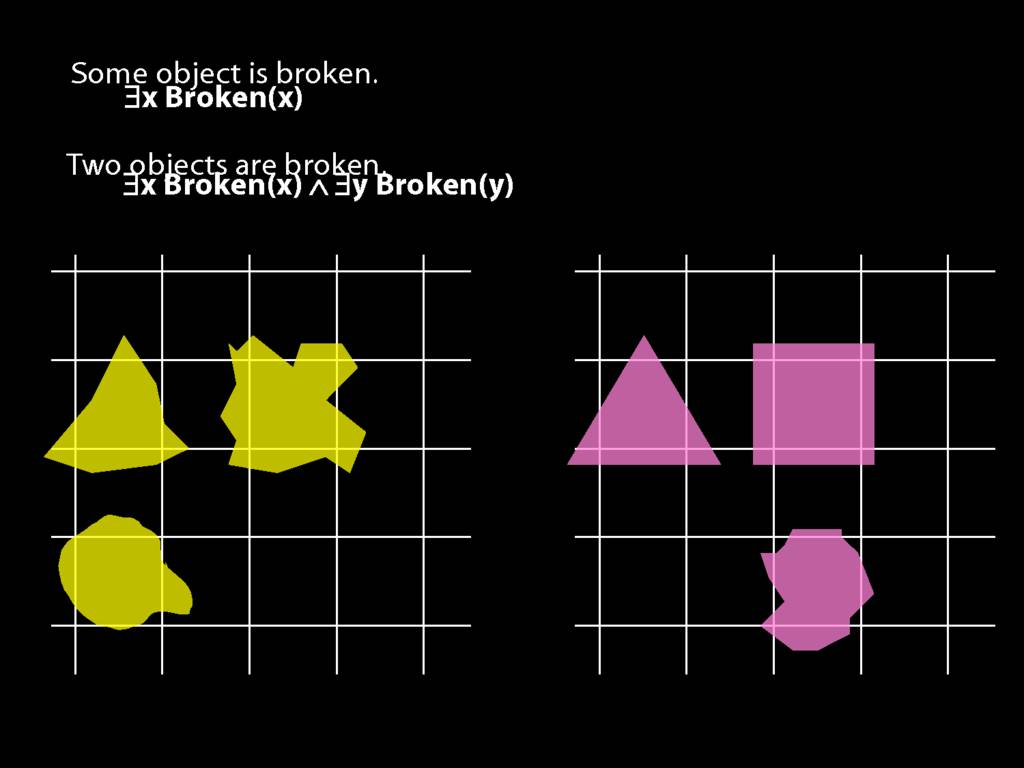
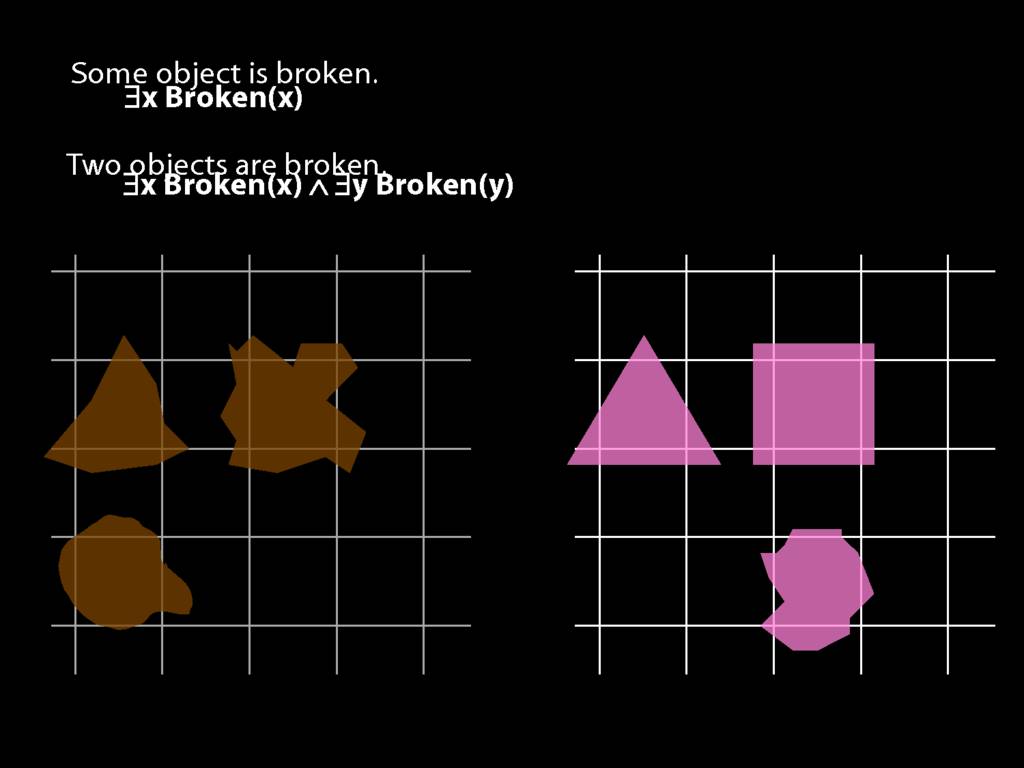
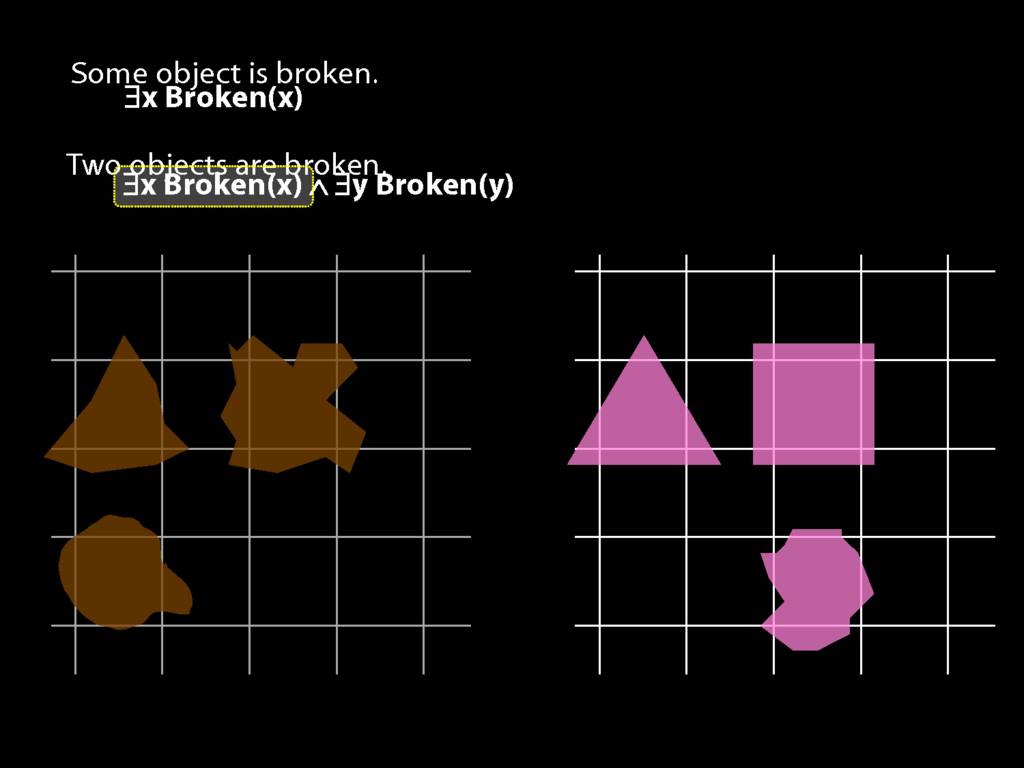
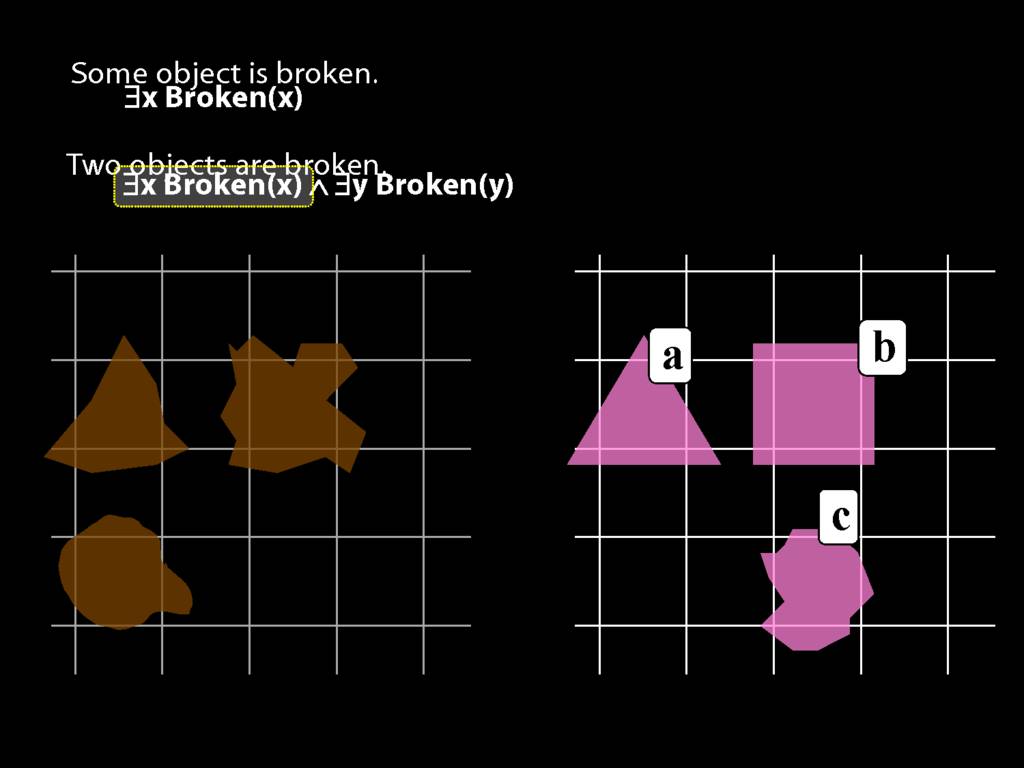
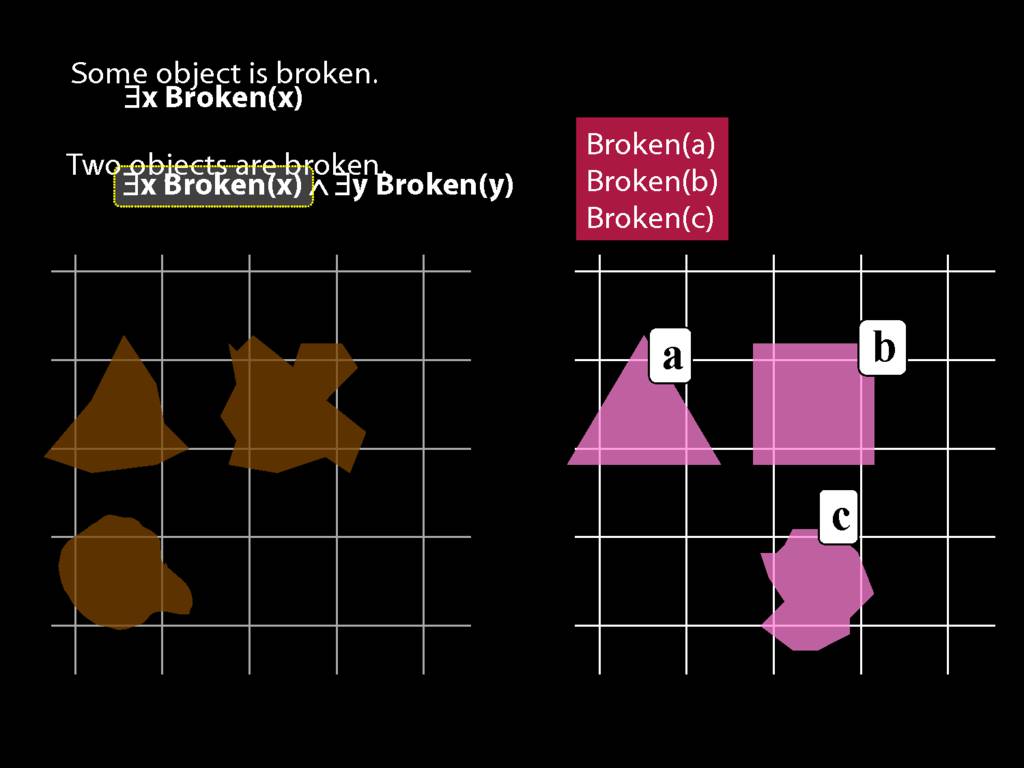
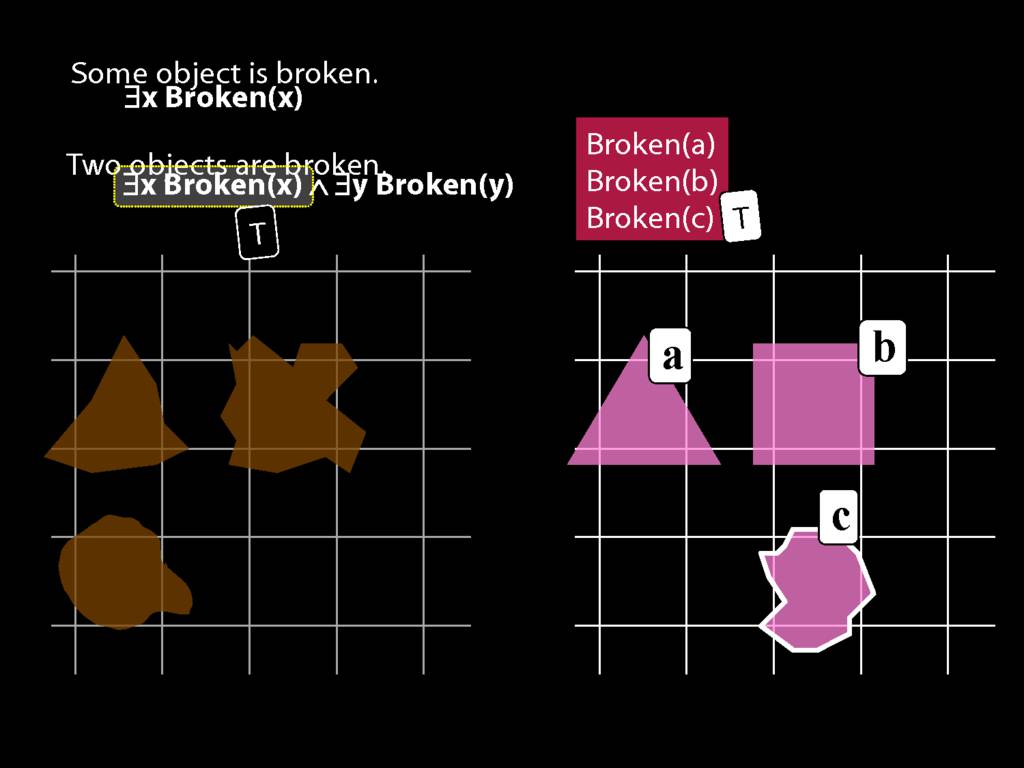
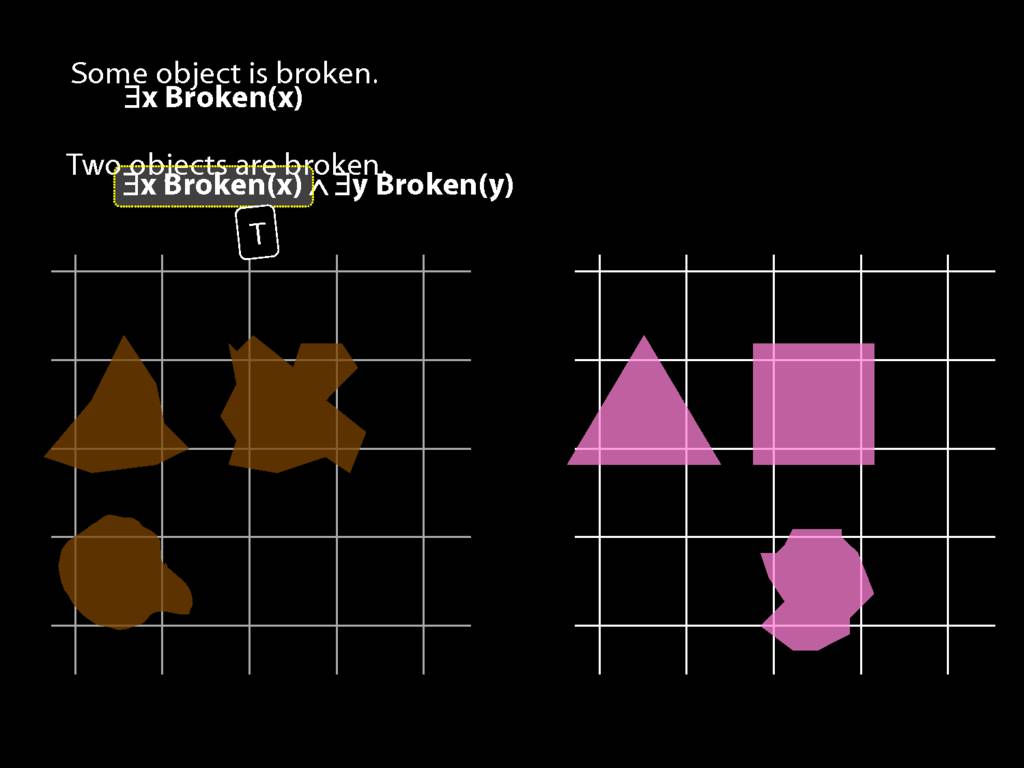
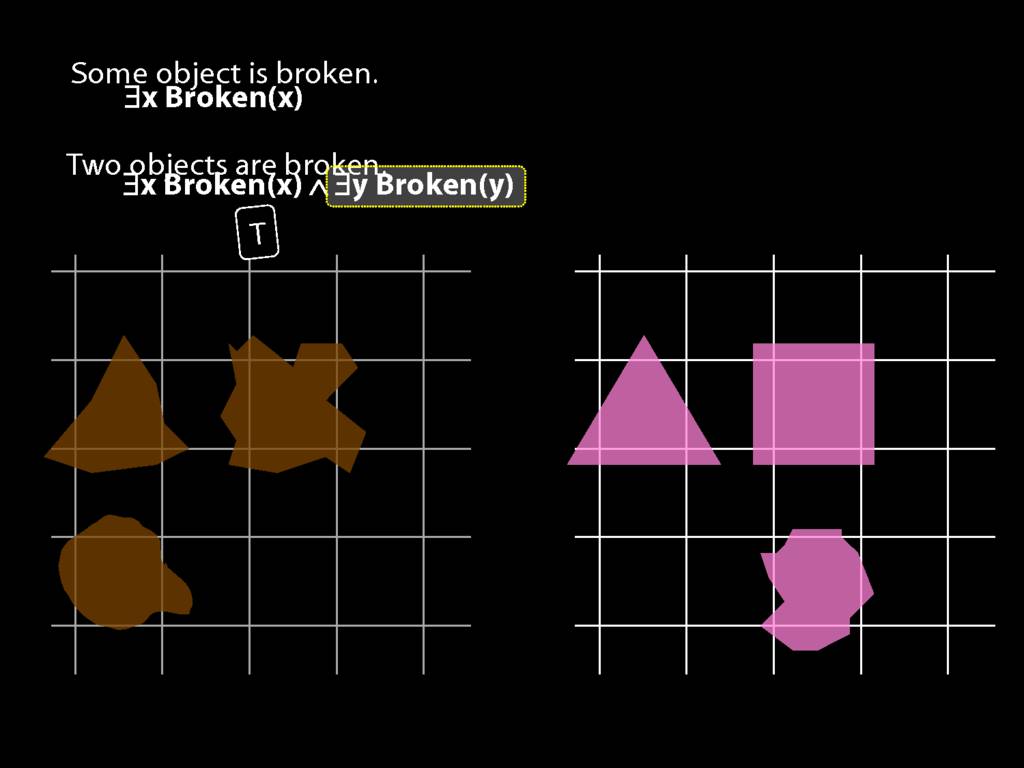
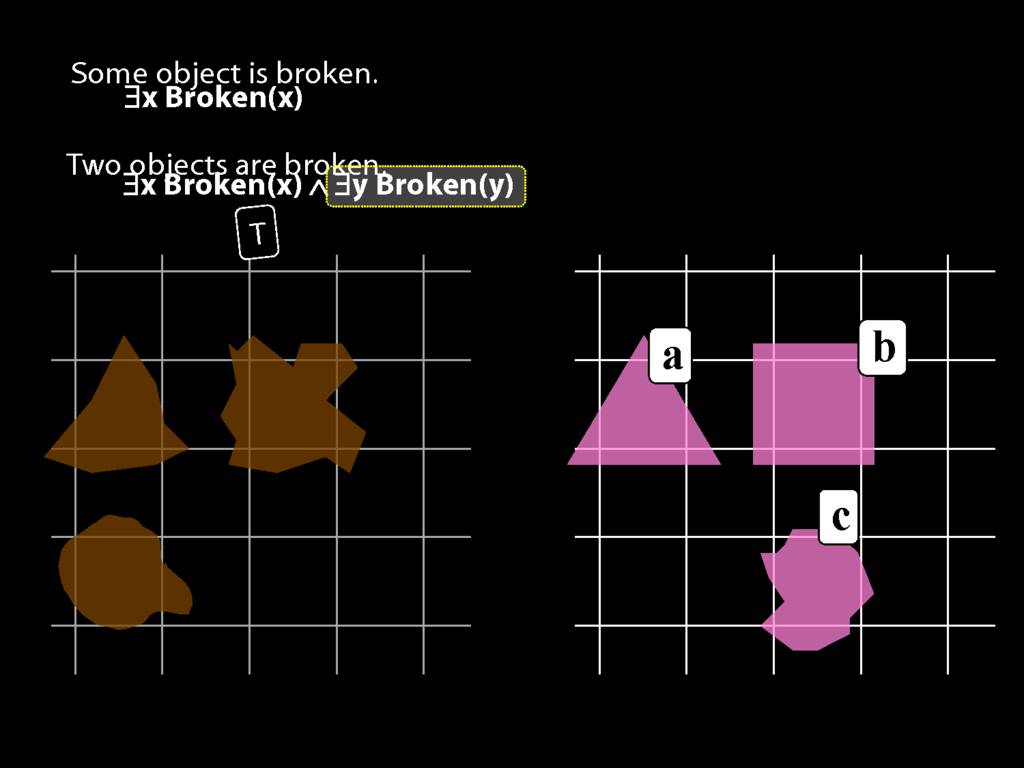
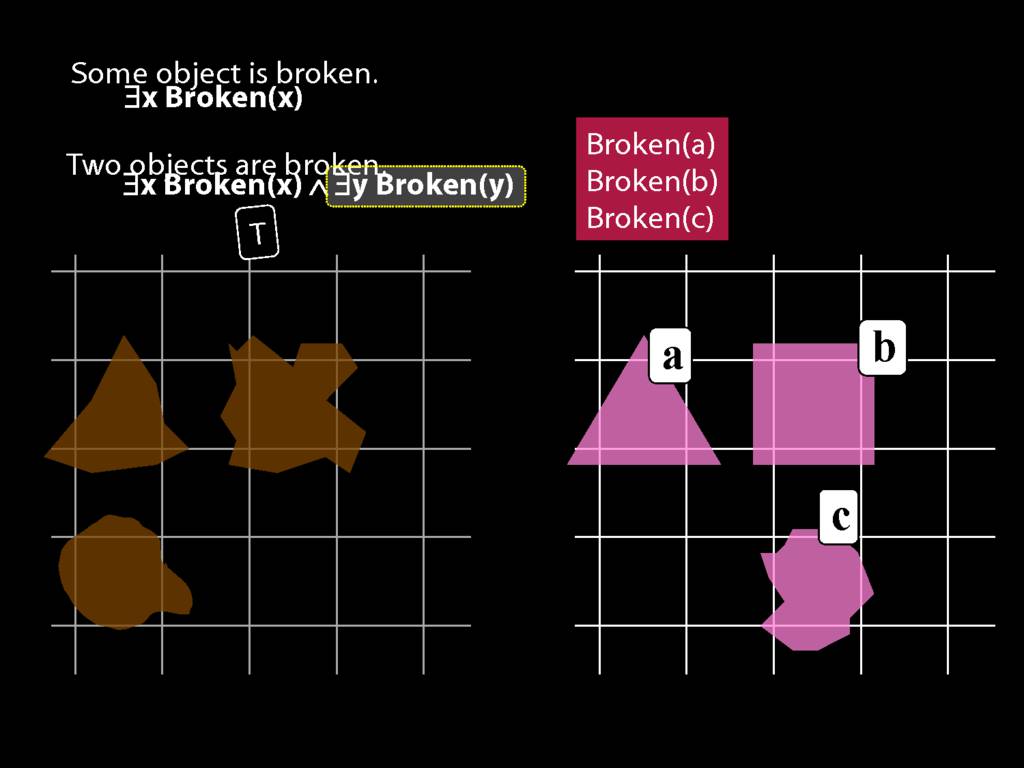
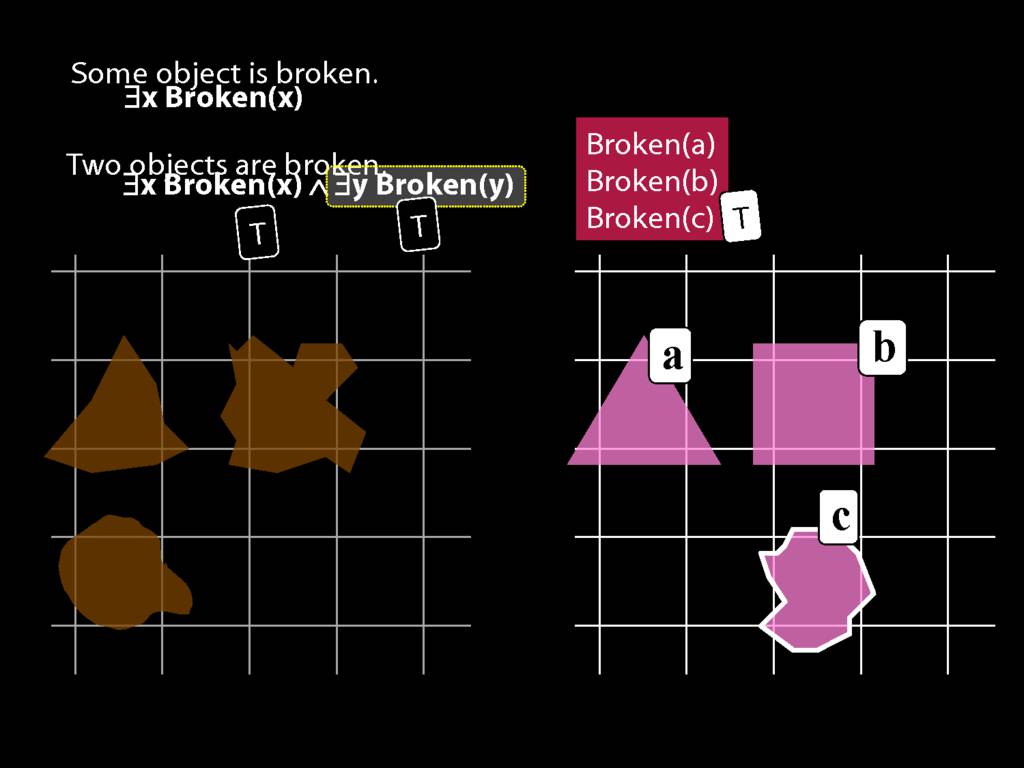
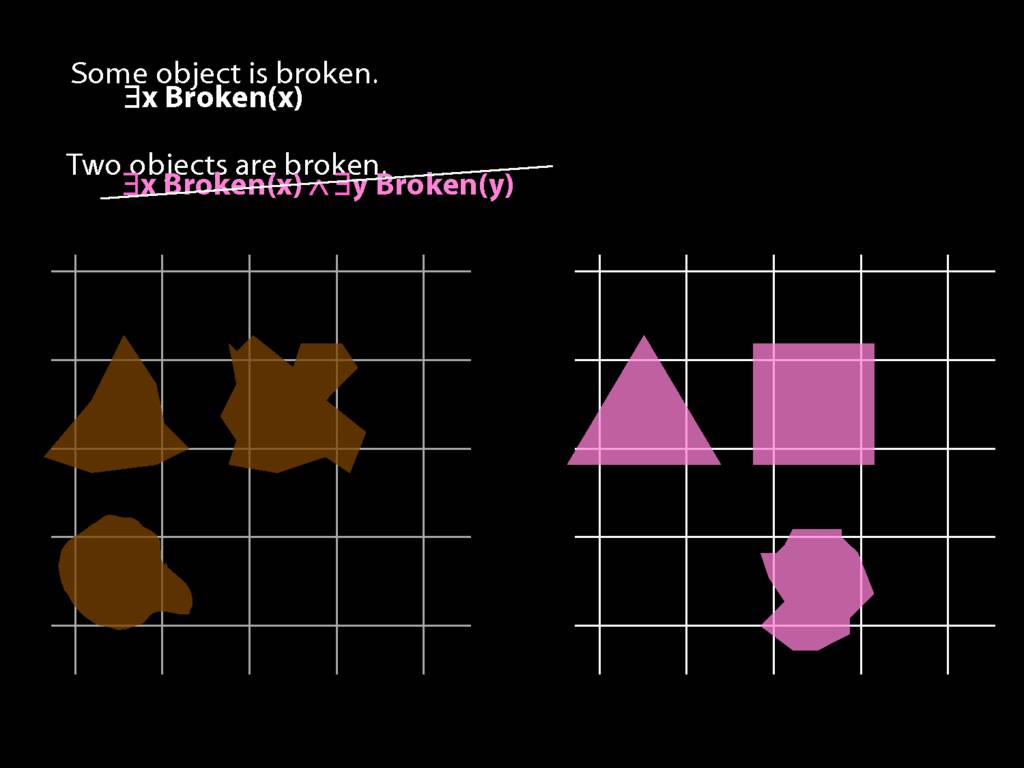
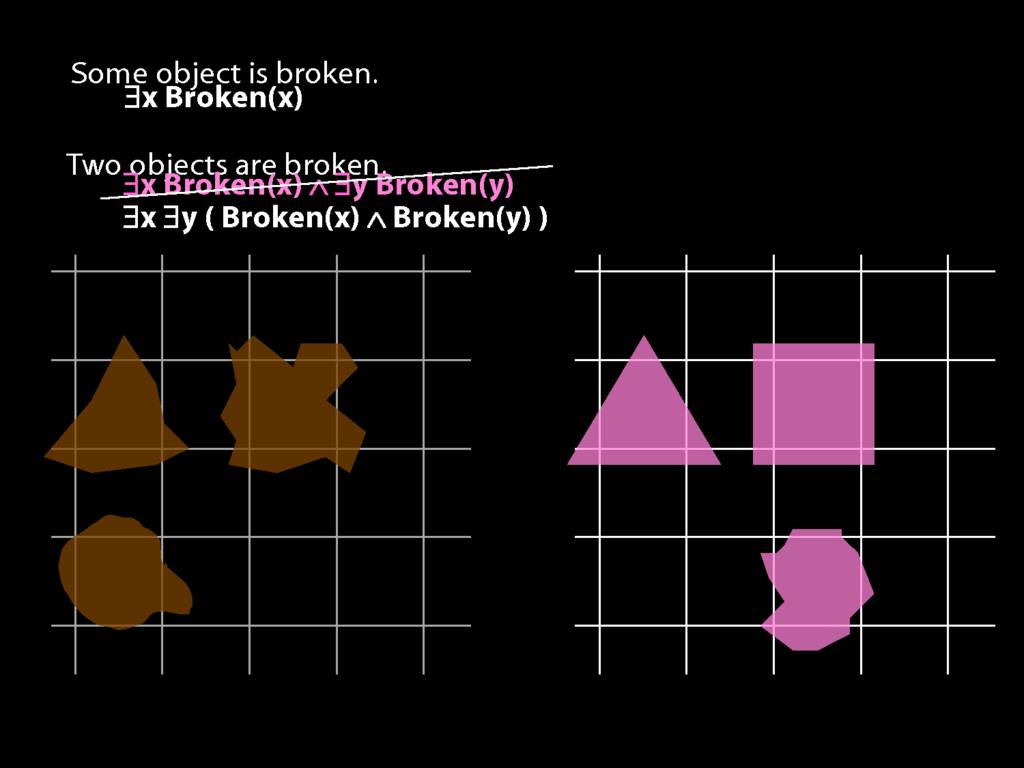
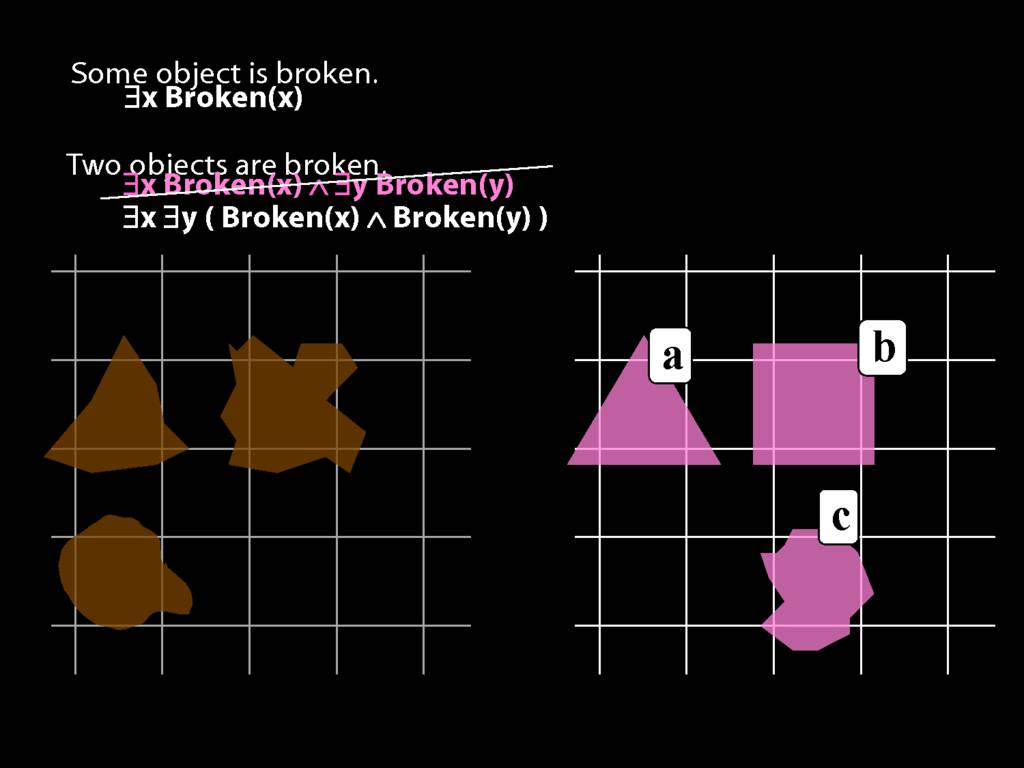
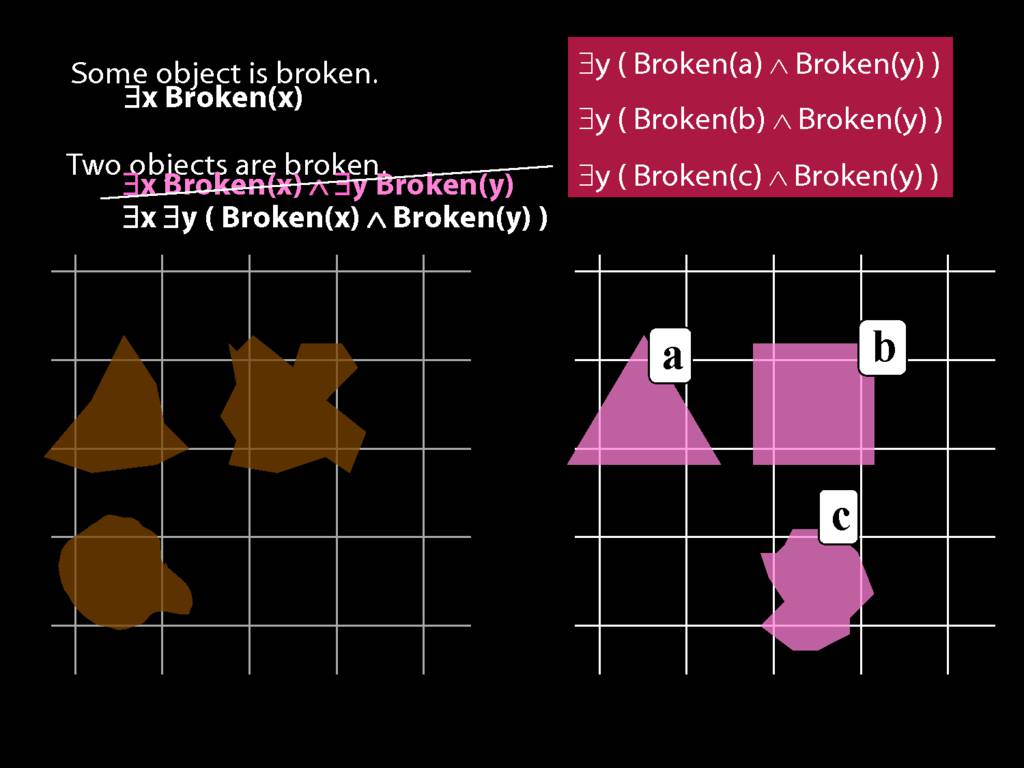
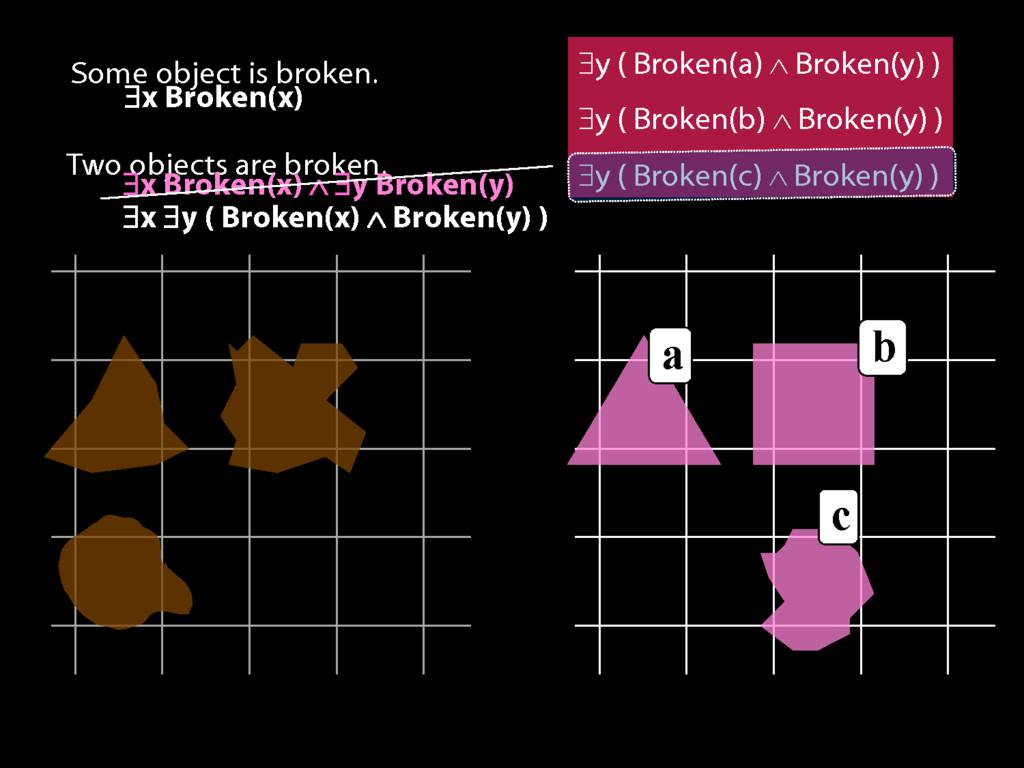
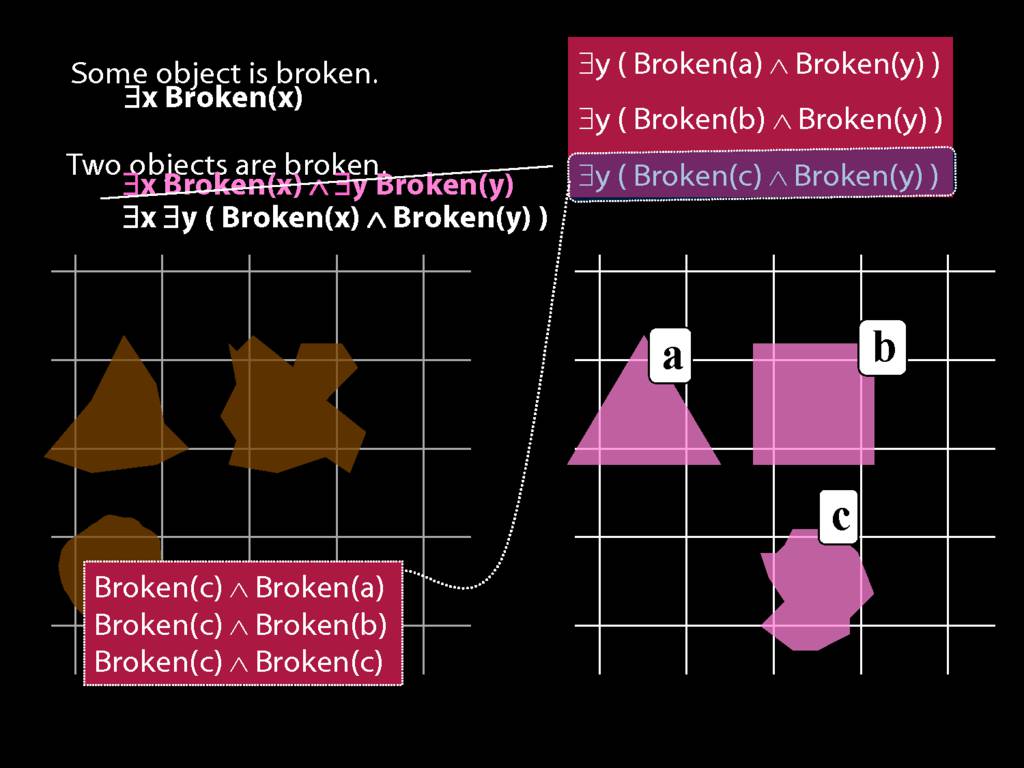
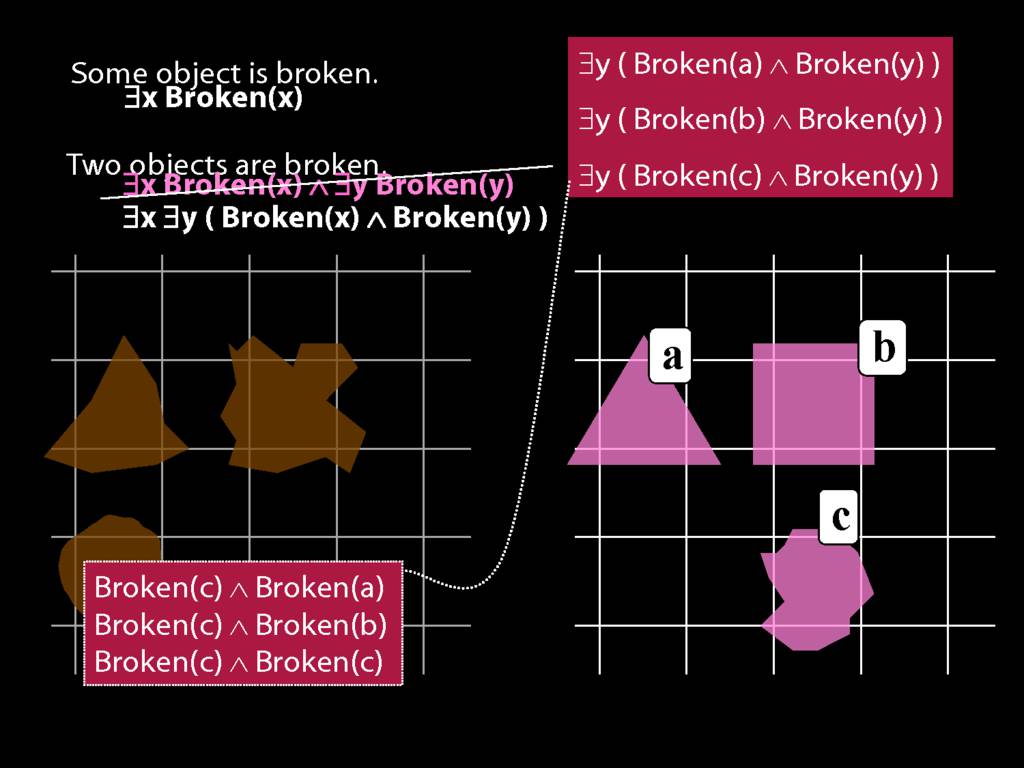
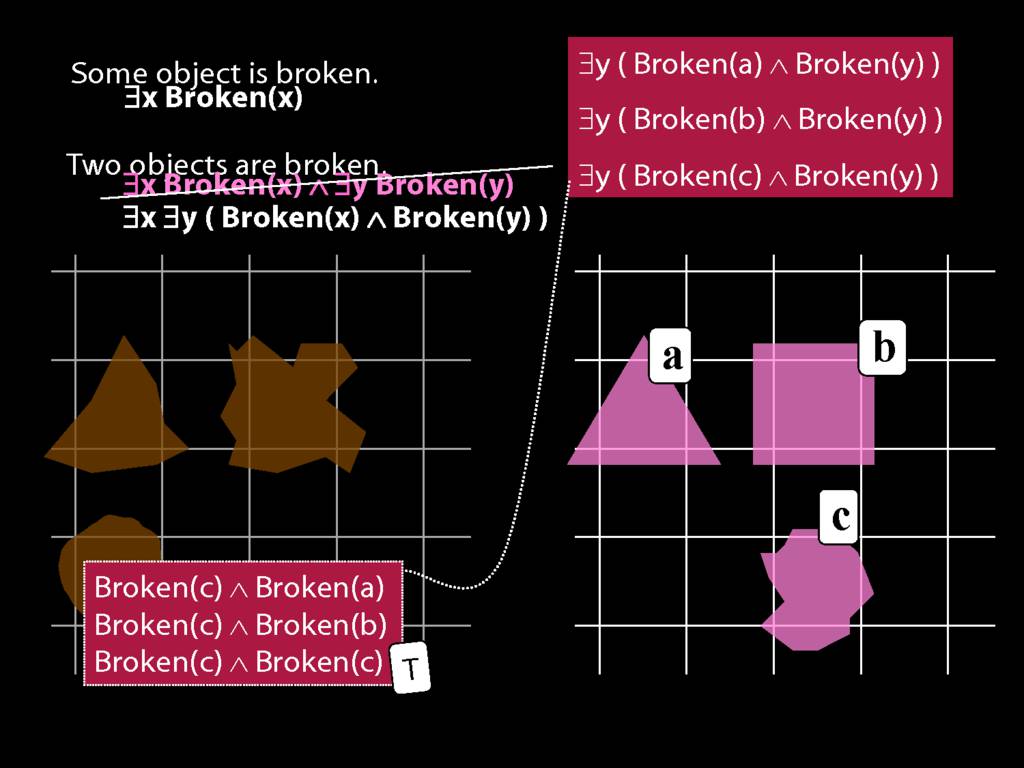
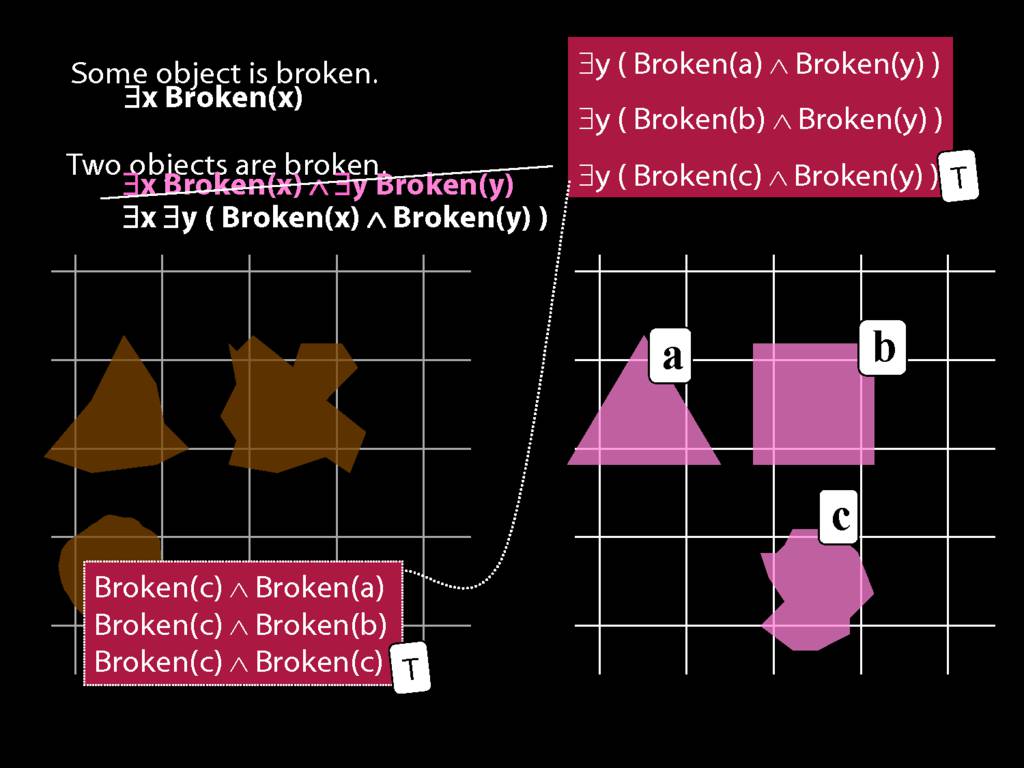
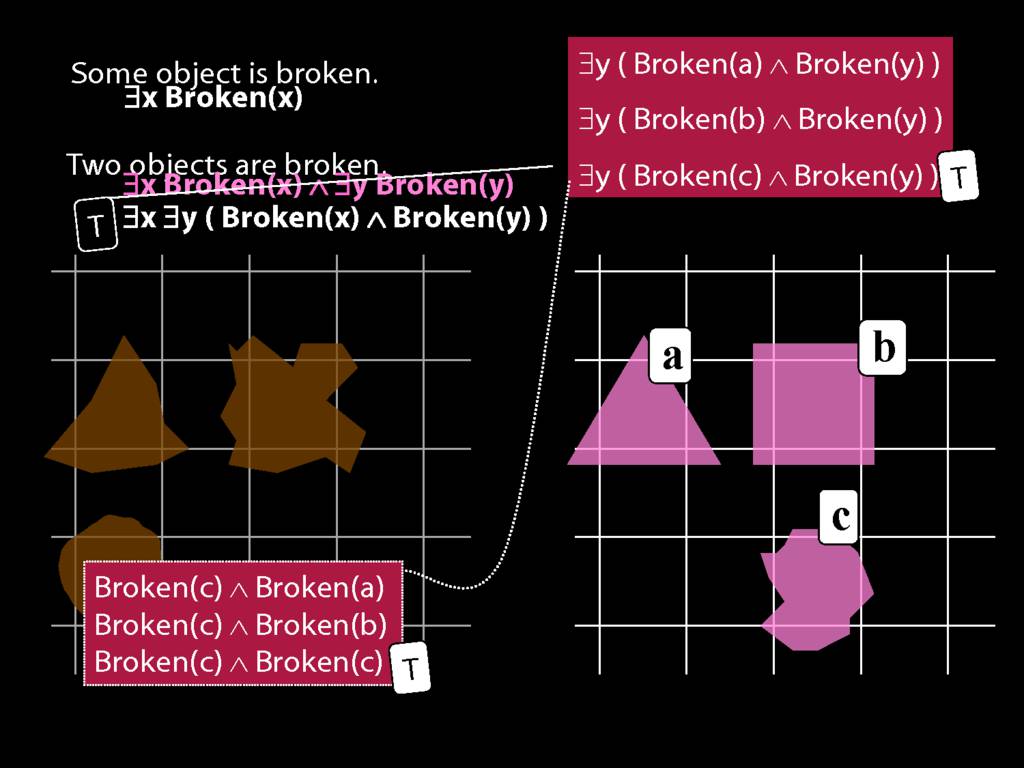
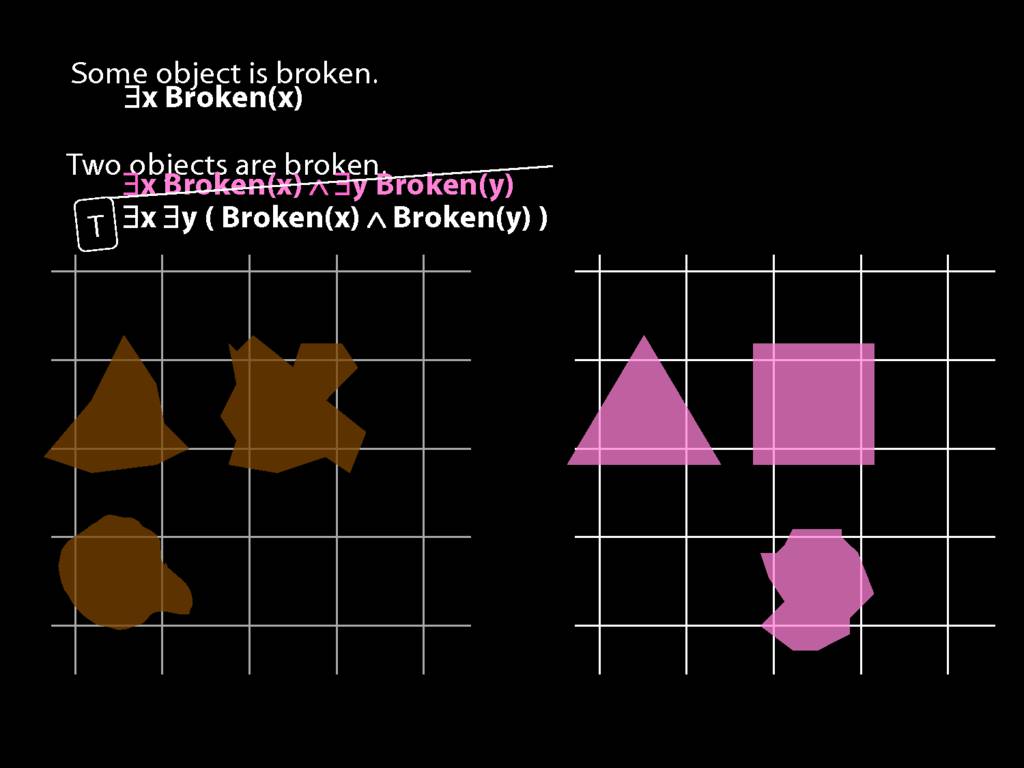
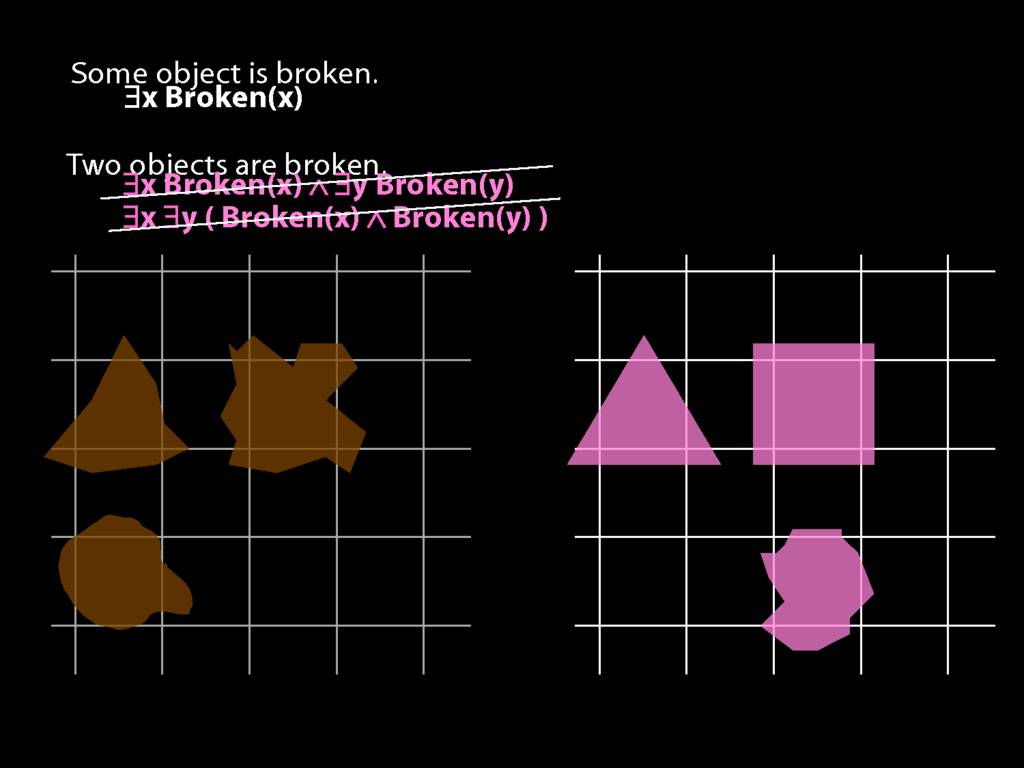
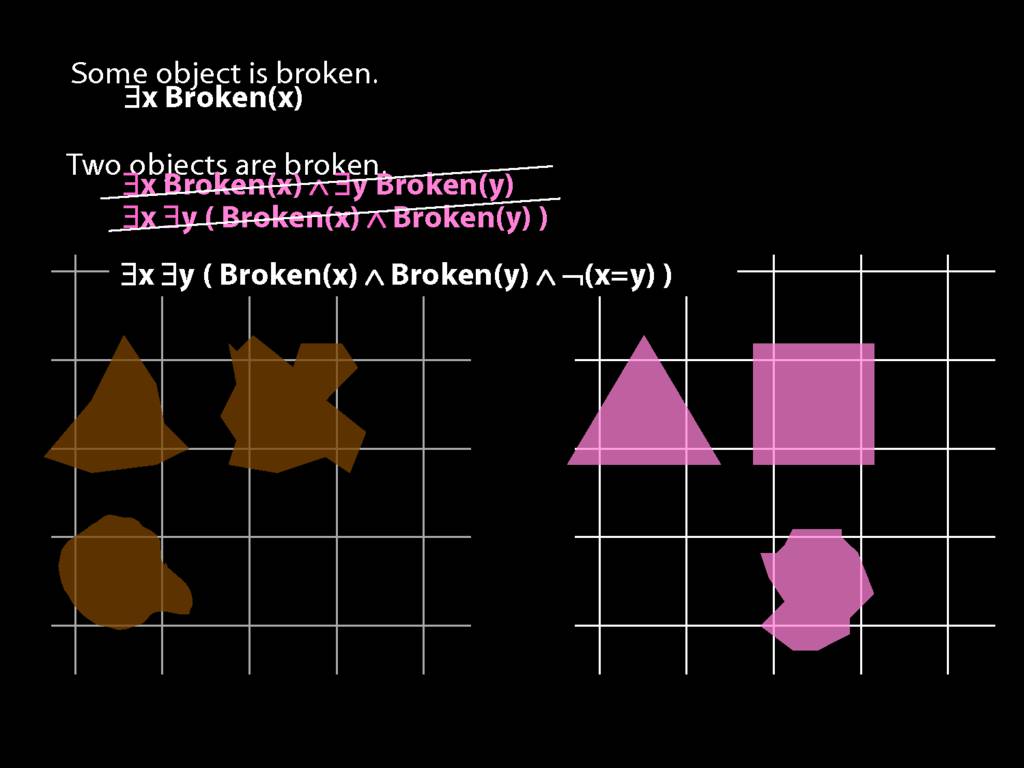
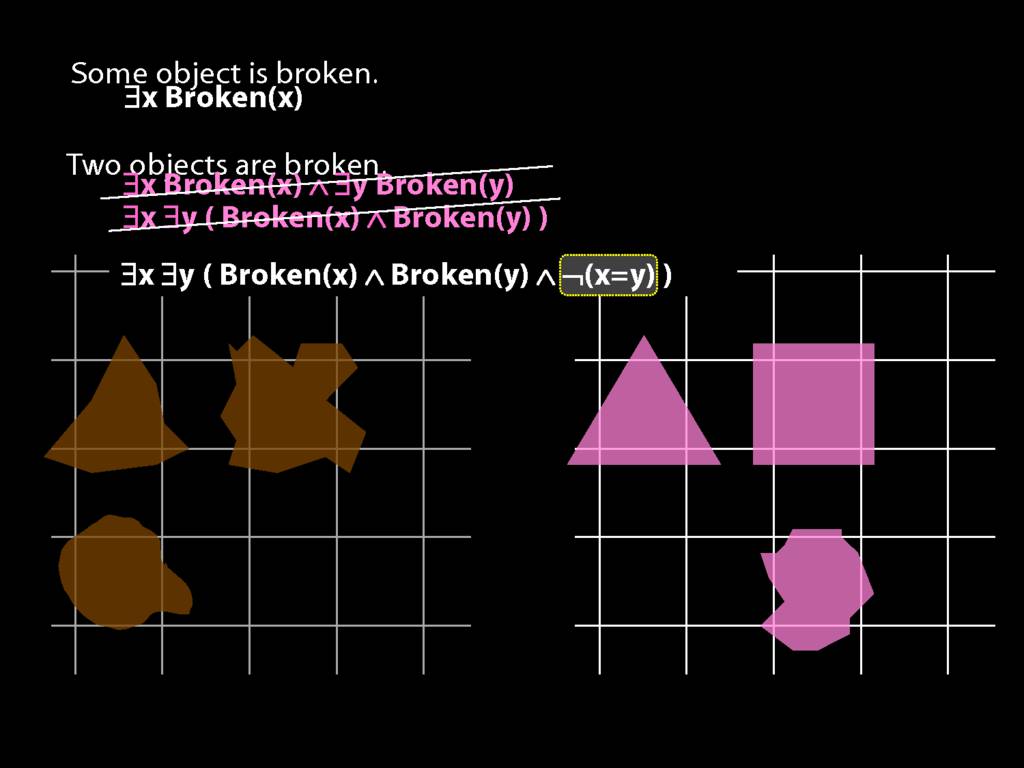
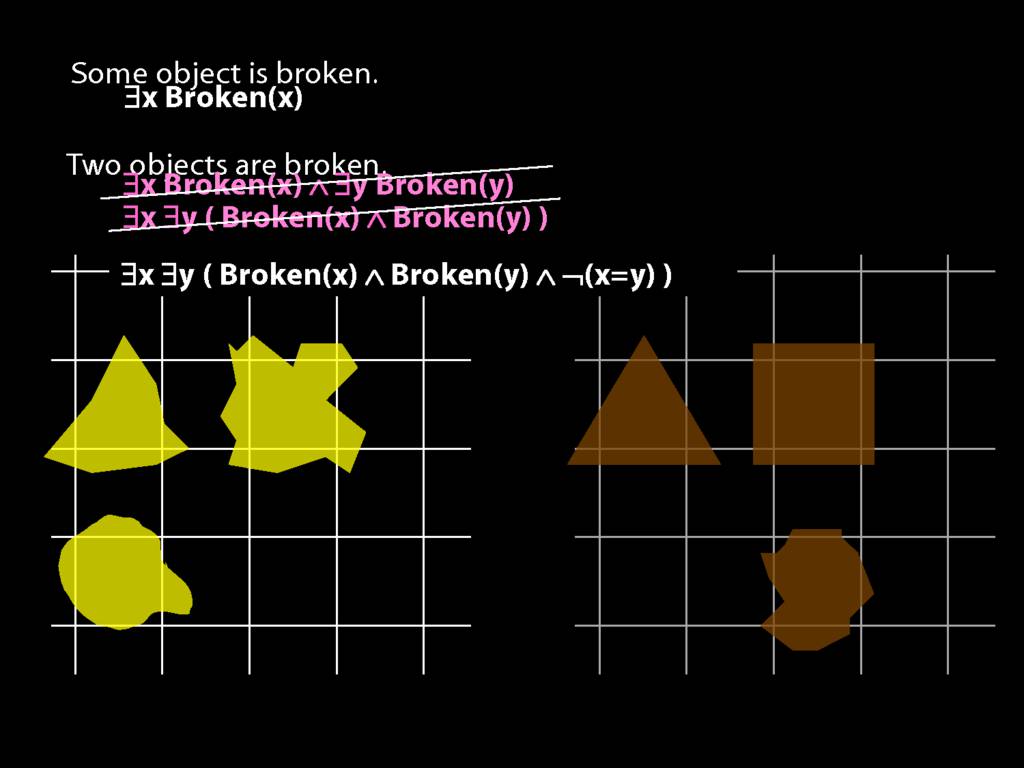
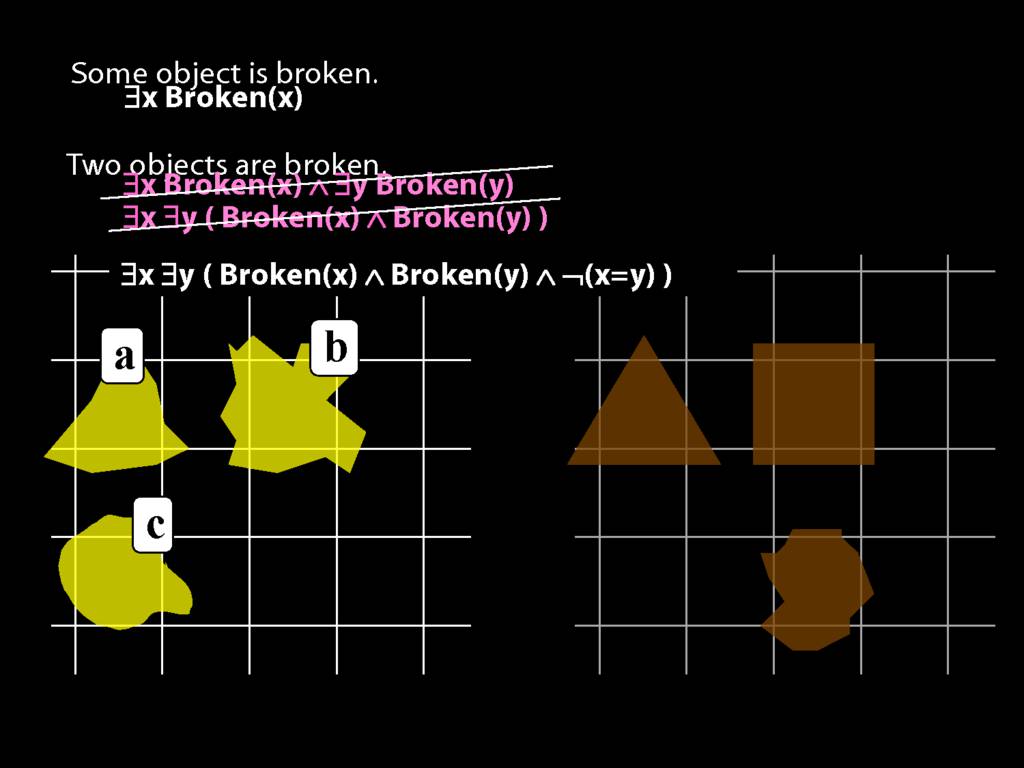
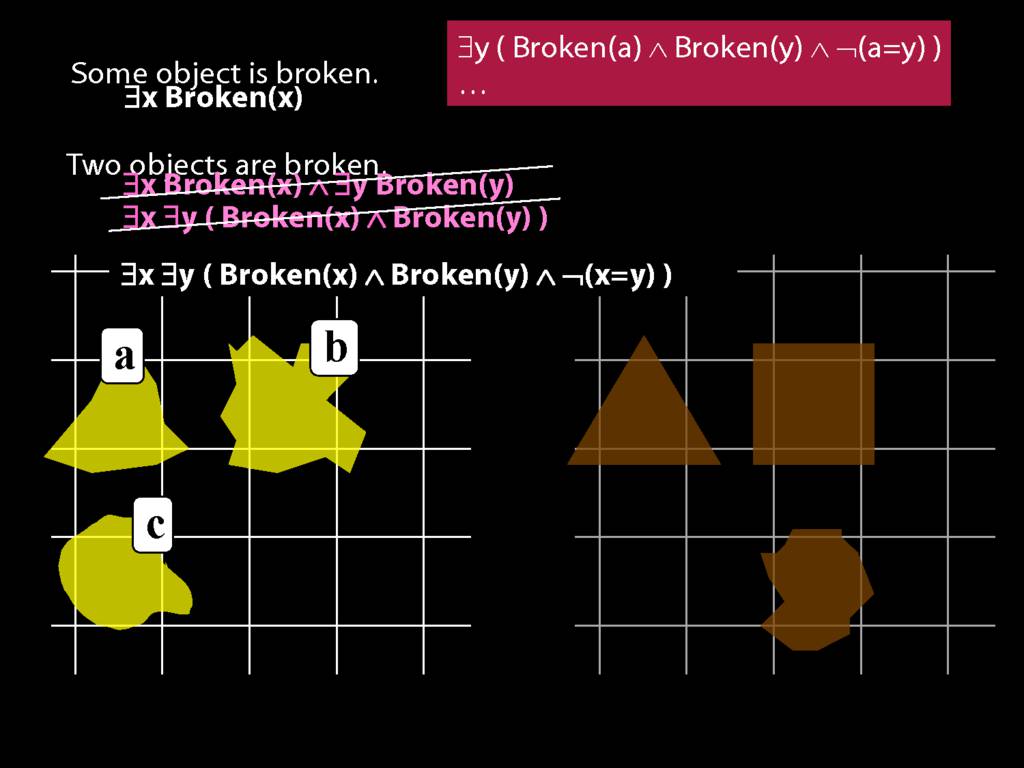
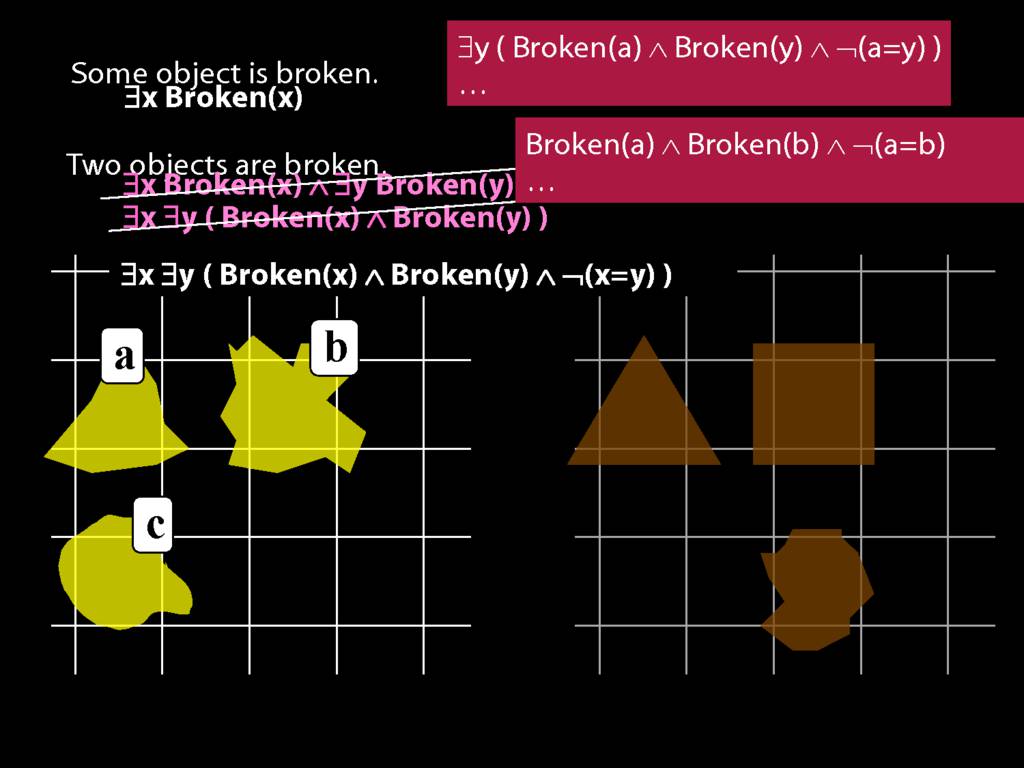
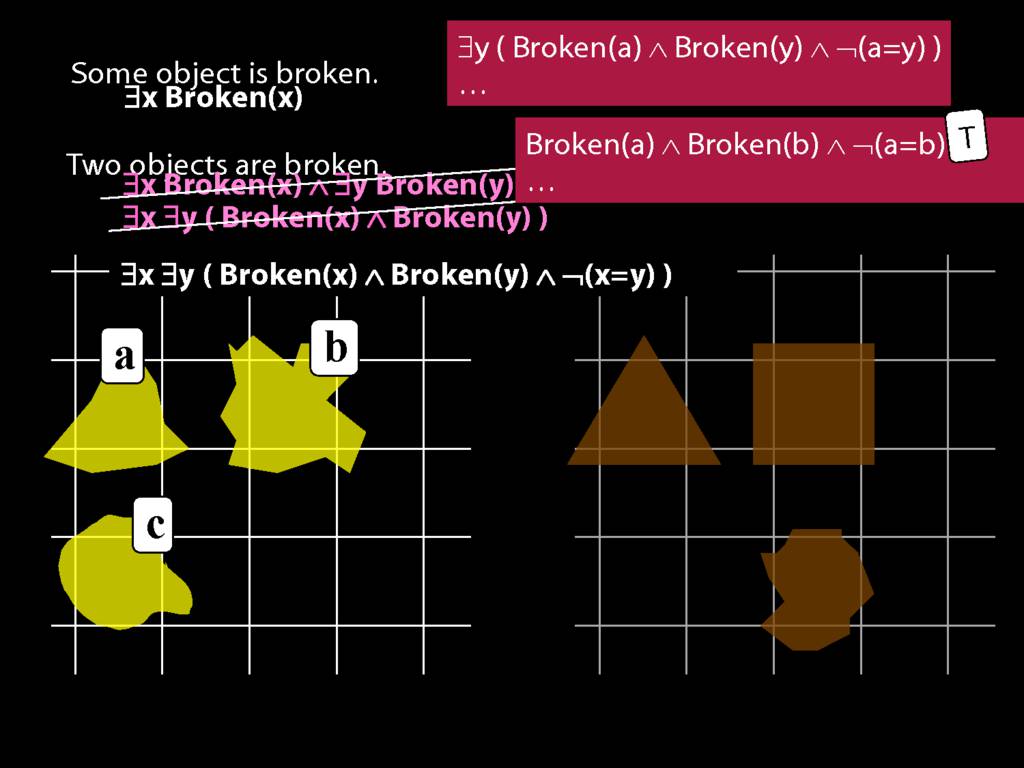
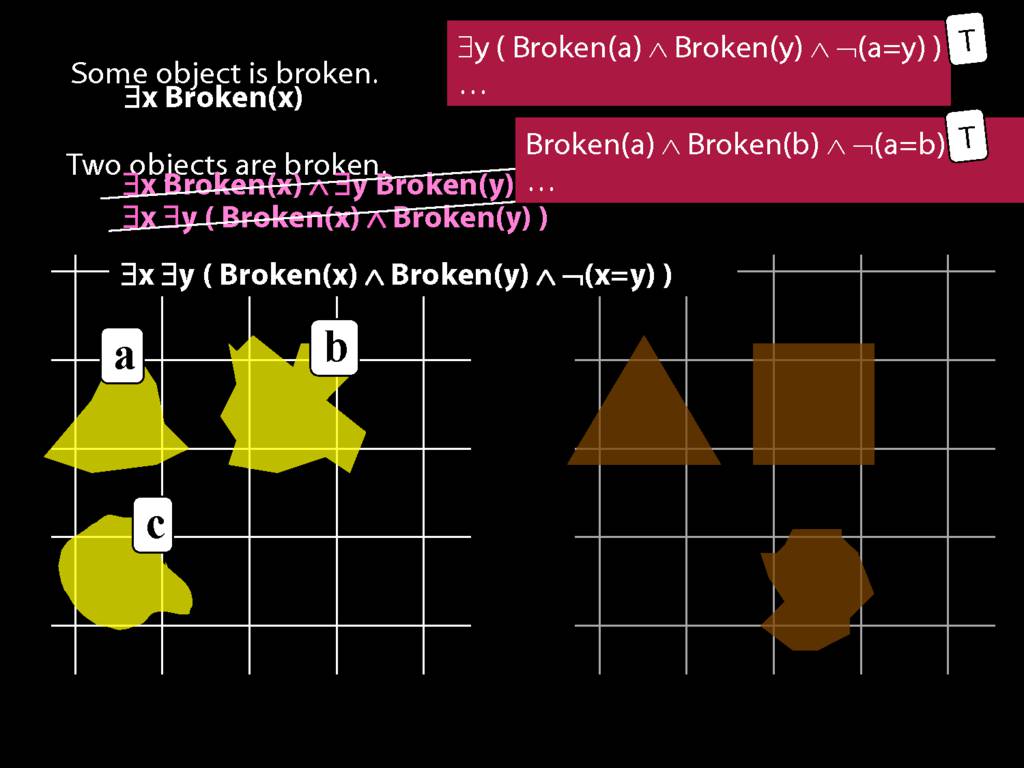
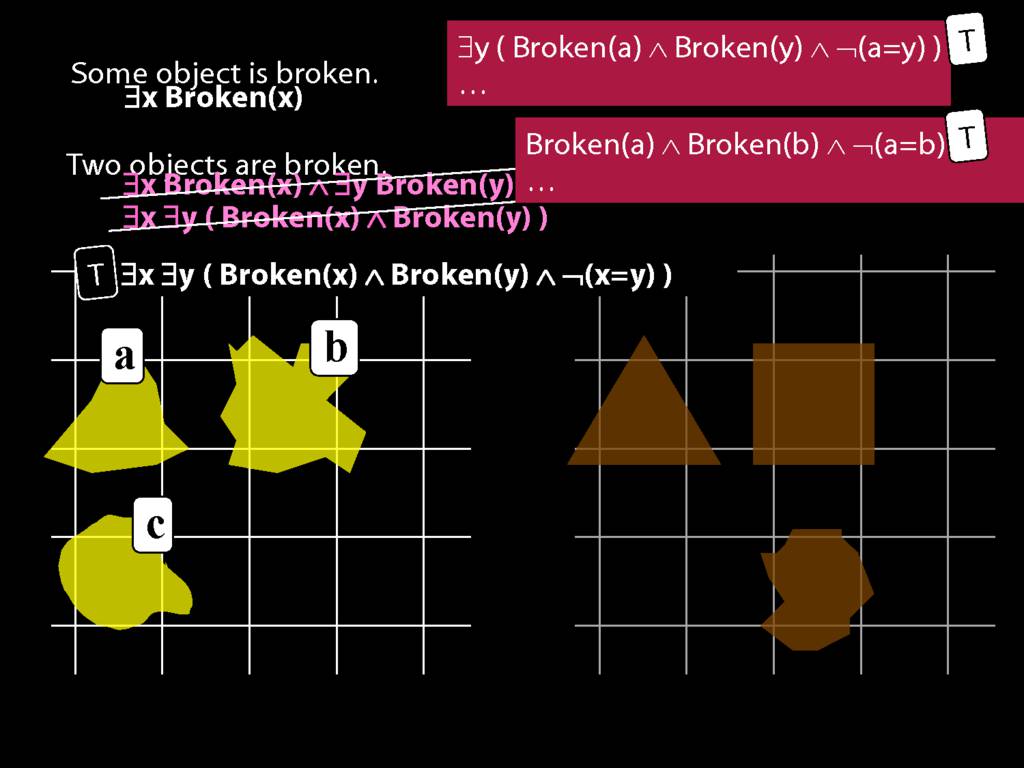
\section{Two Things Are Broken}
\emph{Reading:} §14.1
 
\section{Two Things Are Broken}
To translate sentences involving number into awFOL, use identity. For example,
`Two things are broken' might be translated as:
∃x ∃y ( Broken(x) ∧ Broken(y) ∧ ¬(x=y) )
 

There Is Exactly One

 
\section{There Is Exactly One}
 
\section{There Is Exactly One}
There is one creator (at least one, maybe more).
\hspace{3mm} ∃x Creator(x)
Ahura Mazda is the one and only creator.
\hspace{3mm} Creator(a) ∧ ∀x( Creator(x) → x=a )
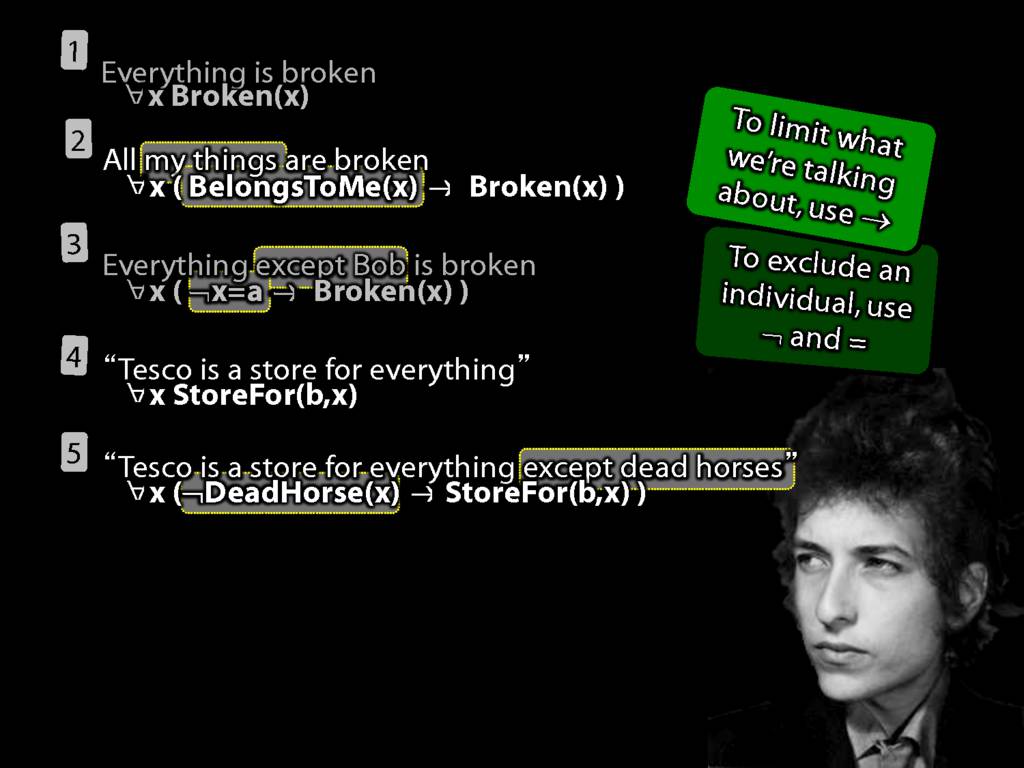
All squares are broken.
\hspace{3mm} ∀x( Sqr(x) → Brkn(x) )
There is one and only one creator.
\hspace{3mm} ∃y( Creator(y) ∧ ∀x( Creator(x) → x=y ) )
\hspace{3mm} or:
\hspace{3mm} ∃y ∀x( Creator(x) ↔ x=y )

There is one creator (at least one, maybe more).

∃x Creator(x)

Ahura Mazda is the one and only creator.

∃y( Creator(a) ∧ ∀x( Creator(x) → x=a )

All squares are broken.

∀x( Sqr(x) → Brkn(x) )

There is one and only one creator.

∃y( Creator(y) ∧ ∀x( Creator(x) → x=y ) )

Look, two quantifiers. But not just two quantifiers, one is existential and the other is universal. Mixed quantifiers!
Here's another, shorter way of expressing the same proposition (these are logically equivalent)

or:

∃y( ∀x( Creator(x) ↔ x=y ) )

Ex: There is one and only one female creator.

Ex: There is one and only one creator and she is female.

14.10--14.12, *14.13
11.10, 11.13
14.2
 

↔ : truth tables and rules

 
\section{↔ : truth tables and rules}
 
\section{↔ : truth tables and rules}
ABA → BB → A(A → B) ∧ (B → A)A ↔ B
​TTTTTT
​TFFTFF
​FTTFFF
​FFTTTT

​1.

A ↔ B

​2.

A

​3.B↔Elim: 1,2
​1.

A ↔ B

​2.

B

​3.A↔Elim: 1,2

How do I intro ↔?

ABA ↔ B
​TTT
​TFF
​FTF
​FFT
ABA → B
​TTT
​TFF
​FTT
​FFT
​1.

A

​2....
​3.B
​4.

B

​5....
​6.A
​7.A ↔ B
​1.

A

​2....
​3.B
​4.A → B
#
 

Variables

 
\section{Variables}
 
\section{Variables}
Names : a, b, c, …
Variables : x, y, z, w, …
Variables are for saying several things about one thing even without specifying which thing it is
NB: `Some x is a horse and x is dead' ain't English.
 

More Dead Horse

 
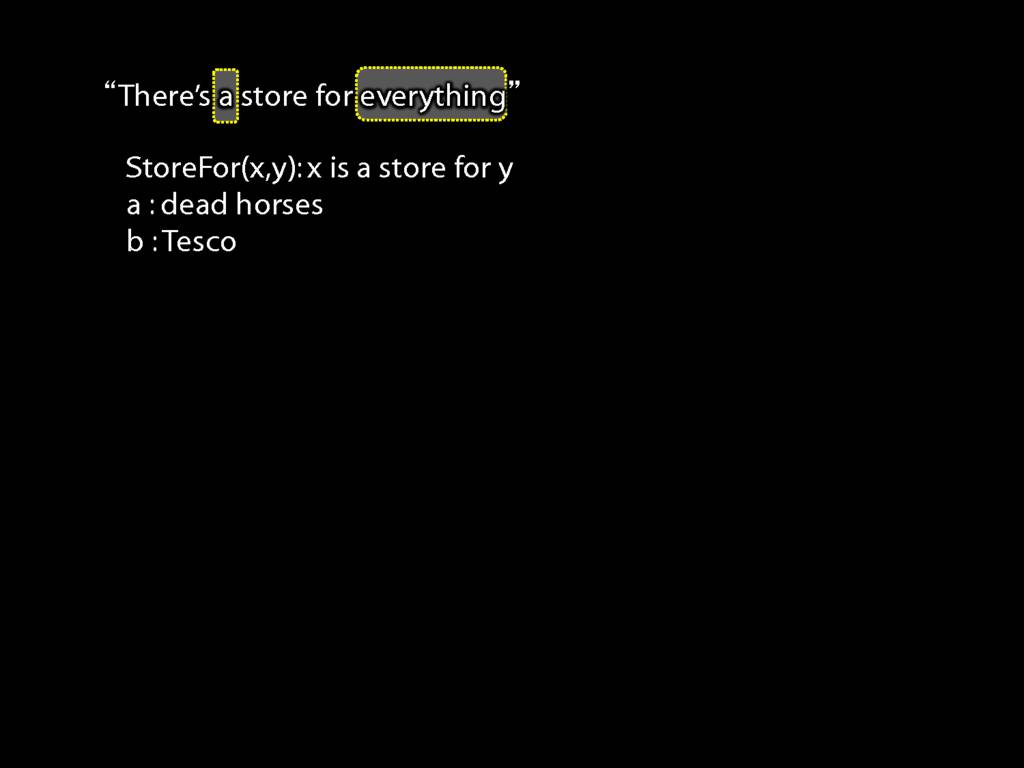
\section{More Dead Horse}
\emph{Reading:} §11.4, §11.5
 
\section{More Dead Horse}
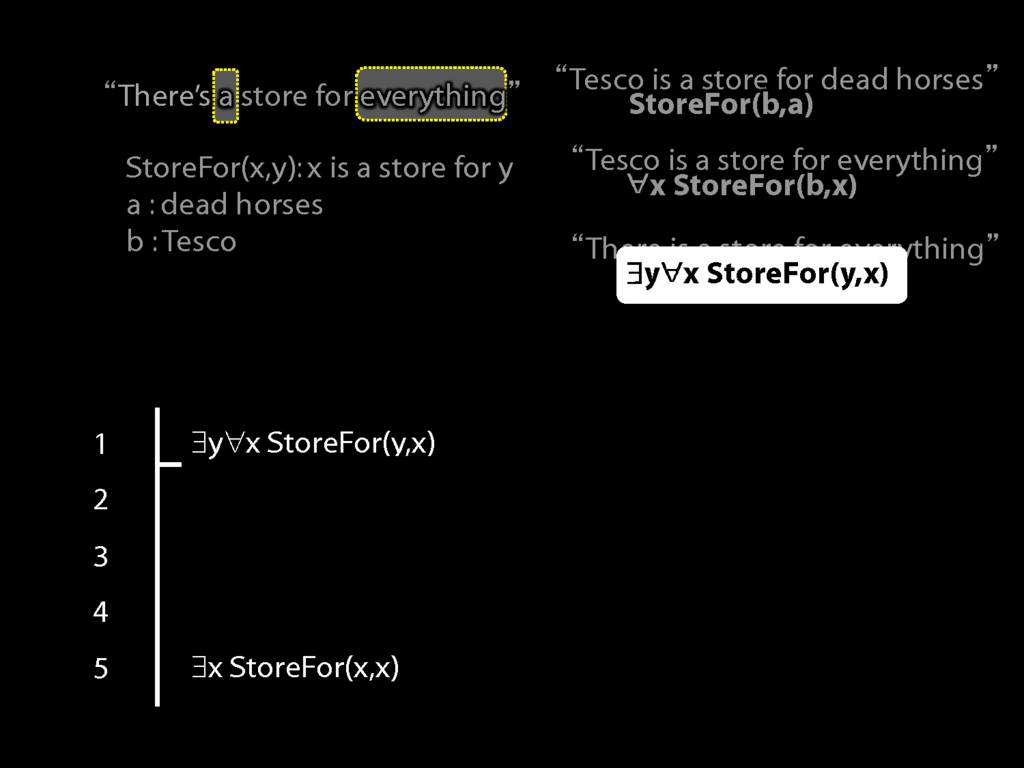
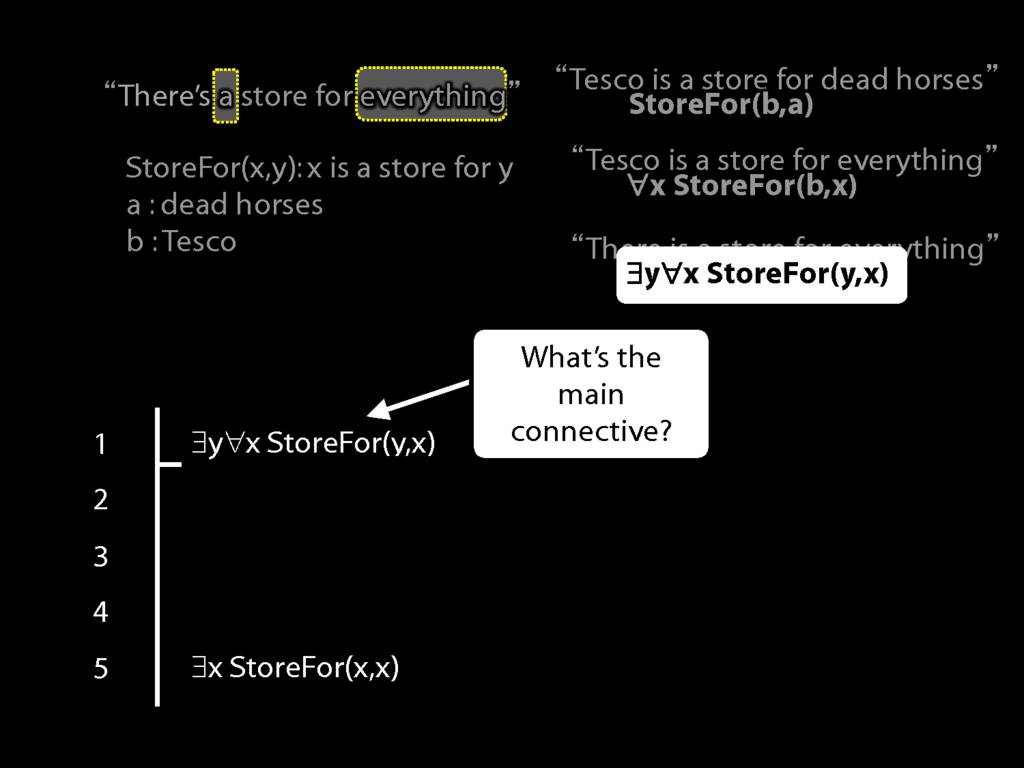
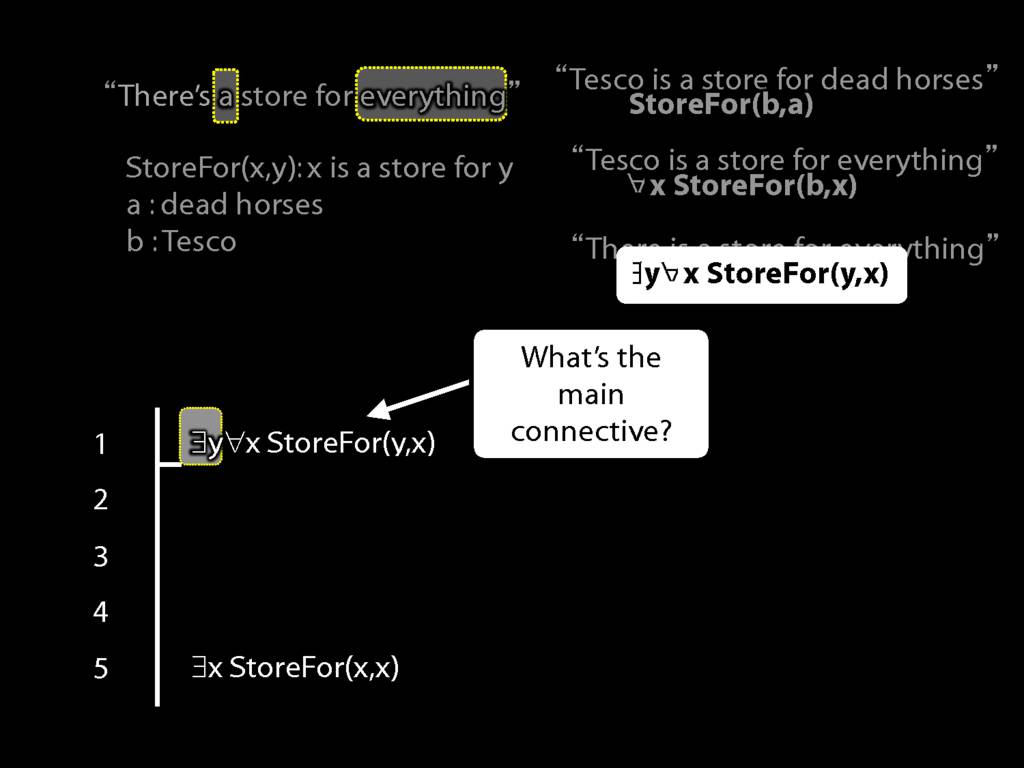
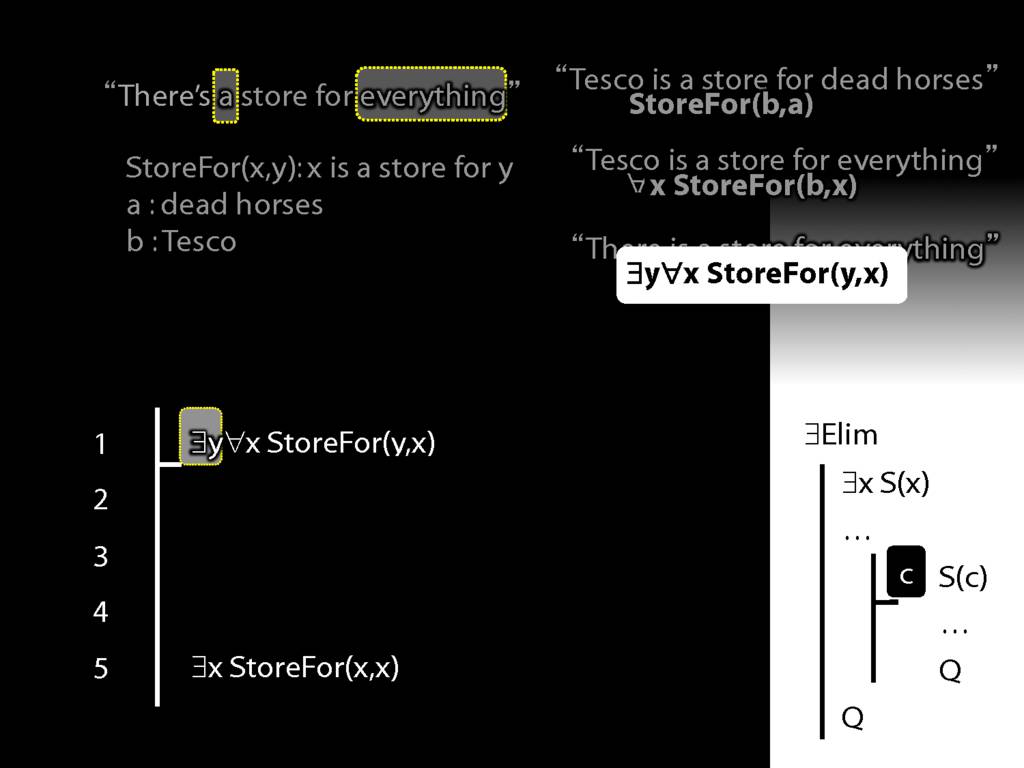
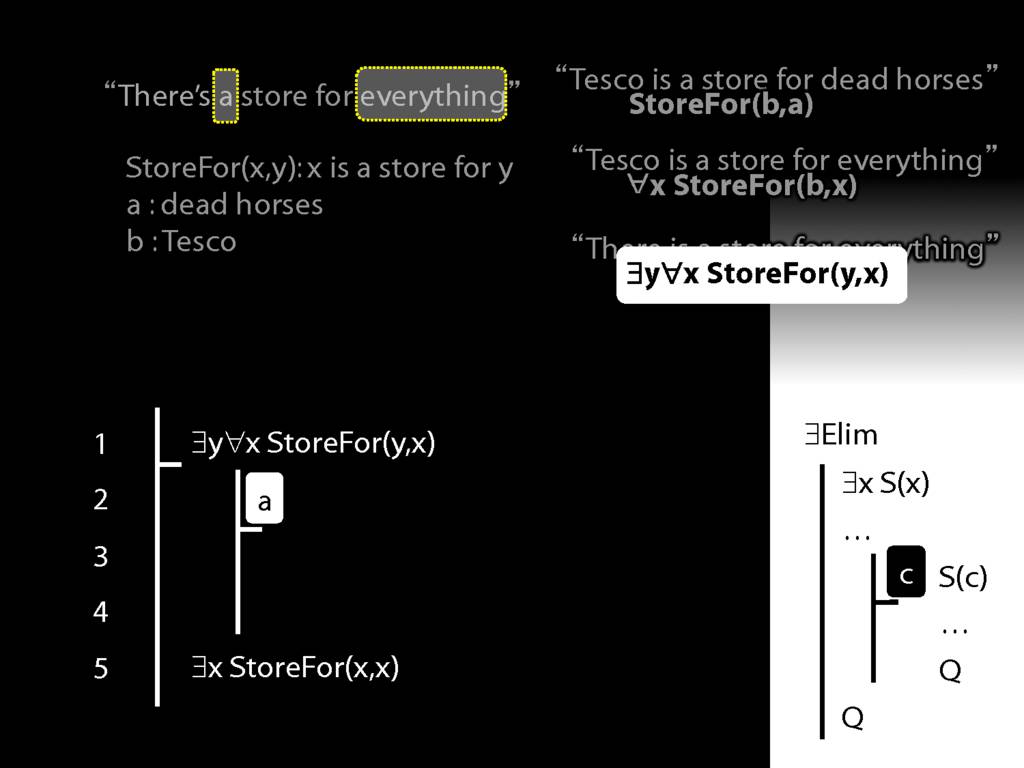
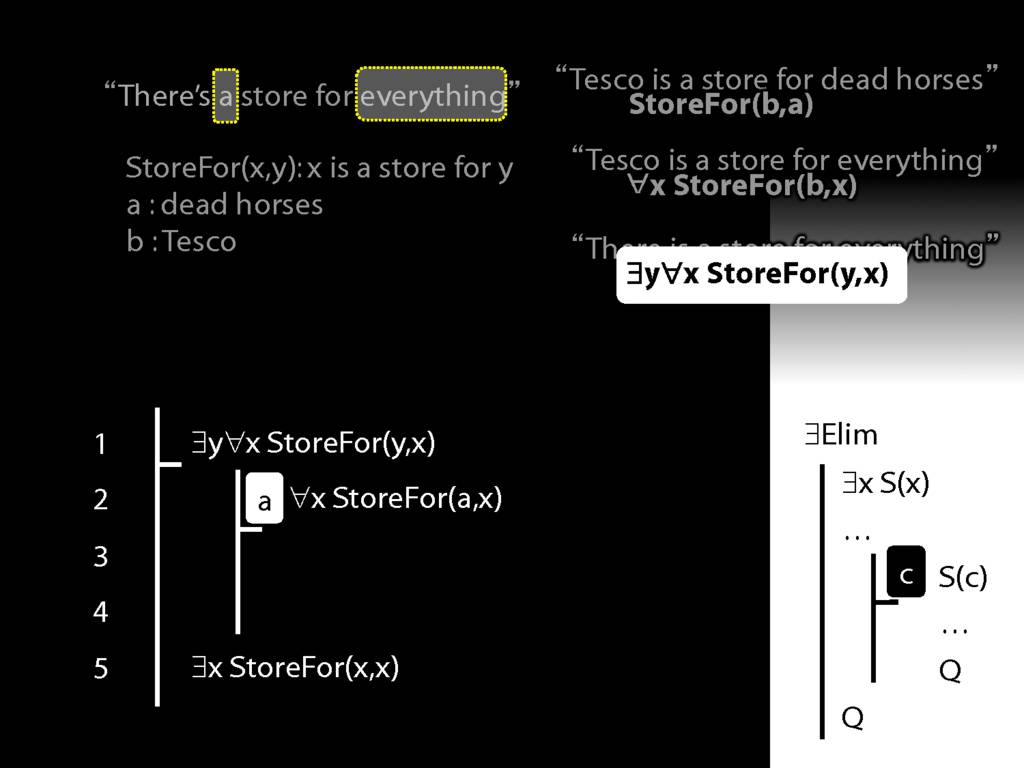
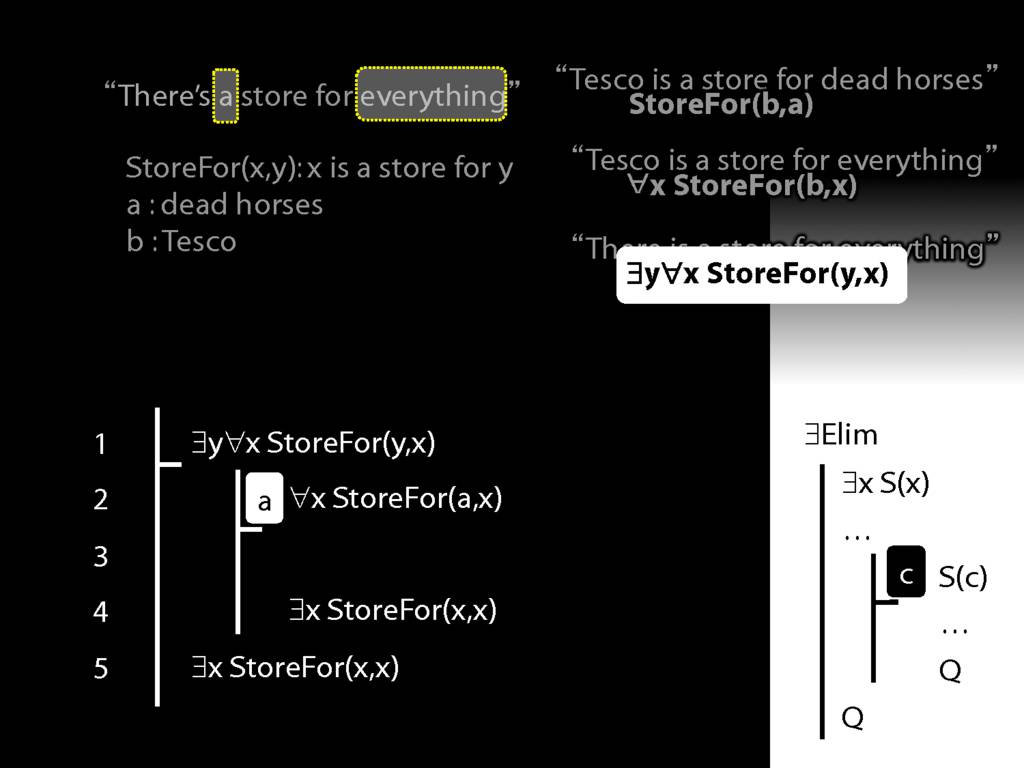
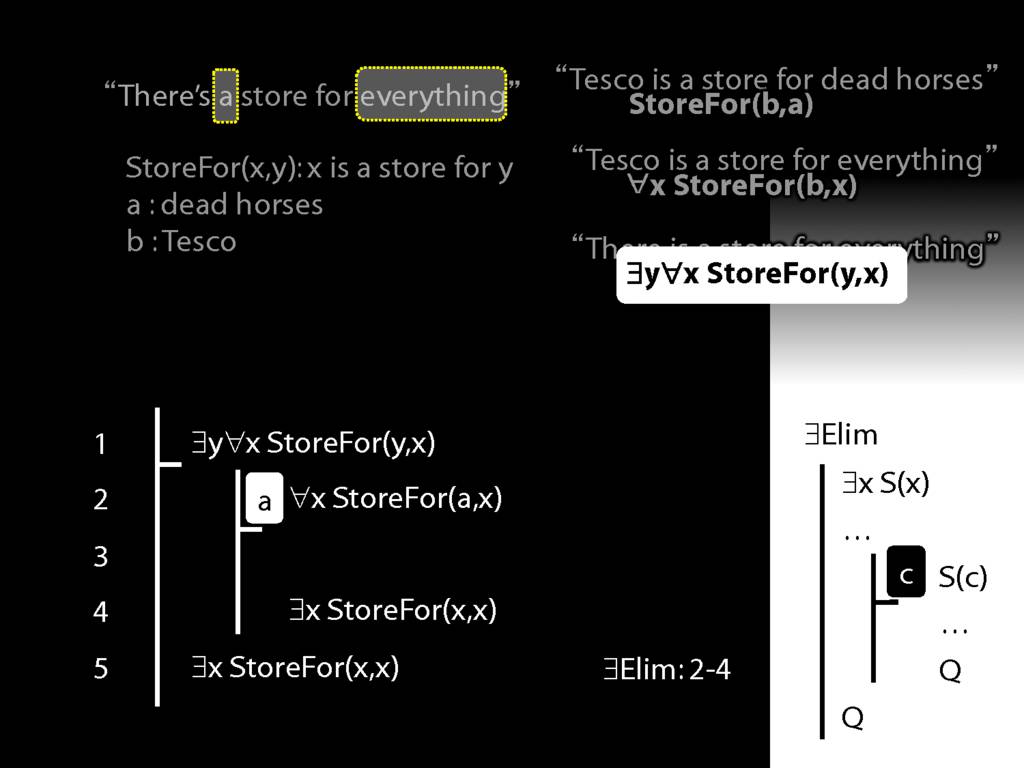
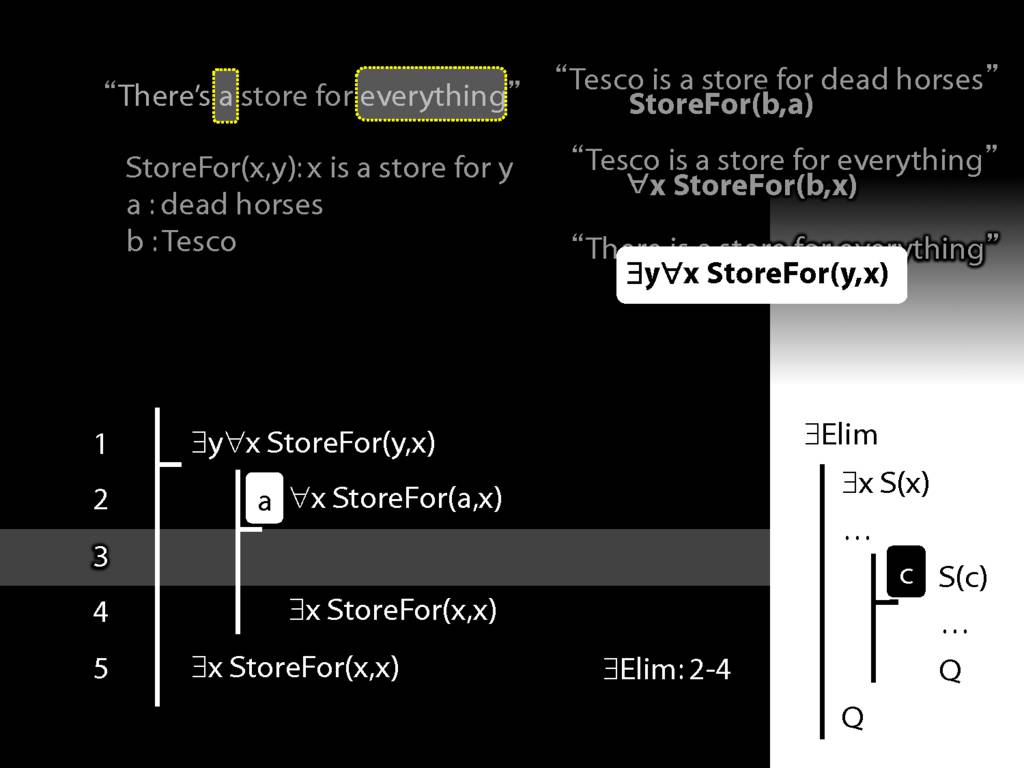
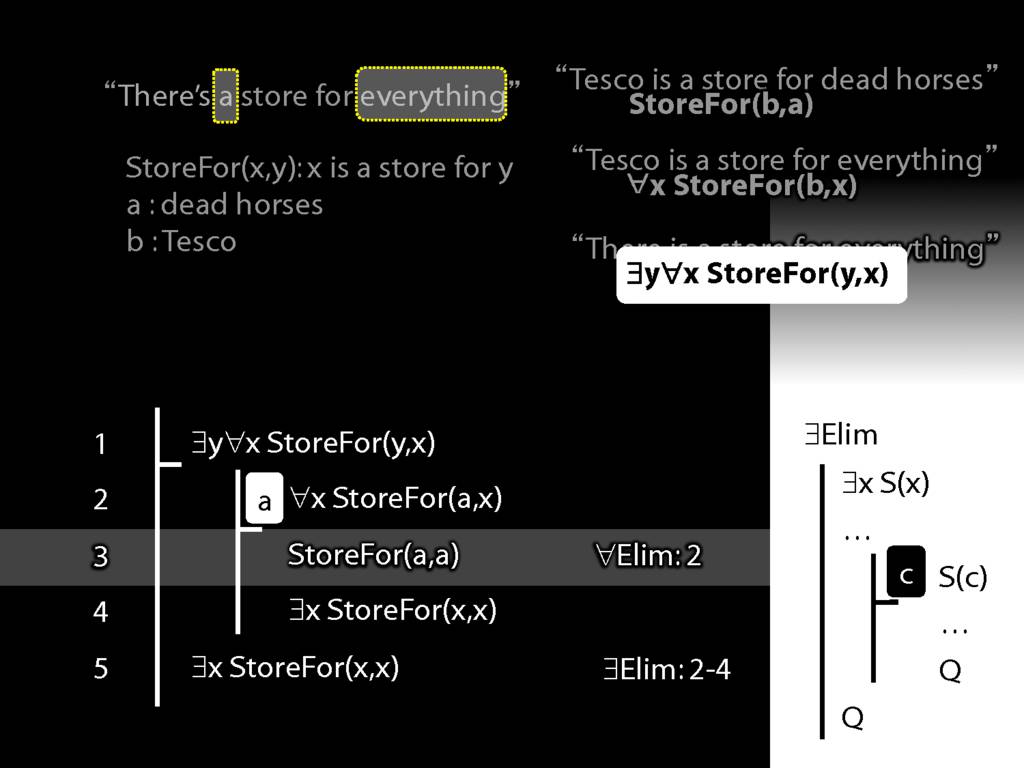
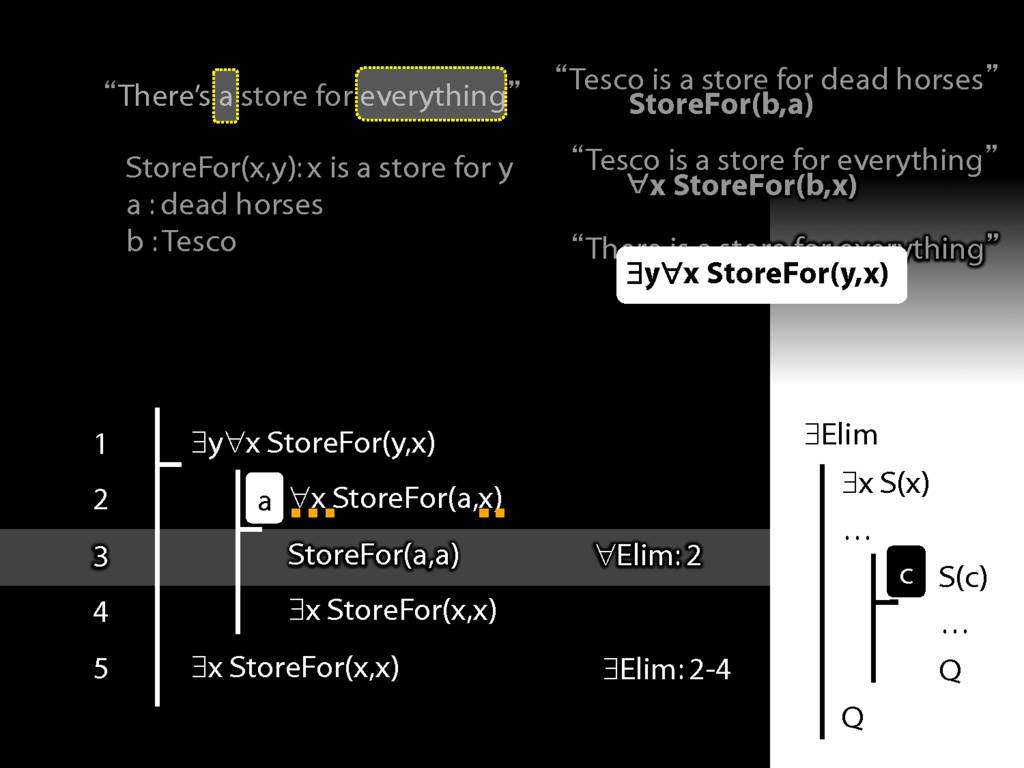
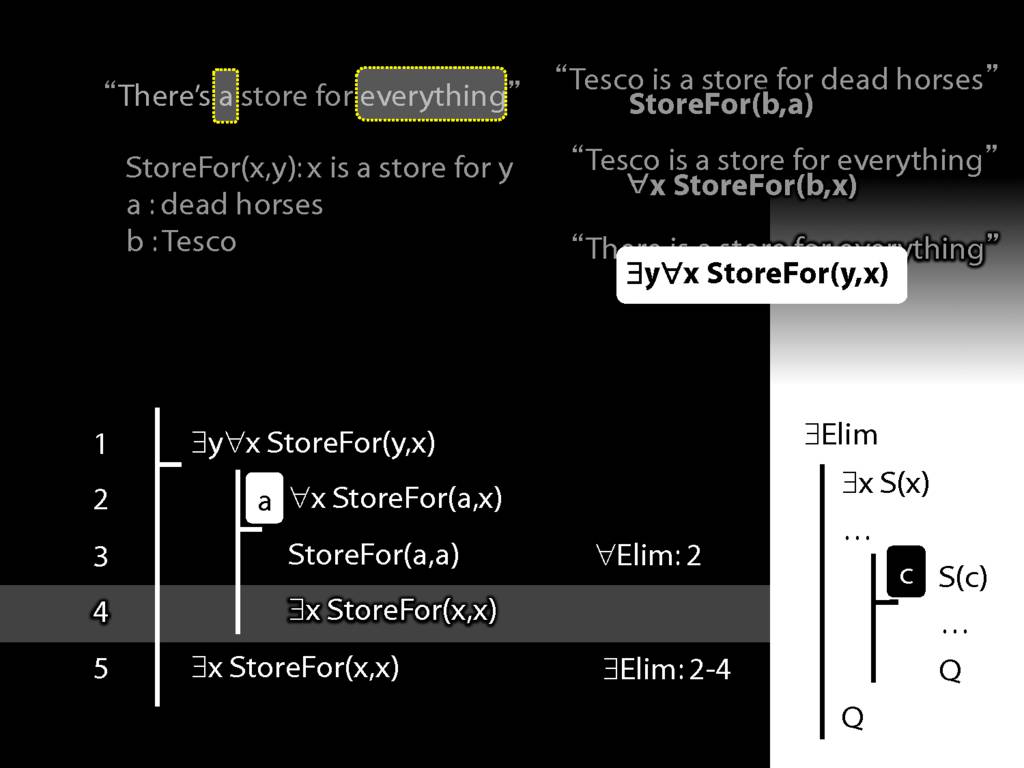
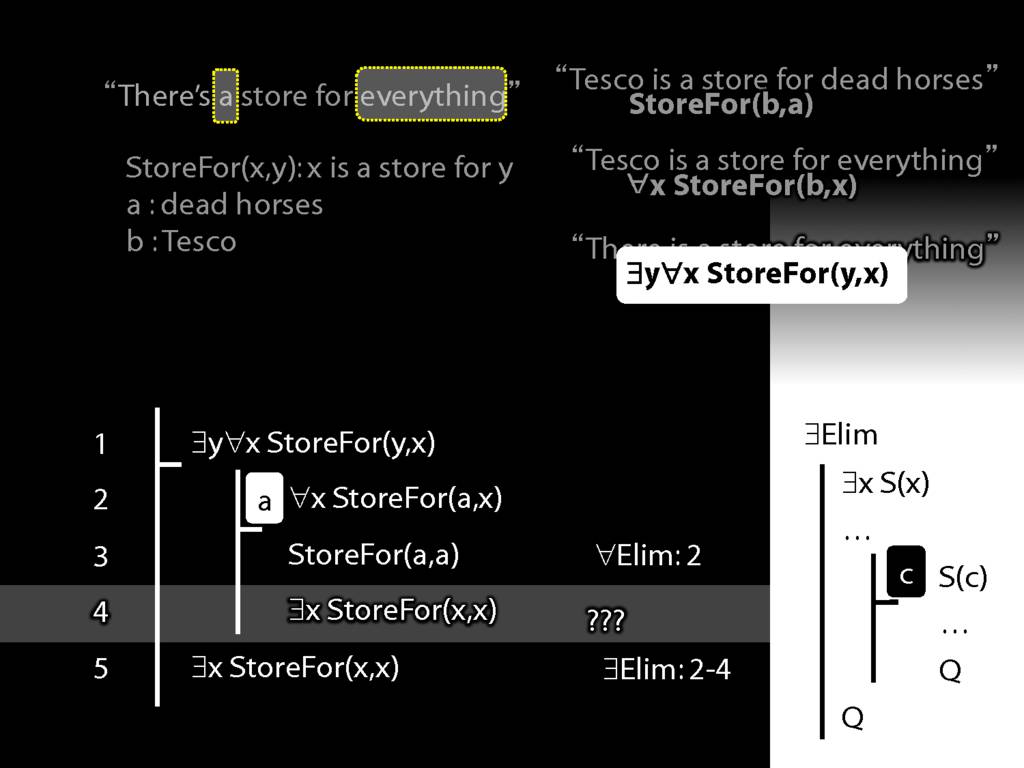
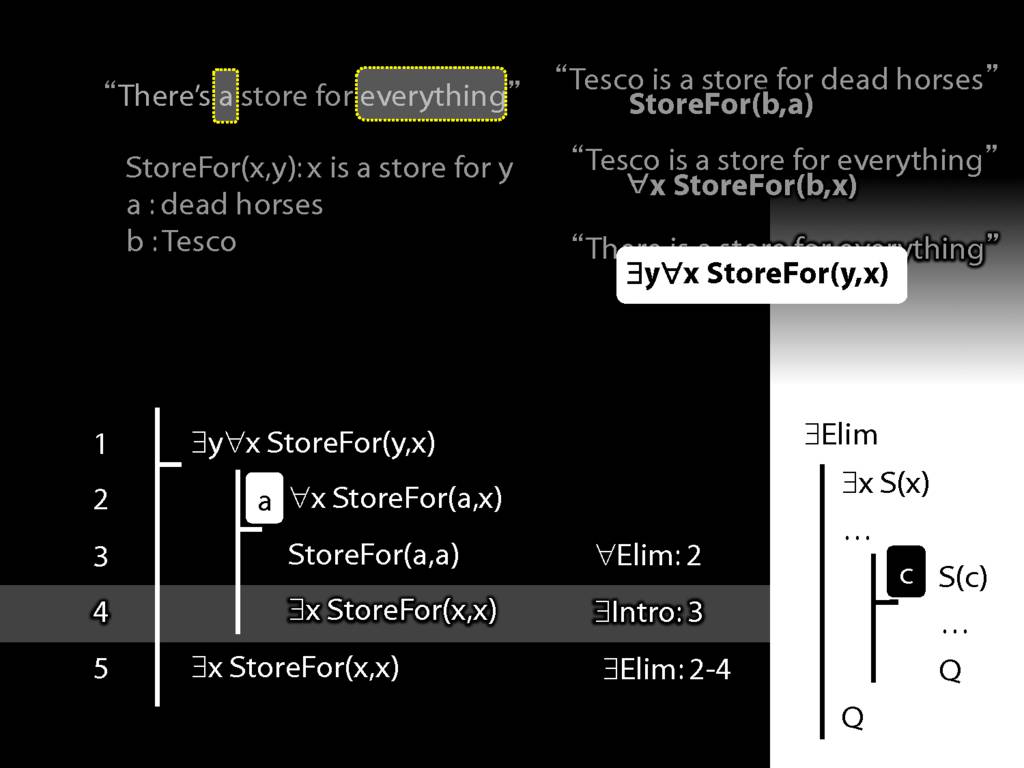
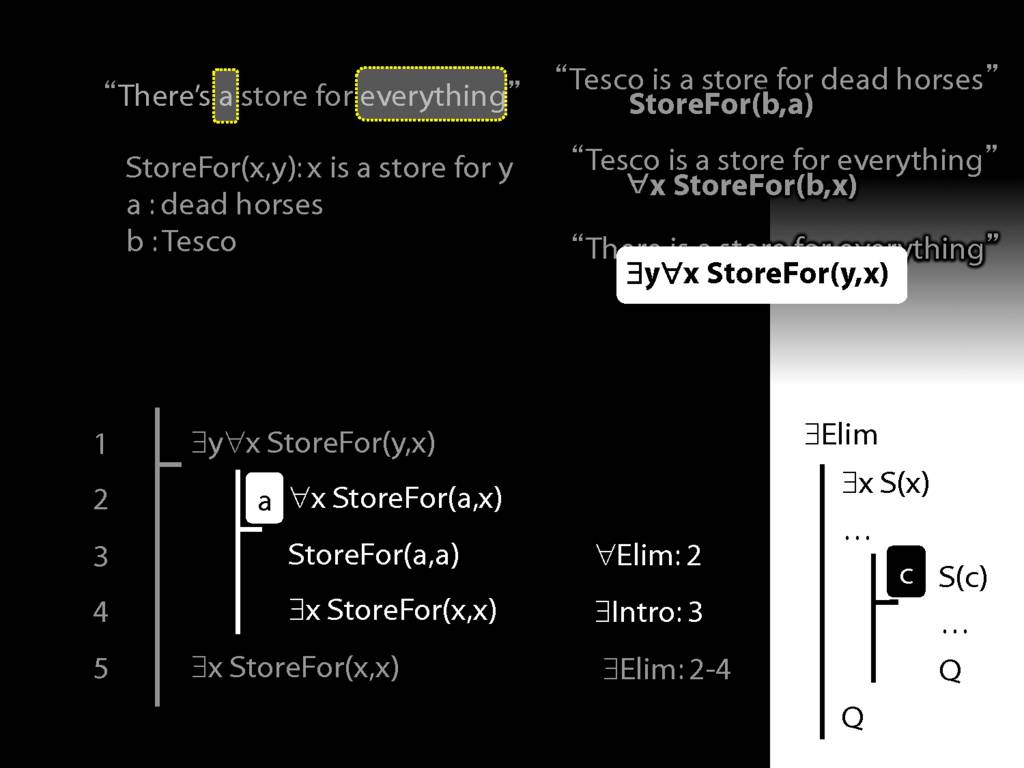
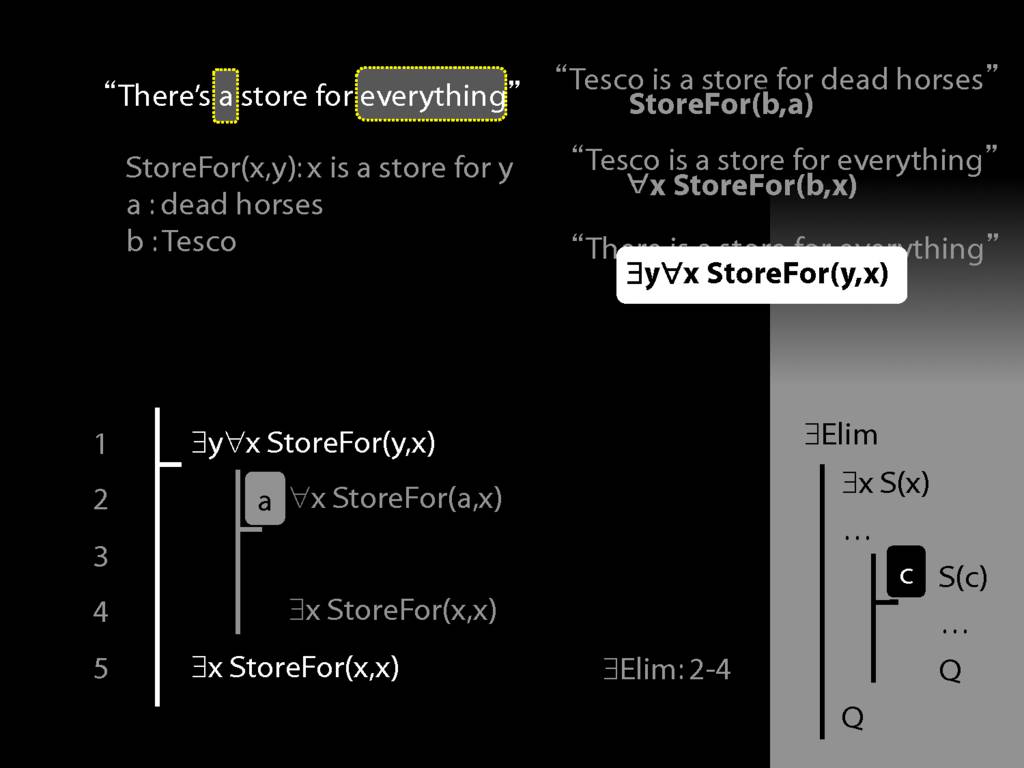
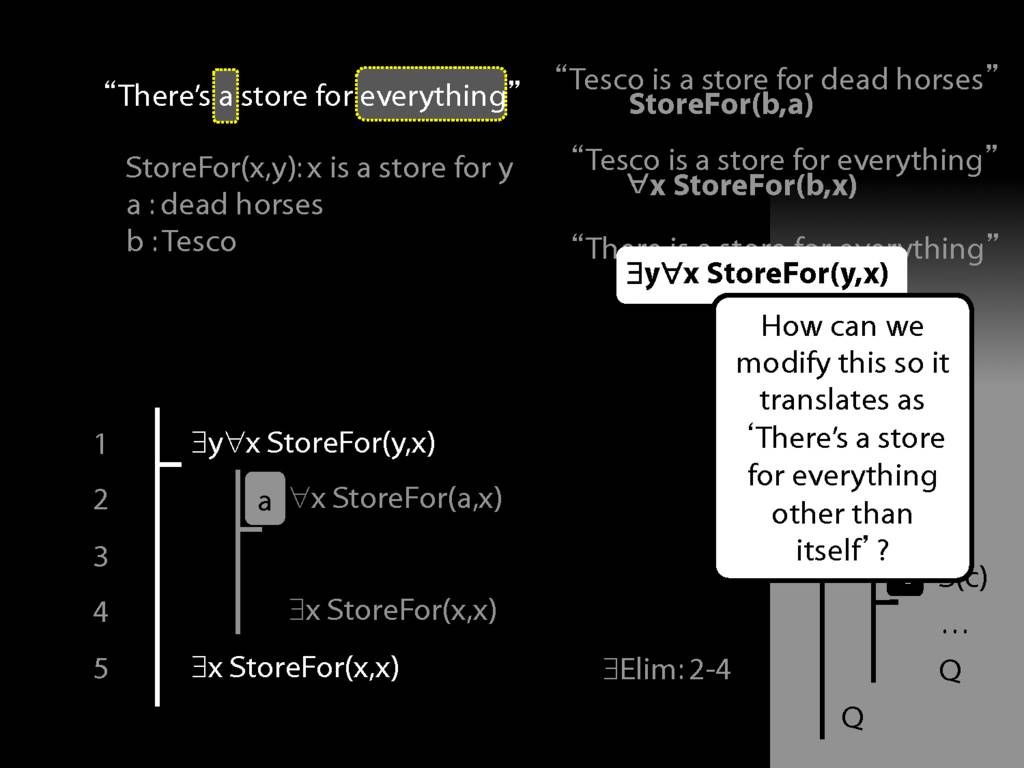
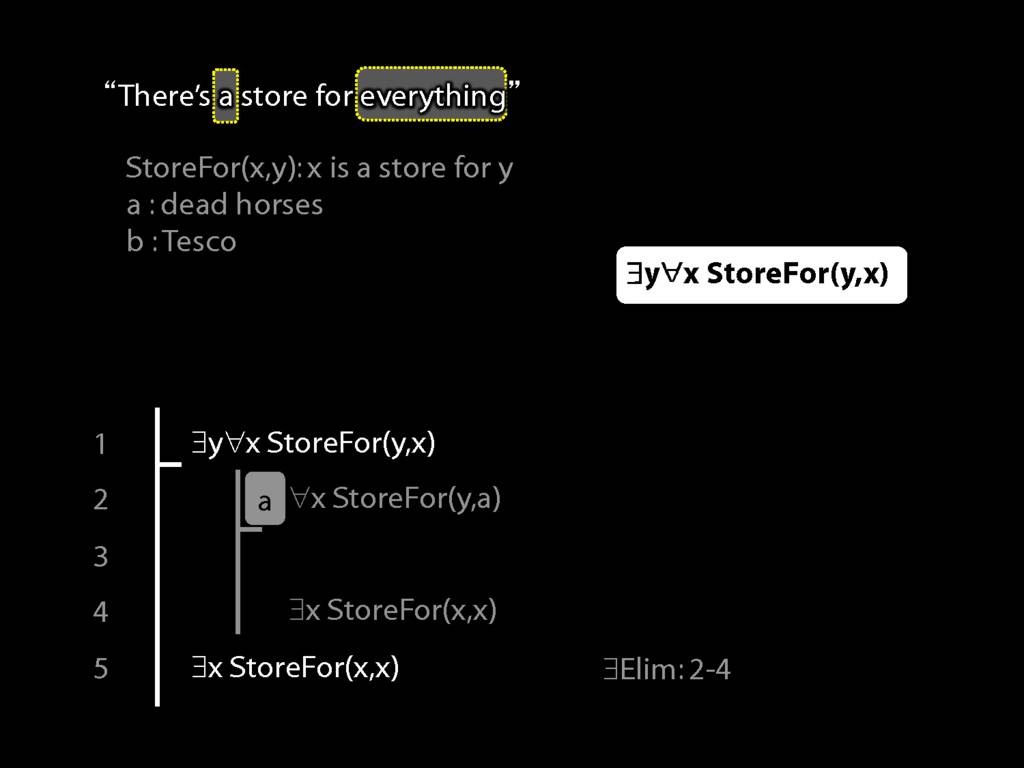
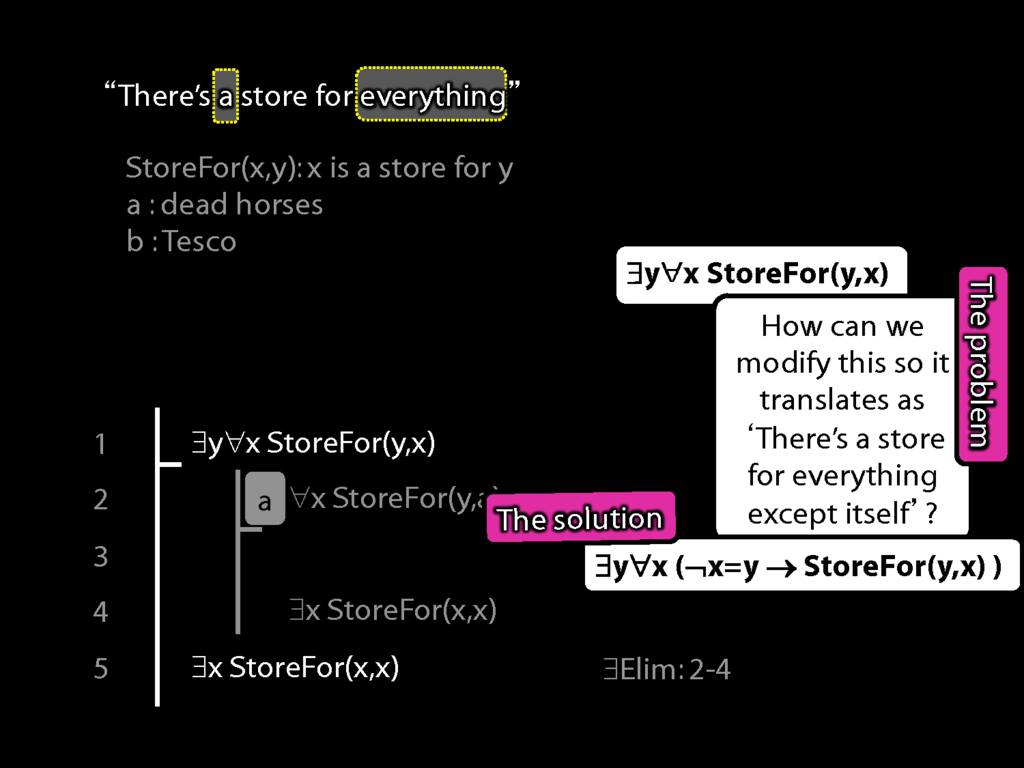
“Tesco is a store for everything”
\hspace{3mm} ∀x StoreFor(b,x)
Tesco is a store for everything except dead horses
\hspace{3mm} ∀x (¬DeadHorse(x) → StoreFor(b,x) )
Tesco is a store for everything except Tesco
\hspace{3mm} ∀x (¬x=b → StoreFor(b,x) )
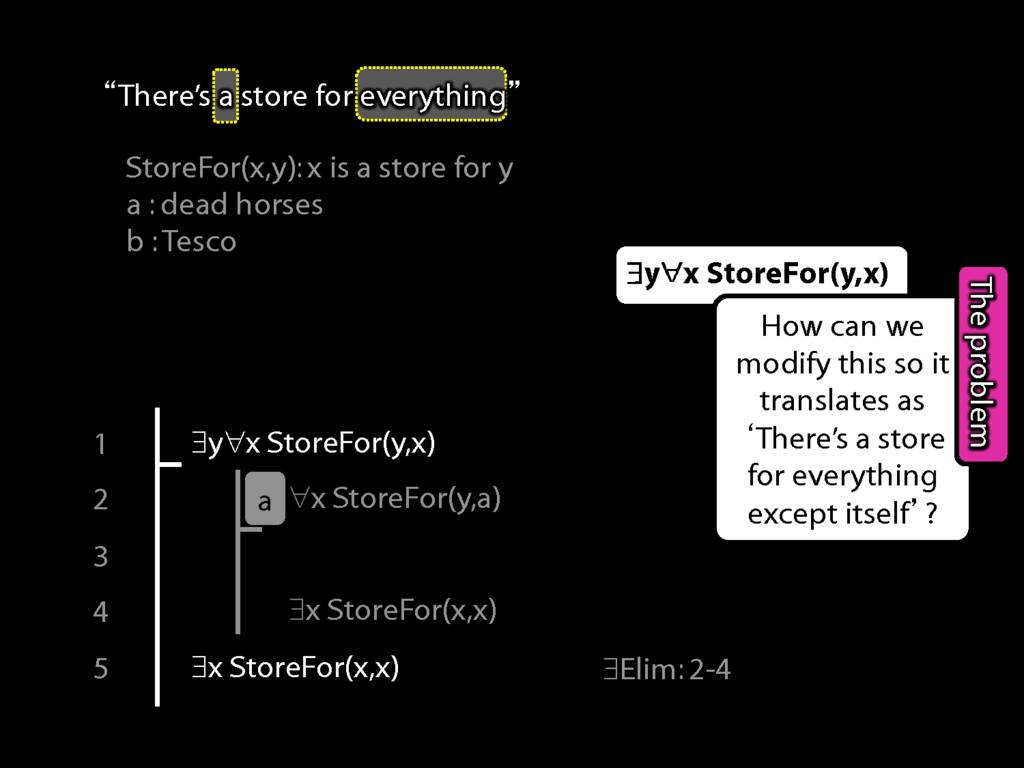
There is a store for everything except itself
\hspace{3mm} ∃y ∀x (¬x=y → StoreFor(y,x) )
 

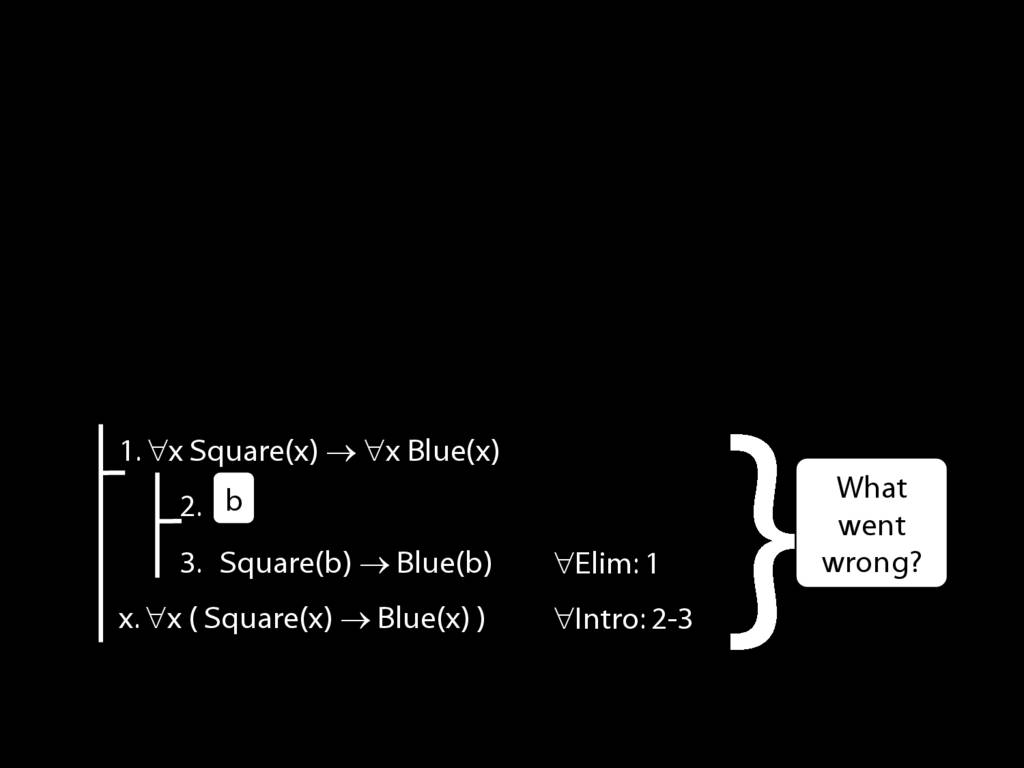
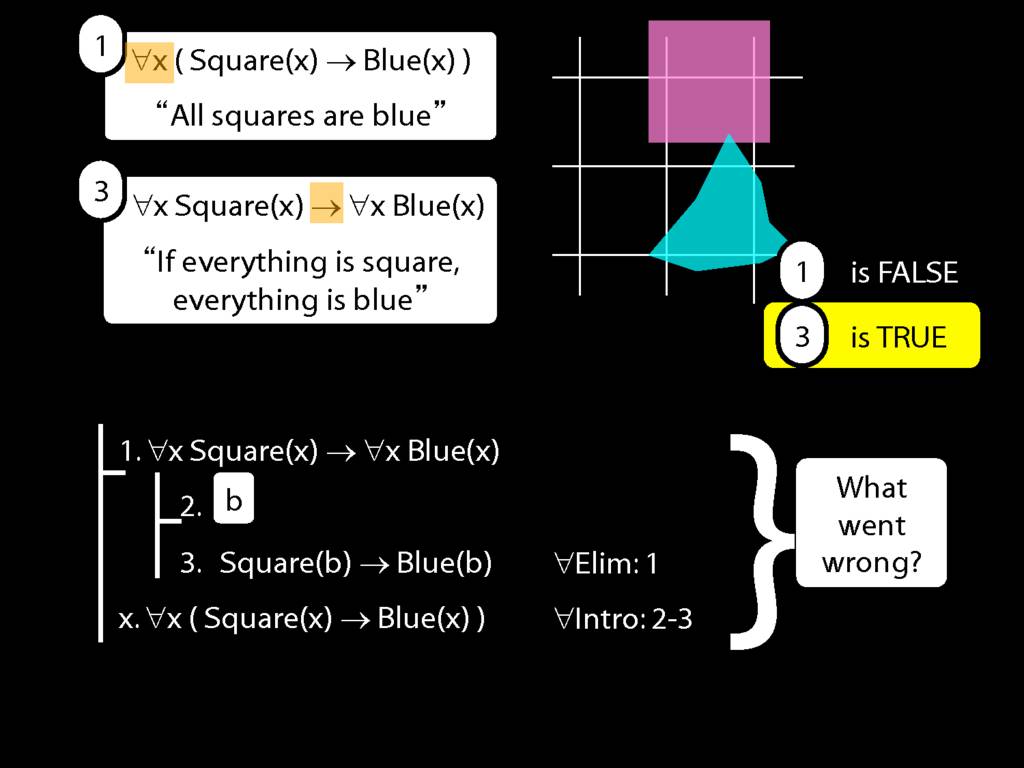
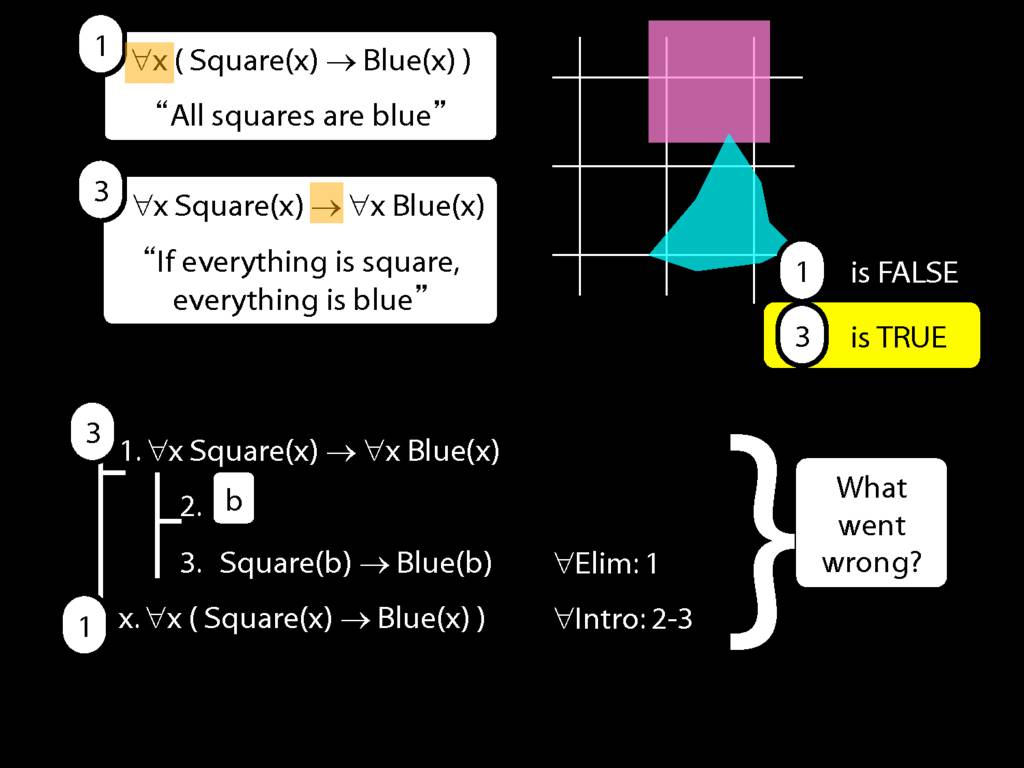
∀Intro: An Incorrect Proof

 
\section{∀Intro: An Incorrect Proof}
\emph{Reading:} §13.1, §13.2
 
\section{∀Intro: An Incorrect Proof}
This proof is wrong, but why?:
There is a counterexample to the argument:
 

Substitution of Equivalents

 
\section{Substitution of Equivalents}
\emph{Reading:} §4.5, §10.3
 
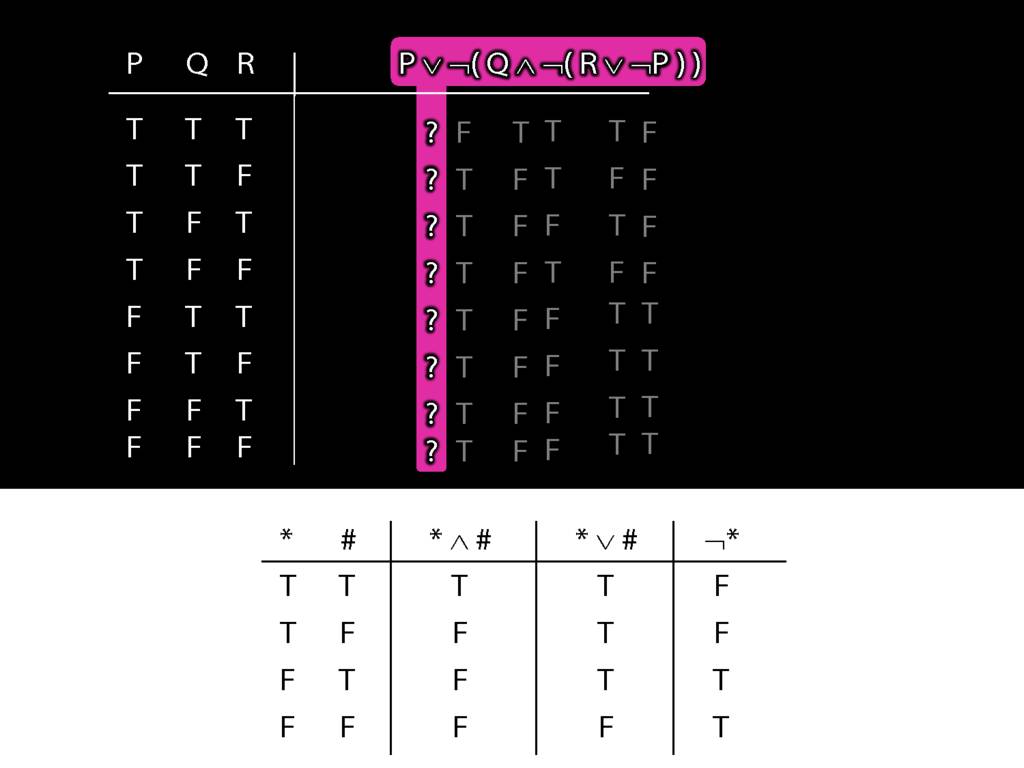
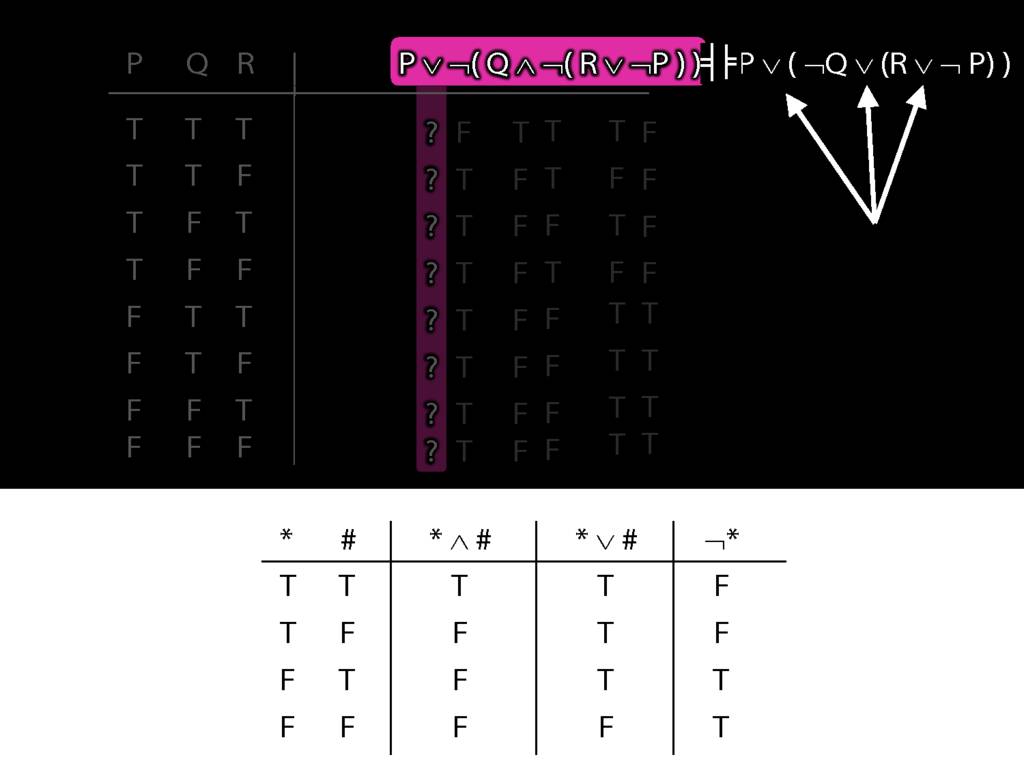
\section{Substitution of Equivalents}
Suppose that φ, ψ and χ are sentences of awFOL. Suppose that φ is logically equivalent to ψ. Let χ[φ/ψ] be the result of replacing, in χ, zero or more occurrences of φ with ψ. The \emph{subsitution theorem} says that χ[φ/ψ] is logically equivalent to χ.

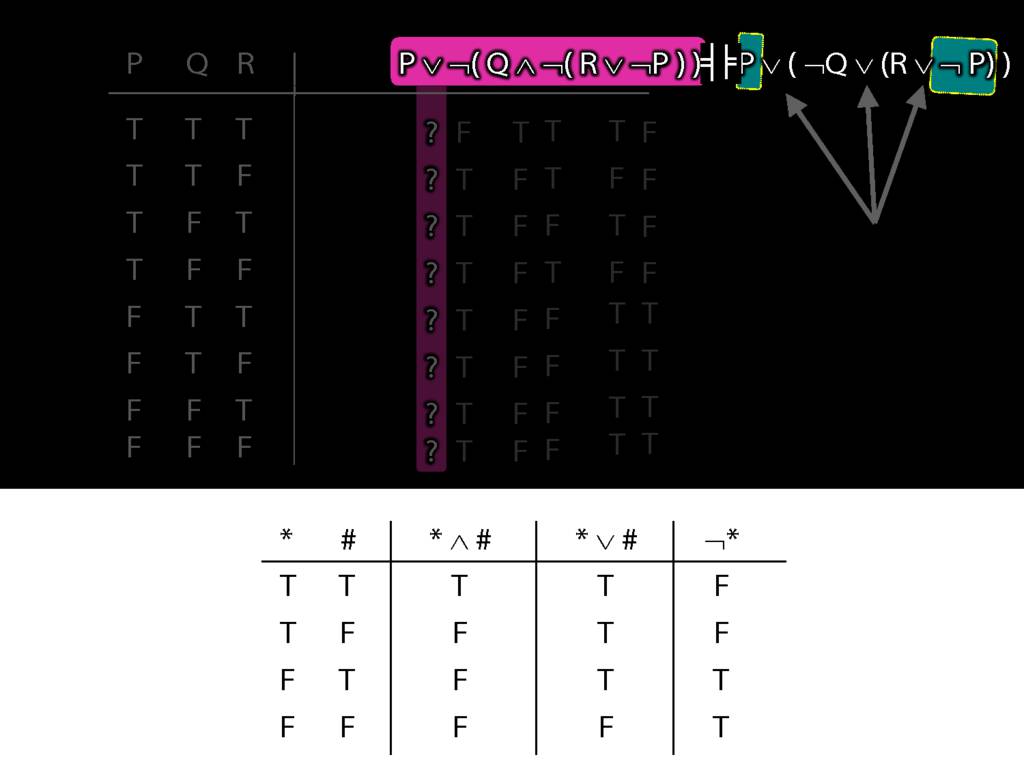
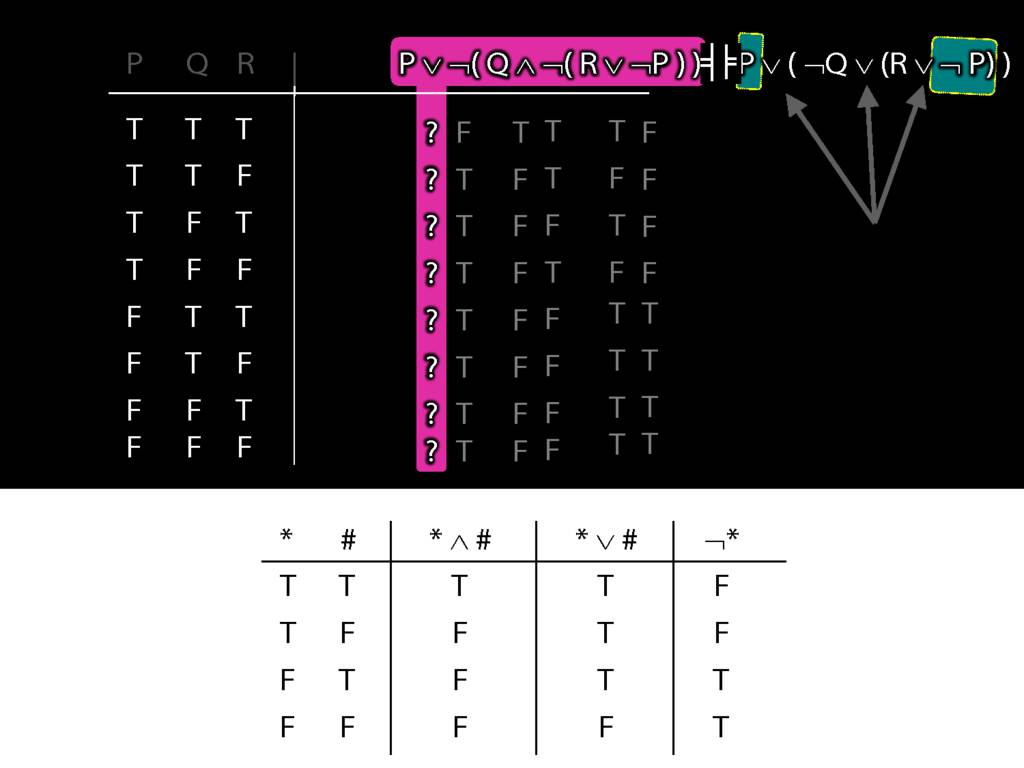
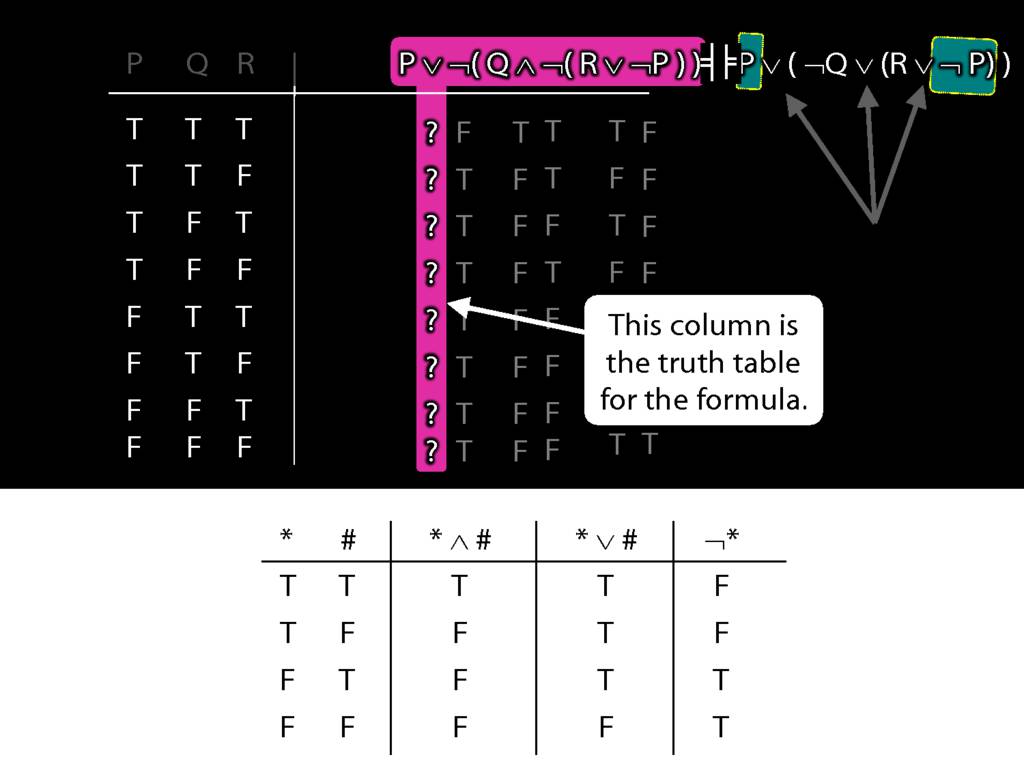
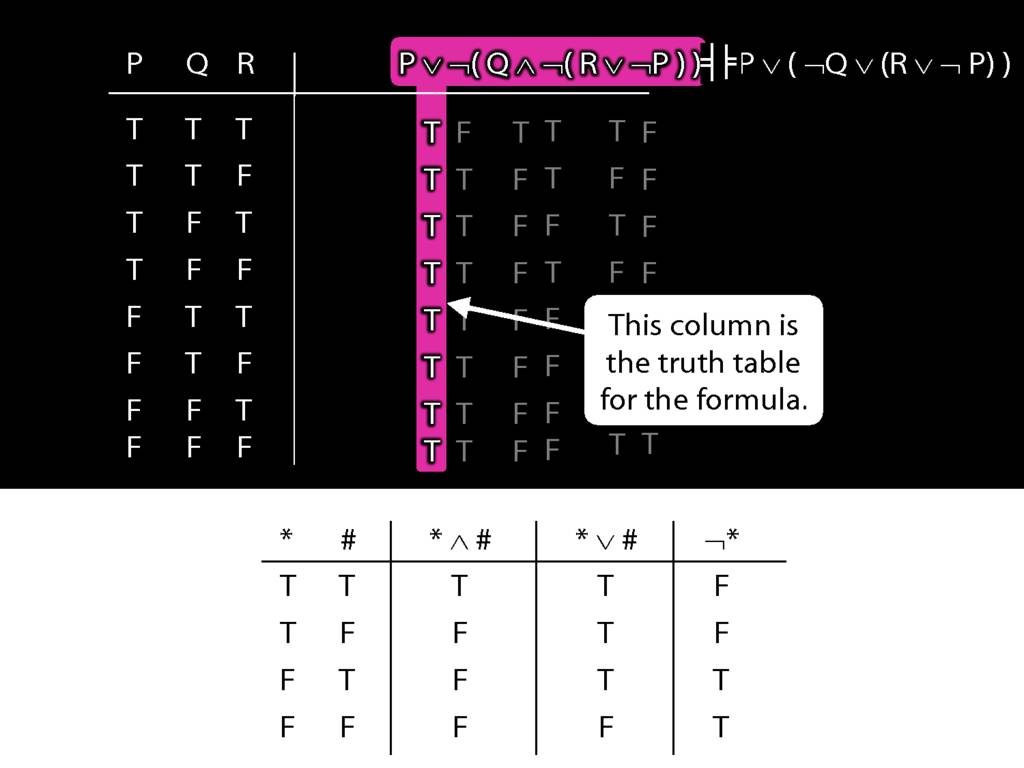
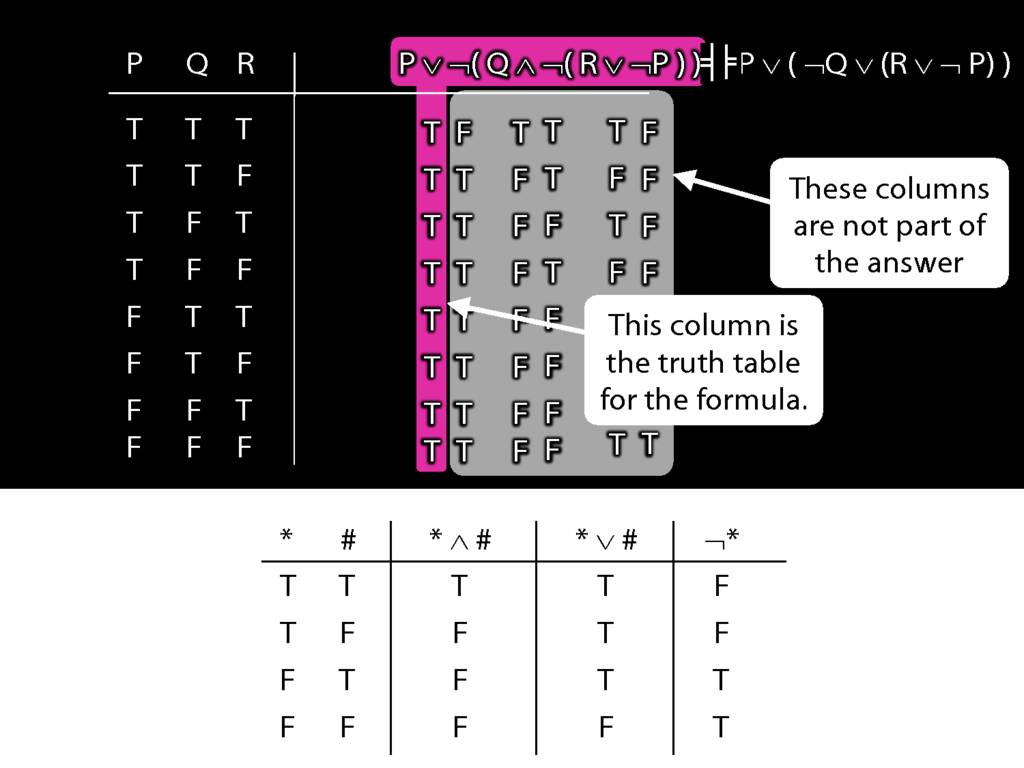
A ∧ B ⫤⊨ ¬(¬A ∨ ¬B)

A ∨ B ⫤⊨ ¬(¬A ∧ ¬B)

A → B ⫤⊨ ¬A ∨ B

¬¬(¬A ∧ ¬B) ⫤⊨ ¬(A ∨ B)

7.25
4.31, 7.25
 

Soundness and Completeness: Statement of the Theorems

 
\section{Soundness and Completeness: Statement of the Theorems}
\emph{Reading:} §8.3, §13.4
 
\section{Soundness and Completeness: Statement of the Theorems}
‘A $\vdash$ B’ means there is a proof of B using premises A
‘$\vdash$ B’ means there is a proof of B using no premises
‘A ⊨ B’ means B is a logical consequence of A
‘⊨ B’ means B is a tautology
‘A ⊨$_{TT}$ B’ means B is a logical consequence of A just in virtue of the meanings of truth-functions (the textbook LPL calls this ‘tautological consequence’)
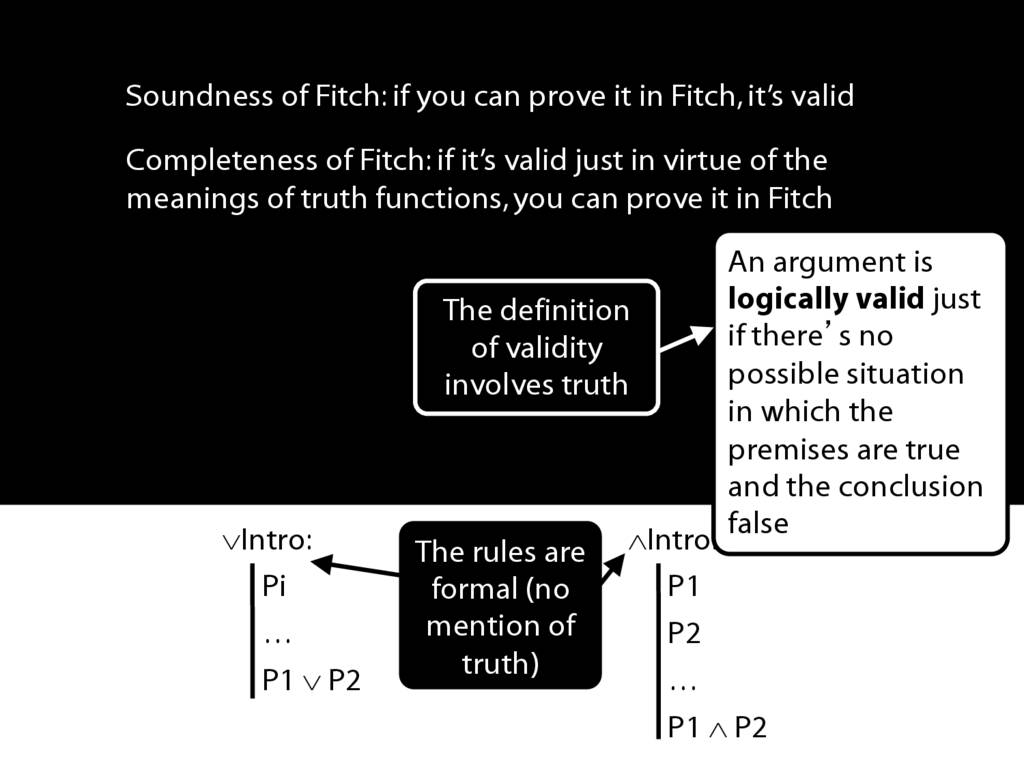
\emph{Soundness}: If A $\vdash$ B then A ⊨ B
\hspace{3mm} i.e. if you can prove it in Fitch, it’s valid
\emph{Completeness}: If A ⊨$_{TT}$ B then A $\vdash$ B
\hspace{3mm} i.e. if it’s valid just in virtue of the meanings of the truth-functional connectives, then you can prove it in Fitch.