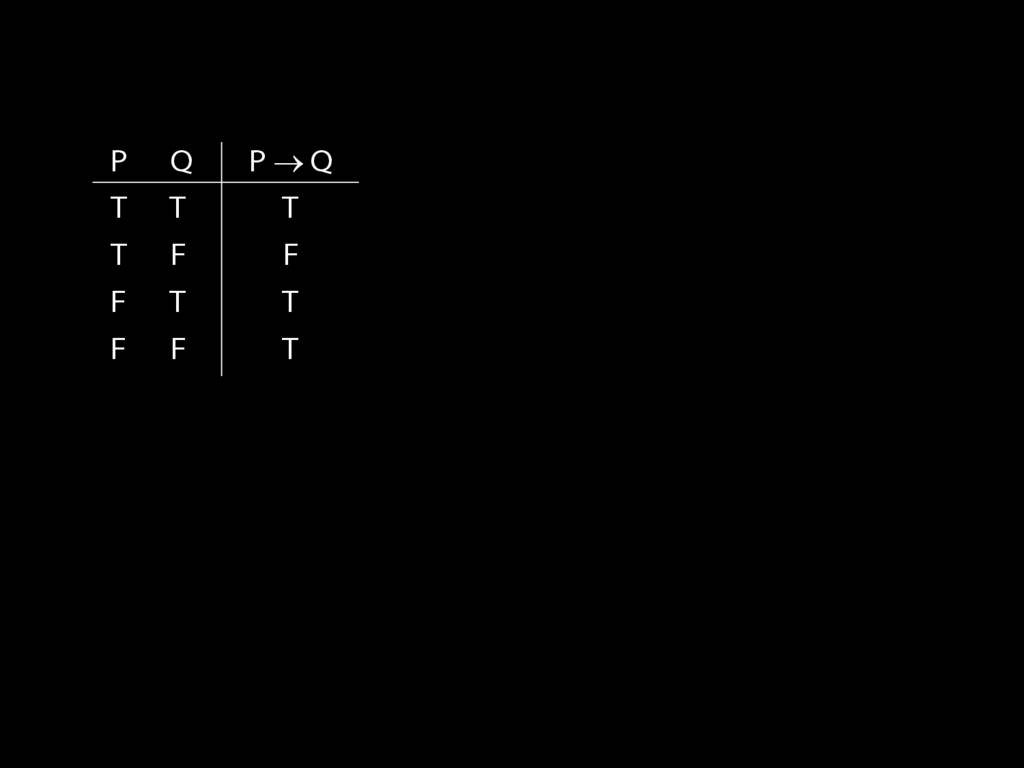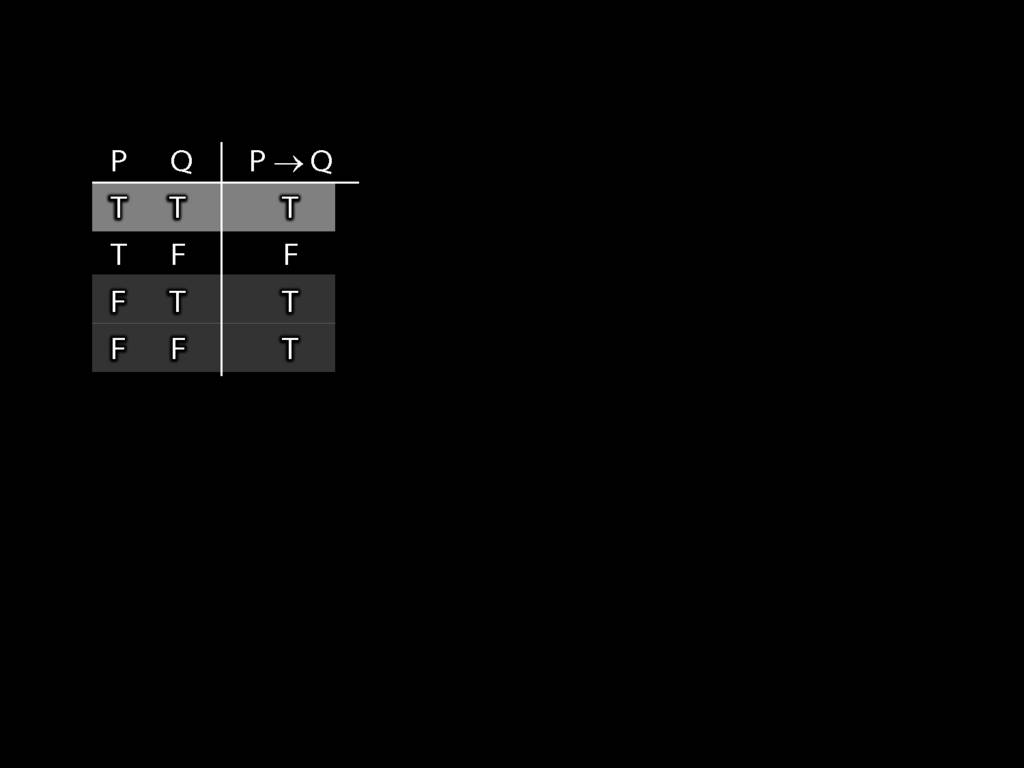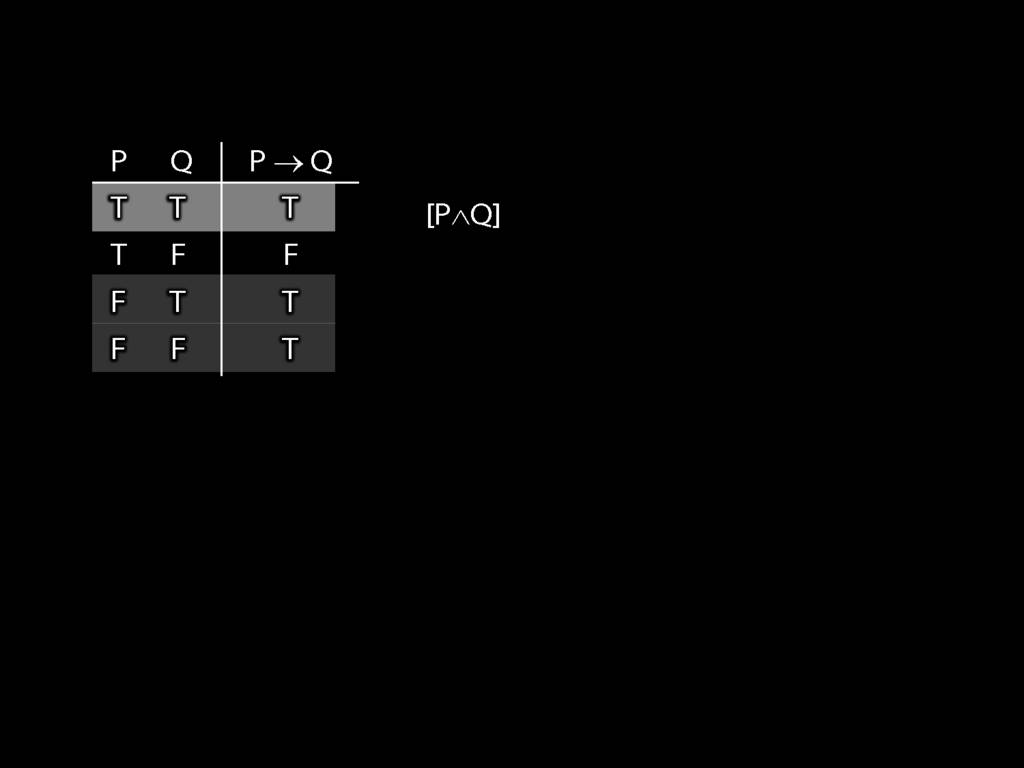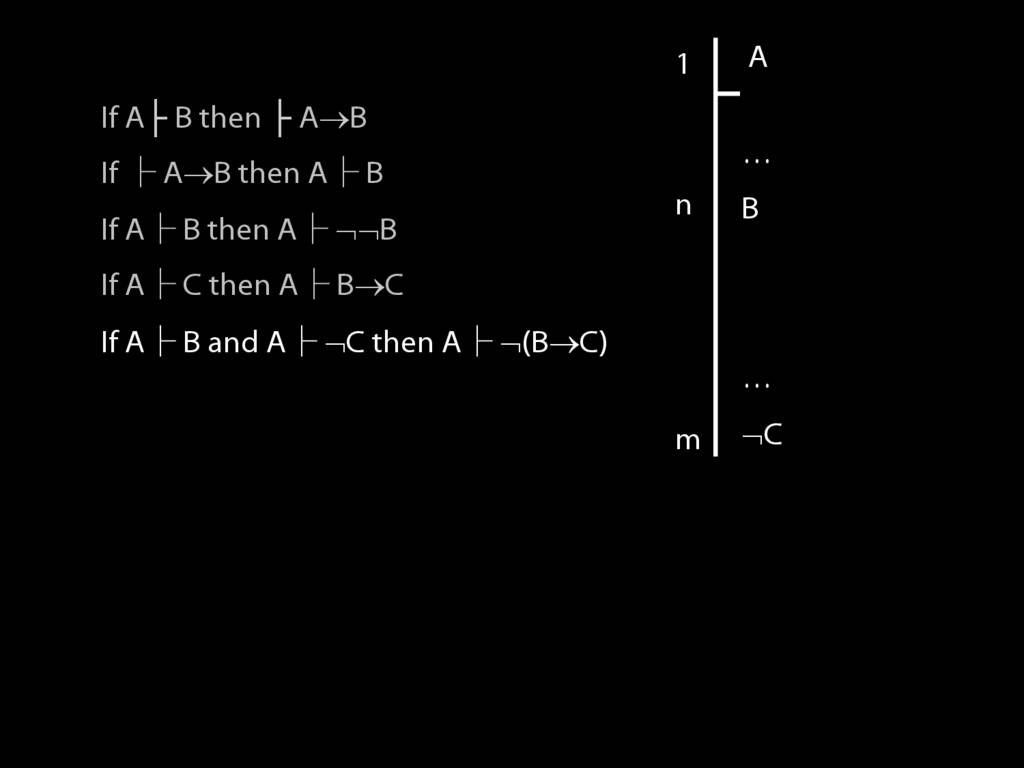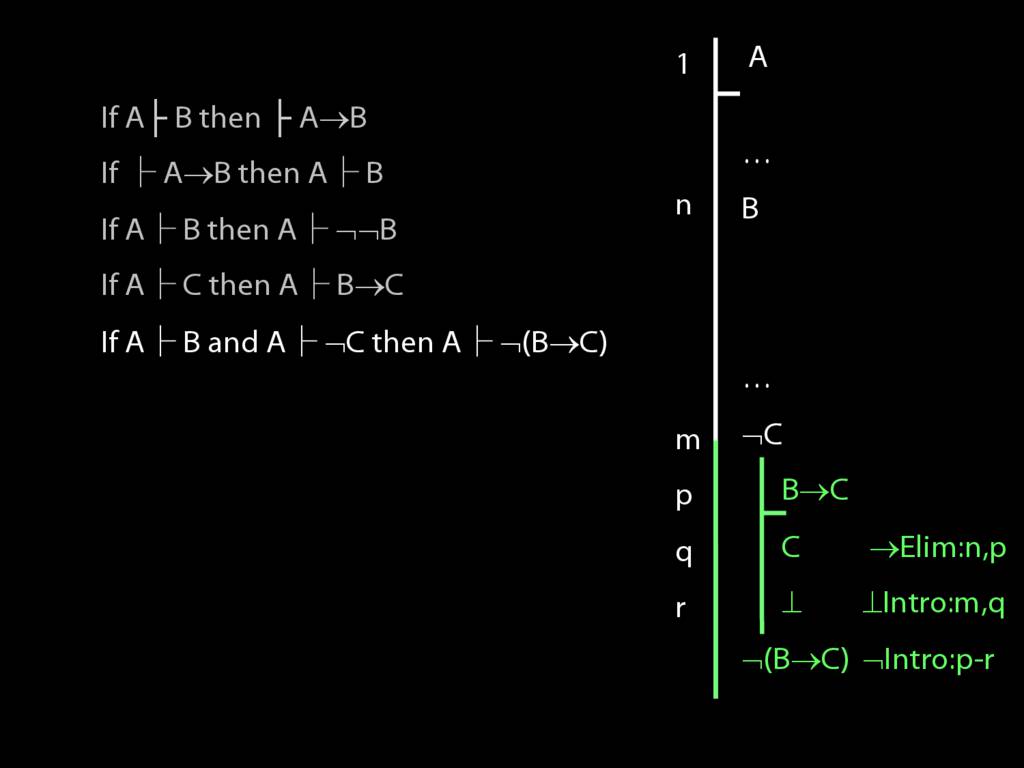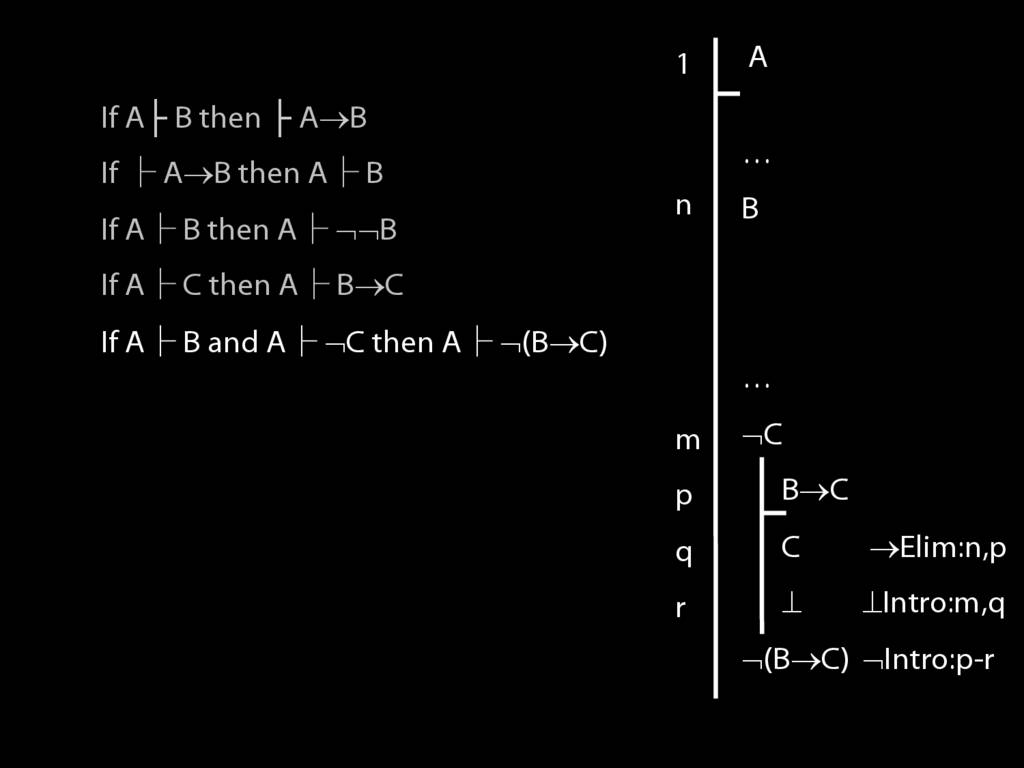\title {Logic I \\ Fast Lecture 07}
\maketitle
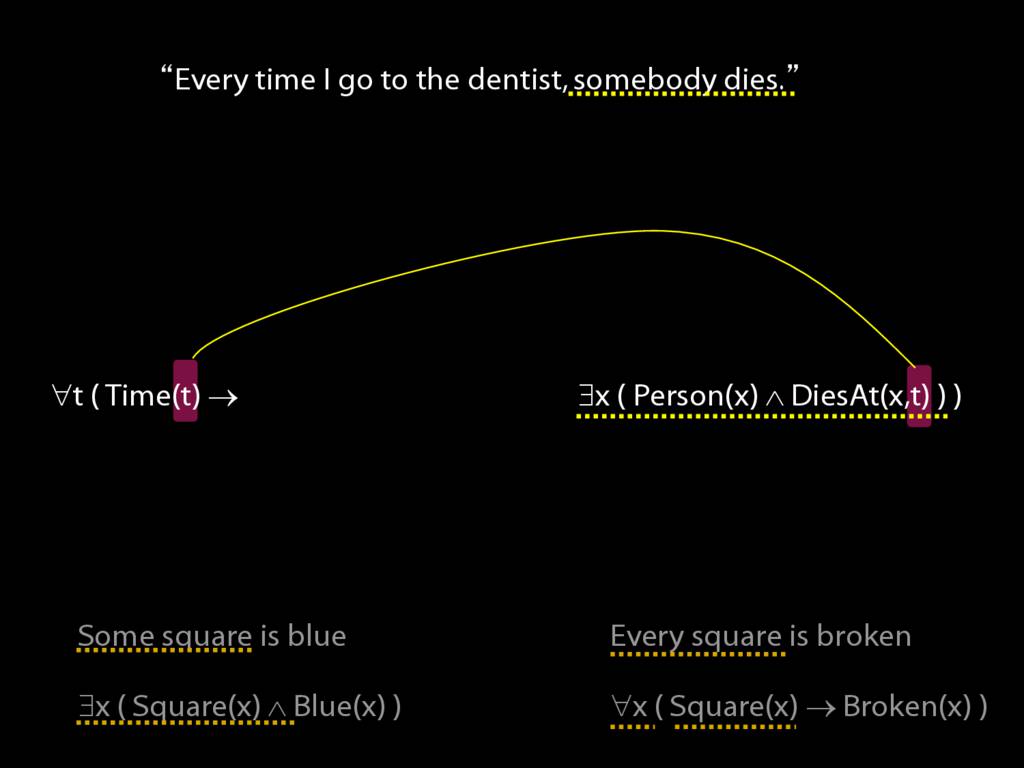
\section{Every Time I Go to the Dentist Someone Dies}
\emph{Reading:} §11.2
\section{Every Time I Go to the Dentist Someone Dies}
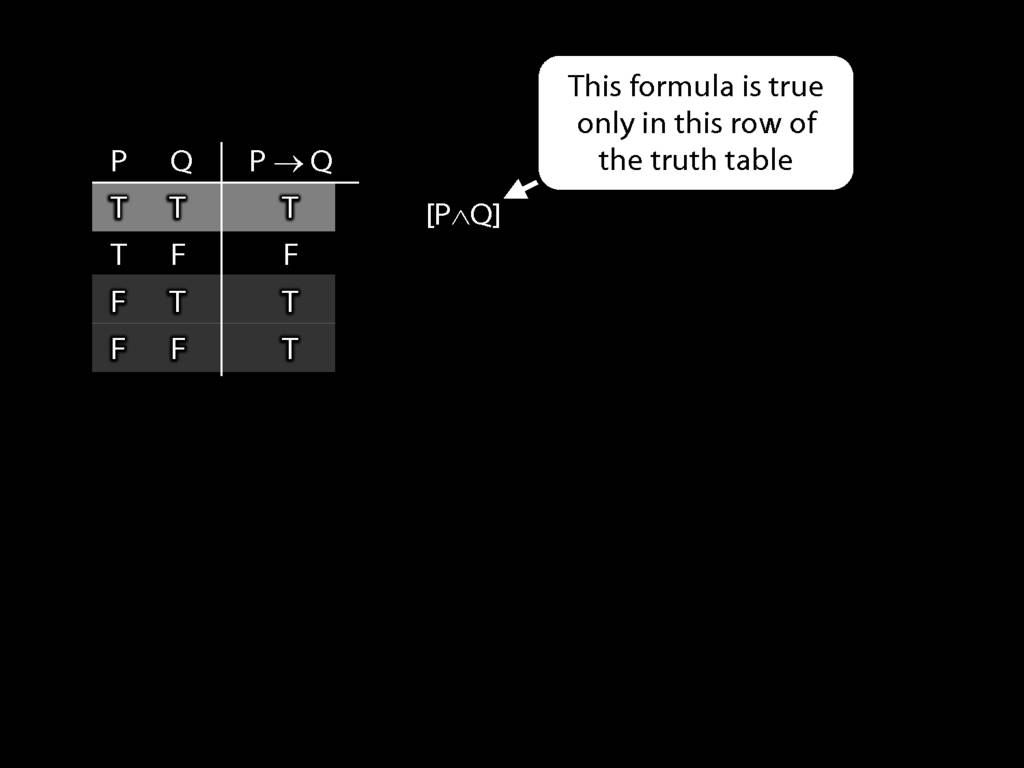
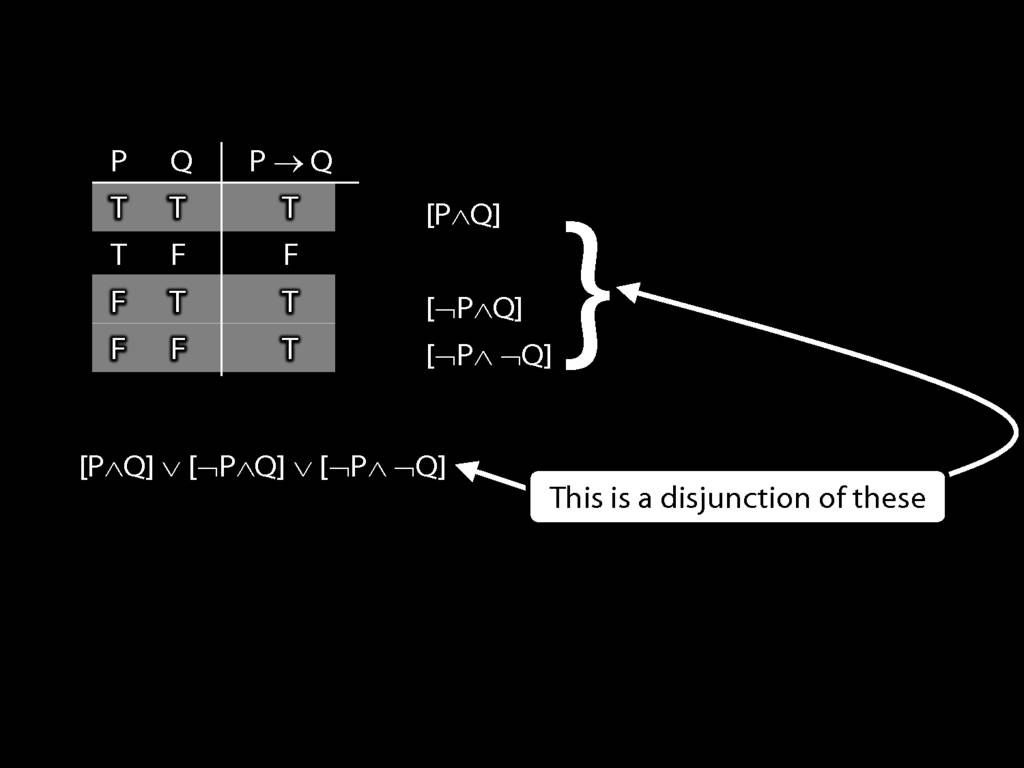
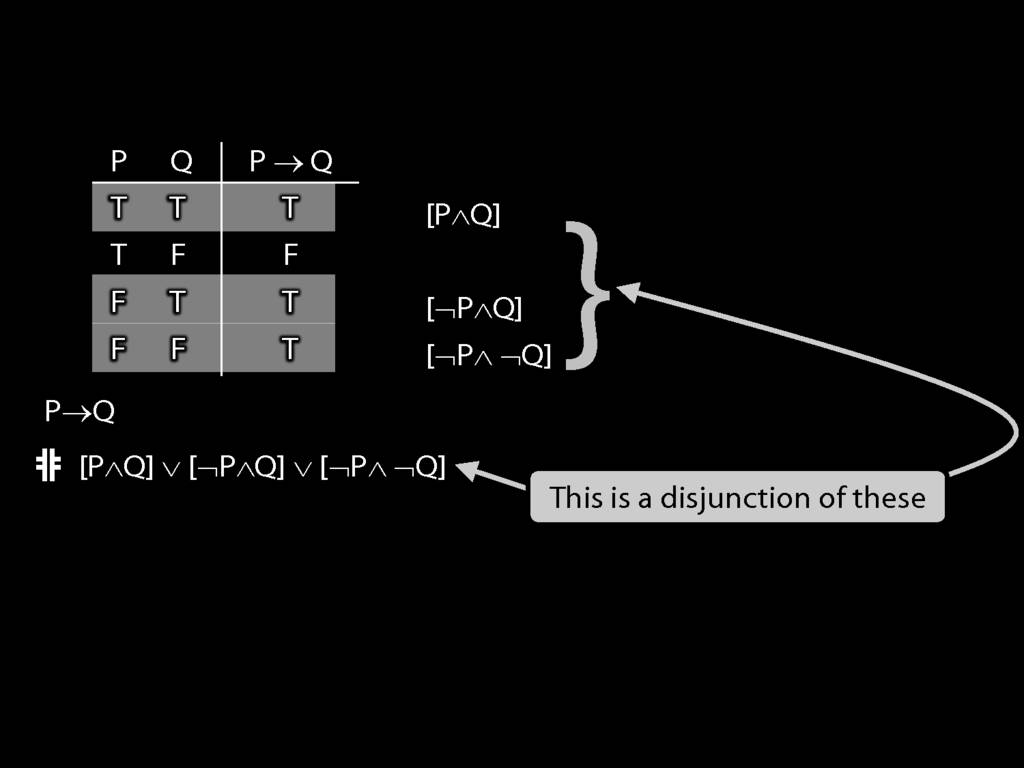
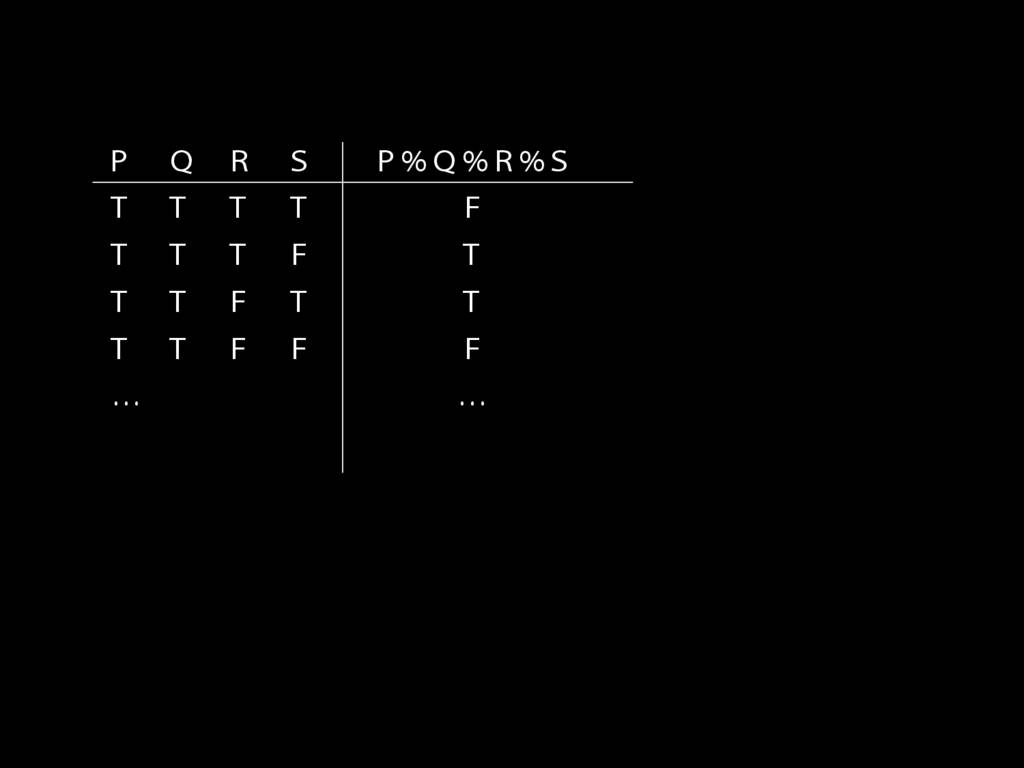
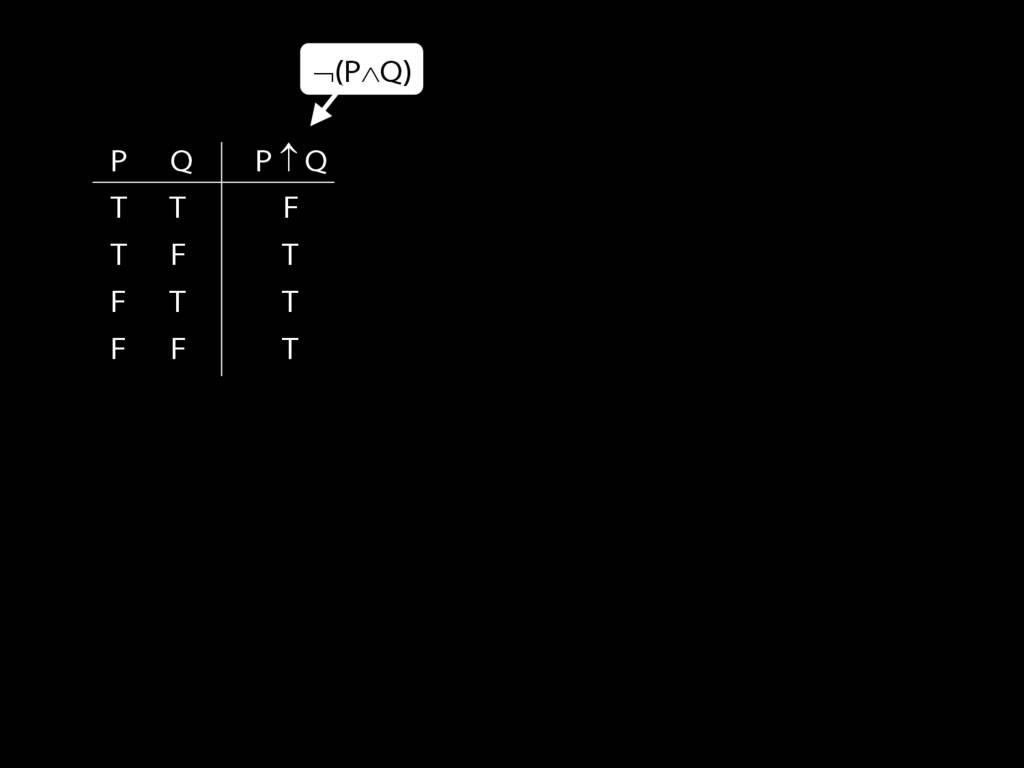
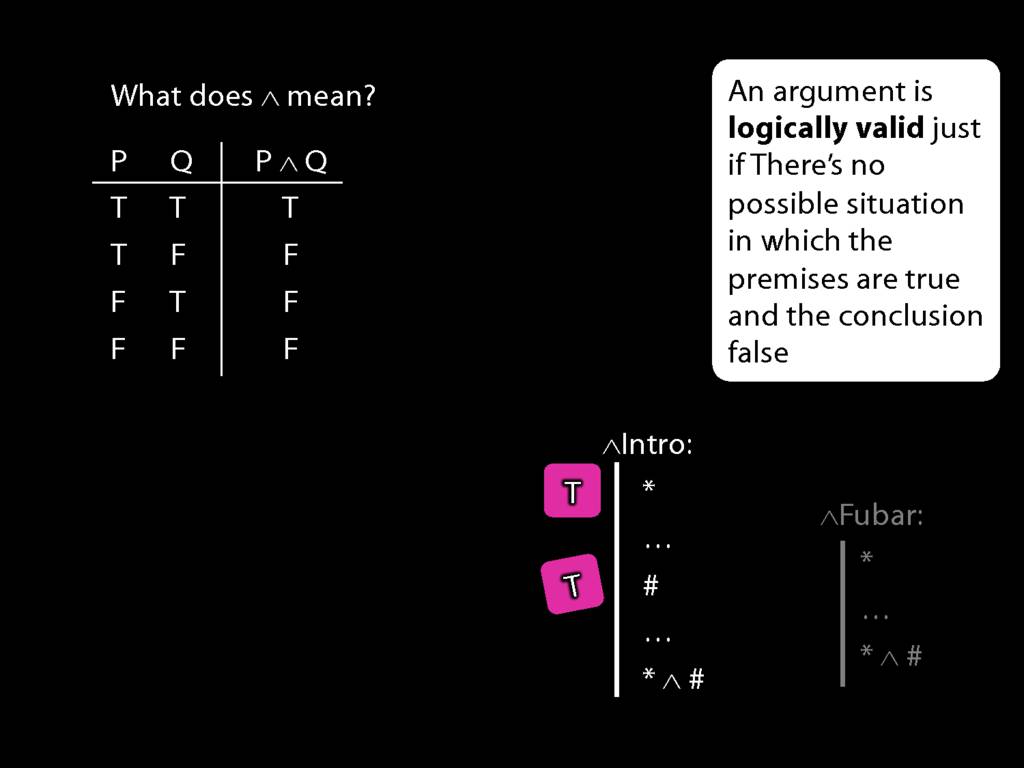
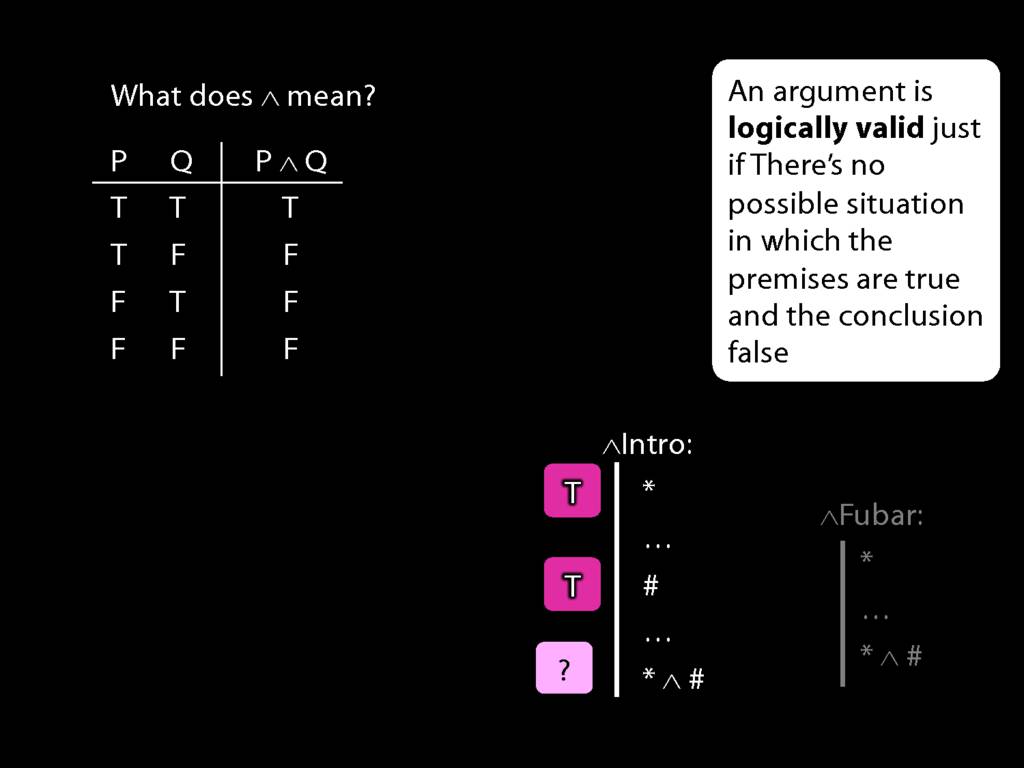
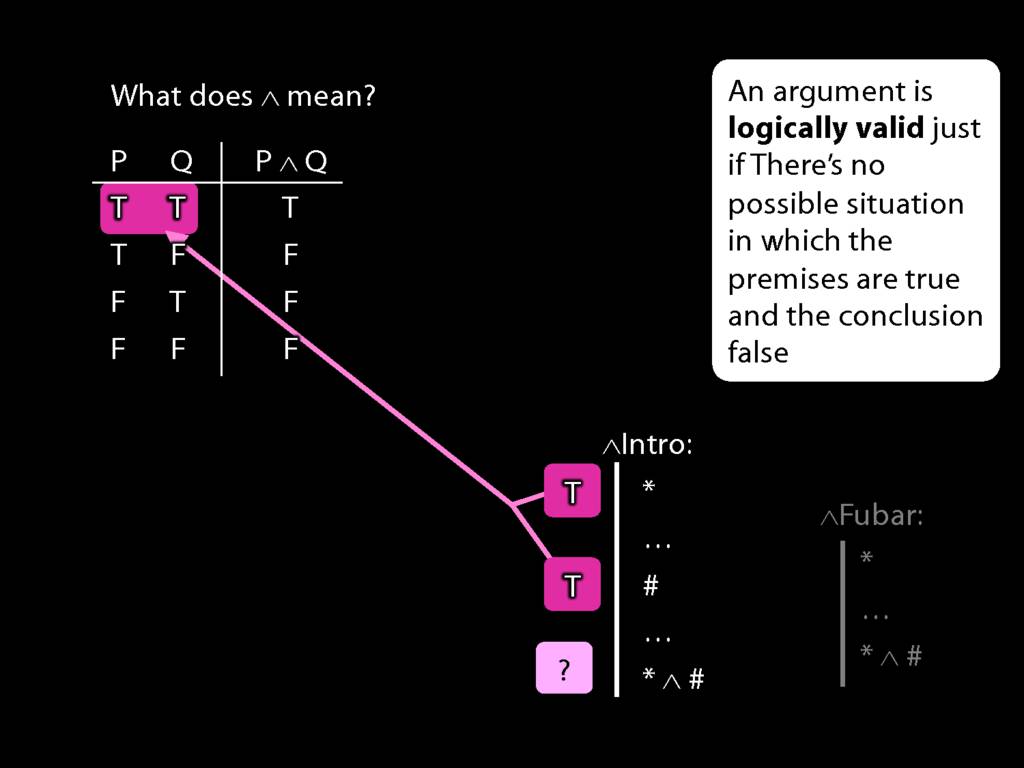
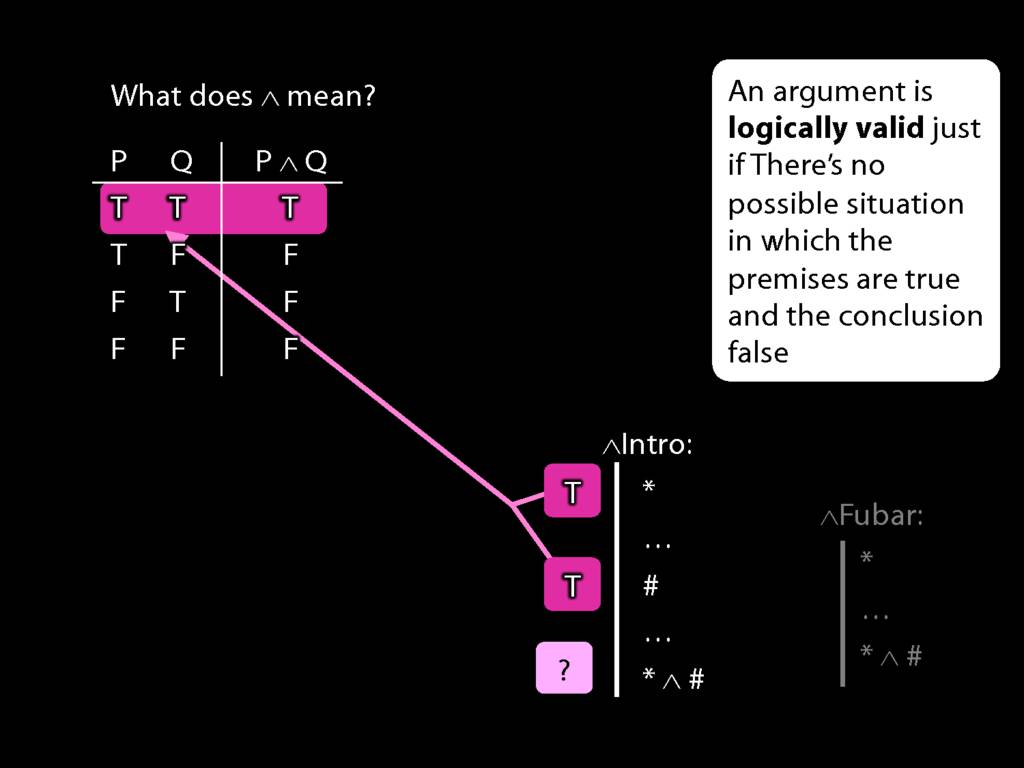
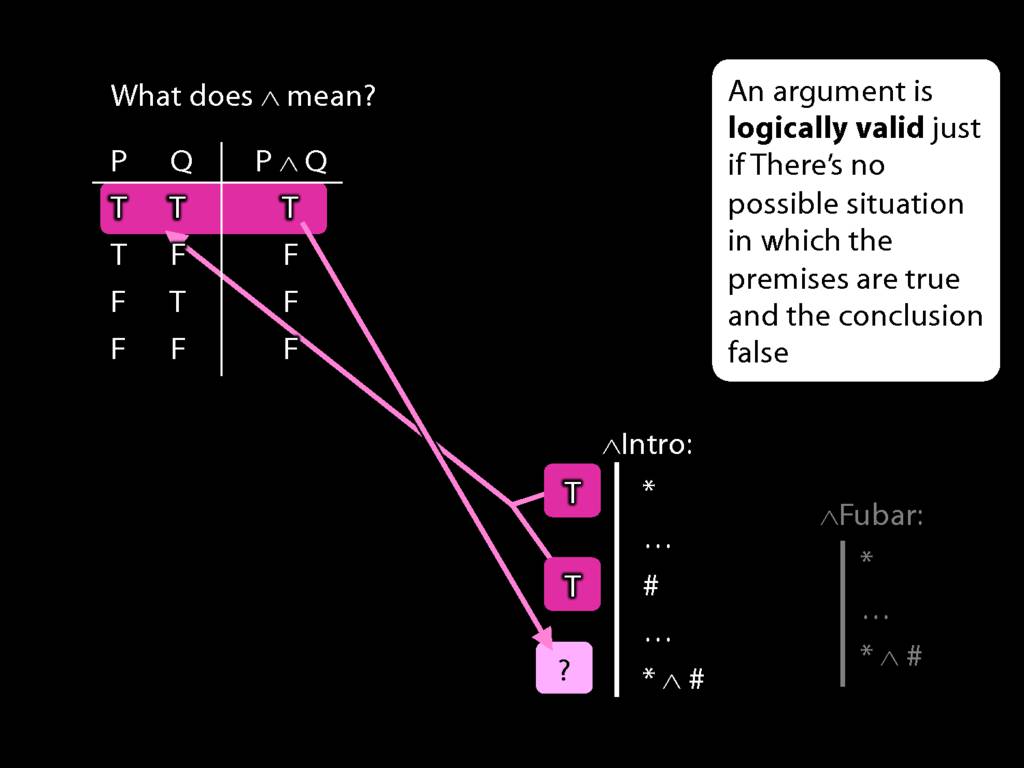
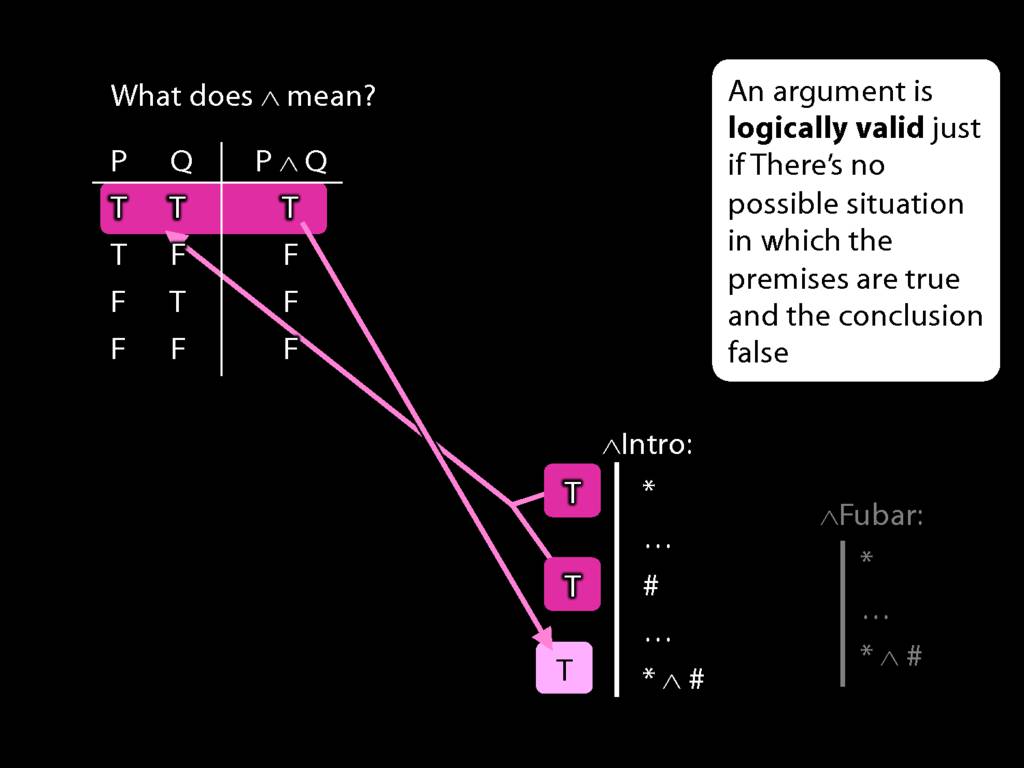
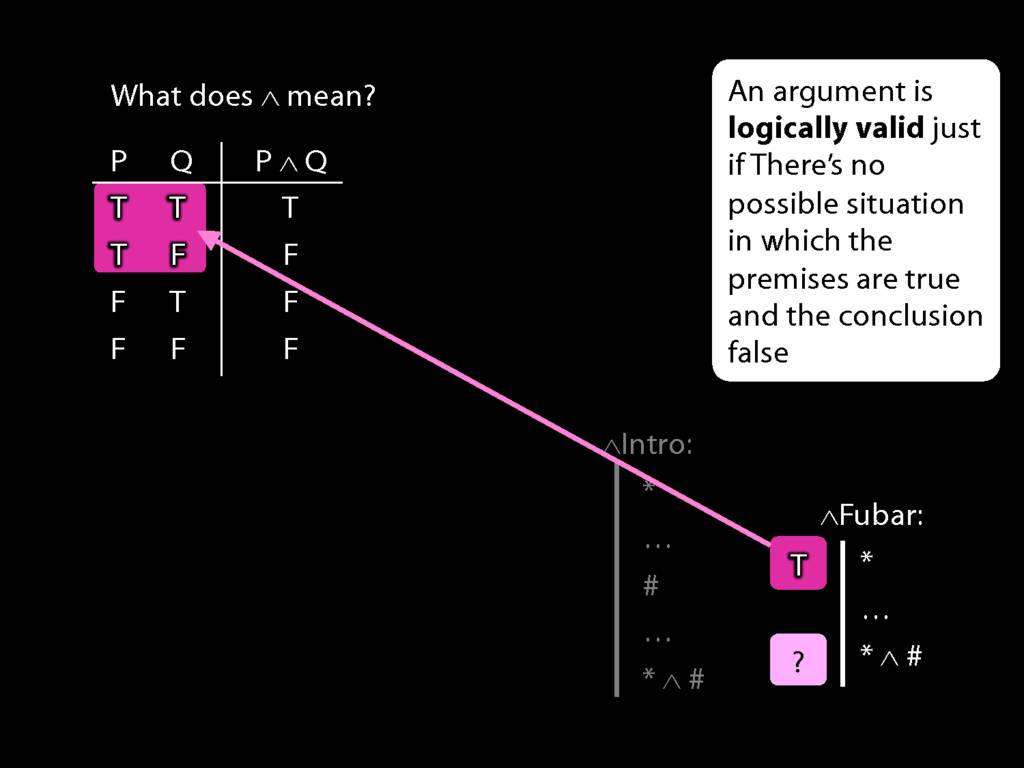
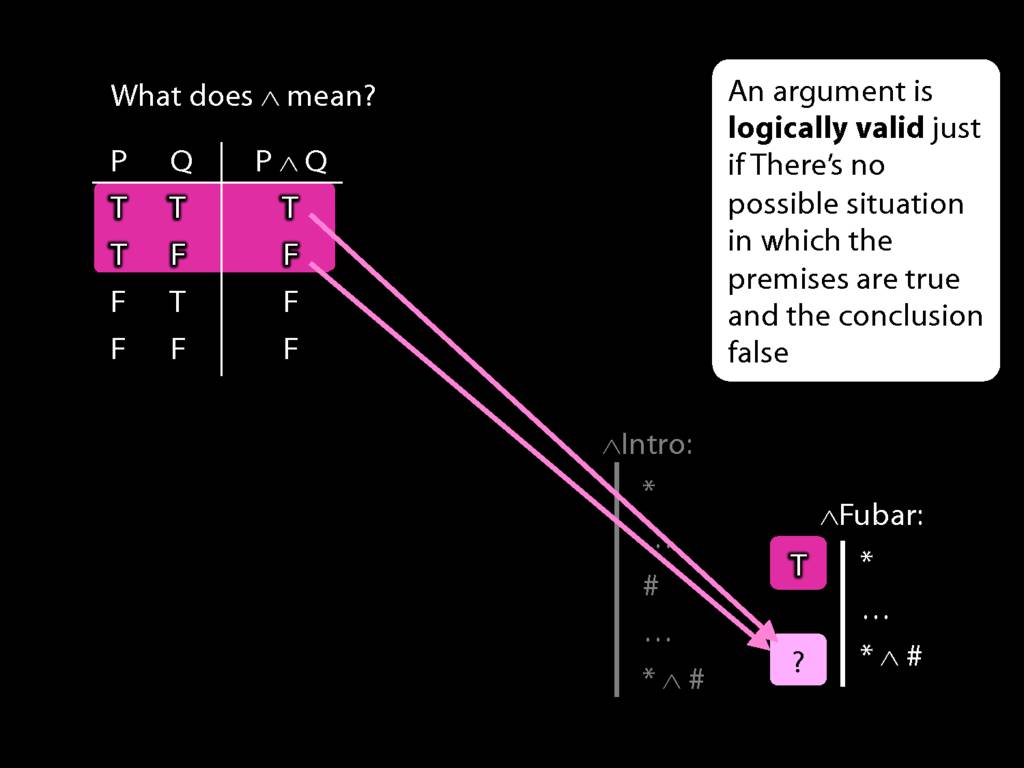
\section{Truth-functional completeness}
\emph{Reading:} §7.4
\section{Truth-functional completeness}
7.25, 7.26, *7.28, 7.29
7.25, 7.26, *7.28, 7.29
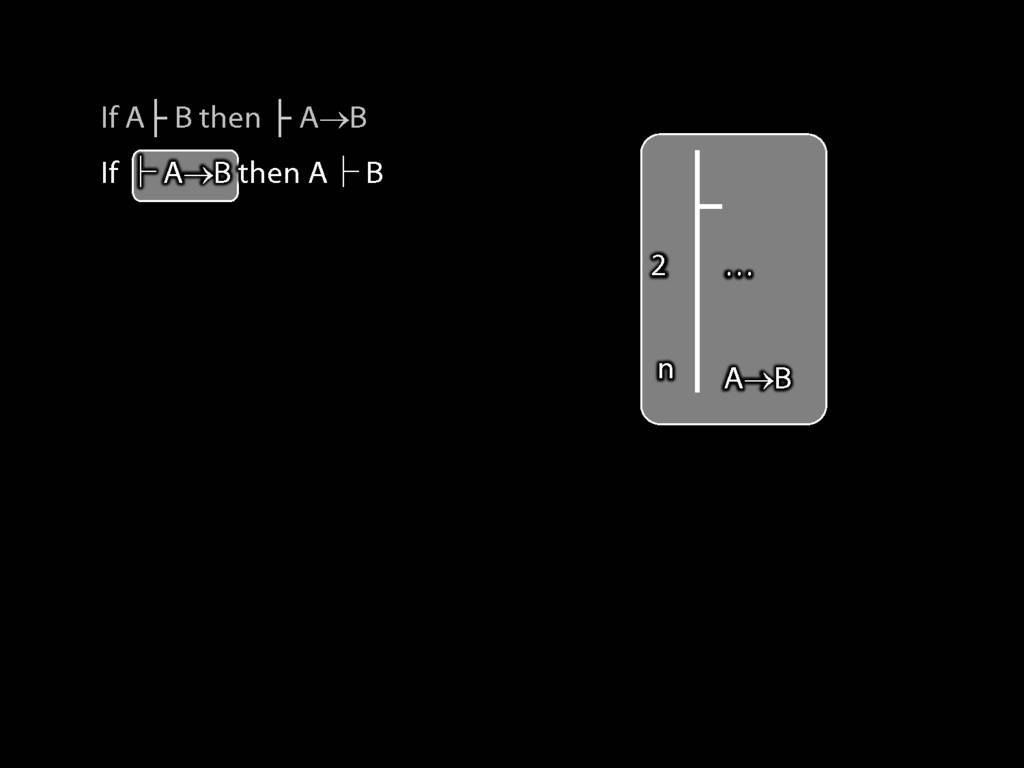
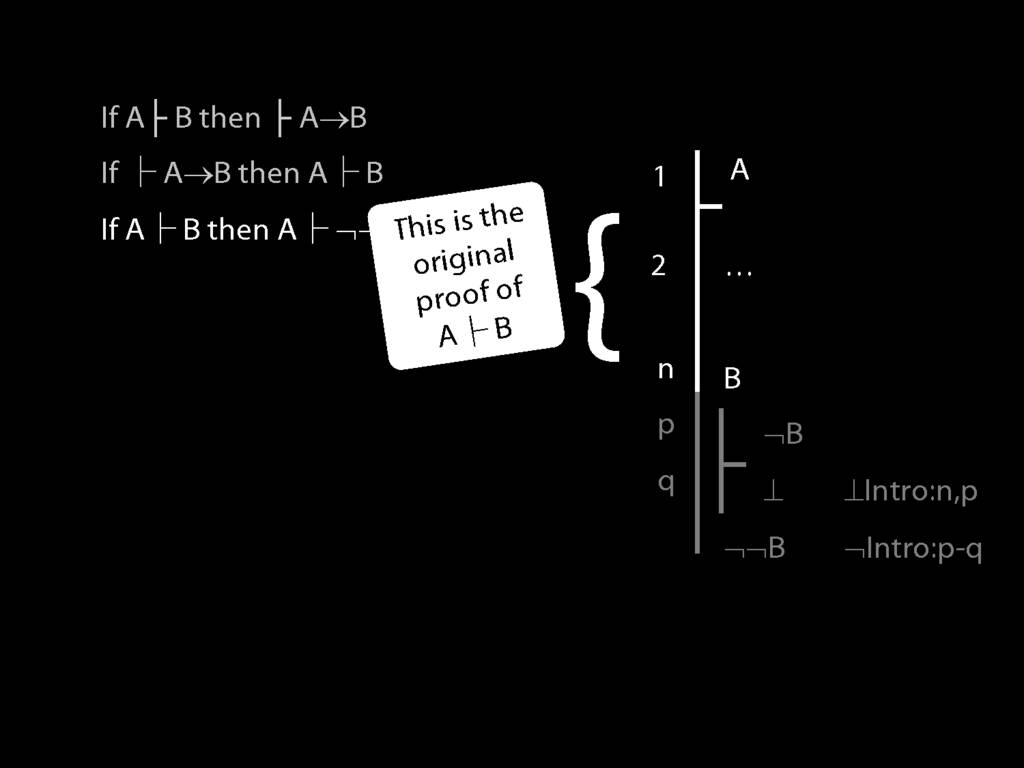
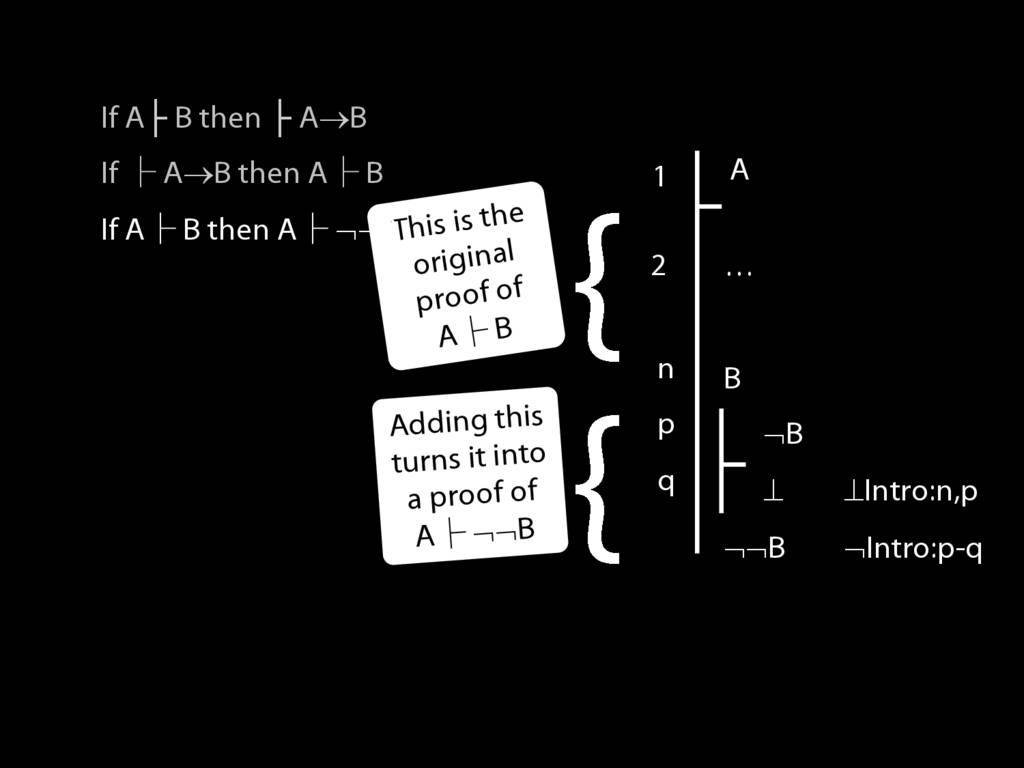
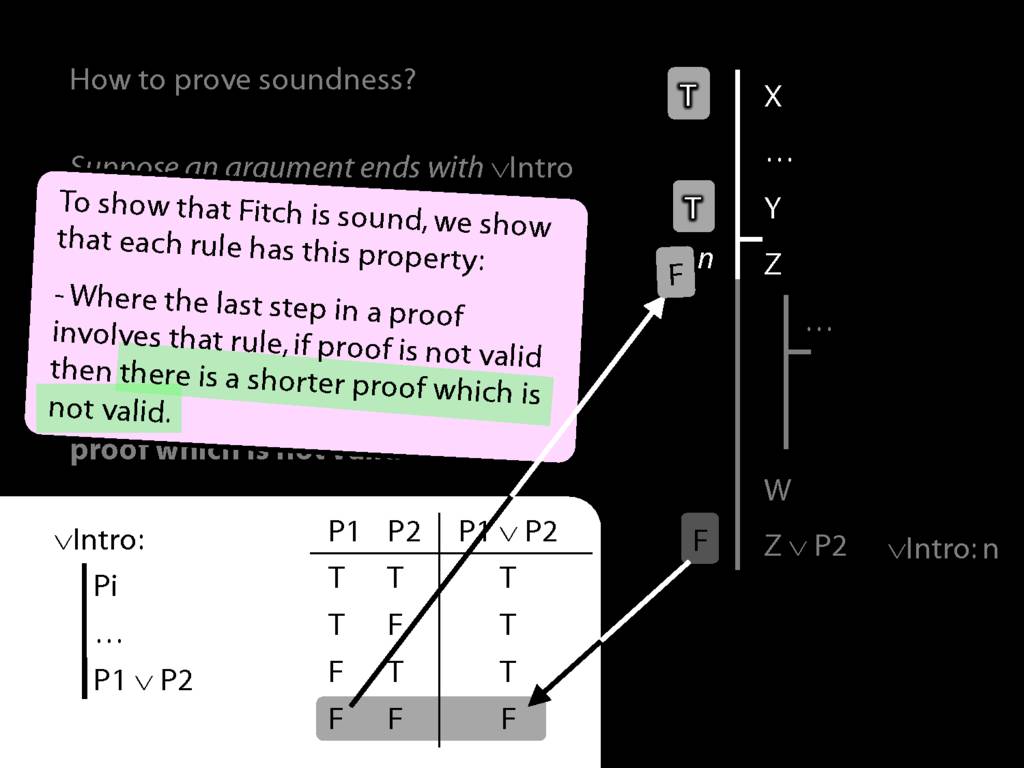
\section{Proofs about Proofs}
\section{Proofs about Proofs}
\section{The Soundness Property and the Fubar Rules (fast)}
\emph{Reading:} §8.3
\section{The Soundness Property and the Fubar Rules (fast)}
7.32
7.32
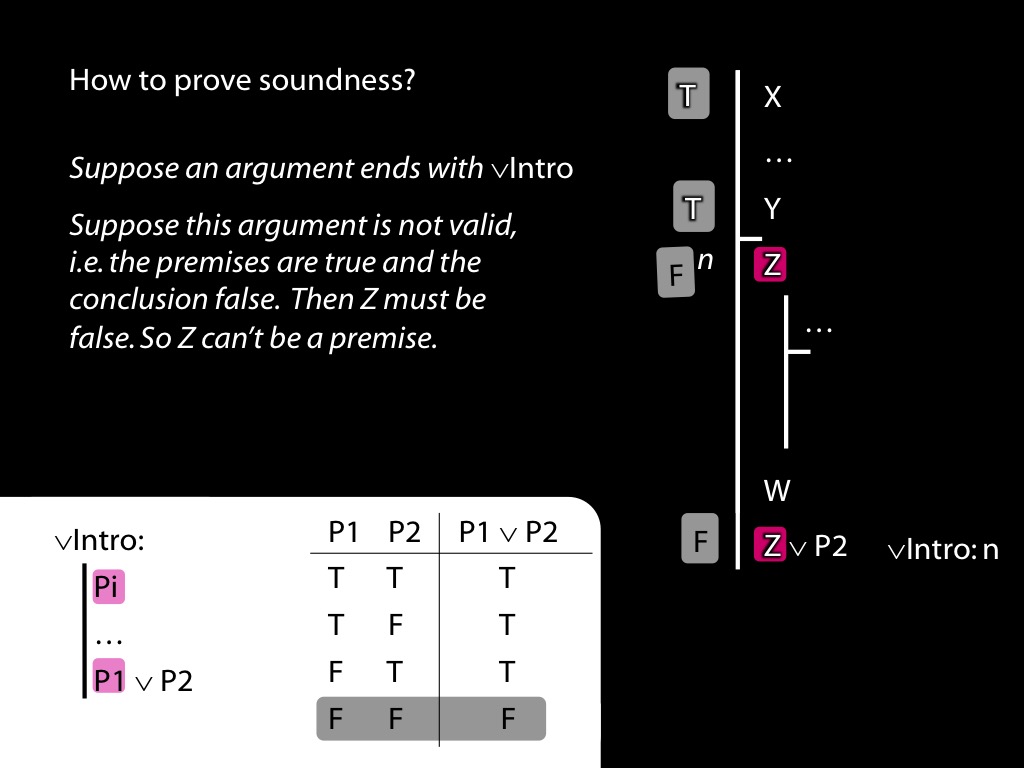
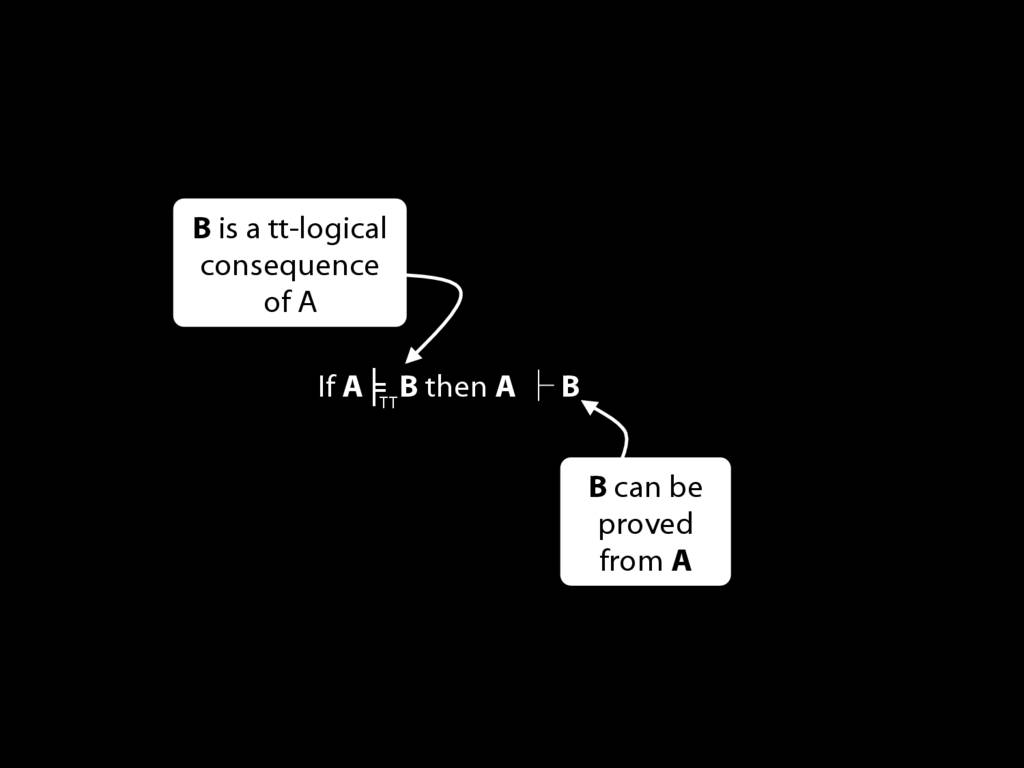
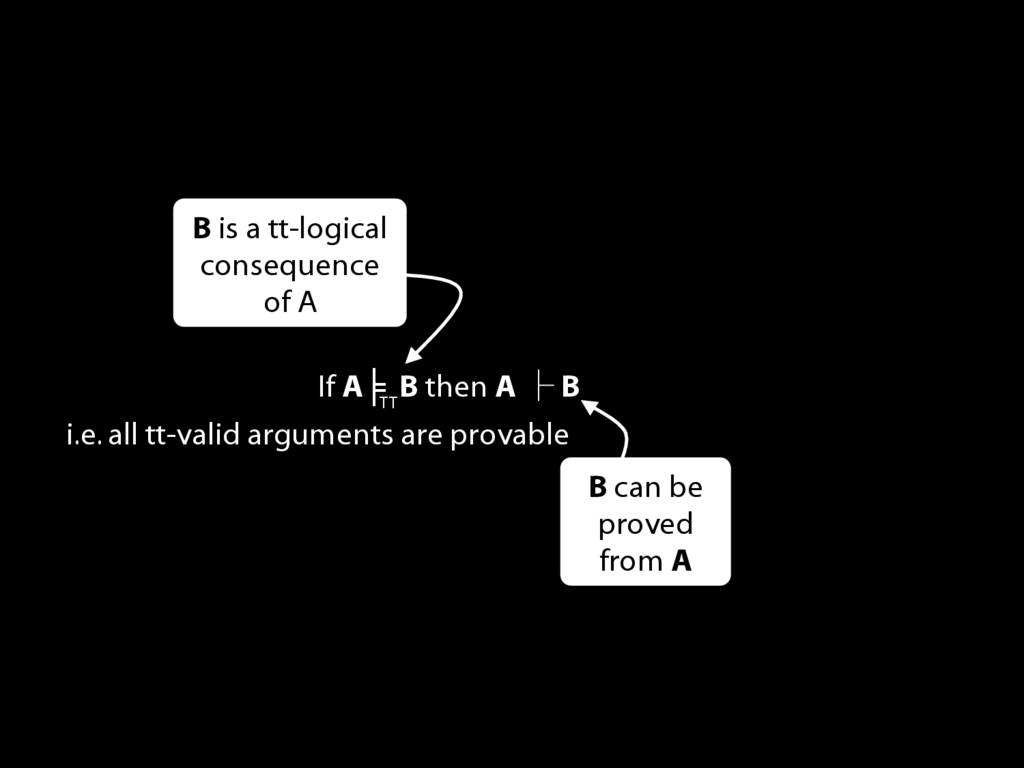
\section{Proof of the Soundness Theorem}
\emph{Reading:} §8.3
\section{Proof of the Soundness Theorem}
\section{The Essence of the Completeness Theorem}
\emph{Reading:} §8.3
\section{The Essence of the Completeness Theorem}
\section{Lemma for the Completeness Theorem}
\emph{Reading:} §8.3
\section{Lemma for the Completeness Theorem}
\section{Proof of the Completeness Theorem}
\emph{Reading:} §8.3, §17.1, §17.2
\section{Proof of the Completeness Theorem}
\section{Proof of Proposition 4 for the Completeness Theorem}
\emph{Reading:} §15.1, §15.6
\section{Proof of Proposition 4 for the Completeness Theorem}
15.33--15.40 (second edition)
15.33, 15.37--15.39 (second edition)
\section{More Records Than the KGB}
\emph{Reading:} §14.1, §14.3
\section{More Records Than the KGB}
\section{The End Is Near}
\emph{Reading:} §14.3
\section{The End Is Near}
14.26, 14.28
14.2
14.4, 14.5
14.10, 14.11
14.26, 14.28
13.51–2, 14.13 %proofs
For each of the following sentences of FOL, give a logically equivalent sentence of idiomatic English using the specified interpretation. Your English sentences should be as concise as possible.
Domain : people and actions
D(x) : x is desirable
V(x) : x is virtuous
A(x) : x is an action
H(x) : x is a person
P(x,y) : x performed y
i. ∀x (( D(x) → V(x) )
ii. ∀x ( (A(x)∧ D(x) ) → V(x) ) )
iii. ∃x ( A(x) ∧ ¬( D(x) → V(x) ) )
*iv. ∃x(H(x)∧∀y((A(y)∧P(x,y))→V(y)))
**v. ¬∃x (∃y (H(x) ∧ P(x,y) ∧ A(y) ∧ ¬V(y)) ∧ ¬∃z[P(x,z) ∧ A(z) ∧ V(z)))