\title {Logic I \\ Lecture 06}
\maketitle
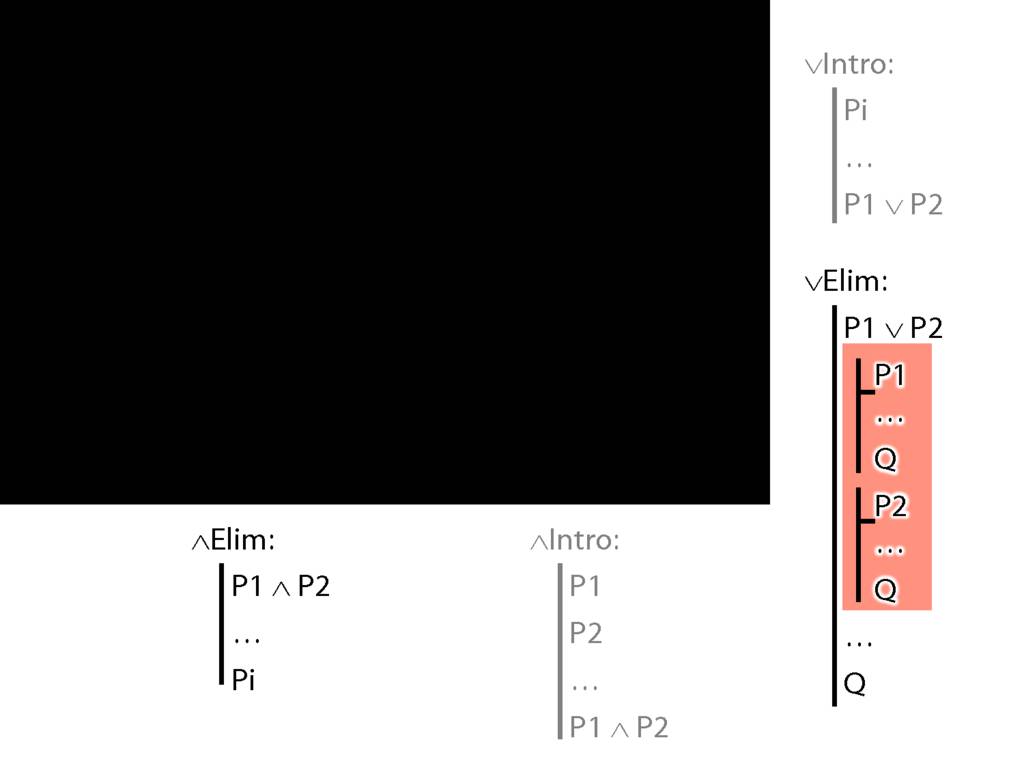
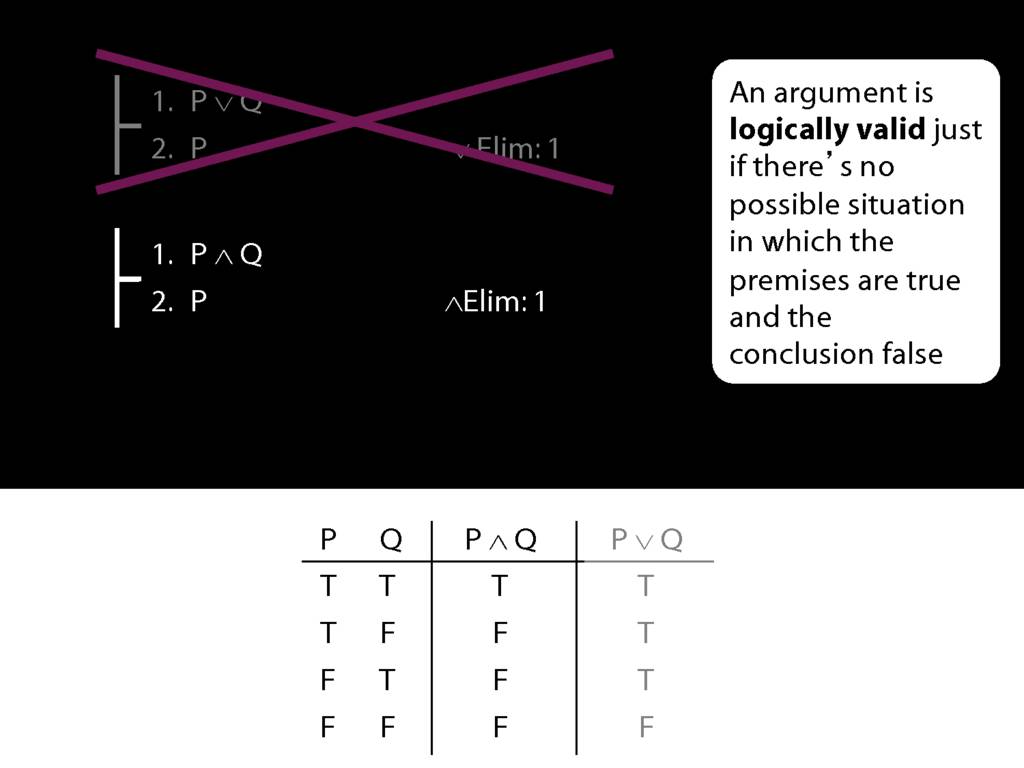
\section{∨Intro and ∨Elim}
\emph{Reading:} §6.2
\section{∨Intro and ∨Elim}
\section{∨Elim and Soundness}
\emph{Reading:} §5.2, §6.2
\section{∨Elim and Soundness}
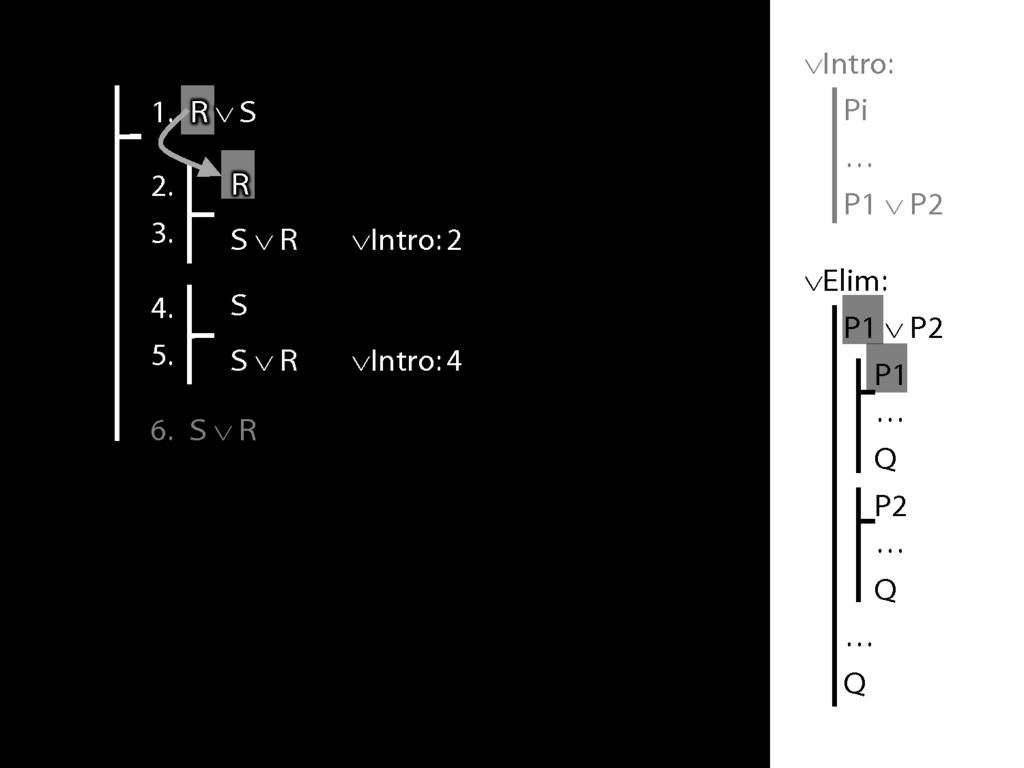
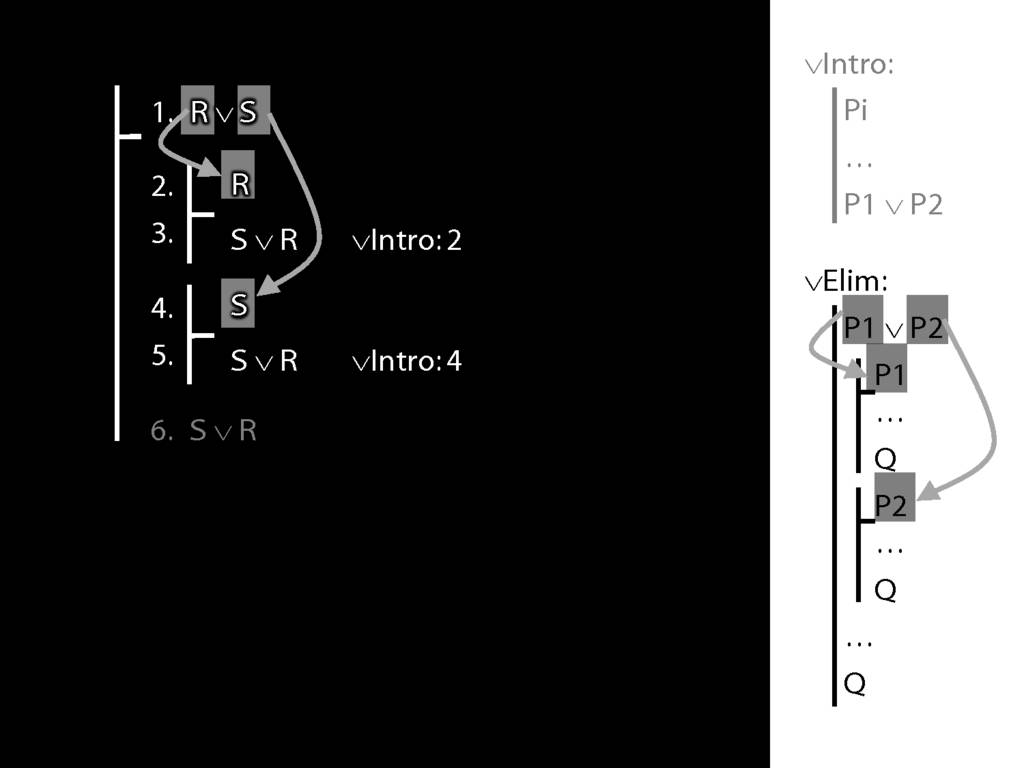
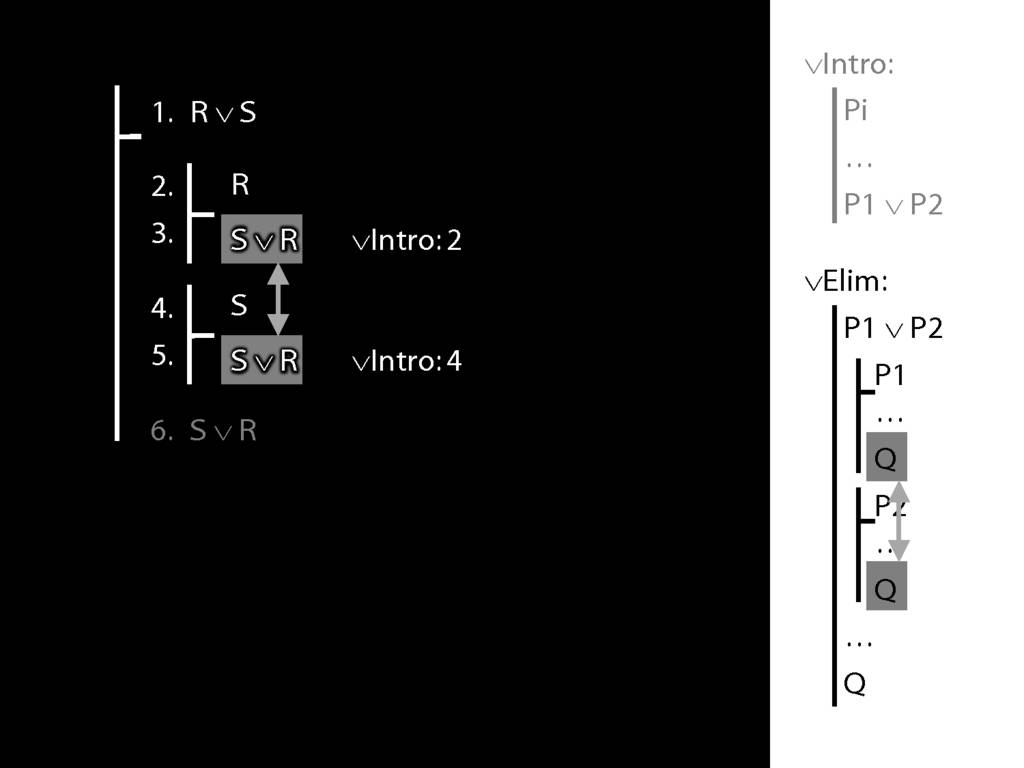
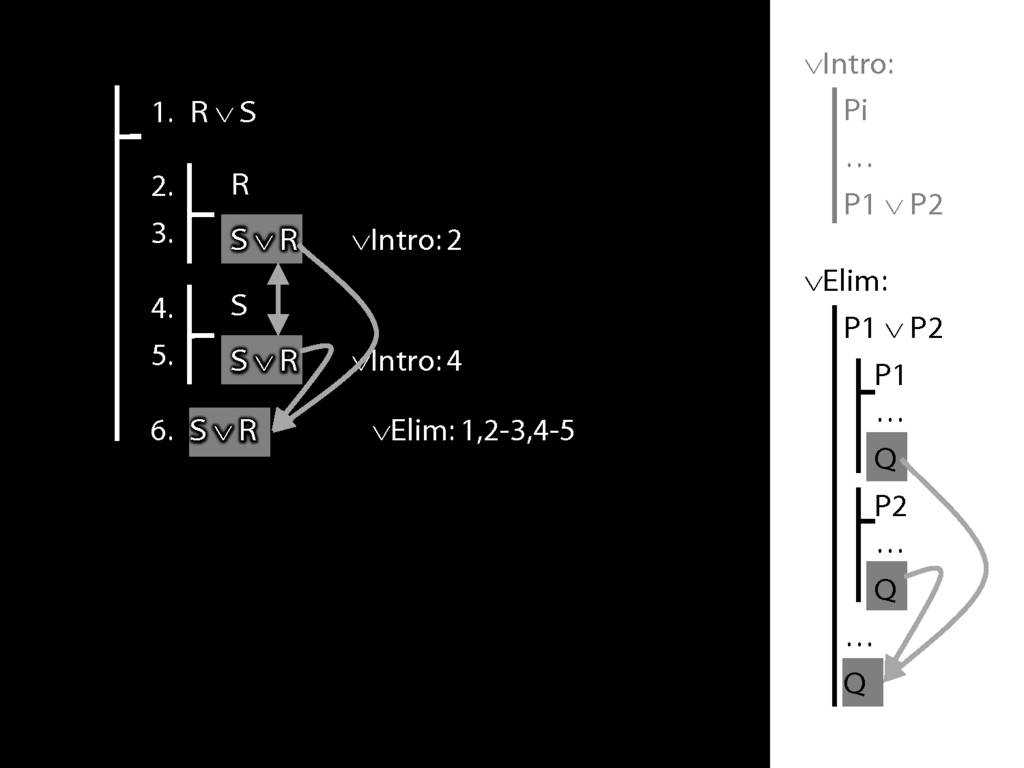
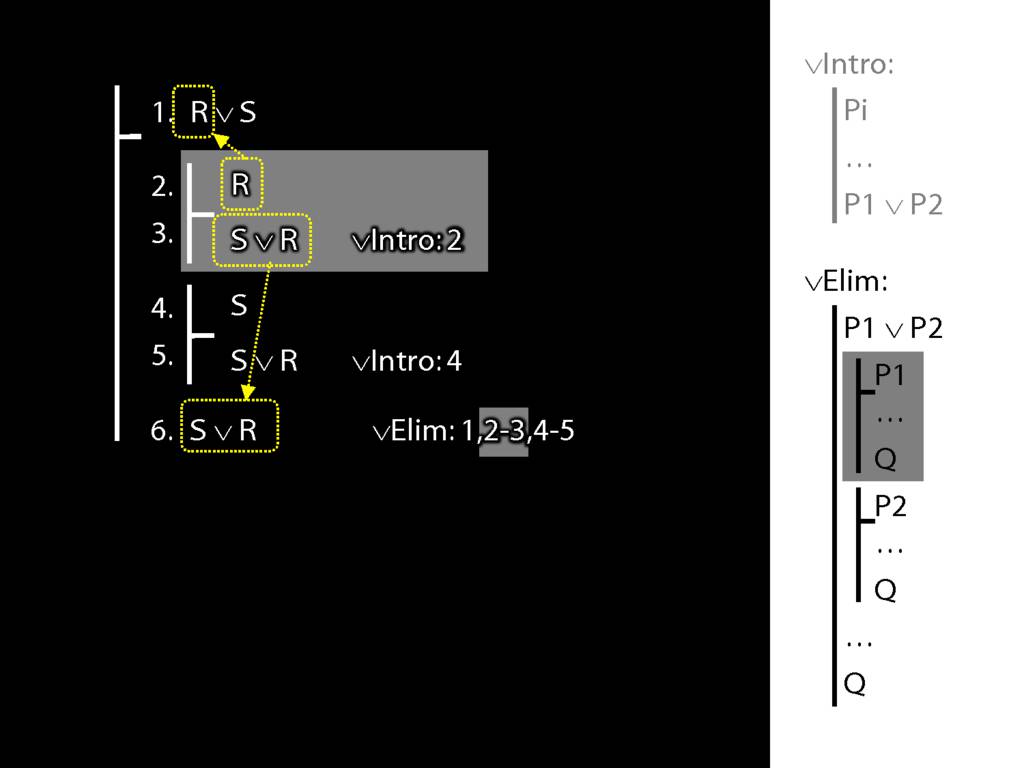
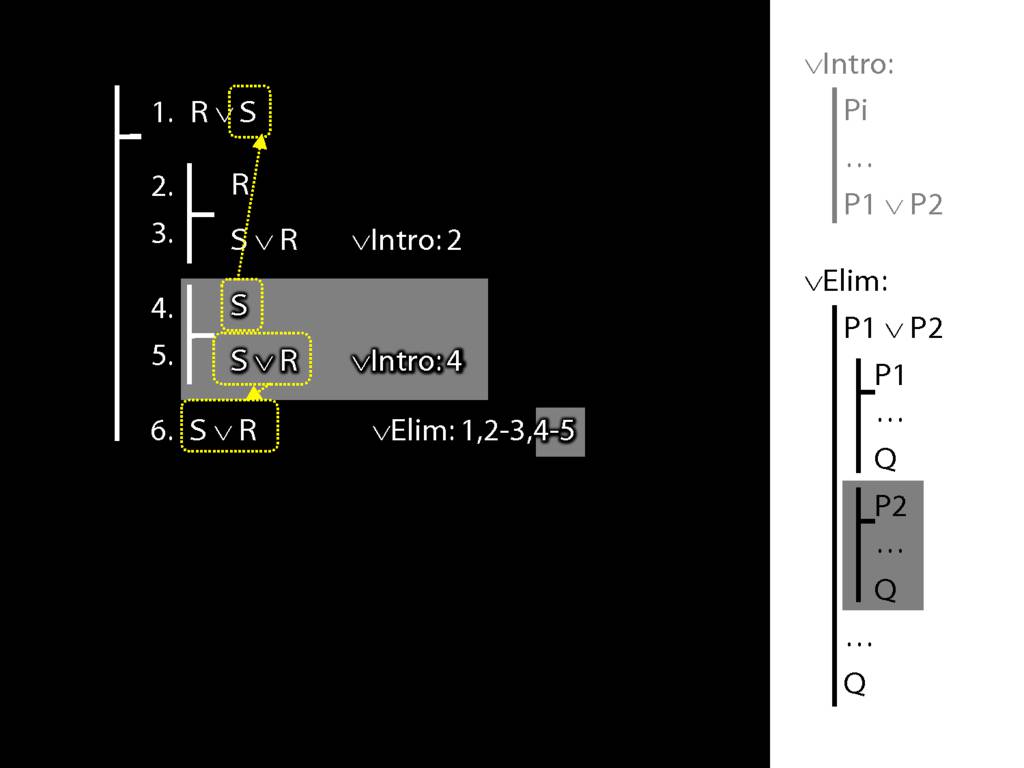
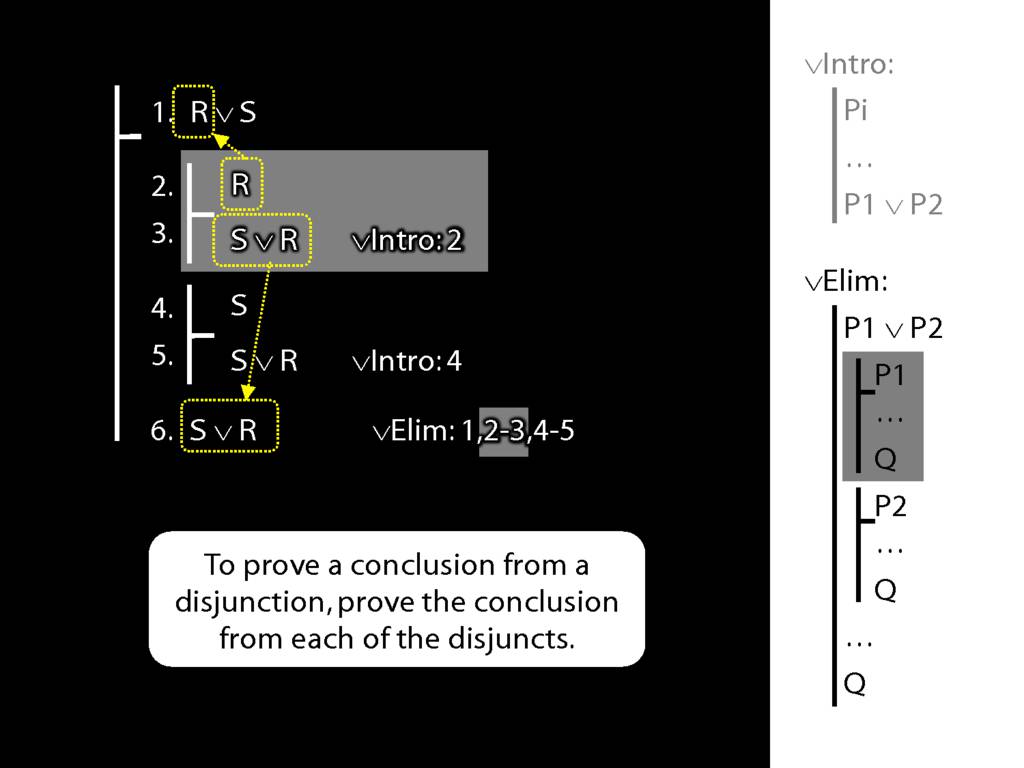
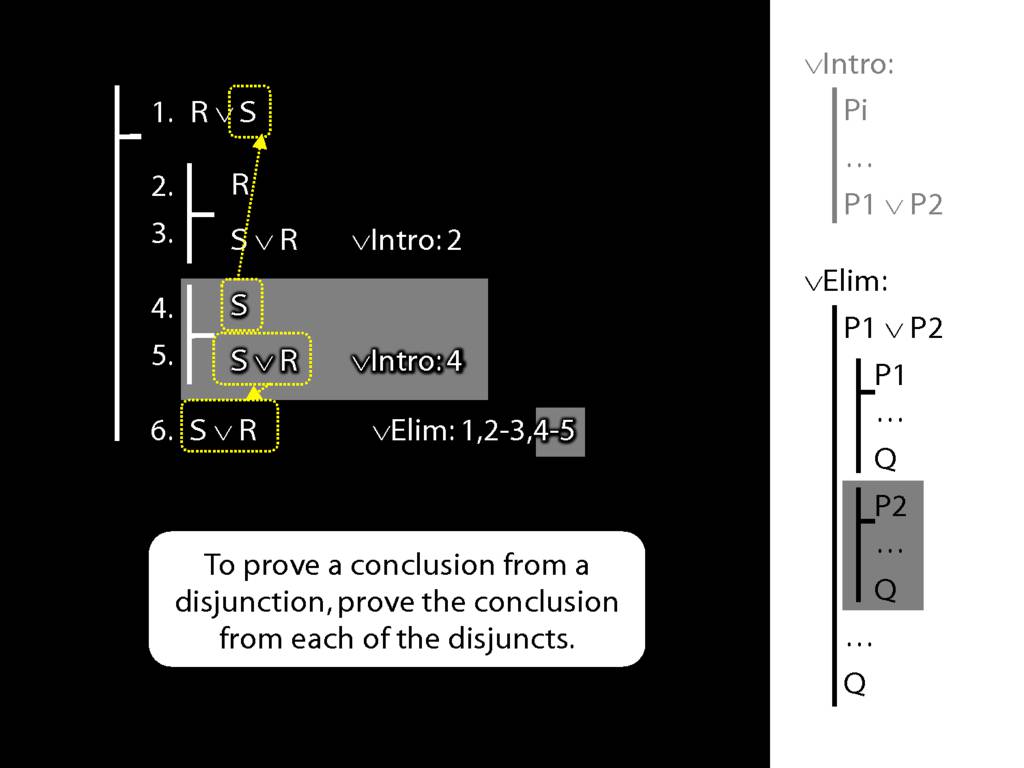
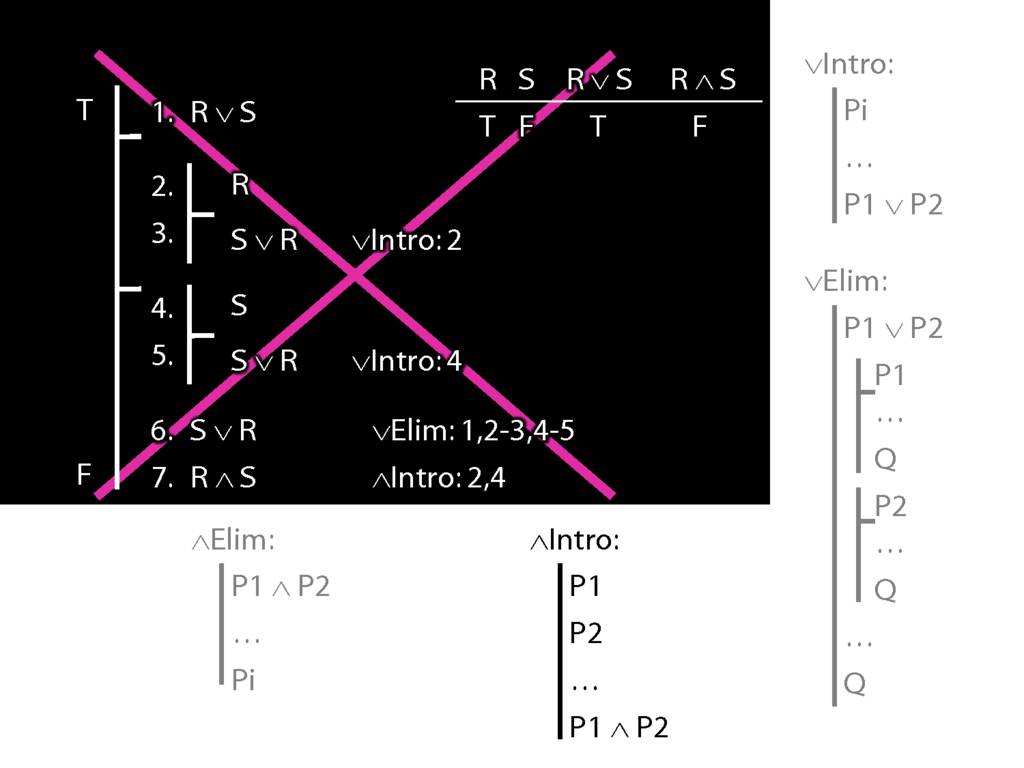
\section{∨Elim: An Example}
\emph{Reading:} §5.2, §6.2
\section{∨Elim: An Example}
5.1--5.6
6.2--6.6
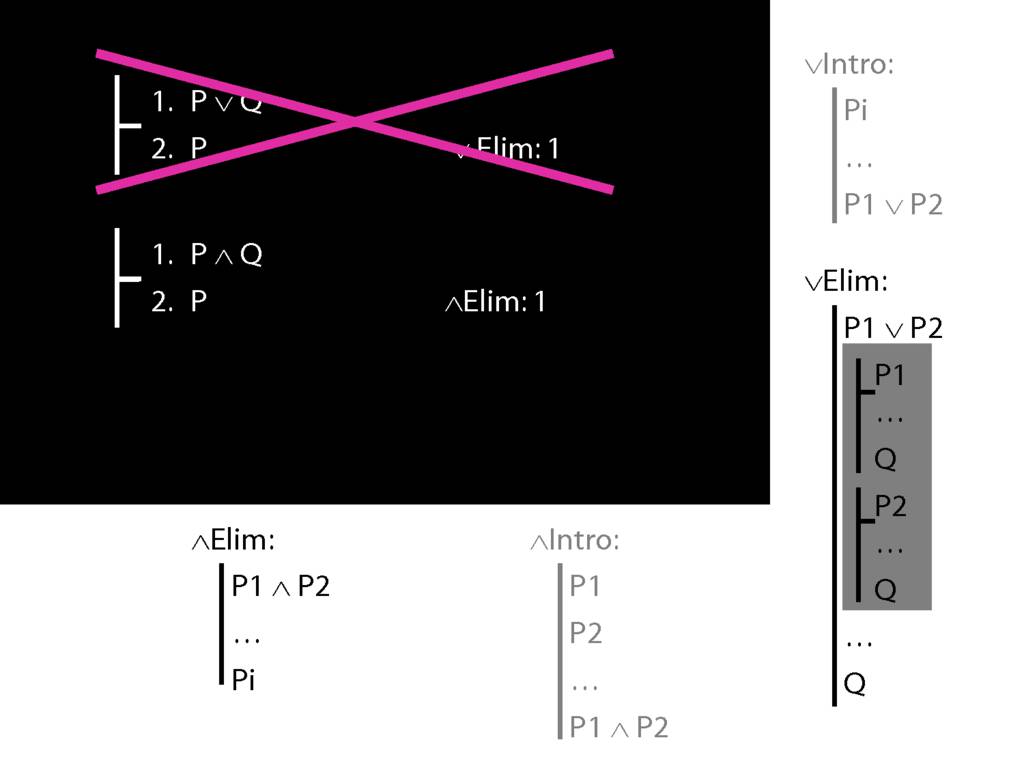
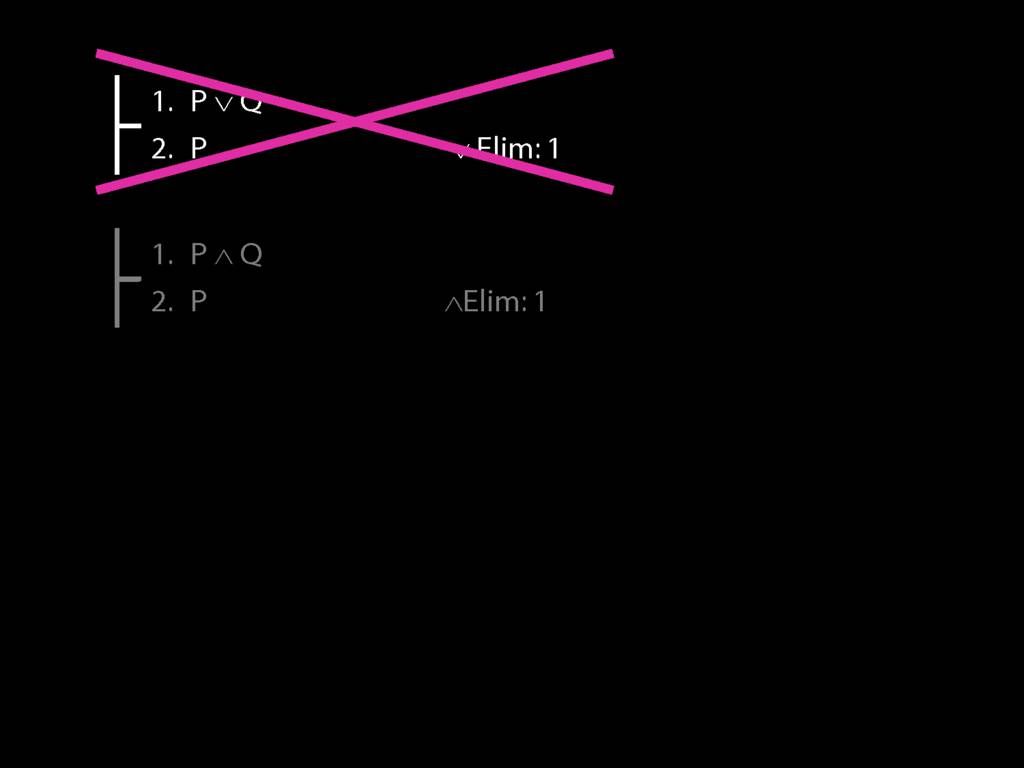
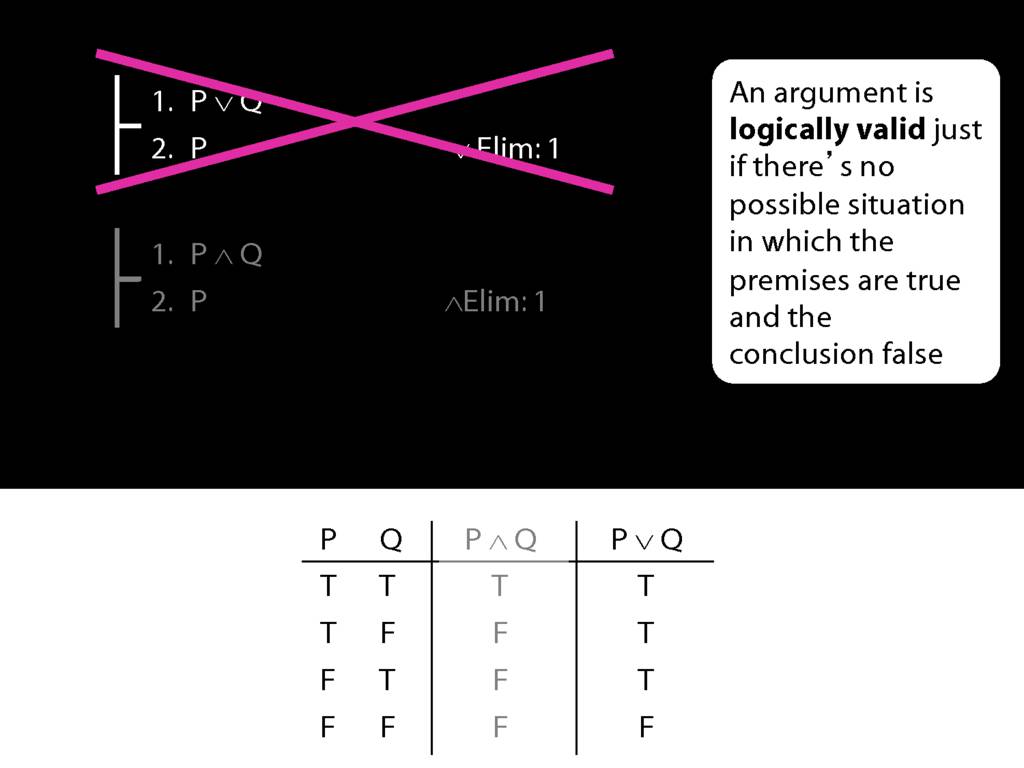
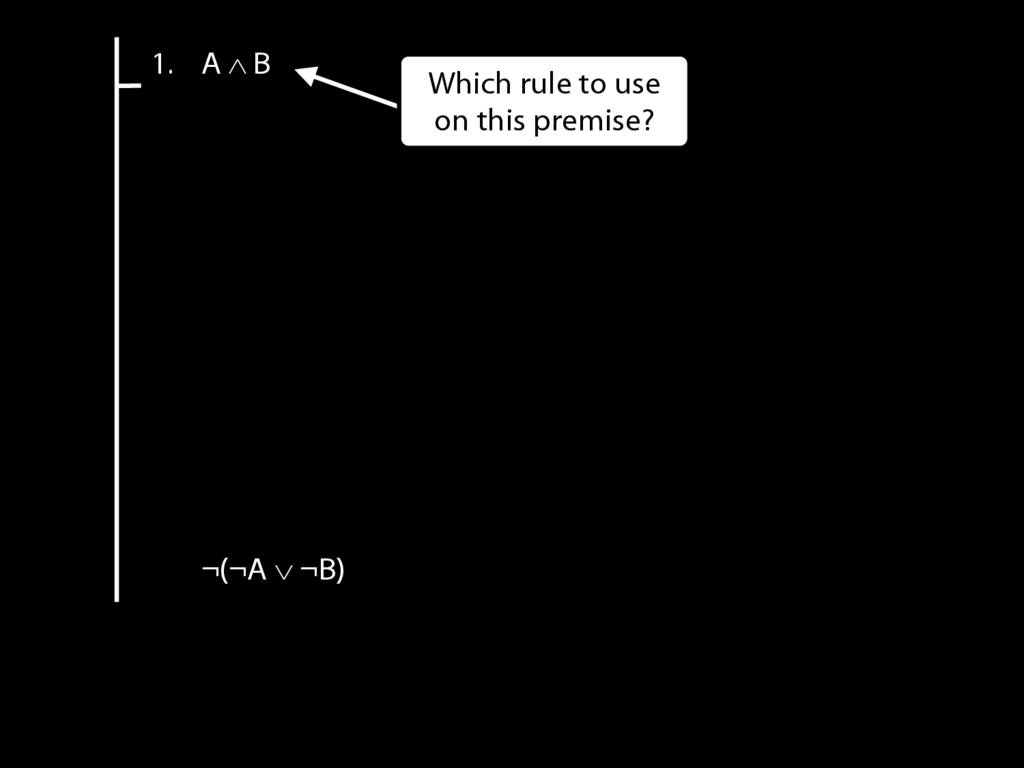
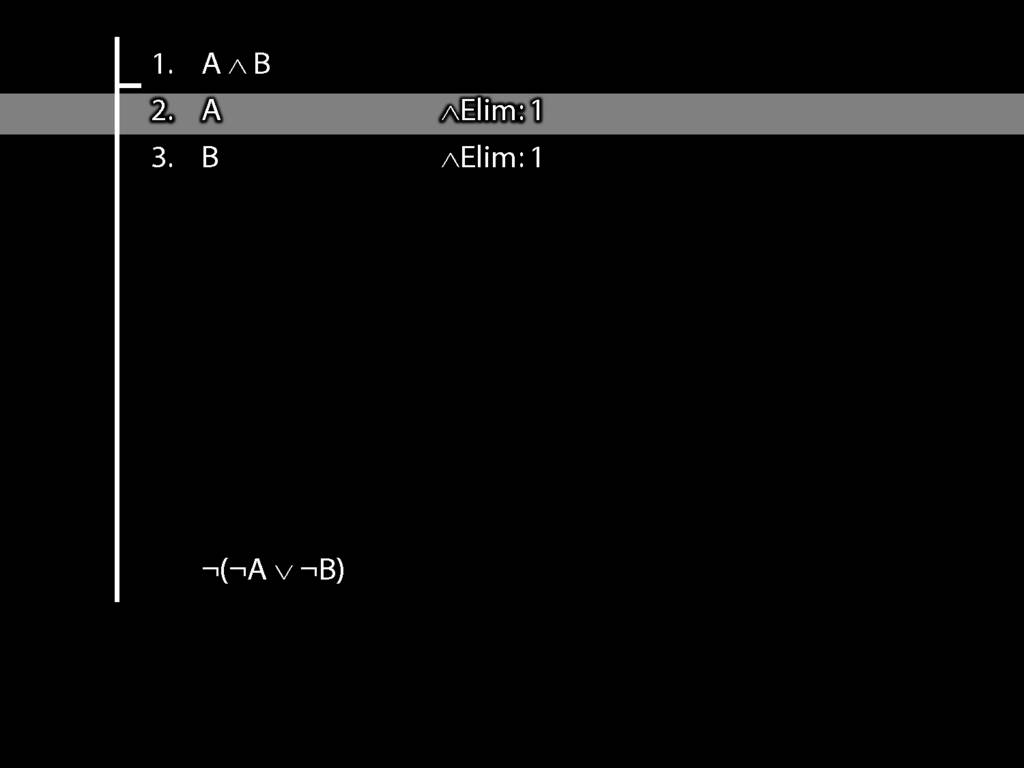
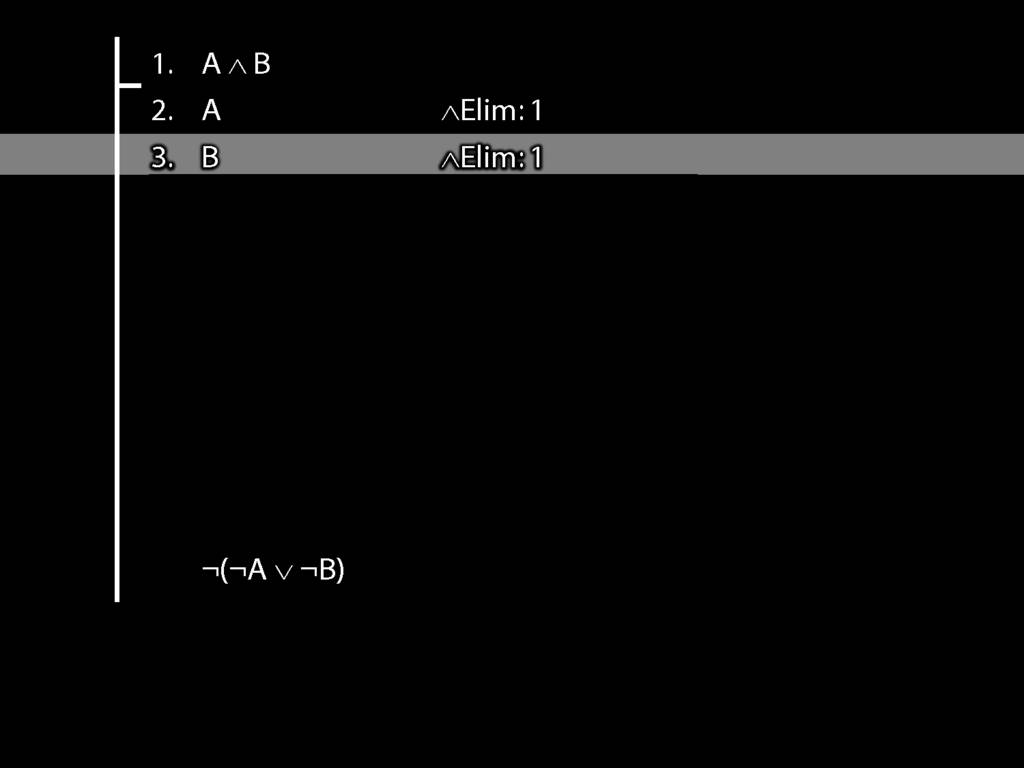
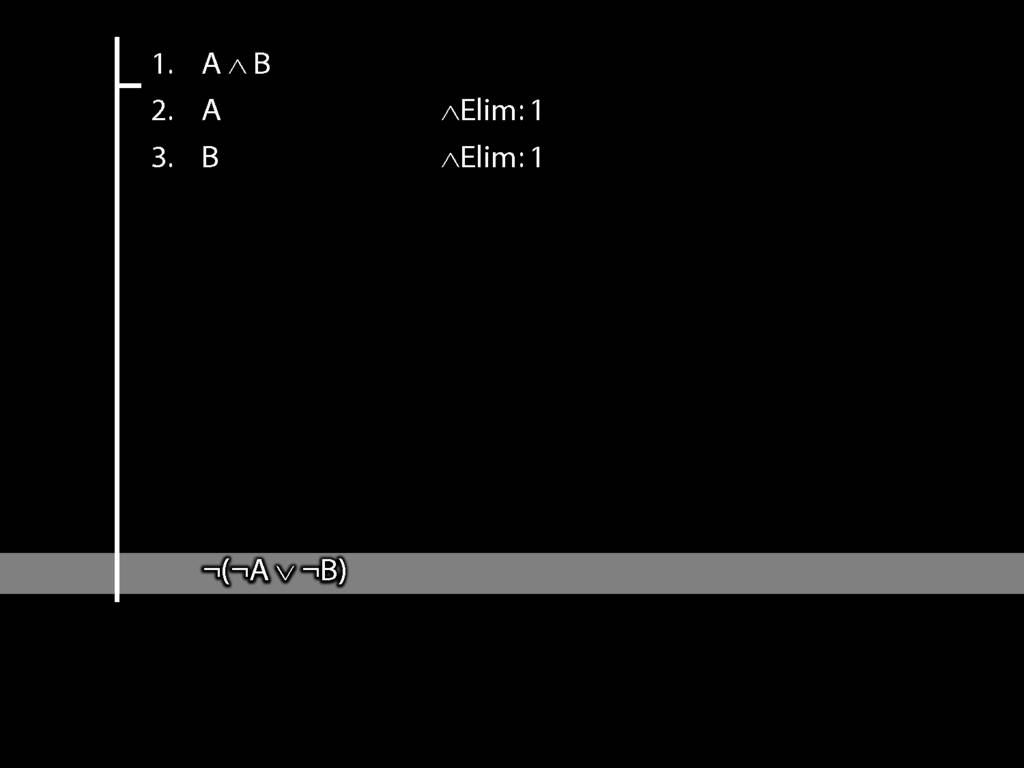
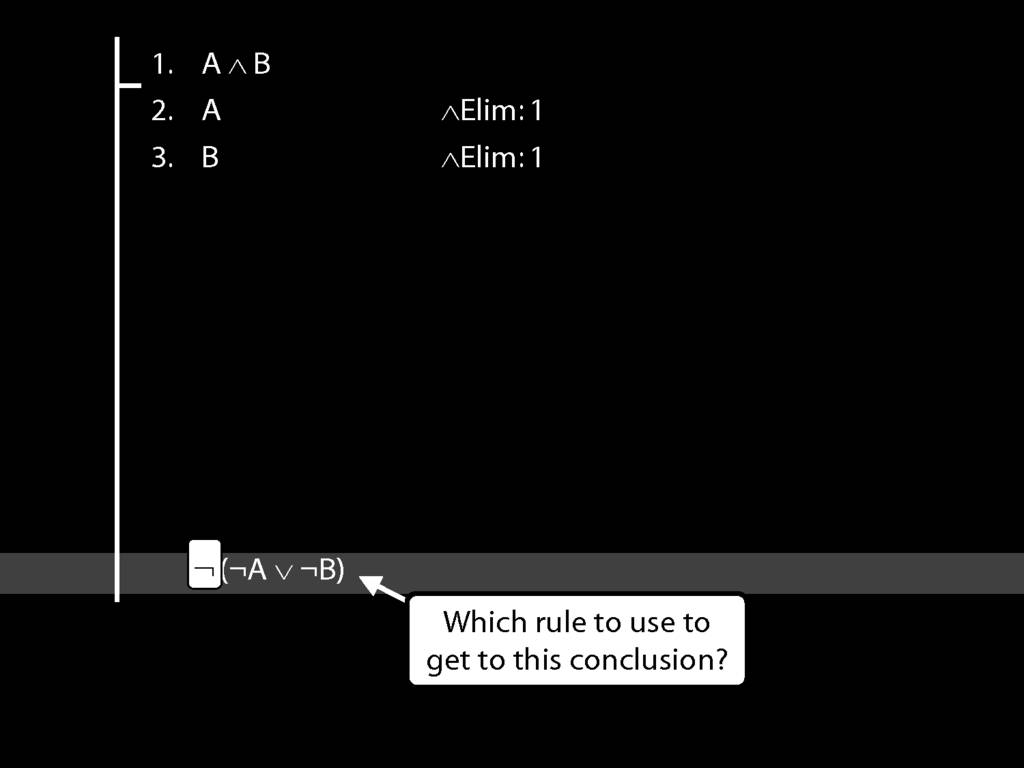
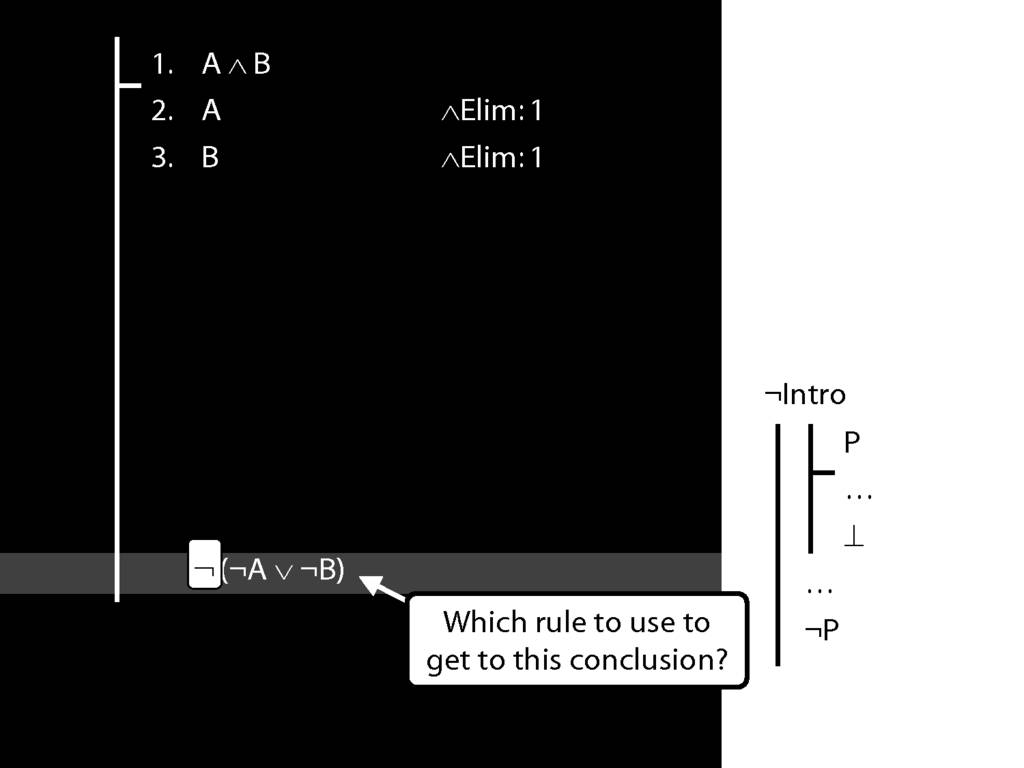
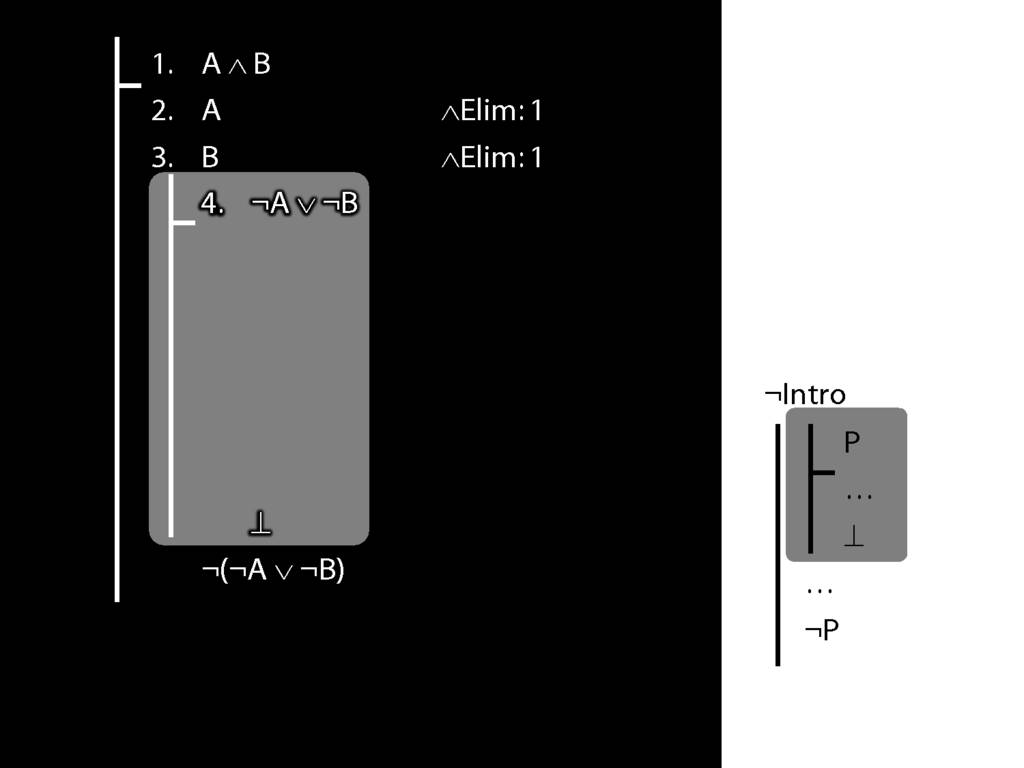
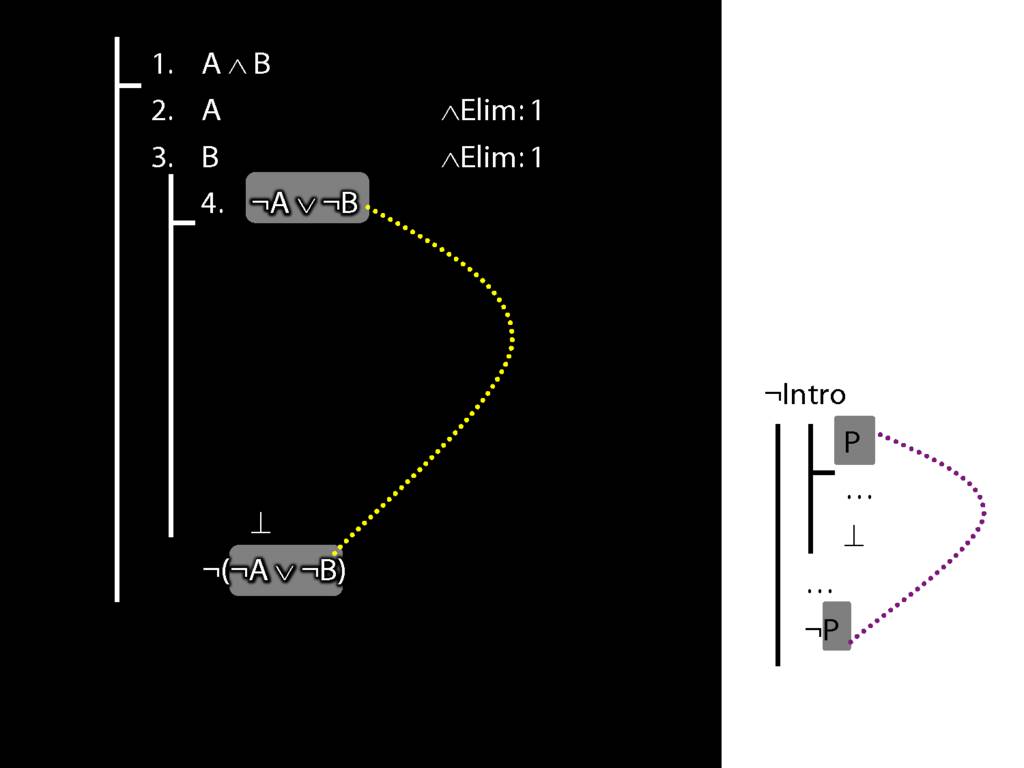
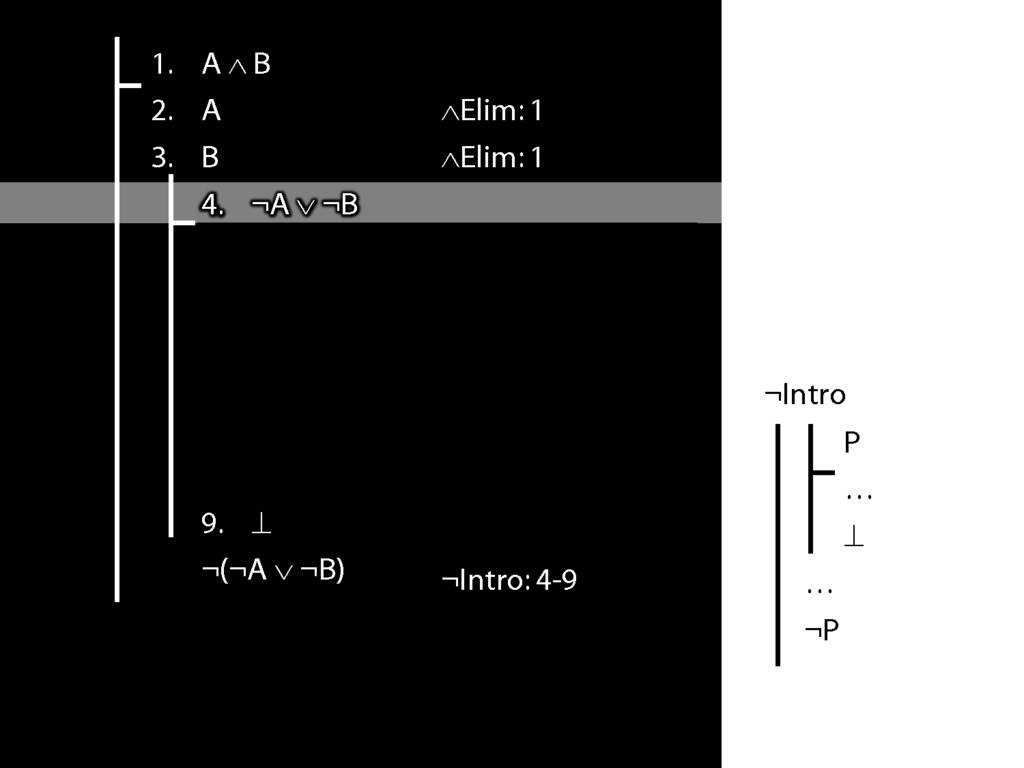
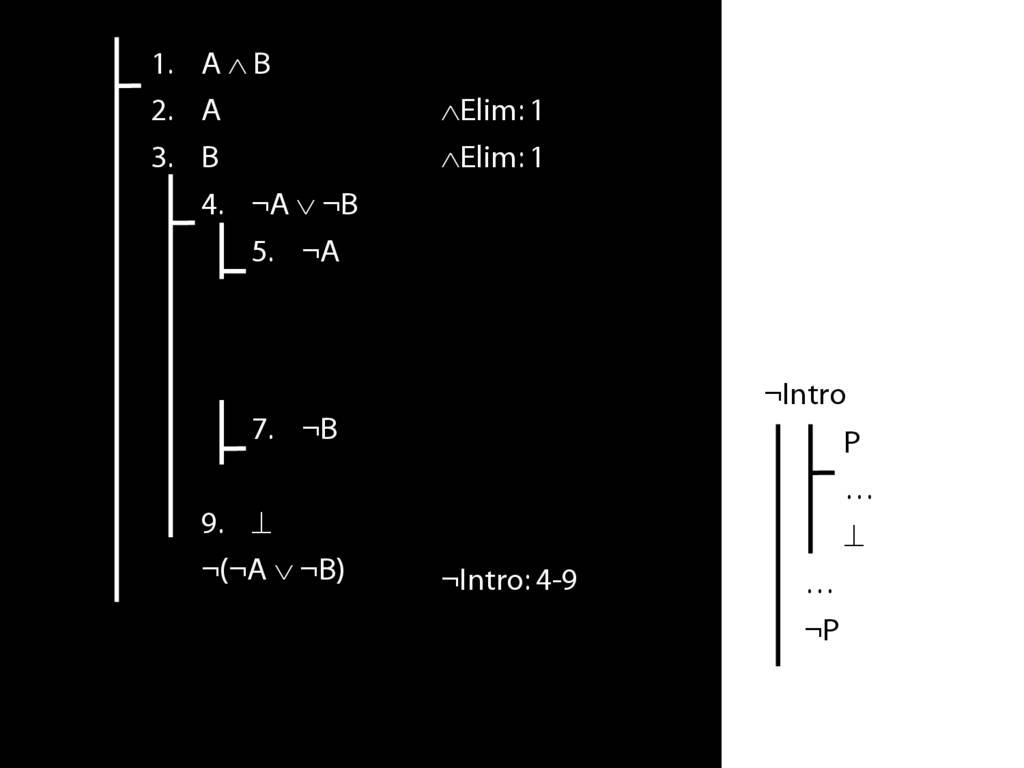
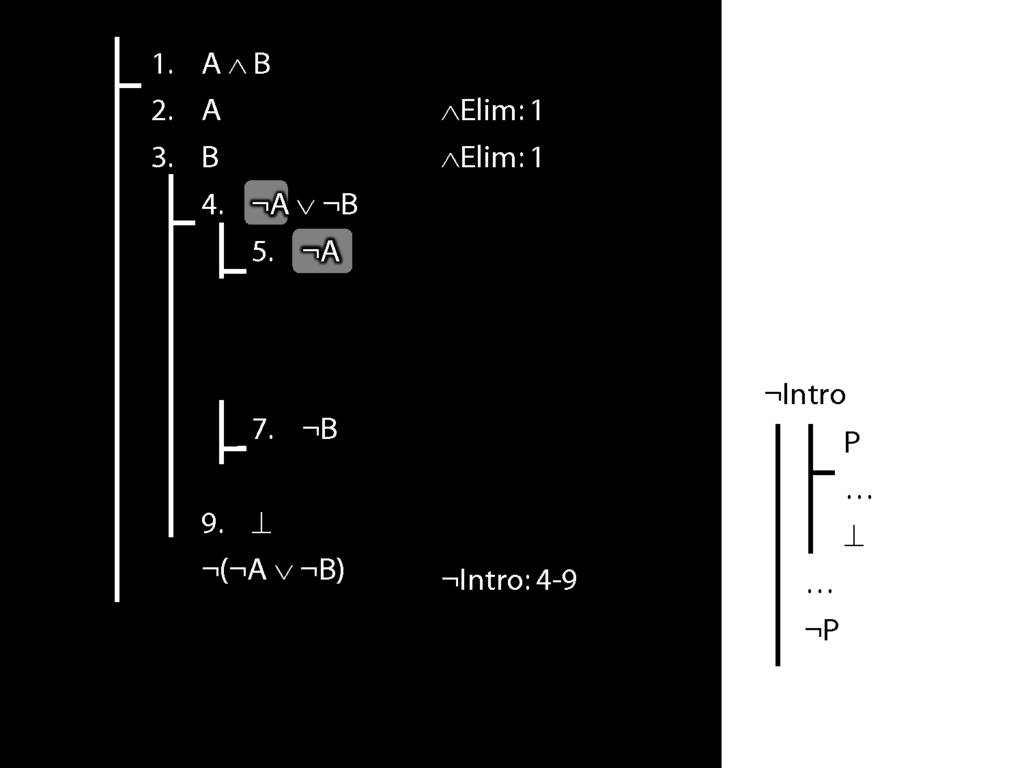
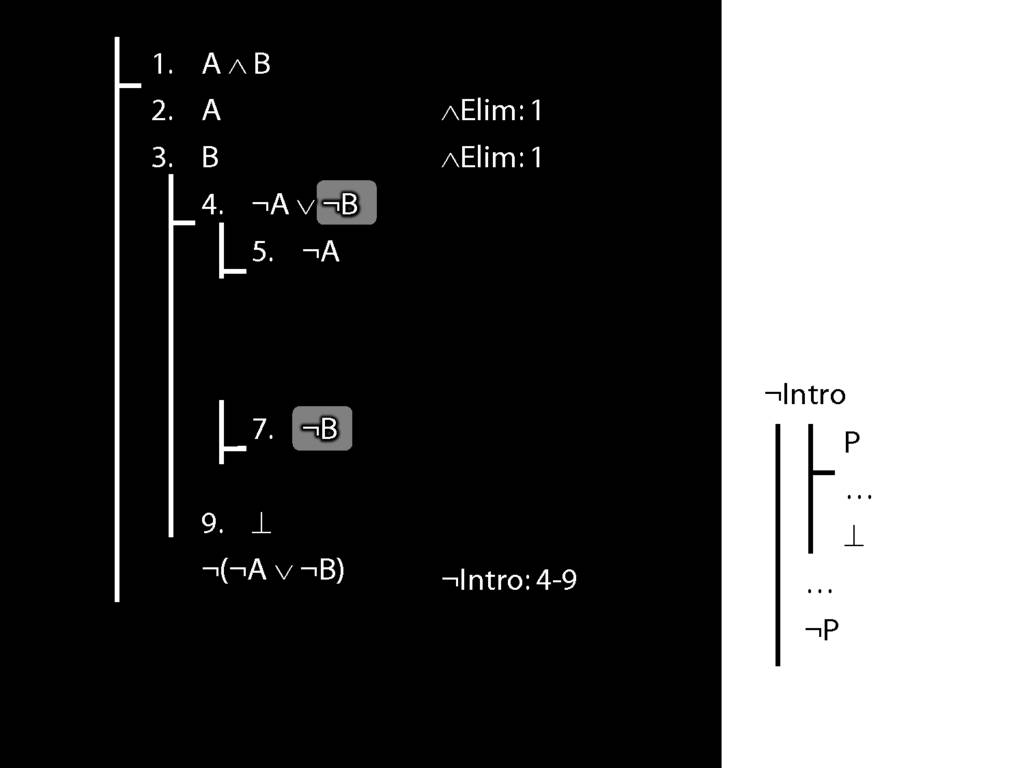
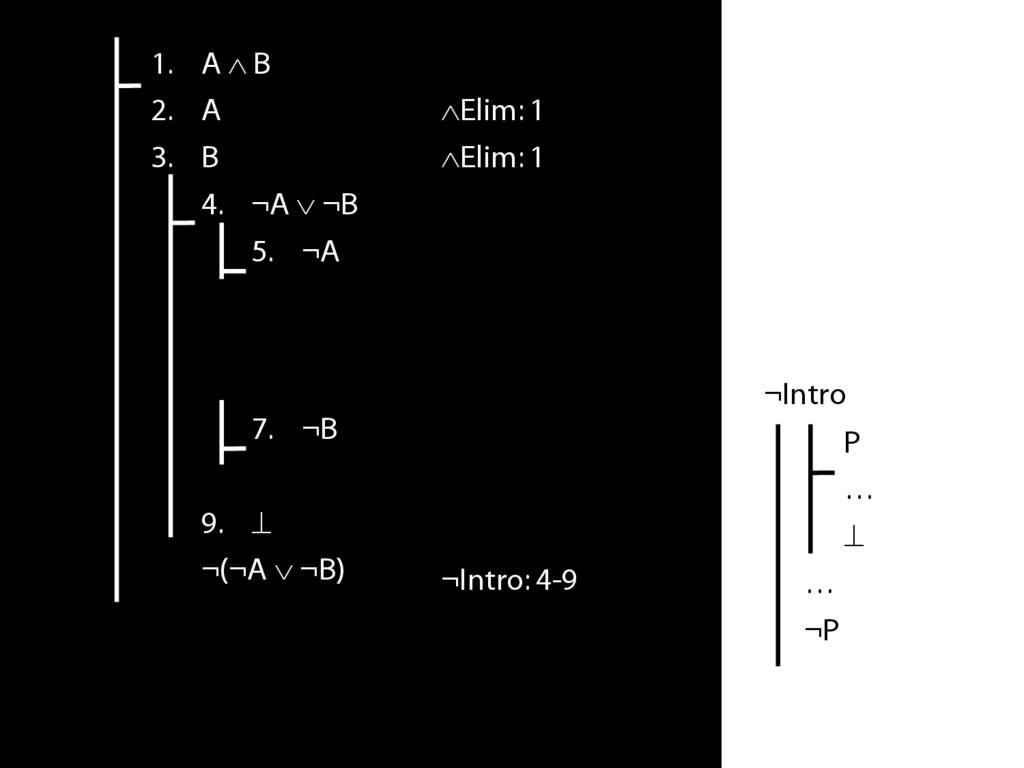
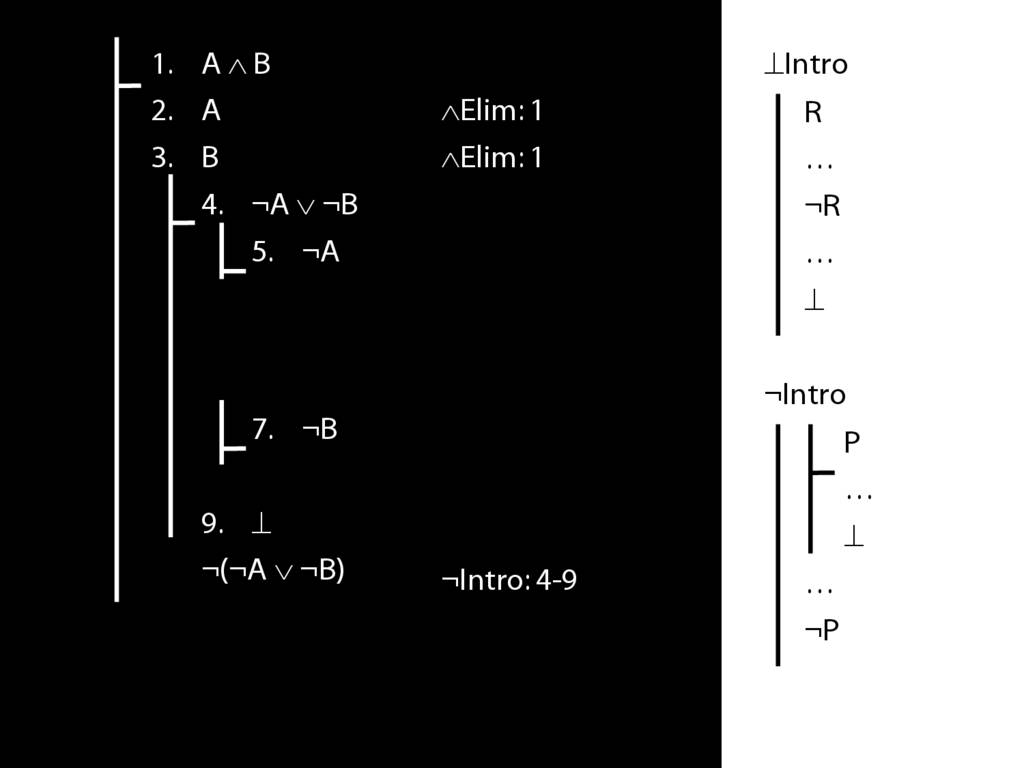
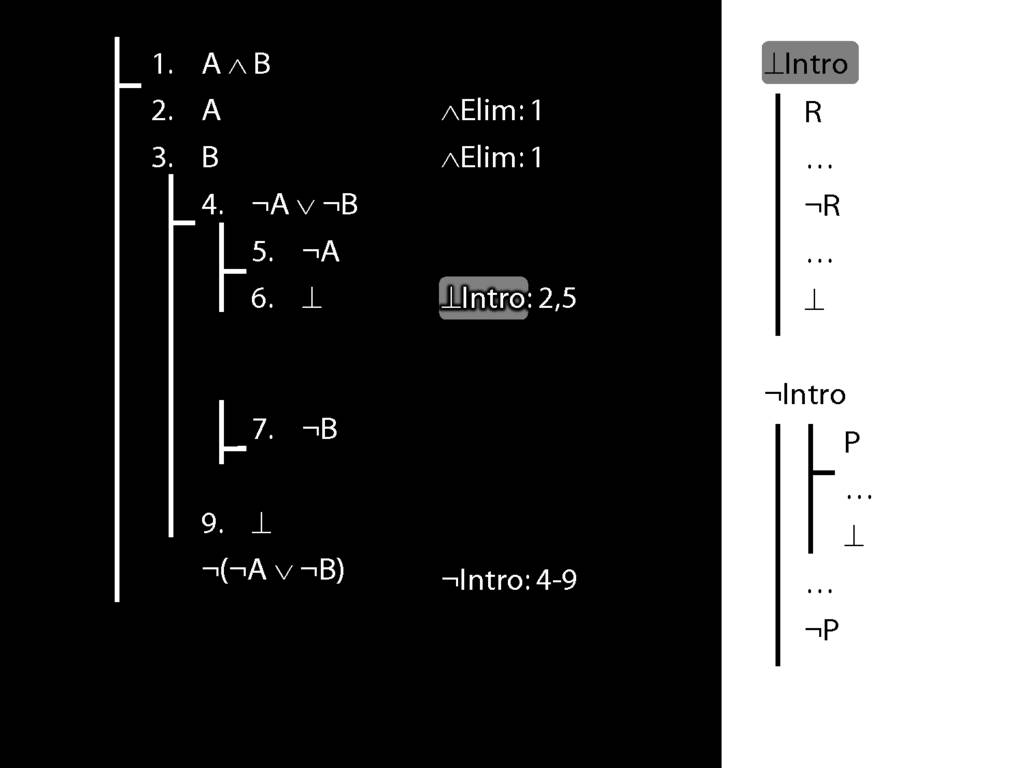
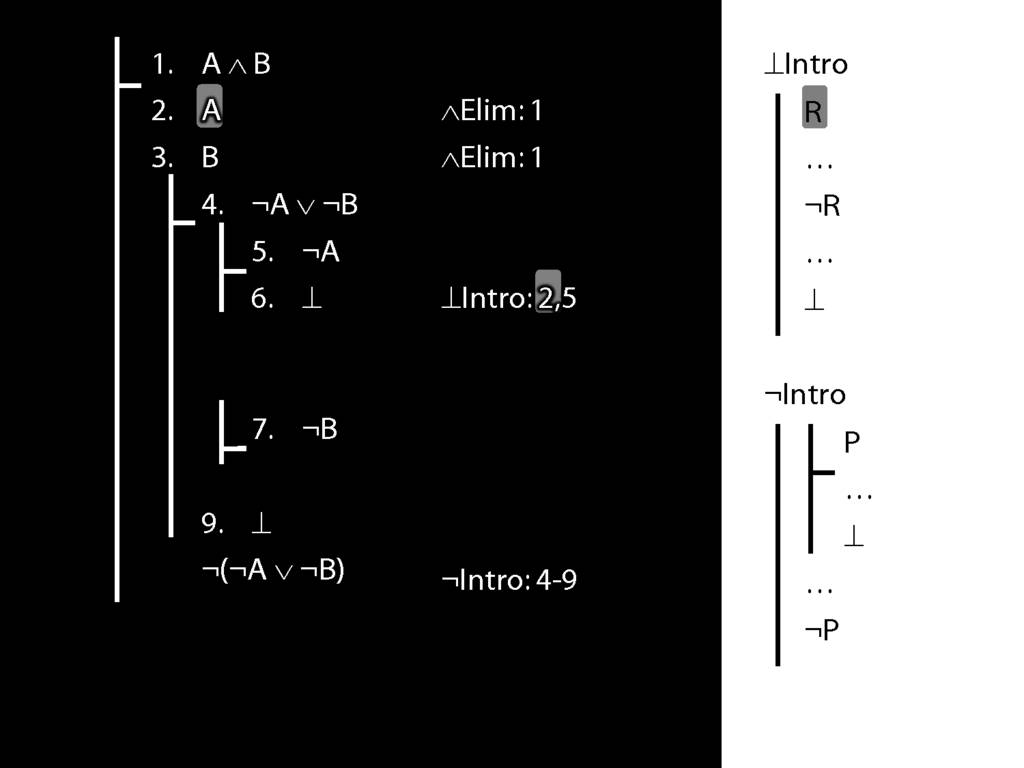
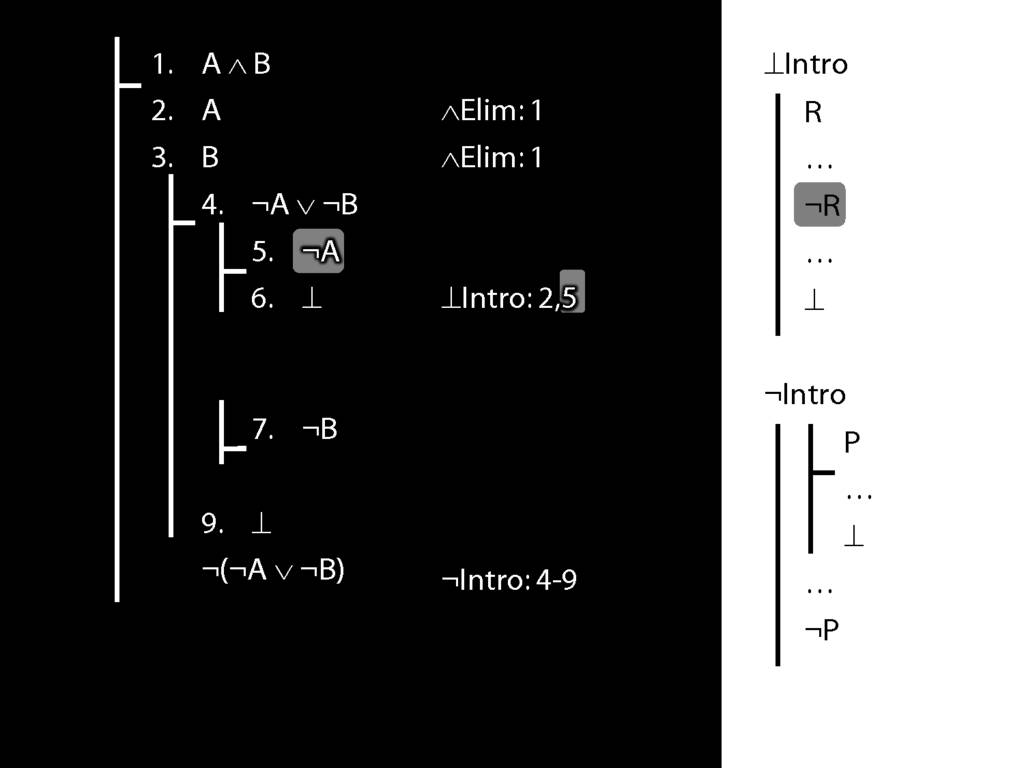
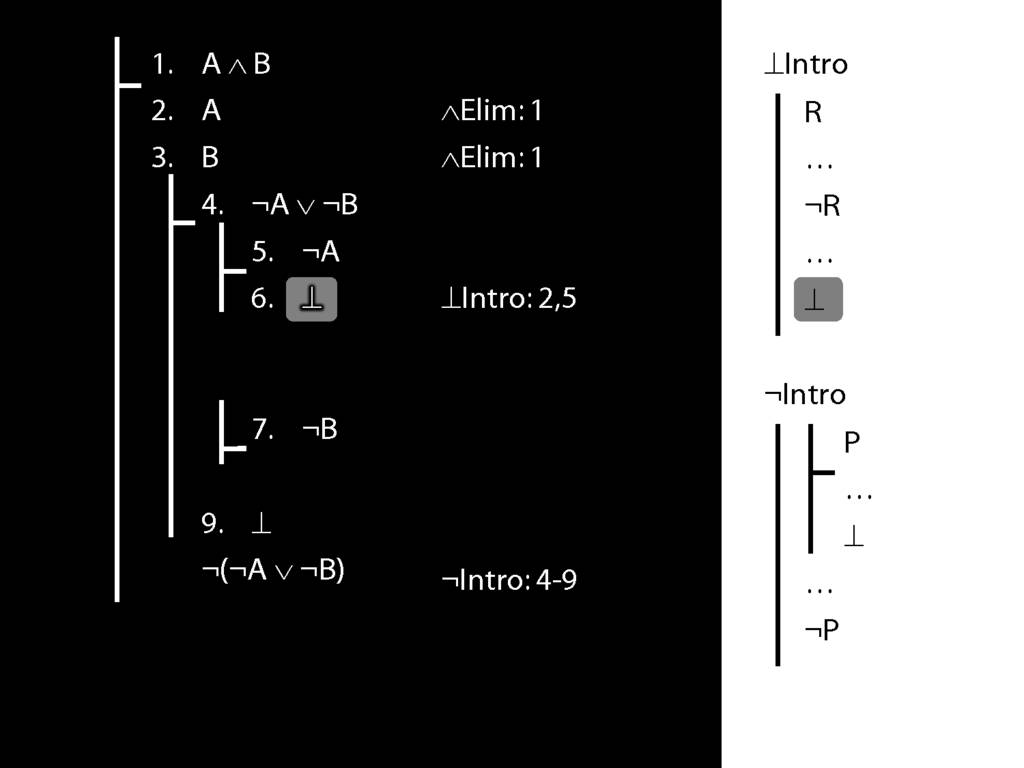
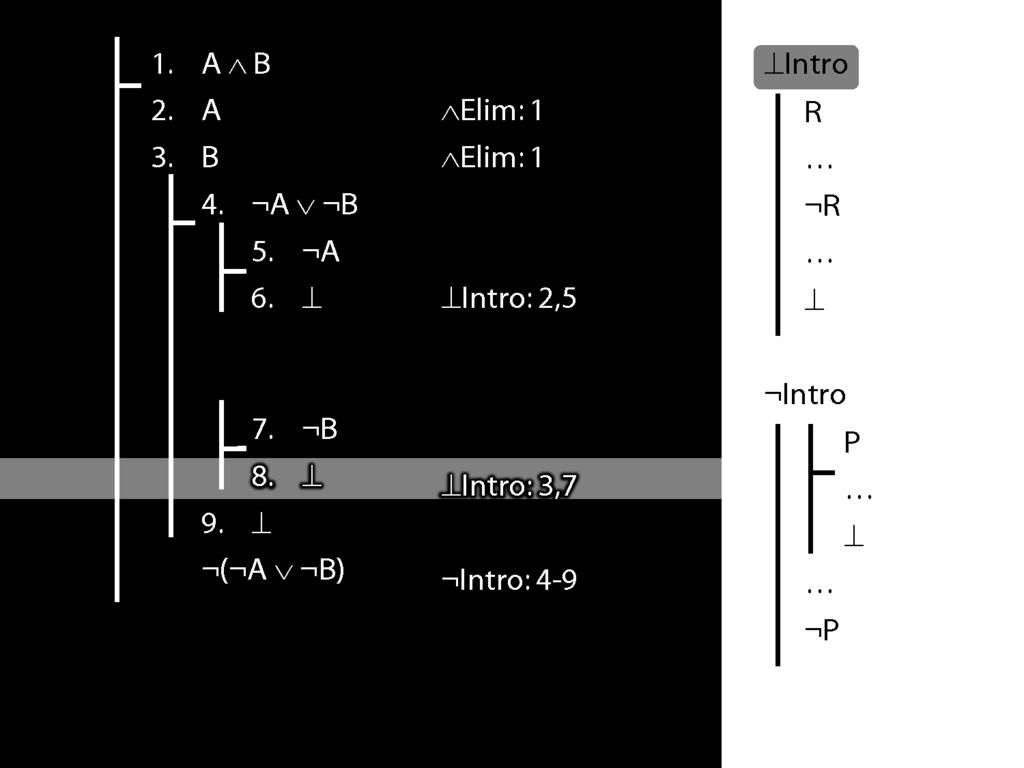
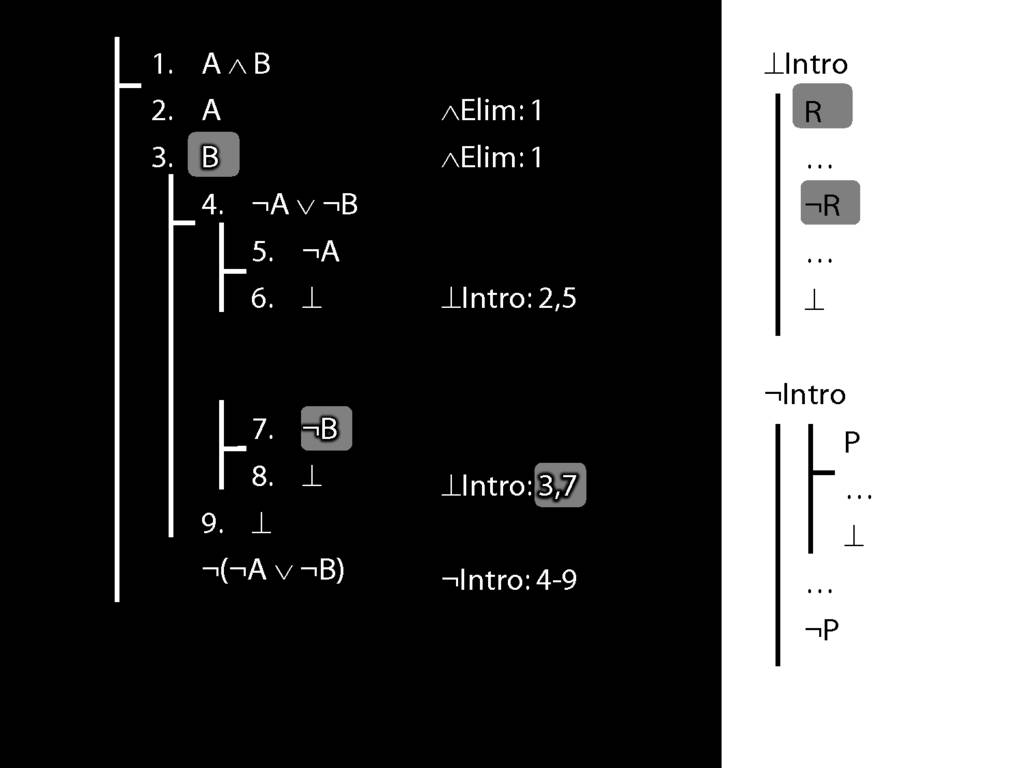
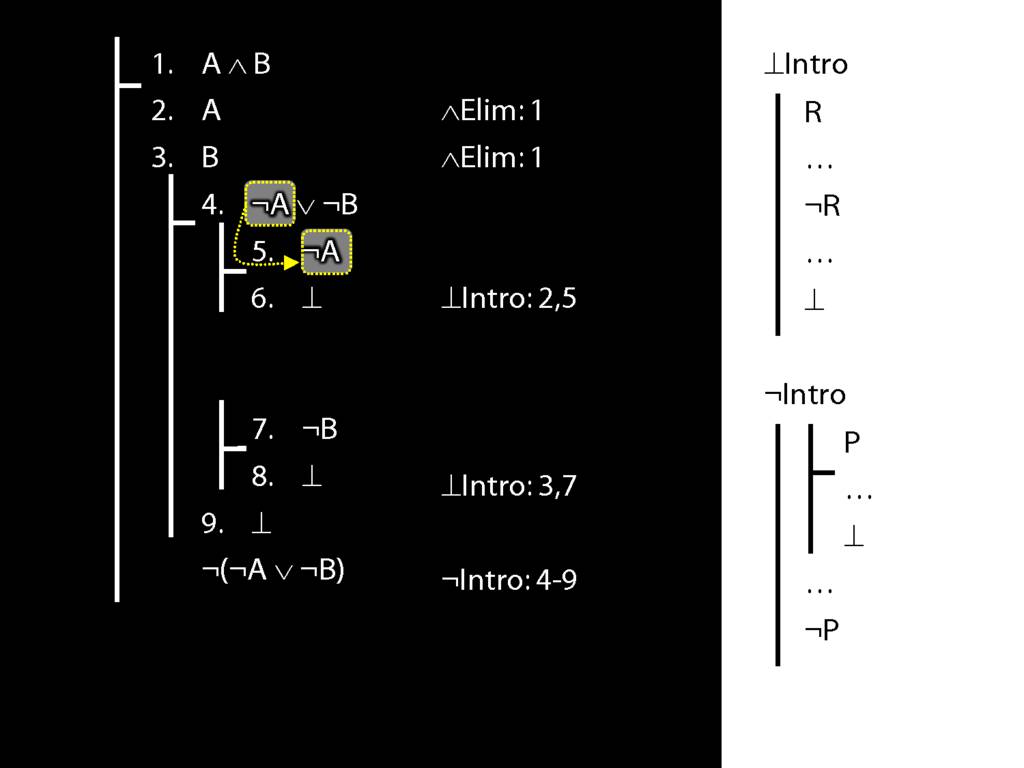
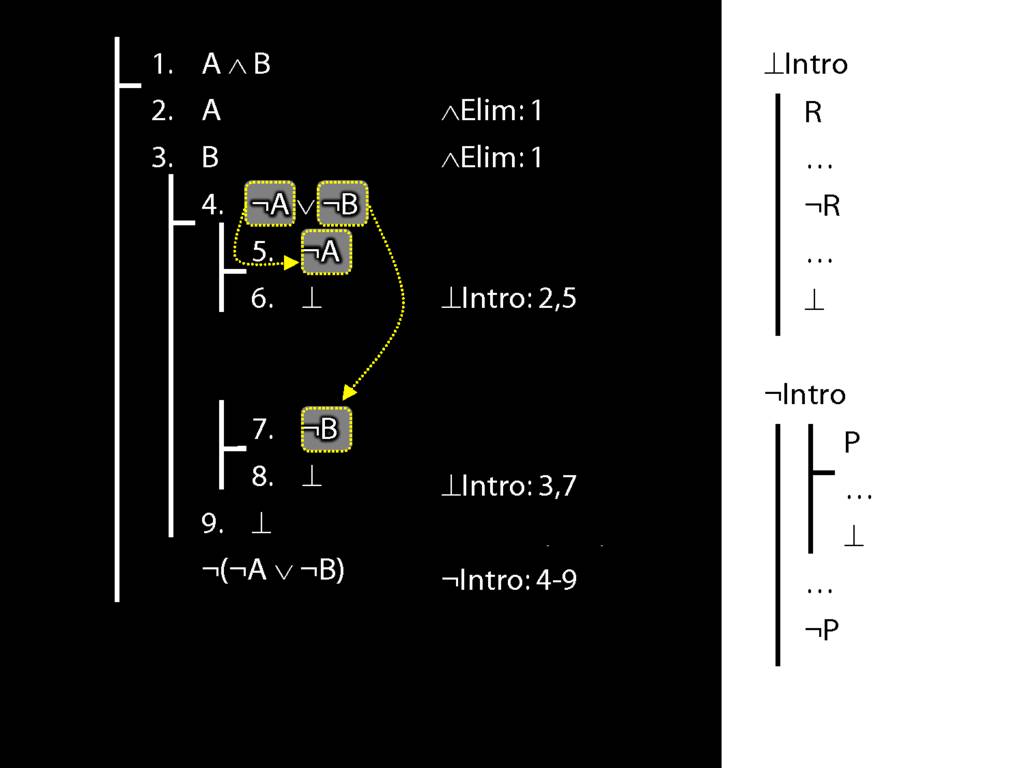
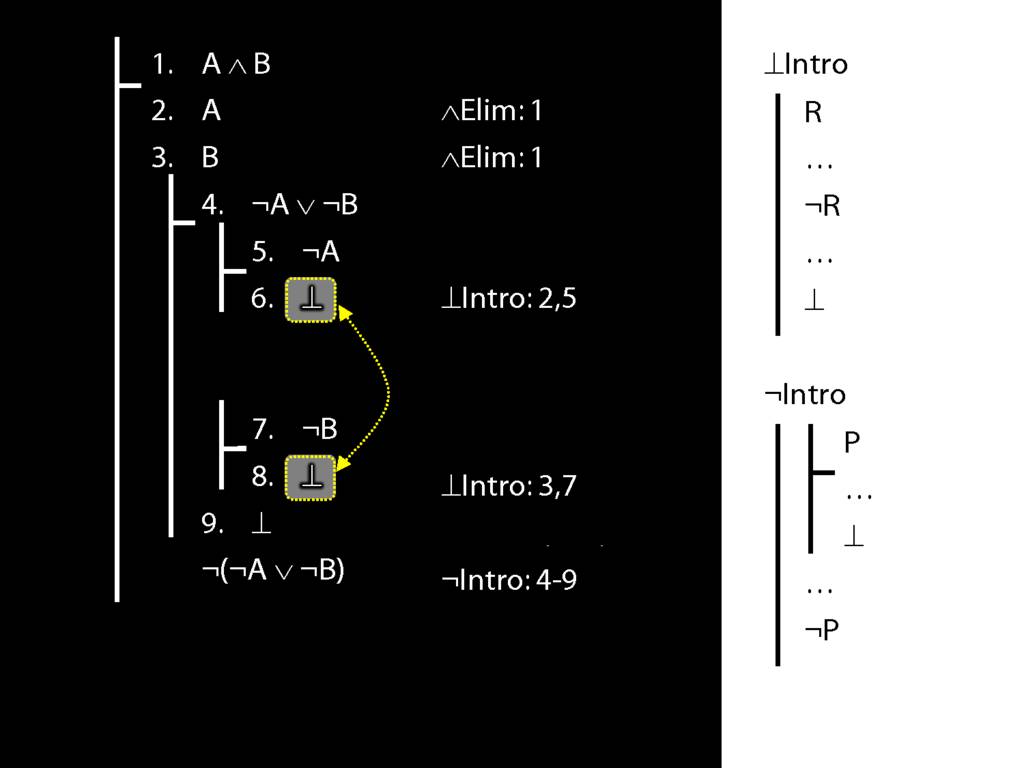
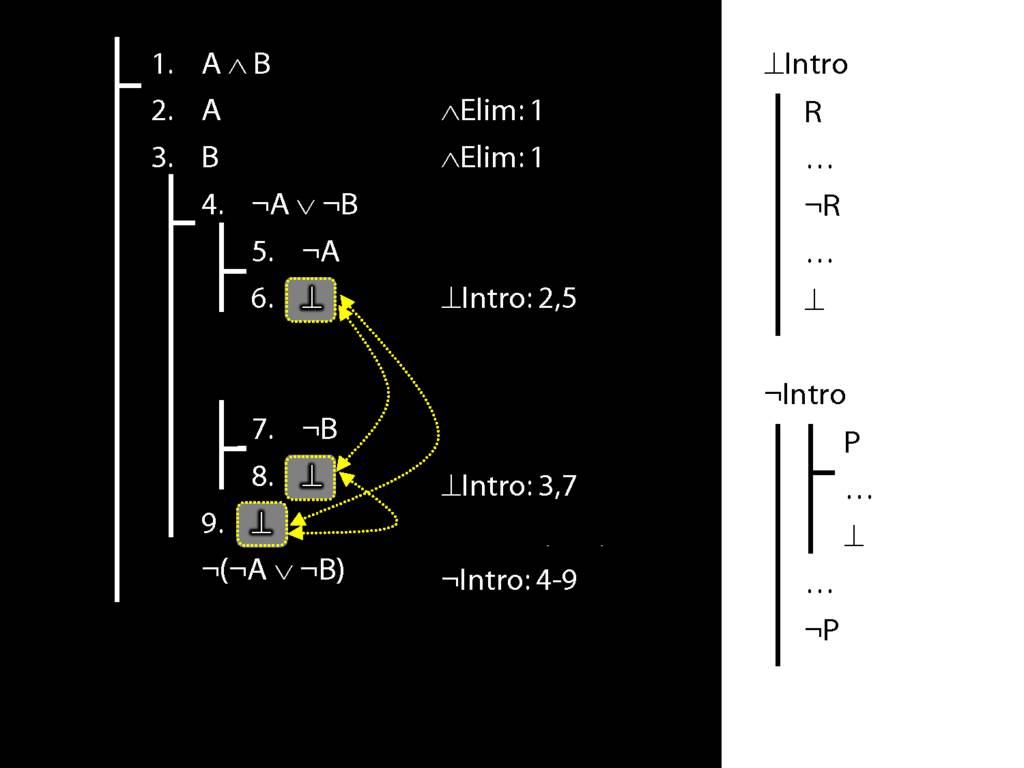
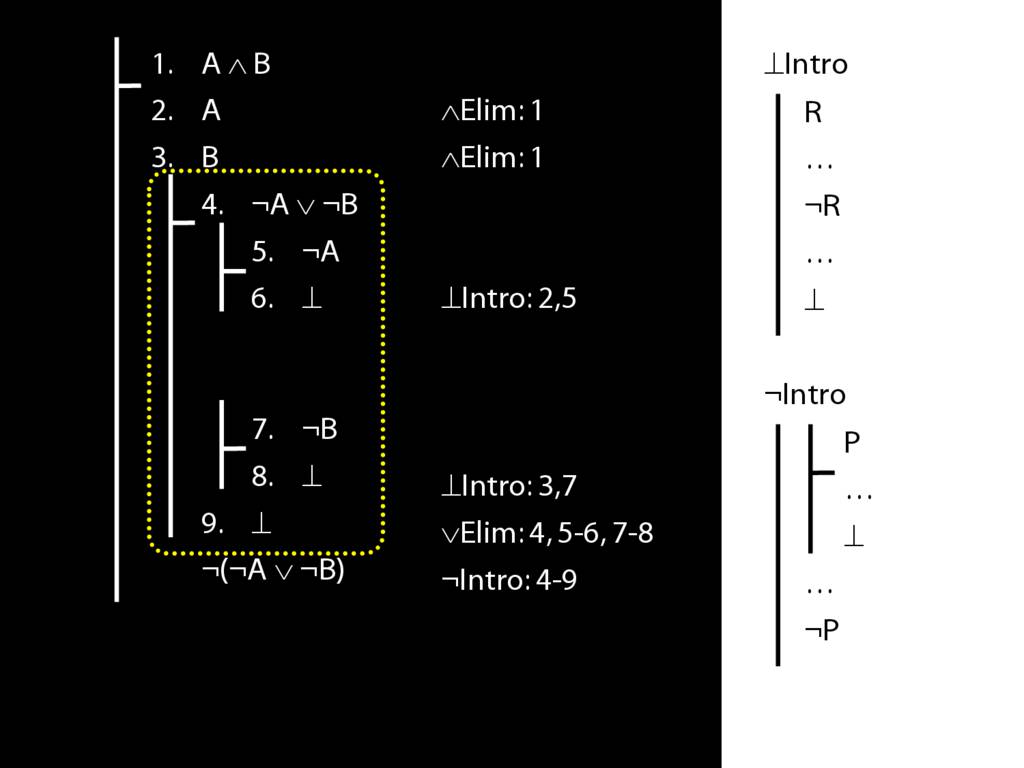
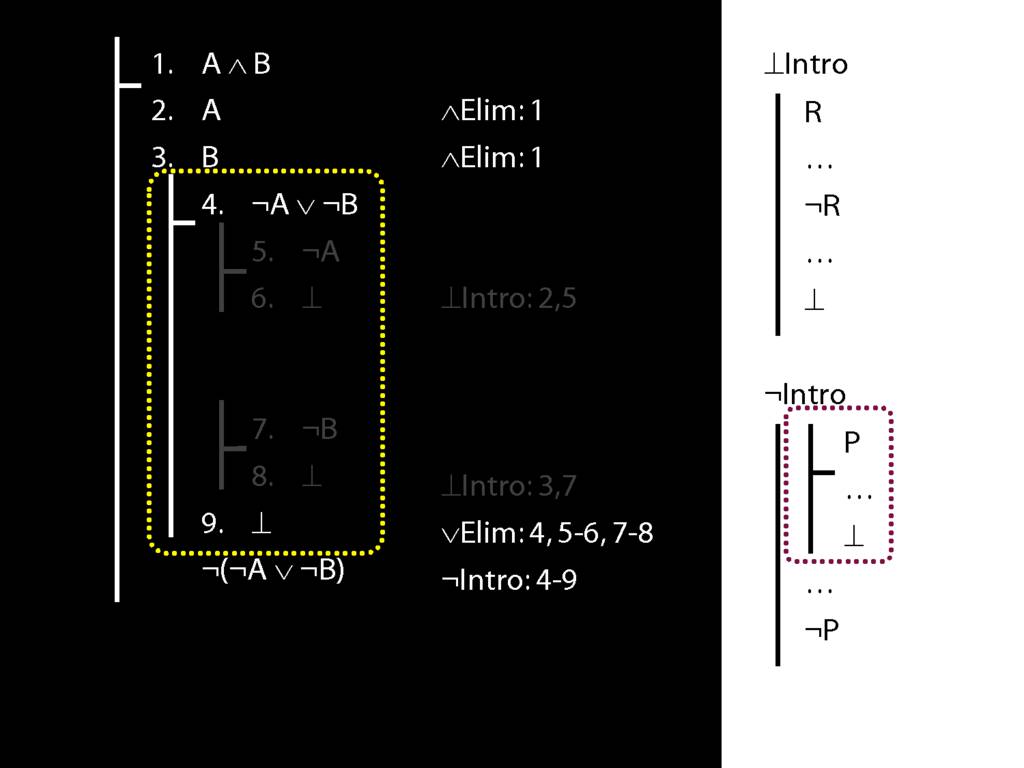
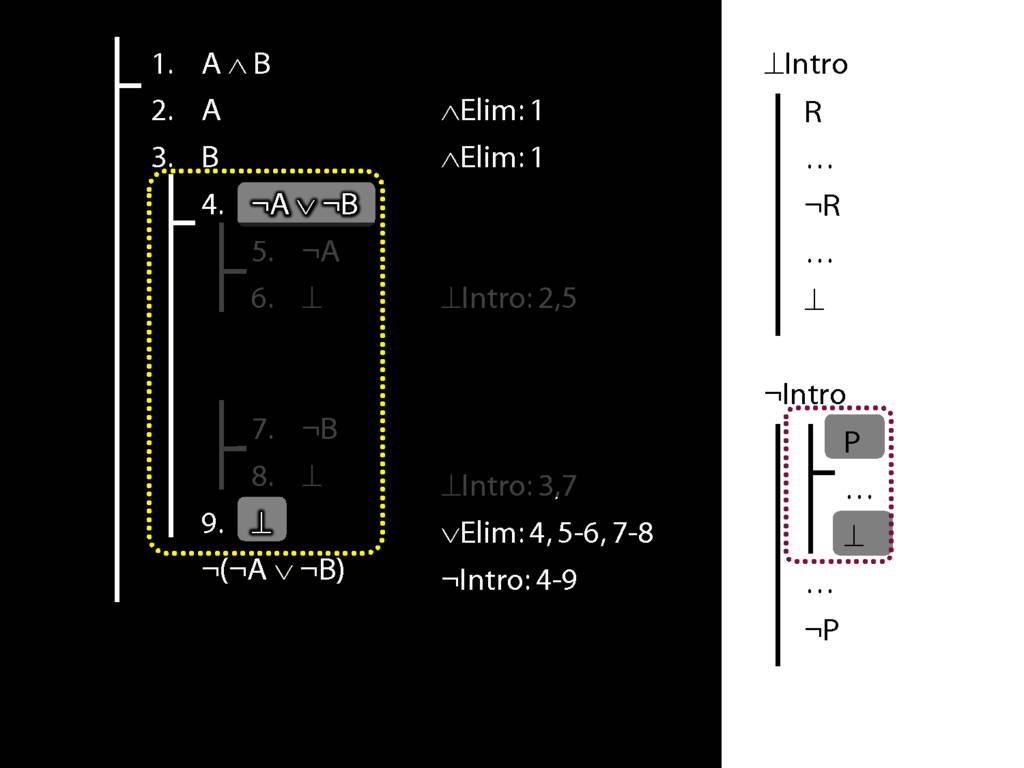
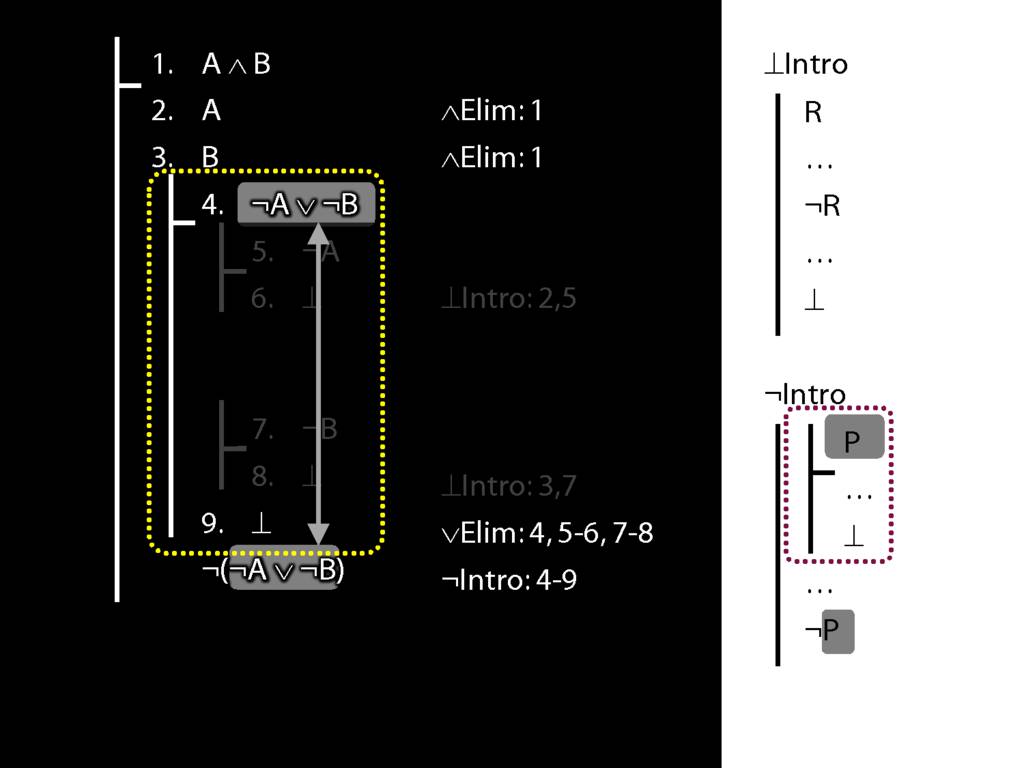
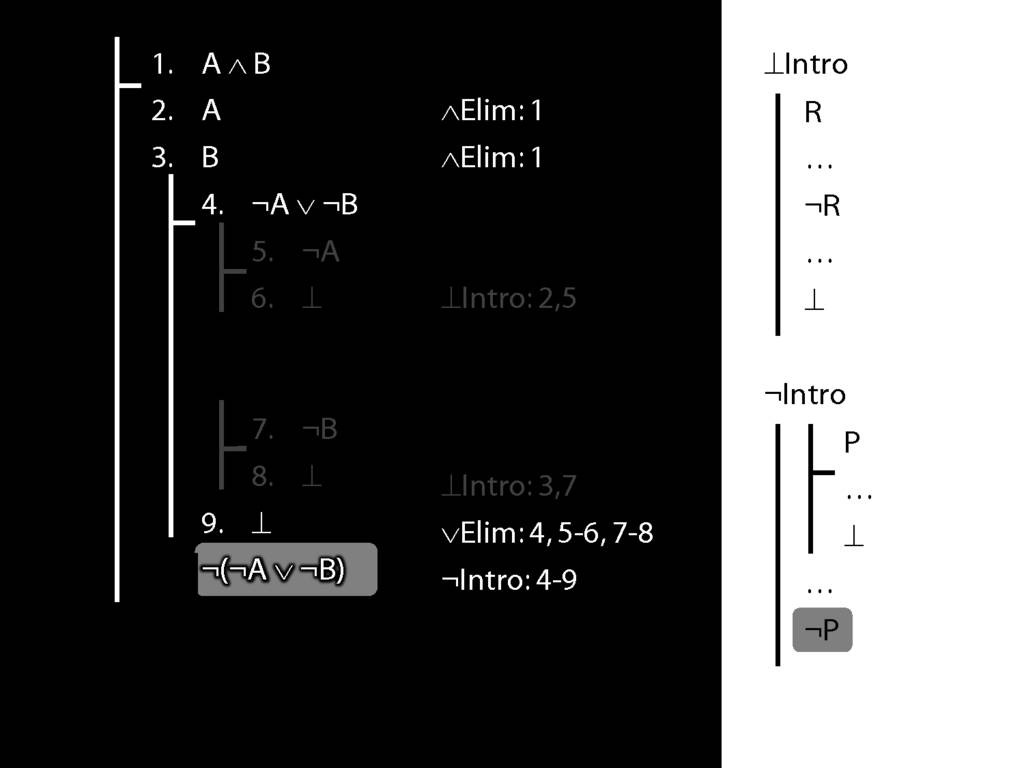
\section{Not Or}
\emph{Reading:} §3.7
\section{Not Or}
3.19
5.18
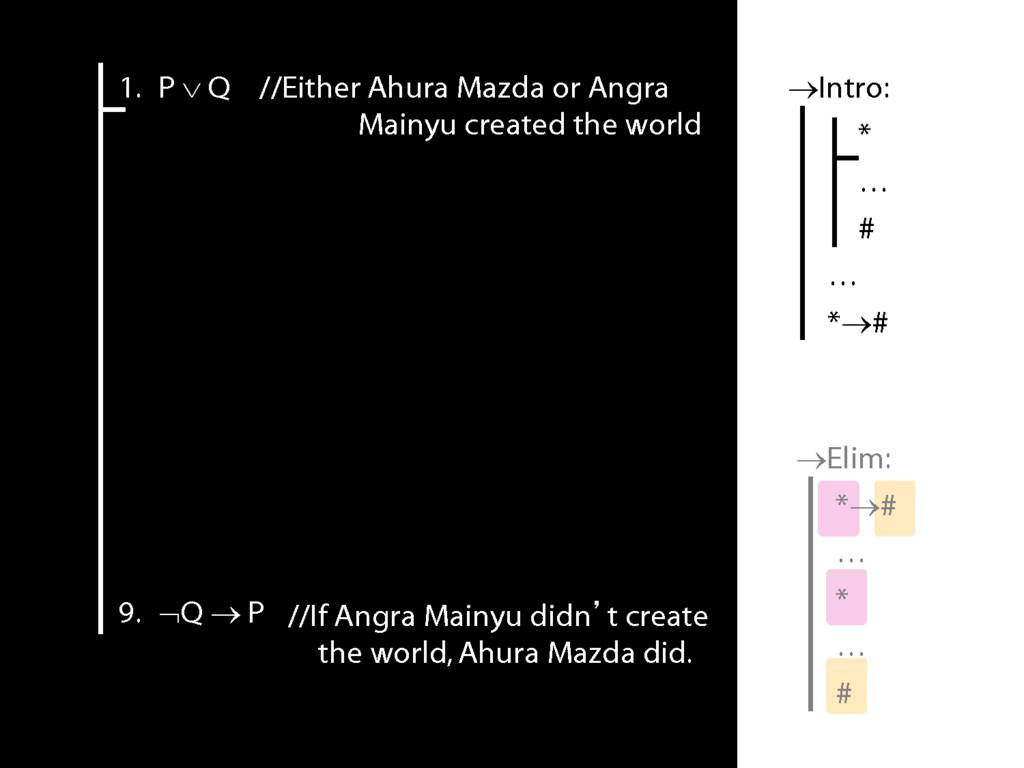
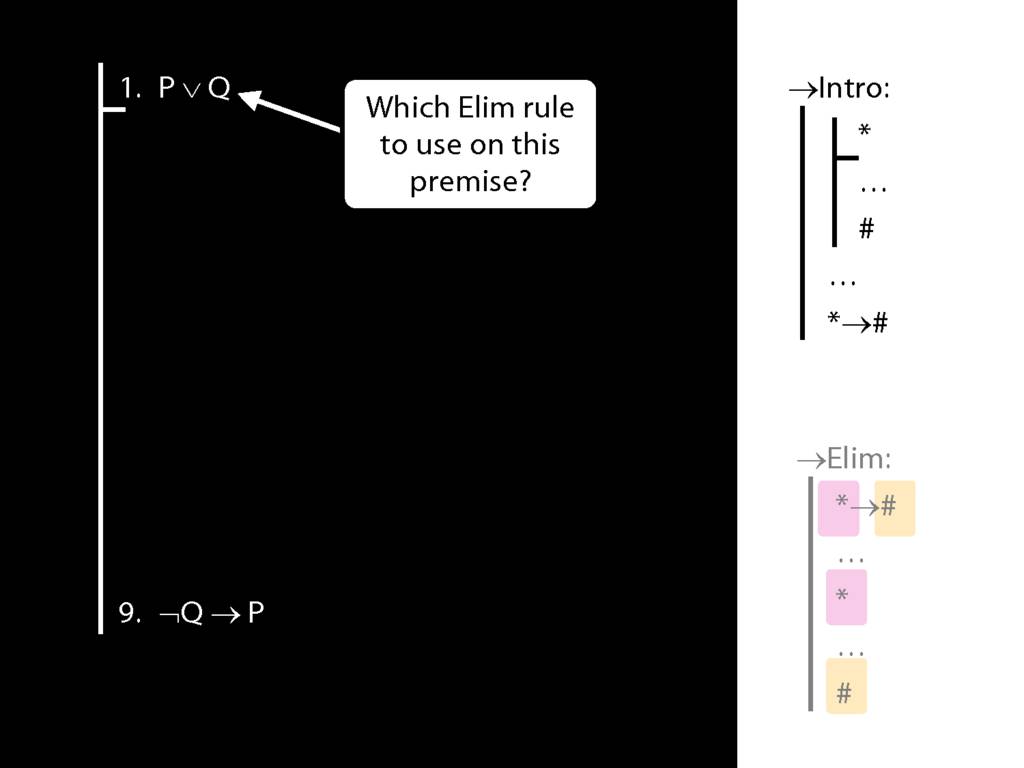
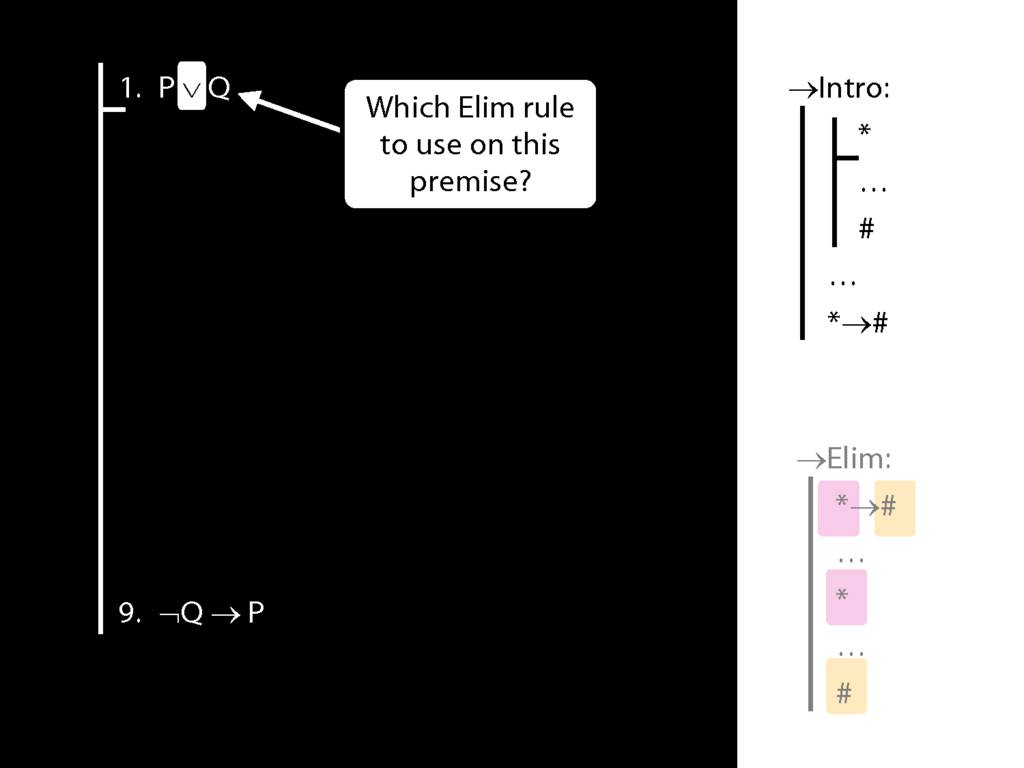
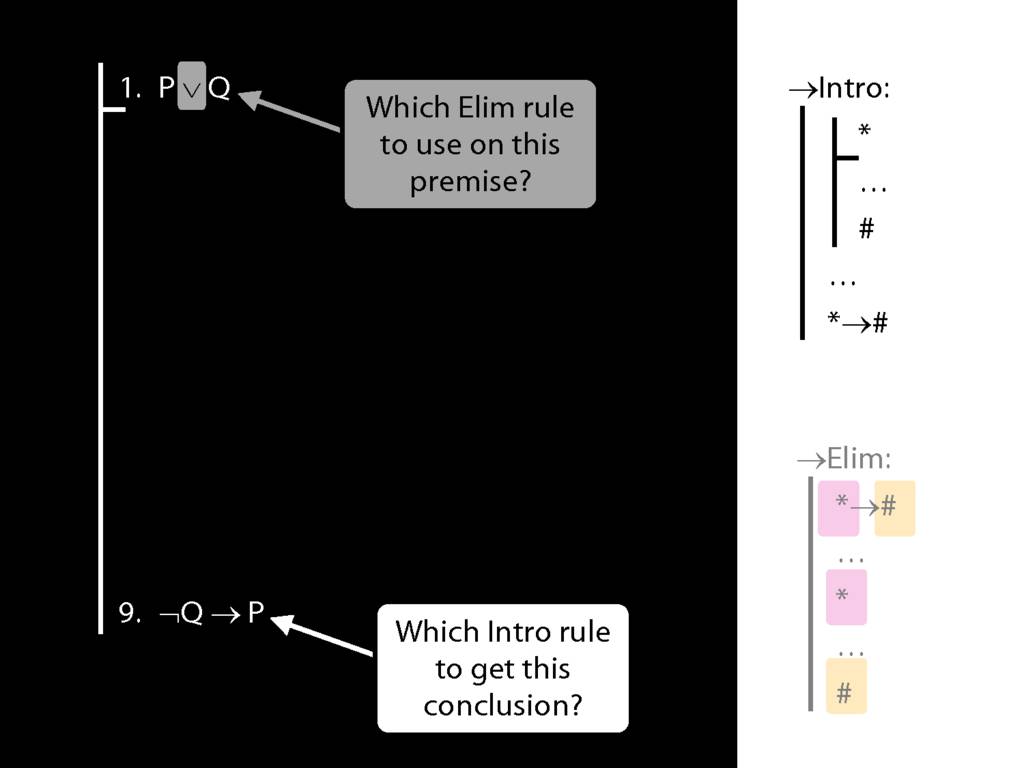
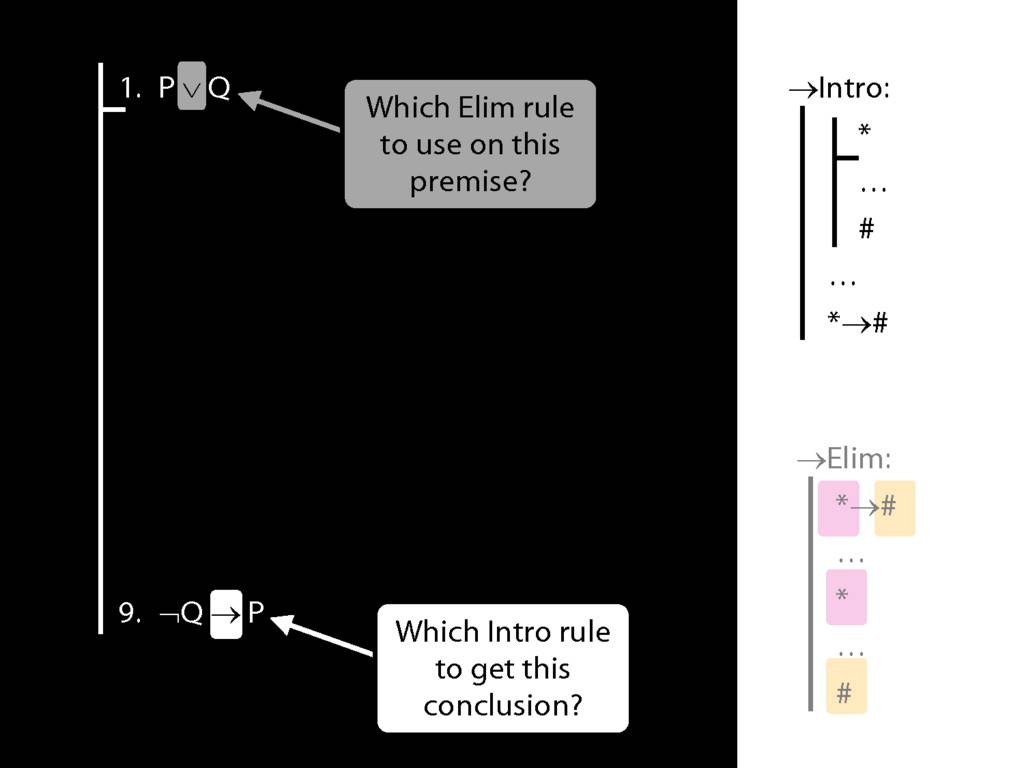
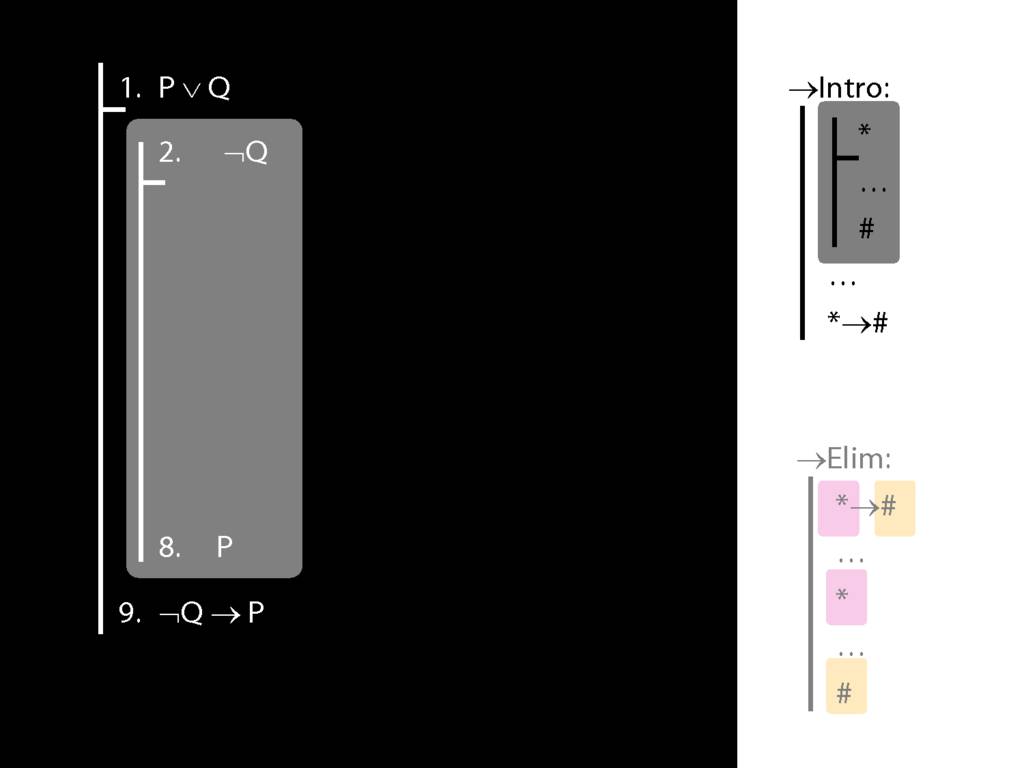
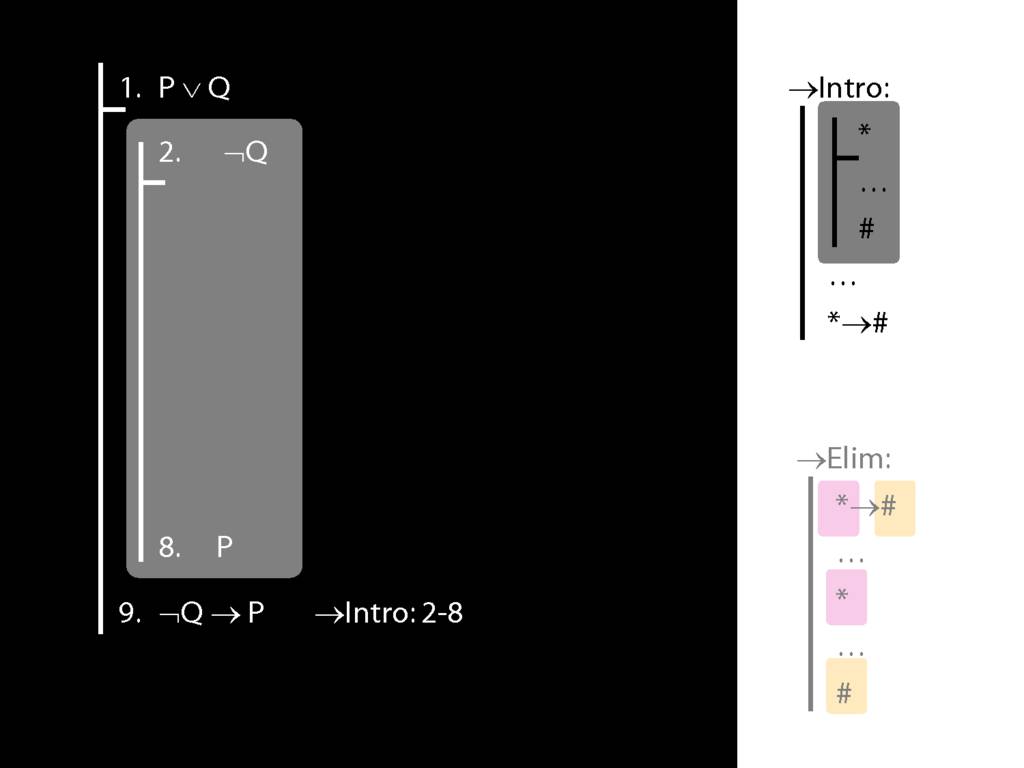
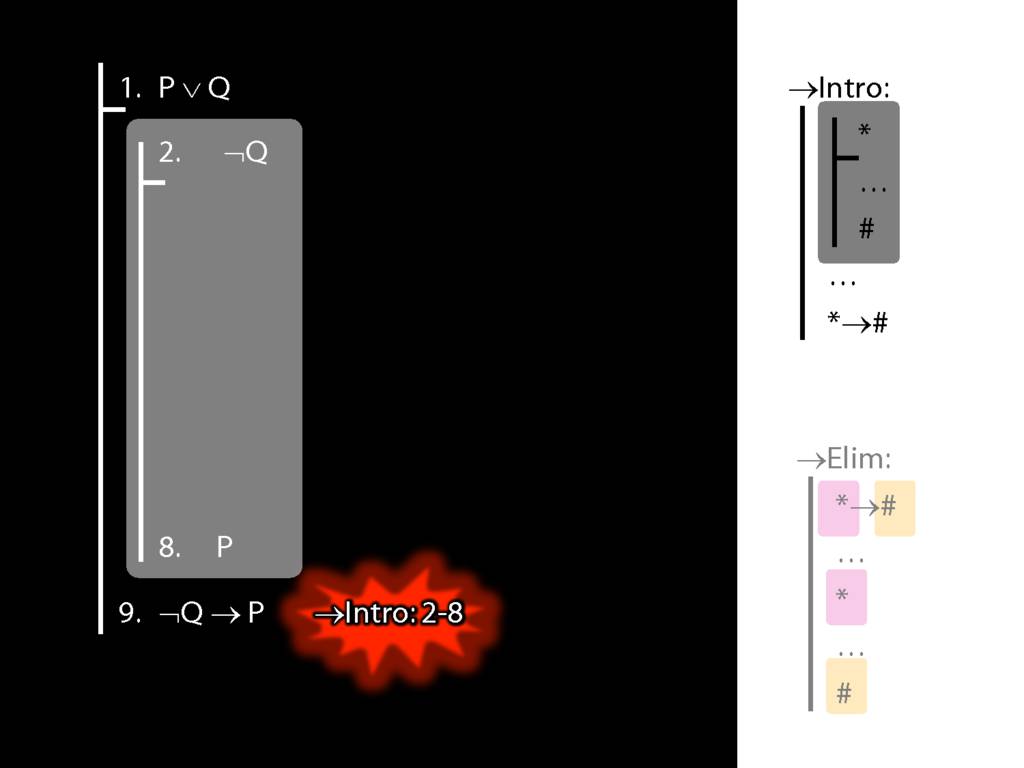
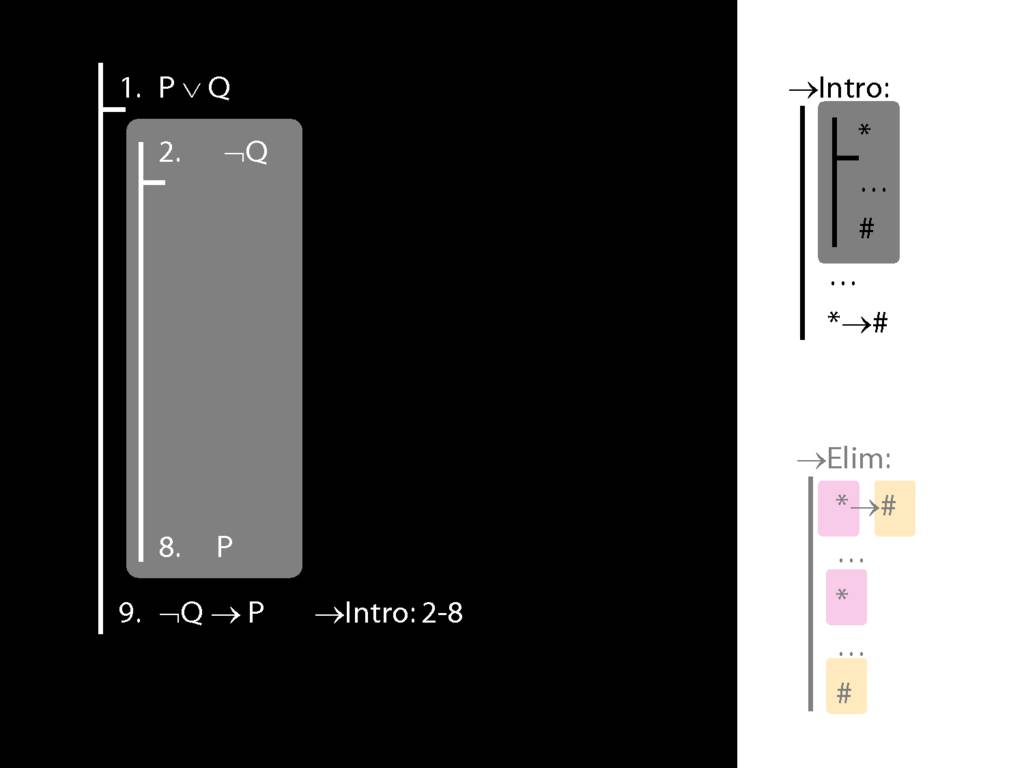
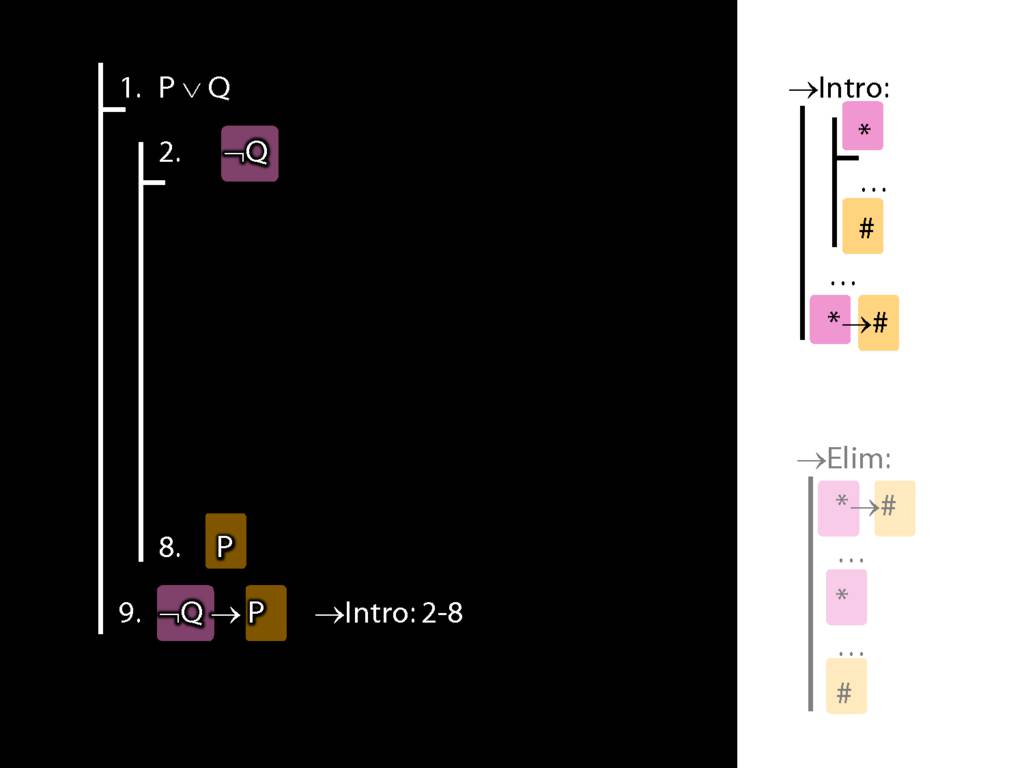
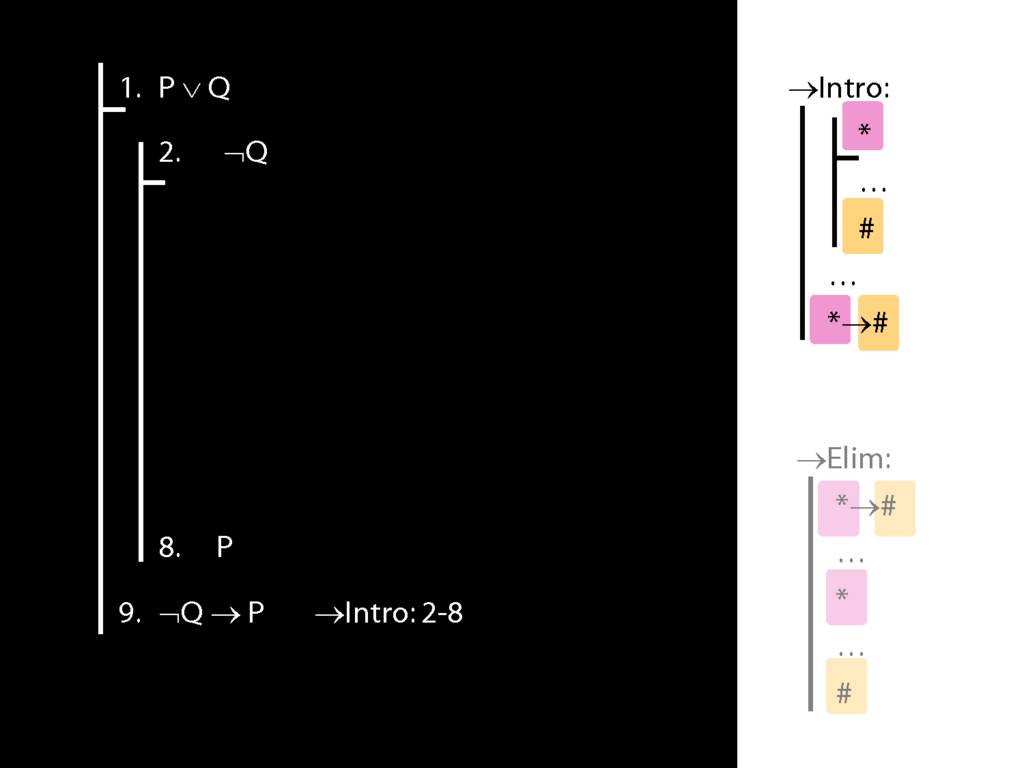
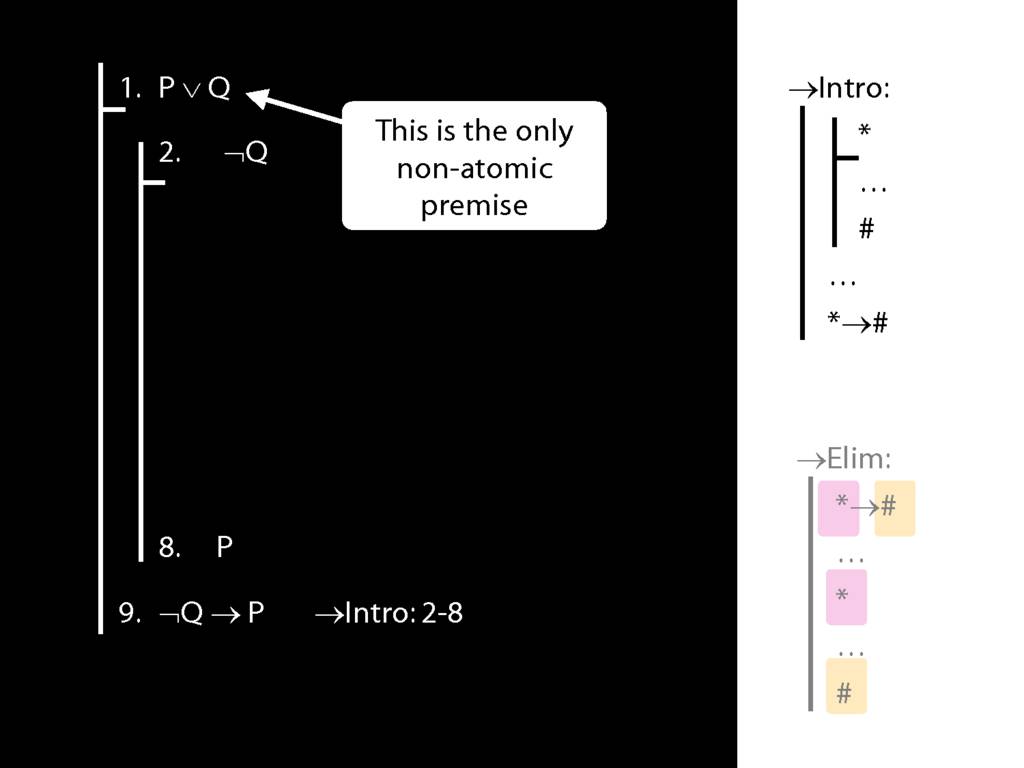
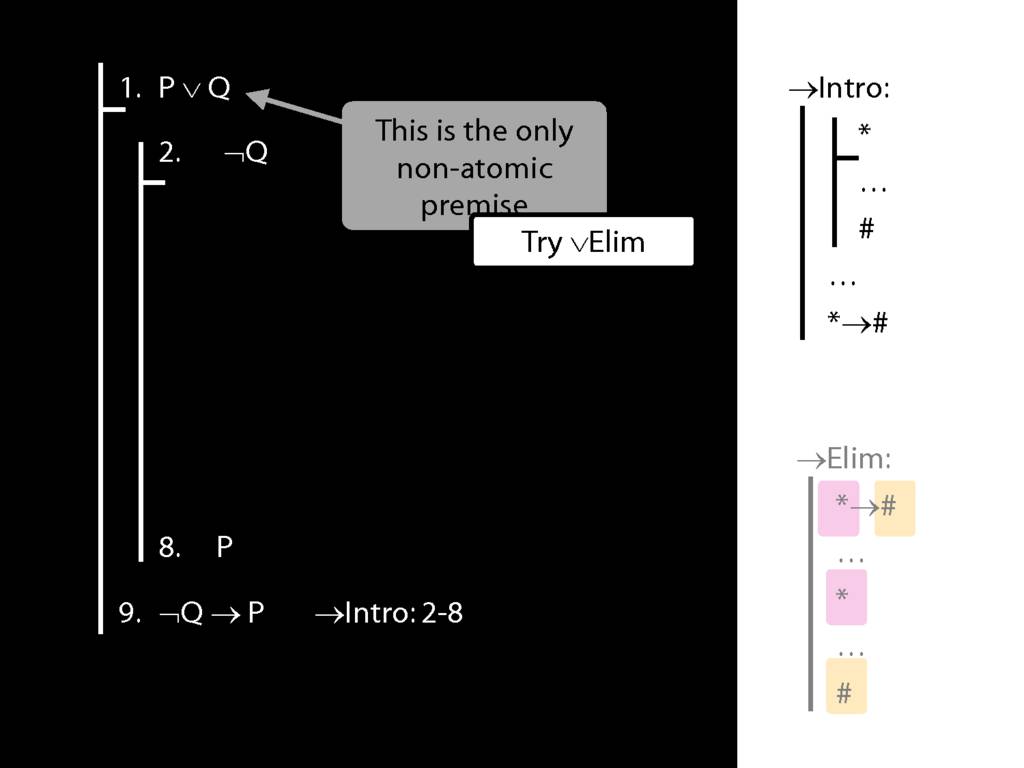
\section{→Intro: An Example}
\section{→Intro: An Example}
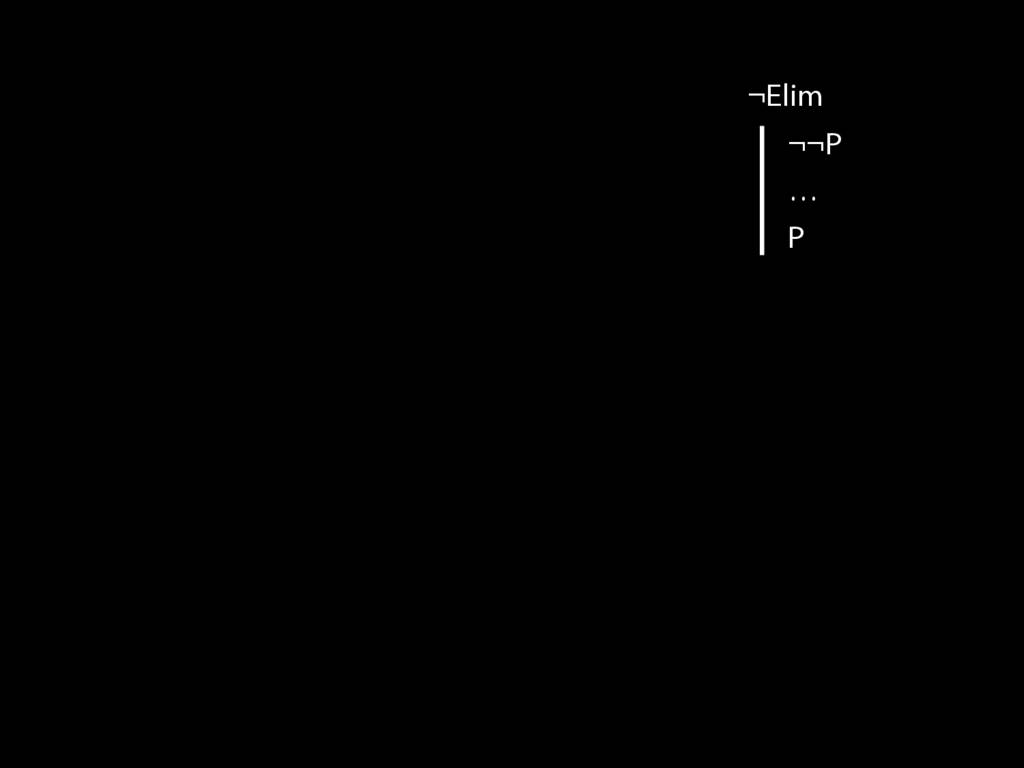
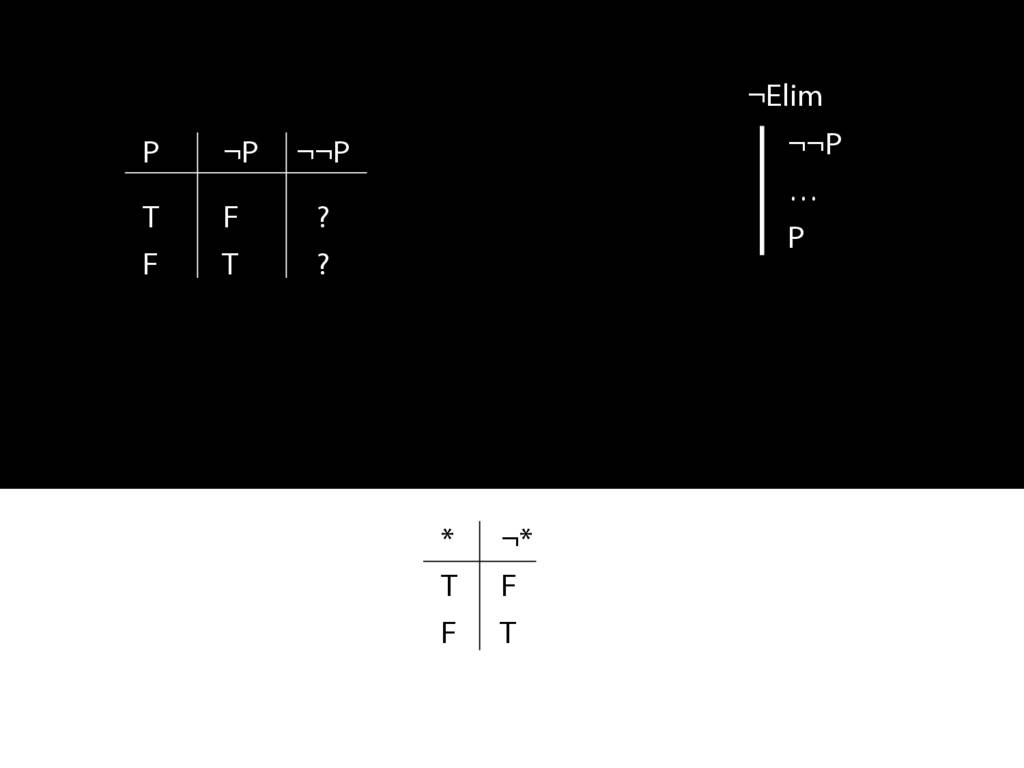
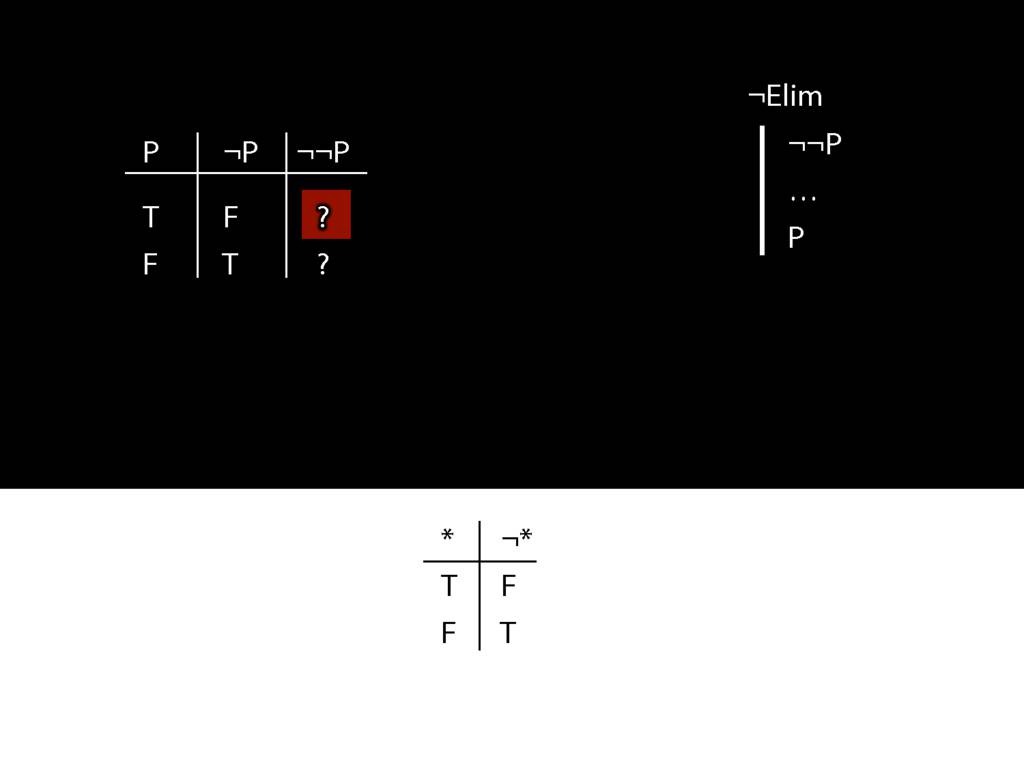
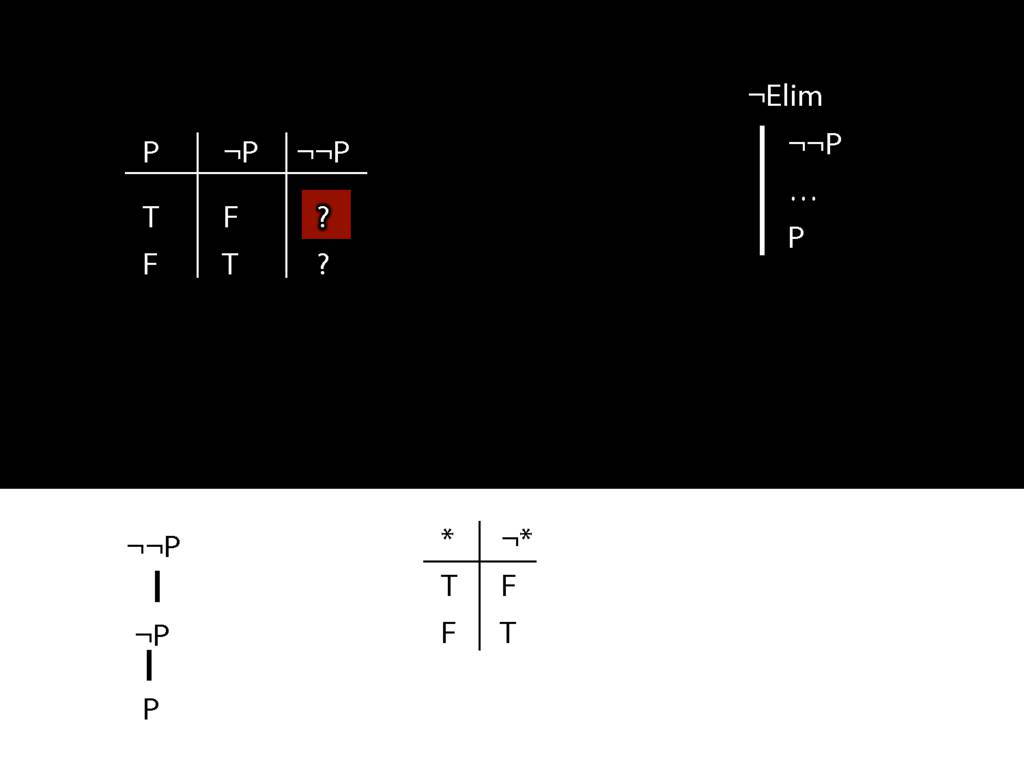
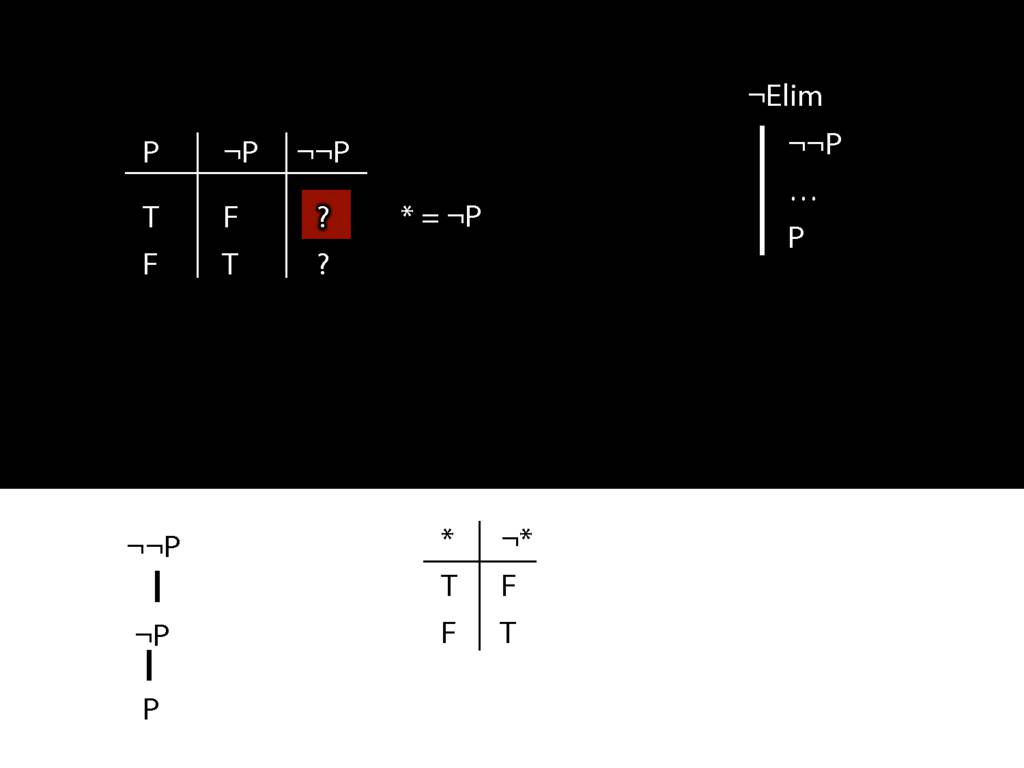
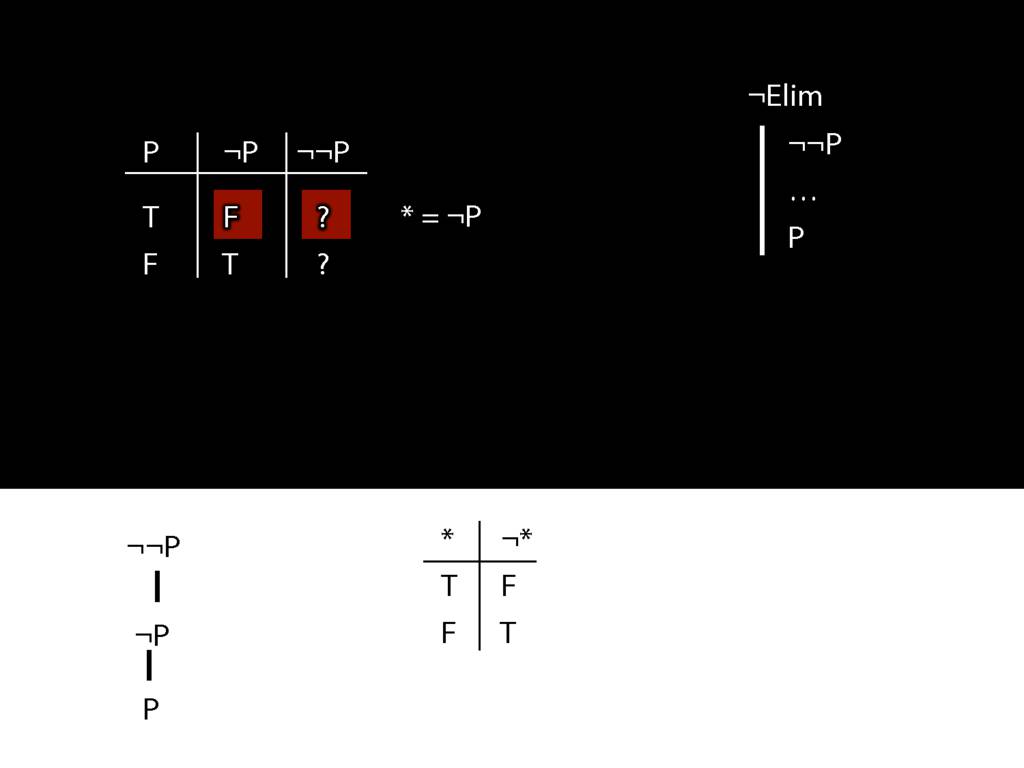
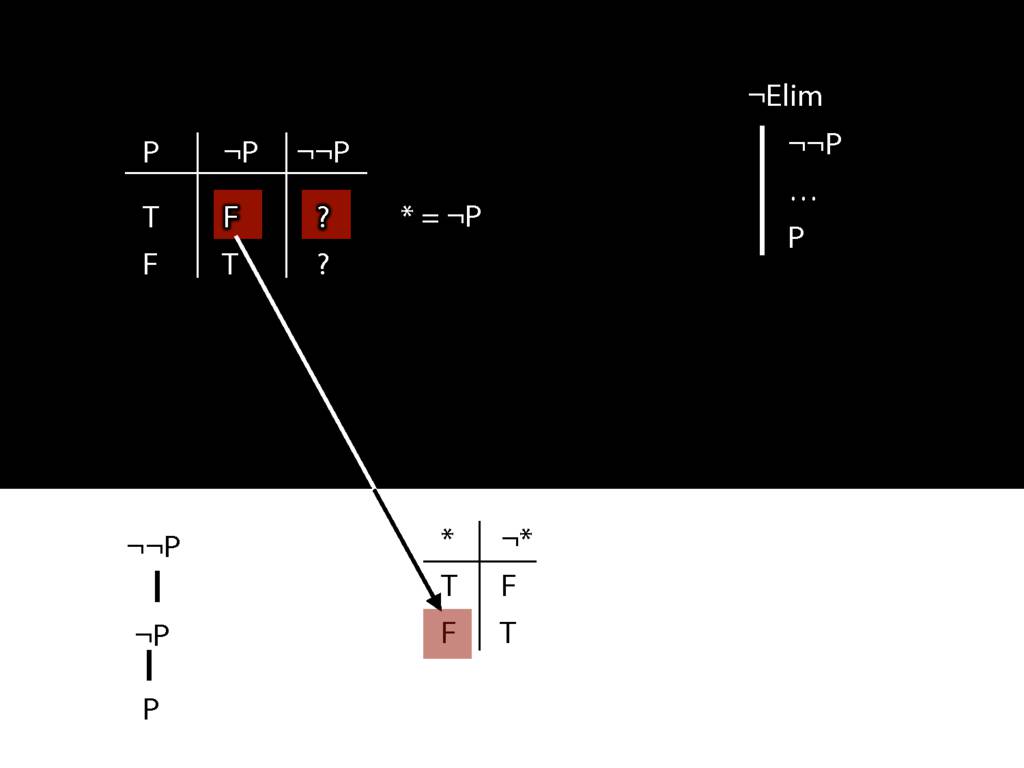
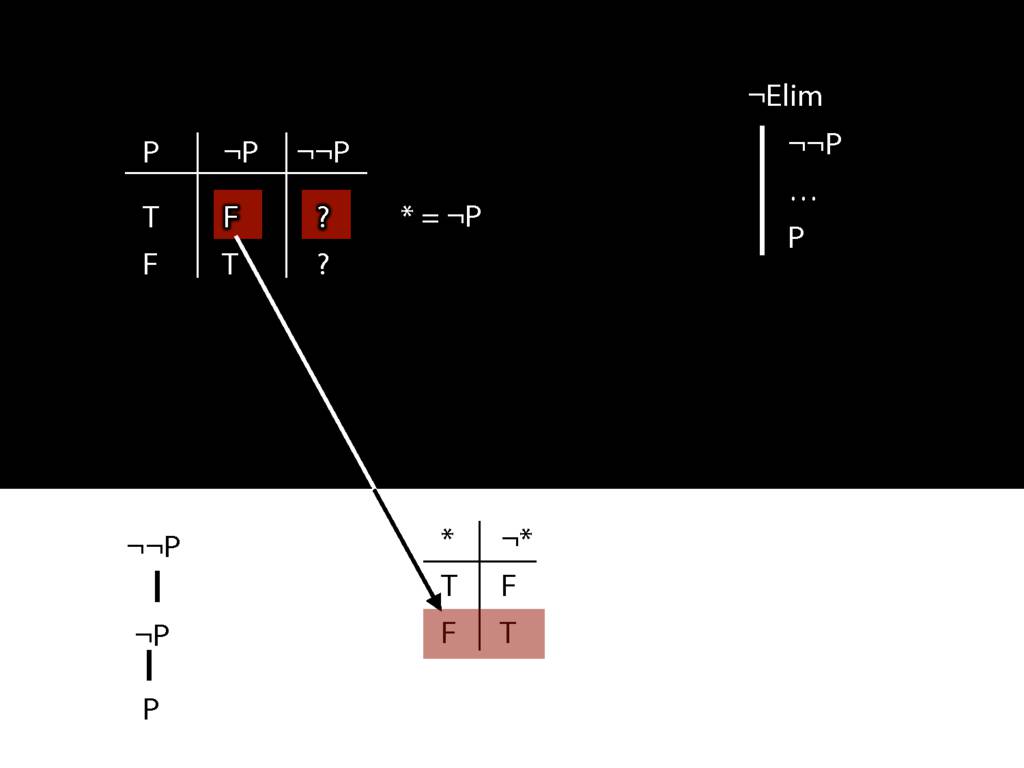
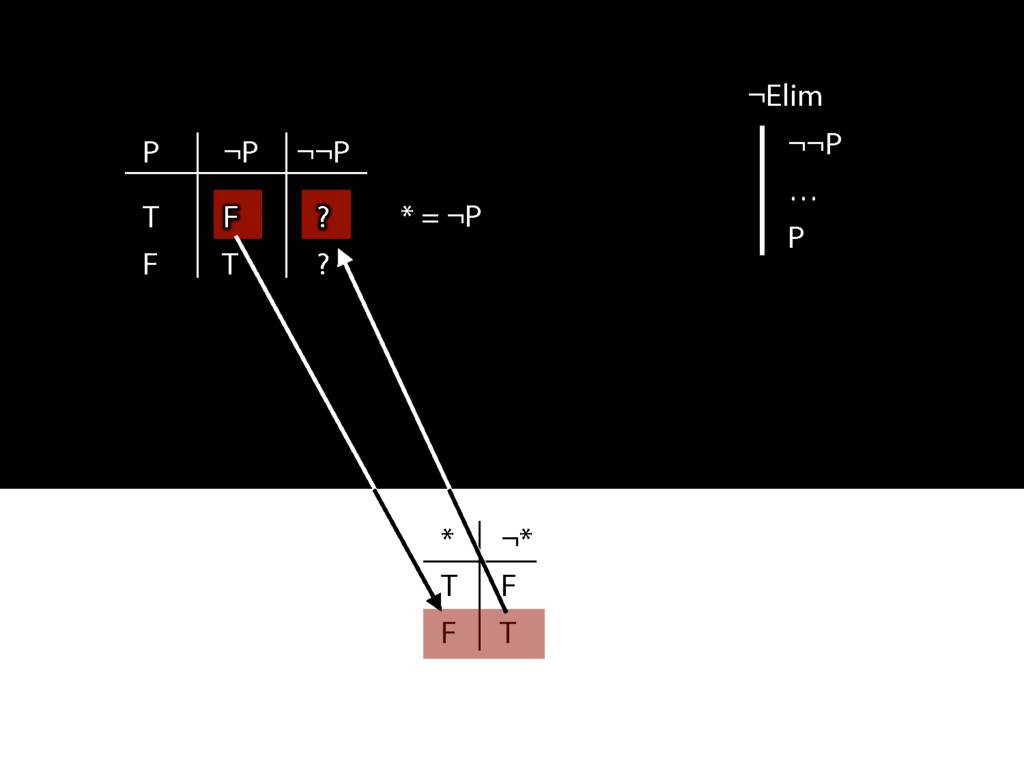
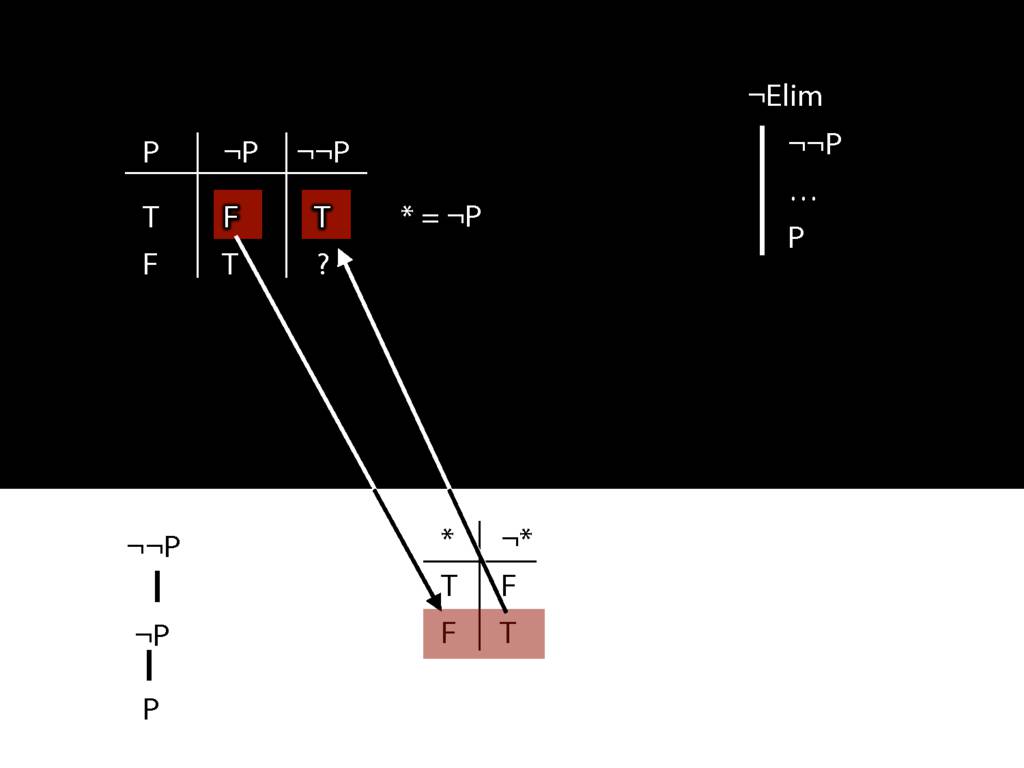
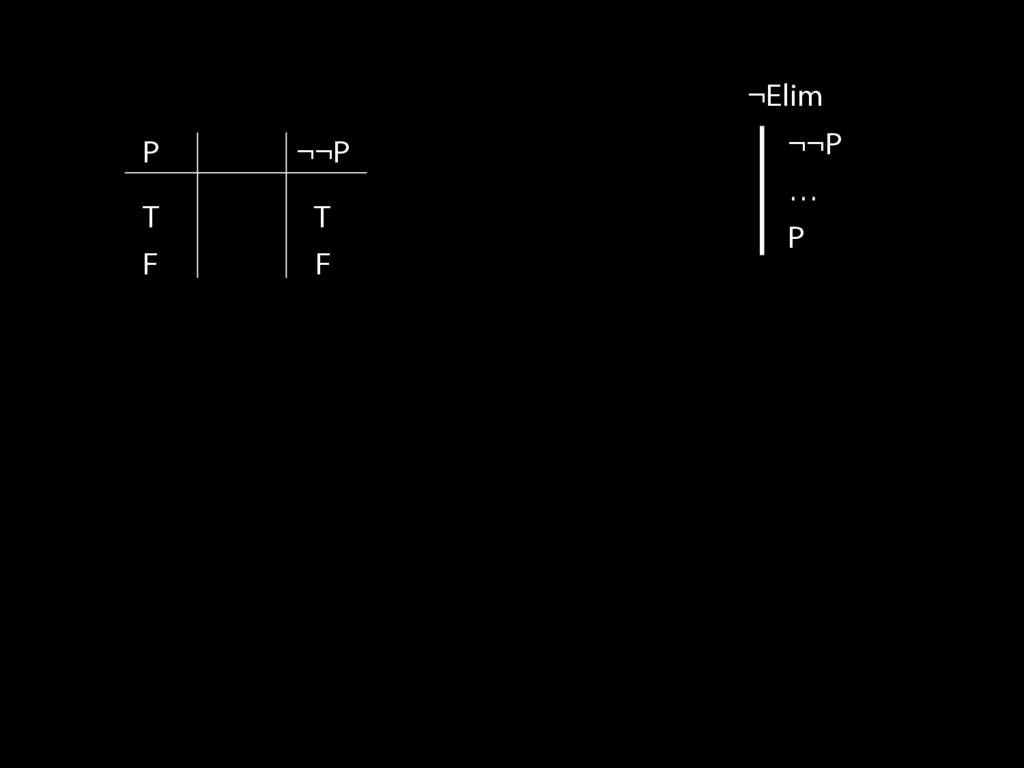
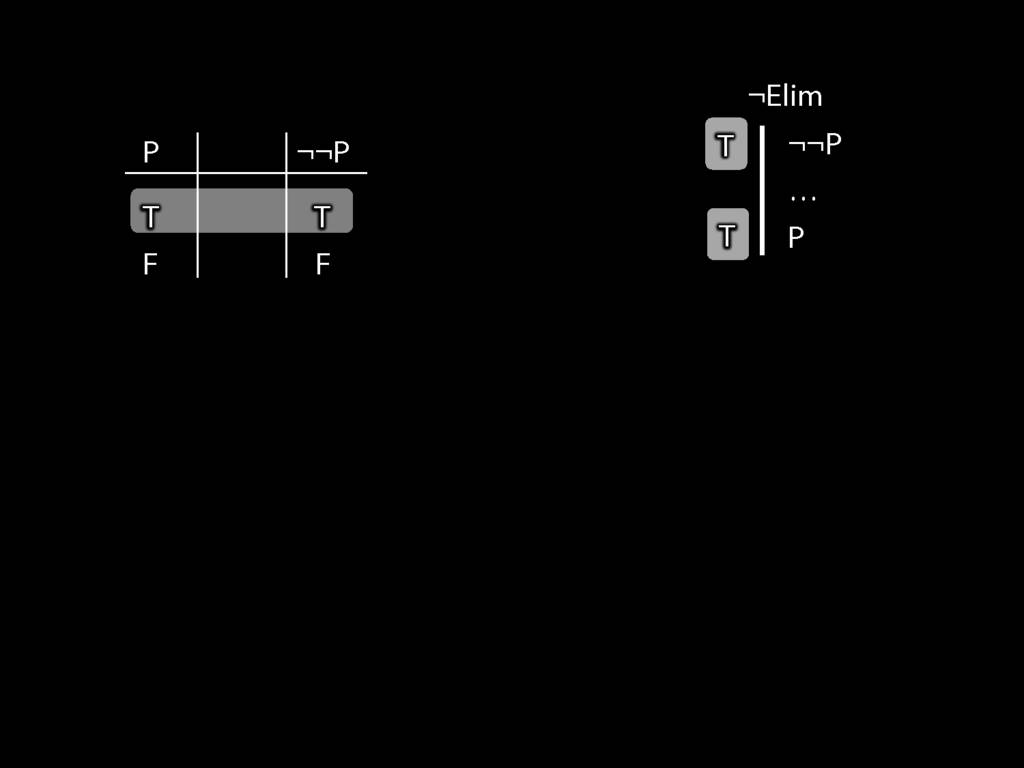
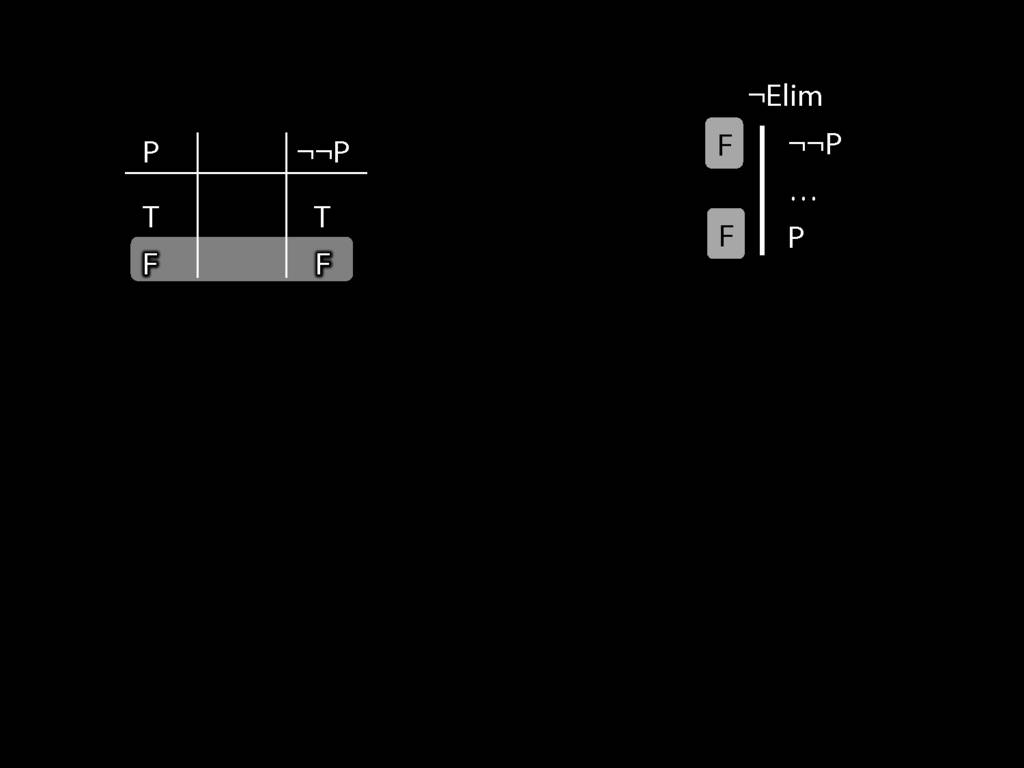
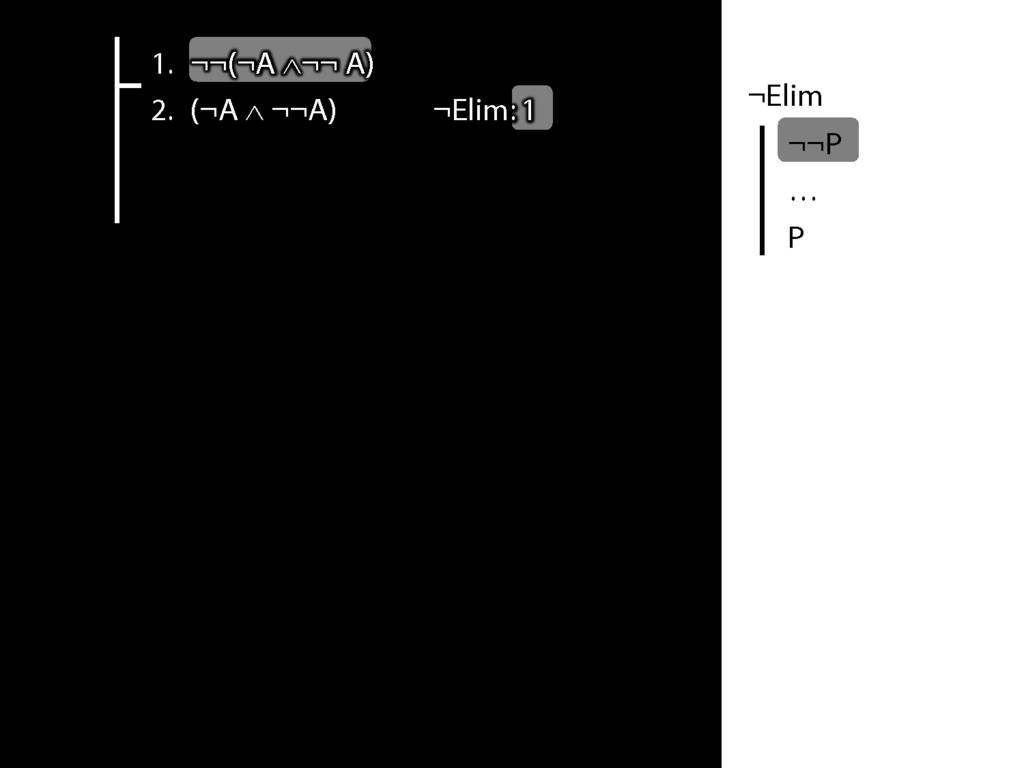
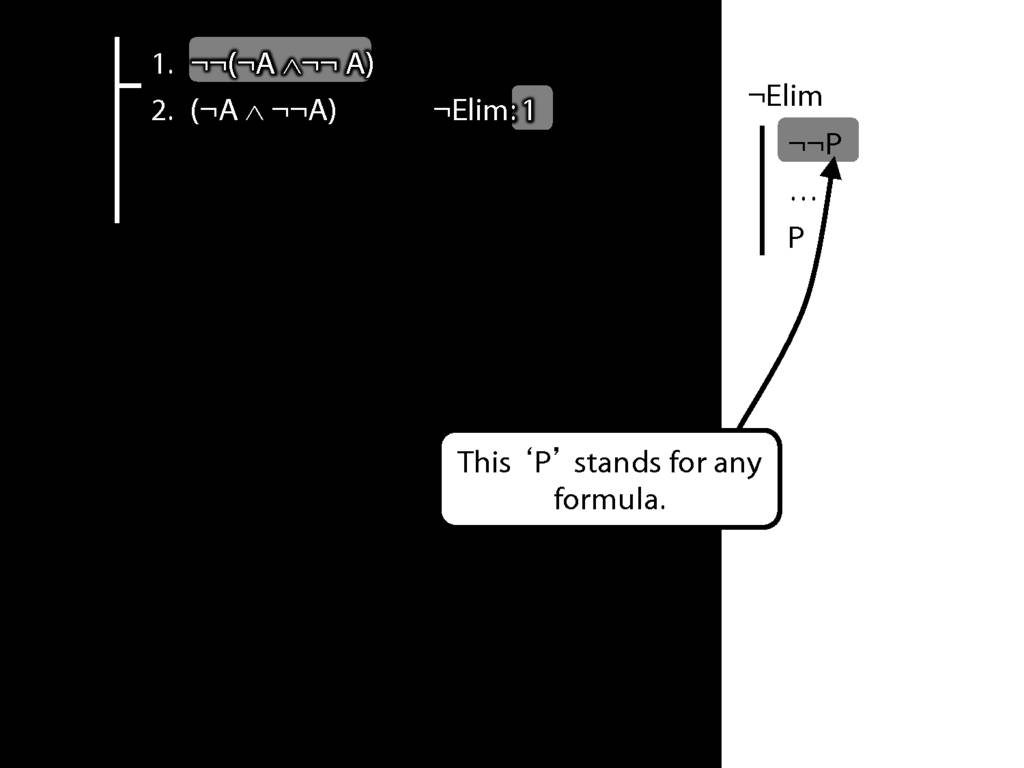
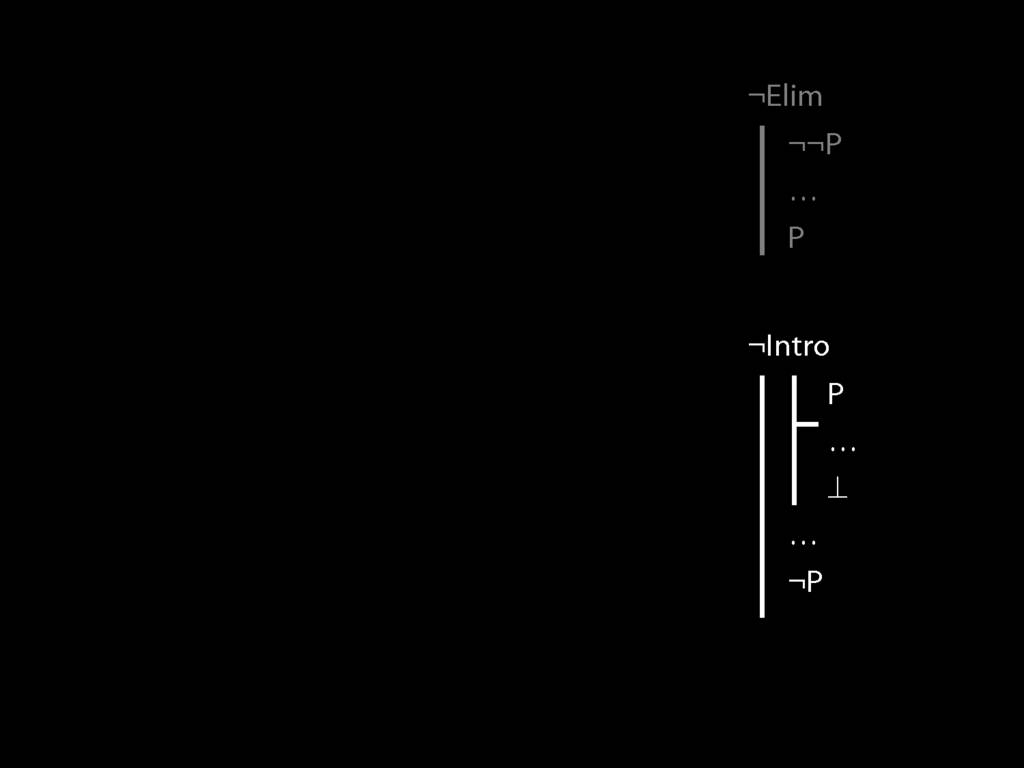
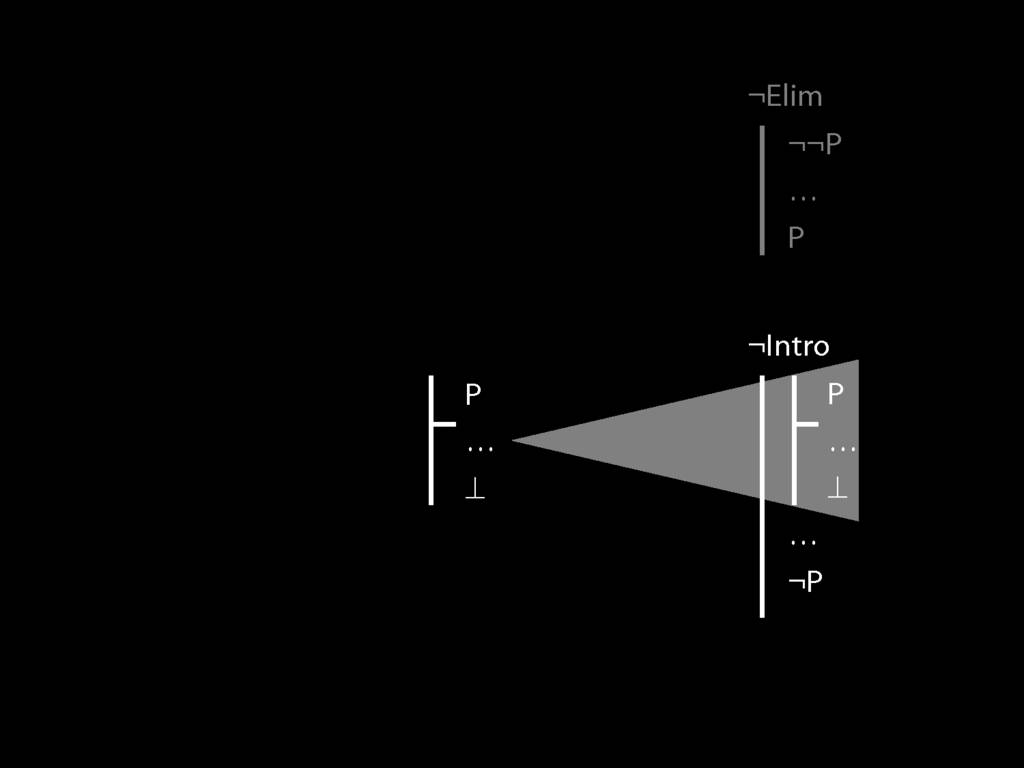
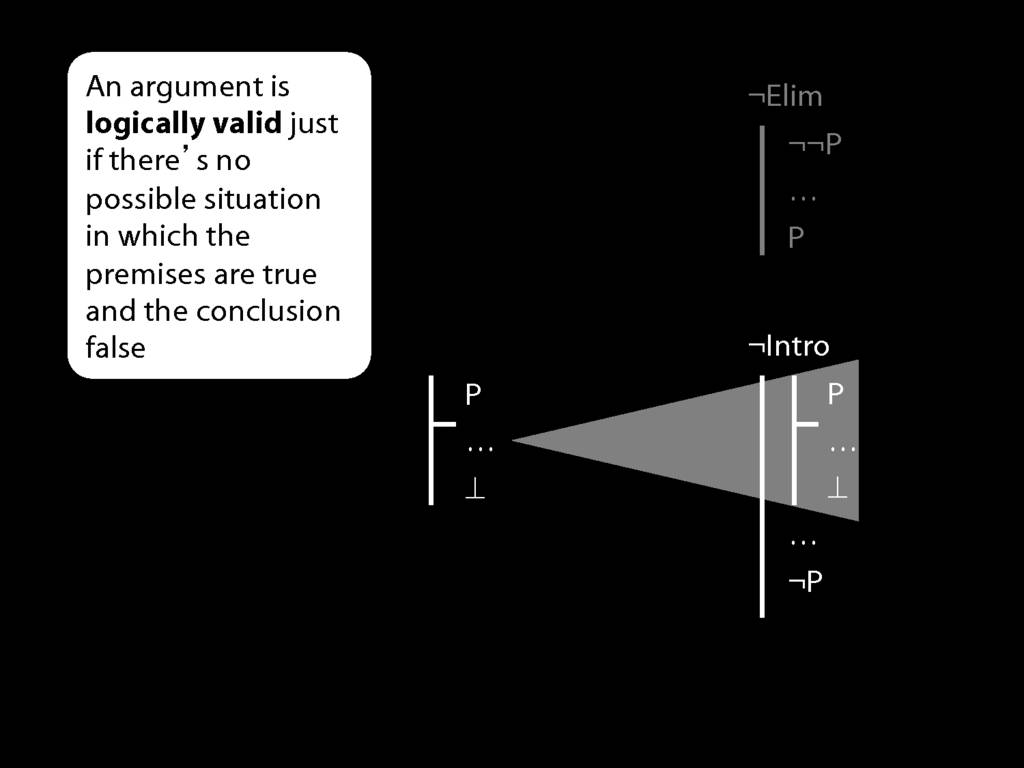
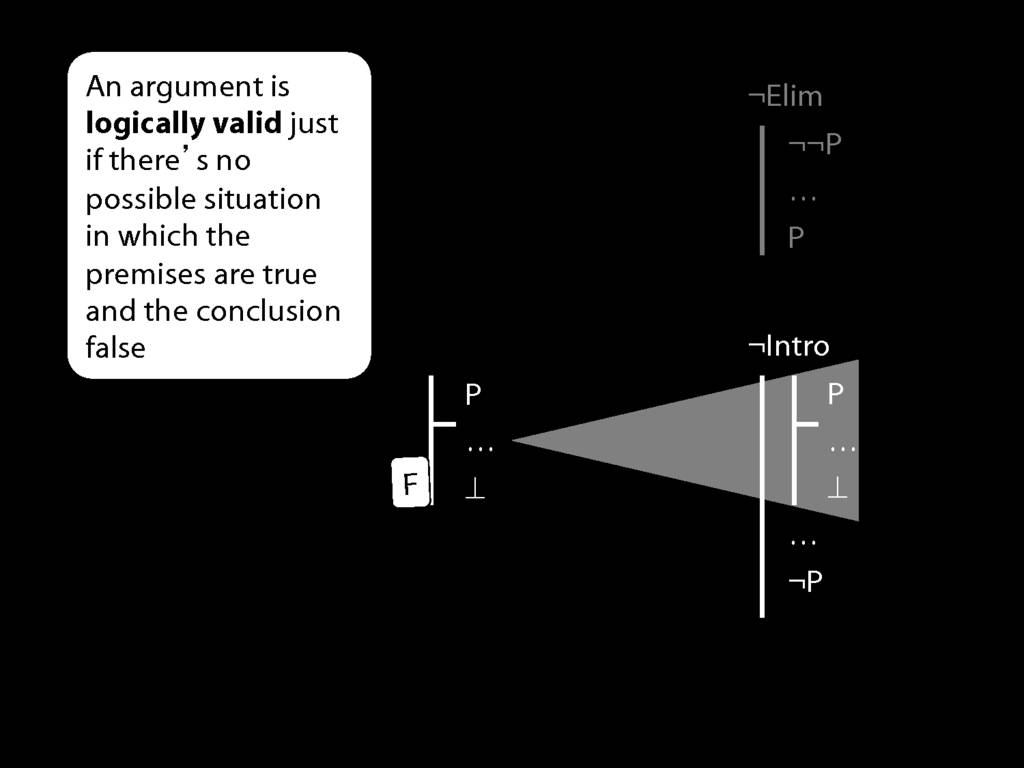
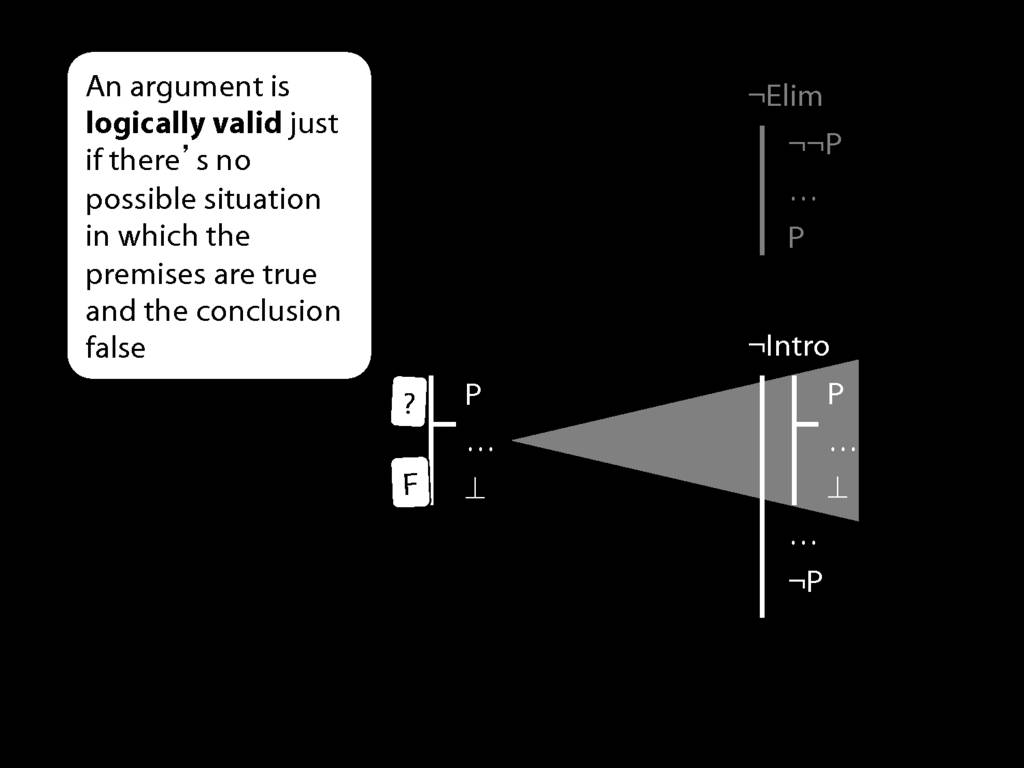
\section{¬Elim}
\emph{Reading:} §6.3
\section{¬Elim}
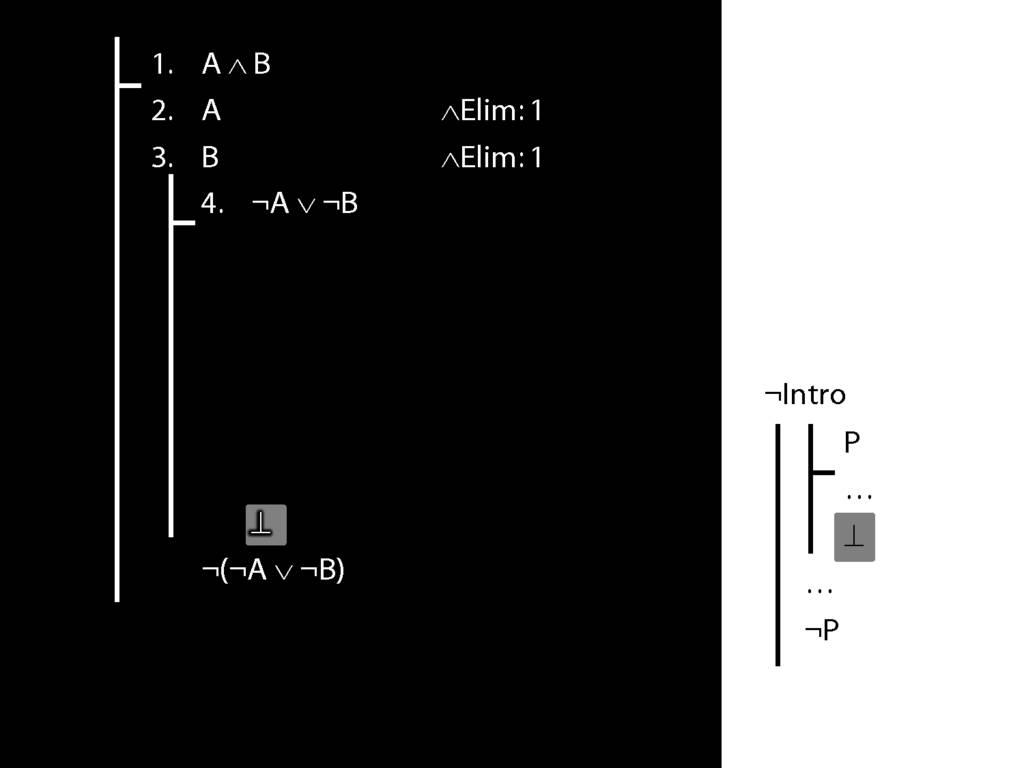
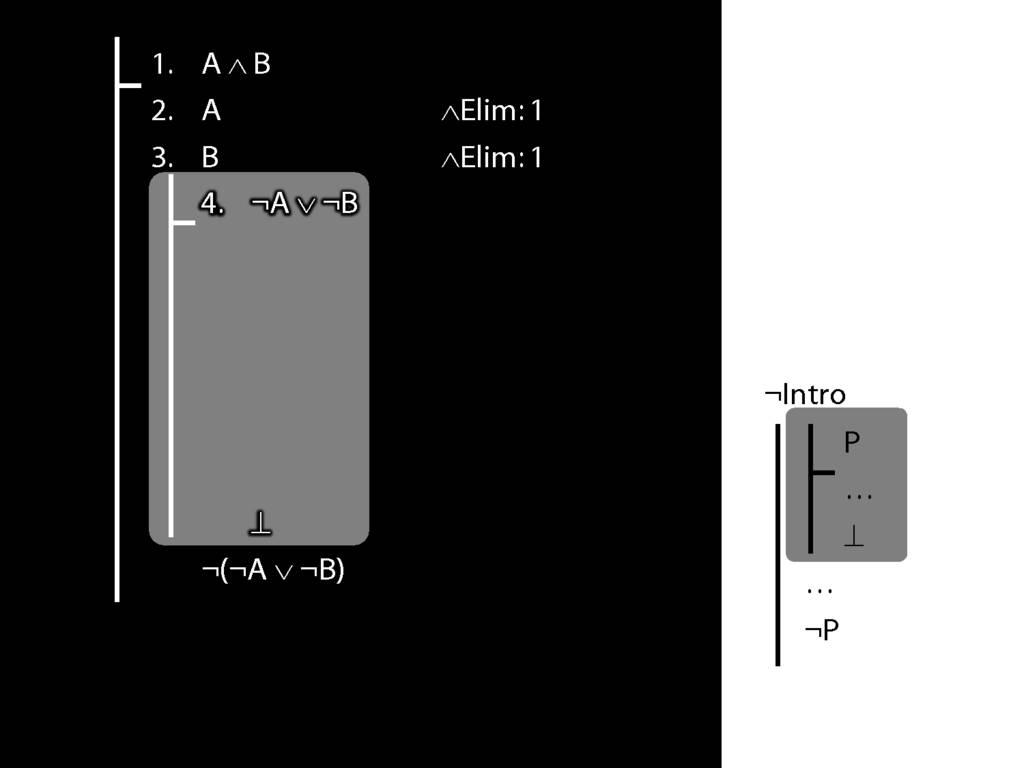
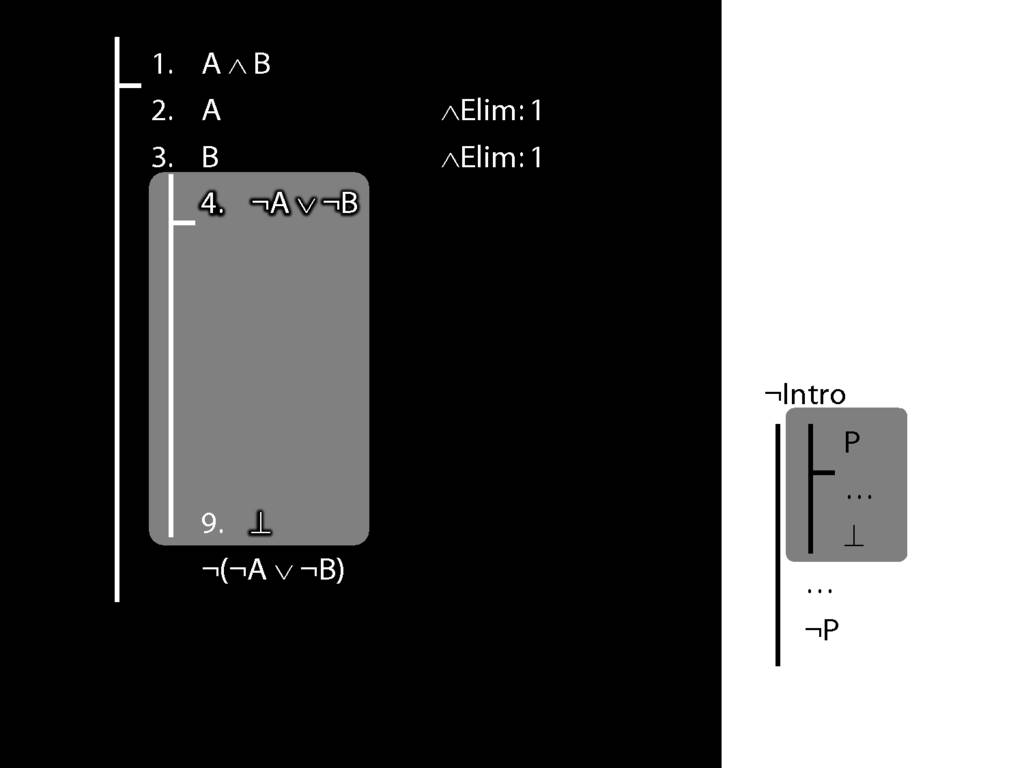
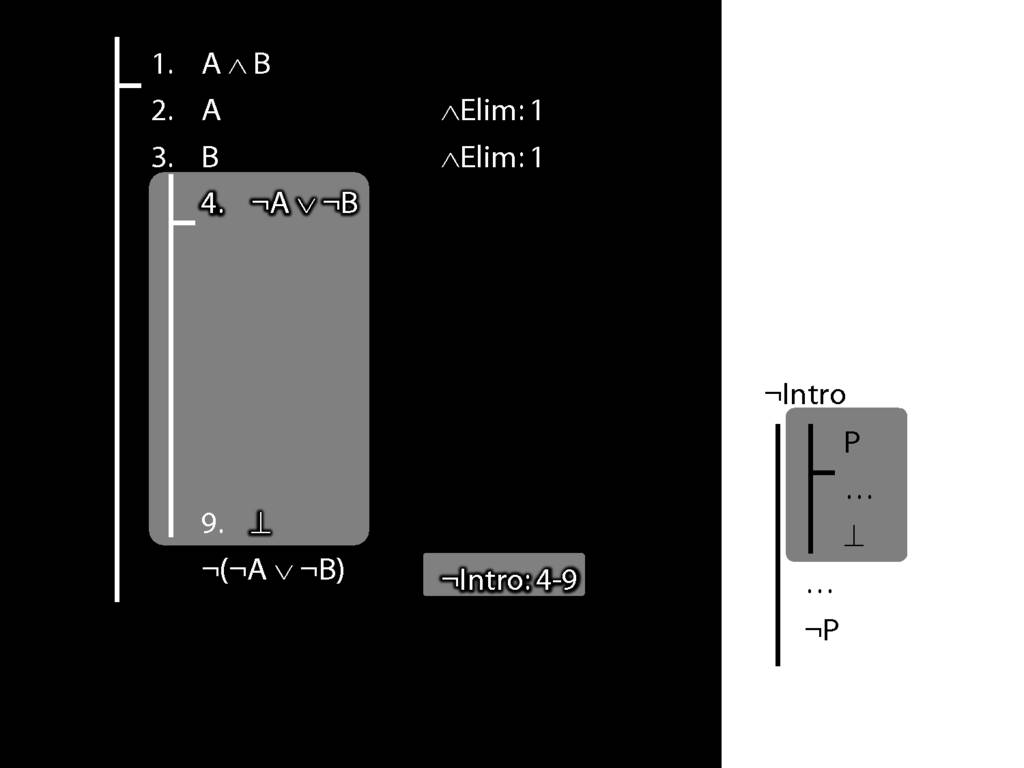
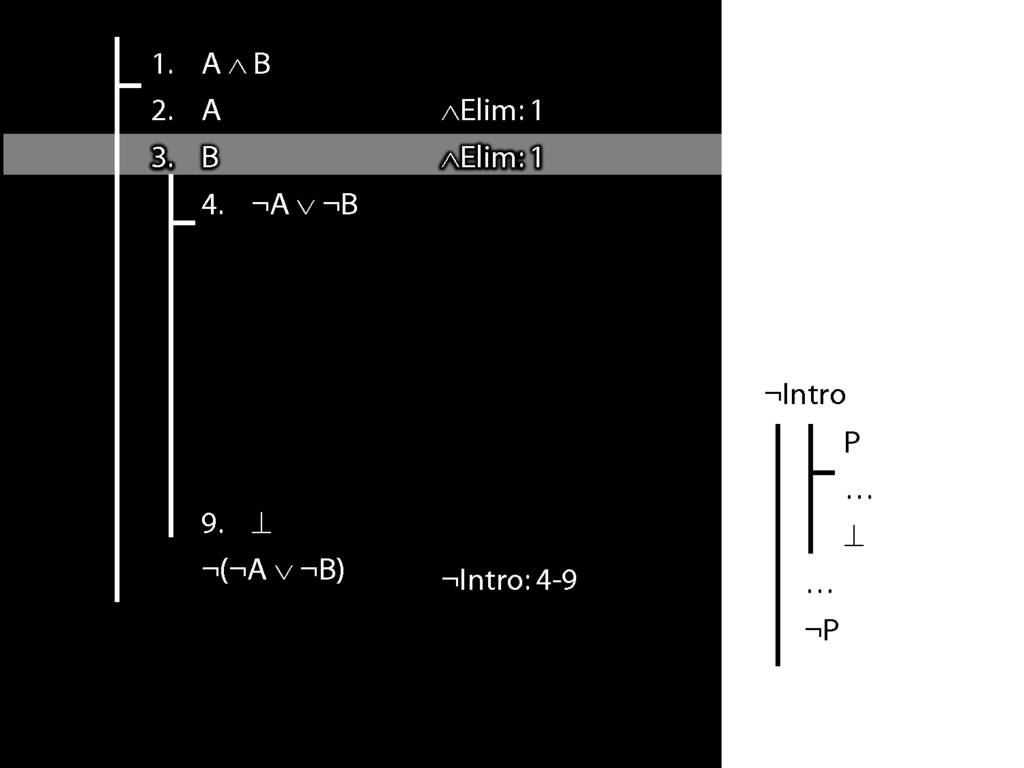
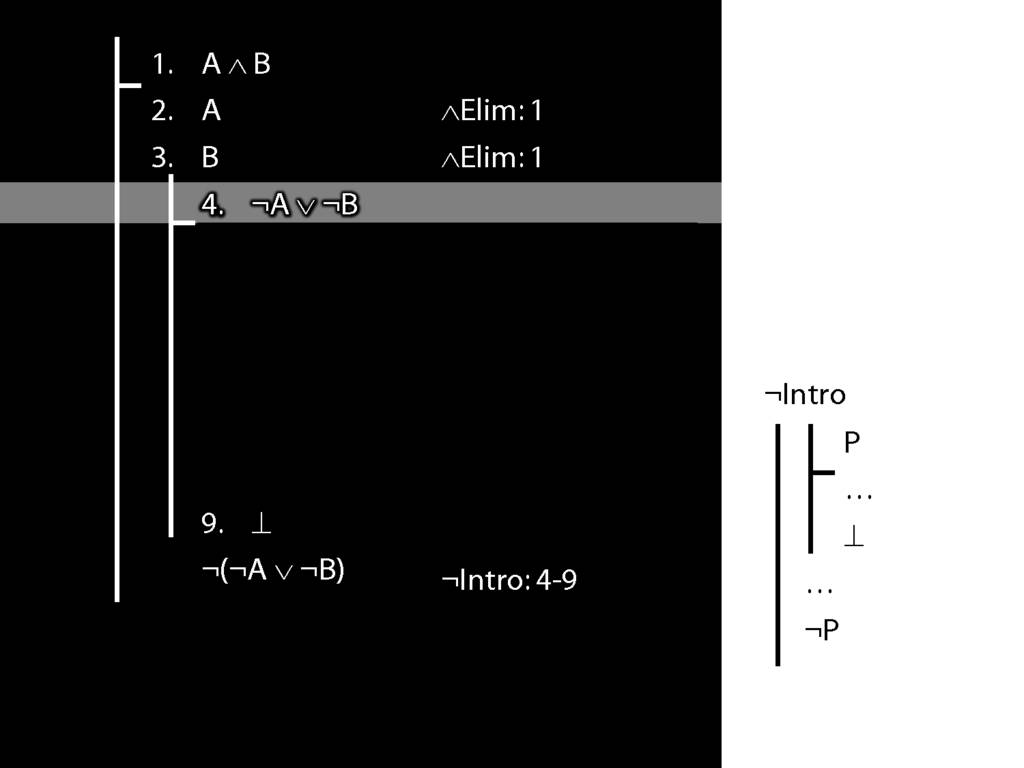
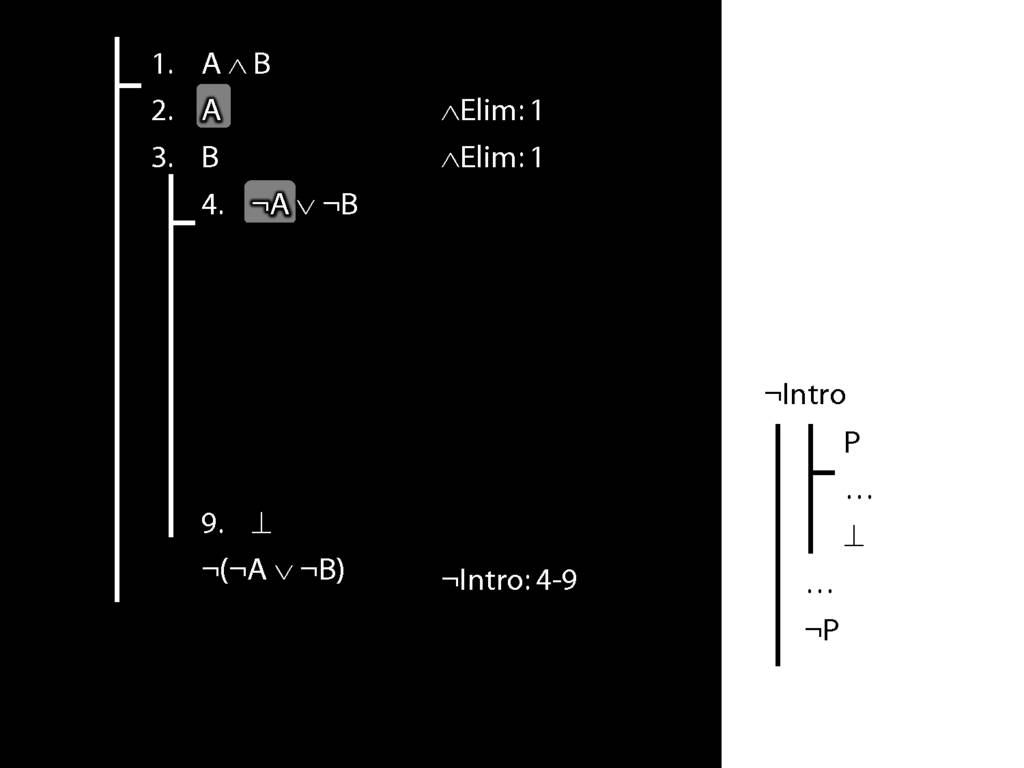
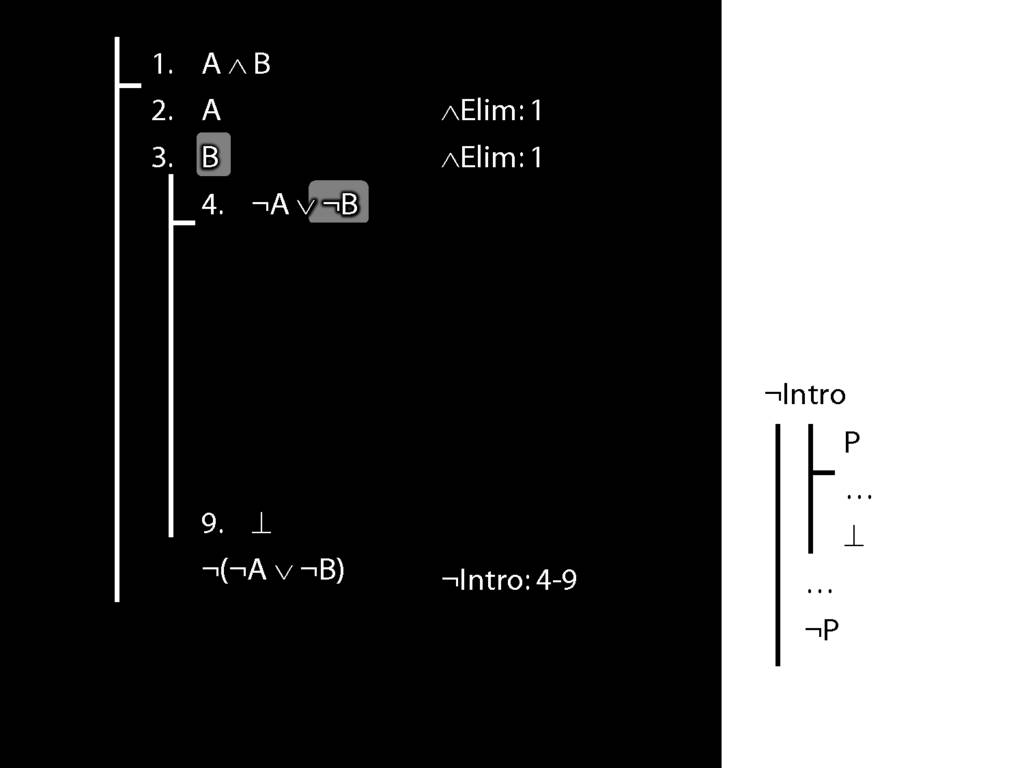
\section{¬Intro}
\emph{Reading:} §5.3, §6.3
\section{¬Intro}
6.7--6.10
*6.11--6.12
6.7--6.12
6.18--6.20
6.24--6.27
*6.40--6.42
\section{¬Intro continued}
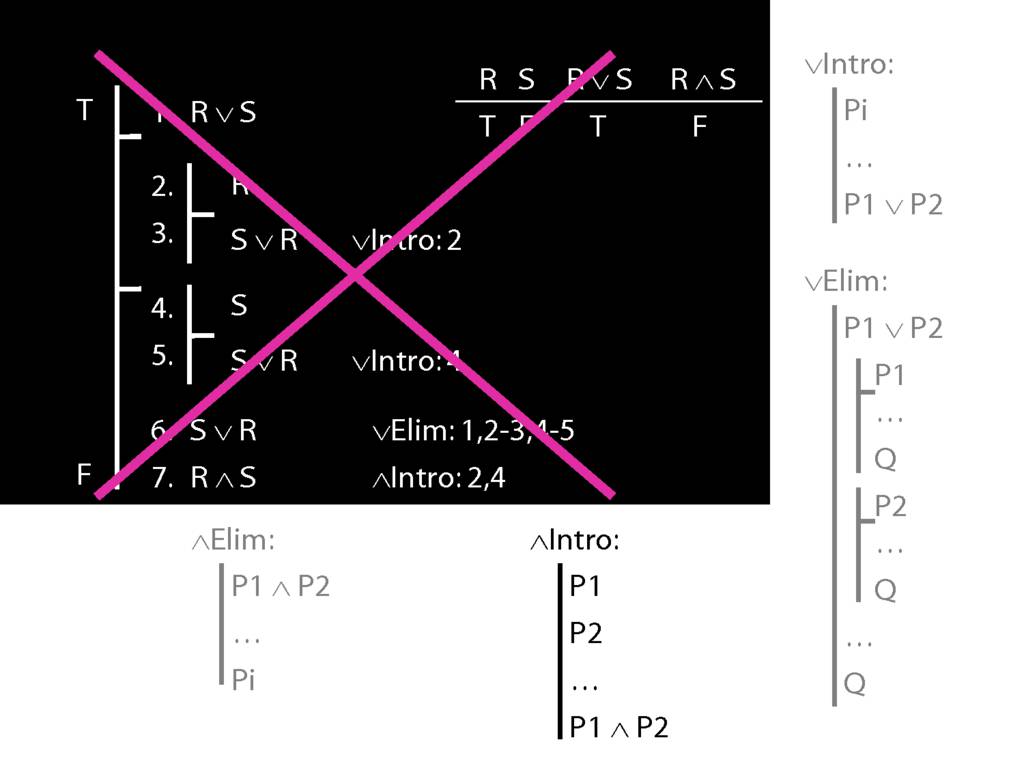
\section{∨Elim: Recap}
\section{Subproofs Are Tricky}
\section{Subproofs Are Tricky}