Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

7.1--7.2, *7.3--7.6
\title {Logic I \\ Lecture 08}
 
\maketitle
 

Logic I

Lecture 08

\def \ititle {Logic I}
\def \isubtitle {Lecture 08}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
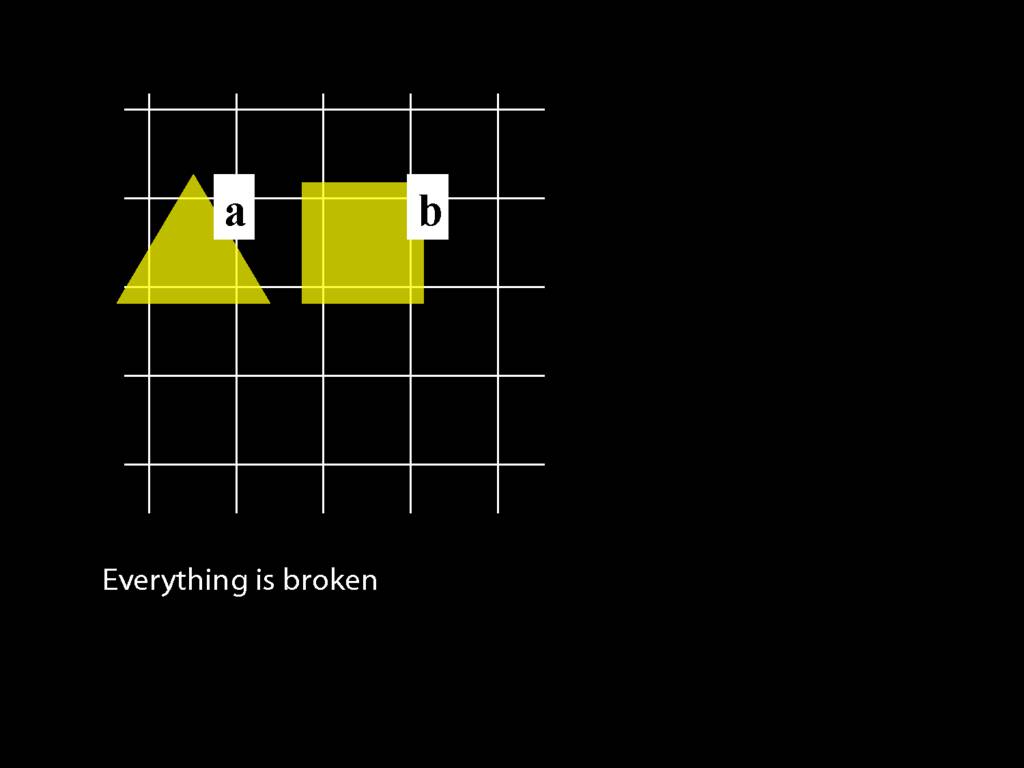
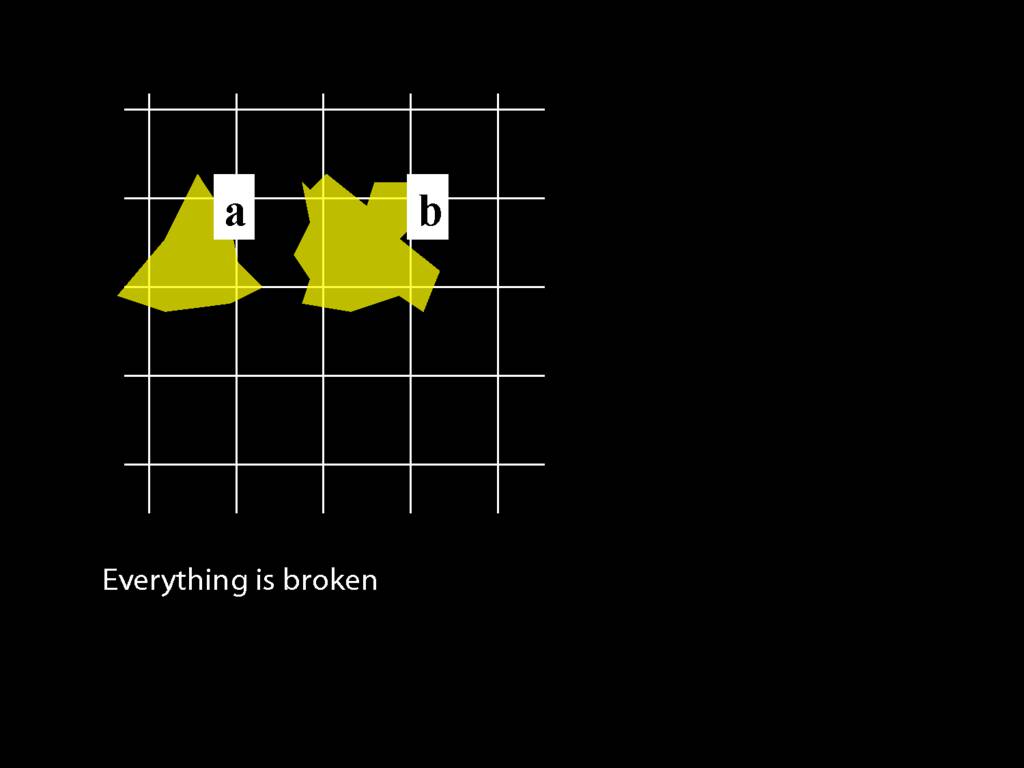
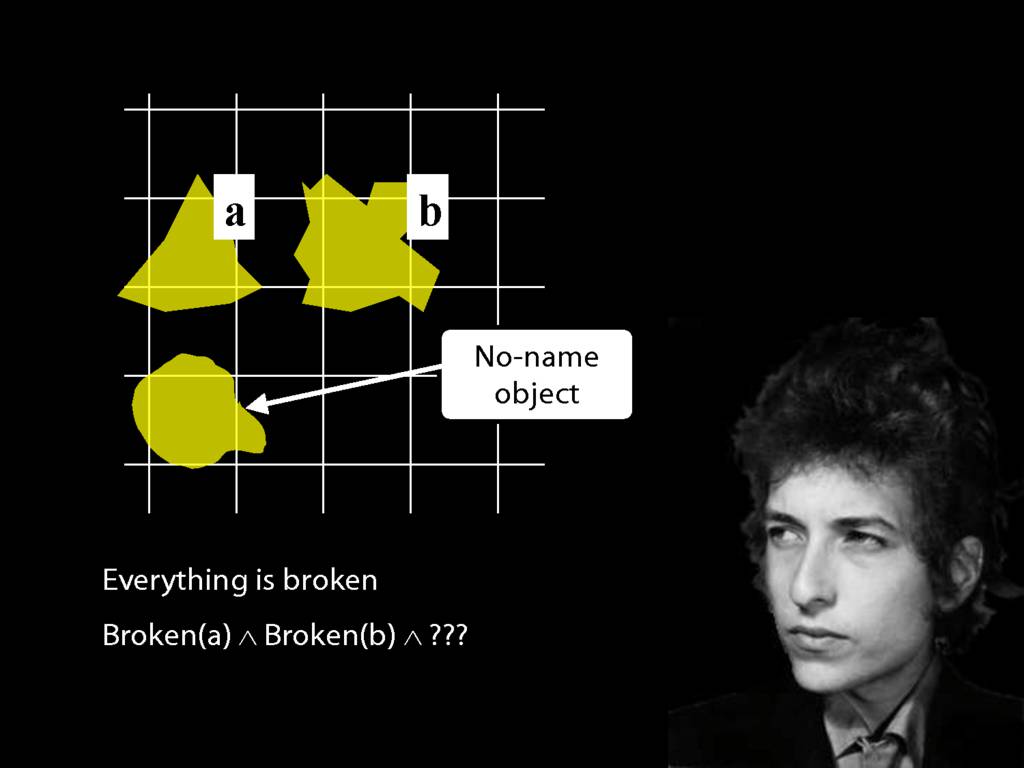
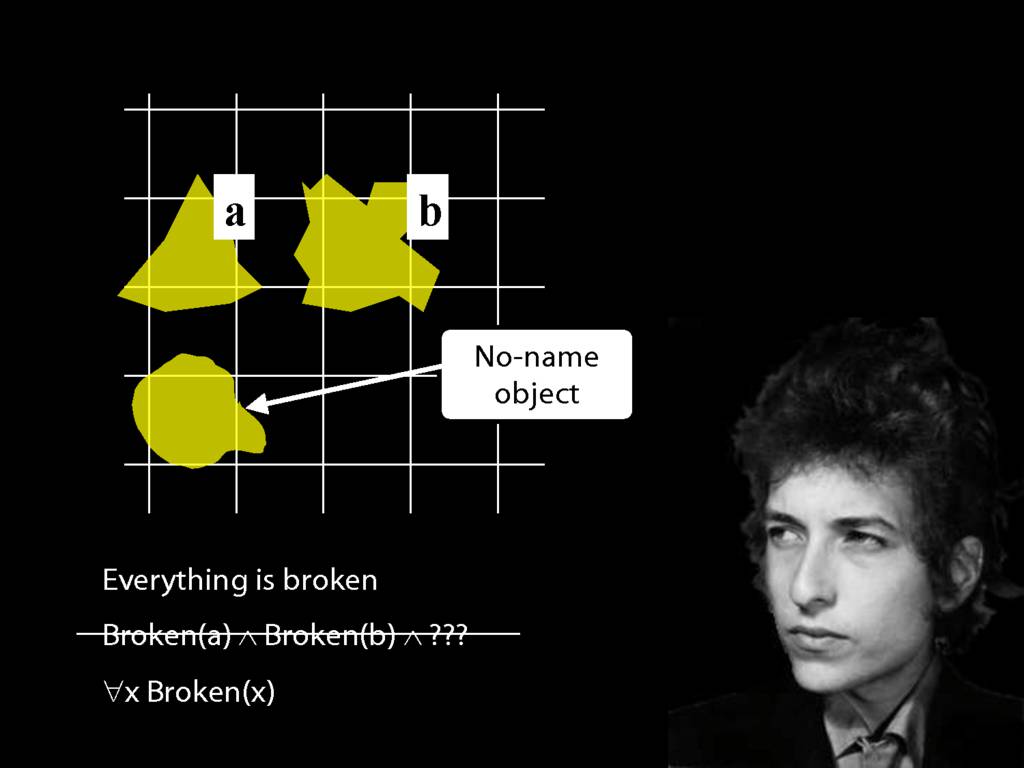
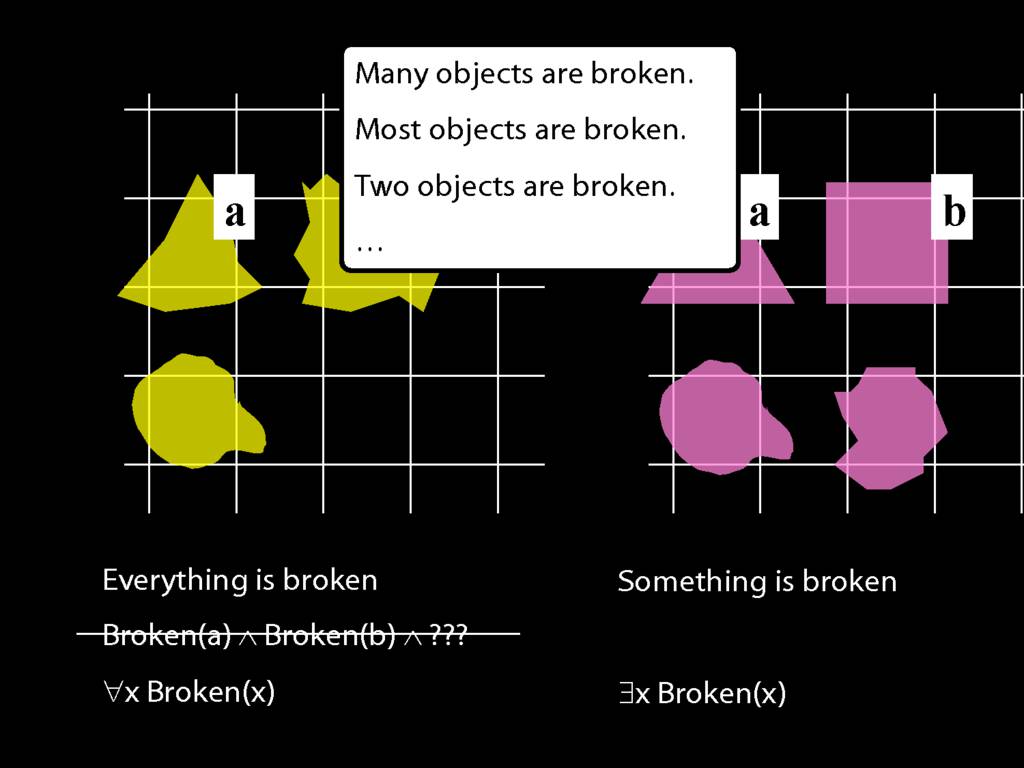
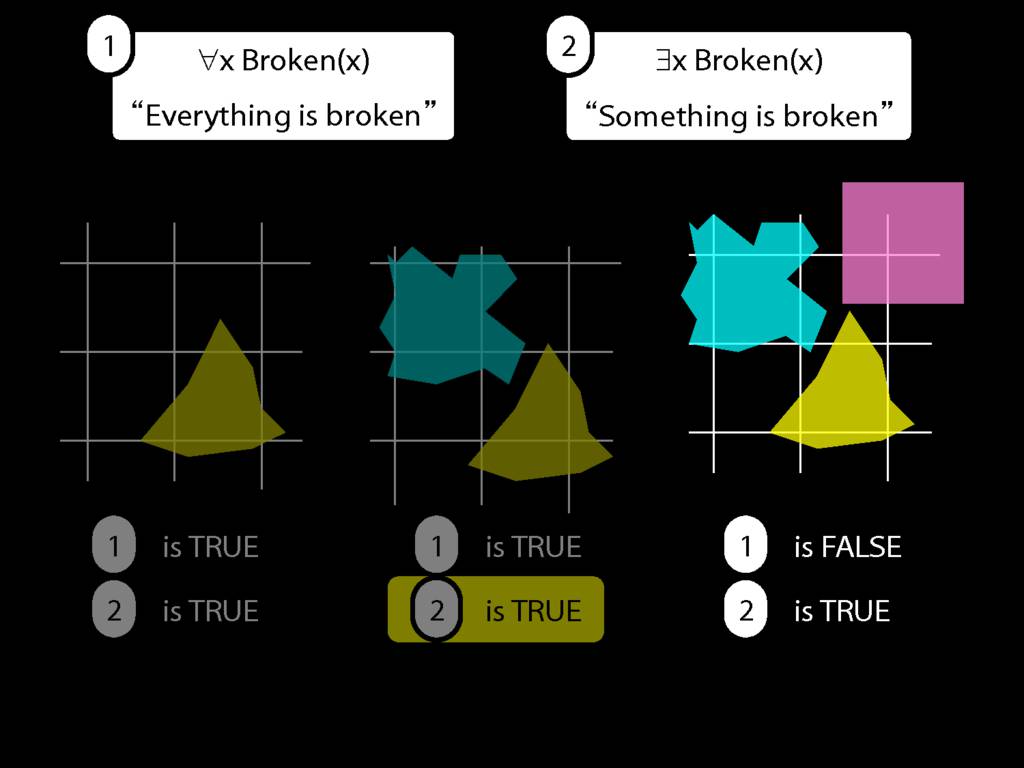
\section{Get Some Quantifiers: Don't Economise}
 

Everything Is Broken

 
\section{Everything Is Broken}
\emph{Reading:} §9.1, §9.2
 
\section{Everything Is Broken}
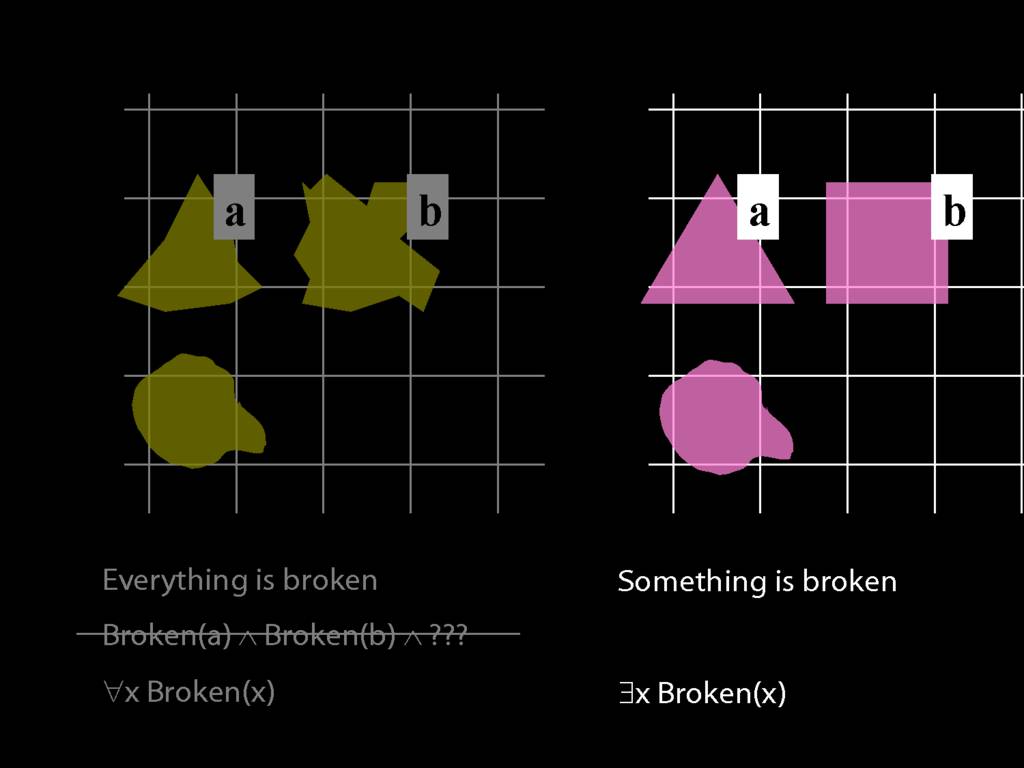
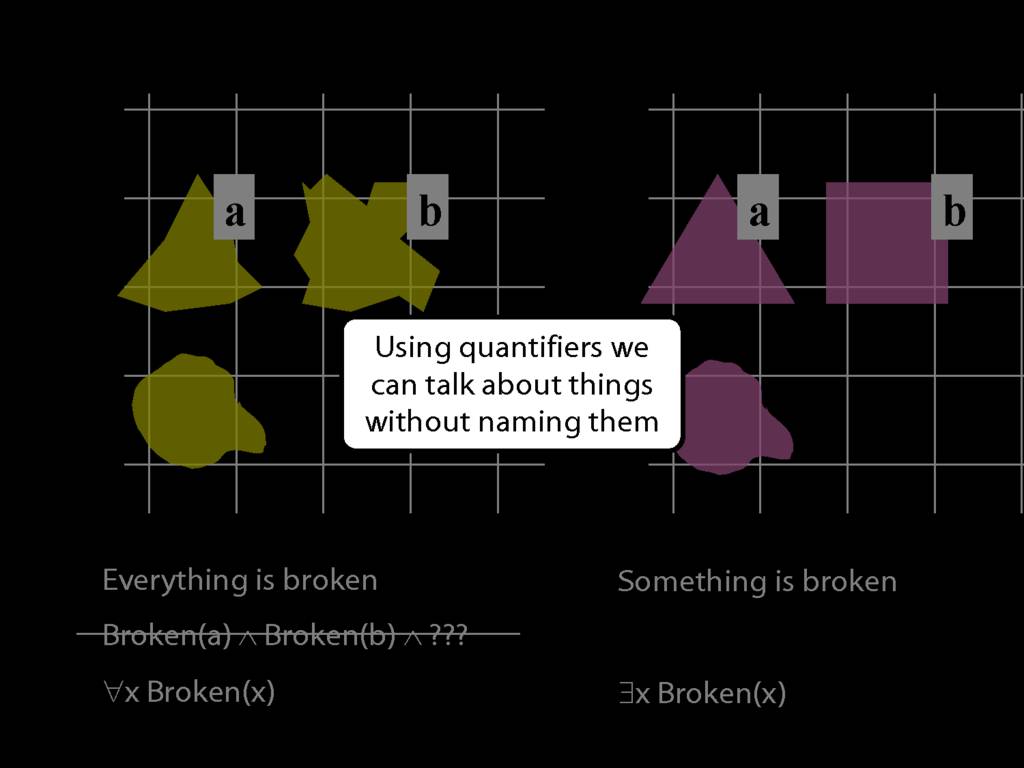
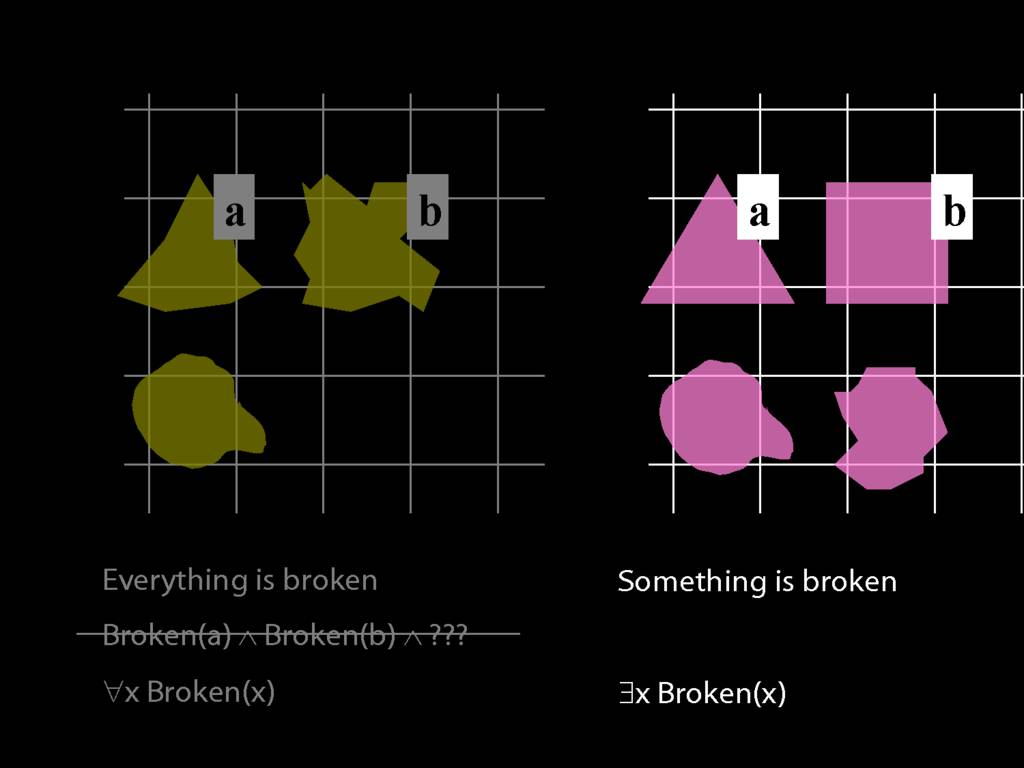
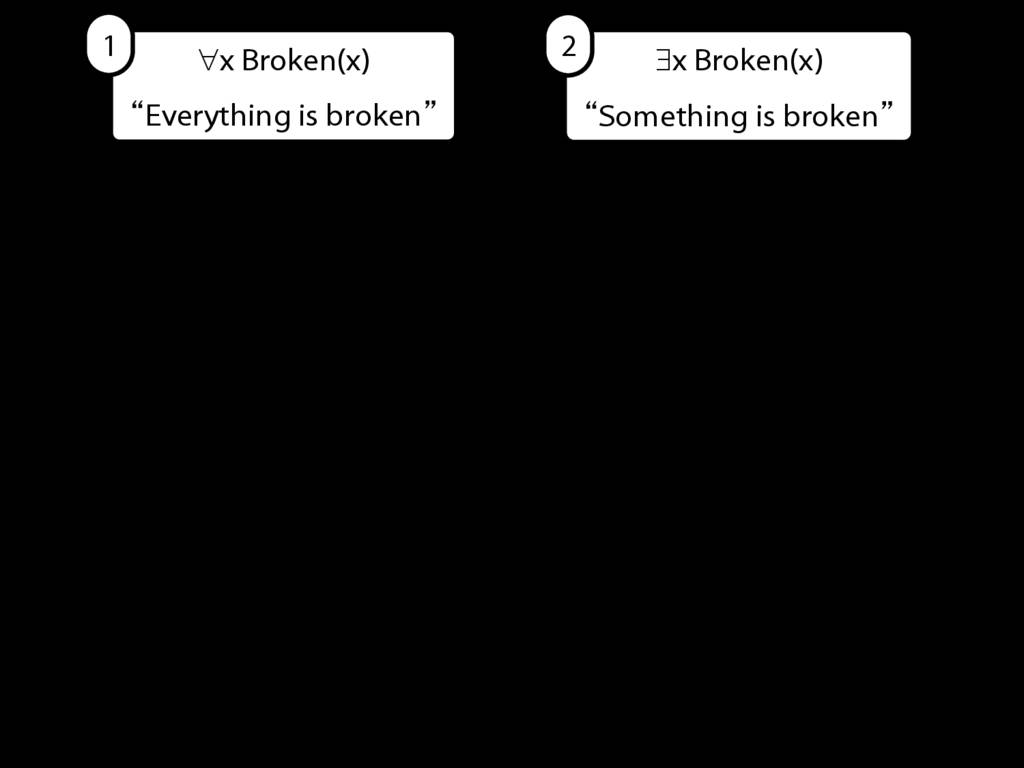
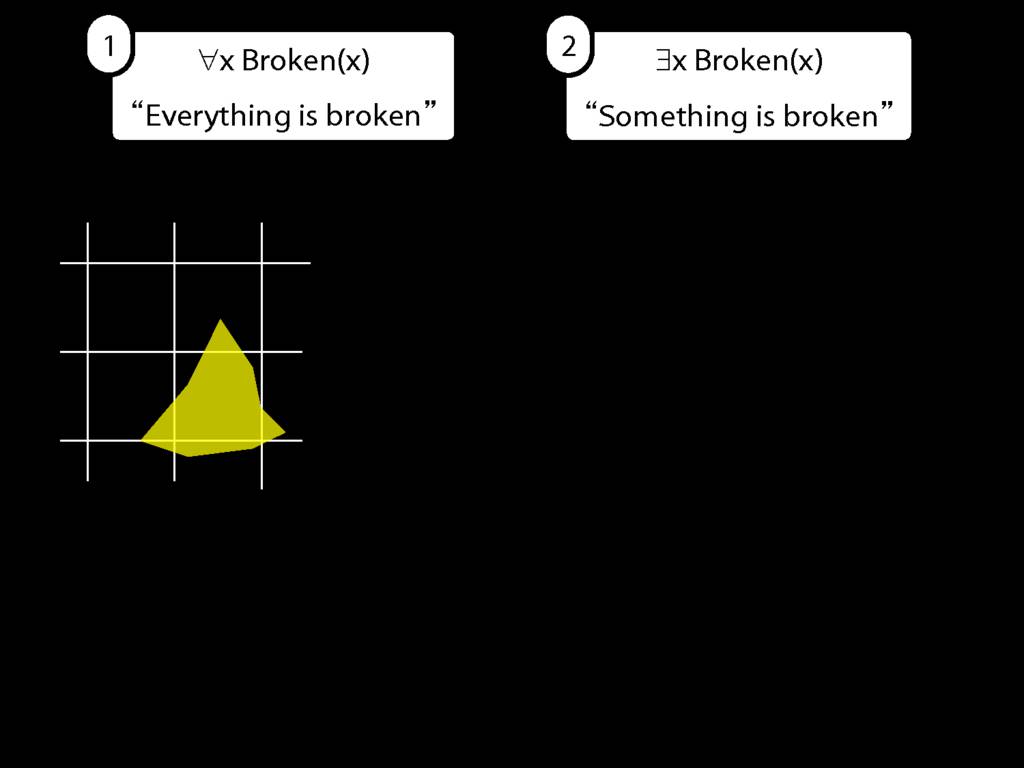
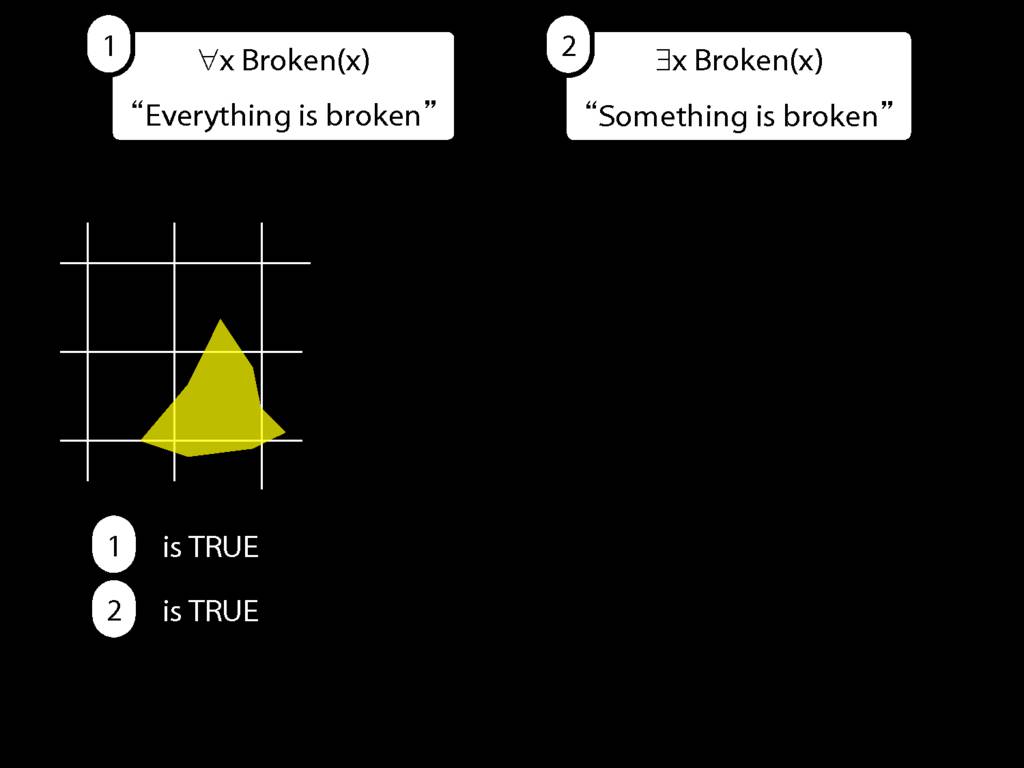
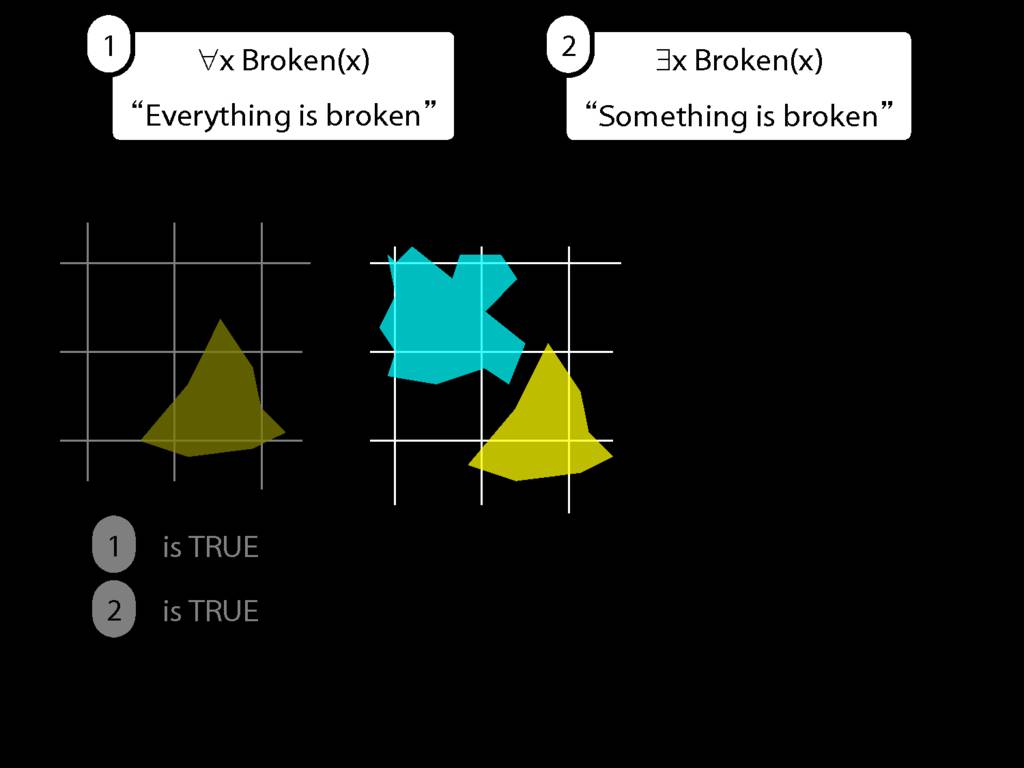
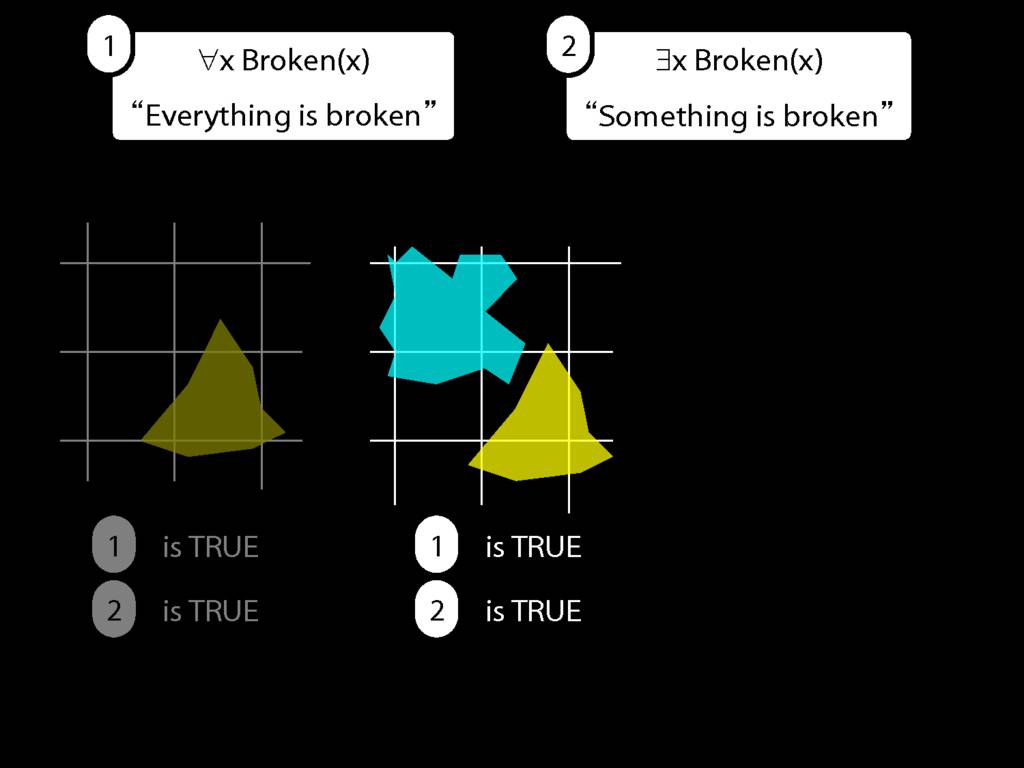
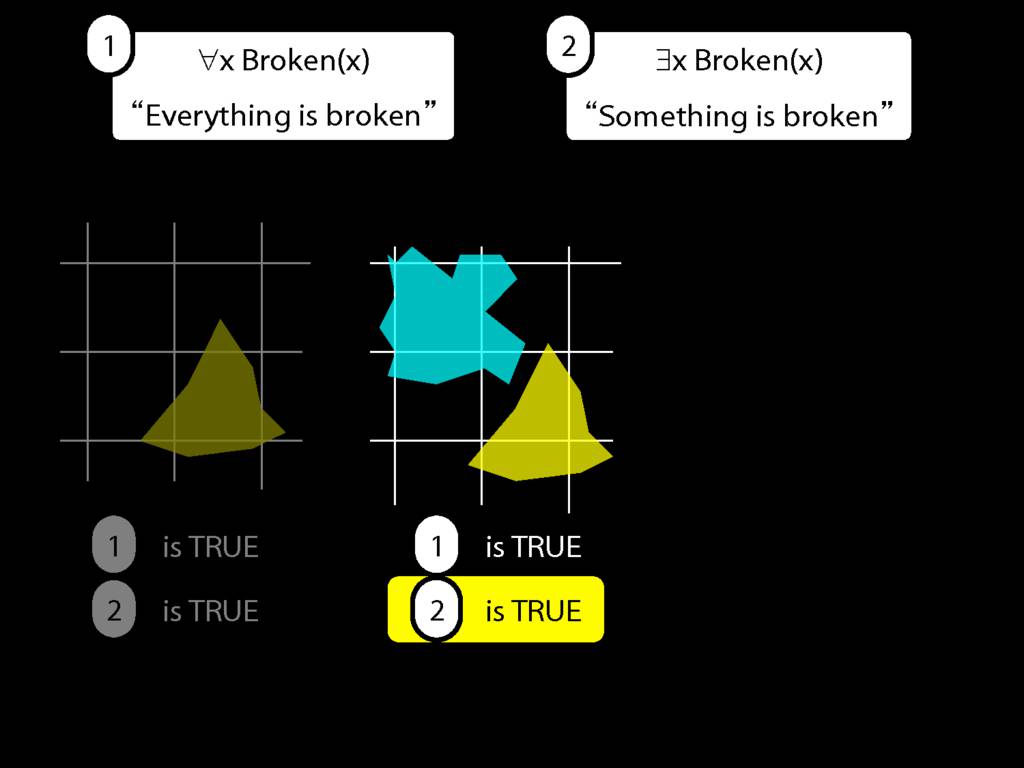
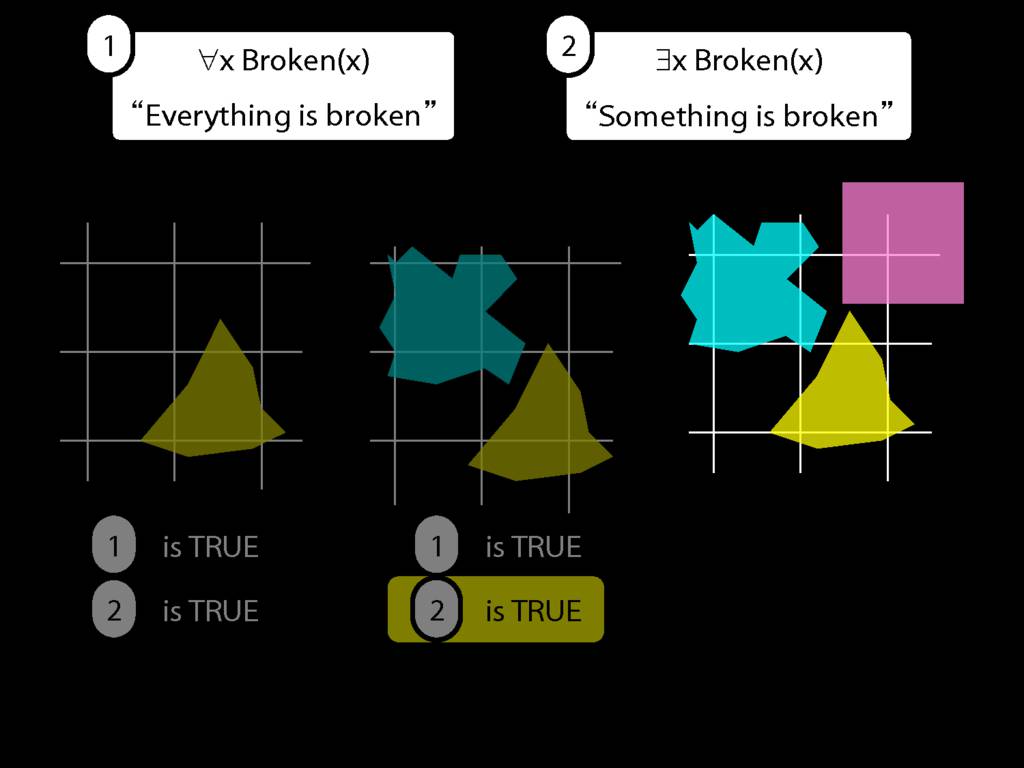
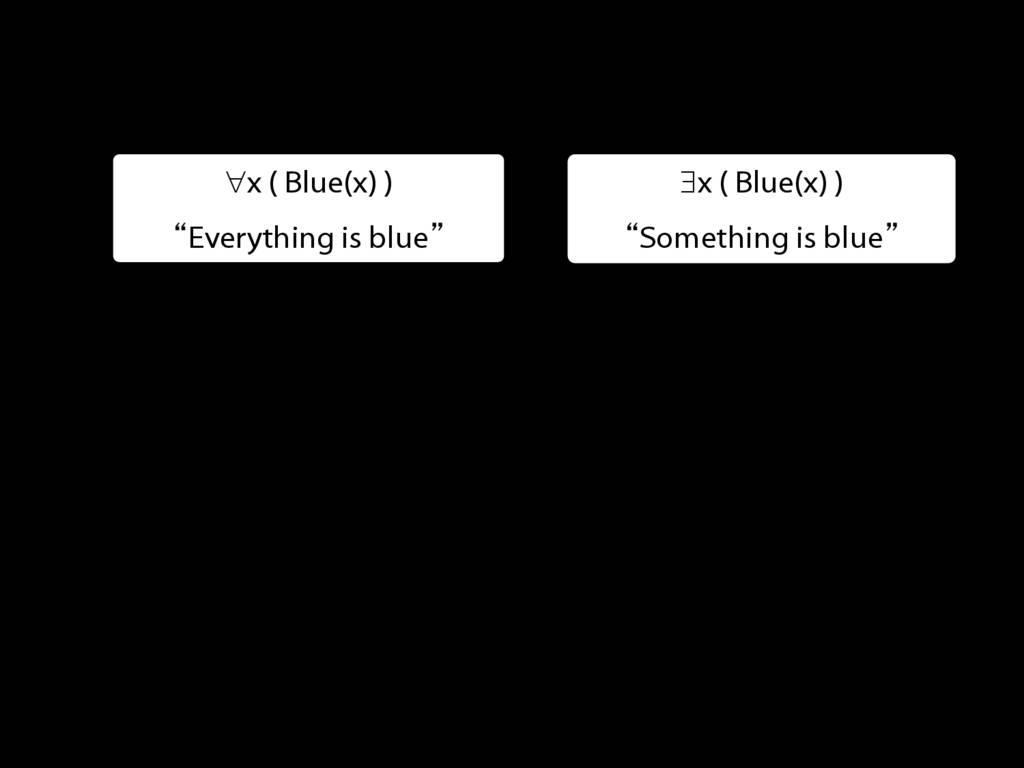
Everything is broken: ∀x Broken(x)
Something is broken: ∃x Broken(x)
9.1 odd numbers only
9.2 even numbers only
9.8–-9.10
 

All Squares Are Blue

 
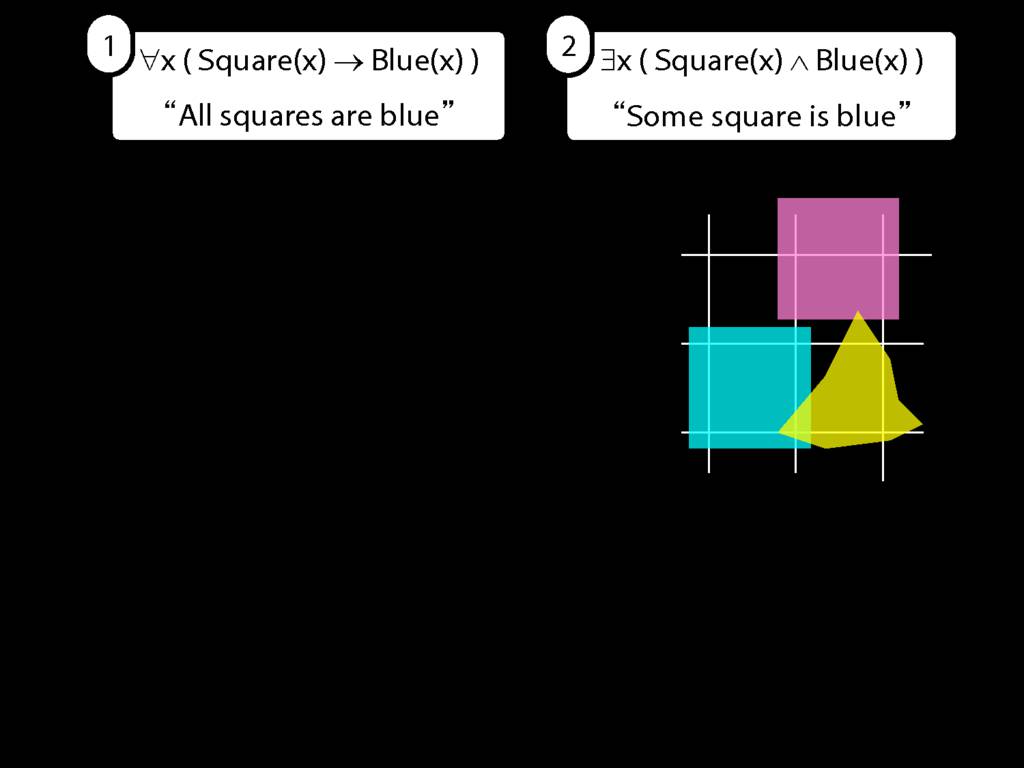
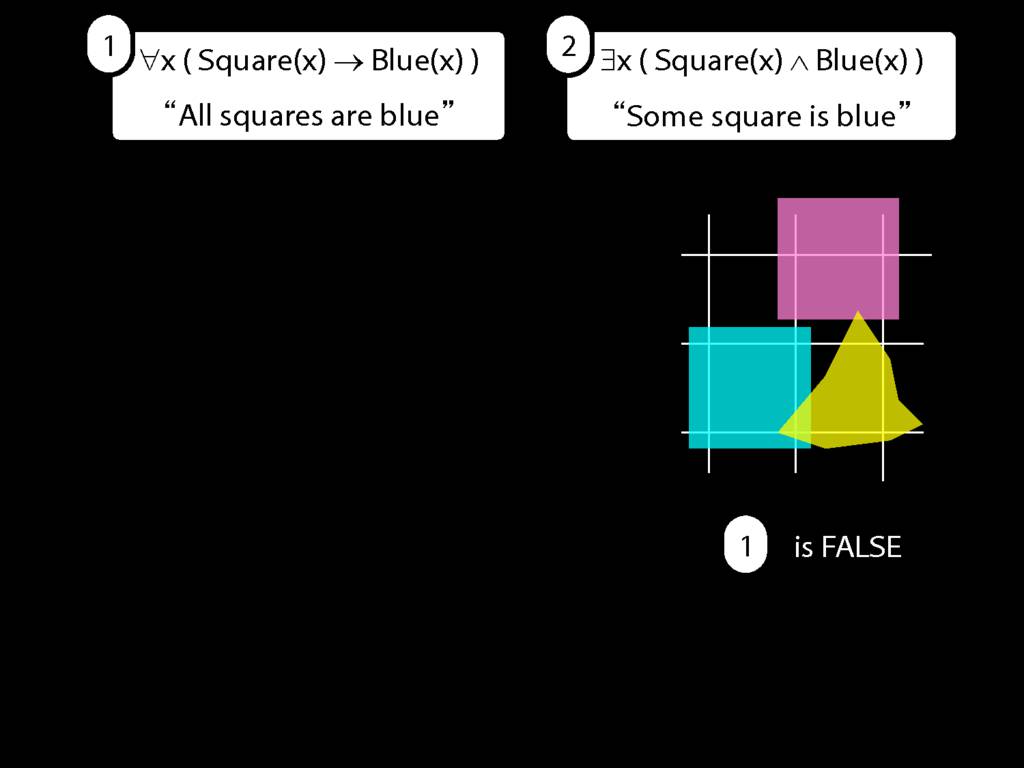
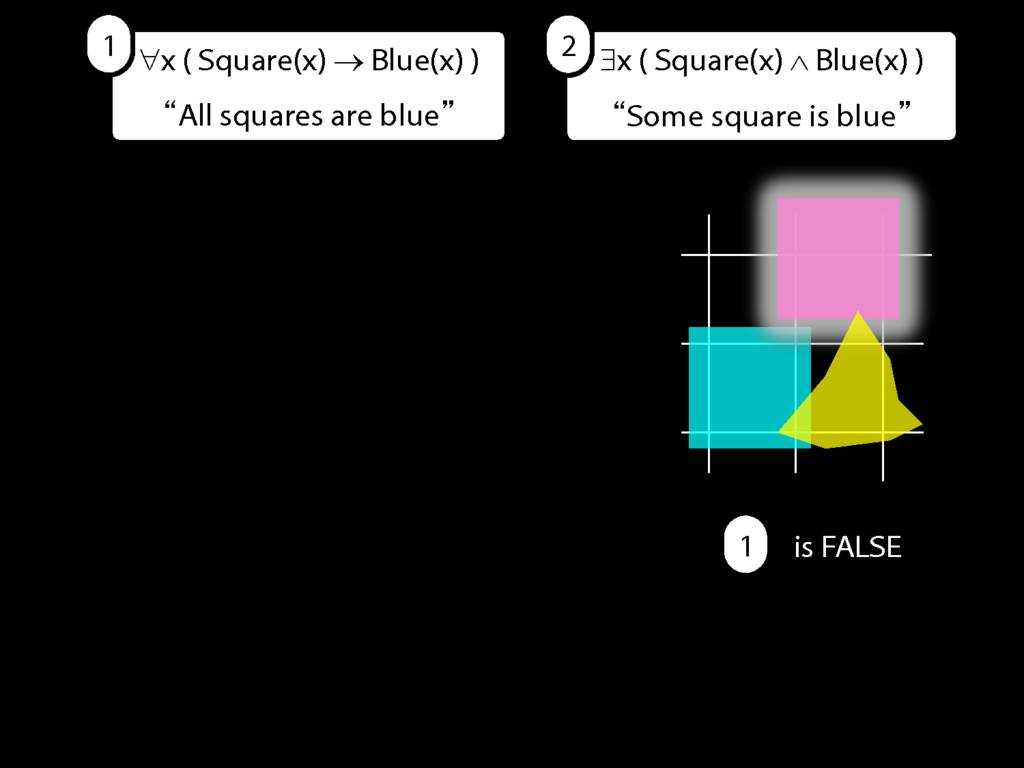
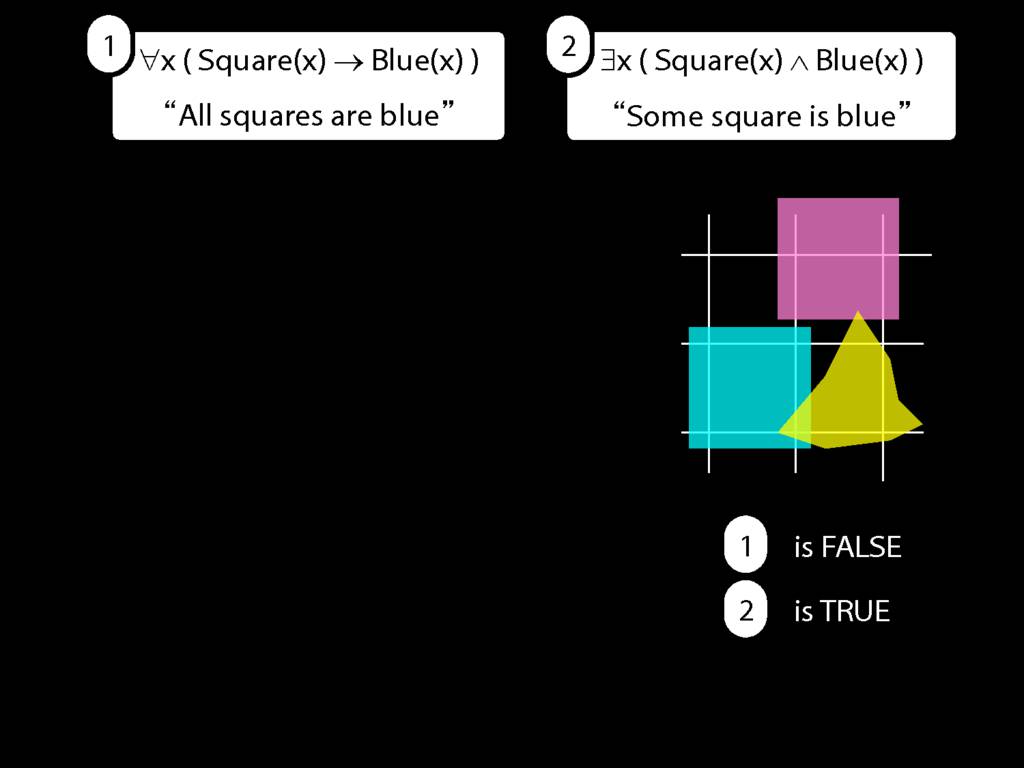
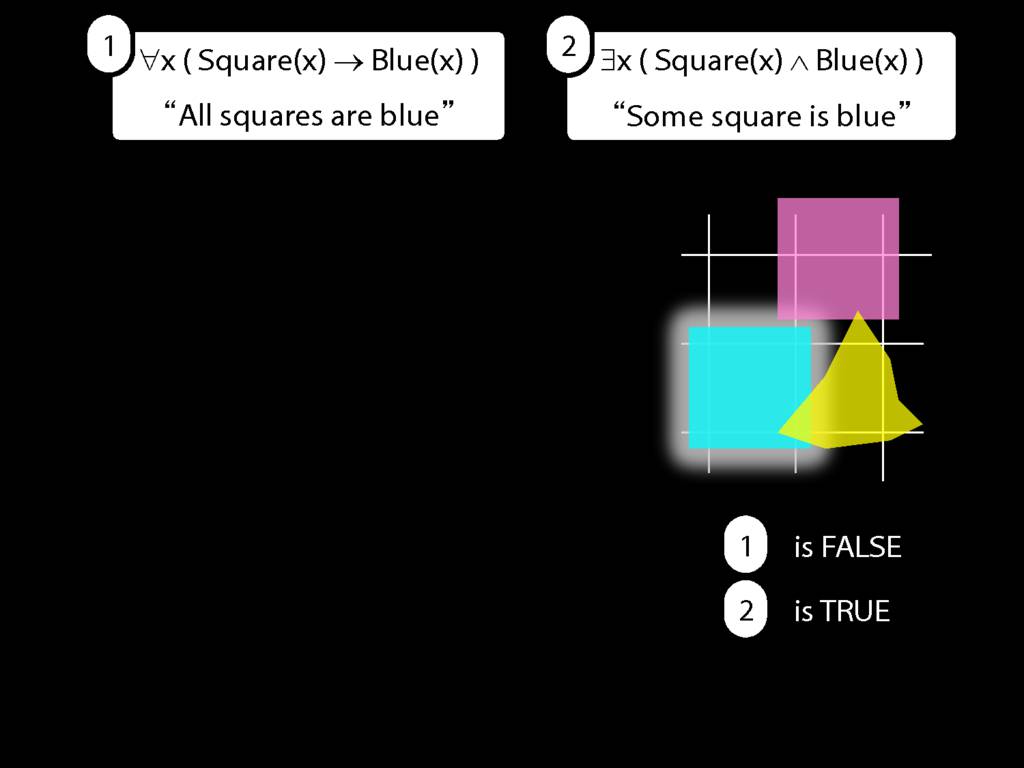
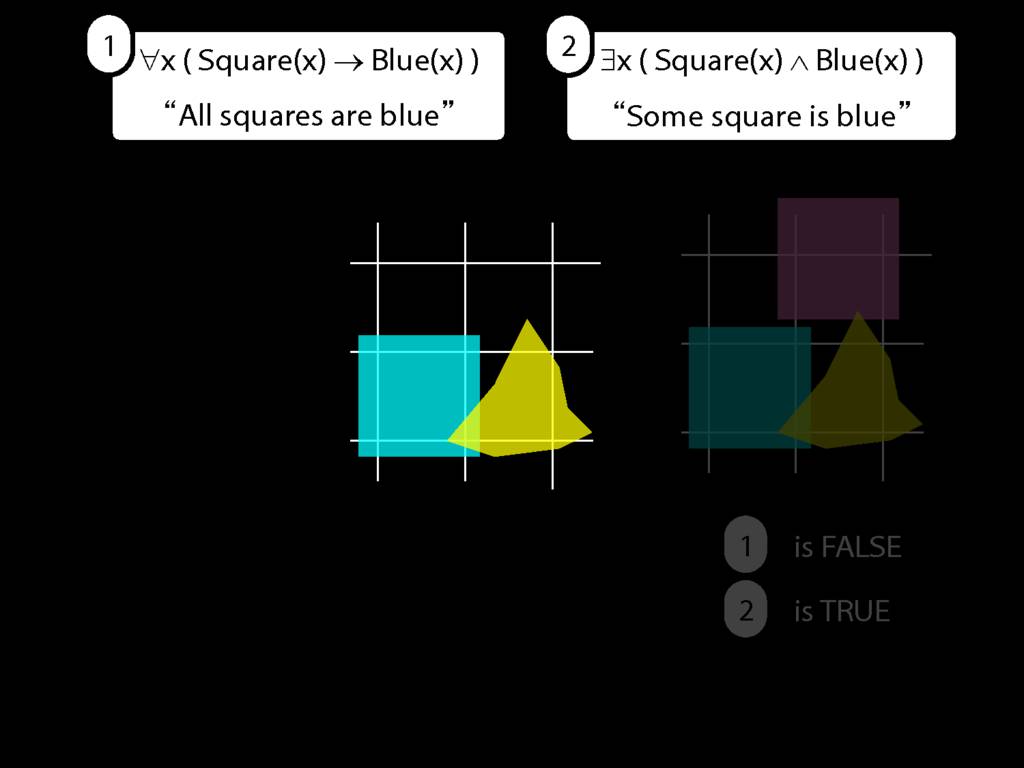
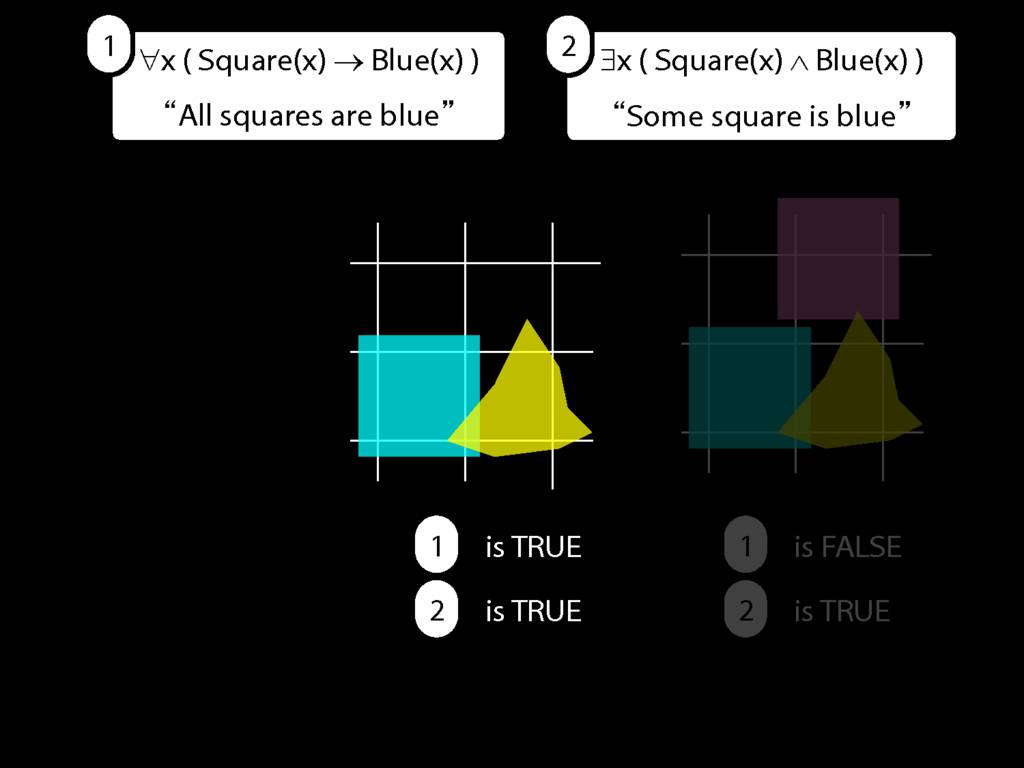
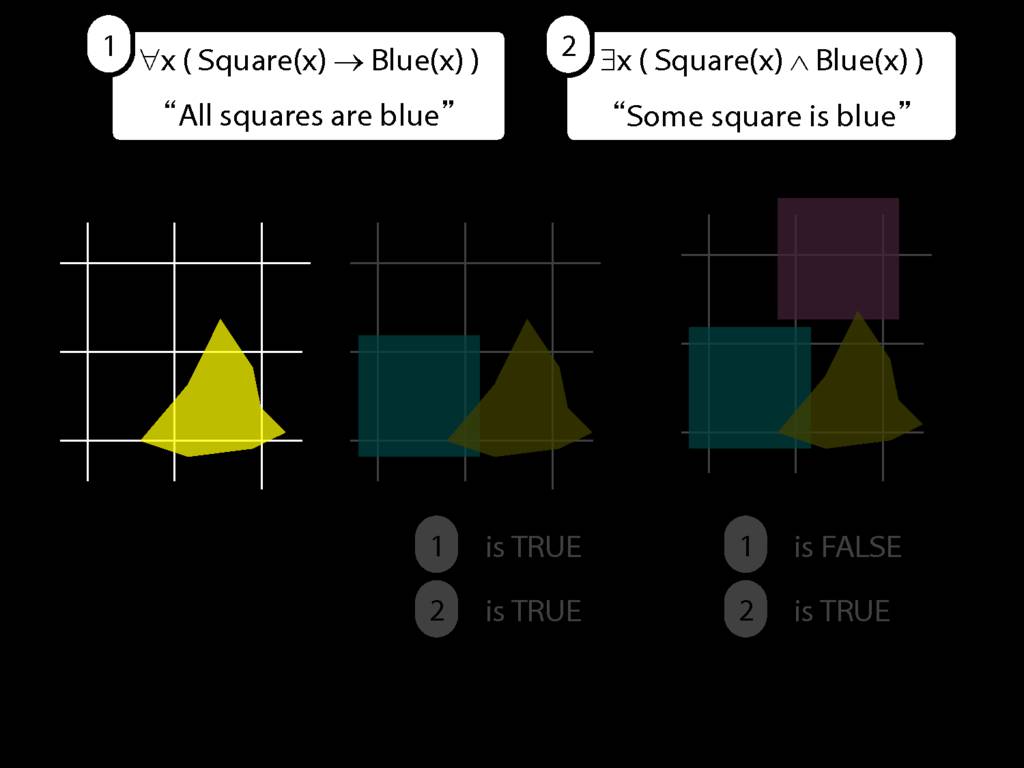
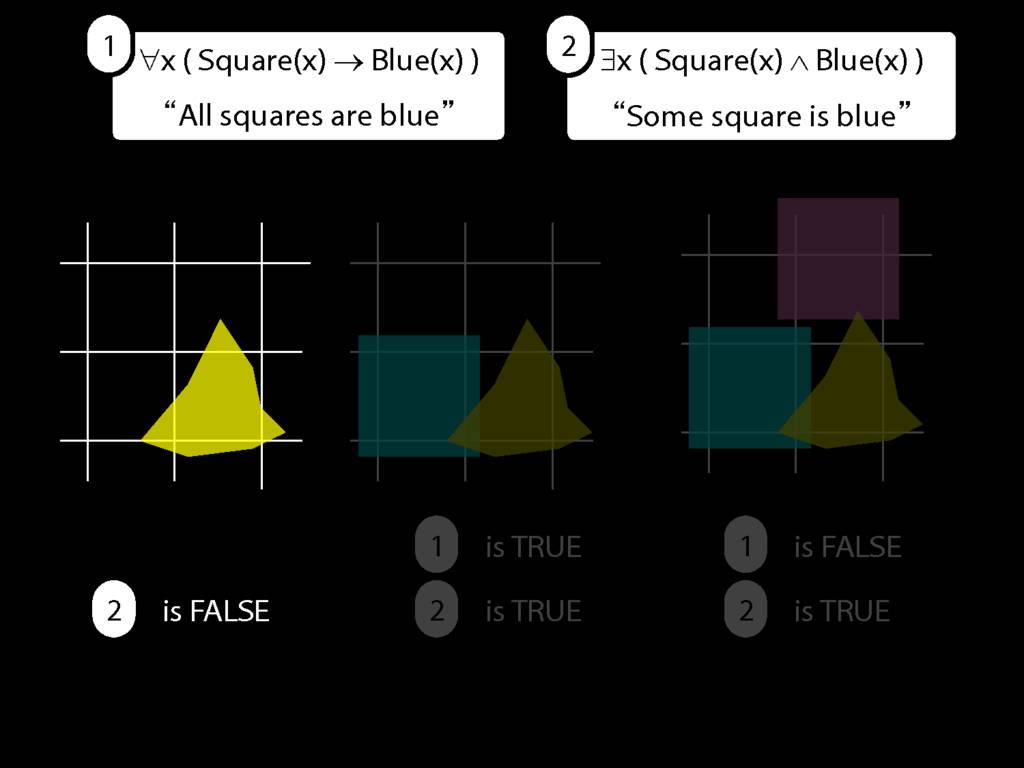
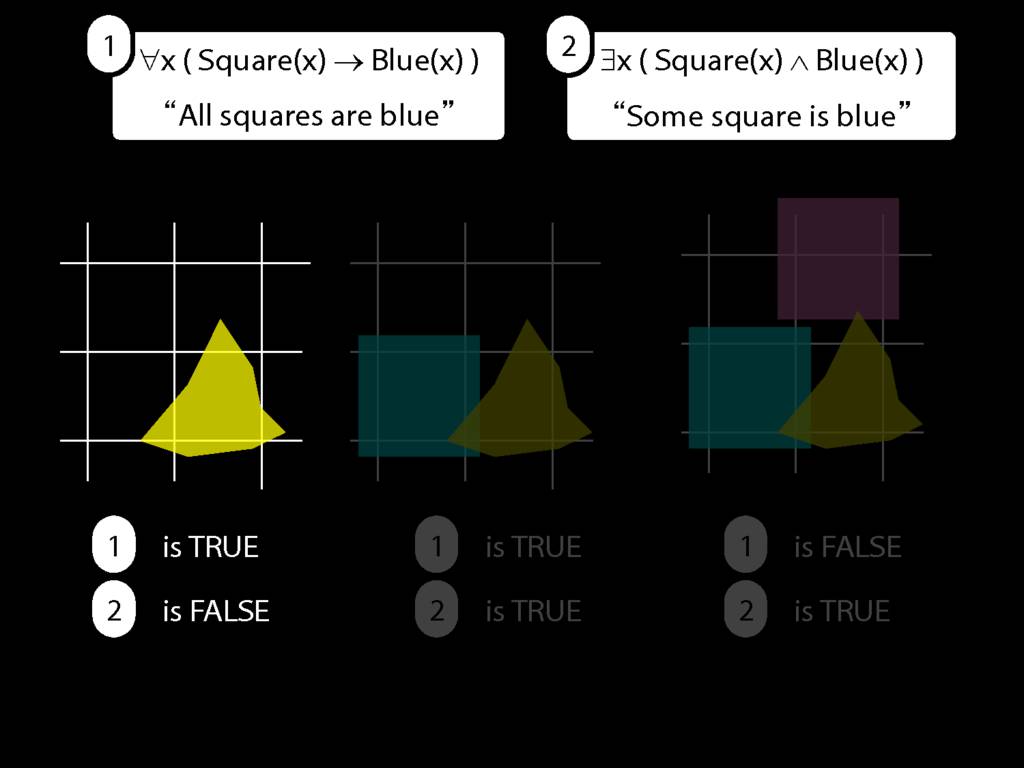
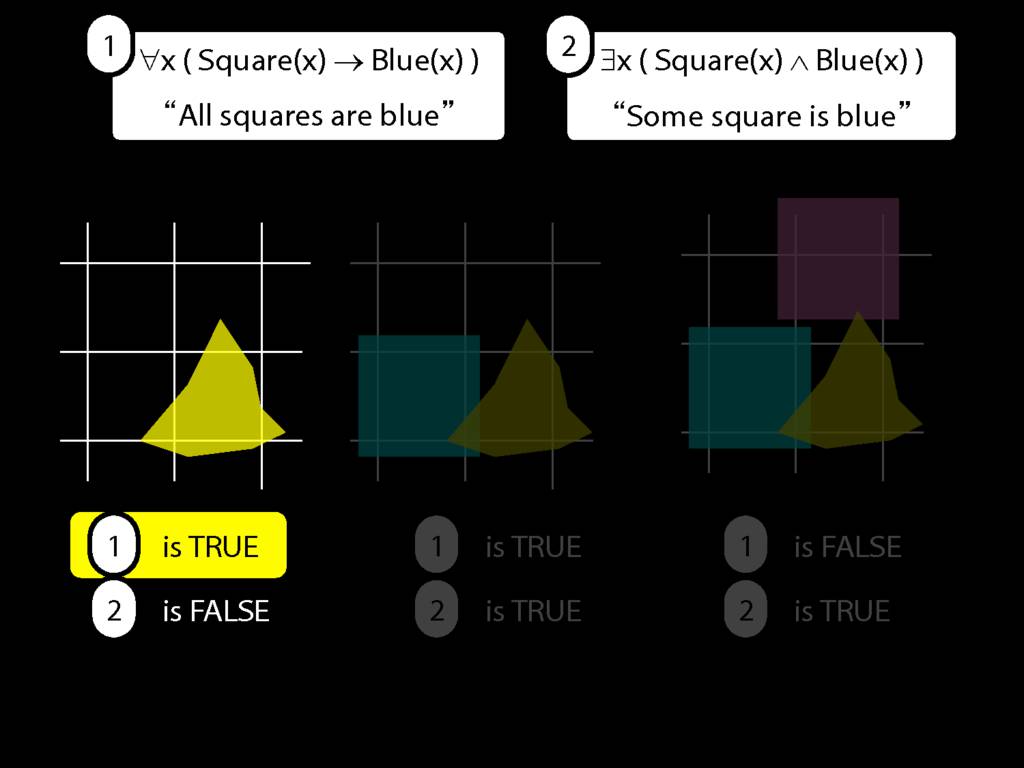
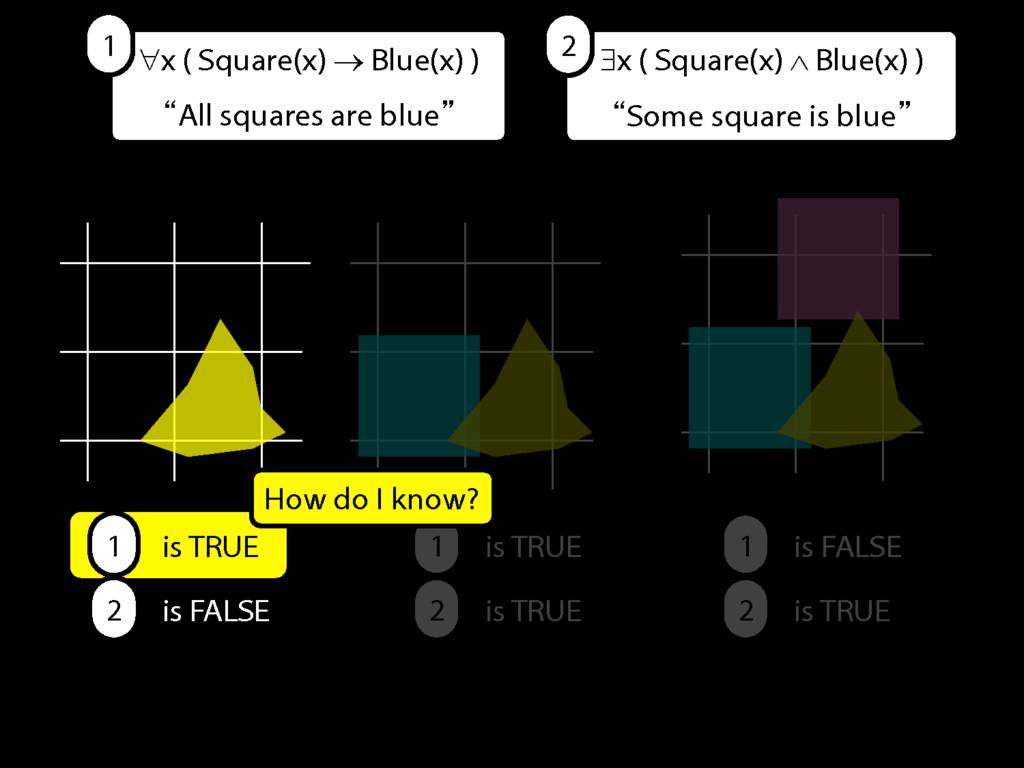
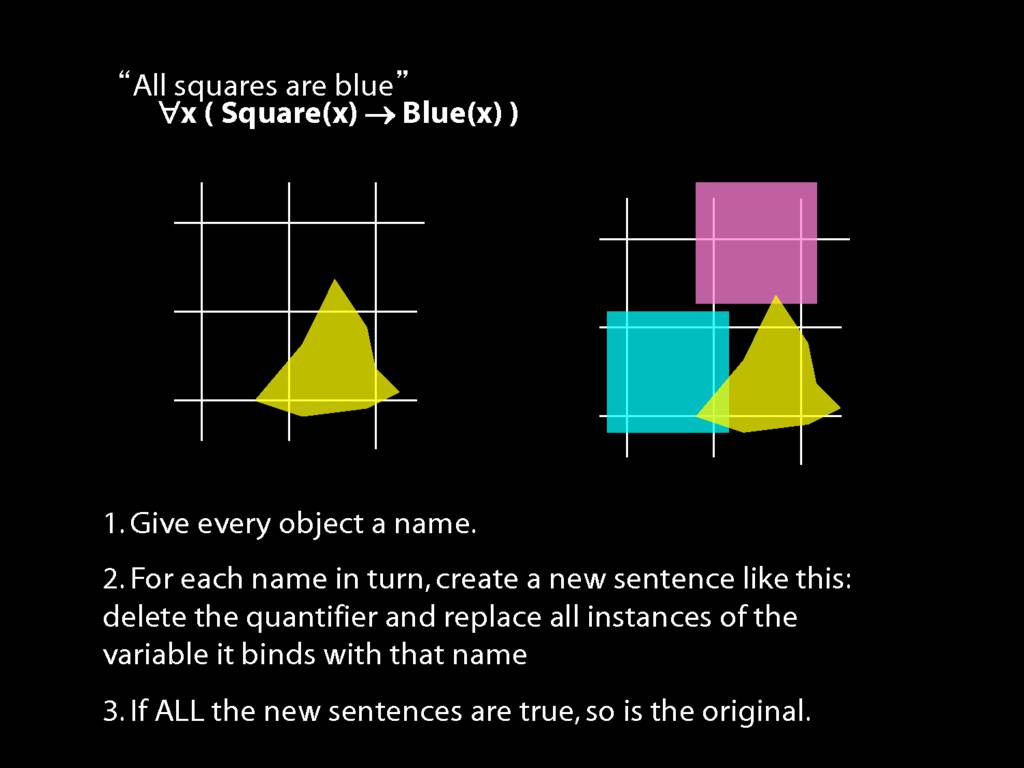
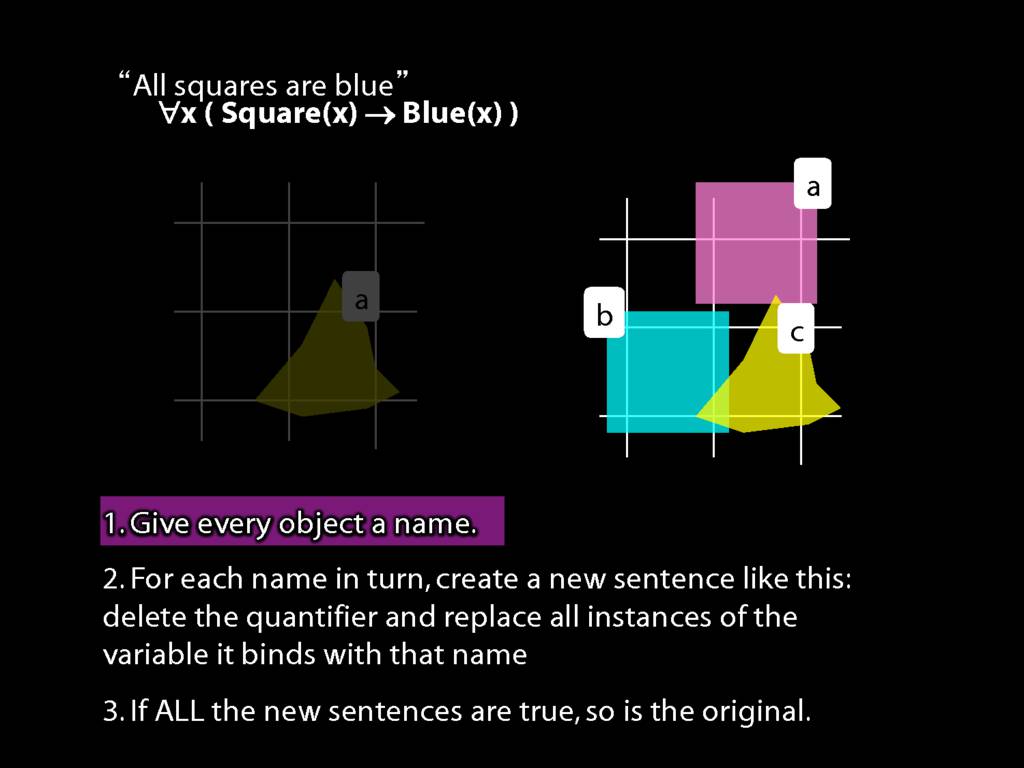
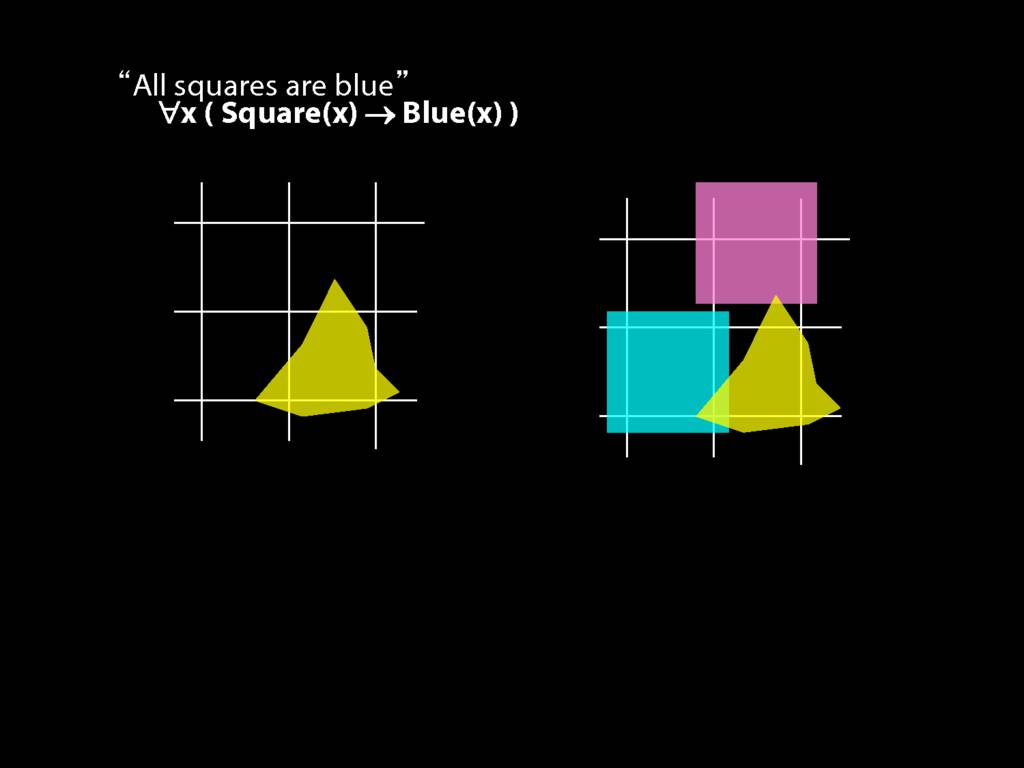
\section{All Squares Are Blue}
\emph{Reading:} §9.2, §9.3, §9.5
 
\section{All Squares Are Blue}
9.4--9.5
9.8--9.10
 

What does ∀ mean?

 
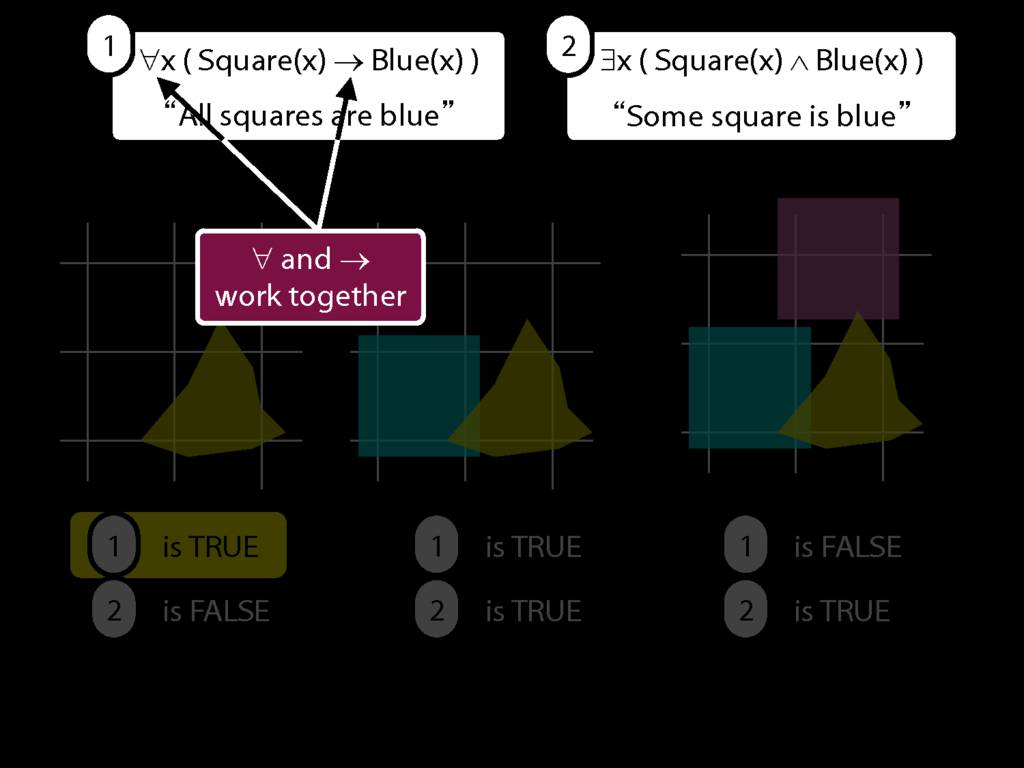
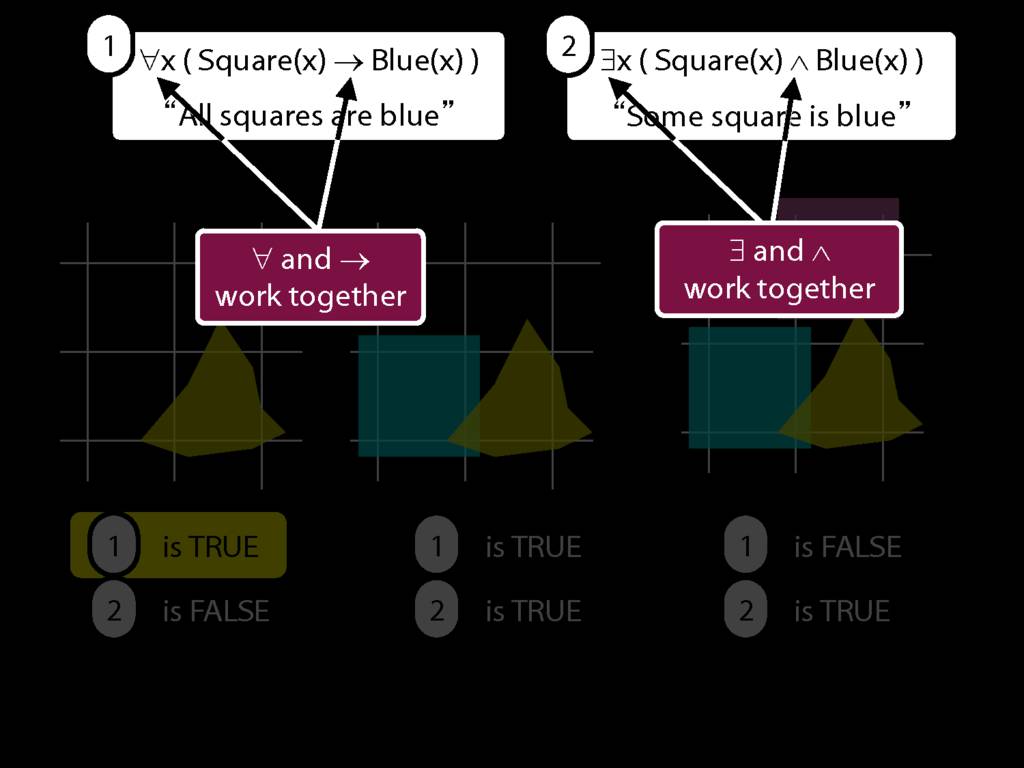
\section{What does ∀ mean?}
\emph{Reading:} §9.4
 
\section{What does ∀ mean?}
We give the meaning of ∀ by specifying what it takes for a sentence containing ∀ to be true:
\begin{enumerate}
\item Give every object a name.
\item For each name in turn, create a new sentence like this: delete the quantifier and replace all instances of the variable it binds with that name.
\item If ALL of the new sentences are true, so is the original sentence.
\end{enumerate}
 

Vegetarians Are Evil

 
\section{Vegetarians Are Evil}
\emph{Reading:} §9.2, §9.3, §9.5
 
\section{Vegetarians Are Evil}
 

Counterexamples with Quantifiers

 
\section{Counterexamples with Quantifiers}
 
\section{Counterexamples with Quantifiers}
Evil(x)HatesMeat(x)Vegetarian(x)
Ayesha (a)no?noyes
ABA → B
​TTT
​TFF
​FTT
​FFT

 

Evil(a) → HatesMeat(a)

HatesMeat(a) → Vegetarian(a)

Vegetarian(a) → Evil(a)

logic support

S0.08

Monday, 08 February 2016

19:00-20:00

I recently compiled all the rules of proofs on a sheet and now use this sheet as a constant reference while working on them. It has improved the way i work substancially so that logic no longer makes me want to die inside ... as much.

 

We knew that it was invalid ...

 
\section{We knew that it was invalid ...}

Hi, we have been working on the logic exercises ... ended in a 15 minute argument between two maths students and two philosophy students

The exercise is 5.6 which says:
'From P ∧ Q and ¬P, infer R'

We knew that it was invalid because of not being able to infer R when it is not involved at all in the premise,

An argument is logically valid just if there’s no possible situation in which the premises are true and the conclusion false.

however the problem arose when we were discussing the premises.

Is it a contradiction to say that ... that P and Q, then have a second statement that says it's not the case that P?

And if so, then if the premises are contradictory does that automatically make the argument invalid by default?

 
\section{DeMorgan: ¬(A ∧ B) ⫤⊨ ¬A ∨ ¬B}
\emph{Reading:} §3.6, §4.2
 
\section{DeMorgan: ¬(A ∧ B) ⫤⊨ ¬A ∨ ¬B}
`$\leftmodels\models$' means `is logically equivalent to', so for now `has the same truth table as'.
A $\leftmodels\models$ ¬¬A
¬(A ∧ B) $\leftmodels\models$ (¬A ∨ ¬B)
¬(A ∨ B) $\leftmodels\models$ (¬A ∧ ¬B)
A → B $\leftmodels\models$ ¬A ∨ B
¬(A → B) $\leftmodels\models$ ¬(¬A ∨ B) $\leftmodels\models$ A ∧ ¬B
Here's a useful equivalence: double negations cancel out (at least in logic).

A ⫤⊨ ¬¬A

is logically equivalent to

i.e. has the same truth table as

A¬A¬¬A
​TFT
​FTF
¬(A ∧ B)    ⫤⊨     (¬A ∨ ¬B)
¬(A ∨ B)⫤⊨(¬A ∧ ¬B)
A → B⫤⊨¬A ∨ B
¬(A → B)⫤⊨¬(¬A ∨ B)    ⫤⊨    A ∧ ¬B
ABA ∧ B¬(A ∧ B)¬A¬B¬A ∨ ¬B
​TTTFFFF
​TFFTFTT
​FTFTTFT
​FFFTTTT
AB¬(A ∨ B)¬A ∧ ¬B
​TTFF
​TFFF
​FTFF
​FFTT
ABA → B¬A ∨ B
​TTTT
​TFFF
​FTTT
​FFTT
ABA → B¬(A → B)¬(¬A ∨ B)A ∧ ¬B
​TTTFFF
​TFFTTT
​FTTFFF
​FFTFFF
3.19
4.15--18
7.1--7.2, *7.3--7.6
3.19
4.31
\usepackage{pdfpages}
\includepdf[pages={1}]{img/rules.pdf}