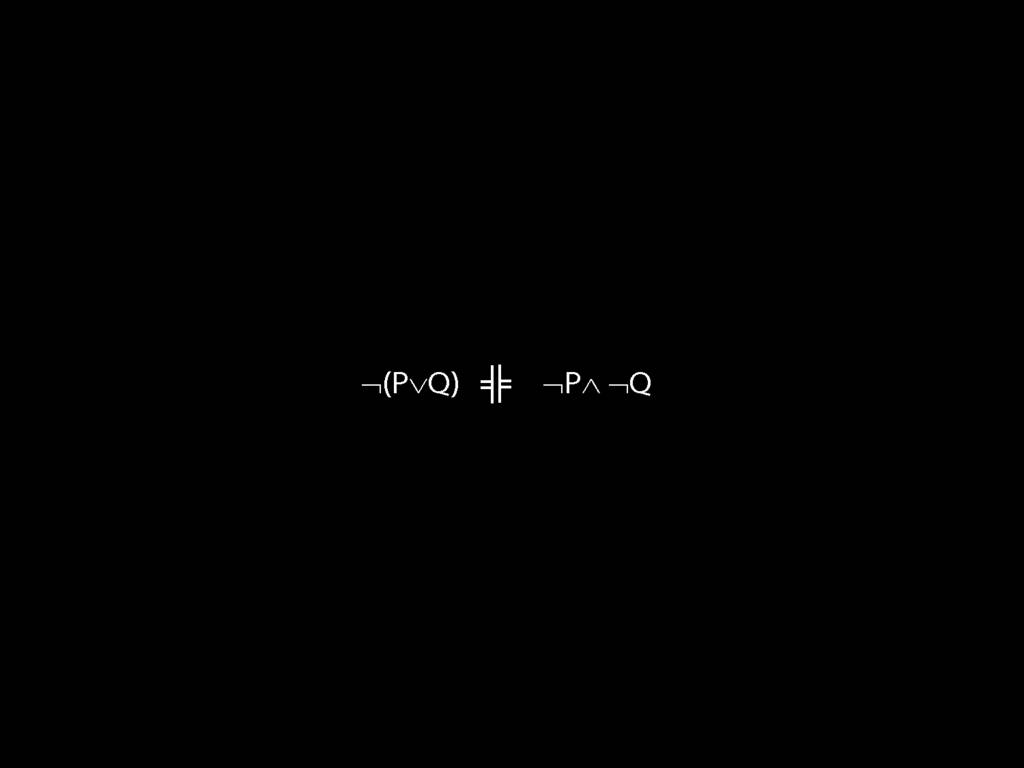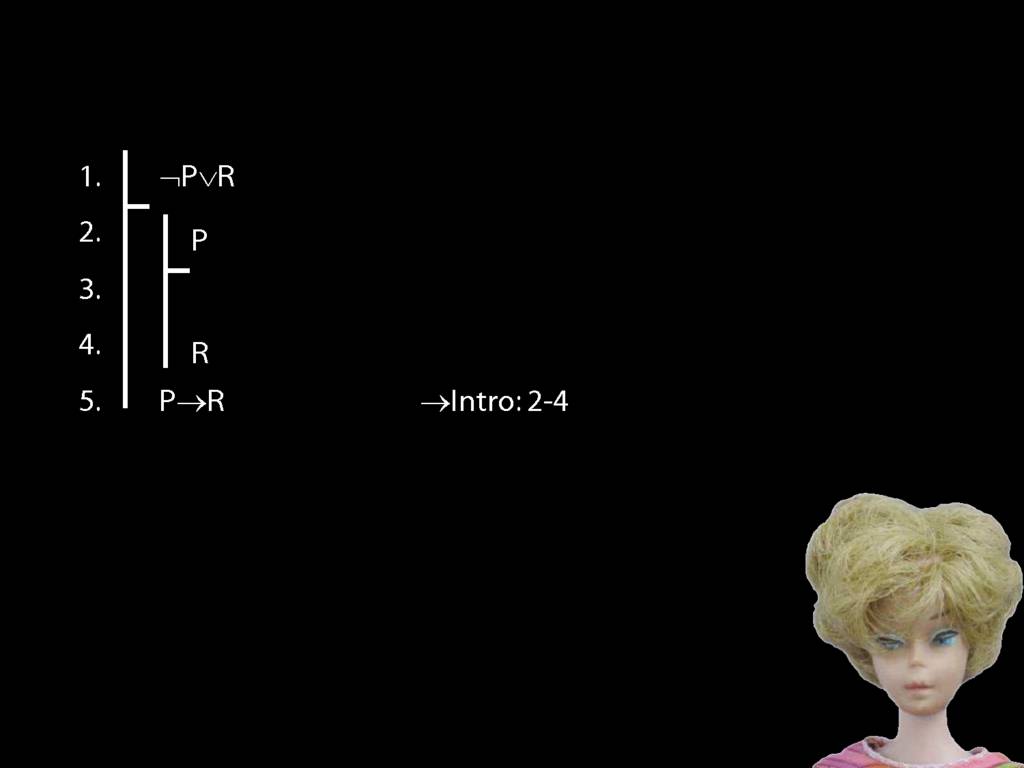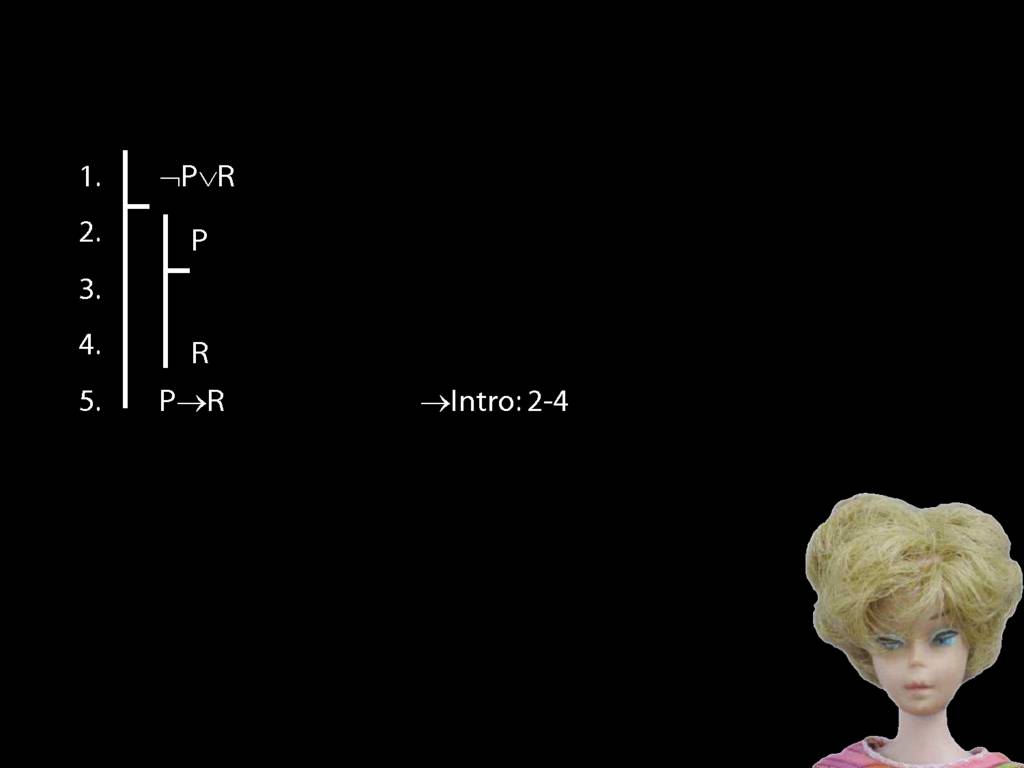Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Lecture 09}
 
\maketitle
 

Logic I

Lecture 09

\def \ititle {Logic I}
\def \isubtitle {Lecture 09}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
\section{Scope: A Mistaken Application of ¬Elim}
 
\section{Scope: A Mistaken Application of ¬Elim}
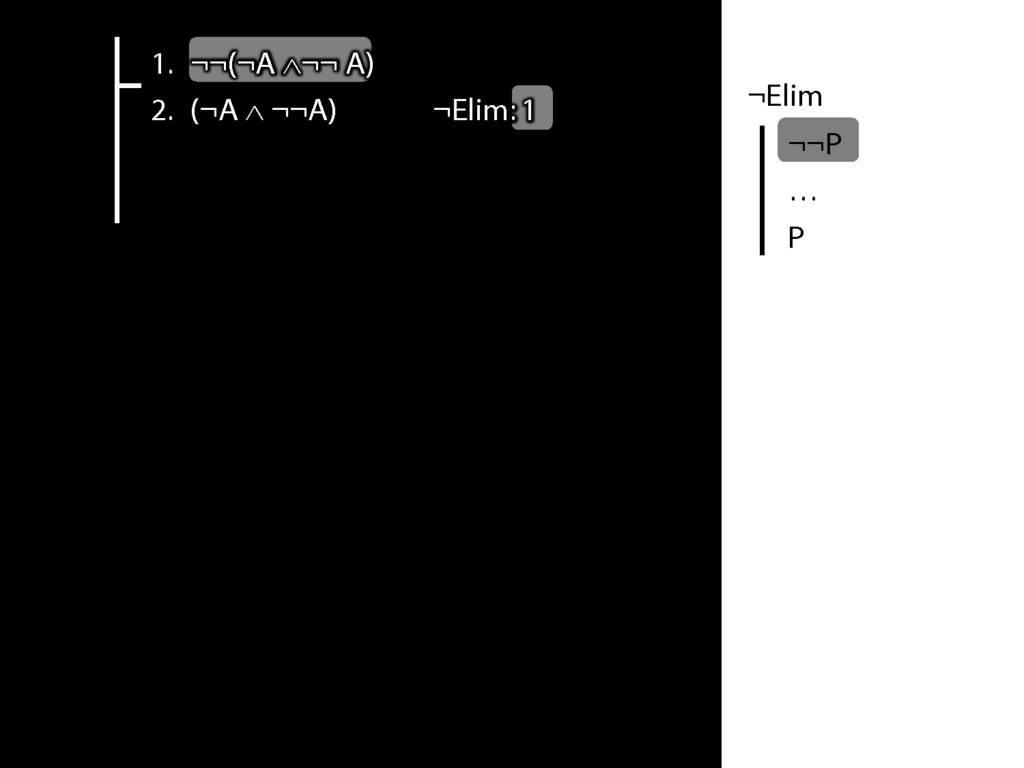
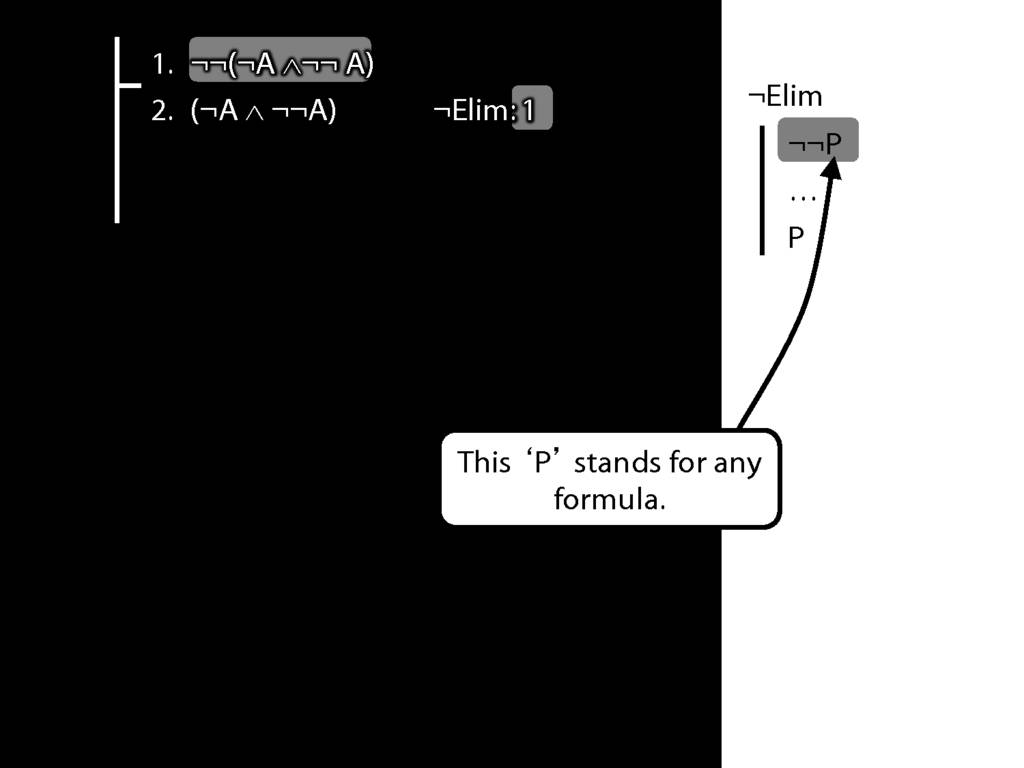
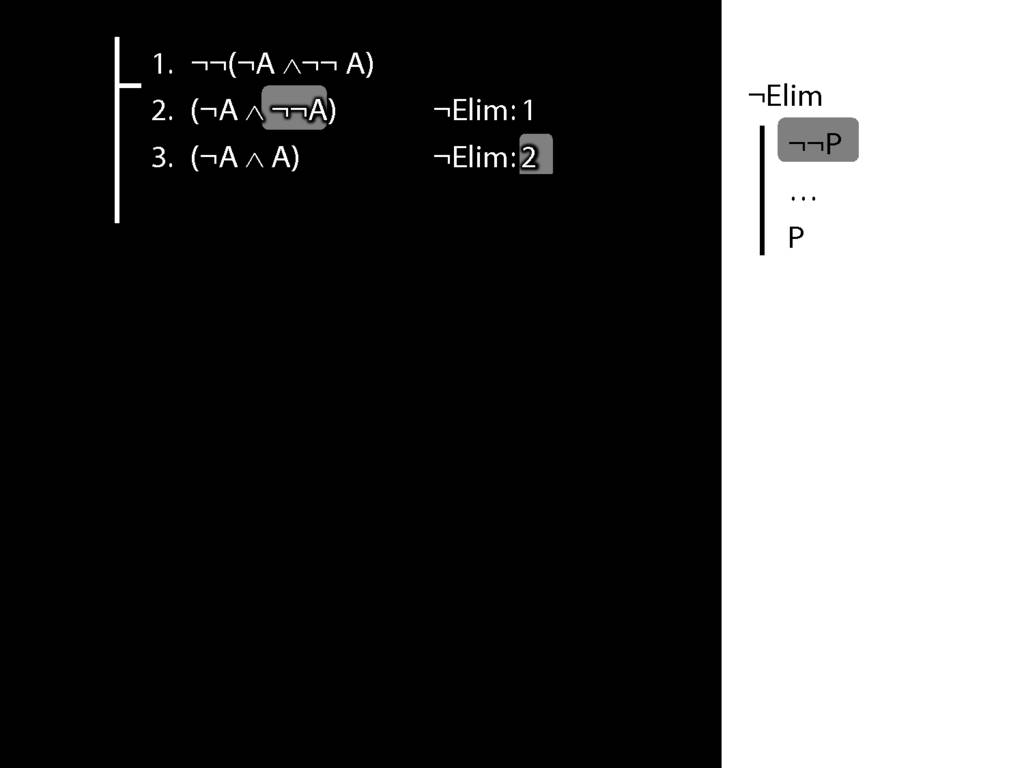
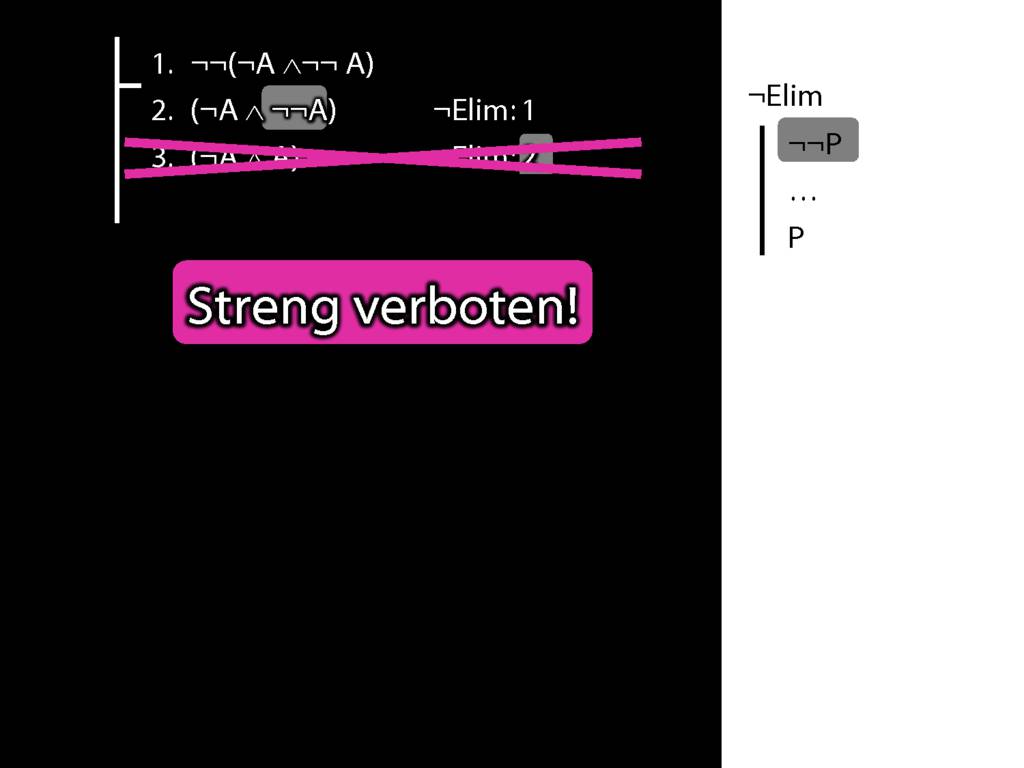
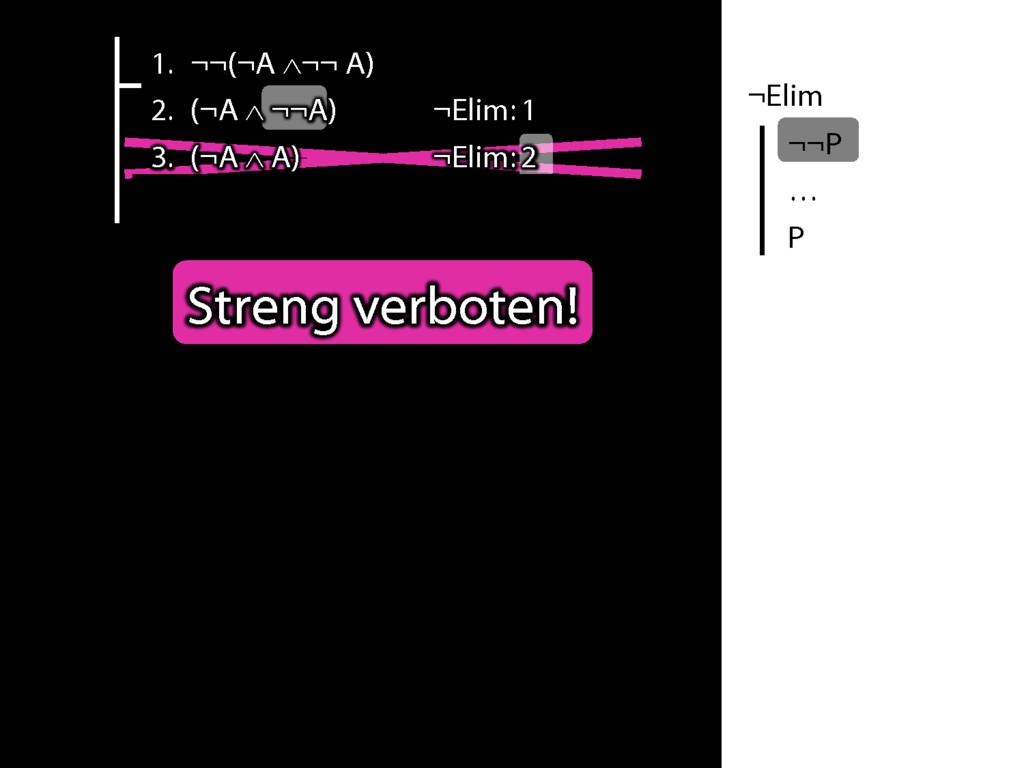
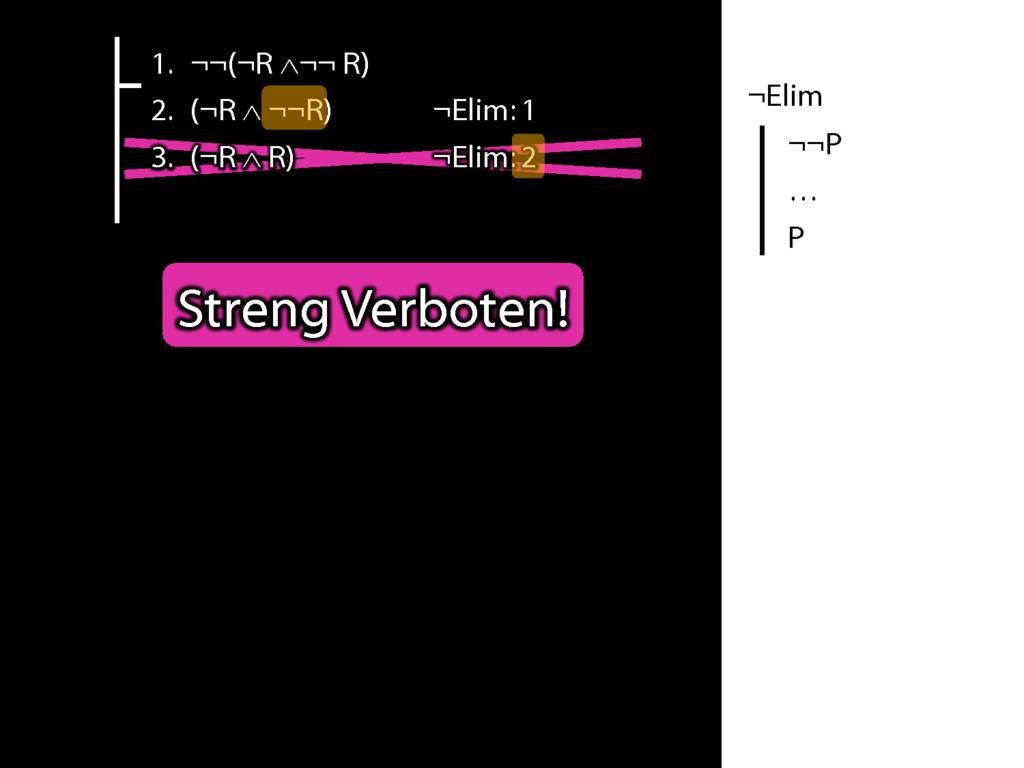
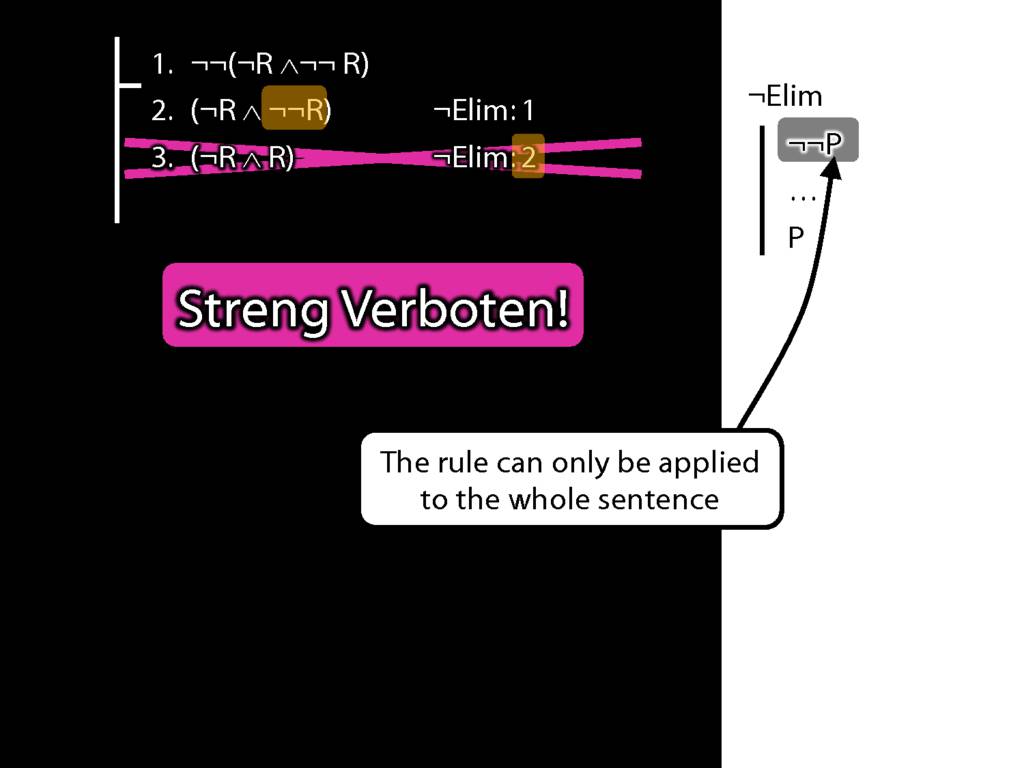
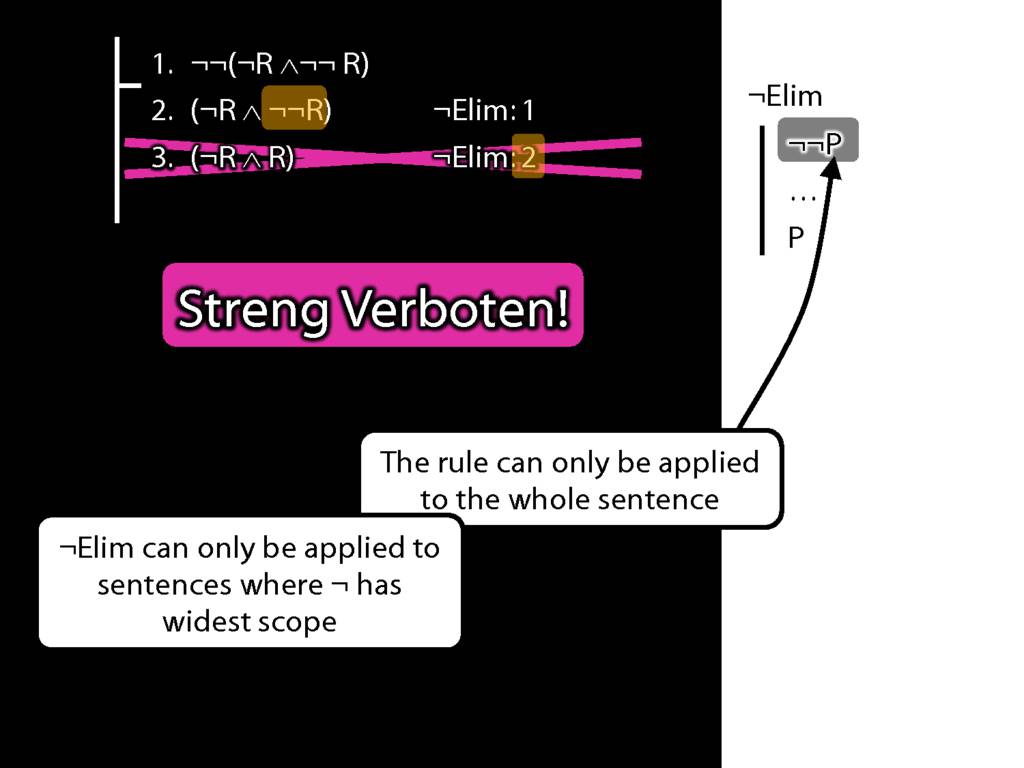
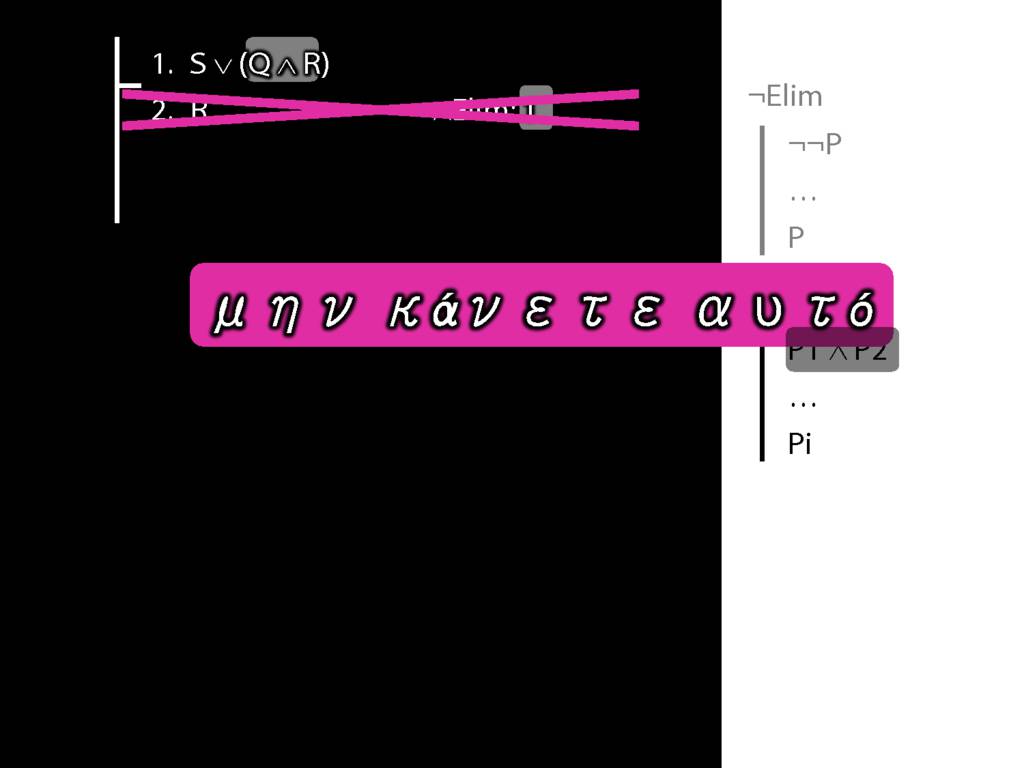
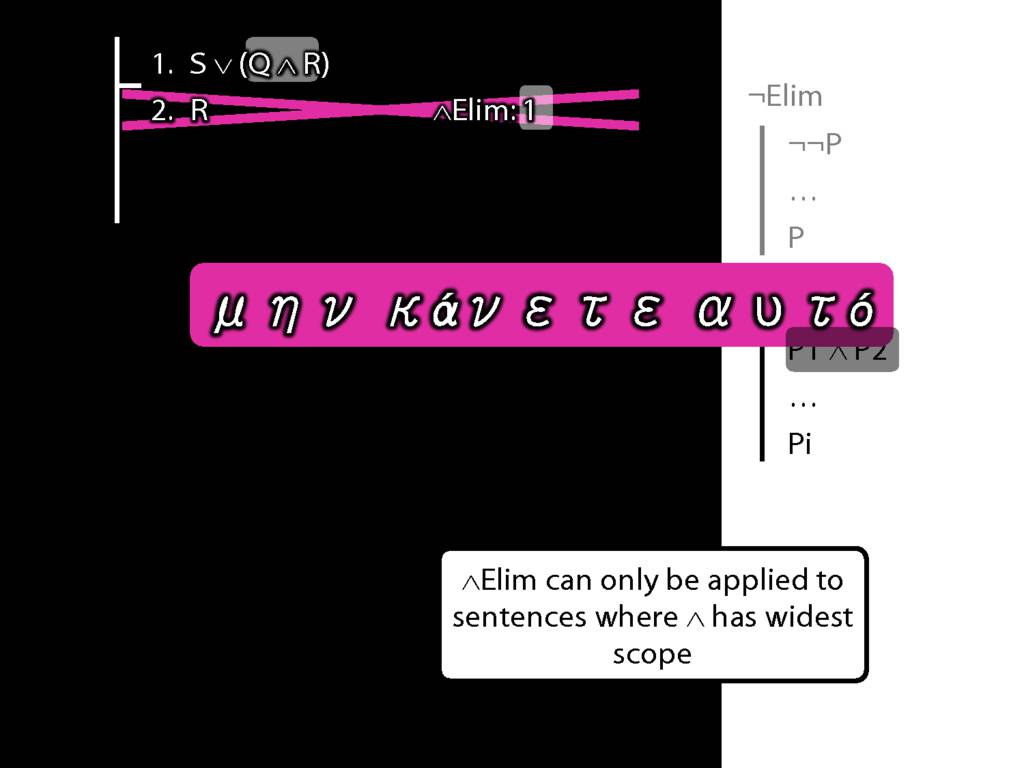
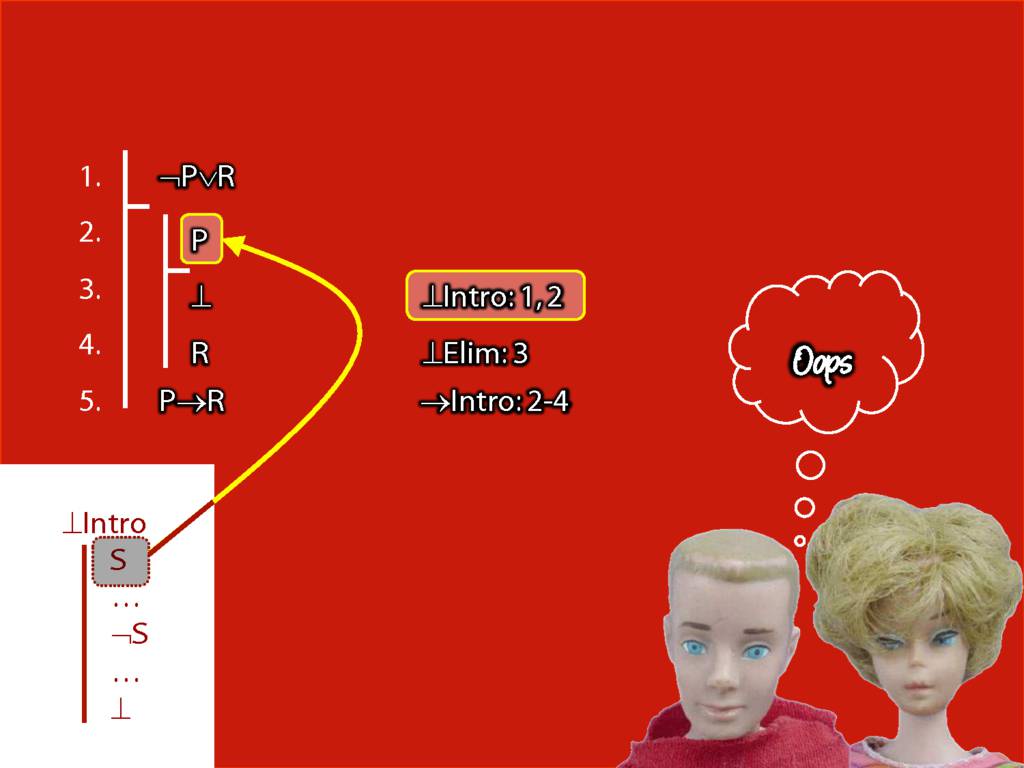
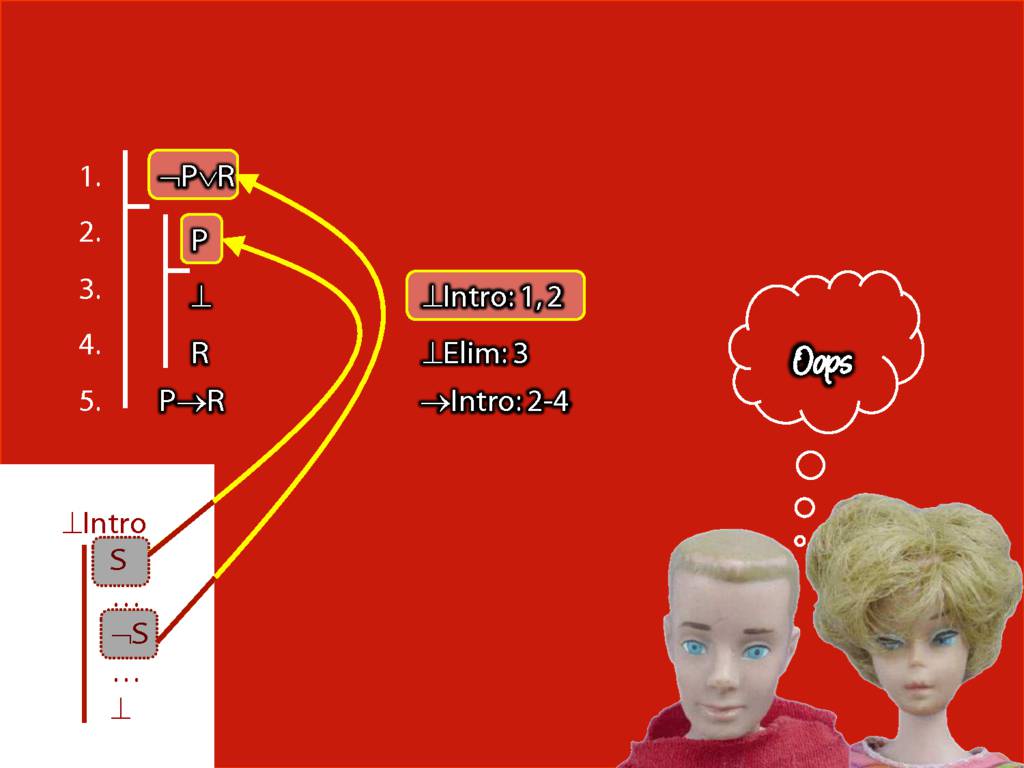
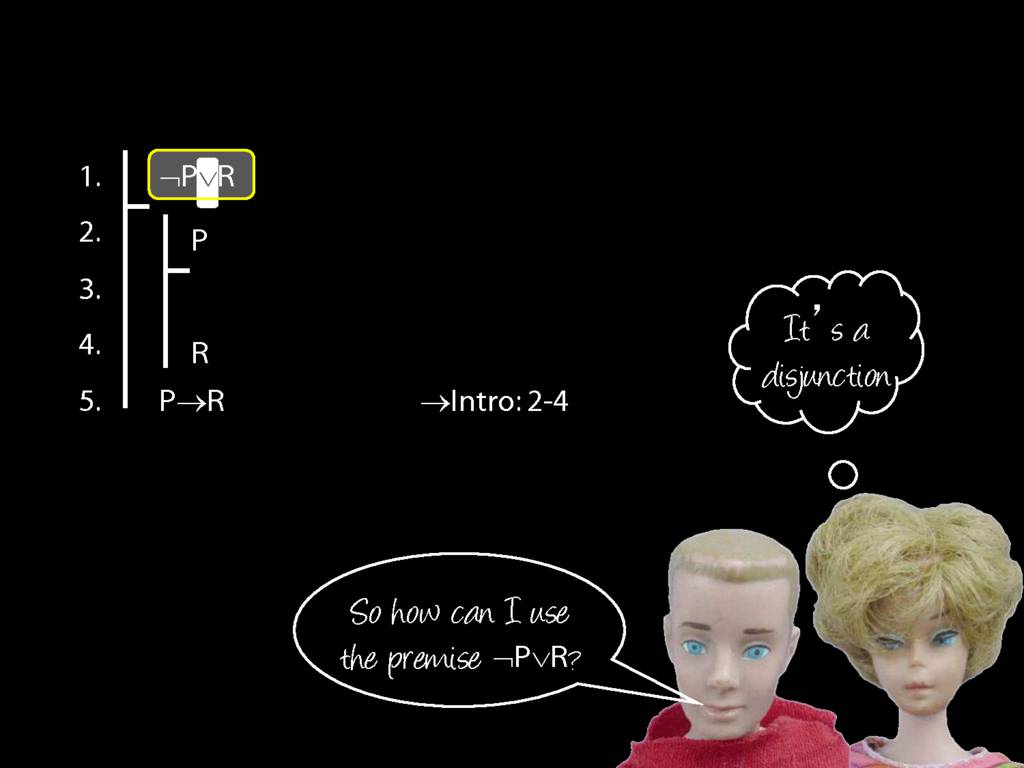
What is wrong with this proof?
6.8
 
\section{Scope}
\emph{Reading:} §3.5
 
\section{Scope}
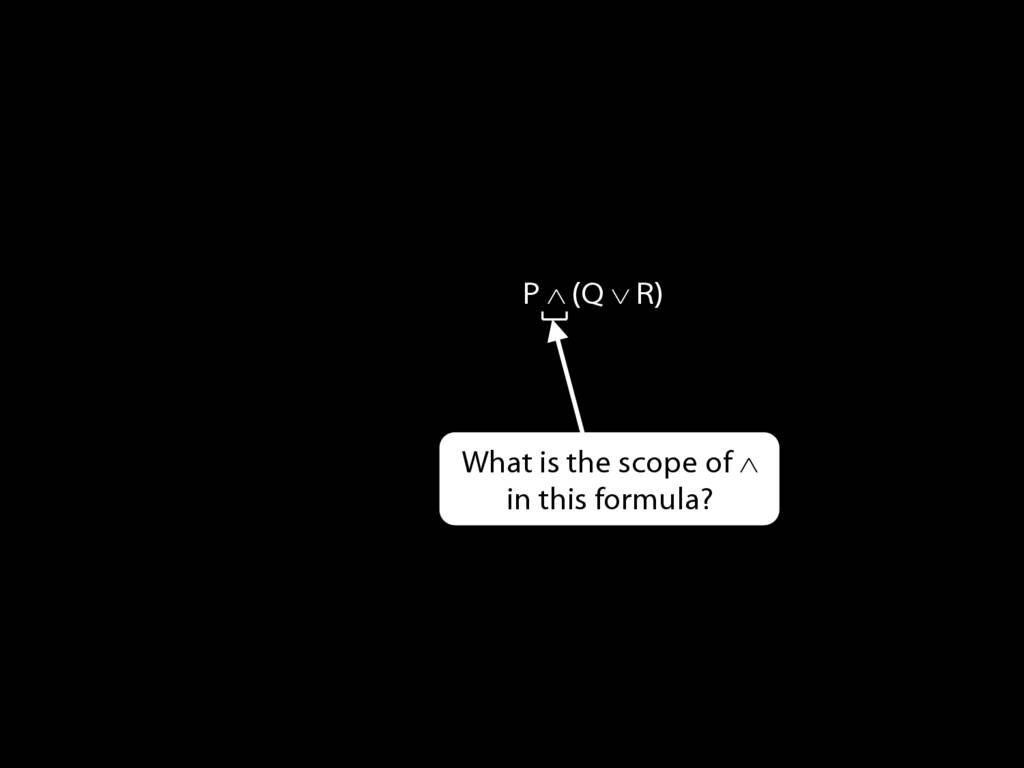
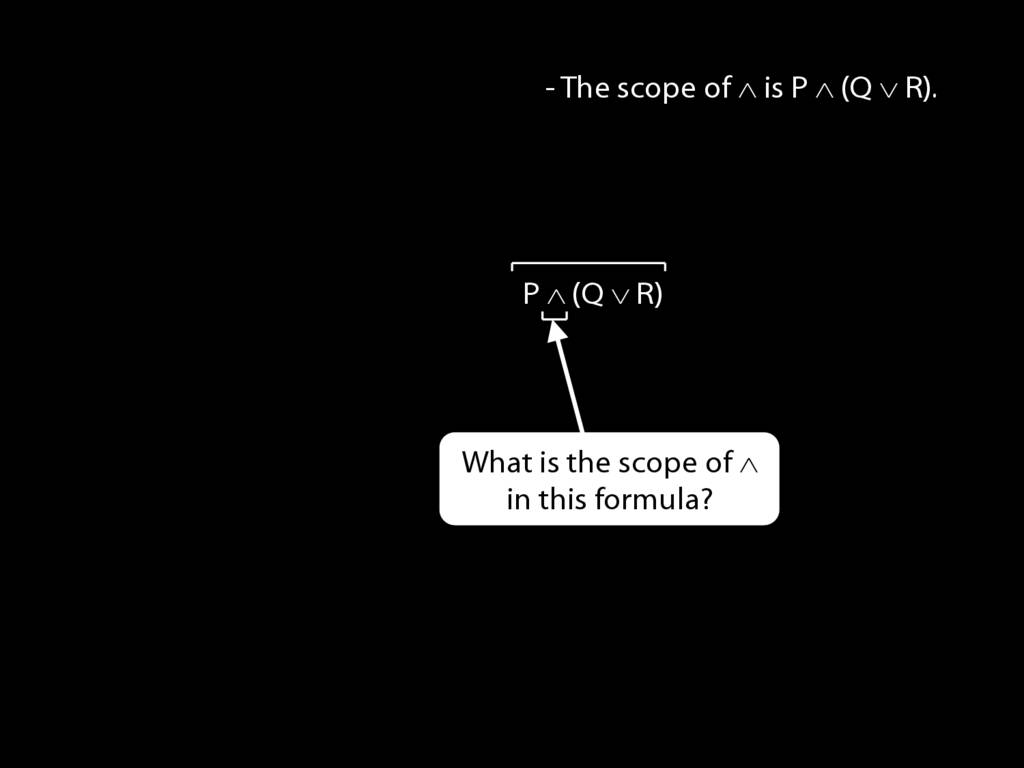
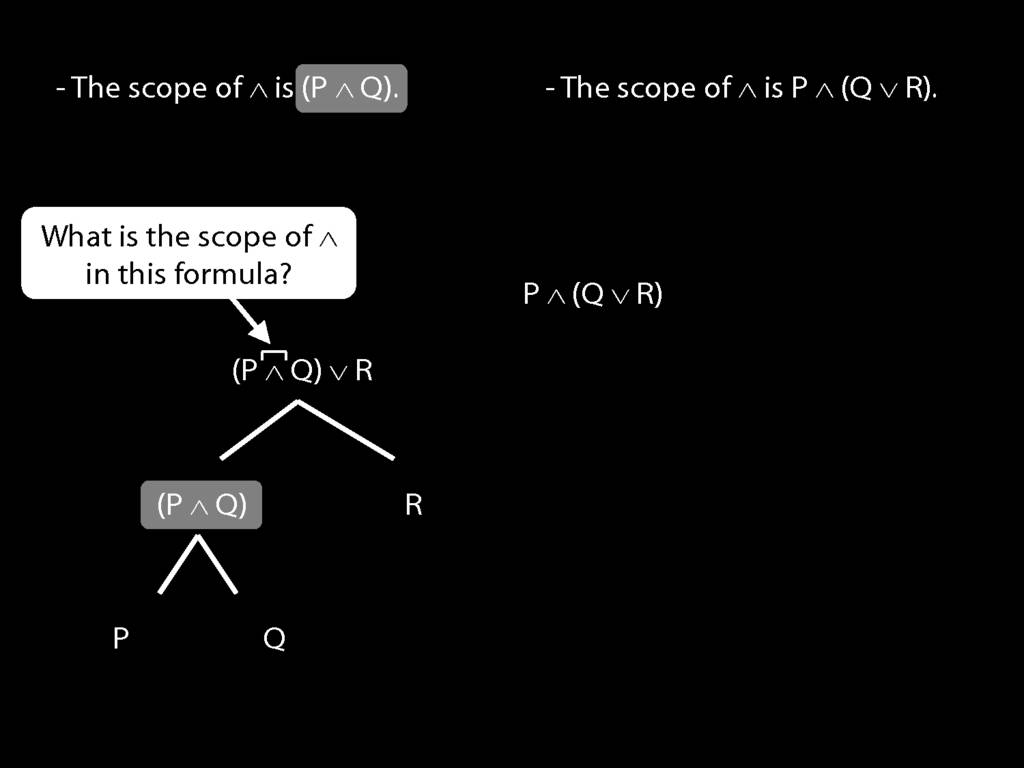
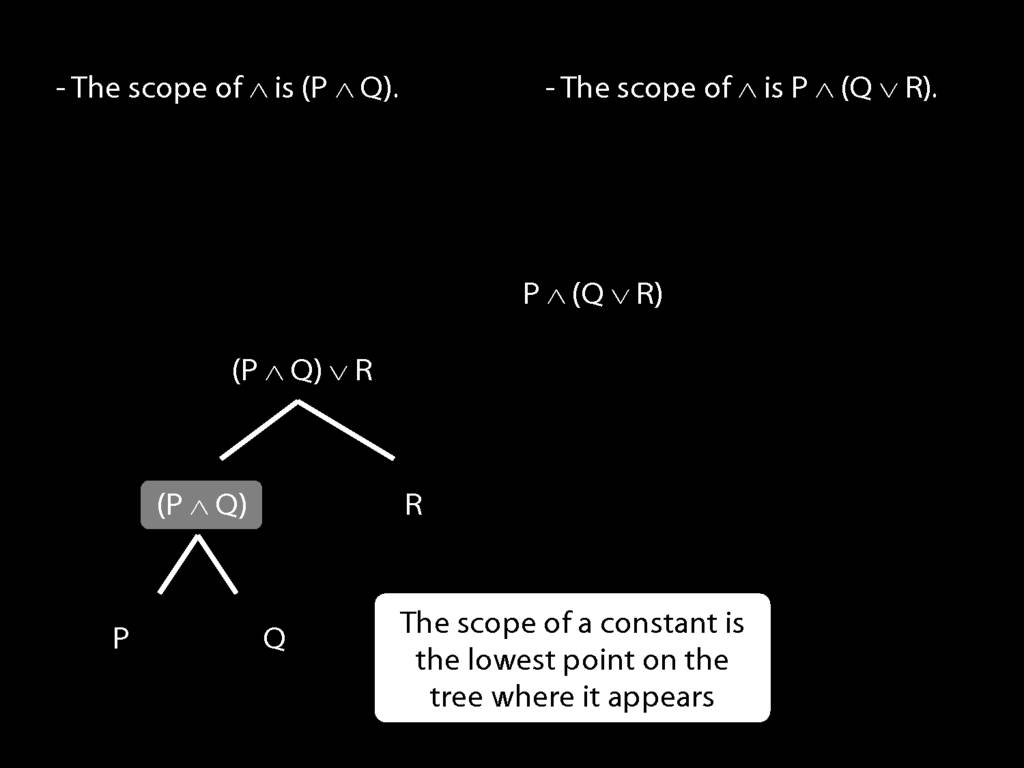
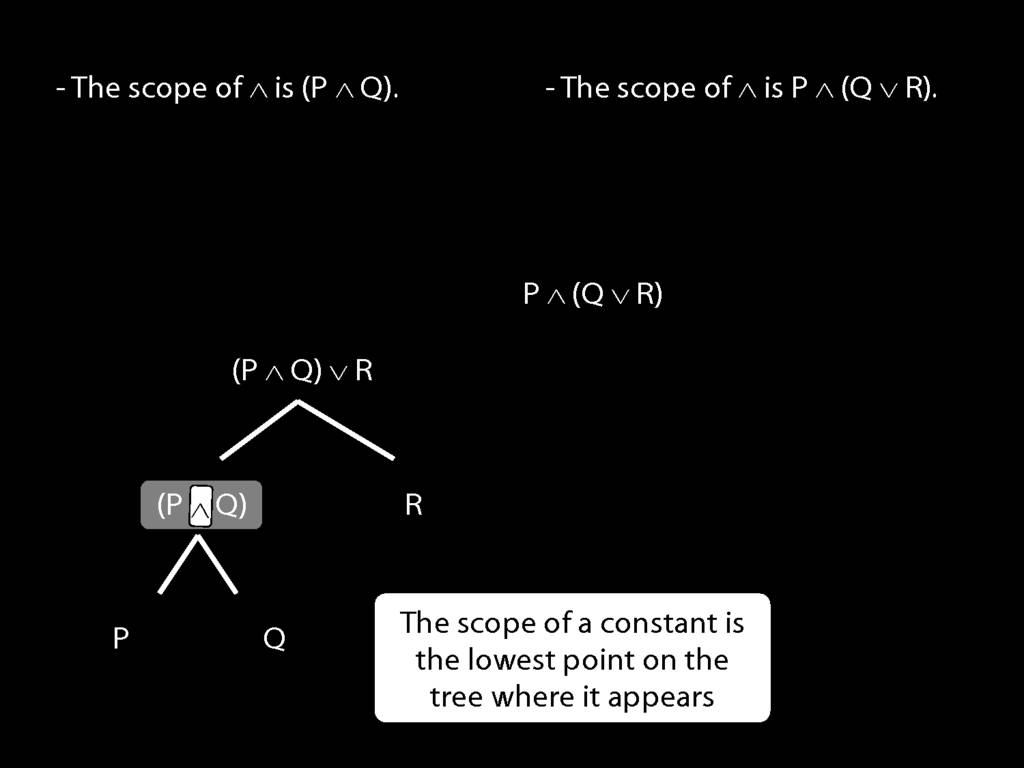
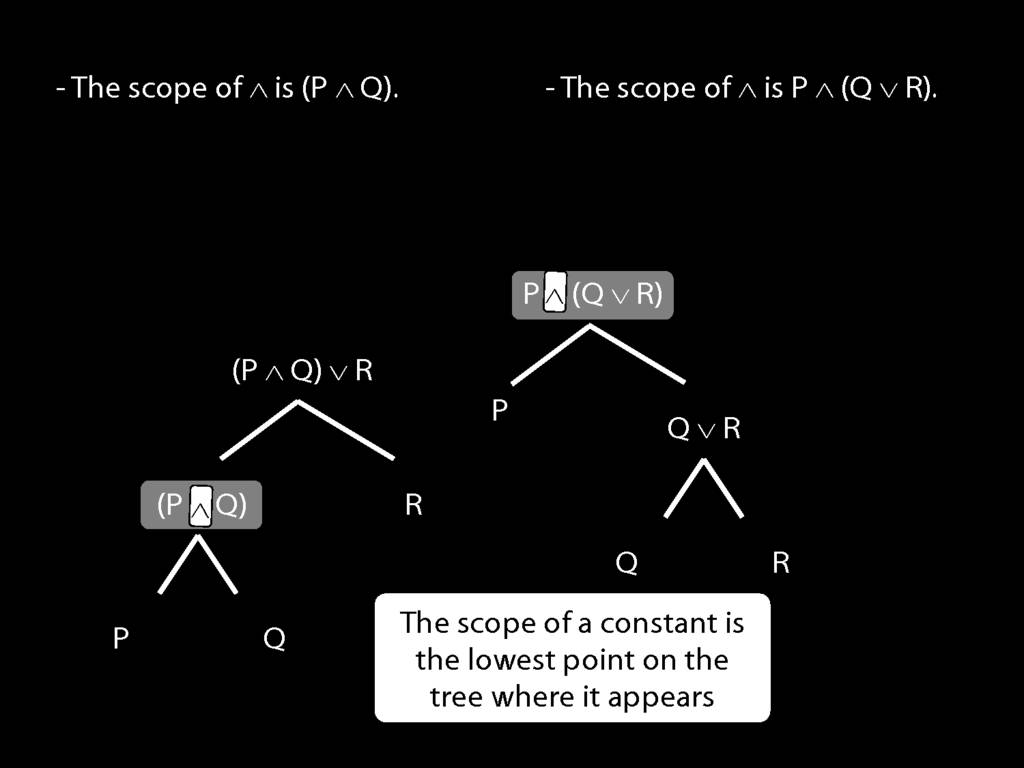
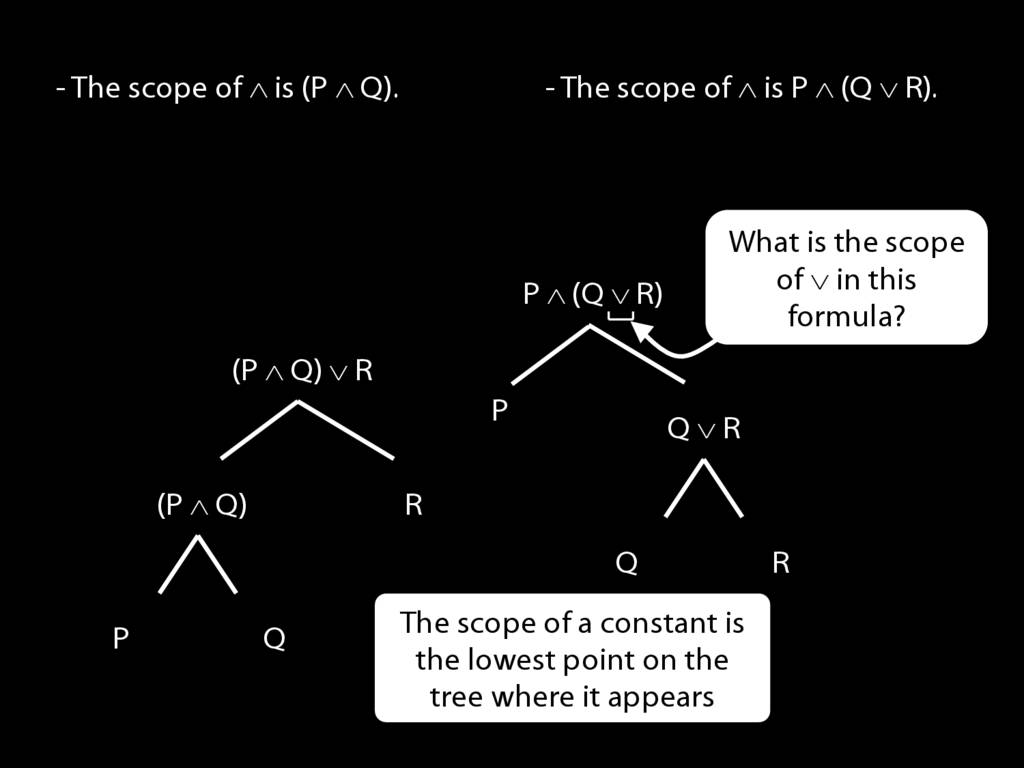
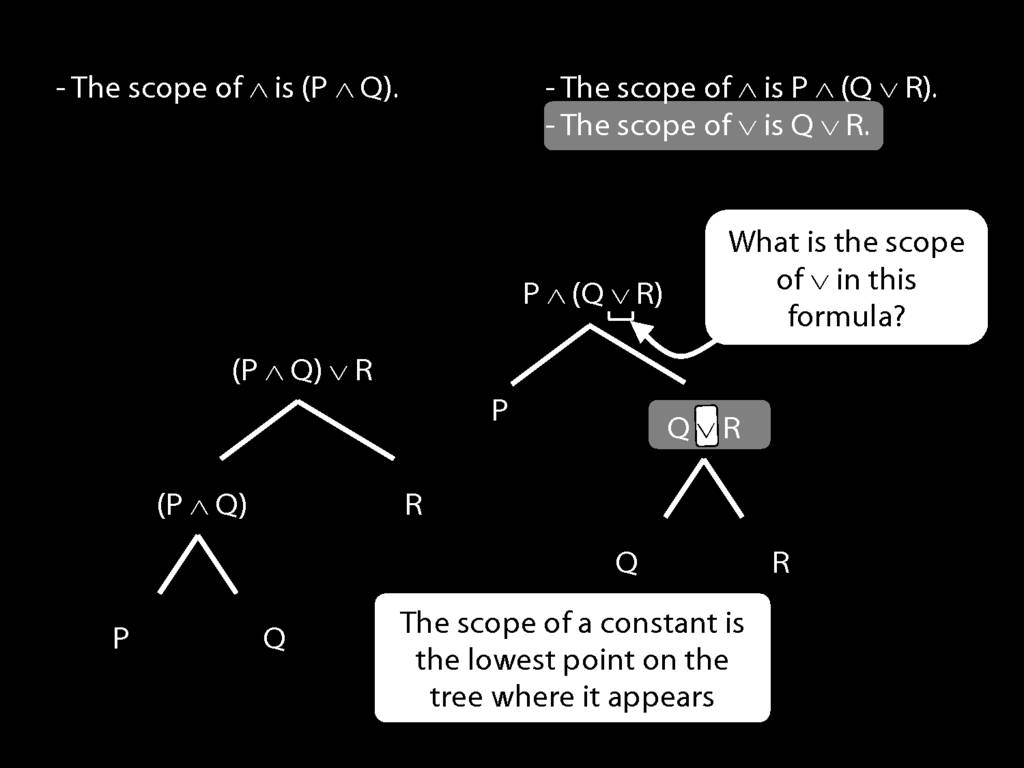
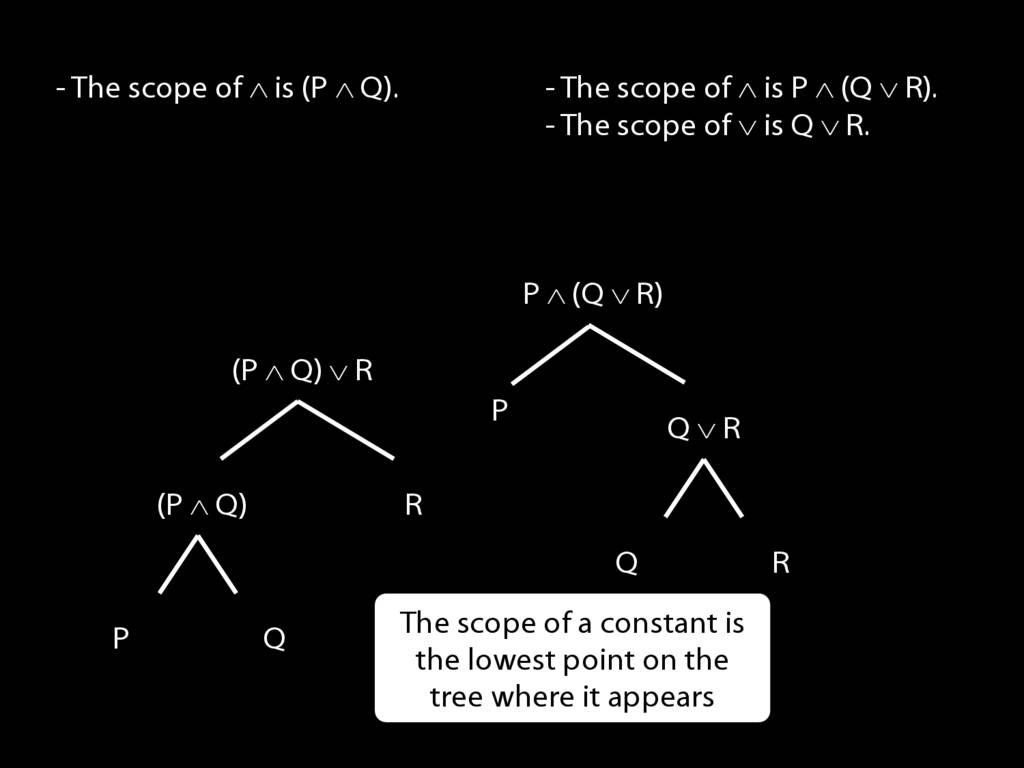
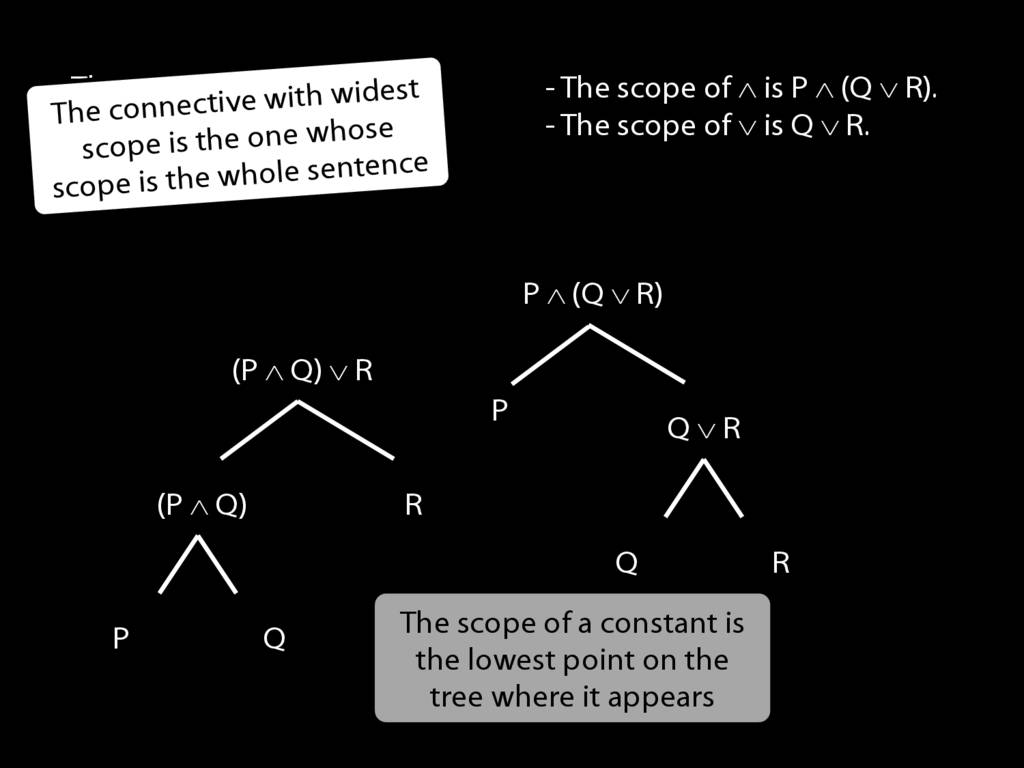
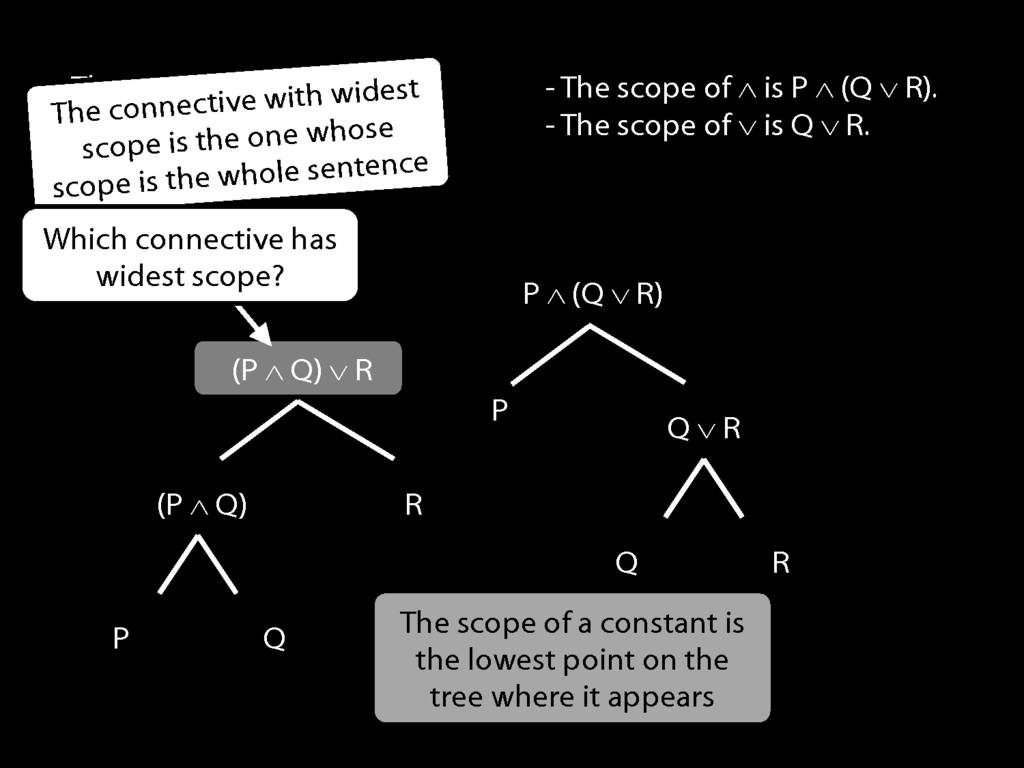
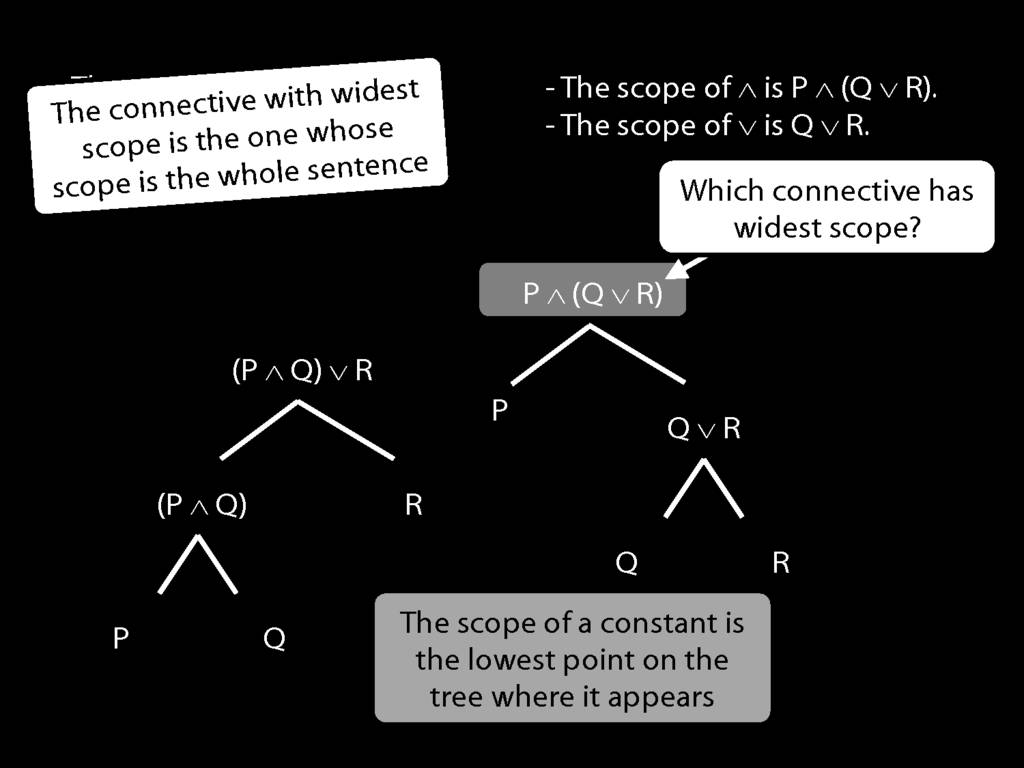
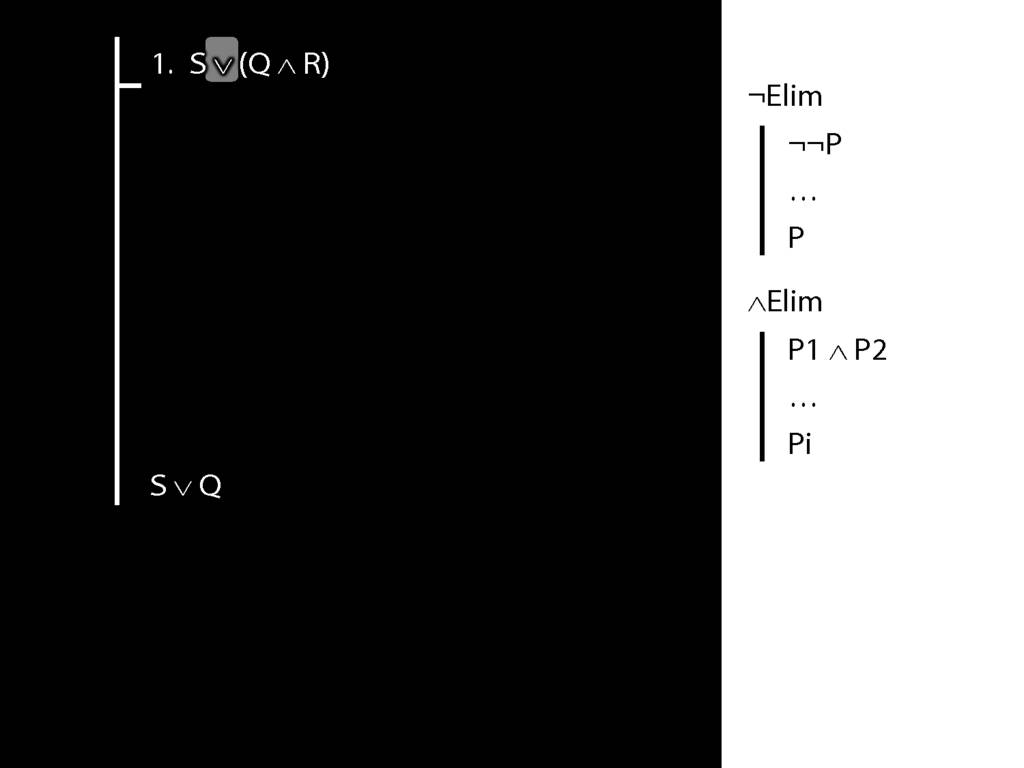
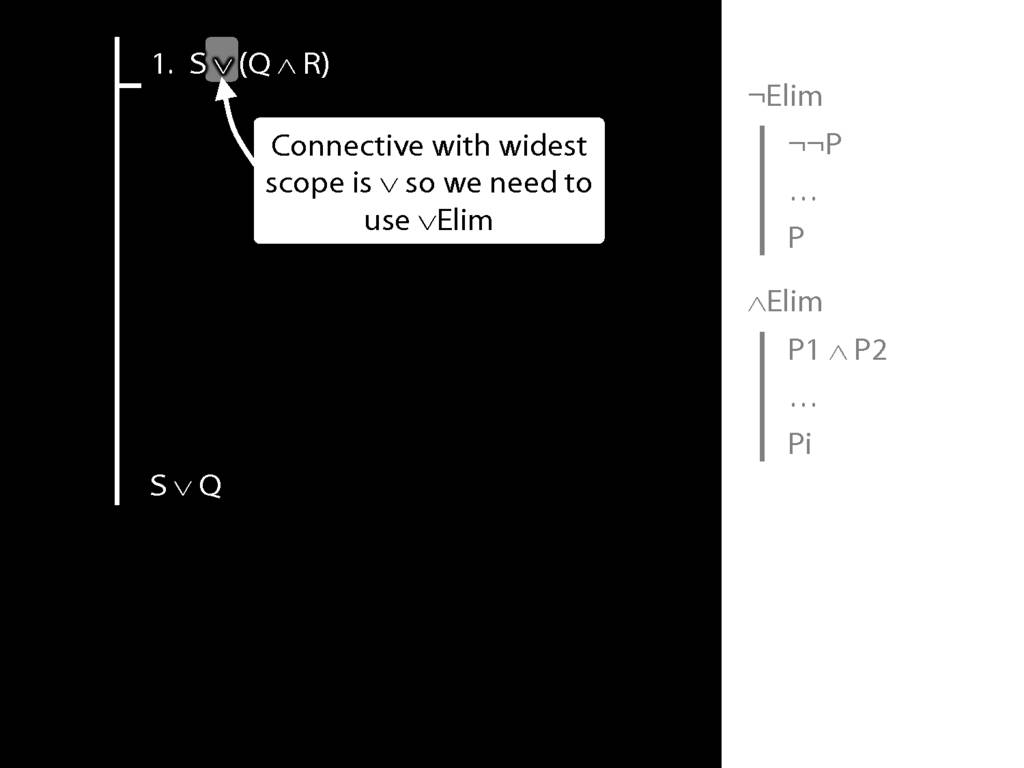
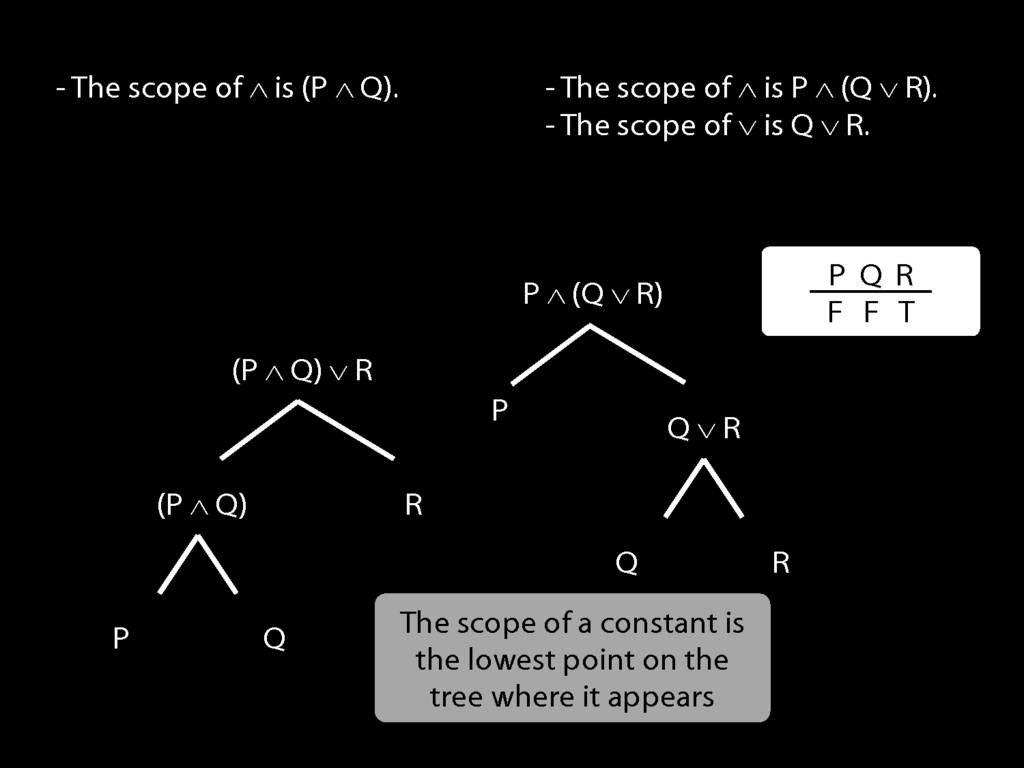
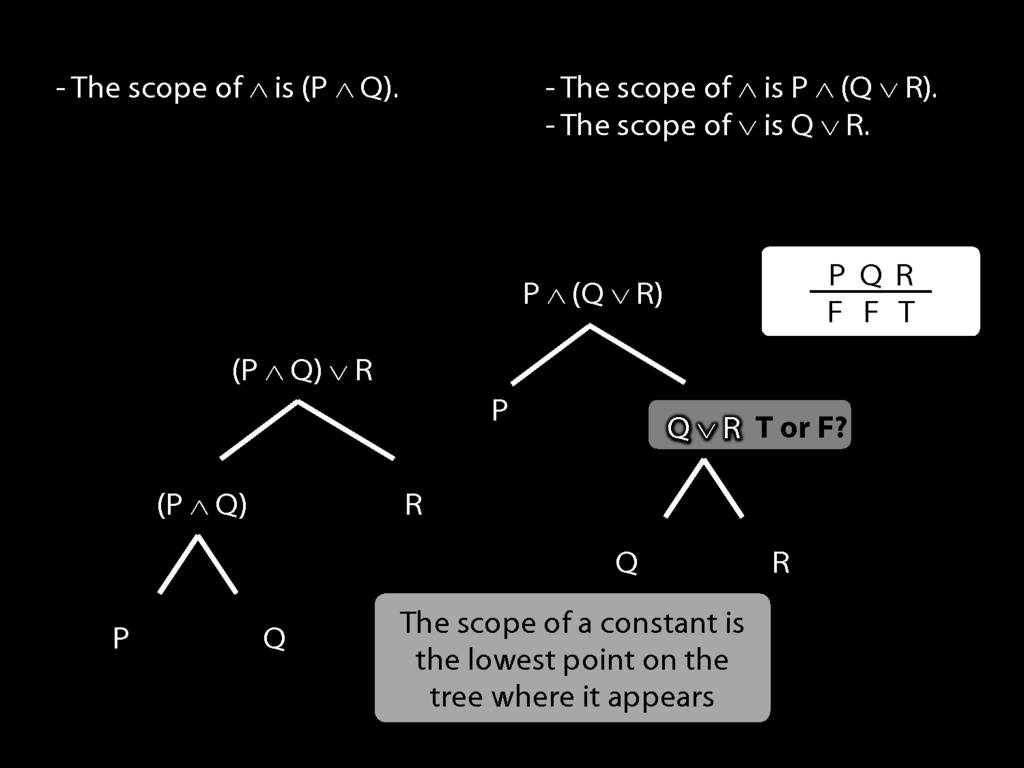
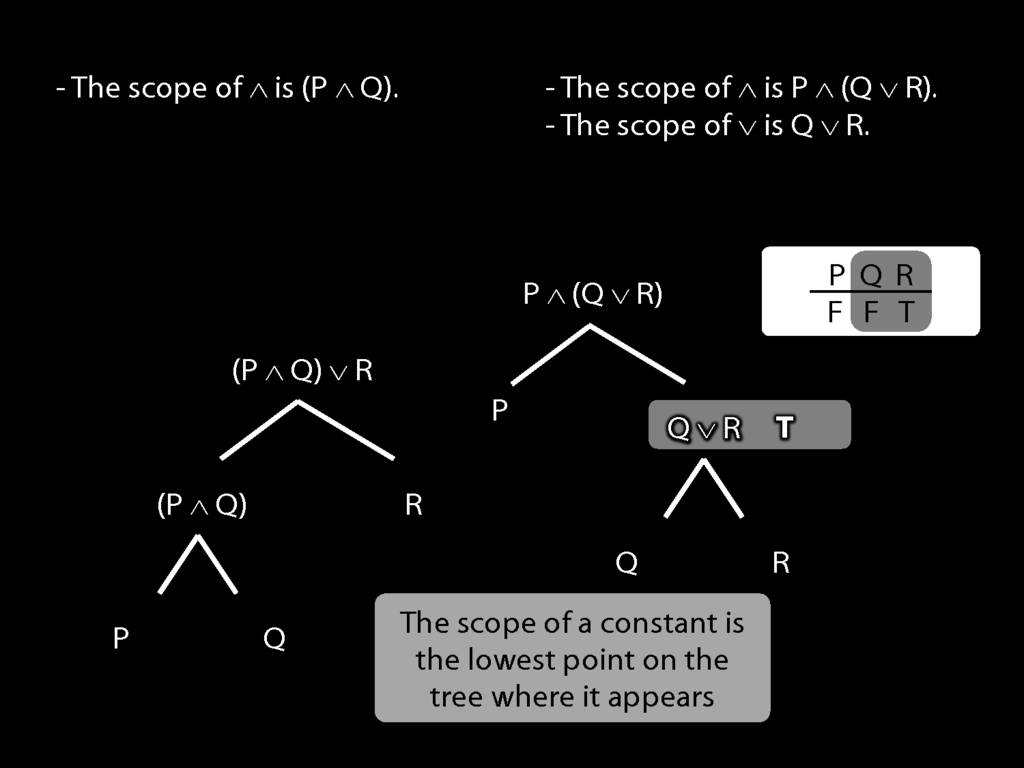
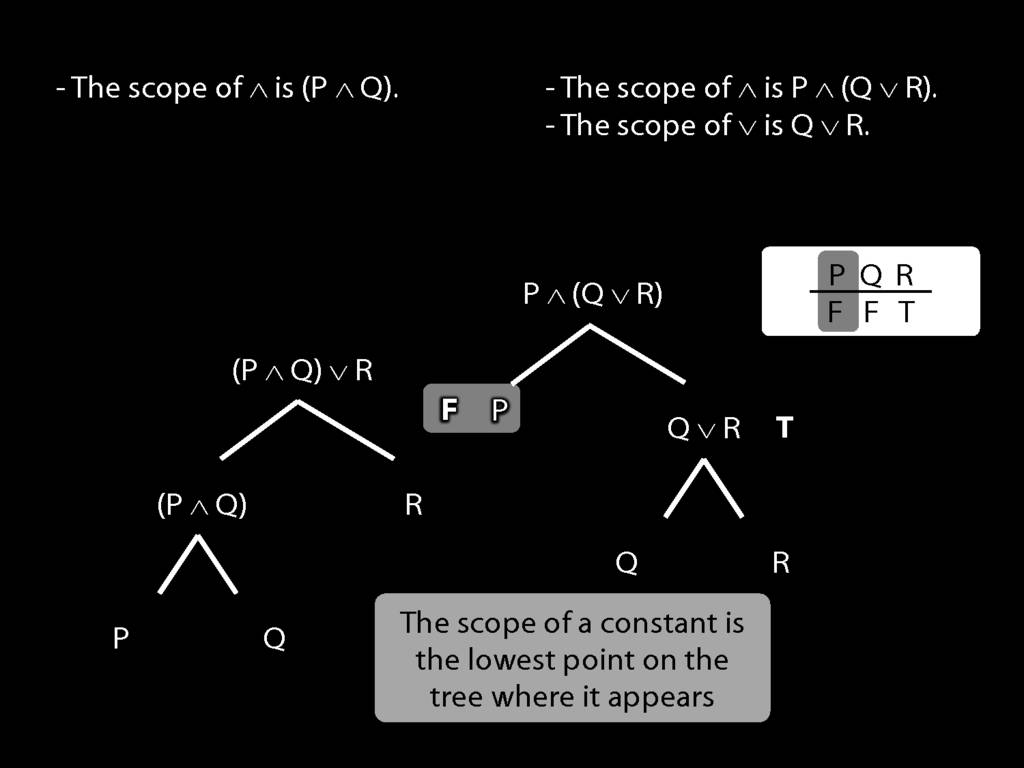
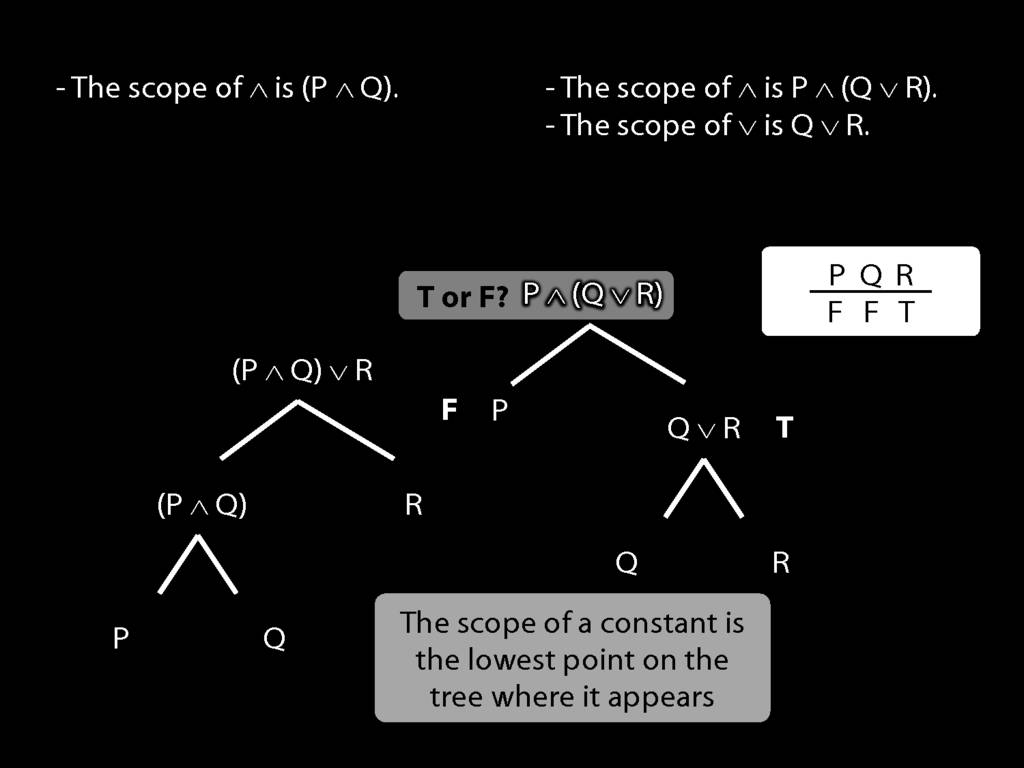
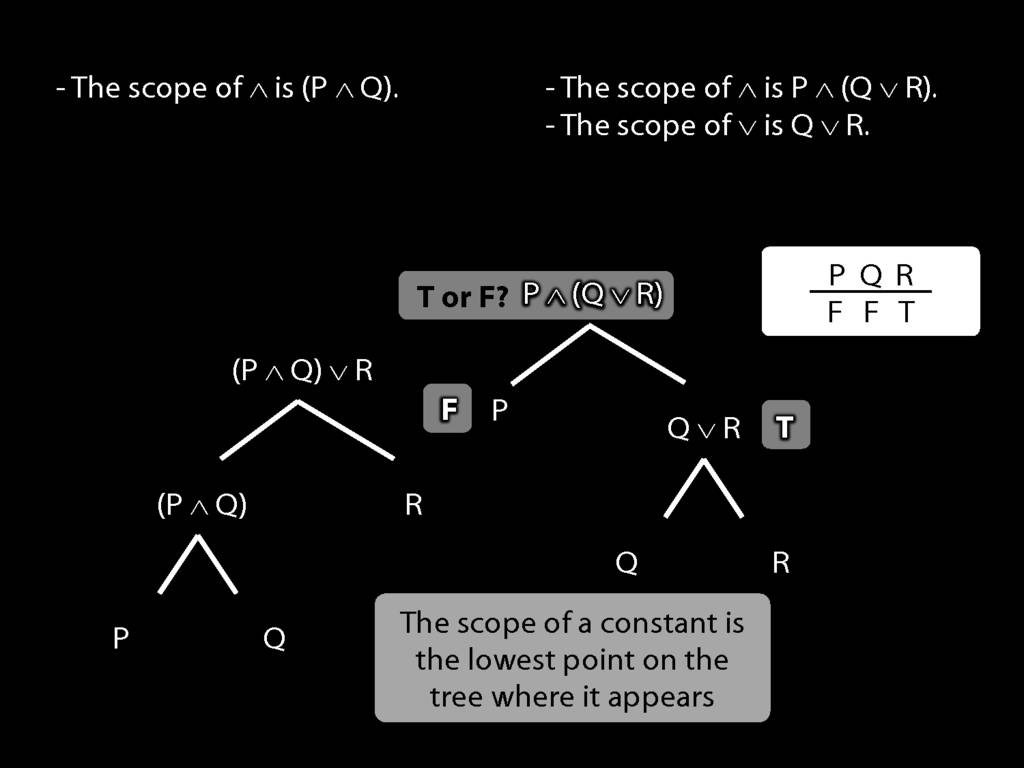
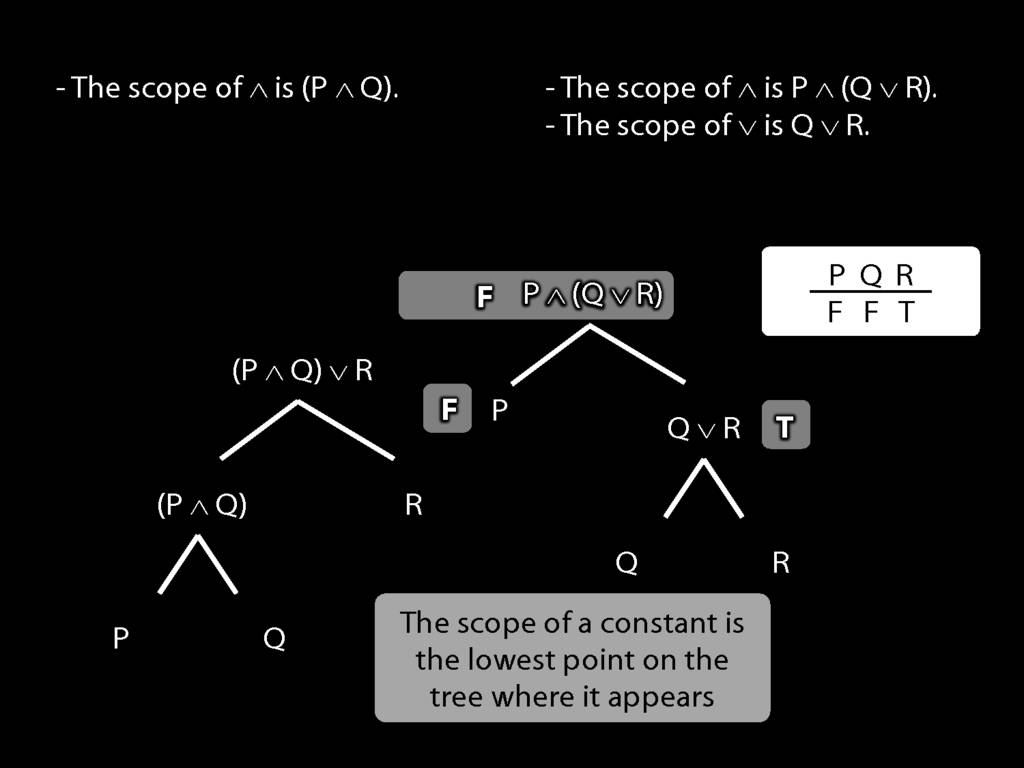
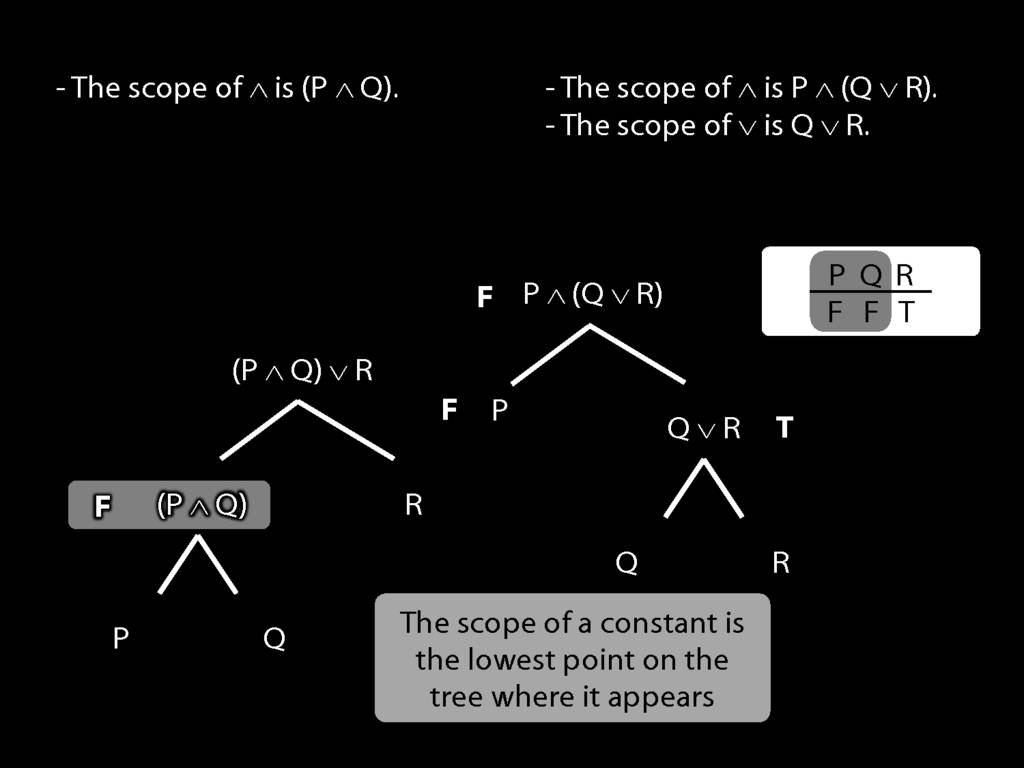
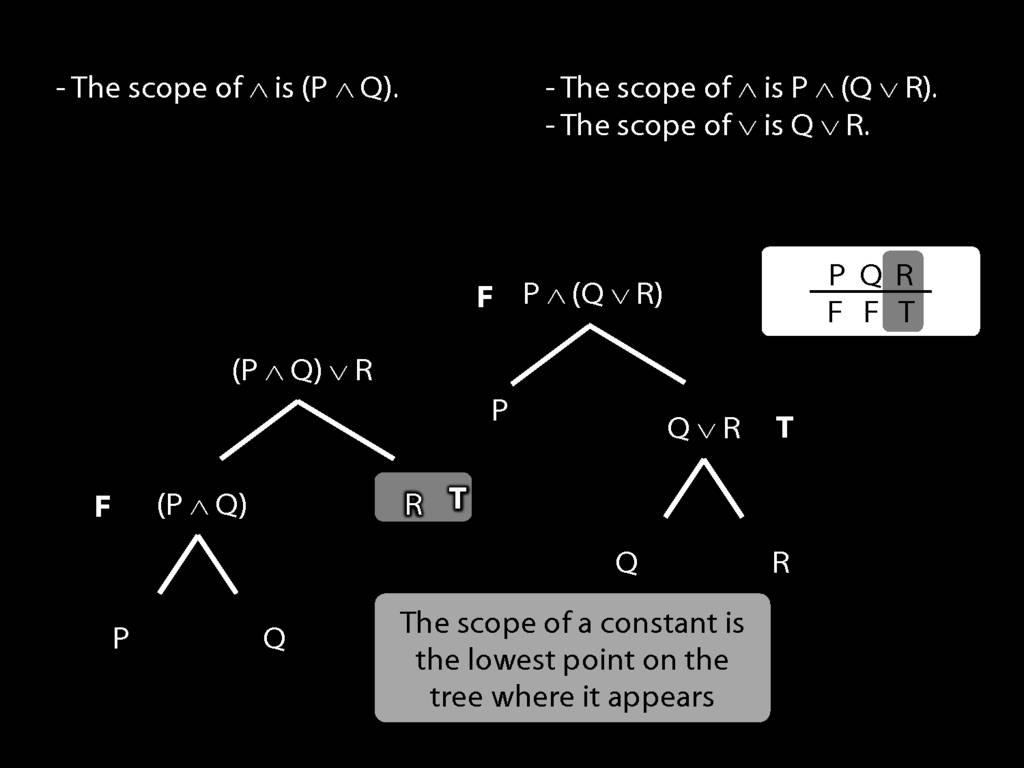
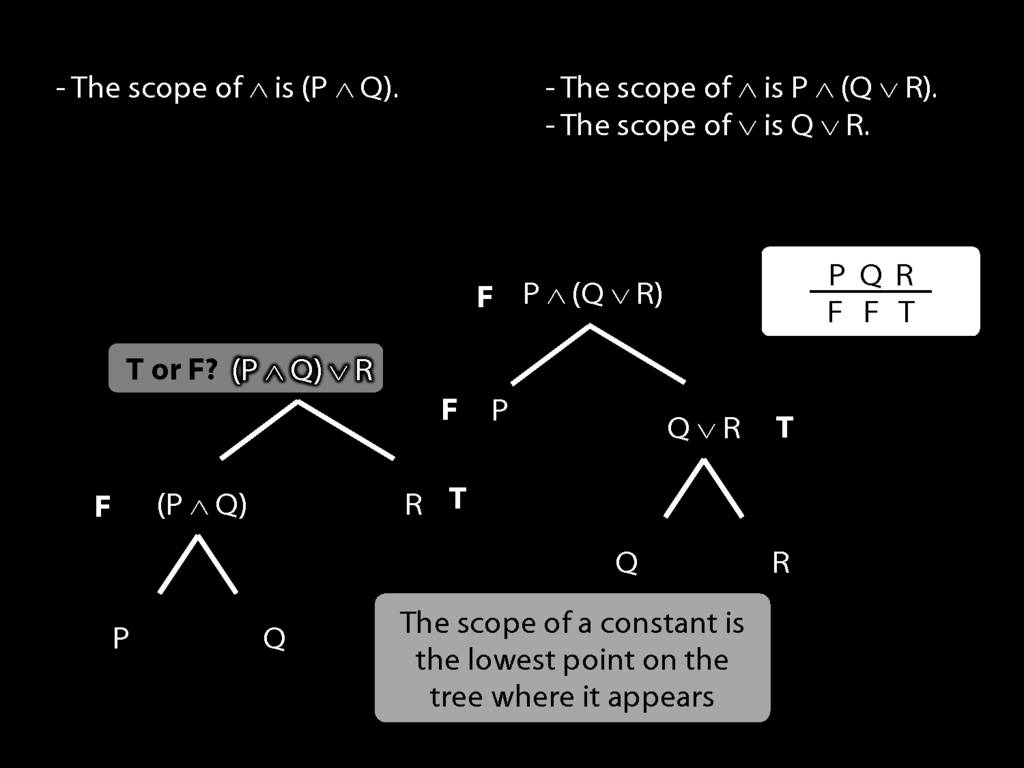
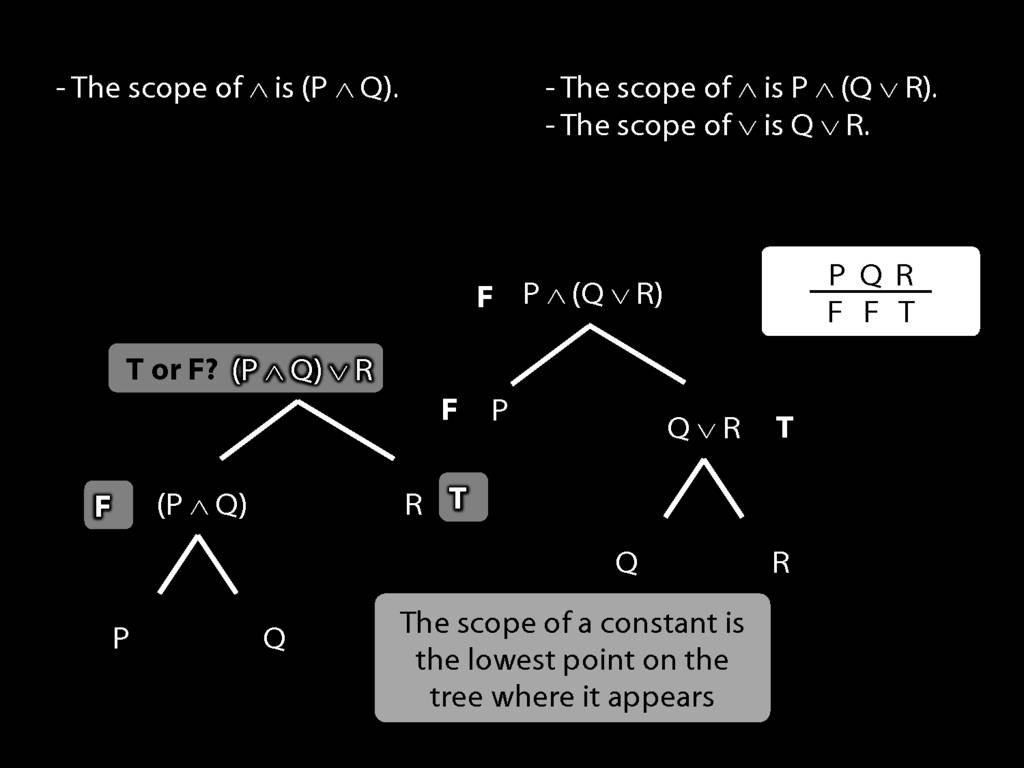
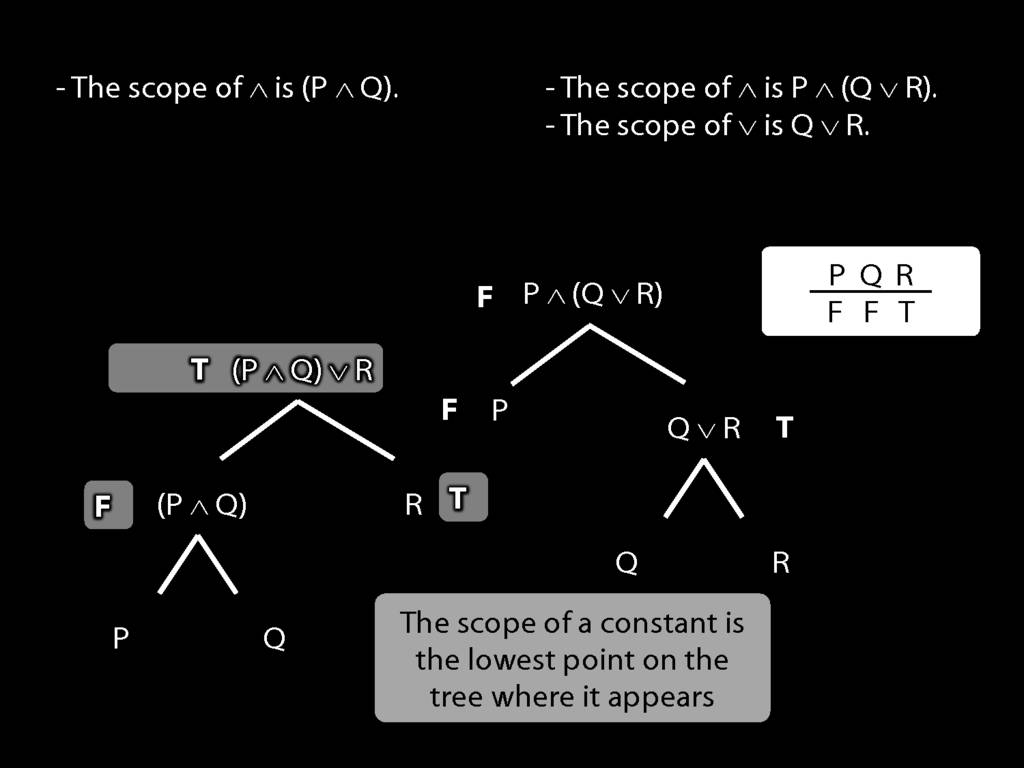
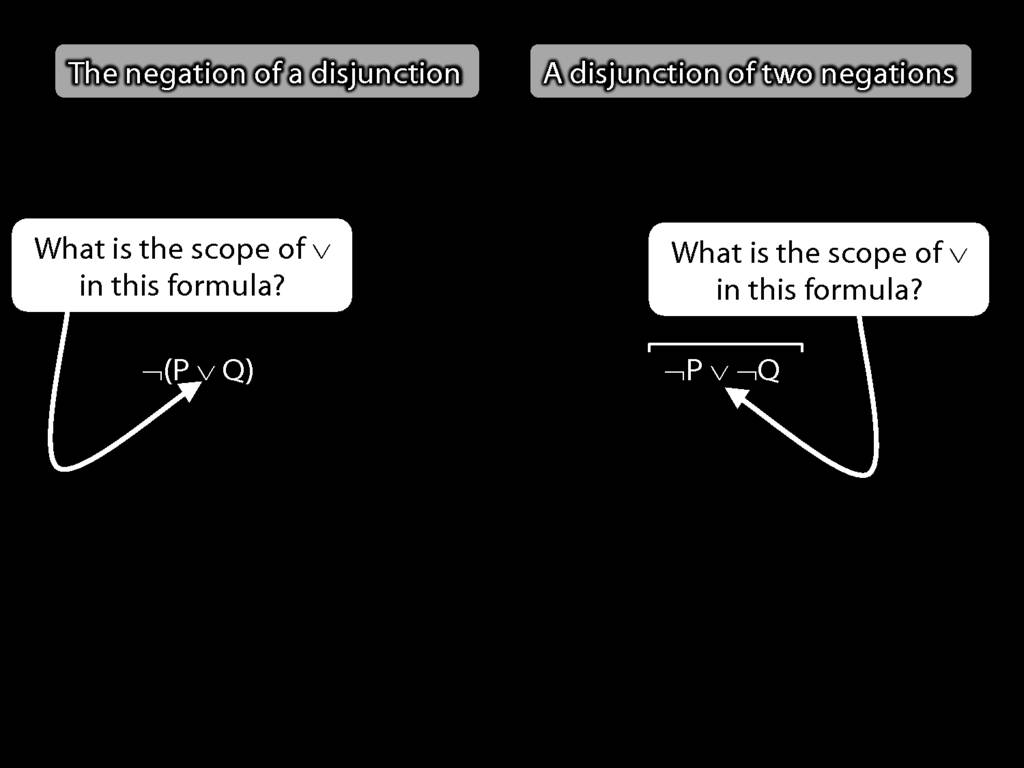
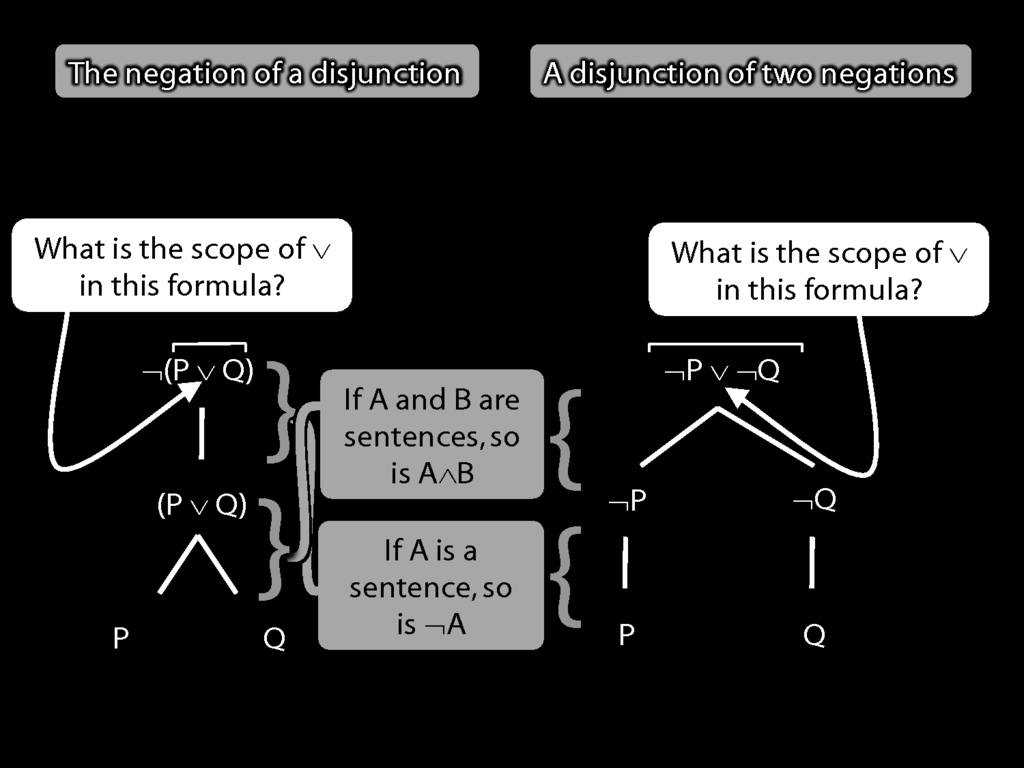
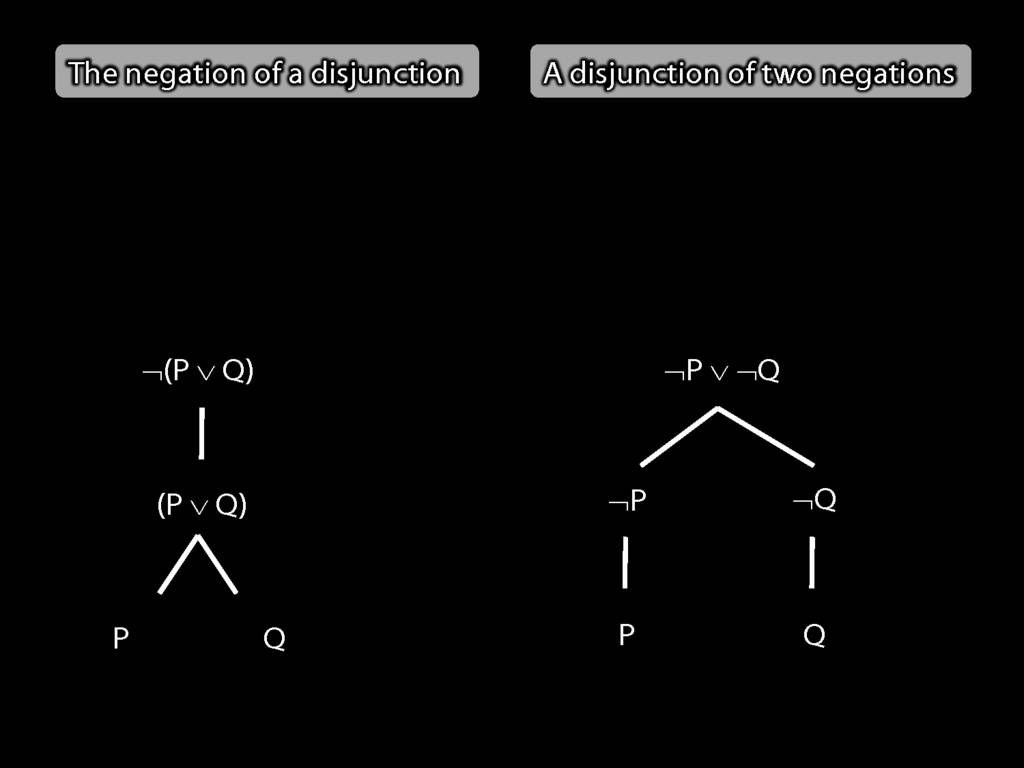
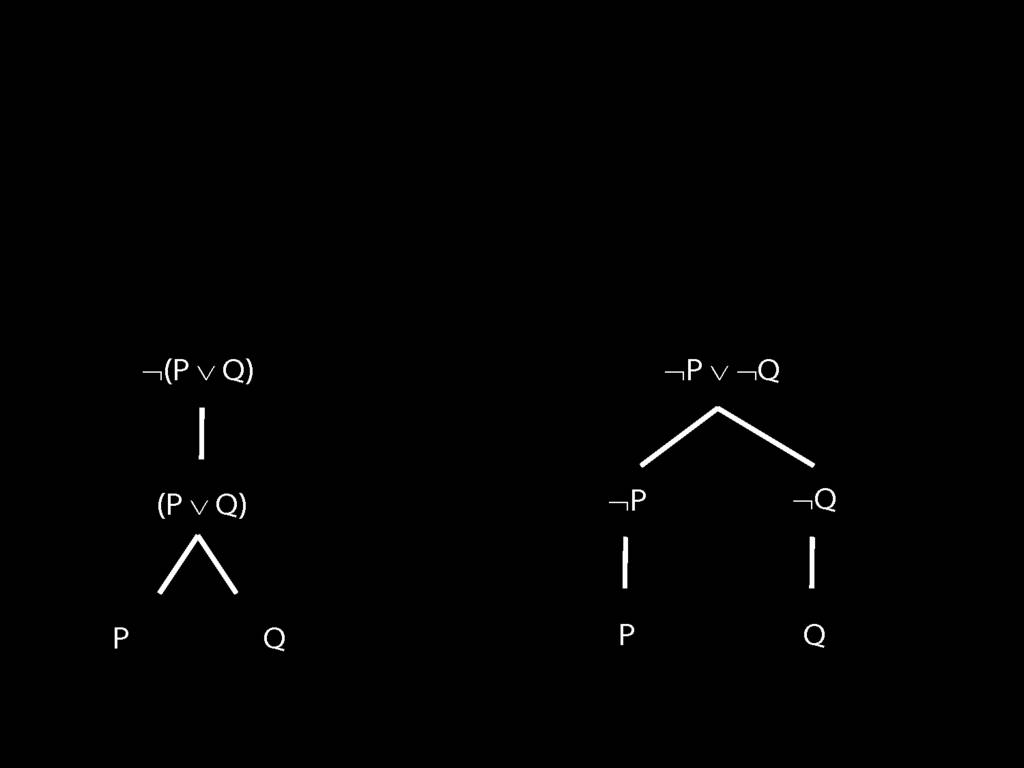
The \emph{scope} of a connective (token) is the sentence containing it lowest in the tree.
The connective with \emph{widest scope} is the one whose scope is the whole sentence.
A rule of proof can only be applied to the connective with widest scope.
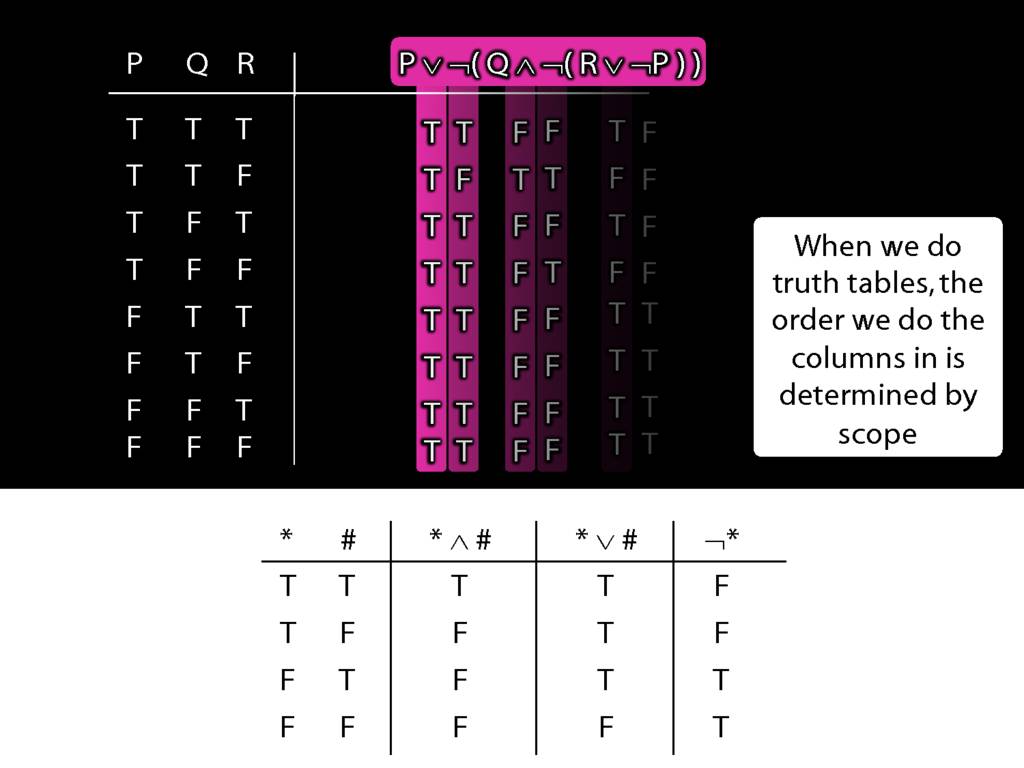
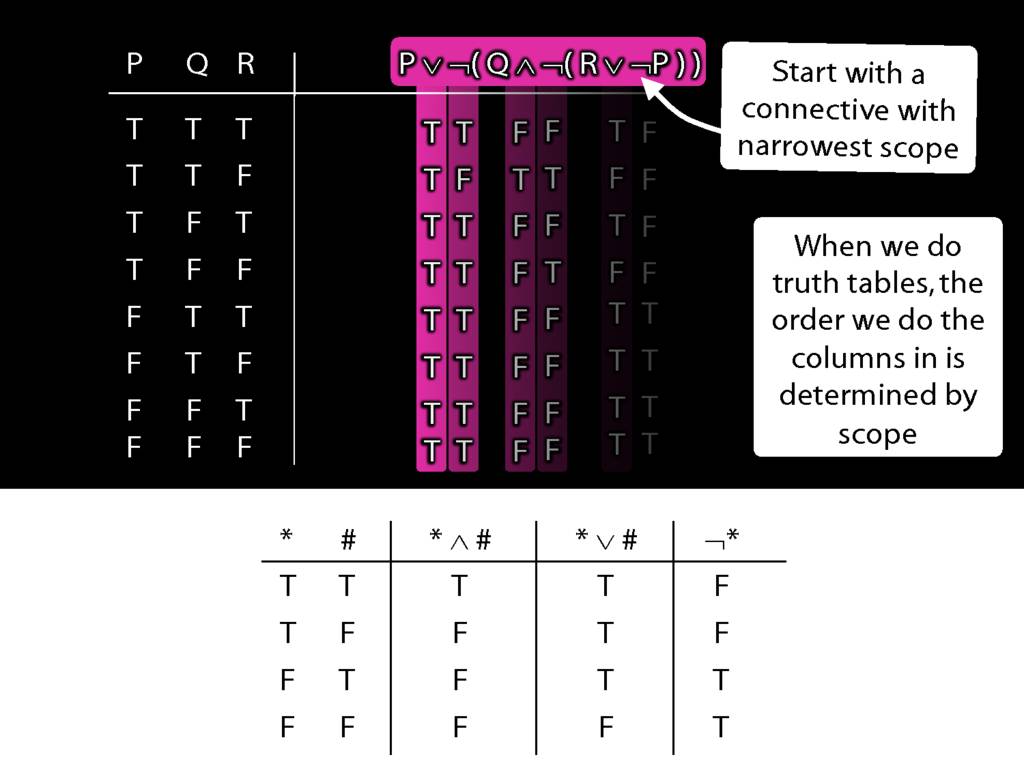
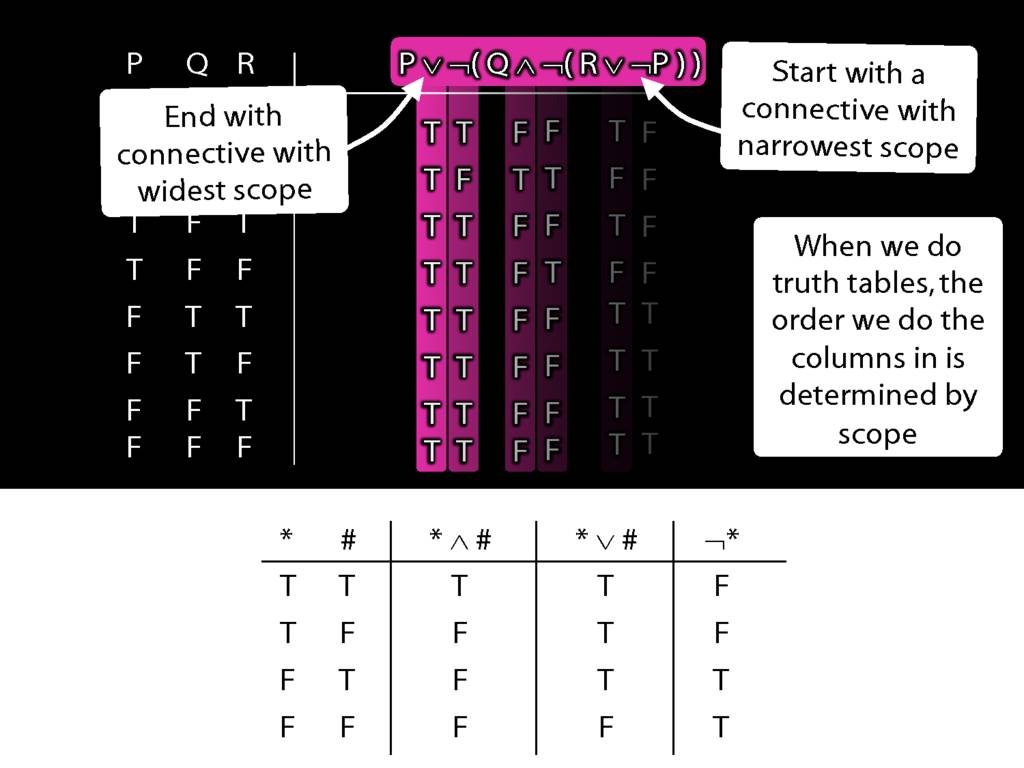
When we do truth tables, the order we do the columns in is determined by scope.
3.14
3.15
 

Scope and Negation

 
\section{Scope and Negation}
\emph{Reading:} §3.5, §3.6
 
\section{Scope and Negation}

No lectures or seminars in reading week (Week 6).

office hours

Tuesdays:

16-17 in S2.40 (Barney)

Wednesdays:

11-12 in S2.40 (Hemdat)

12-13 in S2.40 (Hemdat)

13-14 in S2.40 (Alfonso)

15-16 in S2.40 (Dino)

16-17 in H3.45 (Barney*)

Thursdays:

10-11 in S2.33 (Joe)

12-13 in S2.33 (Joe)

13-14 in S2.40 (Barney)

15-16 in S2.40 (Dino)

 

Proof Example: ¬(P∨Q) therefore ¬P∧¬Q

 
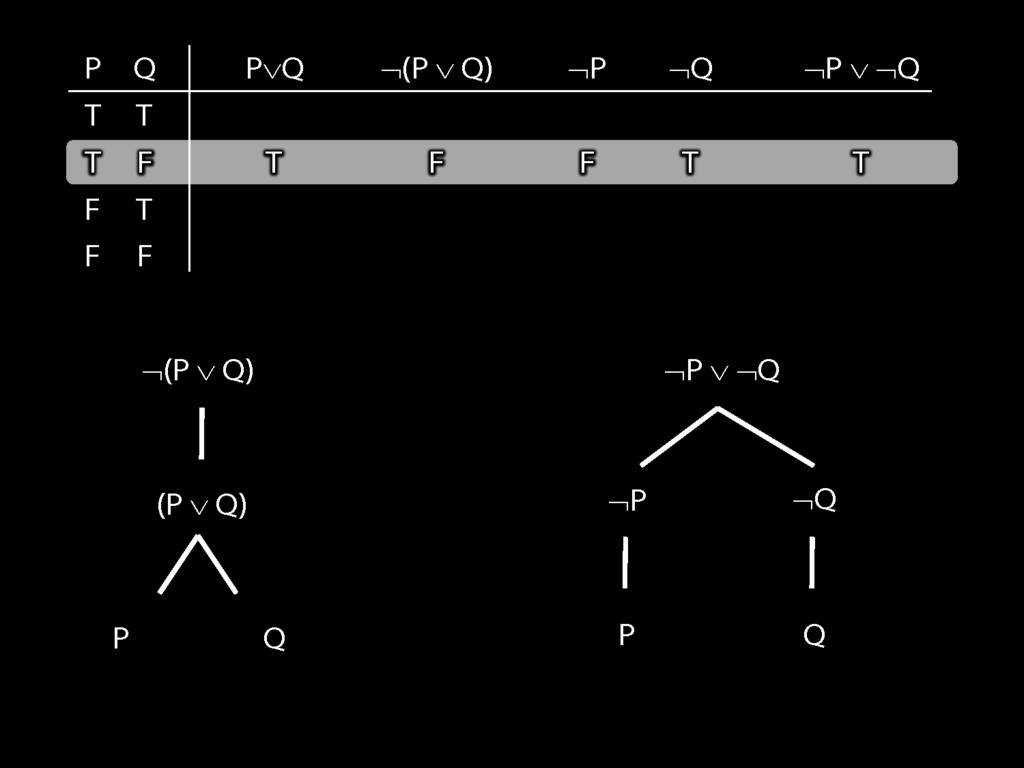
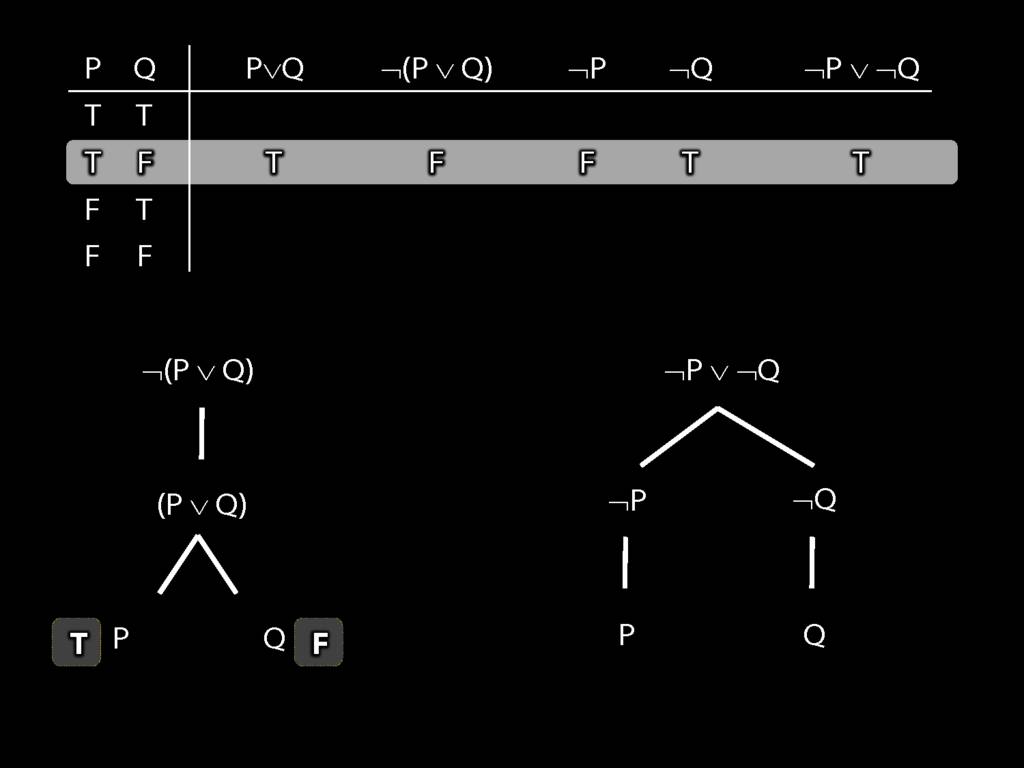
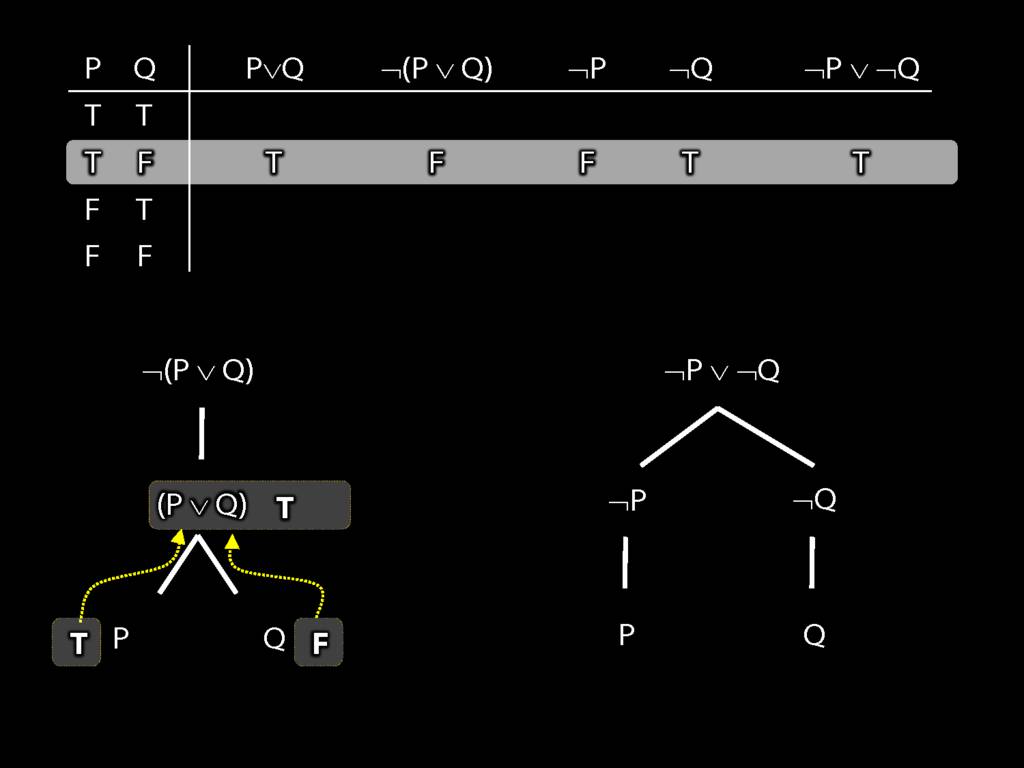
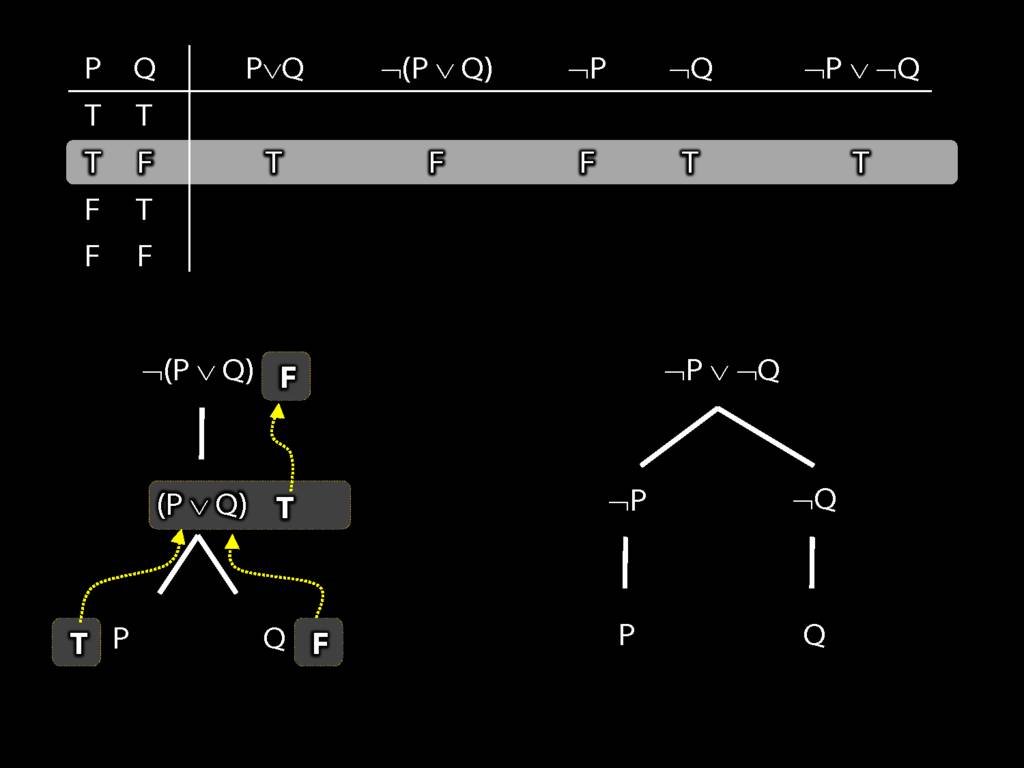
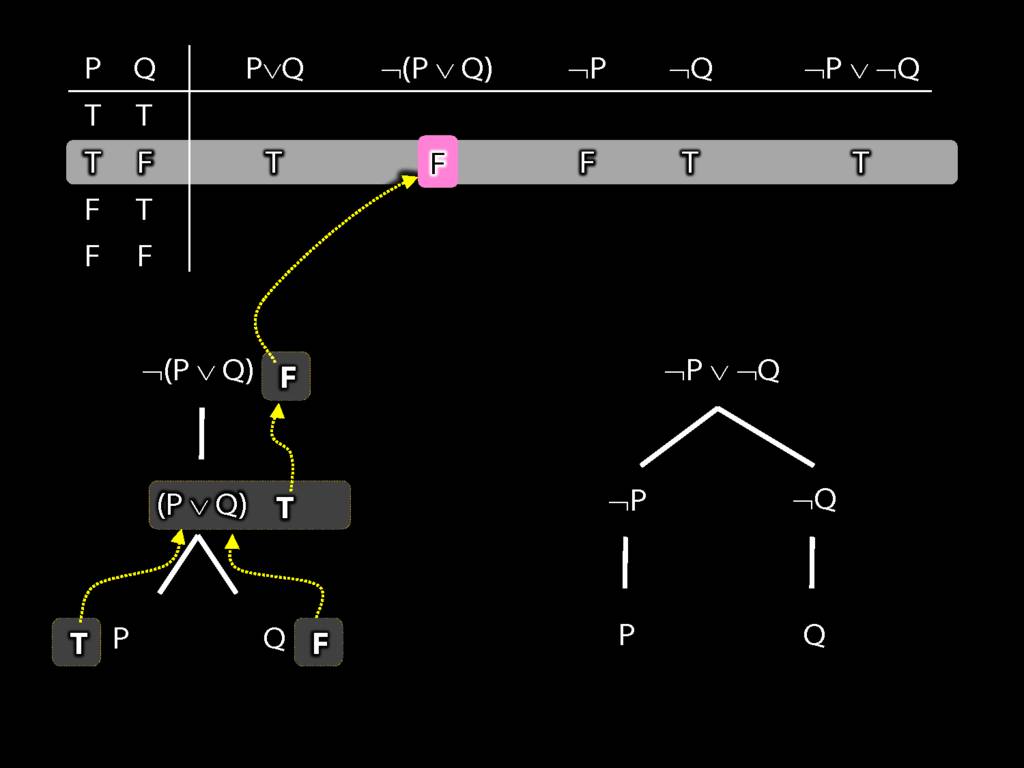
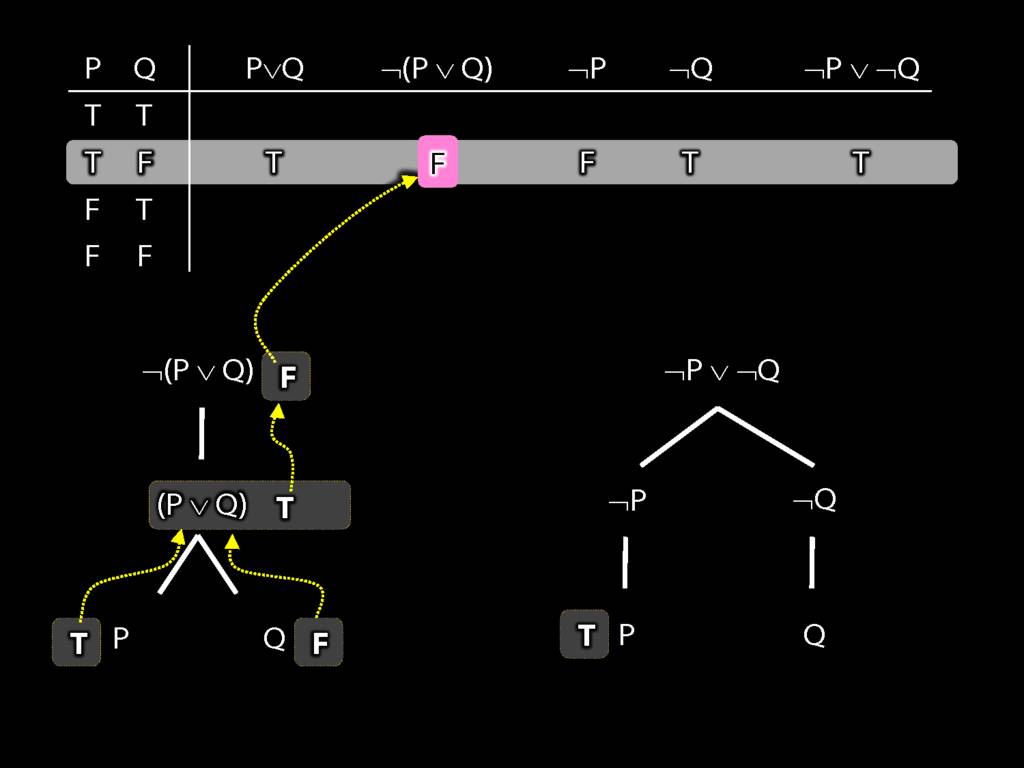
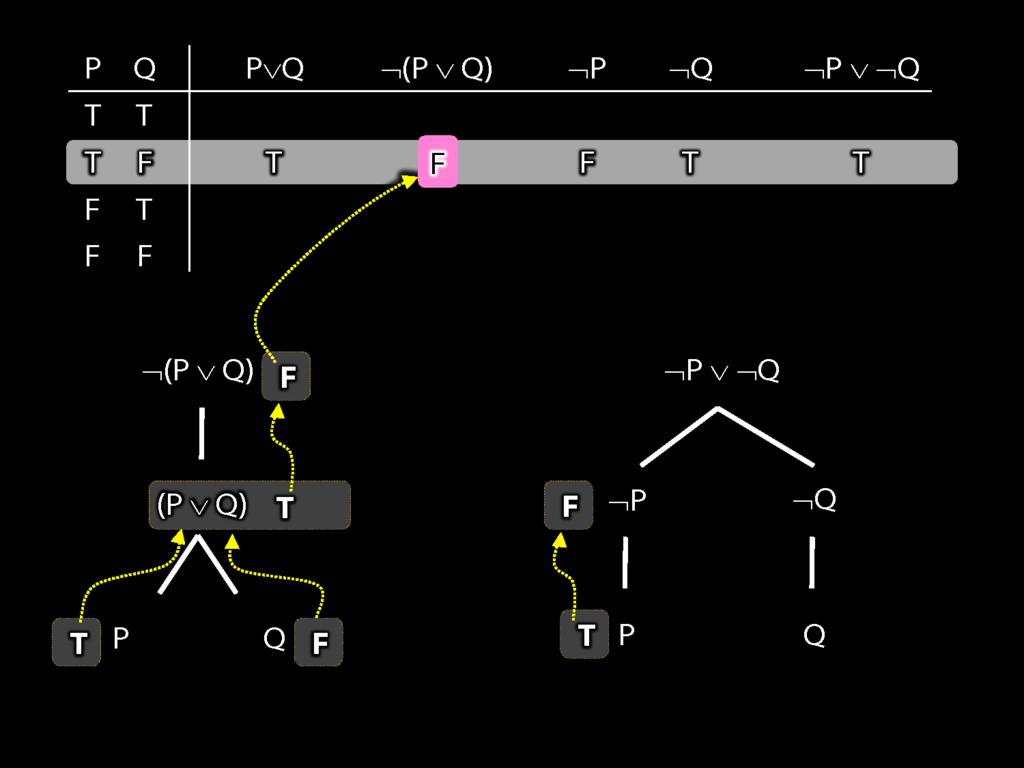
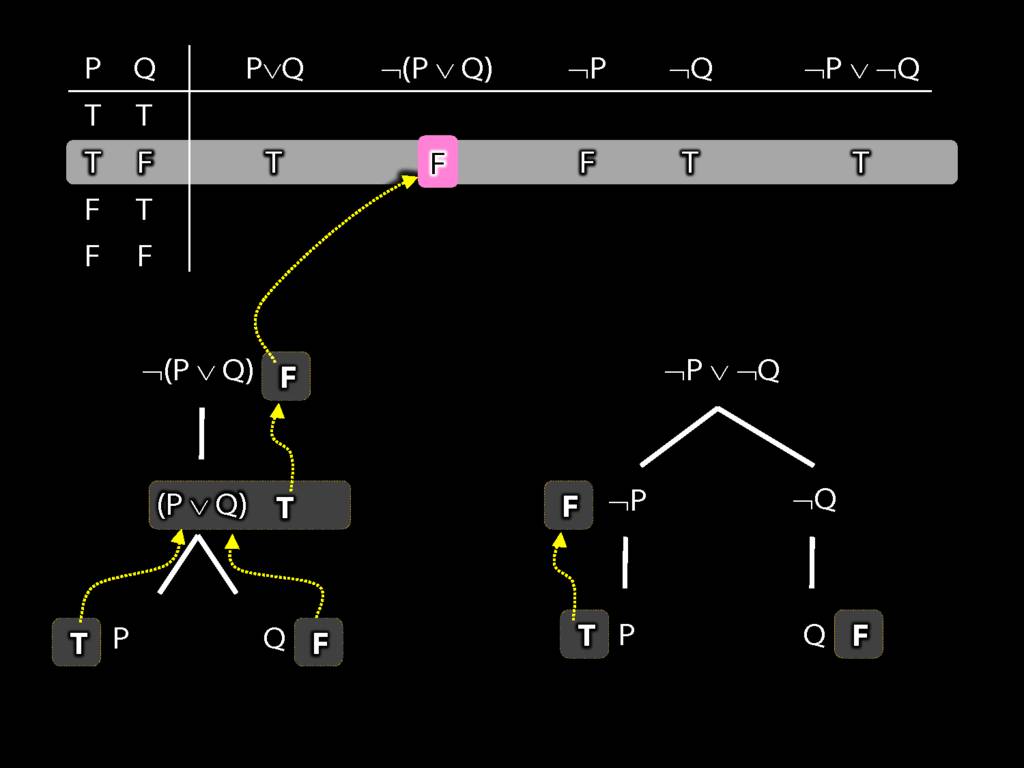
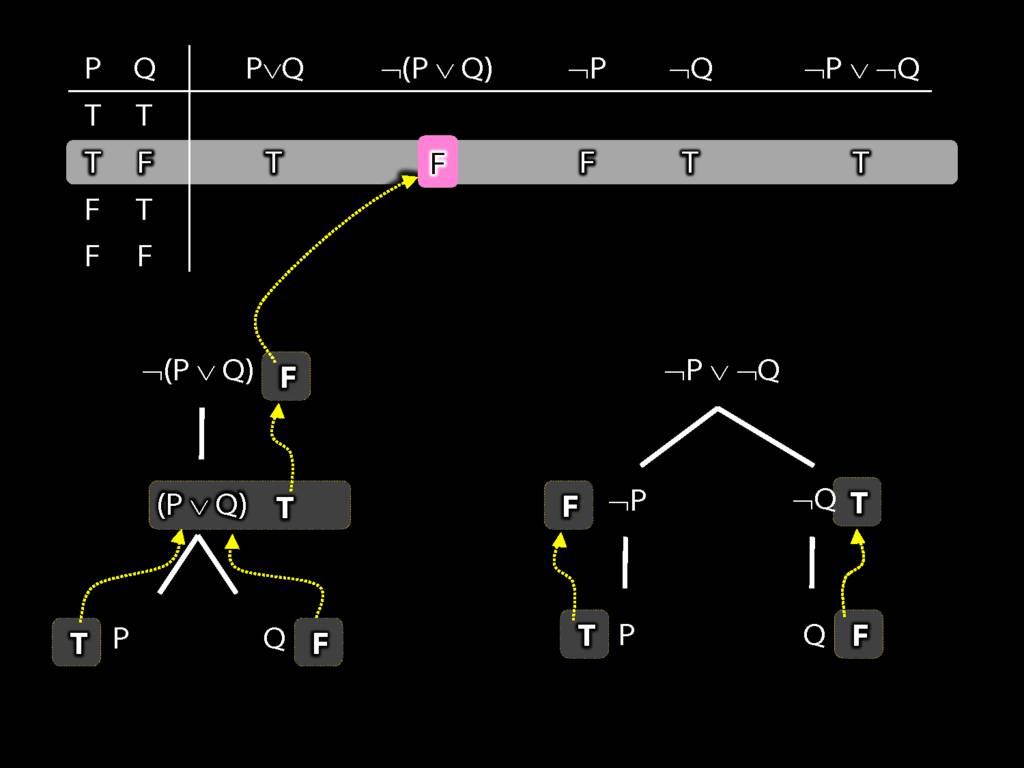
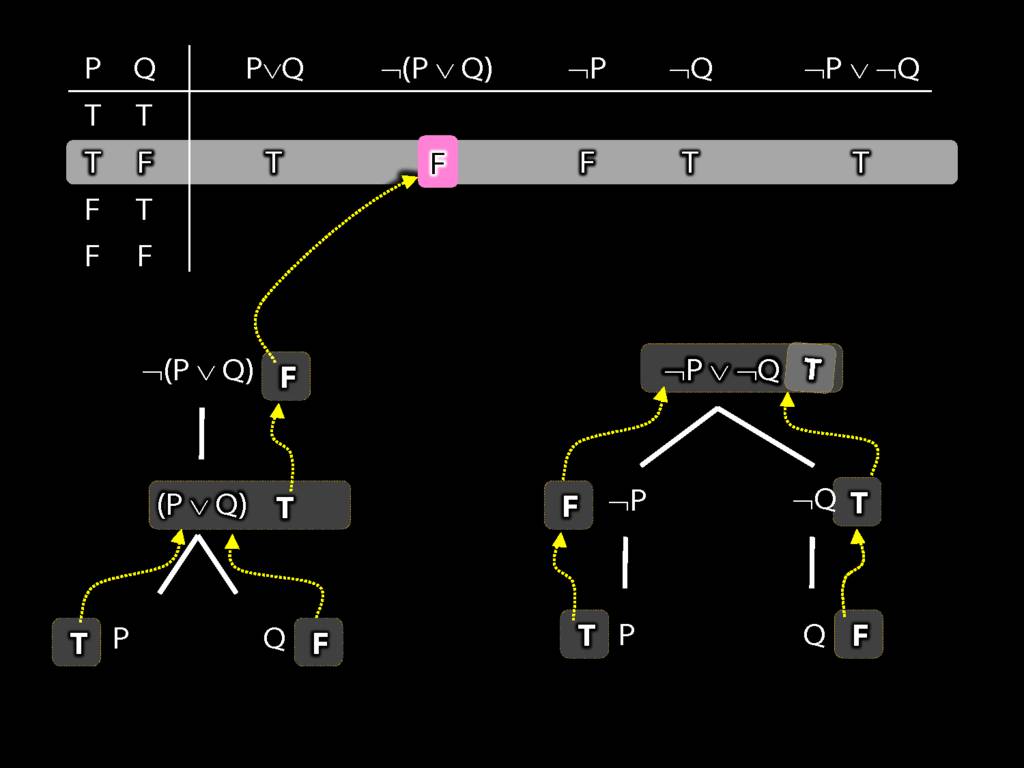
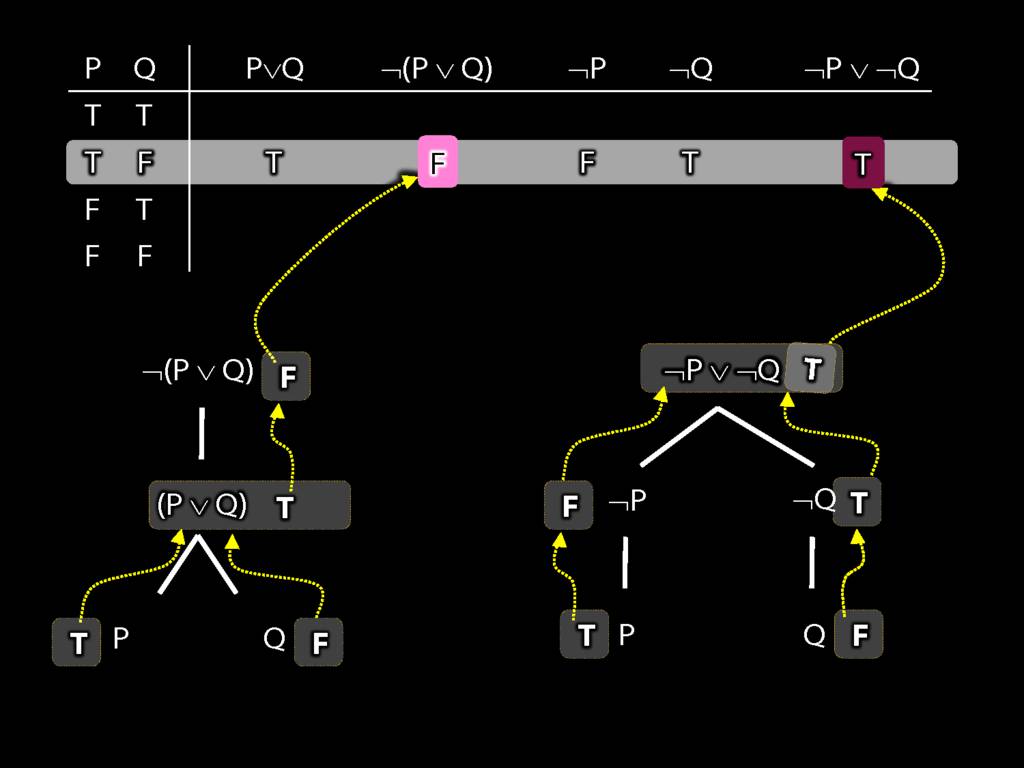
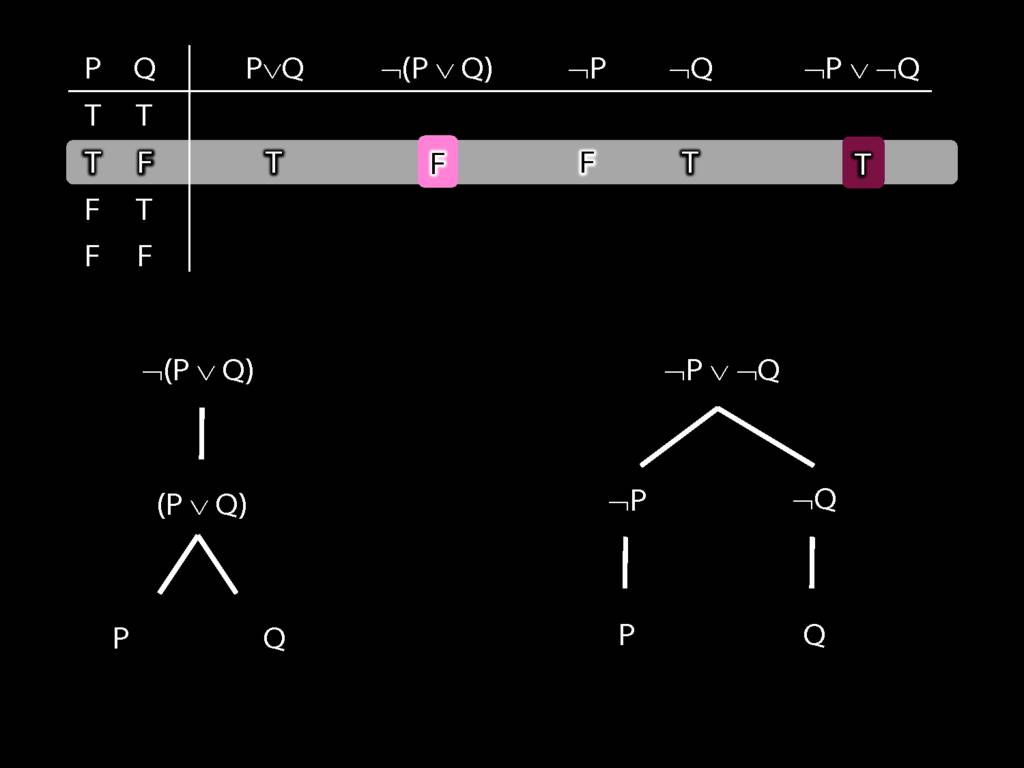
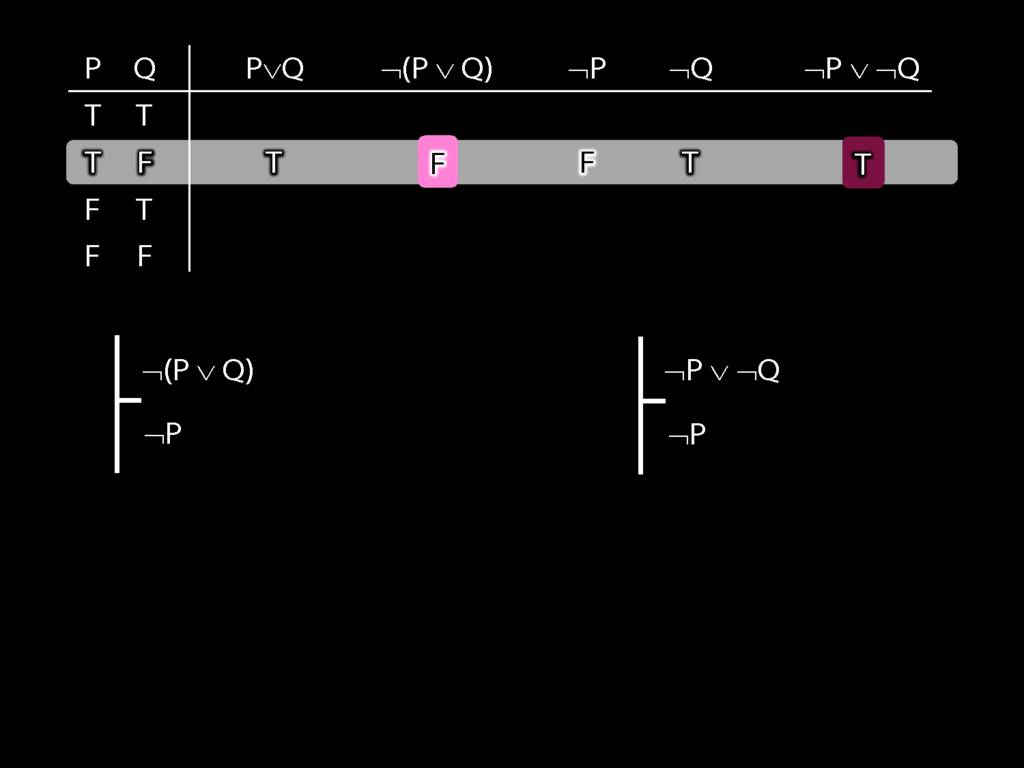
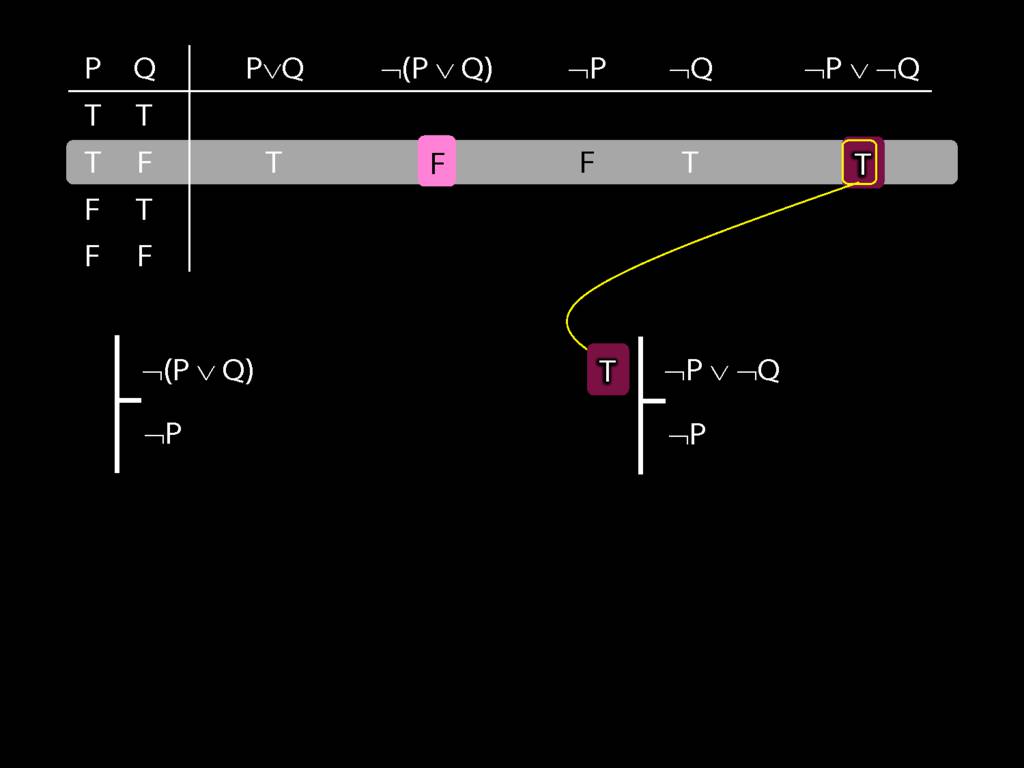
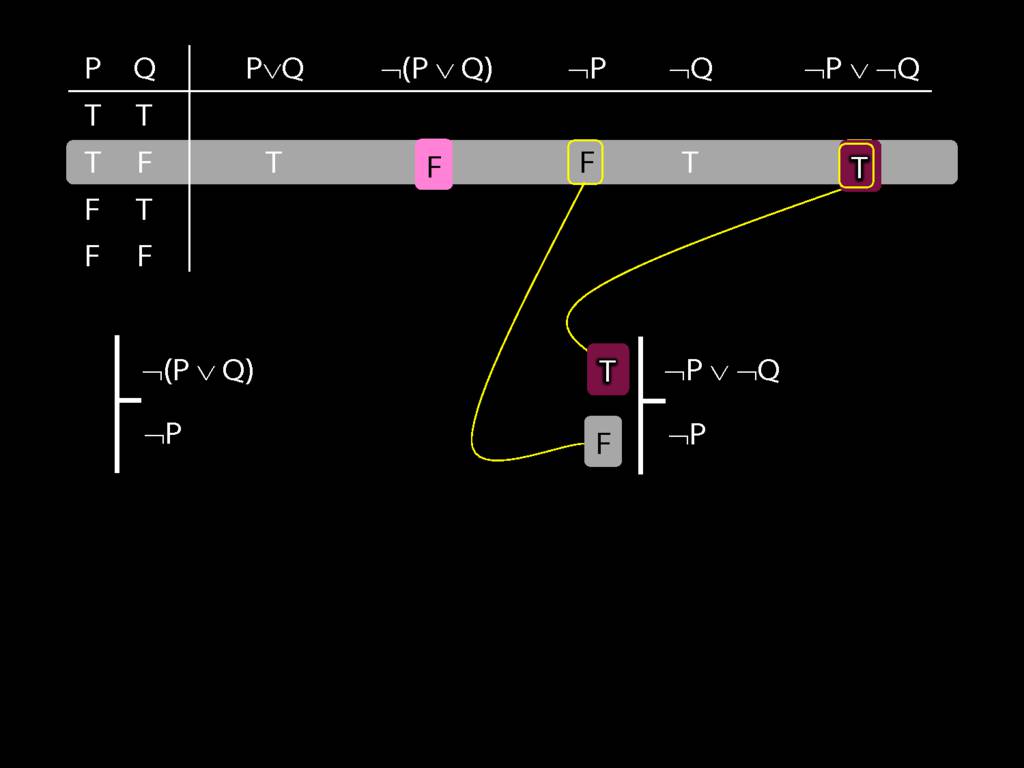
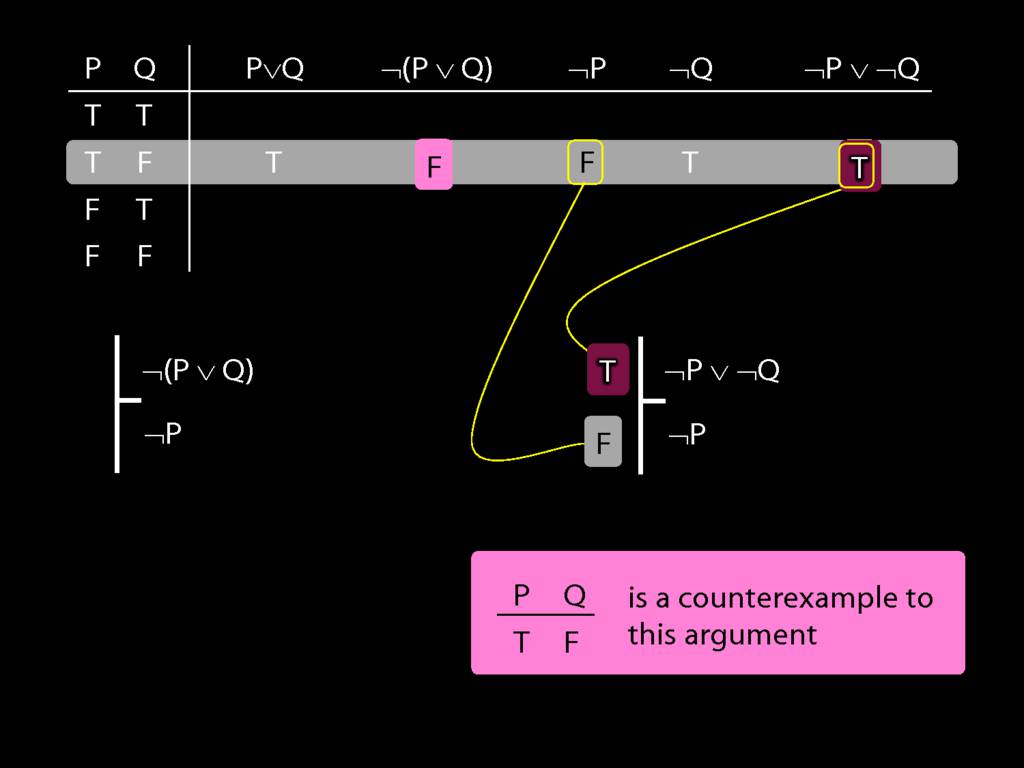
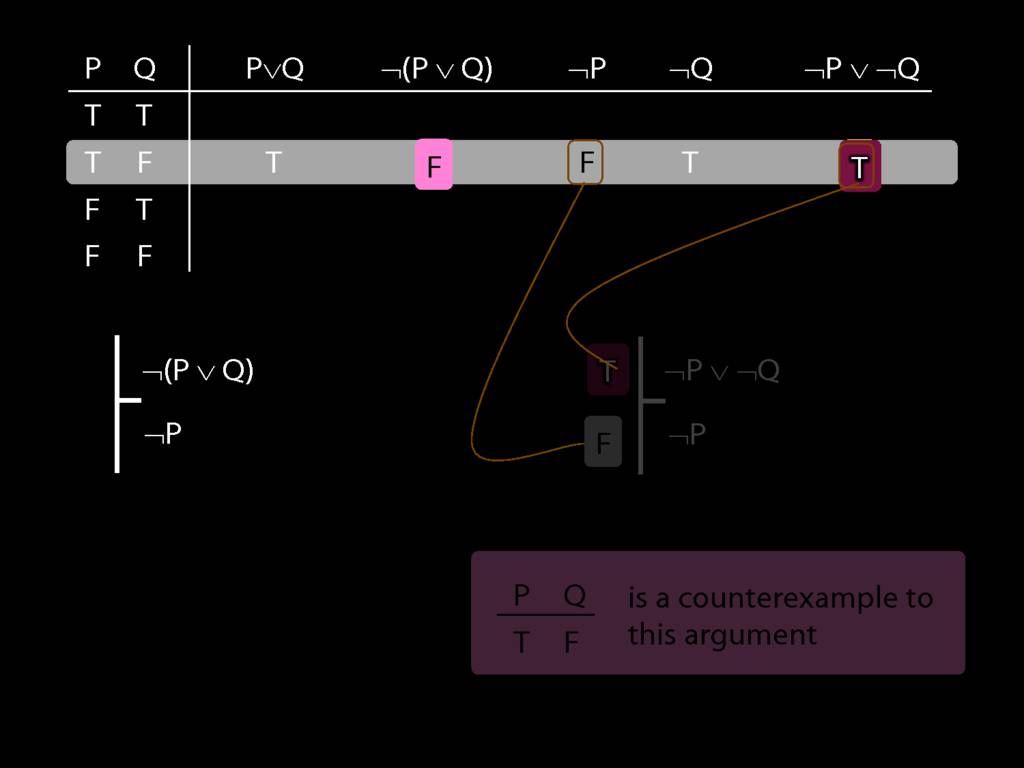
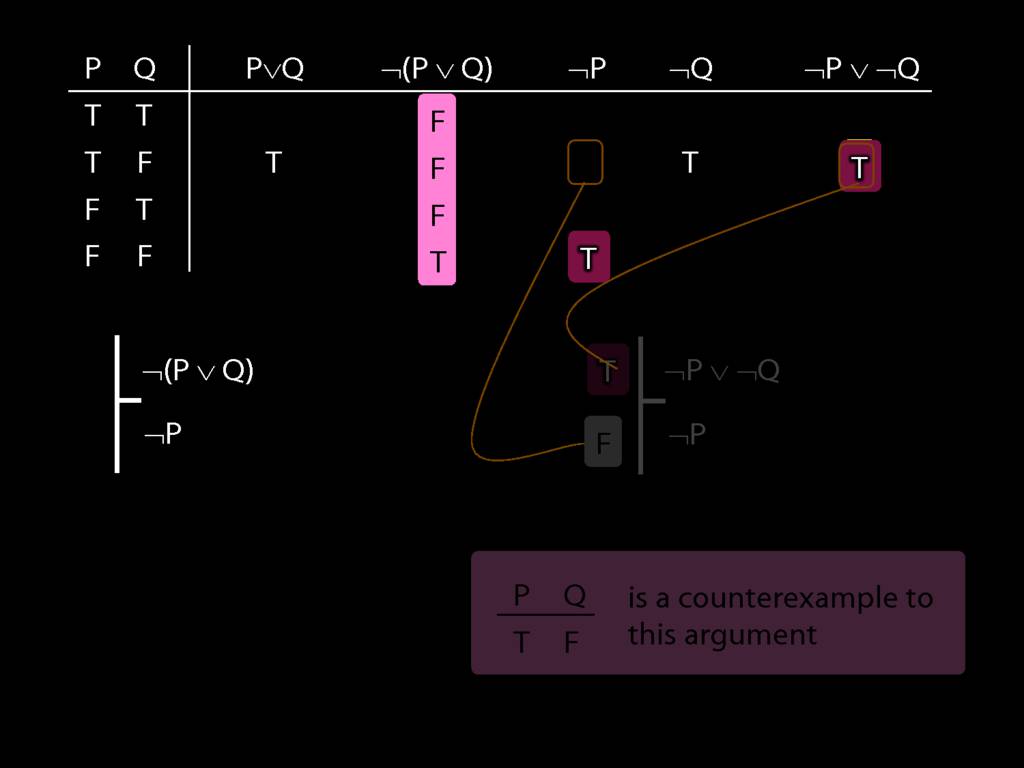
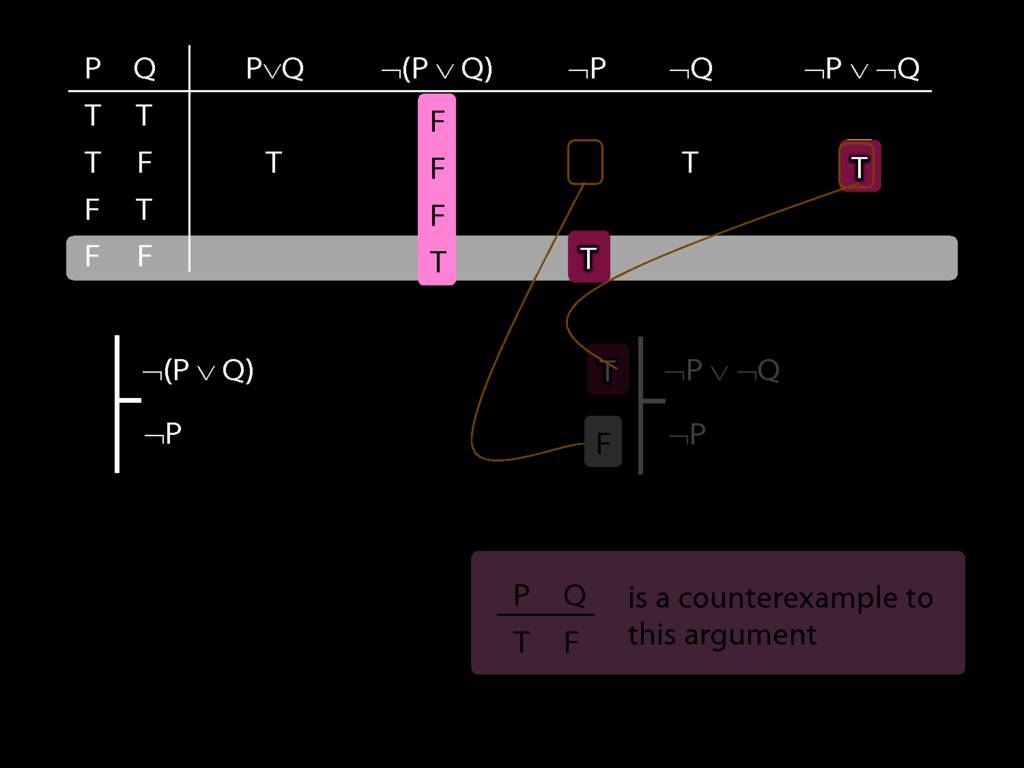
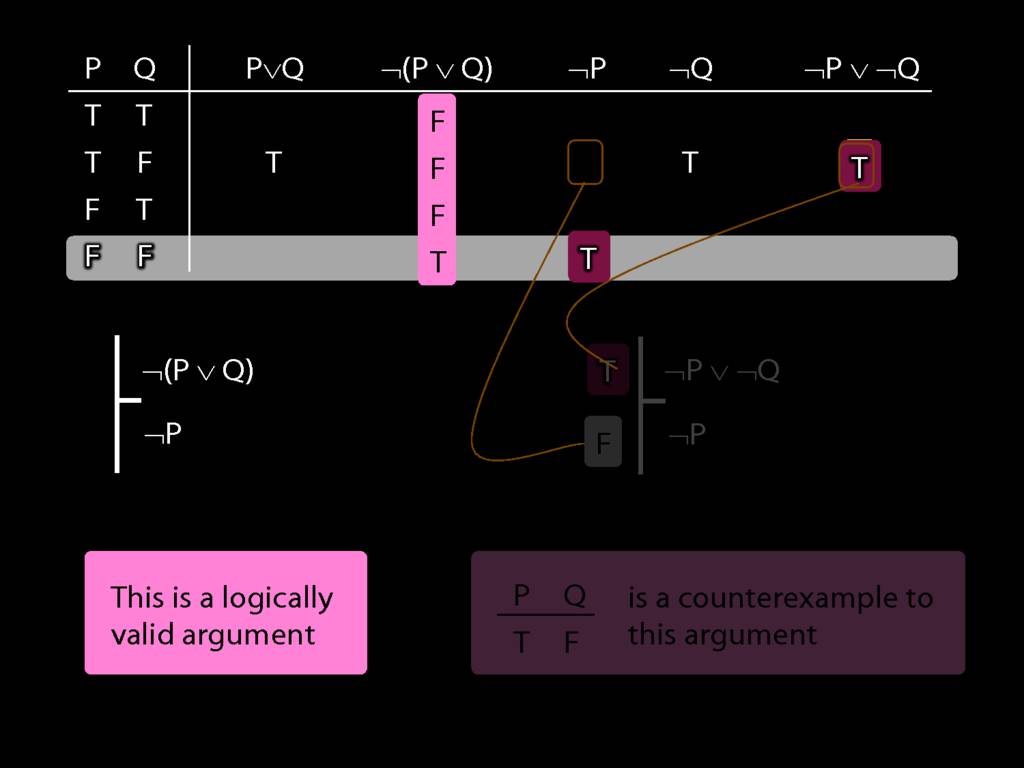
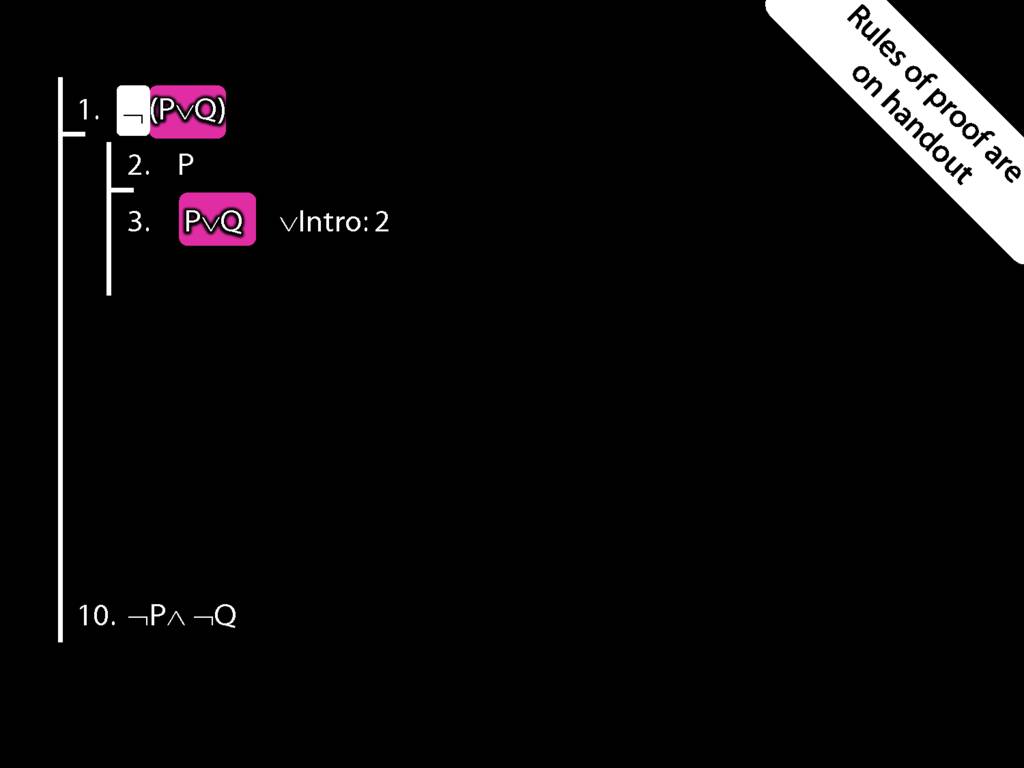
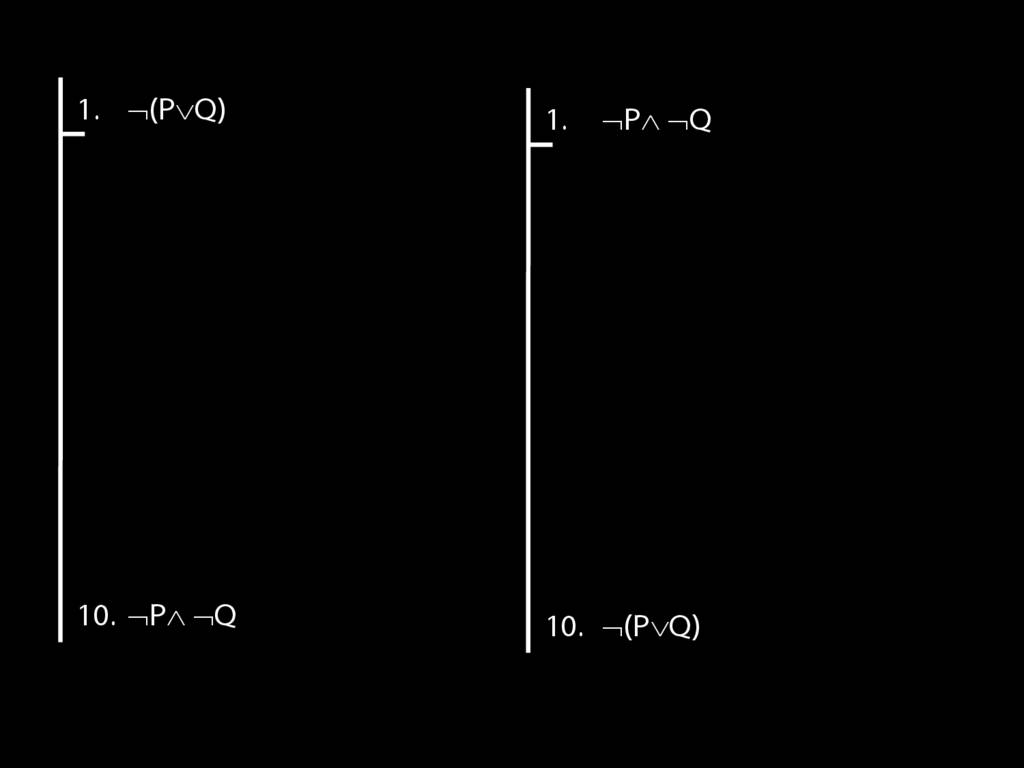
\section{Proof Example: ¬(P∨Q) therefore ¬P∧¬Q}
 
\section{Proof Example: ¬(P∨Q) therefore ¬P∧¬Q}
6.24--6.27
 

I Met a Philosopher

 
\section{I Met a Philosopher}
\emph{Reading:} §9.2, §9.3, §9.5
 
\section{I Met a Philosopher}
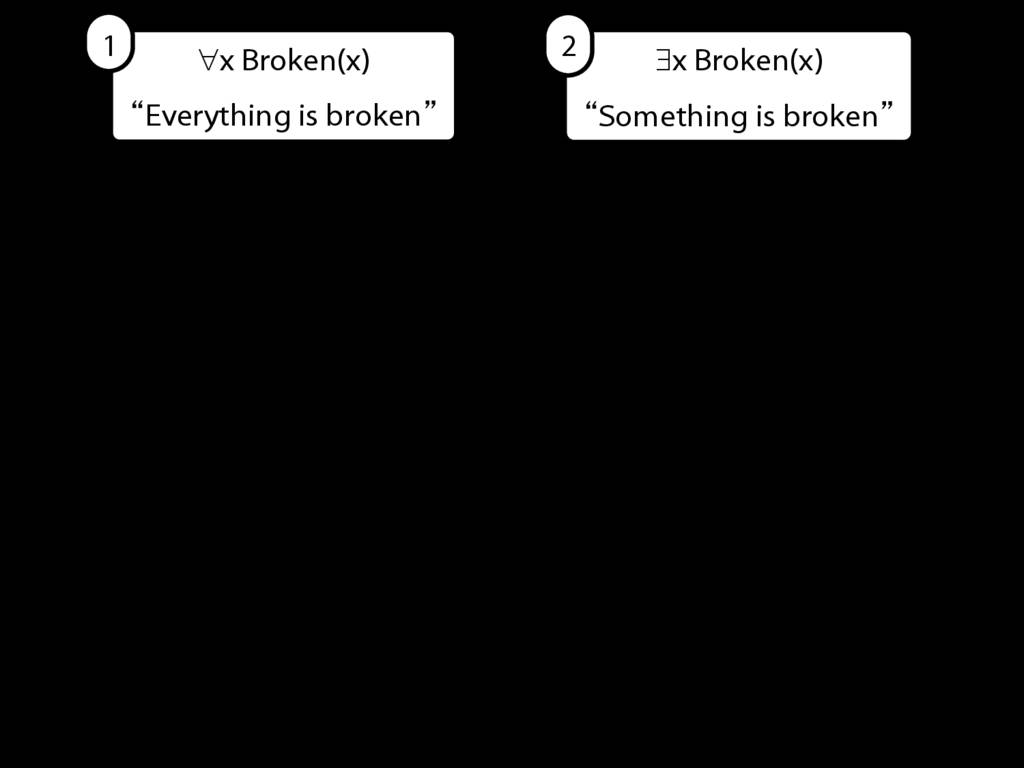
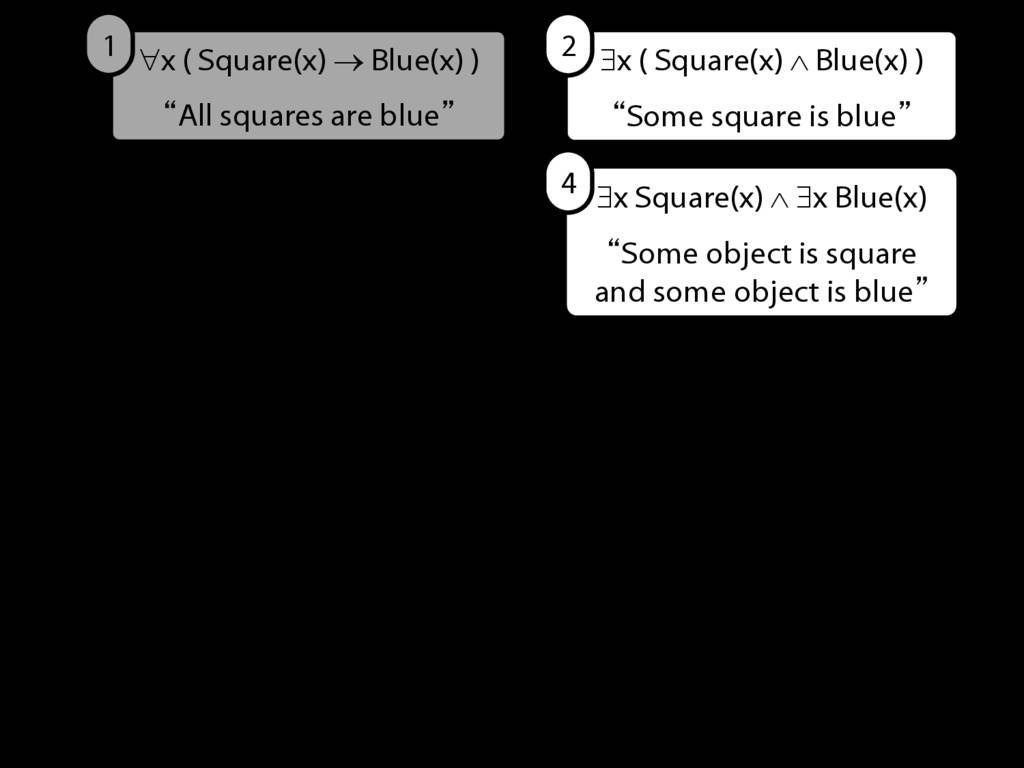
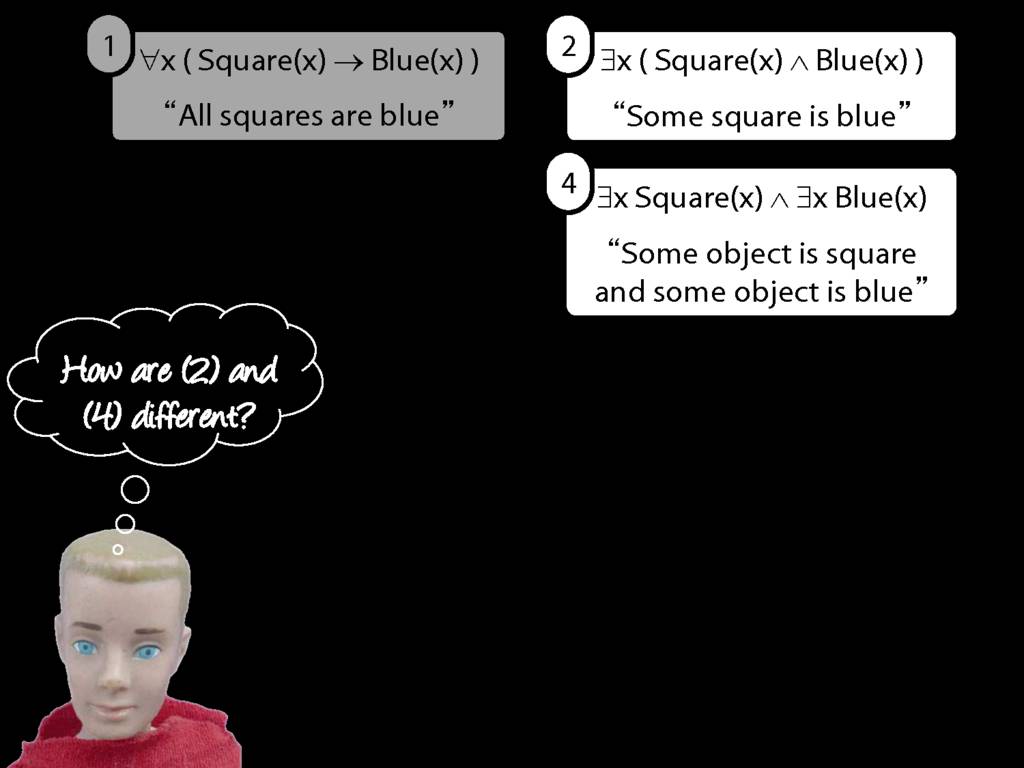
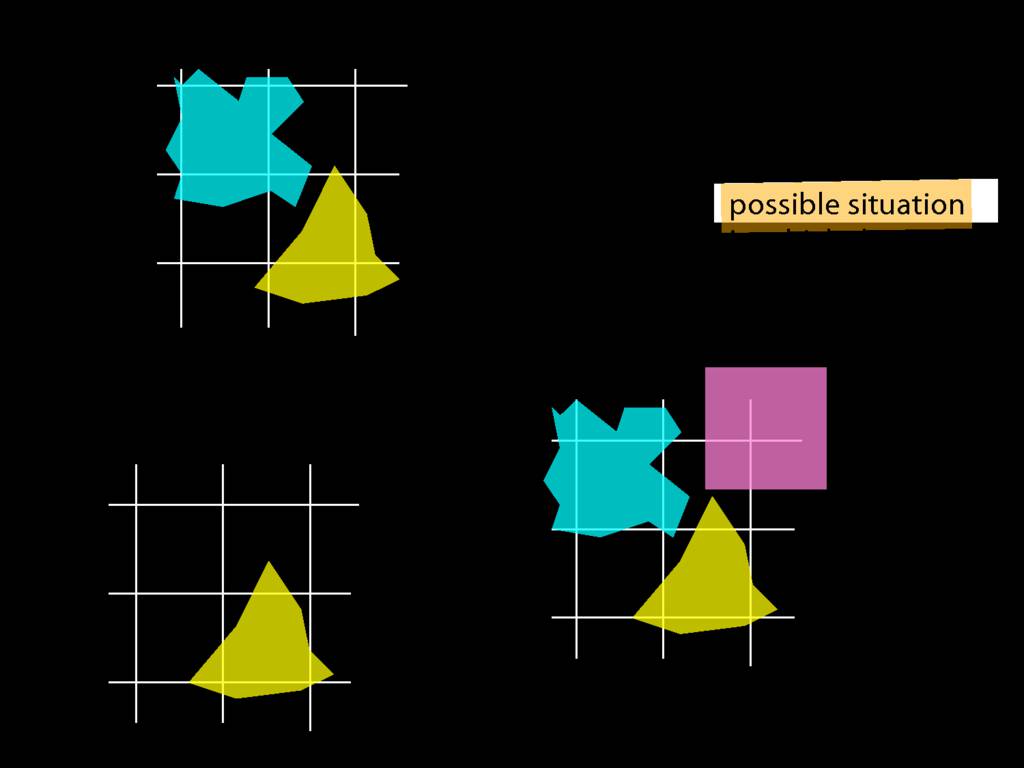
You may remember the two basic forms of quantified sentences we've been considering so far. These are quite limiting. What happens if we want to say, not that everything is broken, but that everything of mine is broken. And how could we say, not just that something is broken, but that a red square is broken (say)?
 

All circles are broken.

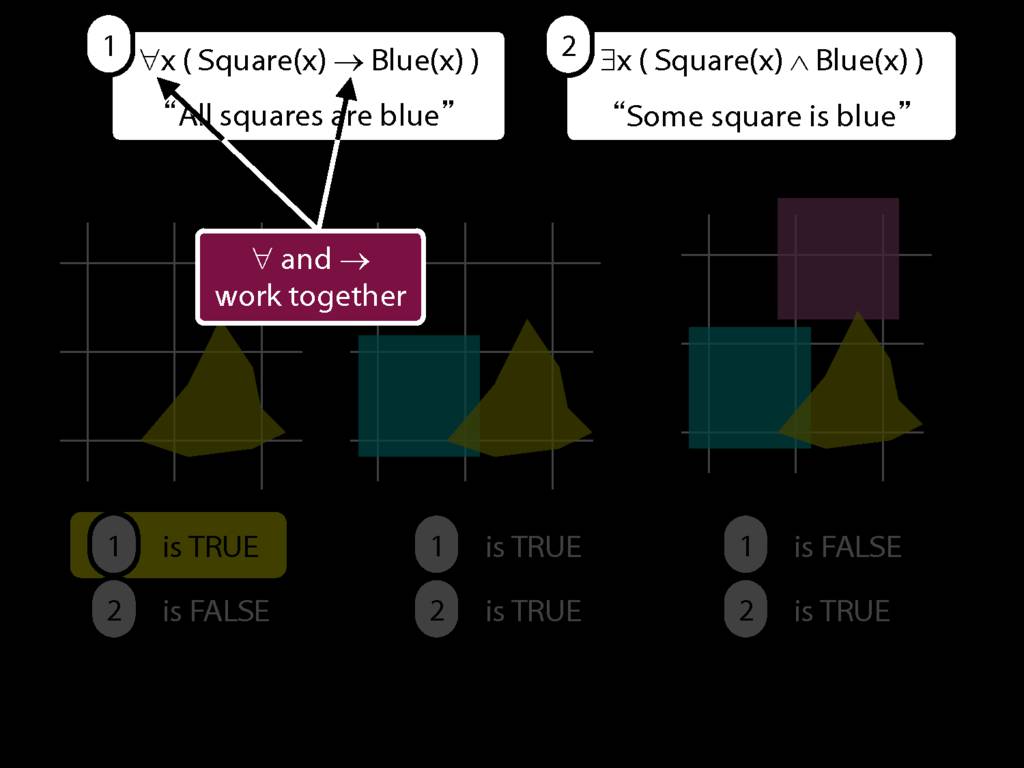
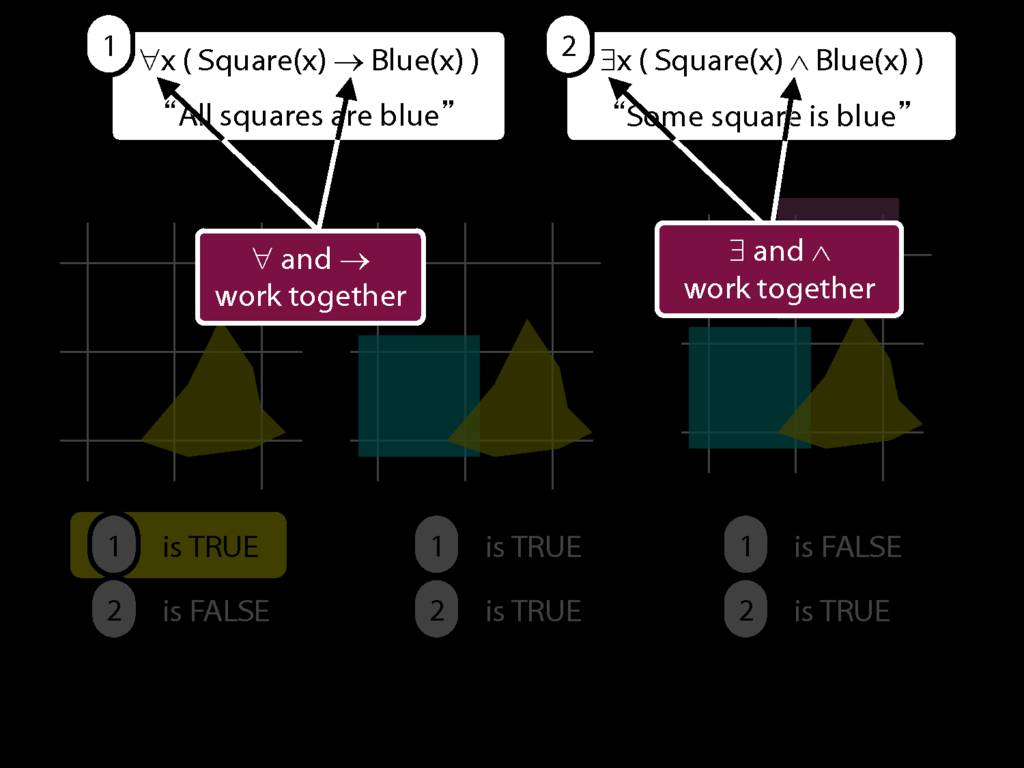
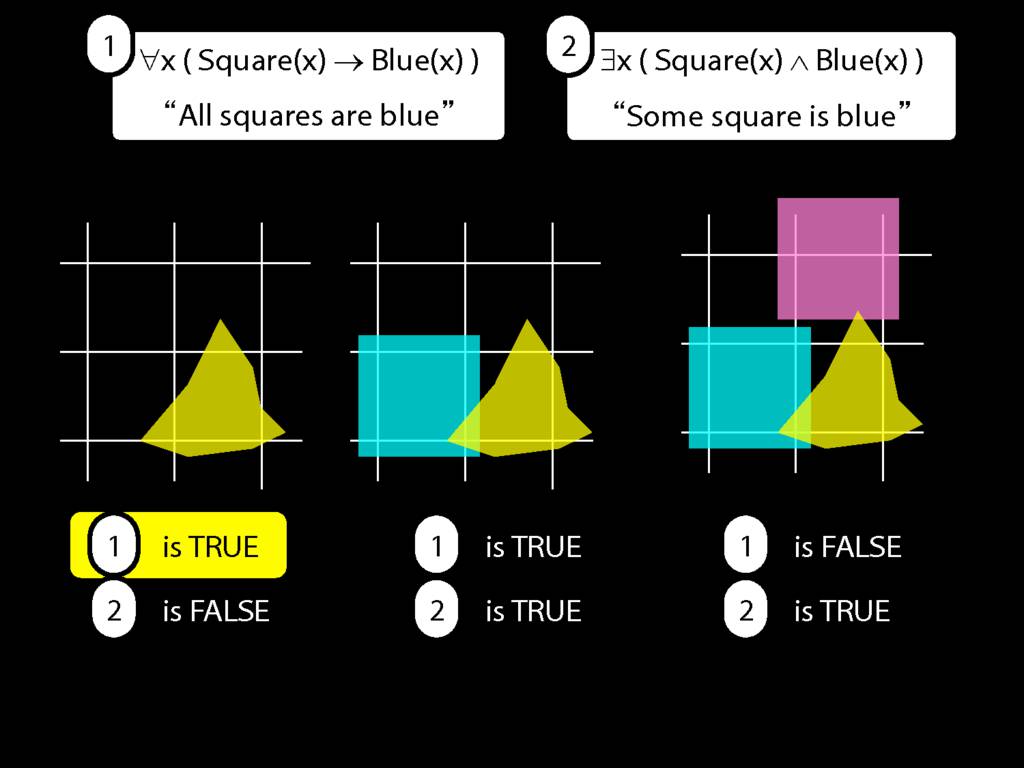
∀x( Circle(x) → Broken(x) )

All idols are dead.

∀x( Idol(x) → Dead(x) )

All who wander are lost.

∀x( Wanderer(x) → Lost(x) )

A square is broken

Something is square and broken

∃x ( Square(x) ∧ Broken(x))

These are variables. I have a terrible conscience about variables because I've been talking about them without explaining what they are.

A red square is broken

Something is red and square and broken

∃x ( Red(x) ∧ Square(x) ∧ Broken(x) )

9.1 odd numbers only
9.2 even numbers only
9.4
9.5
9.8
9.9
9.10
9.12
9.8
9.9
9.10
9.12
9.13
 

Scope and Quantifiers

 
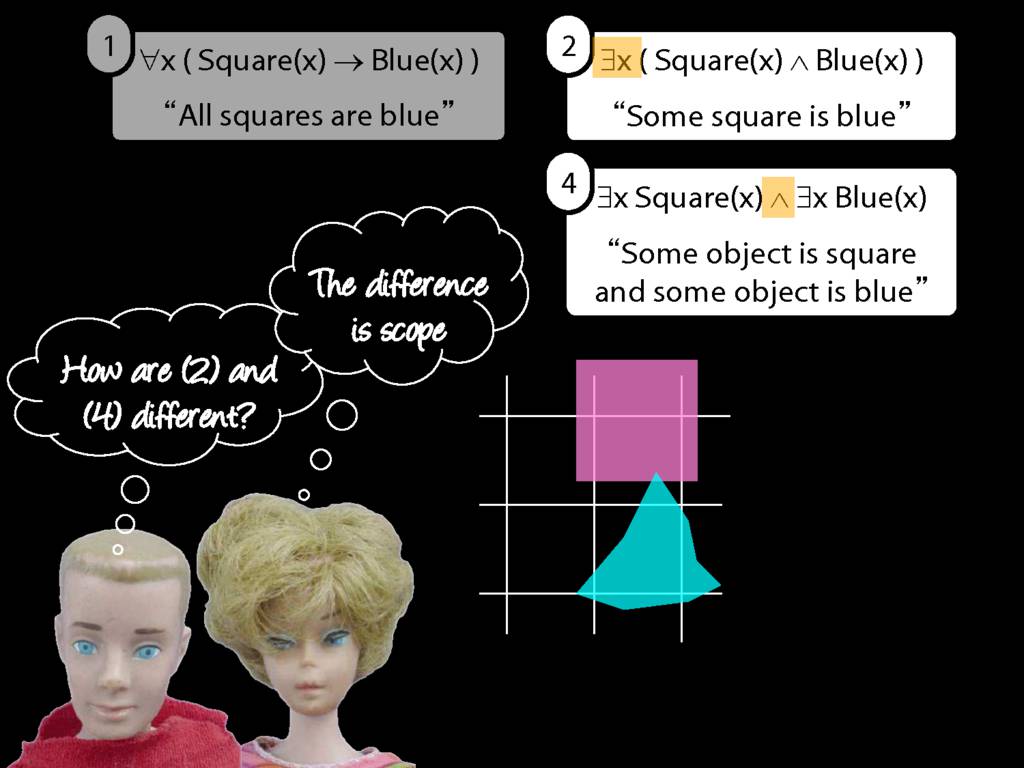
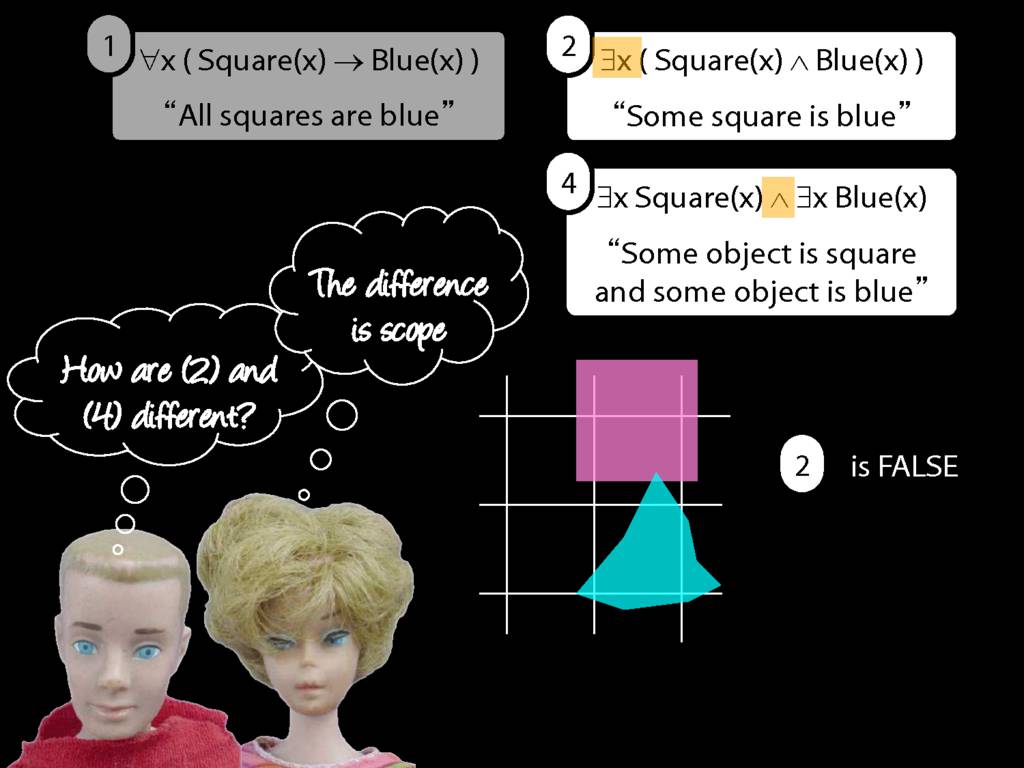
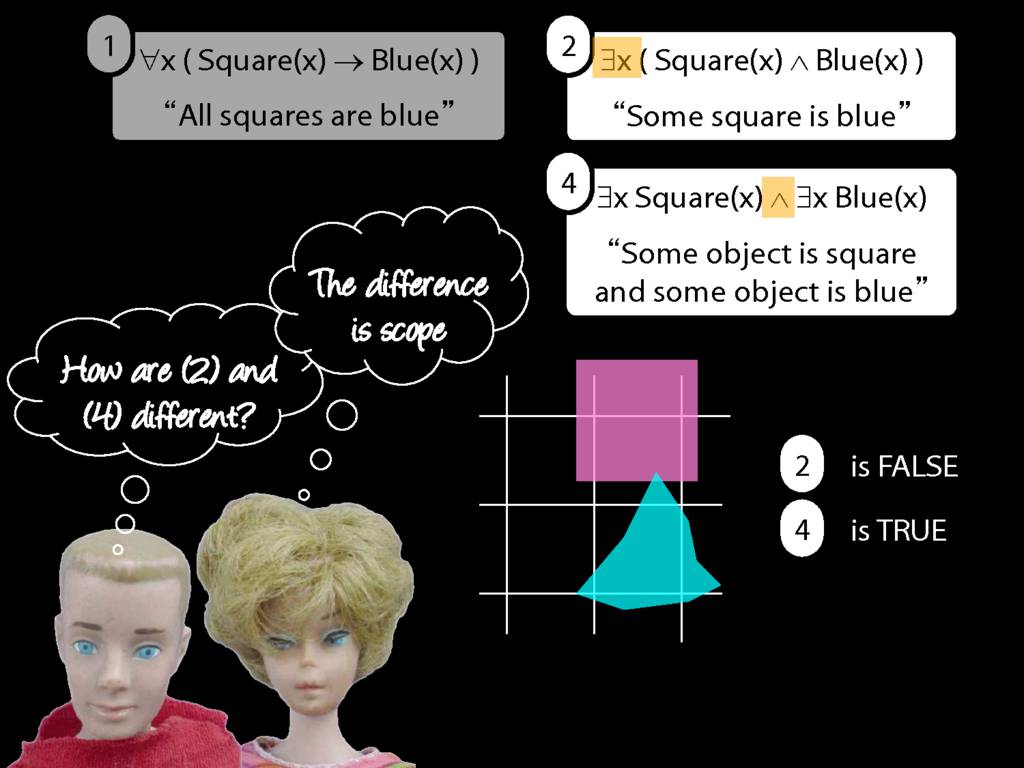
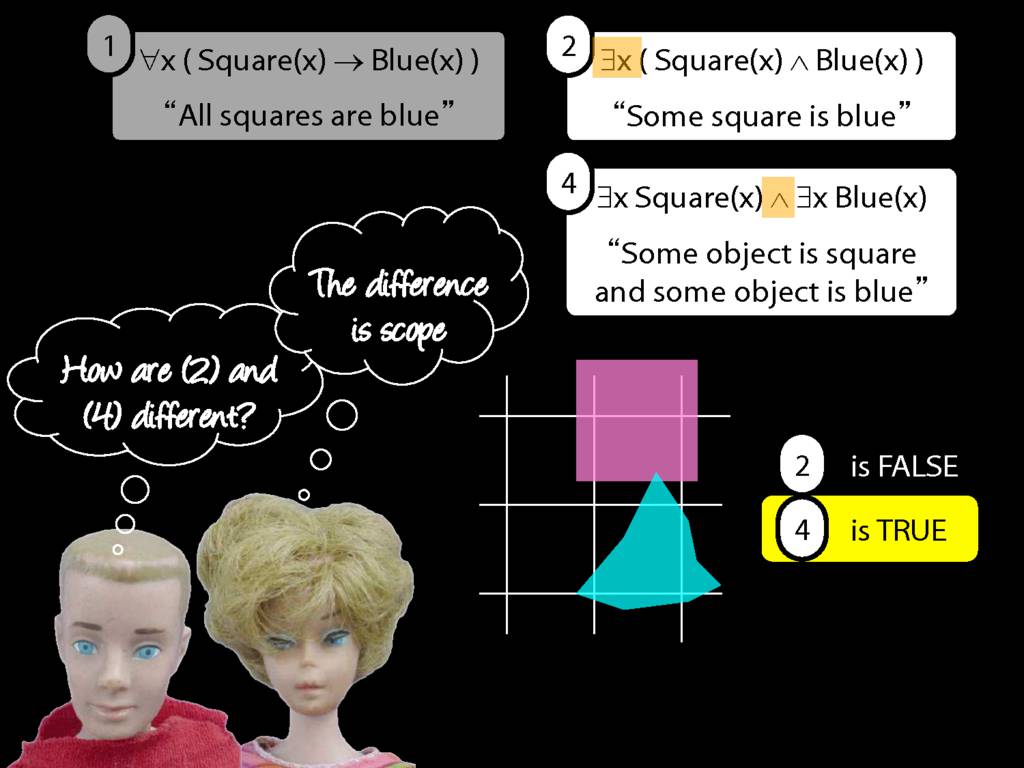
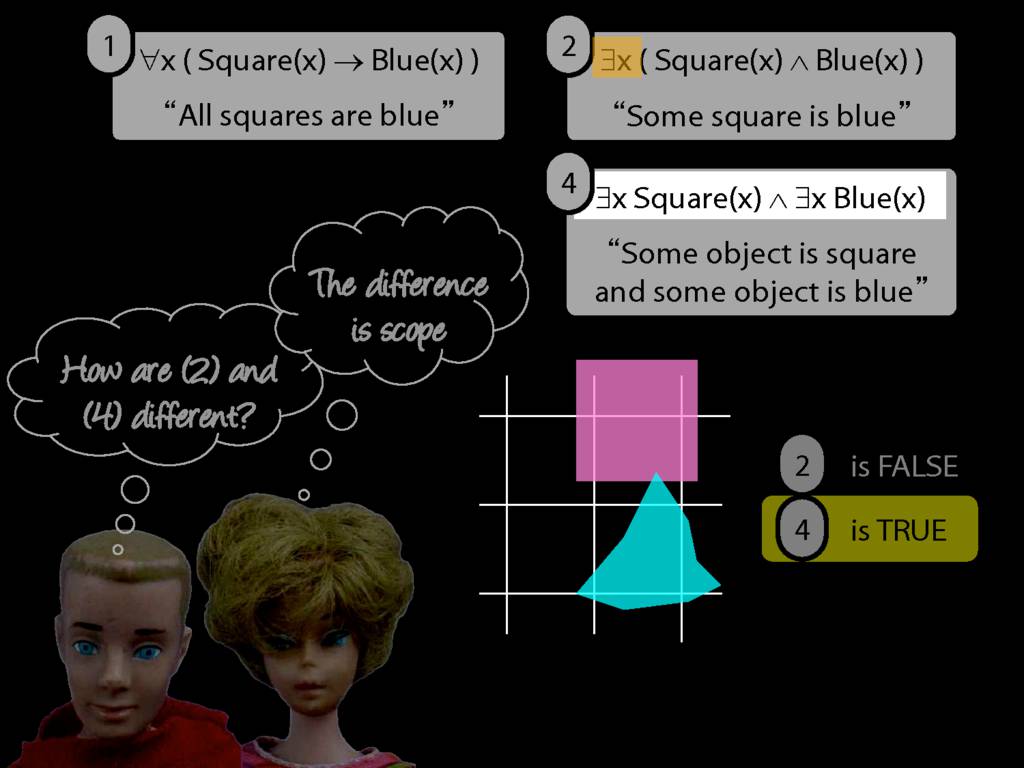
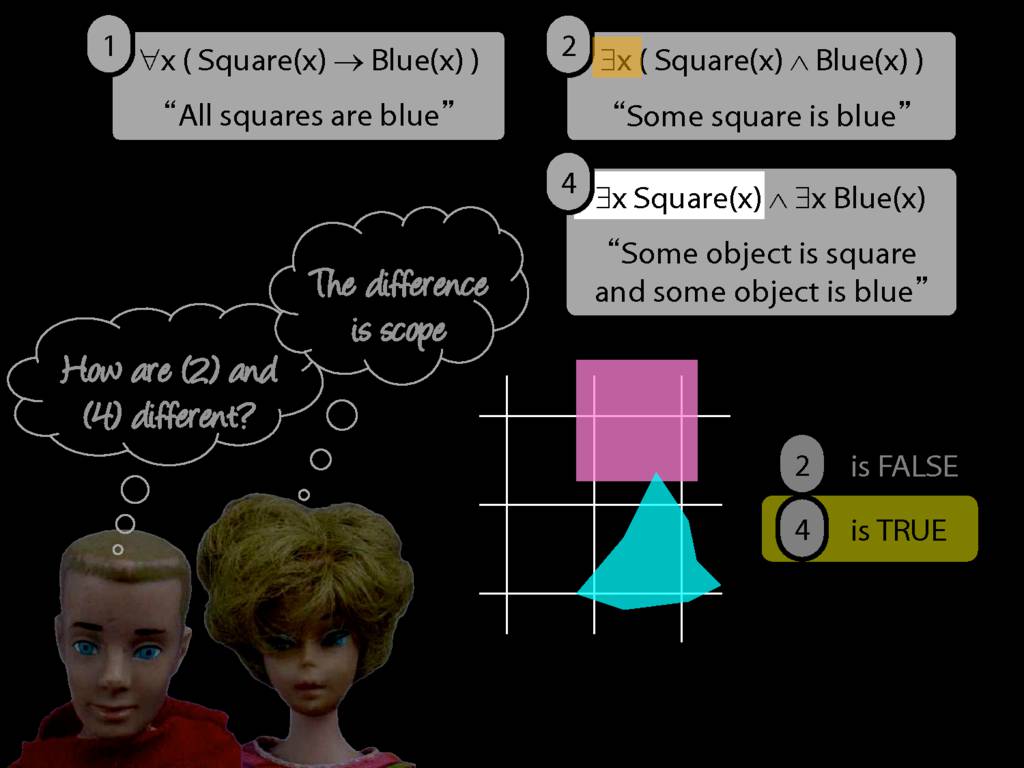
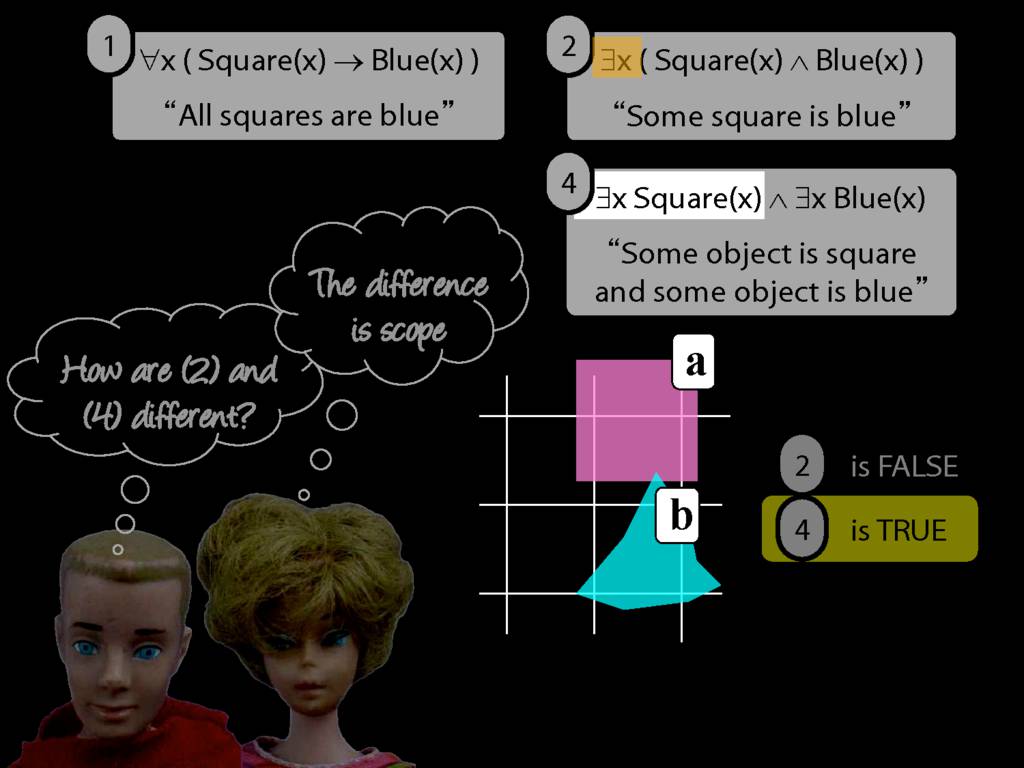
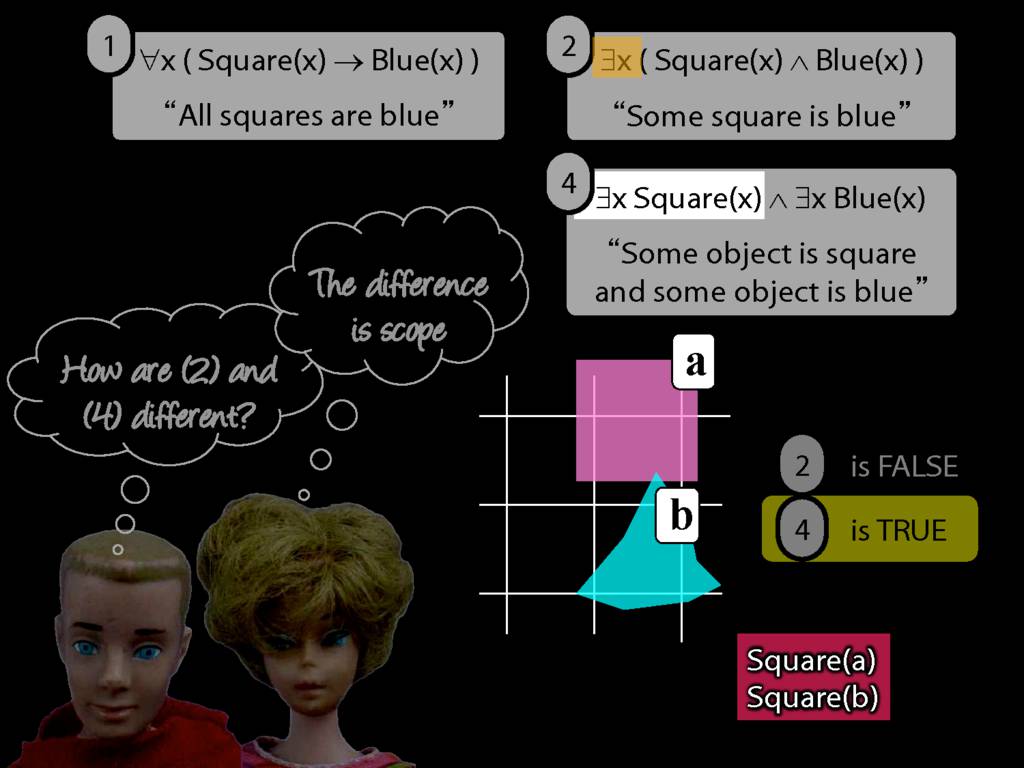
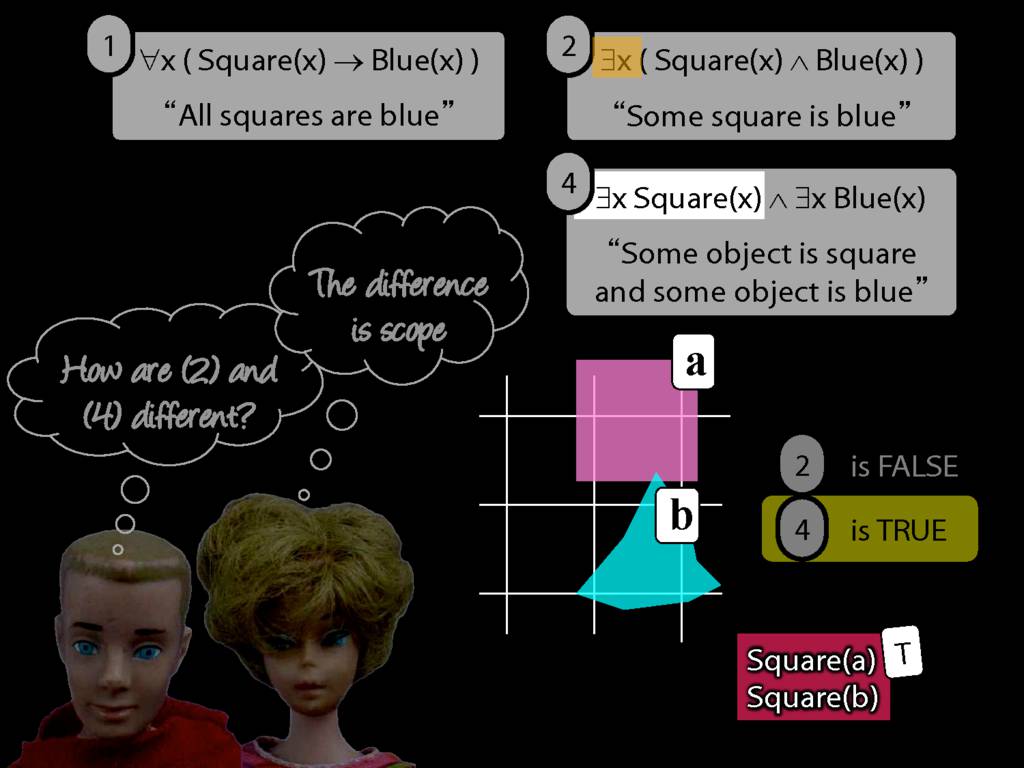
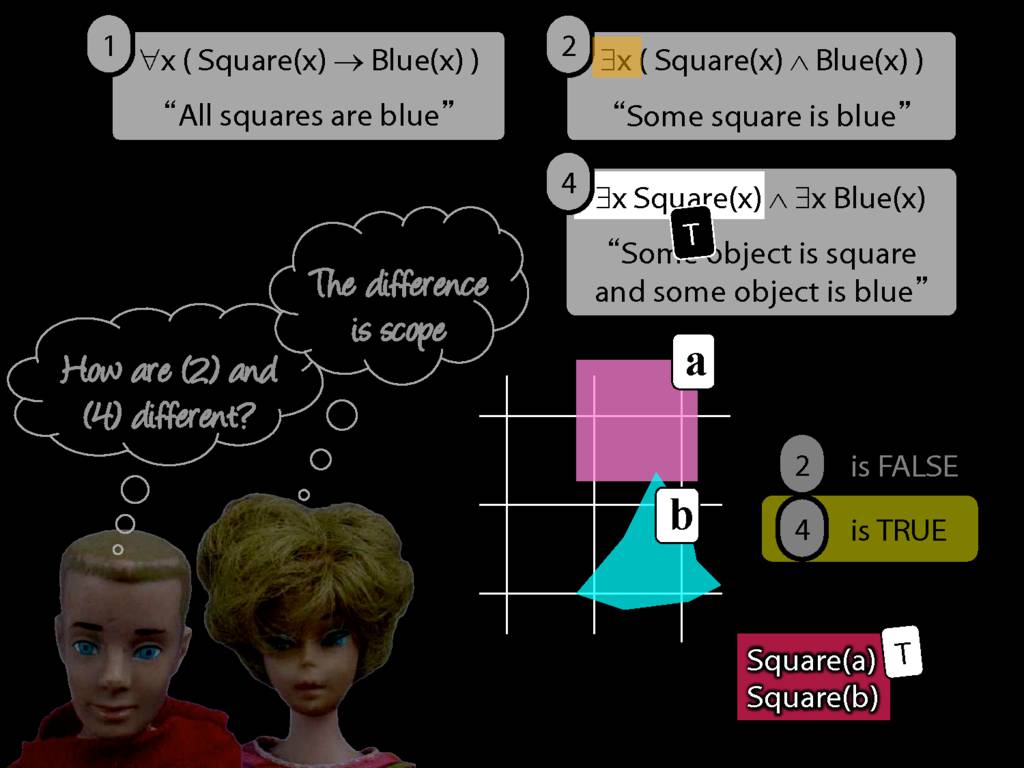
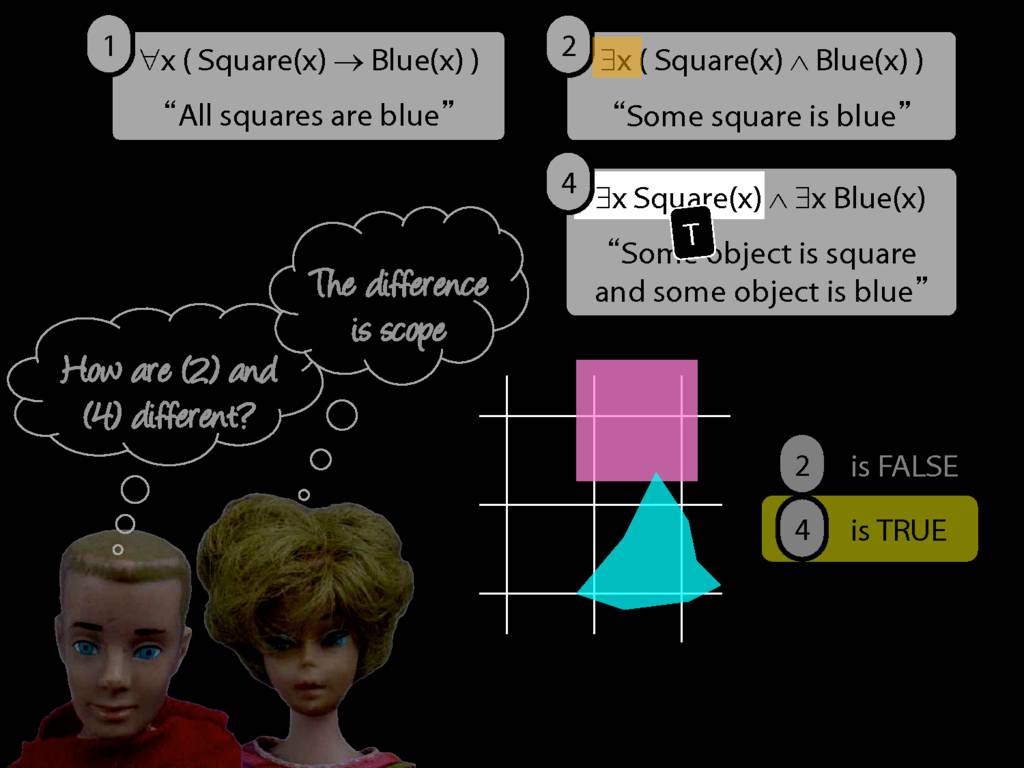
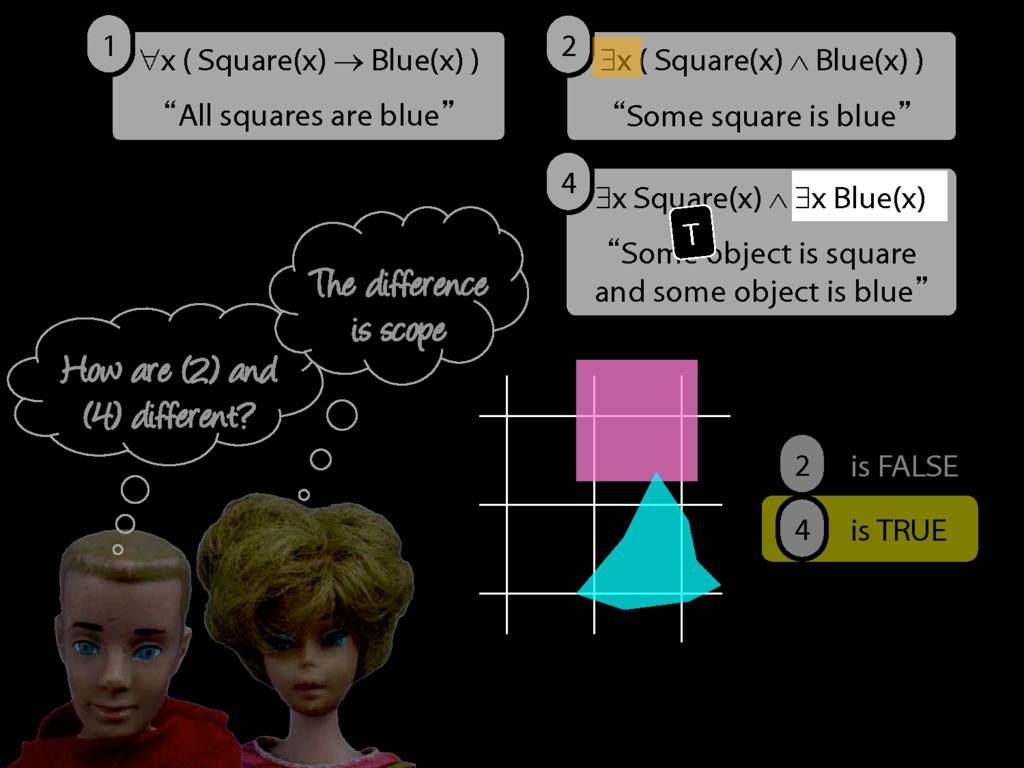
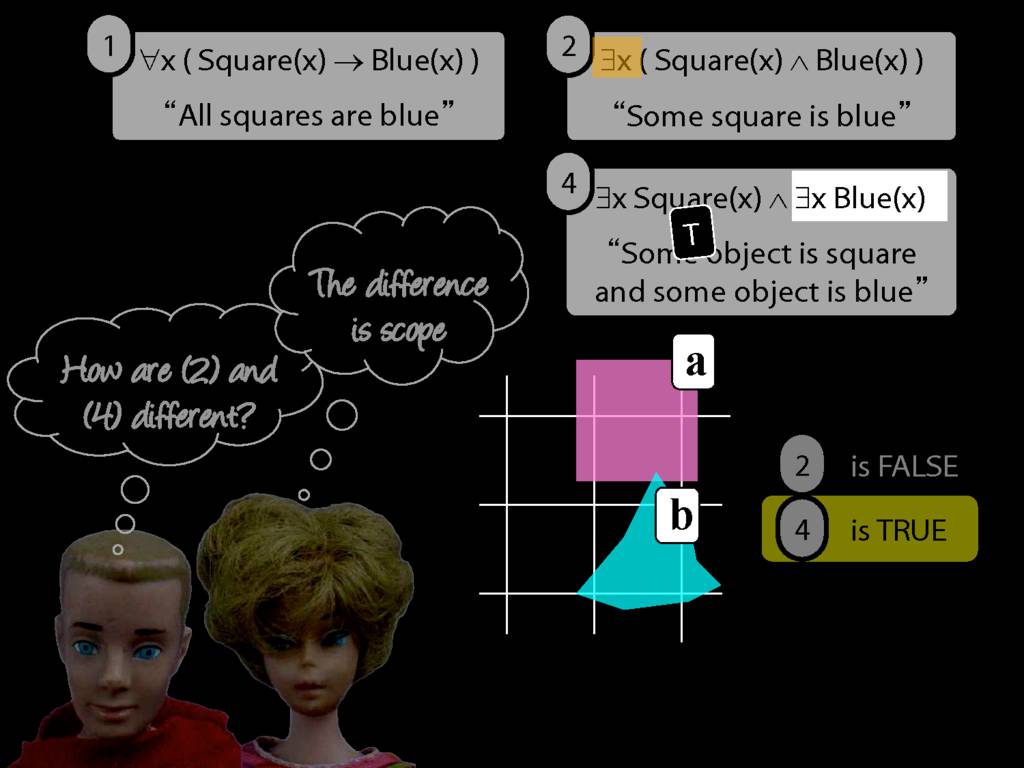
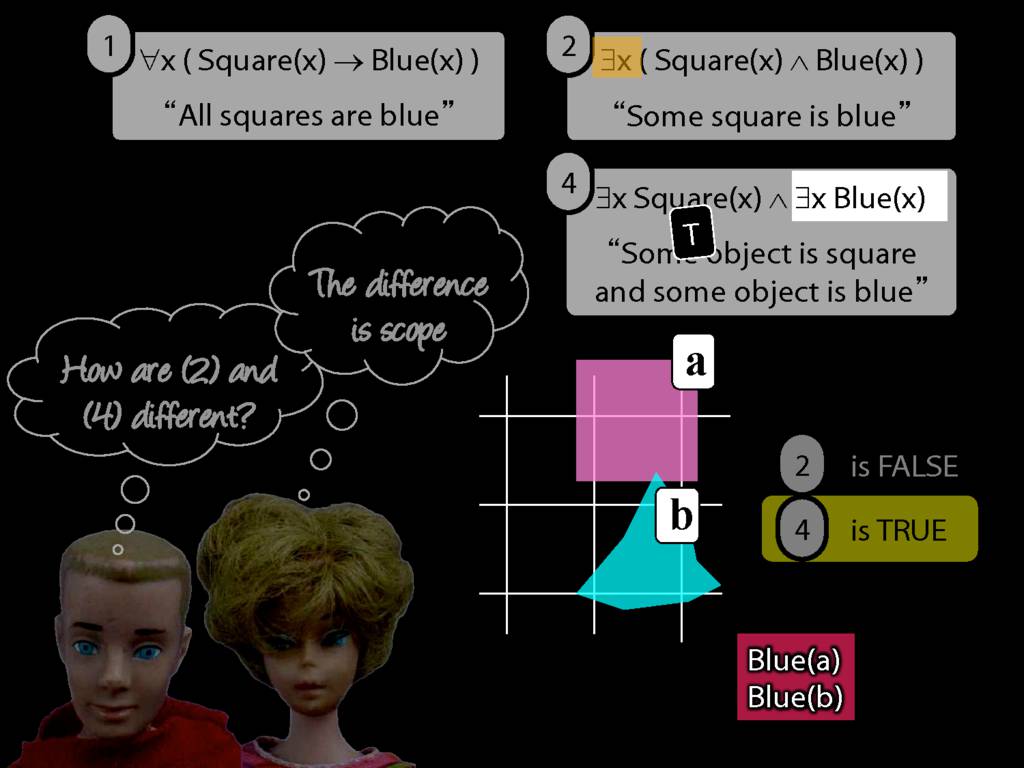
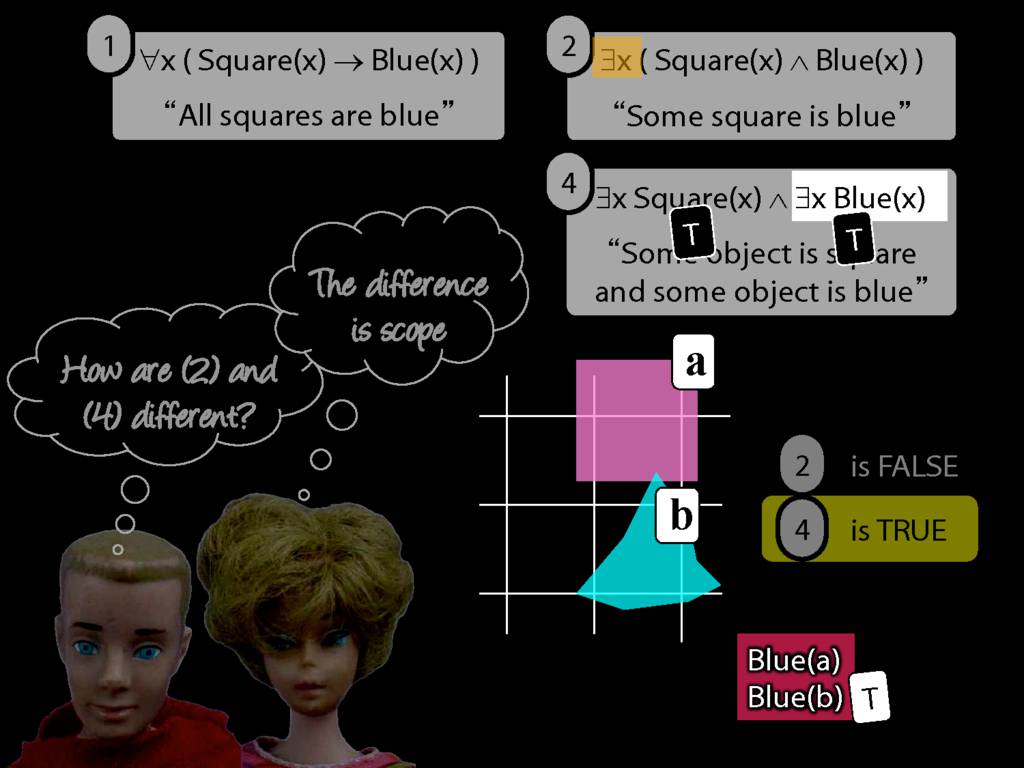
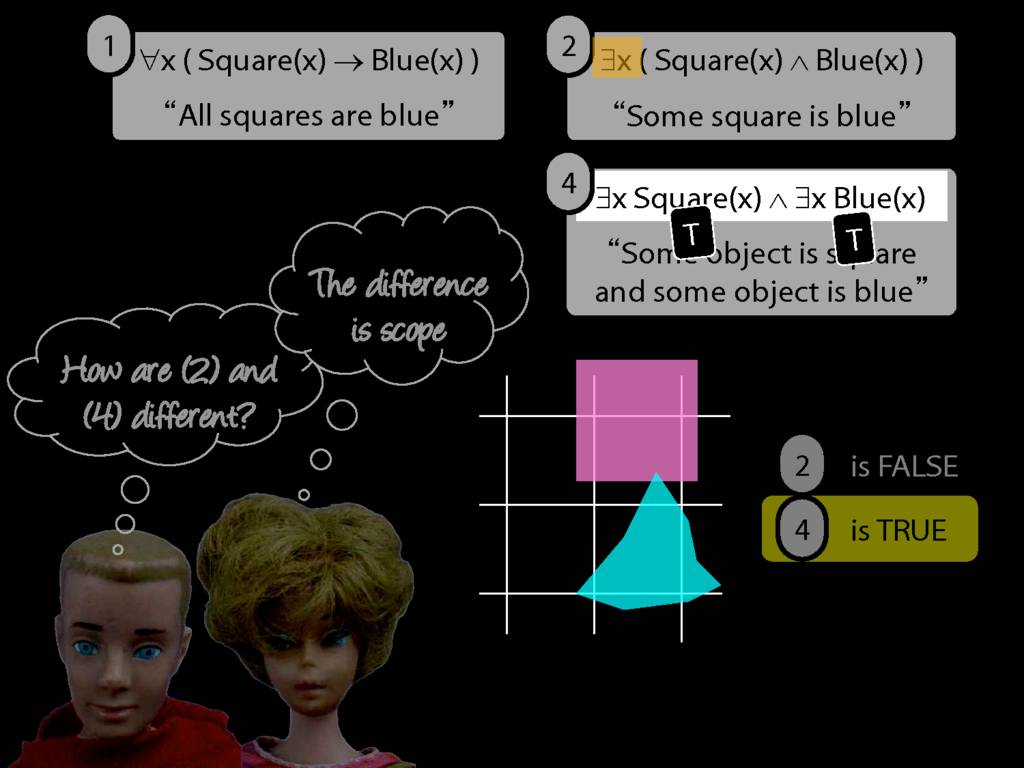
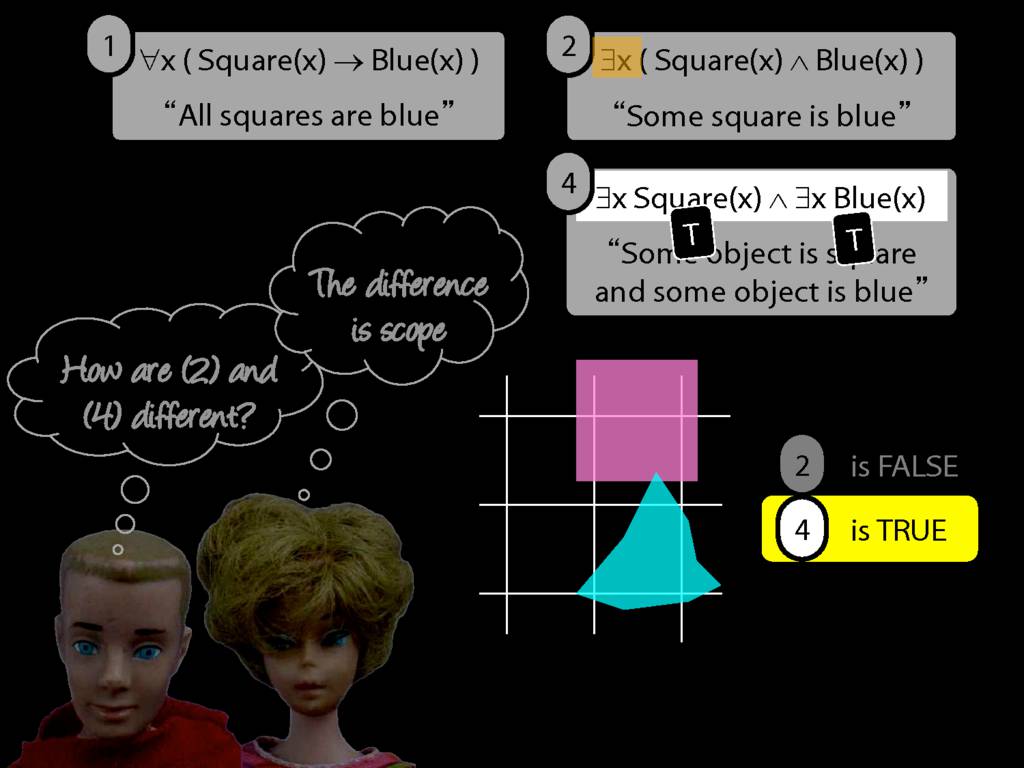
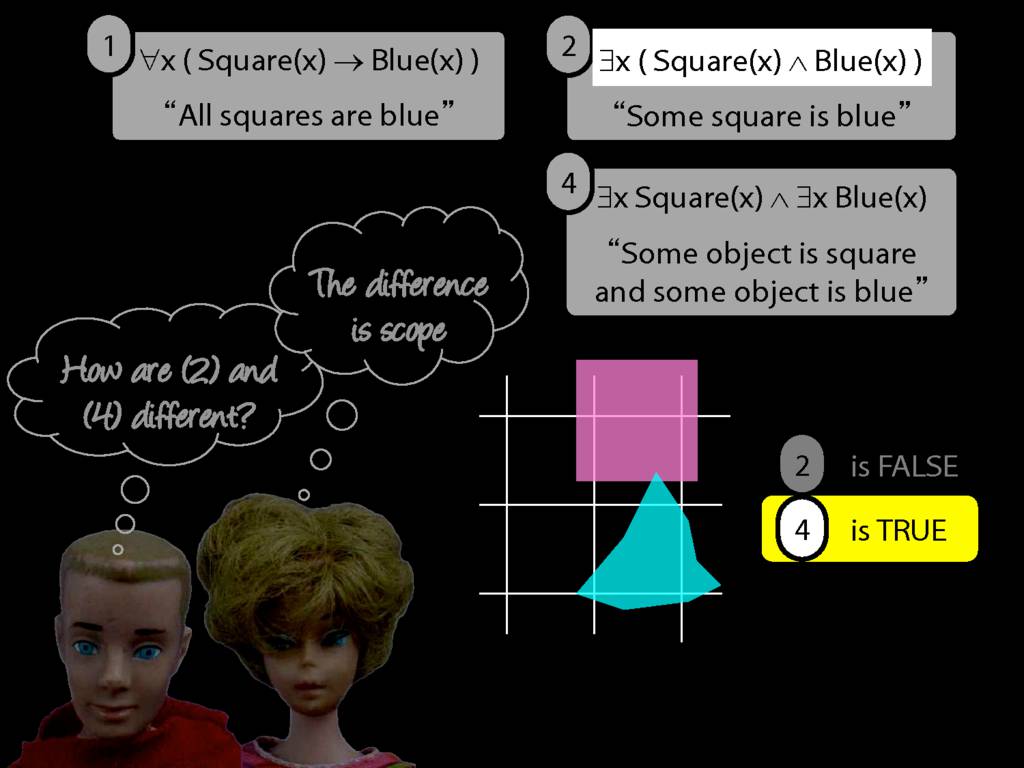
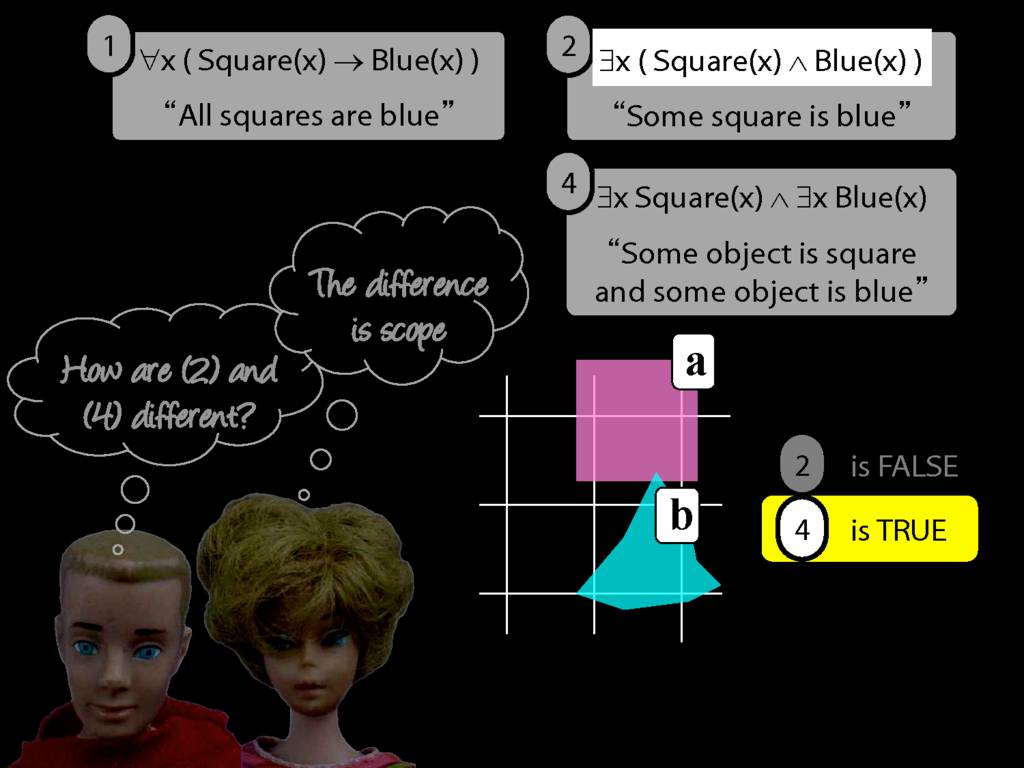
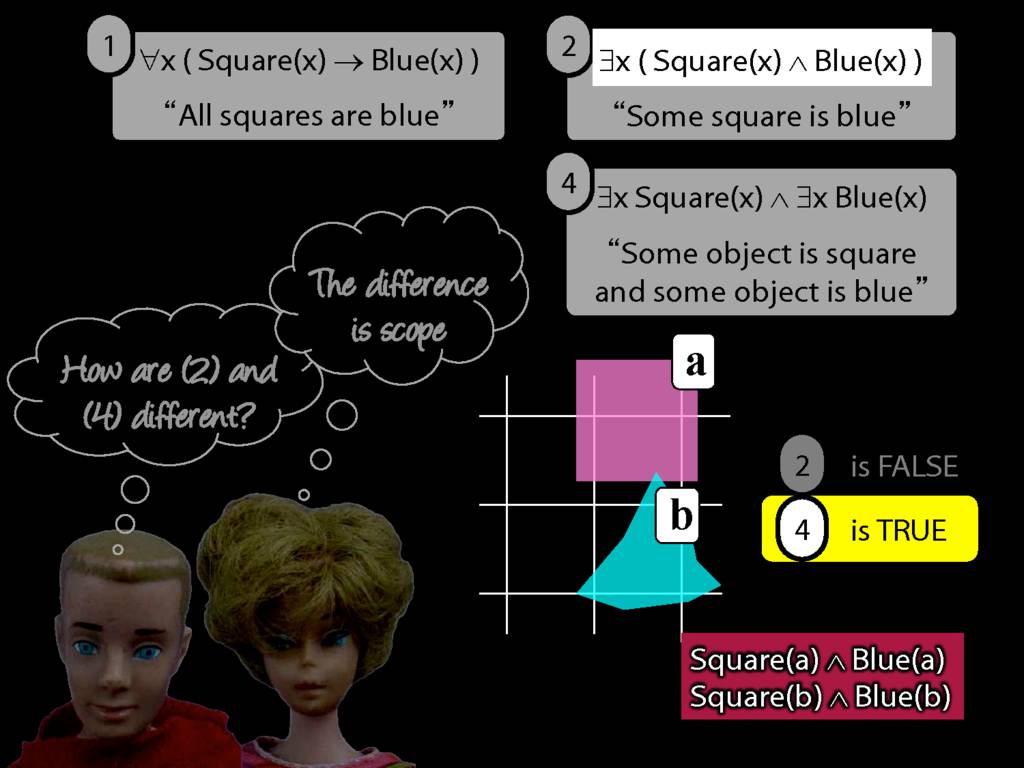
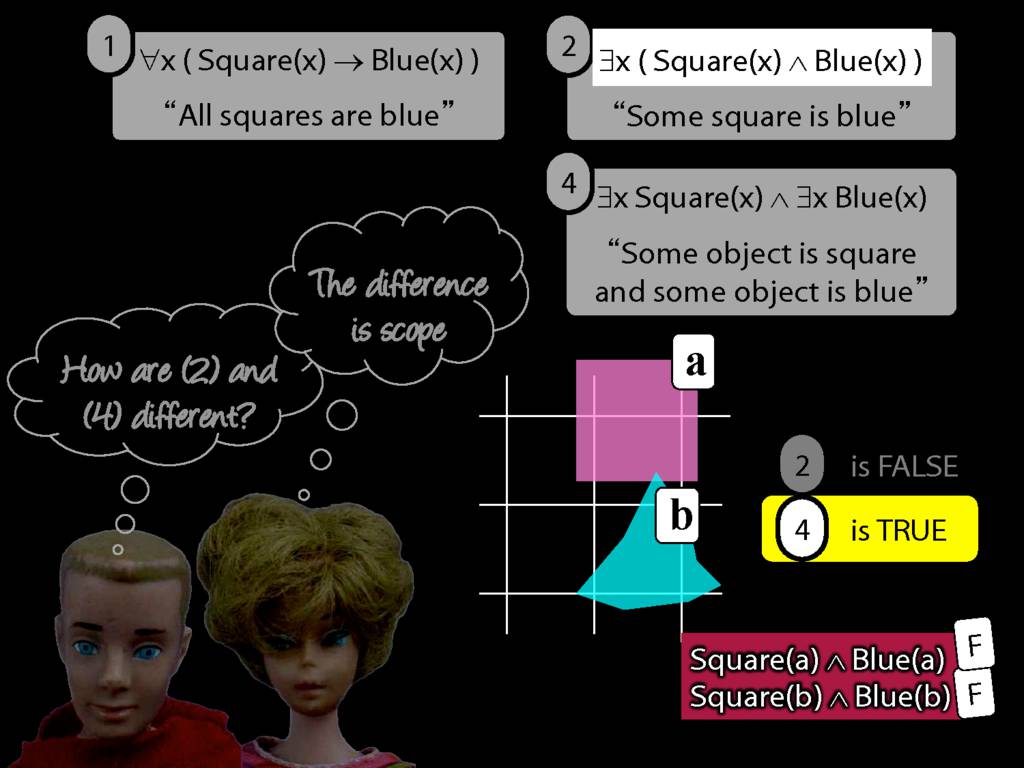
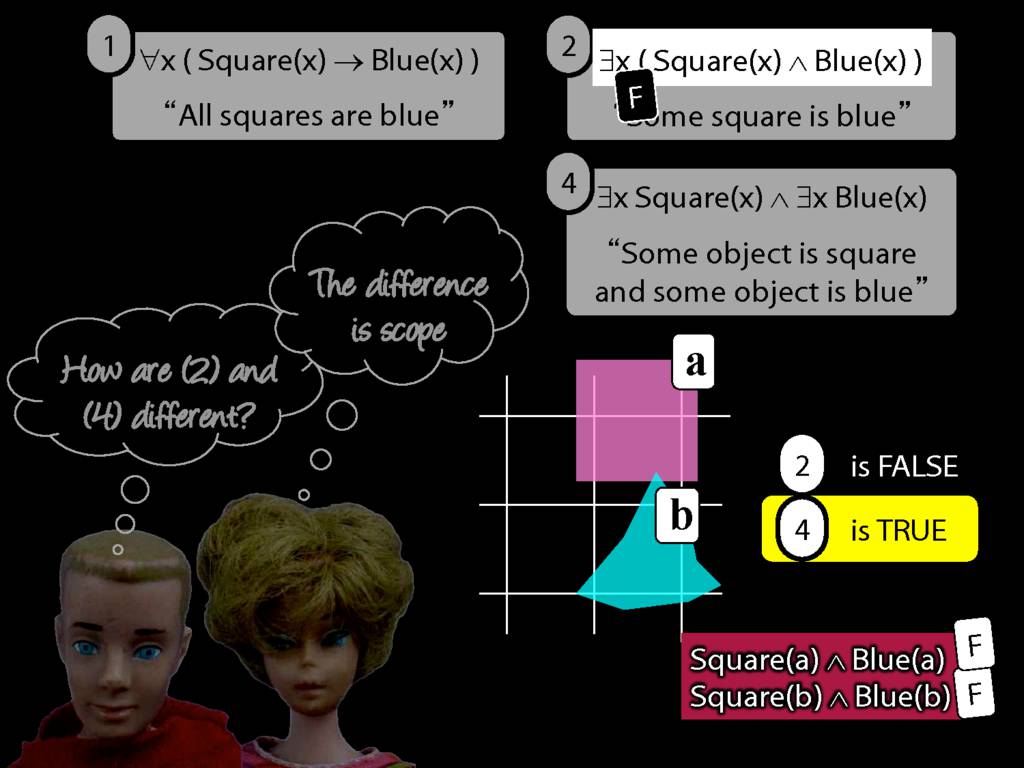
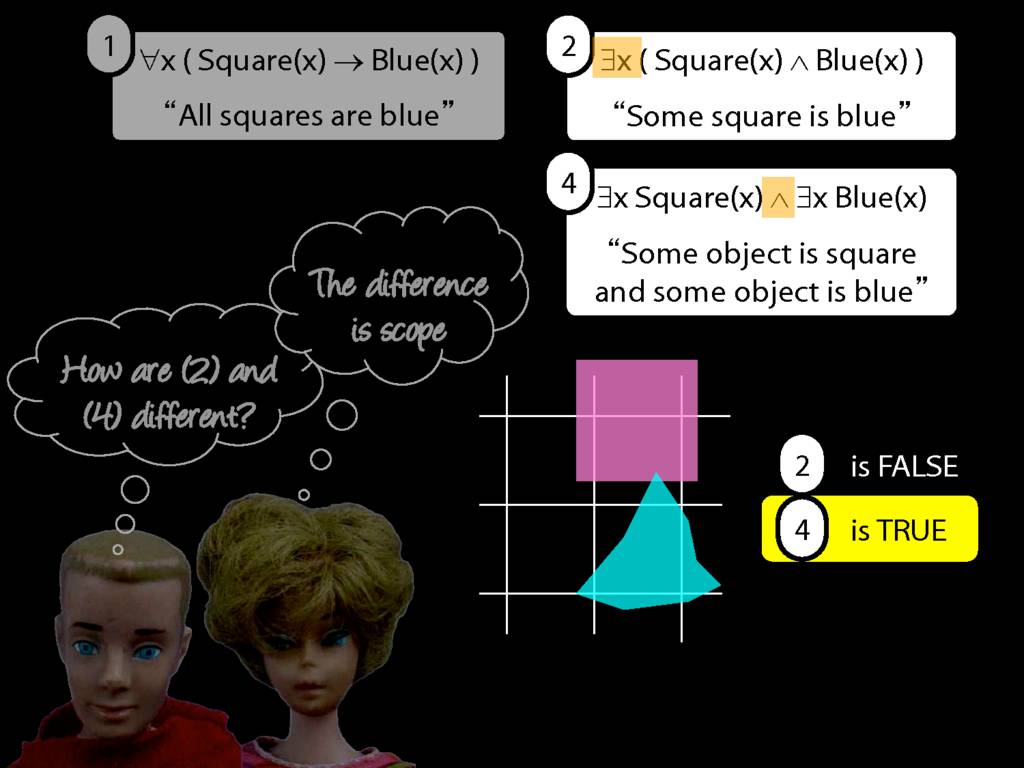
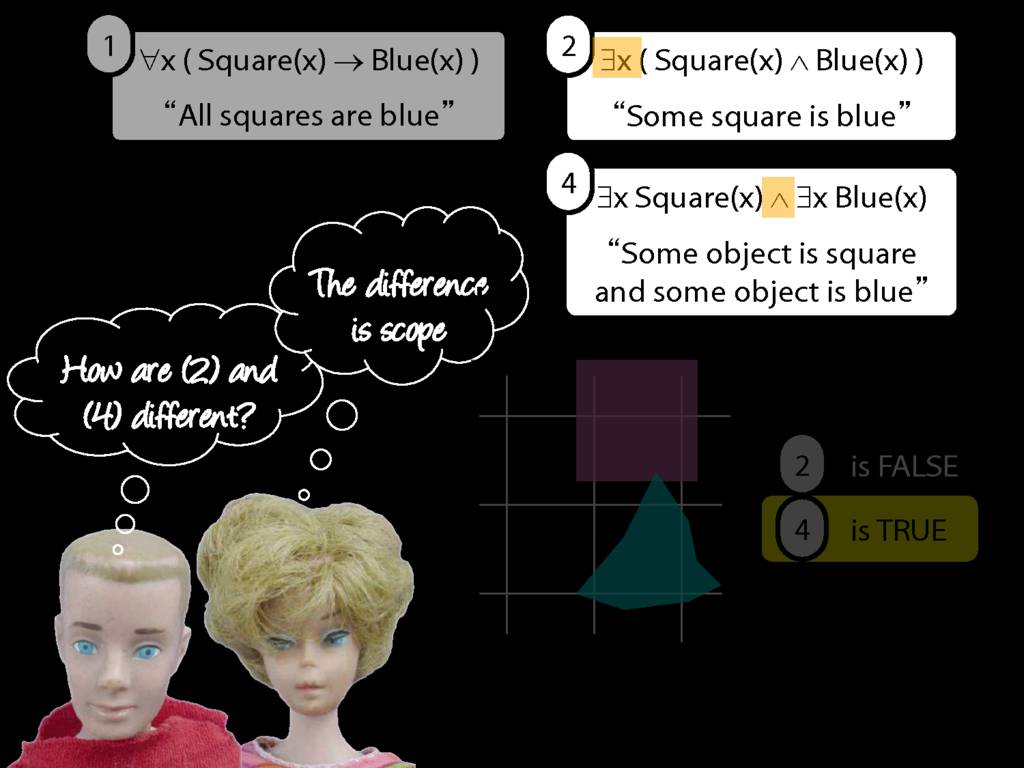
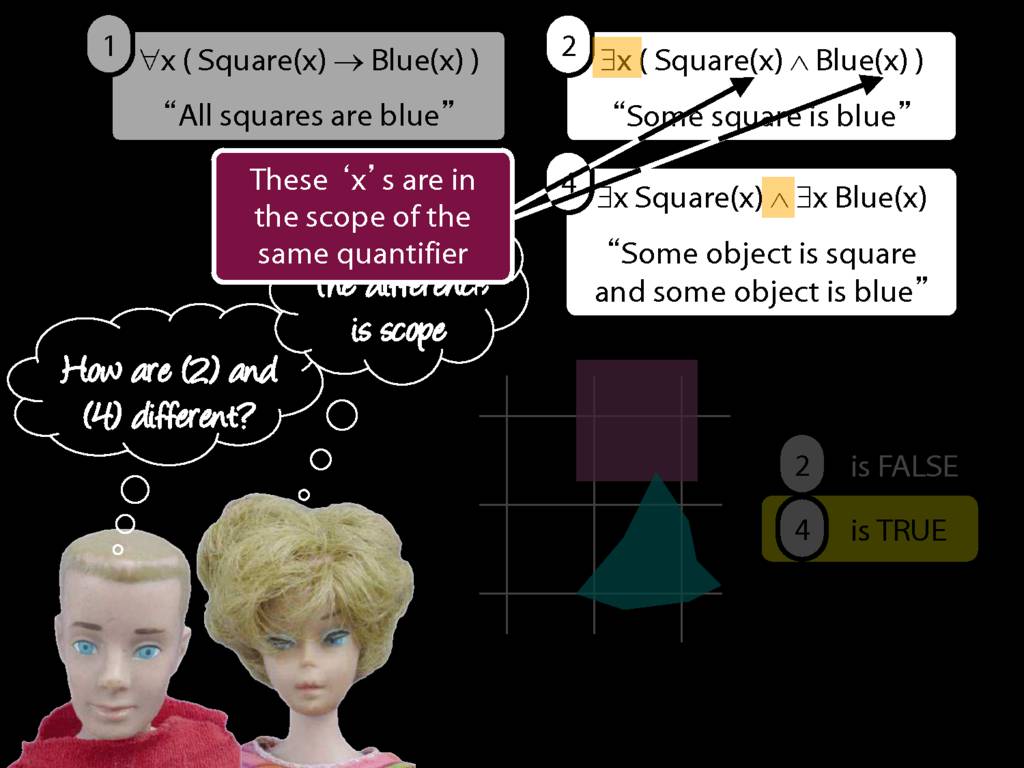
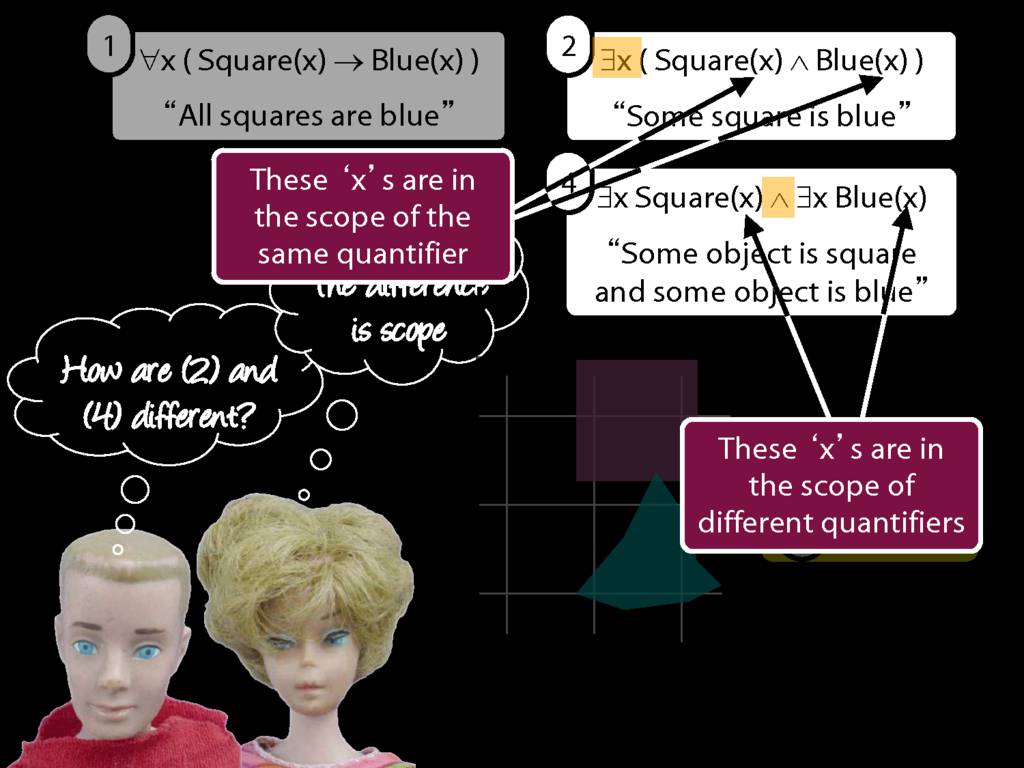
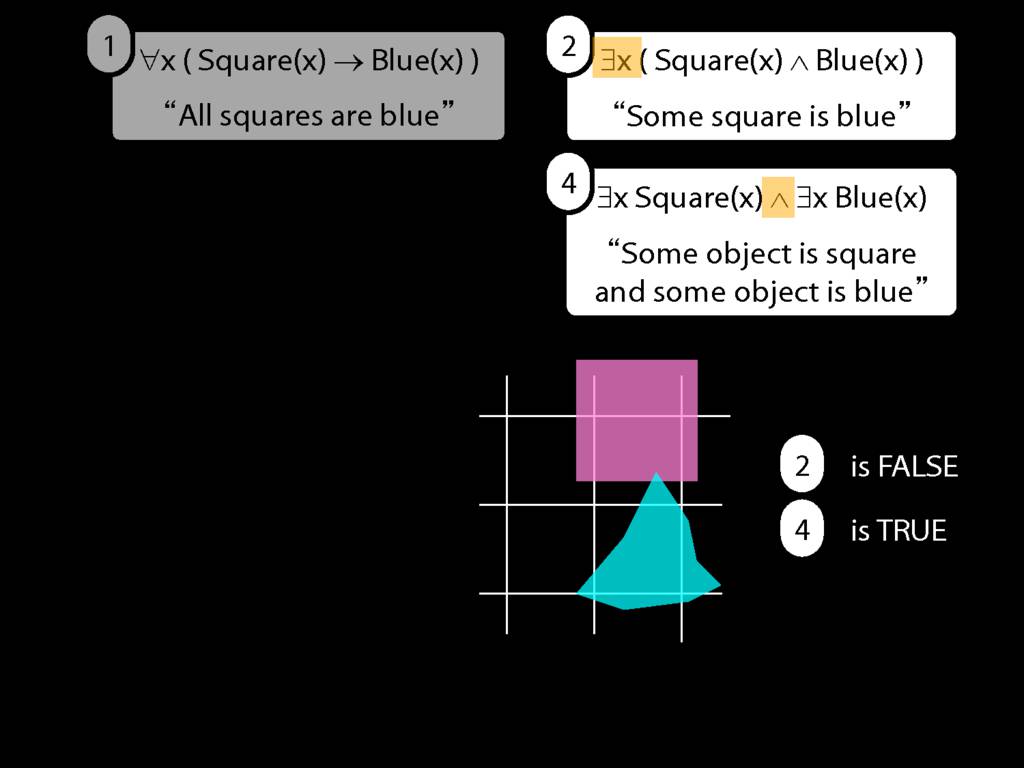
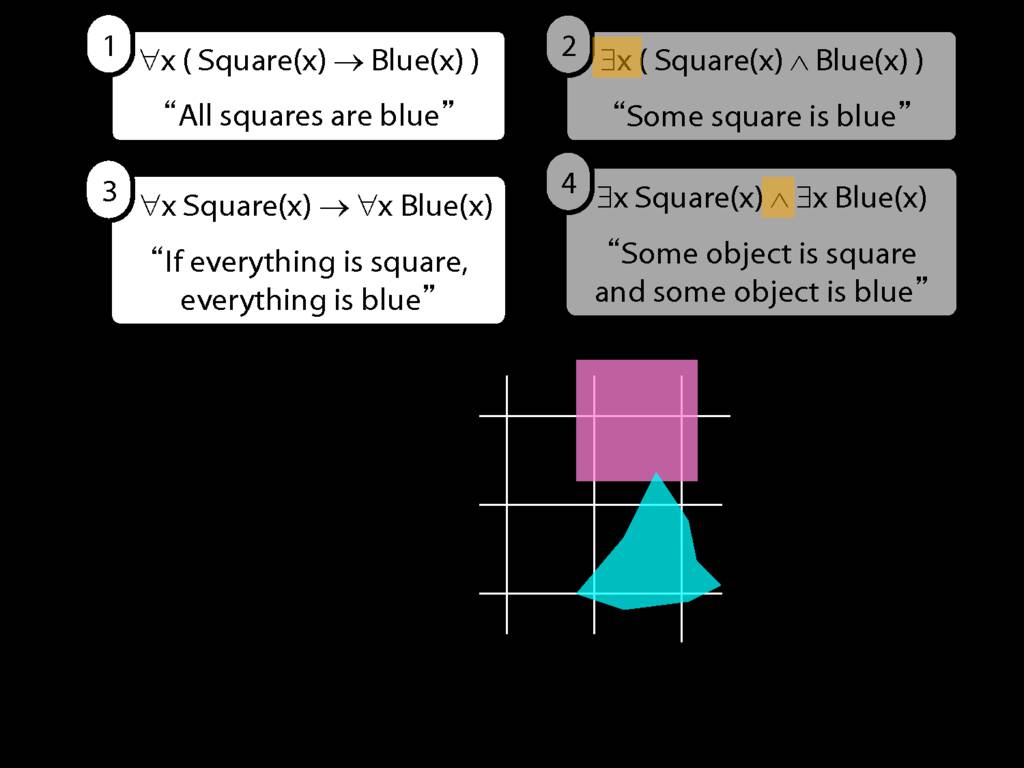
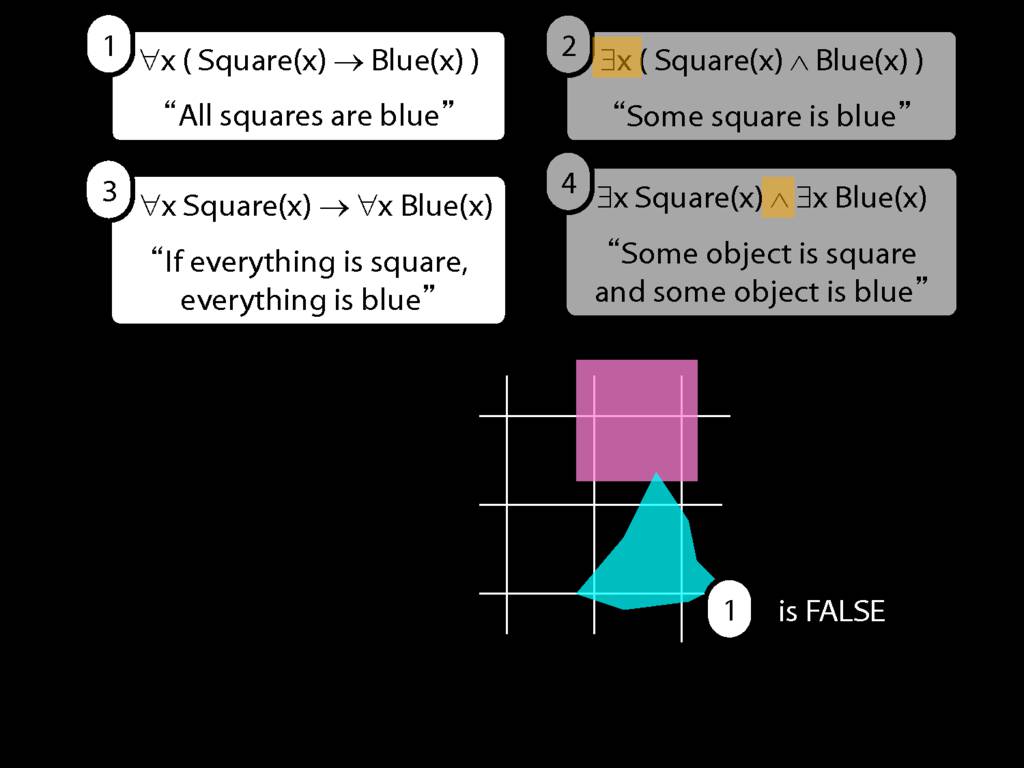
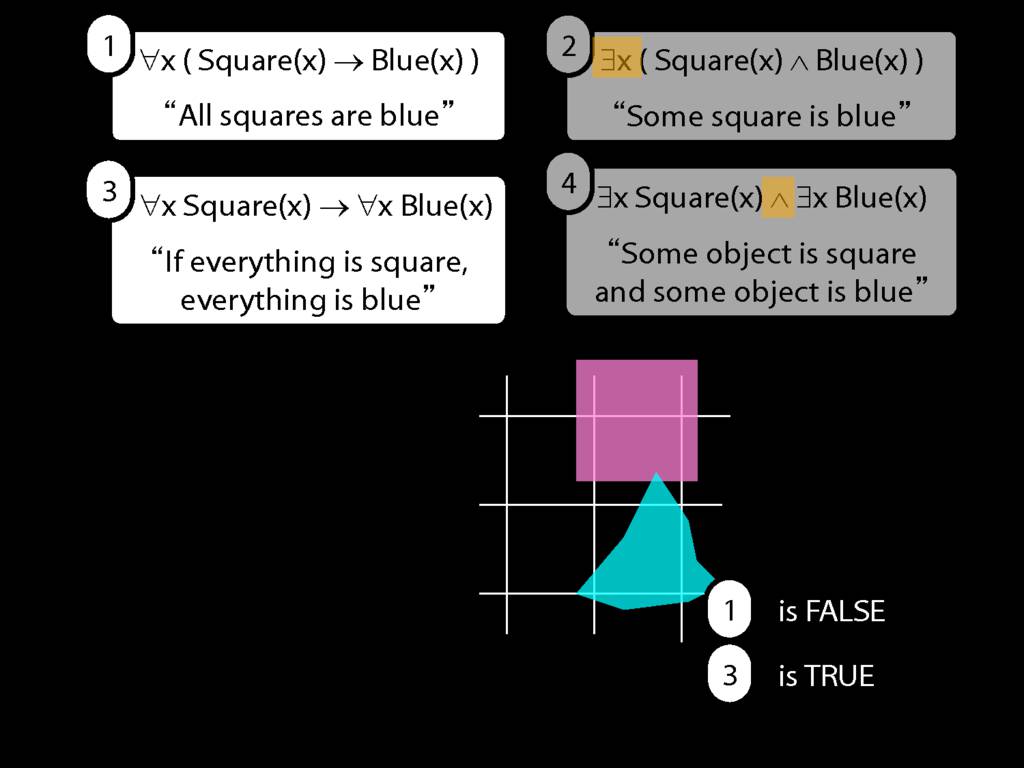
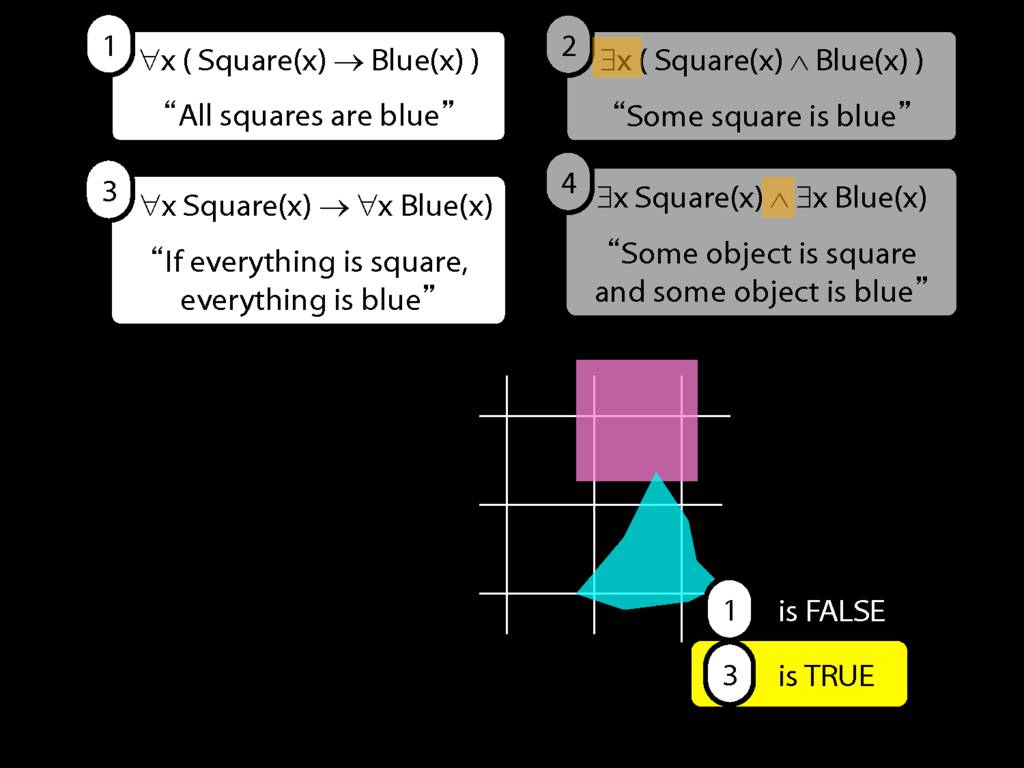
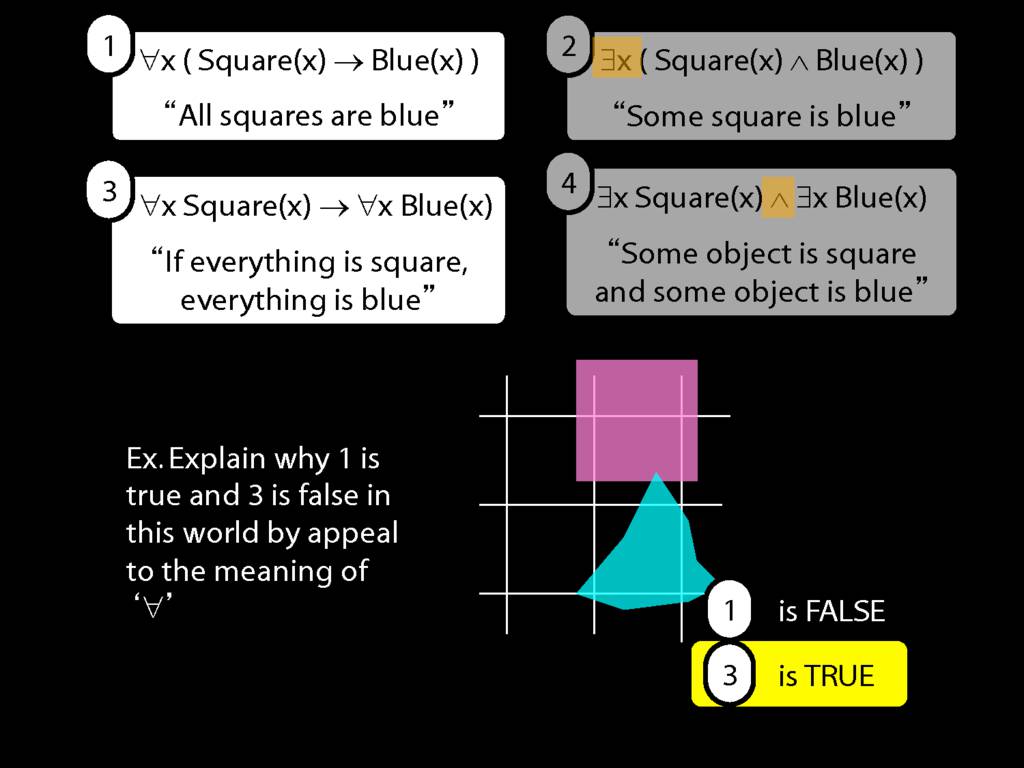
\section{Scope and Quantifiers}
\emph{Reading:} §9.5, §9.6
 
\section{Scope and Quantifiers}
\begin{minipage}{\columnwidth}
Underlining shows the scope of the quantifiers:
\end{minipage}

No lectures or seminars in reading week (Week 6).

 

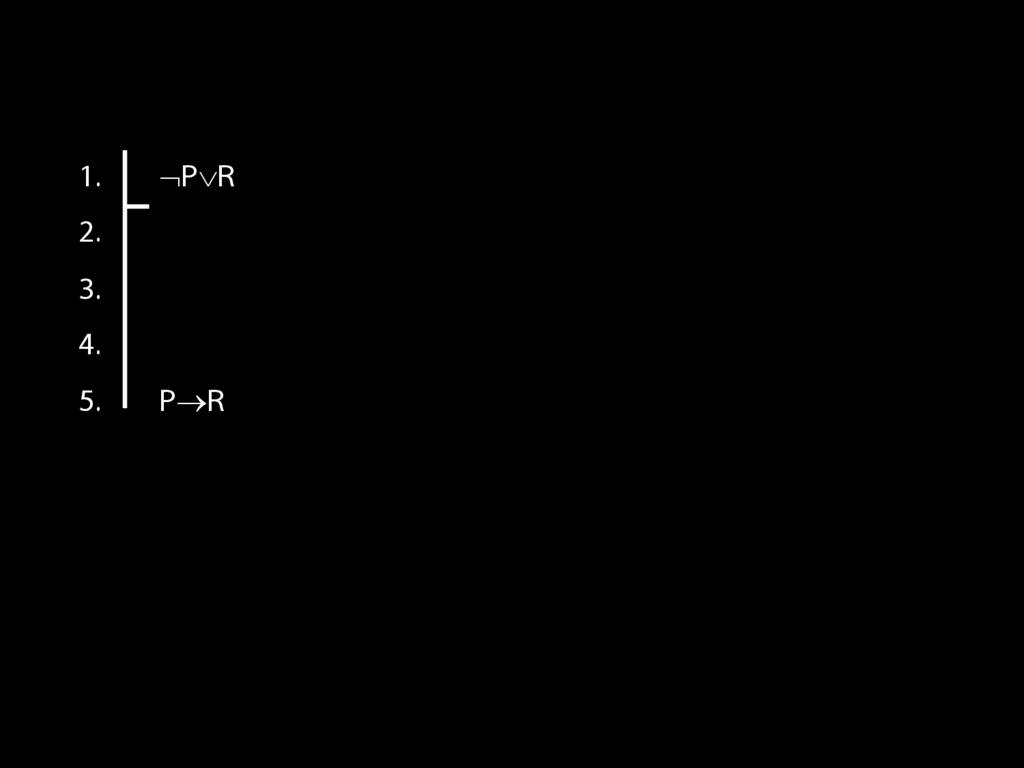
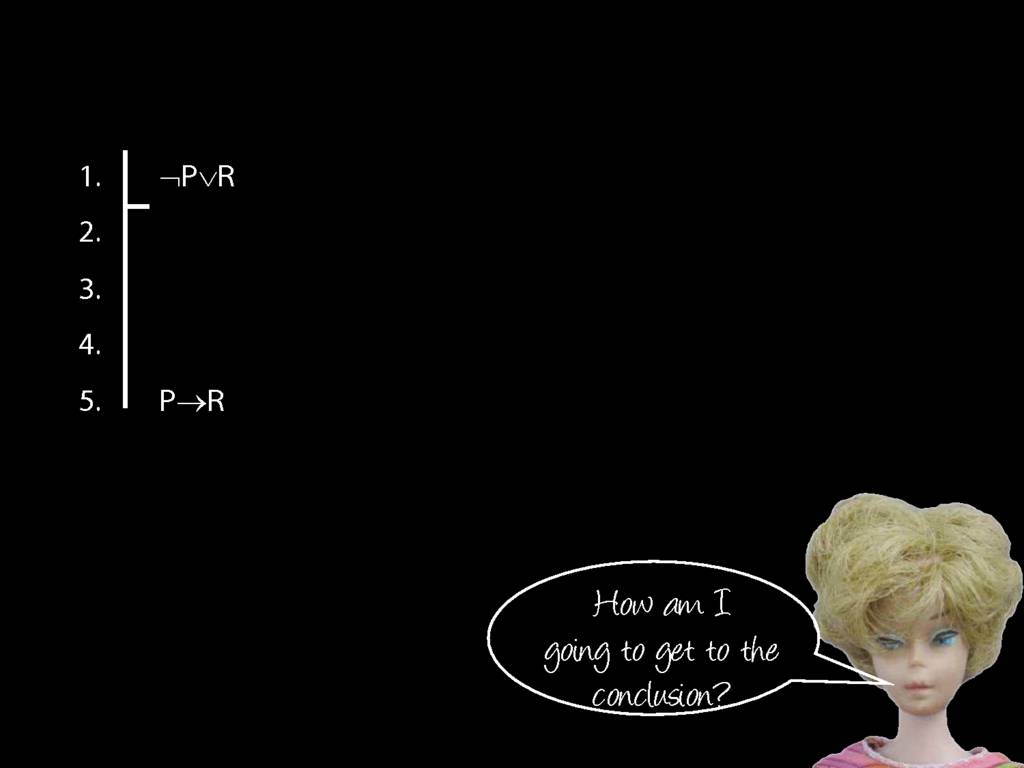
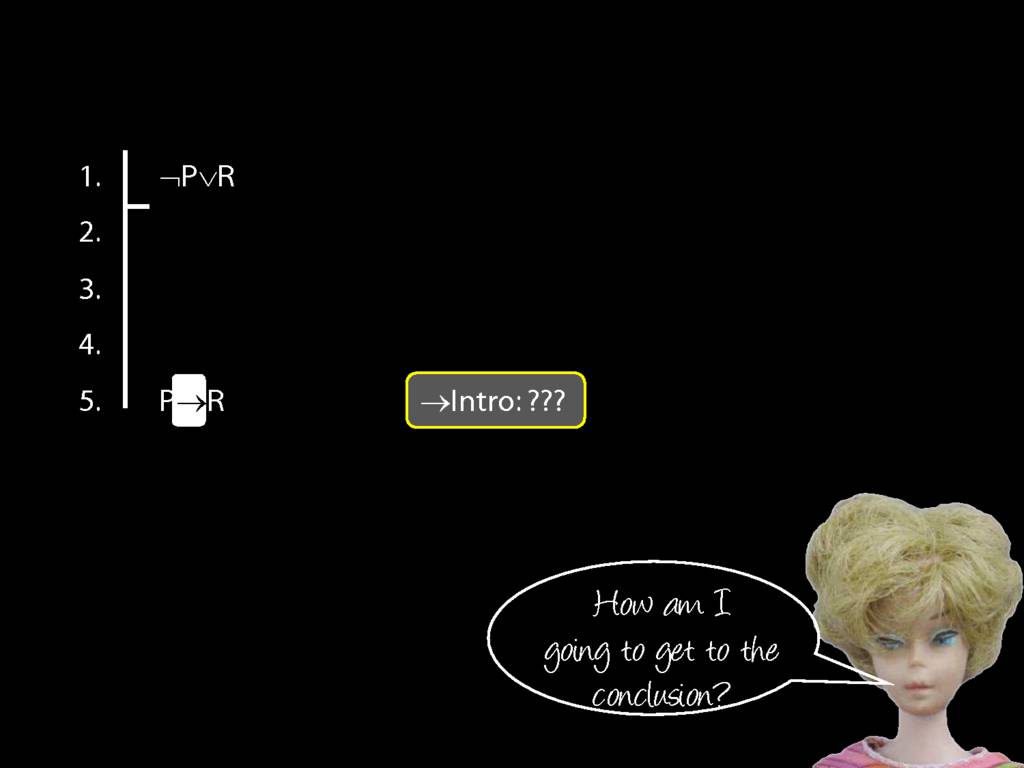
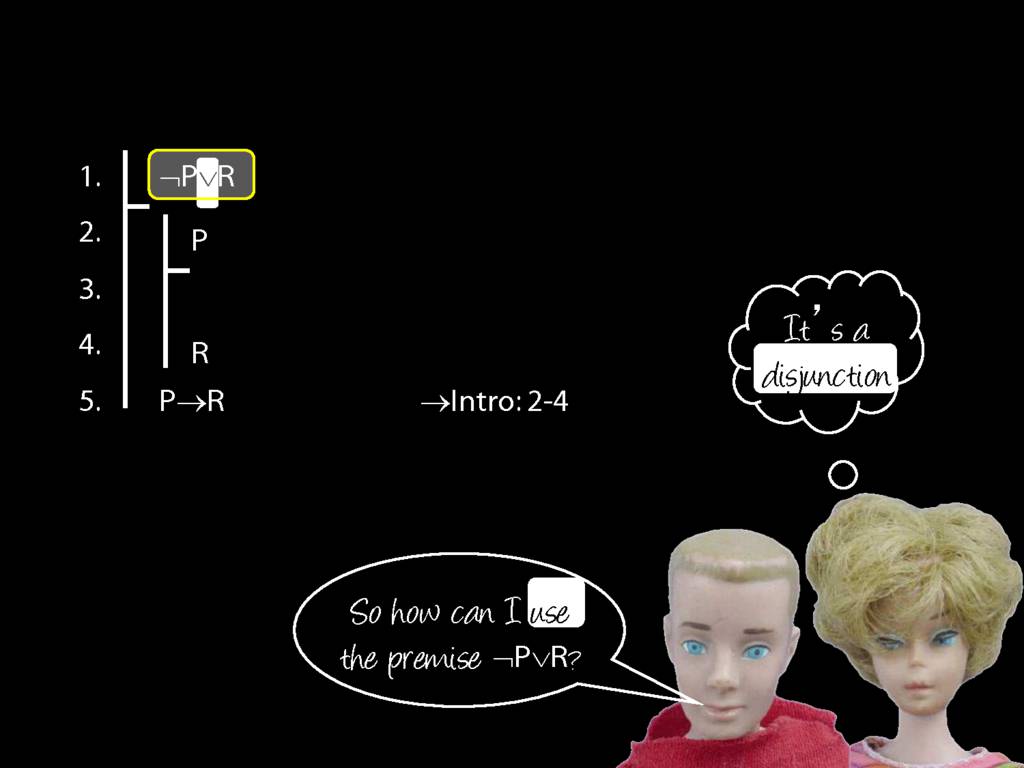
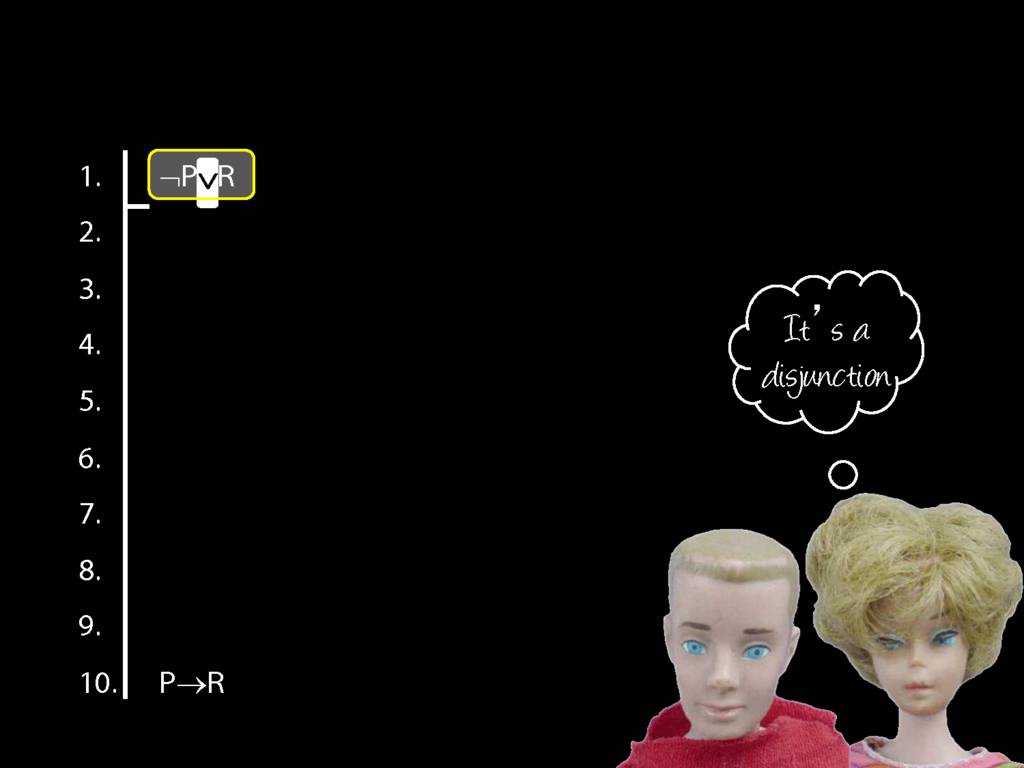
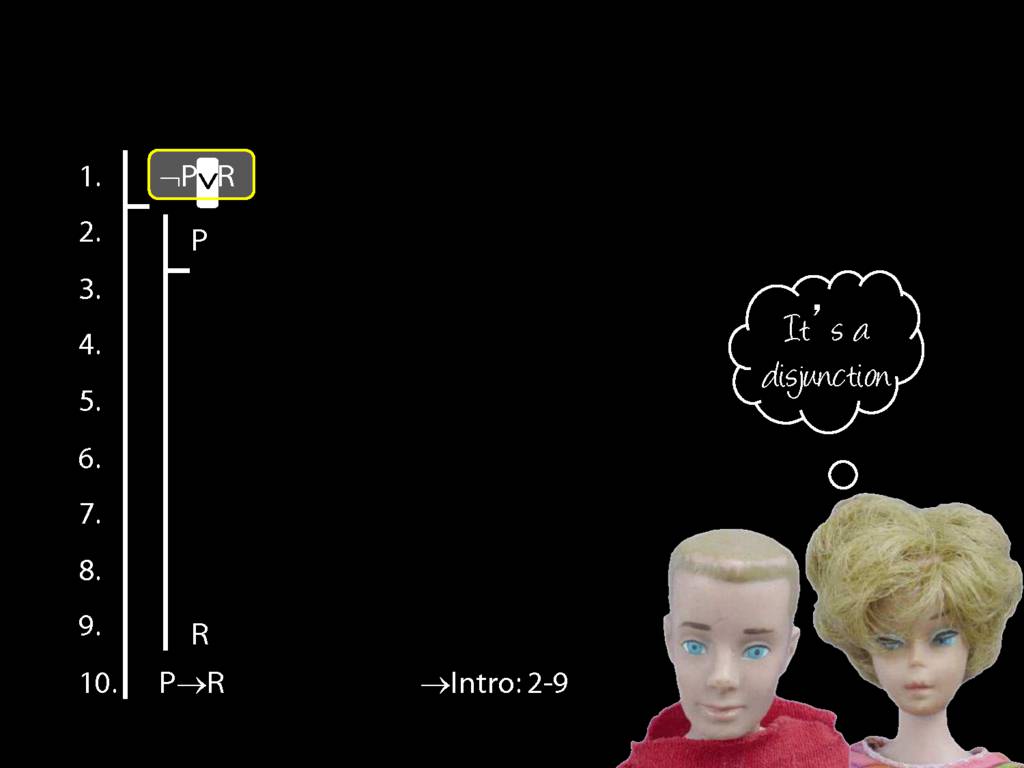
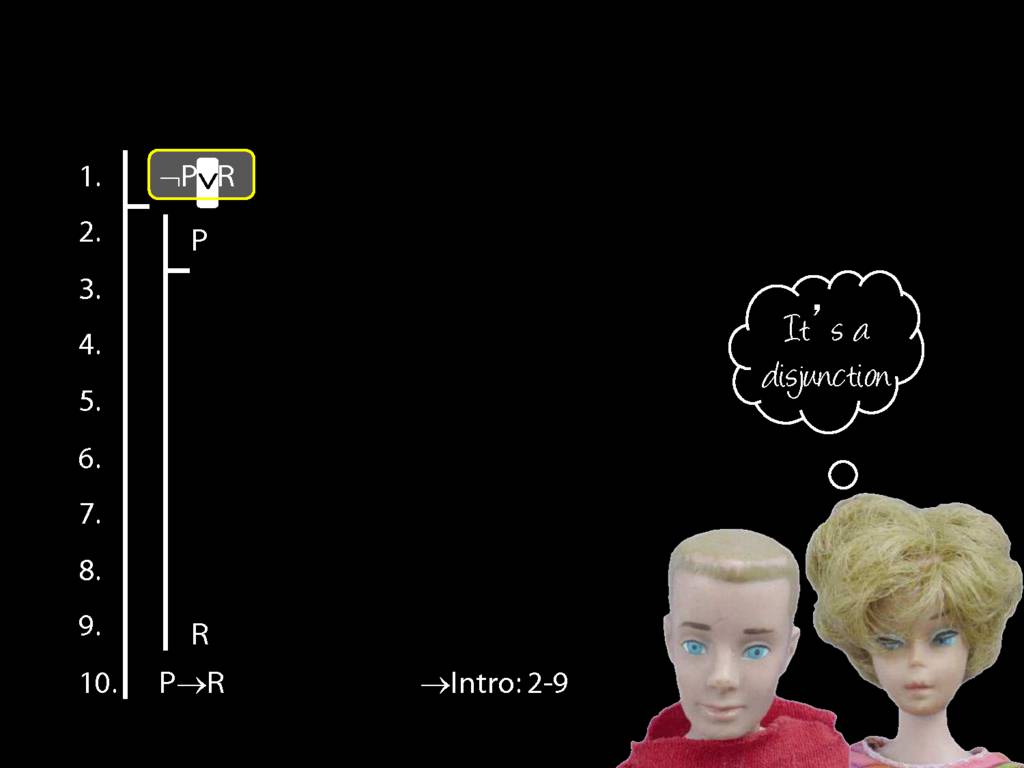
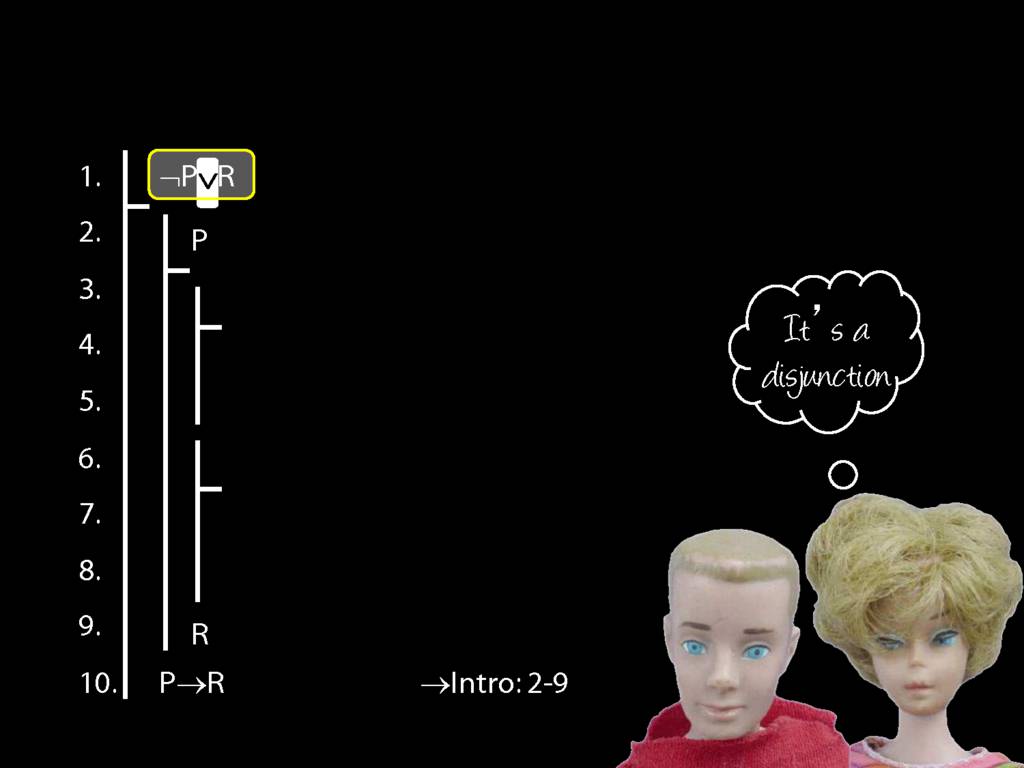
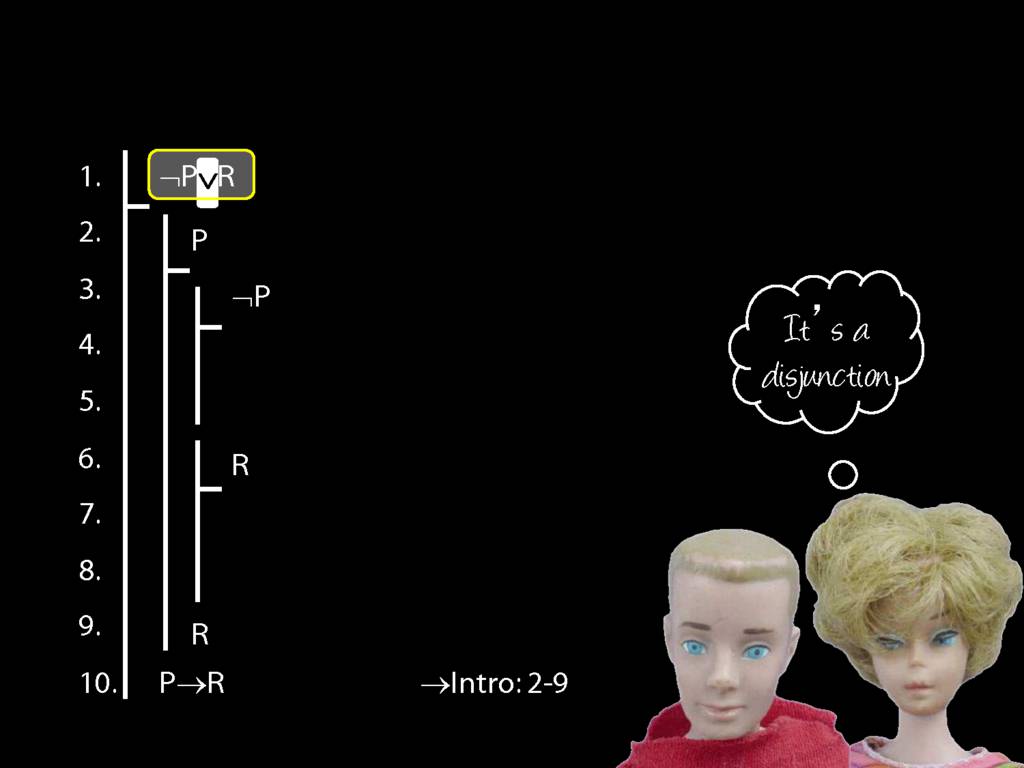
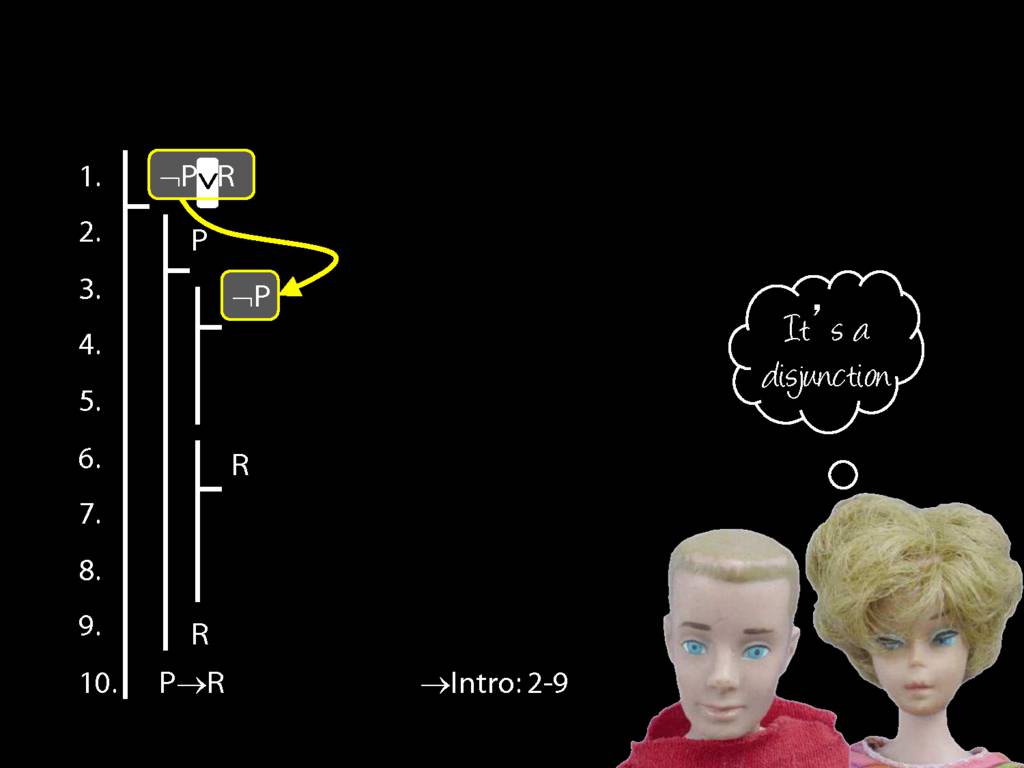
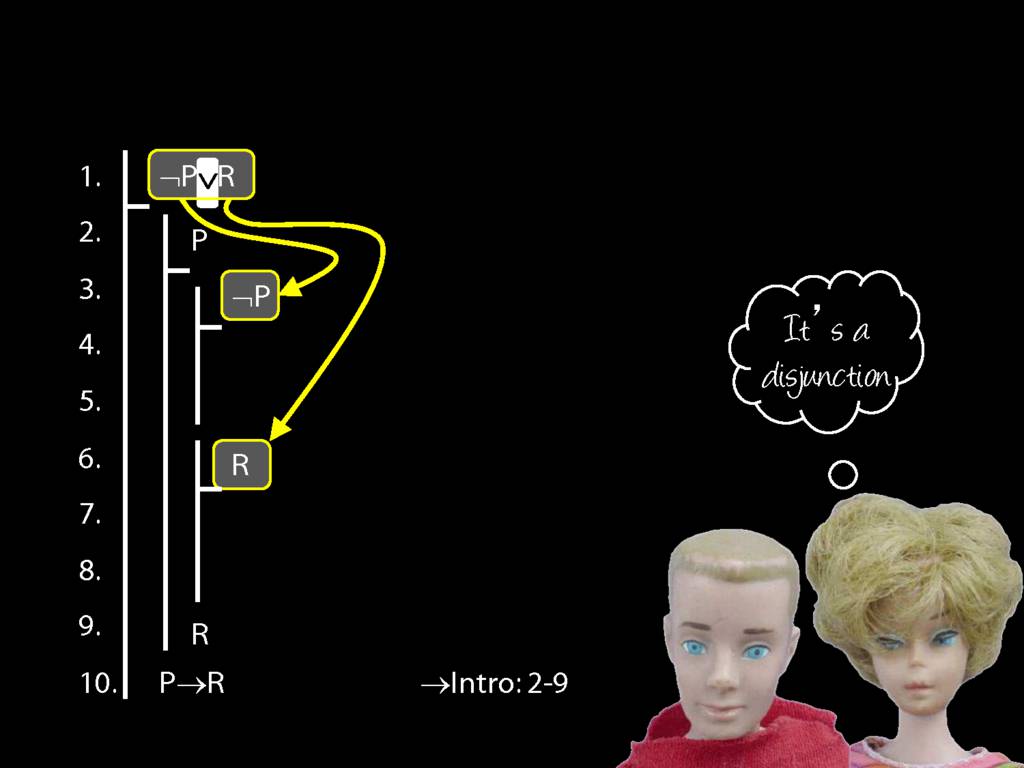
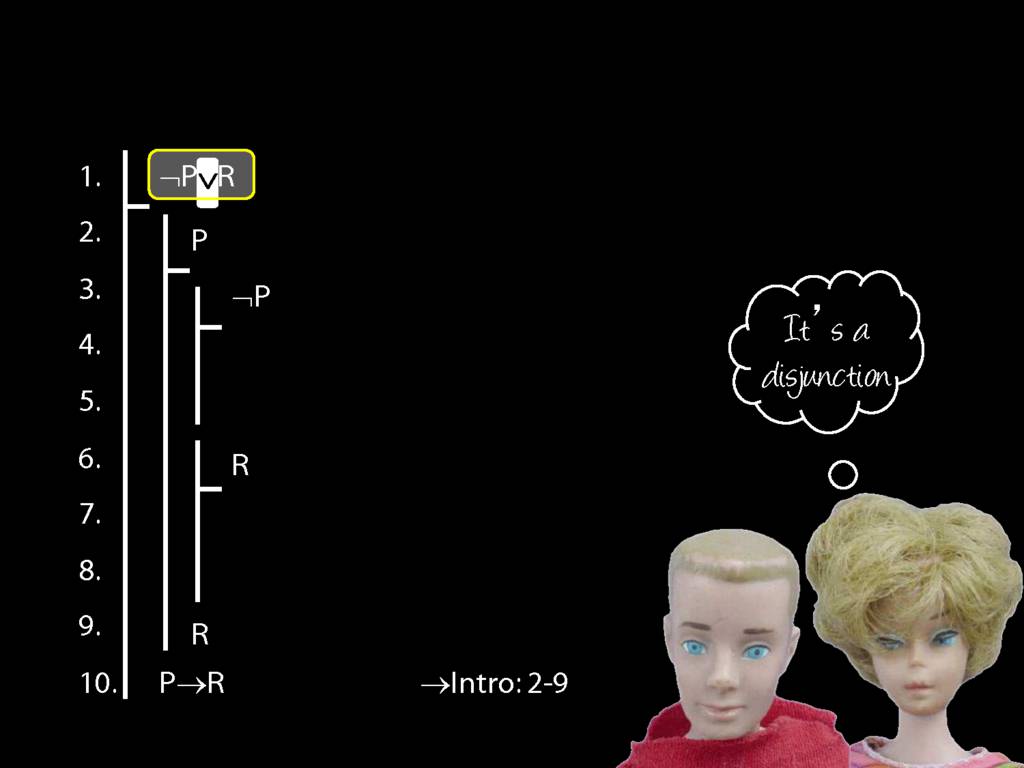
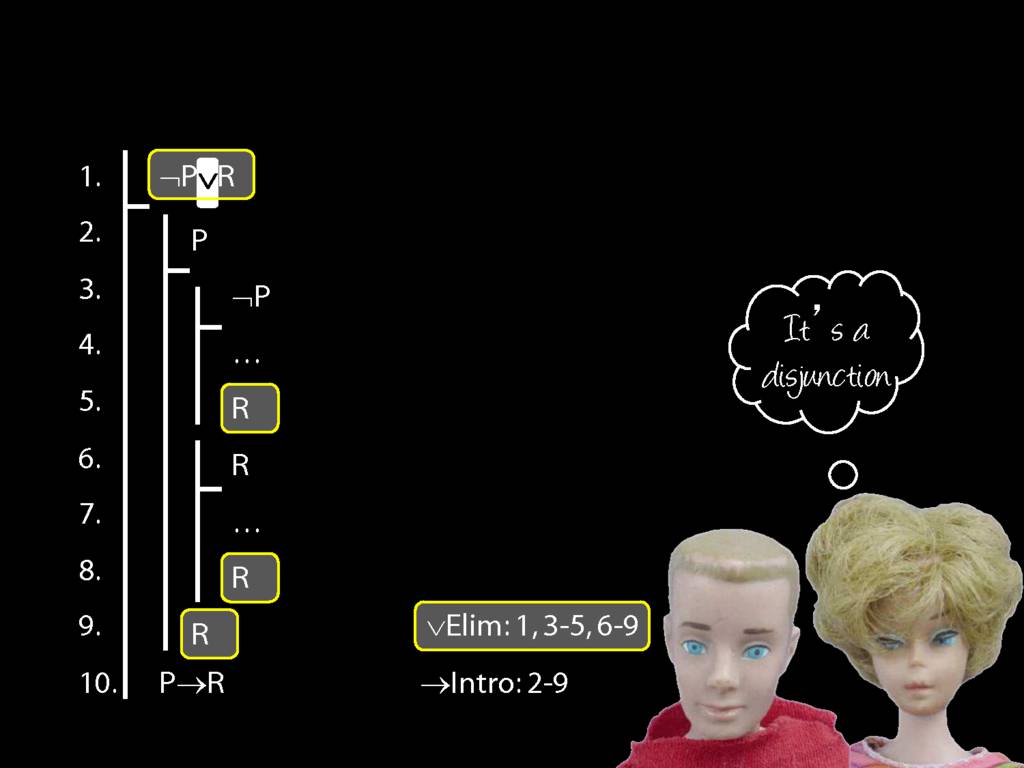
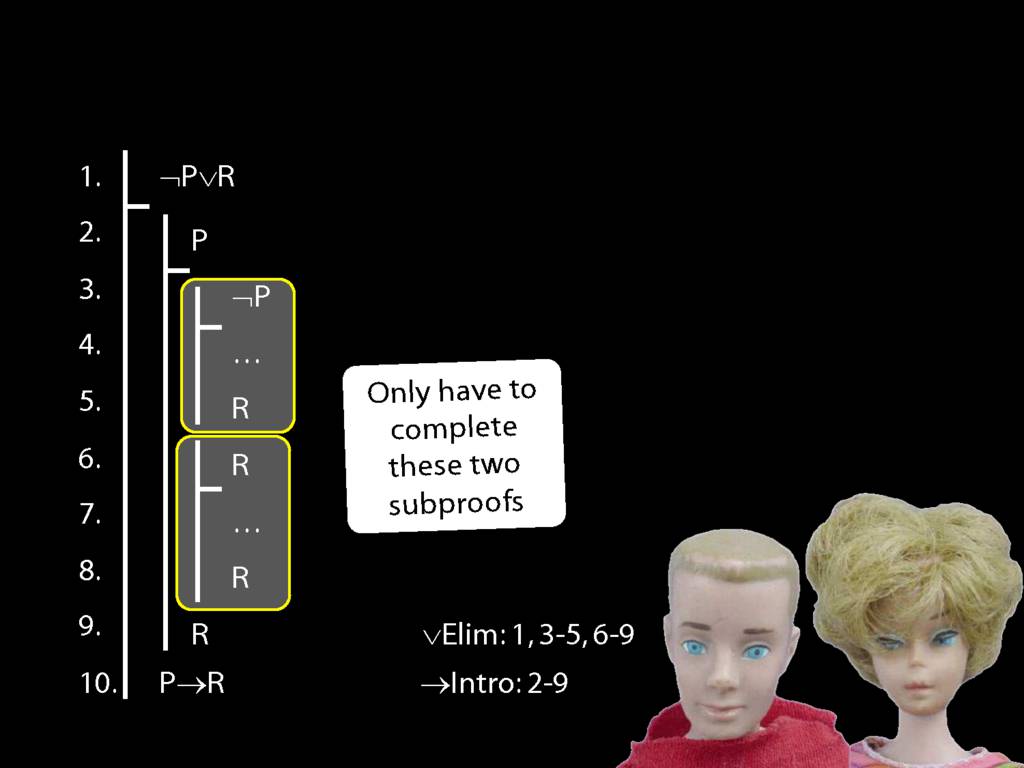
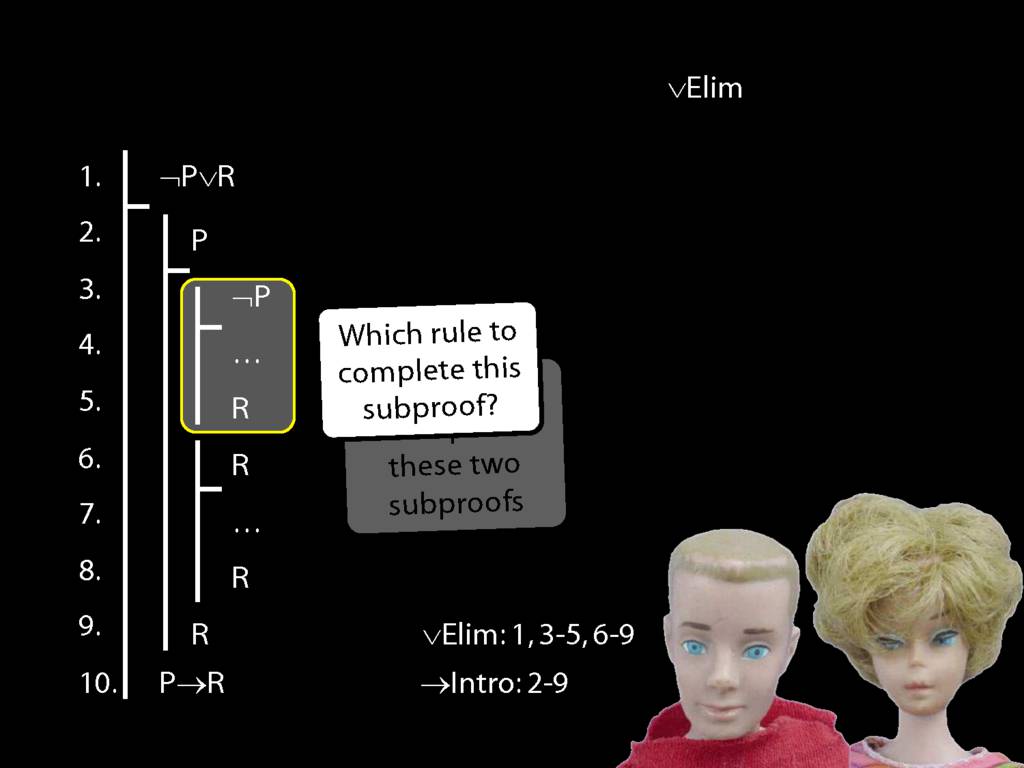
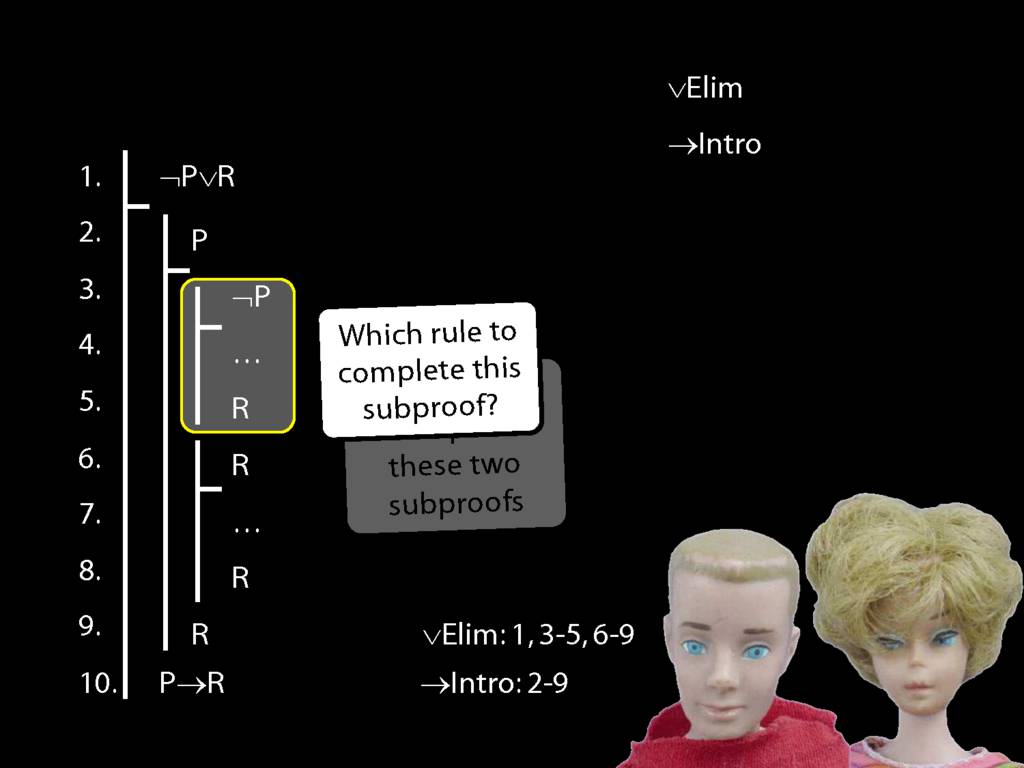
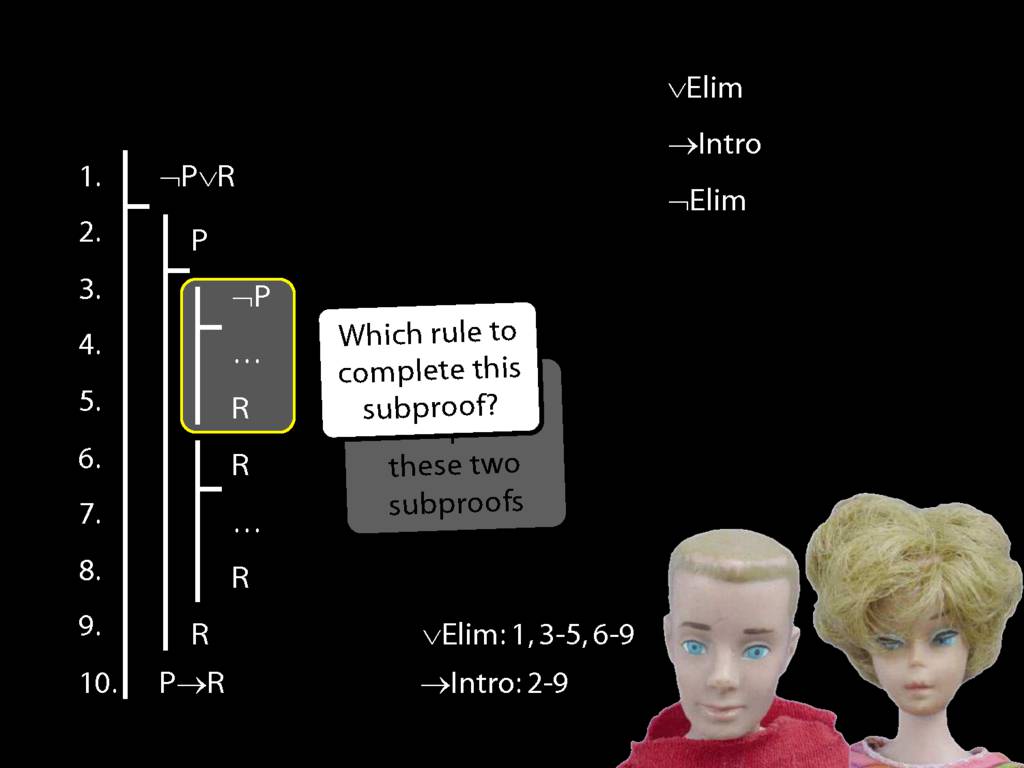
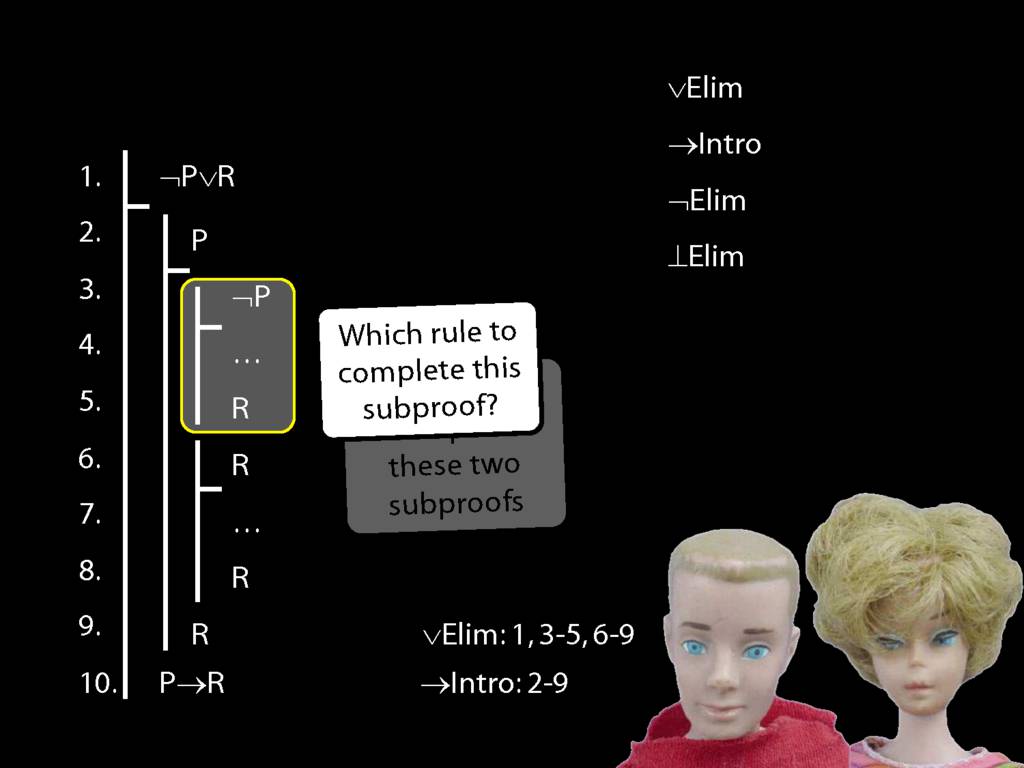
Proof Example: ¬P∨R therefore P→R

 
\section{Proof Example: ¬P∨R therefore P→R}
 
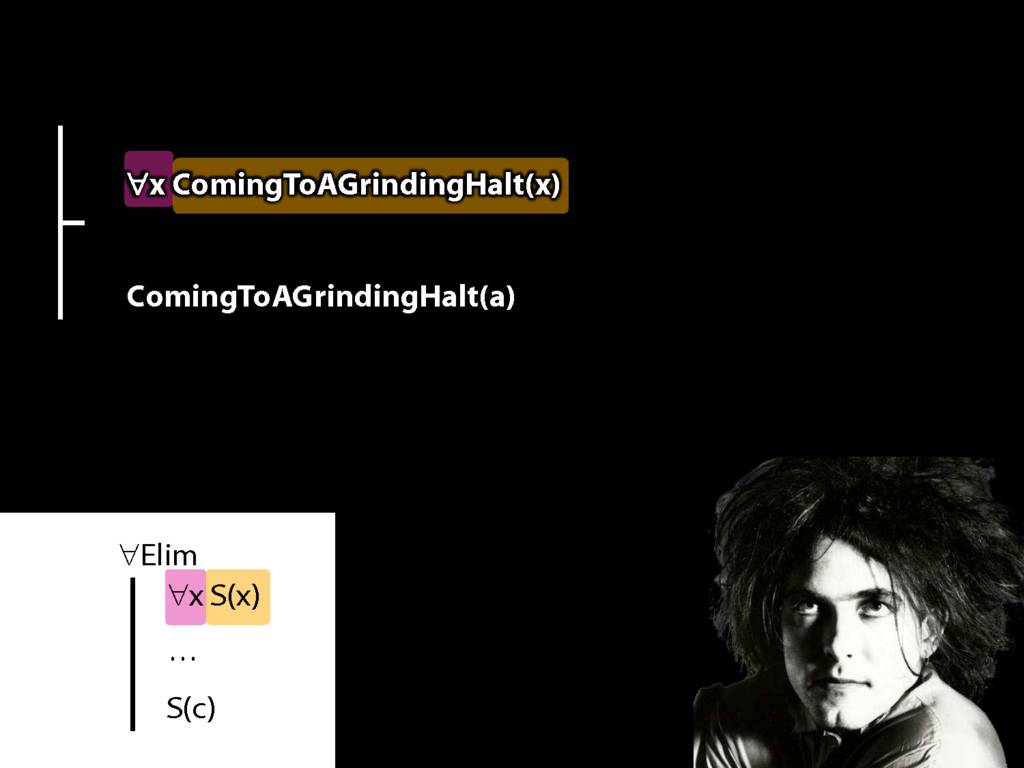
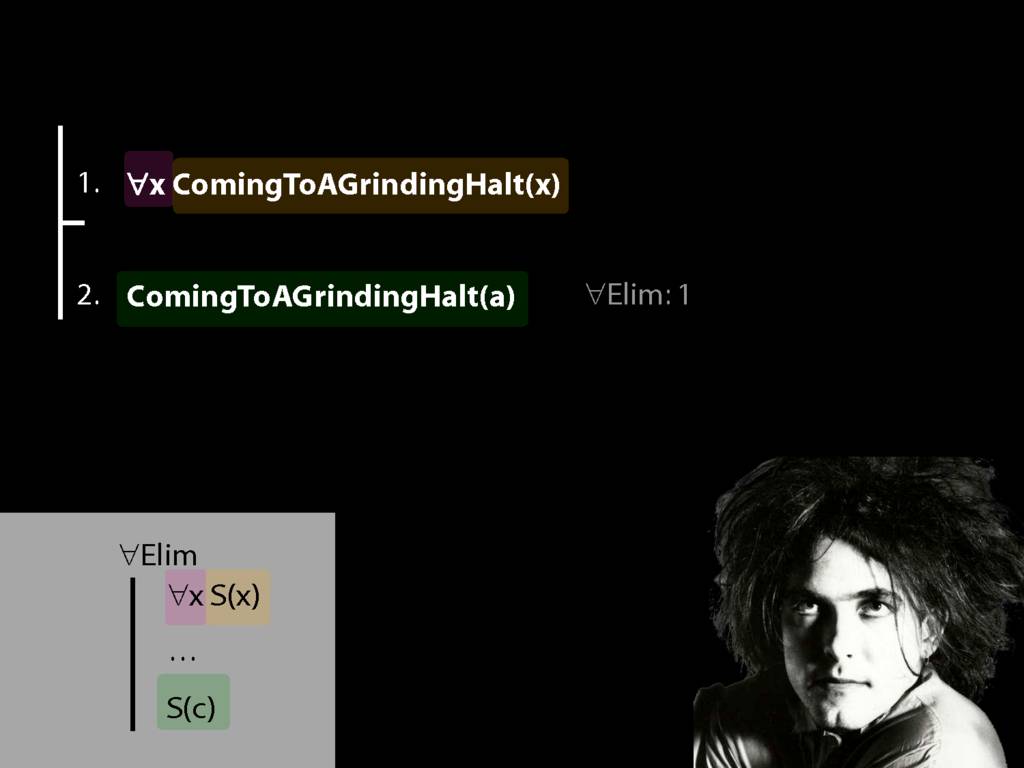
\section{Proof Example: ¬P∨R therefore P→R}
 

∀Elim

 
\section{∀Elim}
\emph{Reading:} §13.1
 
\section{∀Elim}