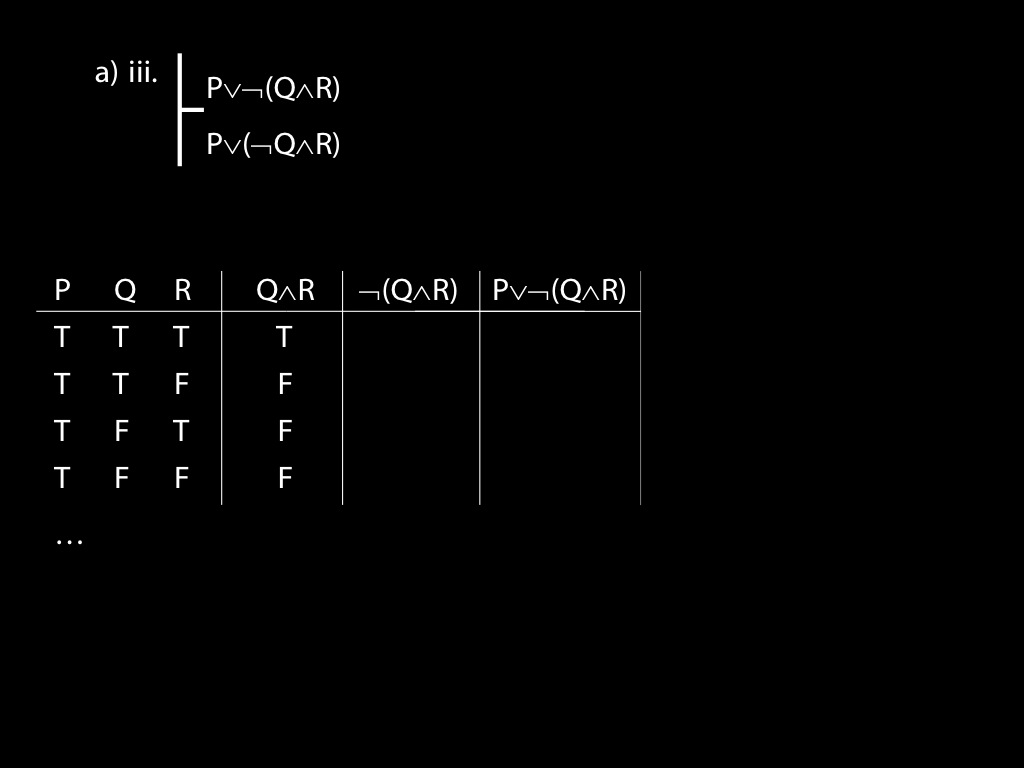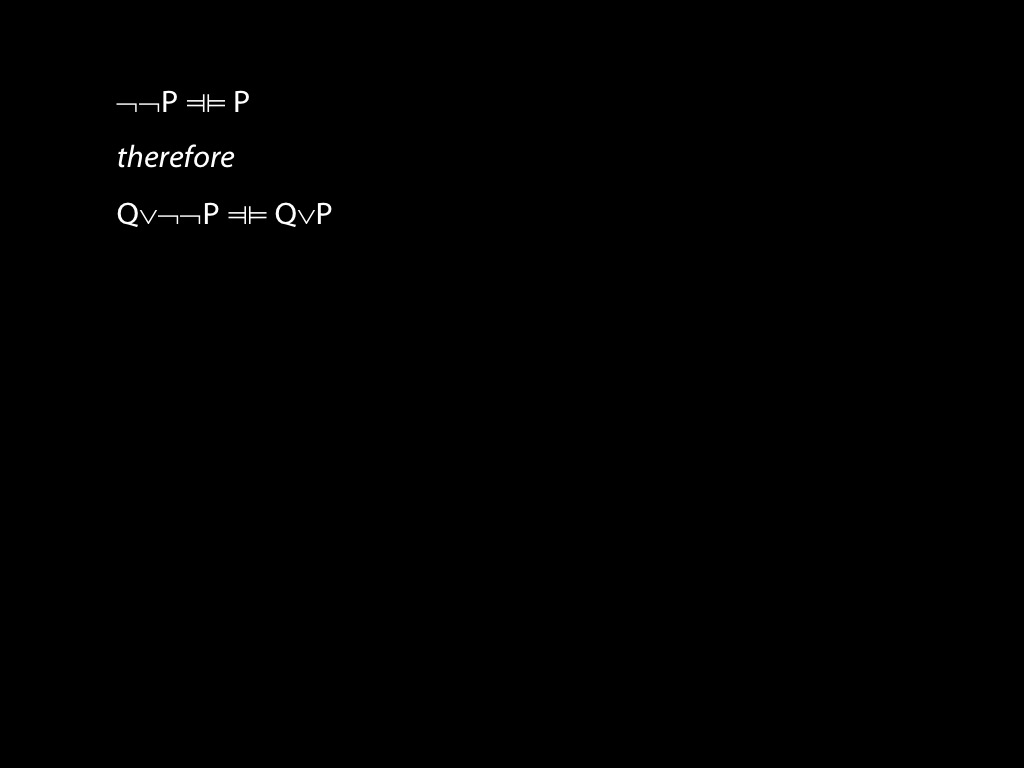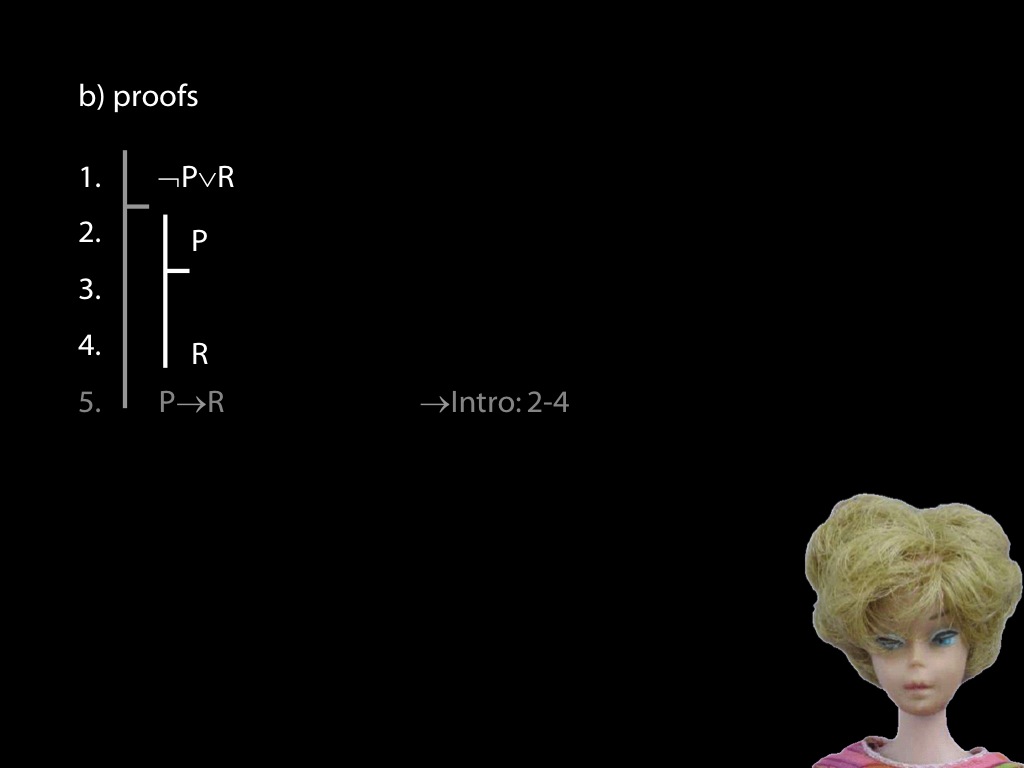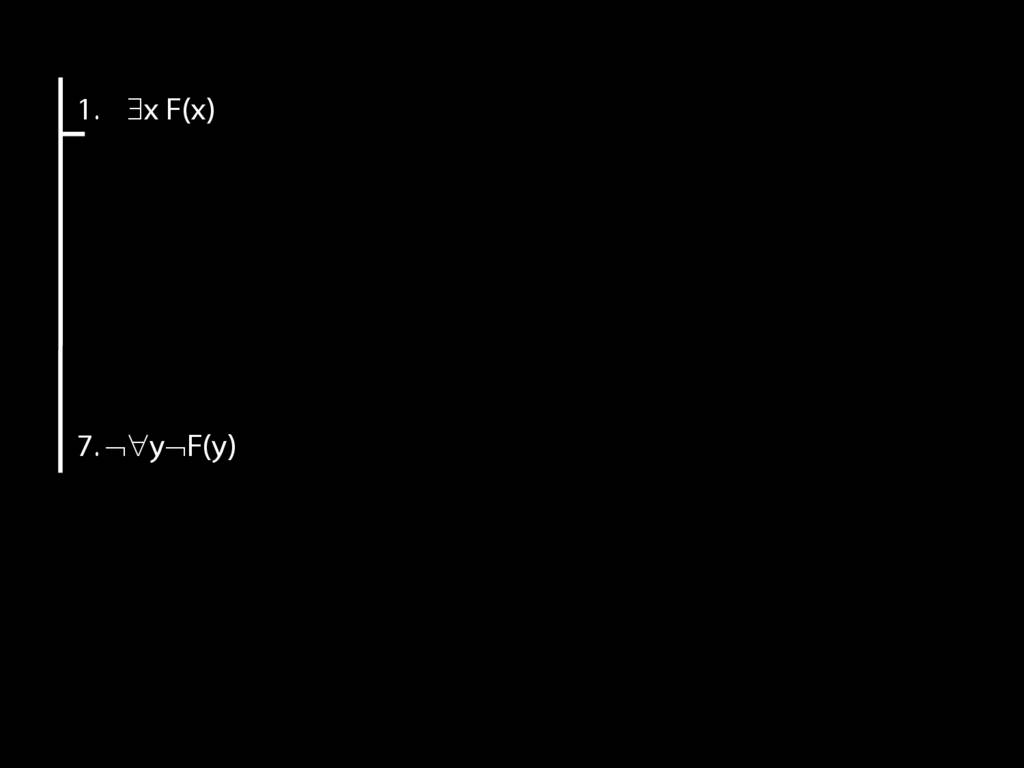\title {Logic I \\ Lecture 17}
\maketitle
\section{Revison: Definitions}
\section{Revison: Definitions}
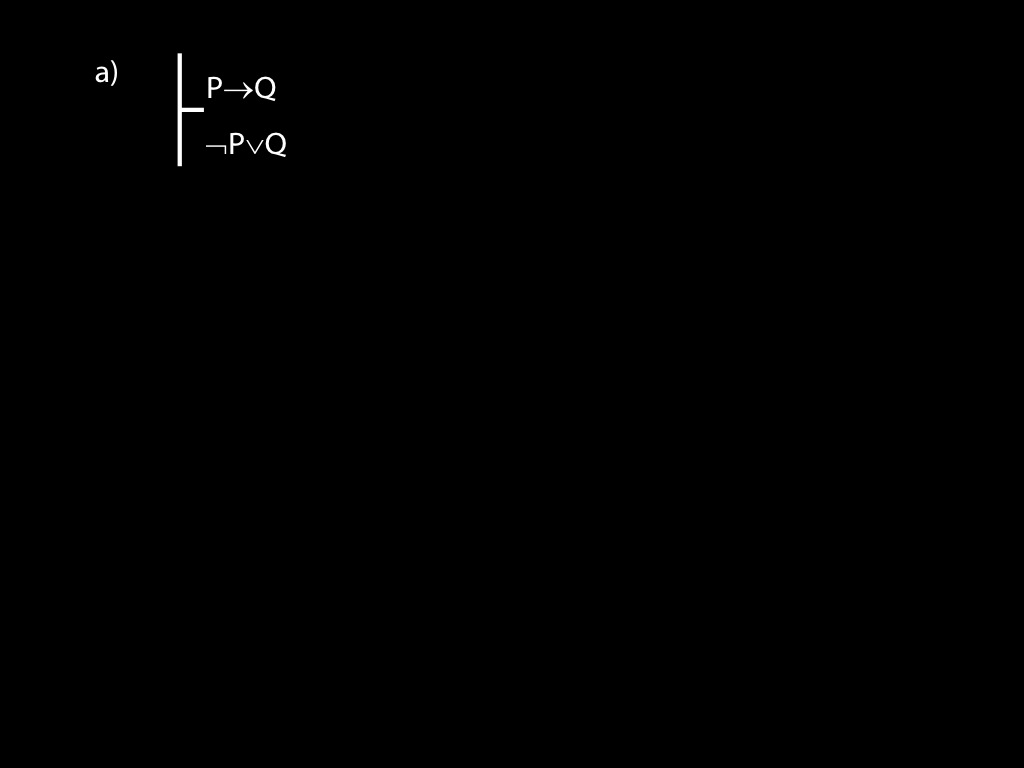
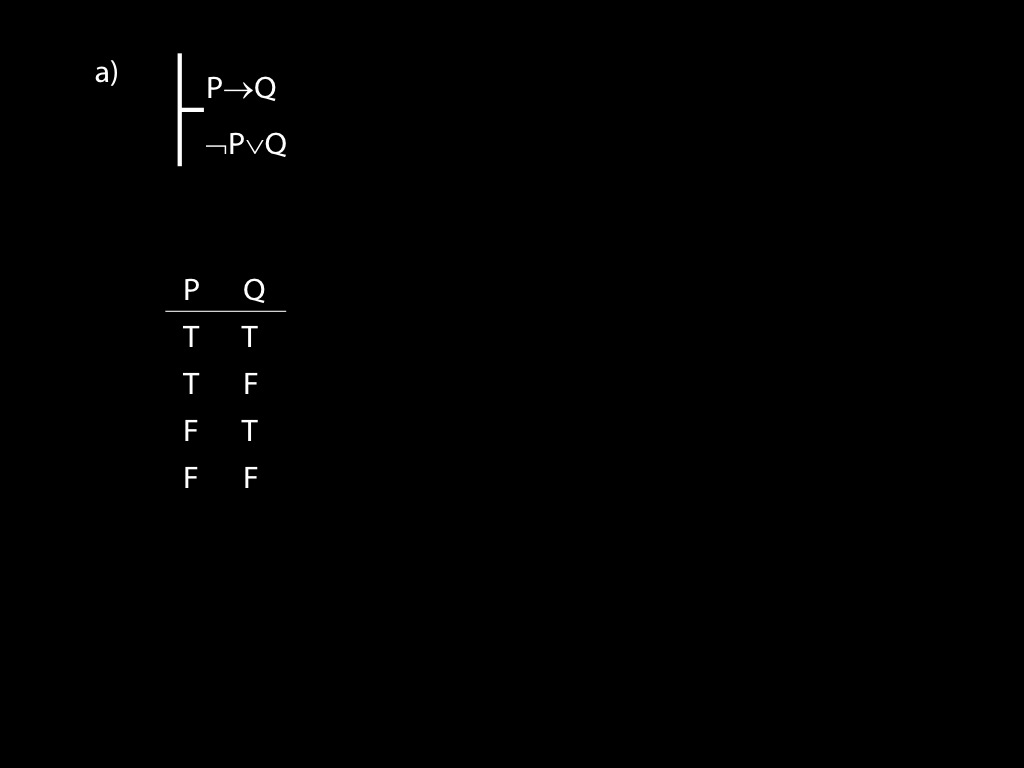
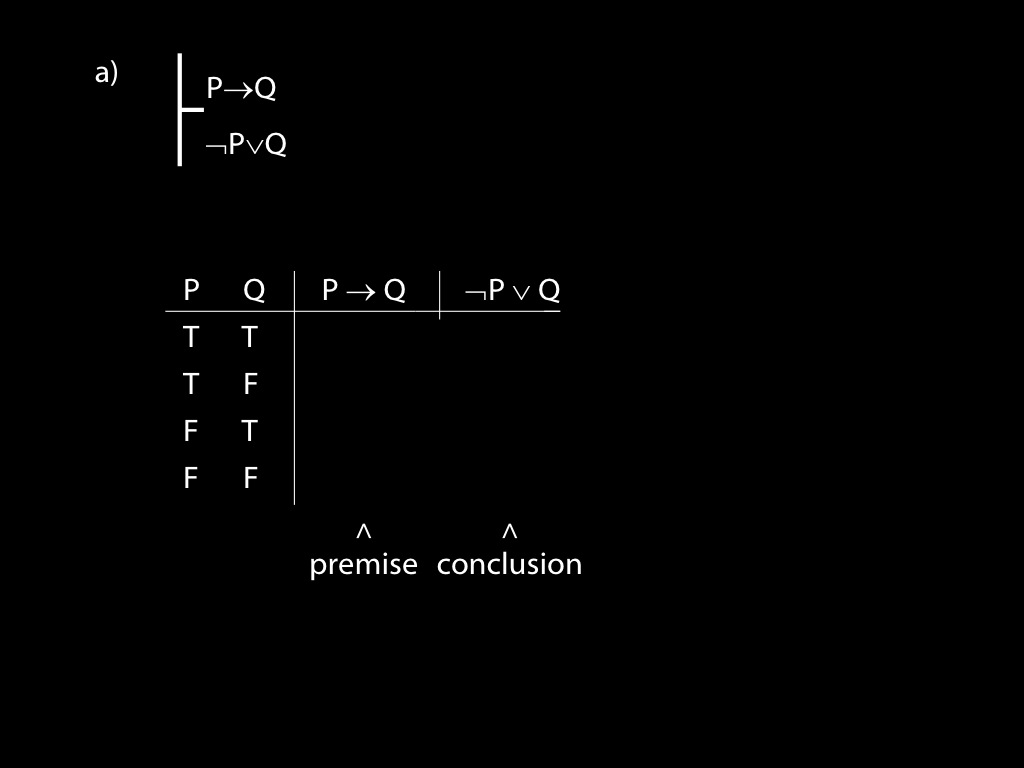
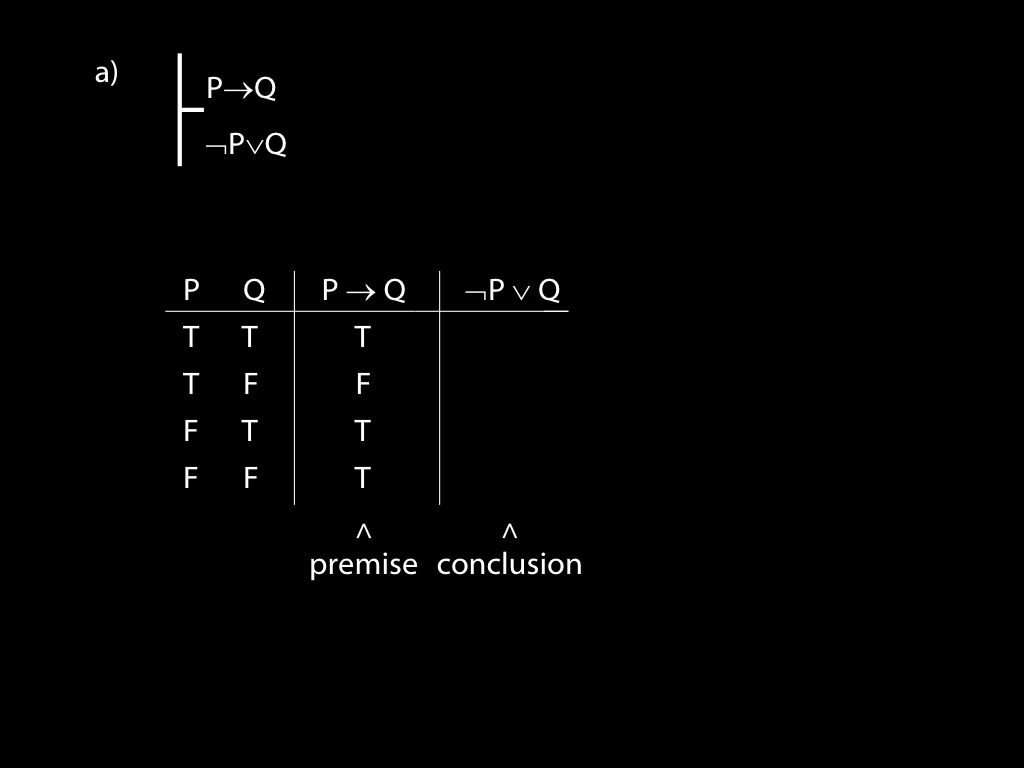
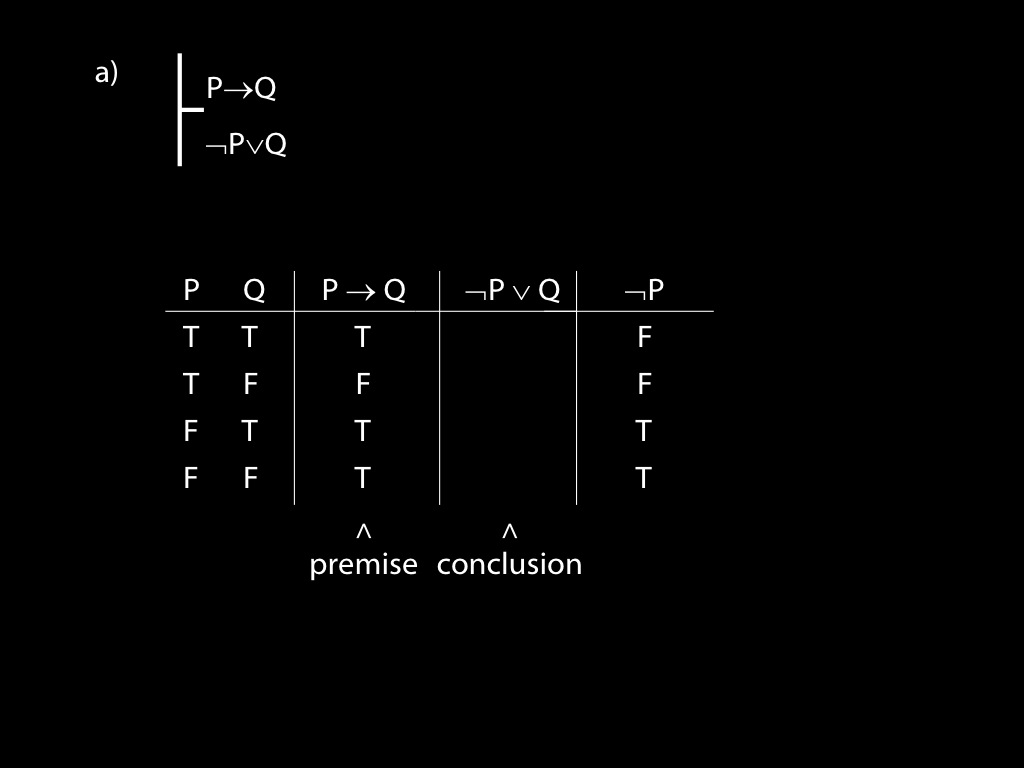
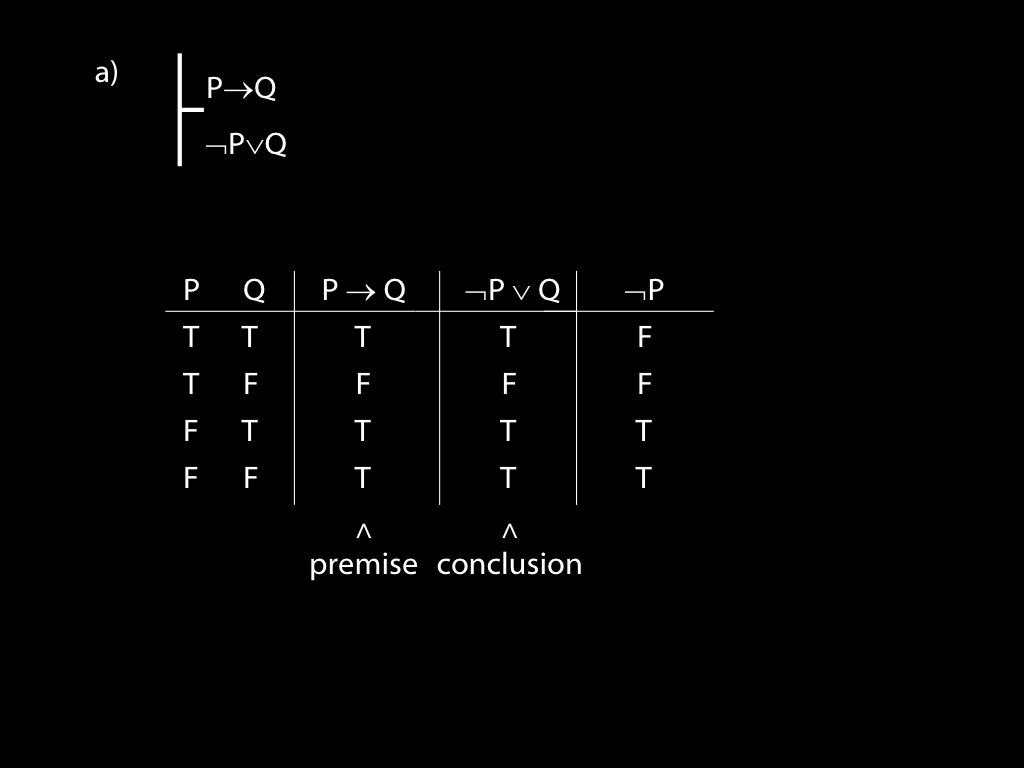
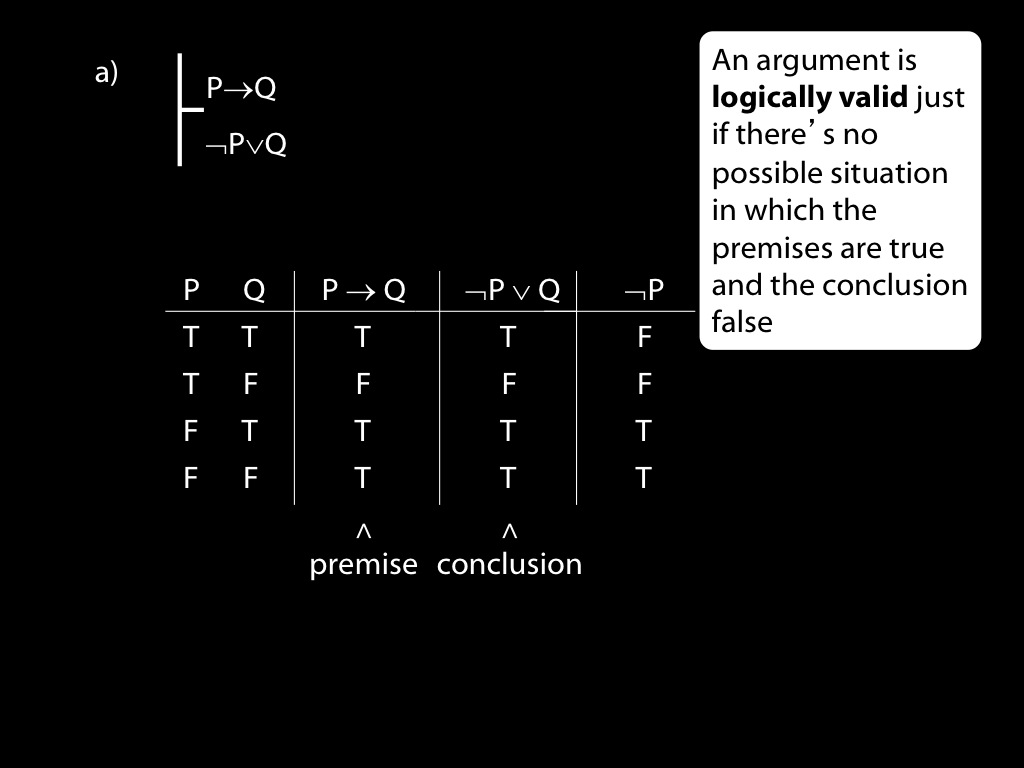
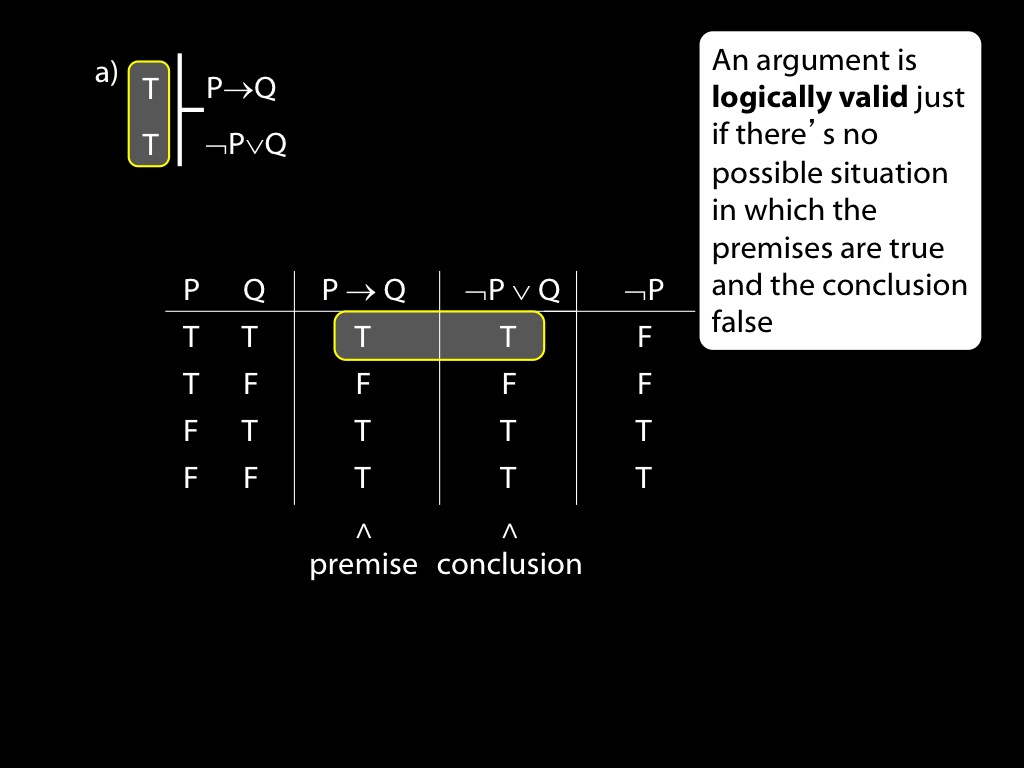
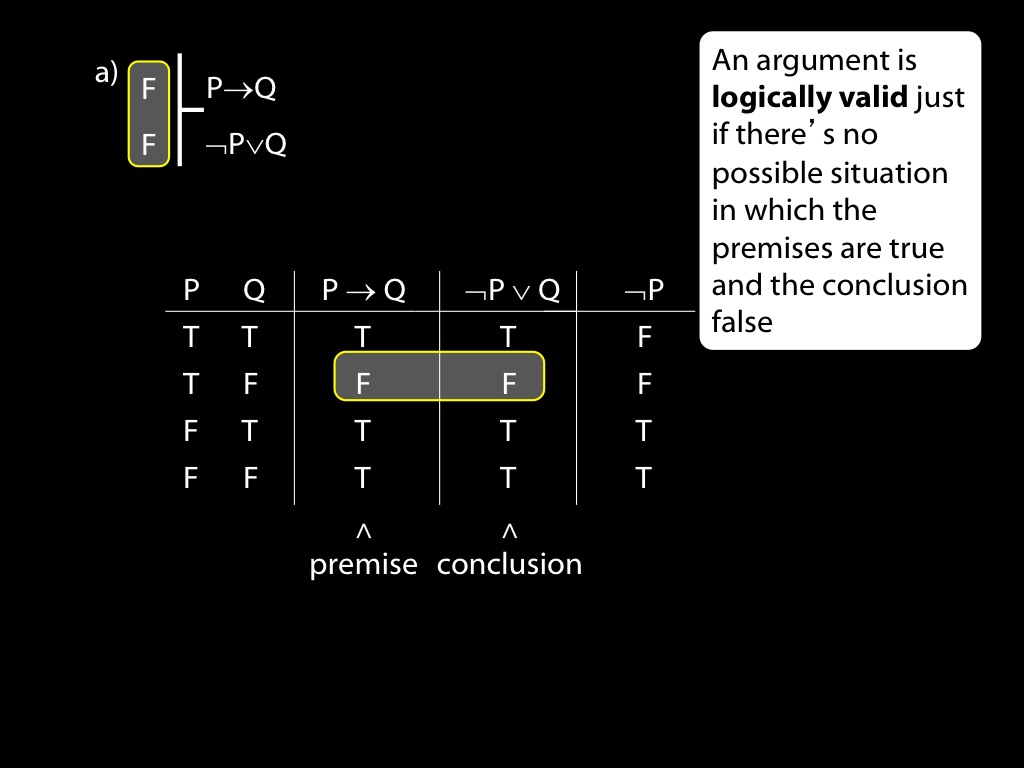
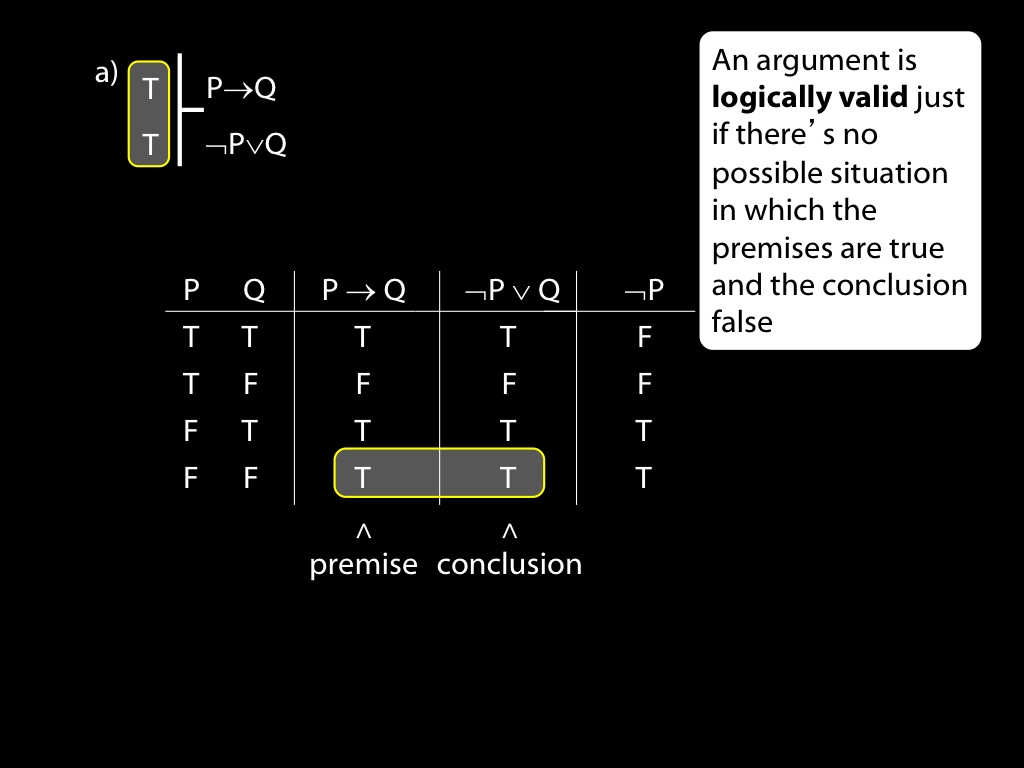
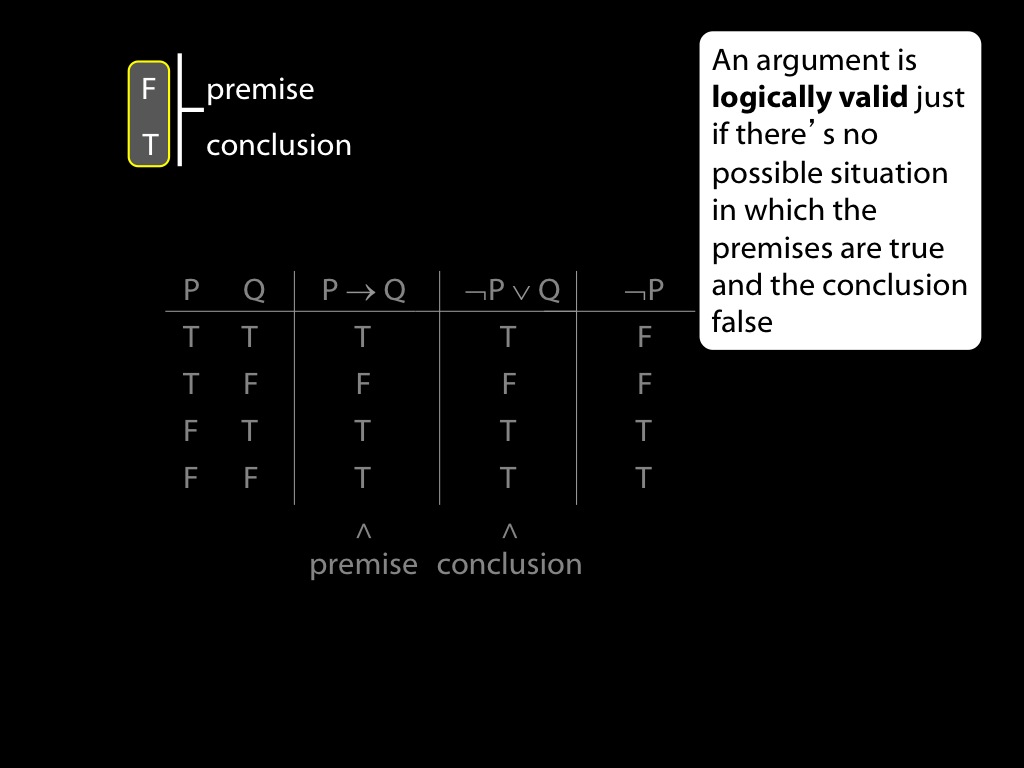
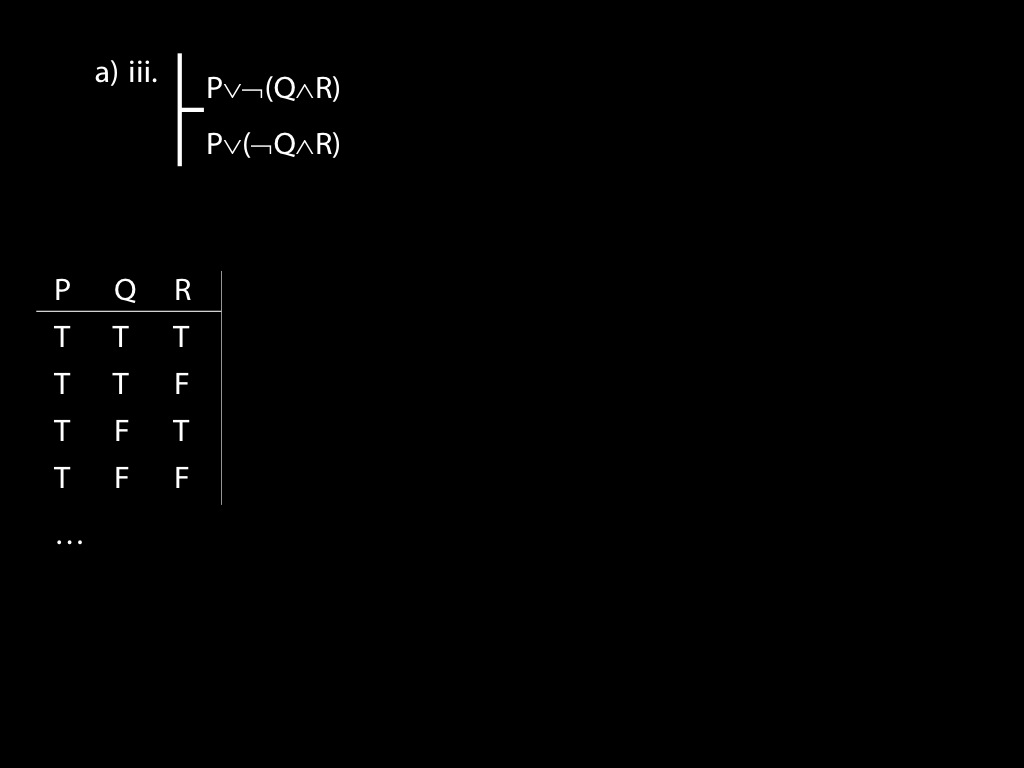
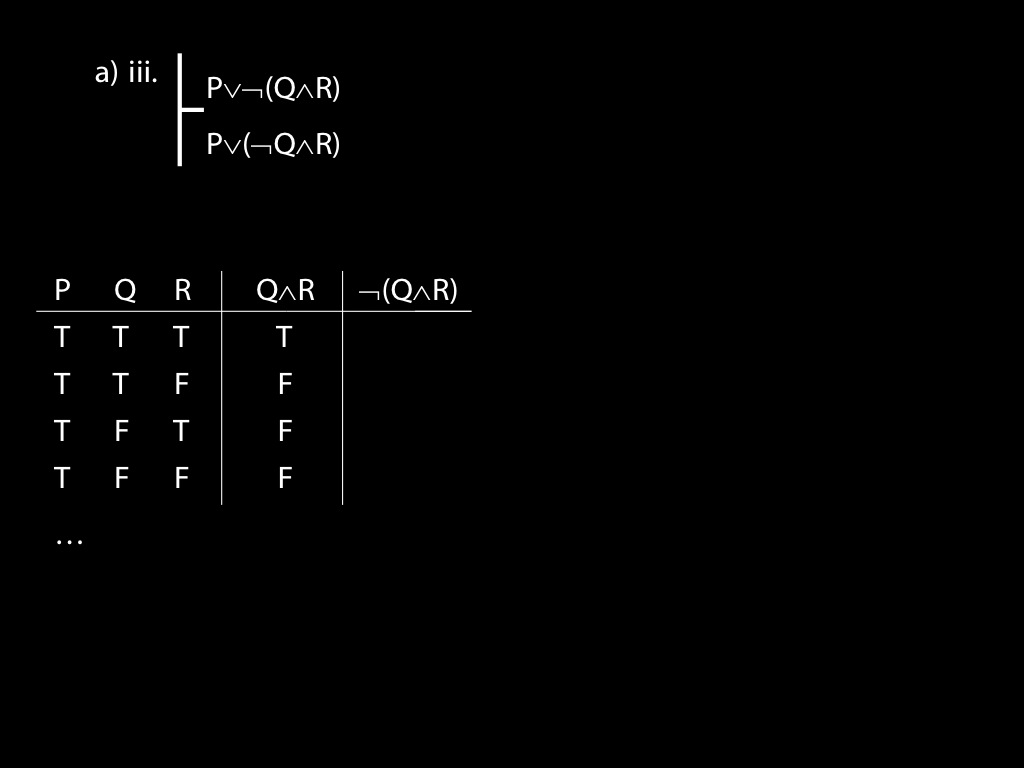
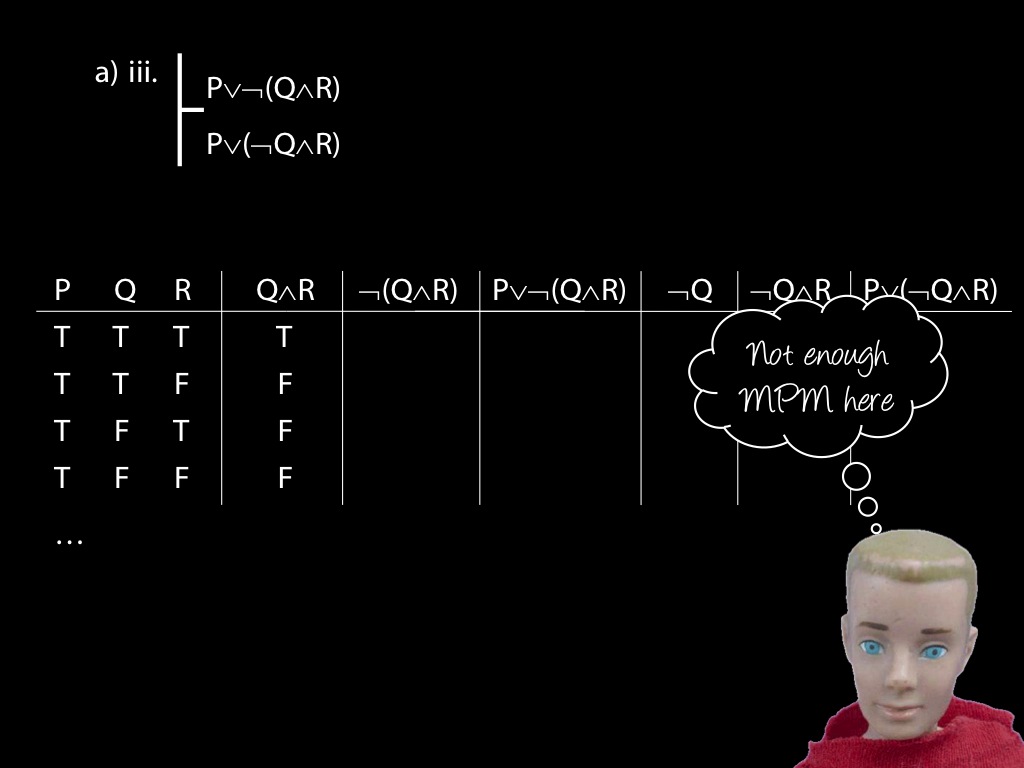
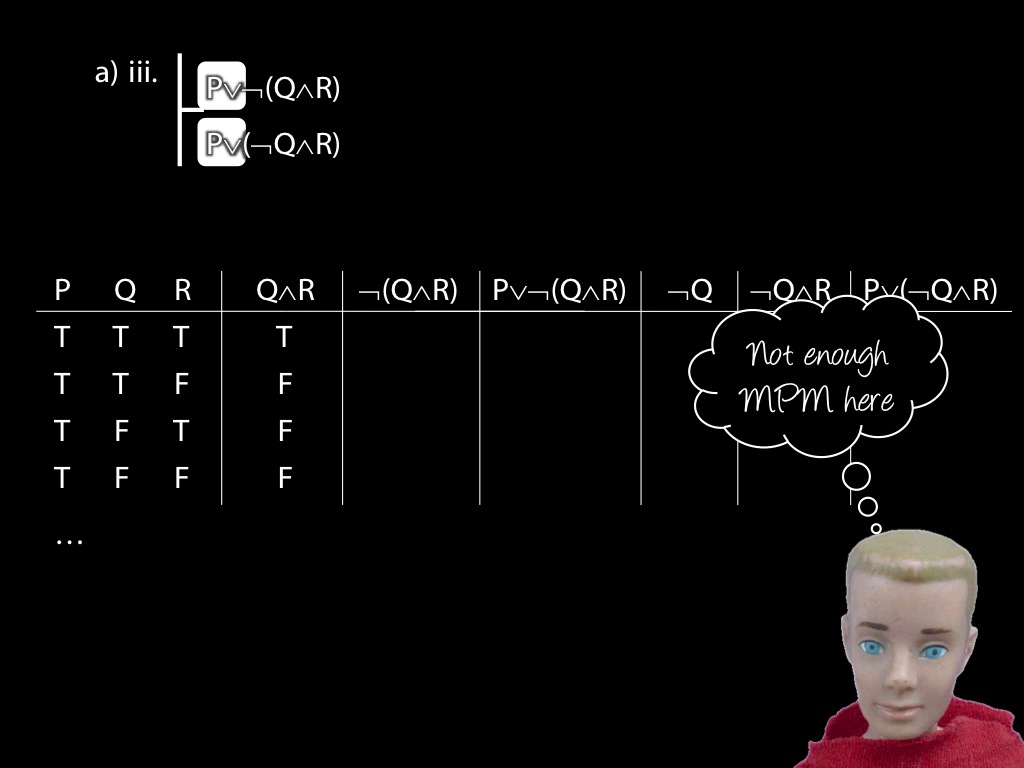
\section{Revison: Truth tables}
\section{Revison: Truth tables}
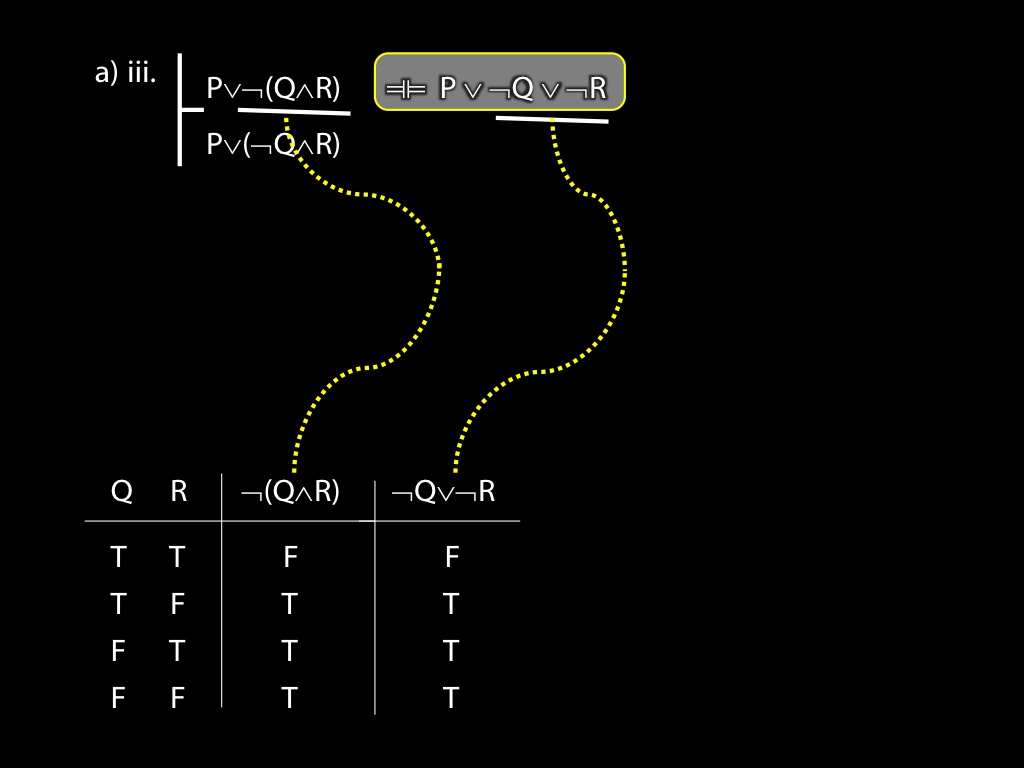
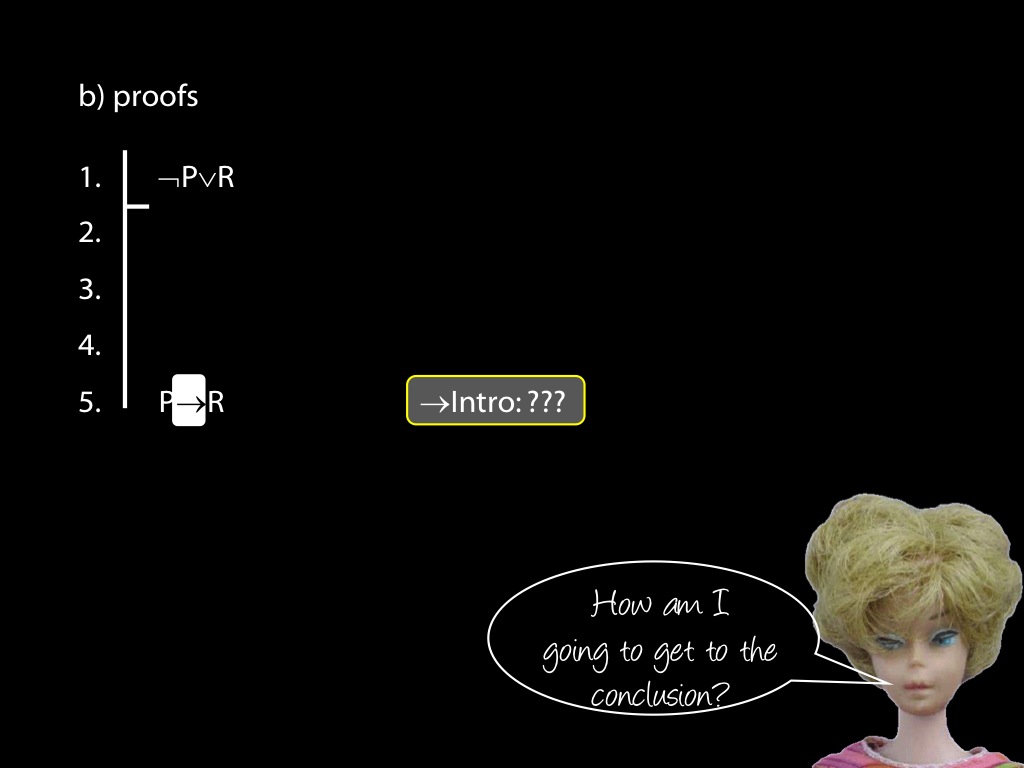
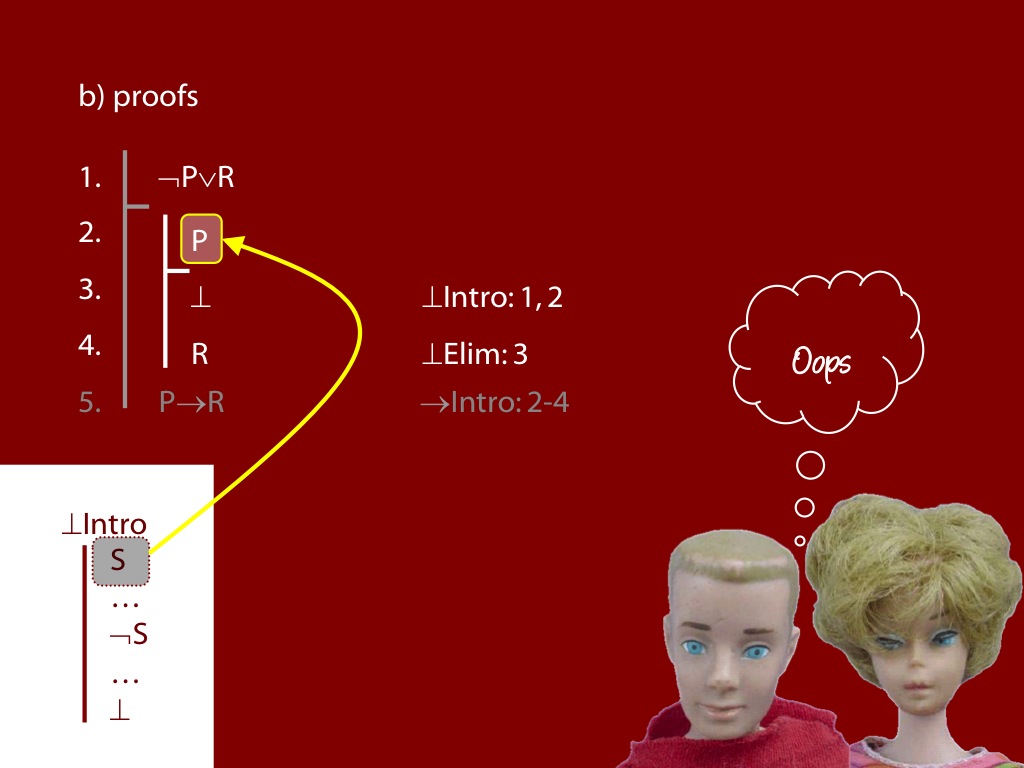
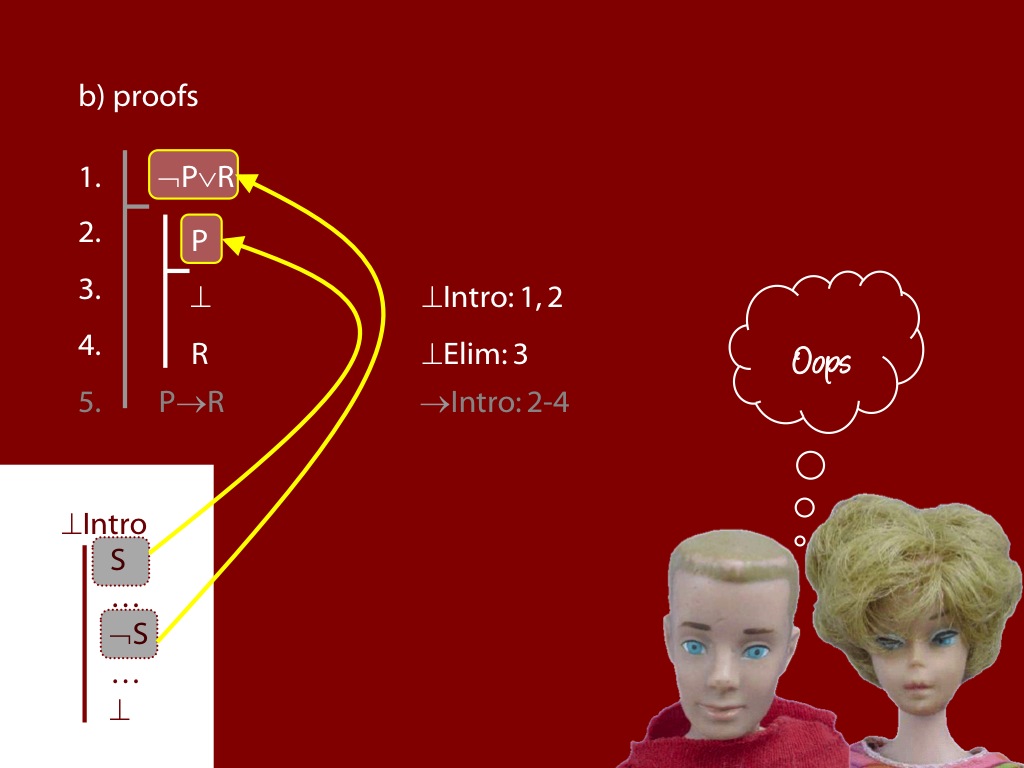
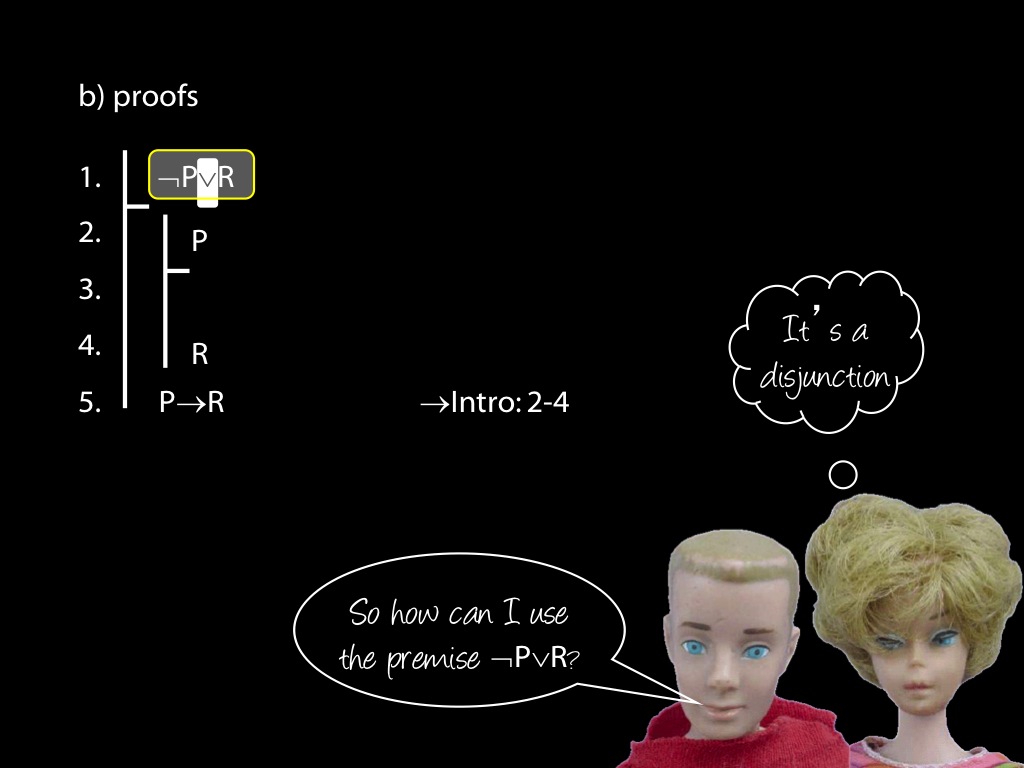
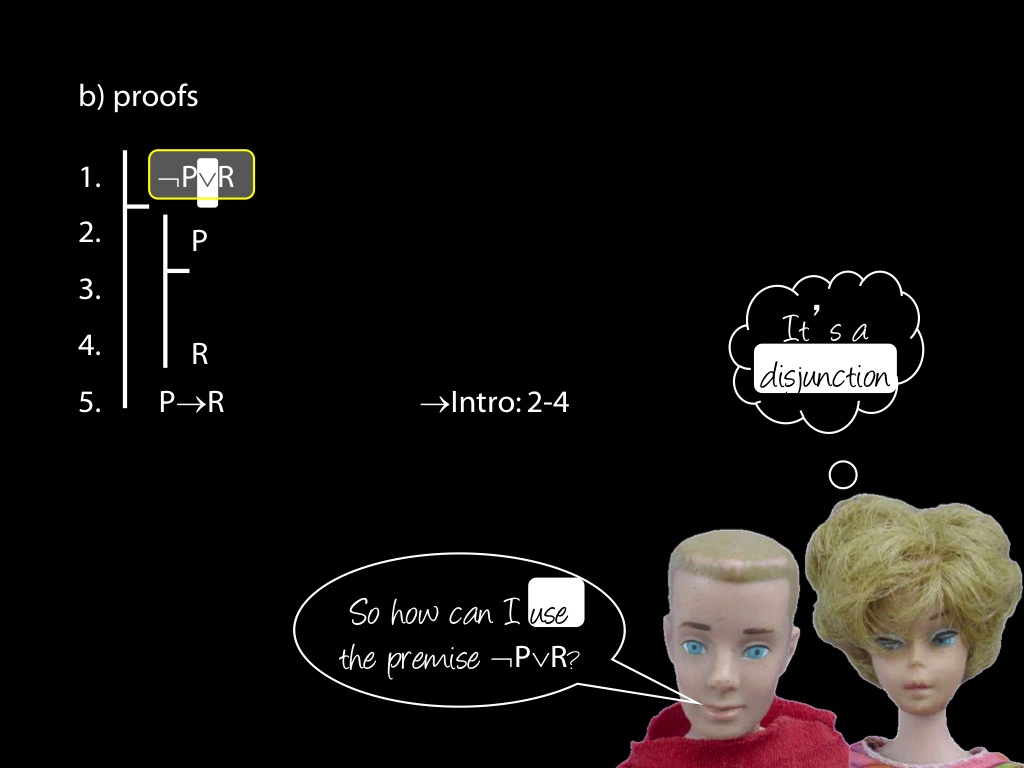
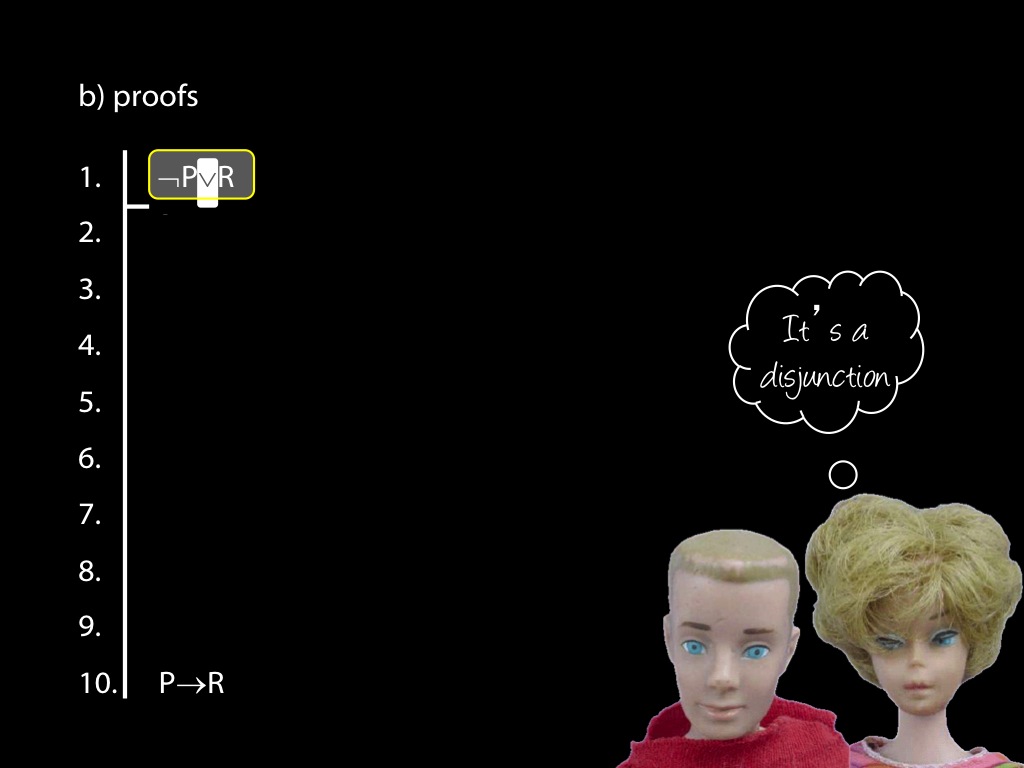
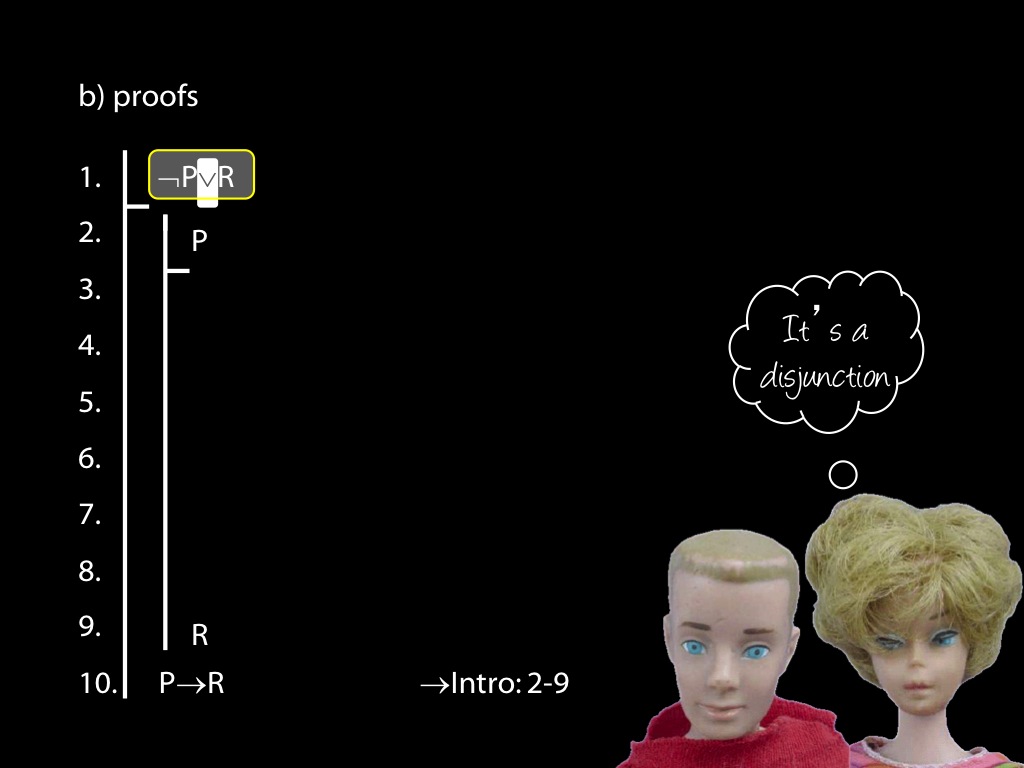
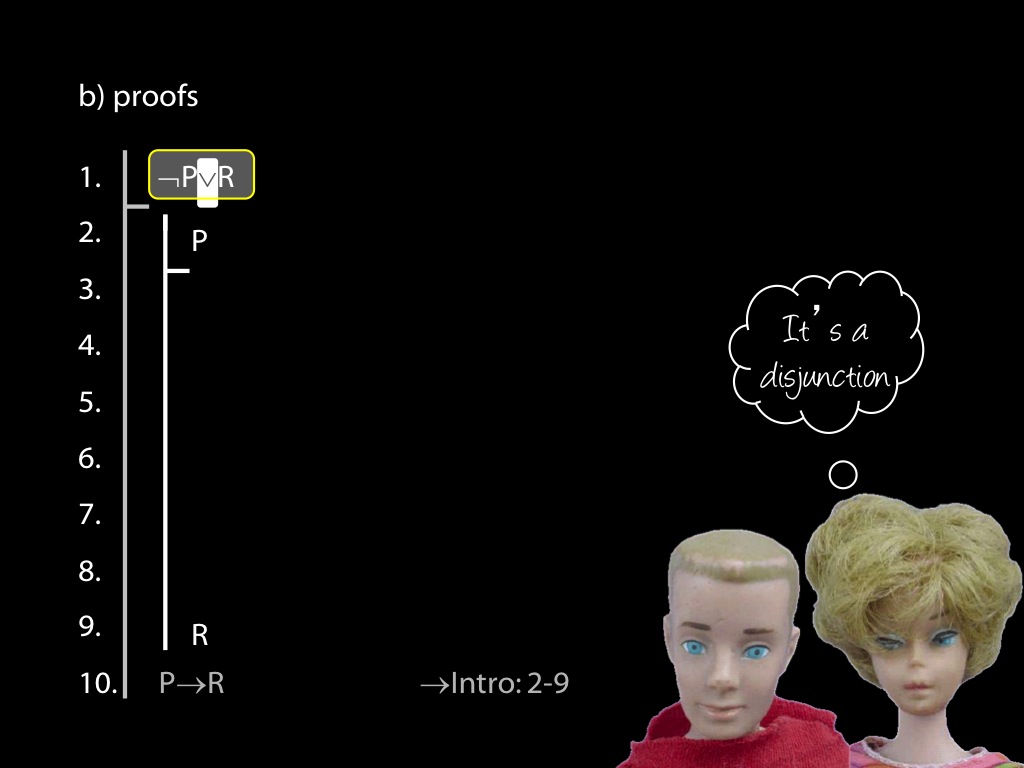
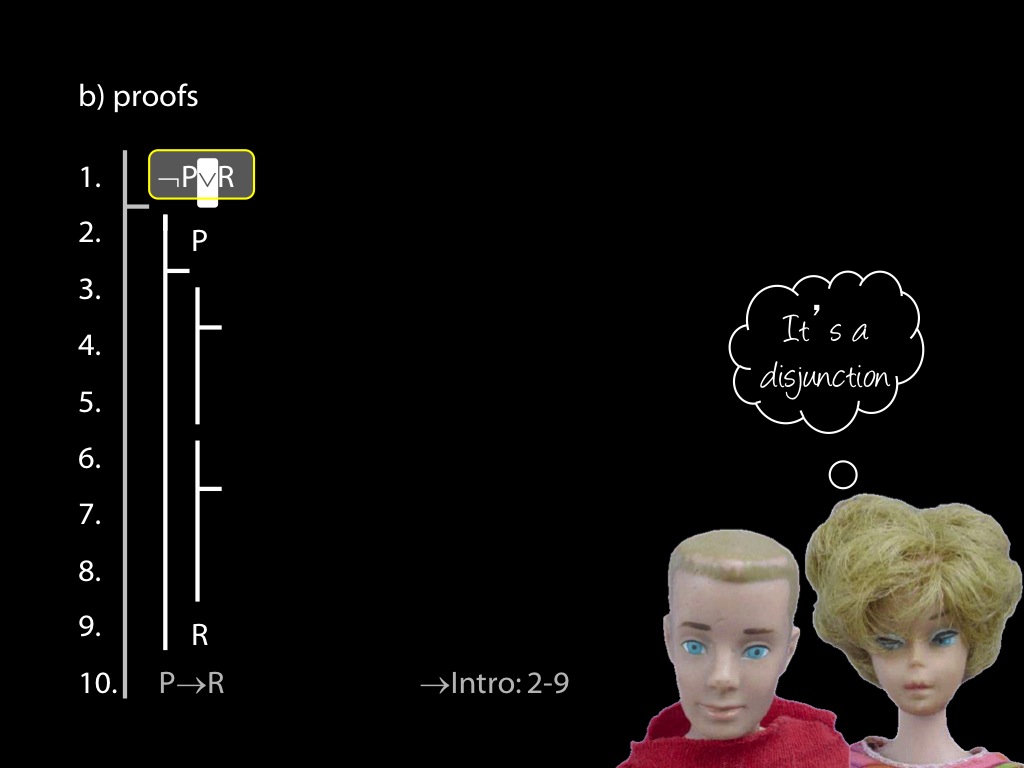
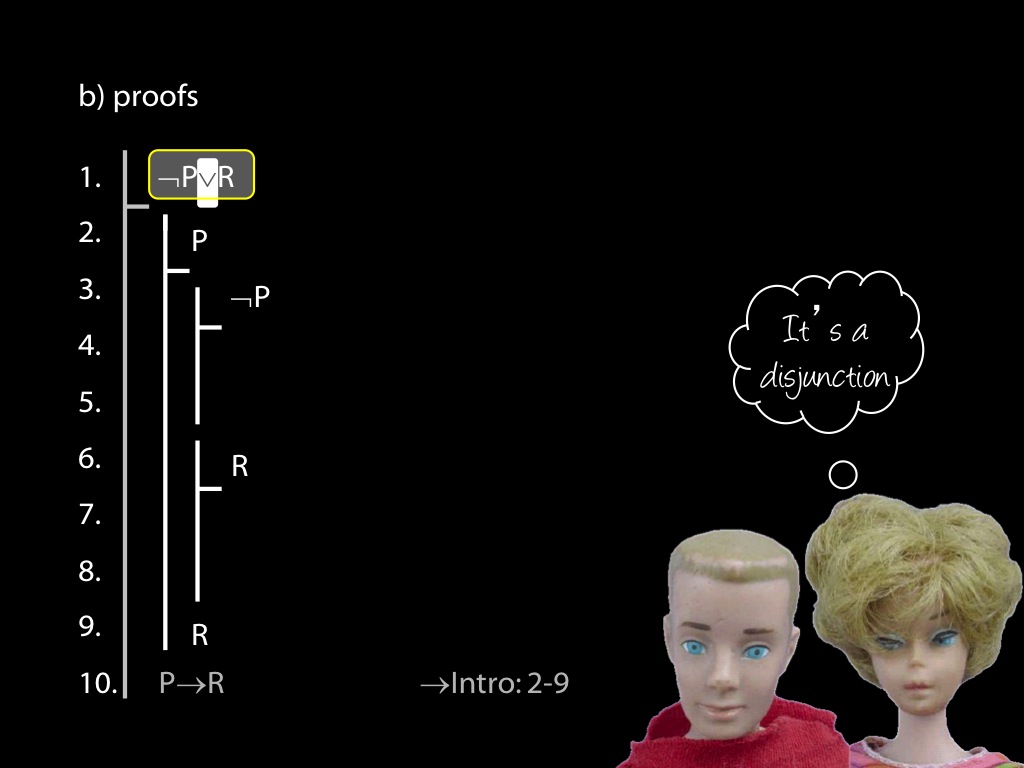
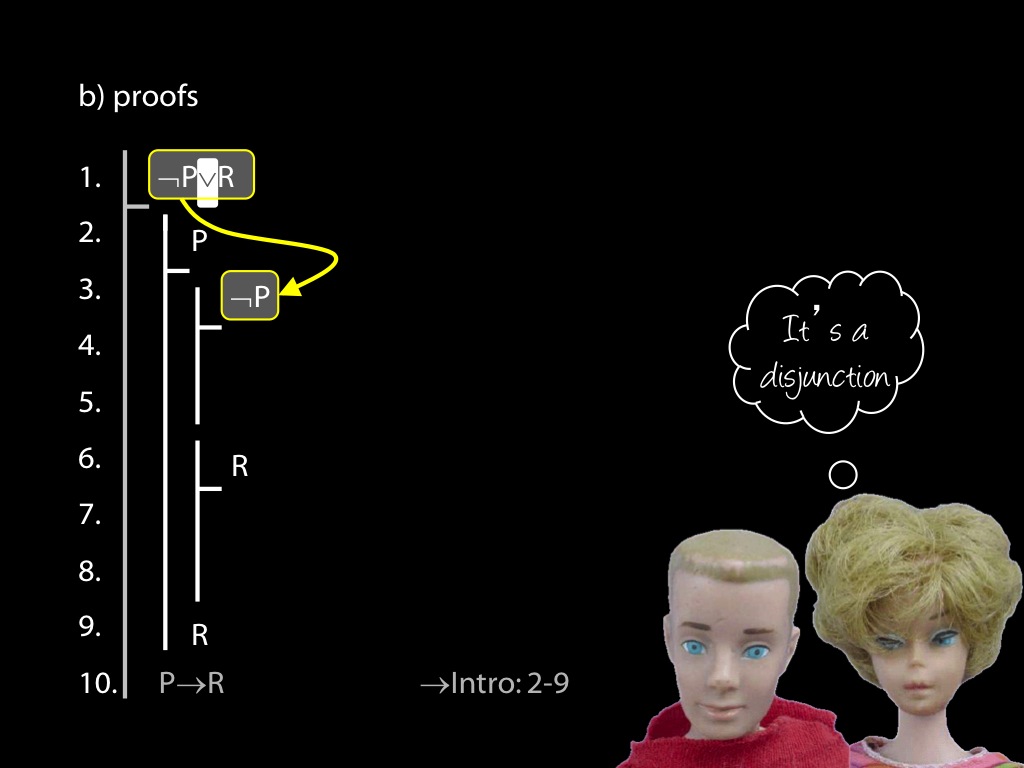
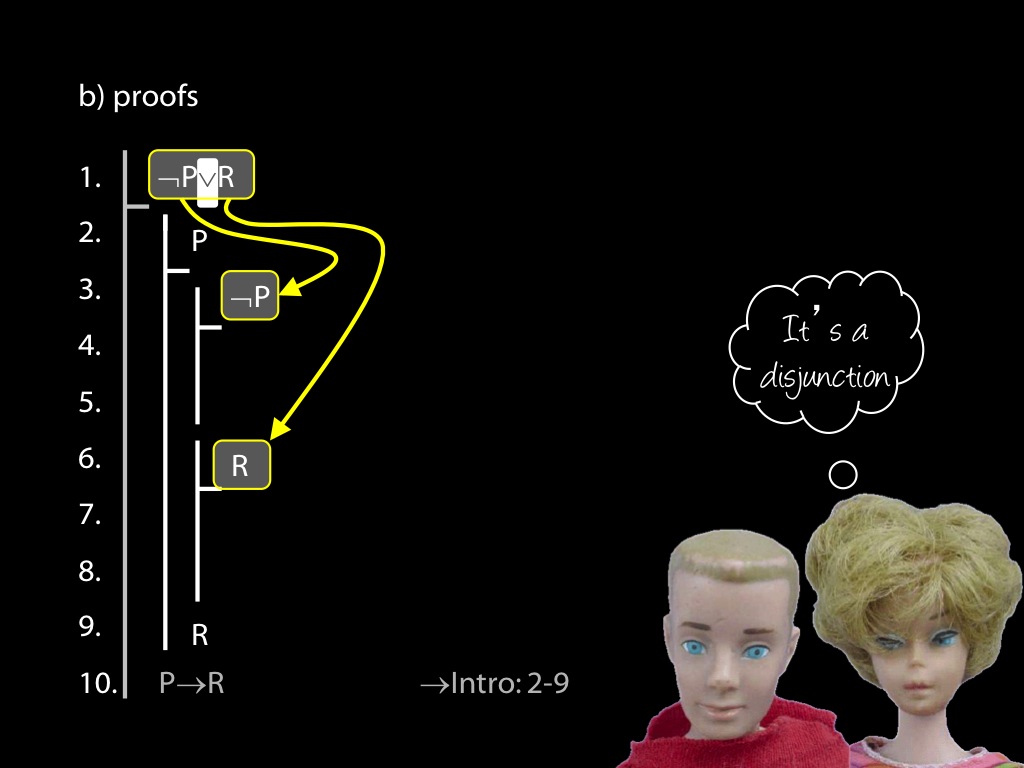
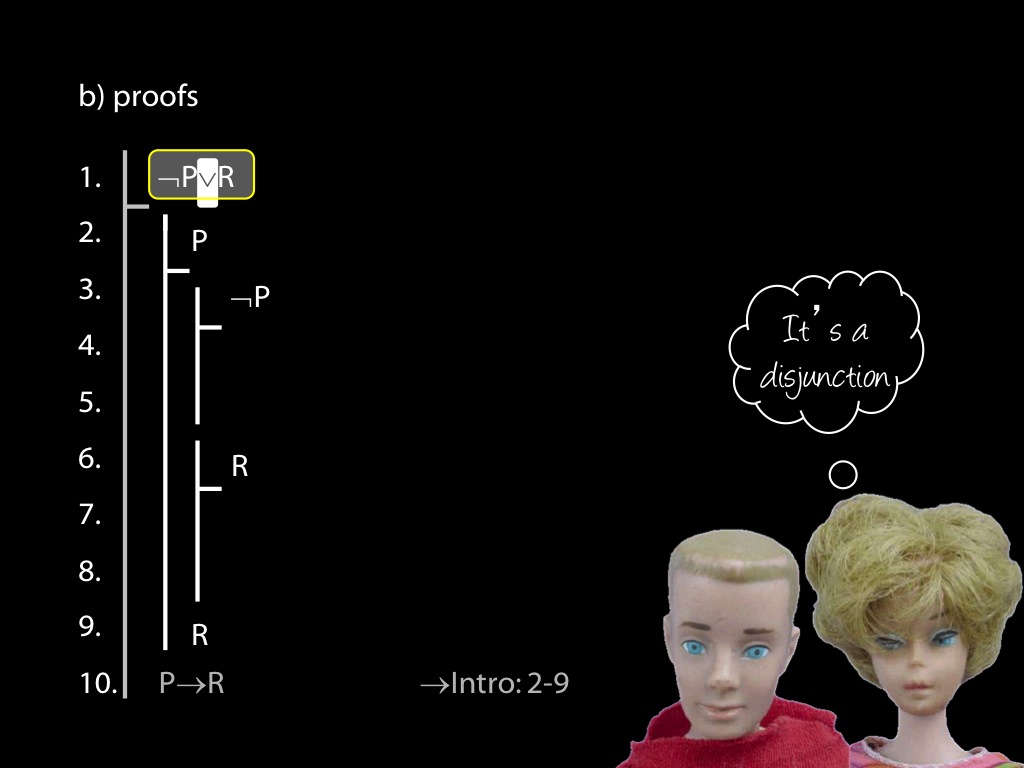
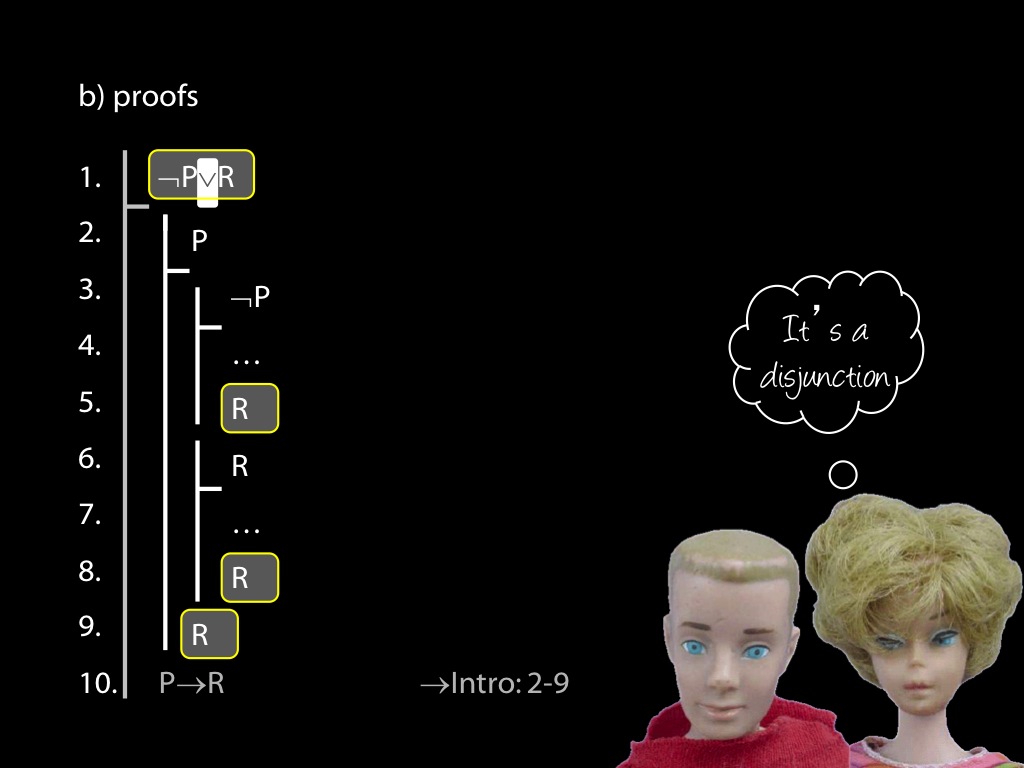
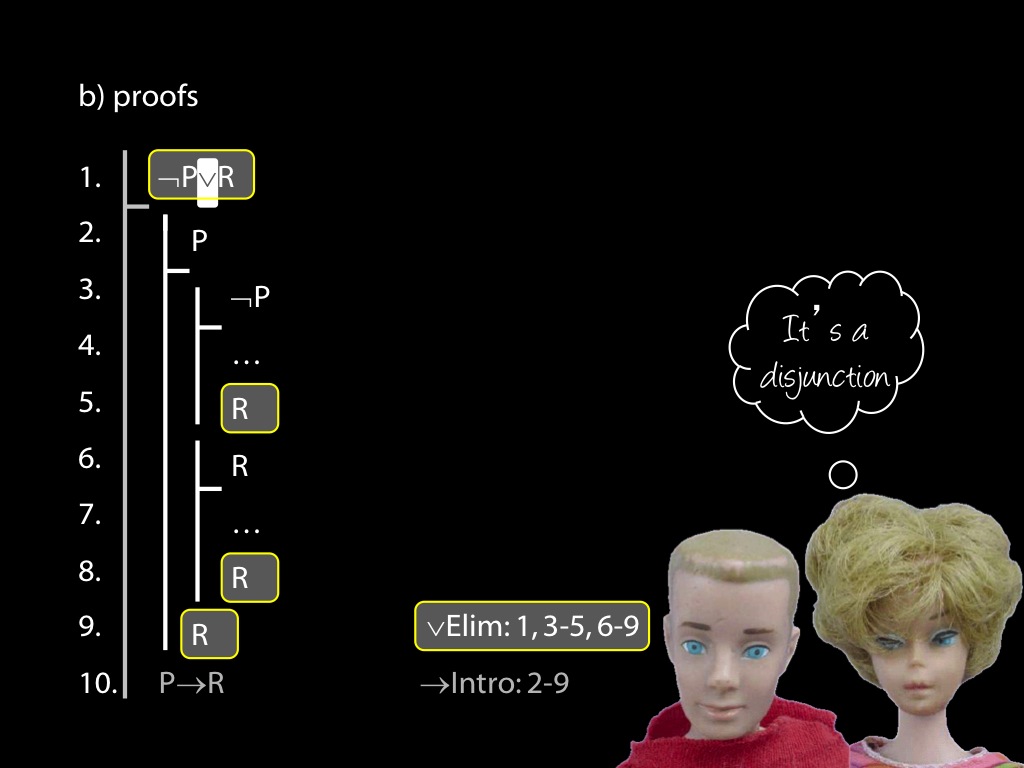
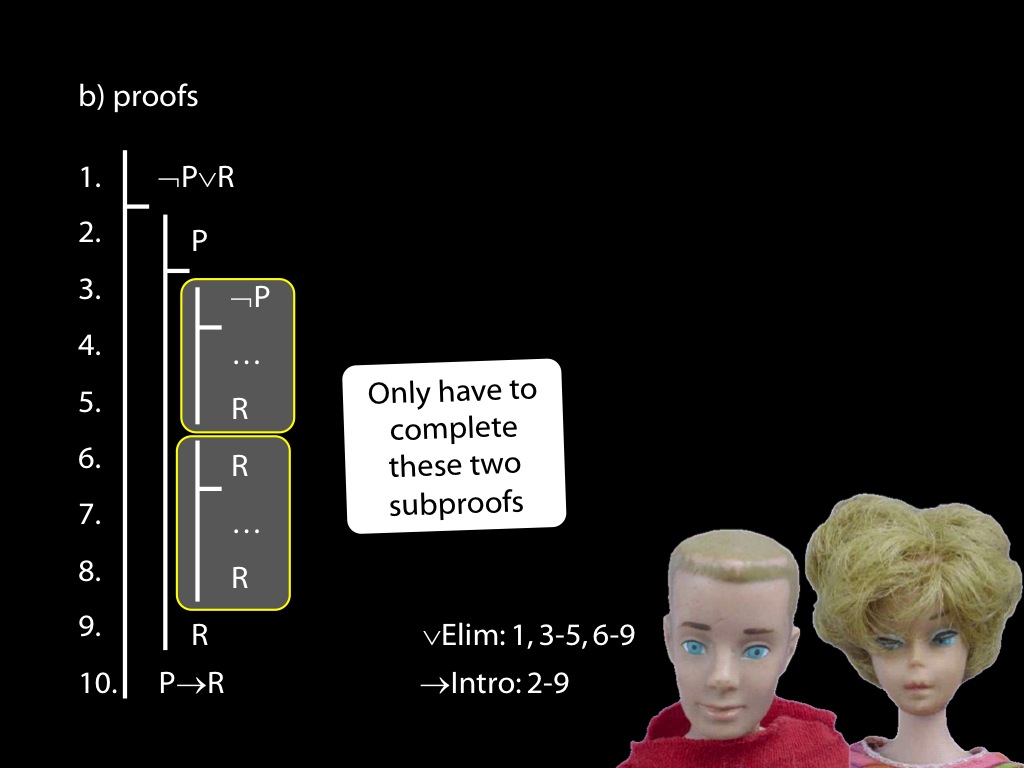
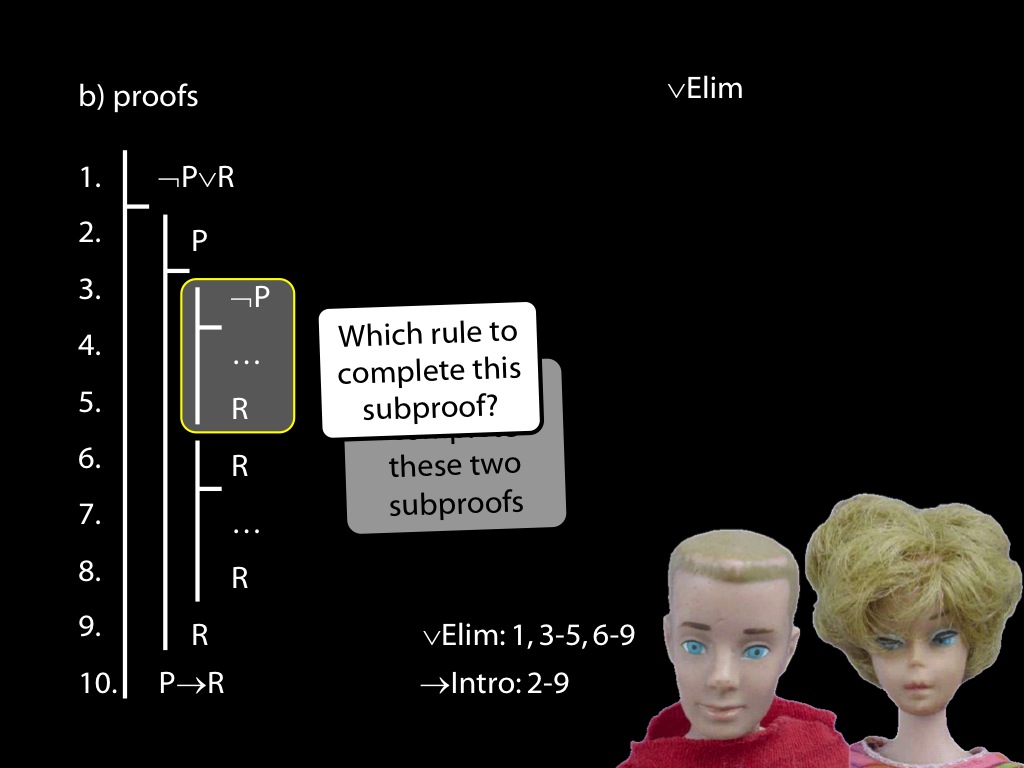
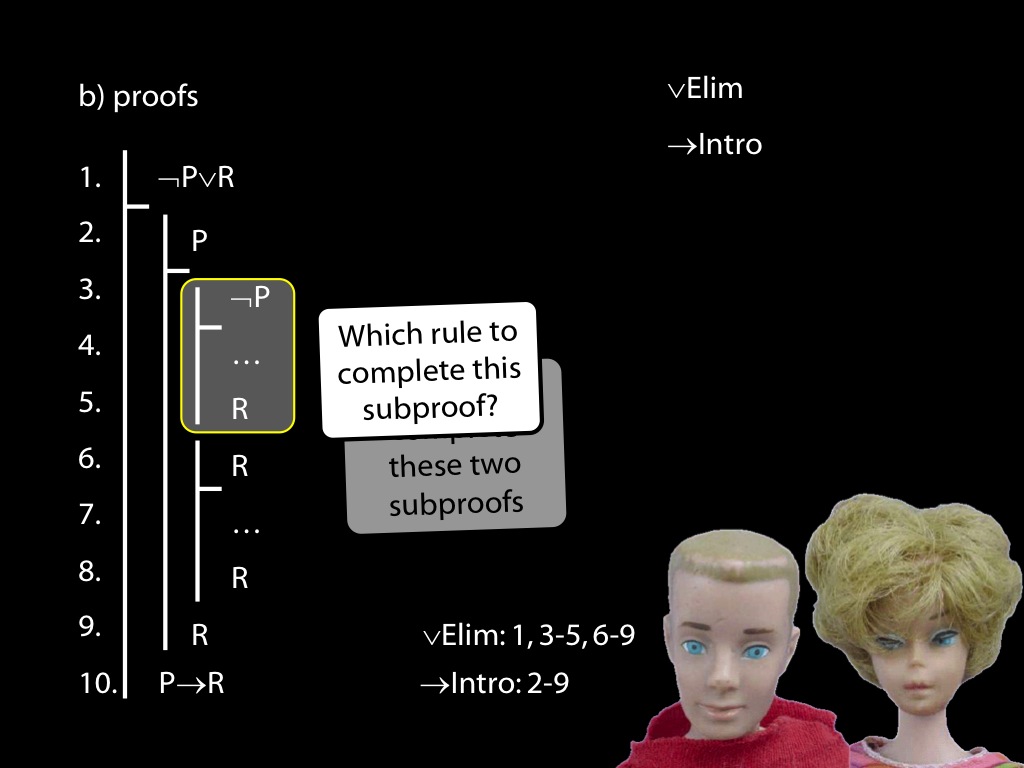
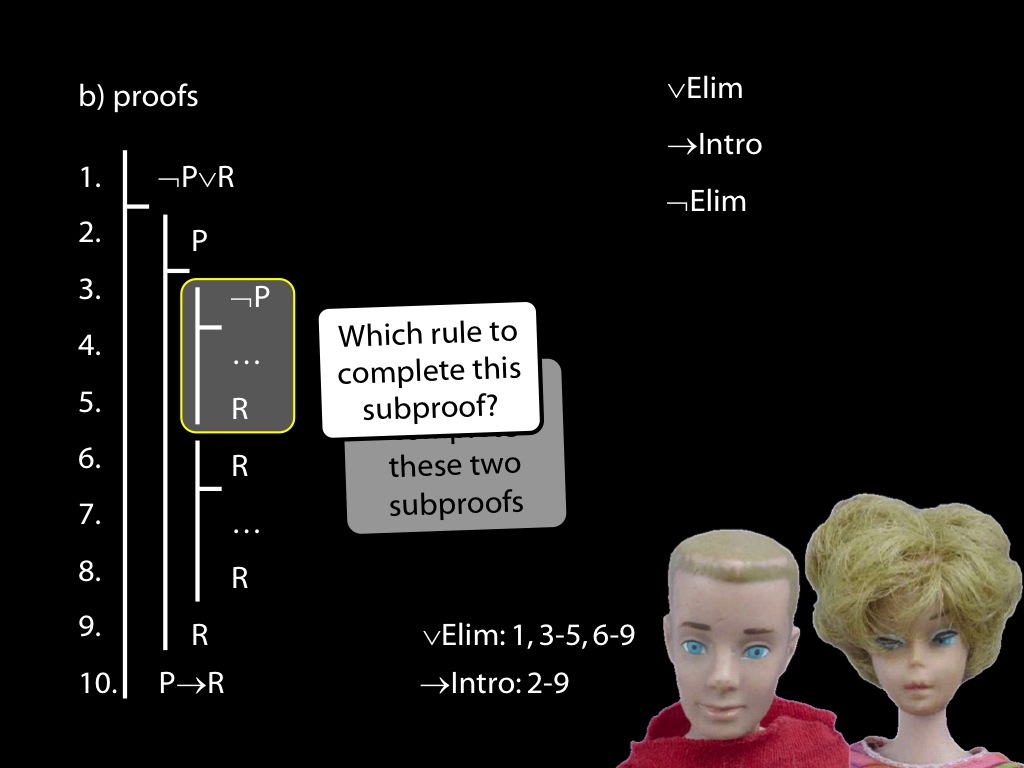
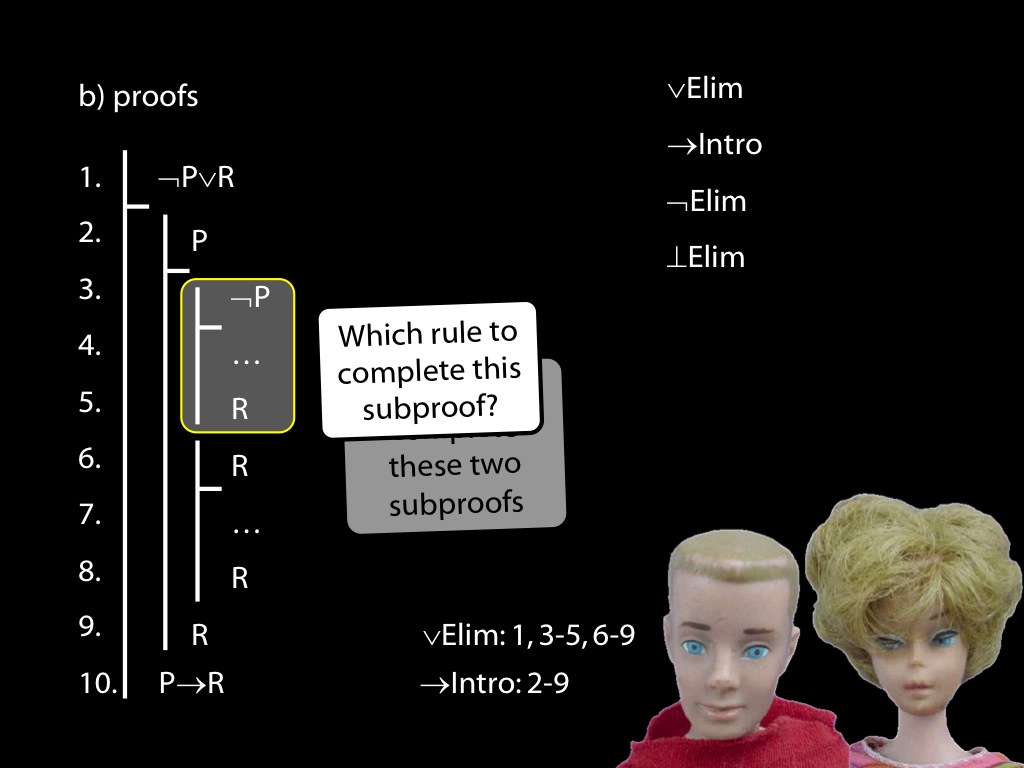
\section{Revison: Proofs (propositional)}
\section{Revison: Proofs (propositional)}
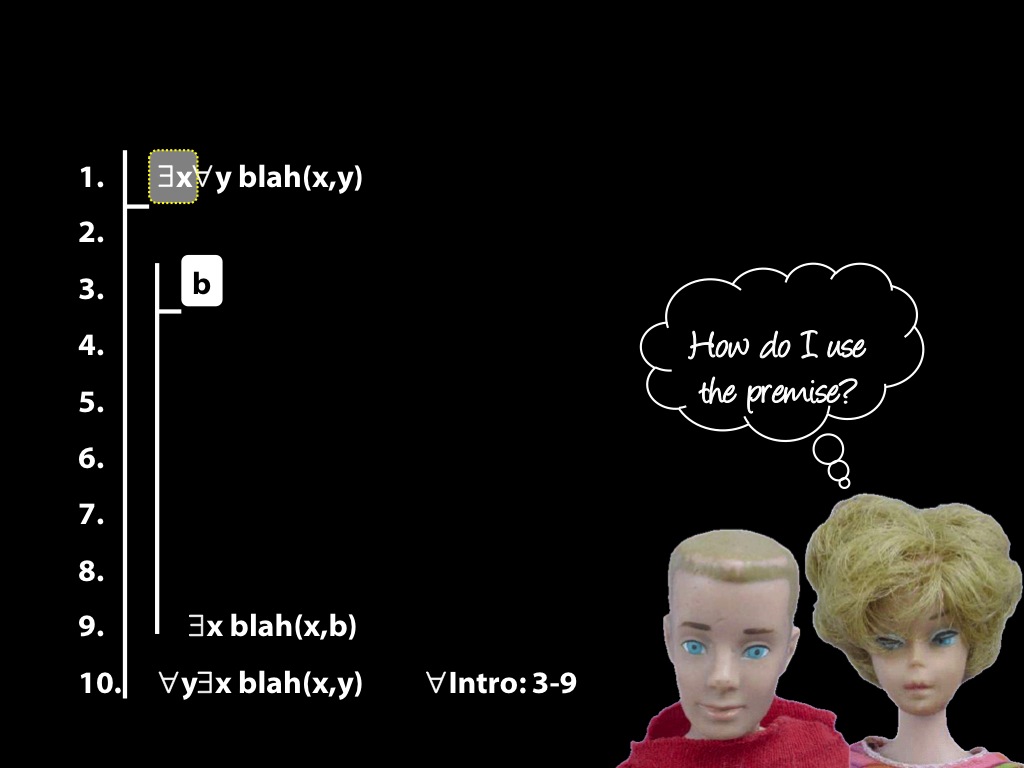
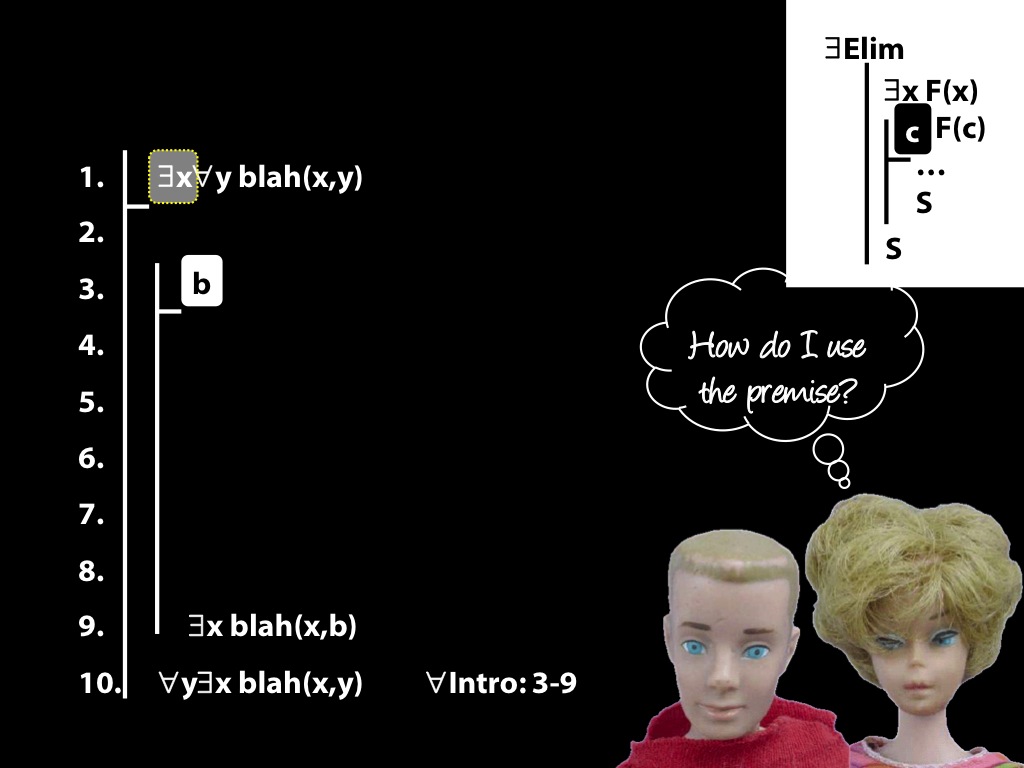
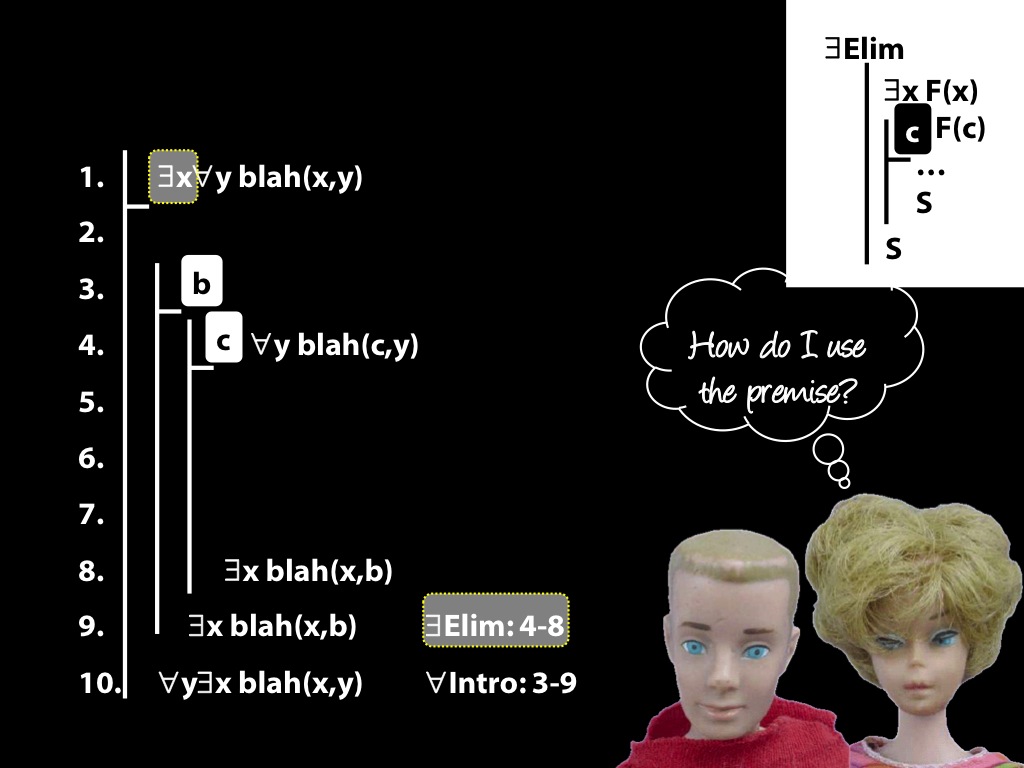
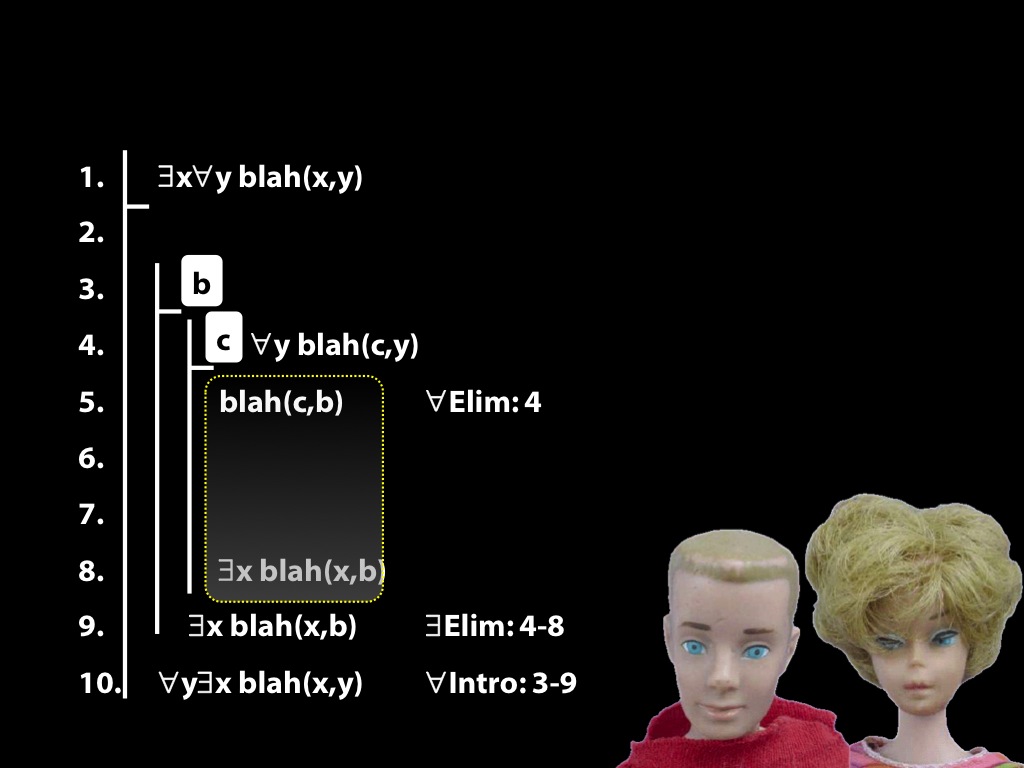
\section{Revison: Proofs (with quantifiers)}
\section{Revison: Proofs (with quantifiers)}
\section{Revison: Translation from English to awFOL}
\section{Revison: Translation from English to awFOL}
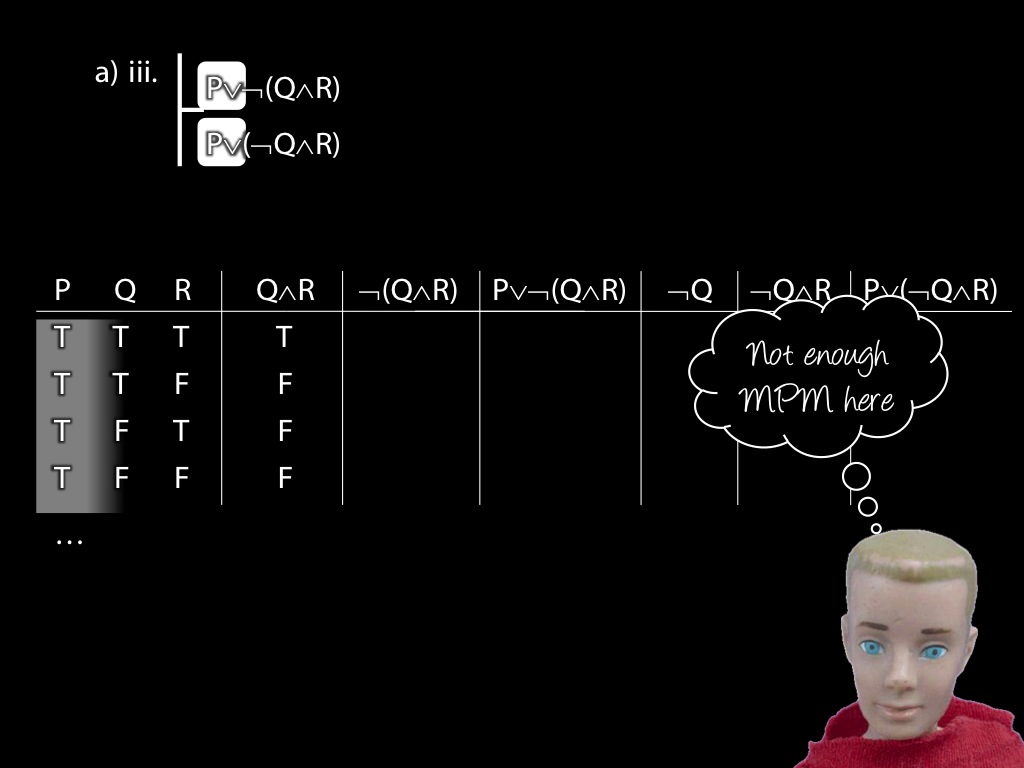
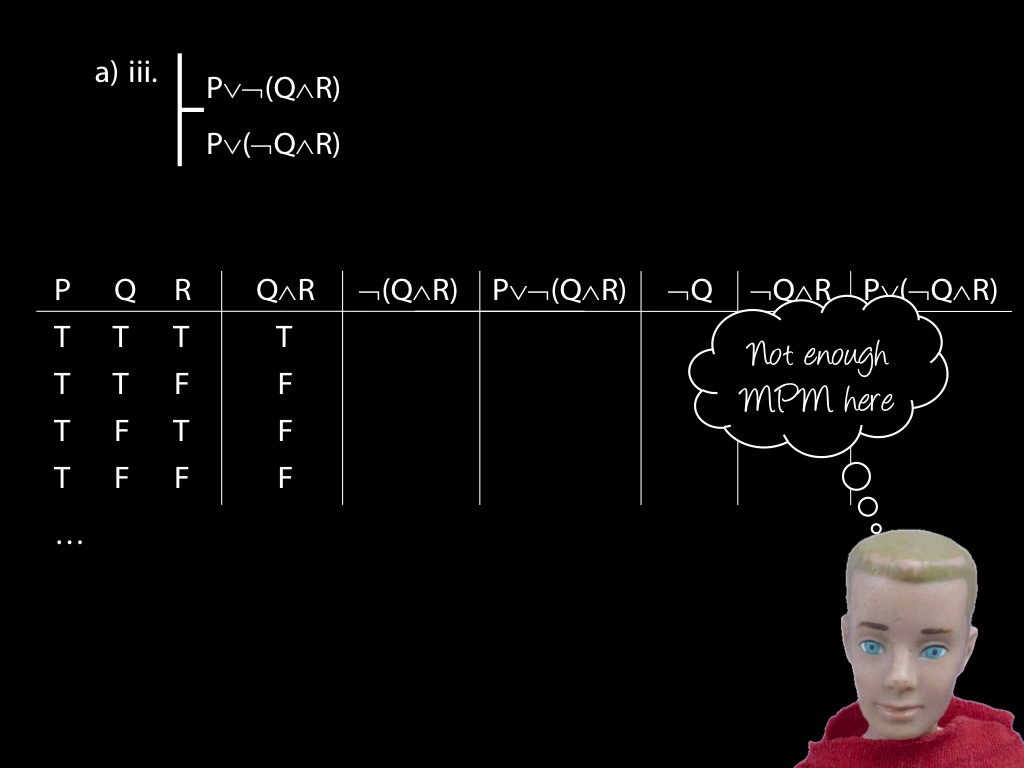
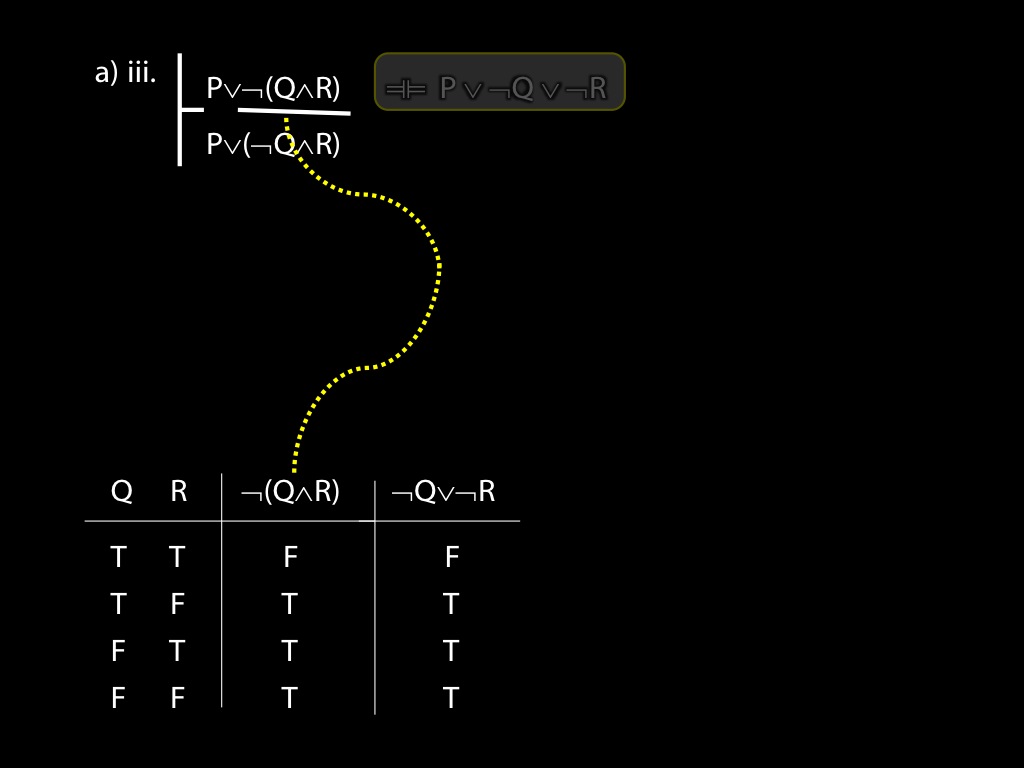
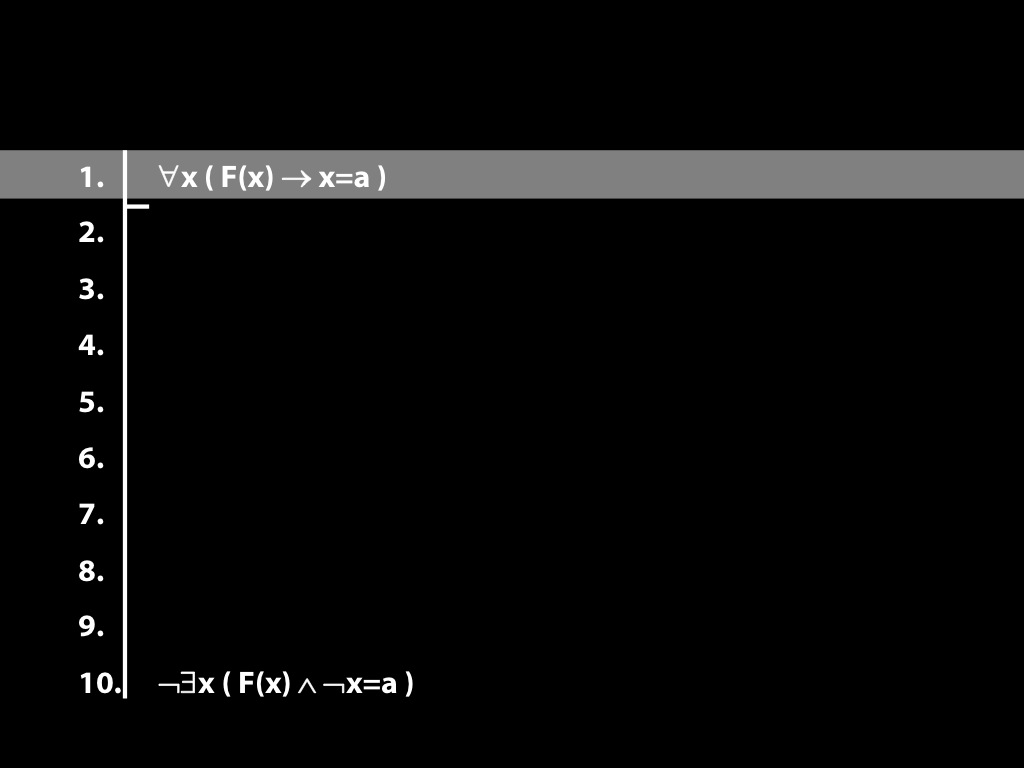
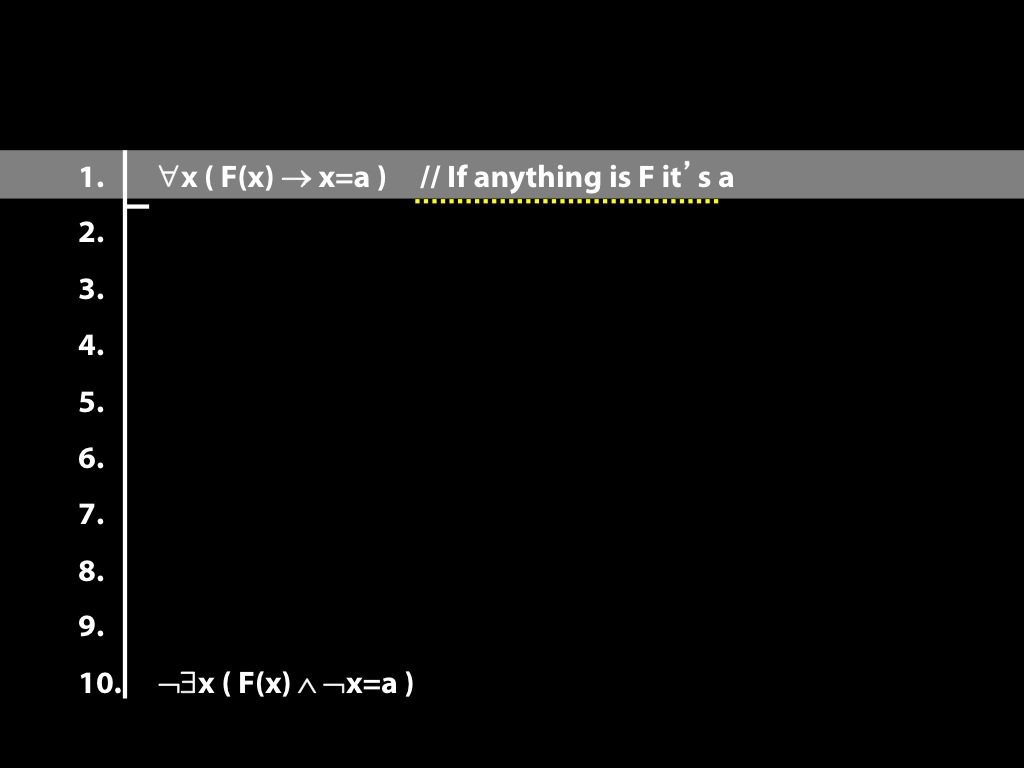
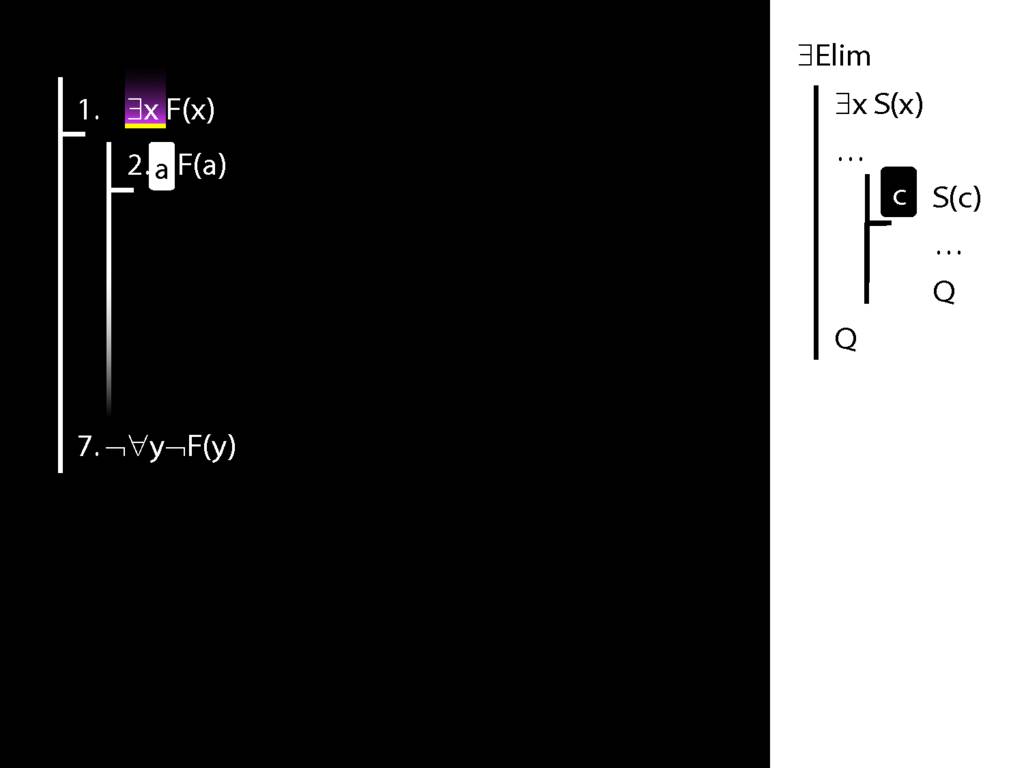
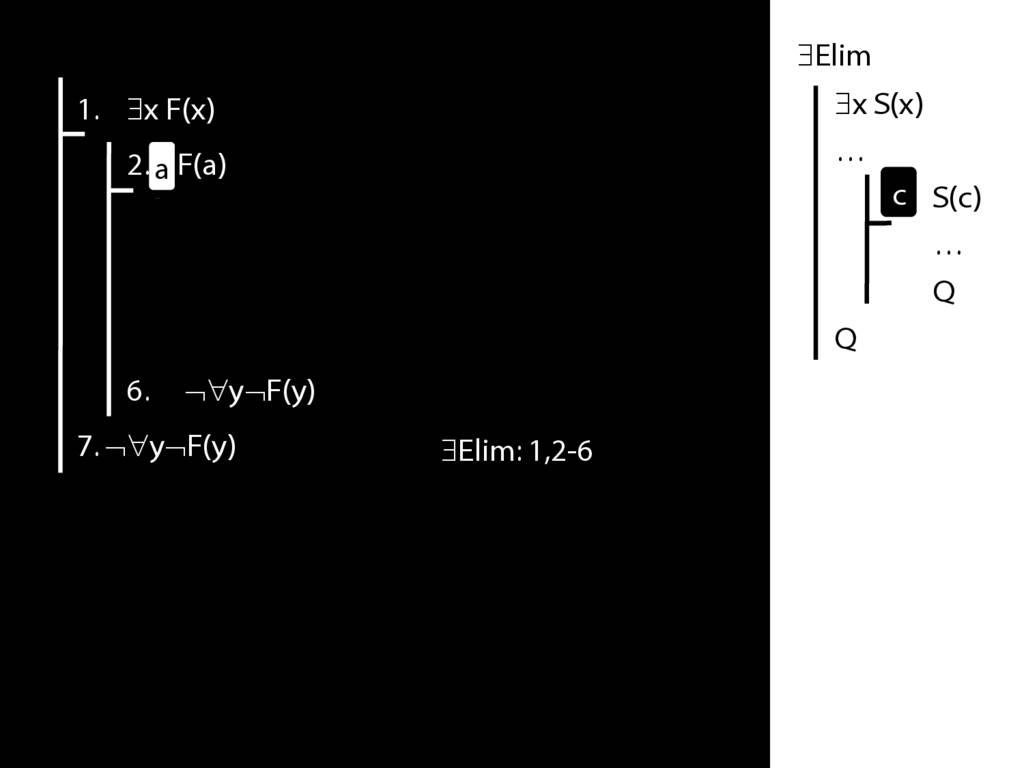
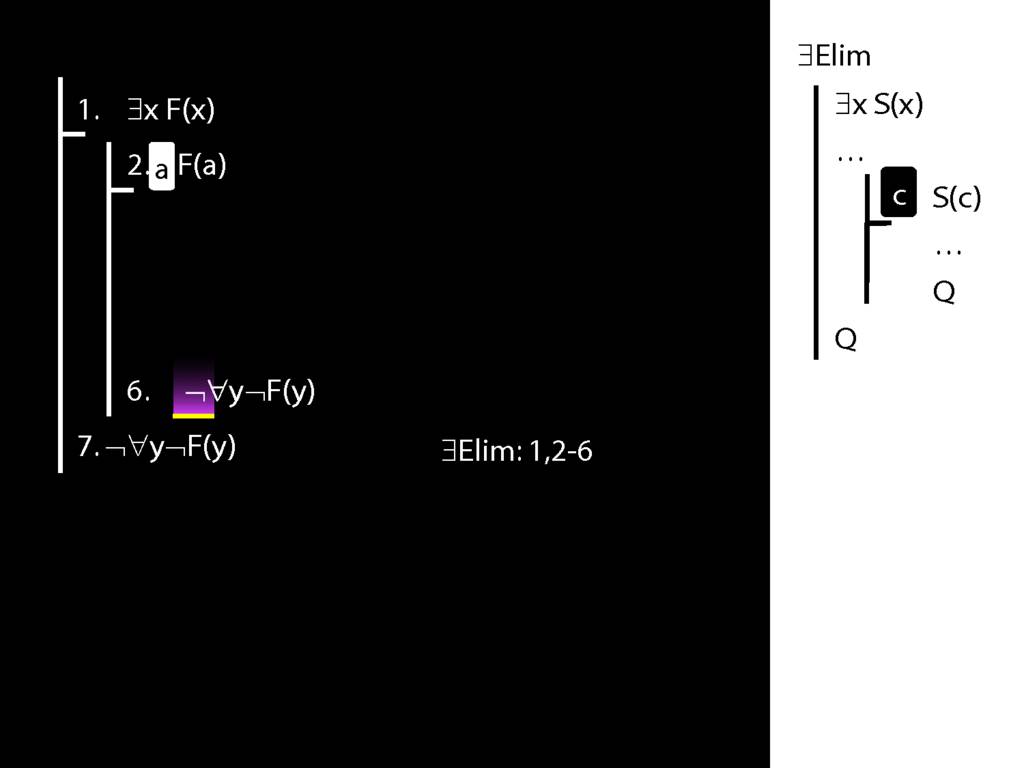
\section{Proof Example: ∃x Dead(x) ⊢ ¬∀x¬ Dead(x).}
\section{Proof Example: ∃x Dead(x) ⊢ ¬∀x¬ Dead(x).}
13.43--13.45
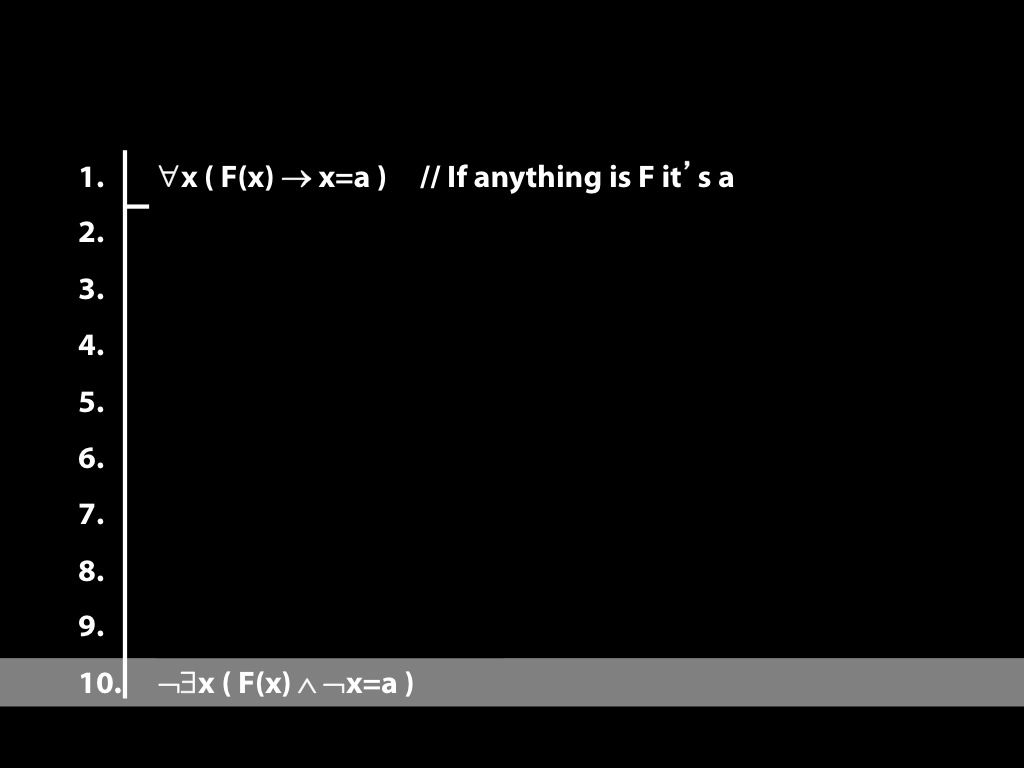
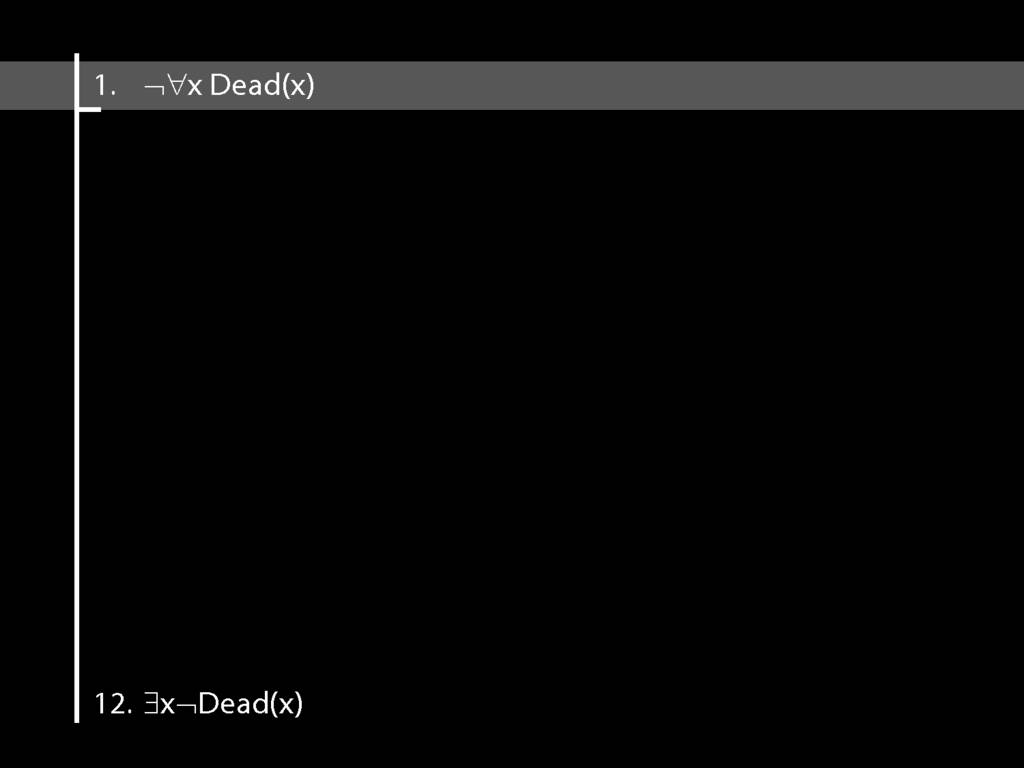
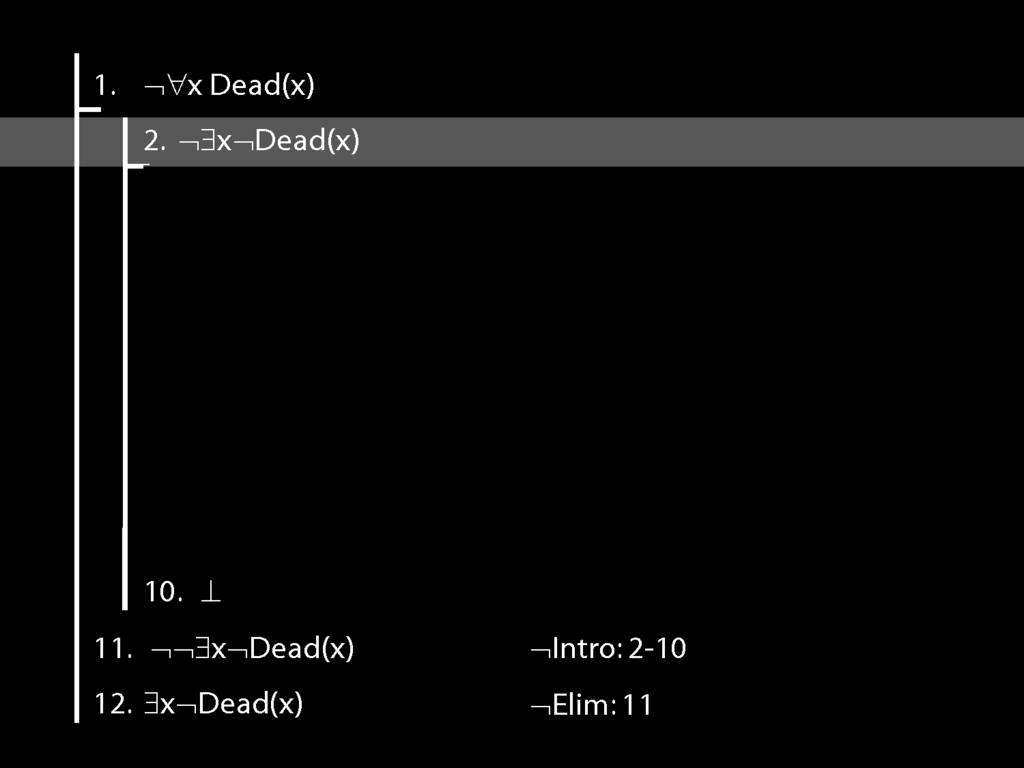
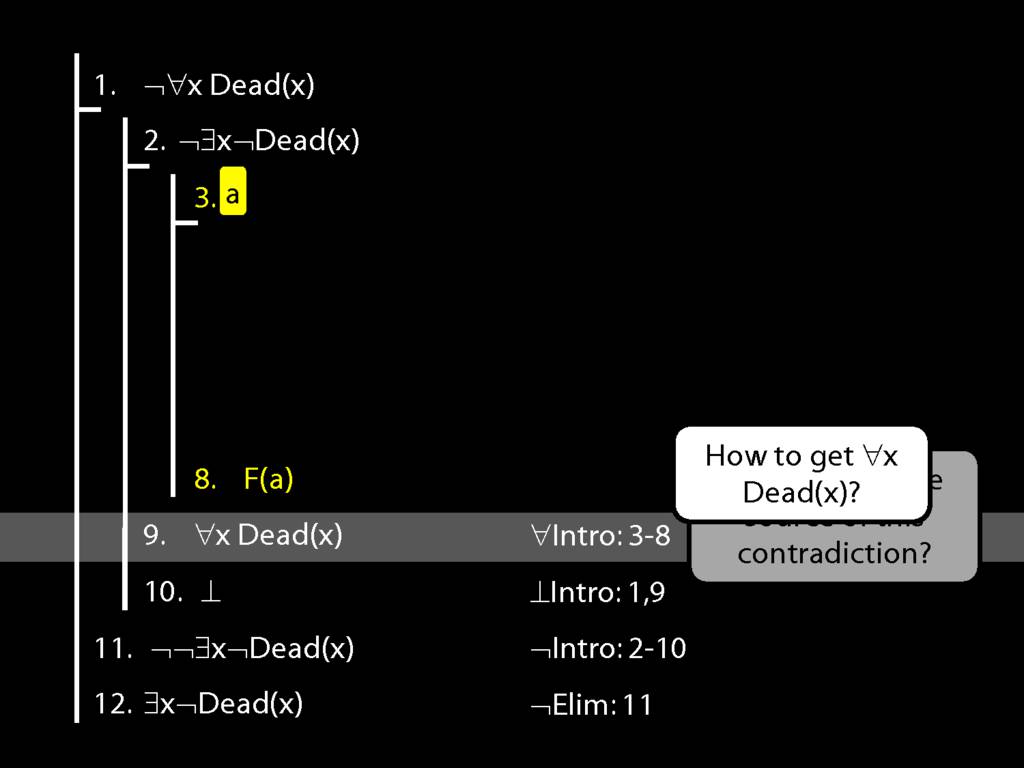
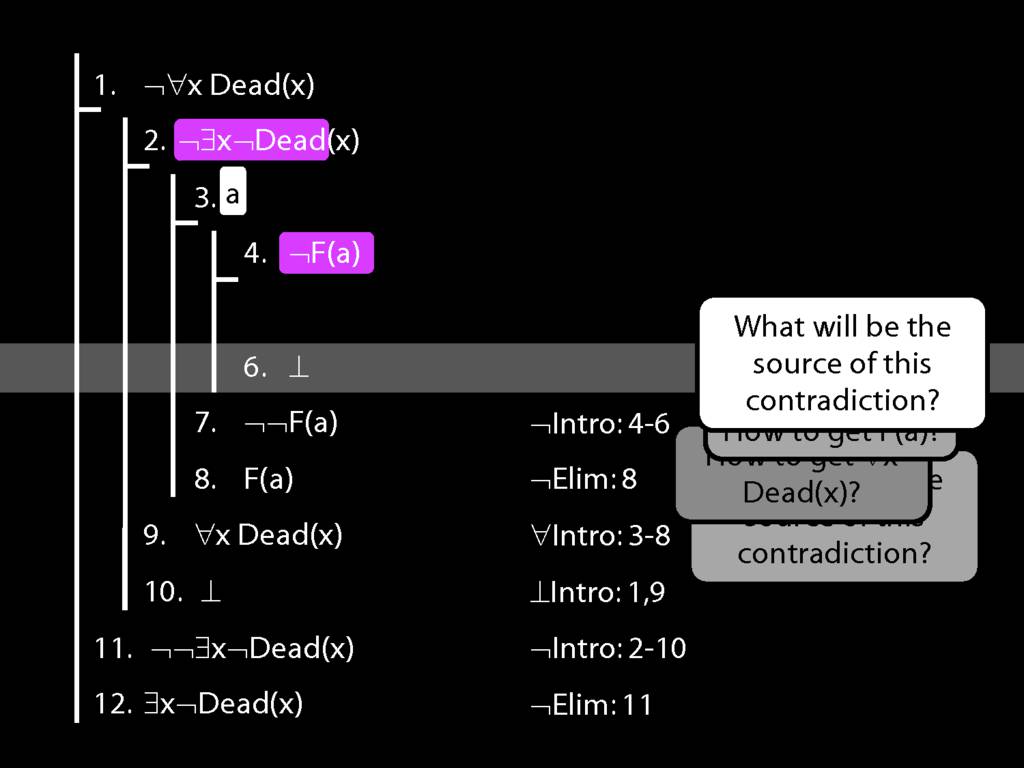
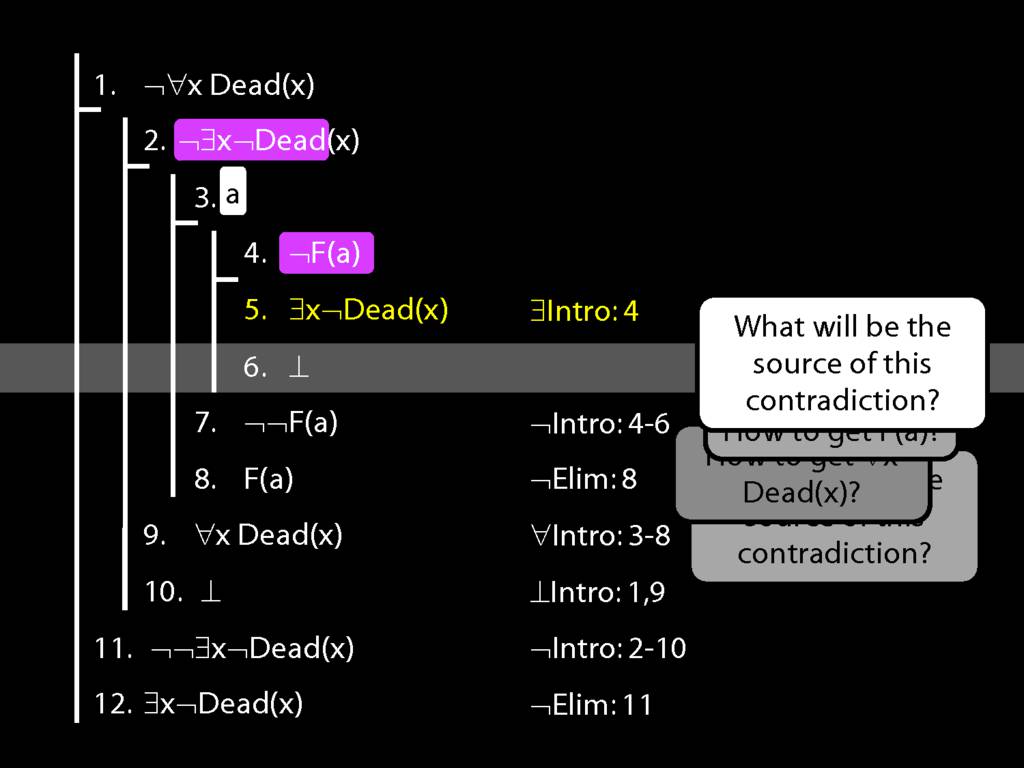
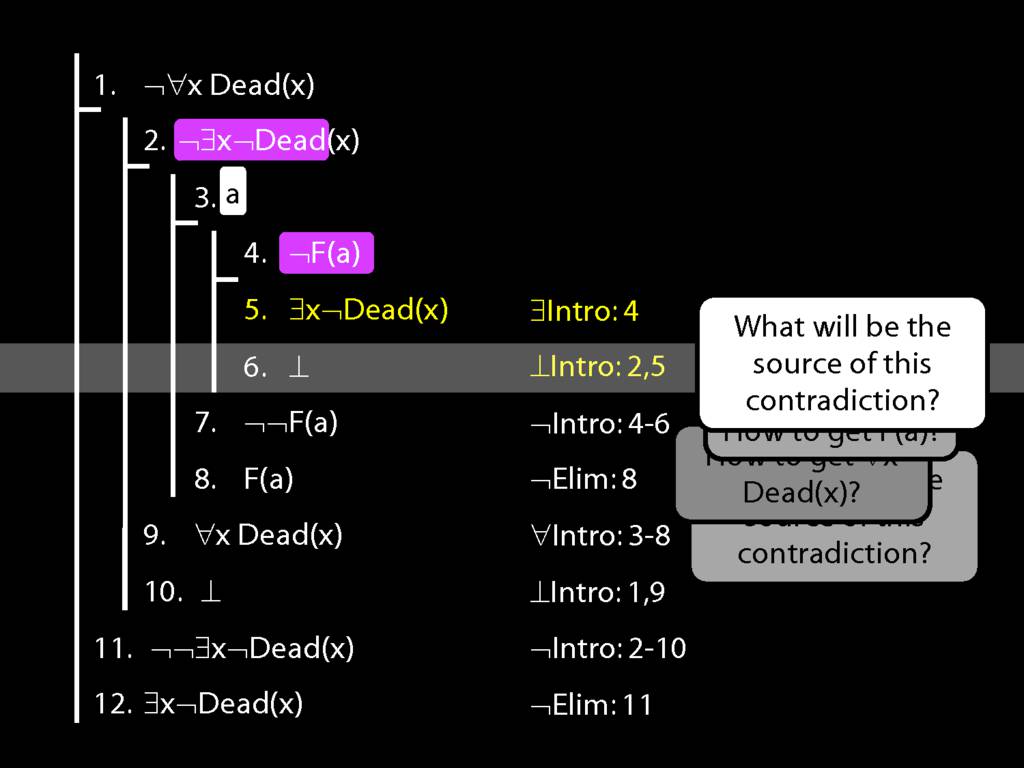
\section{Proof Example: ¬∀x Dead(x) ⊢ ∃x¬ Dead(x).}
\section{Proof Example: ¬∀x Dead(x) ⊢ ∃x¬ Dead(x).}
13.49--13.50
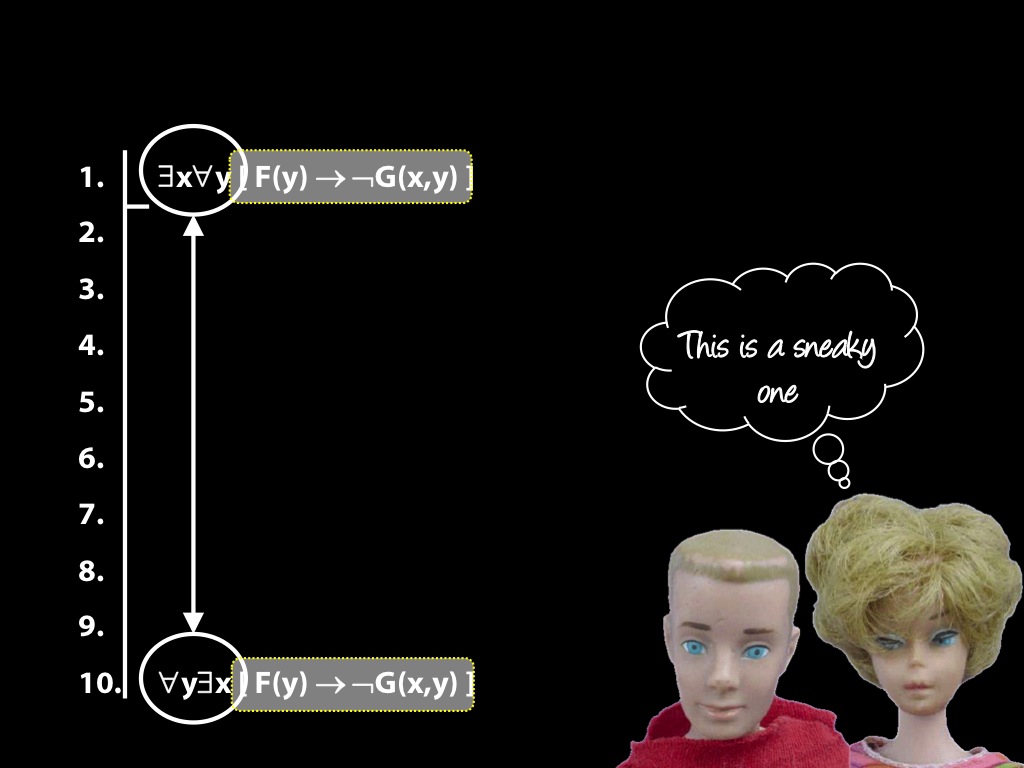
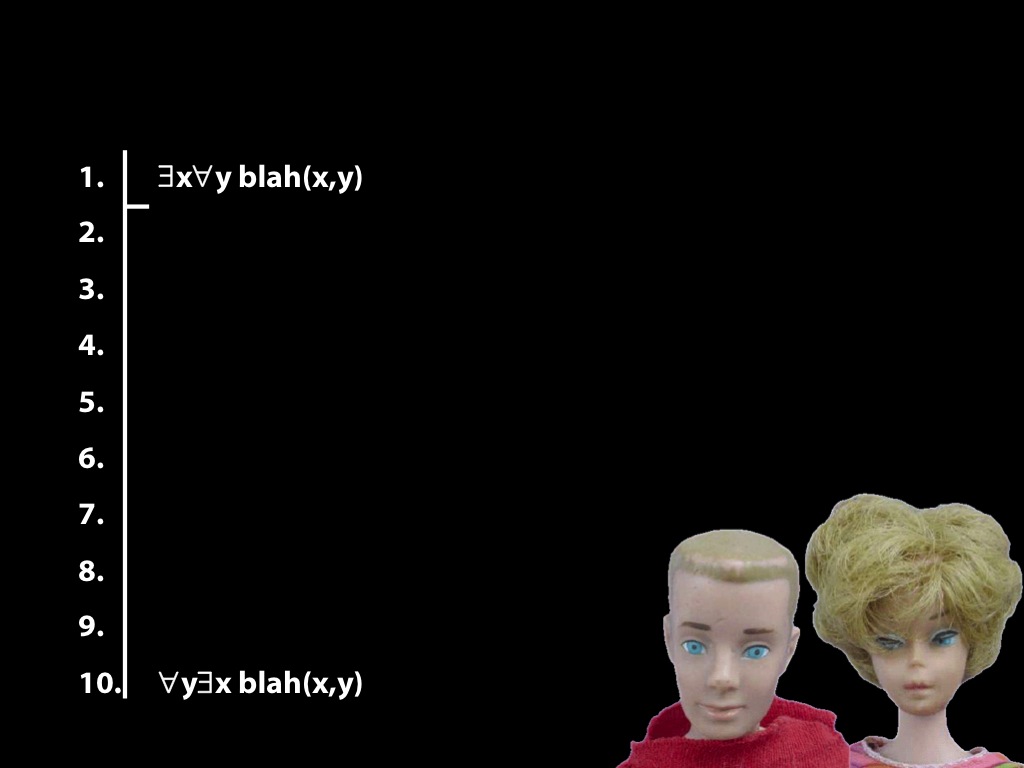
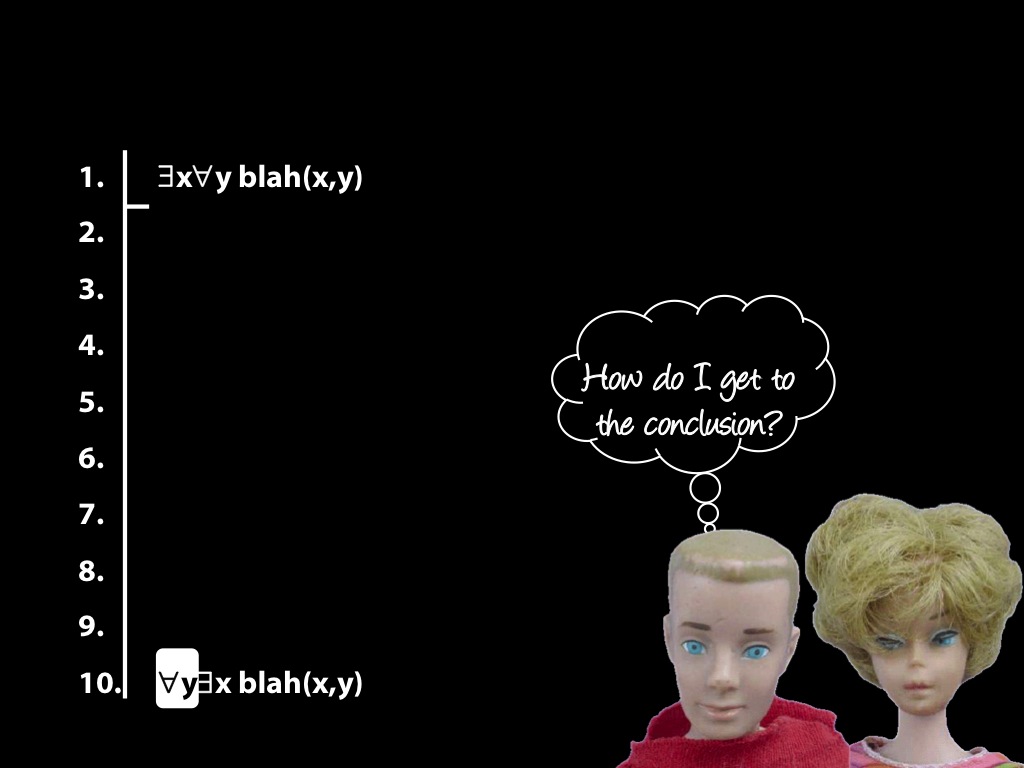
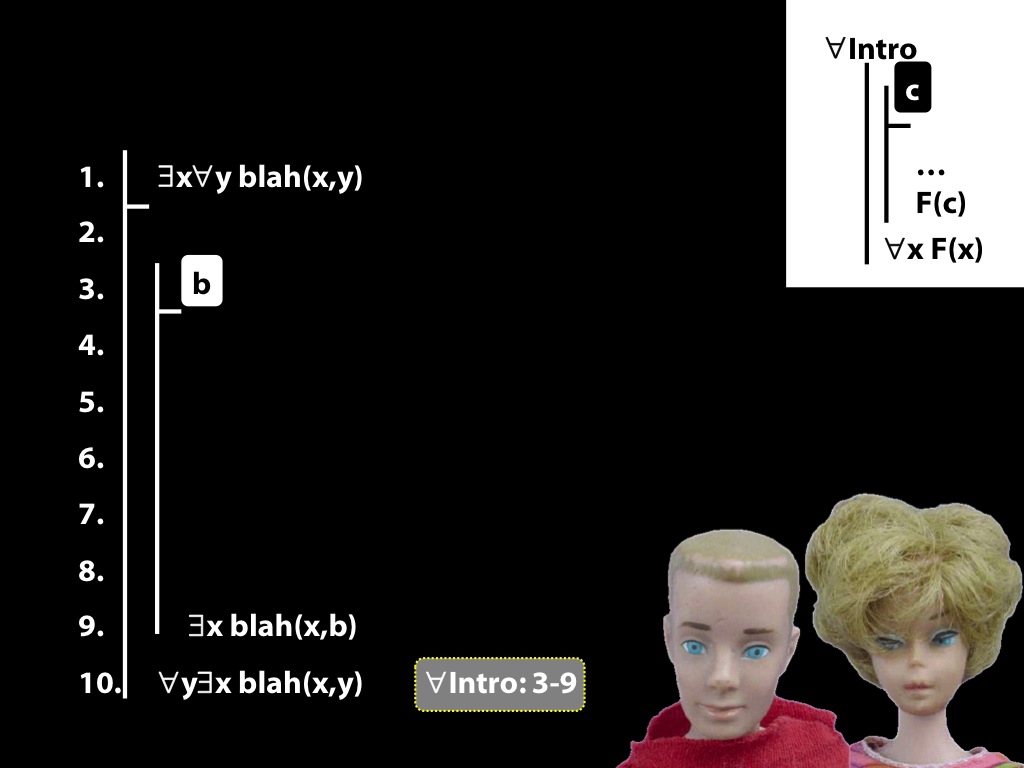
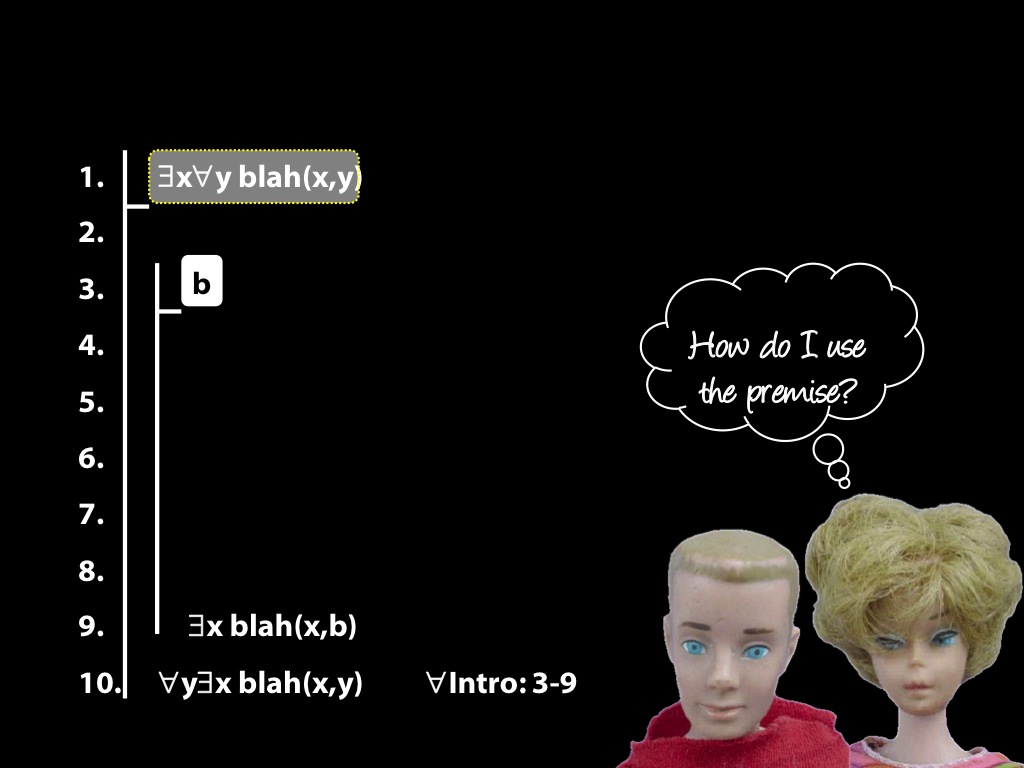
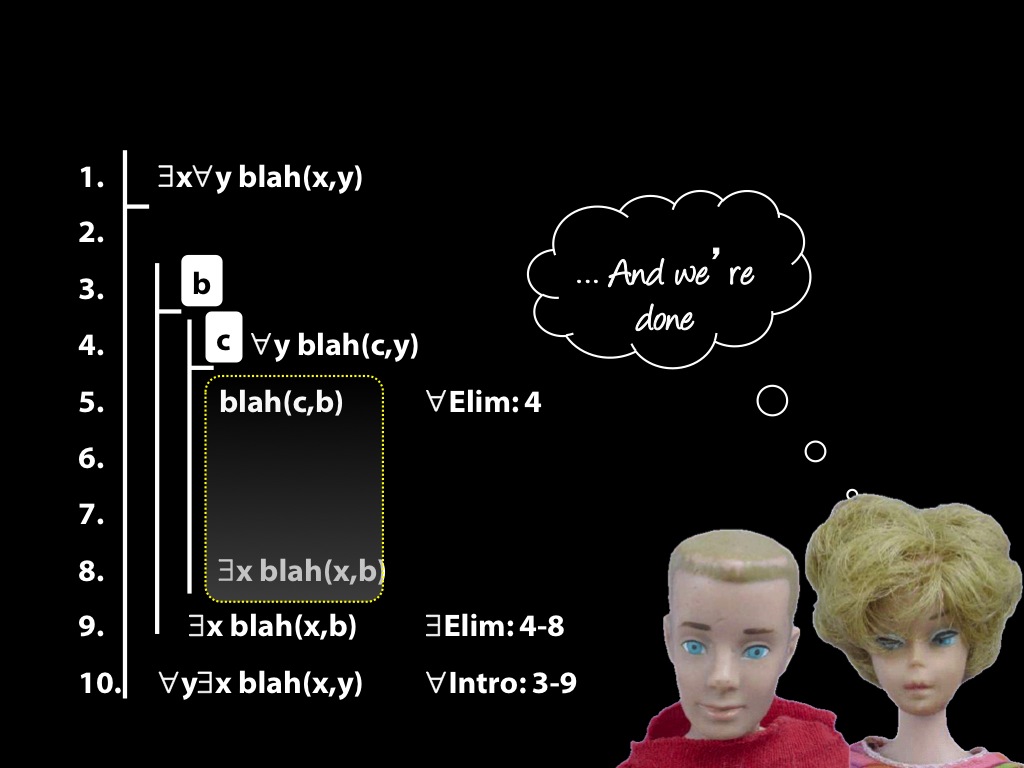
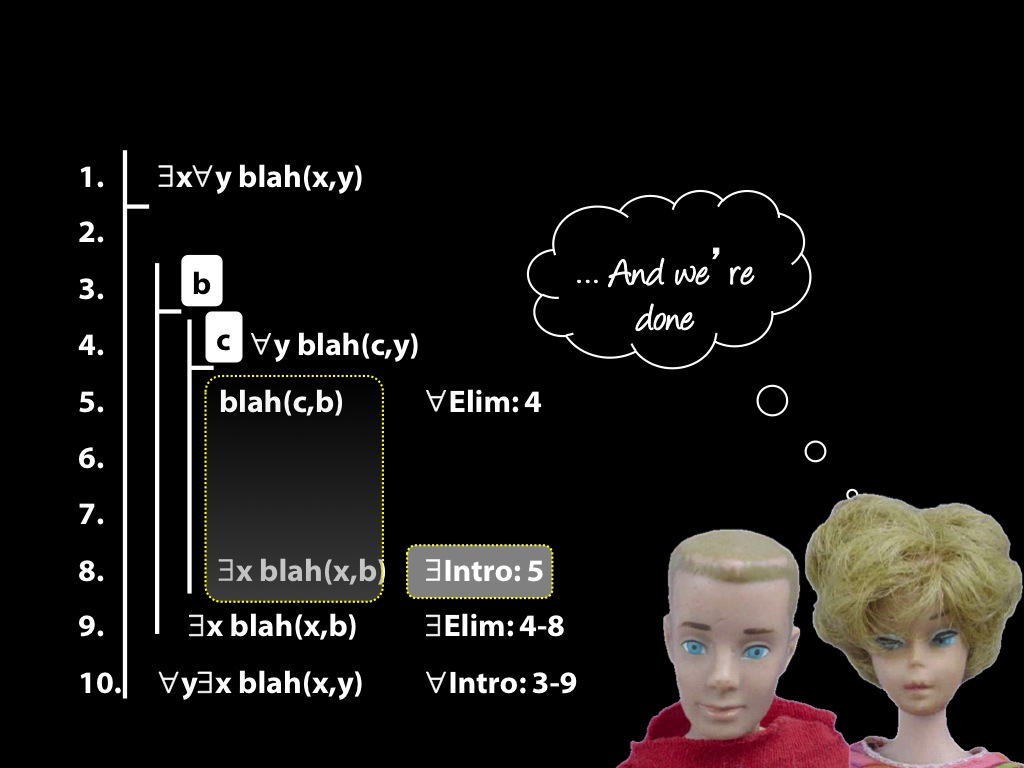
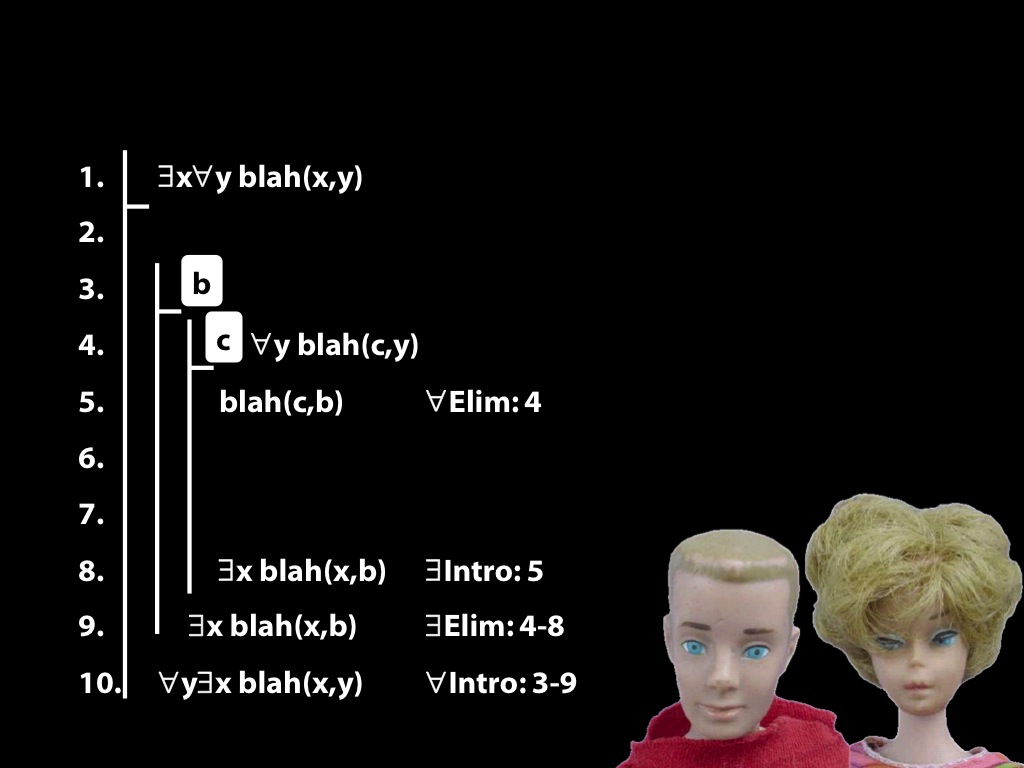
\section{The End Is Near}
\emph{Reading:} §14.3
\section{The End Is Near}
14.26, 14.28
14.2
14.4, 14.5
14.10, 14.11
14.26, 14.28