Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Logic (PH133)}

\maketitle

Logic (PH133)

Lecture 1

[email protected]

\def \ititle {Logic (PH133)}

\def \isubtitle {Lecture 1}

\begin{center}

{\Large

\textbf{\ititle}: \isubtitle

}

\iemail %

\end{center}

Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.

\section{Learning Objectives}

Quick Intro to awFOL

\section{Quick Intro to awFOL}

\emph{Reading:} §1.1, §1.2, §1.3

\section{Quick Intro to awFOL}

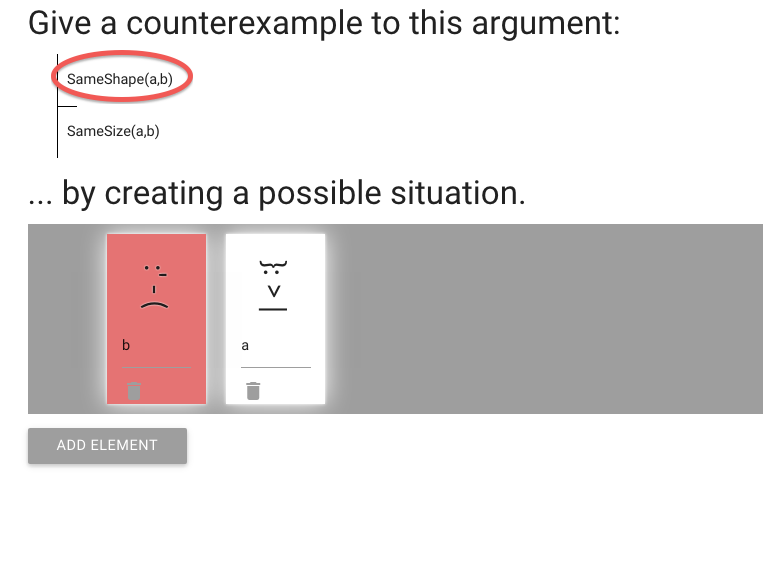
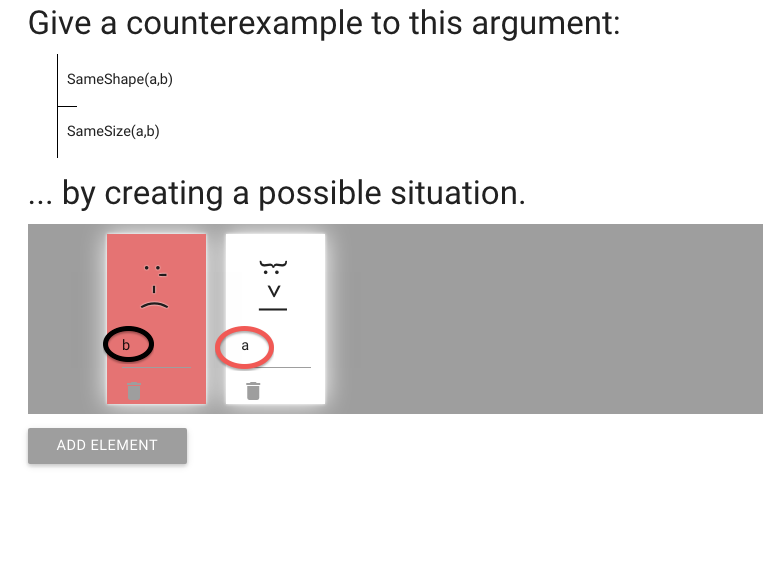
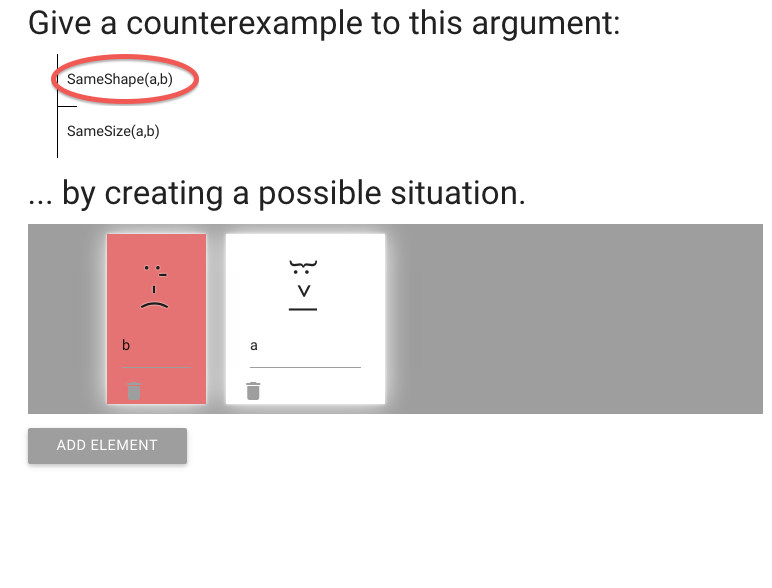
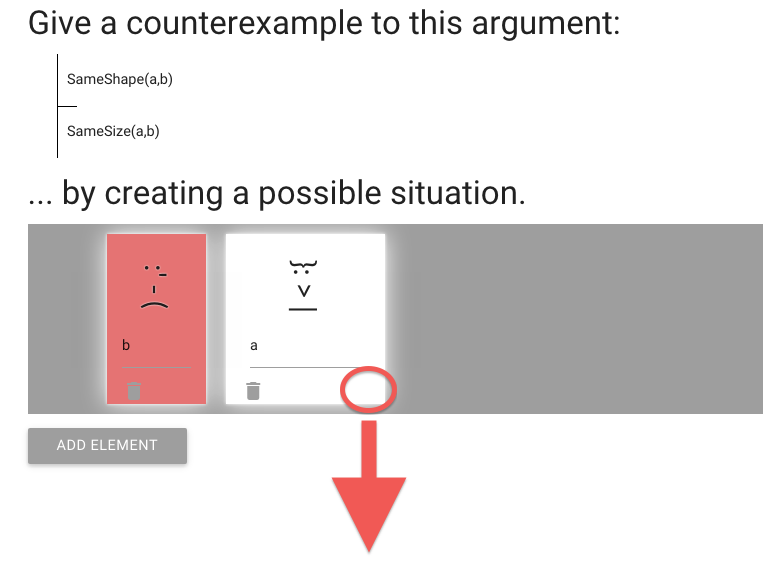
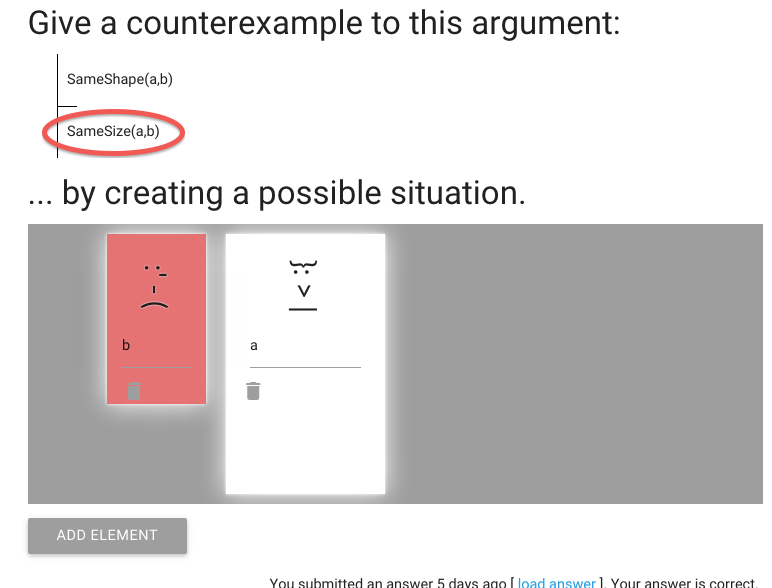
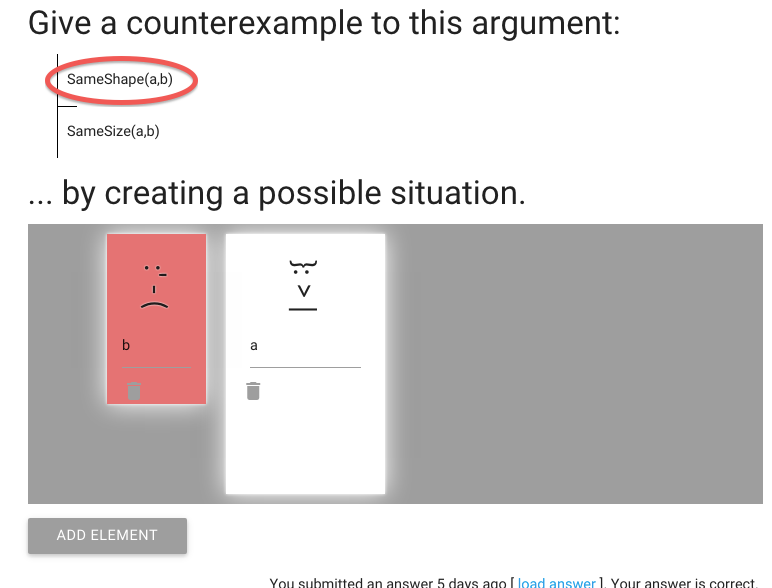
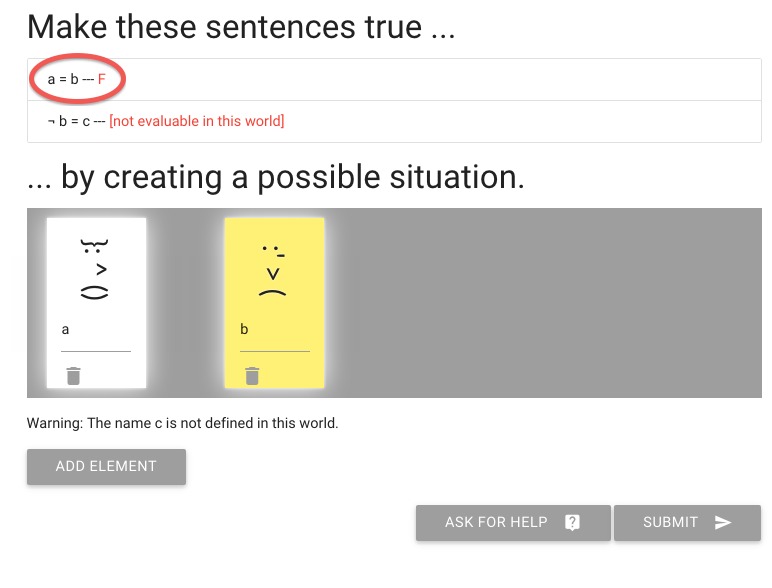
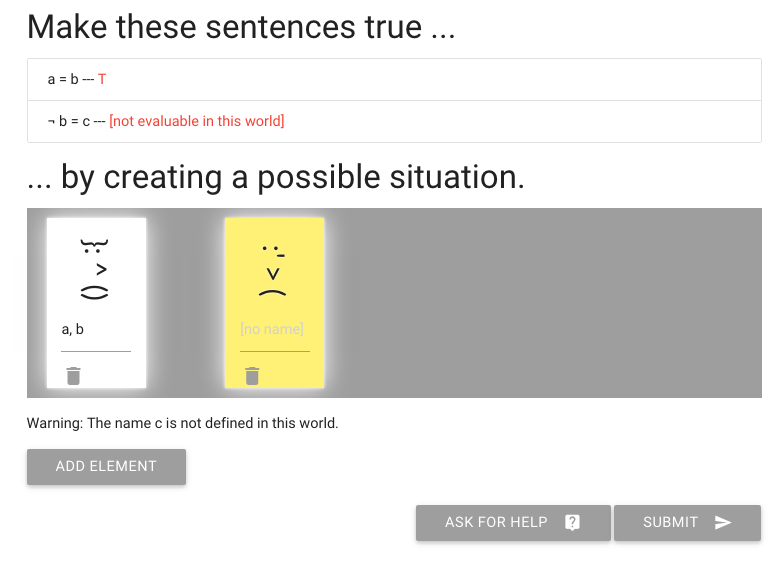
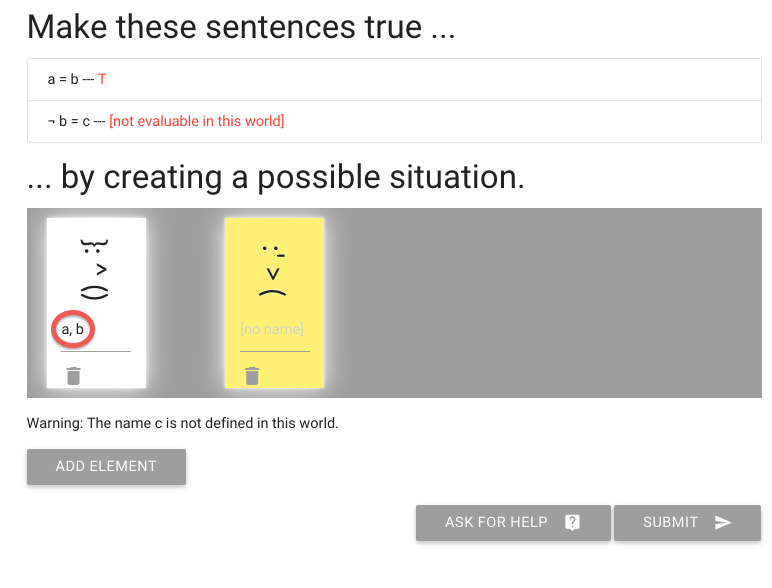
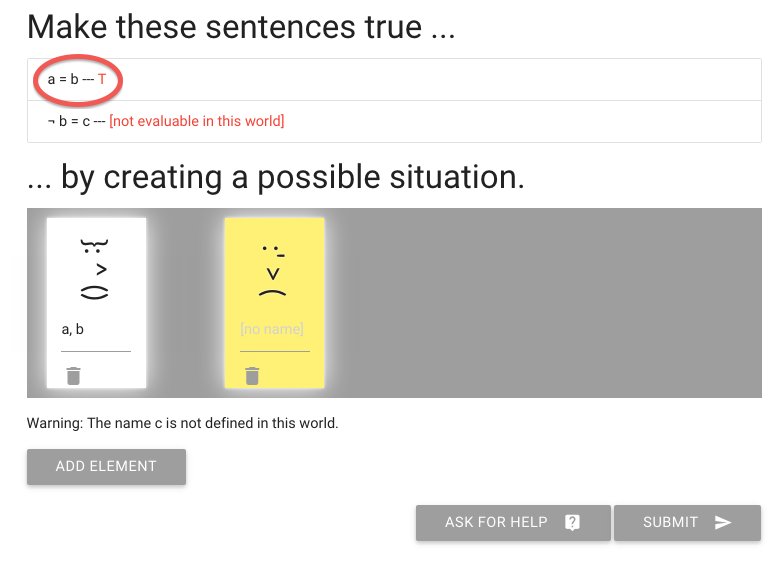
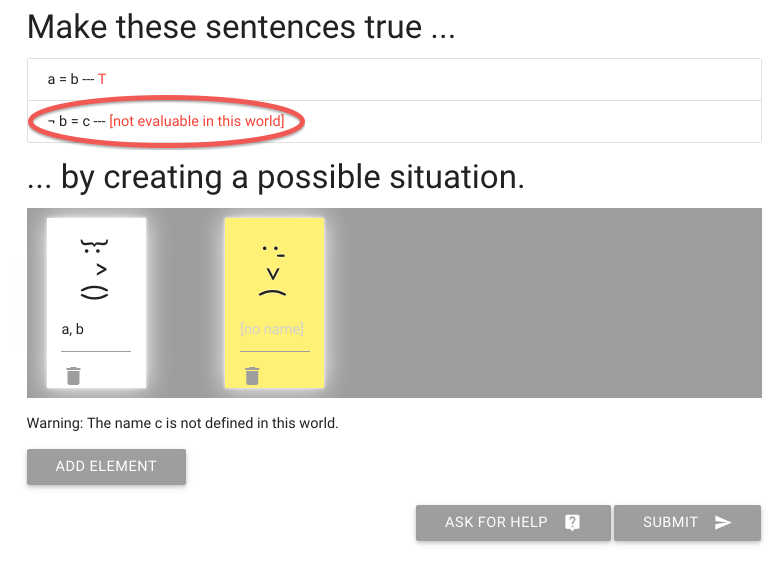
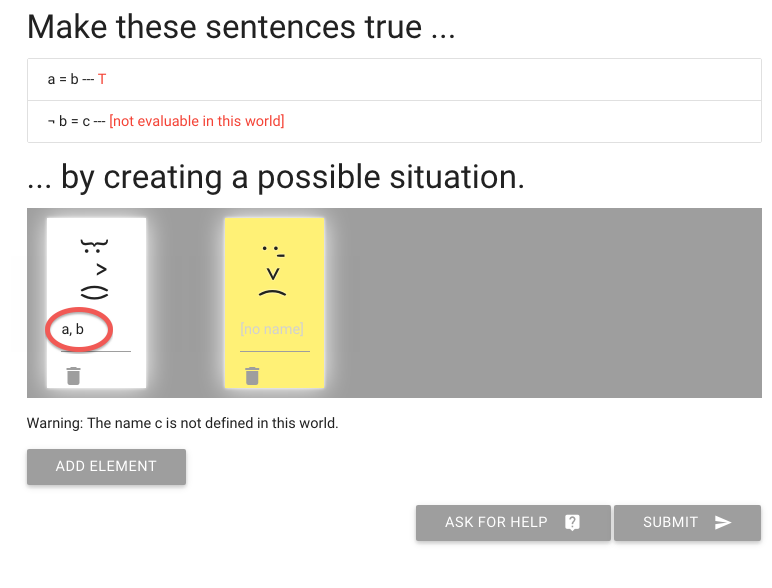
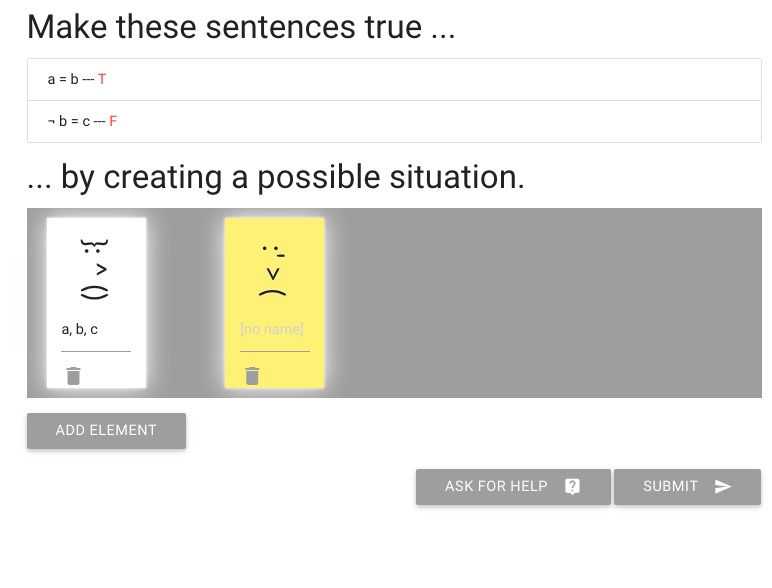
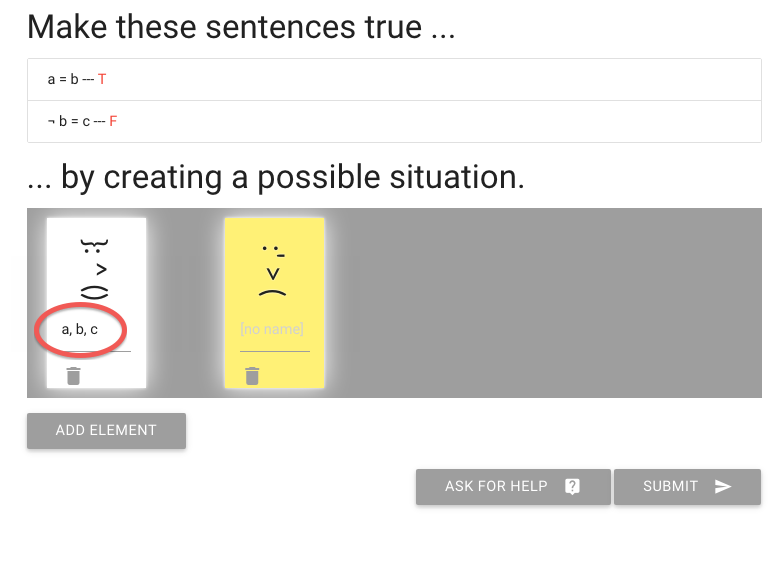
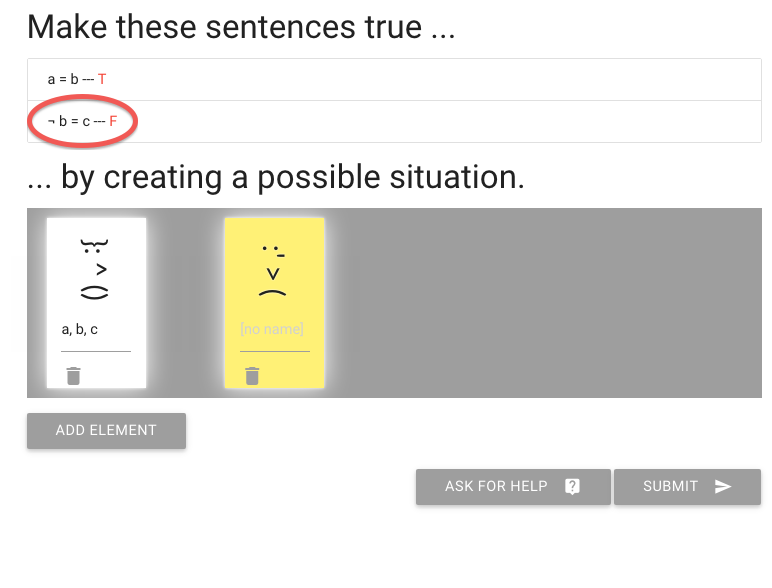
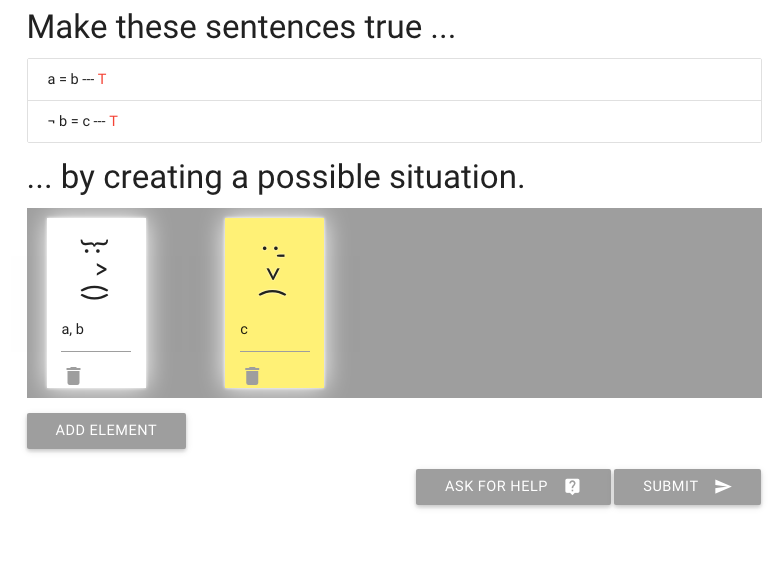
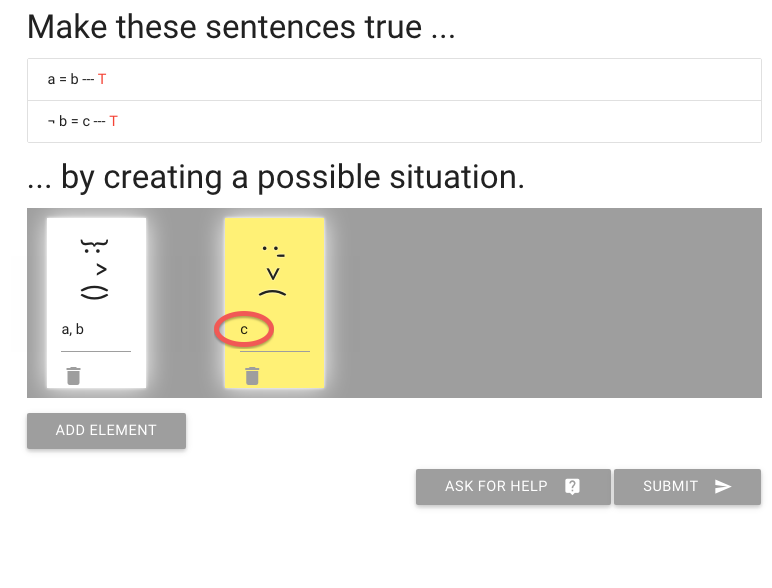
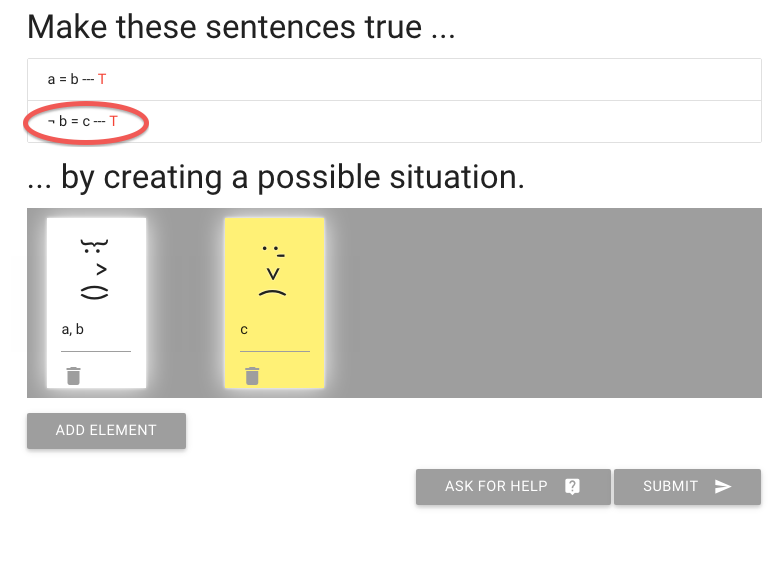
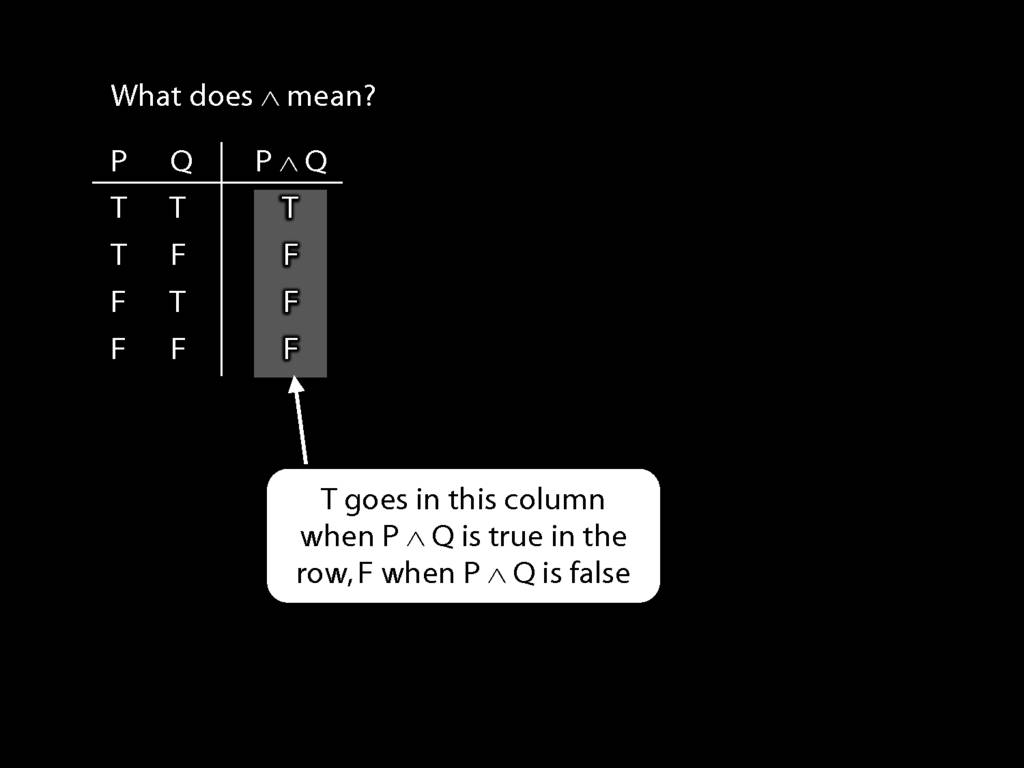
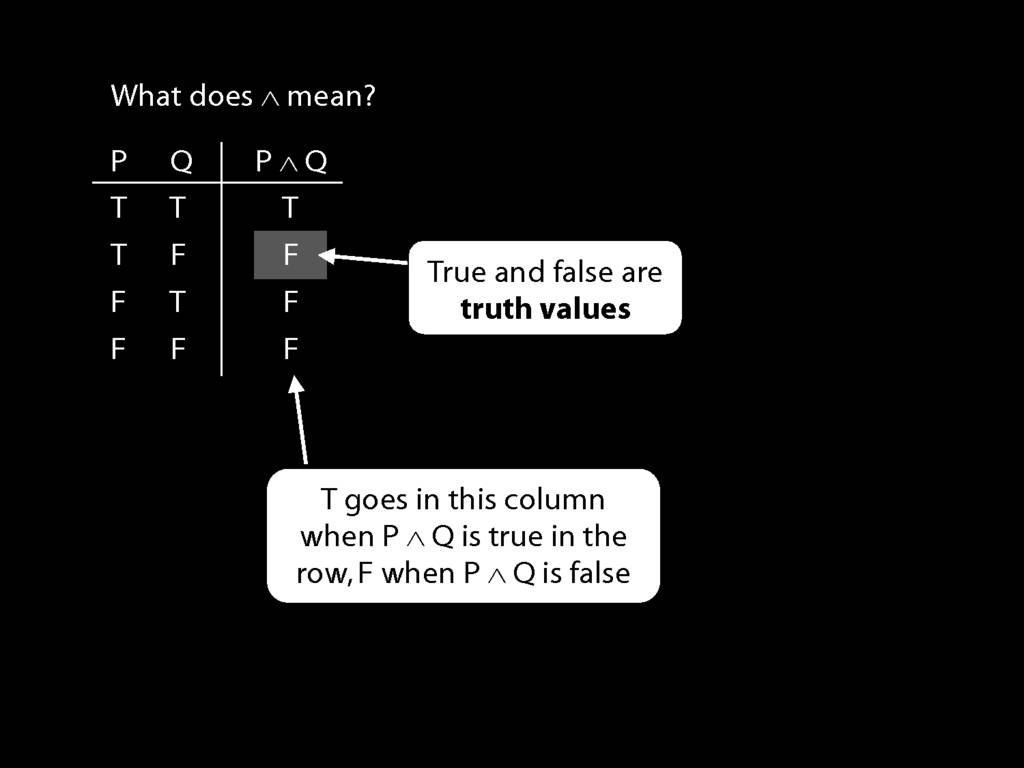
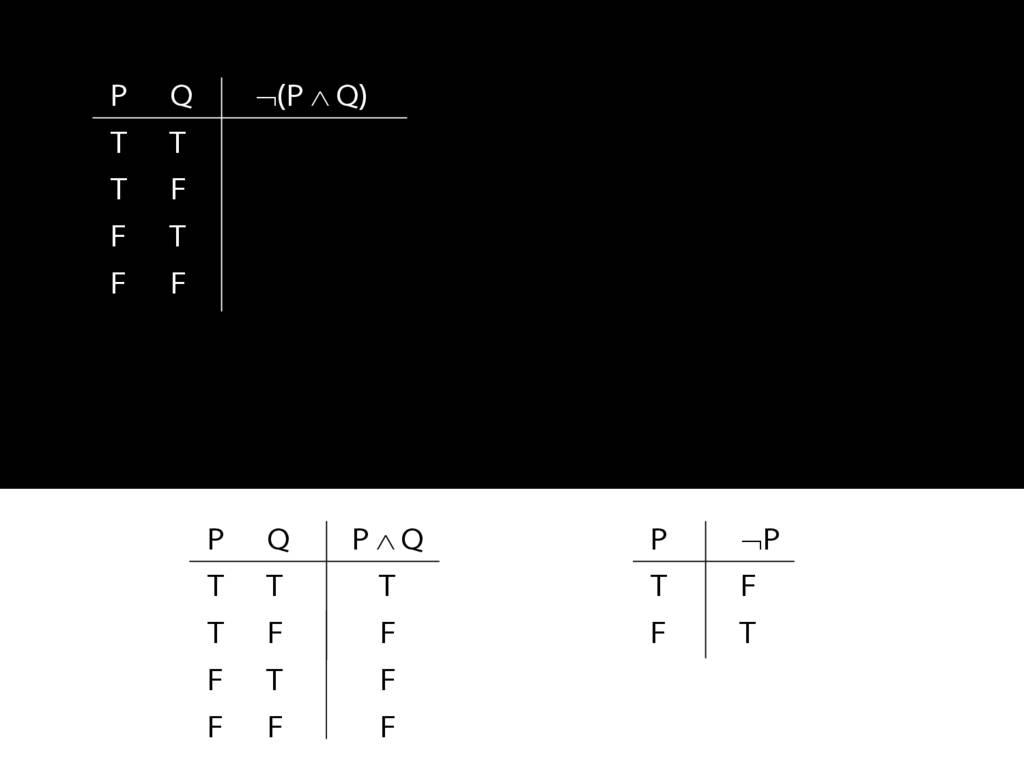
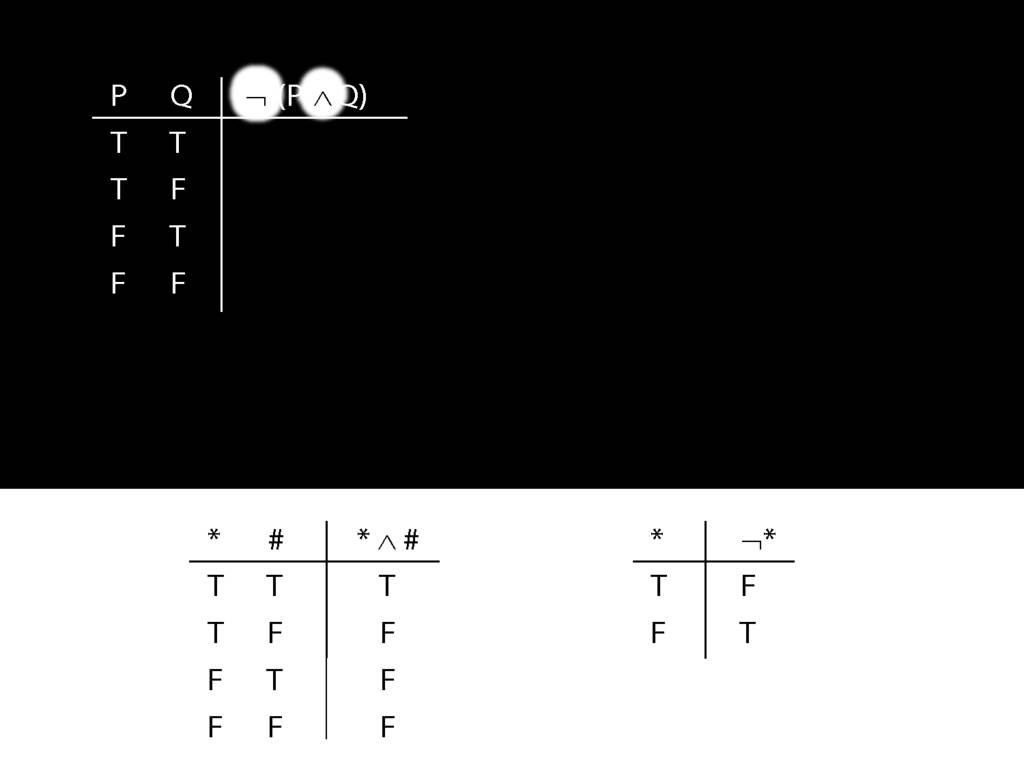
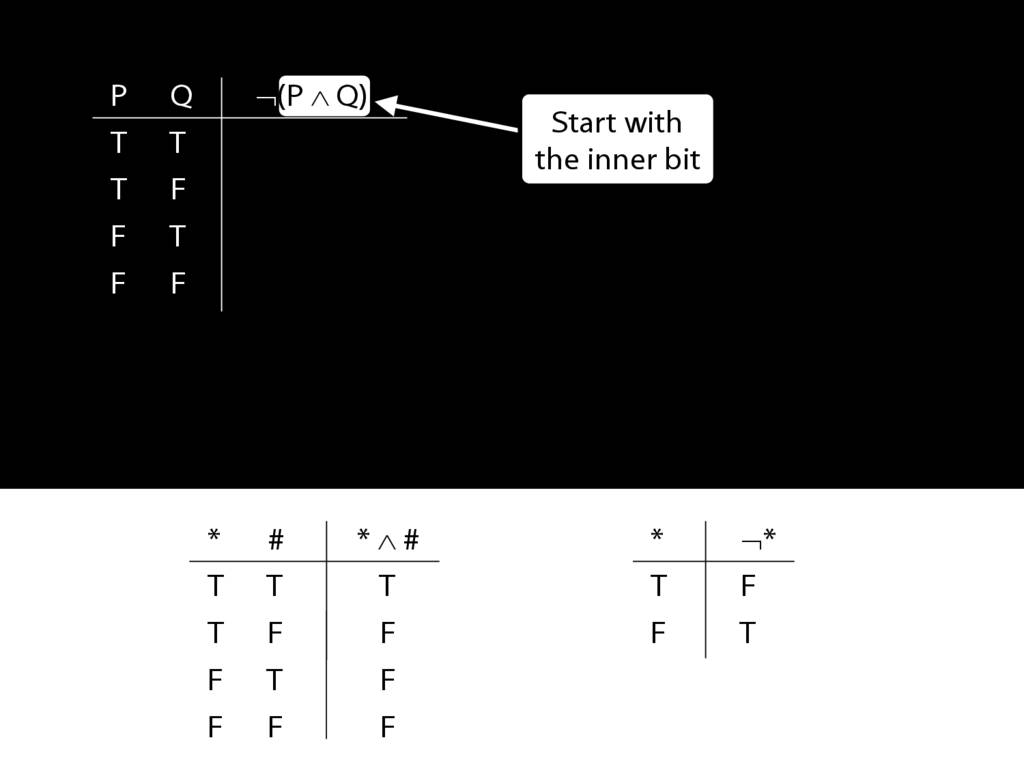
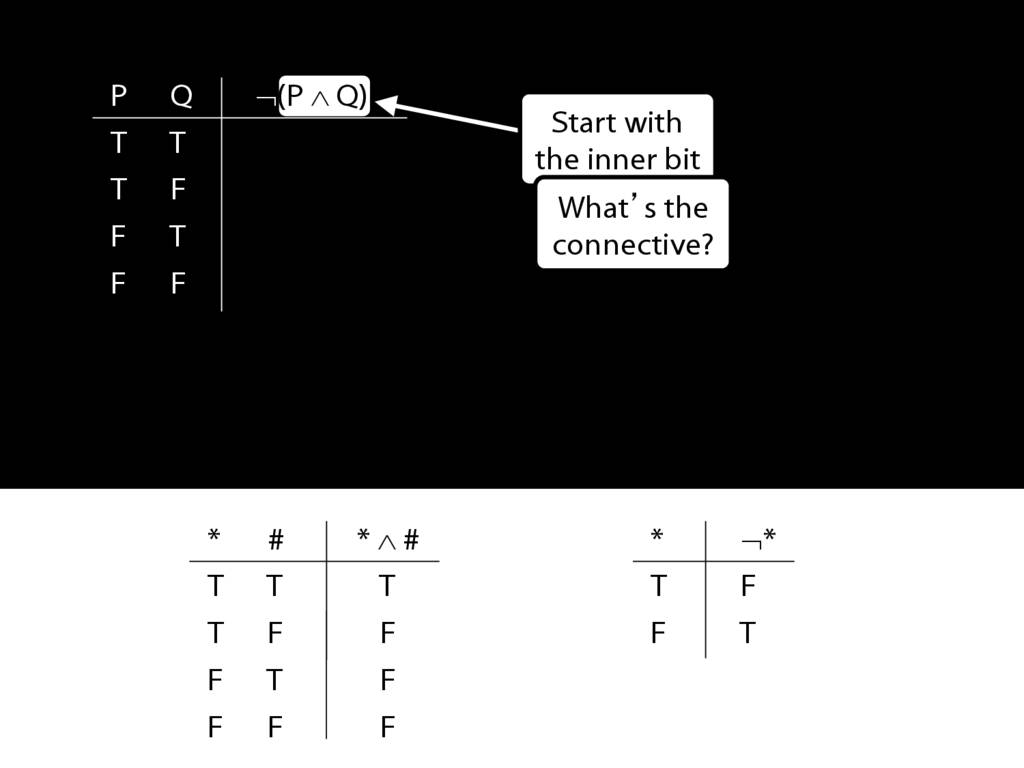
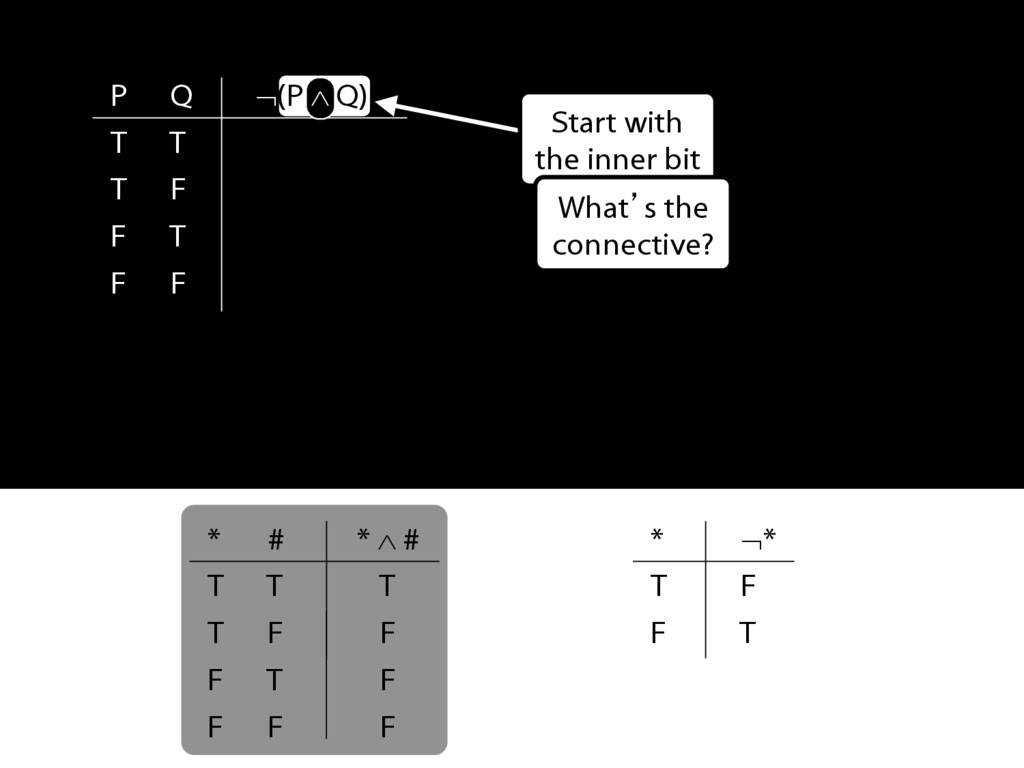
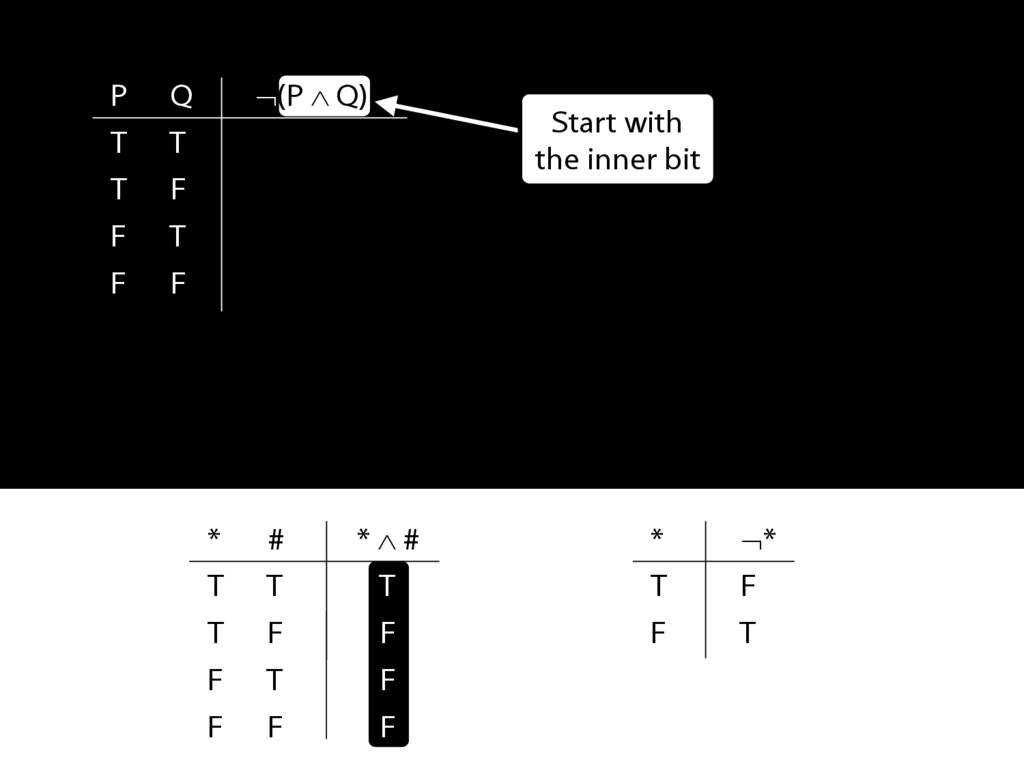
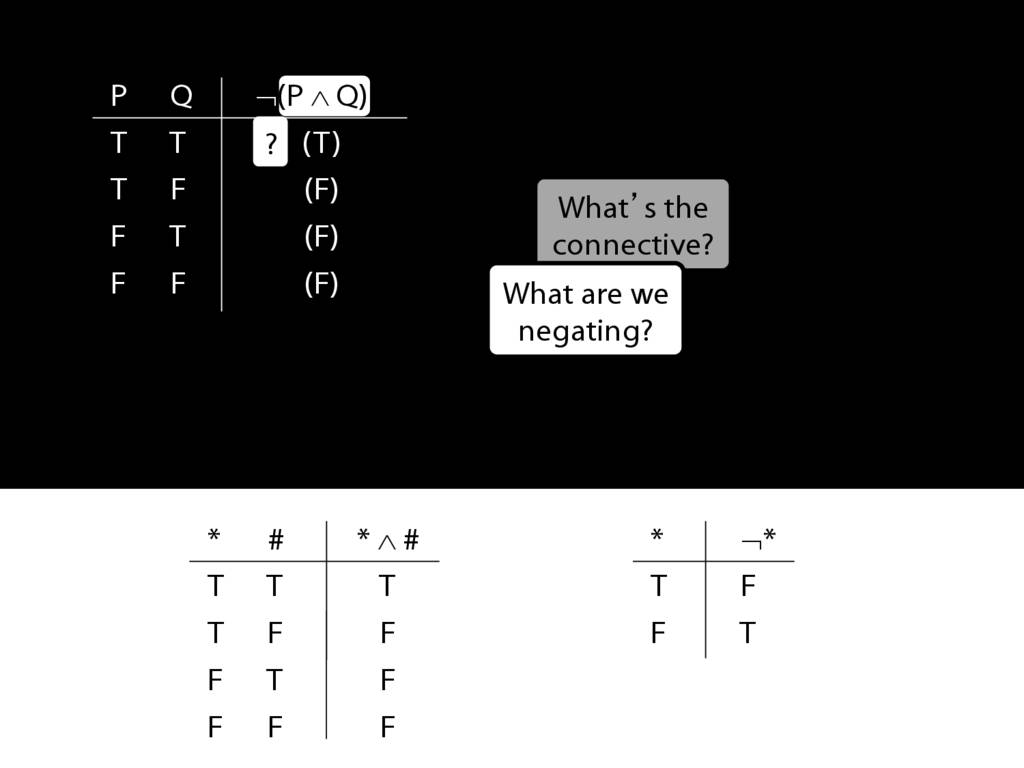
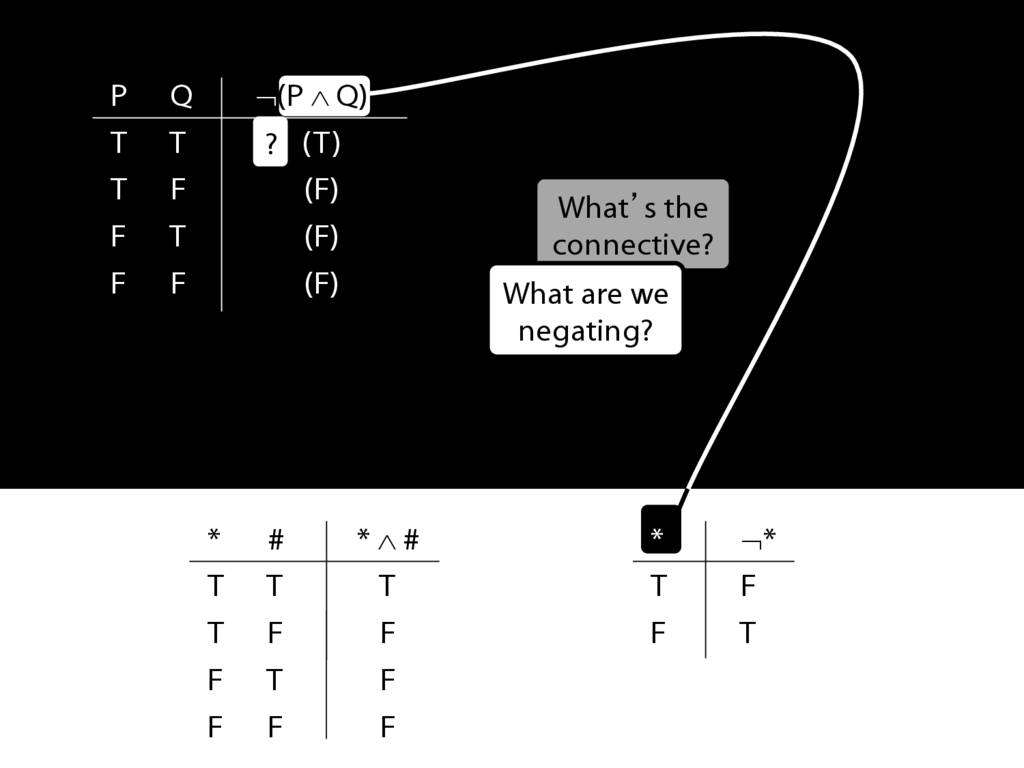
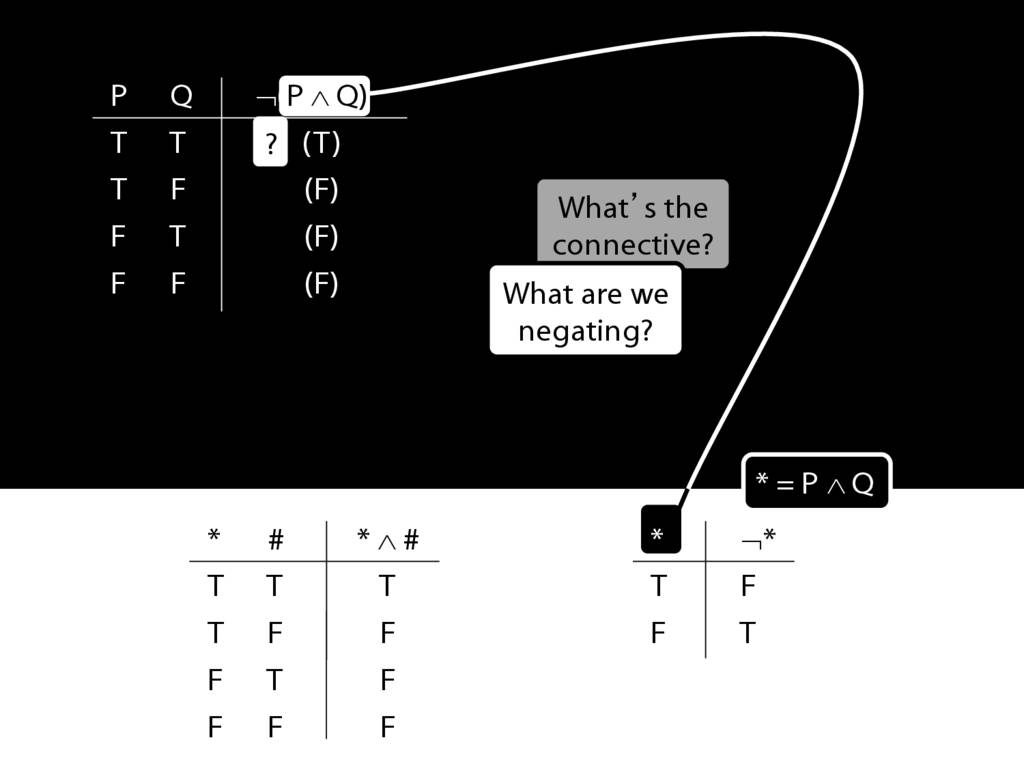
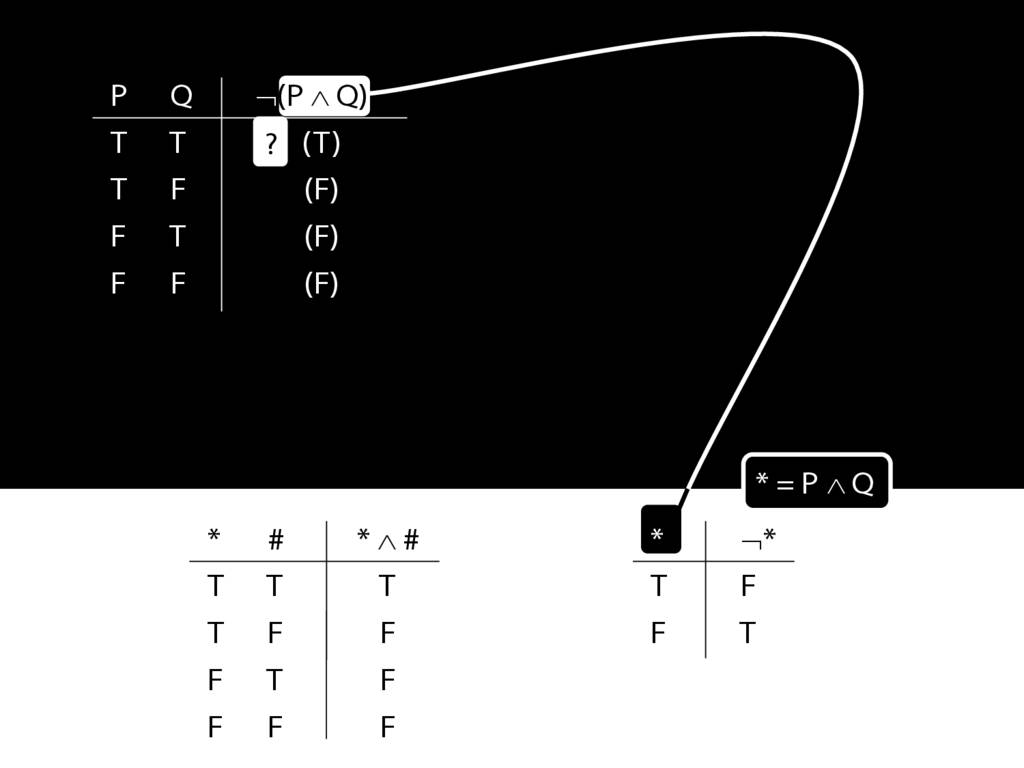
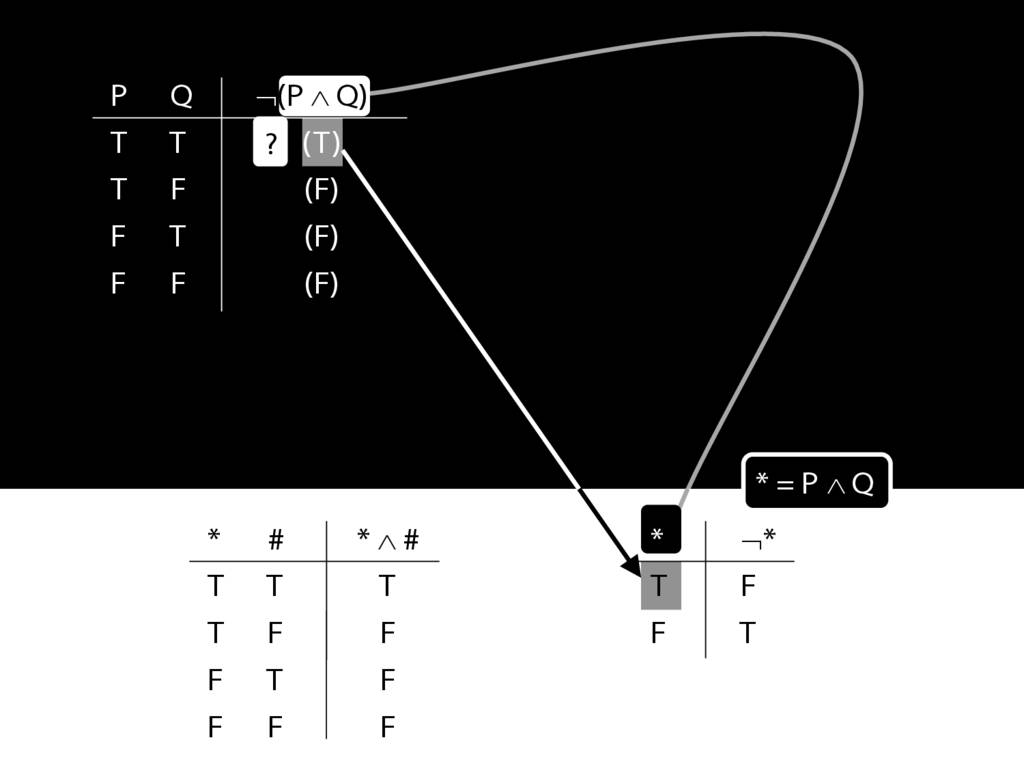
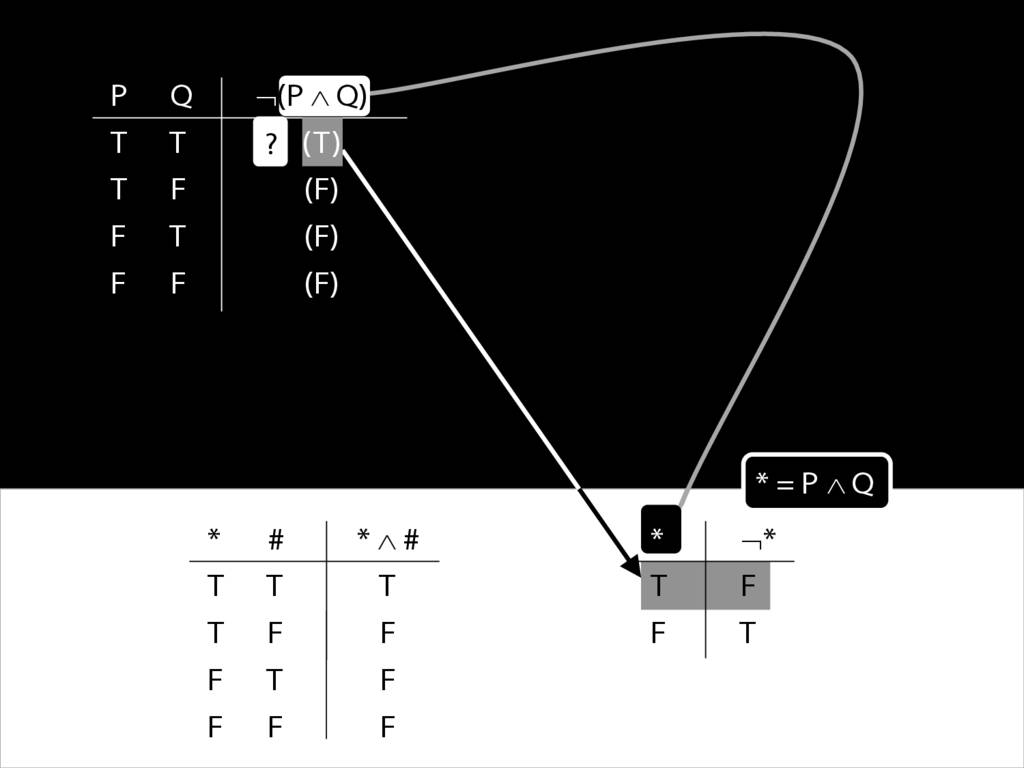
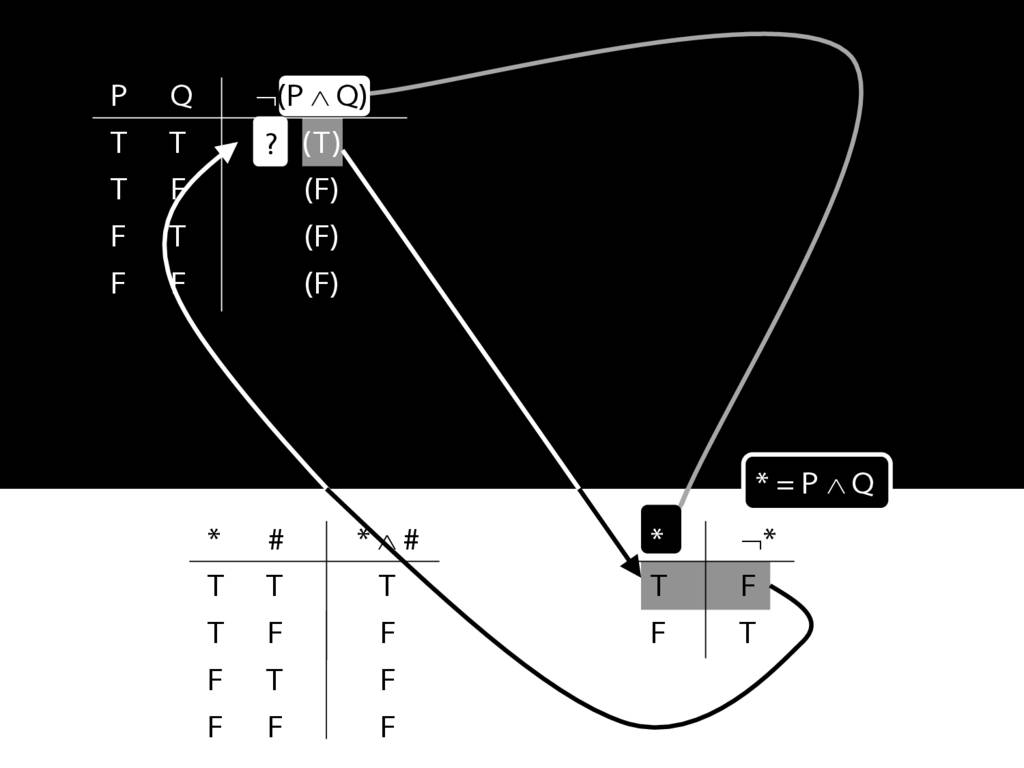
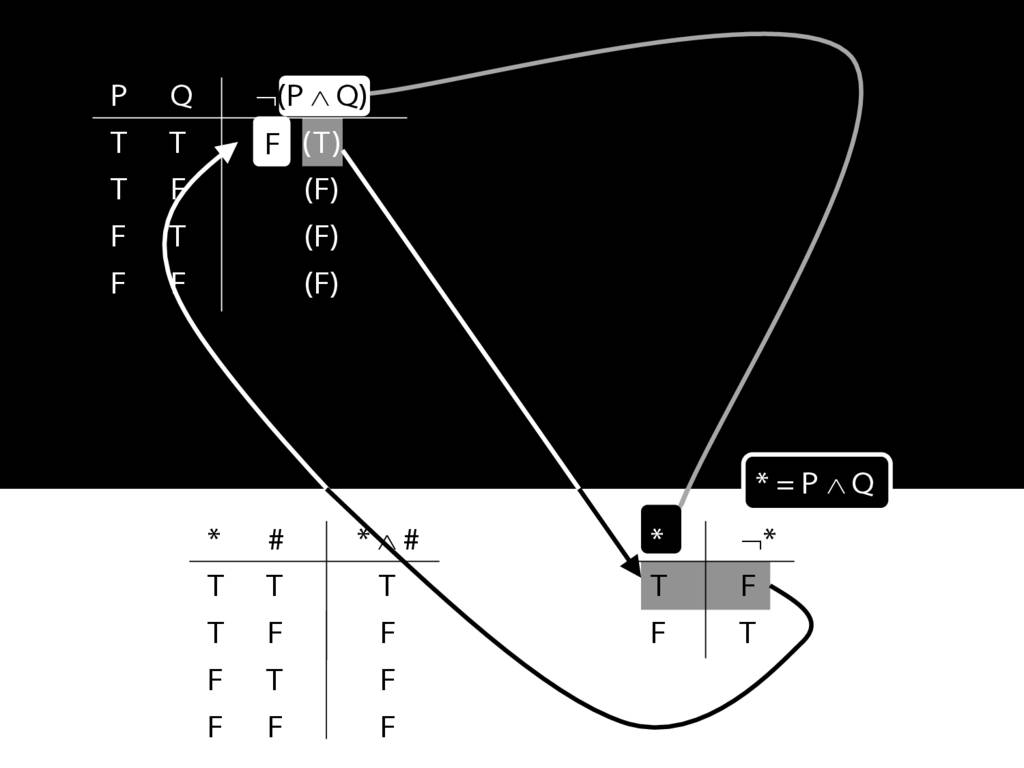
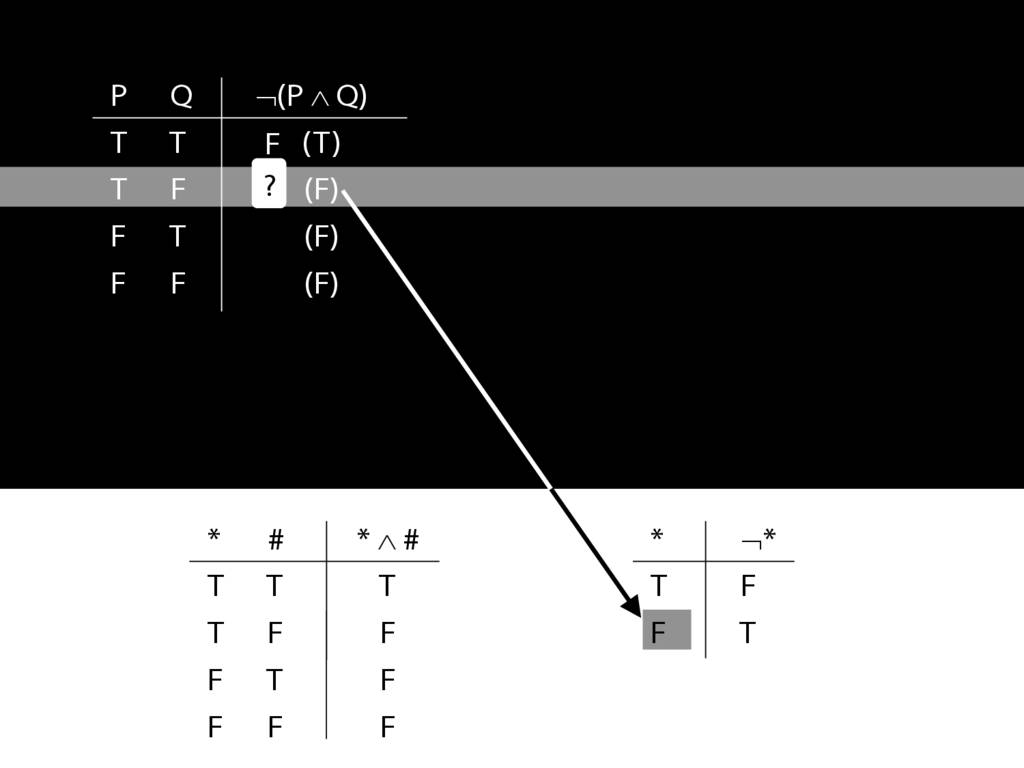
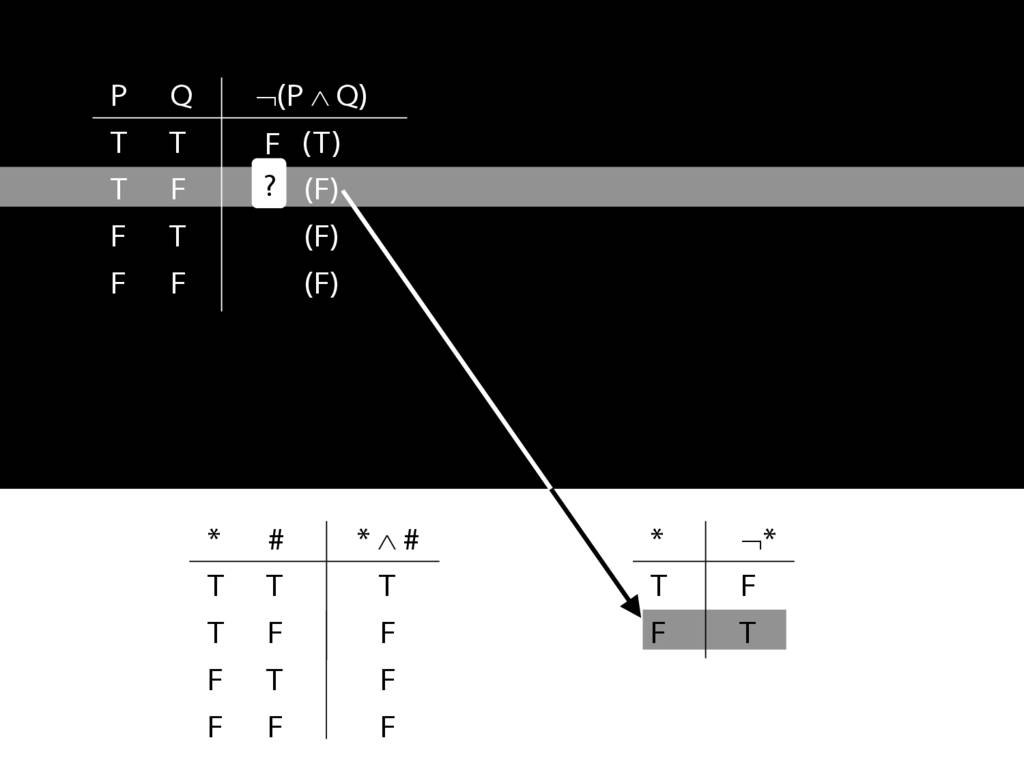
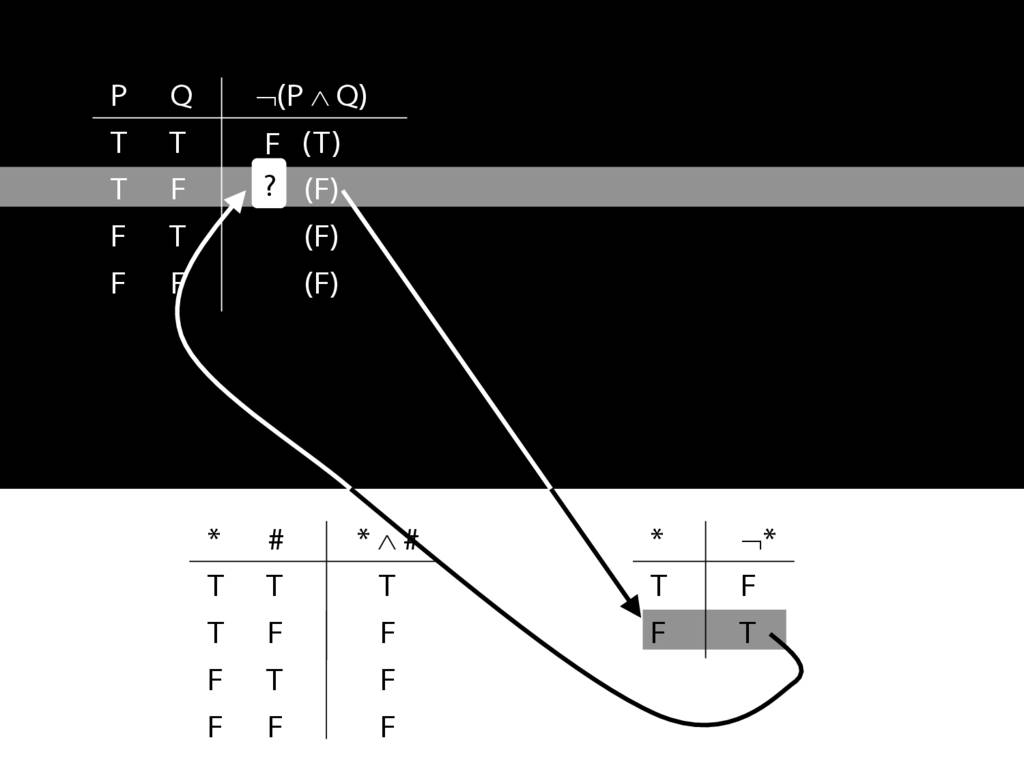
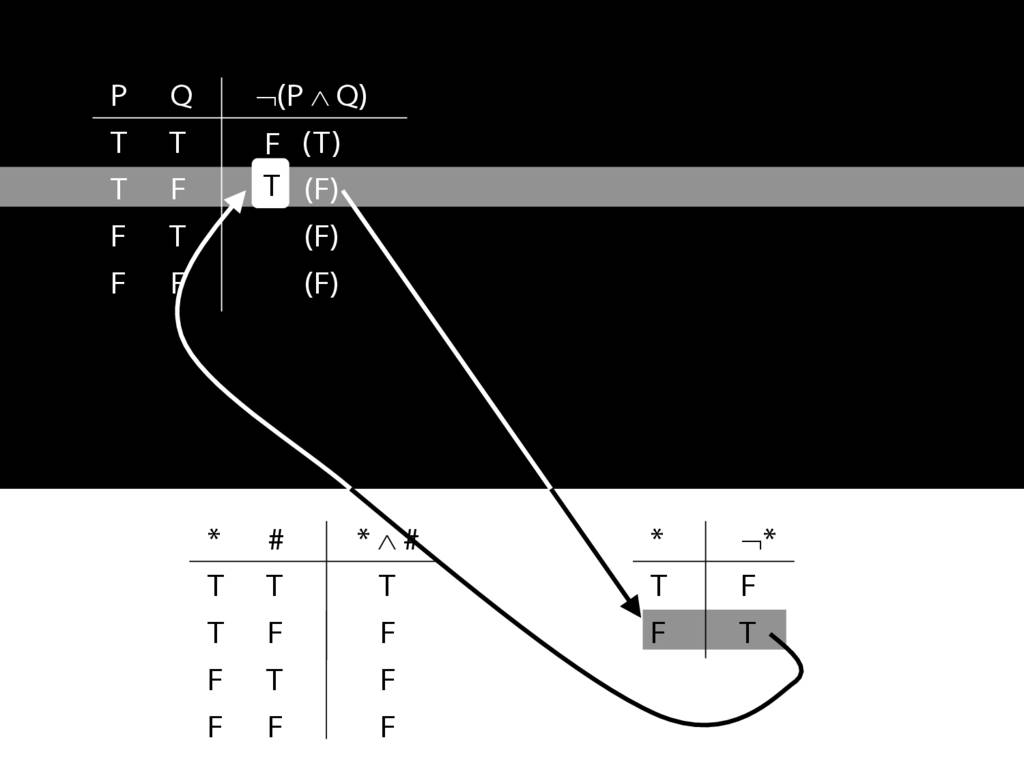
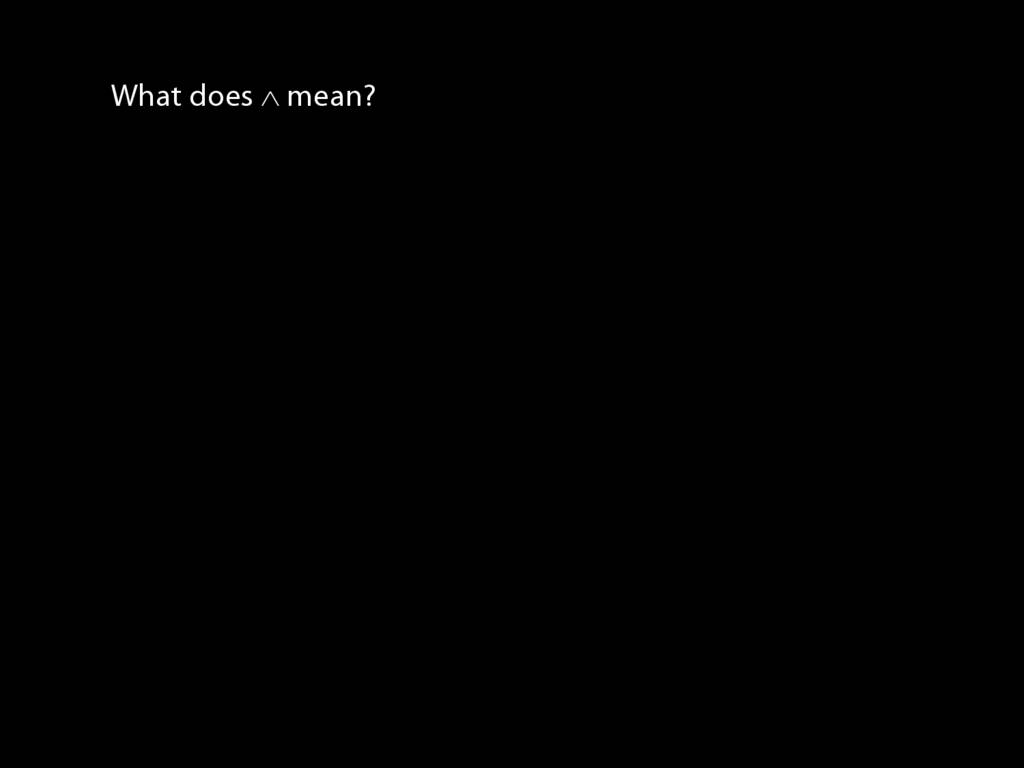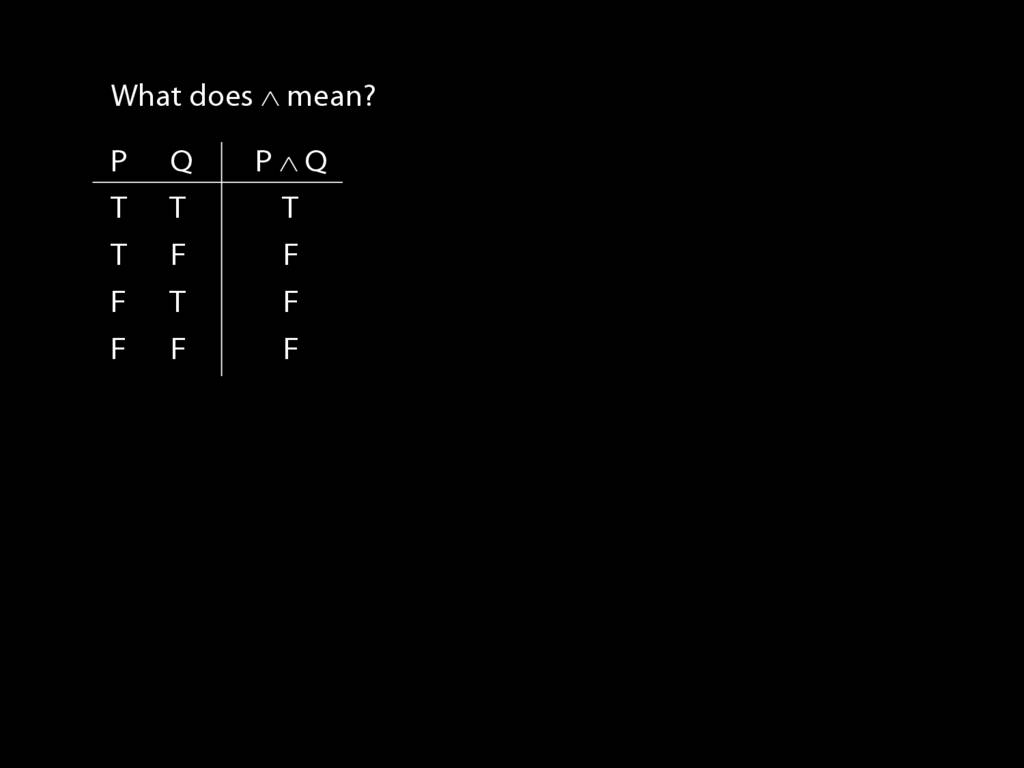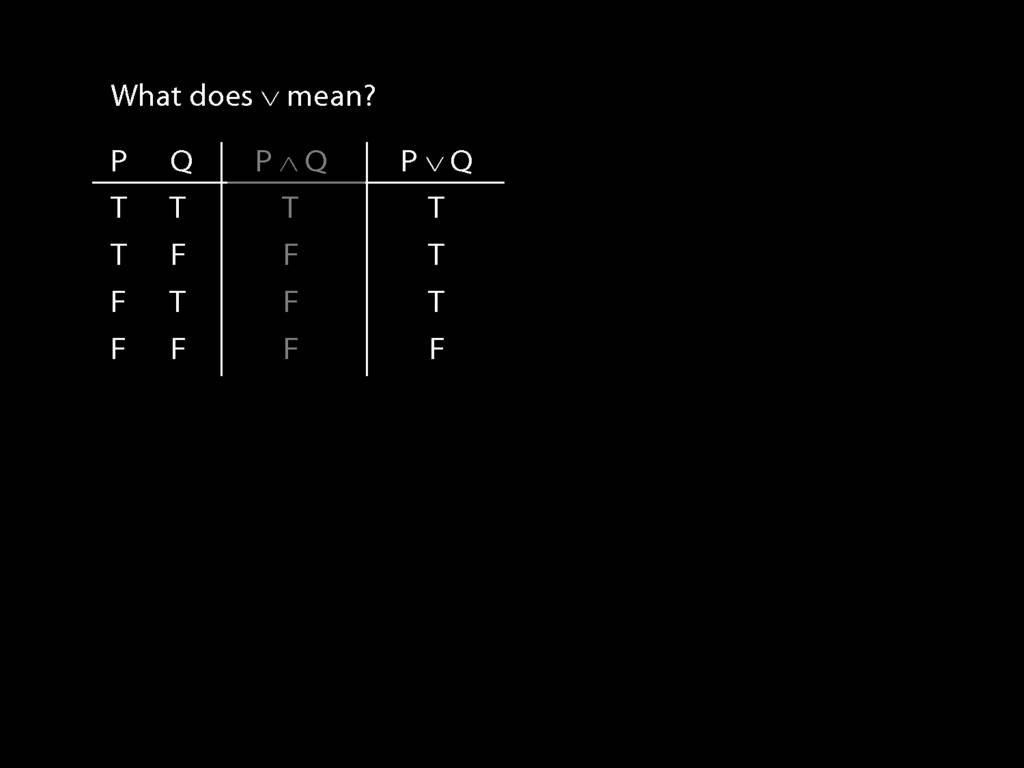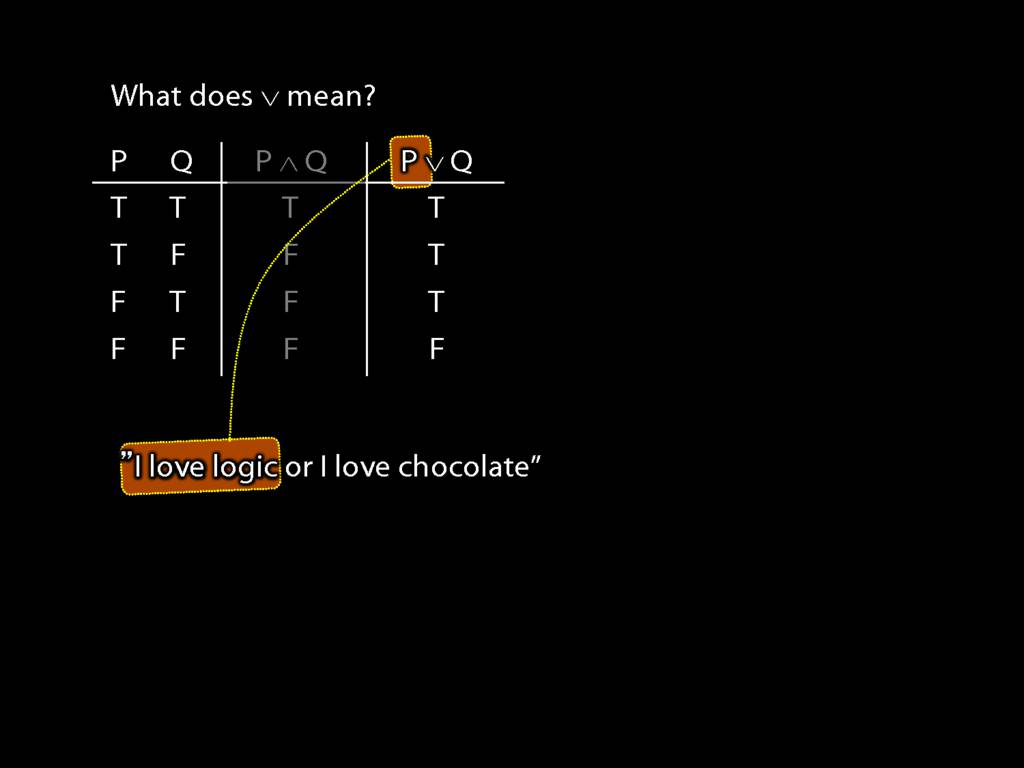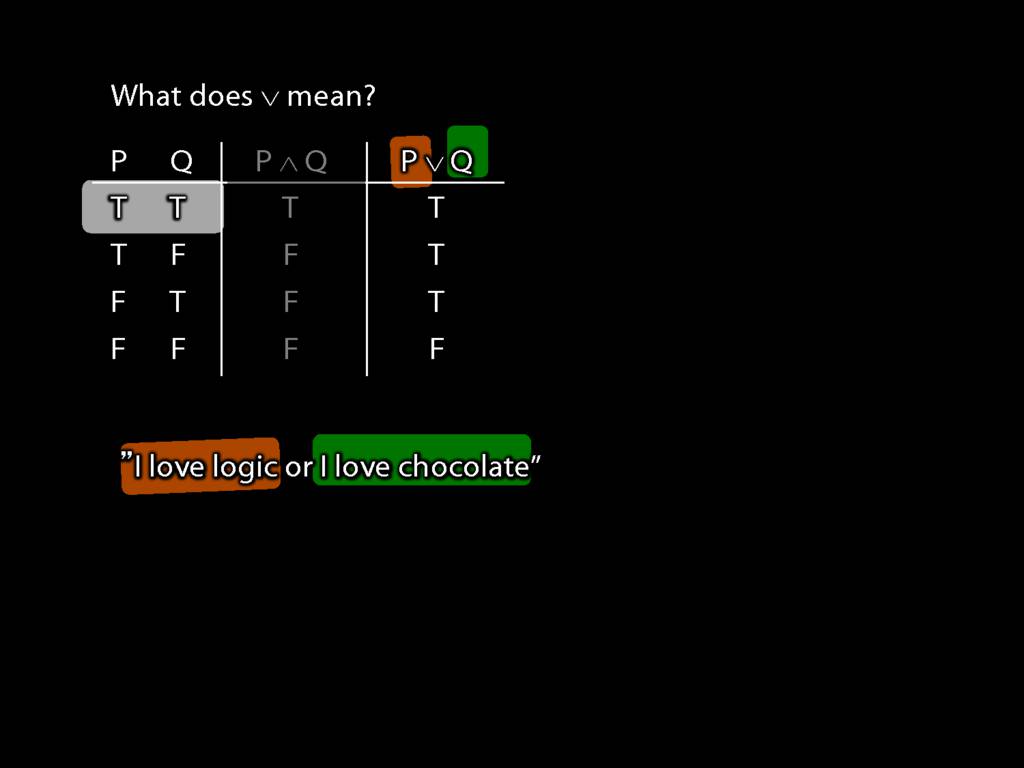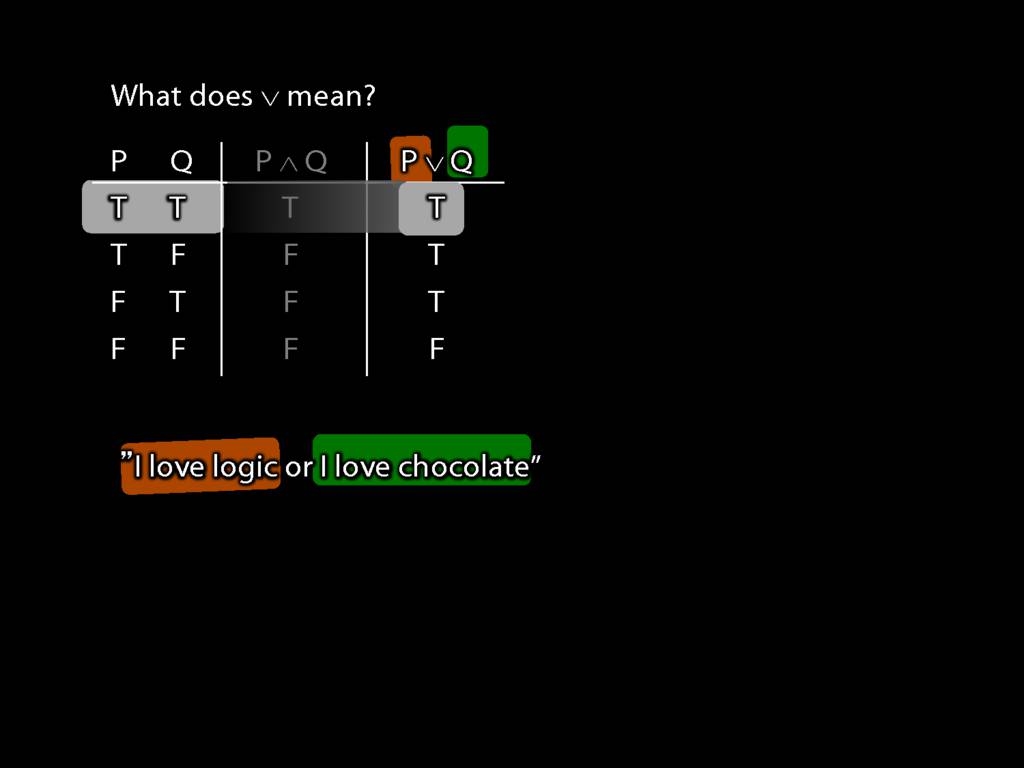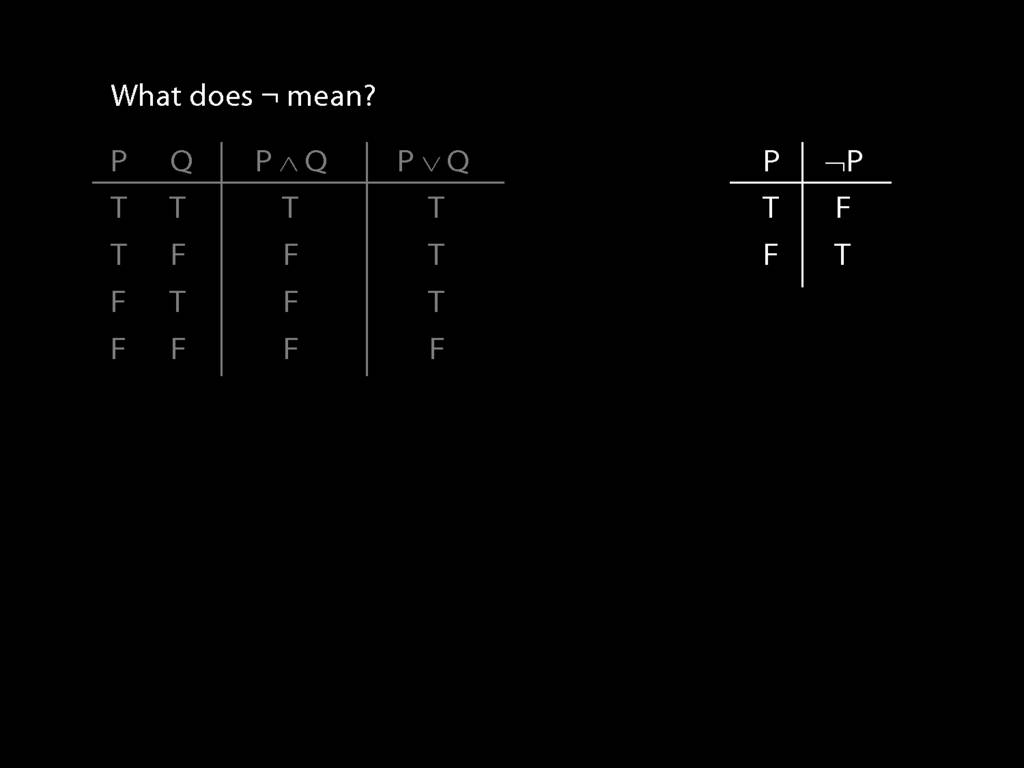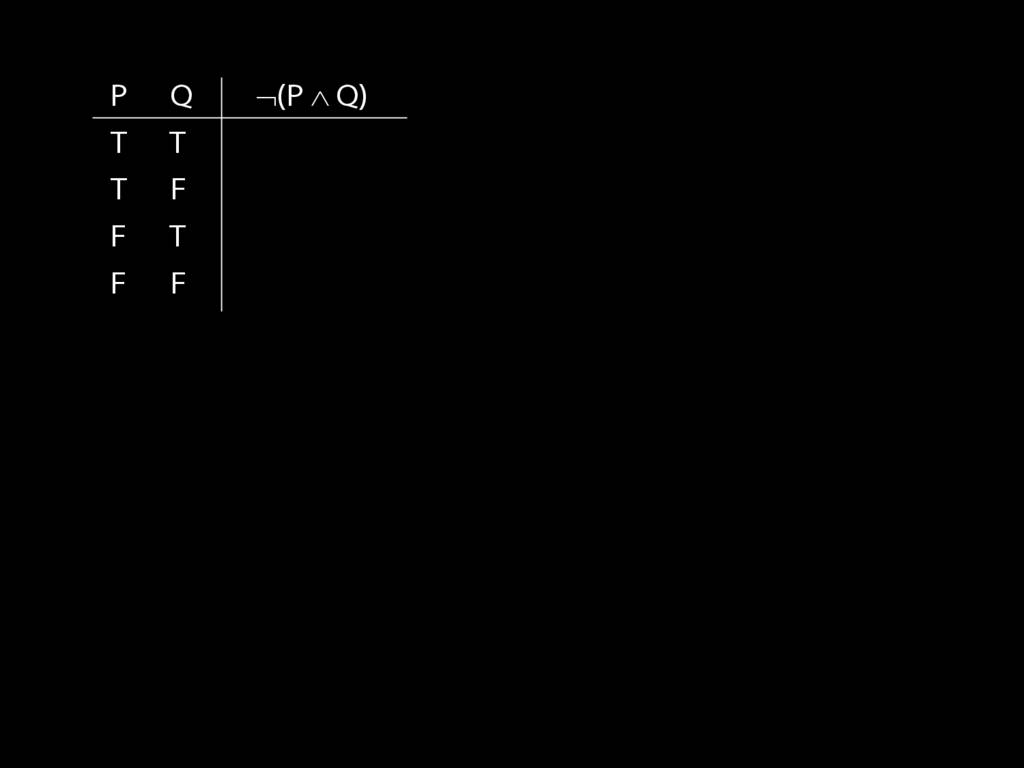John is square

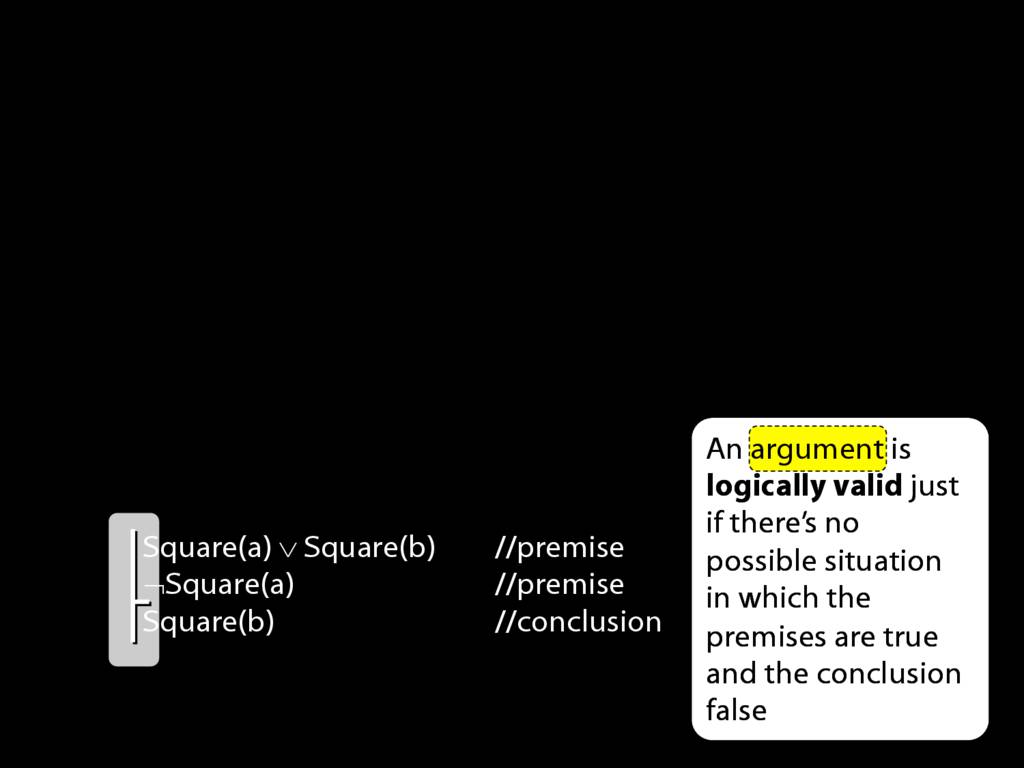
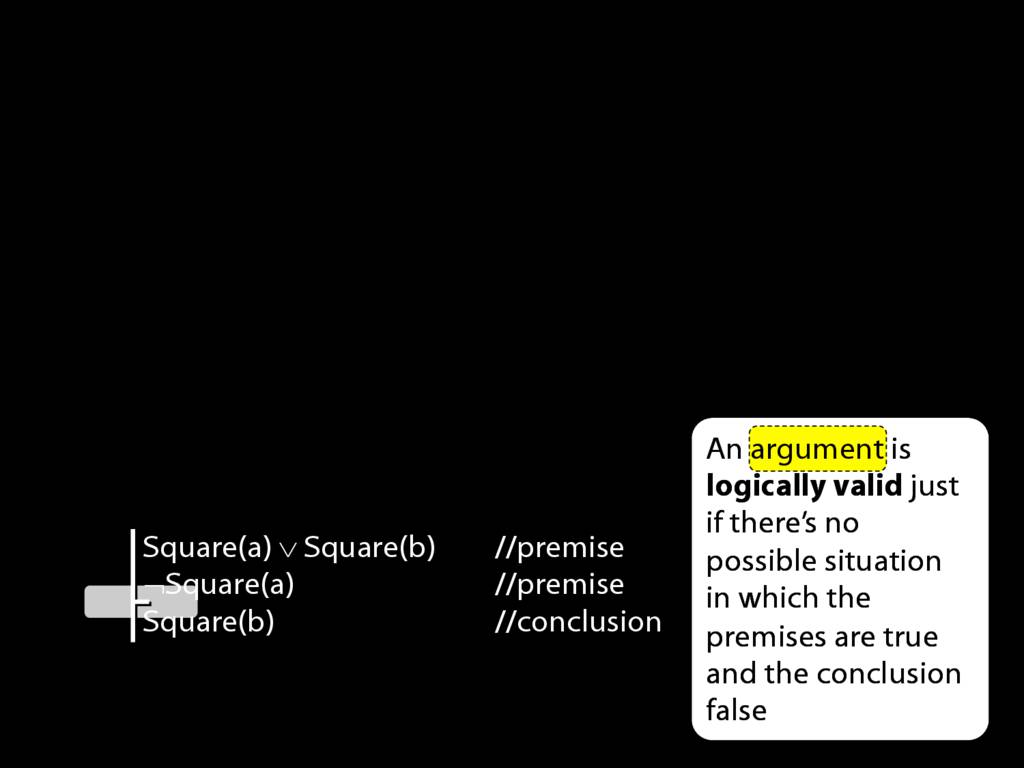
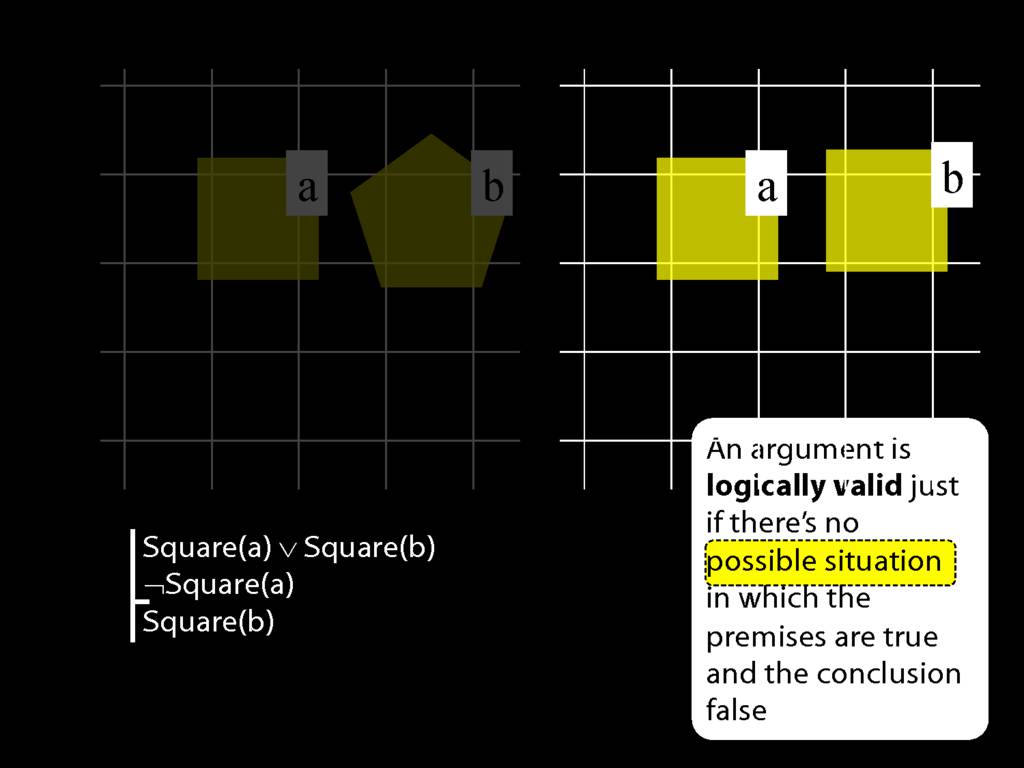
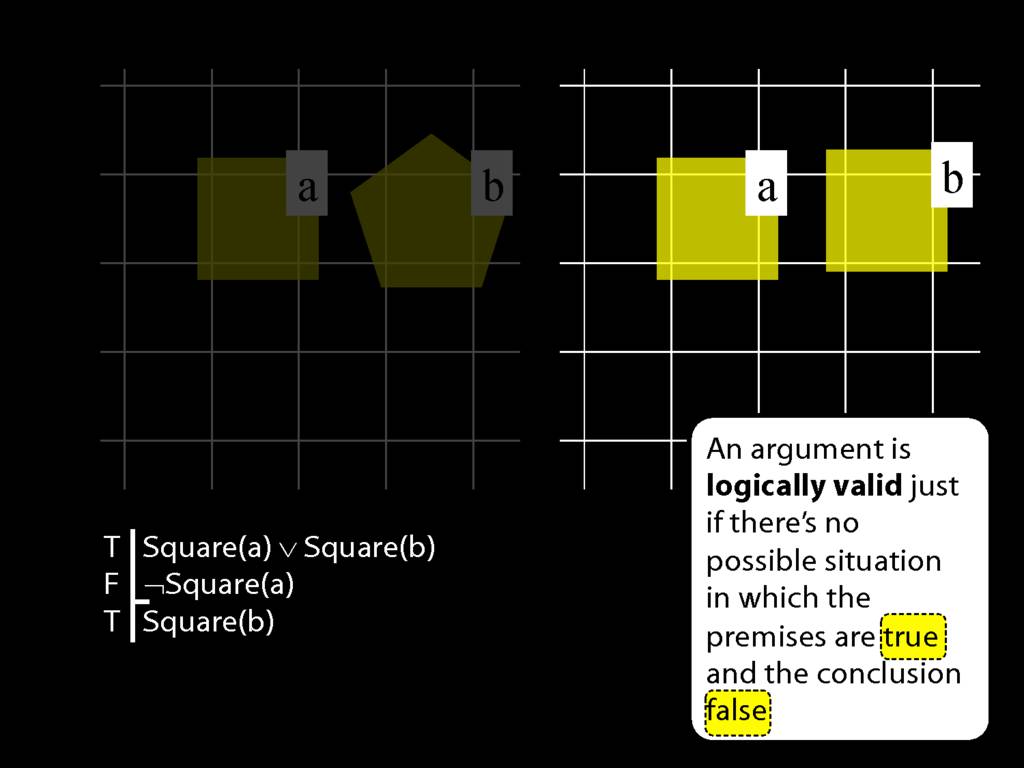
Square( a )

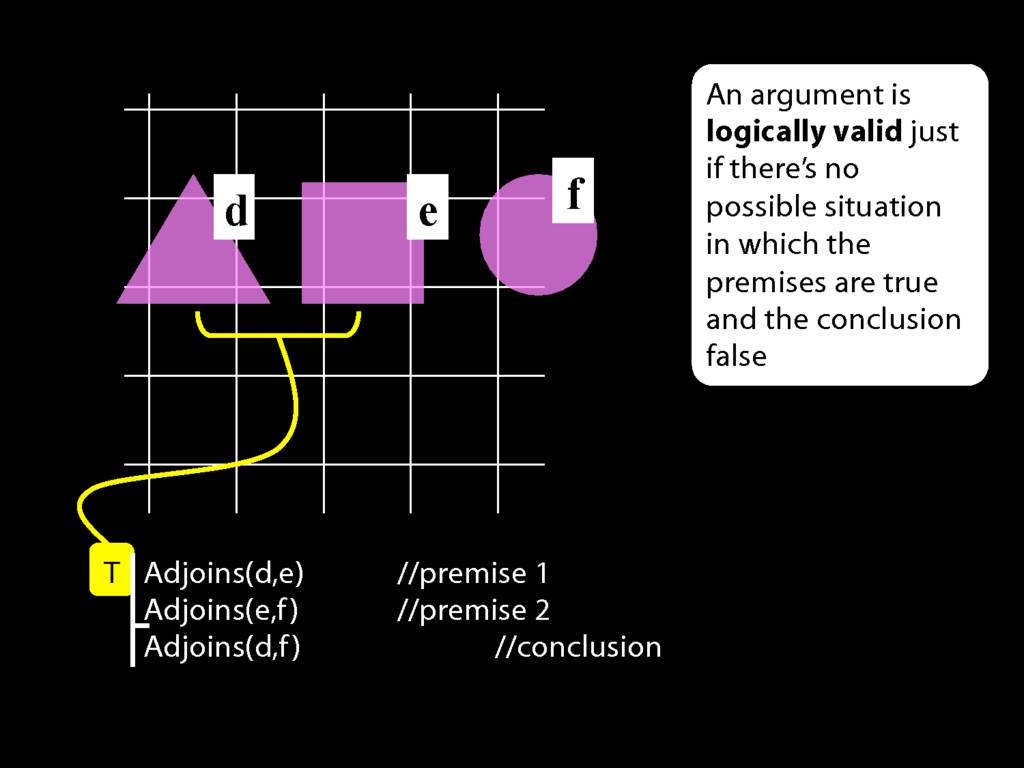
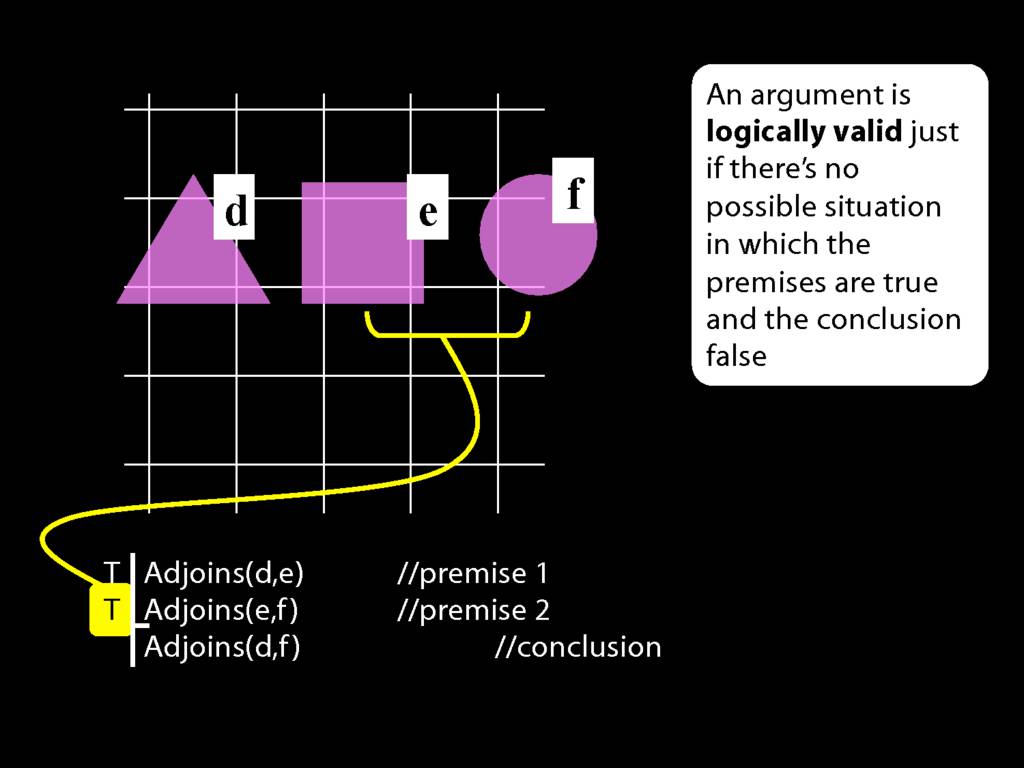
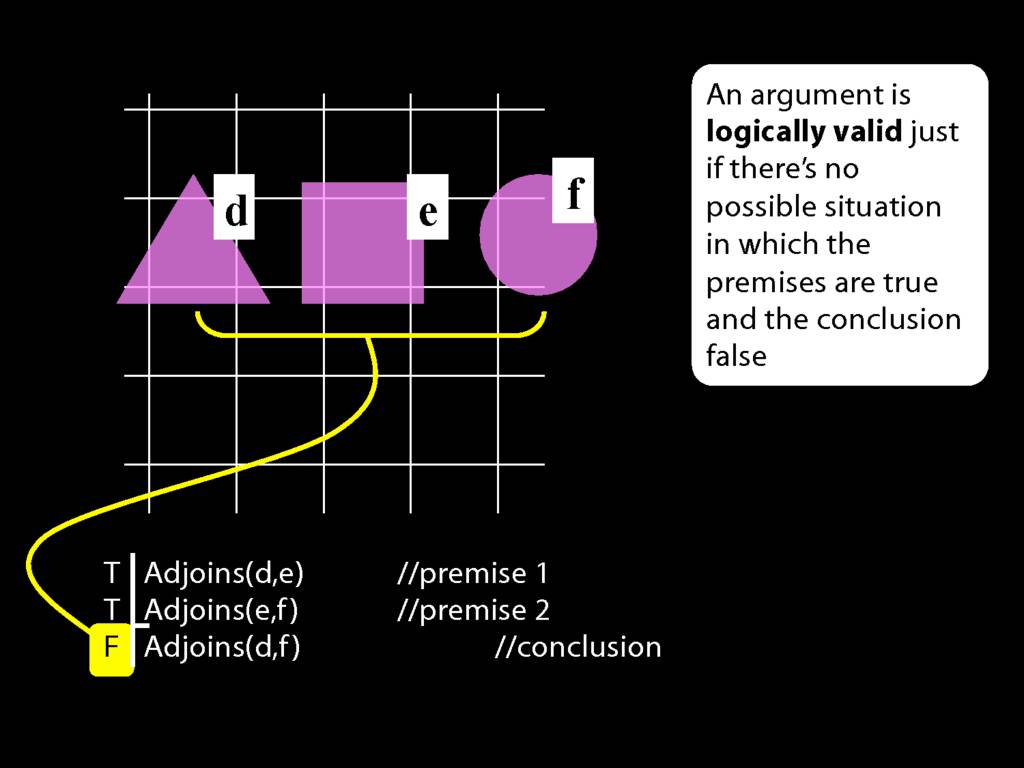
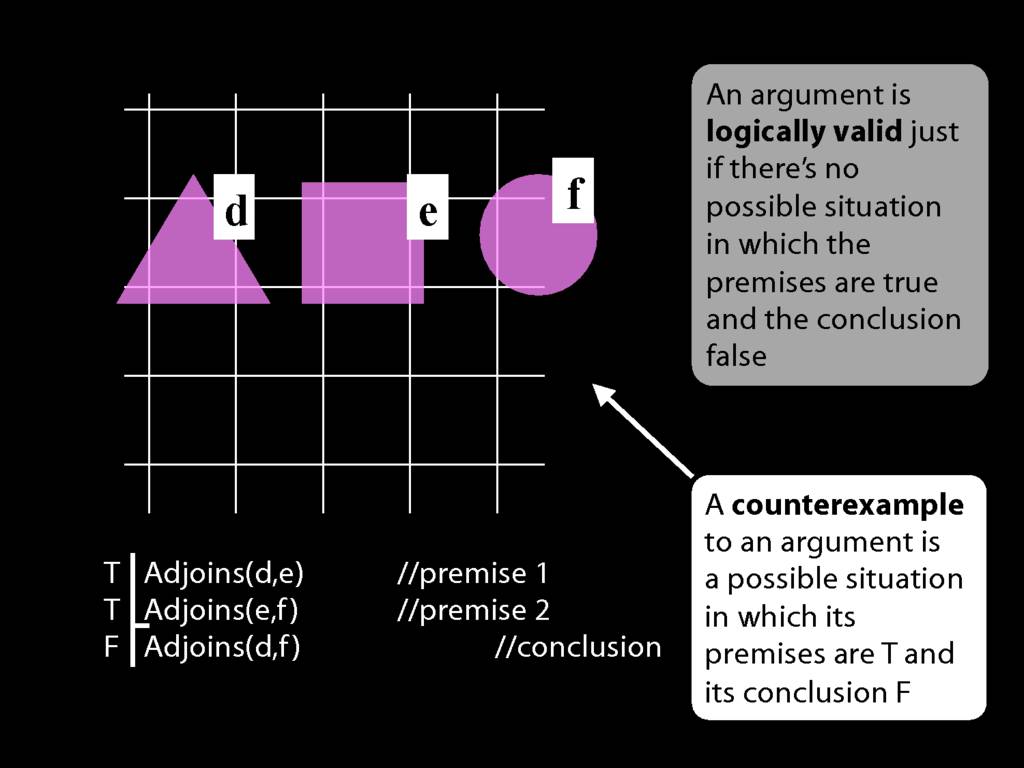
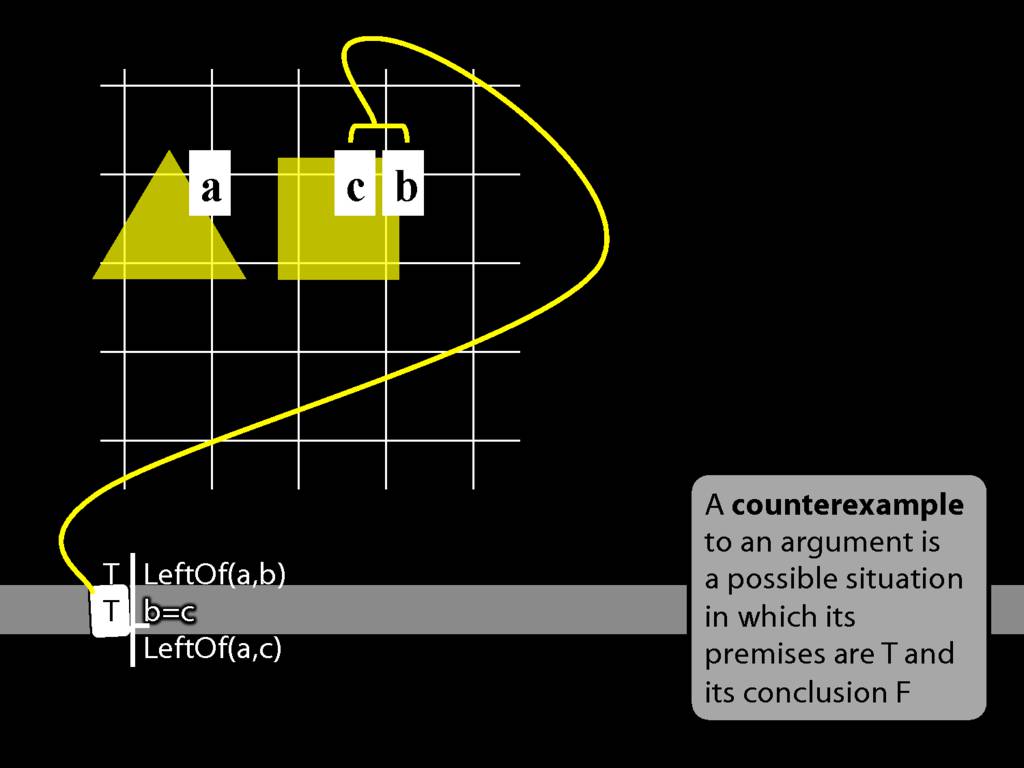
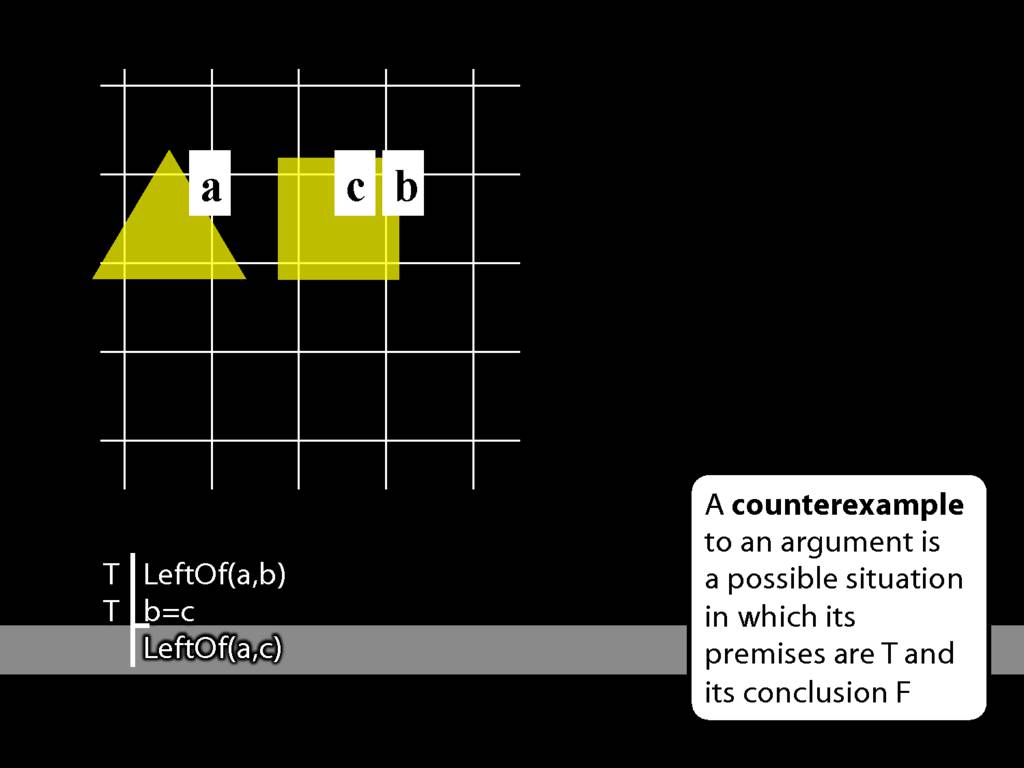
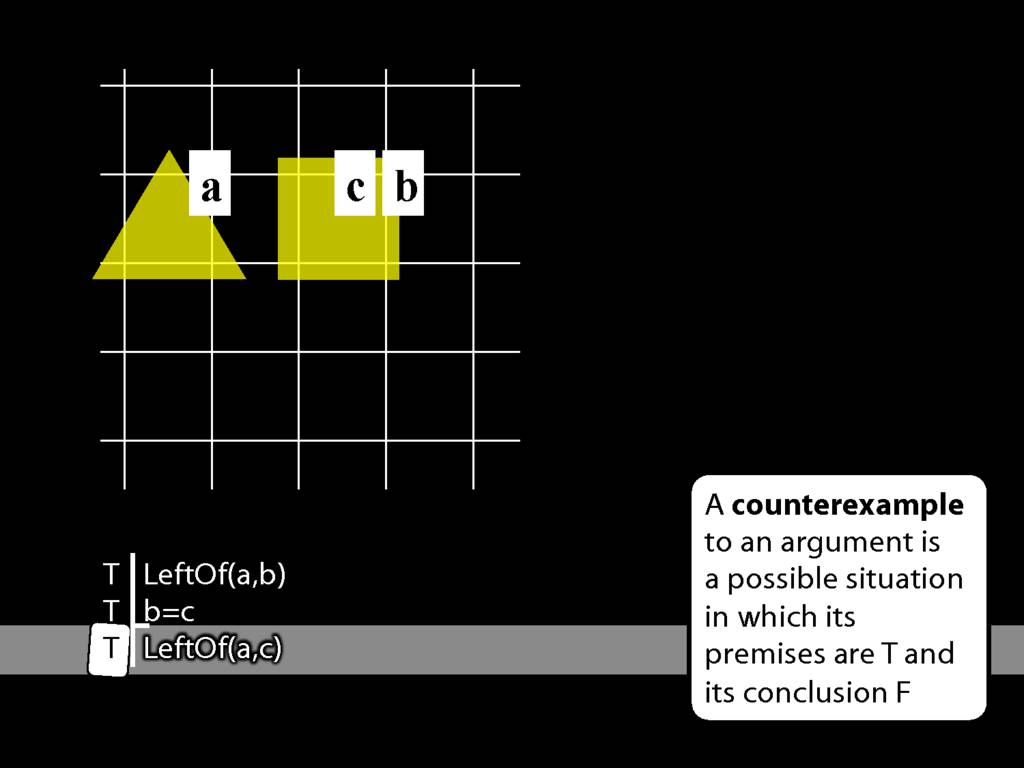
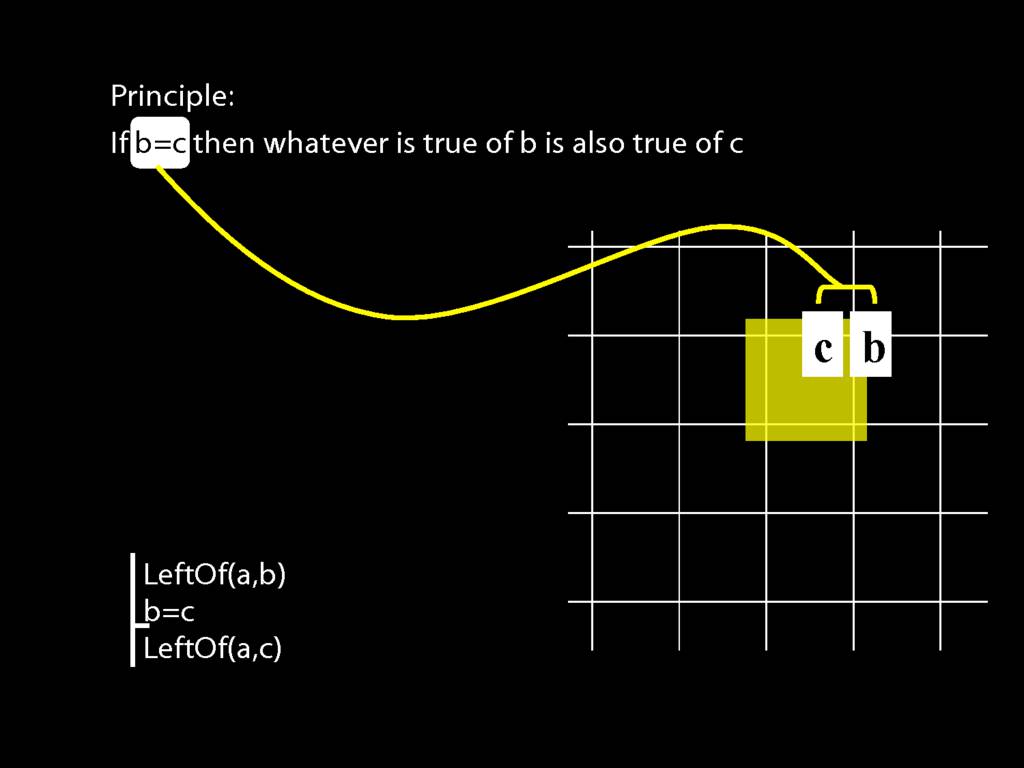
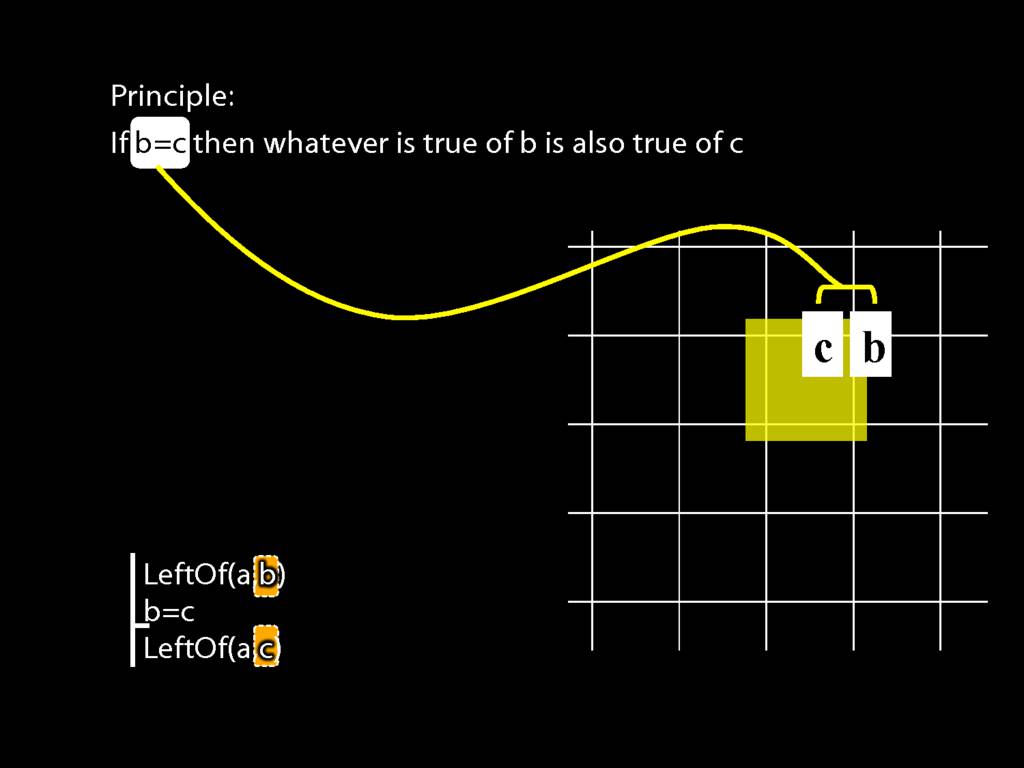
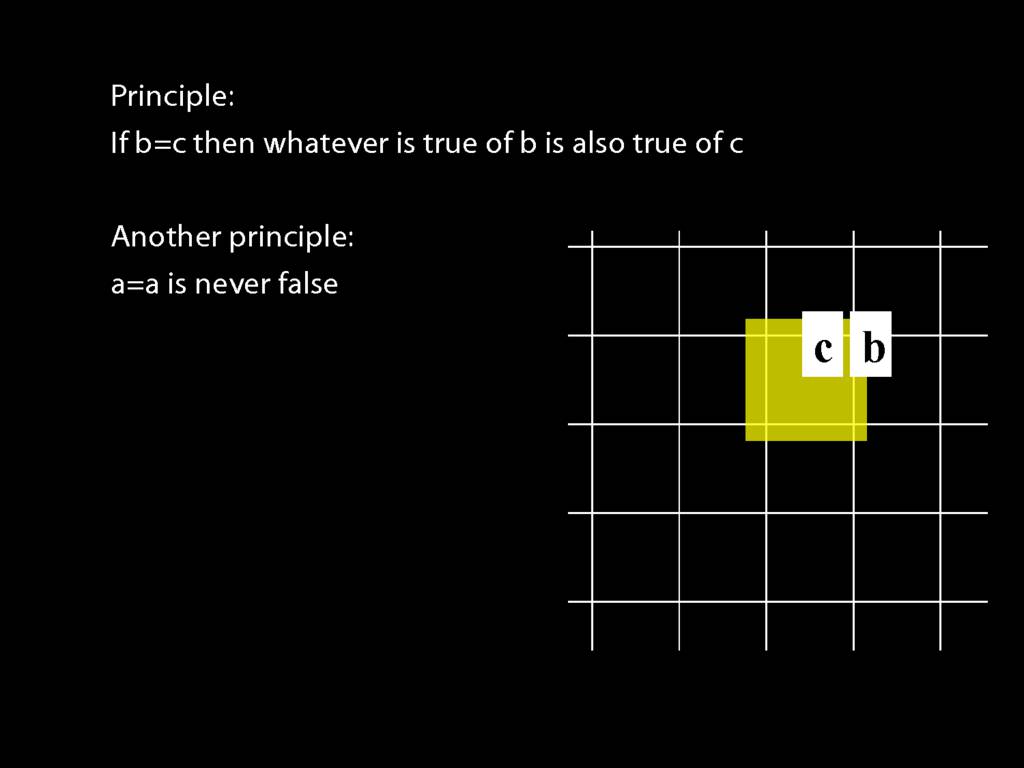
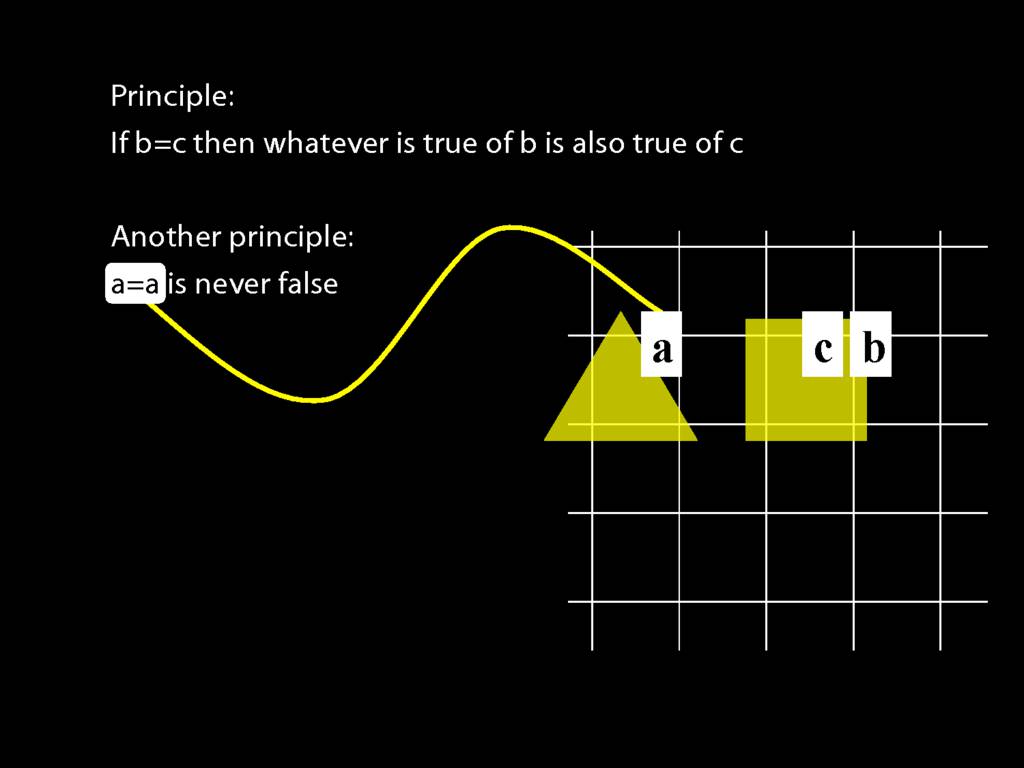
John is to the left of Ayesha

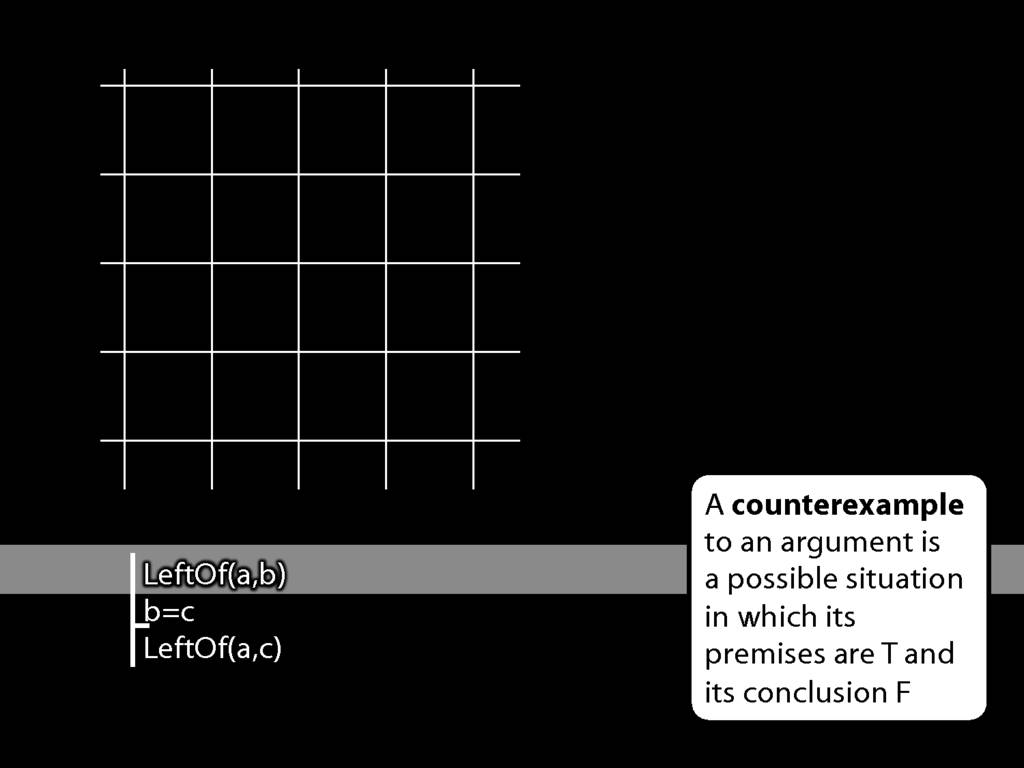
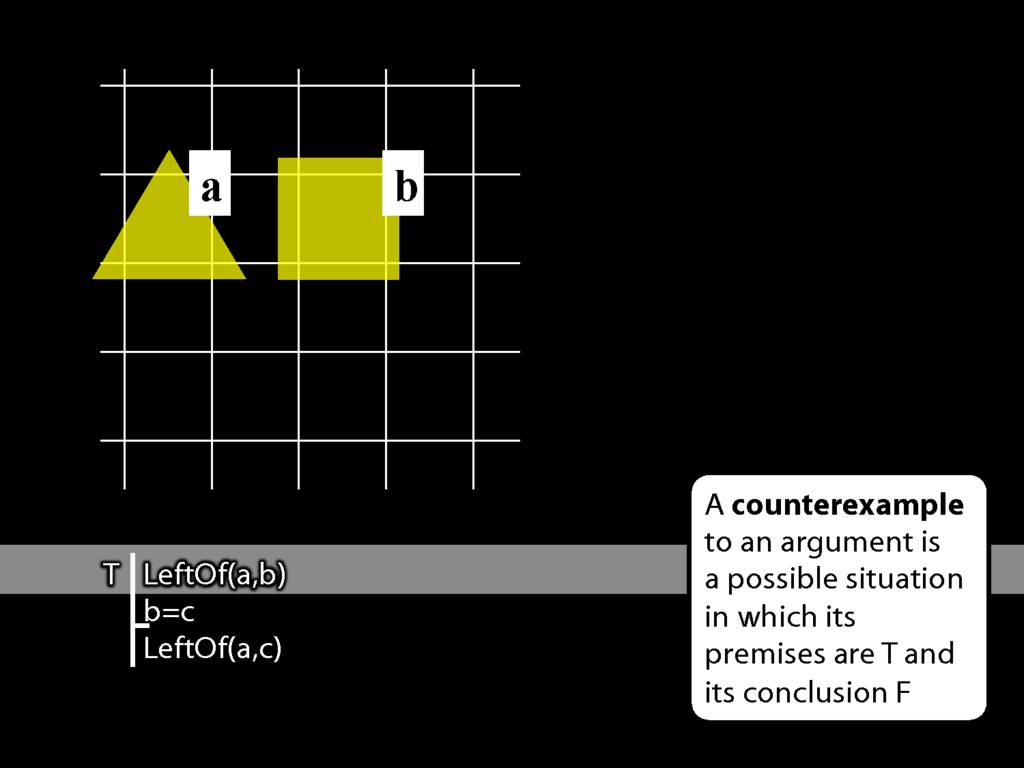
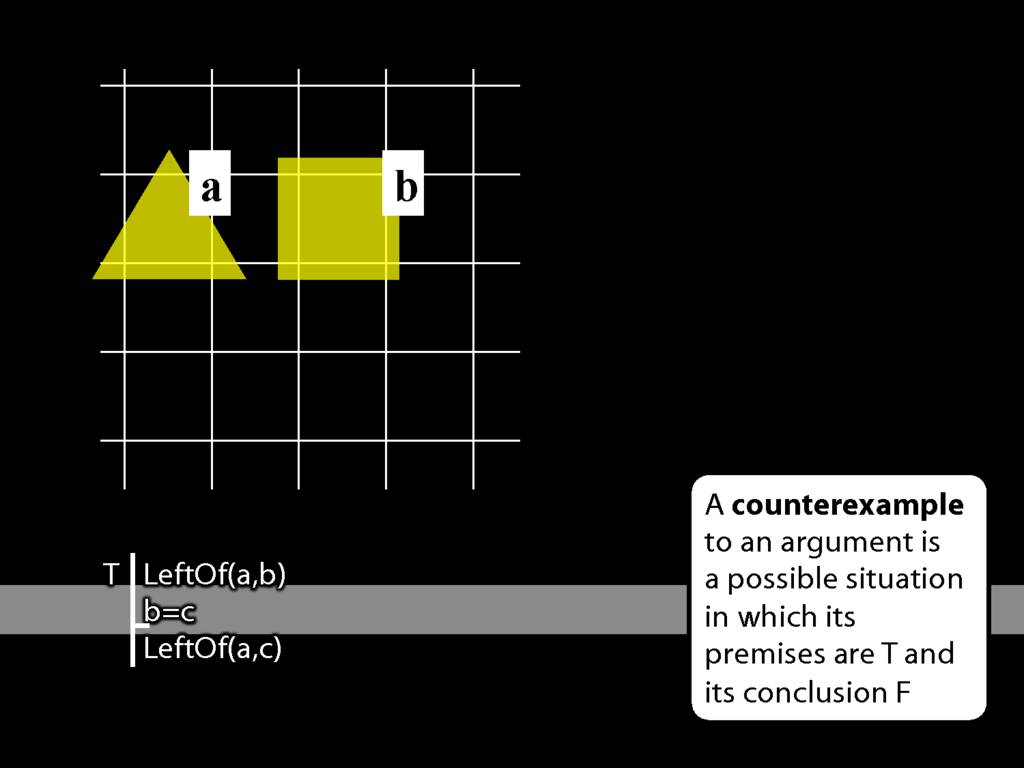
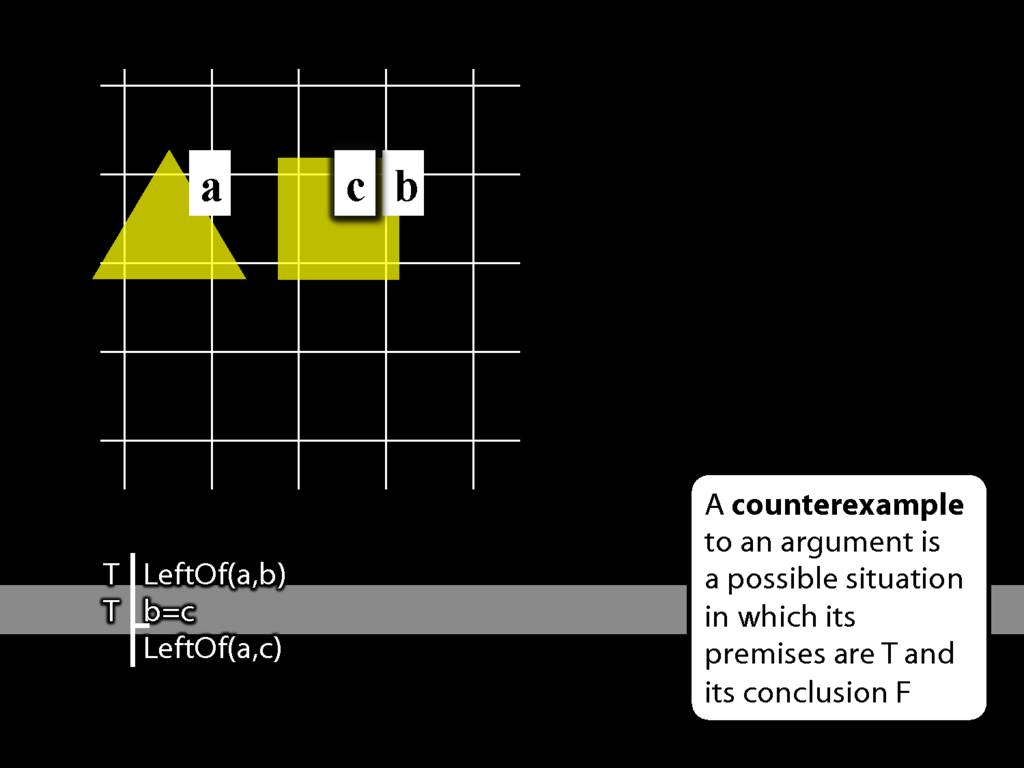
LeftOf( a , b )

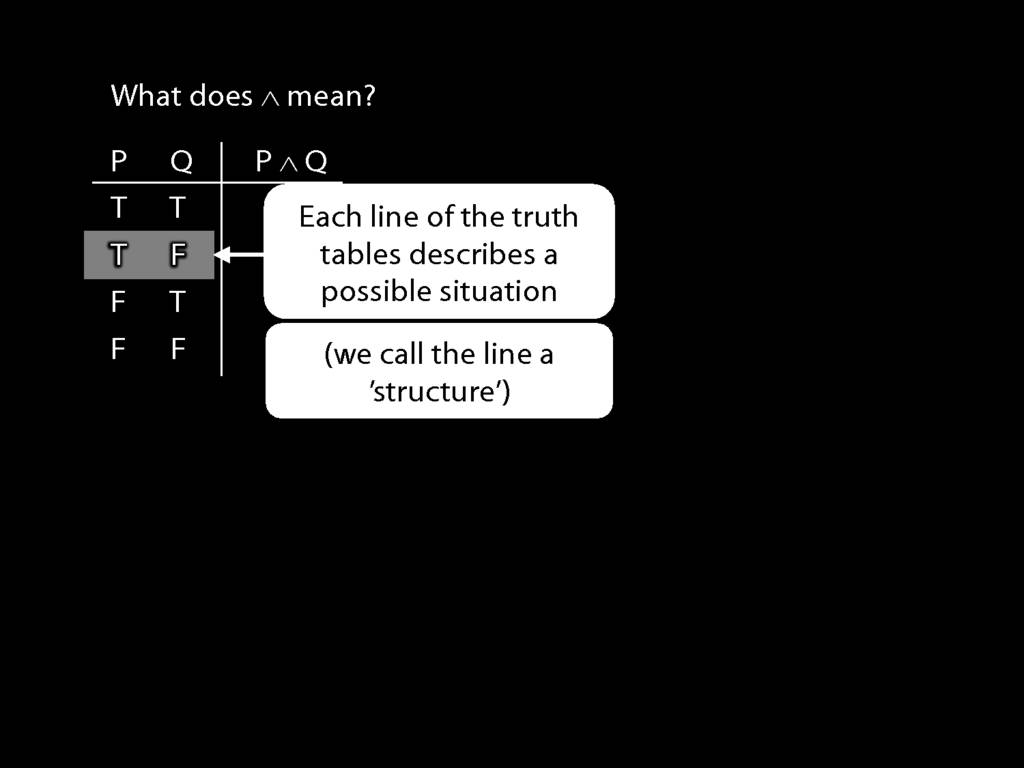
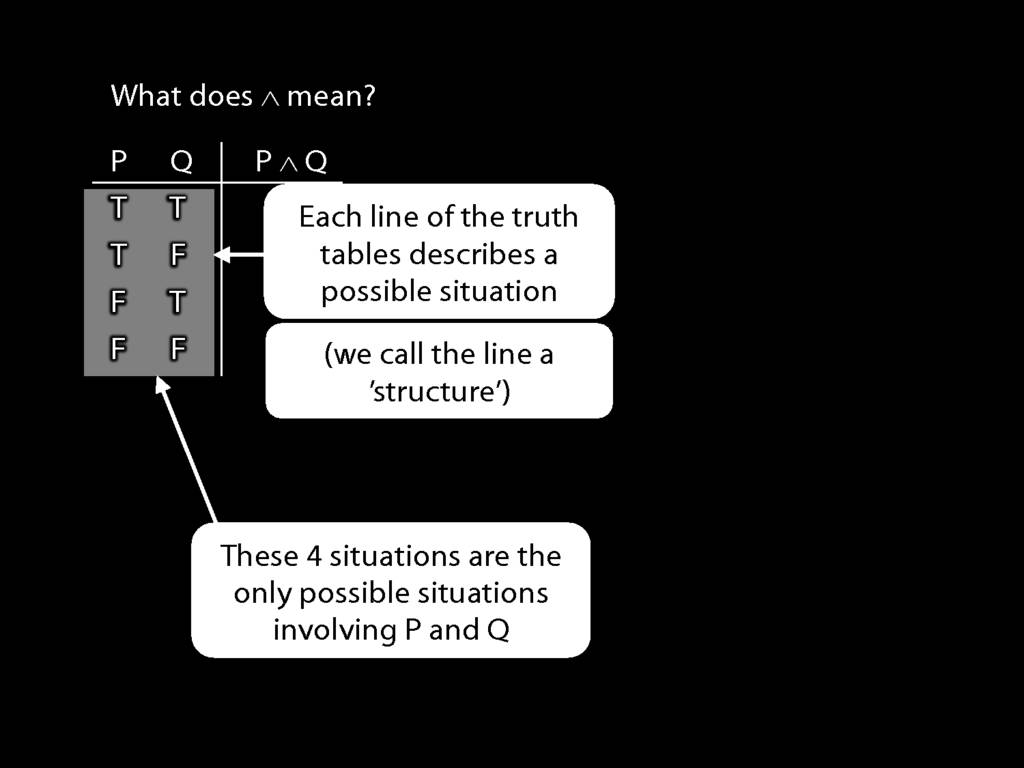
John is square or Ayesha is trinagulra

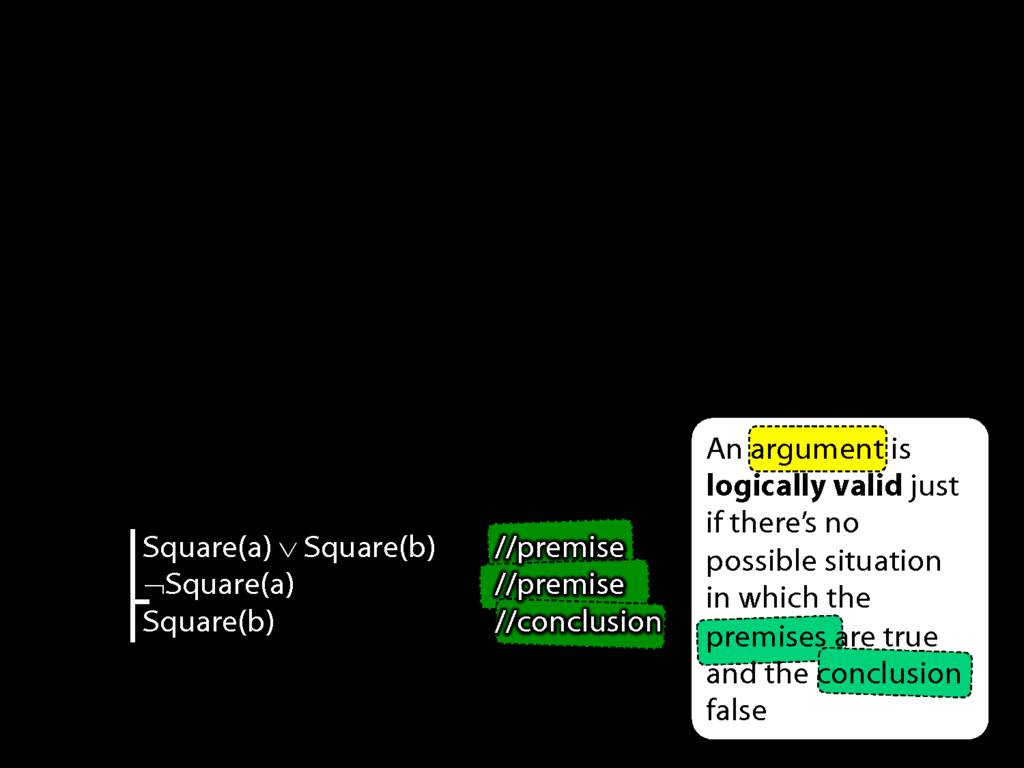
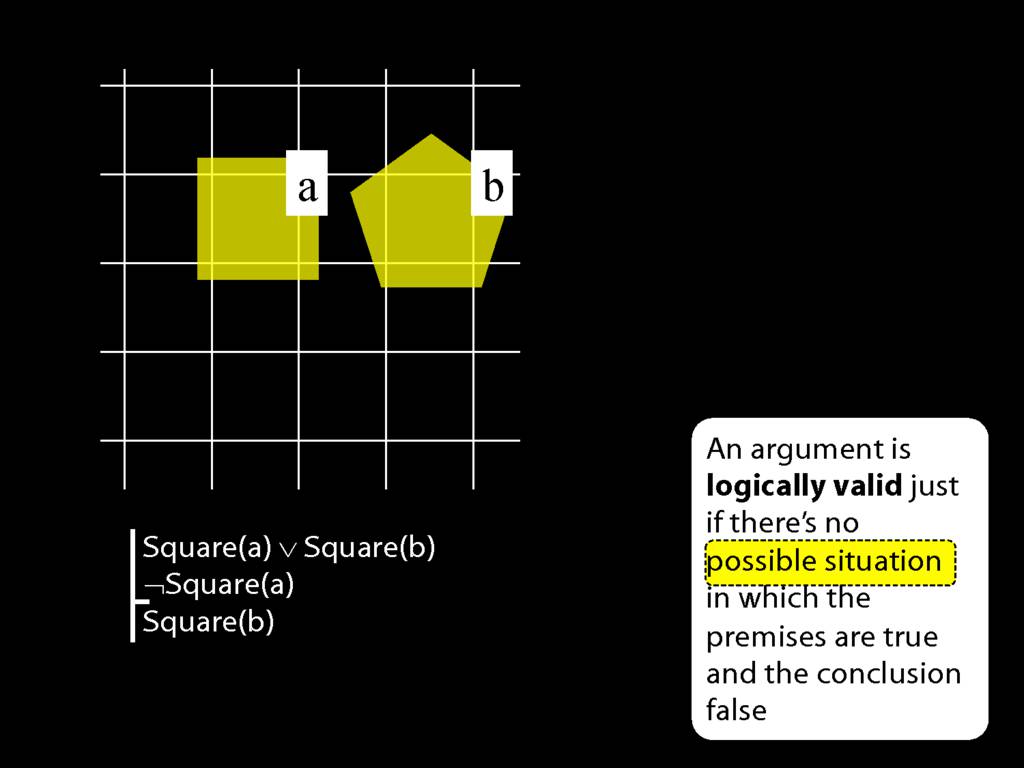
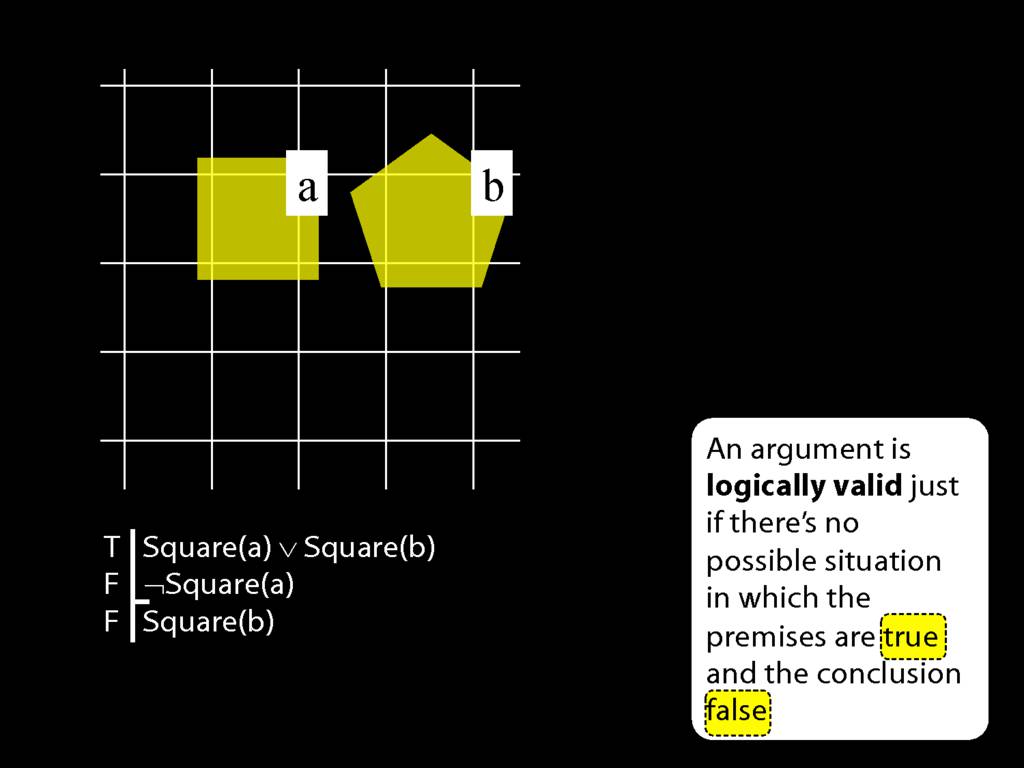
Square( a ) ∨ Trinagulra( b )

name (refers to an object)

predicate (refers to a property)

connective (joins sentences)

sentence (can be true or false)

atomic sentence (no connectives)

non-atomic sentence (contains connectives)

Our approach to studying logic will involve a formal language called awFOL. `FOL' stands for first order language, and I call this particular first-order language `awFOL` because, like nearly all first-order languages used in textbooks, it’s awful. (Where are the binary quantifiers? Why are brackets used with two completely different meanings? ...)

The language of the textbook is called ‘FOL’. ‘awFOL’ is basically the same as FOL except that you can replace symbols with words which makes typing it easier. Also 'FOL' is a really stupid name because there are lots of first-order languages. It's a bit like I ask you what language you speak and instead of saying 'Farsi' or 'English' or 'Cantonese' you say 'Language, I speak Language'. But this is trivial, it doesn't really matter what you call things. Let's move on.

As I was saying, for the purposes of logic we are going to use a formal language. In order to get a sense for this language, let's compare it to English. Take a look at this sentence, John is square.

This is a sentence.

For now a sentence is just something capable of being true or false. (In a longer course we would define what it is to be a sentence more carefully.)

In English there are names ...

... these are terms that function to refer to objects.

There are also predicates, like 'Square'.

Predicates are things that refer to properties. In this case the property is that of being square.

Take a look at this sentence.

Some properties relate several things; for example, being 'to the left of' involves two things rather than one. The expressions for these relational properties are also called predictaes.

By the way, this is also a sentence containing multiple names, 'John' and 'Ayesha'.

Now have a look at this sentence, 'John is square or Ayehsa is triangular' ... or, as I perfer to say, 'trinagulra'. (Did you spot the mistake? Well done.)

Consider the word 'or' in this sentence. It isn't a name or a predicate. It doesn't refer to an object, nor to a property.

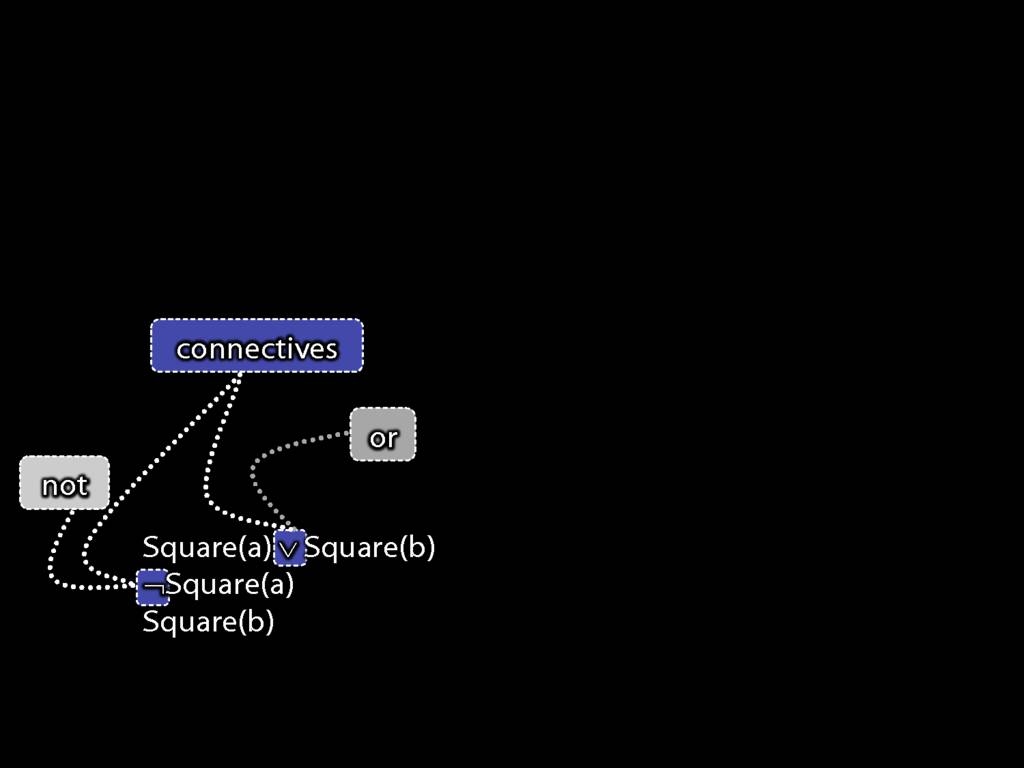
Instead its function is to join two sentences, making a new one. We'll call things like this 'connectives'. A connective is anything that you can combine with zero or more sentences and to make a new sentence.

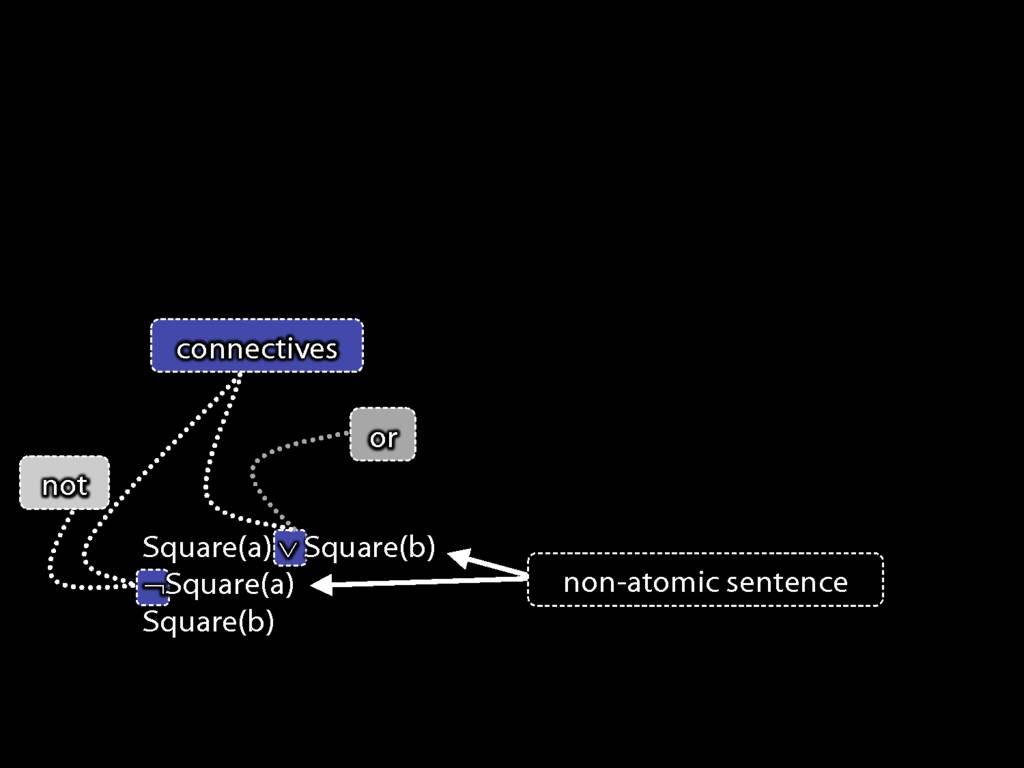
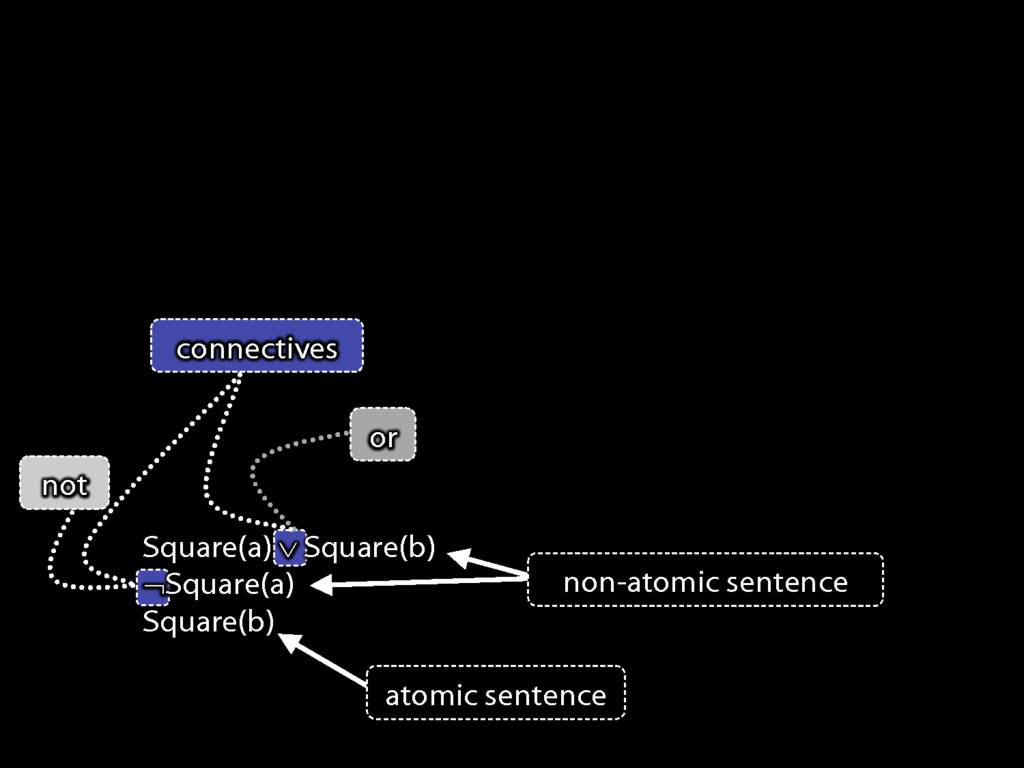
Here's another piece of terminology: a sentence with one or more connectives is 'non-atomic'

And, as you'd expect, a sentence with no connectives is 'atomic';

Now let's see how these sentences look in our formal language, awFOL.

Here's how the equivalent of 'John is square' looks in awFOL.

The whole thing is a sentence of awFOL.

The letter 'a' is a name; just like the English name 'John', the function of 'a' is to refer to an object (in this case, John)

And 'Square( )' is the predicate.

What about 'John is to the left of Ayesha', how can we say something like this in awFOL?

Here's the equivalent of 'John is to the left of Ayesha in awFOL'

Again, the single letters a and b are names.

And 'LeftOf( )' is the predicate. Note that, as in English, the order of the names matters. It affects who we are saying is to the left of who.

Lastly, what is the equivalent of the third sentence in awFOL?

Much as you would expect.

This is a non-atomic sentence (because it contains a connective).

Note that where the English 'or' appears, we use a special symbol. This symbol doesn't do exactly what the English 'or' does, as we'll see later.

Alles klar? Molto bene.

You might be thinking that this English sentence looks, well, ...

... a lot like this awFOL sentence. What's the point of learning a formal language? How will it help us to understand logic?

(It's a bit tricky to answer this question as I haven't yet said what logic is.)

A formal langauge enables us to avoid ambiguity, e.g.:

We need a formal language because ambiguity is awkward to deal with theoretically

\begin{quote}

This is a hospital where doctors are trained.

\end{quote}

A formal langauge also enables us to some avoid appearance--reality problems:

Appearance and reality. We need a formal language because we want a guarantee that a sentence which seems to express a proposition really does express a proposition.

\begin{quote}

Many more people have been to Paris than I have.

\end{quote}

Finally, consider these sentences.

Ayesha doesn’t know diddly squat about logic

Ayesha does know diddly squat about logic

The only difference is an extra negation in the first sentence. Normally you might think that adding a negation changes the meaning, and does so systematically. But this is not true of natural languages like English. We can construct our formal language so that it is true, thereby making our lives simpler insofar as we are interested in reflecting on inferential relations among sentences.

1.1--1.5

*1.6

1.8--1.10

Logically Valid Arguments

\section{Logically Valid Arguments}

\emph{Reading:} §2.1

\section{Logically Valid Arguments}

An argument is \emph{logically valid} just if there’s no possible situation in which the premises are true and the conclusion false

A \emph{connective} joins one or more sentences to make a new sentence. E.g. ‘because’, ‘¬’. The sentences joined by a connective are called \emph{constituent sentences}.

E.g. in ‘P $\lor{}$ Q’,

\begin{quote}

$\lor{}$ is the connective

P, Q are the constituent sentences

\end{quote}

Consider these three sentences.

The first sentence says that John is square or Ayesha is square. The second sentence says John is not square. (I know I just told you John is square; I'm not very consistent, am I?) And the third sentence says Ayesha is square.

Note the symbol; we saw this a moment ago, it's a bit like the English 'or'.

There is also a new symbol in the second sentence, this a bit like the English 'not'.

As you recall, these symbols are called 'connectives'.

Note that the negation connective in the second sentence is making a new sentence from just one sentence. (Connectives can join any number of sentences.)

You may also recall that these first two sentences are non-atomic (they contain connectives), ...

... whereas the third sentence is atomic.

OK, so much for the sentences. So far we've been fixing terminology and getting a feeling for a formal language, which is a tool for studying logic. But I haven't said anything about what logic is.

What is logic? What is this course about?

The answer is here: it's about the notion of logical validity. An argument is logically valid just if there's no possible situation where the premises are true and the conclusion false.

Logic is the study of logical validity. We want to know which arguments have this property, and what means there are of establishing which arguments are valid or not.

Let's go though this slowly. First, what is an argument?

For our purposes, an argument is just a sequence of sentences where zero or more are identified as premises and exactly one is identified as the conclusion.

But what do we mean by premises and conclusions?

A premise is just a sentence that we say is a premise. (That's all there is to being a premise.)

Likewise, a conclusion is just a sentence that we say is a conclusion. How simple is that?

Now we're going to write a lot of arguments so it would be helpful to have a compact way of identifying premises and conclusions ...

... That is the purpose of these lines. The horizontal line specifies that the sentences to its right an argument.

And the vertical line separates the premises from the conclusion.

So this is logic: the study of logical validity. Have we understood the definition yet? Not quite ...

... What do we mean by 'possible situation'?

A possibile situation is just a way that the world is or could be. So consider the situation which is as similar to the actual situation as possible except that you are in Havana smoking a fat cigar rather than attending my lecture. This is a possible situation.

Now possible situations are huge things; in specifying a possible situation, you are specifying something as big as the actual situation, with all the trees, leaves, insects and everything. It is helpful to have a proxy for possible situations, something much simpler than a real possible situation.

For our purposes, a good proxy is often an arrangement of shapes in two dimensional space. For evaluating the argument about John and Ayesha, we can pretend that possible situations are just shapes in space. Thinking of possible situations in this way is simpler, and doesn't ignore anything relevant to this particular argument.

The final concepts in our definition of logical validity are truth and falsity. These concepts are too simple to say anything much illuminating about.

Note that whether a sentence is true or false depends on which possible situation we are talking about. In this possible situation, the first premise is true, the second premise is false and the conclusion is false.

But in this possible situation, ...

... the conclusion is true.

Incidentally, you will sometimes be asked whether a logically valid argument can have one or more false premises and a true conclusion. If you're asked that question, do think about this argument and this possible situation.

So logic is the study of logical validity. As I said before, our overall aims in this course are to discover which arguments have this property, and what means there are of establishing which arguments are valid or not. In doing this our main tool is the formal language awFOL.

2.3, 2.4

Admin

Seminar groups (check email or see module web page)
Exercises
Textbook
Slides and handouts are on the web

Counterexamples

\section{Counterexamples}

\emph{Reading:} §2.5

\section{Counterexamples}

A \emph{counterexample} to an argument is a possible situation in which its premises are T and its conclusion F.

There are no counterexamples to a logically valid argument.

If an argument is not valid, then there is a counterexample to it.

To show that an argument is not logically valid, we specify a counterexample to it.

https://logic-ex.butterfill.com/ex/create/from/SameShape(a,b)/to/SameSize(a,b)

Let’s see how to create counterexamples in this in logic-ex.

We have to create a counterexample to an argument.

So the premise must be true ...

... and the conclusion must be false.

I already put the names in; without having things named ‘a’ and ‘b’ the sentences would not be true or false in our possible situation.

We need to make the conclusion false. At the moment it’s true because a and b are the same size. So let’s change the size of a. Do this by dragging the corner to stretch her.

Now a is wider.

This makes the conclusion false, as we wanted.

But now the premise is false too. (This is often the problem with creating counterexamples.) What can we do?

Let’s make a taller as well by stretching her down. Do this by dragging the corner.

Now a is both wider and taller than b.

So the conclusion is still false ...

... but now the premise is true, just as we wanted.

A counterexample to an argument is a possible situation in which its premises are true and its conclusion is false.

2.8, 2.10, 2.12, 2.21

Identity

\section{Identity}

\emph{Reading:} §2.2

\section{Identity}

Here’s an argument involving identity. Let’s see if it’s valid.

Principle: If b=c then whatever is true of b is also true of c.

Principle: a=a is never false

Suppose we want to find a counterexample. So we need to make make the premises true. Let’s see if we can make them true without making the conclusion true.

Start with an empty world.

Consider the first premise

We want the first premise to be true so we have to put a to the left of b.

What about the second premise? So far the truth-value of the second and third premises are undefined because the name ‘c’ does not yet designate any object in this situation.

Want the second premise to be true so we have to label the b object c as well.

This is what b=c requires--that one and the same object have both labels.

Now, what about the conclusion?

Having made the premises true, the conclusion turns out to be true as well.

This is sort of an informal proof that the argument is valid. If you think about what is involved in making the premises true, you can see that it guarantees the truth of the conclusion as well.

As far as the logic of identity goes, all you need to know are two principles.

This first principle.

You can see that this principle must be true from the meaning of identity: b=c requires that one and the same object have both labels.

And this first principle is exactly what you need to prove the argument we were just looking at.

The second principle says, roughly, that everything is identical to itself.

You can see that this principle must be true from the meaning of identity: a=a requires only that one and the object named 'a' be named 'a', which you can't really avoid. (In case you're thinking there's a tricky issue about what happens if nothing is named 'a', well done. In our system of logic, we rule that possibility out by stipulation to keep things simple.)

These principles are all you need to understand the logical notion of identity. They allow you to do things like prove that identity is a symmetric and transitive relation.

I want to show you quickly how to work with identity in logic-ex.

Let’s add a person to the possible situation

Here I’ve added some names

I’ve called one person ‘a’ and the other ‘b’.

Of course this makes the first sentence false, not true. How do I make it true?

Like this ...

I’ve given one person both names. To give more than one name to a person, simply type multiple names separated by commas or spaces (or both), just as I’ve done here.

And this makes the sentence ‘a=b’ true, of course.

But what about the next sentence, ‘not b=c’?

To make this true or false, I need to give someone the name c. I’m going to add that to the person already known as ‘a’ and ‘b’.

So here you see one person has all three names

Of course this means the second sentence, ‘not b=c’ is false. We need to make that true. How are we going to do that?

Let me re-arrange the names.

You see that I’ve named the other, yellow person c.

And this is enough to make the second sentence true.

2.5, 2.6

Sentence Letters

\section{Sentence Letters}

Recall this argument about Ayesha and John.

The sentence 'Square(b)' occurs twice, once as part of the first premise, and once as the conclusion.

The sentence 'Square(a)' also occurs twice, once as part of the first premise, and once in the second premise.

And there are no other sentences in this argument.

So we can represent this form of argument in a much more general way ...

... by using letters to stand for sentences instead of names and predicates.

Why is this more abstract representation useful?

We don't want to consider arguments one-by-one. We want to be able to say things about a large number of arguments. The use of sentence letters lets us talk abou a much larger class of arguments, all of which are valid in virtue of having this form.

But how far can we go with sentence letters?

Consider this argument. There are three atomic sentences.

So if we wanted to represent it using sentence letters only, we'd have to have three different sentence letters.

But now we have lost what is interesting about this form of argument. After all, any argument with two premises and a conclusion has the form P, Q therefore R. There's nothing interesting we can say about all arguments with *this* form. So where an argument exploits identity, we can't capture what's logically interesting about its form using sentence letters.

The same is true where an argument exploits quantifiers ... this is something we'll get to later in the course.

Truth Tables

\section{Truth Tables}

\emph{Reading:} §3.1, §3.2, §3.3

\section{Truth Tables}

Here's a rough guide to what the connectives mean.

Rough guide:

`$\land{}$' means and

`$\lor{}$' means or

`$\lnot{}$' means not

Why do we need more than this rough guide?

Consider the sentence 'I love logic or I love chocolate'. If I were to say this to you, and it turned out that I loved logic and chocolate both, you might think I had mislead you by saying 'or'. And that might lead you to think that the English sentence is false, and that 'or' sentences are false when the two sentences they conjoin are both true. That is, the English 'or' is exclusive.

But now consider a different example. You say to me, 'You can be my friend if you love logic or chocolate'. Then, as before, it turns out that I love both. In this situation you're not going to deny me friendship. You're not going to say I haven't meet the criterion you specified. No, if I love both then I'm doubly your friend.

This tells us that an English sentence involving 'or' is true when the two sentences conjoined are both true. That is, the English 'or' is inclusive. But now we seems to have contradictory urges. One case urges us to say that the English 'or' is exclusive (false when the things conjoined are both true), the other case urges us to say the opposite. Now the truth is probably that the English 'or' is neither inclusive nor exclusive but much more complex still.

The point of introducing a formal language is to avoid all this complexity. Not because there's anything wrong with the English 'or'--on the contrary, it's complexity is a wonderful thing for communication. But our concern is not communication but logic. Now if we define our symbols just by invoking the meanings of English words, we won't succeed in avoiding the complexity of natural languages like English. We will have merely replaced one sign with another.

This is why we need more than the rough guide

So what does a symbol like ∧ mean?

The answer is given by a truth table.

Each line of the truth table describes a possible situation.

For instance, this line of the truth-table describes the situation where P is true and Q false.

(Strictly speaking, this is not a possible situation but a whole class of possible situations.)

Insofar as we are interested in sentences involving sentence-letters and certain connectives, we need only distinguish possible situations in which the sentence-letters of interest have different truth values. This means that if we are concerned with two sentence letters, there are only four kinds of possible situation that we need to consider.

The Ts and Fs in this column tell us whether the sentence is true or false.

So, for example, we are told that P∧Q is false when P is true and Q false.

These true and false are called truth-values.

To illustrate, suppose I ask you, What is the truth-value of P∧Q in this row (the second row)? What would you say?

What does ∨ mean?

The answer is given by another truth table.

Let's return to the English sentence about loving chocolate or logic. Imagine that instead of 'or' we had the logical symbol for disjunction, ∨.

Then 'I love logic' is P, and ...

... 'I love chocolate' is Q.

Now what happens if they are both true?

The truth-table tells us that their disjunction is also true. So specifying meanings by invoking truth-tables means we don't have to worry about the complexities of natural languages like English.

Note that the truth-tables are stipulations. You can't argue that it is wrong to put a T in the first row of this truth-table. The truth-table is a stipulation about the meanings of the symbol.

The point of a formal language is that it is a thing of our creation. We are free to make whatever stipulations we like about it. By contrast, we can't make stipulations about a natural language like English, because natural languages have lives of their own. In the case of natural language, meaning has to be discovered, not stipulated.

Finally, what do we say about the meaning of our symbol for negation, ¬?

The truth-table specifying its meaning is very simple; it takes true to false and false to true.

3.1, 3.2

3.5, 3.7

3.1, 3.3

3.5, 3.7

Complex Truth Tables

\section{Complex Truth Tables}