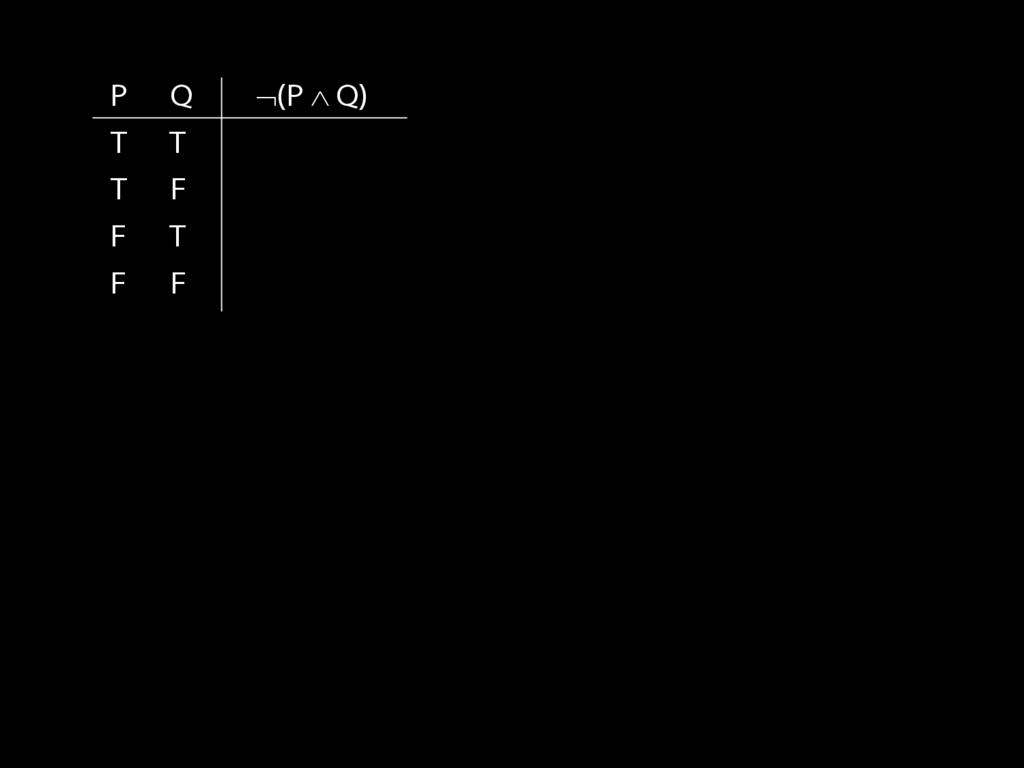Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides

\def \ititle {Logic (PH133)}
\def \isubtitle {Lecture 2}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.

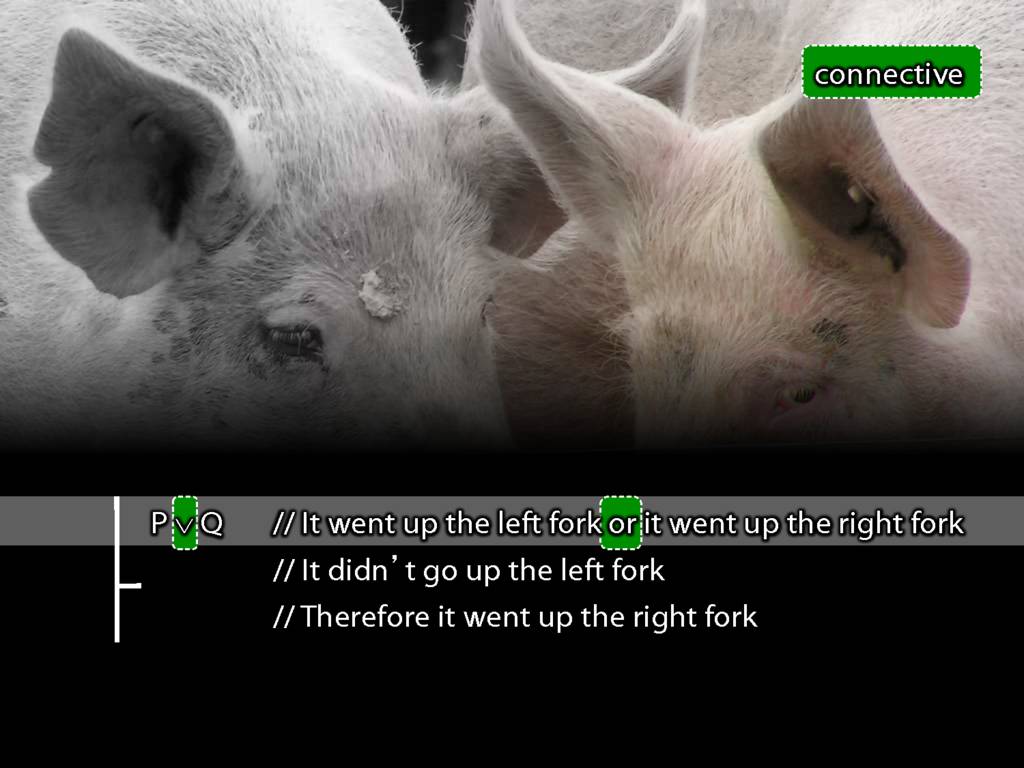
Over the vacation you and I were labouring on a farm and at one point we were herding the pigs.
Just as we almost had them secure, one of them ran off up the lane.
We closed the gate on the others and ran off behind it.
After a short sprint we came to a fork in the road.
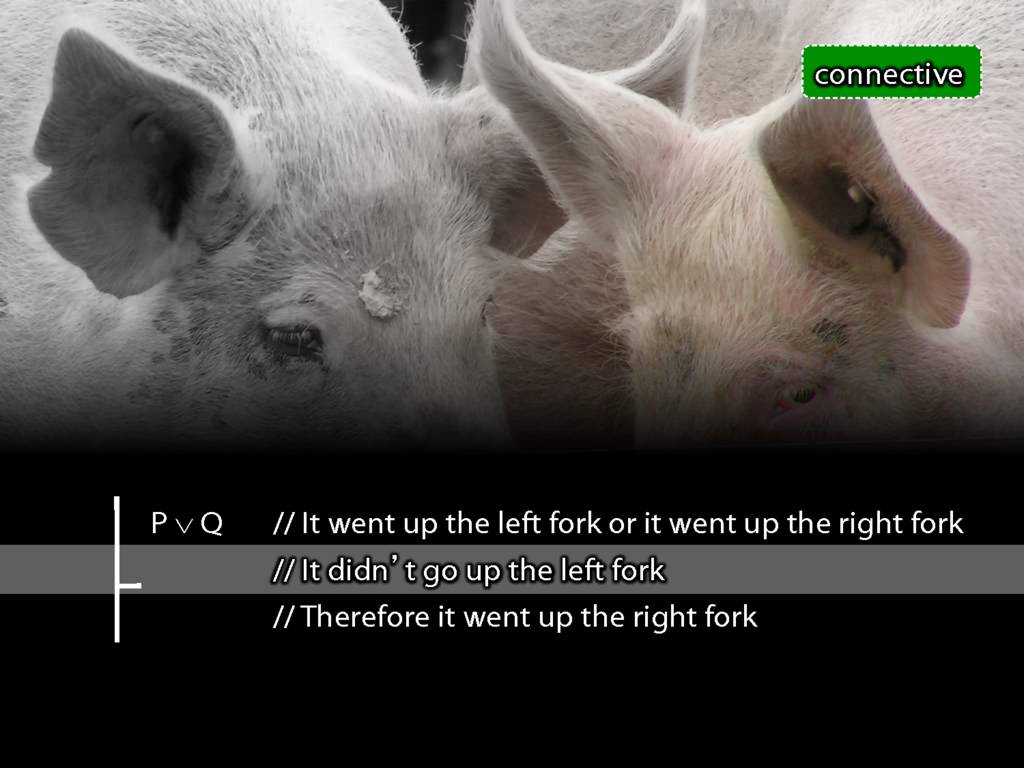
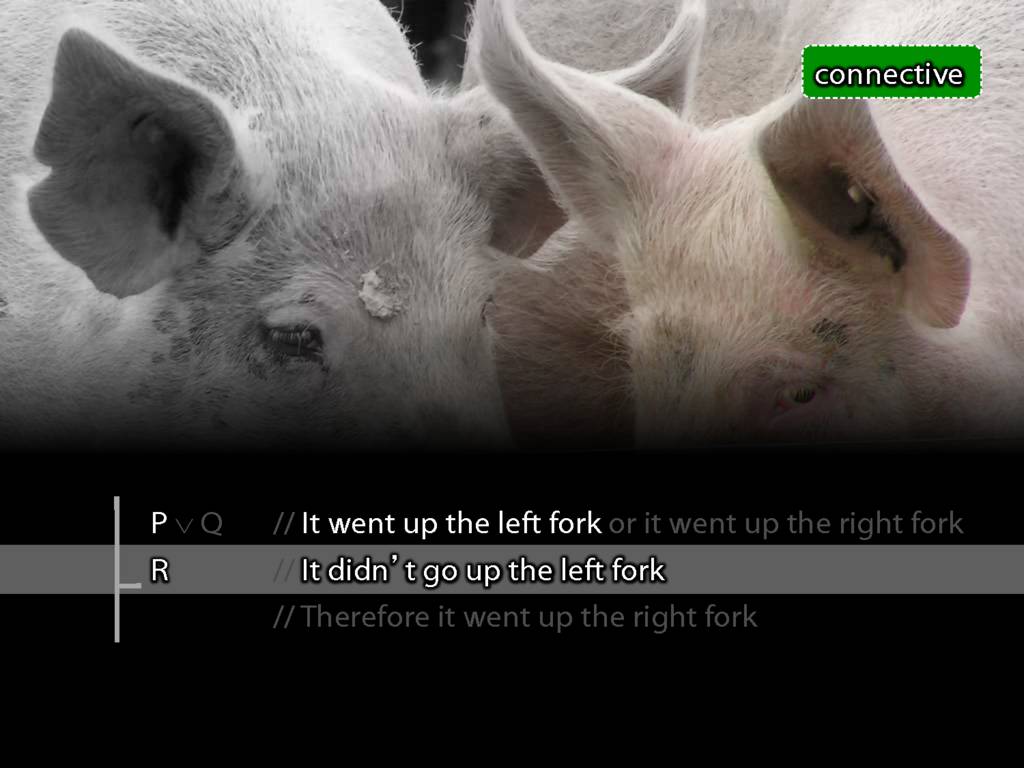
I said, not very insightfully, either it went up the left fork or the right fork.
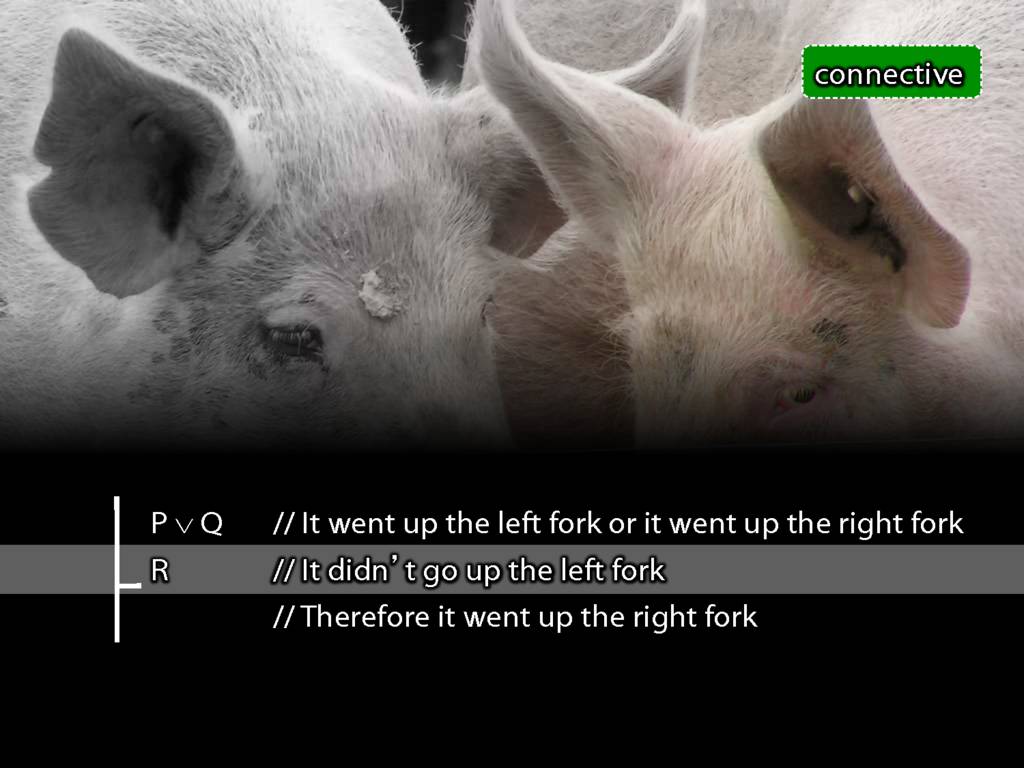
You said, It didnt' go up the left fork.
So we concluded that it went up the right fork and ran off after it.
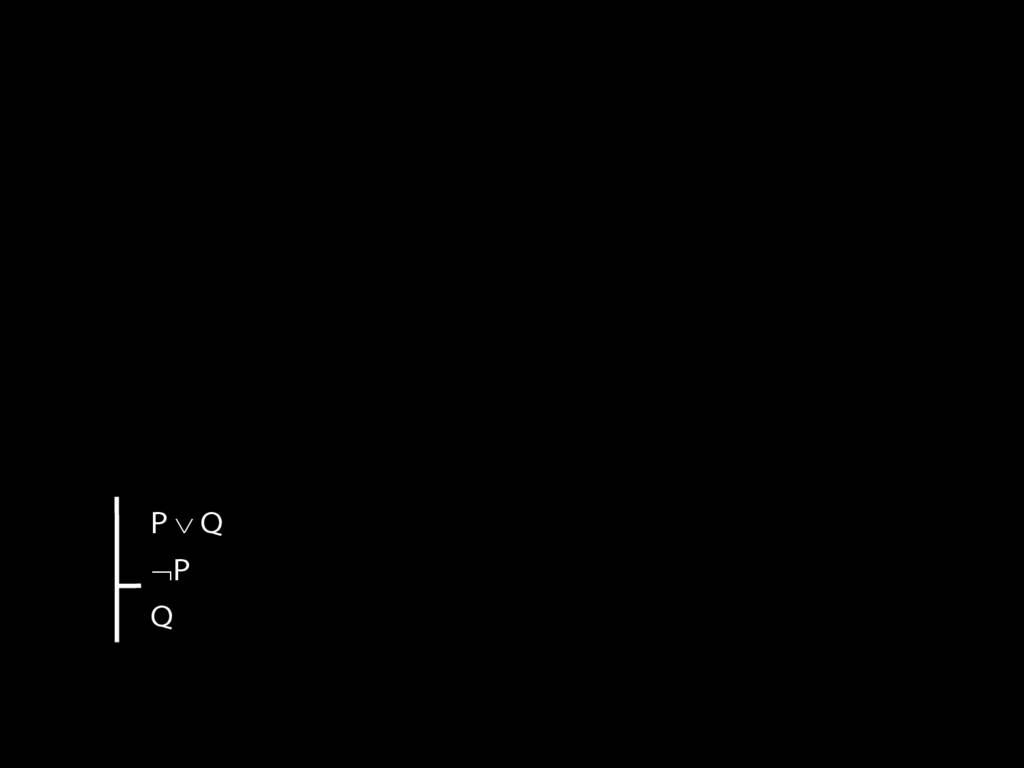
Our exchange is an argument in the sense that we're interested in.
It has two premises and a conclusion.

How can we formalise this argument?
We could introduce a name for the pig and predictates for its actions.
But we don't need to introduce names and predictates.
In the case of this argument, we can formalise it just using letters for sentences.
\section{Logical Validity and Truth Tables}
\emph{Reading:} §4.3
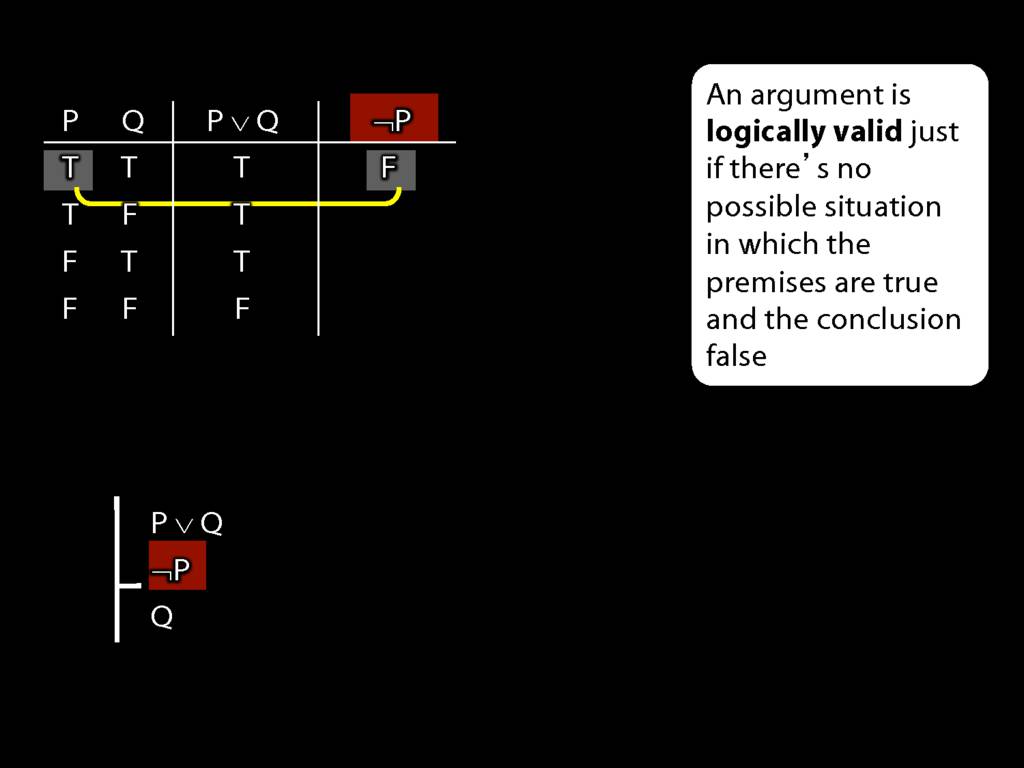
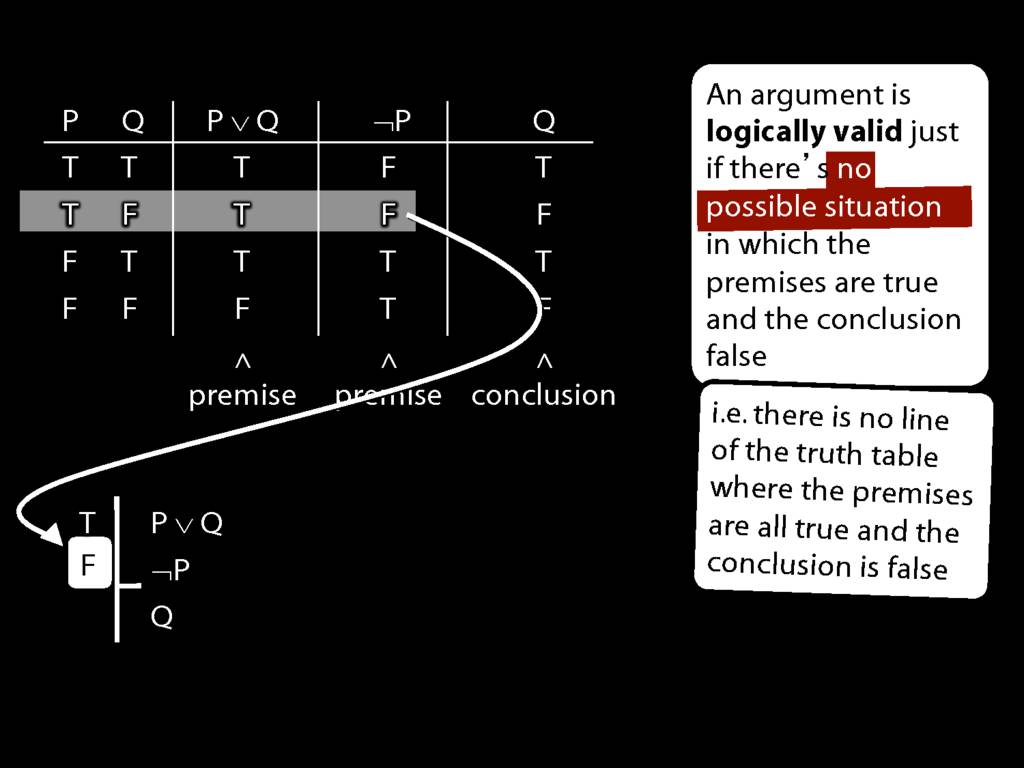
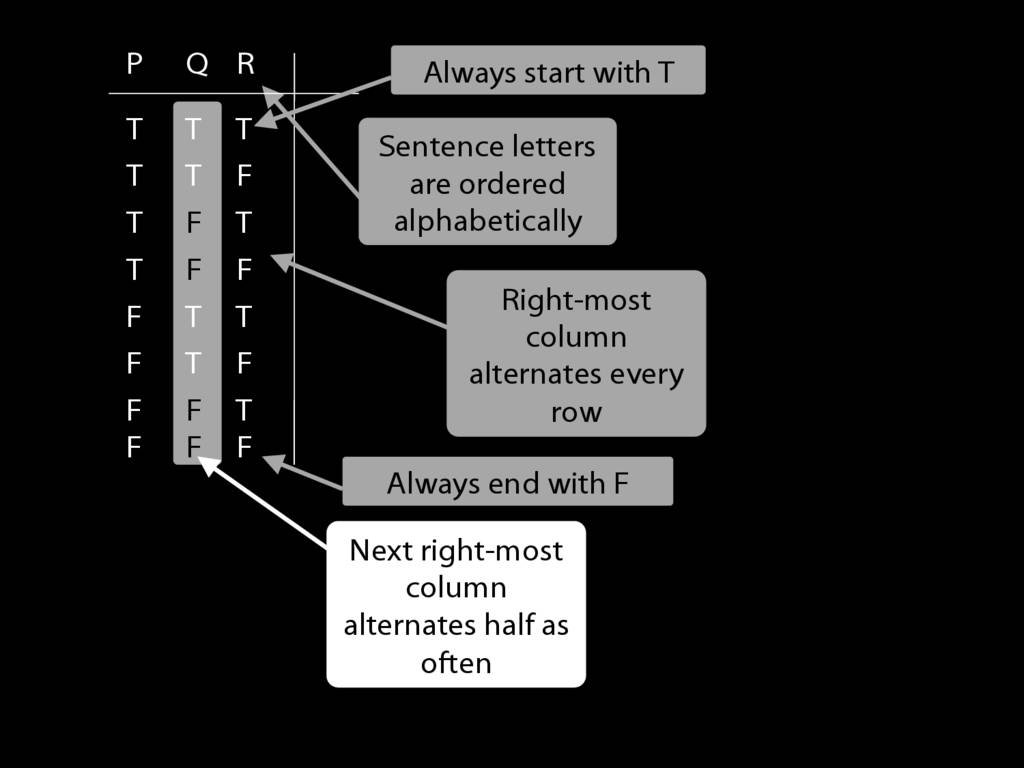
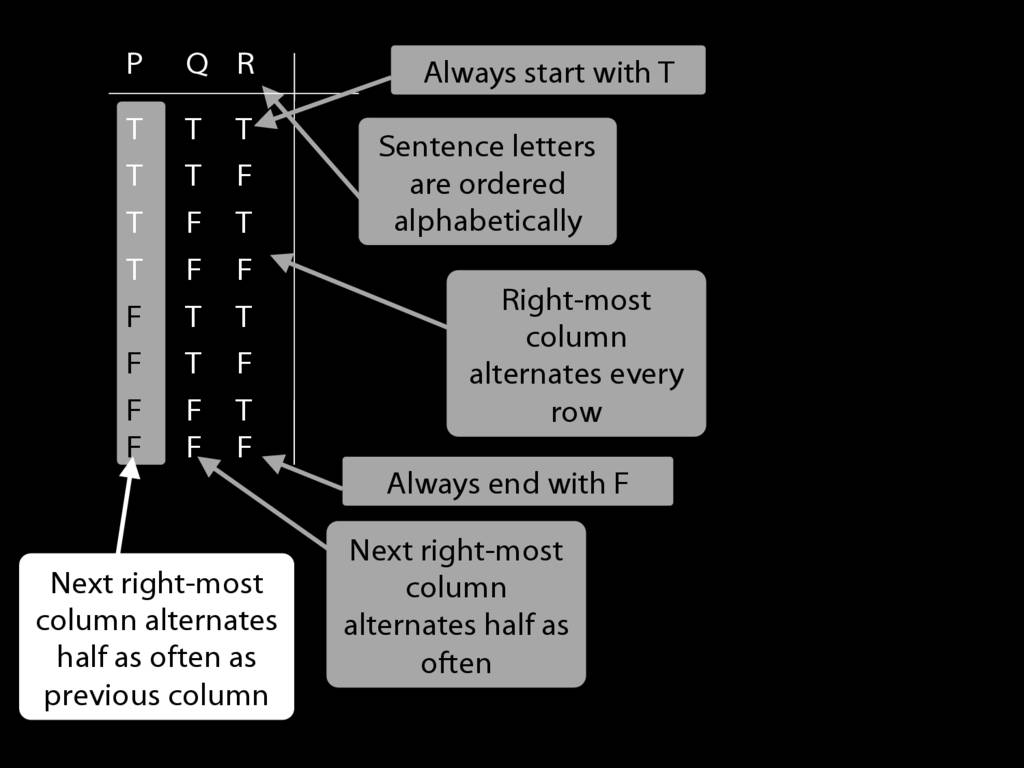
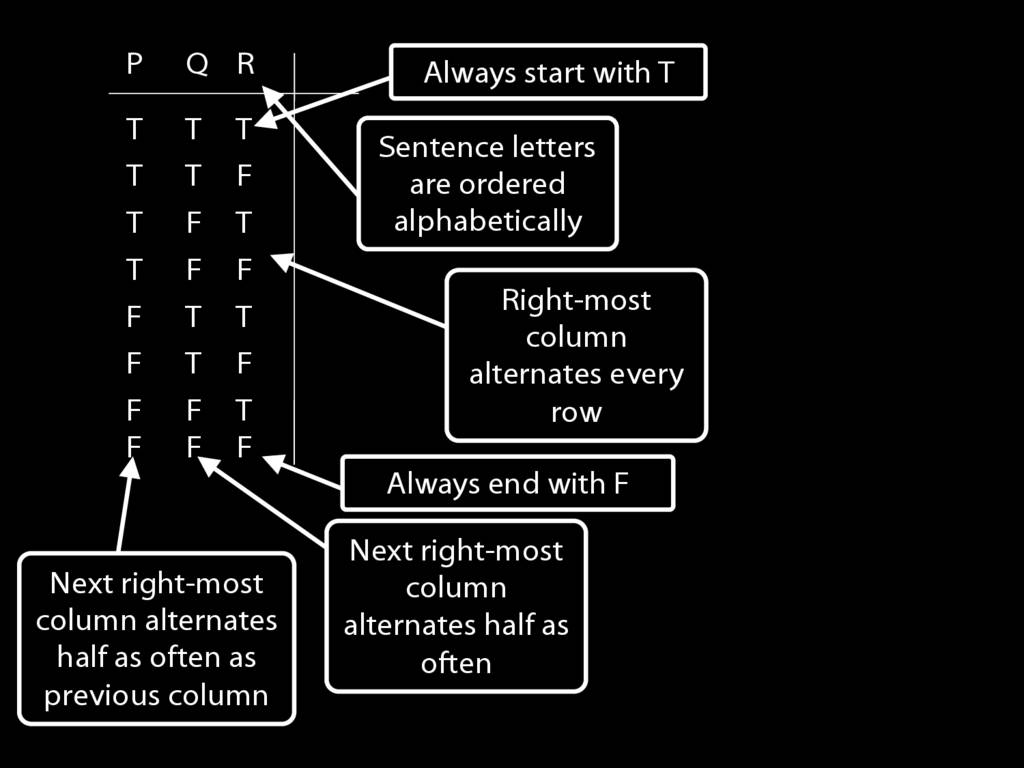
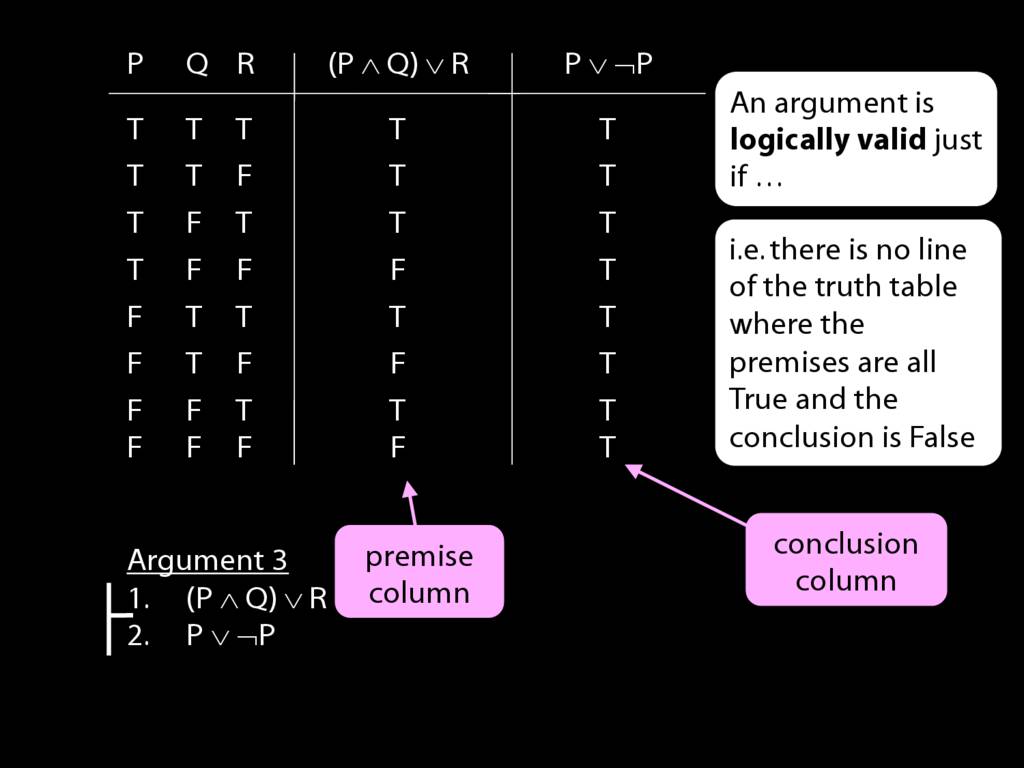
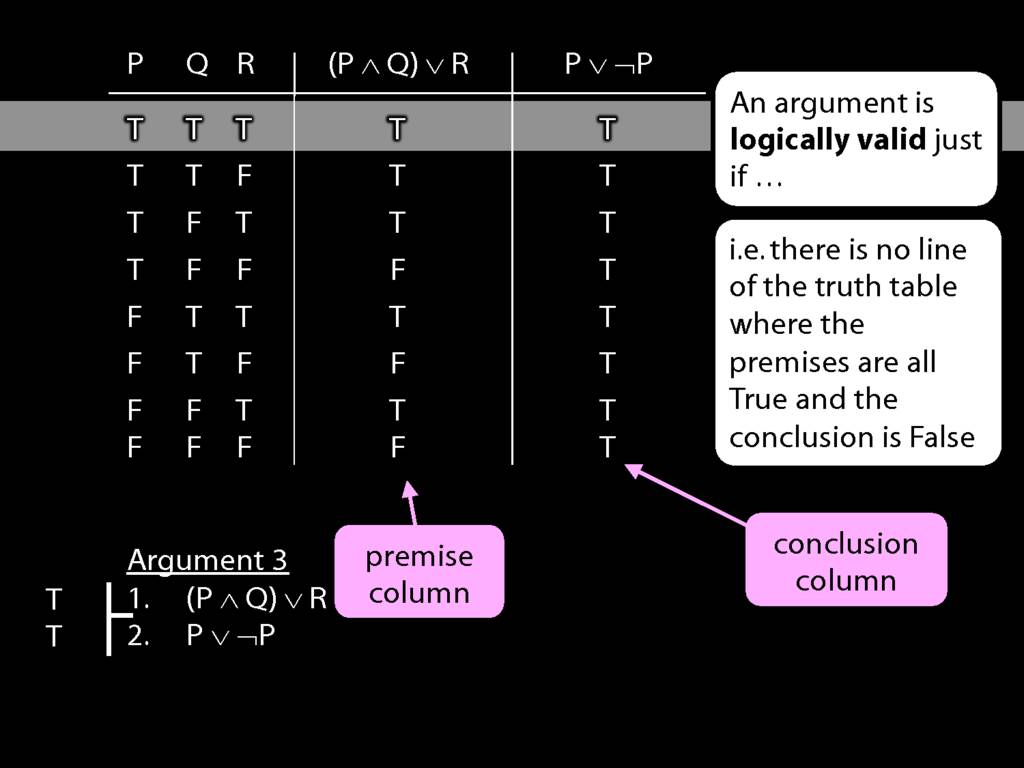
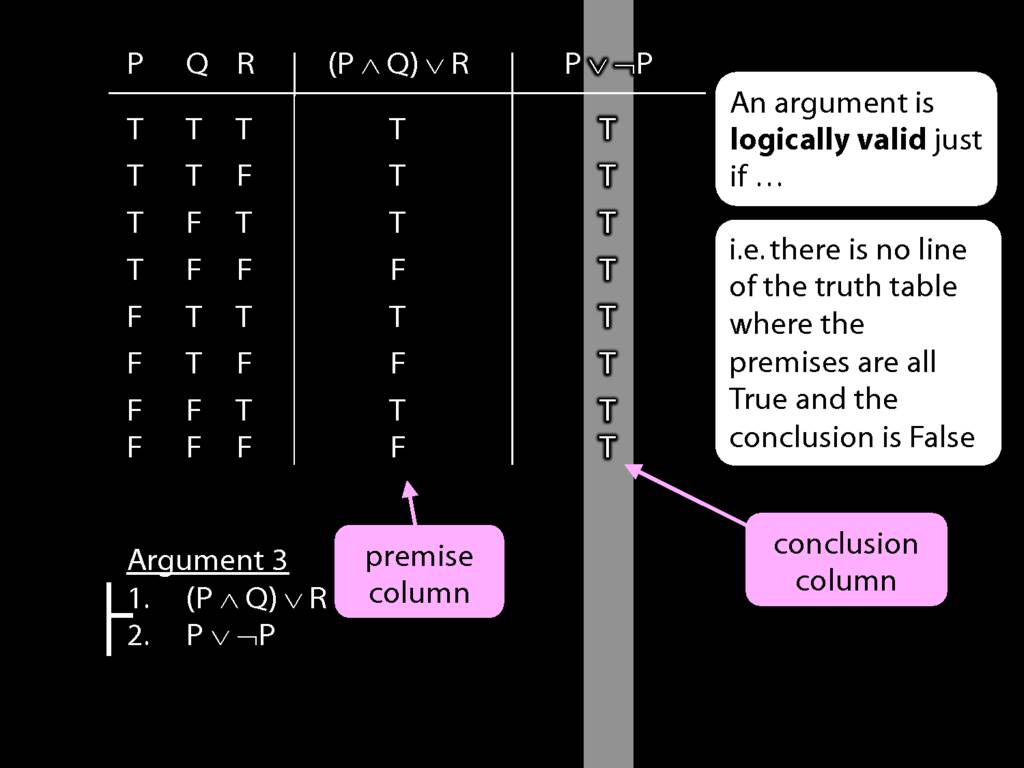
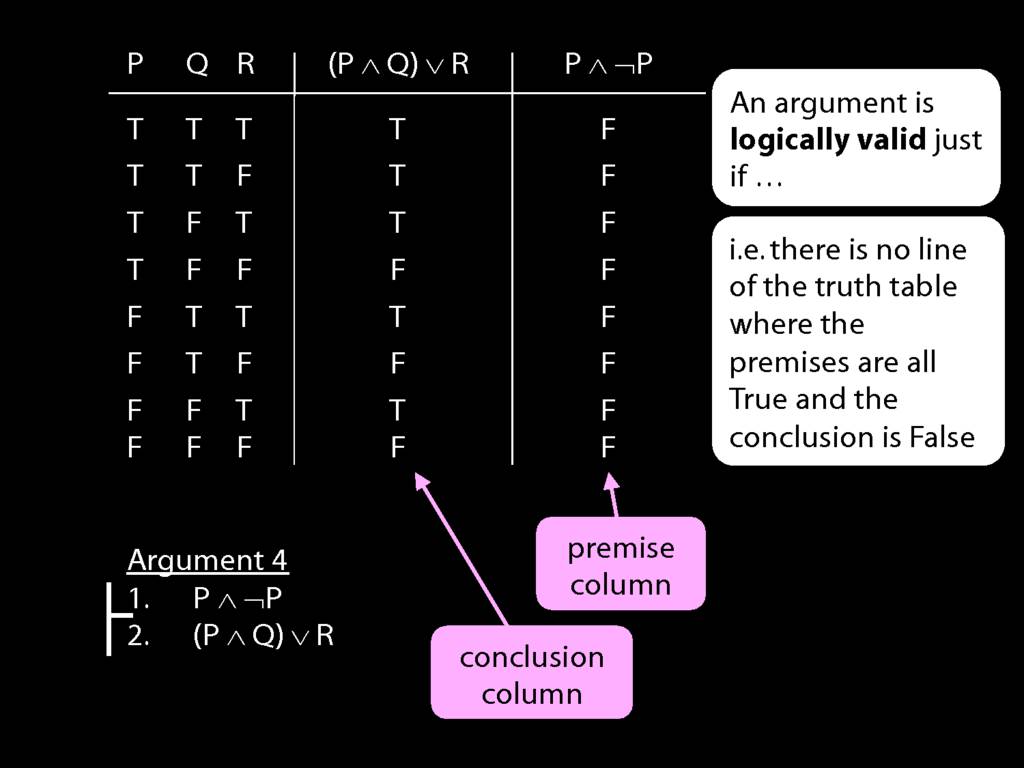
We can use truth tables to establish that
some arguments are logically valid
\begin{minipage}{\columnwidth}
Truth tables can be used to show that an argument is valid. To illustrate ...
\end{minipage}
\begin{minipage}{\columnwidth}
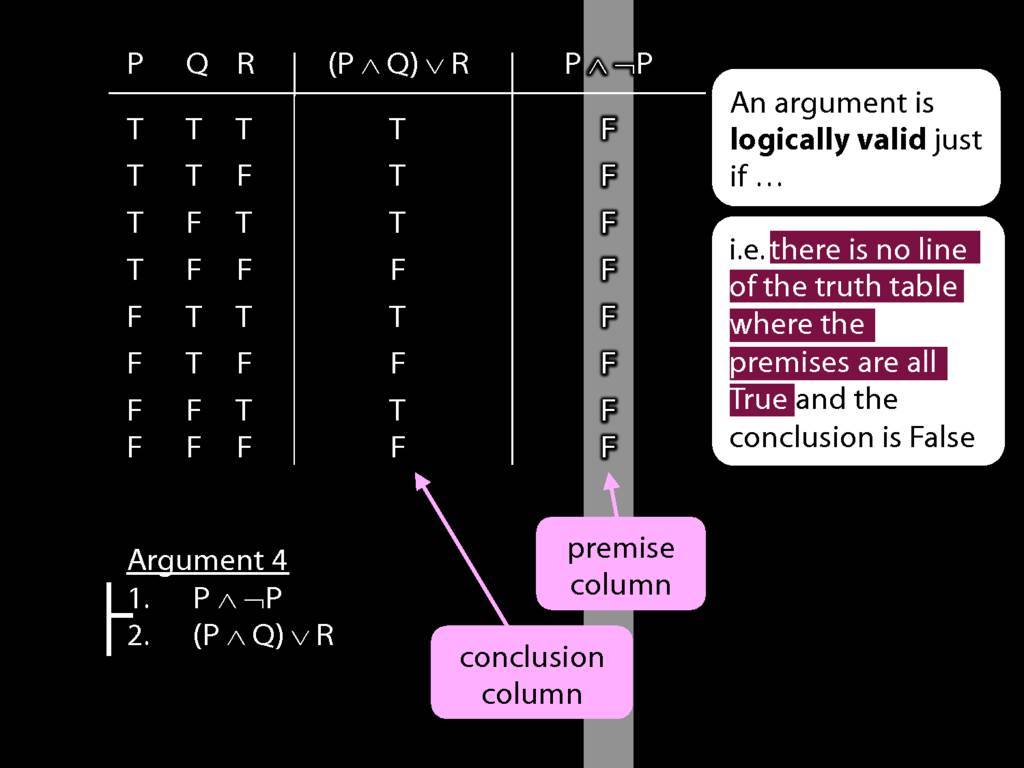
To establish that an argument is valid:
\begin{enumerate}
\item Create truth tables for each premise and the conclusion.
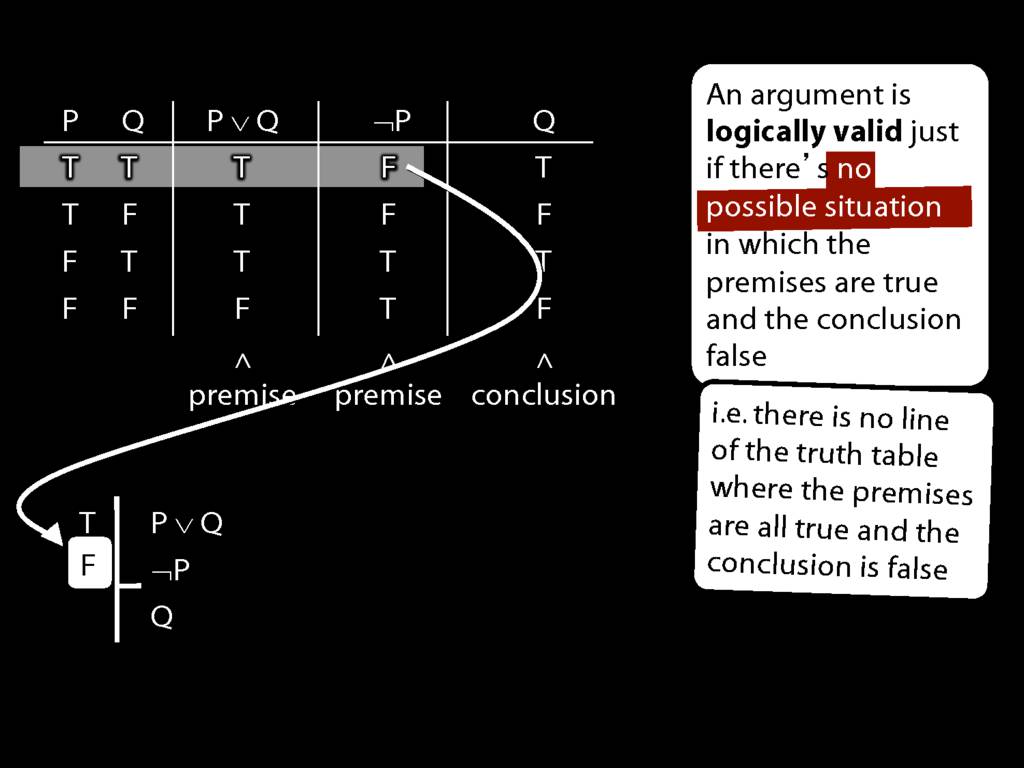
\item Check whether there is a row of the truth table where all premises are true and the conclusion is false.
\item If not, the argument is valid.
\end{enumerate}
\end{minipage}

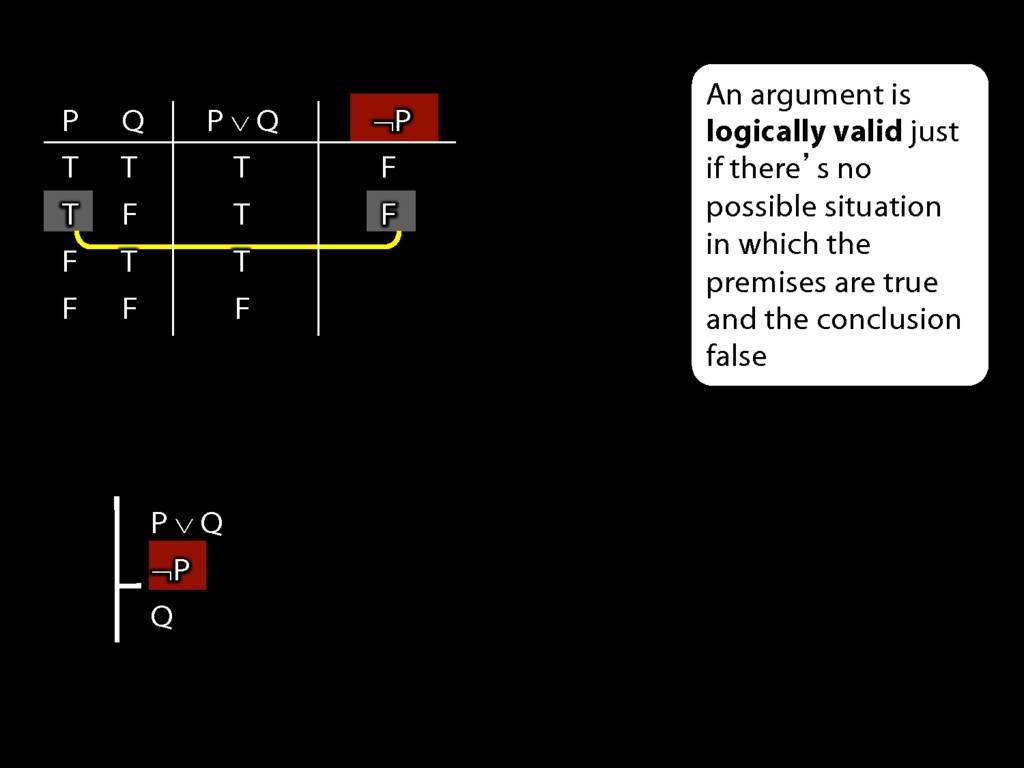
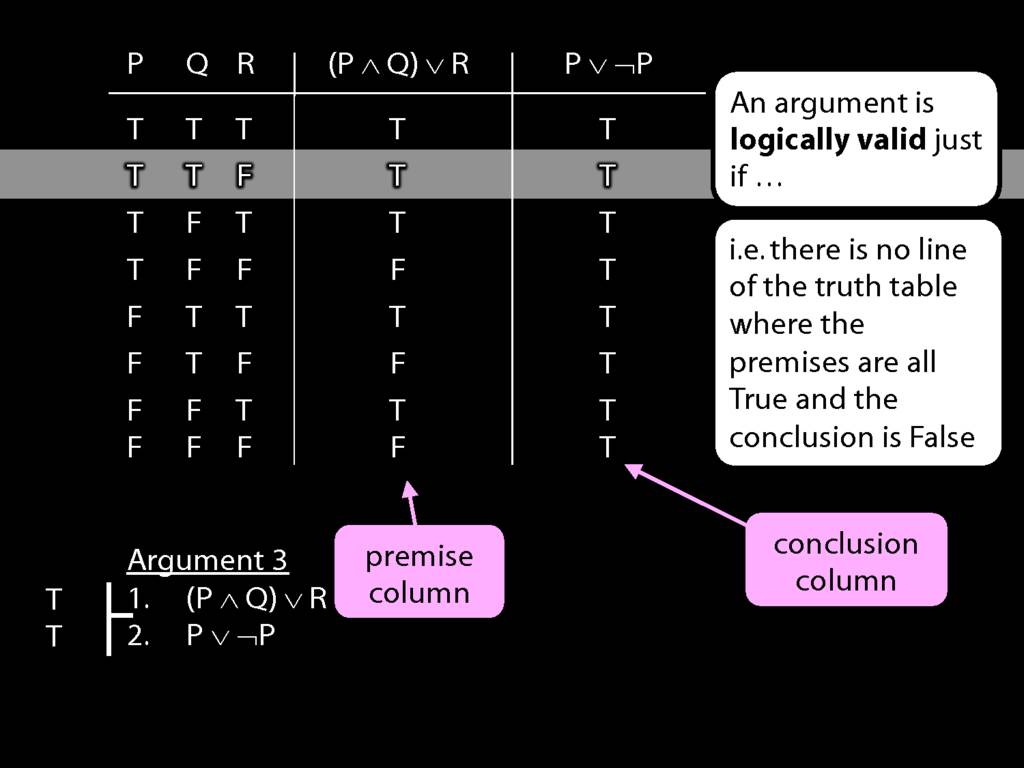
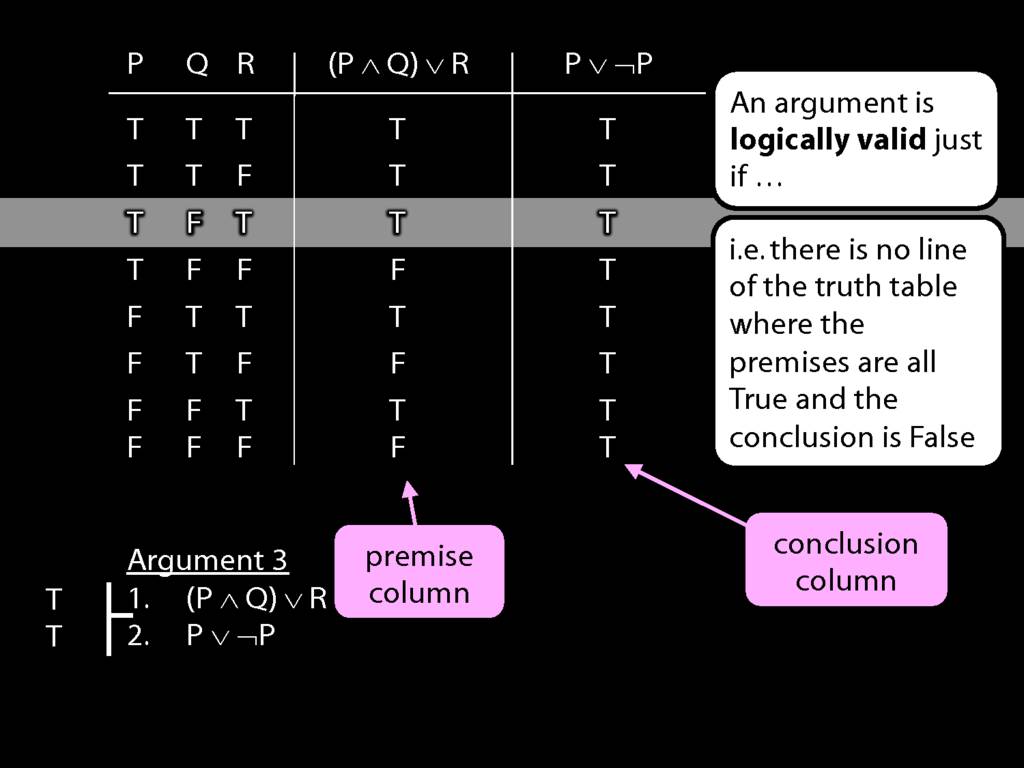
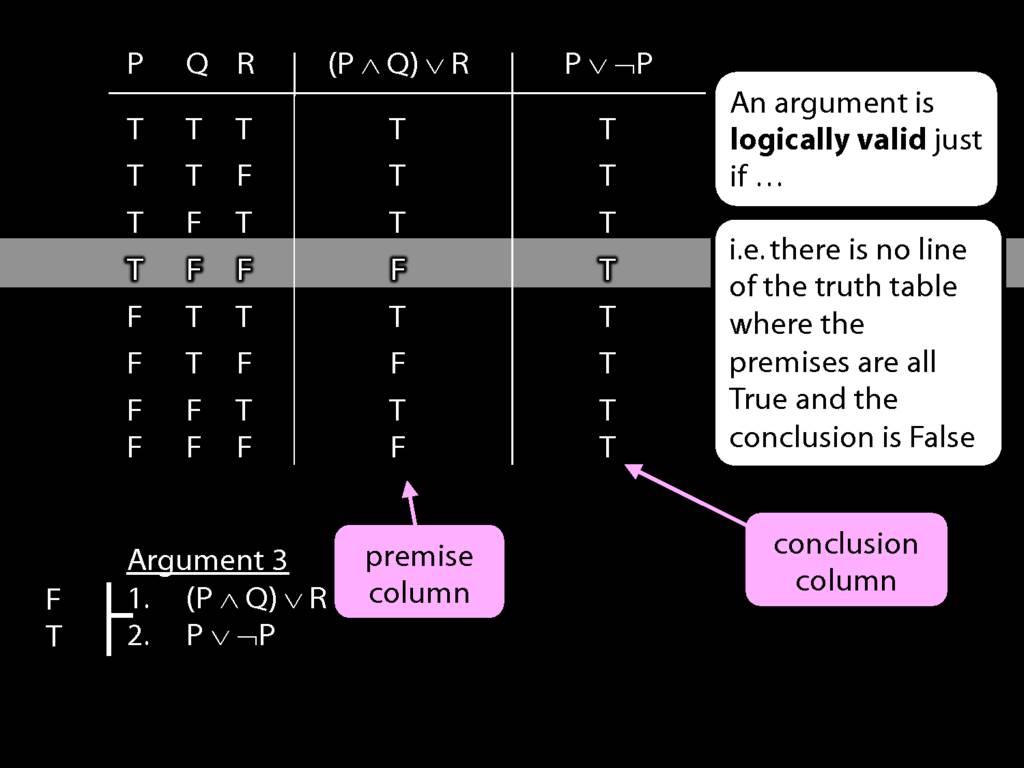
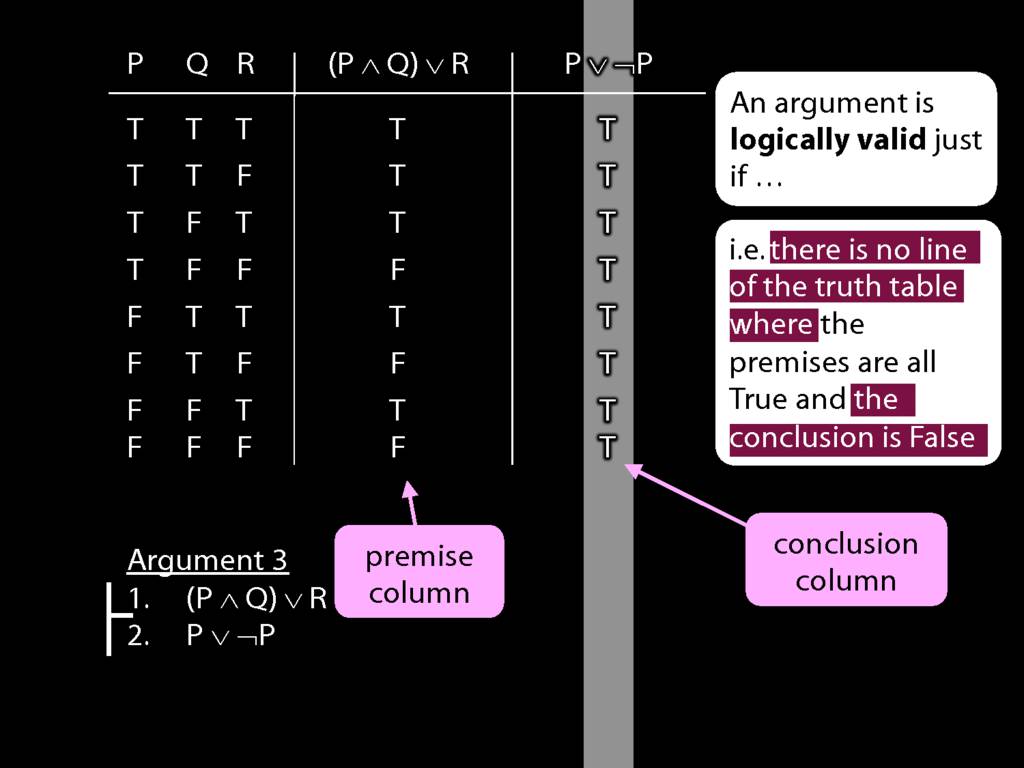
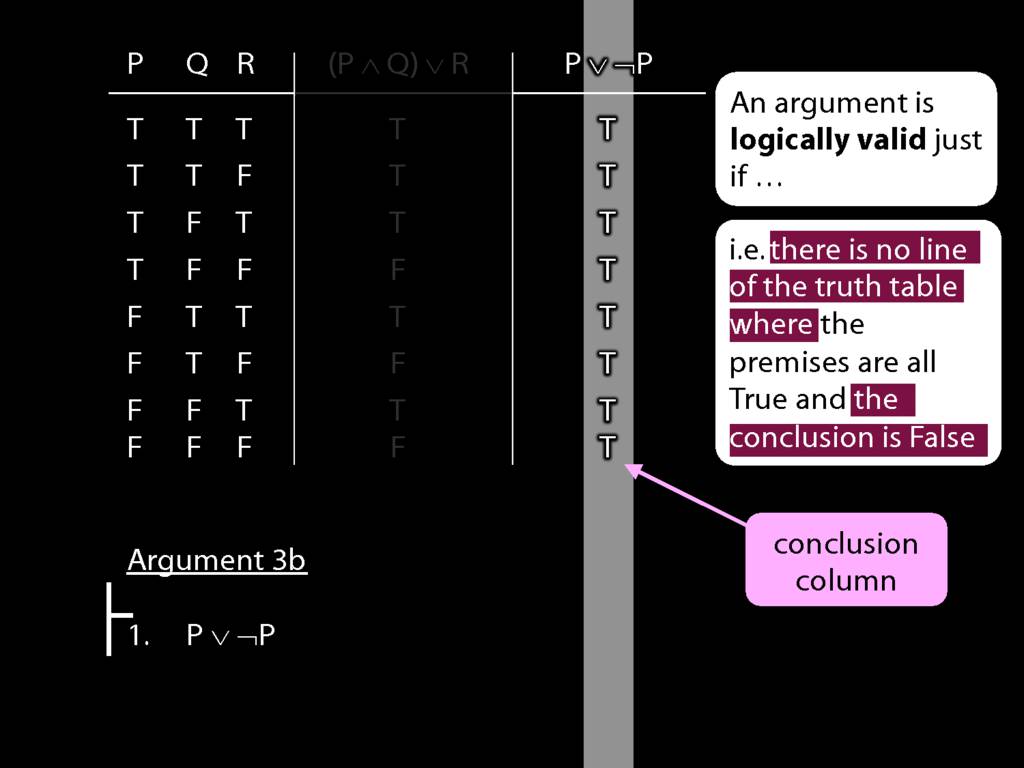
Don’t need to go further, already have a false premise. So this won’t be a situation in which the premises are true and the conclusion false.

This situation is different from the other two: the premises are true in this possible situation, so we had to think about whether the conclusion is true.
But, as you can see, the conclusion is also true. So this is no counterexample.

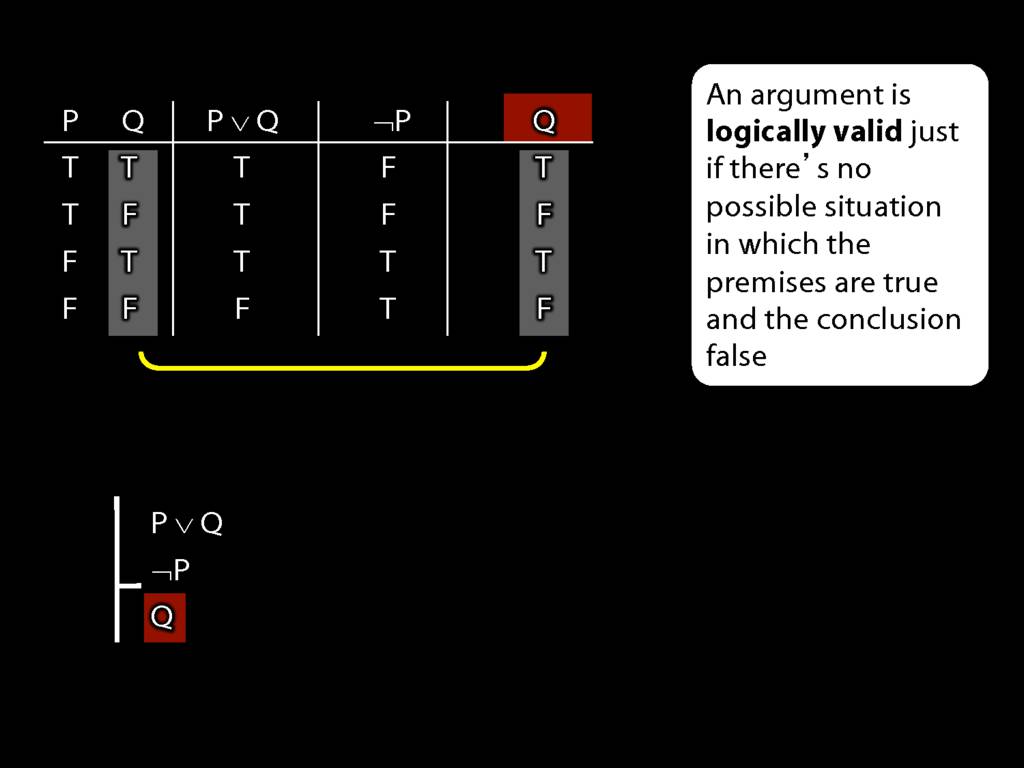
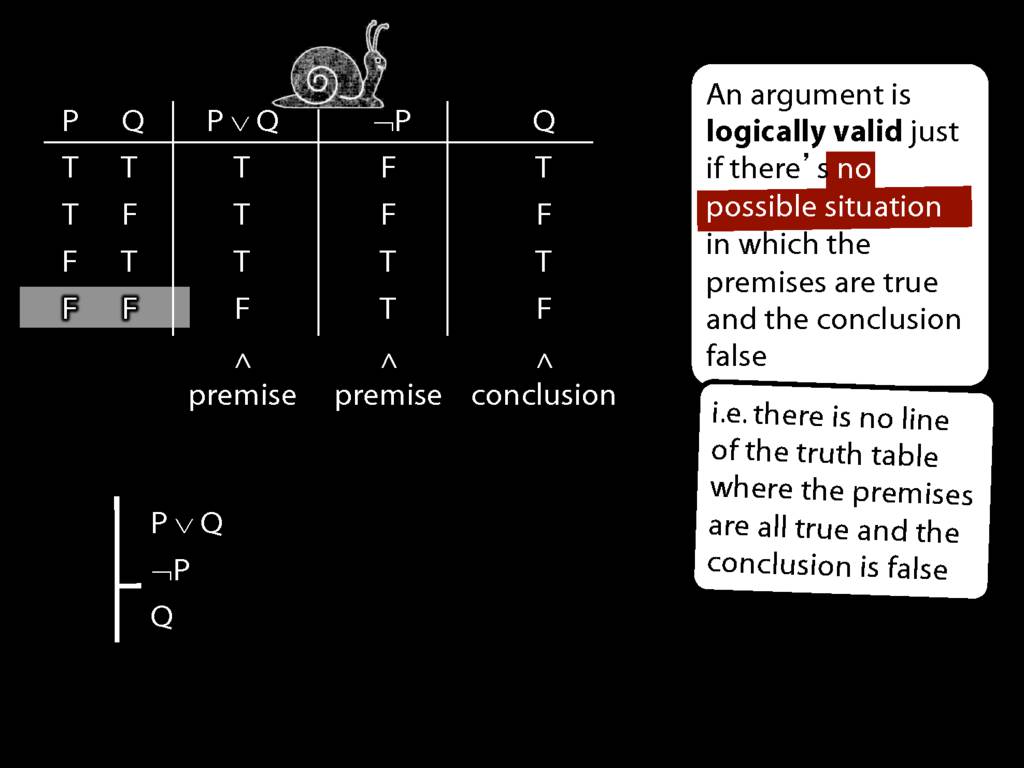
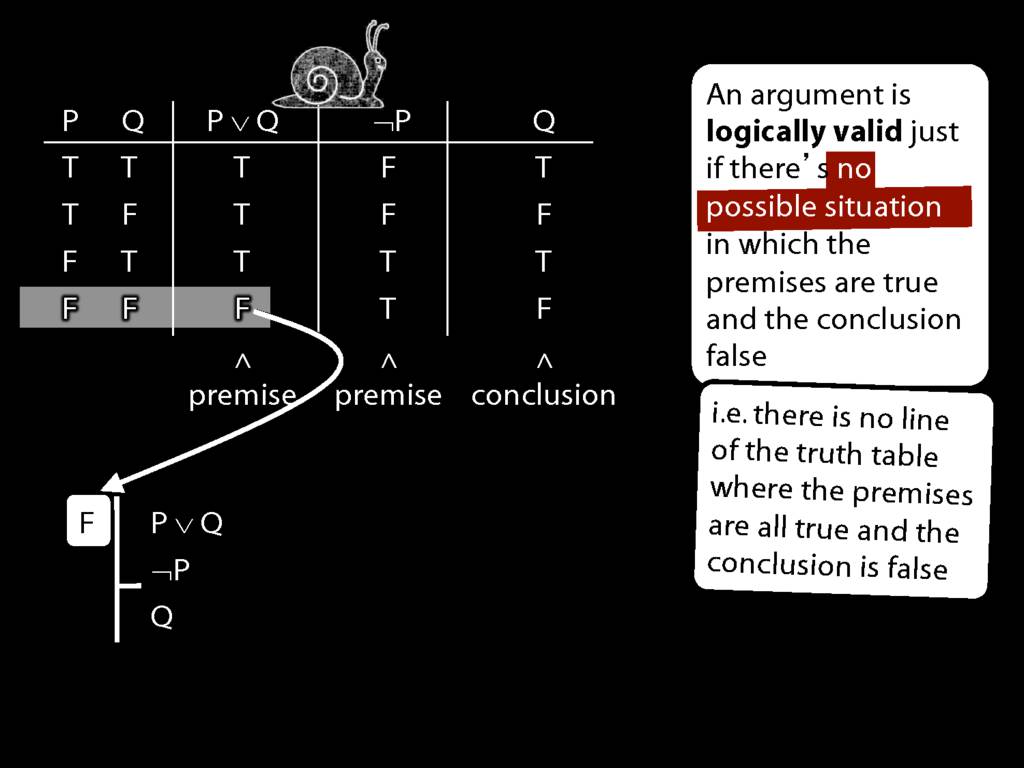
So if someone asked you to show that this argument is valid using truth tables, what would you do?
First, create truth tables for each premise and for the conclusion.
Next, check whether there is any row where the premises are true and the conclusion false.
If not, you can write this:
By inspecting the truth table, there is no row where the premises are true and the conclusion false; therefore, the argument is logically valid.

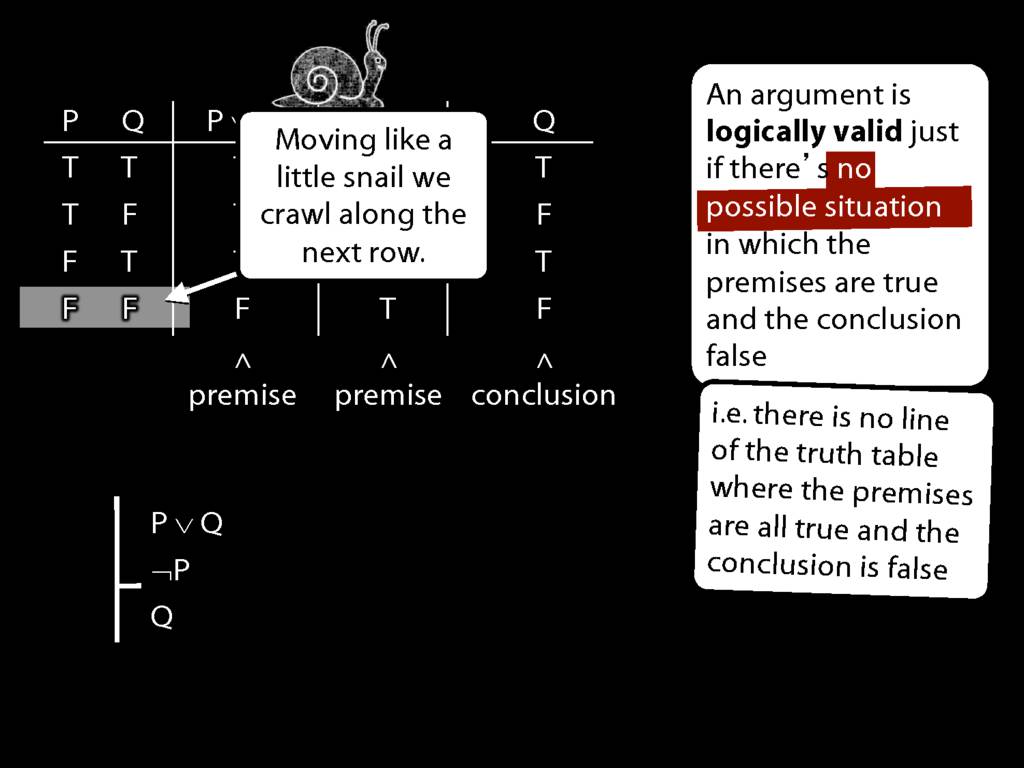
When you're doing truth tables there's a temptation to race through them.

But you shouldn't do that. Be the little snail.
5.1-5.4
\section{Why Logic?}
Logic is a tool for precise expression. In your future life you probably won't use
logical symbols, but, if things go well,
the way you formulate ideas will be guided by your familiarity with
logical structures.
Studying logic also enables you to identify and explain mistakes in reasoning.
You might think that you don't need driving lessons and that you
already know how to think.
That's plausible, but you are probably going to be surrounded by people
who regularly make logical mistakes.
It turns out that even simple logical mistakes are quite common.
Here's a question from an experiment.
Which cards do you need to turn over to confirm the truth of this claim?
I want you all to answer the question.
‘If a card has a vowel on one side, then it has an even number on the other side.’
(Waison & Johnson-Laird 1972)
Well, what's the answer?
The solution is: you need to turn over E and 7
‘Philosophy is thinking in slow motion.’ (John Campbell)

This course is about logical validity; there is also a sister notion, logical truth.
To say that a sentence is logically true is to say that there's no possible situation in which it is false.
(This is slightly different from the definition given in the textbook, but it's equivalent in that the two definitions pick out the same sentences.)
In exploring the notions of logical validity and logic truth, we are exploring the limits of
the world. One reason for studying logic is just that you are curious about what is
possible.

‘Logic pervades the world: the limits of the world are also its limits.’
(Wittgenstein, Tractatus 5.61)
On his album game theory, Black Thought (Tariq Trotter) mentions people of whom it is said that they

‘don’t obey no laws, not even gravity’
(Tariq Trotter, Game Theory track 10)
(The context:
‘I couldn't tell you why I think they constantly after me
Maybe it's cause the news put it to me so graphically
How niggaz don't obey no laws, not even gravity boy’)
Why study logic? It is easy to escape supply and demand--that law applies only to
rational agents,
and we are none of us entirely rational.
It is slightly harder to escape gravity, which was
thought to apply to all physical things although Tariq Trotter claims to have done it
on Game Theory (Livin’ in a New World).
The laws of logic are fundamental in the sense that
absolutely everything is subject to them, even musicians.
After I heard Game Theory I
tried to get the philosophy department to put Tariq forward for an honourary doctorate
so that he could call himself *DR* Black Thought but in the end they gave it to
Professor Peacocke instead.
2013-05-30
RE: Love and Logics
Dear Professor,
Hope you're well. My name is [name removed], a former student.
I just wanted to say thank you for your wonderful lectures on logics. I didn't know logics was so useful that it helped me to find a really nice girlfriend and enables me to win arguments all the time!
Thanks again. Haha.
[name]
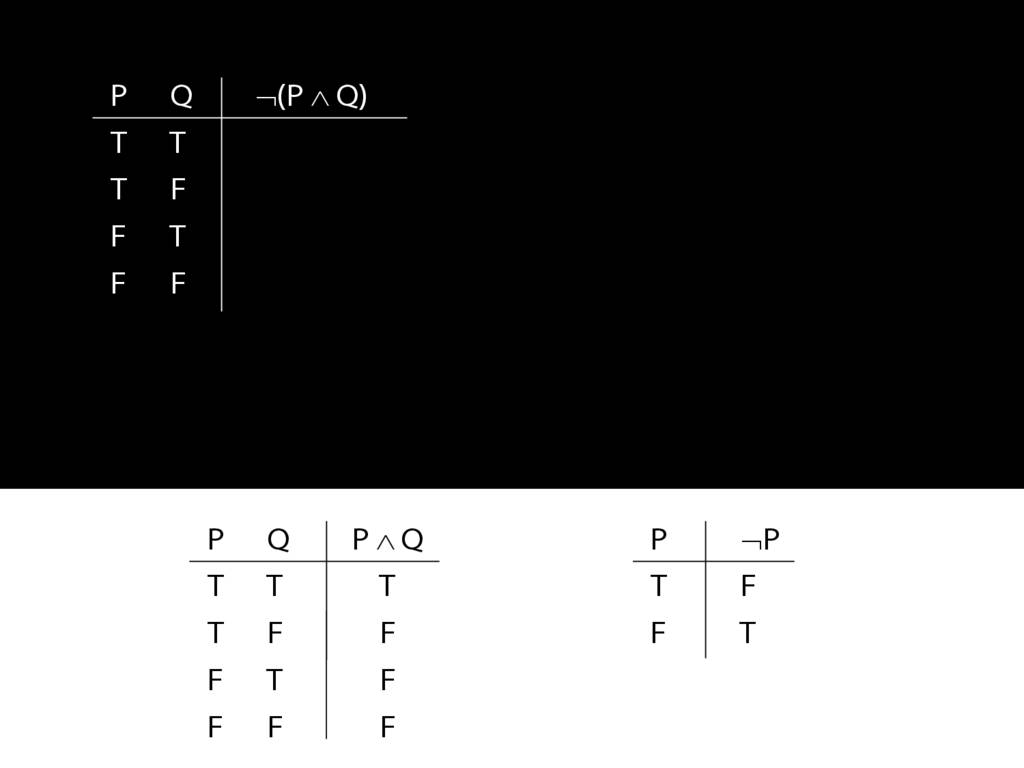
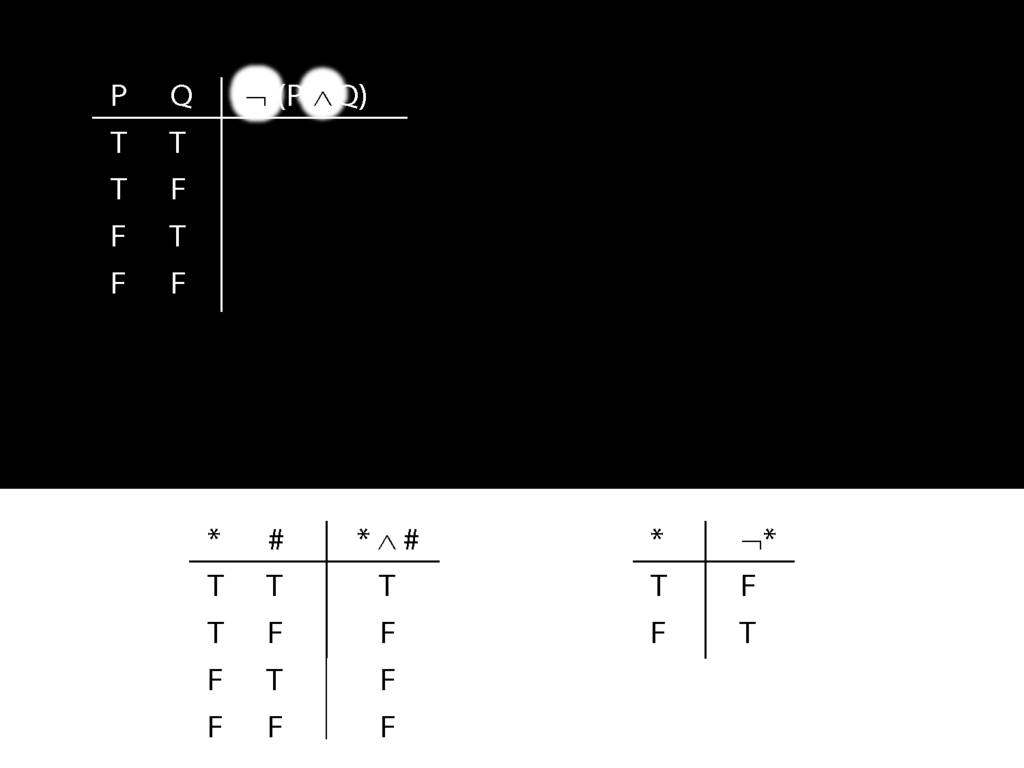
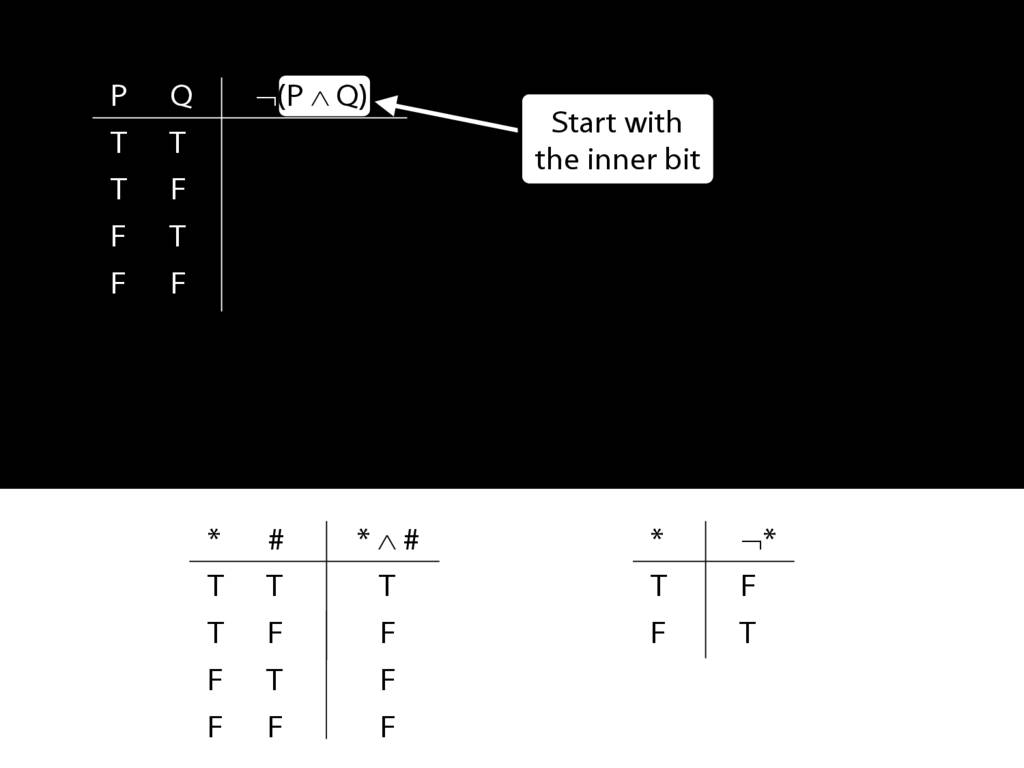
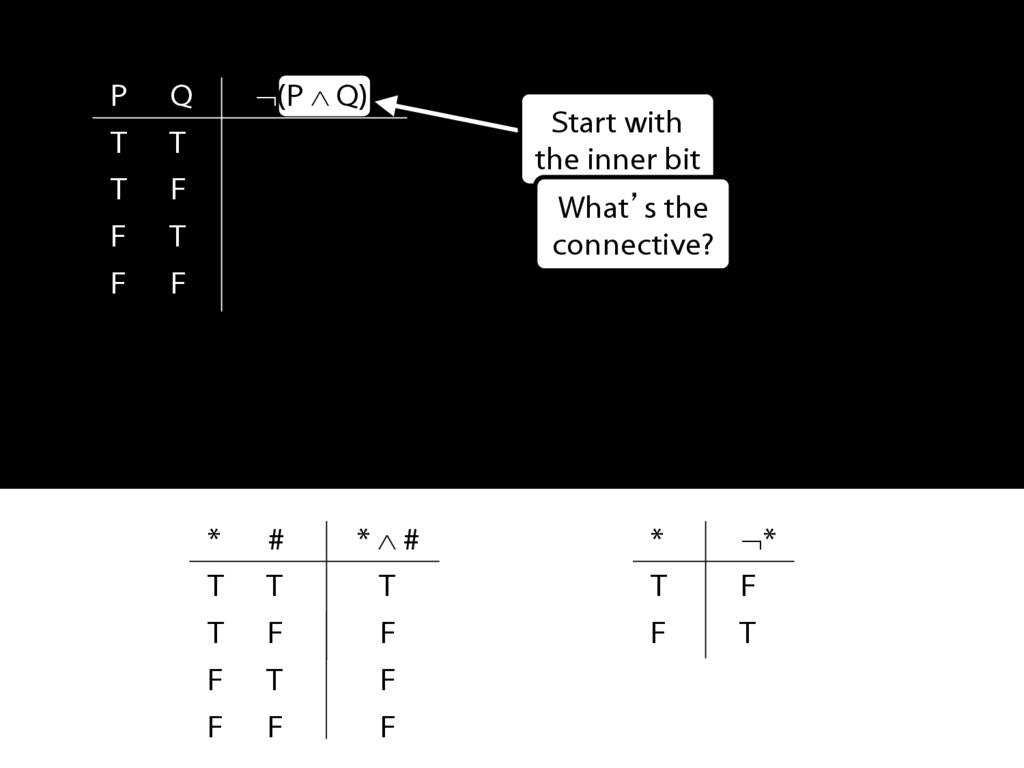
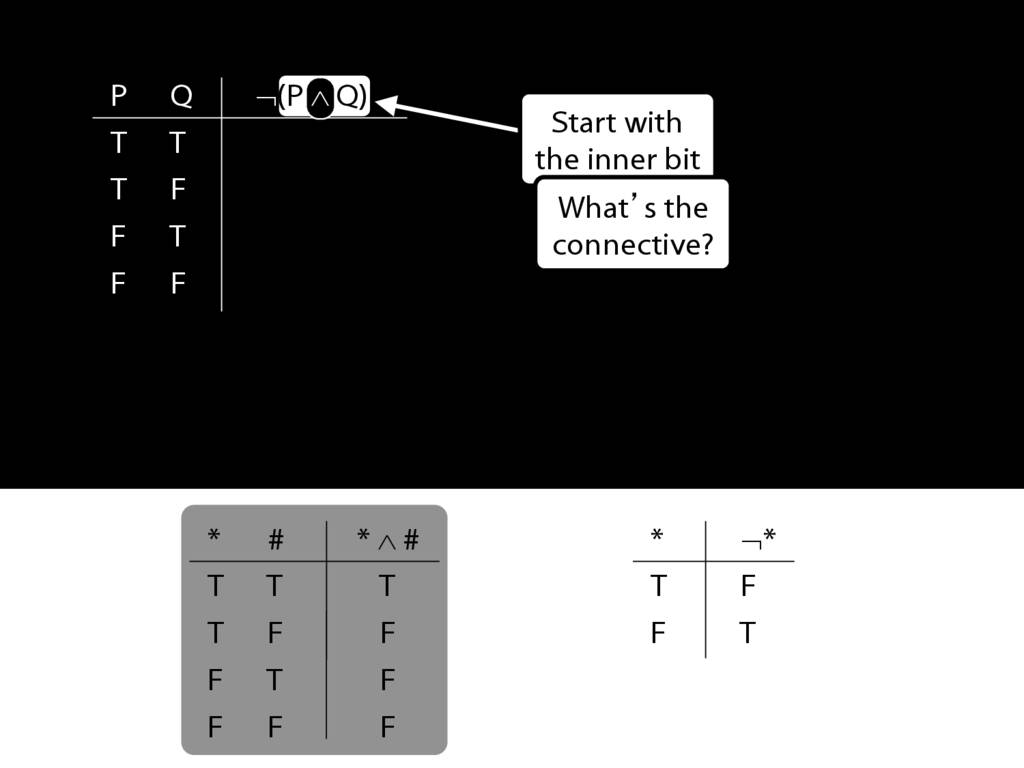
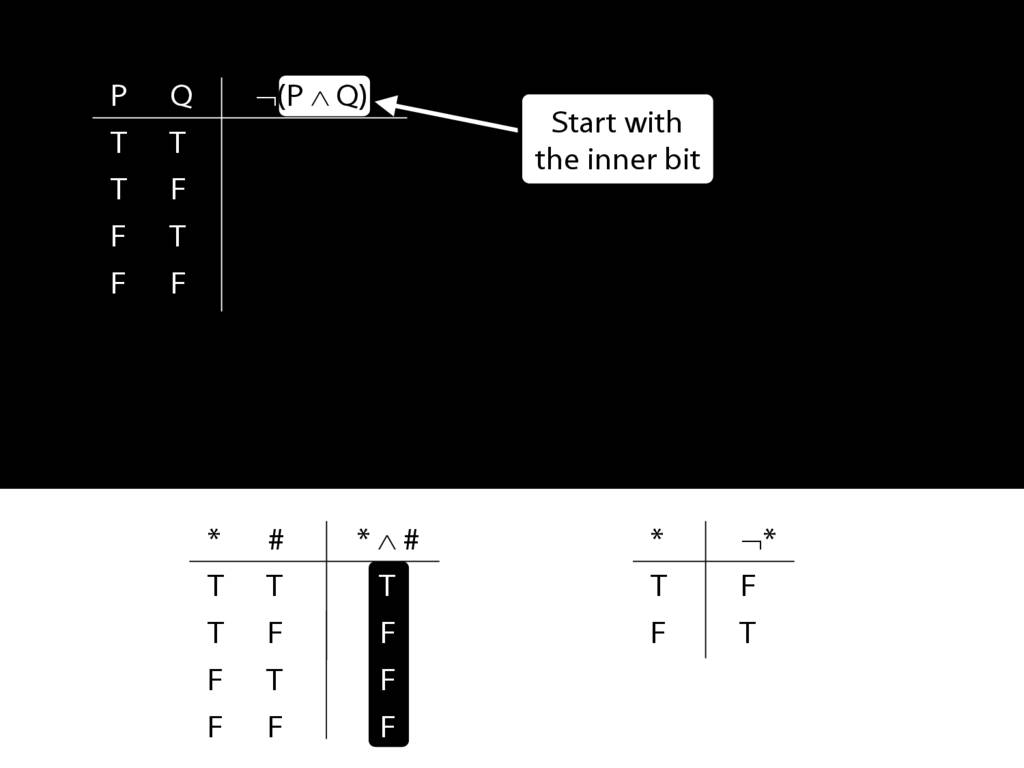
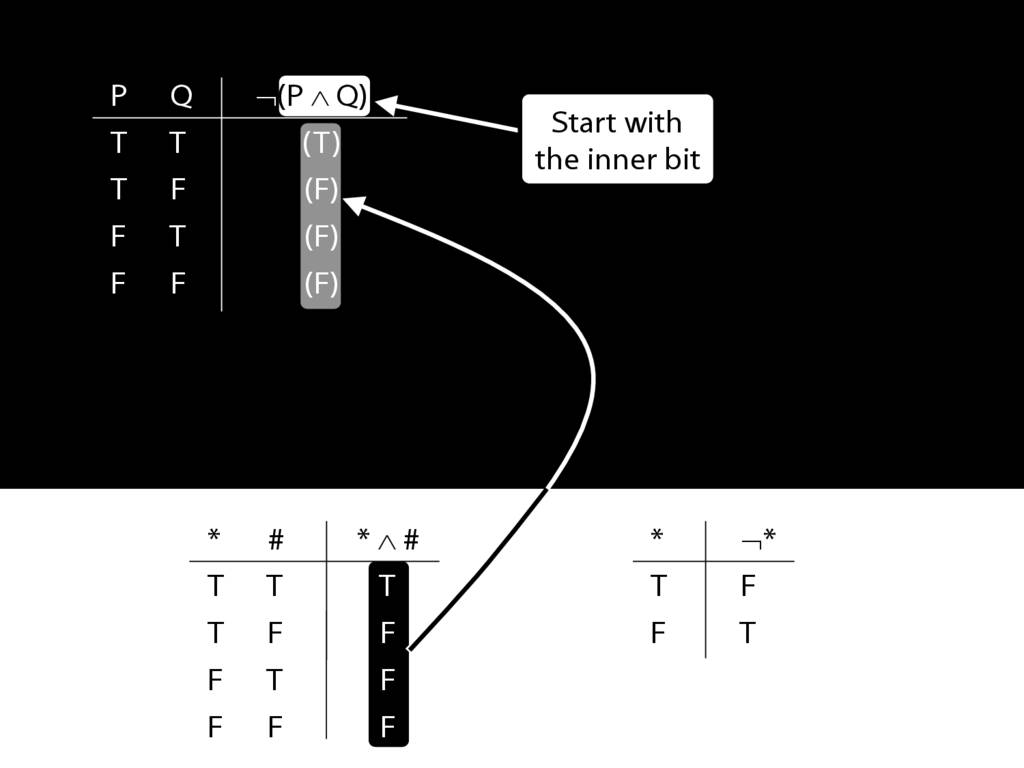
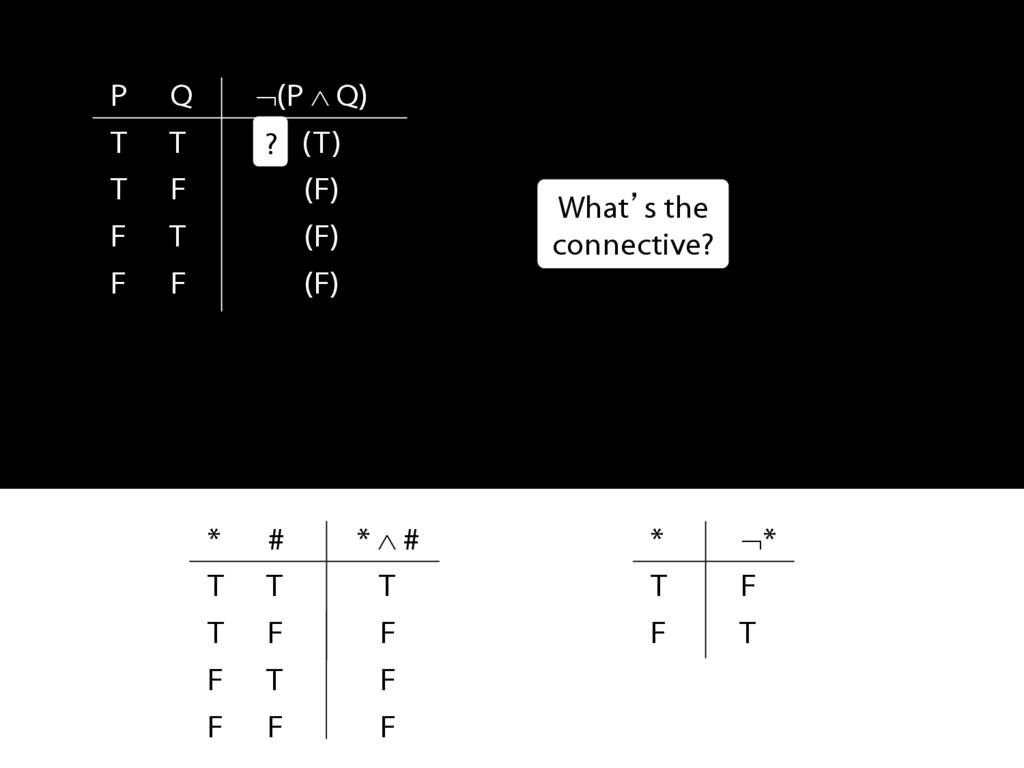
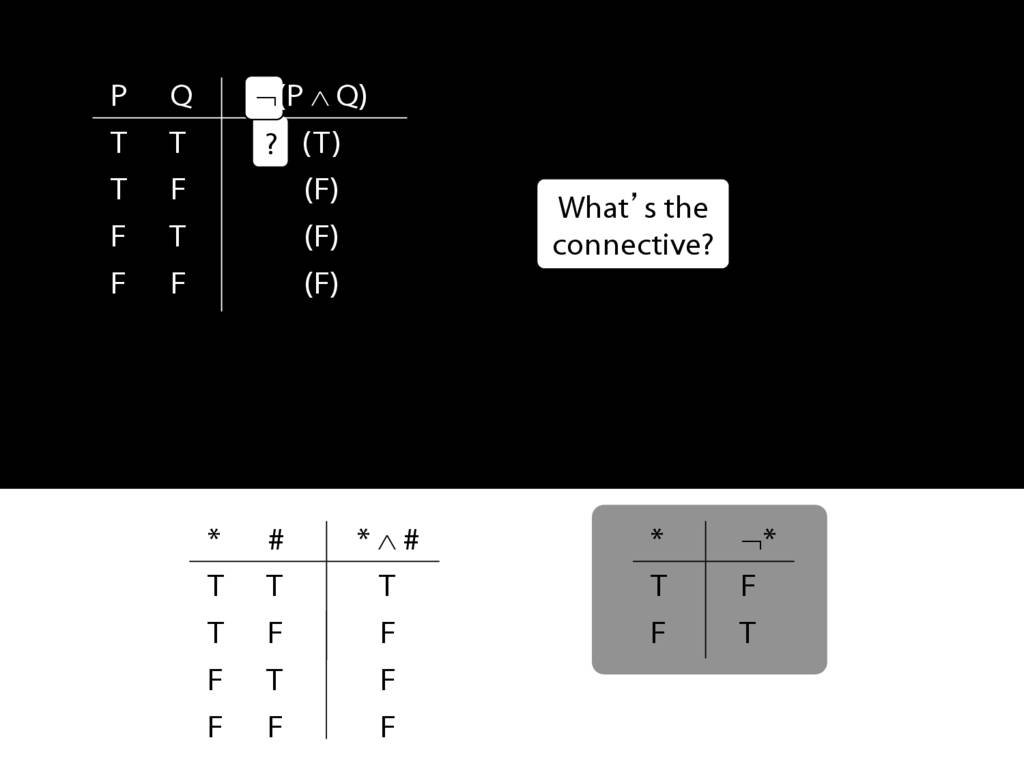
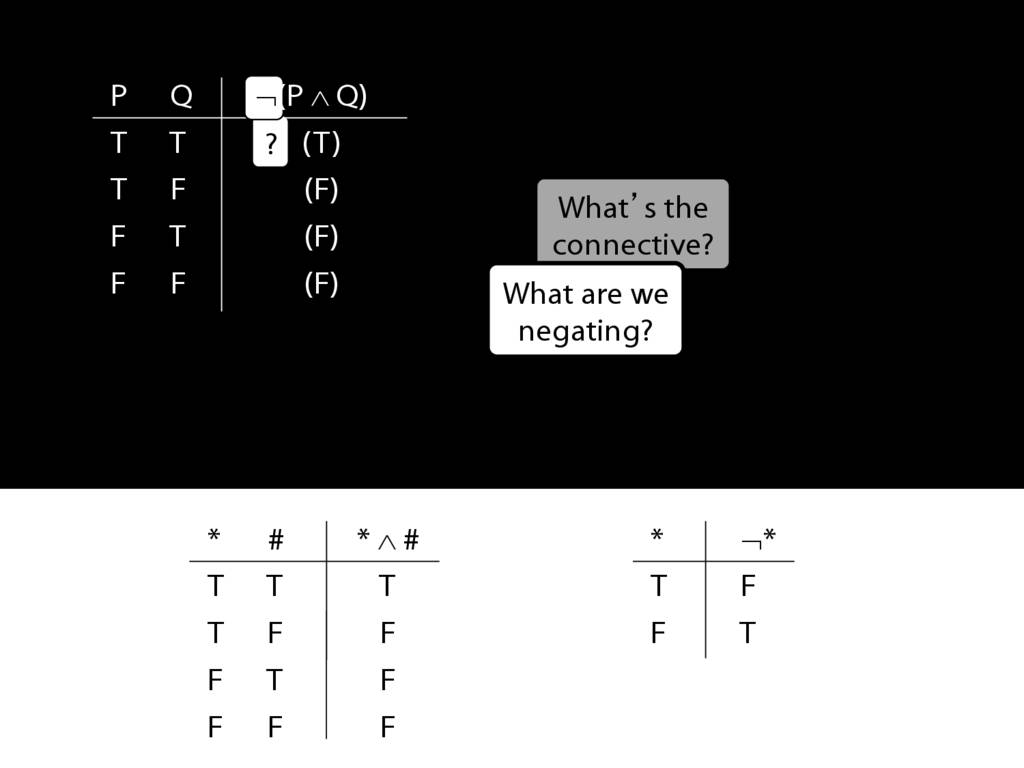
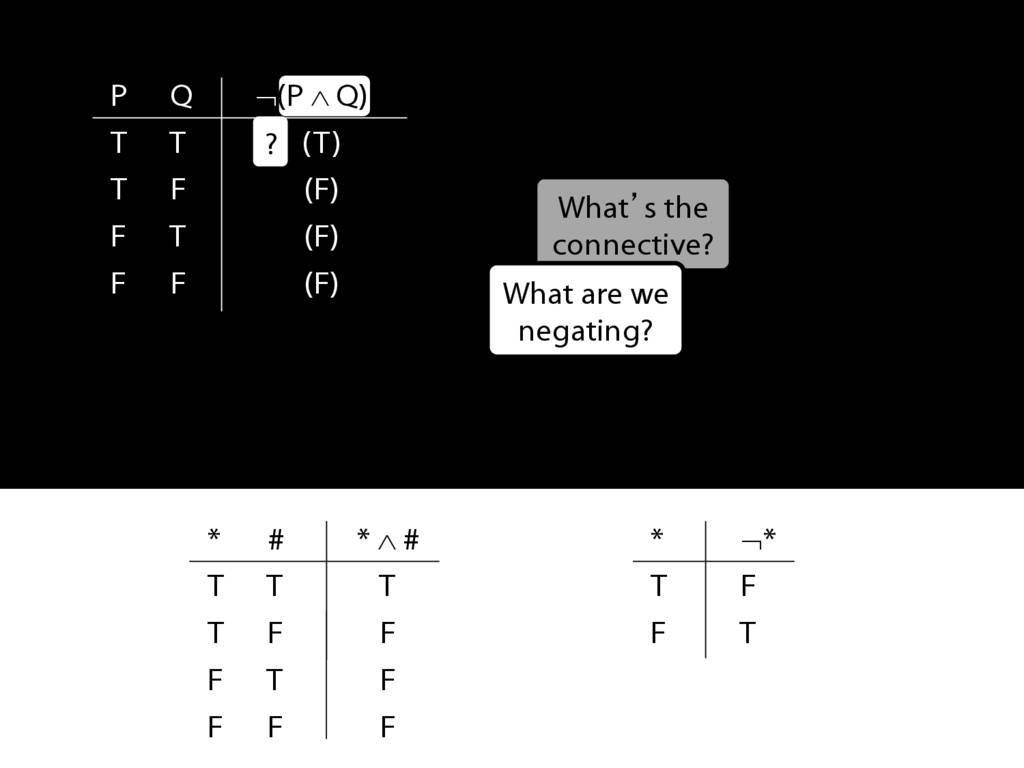
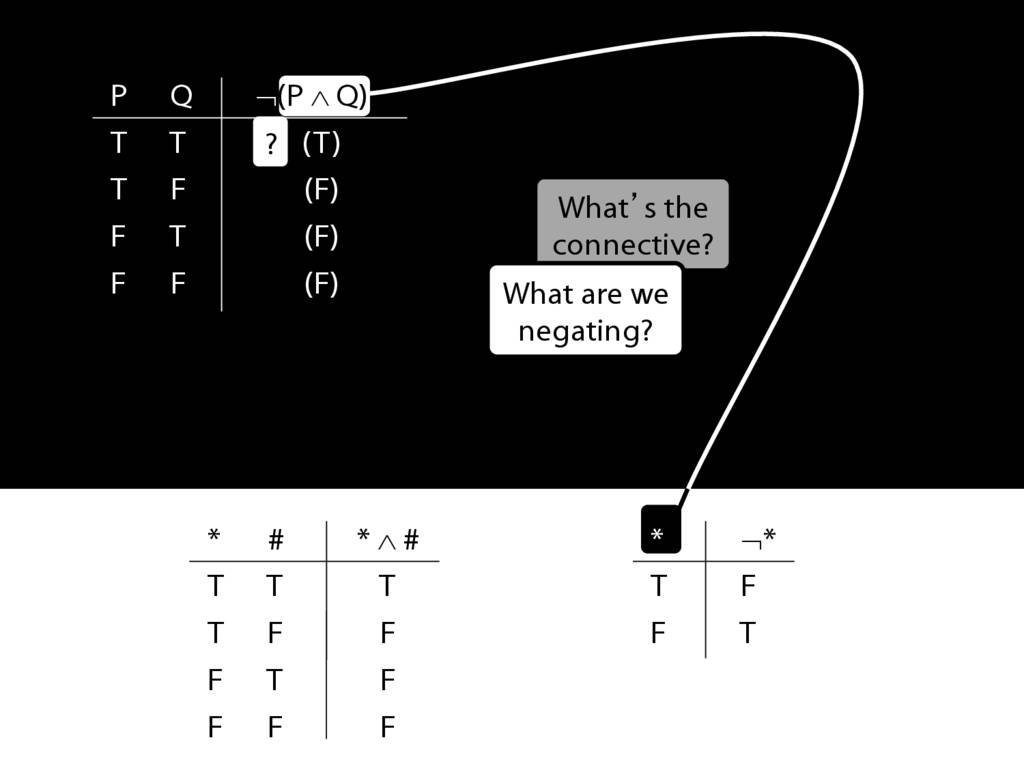
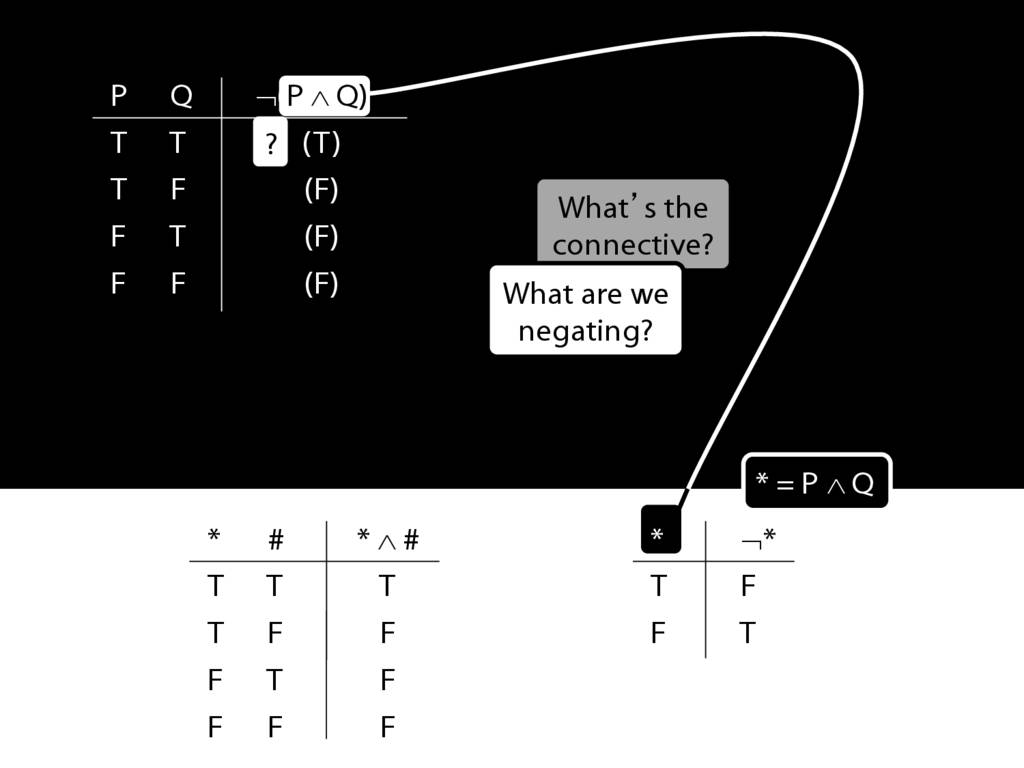
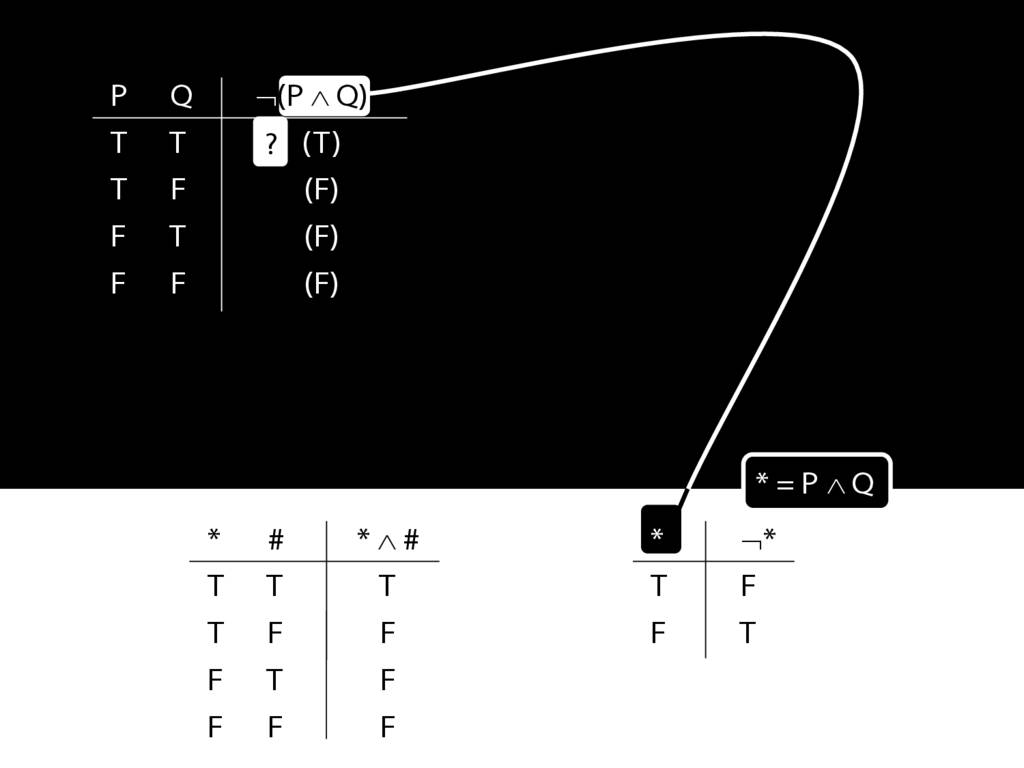
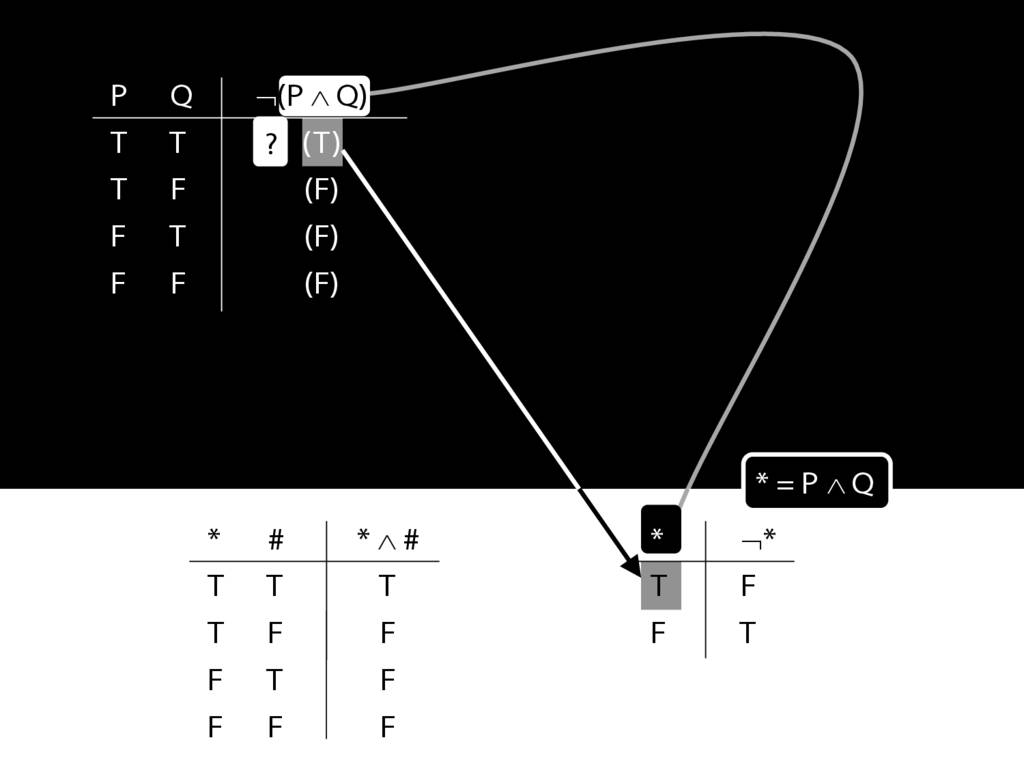
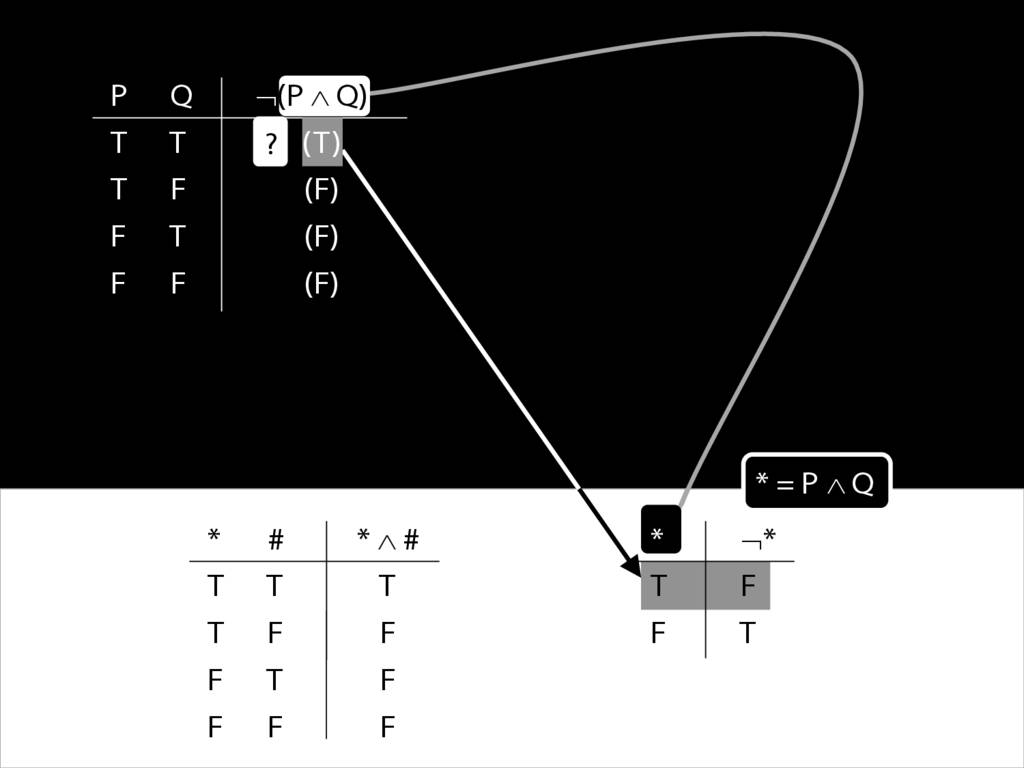
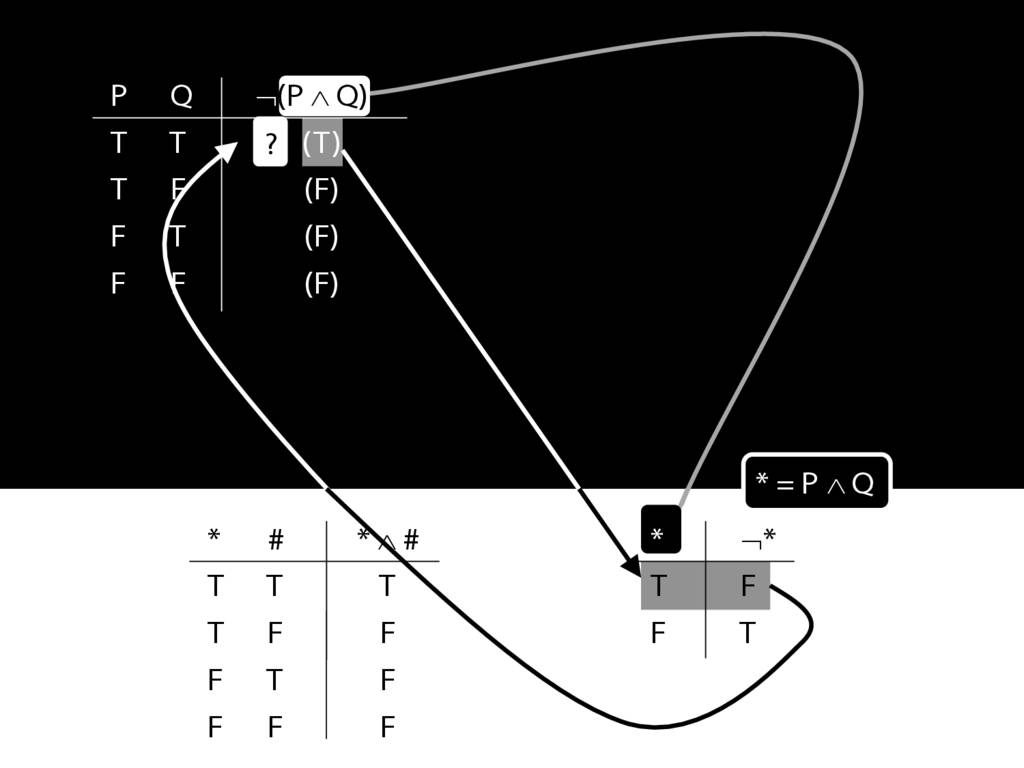
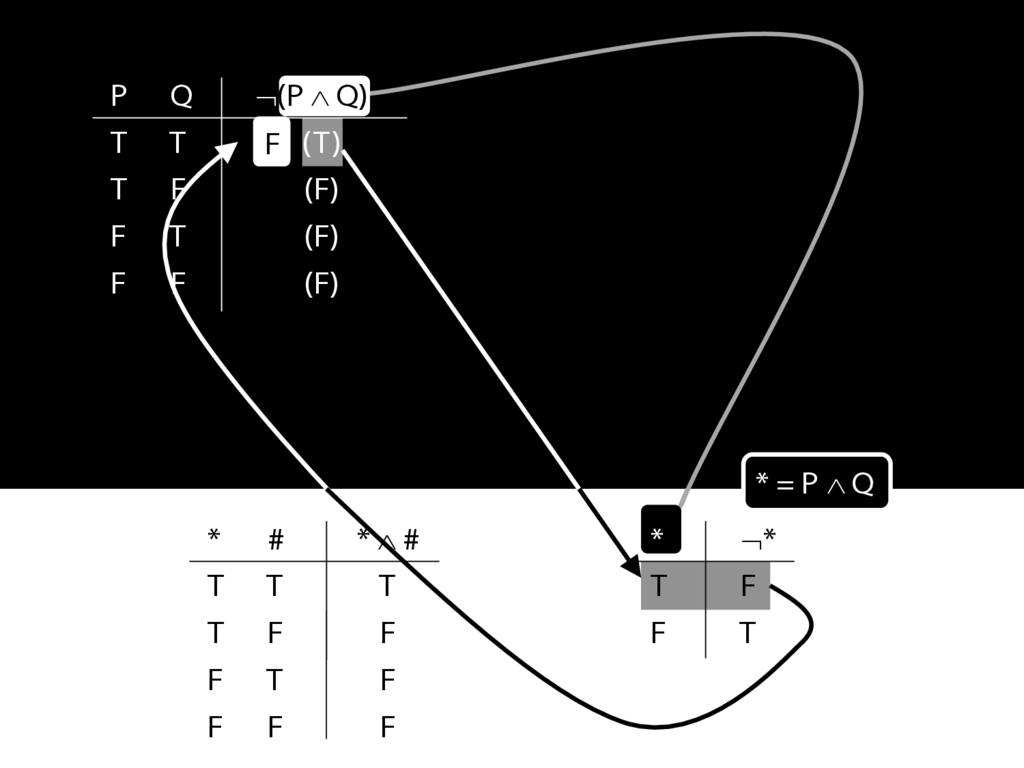
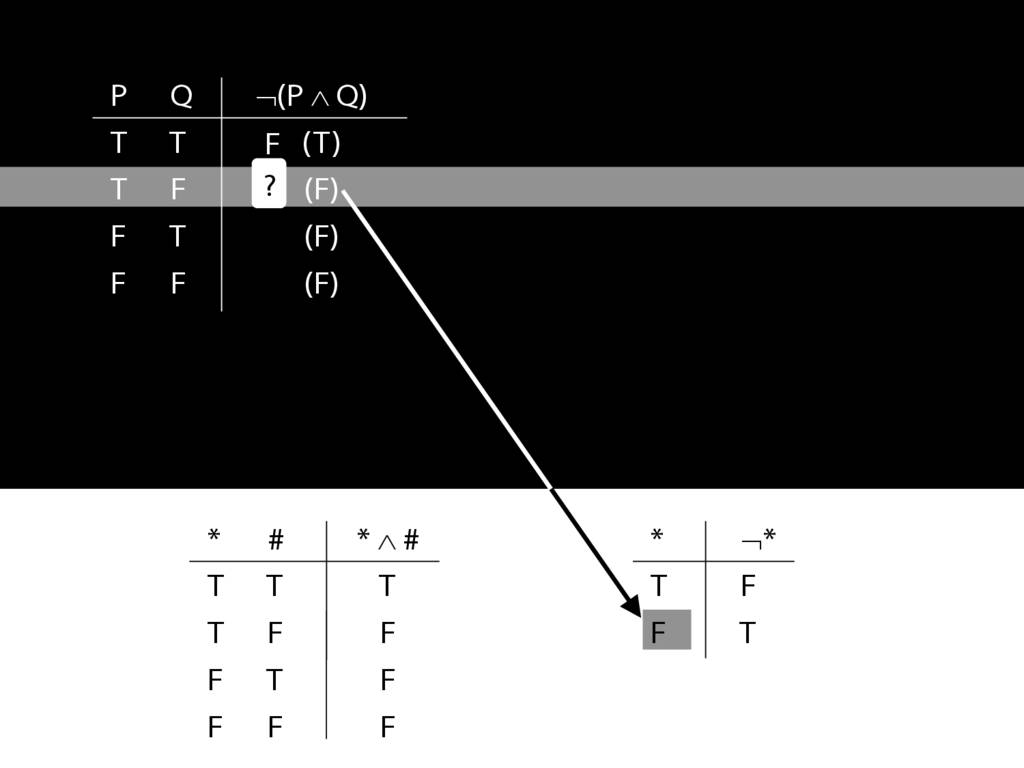
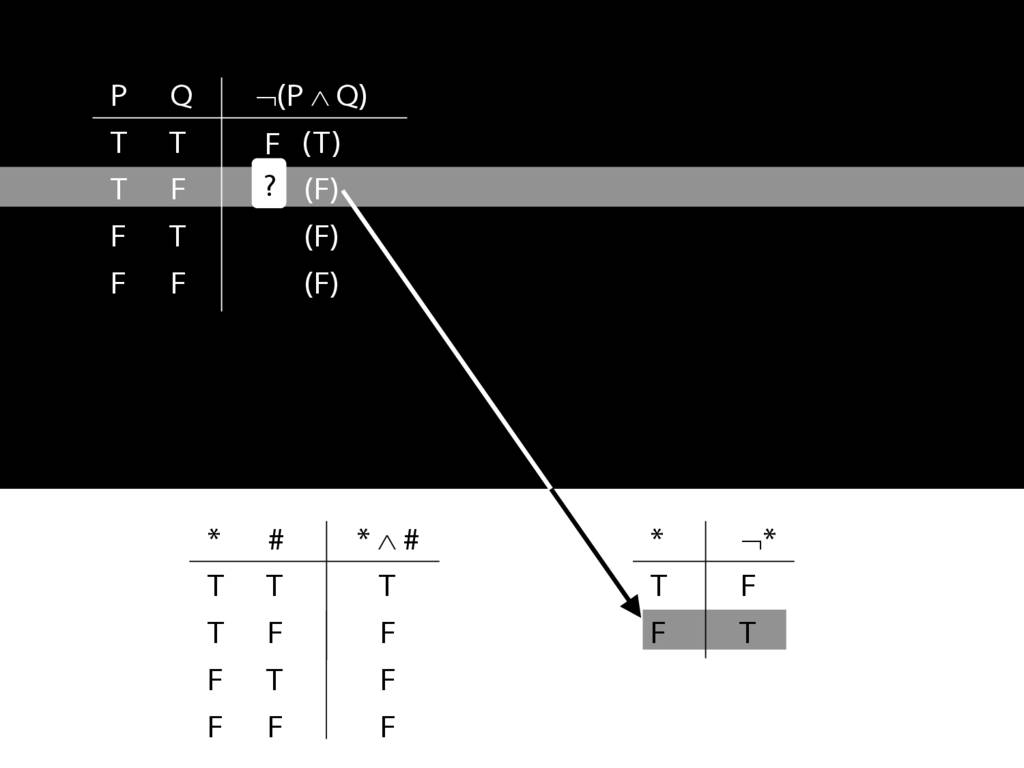
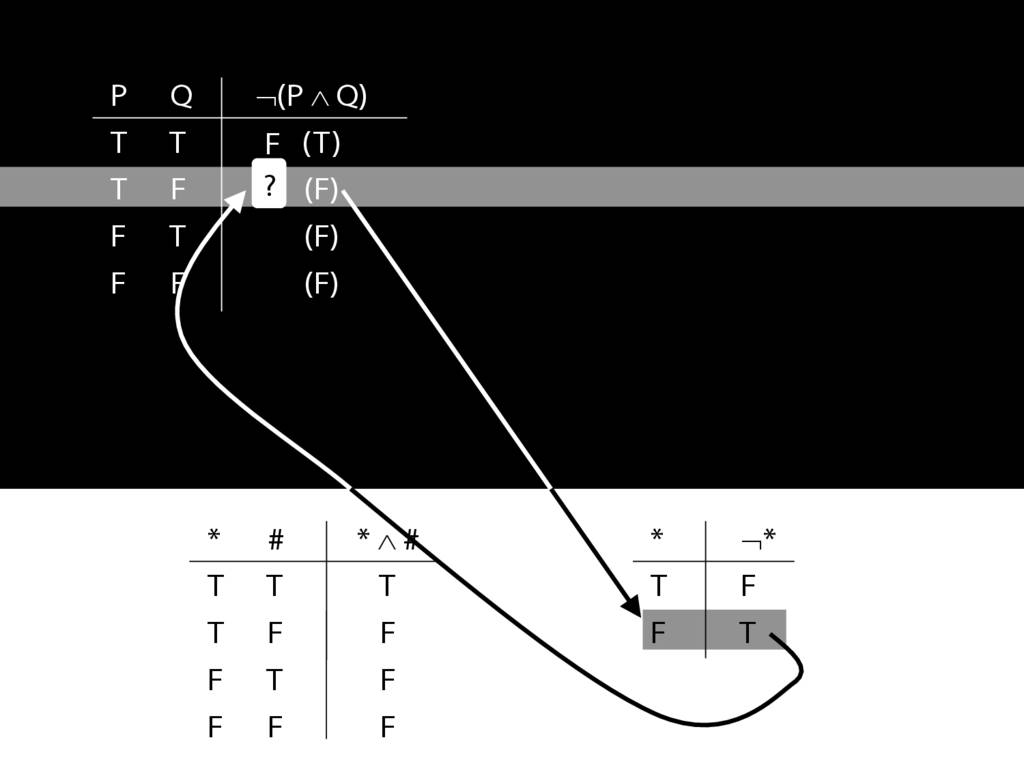
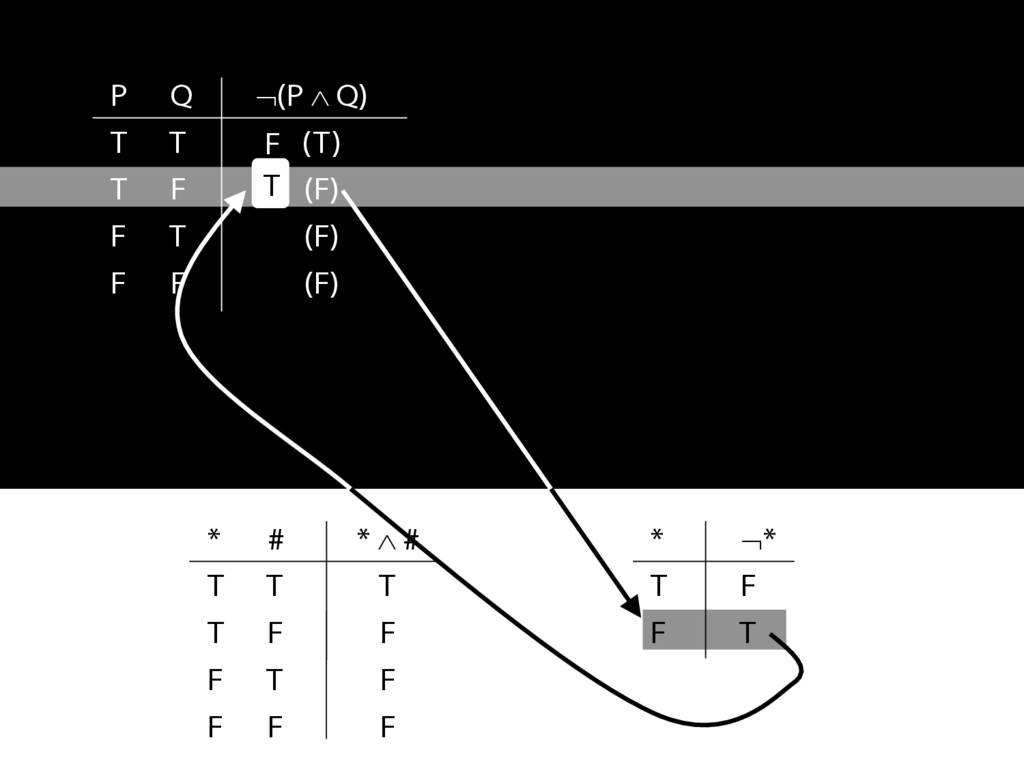
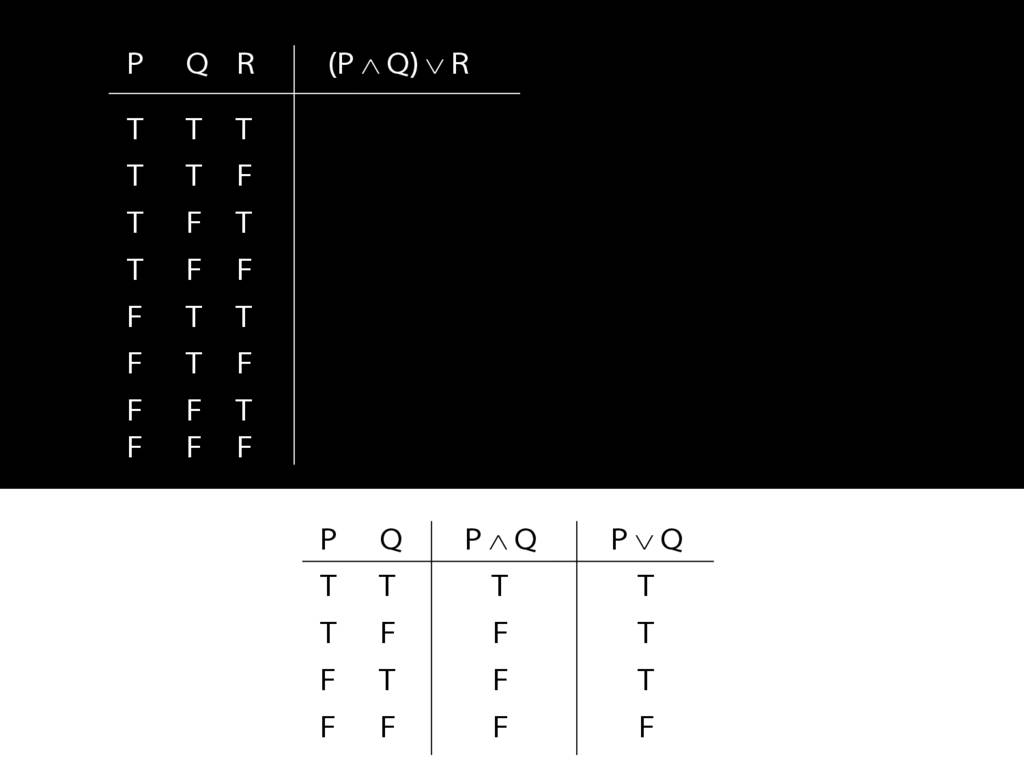
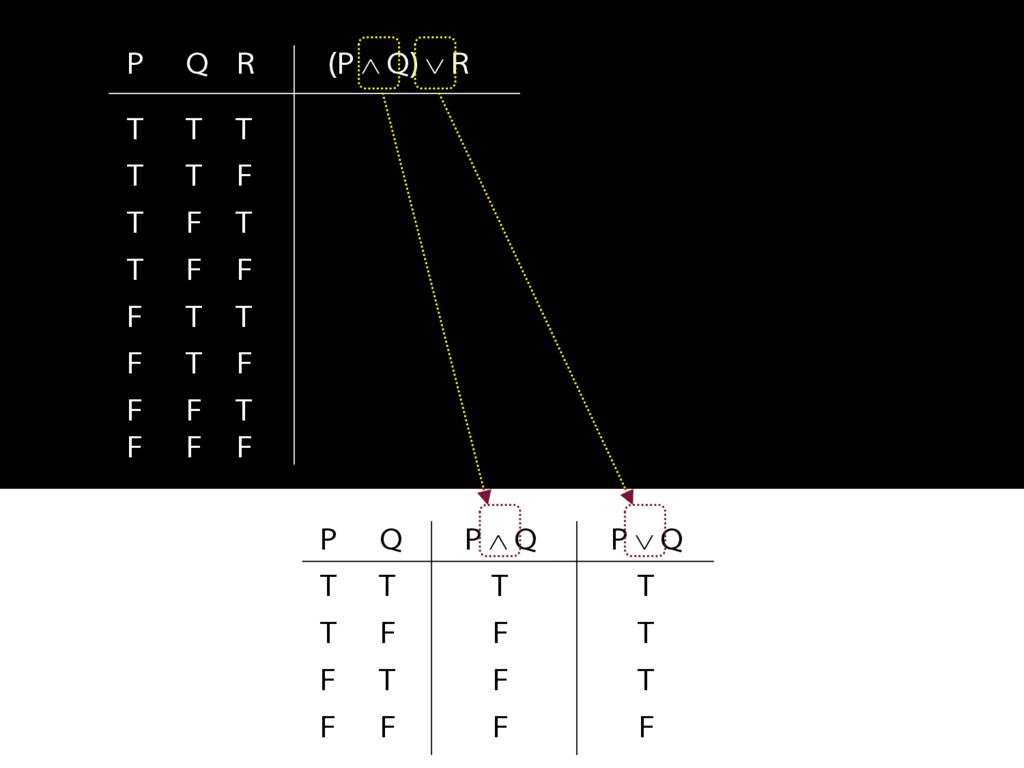
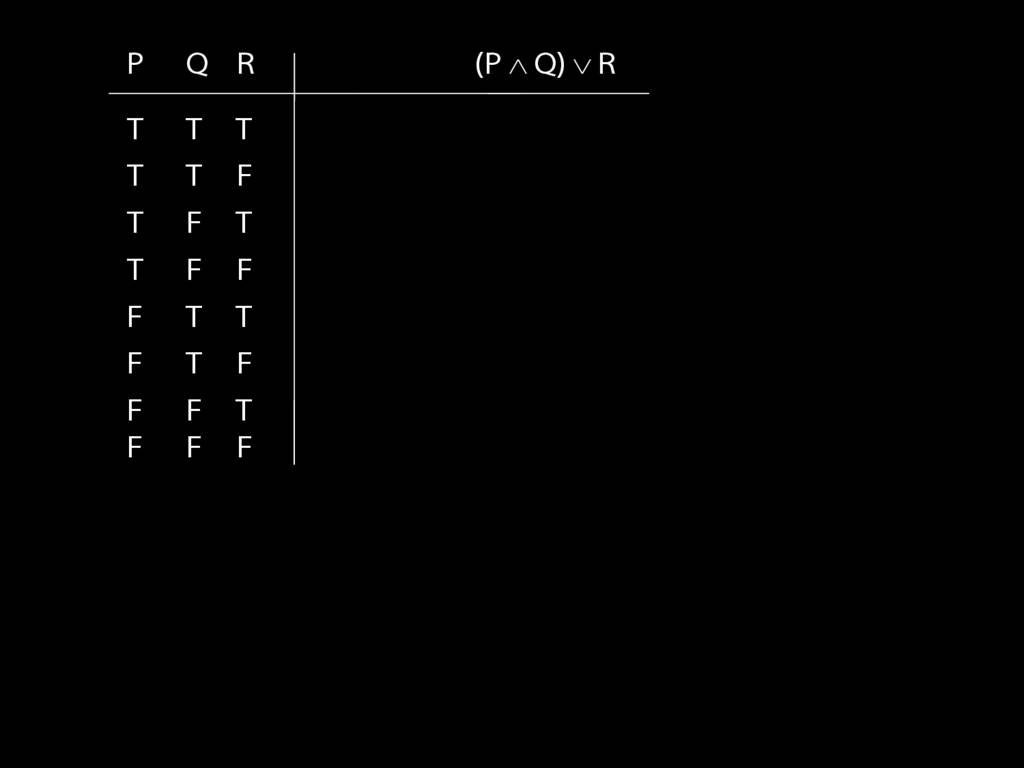
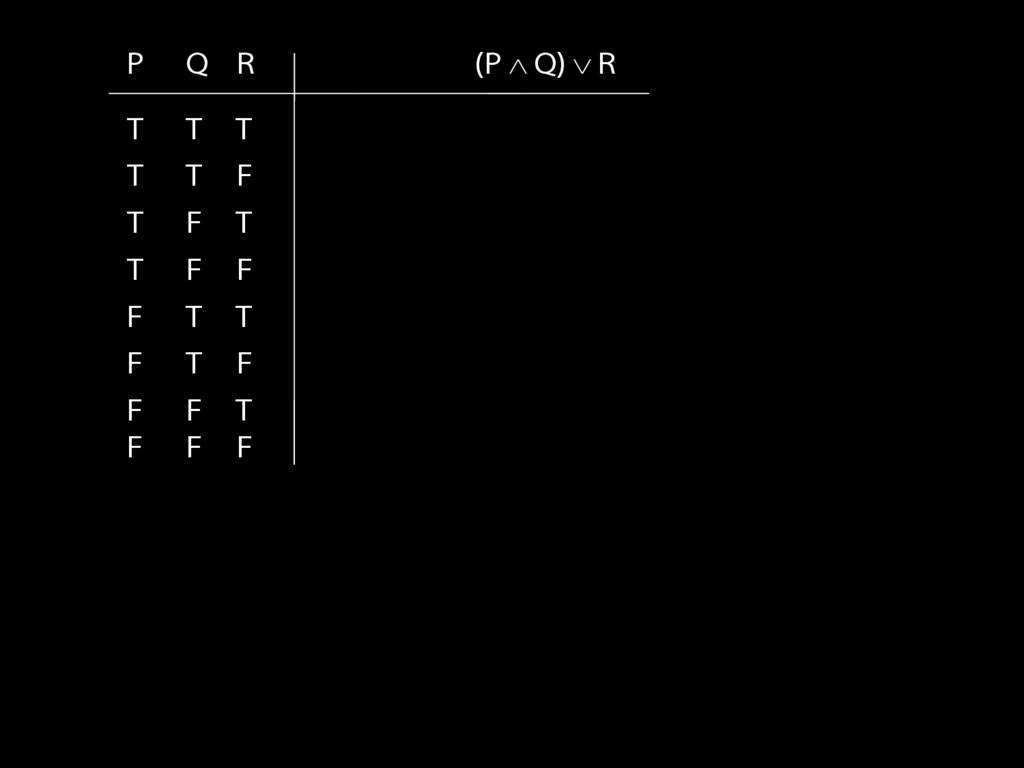
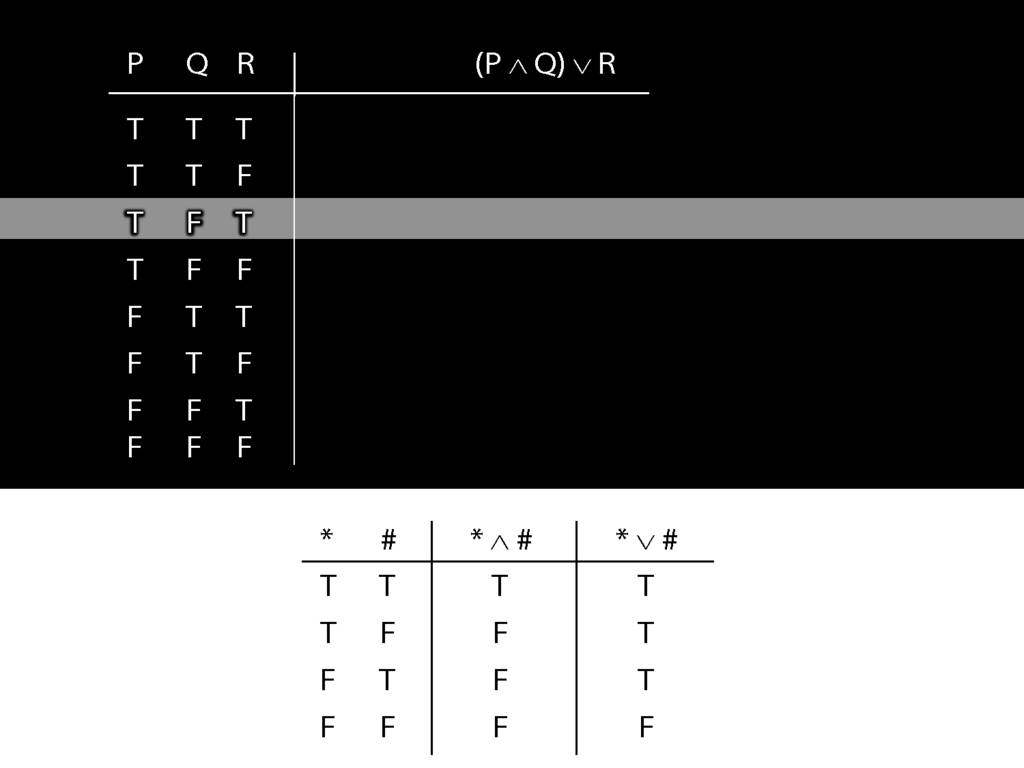
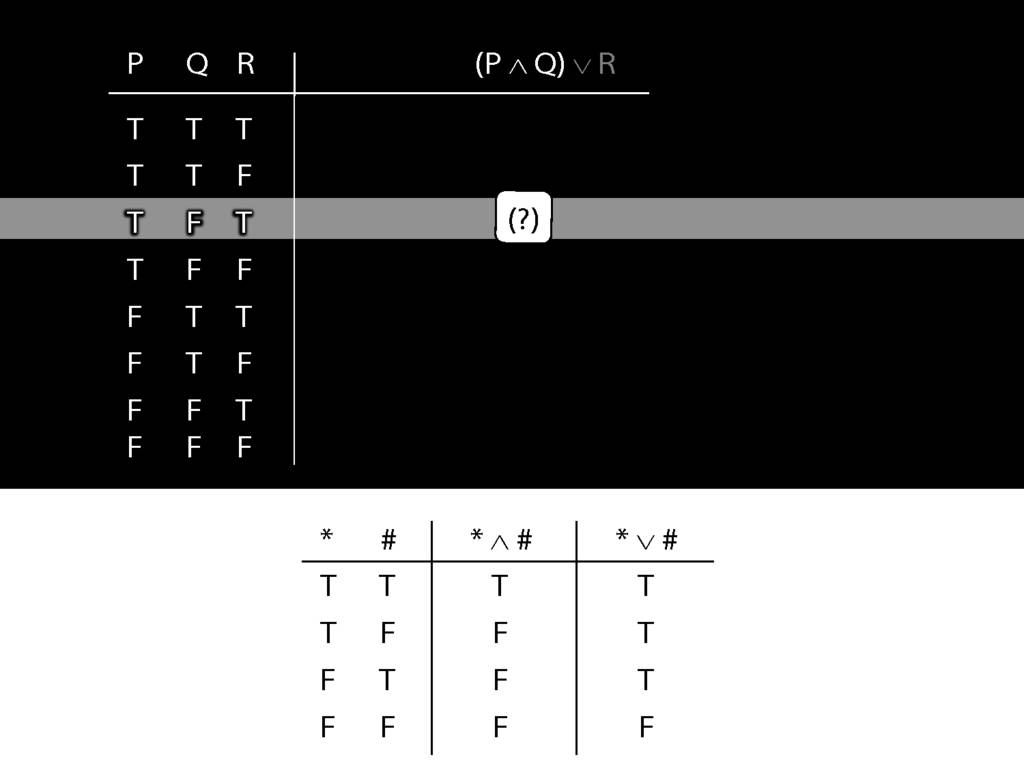
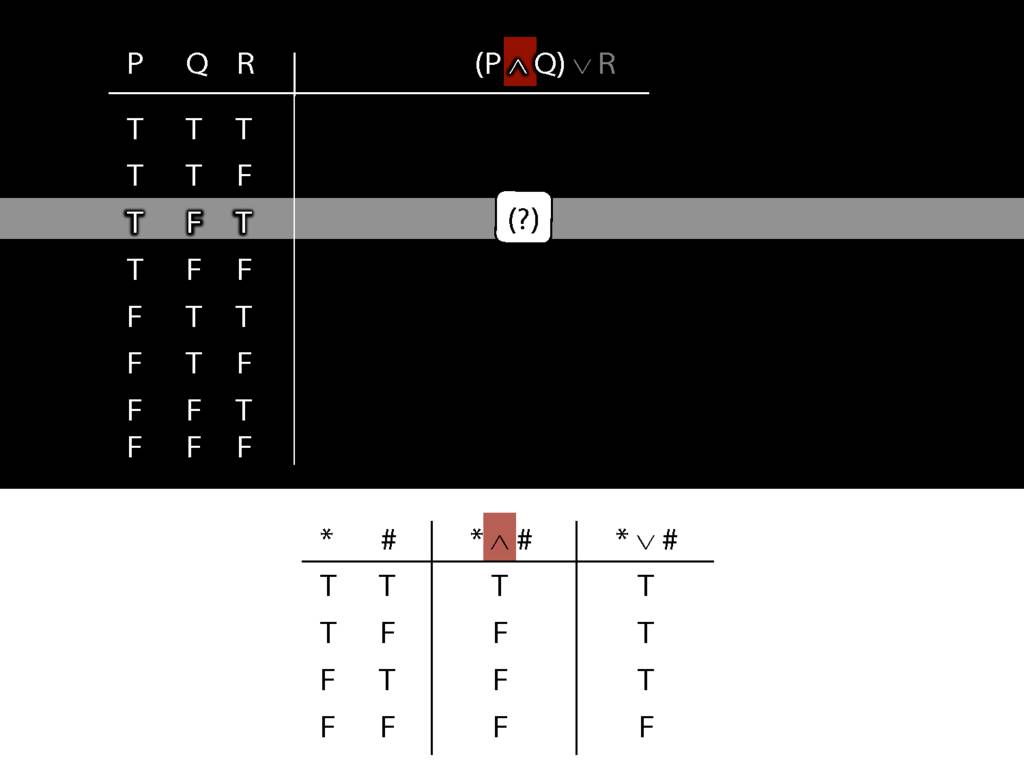
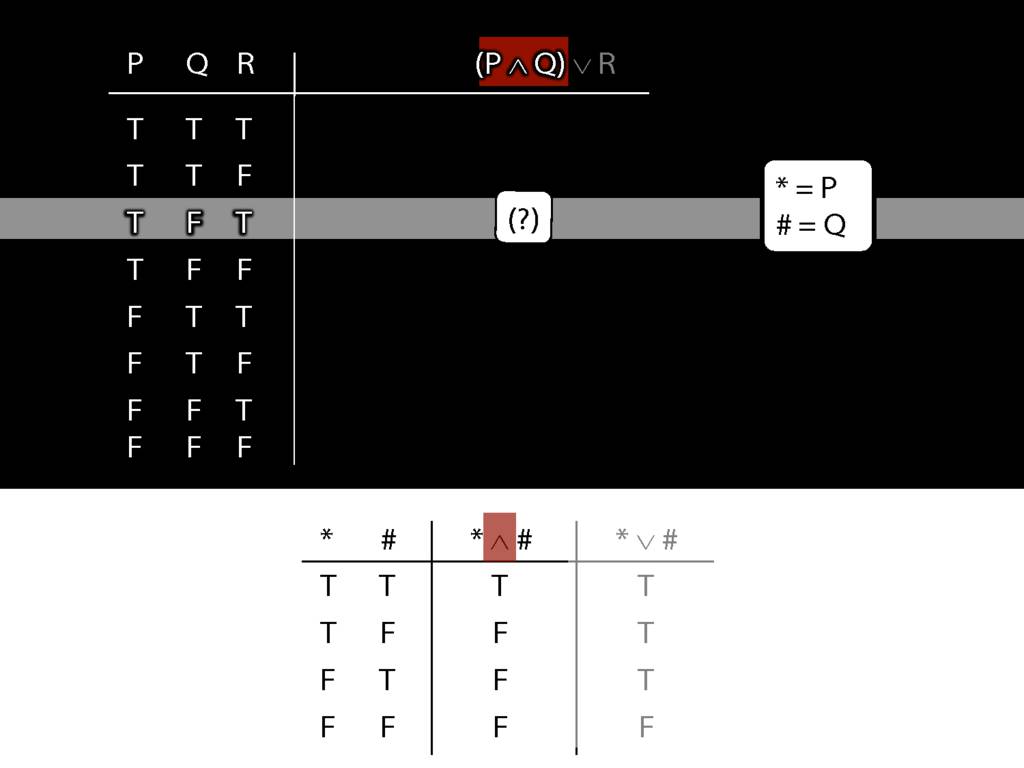
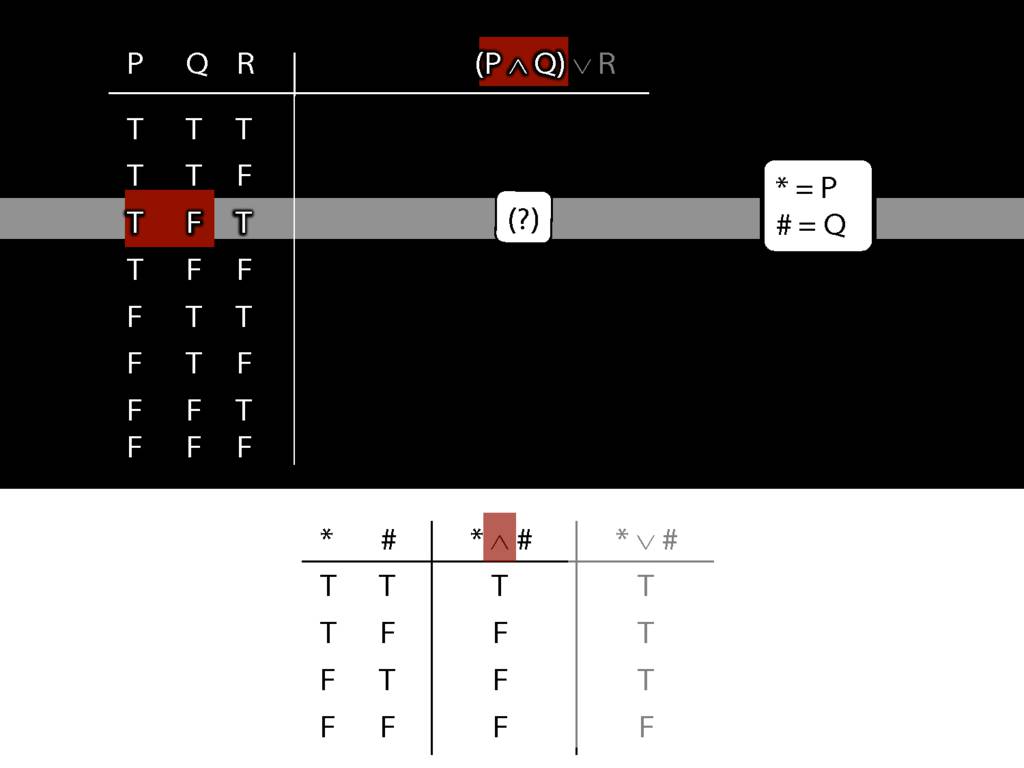
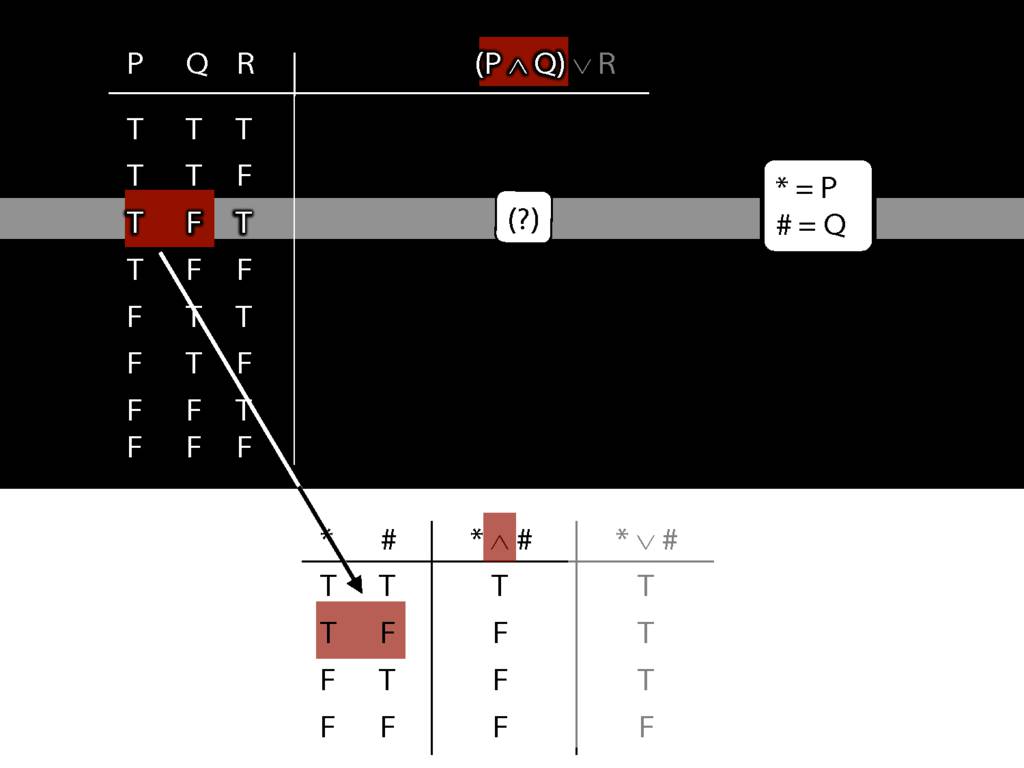
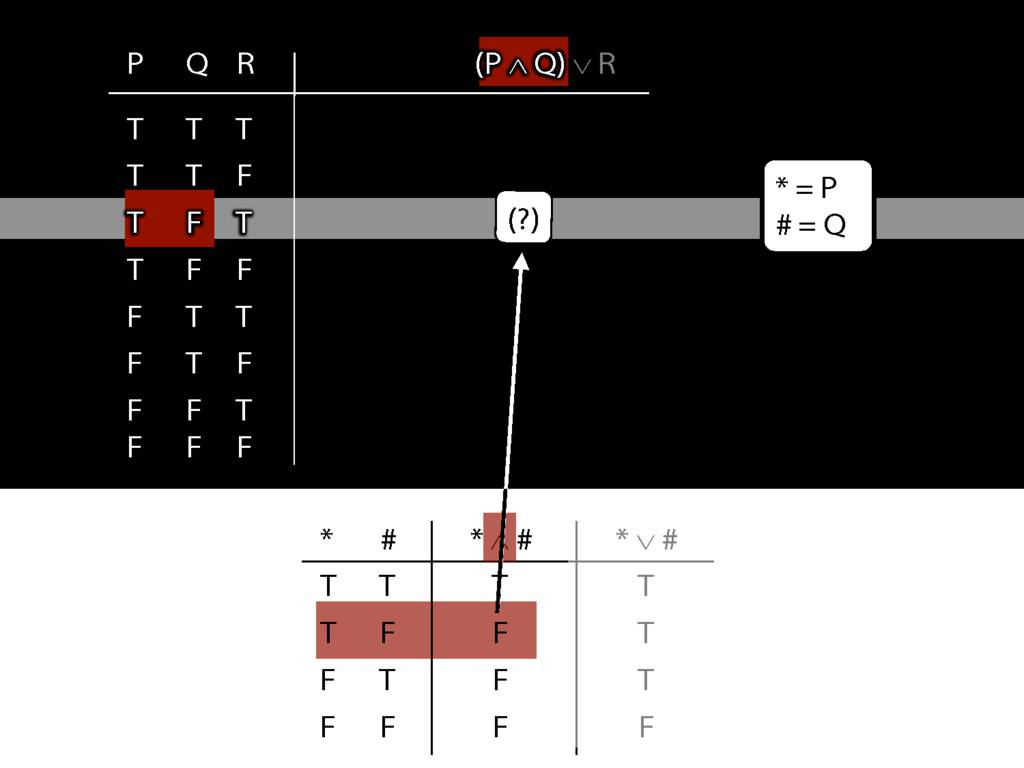
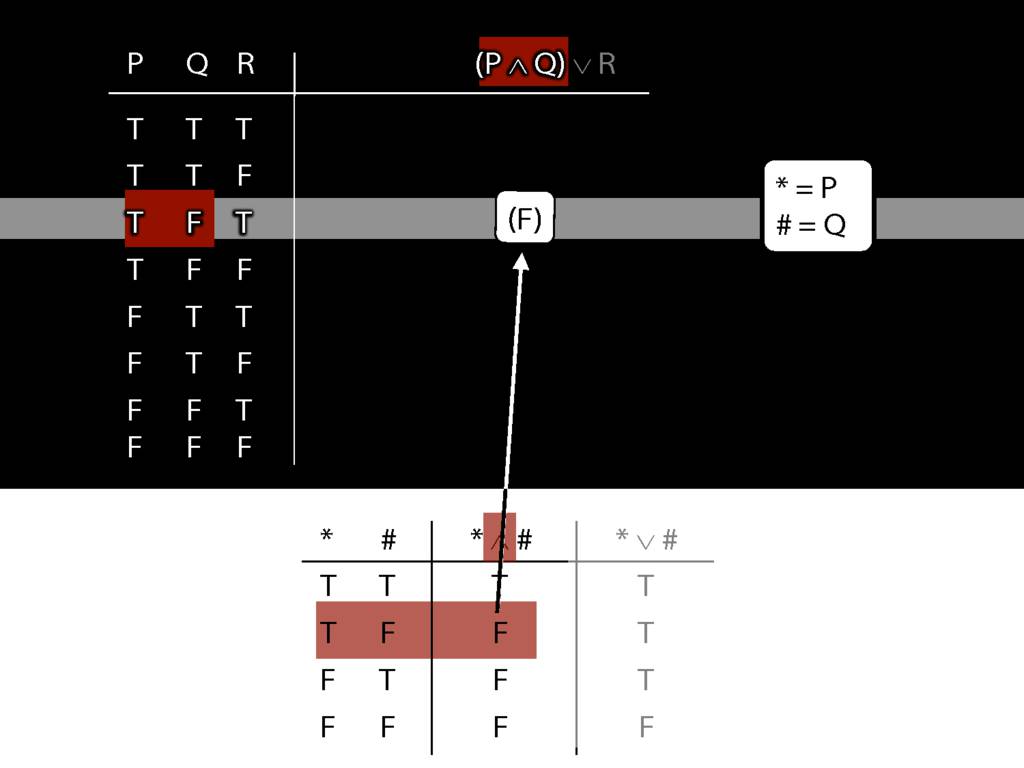
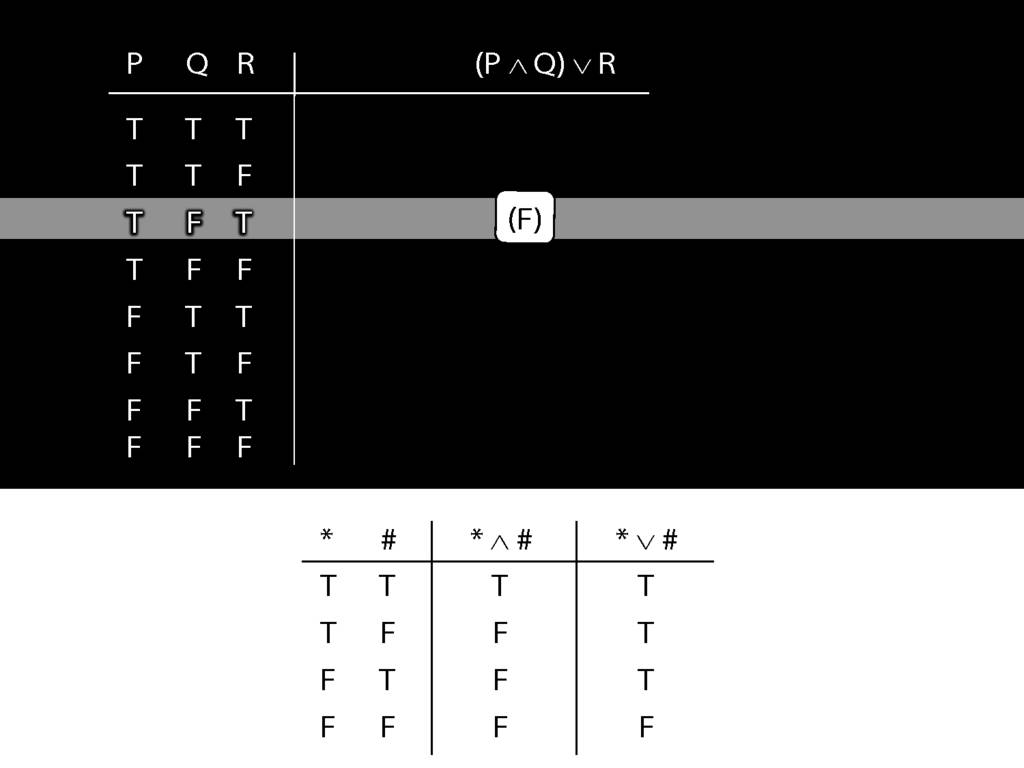
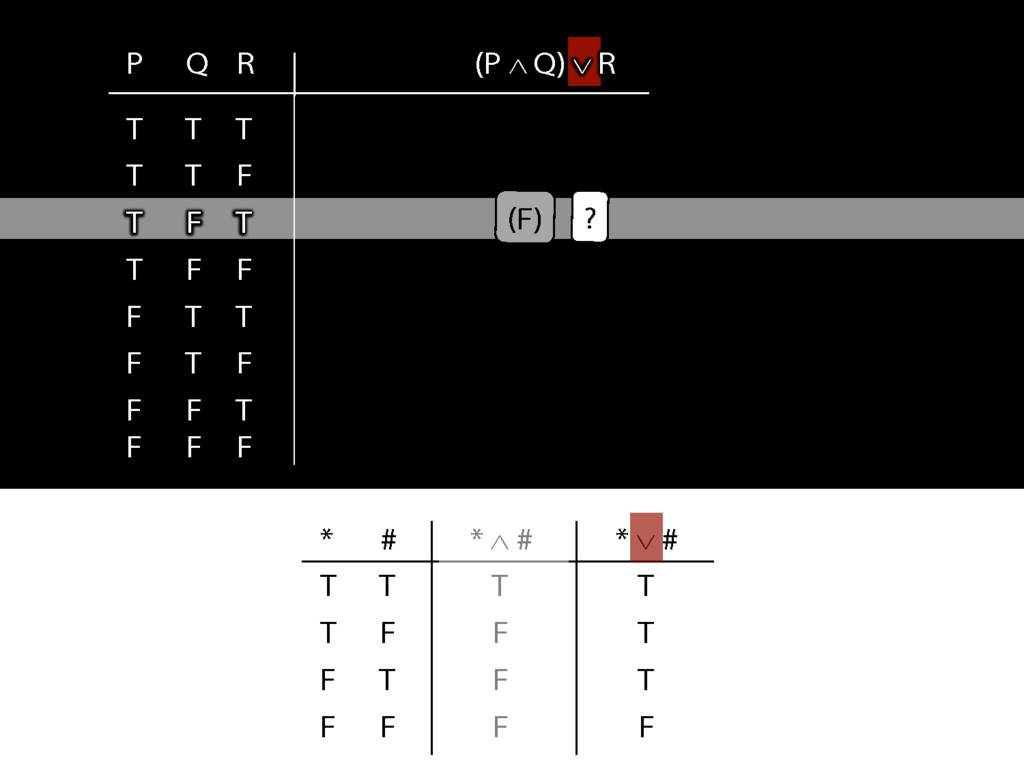
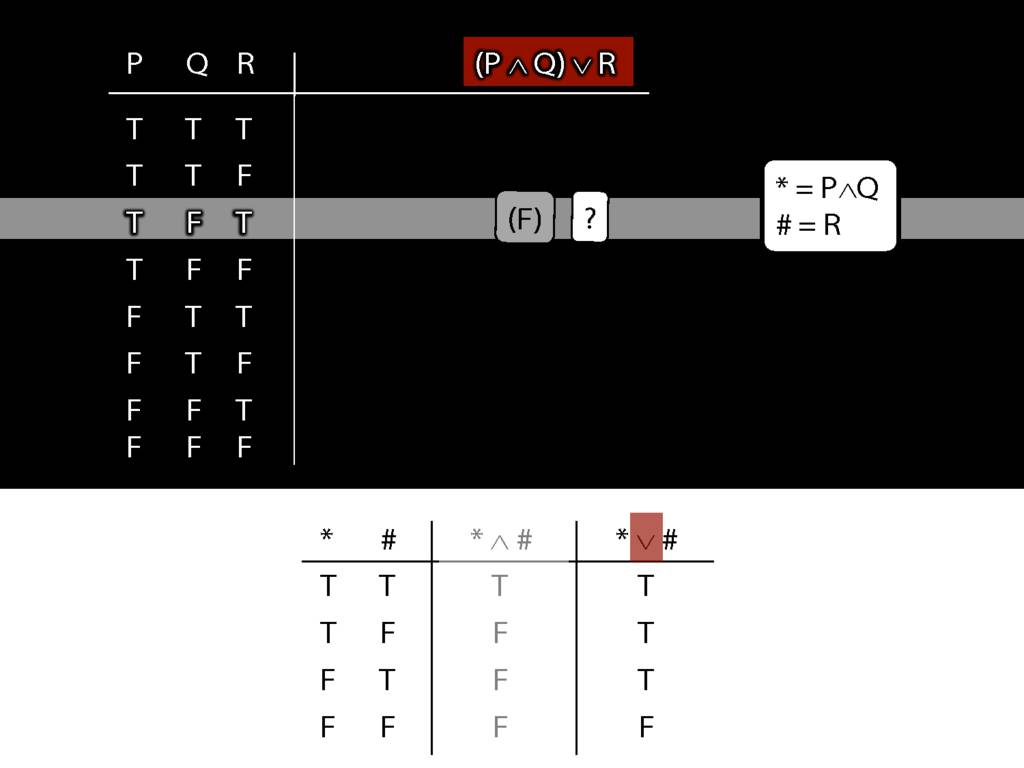
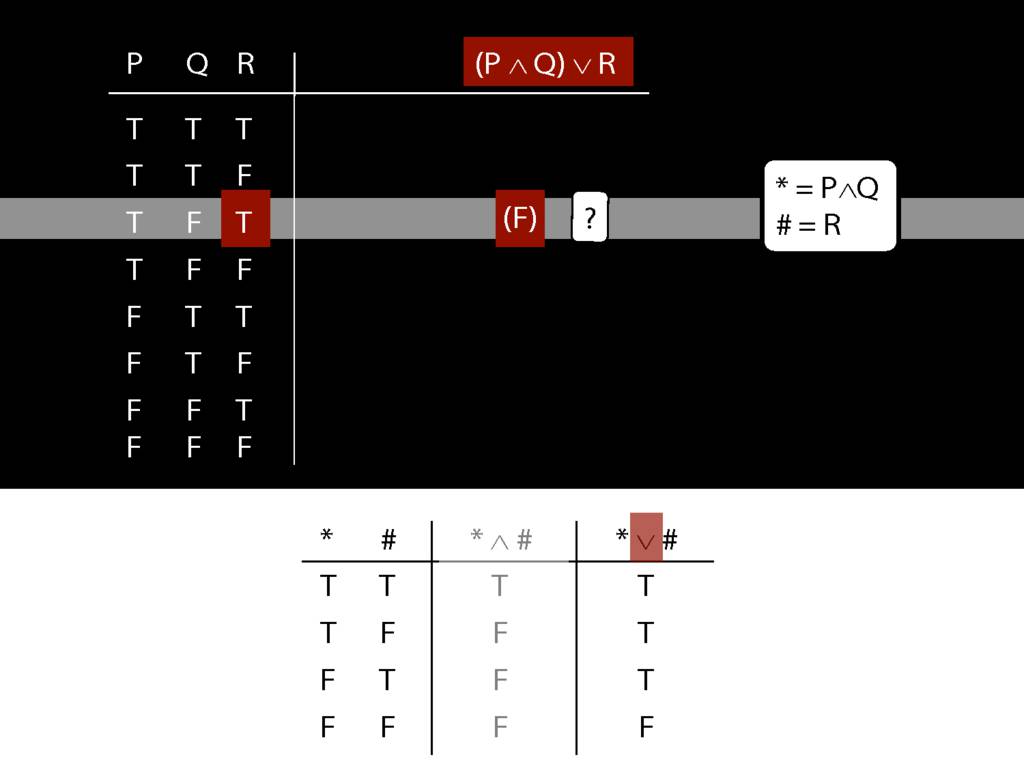
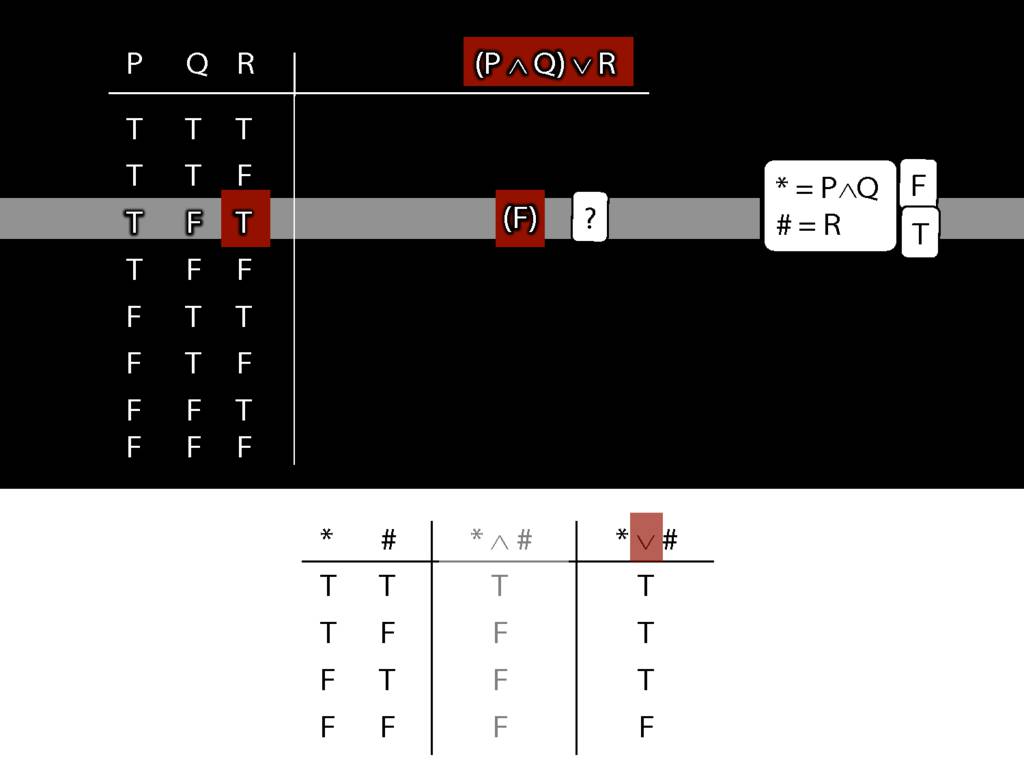
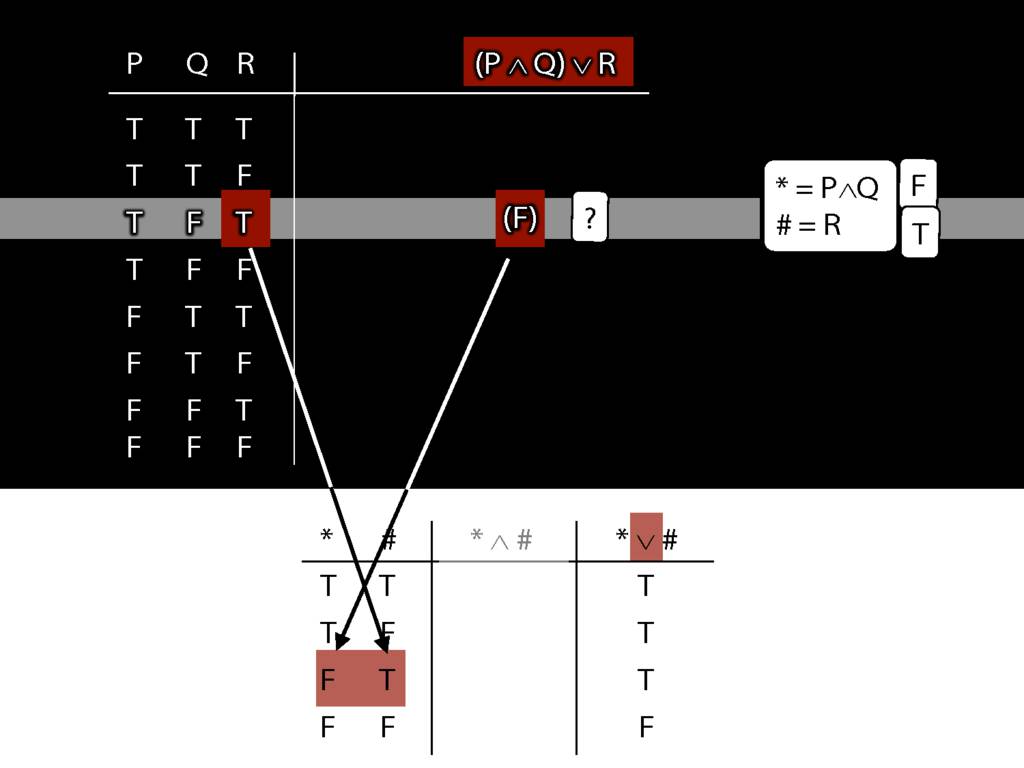
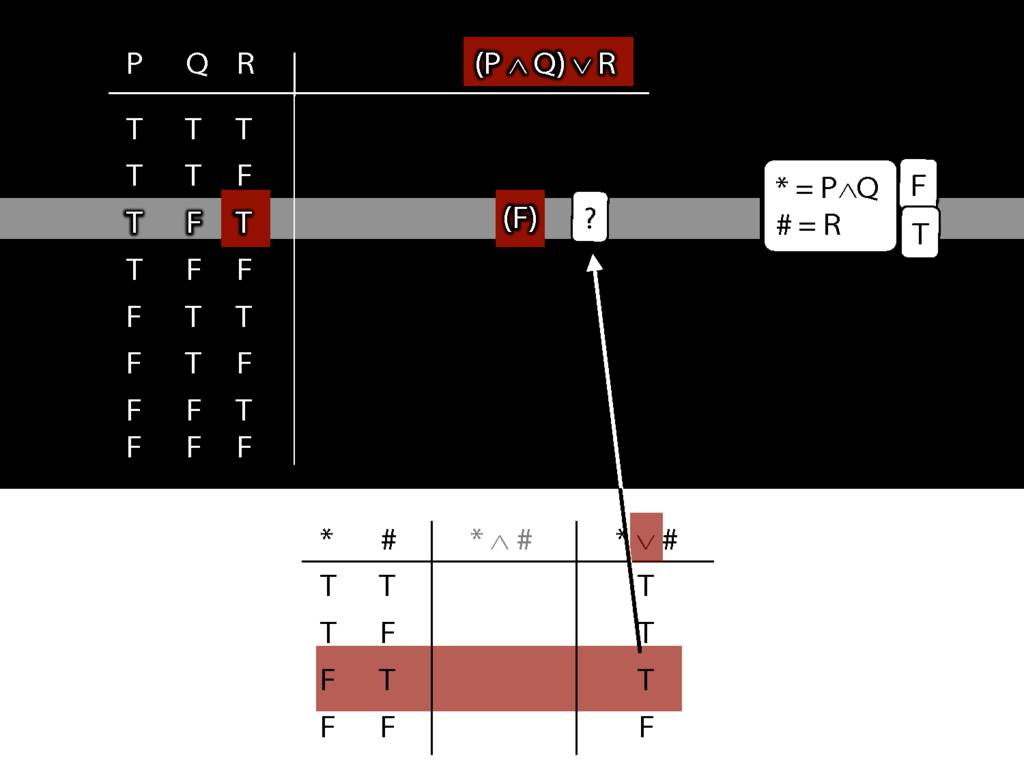
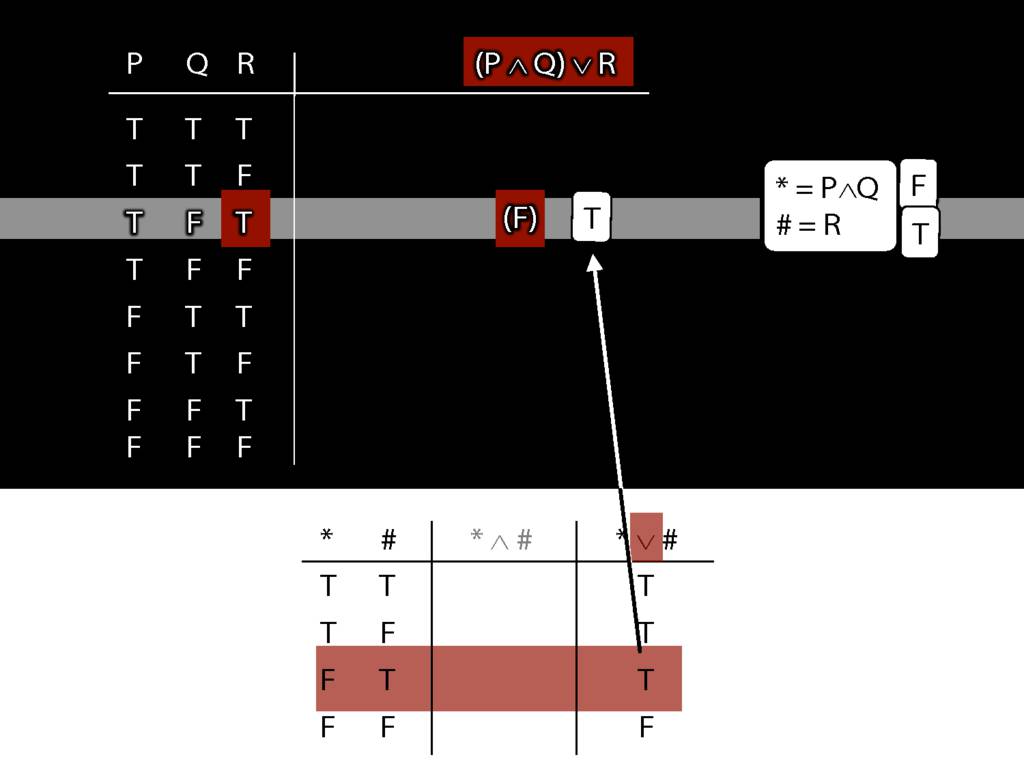
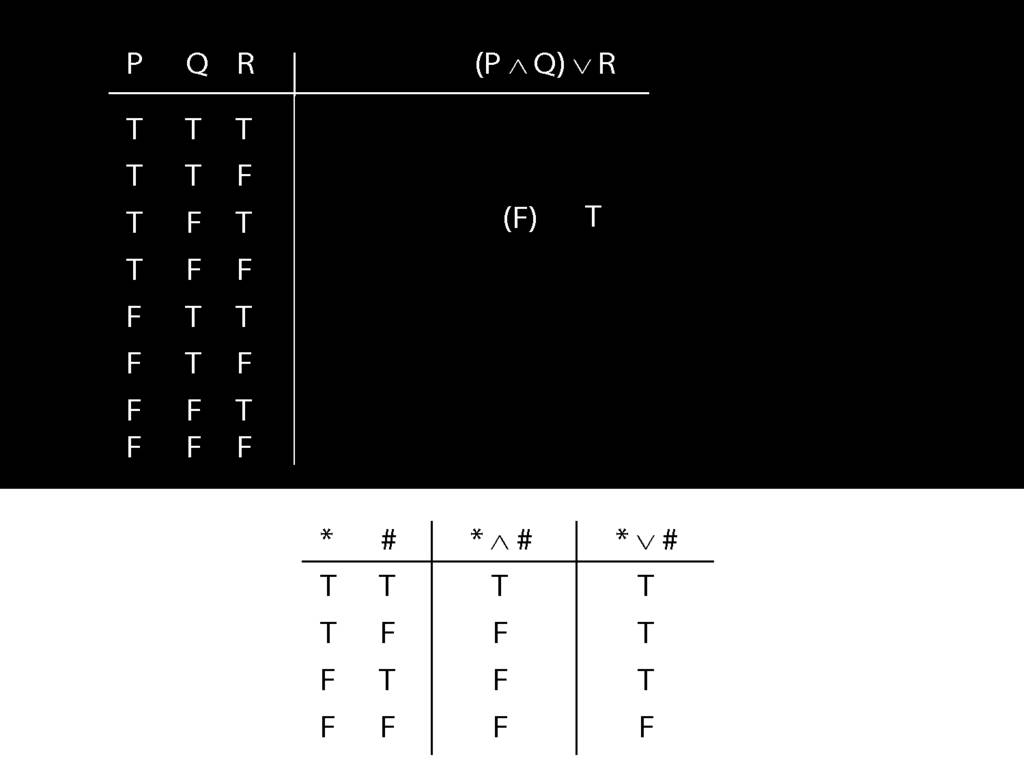
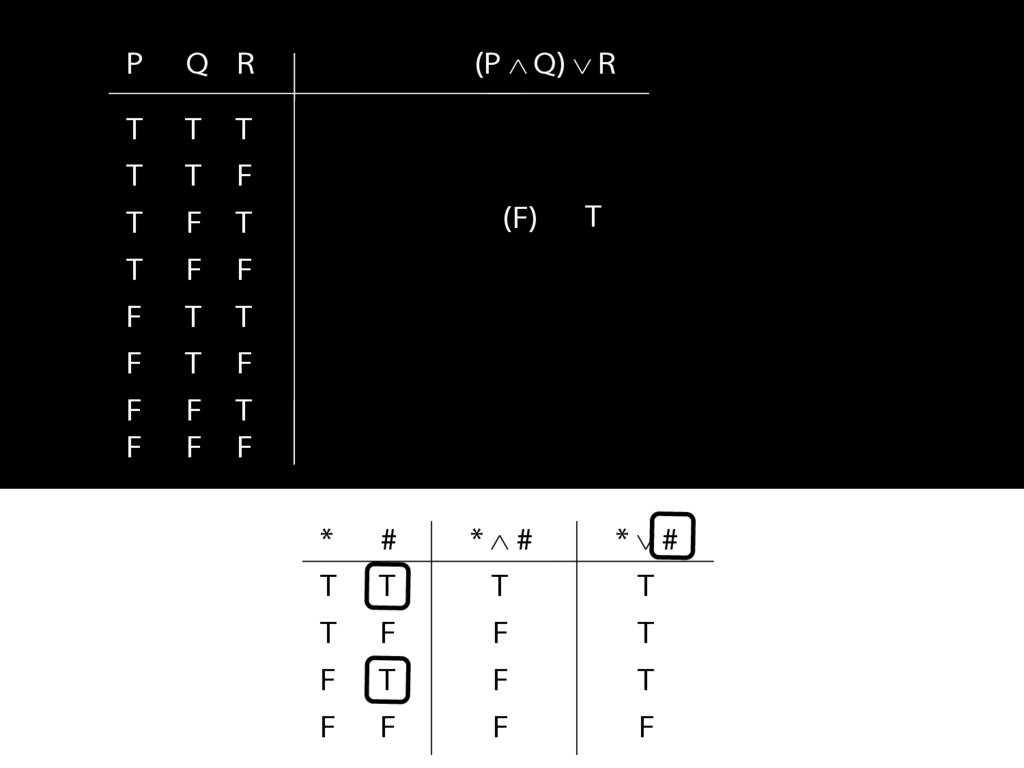
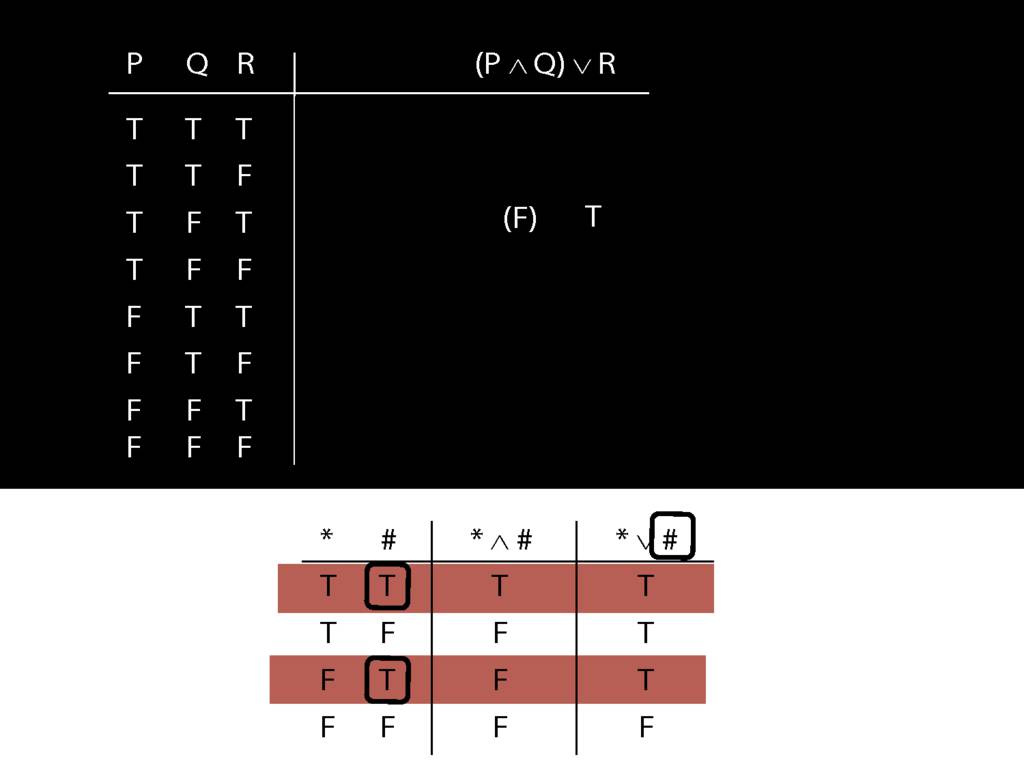
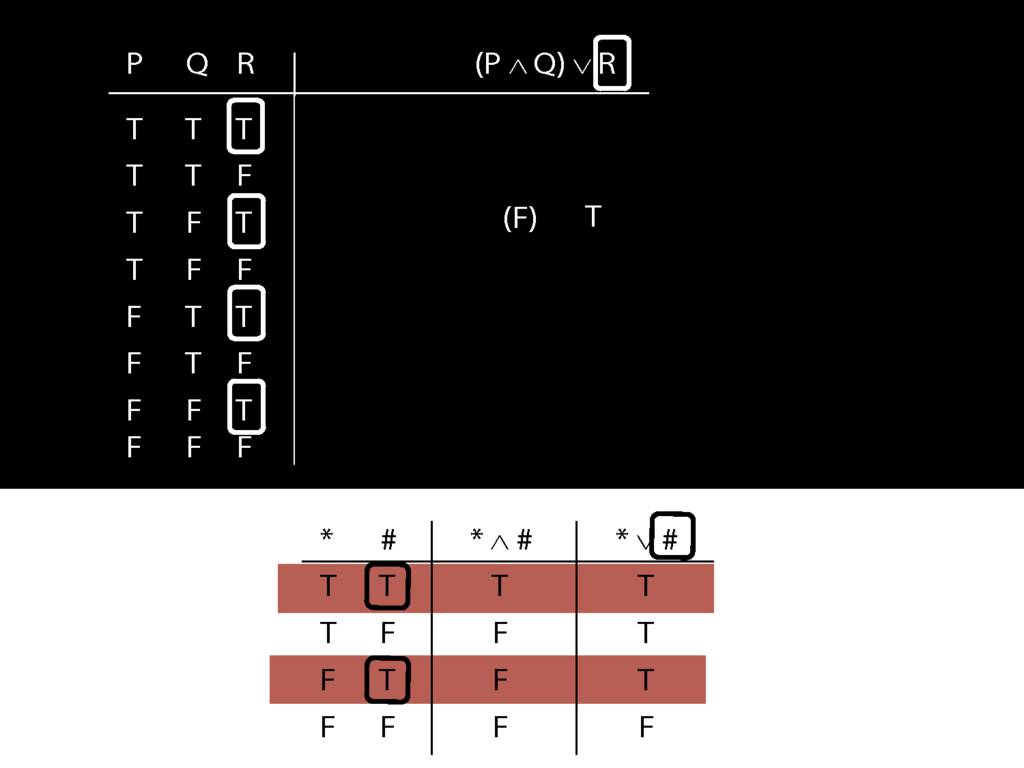
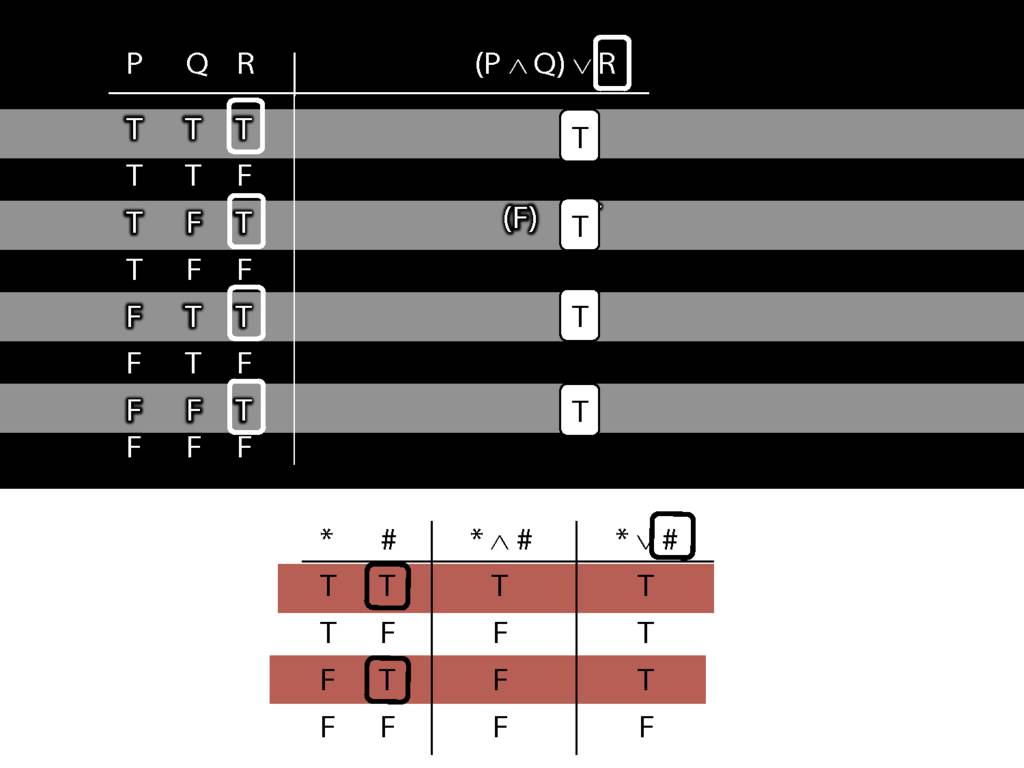
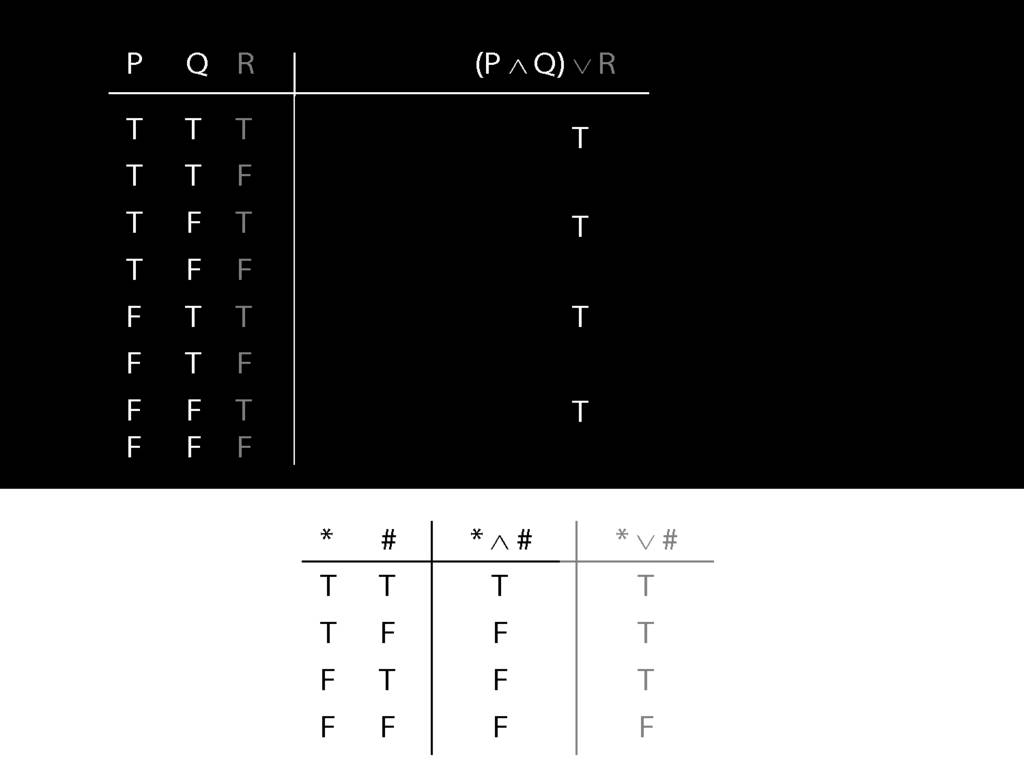
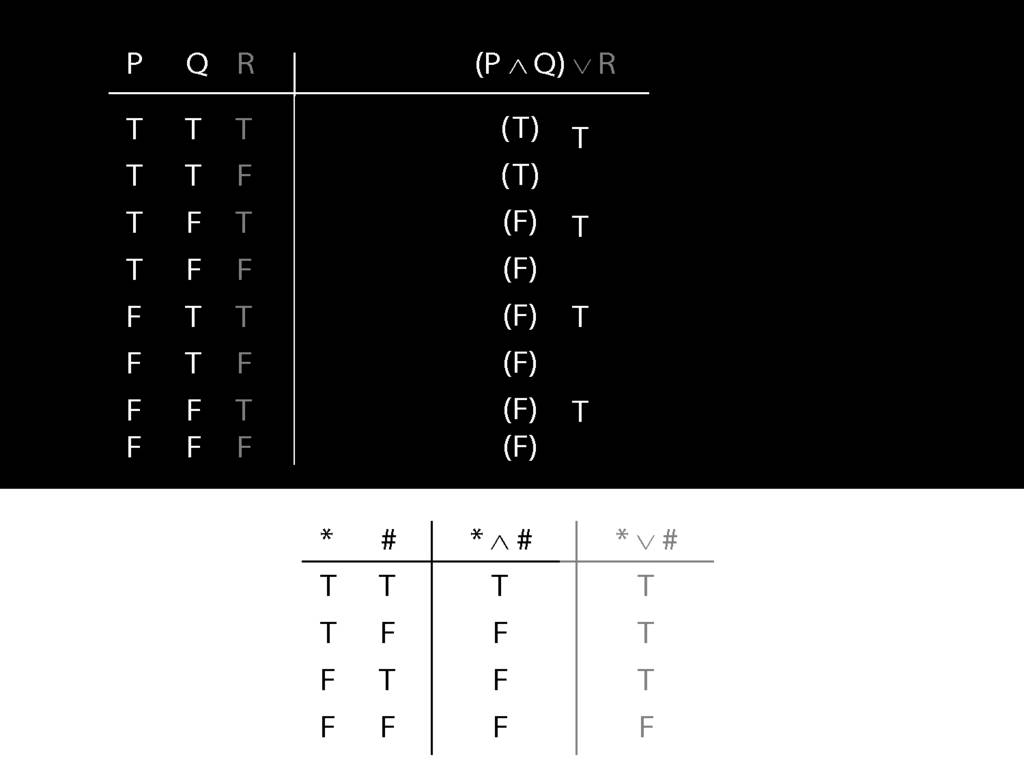
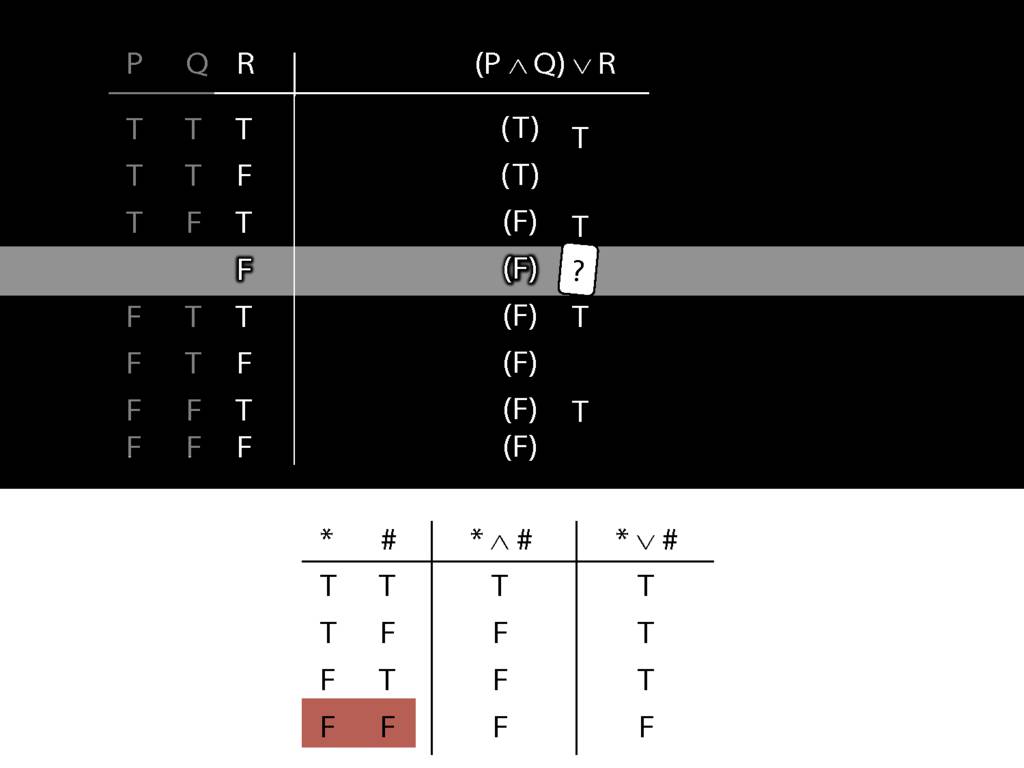
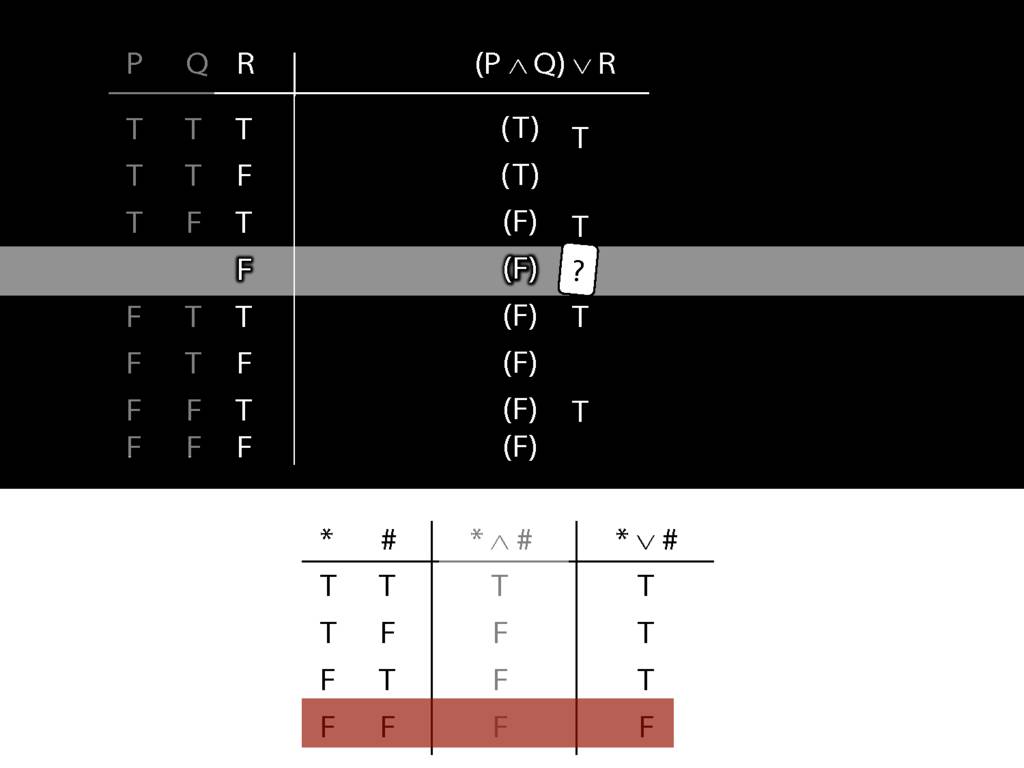
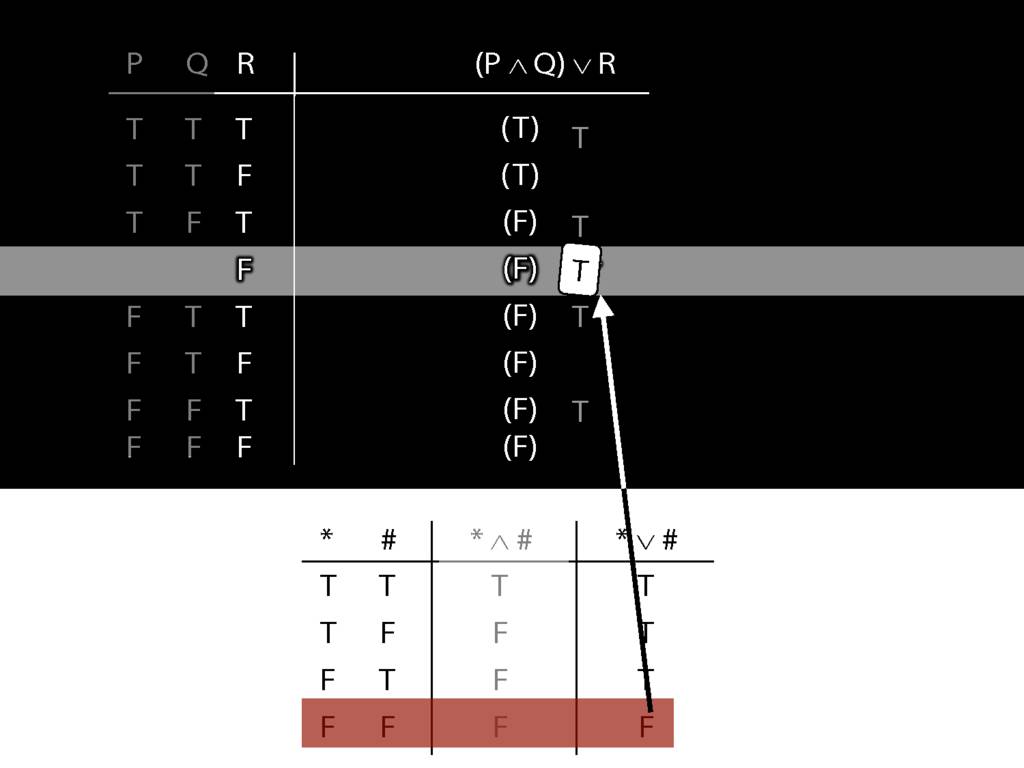
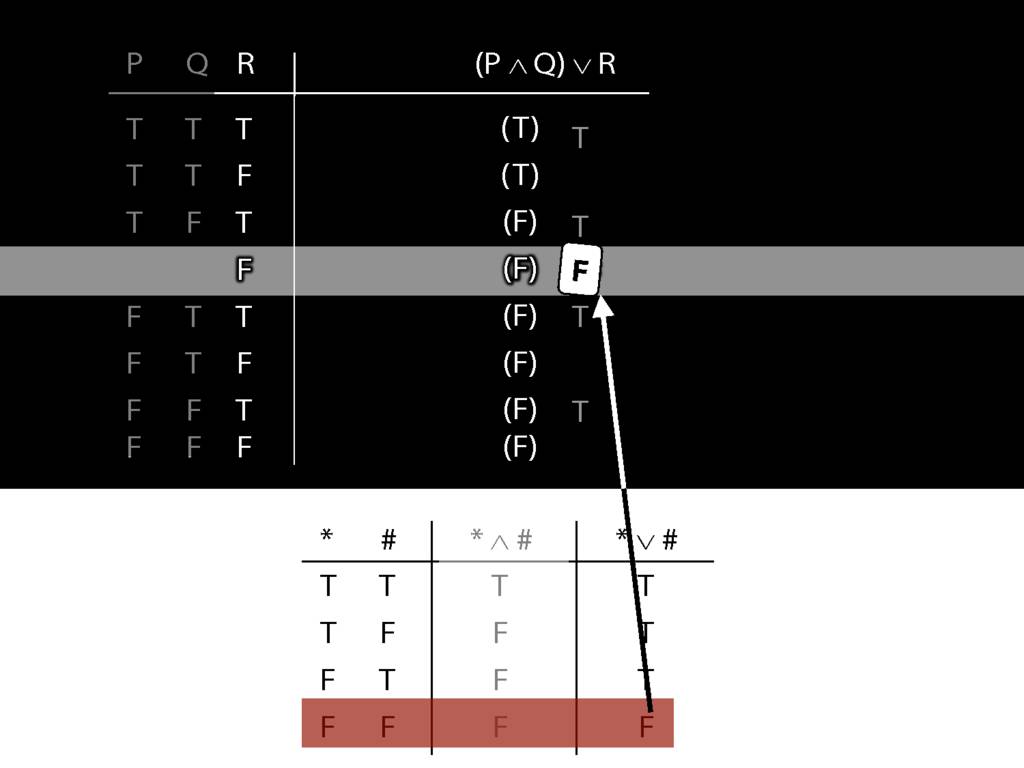
\section{Complex Truth Tables}
\section{Complex Truth Tables}
\emph{Reading:} §3.3, §3.5

\begin{minipage}{\columnwidth}
Complex truth table example:
\end{minipage}
3.12, 3.13
4.4-4.7
4.12-14
3.14, 3.15
\section{Contradictions, Logical Truths and Logical Validity}
\emph{Reading:} §4.1, §4.2, §5.4

P $\lor{}$ ¬P is a \emph{logical truth}
logical truth defined p. 568
P $\land{}$ ¬P is a \emph{contradiction}
contradiction defined p. 564

Unlike say knowledge or truth, where it’s up to you to form a view of your own to a large extent, with logical validity there is a precise and clear definition that we are working with. Of course there are still questions about the nature of logical validity, but to get to those questions you first have to accept its definition.
4.1, 4.2
4.1, 4.2
4.12--4.16