Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
\title {Logic I \\ Logic (PH133)}
\maketitle

\def \ititle {Logic (PH133)}
\def \isubtitle {Lecture 3}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
\section{Formal Proof}
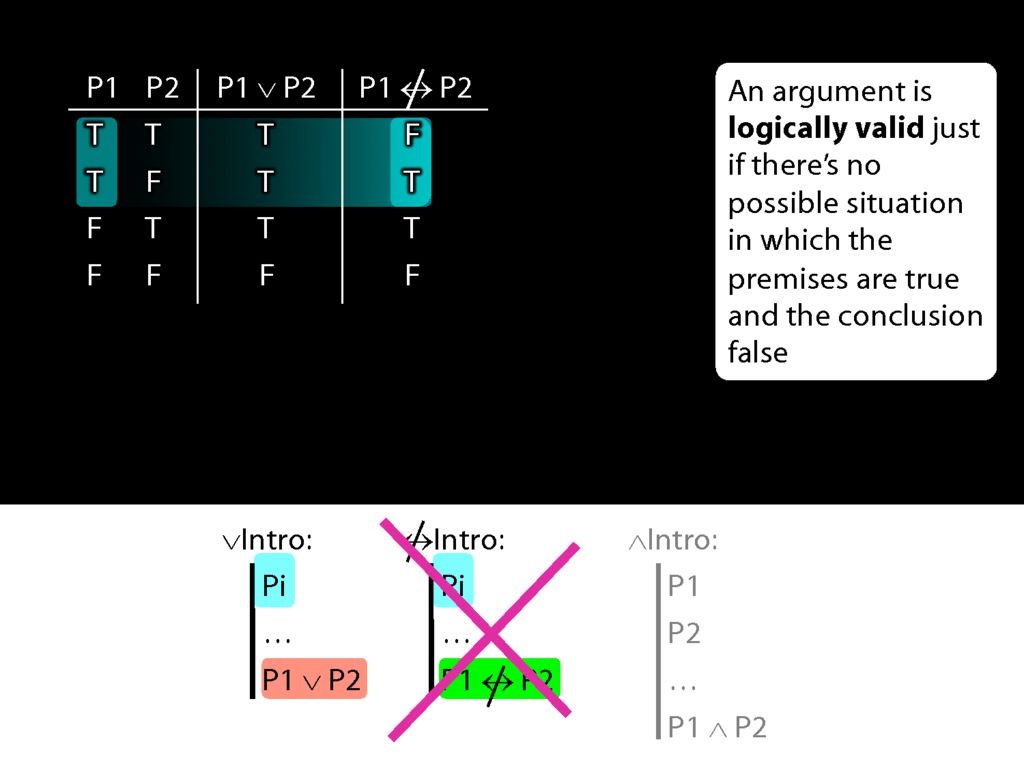
An argument is logically valid just if there’s no possible situation in which the premises are true and the conclusion false.
Two ways to show that an argument is logically valid:
- truth tables
- fitch proof (formal)
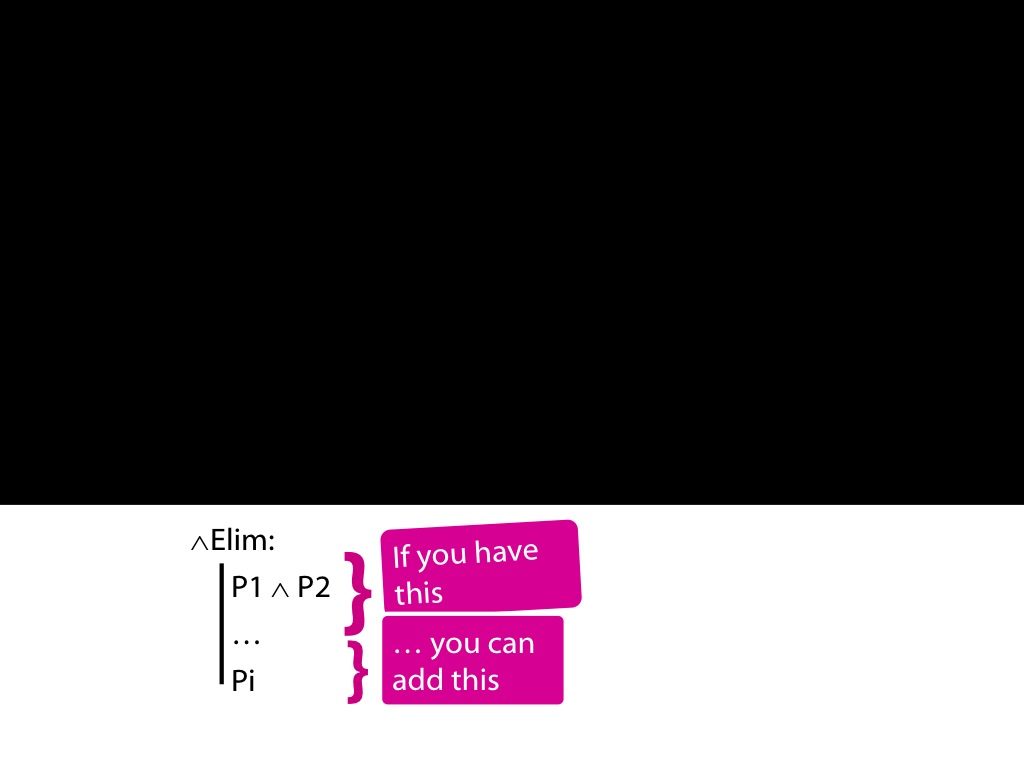
∧Elim
| | P1 ∧ P2 | ||
| | ... | ||
| | Pi |
\section{Translating a Simple Argument}

We're studying a formal system of proof called Fitch.
Here's the first rule of Fitch. It's called conjunction elimimnation.
The rule says that if you have a conjunction of two things in your proof, you can add a new line to your proof containing either one.

So if you something like this in your proof ...
... you can add something matching this.
I'll explain how to use conjunction elimination in a moment. First, let's look at another rule.

This rule is called conjunction introduction.
The rule says that if you have two things in your proof, you can extend your proof by one line to add their conjunction.

So if you these things matching these in your proof ...

... you can add something matching this.

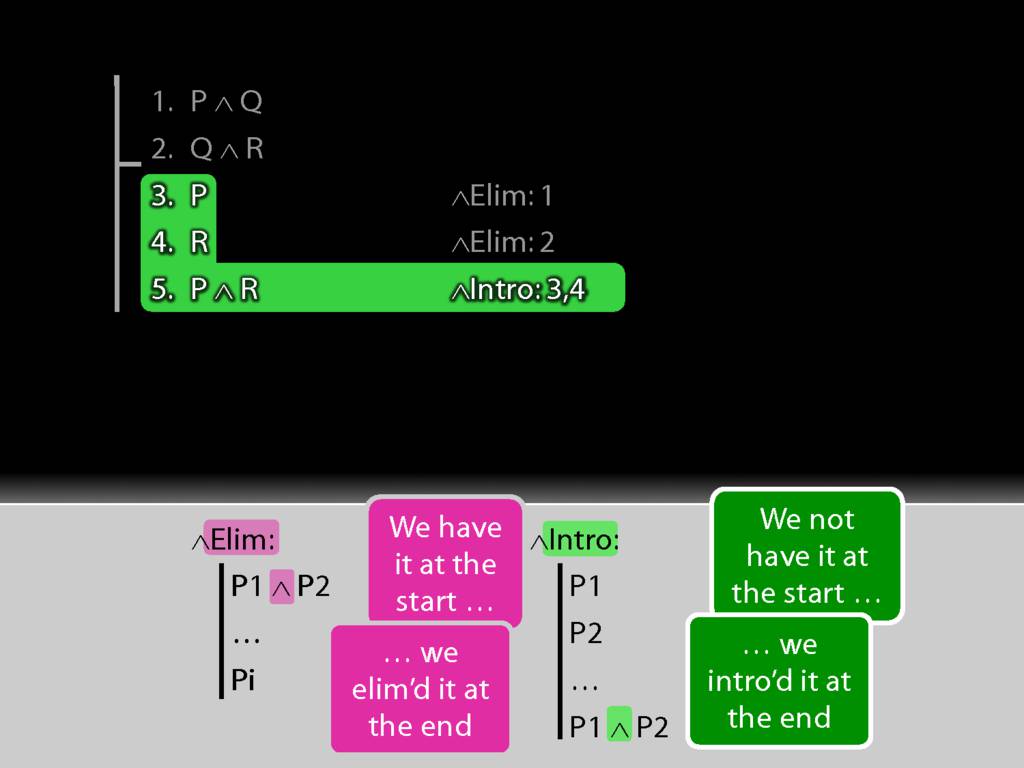
So let's look at an application of our rules of proof.
I want to do this by translating an argument from English into our formal language awFOL.

This doesn’t seem to be true.

But this does seem to be true, or at least horribly plausible.

And this seems right too, maybe.

Now if we take the first two sentences as premises and the second as a conclusion, we have an argument.
Is the argument logically valid?
Apparently not because the premises are true and the conclusion false.
But look what happens when we translate it into awFOL assuming that the english 'and' means the same as the awFOL conjunction symbol, '∧'.

The first premise comes out as P∧Q

Where P stands for the sentence 'The world will overheat'.

And Q stands for 'We will all die'.

What about the second premise?

This comes out as Q∧R.

The key thing is that we're re-using Q because the sentence about the world overheating occurs in both the first
and second premises. Where we have the same English sentence, we have to use the same sentence-letter in awFOL.

Now what about the conclusion?

This is P∧R. Not that both sentences are already familiar.

P occurs in the first premise ...

... and Q occurs in the second premise.

So here's our argument.

Since we're going to do a formal proof, we should use the vertical and horizontal lines.
(Surely you remember that the vertical line runs the length of the argument, and the horizontal line separates premises from conclusion.)


We also need to use line numbers.
\section{Formal Proof: ∧Elim and ∧Intro}
\emph{Reading:} §5.1, §6.1
\section{Formal Proof: ∧Elim and ∧Intro}

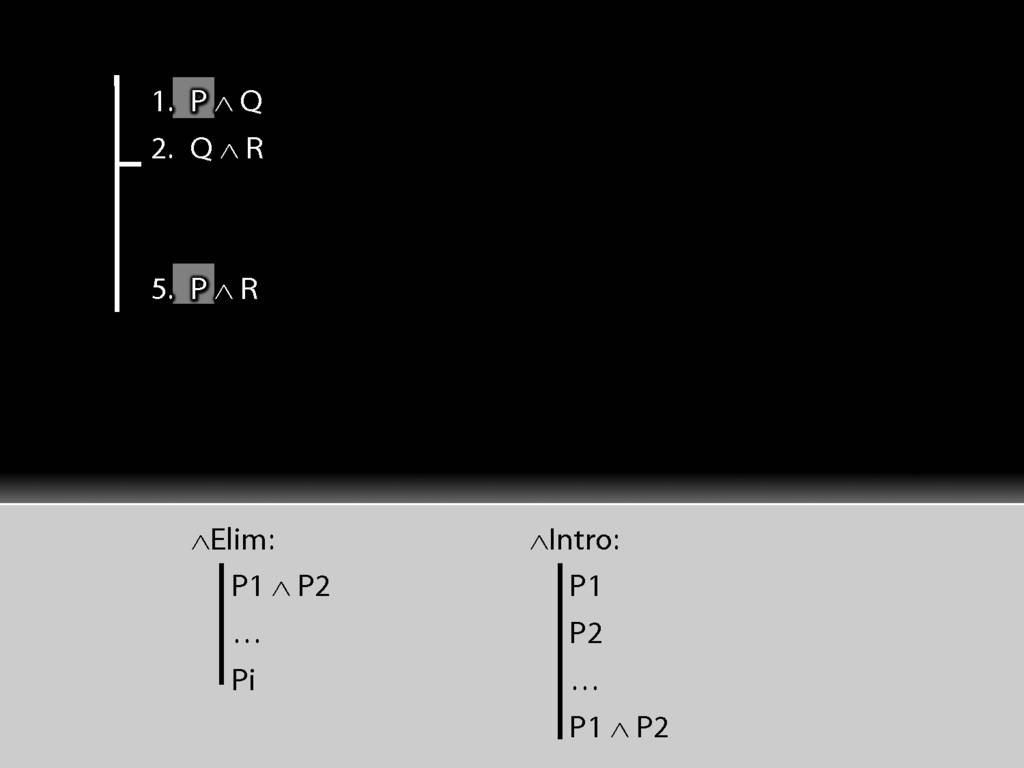
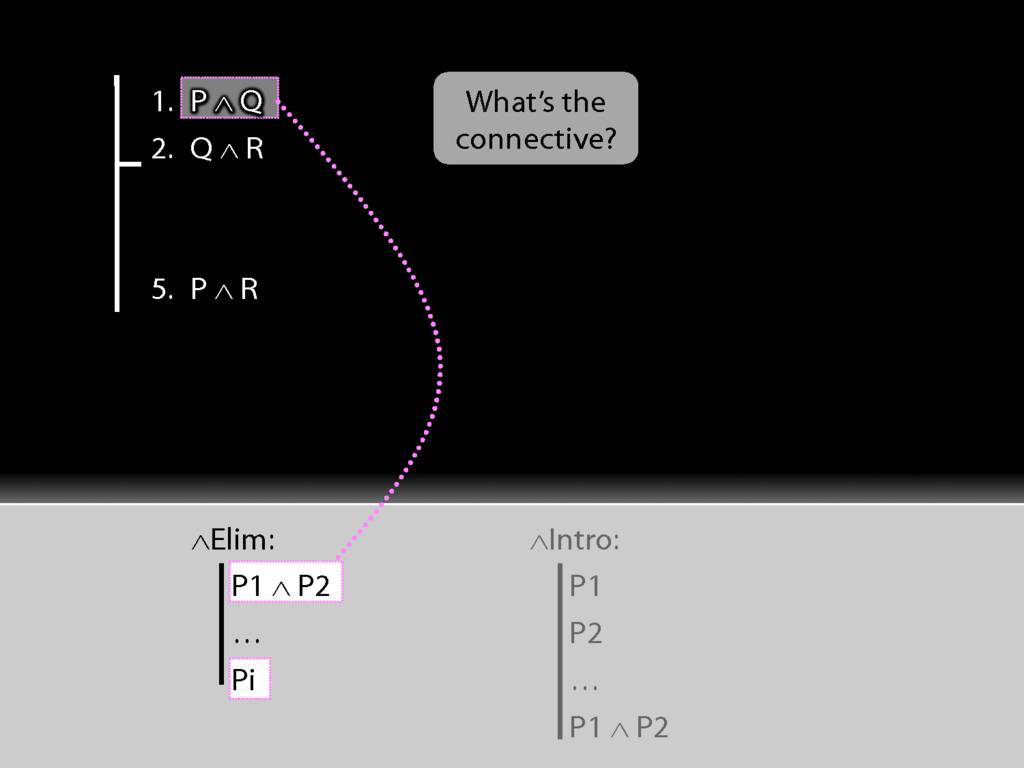
See how we have P in a premise and P in the conclusion?
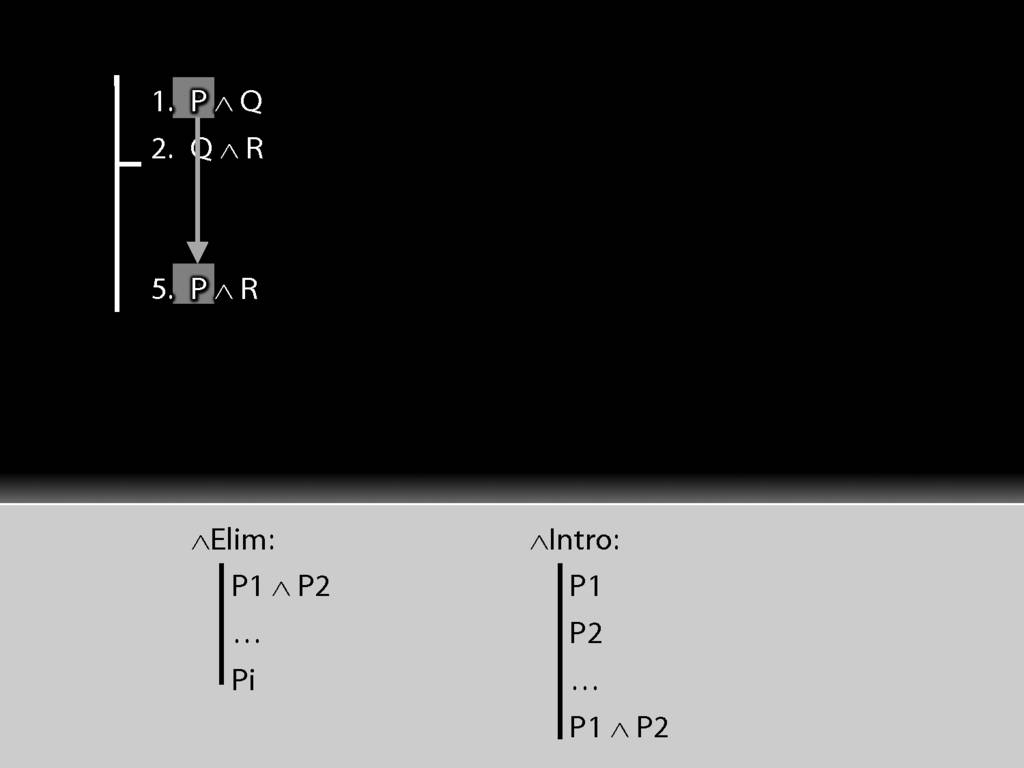
We have to get the P out of the conjunction and back into the conclusion.
How can we get P out of this premise?
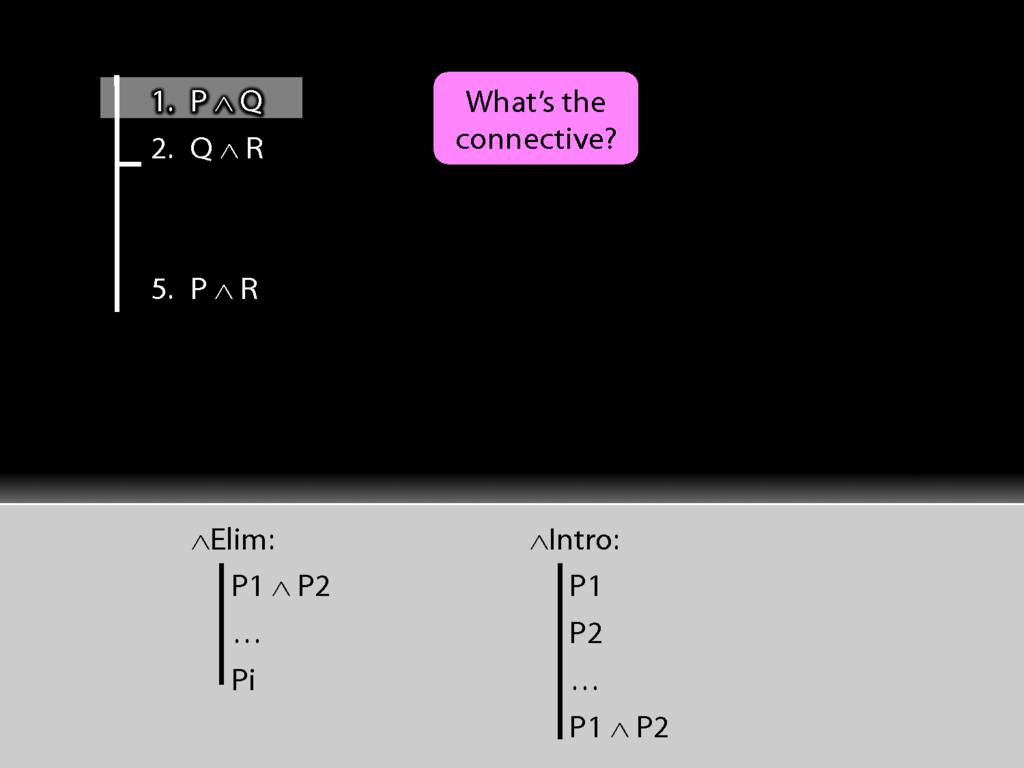
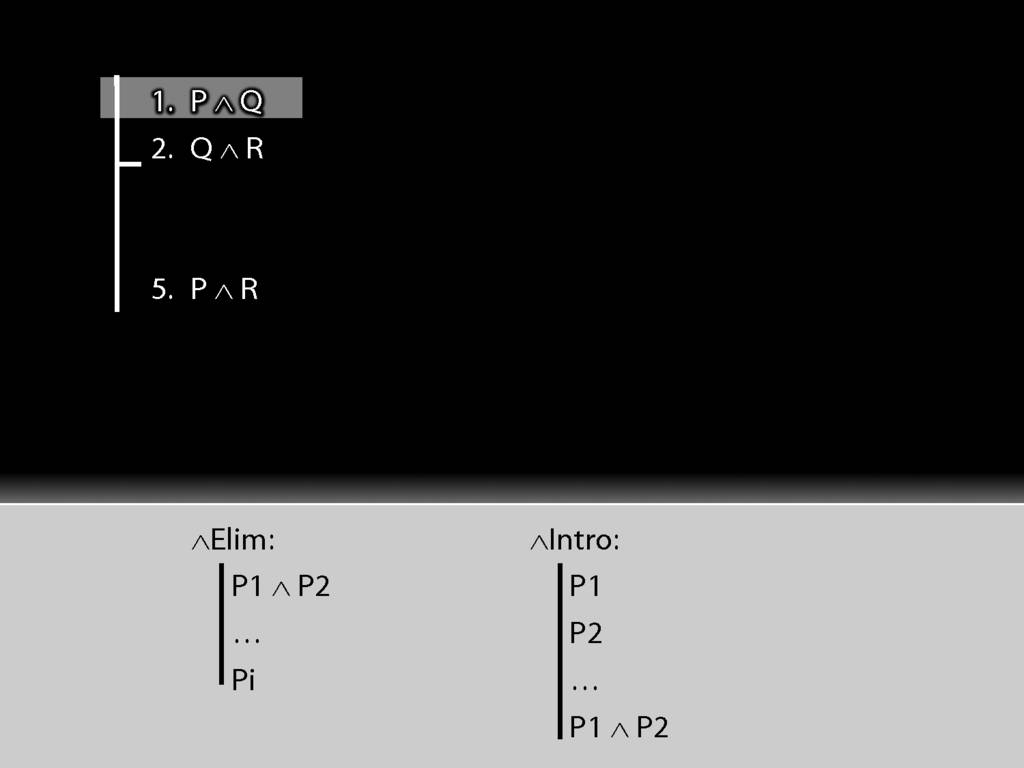
First we have to ask, What's the connective?
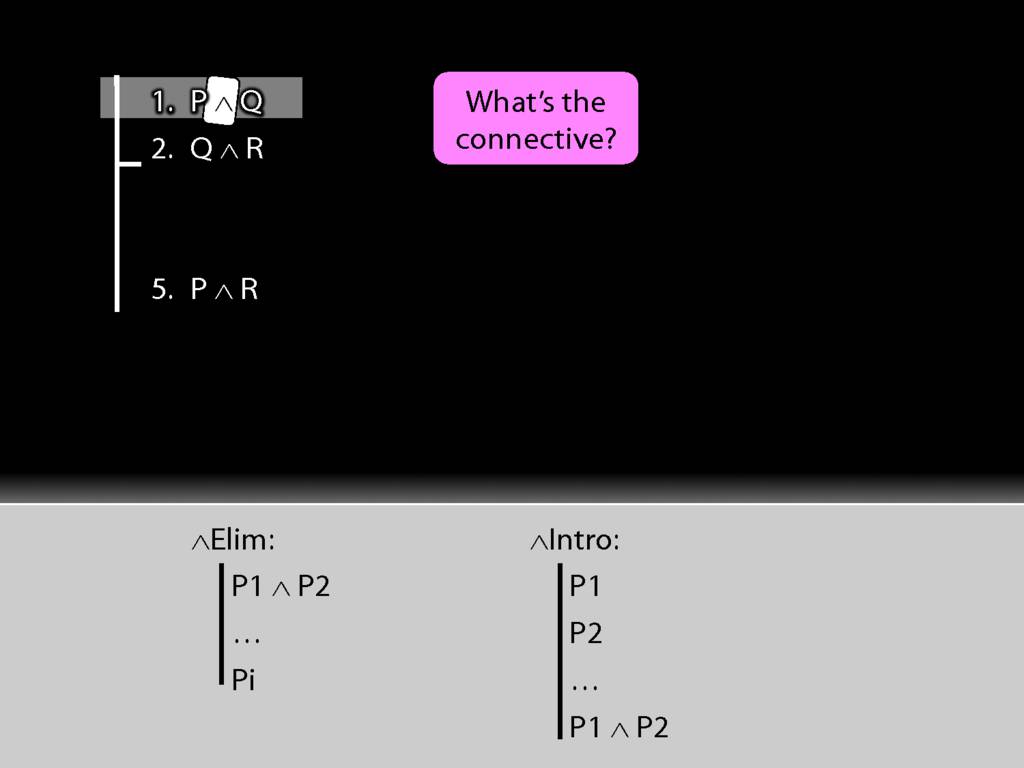
The connective is conjunction. This tells us we want to use a conjunction-rule. But is it the introduction or elimination rule that we need?
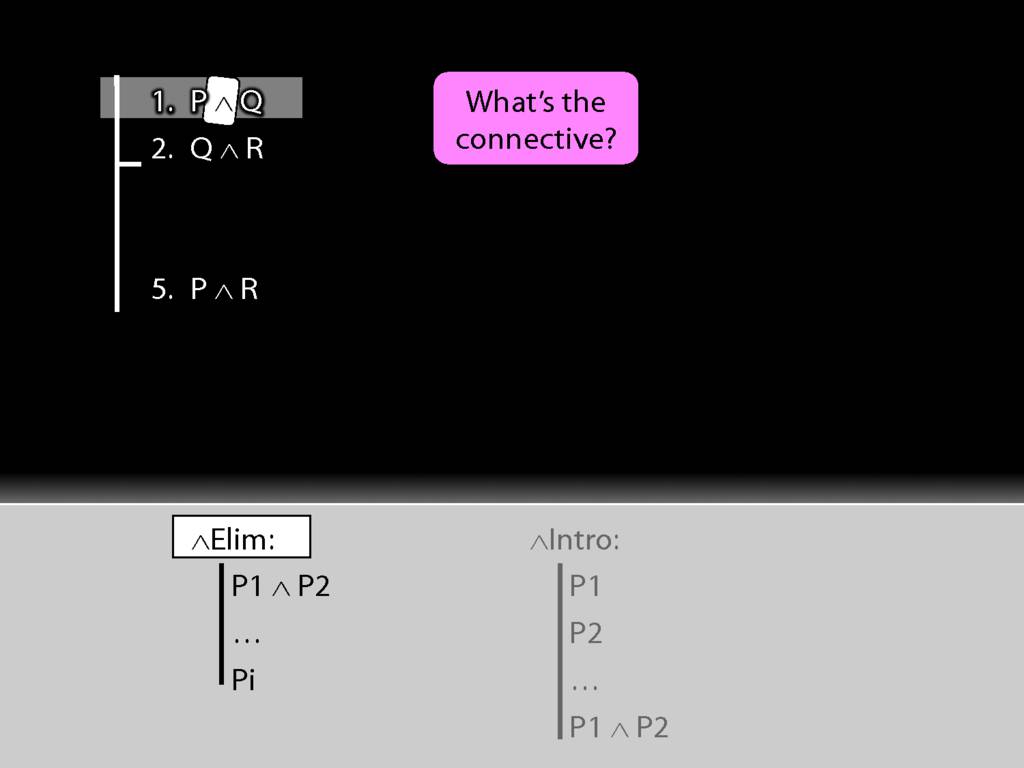
It's elimination. Nearly always we need elimination when we're acting on premises.
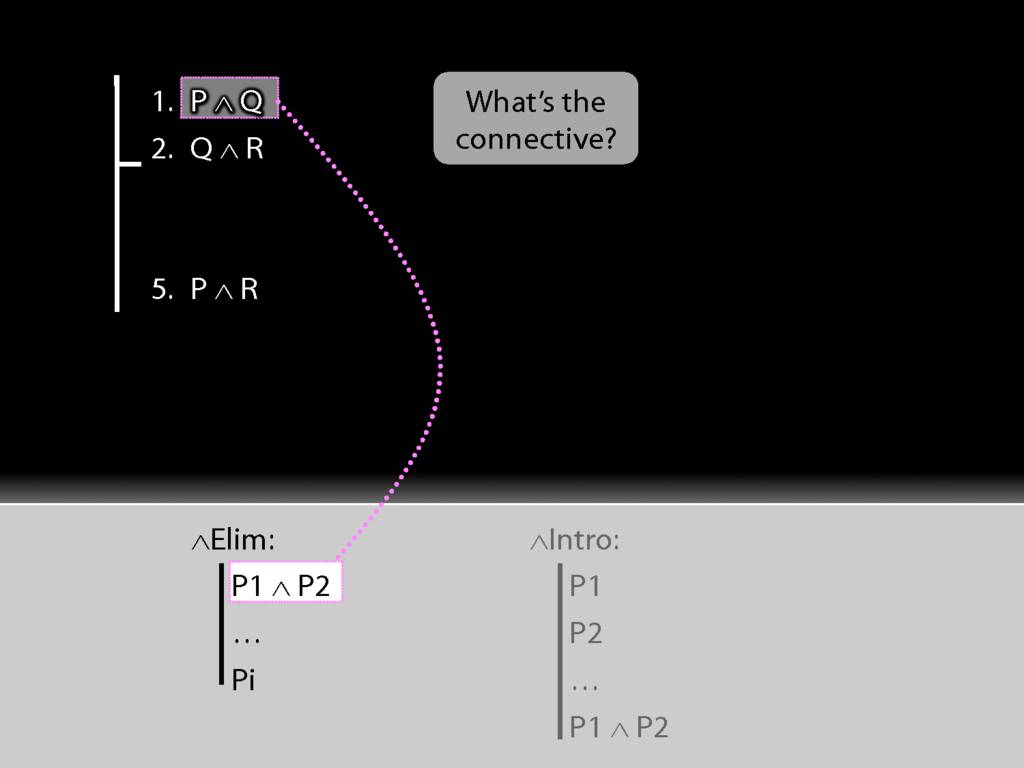
See how the rule matches our premise.
Because we have a match, we can use this rule to add a line to our proof.
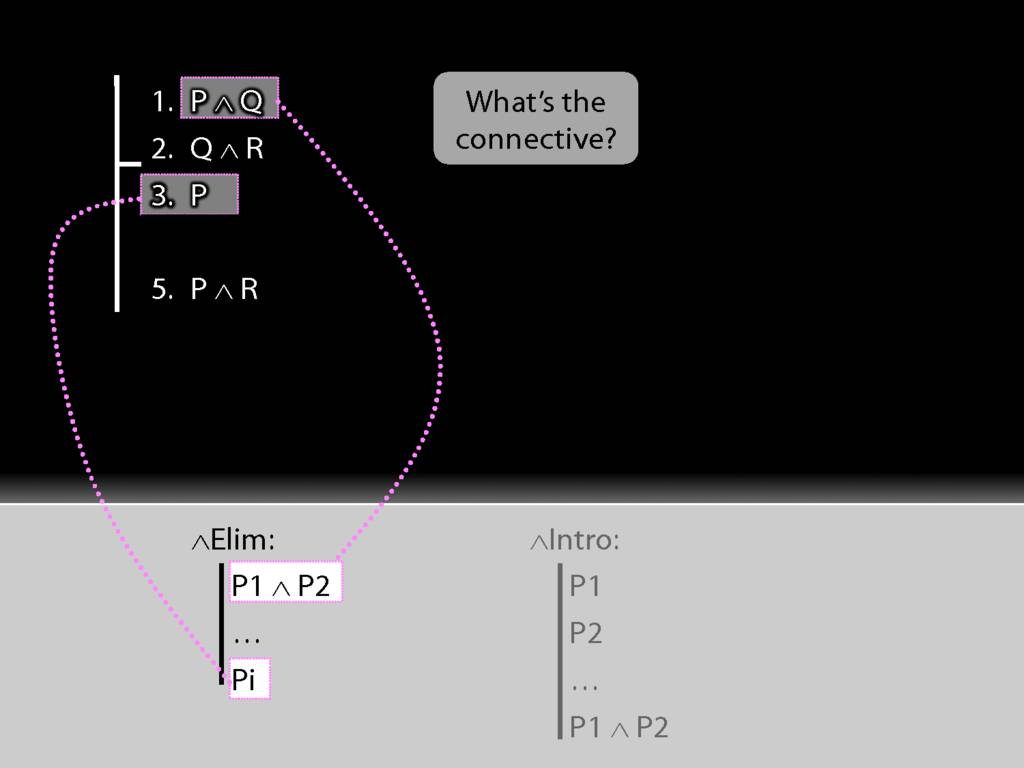
The rule allows us to add 'P' or 'Q' to the proof, but I've chosen to add 'P'.
Now having used the rule we have to explain exactly what we've done. This requires two things ...
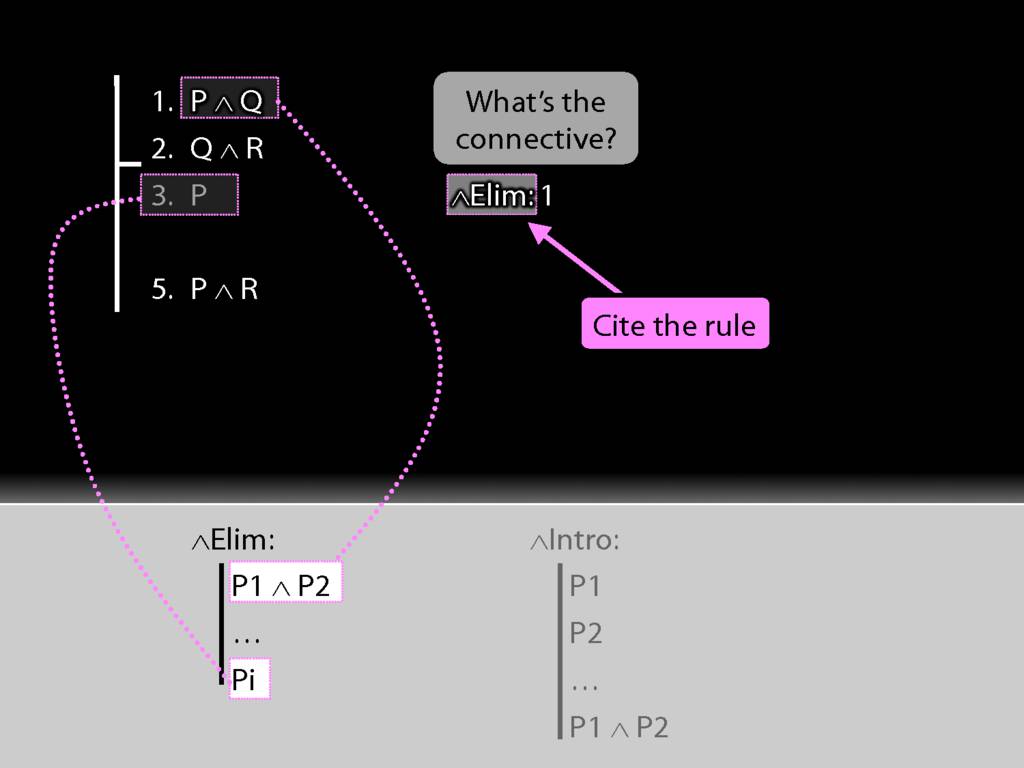
We must cite the rule used.
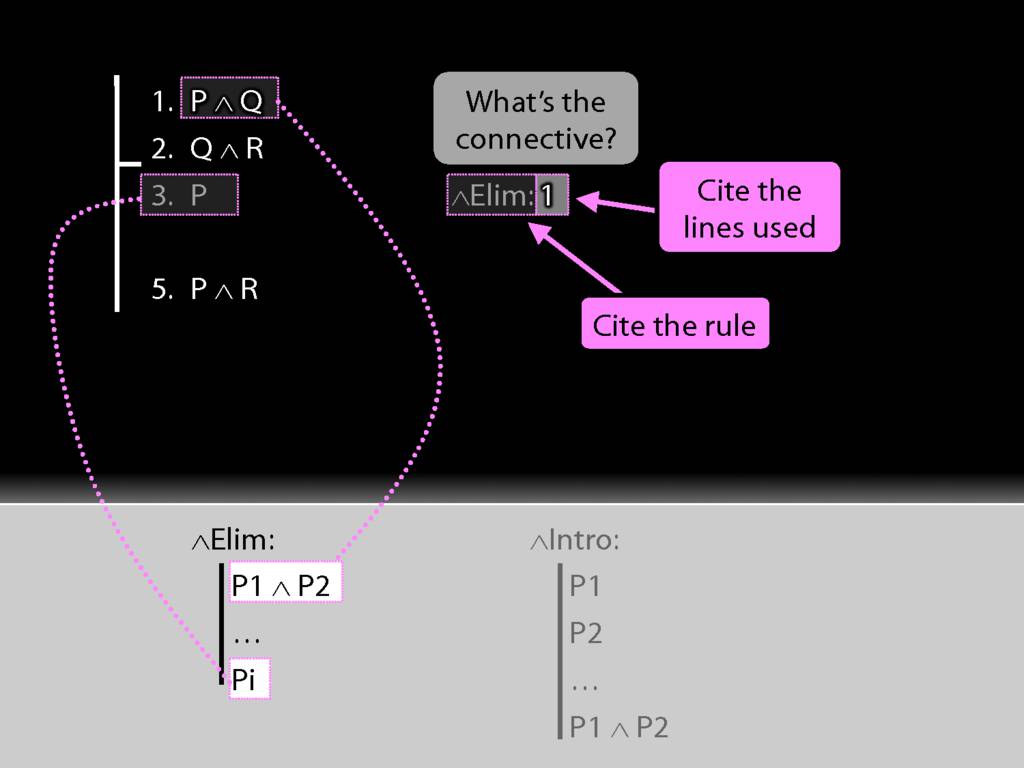
And we must cite the lines we applied the rule to.
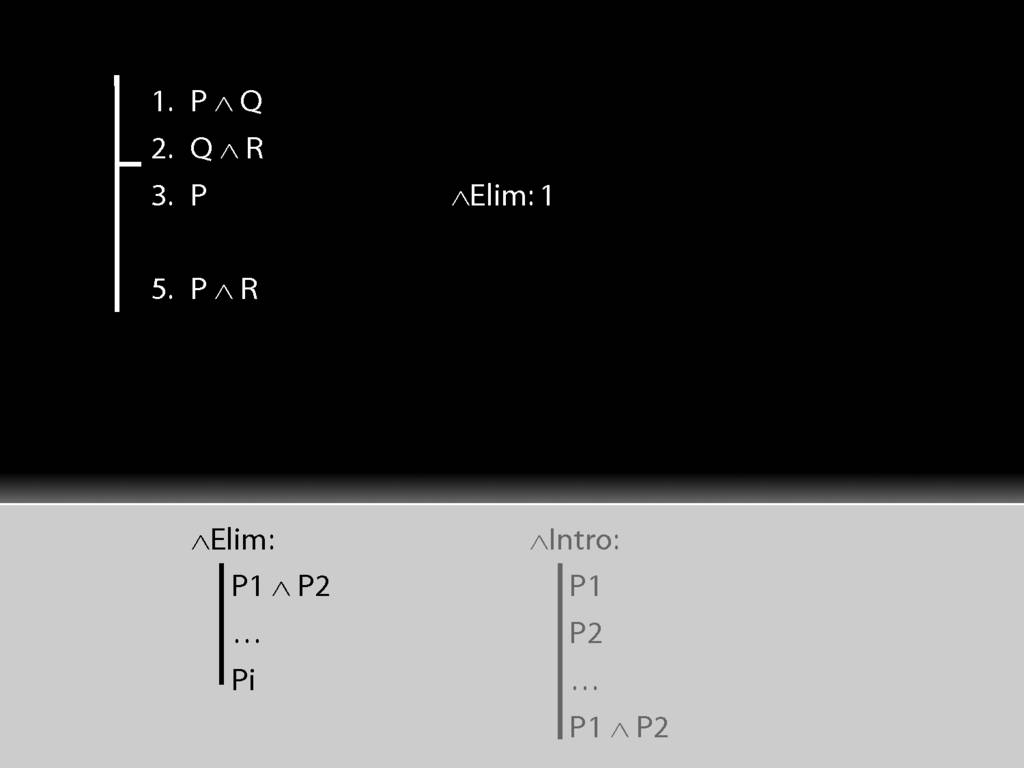
So far so good. Can you see what we should do next?

Getting the R out of the second premise can be done in exactly the same way.
Now, how are we going to get to the conclusion?
In general, we use introduction rules to get to the conclusion. And since this conclusion is a conjunction, we'll use conjunction-intro to get to it.

Look at the rule for conjunction intro.
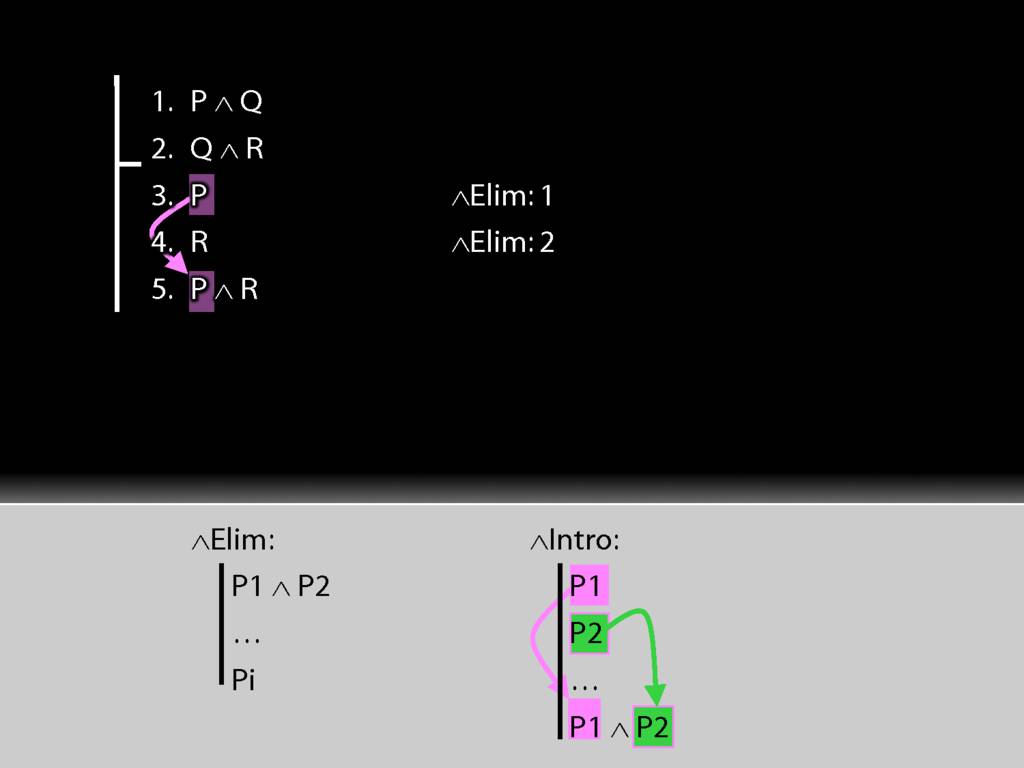
See how our proof fits the pattern of the rule.
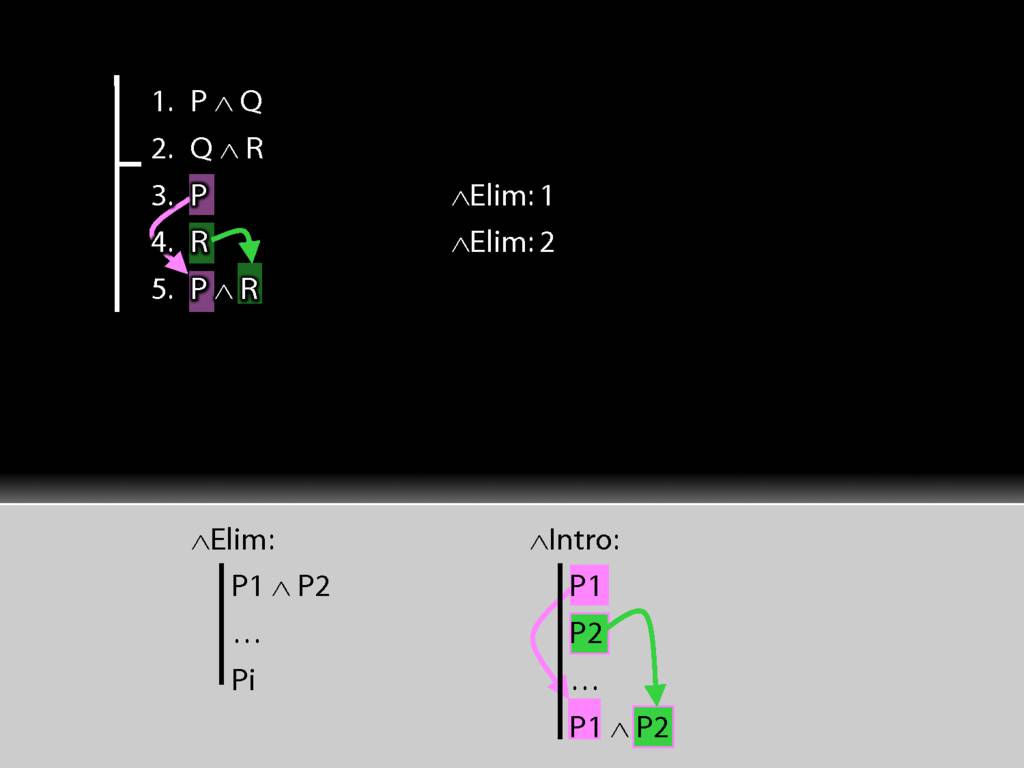
So it turns out we already did what we need for conjunction intro.
All that's left is to explain what we've done. As before this requres two things.
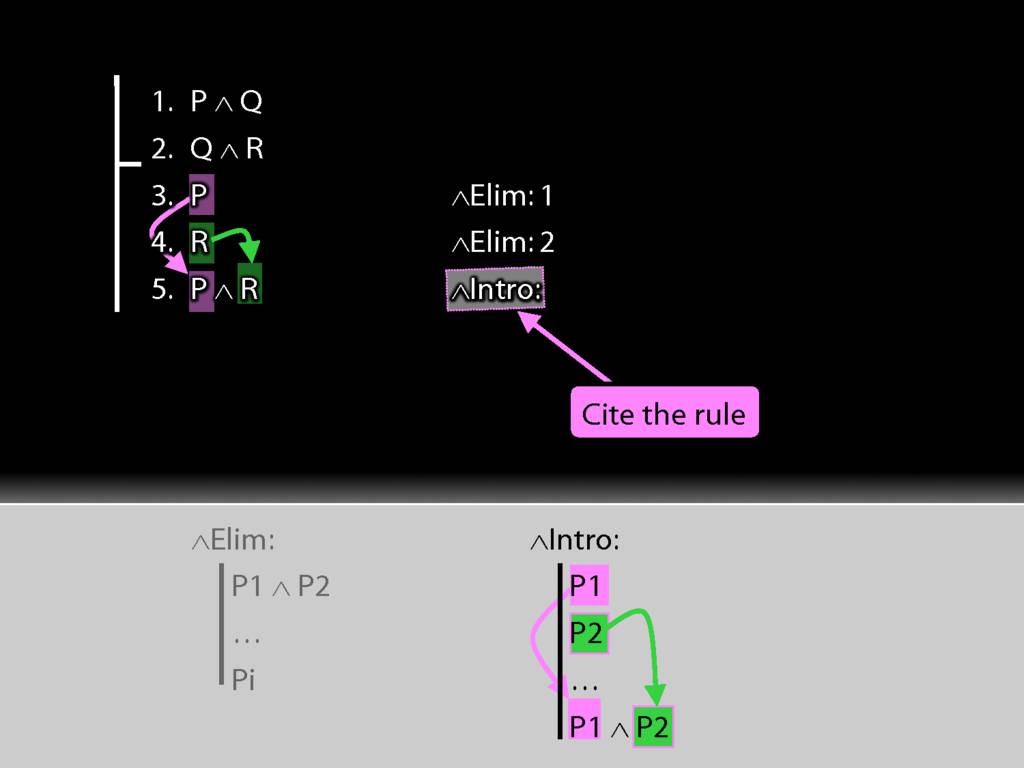
We must cite the rule used.
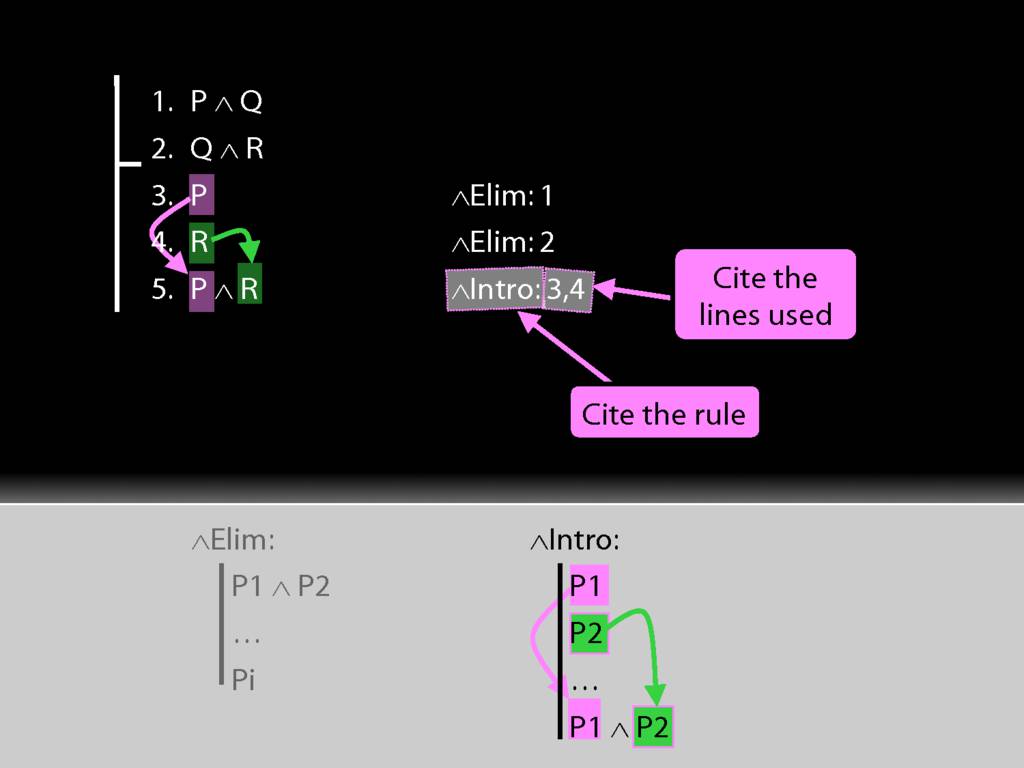
And we must cite the lines we applied the rule to.

Note the pattern of rules that we have for conjunction: introduction and elimination.
For each connective we'll have such a pair of rules, one introduction rule and one elimination rule.

With the elimination rule, we have the connective at the start and we eliminate it in applying the rule.

See how this worked in our proof.

With the introduction rule, we don't have the connective at the start and we introduce it by appling the rule.
Here's how we did it in the proof.
If you've been following all this, you know everything you need to know to use conjunction intro and conjunction elim in proofs.
You also know how to do Fitch proofs. The rest is just a matter of learning more rules.
Now it's possible you haven't entirely been following all this ...

... When I was learning logic, I often didn't immediately understand the lectures and needed
to go back over my notes after each lecture.
Hopefully you will do the same because I don't really have the patience for spoon feeding.
\textbf{Writing a proof in zoxiy}
https://logic-ex.butterfill.com/ex/proof/from/A and B|B and C/to/A and C
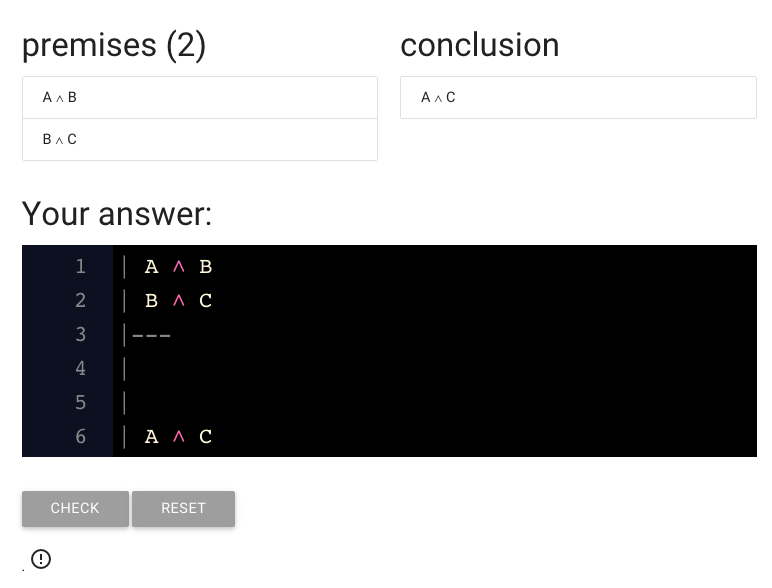
When you start an exercise, you’re already given the basic form of
the proof, with a couple of blank lines.
The box you’re working in is just a text editor.
You can add lines by pressing ‘return’ and delete lines
just like you would in any text editor.
To repeat: the proof is just some text that you edit in the normal way.
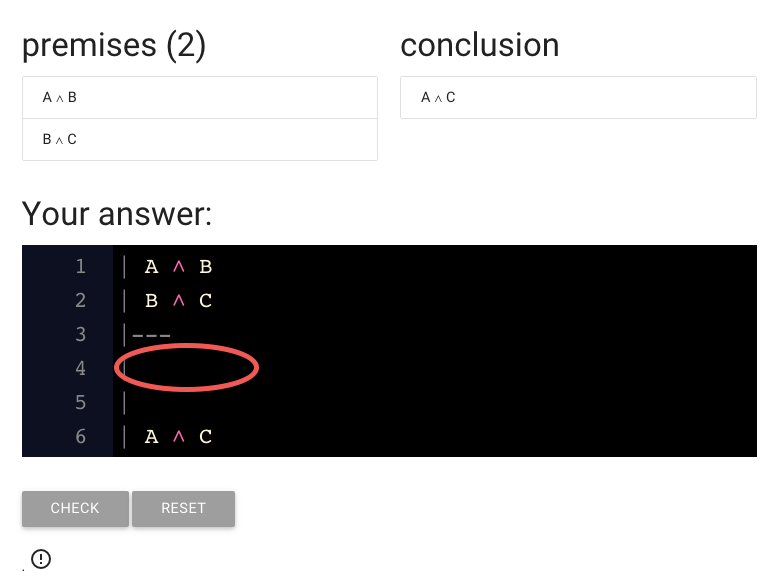
We just need to a step here.
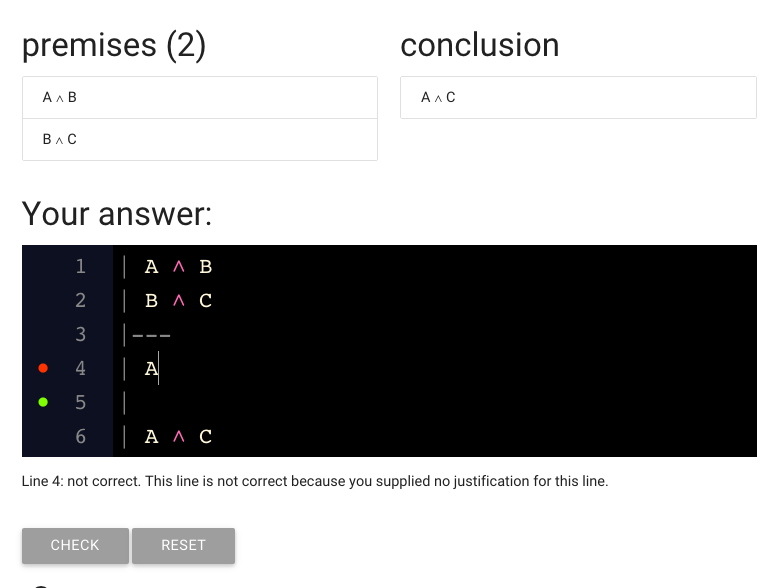
I’ve gone ahead and typed A because we need to derive A from the premises.
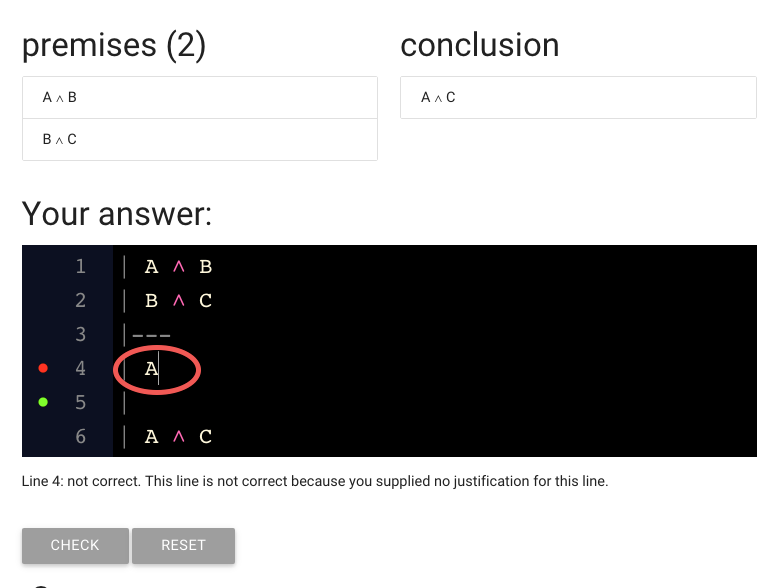
Here’s the A I typed.
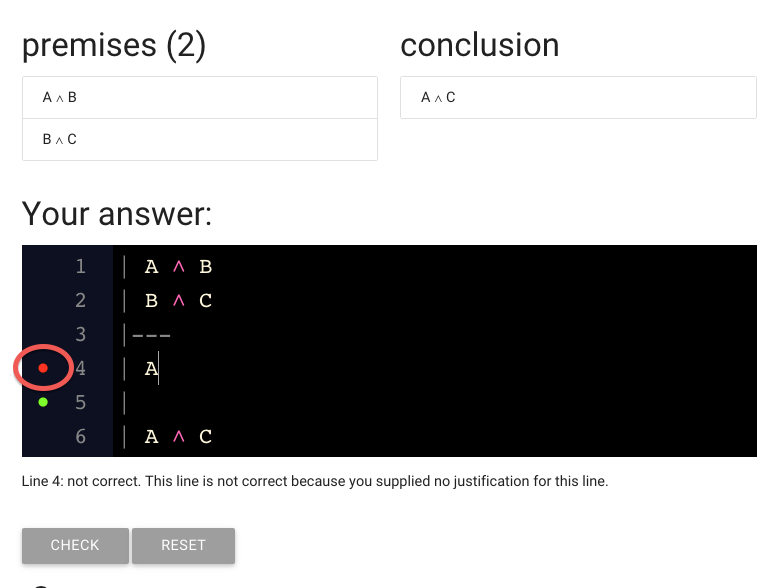
This red dot suggests that there is a problem with the line.
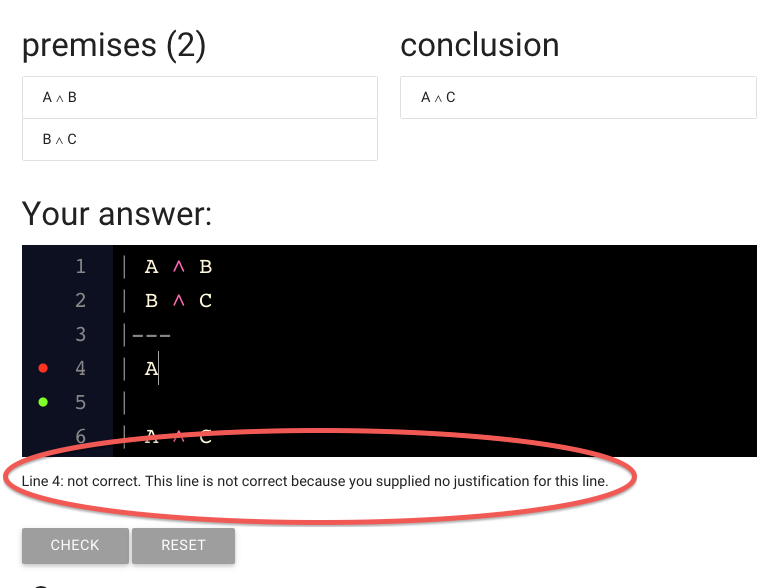
The text under or proof is giving us a clue: we didn’t justify the step yet.
Let’s do that now.
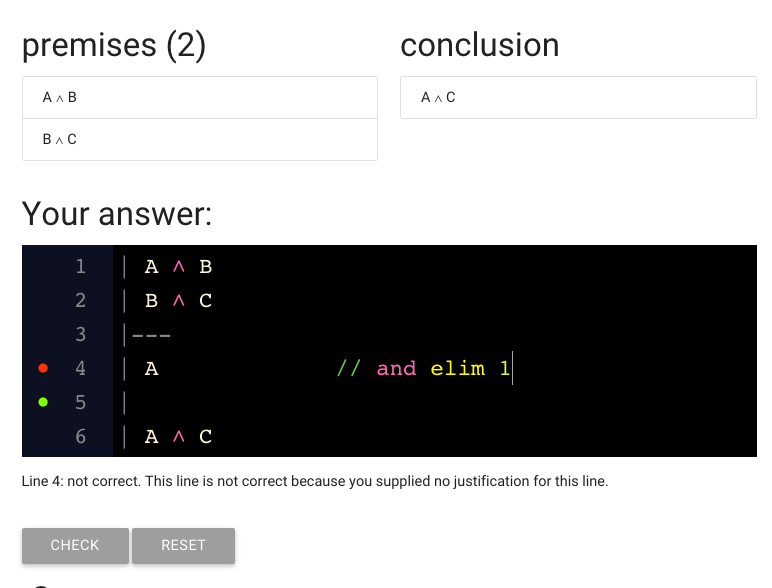
Here I’ve added justification.
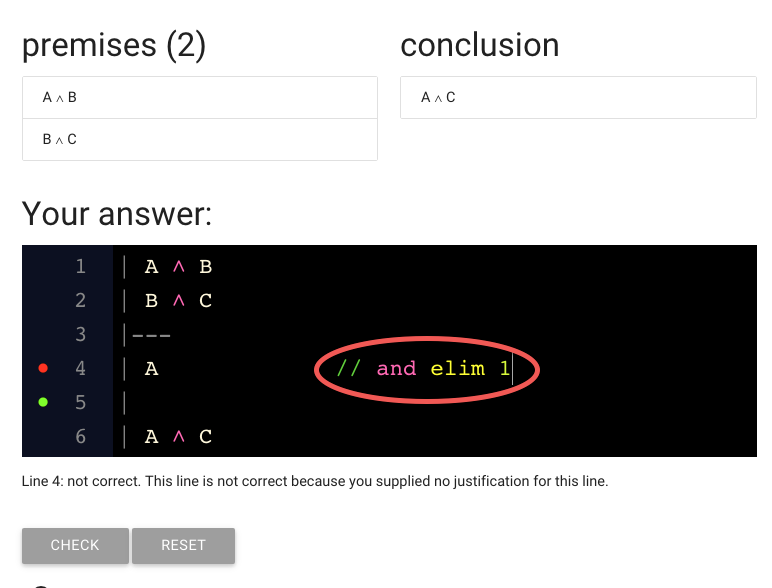
It’s over here on the right (I just added spaces to move it away from the sentence ‘A’).
I want to mention a couple of conventions.
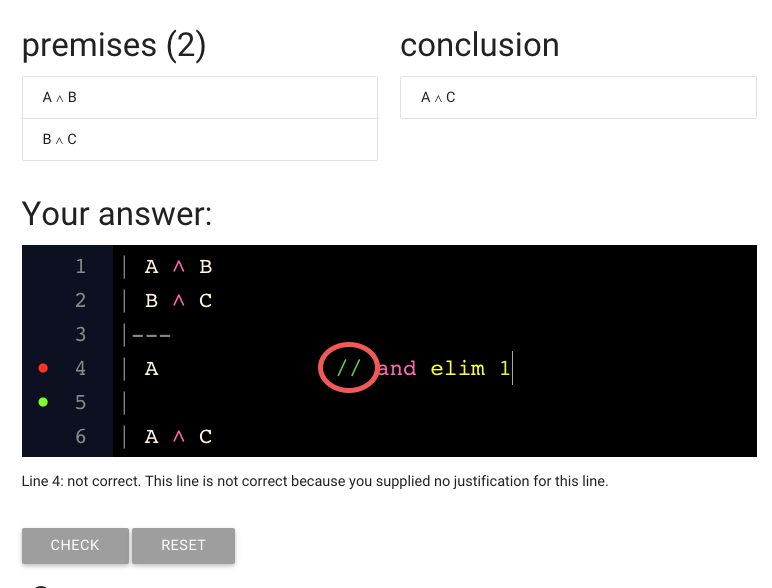
First, justification needs to start with ‘//’. This is to separate justification
from the sentence itself.
If you forget the ‘//’, zoxiy won’t be able to understand your proof and won’t
be able to explain to you what went wrong.
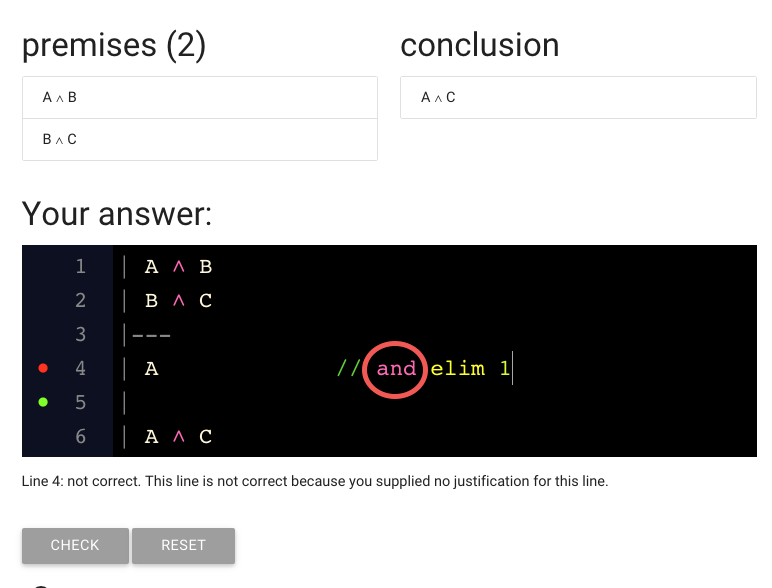
The next thing to note is that I typed the word ‘and’ rather than the symbol
for conjunction (‘∧’). As a convenience, zoxiy will let us use words
rather than making us type symbols. But we can type the symbols if we prefer.
The same is true when we’re writing sentences: you can type ‘A and B’ instead of
‘A ∧ B’ if you like.
This is a handy feature of awFOL vs the language of the textbook we’re using.
awFOL let’s you use words where really there should be a symbol, just to make
it easy to type things.
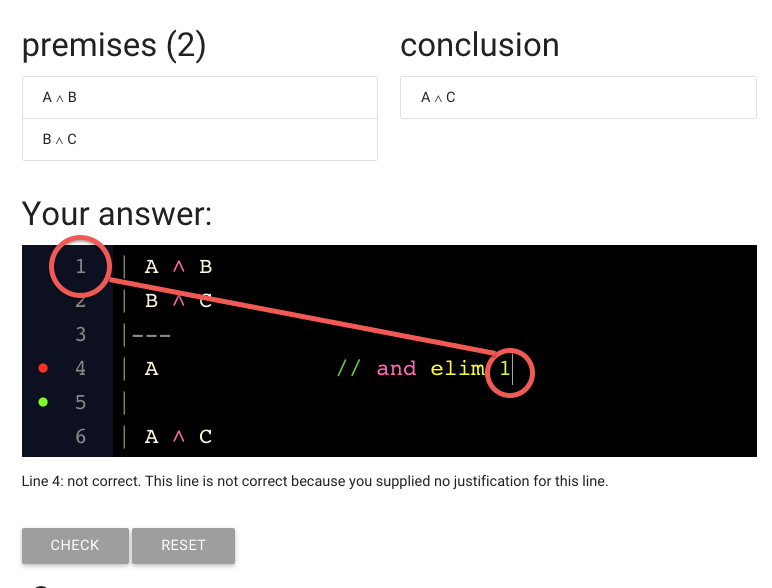
Finally, note that we put a number at the end. This is the number 1,
which refers to the first line.
zoxiy provides line numbers for us (you can add your own
if you prefer, but then you have to be really consistent about
starting each line with a number).
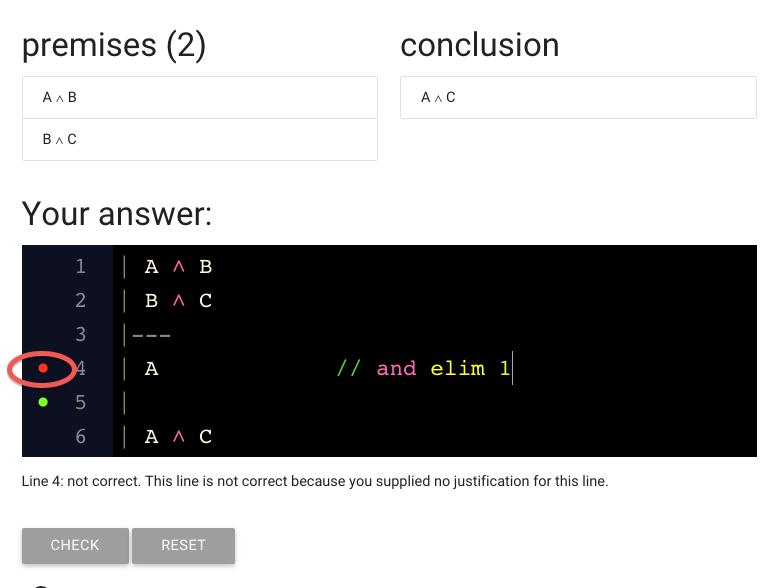
Wait a minute. We still have that red dot and the error message
telling us our line is not justified. But we have added the justification.
What’s going on?
zoxiy might be a bit slow to update. In this situation, just move your
cursor up and down to get zoxiy to check your line again.
Let me do that now ...
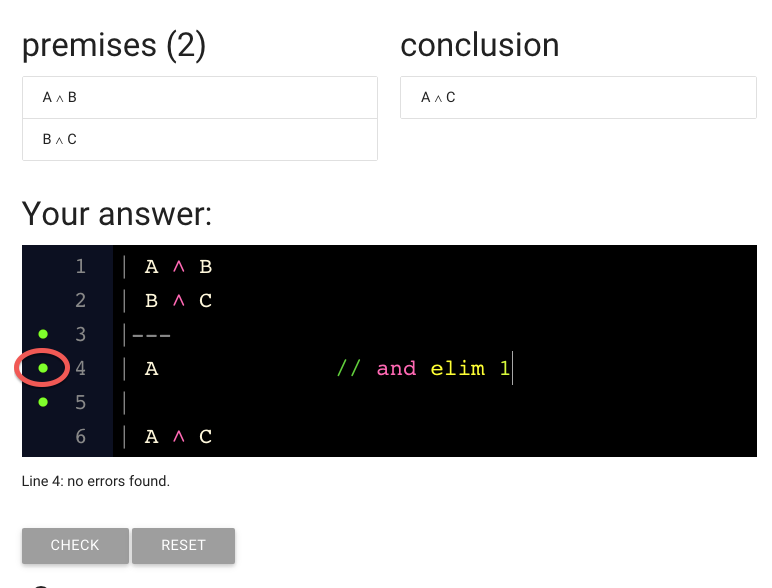
... and the dot has turned green, indicating that this line is ok.
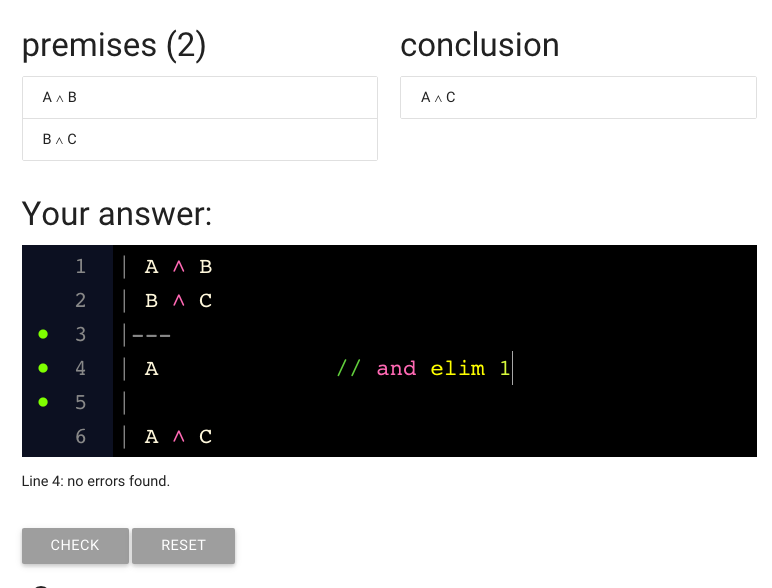
What’s next?
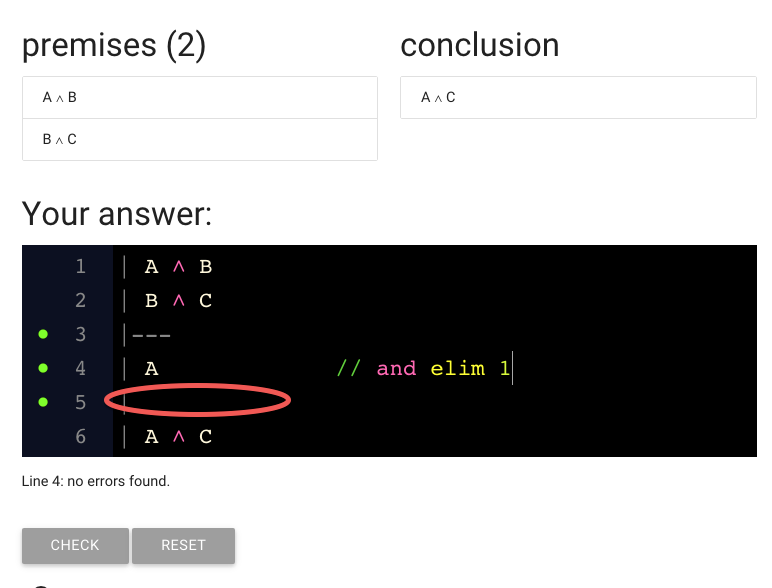
We need to add another step to the proof.
(It just happens that we have the right amount of space for this proof,
but generally you are going to have to add lines to your proof. Do this
with the return key, as mentioned above.)
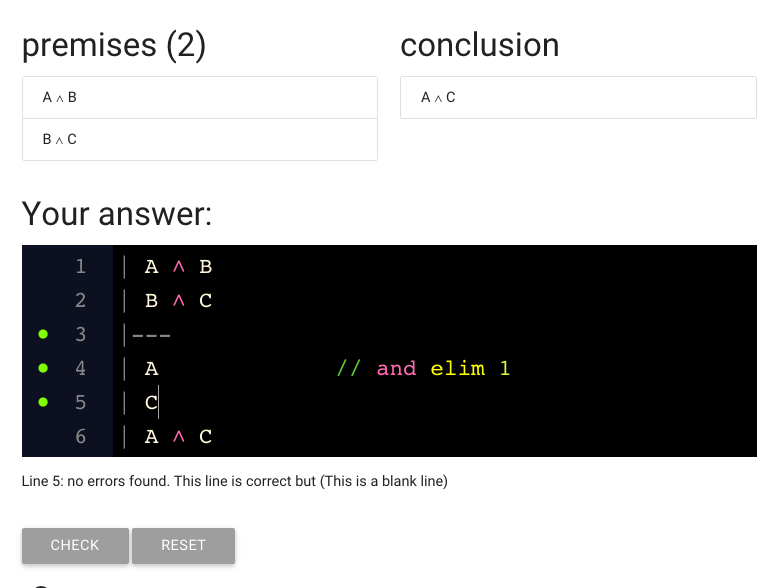
Here I’ve added the setntence we need (‘C’).
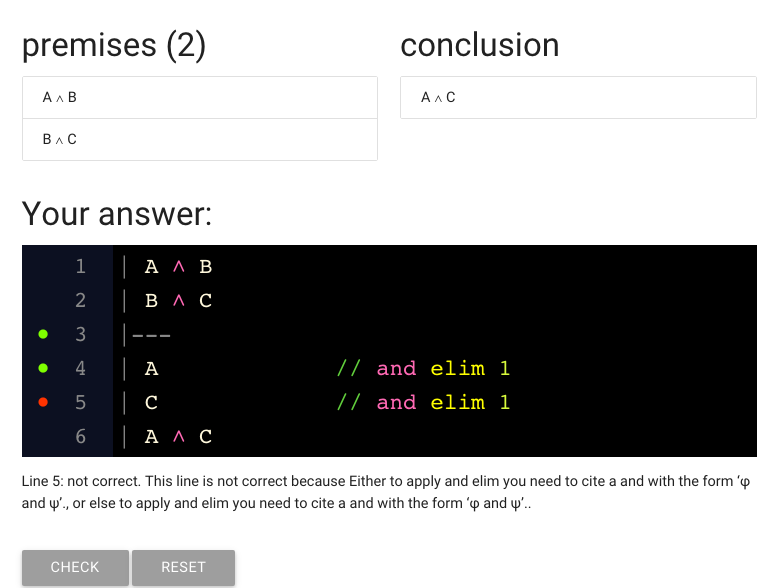
And here’s the justification as well.
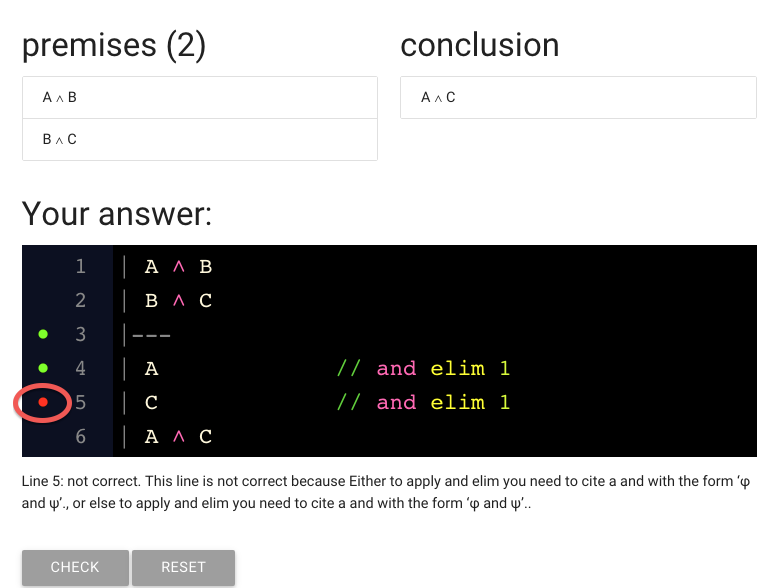
But wait, the red dot is back.
That means there’s something wrong with the line.
What has gone wrong?
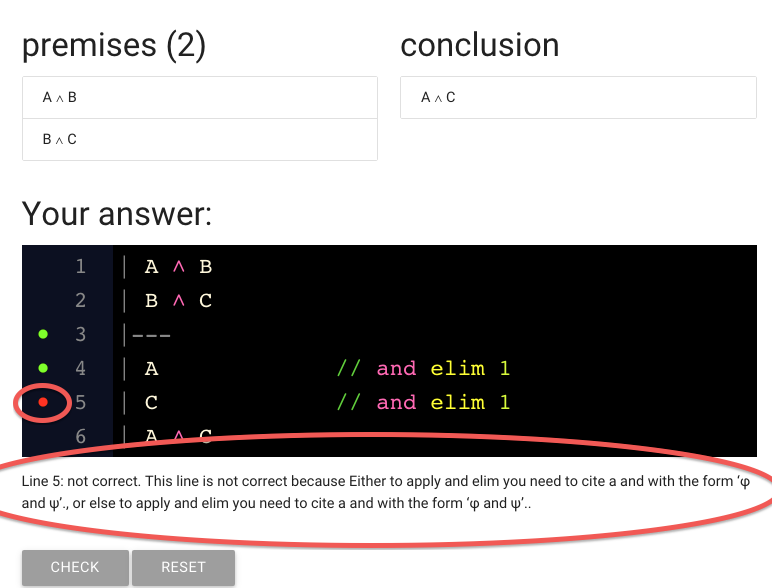
The status message is really unhelpful in this case, as it often will be.
(Maybe it will be improved at some point.)
Sorry about that.
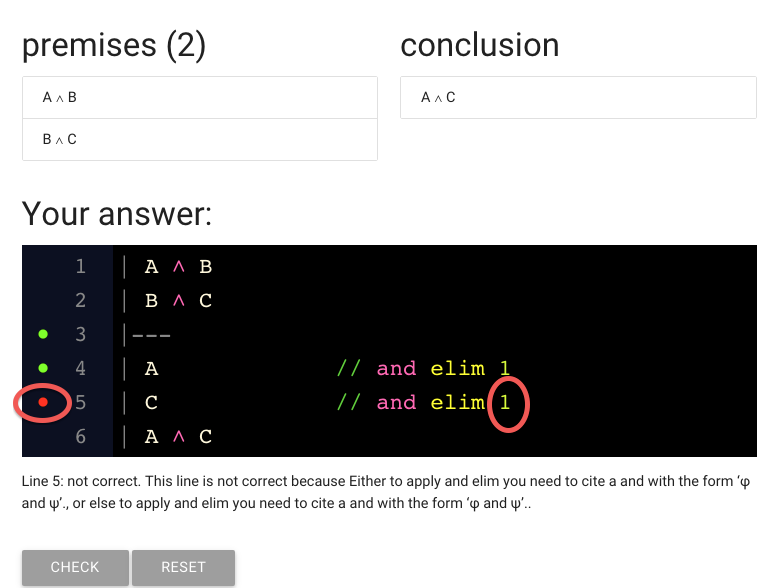
What could have gone wrong? Note that we’re citing line 1.

So let’s have a look at line 1.
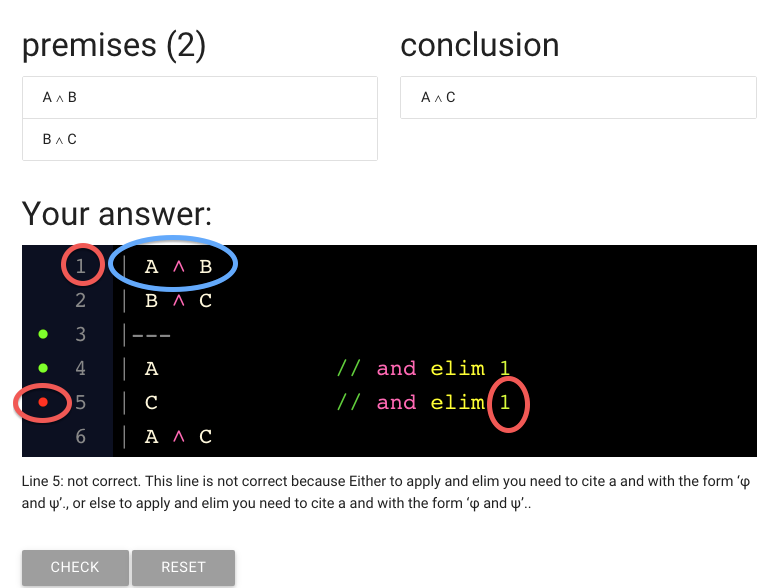
This line contains ‘A and B’.

But actually we’re trying to derive C.
And you can’t derive C from A and B.

The C we want to derive is actually here, in line 2.

So we have to edit the line number.
(This kind of mistake tends to happen to me quite a bit because
I like to copy and paste justification to save typing)
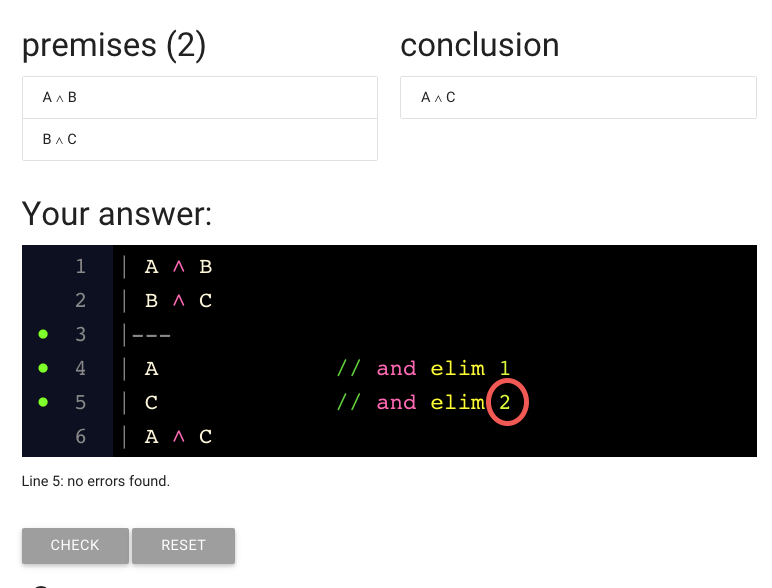
Here I’ve fixed the line number.
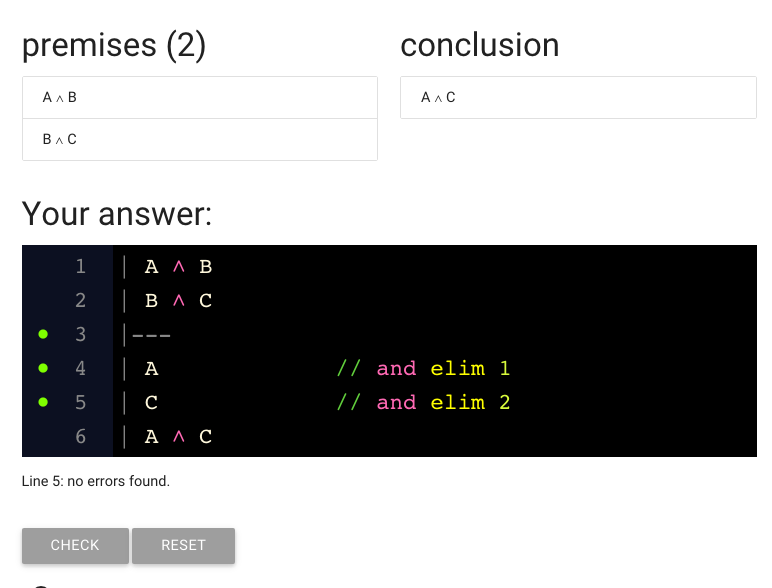
What’s next?
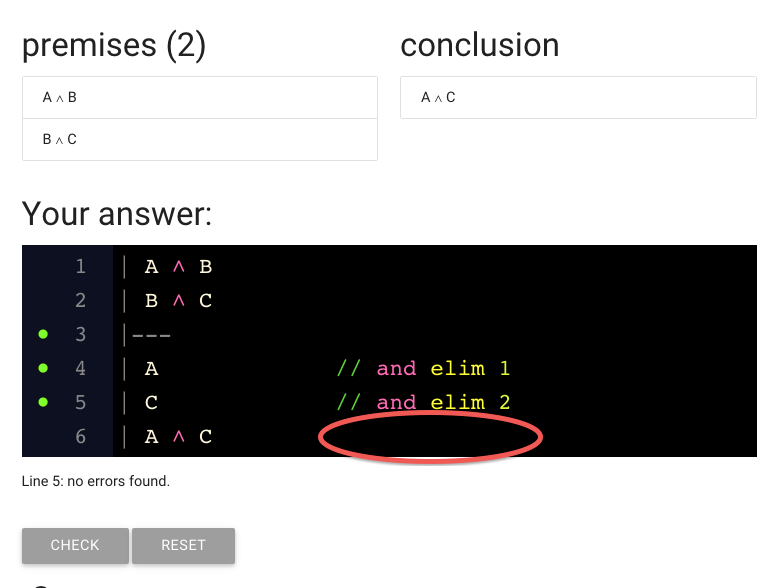
There’s a big whole where the justification for the last line should be.
(Remember that every line of the proof is either a premise or needs justification.)

So I’ve gone ahead and added the justification.

But it hasn’t worked: we’ve got the red dot again.
Unless you’re really good at logic, you’re going to be seeing a lot of the red dot
for a few weeks.
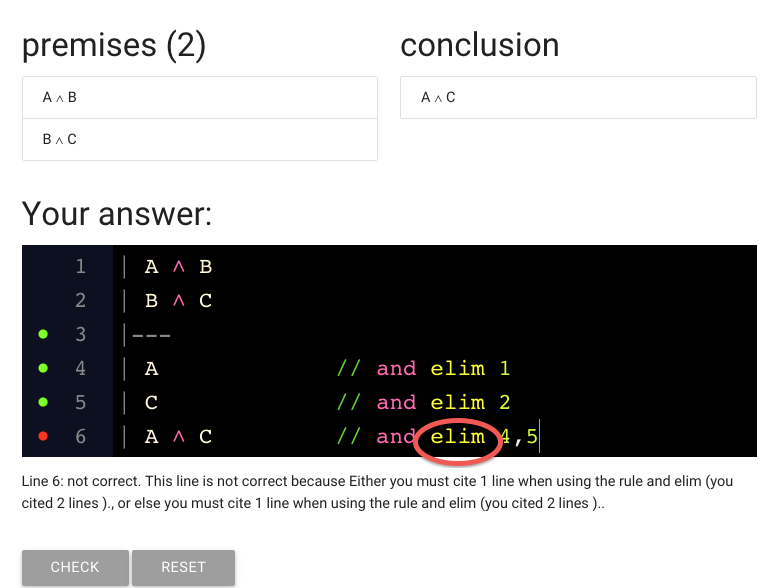
Here’s the mistake: we’re still citing and elim.
But at this point we’re supposed to be *introducing* a conjunction
rather than eliminating one.
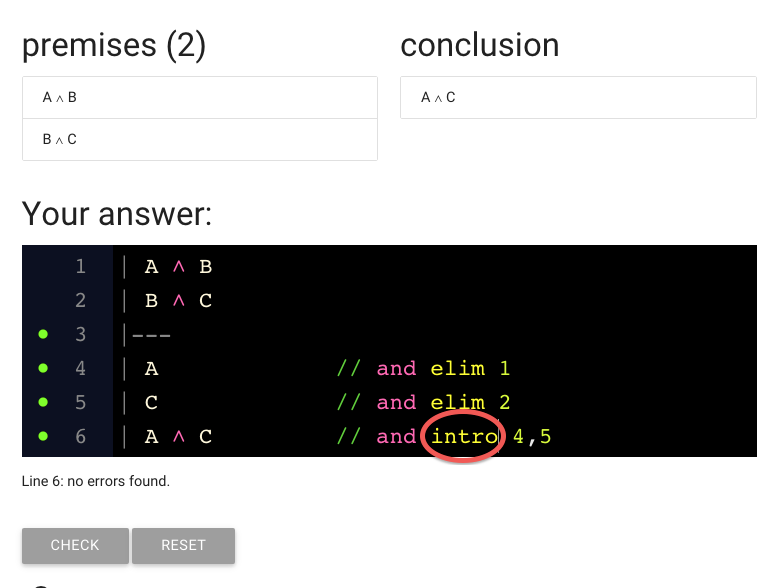
We can fix this just by deleting ‘elim’ and replacing it with ‘intro’
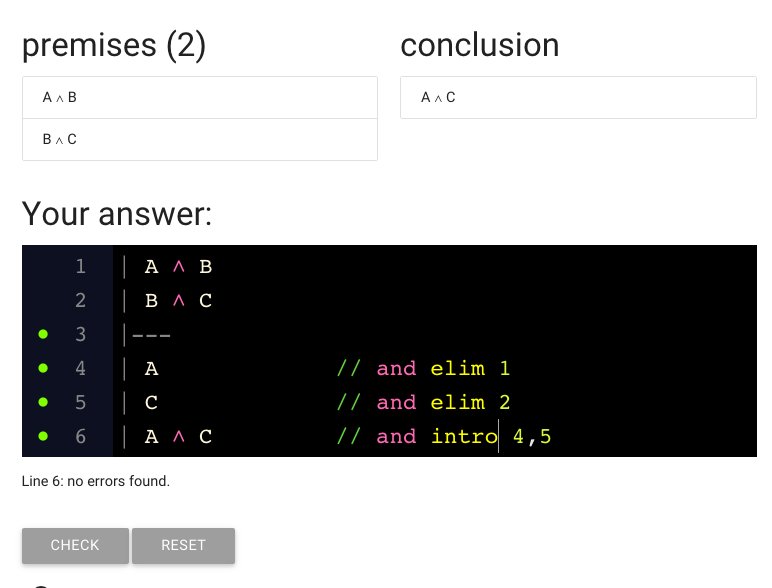
And here’s the finished proof.
This is correct; if you submit it, zoxiy should say your proof is correct.
6.1
5.3--5.6

∧Intro and ∨Intro: Compare and Contrast
\section{∧Intro and ∨Intro: Compare and Contrast}
\emph{Reading:} §6.1
\section{∧Intro and ∨Intro: Compare and Contrast}
How come we can prove only valid arguments?
How come we can prove only valid arguments?

Here is a new rule of proof, called disjunction intro.
∨Intro is saying that if you have any sentence, you can add a line to your proof containing a disjunction of that sentence and any other sentence you like.
Explain ∨Intro with an example: if you know Ayesha is in the garden but don’t want to give this away but do want to speak the truth you can say “Ayesha is in the library or Ayesha is in the garden”.
The transition from 'Ayesha is in the garden' to 'Ayesha is in the garden or Ayesha is in the library' is the transition that disjunction intro allows you to make in formal proofs.
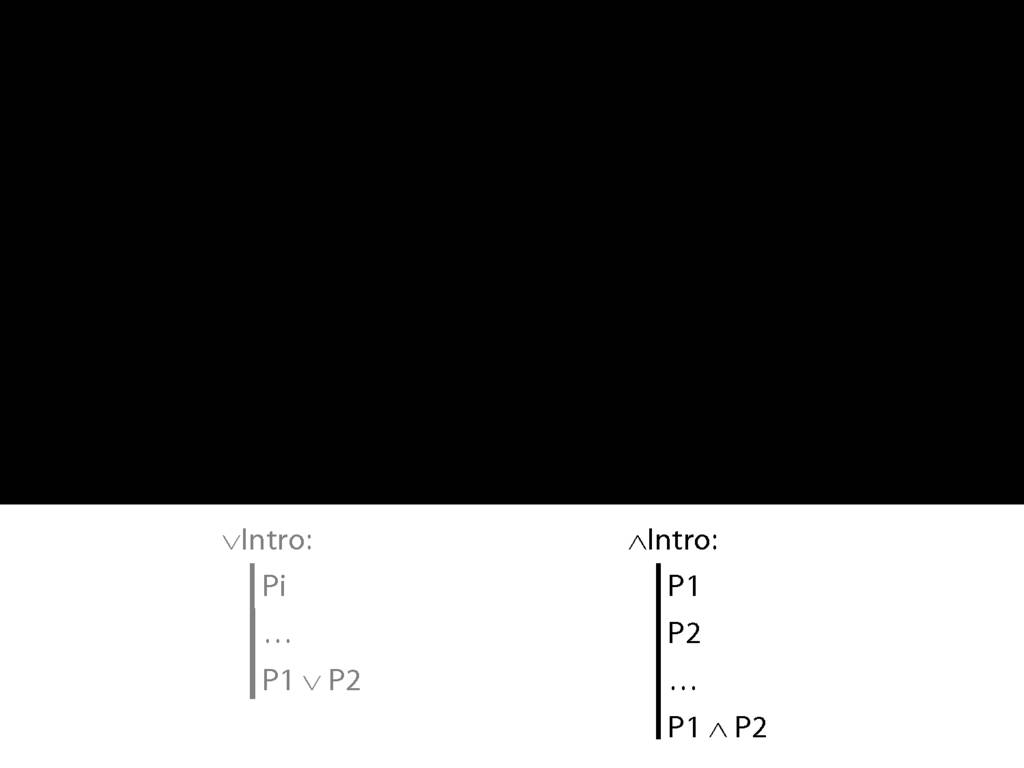
Contrast ∧Intro ...
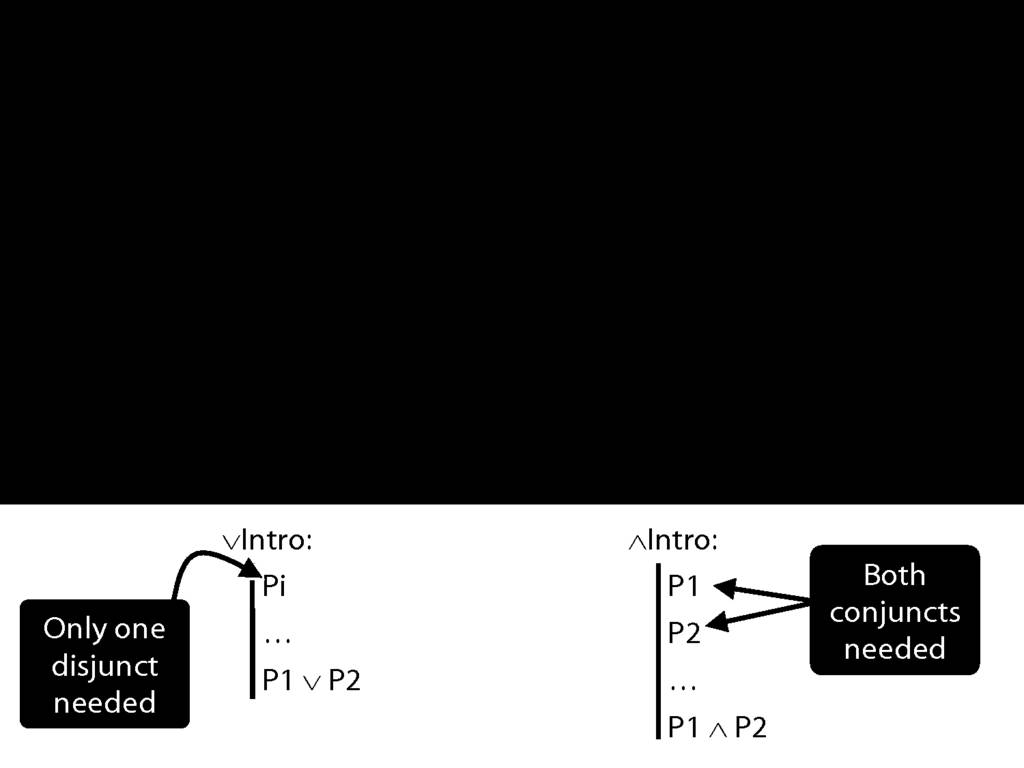
∧Intro is just like ∨Intro except that you need both conjuncts for ∧Intro.
Why should we have set things up like this? Why is using ∧Intro more demanding than using ∨Intro?
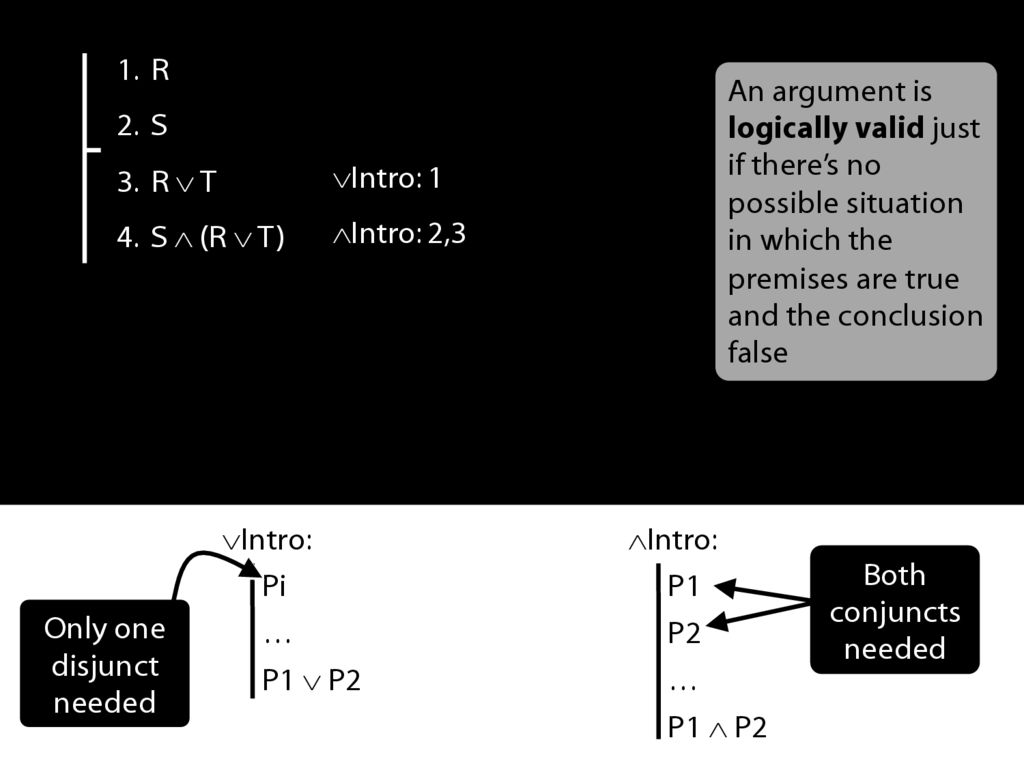
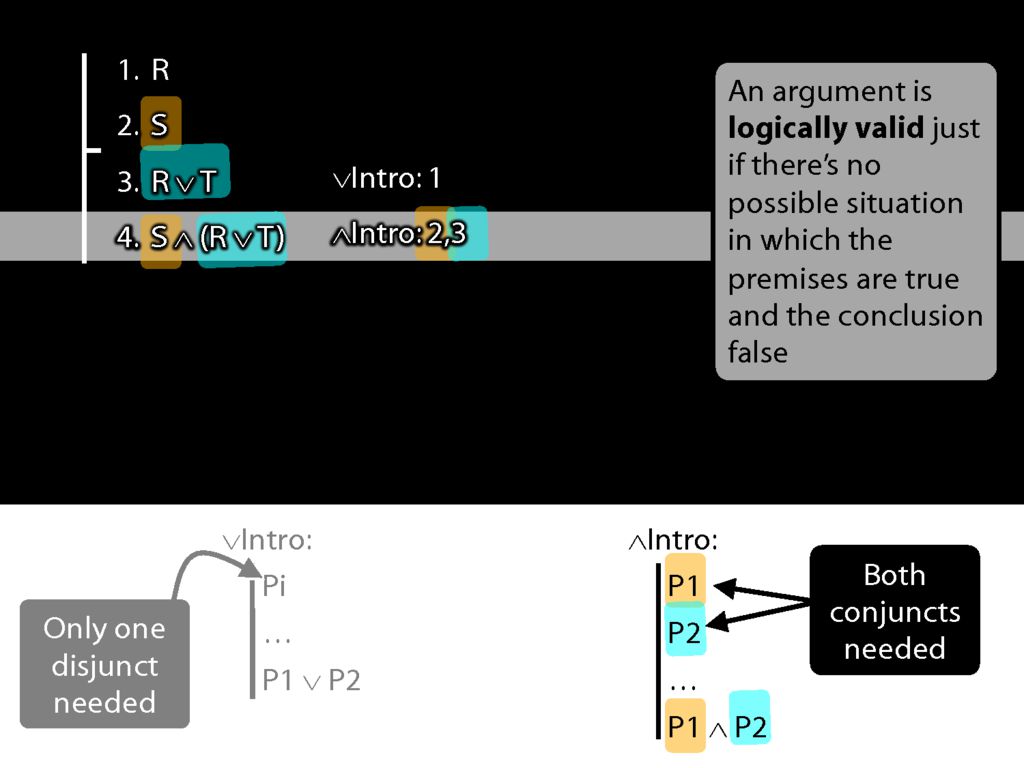
Let's have a look at a proof involving these two rules.
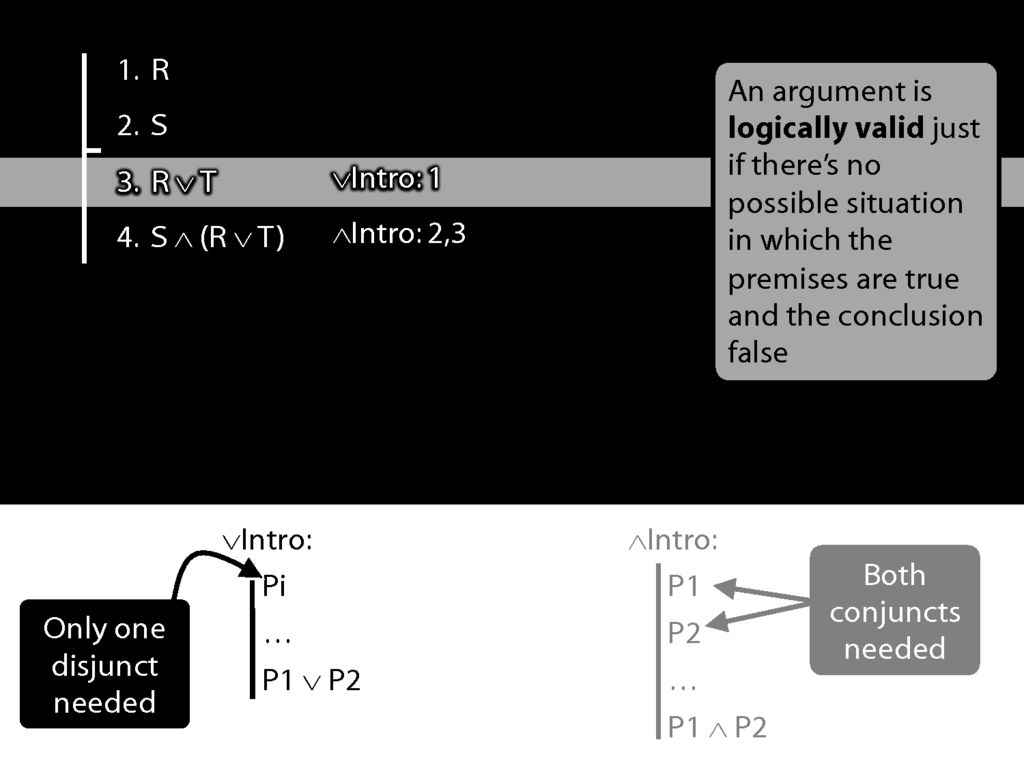
We're using ∨Intro at line 3 to get R∨T.
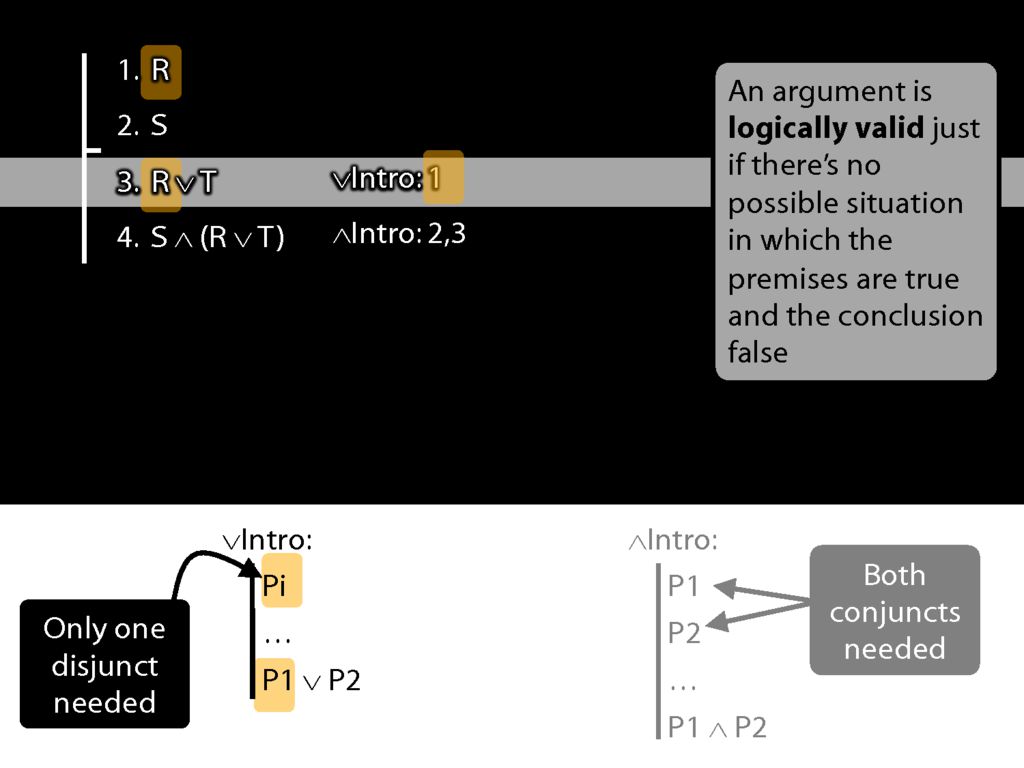
See how what we've done matches the rule. (Sometimes people ask, Where does the T come from? The answer is: it just comes from nowhere.)
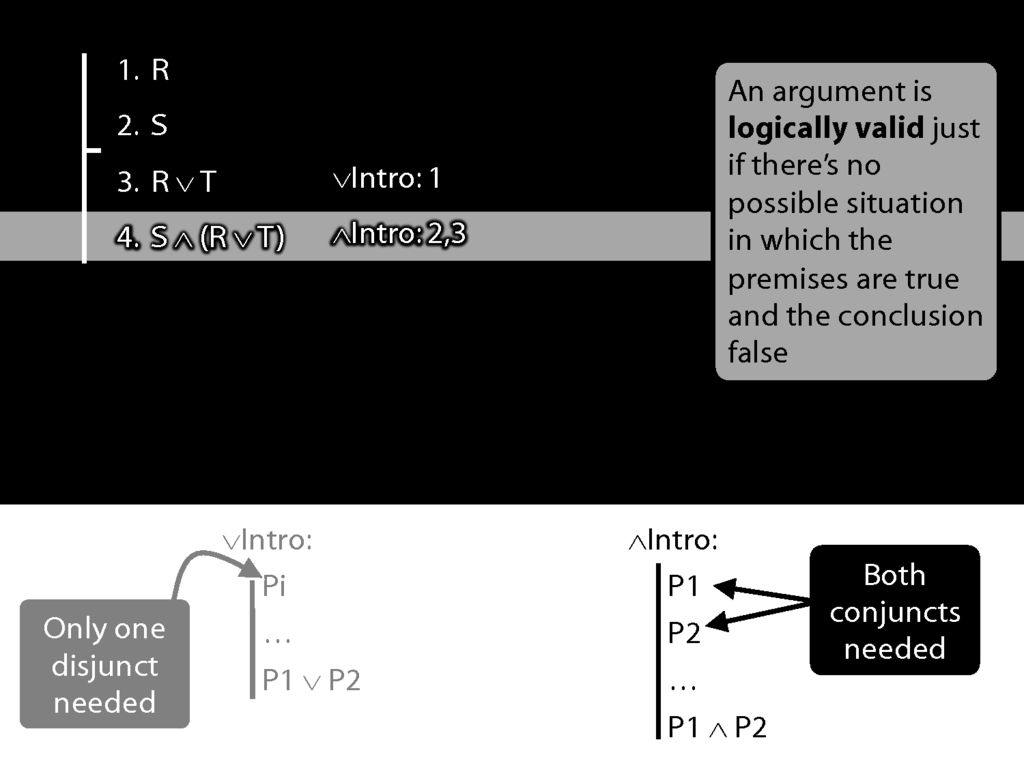
Now we're using ∧Intro.
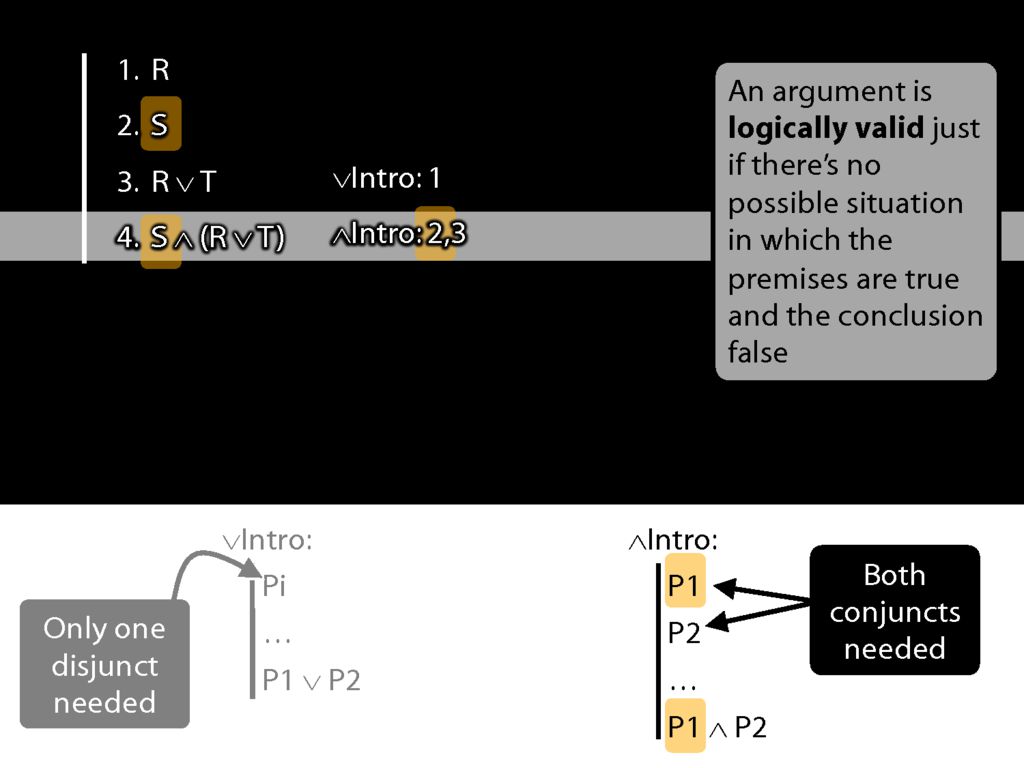
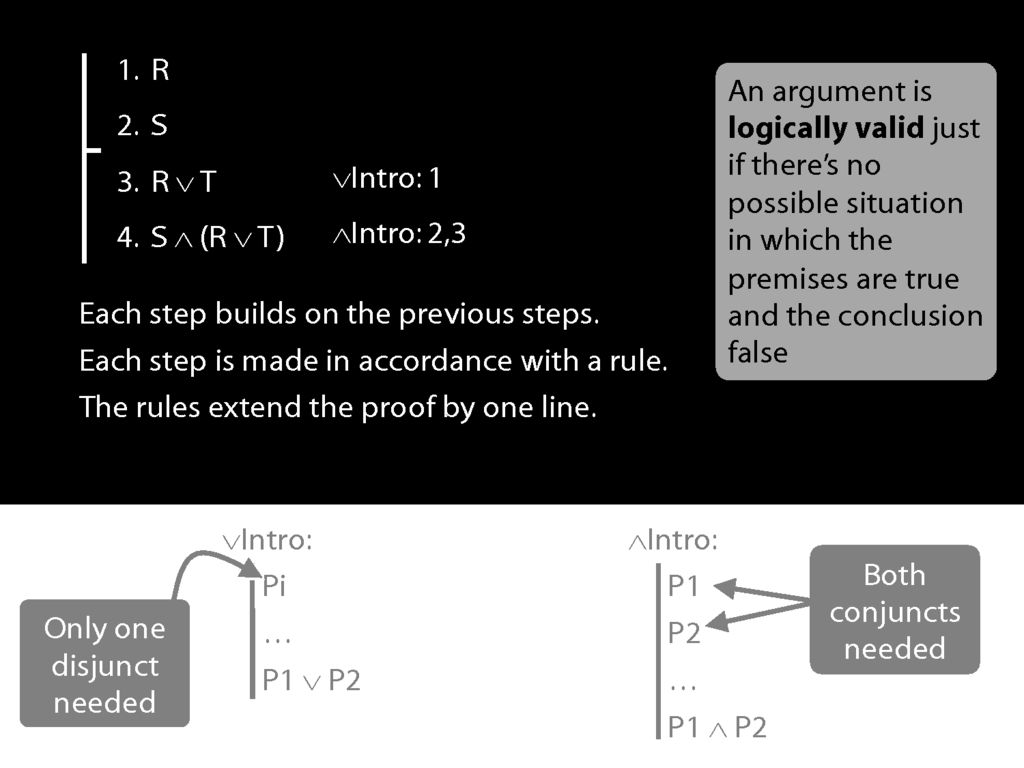
Note some properties of the proof:
Each step builds on the previous steps; each step is made in accordance with a rule; and the rules we've seen so far extend the proof by one line.
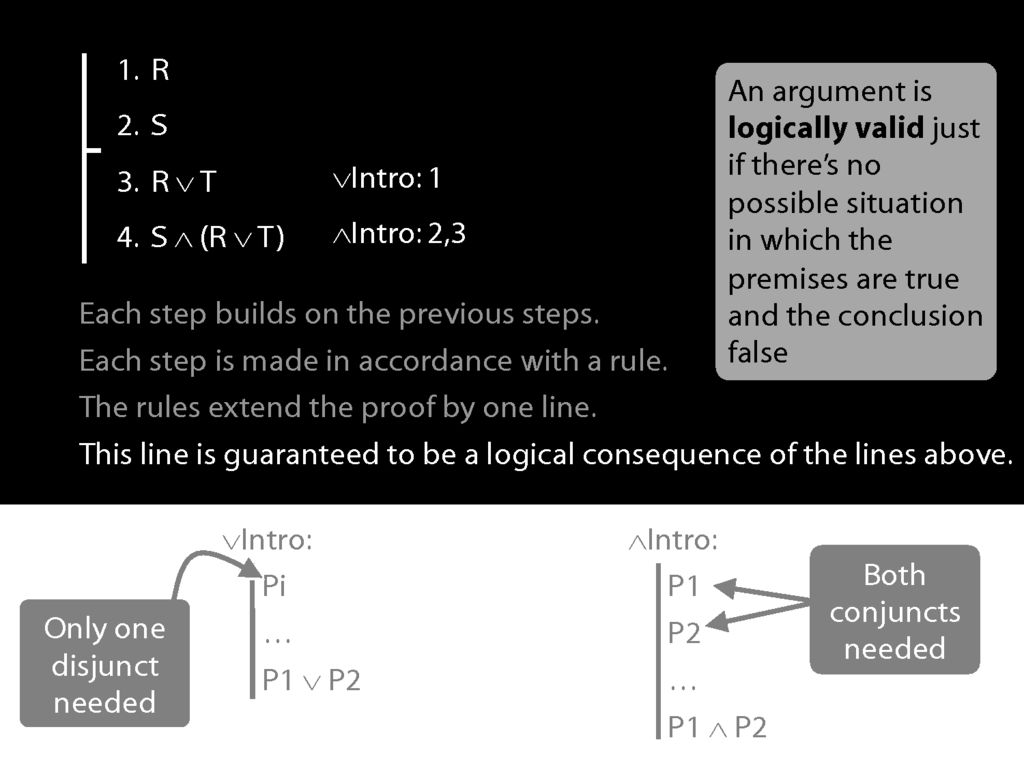
The most important property, though is this: The new line is guaranteed to be a logical consequence of the lines above.

Let me illustrate ...

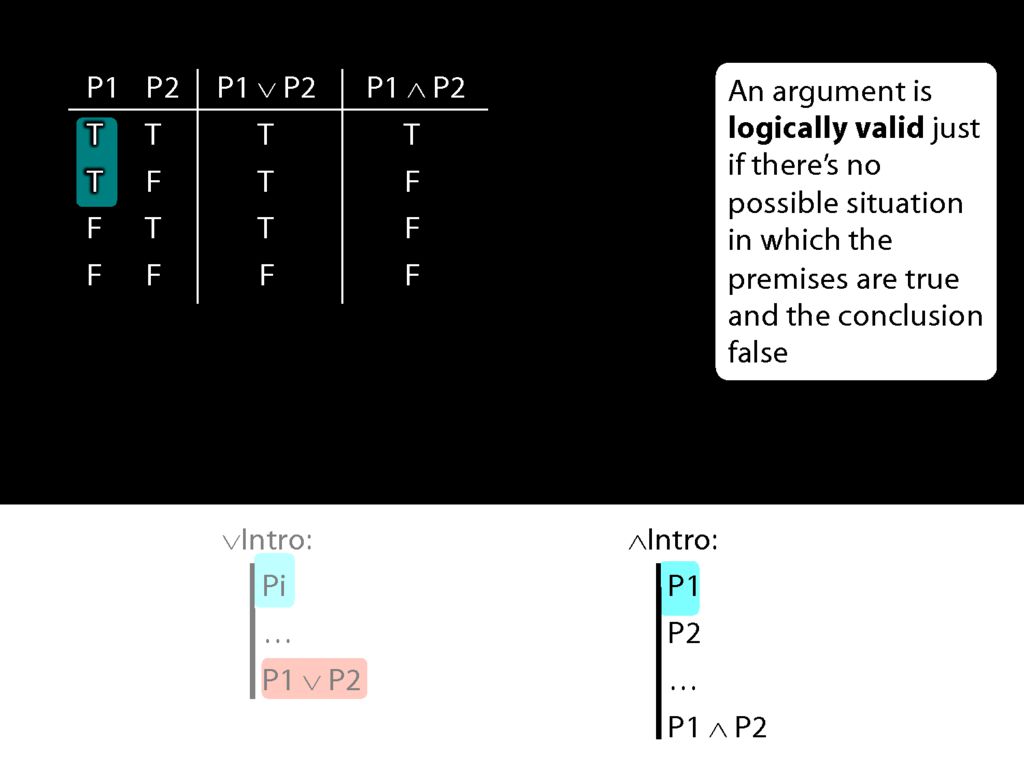
Consider the truth table for disjunction.

What happens when the prerequiste for the disjunction-intro rule is true? In that case, we're in the first two rows of the truth table.
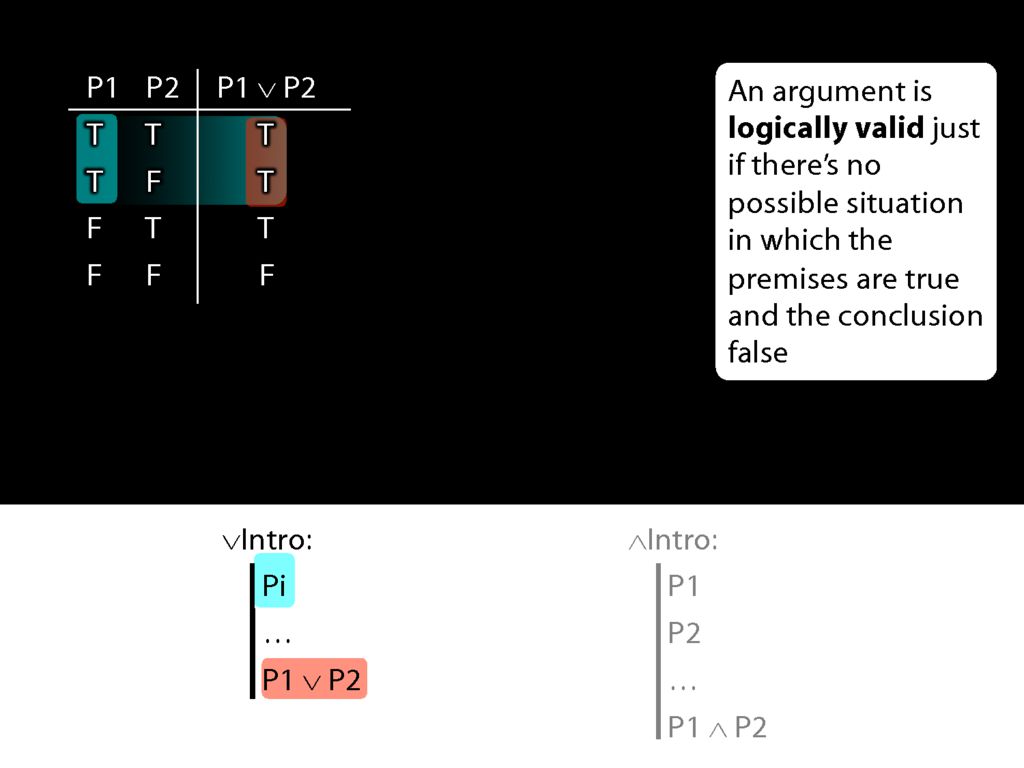
And in those first two rows, the disjunction which the rule adds to the proof is true.
So given the truth table, we can see that disjunction-intro will never take us from a truth to a falsehood; from a truth we can only reach another truth using disjunction-intro.
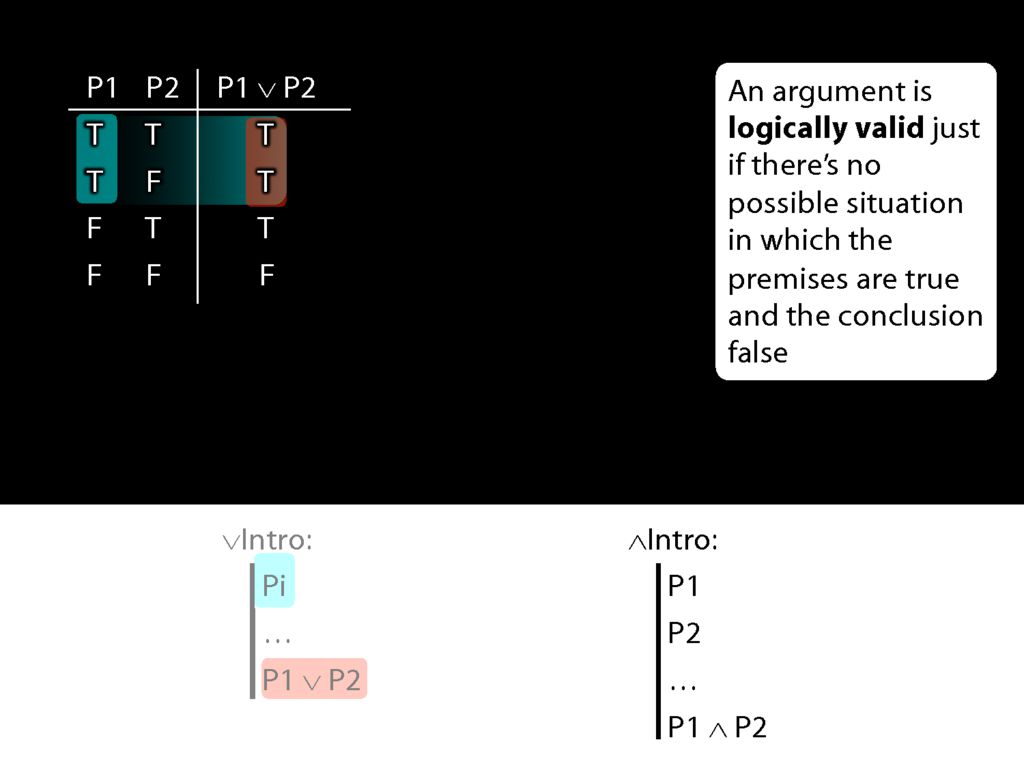
Now look at conjunction intro.
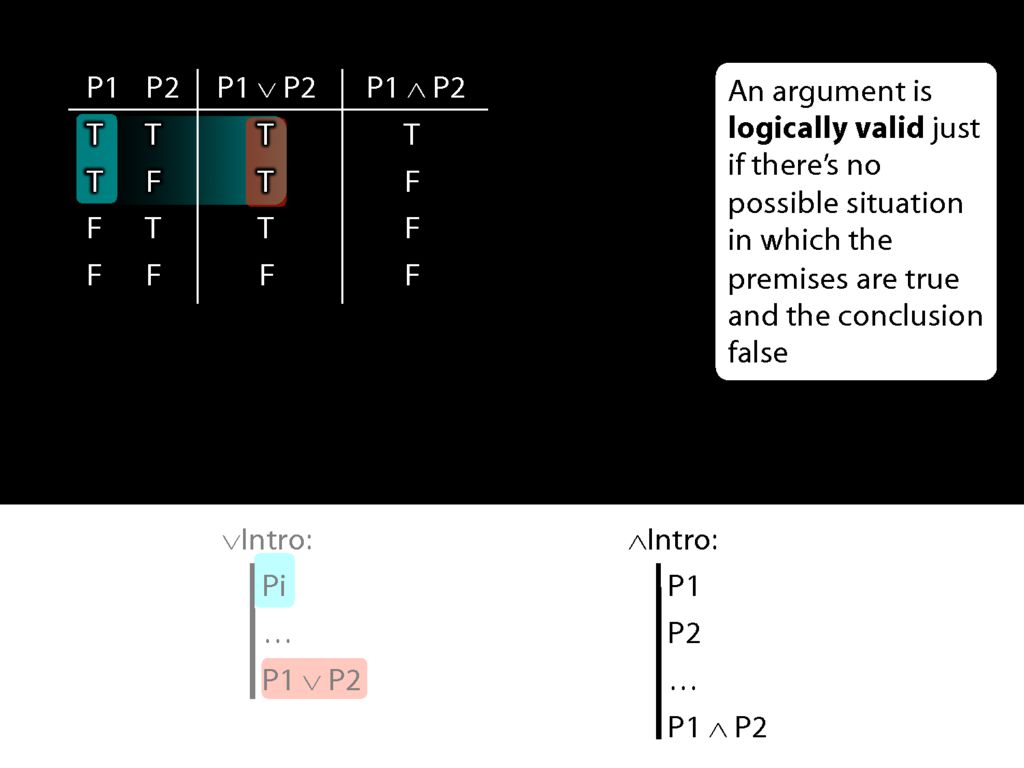
Here's the truth table for conjunction.
Now what happens when the first prerequisite for conjunction introduction is true?
In that case, we're in the first two rows of the truth table.
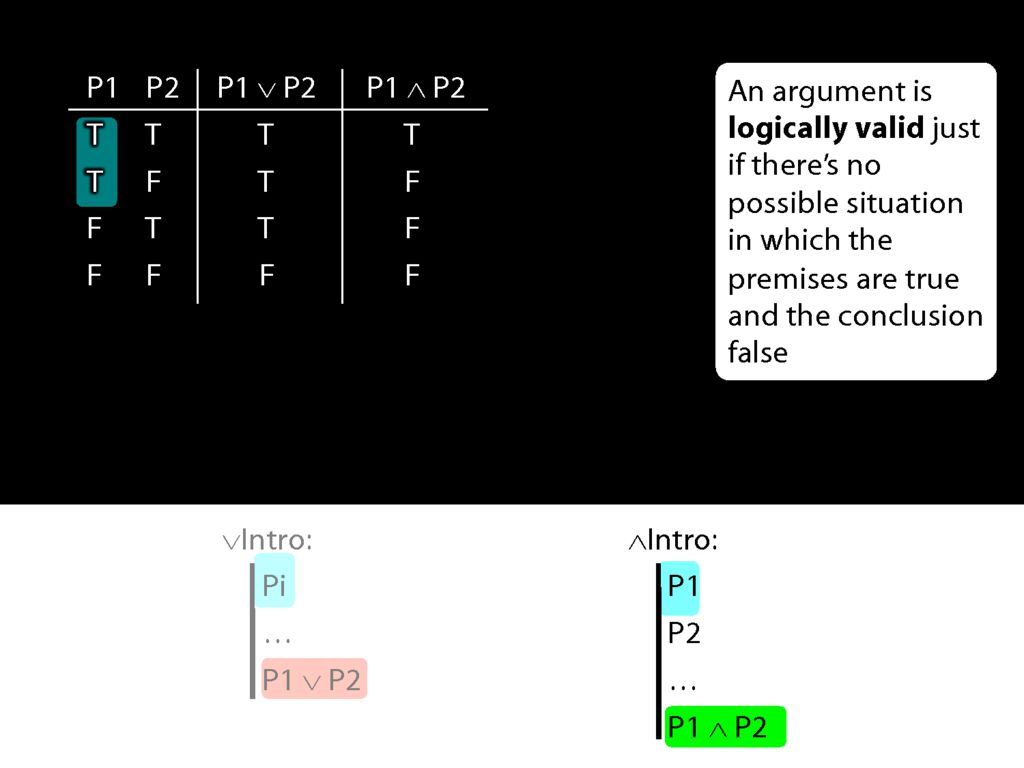
What is the truth value of the conjunction which conjunction-introduction adds to the proof in these rows of the truth table?
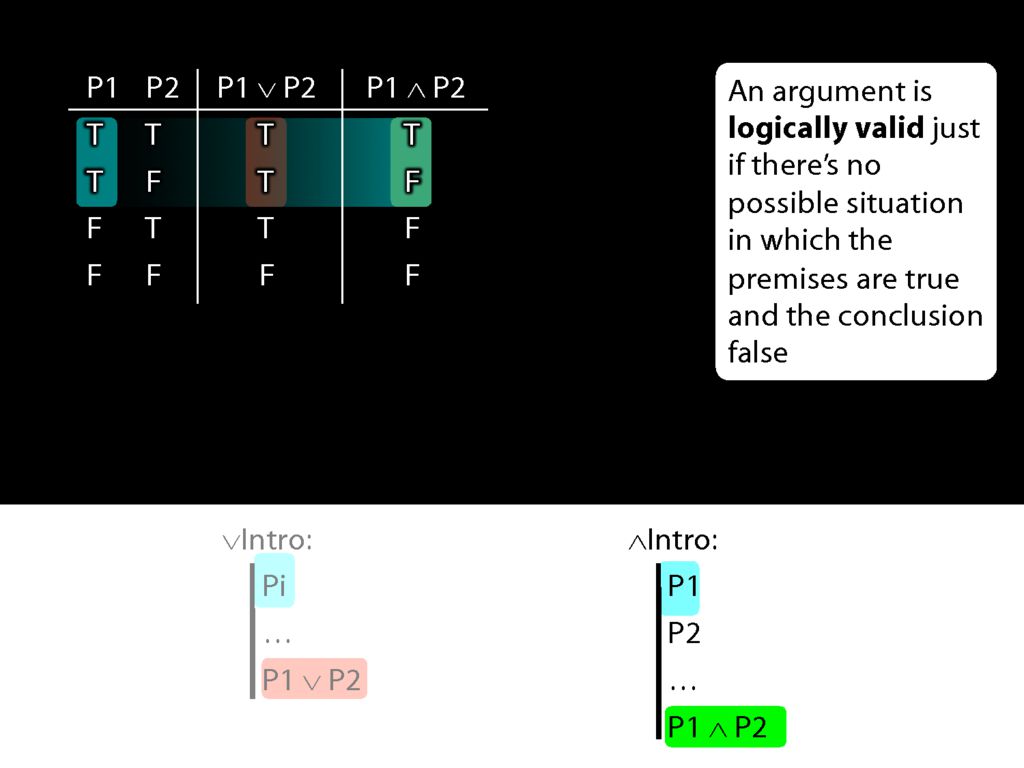
Actually this conjunction is true is one row and false in the other.
So when P1 is true, P1∧P2 is sometimes true and sometimes false.
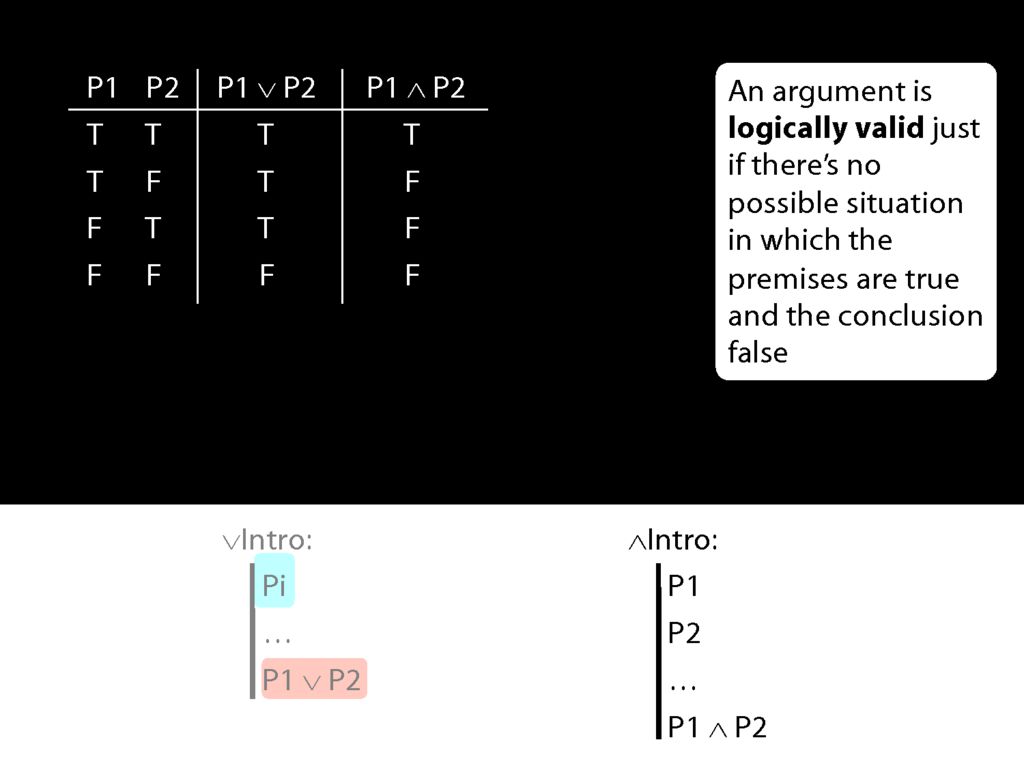
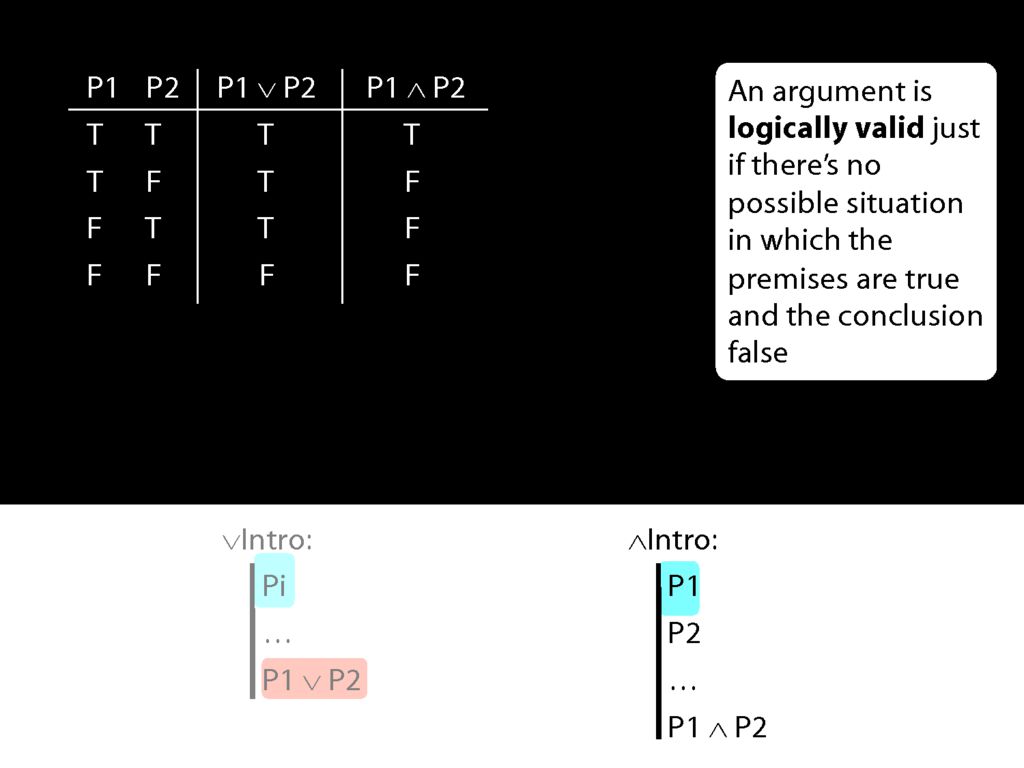
This means that if conjunction-intro required just one conjunct, it would sometimes take us from a truth to a falsehood.
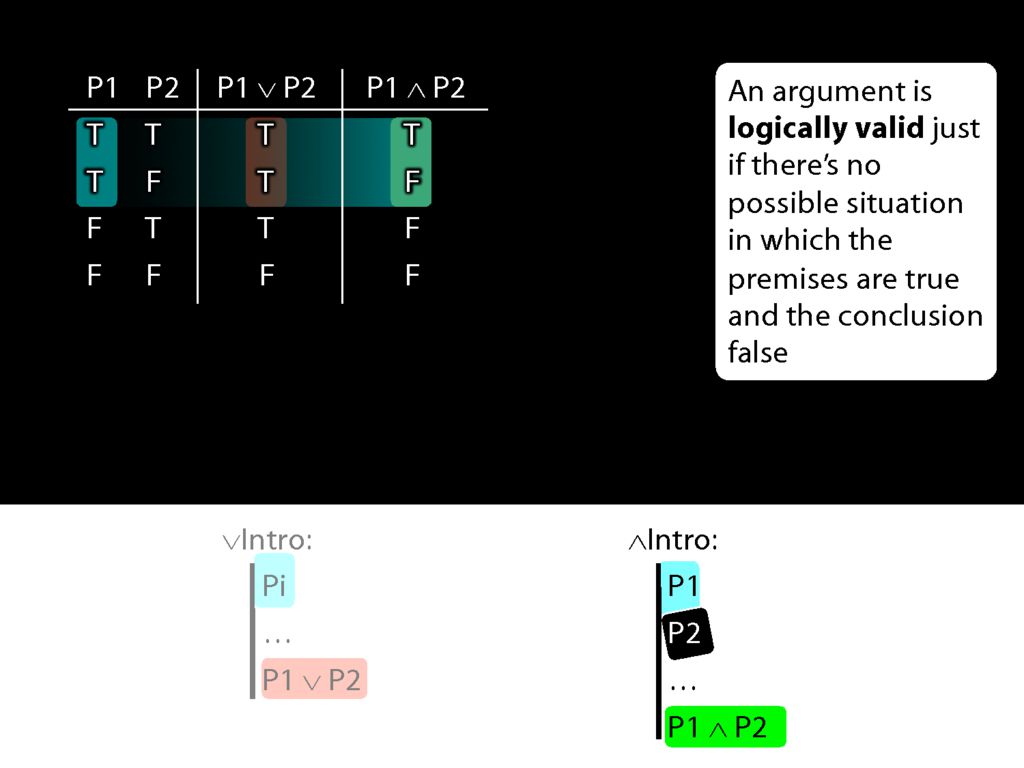
But actually conjunction-intro requires that we already have both conjuncts in our proof.
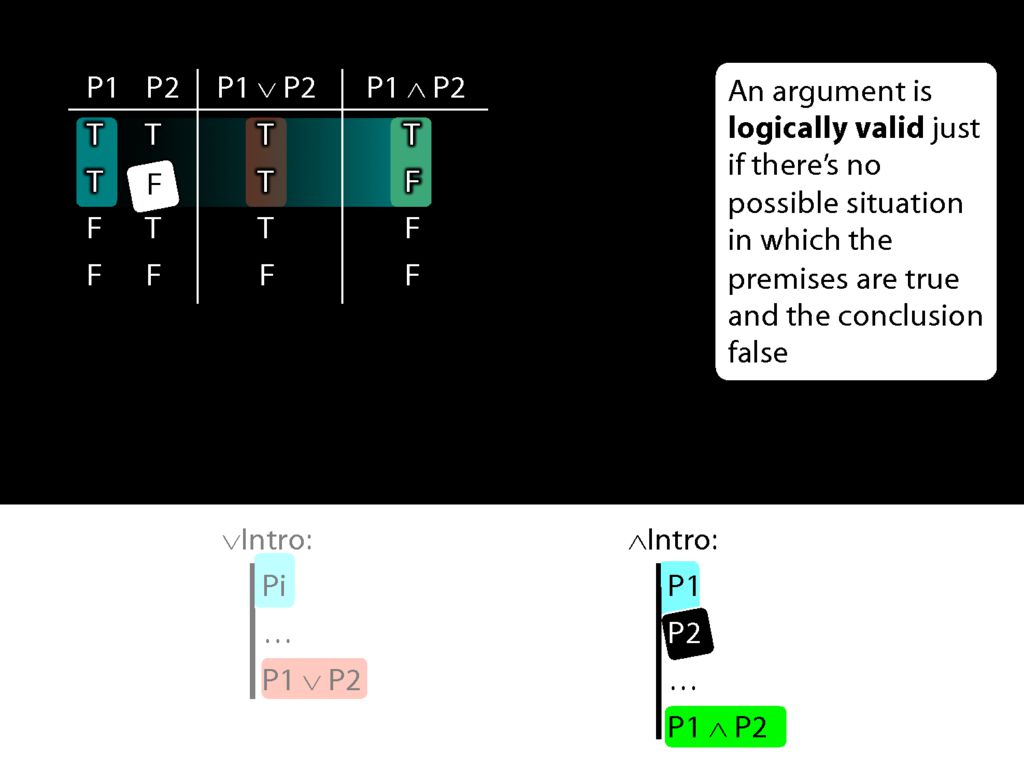
So if both pre-requisites for using conjuncton introduction are true, then we can't be in the second row of the truth table.
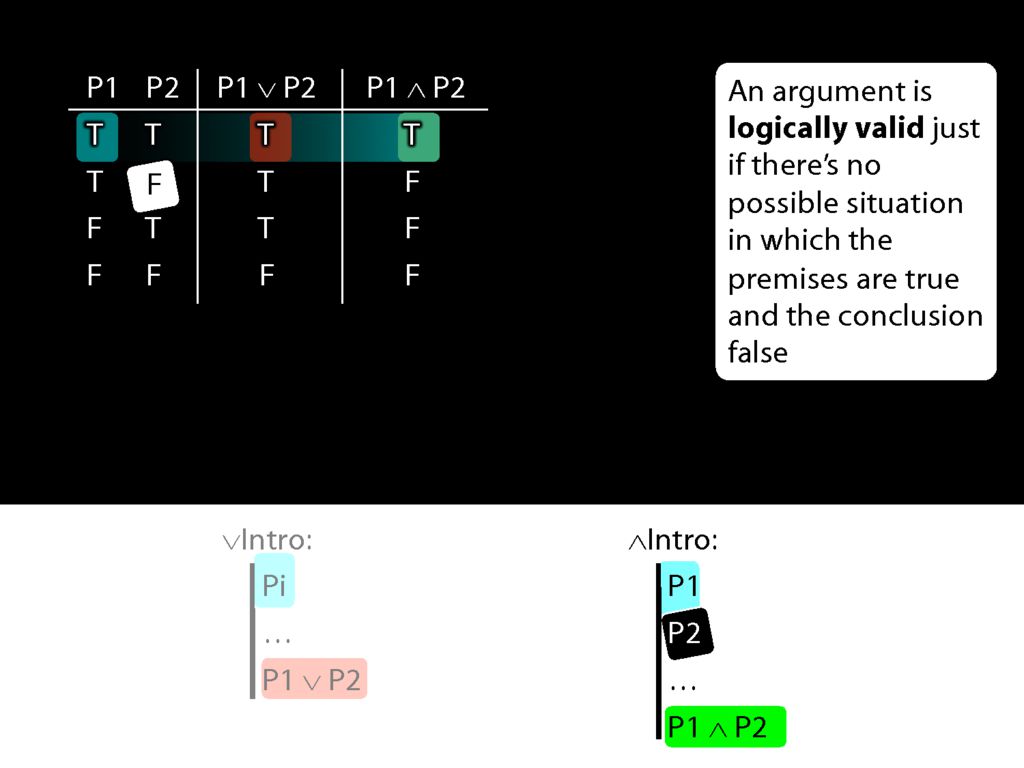
And this means that when everything conjunction-intro requires is true, then the conjunction it allows us to introduce must always be true.
Earlier I asked, Why is using ∧Intro more demanding than using ∨Intro? Now we can see exactly what the answer is.
Speaking entirely formally, we can use whatever rules we like.
But we want our rules to mirror logical validity--given truths, we want them to take us only to truths. We want them never to take us from truth to falsehood.
For this reason, given the truth table for conjunction, ∧Intro has to require that we already have both conjuncts.
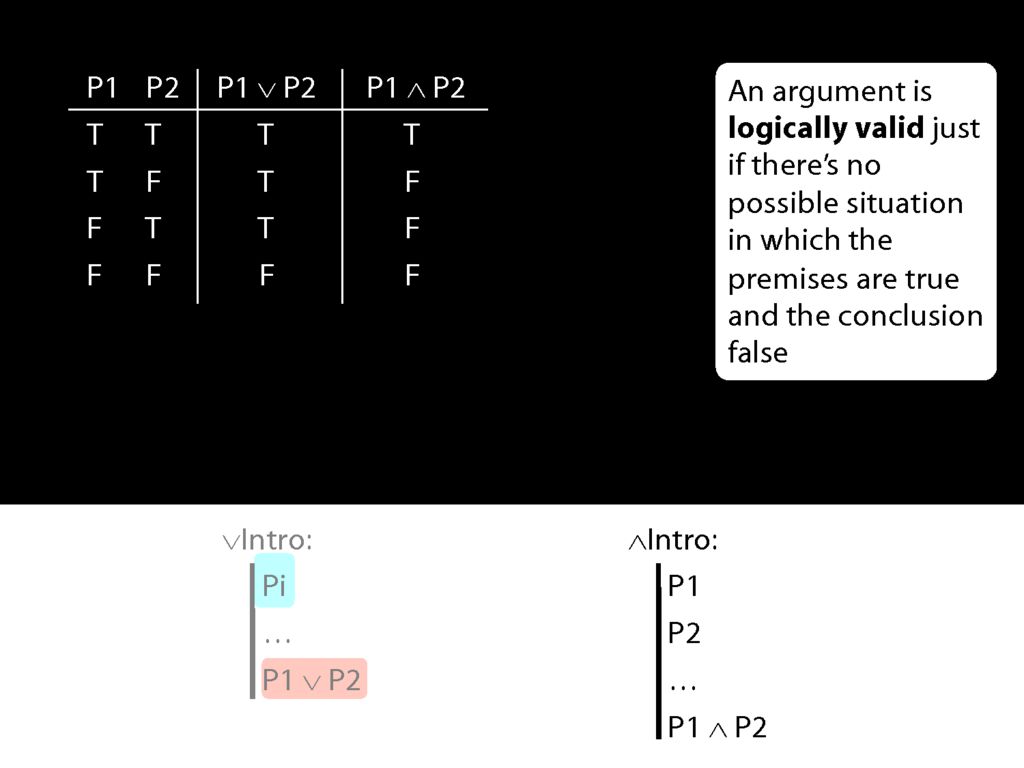
Let me make the same point by introducing a new connective.


Suppose we have a connective called 'is not eqivalent' and we stipulate this introduction rule.
\begin{minipage}{\columnwidth}
Let us define a new connective with this truth table:
\end{minipage}
\begin{minipage}{\columnwidth}
The following rule is unacceptable. Why?
\end{minipage}
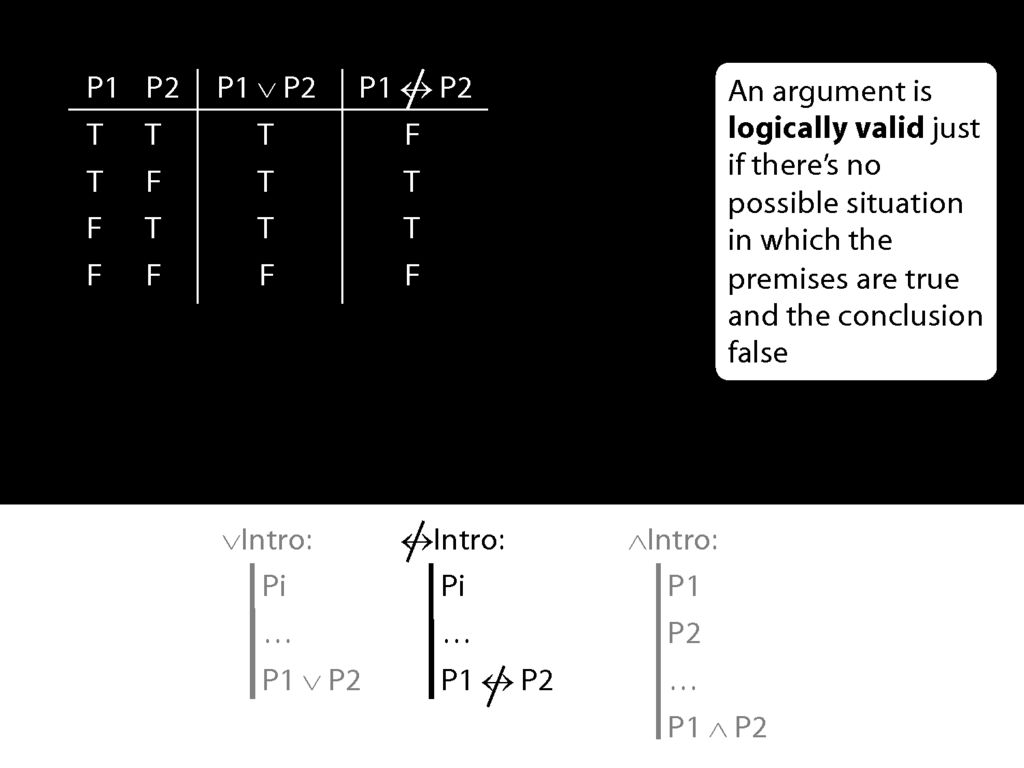
Suppose also that our new connective has this truth table, so that the 'P1 is not eqivalent to P2' is true exactly when P1 and P2 have different truth values.
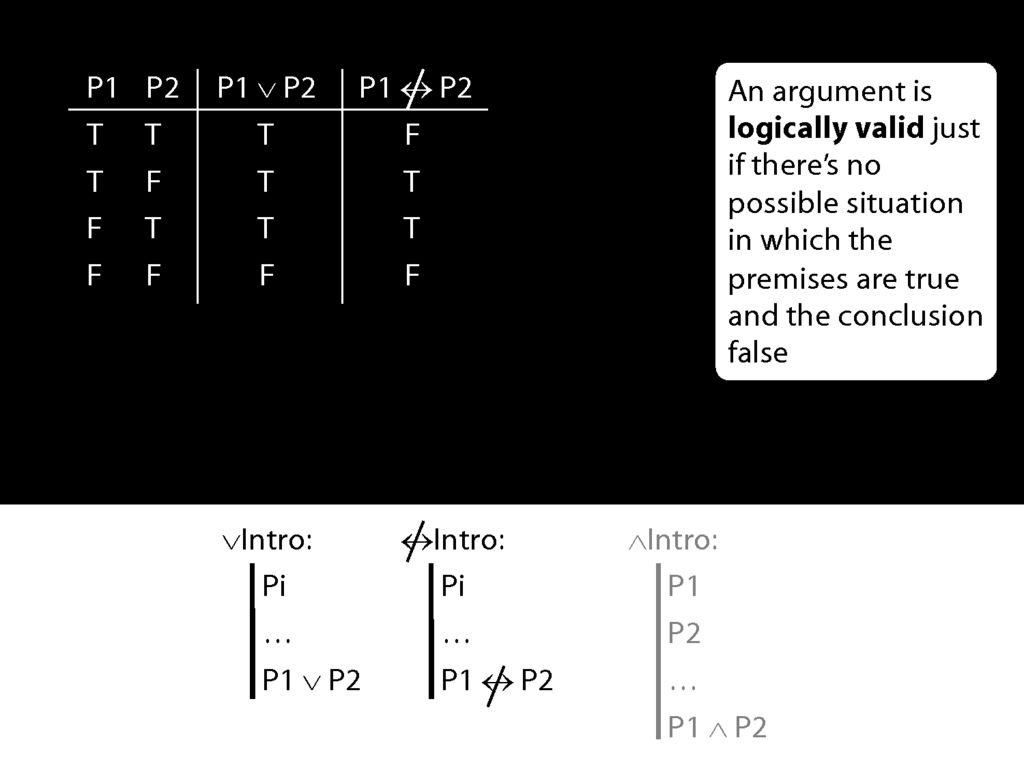
Now the rule for not-equivalent-intro is just like the rule for disjunction-intro.
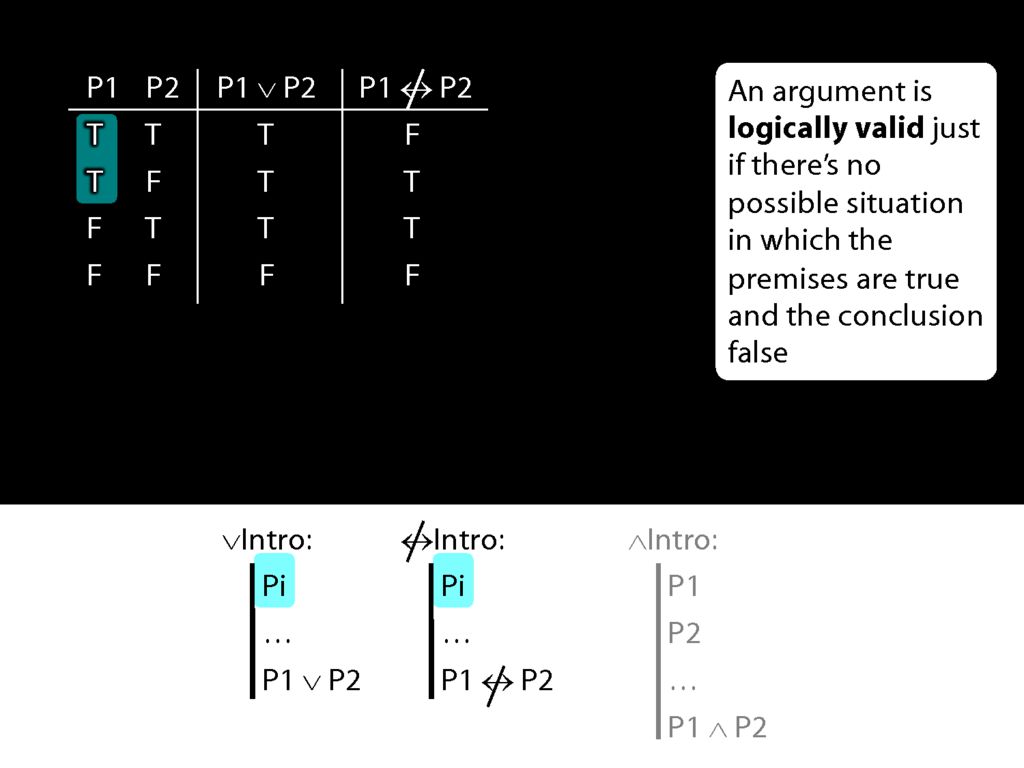
What happens when the prerequsite for these rules is true?
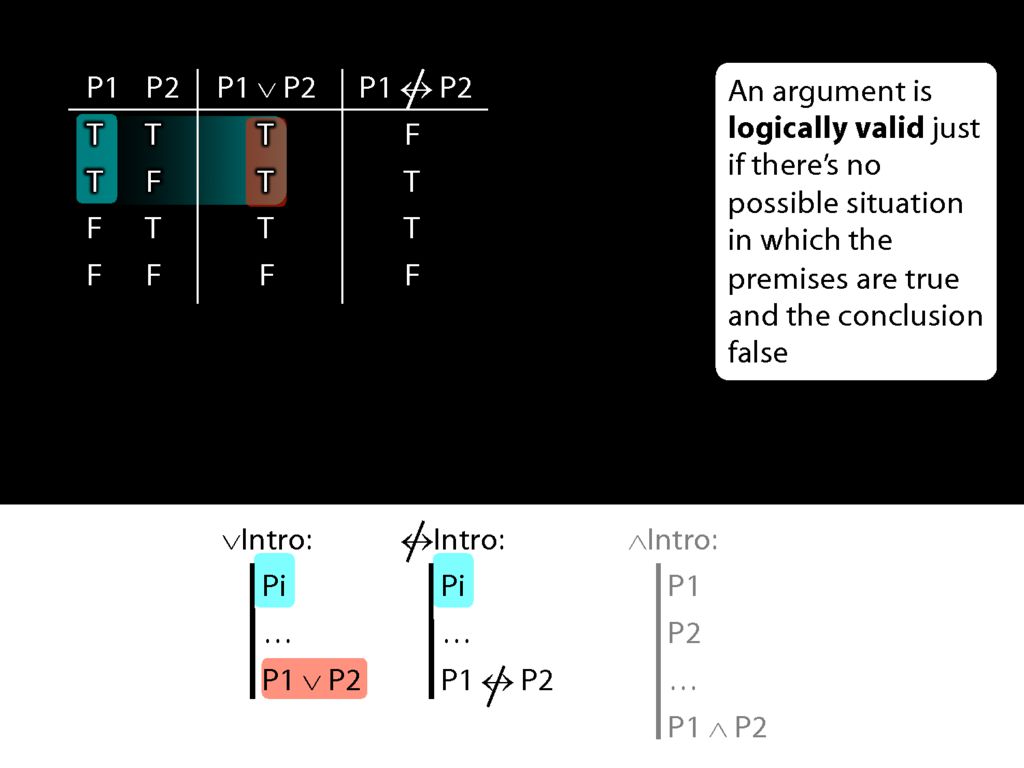
The disjunction that we can introduce with disjunction-intro is true.
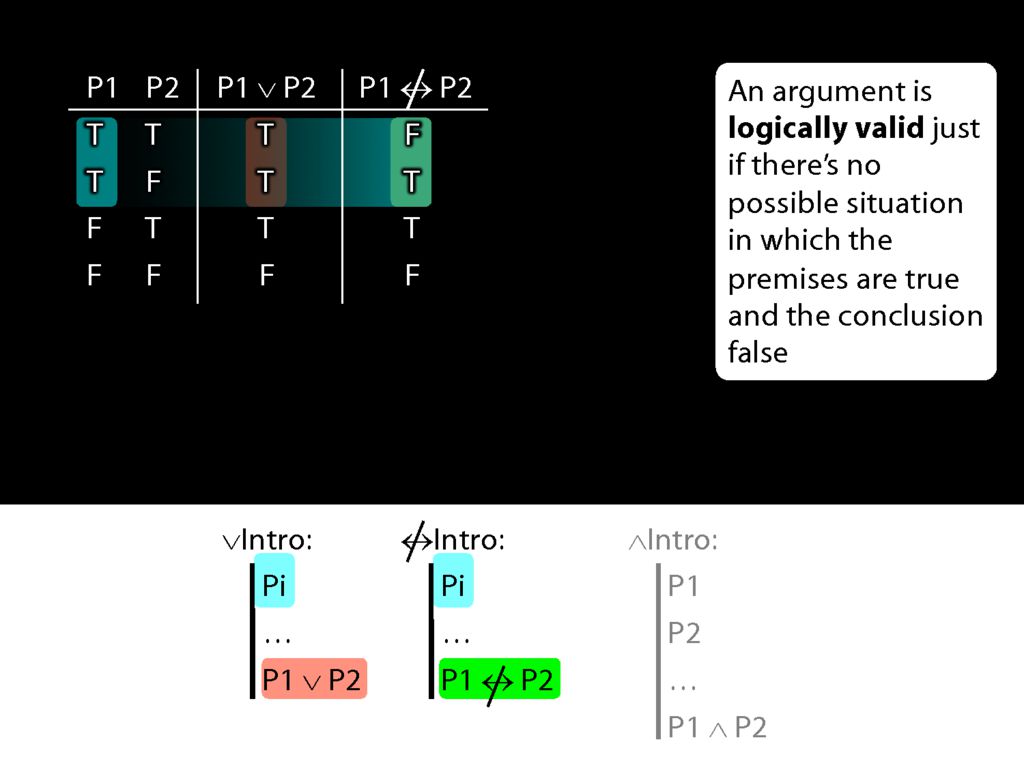
But the sentence that we can introduce with not-equivalent-intro is sometimes false and sometimes true.
So the new rule not-equivalent-intro would allow us to move from truths to falsehoods.
That's why we shouldn't have this rule.

How to Write Proofs
\section{How to Write Proofs}
\section{How to Write Proofs}



Rules of Proof for Identity
\section{Rules of Proof for Identity}
\emph{Reading:} §2.2
\section{Rules of Proof for Identity}

Earlier I said to understand identity as logicians think about it, there are just two principles you need.
These principles correspond to the identity and elimitation rules for identity.
The first principle said that if b=c, then whatever is true of b is also true of c.

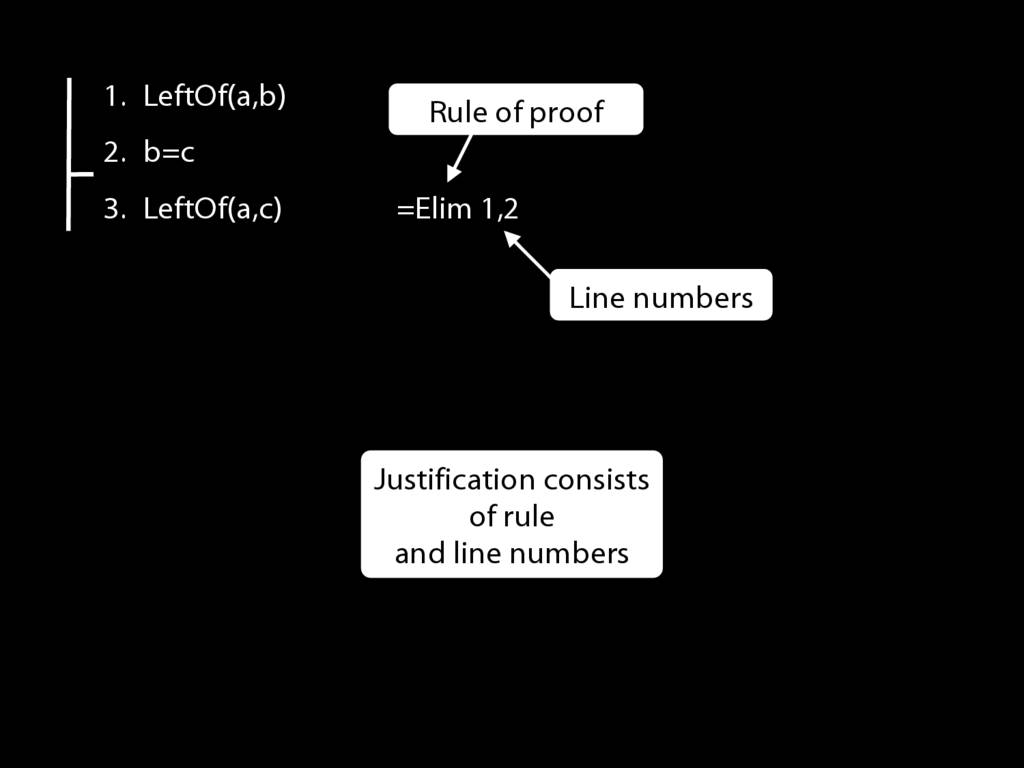
This principle is the rule =Elim.

Then there was another principle, a=a is never false; this is the rule of proof =Intro.

The first rule of proof is expressed just as you would expect:
there are things you have to have already in your proof, and if you have them then you can extend the proof by adding this to it.

But identity intro is a bit different. In this case there are no pre-requisites.
You can use the rule regardless of what you have.
The rule says that any time you like you can add a sentence of this form, so a=a or b=b or whatever.

Let's see how these rules work with a simple proof.
(Everytime I show you new rules, I'll also show you an example of how they're used.)

First I need some line numbers, and maybe a bit of space.
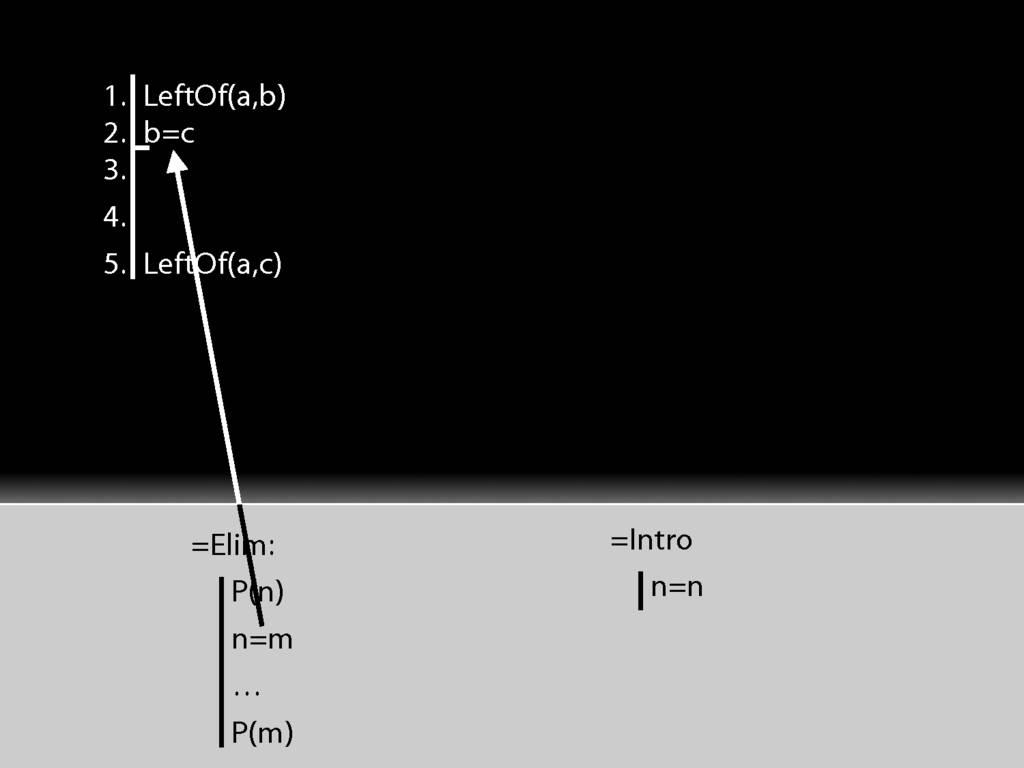
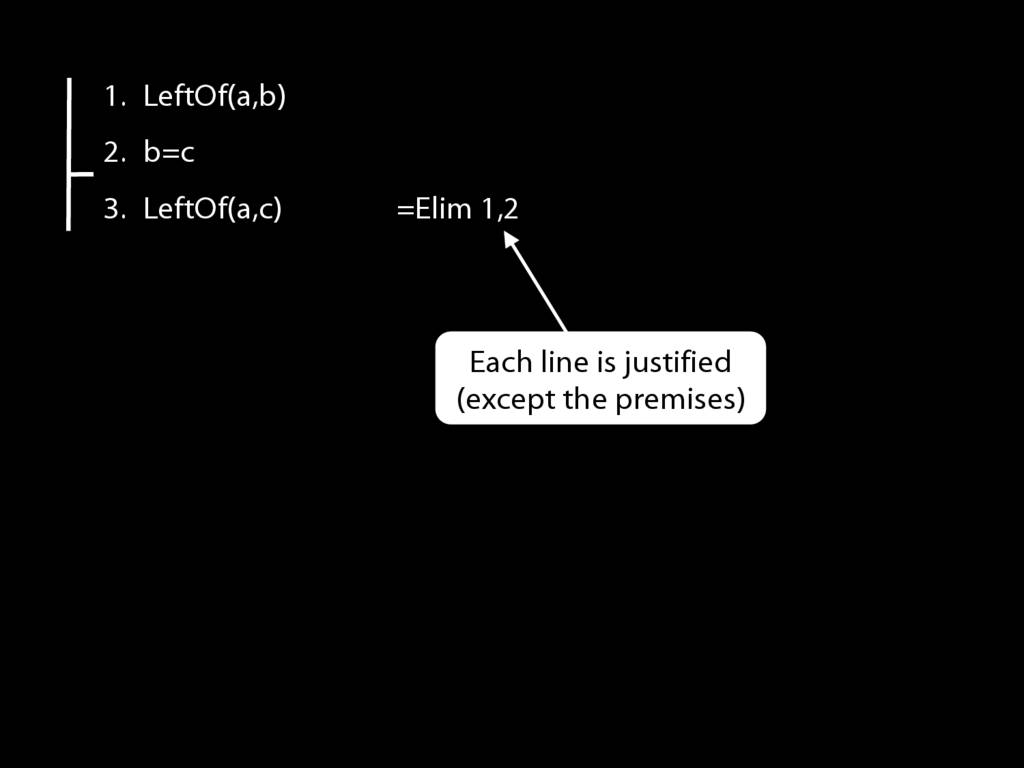
To apply =Elim I need an identity statement; and that's just what I have at line 2.
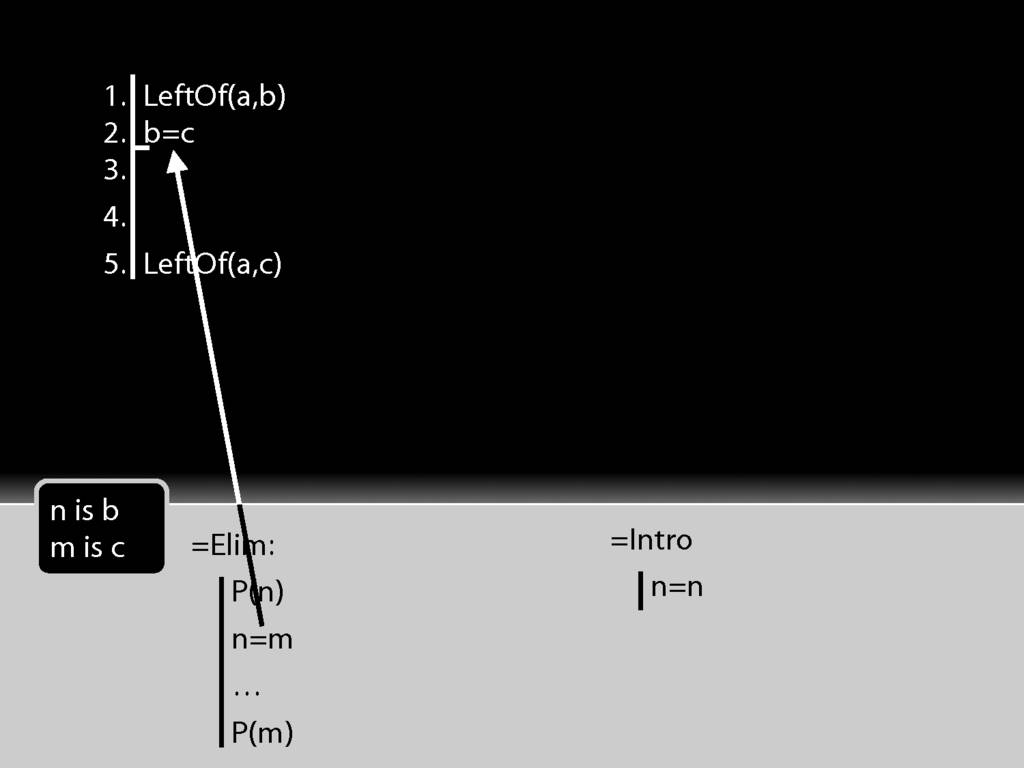
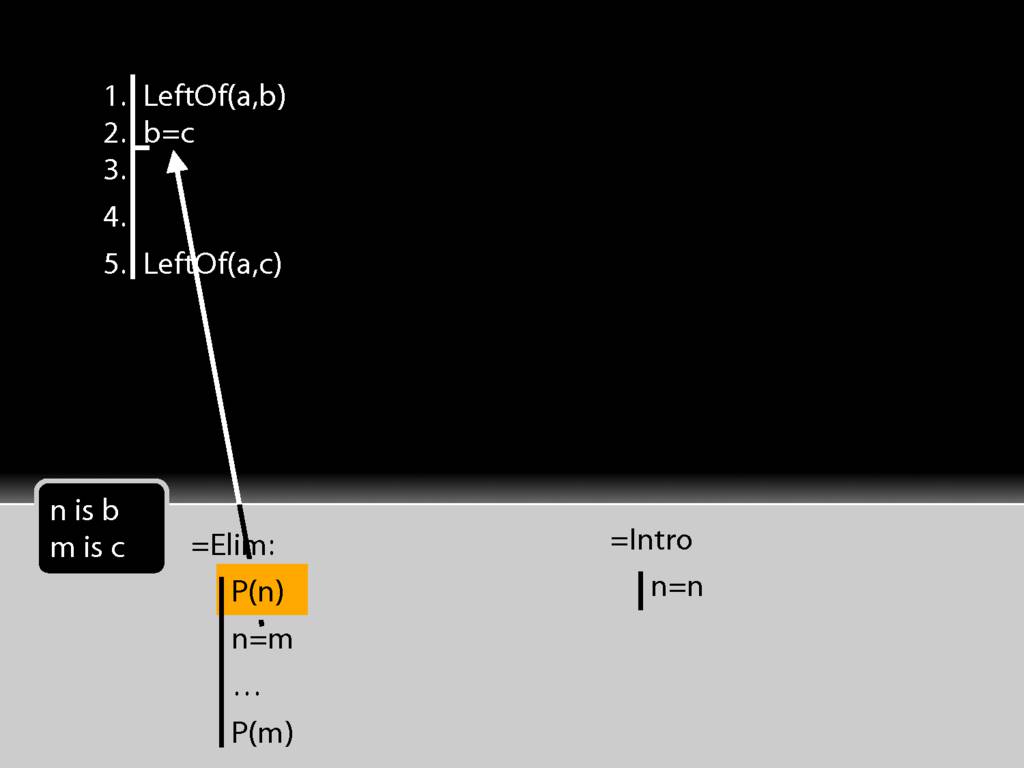
To apply =Elim I also need a statement about the thing named on the left hand side of the identity statement, in this case b.
That's just what I have at line 1 of the proof.
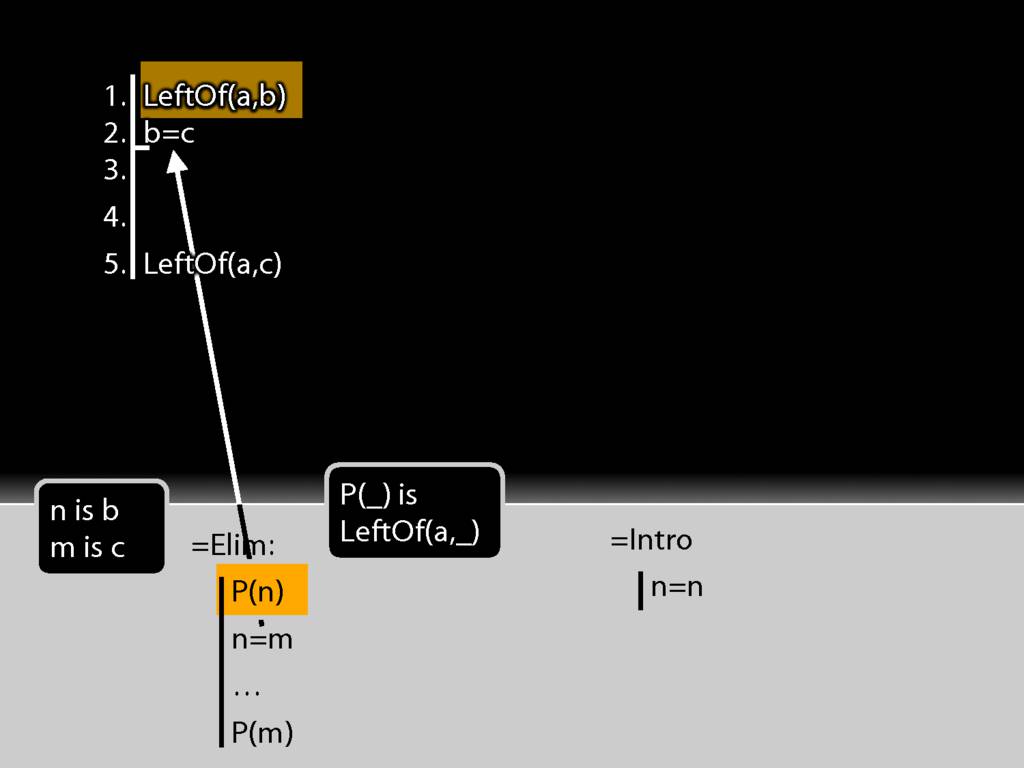
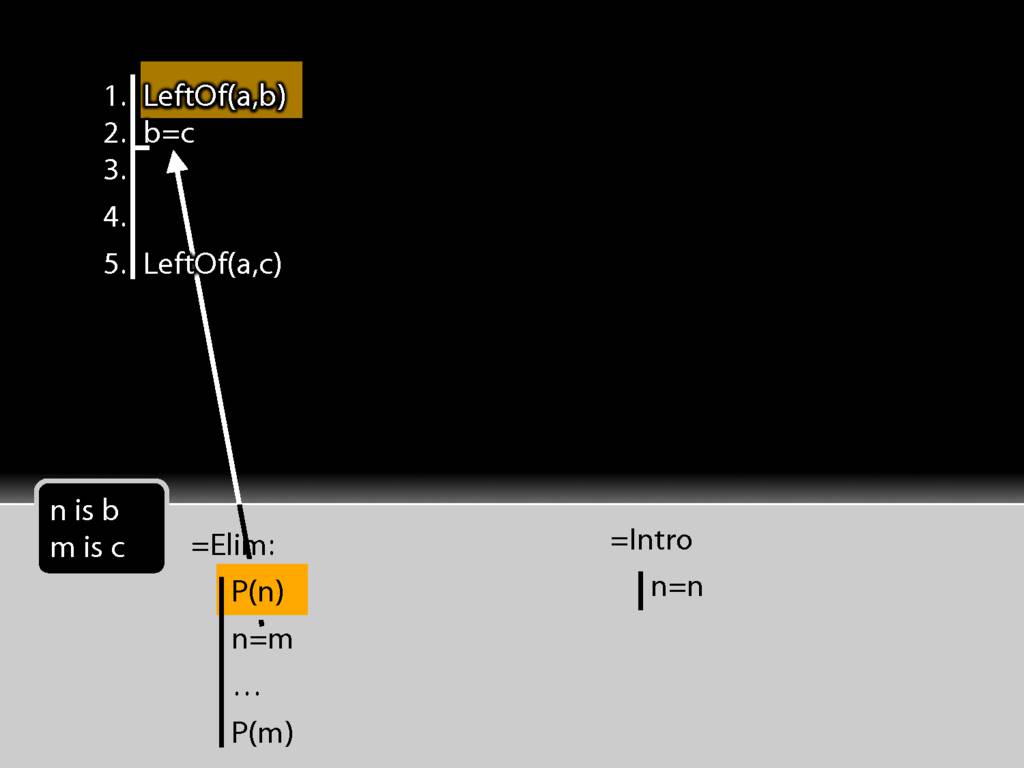
So actually I have both of the things I need to apply =Elim.
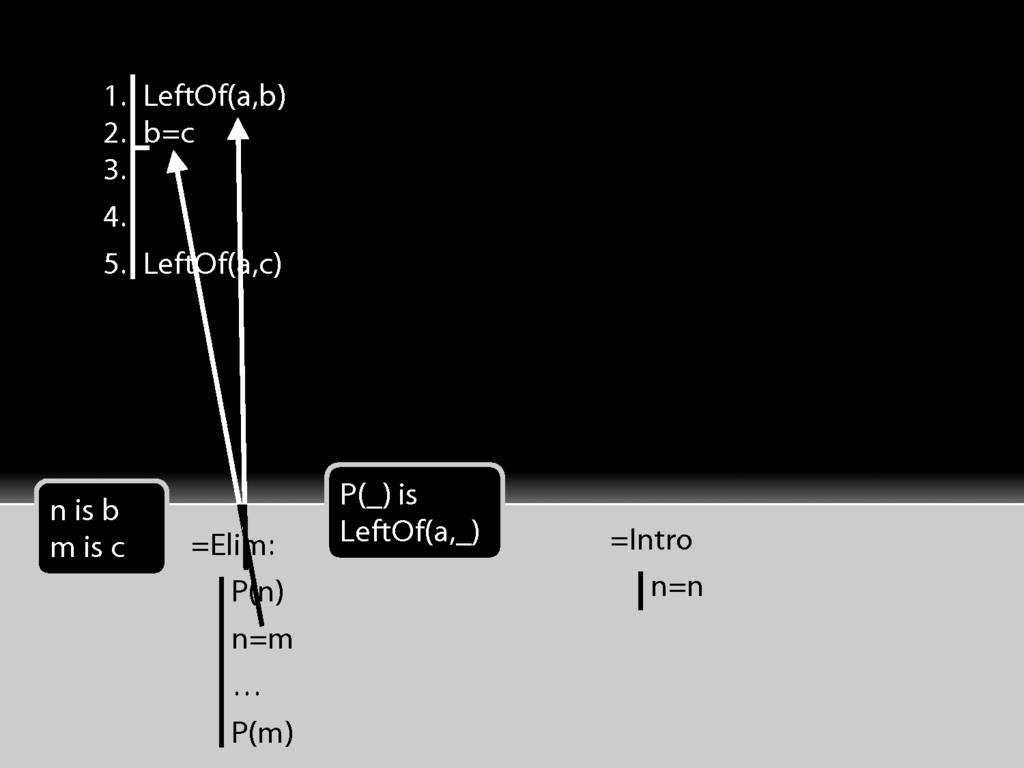
But now look at the conclusion of this argument.
The conclusion is just what =Elim allows me to conclude.
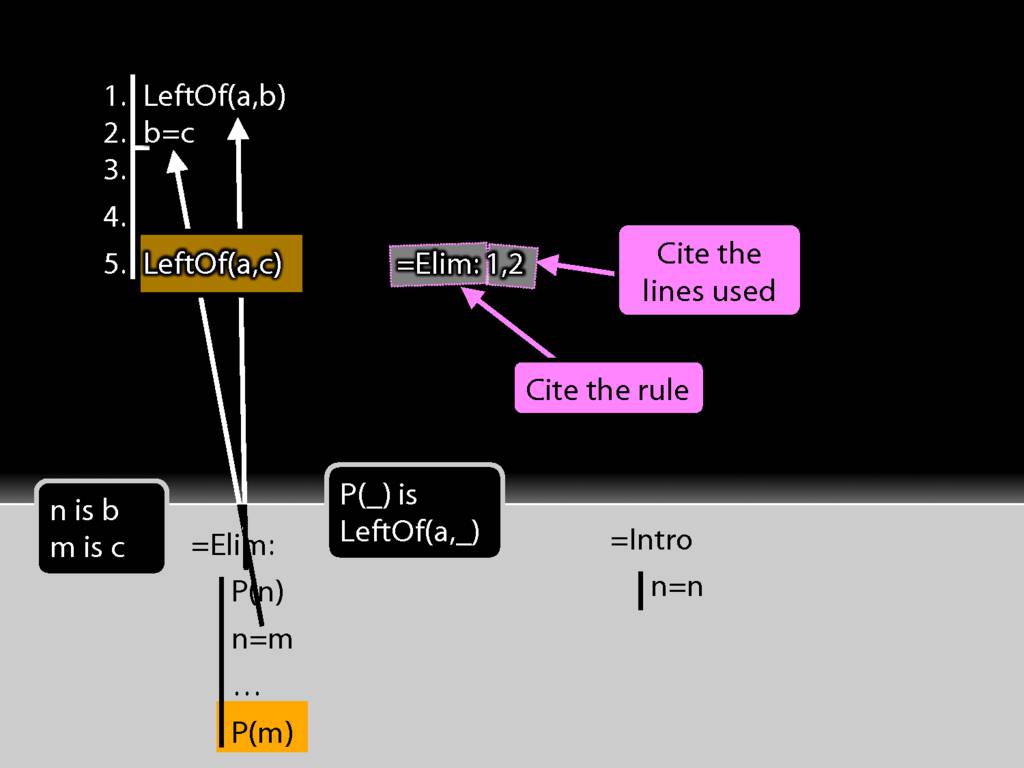
Have I finished the proof? Not yet. I need to justify the step, which involves two things: I need to cite the rule and to cite the lines I've used in applying it.

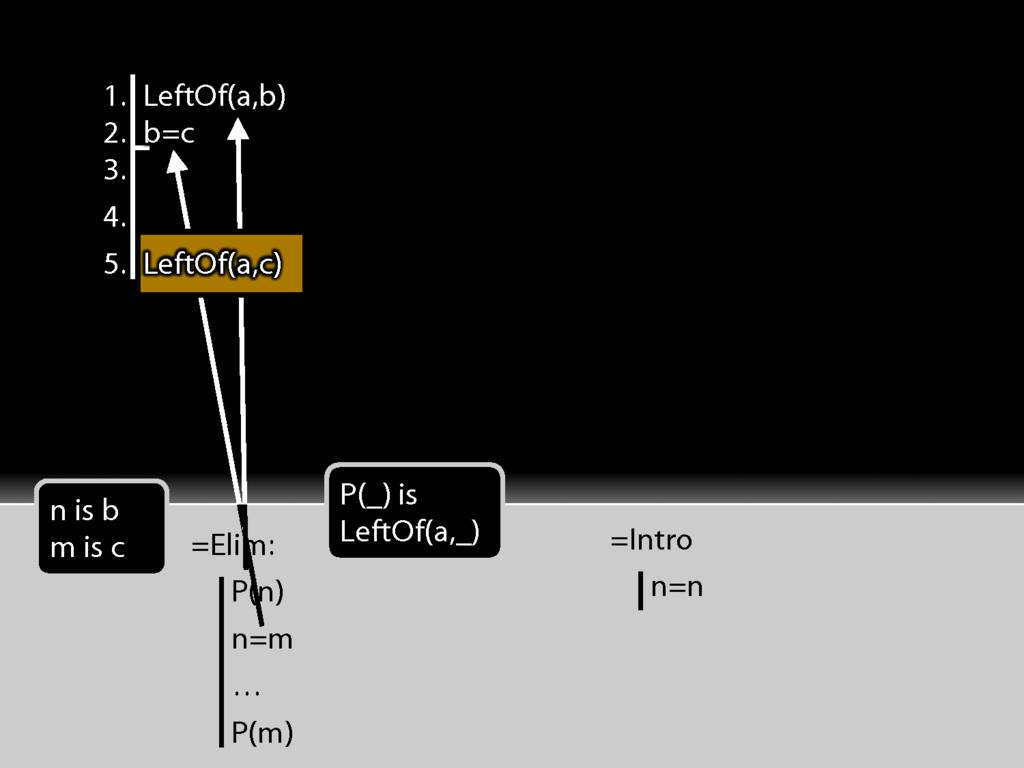
Let's look at the same thing a different way.

The first premise is a statement about b (it says a is left of it) whereas the conclusion is the same statement about c (it says that a is left of it).
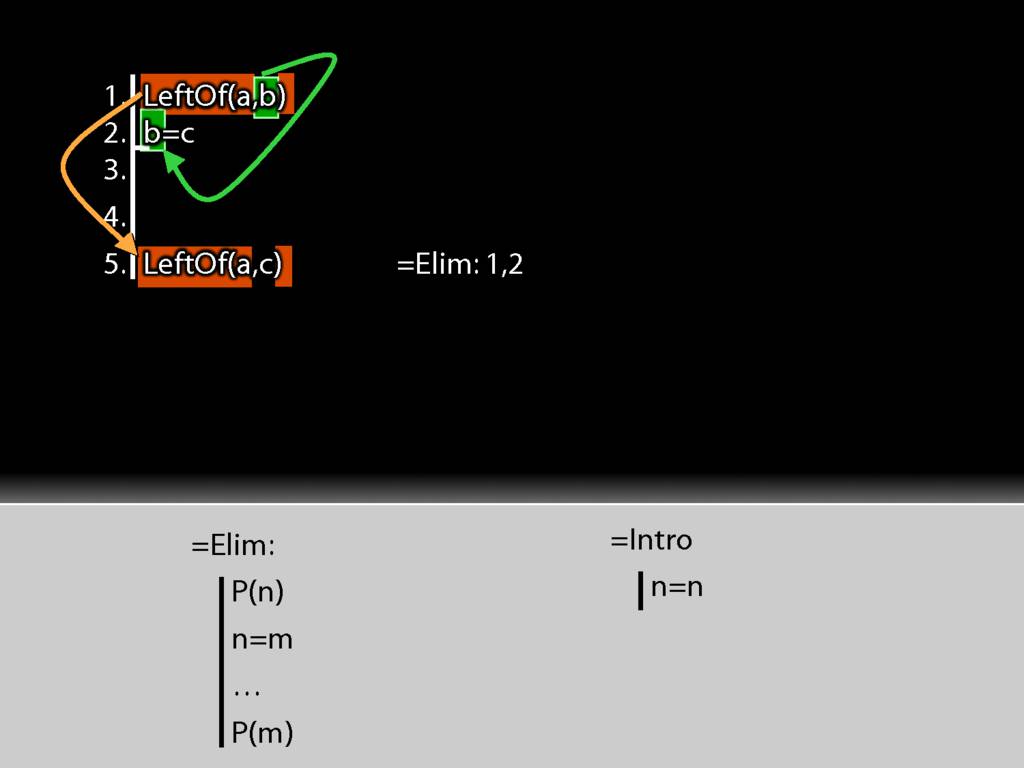
I take the b from the first premise and put it into the identity statement.
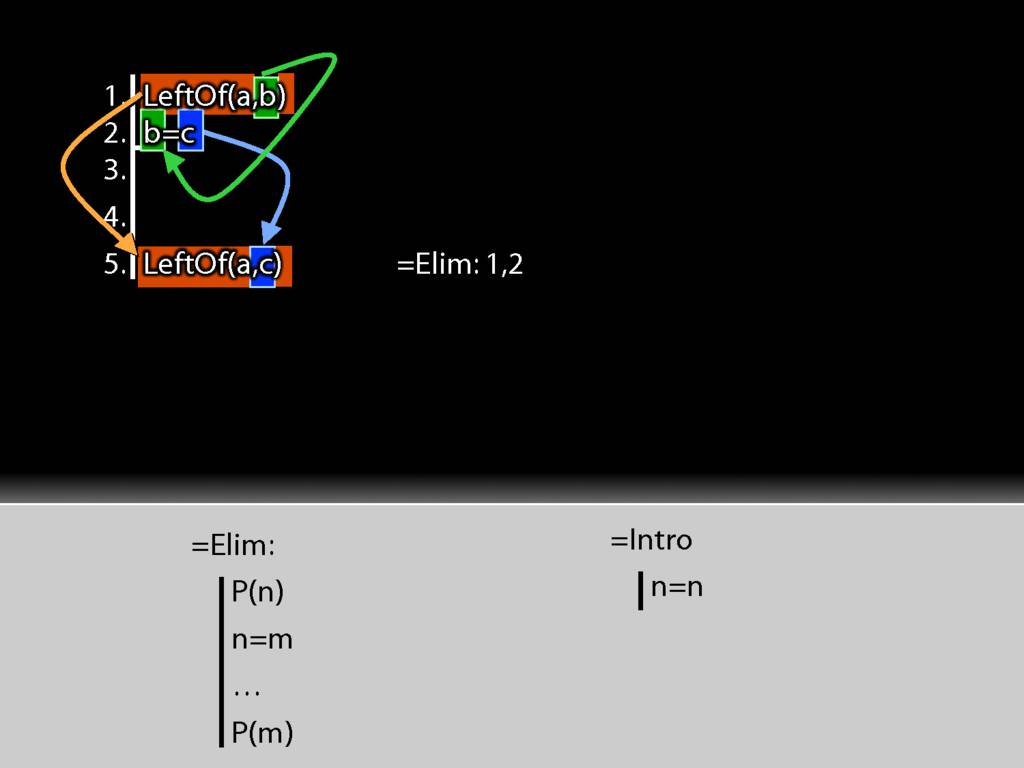
I move accross the identity statement from left to right and find c. And this c I put into the conclusion just where b was earlier.
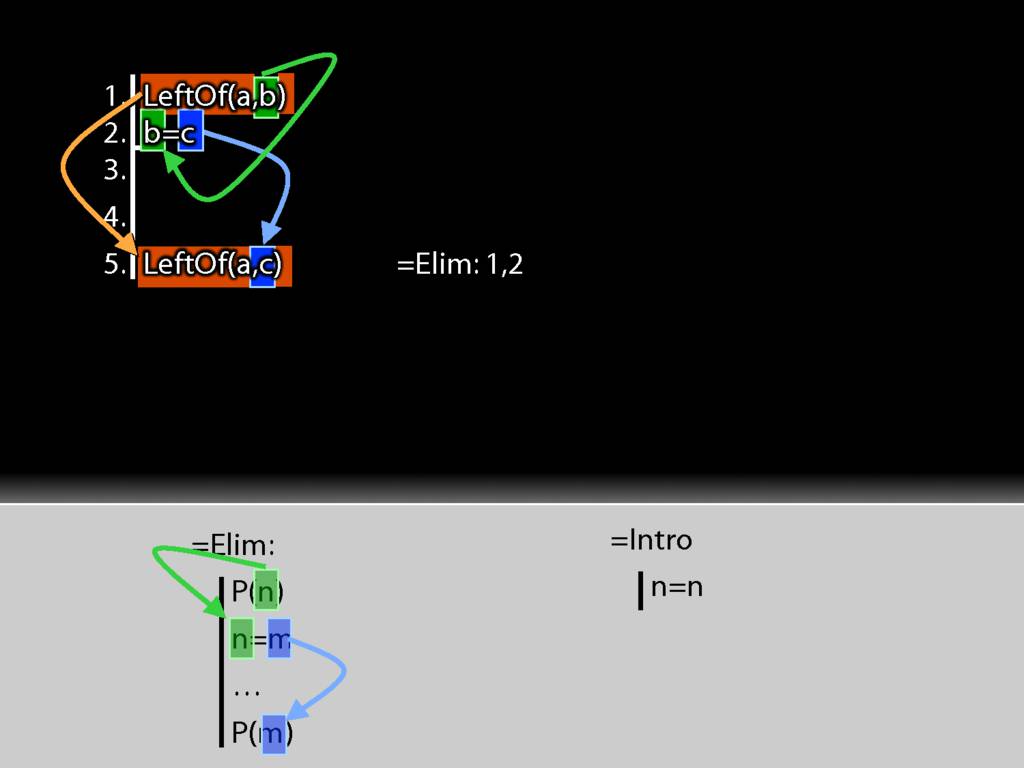
And this is just the pattern I need to make to use =Elim.

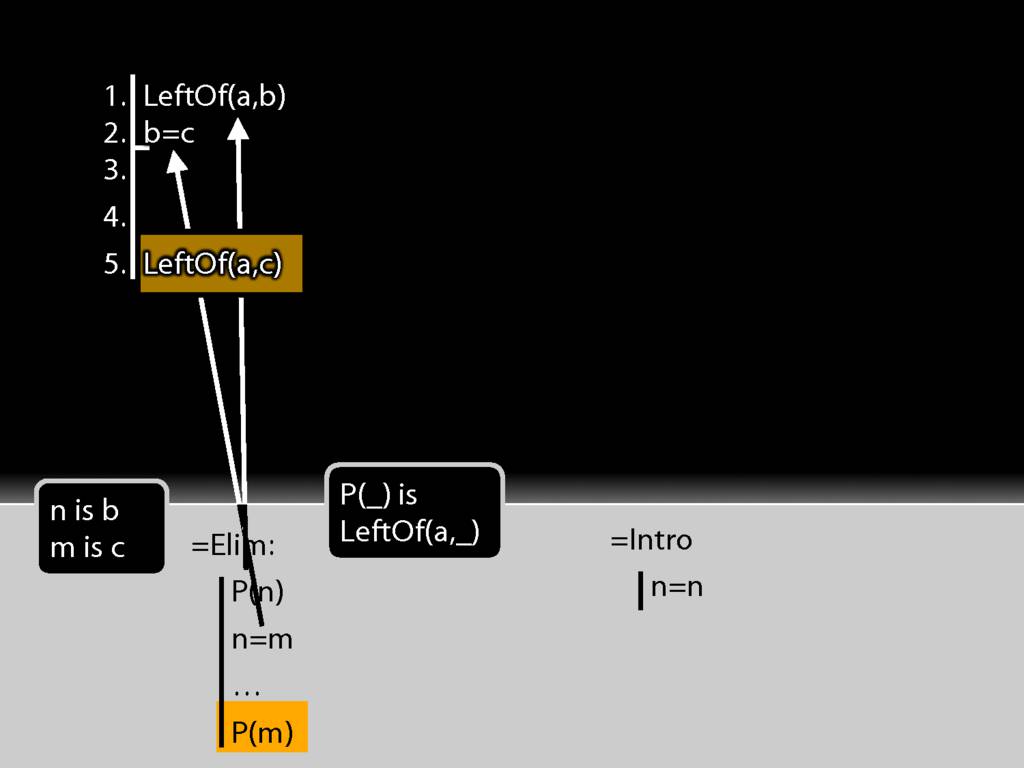
One last thing ...

Look at this thing on your right. It looks much like a proof. But actually it's no more a proof than a toddler's scribble. Why not? (I'll return to this question later.)

Logic Makes Me Die Inside
\section{Logic Makes Me Die Inside}
\emph{Reading:} §2.1
\section{Logic Makes Me Die Inside}

Can I logically valid argument have true premises and a false conclusion?
Let me put this another way ...
Do you use facebook? I’m not on it. I already have a friend, so it didn't seem necessary.
But I was very proud to learn (from a TA) that one year some of my students set up a facebook group for logic.
How cool is that? You love logic so much that you have a facebook group to celebrate.
I'm like the Burial of logic lecturers ...
Or not.
But let's have a closer look at the argument.

One premise, one conclusion.

The funny thing about this argument is not just that there's a counterexample to it, ...

... but that the actual world is a counterexample to it.
So if you think about it, the facebook group was actually for people who love logic after all.
Earlier I asked, Can a logically valid argument have true premises and a false conclusion?
Please think about this question before writing about logic.
So what was logic making me die inside really about?
I think it was probably intended to be a response to the logical validity of two arguments, this one ...
| | P ∧ ¬P | ||
| | Q |
... and this one.
If you are really good, you'll be able to prove both arguments by the end of the course.
In fact, you could prove the argument on your left by the end of today.
In fact, let's see how to do that right away (in unit 270).
| | Q | ||
| | P ∨ ¬P |

¬, ⊥
\section{¬, ⊥}
\emph{Reading:} §6.3
\section{¬, ⊥}

Here are the negation sign and my favourite truth-functional connective, the contradiction sign.

For each of these signs, we want two things: it's truth table and the rules of proof that allow us to exploit it in Fitch proofs.

Here's the truth table for negation: it takes true to false and false to true.
This is a sulky attitude to have, but not quite as sulky as the contradiction sign ...

... which just takes everything to false.
(How great is that?)

Strictly speaking we don't need the contradiction sign because it has the same truth table as P and not P.
(Well, strictly speaking, we only need one connective, but that is another story.)

Let's do contradiction first.

Here is an argument exemplifying the use of the contradiction rules.
We're going to prove it using Fitch, but first, is it valid?

Recall the definition of logical validity.

Now looks at the truth-tables for premise and conclusion.

You can see that there's no possible situation in which the premise is true.
So, surely, there can't be a possible situation in which the premise is true AND the conclusion is false.
So the argument is logically valid.
Now let's prove it.

What shall we do first? The premise is a conjunction, so we can apply conjunction elimination.

This gets us R ...

... and we musn't forget to cite the rule and the line number.

We can also extact not R from the premise ....

... using the same rule, conjunction elim.
But now what happens?

We can introduce a contradiction. Why? What allow us to do this?

Look at the justification given. This tells us that the rule is contradiction intro ...

... and it tells us that the lines are 2 ...

... and 3.

Now how do we get to the conclusion?

Conjunction elimination is made for this purpose.

To eliminate the conjuction, we need to cite the line in which it occurs.

That's good, we've seen the rules contradiction intro and contradiction elim in action. But so far I've not told you what the rules are.

Here's where we used contradiction intro.

The rule says this ...

... that if you have a sentence ...

... and also the negation of that same sentence, then ...

... you can add the contradiction sign in a new line of your proof.

(This works for any sentence, not just sentence letters.)

What about the elim rule, contradiction elim?

Here's how to use it: you need to have a contradiction in your proof somewhere, ...
... and you cite the contradiction ...

... and you can add whatever you want to your proof.
Contradiction elim is a wonderful rule but it comes with a word of caution.
It's quite rare that you will use contradiction elim.
Most of the time, when you have a contradiction in your proof, the rule you actually want is negation introdction.
So be careful when you feel the urge to eliminate a contardiction: always ask yourself whether you shouldn't be introducing negation yet.
(We'll see how to introduce negation later.)

I haven't explain anything about why the rules should work as they do.
My suggestion is that you first learn the rules without thinking about their meaning,
and later we'll discuss how the rules relate to logical validity.
(This is a bit different from the textbook which wants you to think about why the rules are good before you use them.)

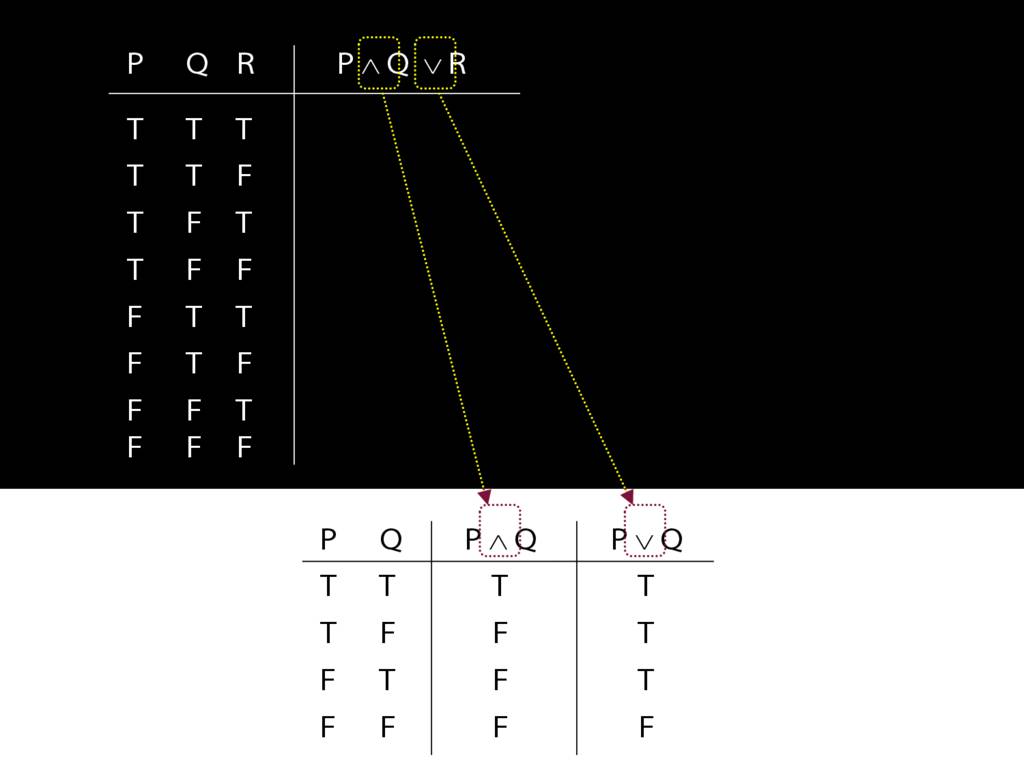
A ∧ B ∨ C
\section{A ∧ B ∨ C}
\emph{Reading:} §3.5
\section{A ∧ B ∨ C}

Here's Johnny Depp having his hair cut in Charlie and the Chocolate Factory.
Mrs B made me watch this film because she fancies Jonny Depp.
Ambiguity can be \emph{lexical}, e.g. `Actor testifies in horse suit'. Ambiguity can also be \emph{syntactic}, e.g. `How to combat the feeling of helplessness with illegal drugs'. (Both examples are from Bucaria, C. (2004), `Lexical and syntactic ambiguity as a source of humor: The case of newspaper headlines', Humour 17(3): 279--309.)

But, to be fair, how could one not?
Anyway, here he's saying 'I need a heir' and holding up a hair.
This is one example of ambiguity.
Note that here the ambiguity can be traced to a single word, 'heir' which sounds just like another word with a different meaning. We might say, the ambiguity is all in the word.

Now contrast a statement like 'two puffins ate six fish'.
This statement is ambiguous because there are two quite different ways of understanding it.
Here you see one interpretation where There were two puffins: and they ate six fish
This interpretation is good for the puffins, less good for the fish.

Here's the other interpretation of 'two puffins ate six fish'. Here it means there were six fish: and two puffins ate them.
So less happy puffins.
Here's the key thing, though. The sentence 'Two puffins ate six fish' is ambiguous but the ambiguity is not due to any particular word. It's not that the word 'puffin' is ambiguous, for example.
This matters because it shows that not all ambiguity is lexical; some of it is, as linguists might say, synatactic or structural.
But why does ambiguity matter to us?
We are constructing a formal language and we want each sentence to have just one truth value, true or false.
In our formal language, we don't want sentences that are true and false.
This means of course that we need to avoid ambiguity.
Insofar as ambiguity is merely lexical--insofar as it is linked to particular words having multiple meanings--it's easy to avoid.
To avoid that sort of ambiguity, lexical ambiguity, we just have to avoid defining words twice. Easy.
But how can we be sure that our formal language involves no syntactic ambiguity?

Consider this thing (it's not a sentence). If we allowed this into our language, we'd have problems.
For one thing, we'd not be able to say what the right way to construct its truth table is.

Now this thing is not a sentence. Instead we have two distinct sentences, (A ∧ B) ∨ C and A ∧ (B ∨ C).
Just a moment ago I asked, How can we be sure that our formal language involves no syntactic ambiguity?
The simplest answer is: because we use brackets.
It's important to realise this, but it's not a very satisfying answer for two reasons.
First, it's not satisfying because we don't know \emph{how} the brackets enable us to avoid ambiguity. The answer doesn't enable us to prove that our language contains no ambiguous sentences.
And, second, it's not satisfying because we haven't said anything yet about what the brackets mean. We can't just throw symbols into our language without explaining them. (This is the down side of having a formal language: we have to say what everything means explicity, since it's a creature of our own creation.)
3.20, 3.21, 3.22
\section{A ∧ B ∨ C: the Truth-tables}
\section{A ∧ B ∨ C: the Truth-tables}
Let us examine how these two sentences, (A and B) or C versus A and (B or C), differ using truth tables.
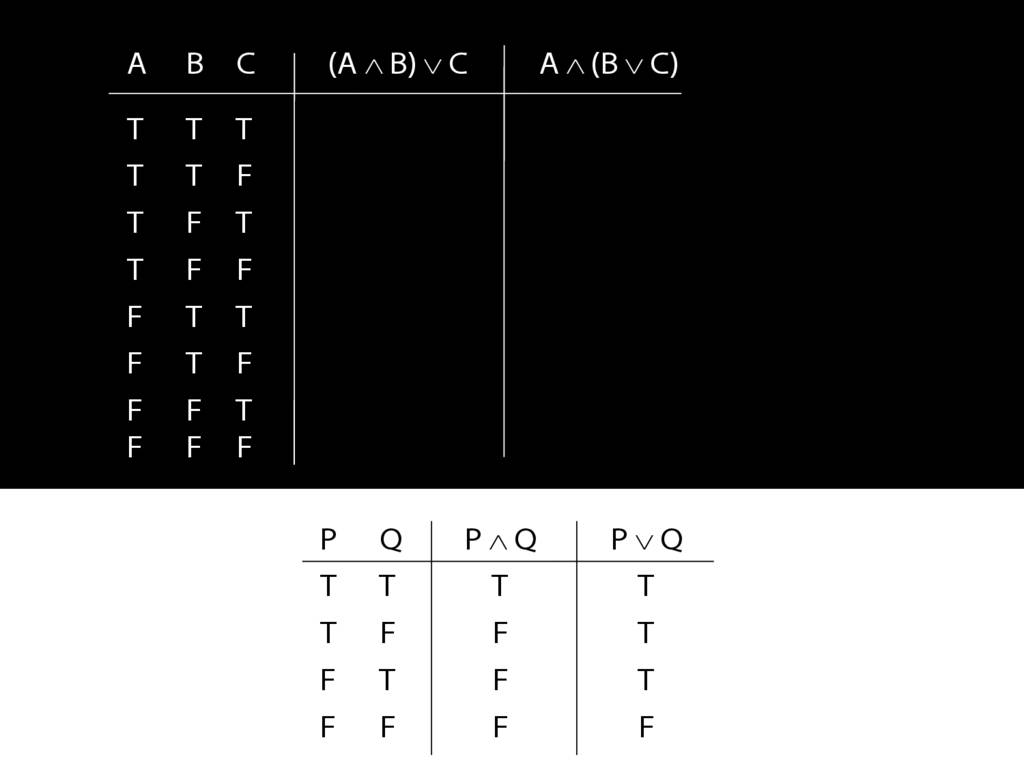
We have quite a few rows to fill in so it's worth thinking about short cuts.
Think about this C on the right hand side of the disjunction.
Whenever a disjunct is true ...

... oops, Ken says he's dying inside.
For most people that would be an exaggeration, but for Ken it's actually an understatement of his problems.
Anyway, I hope it isn't because of logic.

If this is too easy, try an exercise while I'm talking about the truth tables.
Here's one argument ...

... and here's a second argument. Your exercise is to say which is valid and which is not valid.
For the invalid argument, give a counterexample.
For the valid argument, give a Fitch proof.
While you are doing that, the rest of us will go back to thinking about truth tables.
So we were thinking about the right disjunct of the first sentence, C.
What happens when this disjunct is true?
The whole sentence is true, regardless of what the truth value of the other (left) disjunct is.
So in every row of the truth-table in which C is true, ...
... these four rows ...
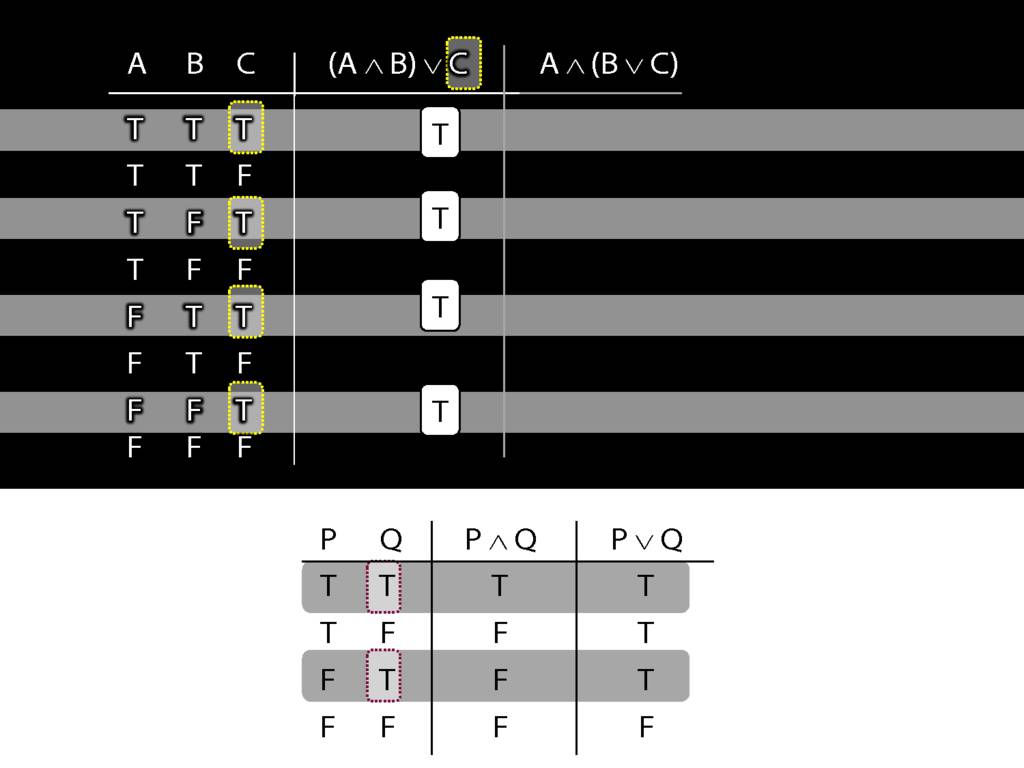
... we know that the whole sentence is true.
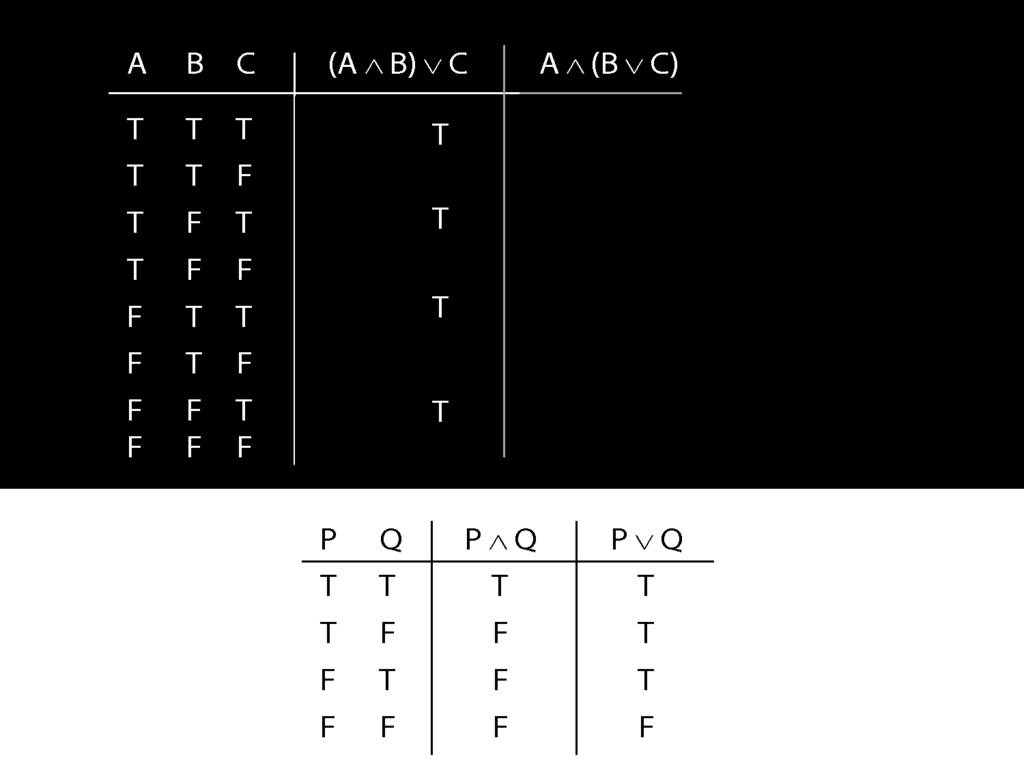
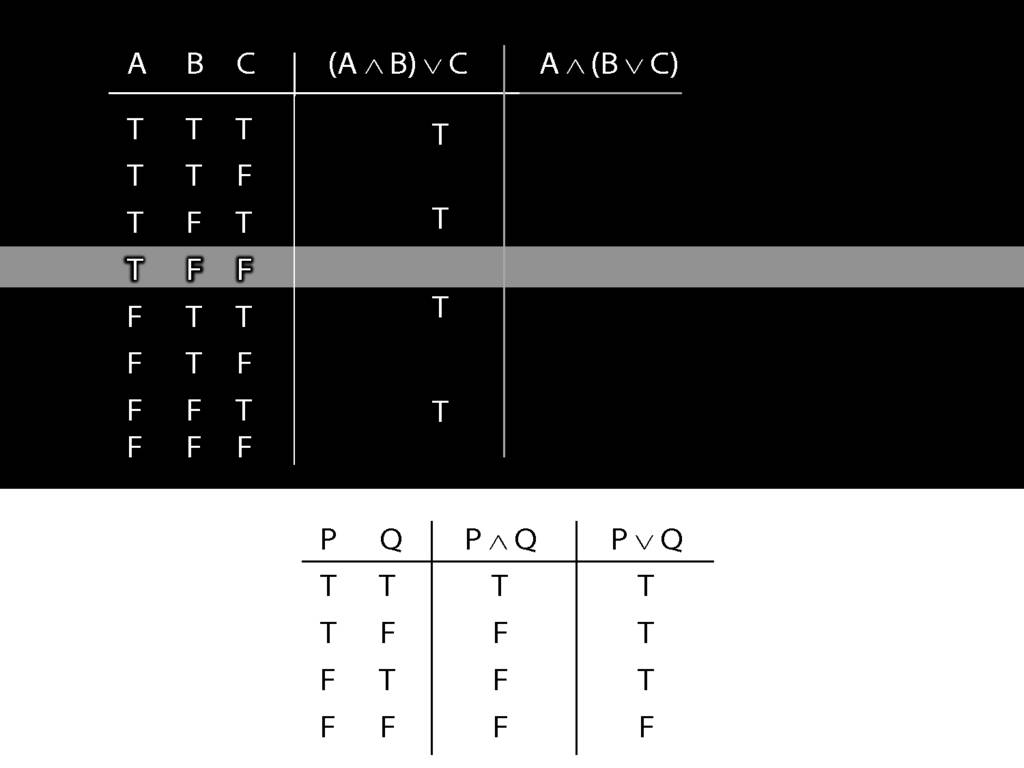
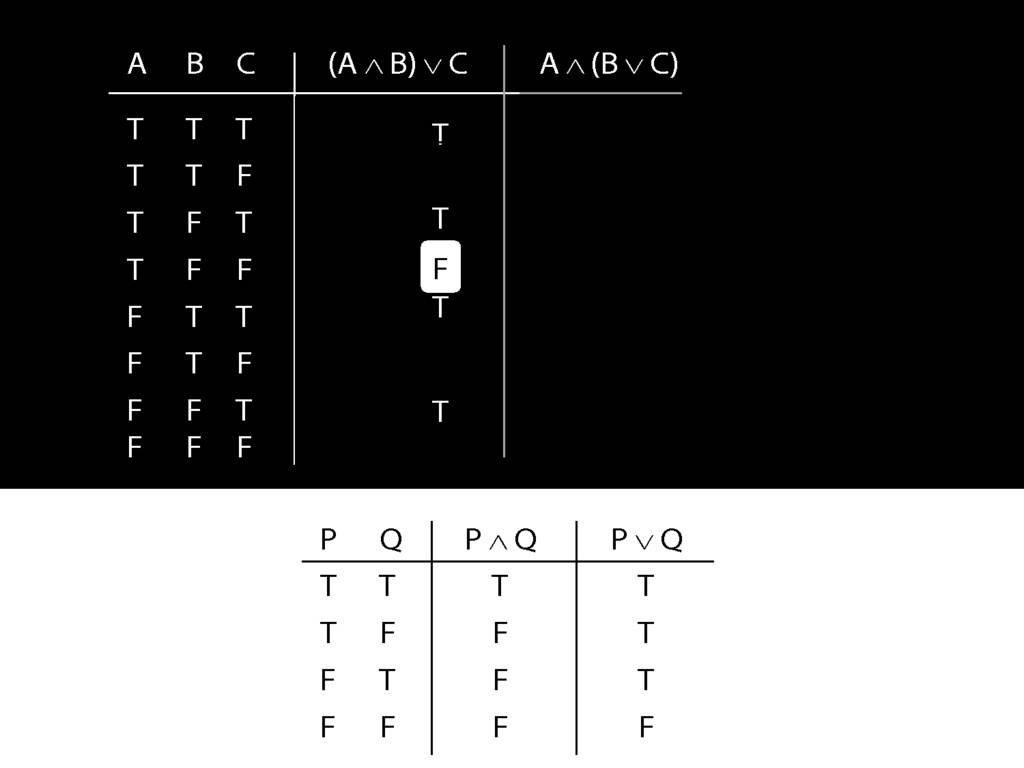
Now consider row four. Here we have to do it the slow way.
We start at a point innermost in the brackets, so with A and B.
What is the truth value of A and B in this row?
That depends on what the main connective in this sentence is, and on what the truth values of A and B are.
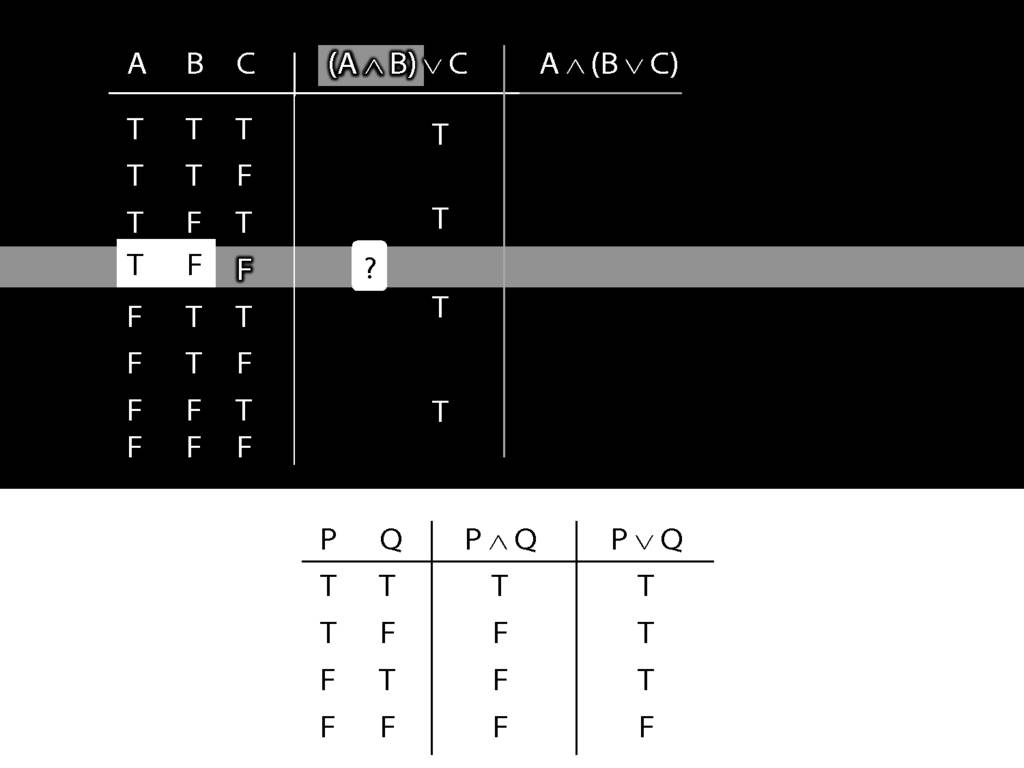
In this row, A is true and B is false.
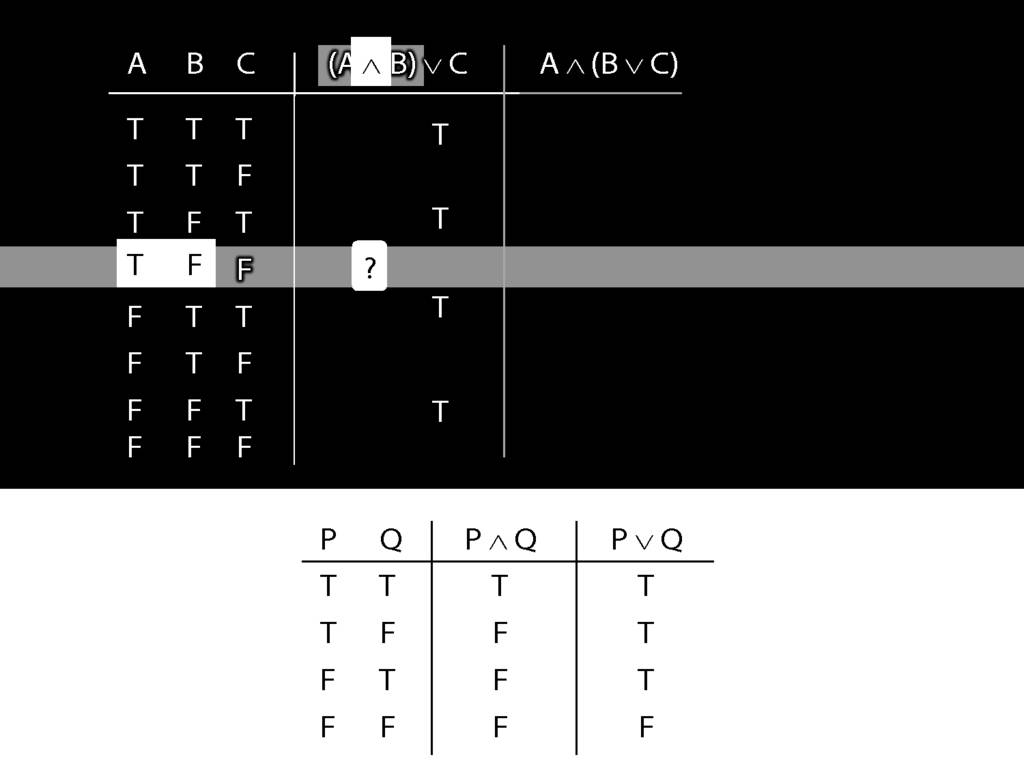
And the connective is conjunction.
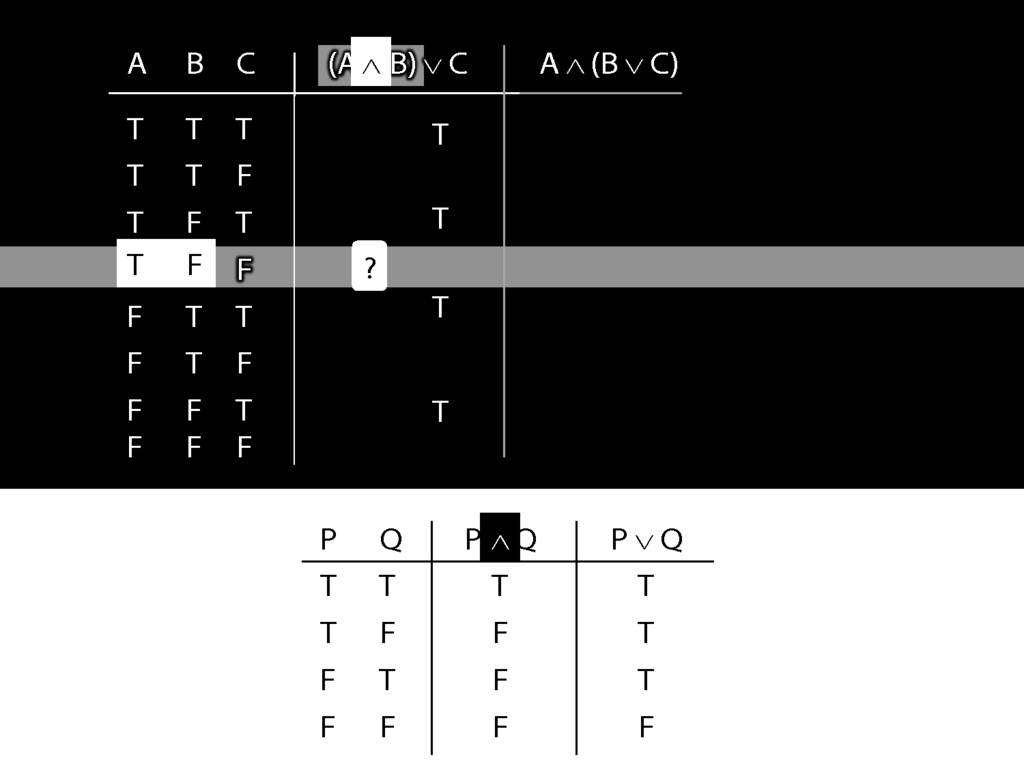
So the truth-table we need to consult is the one for conjunction.
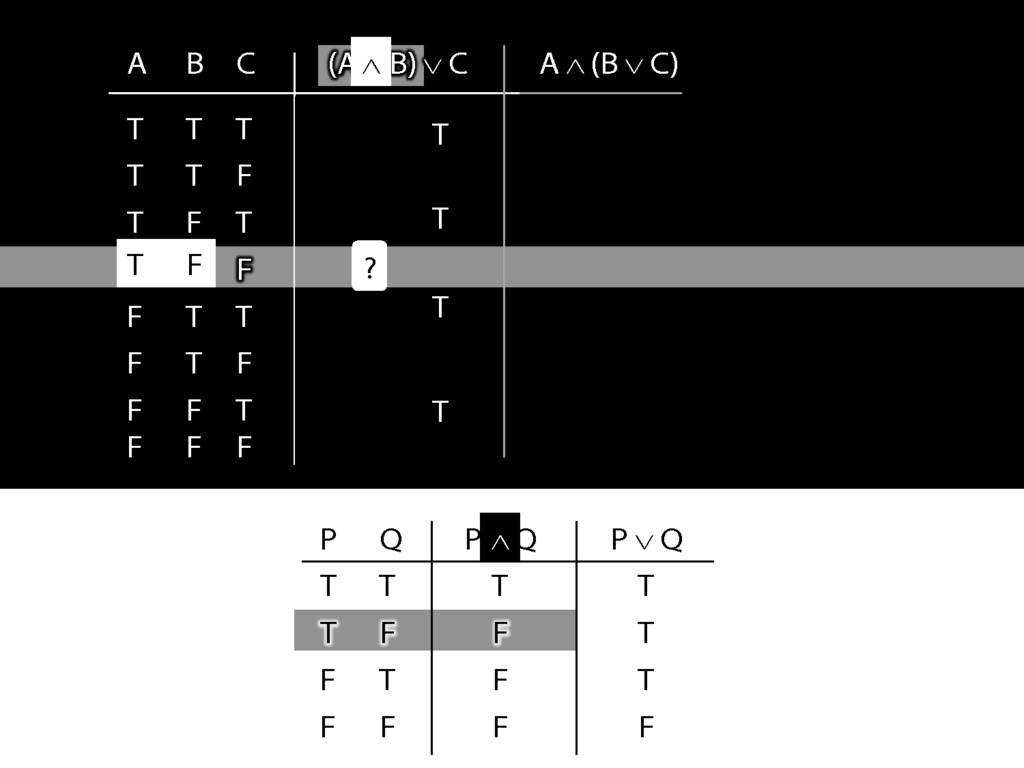
It's the second row that we want because this is the row where A is true and B false.
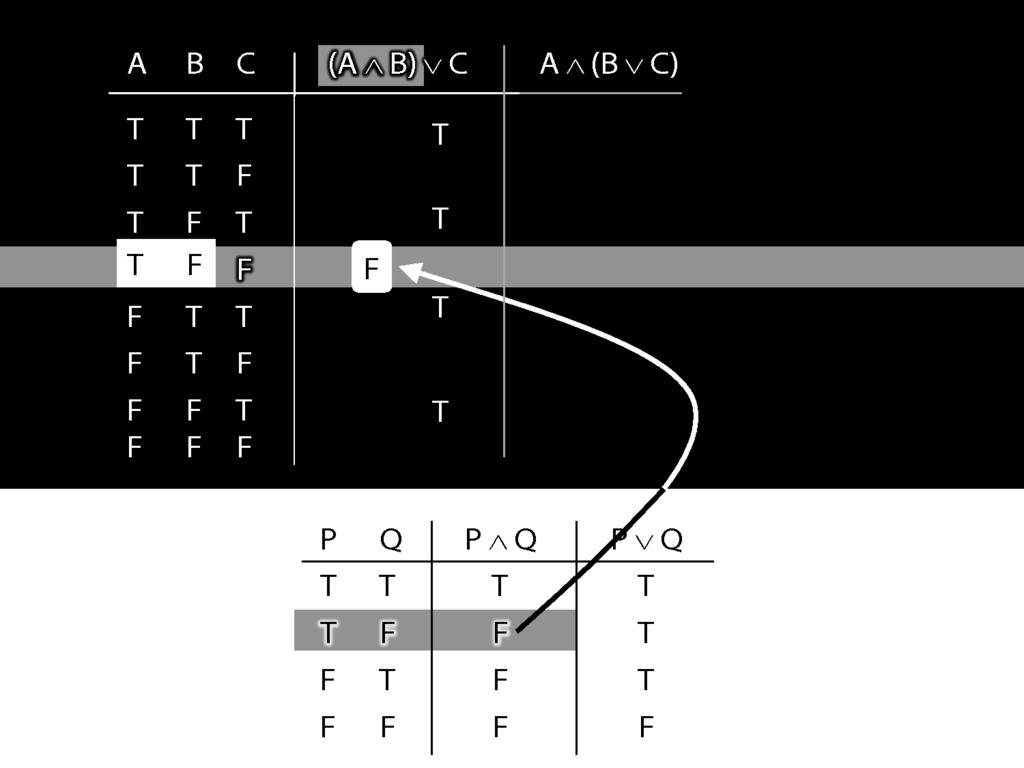
In this row of the truth-table, the conjunction is false.
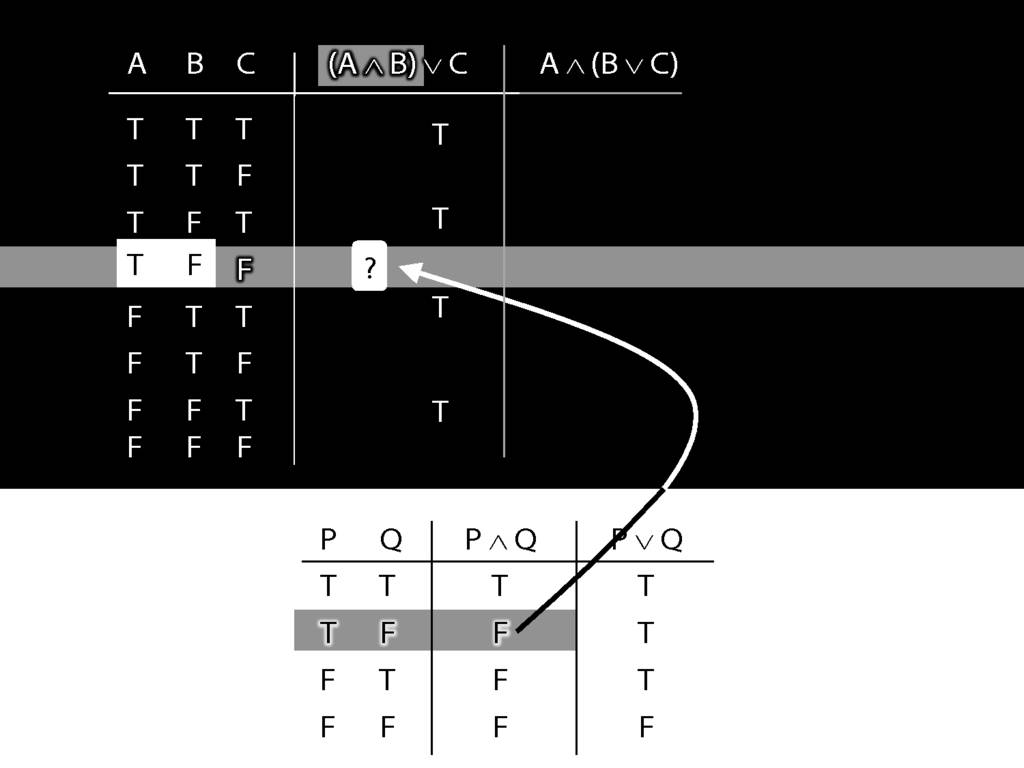
And it's this truth-value that we put into our truth-table for A and B.
Prima!
Bene!
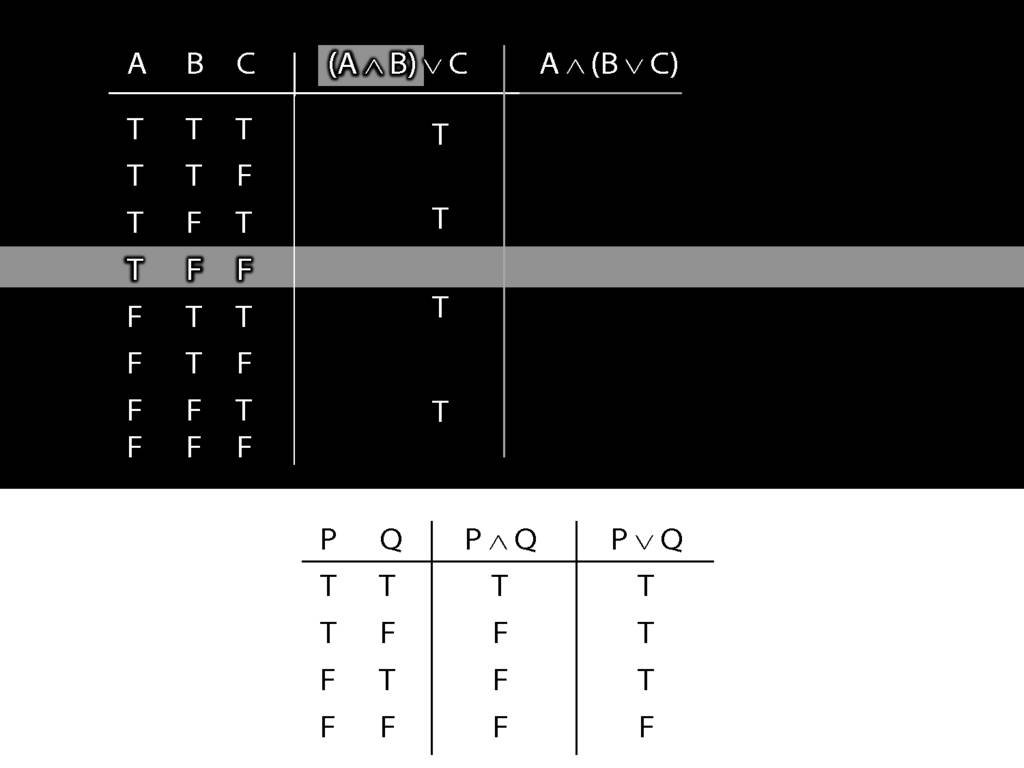
Now we turn to the whole sentence. What is its truth value?
First we have to ask, What is the connective?
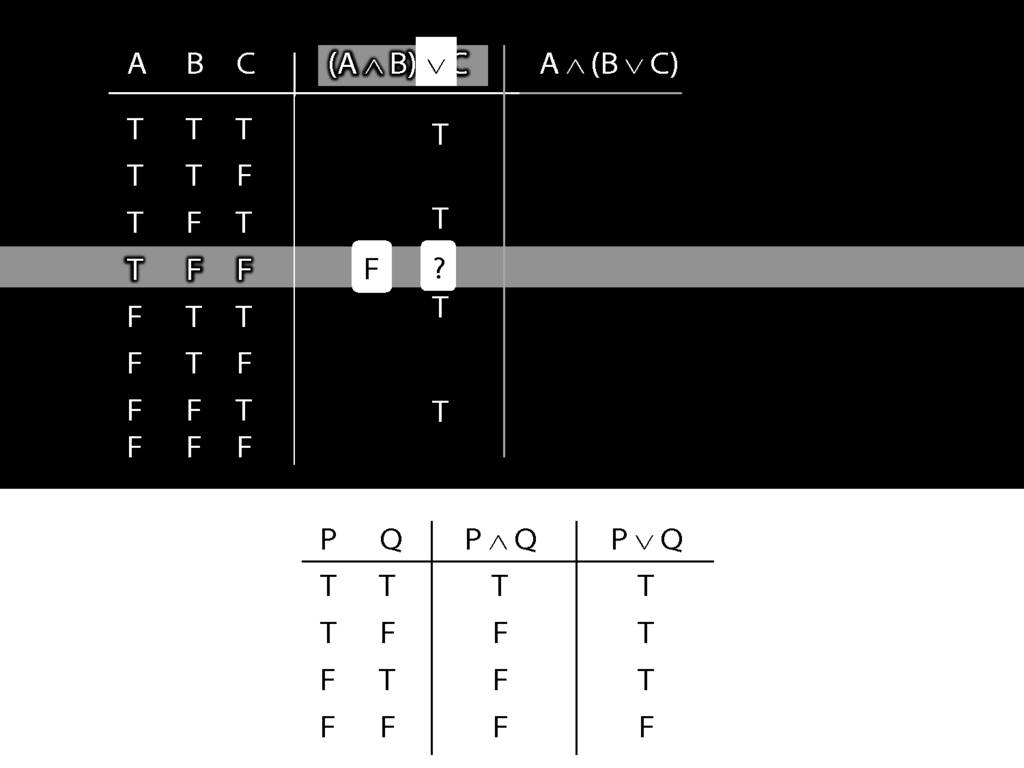
In this case the connective is disjunction.
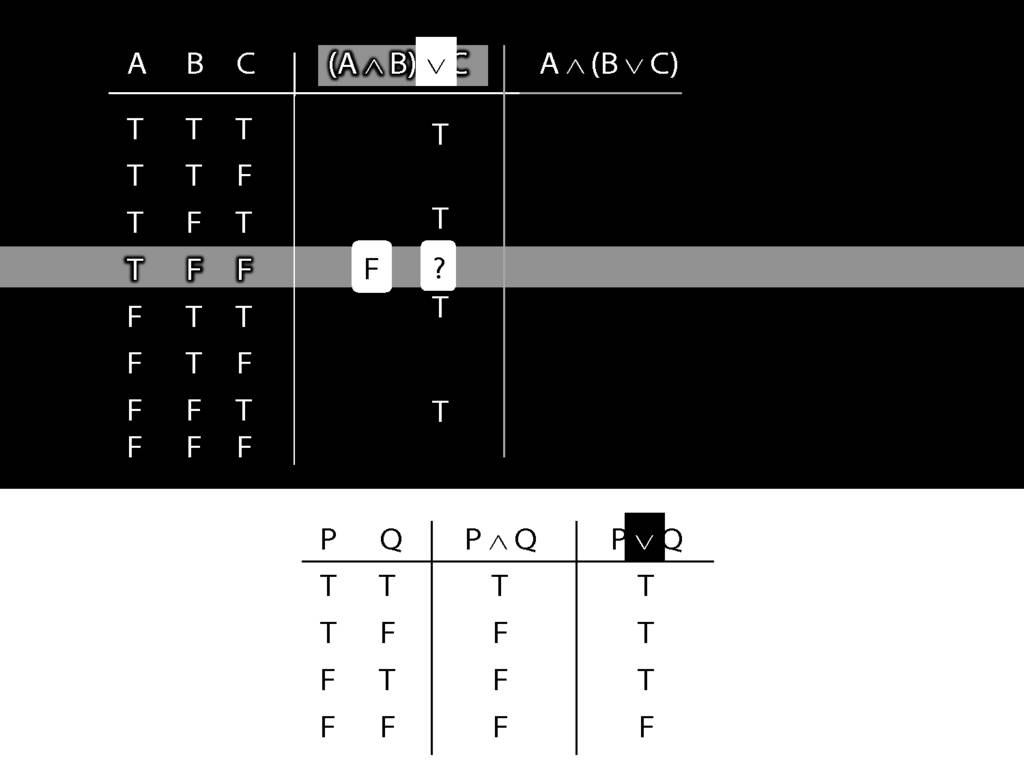
So the truth-table we need to consult is the one for disjunction.
But which row do we need?
In this case, the thing on the left of the disjunction (the left disjunct) is A and B, which is false;
and the thing on the right, C, is also false.
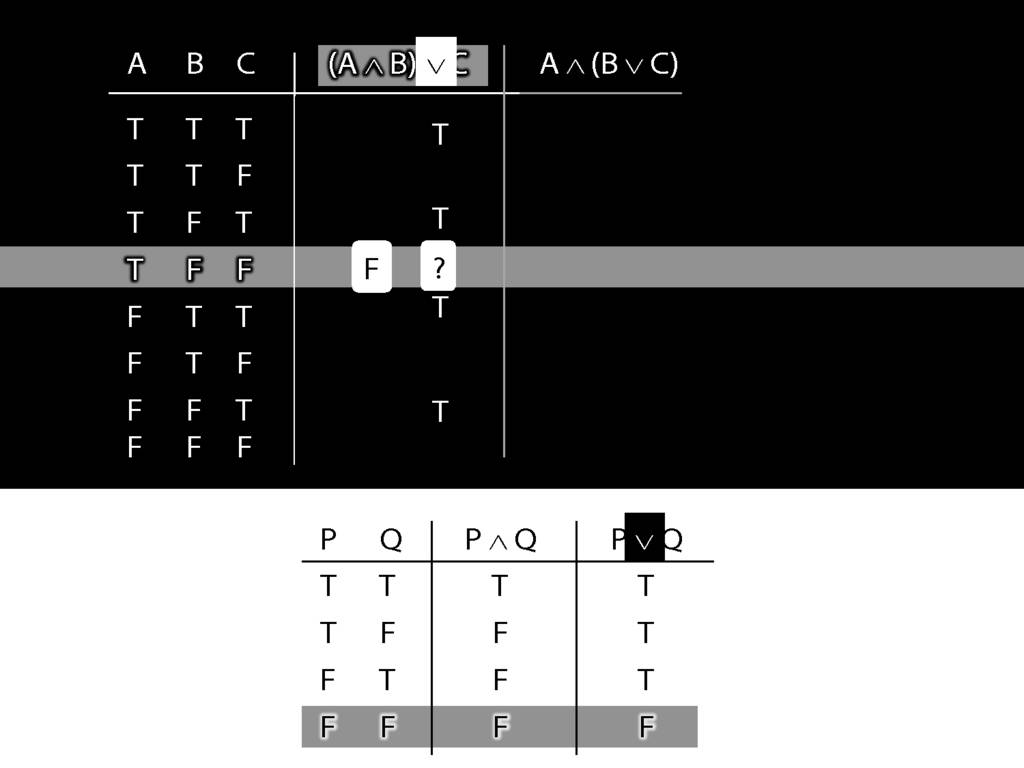
So we're looking at the last row of the truth-table, the one with false and false.
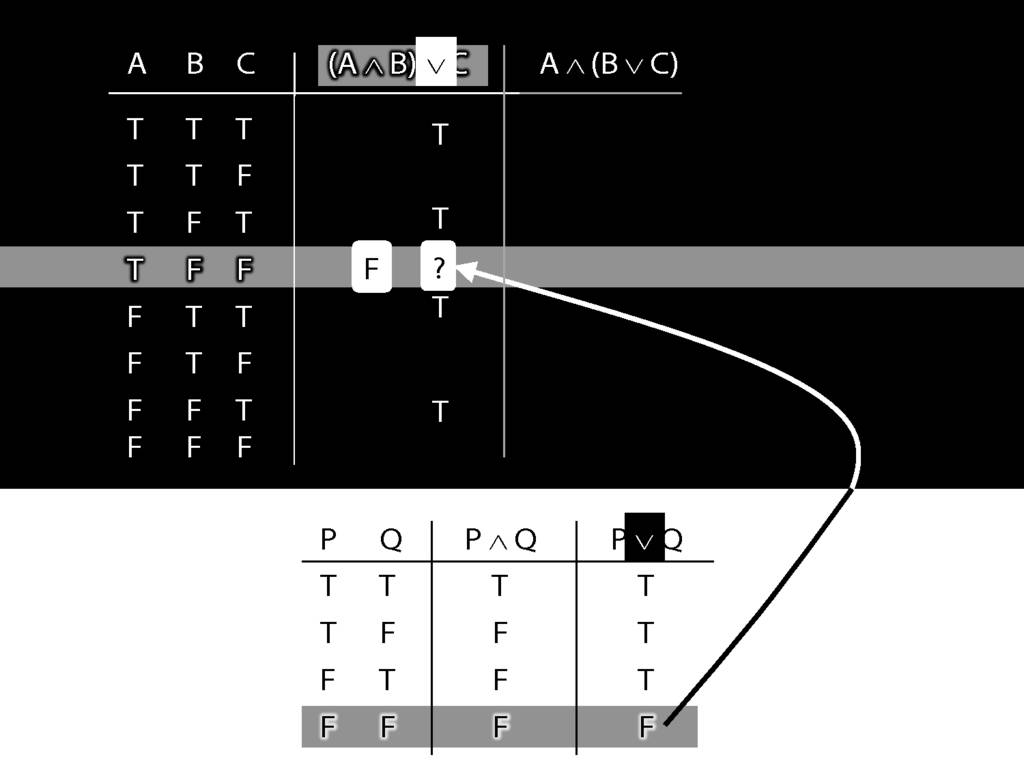
The truth-value in this row is the truth-value we need to put into the truth-table we're working on.
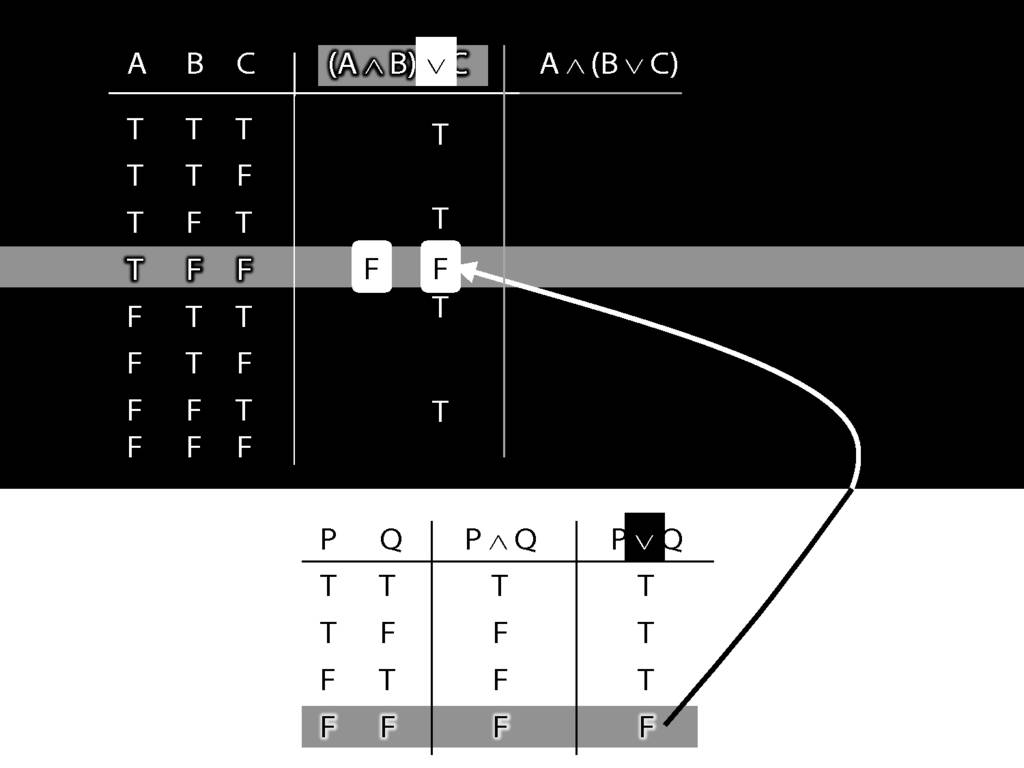
So we know that (A and B) or C is false in this row, where A is true, B is false and C is false.
Sehr gut!
I'll give you the rest of this for free.
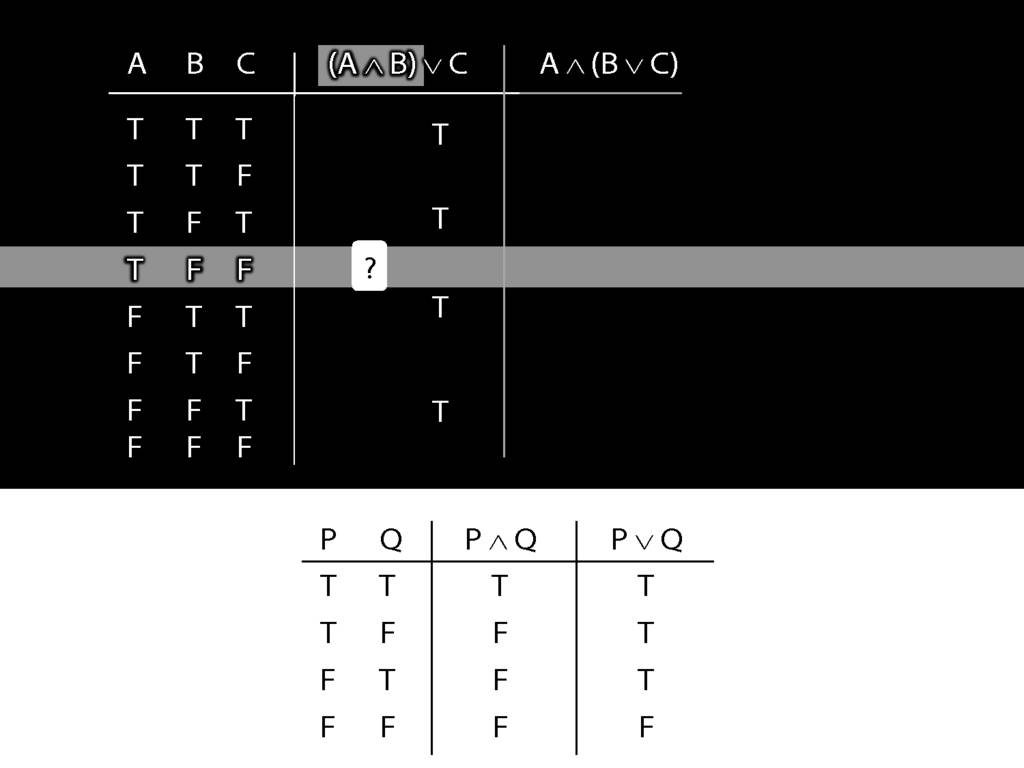
Now think about the other sentence.
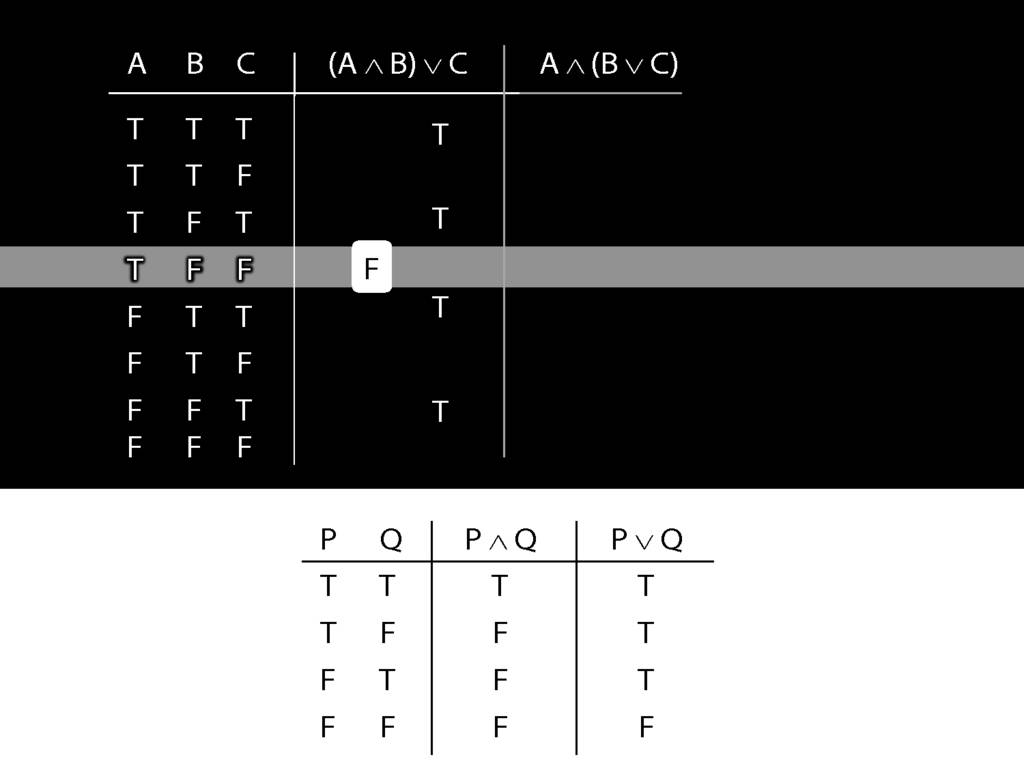
The thing on the left, the left conjunct, is the simplest part.
What happens when this is false?
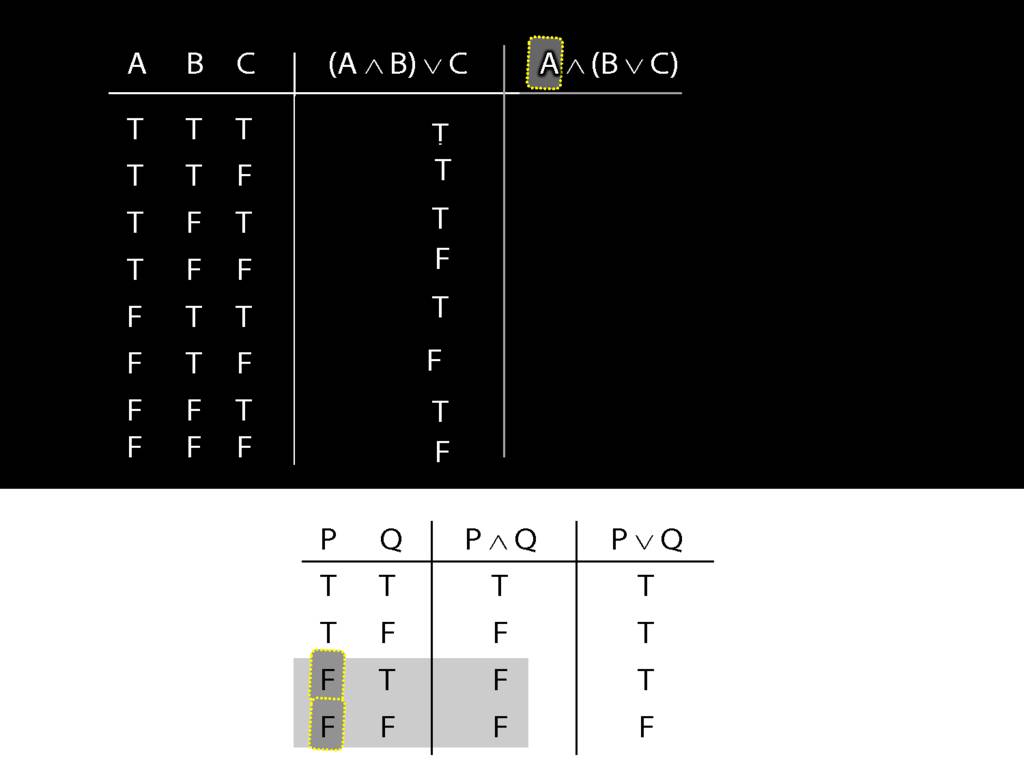
Regardless of what happens on the right, when the left side of a conjunction is false, the whole thing is false.
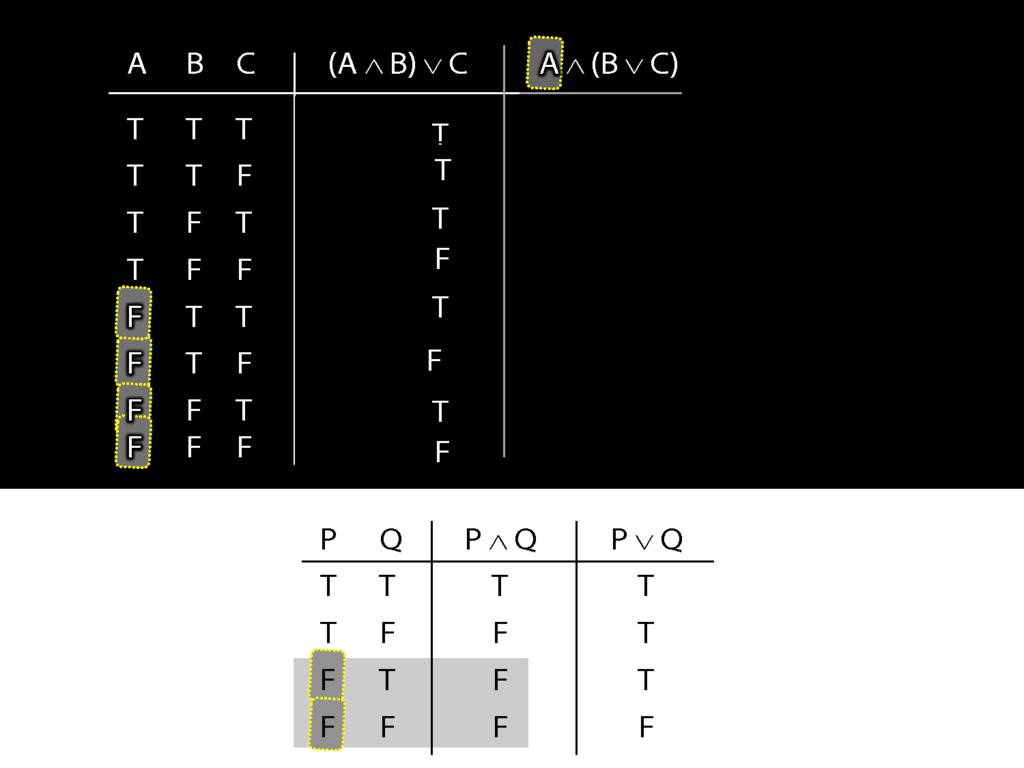
This can save us time. Where is this left side of the conjunction false?
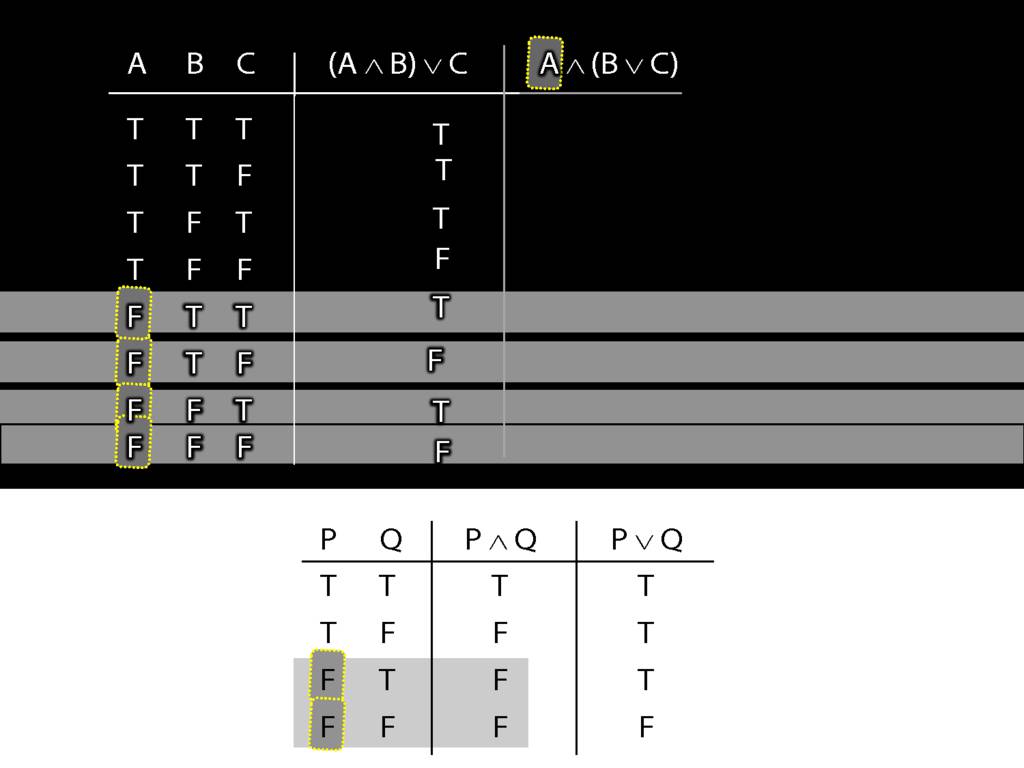
In the bottom four rows.
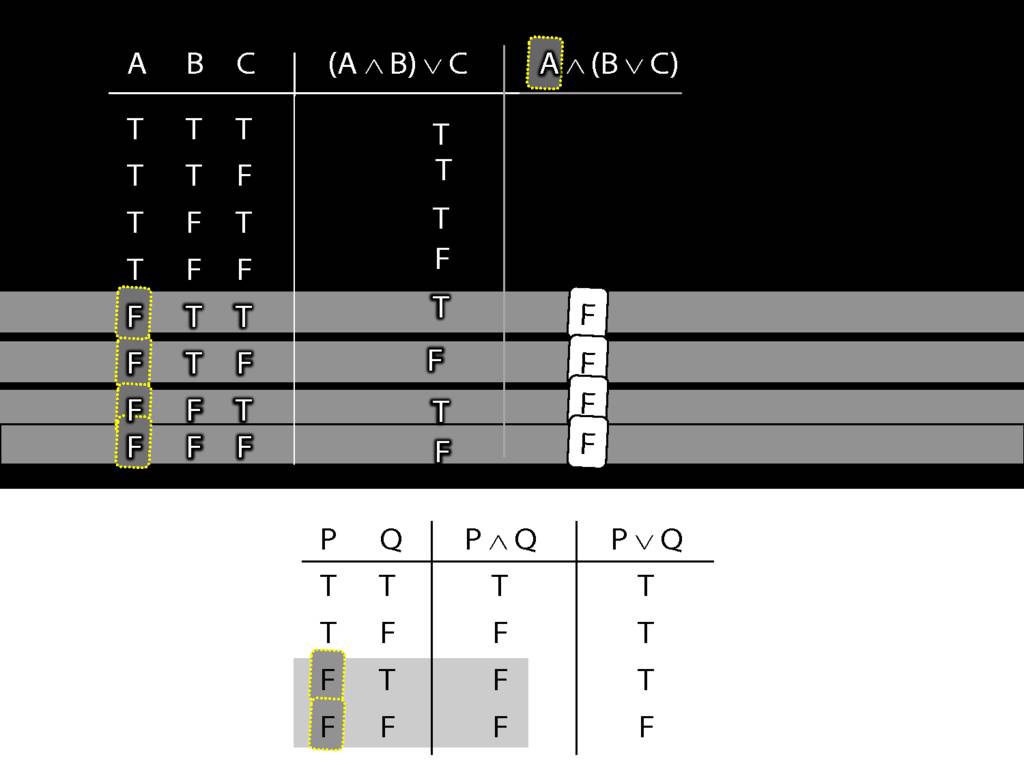
So we can be sure, even without thinking about the right side, that the whole sentence is false in these rows.
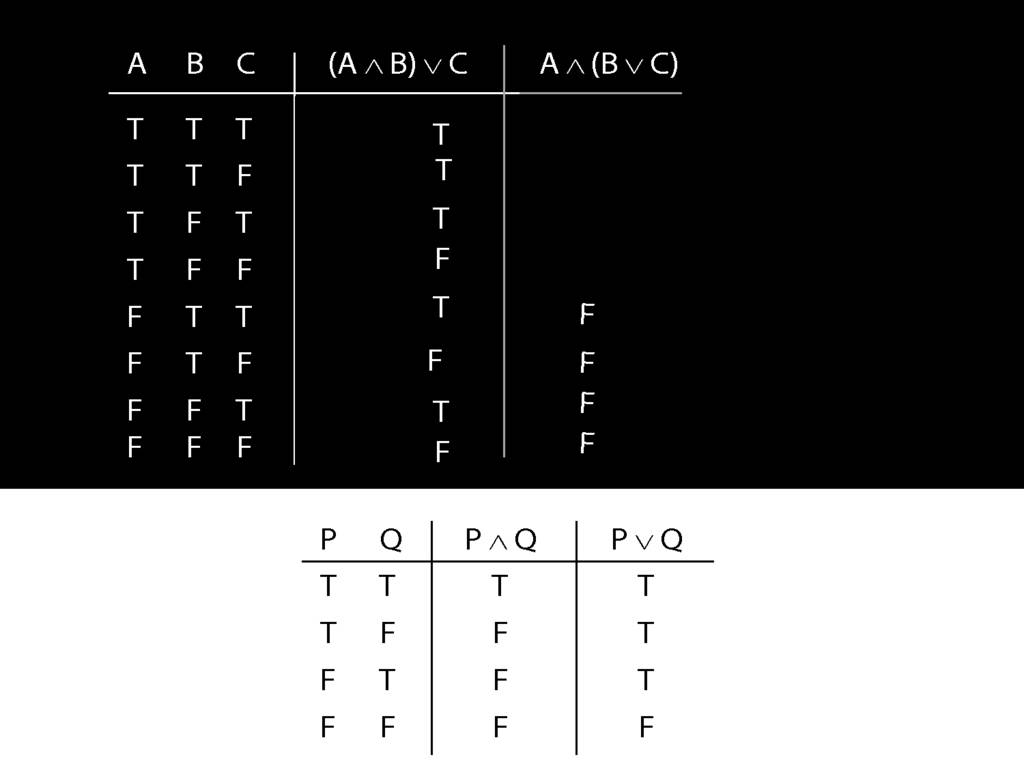
The rest of the truth table probably requires more thought ...
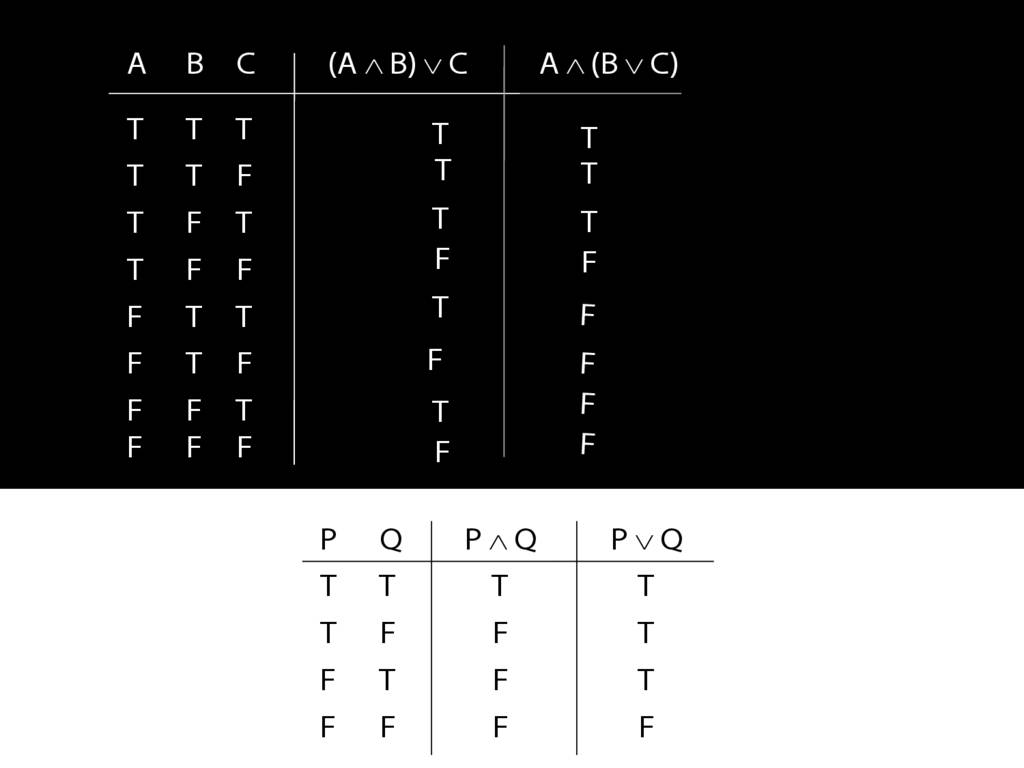
... so here's one I made earlier.
\section{A ∧ B ∨ C: They Are Different}
\section{A ∧ B ∨ C: They Are Different}

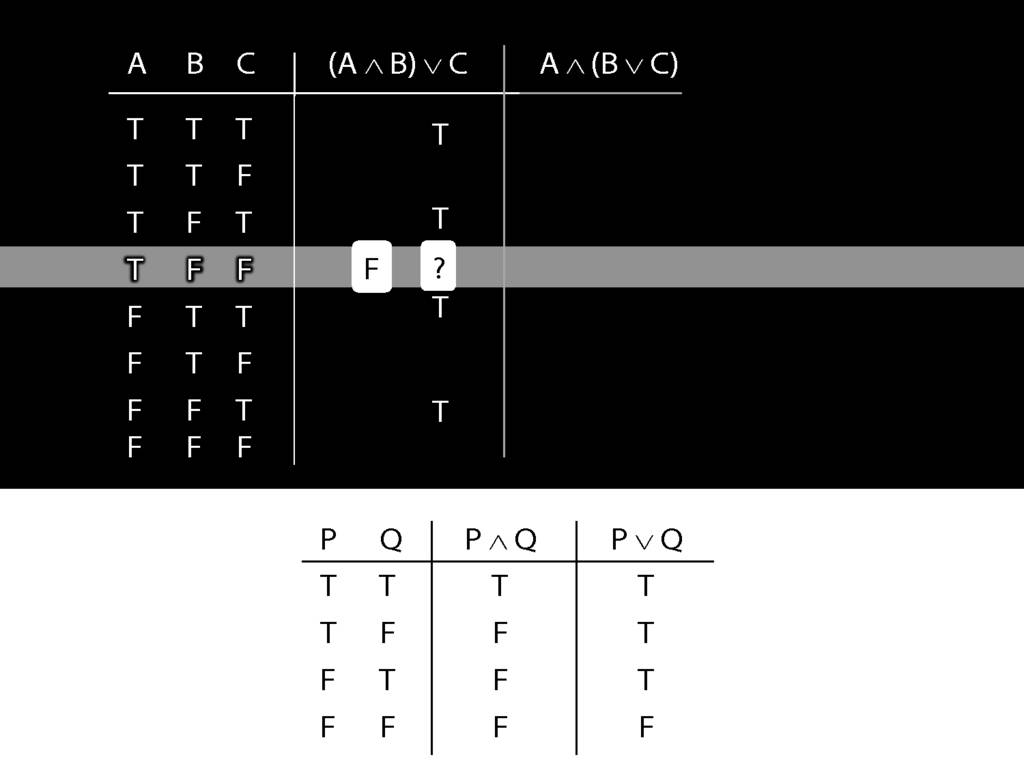
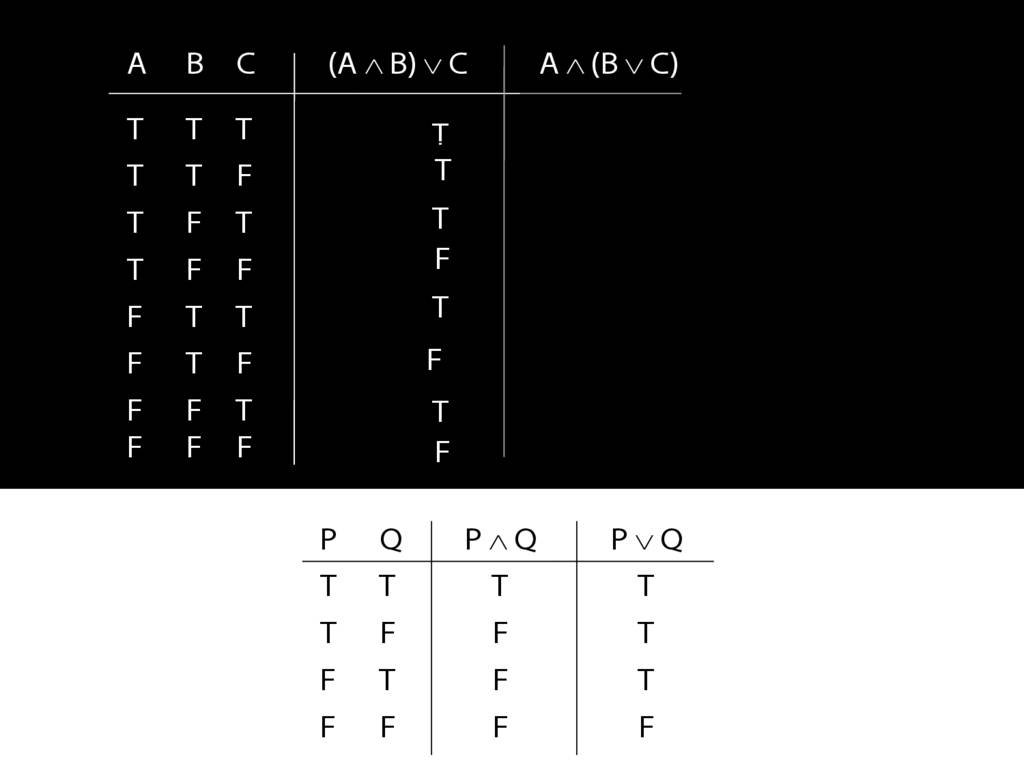
OK, so we have the truth tables. Where do they differ?

The truth-tables differ in rows five and seven only.
So the only difference between these two sentences is the brackets, but
this difference means that the two sentences differ in truth-value.

This also makes a difference to their role in arguments, of course.
Which of these arguments is logically valid?

Recall that for an argument to be logically valid is for ...

Now in the case of truth-tables, for an argument to be logically valid amounts to there being no row of the truth-table where the premise is true and the conclusion false.

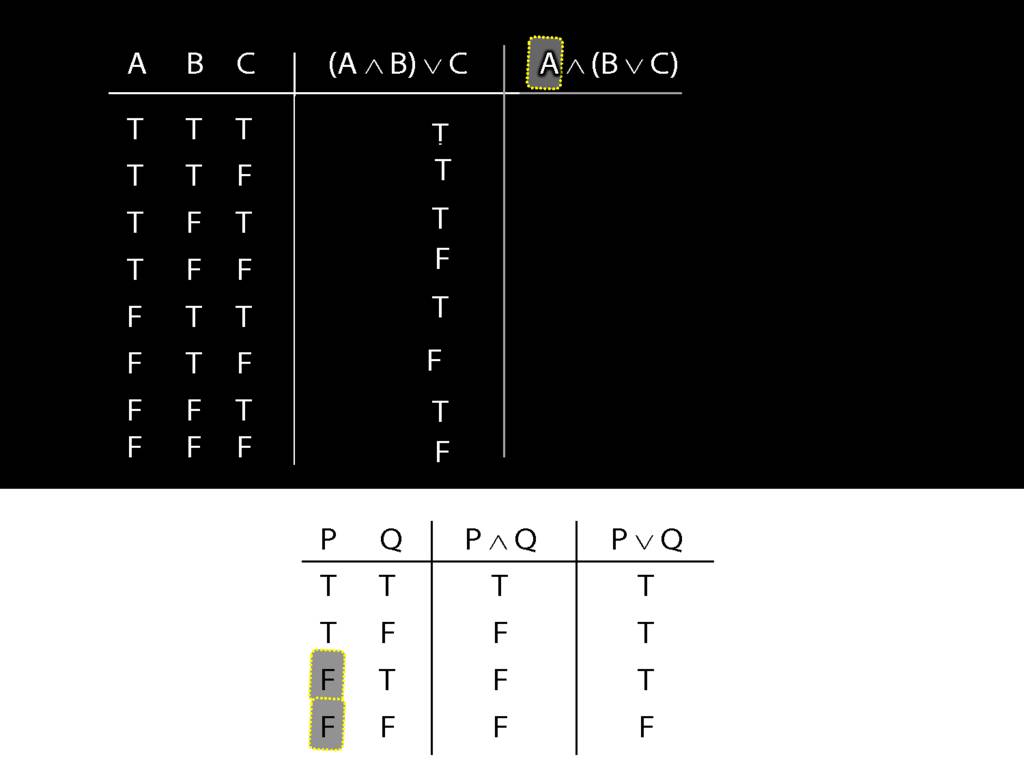
Consider the first argument. Is this valid?
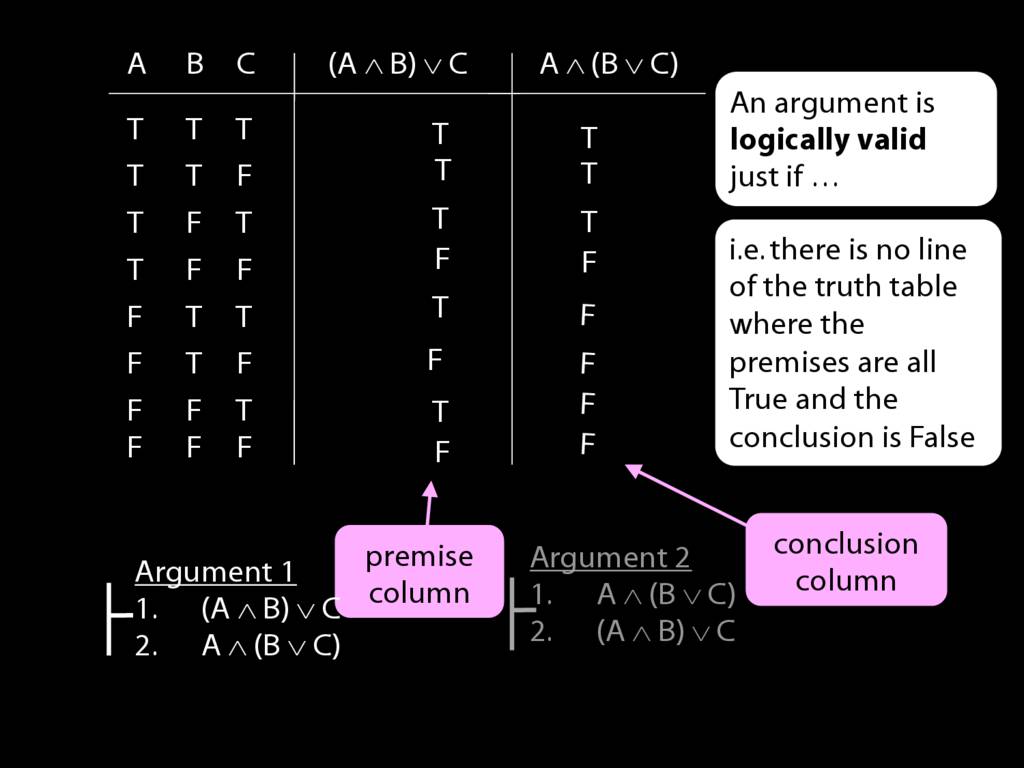
Here's the premise and here's the conclusion.
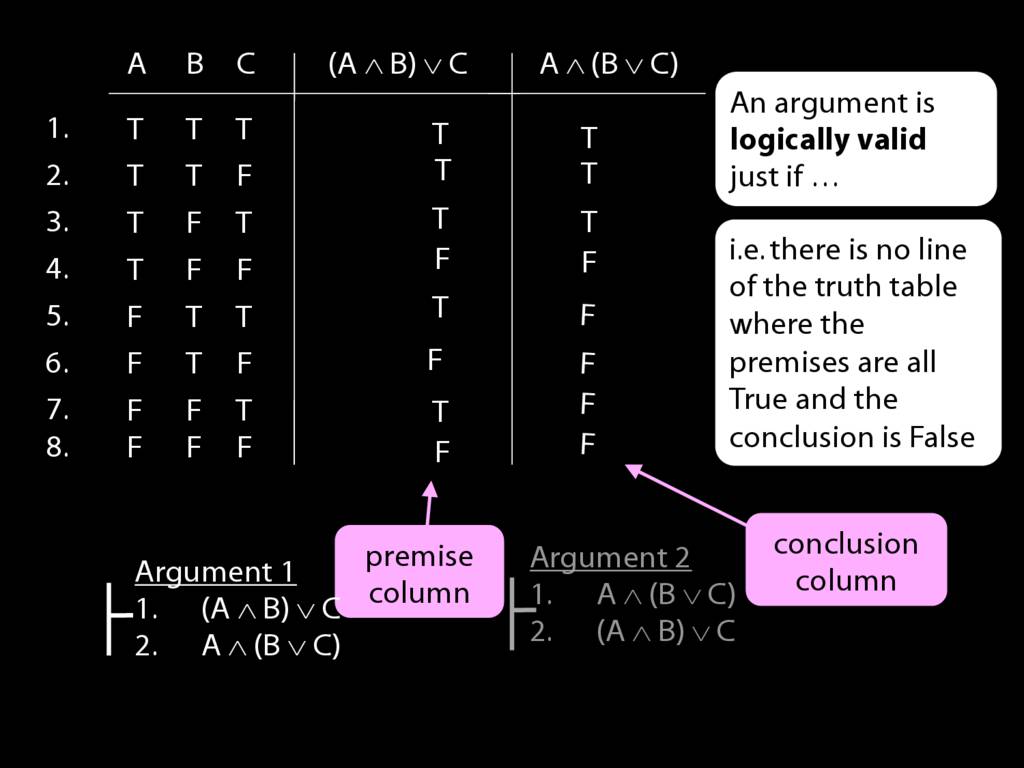
(Let's have some numbers so you can see which lines I'm talking about.)
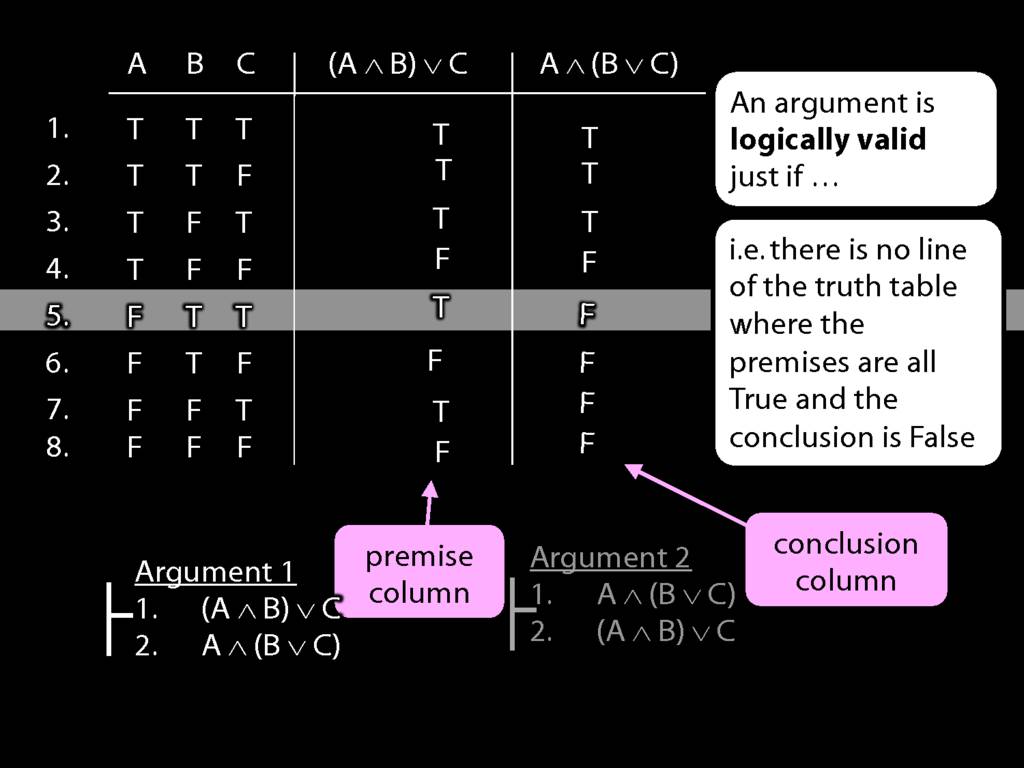
What happens in line five? Here we have true premise and false conclusion.
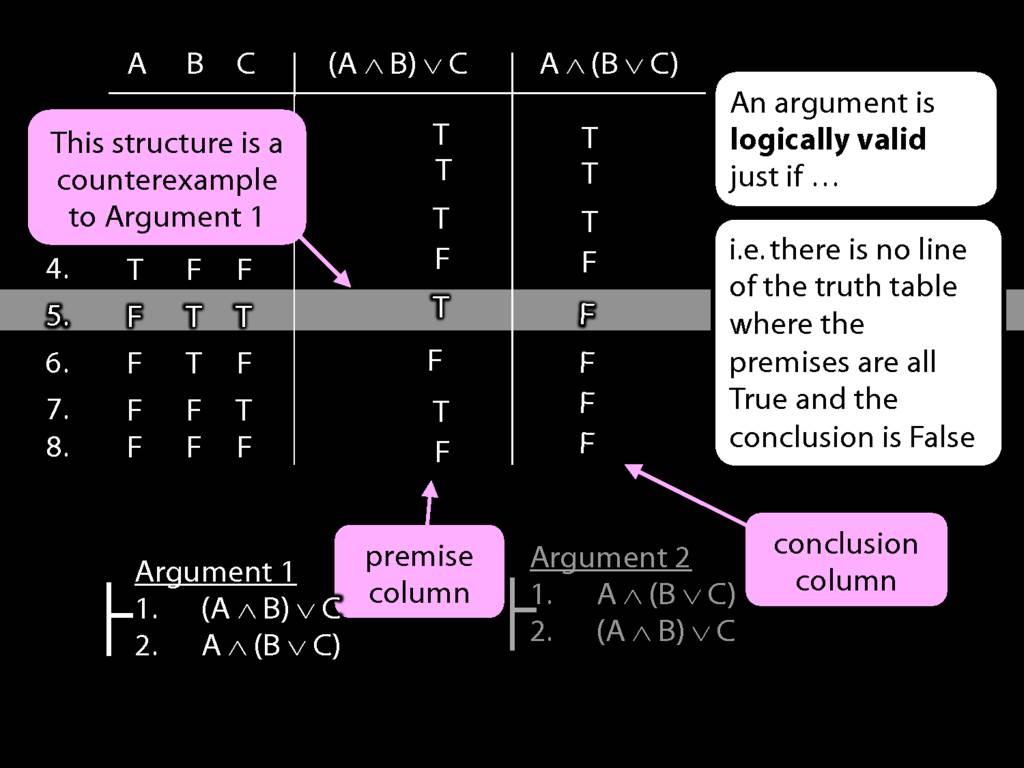
So the argument is not valid, and this row is a counterexample to the argument.
If someone asks you for a counterexample, what do you have to write?
Just this : A false, B true and C true. That's is: you've specified a possibile situation
in which the premises are true and the conclusion false, and that's what a counterexample is.
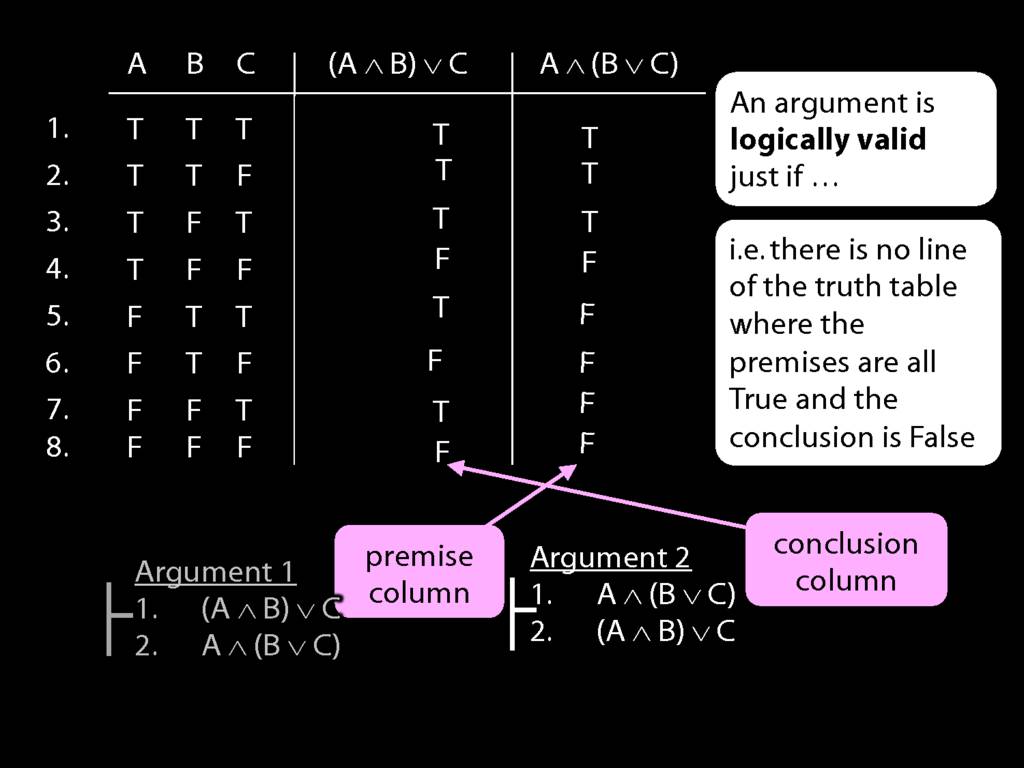
Now look at argument 2. Here the premise and conclusion columns are the other way around.

In the last five rows, the premise is false. So we can ignore these because
we won't find a true premise AND a false conclusion where the premise is false.'
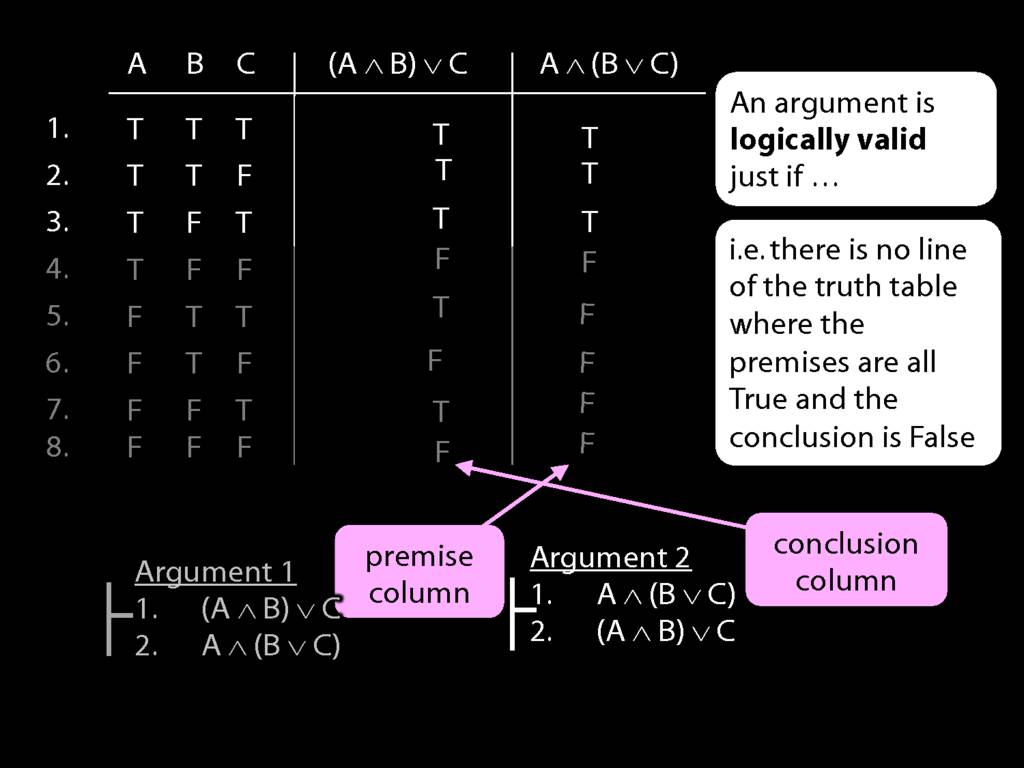
What about the top three rows?

In the top three rows, the premise is true ...
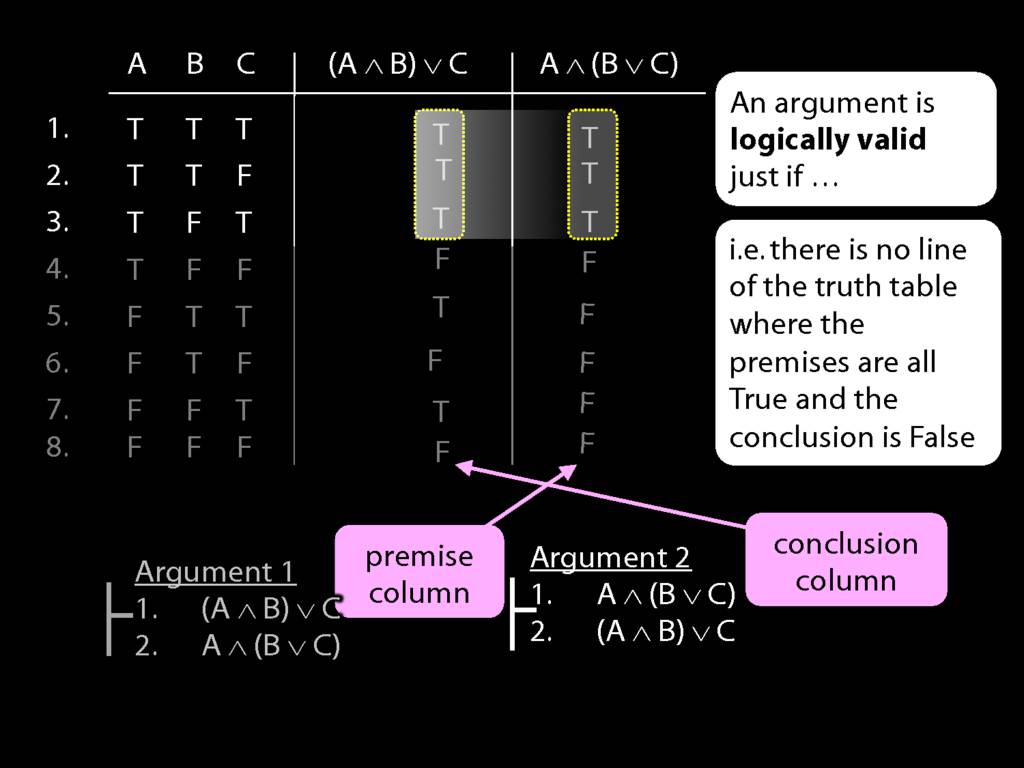
... but so is the conclusion.
So this second argument is clearly logically valid.
(A ∧ B) ∨ C
vs
A ∧ (B ∨ C)
This ends my discussion of these two sentences.
Although they differ only with respect to brackets, they have different truth-tables
and so contribute differently to the validity or not of arguments.
There's a simple message and a complex one.
The simple message is that the brackets matter.
The complex one is that we have more work to do in explaining our formal language, awFOL.
We have more work to do because we haven't yet said what the brackets mean,
although it's clear that they contribute to the meanings of sentences of awFOL.
What is the counterpart of a truth-table for brackets?
In this course we don't have time to worry about this question; we must leave the meaning
of the brackets as something that you get only implicitly.
3.14, 3.15
3.14, 3.15
7.2, 7.5, 7.6

Formal Proof
\section{Formal Proof}

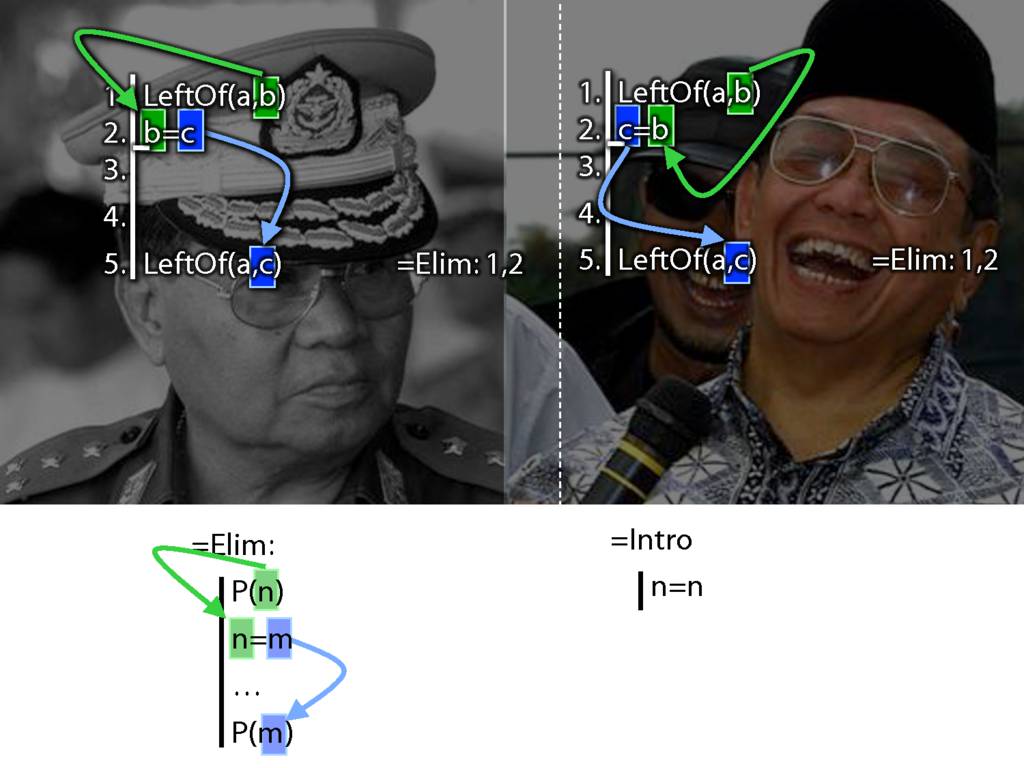
Recall these two diagrams from earlier. The left one is a proof, the right one is not.
Spot the difference.

Yes, the difference is at line 2.
But why is this difference significant?
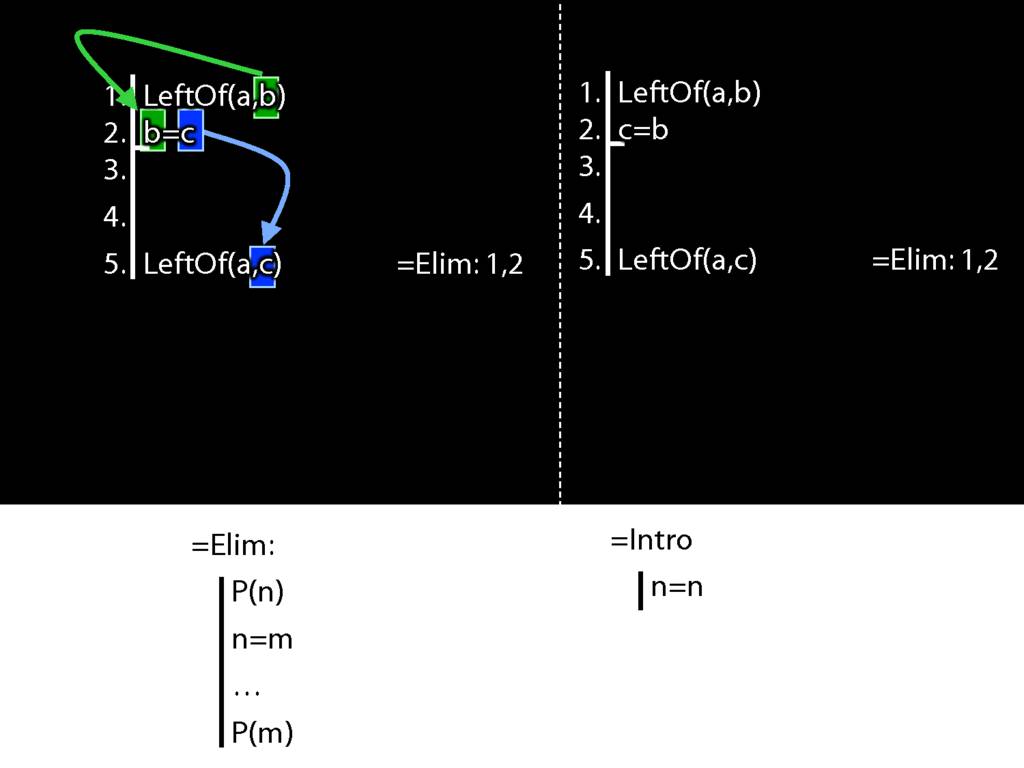
Look what happens in the left diagram (the genuine proof). Do you see the pattern?
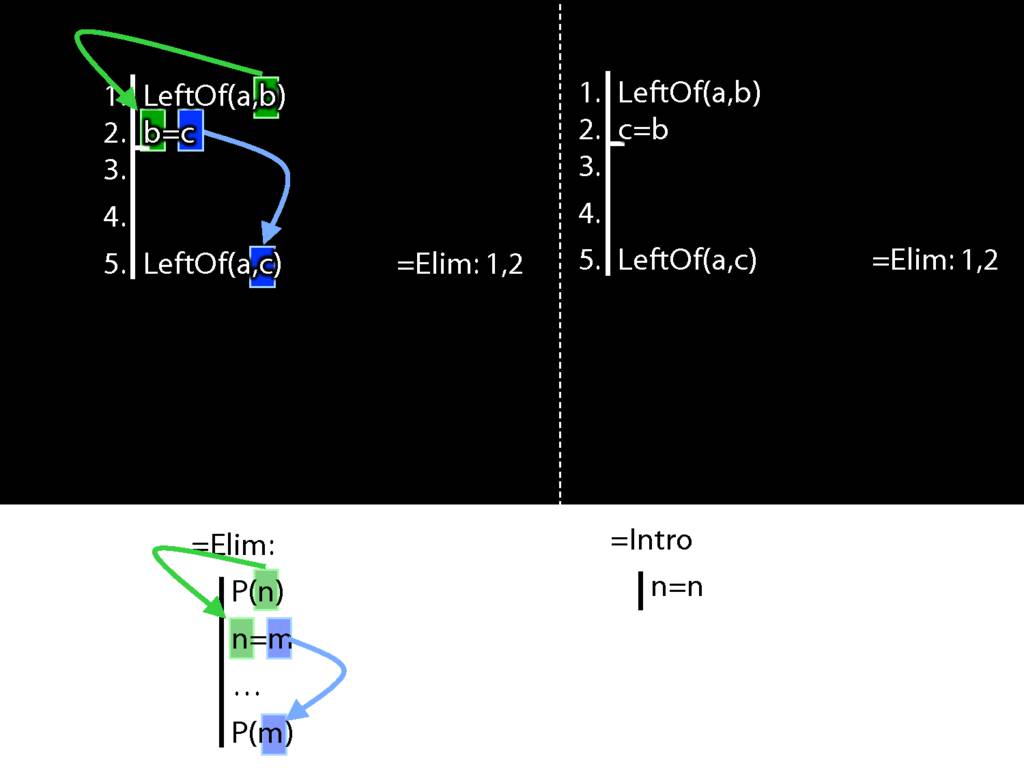
That pattern matches the pattern described by the rule identity elimination (=Elim)
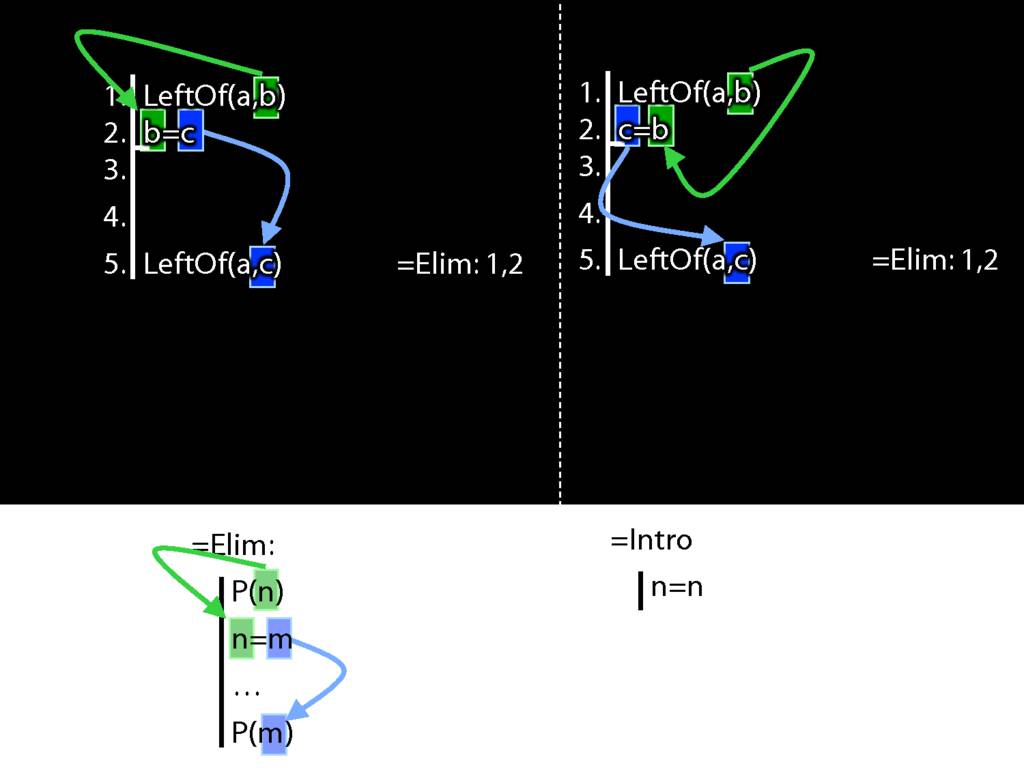
Now look at the pattern in the diagram on the right.
This is a different pattern.
You might protest that b=c and c=b mean the same thing; one can't be true unless the other is.
These sentences do not express different thoughts.
This is true but it is entirely besides the point.
Why is it beside the point?
In studying proof, we're interested in ways of linking the purely formal to the genuinely meaningful.
The proof system Fitch is a formal system of proof.
What we want to show is that, within limits, Fitch captures a notion of logical validity.
This is interesting only because we can describe Fitch entirely without invoking truth or meaning.
So the fact that b=c and c=b mean the same is irrelevant in Fitch.
When you're thinking about Fitch, all you care about is the pattern of symbols.
And b=c is a different pattern from c=b.

This is Abdurrahman Wahid, popularly known Gus Dur, a former president of Indoneisa and one of the most jovial national leaders ever. He was a really nice guy. As president he was infirm and nearly blind. When asked to resign he replied “I need help to step up, let alone step down.” (Economist 2010-01-07 obituary). Unfortunately he died recently (december 30 2009)

And this is Than Schwe, Myanamar’s military ruler.
Guess who I'd pick to marks your logic exam.
One last thing. The argument on your right is logically valid. Can you prove it?