Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
\title {Logic I \\ Logic (PH133)}
\maketitle

\def \ititle {Logic (PH133)}
\def \isubtitle {Lecture 4}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
\section{Everything Is Broken}
\emph{Reading:} §9.1, §9.2
\section{Everything Is Broken}

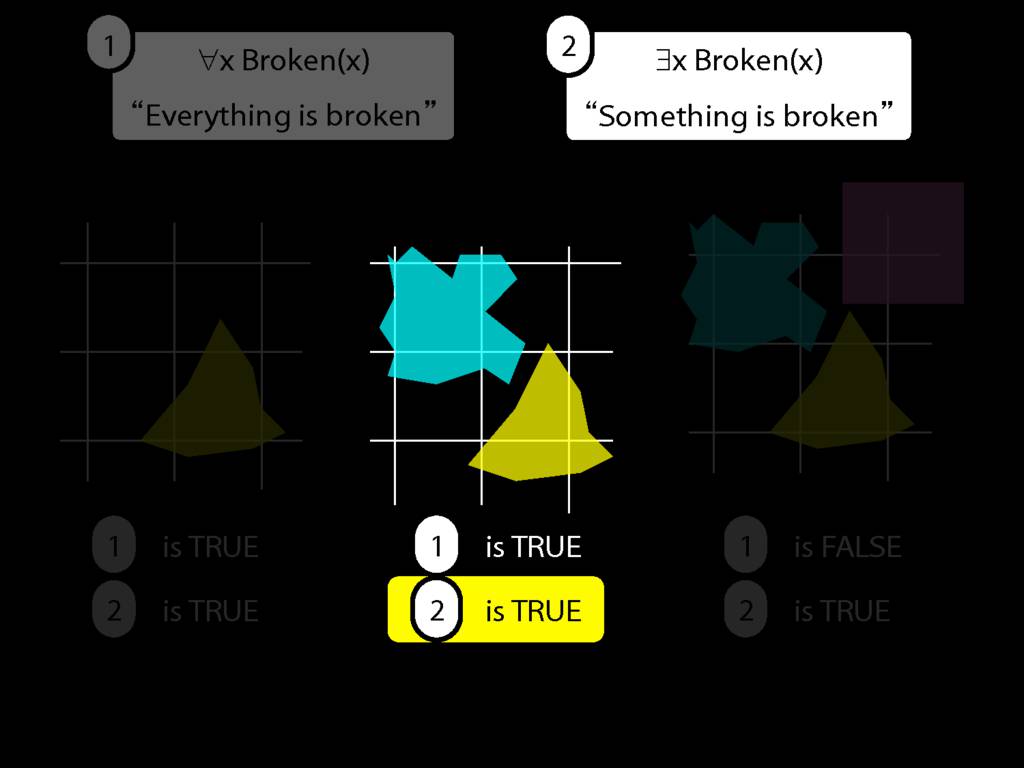
Everything is broken: ∀x Broken(x)
Something is broken: ∃x Broken(x)







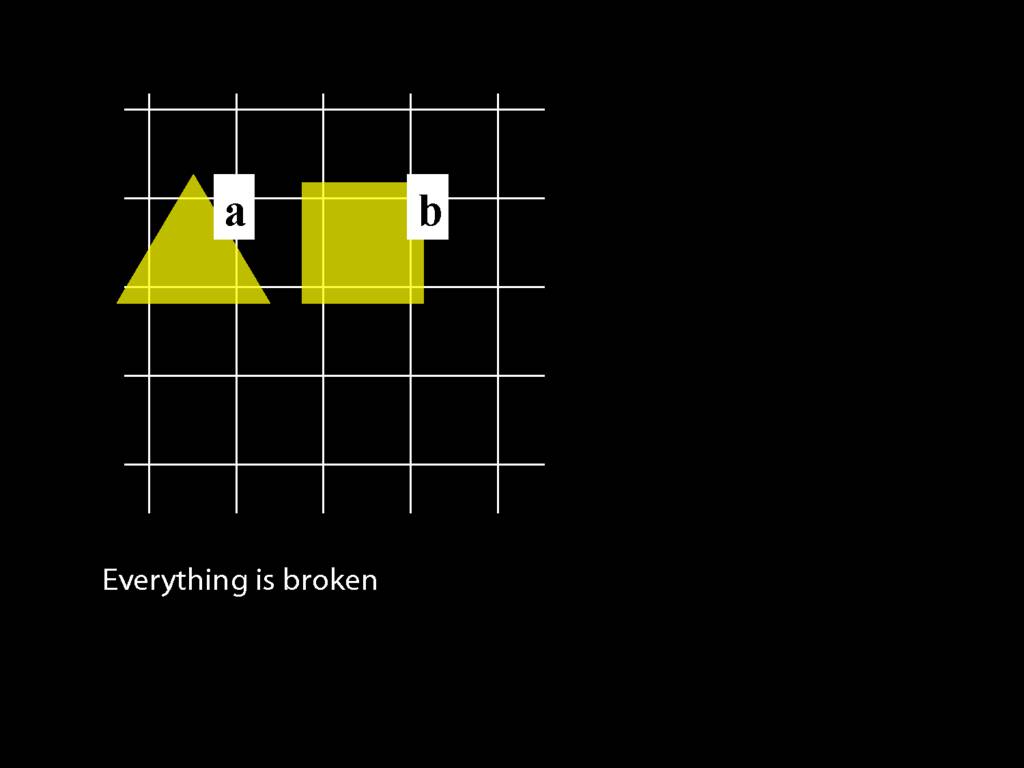
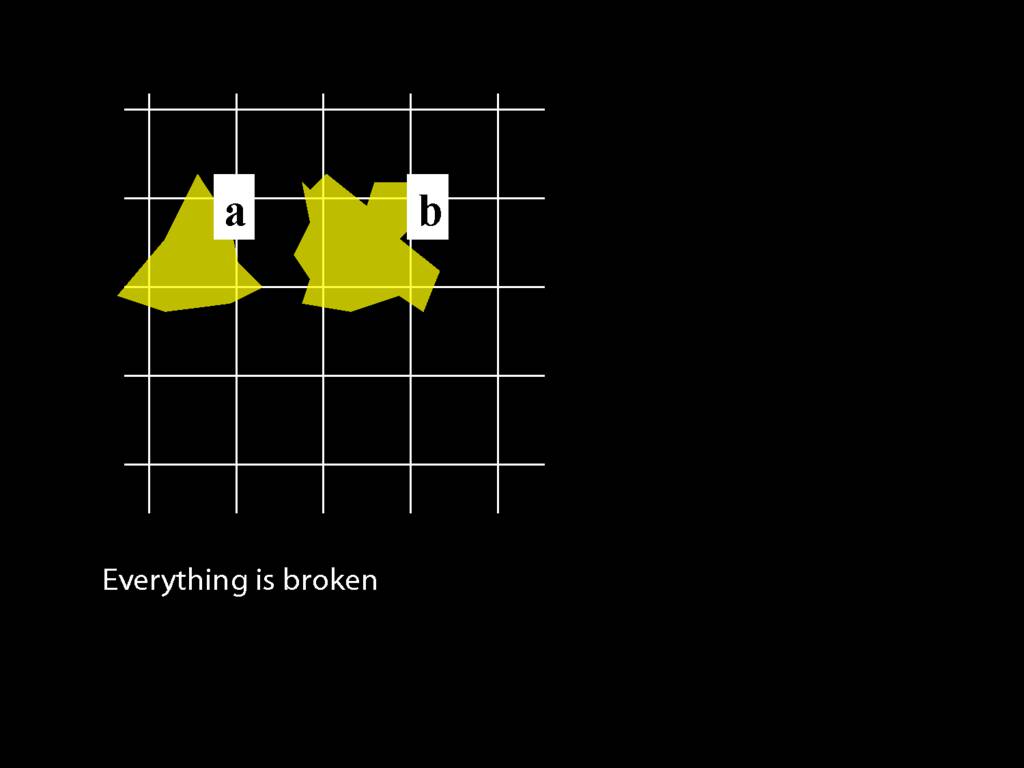



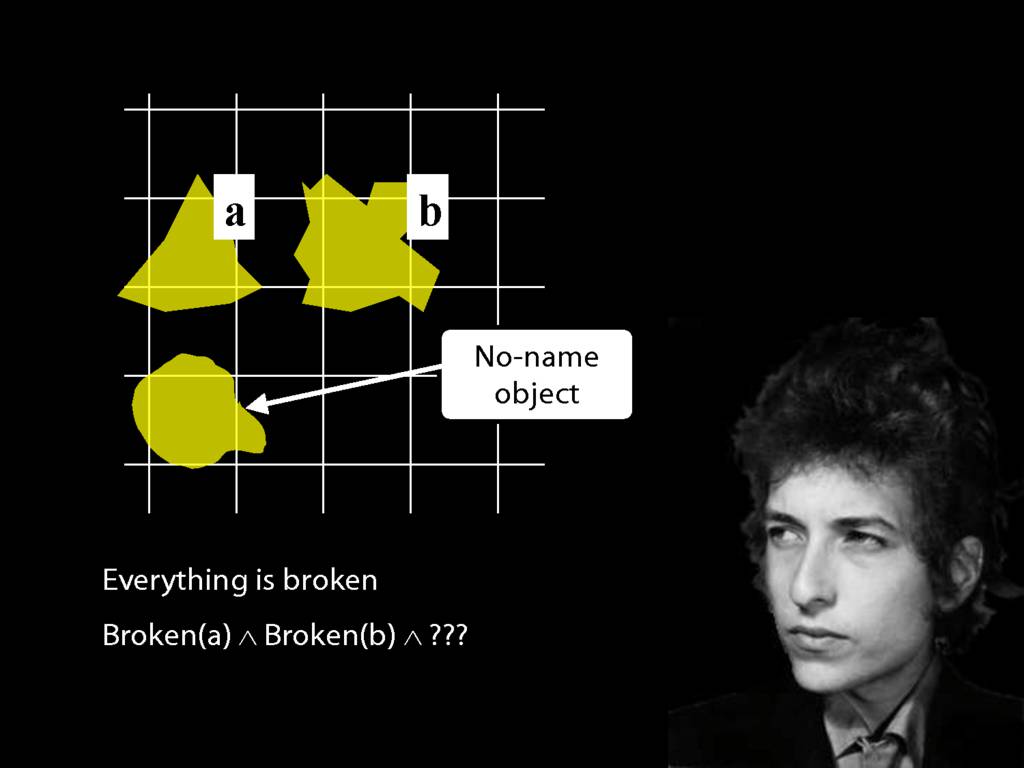
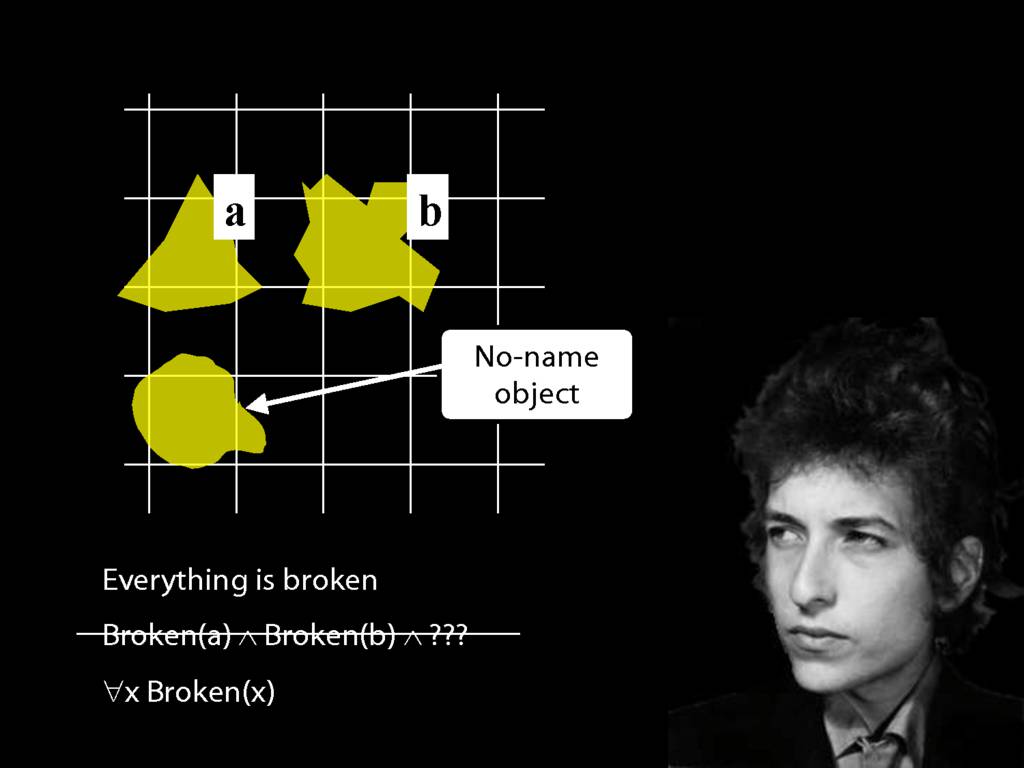
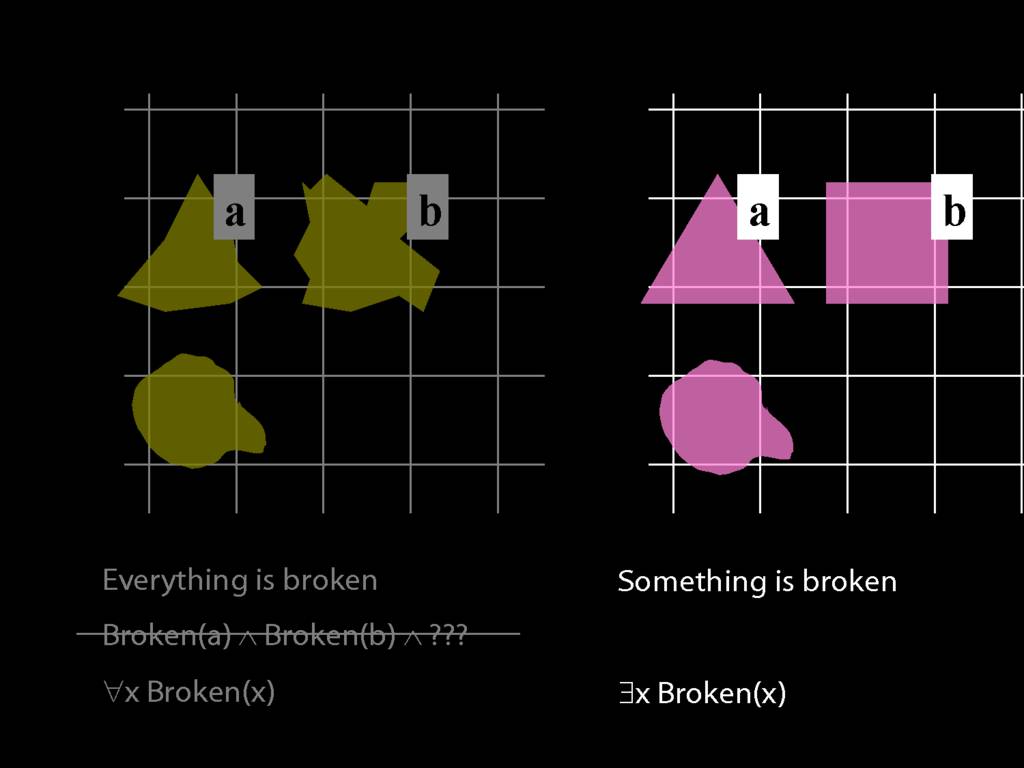
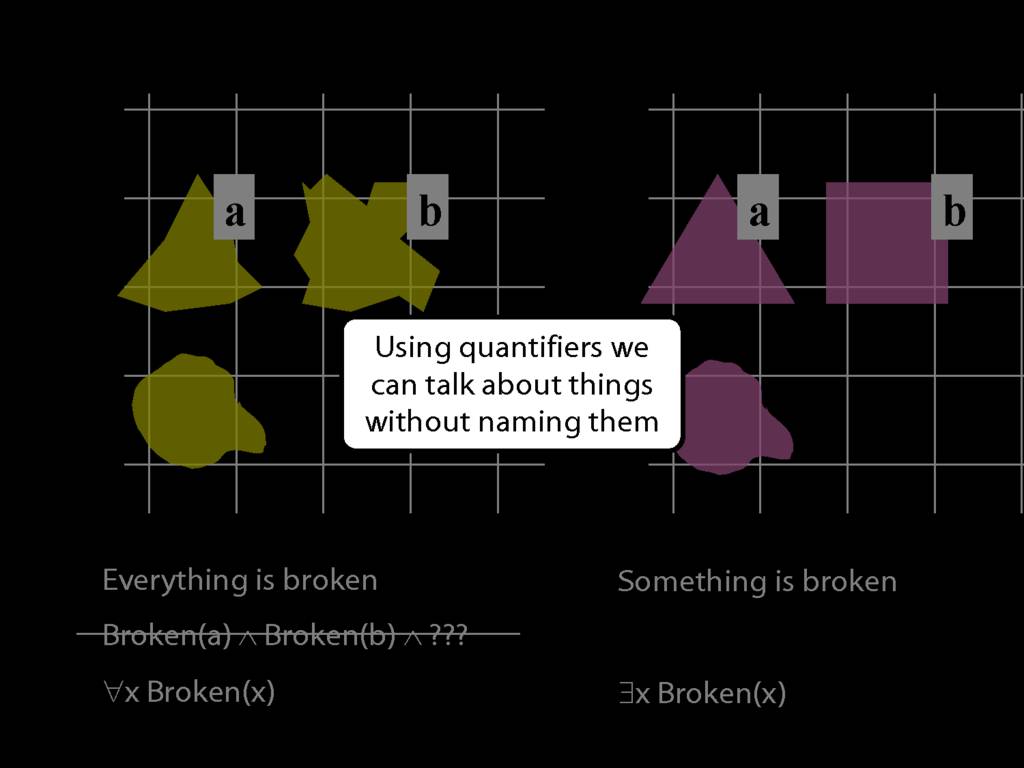
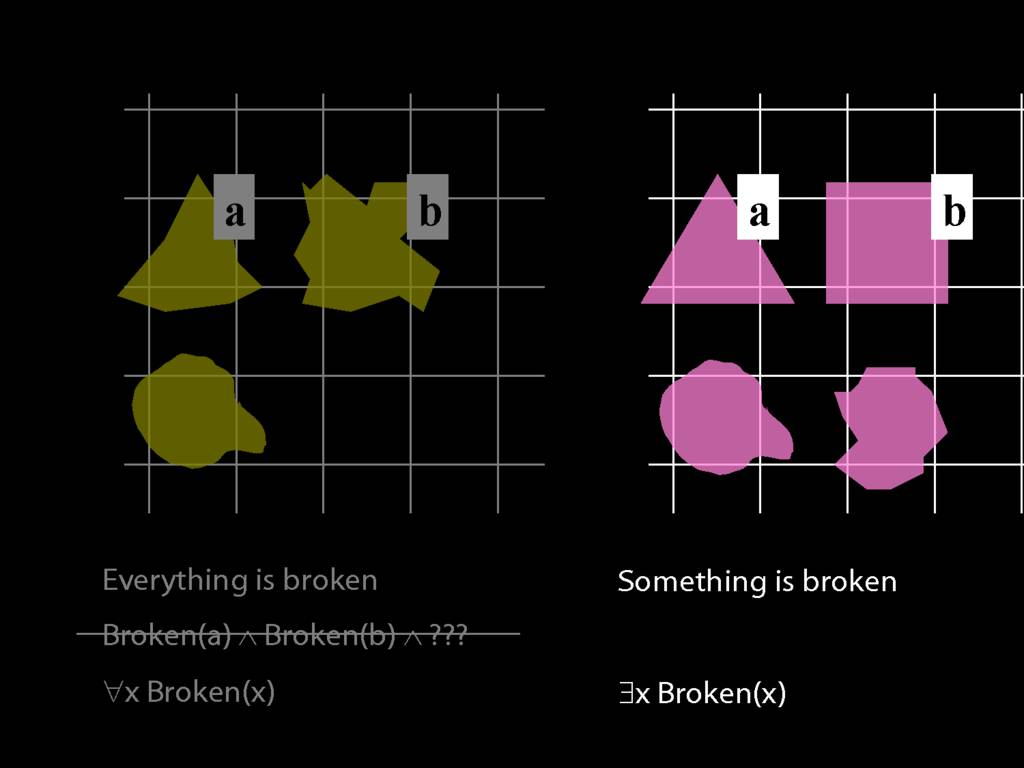
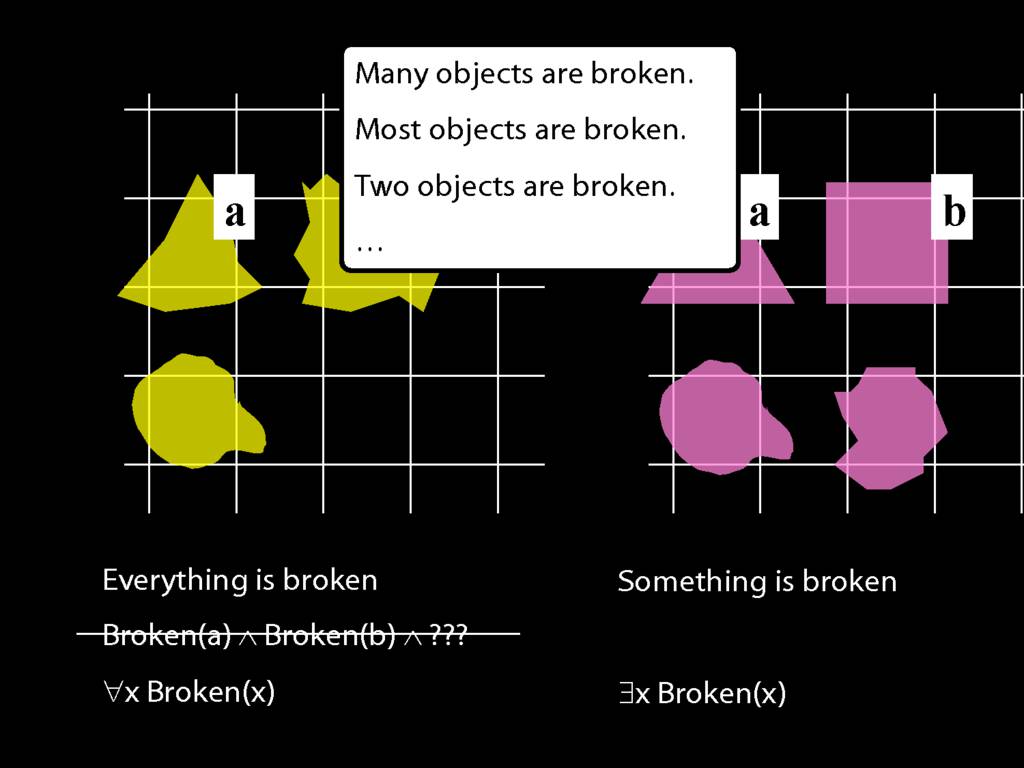


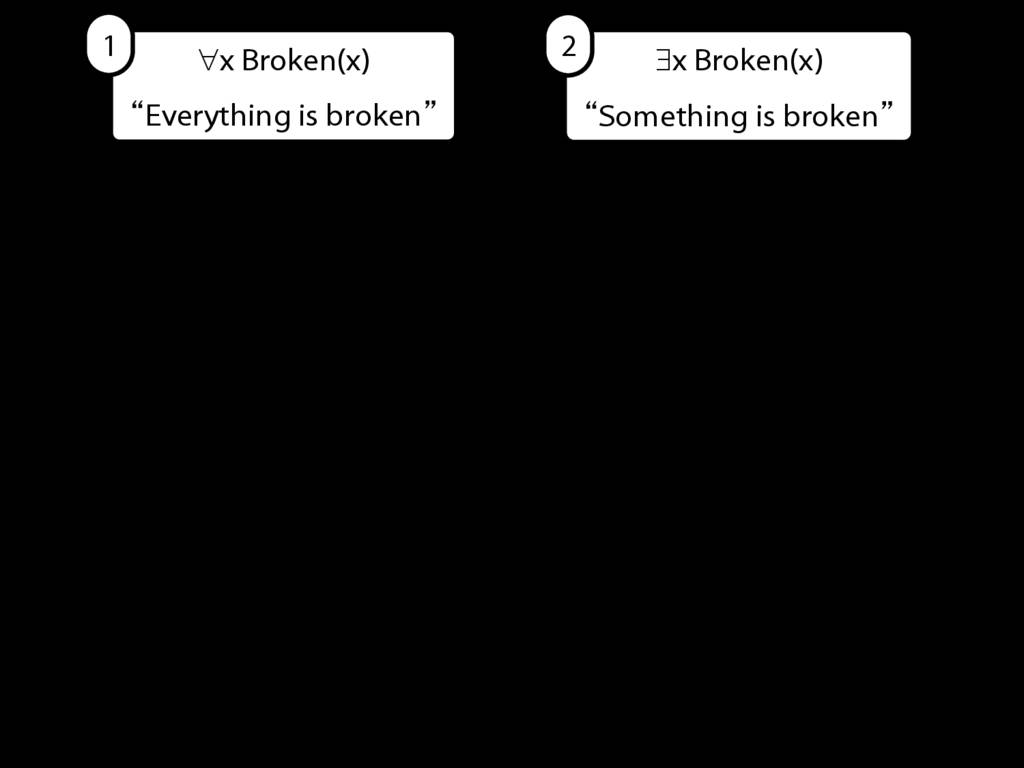
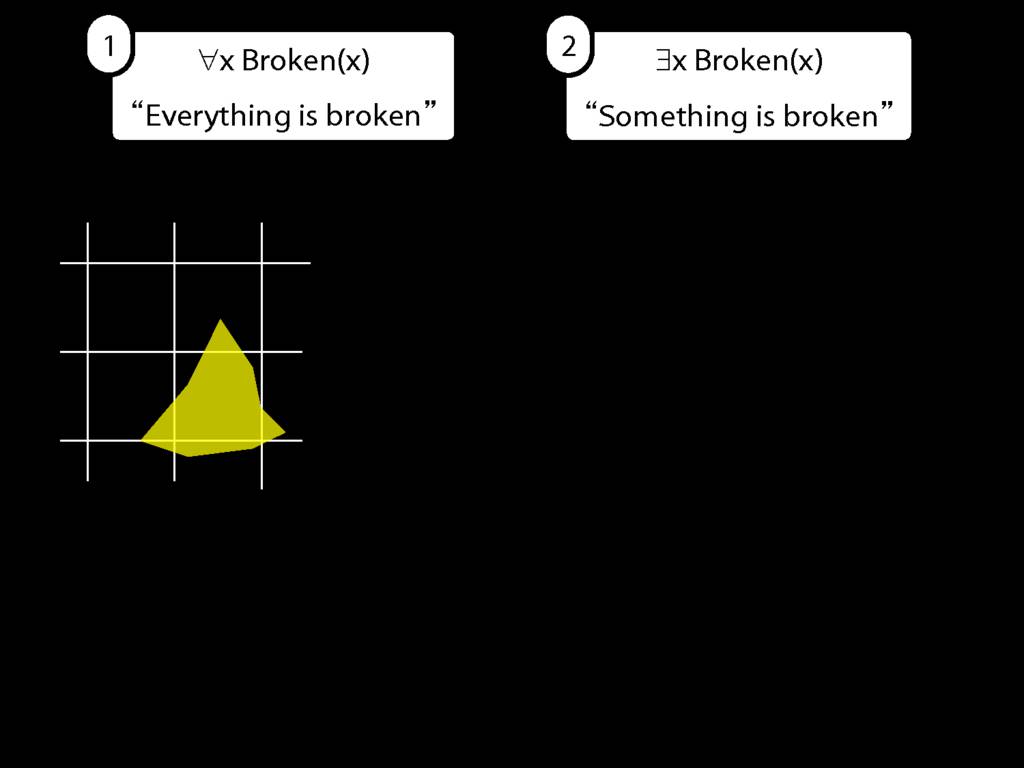
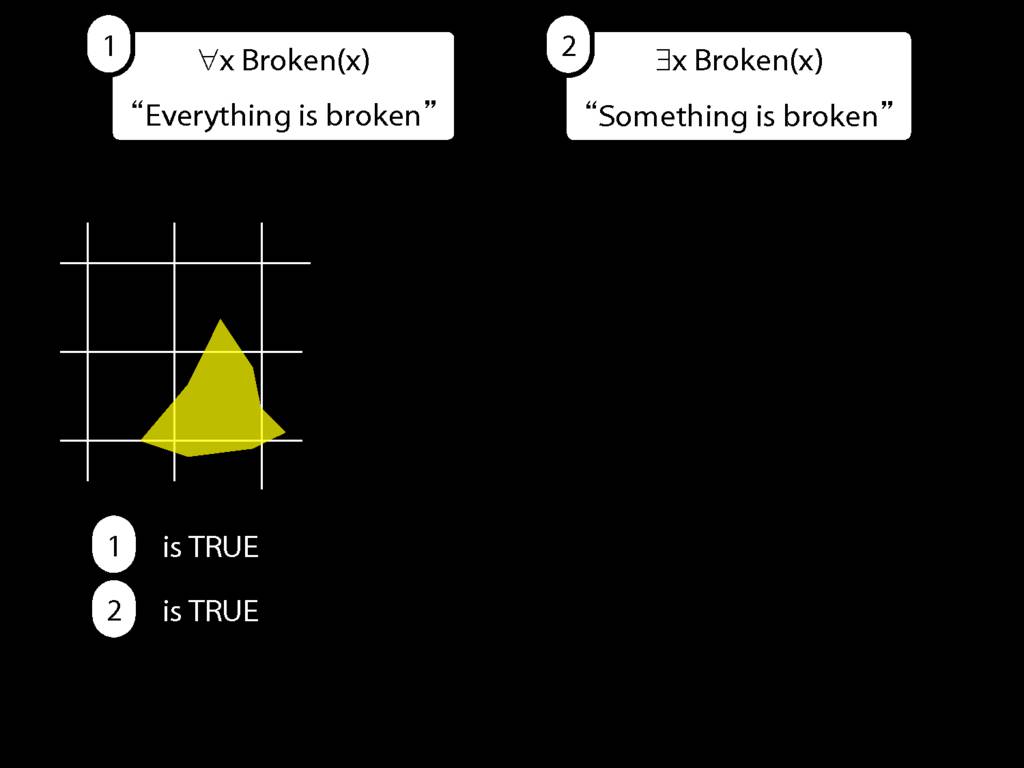
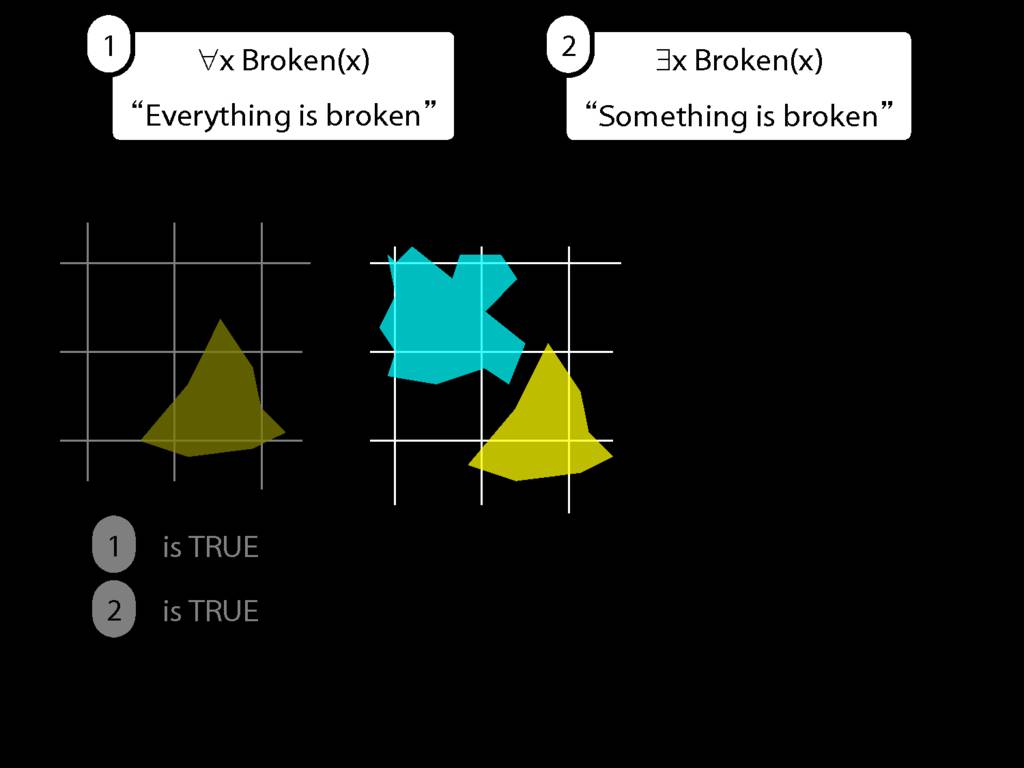
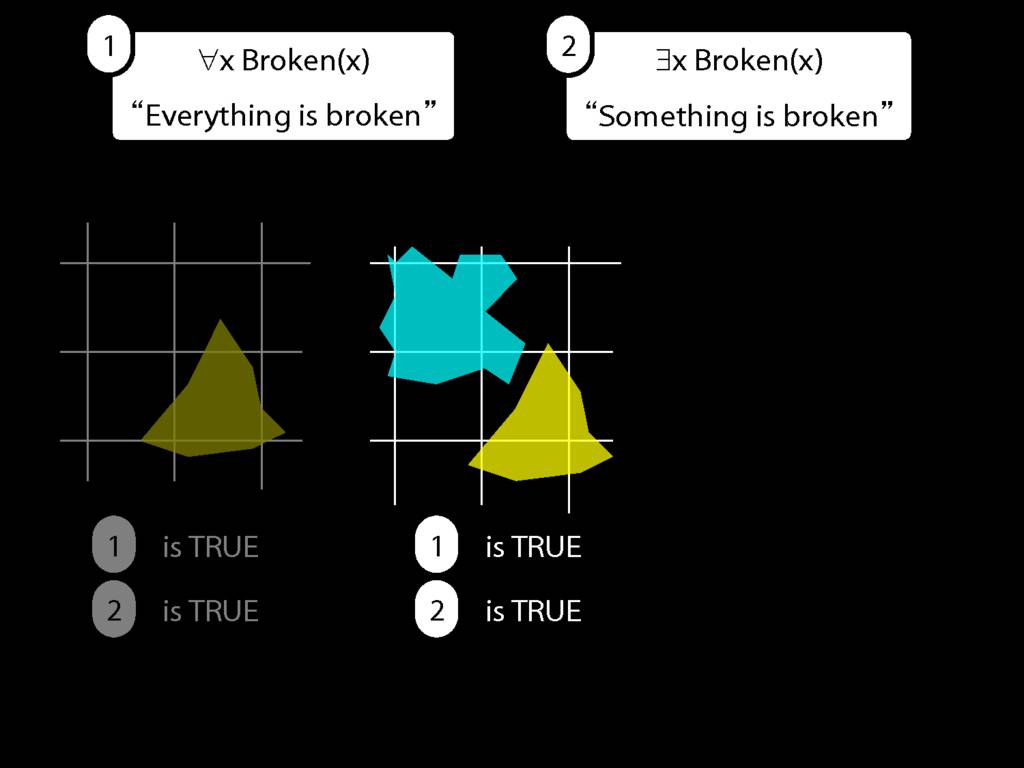
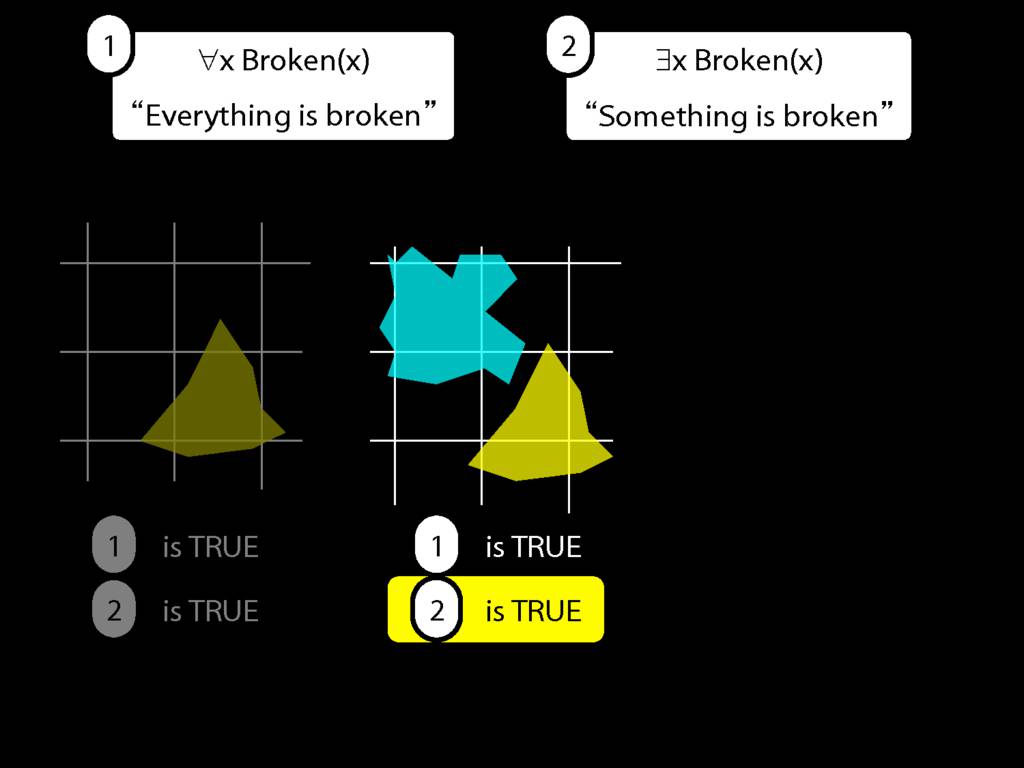
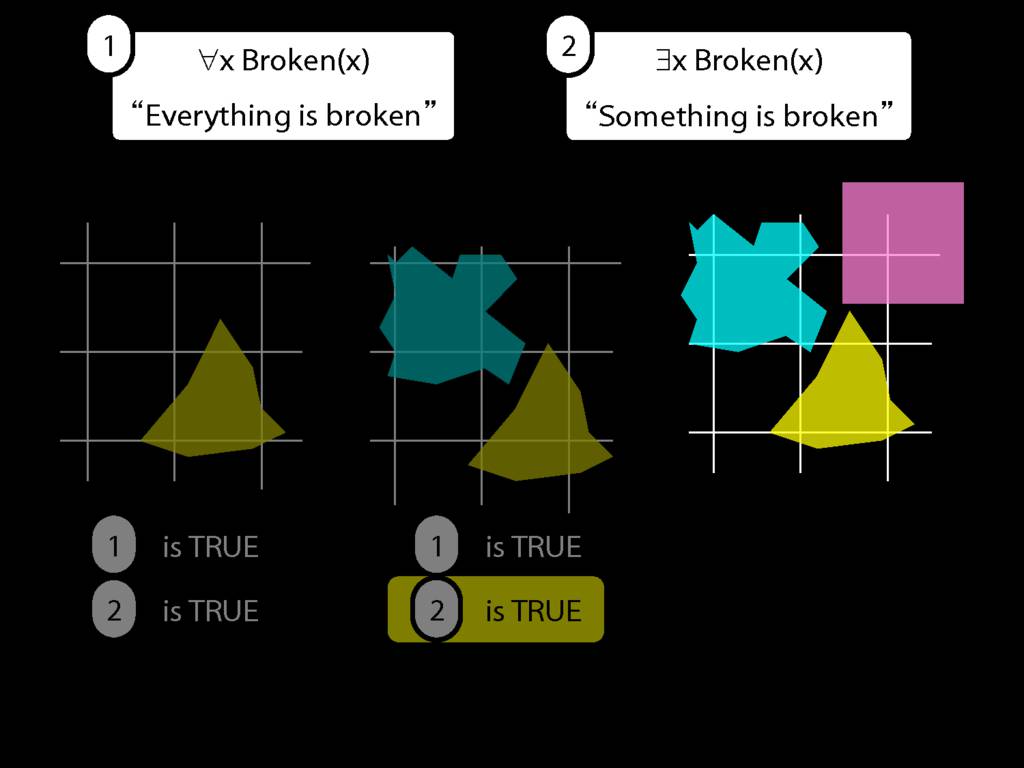
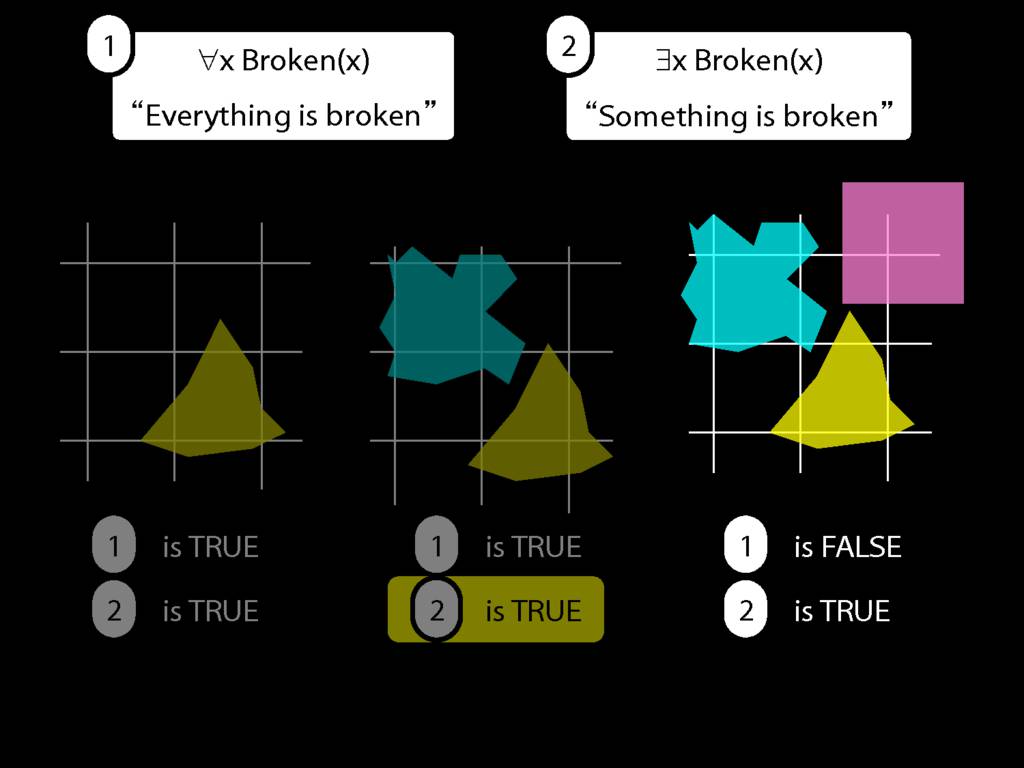
9.1 odd numbers only
9.2 even numbers only
9.8–-9.10
\section{Get Some Quantifiers: Don't Economise}





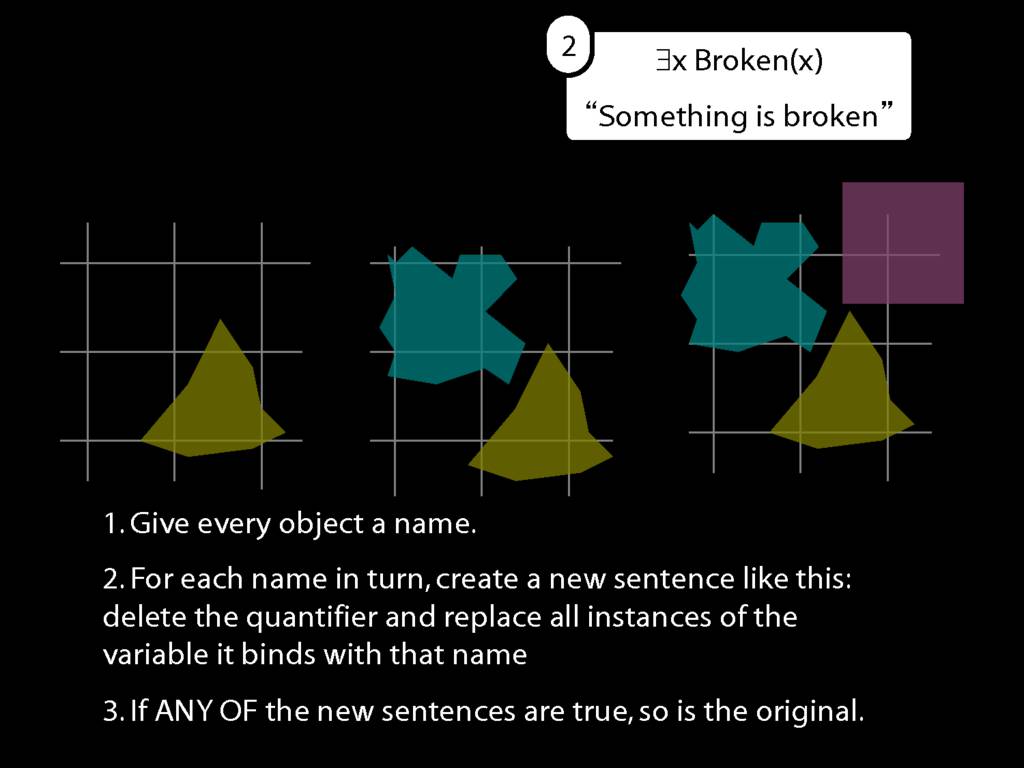
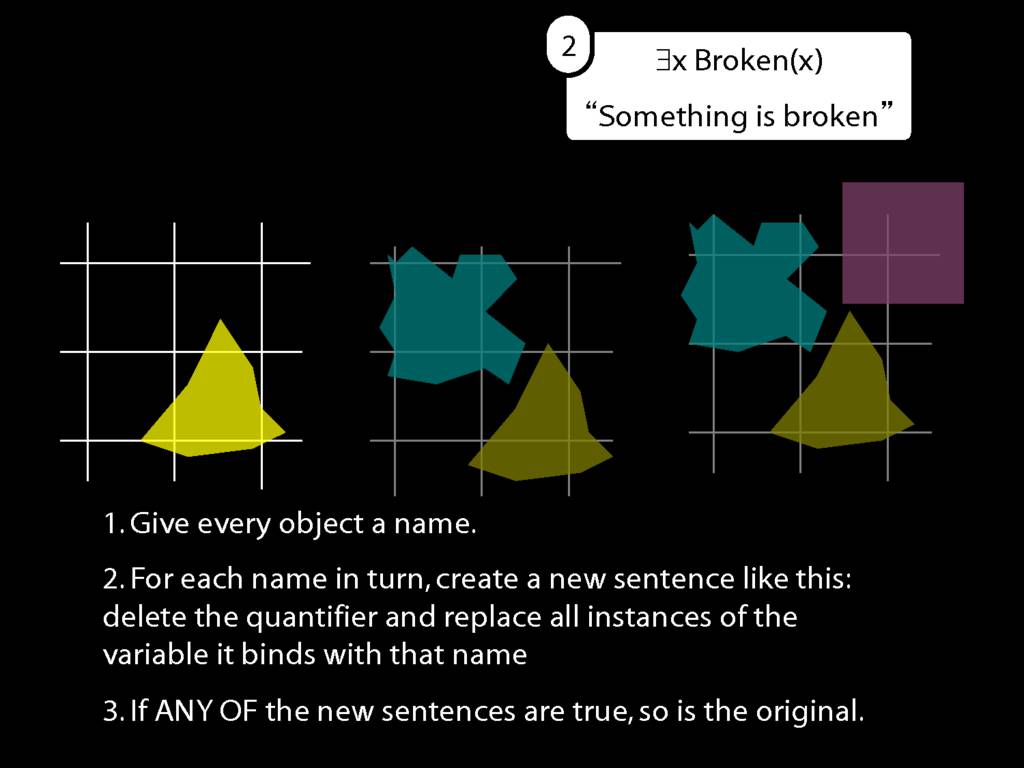
What does ∃ mean?
\section{What does ∃ mean?}
\emph{Reading:} §9.4
\section{What does ∃ mean?}

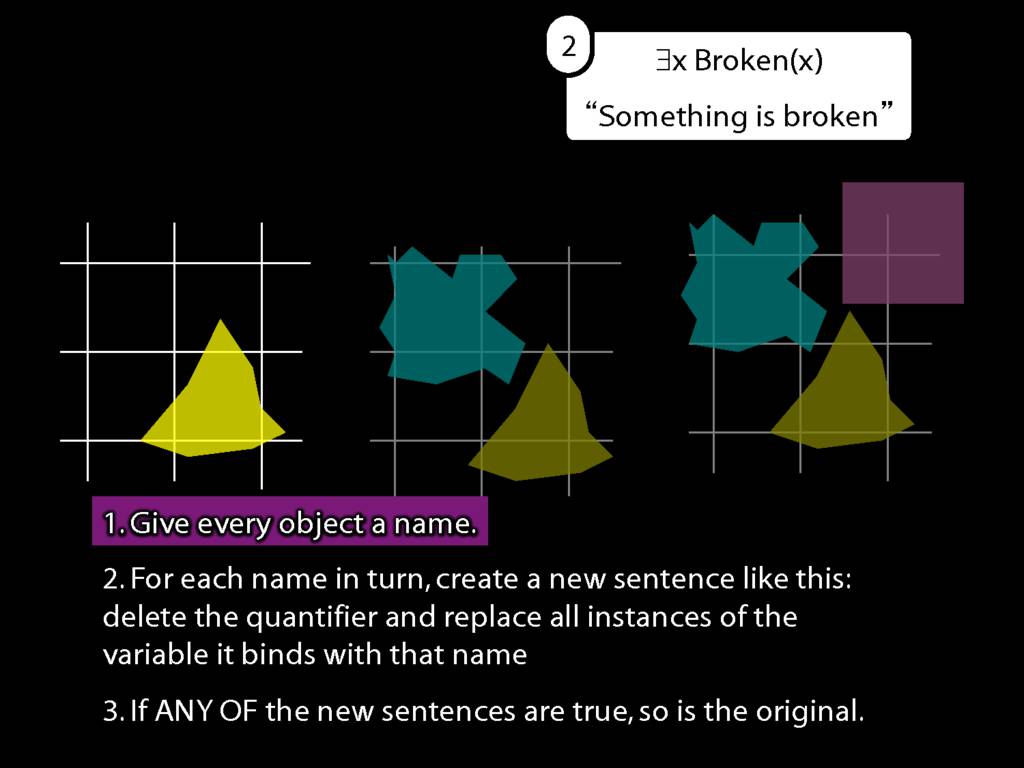
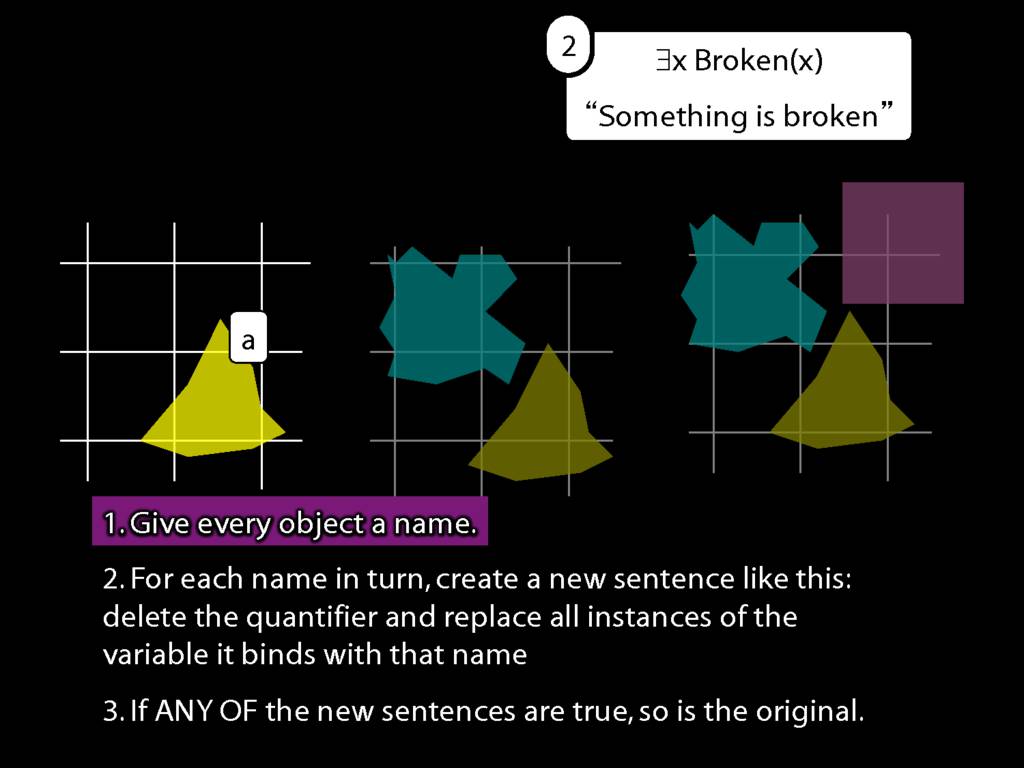
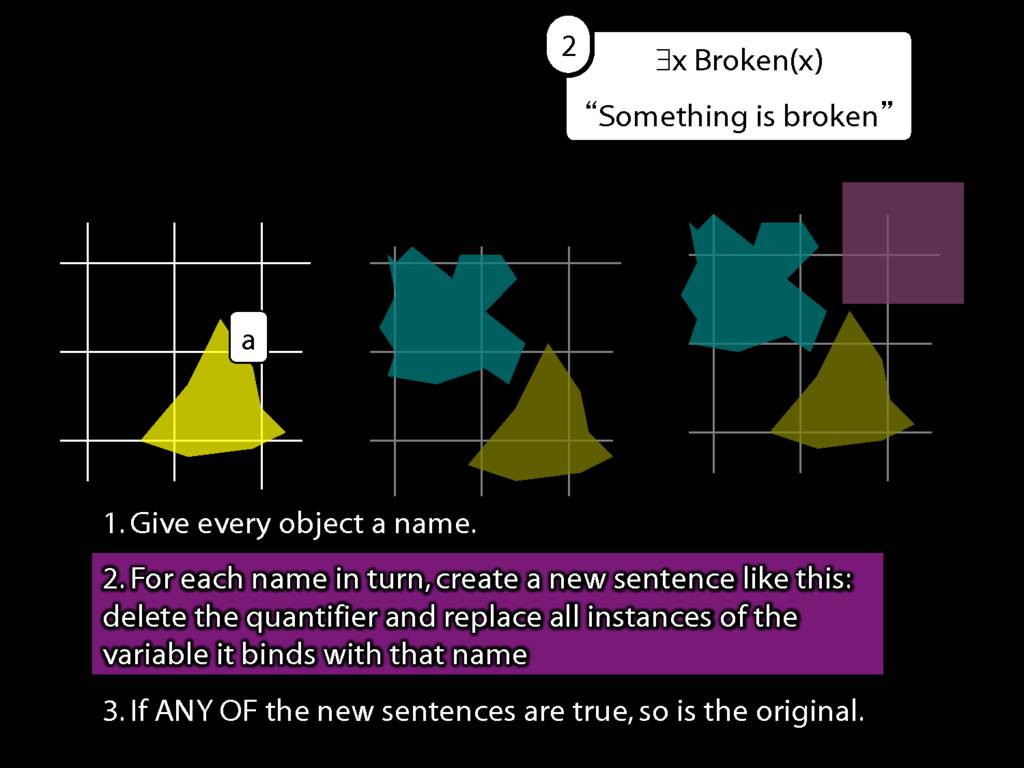
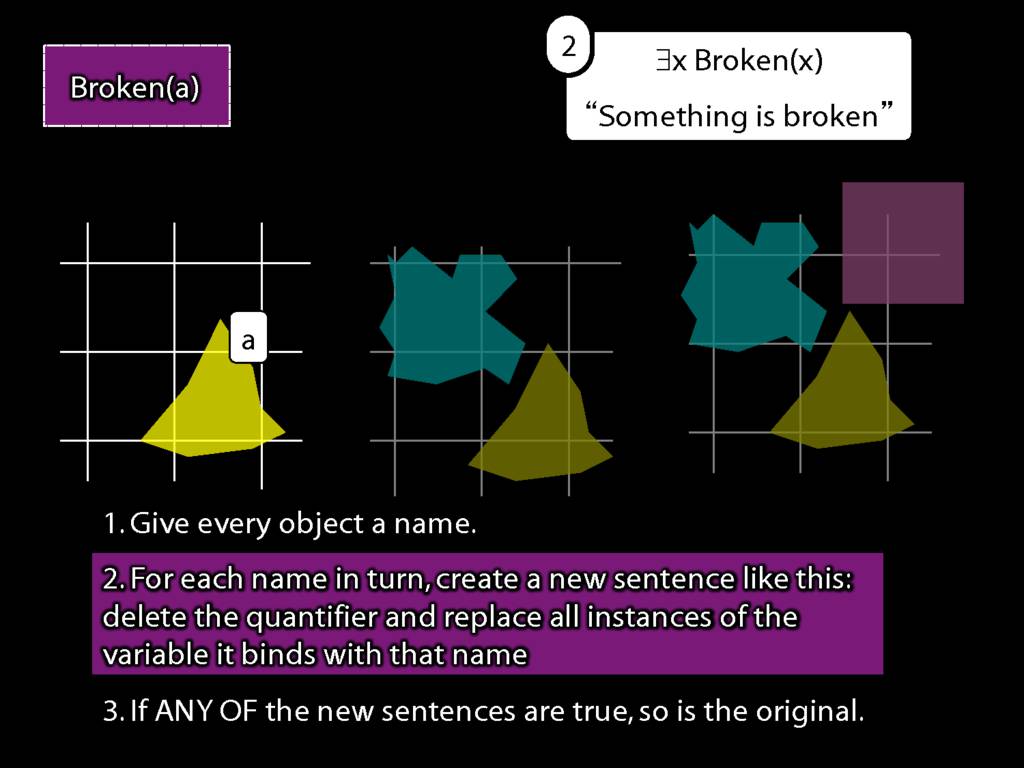
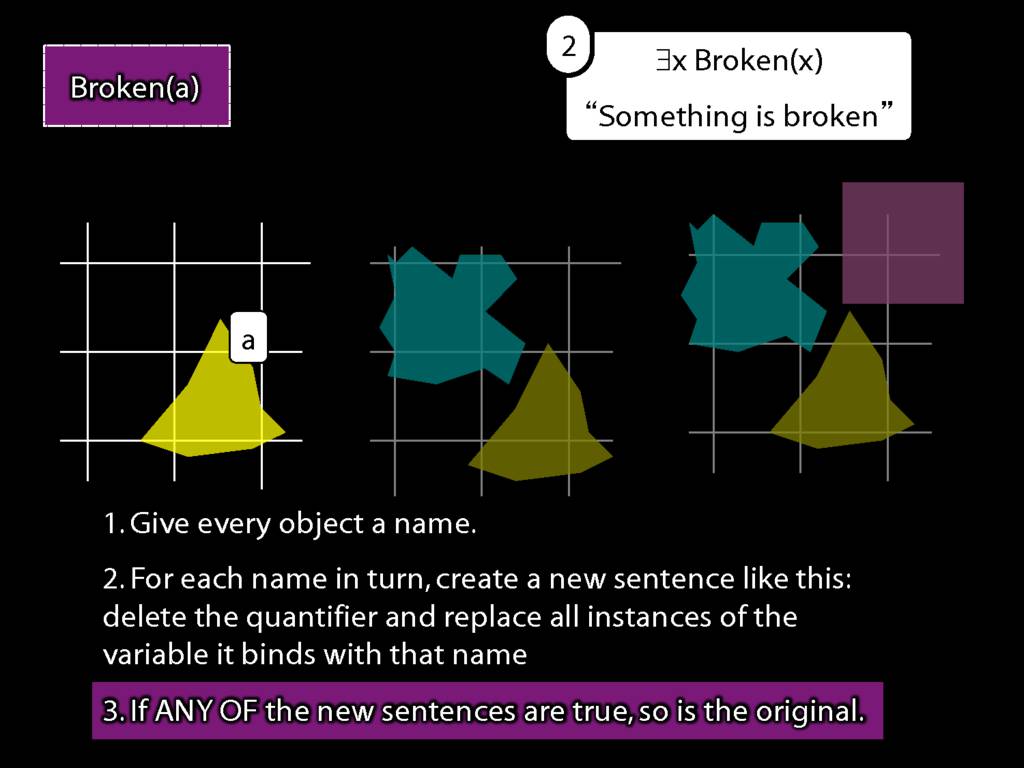
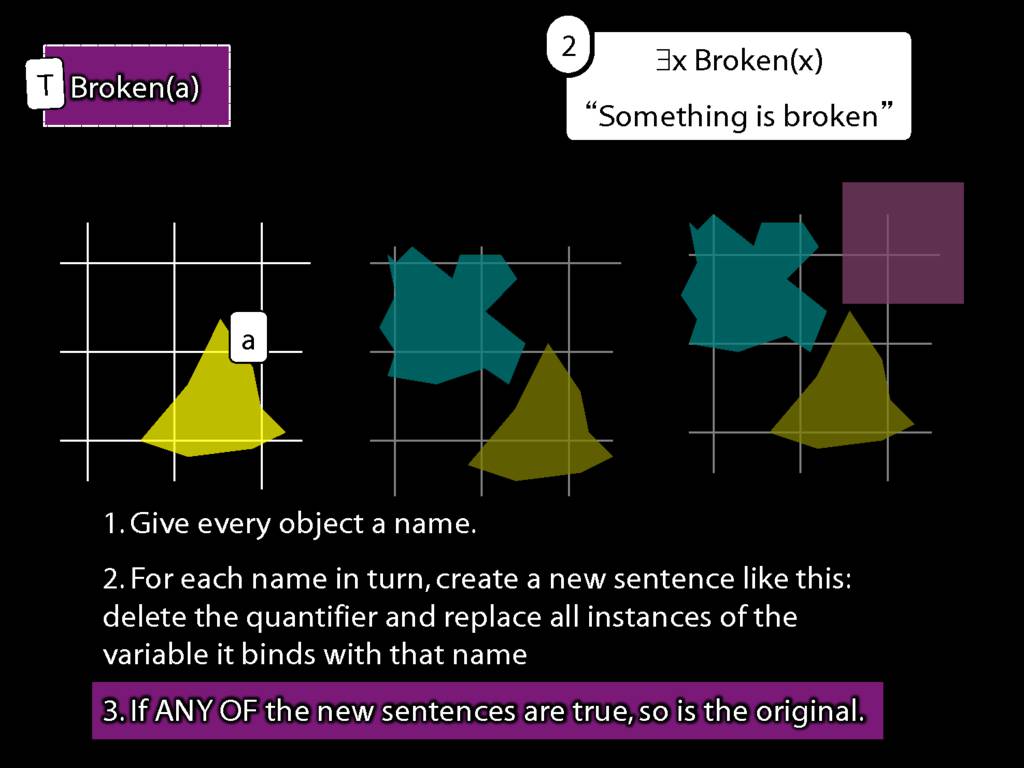
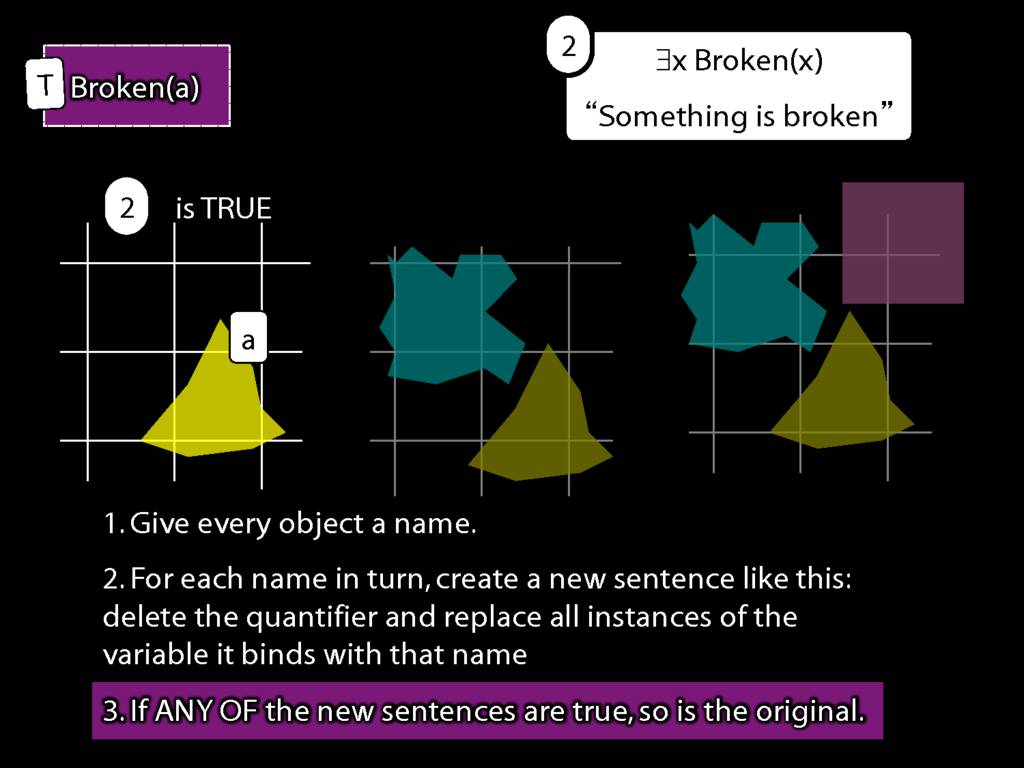
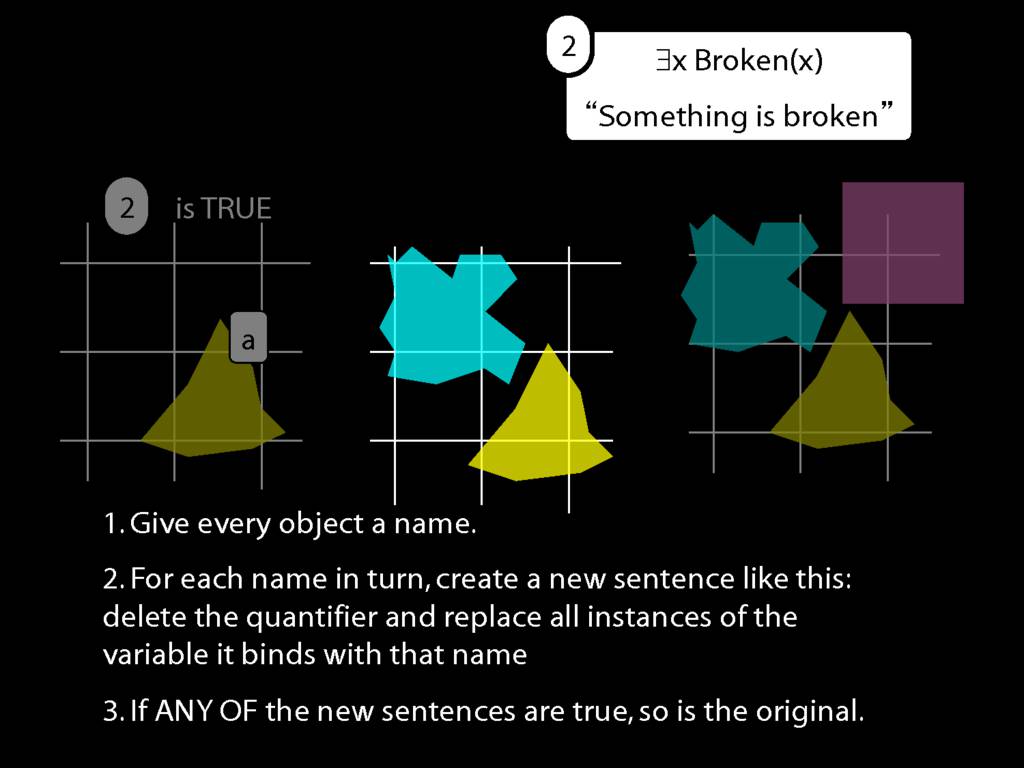
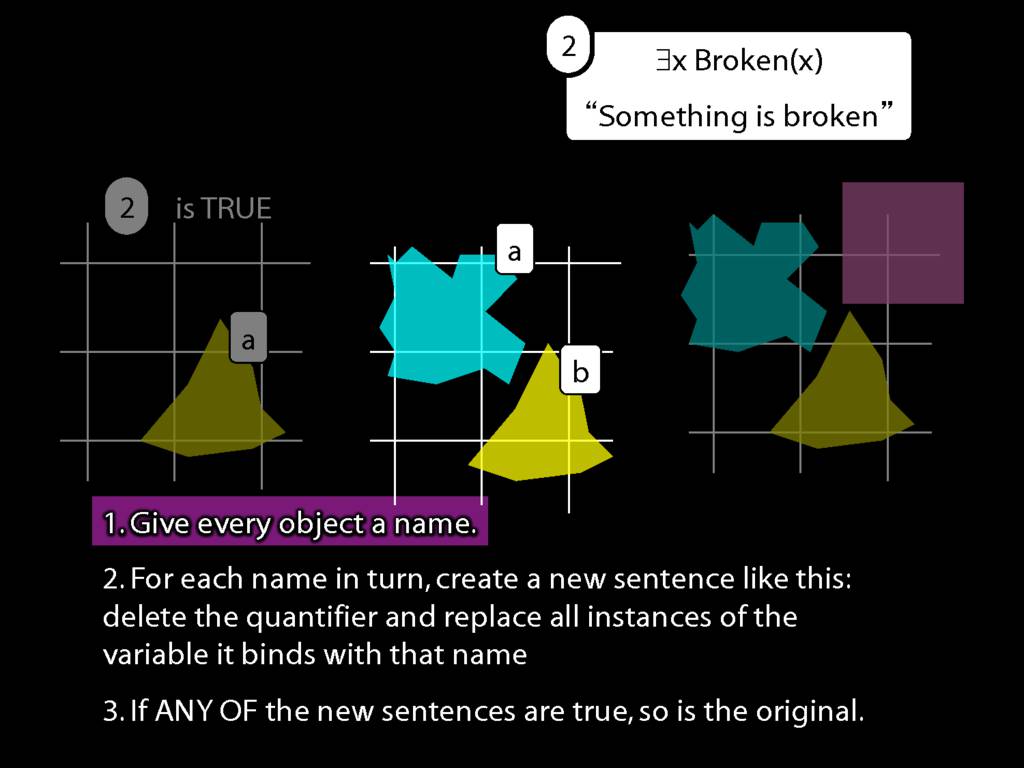
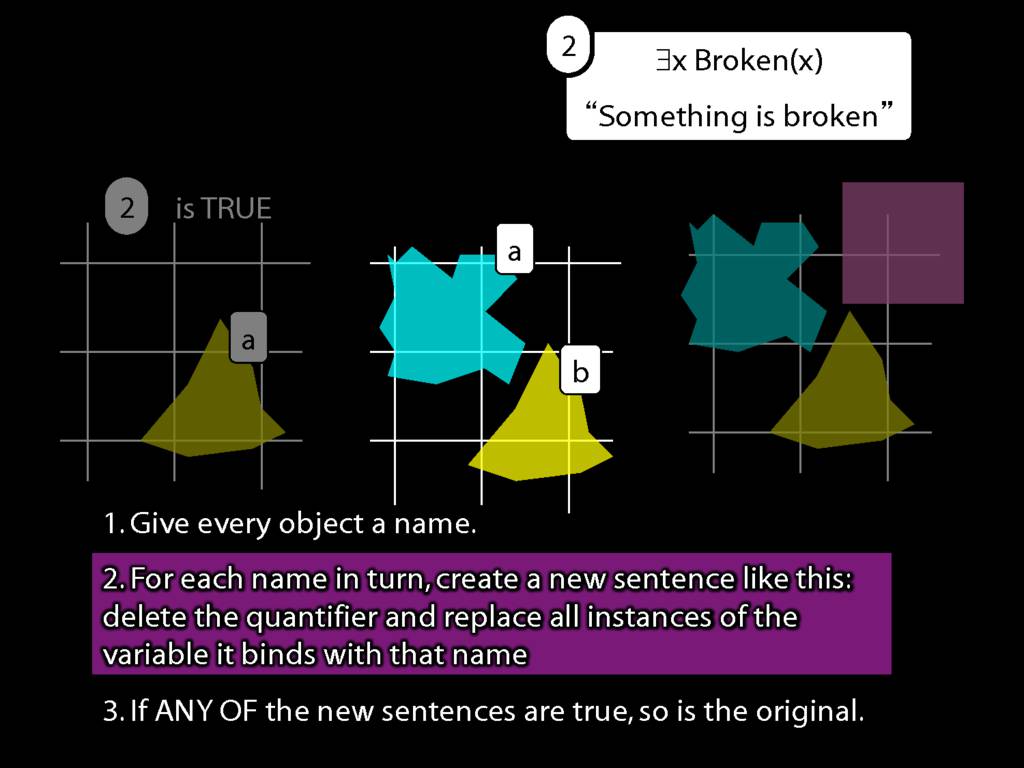
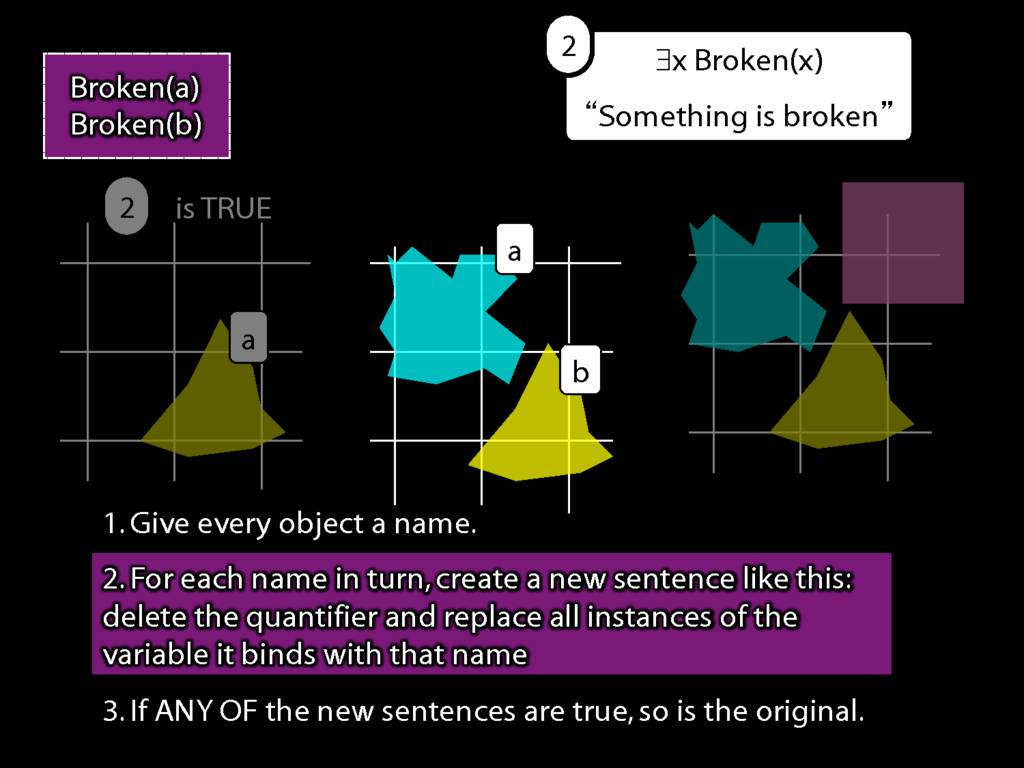
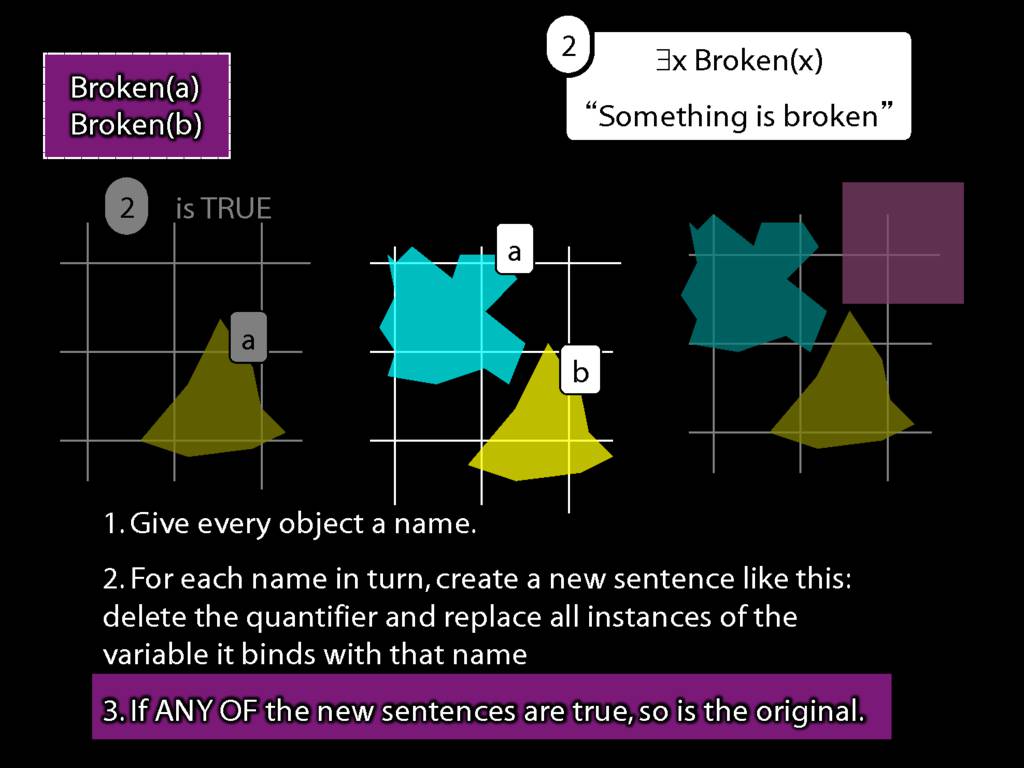
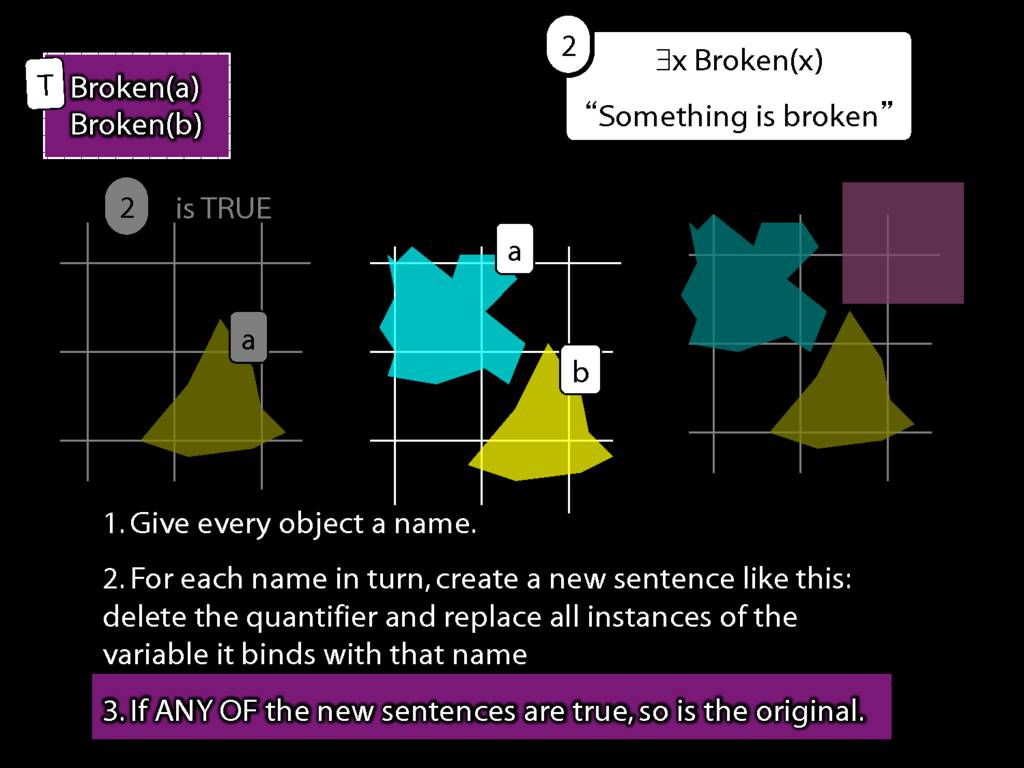
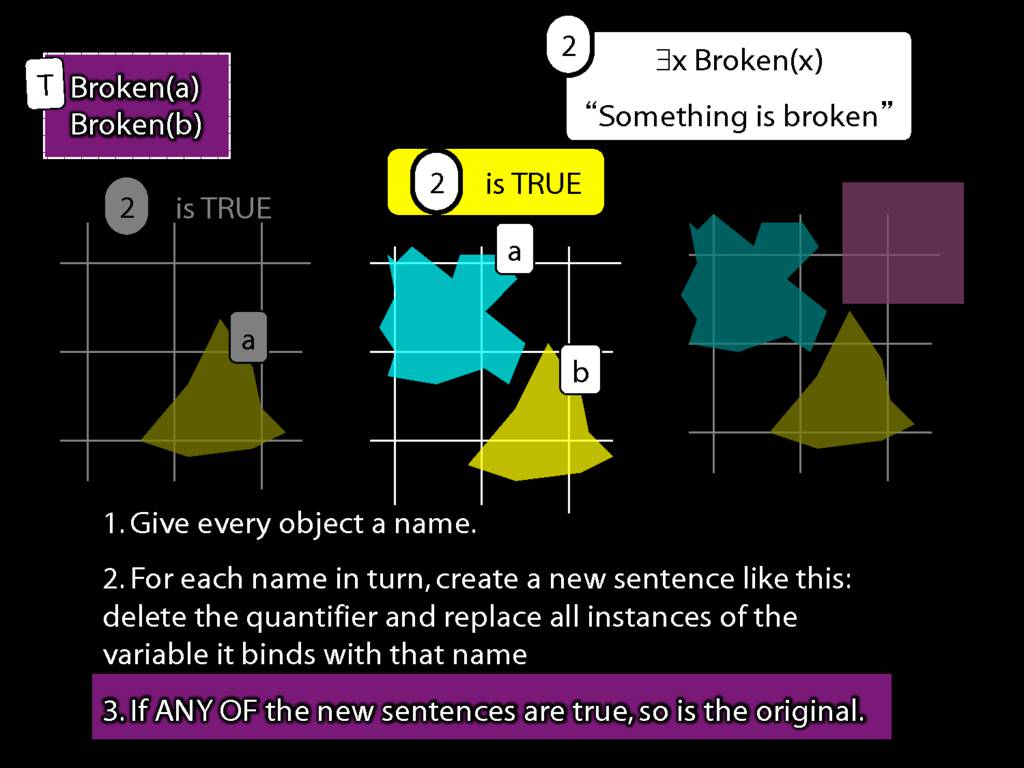
We give the meaning of ∃ by specifying what it takes for a sentence containing ∃ to be true:
\begin{enumerate}
\item Give every object a name.
\item For each name in turn, create a new sentence like this: delete the quantifier and replace all instances of the variable it binds with that name.
\item If ANY of the new sentences are true, so is the original sentence.
\end{enumerate}








Formal Proof
\section{Formal Proof}

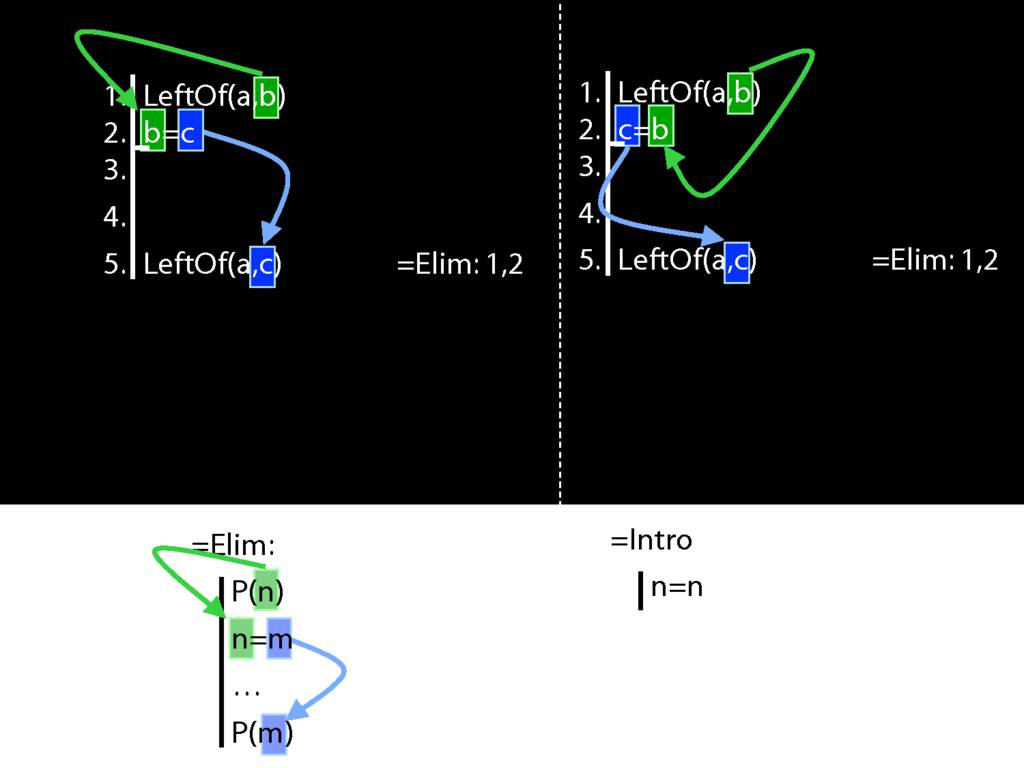
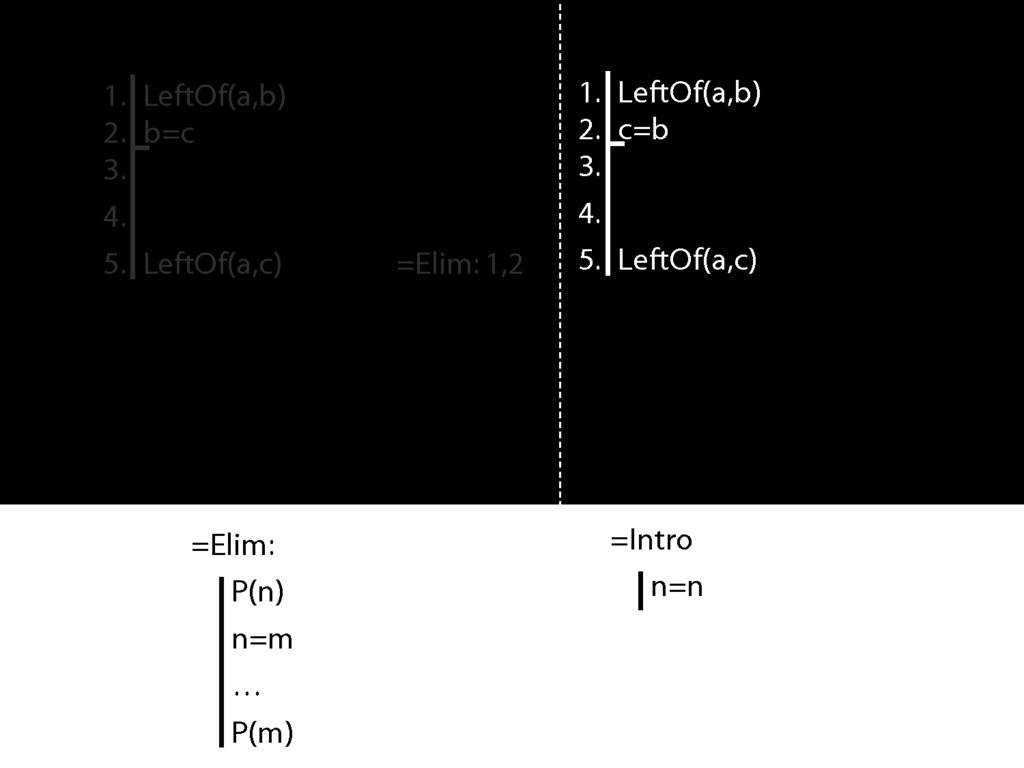
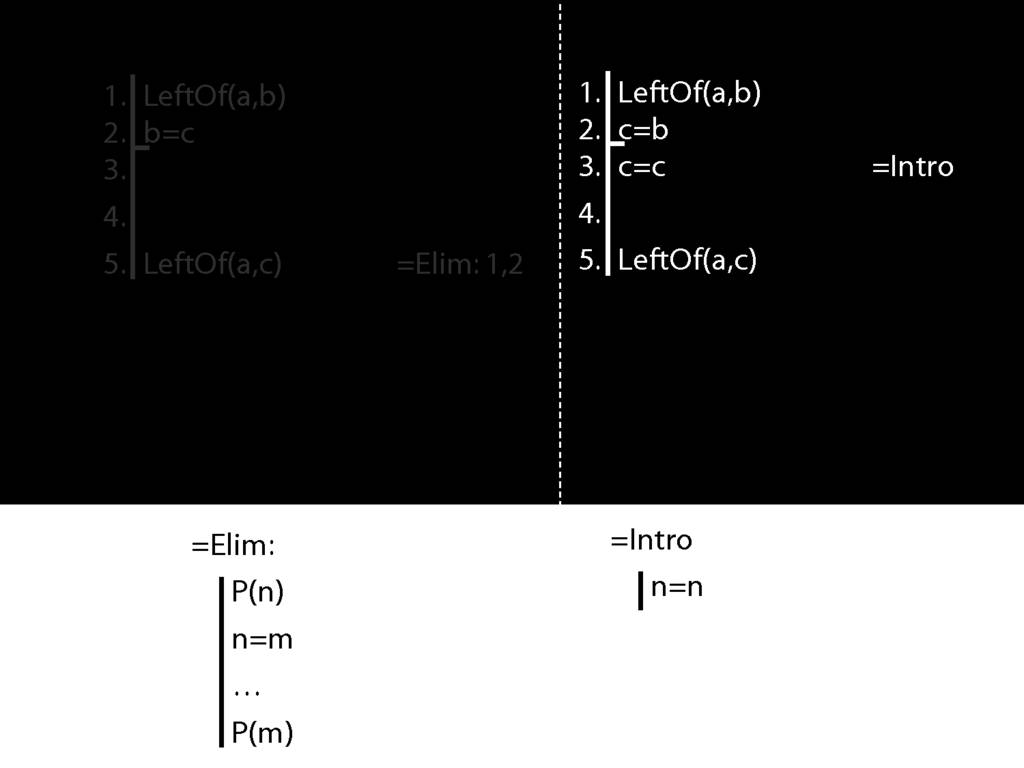
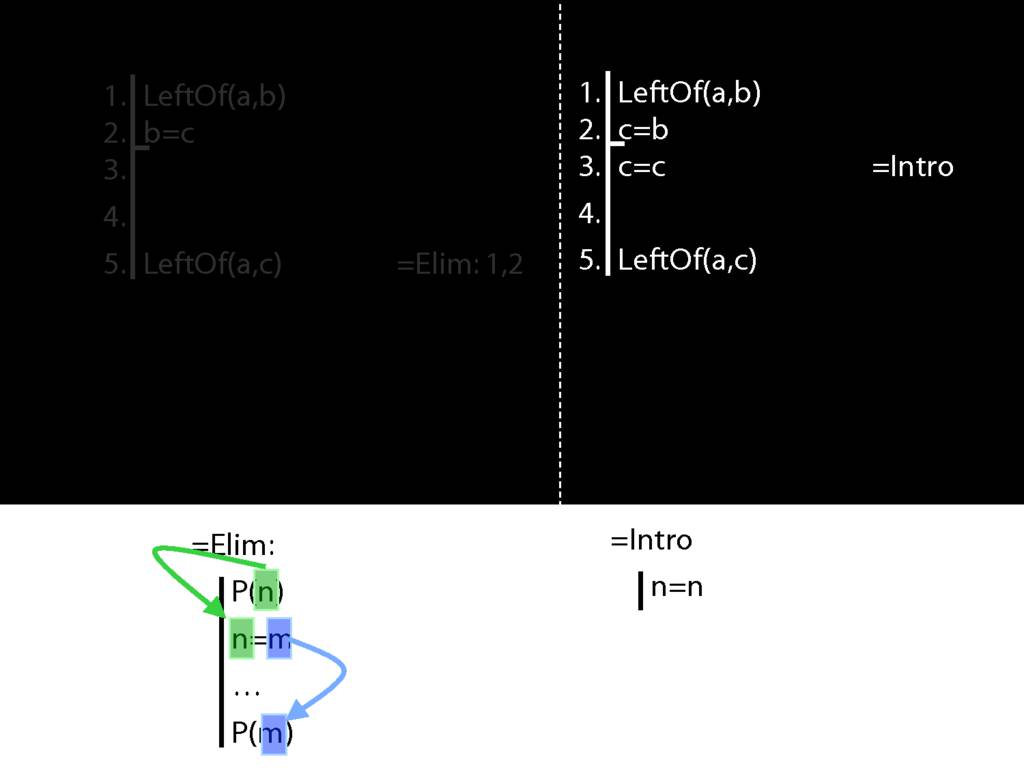
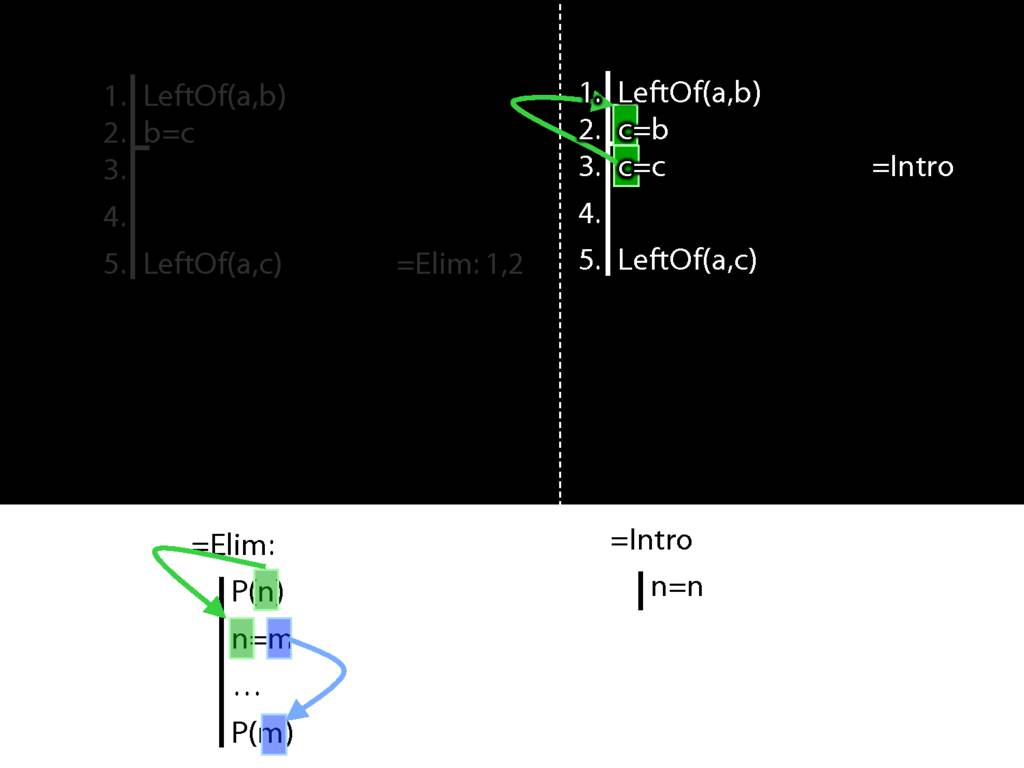
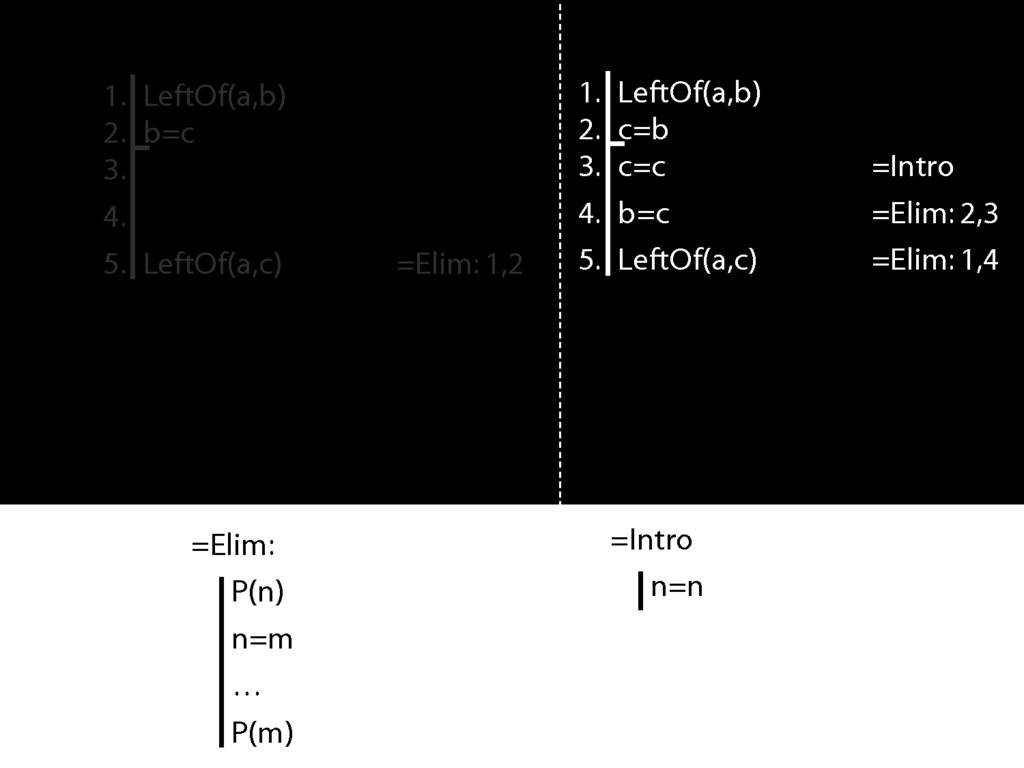
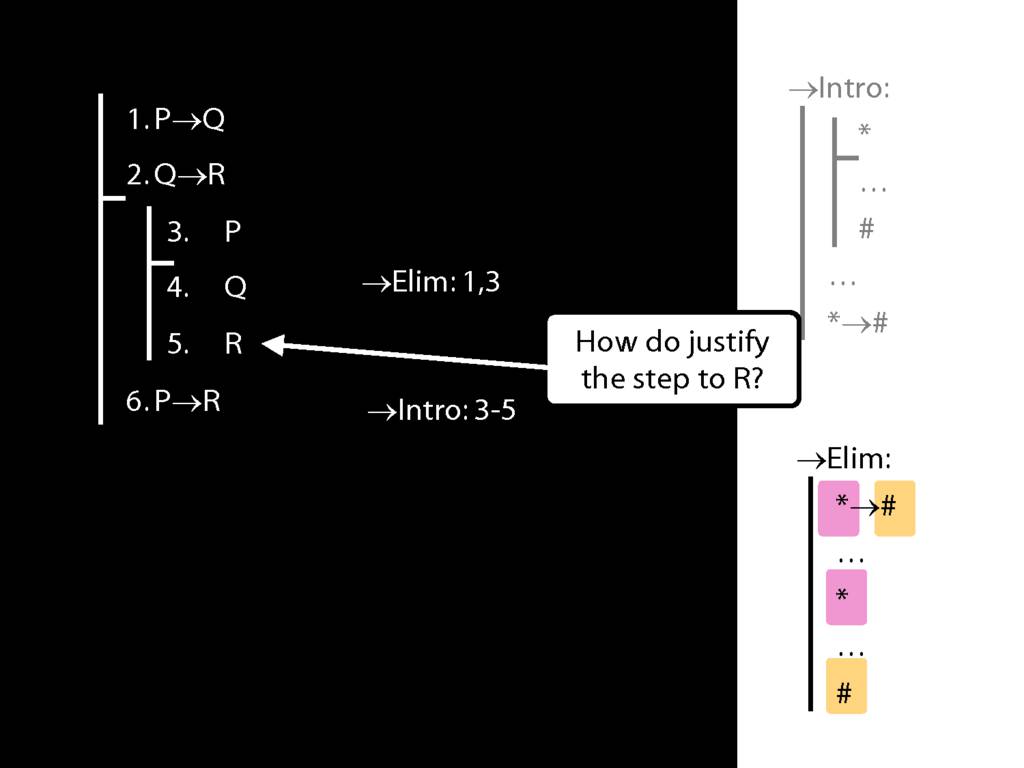
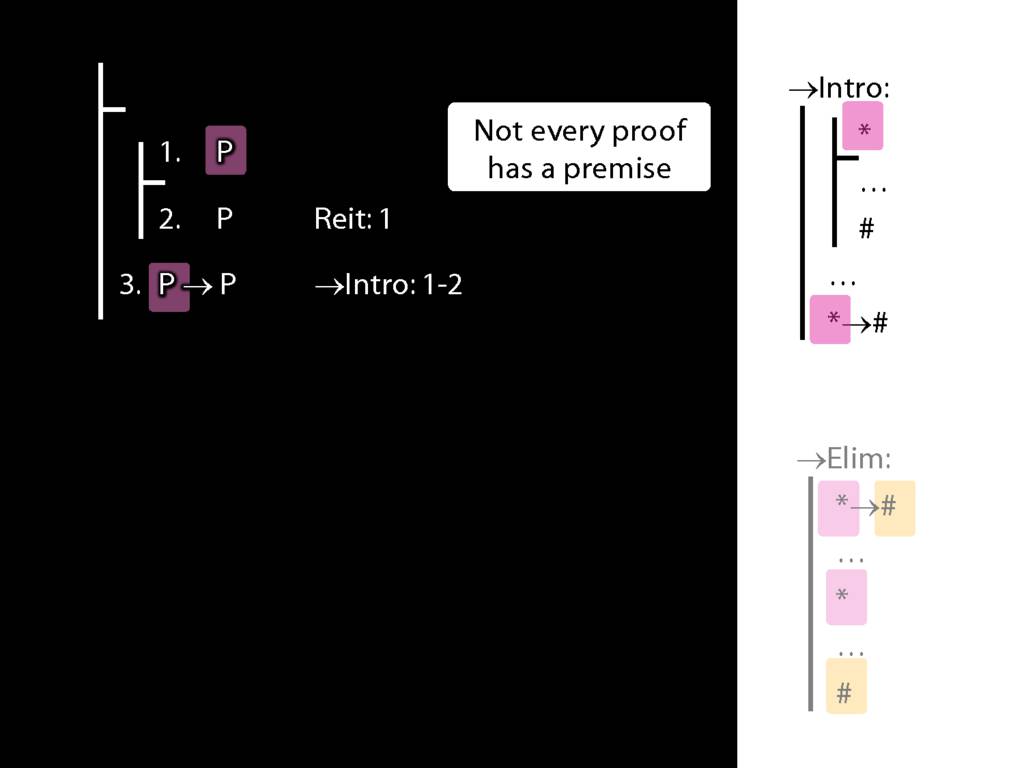
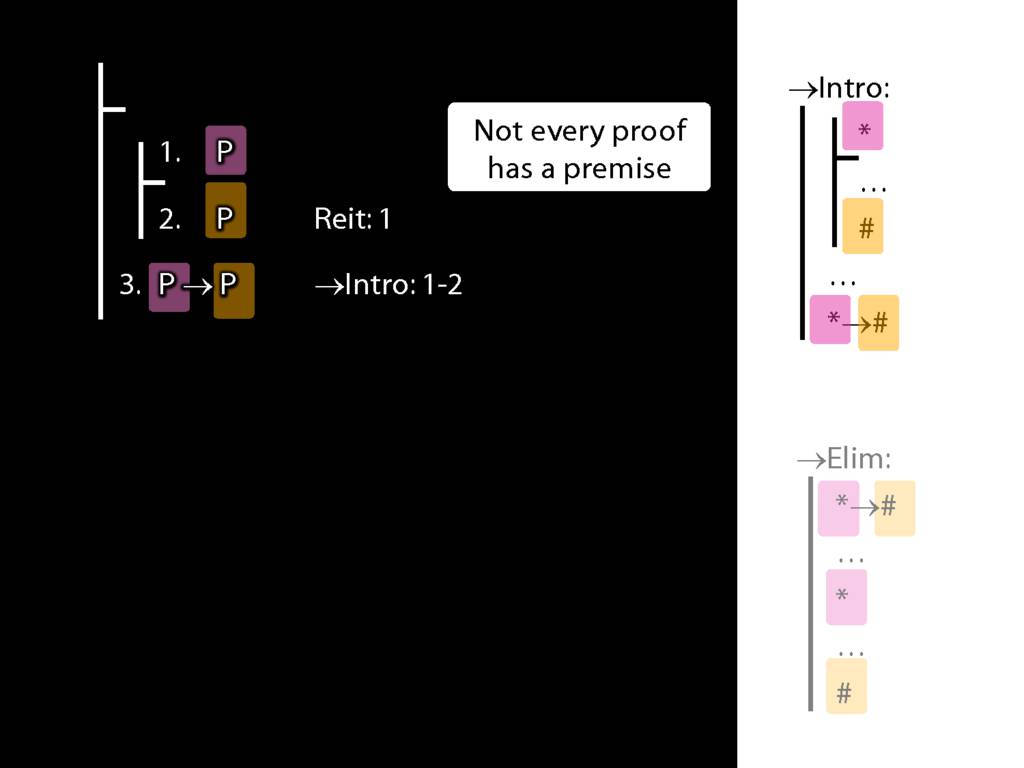
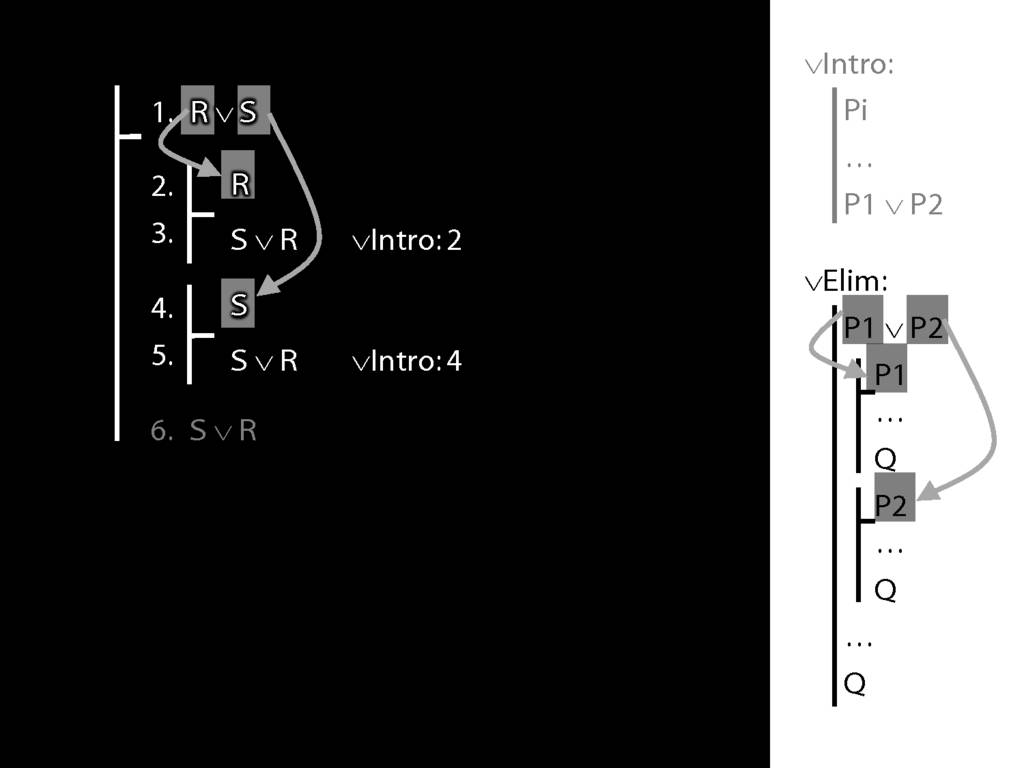
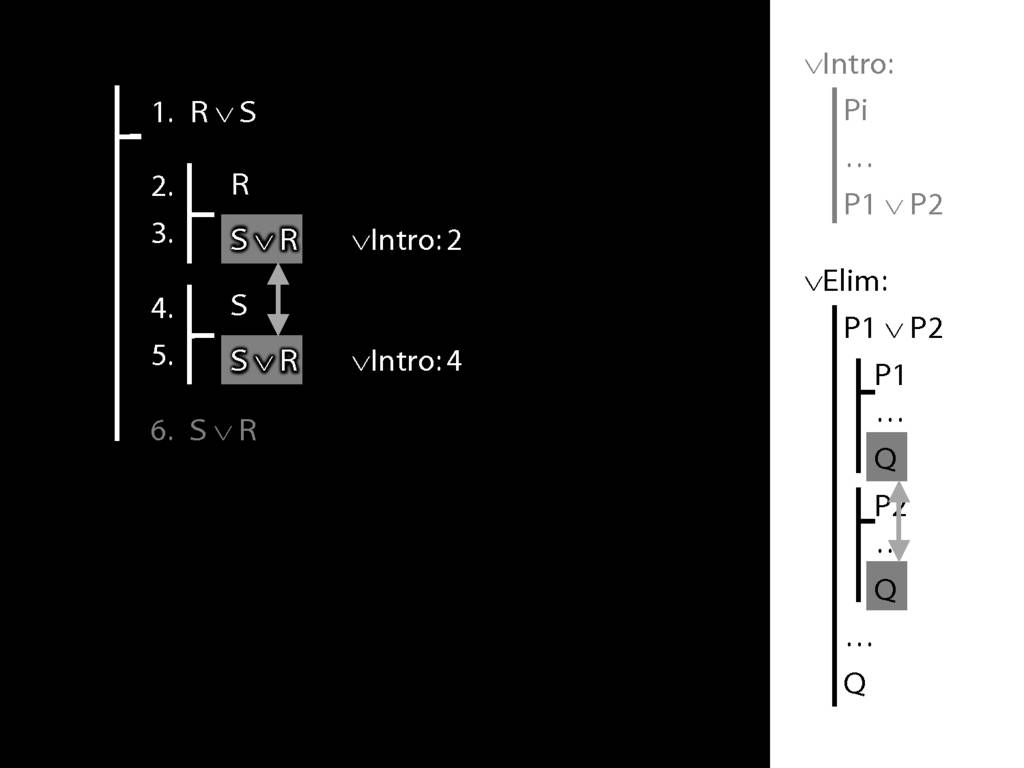
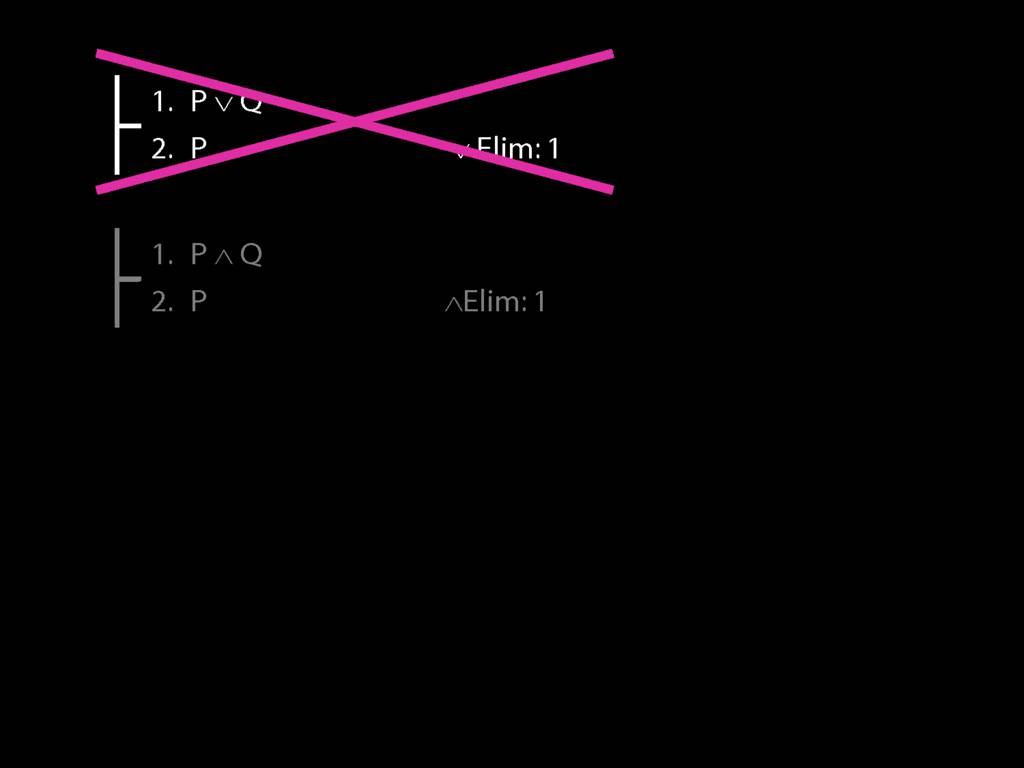
Recall these two diagrams from earlier. The left one is a proof, the right one is not.
Spot the difference.

Yes, the difference is at line 2.
But why is this difference significant?
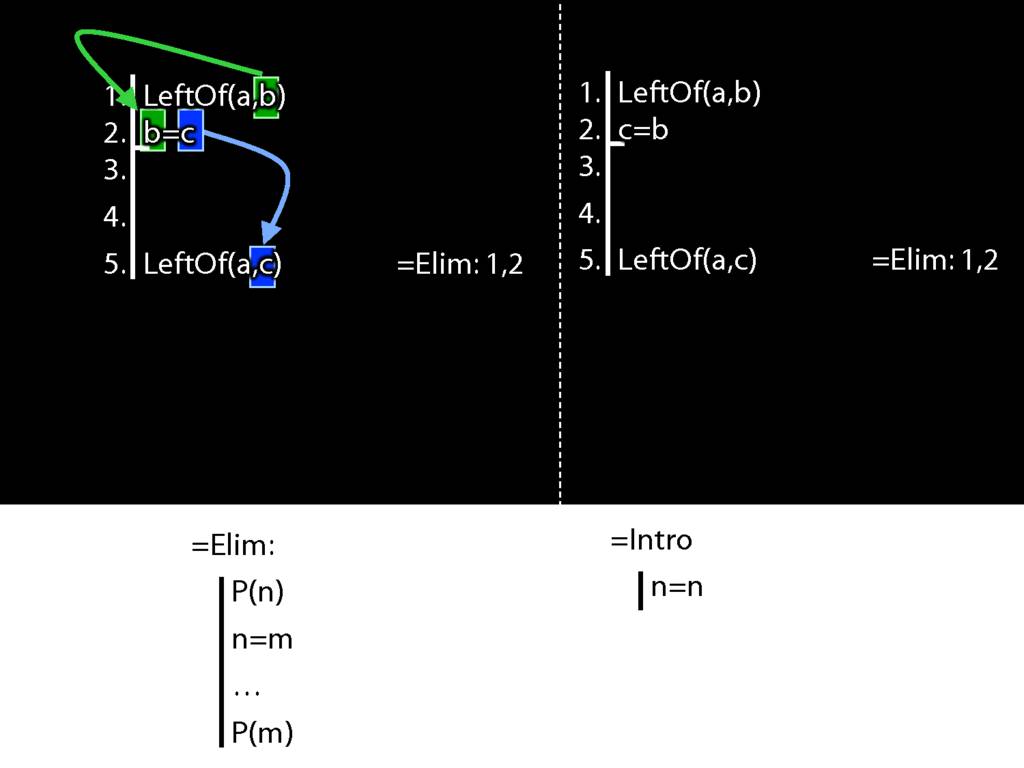
Look what happens in the left diagram (the genuine proof). Do you see the pattern?
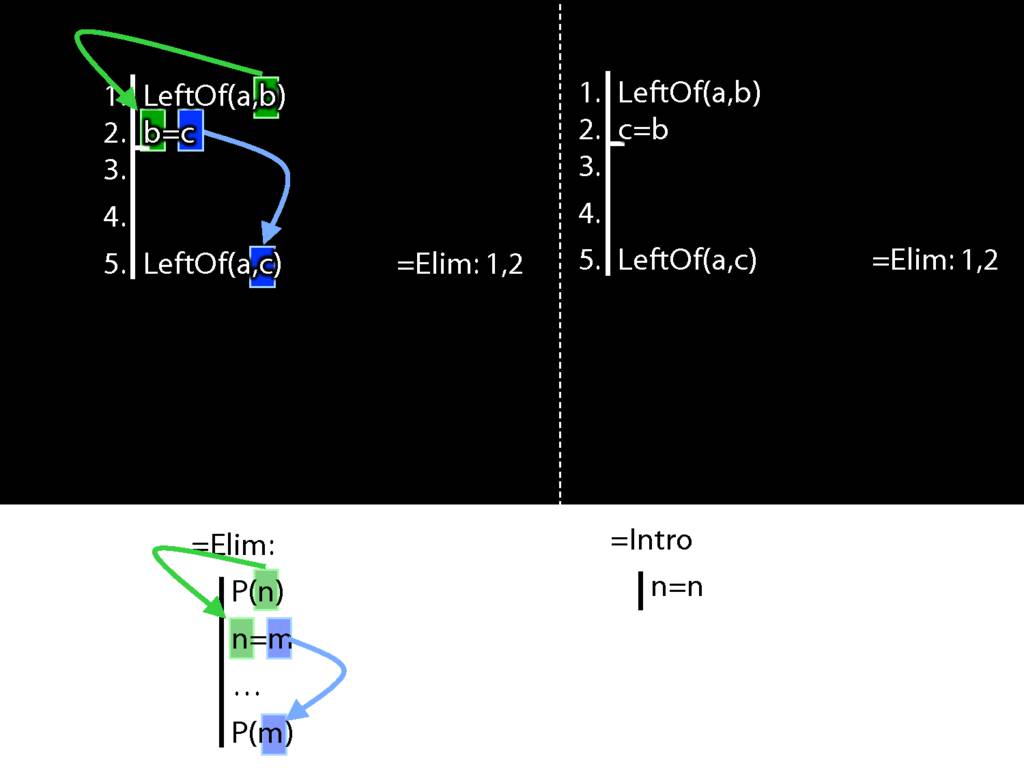
That pattern matches the pattern described by the rule identity elimination (=Elim)
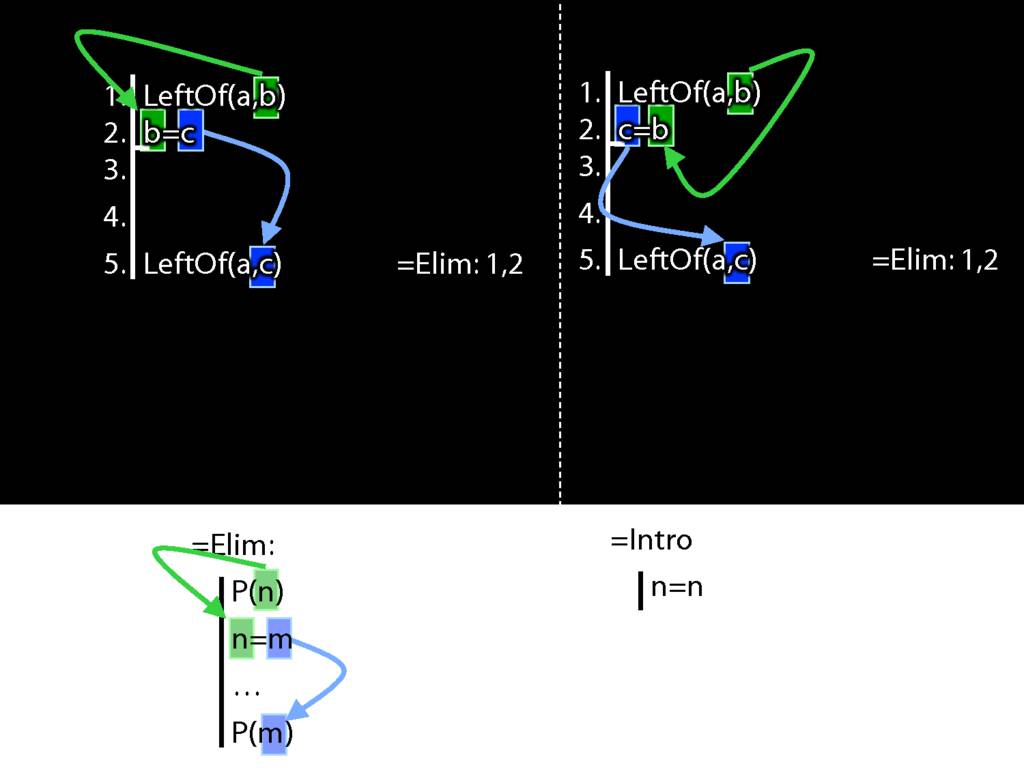
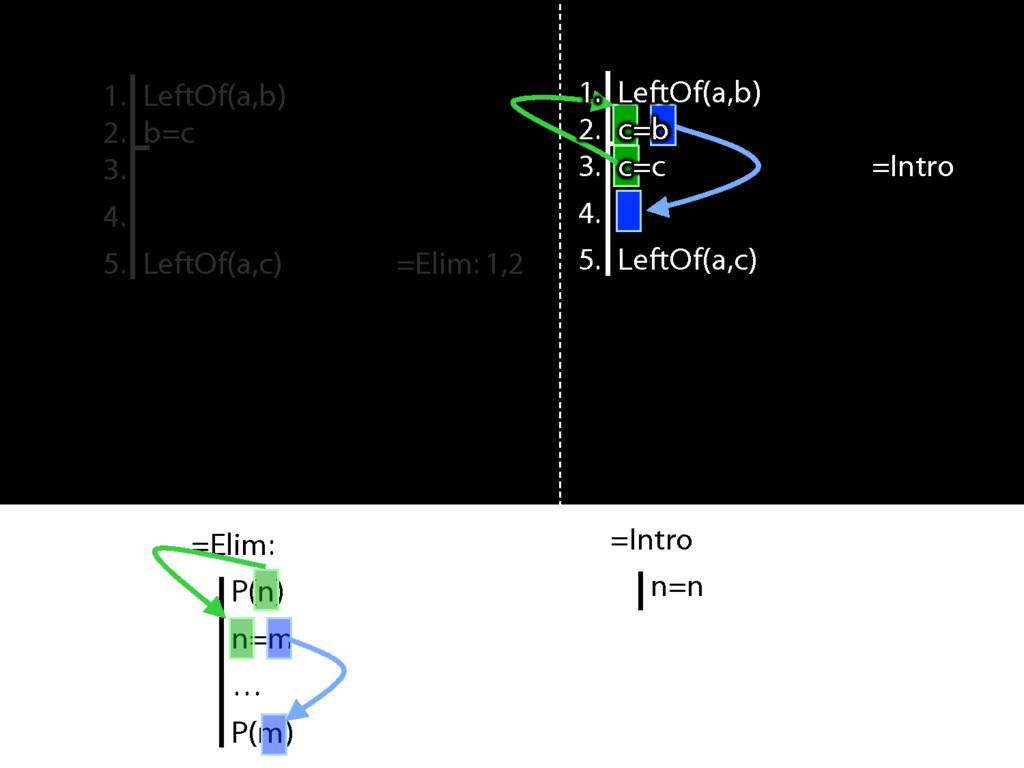
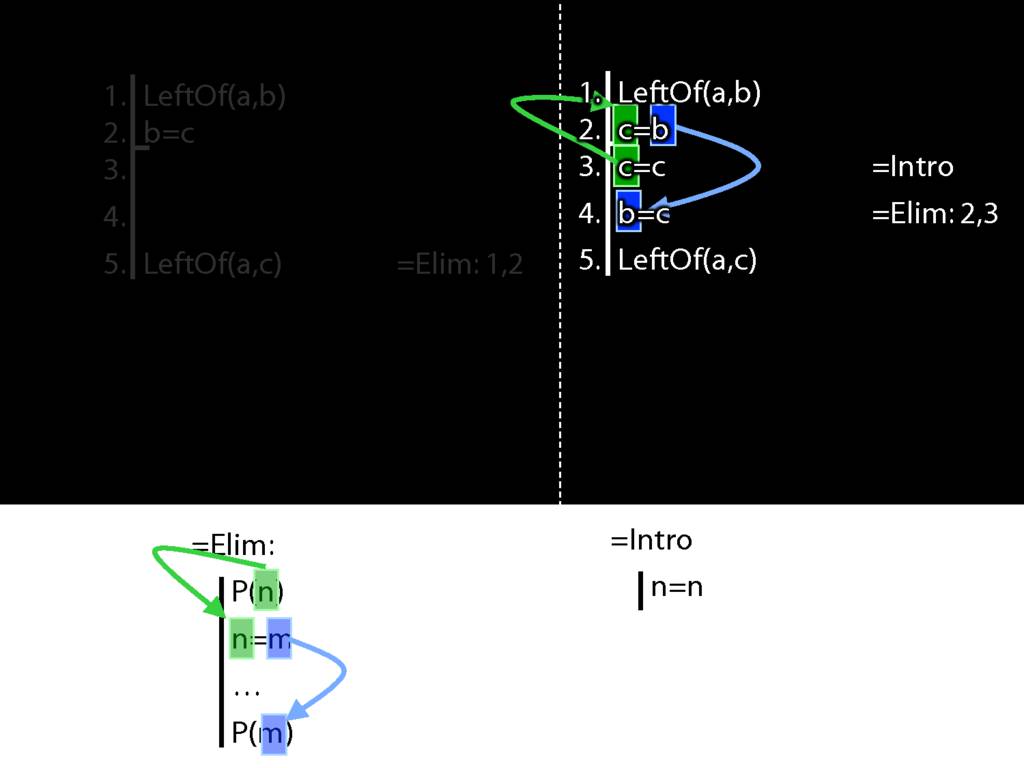
Now look at the pattern in the diagram on the right.
This is a different pattern.
You might protest that b=c and c=b mean the same thing; one can't be true unless the other is.
These sentences do not express different thoughts.
This is true but it is entirely besides the point.
Why is it beside the point?
In studying proof, we're interested in ways of linking the purely formal to the genuinely meaningful.
The proof system Fitch is a formal system of proof.
What we want to show is that, within limits, Fitch captures a notion of logical validity.
This is interesting only because we can describe Fitch entirely without invoking truth or meaning.
So the fact that b=c and c=b mean the same is irrelevant in Fitch.
When you're thinking about Fitch, all you care about is the pattern of symbols.
And b=c is a different pattern from c=b.

This is Abdurrahman Wahid, popularly known Gus Dur, a former president of Indoneisa and one of the most jovial national leaders ever. He was a really nice guy. As president he was infirm and nearly blind. When asked to resign he replied “I need help to step up, let alone step down.” (Economist 2010-01-07 obituary). Unfortunately he died recently (december 30 2009)

And this is Than Schwe, Myanamar’s military ruler.
Guess who I'd pick to marks your logic exam.
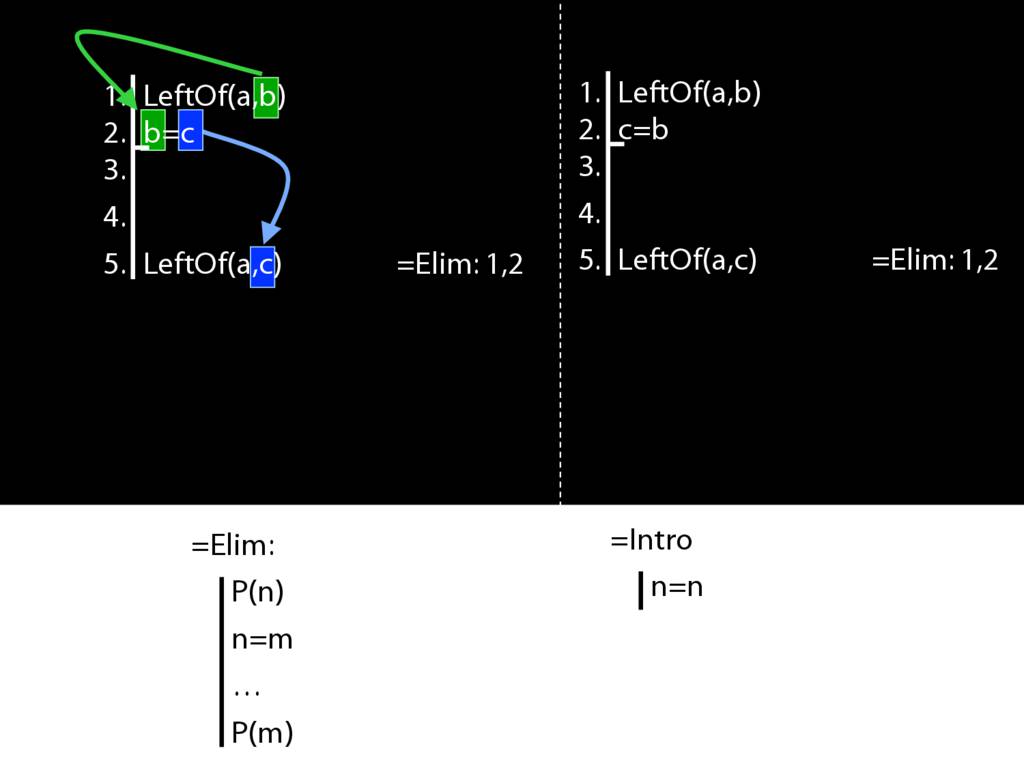
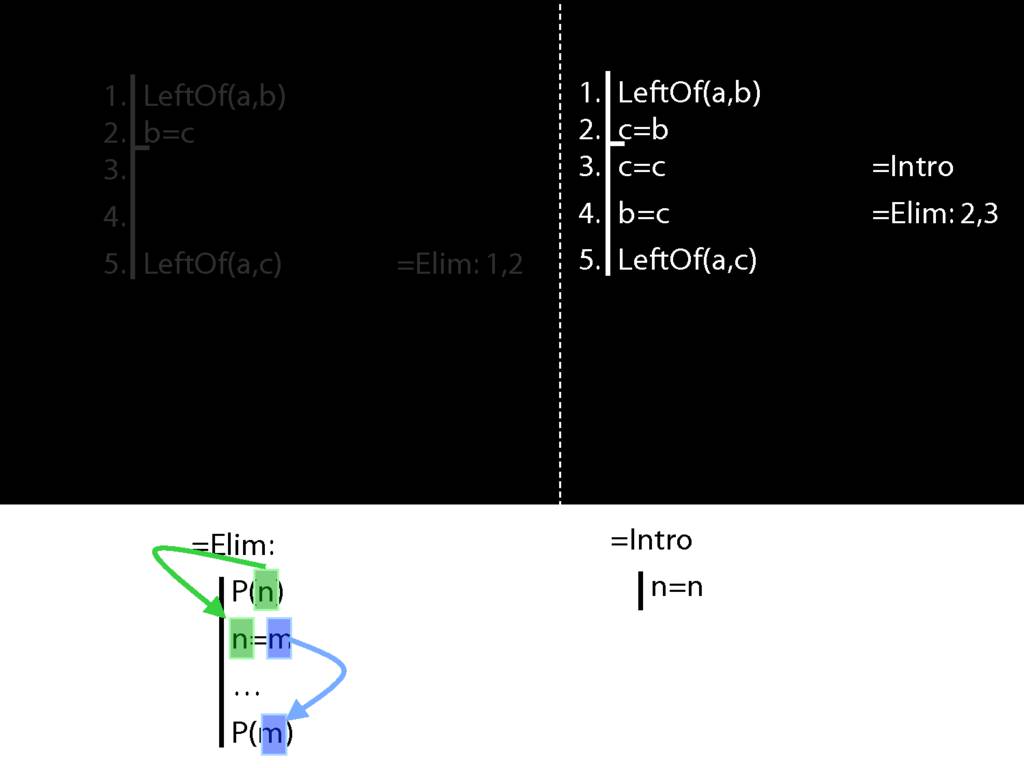
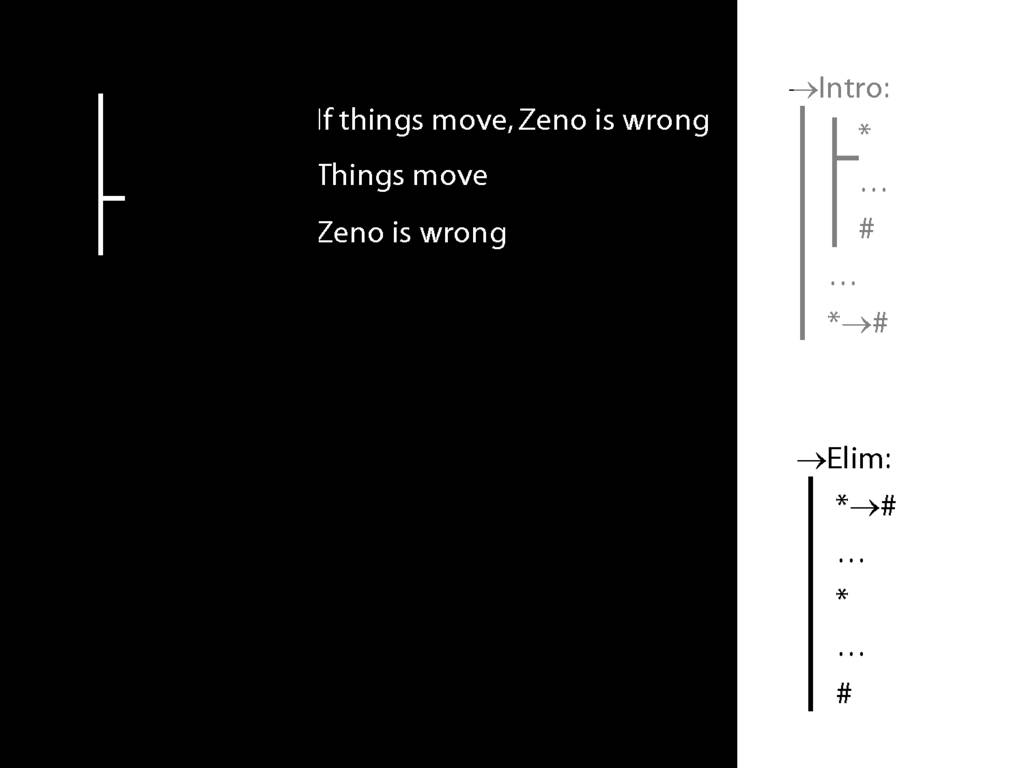
One last thing. The argument on your right is logically valid. Can you prove it?
\section{=Elim Again}

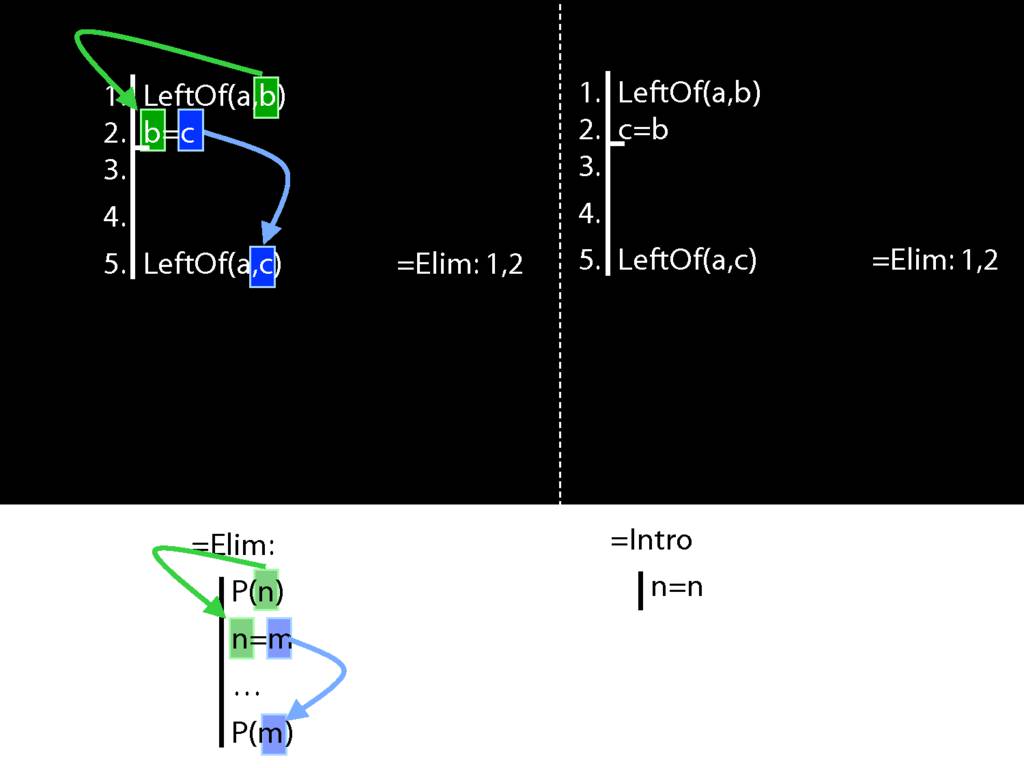

→Intro, →Elim
\section{→Intro, →Elim}
\emph{Reading:} §8.1, §8.2
\section{→Intro, →Elim}




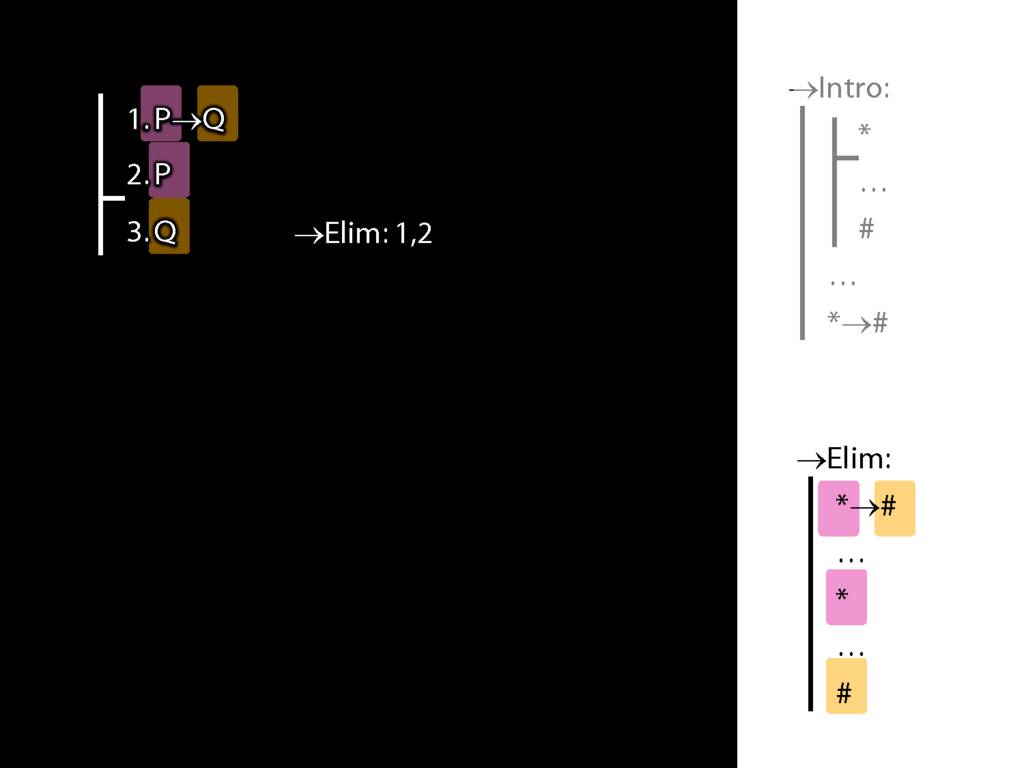


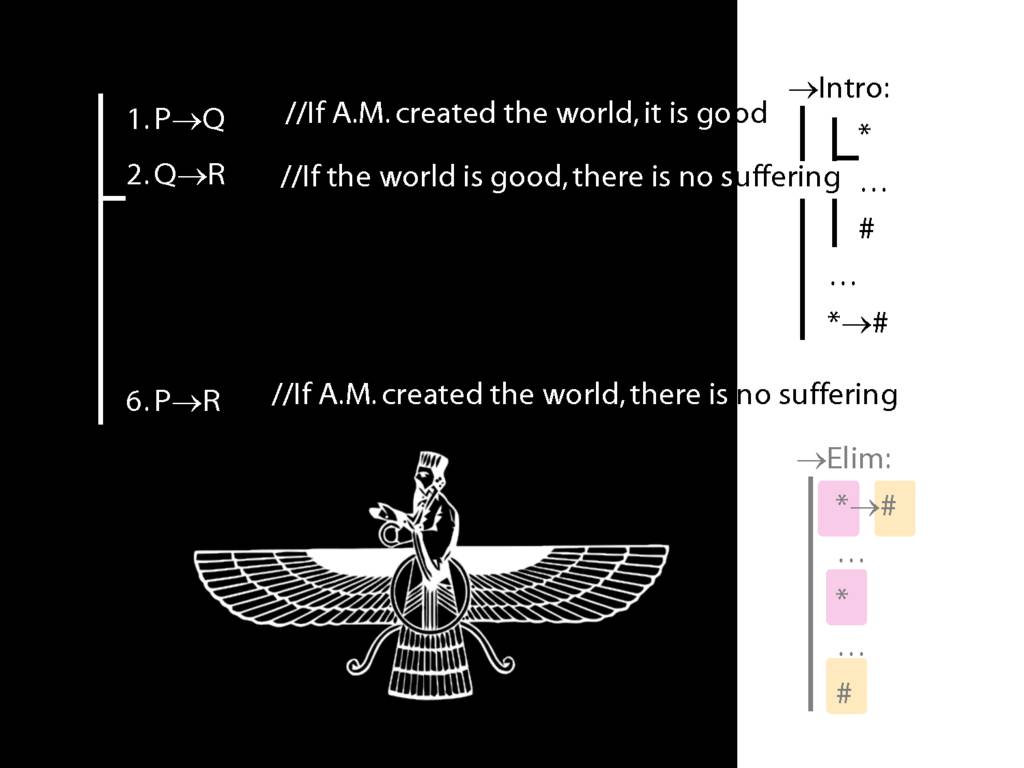
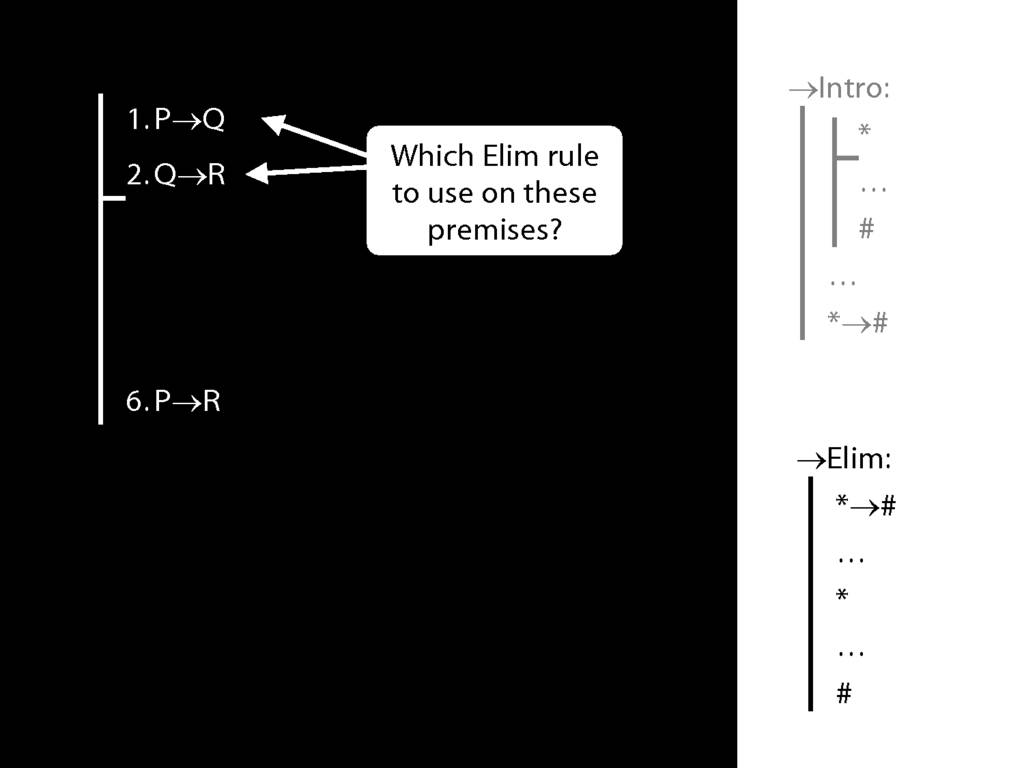
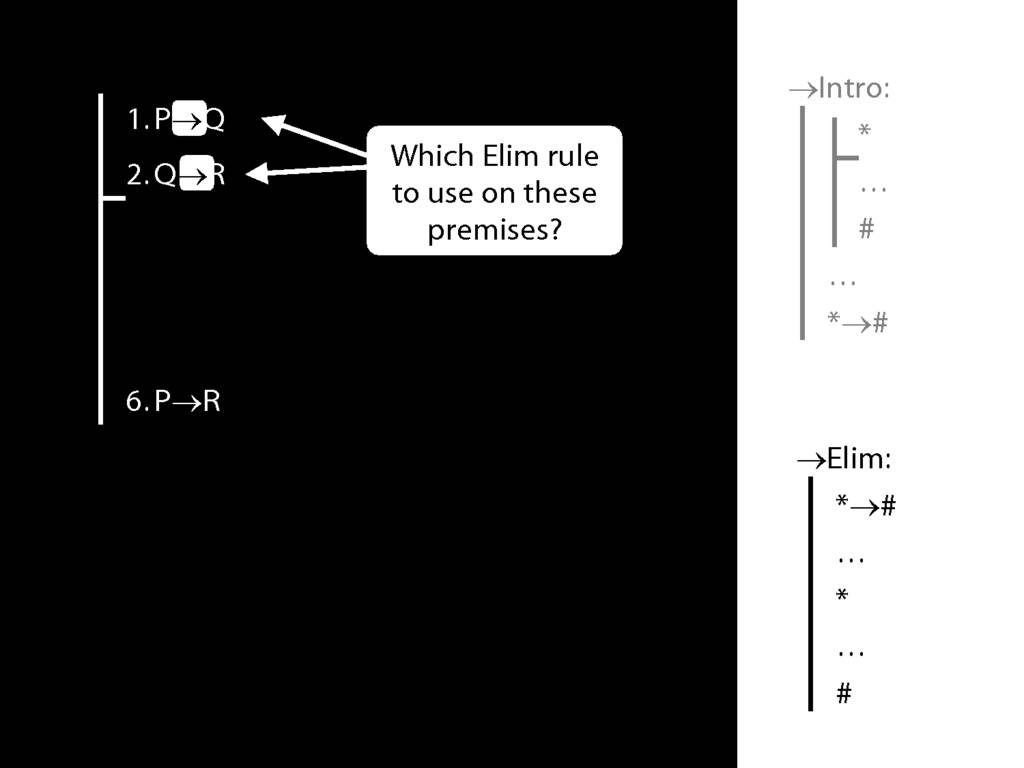
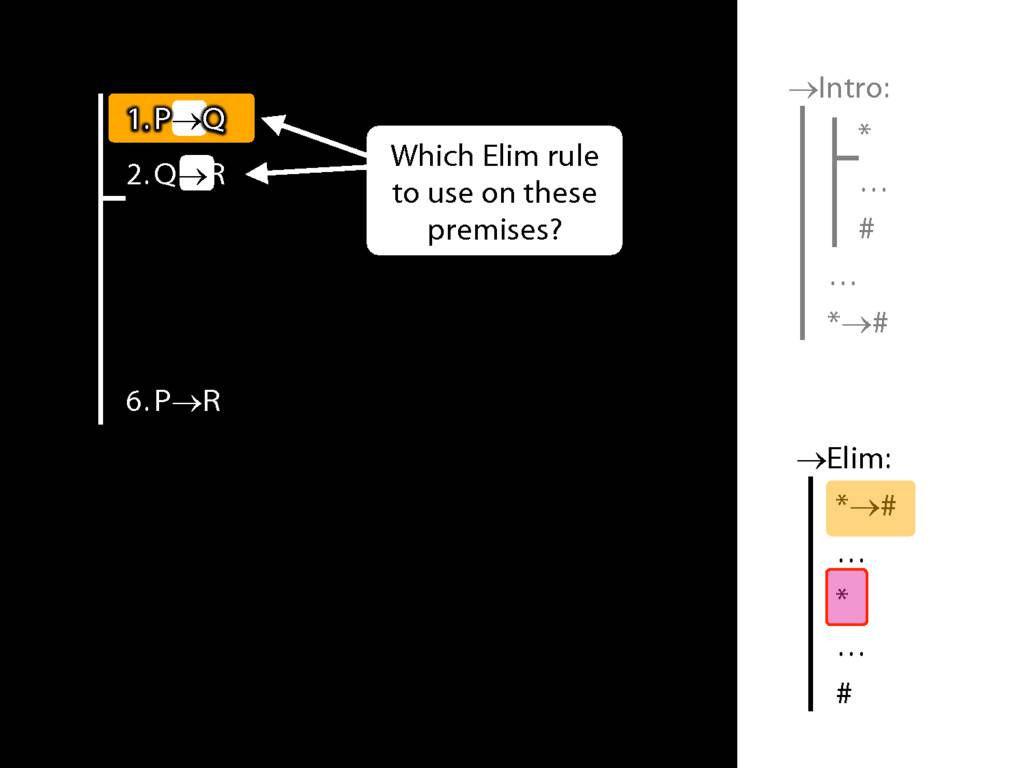
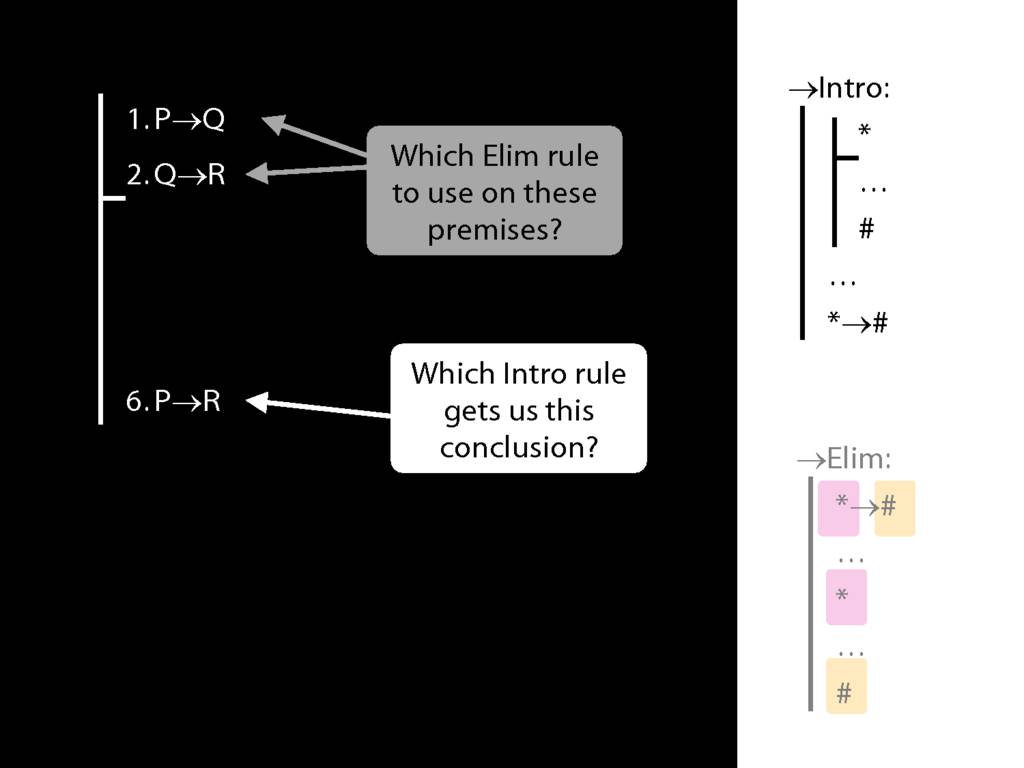
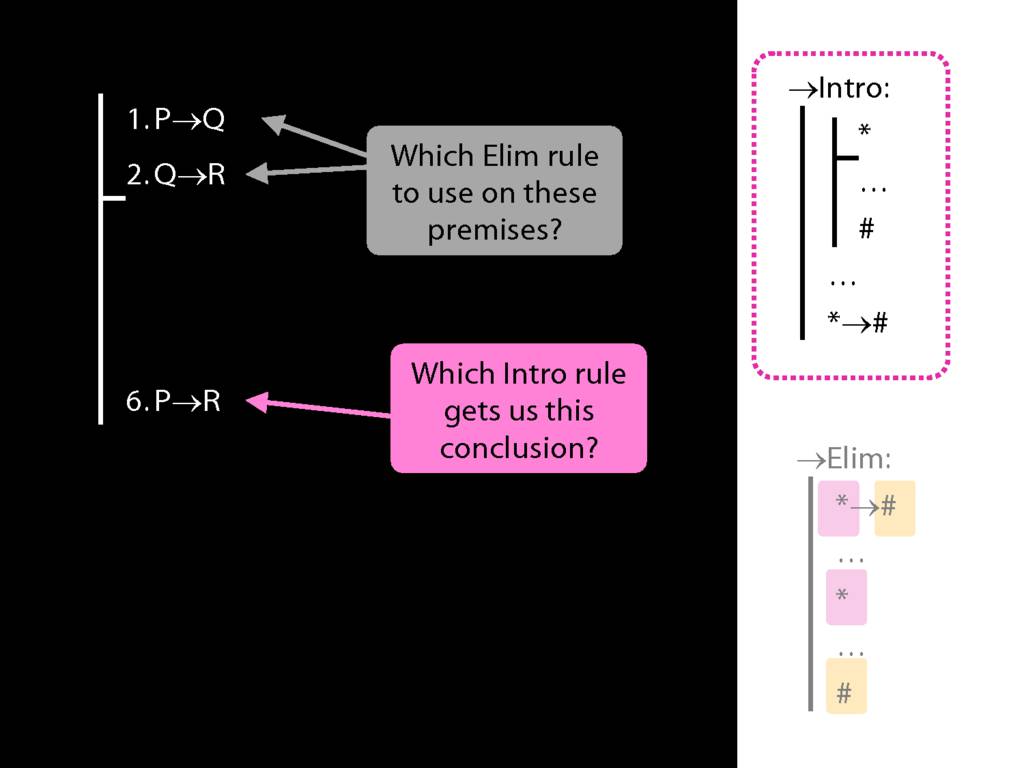
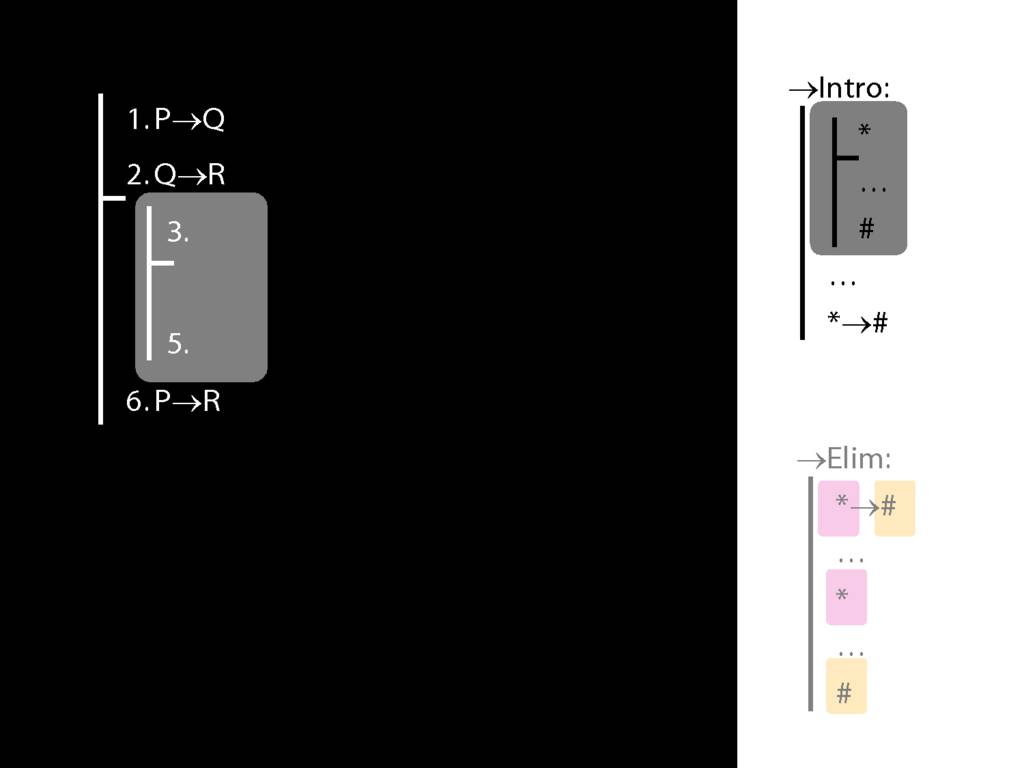
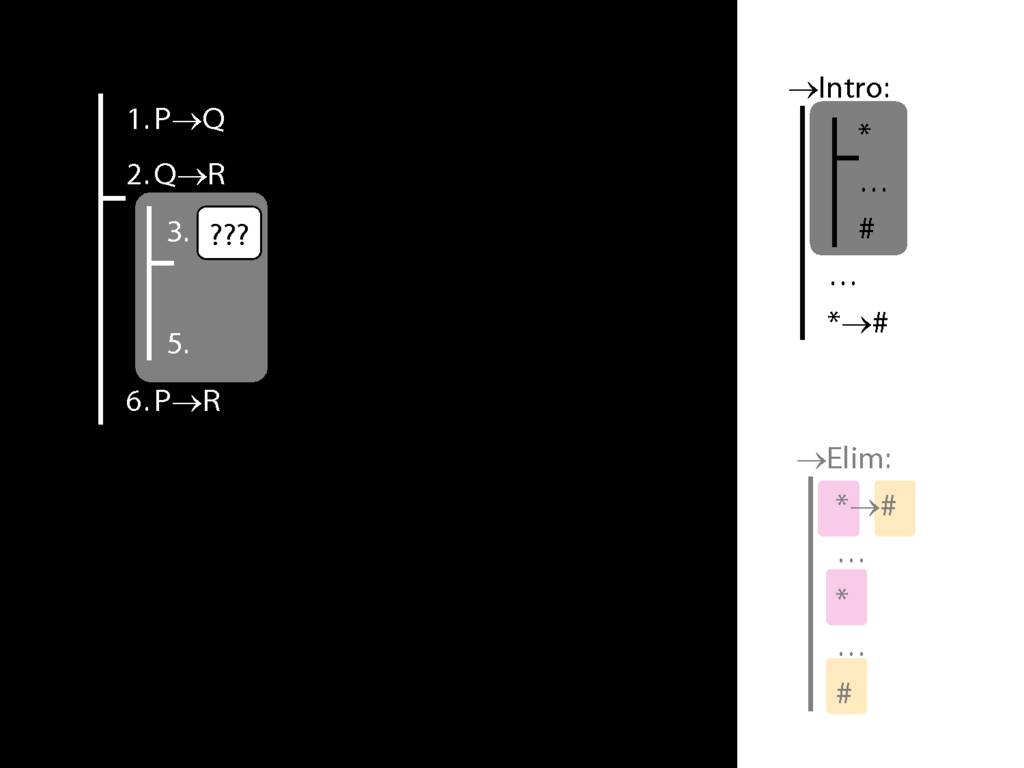
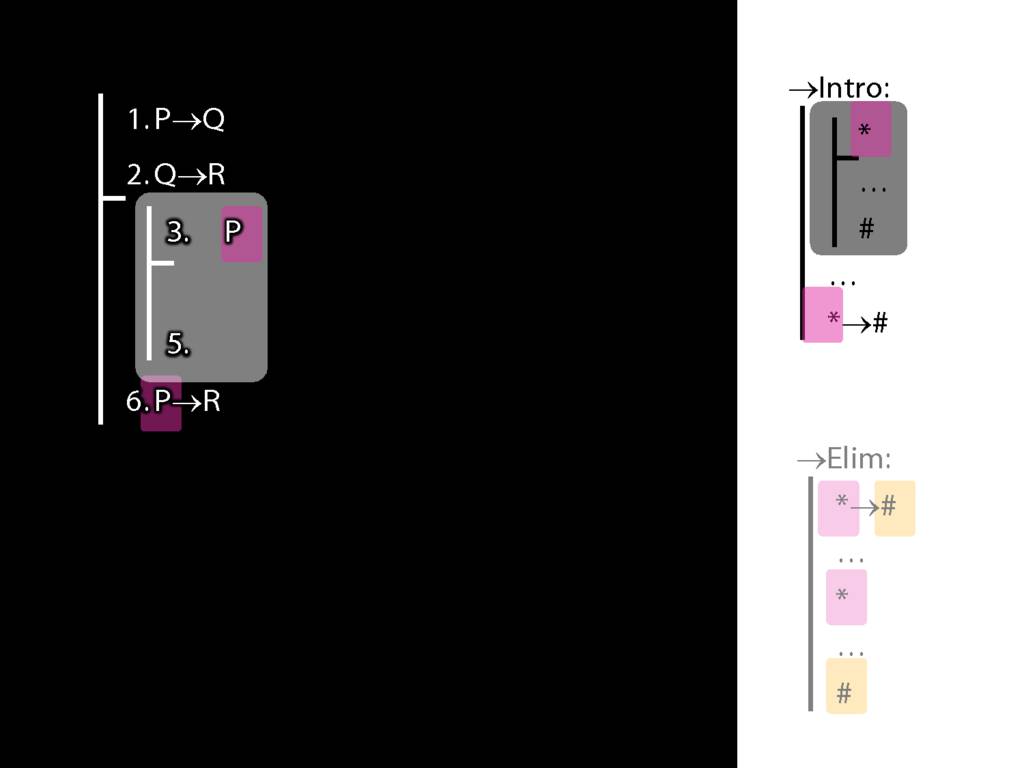
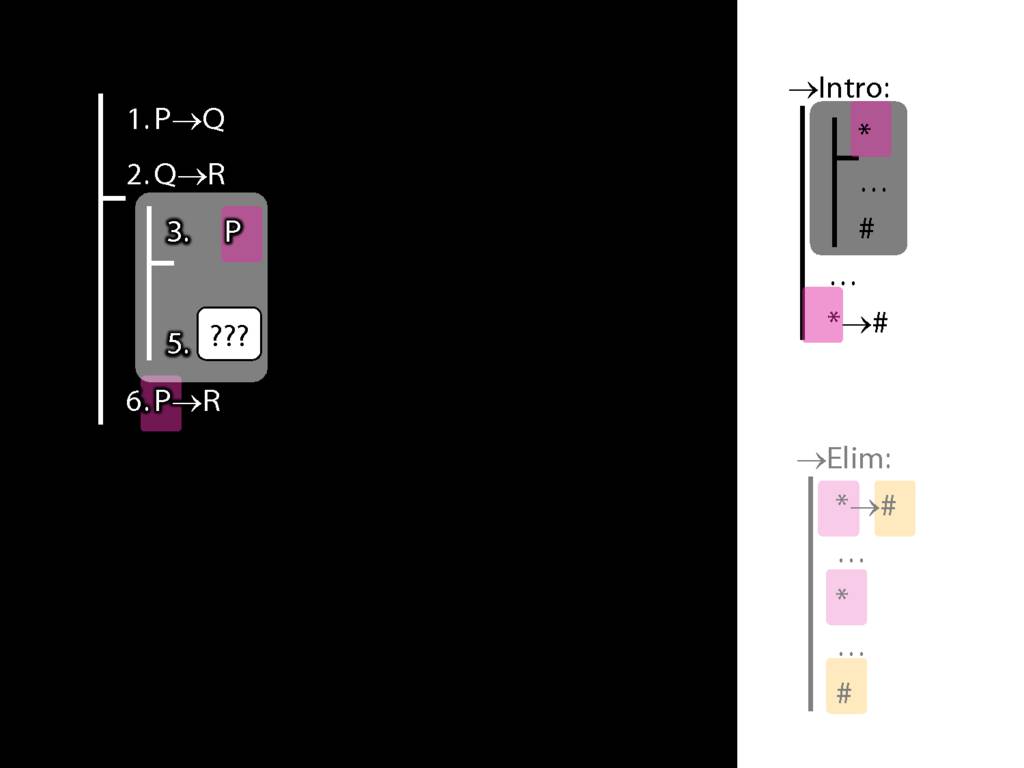
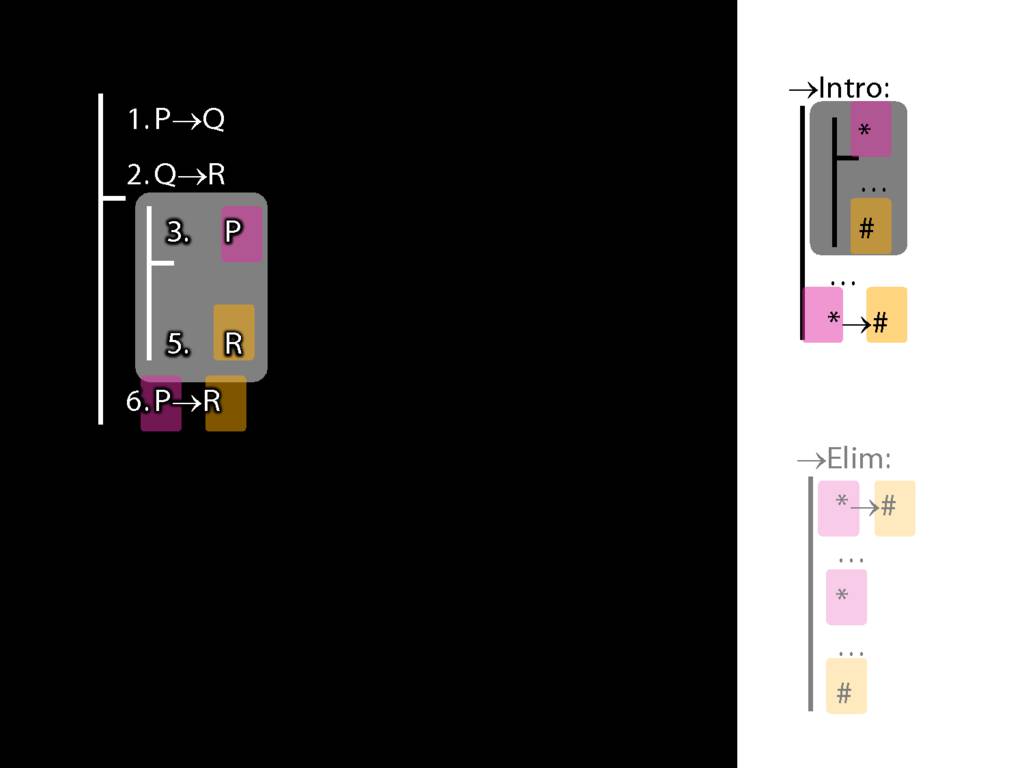
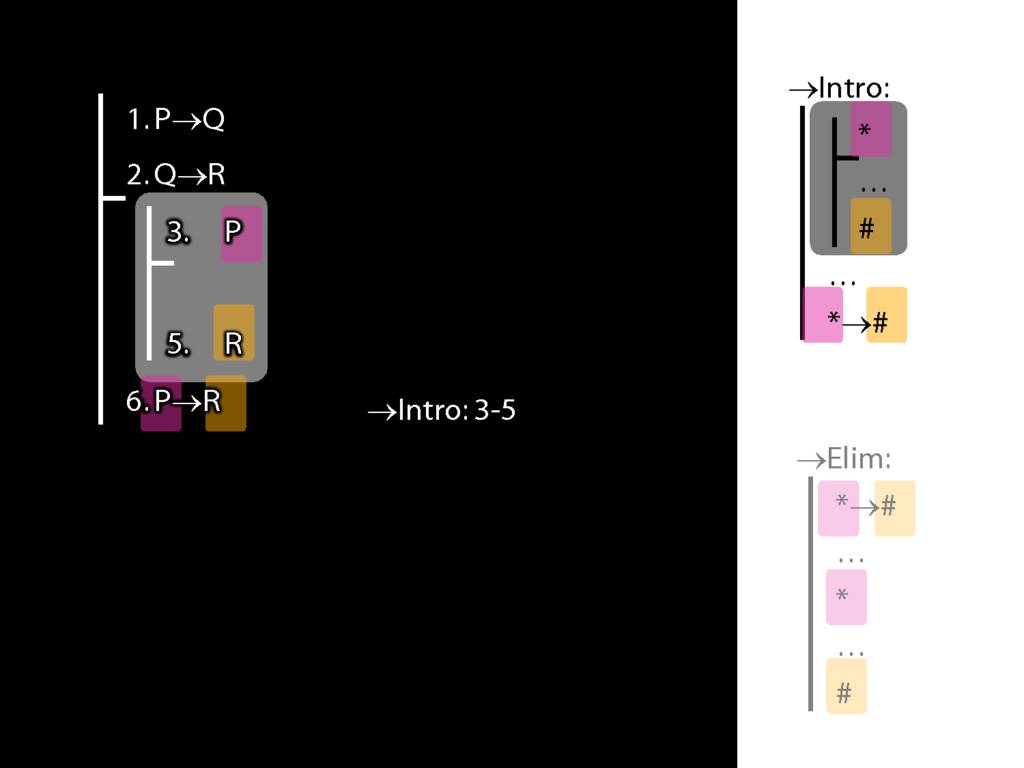
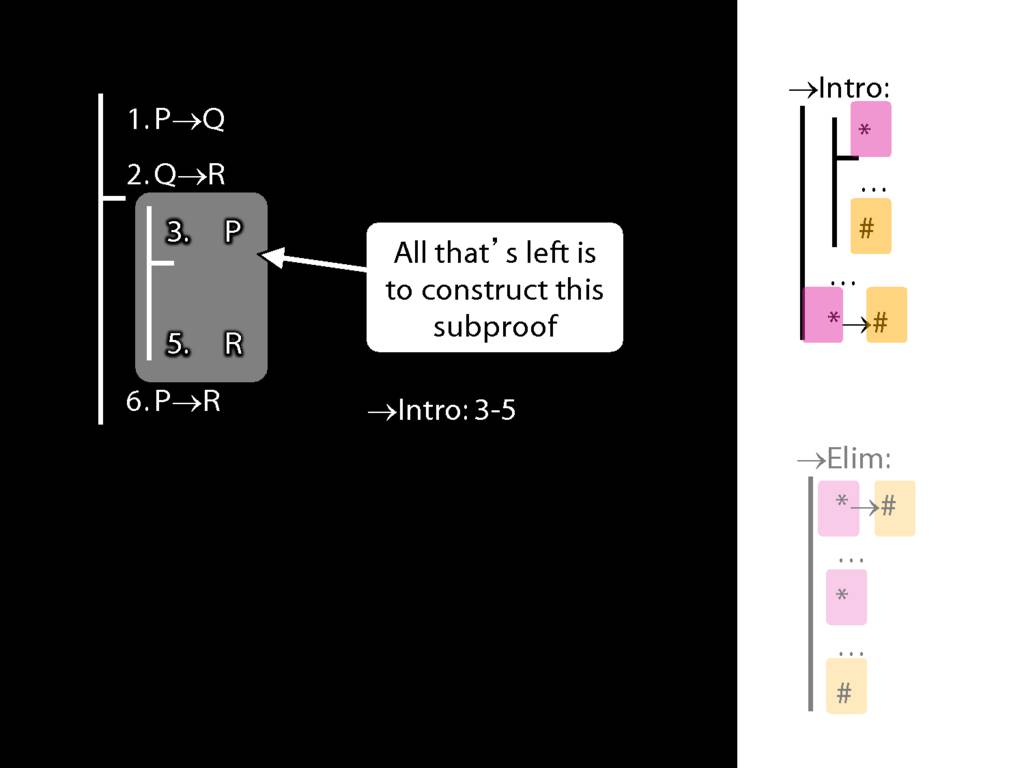
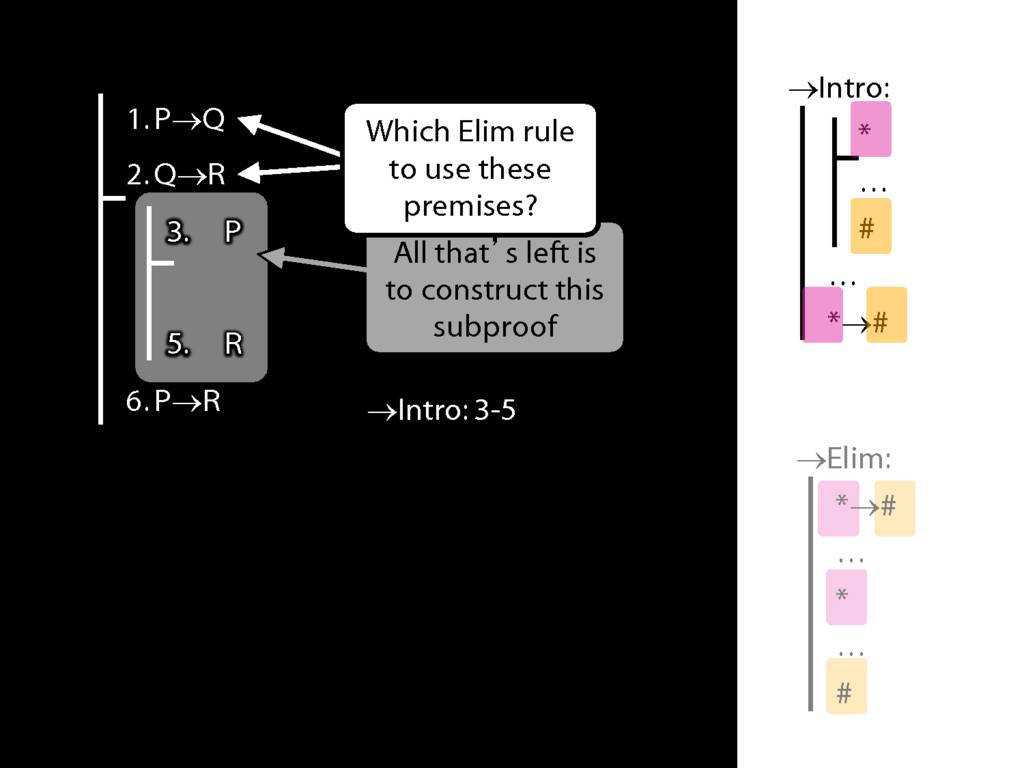
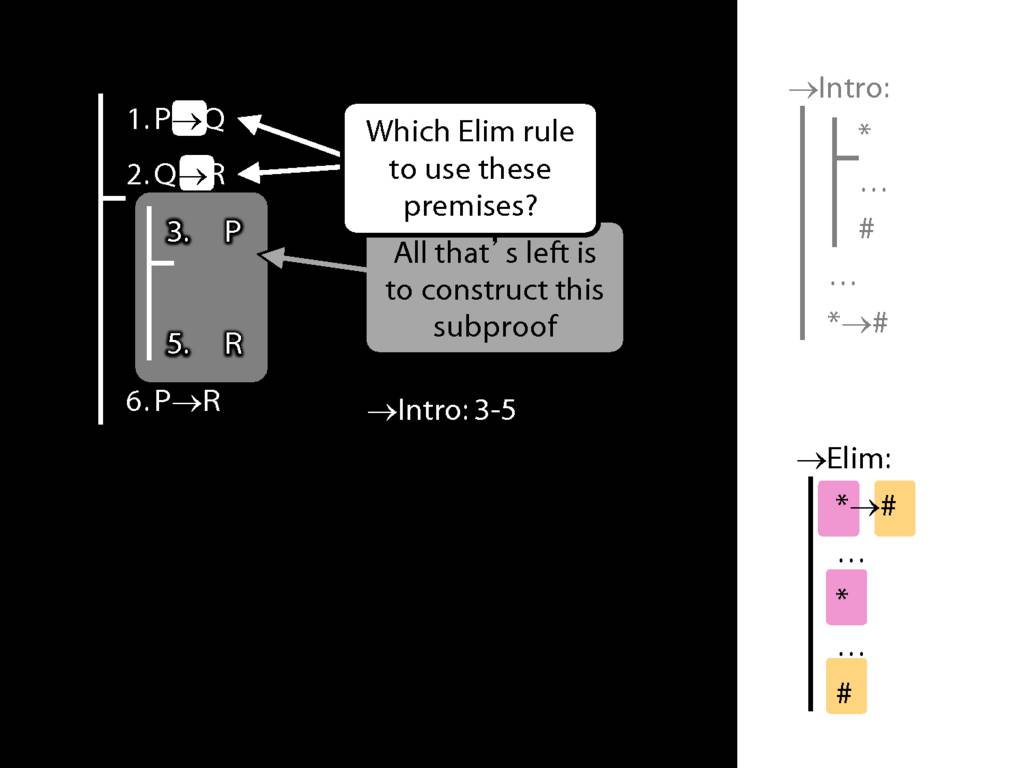
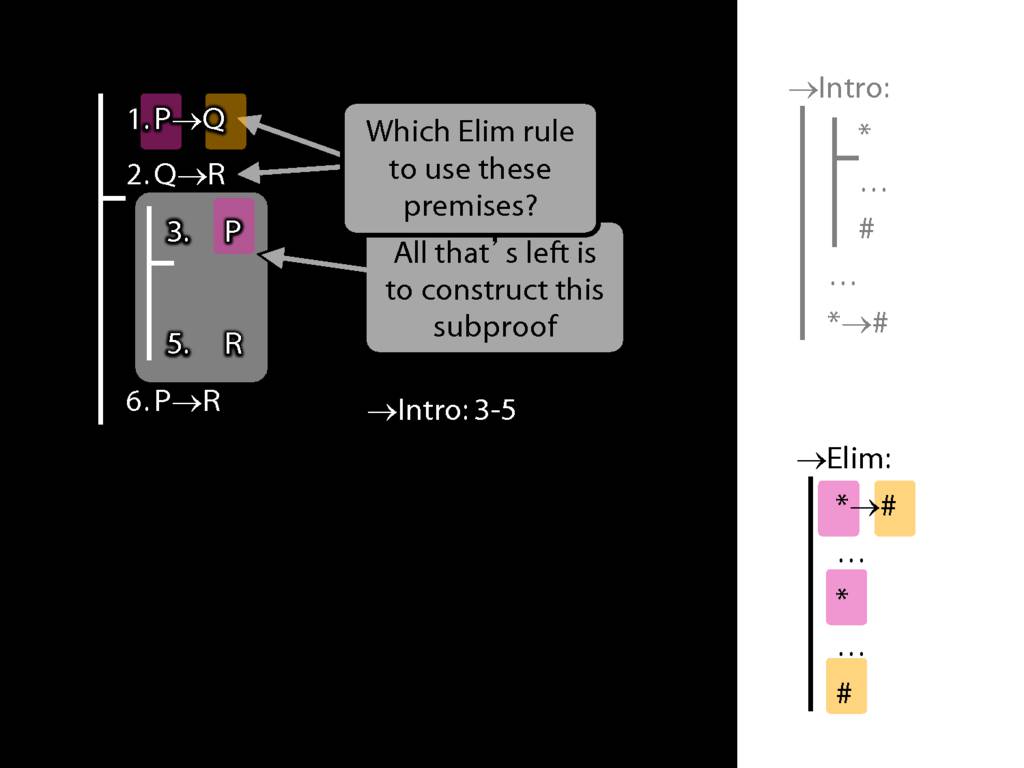
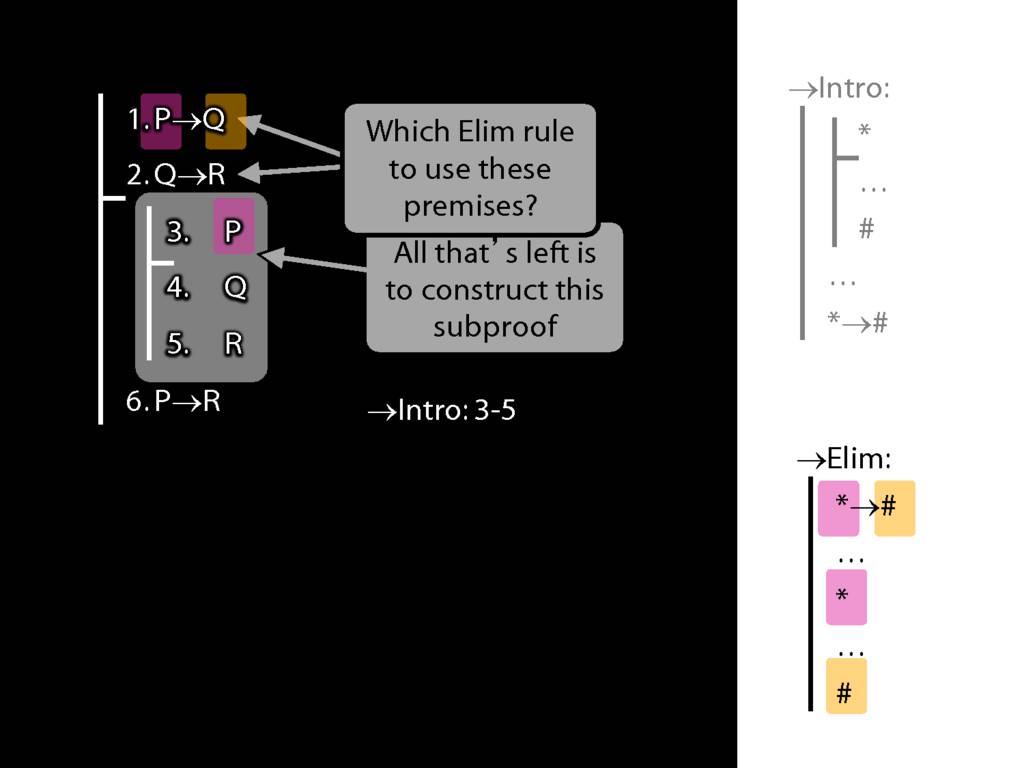
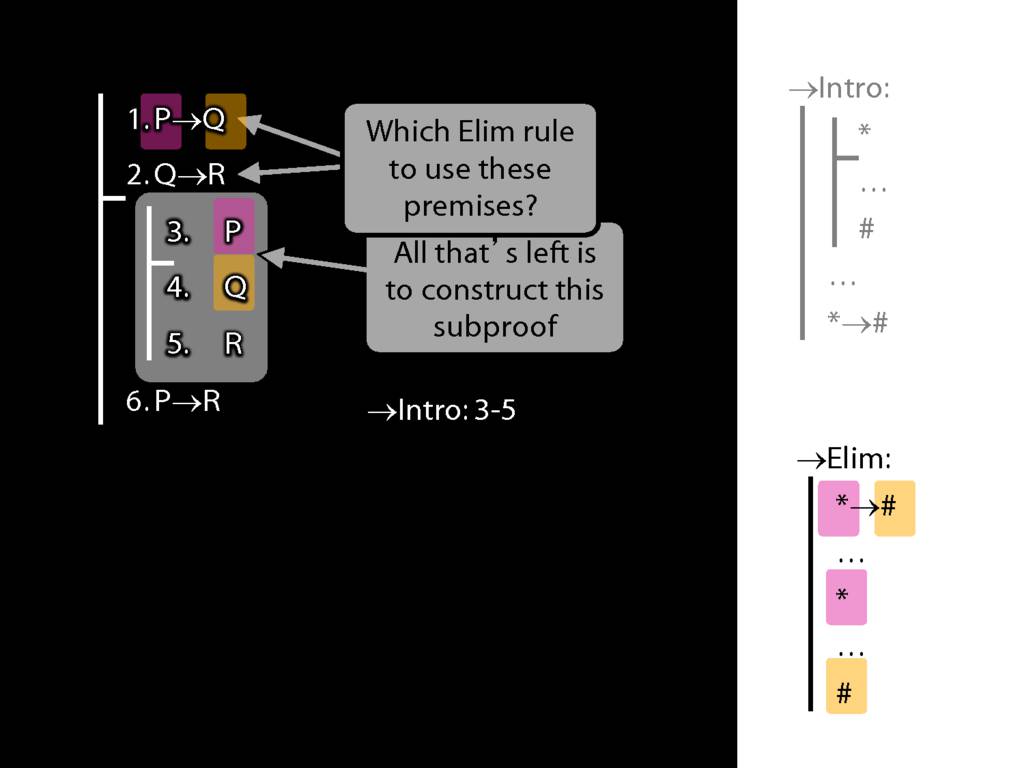
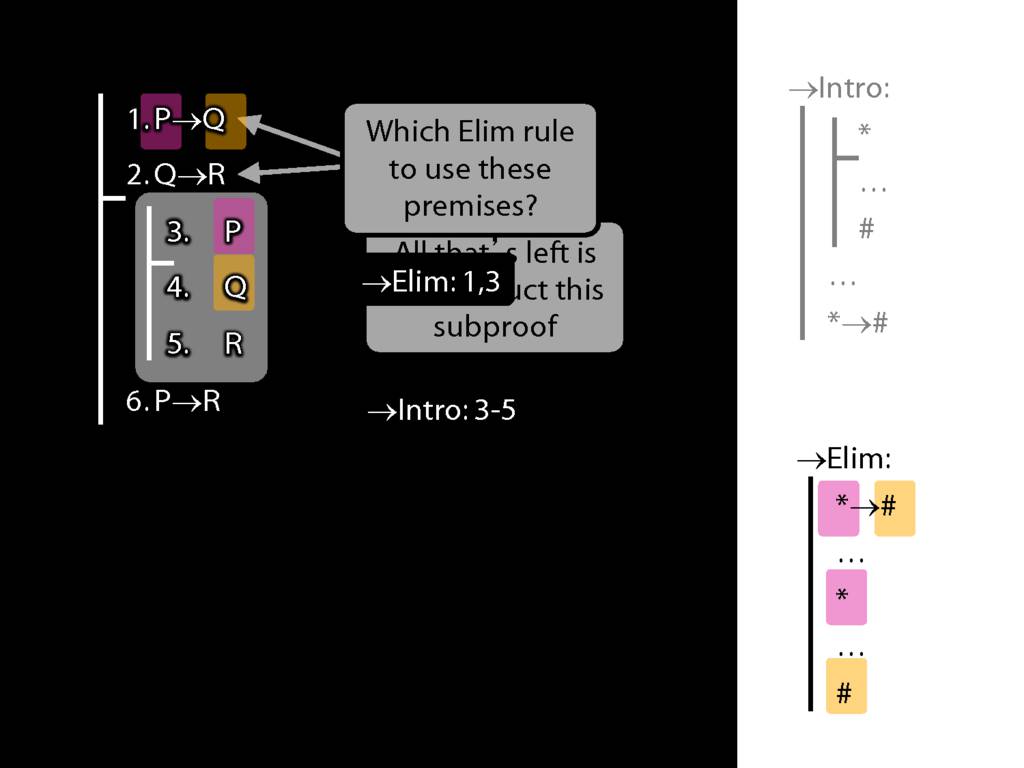
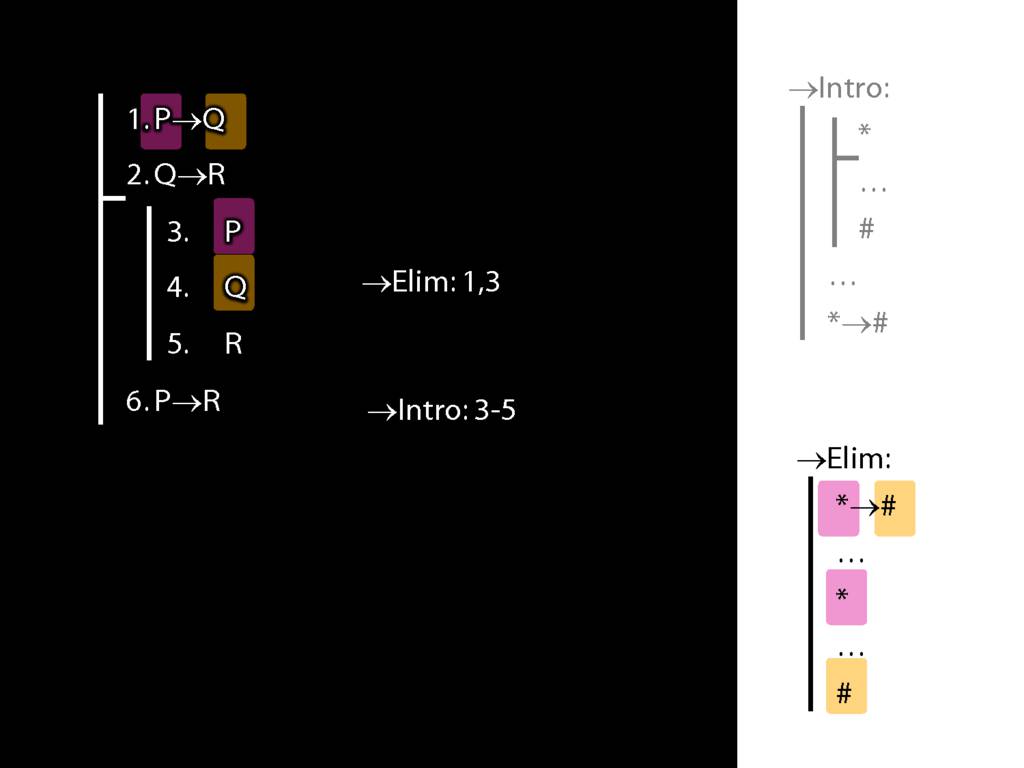


8.20--8.25

Subproofs with zoxiy
\section{Subproofs with zoxiy}
\emph{Reading:} §8.1, §8.2
\section{Subproofs with zoxiy}
https://logic-ex.butterfill.com/ex/proof/from/A arrow B|B arrow C/to/A arrow C
Let’s see how to create proofs with subproofs in this in logic-ex.
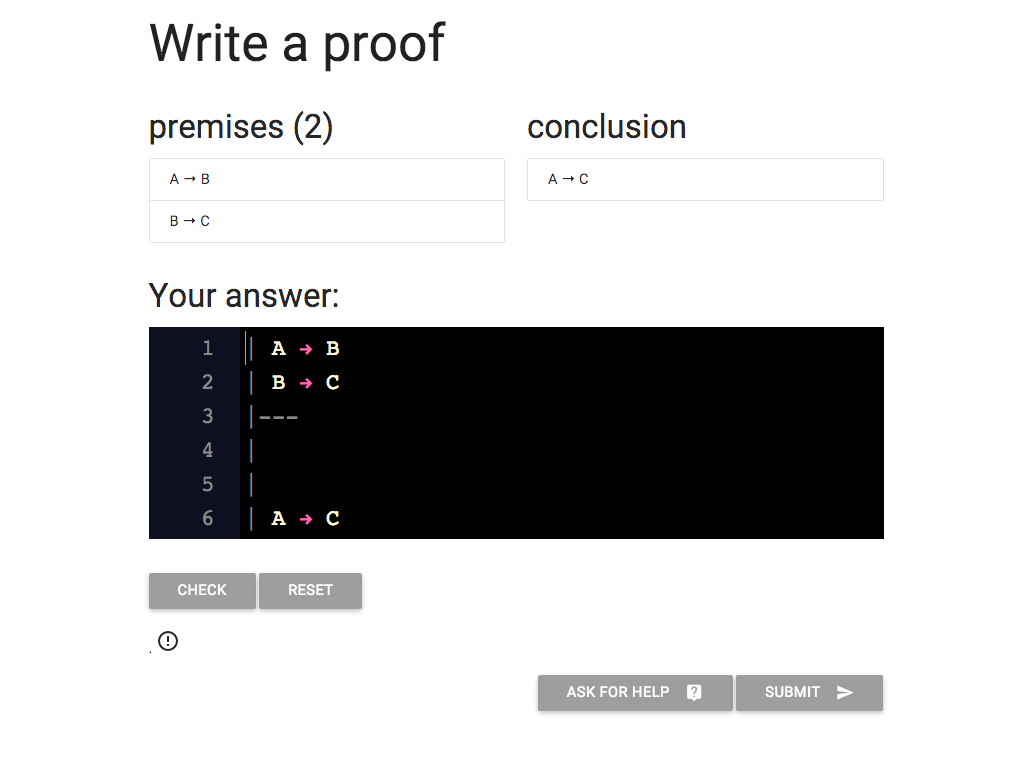
Here we’re asked to write a proof that will
require a subproof. (If you’ve been following the
lectures, you’ve already seen this proof.)
We’re going to create a subproof in order to use the rule arrow intro.
If you don’t already know the rule, please take a look at the rule now
so you can follow what we’re doing.
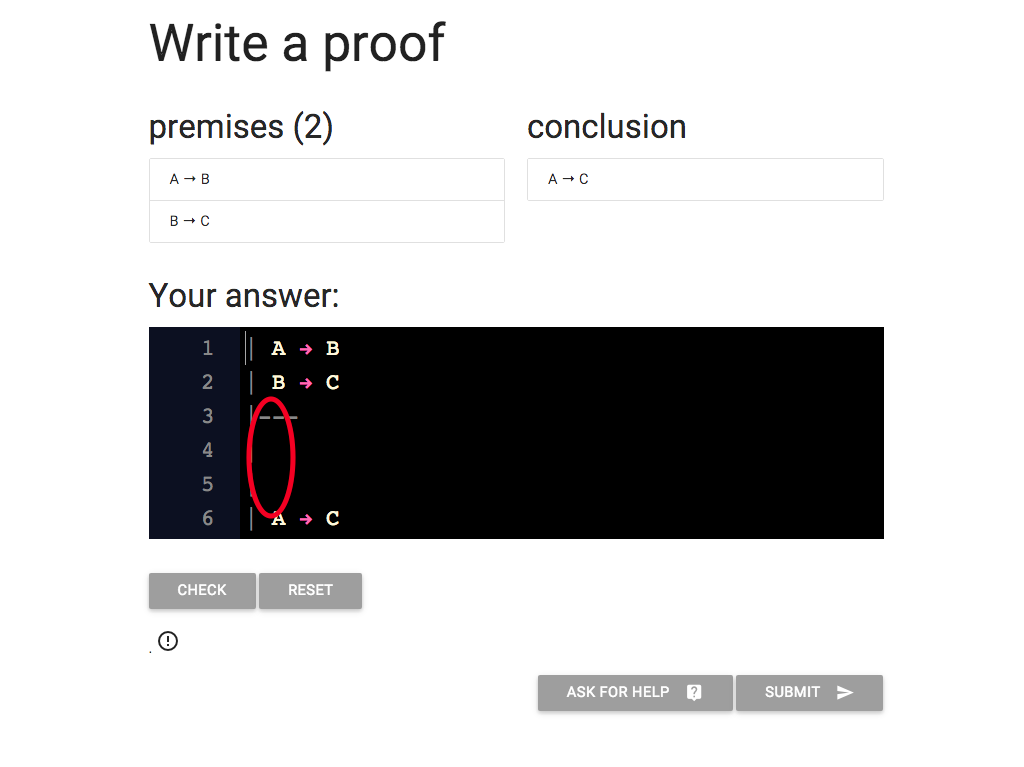
The first thing we need is a bit more space
for our subproof.
Remember that the proof is just a bit of text, and the black box here
is just a text editor.
So to make new lines I just use the enter key.
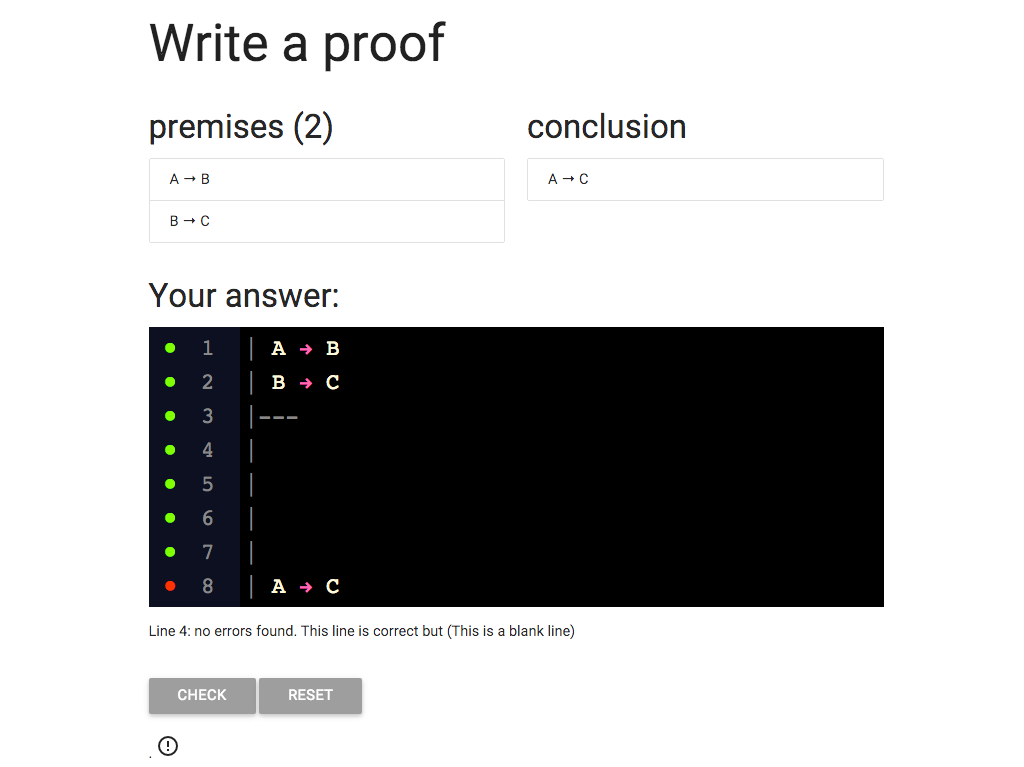
Here I’ve added new lines to the proof.
Each line starts with a vertical bar, ‘|’.
(If you can’t find the vertical bar on your keyboard you
might have to copy and paste it.)
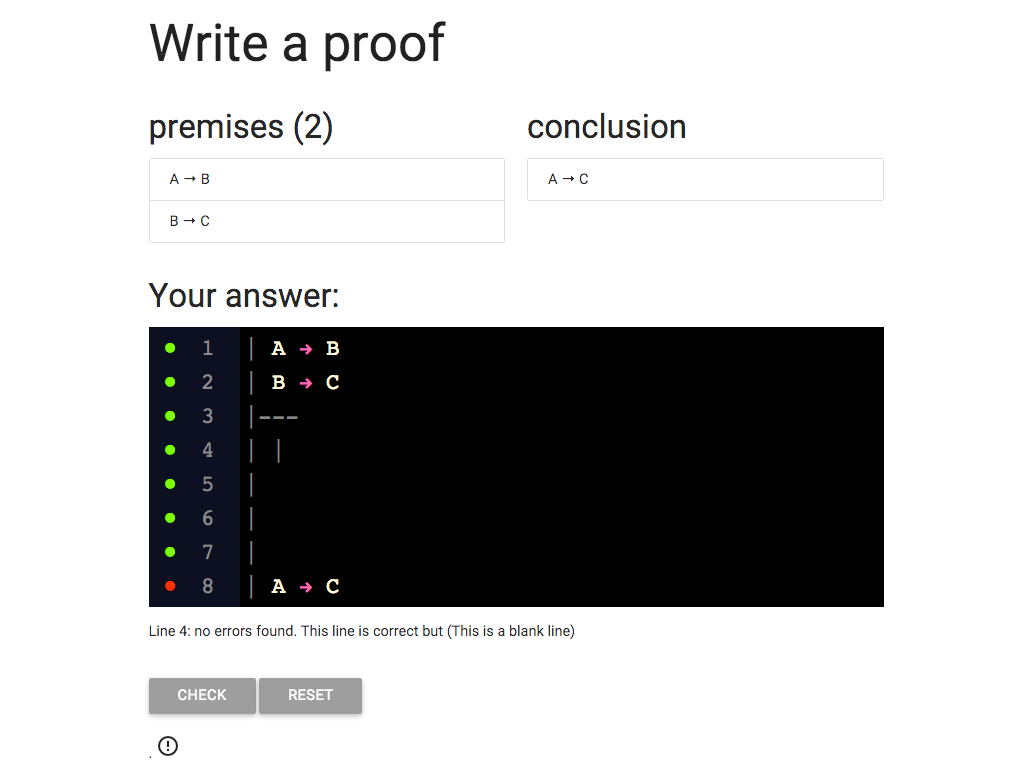
OK, let’s make a subproof.
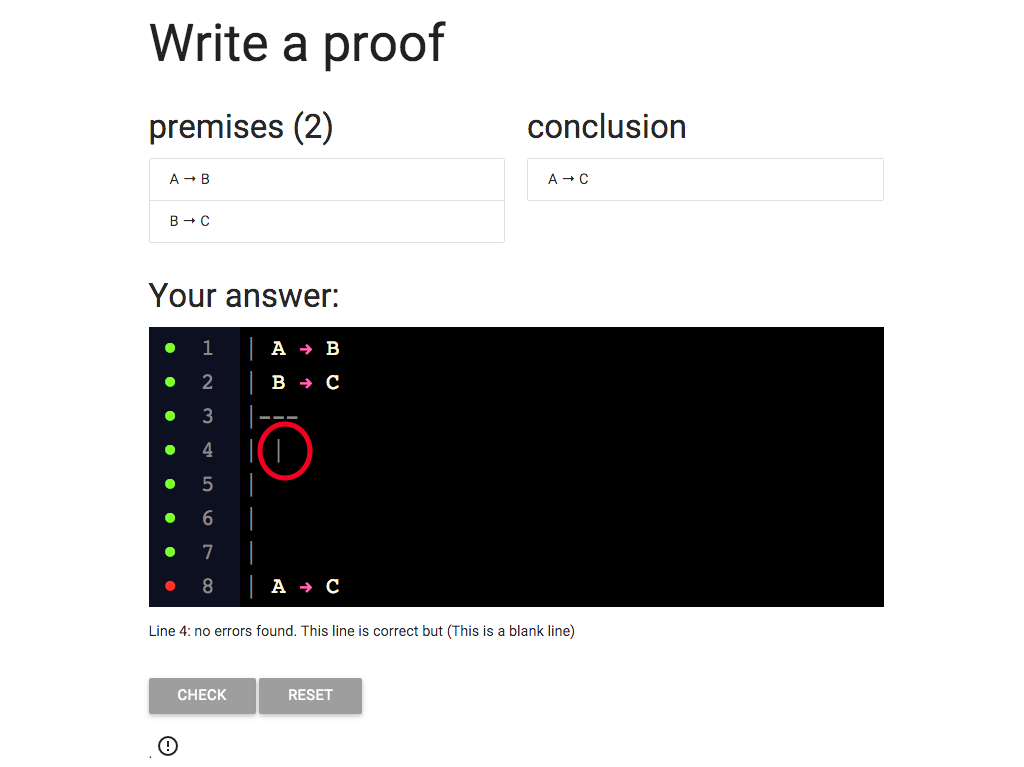
On each line, I need to add a new vertical bar like this one.
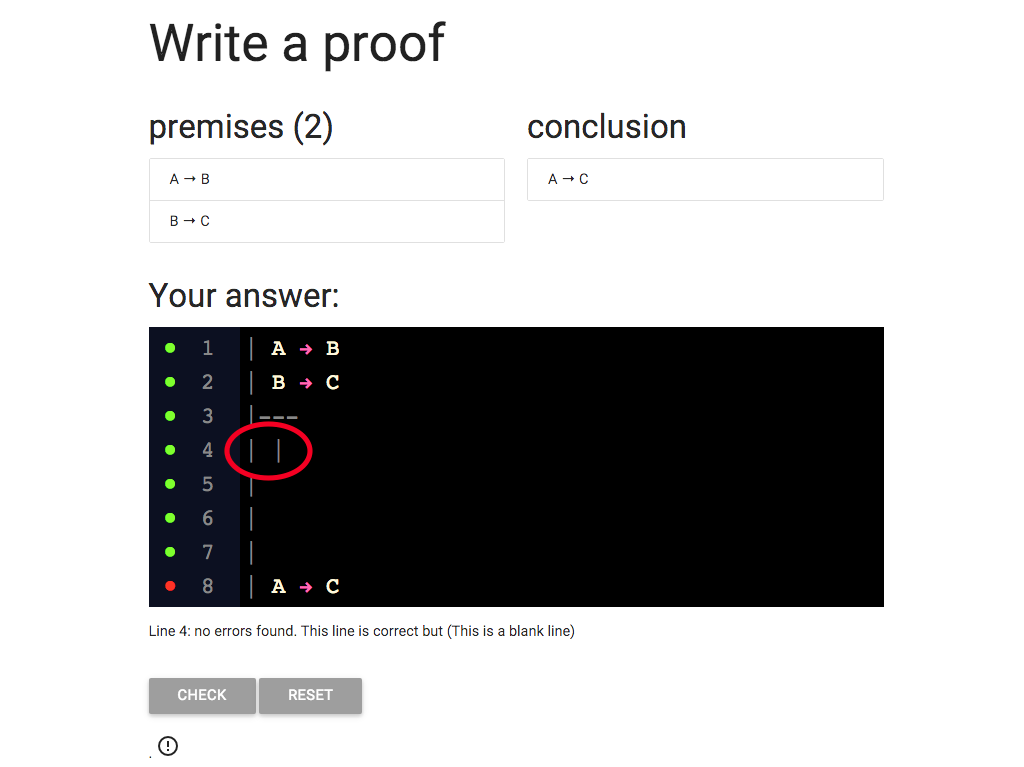
So now, as you can see, there are two vertical bars at the start of line 4.
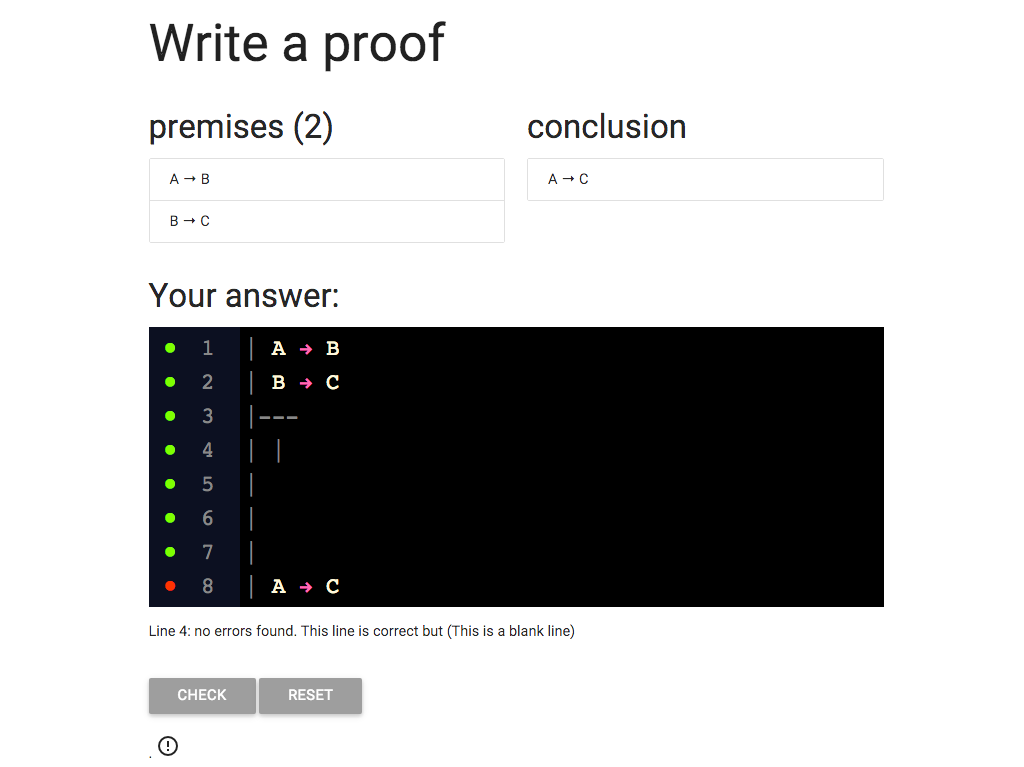
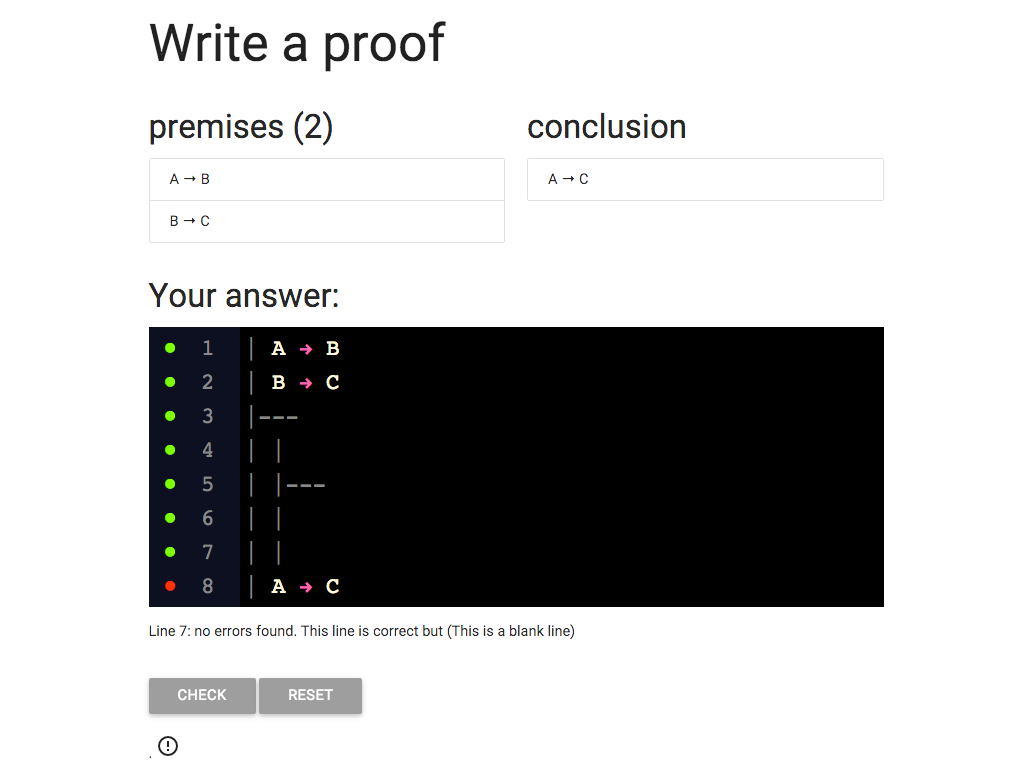
I keep going with adding the extra vertical lines,
and I add the horizontal line as three dashes, ‘-’.
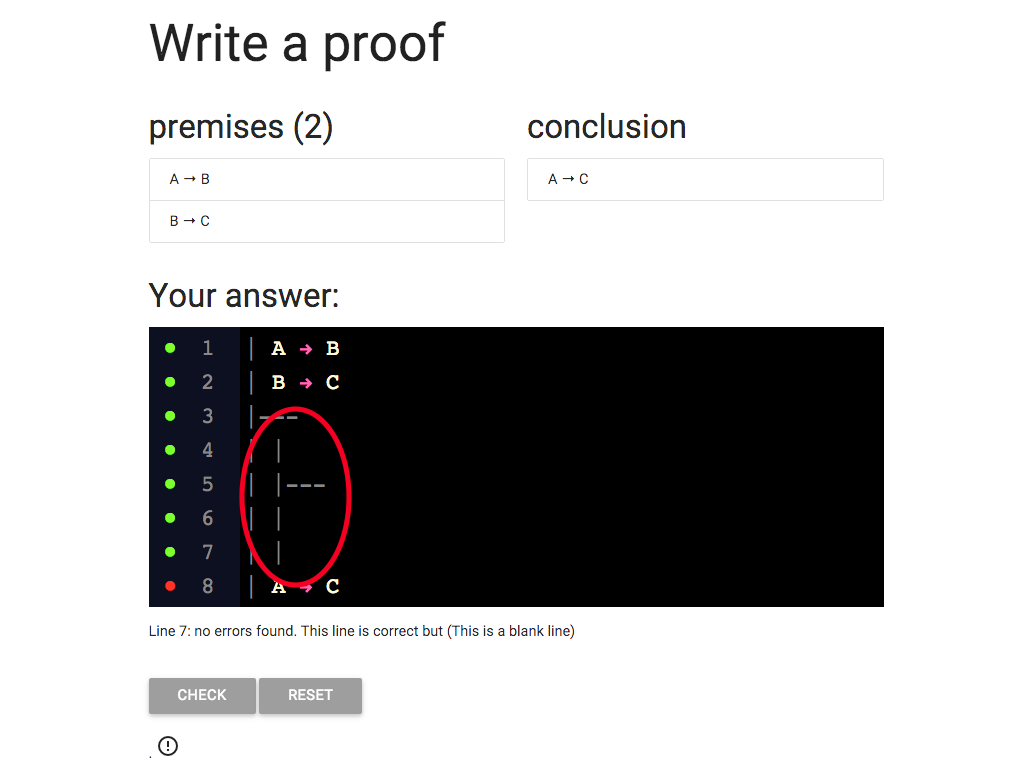
So this is a subproof. It’s just lie the outer proof:
each line that is part of it starts with a vertical bar,
and the premise is seperated from the rest with a horizontal
line comprising three dashses.
What next?
When I’m doing a proof I like to put the premise
and conclusion of the subproof in first.
After all, we already know what these are from the rule
of proof we are using, whereas we will have
to think about what goes in the middle.
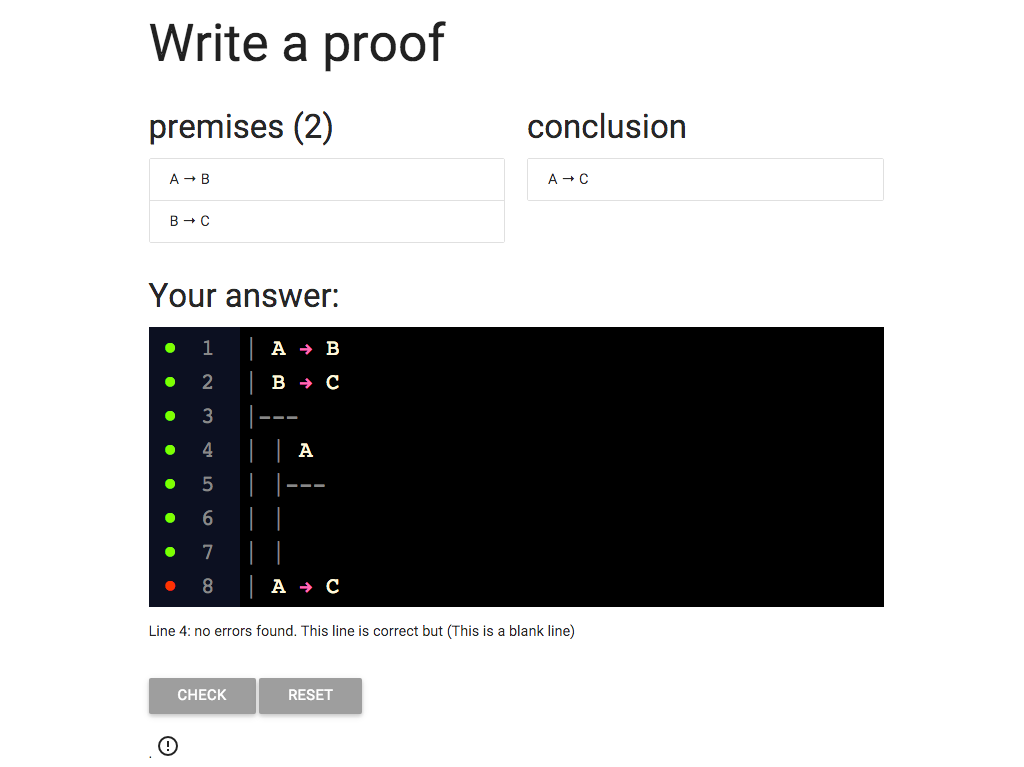
The premise of the subproof is A.

But why is it A?
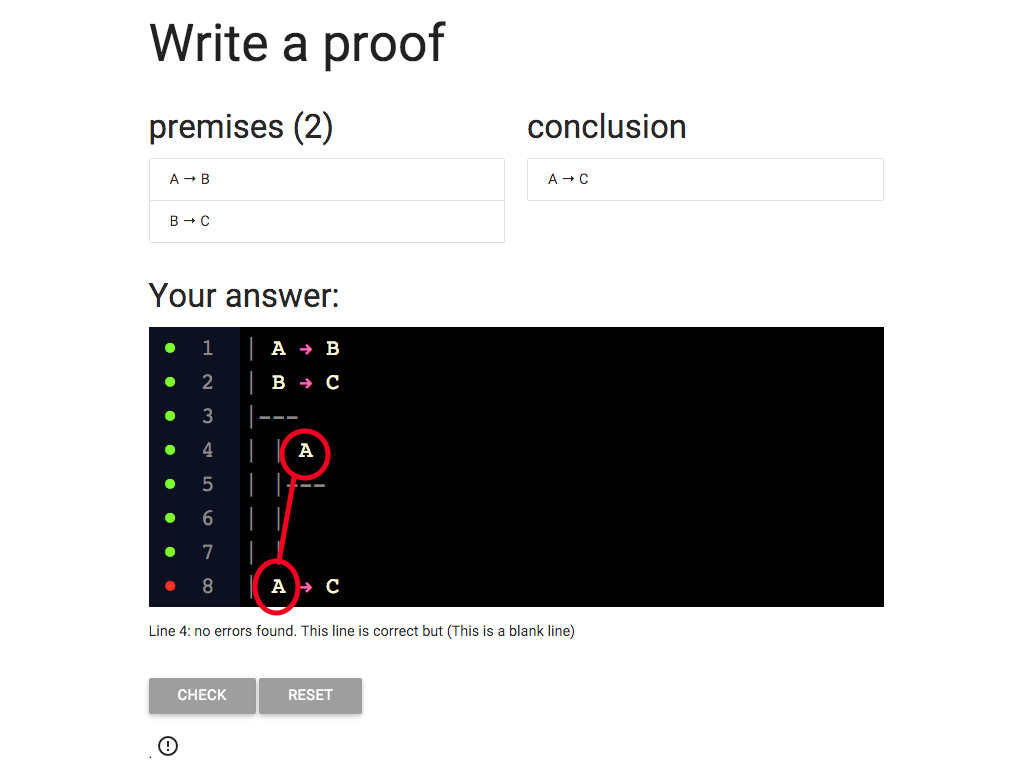
Well A is the thing on the left of the condition.
It’s the *antecedent* of the conditional.
And if you look at the rule for arrow intro, it tells you
that the subproof has to start with the antecdent of the
conditional you want to introduce.
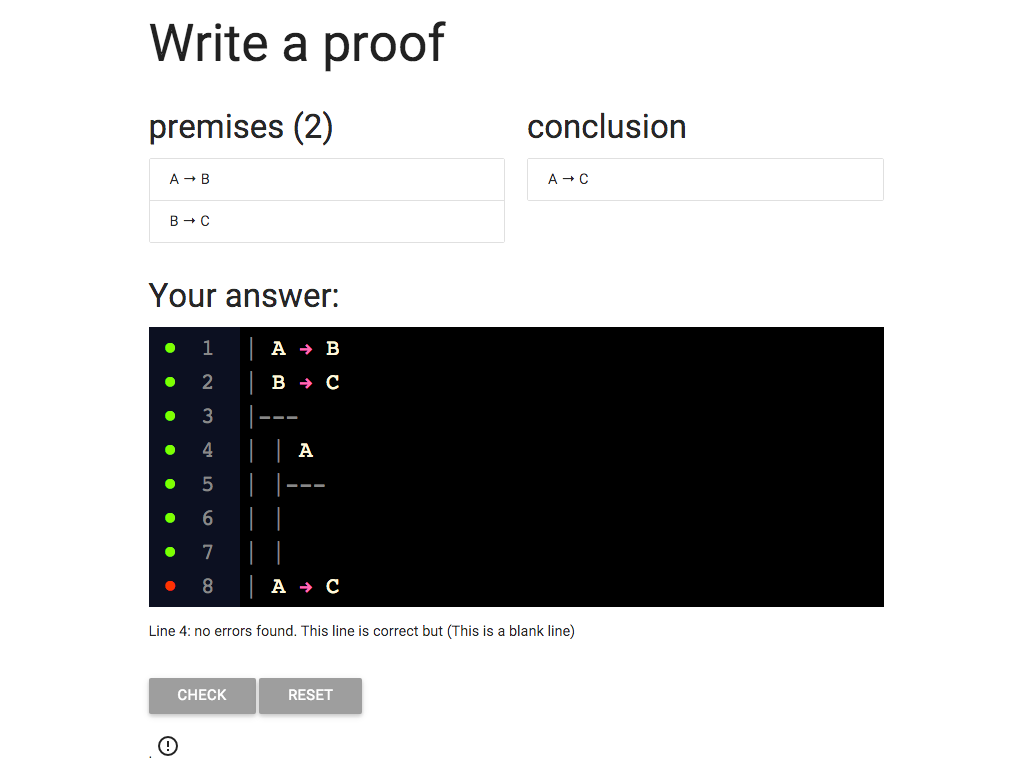
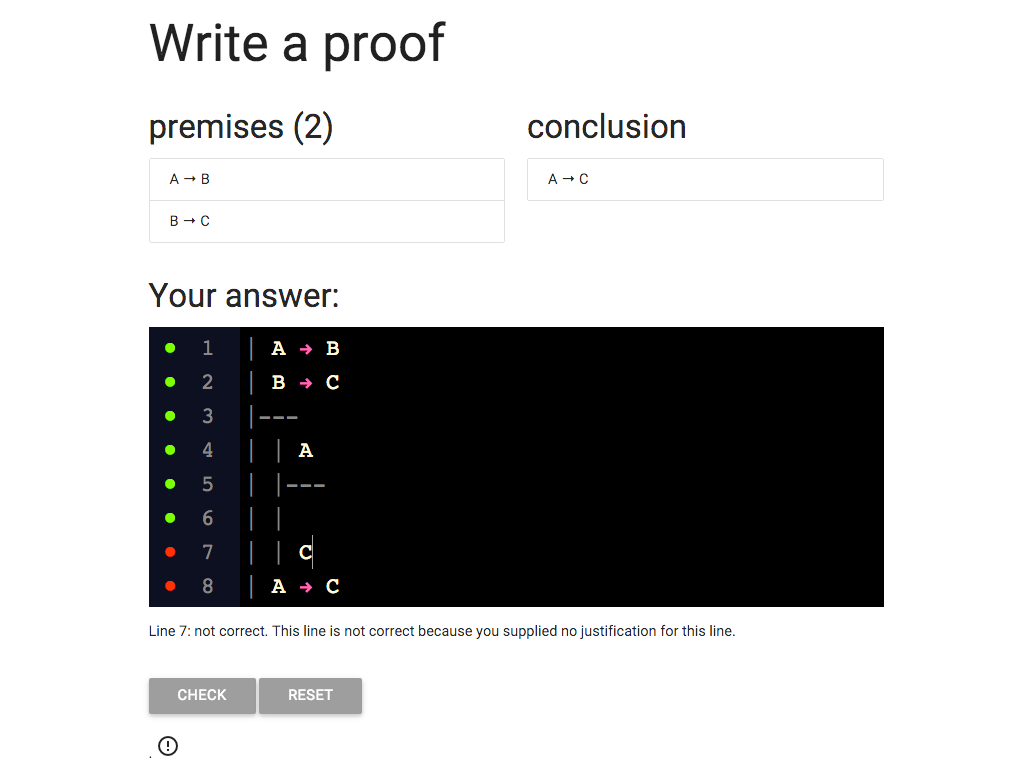
Now for the conclusion of the subproof.
Here I’ve written C.
But why have I written C?
Because C is the thing on the right of the conditional
we are trying to introduce.
It is the *antecdent* of 'A → C '
And the rule for arrow intro tells us that we need a subproof
whose conclusion is the antecdent of the conditional we are
trying to introduce.
So there’s no choice about what to put for the premise and
conclusion of the subproof, we just have to do what the rule tells
us to do.
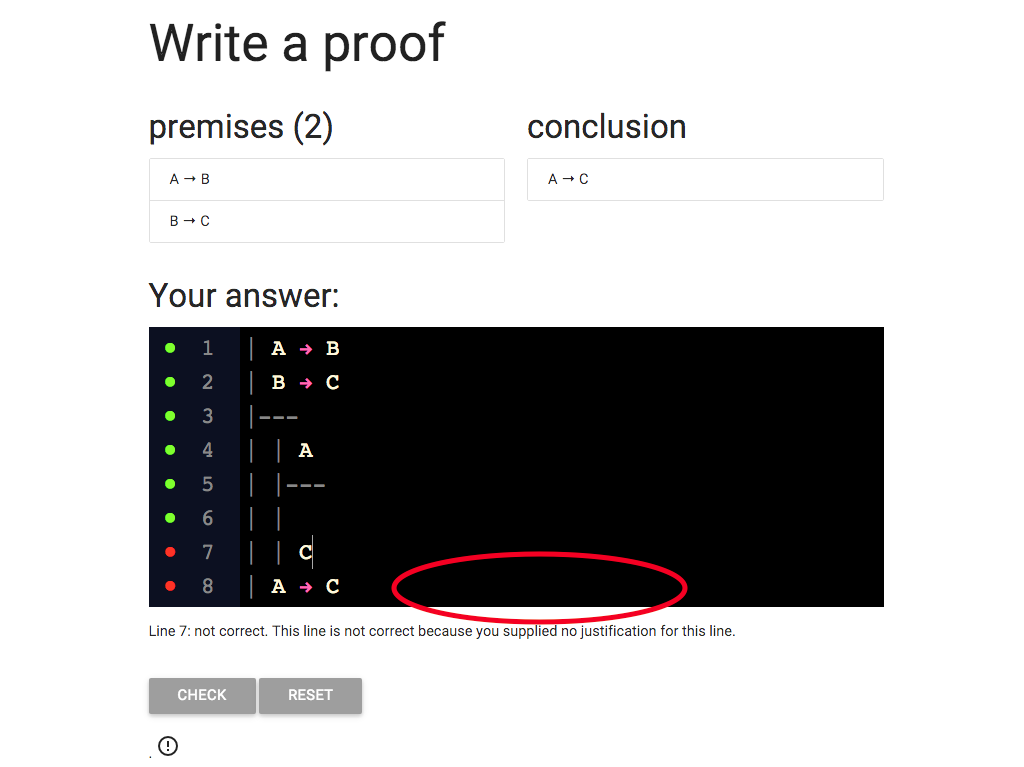
We’re not done with the rule arrow intro yet.
To use the rule it’s not enough to have a subproof: we also neeed
to provide the justification.
What goes here?
As always the rule tells us exactly what to write.
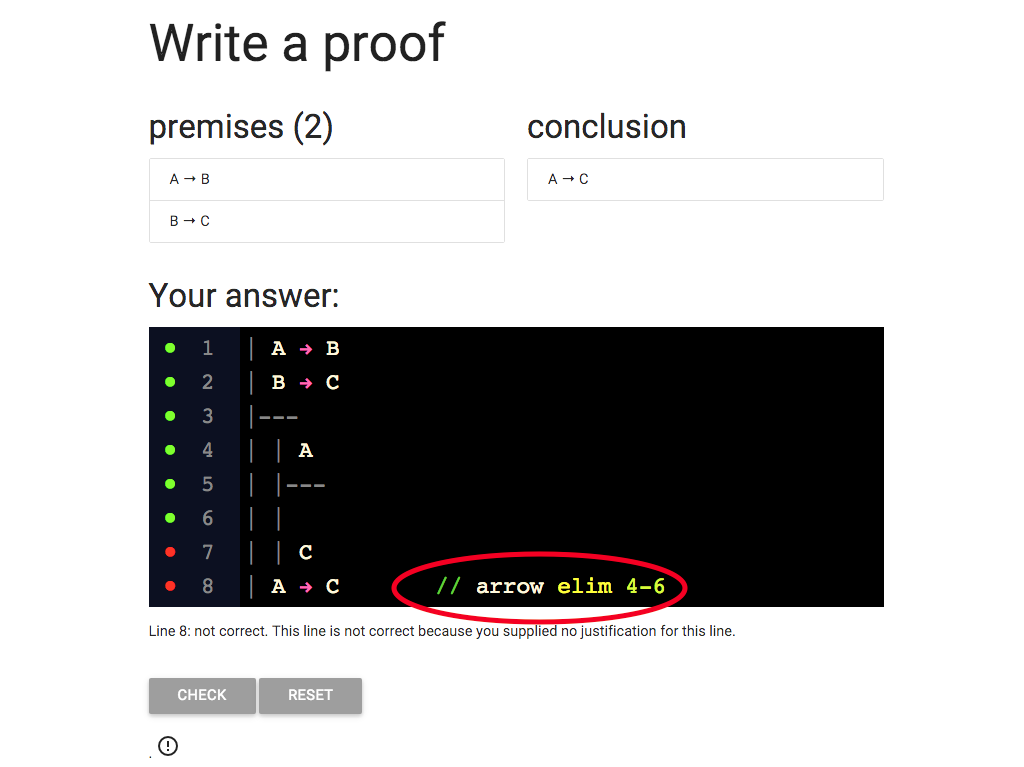
So I’ve filled in the justification.
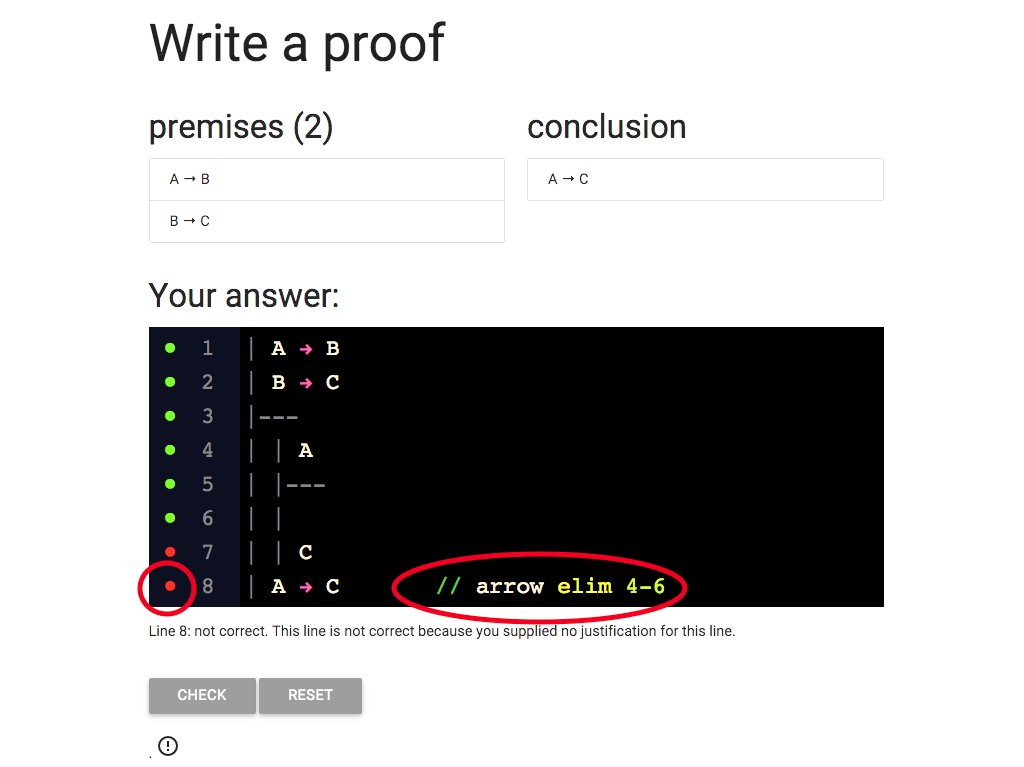
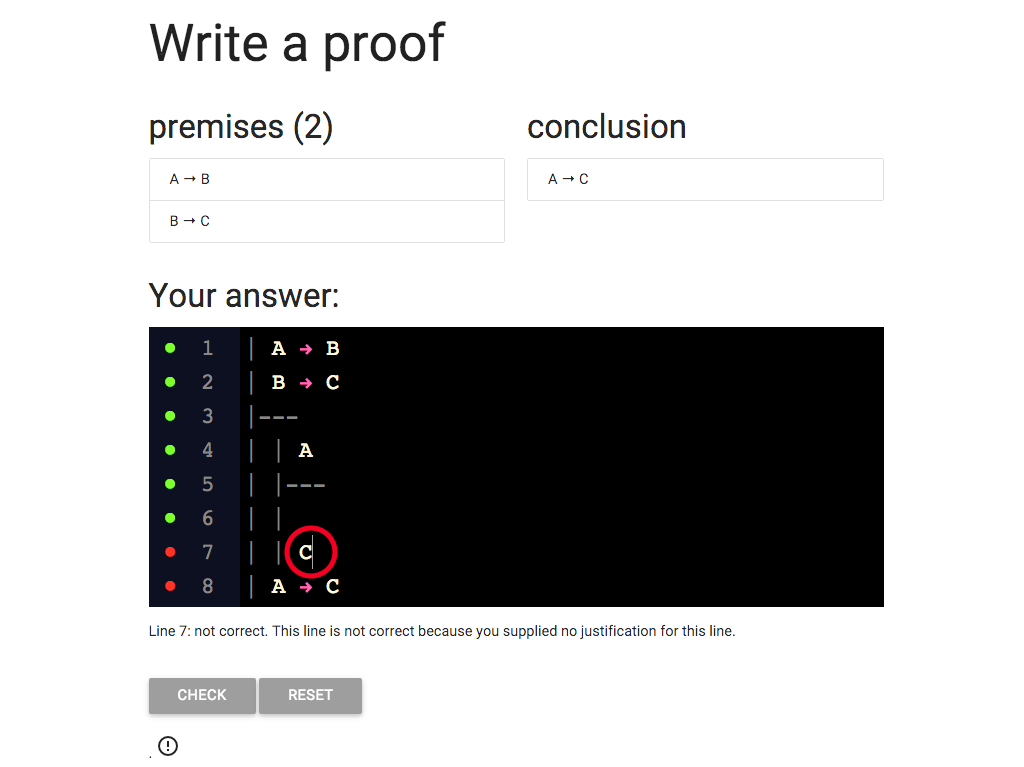
But wait a minute: the red dot means the line is not correct.
Why is it wrong?
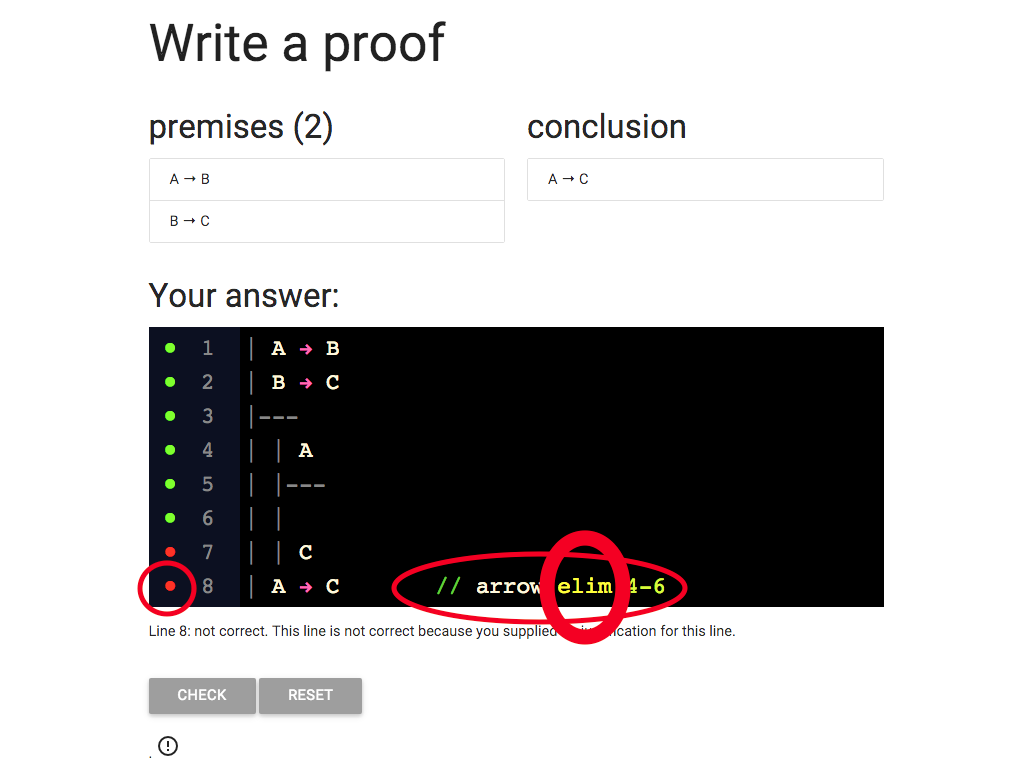
Oops, I wrote arrow elim when I should have written arrow intro.
You might think this doesn’t really matter; I got the ‘arrow’ part write,
I just confused intro and elim, which I do all the time (sorry).
But if you’re a machine, or a logican, it matters.
The software doesn’t do marks for effort, it just cares where what
you’ve written is a proof or not. And if you’ve got a red dot,
you havent’t written a proof.
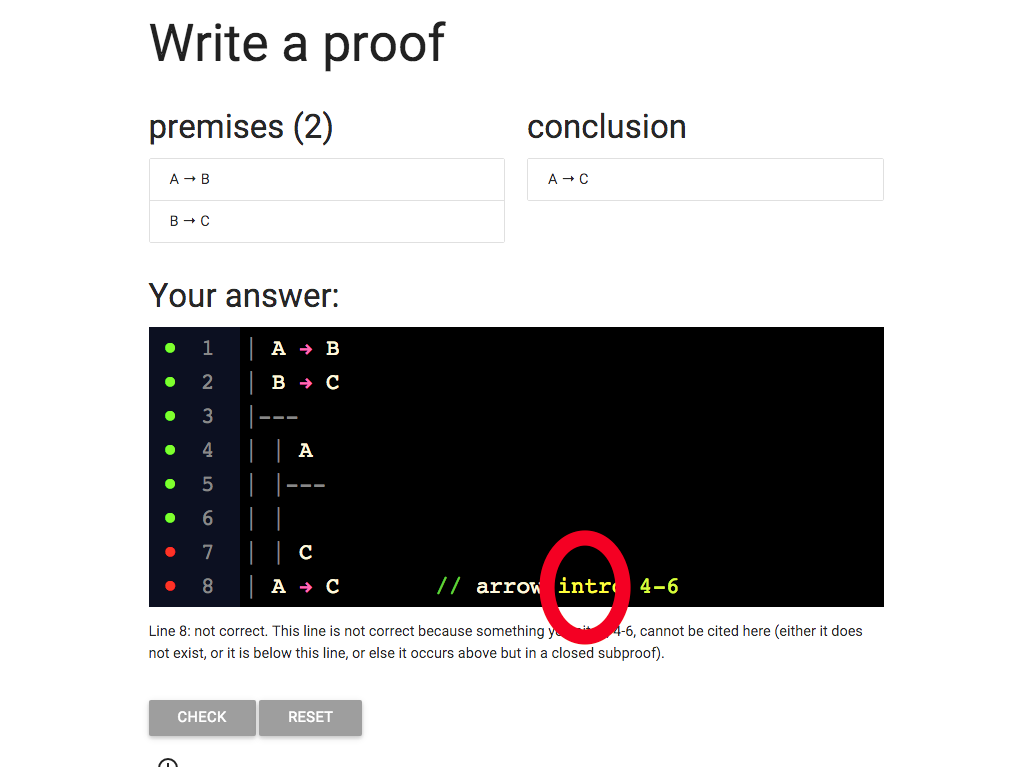
So I’ve changed elim to intro.
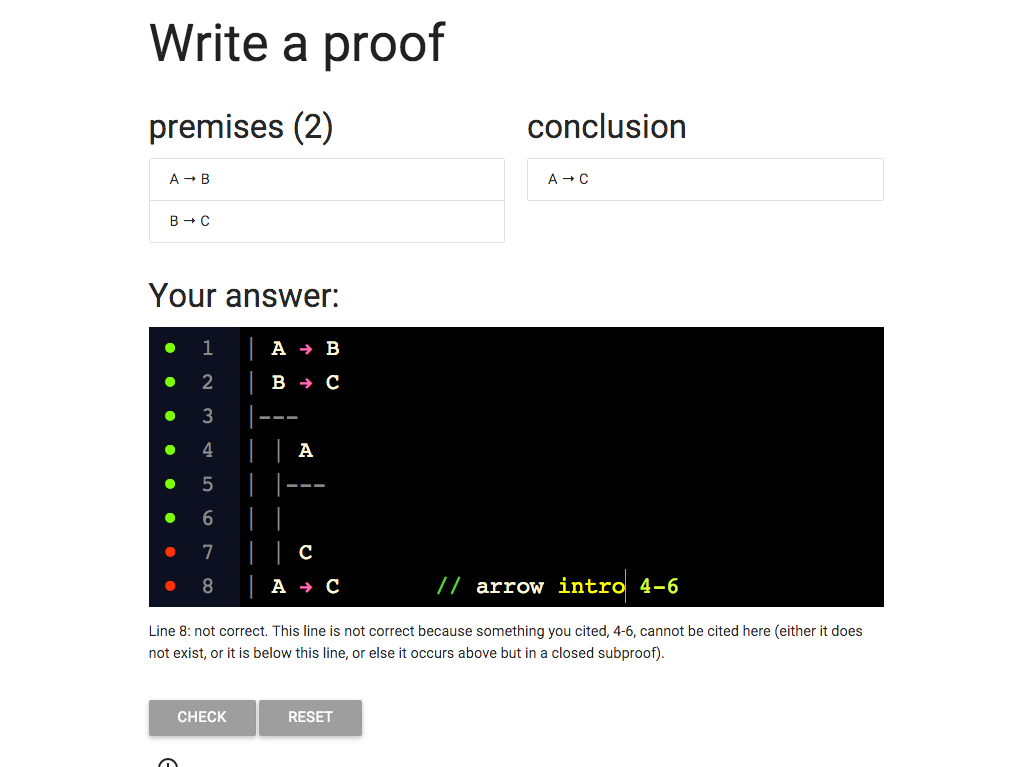
Now I’m citing the right rule ...
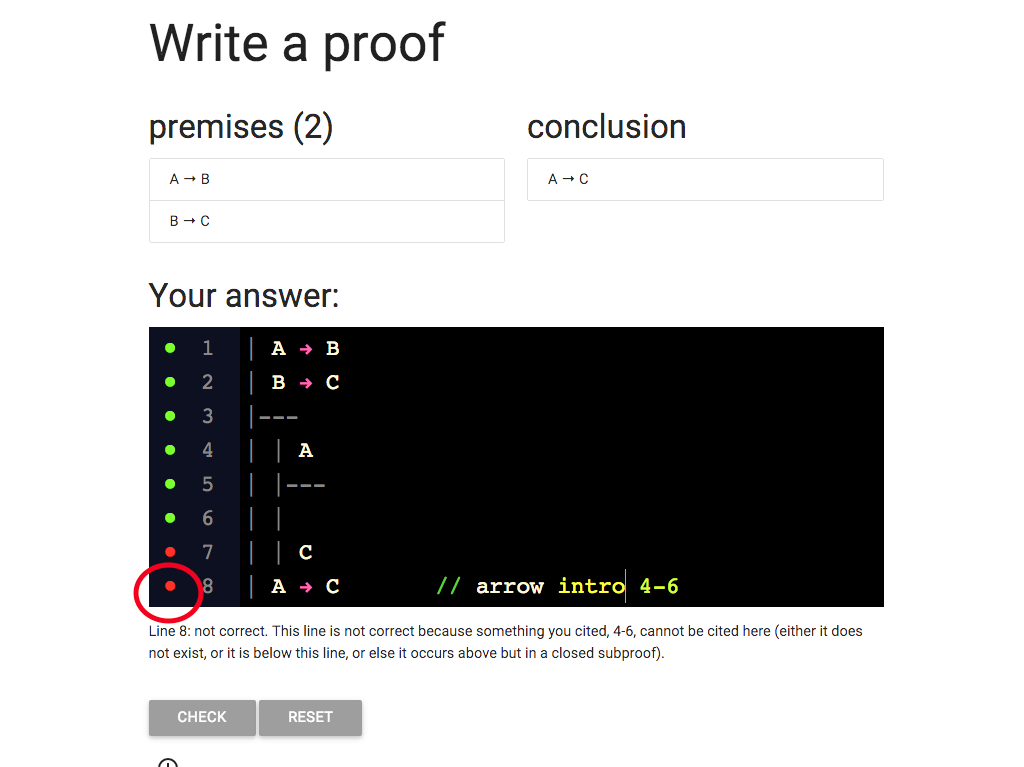
... but I still have that red dot.
What is wrong?
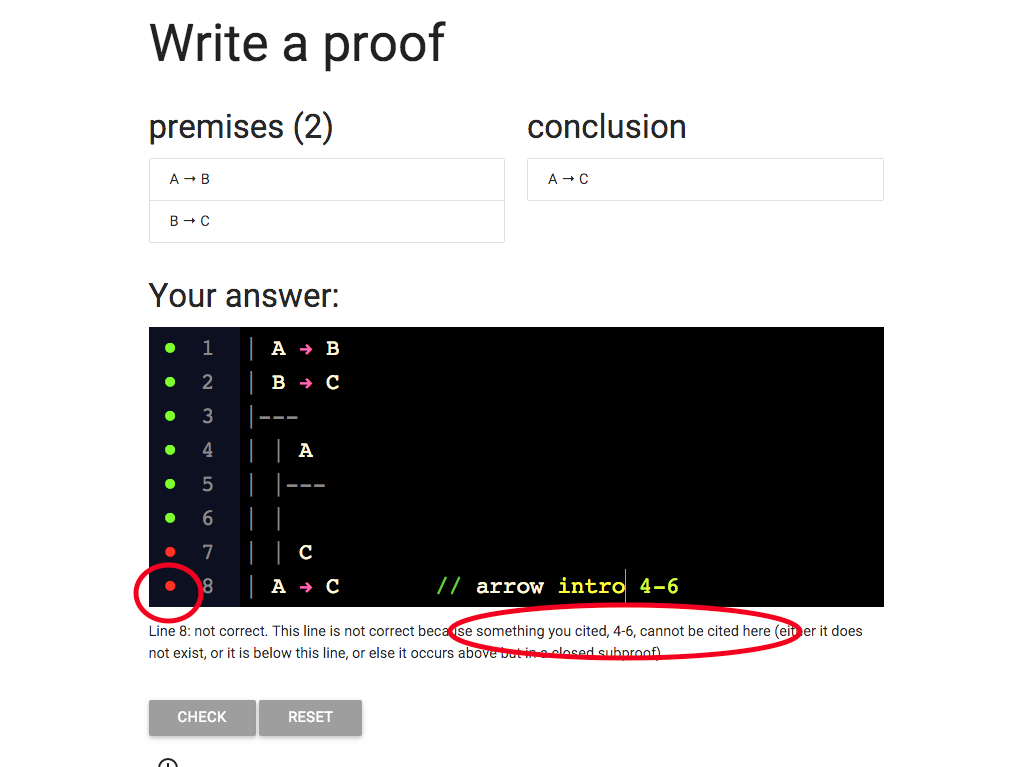
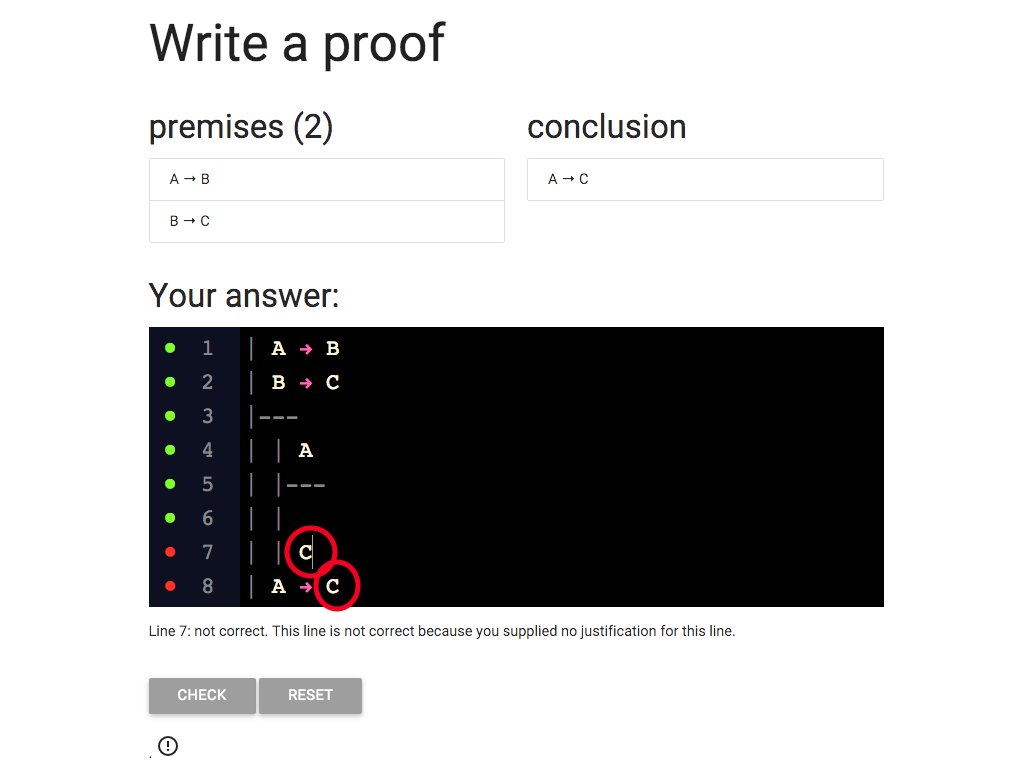
Take a look at the error message.
It tells me that lines 4-6 can’t be cited here.
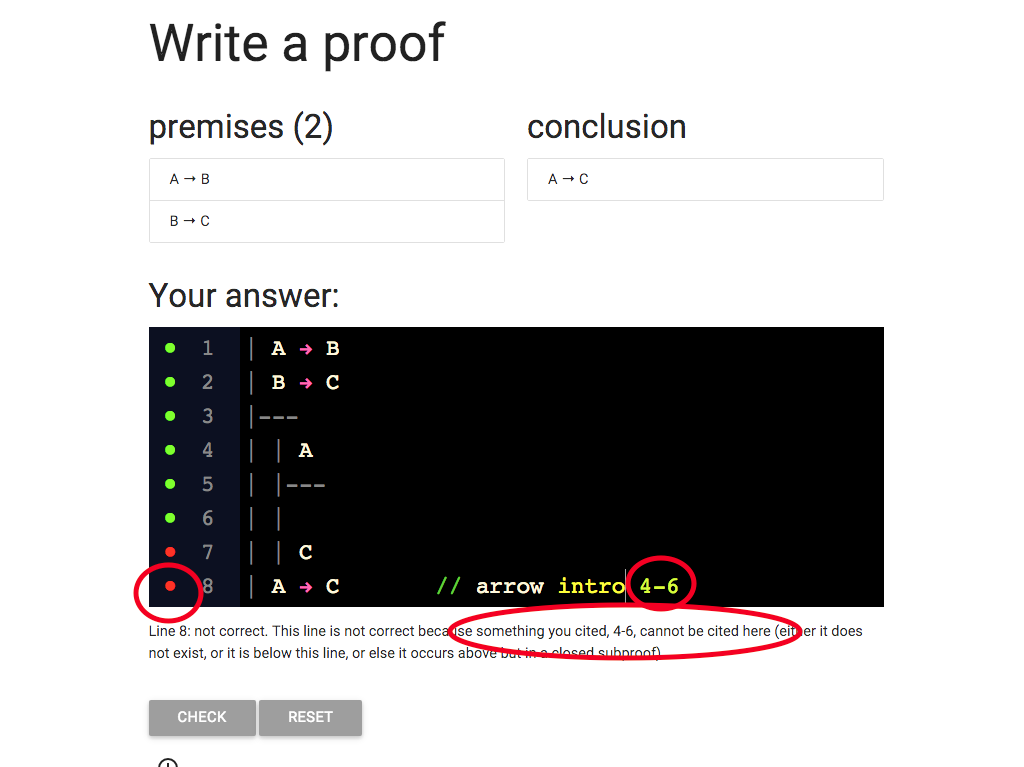
And I am citing lines 4-6, so the message is relevant.
But why can’t I cite them?
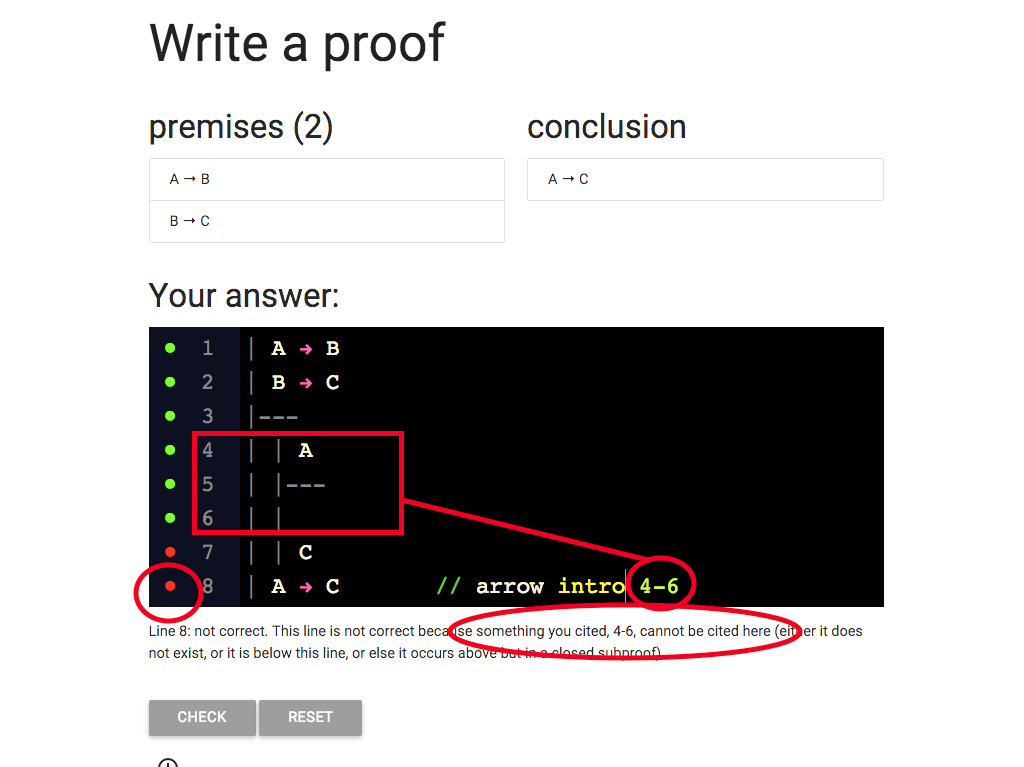
Wait a minute, lines 4-6 are only part of the subproof.
This is a mistake.
I wanted to cite the whole subproof.
And in fact the rules of proof only allow me to cite whole
subproofs.
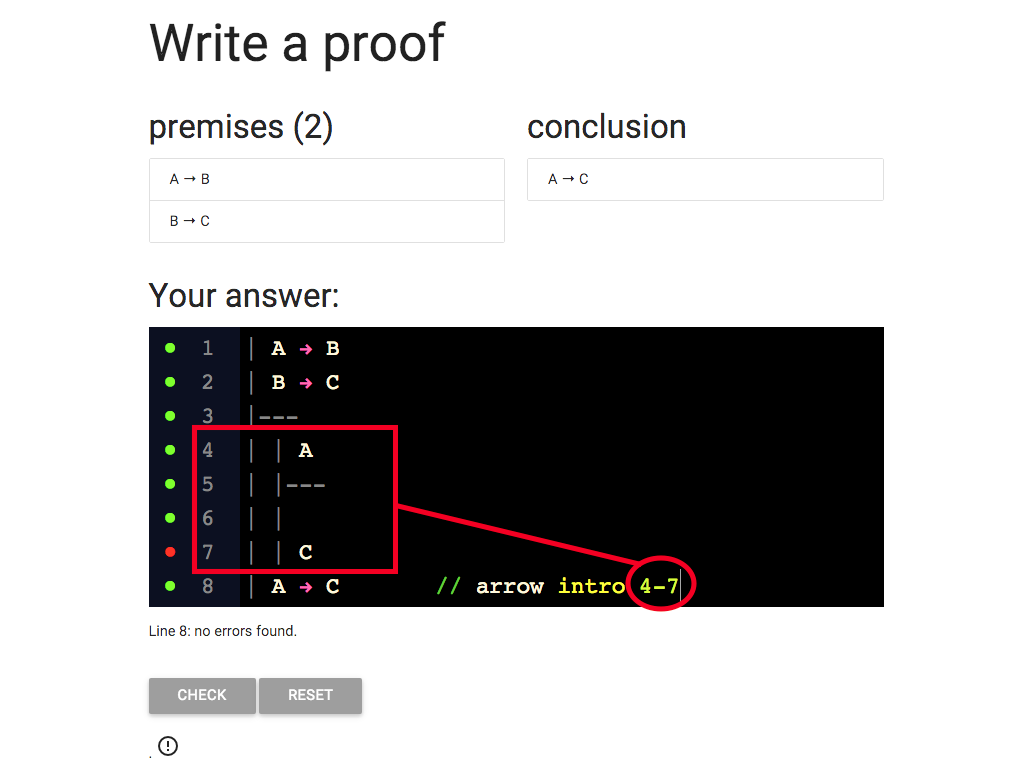
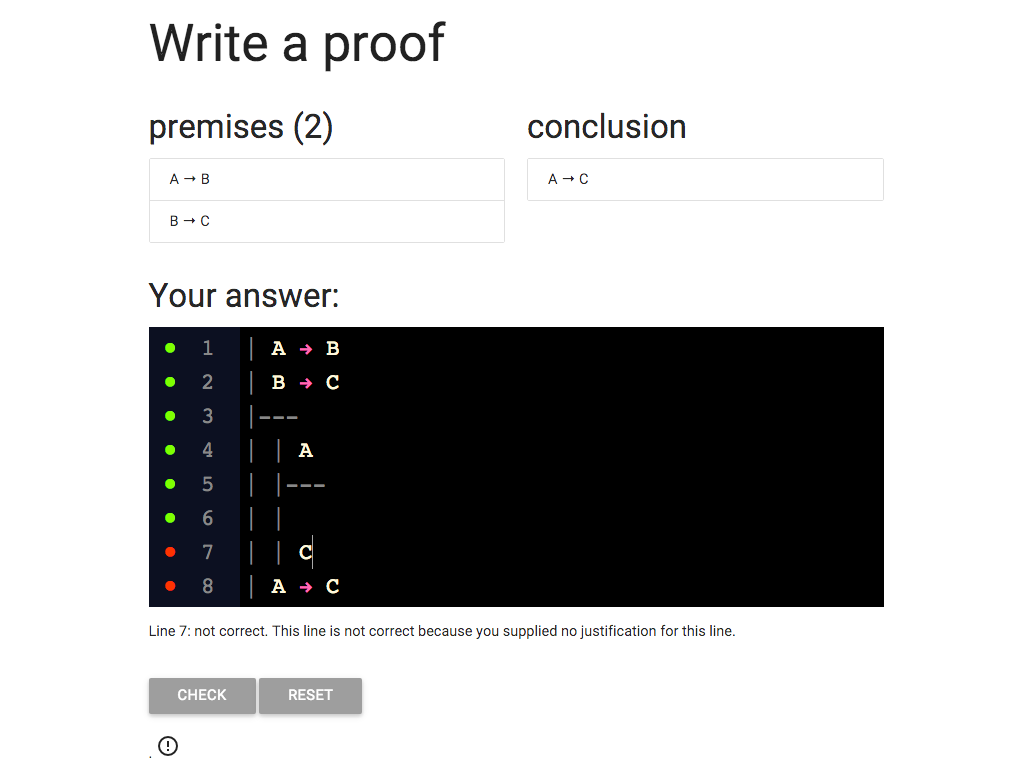
Let’s update so that the justification cites the whole subproof.
That is, it cites lines 4-7
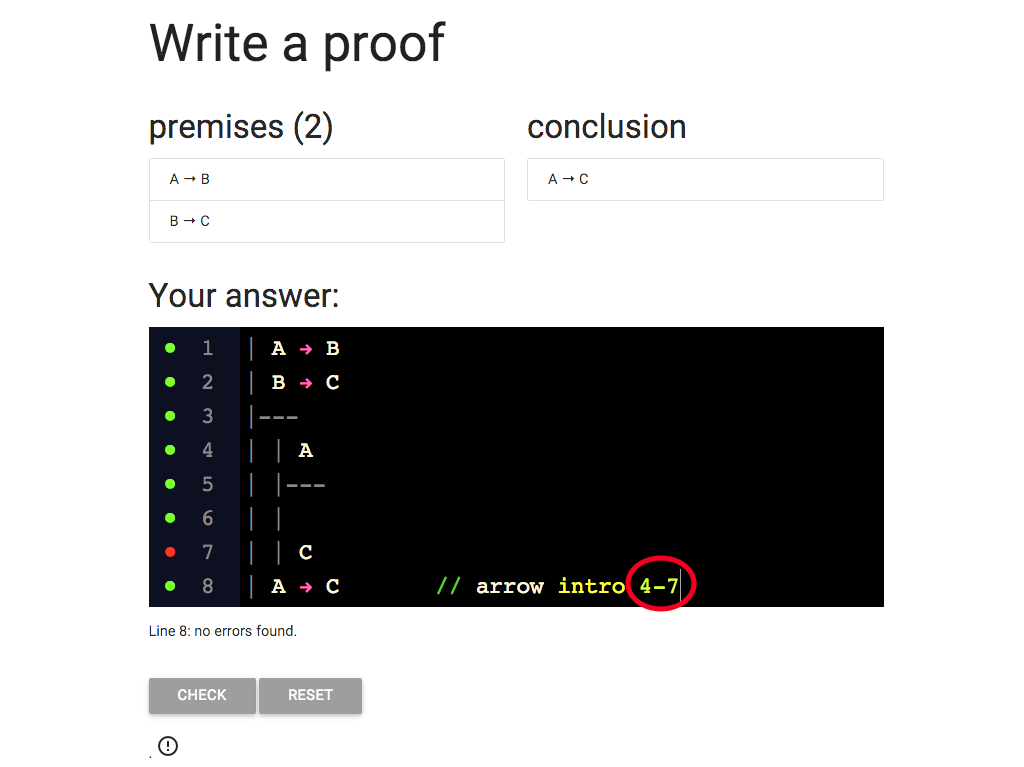
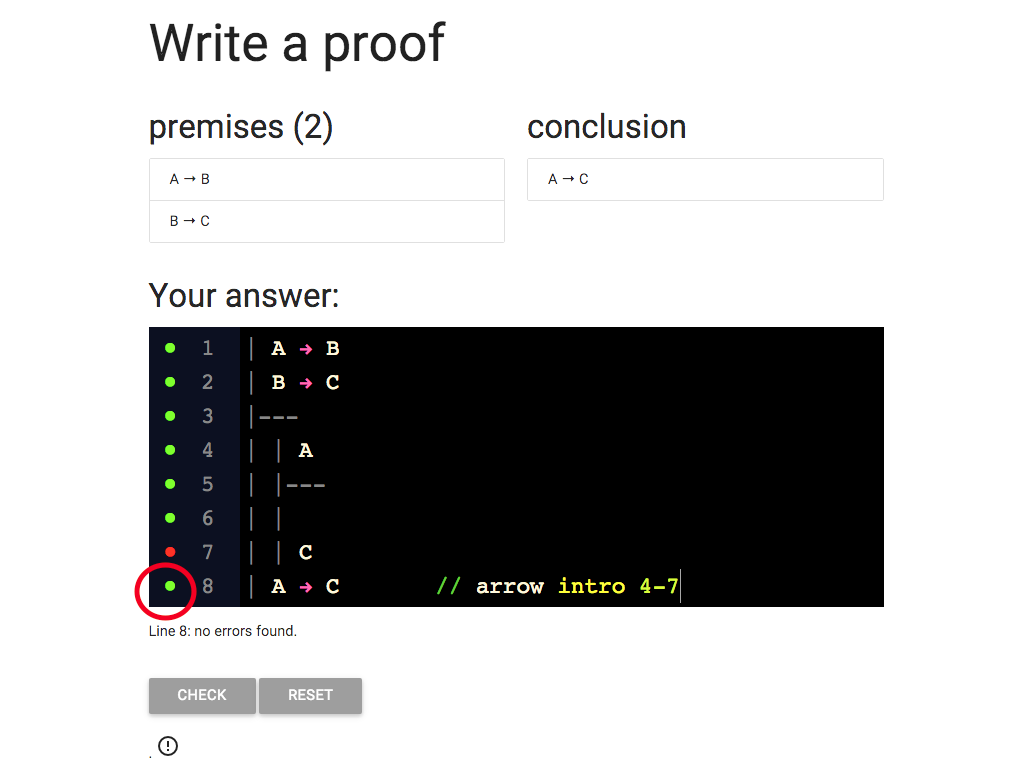
Now I’ve got the grren dot, at last.
Am I done?
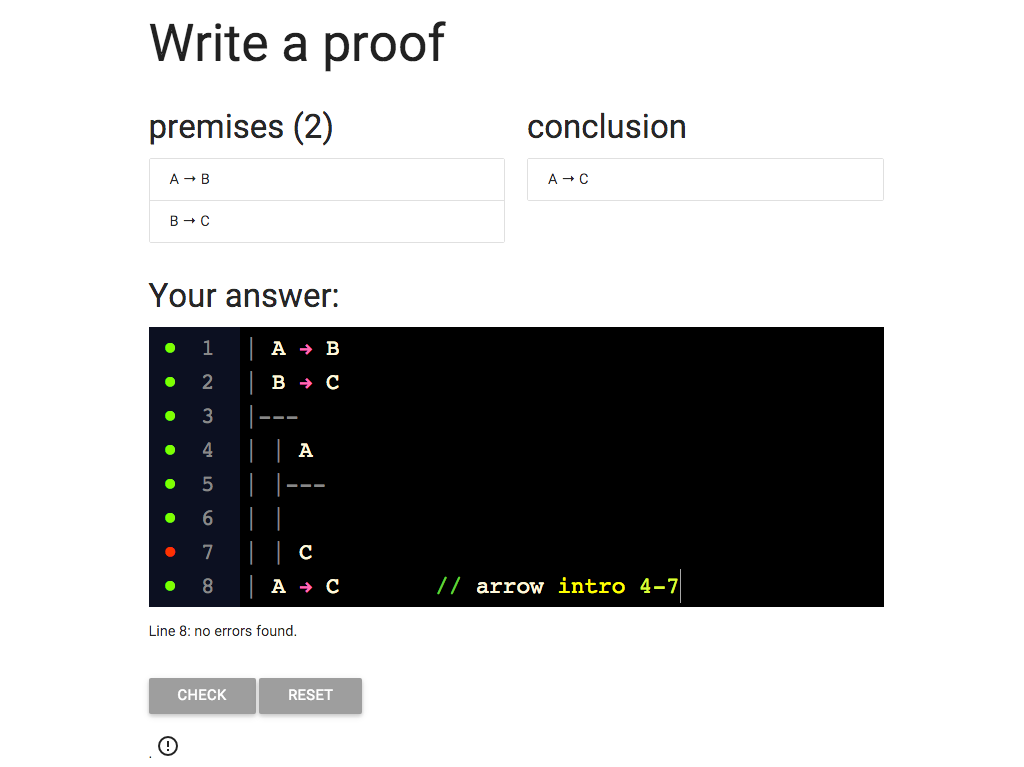
Not quite, I still need to complete the subproof.
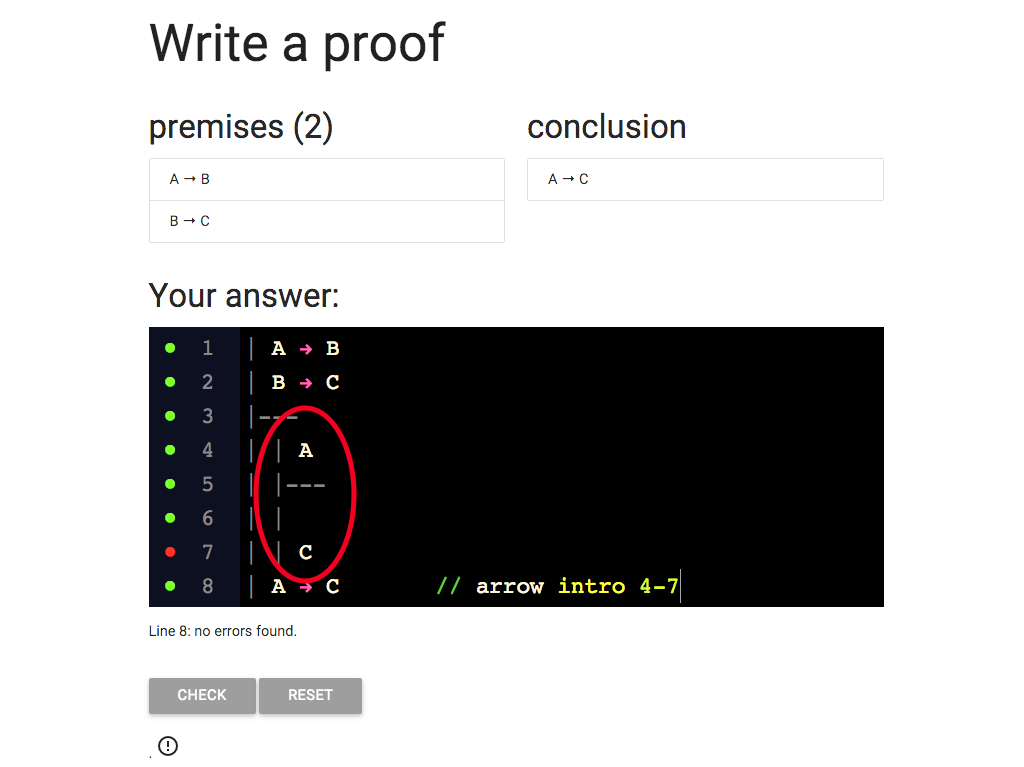
I know that I can get B from
A at line 4 and the conditional ‘A → B’ at line 1.
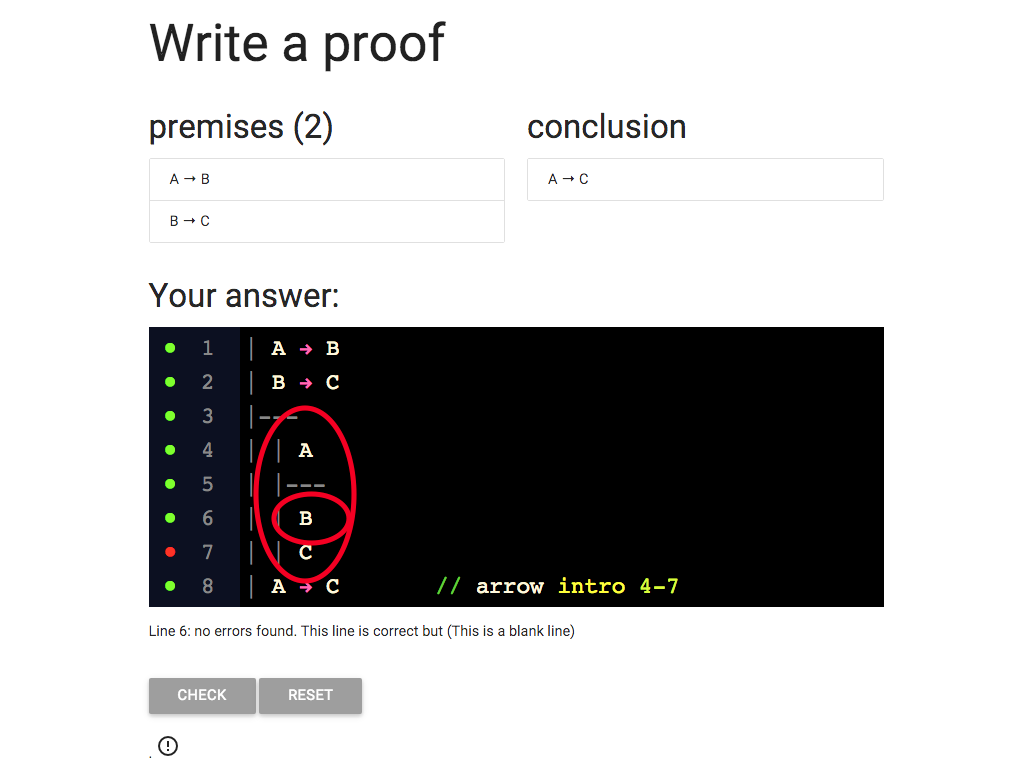
So I’ve added B at line 6.
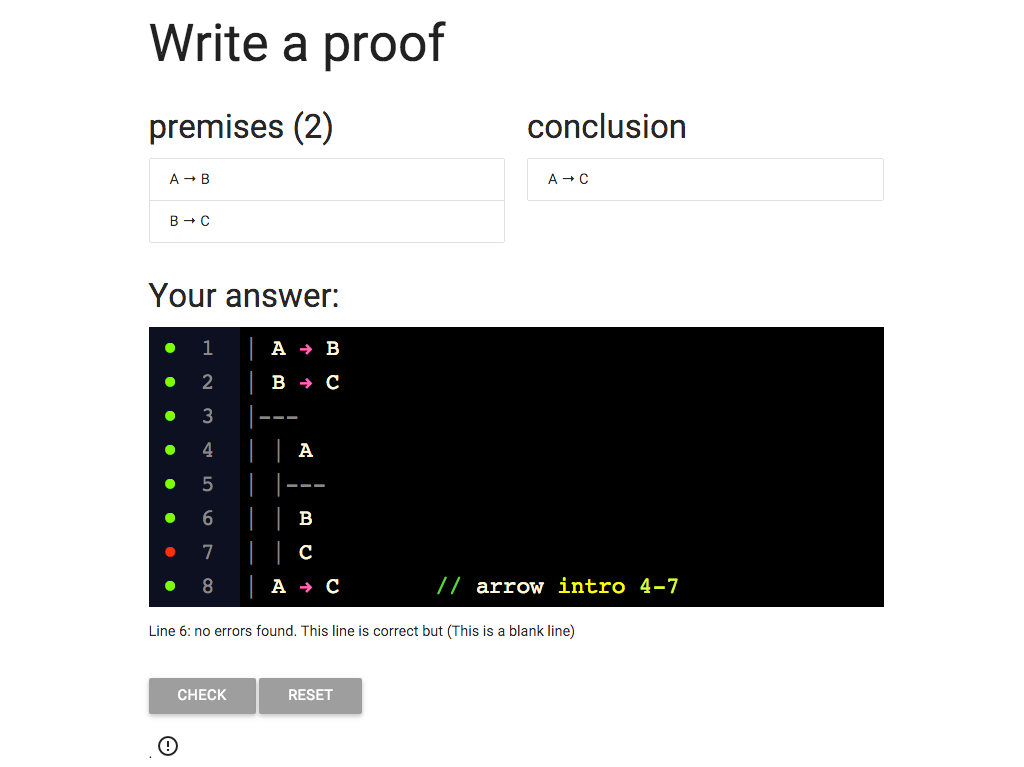
Now I need to give some justification for this line.
What will the justification be?
I’m eliminating the arrow from a conditional sentence, A → B, from line 1, and I have the
antecedent of the conditional at line 4.
So what should I write for the justification?
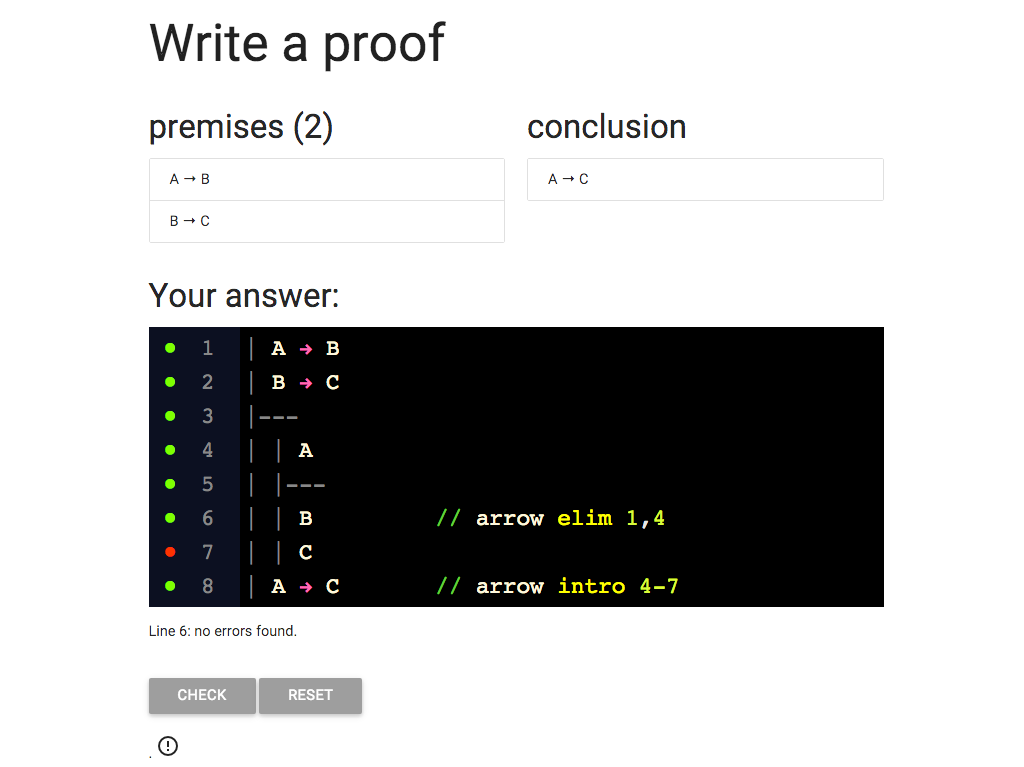
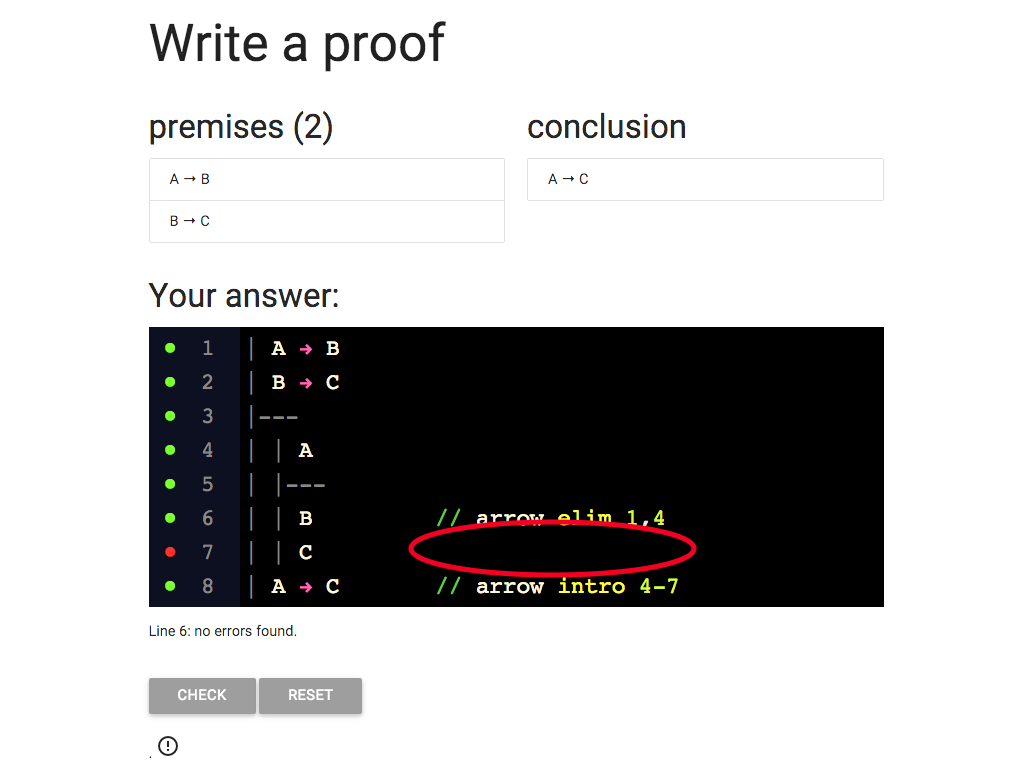
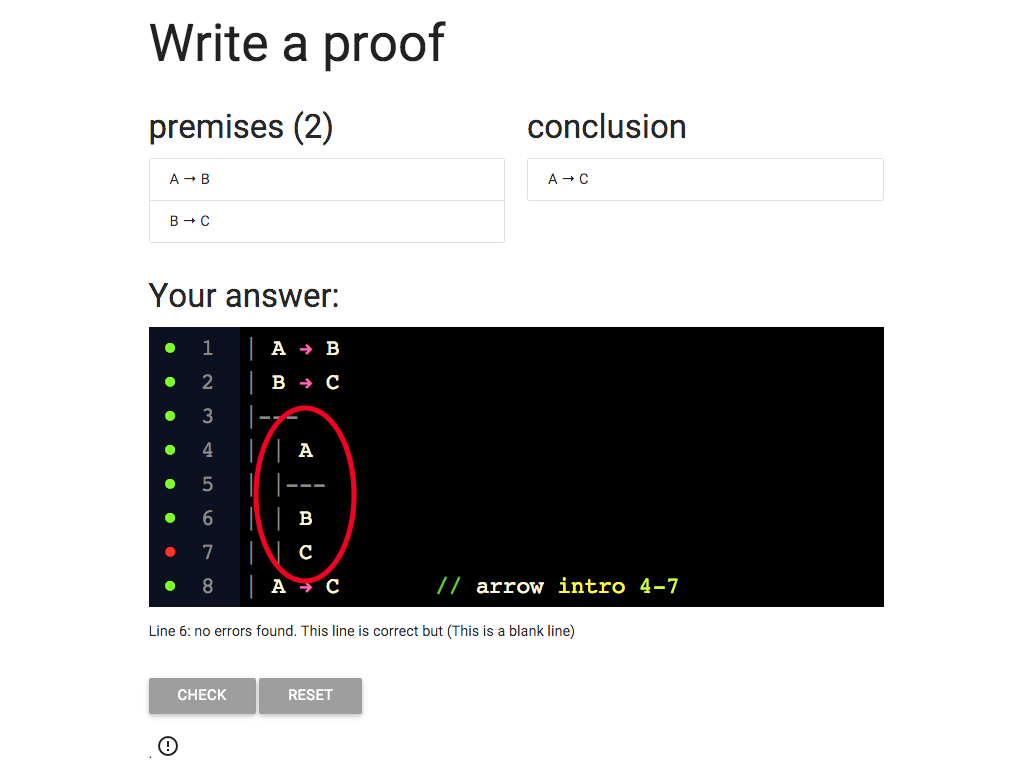
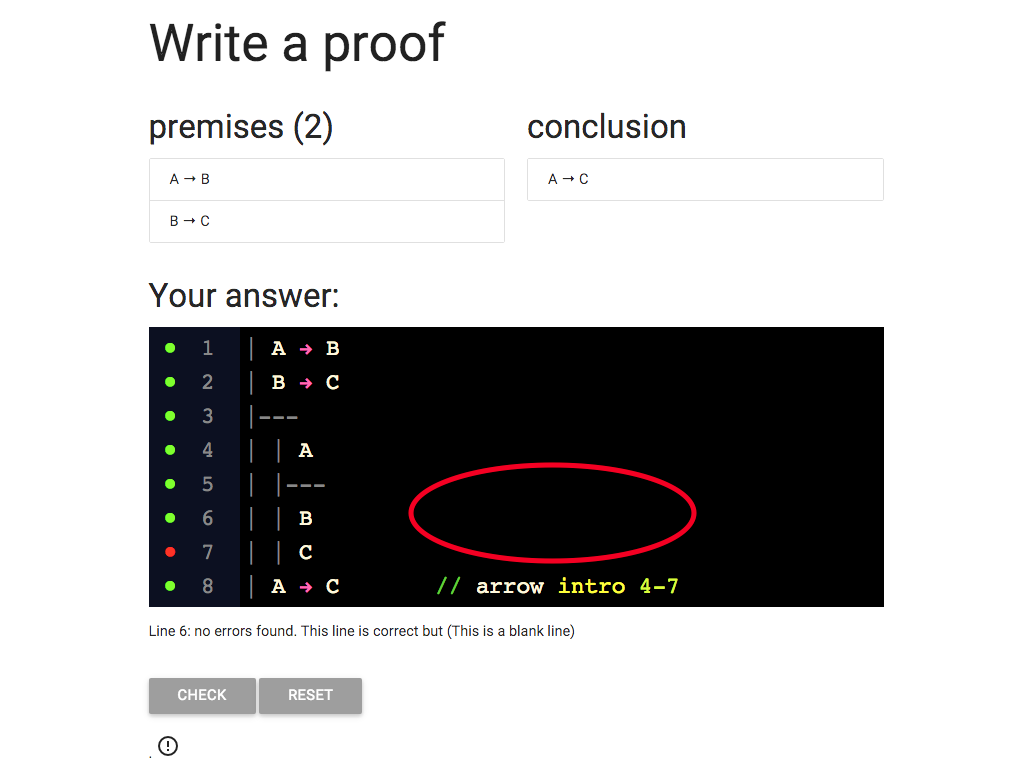
The last thing I need is the justification for the C at line 7.
Where does this come from?
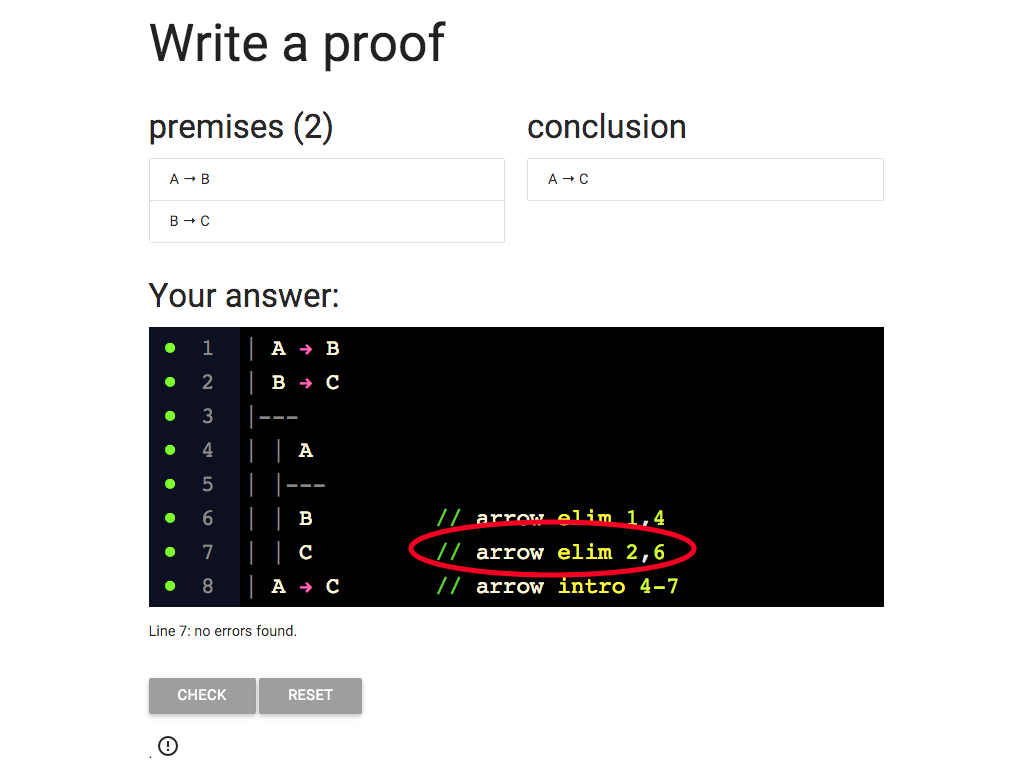
I’m eliminating the arrow from B → C (line 2) and I can do this because
I also have the antecedent, B, at line 6.
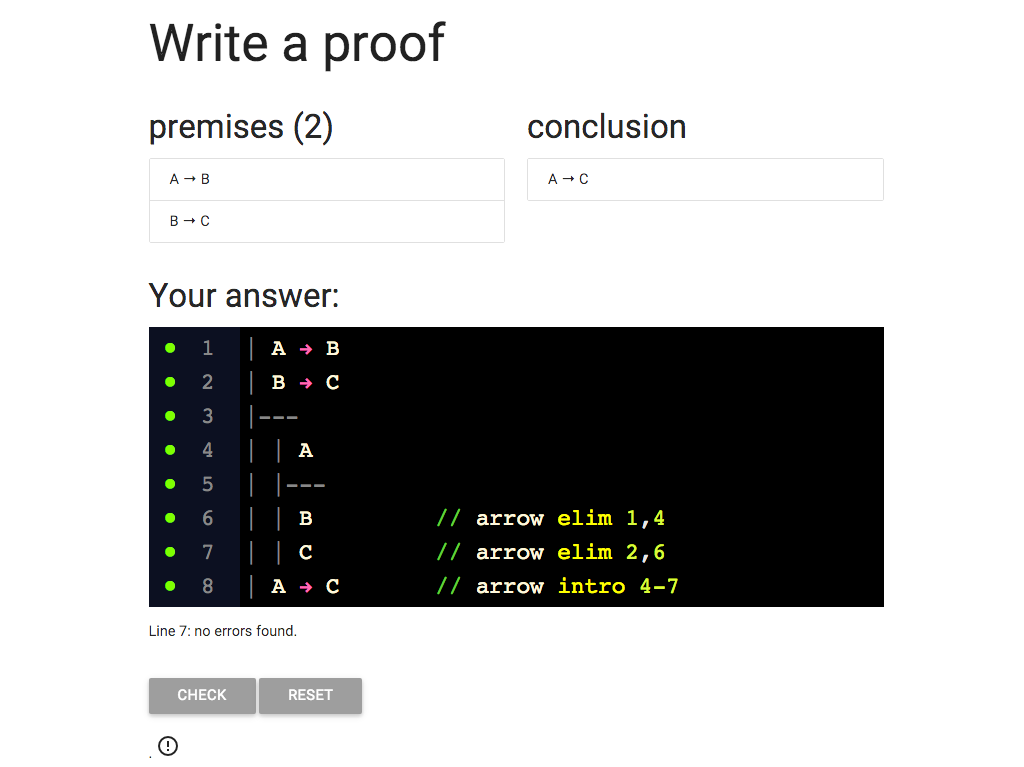
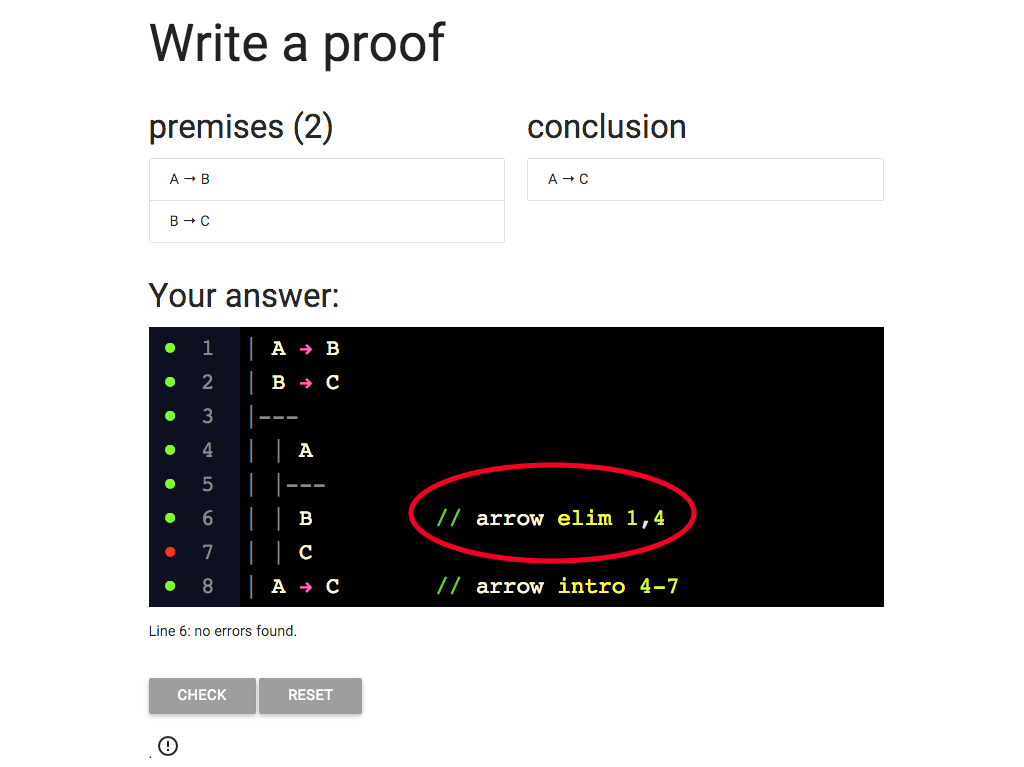
The proof looks ok, lots of green dots, but sometimes the dots don’t
get updated (they’re a bit lazy to avoid making your browser slow down).
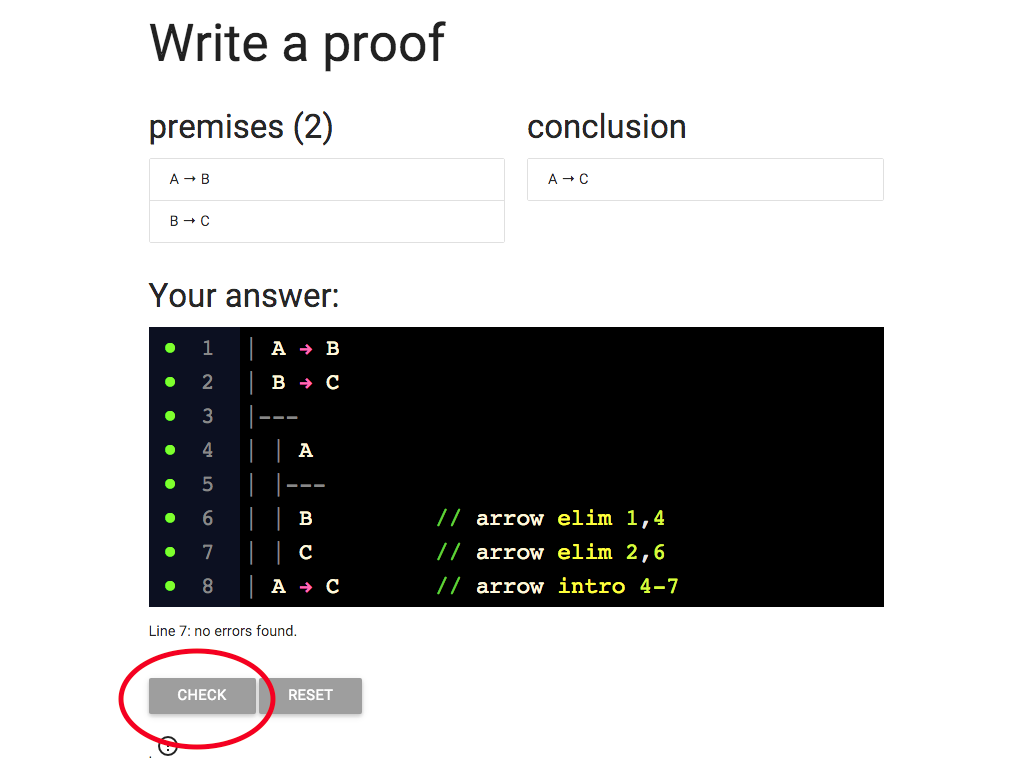
So to be sure I can hit the ‘CHECK’ button.
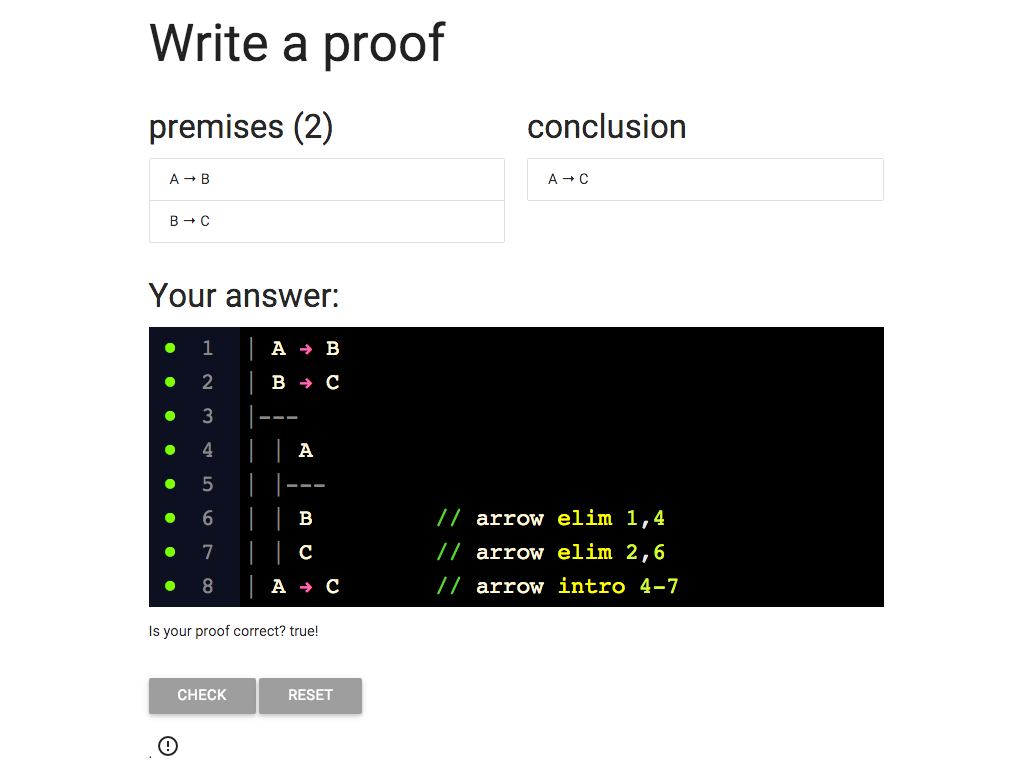
Great, we did it!

∨Elim: An Example
\section{∨Elim: An Example}
\emph{Reading:} §5.2, §6.2
\section{∨Elim: An Example}

To prove a conclusion from a disjunction, prove it from each disjunct.








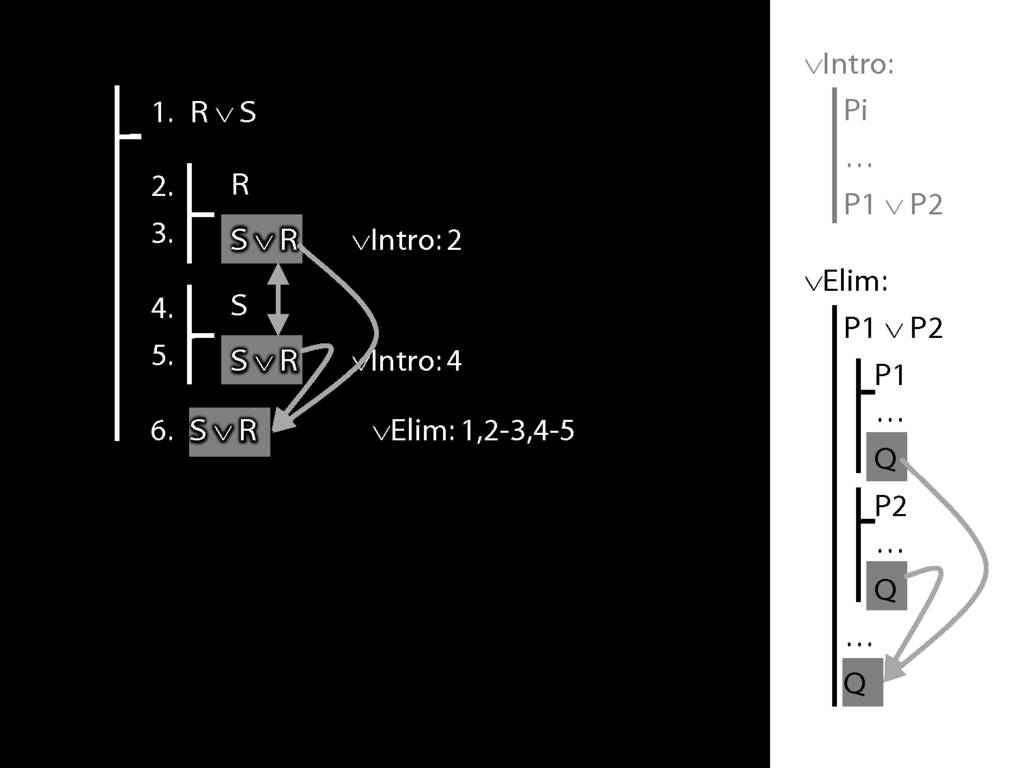



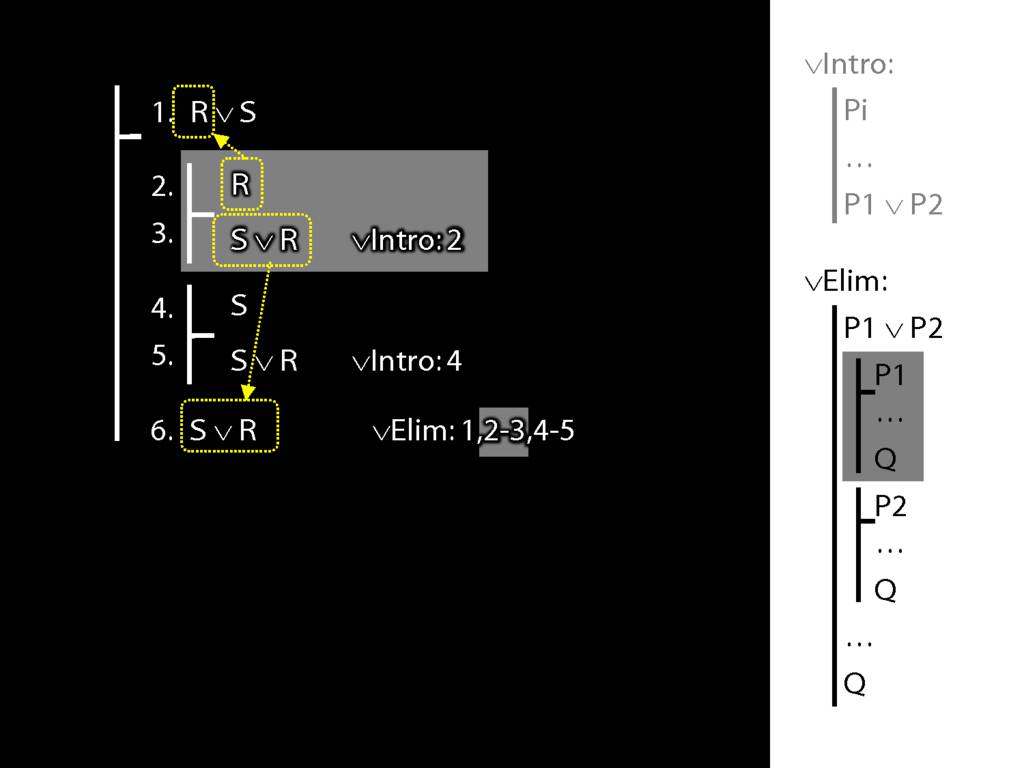

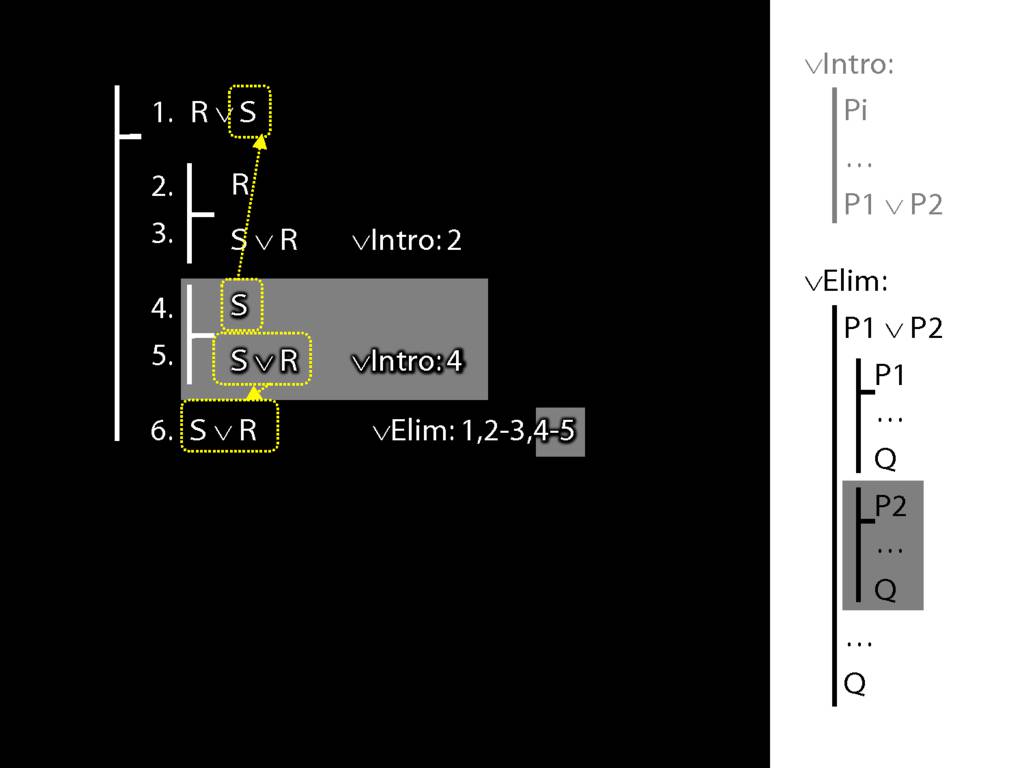

5.1--5.6
6.2--6.6
\section{∨Elim and Soundness}
\emph{Reading:} §5.2, §6.2
\section{∨Elim and Soundness}


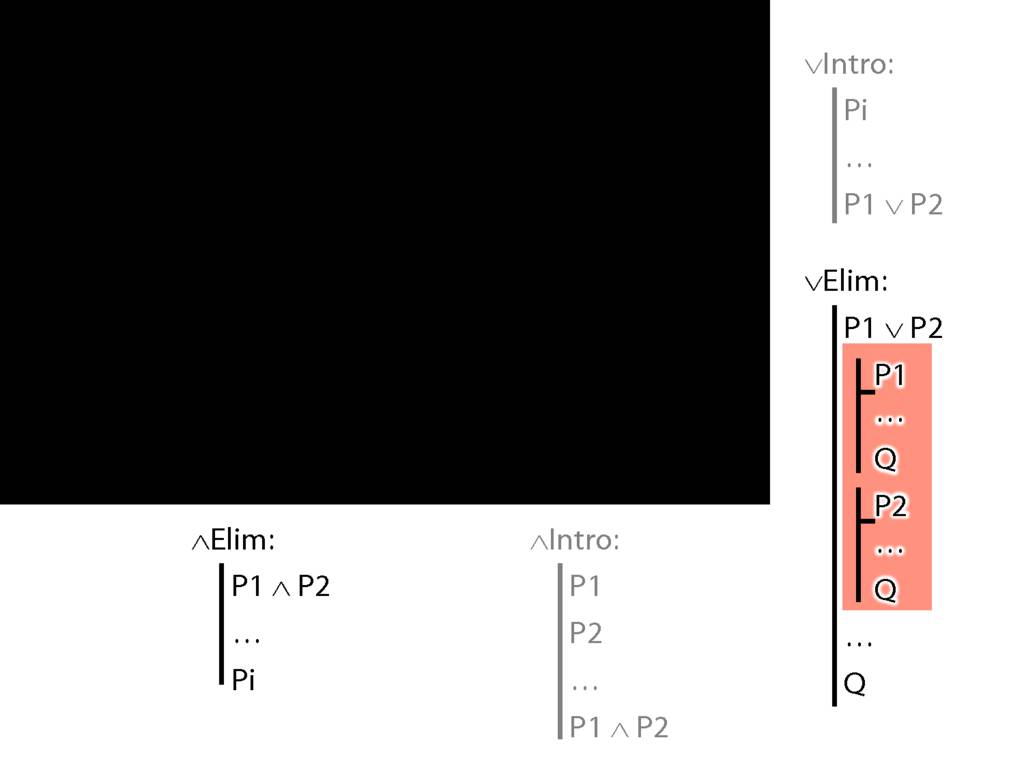





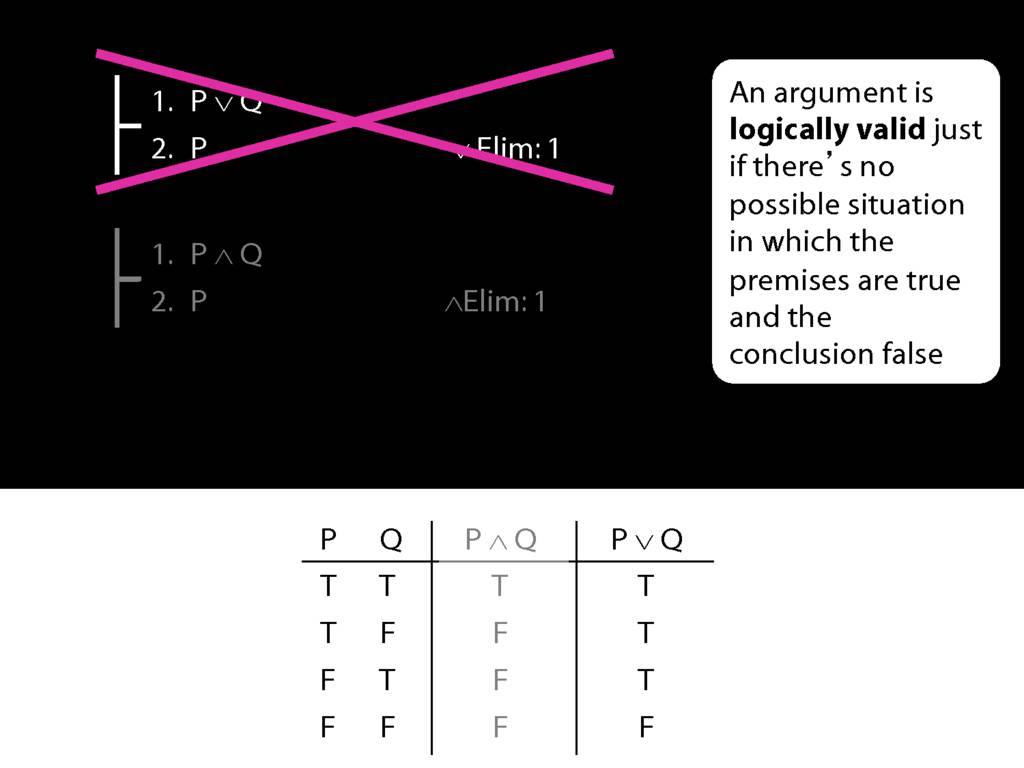

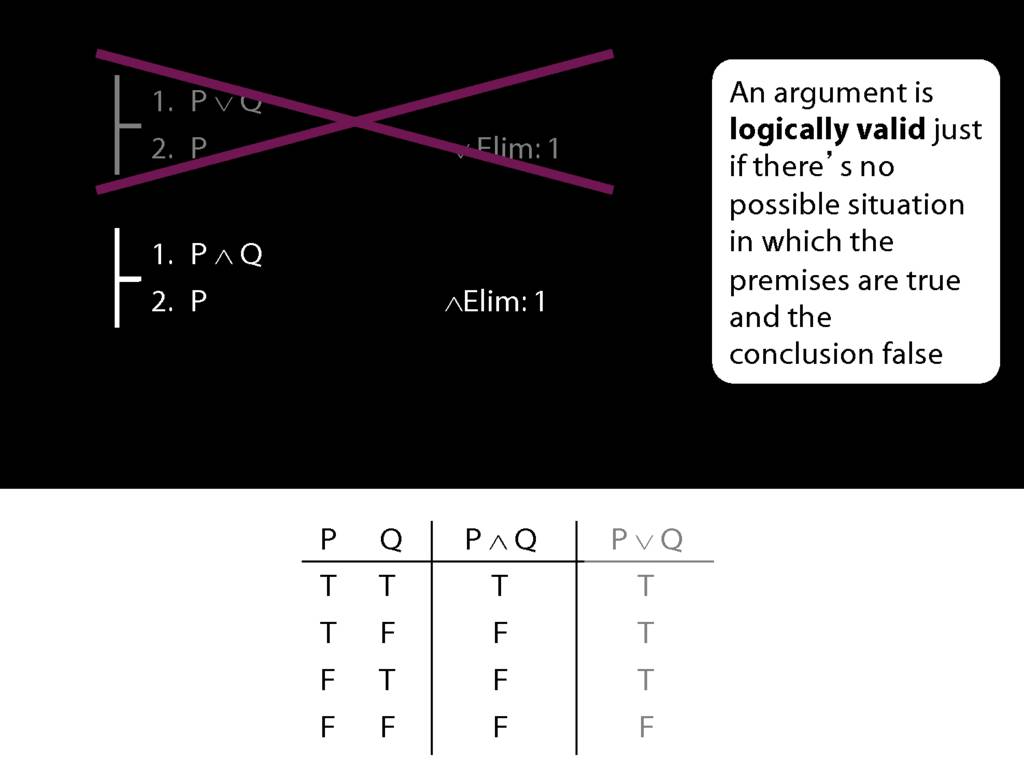
The rules of proof are formal stipulations.
-- but --
Some stipulations allow us to ensure we can only prove logically valid arguments.