Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Logic (PH133)}
 
\maketitle
 

Logic (PH133)

Lecture 6

\def \ititle {Logic (PH133)}
\def \isubtitle {Lecture 6}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
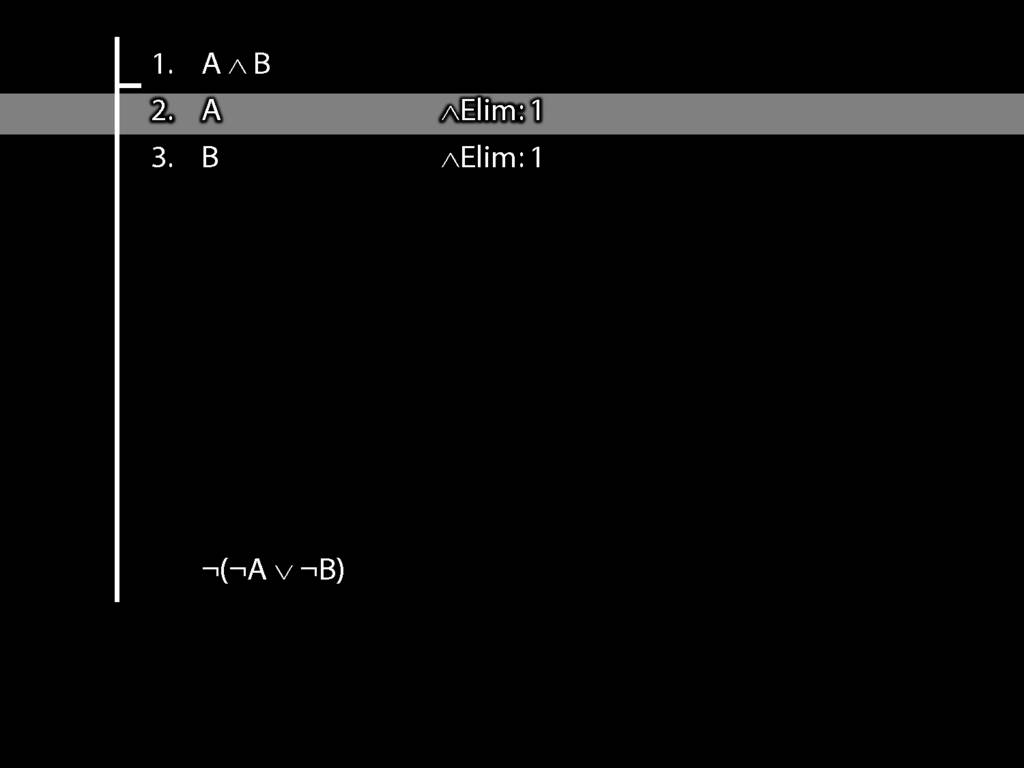
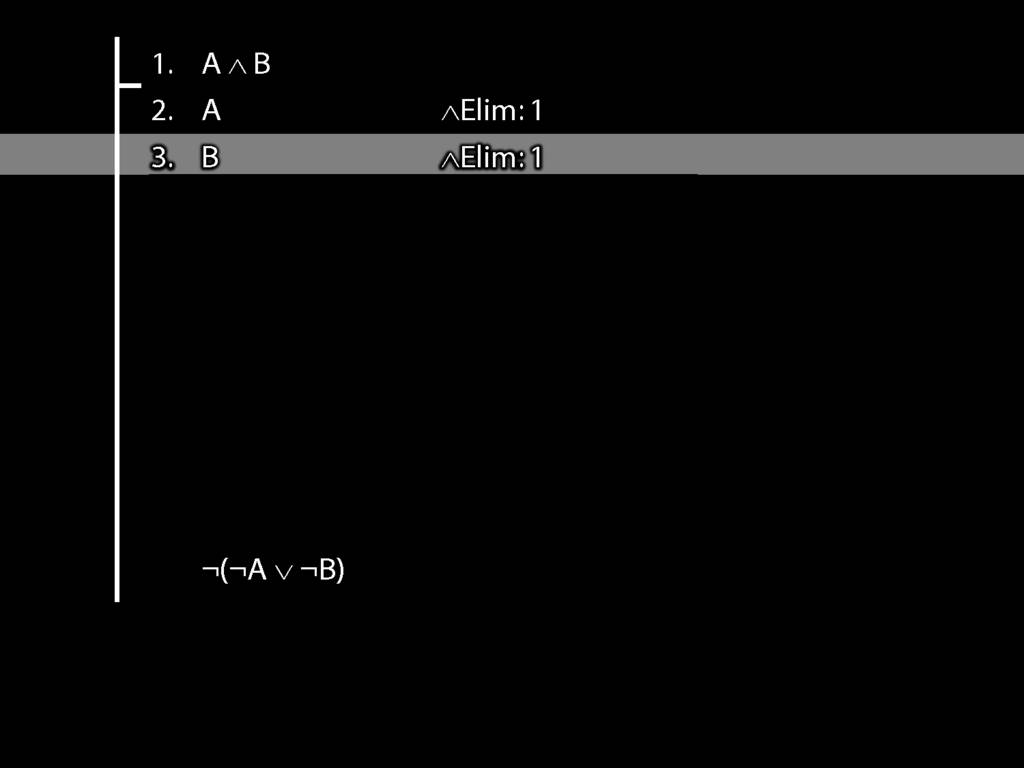
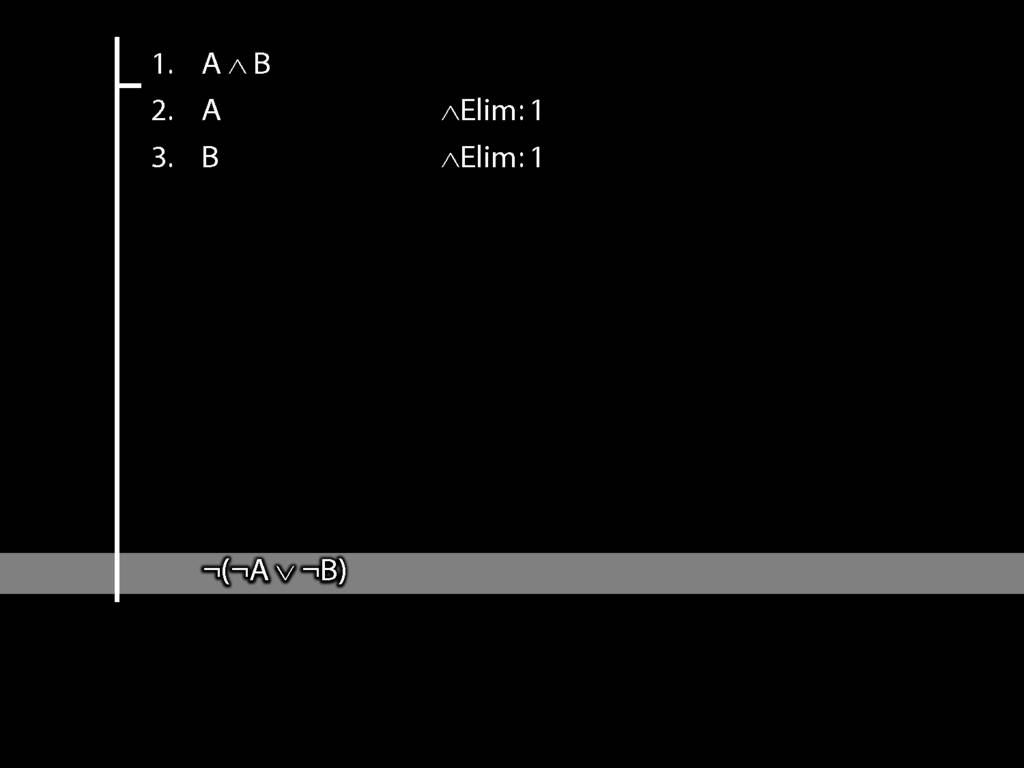
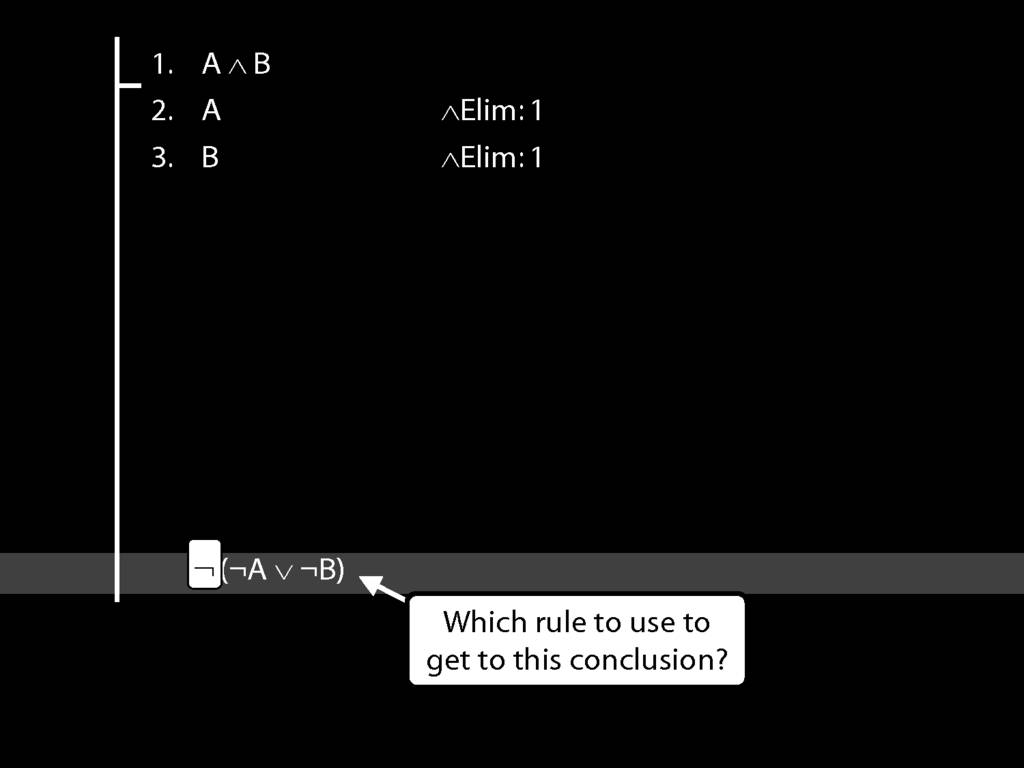
\section{DeMorgan: ¬(A ∧ B) ⫤⊨ ¬A ∨ ¬B}
\emph{Reading:} §3.6, §4.2
 
\section{DeMorgan: ¬(A ∧ B) ⫤⊨ ¬A ∨ ¬B}
`$\leftmodels\models$' means `is logically equivalent to', so for now `has the same truth table as'.
A $\leftmodels\models$ ¬¬A
¬(A ∧ B) $\leftmodels\models$ (¬A ∨ ¬B)
¬(A ∨ B) $\leftmodels\models$ (¬A ∧ ¬B)
A → B $\leftmodels\models$ ¬A ∨ B
¬(A → B) $\leftmodels\models$ ¬(¬A ∨ B) $\leftmodels\models$ A ∧ ¬B
Here's a useful equivalence: double negations cancel out (at least in logic).

A ⫤⊨ ¬¬A

is logically equivalent to

i.e. has the same truth table as

A¬A¬¬A
​TFT
​FTF
¬(A ∧ B)    ⫤⊨     (¬A ∨ ¬B)
¬(A ∨ B)⫤⊨(¬A ∧ ¬B)
A → B⫤⊨¬A ∨ B
¬(A → B)⫤⊨¬(¬A ∨ B)    ⫤⊨    A ∧ ¬B
ABA ∧ B¬(A ∧ B)¬A¬B¬A ∨ ¬B
​TTTFFFF
​TFFTFTT
​FTFTTFT
​FFFTTTT
AB¬(A ∨ B)¬A ∧ ¬B
​TTFF
​TFFF
​FTFF
​FFTT
ABA → B¬A ∨ B
​TTTT
​TFFF
​FTTT
​FFTT
ABA → B¬(A → B)¬(¬A ∨ B)A ∧ ¬B
​TTTFFF
​TFFTTT
​FTTFFF
​FFTFFF
3.19
4.15--18
7.1--7.2, *7.3--7.6
3.19
4.31
 

Negation and the arrow: A → ¬B ⊭ ¬(A → B)

 
\section{Negation and the arrow: A → ¬B ⊭ ¬(A → B)}
\emph{Reading:} §3.6
 
\section{Negation and the arrow: A → ¬B ⊭ ¬(A → B)}

A → ¬B ⊭ ¬(A → B)

is not a logical consequence of

i.e.
​

A → ¬B

​¬(A → B)
is not a logically valid argument
ABA → ¬BA → B¬(A → B)
​TTFTF
​TFTFT
​FTTTF
​FFTTF

A → ¬B ⊭ ¬(A → B)

#
 

↔ : truth tables and rules

 
\section{↔ : truth tables and rules}
 
\section{↔ : truth tables and rules}
ABA → BB → A(A → B) ∧ (B → A)A ↔ B
​TTTTTT
​TFFTFF
​FTTFFF
​FFTTTT

​1.

A ↔ B

​2.

A

​3.B↔Elim: 1,2
​1.

A ↔ B

​2.

B

​3.A↔Elim: 1,2

How do I intro ↔?

ABA ↔ B
​TTT
​TFF
​FTF
​FFT
ABA → B
​TTT
​TFF
​FTT
​FFT
​1.

A

​2....
​3.B
​4.

B

​5....
​6.A
​7.A ↔ B
​1.

A

​2....
​3.B
​4.A → B
#
 

All Cats Are Grey

 
\section{All Cats Are Grey}
 
\section{All Cats Are Grey}

Everything is broken

∀x Broken(x)

All squares are broken.

∀x ( Square(x) → Broken(x) )

Everything of mine is broken.

∀x ( ThingofMine(x) → Broken(x) )

Everybody loves chocolate or logic..

∀x ( Person(x) → LovesChocolateOrLogic(x) )

 

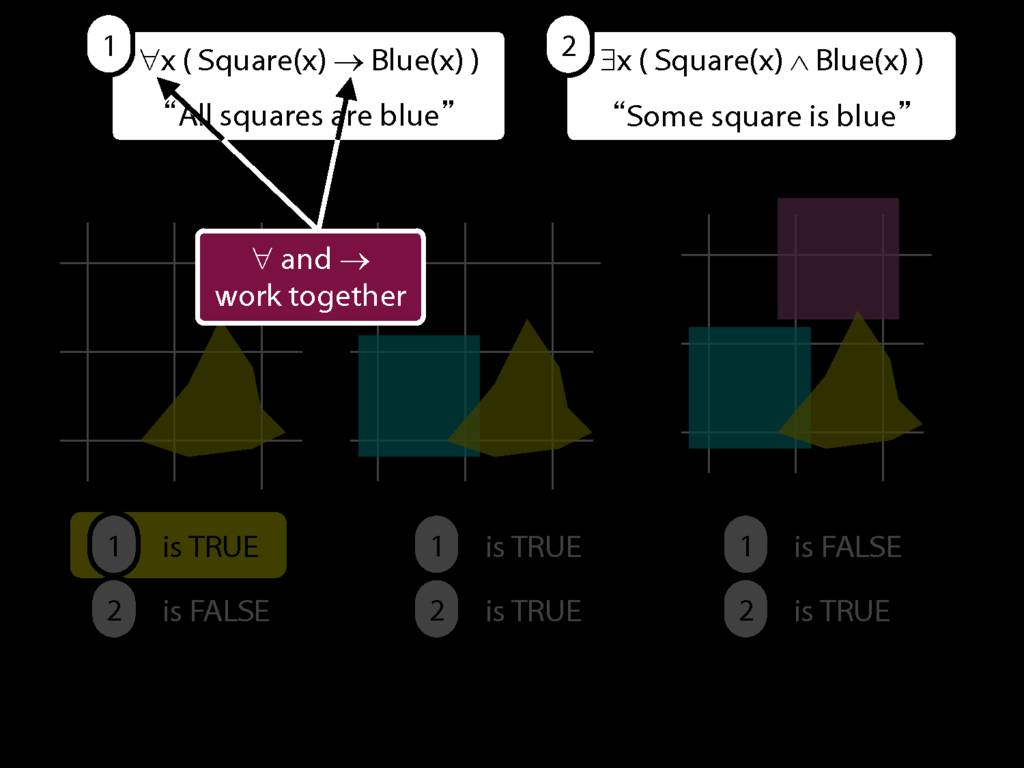
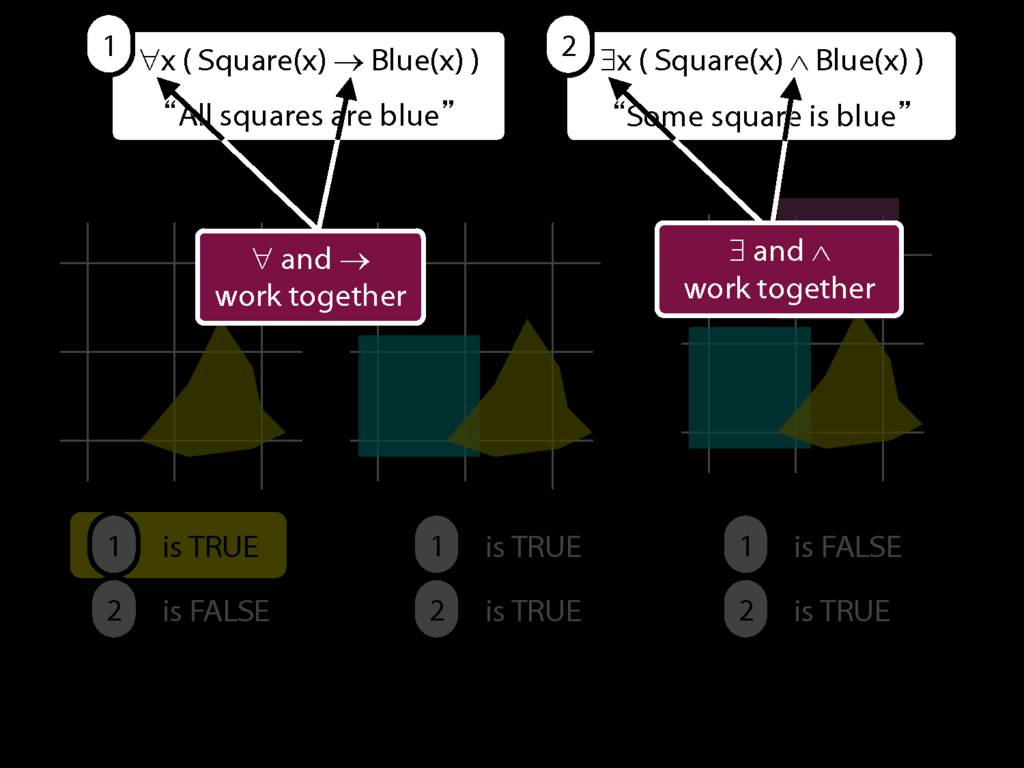
universal:arrow, existential:conjunction

 
\section{universal:arrow, existential:conjunction}
 

Don't use ∃ with →

 
\section{Don't use ∃ with →}
 
\section{Don't use ∃ with →}
\begin{minipage}{\columnwidth}
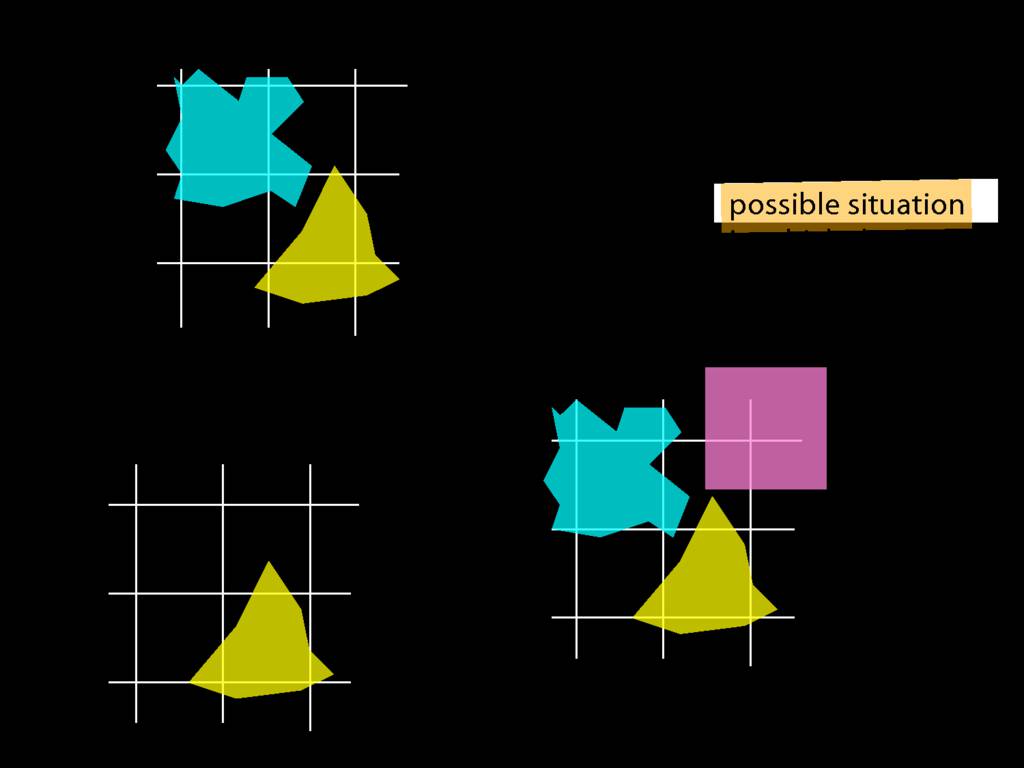
Is true ∃x(Square(x) → Broken(x)) in this world?
\end{minipage}
∃x(Square(x) → Broken(x))
\hspace{3mm} ⫤⊨
∃x(¬Square(x) ∨ Broken(x))
\hspace{3mm} ⫤⊨
∃x(¬Square(x)) ∨ ∃x(Broken(x))

1.

∀x(Square(x) ∧ Broken(x))

2.

∀x(Square(x) → Broken(x))

⫤⊨
3.
∀x(¬Square(x) ∨ Broken(x))

4.
∃x(Square(x) ∧ Broken(x))

5.
∃x(Square(x) → Broken(x))

⫤⊨
6.
∃x(¬Square(x) ∨ Broken(x))

⫤⊨
7.
∃x(¬Square(x)) ∨ ∃x(Broken(x))

nb
∀x(¬Square(x) ∨ Broken(x)) ⊭ ∀x(¬Square(x)) ∨ ∀x(Broken(x))

1. is false

2. is true

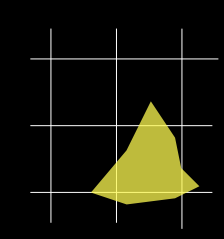
4. is false

5. is ???

#
9.10
9.15--9.17
*9.18--9
9.10
 

¬Intro

 
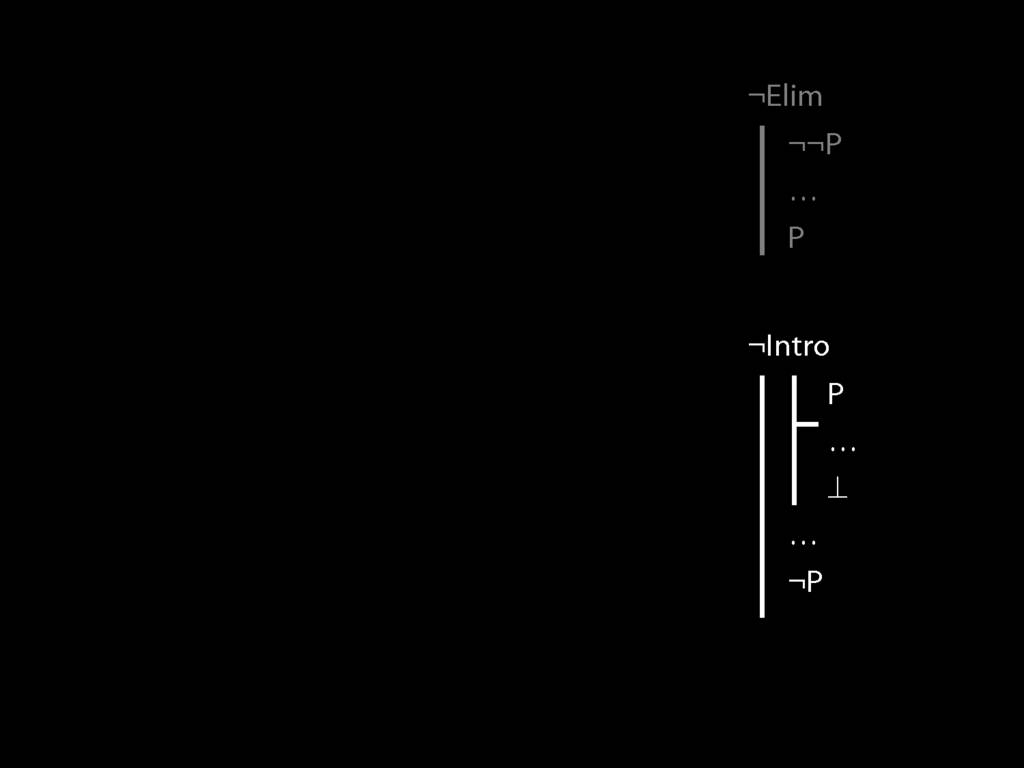
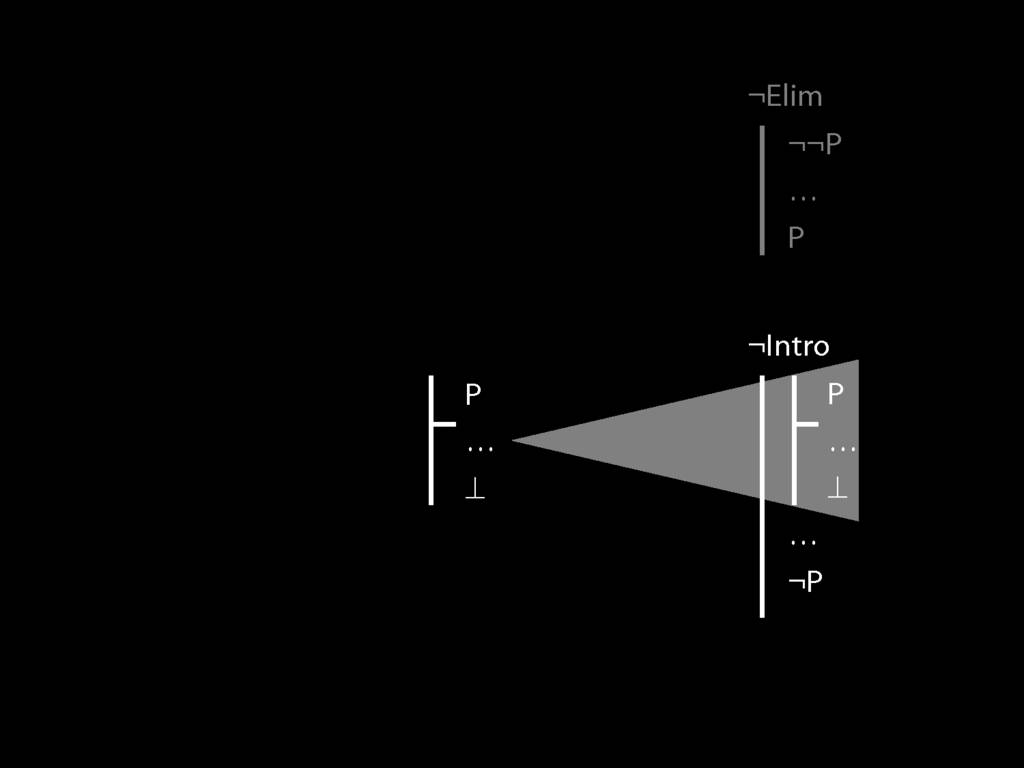
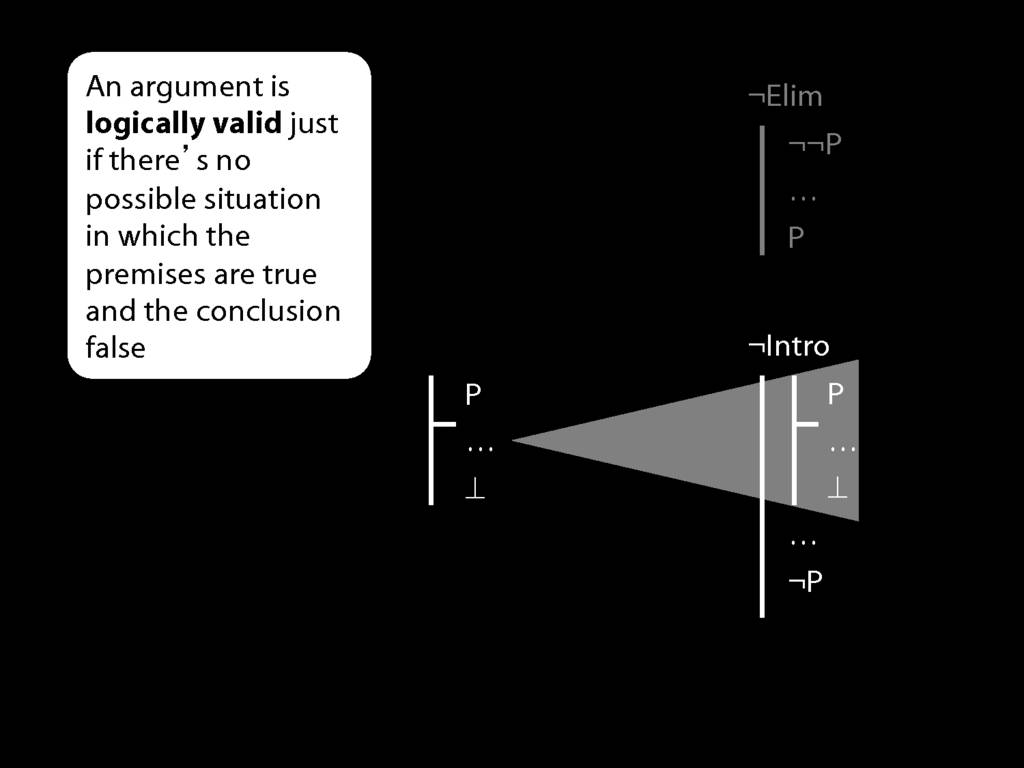
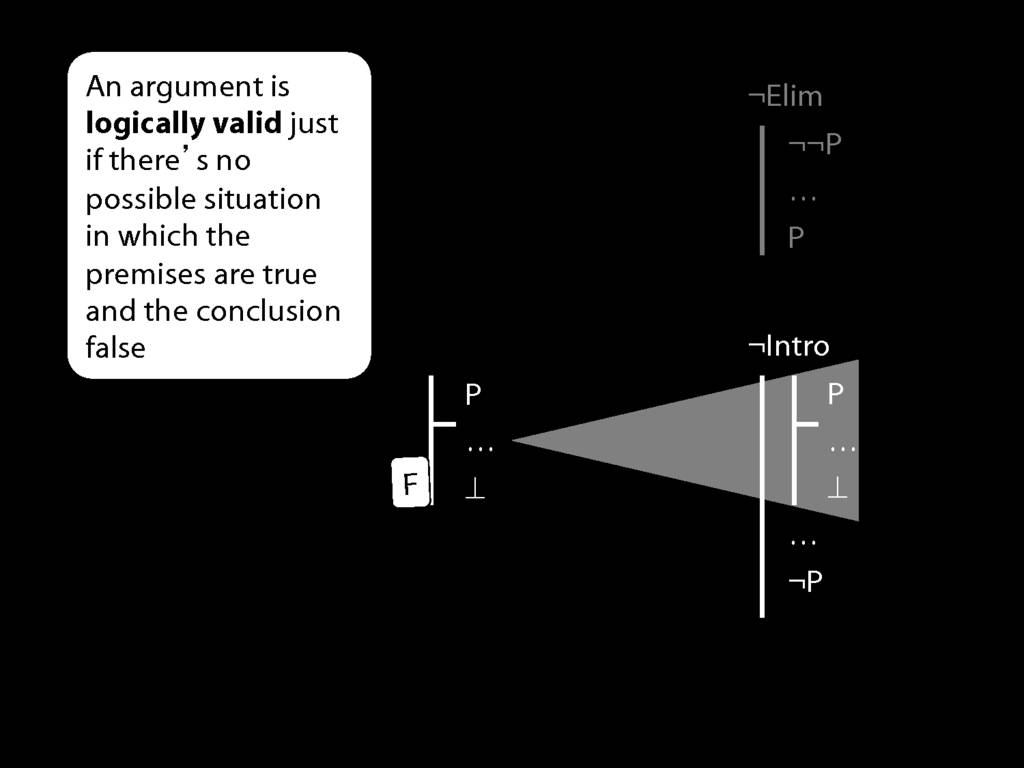
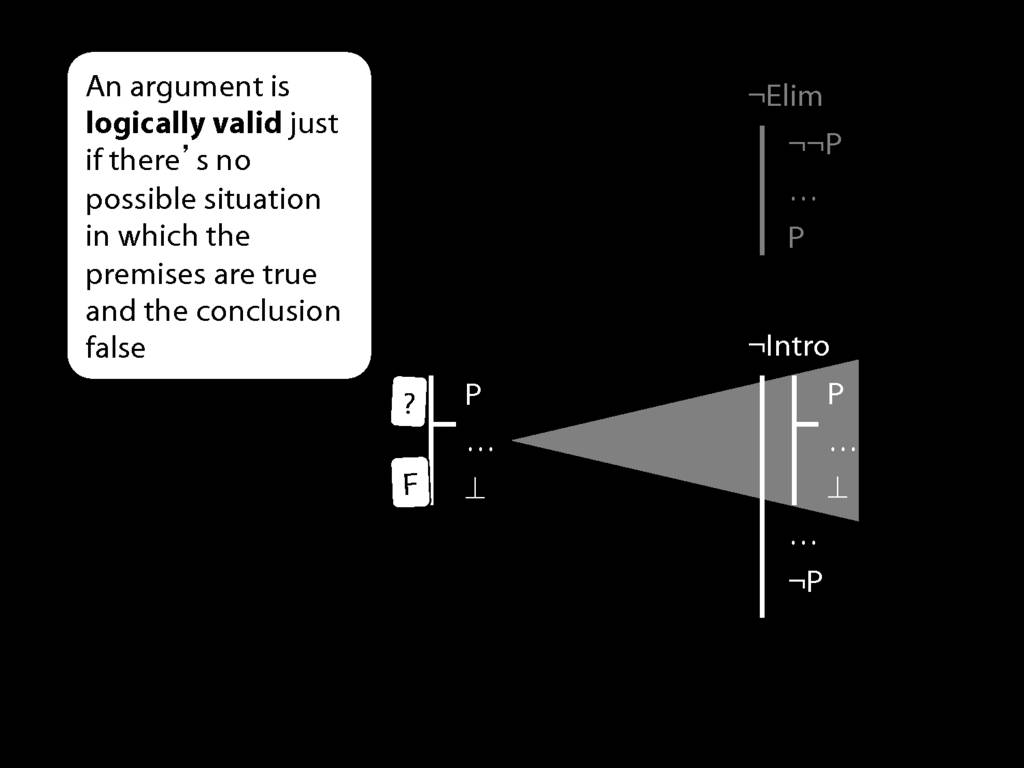
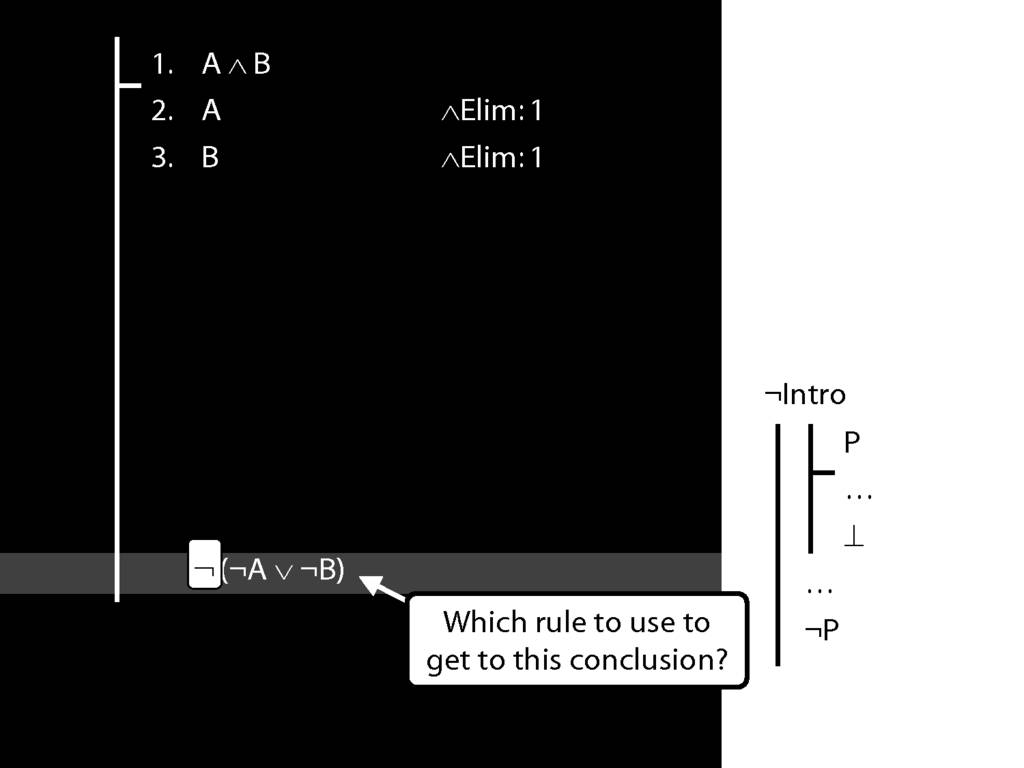
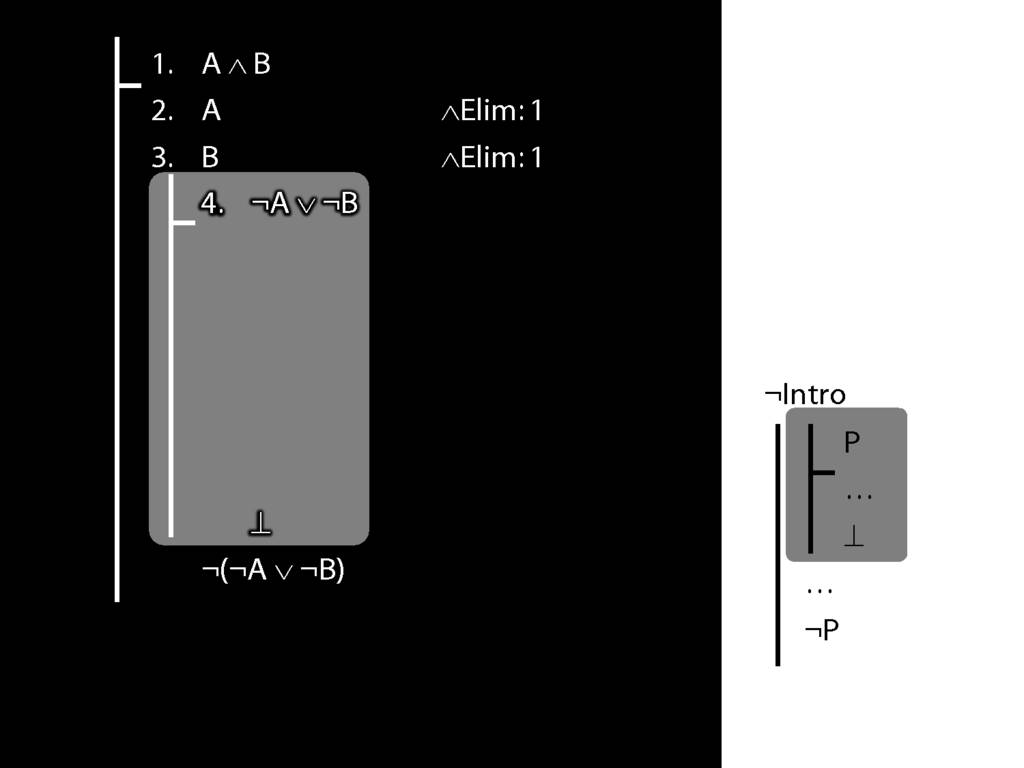
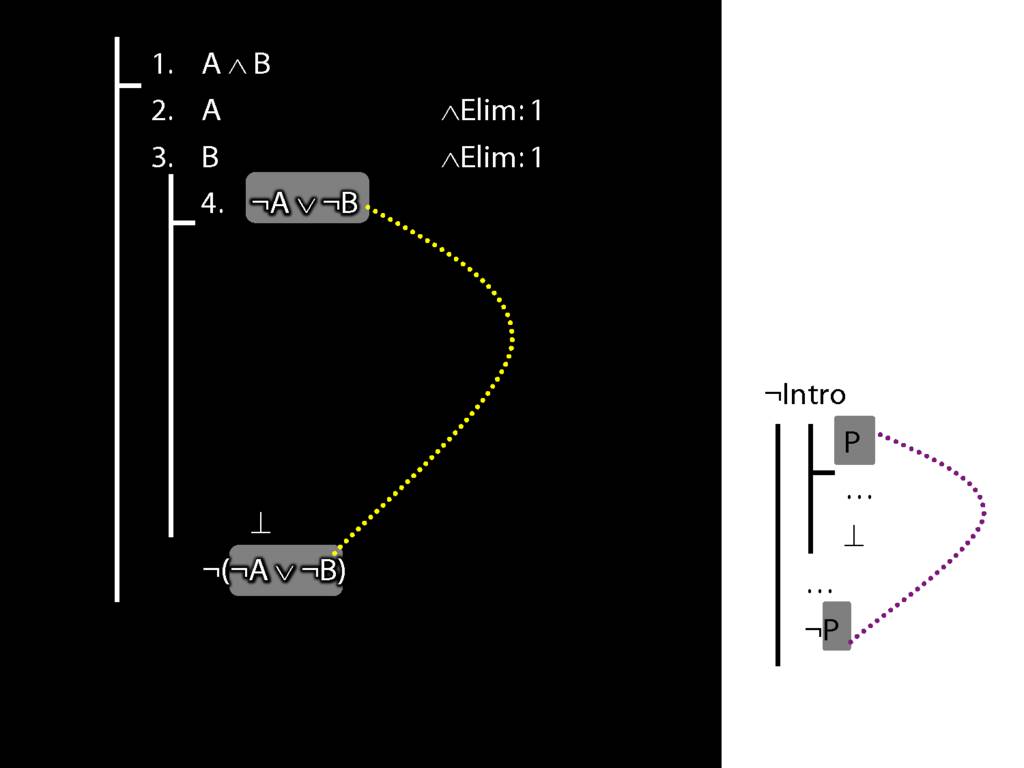
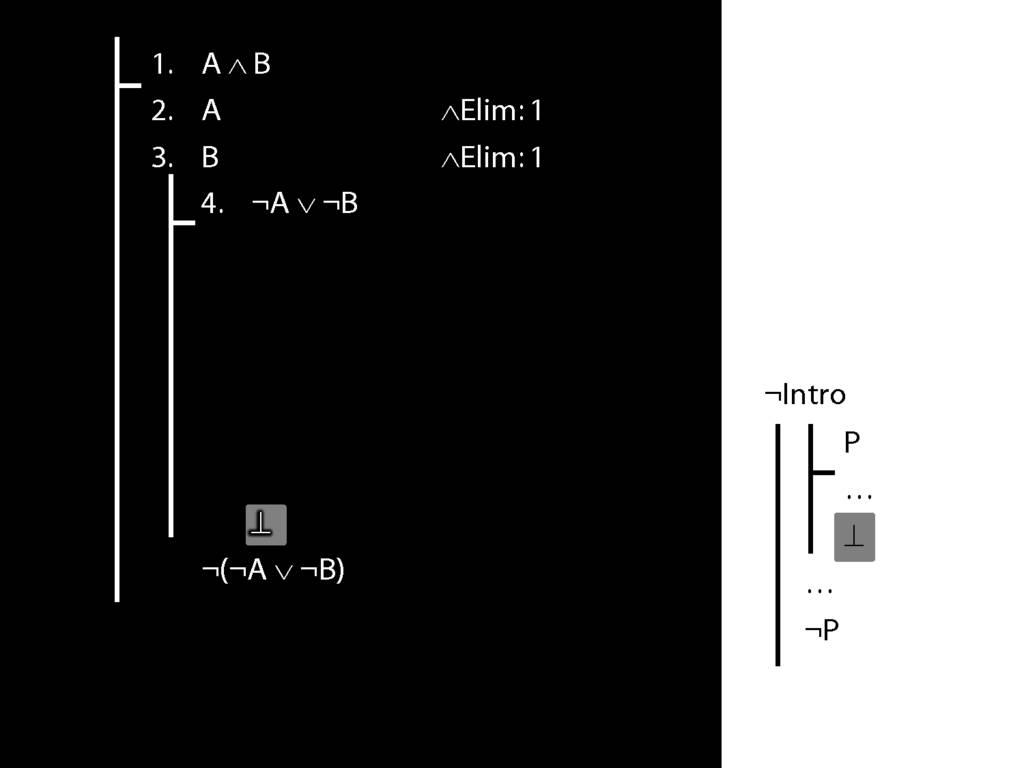
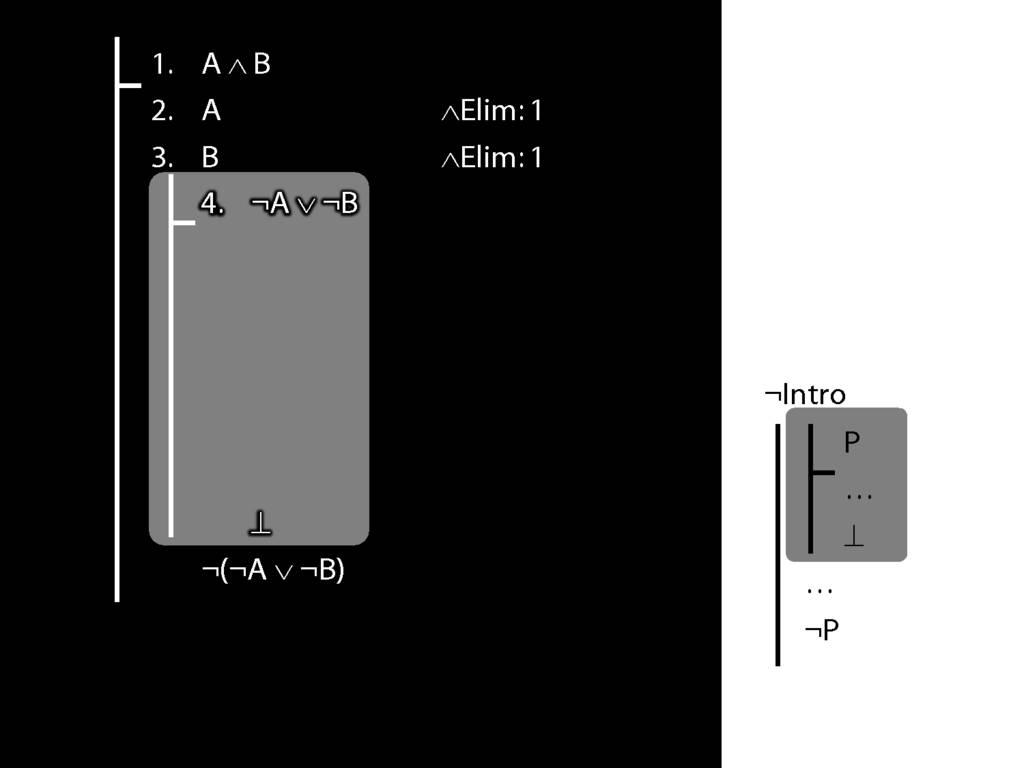
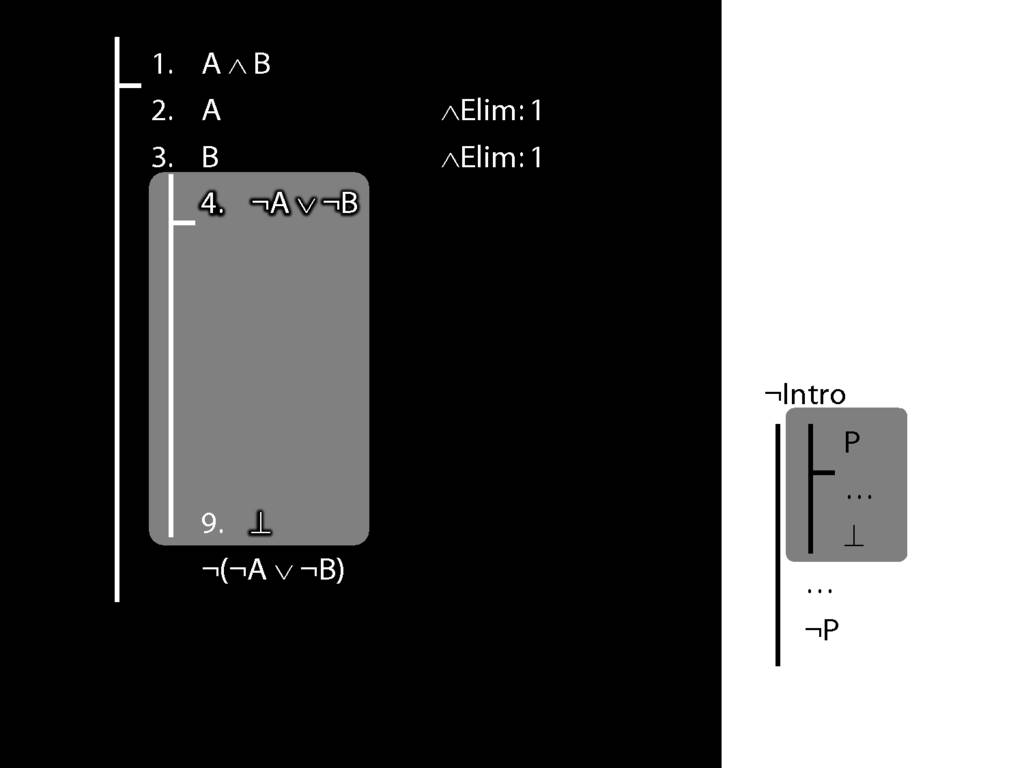
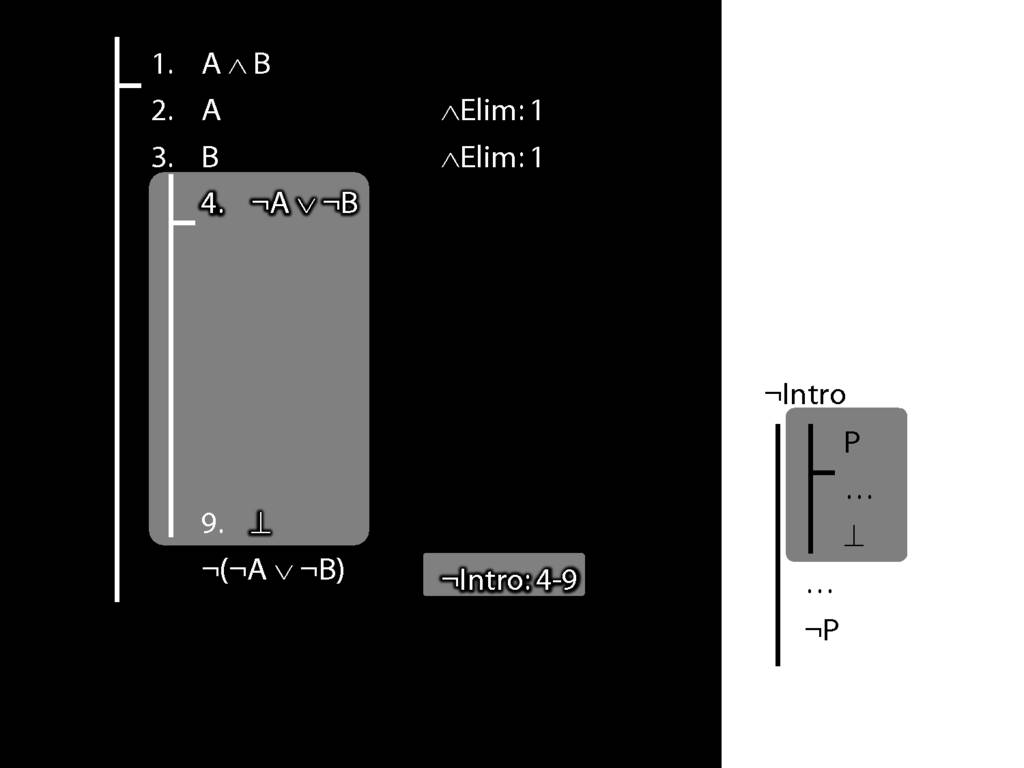
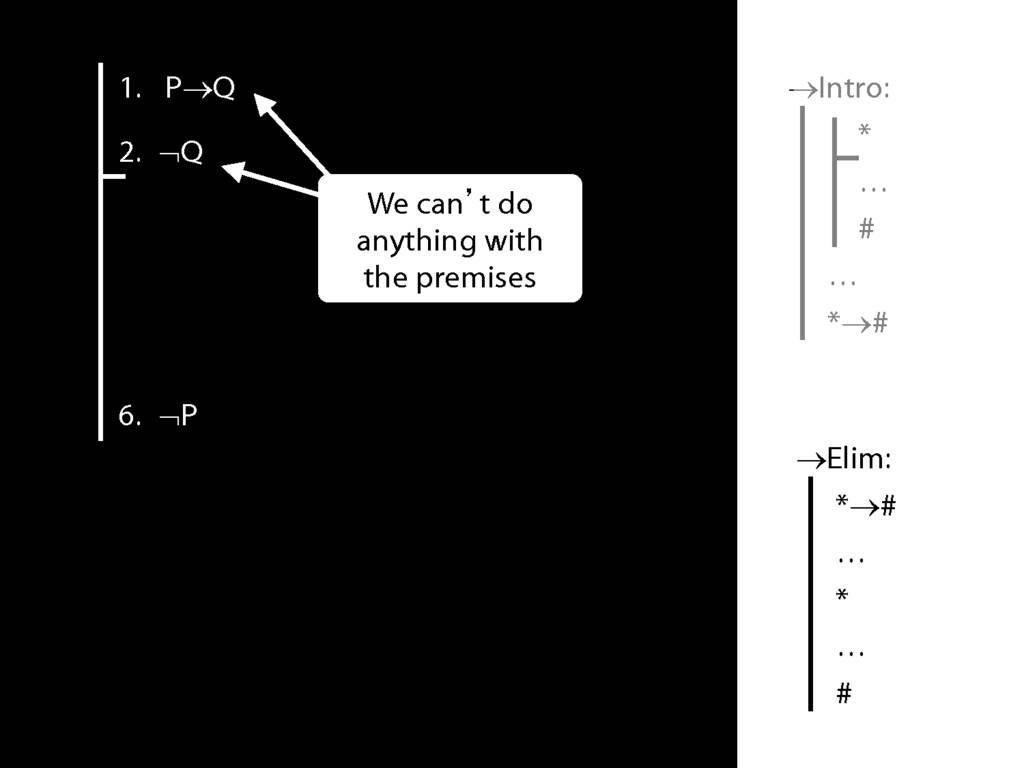
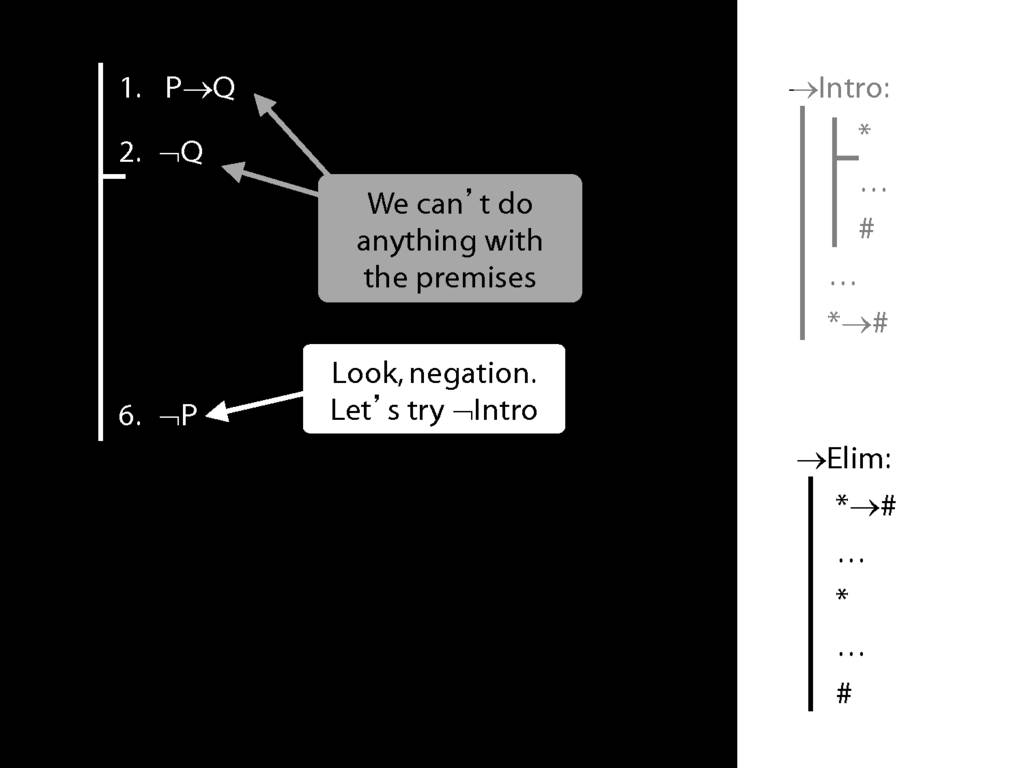
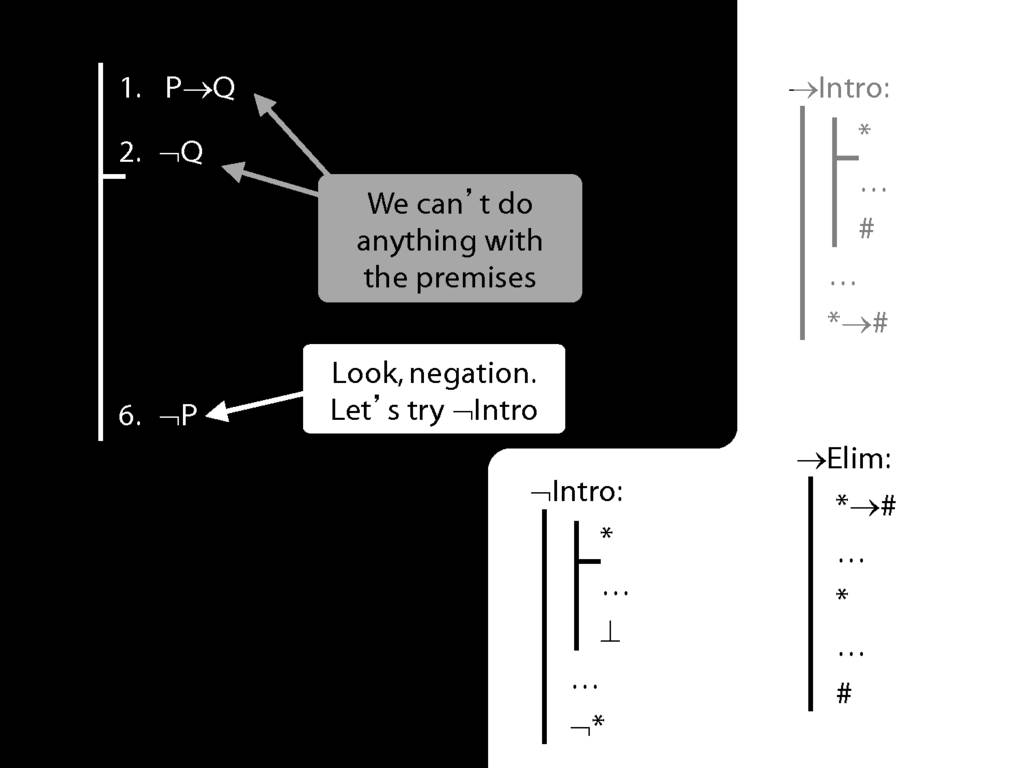
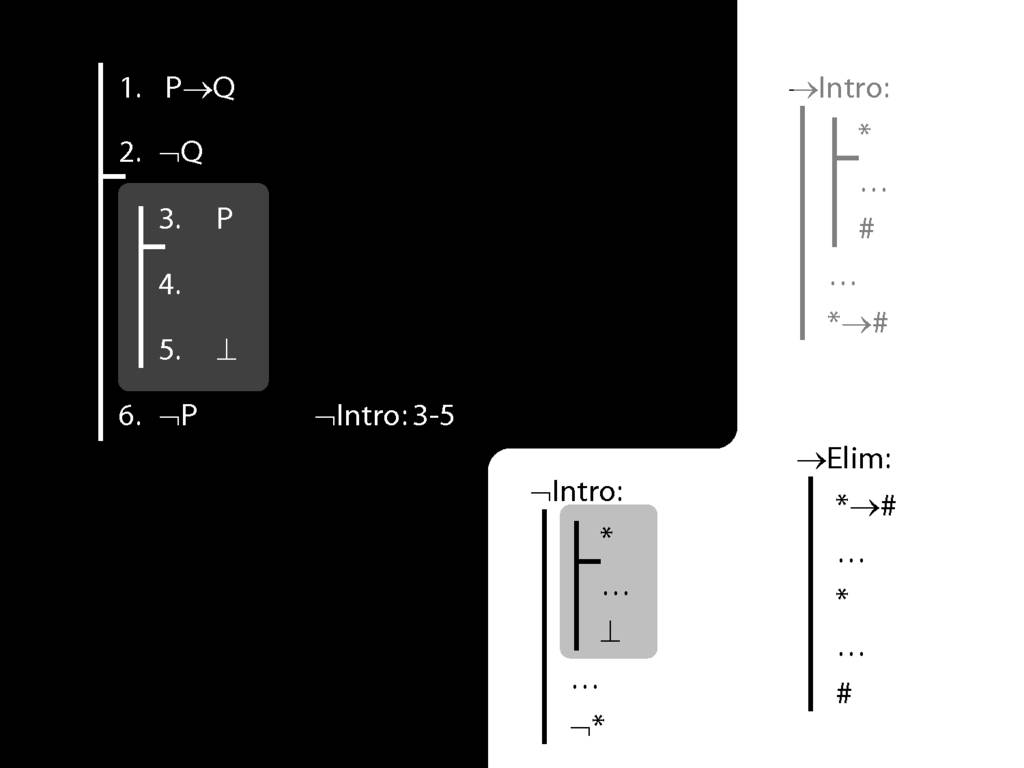
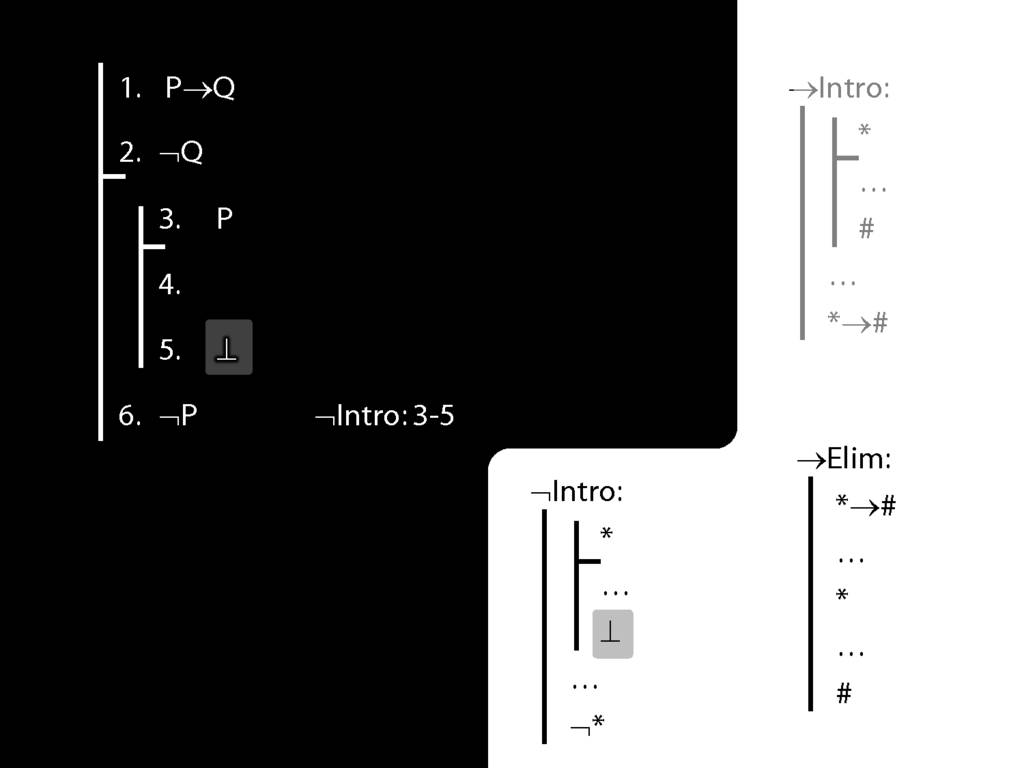
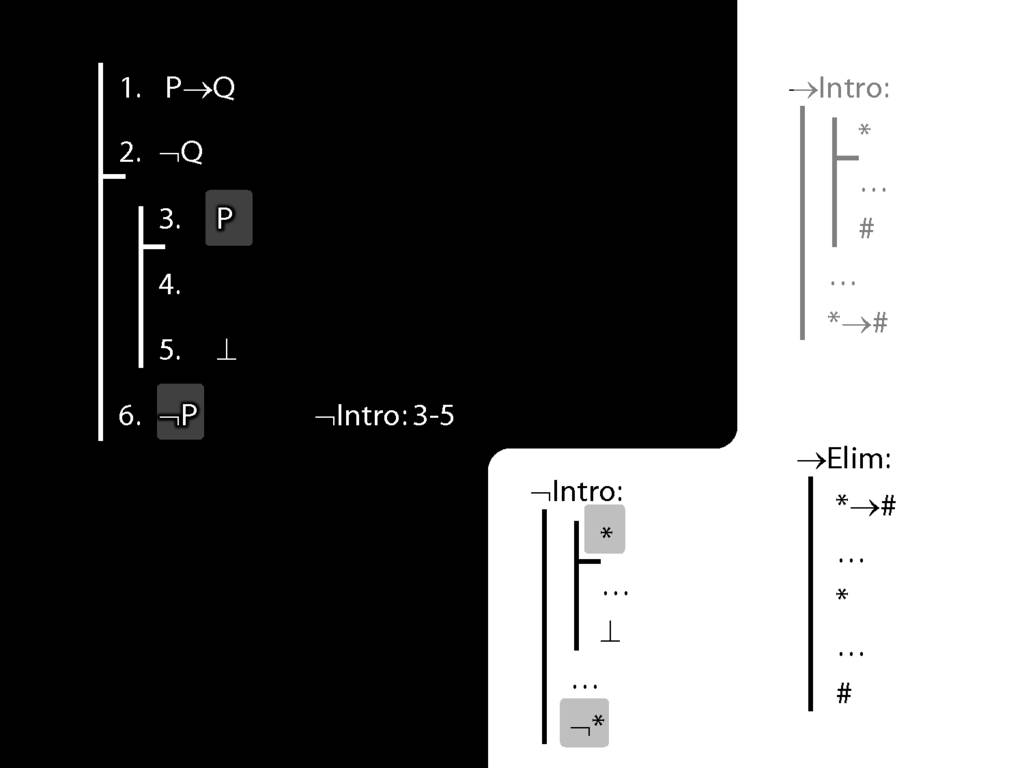
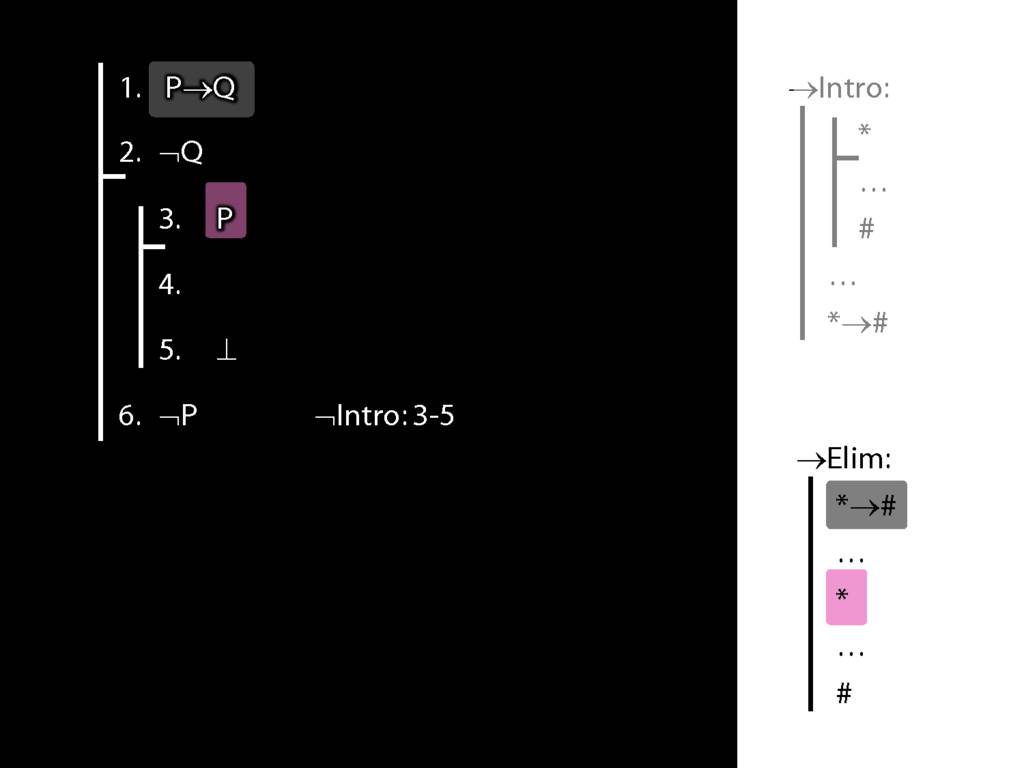
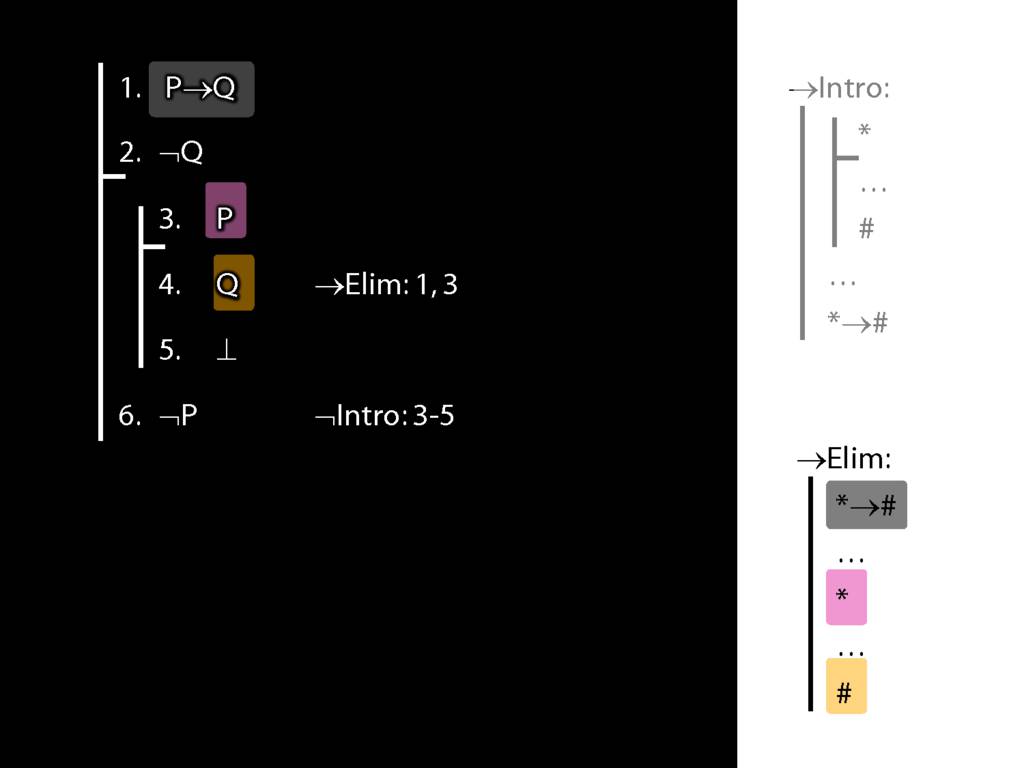
\section{¬Intro}
\emph{Reading:} §5.3, §6.3
 
\section{¬Intro}
6.7--6.10
*6.11--6.12
6.7--6.12
6.18--6.20
6.24--6.27
*6.40--6.42

Joint Action:

Which forms of shared agency underpin our social nature?

(Autumn Term)

Social Cognition:

What makes others’ minds and actions intelligible to us?

(Spring Term)

Origins of Mind: Philosophical Issues in Cognitive Development (PH357)

(http://origins-of-mind.butterfill.com)

 

¬Intro Proof Example

 
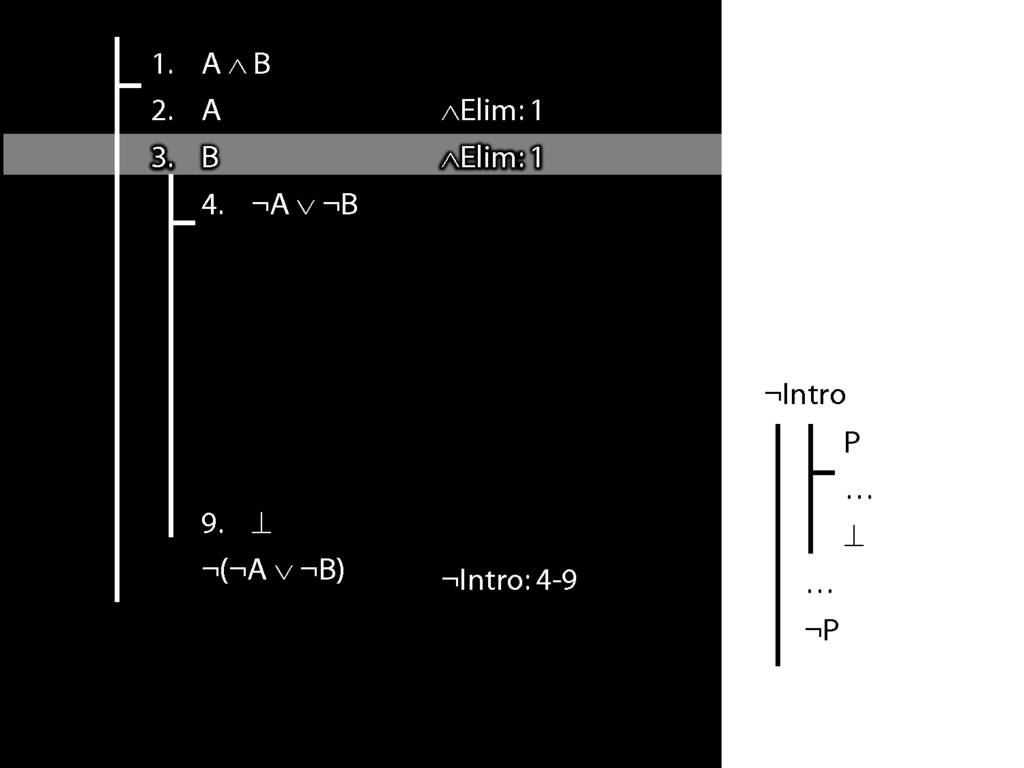
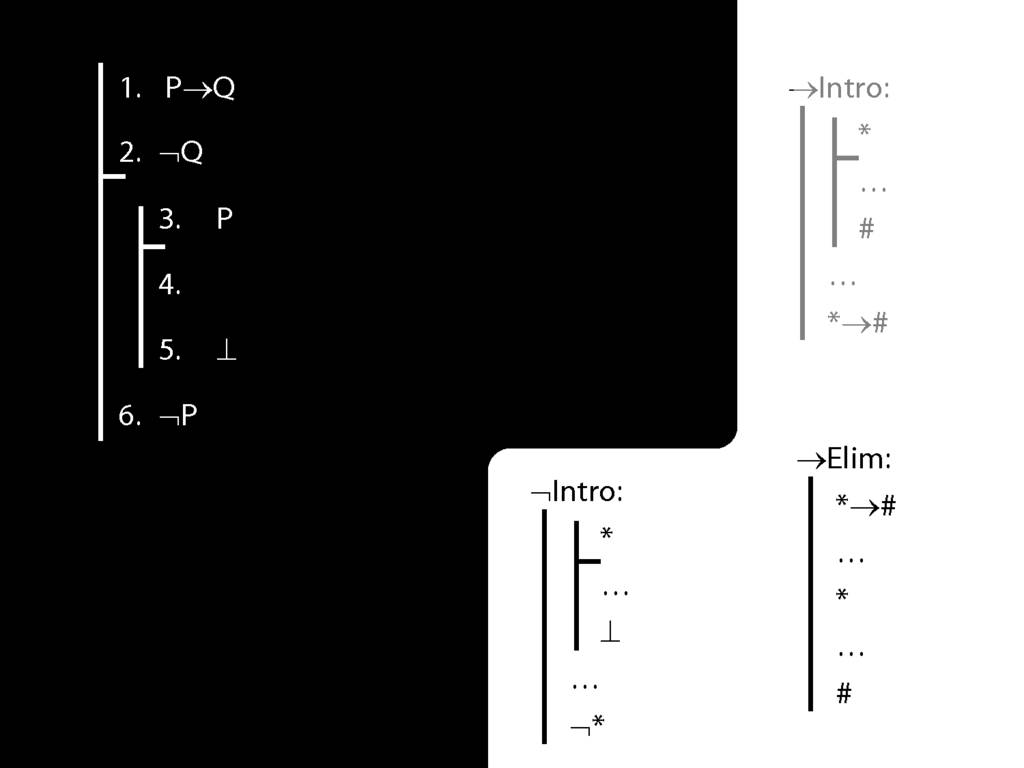
\section{¬Intro Proof Example}
\emph{Reading:} §5.3, §6.3
 
\section{¬Intro Proof Example}
6.24--6.26
 

Subproofs Are Tricky

 
\section{Subproofs Are Tricky}
 
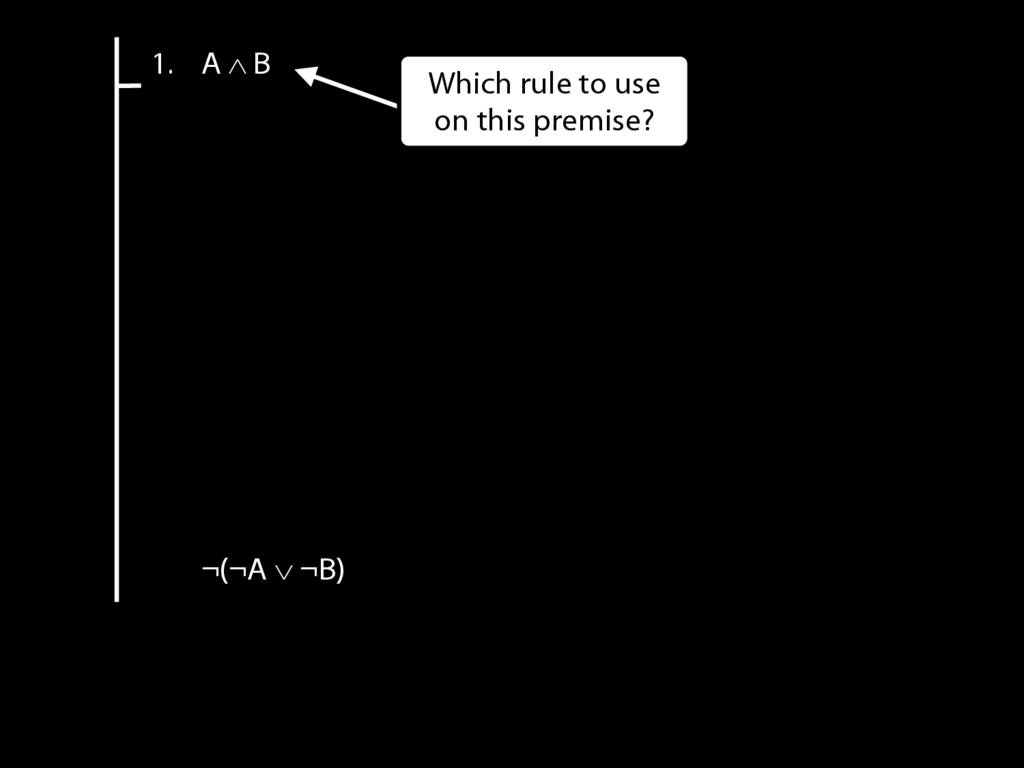
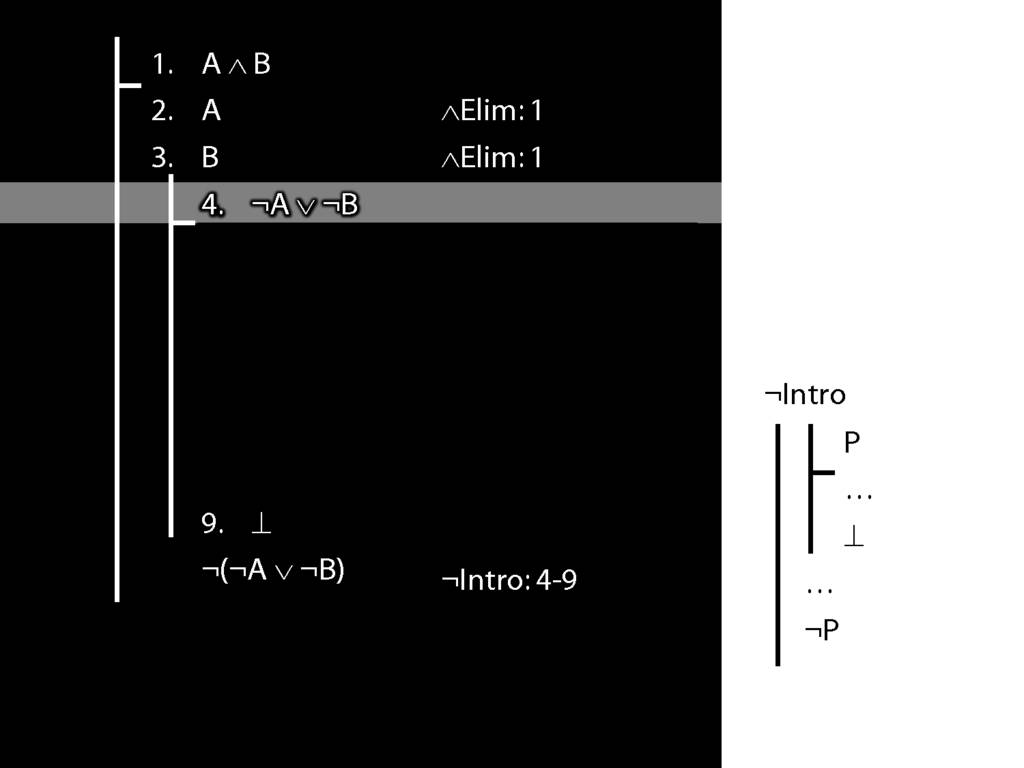
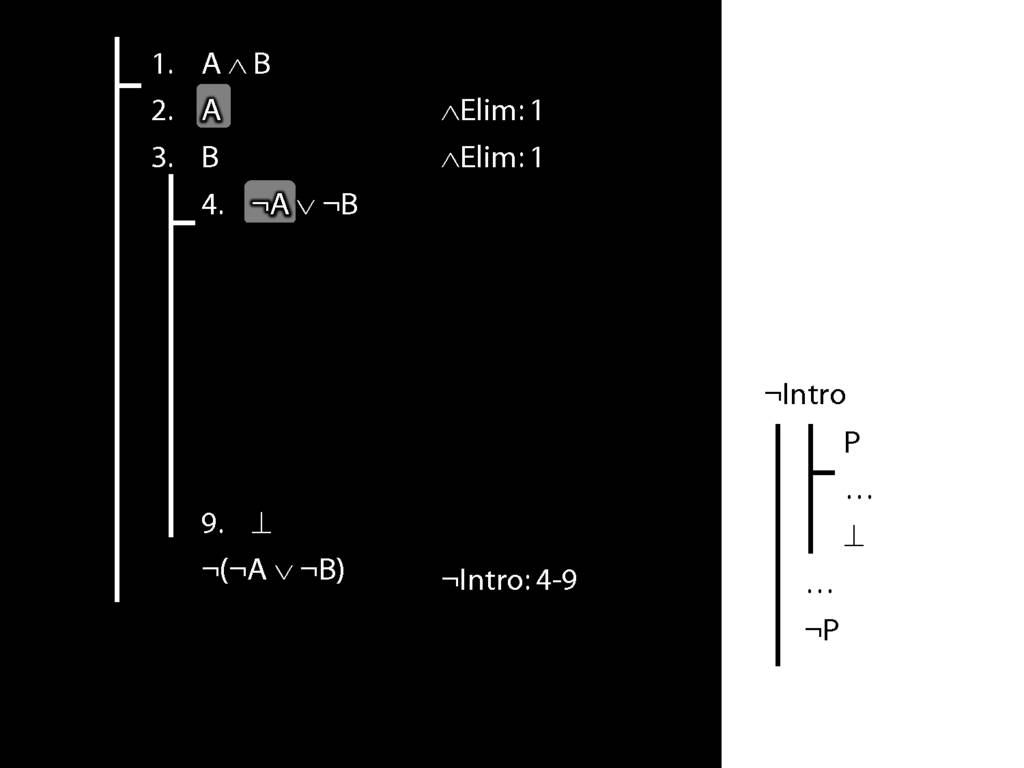
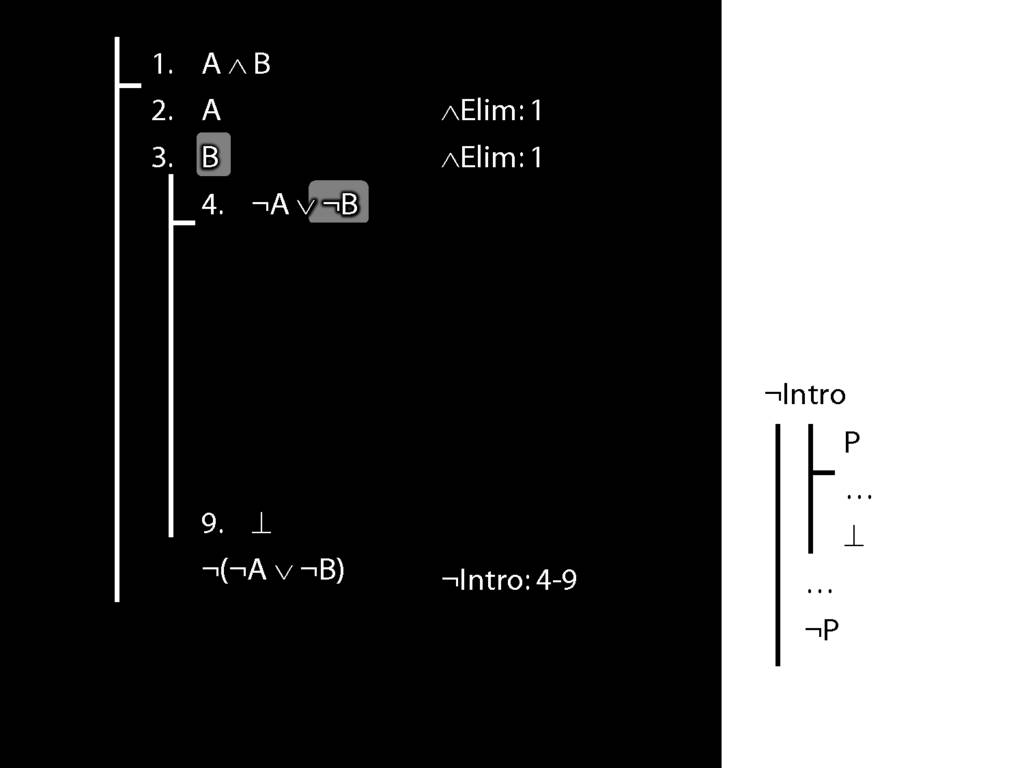
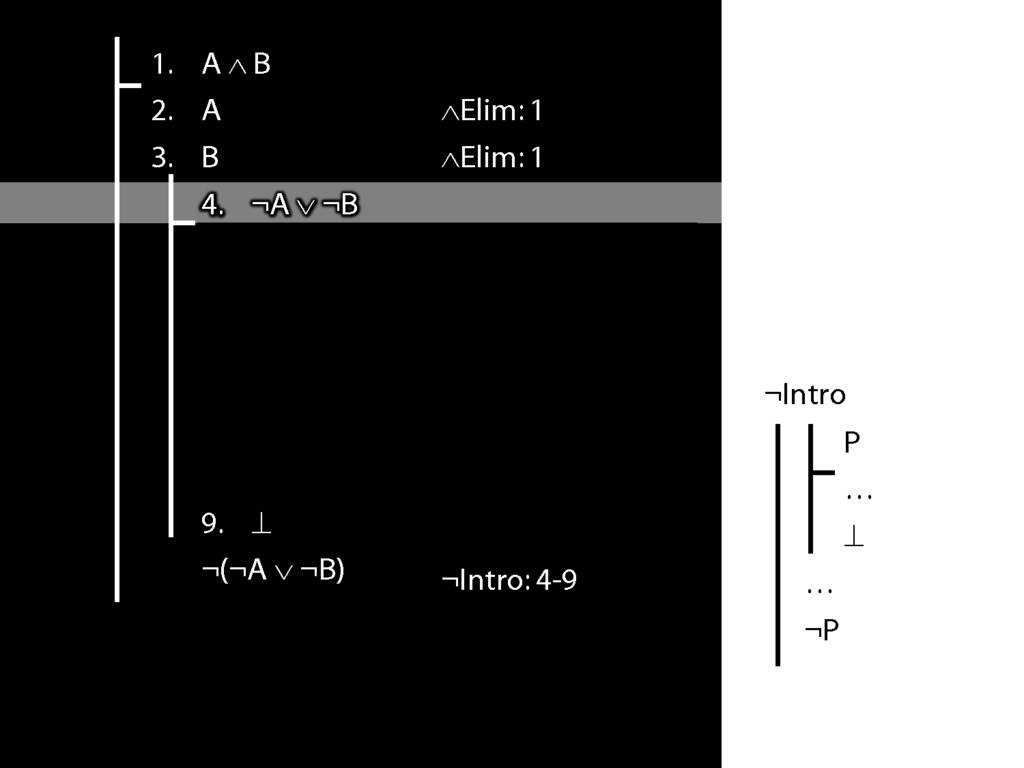
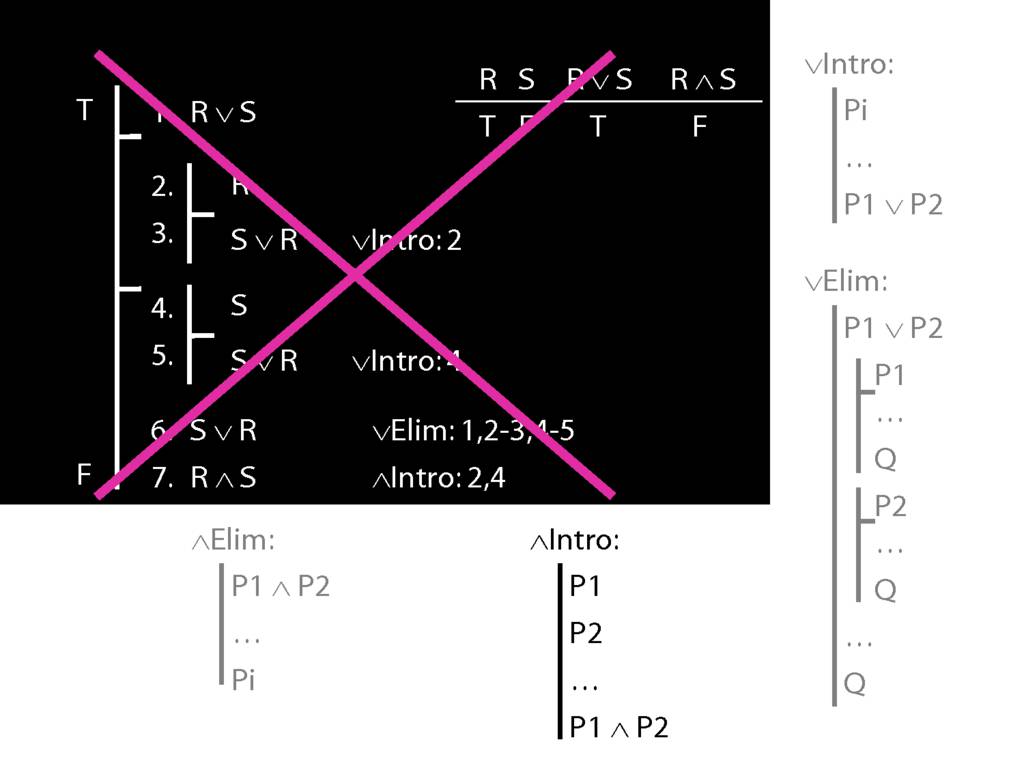
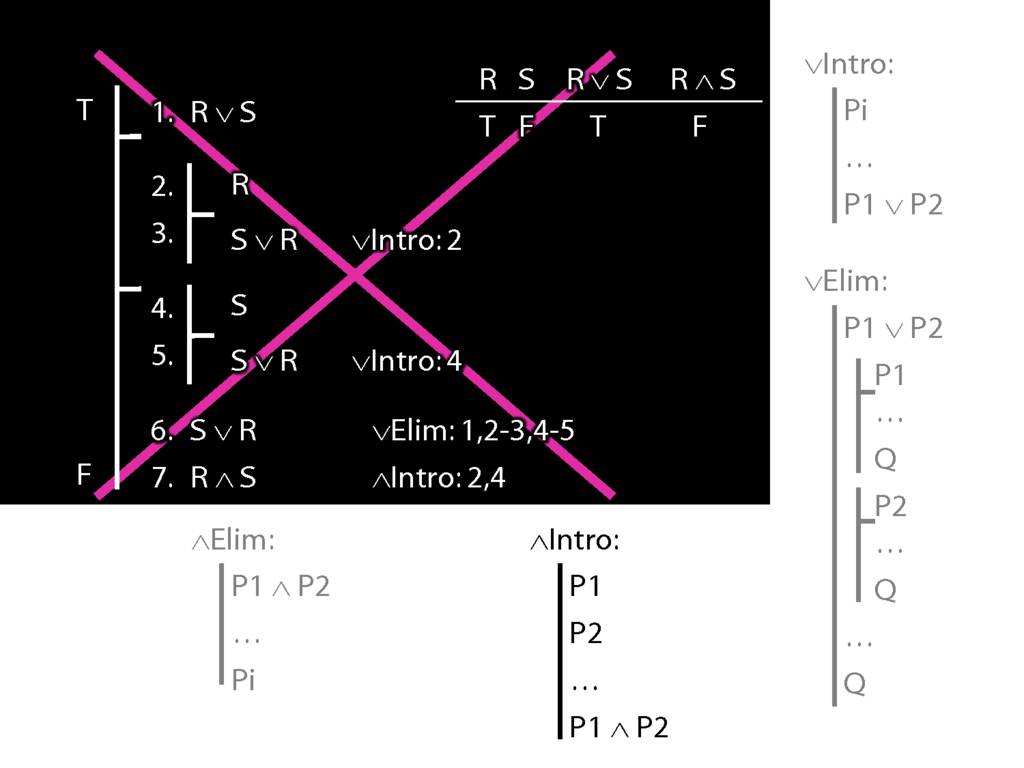
\section{Subproofs Are Tricky}
What is wrong with the following apparent proof?
 

∀Elim

 
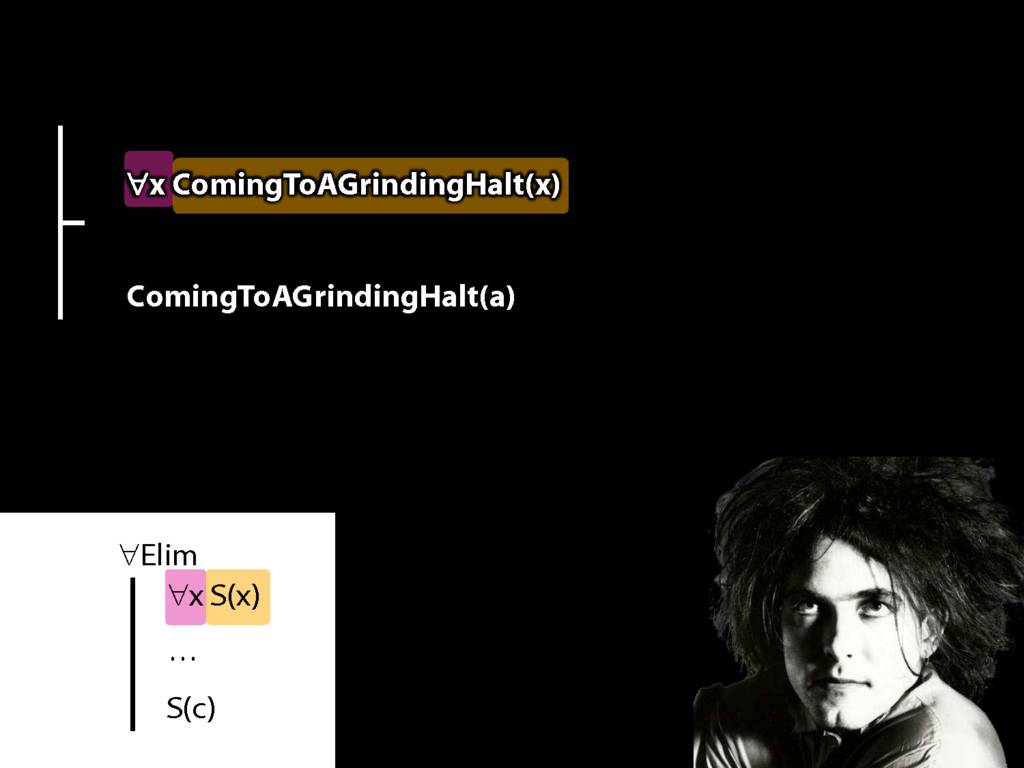
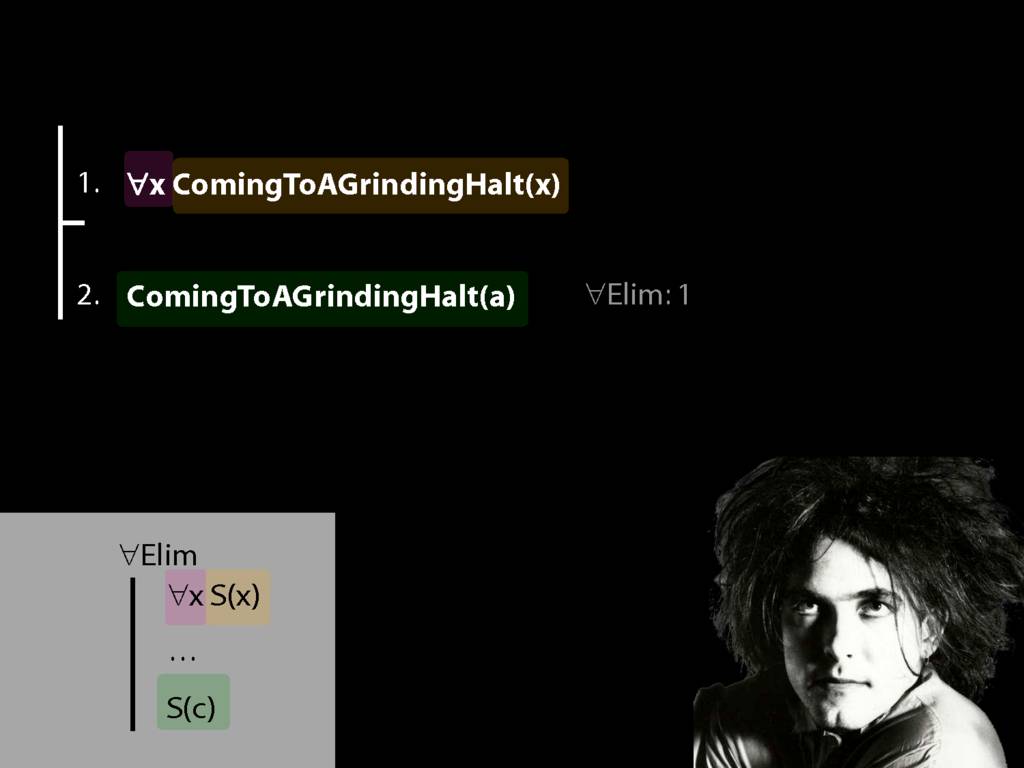
\section{∀Elim}
\emph{Reading:} §13.1
 
\section{∀Elim}