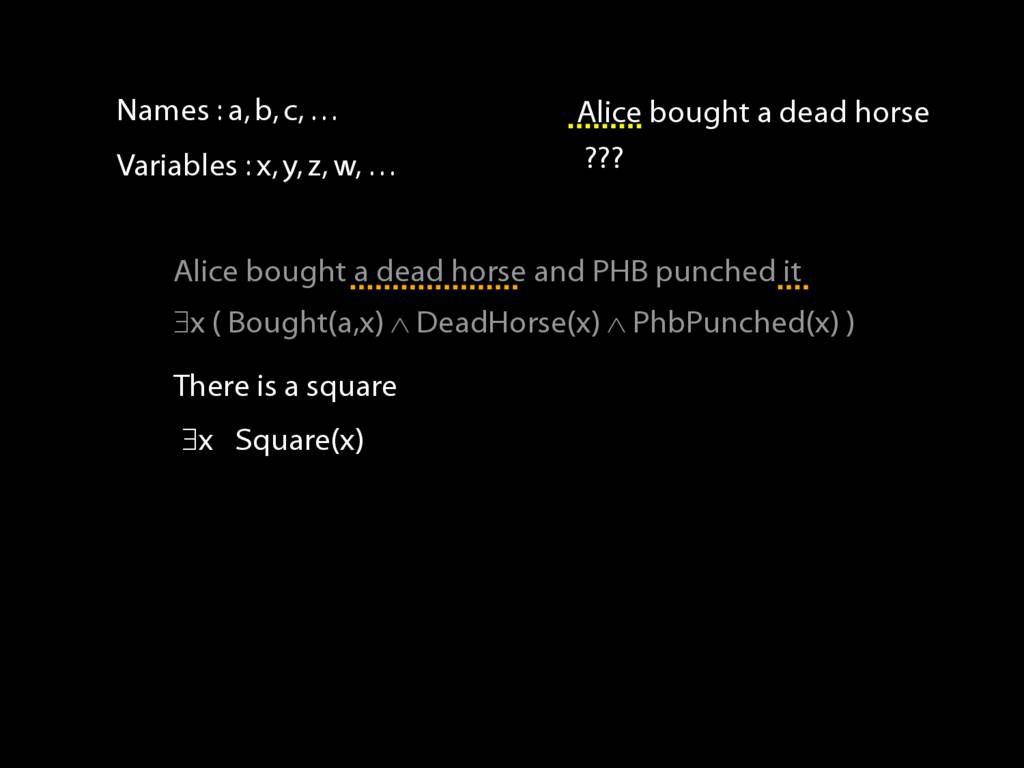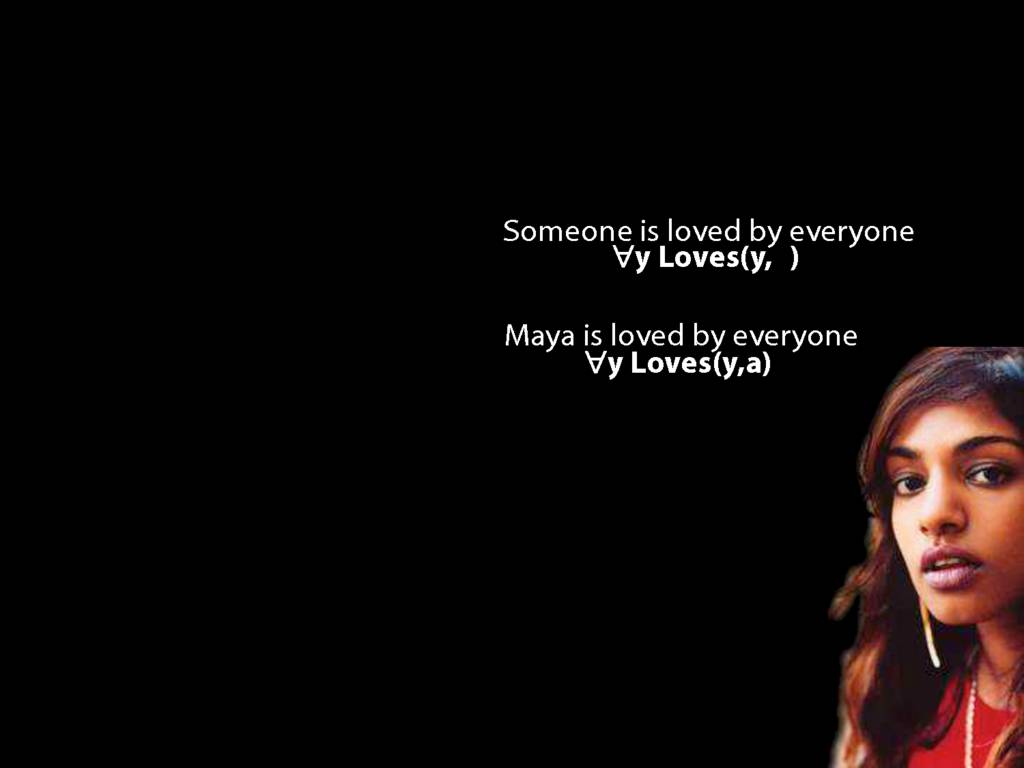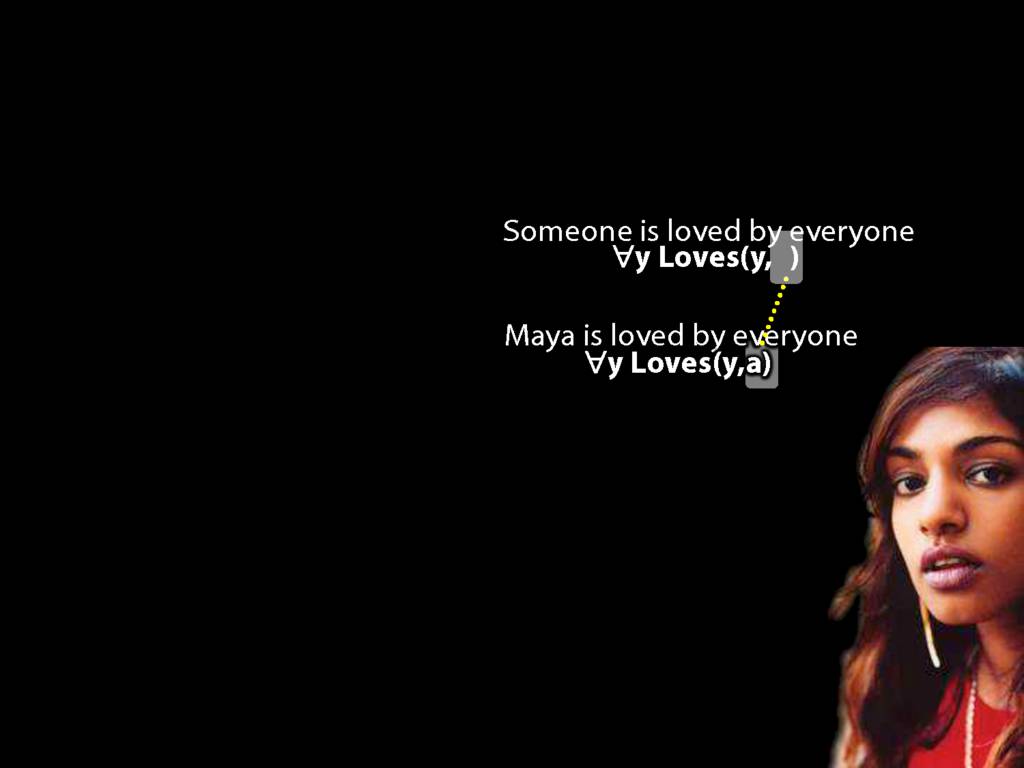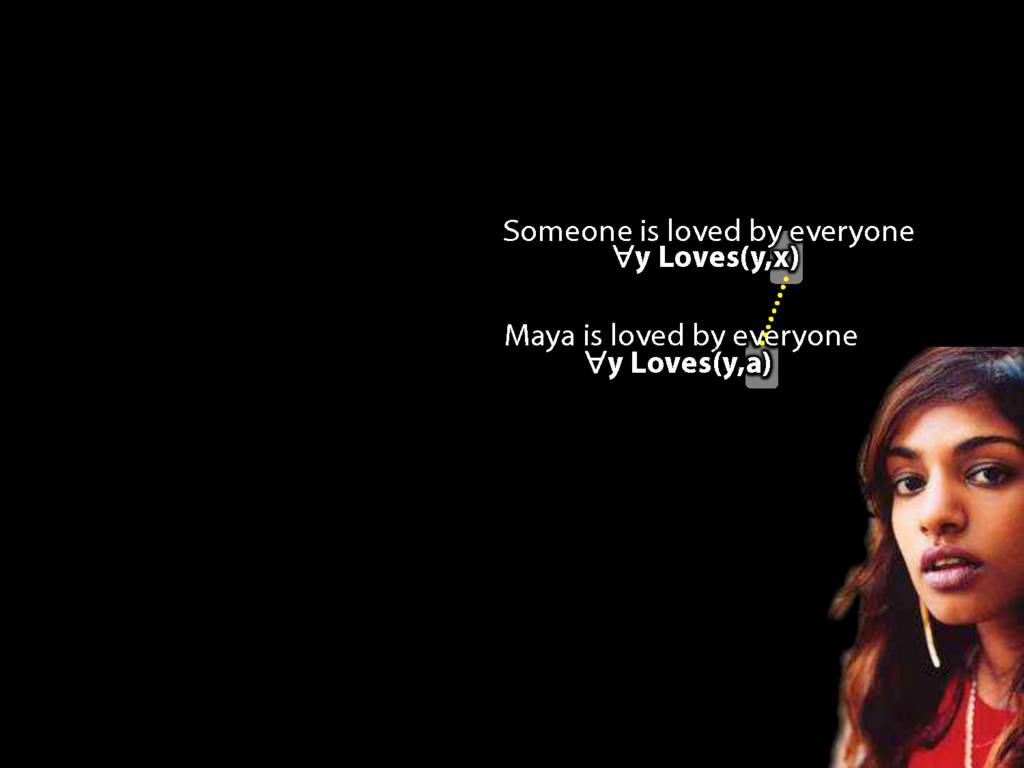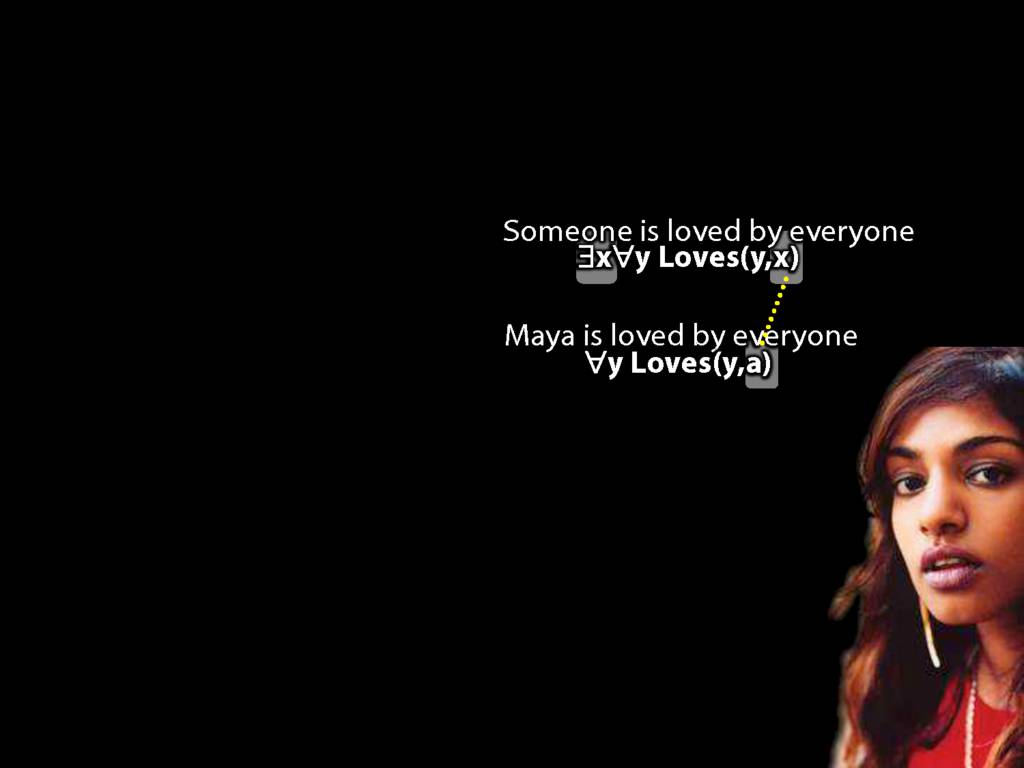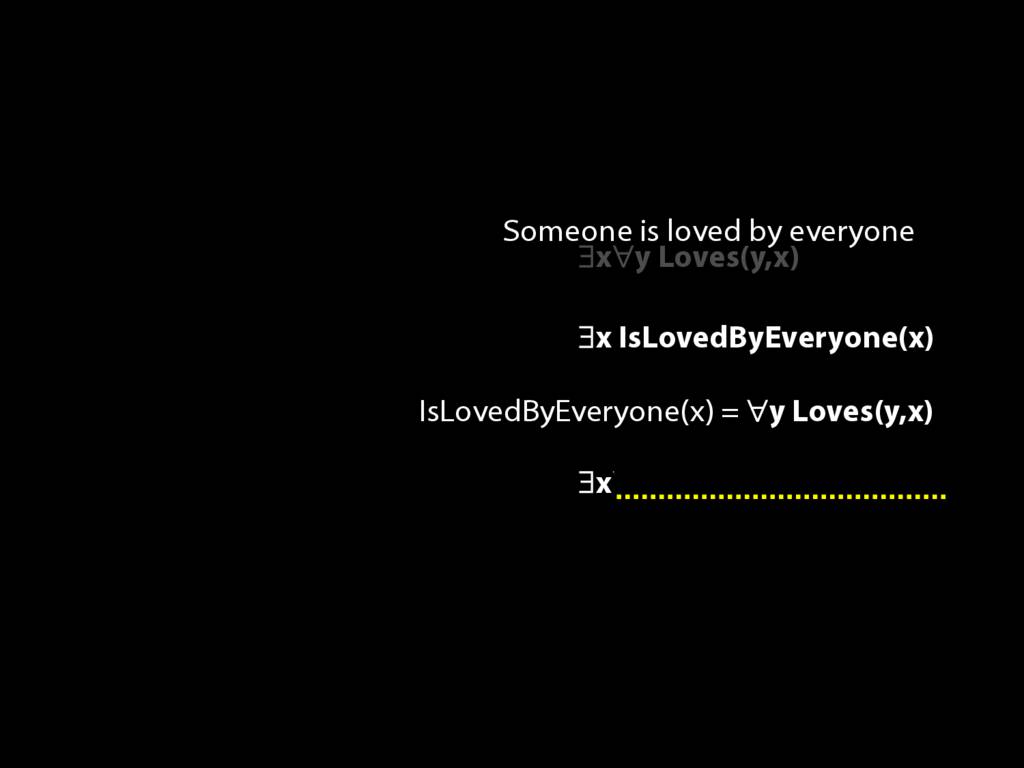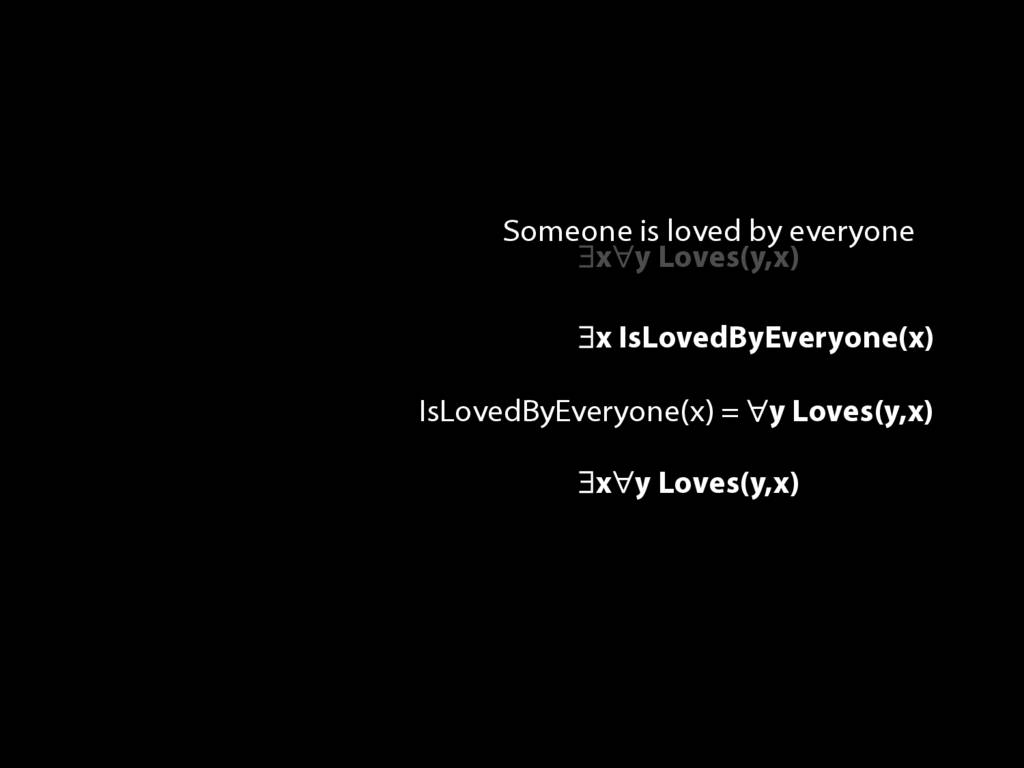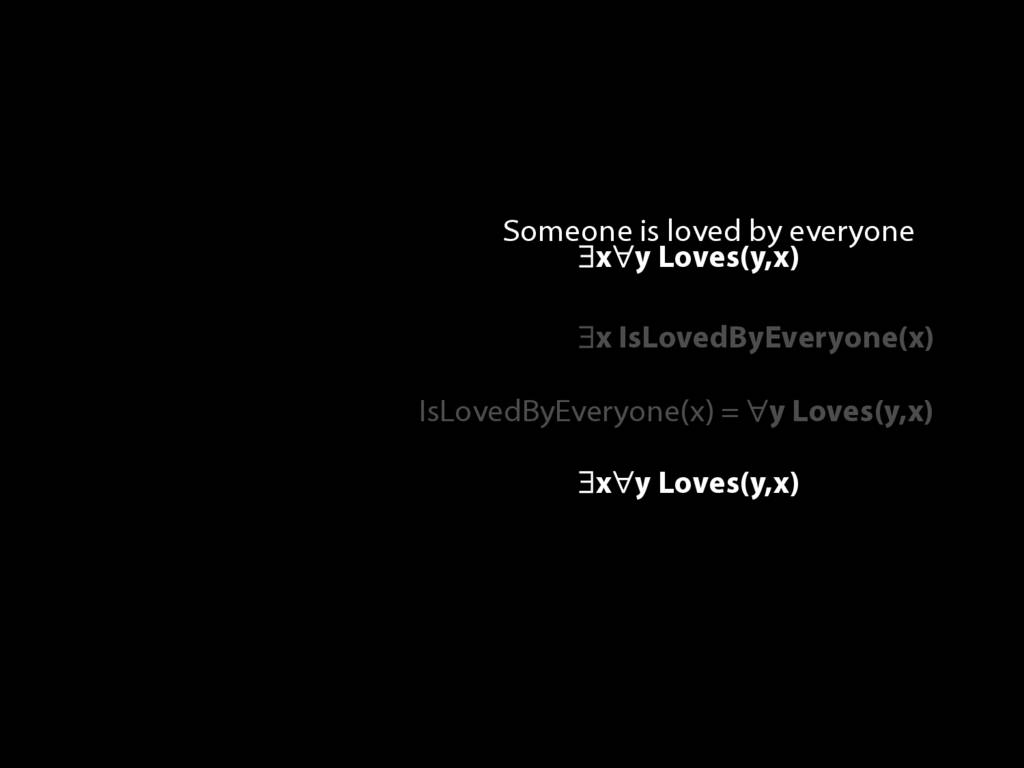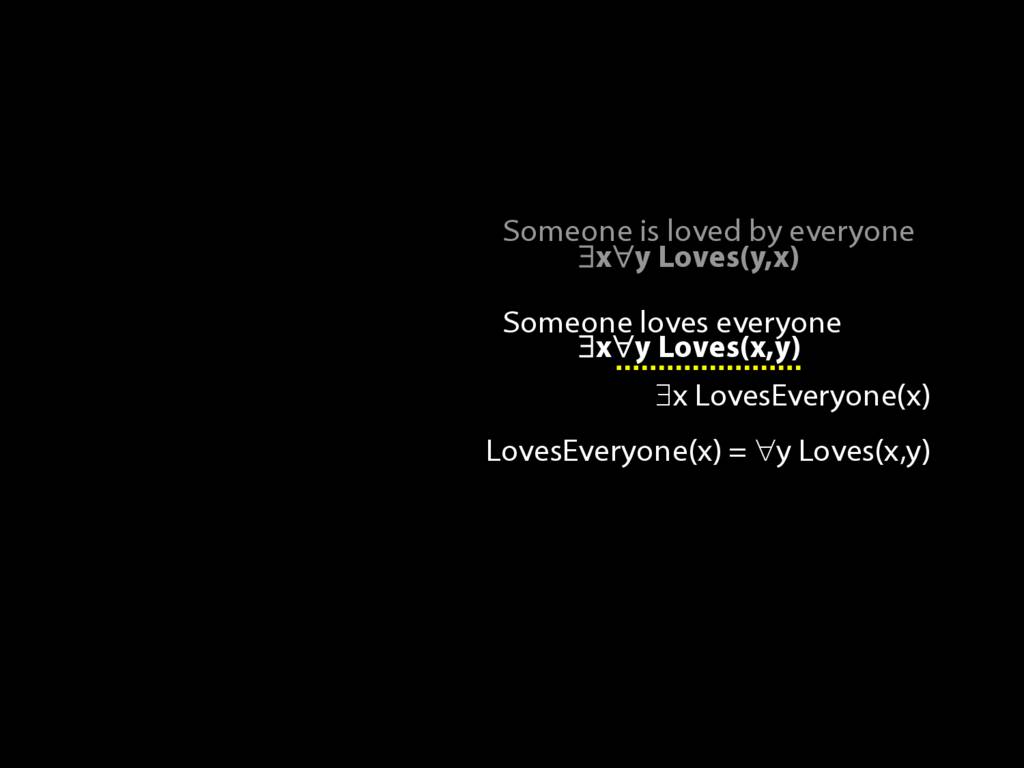Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Logic (PH133)}
 
\maketitle
 

Logic (PH133)

Lecture 8

\def \ititle {Logic (PH133)}
\def \isubtitle {Lecture 8}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
\section{Subproofs Are Tricky: The Answer}
 
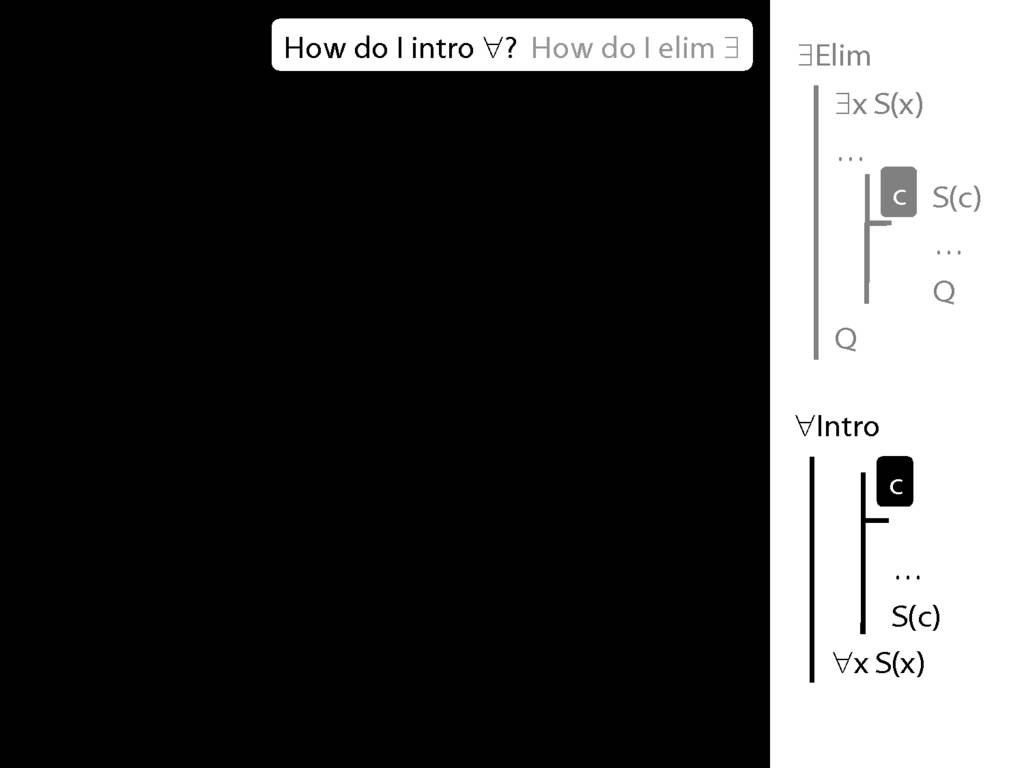
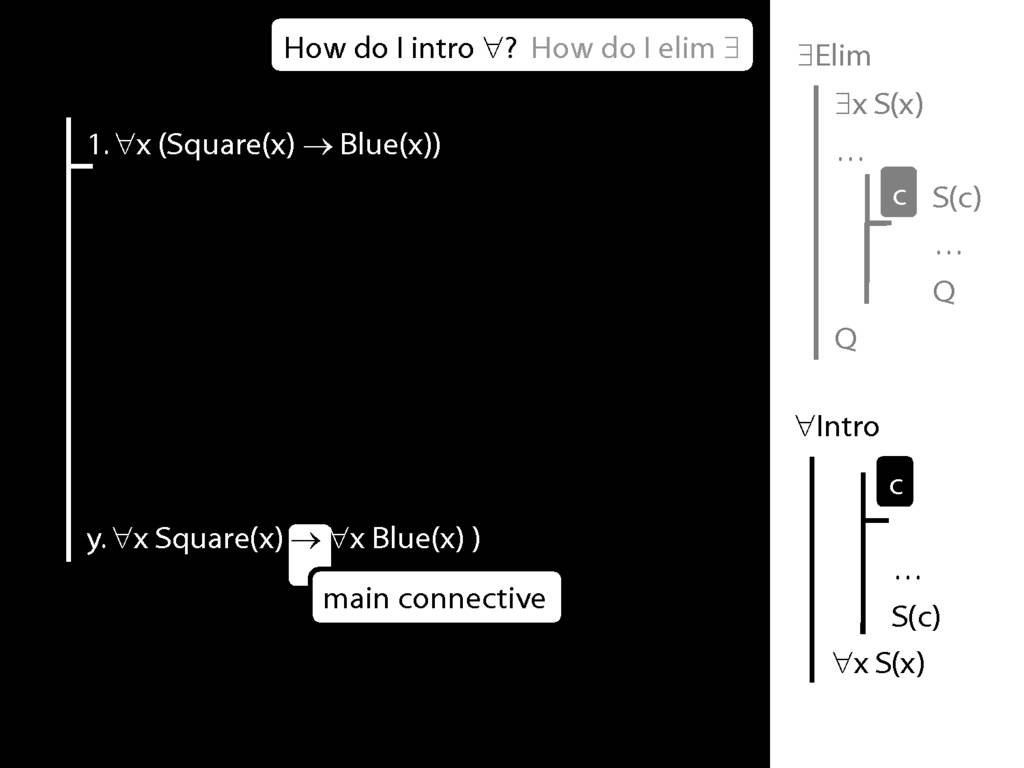
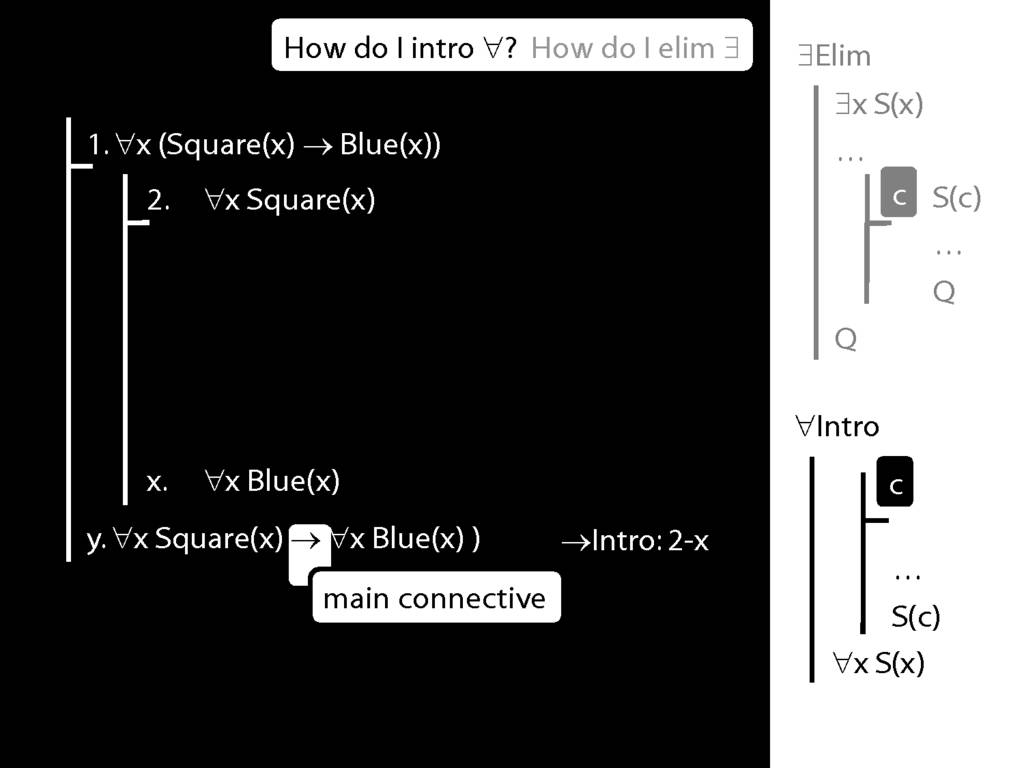
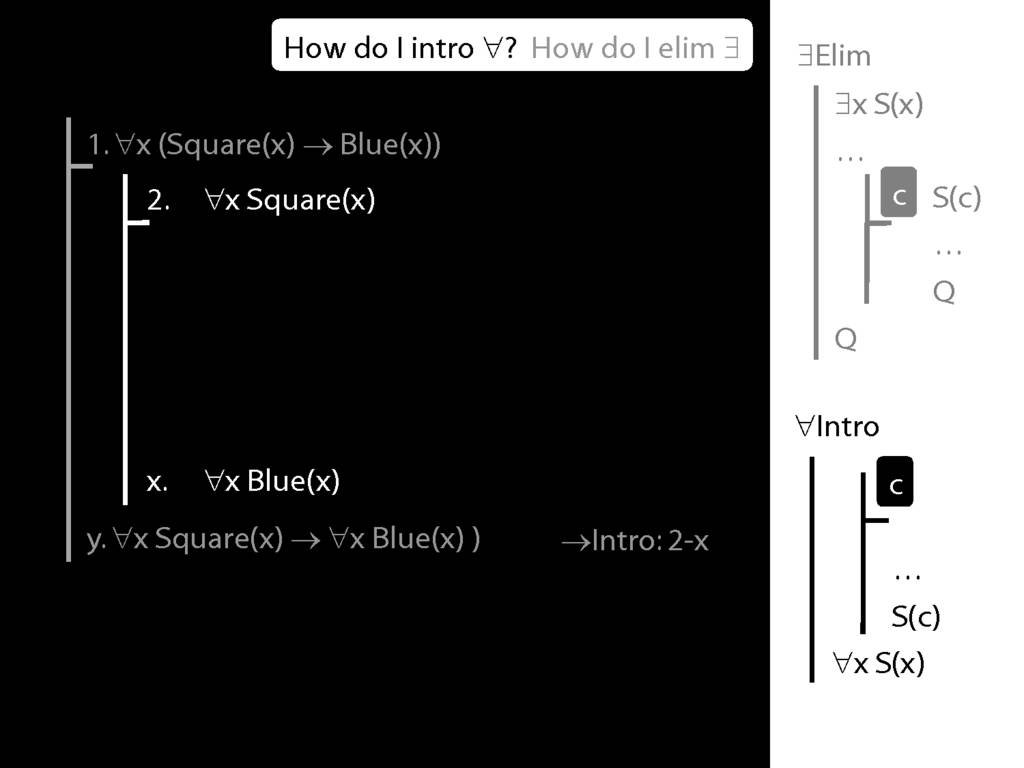
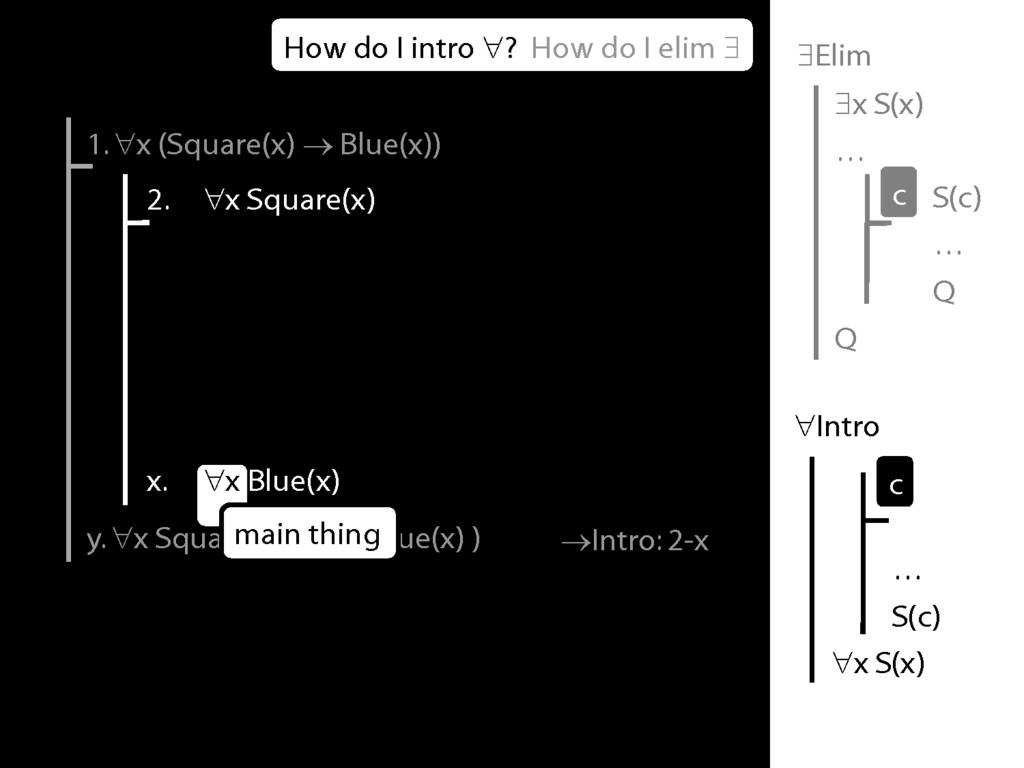
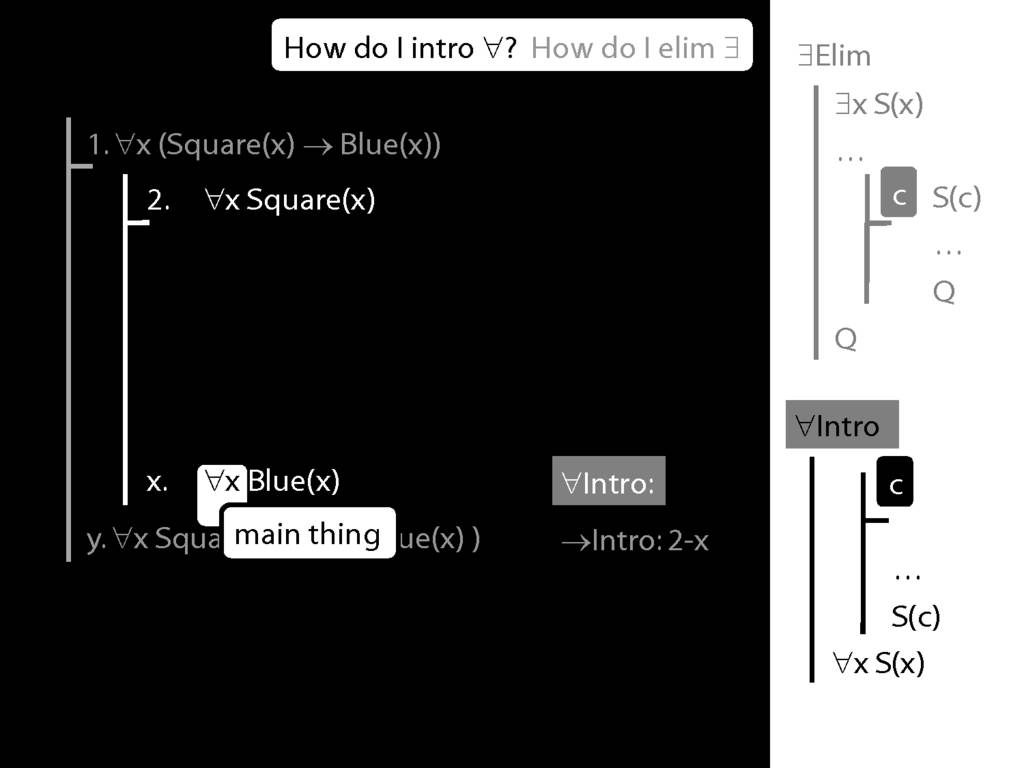
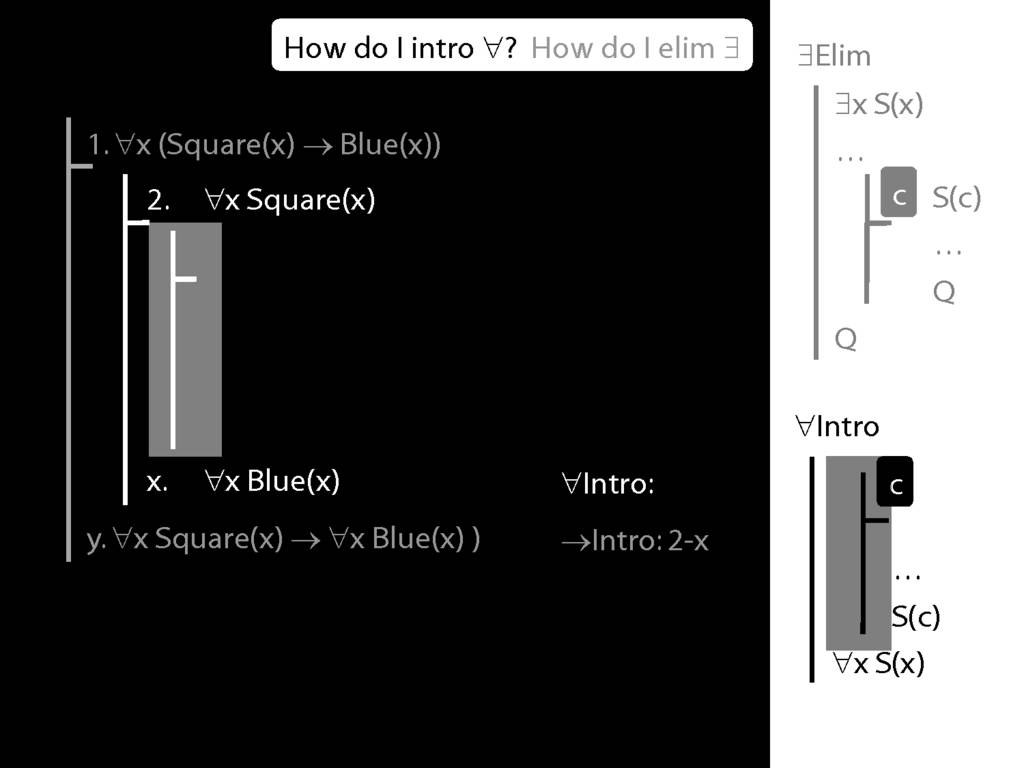
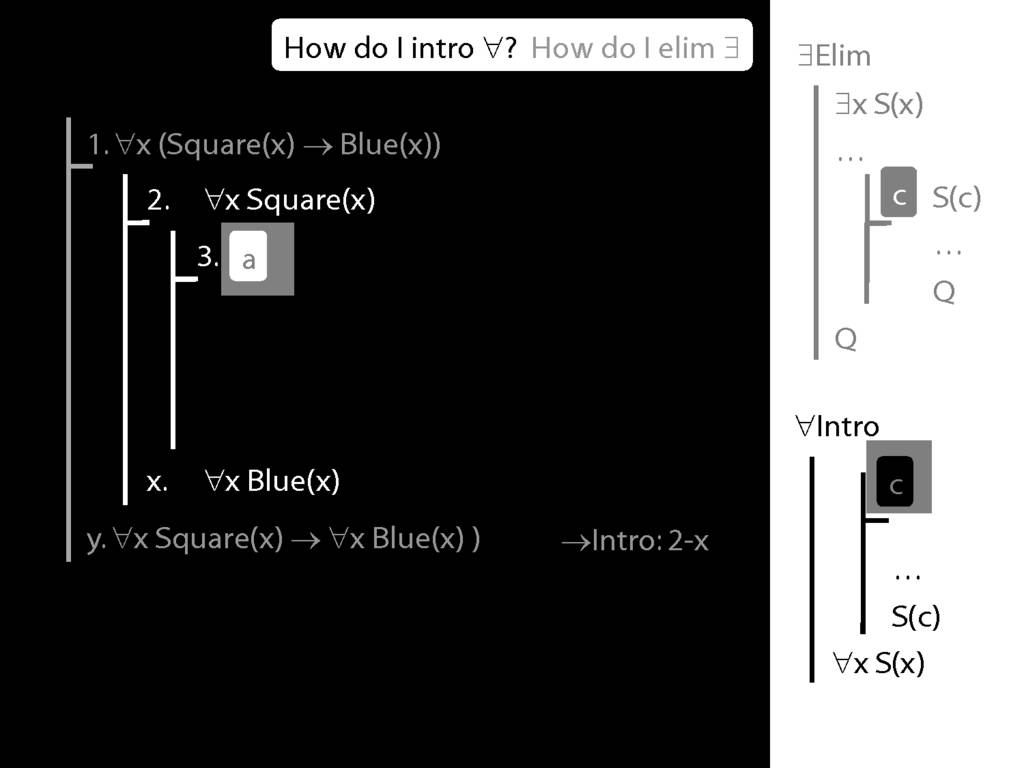
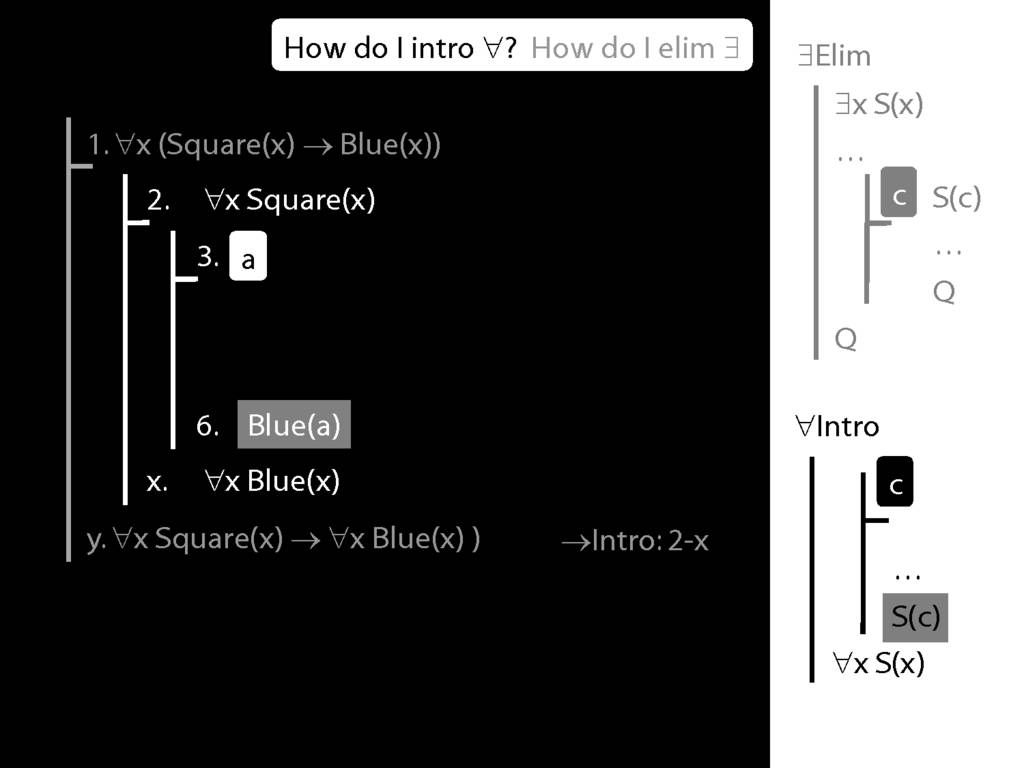
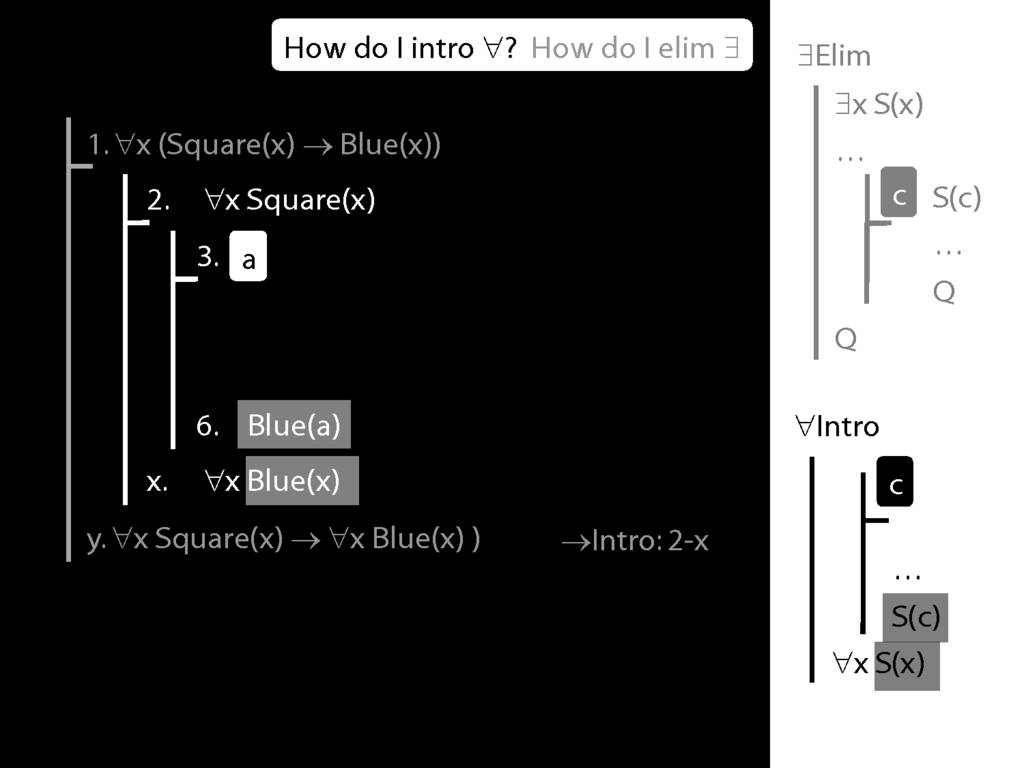
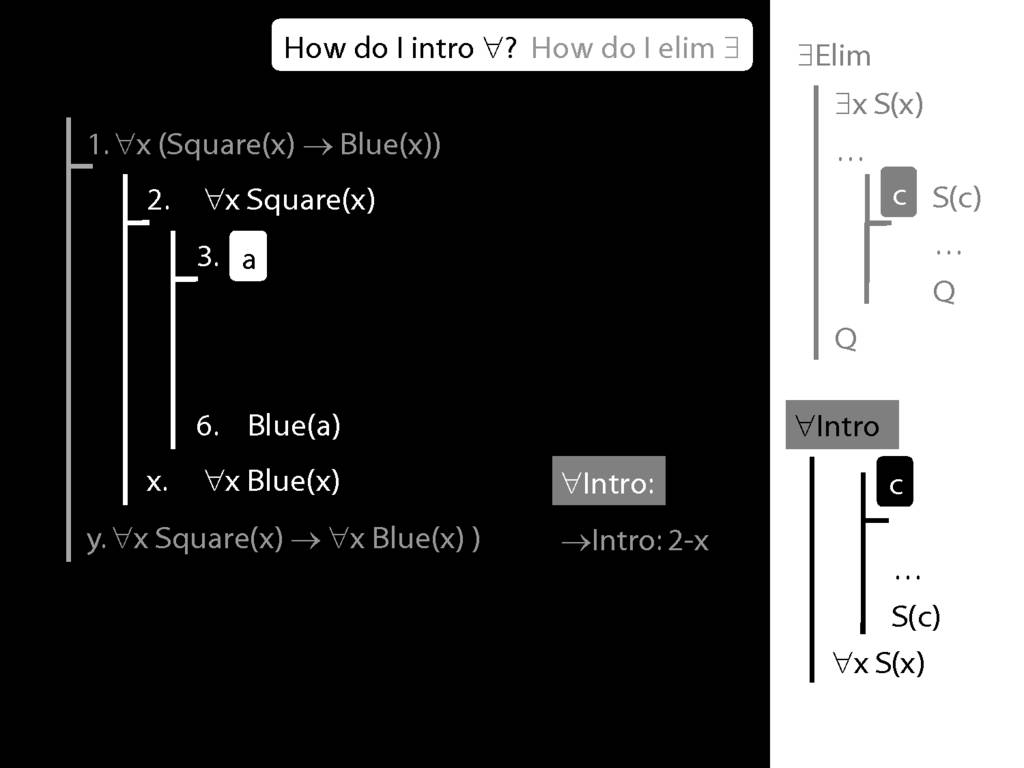
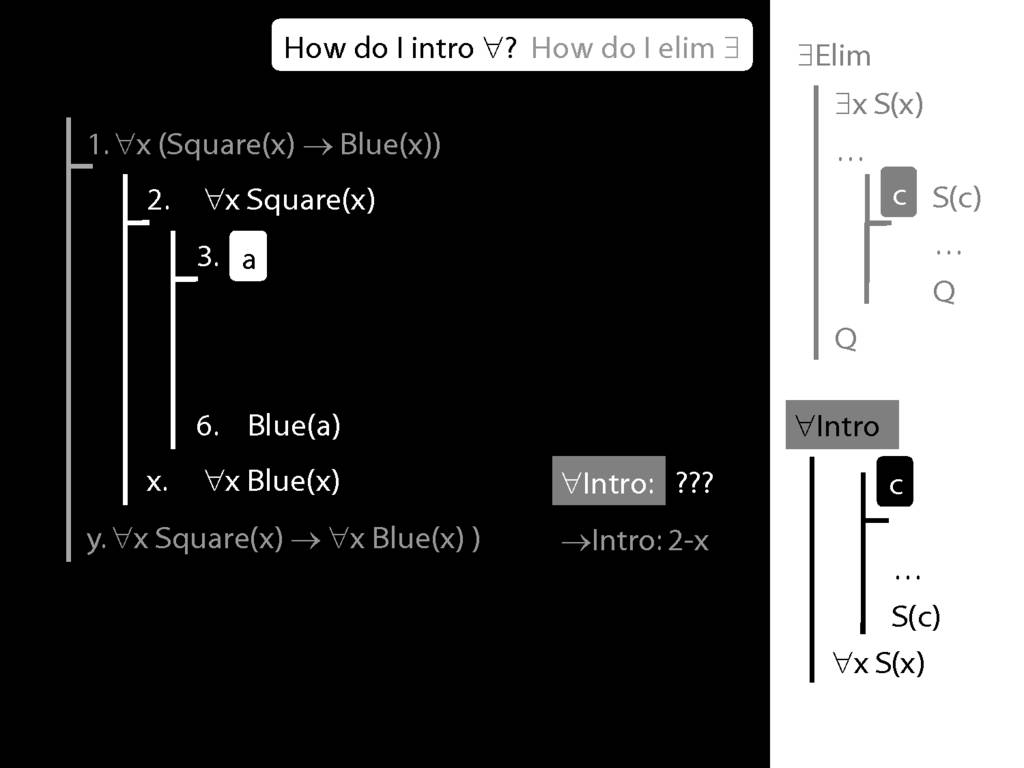
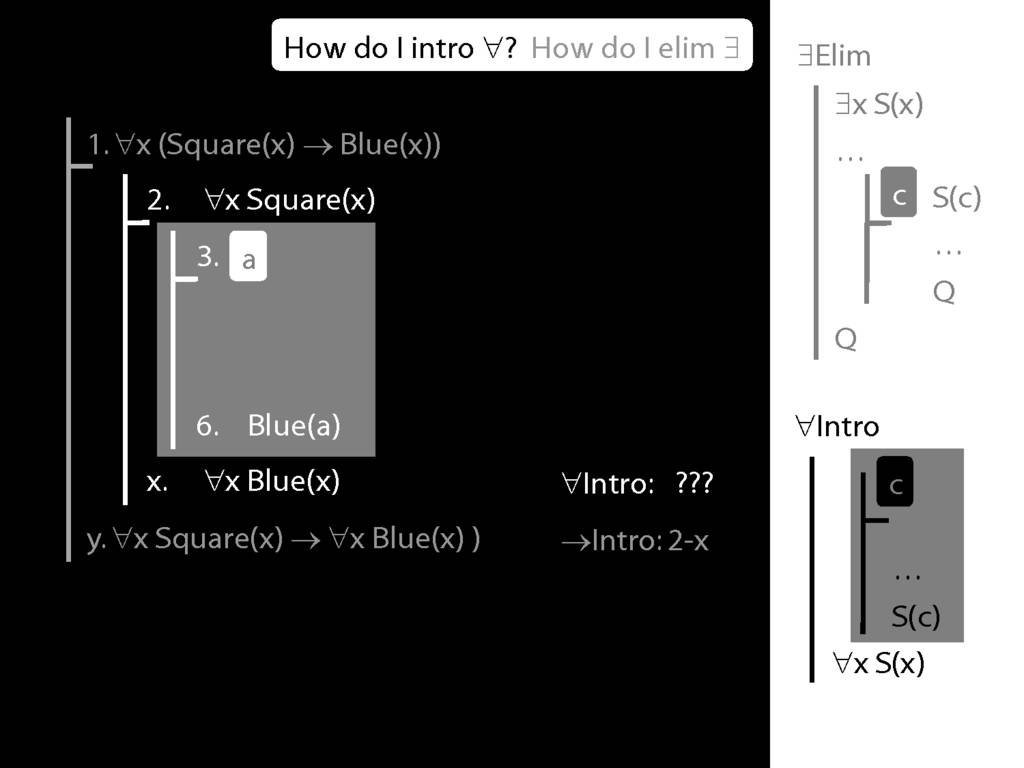
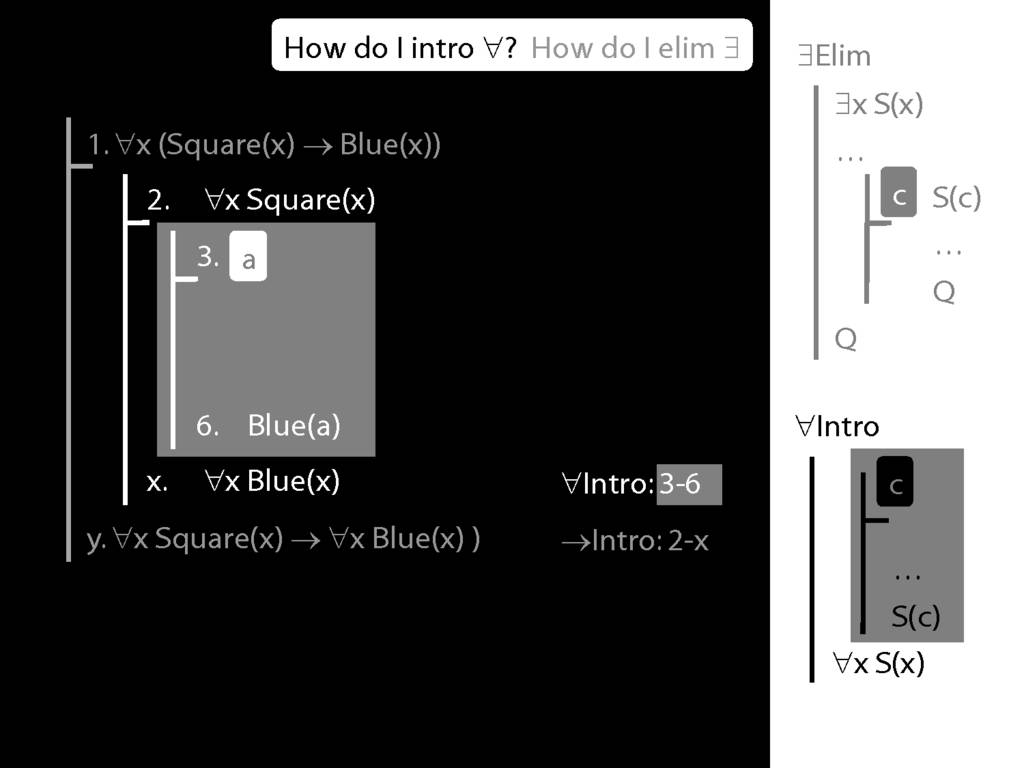
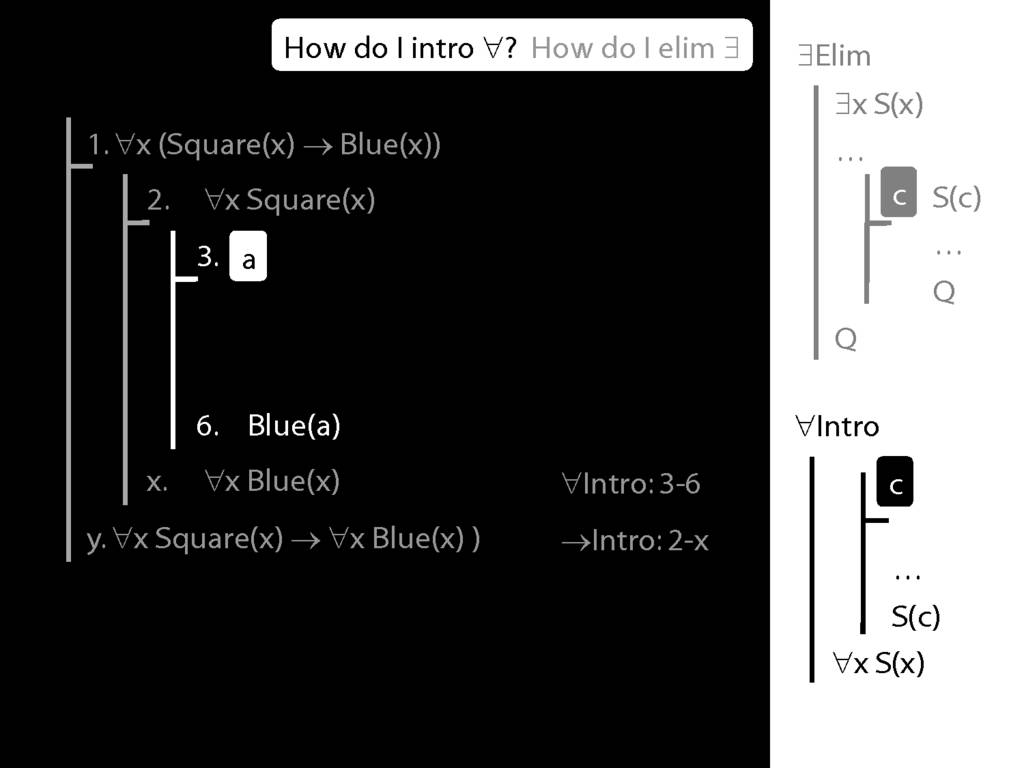
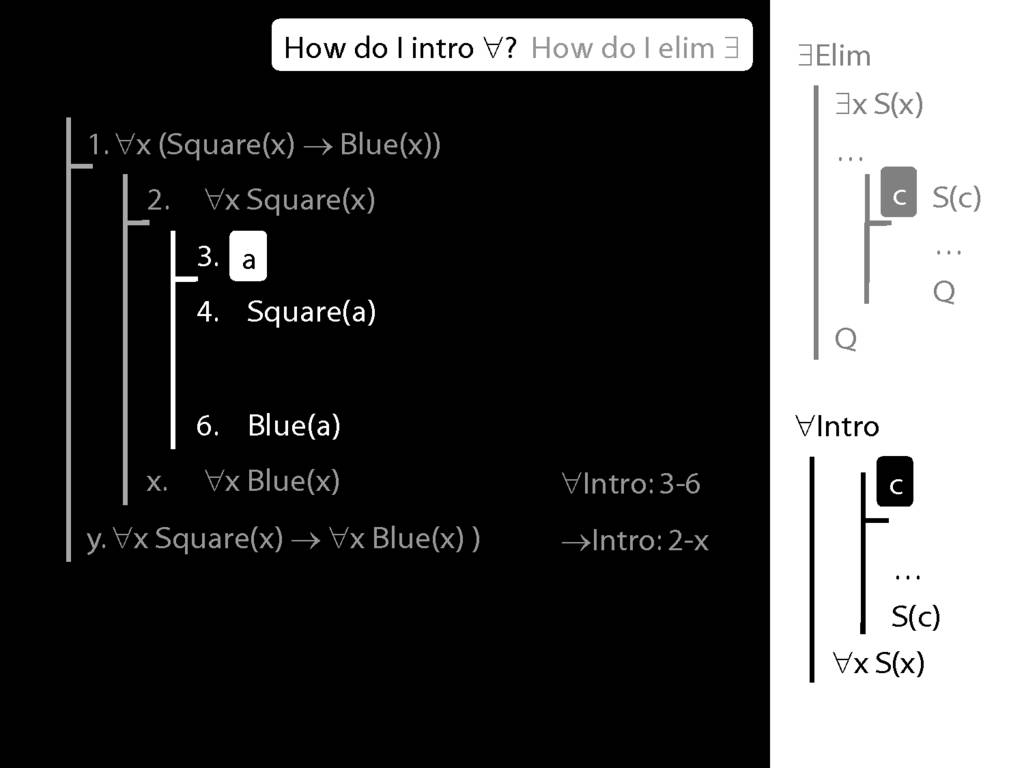
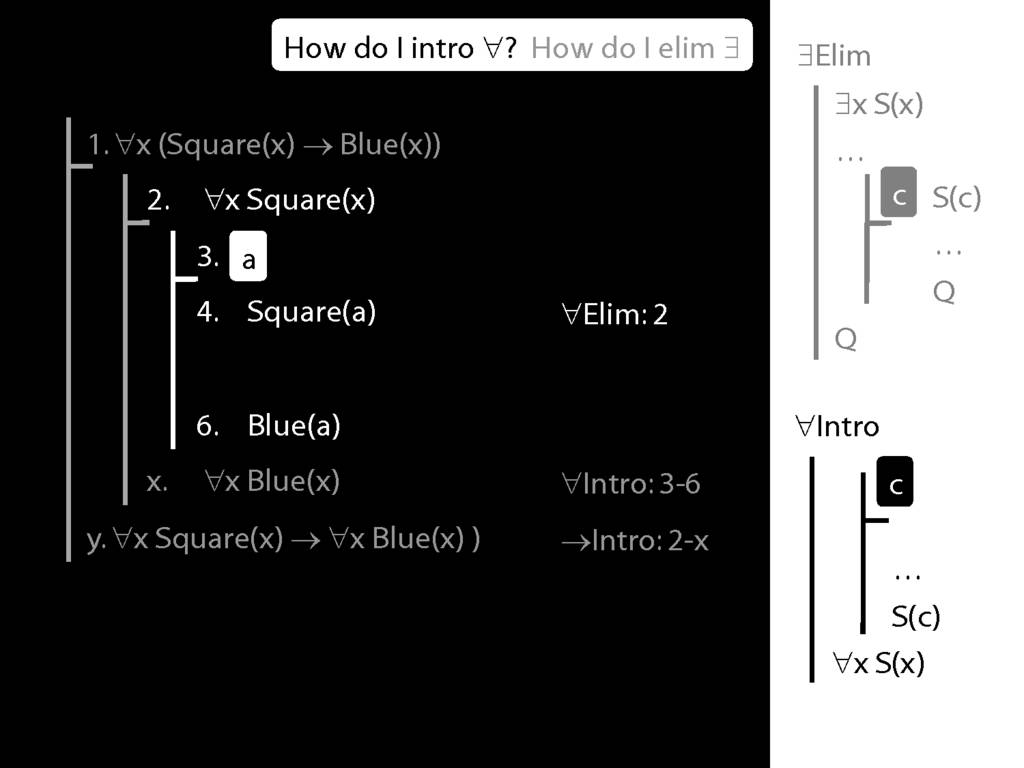
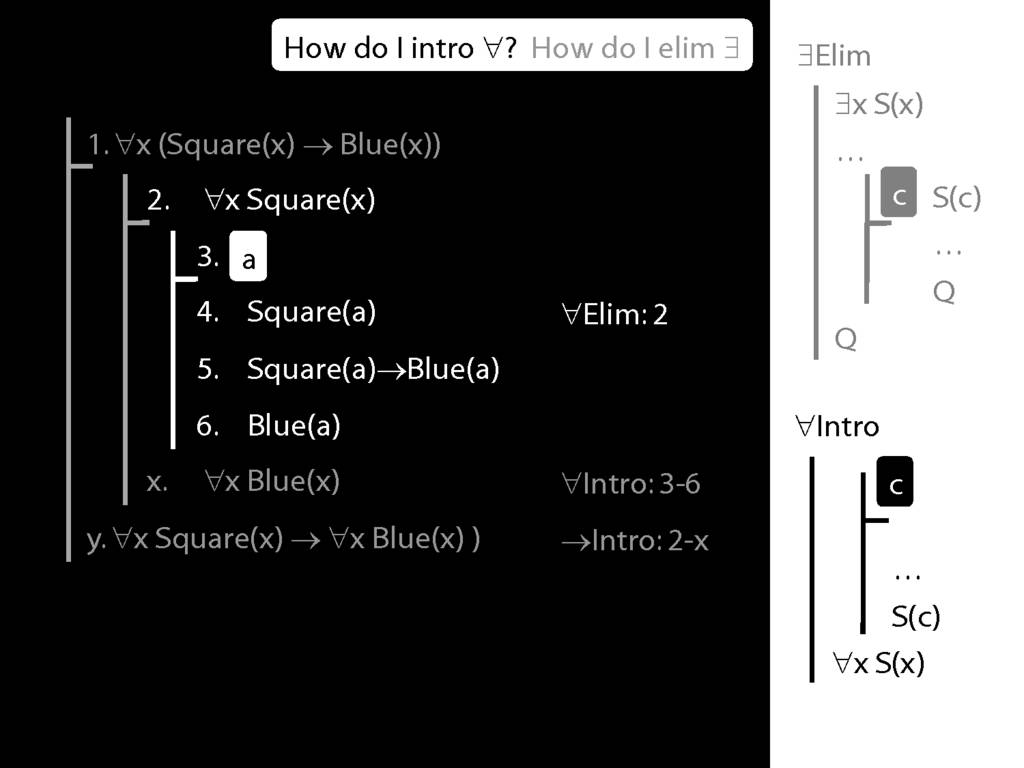
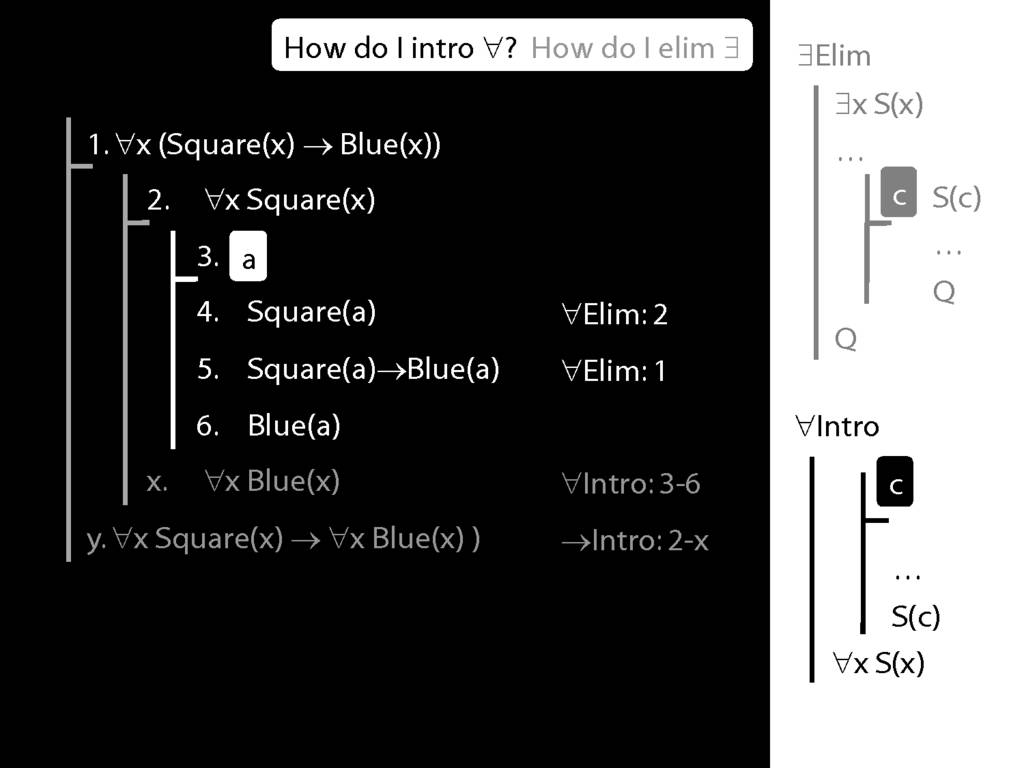
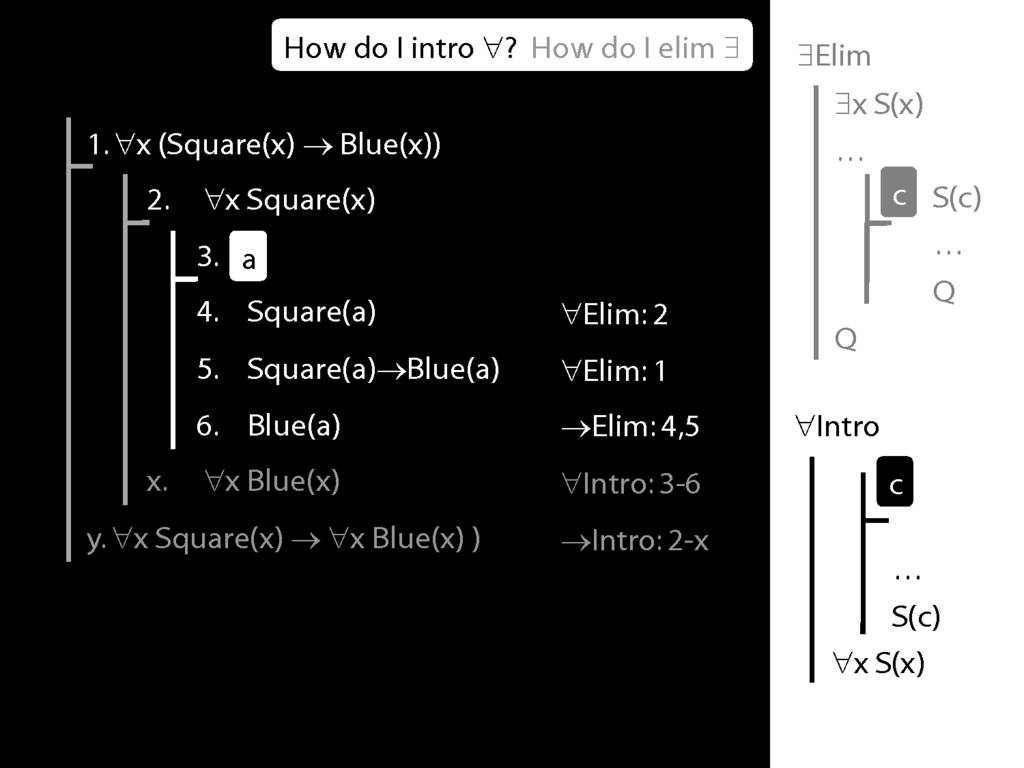
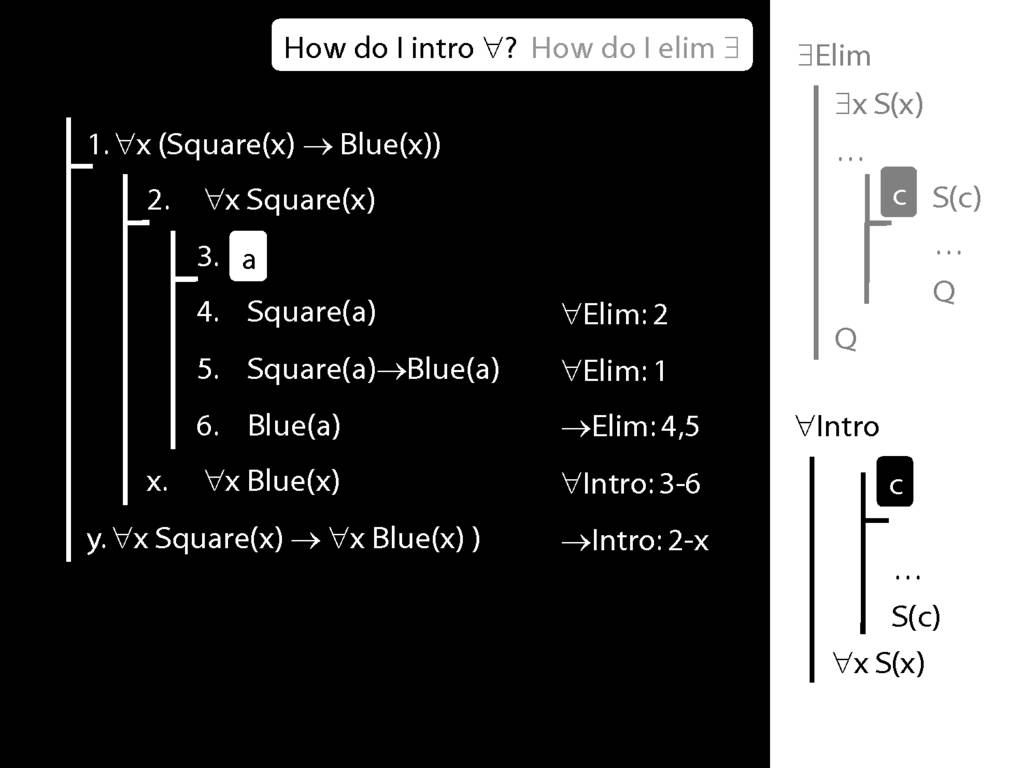
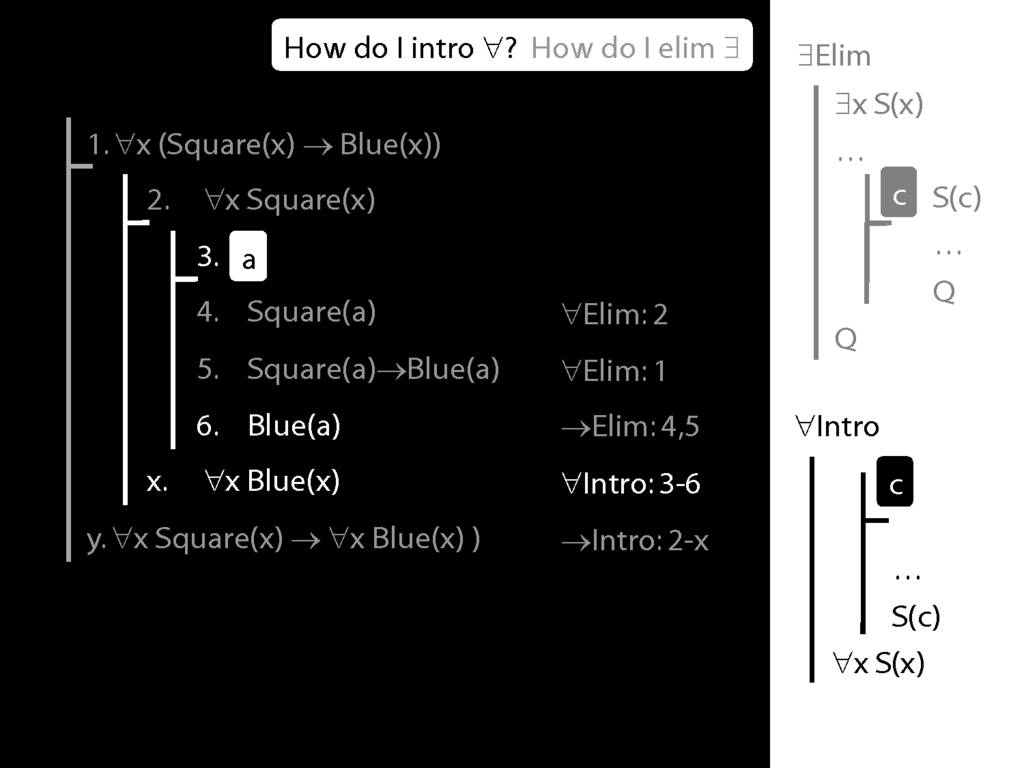
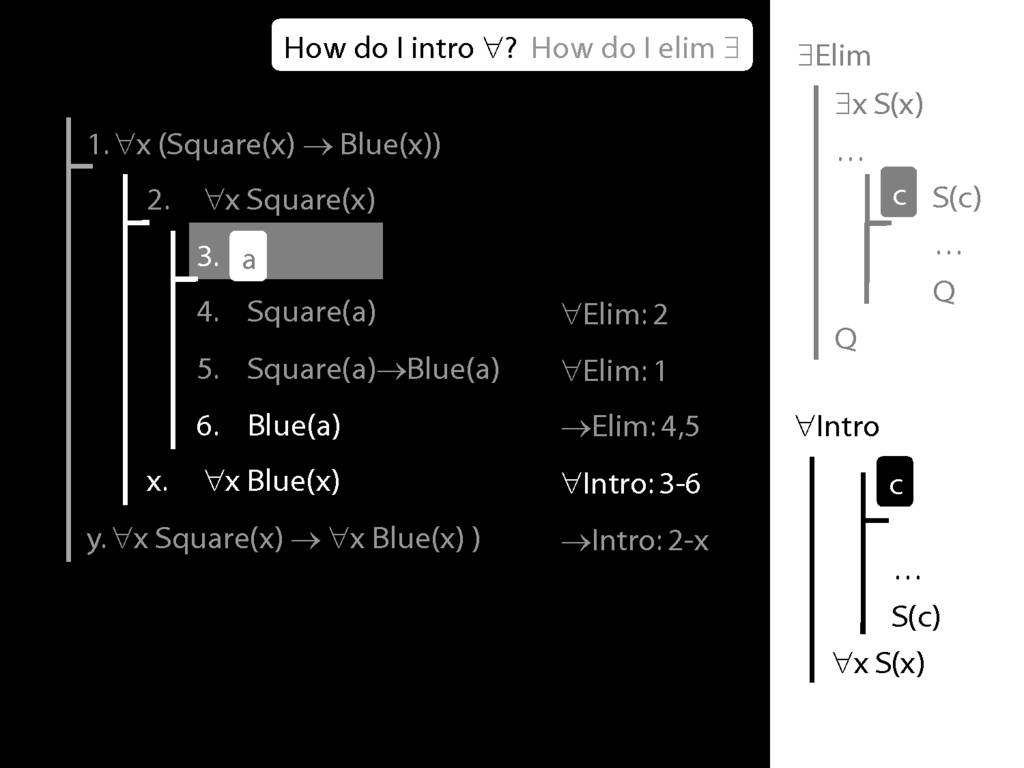
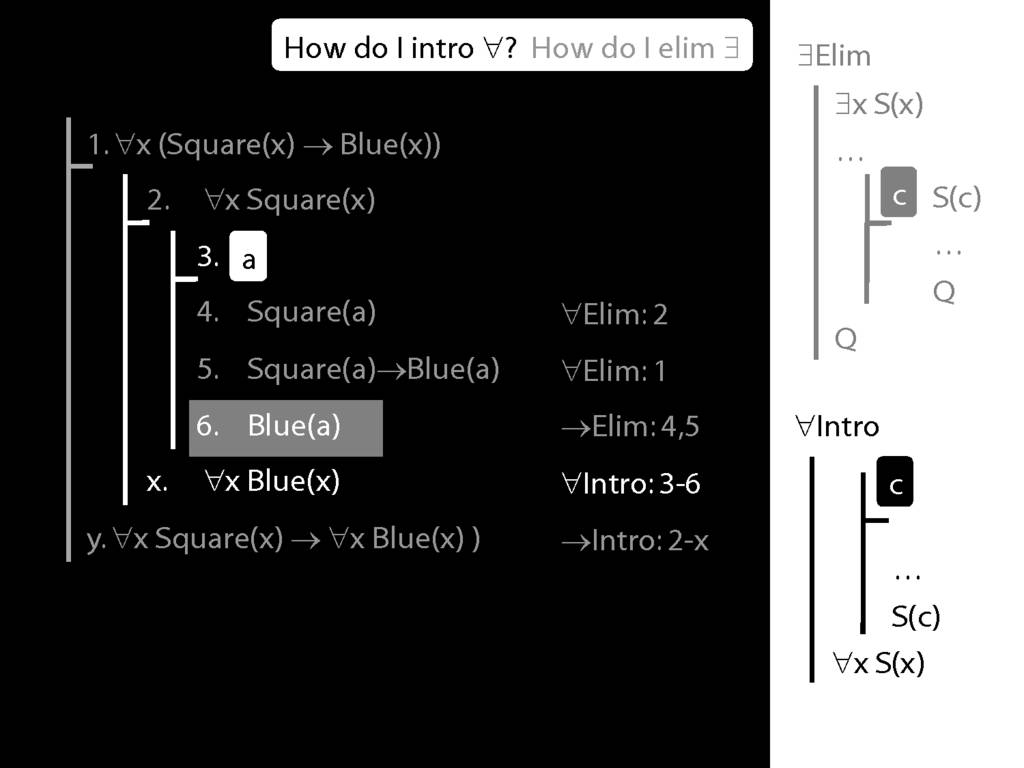
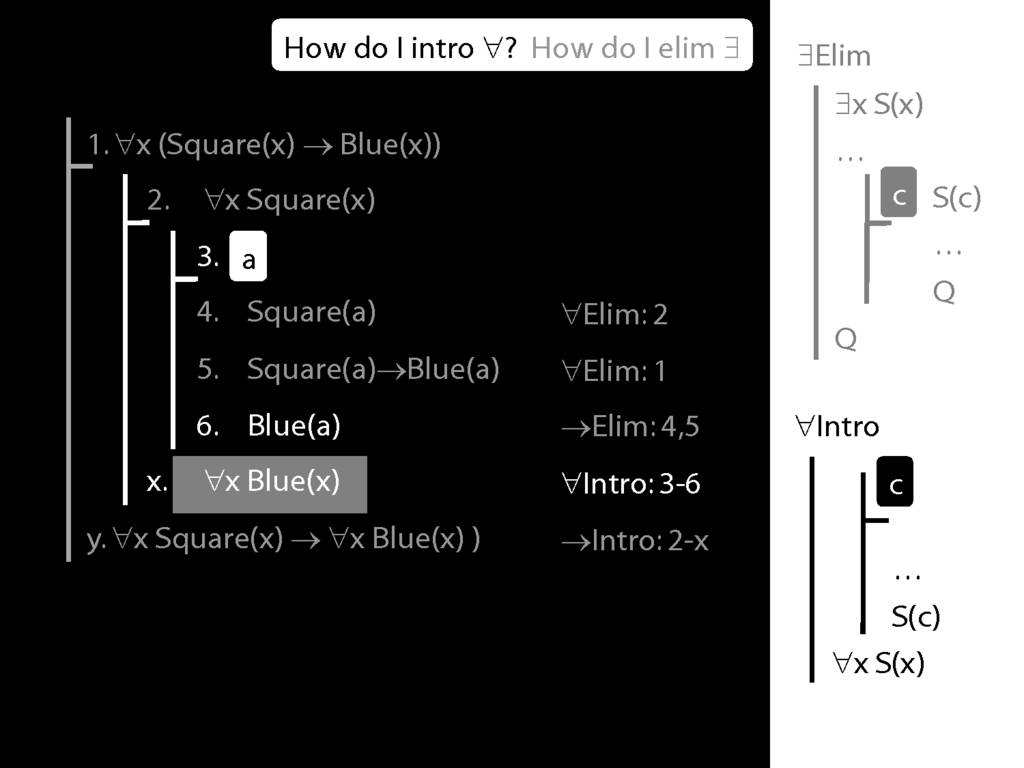
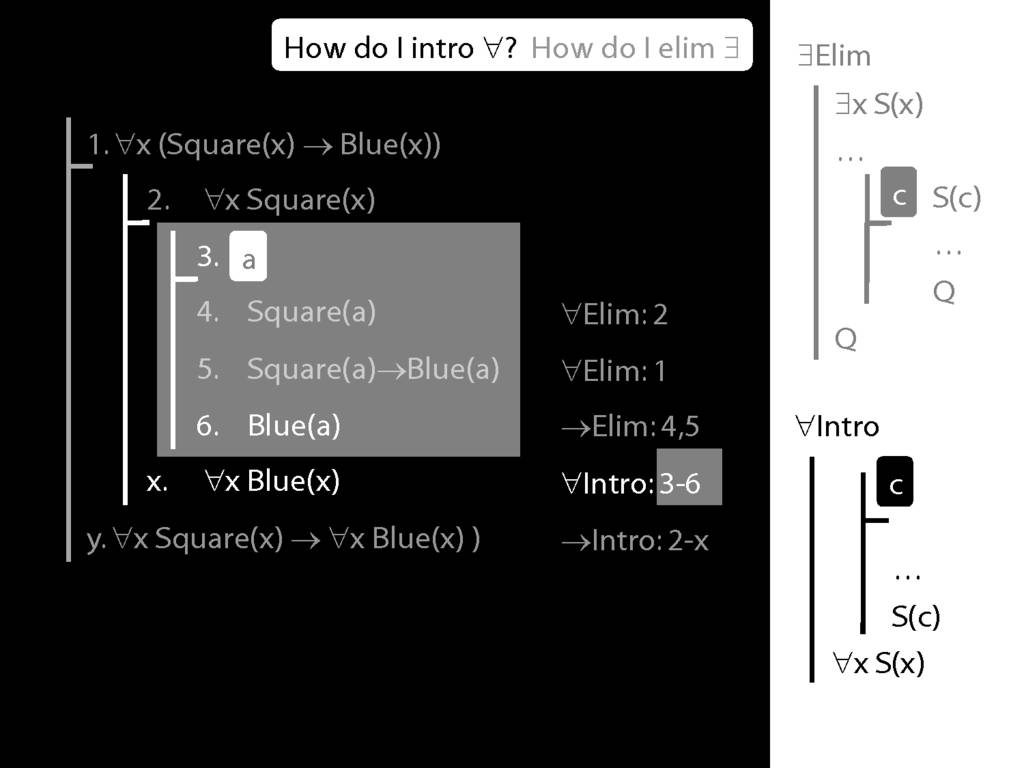
\section{Subproofs Are Tricky: The Answer}
 

∀Intro

 
\section{∀Intro}
\emph{Reading:} §12.1, §12.3, §13.1
 
\section{∀Intro}
\begin{minipage}{\columnwidth}
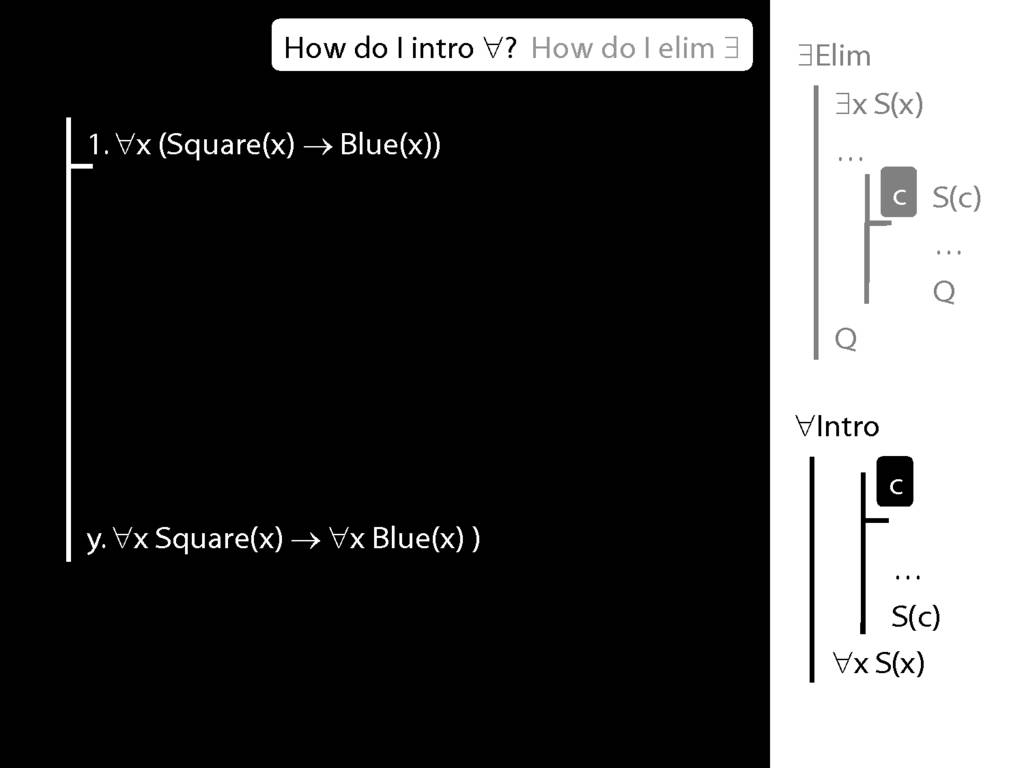
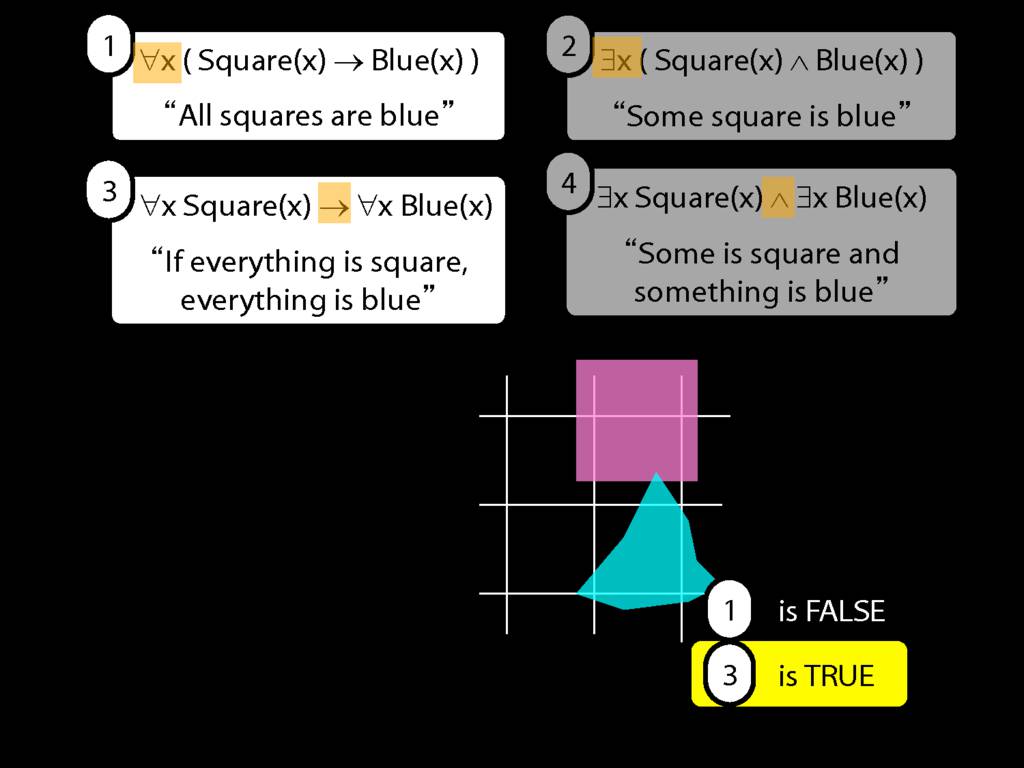
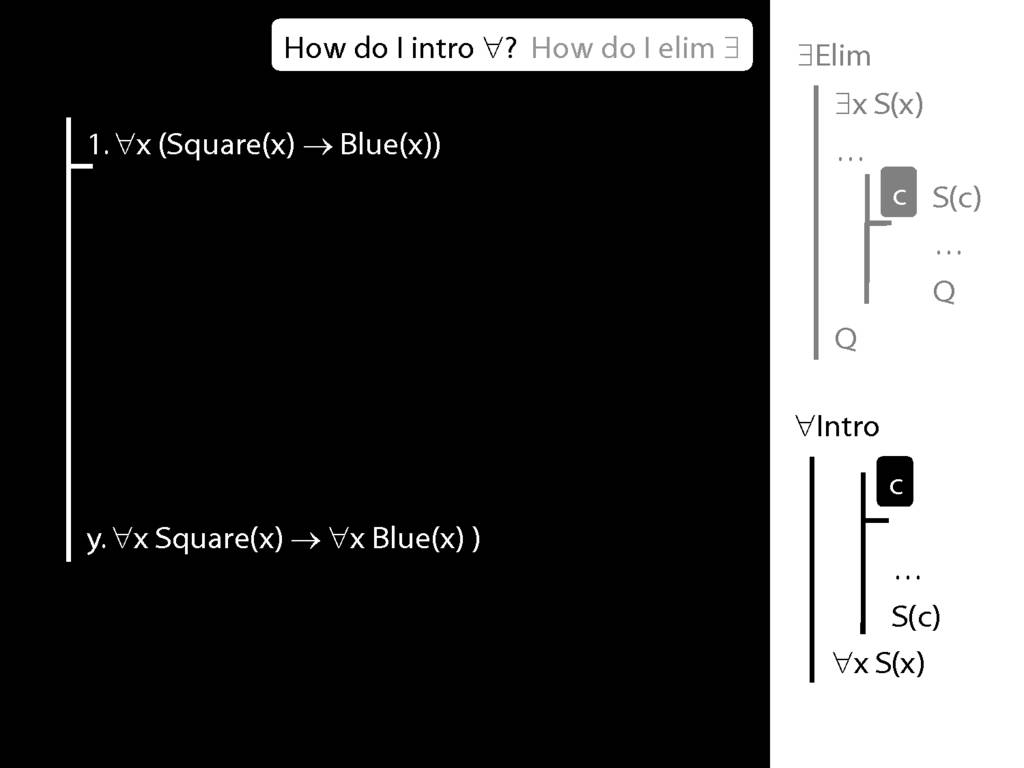
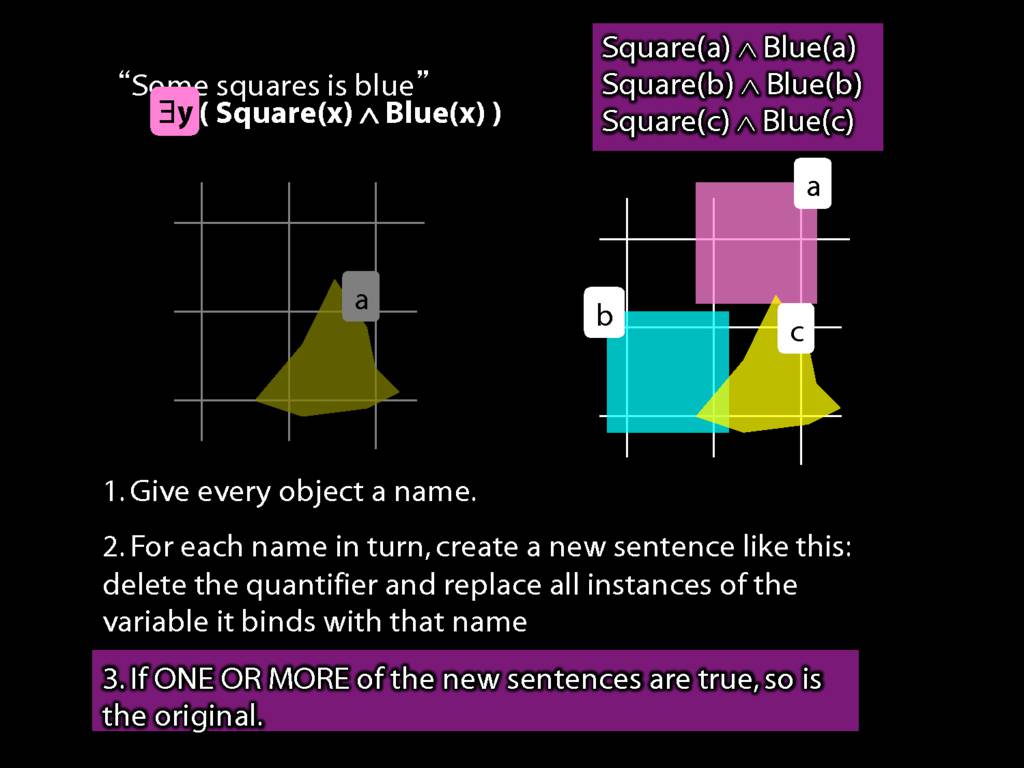
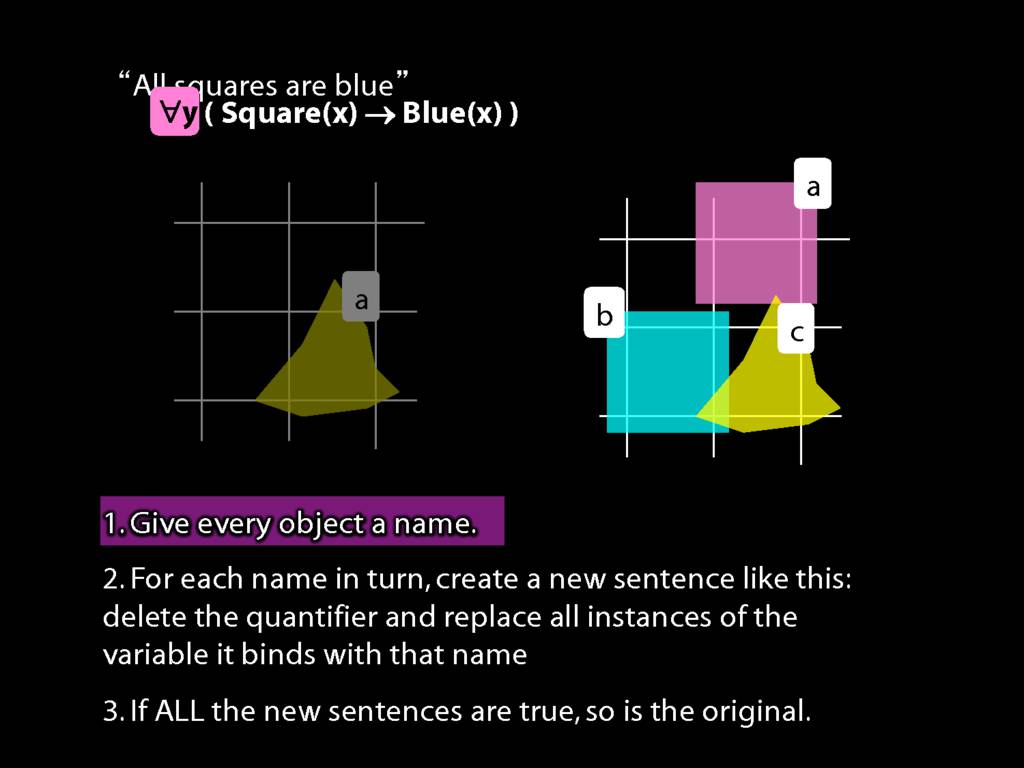
Why is this proof incorrect?
\end{minipage}
12.4--12.5
*12.6--12.7
12.9--12.10
 

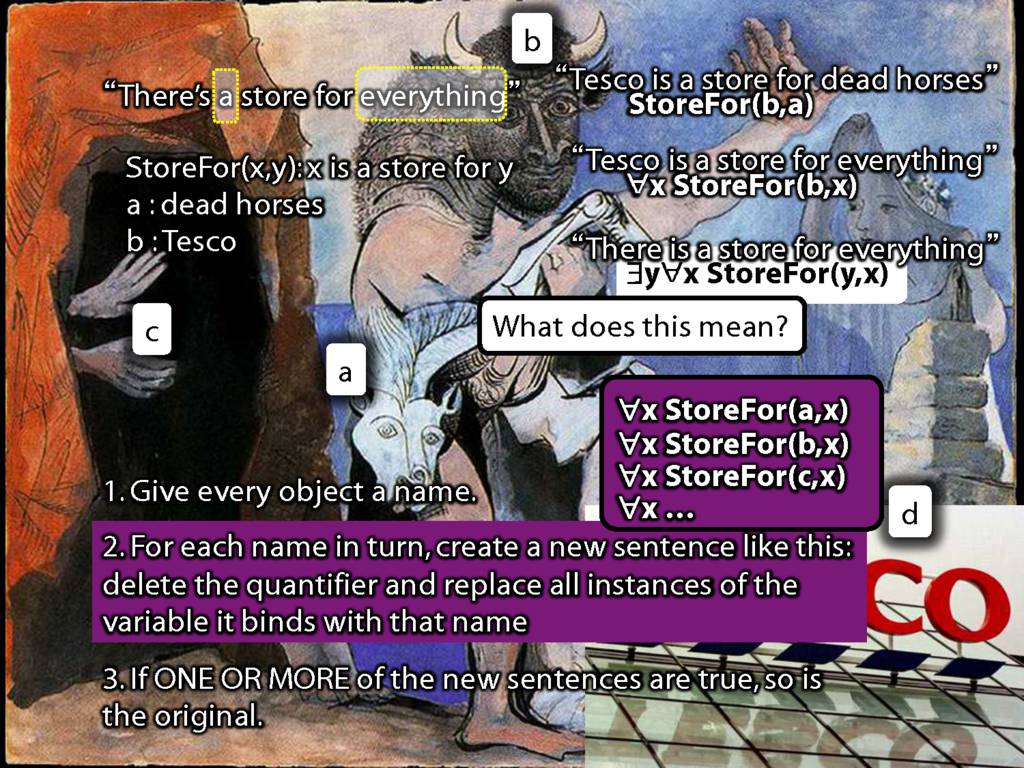
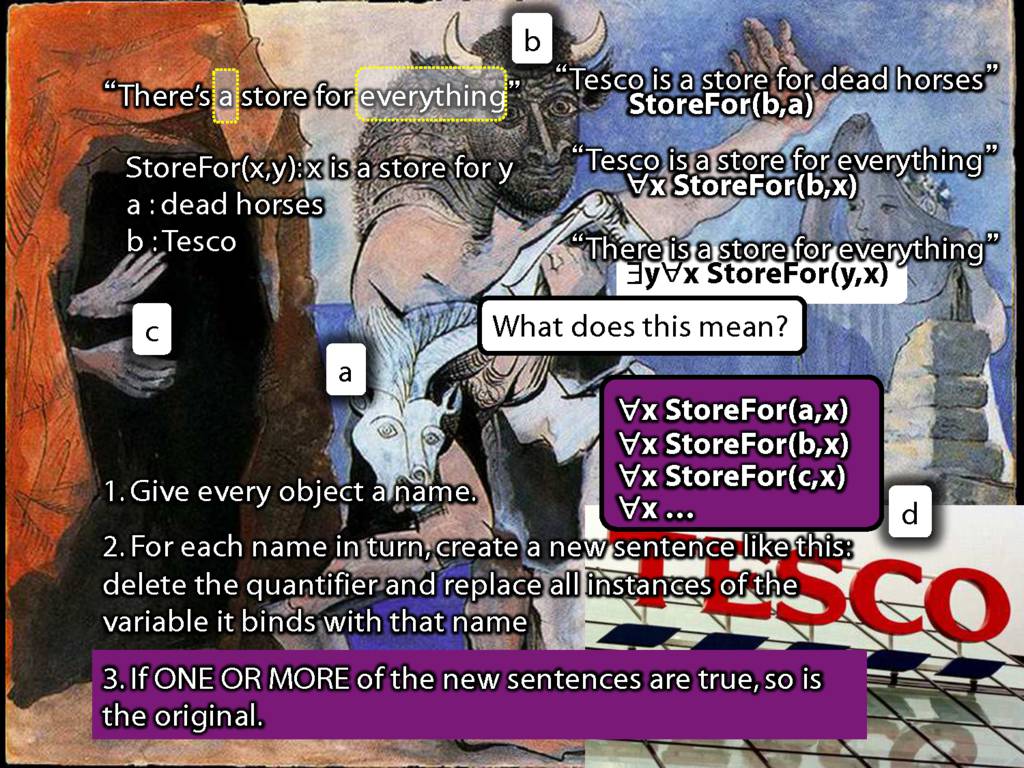
There Is a Store for Everything

 
\section{There Is a Store for Everything}
\emph{Reading:} §11.2, §11.3
 
\section{There Is a Store for Everything}
There is a store for everything:
\hspace{3mm} ∃y∀x StoreFor(y,x)
\hspace{3mm} ∀y∃x StoreFor(x,y)
Other sentences to translate:
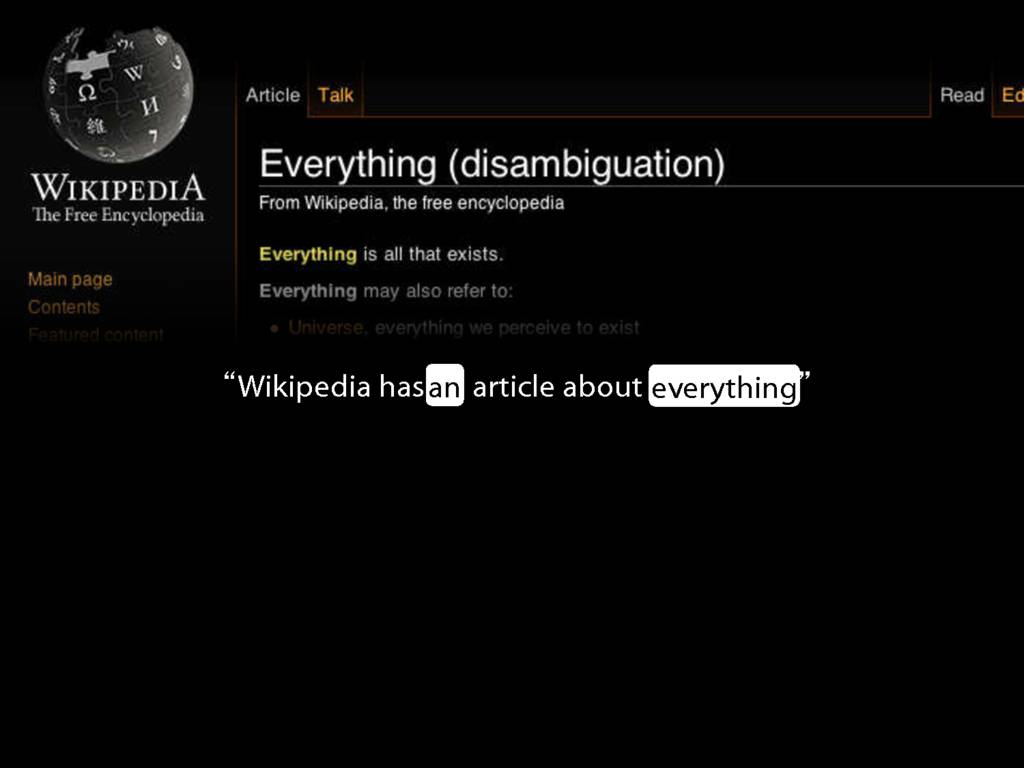
\hspace{3mm} Wikipedia has an article about everything
\hspace{3mm} Everyone hurts someone they love
\hspace{3mm} Someone hurts everyone she loves
11.3
11.4, 11.8, 11.9
11.11, 11.13, *11.10
11.8, 11.9, *11.11
 

Variables

 
\section{Variables}
 
\section{Variables}
Names : a, b, c, …
Variables : x, y, z, w, …
Variables are for saying several things about one thing even without specifying which thing it is
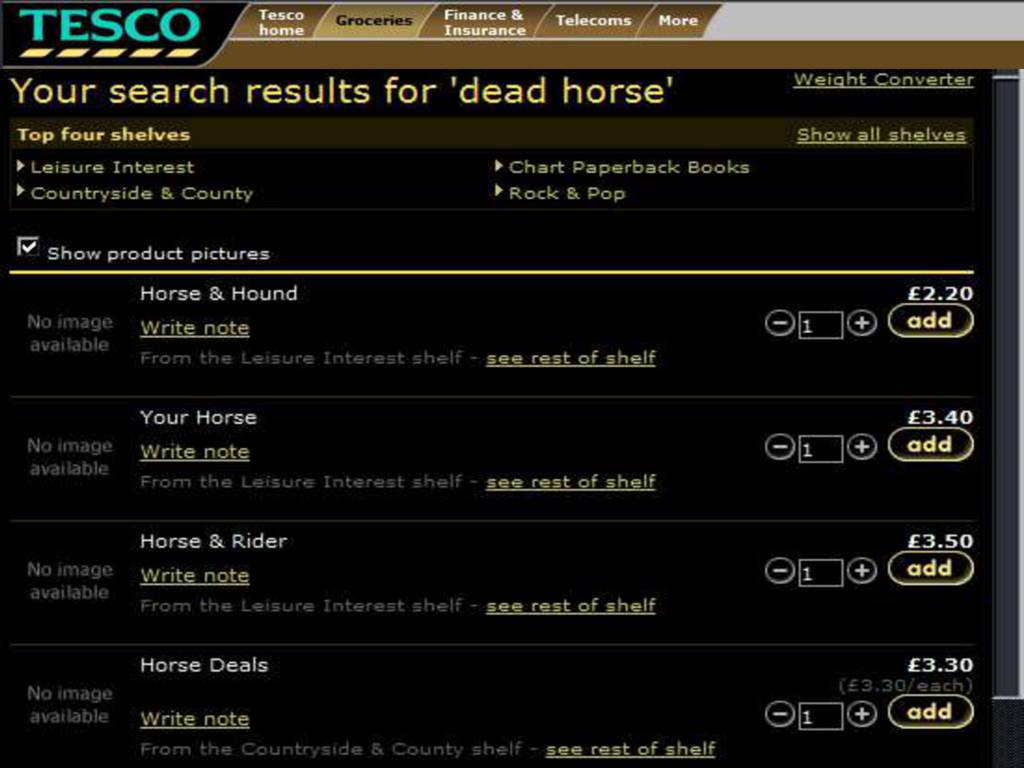
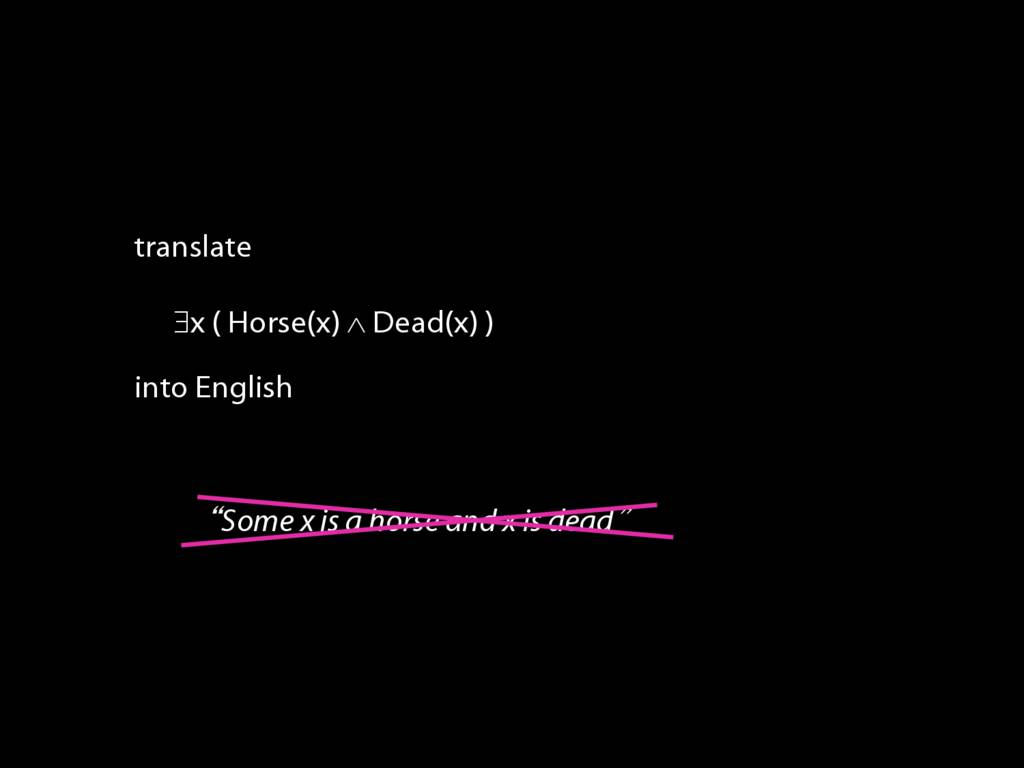
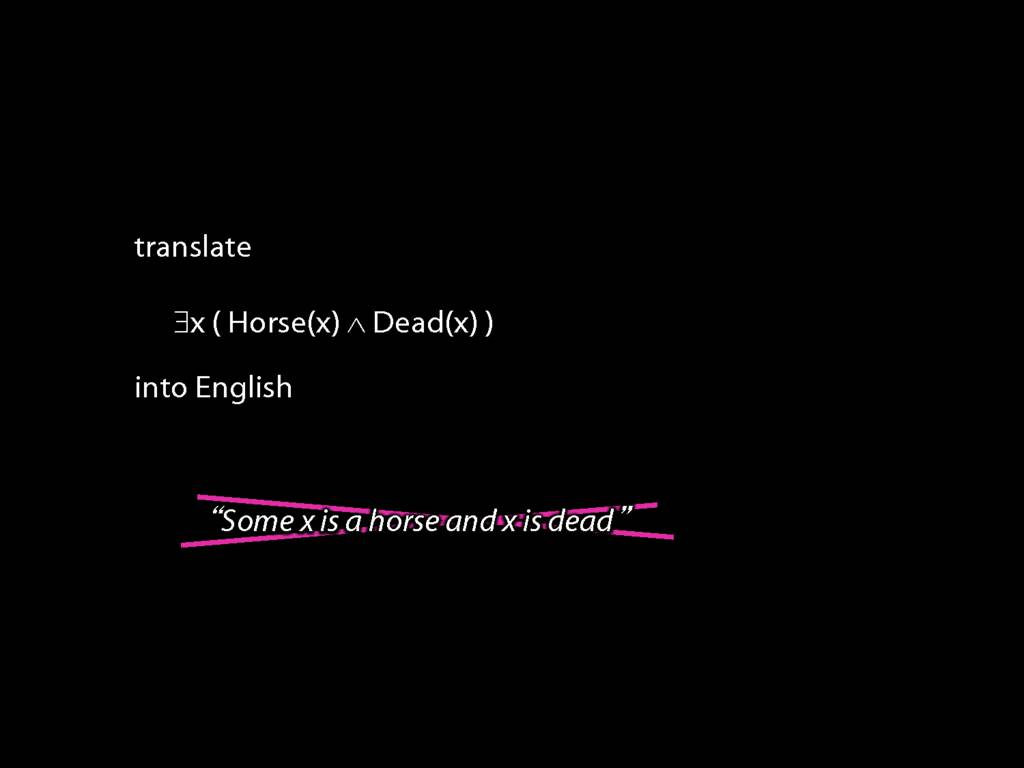
NB: `Some x is a horse and x is dead' ain't English.
 

Loving and Being Loved

 
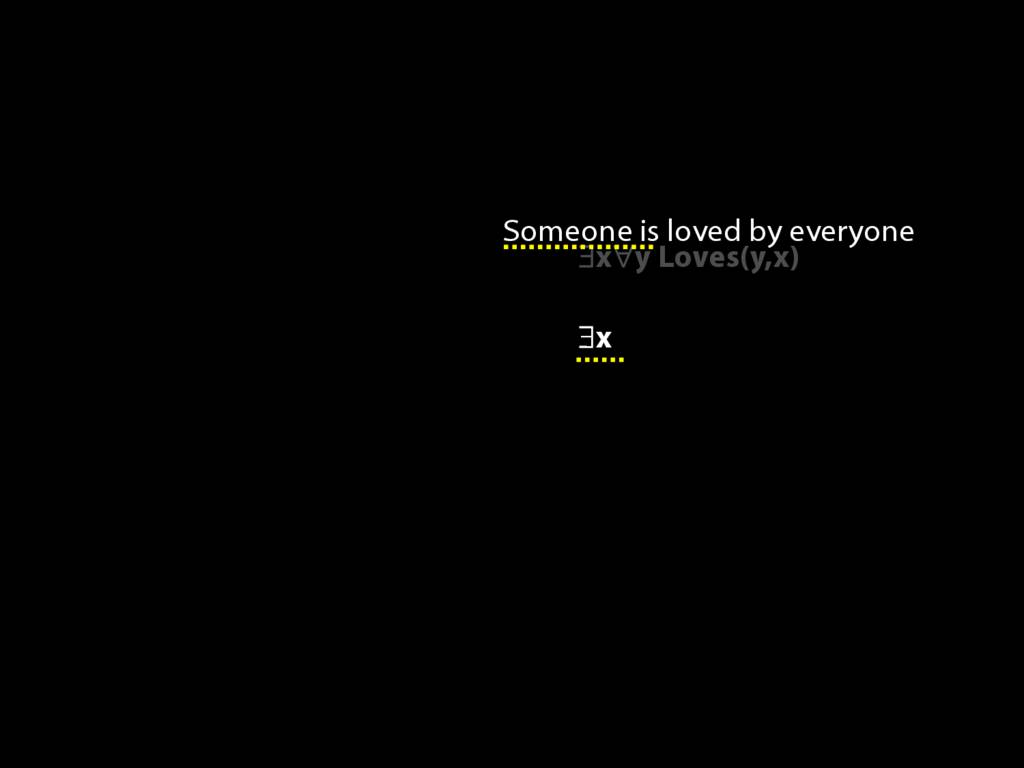
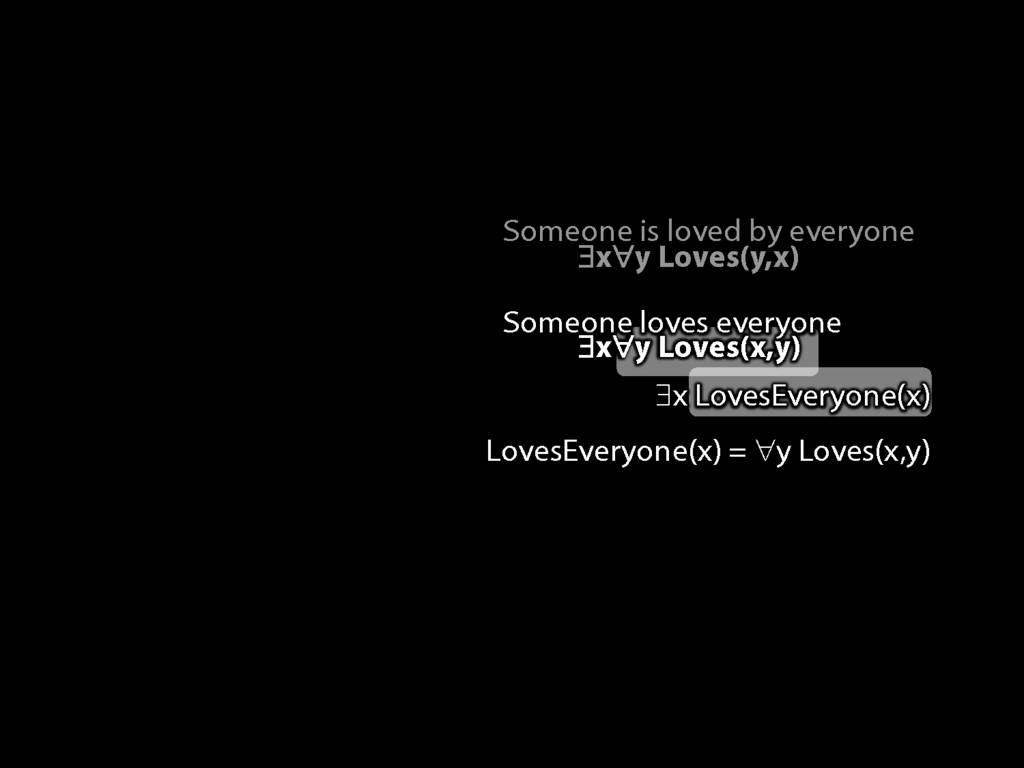
\section{Loving and Being Loved}
\emph{Reading:} §11.2, §11.3
 
\section{Loving and Being Loved}
 

Somebody Is Not Dead

 
\section{Somebody Is Not Dead}
 
\section{Somebody Is Not Dead}
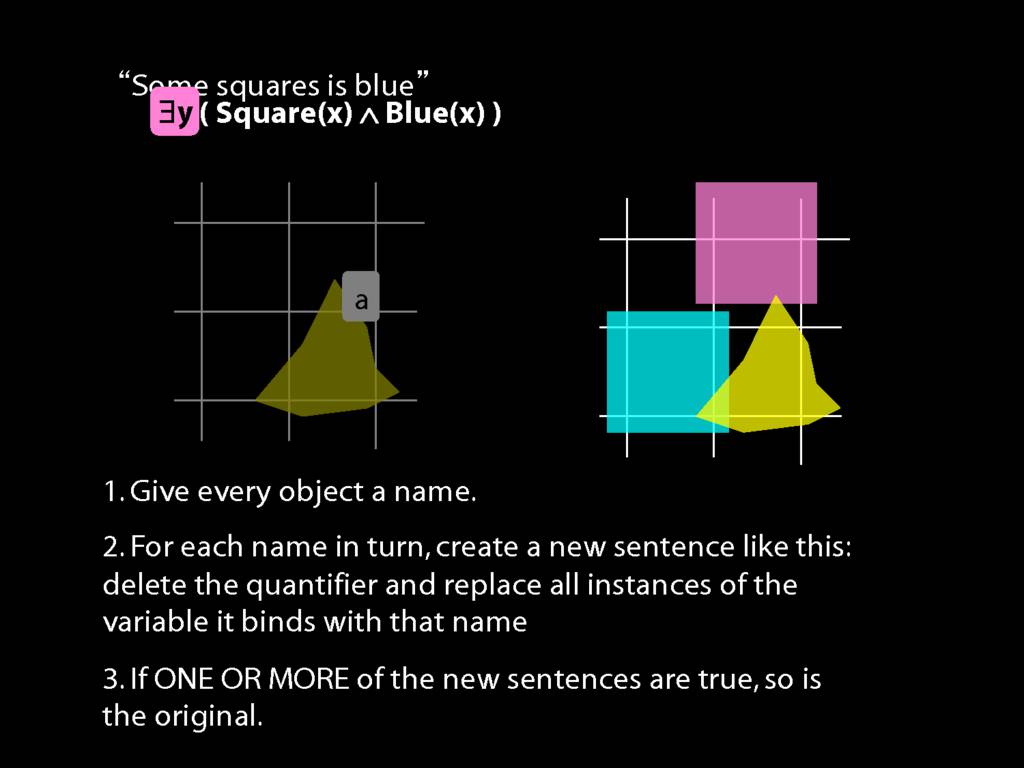
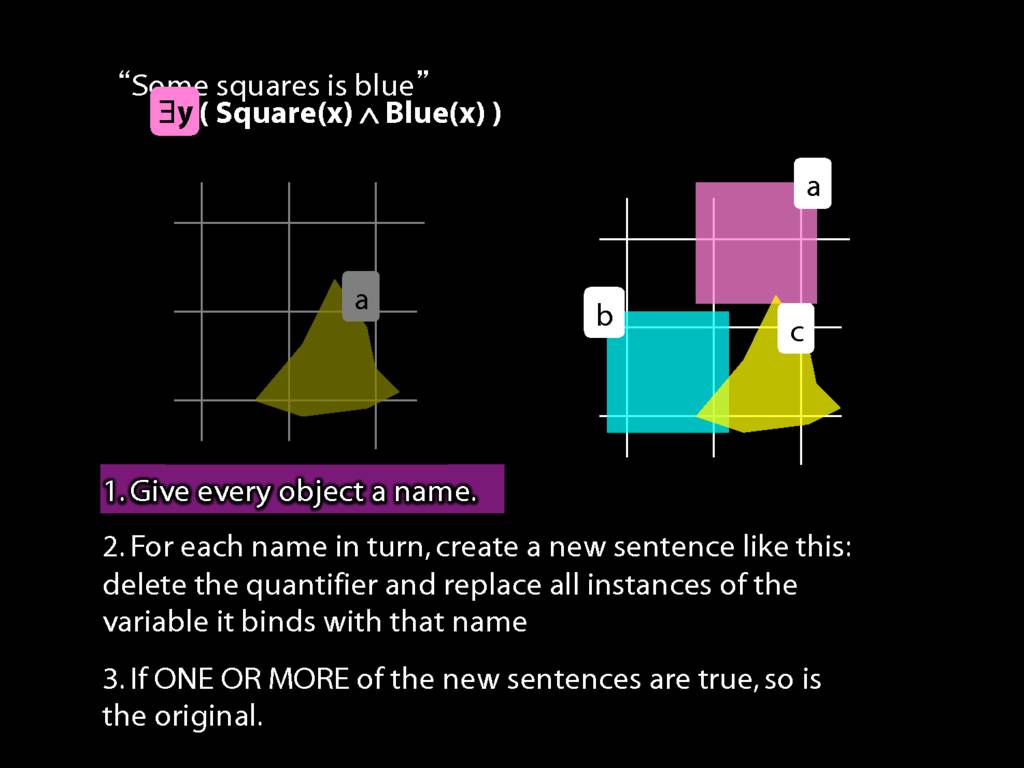
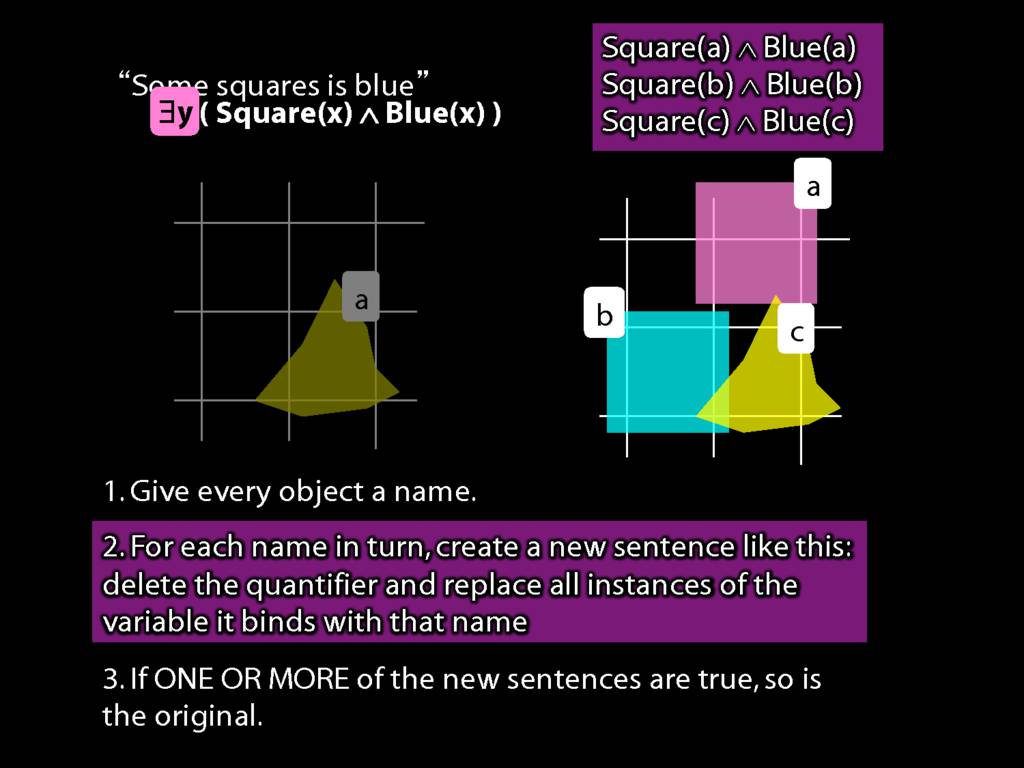
Some person is dead.
\hspace{5mm} ∃x(Person(x) ∧ Dead(x))
Some person is not dead.
\hspace{5mm} ∃x(Person(x) ∧ ¬Dead(x))
No person is dead.
\hspace{5mm} ¬∃x(Person(x) ∧ Dead(x))
Every person is dead.
\hspace{5mm} ∀x(Person(x) → Dead(x))
Every person is not dead.
\hspace{5mm} ∀x(Person(x) → ¬Dead(x))
Not every person is dead.
\hspace{5mm} ¬∀x(Person(x) → Dead(x))

Some person is dead.

∃x(Person(x) ∧ Dead(x))

Some person is not dead.

∃x(Person(x) ∧ ¬Dead(x))

No person is dead.

¬∃x(Person(x) ∧ Dead(x))

Every person is dead.

∀x(Person(x) → Dead(x))

Every person is not dead.

∀x(Person(x) → ¬Dead(x))

Not every person is dead.

¬∀x(Person(x) → Dead(x))

#
 

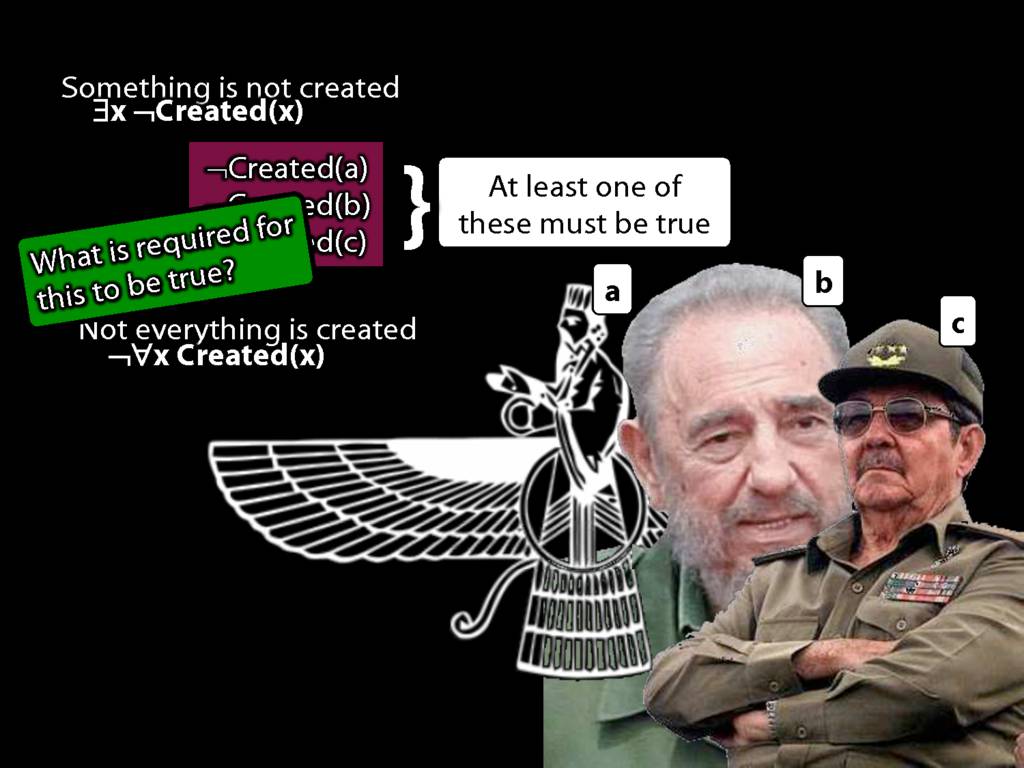
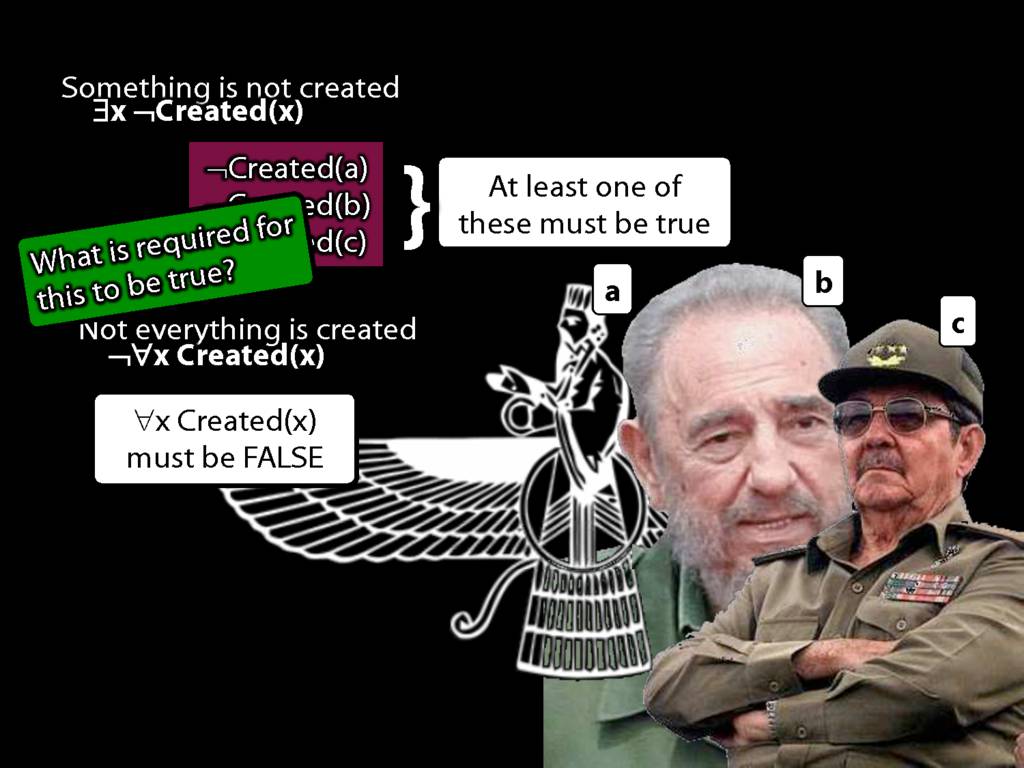
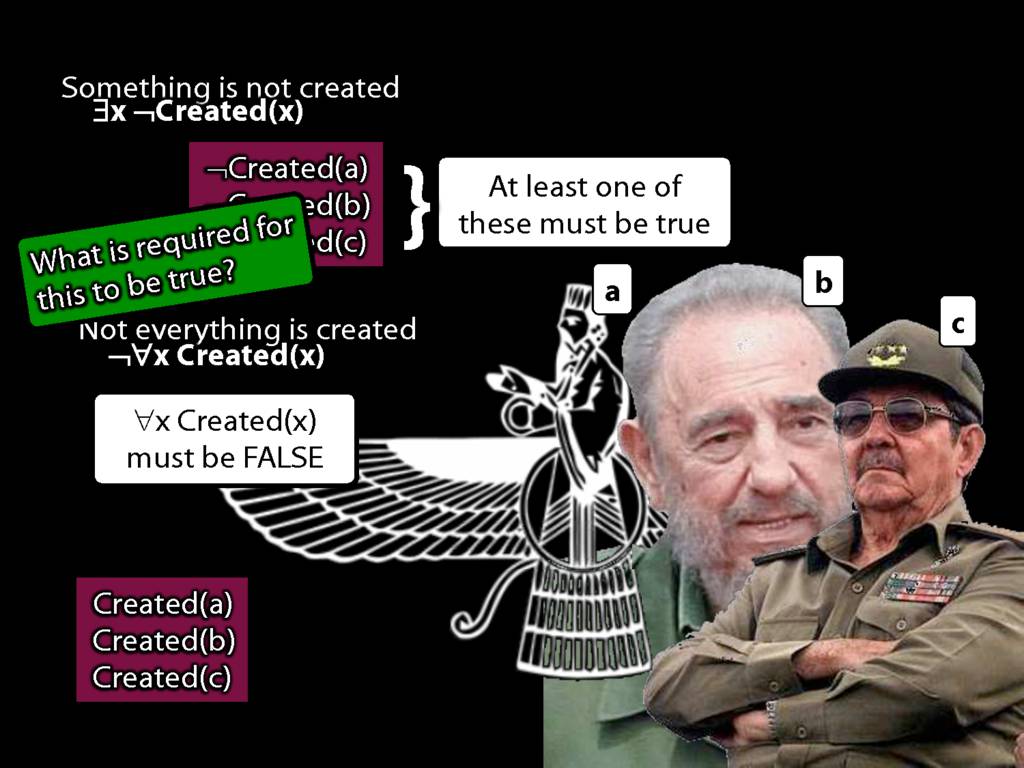
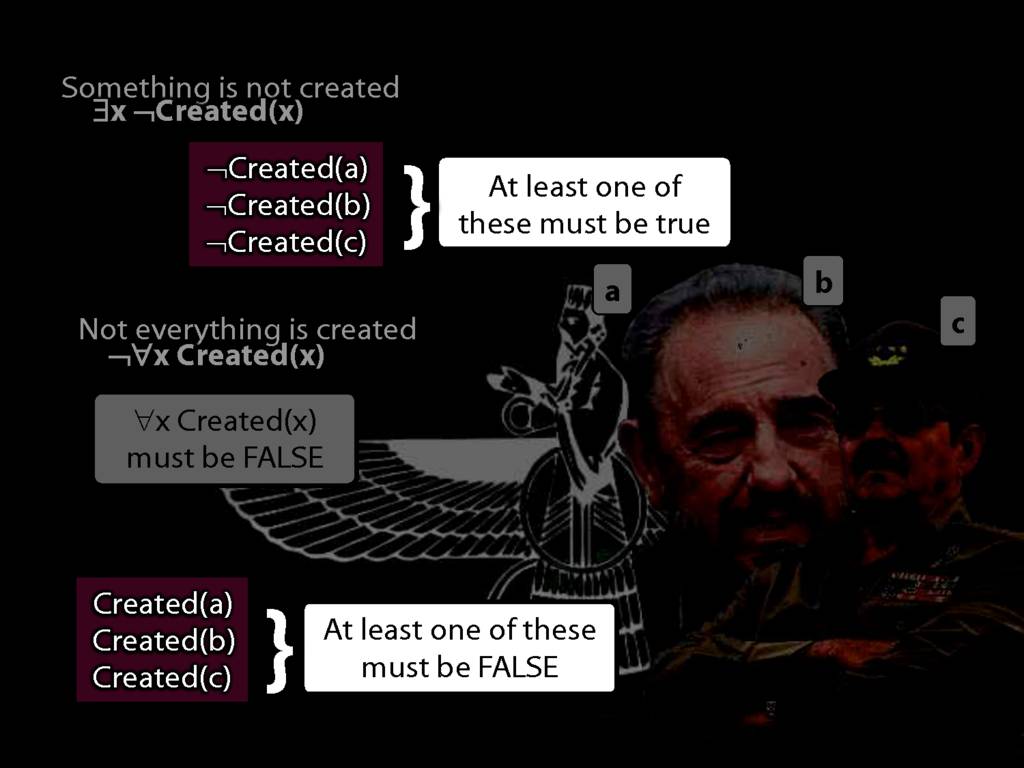
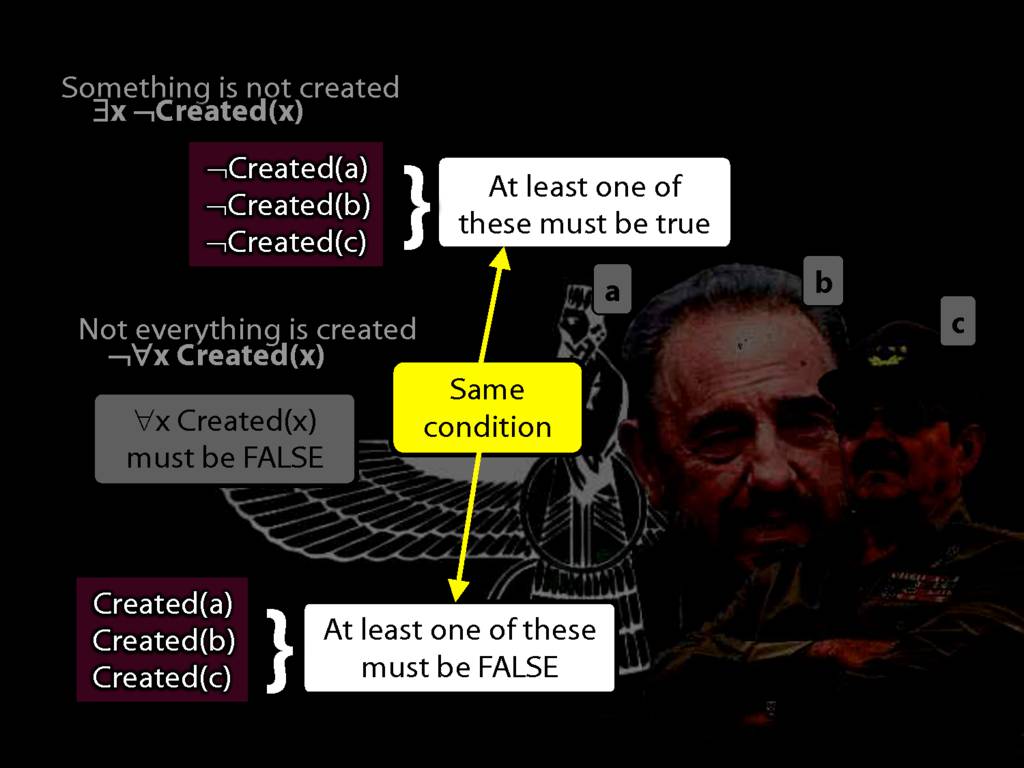
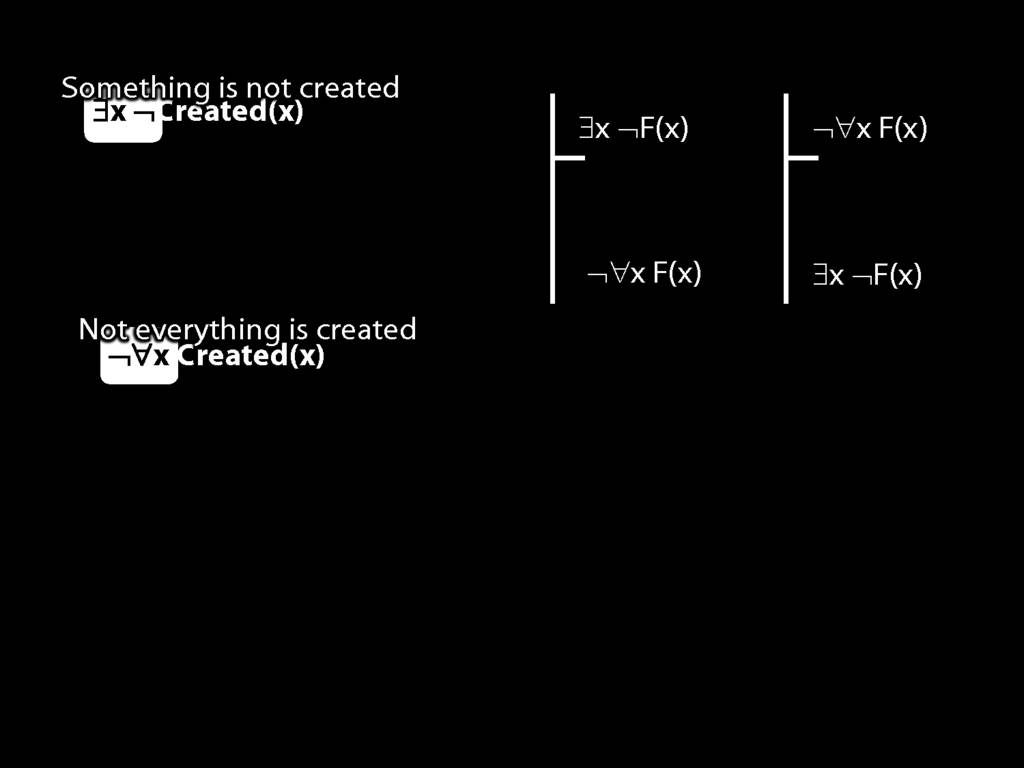
Quantifier Equivalences: ¬∀x Created(x) ⫤⊨ ∃x ¬Created(x)

 
\section{Quantifier Equivalences: ¬∀x Created(x) ⫤⊨ ∃x ¬Created(x)}
\emph{Reading:} §10.1, §10.3, §10.4
 
\section{Quantifier Equivalences: ¬∀x Created(x) ⫤⊨ ∃x ¬Created(x)}
 
\section{The End Is Near}
\emph{Reading:} §14.3
 
\section{The End Is Near}
‘The’ can be a quantifier, e.g. ‘the square is broken’. How to formalise it?
The square is broken \\ ⫤⊨ There is exactly one square and it is broken
Recall that we can translate `There is exactly one square' as:
\hspace{5mm} ∃x ( Square(x) ∧ ∀y ( Square(y) → x=y ) )
So `There is exactly one square and it's broken':
\hspace{5mm} ∃x ( Sqr(x) ∧ ∀y ( Sqr(y) → x=y ) ∧ Broken(x) )

There is an end, and all ends are this end, and it is near.

∃x ( End(x) ∧ ∀y ( End(y) → x=y ) ∧ Near(x) )

14.26, 14.28
14.2
14.4, 14.5
14.10, 14.11
14.26, 14.28