Last summer you and I were working on a farm herding pigs.
One evening we had almost got all of the pigs back into their sty for the night
when one of them escaped and ran off down the lane.
We closed the gate to secure the other pigs and ran off after
the escaped pig.
After a while we came to a fork in the lane.
I said, Either it went up the left fork or it went up the right fork.
You then said, It didn’t go up the left fork.
So off we ran up the right fork.
\textbf{Argument 1:} \begin{quote} Either it went up the left fork or it went up the right fork.
It didn’t go up the left fork.
therefore:
It went up the right fork. \end{quote}
\textbf{Argument 2:} \begin{quote} Either it went up the left fork or it went up the right fork.
The left fork is unsuitable for pigs.
therefore:
It went up the right fork. \end{quote}
\begin{minipage}{\columnwidth}
\textbf{awFOL version of Argument 1:}
\end{minipage}
Here is our reasoning in the form of an argument.
It has two premises.
And a conclusion.
For our purposes, an argument is any number of premises followed by a conclusion.
And a premise is any statement we specify as a premise; likewise,
a conclusion is any statement we specify to be a conclusion.
So this is a very broad notion of ‘argument’.
It wouldn’t satisfy a visitor to the argument clinic,
but it will do well enough for our purposes.
This argument has an interesting property: it is logically valid.
That is: there is no possible situation in which the premises are true
and the conclusion false.
Of course, we might be wrong in saying that either the pig went up the
left fork or it went up the right fork.
Perhaps it is hiding in the hedge having a laugh at our expense.
But this isn’t relevant to logical validity.
What matters for logical validity is just that the conclusion
can’t be false *if* the premises are true.
Contrast this argument (Argument 2 on the handout).
This argument is not logically valid.
After all, a sufficiently contrary pig could take the left
fork despite its unsuitability for pigs.
So although Argument 2 is a perfectly good argument in some ways,
it is not logically valid.
There is a possible situation involving a contrary pig in which the
premises are true but the conclusion is false.
This is a course about logical validity.
We are going to investigate which arguments are valid and which are not.
It would be quite slow to do this one argument at a time.
Imagine having considered this argument about the pigs,
we had to consider essentially the same argument for the ducks,
the geese, the cows, the sheep, the ostriches, the crocodiles,
and all the other farm animals we were looking after.
(Don’t ask what the crocodiles were doing on the farm.)
But luckily this won’t be necessary because
we can think about many arguments as sharing a single form.
If you think about it, the pigs are a bit extraneous.
When it comes to logically validity,
any argument like this will be logically valid.
Really, it’s validity just depends on the ‘or’ and ‘not’ features.
As I said, this is a course about logical validity.
Logic is the study of logical validity.
We want to know which arguments have this property,
and what means there are of establishing which arguments are valid or not.
To make this easier, we will adopt some formal notation.
We will draw arguments like this, with the vertical and horizontal lines,
and we will use symbols instead of words.
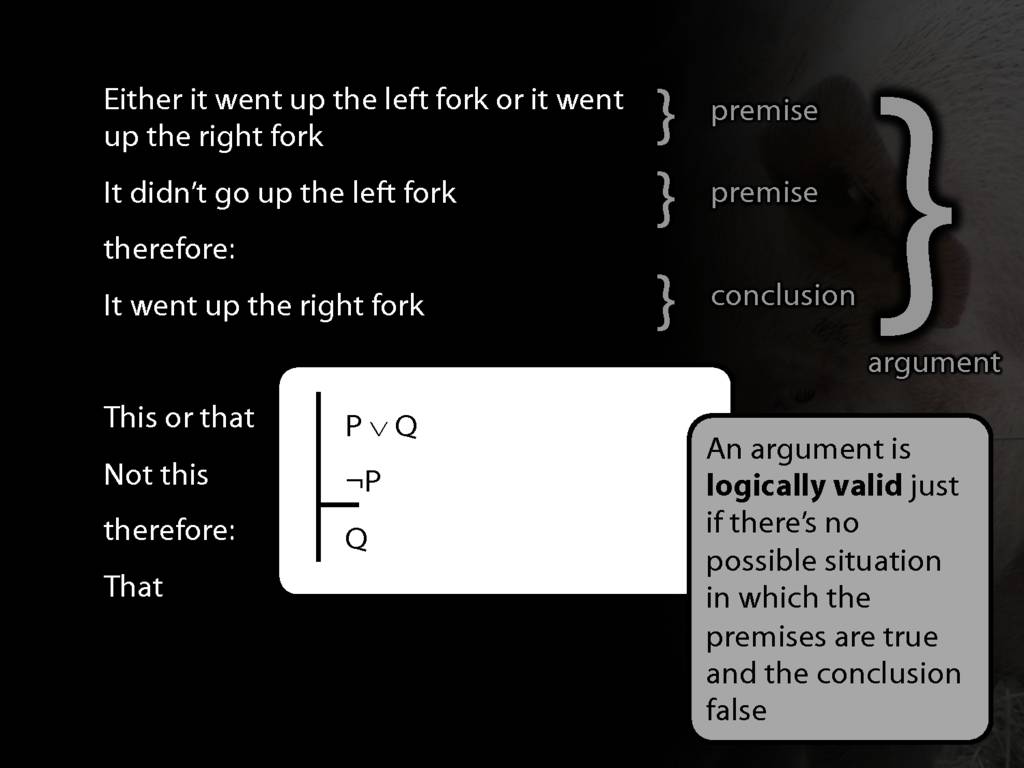
Instead of ‘this’ and ‘that’, we will also use letters like P and Q to stand
for propositions.
I’ll explain all this later in detail; I just wanted
to show you what it will look like.
So what is this course about?
It’s very simple.
We are going to learn to use some formal tools in order to
to investigate which arguments are logically valid and which are not.