Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
Logically Valid Arguments

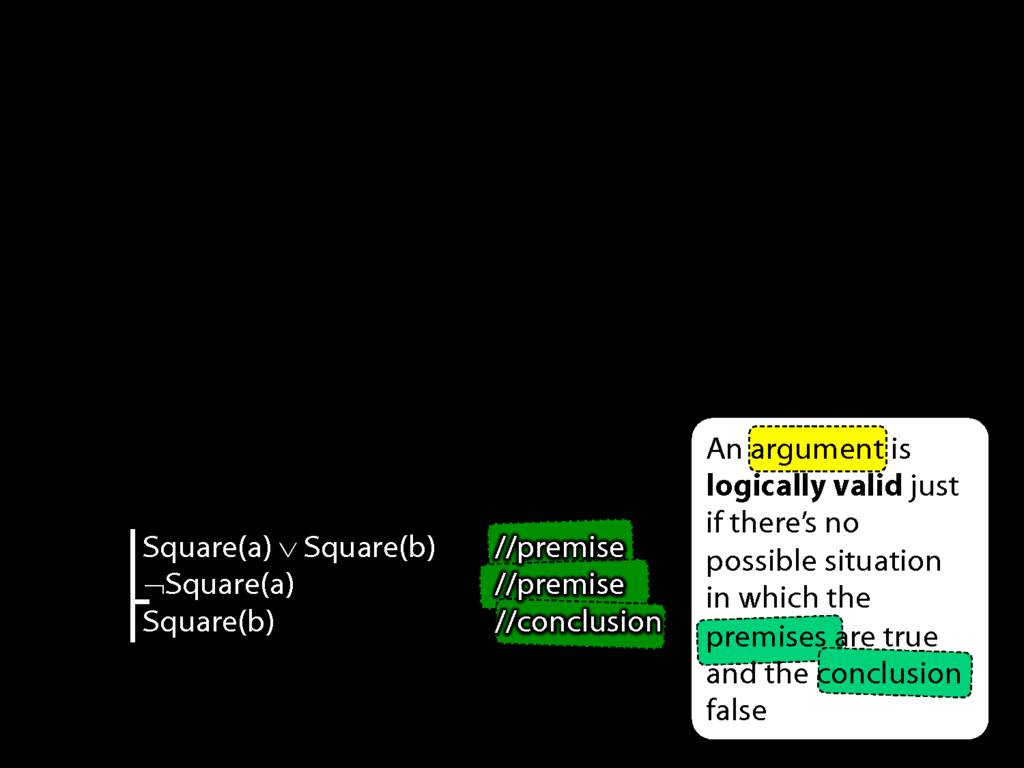
An argument is \emph{logically valid} just if there’s no possible situation in which the premises are true and the conclusion false
A \emph{connective} joins one or more sentences to make a new sentence. E.g. ‘because’, ‘¬’. The sentences joined by a connective are called \emph{constituent sentences}.
E.g. in ‘P $\lor{}$ Q’,
\begin{quote}
$\lor{}$ is the connective
P, Q are the constituent sentences
\end{quote}
Consider these three sentences.
The first sentence says that John is square or Ayesha is square.
The second sentence says John is not square. (I know I just told you John is square; I'm not very consistent, am I?)
And the third sentence says Ayesha is square.

Note the symbol; we saw this a moment ago, it's a bit like the English 'or'.

There is also a new symbol in the second sentence, this a bit like the English 'not'.
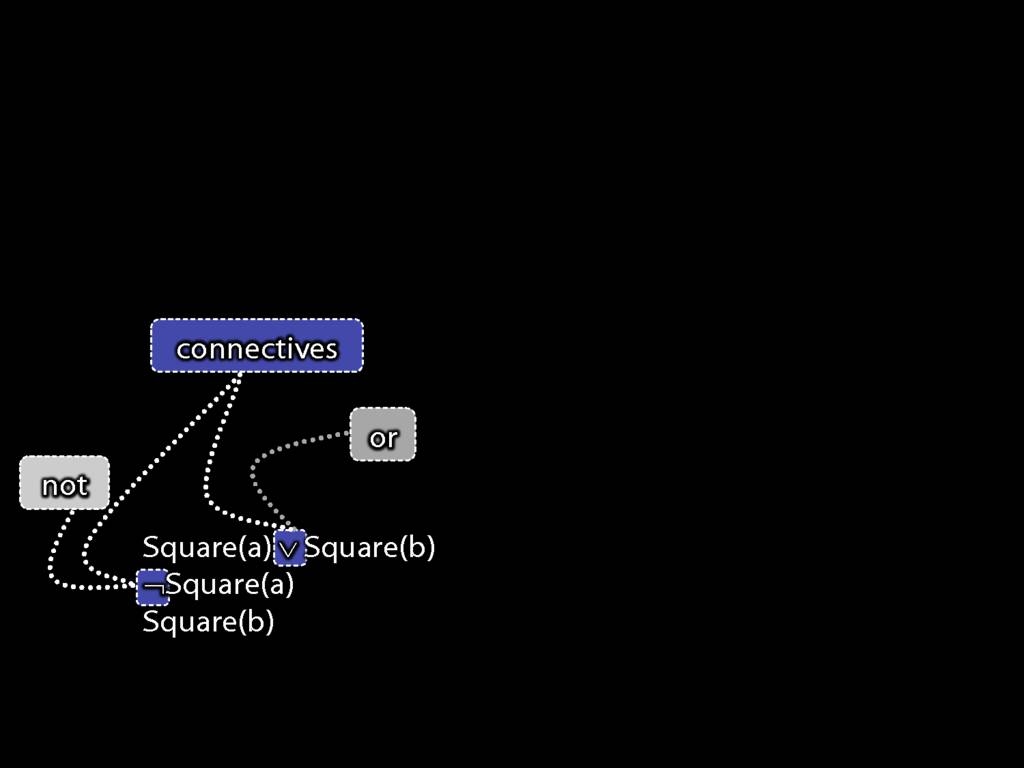
As you recall, these symbols are called 'connectives'.
Note that the negation connective in the second sentence is making a new sentence from just one sentence. (Connectives can join any number of sentences.)
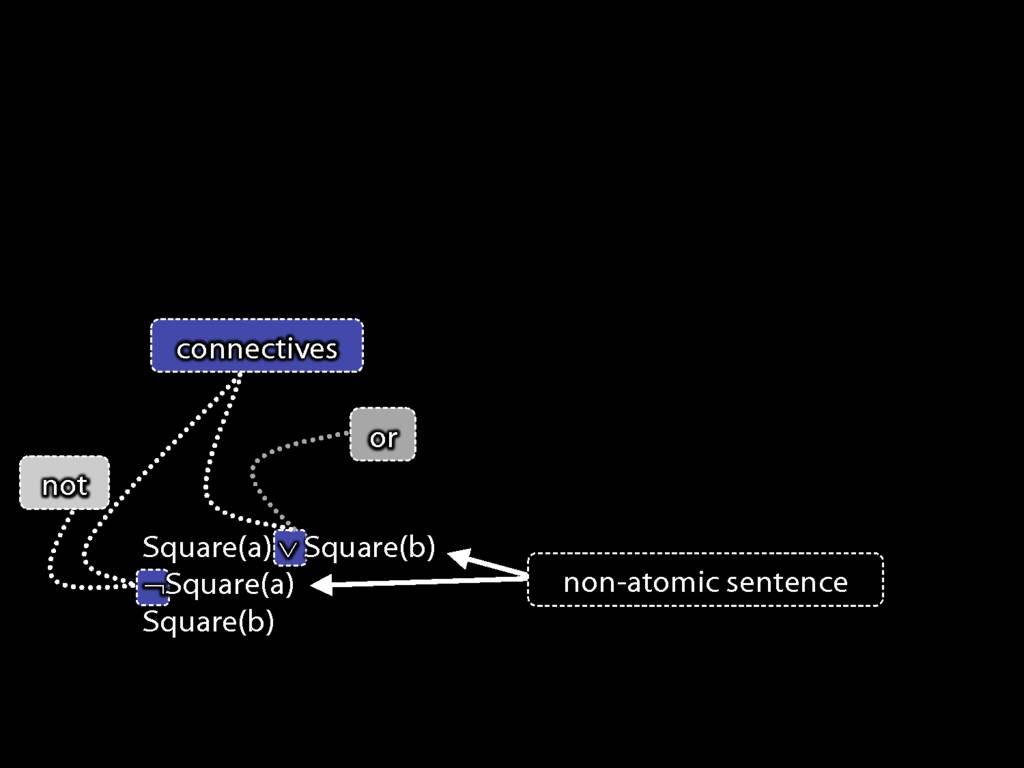
You may also recall that these first two sentences are non-atomic (they contain connectives), ...
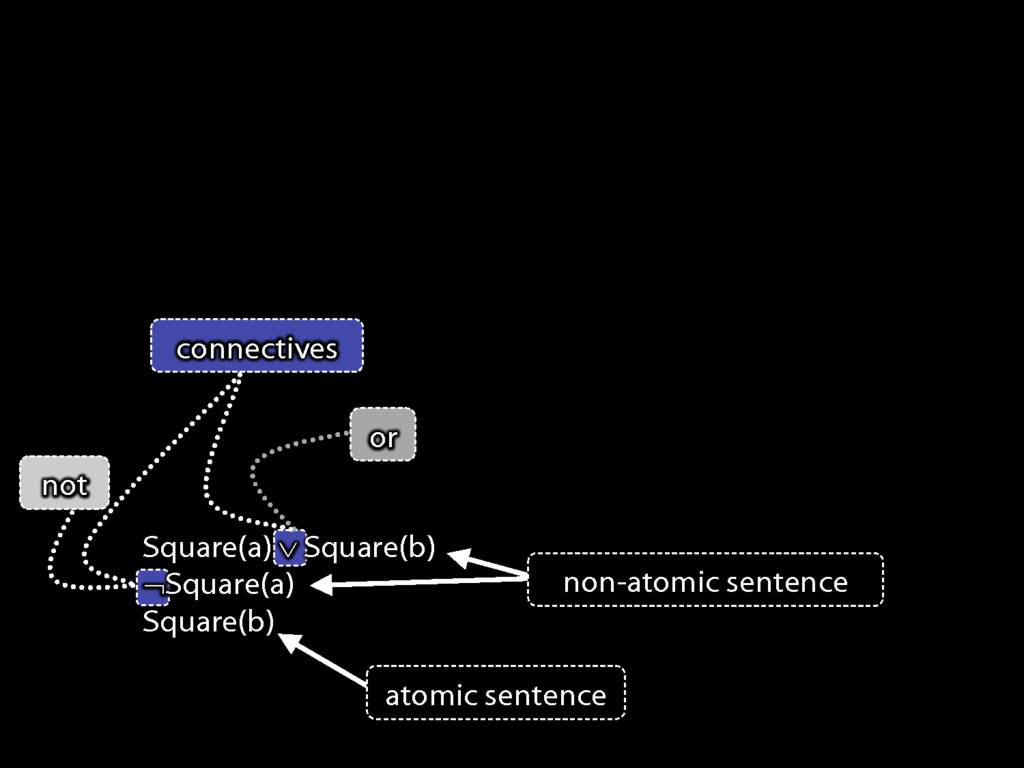
... whereas the third sentence is atomic.

OK, so much for the sentences.
So far we've been fixing terminology and getting a feeling for a formal language, which is a tool for studying logic.
But I haven't said anything about what logic is.
What is logic? What is this course about?
The answer is here: it's about the notion of logical validity. An argument is logically valid just if there's no possible situation where the premises are true and the conclusion false.
Logic is the study of logical validity. We want to know which arguments have this property, and what means there are of establishing which arguments are valid or not.

Let's go though this slowly. First, what is an argument?
For our purposes, an argument is just a sequence of sentences where zero or more are identified as premises and exactly one is identified as the conclusion.
But what do we mean by premises and conclusions?
A premise is just a sentence that we say is a premise. (That's all there is to being a premise.)
Likewise, a conclusion is just a sentence that we say is a conclusion. How simple is that?

Now we're going to write a lot of arguments so it would be helpful to have a compact way of identifying premises and conclusions ...
... That is the purpose of these lines. The horizontal line specifies that the sentences to its right an argument.
And the vertical line separates the premises from the conclusion.

So this is logic: the study of logical validity. Have we understood the definition yet? Not quite ...

... What do we mean by 'possible situation'?
A possibile situation is just a way that the world is or could be.
So consider the situation which is as similar to the actual situation as possible except that you are in Havana smoking a fat cigar rather than attending my lecture.
This is a possible situation.
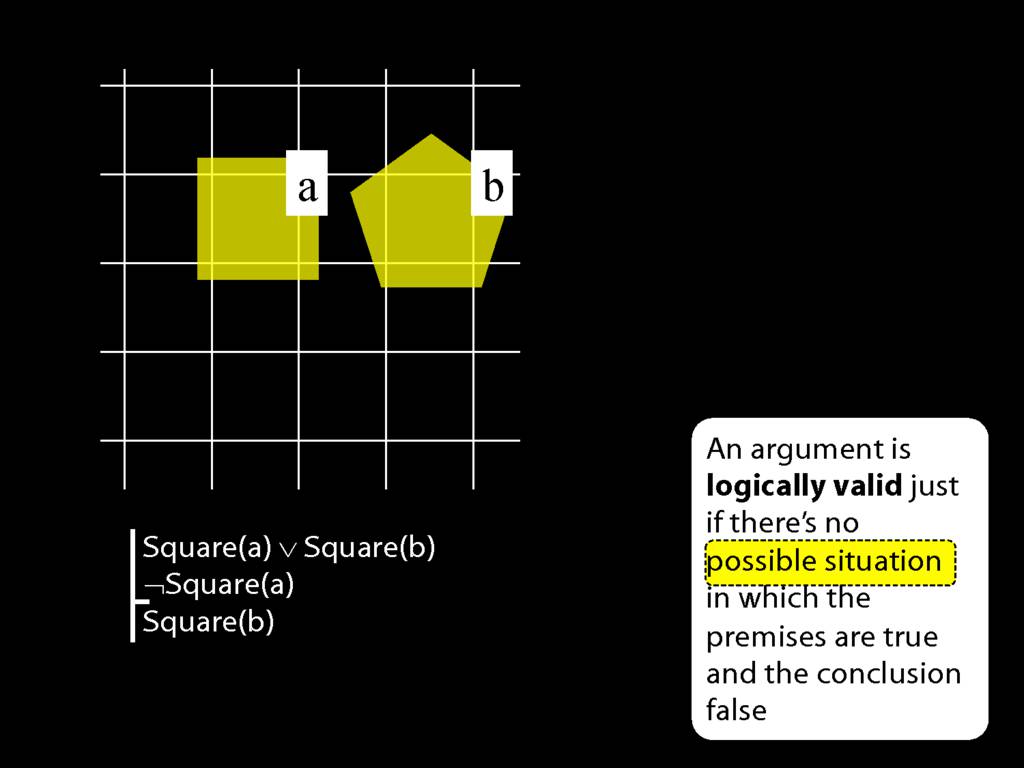
Now possible situations are huge things; in specifying a possible situation, you are specifying something as big as the actual situation,
with all the trees, leaves, insects and everything.
It is helpful to have a proxy for possible situations, something much simpler than a real possible situation.
For our purposes, a good proxy is often an arrangement of shapes in two dimensional space.
For evaluating the argument about John and Ayesha, we can pretend that possible situations are just shapes in space.
Thinking of possible situations in this way is simpler, and doesn't ignore anything relevant to this particular argument.
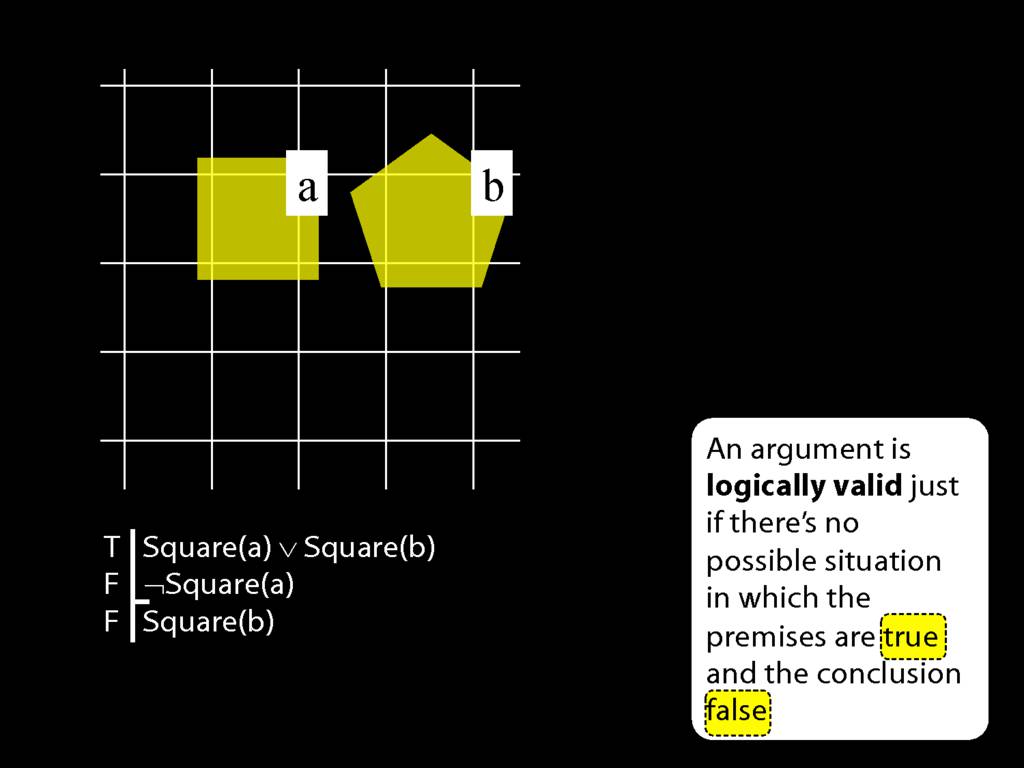
The final concepts in our definition of logical validity are truth and falsity.
These concepts are too simple to say anything much illuminating about.
Note that whether a sentence is true or false depends on which possible situation we are talking about.
In this possible situation, the first premise is true, the second premise is false and the conclusion is false.
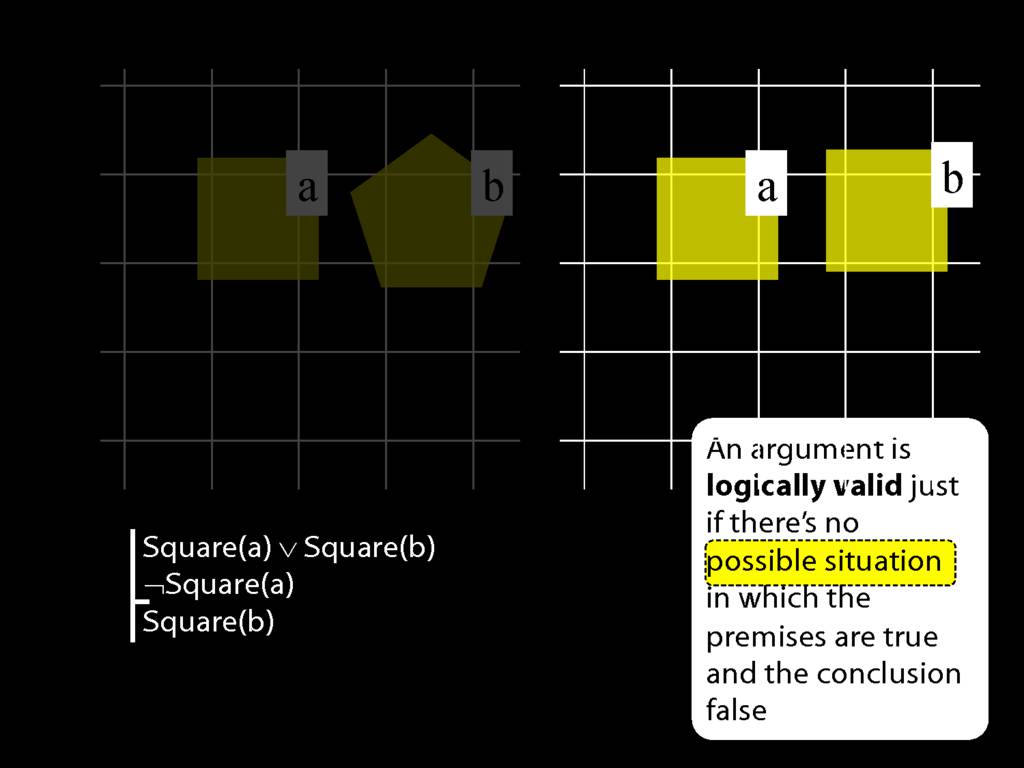
But in this possible situation, ...
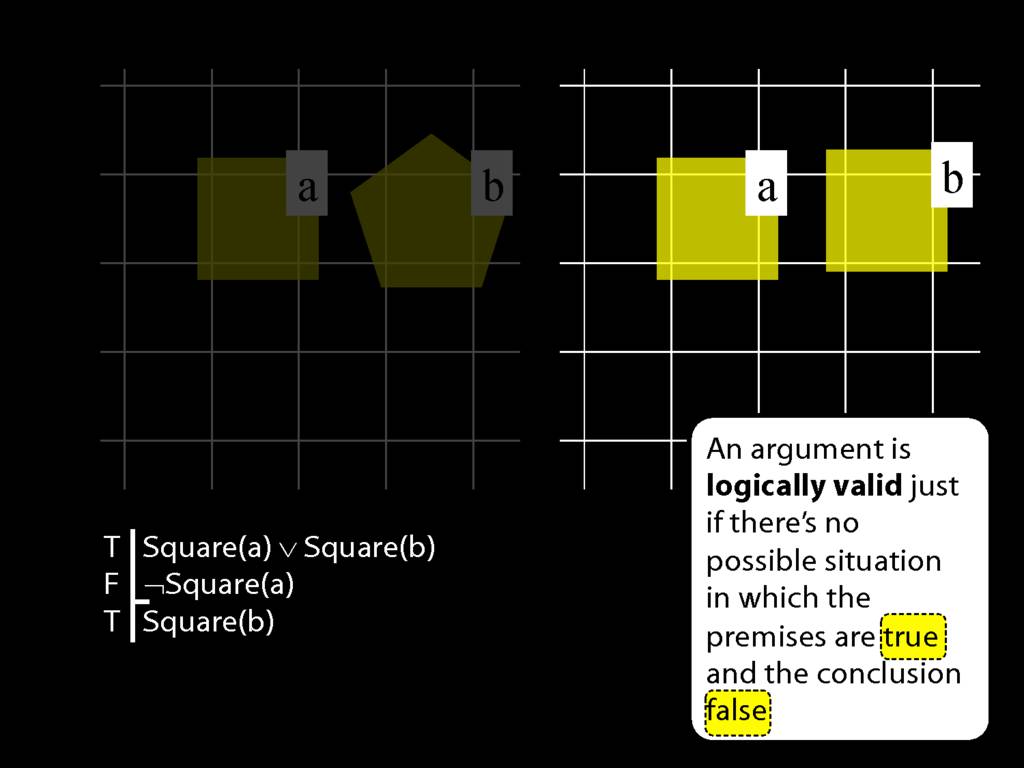
... the conclusion is true.
Incidentally, you will sometimes be asked whether a logically valid argument can have one or more false premises and a true conclusion.
If you're asked that question, do think about this argument and this possible situation.

So logic is the study of logical validity.
As I said before,
our overall aims in this course are to
discover which arguments have this property,
and what means there are of establishing which arguments are valid or not.
In doing this our main tool is the formal language awFOL.
2.3, 2.4