Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
Contradictions, Logical Truths and Logical Possibilities
A \emph{contradiction} is a sentence that is
false in all possible situations.
A \emph{logical truth} is a sentence that is
true in all possible situations.
A \emph{logical possibility} is a sentence that is
true in one or more possible situations.
contradiction
A sentence that is false in all possible situations.
E.g.
| A | A ∧ ¬A |
| T | F |
| F | F |
logical truth
A sentence that is true in all possible situations.
E.g.
| A | A ∨ ¬A |
| T | T |
| F | T |
logical possibility
a sentence that is true in one or more possible situations.
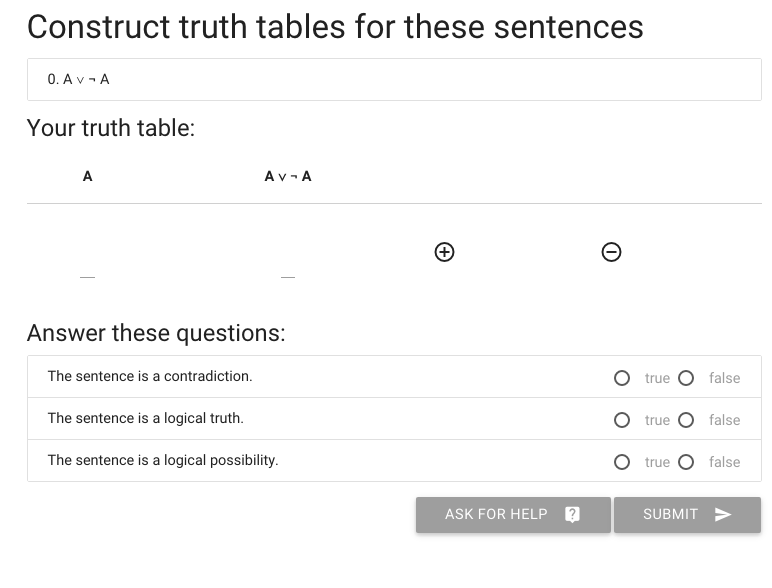
I’ll illustrate how this works in logic-ex.
Let’s say we want to construct the truth table for A or not A.
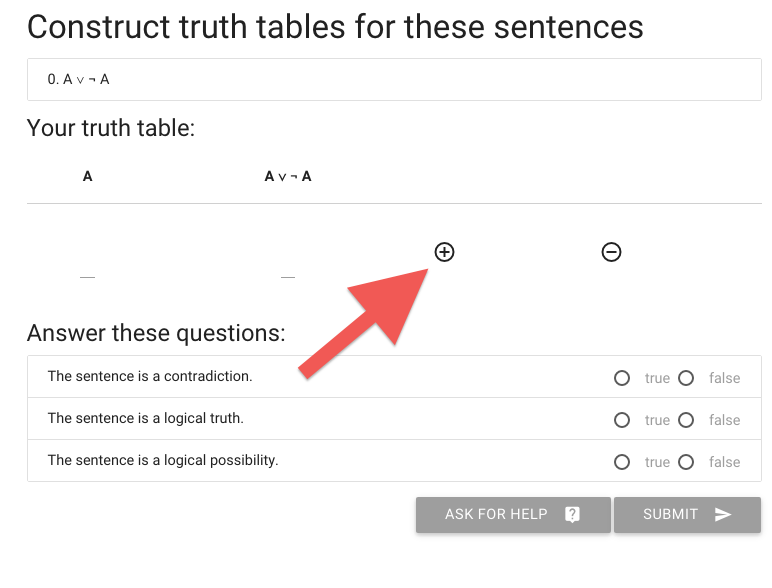
The first thing I need is more rows, so I hit the circled plus thing.
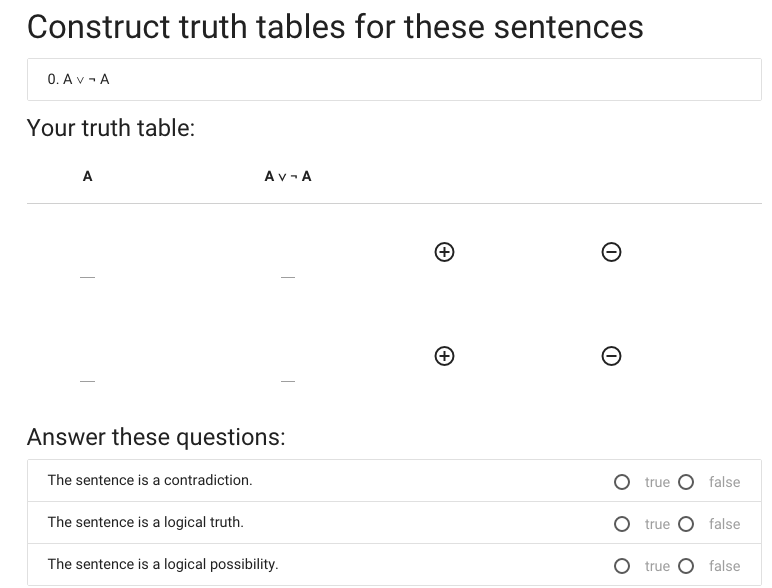
Now I’ve got a second row, and in this case two rows is enough.
Time to start filling in values ...
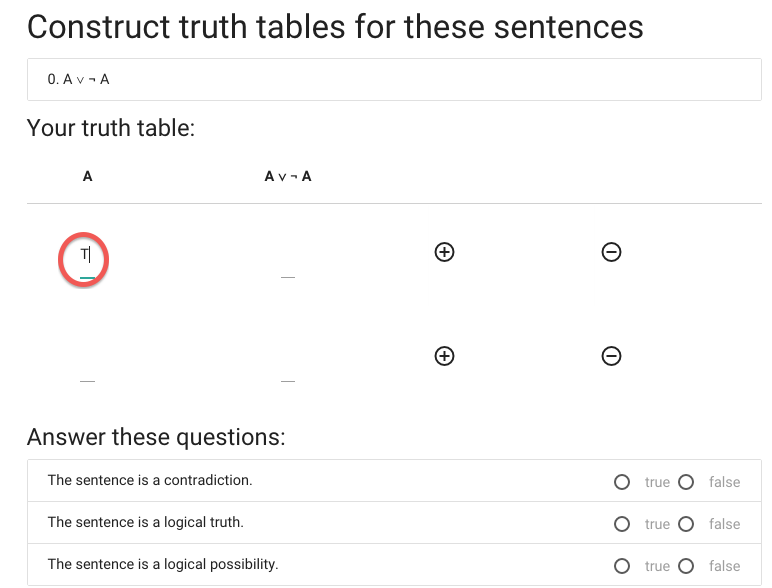
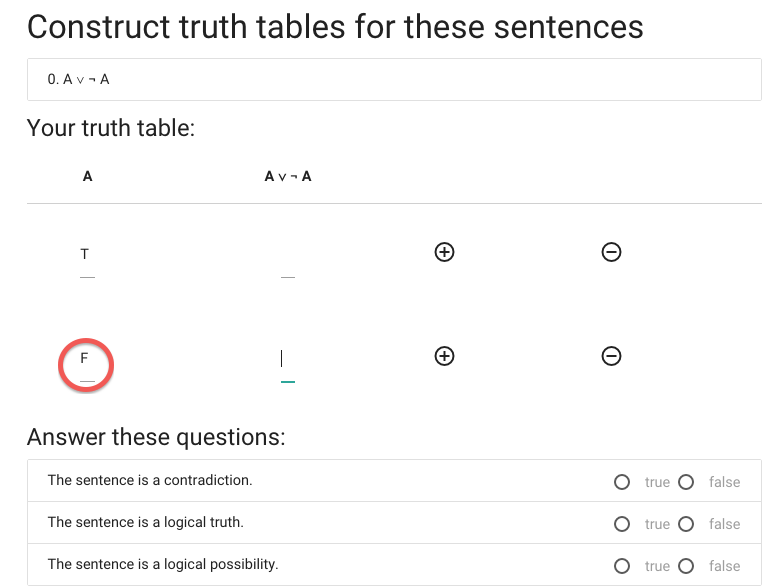
I’m doing the reference columns first because these are always the same
and I don’t need to work out what the values are.
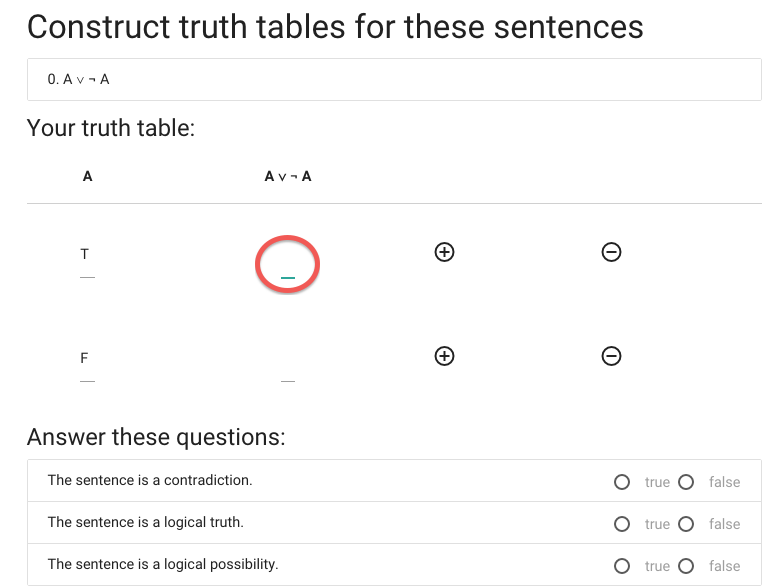
Now I have to enter the value of A or not A when A is true.
You might be able to compute this in value in your head, but
that won’t always be the case. I expect that, often, before
you enter a value in the table in zoxiy you will have taken
a pencil and paper and worked out the truth table step by step.
So what you enter will often be something that took quite a bit
of work to compute.
Or you could just guess. But this is not generally a good strategy
because I take the view that a truth table is either right or wrong,
and if you are really guessing you only have a 1/16 chance of being
right for most truth tables.
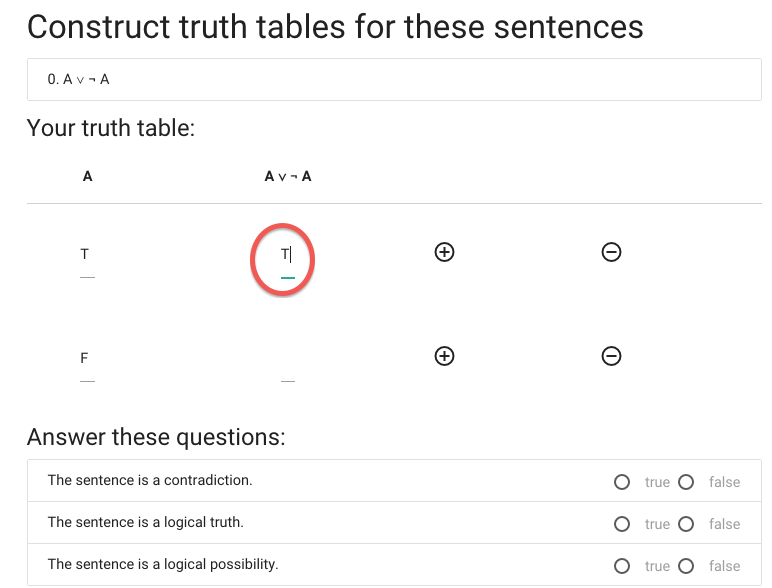
Anyway, I think it’s true.
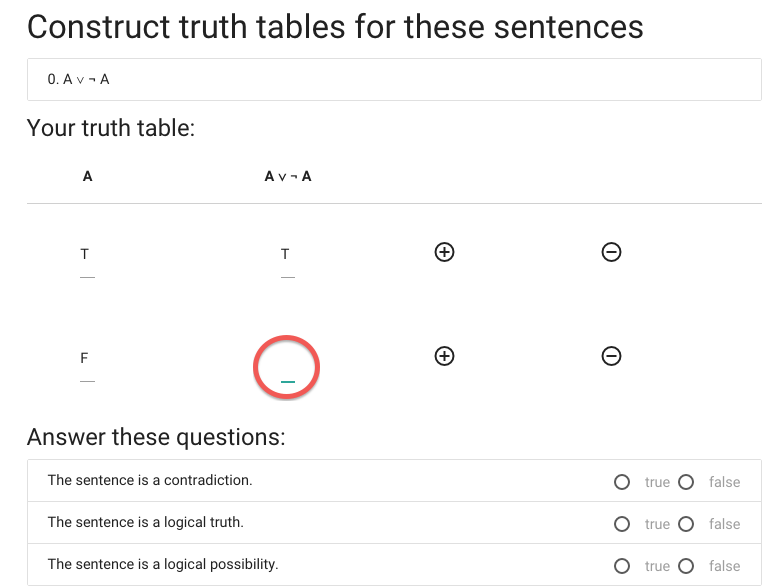
Now for the last truth value.
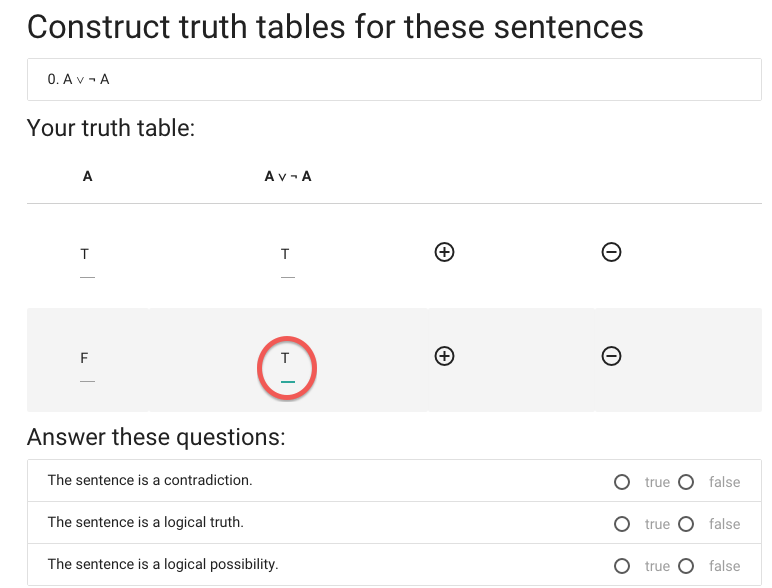
This is also true.
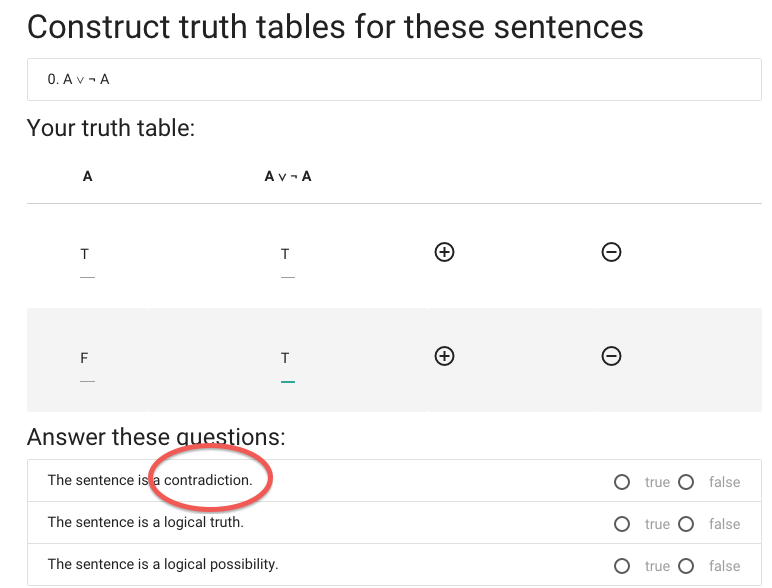
We’re not done yet, we now have to say whether the
sentence is a contradiction.
A \emph{contradiction} is a sentence that is
false in all possible situations.
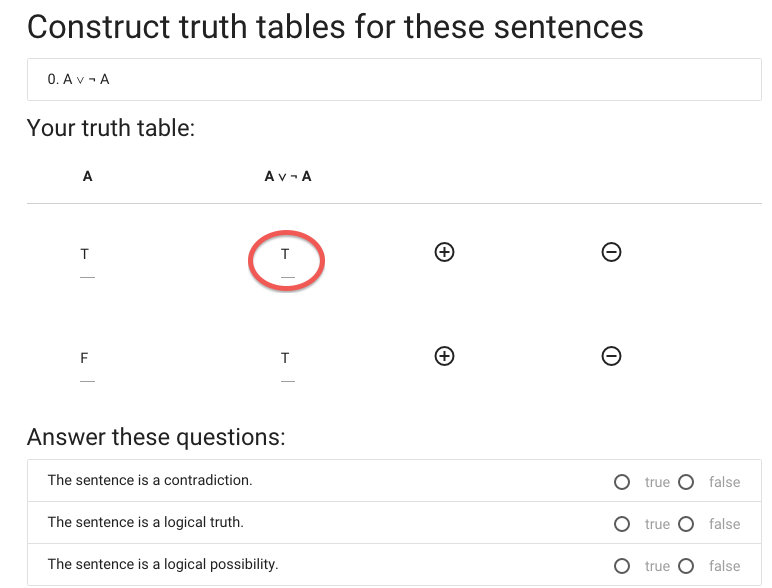
This sentence isn’t
false in all possible situations ...
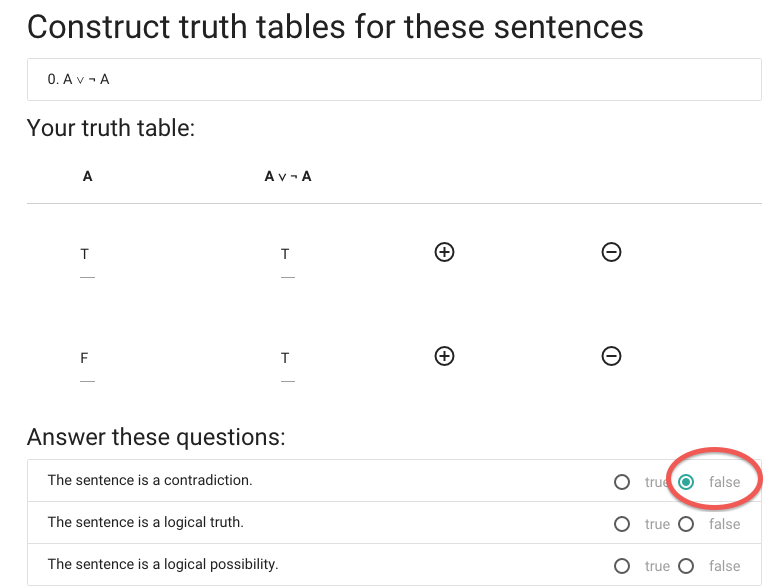
... so it isn’t a contradiction.
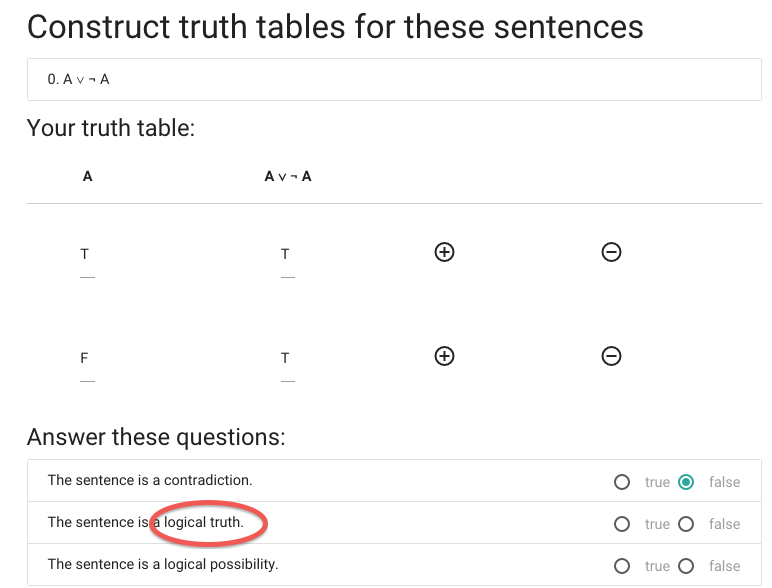
Next we have to specify whether ‘A or not A’ is a logical truth.
A \emph{logical truth} is a sentence that is
true in all possible situations.
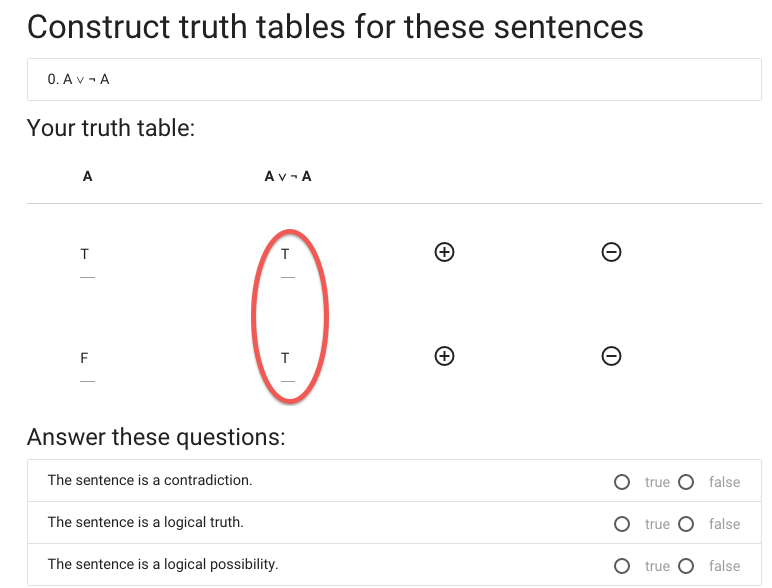
This sentence is true in all possible situations ...
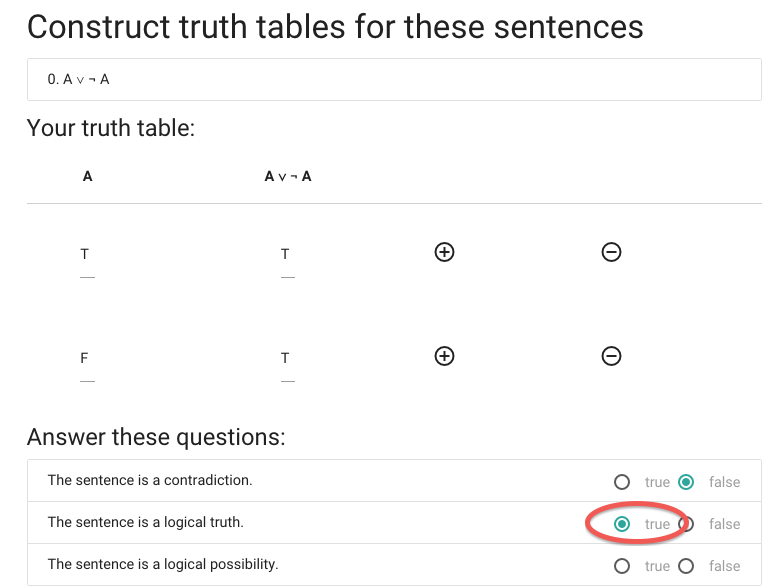
... so this sentence is a logical truth.
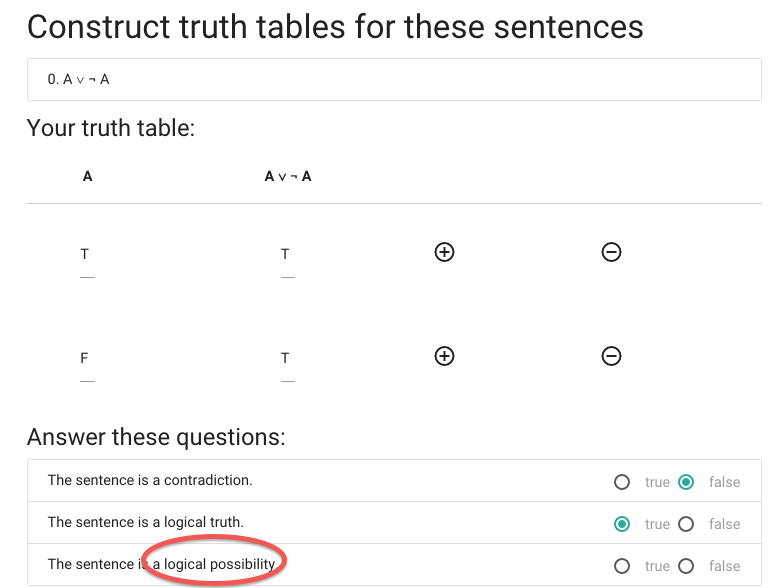
Finally, we’re asked whether the sentence is a logical possibility.
A \emph{logical possibility} is a sentence that is
true in one or more possible situations.

This sentence is true in at least one possible situation ...
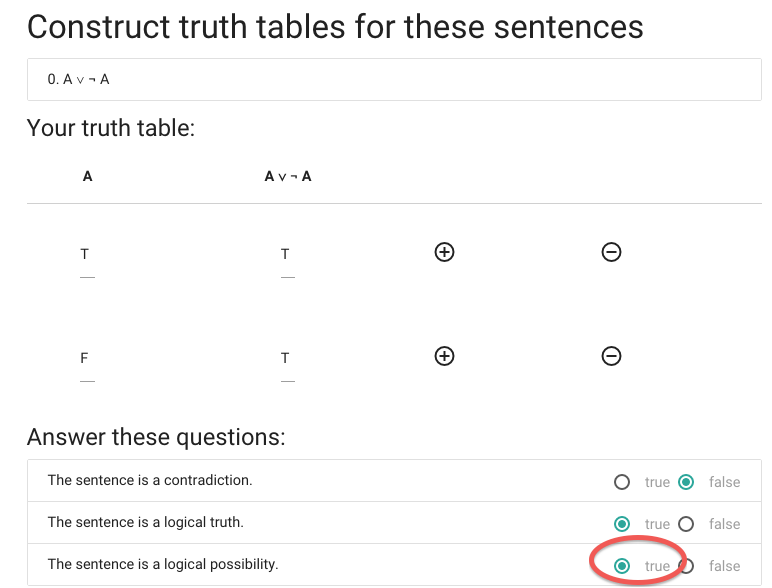
... so this sentence is a logical possibility.
2.5, 2.6