Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
Logical Validity and Truth Tables
We can use truth tables to establish that
some arguments are logically valid
\begin{minipage}{\columnwidth}
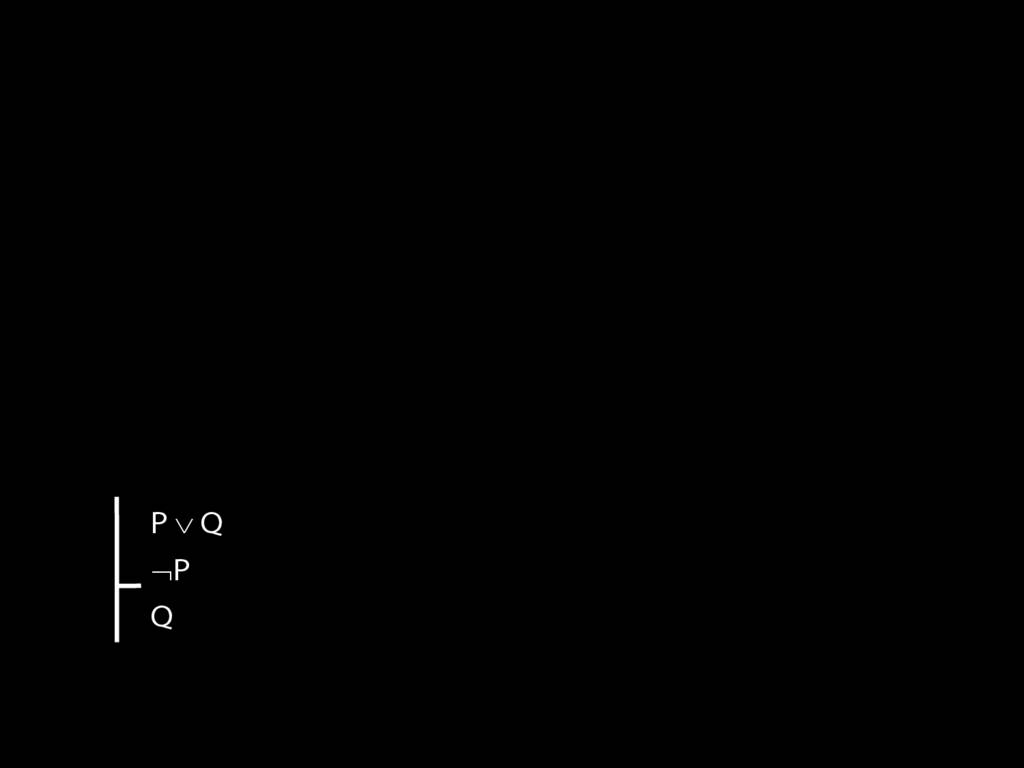
Truth tables can be used to show that an argument is valid. To illustrate ...
\end{minipage}
\begin{minipage}{\columnwidth}
To establish that an argument is valid:
\begin{enumerate}
\item Create truth tables for each premise and the conclusion.
\item Check whether there is a row of the truth table where all premises are true and the conclusion is false.
\item If not, the argument is valid.
\end{enumerate}
\end{minipage}








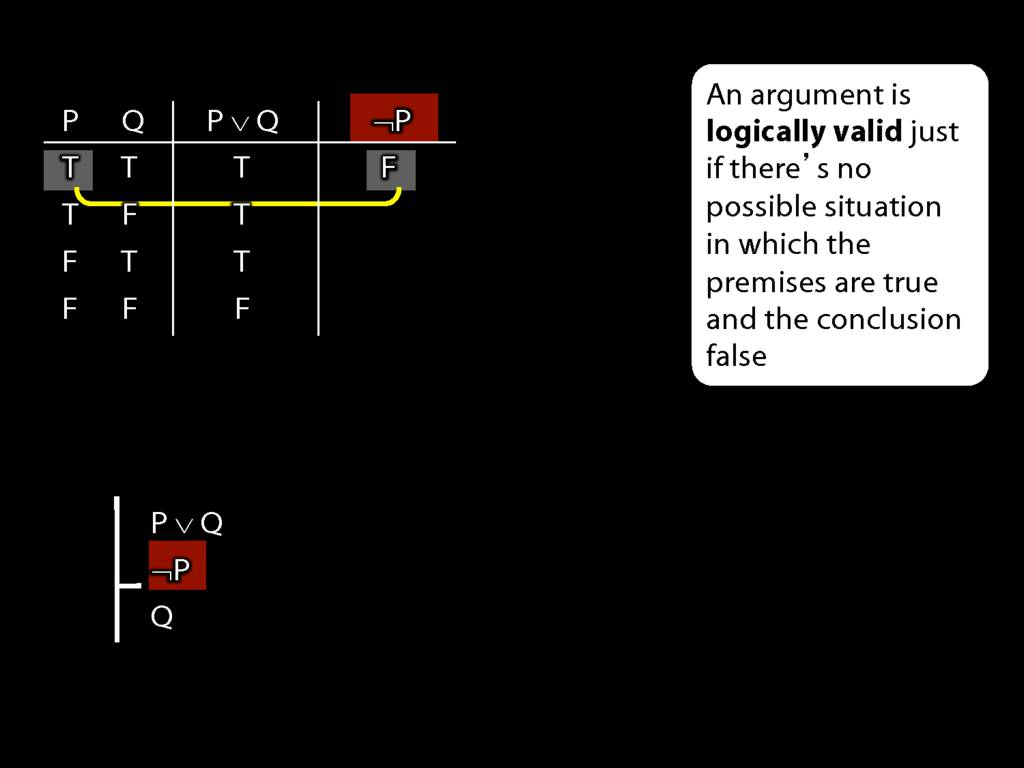
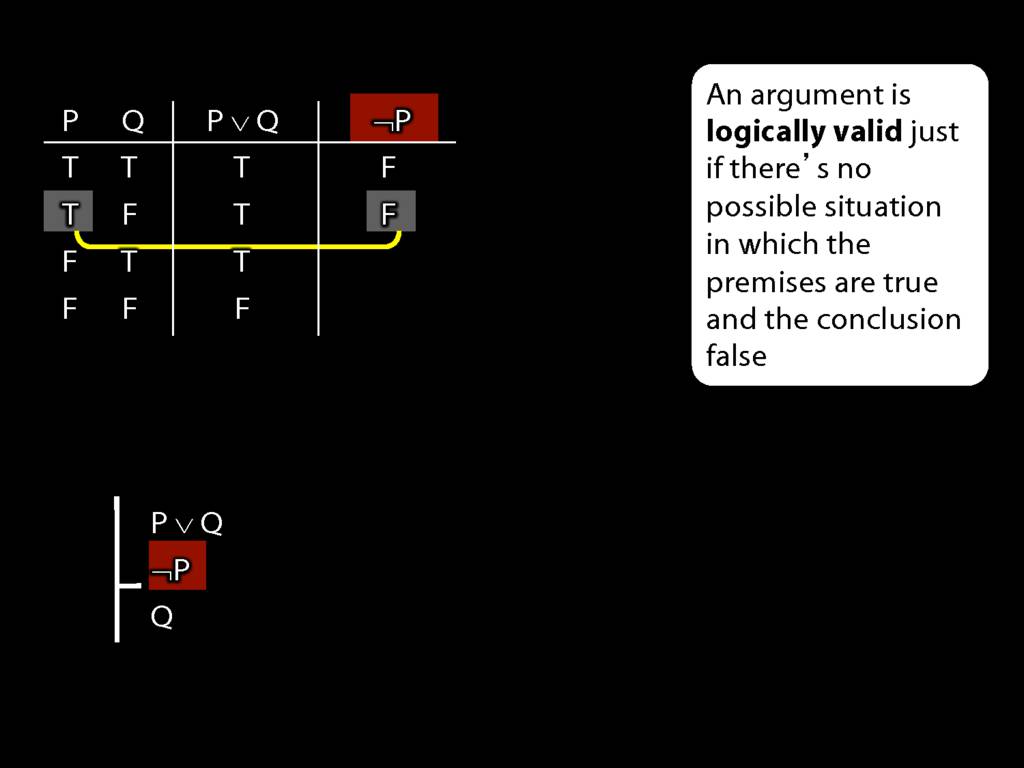



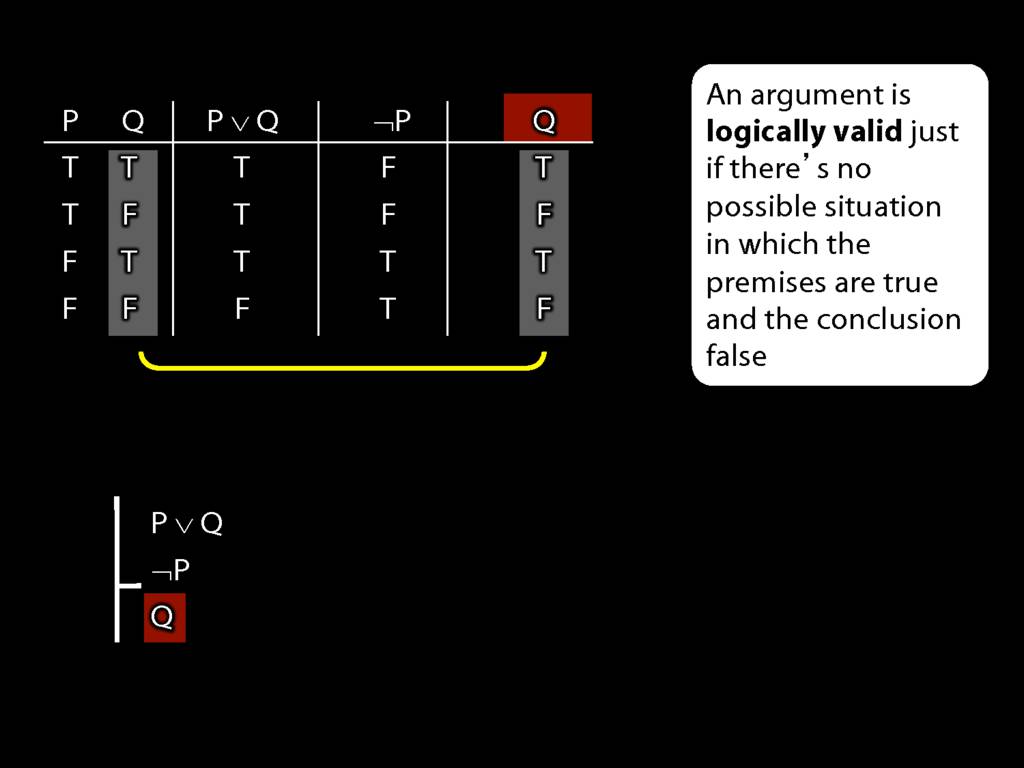





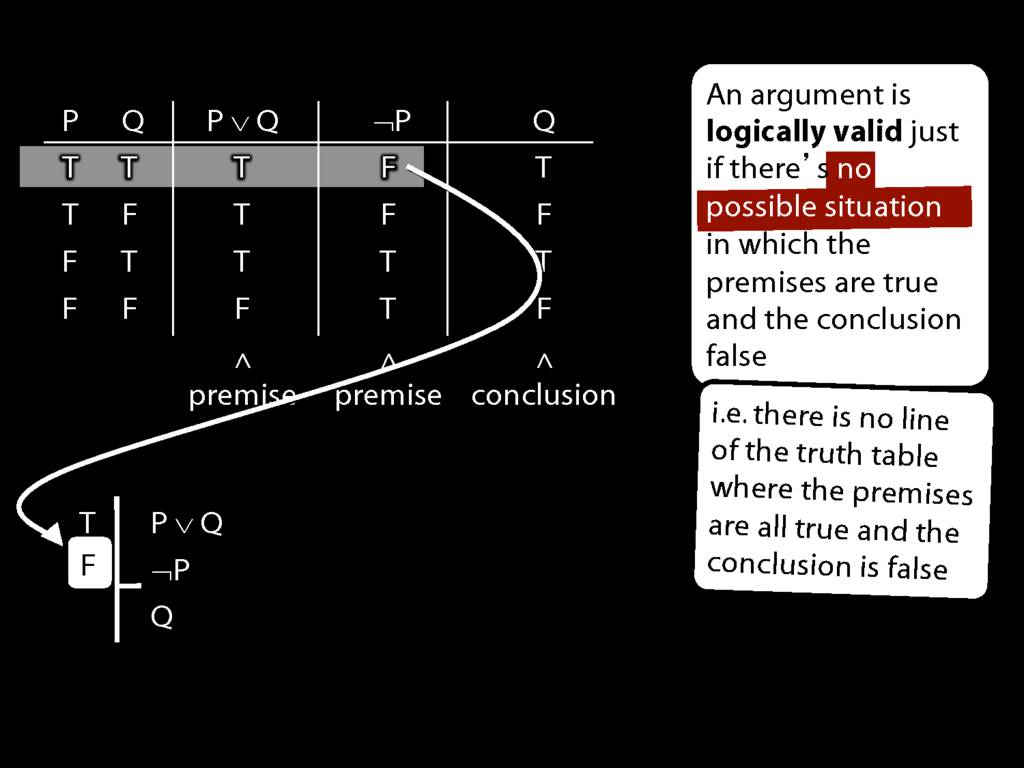

Don’t need to go further, already have a false premise. So this won’t be a situation in which the premises are true and the conclusion false.


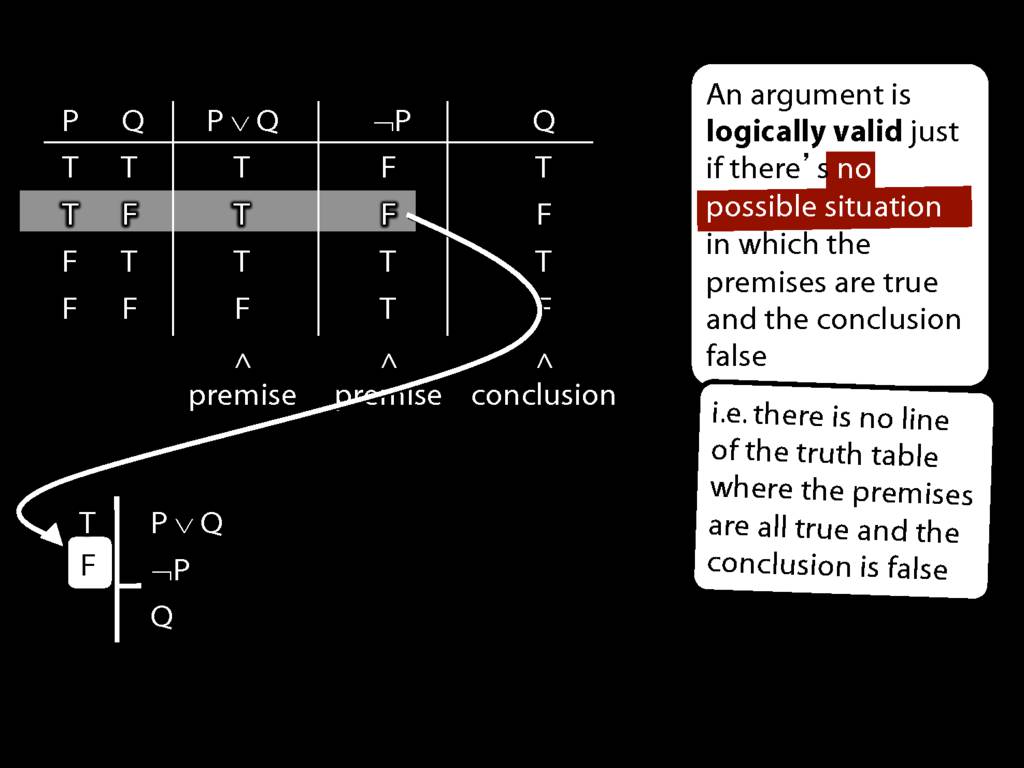





This situation is different from the other two: the premises are true in this possible situation, so we had to think about whether the conclusion is true.
But, as you can see, the conclusion is also true. So this is no counterexample.

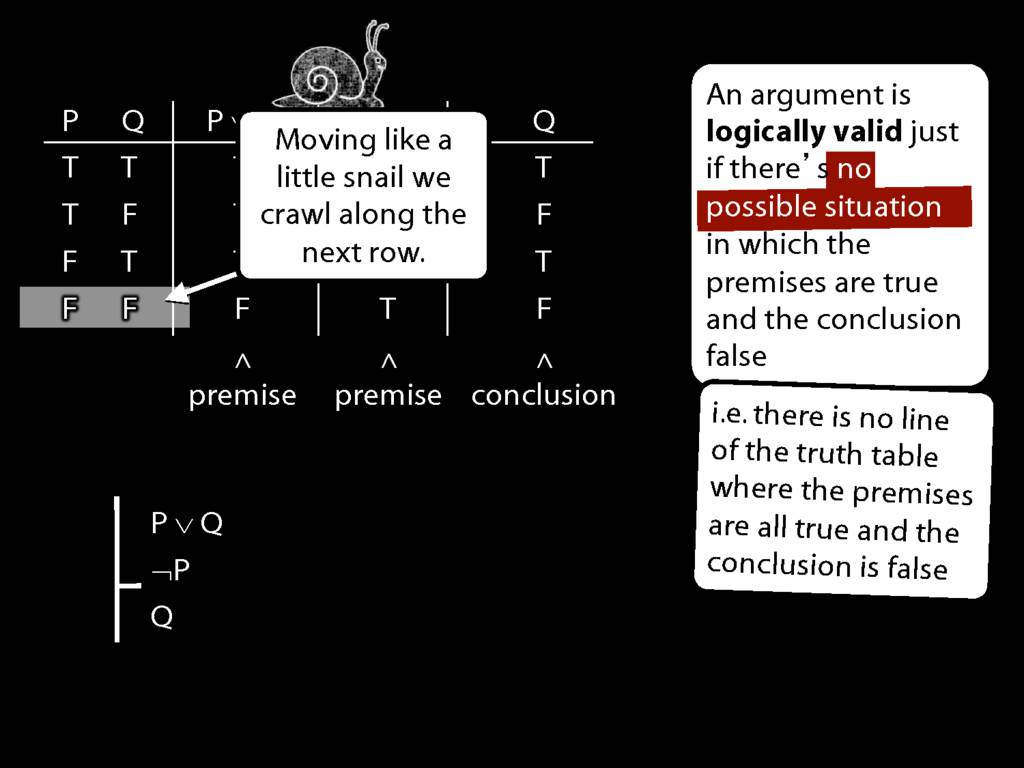
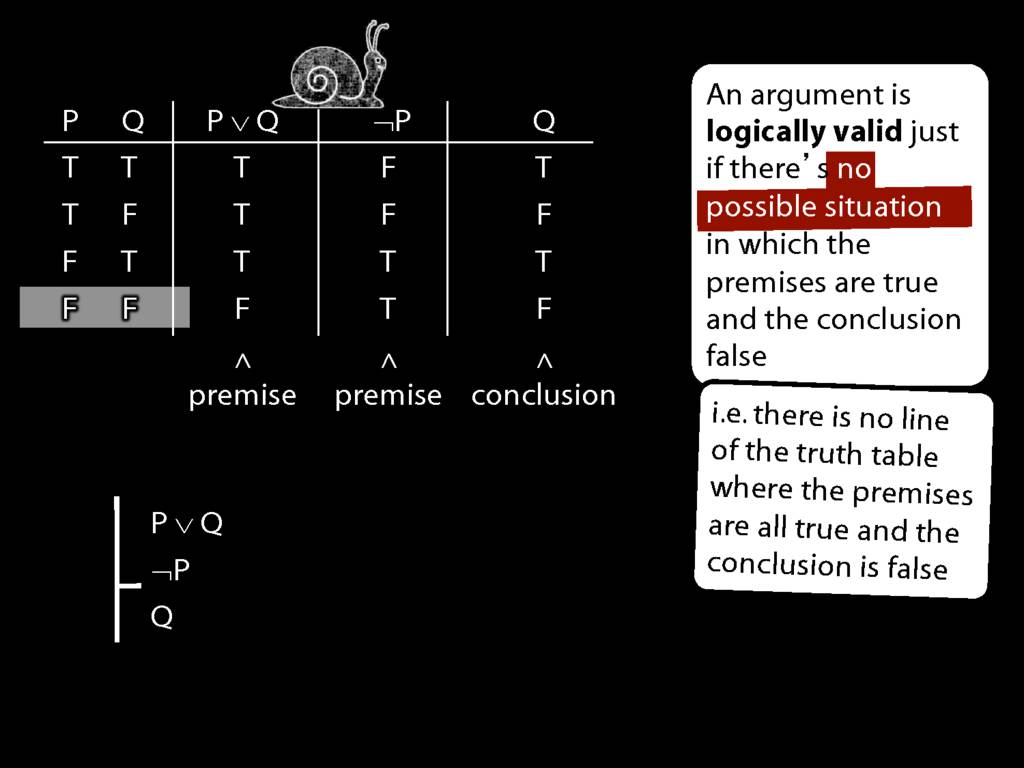
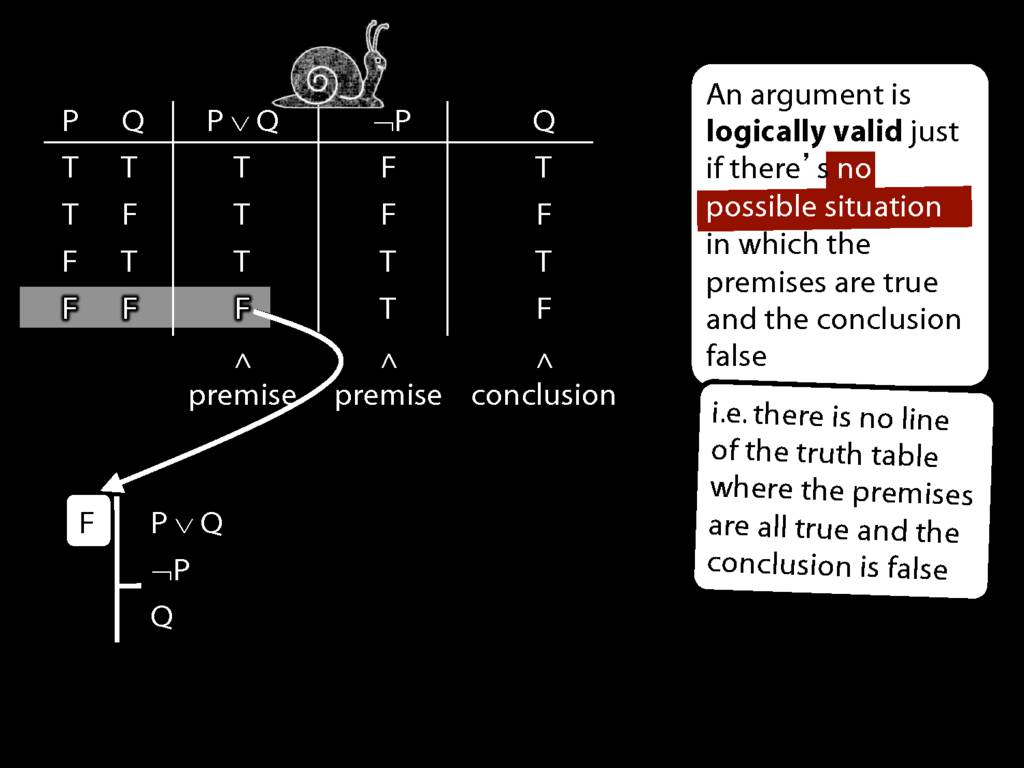

So if someone asked you to show that this argument is valid using truth tables, what would you do?
First, create truth tables for each premise and for the conclusion.
Next, check whether there is any row where the premises are true and the conclusion false.
If not, you can write this:
By inspecting the truth table, there is no row where the premises are true and the conclusion false; therefore, the argument is logically valid.


When you're doing truth tables there's a temptation to race through them.

But you shouldn't do that. Be the little snail.
5.1-5.4