A ∧ B ∨ C: They Are Different

Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

A ∧ B ∨ C: They Are Different

OK, so we have the truth tables. Where do they differ?

The truth-tables differ in rows five and seven only.

So the only difference between these two sentences is the brackets, but this difference means that the two sentences differ in truth-value.

This also makes a difference to their role in arguments, of course.

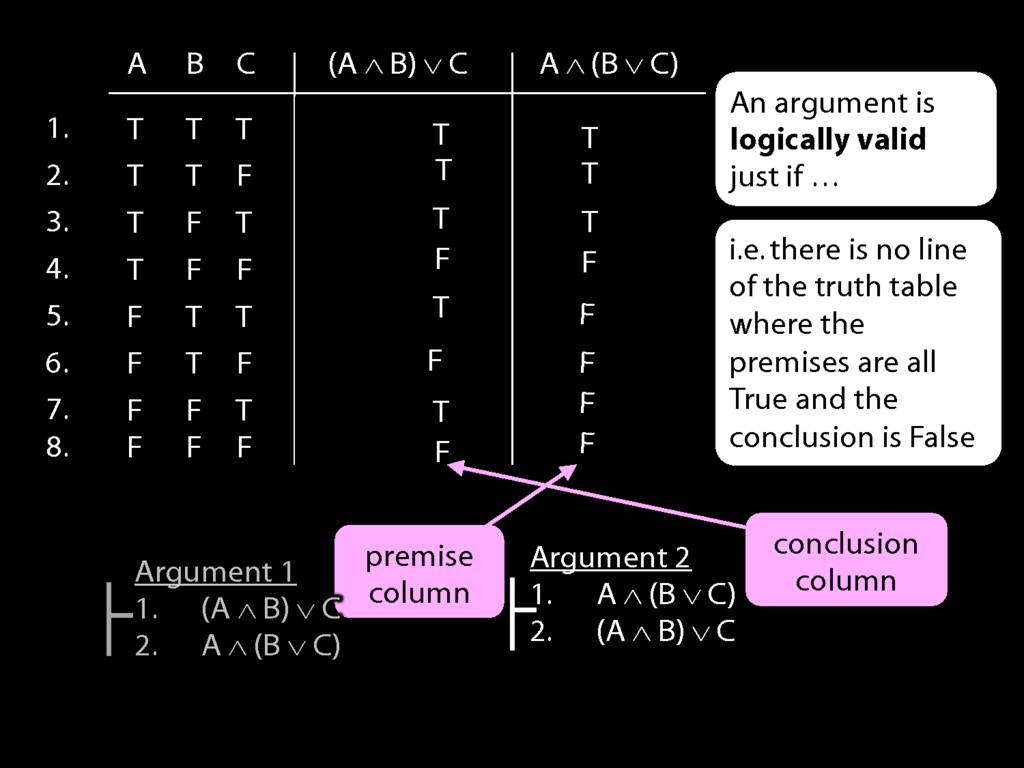
Which of these arguments is logically valid?

Recall that for an argument to be logically valid is for ...

Now in the case of truth-tables, for an argument to be logically valid amounts to there being no row of the truth-table where the premise is true and the conclusion false.

Consider the first argument. Is this valid?

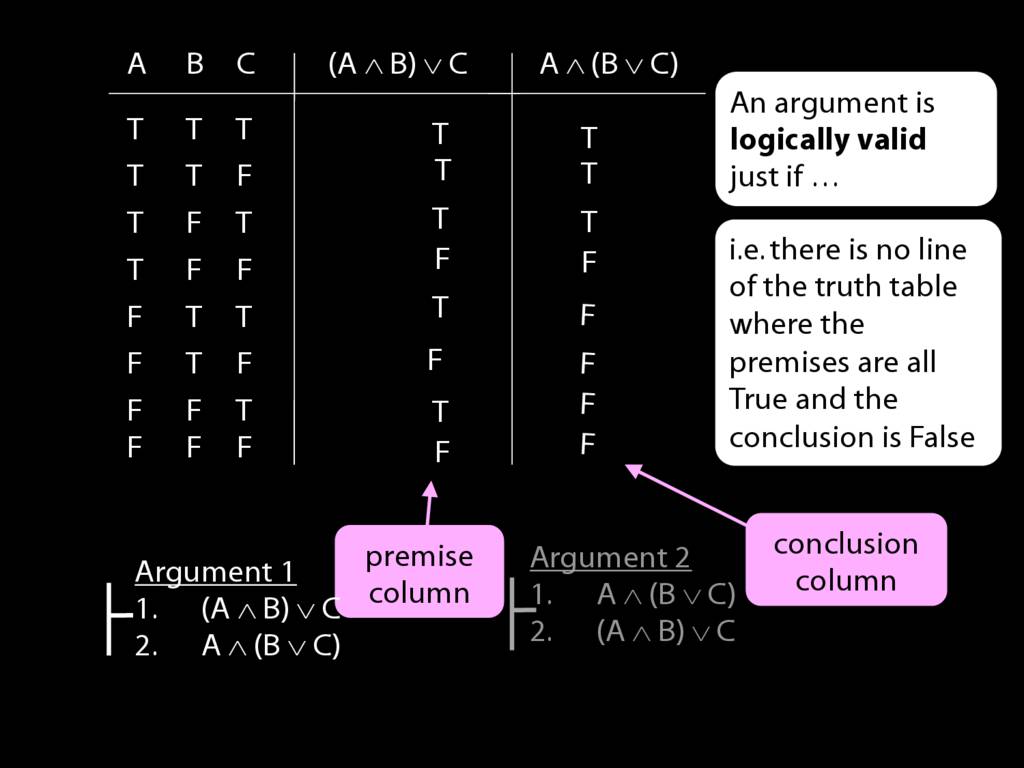
Here's the premise and here's the conclusion.

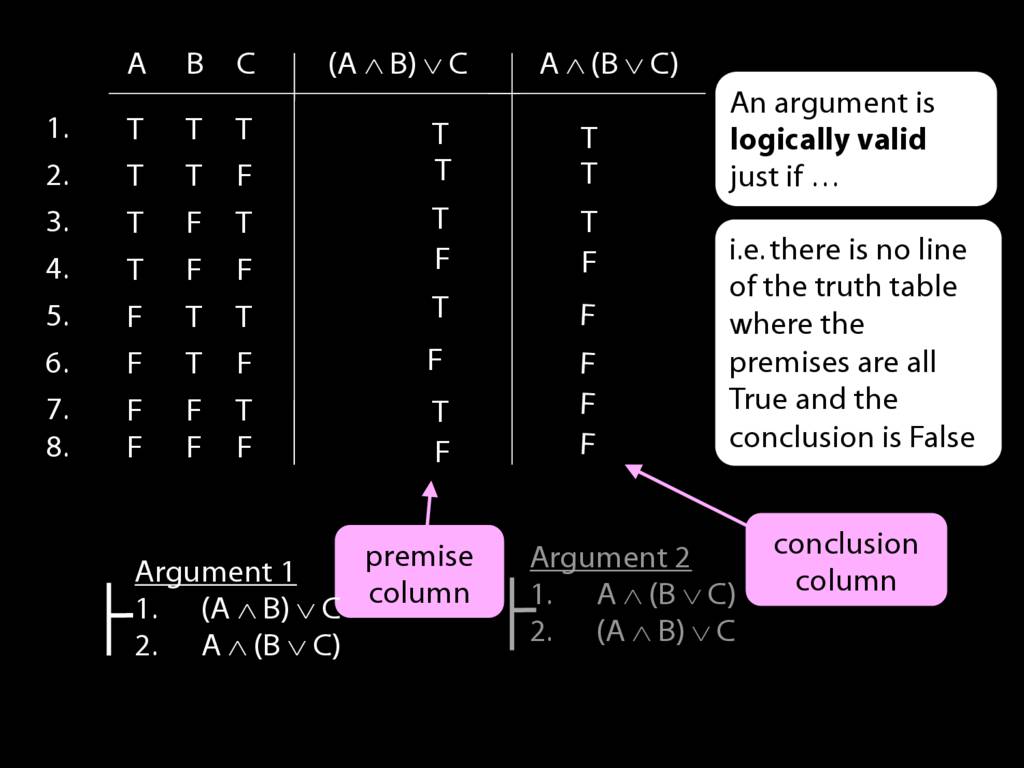
(Let's have some numbers so you can see which lines I'm talking about.)

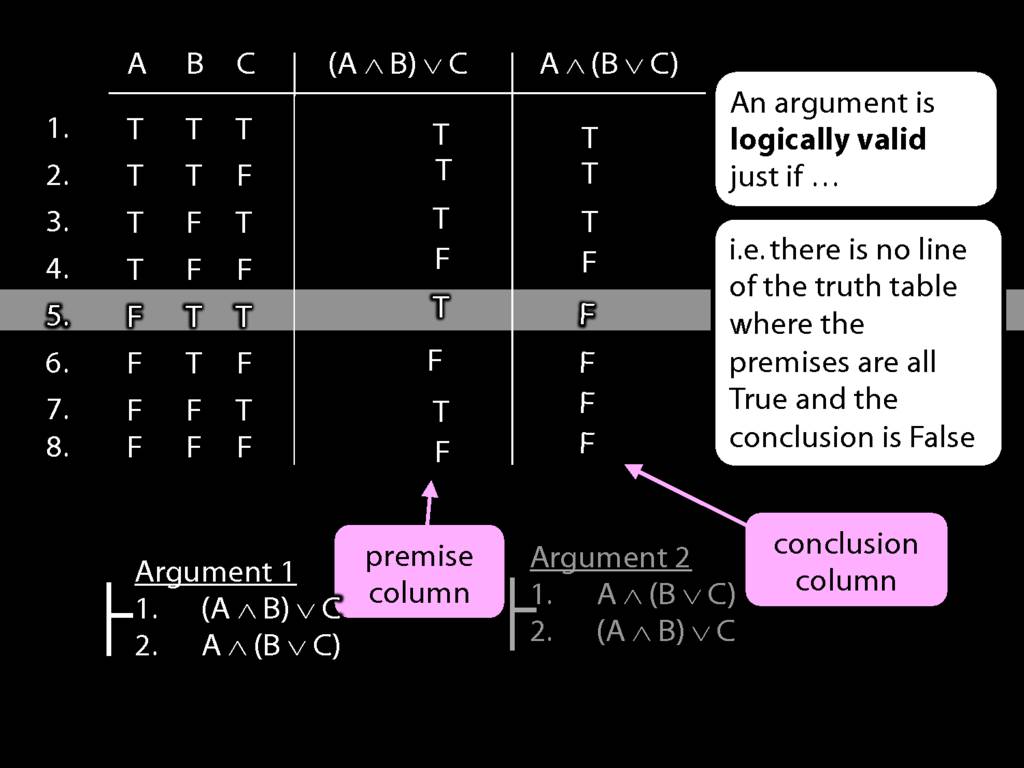
What happens in line five? Here we have true premise and false conclusion.

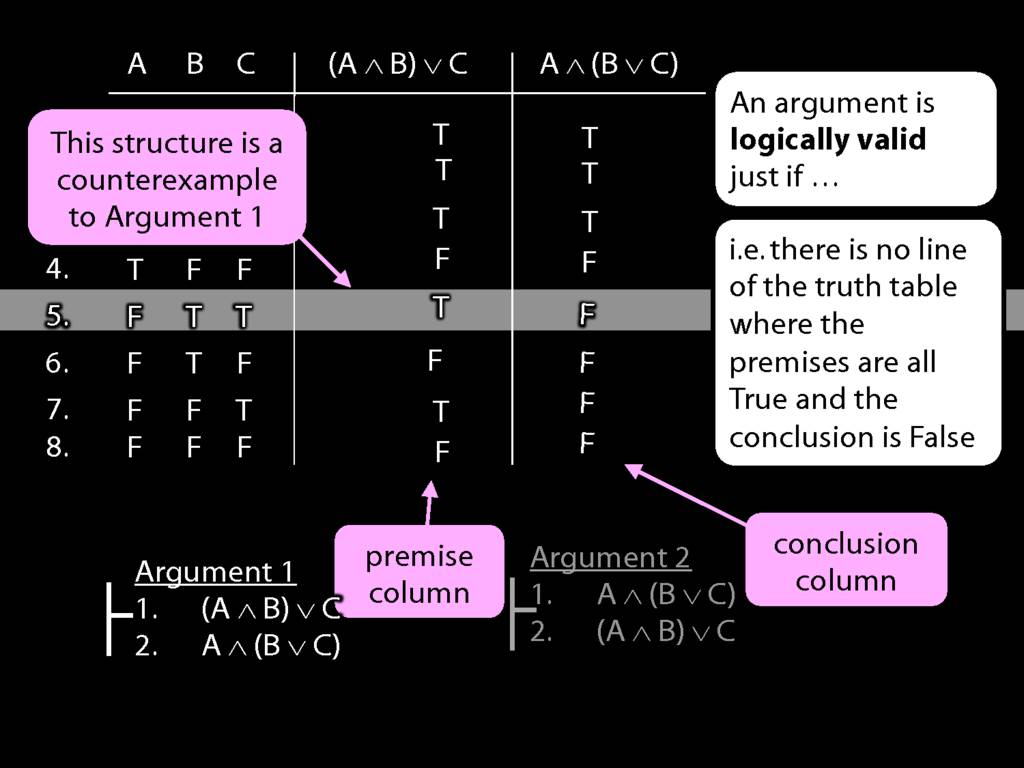
So the argument is not valid, and this row is a counterexample to the argument.

If someone asks you for a counterexample, what do you have to write? Just this : A false, B true and C true. That's is: you've specified a possibile situation in which the premises are true and the conclusion false, and that's what a counterexample is.

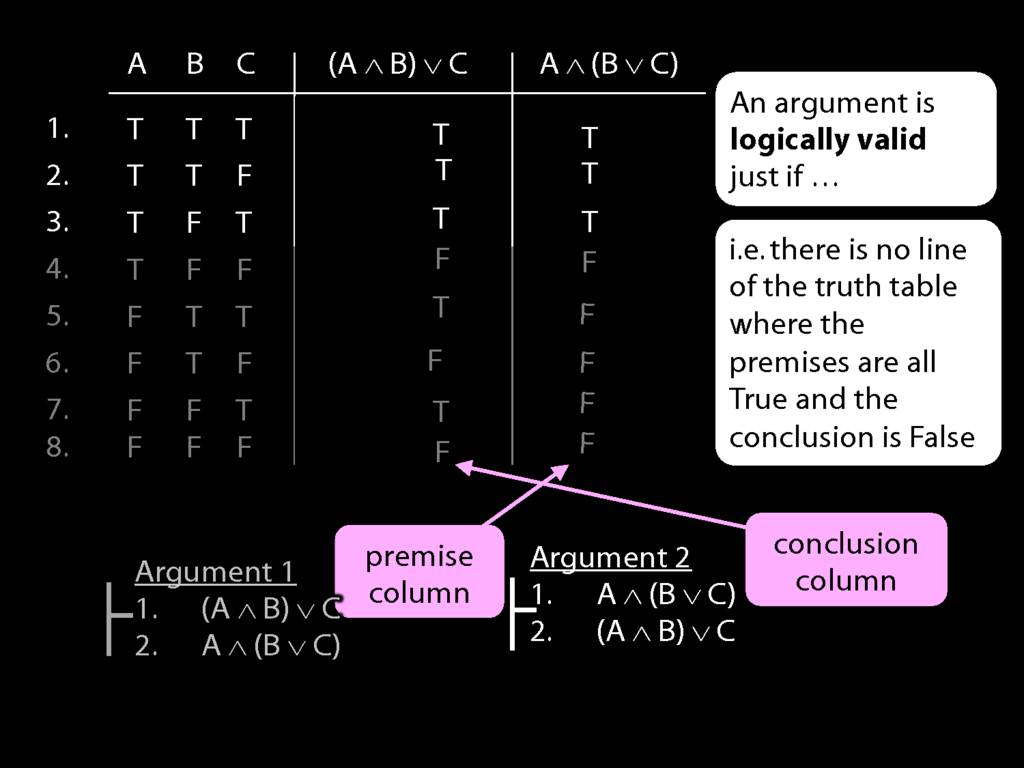
Now look at argument 2. Here the premise and conclusion columns are the other way around.

In the last five rows, the premise is false. So we can ignore these because we won't find a true premise AND a false conclusion where the premise is false.'

What about the top three rows?

In the top three rows, the premise is true ...

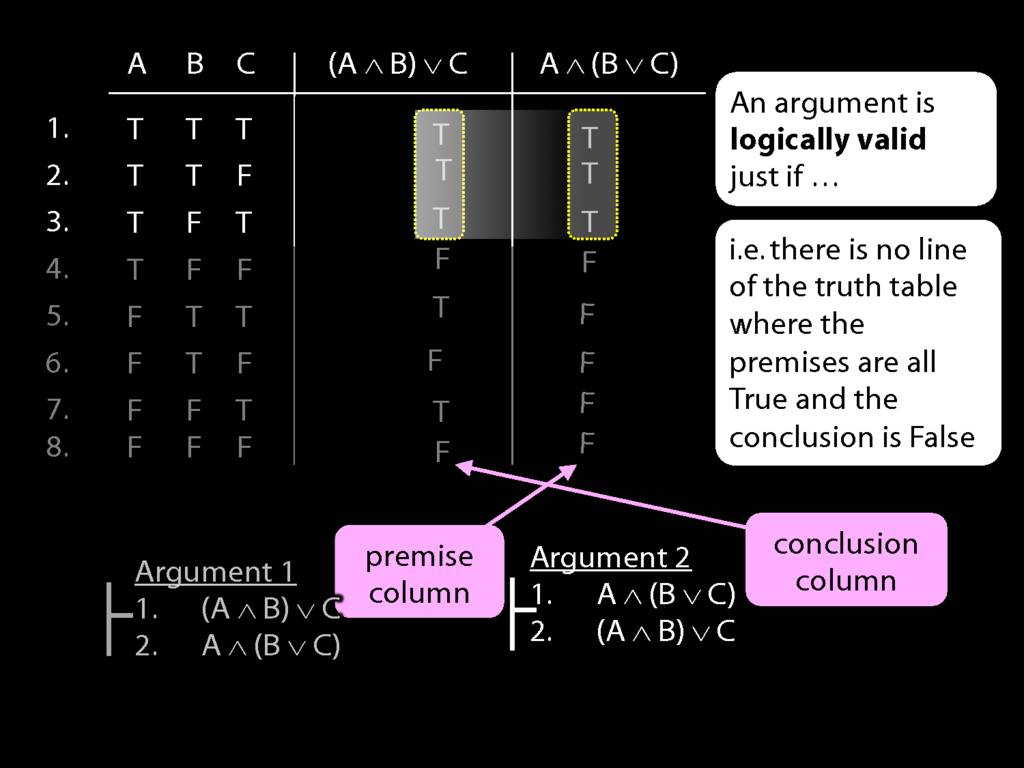
... but so is the conclusion.

So this second argument is clearly logically valid.

(A ∧ B) ∨ C

A ∧ (B ∨ C)

This ends my discussion of these two sentences. Although they differ only with respect to brackets, they have different truth-tables and so contribute differently to the validity or not of arguments.

There's a simple message and a complex one. The simple message is that the brackets matter. The complex one is that we have more work to do in explaining our formal language, awFOL. We have more work to do because we haven't yet said what the brackets mean, although it's clear that they contribute to the meanings of sentences of awFOL. What is the counterpart of a truth-table for brackets? In this course we don't have time to worry about this question; we must leave the meaning of the brackets as something that you get only implicitly.

3.14, 3.15

7.2, 7.5, 7.6