Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
Translating a Simple Argument

We're studying a formal system of proof called Fitch.
Here's the first rule of Fitch. It's called conjunction elimimnation.
The rule says that if you have a conjunction of two things in your proof, you can add a new line to your proof containing either one.

So if you something like this in your proof ...
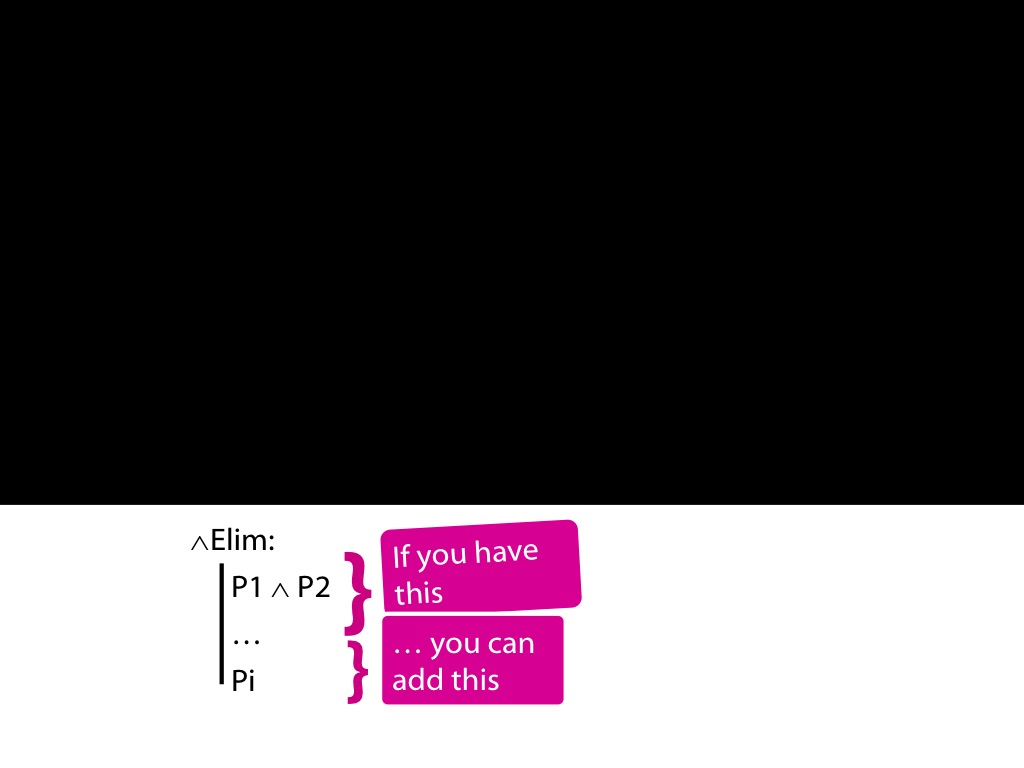
... you can add something matching this.
I'll explain how to use conjunction elimination in a moment. First, let's look at another rule.

This rule is called conjunction introduction.
The rule says that if you have two things in your proof, you can extend your proof by one line to add their conjunction.

So if you these things matching these in your proof ...

... you can add something matching this.

So let's look at an application of our rules of proof.
I want to do this by translating an argument from English into our formal language awFOL.

This doesn’t seem to be true.

But this does seem to be true, or at least horribly plausible.

And this seems right too, maybe.

Now if we take the first two sentences as premises and the second as a conclusion, we have an argument.
Is the argument logically valid?
Apparently not because the premises are true and the conclusion false.
But look what happens when we translate it into awFOL assuming that the english 'and' means the same as the awFOL conjunction symbol, '∧'.

The first premise comes out as P∧Q

Where P stands for the sentence 'The world will overheat'.

And Q stands for 'We will all die'.

What about the second premise?

This comes out as Q∧R.

The key thing is that we're re-using Q because the sentence about the world overheating occurs in both the first
and second premises. Where we have the same English sentence, we have to use the same sentence-letter in awFOL.

Now what about the conclusion?

This is P∧R. Not that both sentences are already familiar.

P occurs in the first premise ...

... and Q occurs in the second premise.

So here's our argument.

Since we're going to do a formal proof, we should use the vertical and horizontal lines.
(Surely you remember that the vertical line runs the length of the argument, and the horizontal line separates premises from conclusion.)


We also need to use line numbers.