Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
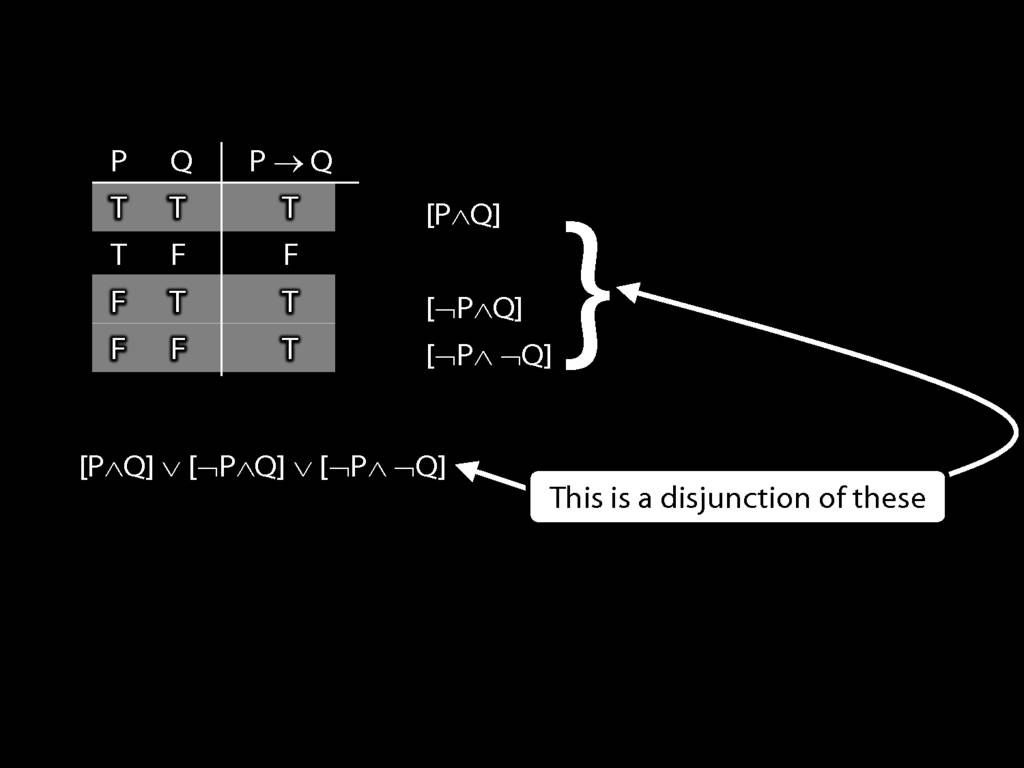
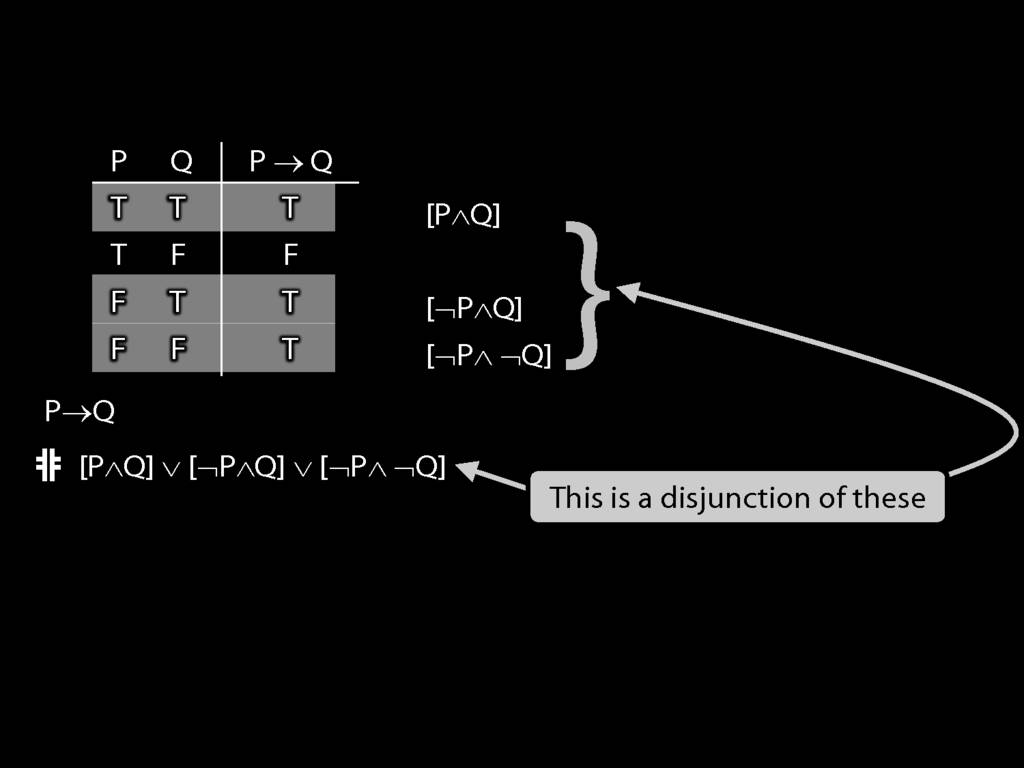
Truth-functional completeness

‘A set of truth-functors is said to be \emph{expressively adequate} (or sometimes \emph{functionally complete}) iff, for every truth-function whatever, there is a formula containing only those truth-functors which express that truth-function, i.e. which has as its truth-table the truth-table specifying that function.’ (Bostock, \emph{Intermediate Logic} p. 45)
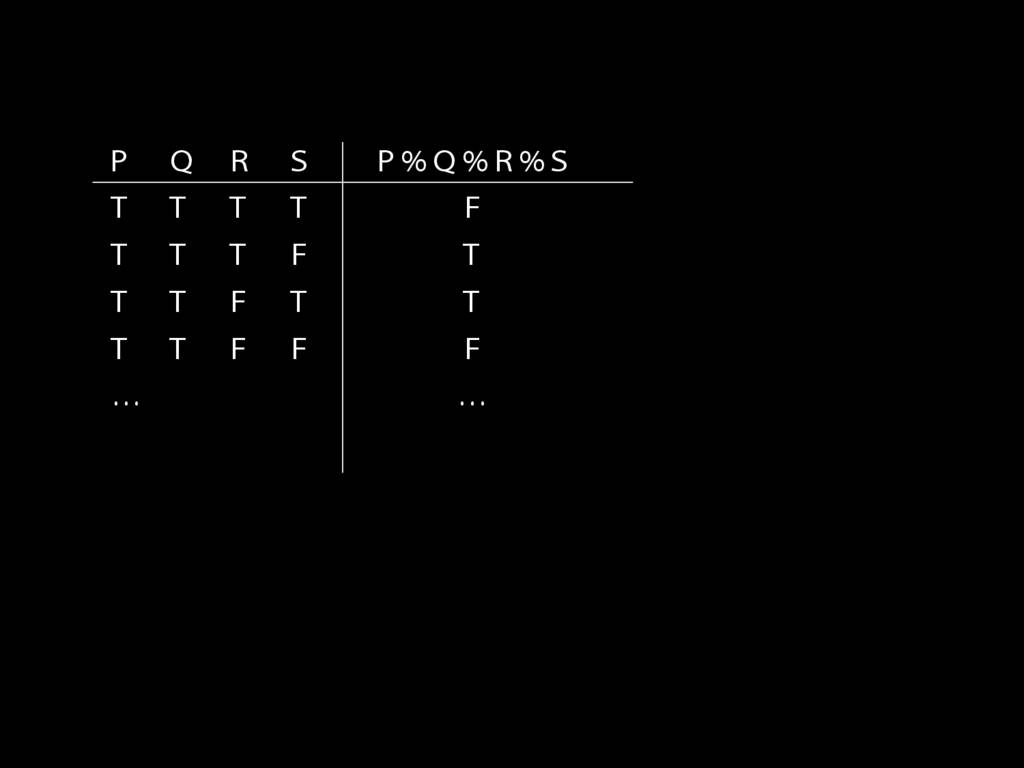
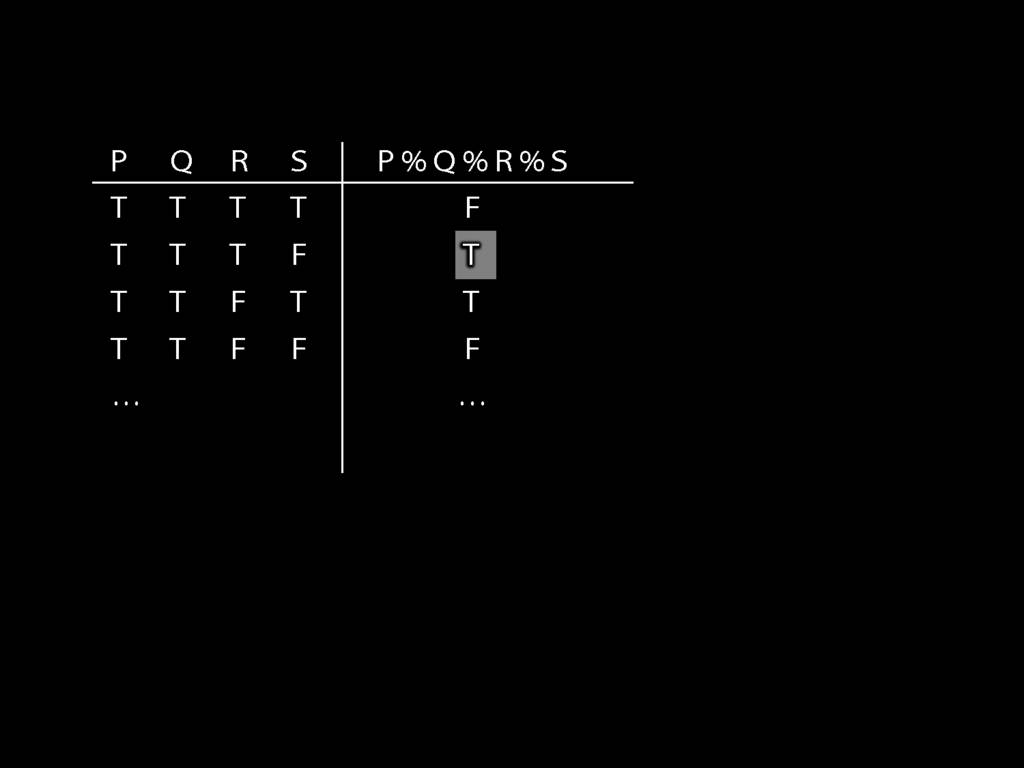
Illustration of the proof that $\{$¬, ∧, ∨$\}$ is truth-functionally complete:
\emph{Exercise} assuming $\{$¬,∨,∧$\}$ is truth-functionally complete, show that $\{$¬,∨$\}$ is.

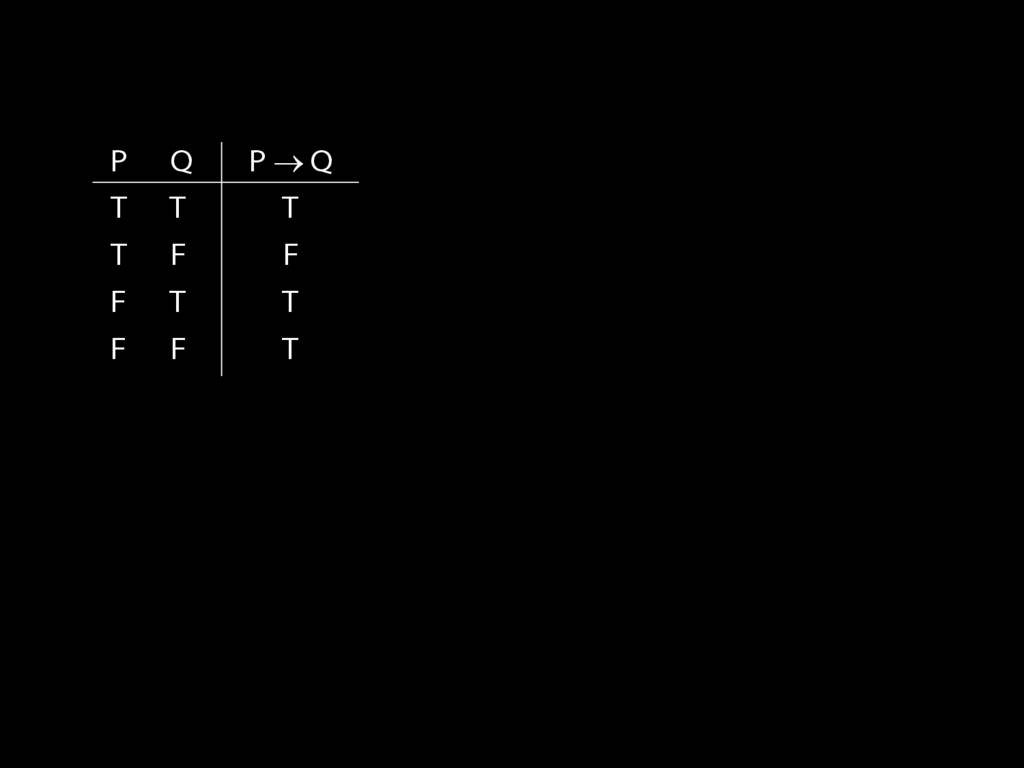

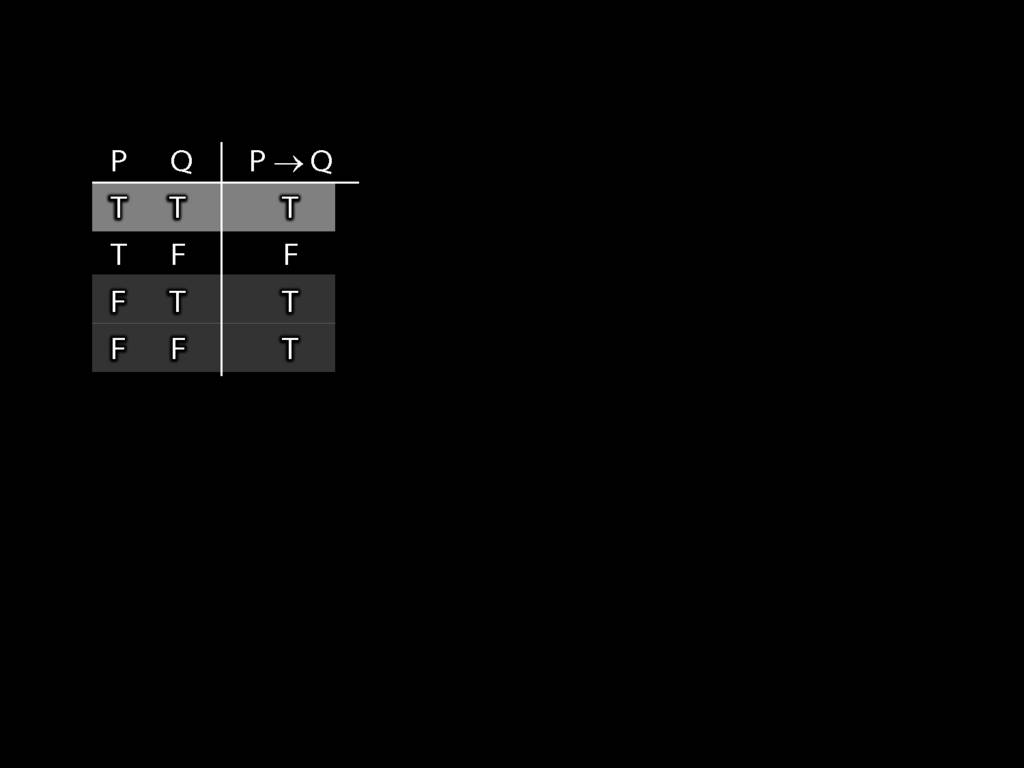
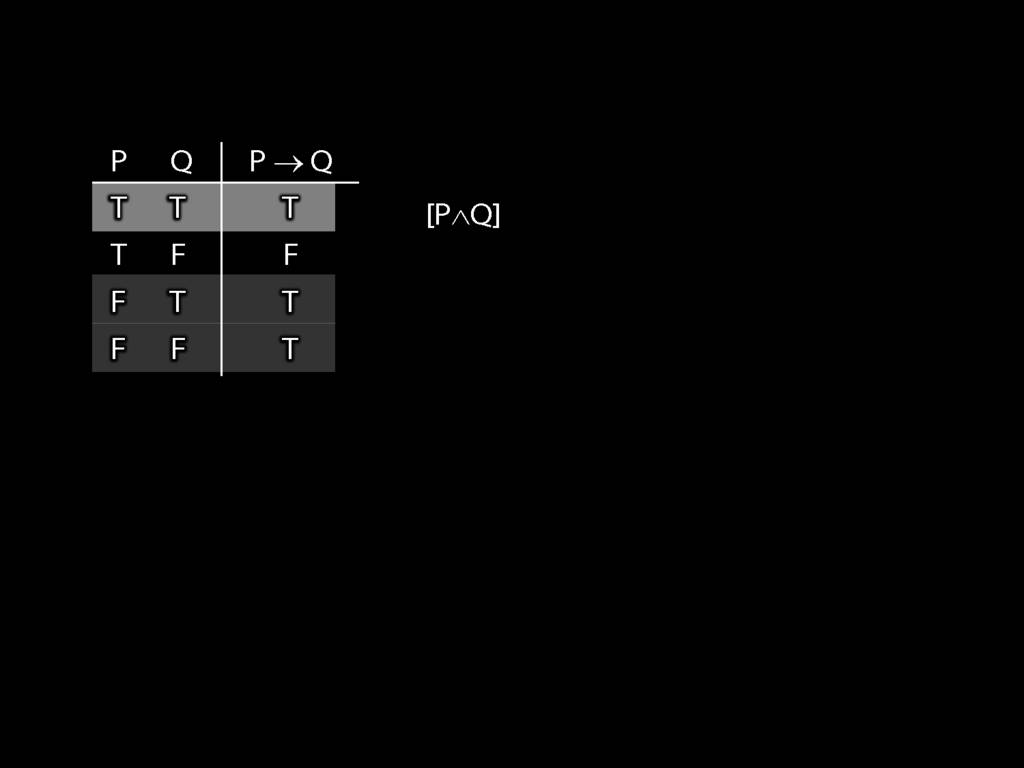
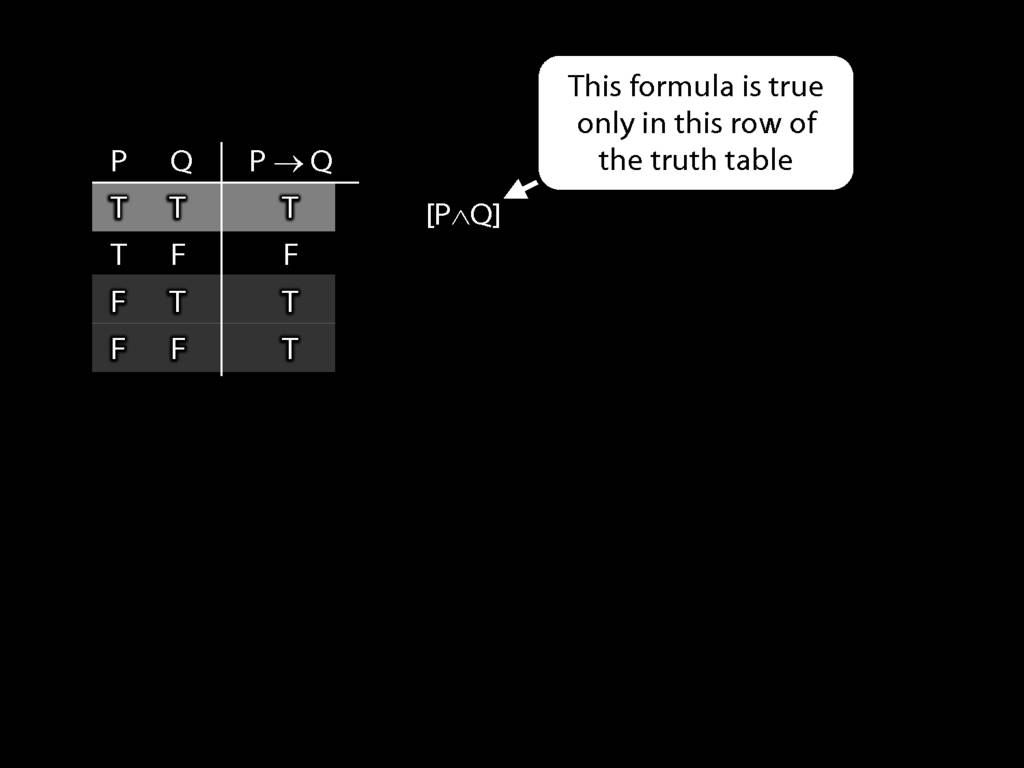








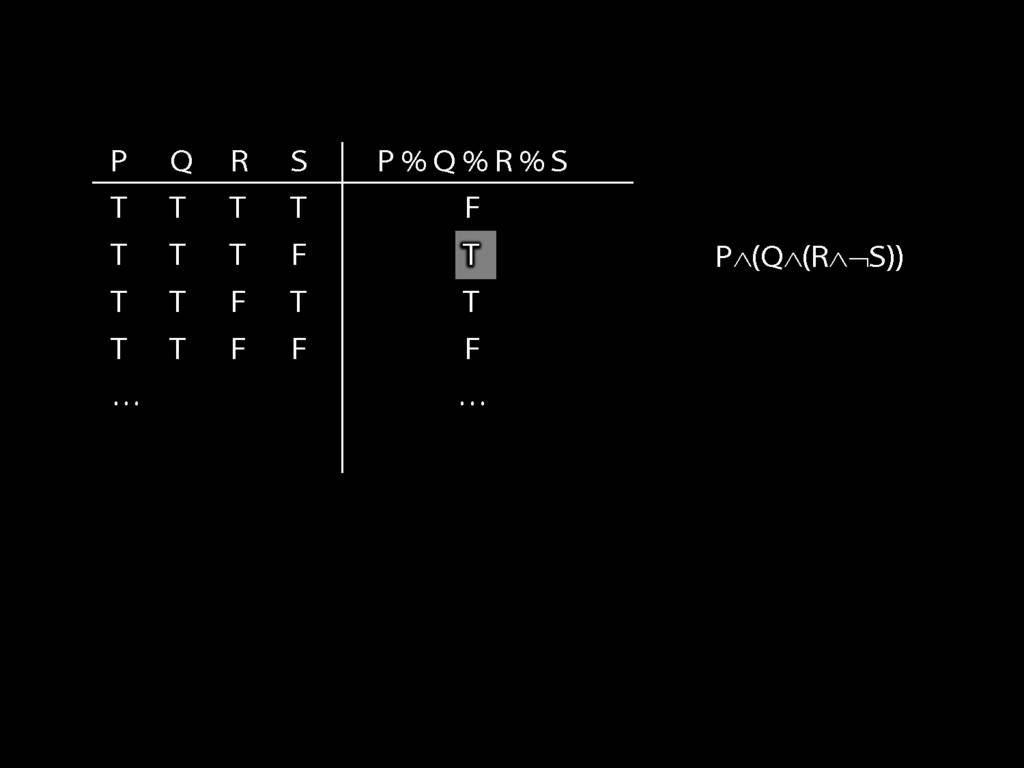
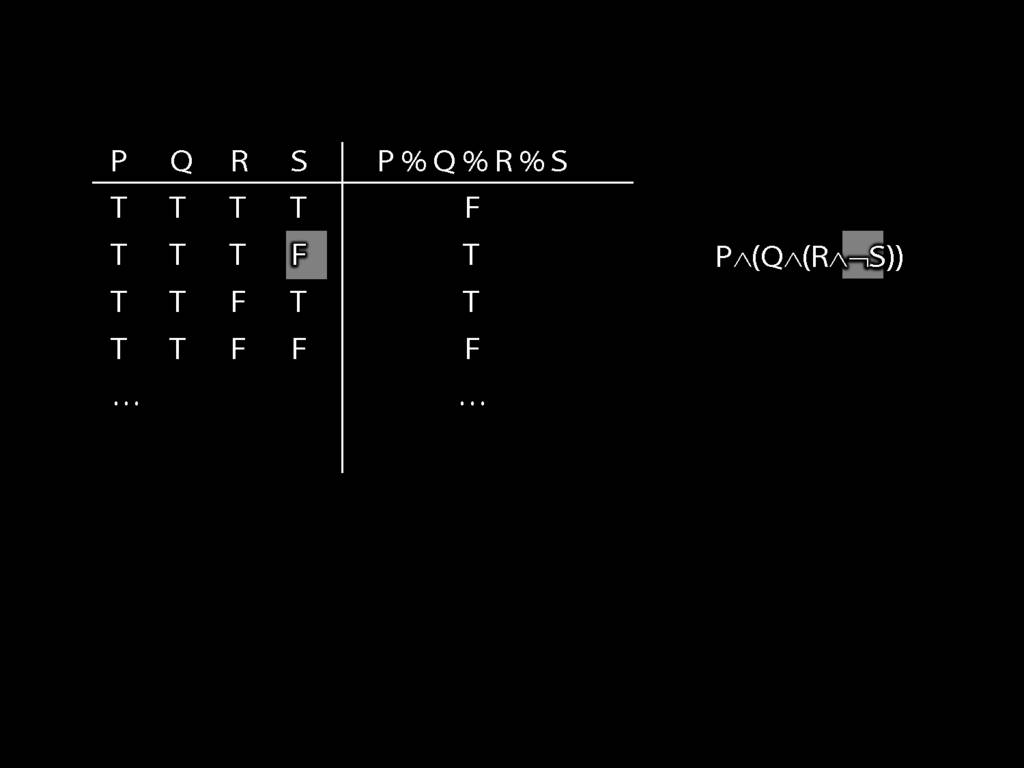


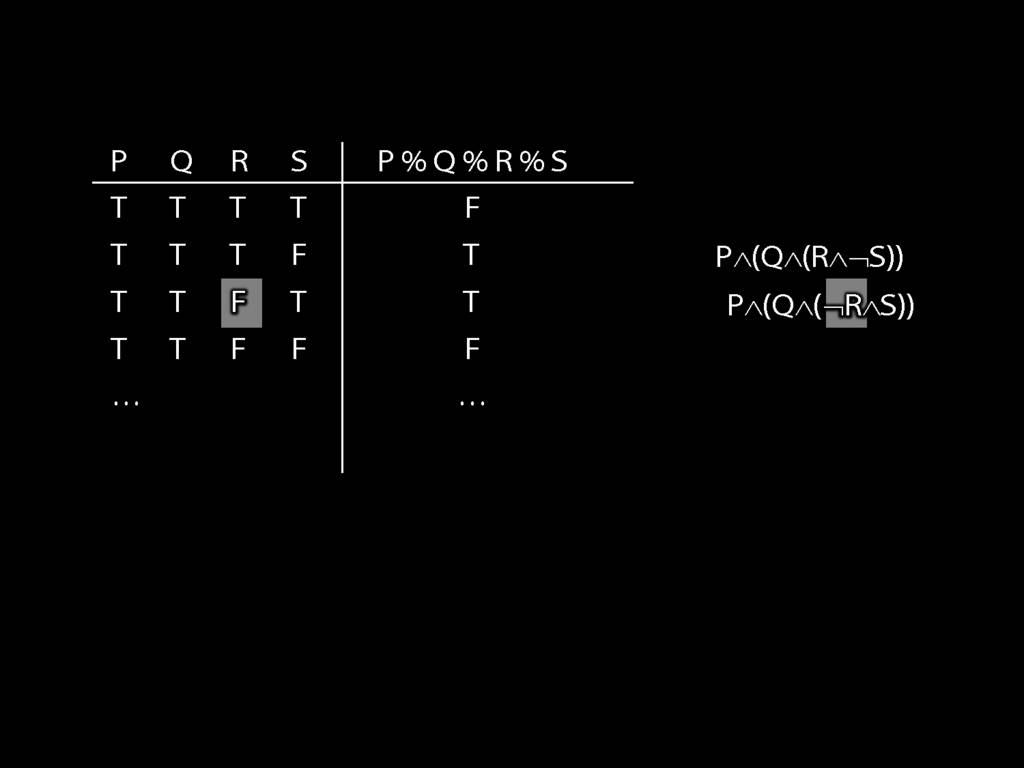












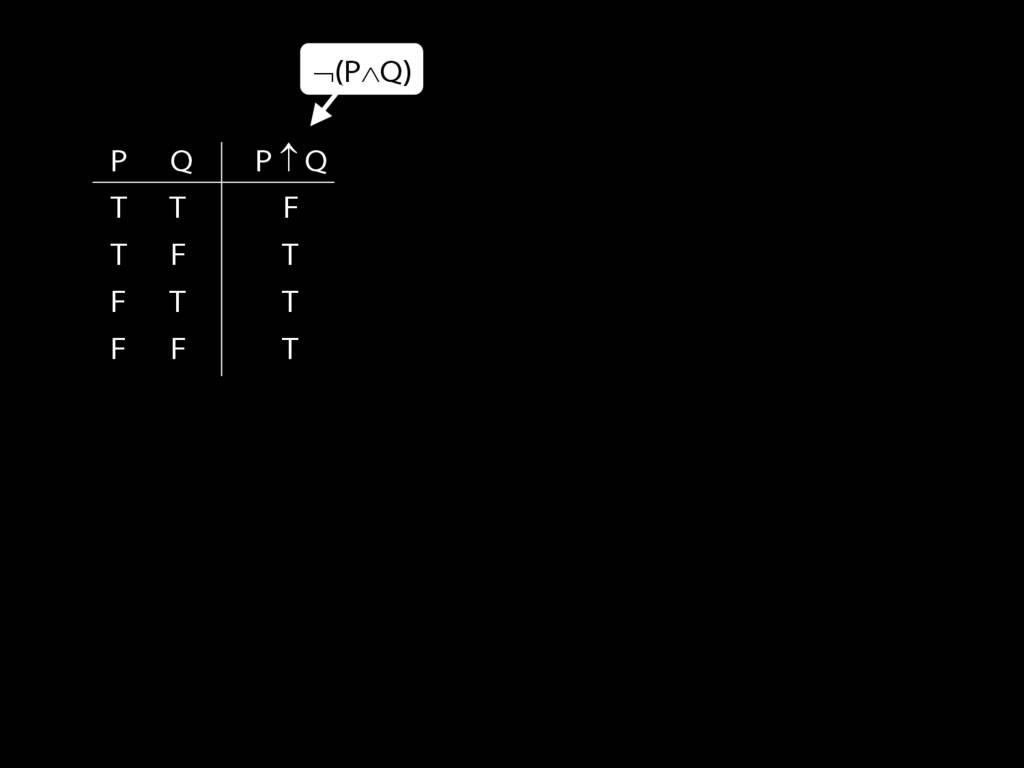



7.25, 7.26, *7.28, 7.29
7.25, 7.26, *7.28, 7.29