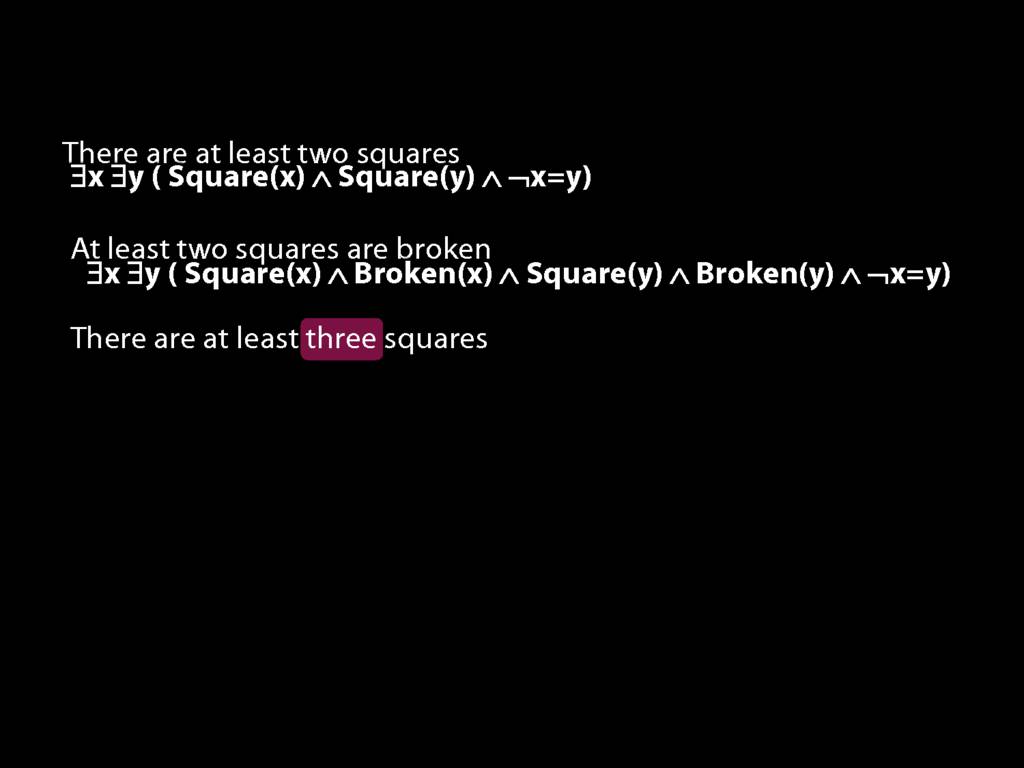
There are at least two squares:
\hspace{5mm} ∃x ∃y ( Square(x) ∧ Square(y) ∧ ¬x=y )
At least two squares are broken:
\hspace{5mm} ∃x ∃y (
\hspace{10mm} Square(x) ∧ Broken(x)
\hspace{10mm} ∧
\hspace{10mm} Square(y) ∧ Broken(y)
\hspace{10mm} ∧
\hspace{10mm} ¬x=y
\hspace{5mm} )
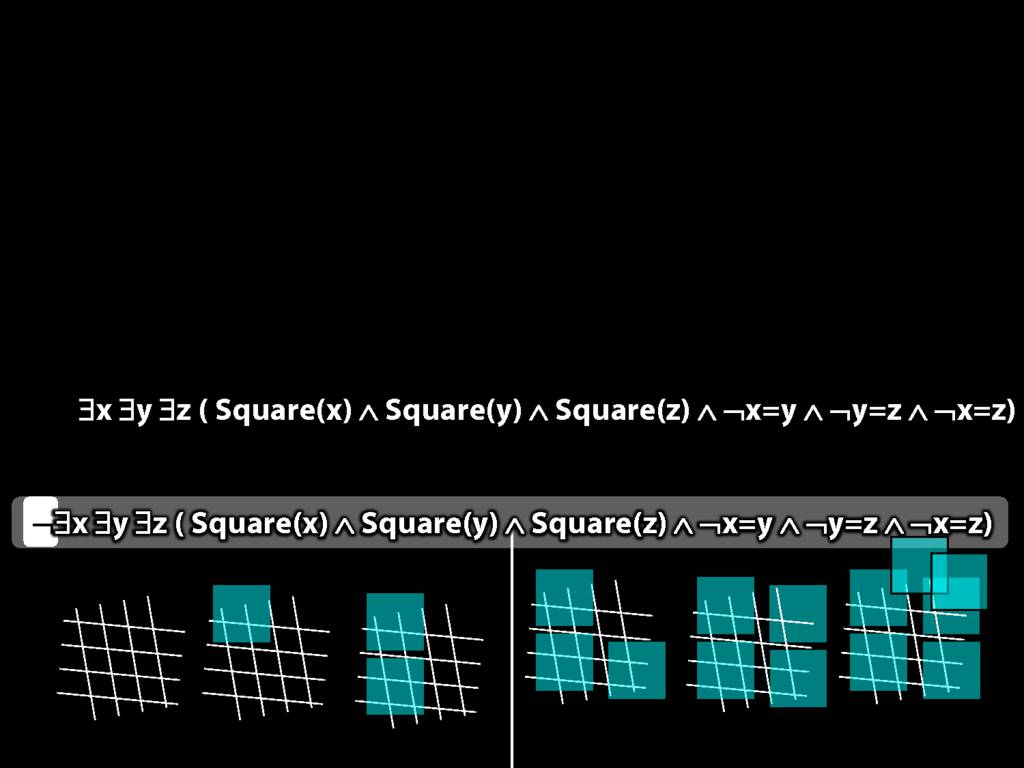
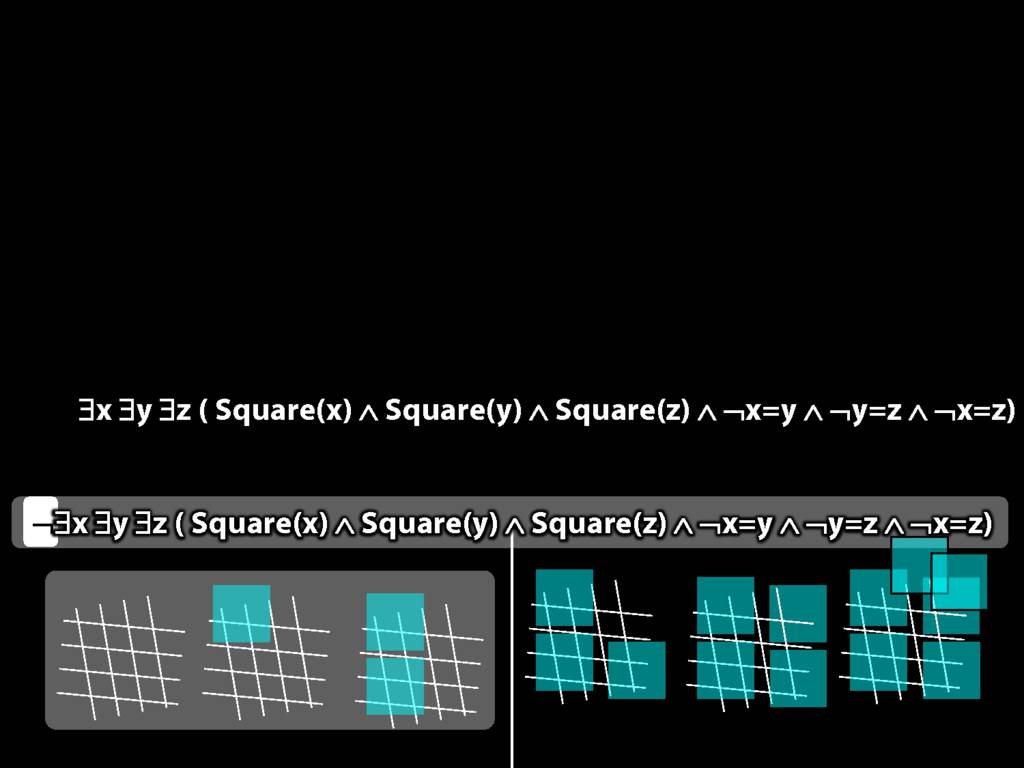
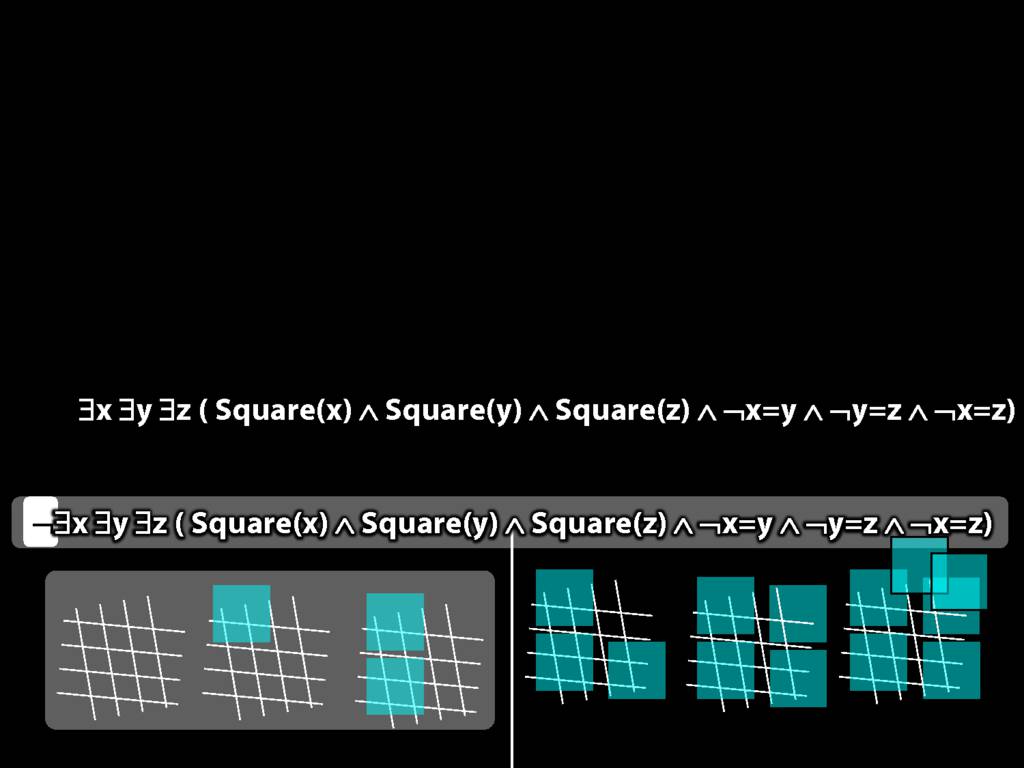
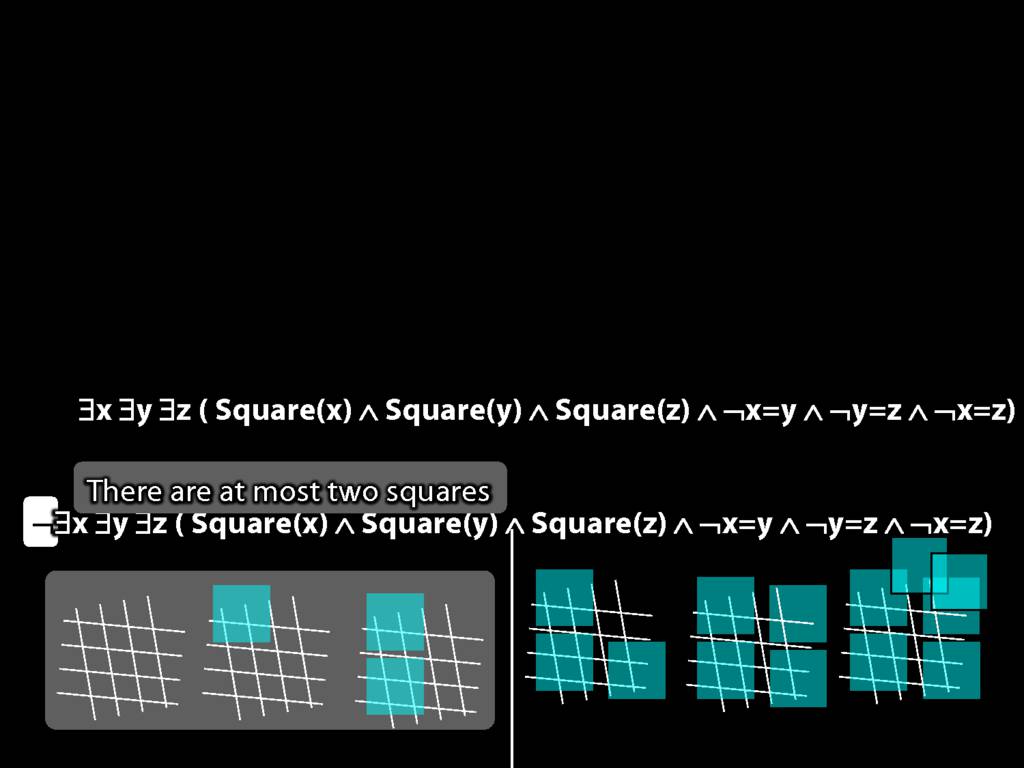
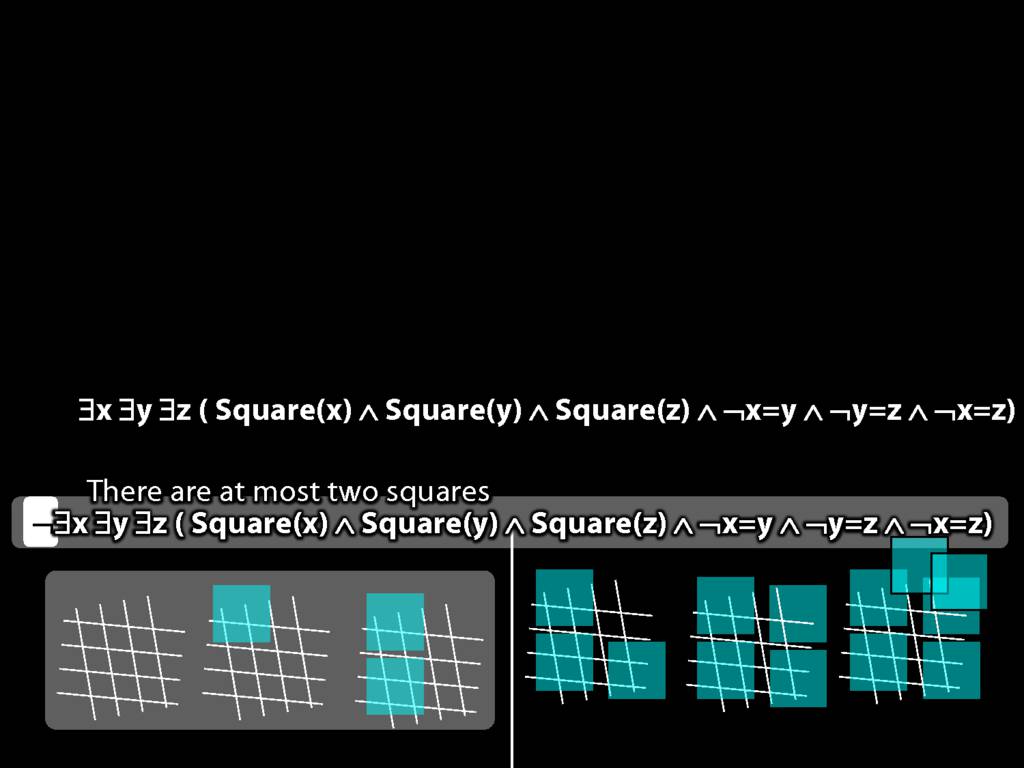
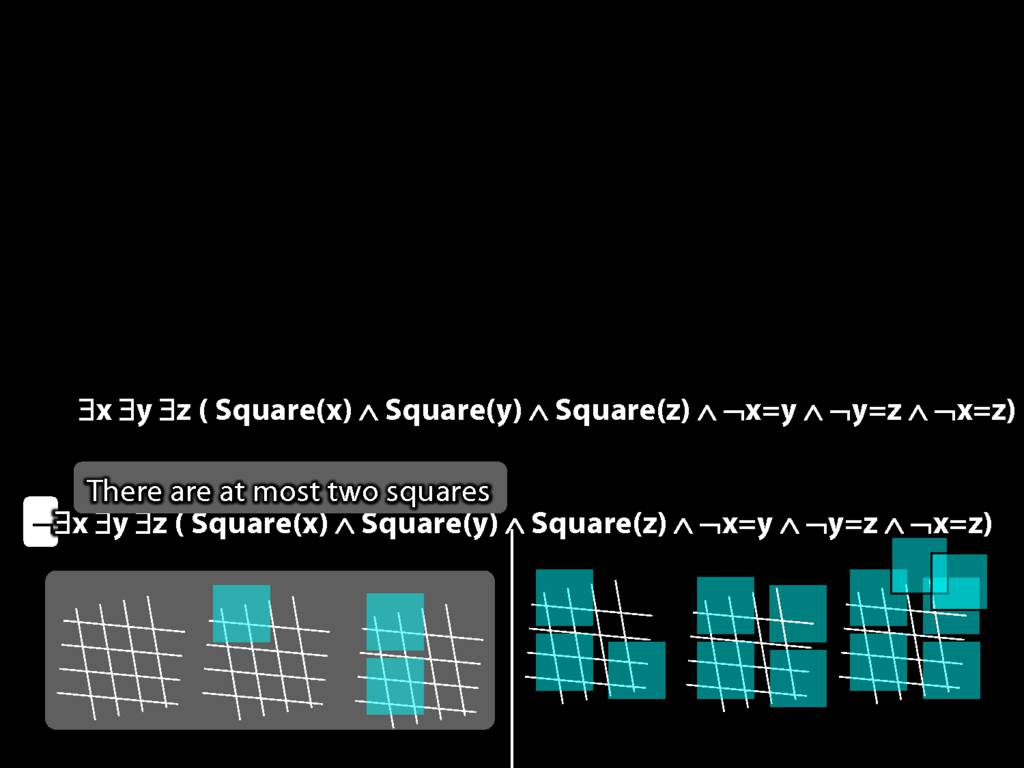
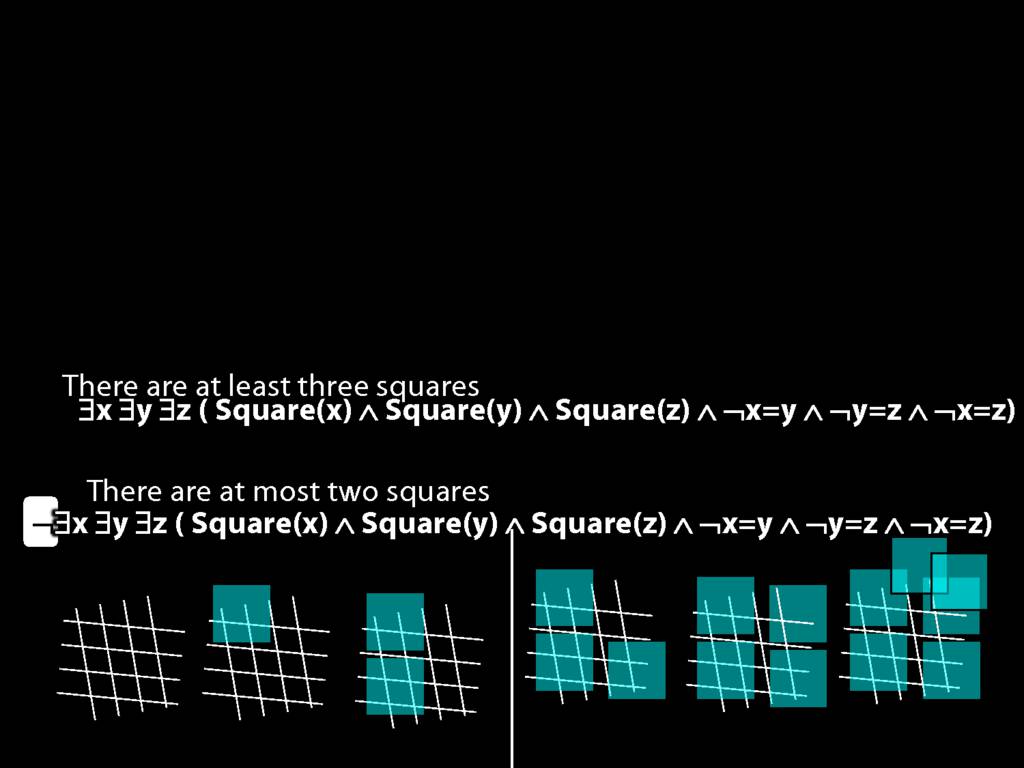
There are at least three squares:
\hspace{5mm} ∃x ∃y ∃z (
\hspace{10mm} Square(x) ∧ Square(y) ∧ Square(z)
\hspace{10mm} ∧
\hspace{10mm} ¬x=y ∧ ¬y=z ∧ ¬x=z
\hspace{5mm} )
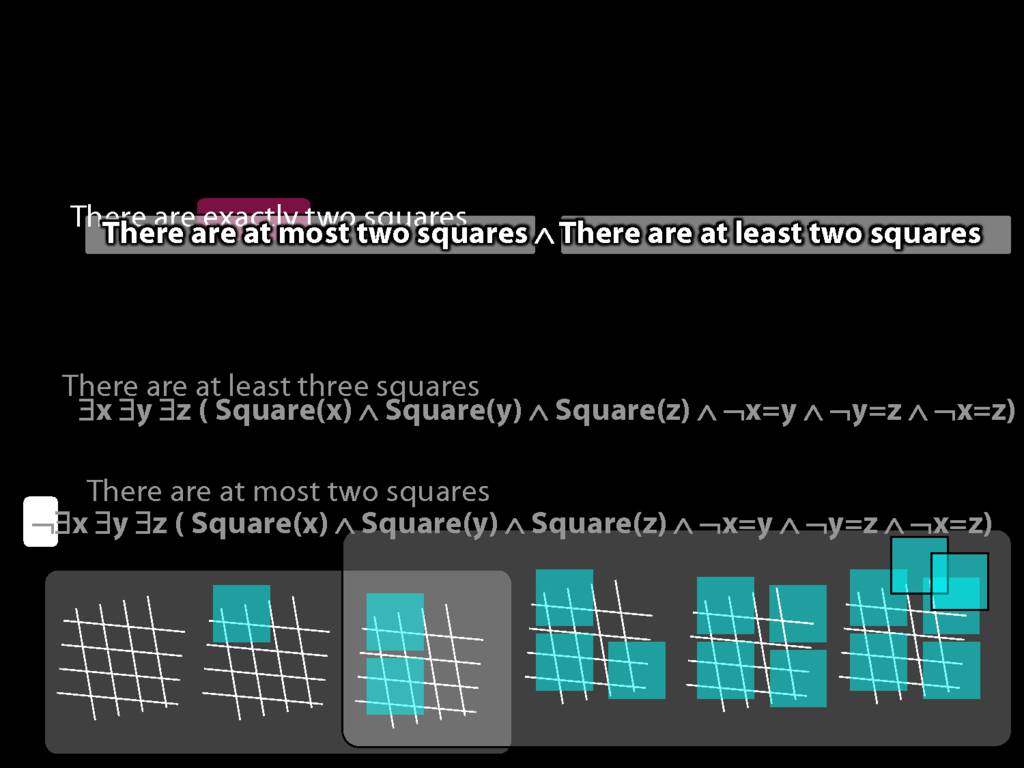
There are at most two squares:
\hspace{5mm} ¬There are at least three squares
\hspace{5mm} ¬∃x ∃y ∃z ( Square(x) ∧ Square(y) ∧ Square(z) ∧ ¬x=y ∧ ¬y=z ∧ ¬x=z)
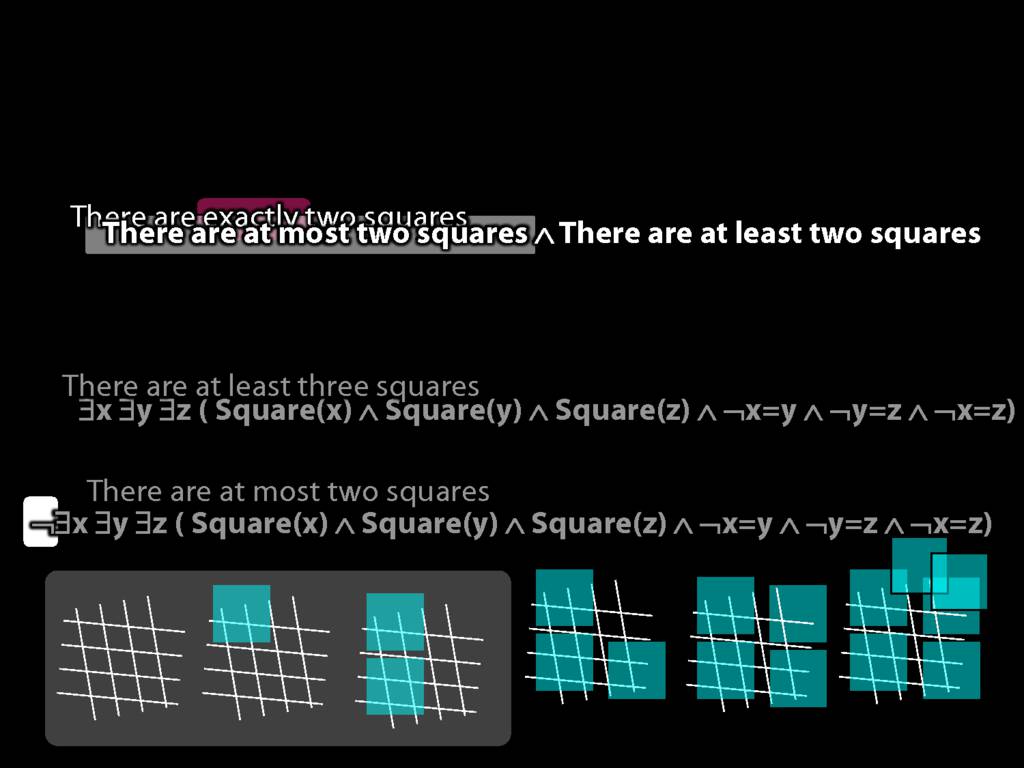
There are exactly two squares:
\hspace{5mm} There are at most two squares ∧ There are at least two squares
\textbf{Number: alternatives}
There is at most one square:
\hspace{5mm} ∀x ∀y ( (Square(x) ∧ Square(y)) → x=y )
There are at most two squares:
\hspace{5mm} ∀x ∀y ∀z (
\hspace{10mm} (Square(x) ∧ Square(y) ∧ Square(z))
\hspace{10mm} →
\hspace{10mm} (x=y ∨ y=z ∨ x=z)
\hspace{5mm} )
There is exactly one square:
\hspace{5mm} ∃x ( Square(x) ∧ ∀y( Square(y) → x=y ) )
There are exactly two squares:
\hspace{5mm} ∃x∃y (
\hspace{10mm} Square(x) ∧ Square(y) ∧ ¬x=y
\hspace{10mm} ∧
\hspace{10mm} ∀z( Square(z) → (z=x ∨ z=y) )
\hspace{5mm} )
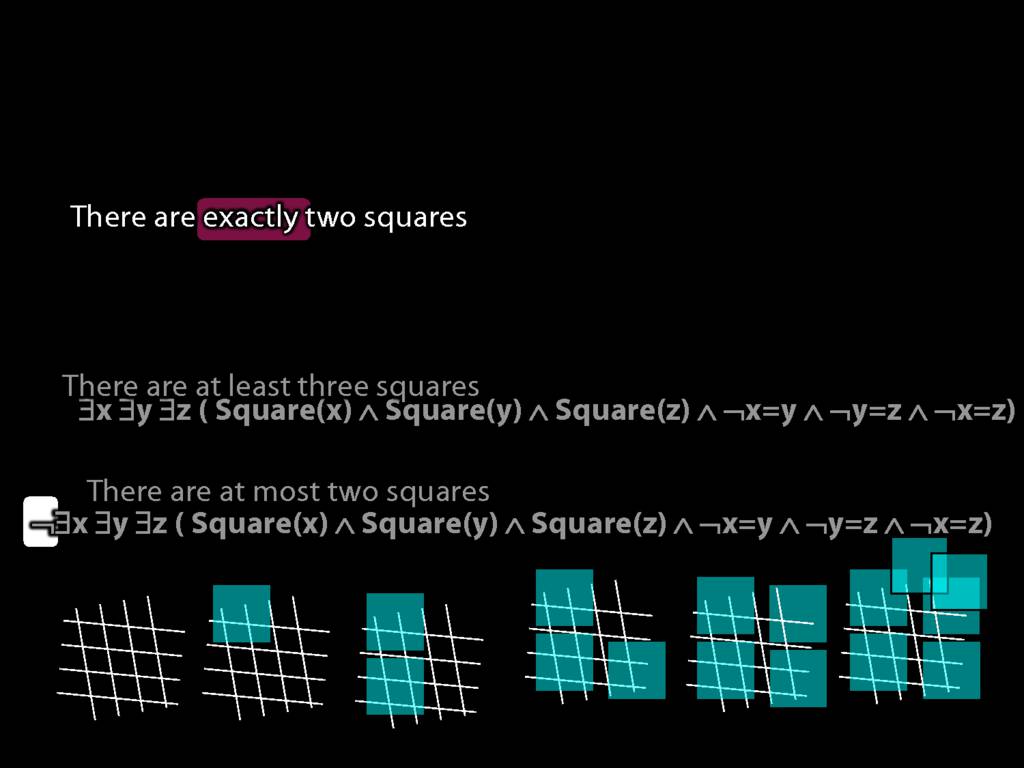
14.2--14.3
14.4--14.5
14.10--14.11