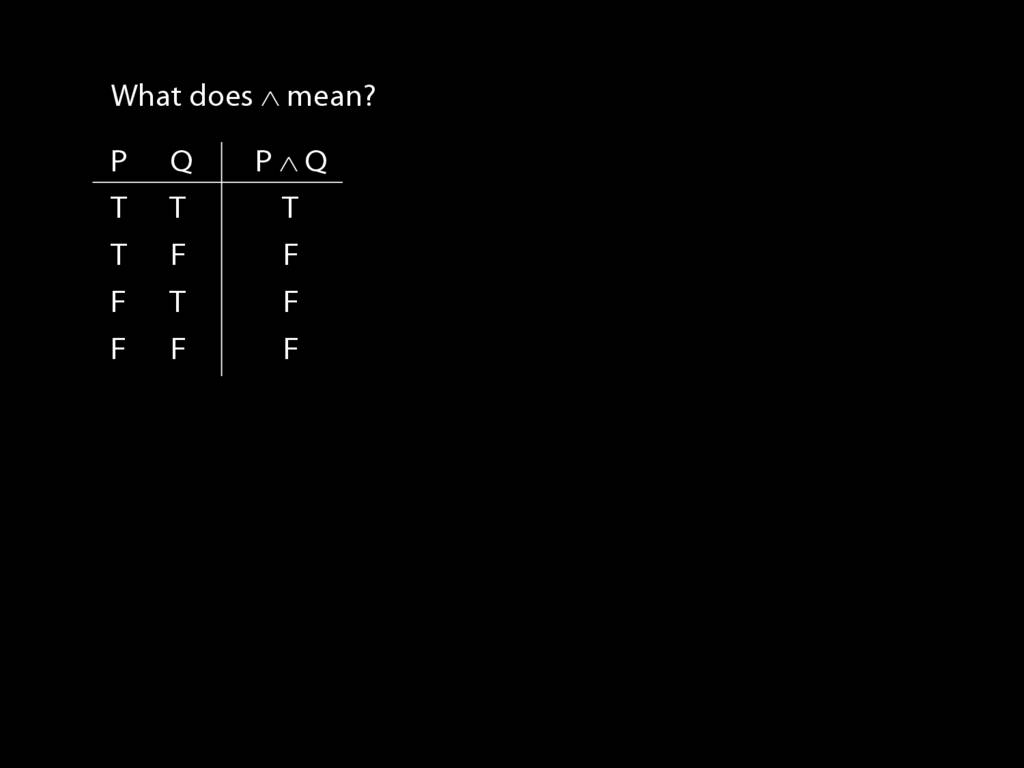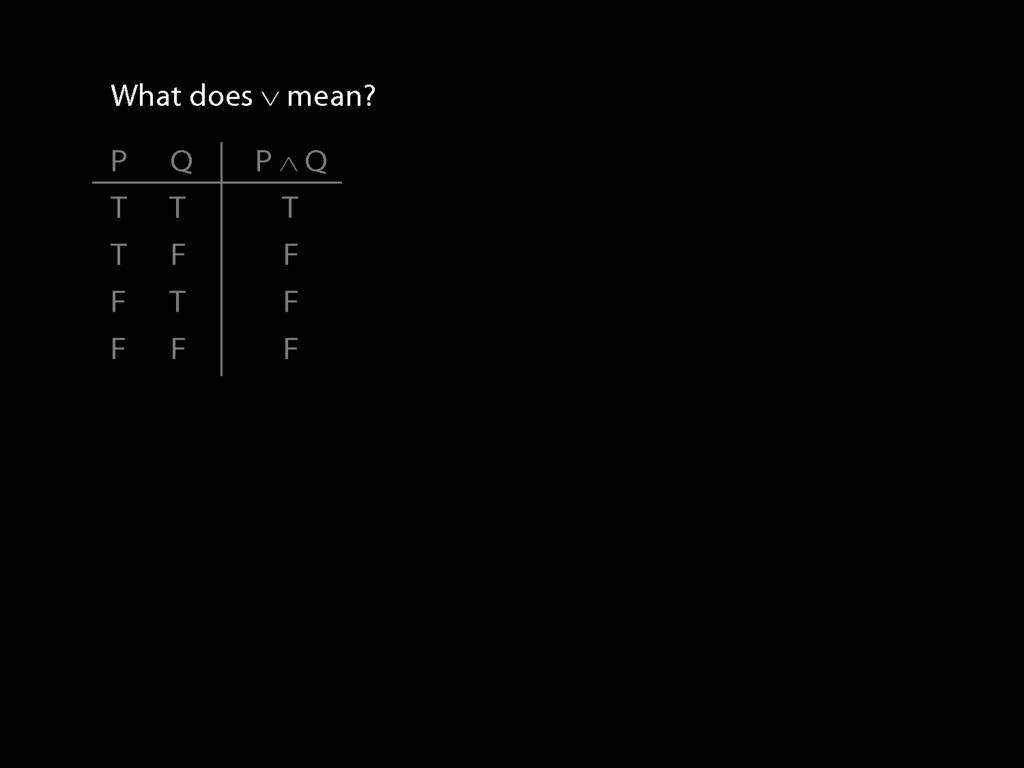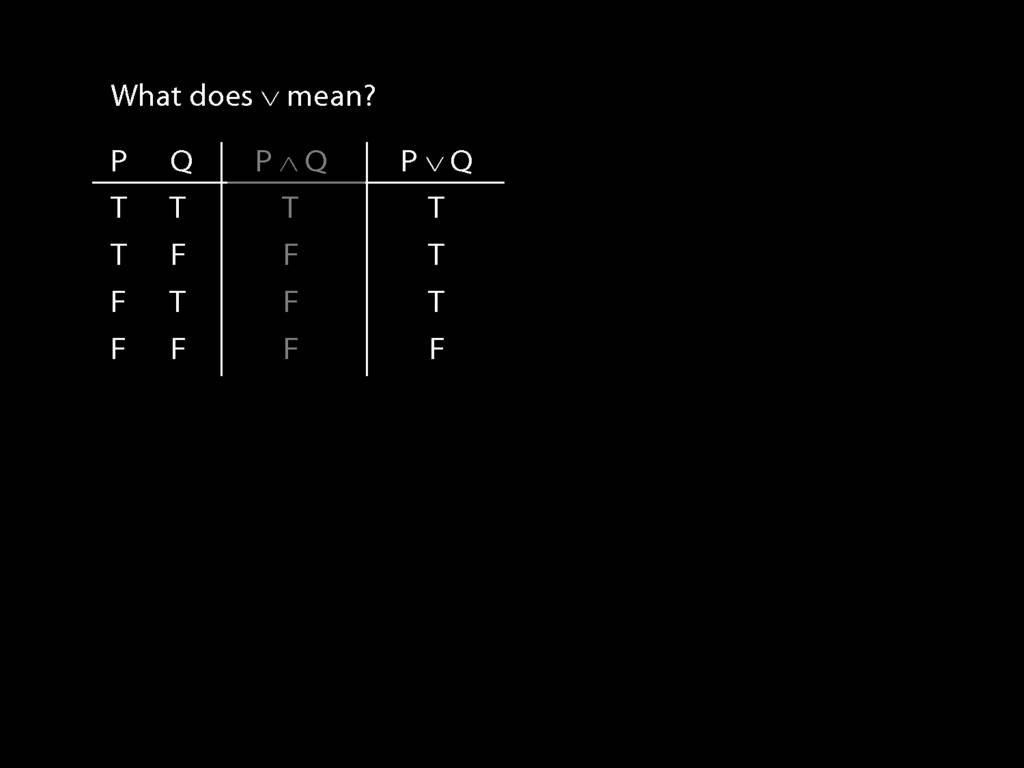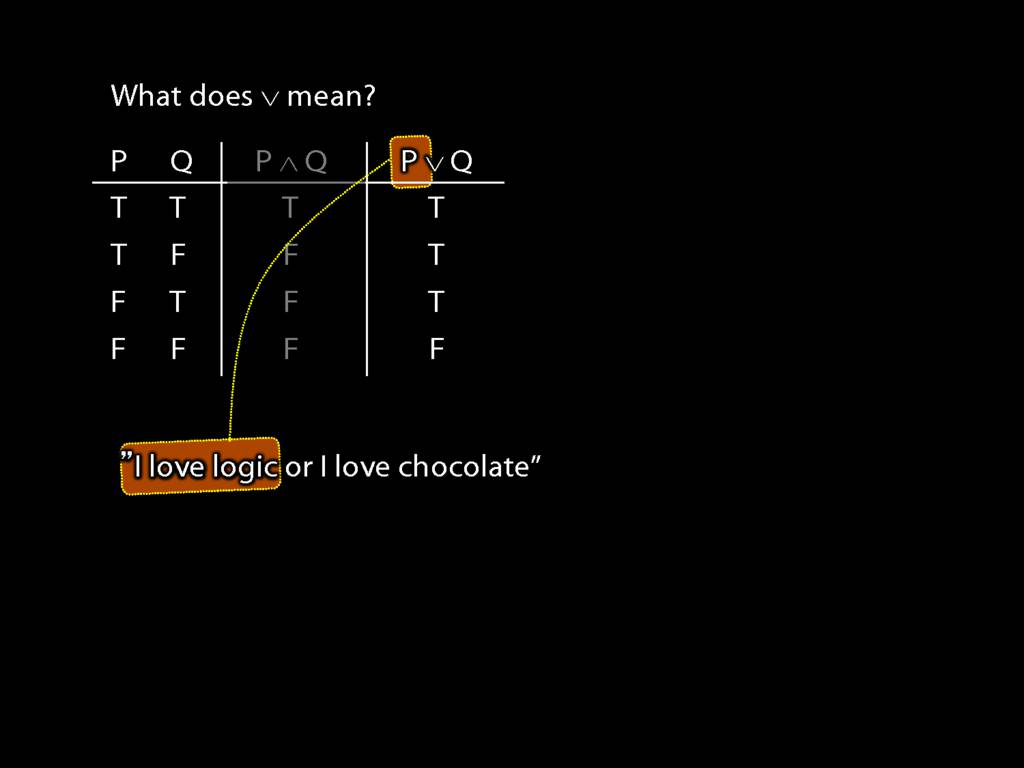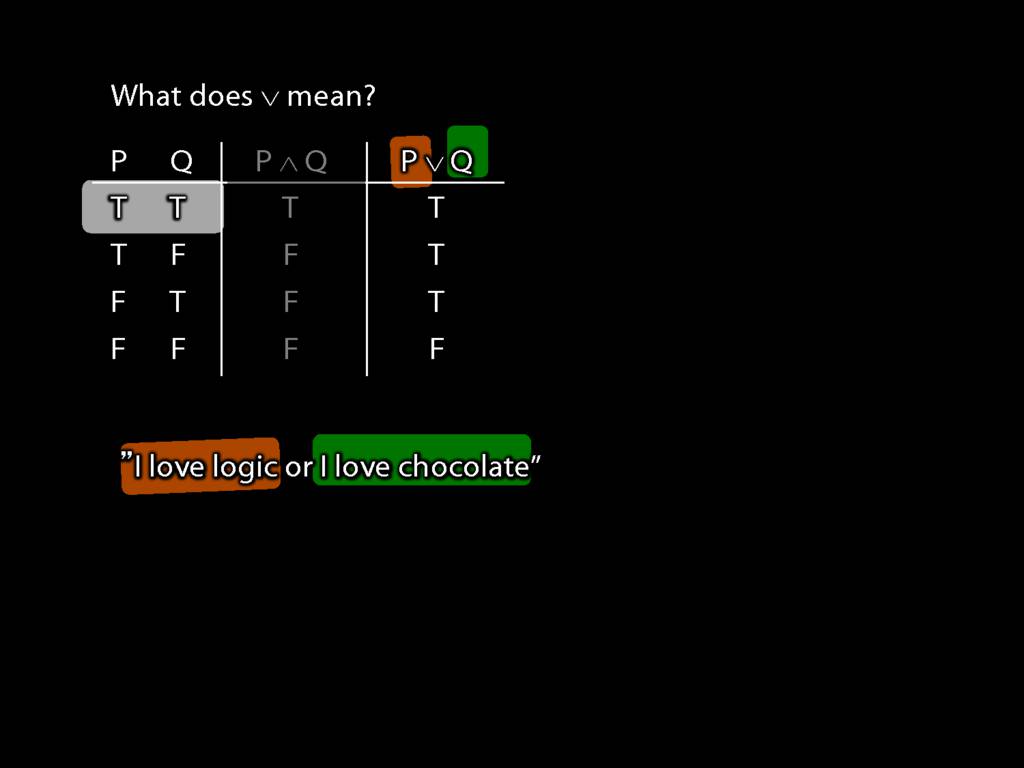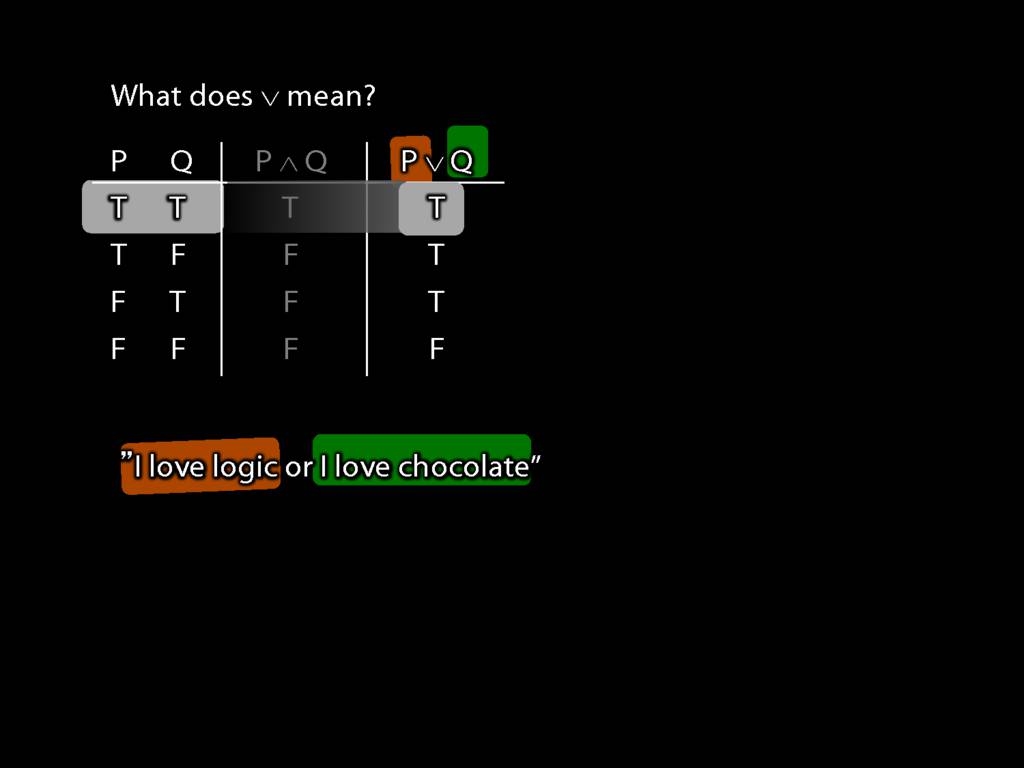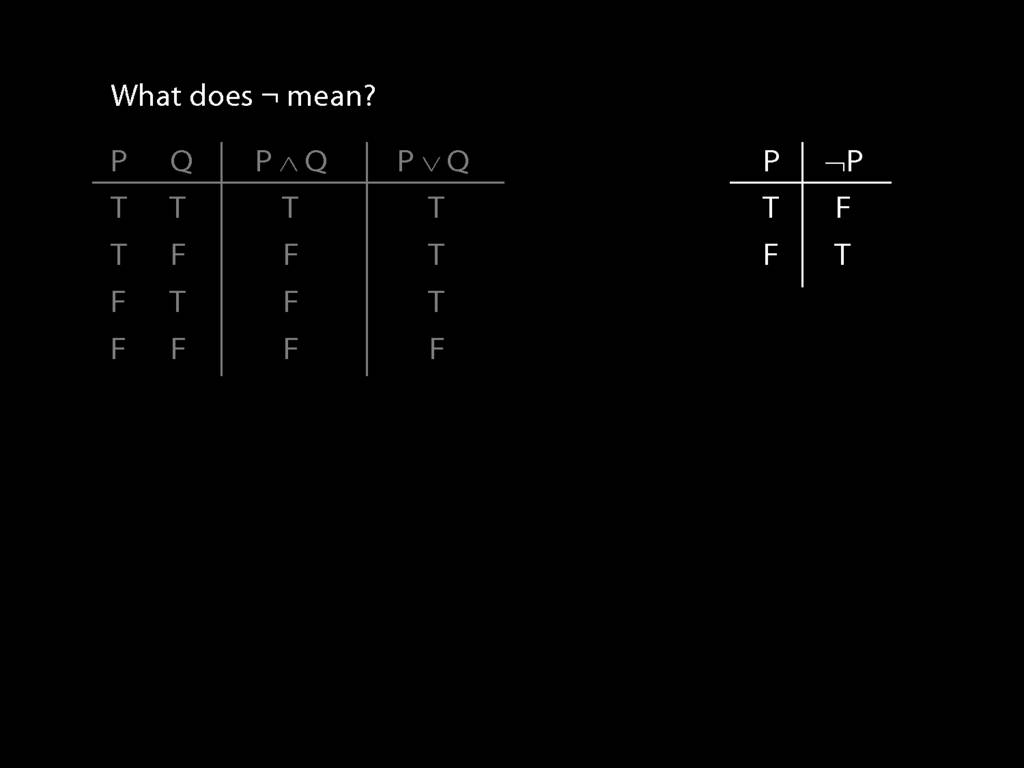Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides

\def \ititle {Logic I}
\def \isubtitle {Fast Lecture 01}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
\section{Terminology}
\section{Logically Valid Arguments}
\emph{Reading:} §2.1

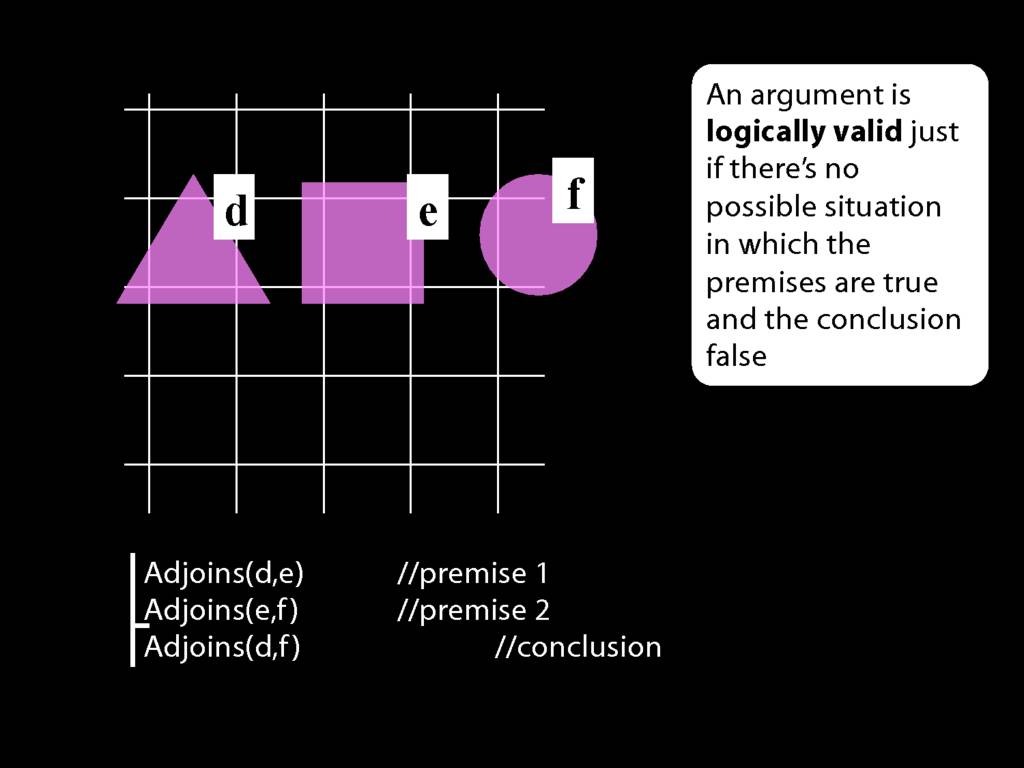
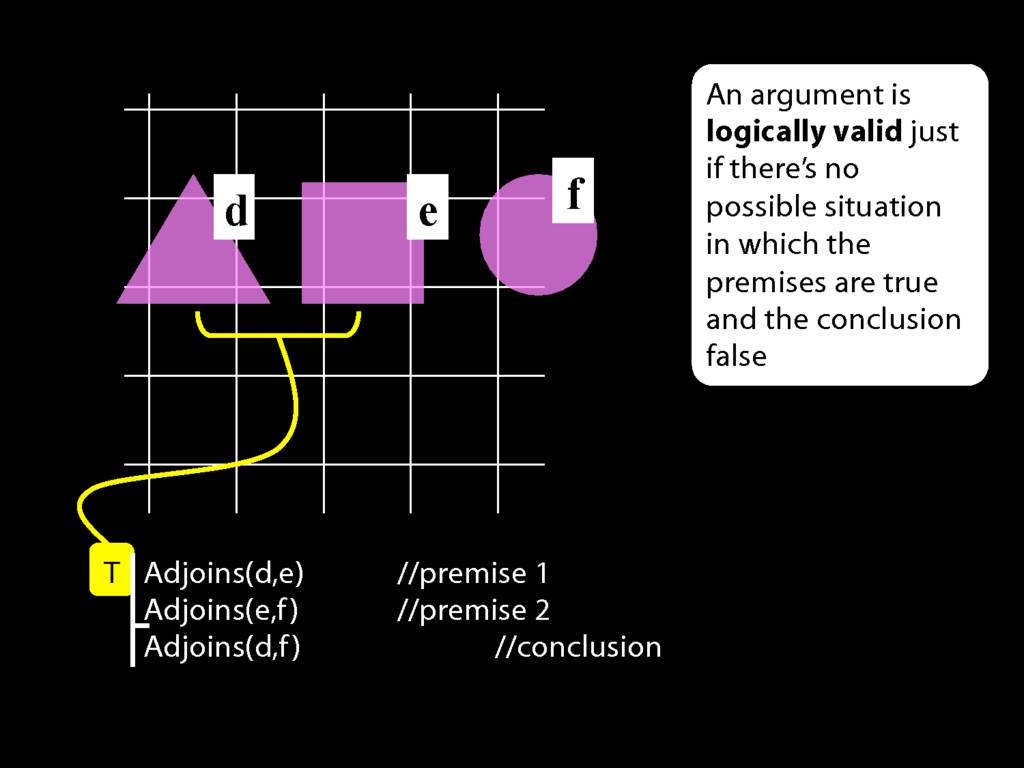
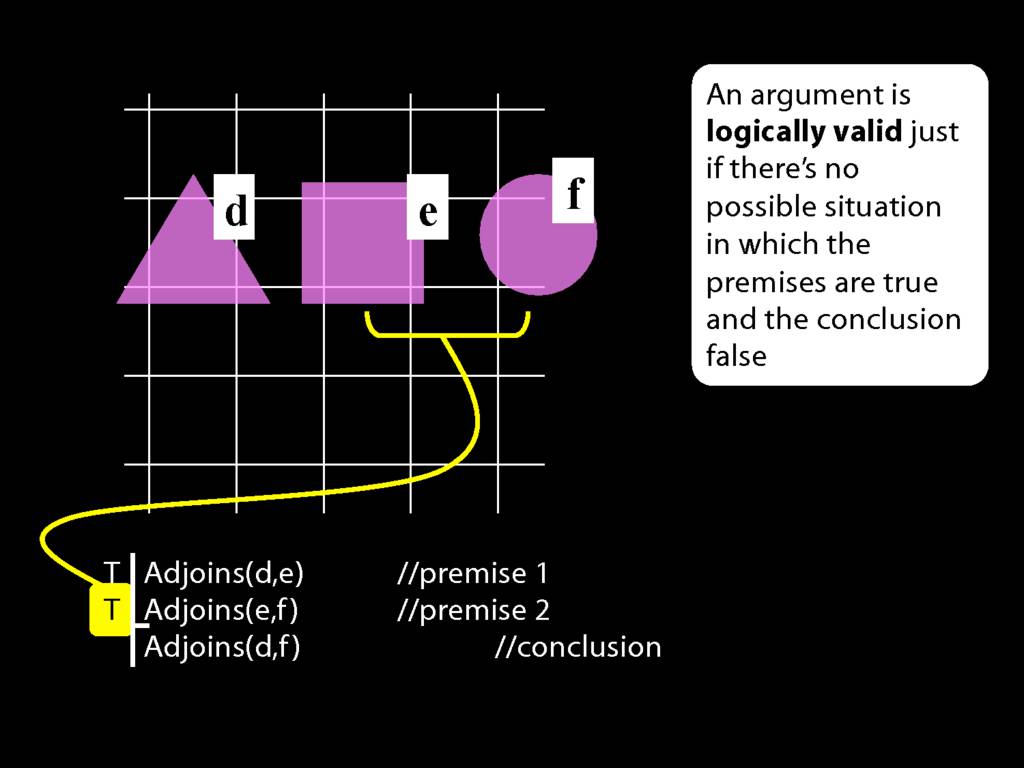
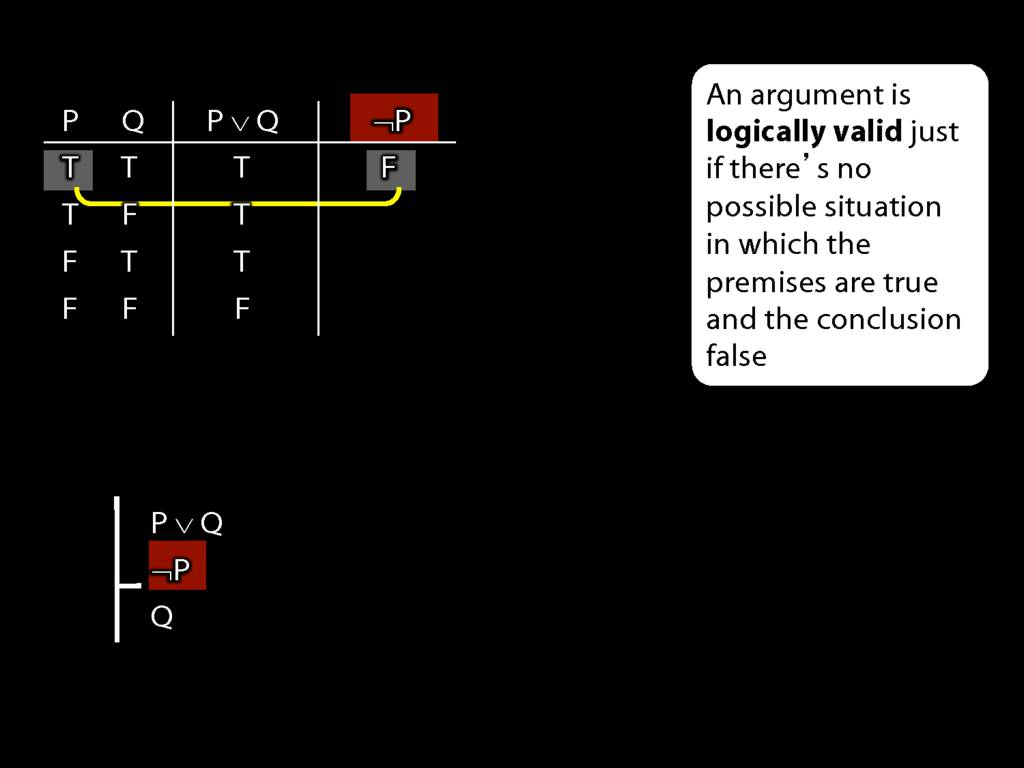
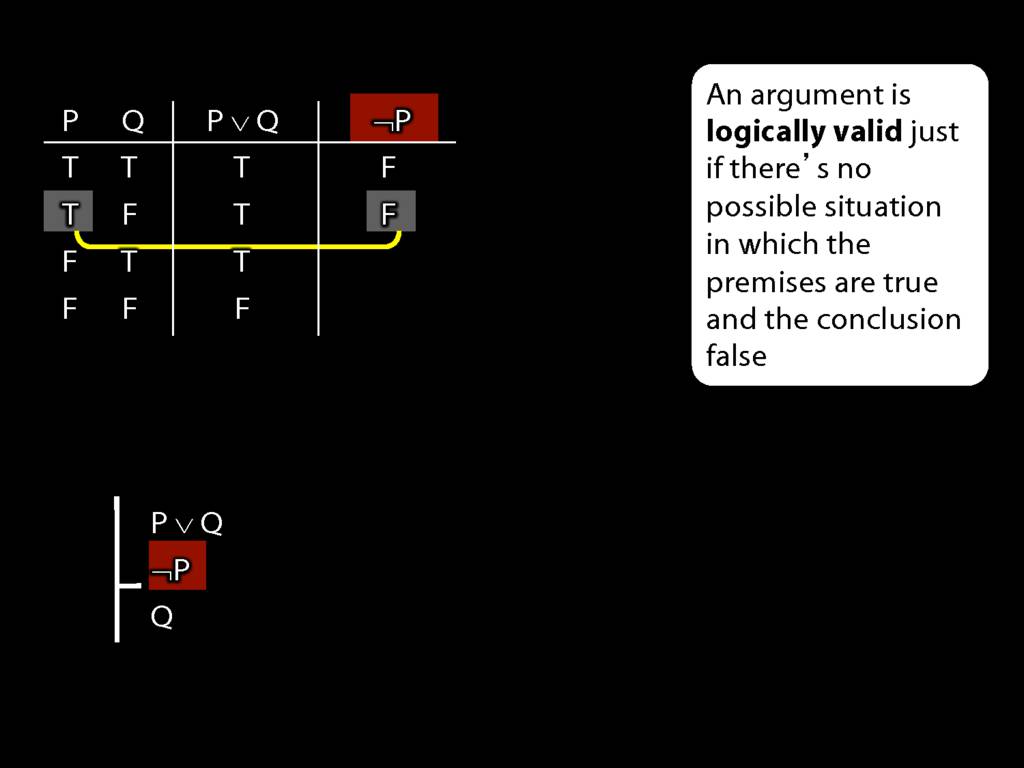
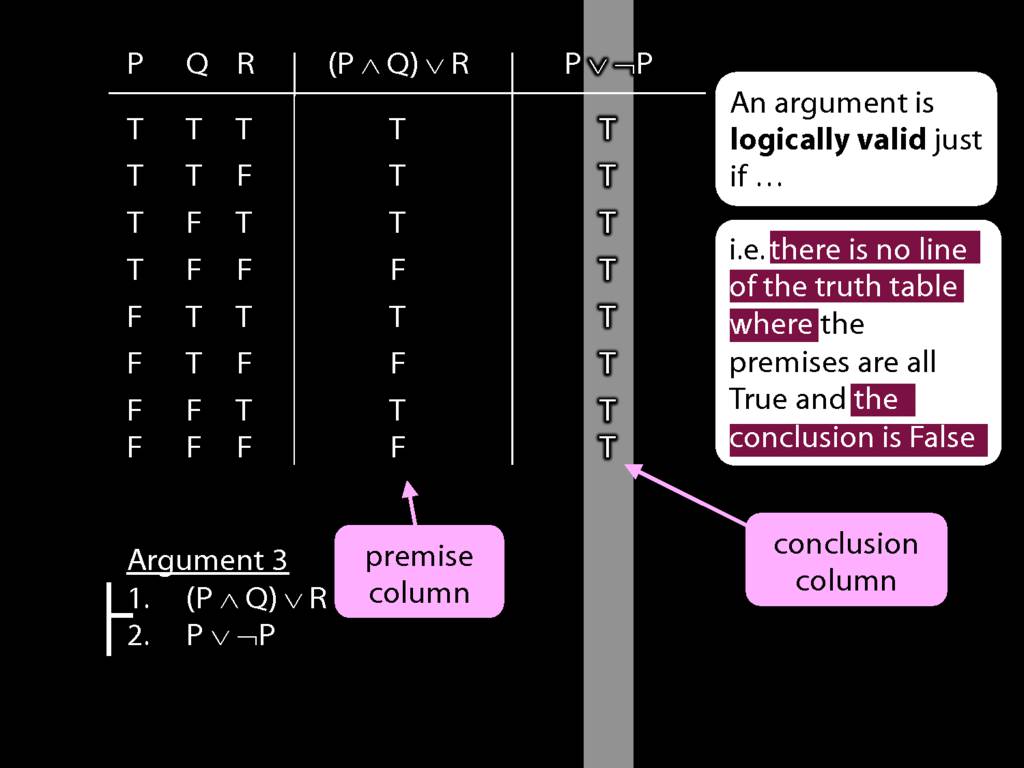
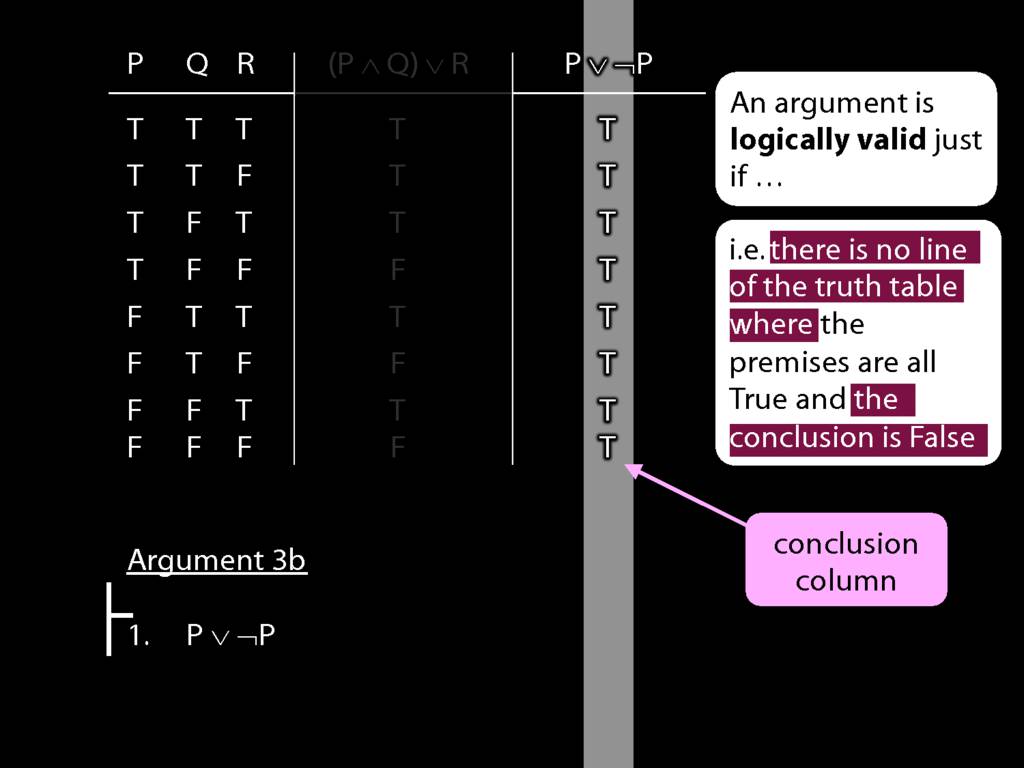
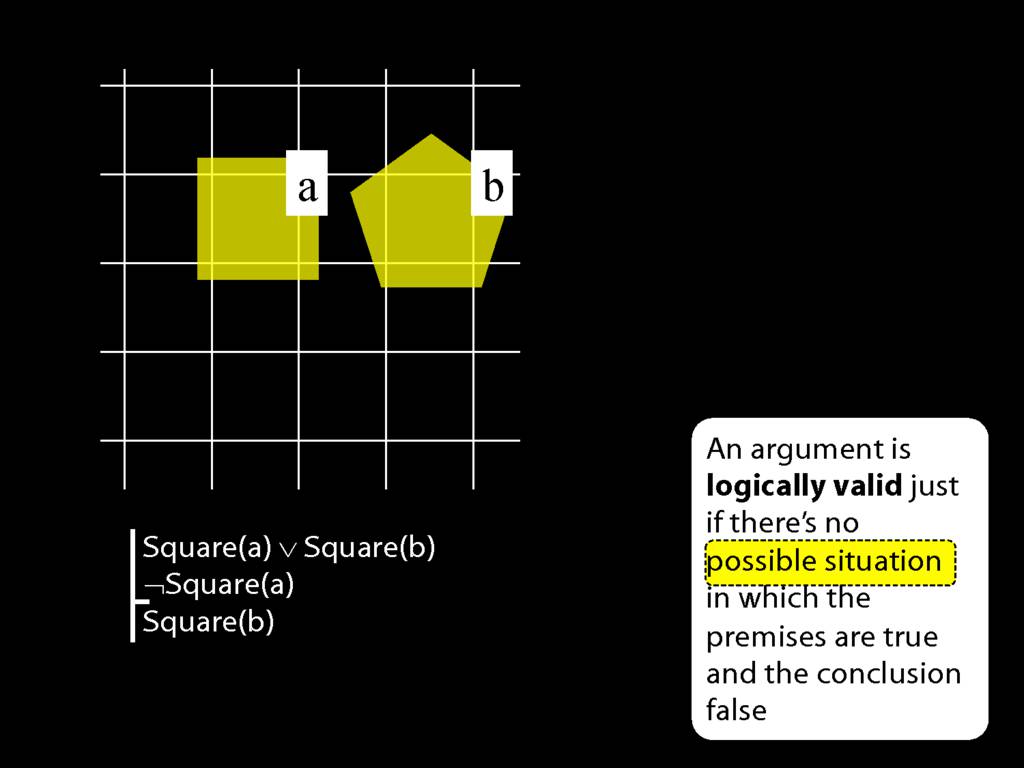
An argument is \emph{logically valid} just if there’s no possible situation in which the premises are true and the conclusion false
A \emph{connective} joins one or more sentences to make a new sentence. E.g. ‘because’, ‘¬’. The sentences joined by a connective are called \emph{constituent sentences}.
E.g. in ‘P $\lor{}$ Q’,
\begin{quote}
$\lor{}$ is the connective
P, Q are the constituent sentences
\end{quote}
Consider these three sentences.
The first sentence says that John is square or Ayesha is square.
The second sentence says John is not square. (I know I just told you John is square; I'm not very consistent, am I?)
And the third sentence says Ayesha is square.

Note the symbol; we saw this a moment ago, it's a bit like the English 'or'.

There is also a new symbol in the second sentence, this a bit like the English 'not'.
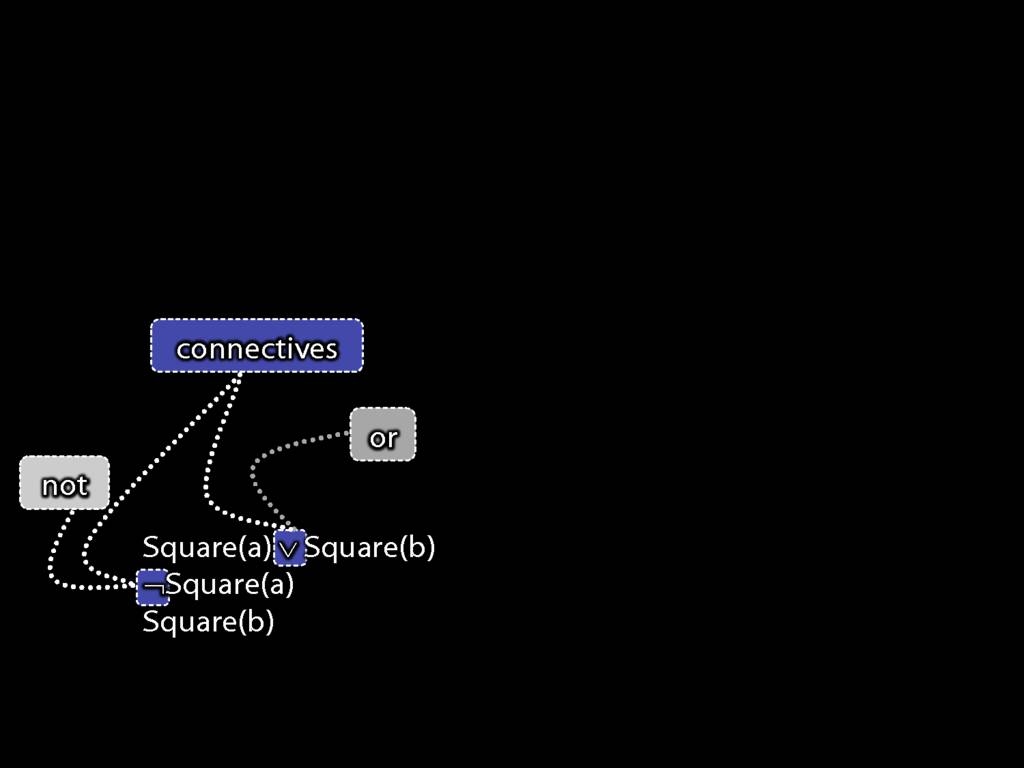
As you recall, these symbols are called 'connectives'.
Note that the negation connective in the second sentence is making a new sentence from just one sentence. (Connectives can join any number of sentences.)
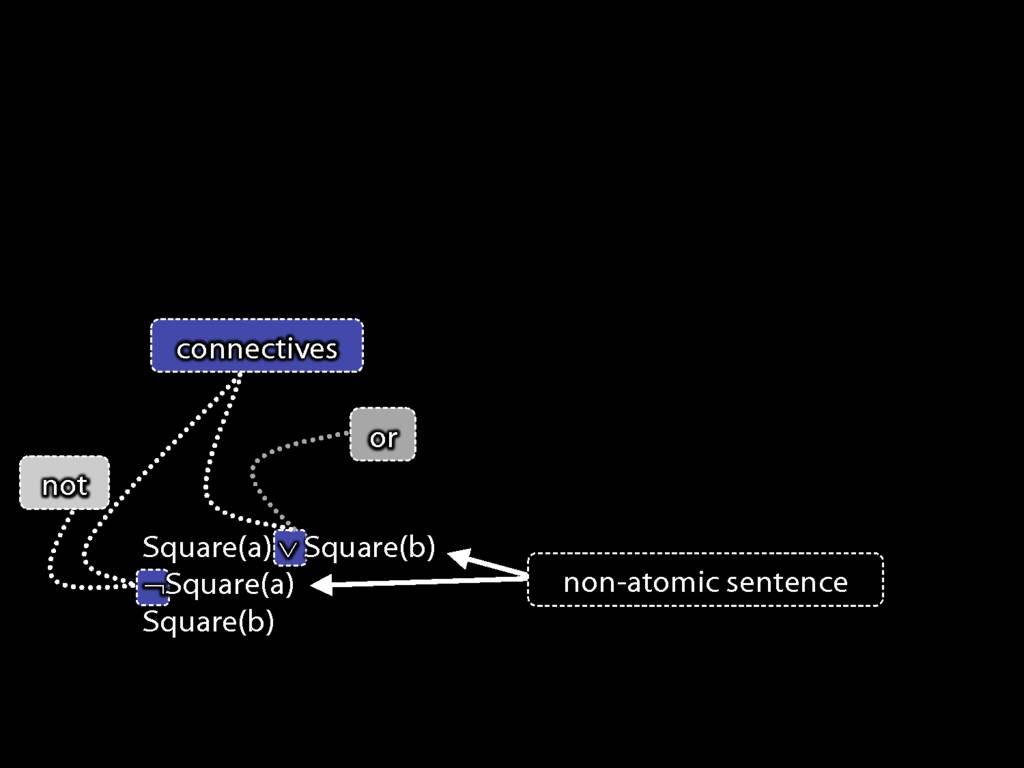
You may also recall that these first two sentences are non-atomic (they contain connectives), ...
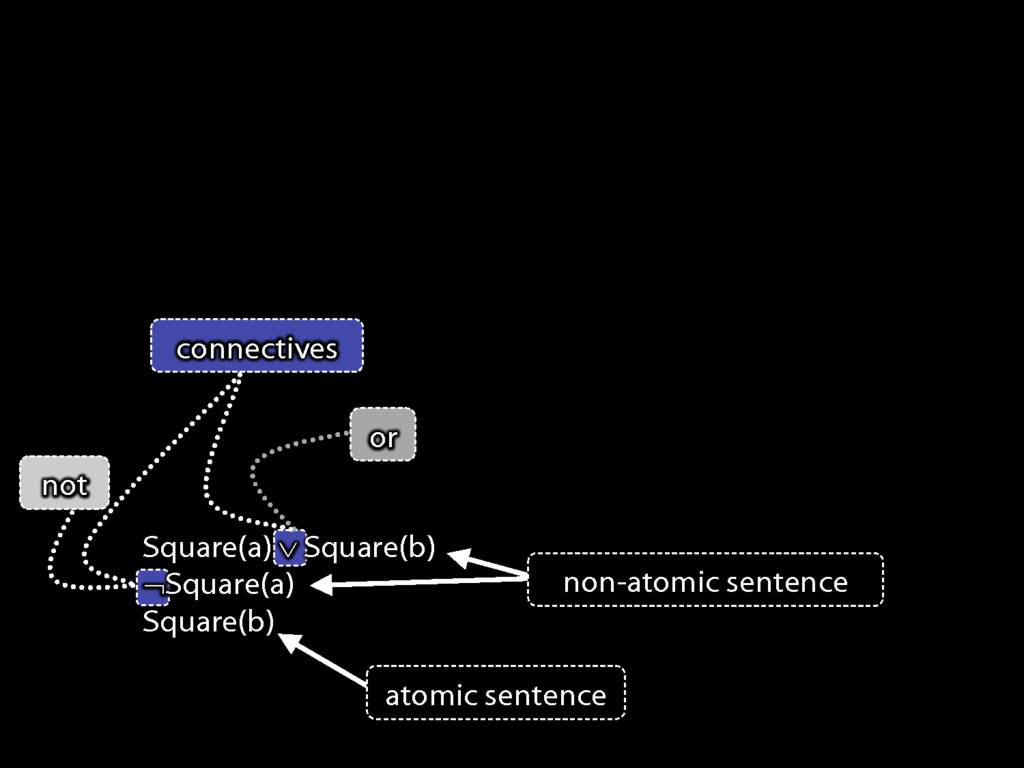
... whereas the third sentence is atomic.

OK, so much for the sentences.
So far we've been fixing terminology and getting a feeling for a formal language, which is a tool for studying logic.
But I haven't said anything about what logic is.
What is logic? What is this course about?
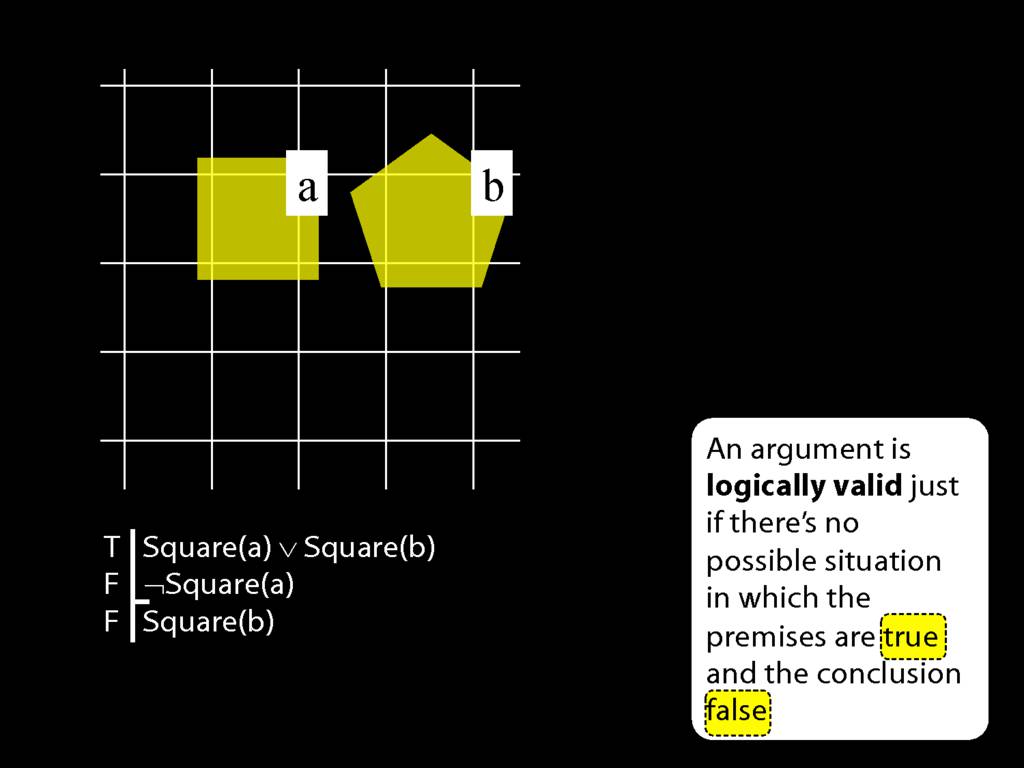
The answer is here: it's about the notion of logical validity. An argument is logically valid just if there's no possible situation where the premises are true and the conclusion false.
Logic is the study of logical validity. We want to know which arguments have this property, and what means there are of establishing which arguments are valid or not.

Let's go though this slowly. First, what is an argument?
For our purposes, an argument is just a sequence of sentences where zero or more are identified as premises and exactly one is identified as the conclusion.
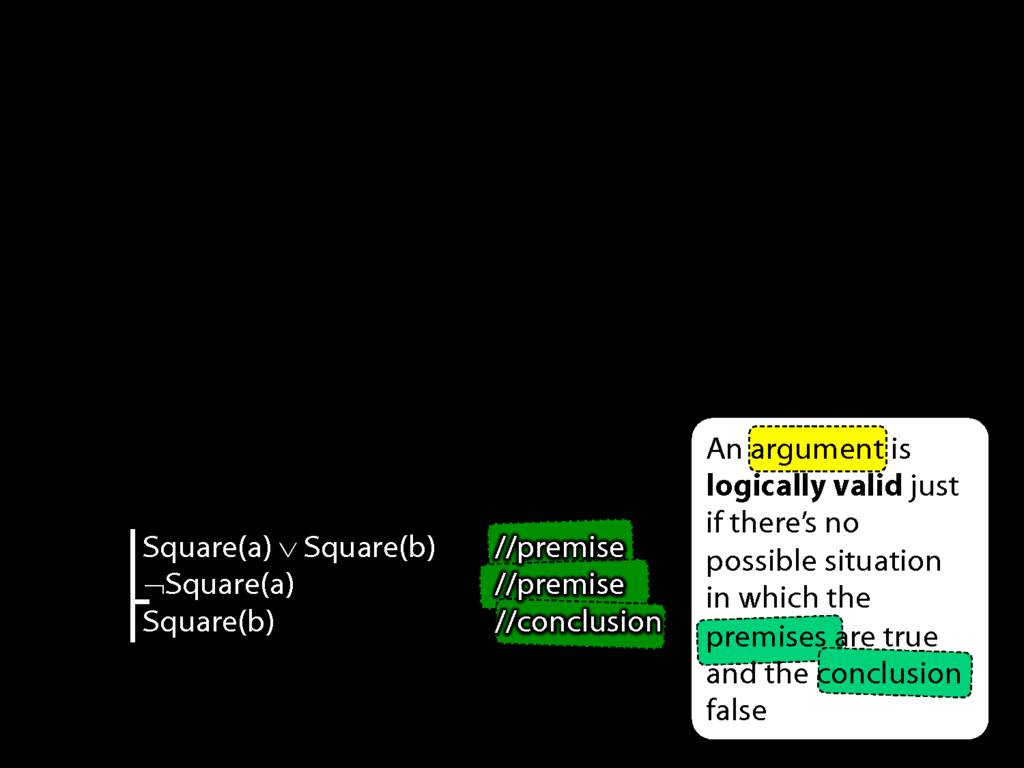
But what do we mean by premises and conclusions?
A premise is just a sentence that we say is a premise. (That's all there is to being a premise.)
Likewise, a conclusion is just a sentence that we say is a conclusion. How simple is that?

Now we're going to write a lot of arguments so it would be helpful to have a compact way of identifying premises and conclusions ...
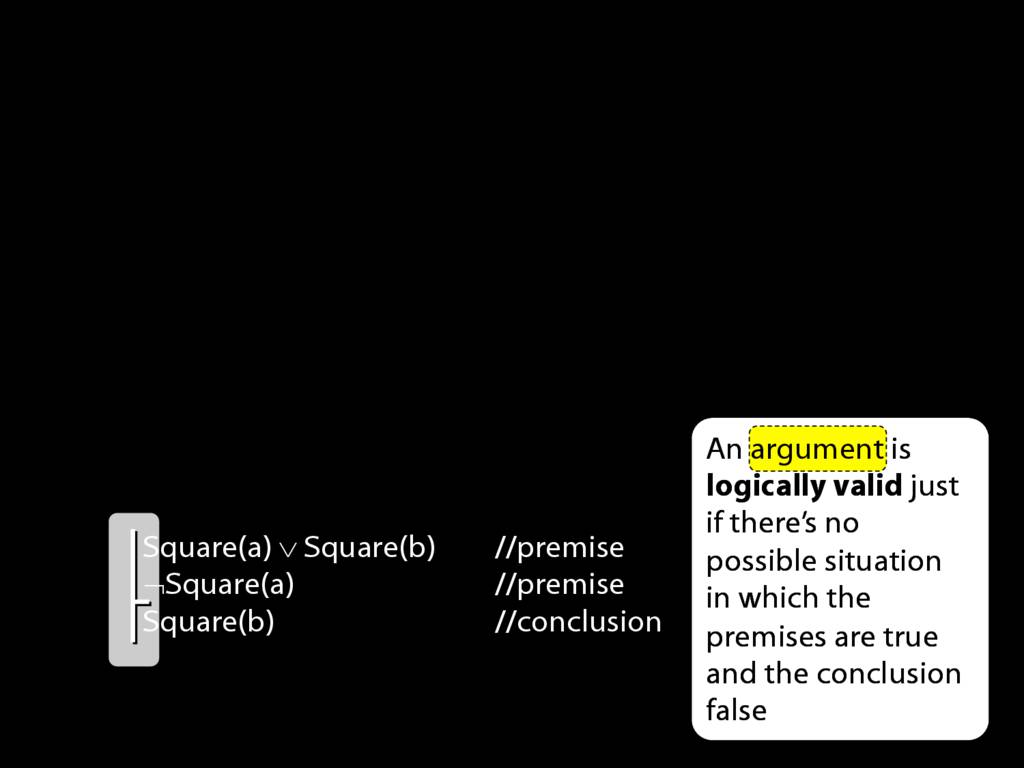
... That is the purpose of these lines. The horizontal line specifies that the sentences to its right an argument.
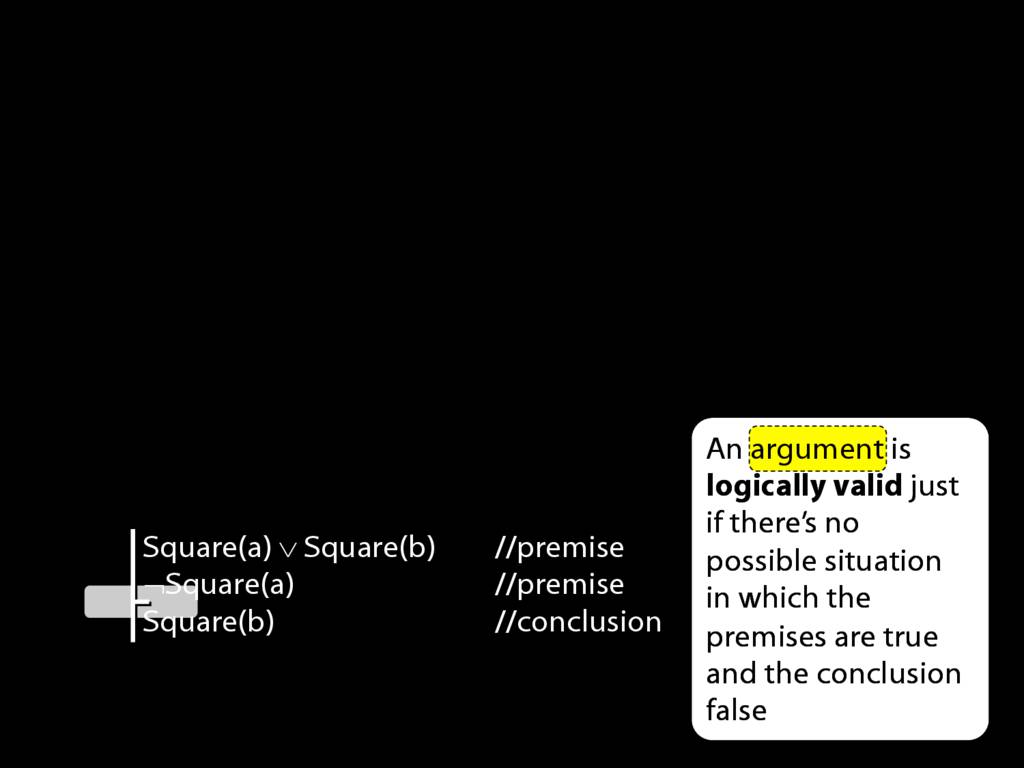
And the vertical line separates the premises from the conclusion.

So this is logic: the study of logical validity. Have we understood the definition yet? Not quite ...

... What do we mean by 'possible situation'?
A possibile situation is just a way that the world is or could be.
So consider the situation which is as similar to the actual situation as possible except that you are in Havana smoking a fat cigar rather than attending my lecture.
This is a possible situation.
Now possible situations are huge things; in specifying a possible situation, you are specifying something as big as the actual situation,
with all the trees, leaves, insects and everything.
It is helpful to have a proxy for possible situations, something much simpler than a real possible situation.
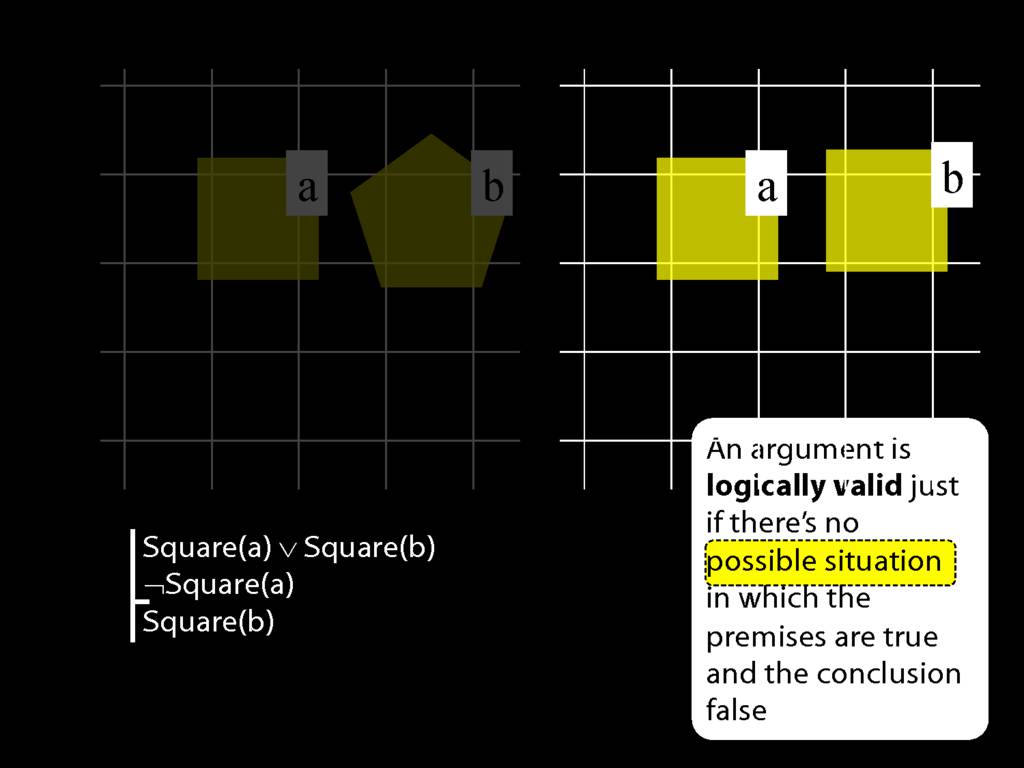
For our purposes, a good proxy is often an arrangement of shapes in two dimensional space.
For evaluating the argument about John and Ayesha, we can pretend that possible situations are just shapes in space.
Thinking of possible situations in this way is simpler, and doesn't ignore anything relevant to this particular argument.
The final concepts in our definition of logical validity are truth and falsity.
These concepts are too simple to say anything much illuminating about.
Note that whether a sentence is true or false depends on which possible situation we are talking about.
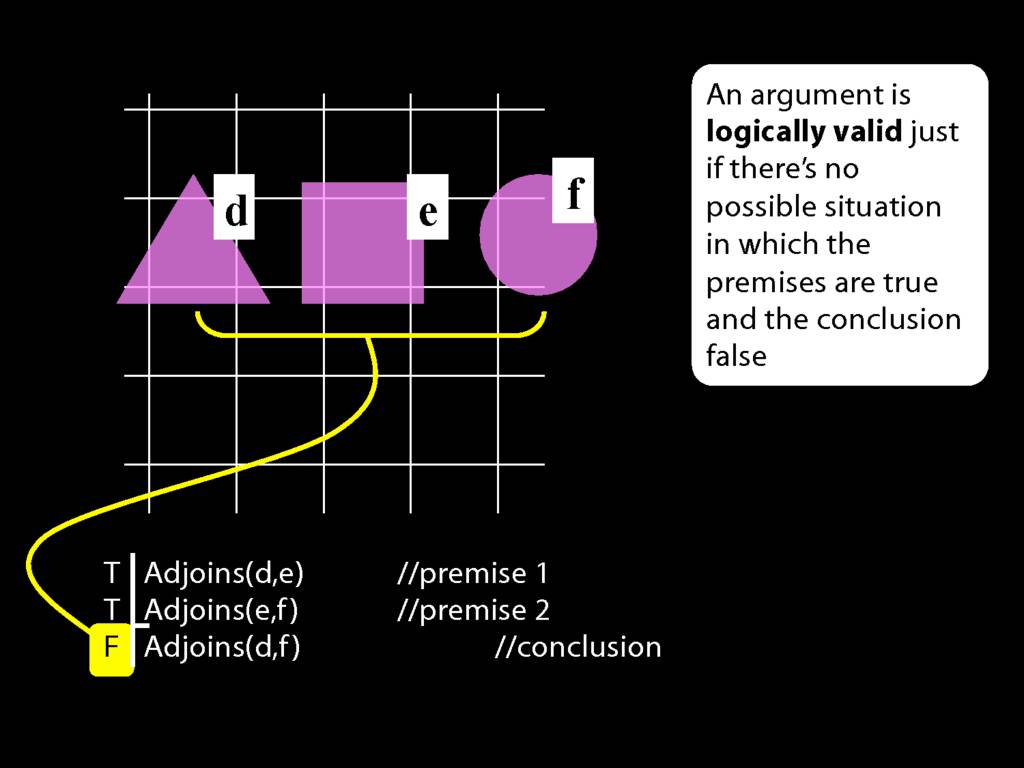
In this possible situation, the first premise is true, the second premise is false and the conclusion is false.
But in this possible situation, ...
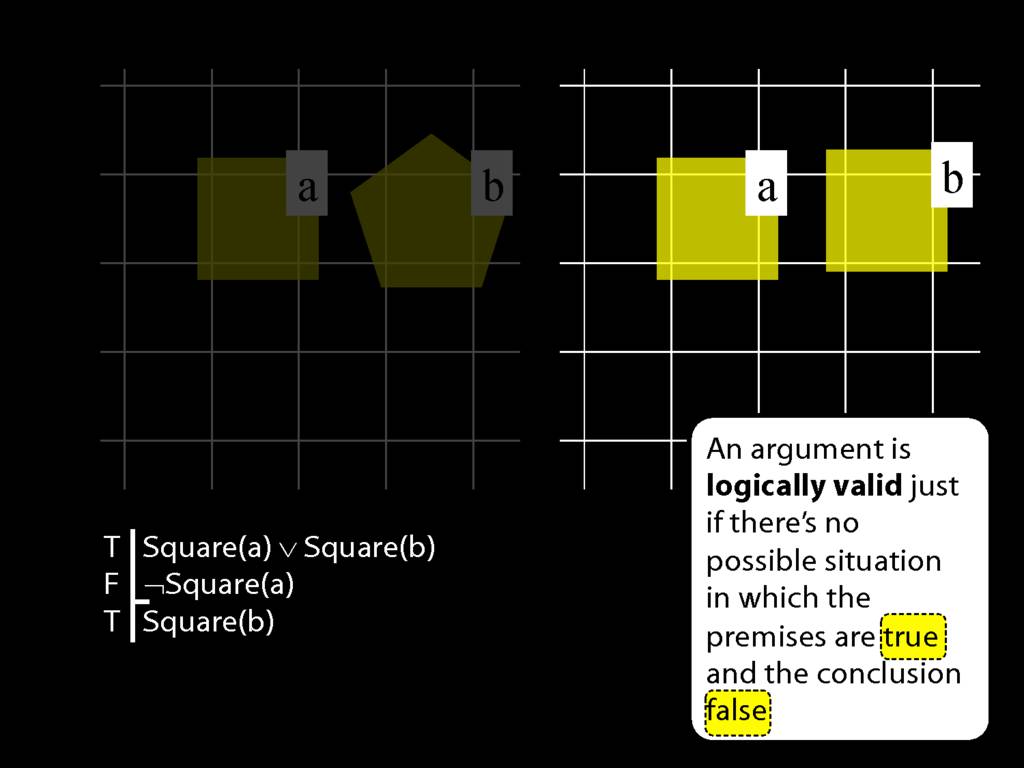
... the conclusion is true.
Incidentally, you will sometimes be asked whether a logically valid argument can have one or more false premises and a true conclusion.
If you're asked that question, do think about this argument and this possible situation.

So logic is the study of logical validity.
As I said before,
our overall aims in this course are to
discover which arguments have this property,
and what means there are of establishing which arguments are valid or not.
In doing this our main tool is the formal language awFOL.
2.3, 2.4
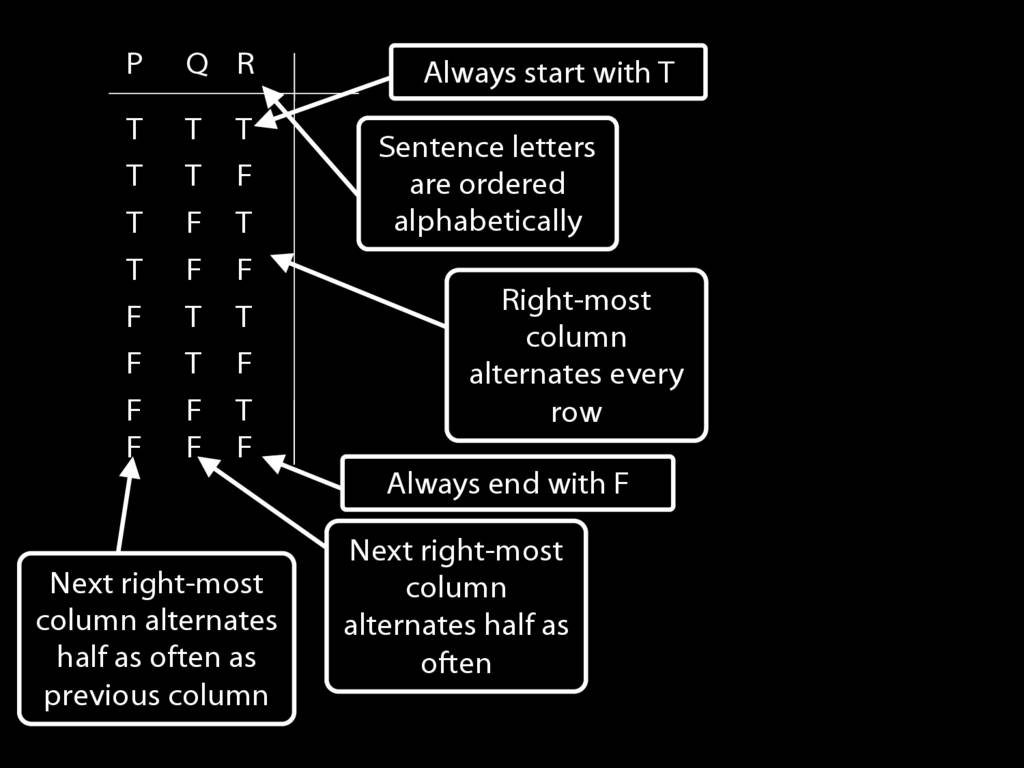
\section{Sentence Letters}

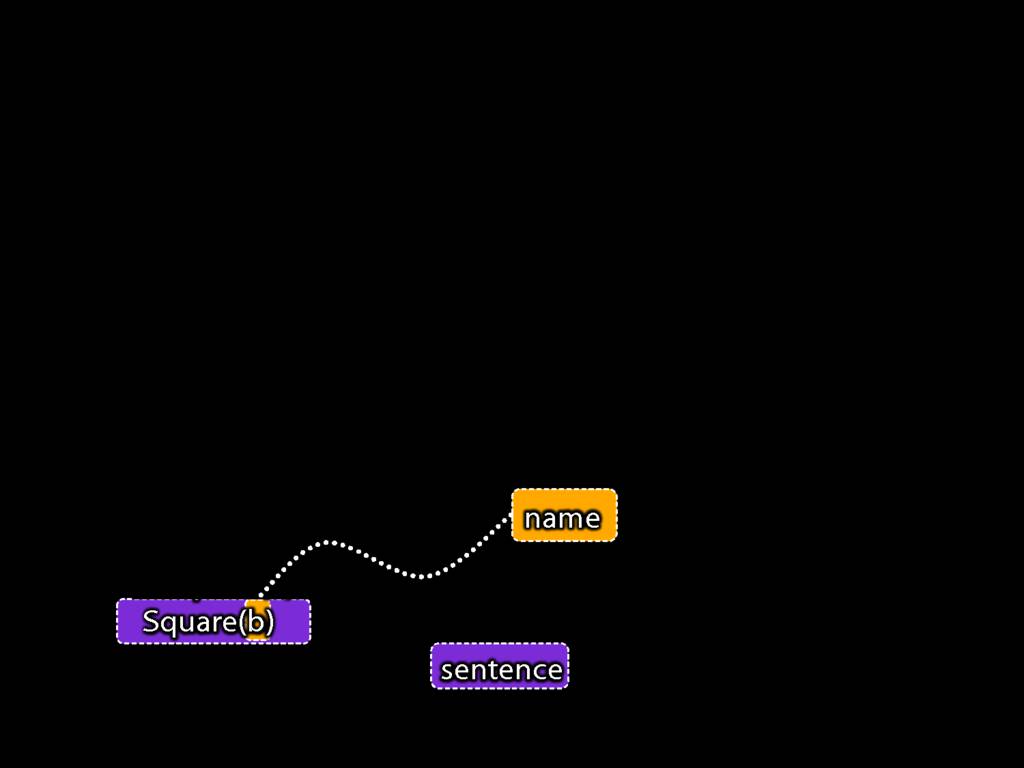
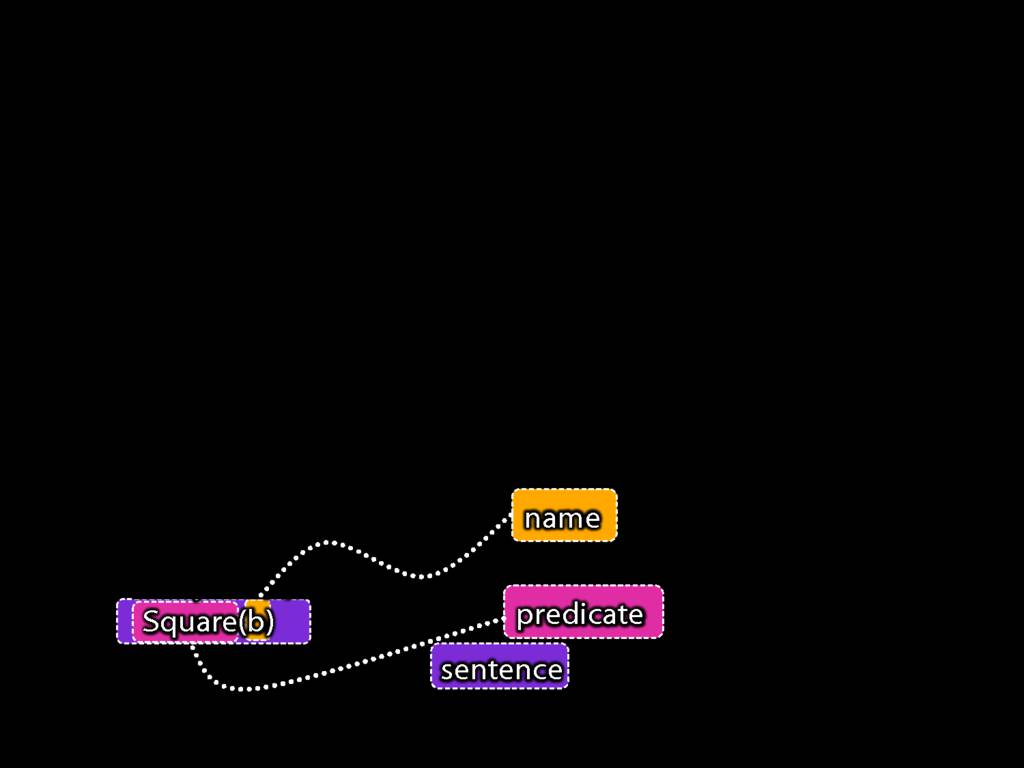
Recall this argument about Ayesha and John.

The sentence 'Square(b)' occurs twice, once as part of the first premise, and once as the conclusion.

The sentence 'Square(a)' also occurs twice, once as part of the first premise, and once in the second premise.
And there are no other sentences in this argument.
So we can represent this form of argument in a much more general way ...

... by using letters to stand for sentences instead of names and predicates.
Why is this more abstract representation useful?
We don't want to consider arguments one-by-one. We want to be able to
say things about a large number of arguments. The use of sentence letters lets us talk abou a much larger class
of arguments, all of which are valid in virtue of having this form.

But how far can we go with sentence letters?

Consider this argument. There are three atomic sentences.

So if we wanted to represent it using sentence letters only, we'd have to have three different sentence letters.
But now we have lost what is interesting about this form of argument.
After all, any argument with two premises and a conclusion has the form P, Q therefore R.
There's nothing interesting we can say about all arguments with *this* form.
So where an argument exploits identity, we can't capture what's logically interesting about its form using sentence letters.

The same is true where an argument exploits quantifiers ... this is something we'll get to later in the course.

- Seminar groups
- Exercises
- Textbook
- Assessment (100% exam)
- Regular lectures
- Web: http://logic-1.butterfill.com
\section{zoxiy}
http://logic-1.butterfill.com
There are logic exercises associated with each lecture.
After each lecture (or before, if you prefer), you should
complete the associated exercises.
You can find links to the exercises for each lecture at:
\url{http://logic-1.butterfill.com}
To complete the exercises you need to register at
\url{https://logic-ex.butterfill.com}
(If you don’t want to do this, you can complete the
alternative textbook exercises on paper.
These are also specified for each lecture at \url{http://logic-1.butterfill.com}).
Seminars will discuss exercises associated with
the previous week’s lectures. As your seminar tutor will
track your progress and mark your exercises, you should
be sure to \textbf{complete the exercises by 2pm on the day before
your seminar}.

Here is the web page describing the logic lectures at
http://logic-1.butterfill.com
This is for the regular (twice-weekly) lectures
You might need to switch to the fast set of lectures,
for which there are different exercises.
(Choose the right page for the lectures you are attending.)
For each set of lectures, you can choose between ‘regular
exercises’ and ‘fast exercises’.
The ‘normal’ exercises are aimed at students who did not take a
mathematical subject at A-Level or equivalent. The ‘fast’
exercises are for students who find logic relatively easy and
want to focus on more difficult questions.
You can switch between fast and normal exercises at any time.
When you hit the link for ‘regular exercises’, you’re told to sign in.
But you can’t because you don’t yet have a password.
You need to register the first time you use logic-ex.
This is the registration form.
Note that this isn’t a secure web page (no ssl).
The email you use should be your university email.
Otherwise your tutor won’t know who you are and won’t
grade your work.

After you sign up, you might be taken to the wrong page.
So go back to http://logic-1.butterfill.com and hit the
exercises link again.
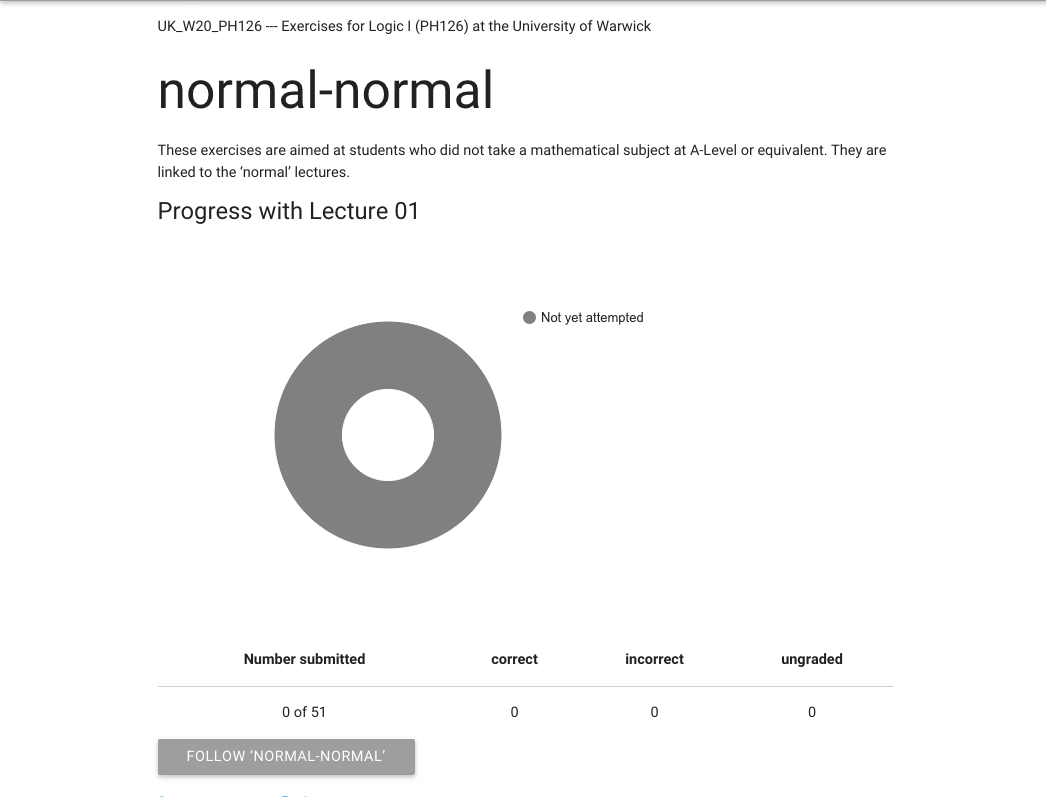
Now we’ve made it into zoxiy.
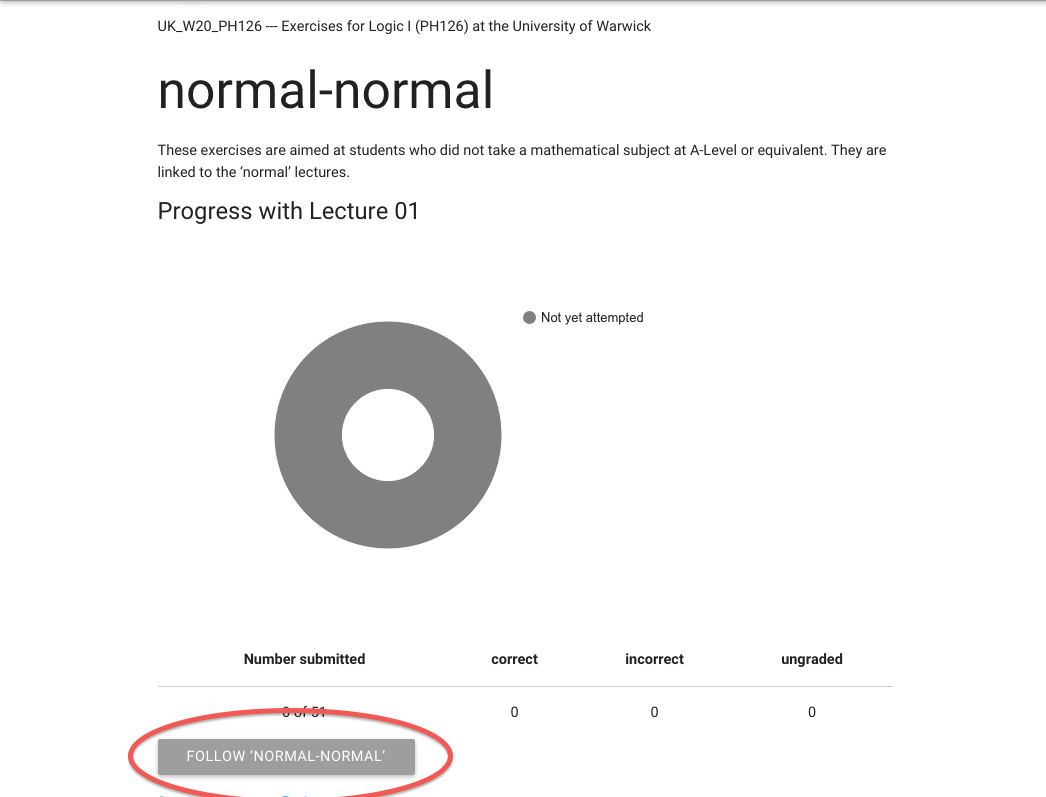
Here’s my motivational progress donut.
It’s very motivating.
Selecting ‘follow’ will make it easier to find the
exercises later, so I’ll do that.
Scroll down to see the exercises.

Here are the exercises.
Each of the links is an exercise.
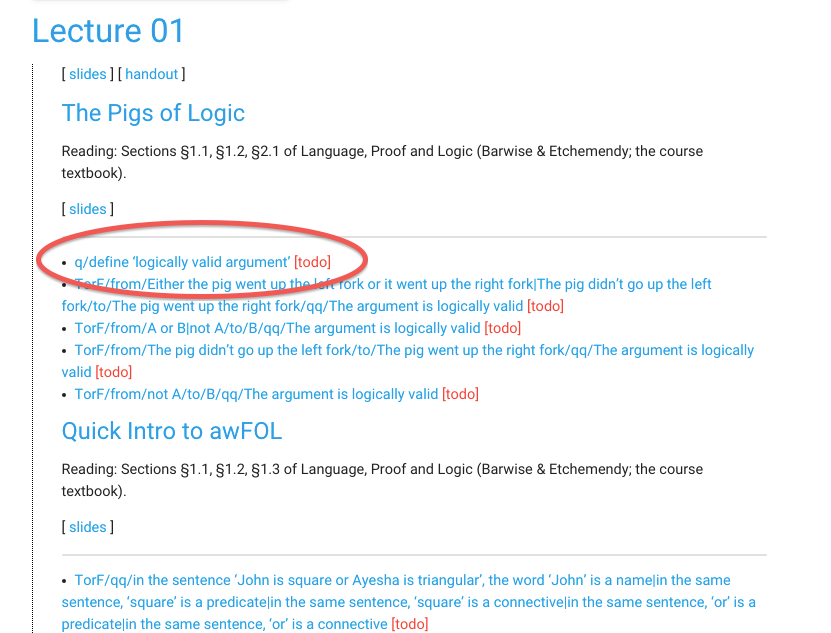
Click on the first exercise link
to get started.
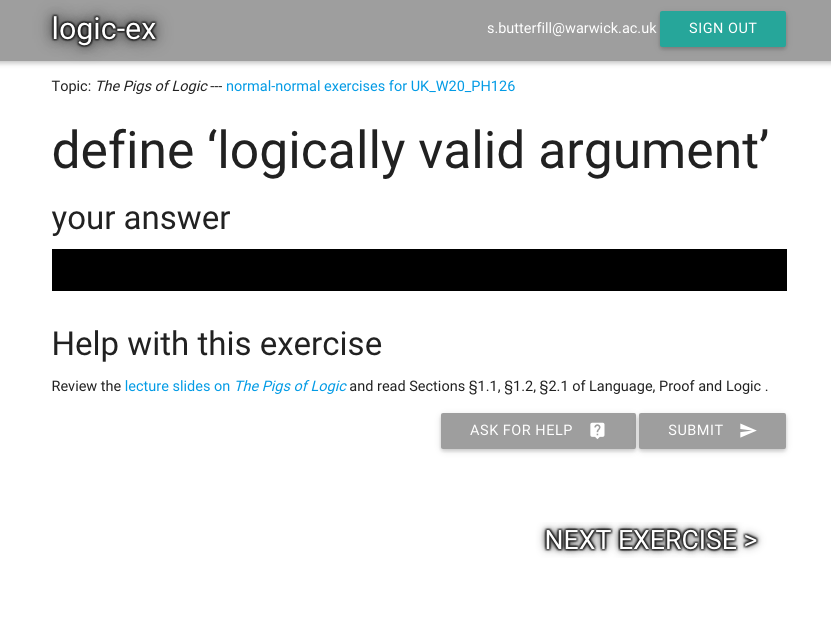
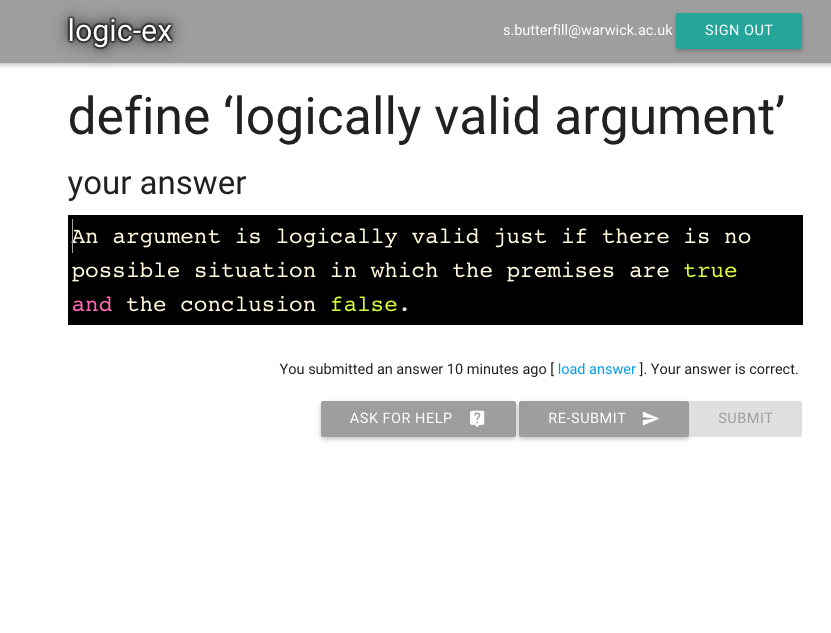
Oh look, it’s asking me to define logically valid argument.
This is the first exercise, so it must be important.
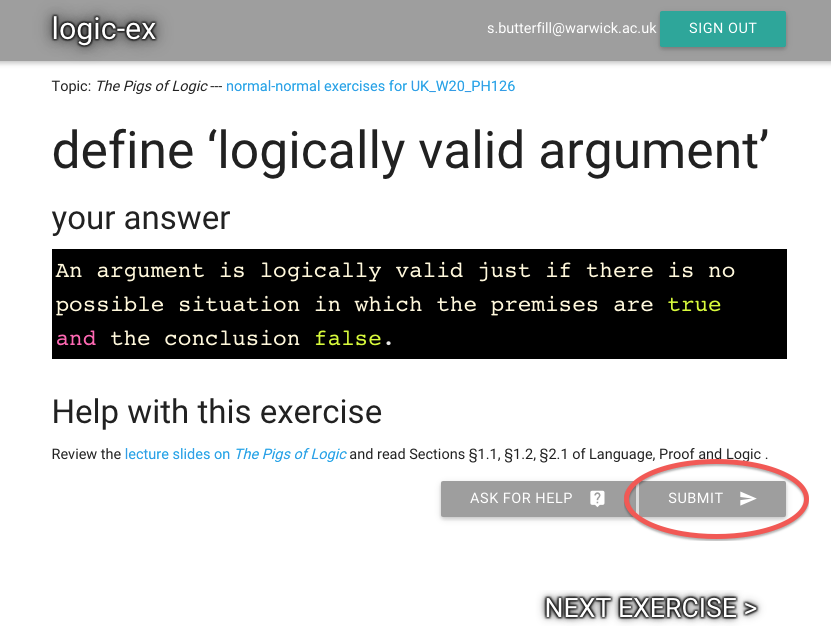
Submit the exercise by pressing the button.

After you submit, it should tell you you answered the question.
This can take a while to come up.
Sometimes it will tell you whether you were right or wrong, but
this time it doesn’t.

You can go direct to the next exercise.
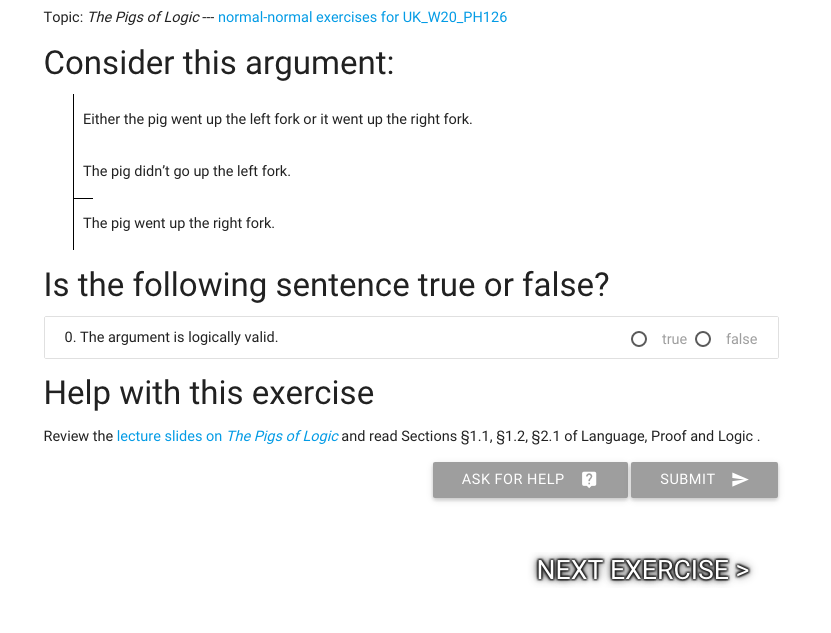
I’m not going to do this one now, I’ll save it for later.
Instead I want to go back to the list of exercises.
My progress has been updated
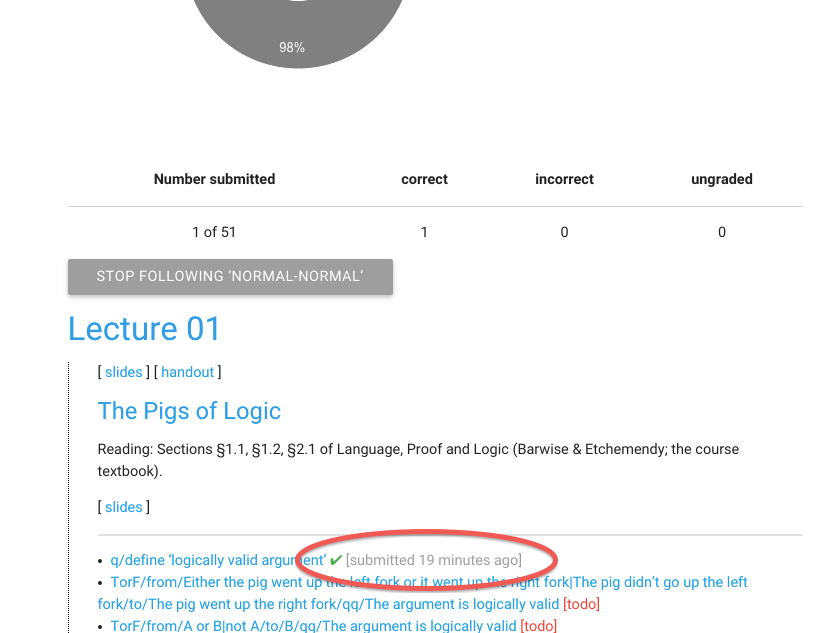
If I scroll down, I can also see that it recorded that I submitted
the exercise here. (So I can easily see where to start from next time.)

But go back up, I want to show you something else.
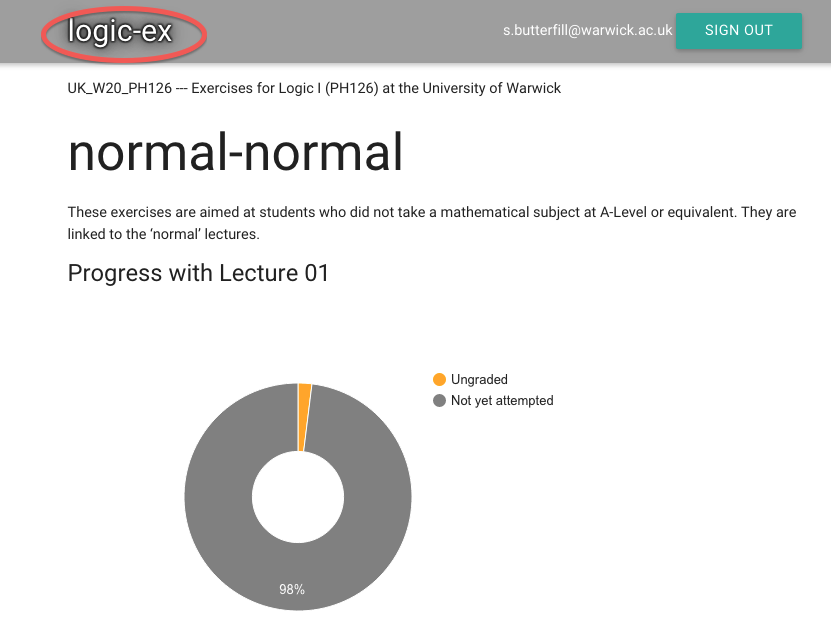
Click on ‘zoxiy’ (top left) to get to the home page.
Here’s what I see when I go to \url{https://logic-ex.butterfill.com}.
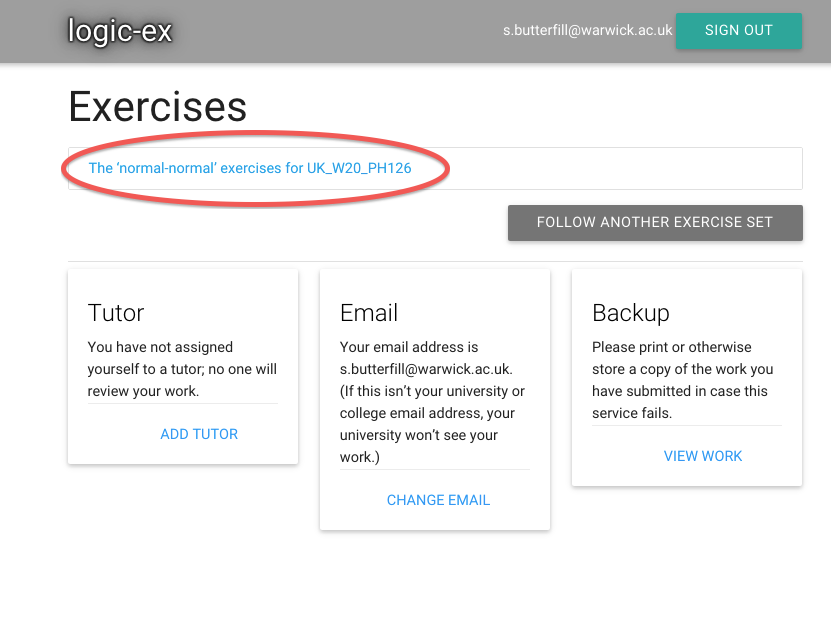
There’s a link that will take me straight to the exercises I’m
currently working on (the normal exercises for the normal lectures).
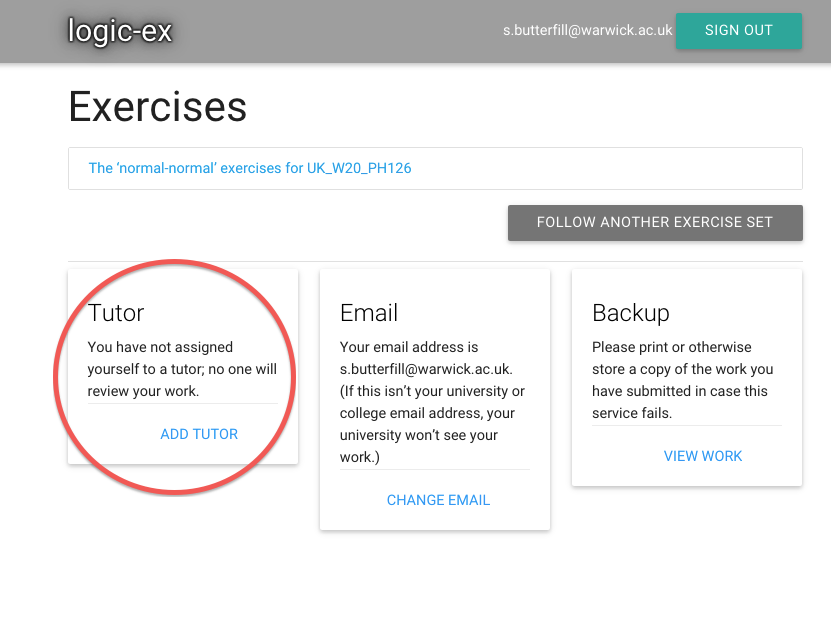
Also, I need to tell zoxiy who my tutor is so that she can mark
my work and check my progress.
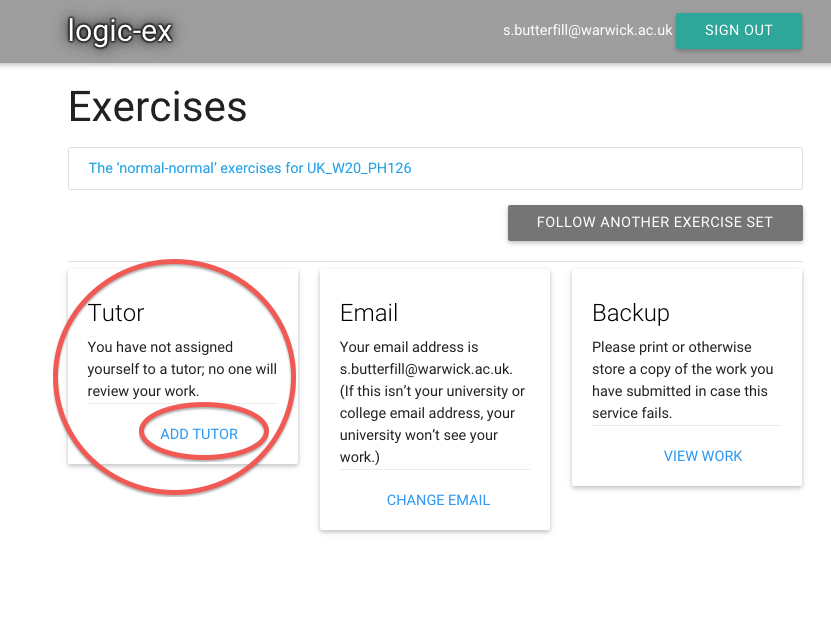
Let’s see how the page changes once I’ve done that...
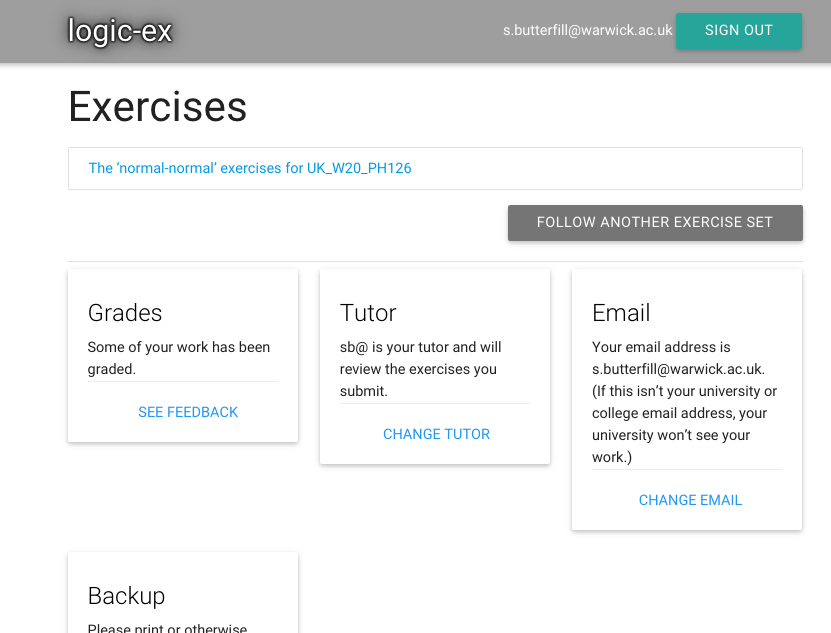
I added my tutor a while ago, and in the meantime she’s graded my answer.
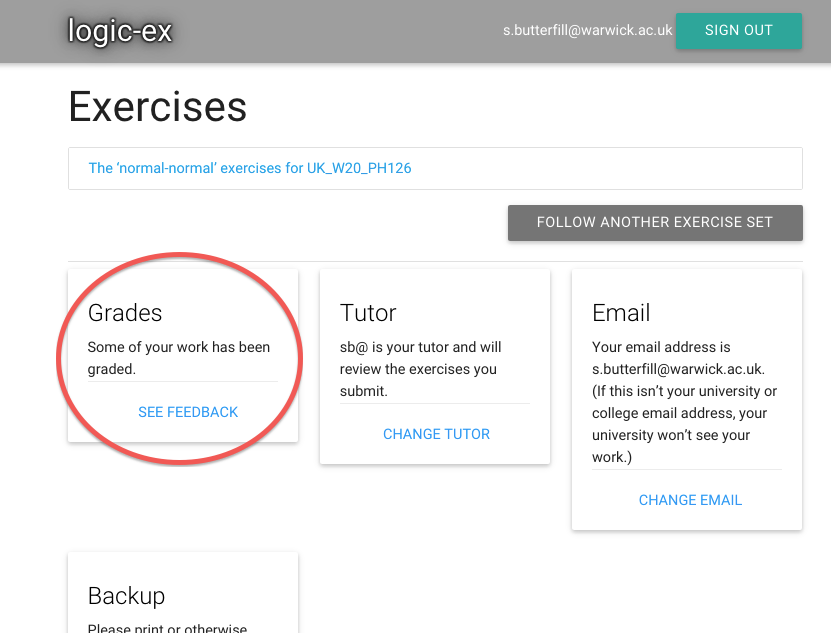
I can tell she’s graded my answer because there’s a message.
(This message only appears when there are new grades, grades I haven’t seen yet.)
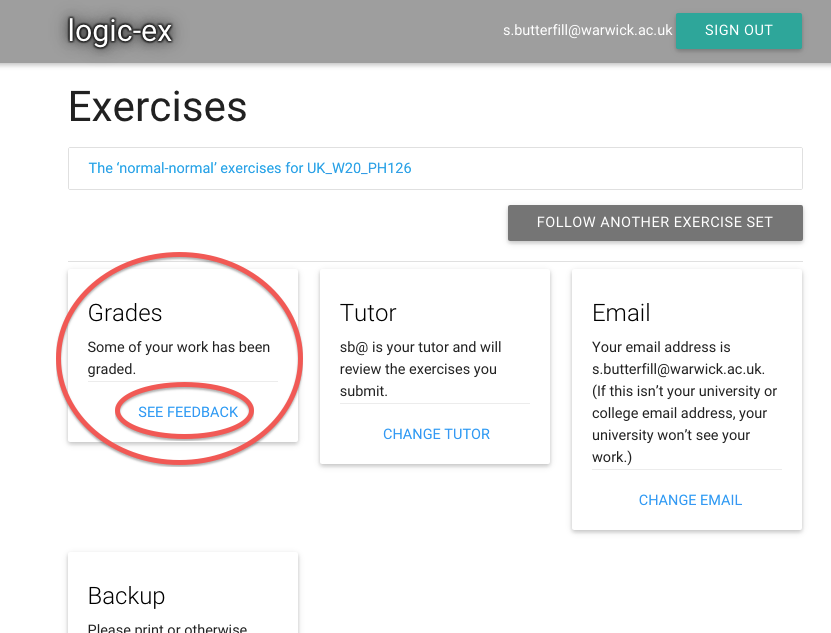
Follow the link to see the feedback.
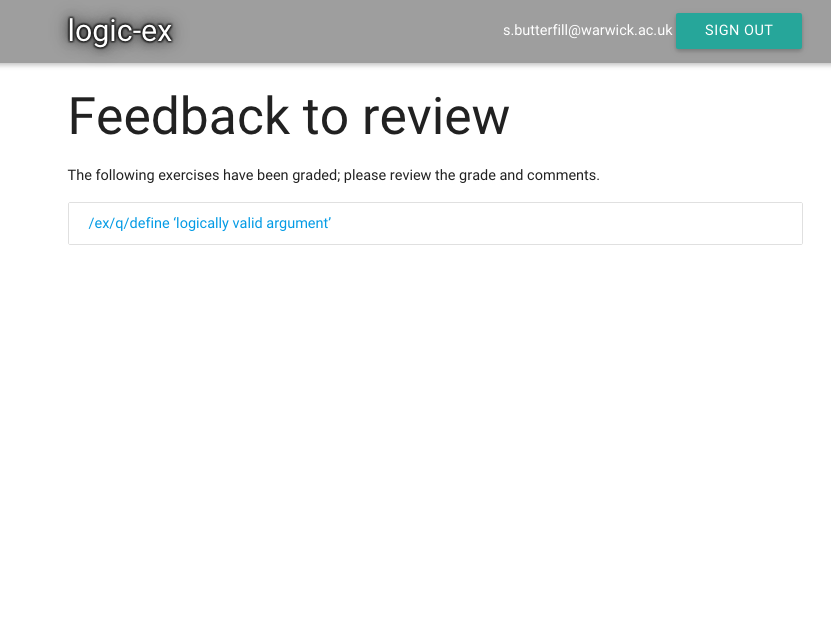
The exercise I just submitted has already been marked.
(Usually your work will be marked an hour or two before your seminar.)
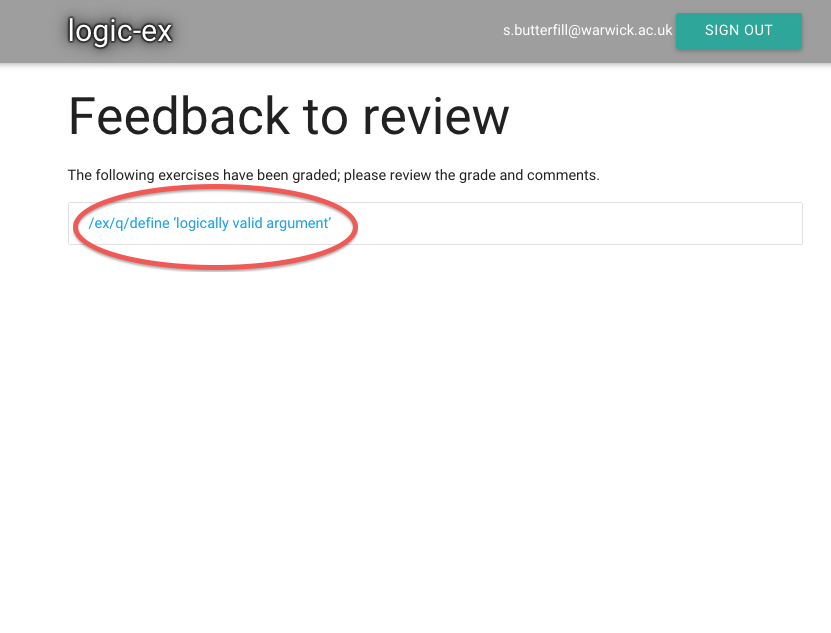
Let’s see whether I got it right ...
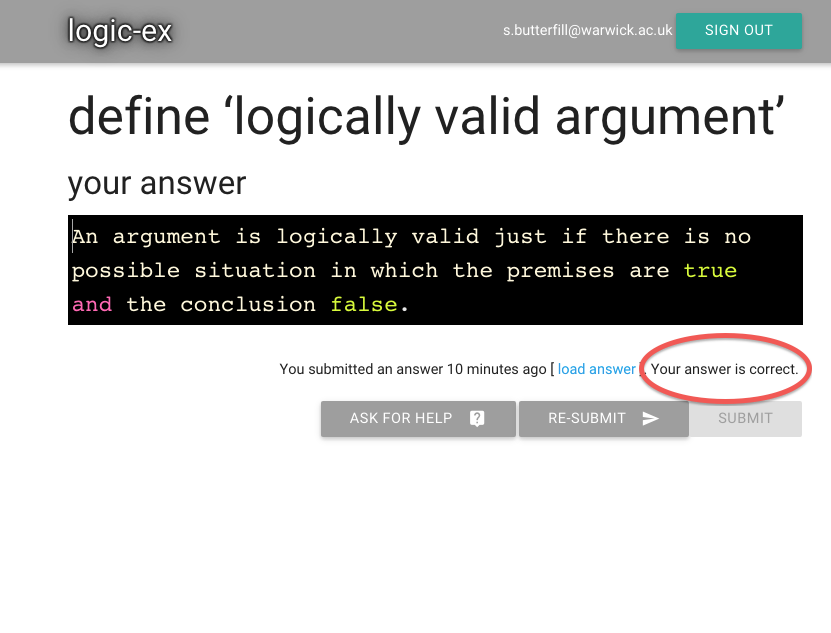
And look, it’s been marked correct

zoxiy: Creating Possible Situations
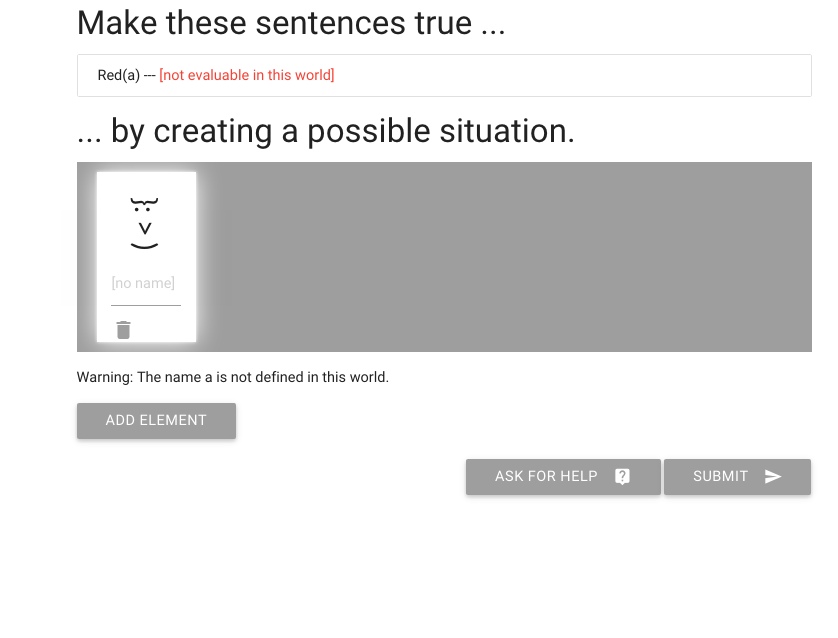
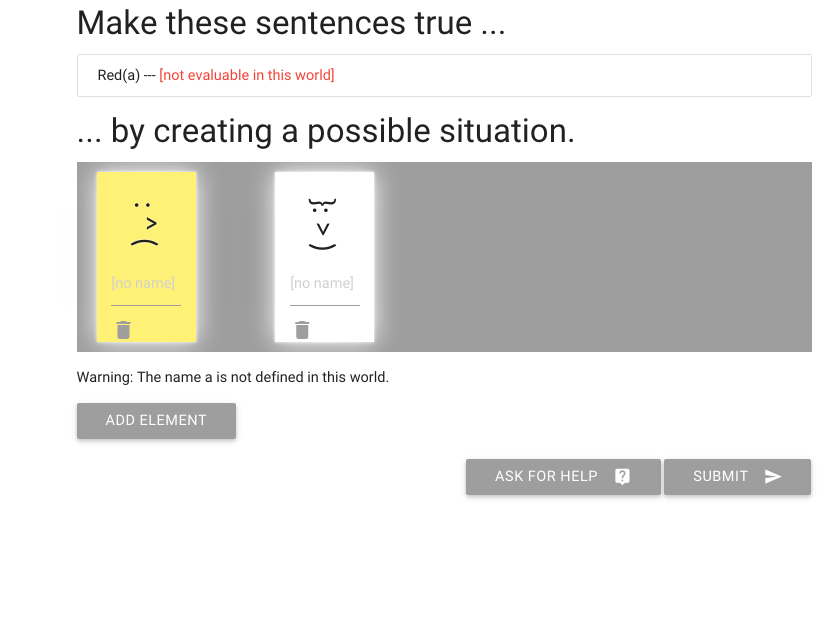
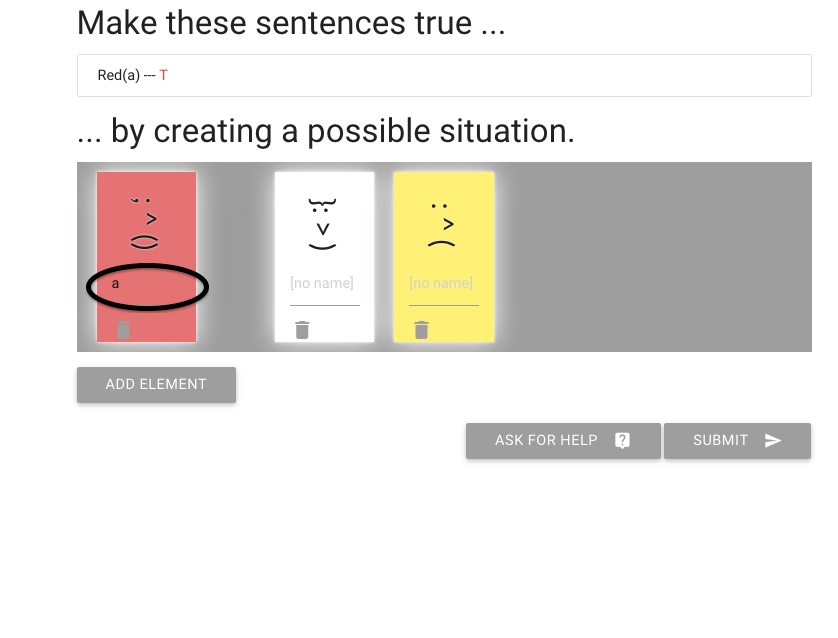
Here is the exercise. We have to make the sentence `Red(a)` true.
How do we get a red person? We can’t change the colour of people,
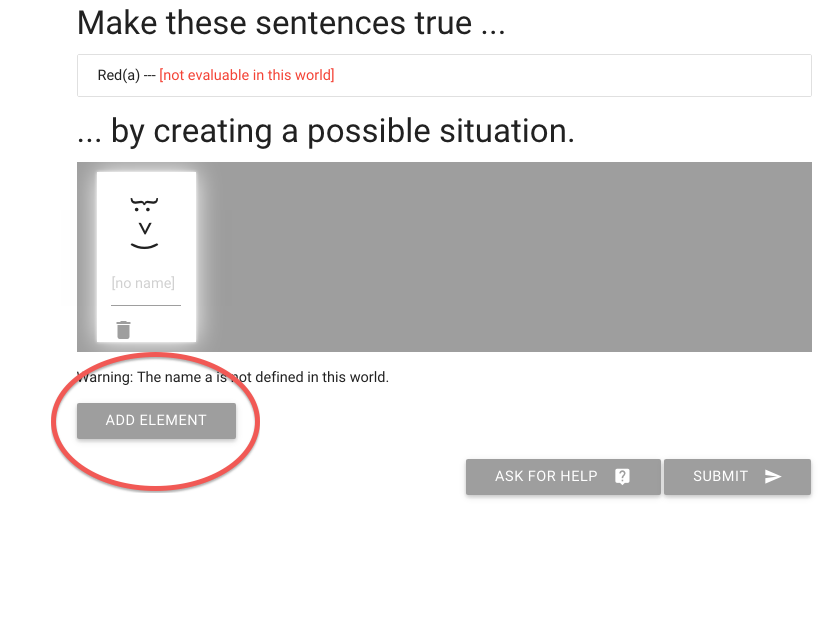
so we just add an element until we find a red one.
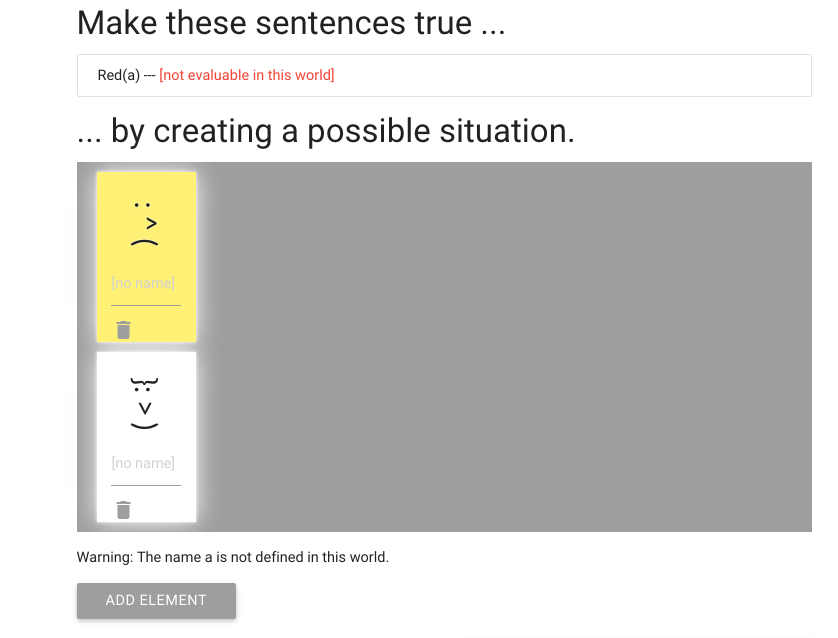
The first one we add is yellow, which is no good.
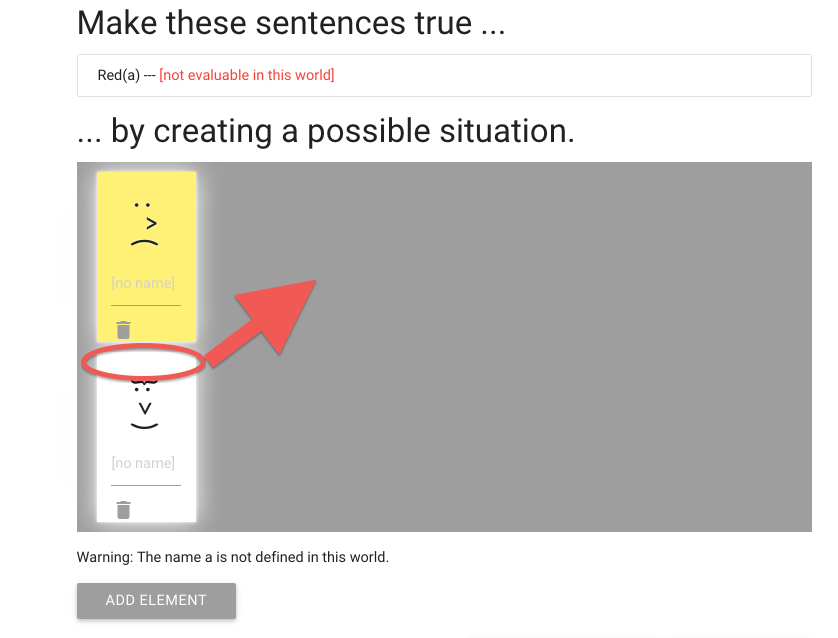
You can move people around by dragging their heads.
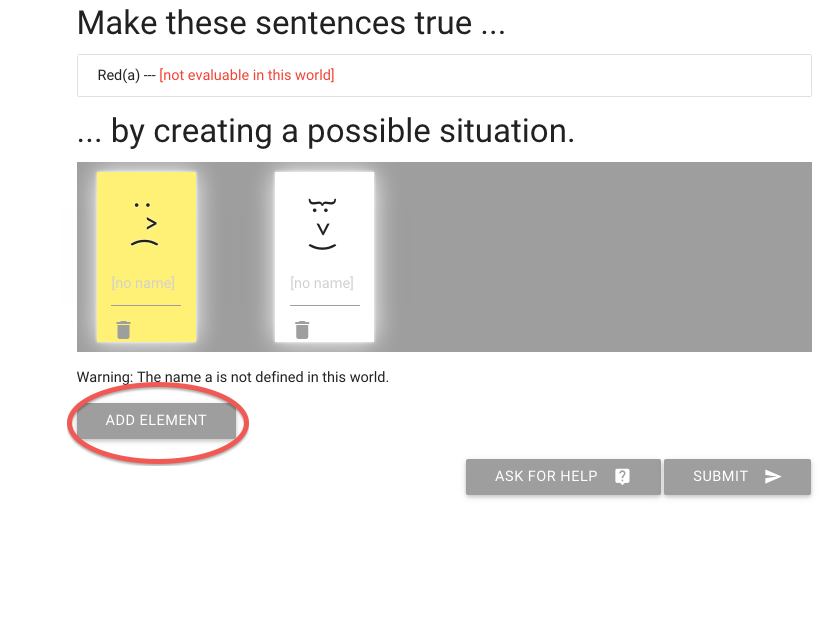
Now I’m going to add another element; hope it’s red.
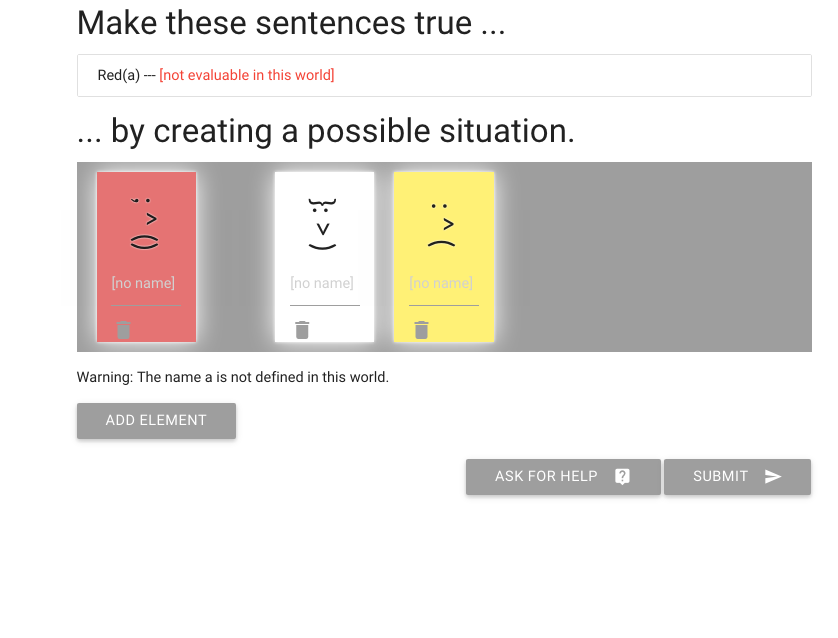
Good, it is.
But I’m not done yet.
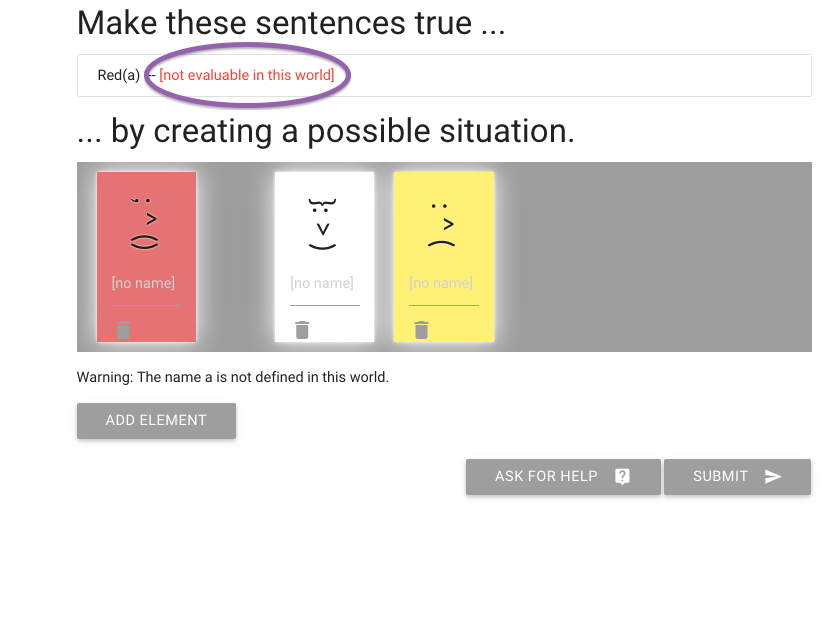
It’s telling me that the sentence isn’t true or false,
that it can’t be evaluated in this possible situation.
What can I do?
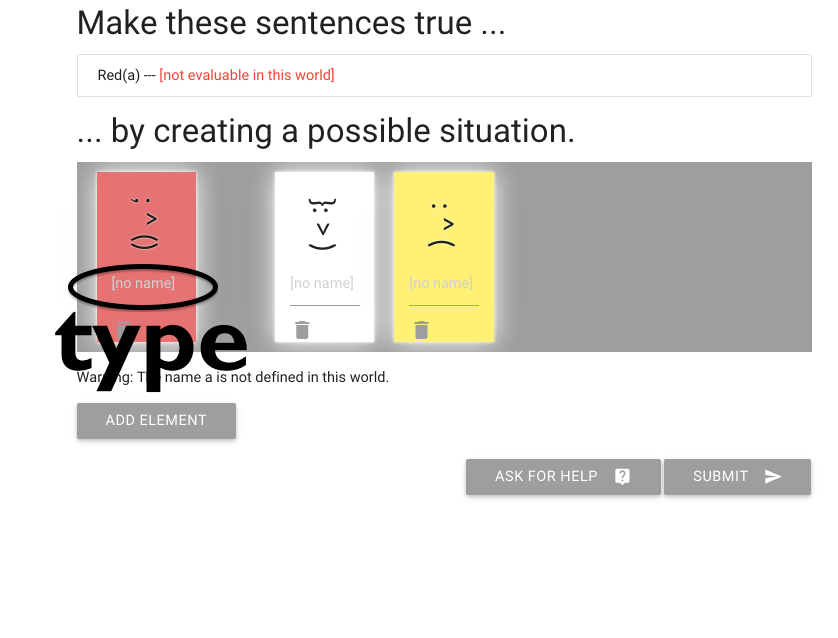
I need to give the red element a name by typing here.
(I’m going to call it ‘a’).
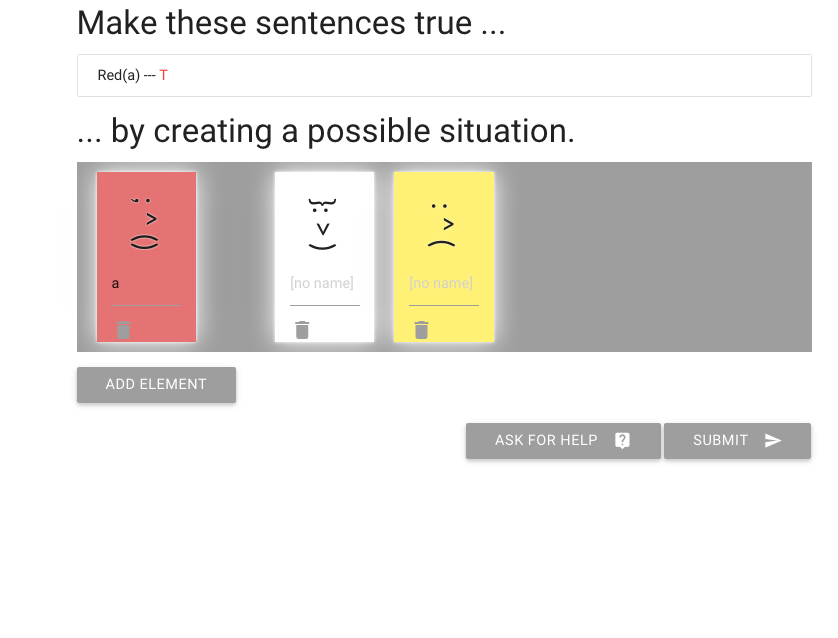
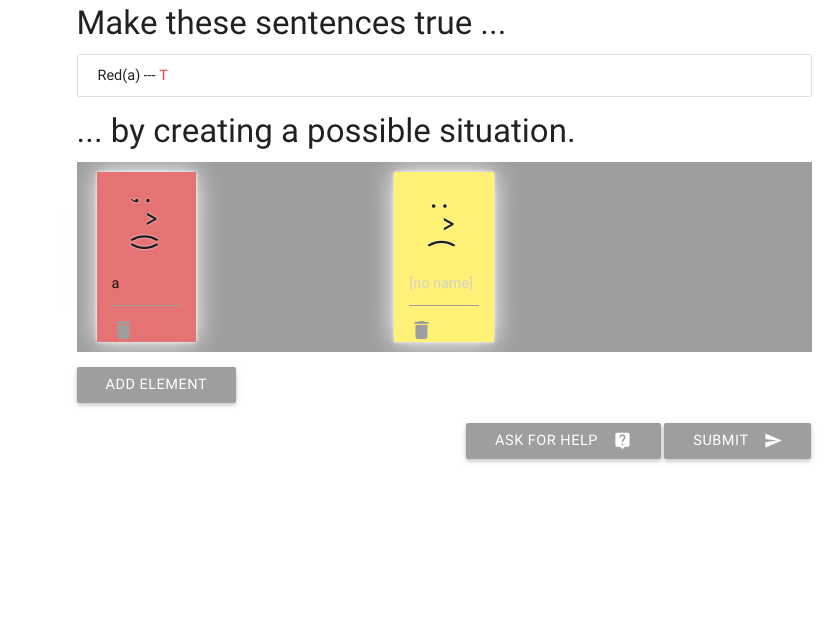
And I’m done with the exercise.
But let me just show you a couple of things that
might be useful with some of the exercises.
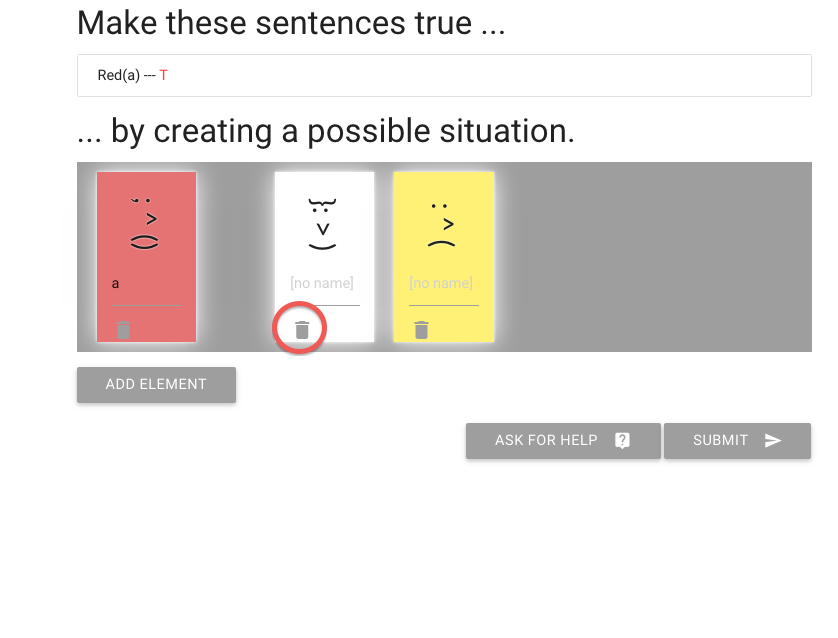
I can delete people that I don’t need like this one.
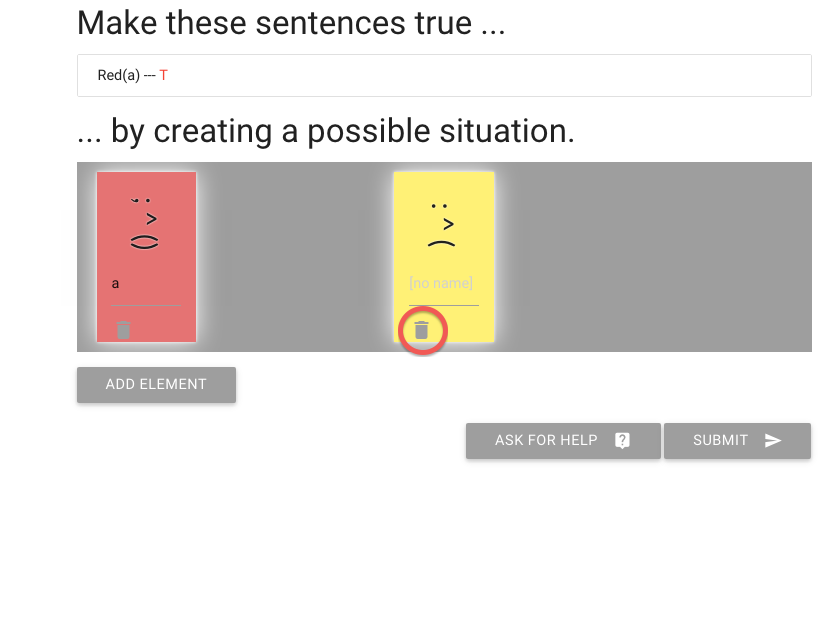
Let’s erase another person.
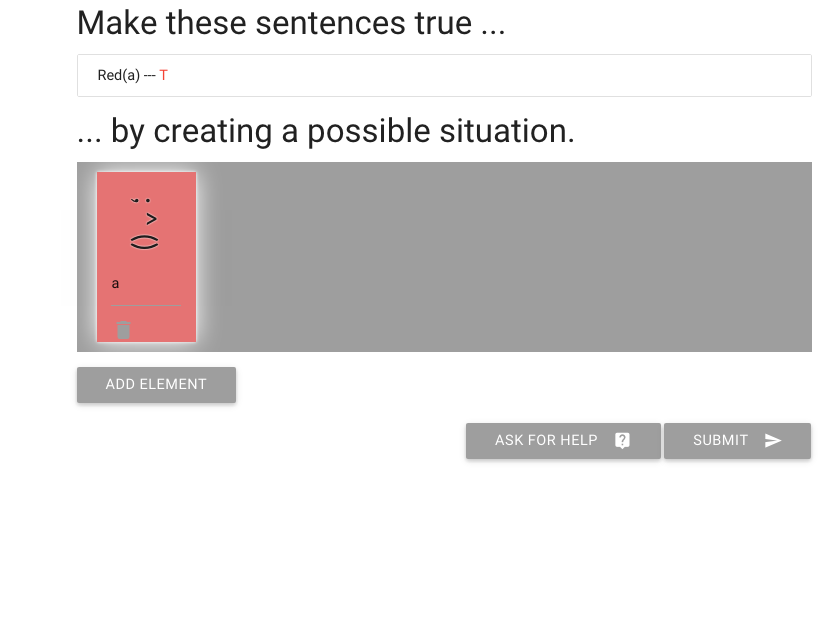
Lastly, I have to say I don’t really like this person’s face.
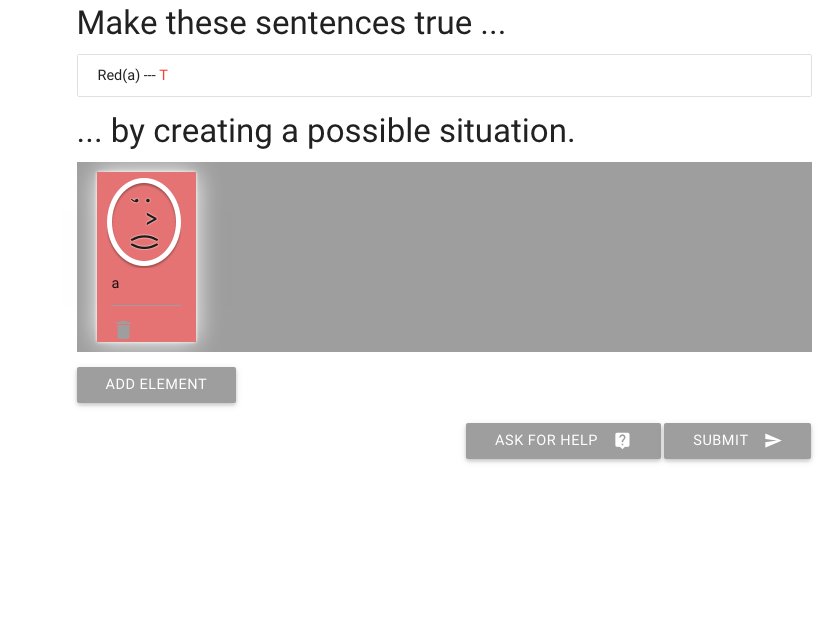
But I can change it by clicking on the eyes, nose and mouth.
This is how I make someone happy or sad.
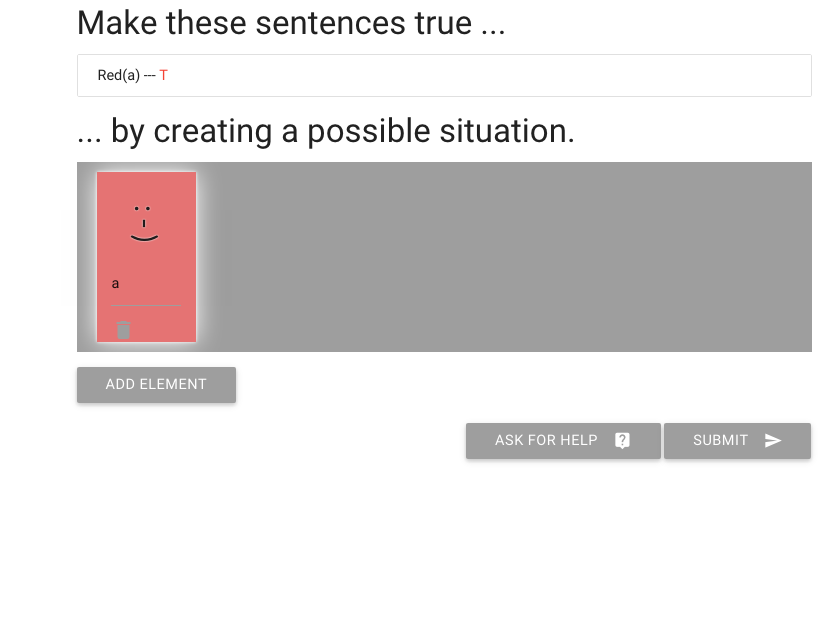
Now the red person is happy.
\section{Counterexamples}
\emph{Reading:} §2.5

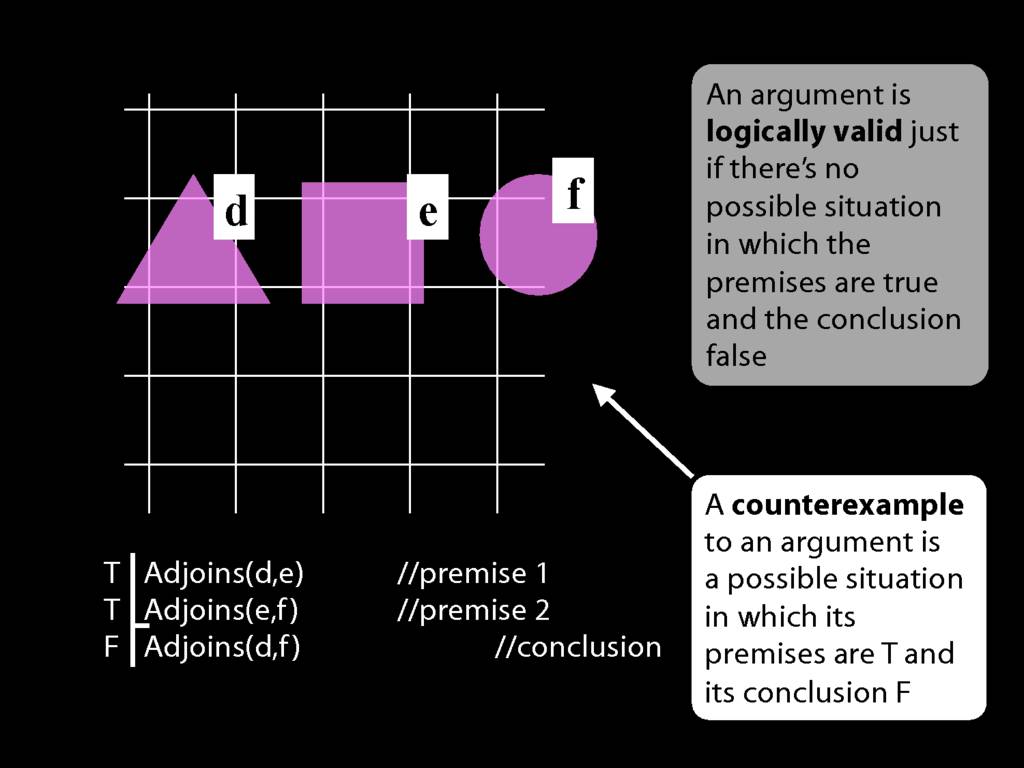
A \emph{counterexample} to an argument is a possible situation in which its premises are T and its conclusion F.
There are no counterexamples to a logically valid argument.
If an argument is not valid, then there is a counterexample to it.
To show that an argument is not logically valid, we specify a counterexample to it.

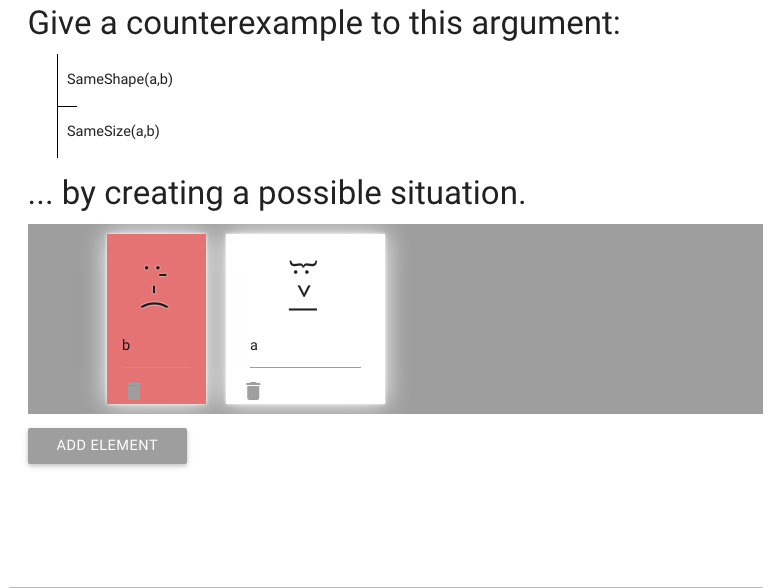
We have to create a counterexample to an argument.
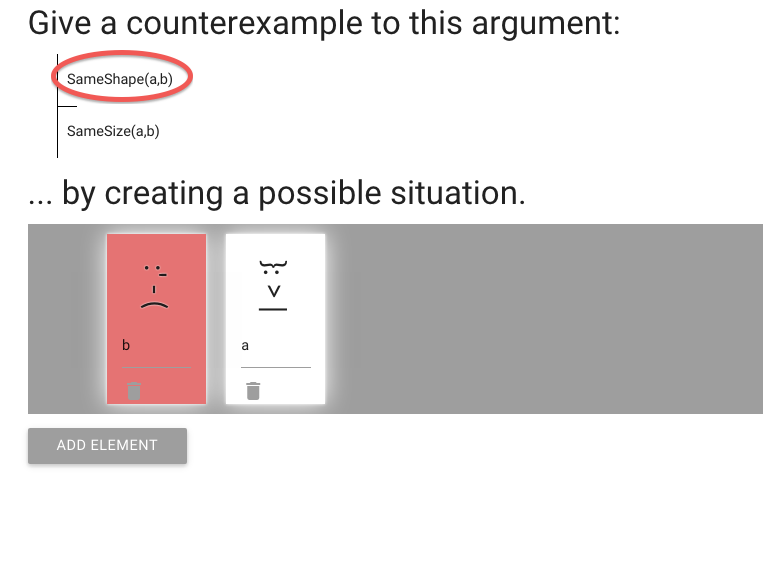
So the premise must be true ...

... and the conclusion must be false.
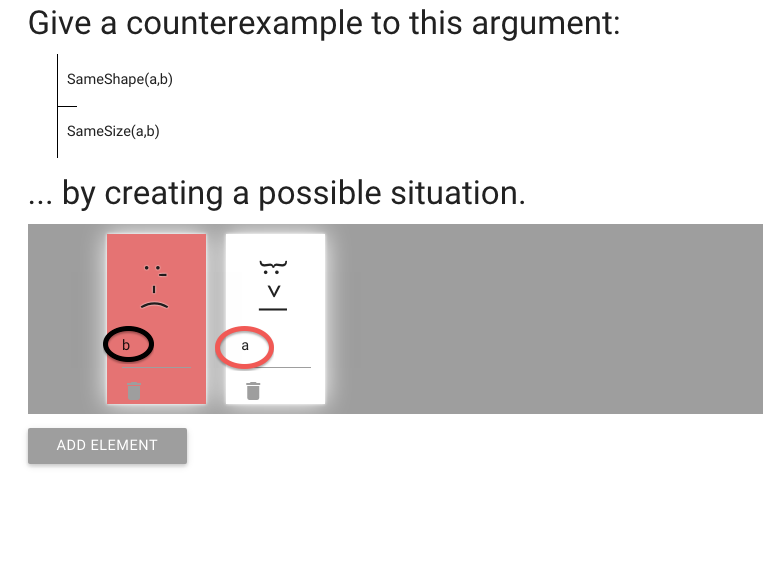
I already put the names in; without having things named ‘a’ and ‘b’
the sentences would not be true or false in our possible situation.
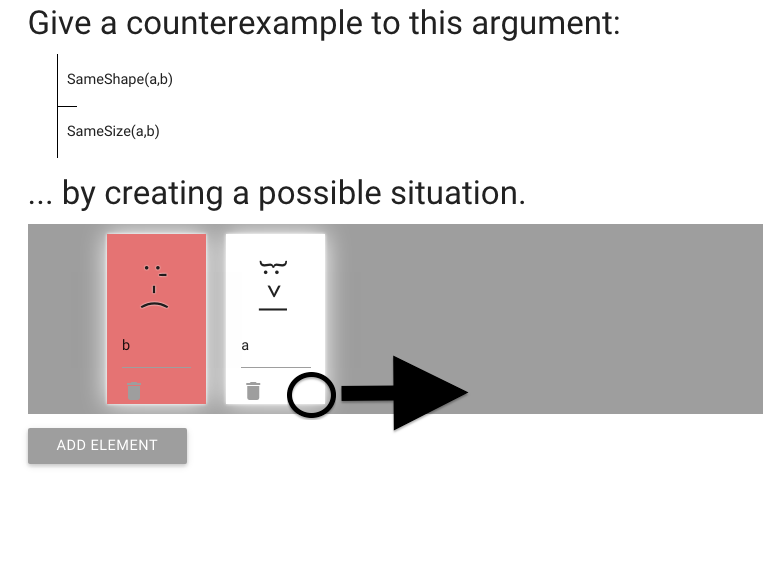
We need to make the conclusion false.
At the moment it’s true because a and b are the same size.
So let’s change the size of a.
Do this by dragging the corner to stretch her.

This makes the conclusion false, as we wanted.
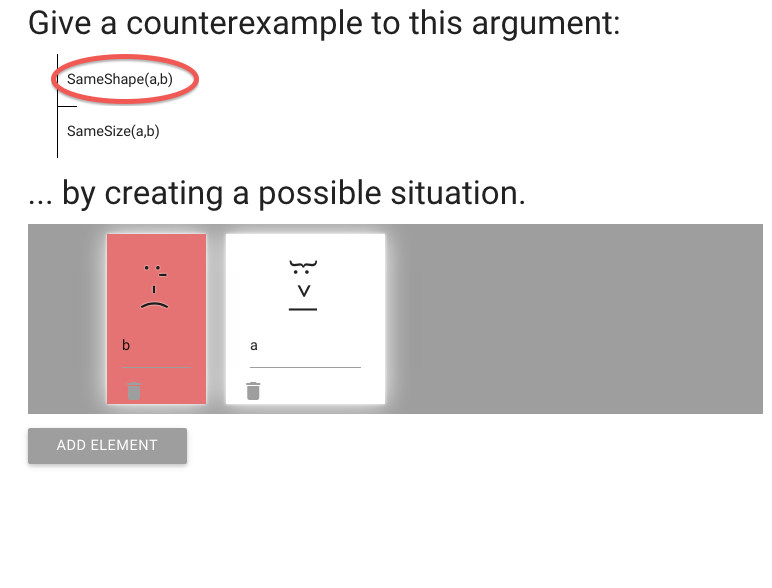
But now the premise is false too.
(This is often the problem with creating counterexamples.)
What can we do?
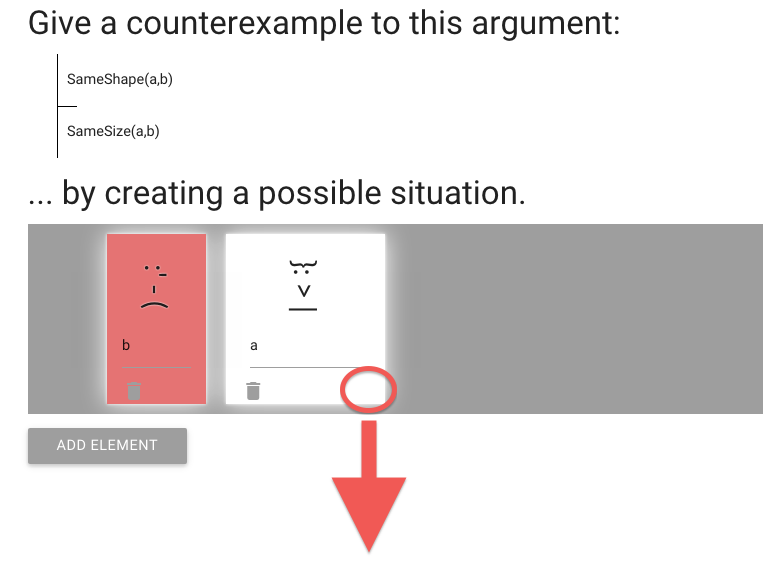
Let’s make a taller as well by stretching her down.
Do this by dragging the corner.

Now a is both wider and taller than b.
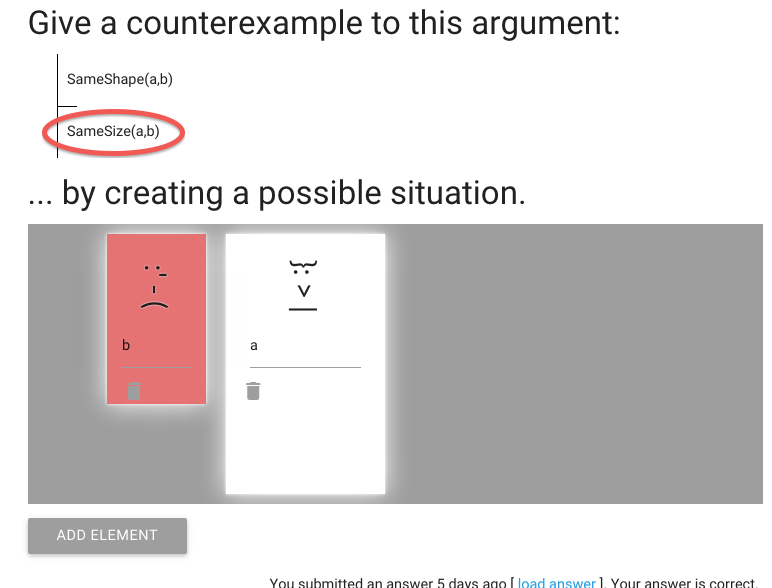
So the conclusion is still false ...
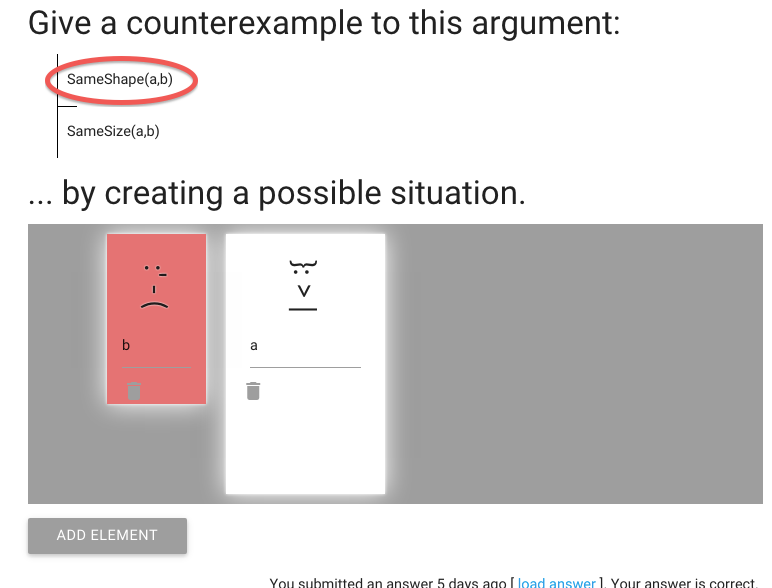
... but now the premise is true, just as we wanted.
A counterexample to an argument is a possible situation in which
its premises are true and its conclusion is false.
2.8, 2.10, 2.12, 2.21
2.8, 2.10, 2.12, 2.21
\section{Identity}
\emph{Reading:} §2.2

Here’s an argument involving identity. Let’s see if it’s valid.
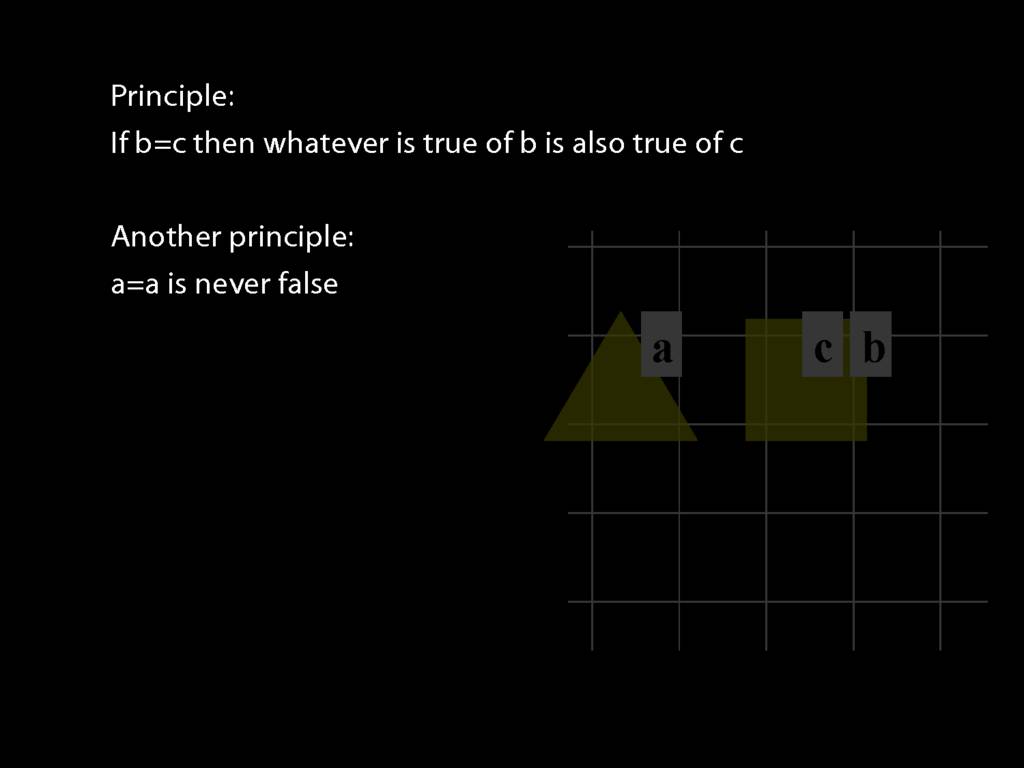
Principle: If b=c then whatever is true of b is also true of c.
Principle: a=a is never false

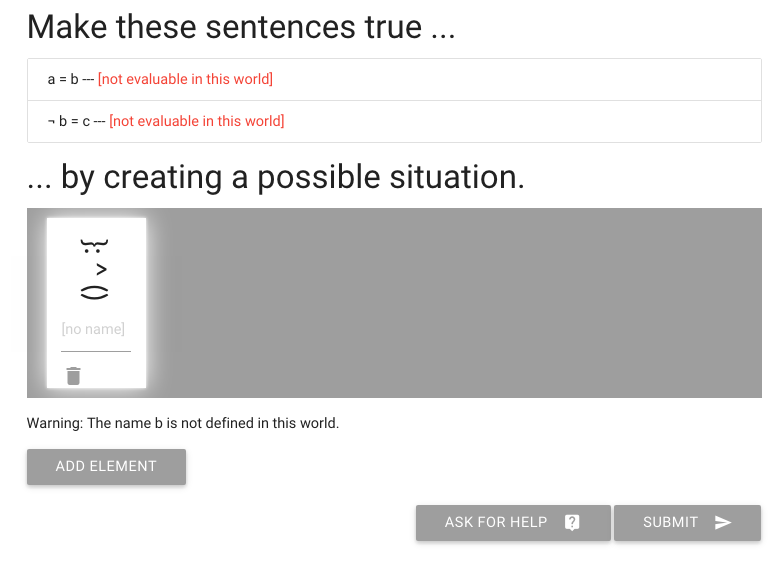
Suppose we want to find a counterexample. So we need to make make the premises true. Let’s see if we can make them true without making the conclusion true.

Start with an empty world.
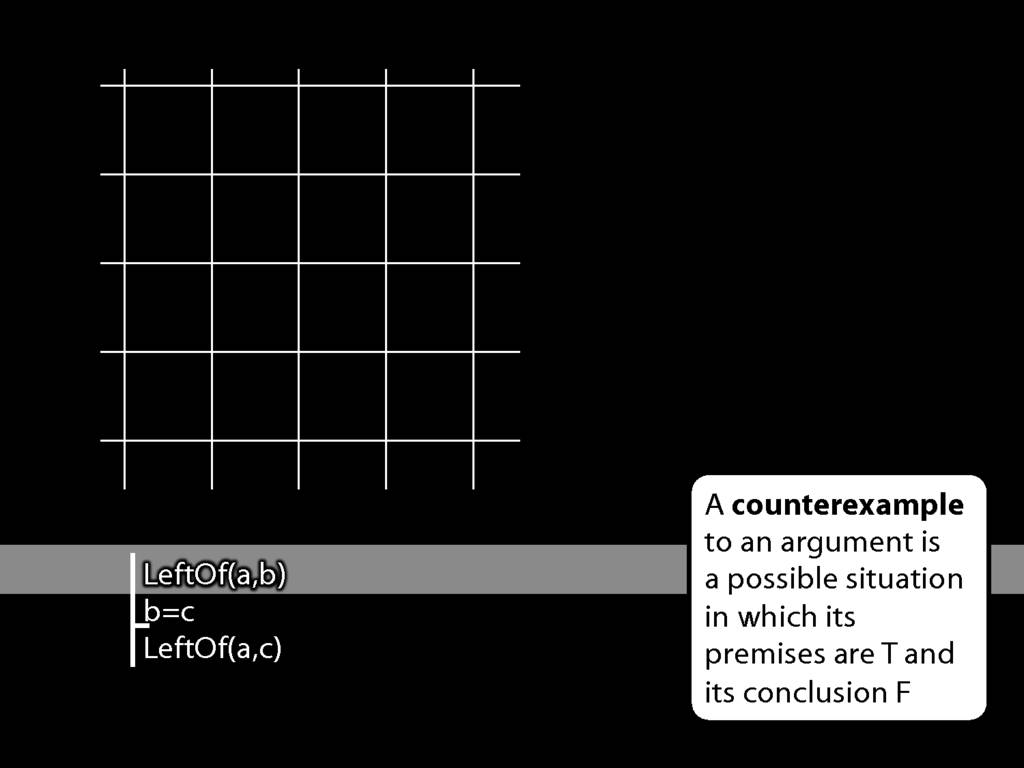
Consider the first premise
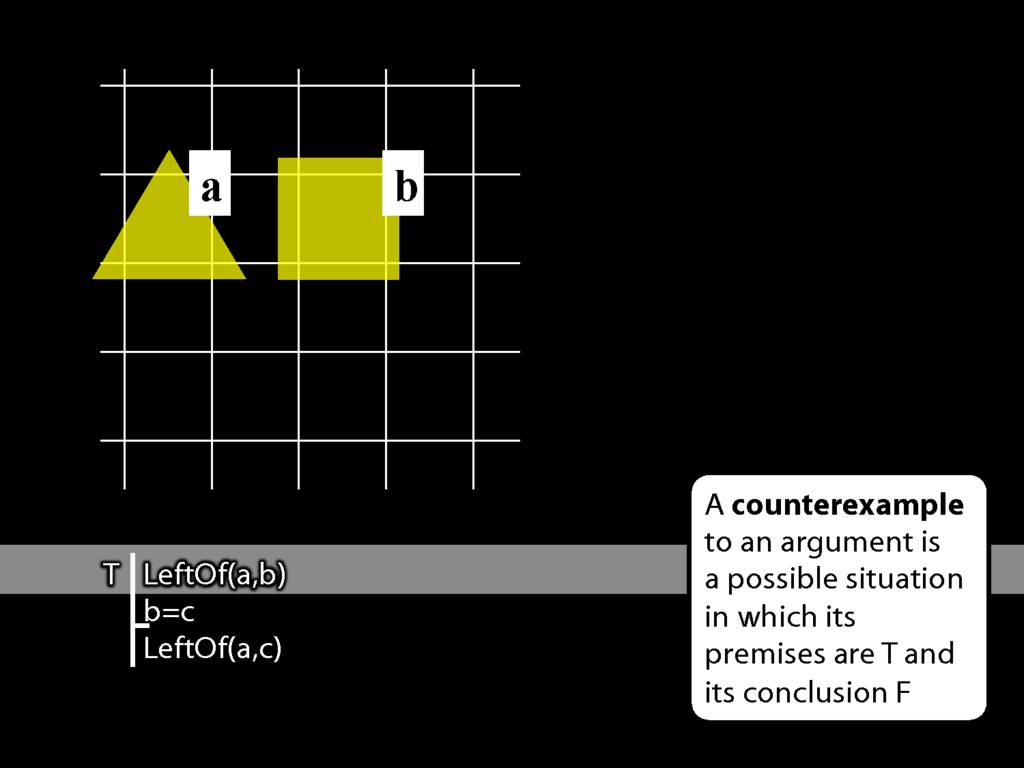
We want the first premise to be true so we have to put a to the left of b.
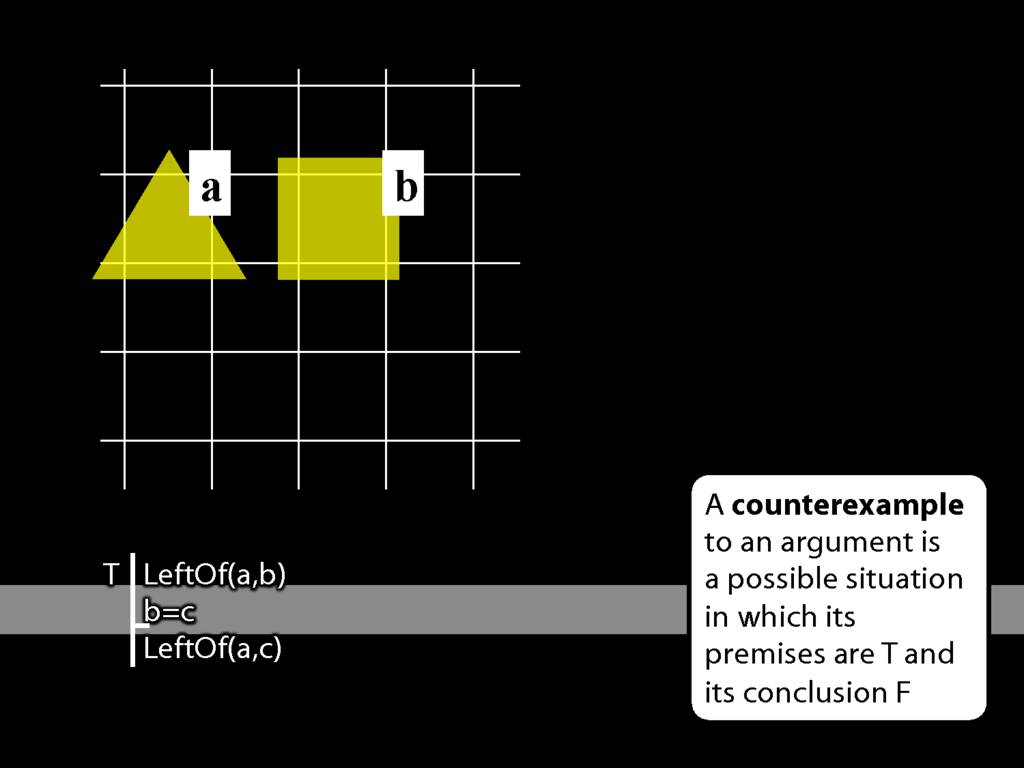
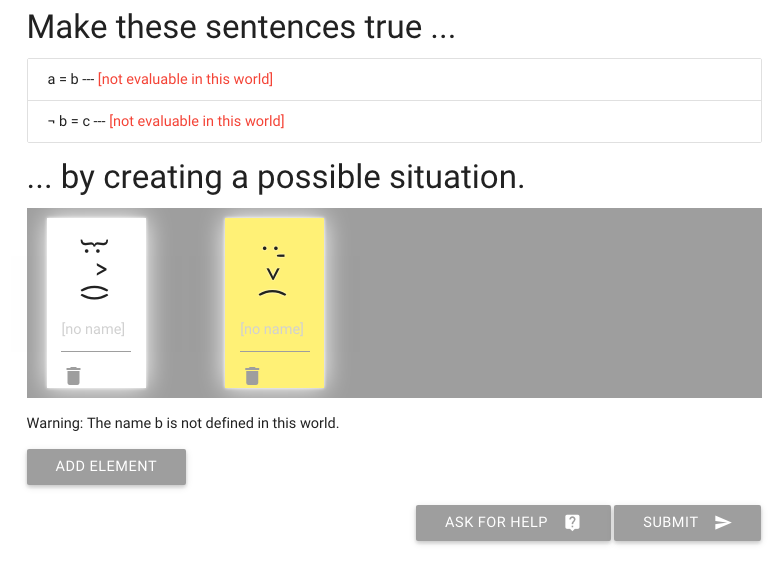
What about the second premise? So far the truth-value of the second and third premises are undefined because the name ‘c’ does not yet designate any object in this situation.
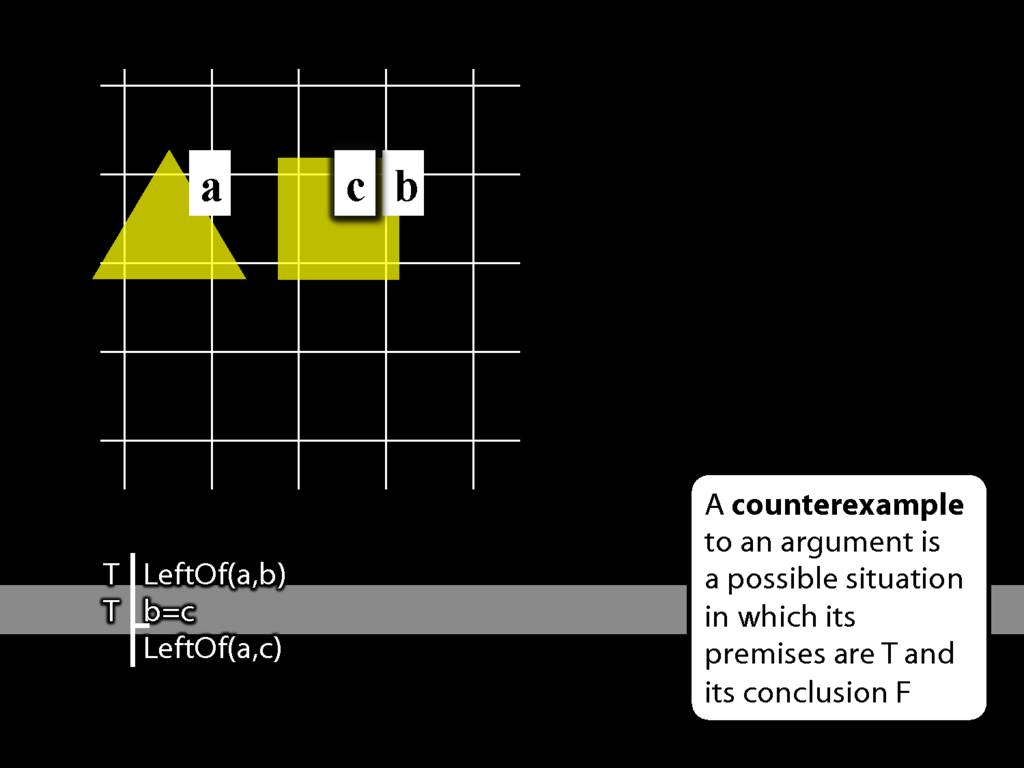
Want the second premise to be true so we have to label the b object c as well.
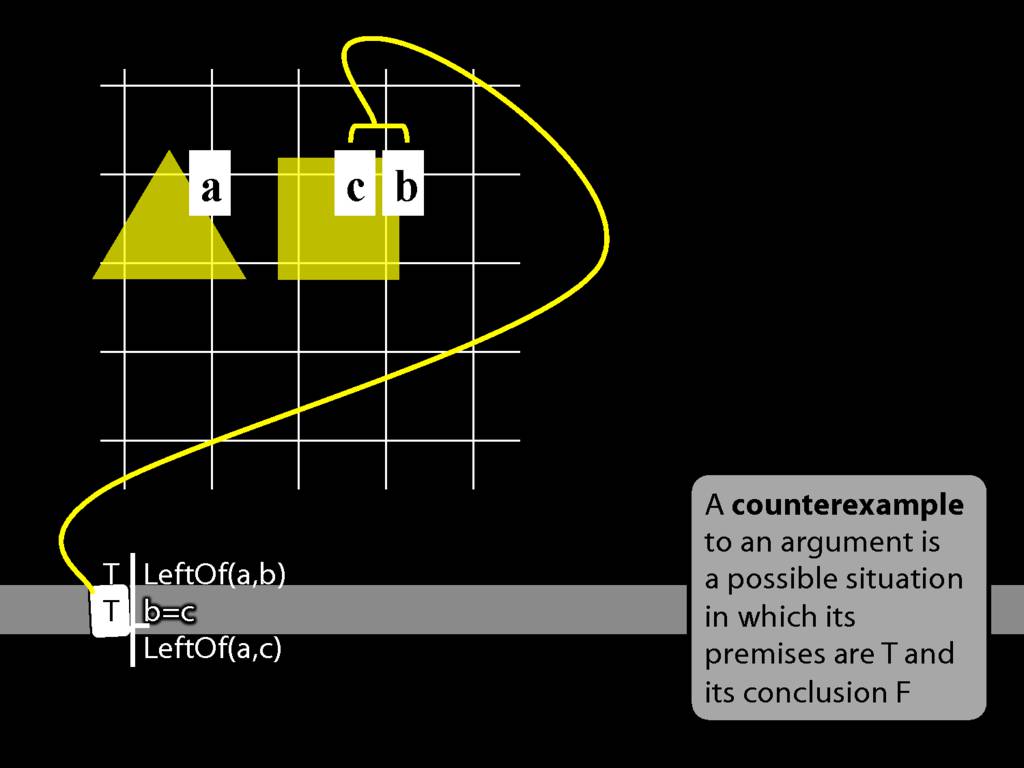
This is what b=c requires--that one and the same object have both labels.
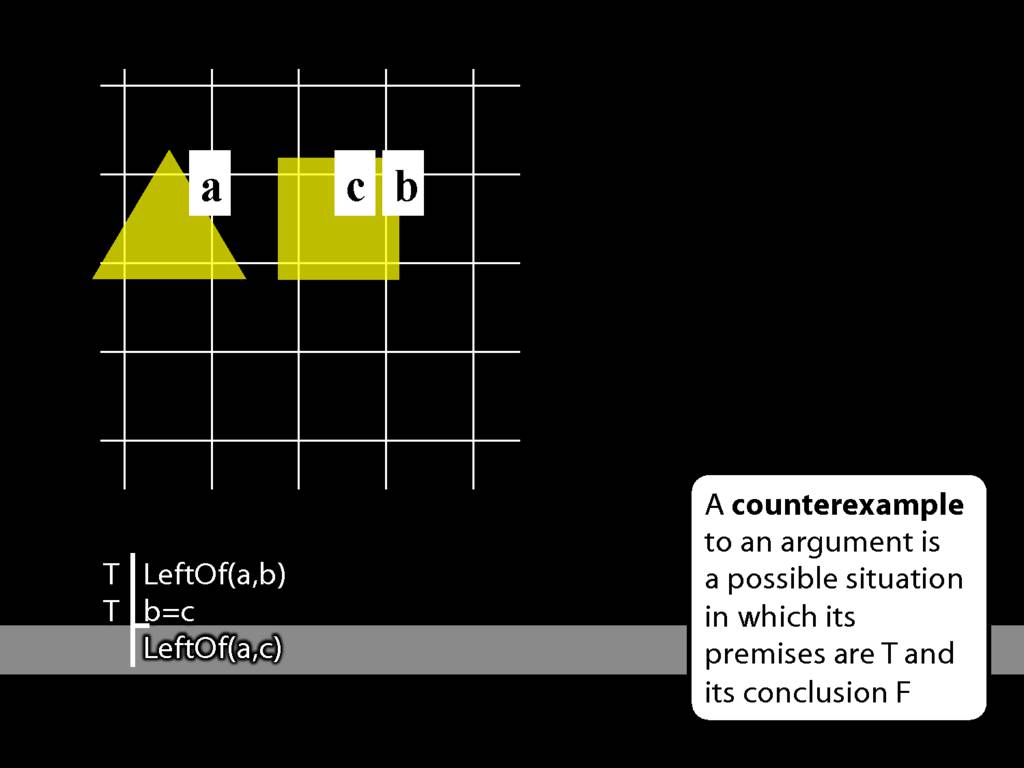
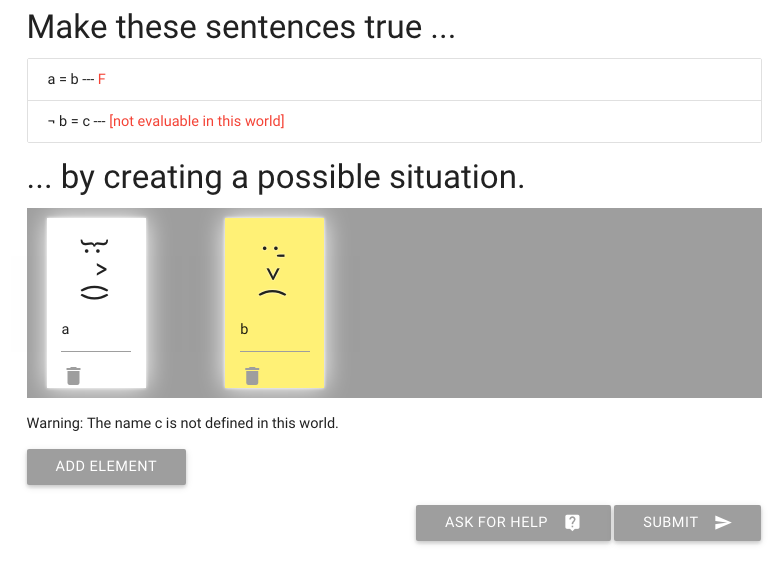
Now, what about the conclusion?
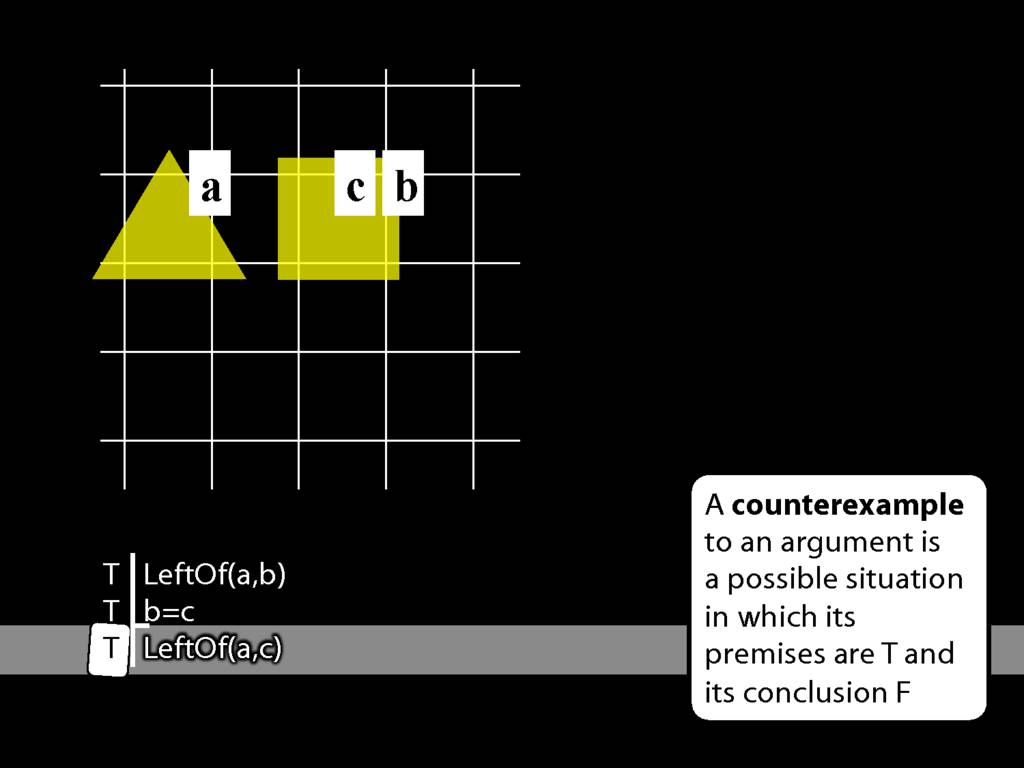
Having made the premises true, the conclusion turns out to be true as well.
This is sort of an informal proof that the argument is valid. If you think about what is involved in making the premises true, you can see that it guarantees the truth of the conclusion as well.

As far as the logic of identity goes, all you need to know are two principles.
This first principle.
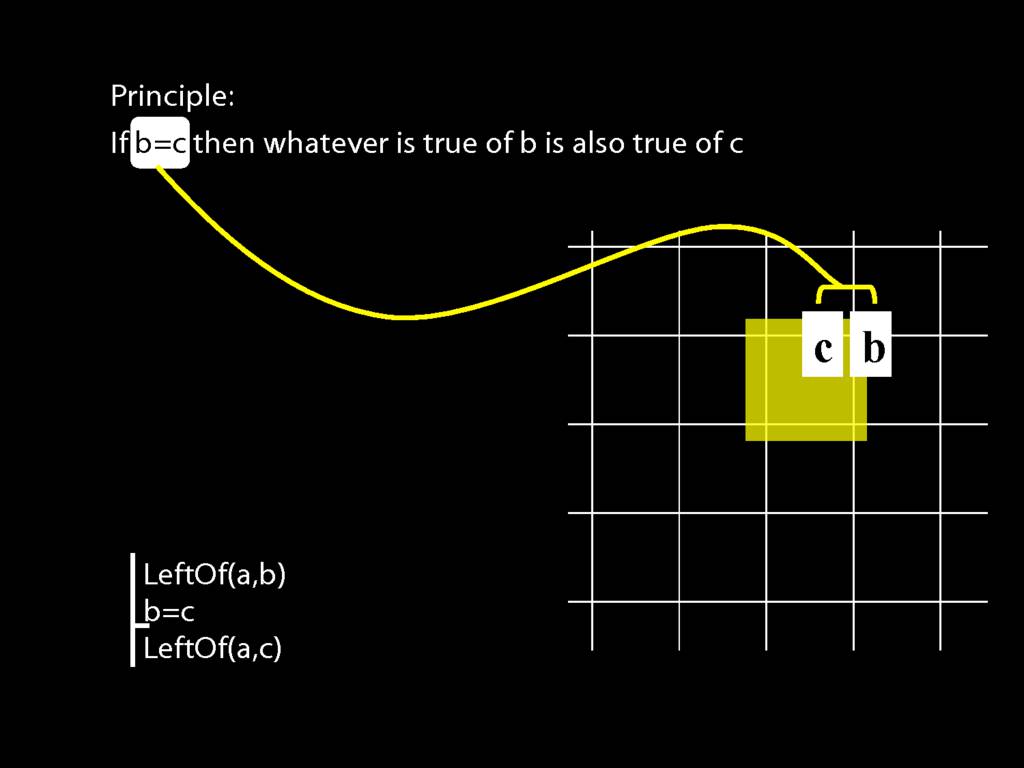
You can see that this principle must be true from the meaning of identity: b=c requires that one and the same object have both labels.
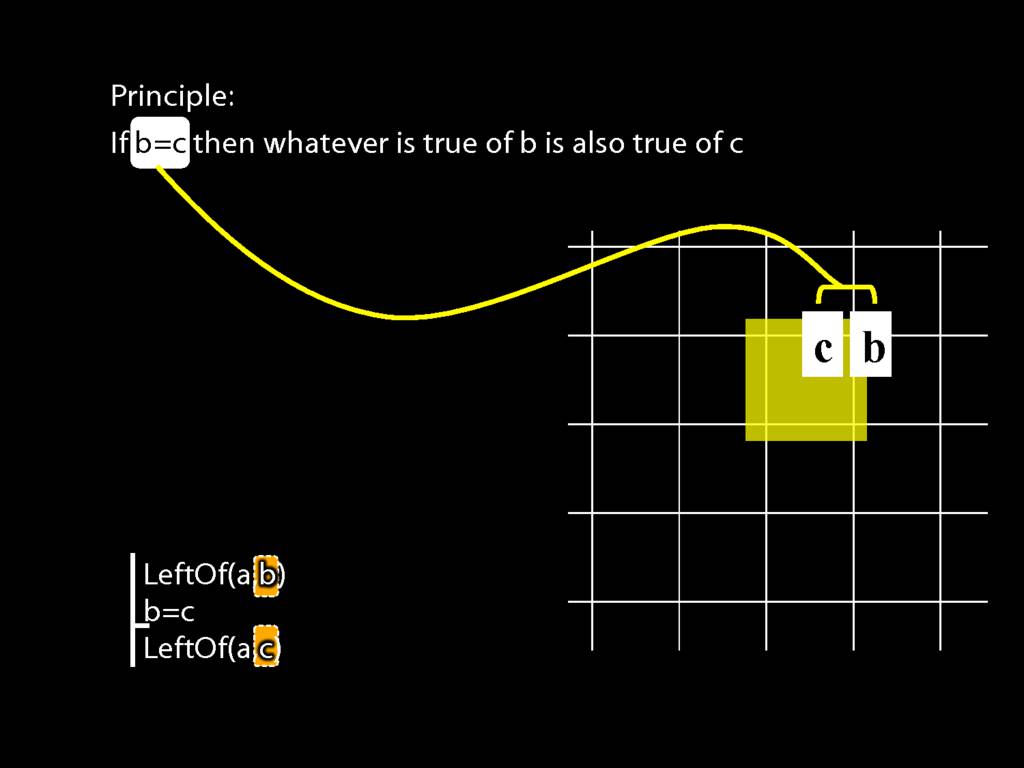
And this first principle is exactly what you need to prove the argument we were just looking at.
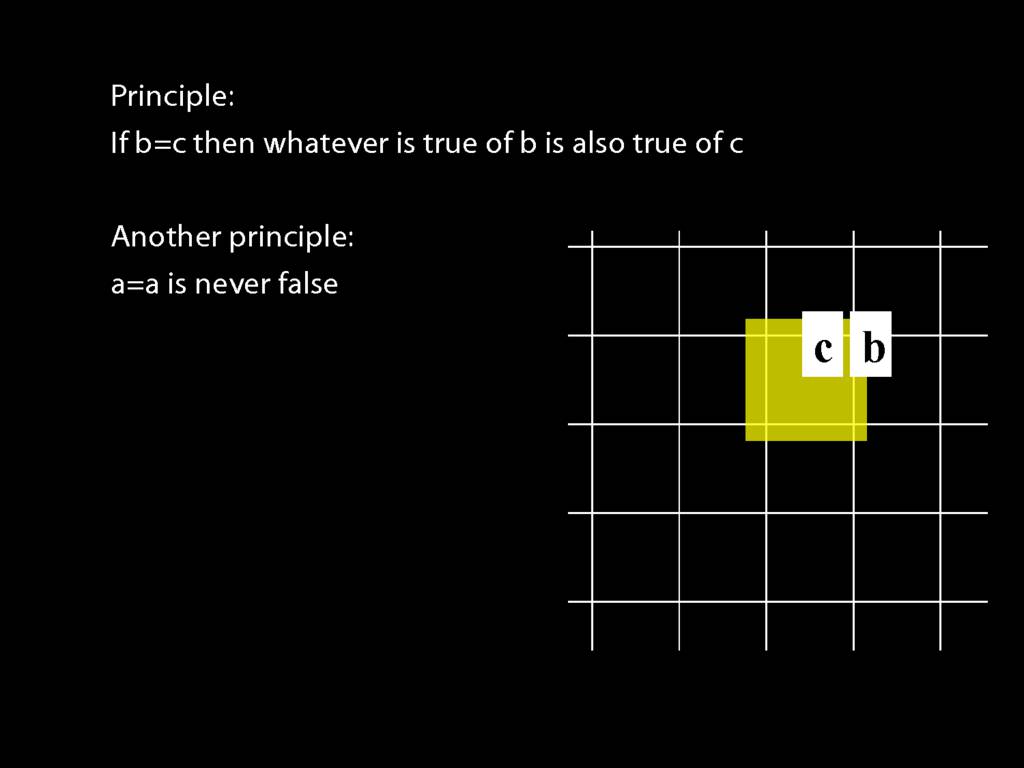
The second principle says, roughly, that everything is identical to itself.
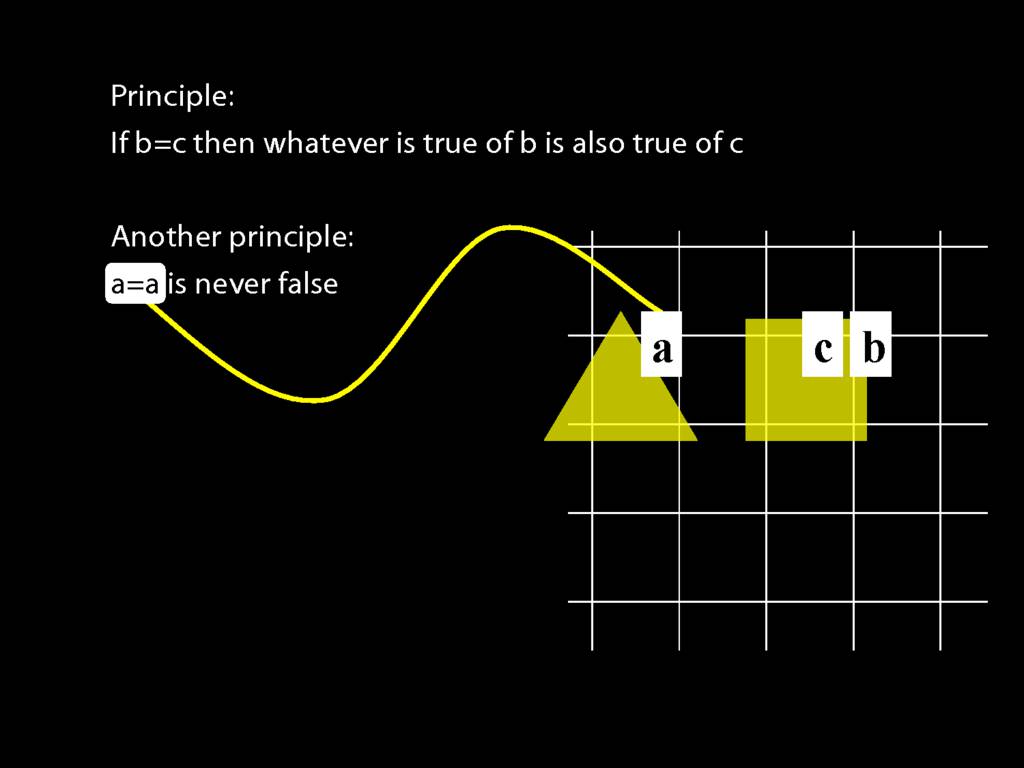
You can see that this principle must be true from the meaning of identity: a=a requires only that one and the object named 'a' be named 'a', which you can't really avoid. (In case you're thinking there's a tricky issue about what happens if nothing is named 'a', well done. In our system of logic, we rule that possibility out by stipulation to keep things simple.)
These principles are all you need to understand the logical notion of identity. They allow you to do things like prove that identity is a symmetric and transitive relation.
I want to show you quickly how to work with identity in logic-ex.
Let’s add a person to the possible situation
Here I’ve added some names
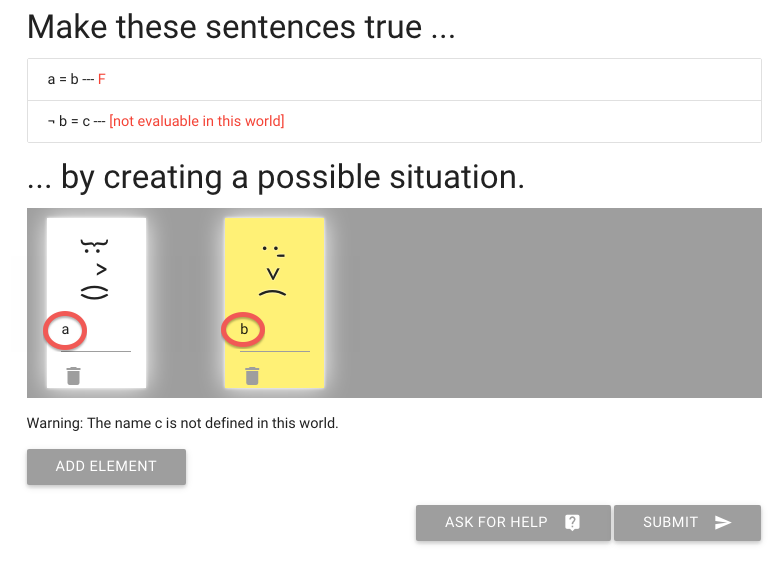
I’ve called one person ‘a’ and the other ‘b’.
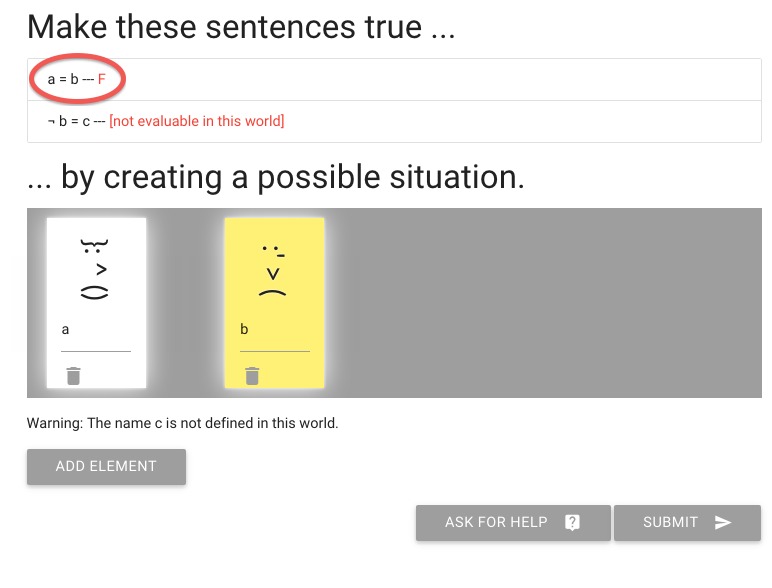
Of course this makes the first sentence false, not true.
How do I make it true?
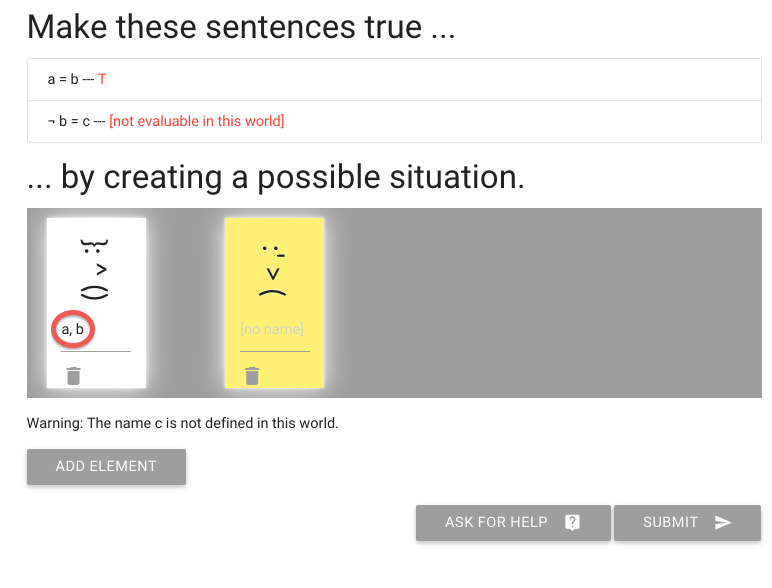
I’ve given one person both names.
To give more than one name to a person, simply type multiple names
separated by commas or spaces (or both), just as I’ve done here.
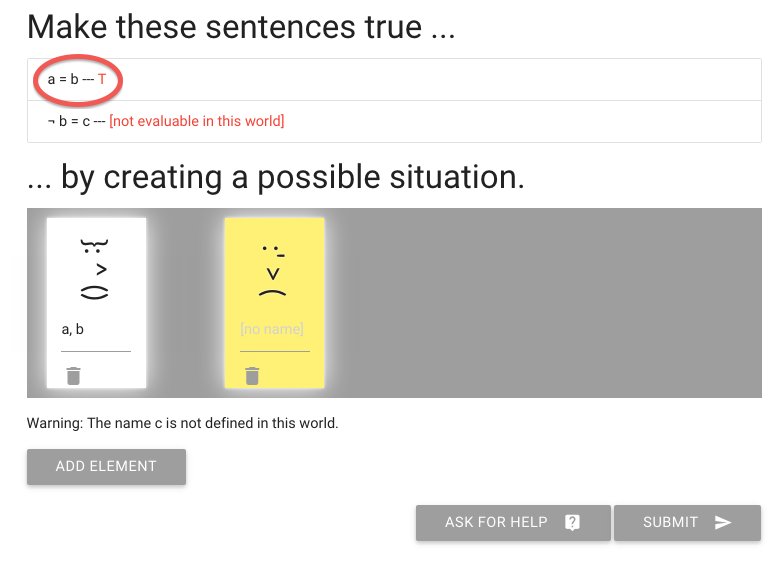
And this makes the sentence ‘a=b’ true, of course.
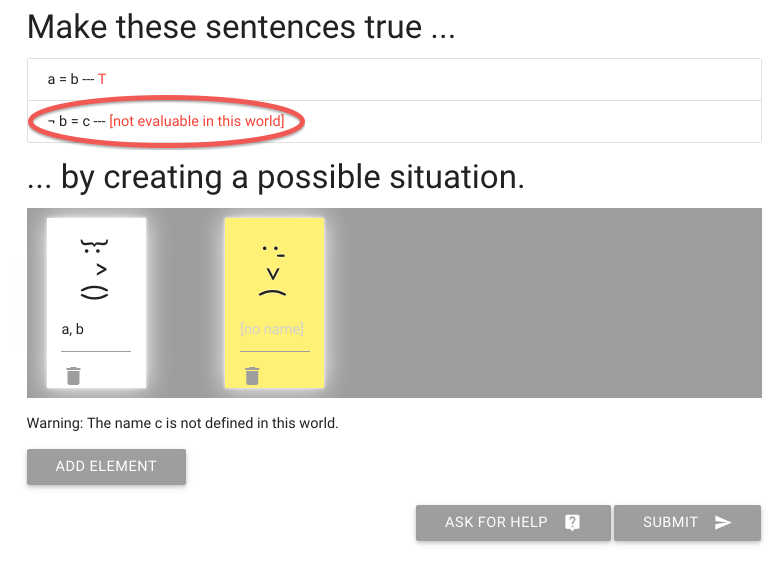
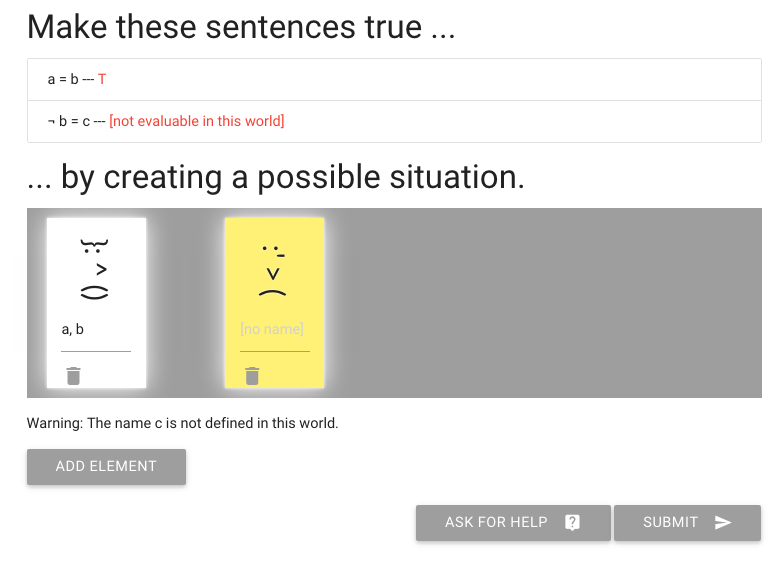
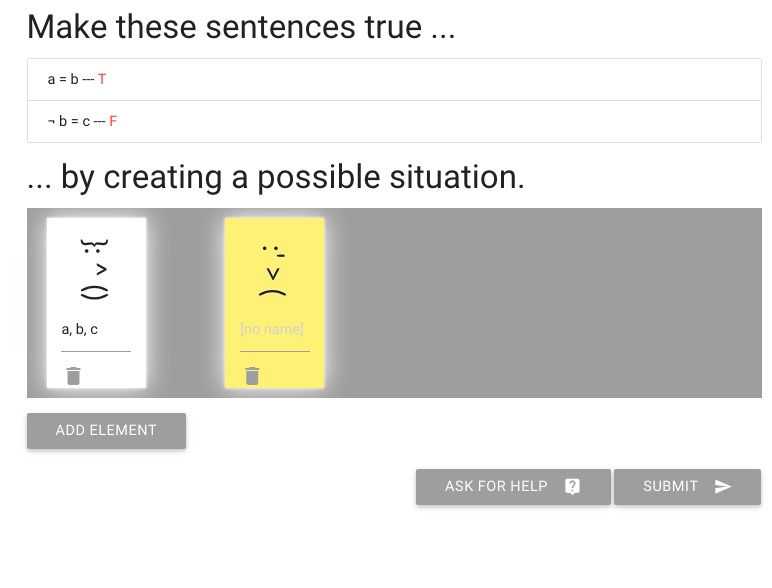
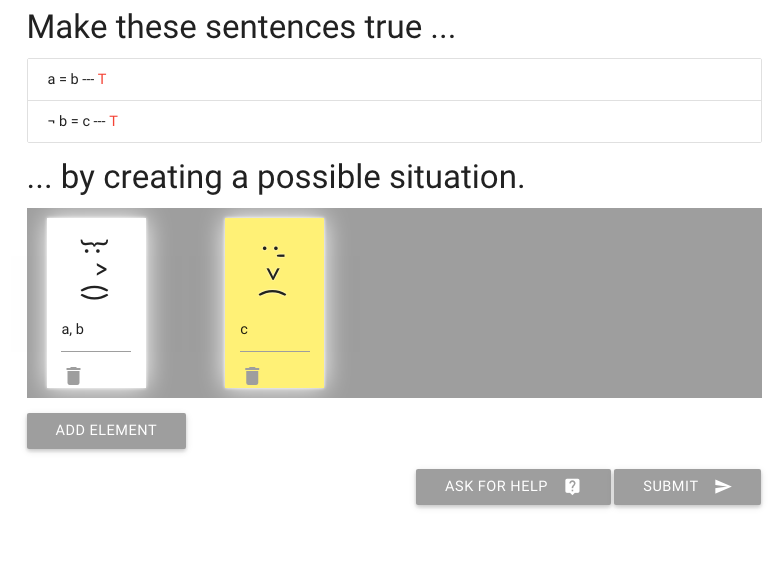
But what about the next sentence, ‘not b=c’?
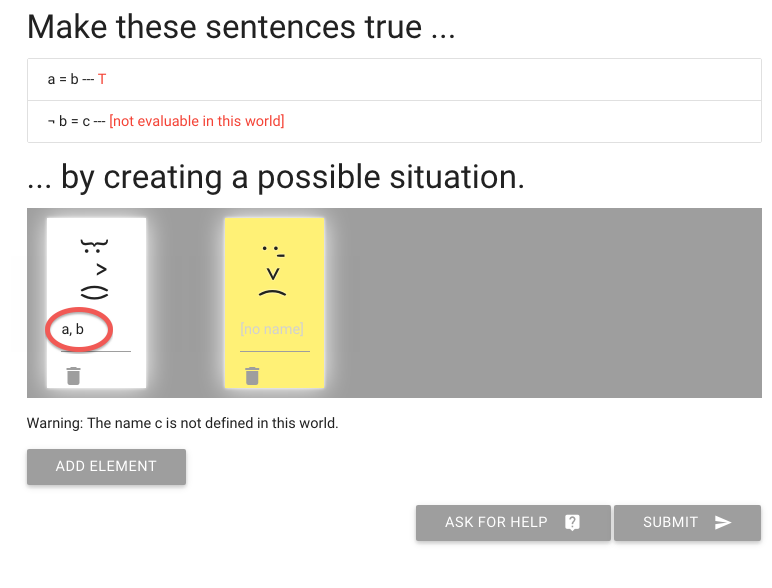
To make this true or false, I need to give someone the name c.
I’m going to add that to the person already known as ‘a’ and ‘b’.
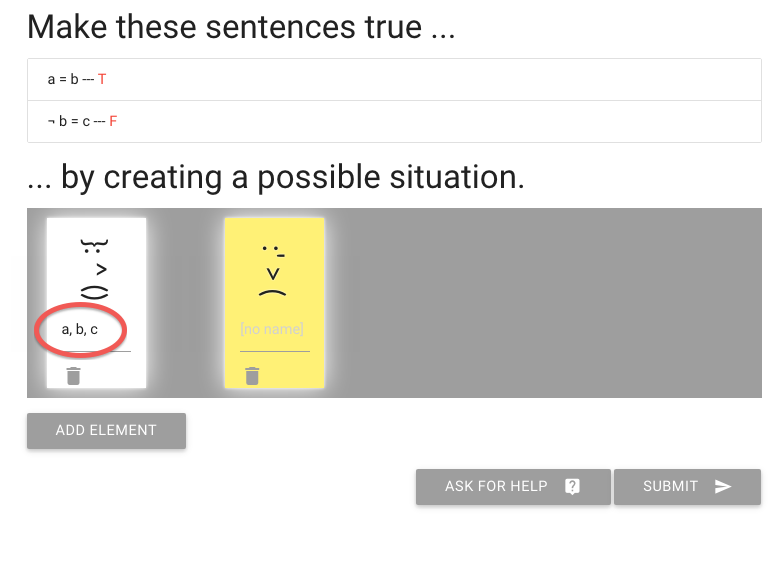
So here you see one person has all three names
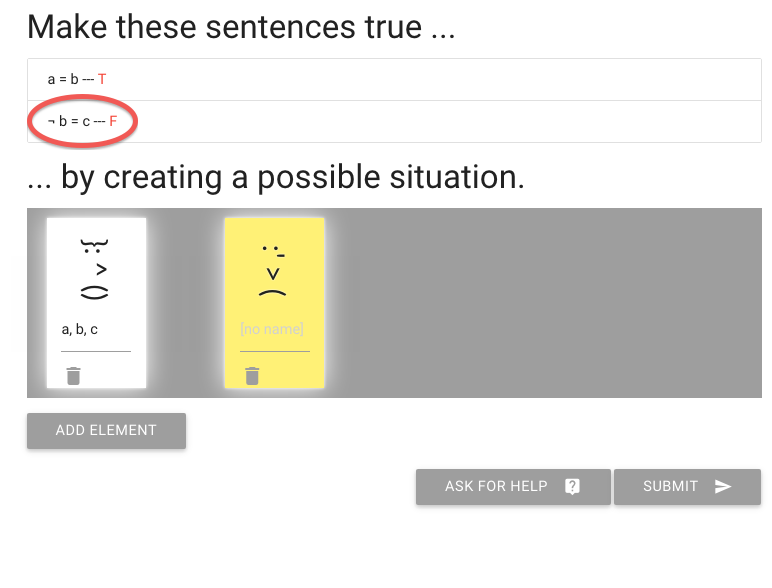
Of course this means the second sentence, ‘not b=c’ is false.
We need to make that true.
How are we going to do that?
Let me re-arrange the names.
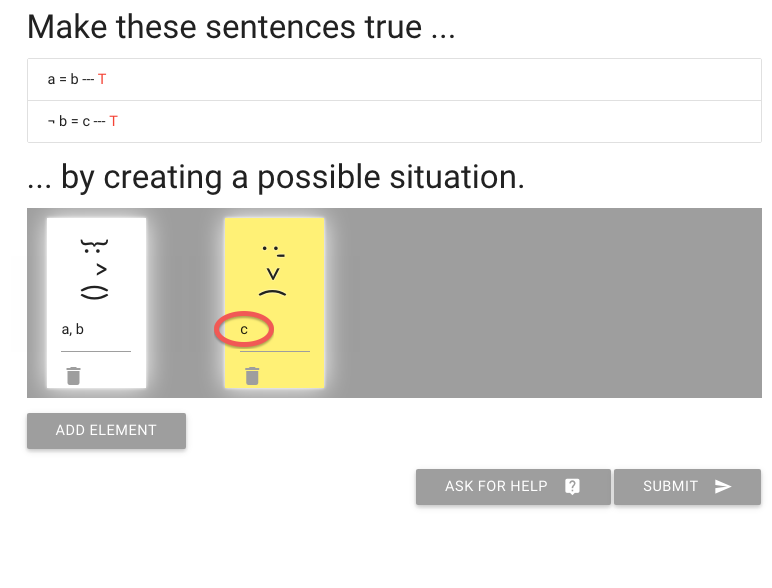
You see that I’ve named the other, yellow person c.
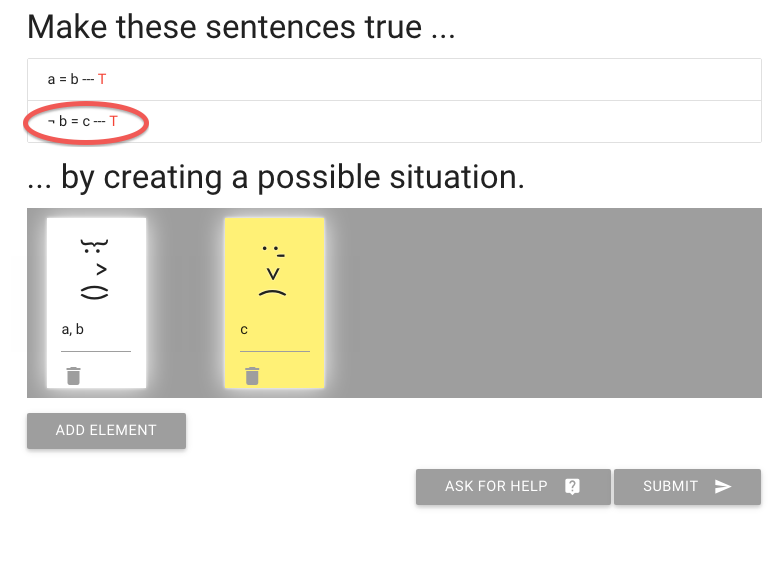
And this is enough to make the second sentence true.
2.5, 2.6
\section{Truth Tables}
\emph{Reading:} §3.1, §3.2, §3.3

Here's a rough guide to what the connectives mean.
Rough guide:
`$\land{}$' means and
`$\lor{}$' means or
`$\lnot{}$' means not

Why do we need more than this rough guide?
Consider the sentence 'I love logic or I love chocolate'.
If I were to say this to you, and it turned out that I loved logic and chocolate both,
you might think I had mislead you by saying 'or'. And that might lead you to think
that the English sentence is false, and that 'or' sentences are false when the two sentences
they conjoin are both true. That is, the English 'or' is exclusive.

But now consider a different example. You say to me, 'You can be my friend if you love logic or chocolate'.
Then, as before, it turns out that I love both.
In this situation you're not going to deny me friendship. You're not going to say I haven't meet the criterion you specified.
No, if I love both then I'm doubly your friend.
This tells us that an English sentence involving 'or' is true when the two sentences
conjoined are both true. That is, the English 'or' is inclusive.
But now we seems to have contradictory urges. One case urges us to say that the English 'or' is exclusive
(false when the things conjoined are both true), the other case urges us to say the opposite.
Now the truth is probably that the English 'or' is neither inclusive nor exclusive but much more complex still.
The point of introducing a formal language is to avoid all this complexity.
Not because there's anything wrong with the English 'or'--on the contrary, it's complexity is a wonderful thing for communication.
But our concern is not communication but logic.
Now if we define our symbols just by invoking the meanings of English words, we won't succeed in avoiding the complexity of
natural languages like English. We will have merely replaced one sign with another.
This is why we need more than the rough guide
So what does a symbol like ∧ mean?
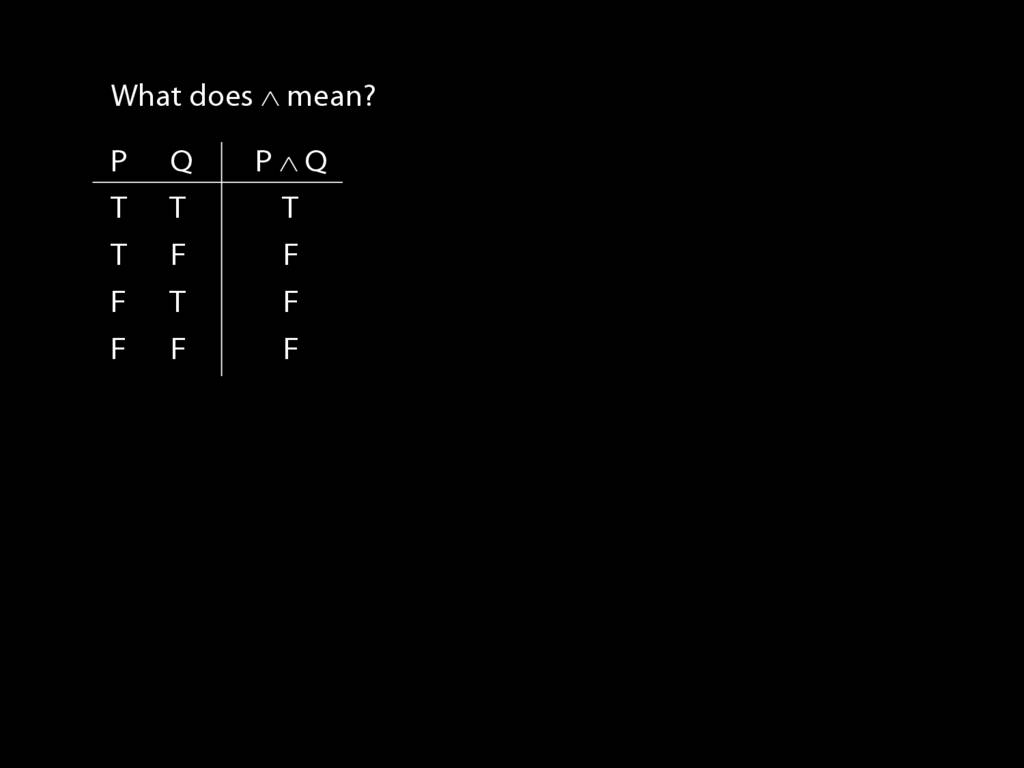
The answer is given by a truth table.
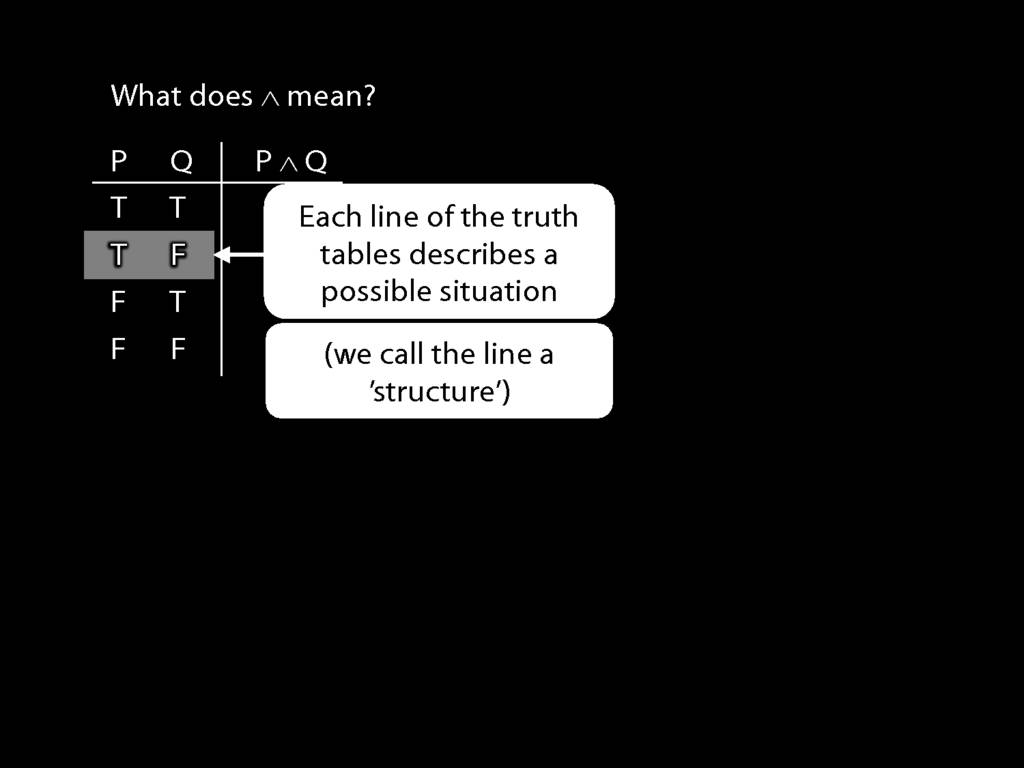
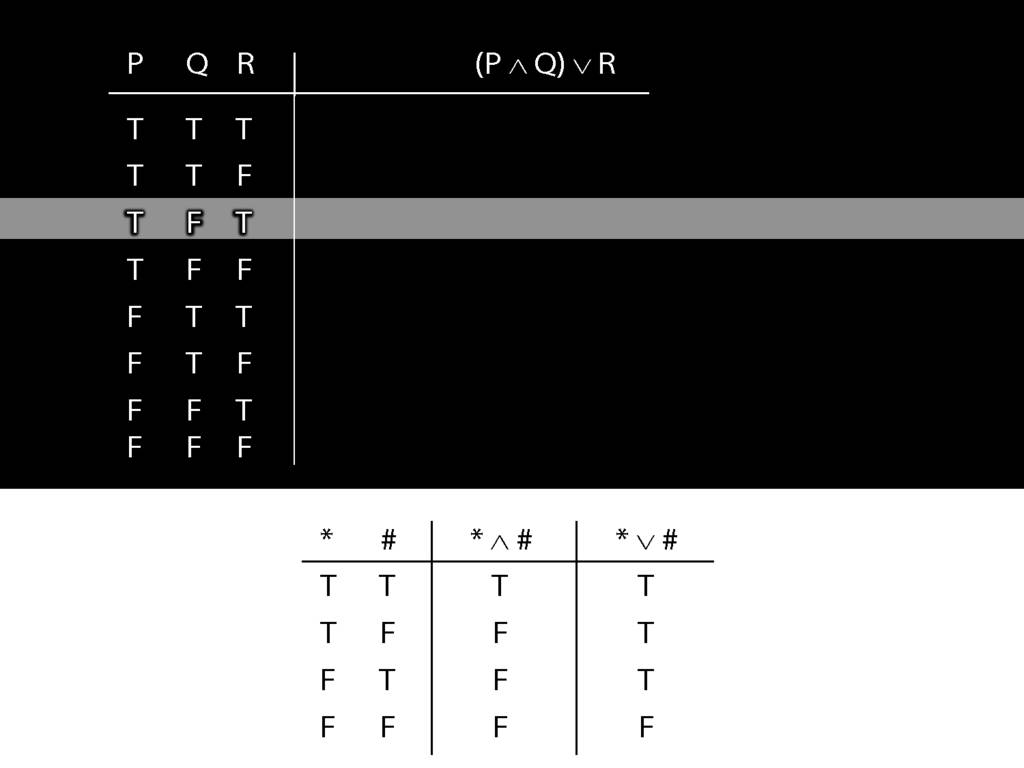
Each line of the truth table describes a possible situation.
For instance, this line of the truth-table describes the situation where P is true and Q false.
(Strictly speaking, this is not a possible situation but a whole class of possible situations.)
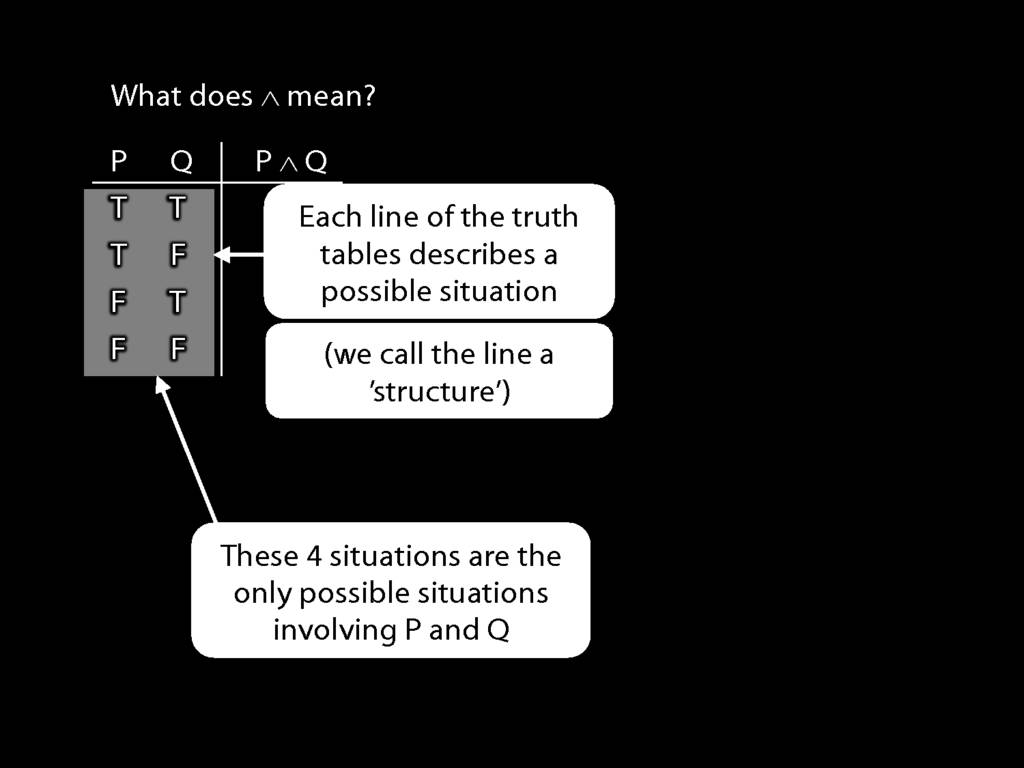
Insofar as we are interested in sentences involving sentence-letters and certain connectives,
we need only distinguish possible situations in which the sentence-letters of interest have different truth values.
This means that if we are concerned with two sentence letters, there are only four kinds of possible situation that we
need to consider.
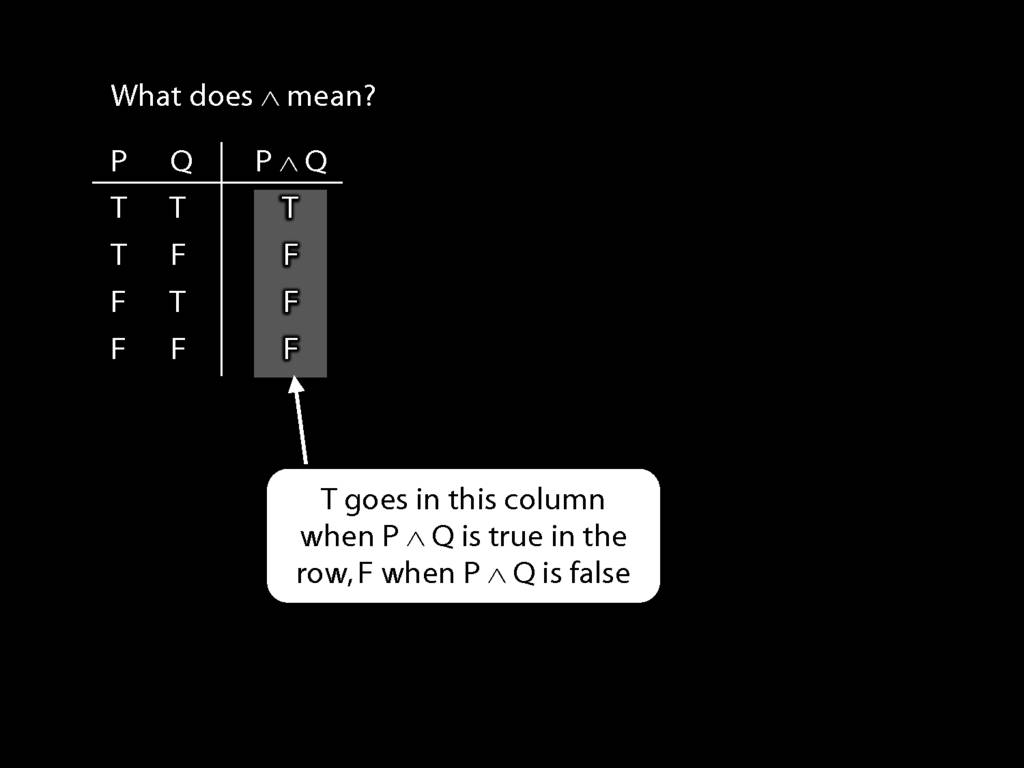
The Ts and Fs in this column tell us whether the sentence is true or false.
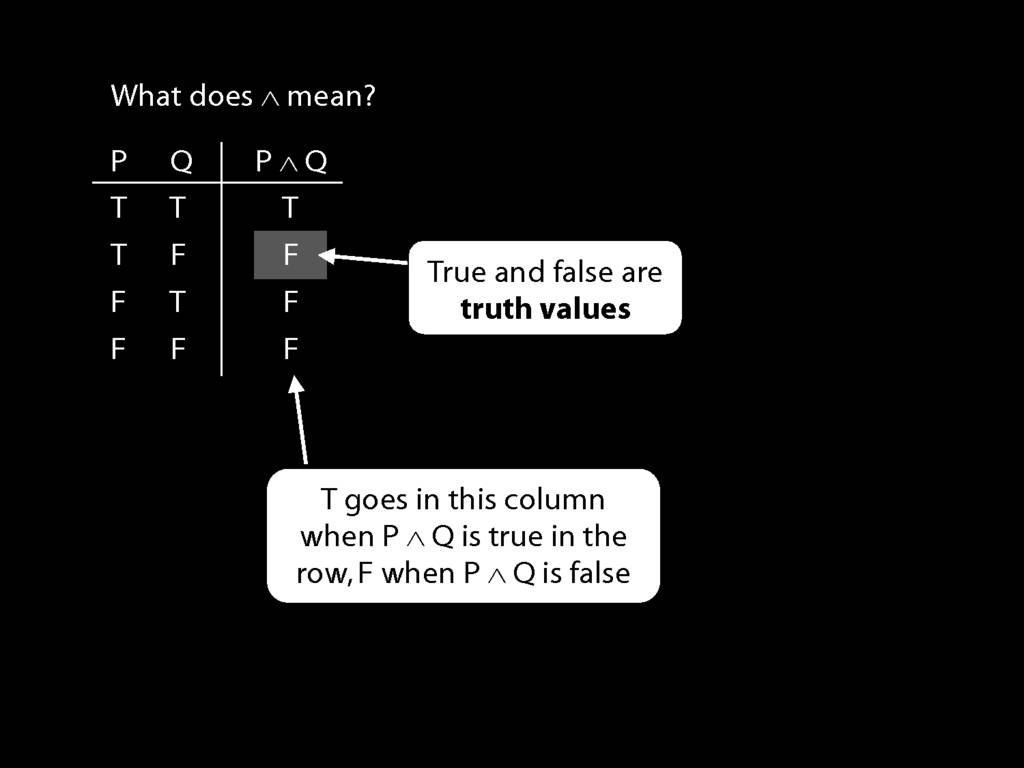
So, for example, we are told that P∧Q is false when P is true and Q false.
These true and false are called truth-values.
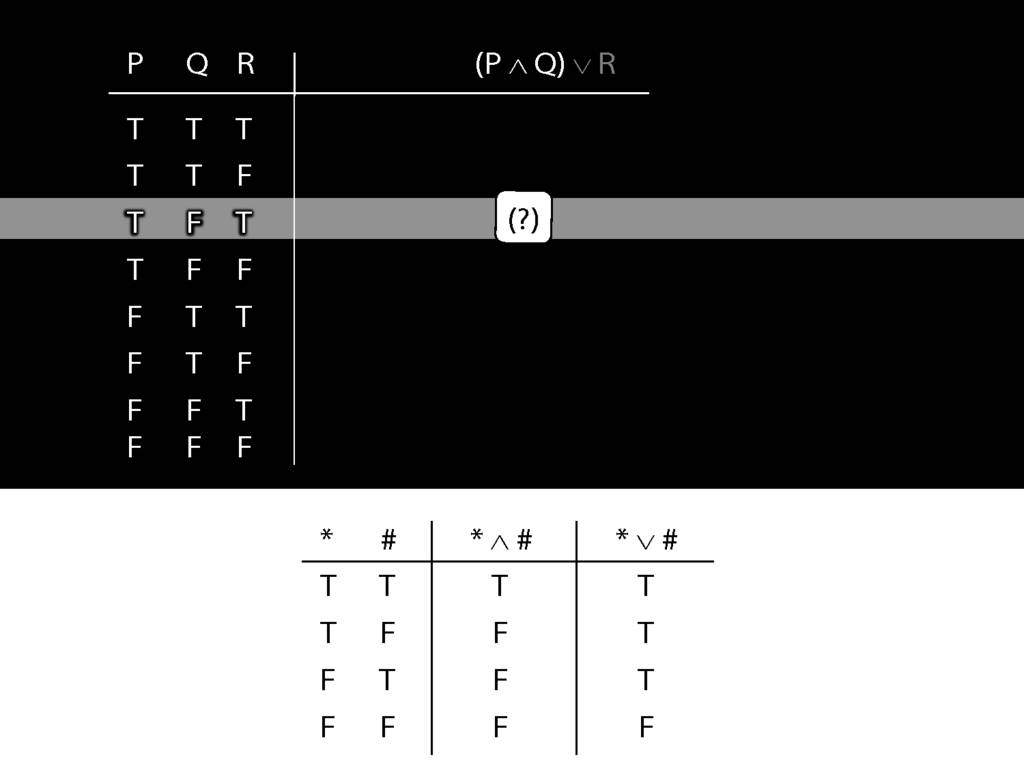
To illustrate, suppose I ask you, What is the truth-value of P∧Q in this row (the second row)? What would you say?
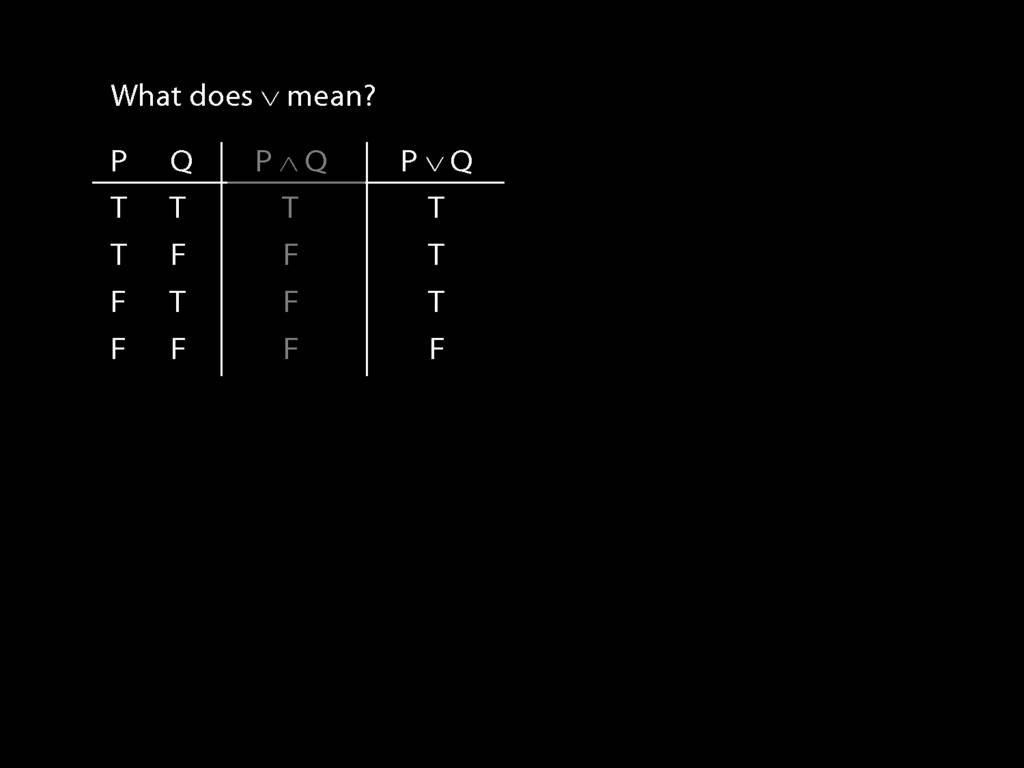
The answer is given by another truth table.

Let's return to the English sentence about loving chocolate or logic.
Imagine that instead of 'or' we had the logical symbol for disjunction, ∨.
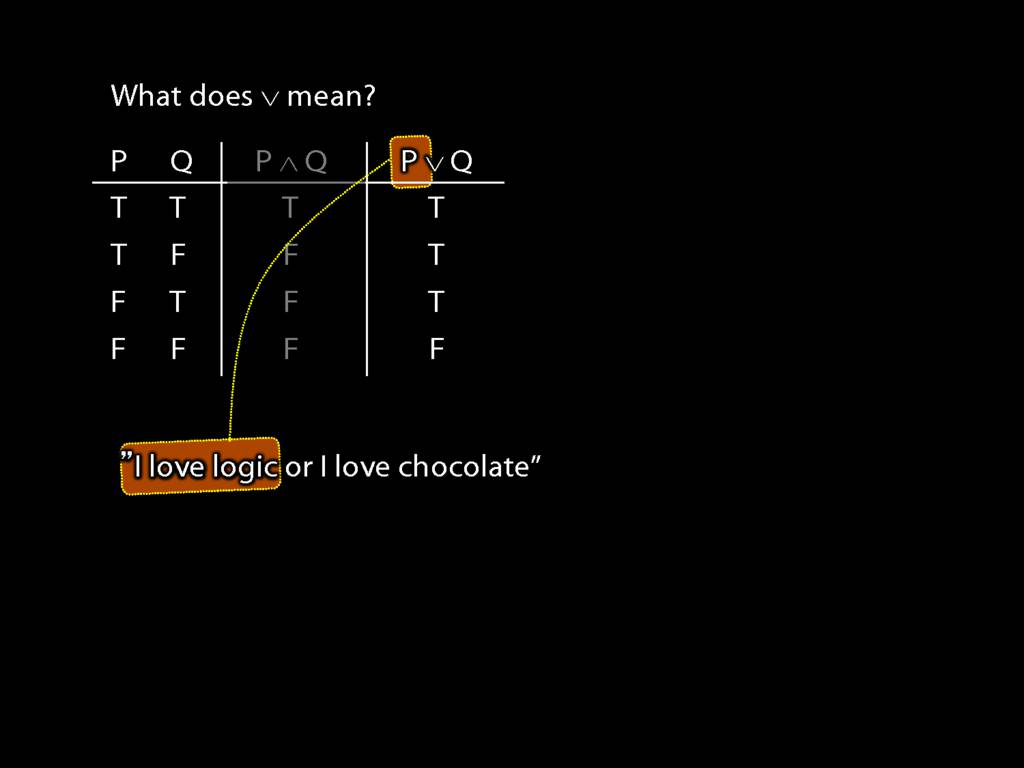
Then 'I love logic' is P, and ...

... 'I love chocolate' is Q.
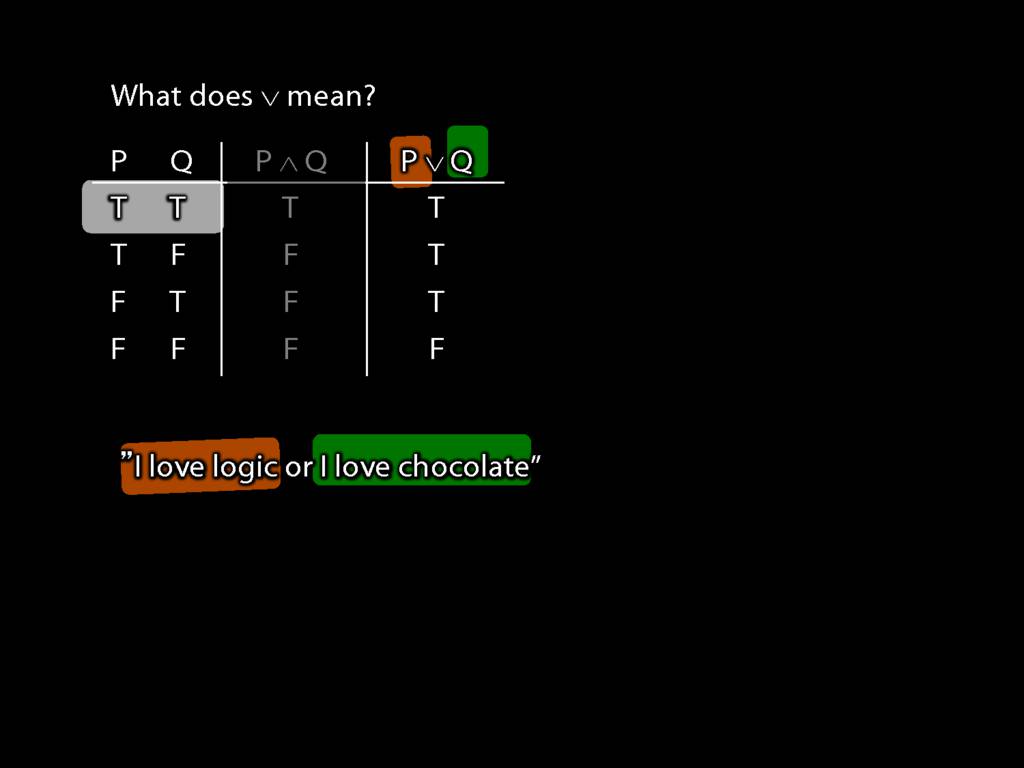
Now what happens if they are both true?
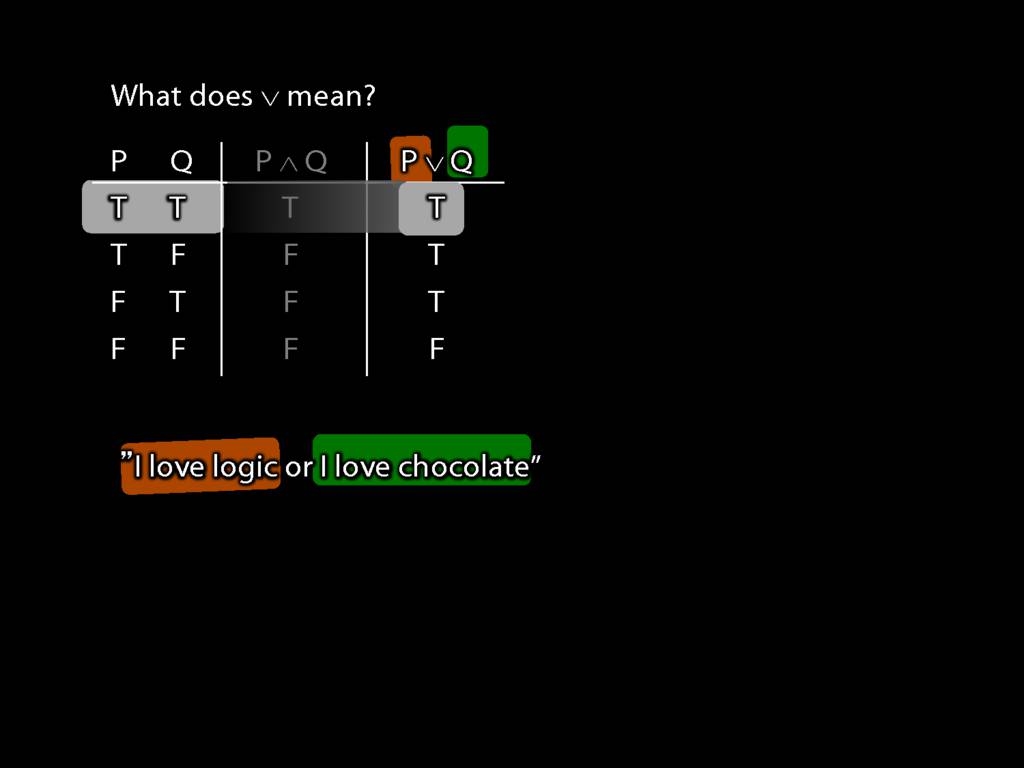
The truth-table tells us that their disjunction is also true.
So specifying meanings by invoking truth-tables means we don't have to worry about
the complexities of natural languages like English.
Note that the truth-tables are stipulations.
You can't argue that it is wrong to put a T in the first row of this truth-table.
The truth-table is a stipulation about the meanings of the symbol.
The point of a formal language is that it is a thing of our creation.
We are free to make whatever stipulations we like about it.
By contrast, we can't make stipulations about a natural language like English,
because natural languages have lives of their own.
In the case of natural language, meaning has to be discovered, not stipulated.
Finally, what do we say about the meaning of our symbol for negation, ¬?
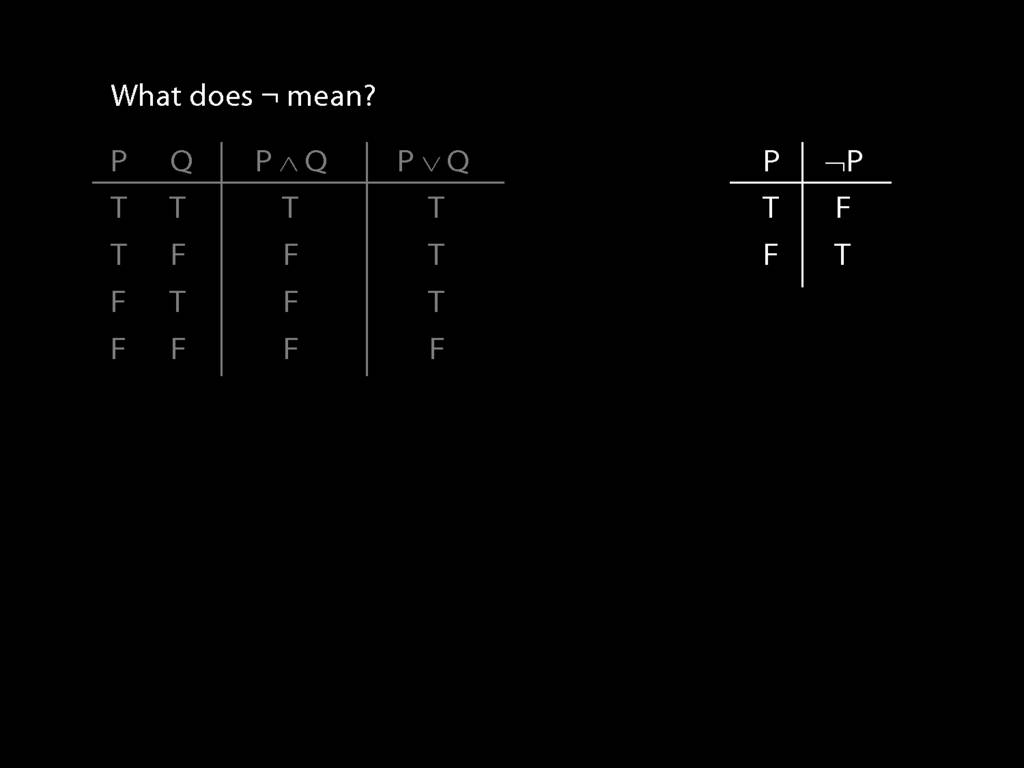
The truth-table specifying its meaning is very simple; it takes true to false and false to true.
3.1, 3.2
3.5, 3.7
3.1, 3.3
3.5, 3.7
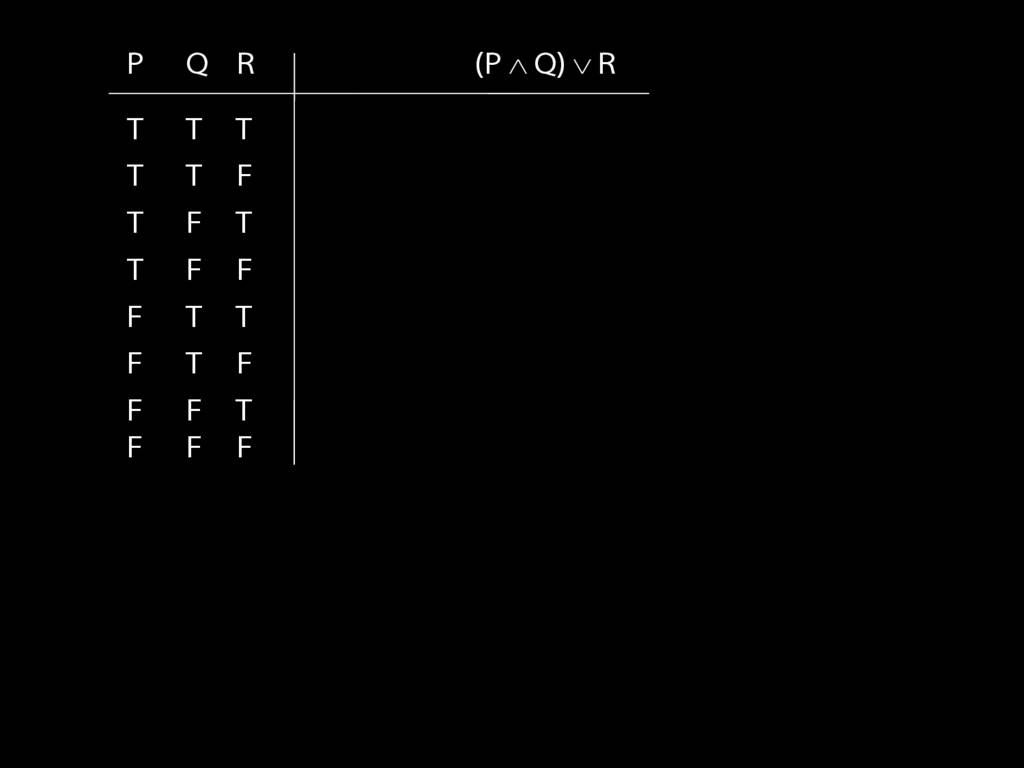
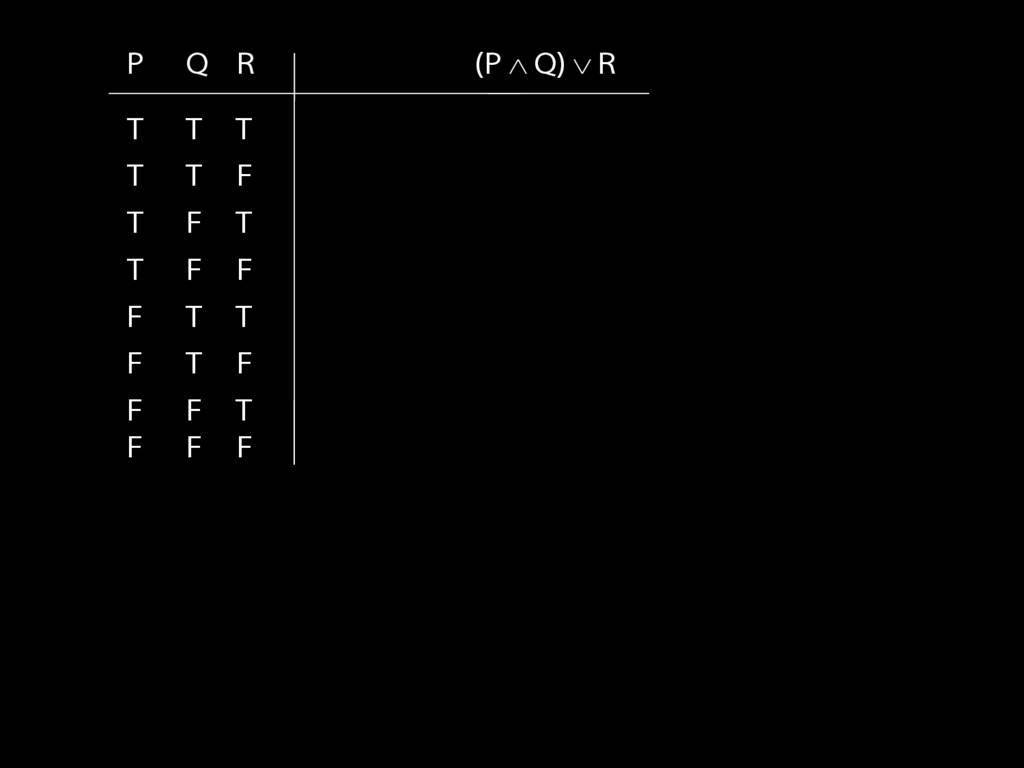
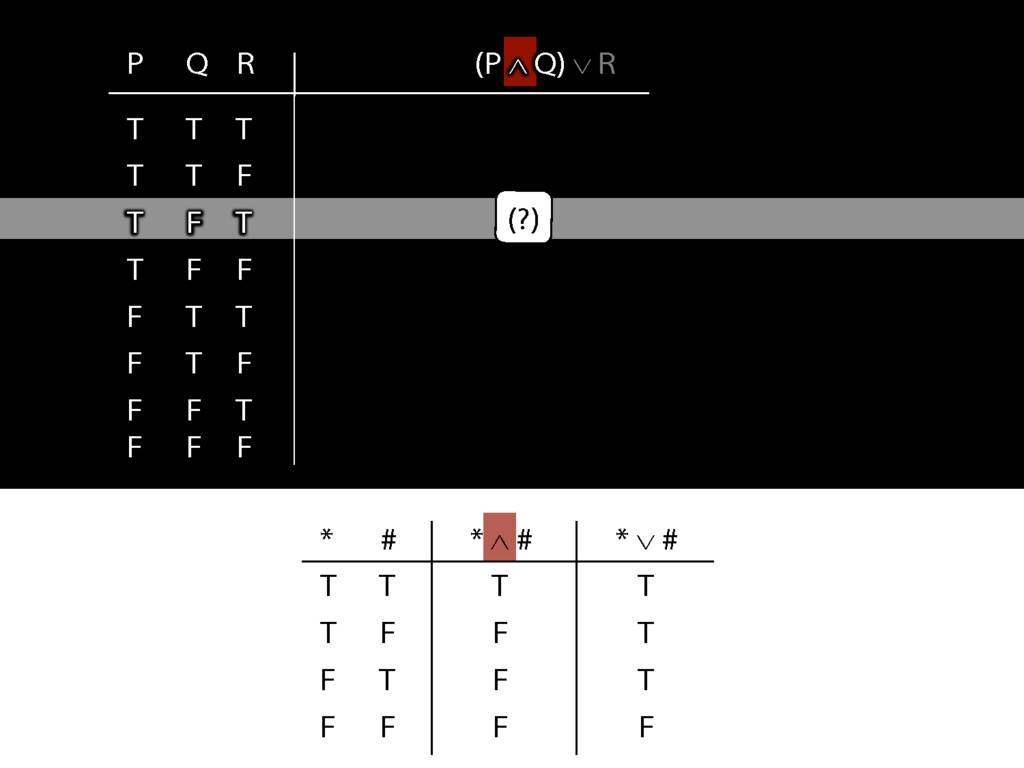
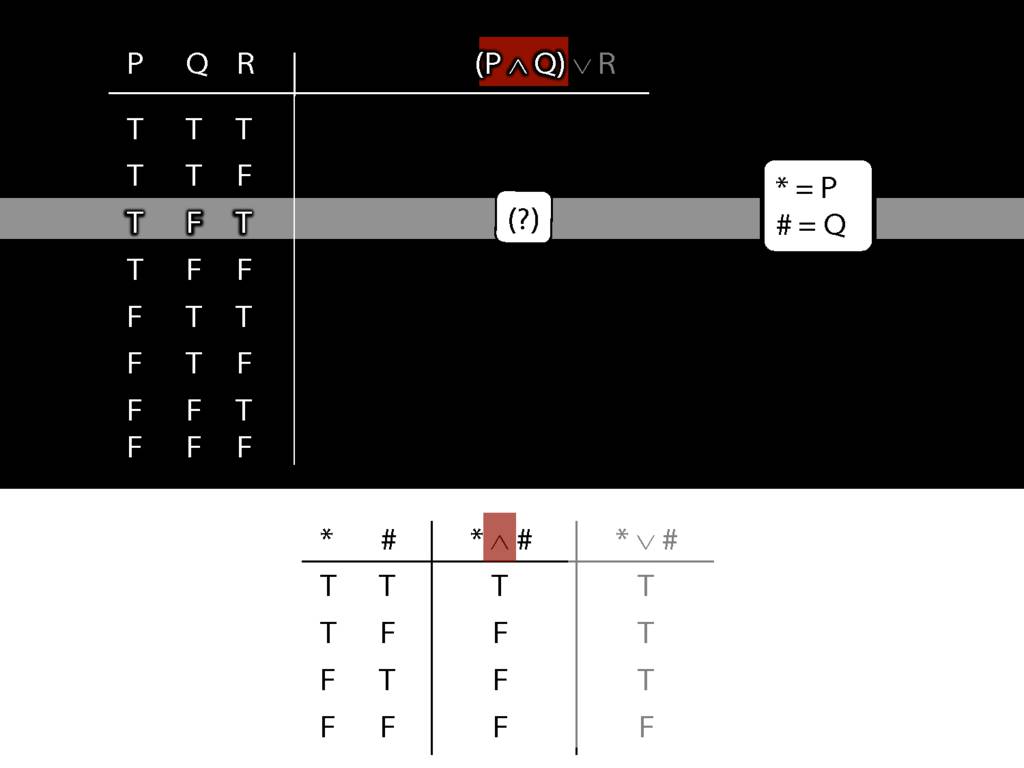
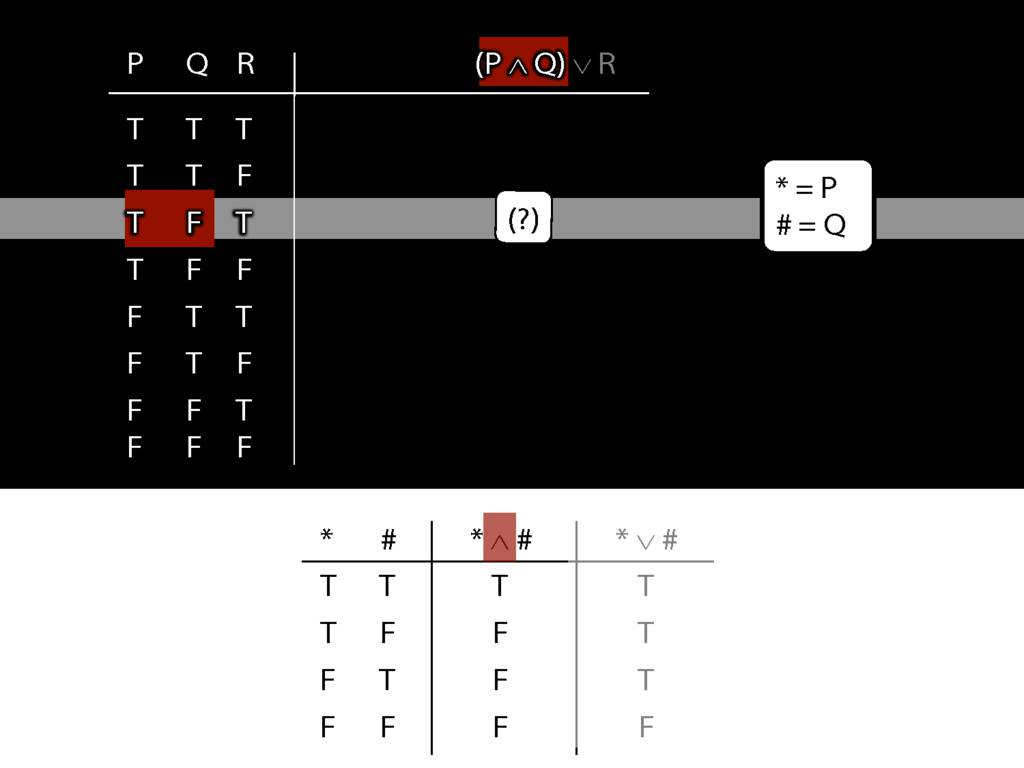
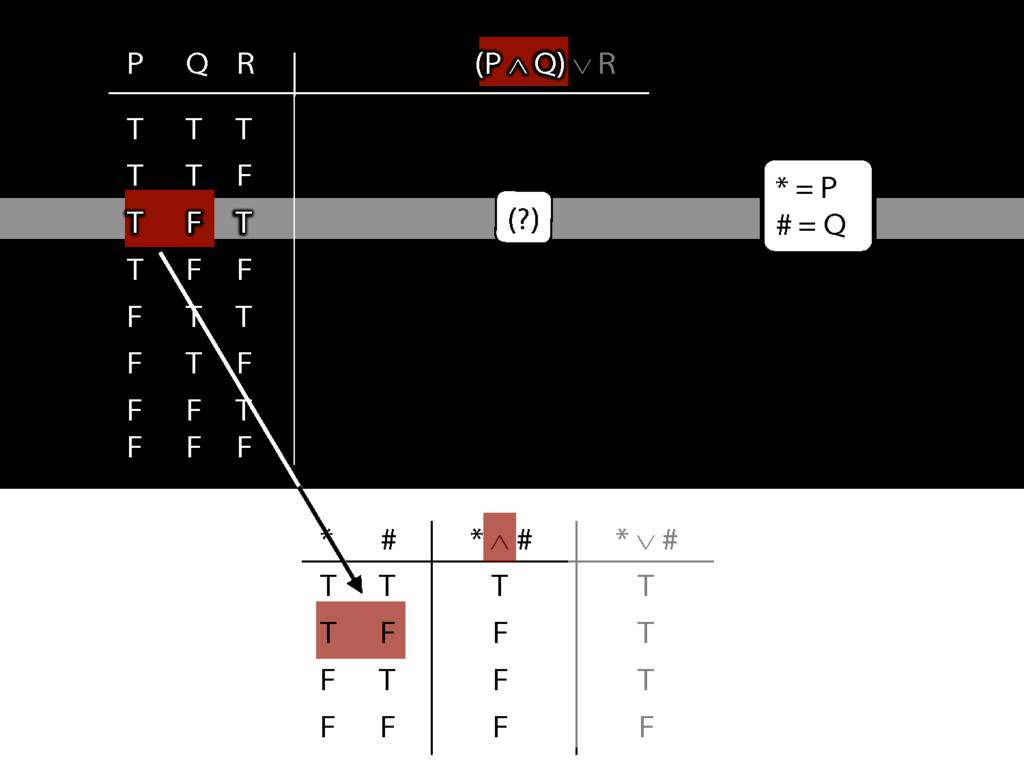
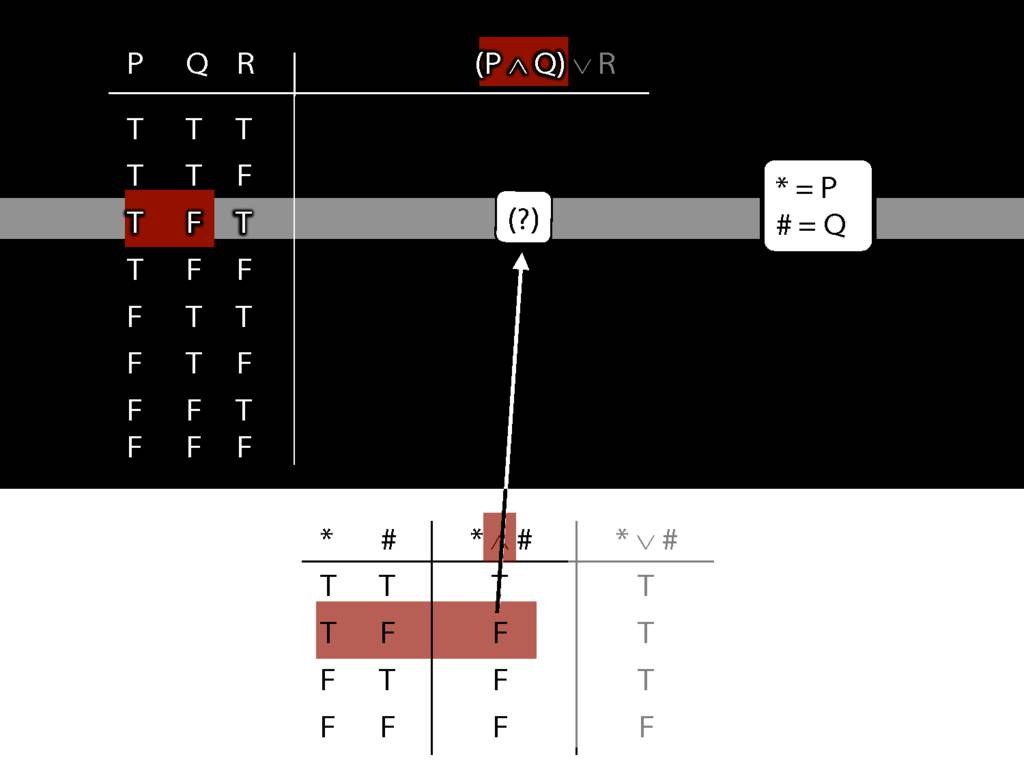
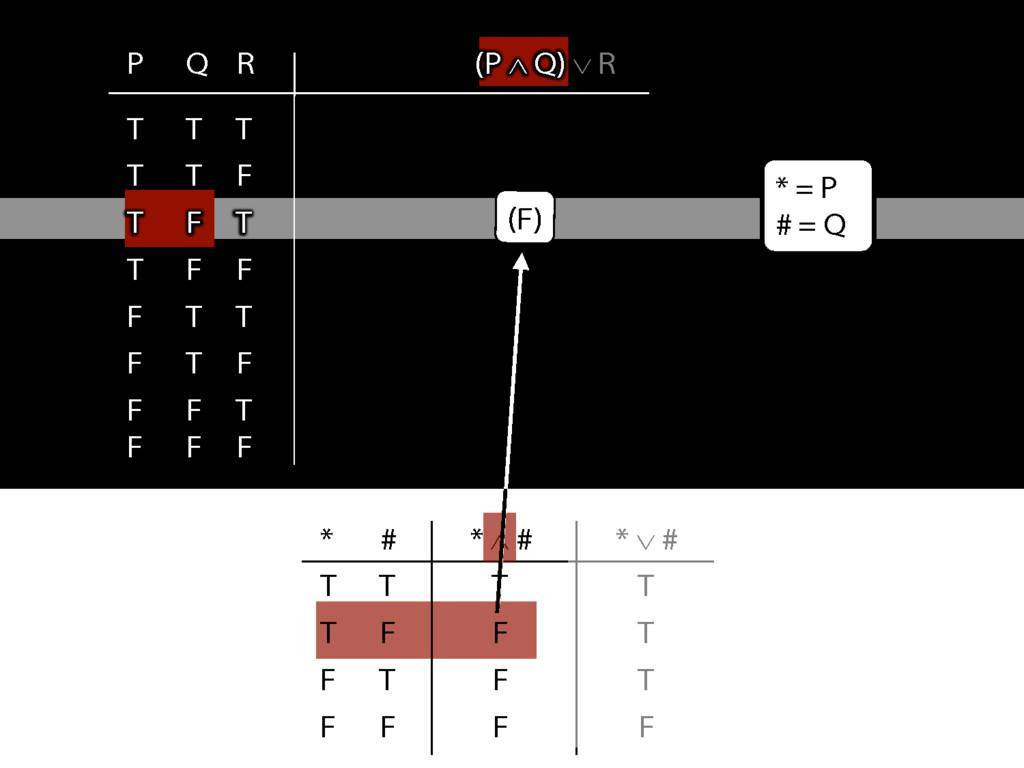
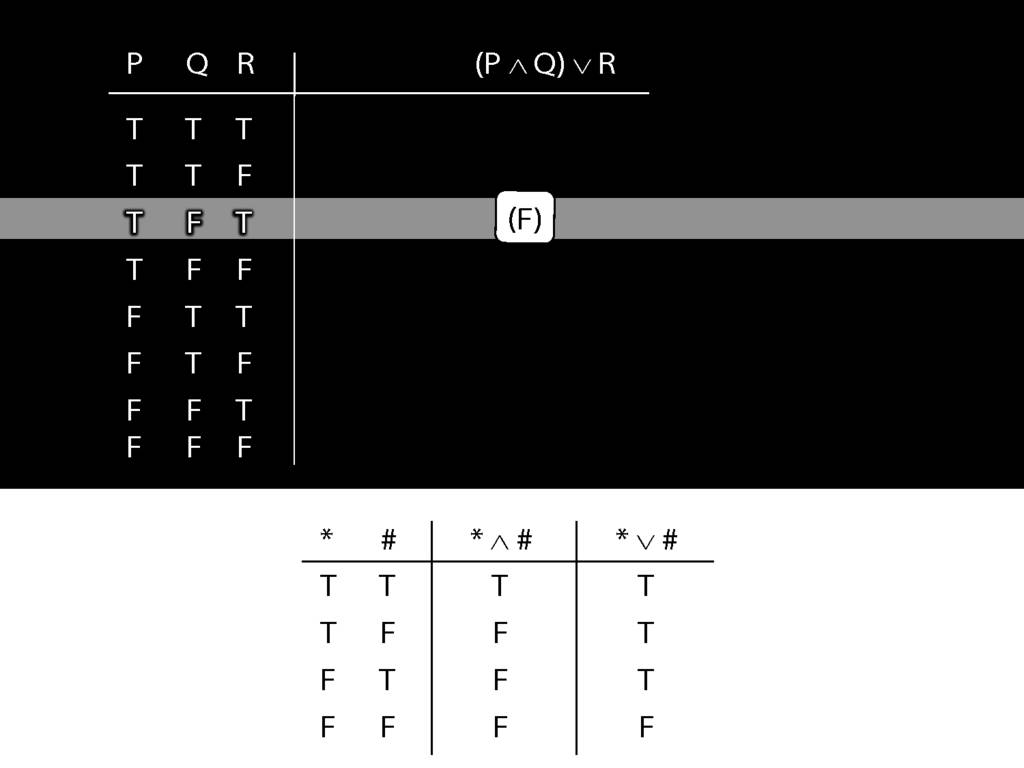
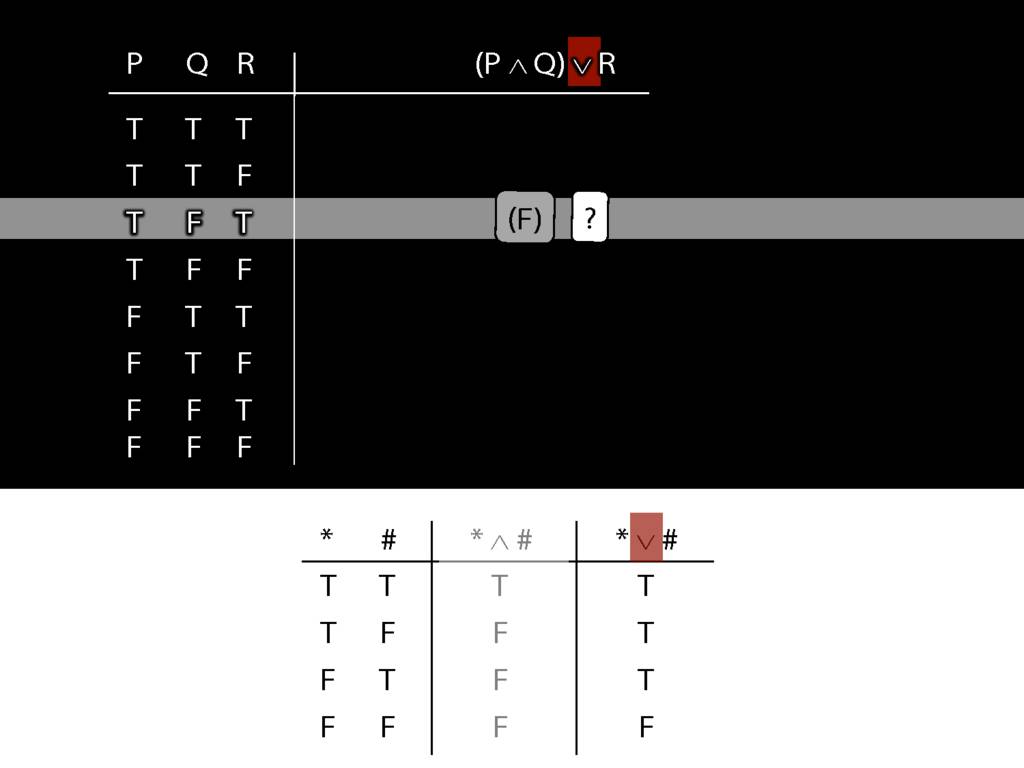
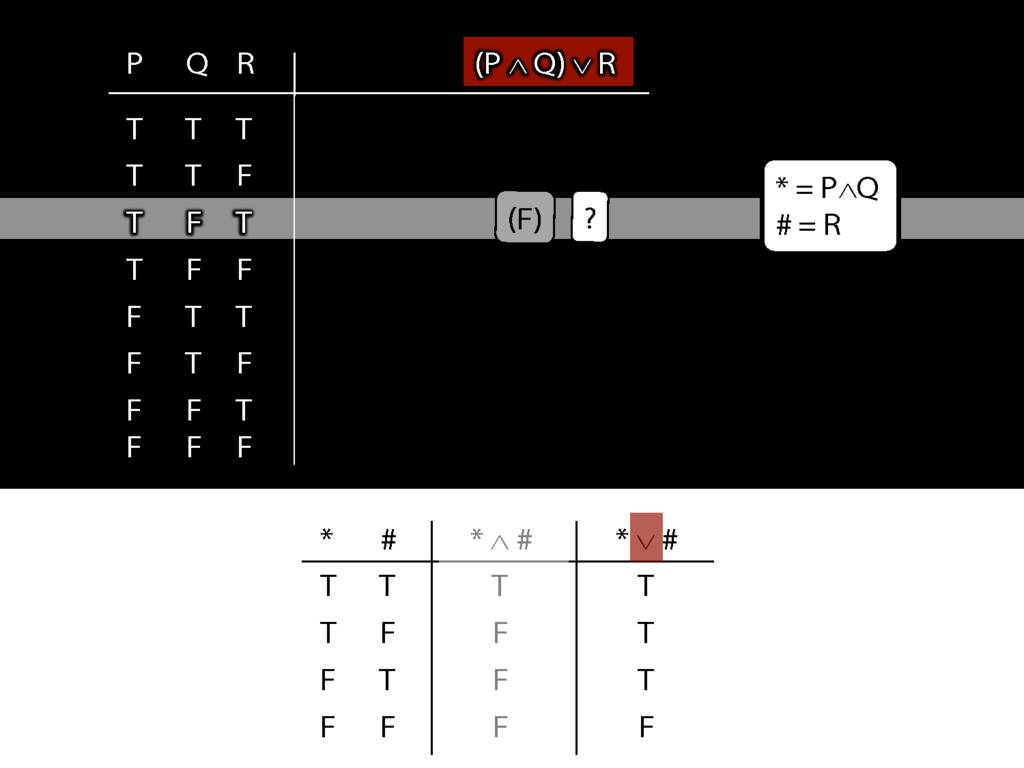
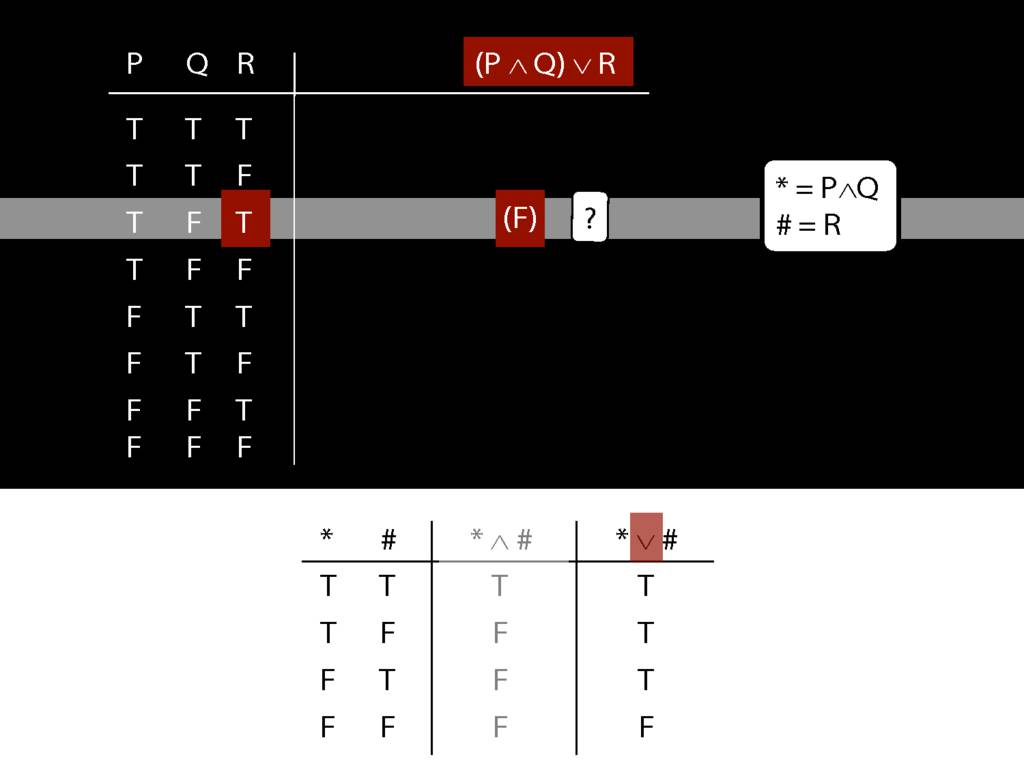
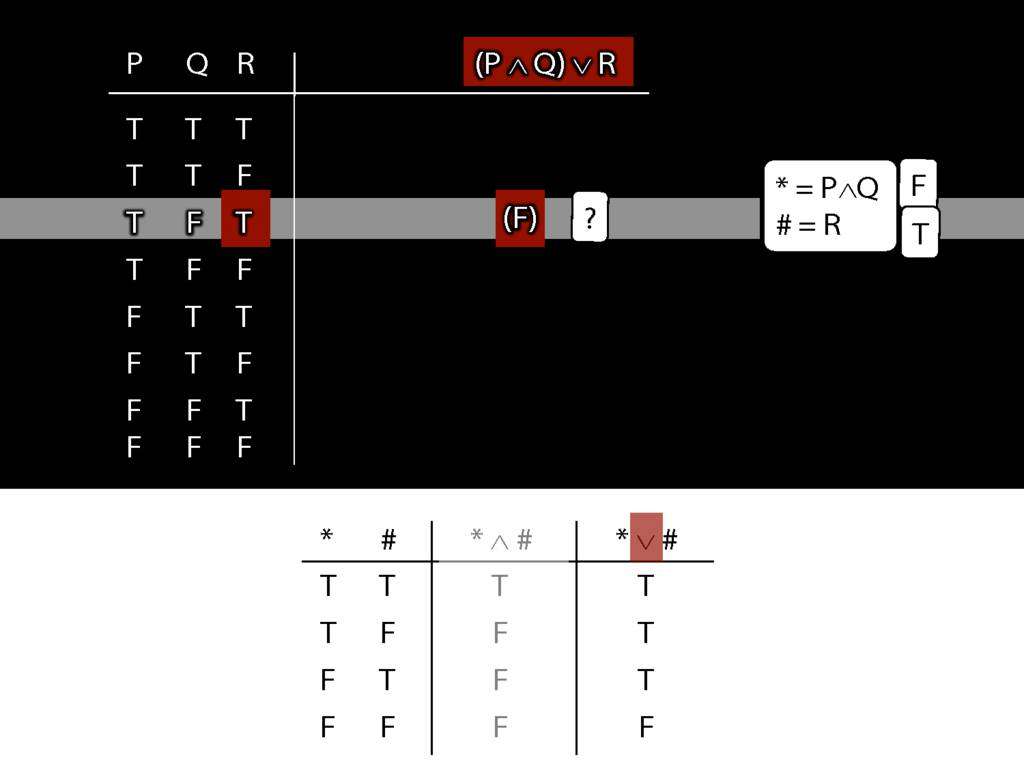
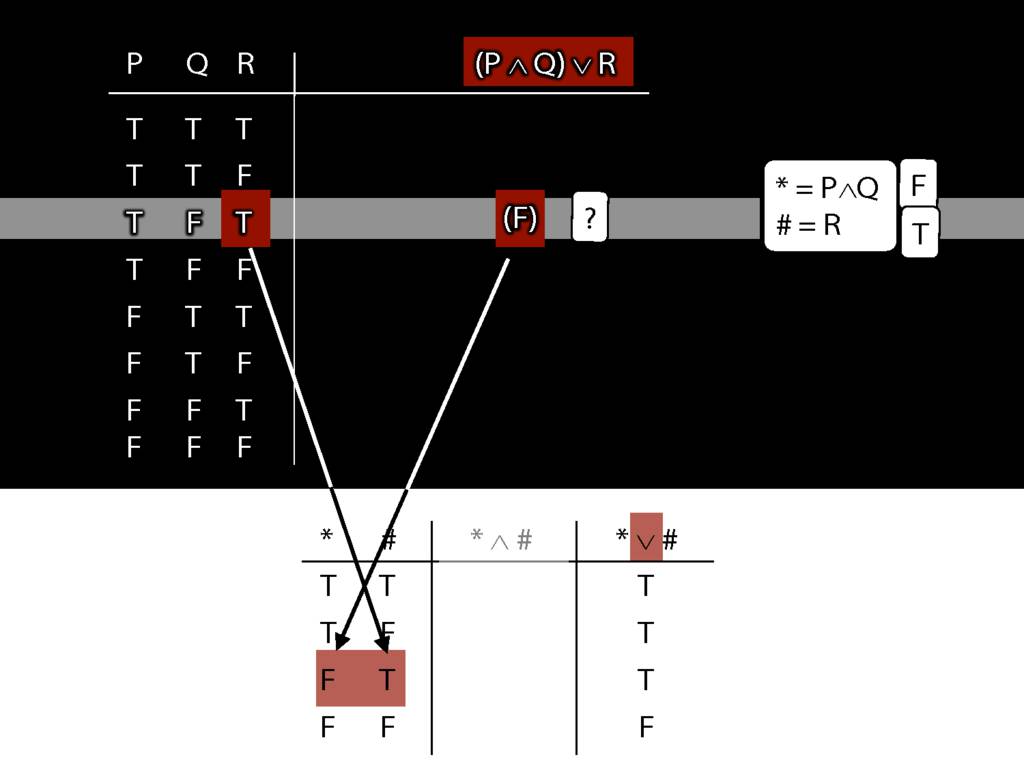
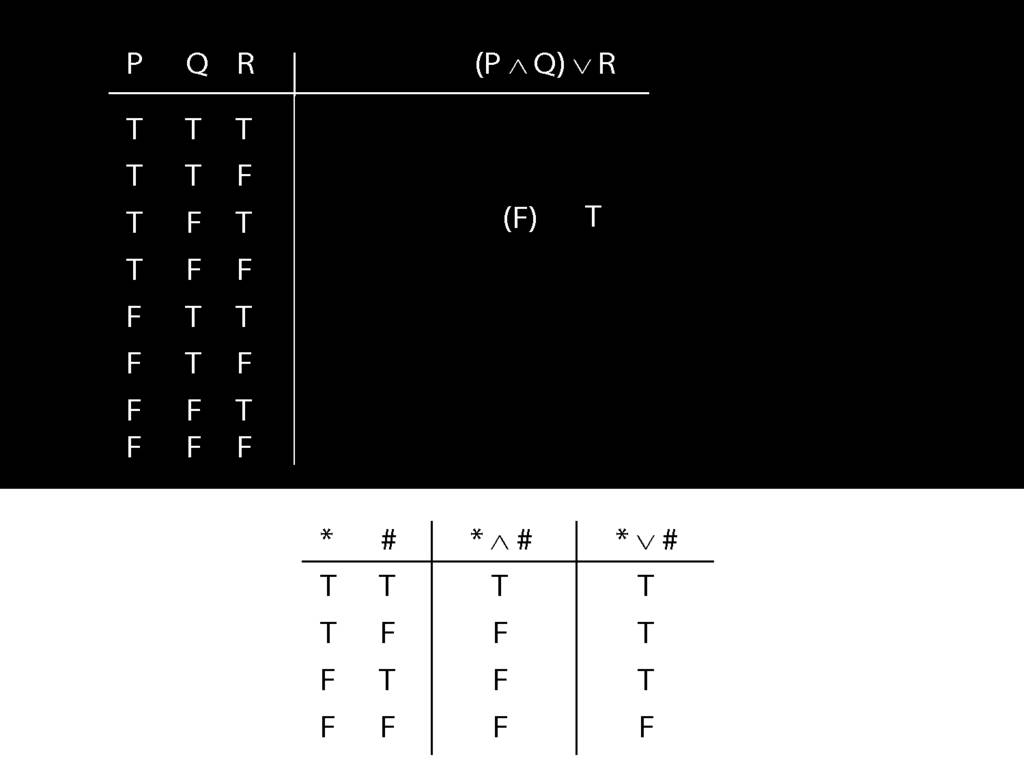
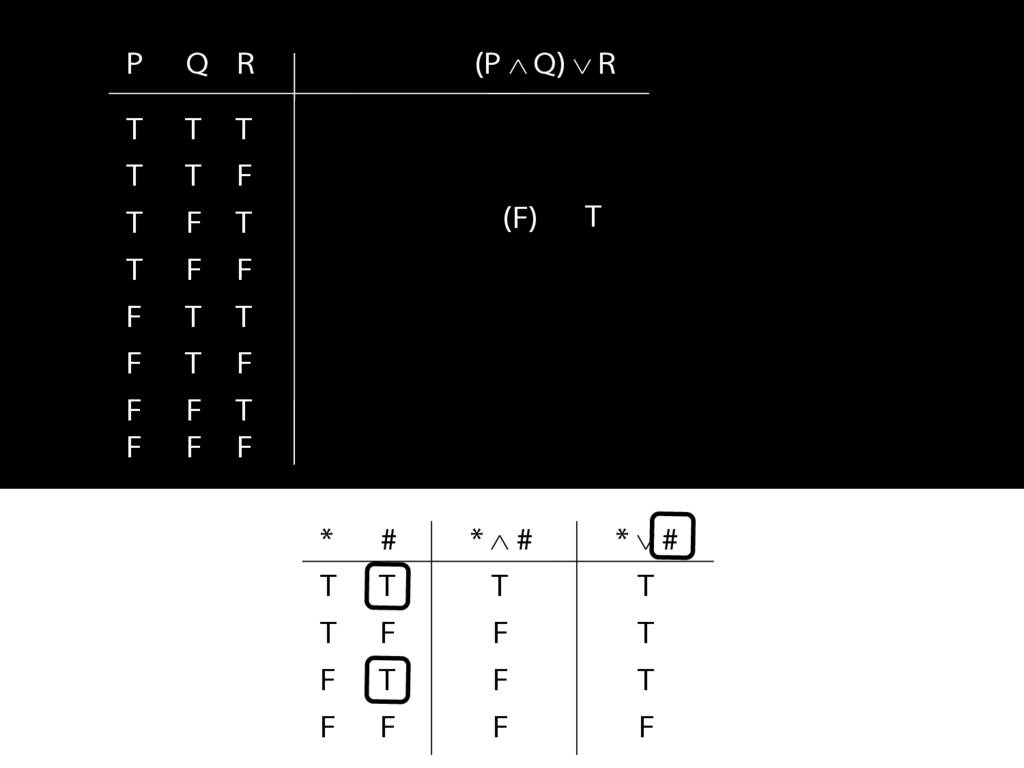
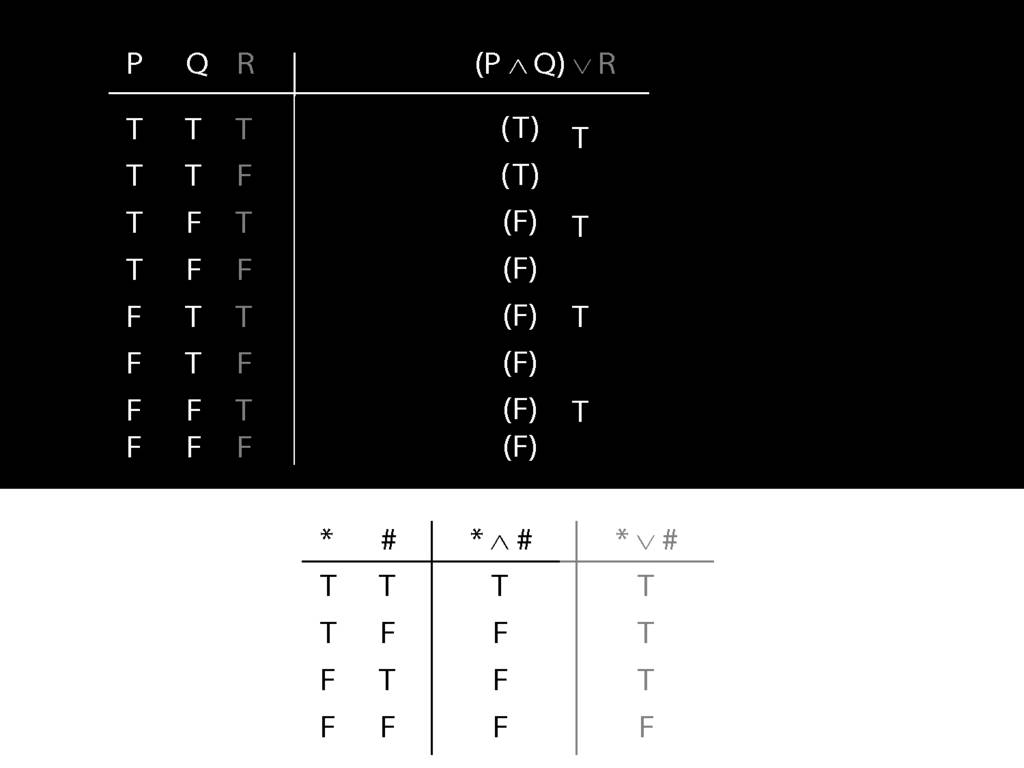
\section{Complex Truth Tables}
\emph{Reading:} §3.3, §3.5

\begin{minipage}{\columnwidth}
Complex truth table example:
\end{minipage}
3.12, 3.13
4.4-4.7
4.12-14
3.14, 3.15

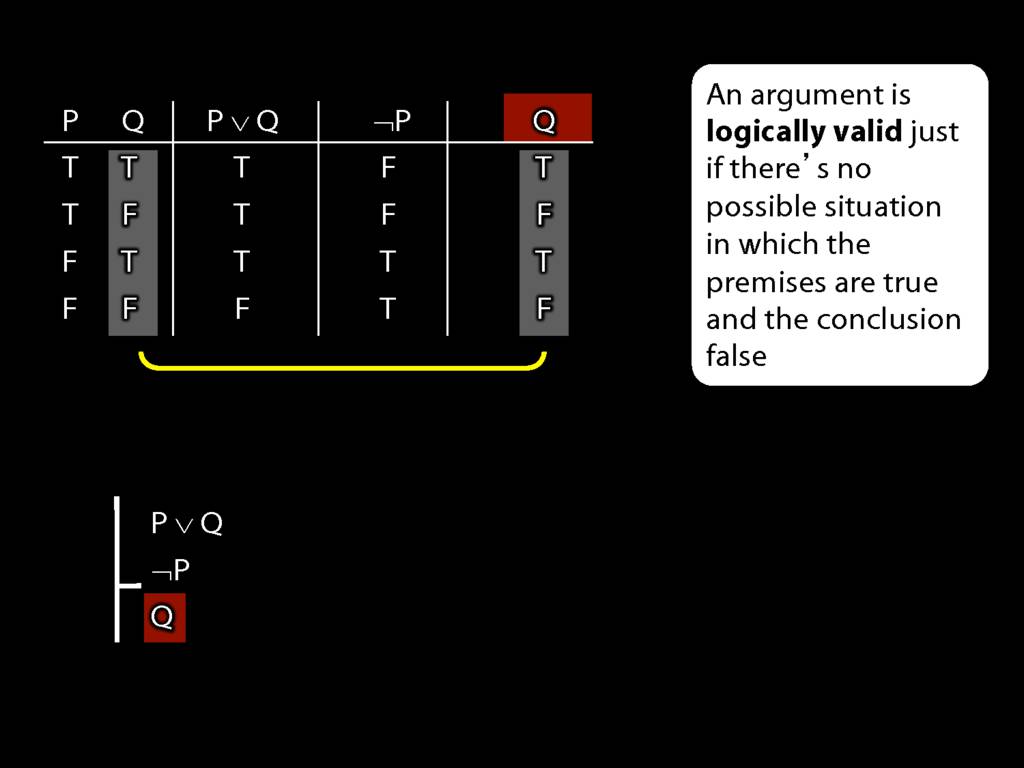
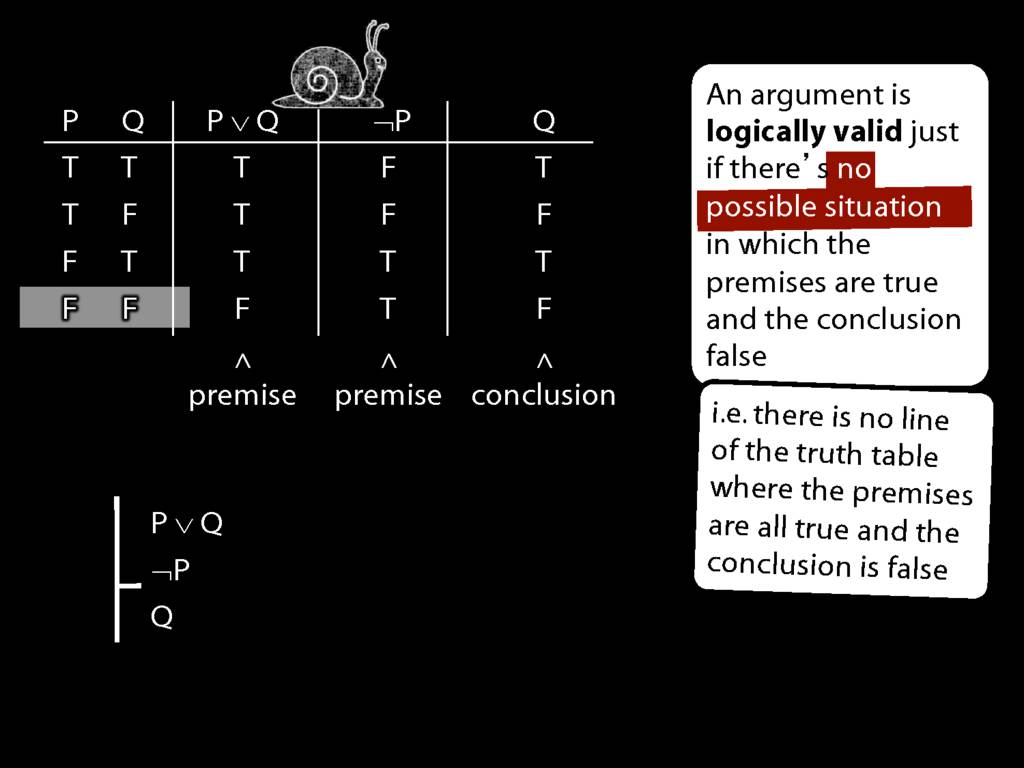
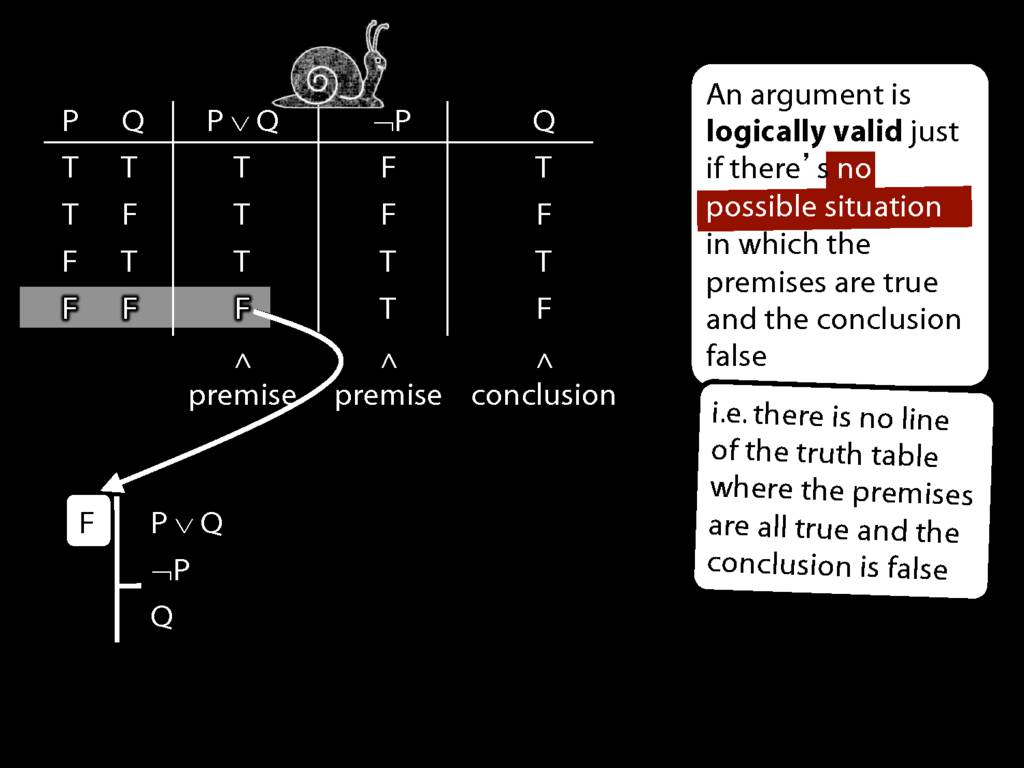
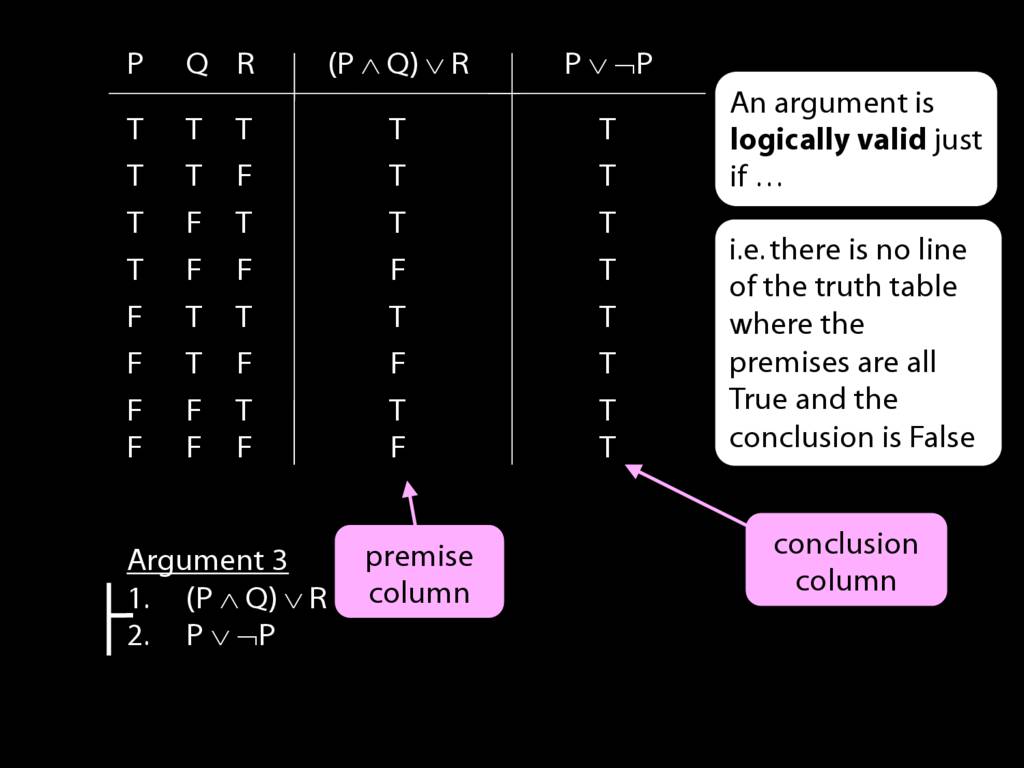
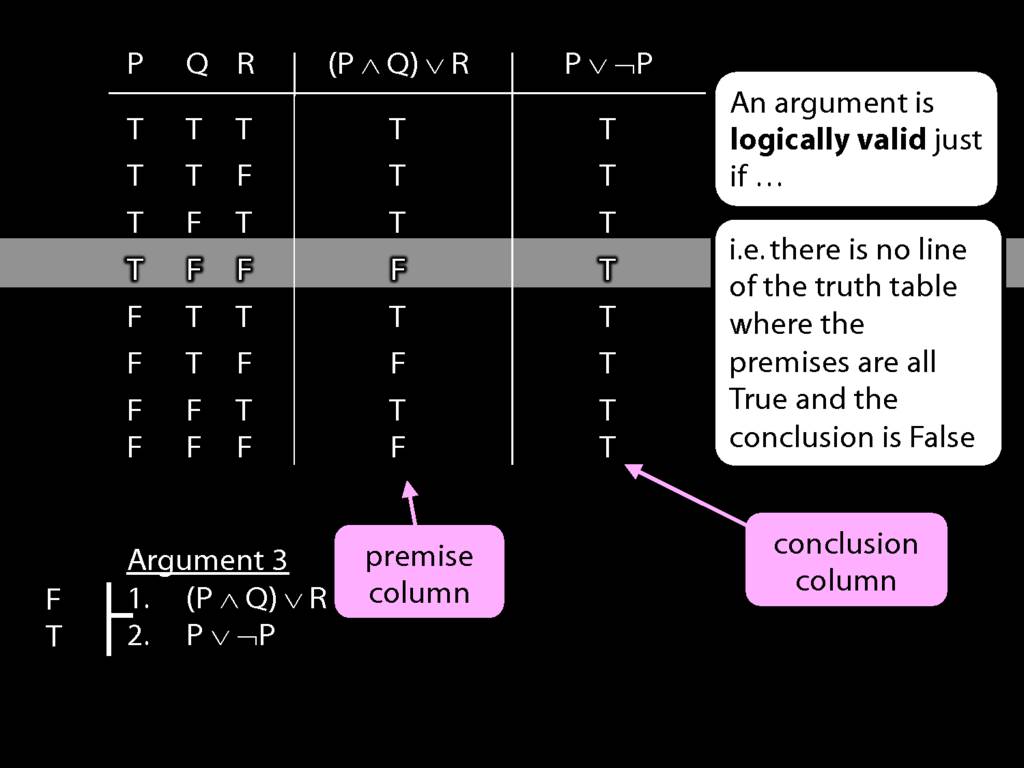
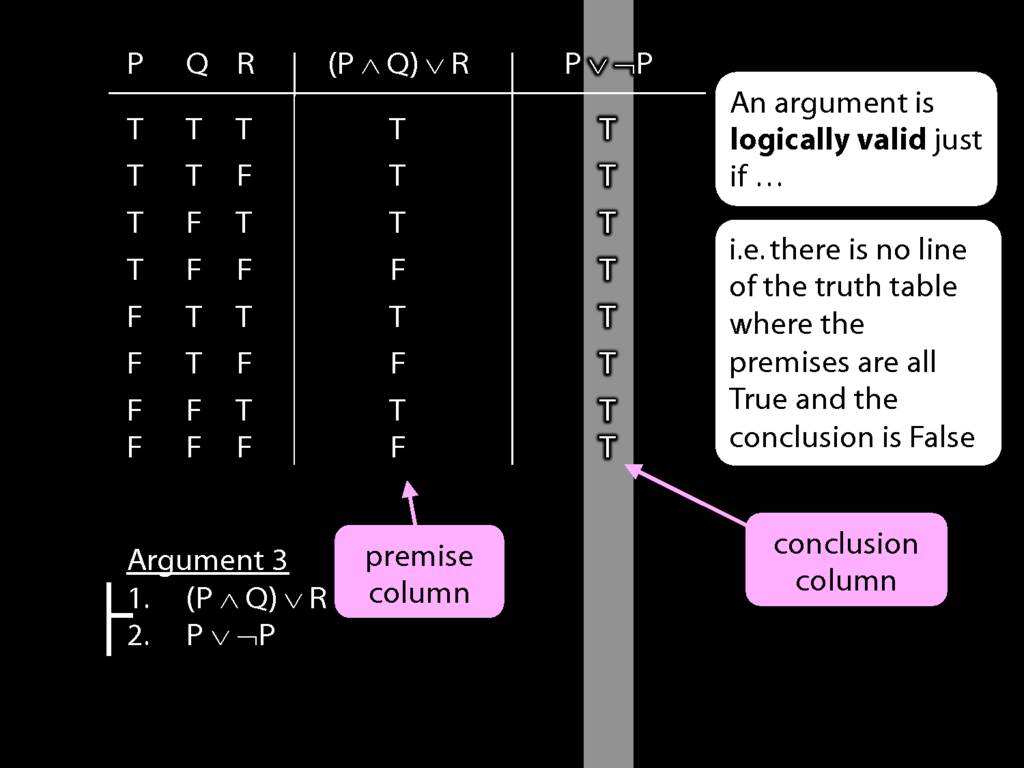
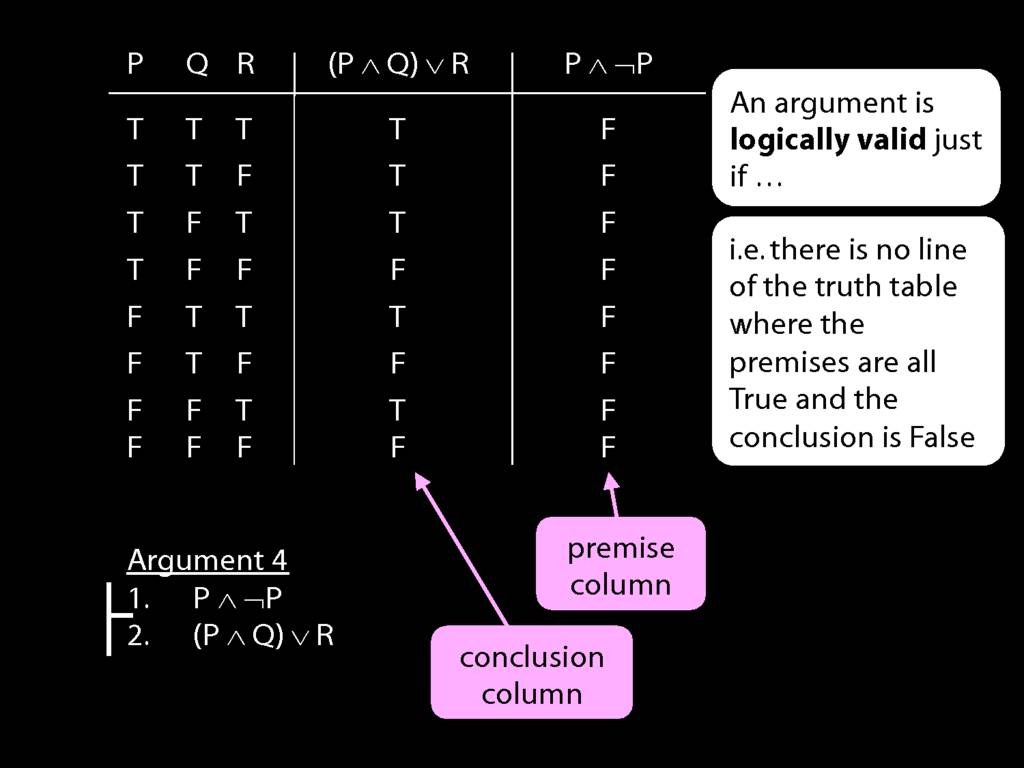
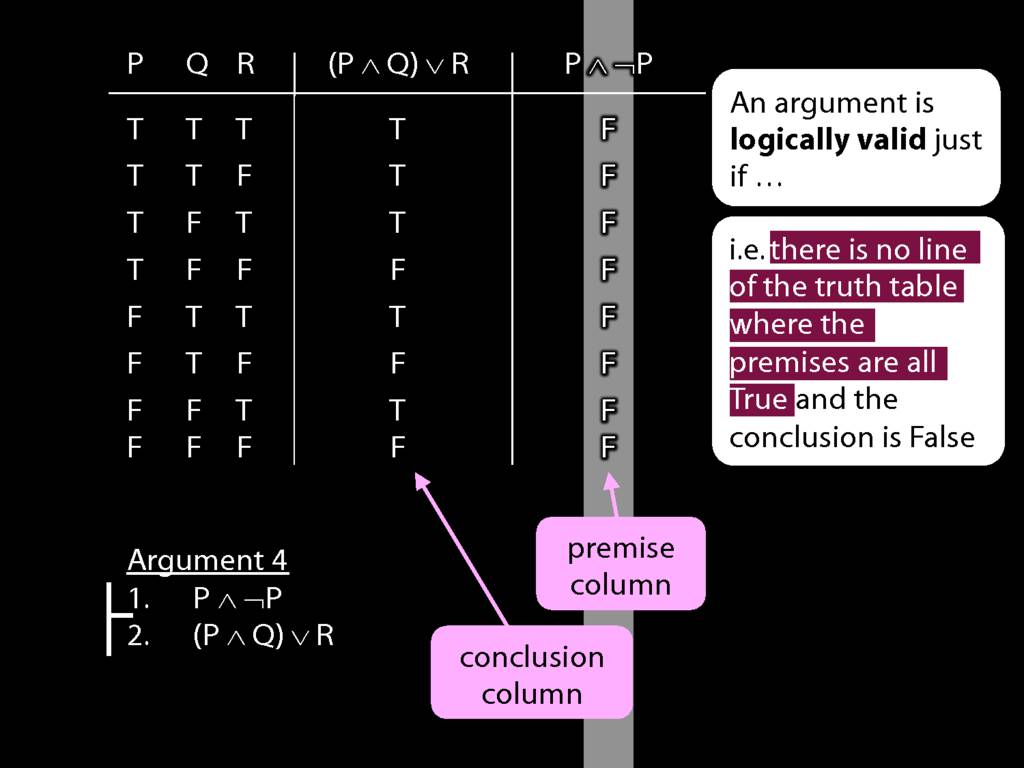
Logical Validity and Truth Tables
\section{Logical Validity and Truth Tables}
\emph{Reading:} §4.3
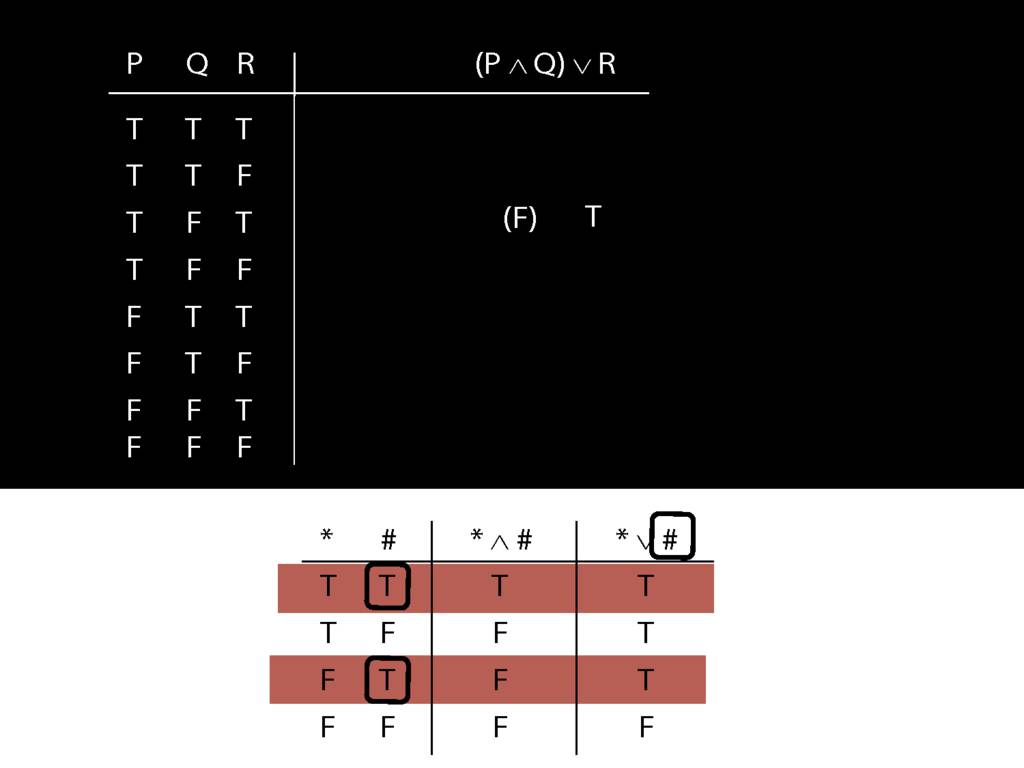
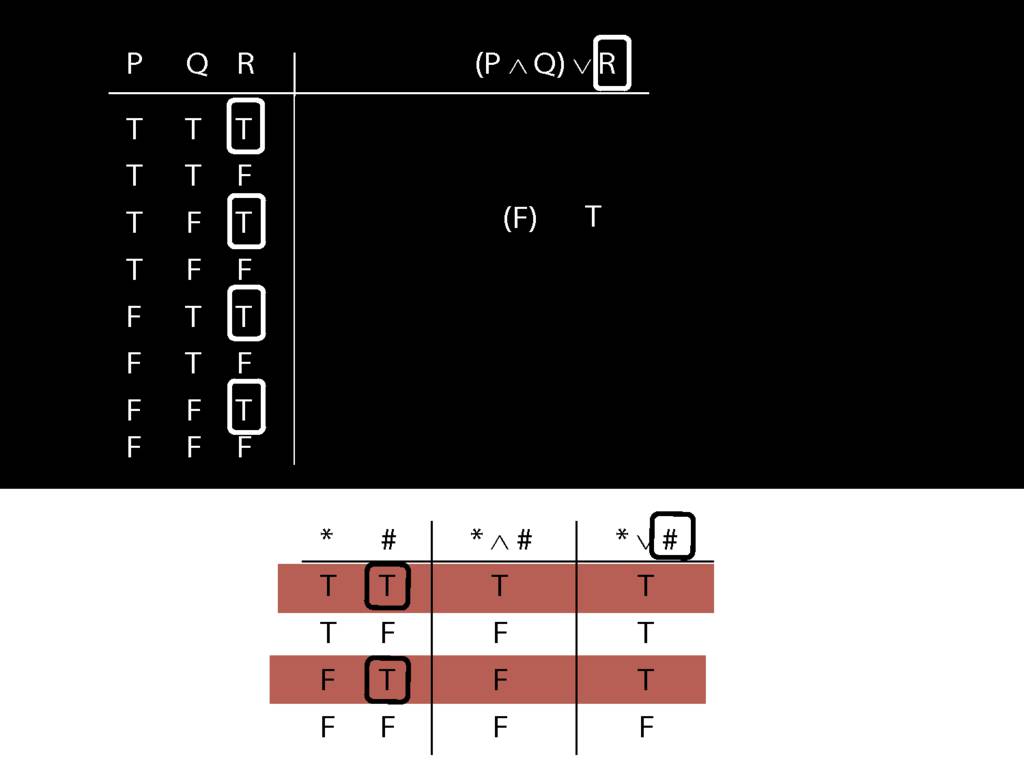
We can use truth tables to establish that
some arguments are logically valid
\begin{minipage}{\columnwidth}
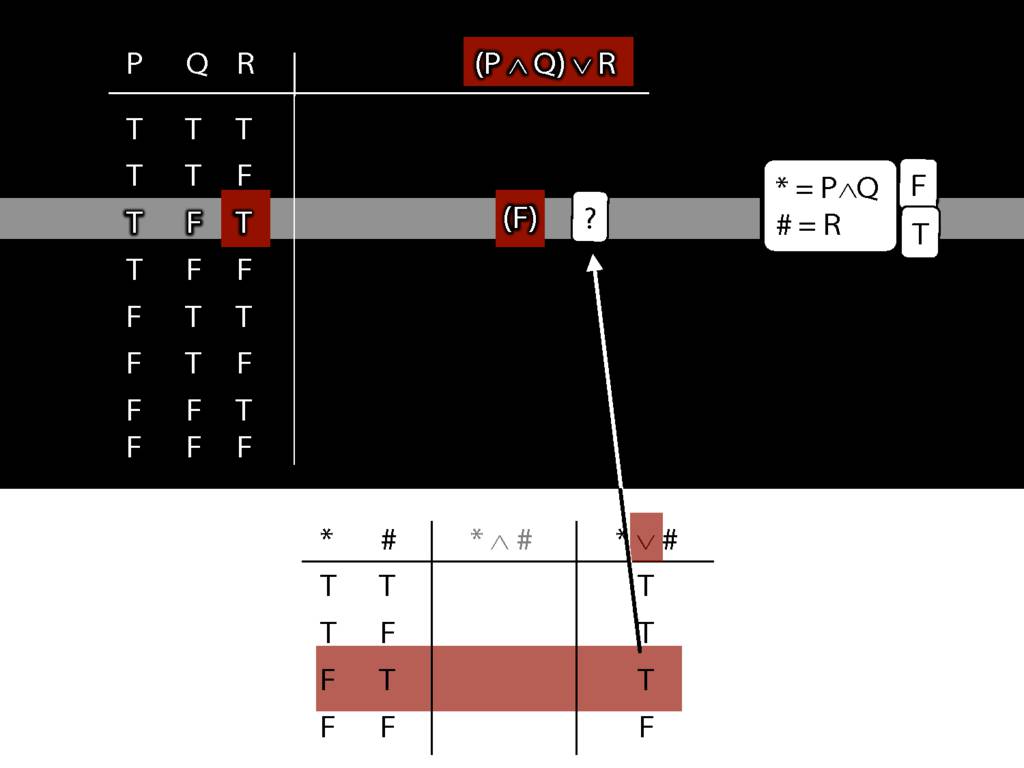
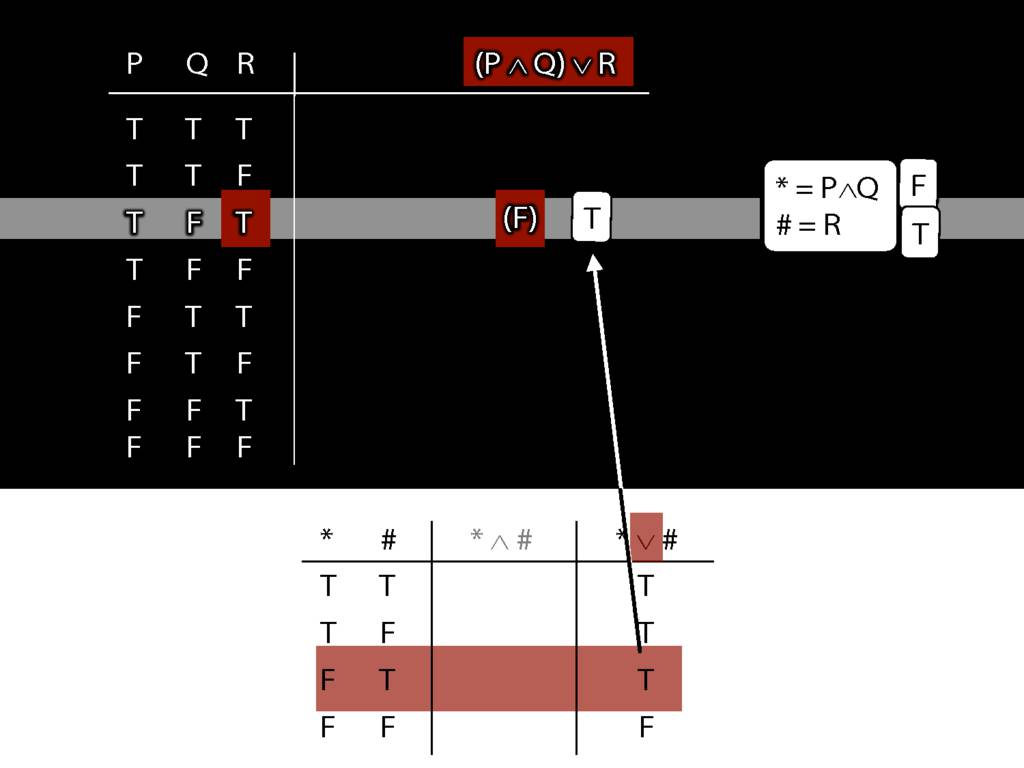
Truth tables can be used to show that an argument is valid. To illustrate ...
\end{minipage}
\begin{minipage}{\columnwidth}
To establish that an argument is valid:
\begin{enumerate}
\item Create truth tables for each premise and the conclusion.
\item Check whether there is a row of the truth table where all premises are true and the conclusion is false.
\item If not, the argument is valid.
\end{enumerate}
\end{minipage}

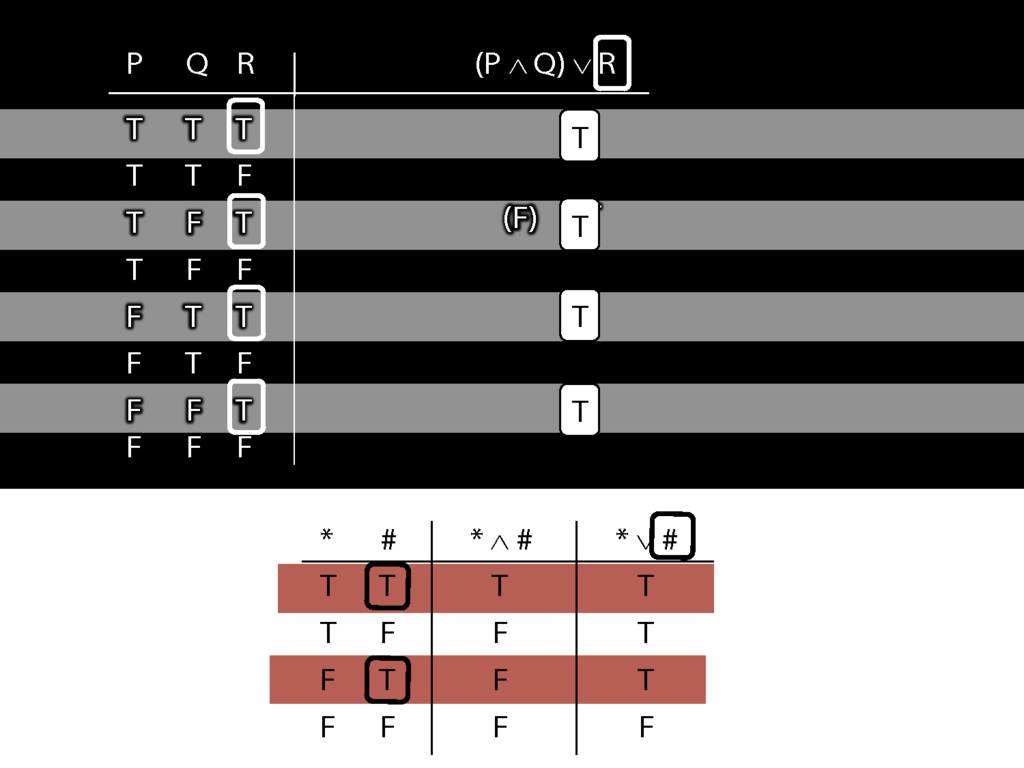
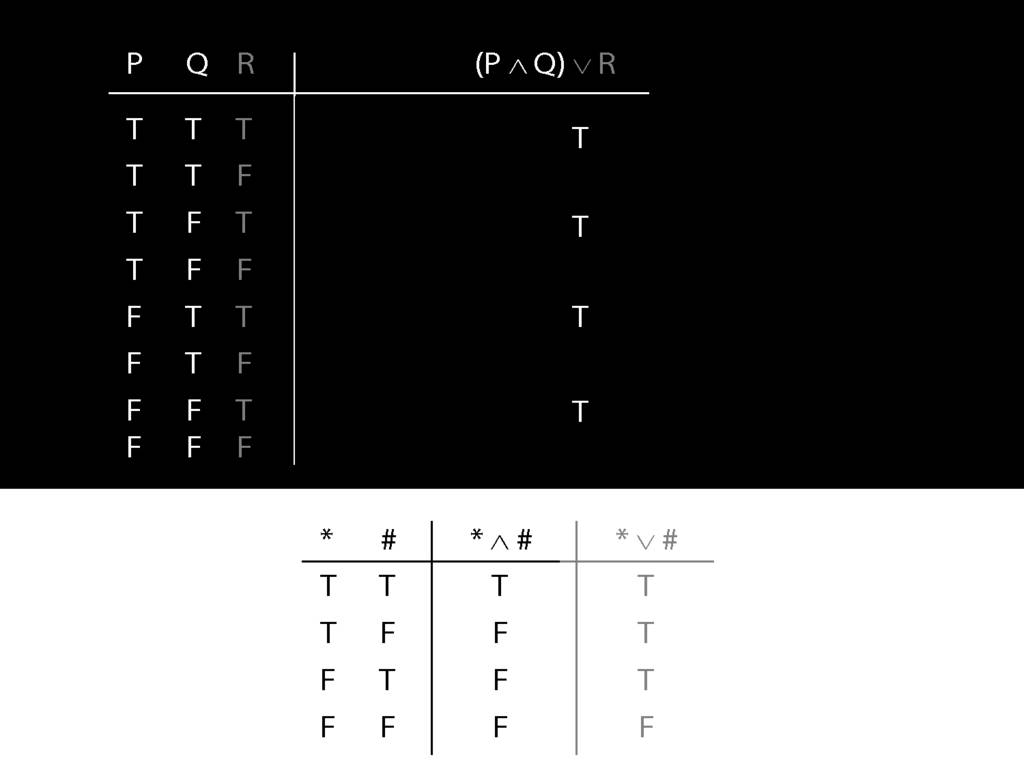
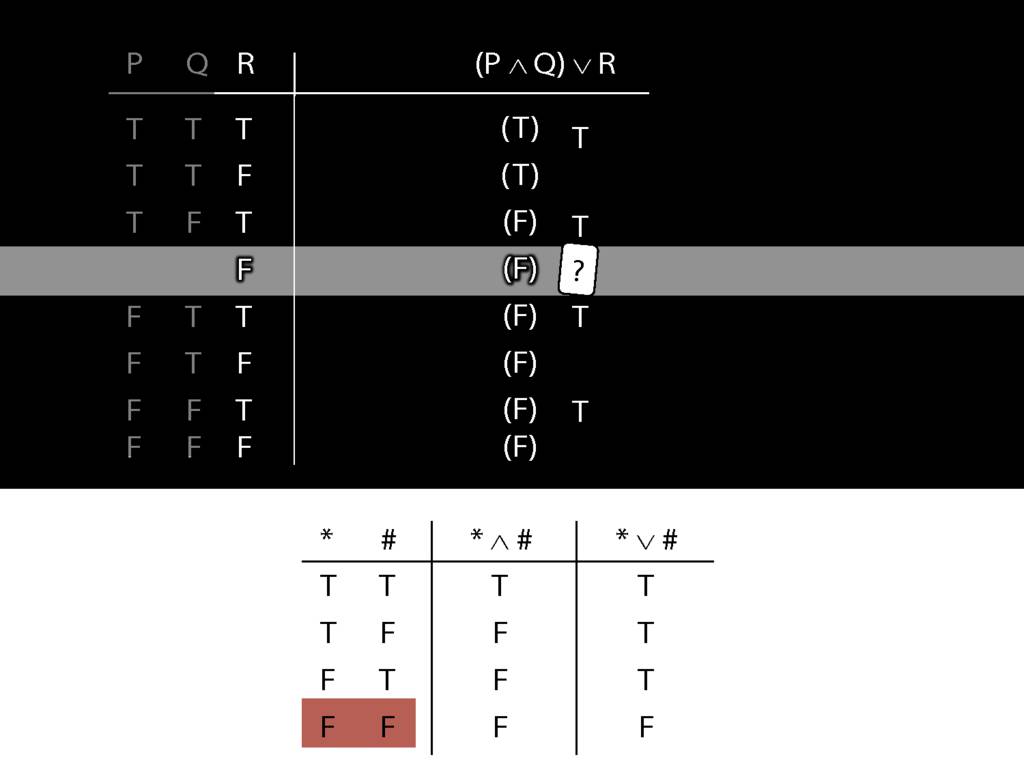
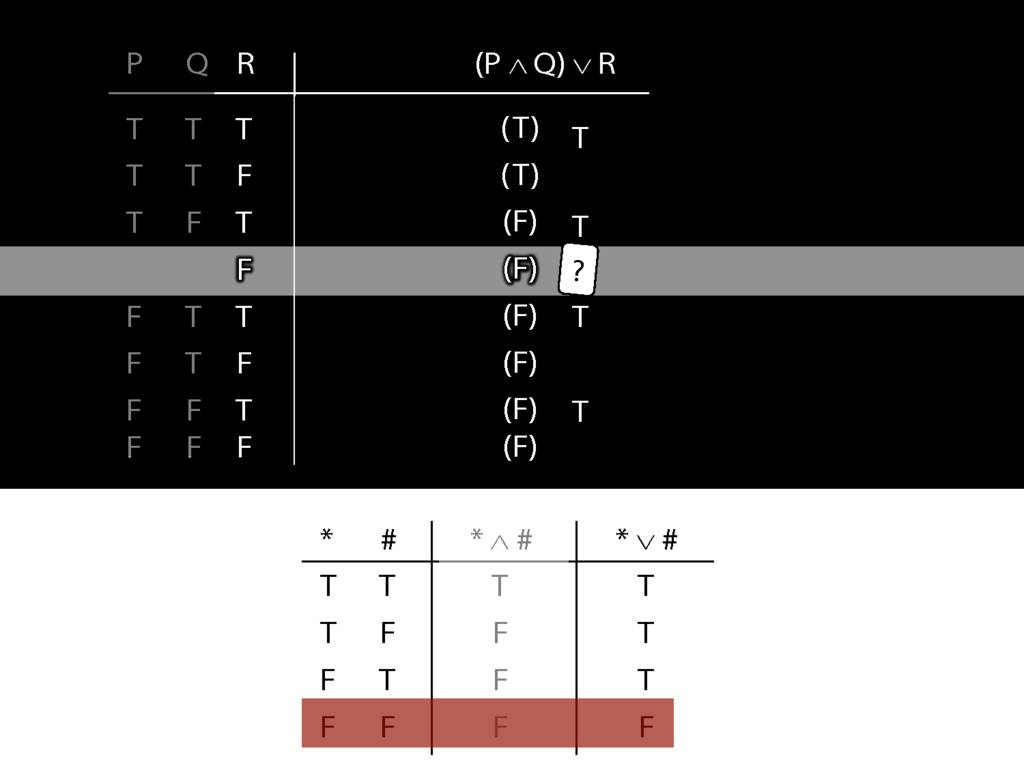
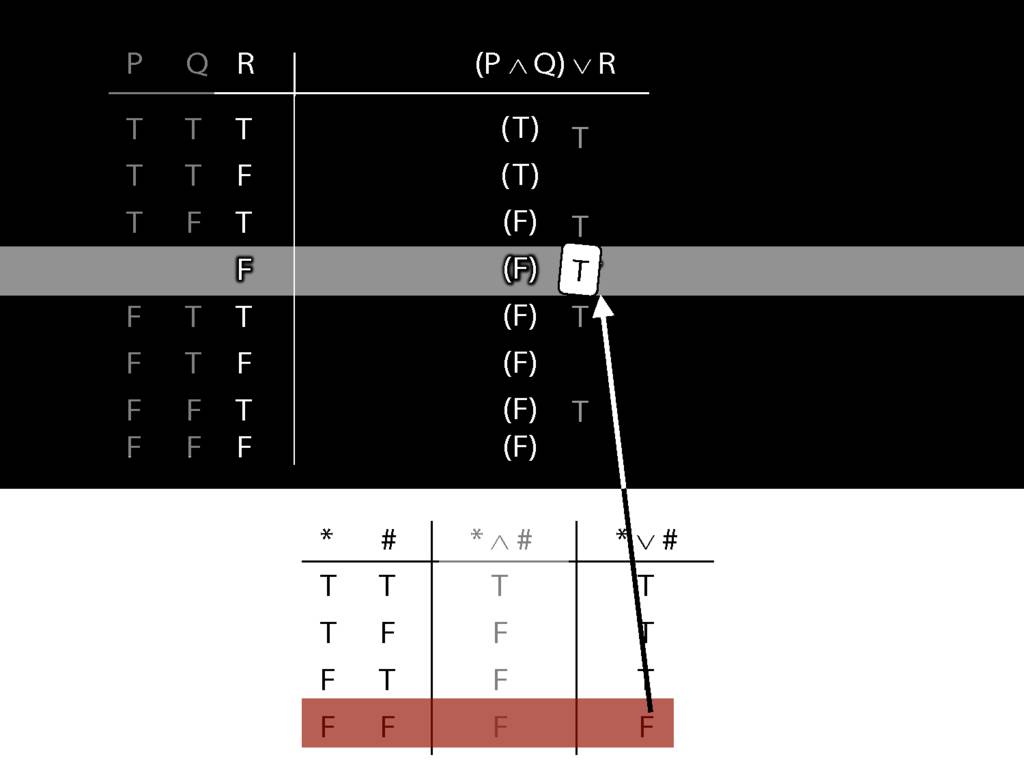
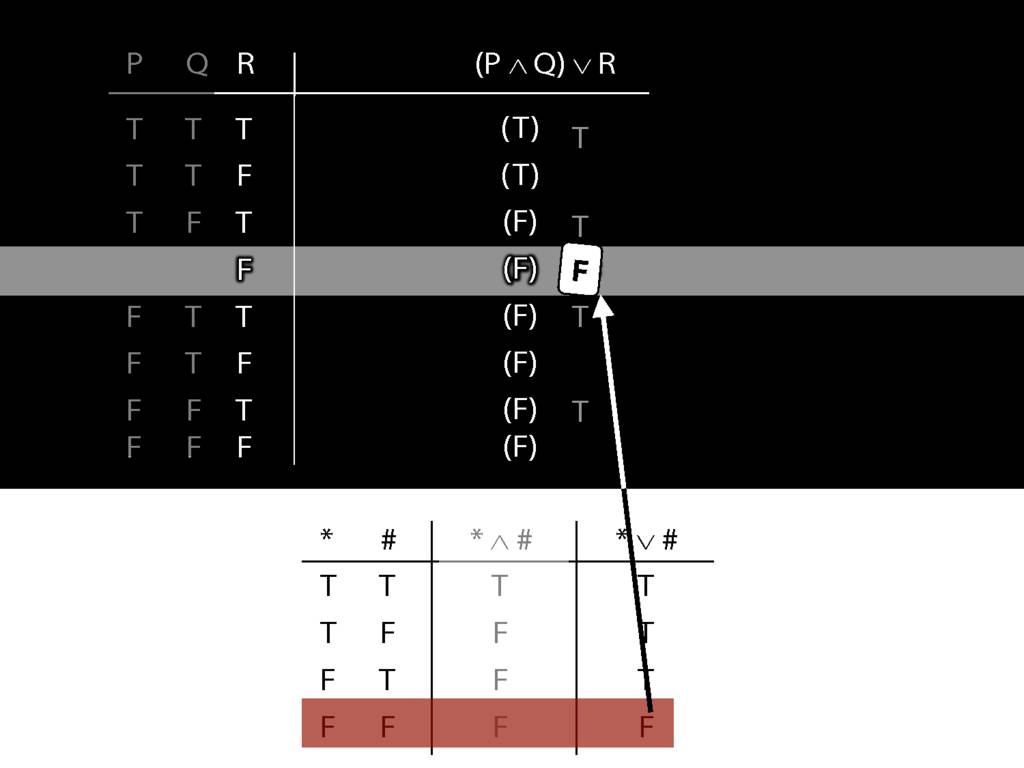
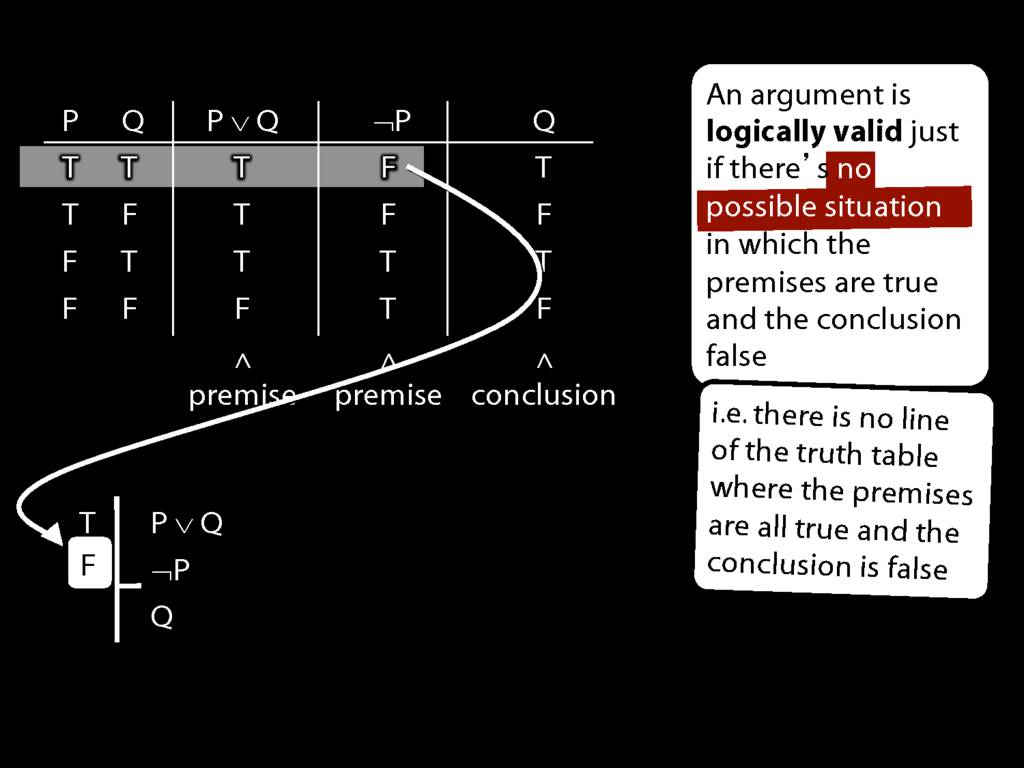
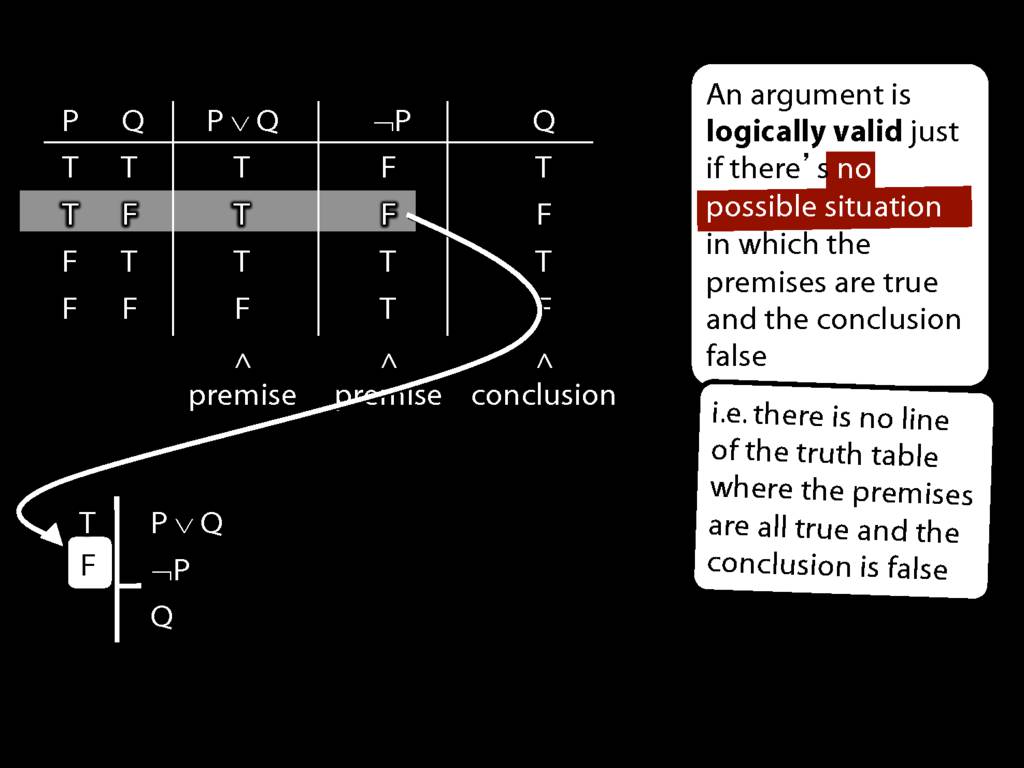
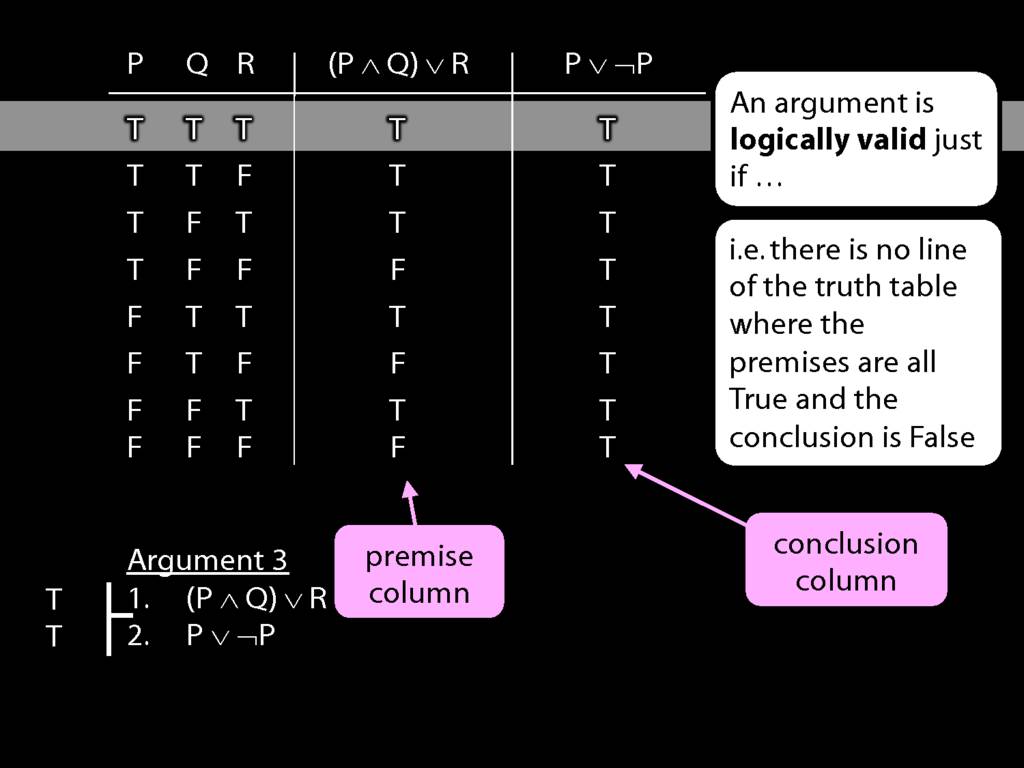
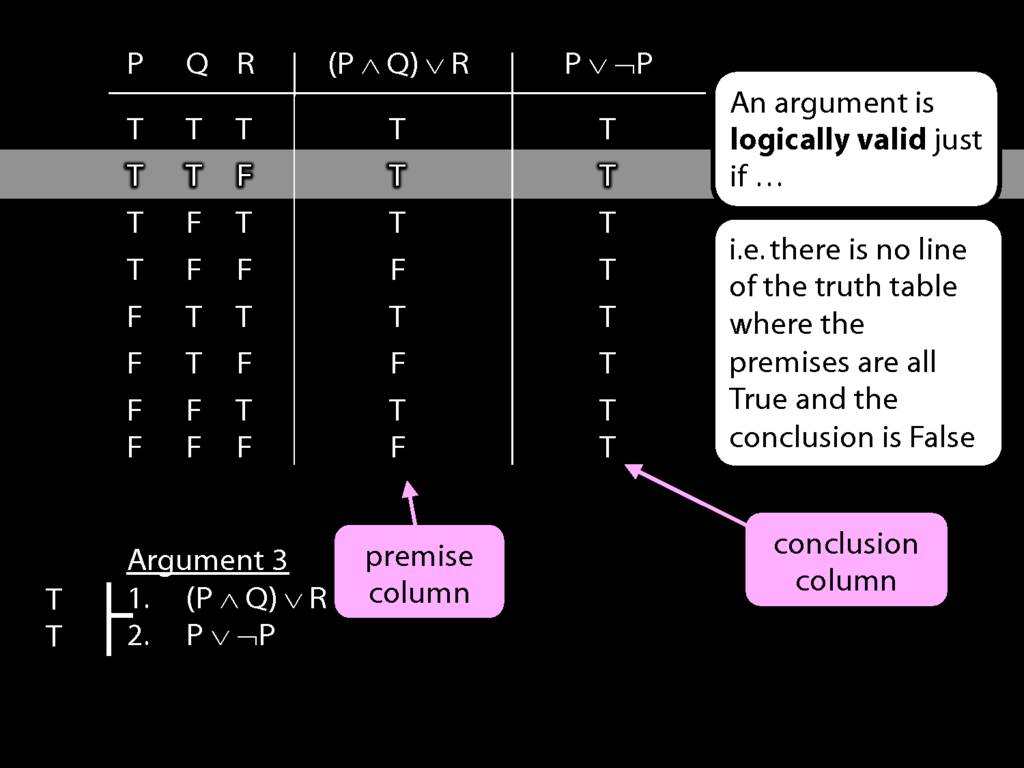
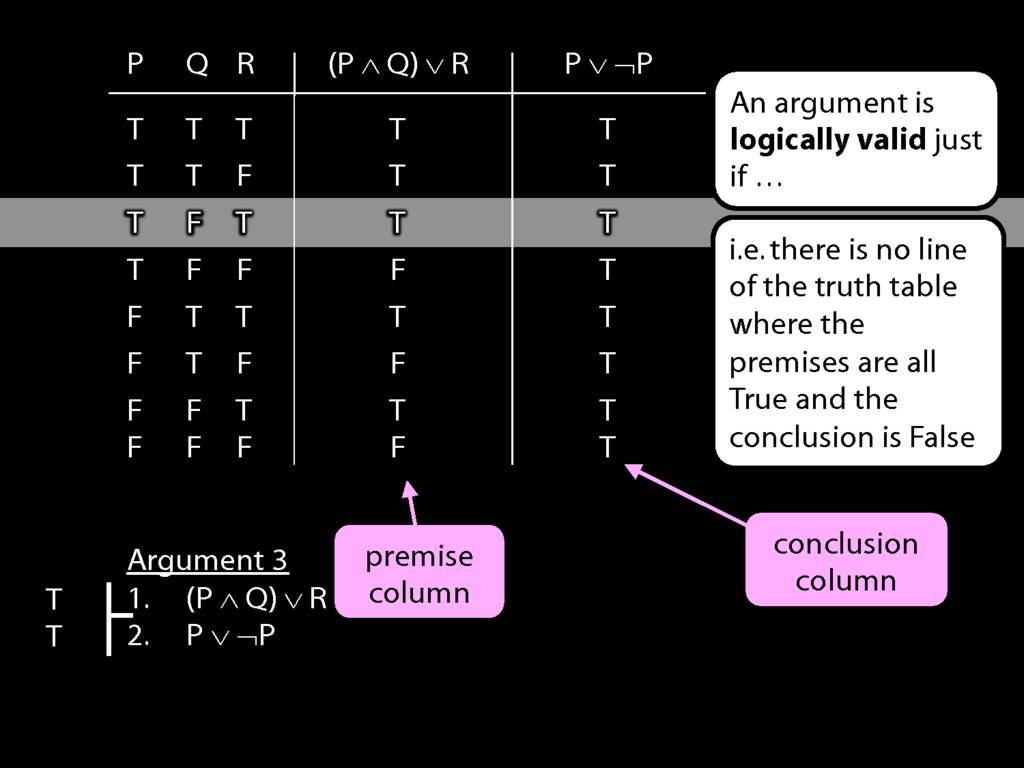
Don’t need to go further, already have a false premise. So this won’t be a situation in which the premises are true and the conclusion false.

This situation is different from the other two: the premises are true in this possible situation, so we had to think about whether the conclusion is true.
But, as you can see, the conclusion is also true. So this is no counterexample.

So if someone asked you to show that this argument is valid using truth tables, what would you do?
First, create truth tables for each premise and for the conclusion.
Next, check whether there is any row where the premises are true and the conclusion false.
If not, you can write this:
By inspecting the truth table, there is no row where the premises are true and the conclusion false; therefore, the argument is logically valid.

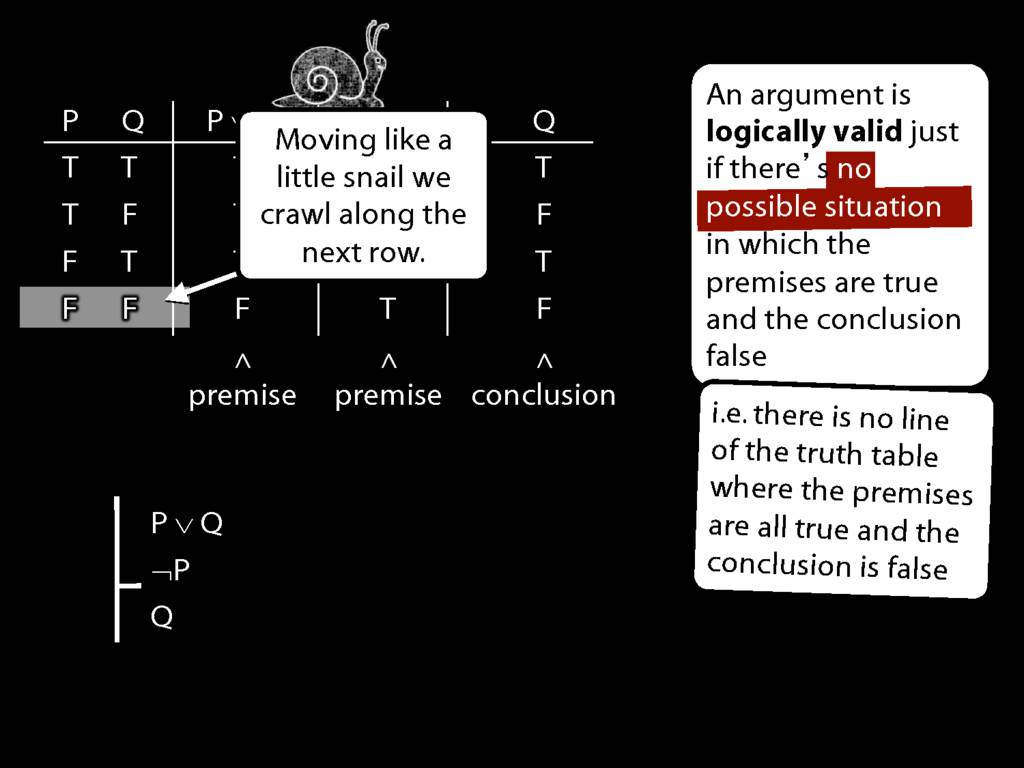
When you're doing truth tables there's a temptation to race through them.

But you shouldn't do that. Be the little snail.
5.1-5.4

Contradictions, Logical Truths and Logical Possibilities
\section{Contradictions, Logical Truths and Logical Possibilities}
\emph{Reading:} §2.2
A \emph{contradiction} is a sentence that is
false in all possible situations.
A \emph{logical truth} is a sentence that is
true in all possible situations.
A \emph{logical possibility} is a sentence that is
true in one or more possible situations.
contradiction
A sentence that is false in all possible situations.
logical truth
A sentence that is true in all possible situations.
logical possibility
a sentence that is true in one or more possible situations.
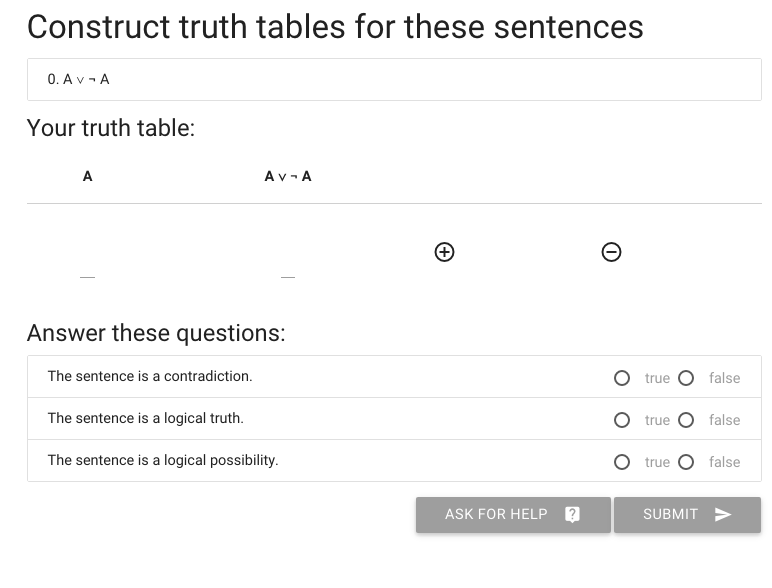
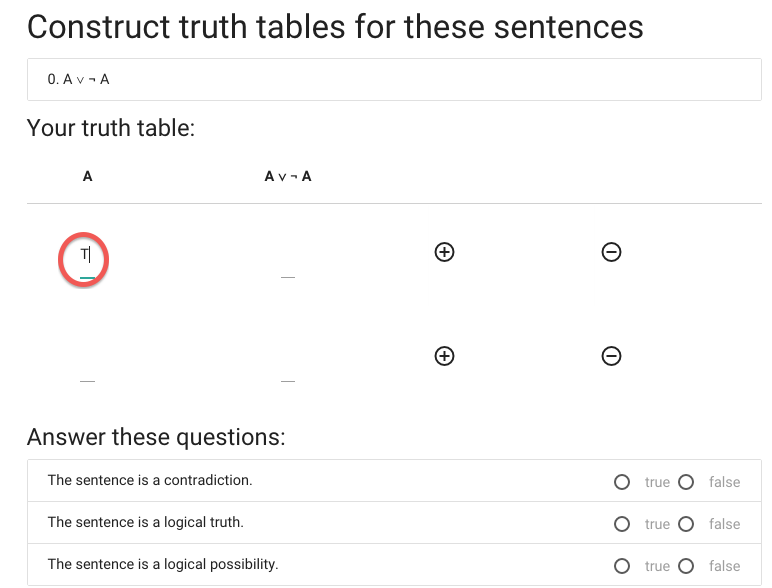
I’ll illustrate how this works in logic-ex.
Let’s say we want to construct the truth table for A or not A.
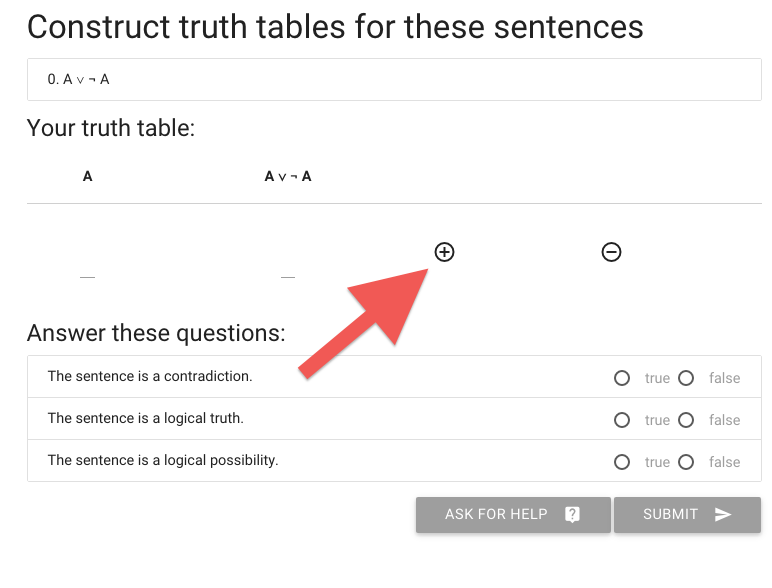
The first thing I need is more rows, so I hit the circled plus thing.
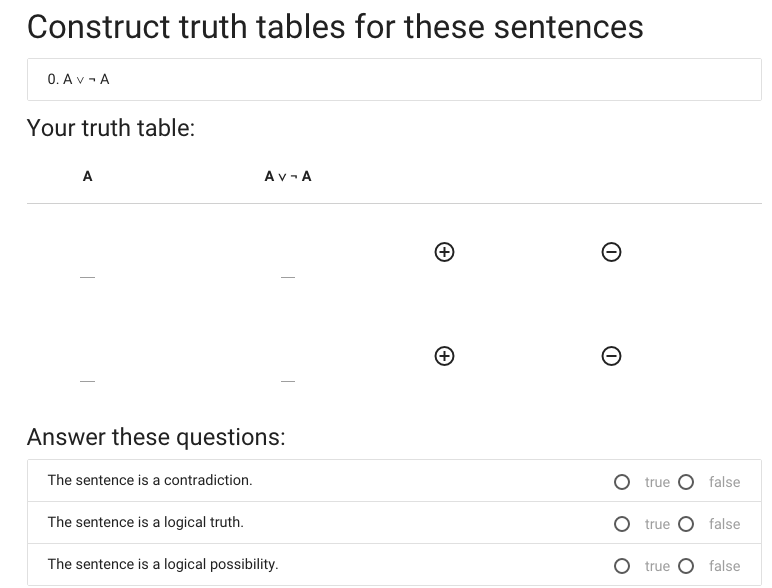
Now I’ve got a second row, and in this case two rows is enough.
Time to start filling in values ...
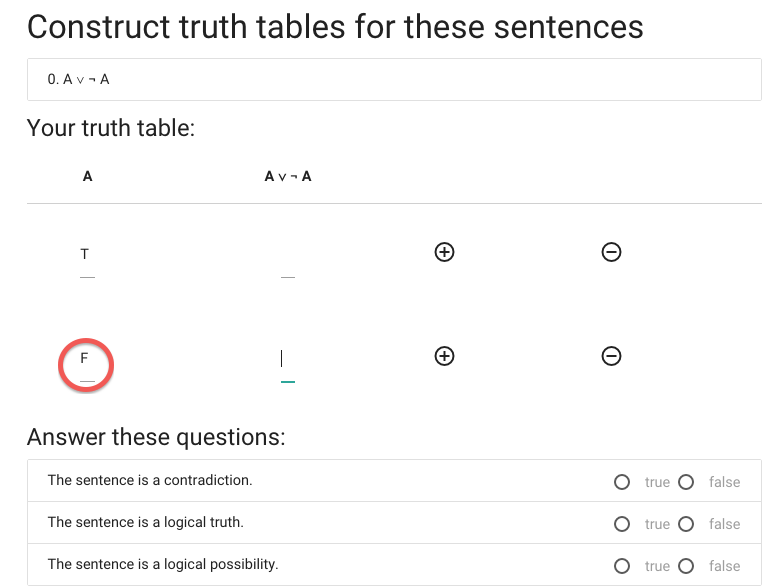
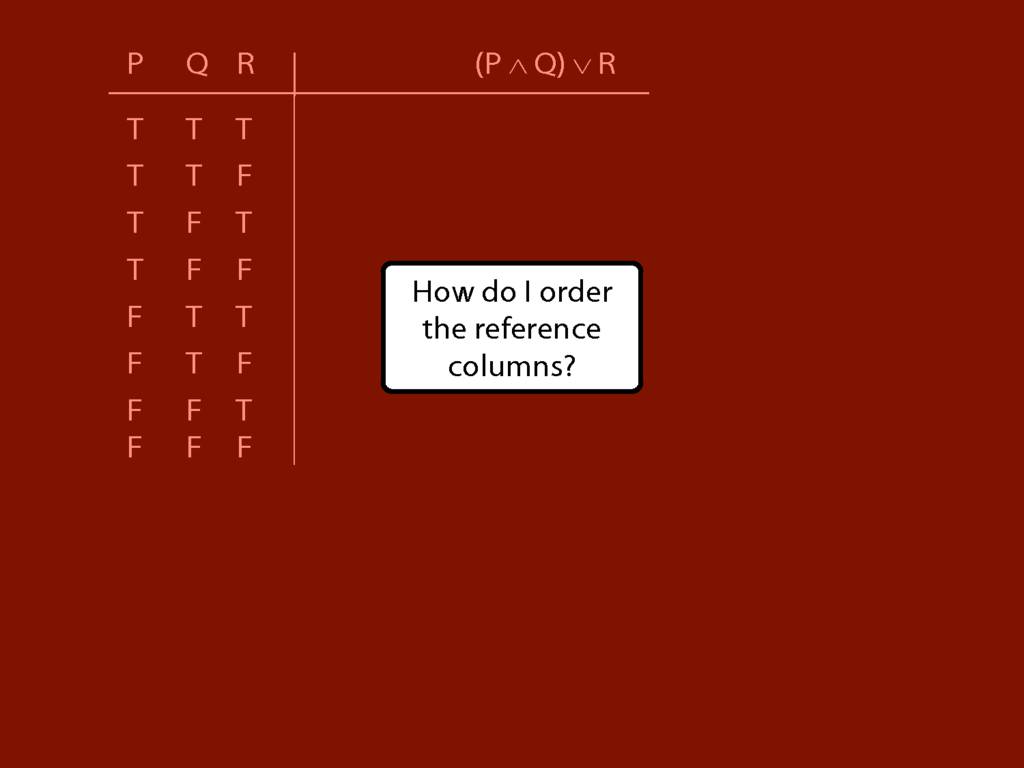
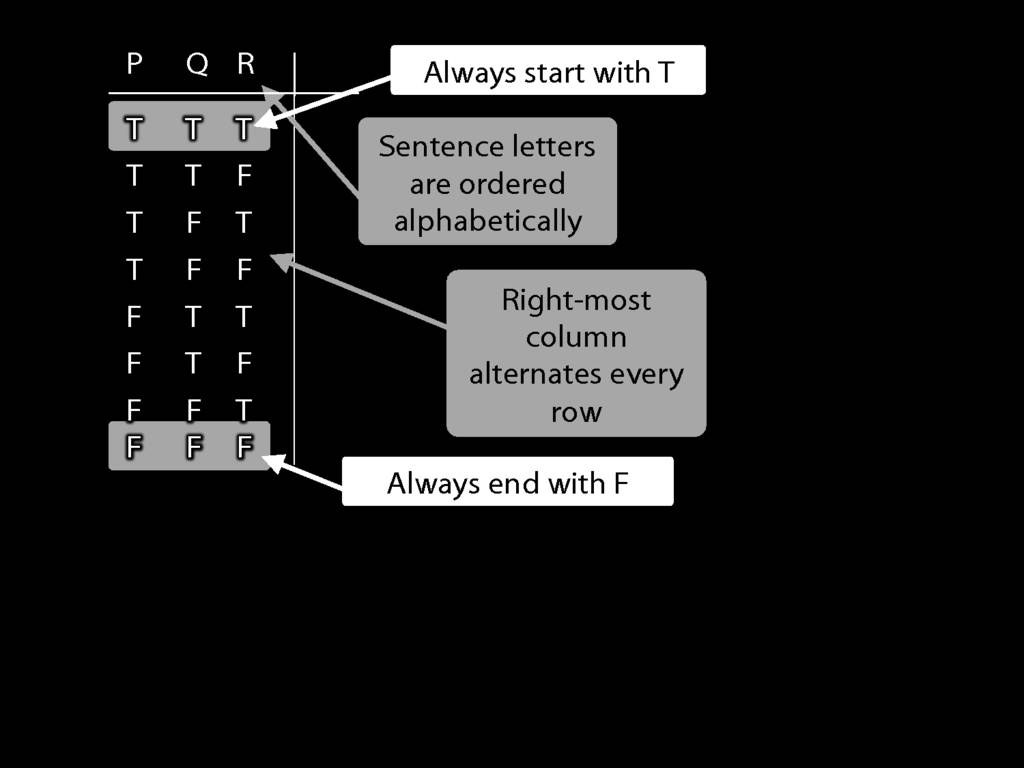
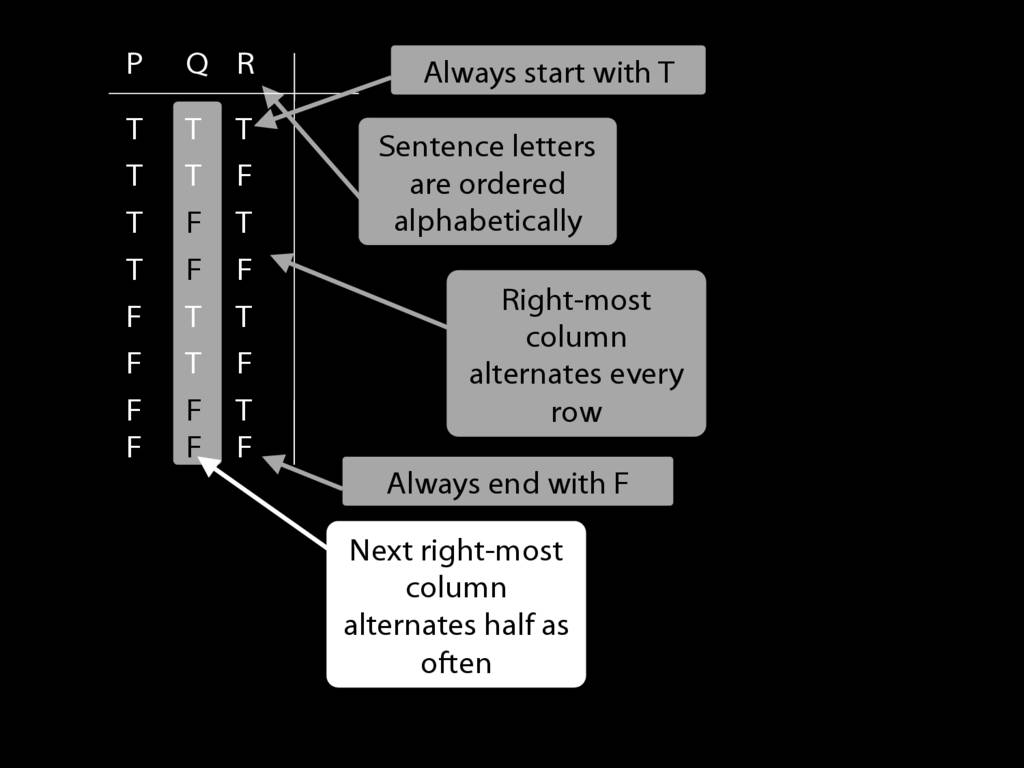
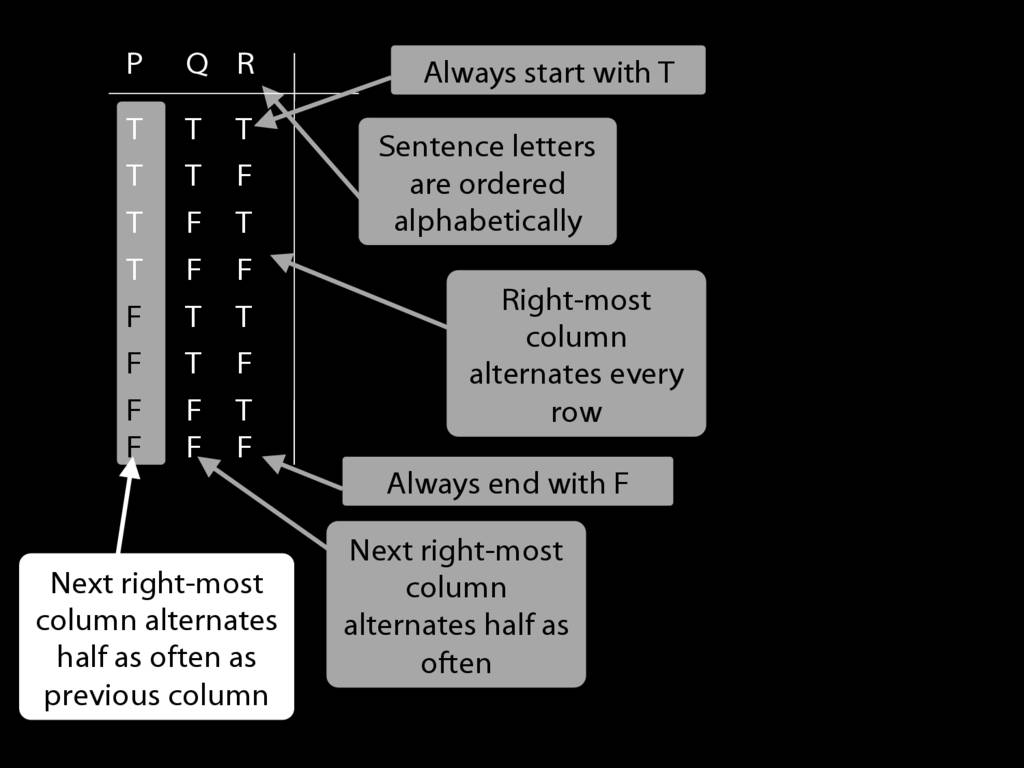
I’m doing the reference columns first because these are always the same
and I don’t need to work out what the values are.
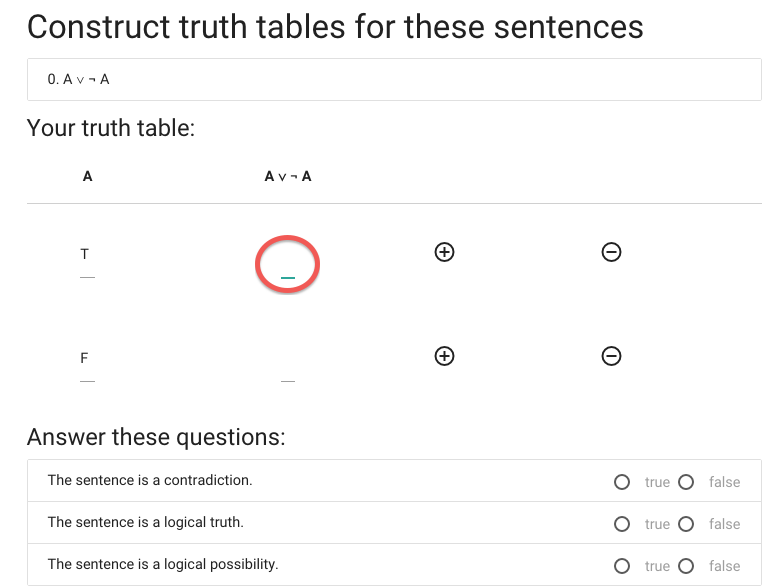
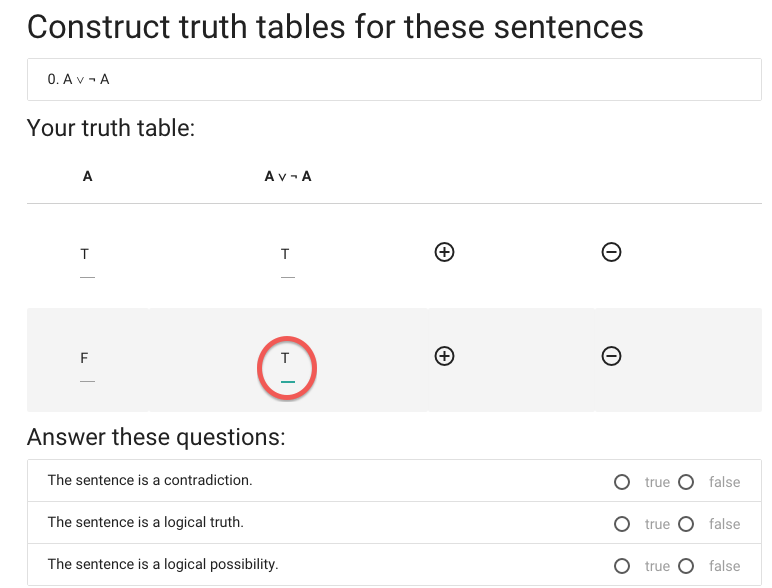
Now I have to enter the value of A or not A when A is true.
You might be able to compute this in value in your head, but
that won’t always be the case. I expect that, often, before
you enter a value in the table in zoxiy you will have taken
a pencil and paper and worked out the truth table step by step.
So what you enter will often be something that took quite a bit
of work to compute.
Or you could just guess. But this is not generally a good strategy
because I take the view that a truth table is either right or wrong,
and if you are really guessing you only have a 1/16 chance of being
right for most truth tables.
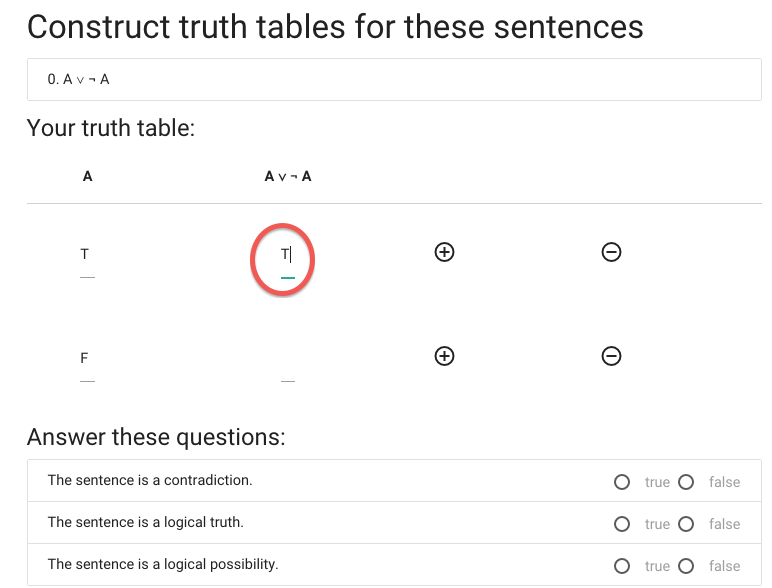
Anyway, I think it’s true.
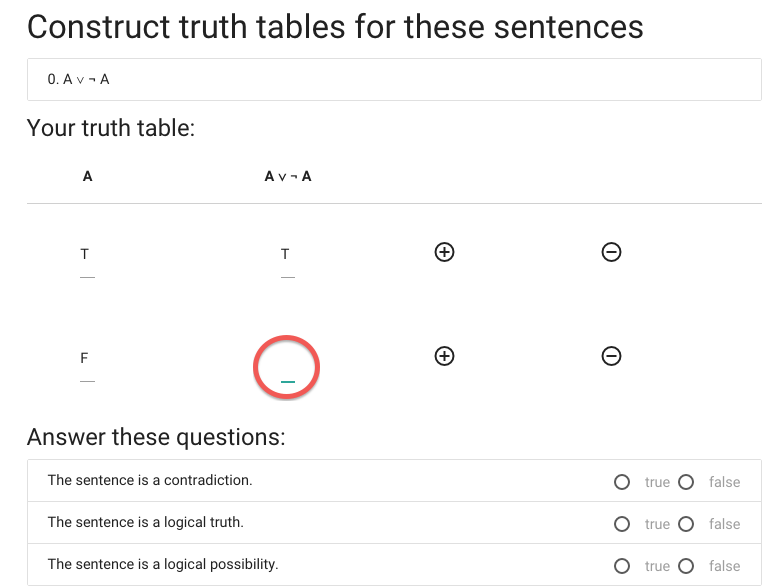
Now for the last truth value.
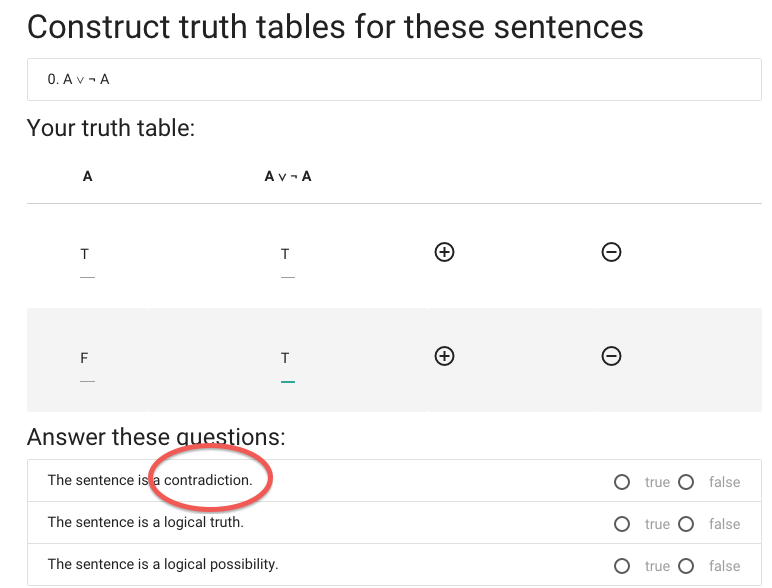
We’re not done yet, we now have to say whether the
sentence is a contradiction.
A \emph{contradiction} is a sentence that is
false in all possible situations.
This sentence isn’t
false in all possible situations ...
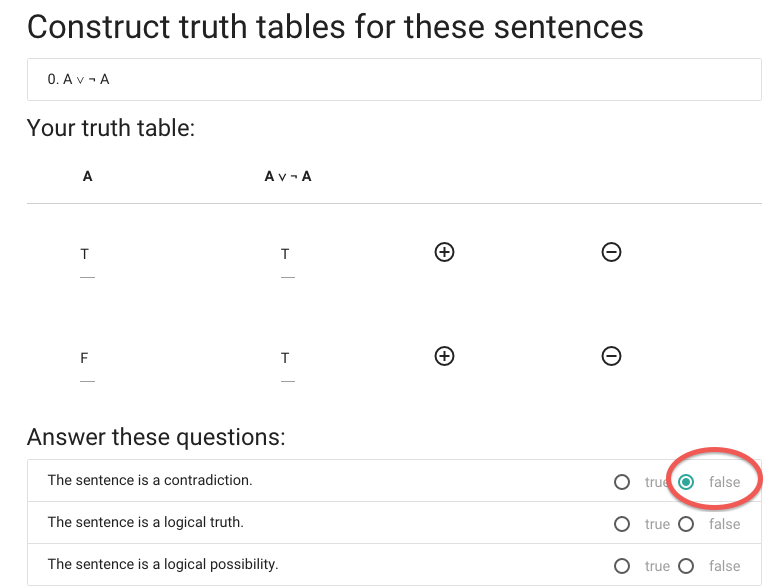
... so it isn’t a contradiction.
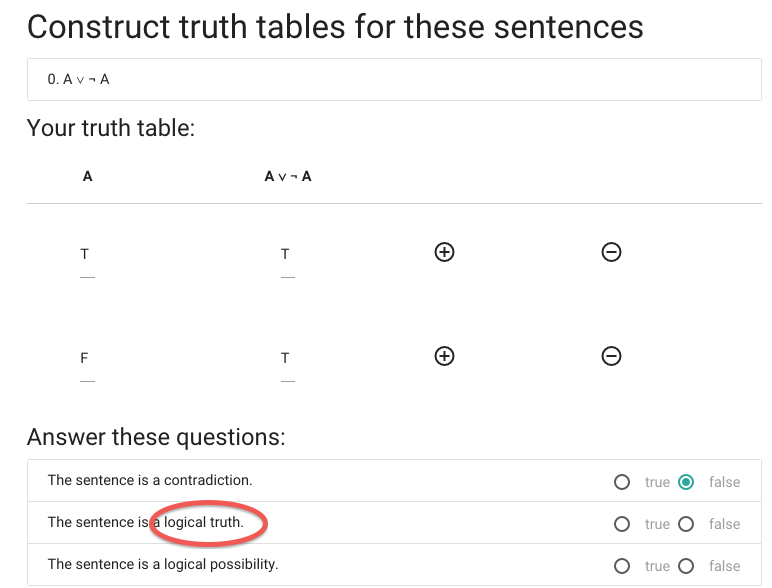
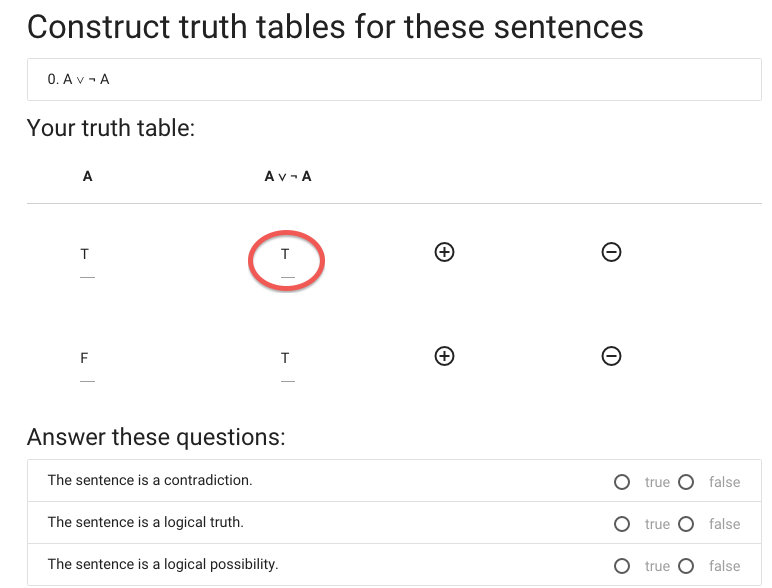
Next we have to specify whether ‘A or not A’ is a logical truth.
A \emph{logical truth} is a sentence that is
true in all possible situations.
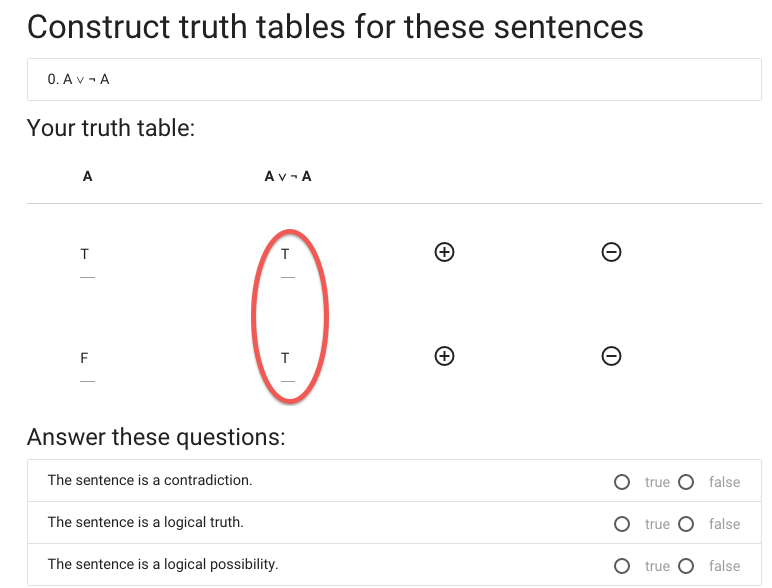
This sentence is true in all possible situations ...
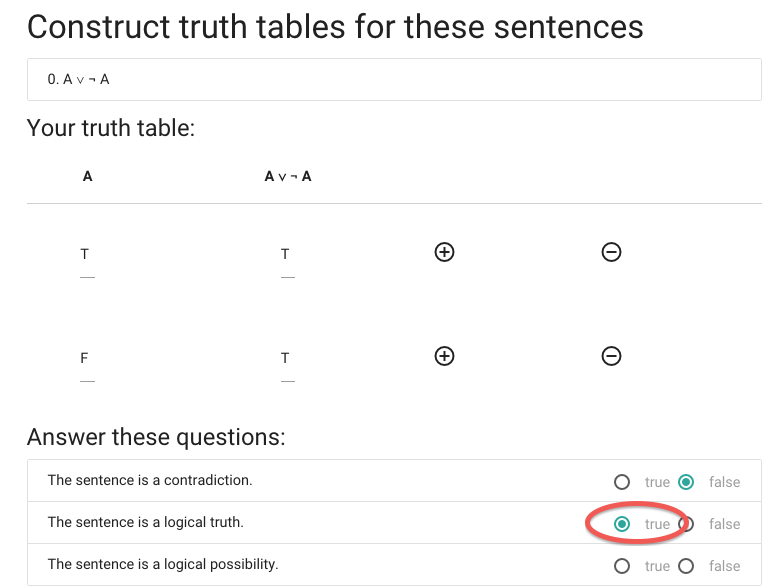
... so this sentence is a logical truth.
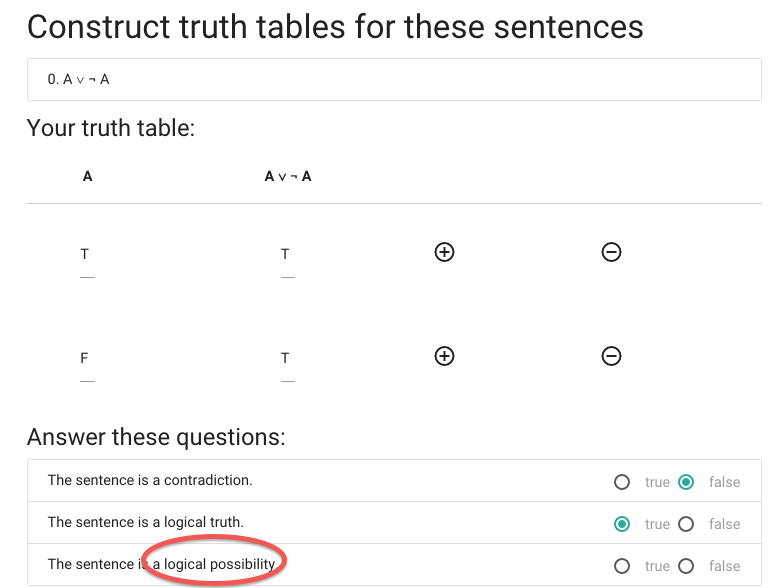
Finally, we’re asked whether the sentence is a logical possibility.
A \emph{logical possibility} is a sentence that is
true in one or more possible situations.

This sentence is true in at least one possible situation ...
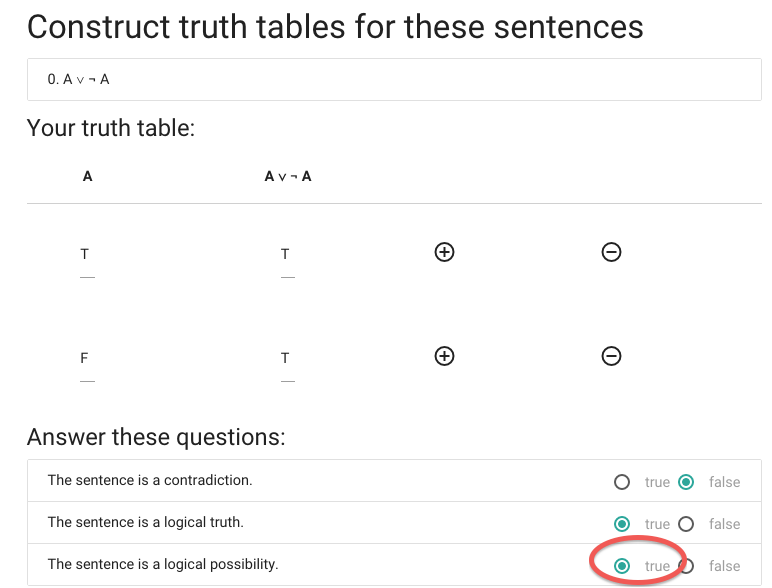
... so this sentence is a logical possibility.
2.5, 2.6
\section{Contradictions, Logical Truths and Logical Validity}
\emph{Reading:} §4.1, §4.2, §5.4

P $\lor{}$ ¬P is a \emph{logical truth}
logical truth defined p. 568
P $\land{}$ ¬P is a \emph{contradiction}
contradiction defined p. 564

Unlike say knowledge or truth, where it’s up to you to form a view of your own to a large extent, with logical validity there is a precise and clear definition that we are working with. Of course there are still questions about the nature of logical validity, but to get to those questions you first have to accept its definition.
4.1, 4.2
4.1, 4.2
4.12--4.16