Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides


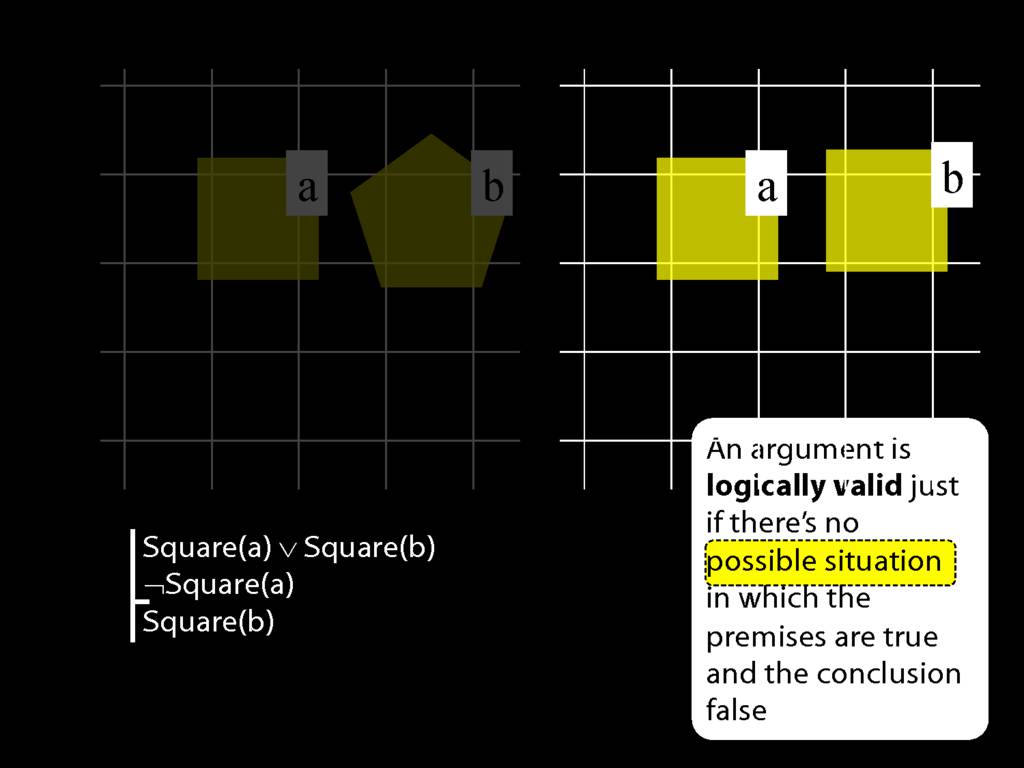
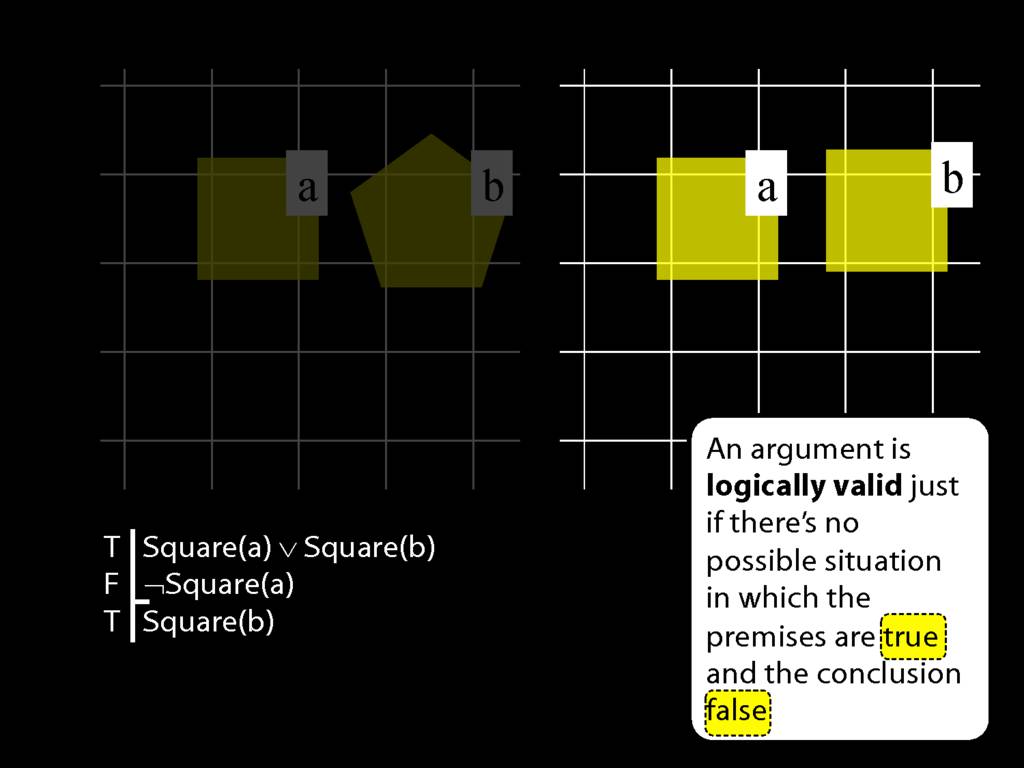
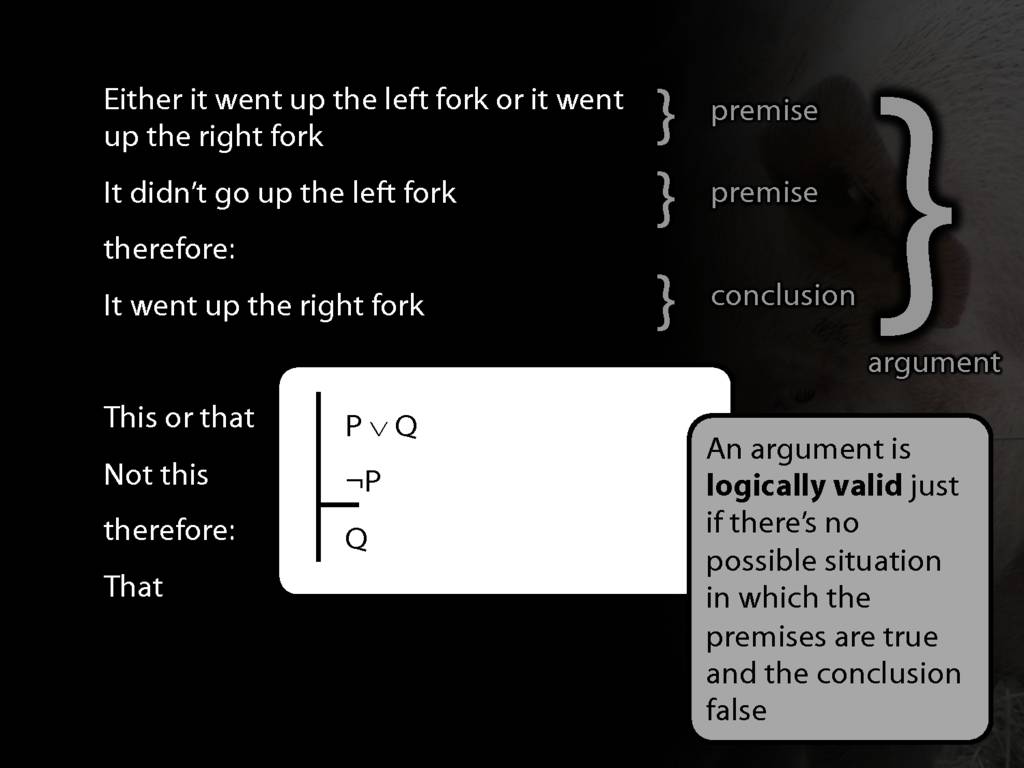
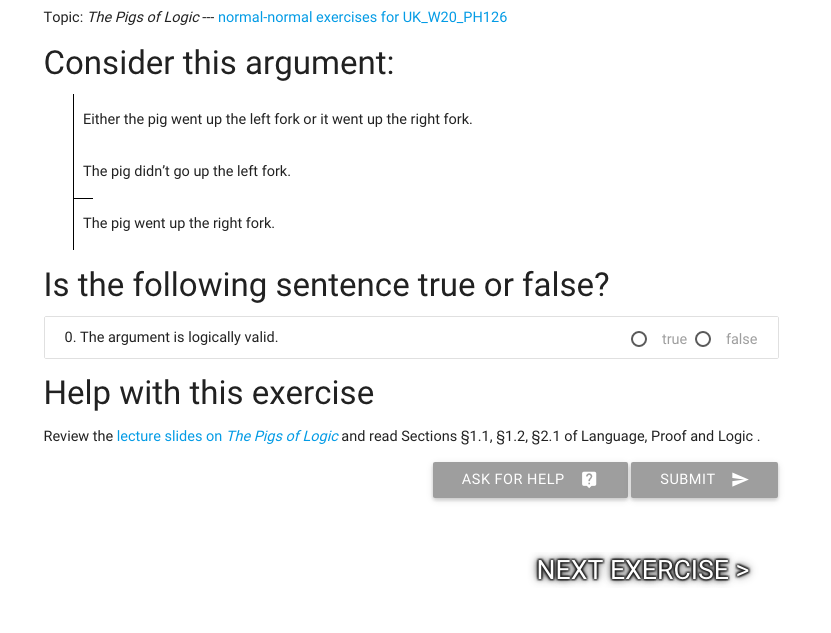
\textbf{Argument 1:} \begin{quote} Either it went up the left fork or it went up the right fork.
It didn’t go up the left fork.
therefore:
It went up the right fork. \end{quote}
\textbf{Argument 2:} \begin{quote} Either it went up the left fork or it went up the right fork.
The left fork is unsuitable for pigs.
therefore:
It went up the right fork. \end{quote}














Why Logic?
why logic?
precise expression
‘If a card has a vowel on one side, then it has an even number on the other side.’
(Waison & Johnson-Laird 1972)
E
K
4
7
‘Philosophy is thinking in slow motion.’ (John Campbell)


‘Logic pervades the world: the limits of the world are also its limits.’
(Wittgenstein, Tractatus 5.61)

‘don’t obey no laws, not even gravity’
(Tariq Trotter, Game Theory track 10)
2013-05-30
RE: Love and Logics
Dear Professor,
Hope you're well. My name is [name removed], a former student.
I just wanted to say thank you for your wonderful lectures on logics. I didn't know logics was so useful that it helped me to find a really nice girlfriend and enables me to win arguments all the time!
Thanks again. Haha.
[name]

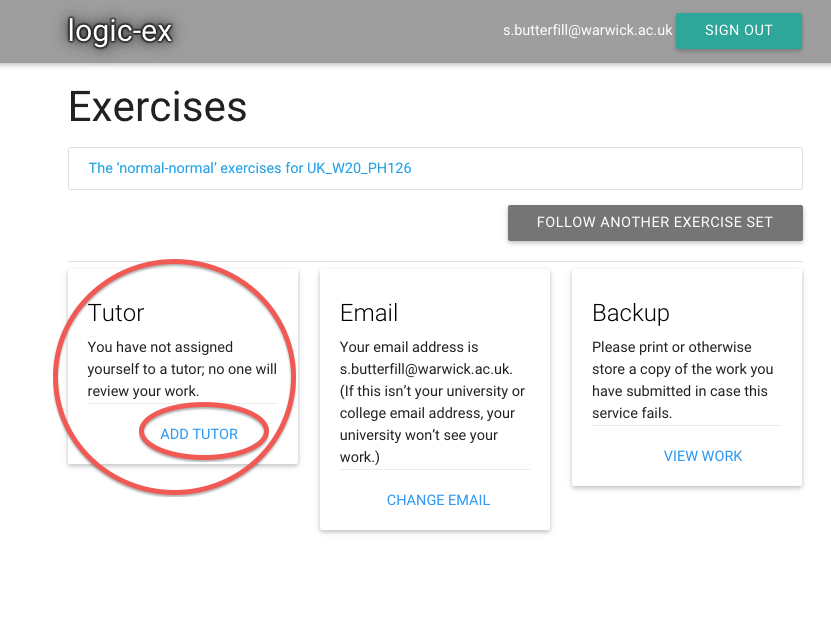
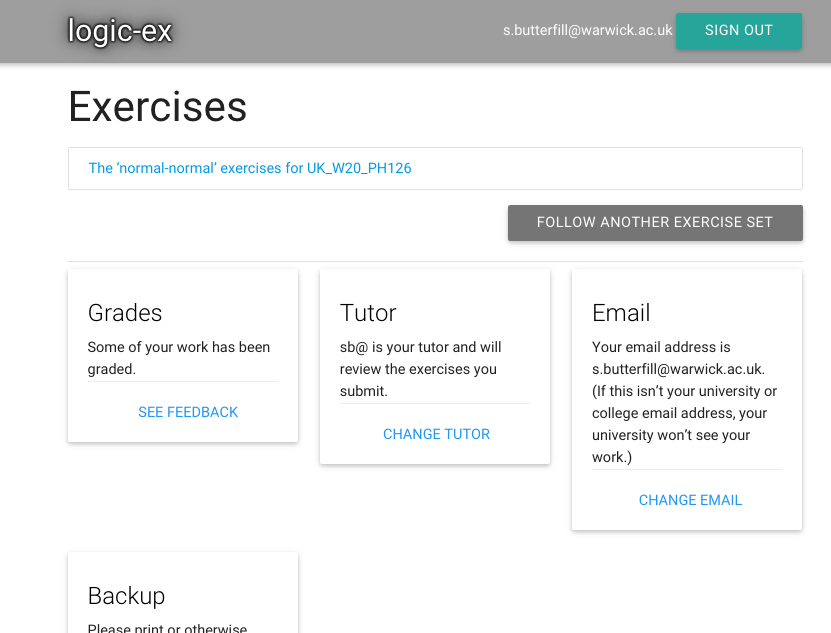
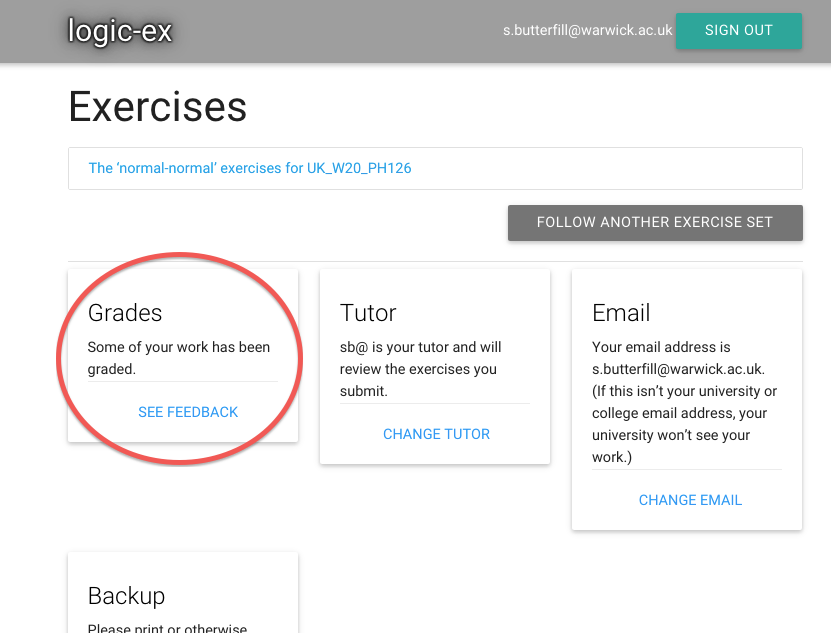
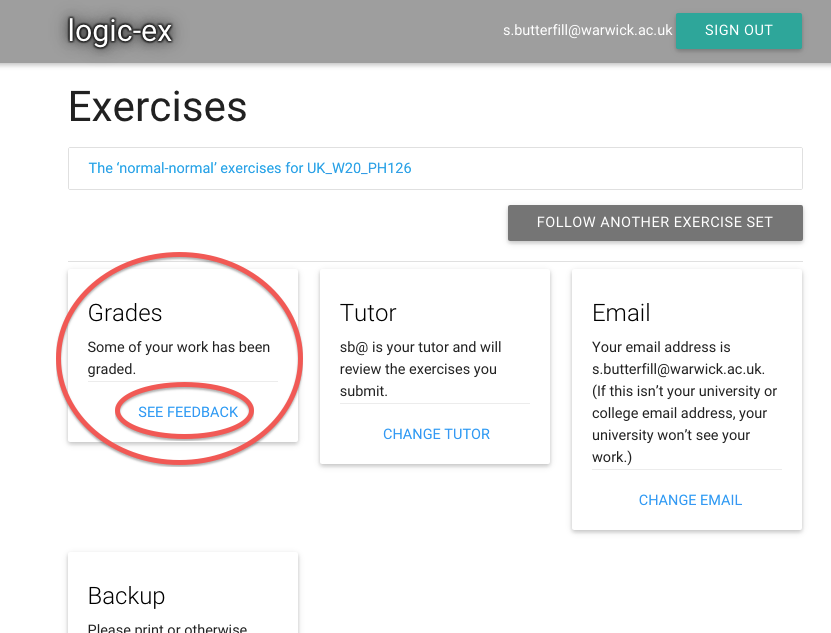
Admin
- Lectures: normal and fast-track
- Seminar groups
- Textbook
- Web: https://logic-1.butterfill.com
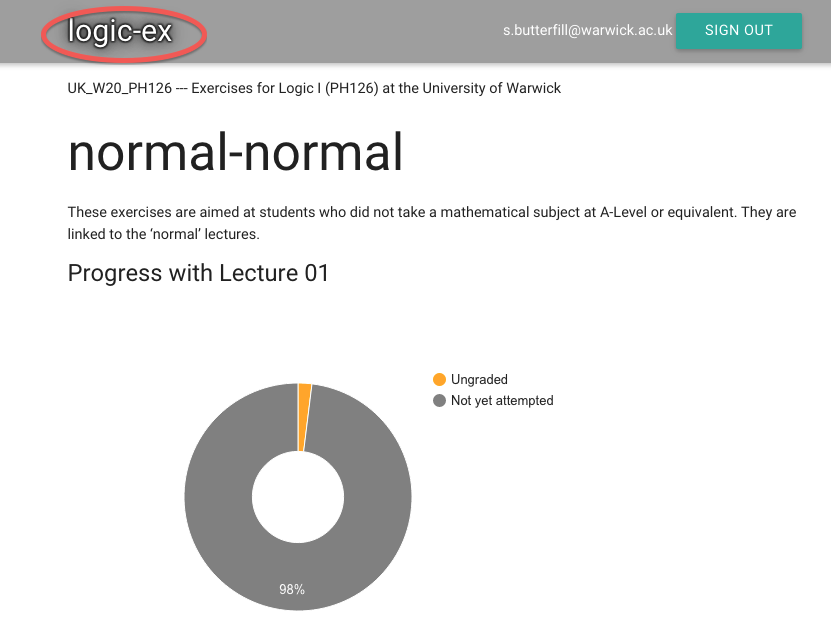
- Exercises
sent: 03:55 29/08/2008
subject: [none]
Dear Stephen,
I am retaking starting logic on tuesday, and I wonder if you could explain to me the difference between contingent, tatologous and inconsistent in terms of truth table results, as I cannot find this information anywhere else?
Many Thanks,
---


zoxiy
http://logic-1.butterfill.com








Quick Intro to awFOL
John is square
Square( a )
John is to the left of Ayesha
LeftOf( a , b )
John is square or Ayesha is trinagulra
Square( a ) ∨ Trinagulra( b )
name (refers to an object)
predicate (refers to a property)
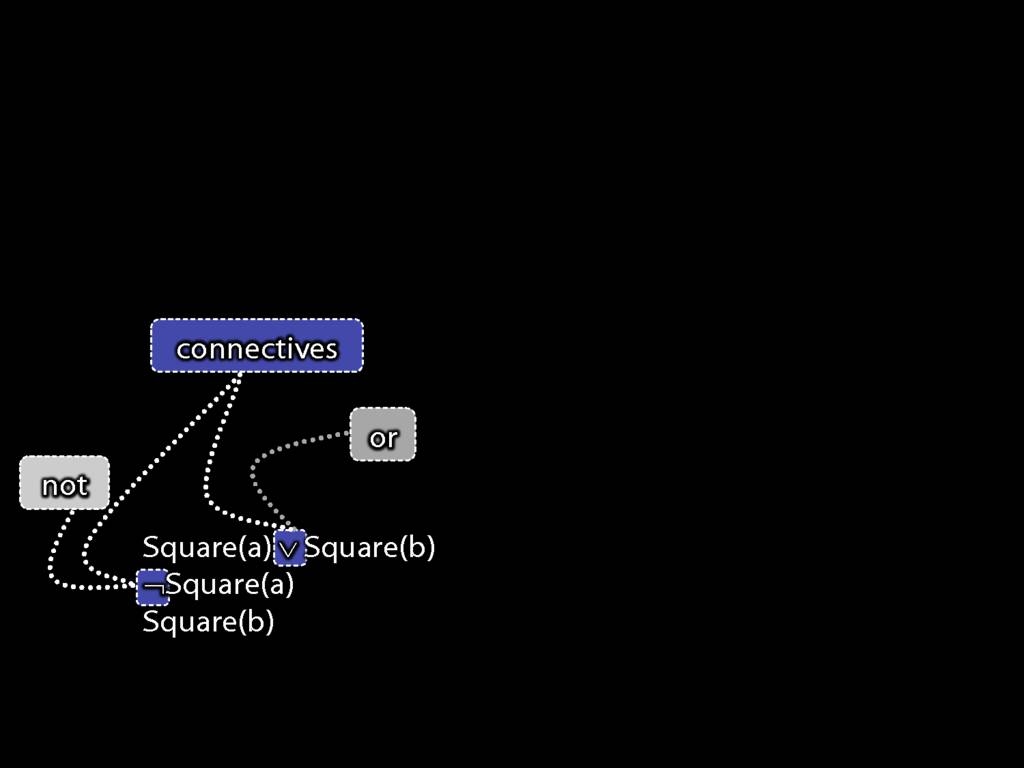
connective (joins sentences)
sentence (can be true or false)
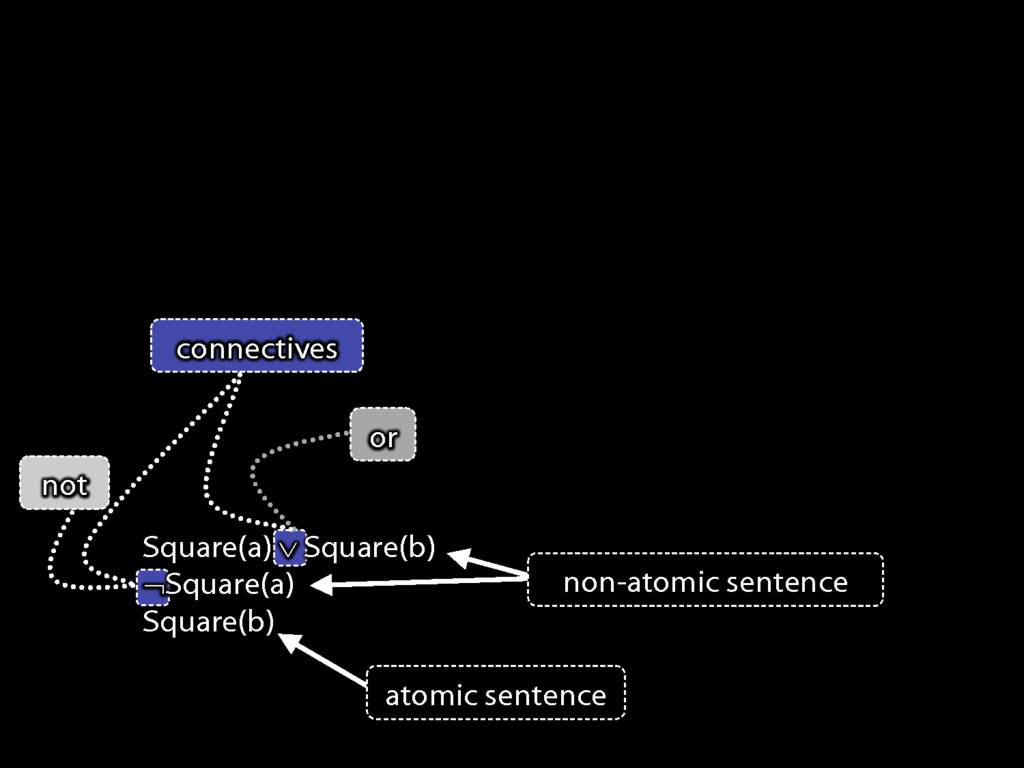
atomic sentence (no connectives)
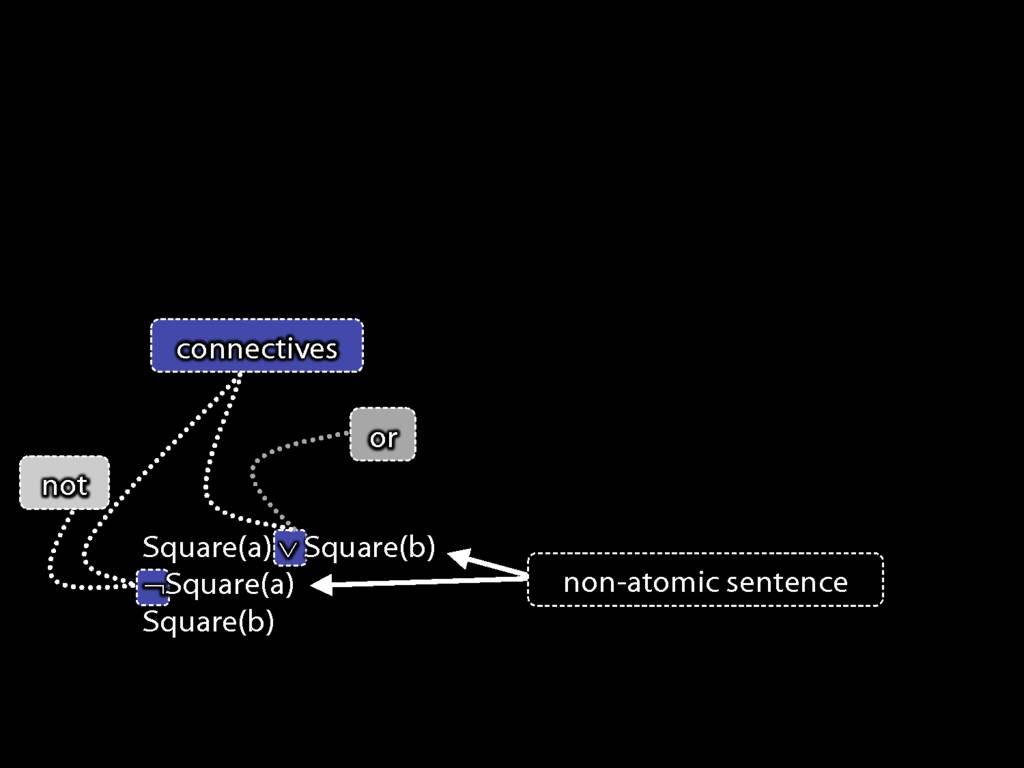
non-atomic sentence (contains connectives)
This is a hospital where doctors are trained.
Many more people have been to Paris than I have.
Ayesha doesn’t know diddly squat about logic
Ayesha does know diddly squat about logic

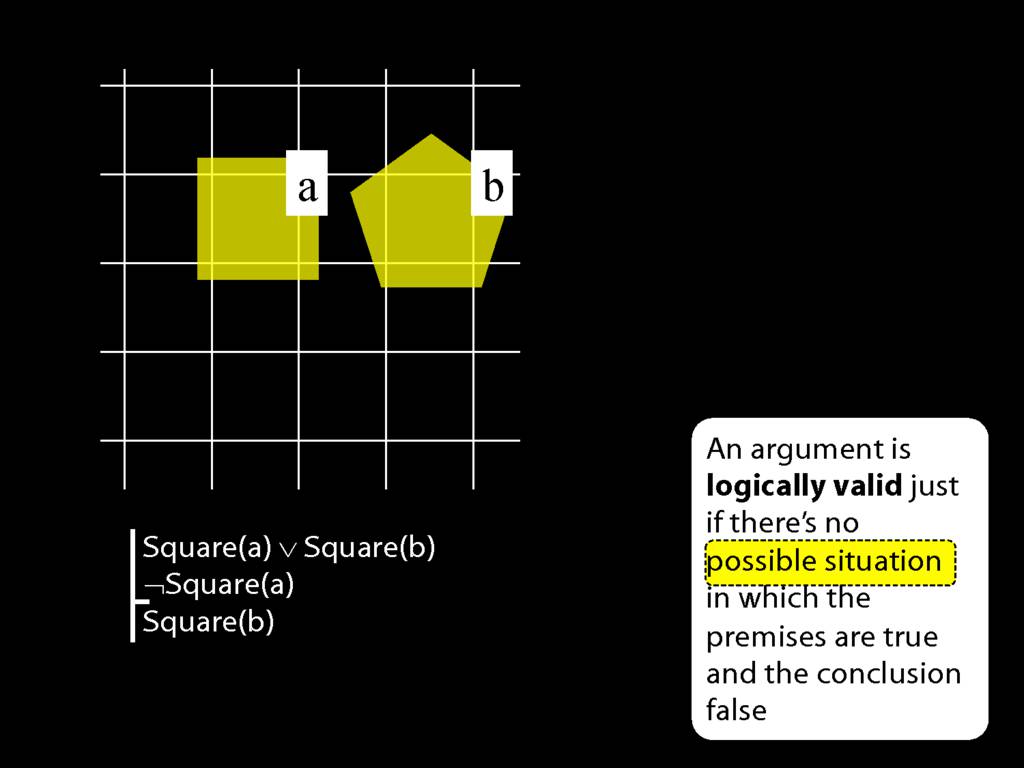
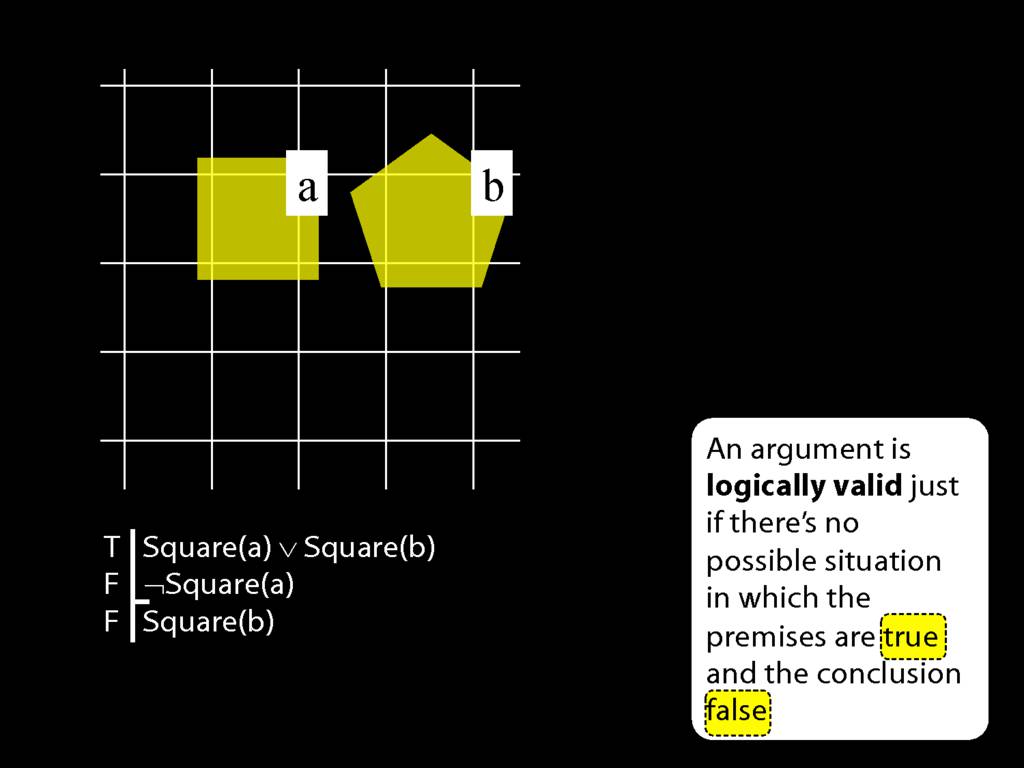
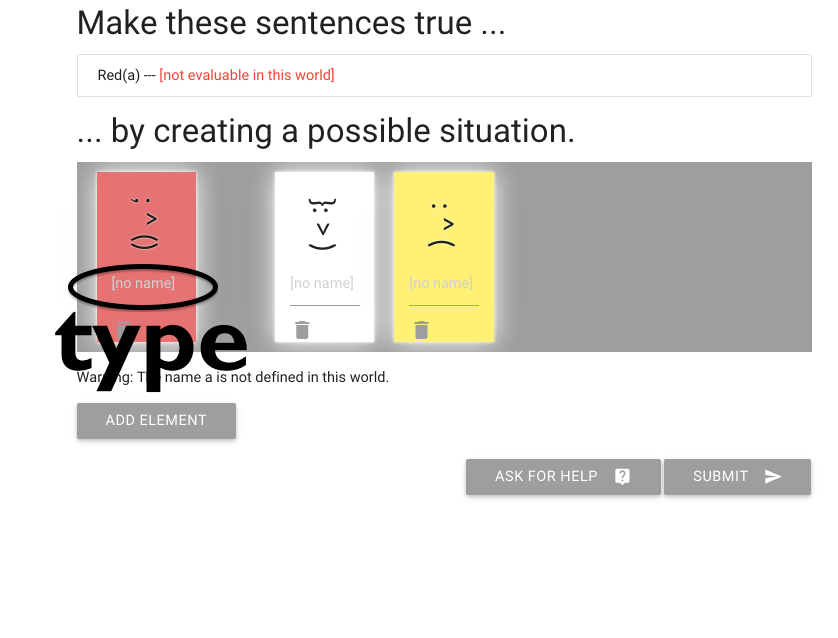
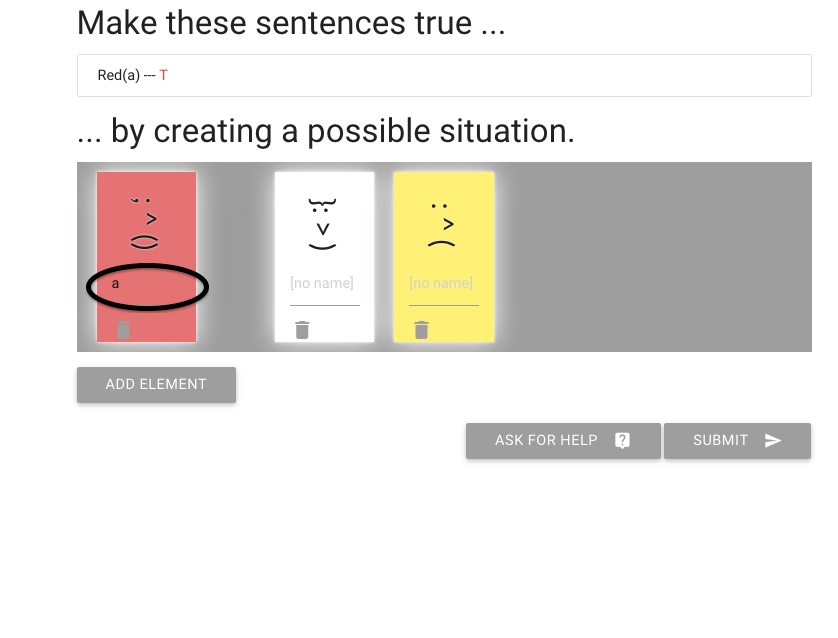
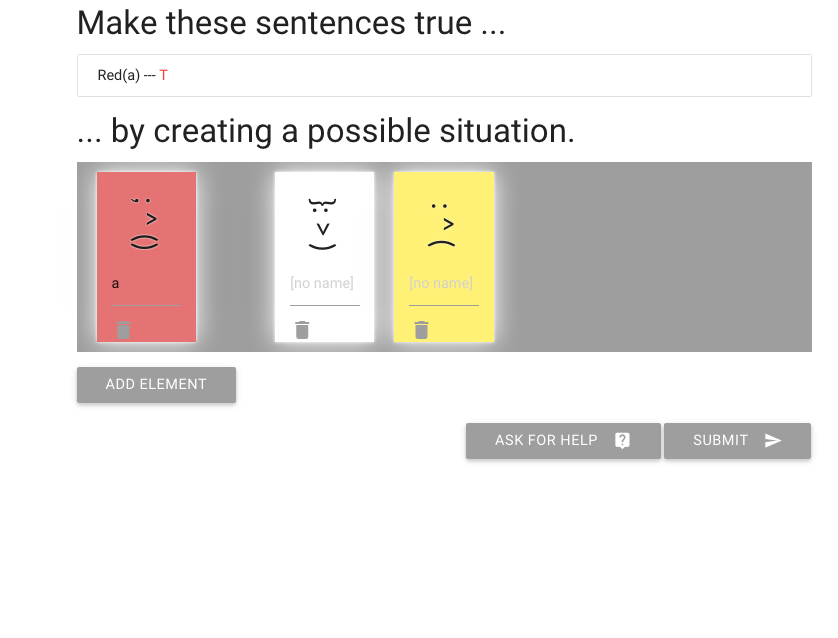
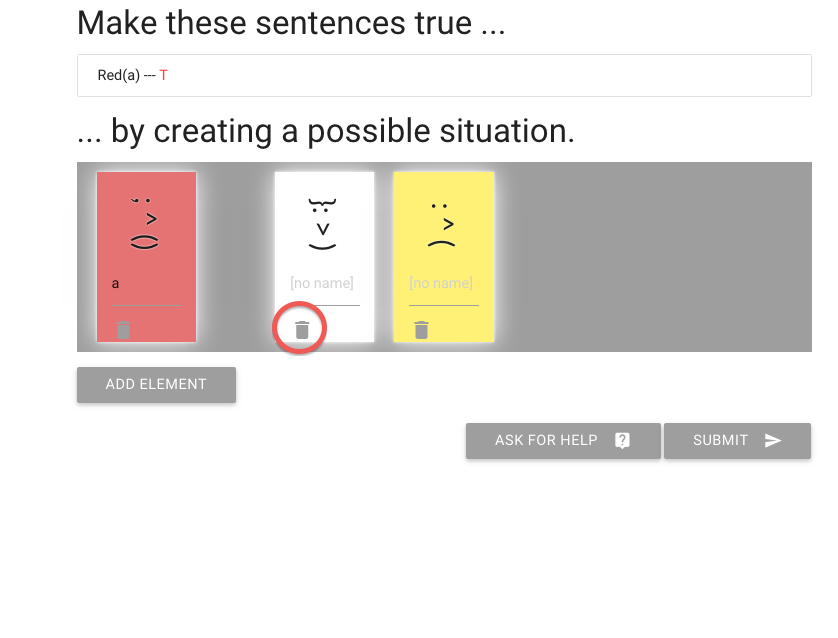
zoxiy: Creating Possible Situations
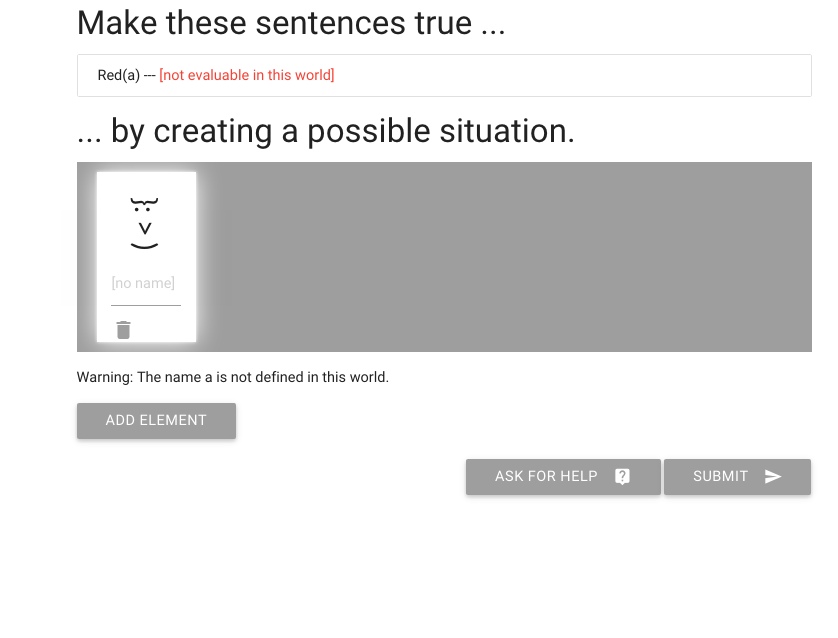
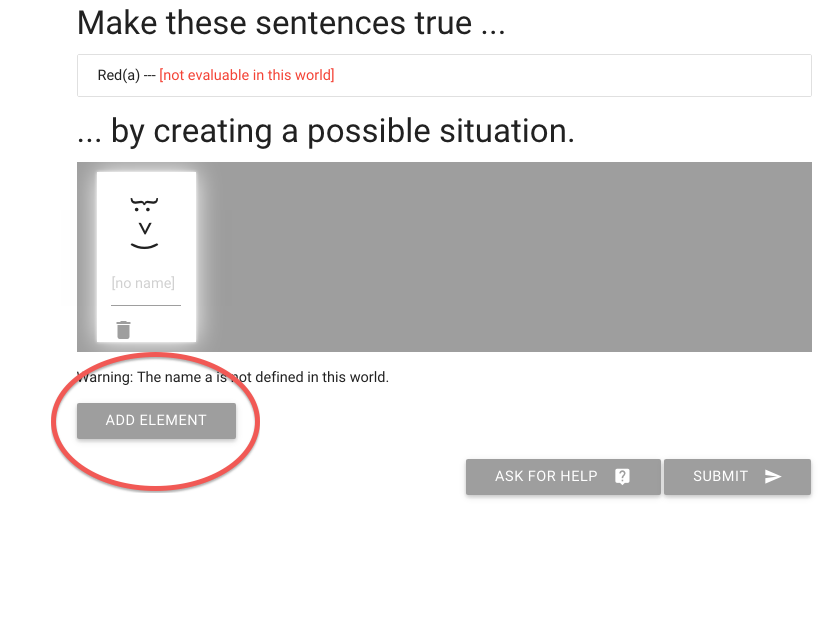
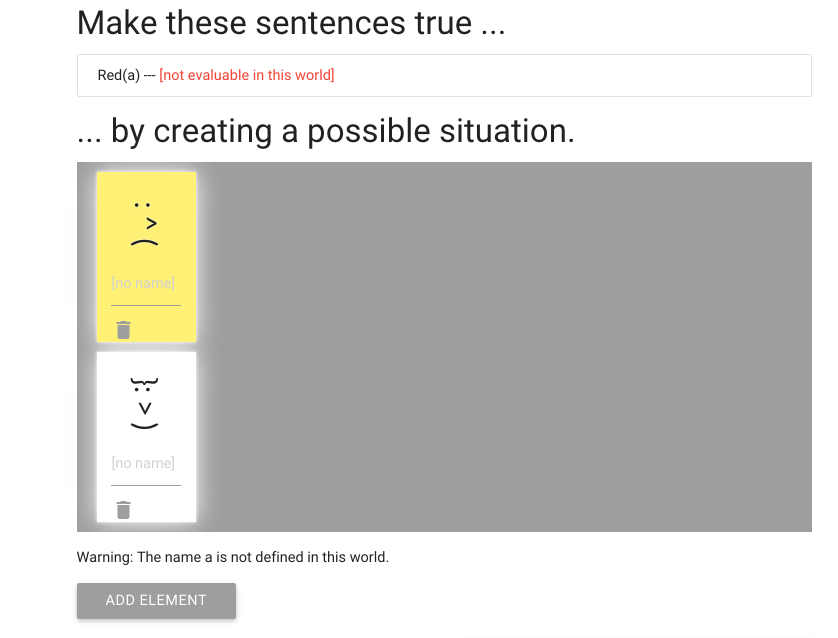
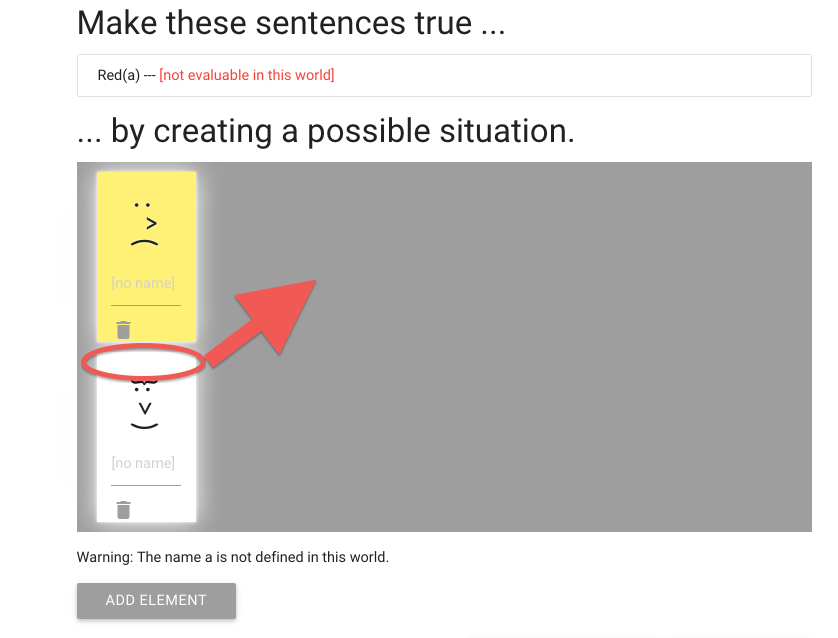
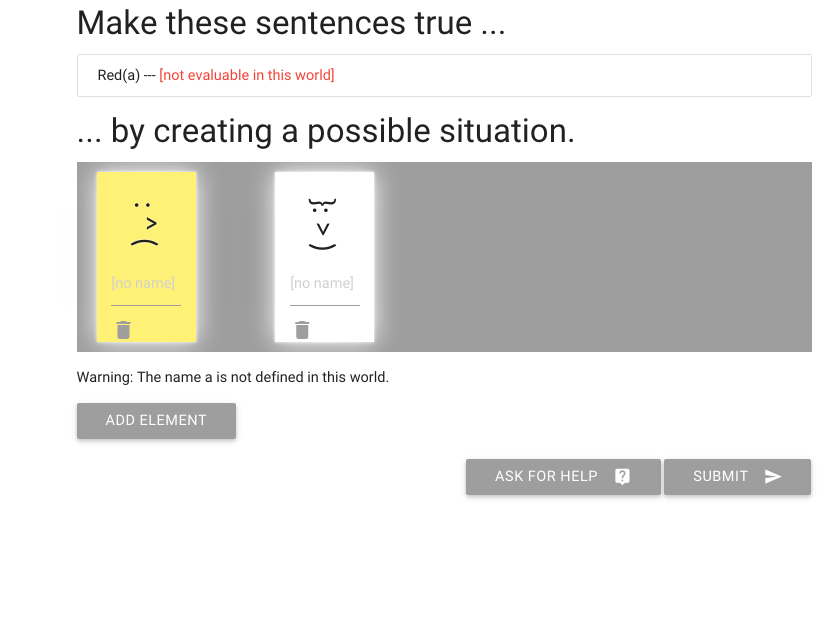
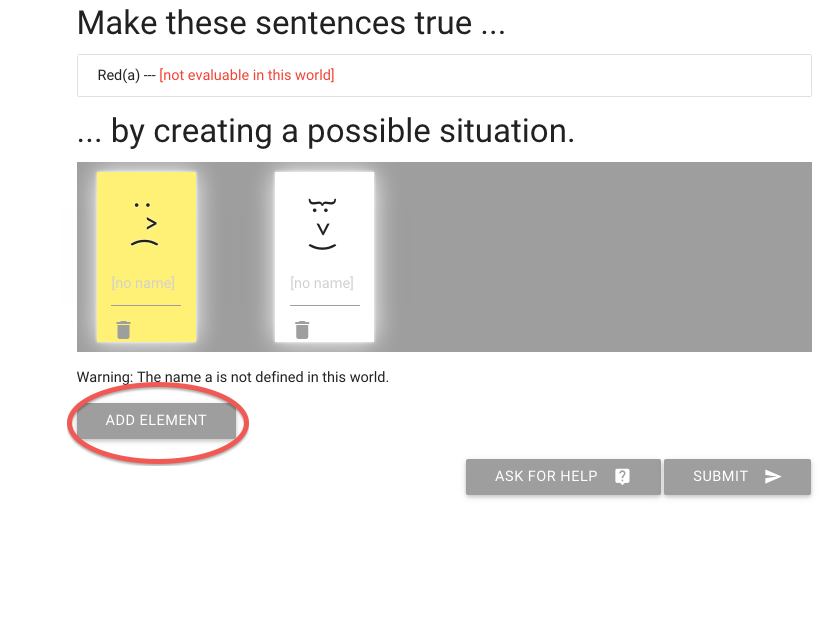
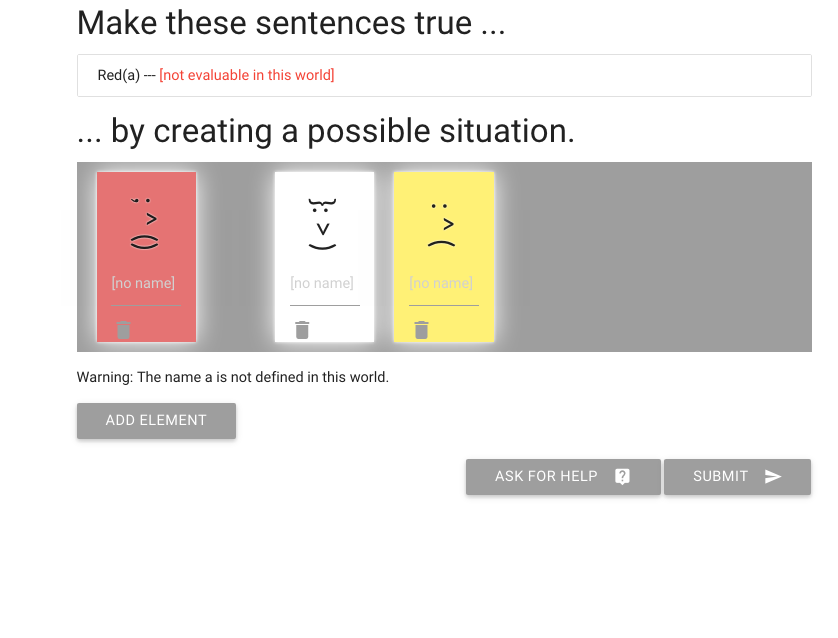
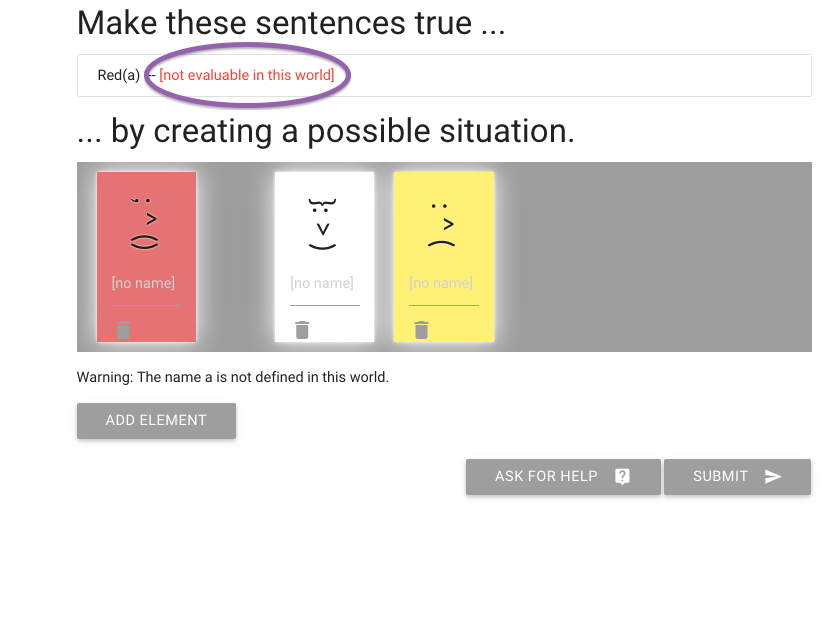
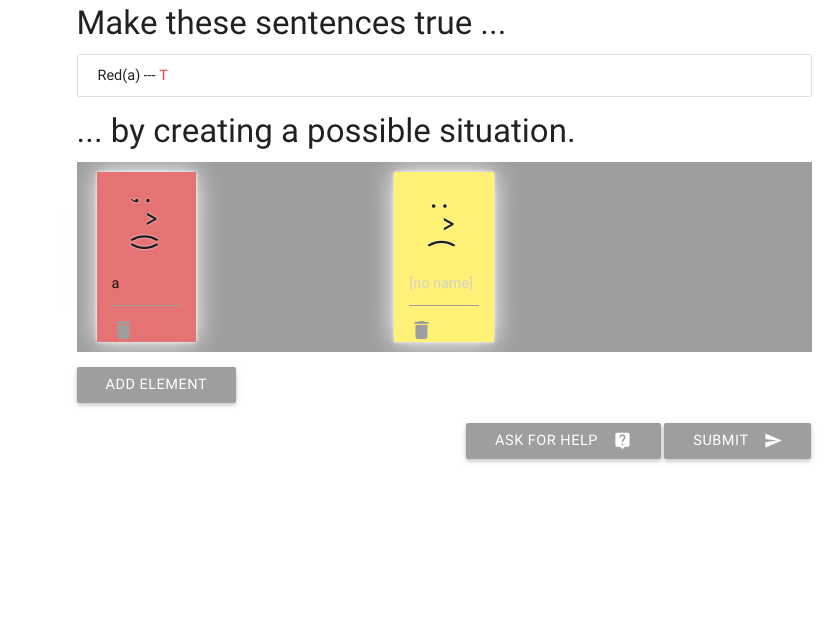
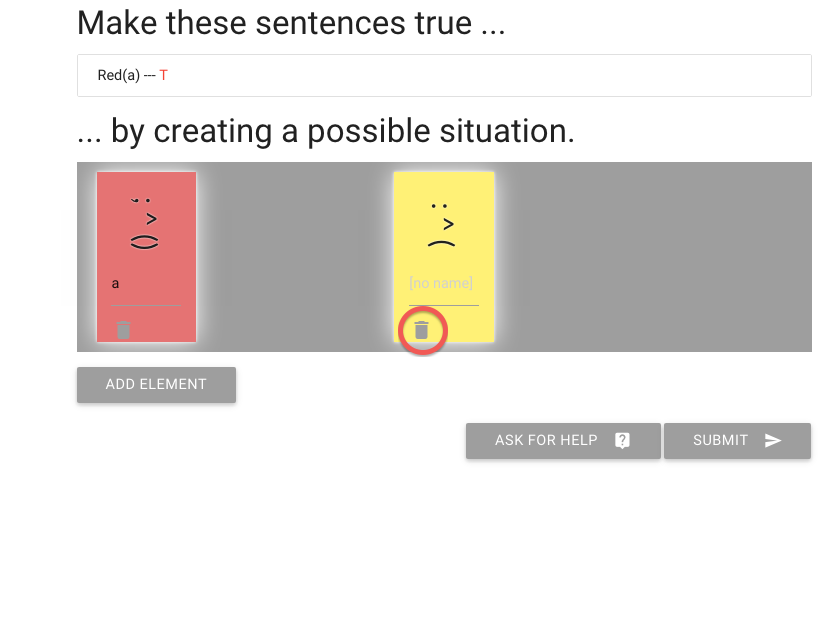
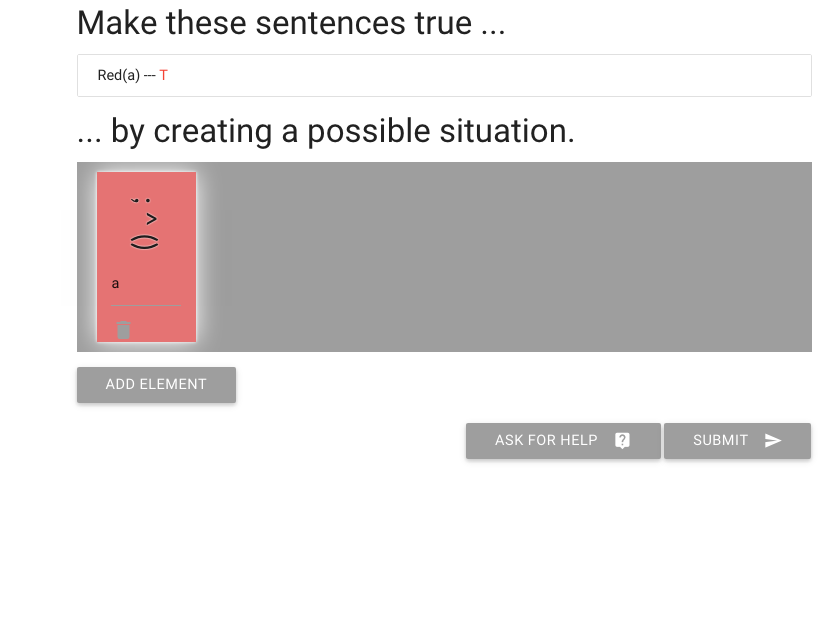
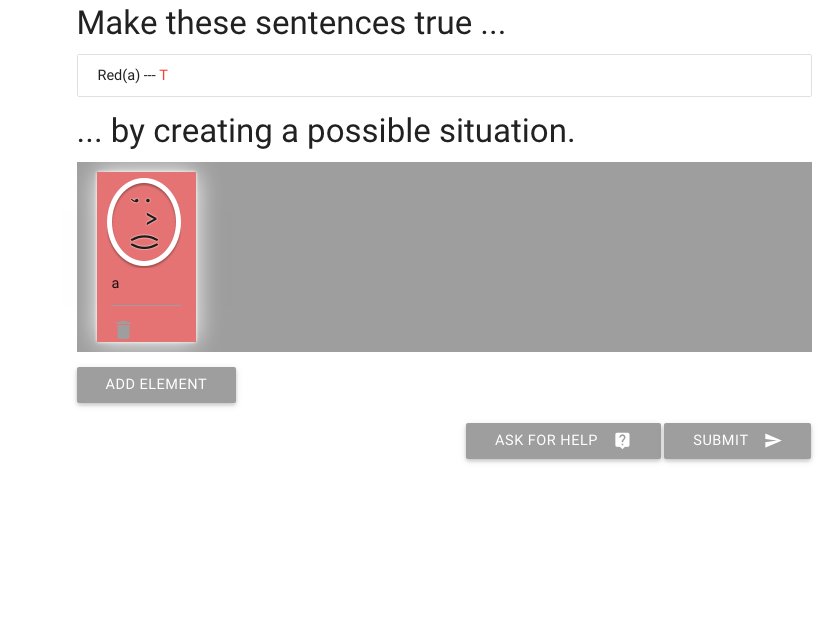

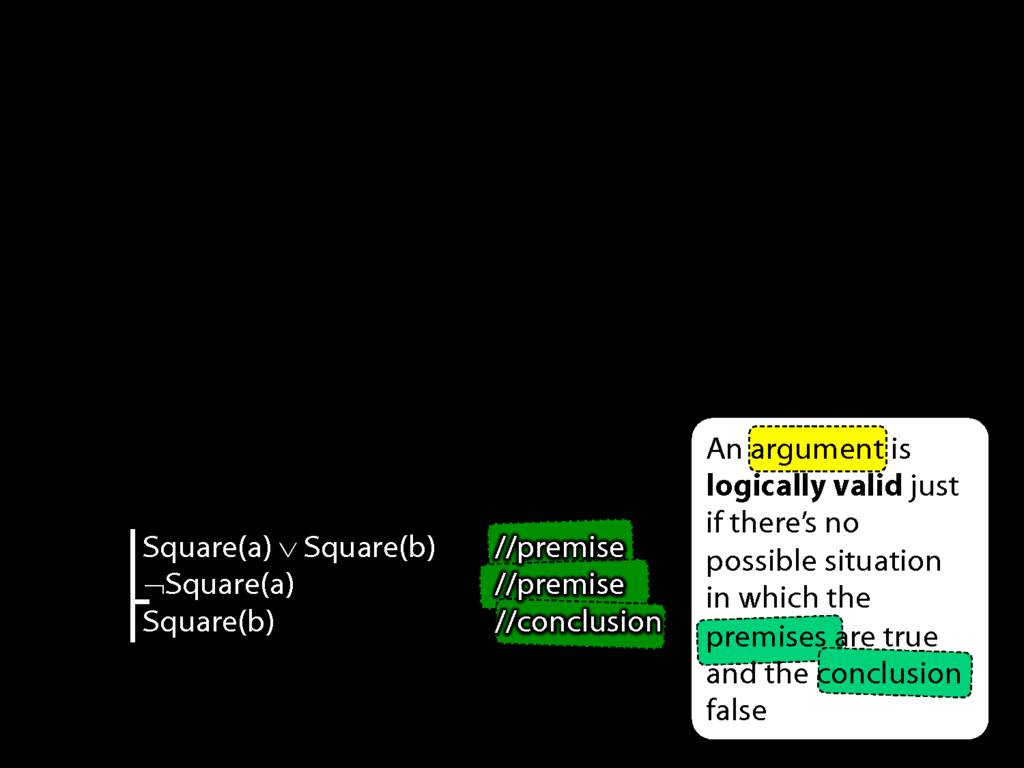
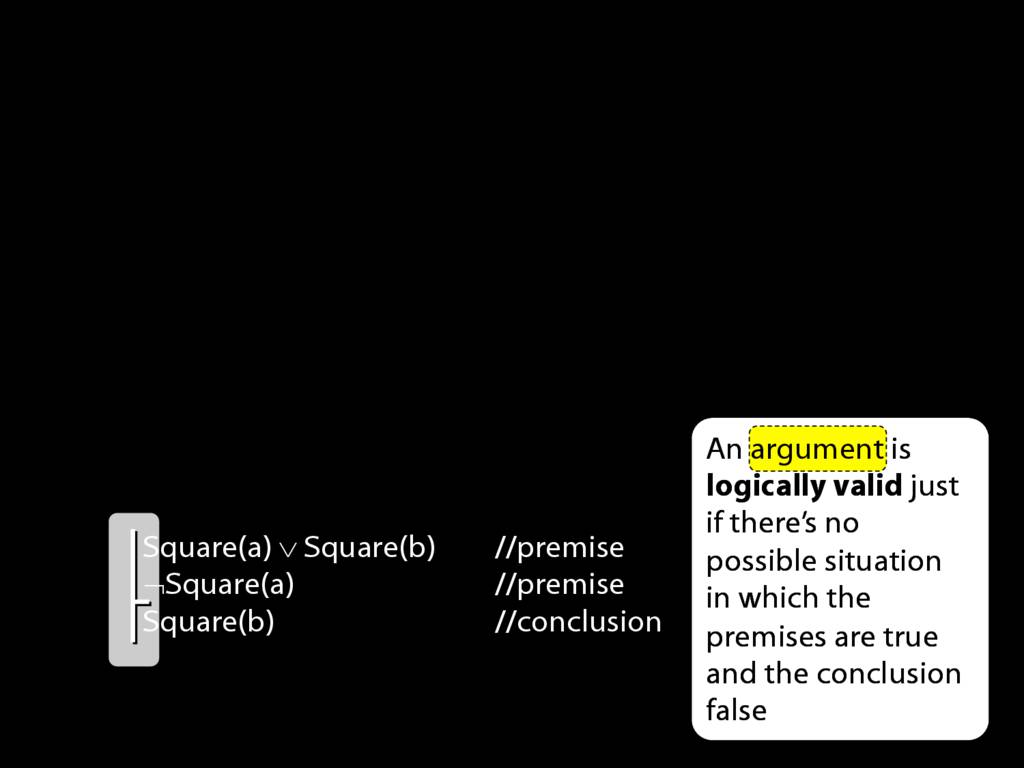
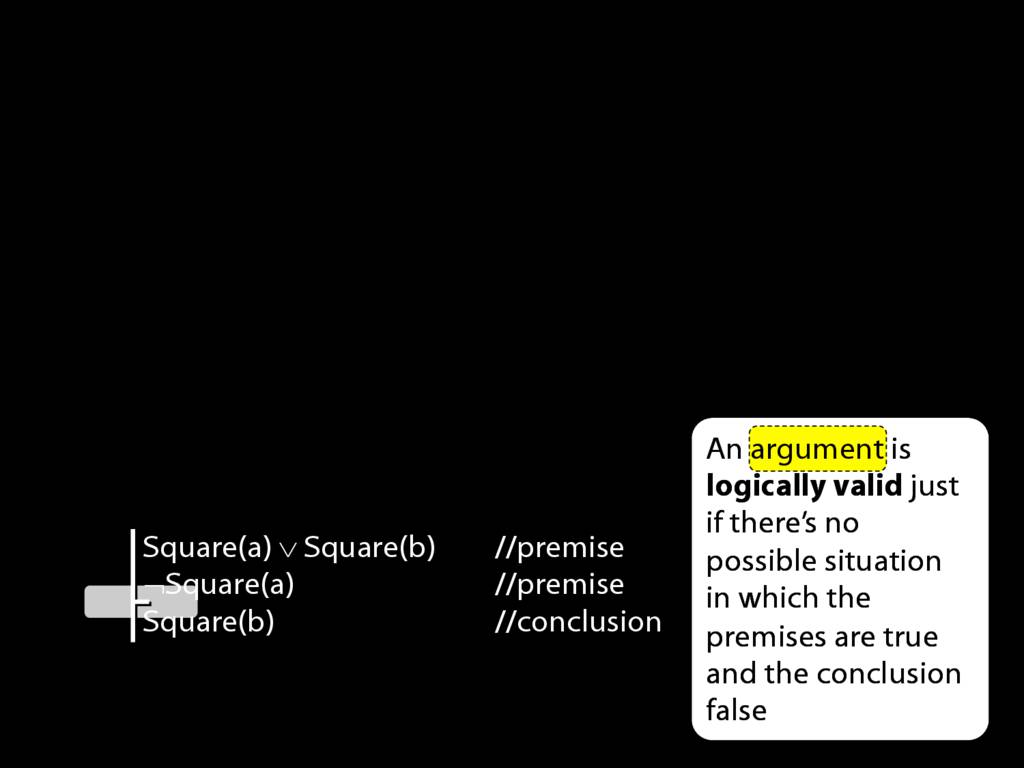
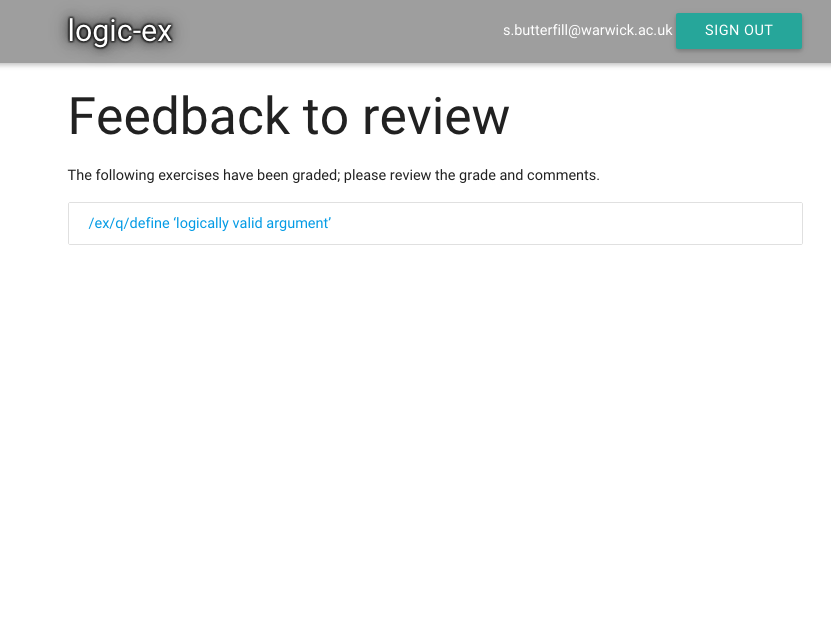
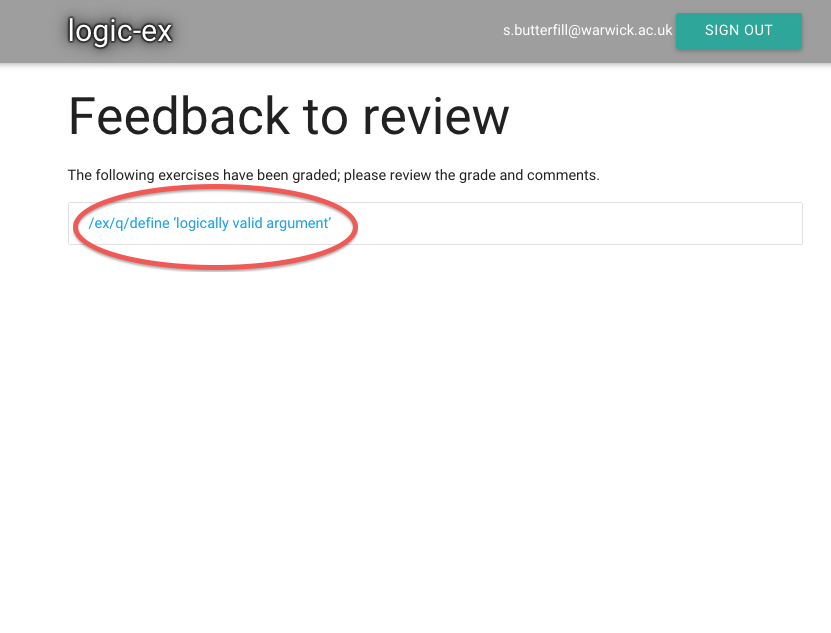
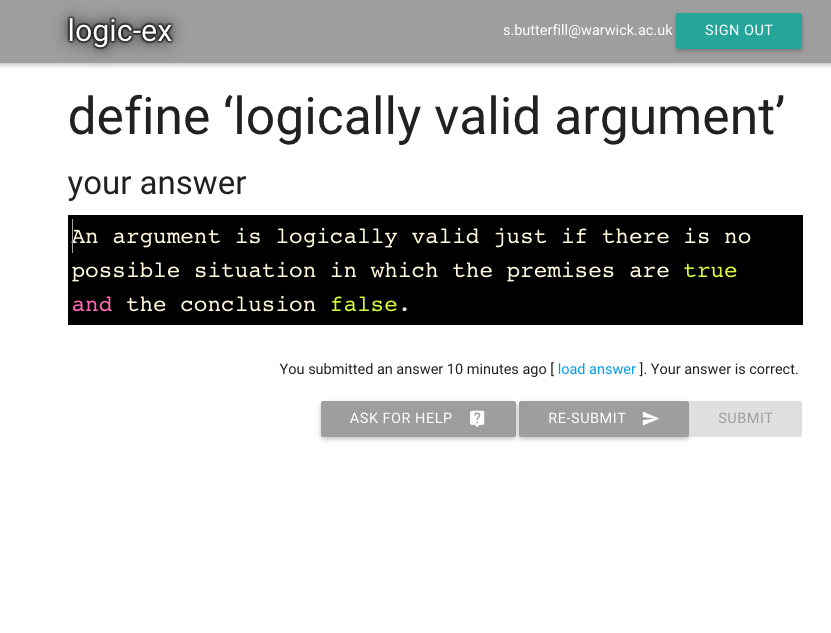
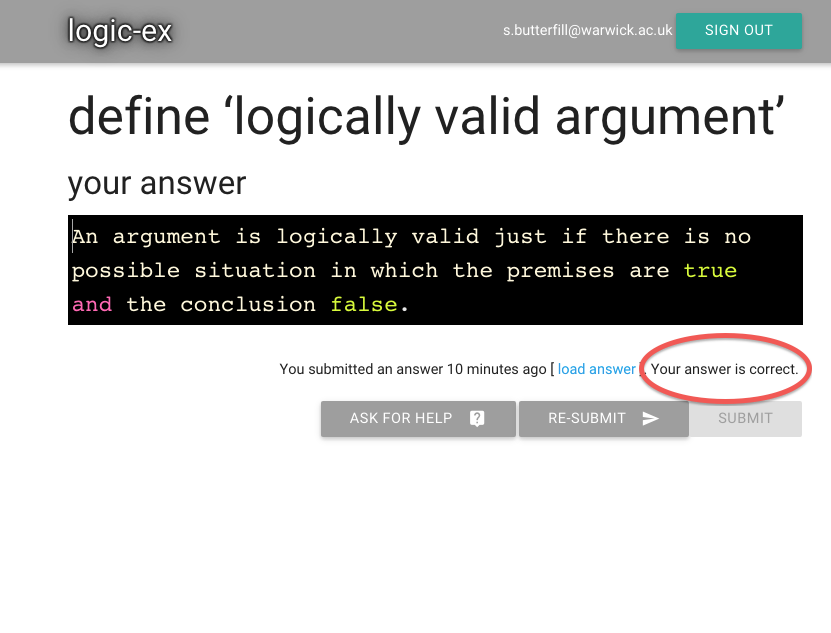
Logically Valid Arguments