Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Lecture 12}
 
\maketitle
 

Logic I

Lecture 12

\def \ititle {Logic I}
\def \isubtitle {Lecture 12}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
9.20
13.1--13.4, 13.10--13.15, *13.16
 
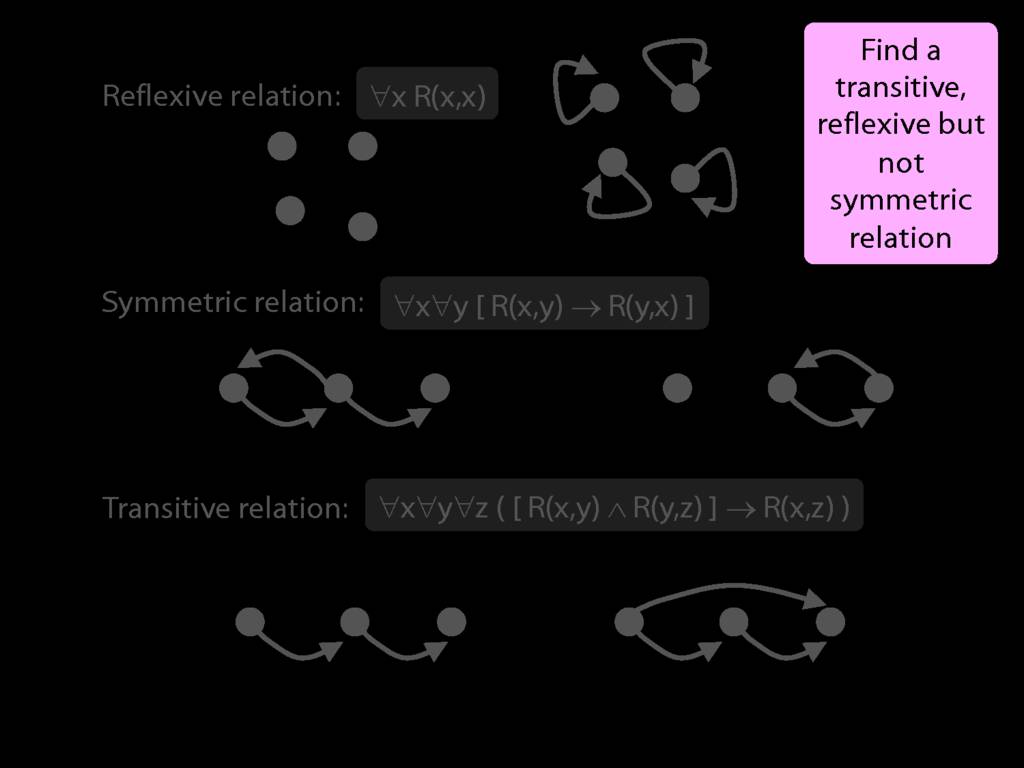
\section{Relations: Reflexive, Symmetric}
\emph{Reading:} §15.1, §15.6
 
\section{Relations: Reflexive, Symmetric}
A \emph{reflexive} relation is one that everything bears to itself. (E.g. everything is the SameShape as itself. E.g. of non-reflexive: not everything is LeftOf itself).
A \emph{symmetric} relation is one such that if x bears it to y, then y bears it to x. (E.g. Adjacent(x,y) is symmetric, LeftOf(x,y) is not symmetric.)
 
\section{Relations: Transitivity}
\emph{Reading:} §15.1, §15.6
 
\section{Relations: Transitivity}
A \emph{transitive} relation is one such that if x bears it to y and y bears it to z then x bears it to z. (E.g. LeftOf is transitive; NotAdjacent is not transitive.)
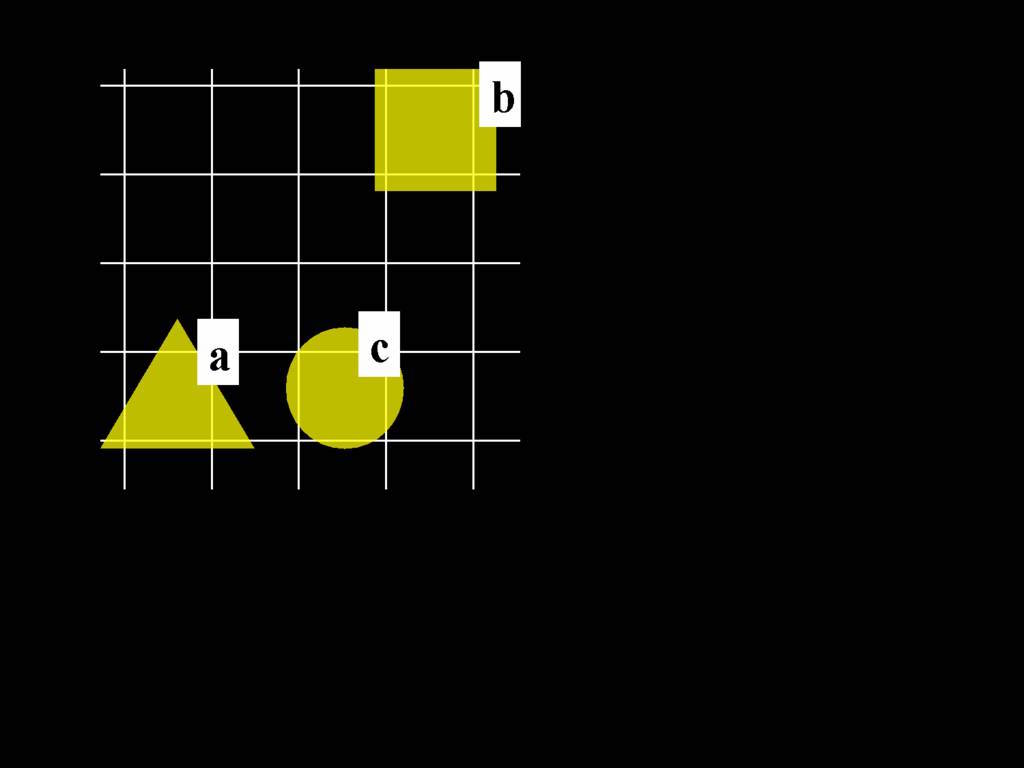
\begin{minipage}{\columnwidth}
If NotAdjacent were transitive, the following argument would be logically valid:
\end{minipage}
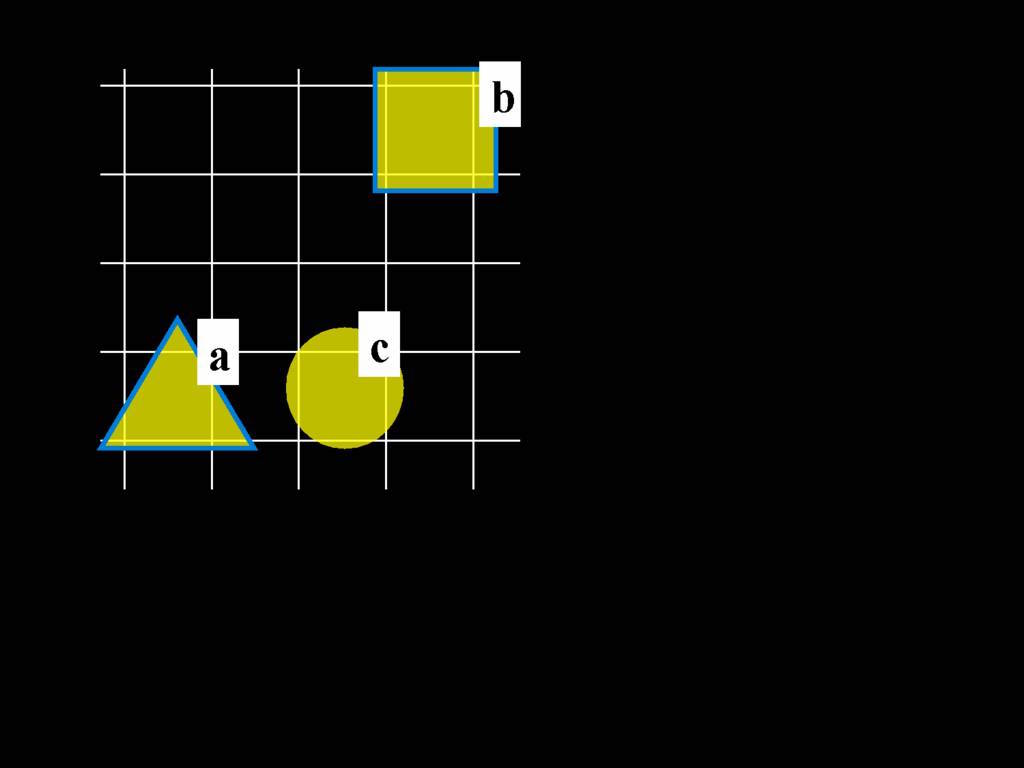
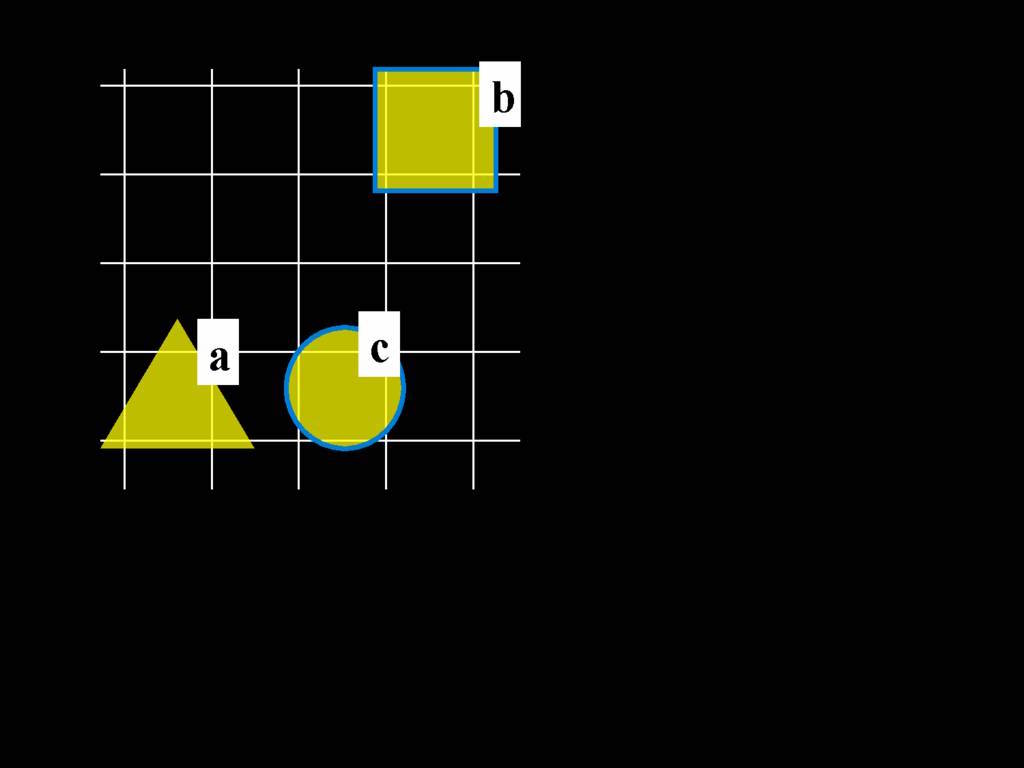
\begin{minipage}{\columnwidth}
A counterexample to this argument:
\end{minipage}

express the counterexample formally

 

Domain

{0, 1, 2}

Names

a : 0

b : 1

c : 2

Predicates

NotAdjacent : {

<0,1>, <1,2>,

<1,0>, <2,1>

}

 

Domain

{0, 1, 2}

Names

a : 0

b : 1

c : 2

Predicates

NotAdjacent : {

<0,1>, <1,2>,

<1,0>, <2,1>

}

 

Domain

{0, 1, 2}

Names

a : 0

b : 1

c : 2

Predicates

NotAdjacent : {

<0,1>, <1,2>,

<1,0>, <2,1>

}

 

Relations: Some Examples

 
\section{Relations: Some Examples}
\emph{Reading:} §15.1, §15.6
 
\section{Relations: Some Examples}
Artificial relations ...
EqualToOrLeftOf(x, y) iff
\hspace{3mm} x = y or LeftOf(x, y)
EqualToOrAdjacent(x, y) iff
\hspace{3mm} x=y or Adjacent(x, y)
JohnOrAyesha(x, y) iff
\hspace{3mm} x = John and y = Ayesha
\hspace{3mm} or x = Ayesha and y = John
JohnToAyesha(x, y) iff
\hspace{3mm} x = John and y = Ayesha
 

Defining Relations Using Dot-Arrow Diagrams

 
\section{Defining Relations Using Dot-Arrow Diagrams}
 

Expressing Relations with Quantifiers

 
\section{Expressing Relations with Quantifiers}
\emph{Reading:} §15.1, §15.6
 
\section{Expressing Relations with Quantifiers}
\begin{minipage}{\columnwidth}
A \emph{reflexive} relation is one that everything bears to itself. (E.g. SameShape)
reflexive: ∀x R(x,x)
\end{minipage}
\begin{minipage}{\columnwidth}
A \emph{symmetric} relation is one such that if x bears it to y, then y bears it to x. (E.g. Adjacent(x,y))
symmetric: ∀x∀y ( R(x,y) → R(y,x) )
\end{minipage}
\begin{minipage}{\columnwidth}
A \emph{transitive} relation is one such that if x bears it to y and y bears it to z then x bears it to z. (E.g. LeftOf is transitive; DifferentShape is not transitive)
transitive: ∀x∀y∀z ( ( R(x,y) ∧ R(y,z) ) → R(x,z) )
\end{minipage}
15.33--15.40 (second edition)
15.33, 15.37--15.39 (second edition)

feedback

‘You could recommend an introduction to logic or an introduction to thinking about logic’

  1. Stephen Read,Thinking about Logic
  2. Mark Sainsbury,Logical Forms

 

Negating Identity

 
\section{Negating Identity}
 
\section{Negating Identity}

¬a=b

¬(a=b)

} these mean the same thing

Ayesha is not Beatrice.

It’s not true that: Ayesha is Beatrice

Ayesha is this: not Beatrice (?)

a=¬b <== don’t do this!

(¬a)=b <== don’t do this either!

 

There Does Not Exist

 
\section{There Does Not Exist}
 
\section{There Does Not Exist}
Something is not dead:
\hspace{3mm} ∃x ¬Dead(x)
Nothing is dead:
\hspace{3mm} ¬∃x Dead(x)
Everything is not broken:
\hspace{3mm} ∀x ¬Broken(x)
Not everything is broken:
\hspace{3mm} ¬∀x Broken(x)

Something is dead.

∃x Dead(x)

Something is not dead.

∃x ¬Dead(x)

Nothing is dead.

¬∃x Dead(x)

​1.

​2.a=a=Intro
​3.∃x (x=x)∃Intro: 2

Everything is broken.

∀x Broken(x)

Everything is not broken.

∀x ¬Broken(x)

Not everything is broken.

¬∀x Broken(x)

​1.

¬∃x Dead(x)

​2.

Dead(a)

​3.∃x Dead(x)∃Intro: 2
​4.⊥⊥Intro: 1,3
​5.¬Dead(a)¬Intro: 2-4
​6.∃x ¬Dead(x)∃Intro: 5
​1.

∃x ¬Dead(x)

​2.¬∃x Dead(x)

Counterexample:

Domain: {Ayesha, Beatrice}

Dead : { <Beatrice> }

a : Ayesha ; b : Beatrice

... Dead(b) is true; so the conclusion, ¬∃x Dead(x), is false

... and ¬Dead(a) is true; so the premise, ∃x ¬Dead(x), is true

9.12
9.18--9.19
 

Expressing Counterexamples Formally

 
\section{Expressing Counterexamples Formally}
\emph{Reading:} §15.1, §15.6
 
\section{Expressing Counterexamples Formally}
Give a counterexample to this argument:
Informally:
Formally:
\hspace{3mm} Domain: \{a, b\}
\hspace{3mm} R: \{<a,a>, <a,b>, <b,b>\}
Here’s a quick look at how to enter the counterexample in zoxiy. If you want more detail, please see the user guide (which is linked to on the home page of zoxiy).

 

Summary of Relations

 
\section{Summary of Relations}
 

Proof Example: A∧B therefore ¬(¬A∨¬B).

 
\section{Proof Example: A∧B therefore ¬(¬A∨¬B).}
 
\section{Proof Example: A∧B therefore ¬(¬A∨¬B).}
 

Proof Example: P therefore ¬¬P.

 
\section{Proof Example: P therefore ¬¬P.}
 
\section{Proof Example: P therefore ¬¬P.}
 

Proof Example: S∨(Q∧R) therefore S∨Q.

 
\section{Proof Example: S∨(Q∧R) therefore S∨Q.}
 
\section{Proof Example: S∨(Q∧R) therefore S∨Q.}