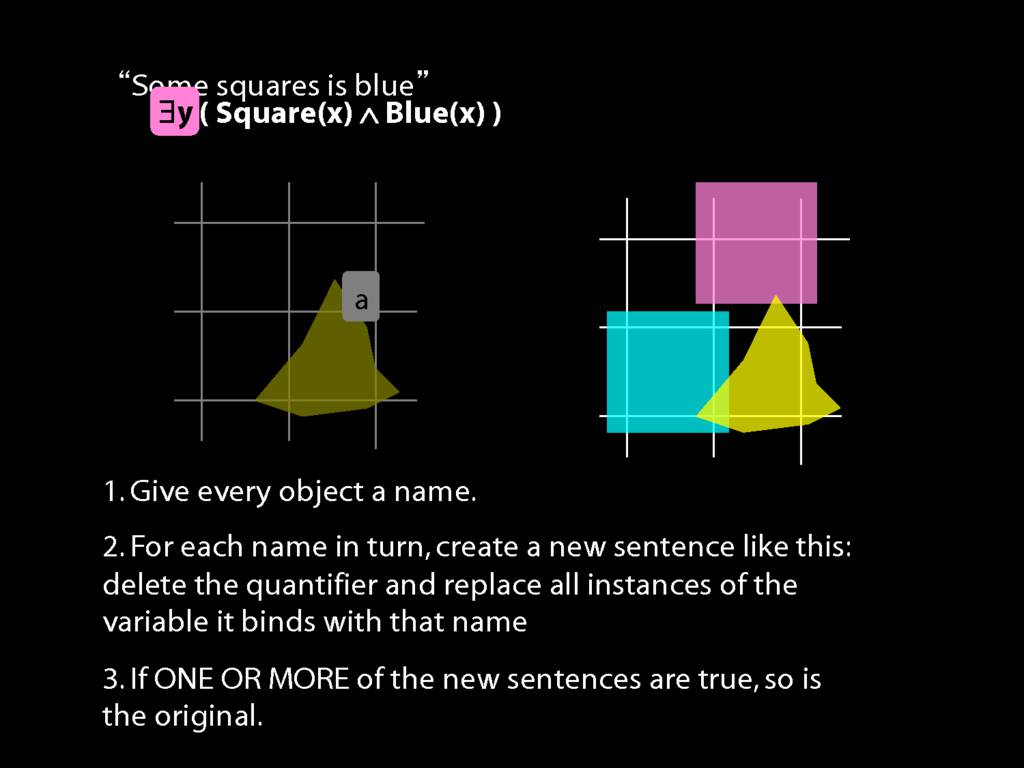
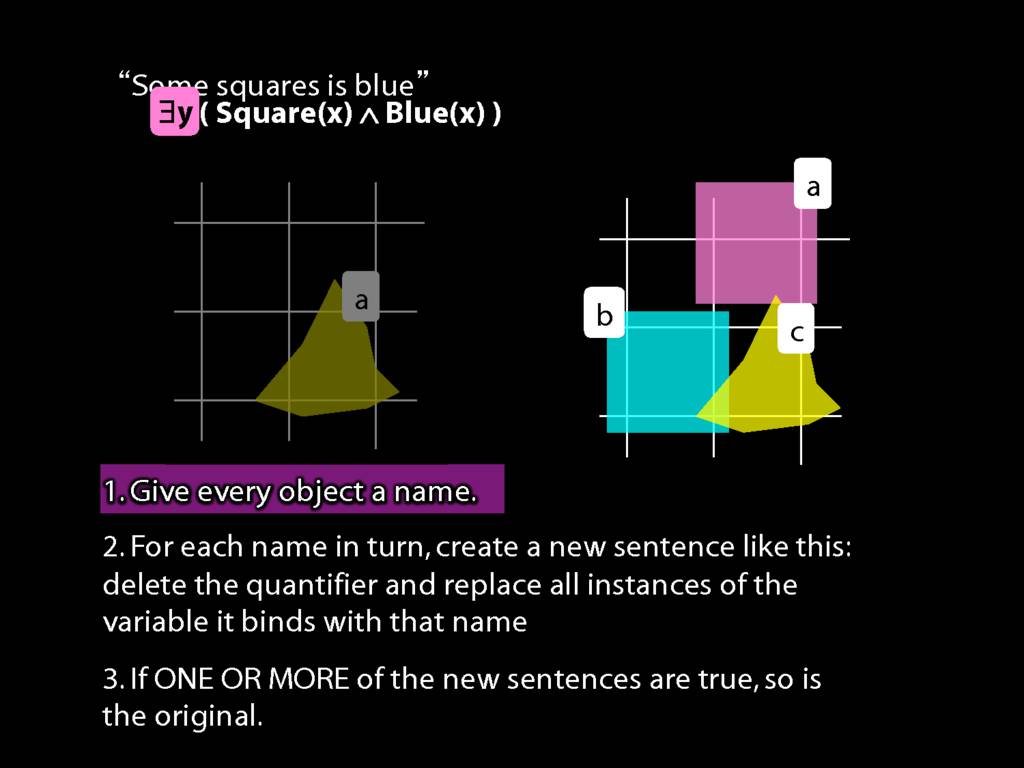
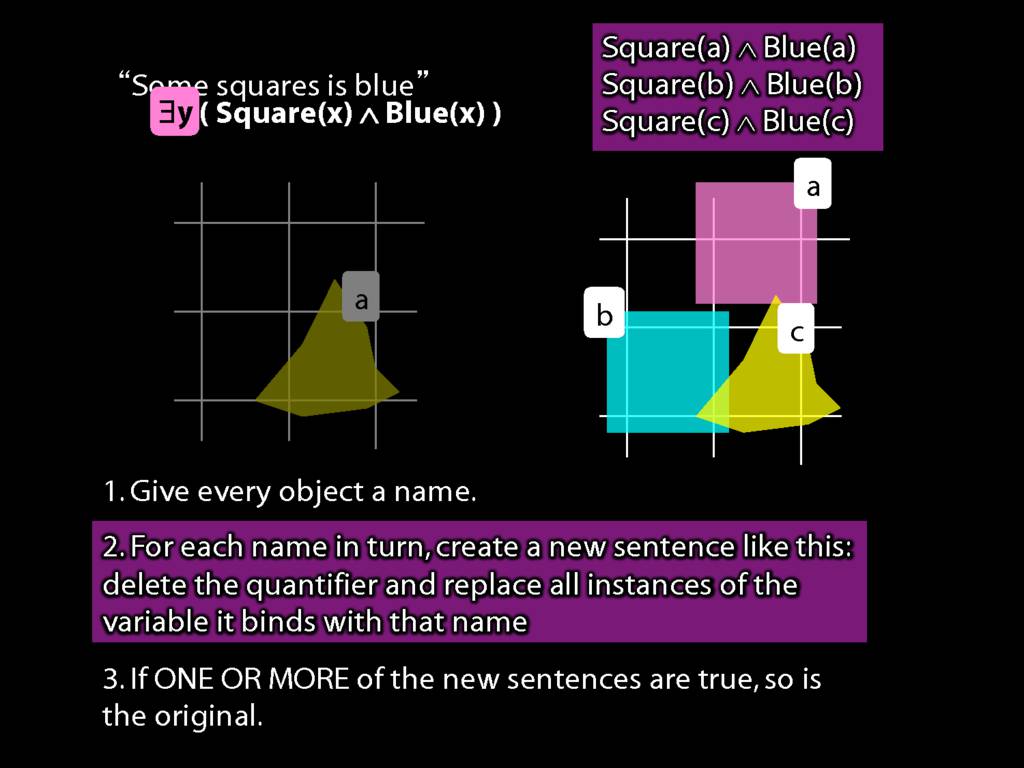
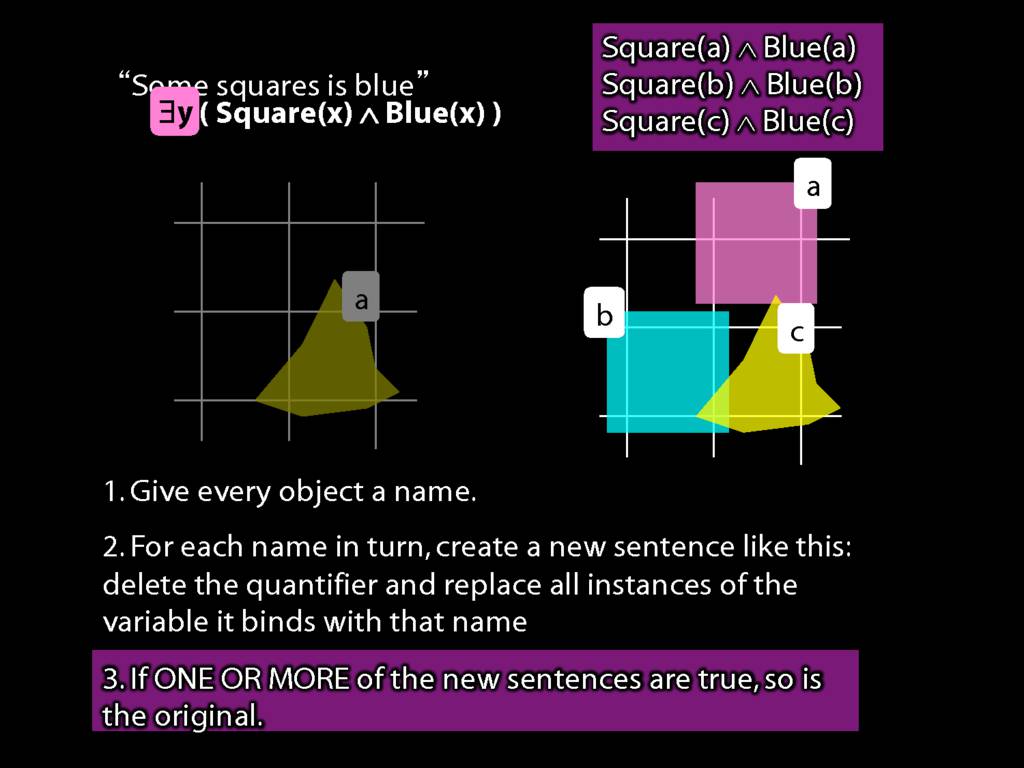
\title {Logic I \\ Lecture 13}
\maketitle
10.24–7, *10.28–9
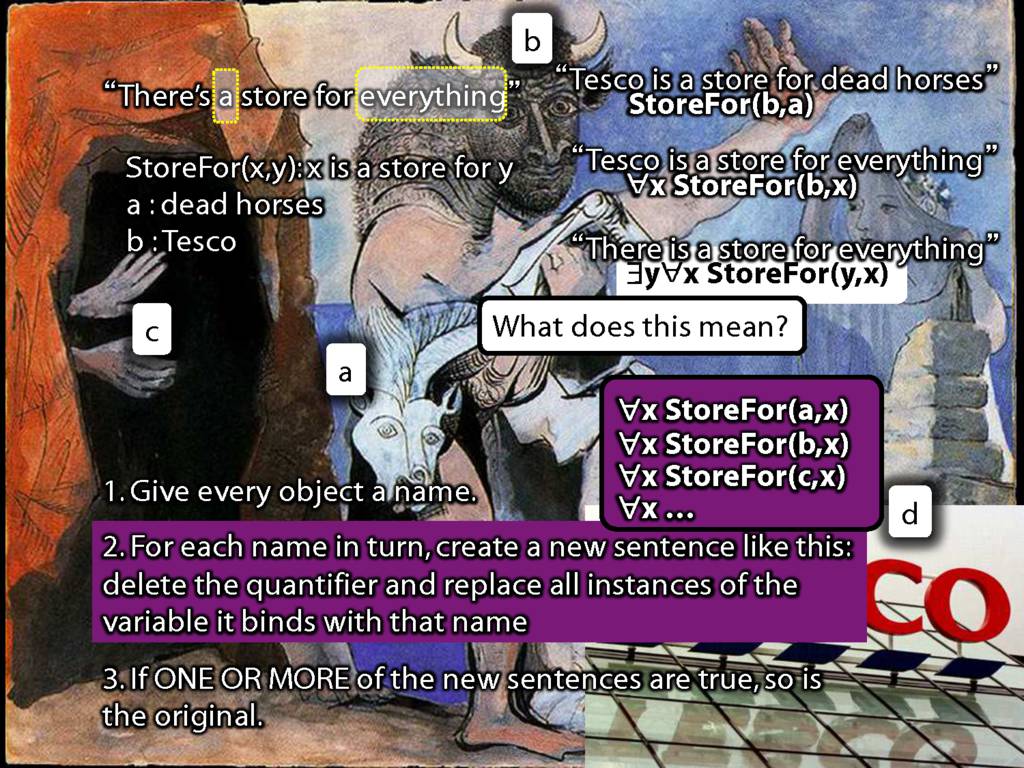
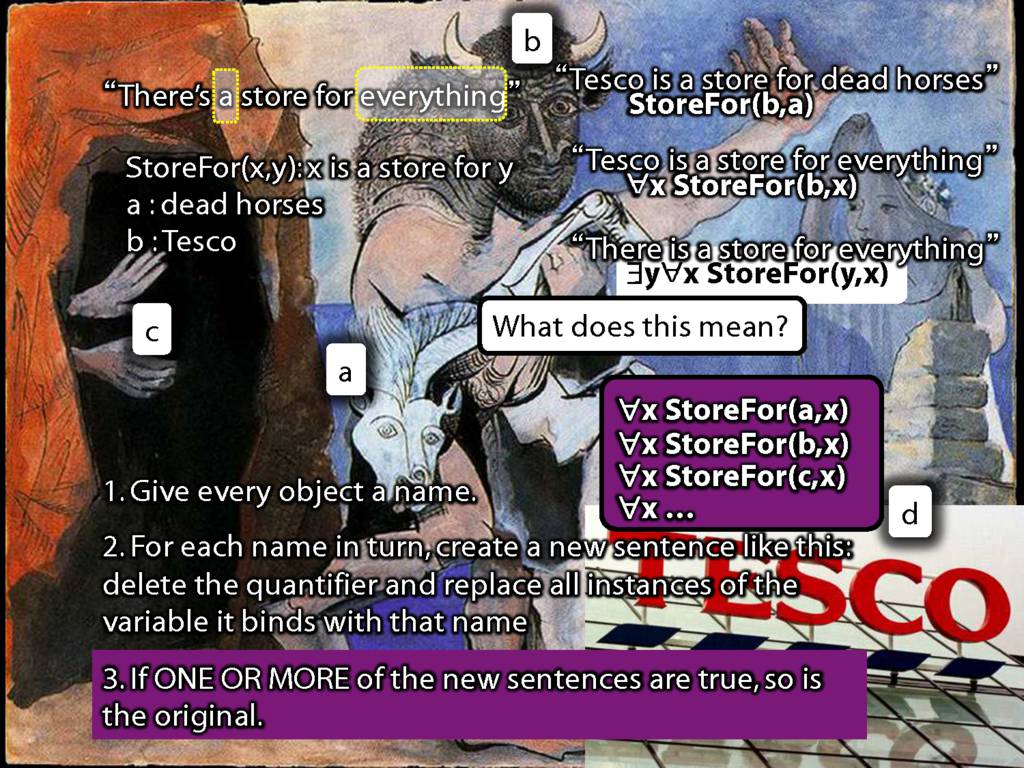
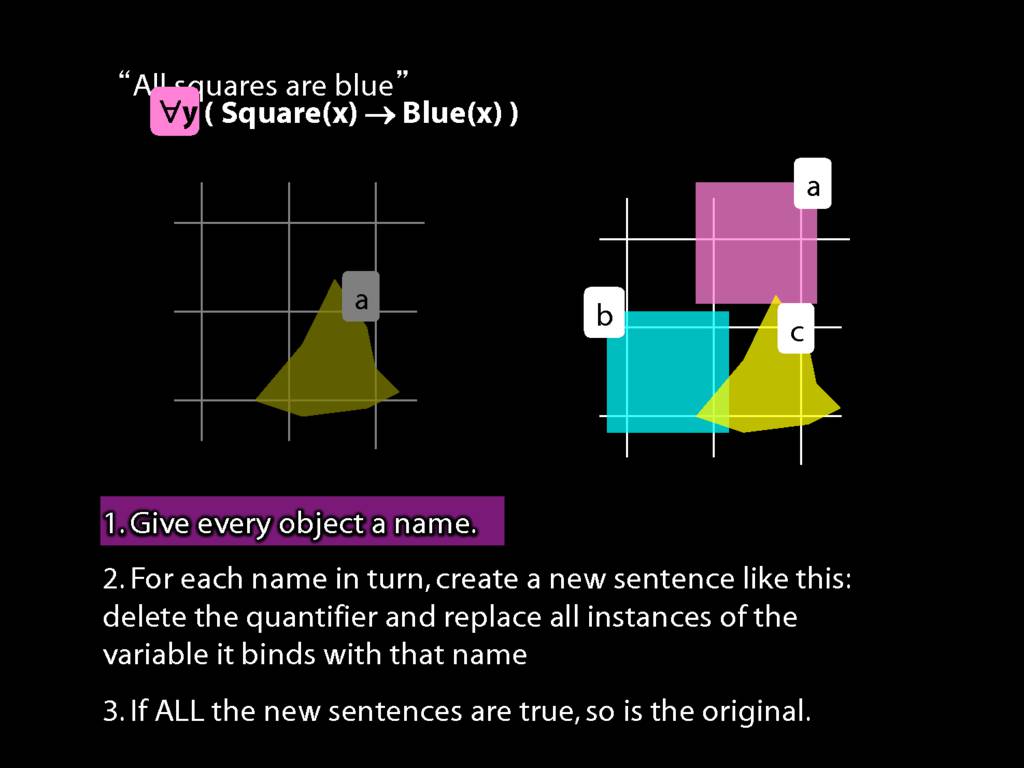
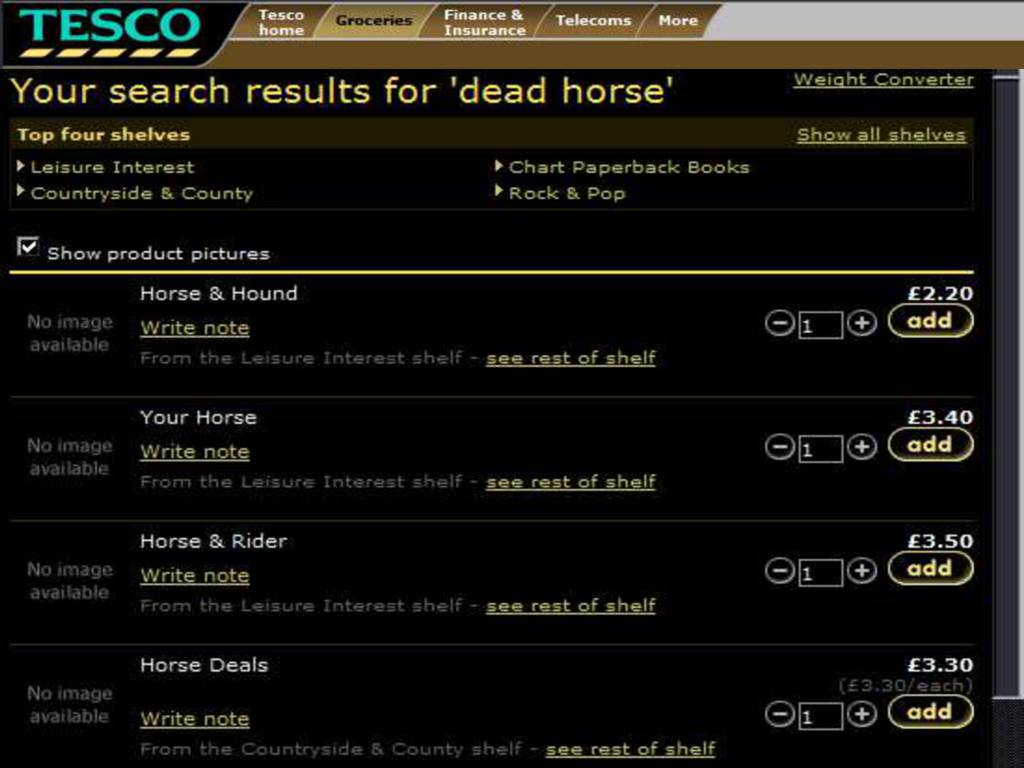
\section{There Is a Store for Everything}
\emph{Reading:} §11.2, §11.3
\section{There Is a Store for Everything}
11.3
11.4, 11.8, 11.9
11.11, 11.13, *11.10
11.8, 11.9, *11.11
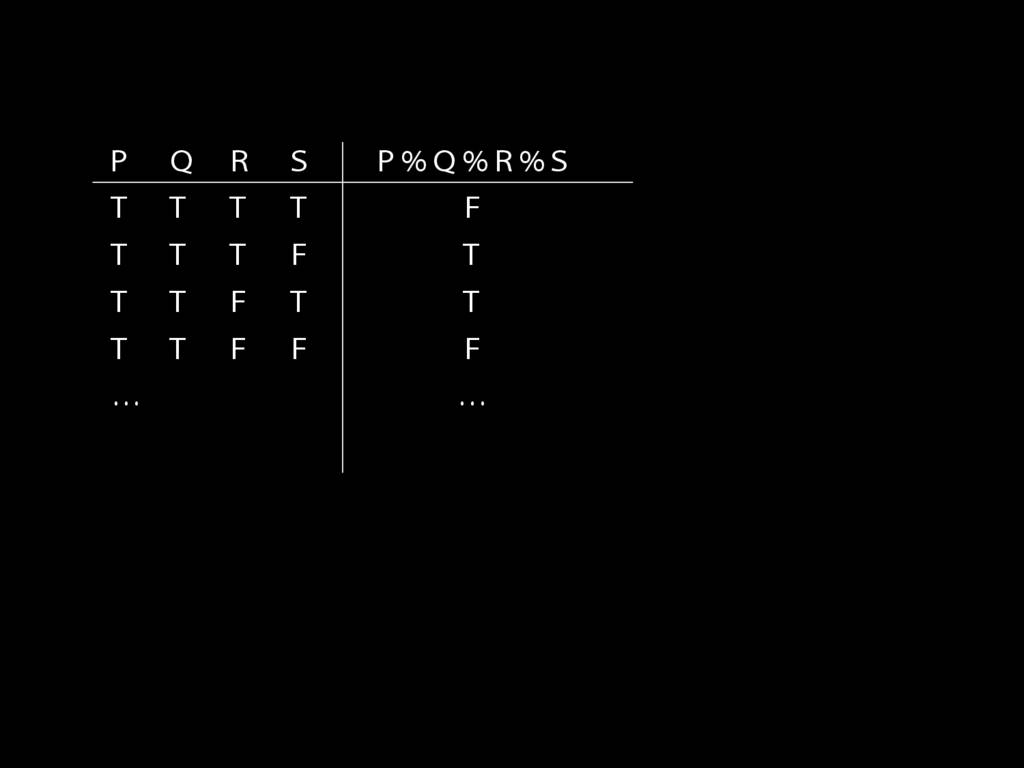
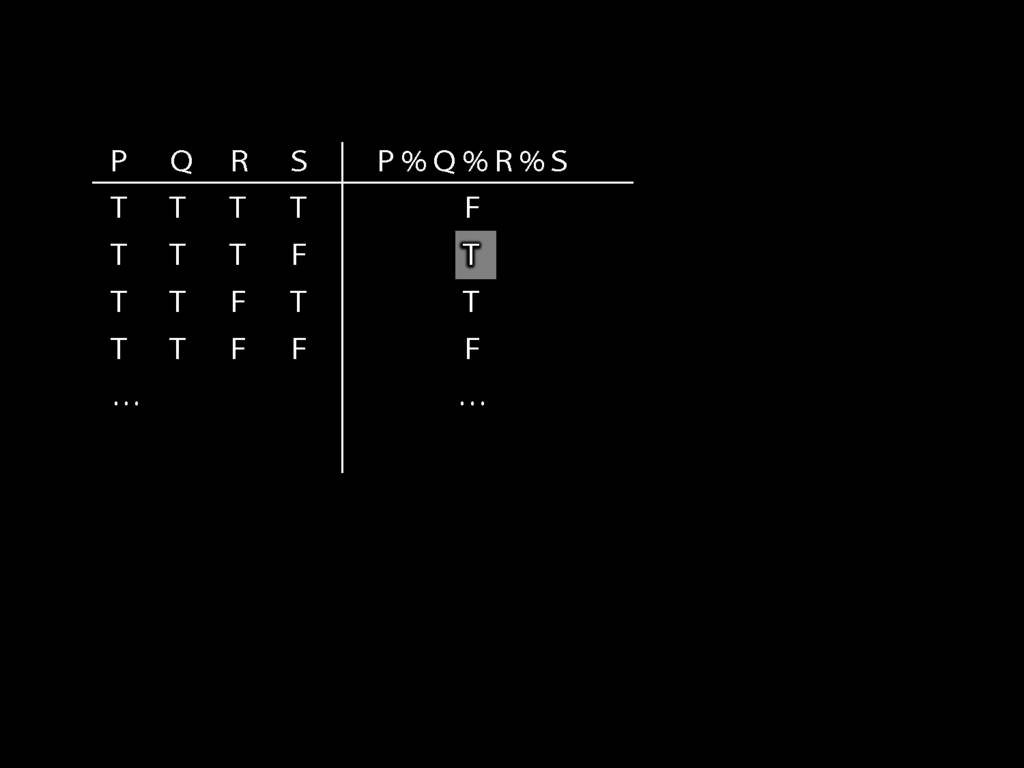
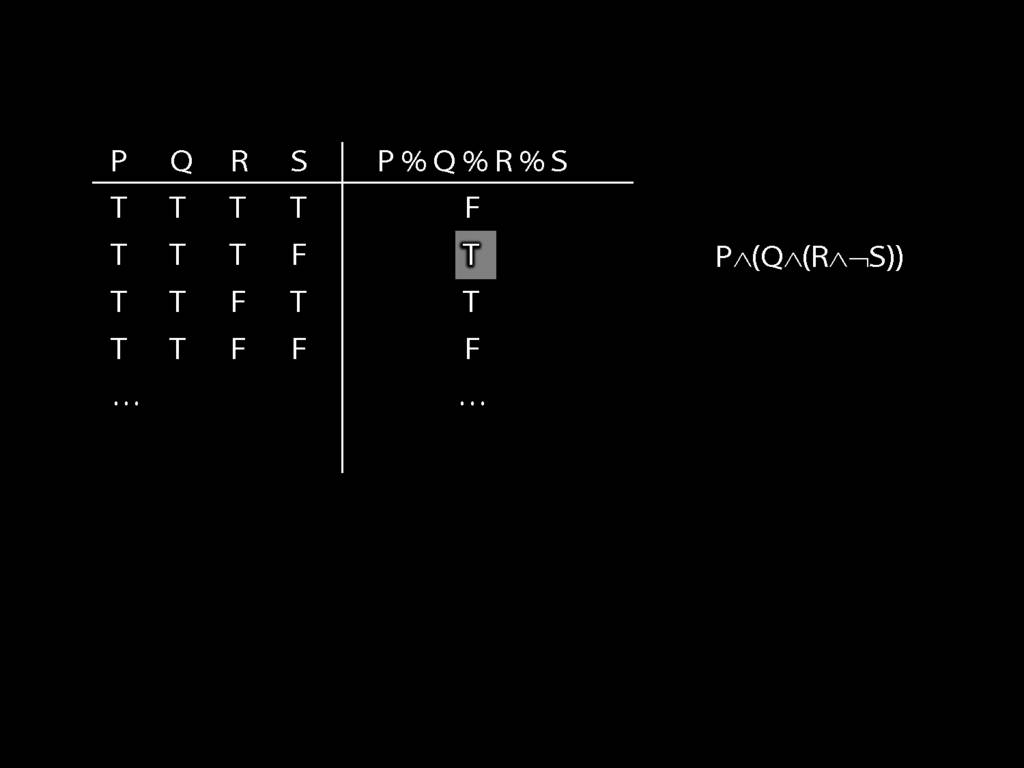
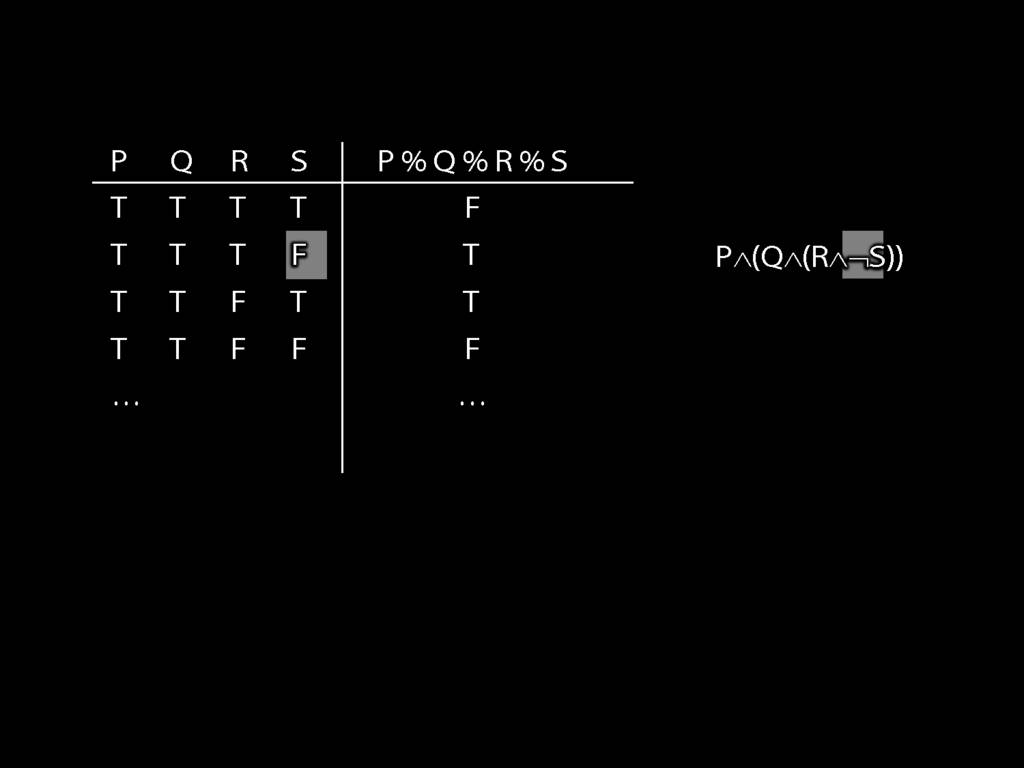
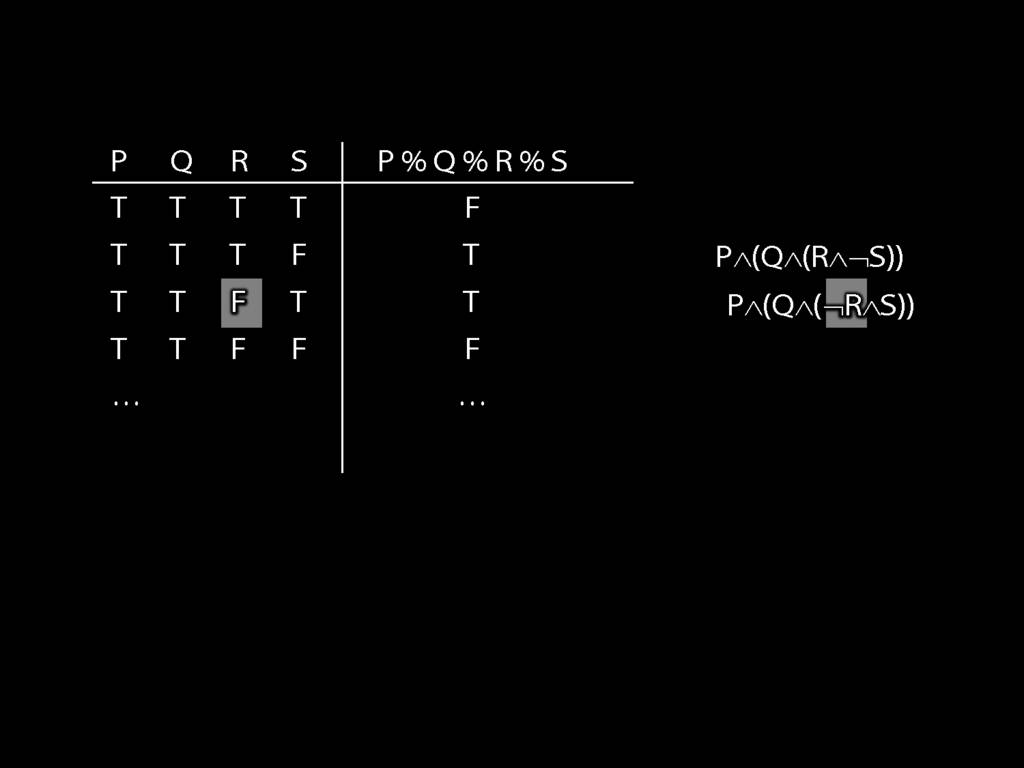
\section{How Big Is a Truth-Table?}
\section{How Big Is a Truth-Table?}
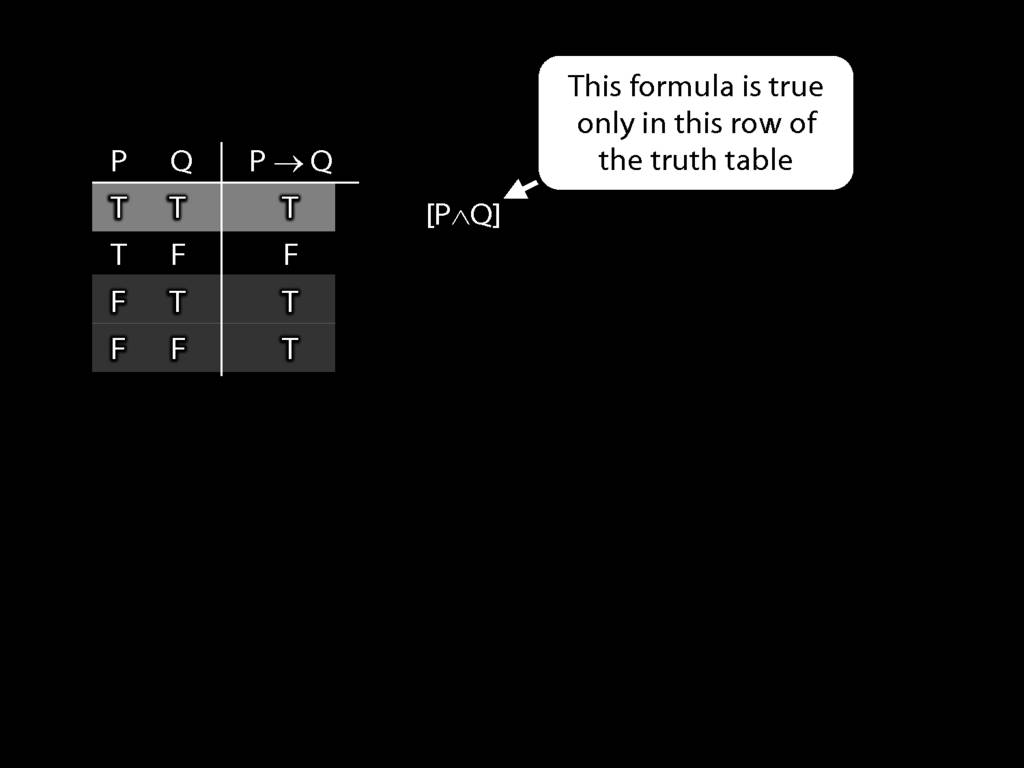
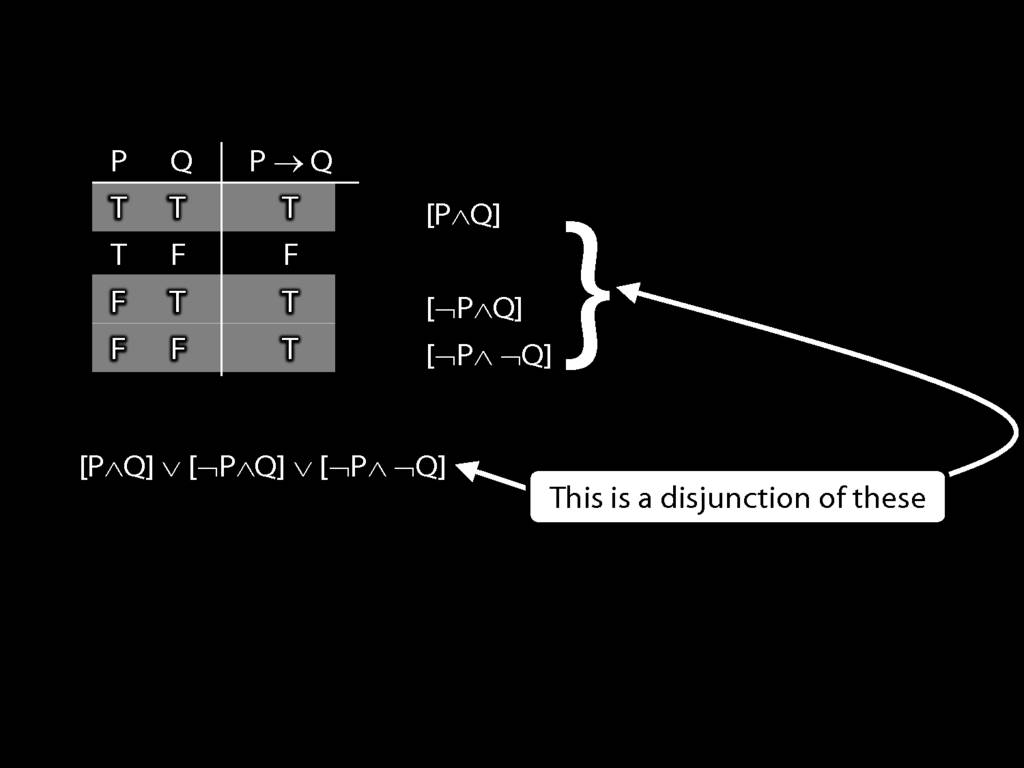
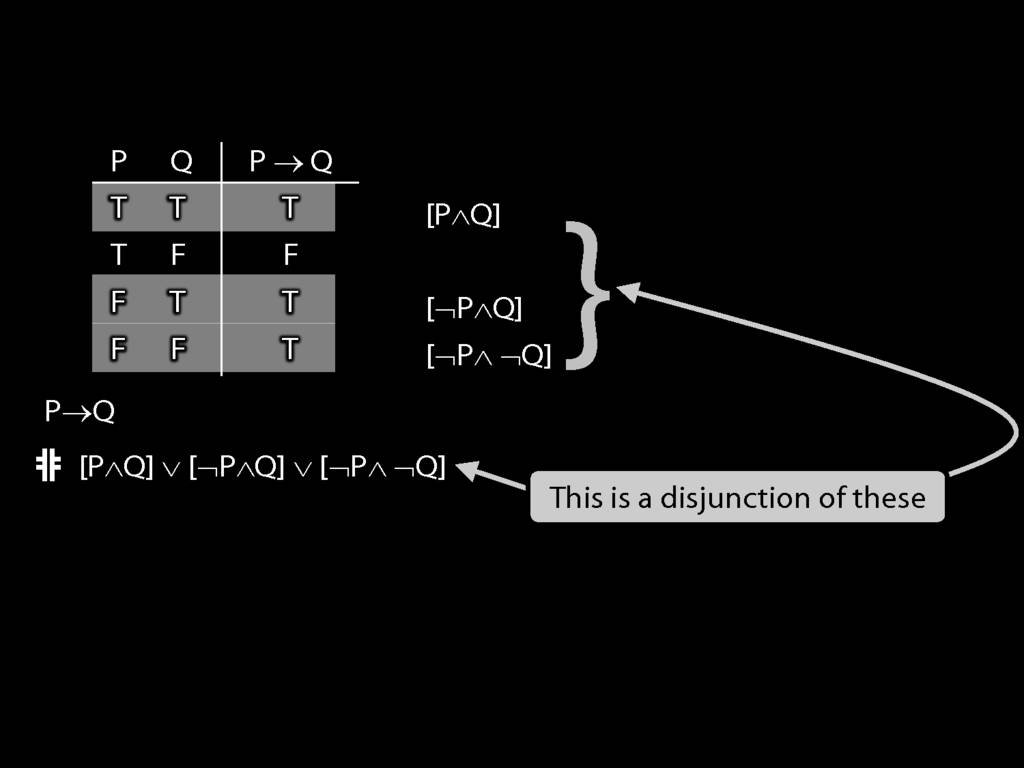
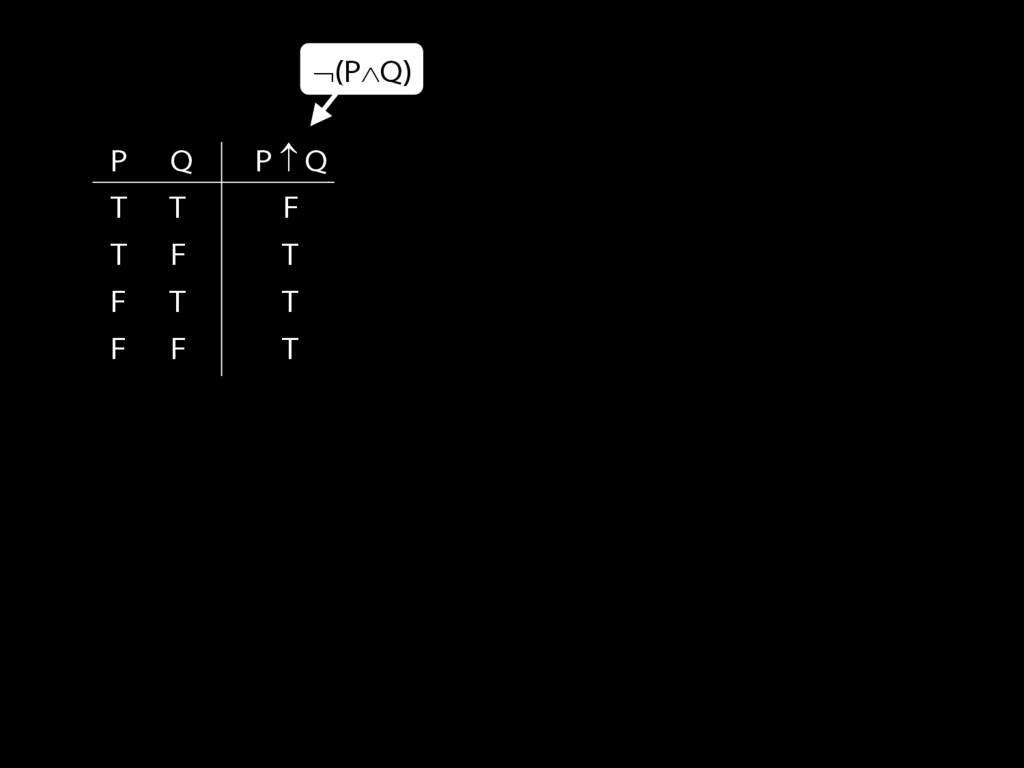
\section{Truth-functional completeness}
\emph{Reading:} §7.4
\section{Truth-functional completeness}
7.25, 7.26, *7.28, 7.29
7.25, 7.26, *7.28, 7.29