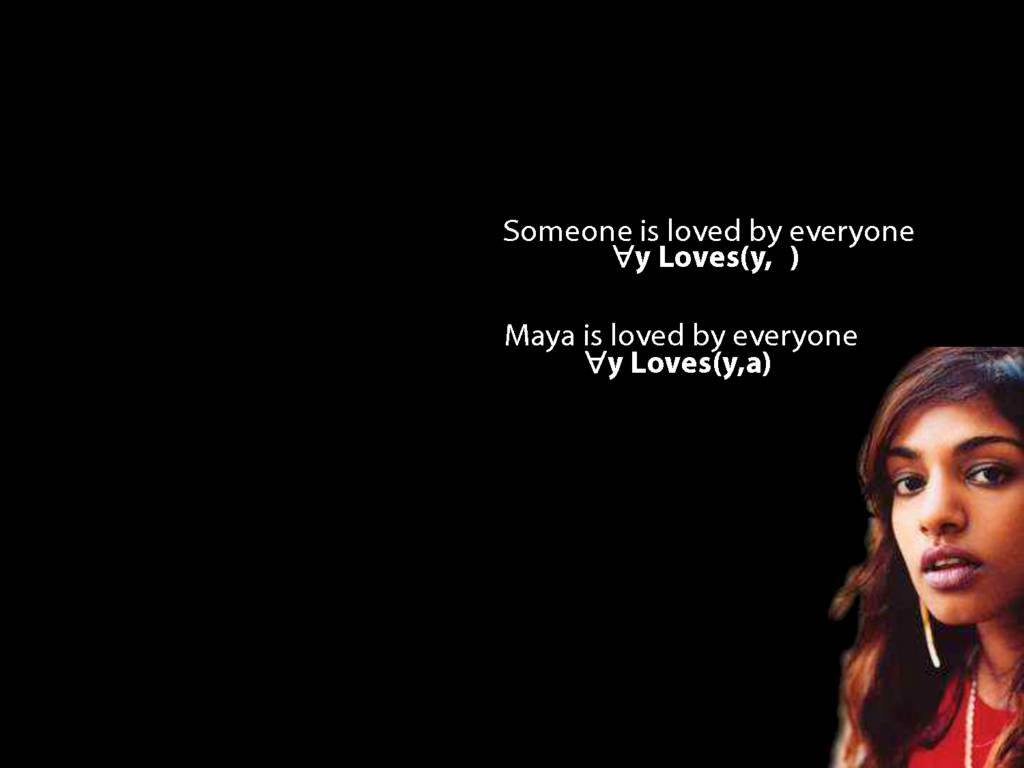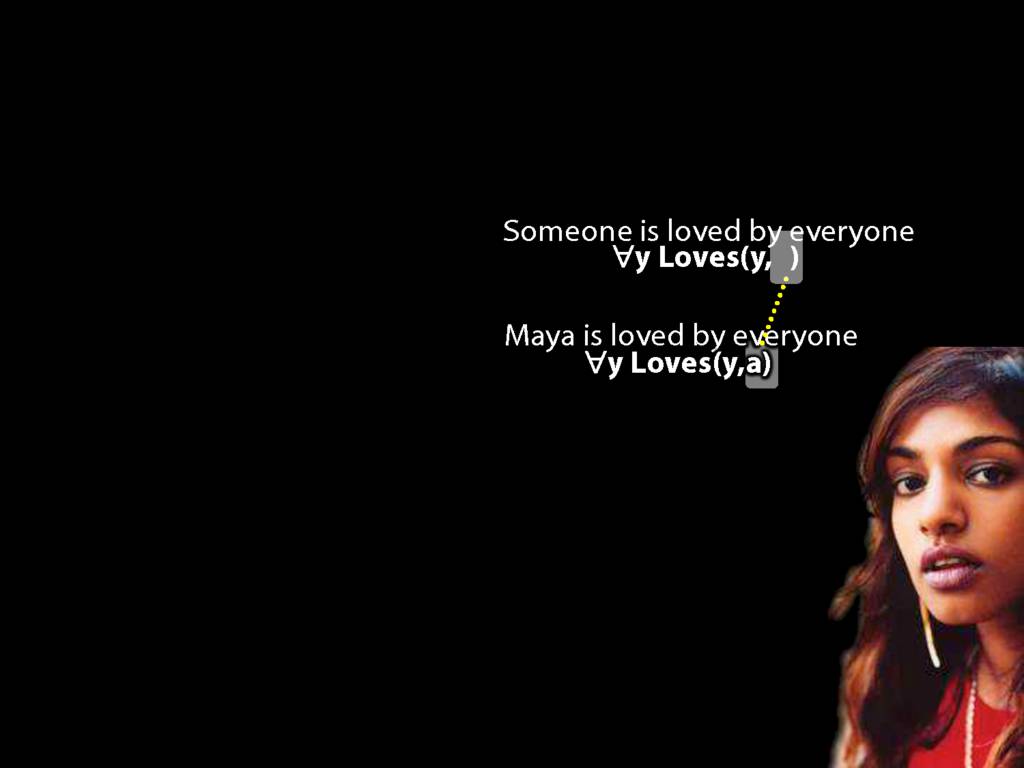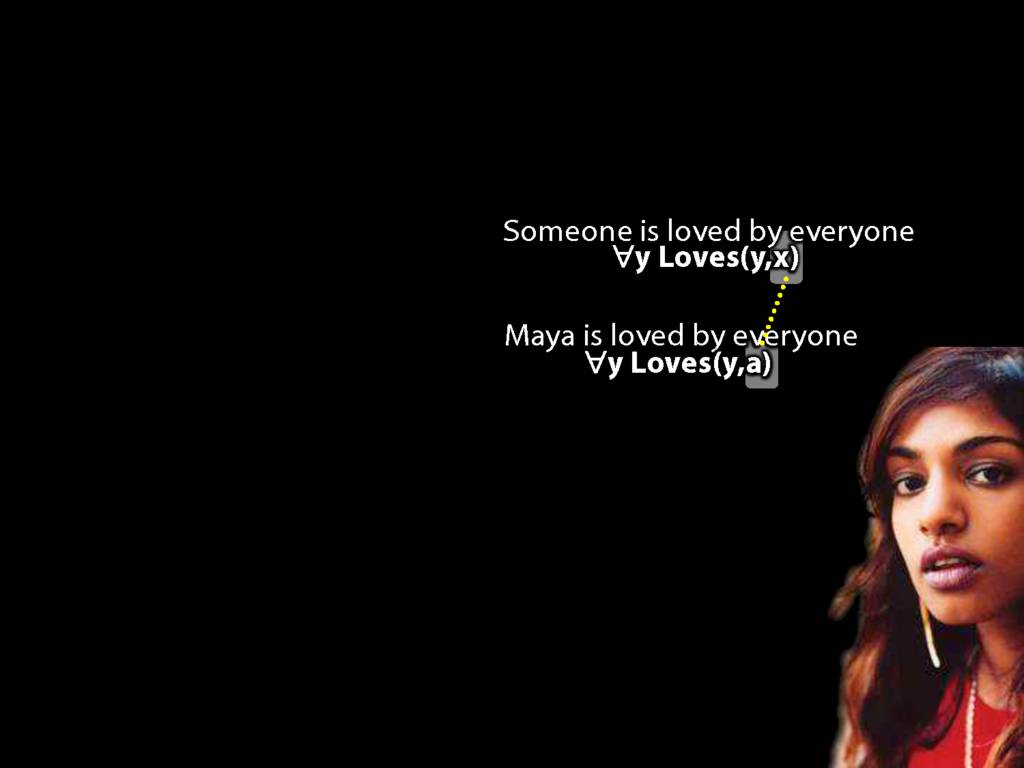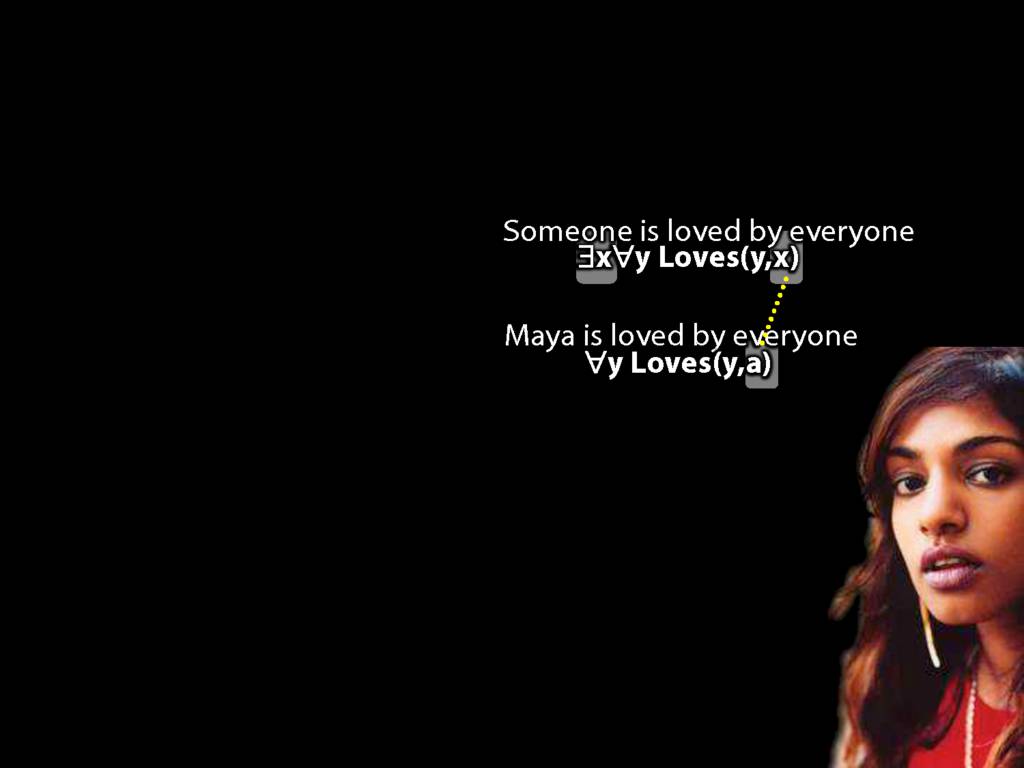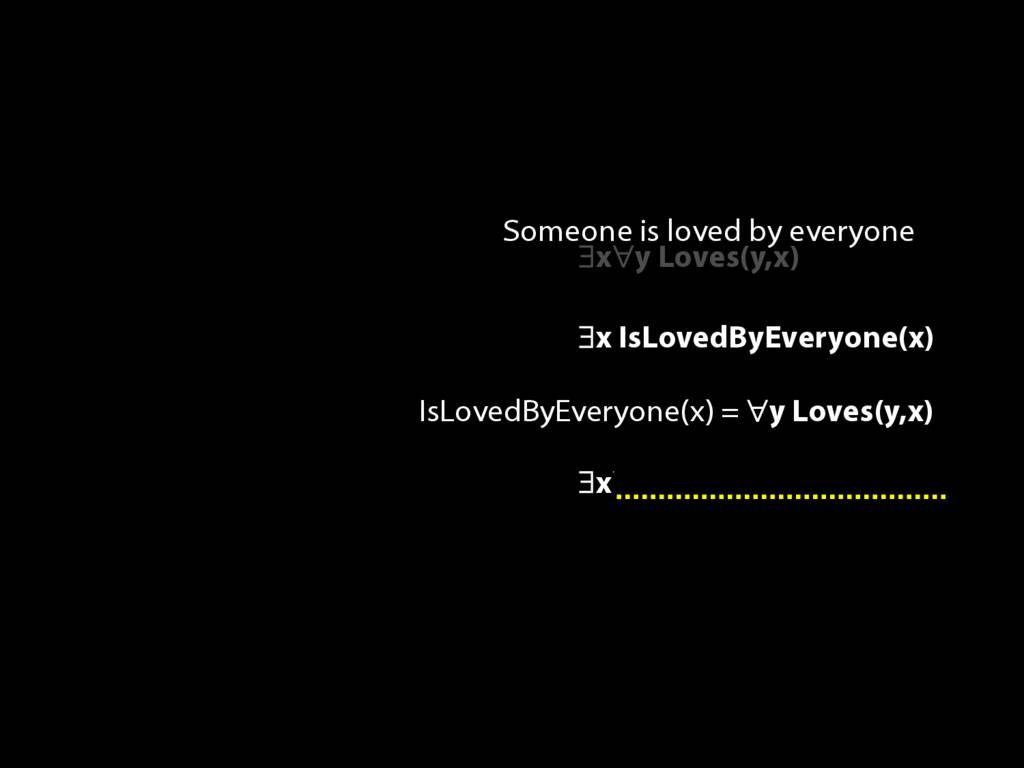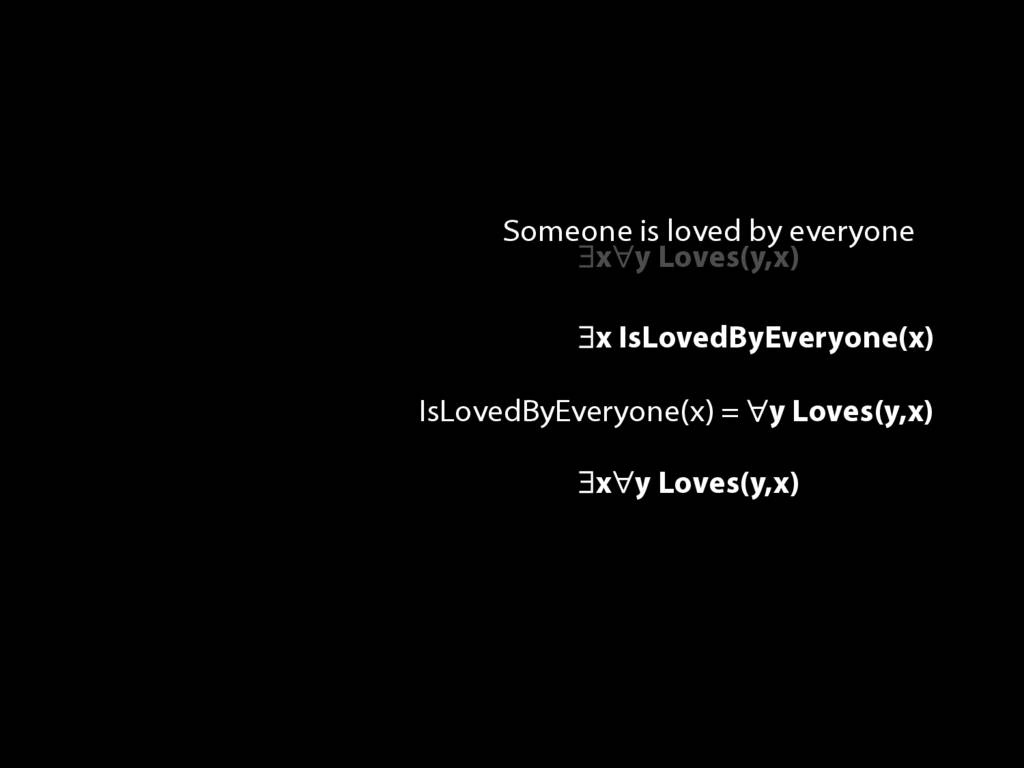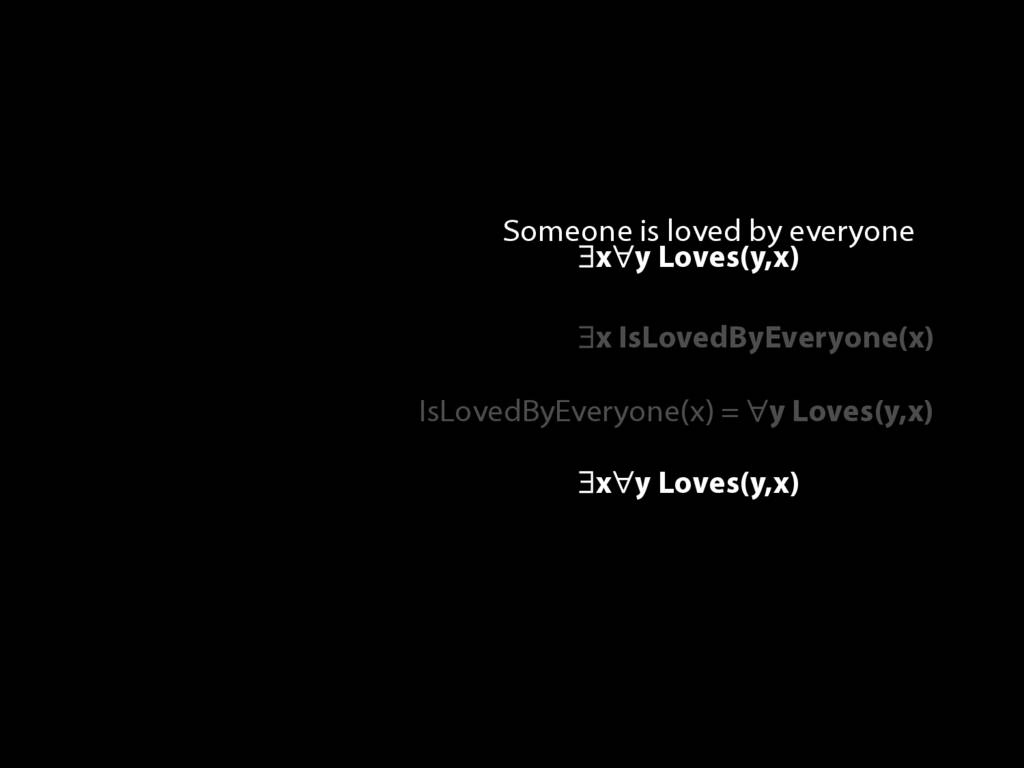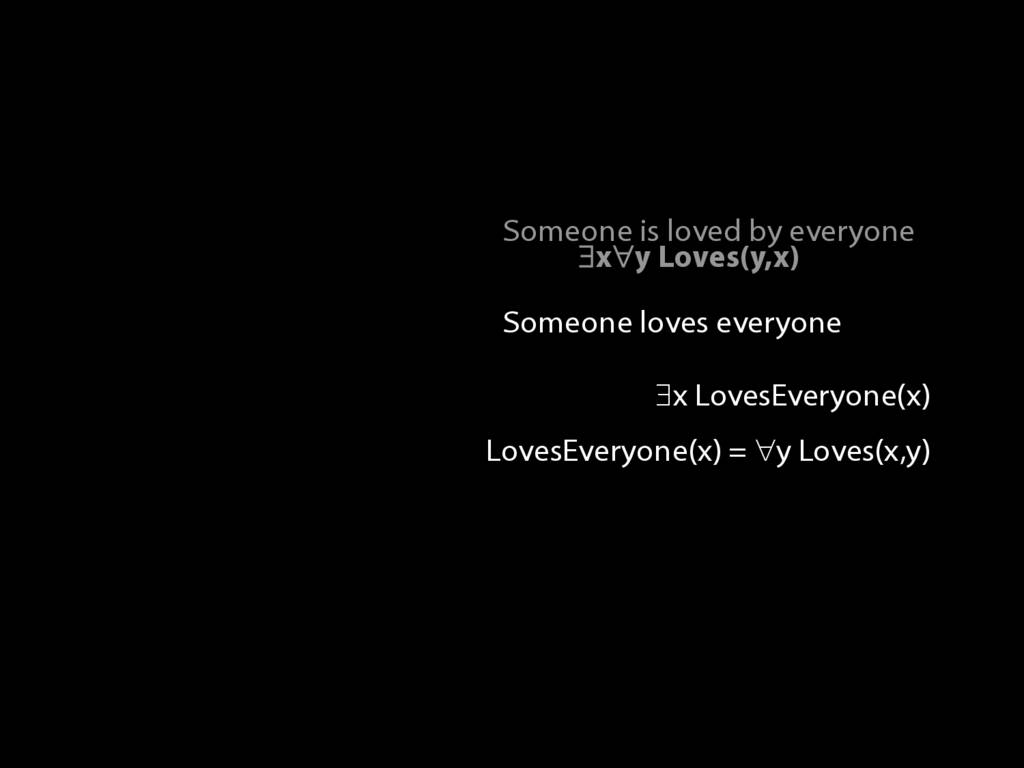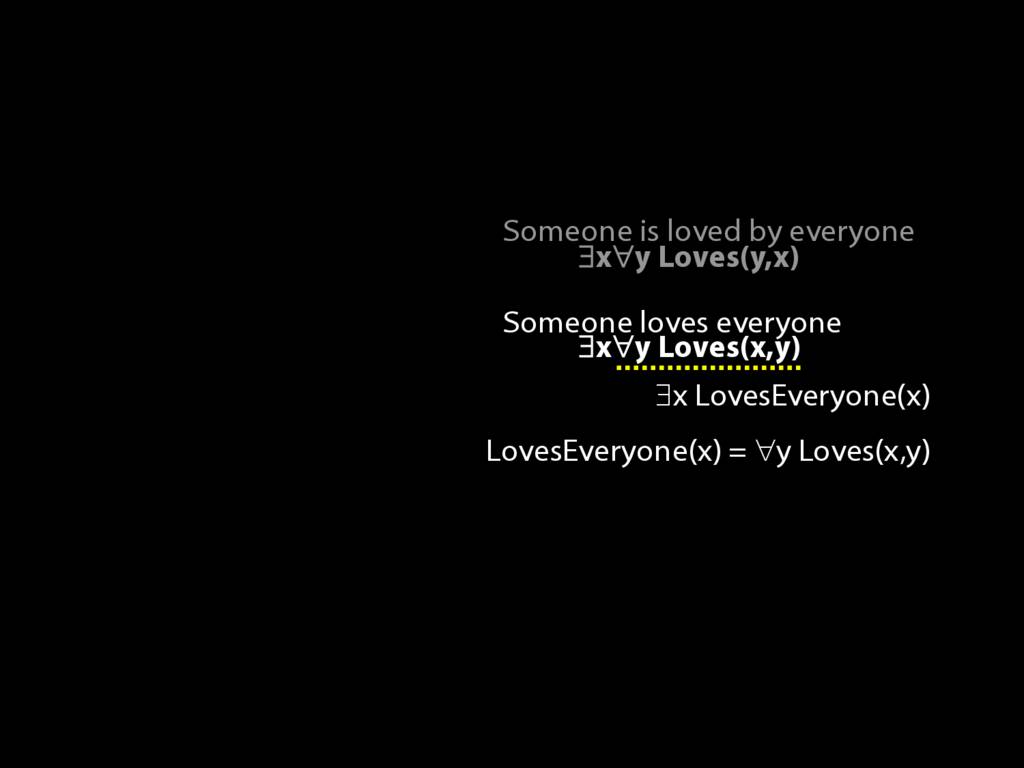Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

\title {Logic I \\ Lecture 14}
 
\maketitle
 

Logic I

Lecture 14

\def \ititle {Logic I}
\def \isubtitle {Lecture 14}
\begin{center}
{\Large
\textbf{\ititle}: \isubtitle
}
 
\iemail %
\end{center}
Readings refer to sections of the course textbook, \emph{Language, Proof and Logic}.
 
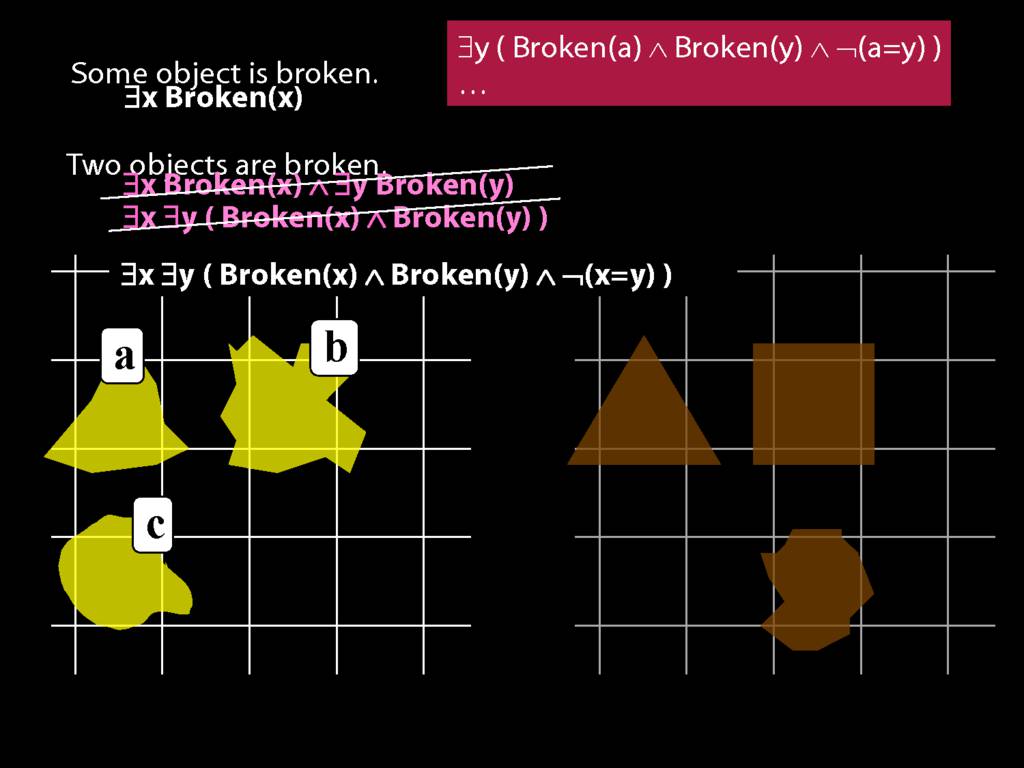
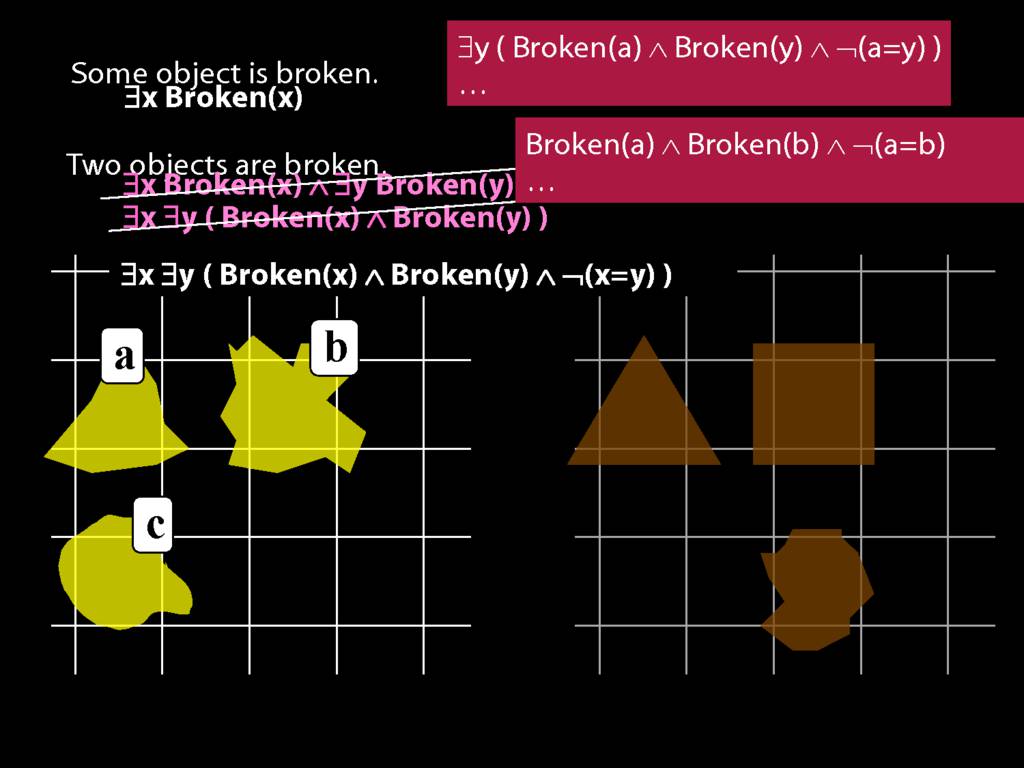
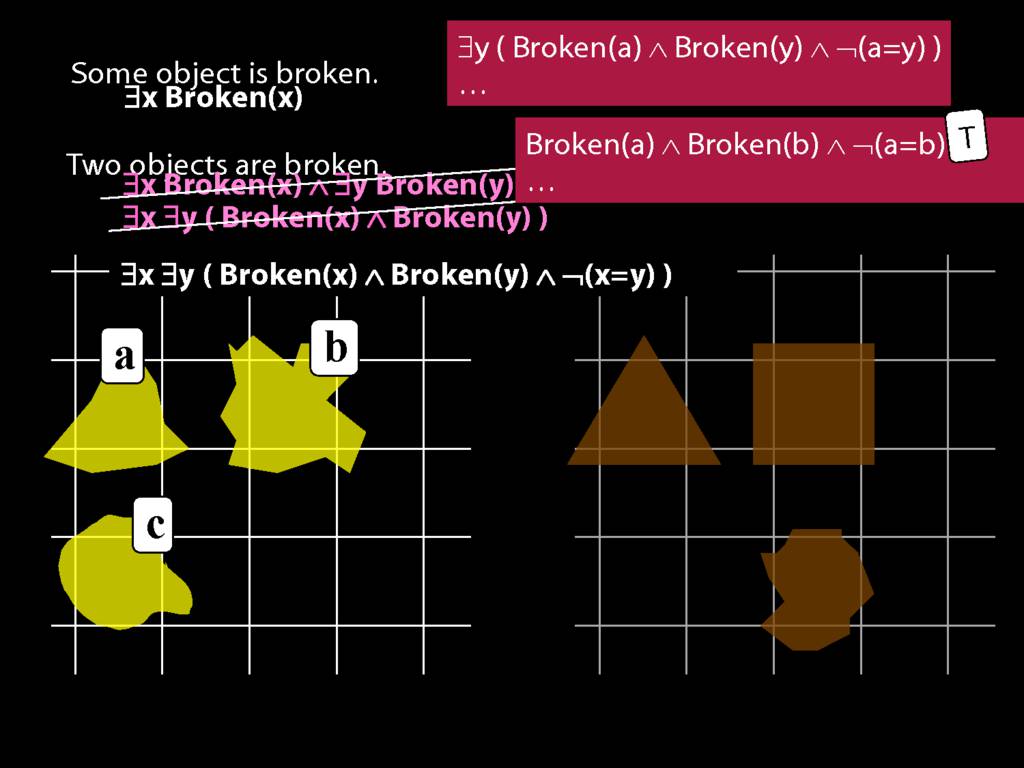
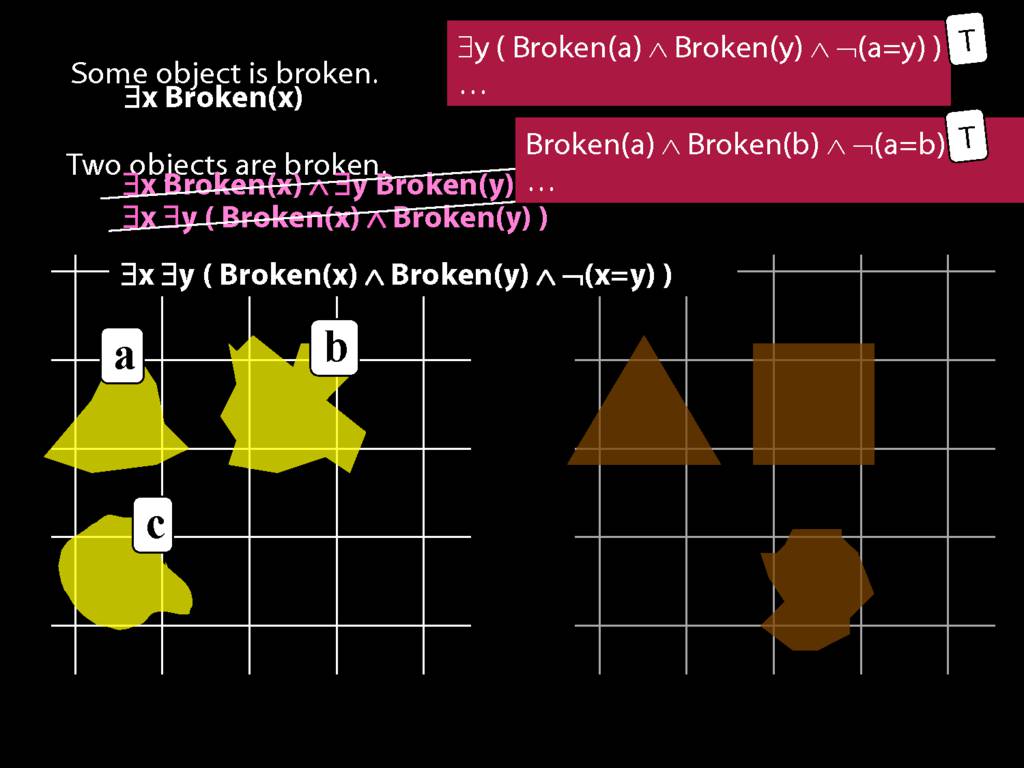
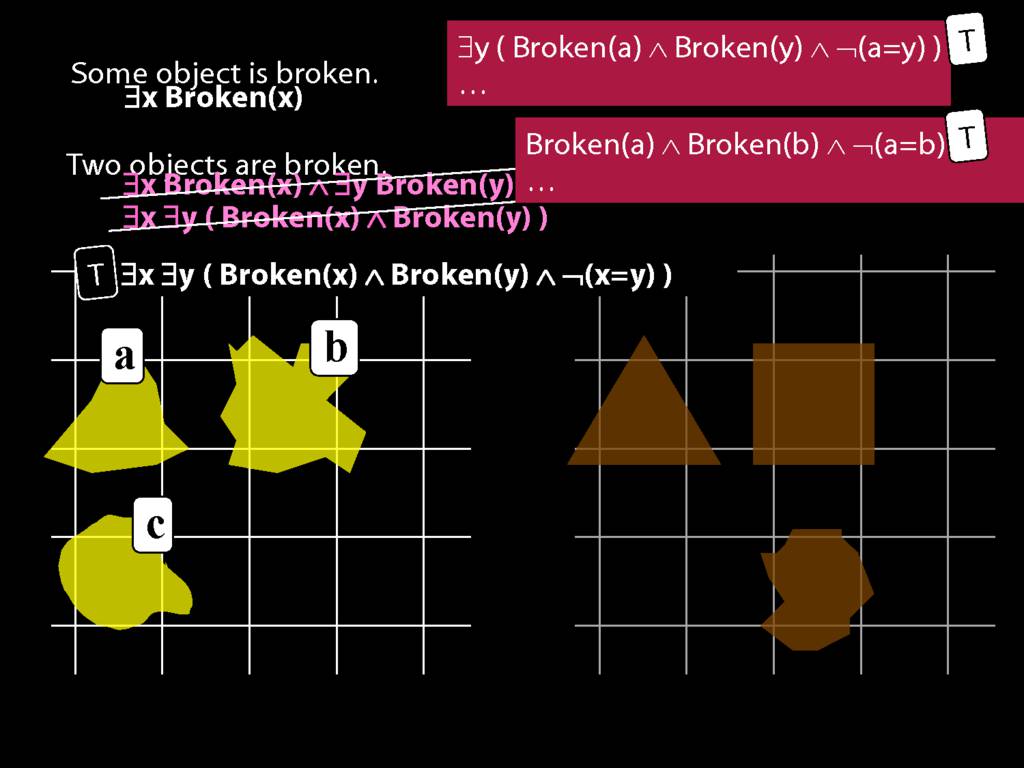
\section{Two Things Are Broken}
\emph{Reading:} §14.1
 
\section{Two Things Are Broken}
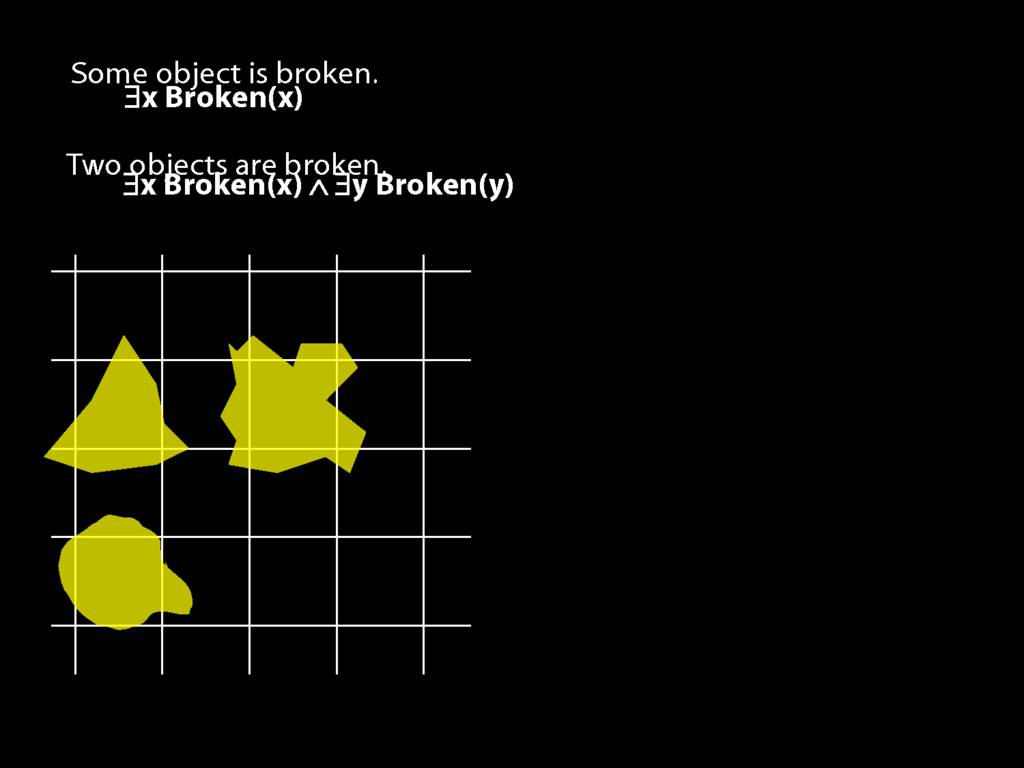
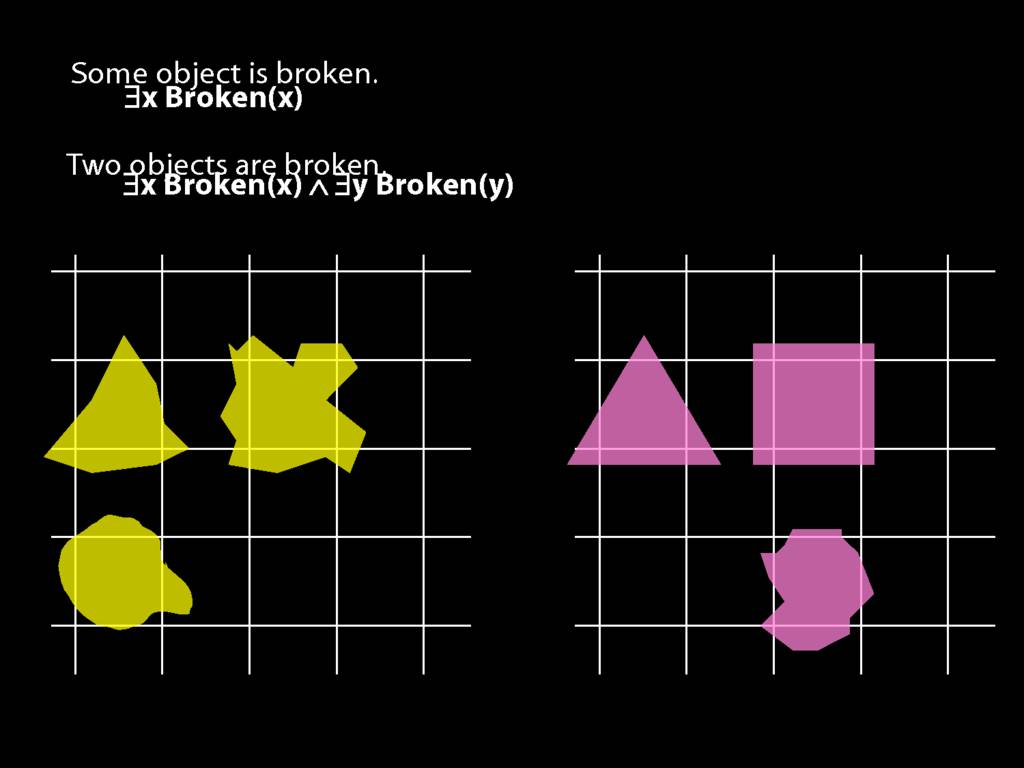
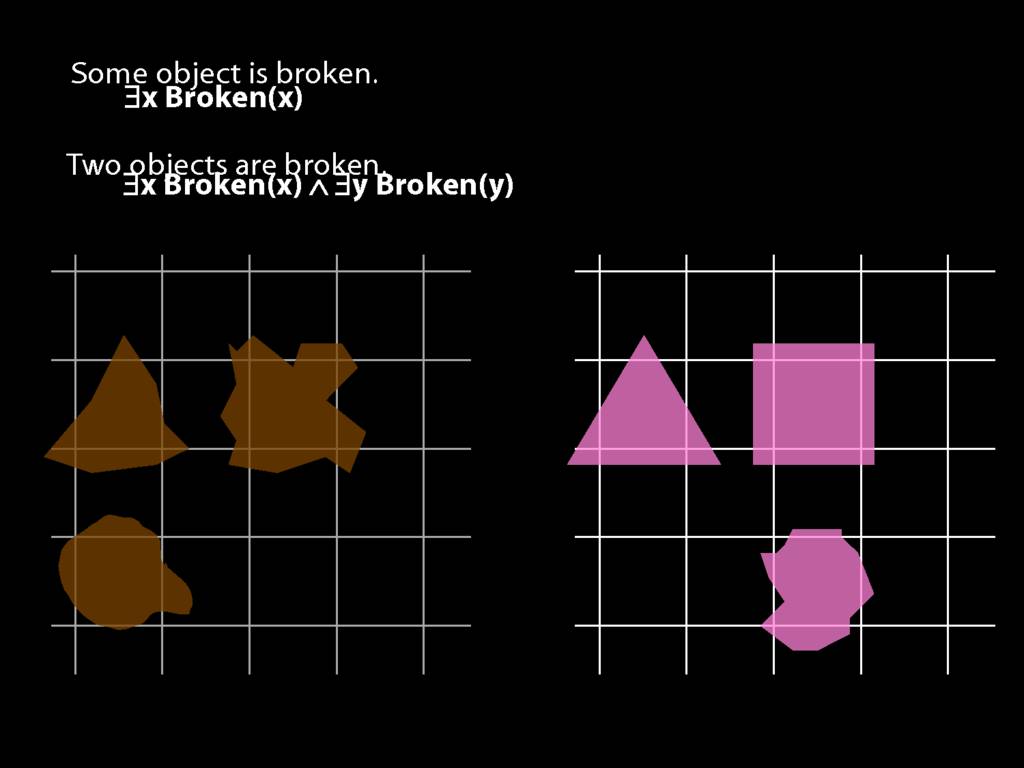
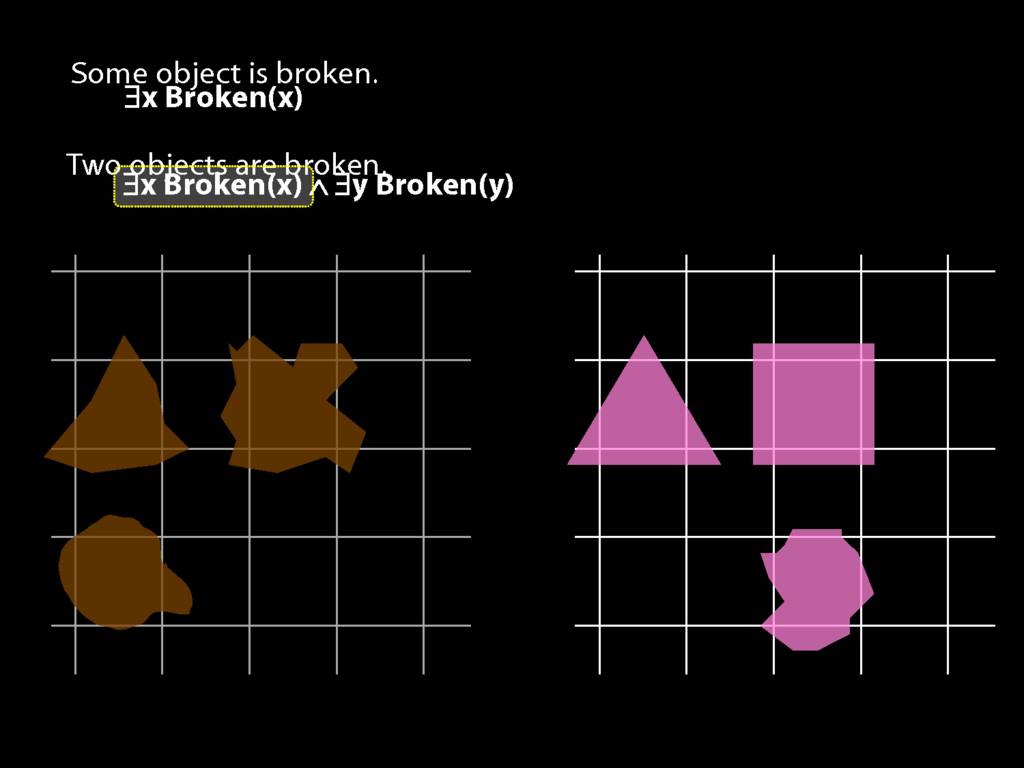
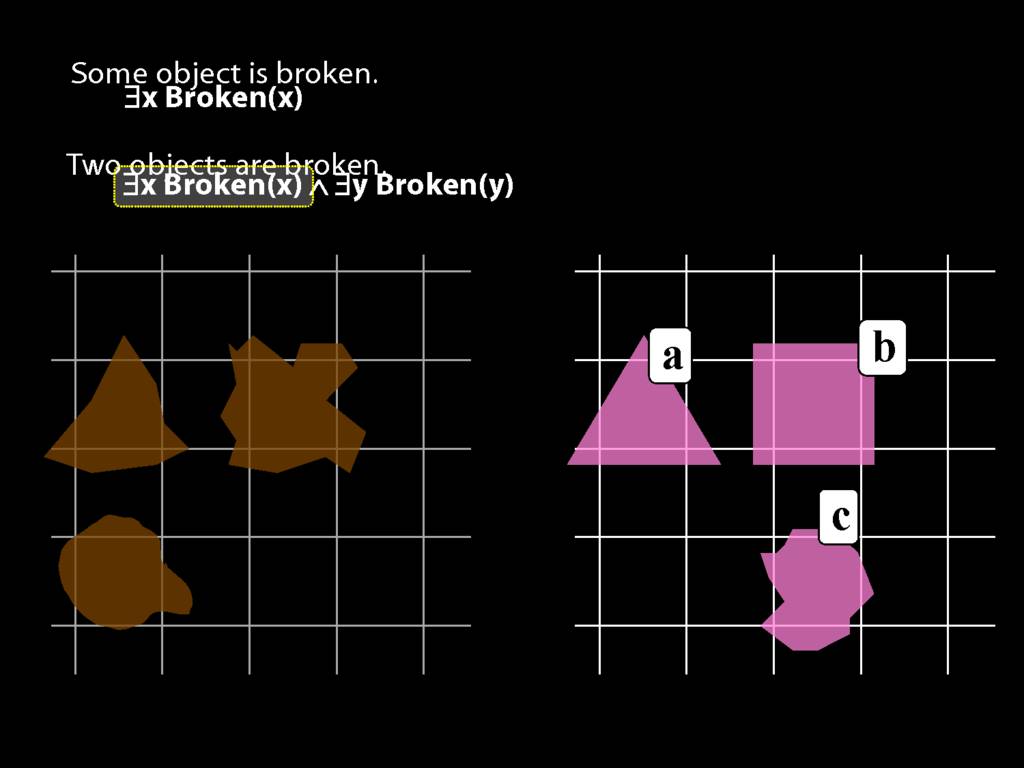
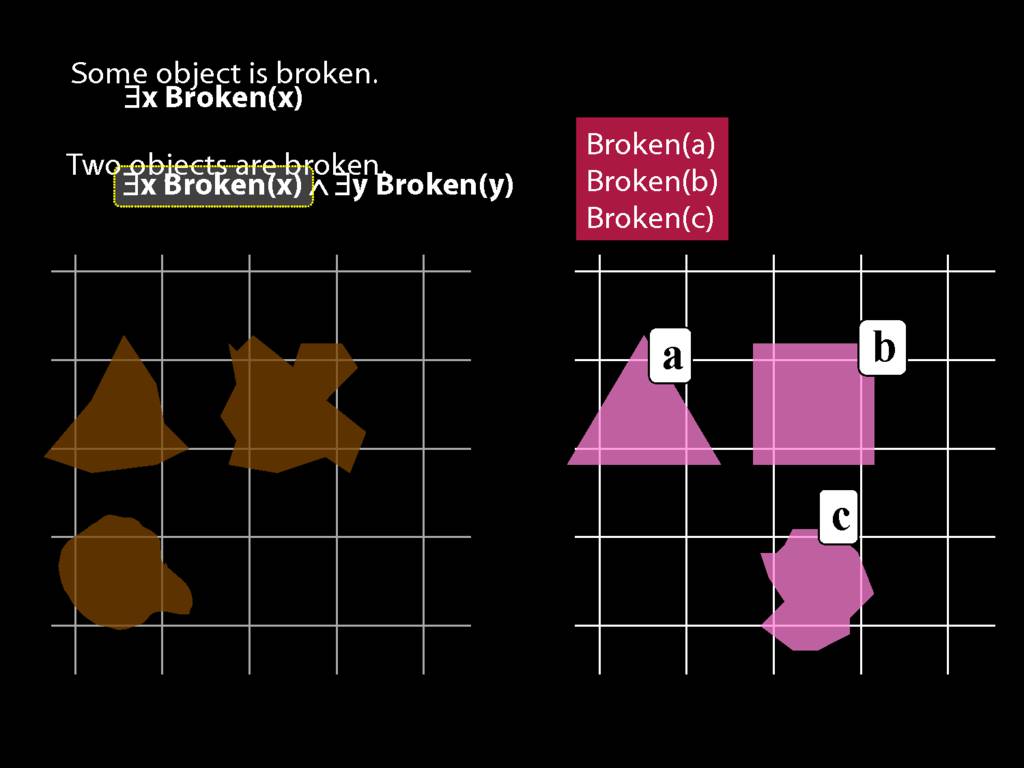
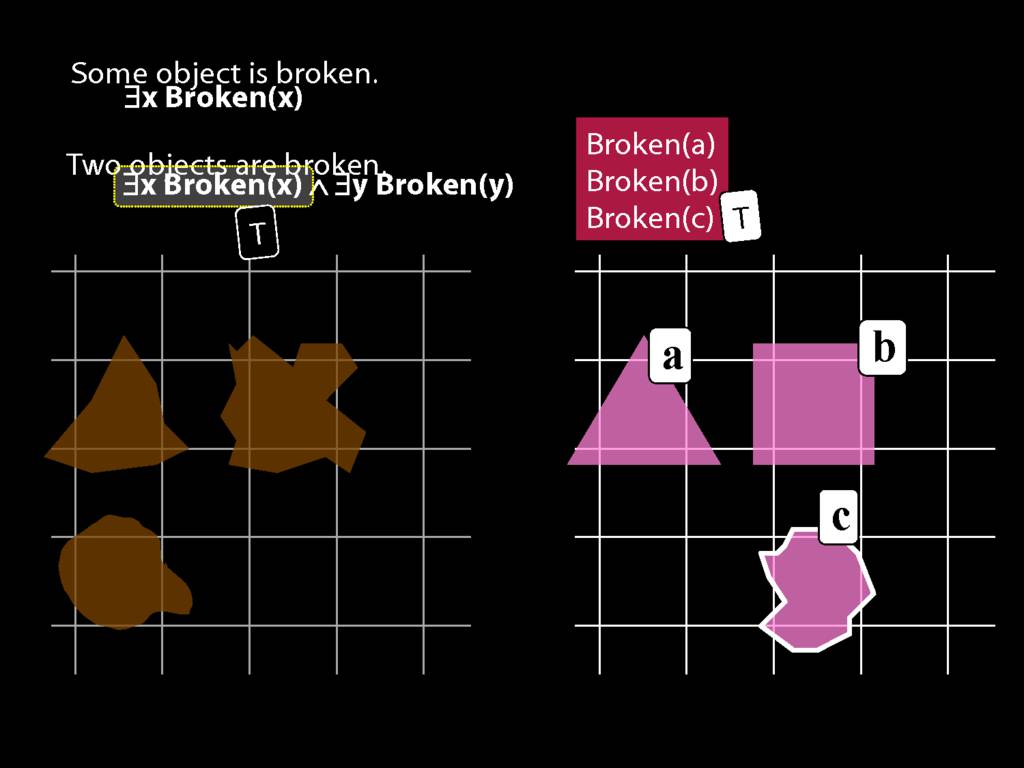
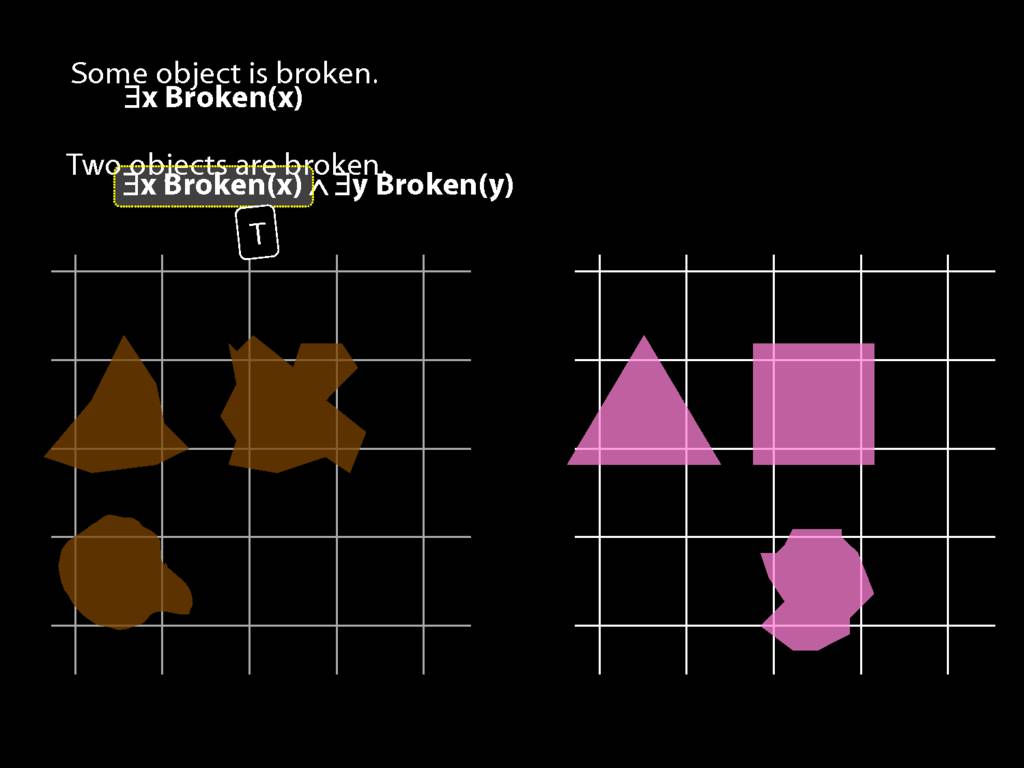
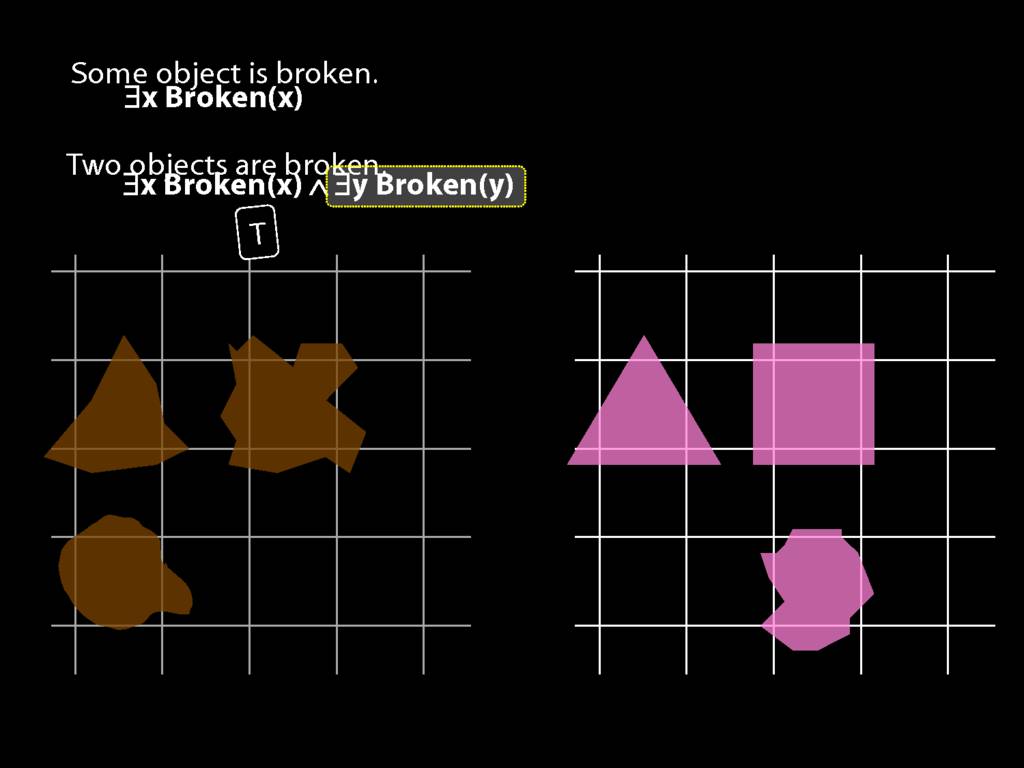
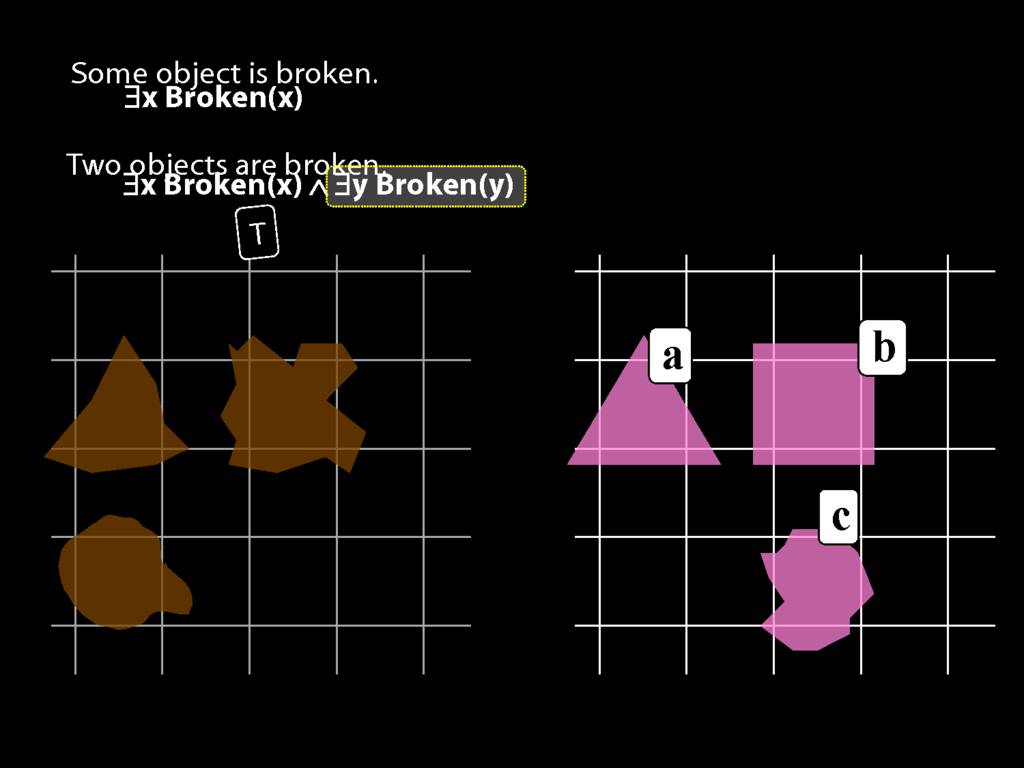
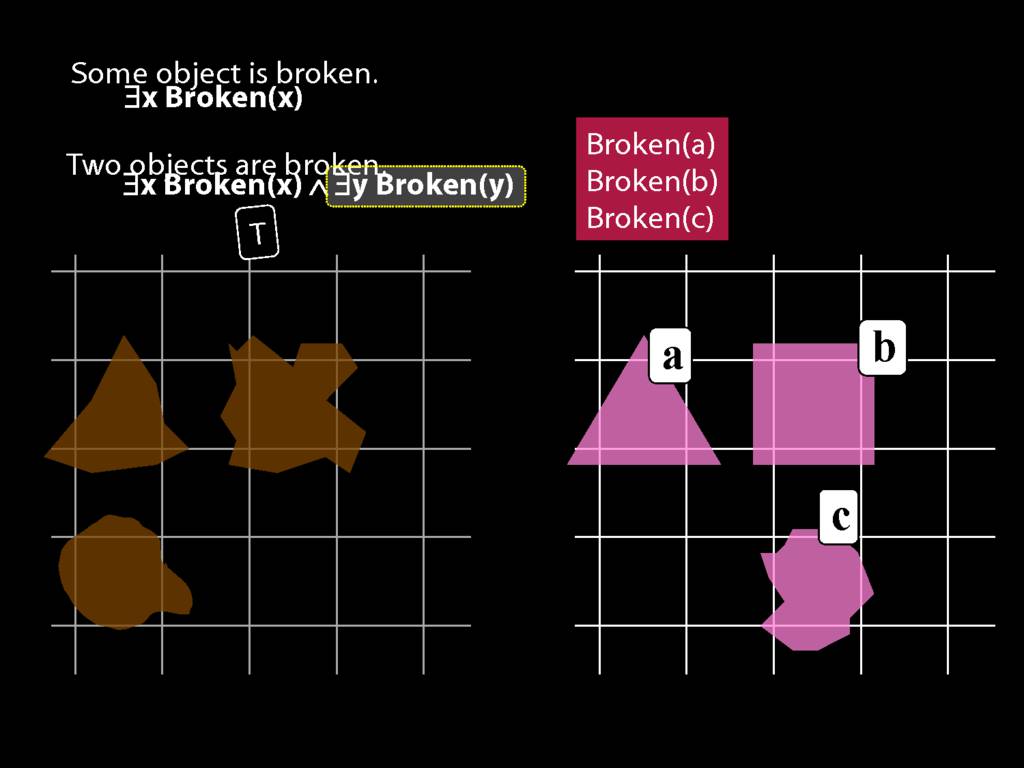
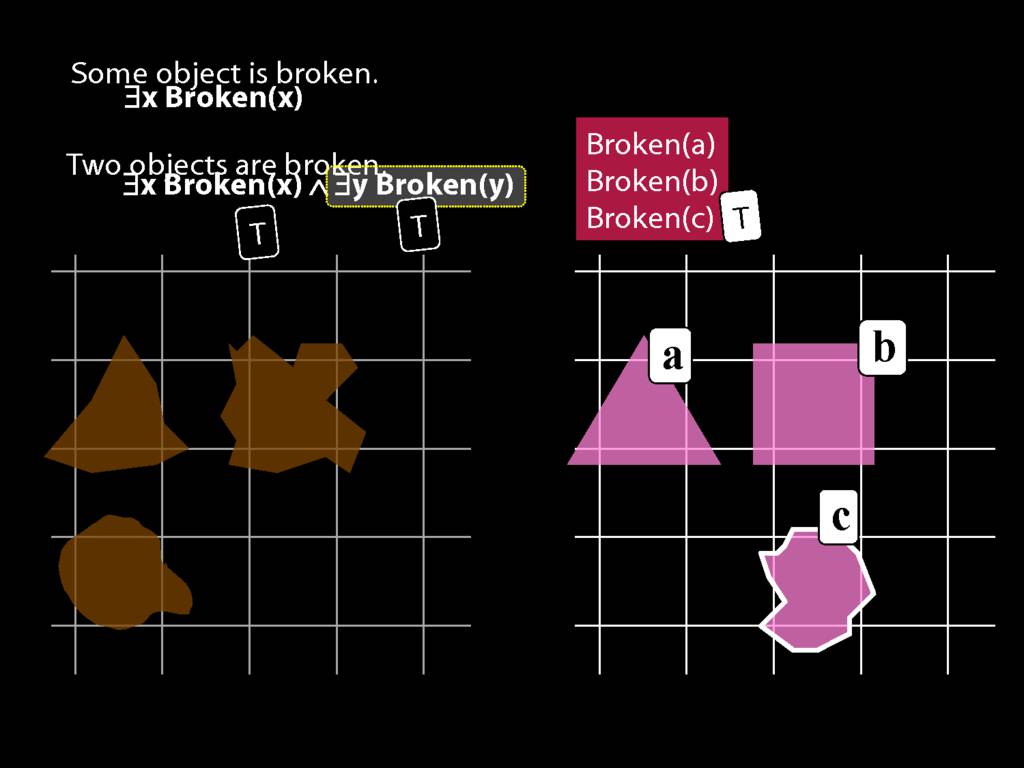
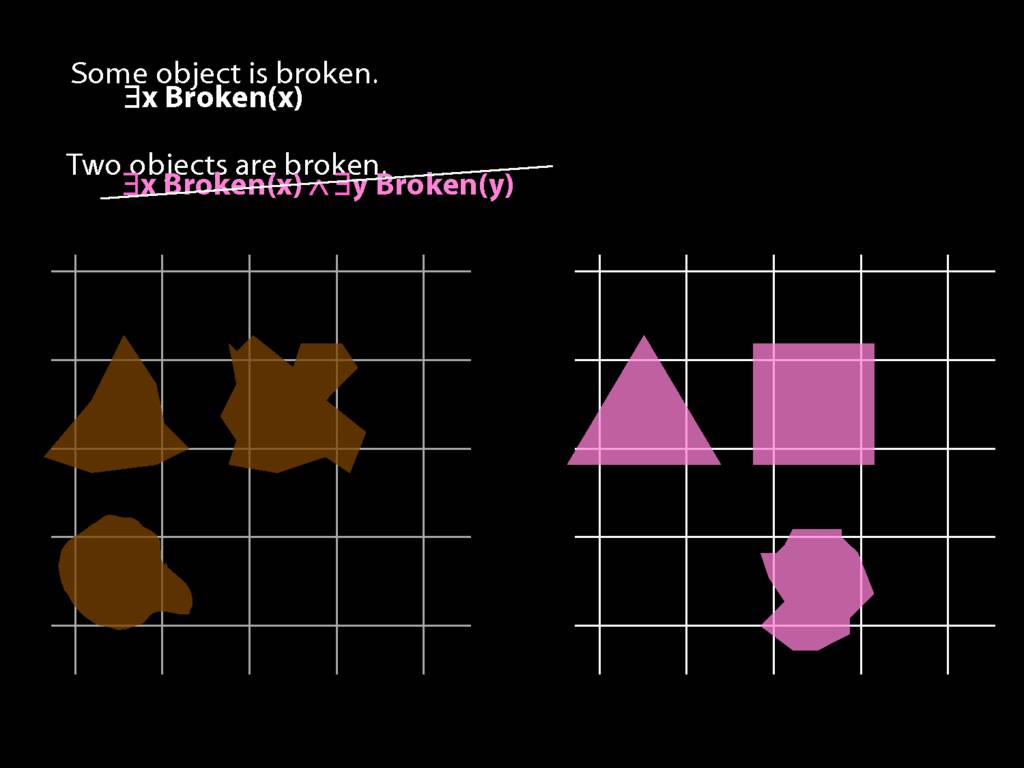
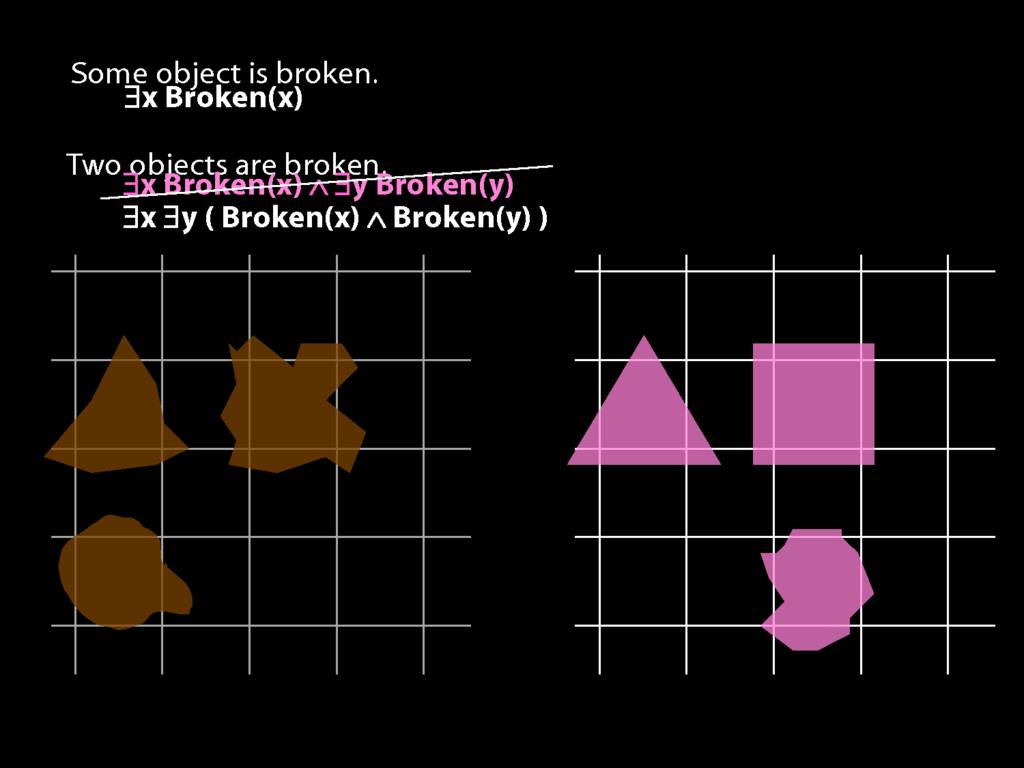
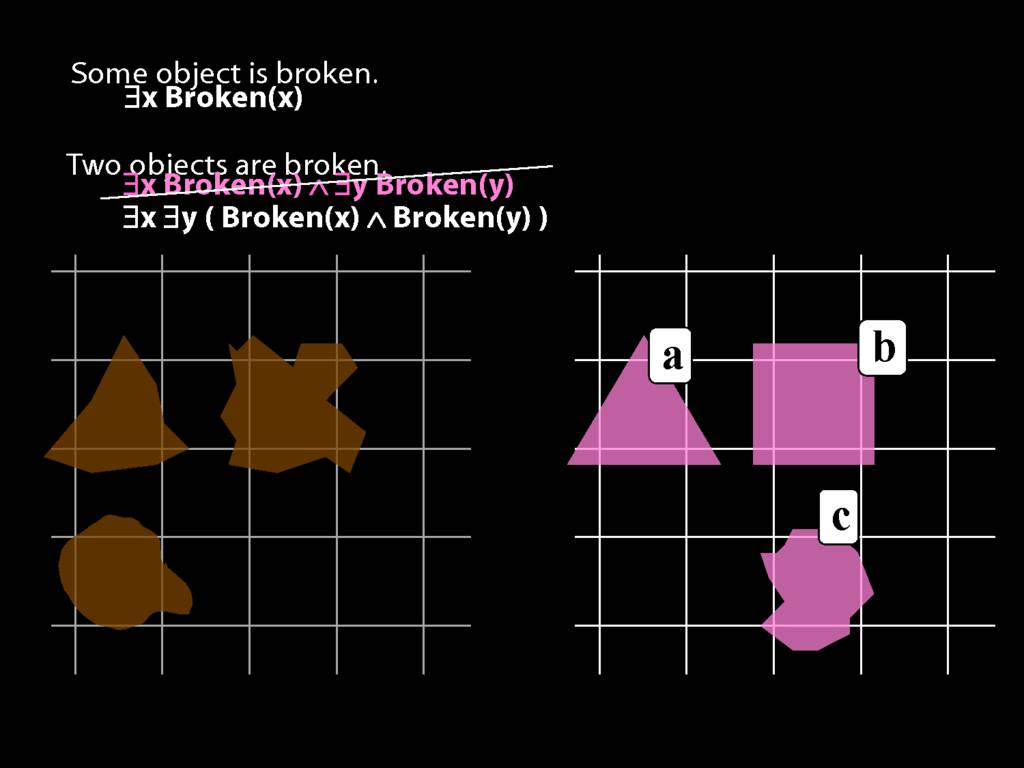
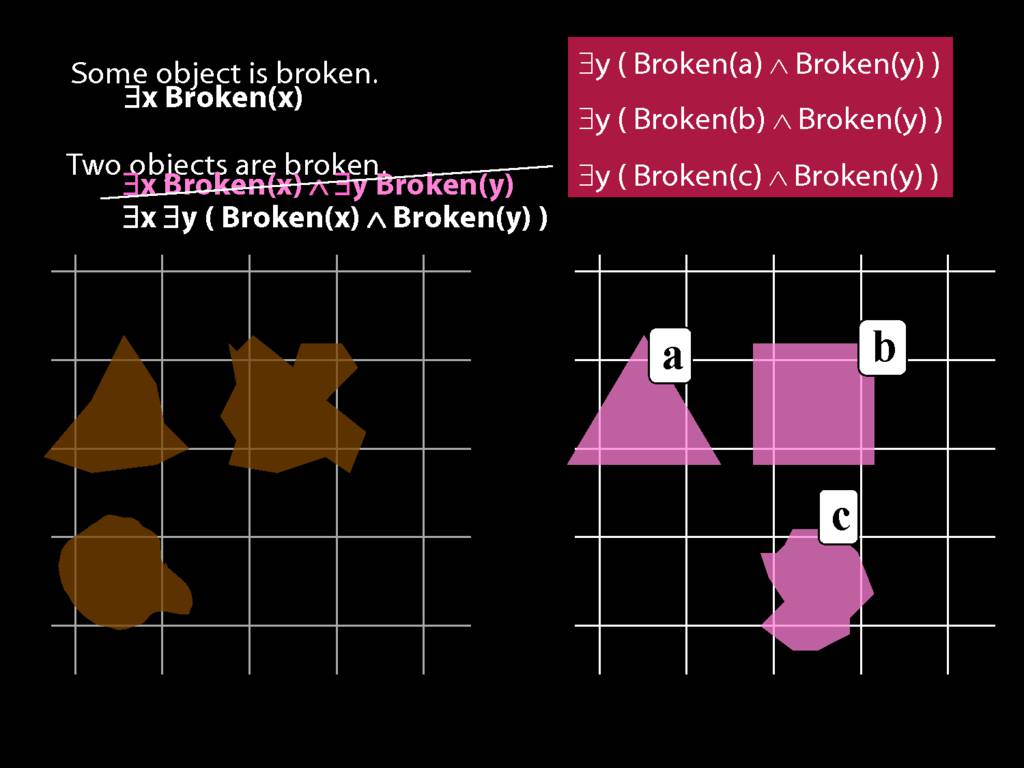
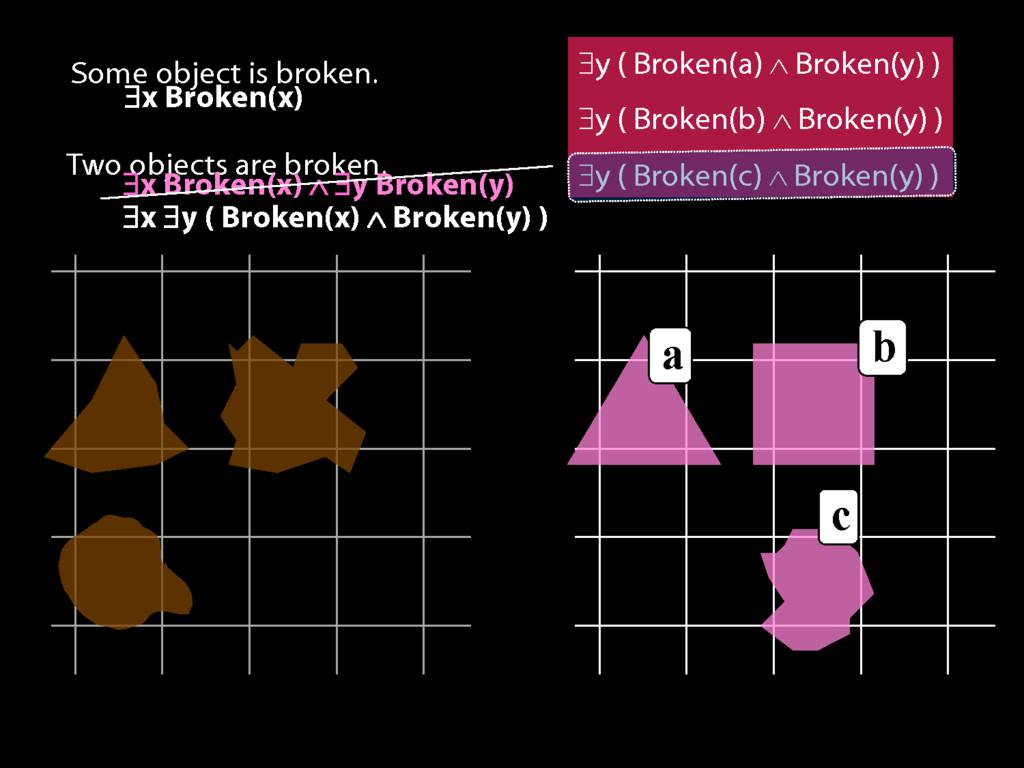
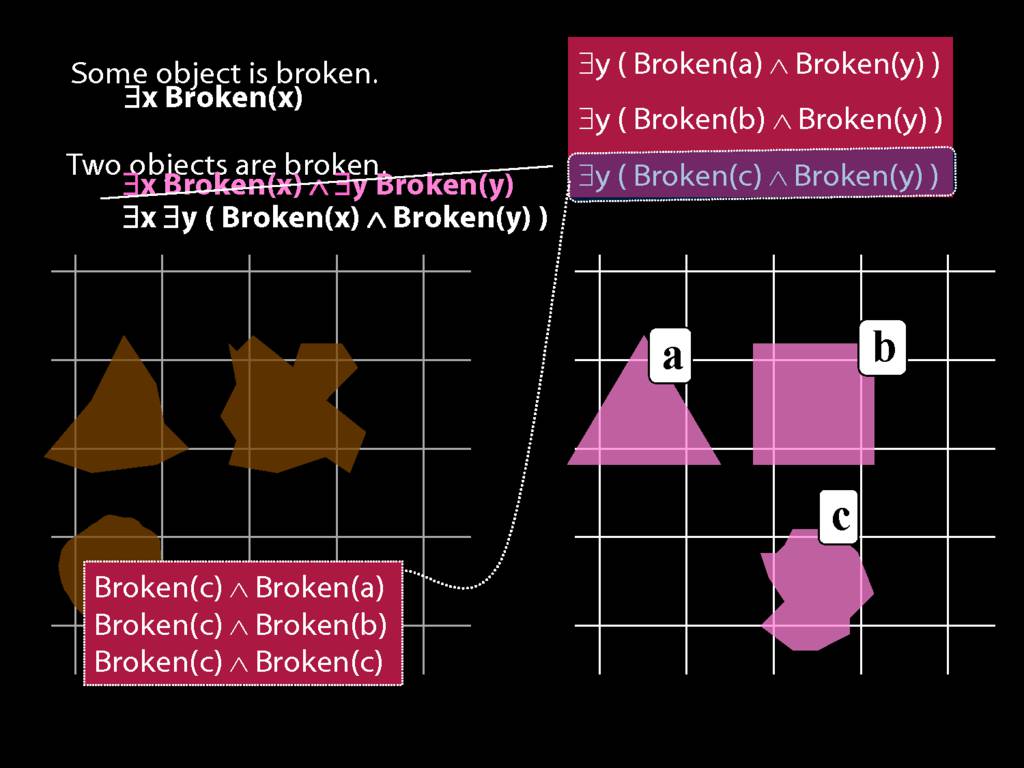
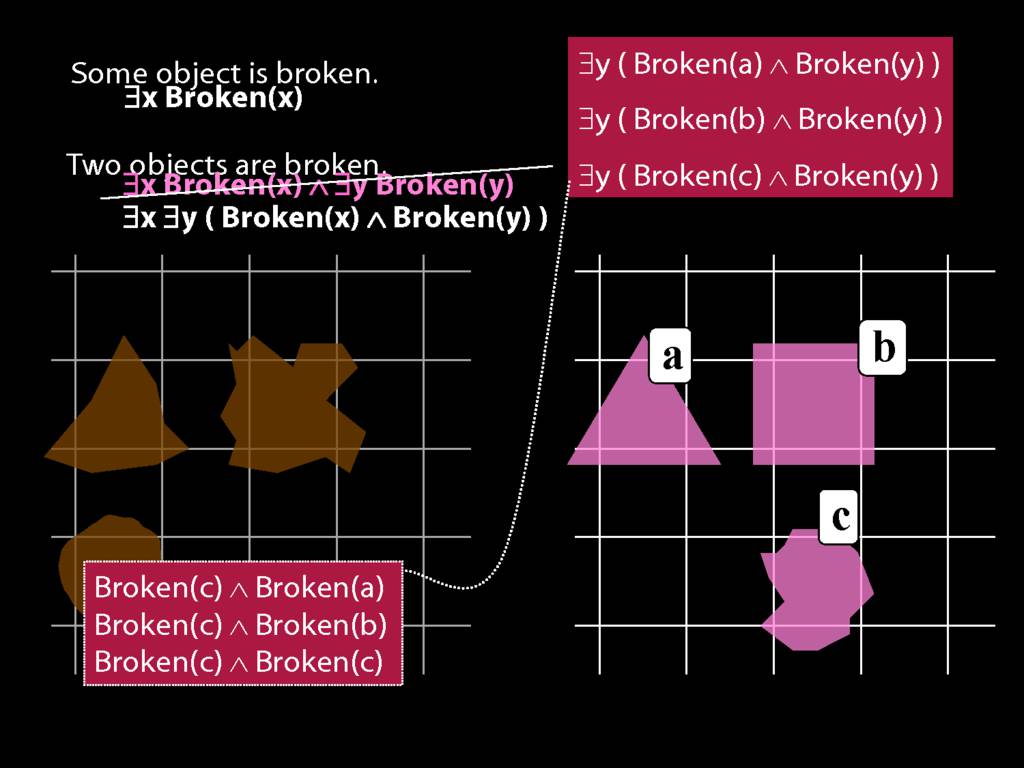
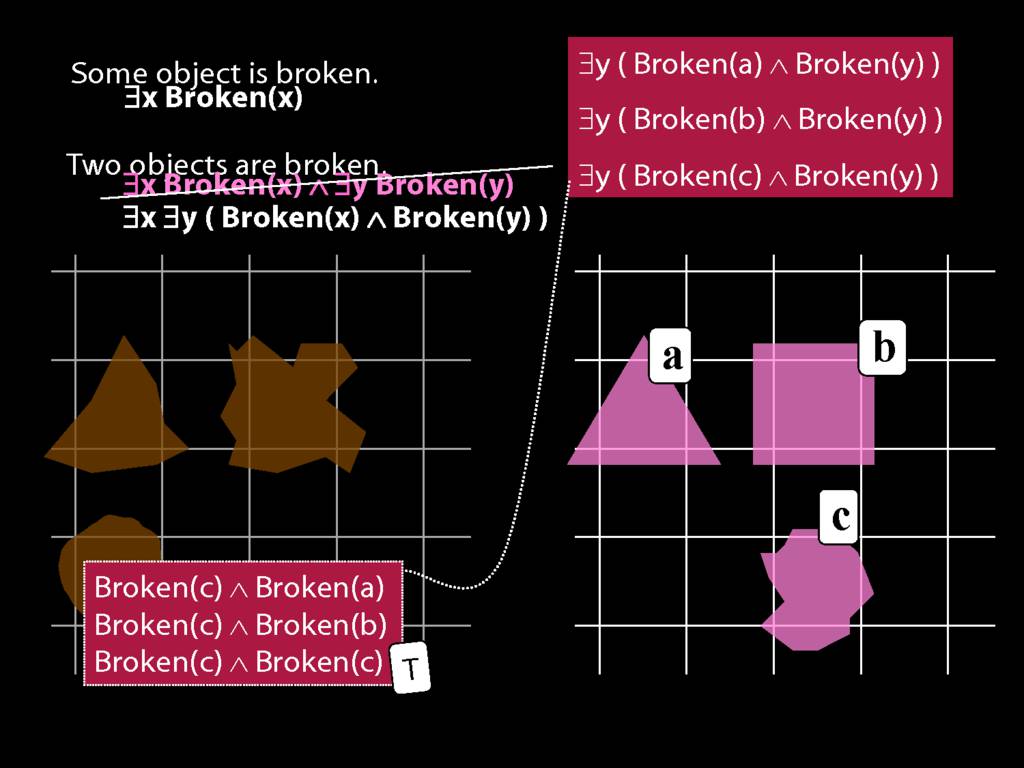
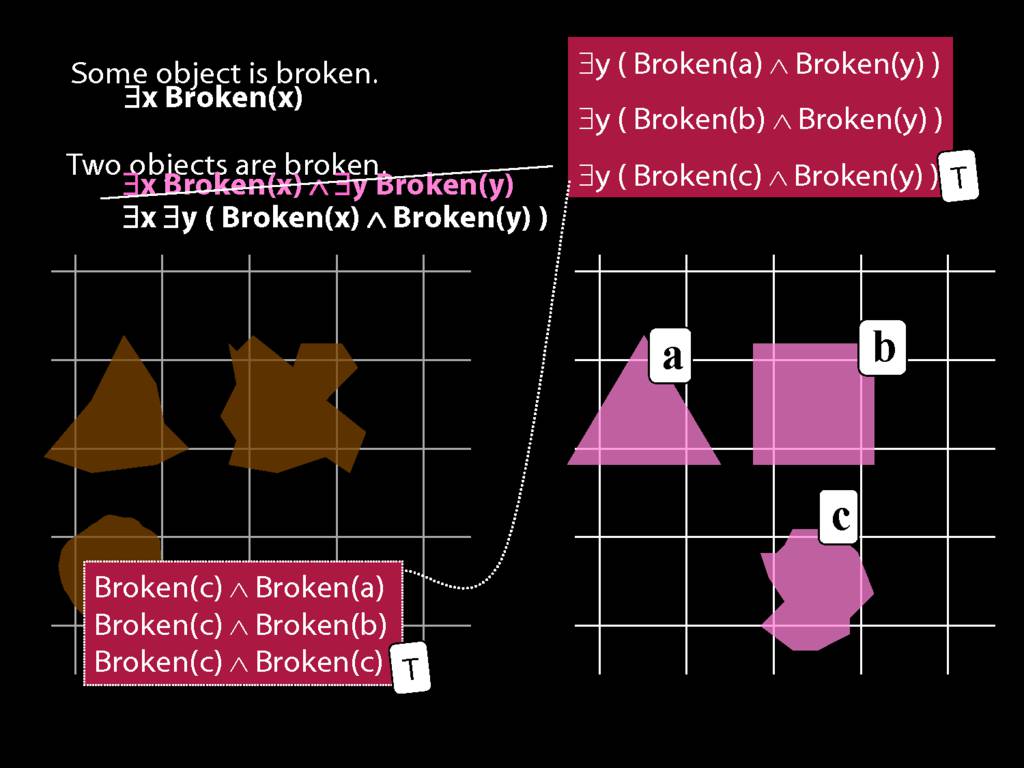
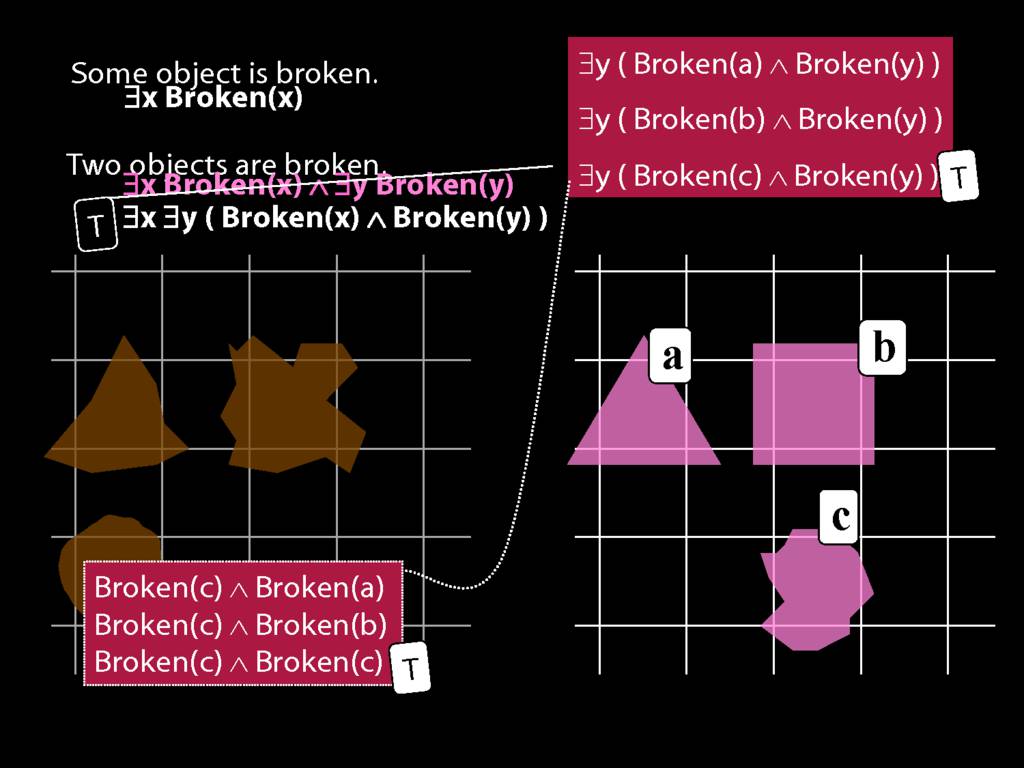
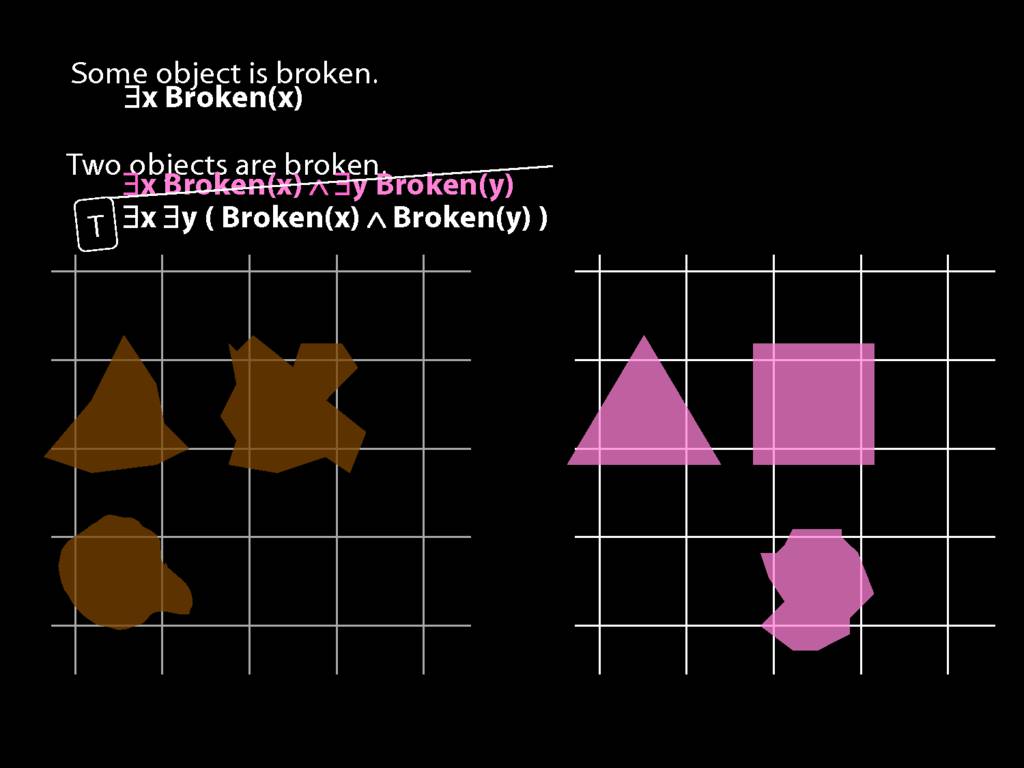
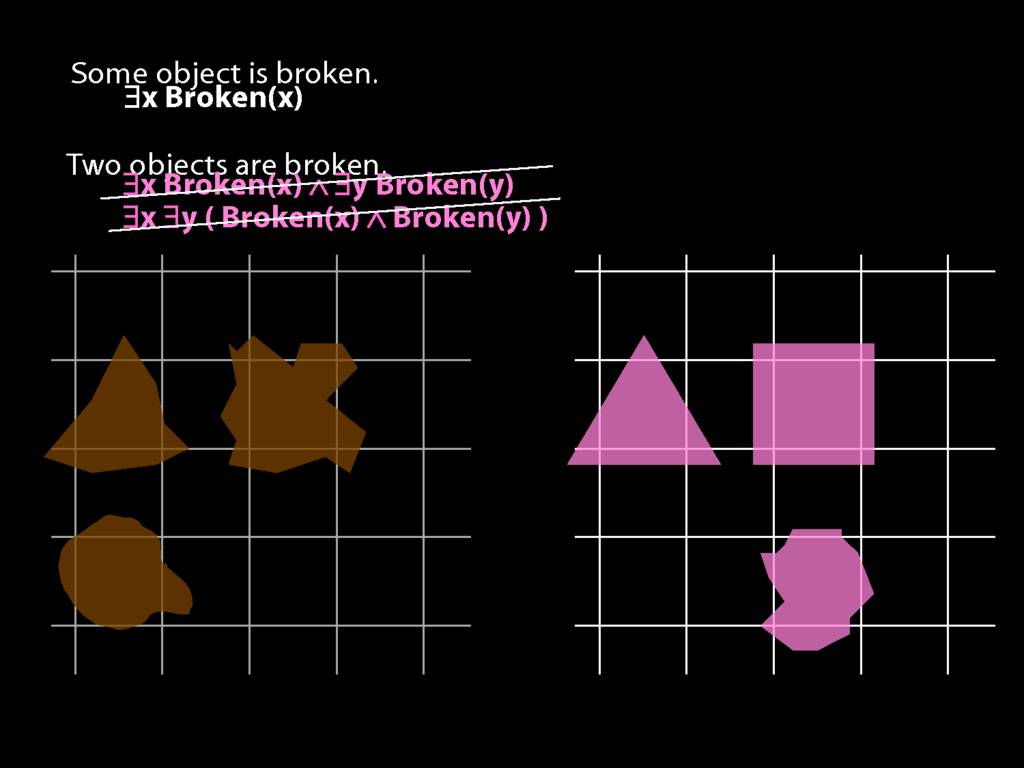
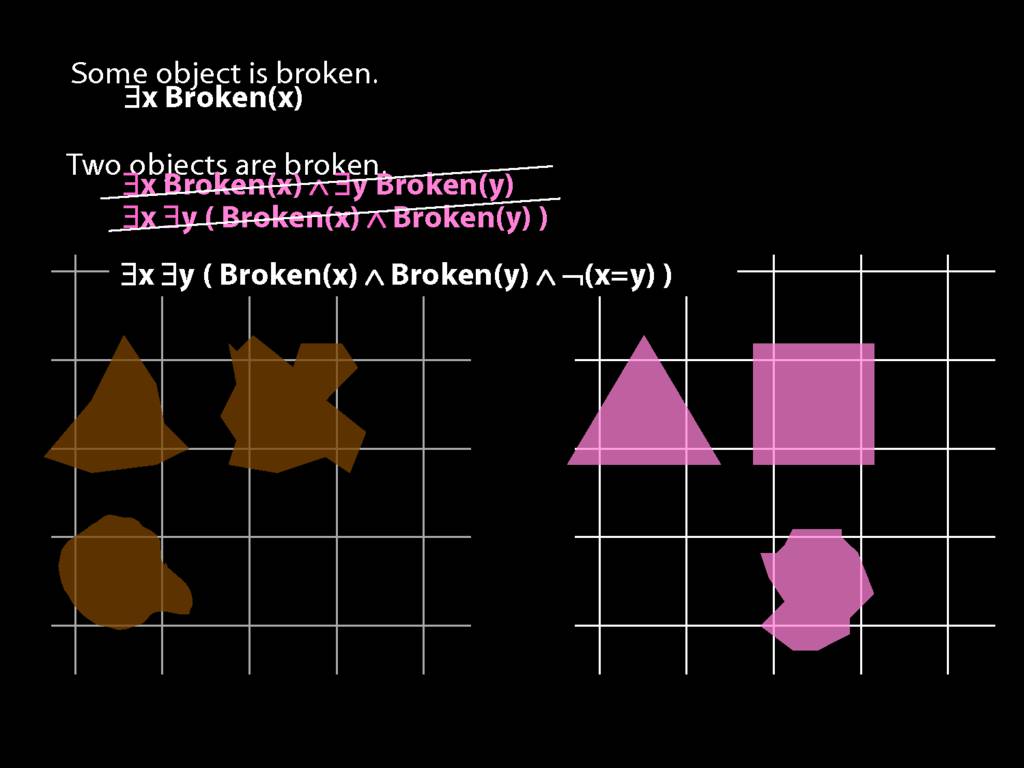
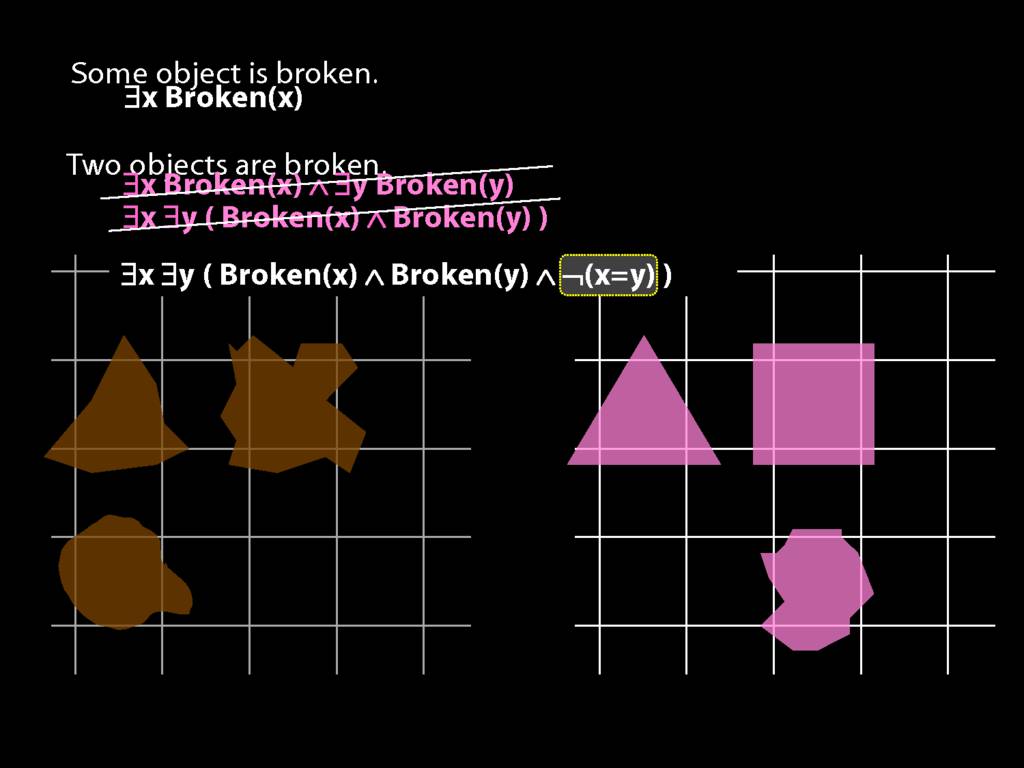
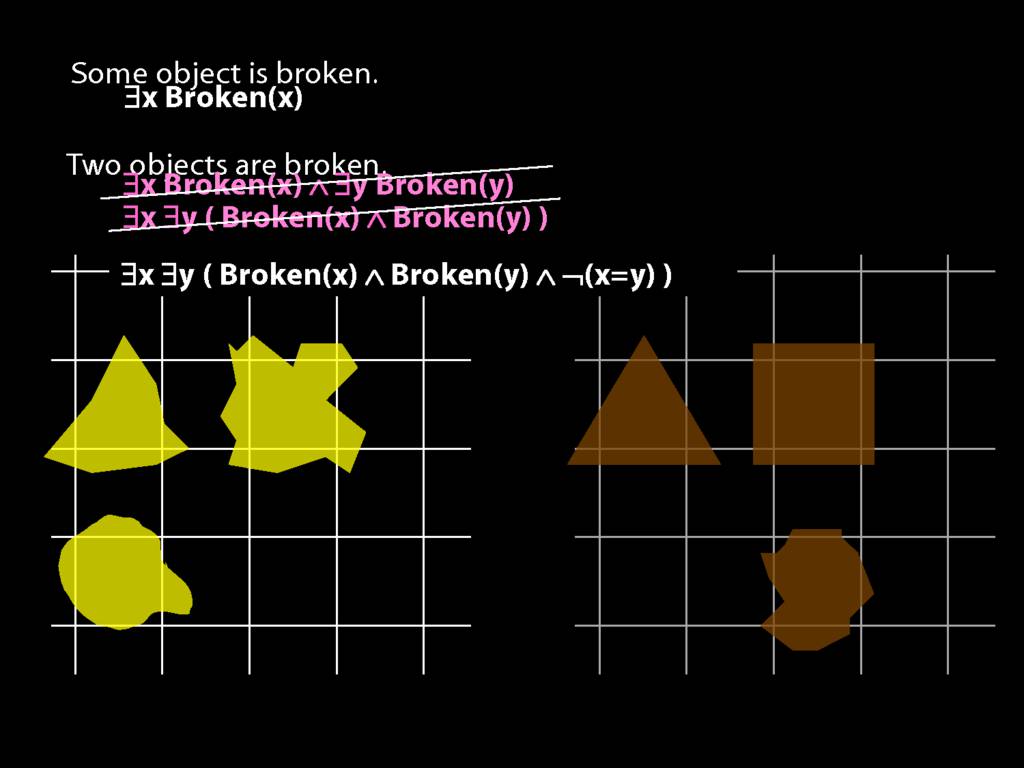
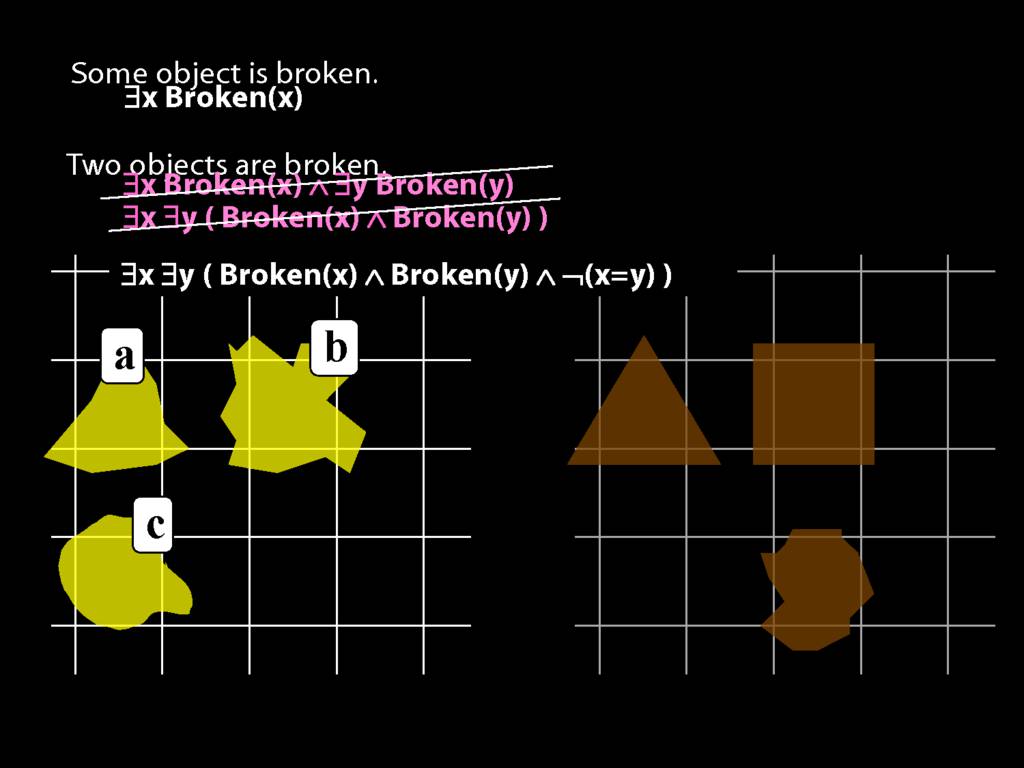
To translate sentences involving number into awFOL, use identity. For example,
`Two things are broken' might be translated as:
∃x ∃y ( Broken(x) ∧ Broken(y) ∧ ¬(x=y) )
 

Loving and Being Loved

 
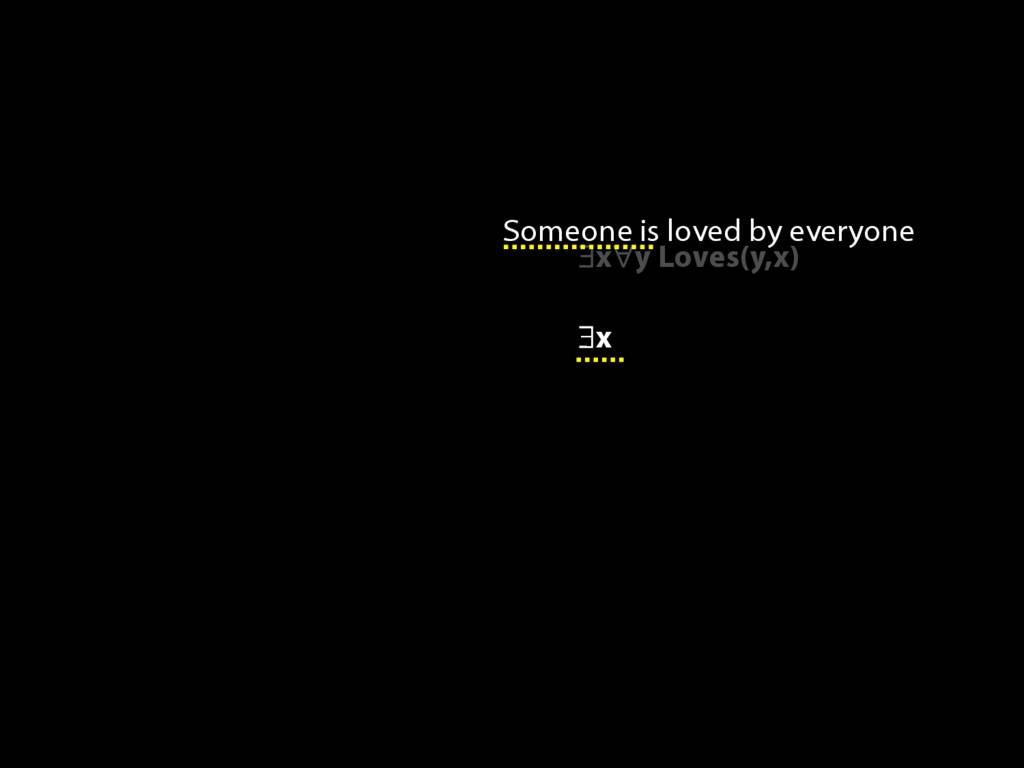
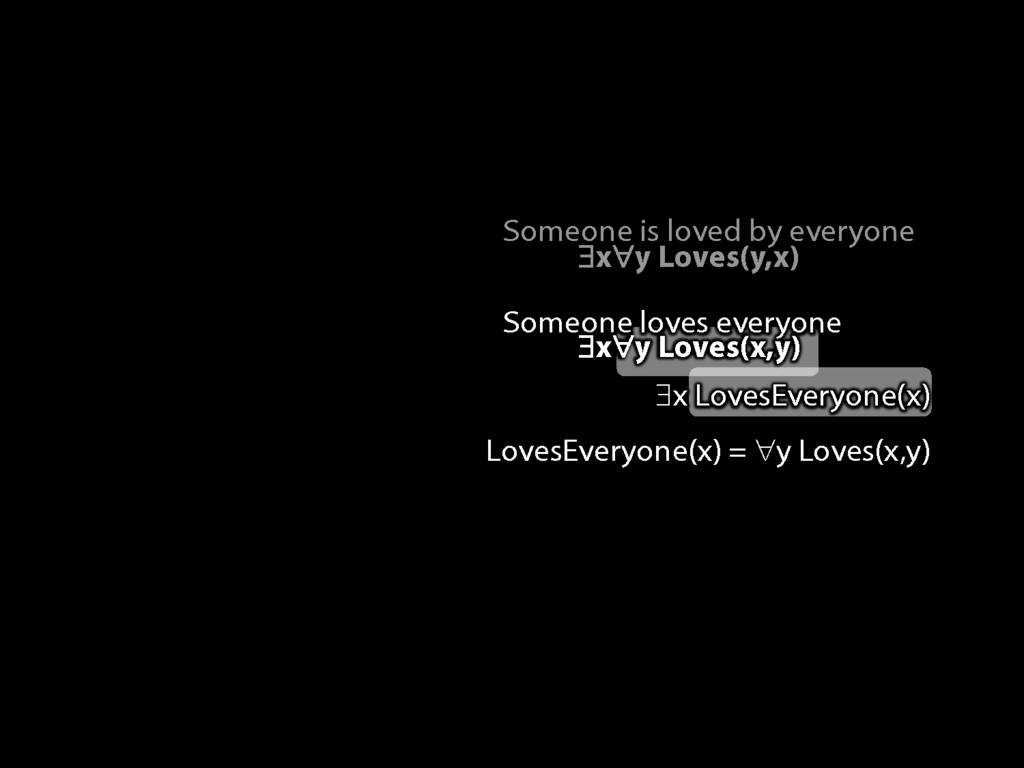
\section{Loving and Being Loved}
\emph{Reading:} §11.2, §11.3
 
\section{Loving and Being Loved}
 

Somebody Is Not Dead

 
\section{Somebody Is Not Dead}
 
\section{Somebody Is Not Dead}
Some person is dead.
\hspace{5mm} ∃x(Person(x) ∧ Dead(x))
Some person is not dead.
\hspace{5mm} ∃x(Person(x) ∧ ¬Dead(x))
No person is dead.
\hspace{5mm} ¬∃x(Person(x) ∧ Dead(x))
Every person is dead.
\hspace{5mm} ∀x(Person(x) → Dead(x))
Every person is not dead.
\hspace{5mm} ∀x(Person(x) → ¬Dead(x))
Not every person is dead.
\hspace{5mm} ¬∀x(Person(x) → Dead(x))

Some person is dead.

∃x(Person(x) ∧ Dead(x))

Some person is not dead.

∃x(Person(x) ∧ ¬Dead(x))

No person is dead.

¬∃x(Person(x) ∧ Dead(x))

Every person is dead.

∀x(Person(x) → Dead(x))

Every person is not dead.

∀x(Person(x) → ¬Dead(x))

Not every person is dead.

¬∀x(Person(x) → Dead(x))

#
 

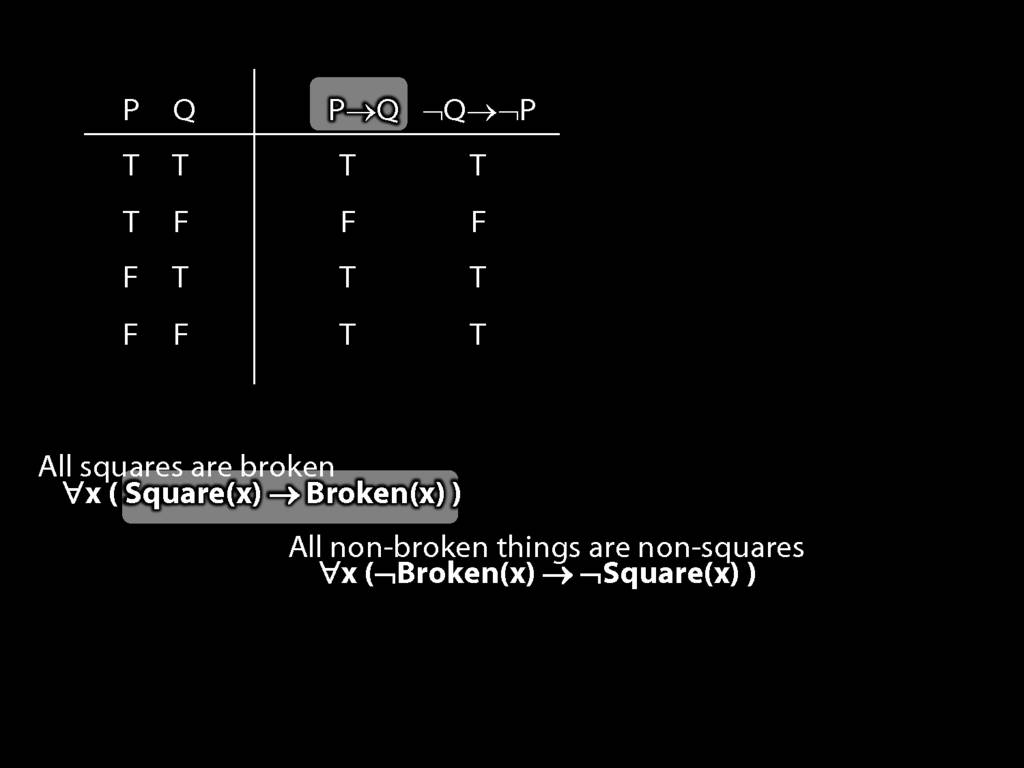
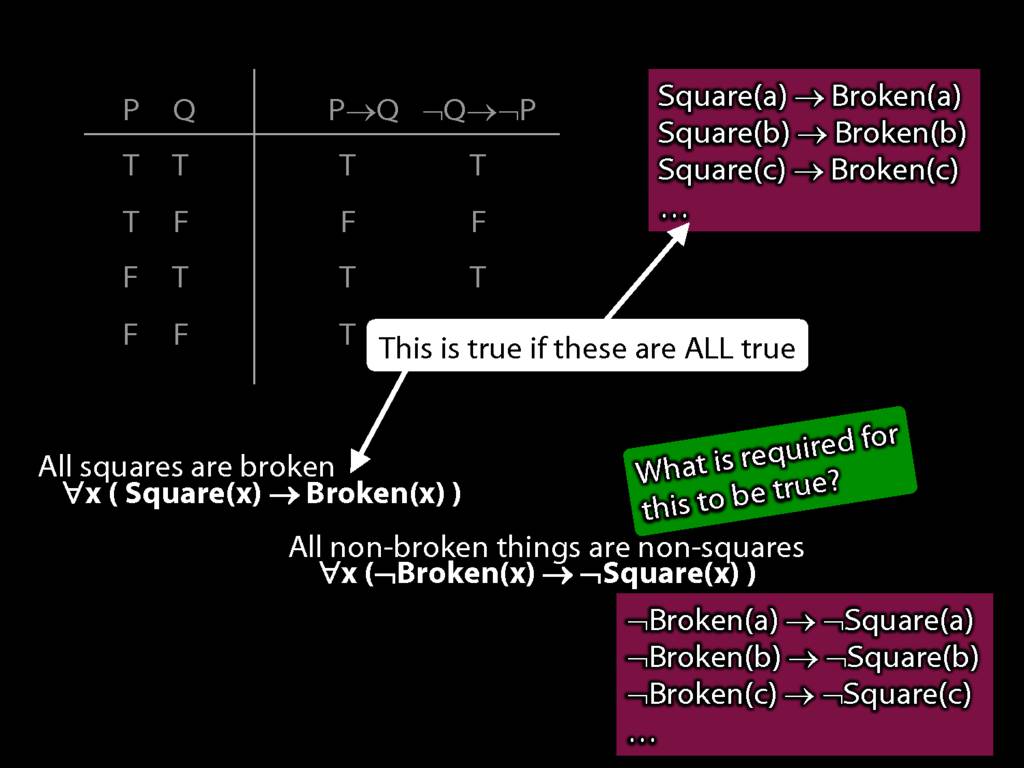
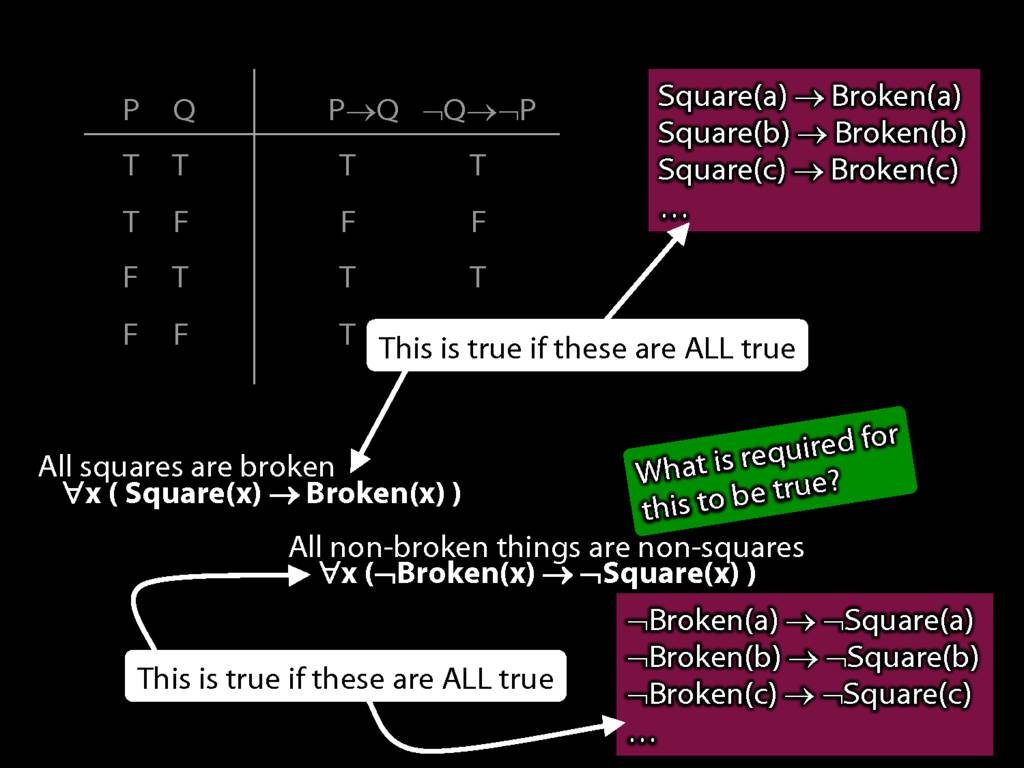
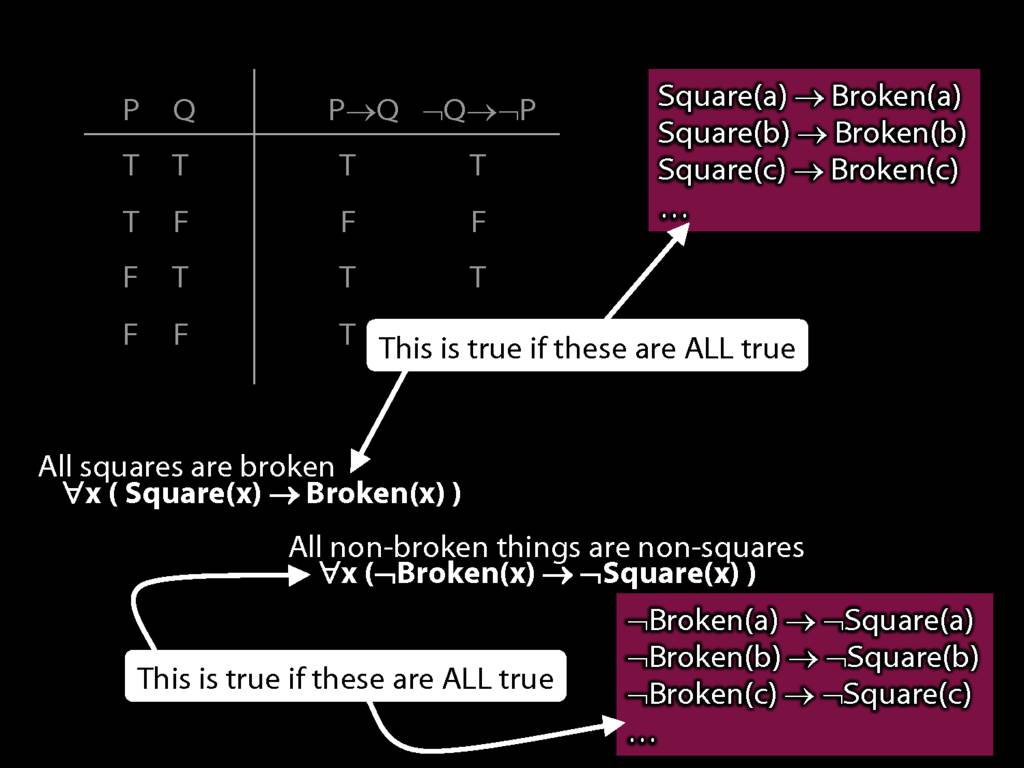
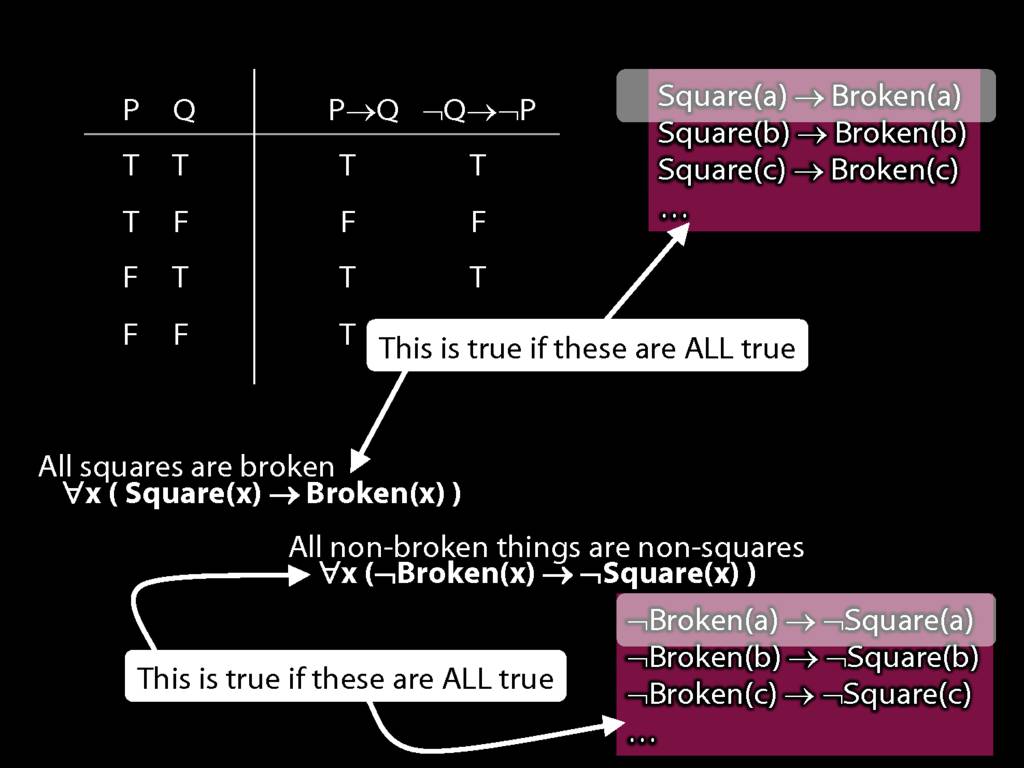
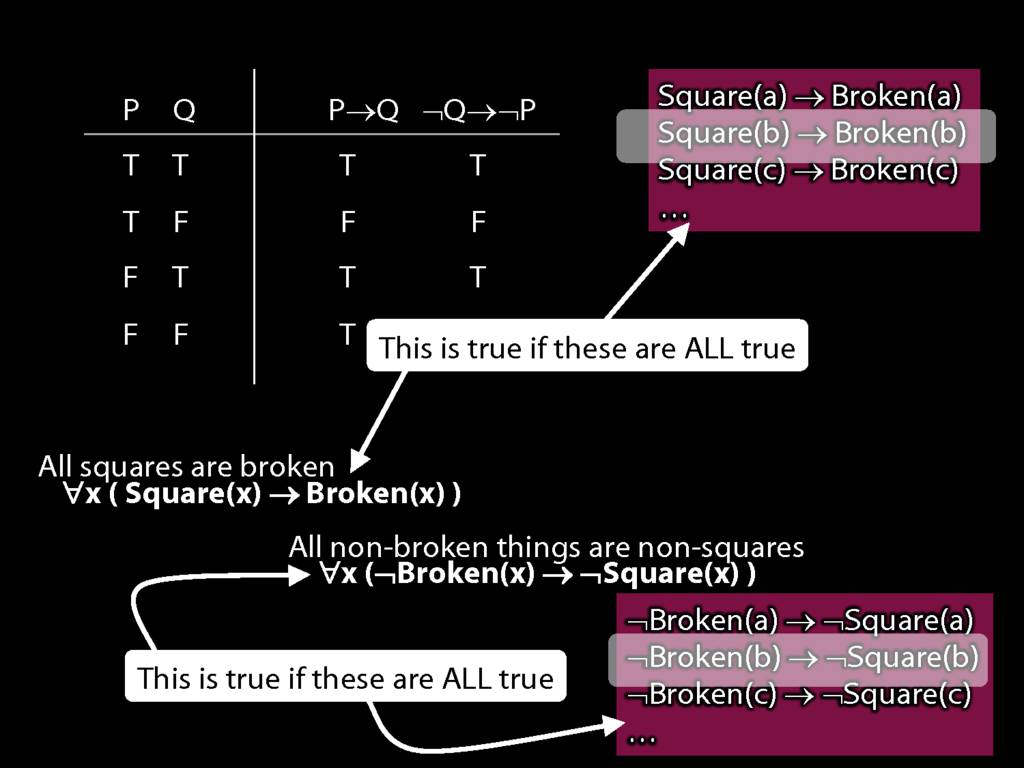
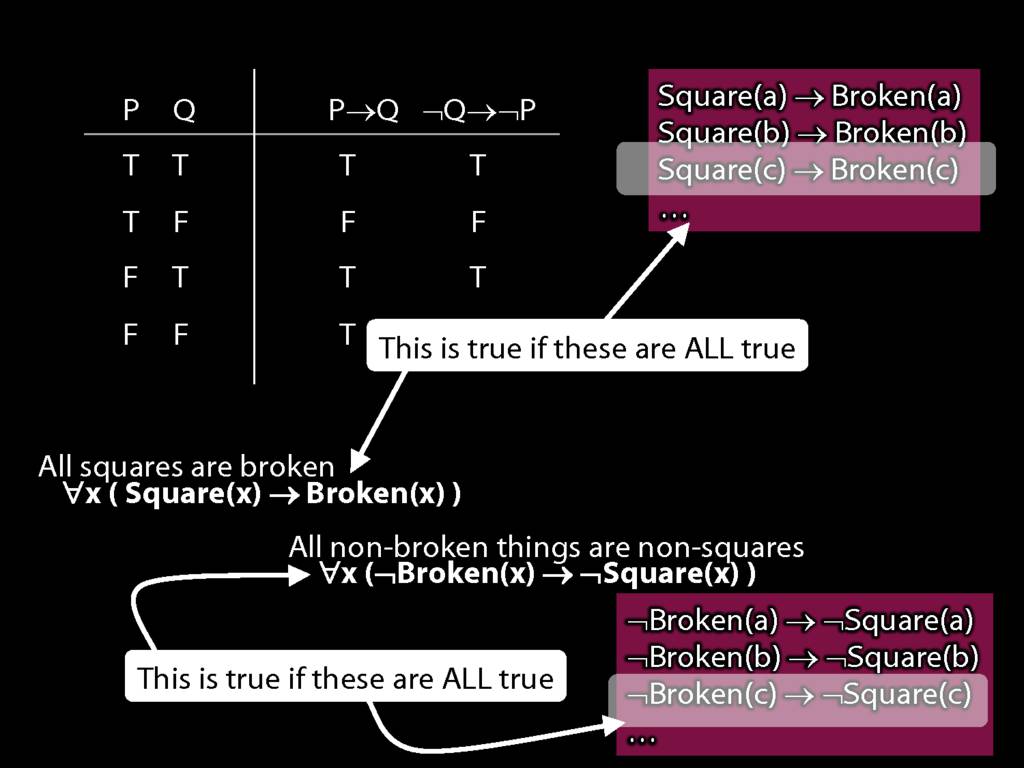
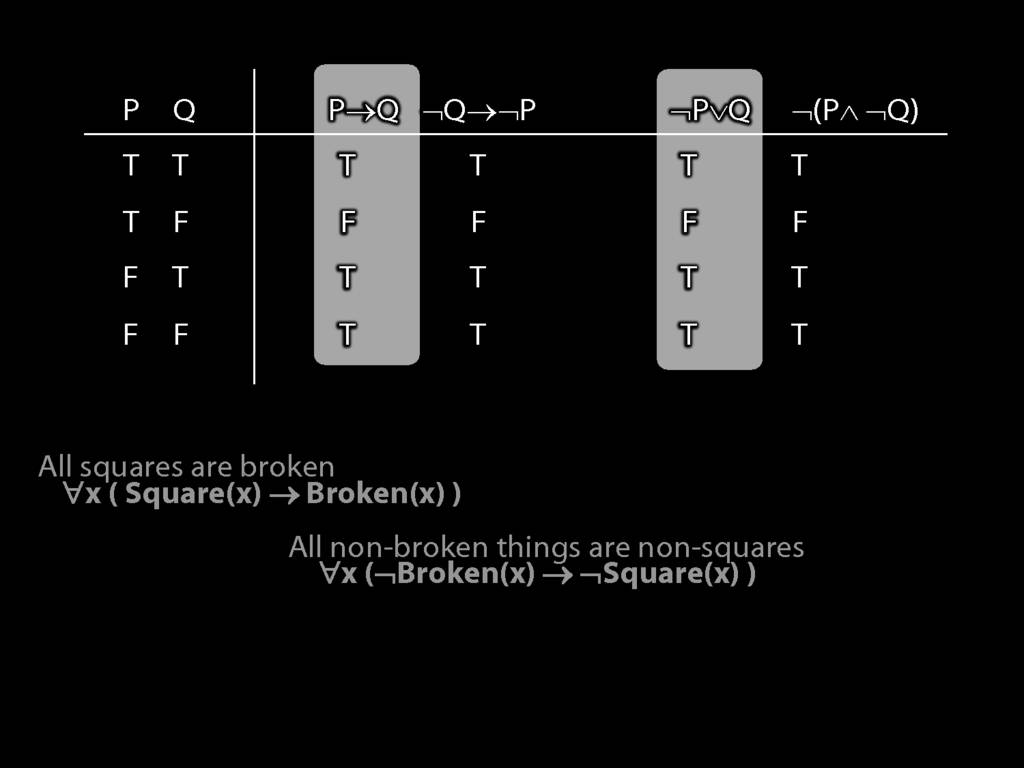
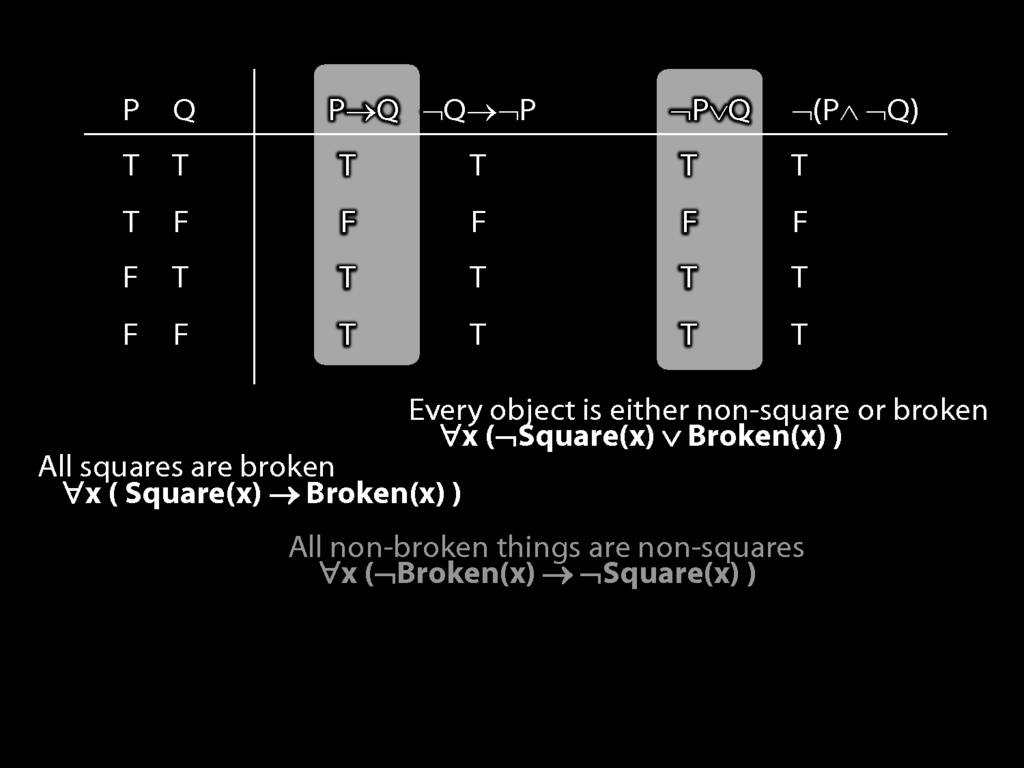
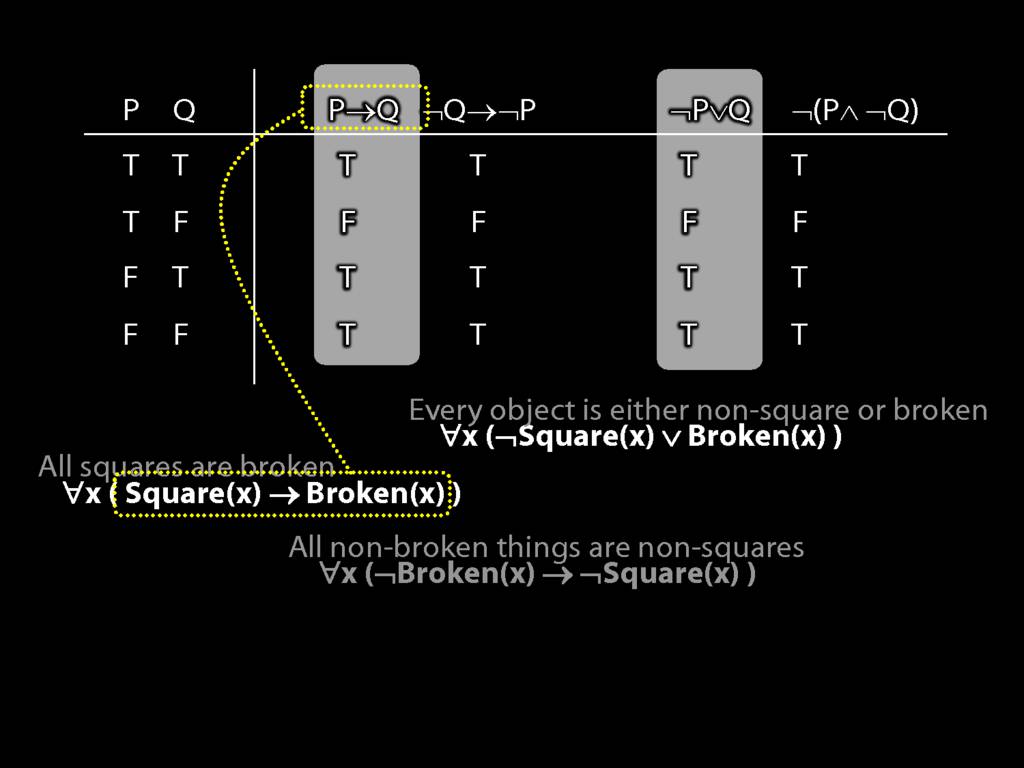
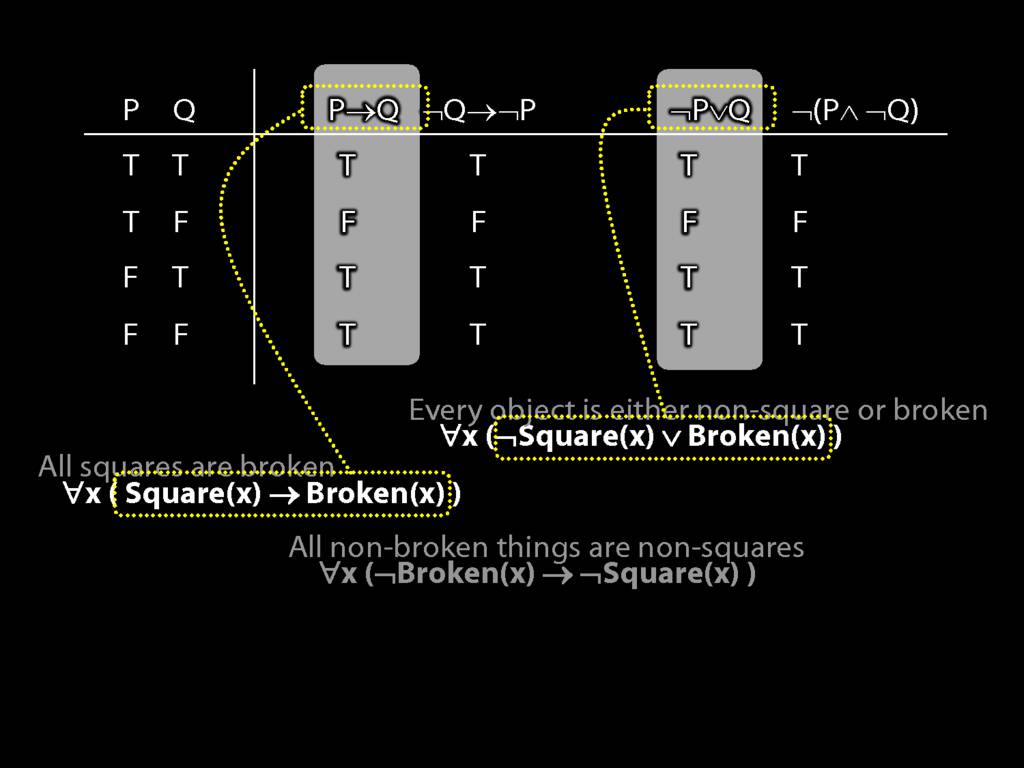
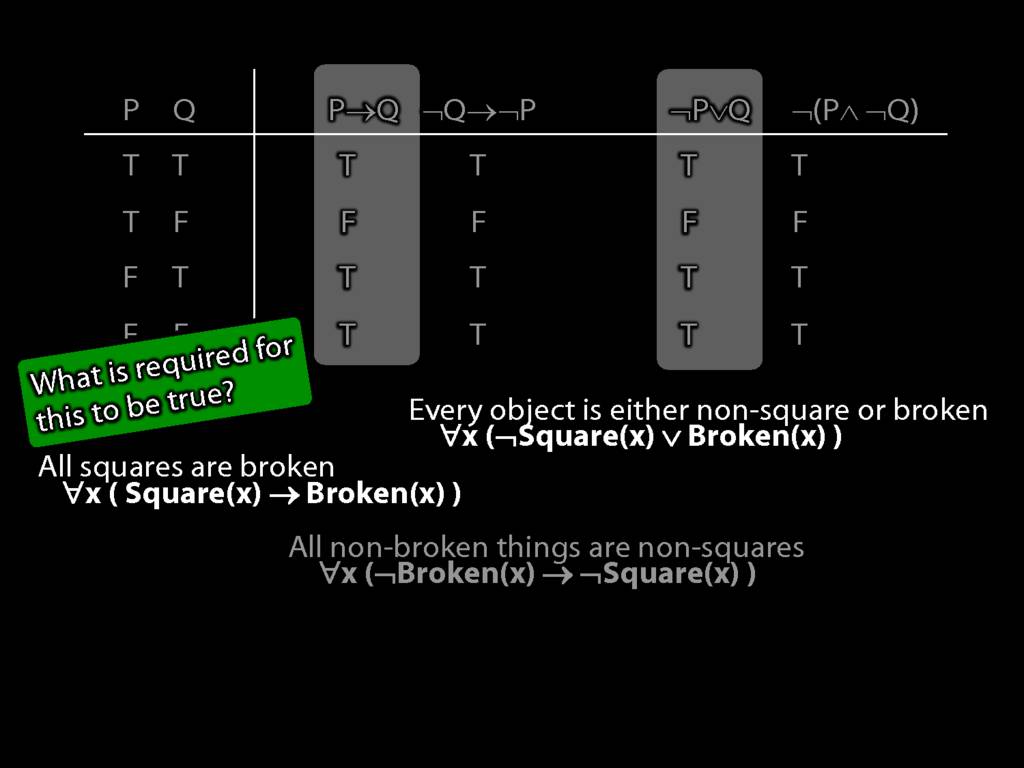
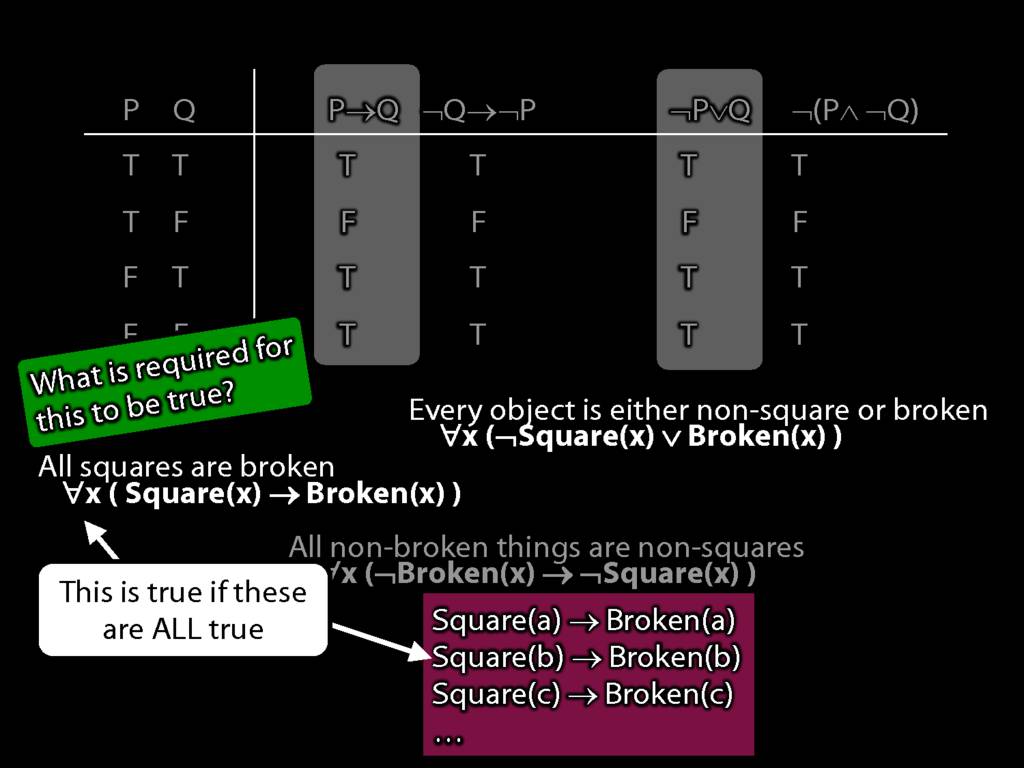
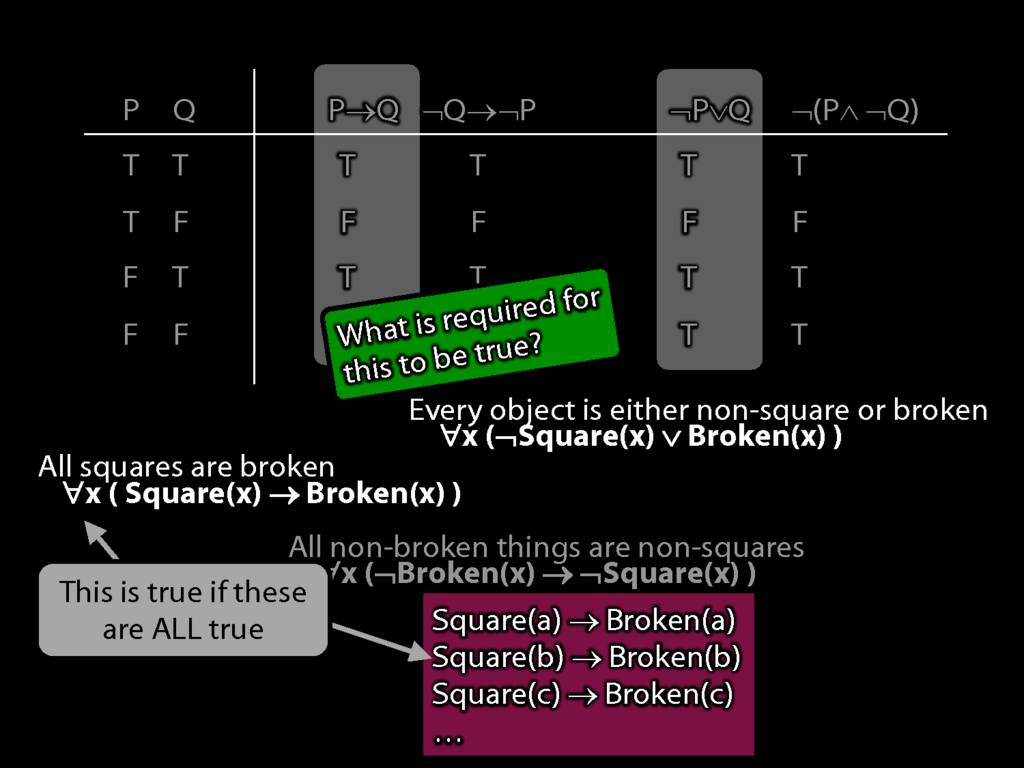
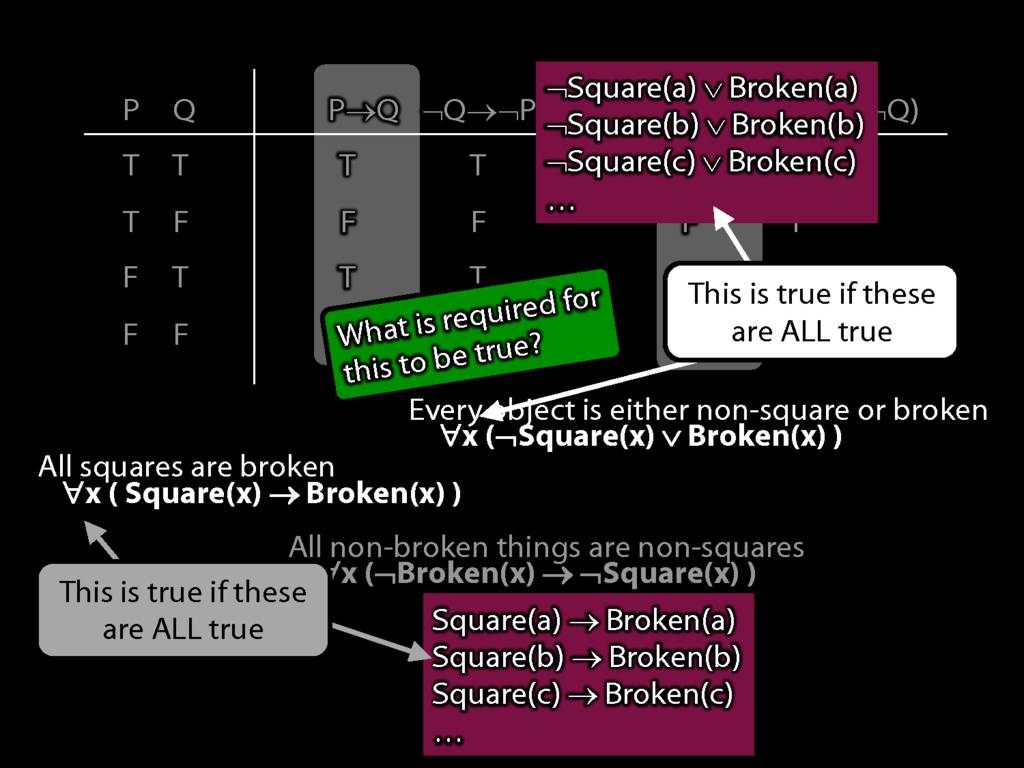
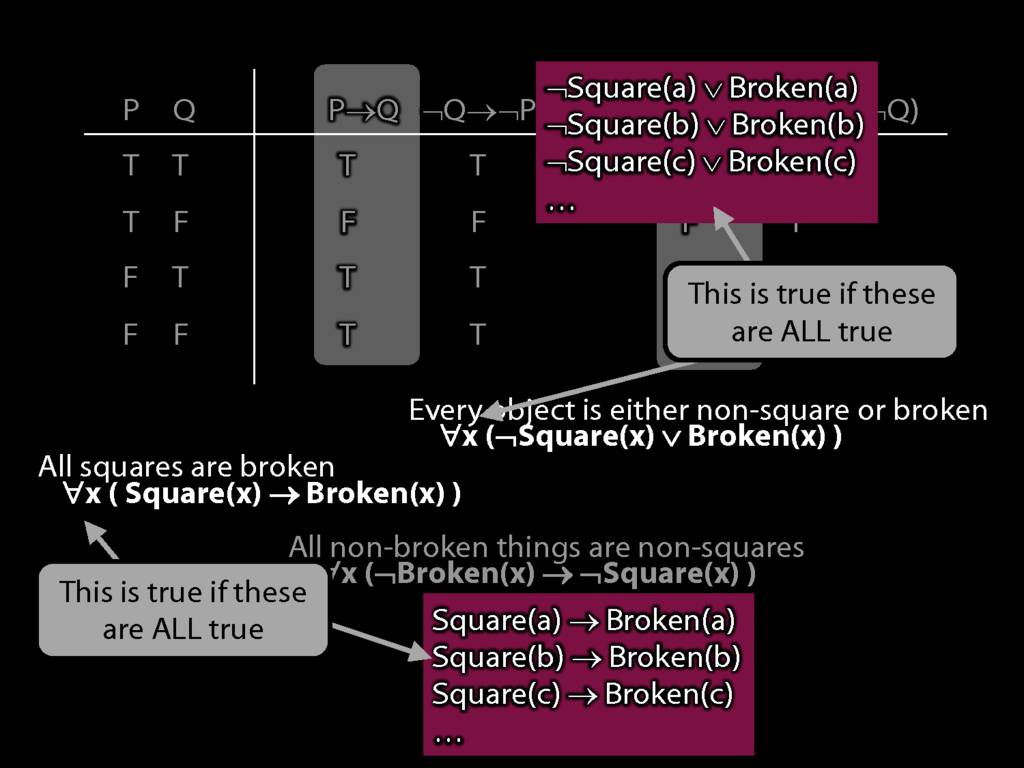
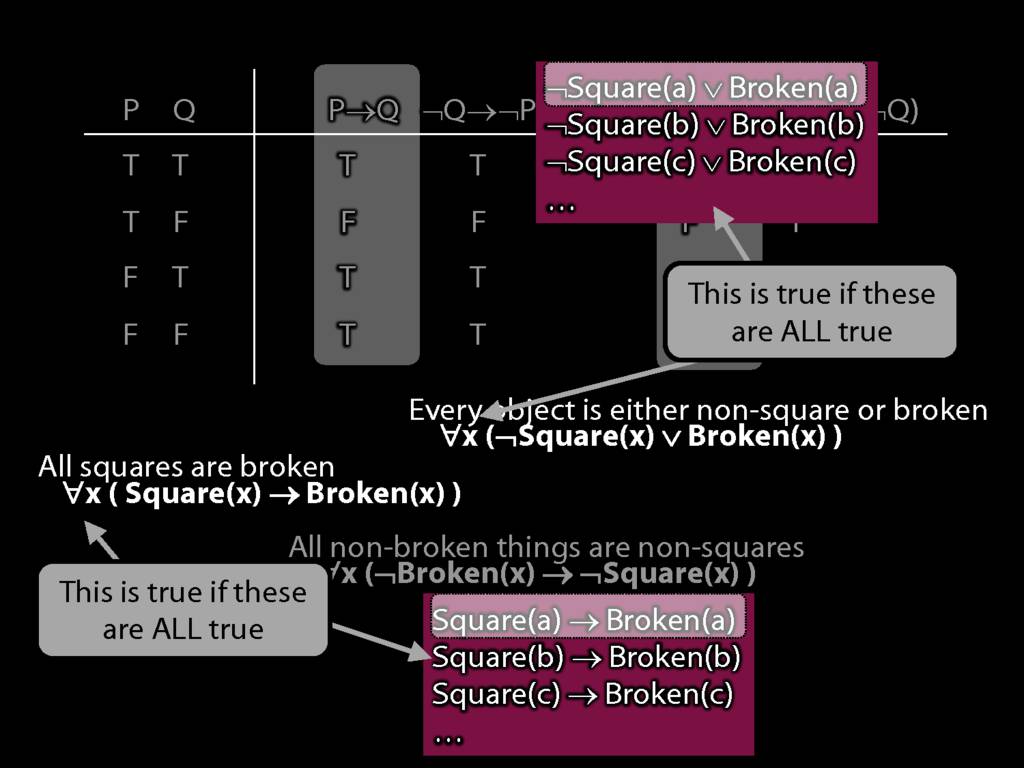
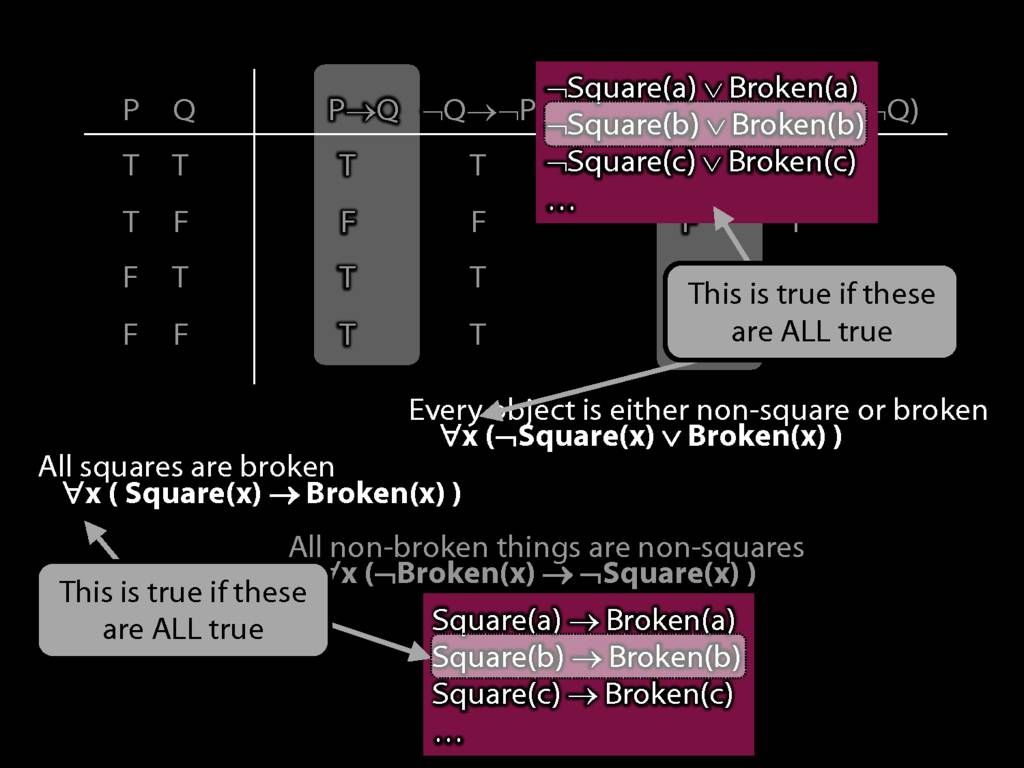
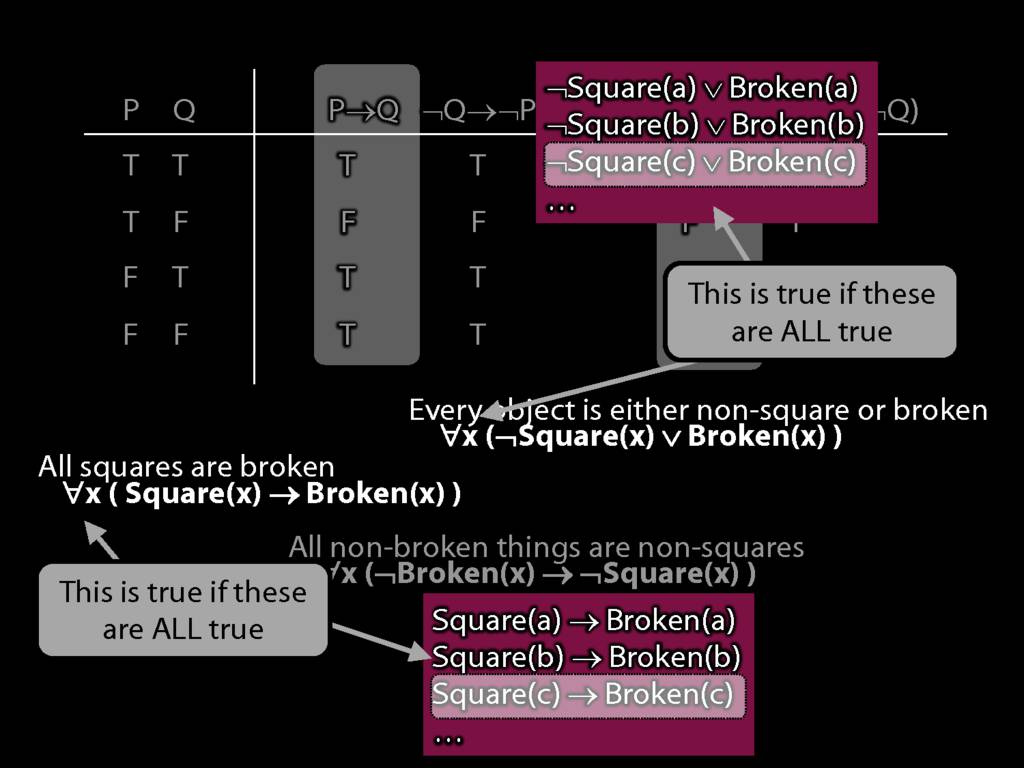
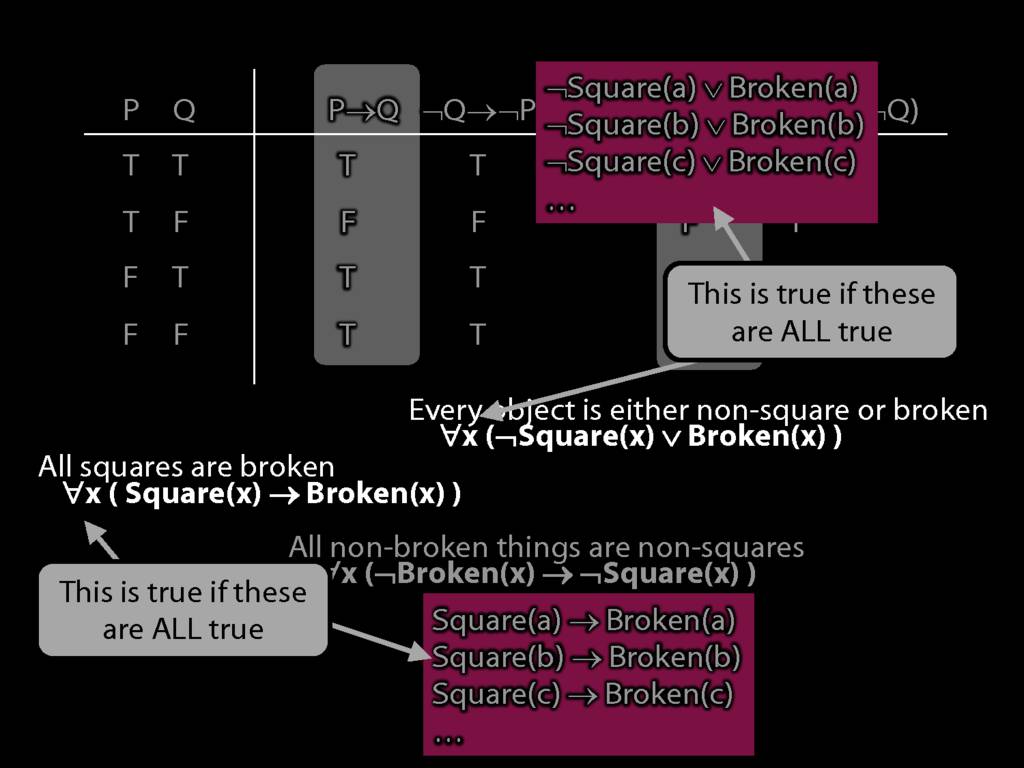
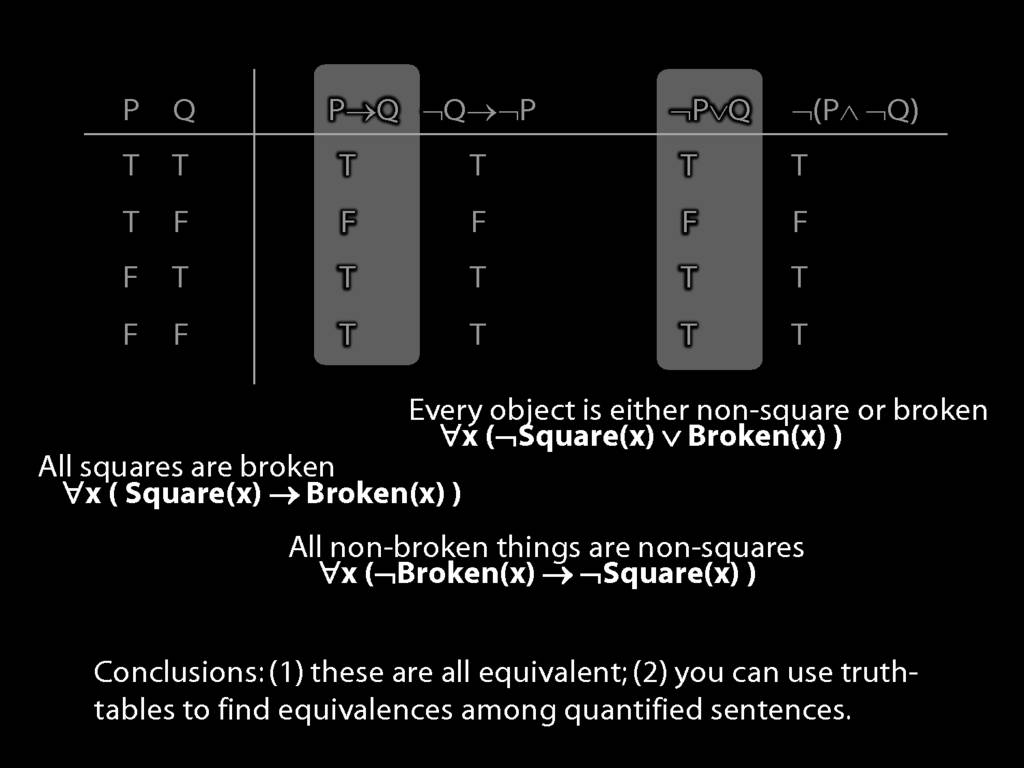
Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))

 
\section{Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))}
\emph{Reading:} §10.3
 
\section{Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Broken(x) → ¬Square(x))}
10.20, 10.22
 
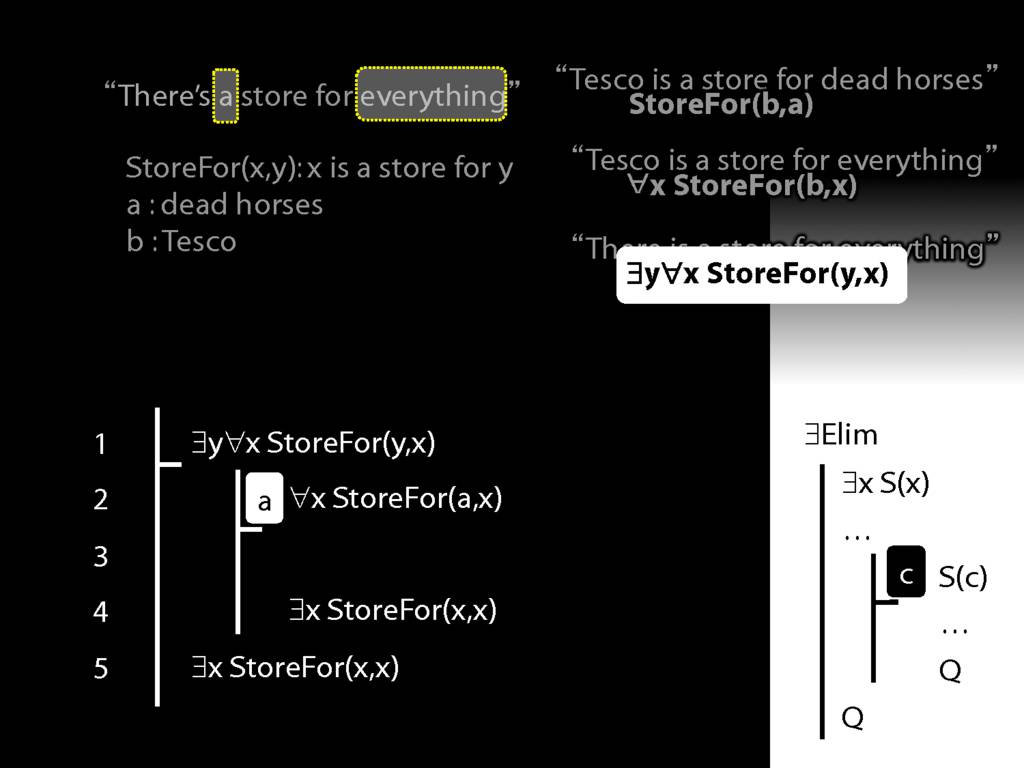
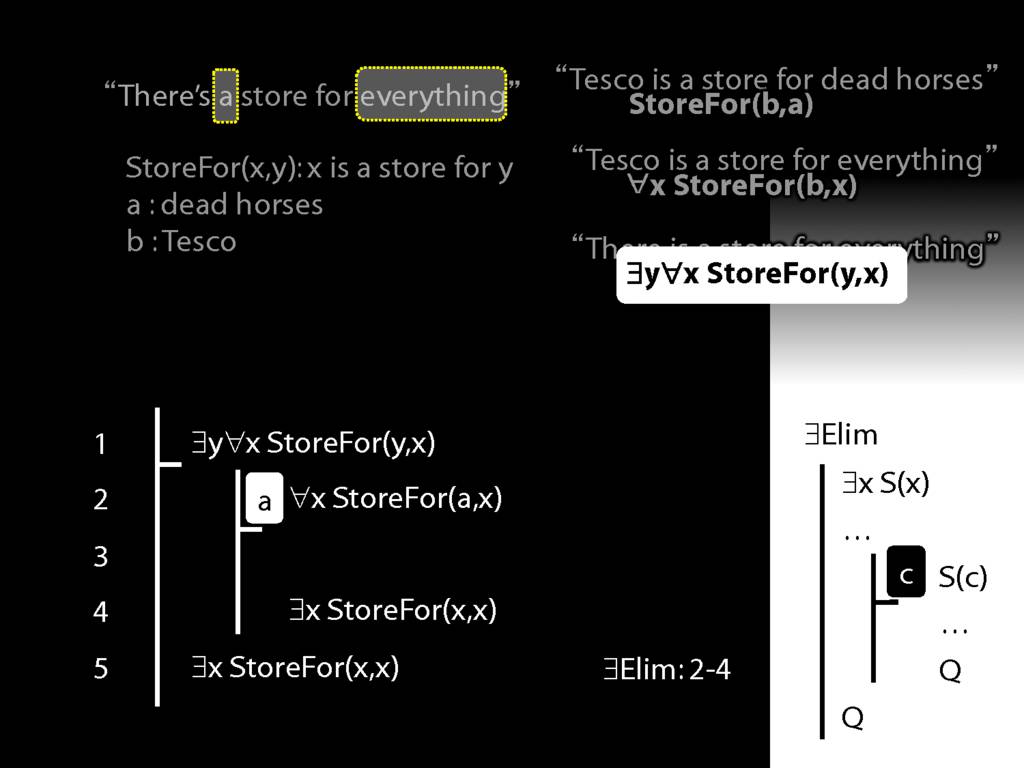
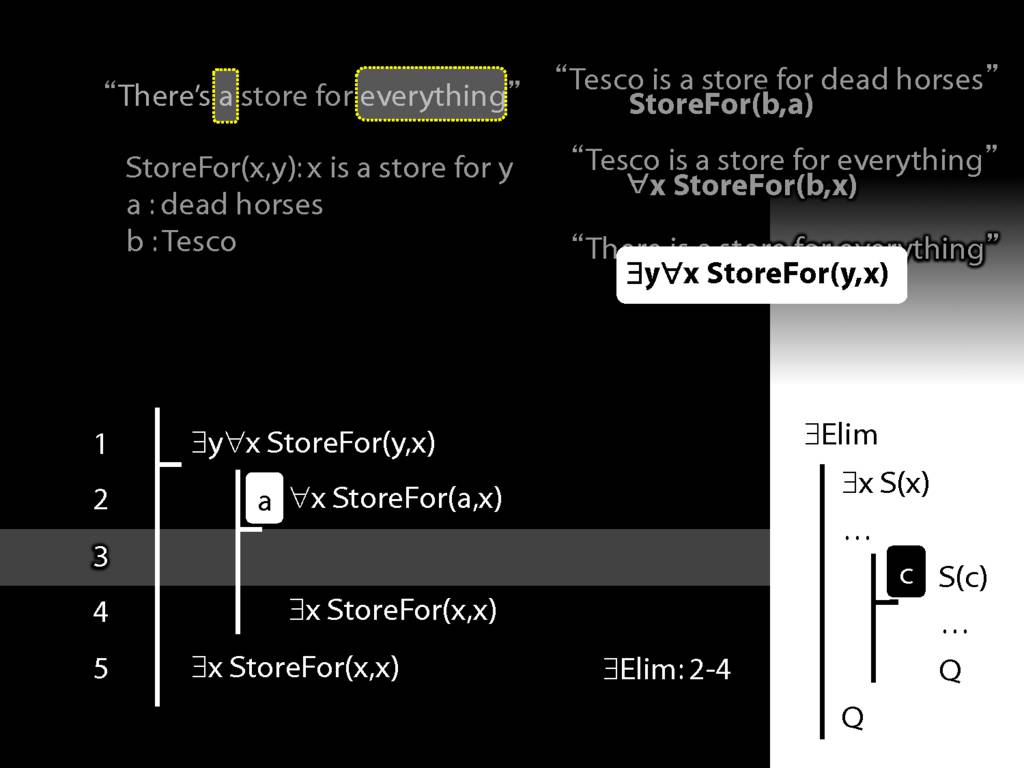
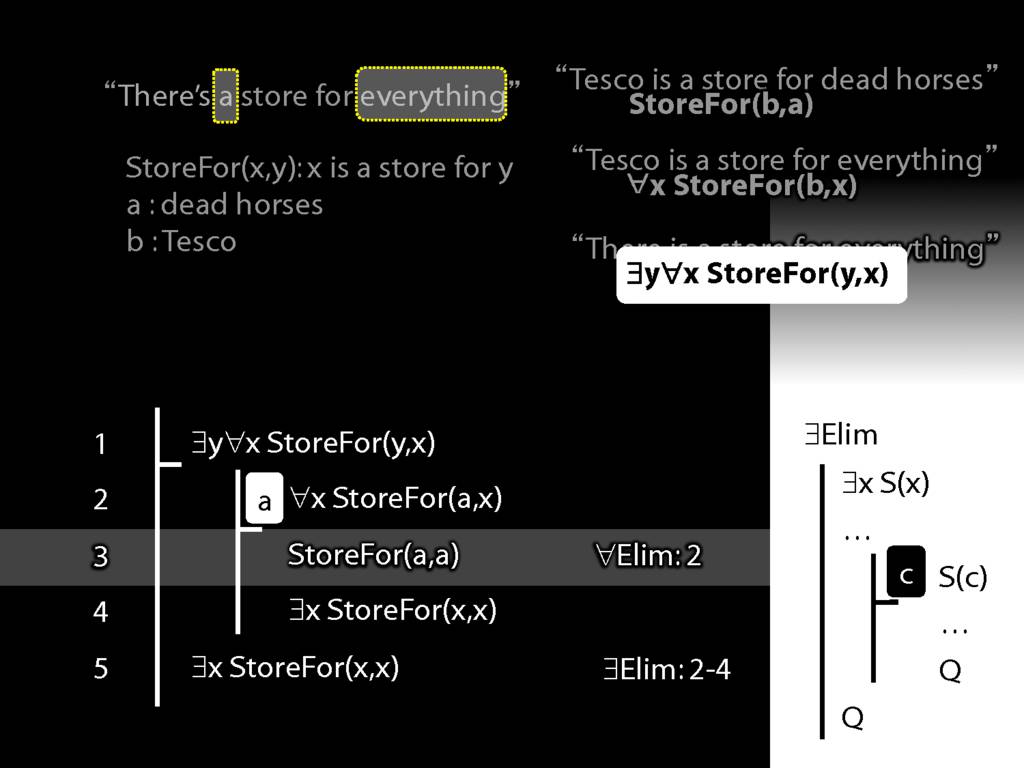
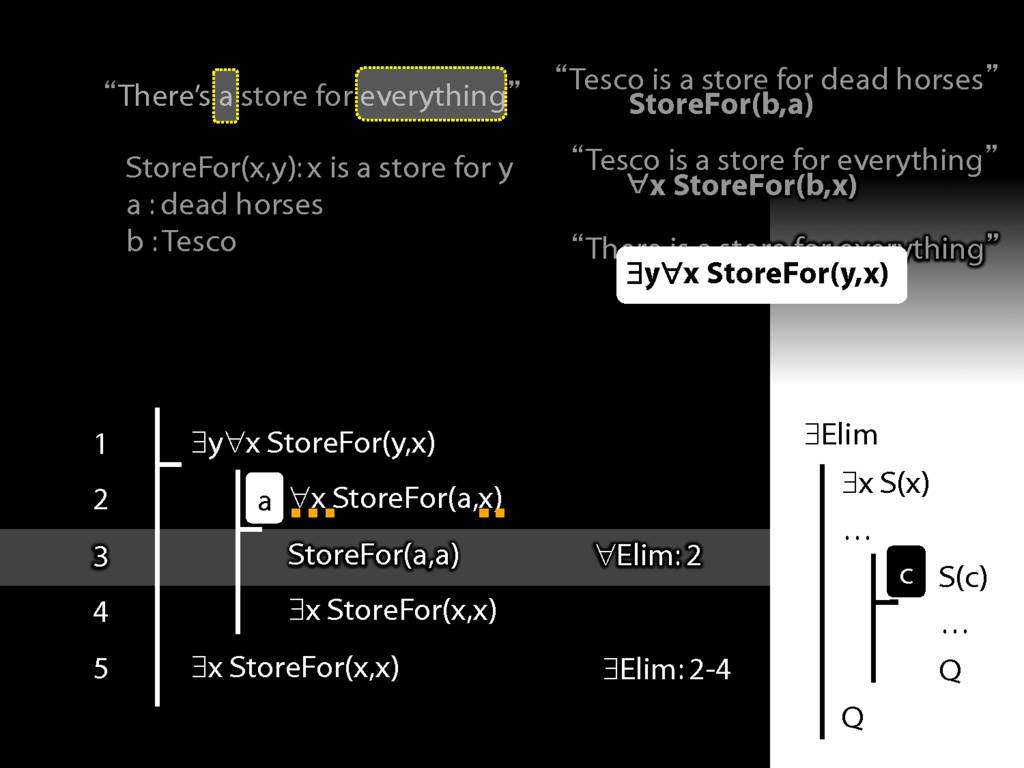
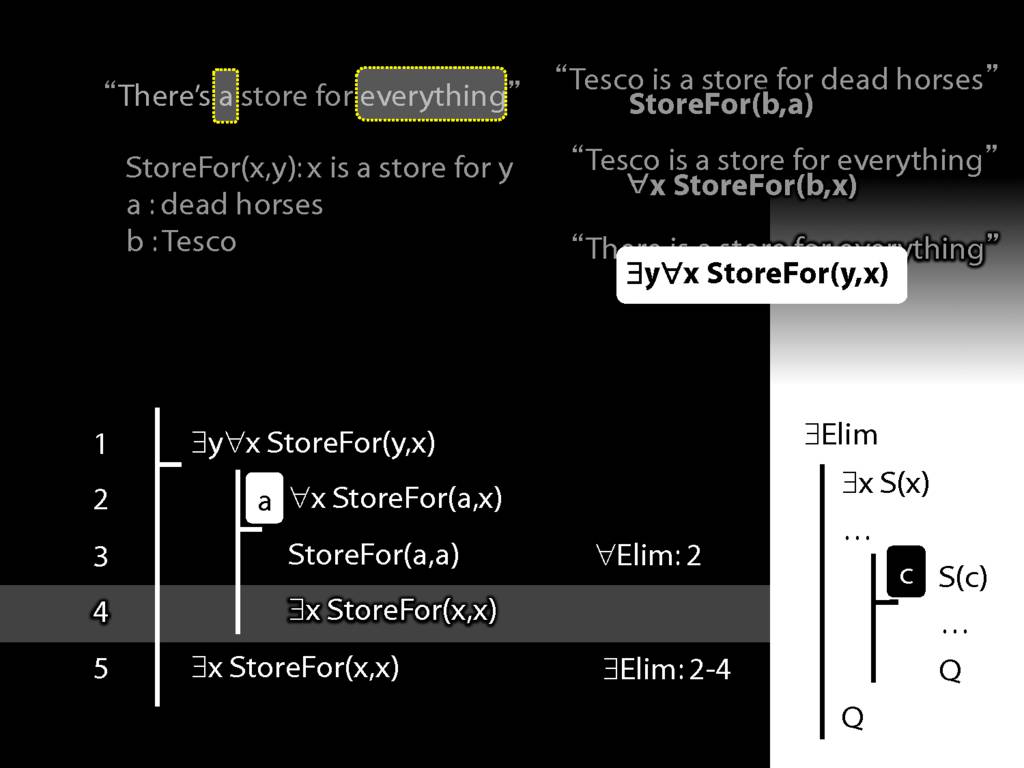
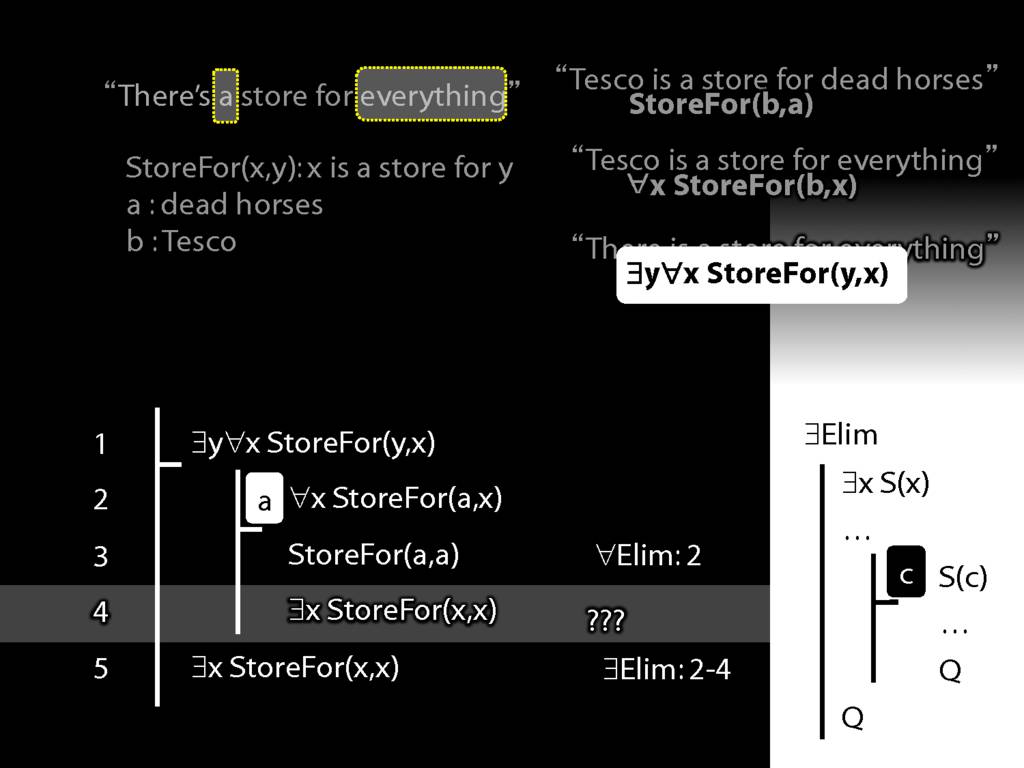
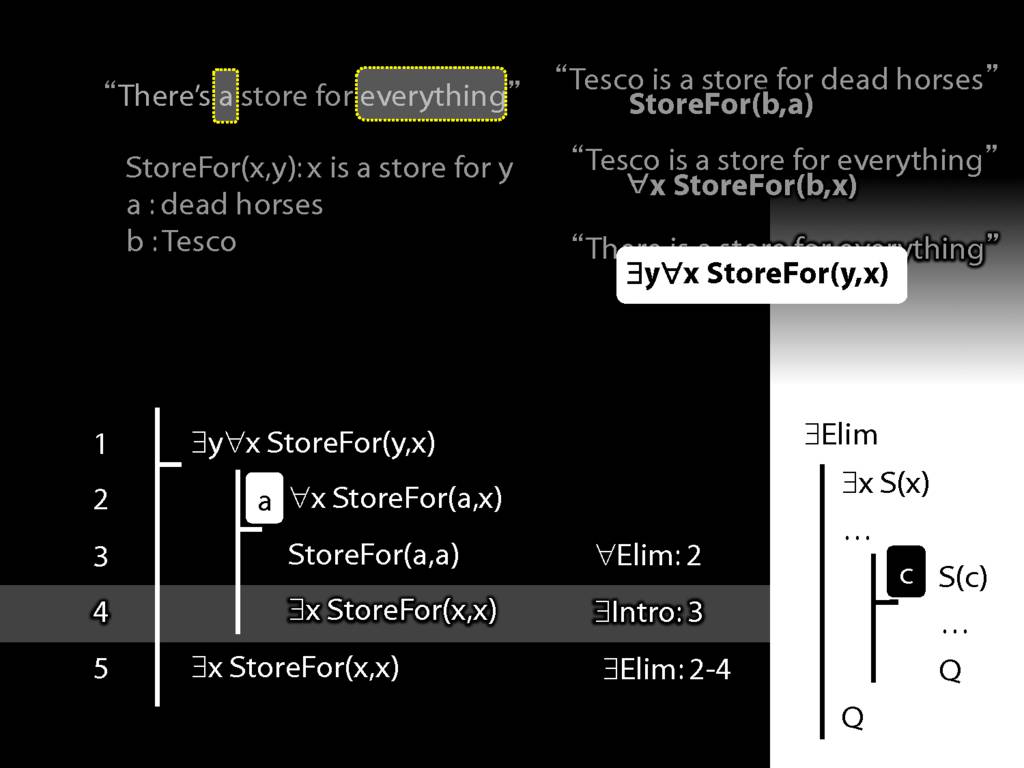
\section{Quantifier Equivalences: ∀x(Square(x) → Broken(x)) ⫤⊨ ∀x(¬Square(x) ∨ Broken(x))}
 

More Dead Horse

 
\section{More Dead Horse}
\emph{Reading:} §11.4, §11.5
 
\section{More Dead Horse}
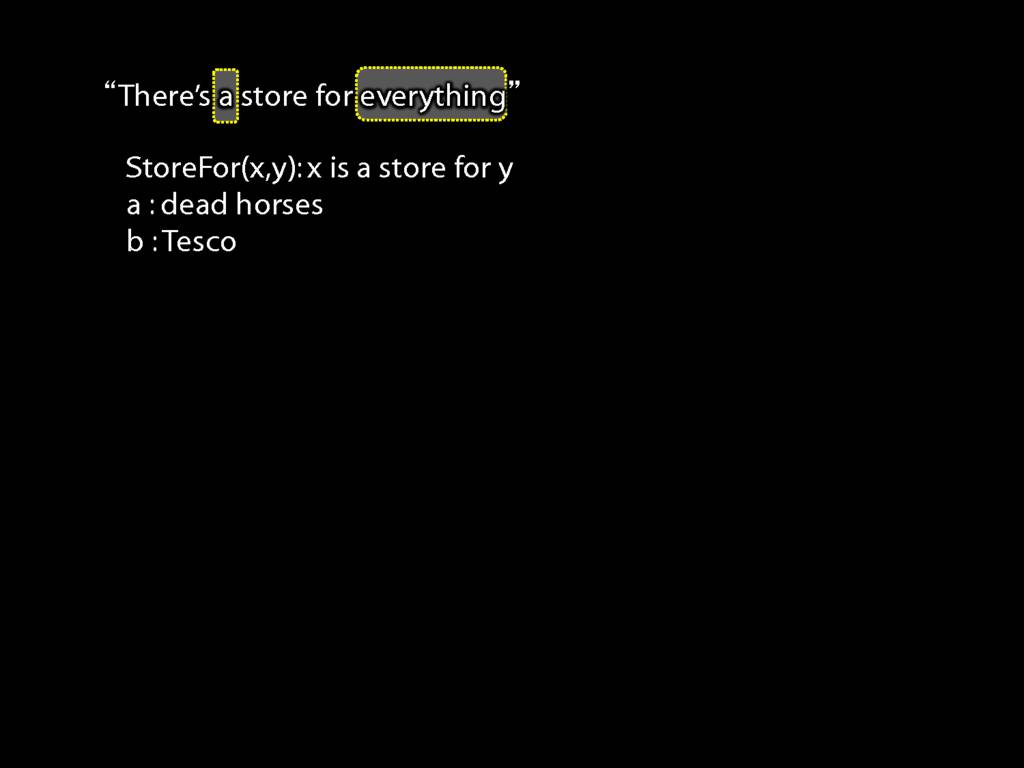
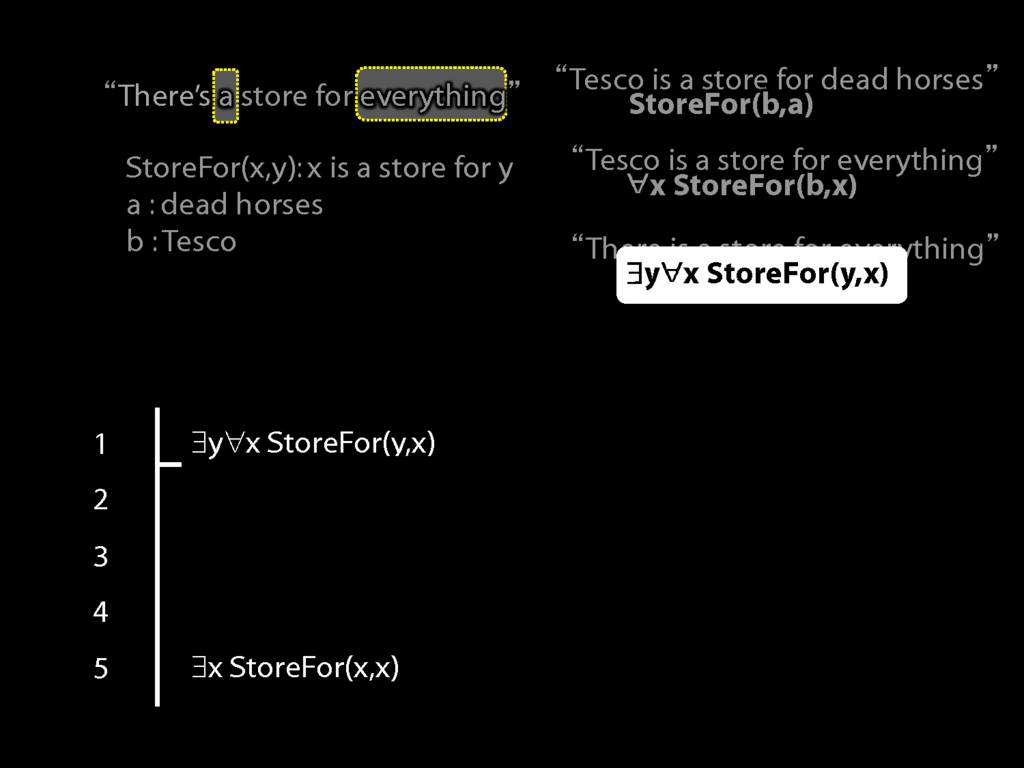
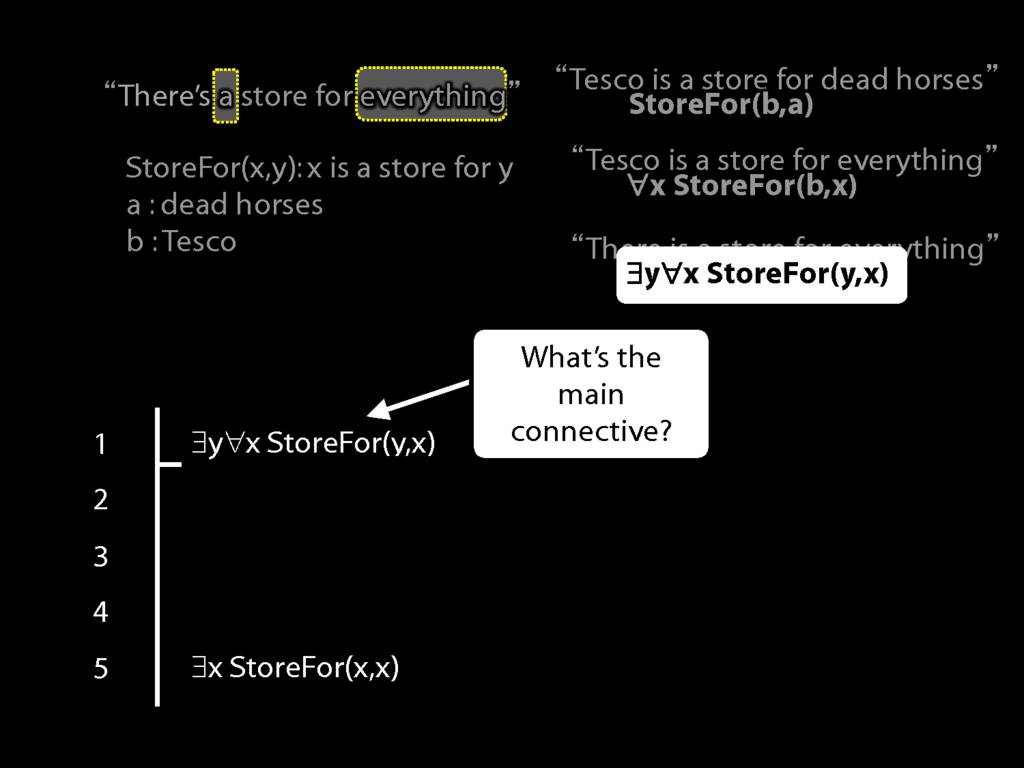
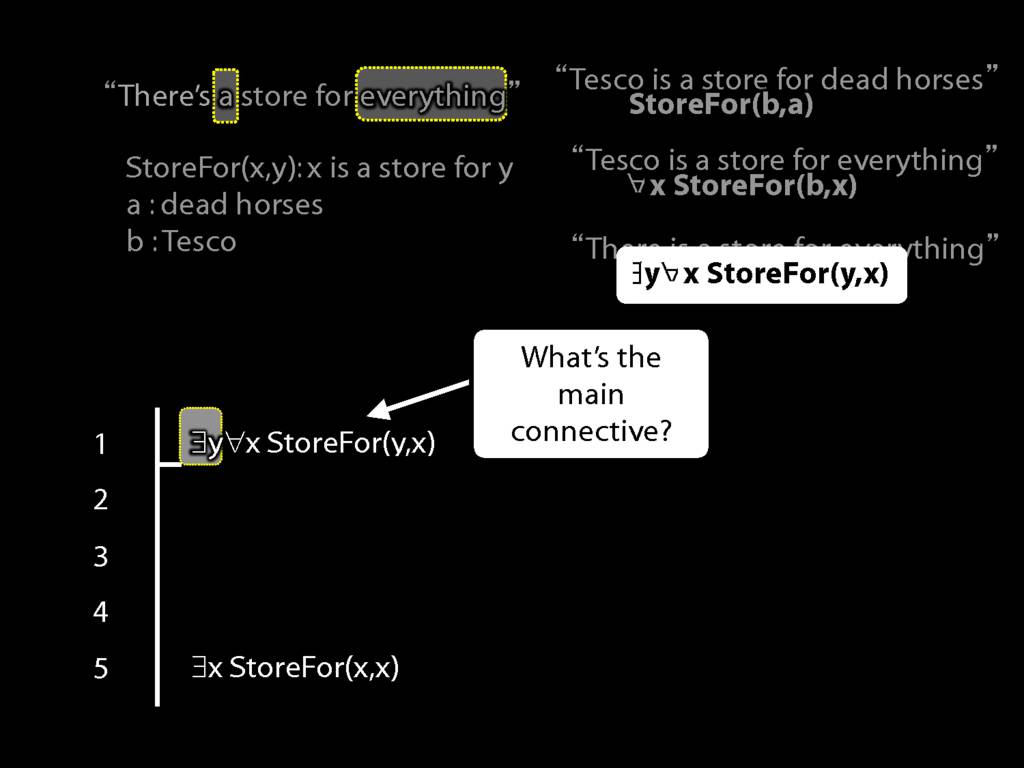
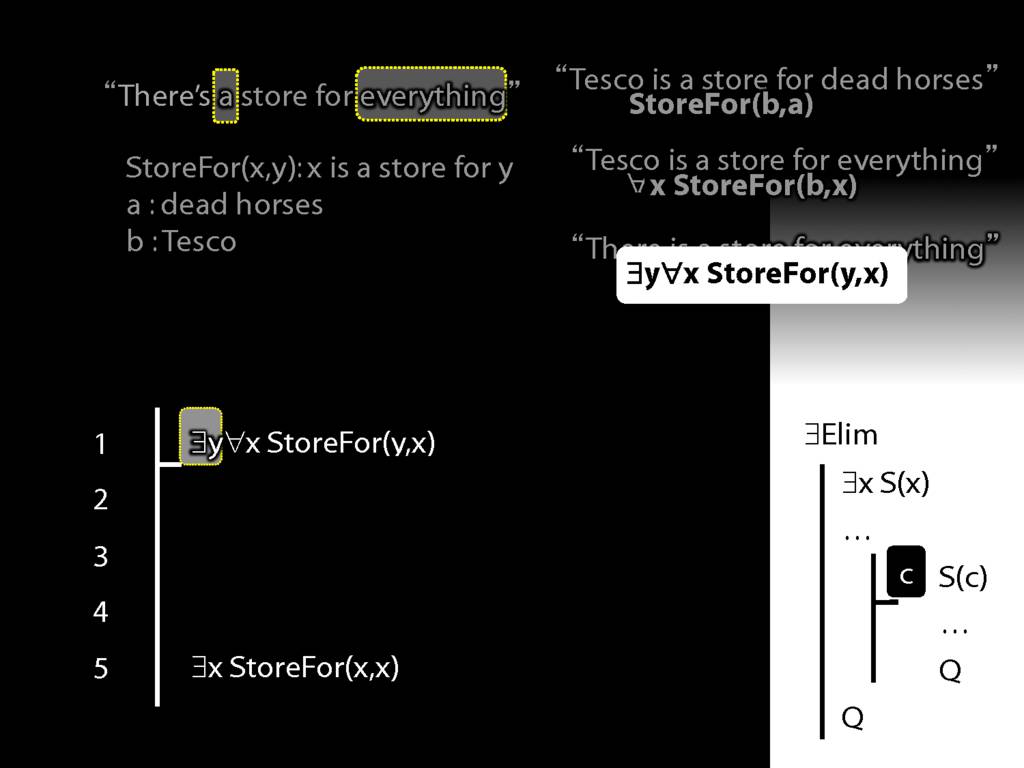
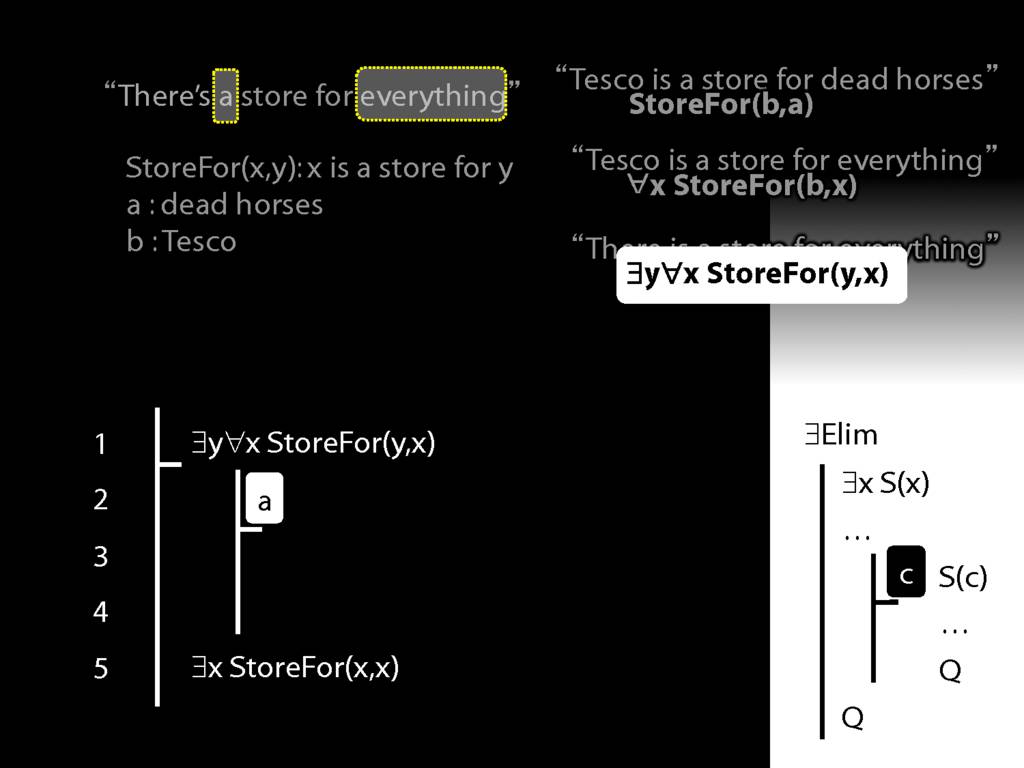
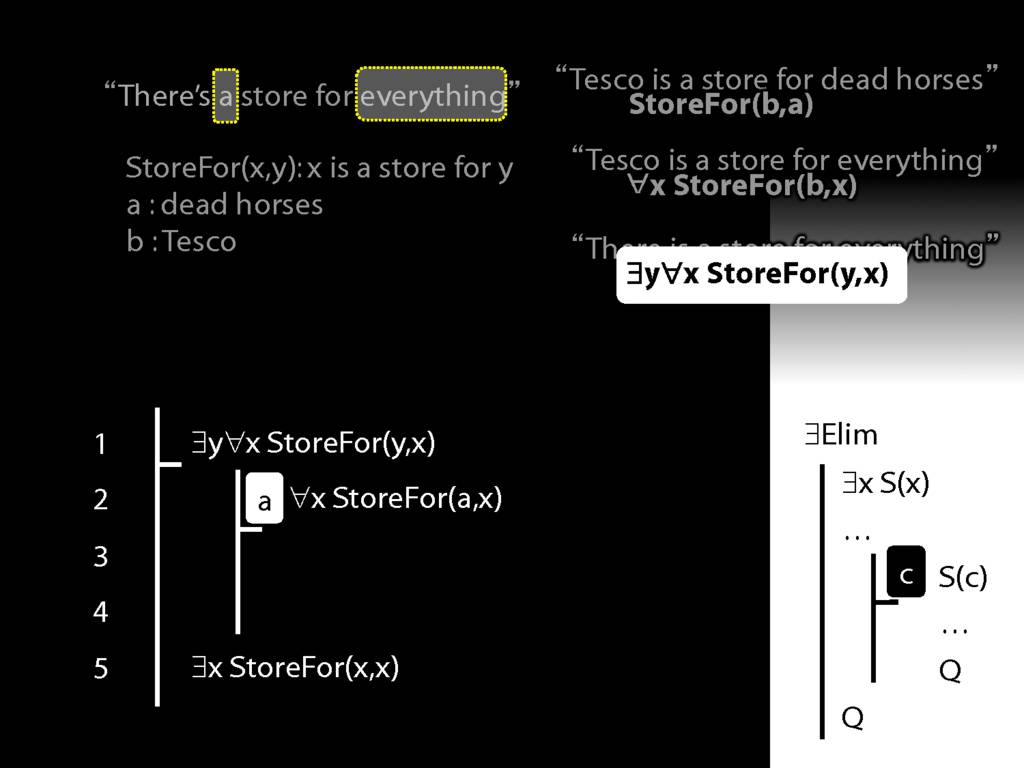
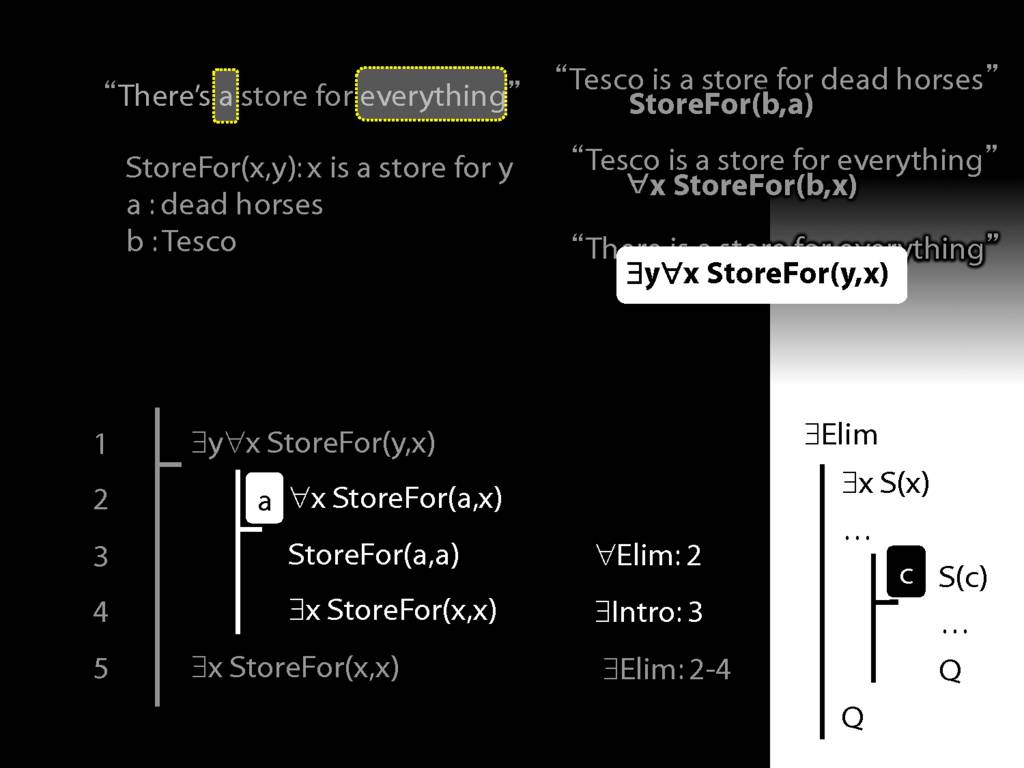
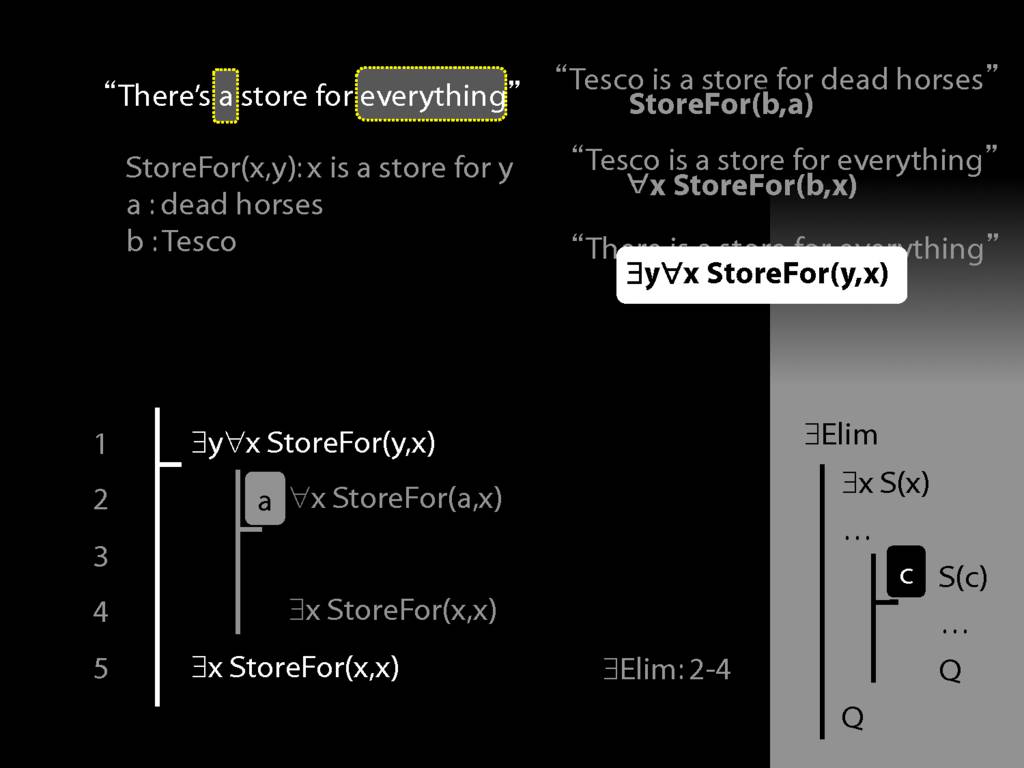
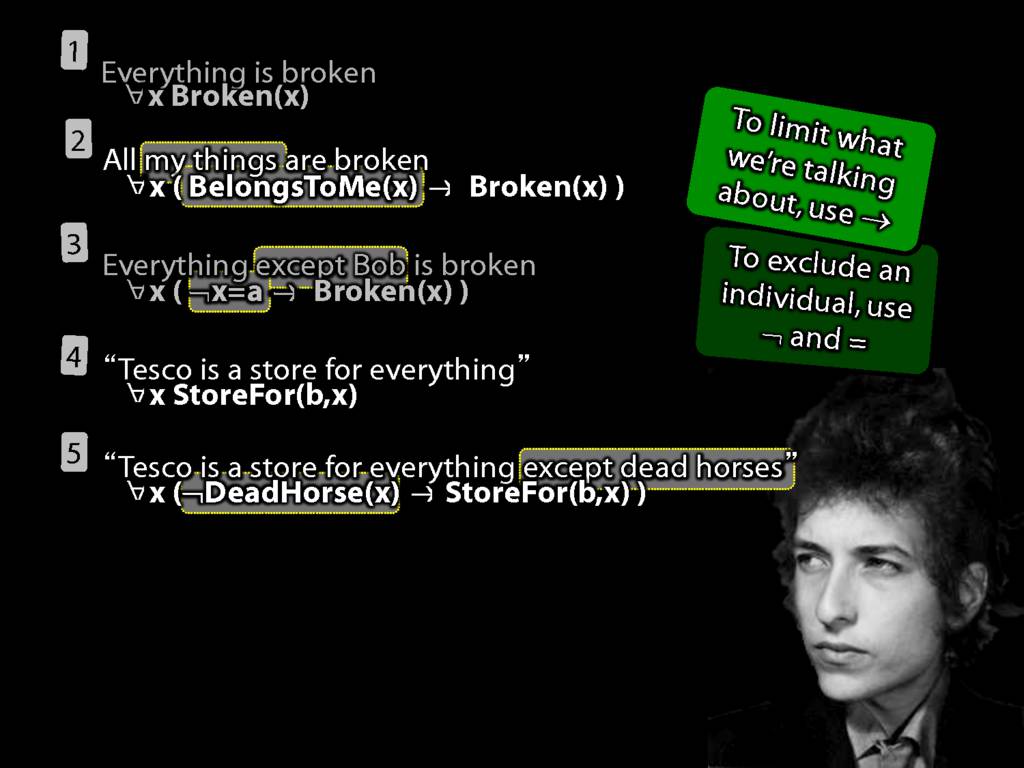
“Tesco is a store for everything”
\hspace{3mm} ∀x StoreFor(b,x)
Tesco is a store for everything except dead horses
\hspace{3mm} ∀x (¬DeadHorse(x) → StoreFor(b,x) )
Tesco is a store for everything except Tesco
\hspace{3mm} ∀x (¬x=b → StoreFor(b,x) )
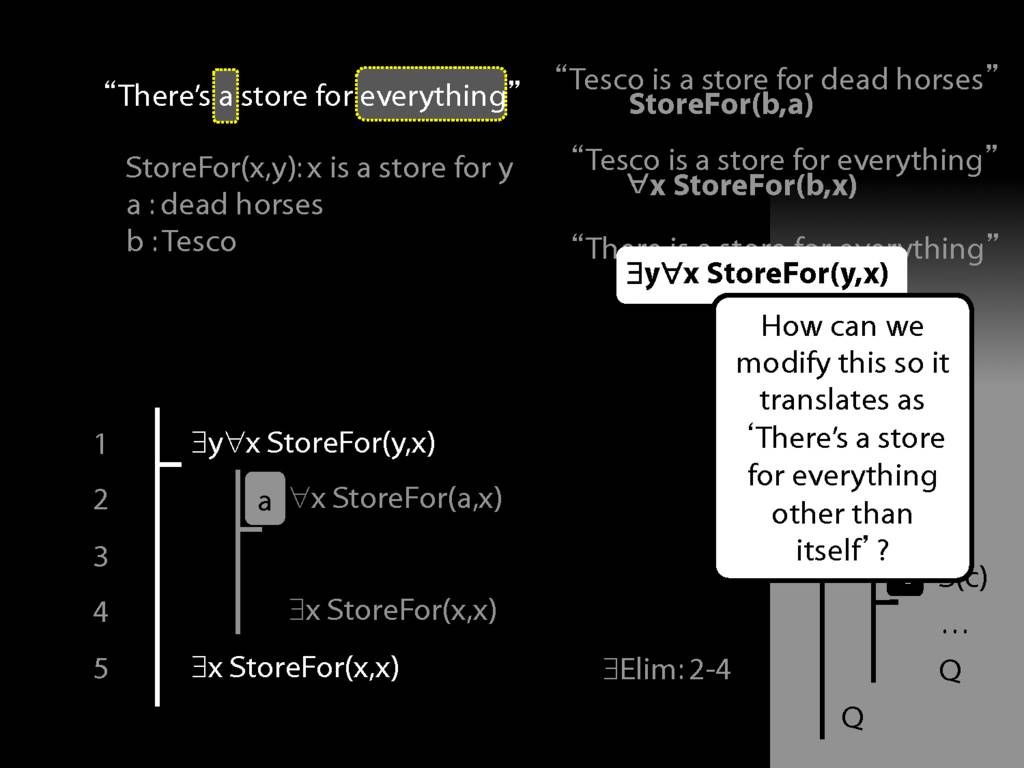
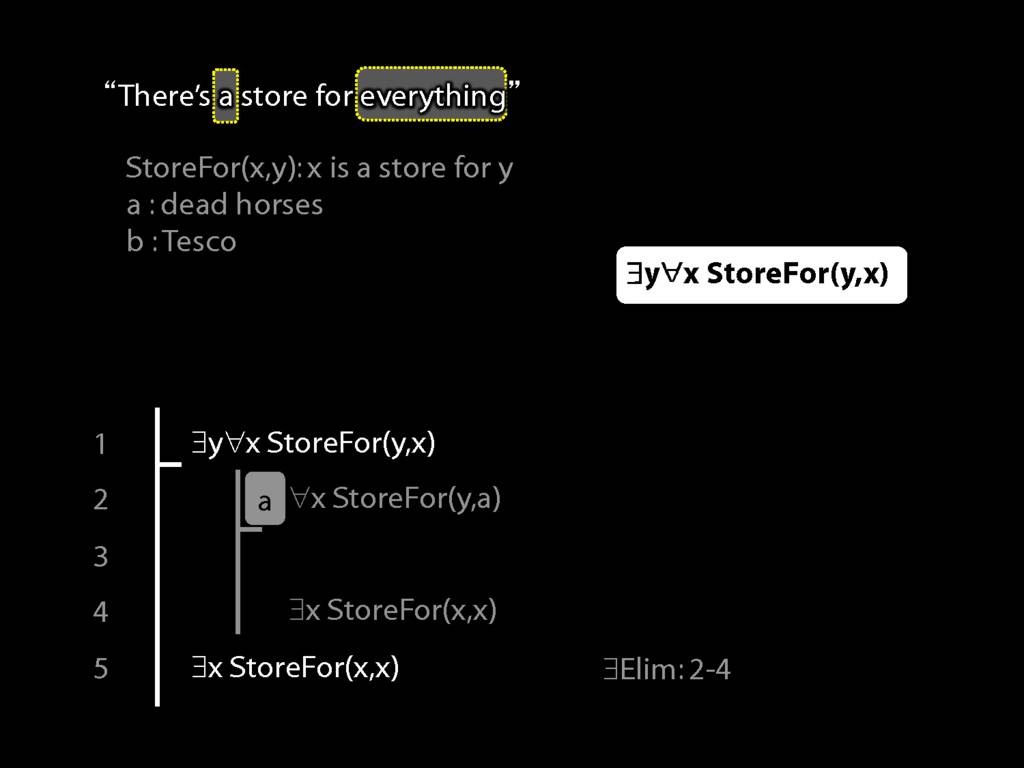
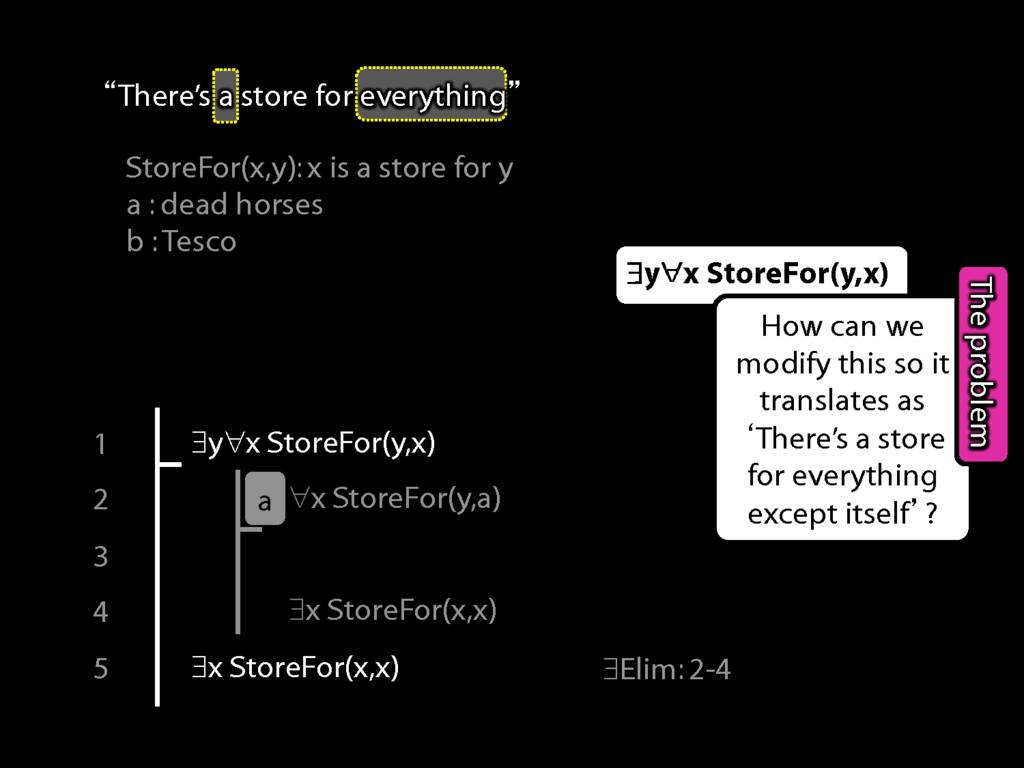
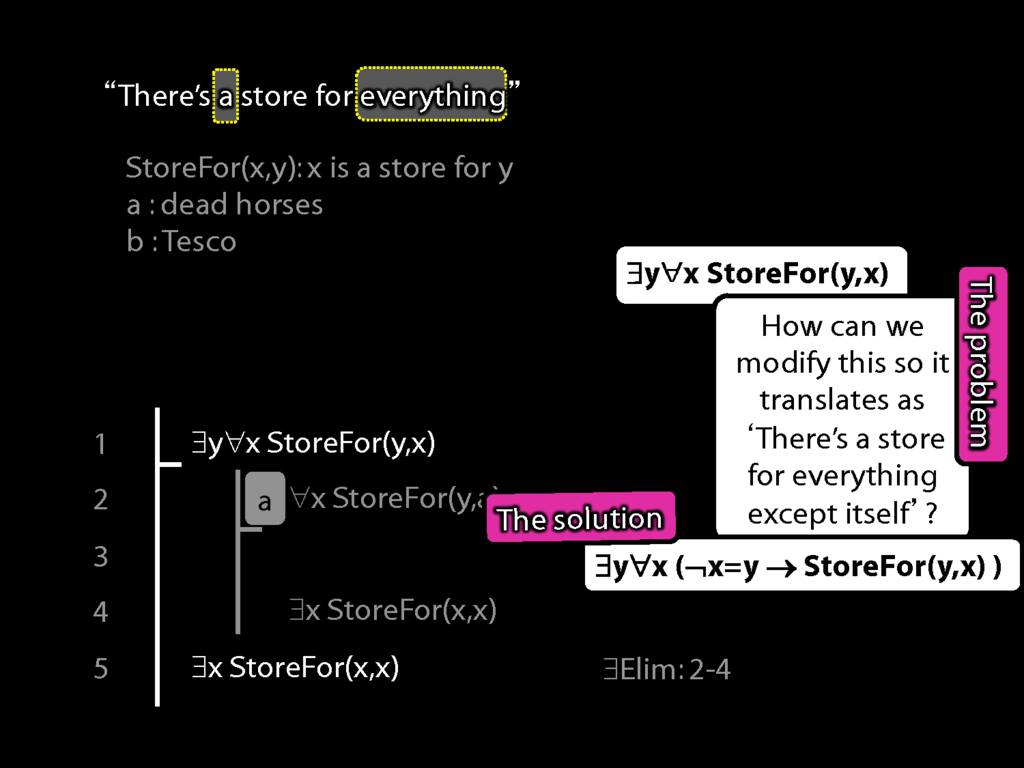
There is a store for everything except itself
\hspace{3mm} ∃y ∀x (¬x=y → StoreFor(y,x) )