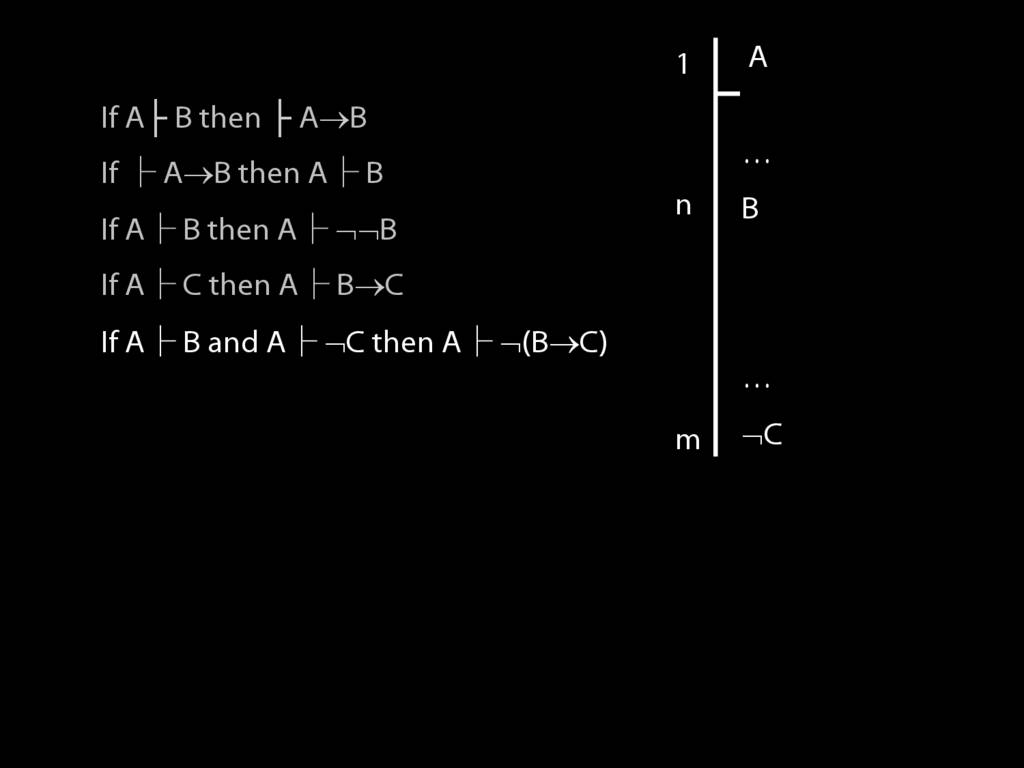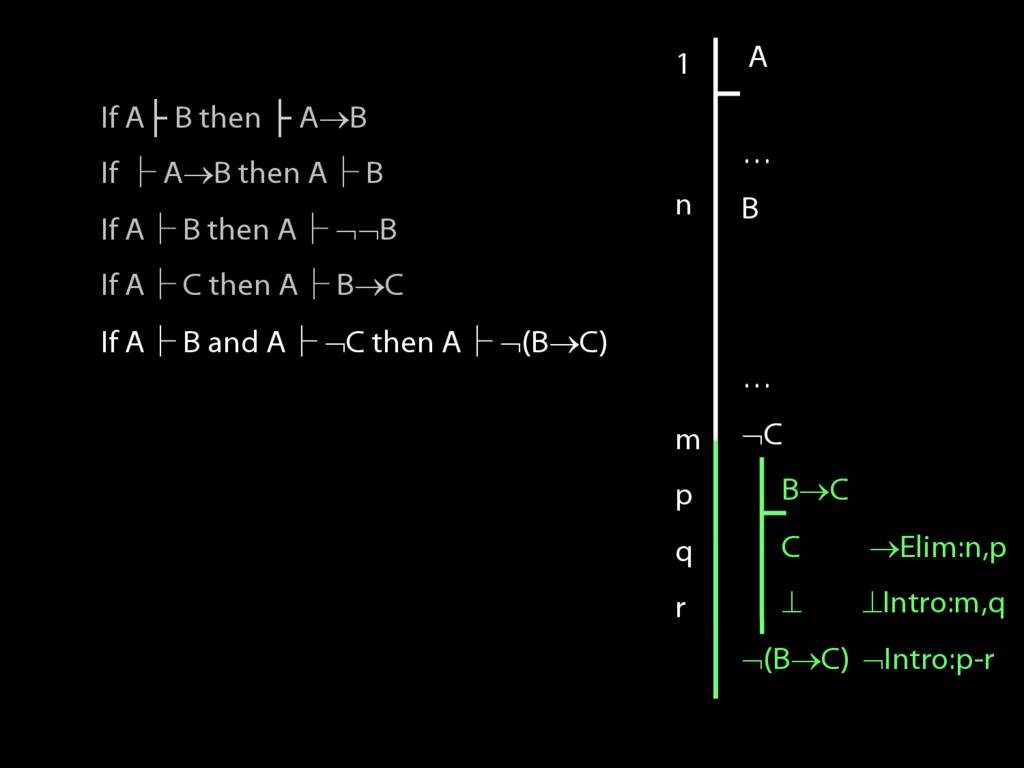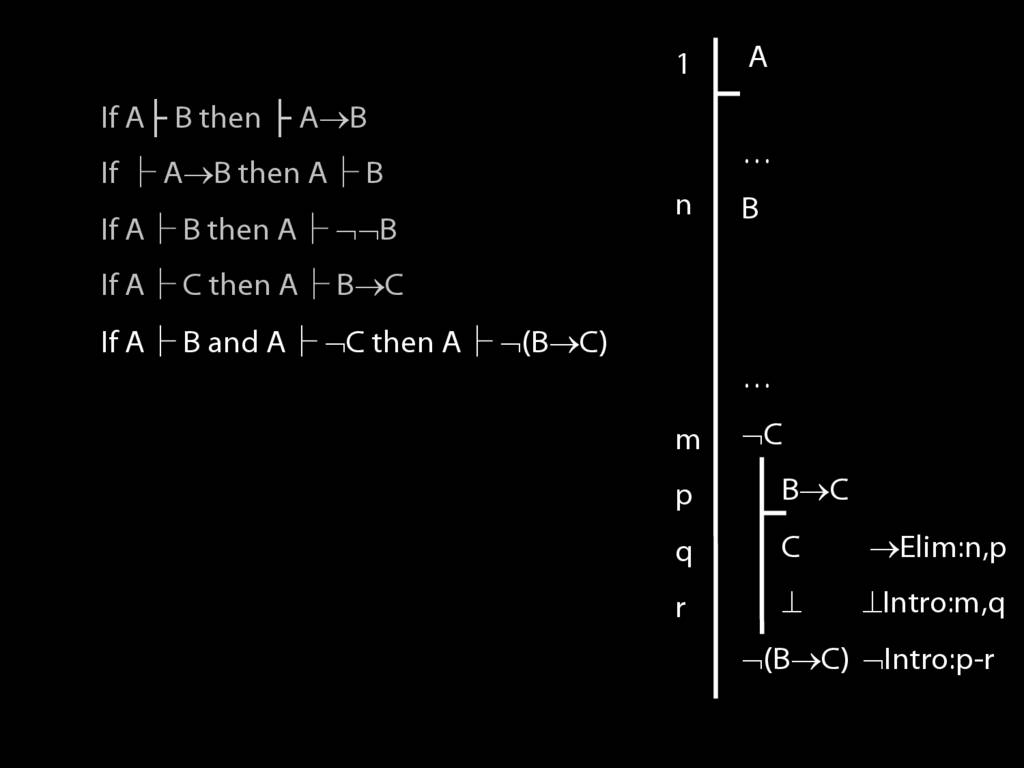\title {Logic I \\ Lecture 16}
\maketitle
\section{There Is Exactly One}
\section{There Is Exactly One}
14.10--14.12, *14.13
11.10, 11.13
14.2
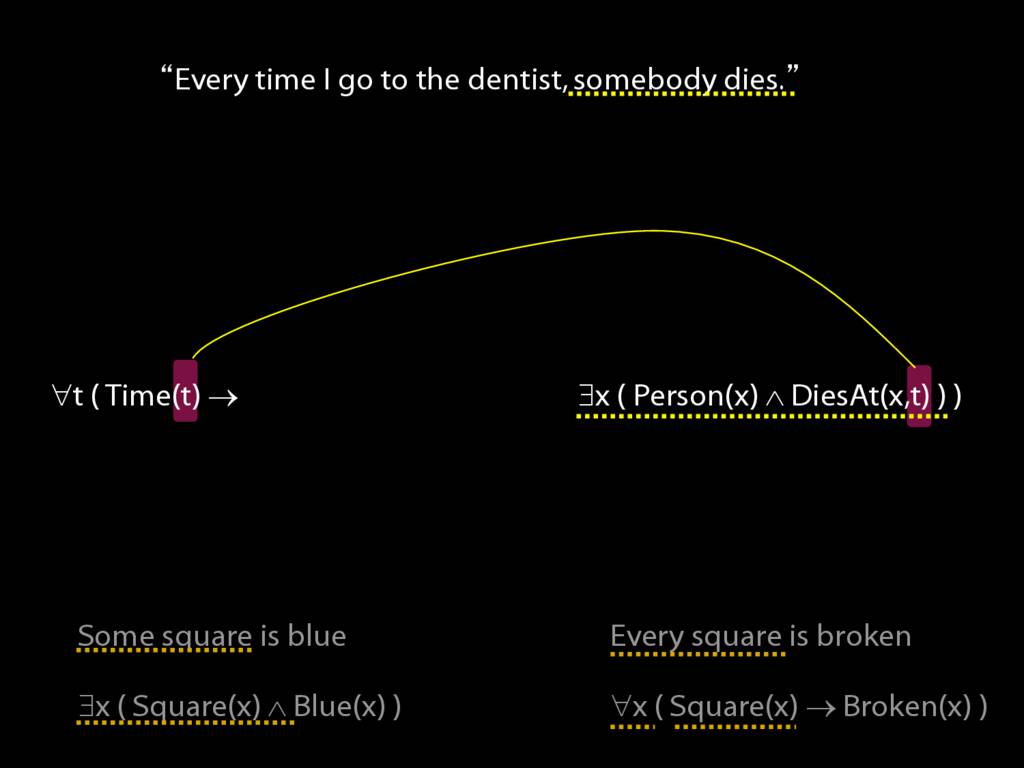
\section{Every Time I Go to the Dentist Someone Dies}
\emph{Reading:} §11.2
\section{Every Time I Go to the Dentist Someone Dies}
\section{Could There Be Nothing?}
\emph{Reading:} §13.2
\section{Could There Be Nothing?}
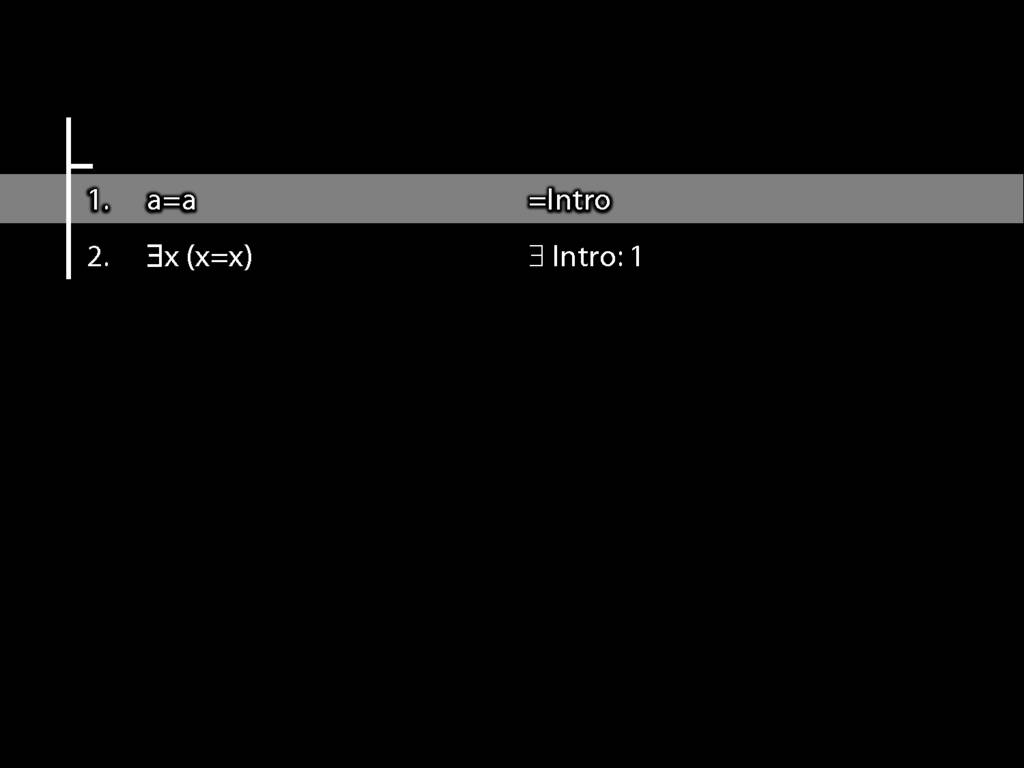
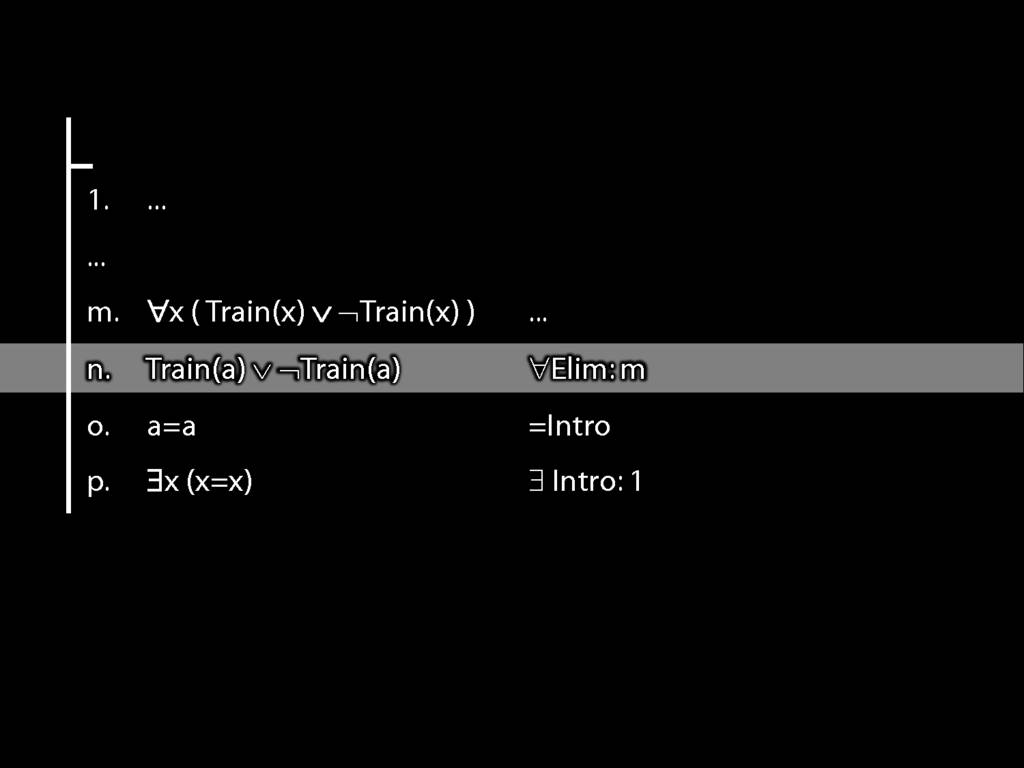
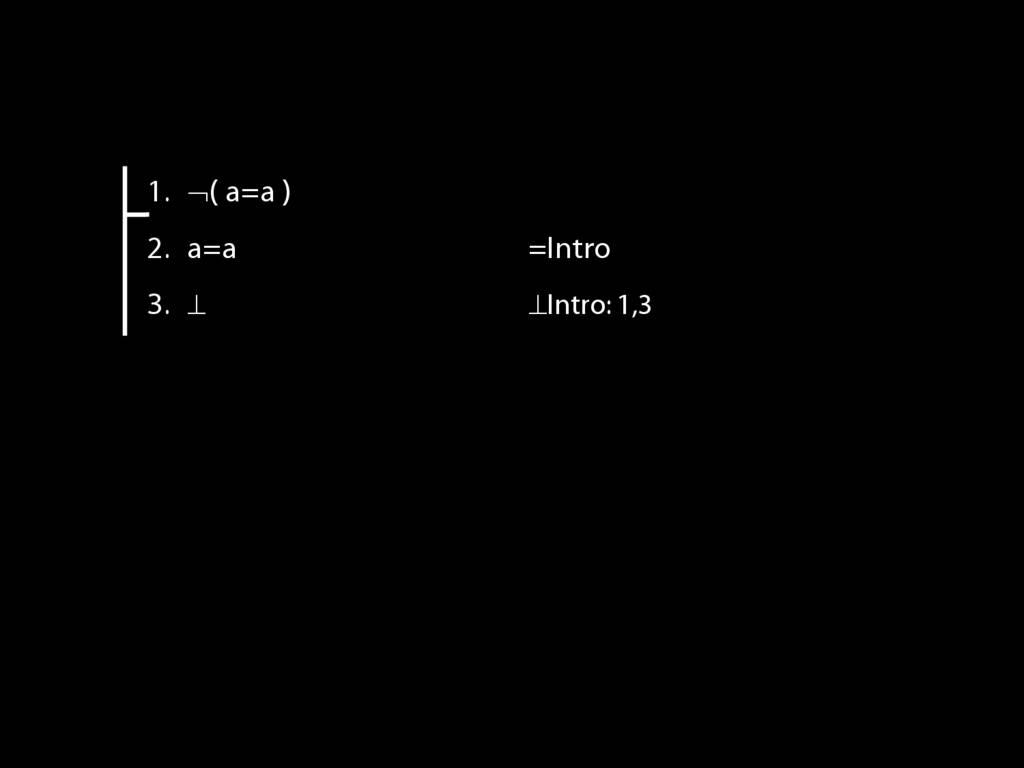
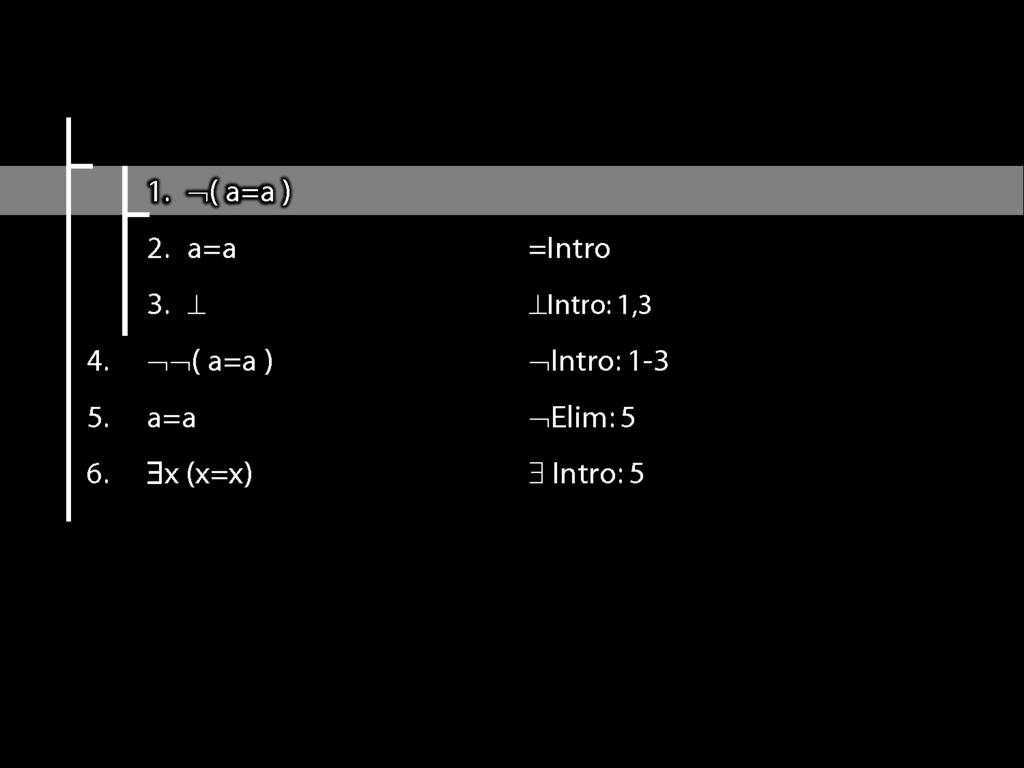
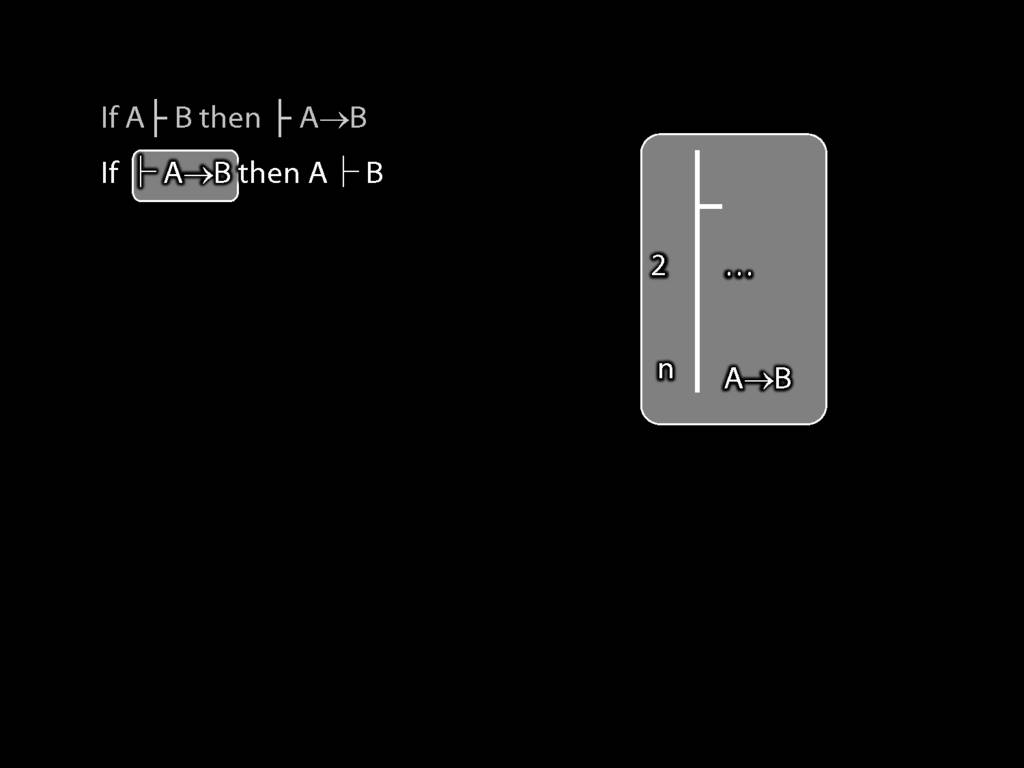
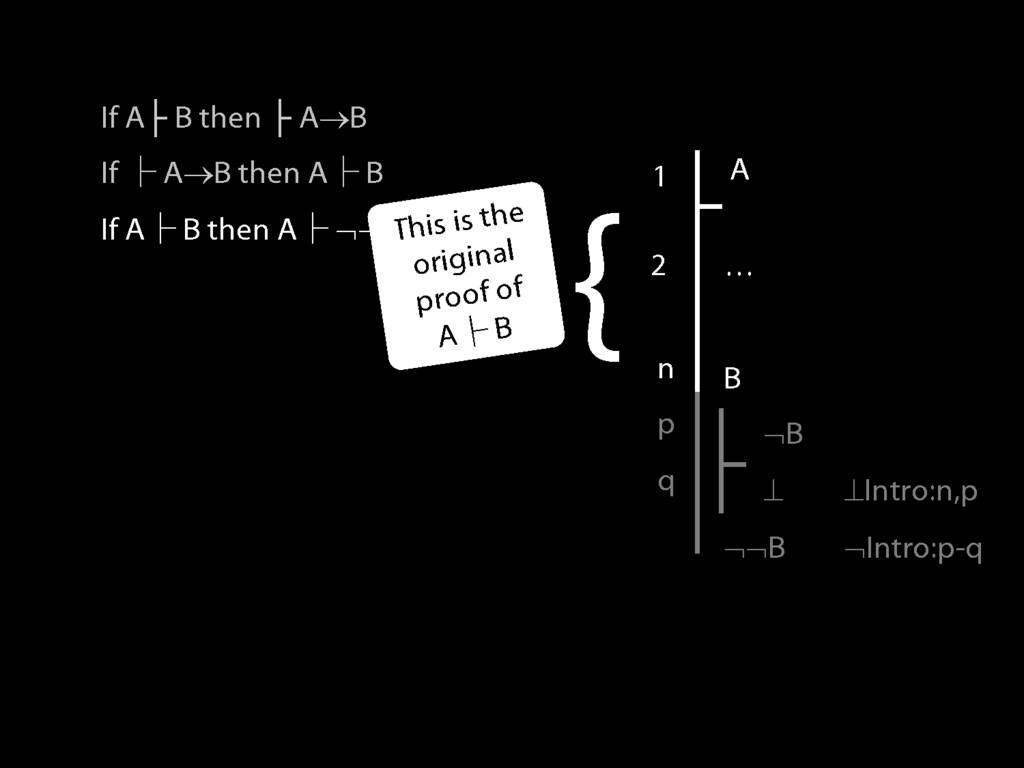
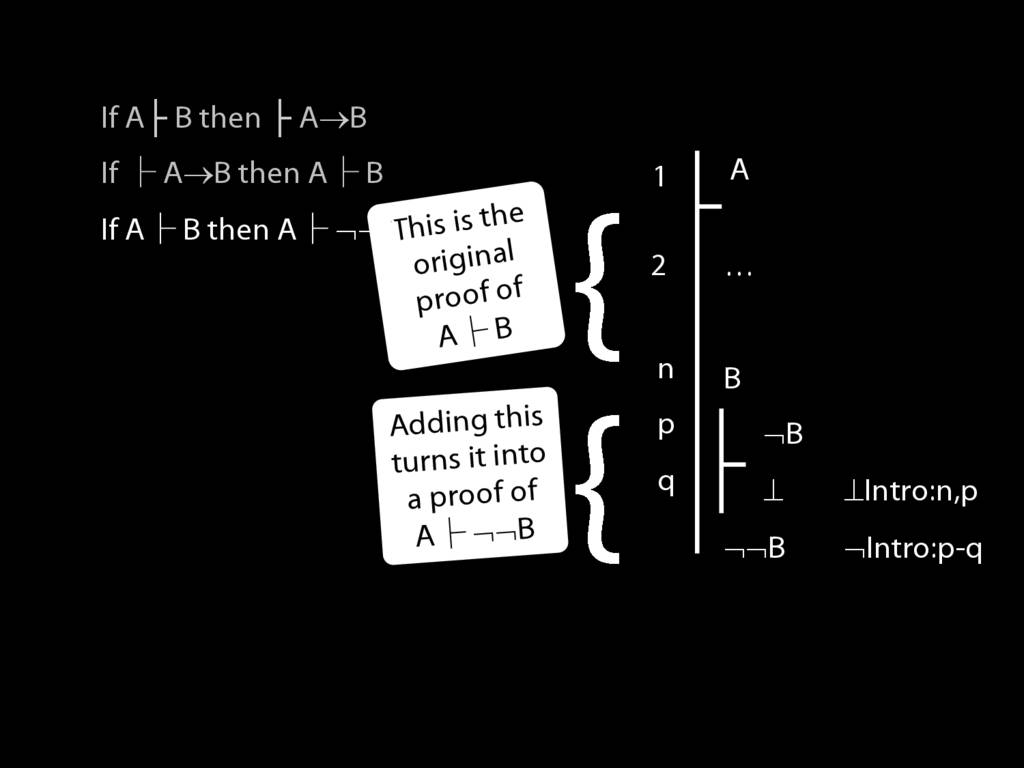
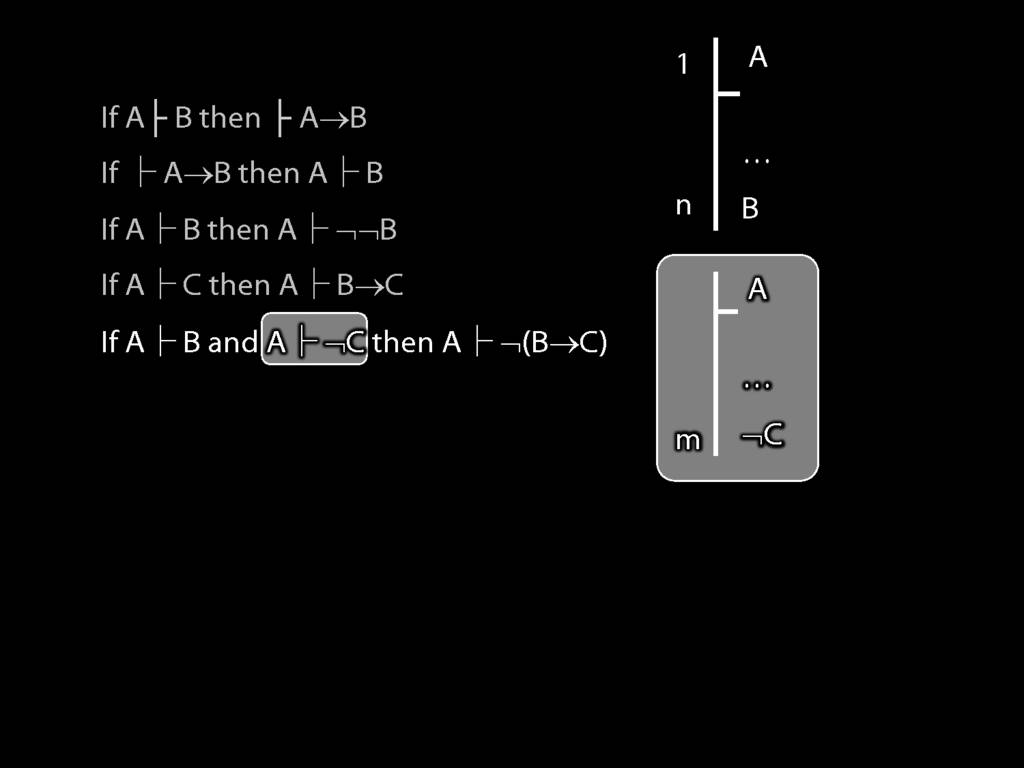
\section{Proofs about Proofs}
\section{Proofs about Proofs}
\section{Does ‘if’ mean what ‘→’ means?}
\emph{Reading:} §7.3
\section{Does ‘if’ mean what ‘→’ means?}