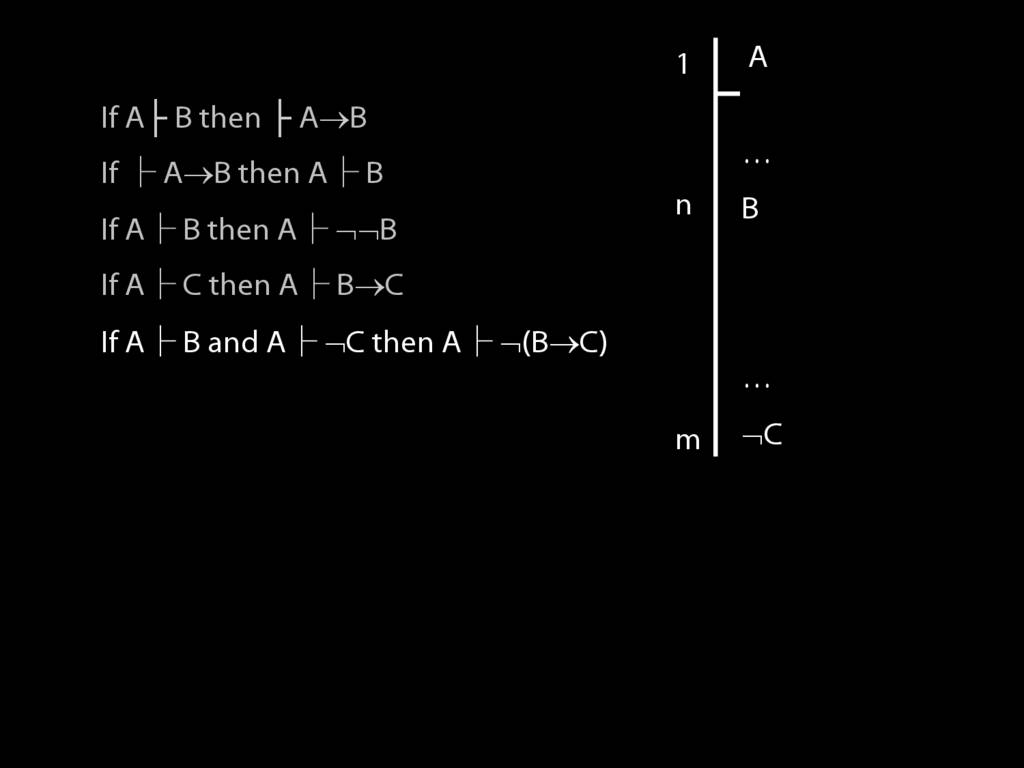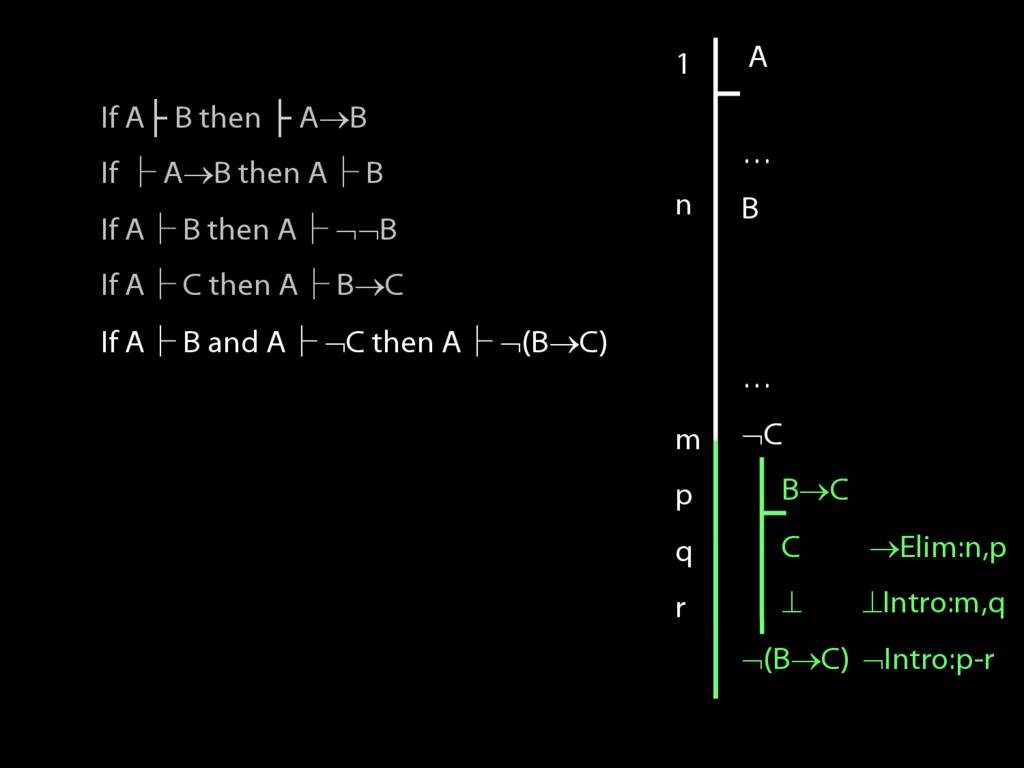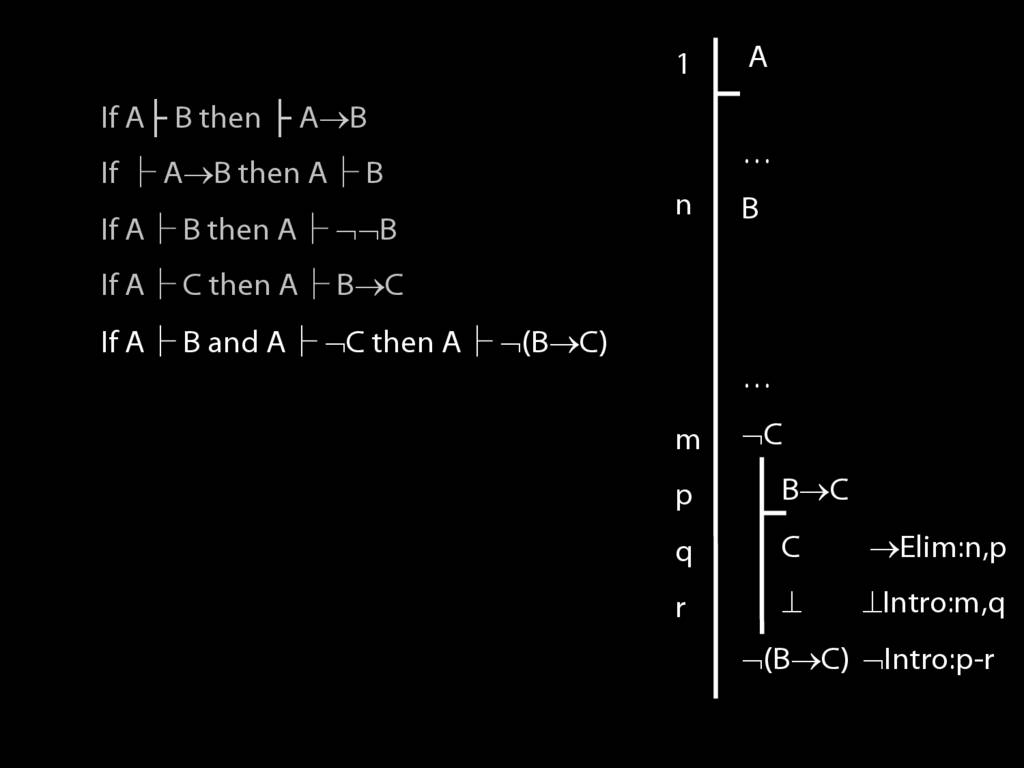\title {Logic I \\ Lecture 18}
\maketitle
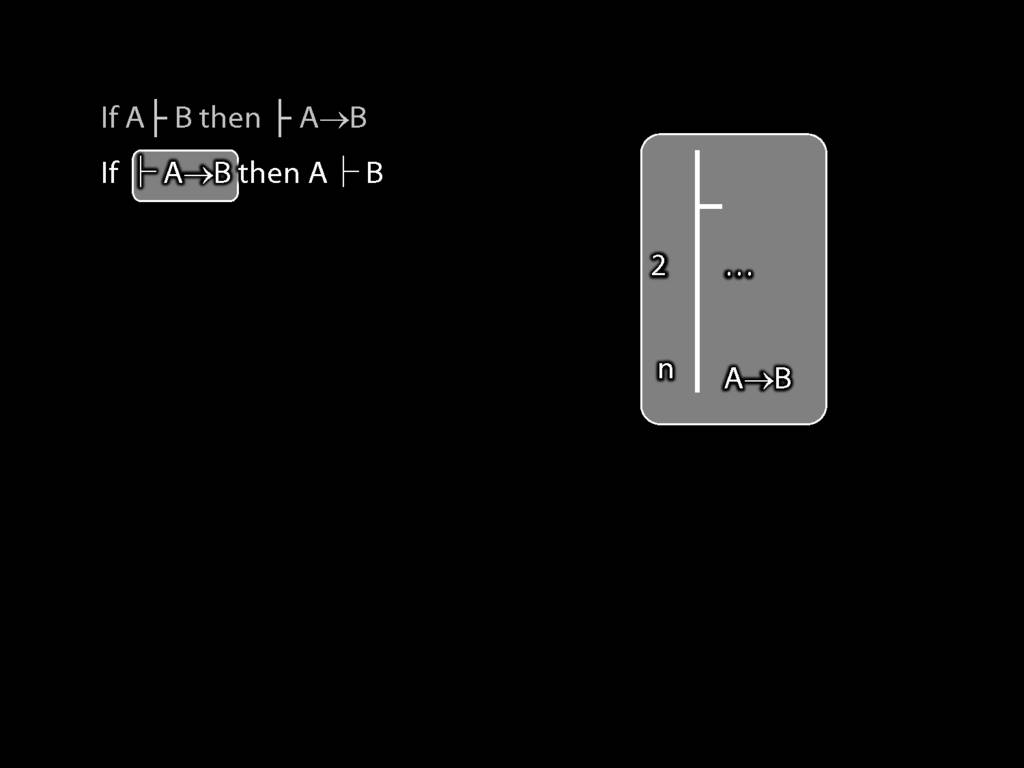
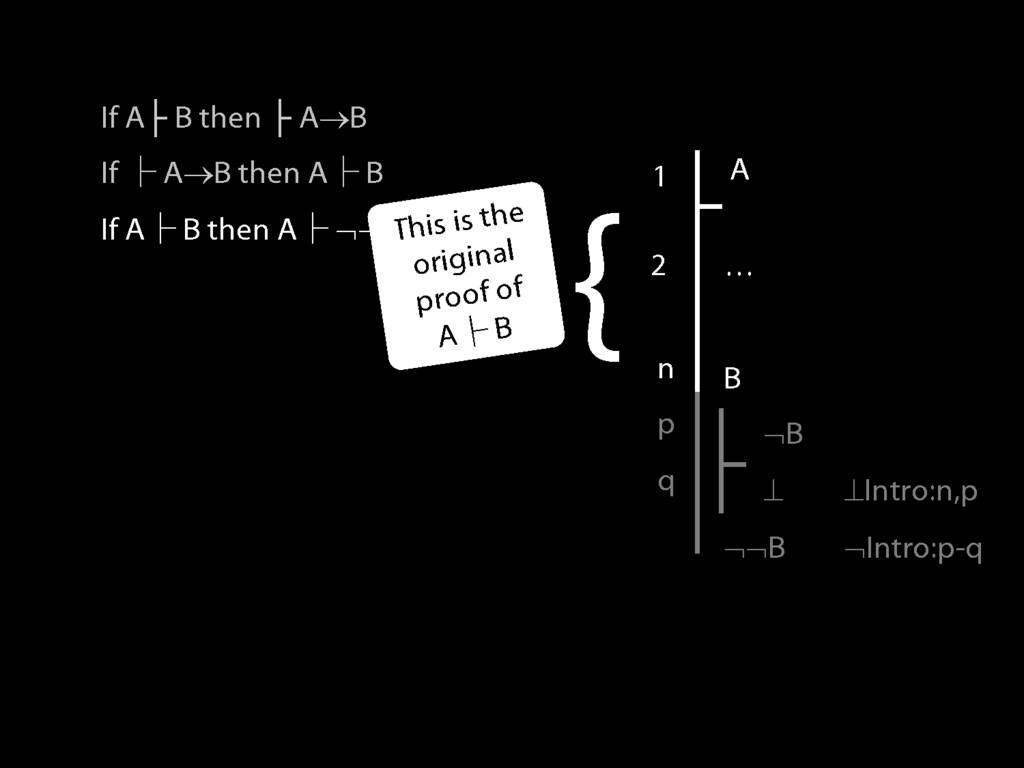
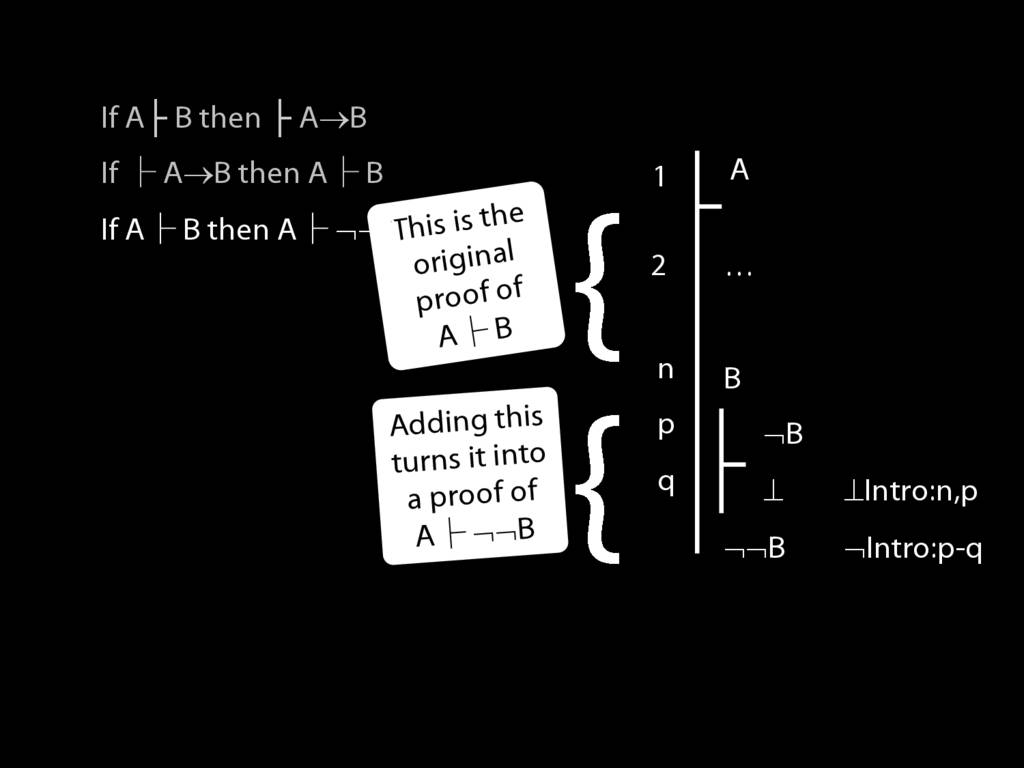
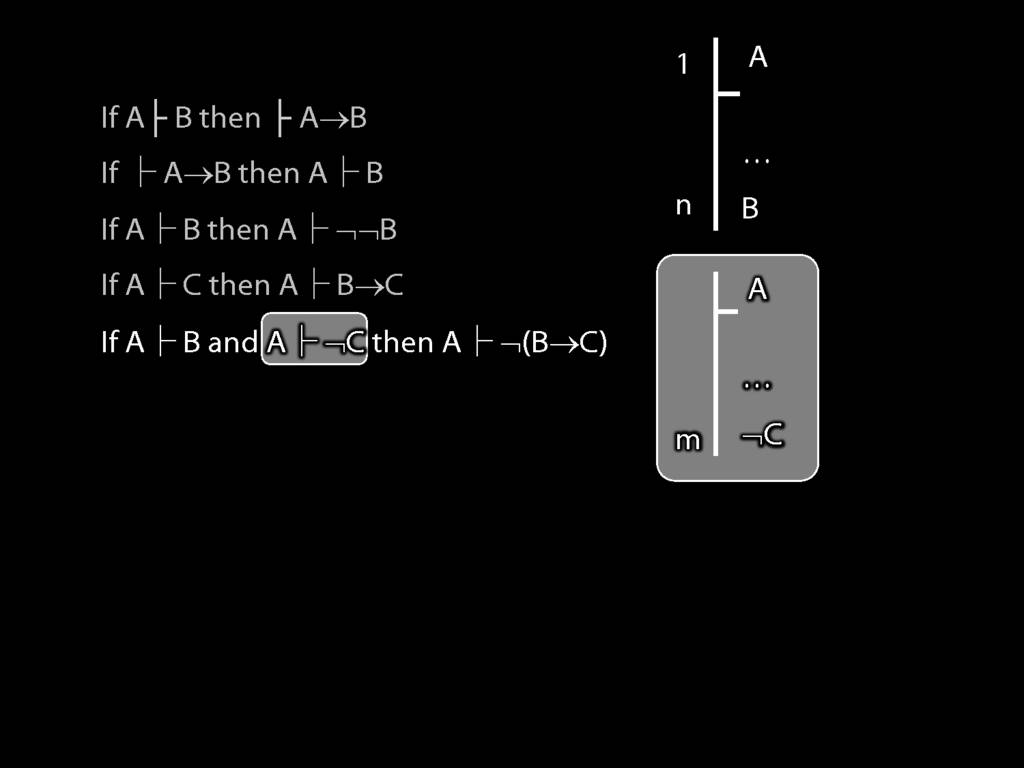
\section{Proofs about Proofs}
\section{Proofs about Proofs}
\section{A ⊨ ⊥}
\section{A ⊨ ⊥}
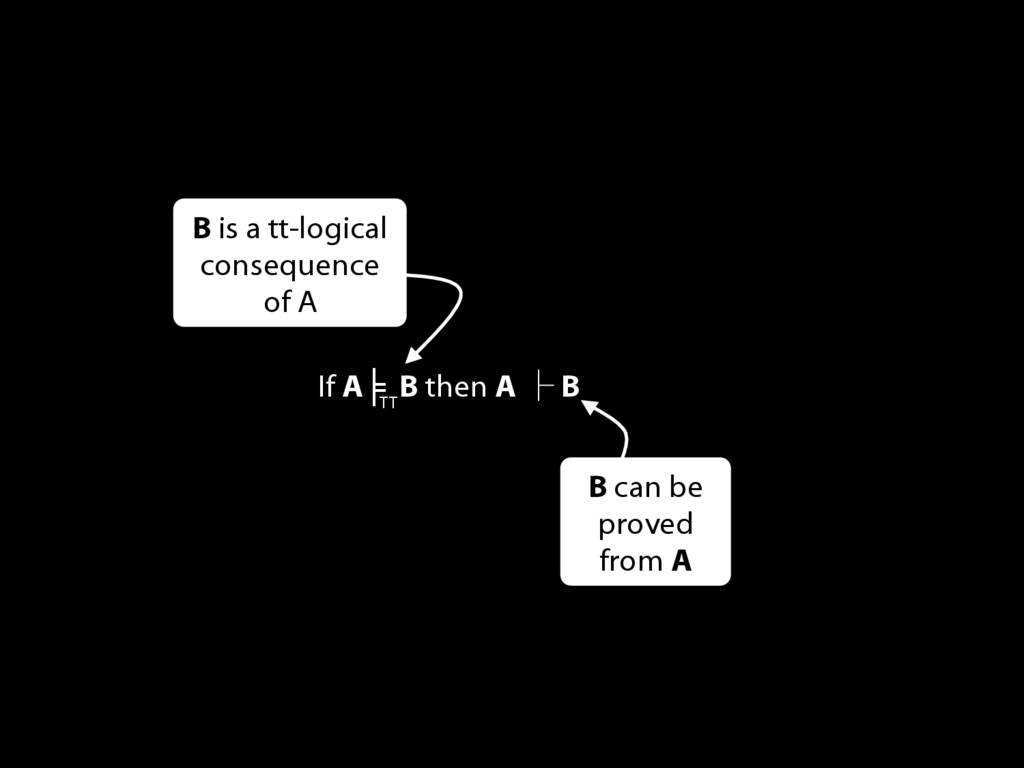
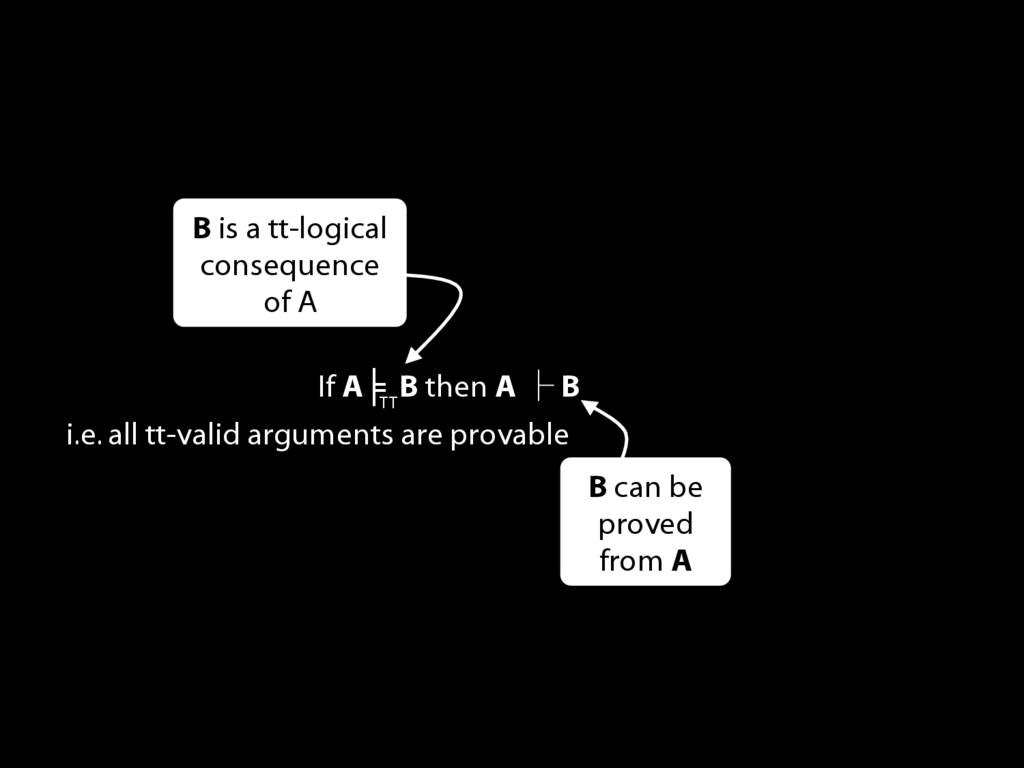
\section{If (A ⊬ ⊥ entails A ⊭TT ⊥) then (A ⊨TT B entails A ⊢ B) }
\section{If (A ⊬ ⊥ entails A ⊭TT ⊥) then (A ⊨TT B entails A ⊢ B) }
\section{The Essence of the Completeness Theorem}
\emph{Reading:} §8.3
\section{The Essence of the Completeness Theorem}
\section{Lemma for the Completeness Theorem}
\emph{Reading:} §8.3
\section{Lemma for the Completeness Theorem}
\section{Proof of the Completeness Theorem}
\emph{Reading:} §8.3, §17.1, §17.2
\section{Proof of the Completeness Theorem}
\section{Proof of Proposition 4 for the Completeness Theorem}
\emph{Reading:} §15.1, §15.6
\section{Proof of Proposition 4 for the Completeness Theorem}
15.33--15.40 (second edition)
15.33, 15.37--15.39 (second edition)