Recall these two diagrams from earlier. The left one is a proof, the right one is not.

Spot the difference.

Yes, the difference is at line 2.

But why is this difference significant?

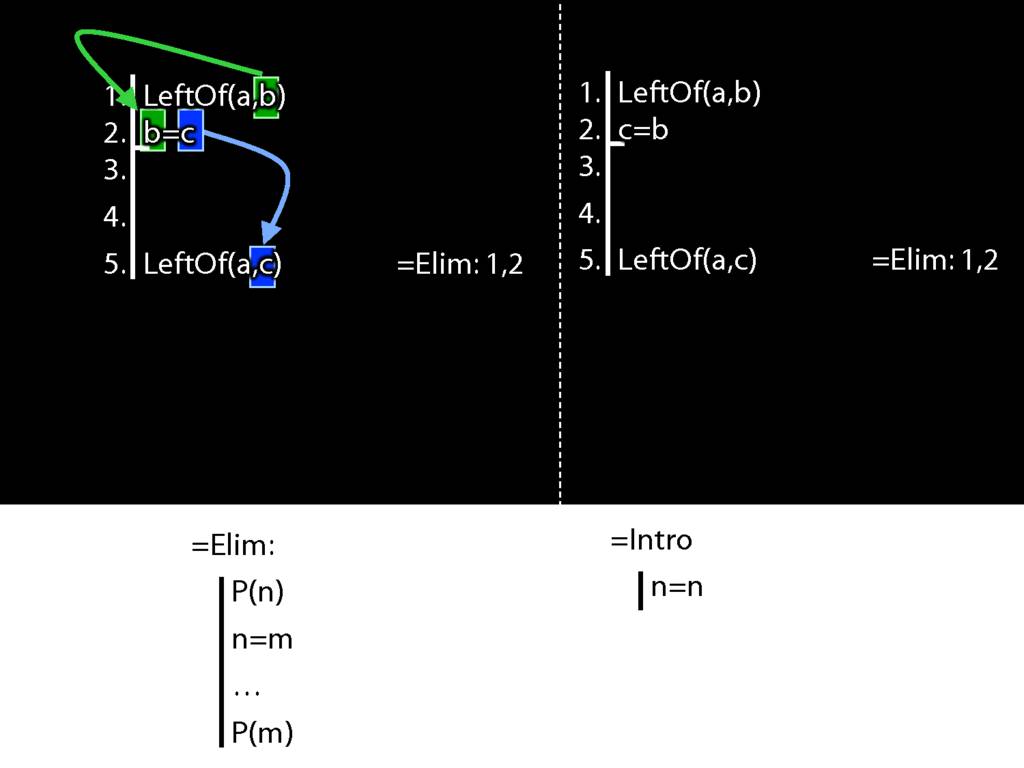
Look what happens in the left diagram (the genuine proof). Do you see the pattern?

That pattern matches the pattern described by the rule identity elimination (=Elim)

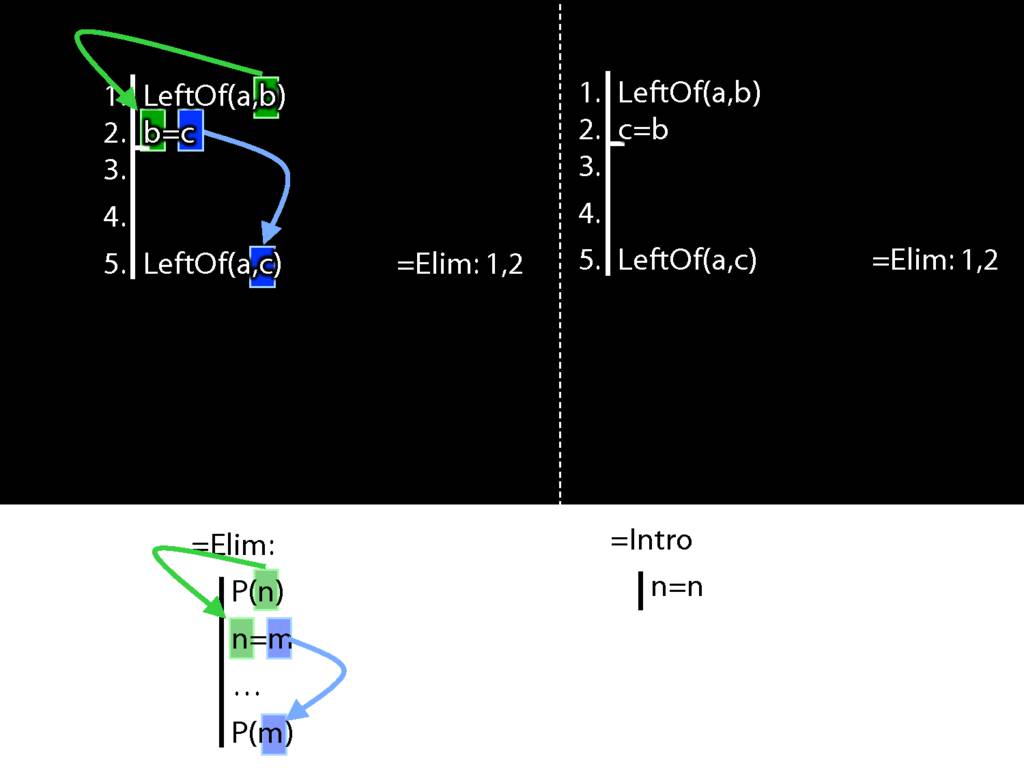
Now look at the pattern in the diagram on the right.

This is a different pattern.

You might protest that b=c and c=b mean the same thing; one can't be true unless the other is. These sentences do not express different thoughts. This is true but it is entirely besides the point.

Why is it beside the point? In studying proof, we're interested in ways of linking the purely formal to the genuinely meaningful. The proof system Fitch is a formal system of proof. What we want to show is that, within limits, Fitch captures a notion of logical validity. This is interesting only because we can describe Fitch entirely without invoking truth or meaning.

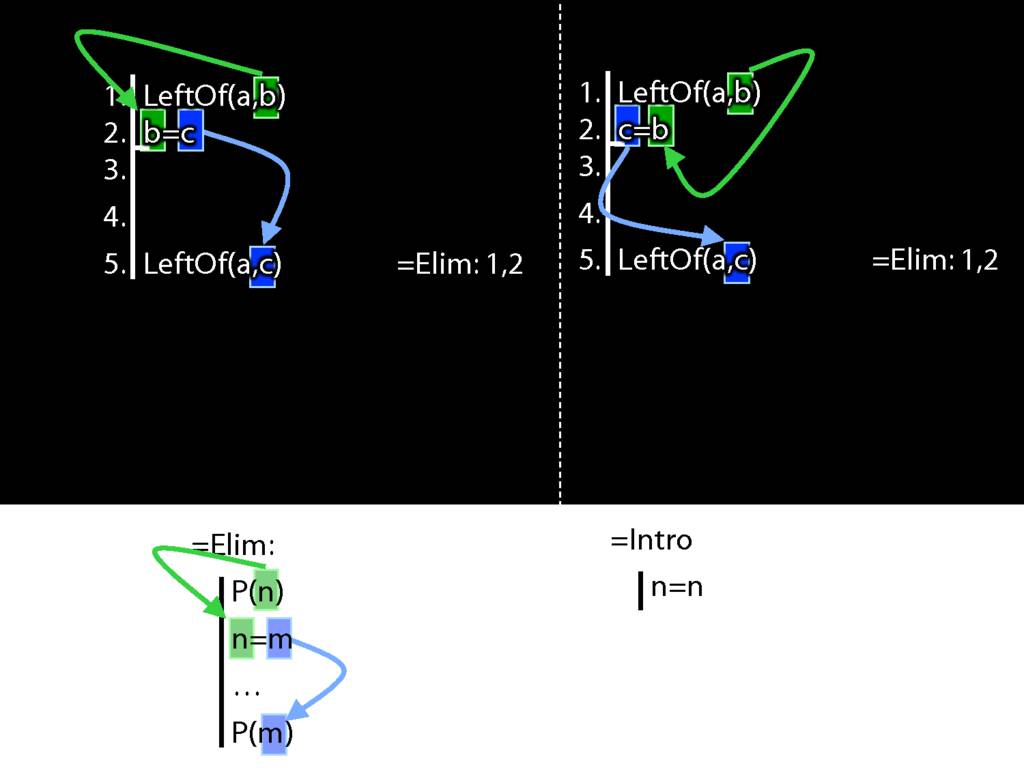
So the fact that b=c and c=b mean the same is irrelevant in Fitch. When you're thinking about Fitch, all you care about is the pattern of symbols. And b=c is a different pattern from c=b.

This is Abdurrahman Wahid, popularly known Gus Dur, a former president of Indoneisa and one of the most jovial national leaders ever. He was a really nice guy. As president he was infirm and nearly blind. When asked to resign he replied “I need help to step up, let alone step down.” (Economist 2010-01-07 obituary). Unfortunately he died recently (december 30 2009)

And this is Than Schwe, Myanamar’s military ruler.

Guess who I'd pick to marks your logic exam.

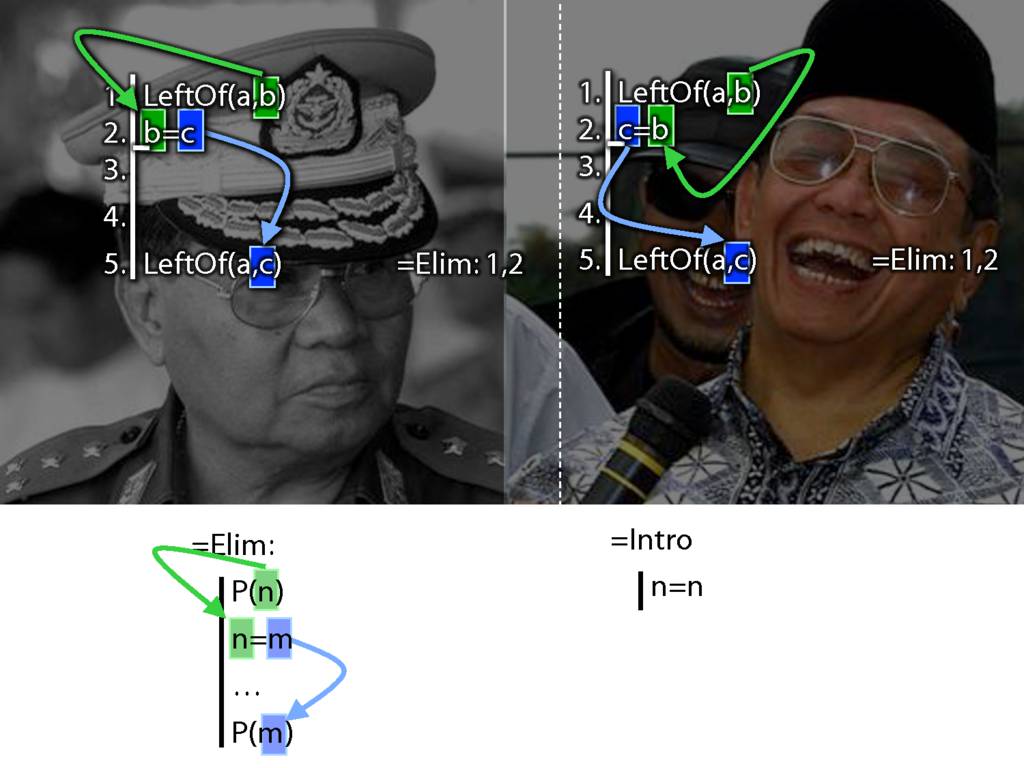
One last thing. The argument on your right is logically valid. Can you prove it?