Here's Johnny Depp having his hair cut in Charlie and the Chocolate Factory.
Mrs B made me watch this film because she fancies Jonny Depp.
Ambiguity can be \emph{lexical}, e.g. `Actor testifies in horse suit'. Ambiguity can also be \emph{syntactic}, e.g. `How to combat the feeling of helplessness with illegal drugs'. (Both examples are from Bucaria, C. (2004), `Lexical and syntactic ambiguity as a source of humor: The case of newspaper headlines', Humour 17(3): 279--309.)
But, to be fair, how could one not?
Anyway, here he's saying 'I need a heir' and holding up a hair.
This is one example of ambiguity.
Note that here the ambiguity can be traced to a single word, 'heir' which sounds just like another word with a different meaning. We might say, the ambiguity is all in the word.
Now contrast a statement like 'two puffins ate six fish'.
This statement is ambiguous because there are two quite different ways of understanding it.
Here you see one interpretation where There were two puffins: and they ate six fish
This interpretation is good for the puffins, less good for the fish.
Here's the other interpretation of 'two puffins ate six fish'. Here it means there were six fish: and two puffins ate them.
So less happy puffins.
Here's the key thing, though. The sentence 'Two puffins ate six fish' is ambiguous but the ambiguity is not due to any particular word. It's not that the word 'puffin' is ambiguous, for example.
This matters because it shows that not all ambiguity is lexical; some of it is, as linguists might say, synatactic or structural.
But why does ambiguity matter to us?
We are constructing a formal language and we want each sentence to have just one truth value, true or false.
In our formal language, we don't want sentences that are true and false.
This means of course that we need to avoid ambiguity.
Insofar as ambiguity is merely lexical--insofar as it is linked to particular words having multiple meanings--it's easy to avoid.
To avoid that sort of ambiguity, lexical ambiguity, we just have to avoid defining words twice. Easy.
But how can we be sure that our formal language involves no syntactic ambiguity?
Consider this thing (it's not a sentence). If we allowed this into our language, we'd have problems.
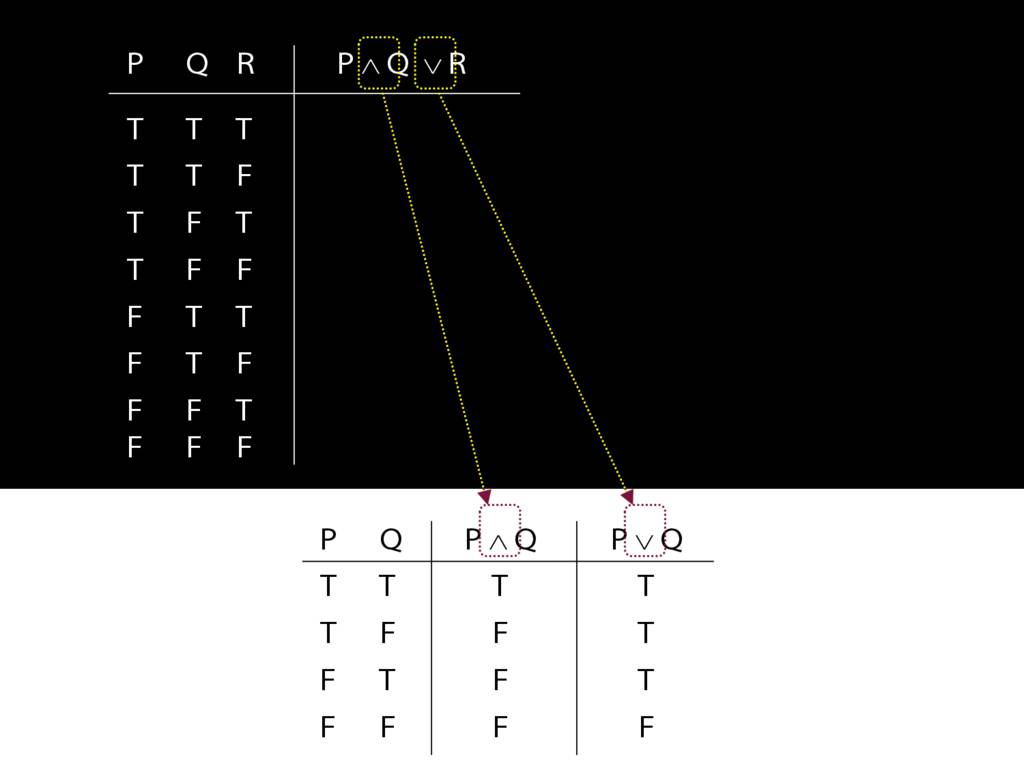
For one thing, we'd not be able to say what the right way to construct its truth table is.
Now this thing is not a sentence. Instead we have two distinct sentences, (A ∧ B) ∨ C and A ∧ (B ∨ C).
Just a moment ago I asked, How can we be sure that our formal language involves no syntactic ambiguity?
The simplest answer is: because we use brackets.
It's important to realise this, but it's not a very satisfying answer for two reasons.
First, it's not satisfying because we don't know \emph{how} the brackets enable us to avoid ambiguity. The answer doesn't enable us to prove that our language contains no ambiguous sentences.
And, second, it's not satisfying because we haven't said anything yet about what the brackets mean. We can't just throw symbols into our language without explaining them. (This is the down side of having a formal language: we have to say what everything means explicity, since it's a creature of our own creation.)
3.20, 3.21, 3.22