Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
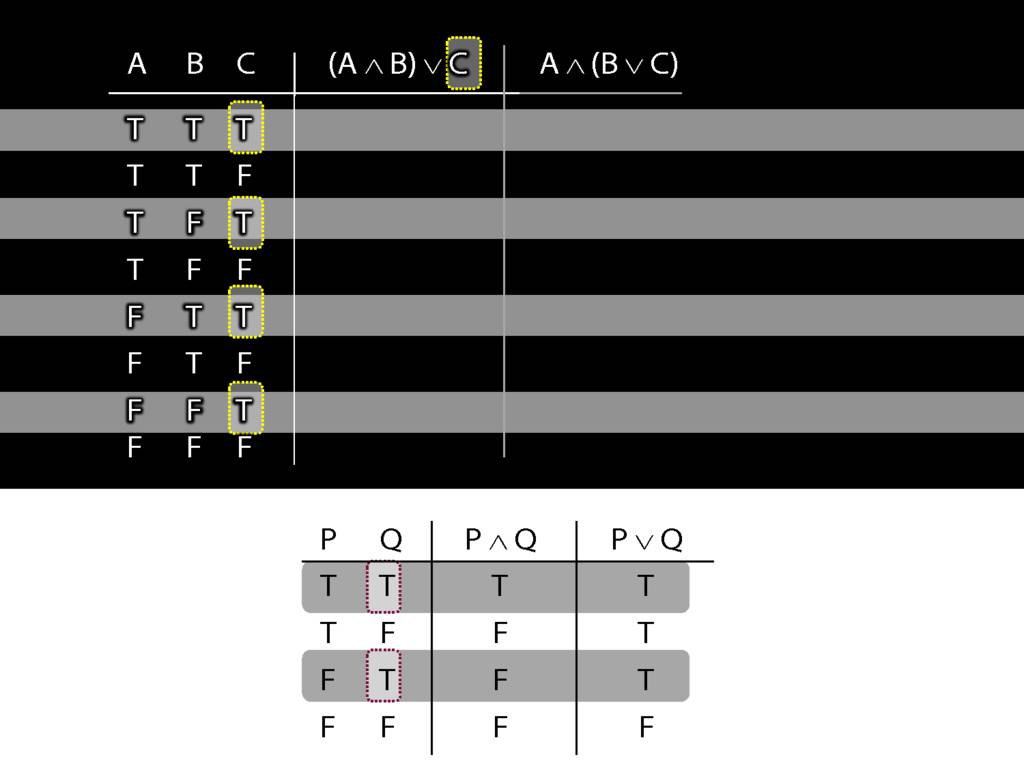
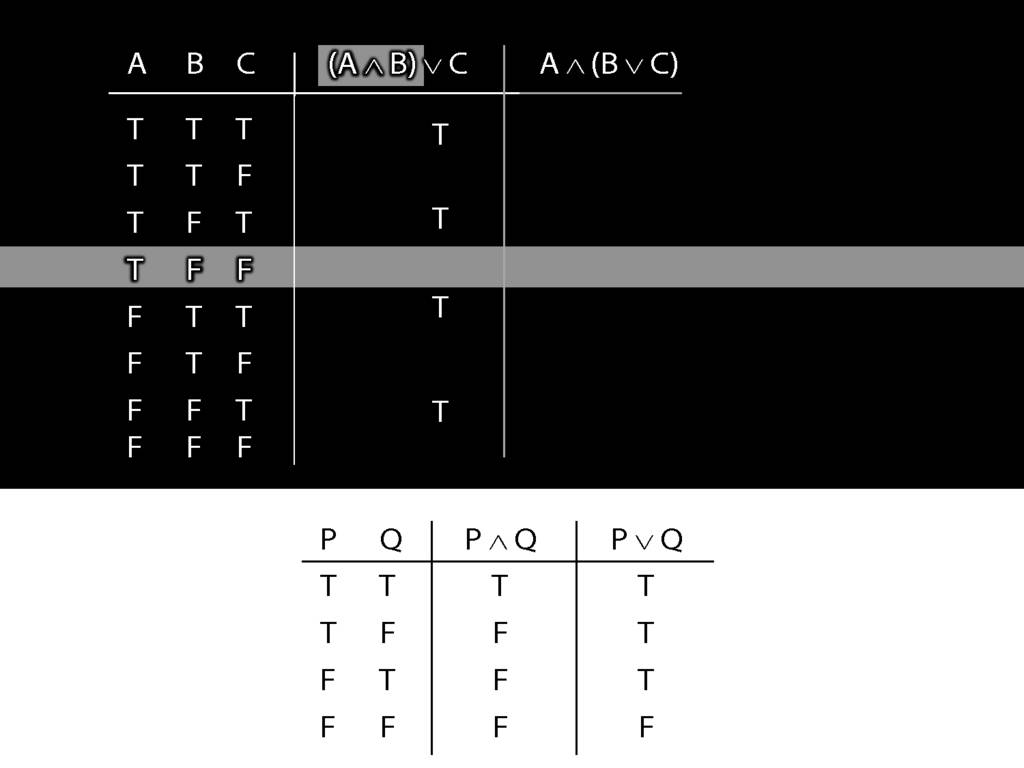
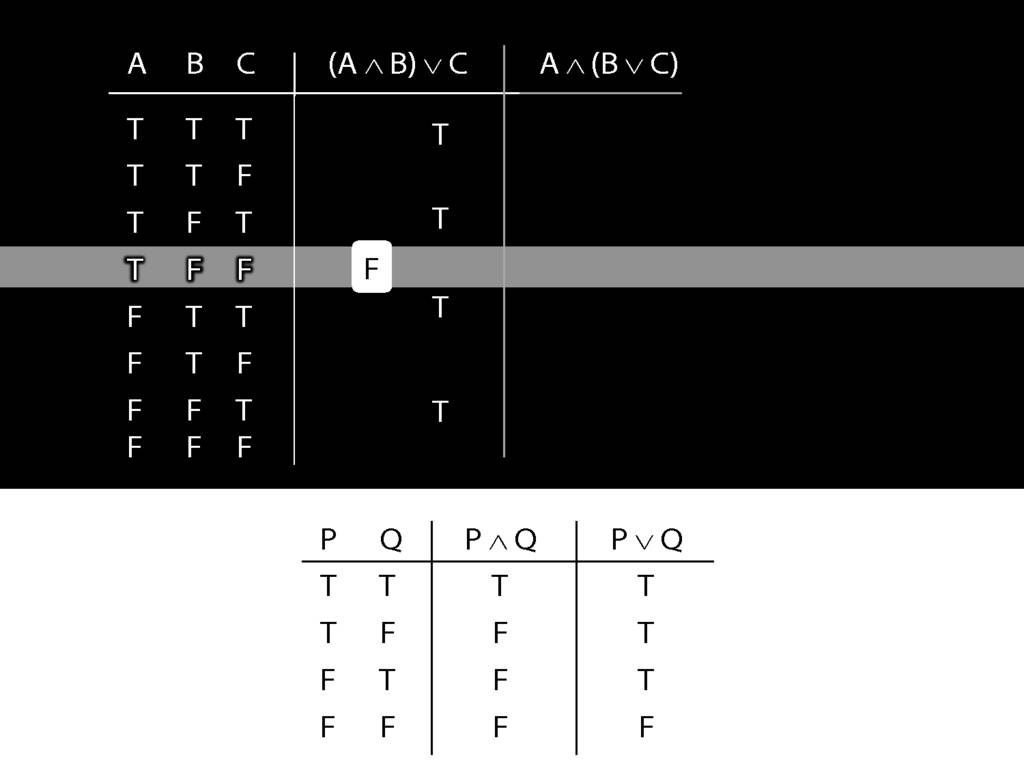
A ∧ B ∨ C: the Truth-tables
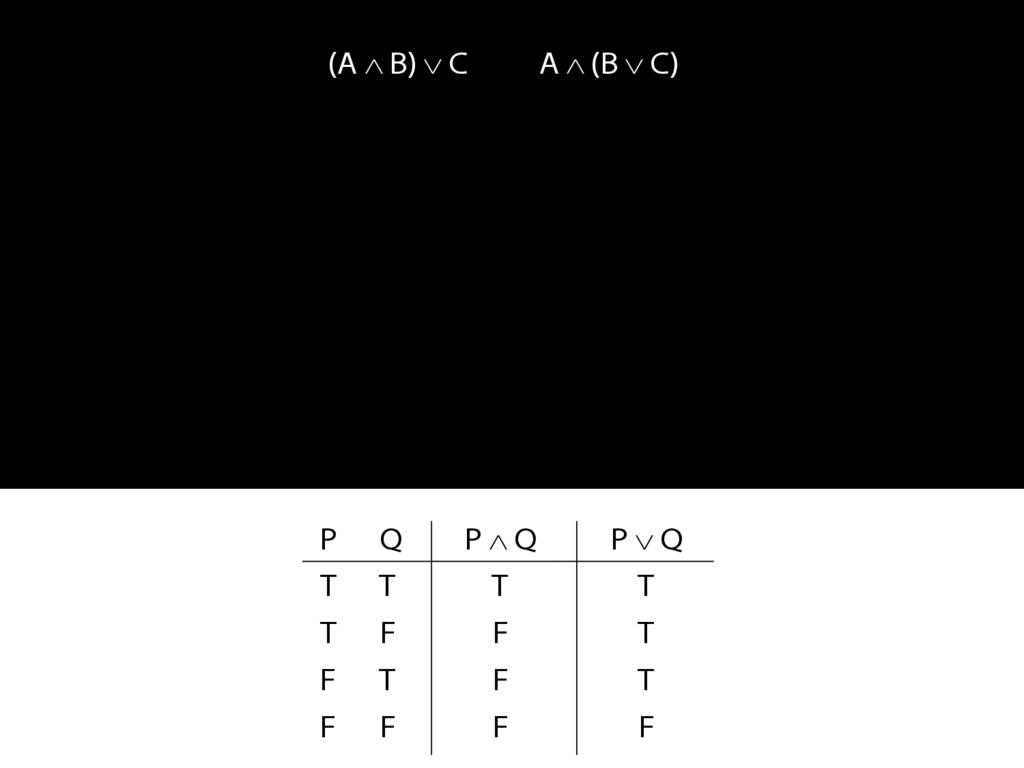
Let us examine how these two sentences, (A and B) or C versus A and (B or C), differ using truth tables.
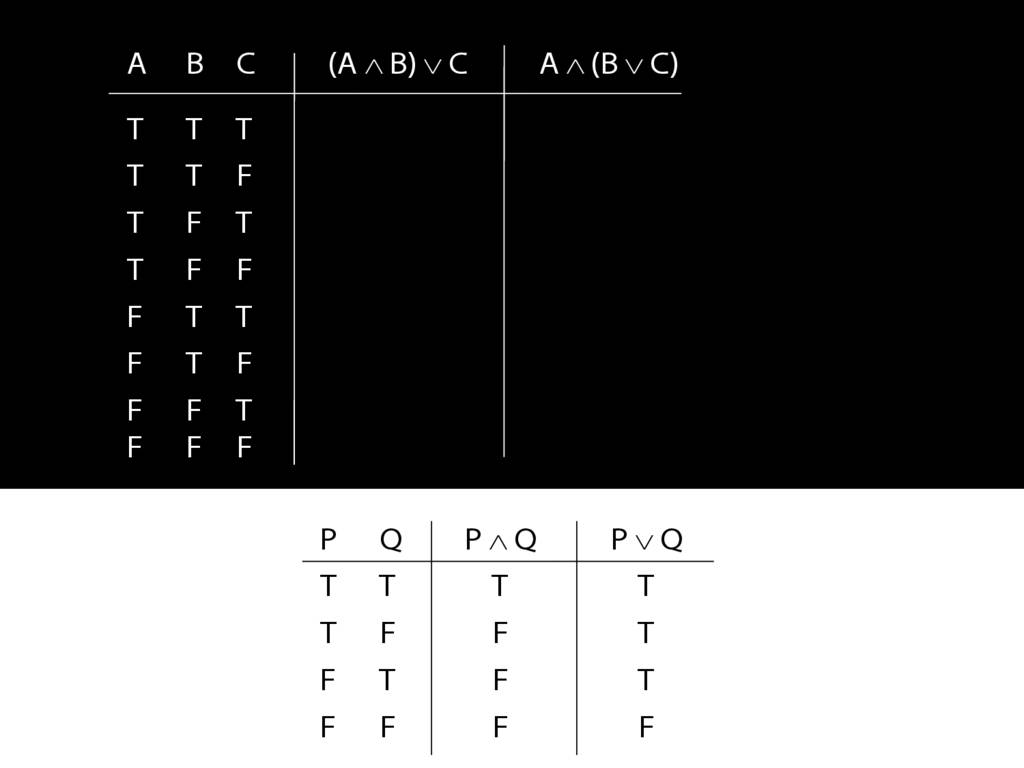
We have quite a few rows to fill in so it's worth thinking about short cuts.
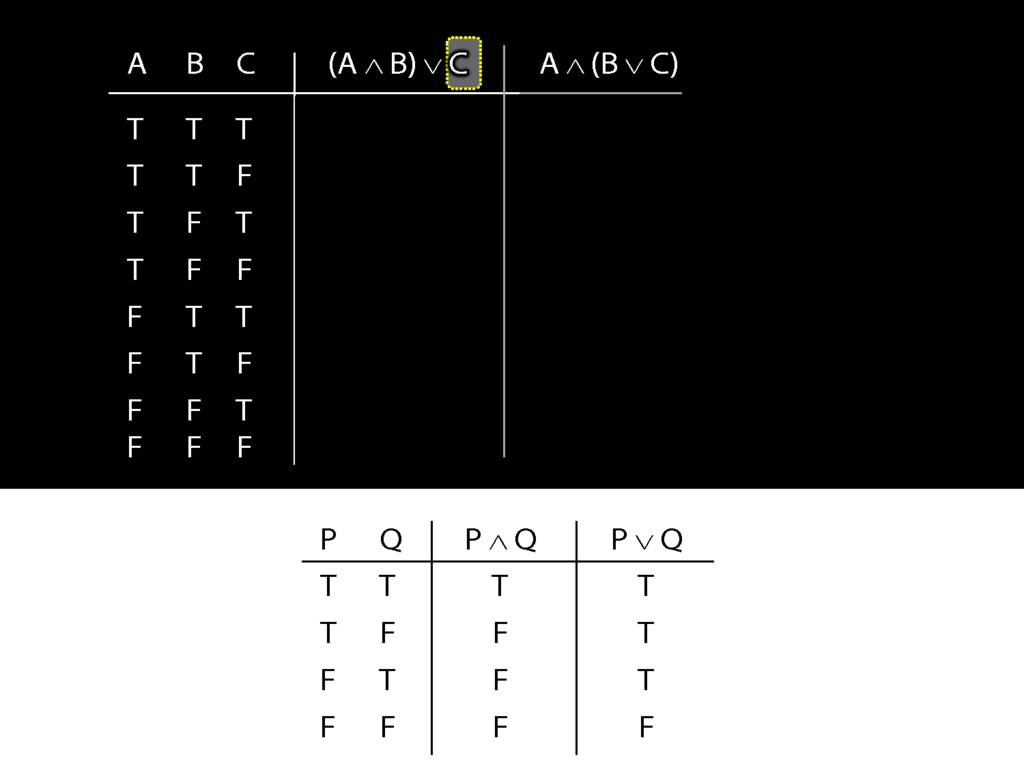
Think about this C on the right hand side of the disjunction.
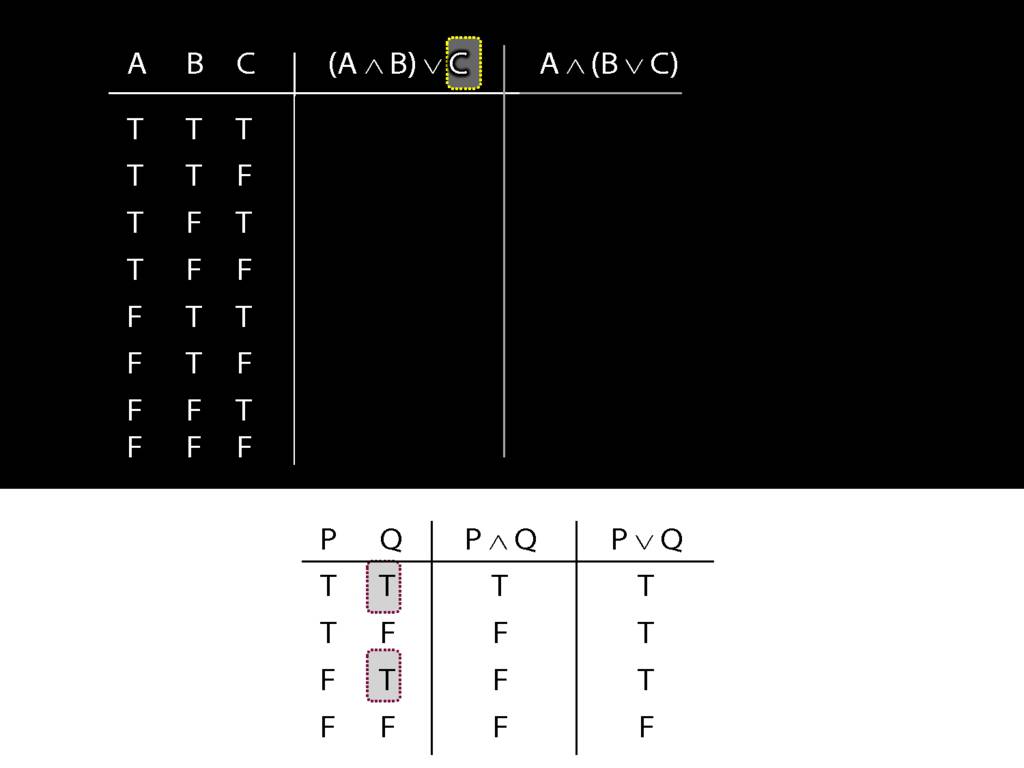
Whenever a disjunct is true ...

... oops, Ken says he's dying inside.
For most people that would be an exaggeration, but for Ken it's actually an understatement of his problems.
Anyway, I hope it isn't because of logic.

If this is too easy, try an exercise while I'm talking about the truth tables.
Here's one argument ...

... and here's a second argument. Your exercise is to say which is valid and which is not valid.
For the invalid argument, give a counterexample.
For the valid argument, give a Fitch proof.
While you are doing that, the rest of us will go back to thinking about truth tables.
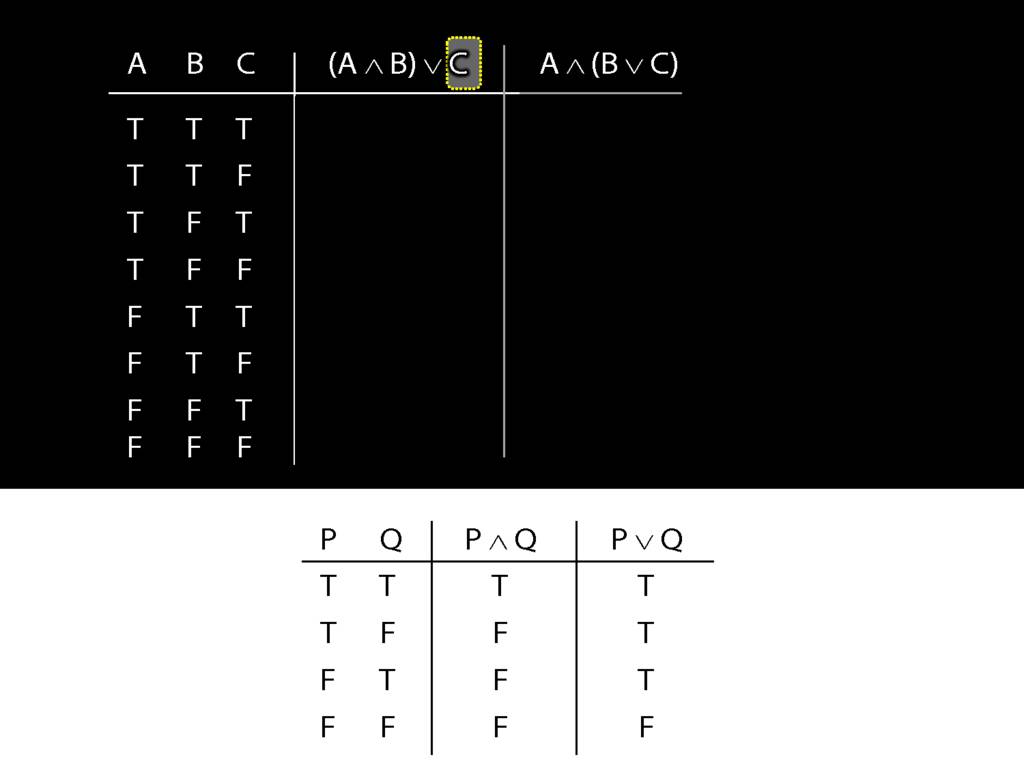
So we were thinking about the right disjunct of the first sentence, C.
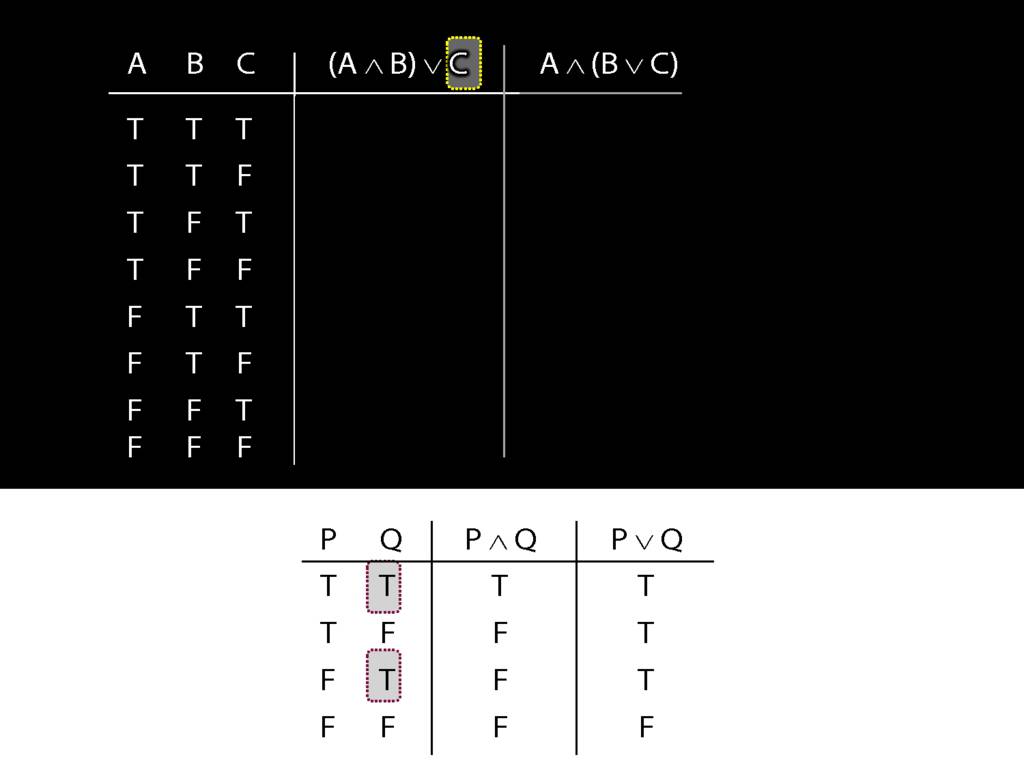
What happens when this disjunct is true?
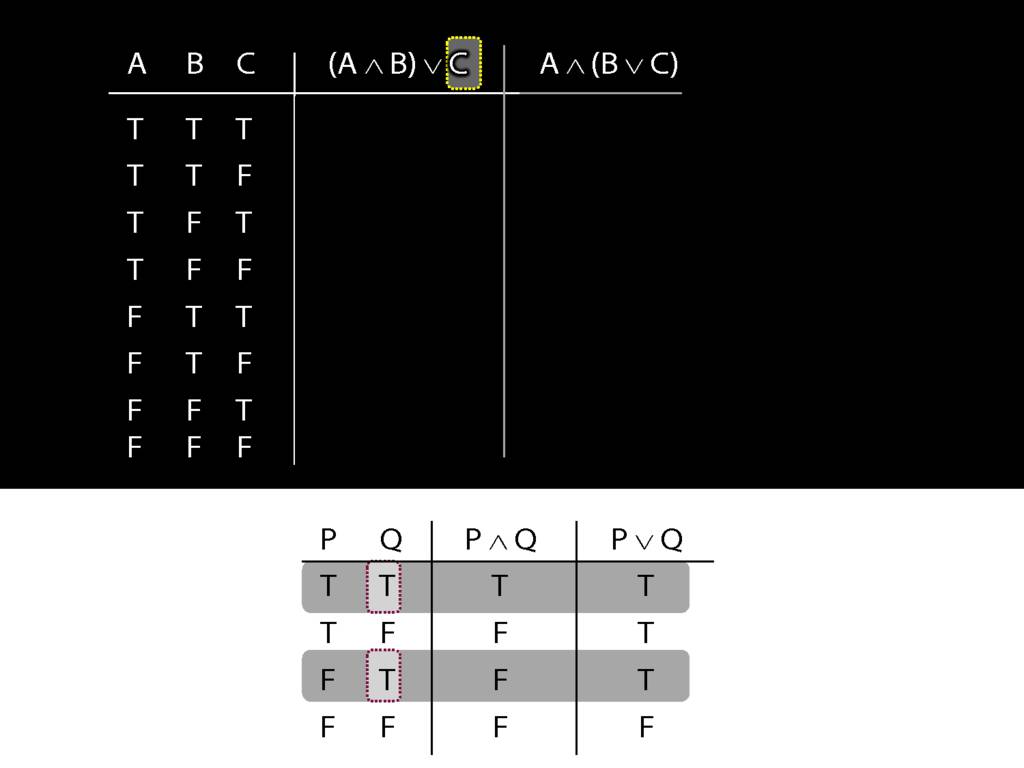
The whole sentence is true, regardless of what the truth value of the other (left) disjunct is.
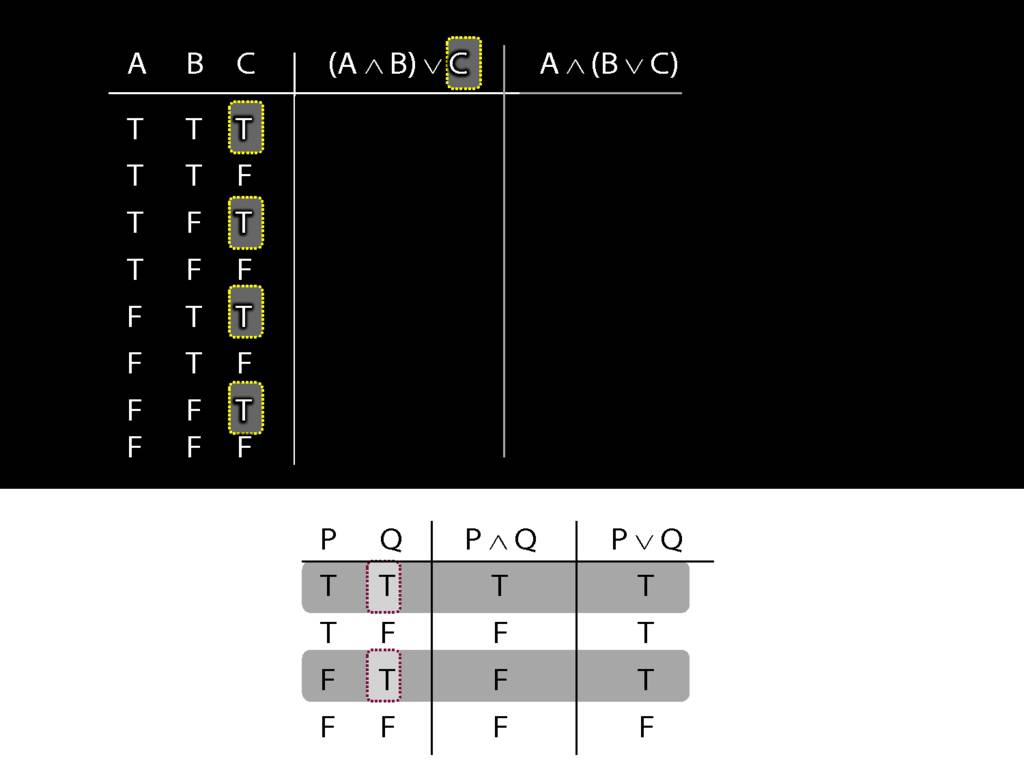
So in every row of the truth-table in which C is true, ...
... these four rows ...
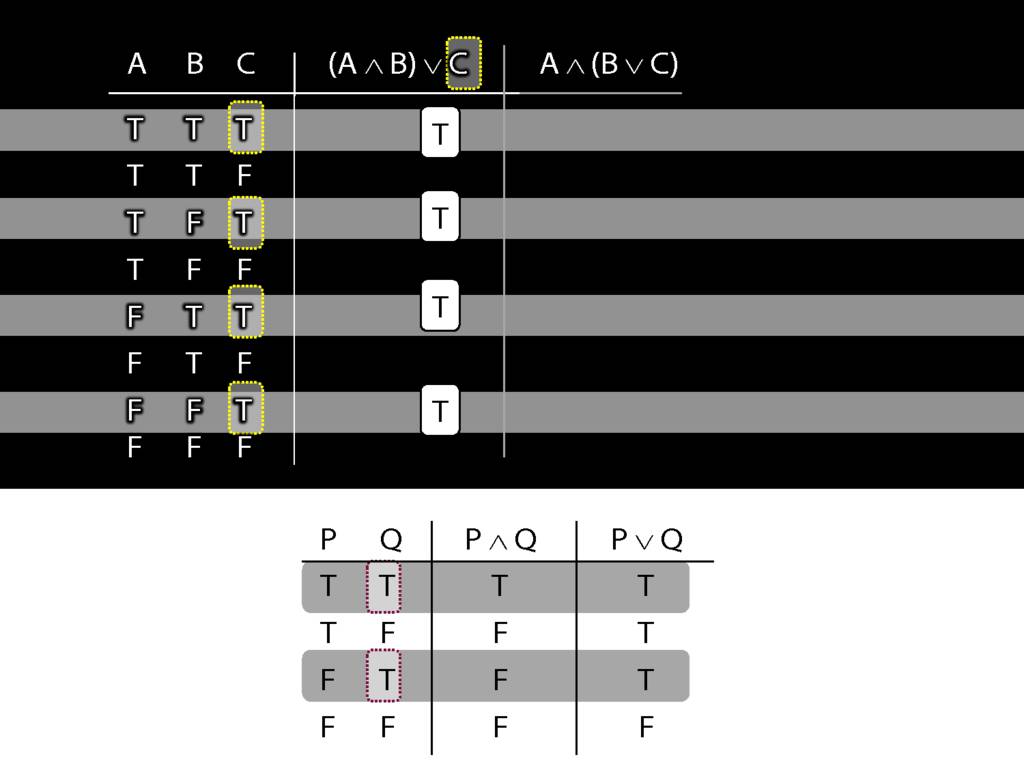
... we know that the whole sentence is true.
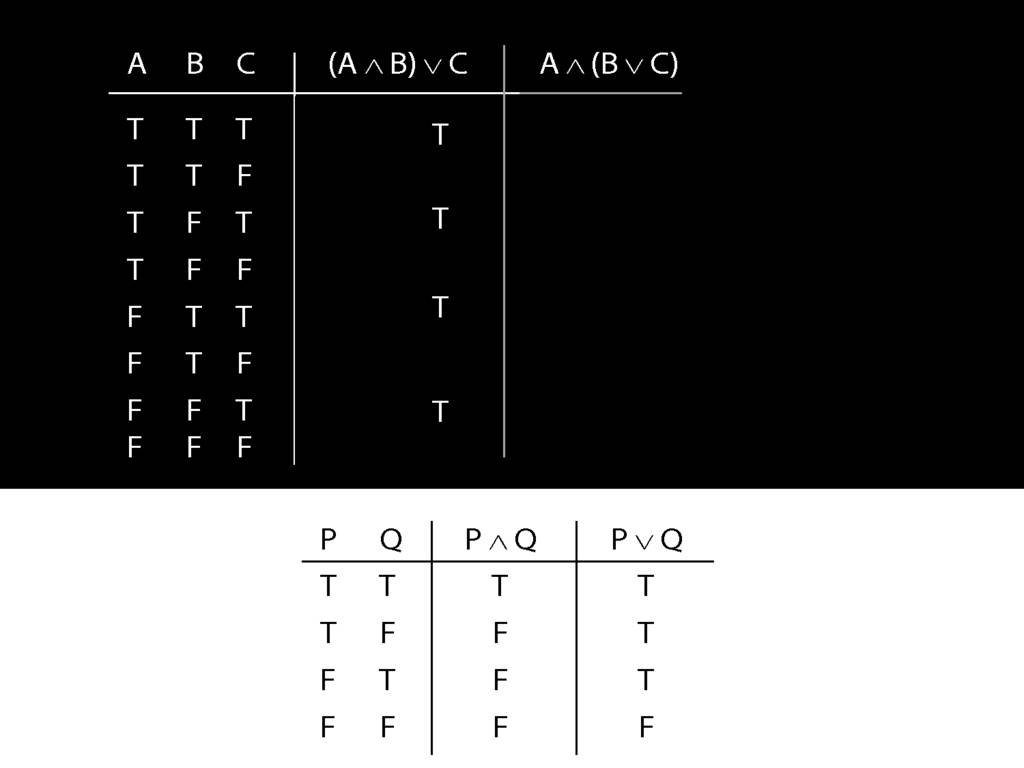
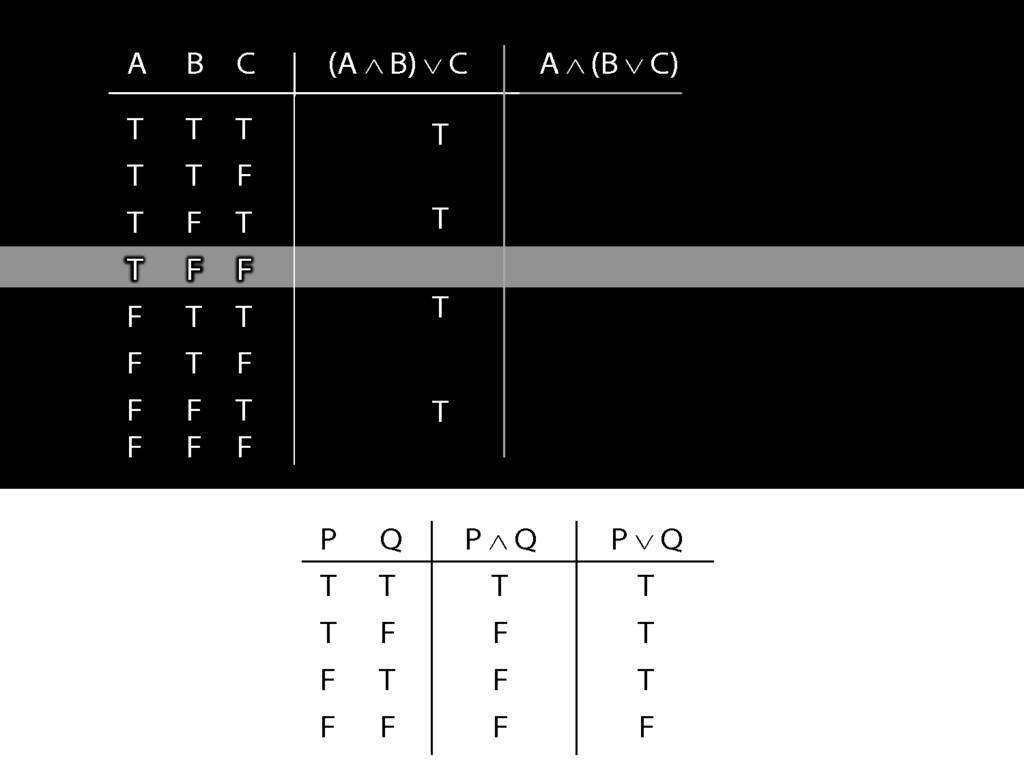
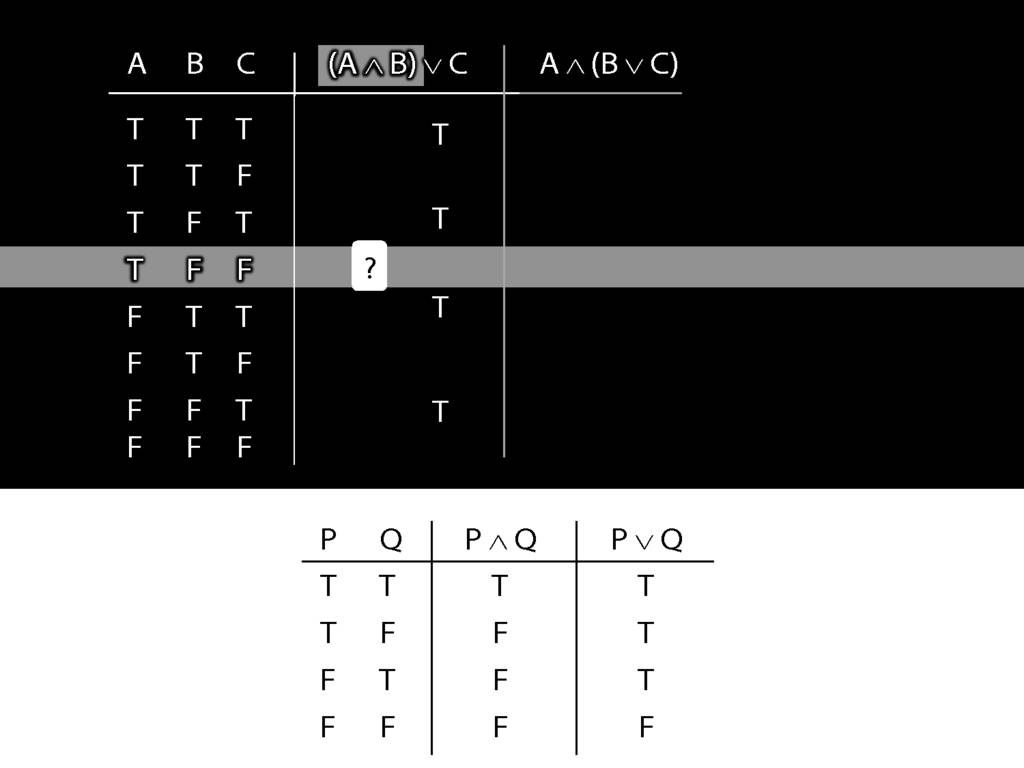
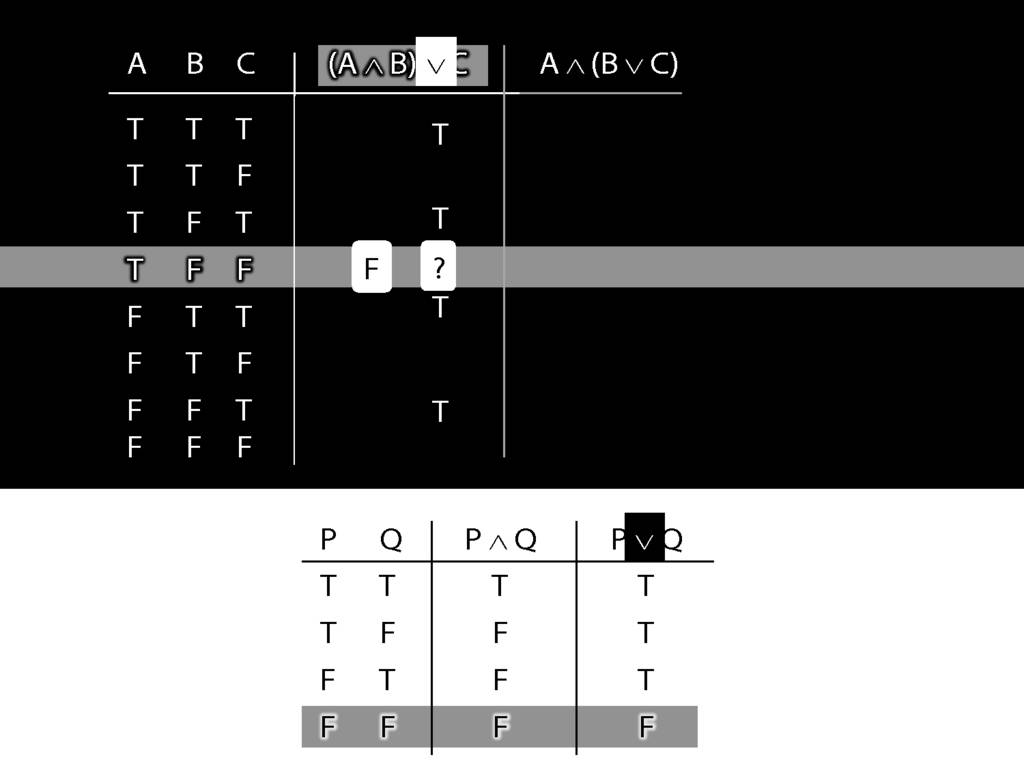
Now consider row four. Here we have to do it the slow way.
We start at a point innermost in the brackets, so with A and B.
What is the truth value of A and B in this row?
That depends on what the main connective in this sentence is, and on what the truth values of A and B are.
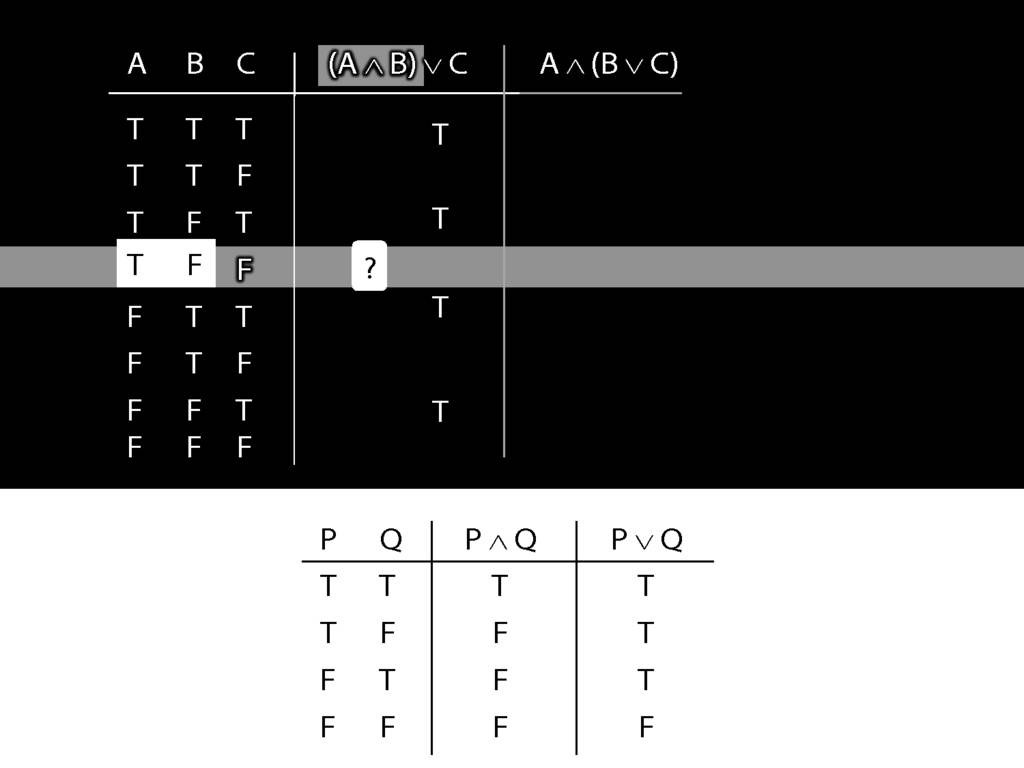
In this row, A is true and B is false.
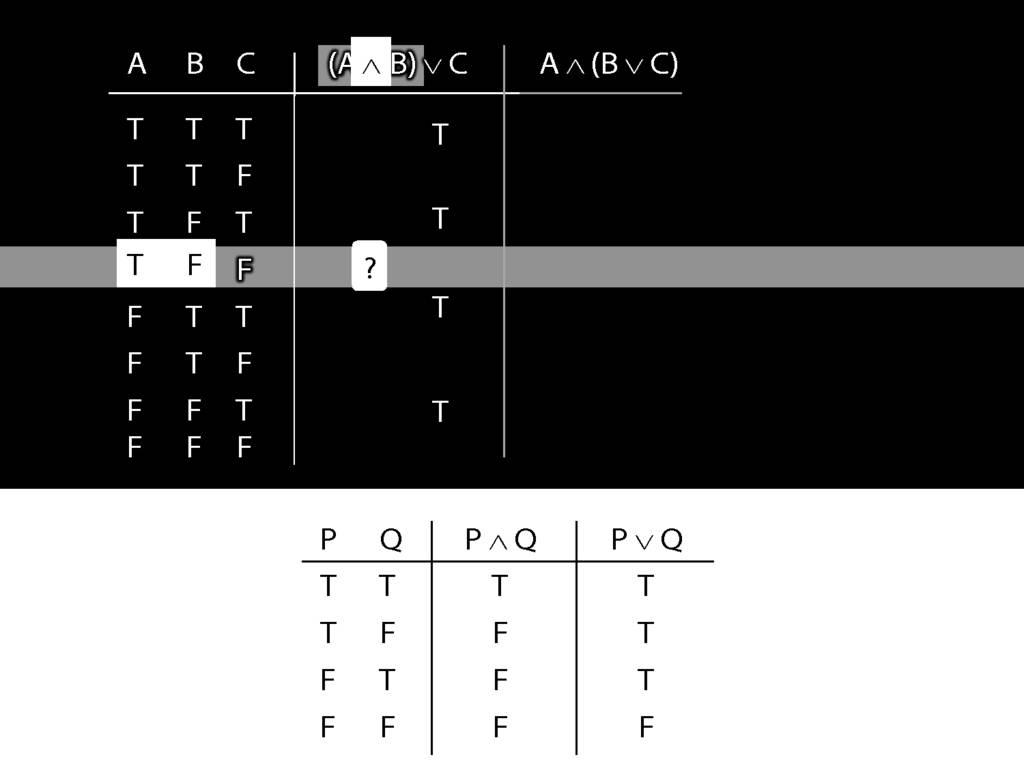
And the connective is conjunction.
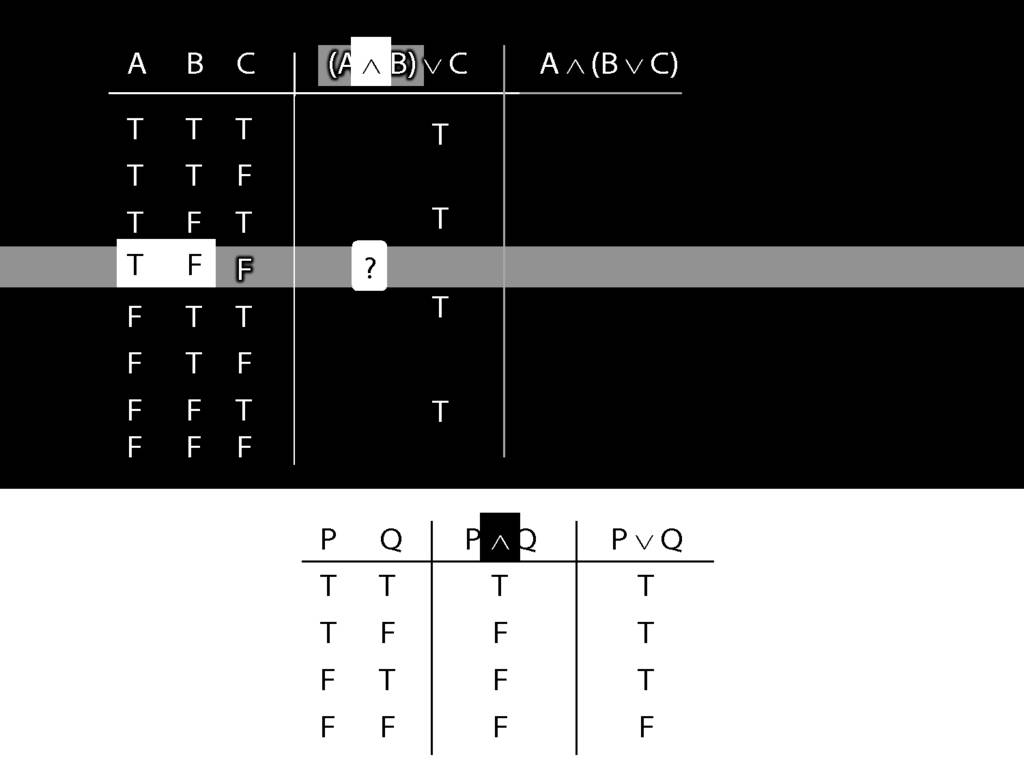
So the truth-table we need to consult is the one for conjunction.
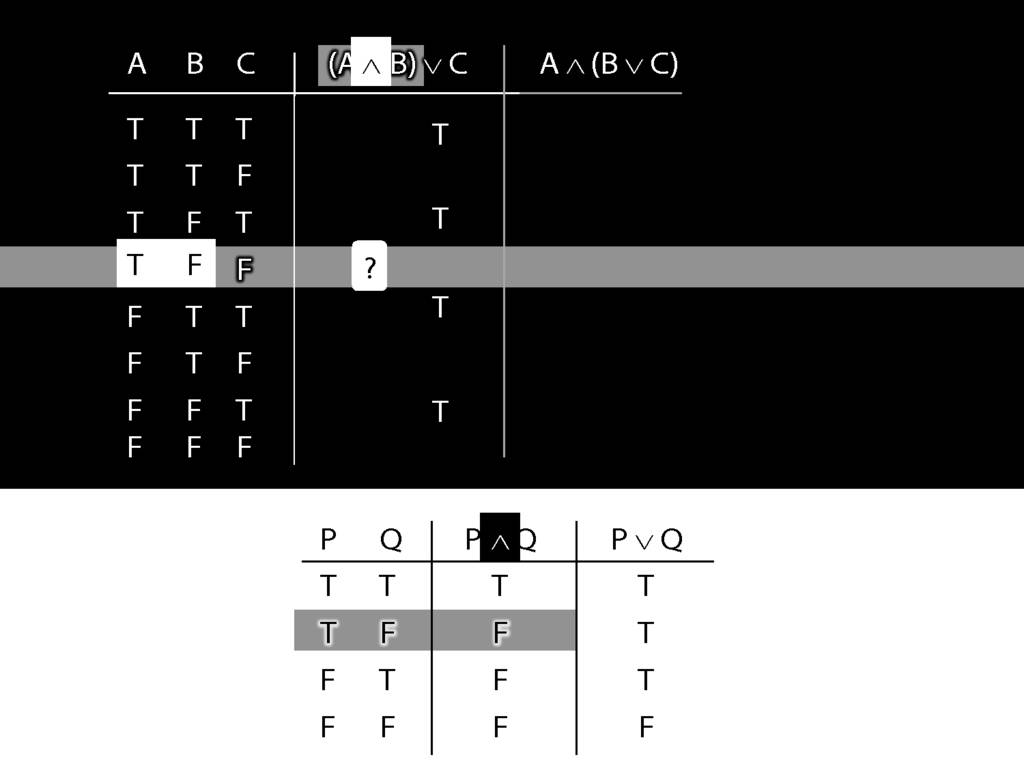
It's the second row that we want because this is the row where A is true and B false.
In this row of the truth-table, the conjunction is false.
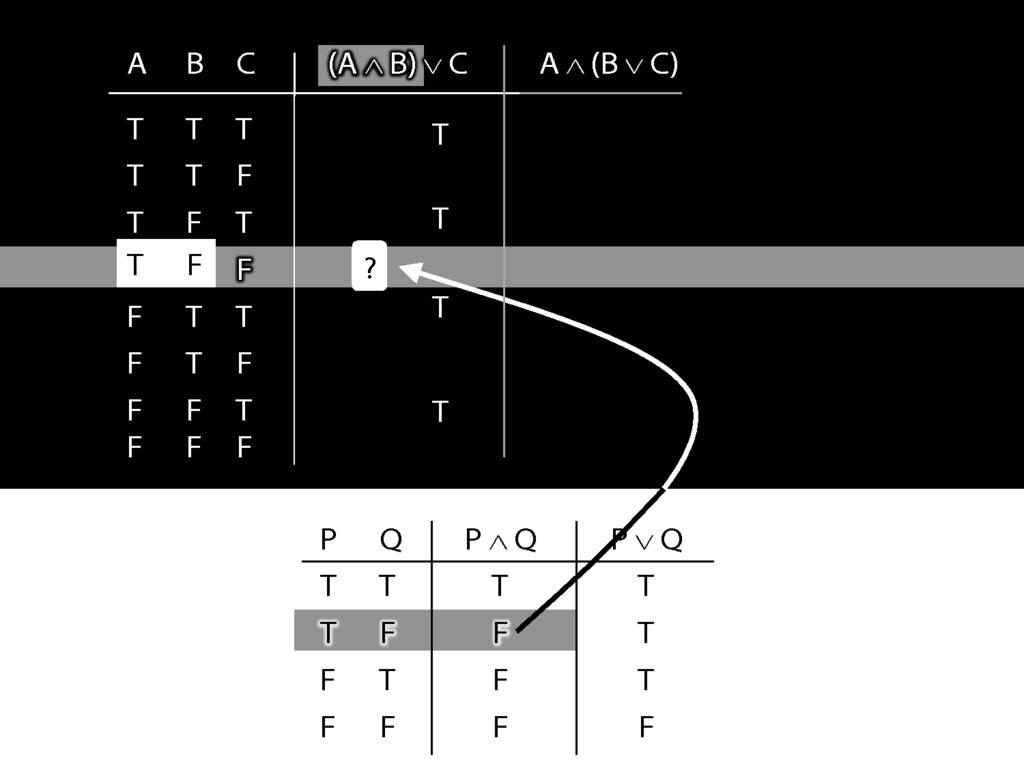
And it's this truth-value that we put into our truth-table for A and B.
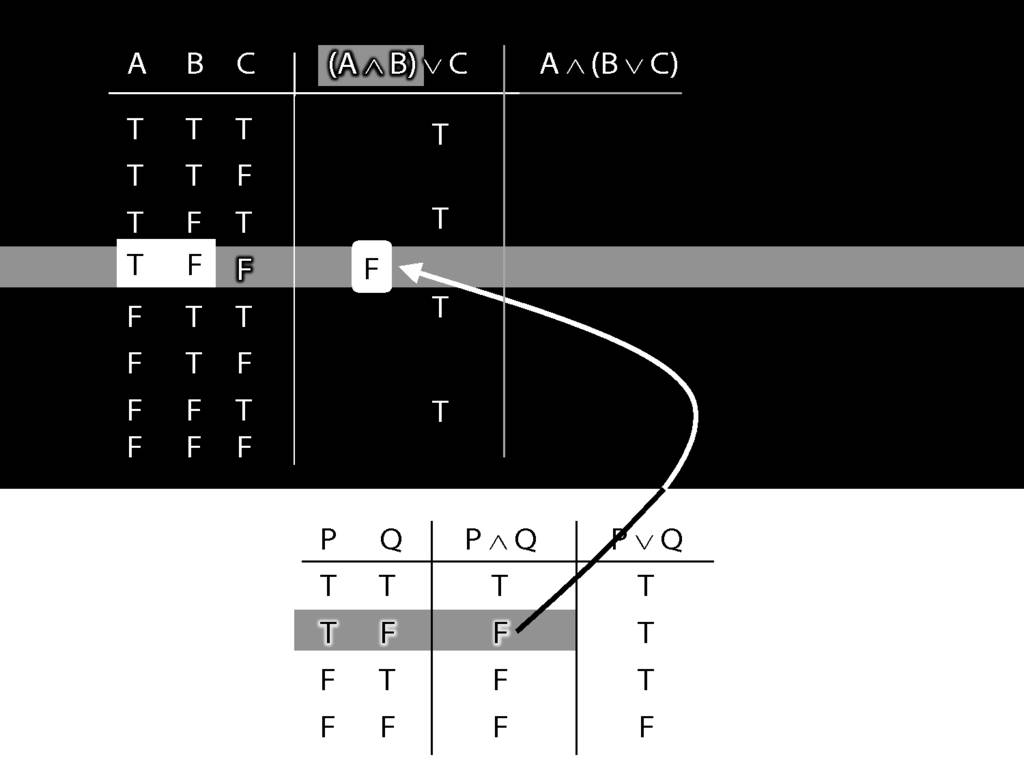
Prima!
Bene!
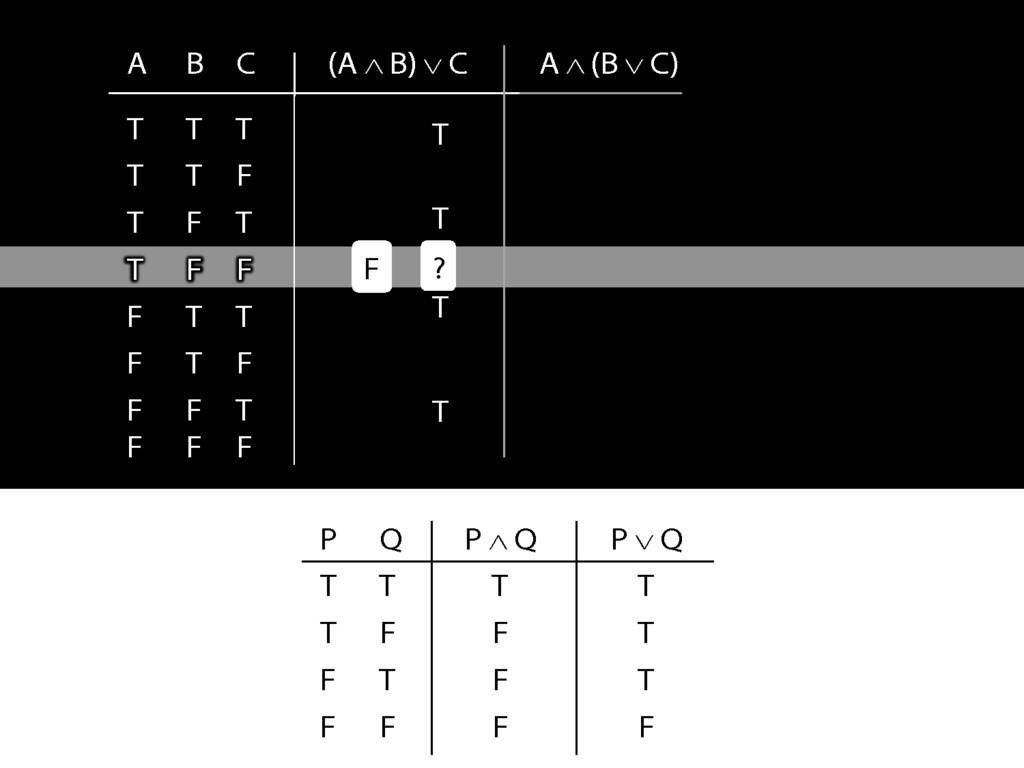
Now we turn to the whole sentence. What is its truth value?
First we have to ask, What is the connective?
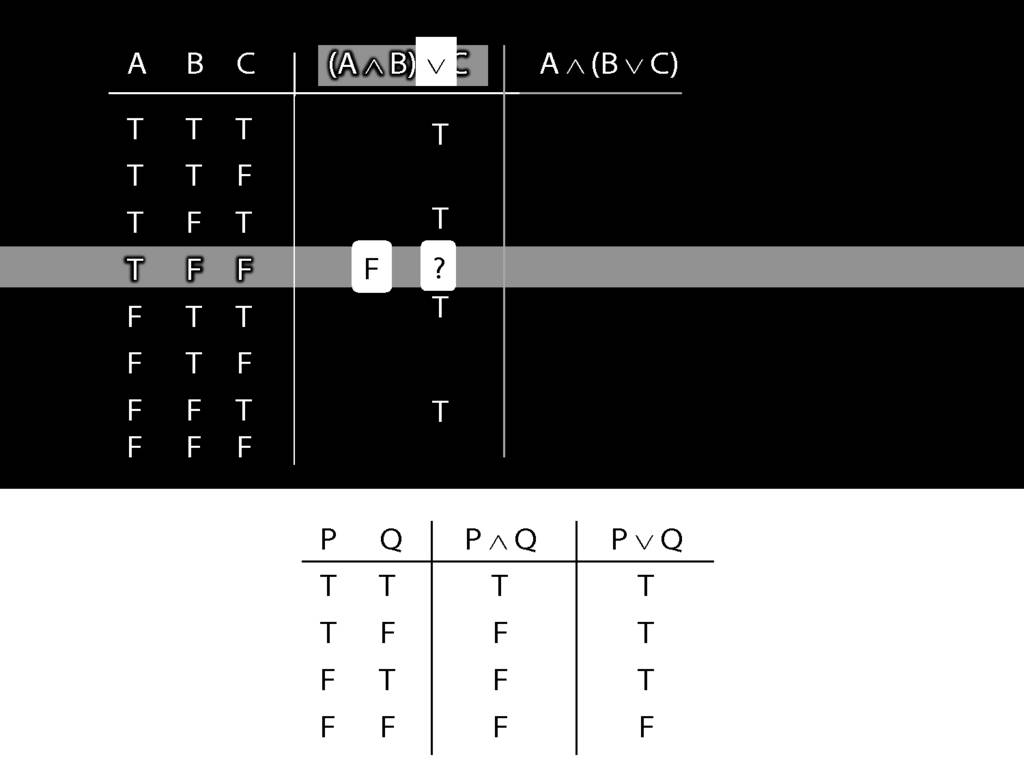
In this case the connective is disjunction.
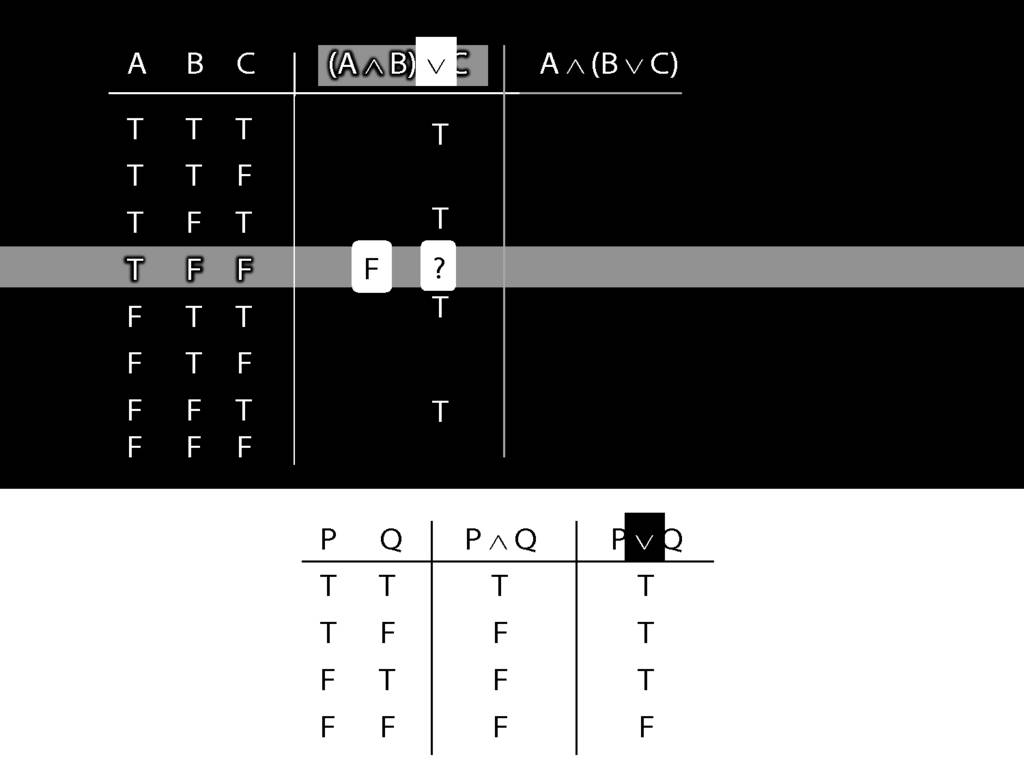
So the truth-table we need to consult is the one for disjunction.
But which row do we need?
In this case, the thing on the left of the disjunction (the left disjunct) is A and B, which is false;
and the thing on the right, C, is also false.
So we're looking at the last row of the truth-table, the one with false and false.
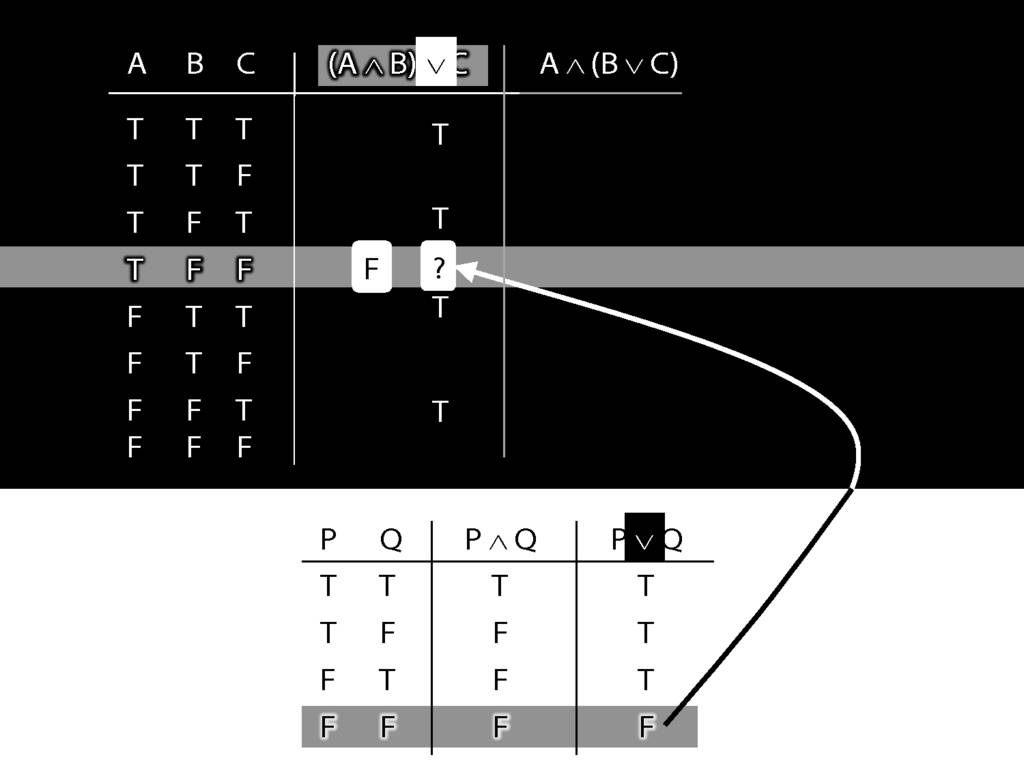
The truth-value in this row is the truth-value we need to put into the truth-table we're working on.
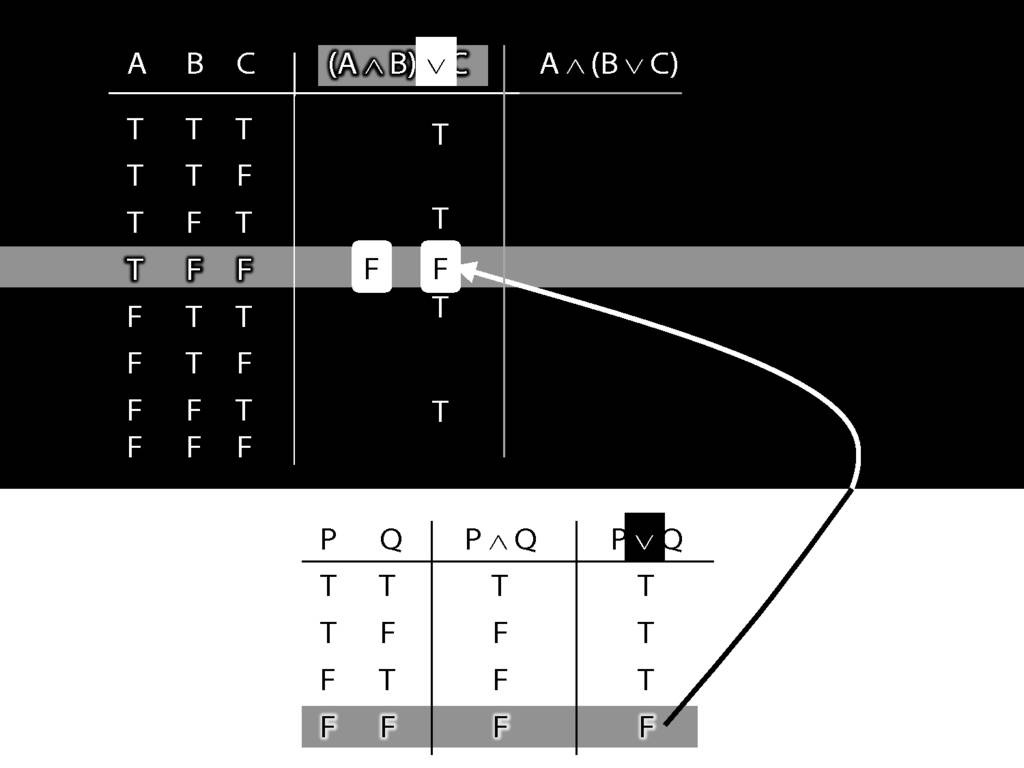
So we know that (A and B) or C is false in this row, where A is true, B is false and C is false.
Sehr gut!
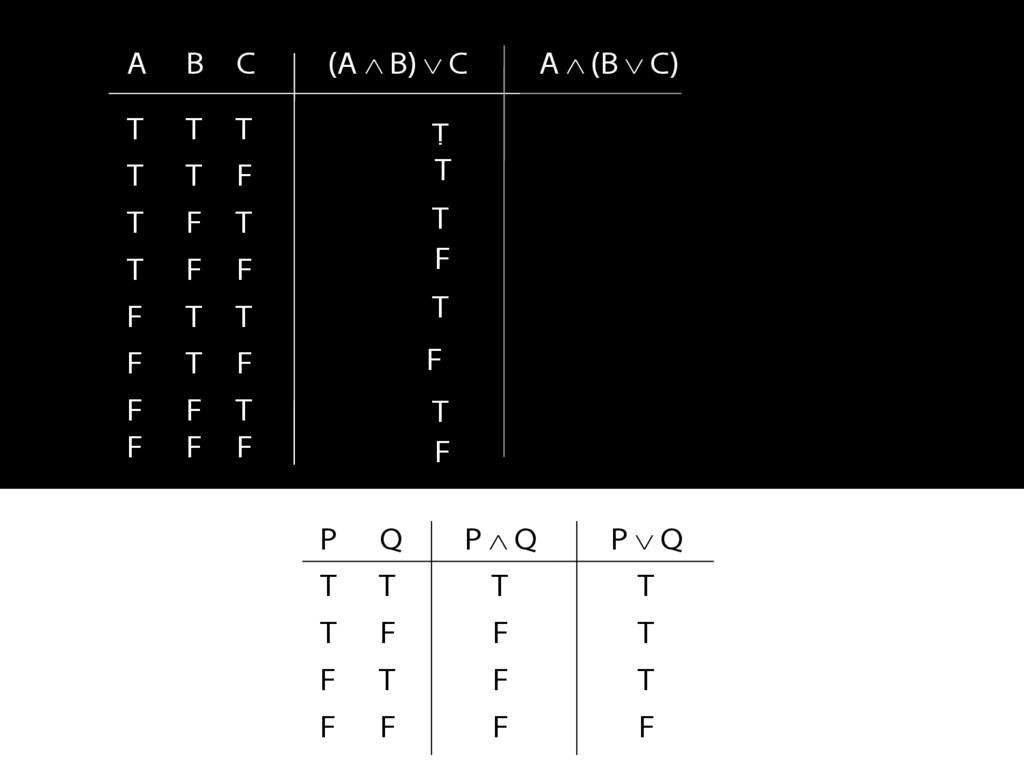
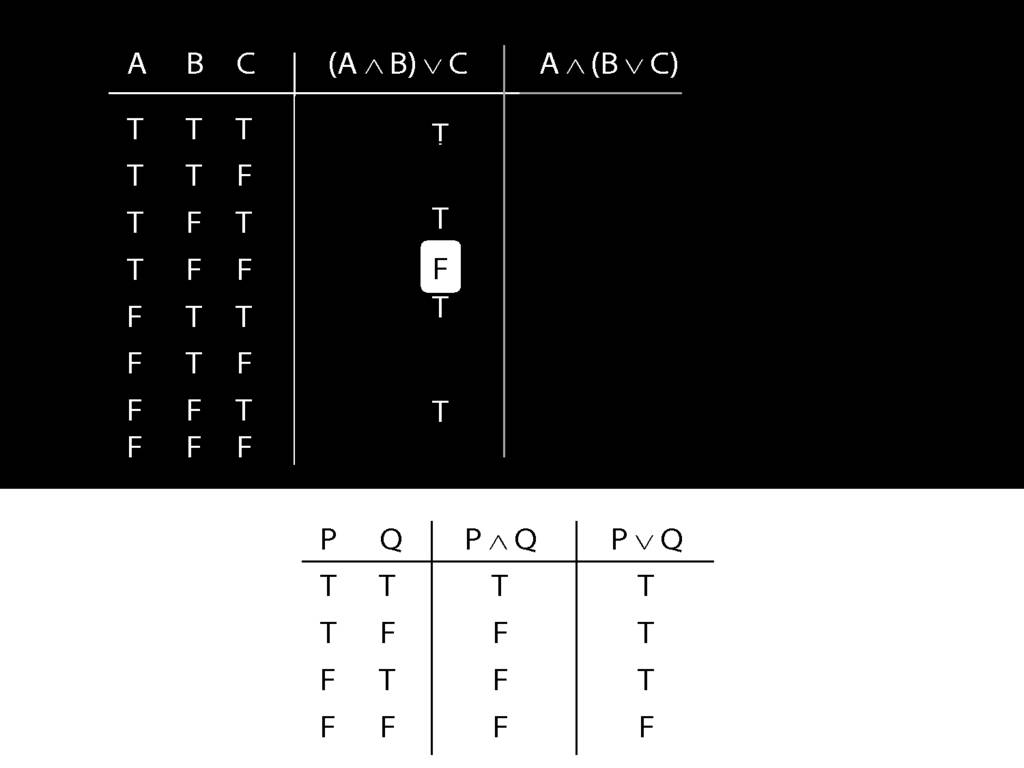
I'll give you the rest of this for free.
Now think about the other sentence.
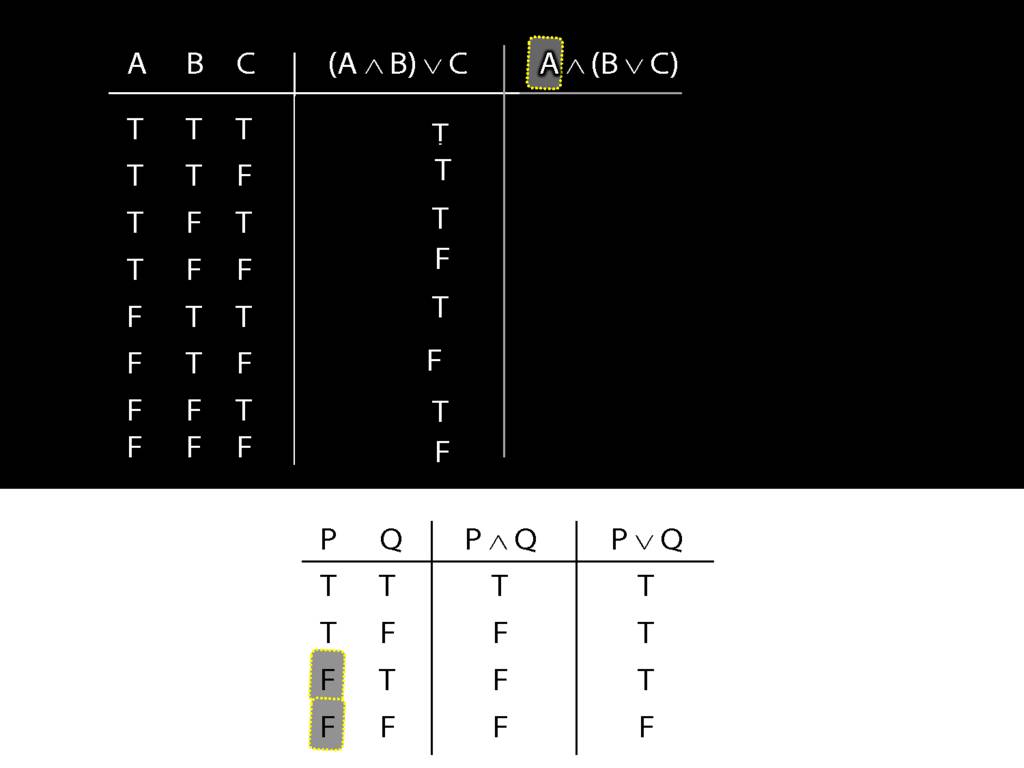
The thing on the left, the left conjunct, is the simplest part.
What happens when this is false?
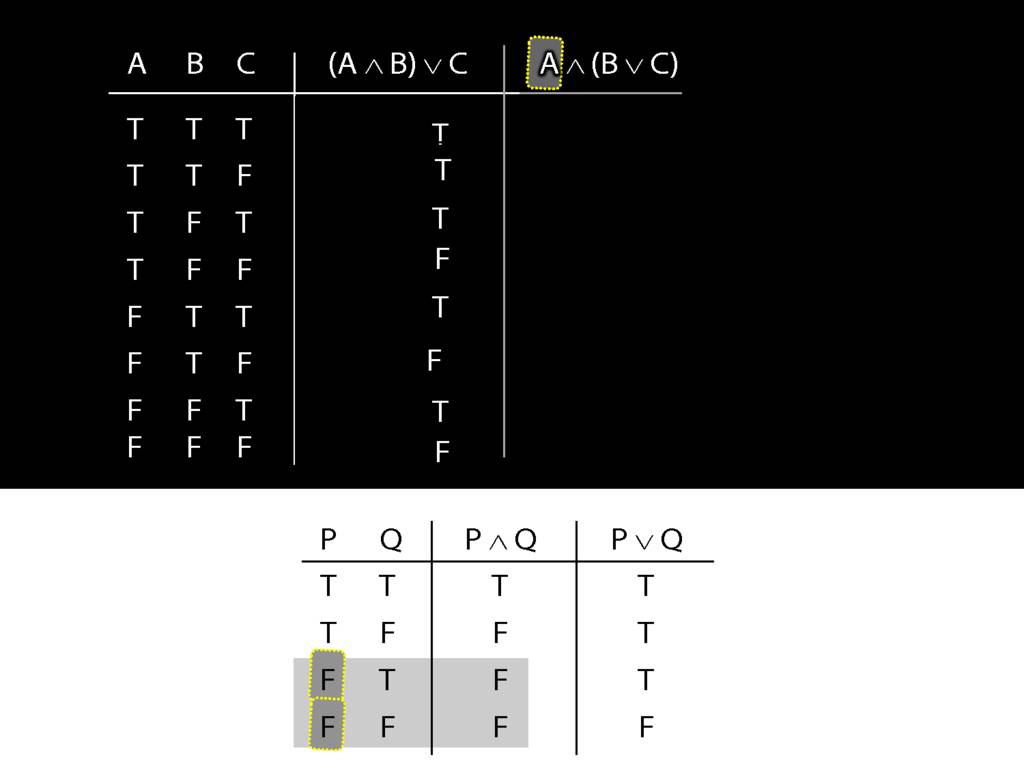
Regardless of what happens on the right, when the left side of a conjunction is false, the whole thing is false.
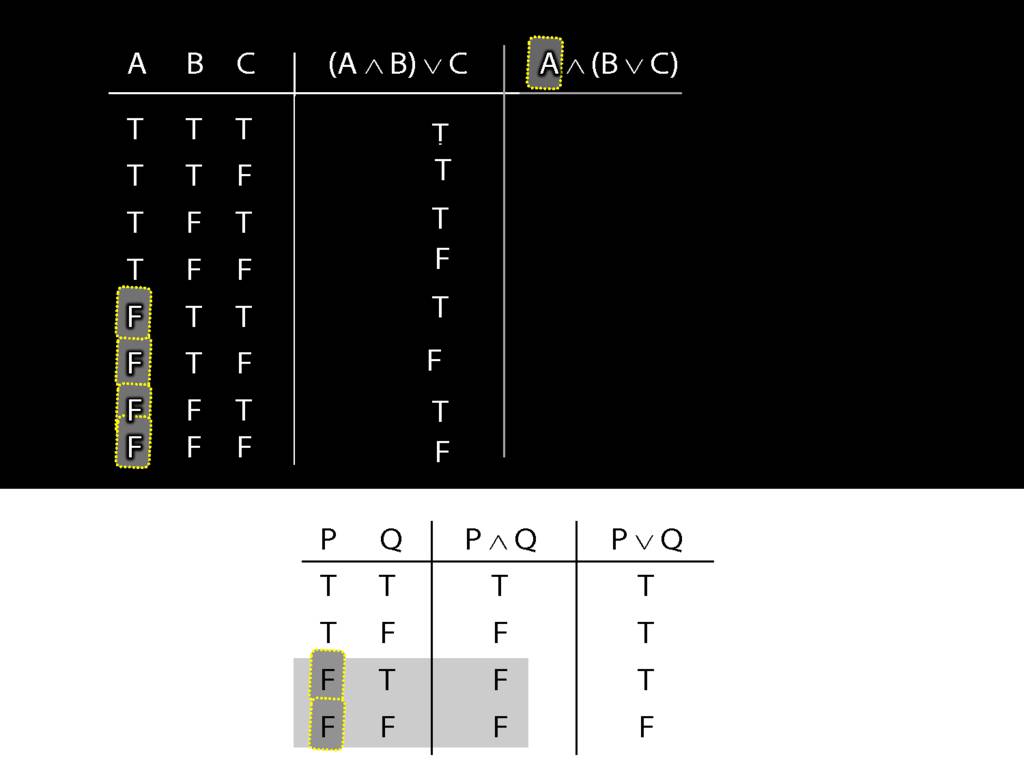
This can save us time. Where is this left side of the conjunction false?
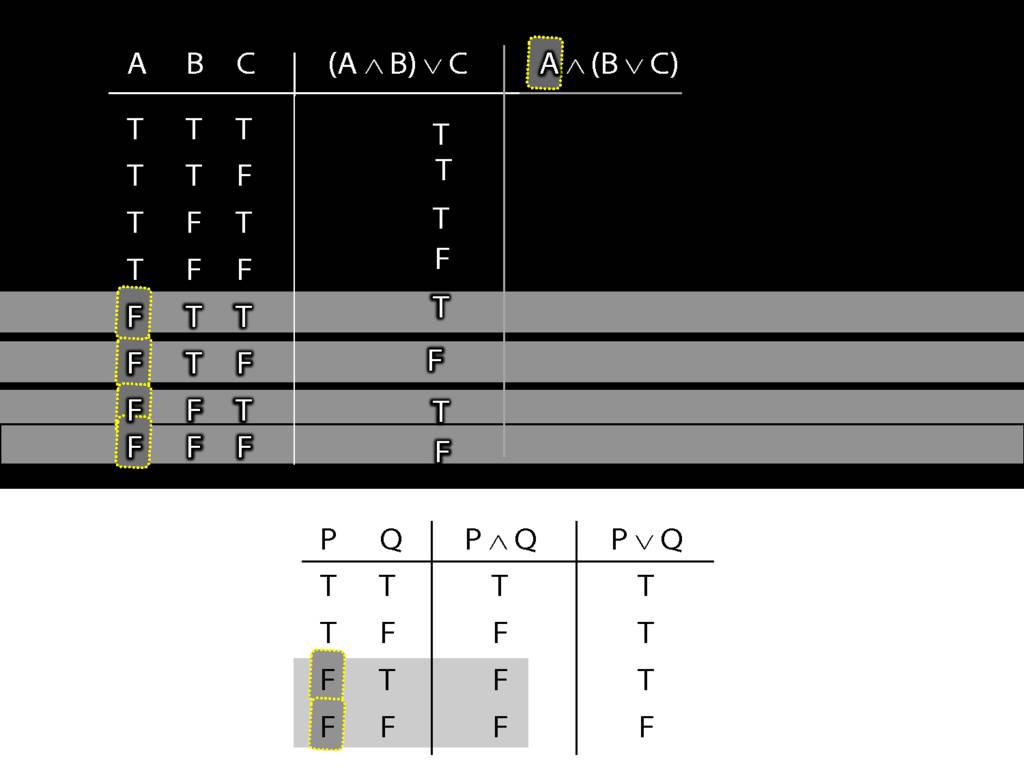
In the bottom four rows.
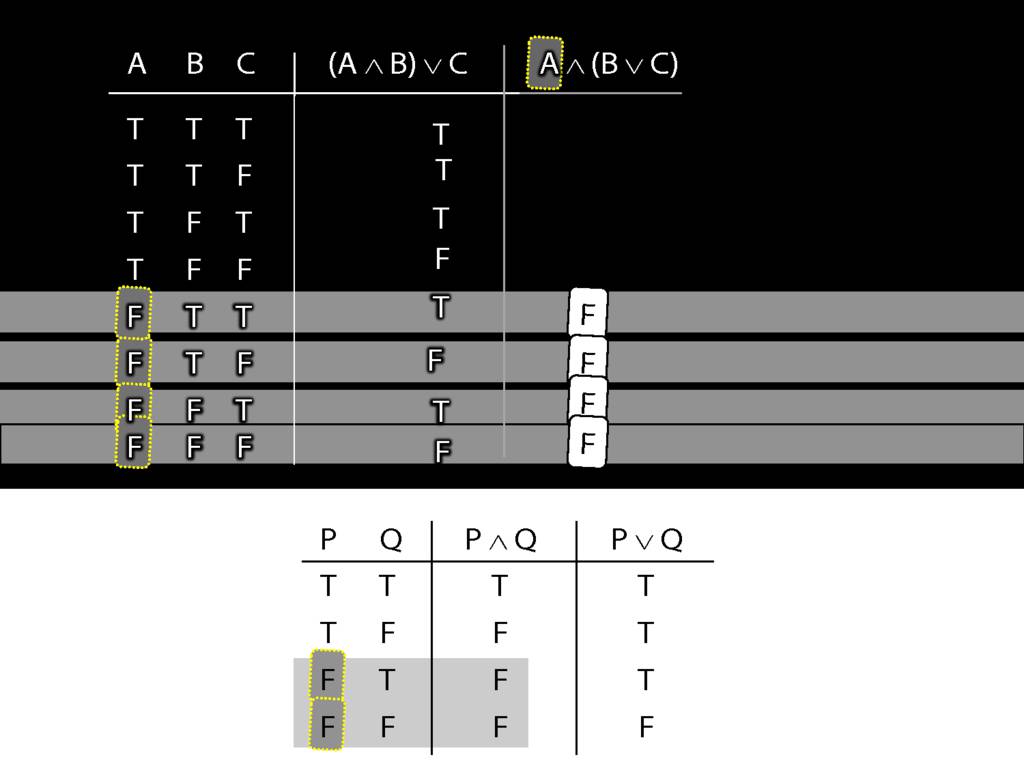
So we can be sure, even without thinking about the right side, that the whole sentence is false in these rows.
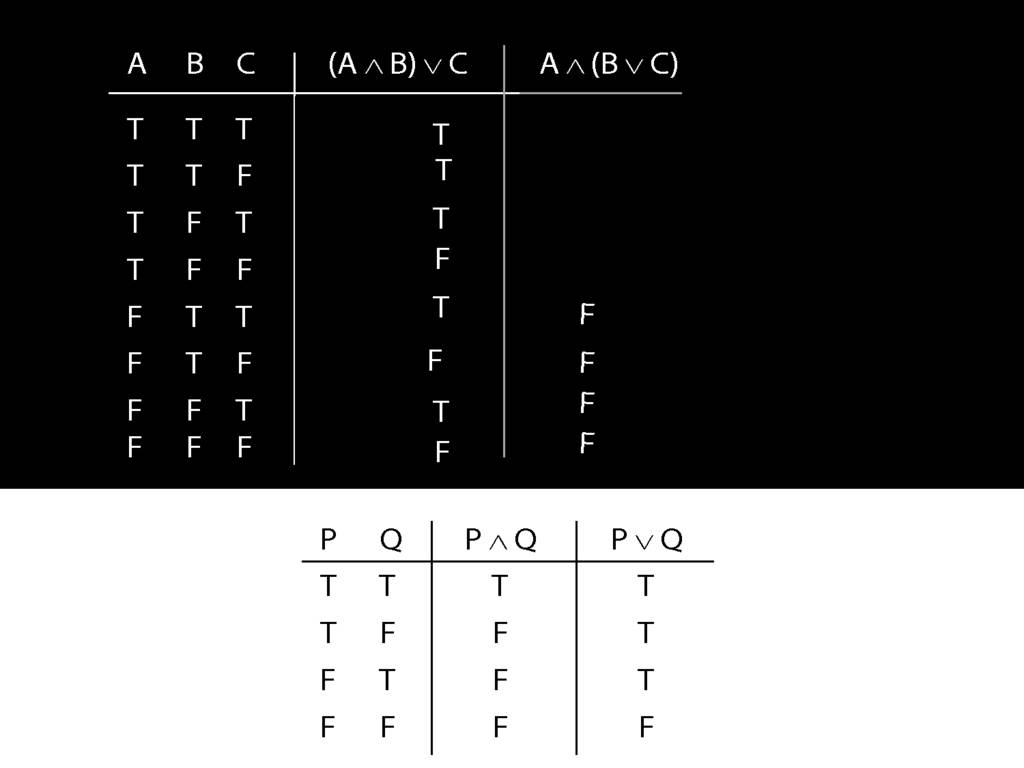
The rest of the truth table probably requires more thought ...
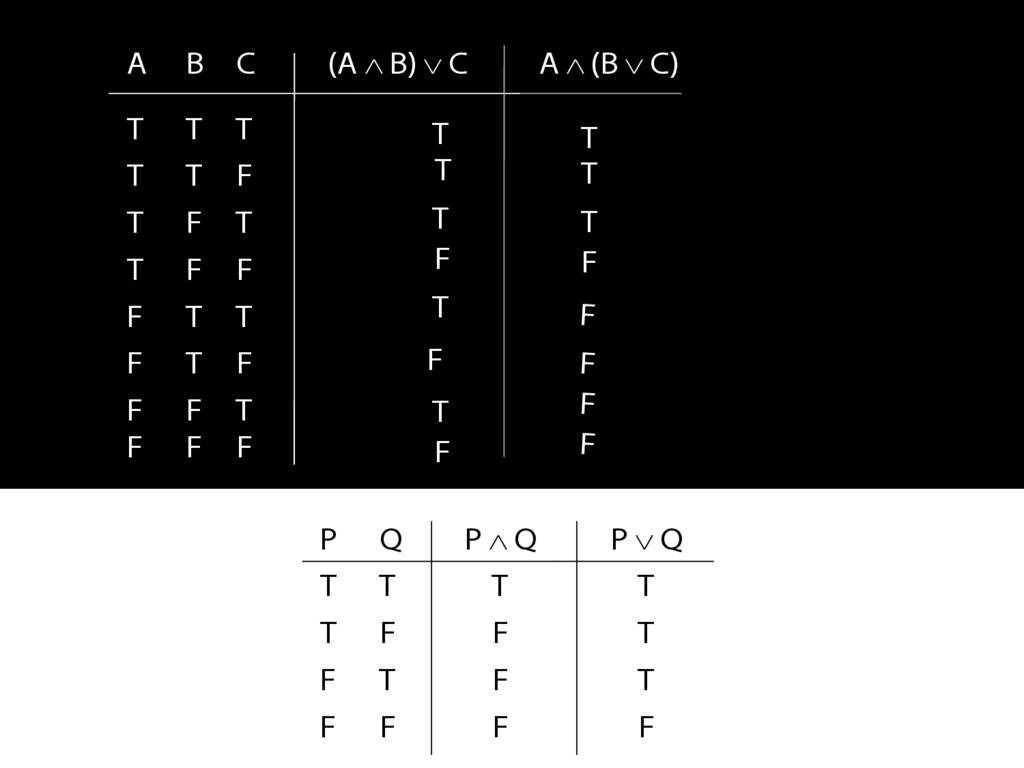
... so here's one I made earlier.