‘A $\vdash$ B’ means there is a proof of B using premises A
‘$\vdash$ B’ means there is a proof of B using no premises
‘A ⊨ B’ means B is a logical consequence of A
‘⊨ B’ means B is a tautology
‘A ⊨$_{TT}$ B’ means B is a logical consequence of A just in virtue of the meanings of truth-functions (the textbook LPL calls this ‘tautological consequence’)
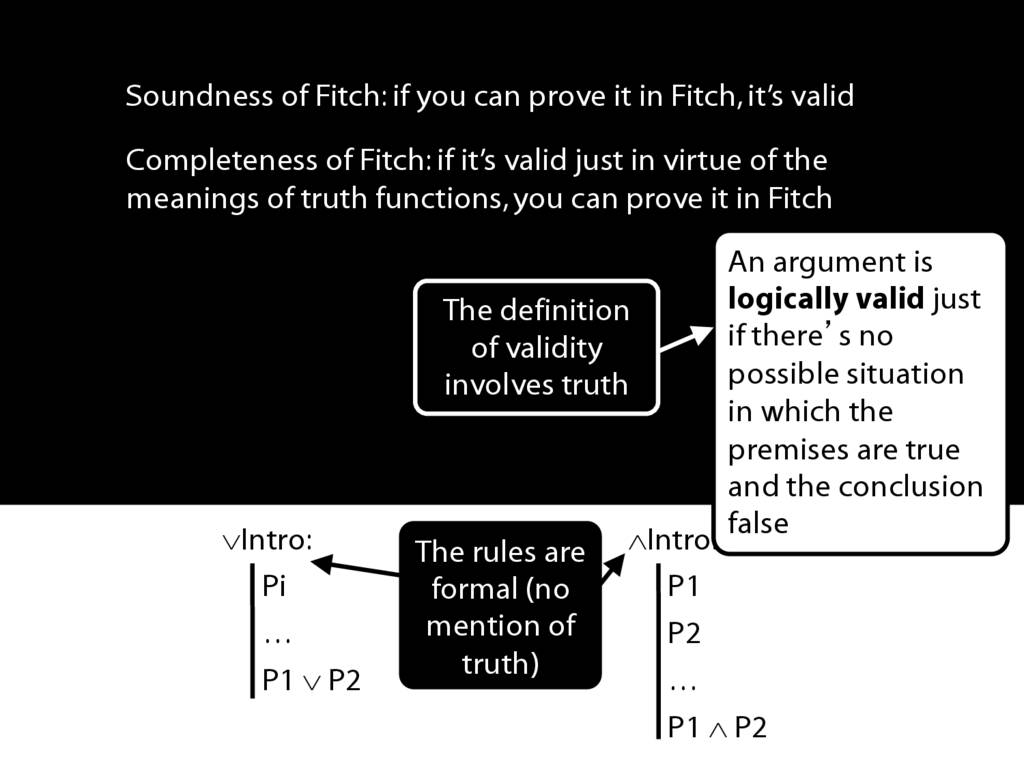
\emph{Soundness}: If A $\vdash$ B then A ⊨ B
\hspace{3mm} i.e. if you can prove it in Fitch, it’s valid
\emph{Completeness}: If A ⊨$_{TT}$ B then A $\vdash$ B
\hspace{3mm} i.e. if it’s valid just in virtue of the meanings of the truth-functional connectives, then you can prove it in Fitch.
