Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
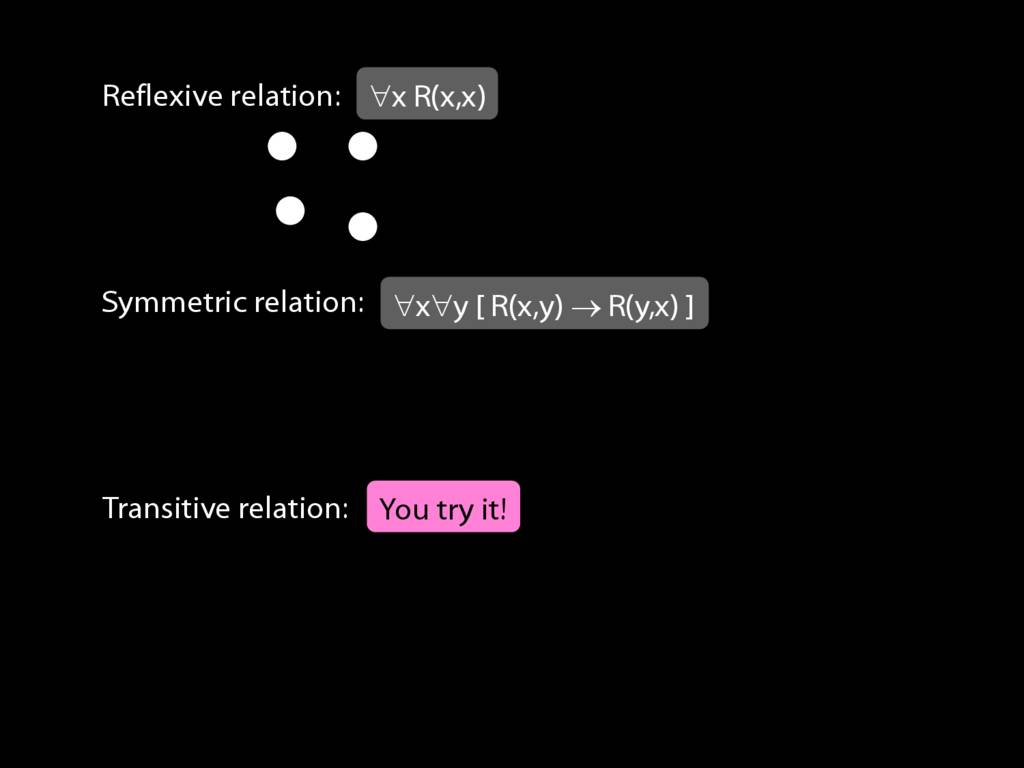
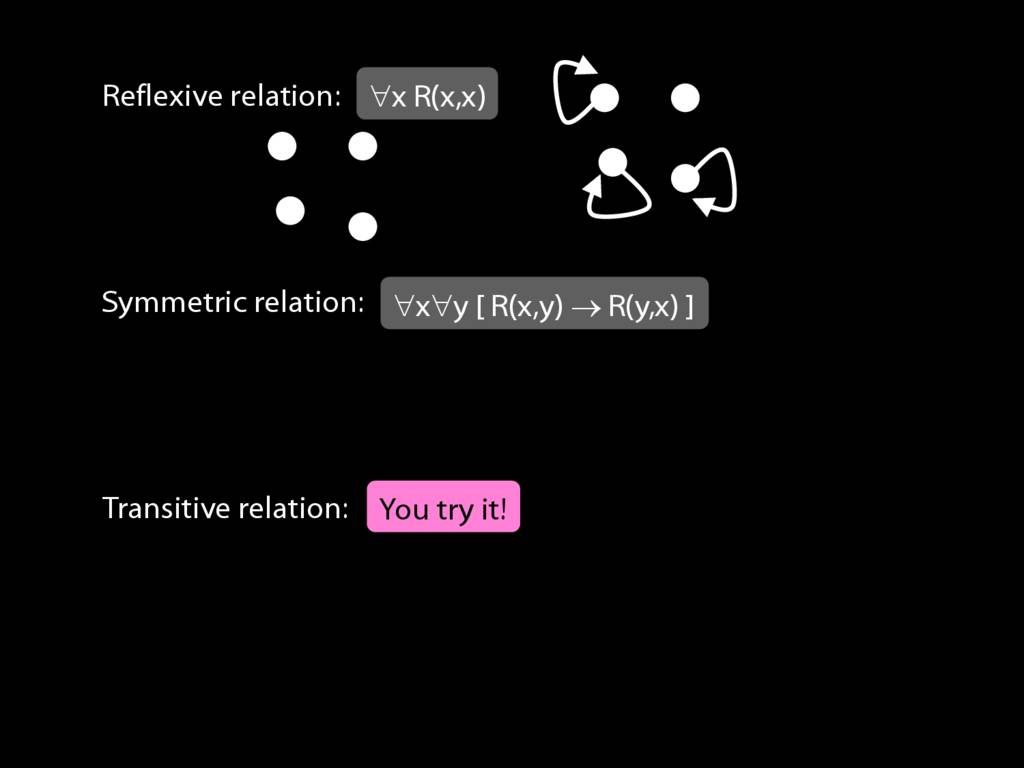
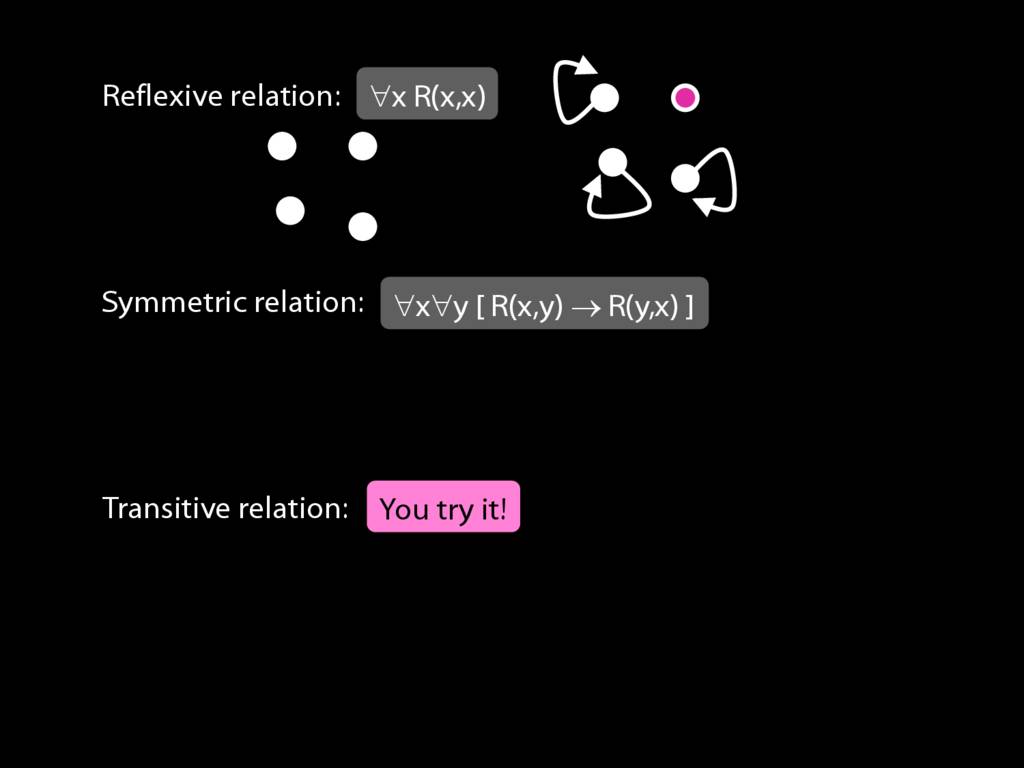
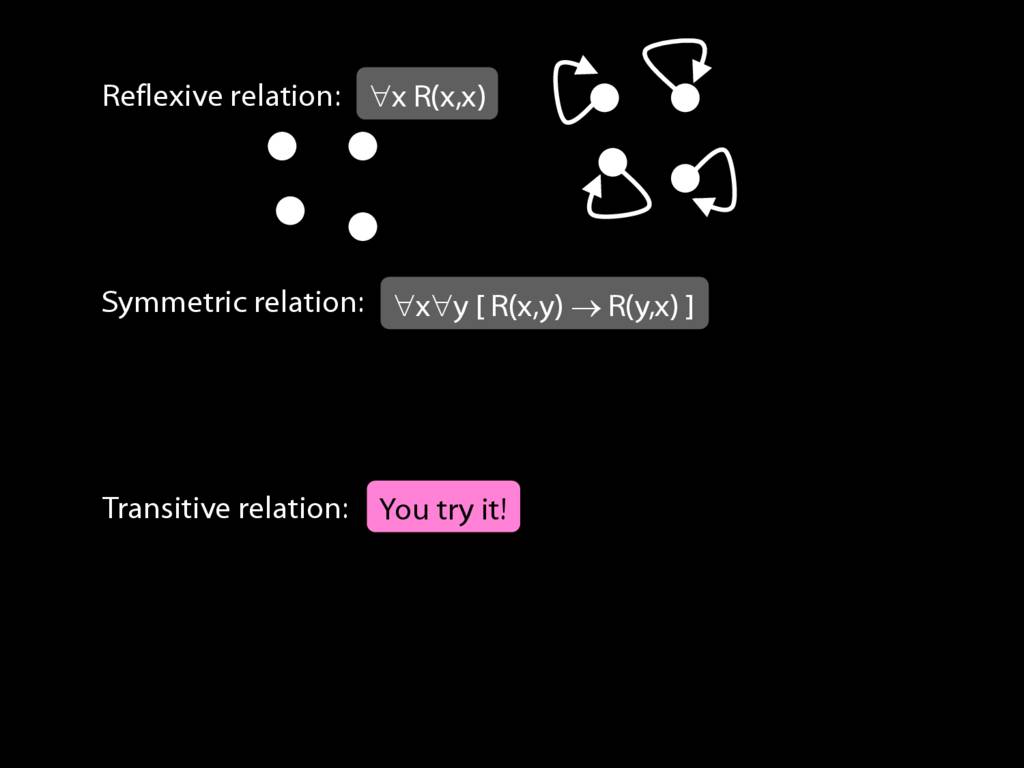
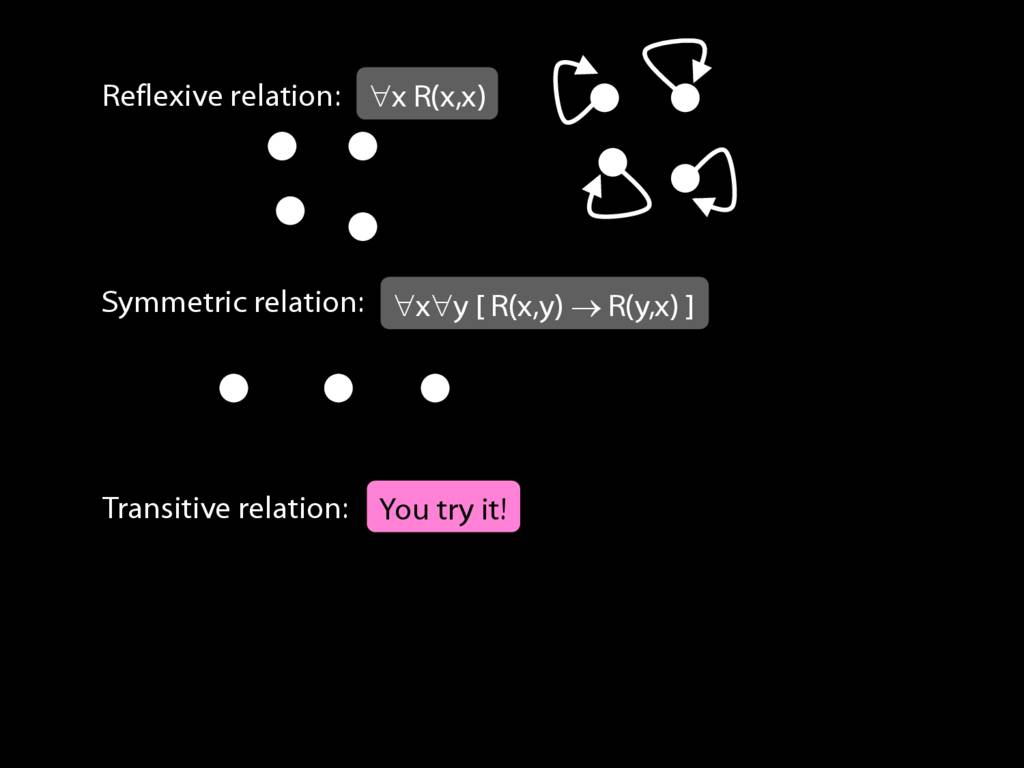
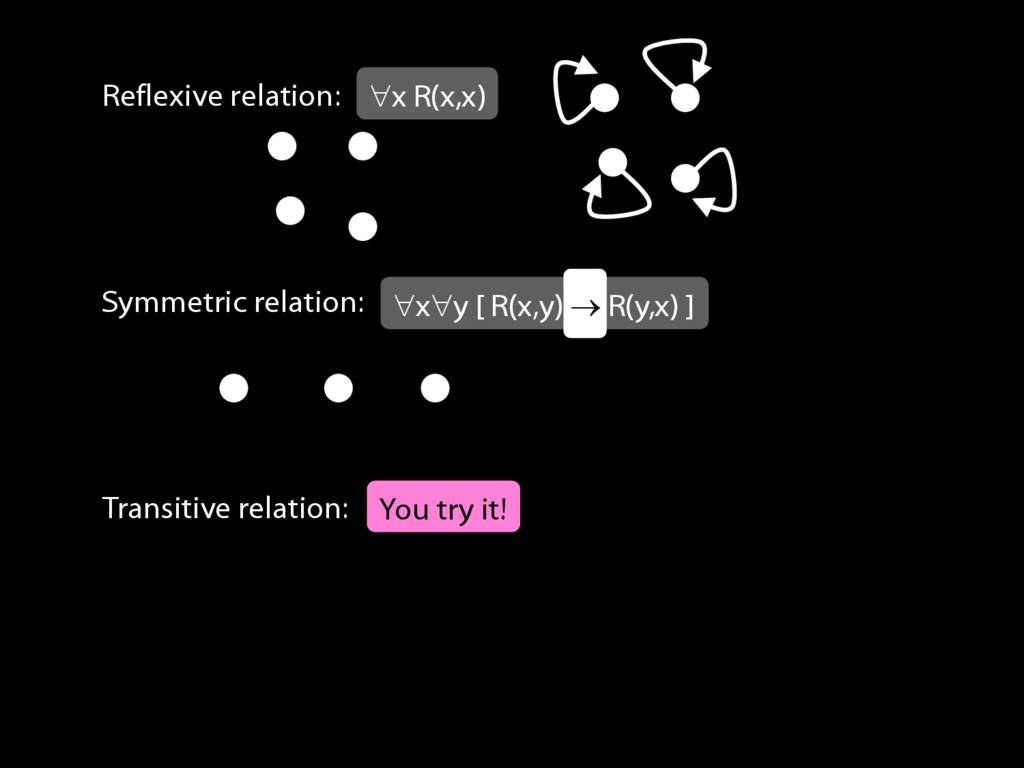
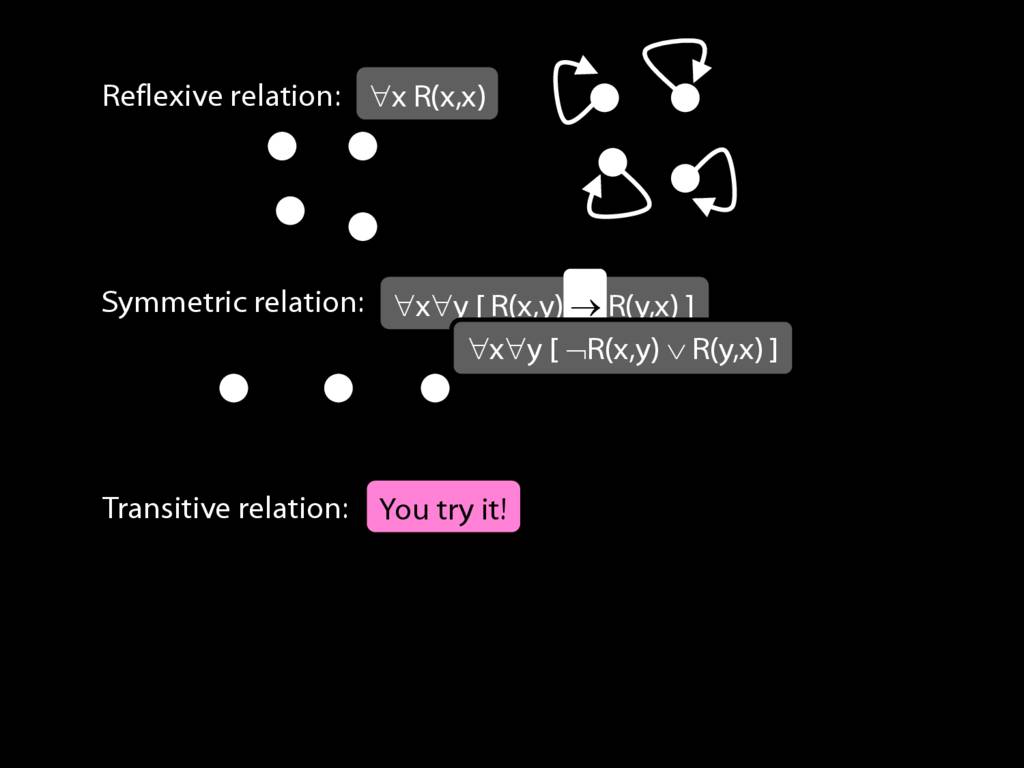
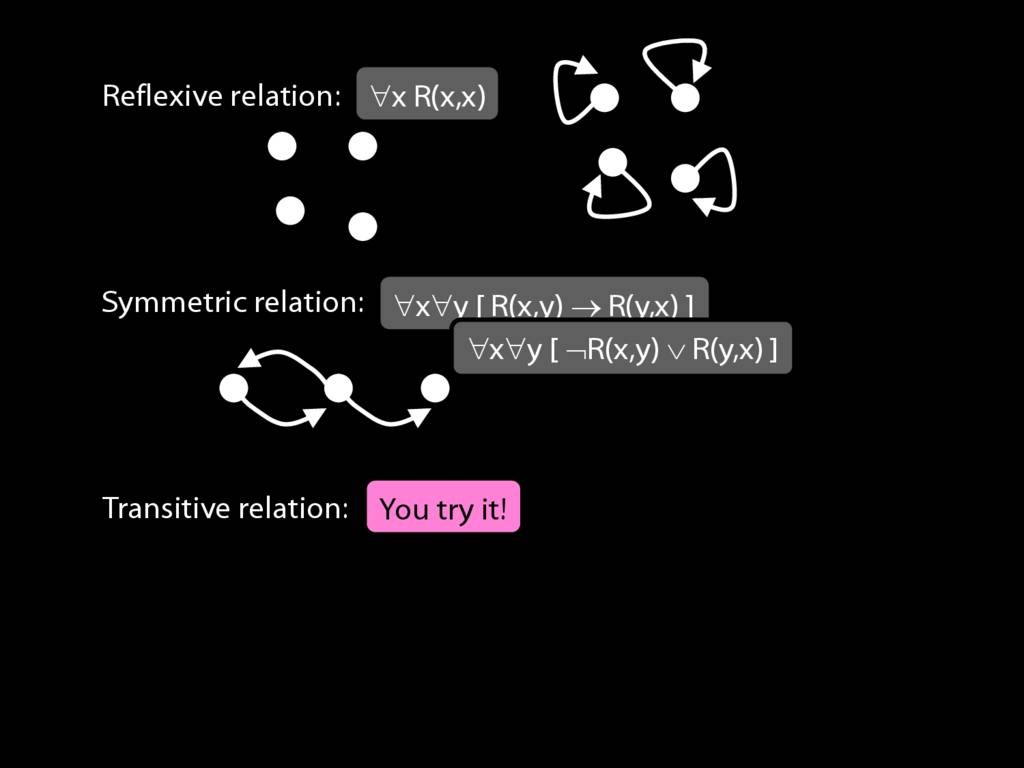
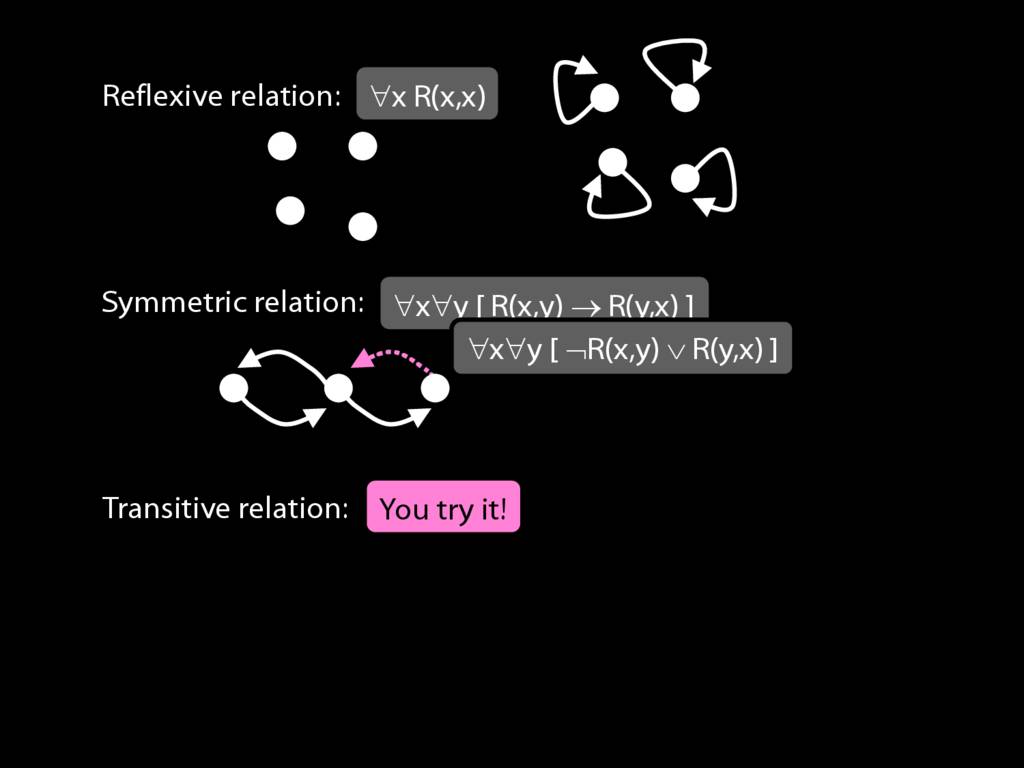
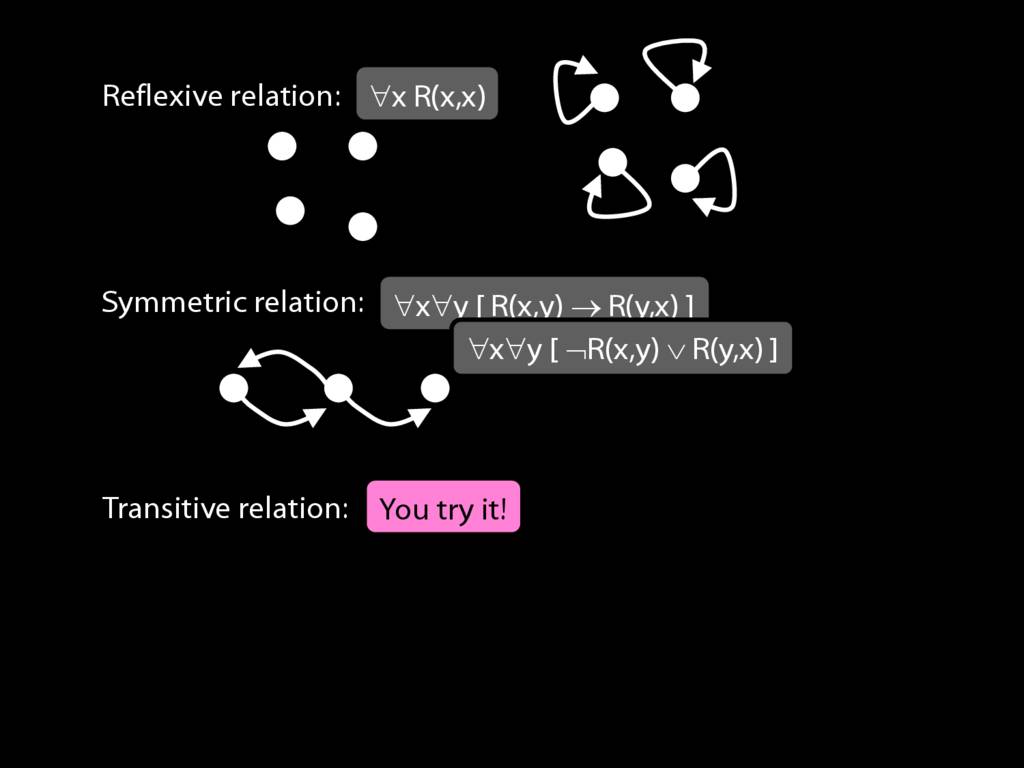
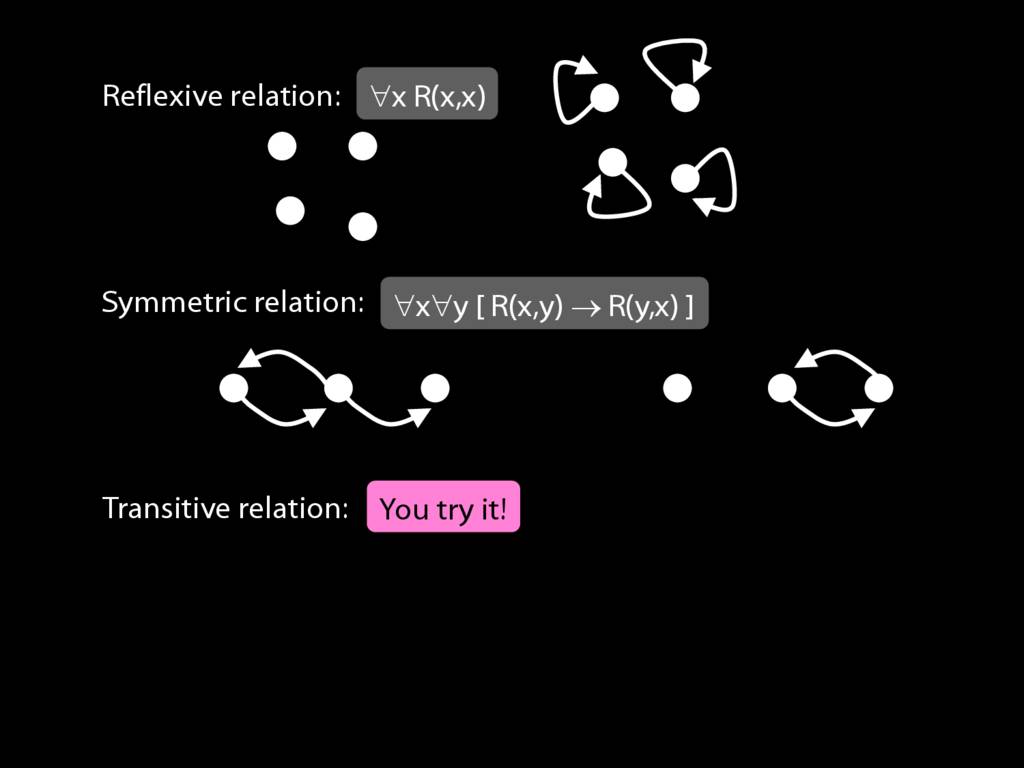
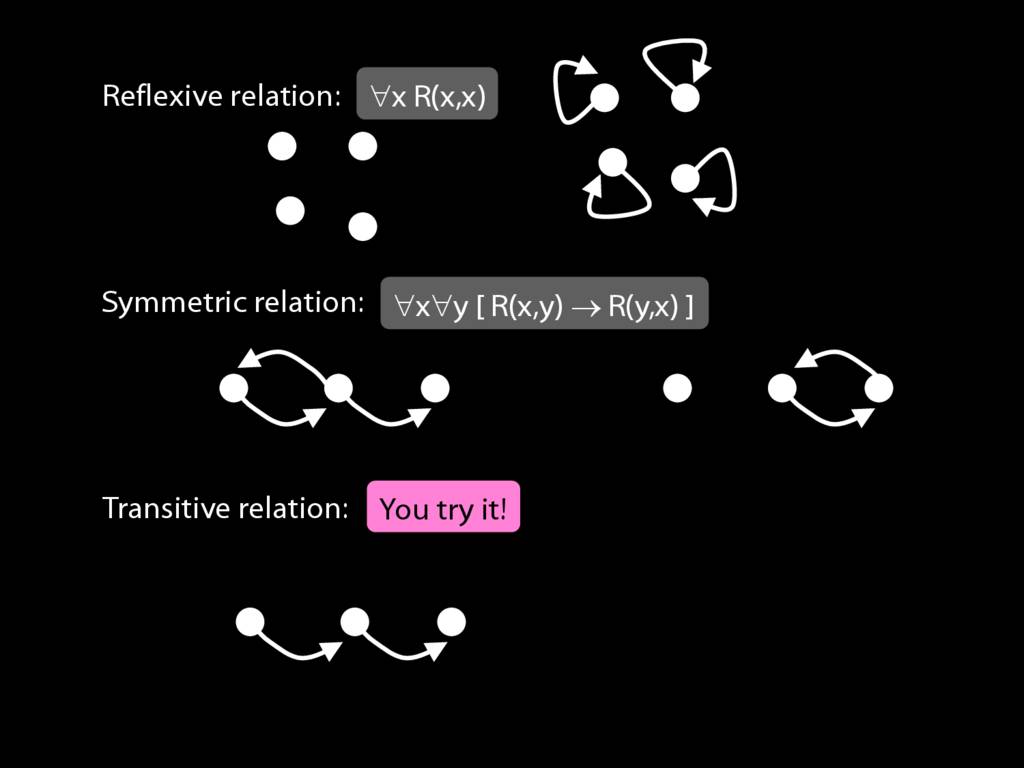
Expressing Relations with Quantifiers

\begin{minipage}{\columnwidth}
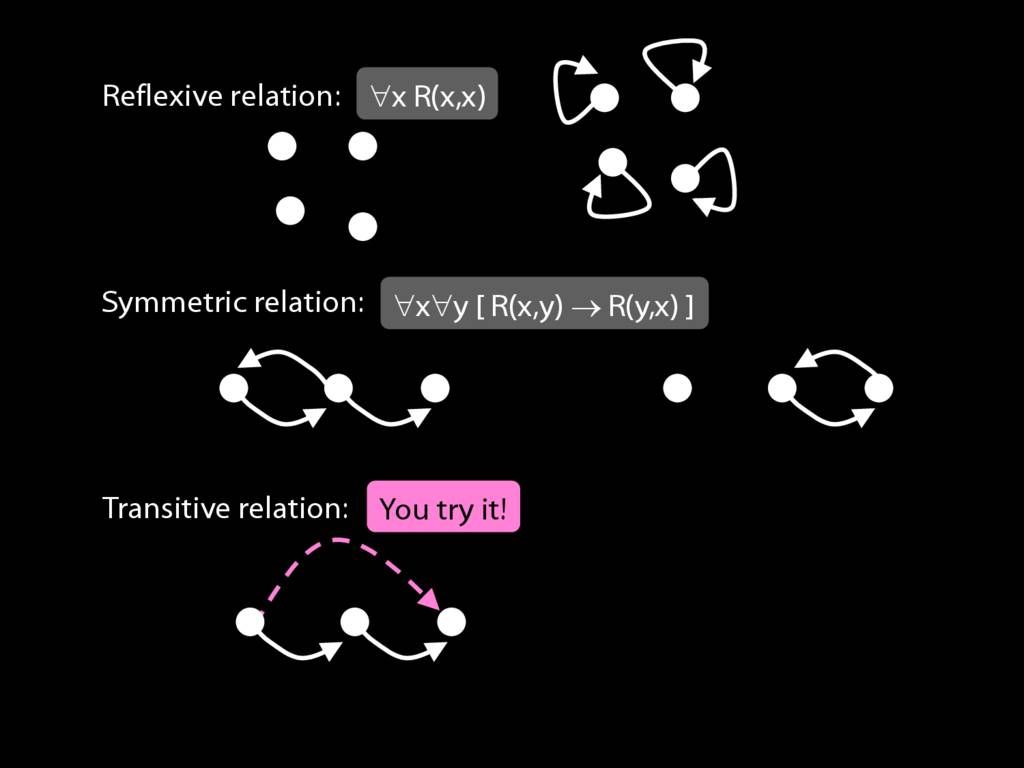
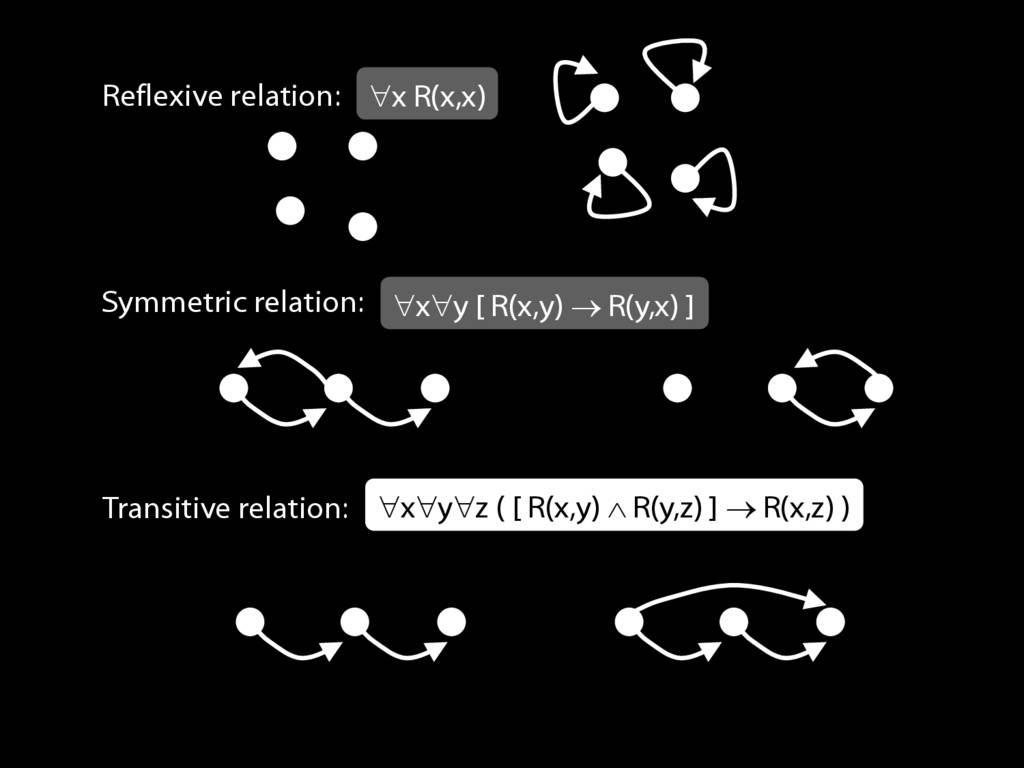
A \emph{reflexive} relation is one that everything bears to itself. (E.g. SameShape)
reflexive: ∀x R(x,x)
\end{minipage}
\begin{minipage}{\columnwidth}
A \emph{symmetric} relation is one such that if x bears it to y, then y bears it to x. (E.g. Adjacent(x,y))
symmetric: ∀x∀y ( R(x,y) → R(y,x) )
\end{minipage}
\begin{minipage}{\columnwidth}
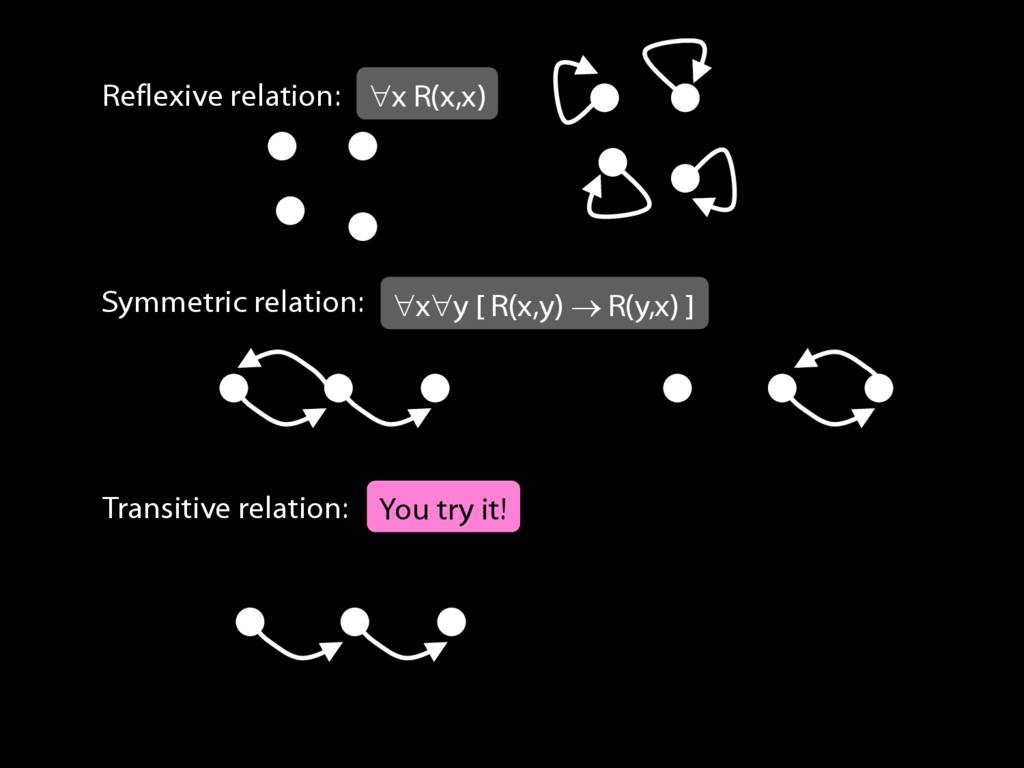
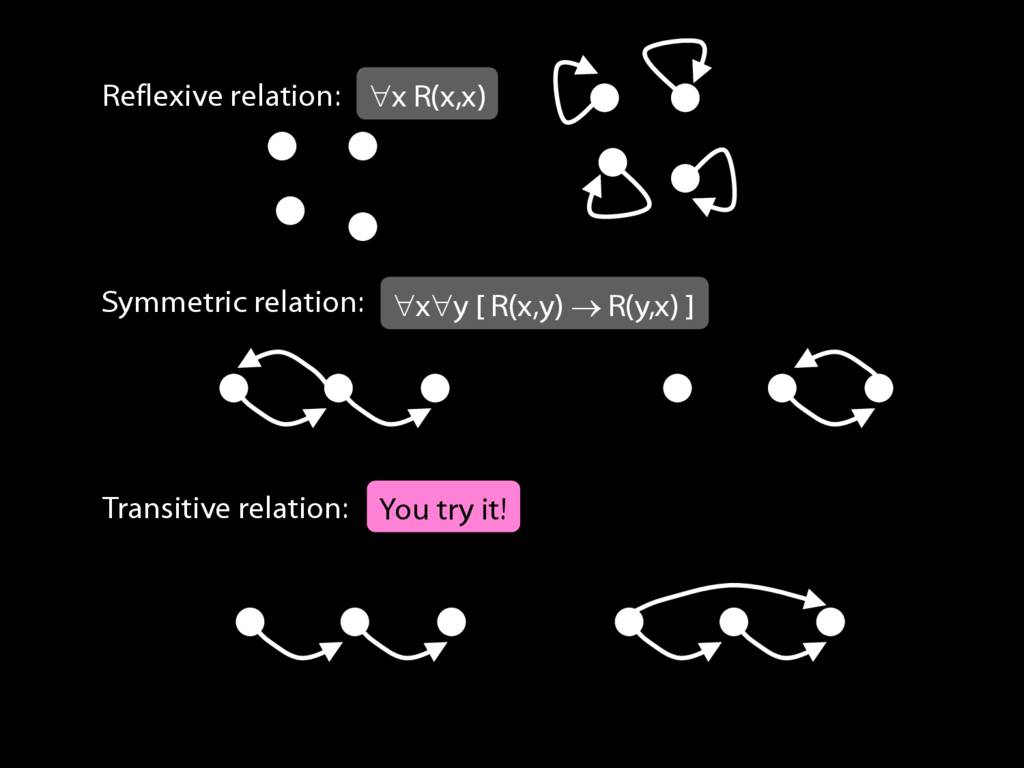
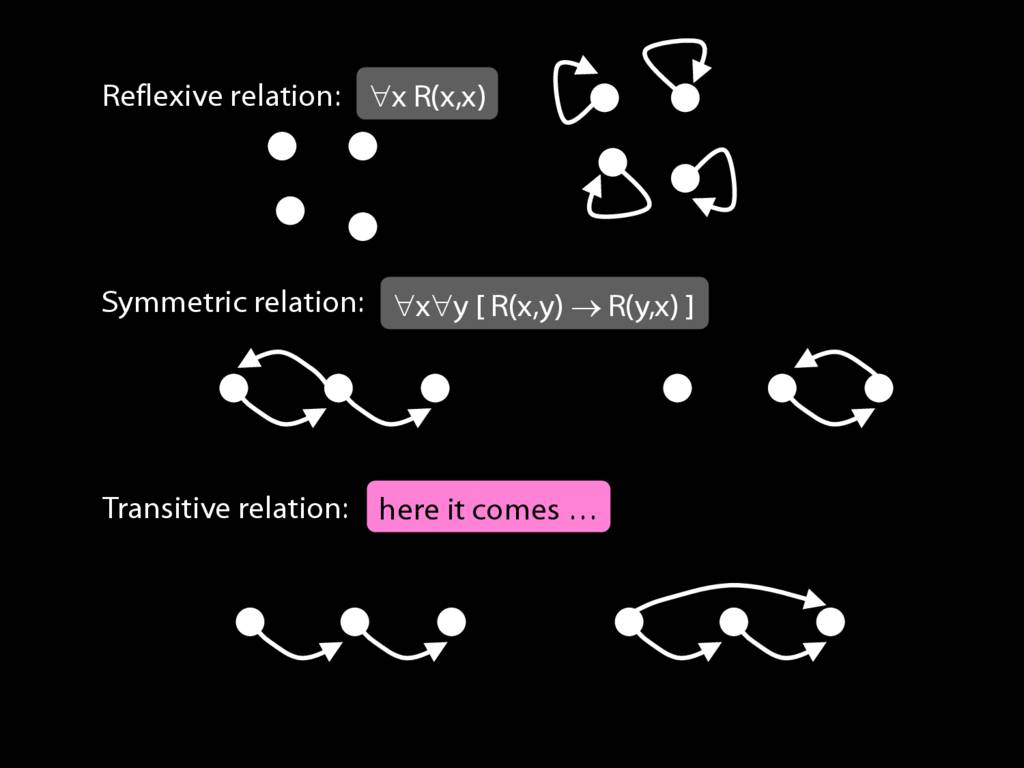
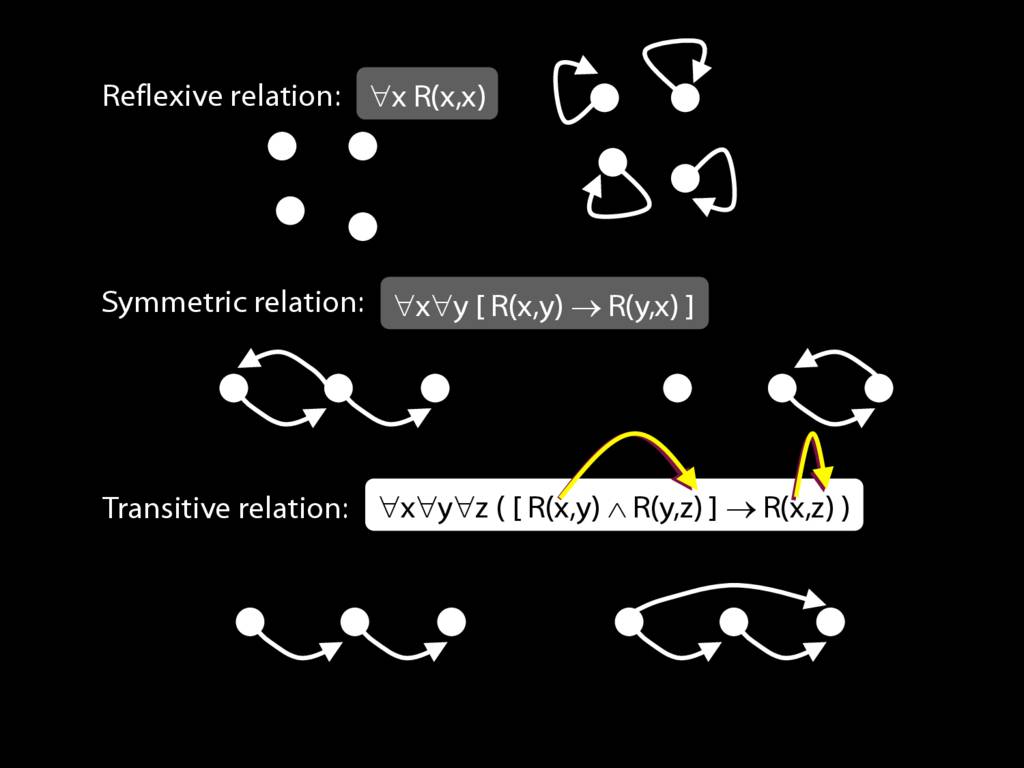
A \emph{transitive} relation is one such that if x bears it to y and y bears it to z then x bears it to z. (E.g. LeftOf is transitive; DifferentShape is not transitive)
transitive: ∀x∀y∀z ( ( R(x,y) ∧ R(y,z) ) → R(x,z) )
\end{minipage}









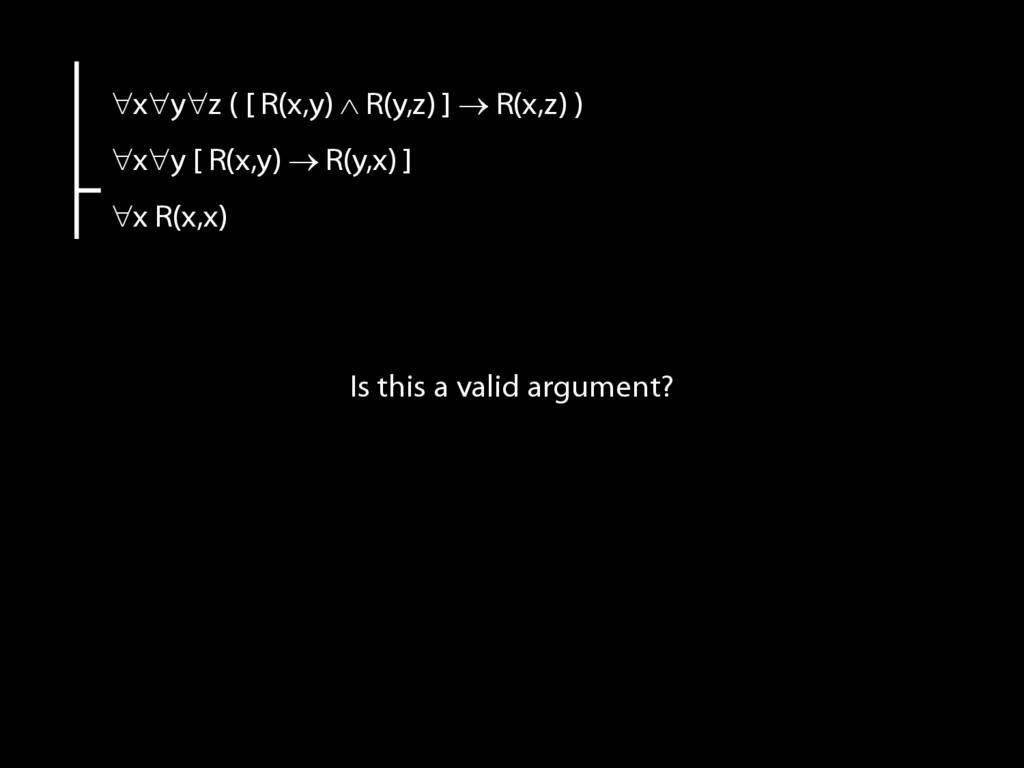




15.33--15.40 (second edition)
15.33, 15.37--15.39 (second edition)