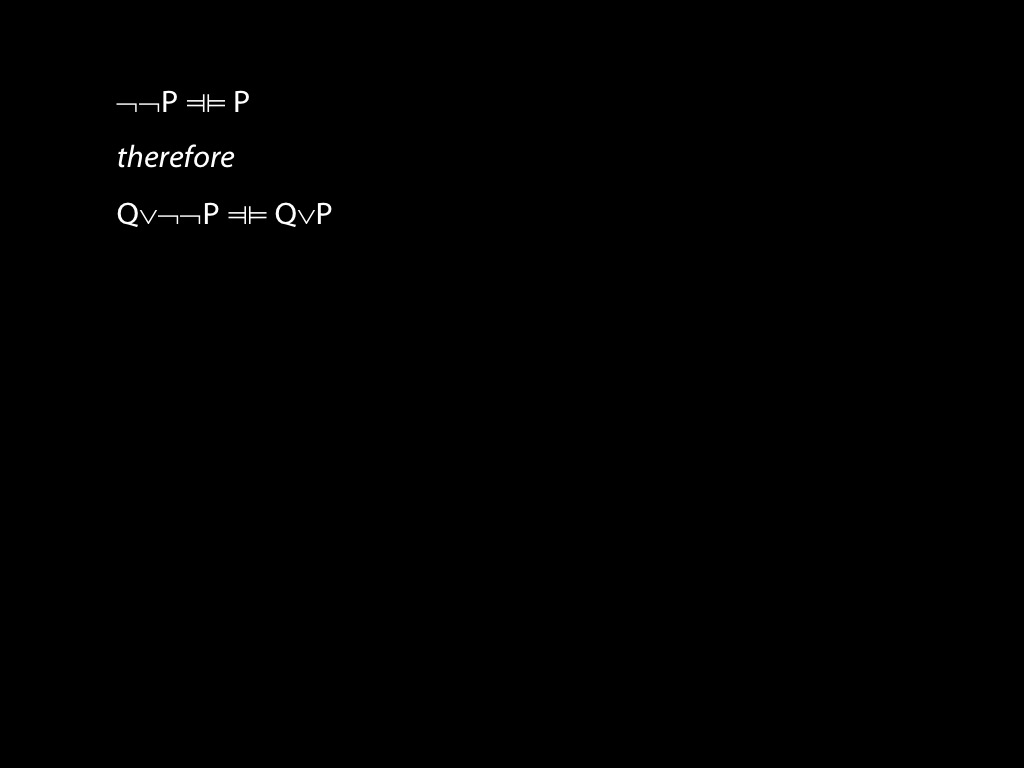Press the right key for the next slide (or swipe left)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)
Press m or double tap to see a menu of slides
Revison: Truth tables
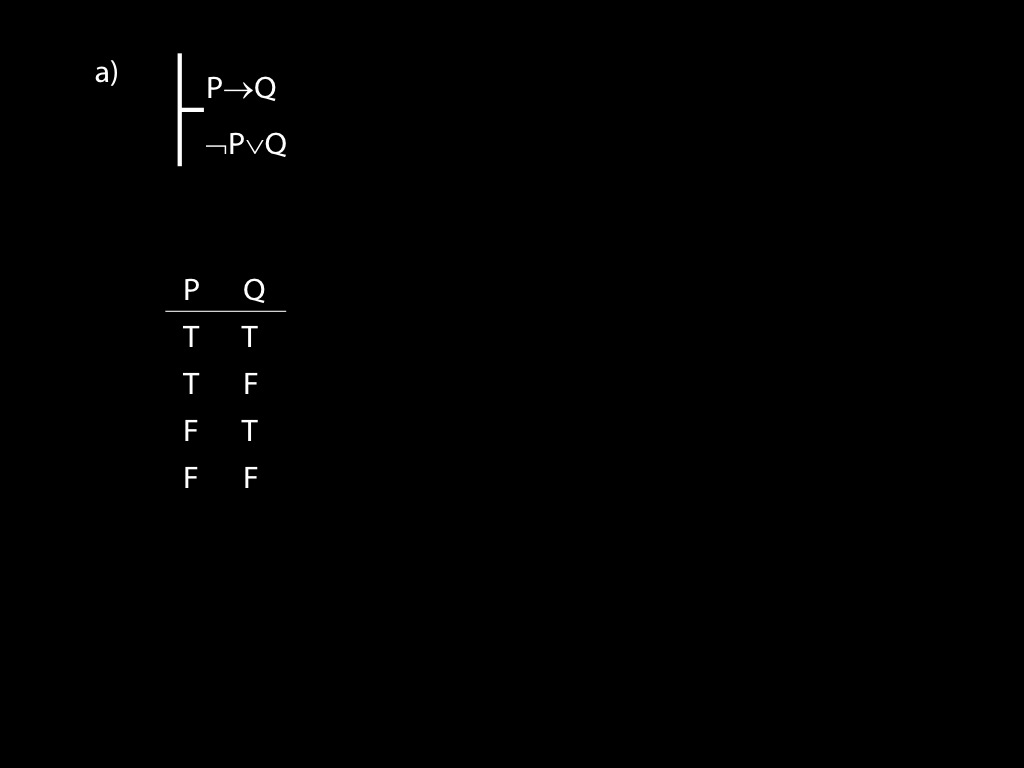
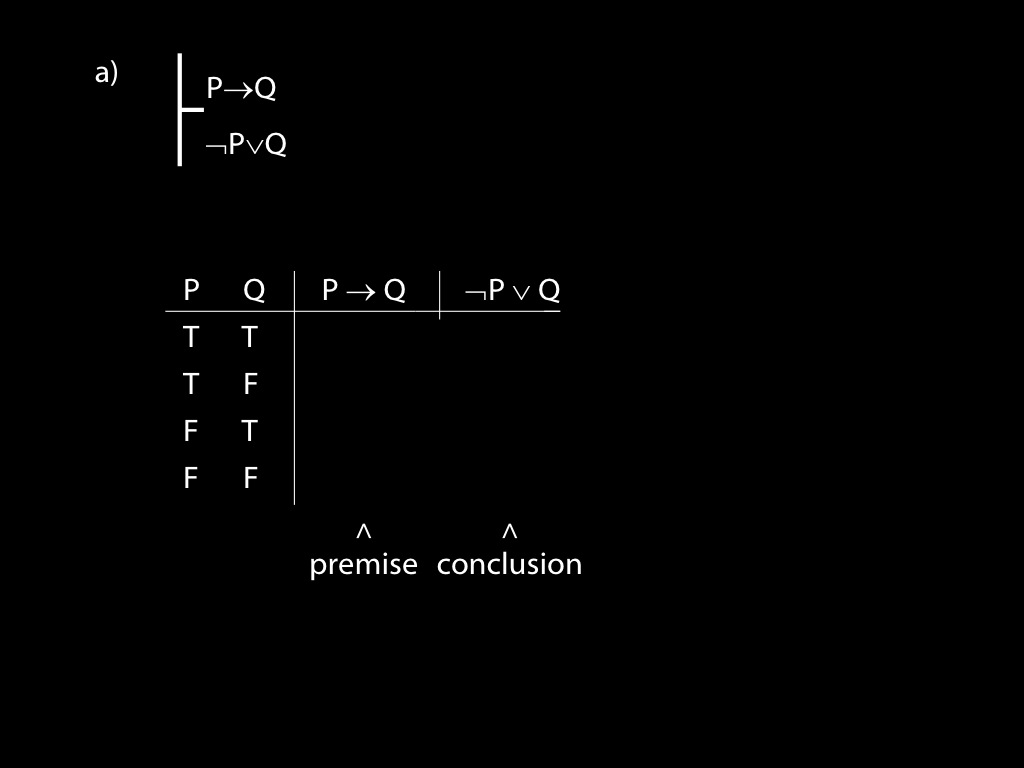
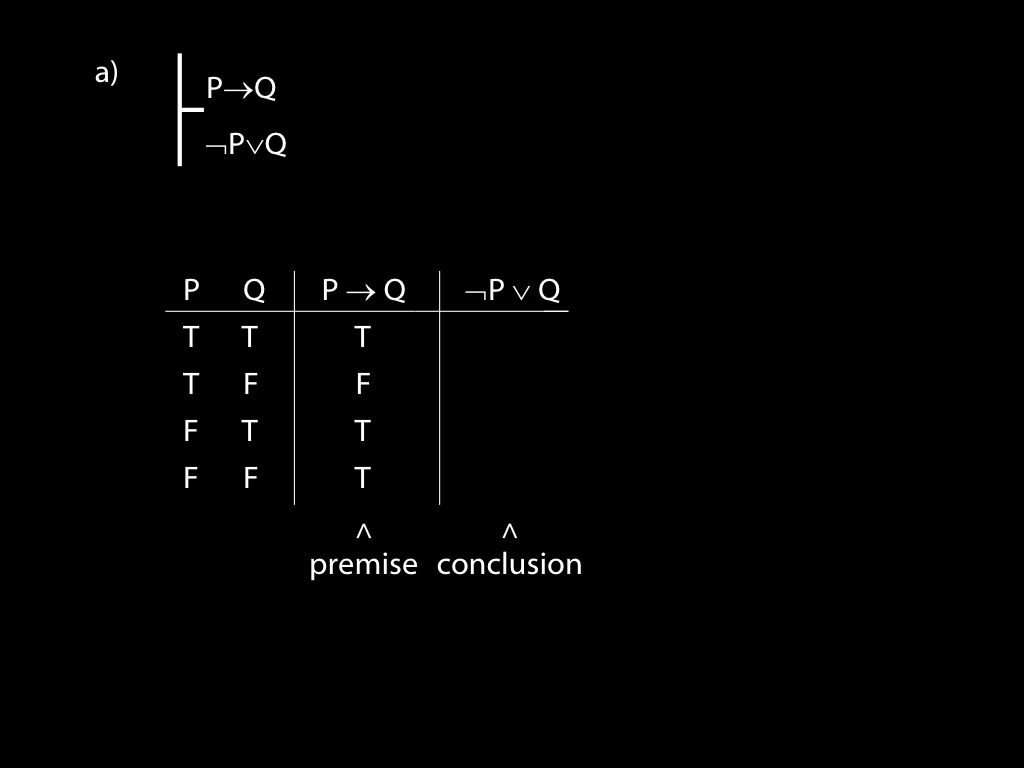
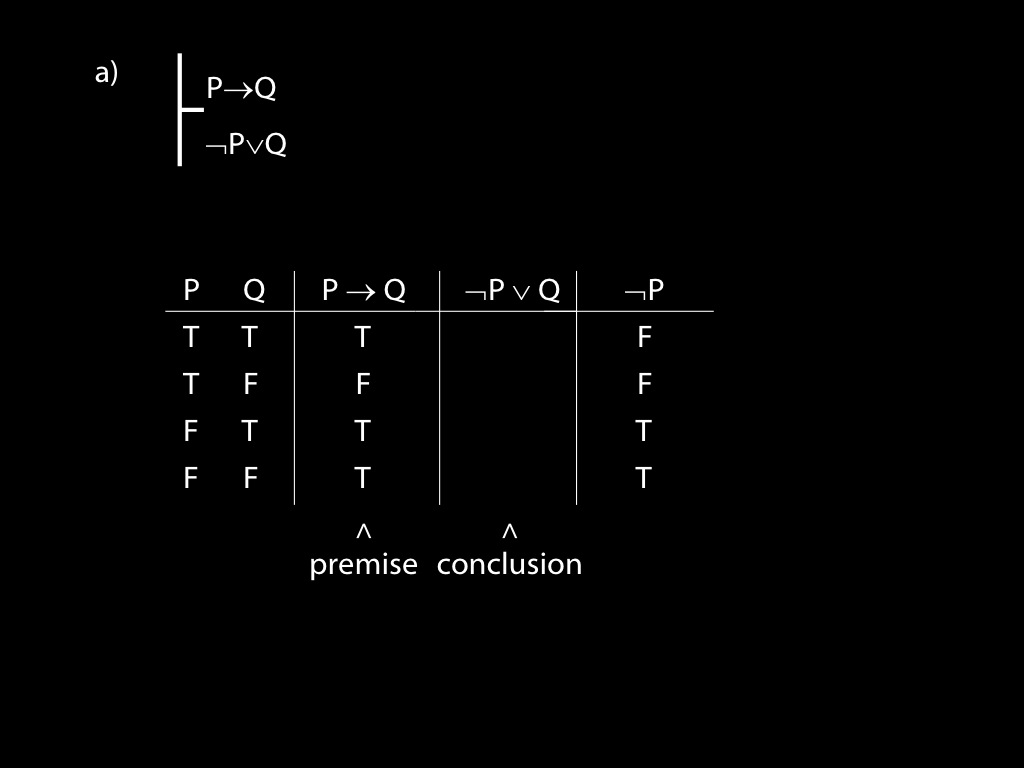
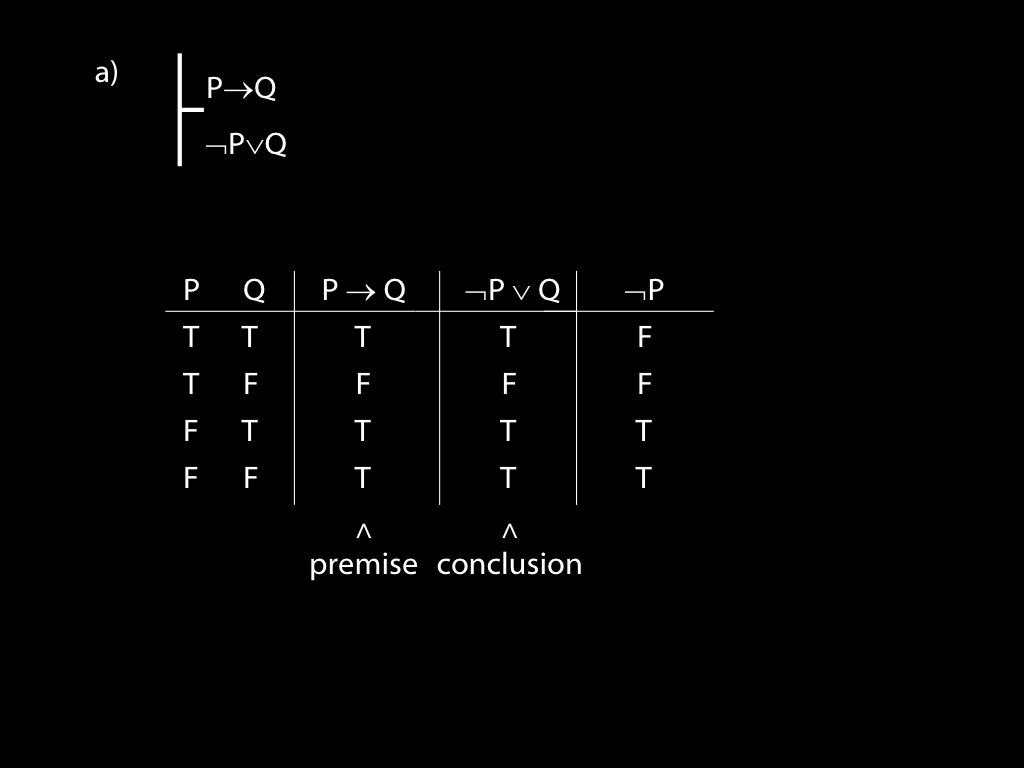
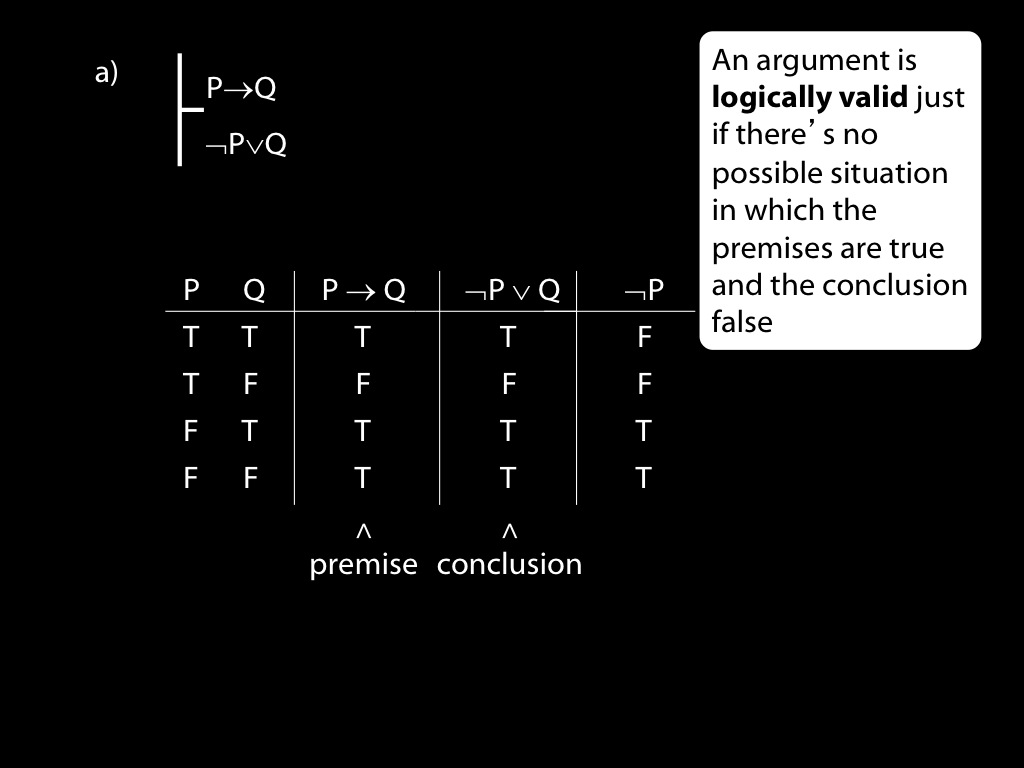
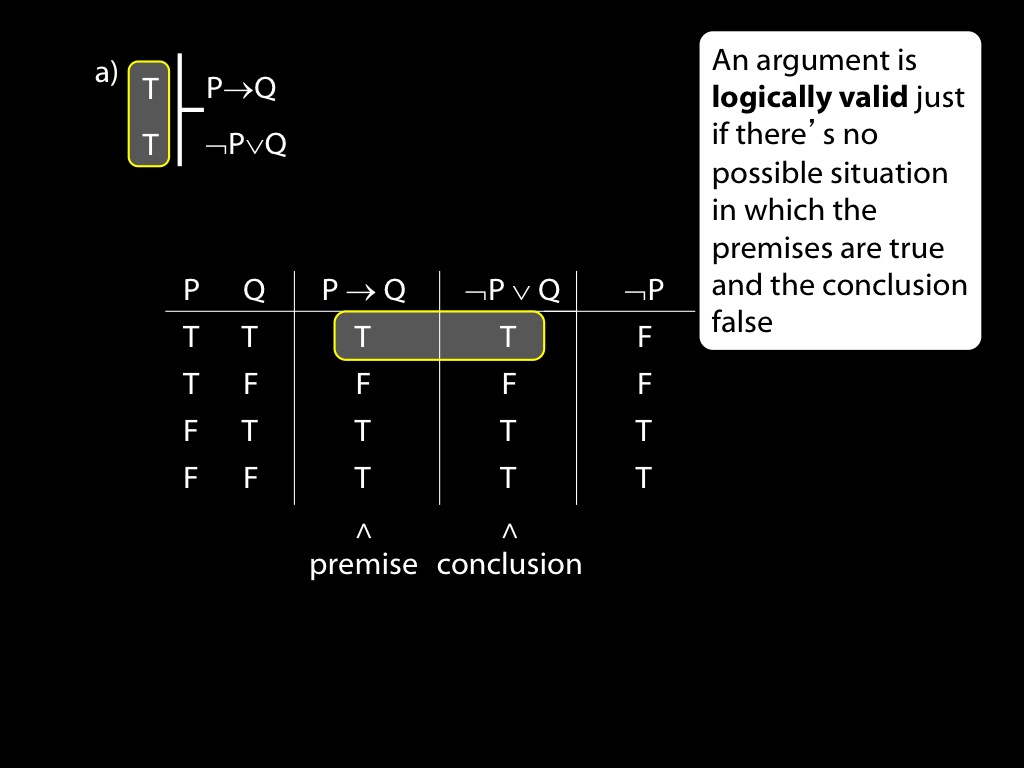
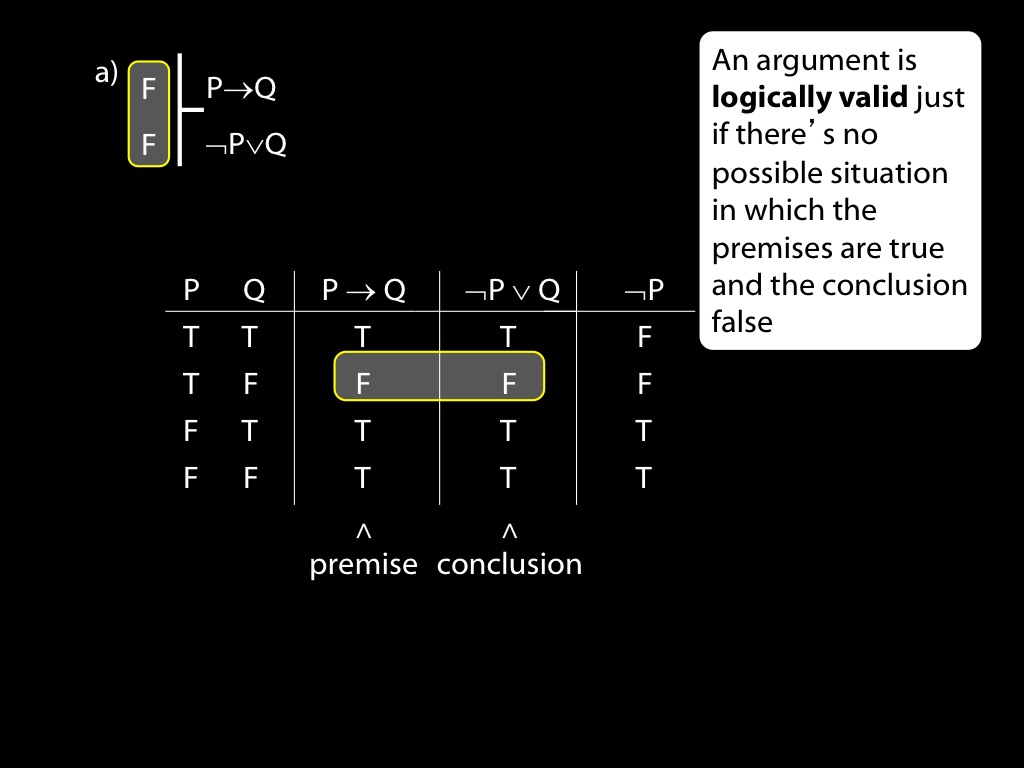
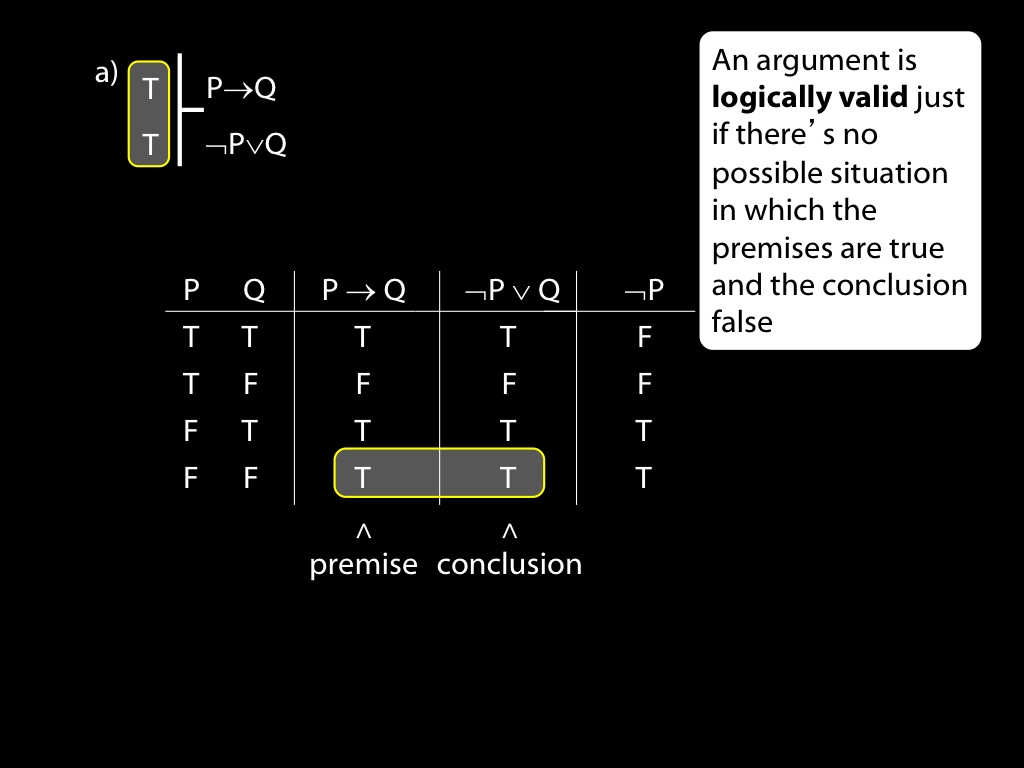
Use truth tables to establish whether the following arguments are valid. If any arguments are invalid, state counterexamples to them. If any arguments are valid, explain carefully using the truth tables why they are valid.
\begin{enumerate}
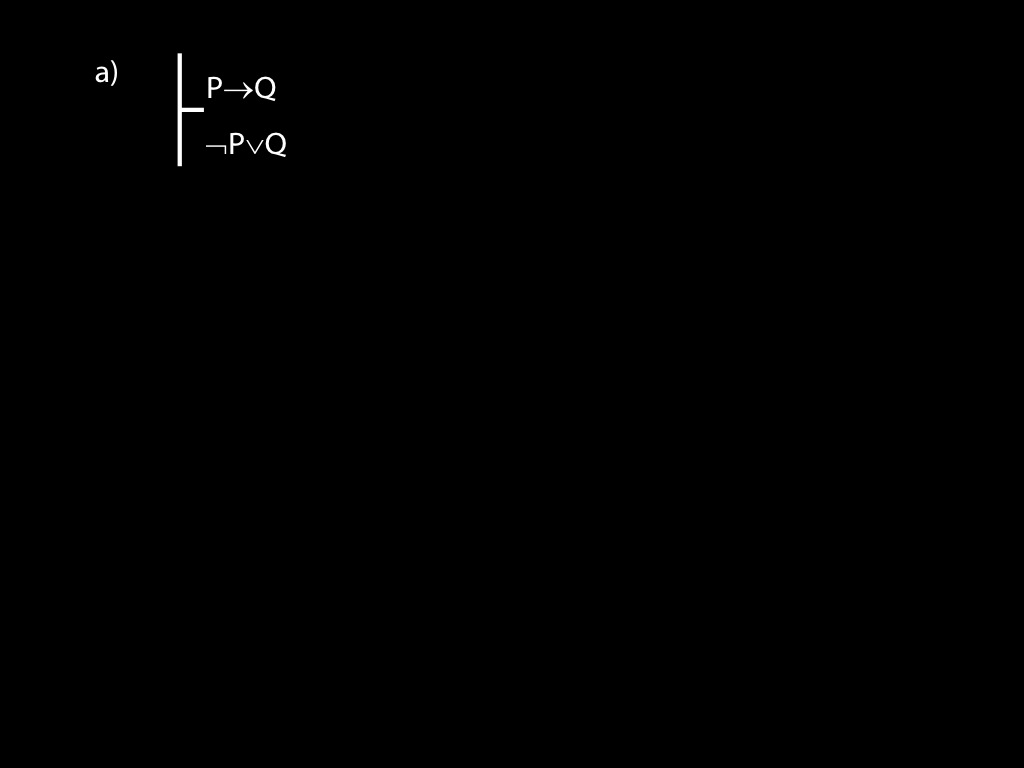
\item
\begin{equation*}
\begin{fitch}
\fh P \to Q \\
\fa \lnot P \lor Q \\
\end{fitch}
\end{equation*}
\item
\begin{equation*}
\begin{fitch}
\fh P ↔ (Q \to Q) \\
\fa P \lor Q \\
\end{fitch}
\end{equation*}
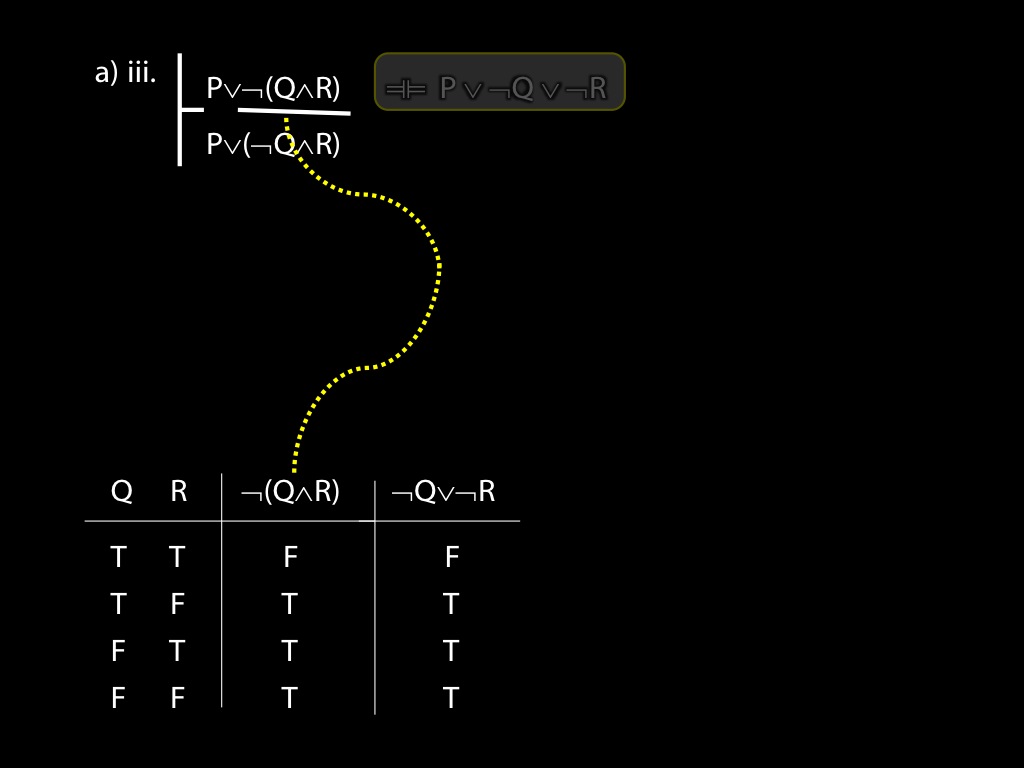
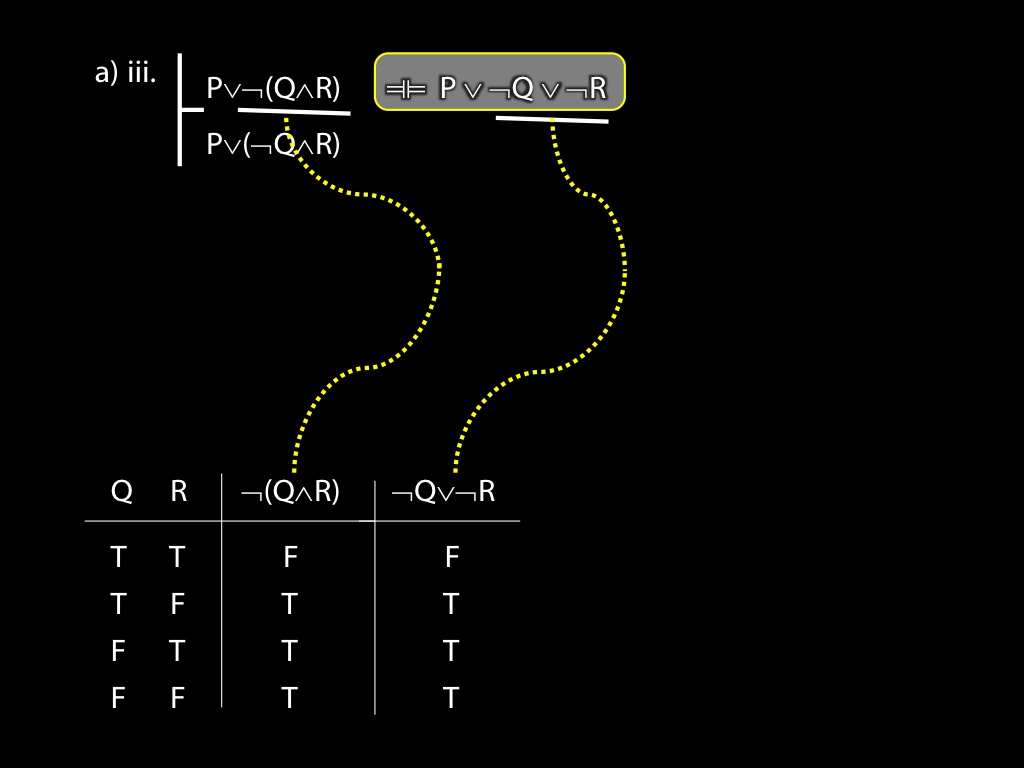
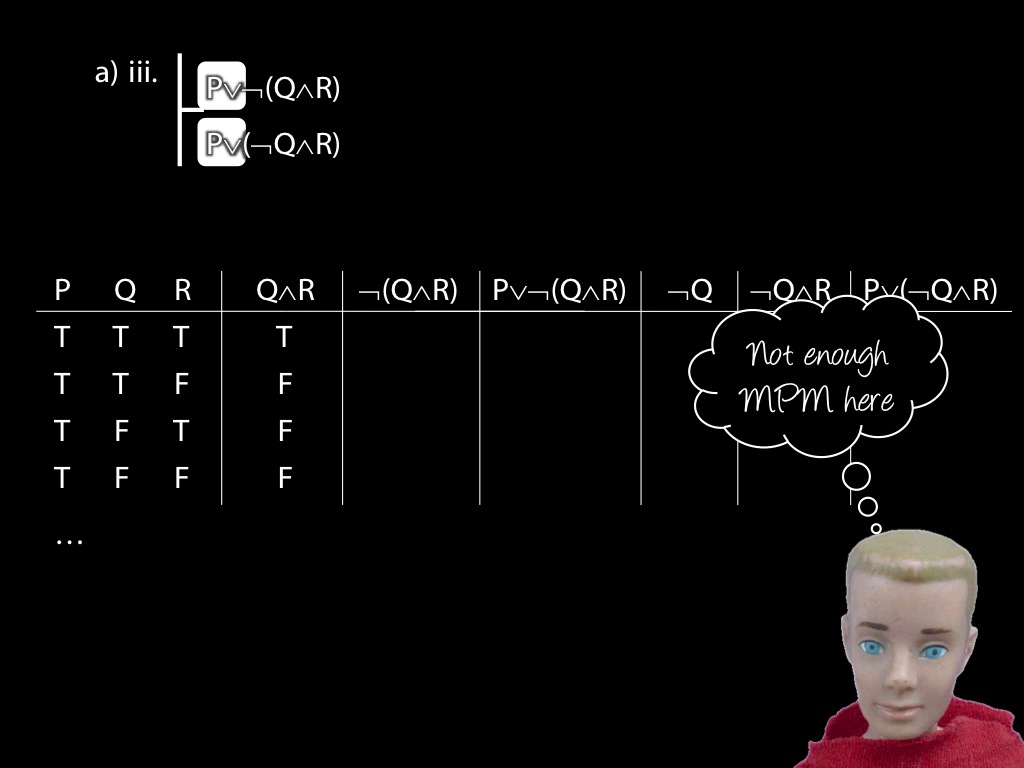
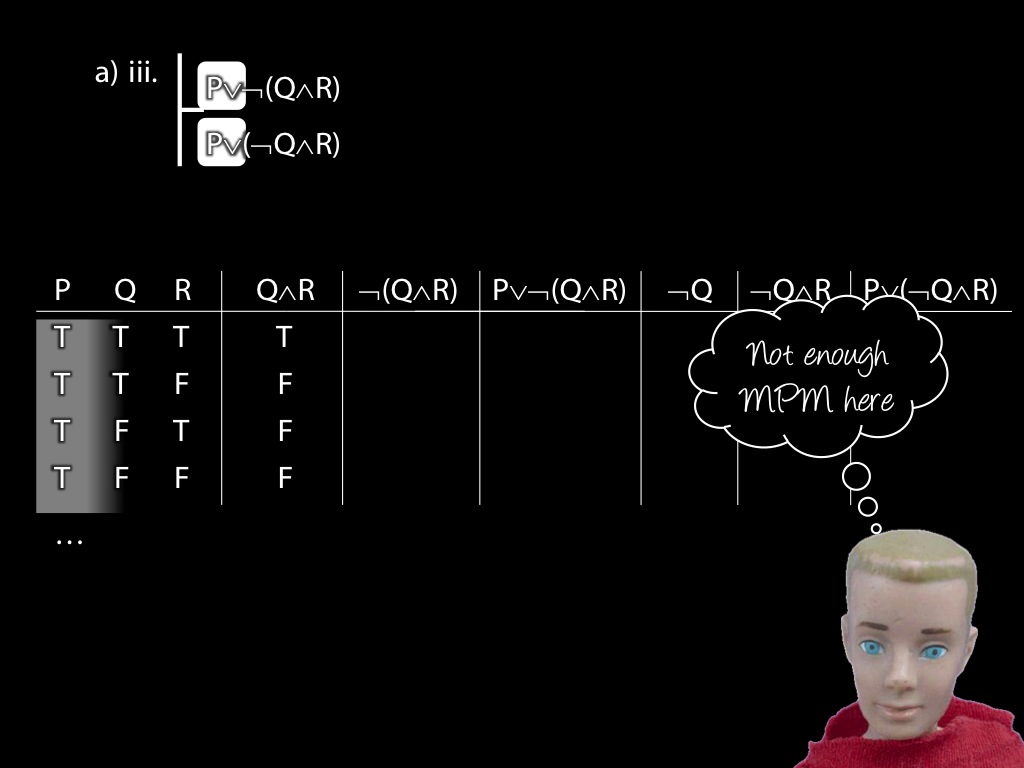
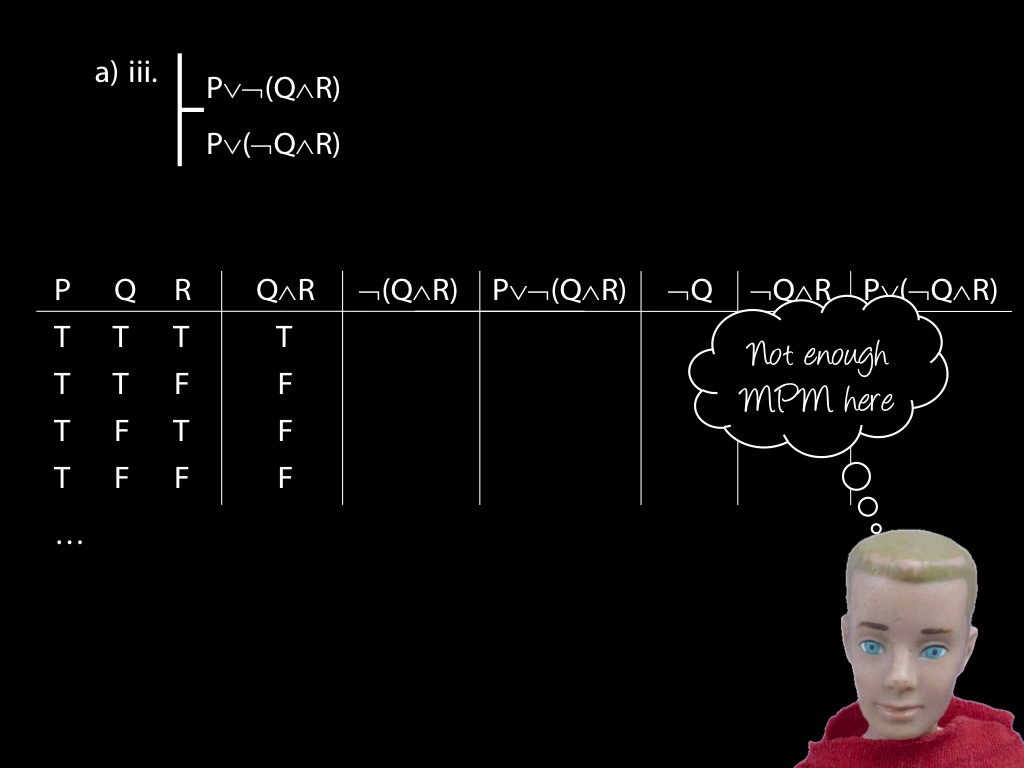
\item
\begin{equation*}
\begin{fitch}
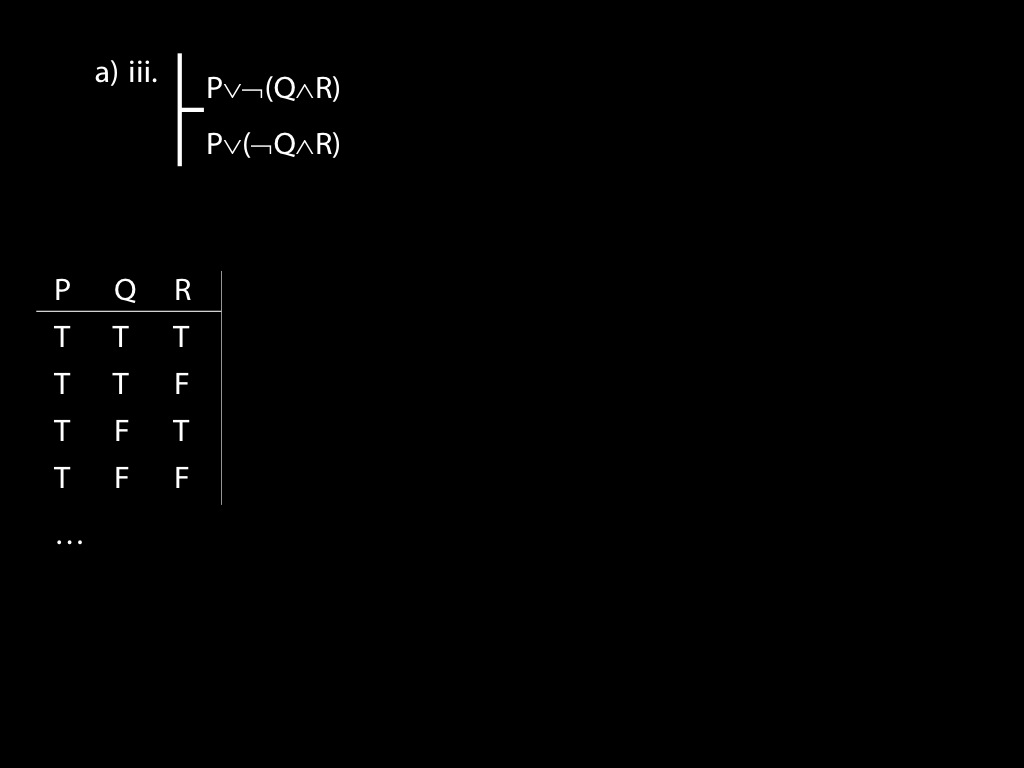
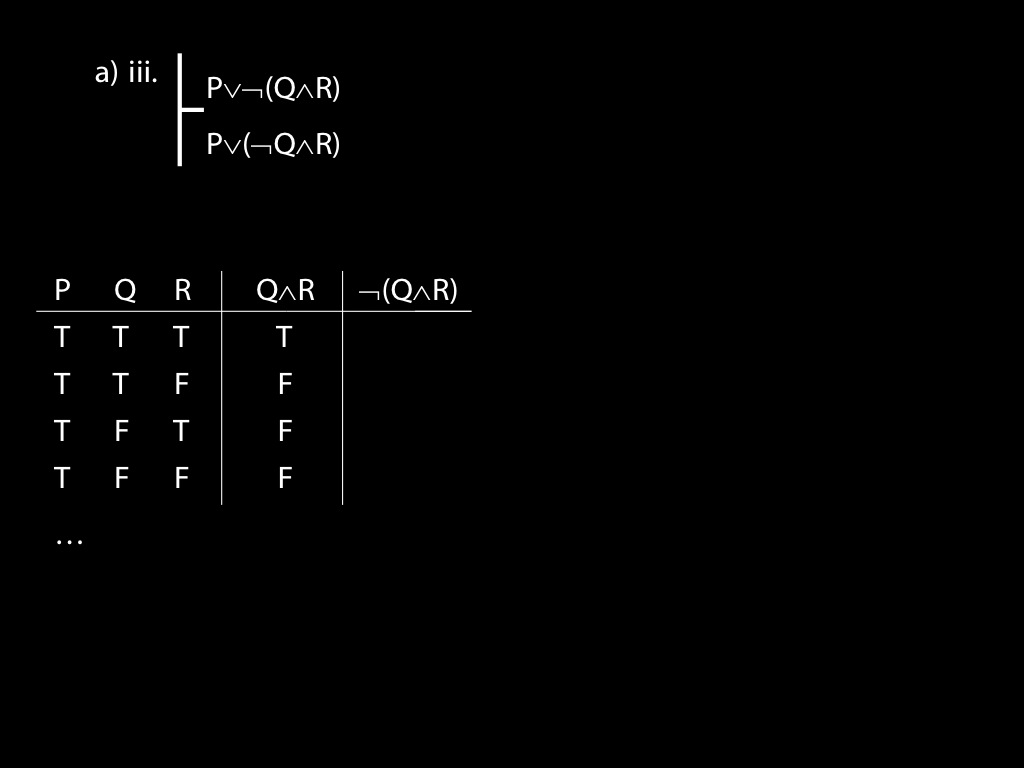
\fh P \lor \lnot(Q \land R) \\
\fa P \lor (\lnot Q \land R) \\
\end{fitch}
\end{equation*}
\end{enumerate}



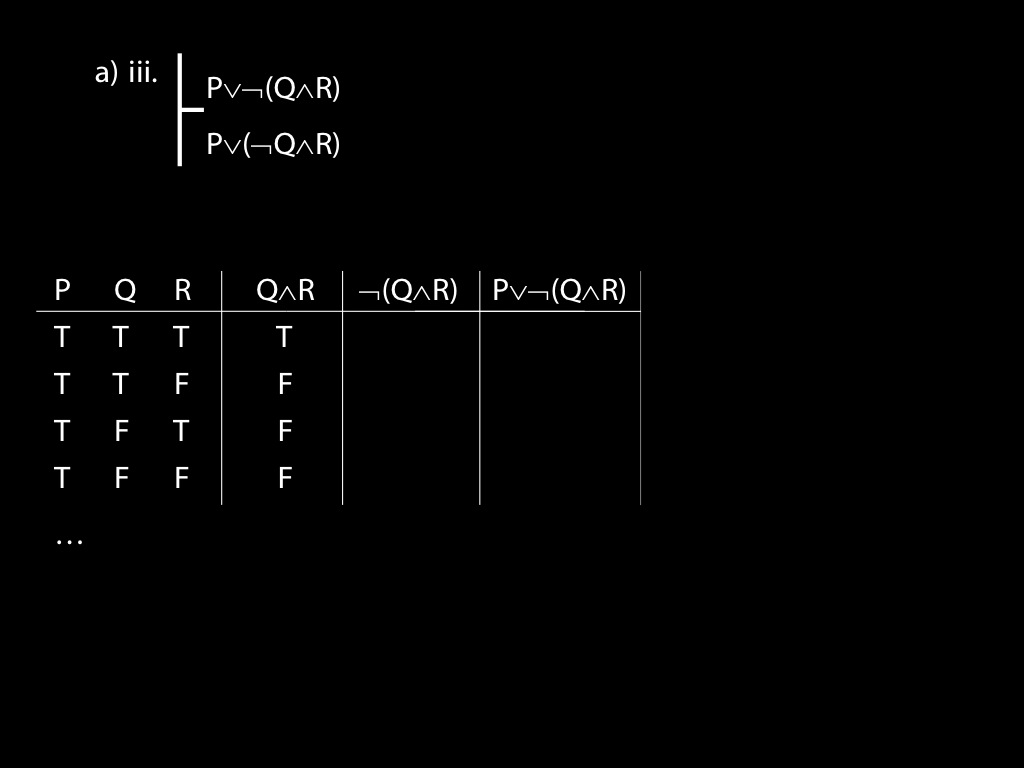




substituion of equivalents